«Уравнение с одной переменной». 9-й класс
Используемая технология: Блочно-модульное обучение.
Для средней общеобразовательной школы.
Автор учебника Макарычев Ю.Н., 3 часа в неделю.
- Информационный блок : выдержка из КТП
№ |
Содержание учебного материала |
Кол-во часов |
Тип урока |
Планируемый результат |
|
базовый |
повышенный |
||||
§5. Уравнения с одной
переменной, 6 часов. Уравнения с одной
переменной, 6 часов. |
|||||
| 1. | Целое уравнение и его корни. | 1 |
Урок-лекция (формирование понятий). | Формирование понятия уравнение высших степеней, умение решать биквадратные уравнения. |
Формирование понятия уравнения высших степеней, их типы; умение безошибочно находить способ решения уравнения, определяя для этого его тип. |
| 2. | Решение уравнений высших степеней. | 1 |
Урок-отработка лекции. | ||
2 |
Урок-диагностика знаний (с\р). |
||||
| 3. | Решение целых уравнений с параметрами. | 1 |
Урок-коррекция ( РНО). |
||
| 4. | Проверочная работа. | 1 |
Урок- контроля ЗУН | ||
Образовательные |
Развивающие |
Воспитывающие |
Сформировать понятие и закрепить знания учащихся по теме “Уравнения с одной переменной”; Умения составлять алгоритм решения уравнения; Закрепить умения и навыки решать
уравнения высших степеней с использованием
разных приемов, в нестандартных ситуациях. |
Развивать умения пользоваться опорным конспектом и вспомогательной литературой для постановки задачи и ее выполнения в ходе решения; Развивать внимательность, собранность и аккуратность; Развивать умения работать самостоятельно и в микро группах, ставить перед собой цель и делать выводы, выполнять безошибочно необходимые арифметические вычисления |
Чувство ответственности; Умение работать в микро группе; Культура труда, аккуратность. |
- Дидактические разработки урока.
1. Урок-лекция. На этом уроке обзорно рассматриваются следующие вопросы:
- Понятие целого уравнения, корни уравнения, повторить способы решения уже известных уравнений;
- Рассмотреть все виды уравнений высших степеней, уметь определять количество корней уравнения;
- Разобрать алгоритмы решения уравнений высших
степеней.

- Составить опорный конспект урока. (д\з)
2. Урок-отработка лекции
.На этом уроке разбираются и отрабатываются основные понятия, приемы и способы, о которых говорилось на первом уроке (пошаговая отработка лекции). Привожу пример лучшего опорного конспекта, составленного учащимися.
Опорный конспект урока по теме:
“Целое уравнение. Уравнения высших степеней”.
Основные методы решений уравнений. |
|
Разложение на множители. |
Введение новой переменной. |
Ключевые понятия:
уравнение, корень уравнения, решить уравнение, равносильные уравнение.
Виды уравнений:
№ |
Название уравнения |
Общий вид |
пример |
1. |
Биквадратное |
ах4+ вх2 + с = 0 замена х2=t обратная замена переменных |
3х4— 5х2 + 8=0 3 t2— 5 t +8=0 |
2. |
Уравнение, сводящееся к
квадратному с помощью замены выражения. |
(х2— 3х)2 + 5(х2— 3х) = 2 замена (х2— 3х) = а а2 + 5а = 2 а2 + 5а — 2 = 0 |
|
3. |
Уравнение, решая которое используем метод группировки слагаемых. |
Прием группировки 3(х-5) –х(х-5)=(х-5)(3-х) |
3х-15-х2+5х=0 3(х-5) + х(-х+5)=0 3(х-5) – х(х-5)=0 (х-5)(3-х)=0х — 5=0 или 3 — х=0 |
4. |
Симметрическое (возвратное) |
а х4+вх3+сх2+вх+а=0 сгруппируема х4+ а +вх3+ вх+ с=0а(х4+1) + в(х3+х) + с=0 делим все уравнение на х2 а(х2+) + в(х+)+с=0 замена х += к ; х2+= к – 2 а(к-2) + вк + с = 0 найдем к обратная замена |
х4+5х3+4х2-5х-1=0 |
5. |
Уравнение с использованием способа деления углом многочлена на одночлен (т.Безу) |
Любой многочлен. Если не удалось решить перечисленными способами, тогда применяем данный прием. |
х3 +6х +4х2+3=0 подробно рассмотреть решение в конспекте. |
Далее учащиеся разбиваются на микро группы и выполняют предложенное учителем задание.
Задание 1: Определить вид уравнения.
№ |
пример |
Вид уравнения |
1. |
(х-2)6— 19(х-2)3= 216 |
|
2. |
3х3— 7х2-7х +3 =0 |
|
3. |
2х4-х3-9х2+13х -5=0 |
|
4. |
х(х+1)(х+2)(х+3)=0,5625 |
|
5. |
6х4-5х3-38х2-5х + 6 = 0 |
|
6. |
(х2+5)2 – 36 = 0 |
|
7. |
х4 + 2х2 – 24 = 0 |
|
8. |
||
9. |
а2х4— (а2 + 1)х2 + 1 = 0 |
Задание 2: Решить уравнения.
Оценка |
Вариант 1 |
Вариант 2 |
“3” |
№7 |
№6 |
“4” |
№1 |
№2 |
“5” |
№5 |
№8 |
Проверка решений у учителя. Выставление оценок.
Выставление оценок.
Домашнее задание.
Уровень |
Решить уравнение. |
“3” |
По учебнику, авторы Ю.Н.Макарычев и др. №234(а,б),247а,248а |
“4” |
№3,№4,№5 |
“5” |
№9,№4,№6 |
3. Урок-диагностика знаний
.На этом уроке учащимся предлагается самостоятельно выполнить работу с целью определения уровня владения новым материалом. Каждому выдается разработка модуля урока, учащийся сам выбирает темп работы и по окончанию урока (2 часа) получает оценку.
Комментарий: У учителя разработка с
ответами, учащимся же выдается без ответов.
Разработка модуля урока по теме: ” Решение уравнений высших степеней”, 9 класс.
ДЛЯ УЧИТЕЛЯ
Для успешного освоения данной темы:
На ”3” нужно выполнить таблицы №1,№2,№3
На “4” нужно выполнить таблицы №1- 4
На “5” нужно выполнить все задания.
Желаю УДАЧИ всем!!!
Блок №1. Решить различные уравнения уже известными способами.
Цель: Закрепить знания и умения, полученные ранее.
Таблица №1 служит разминкой для дальнейшего решения уравнений более высокой степени. Следует решить два уравнения из таблицы, проверить результат и если вы успешно справились, то перейти к следующему заданию.
ТАБЛИЦА №1
| 1. (х+5)(3х-6) = 0 2. х2— 6х = 0 3. (8х –1)2— х(64х + 1) = 12 4. х –5 + 4х-1 = 1 2 3 5. |
Блок №2. Решить уравнения, сделав замену переменных.
Цель: Закрепить способ решения уравнений, используя замену переменных.
Пример- образец №1. Решить уравнение (х2+2х)2 — 2(х2+ 2х) = 3
Решение: Запишем равносильное данному уравнение (х2+ 2х)2 – (х2+ 2х) –3 =0, сделаем замену переменных, выражения в скобках одинаковые, поэтому можно записать:
Замена: х2 + 2х =у
Перепишем получившееся уравнение и решим его.
у2— 2у – 3= 0
Д= в2— 4ас= (-2)2— 4·1·(-3)= 16
у= 3, у= -1
Вернемся теперь к переменной х, сделаем обратную замену и решим два уранения.
Обратная замена:
Ответ: 1, -3, -1.
ТАБЛИЦА №2
Вариант 1 |
Вариант 2 |
1. (х2 +6х)2 –5 (х2 +6х) = 24 (х2 +6х)2 –5 (х2 +6х) = 242. (х2+2)2– (х2+2) = 12 |
1. (х2 –5)2 –5 (х2 –5) – 36 =0 2. (х2 –4х)2 + 9(х2-4х) = — 20 |
Блок №3. Решение биквадратных уравнений.
Цель: Закрепить способ решения биквадратных уравнений.
| Уравнение вида ах4+вх2+с=0, где а,в,с – числа, х – неизвестная переменная называется биквадратным уравнением. Решение биквадратного уравнения с помощью замены переменной сводится к решению квадратного уравнения. |
Пример-образец №2 Решить биквадратное уравнение х4 – 5х2 +4 = 0
Решение: х4 –5х2 +4 =0, биквадратное
уравнение, сделаем замену переменной и решим
получившееся квадратное уравнение.
Замена: х2= t >= 0
t2-5t +4 = 0
D= 9
t= 4, t= 1
Оба корня положительные, поэтому удовлетворяют условию t >= 0.
Обратная замена:
Ответ: ± 2, ± 1.
ТАБЛИЦА №3
Вариант 1 |
Вариант2 |
| 1. х4 – 2х2— 3 =0 2. 5у4 – 5у2 + 2 = 0 3. х4 –4х2 + 4 = 0 |
1. х4 – 5х2 — 36 = 0 2. у4 – 6у2 + 8 = 0 3. 2х4 – 9х2 + 4 = 0 |
Блок №4. Решить уравнения высшей степени.
Цель: Закрепить разные способы решения
уравнений высших степеней.
Если ребята вы добрались до 4 блока, поздравляю вас, вы делаете успехи. Сейчас вам предстоит самостоятельно выбирать способ решения, переменную, которую нужно заменить.
КАРТОЧКА №4
Вариант 1 |
Вариант 2 |
| 1. (х2 +2х)(х2 +2х +2)
= 3 2. х4 – 9х2 + 18 =0 3. (х2 –х-16)(х2-х+2) =88 |
1. (х2 +х)(х2 +х — 5)
= 84 2. х4 – 20х2 +100 =0 3. (2х2 +7х –8)(2х2 +7х – 3) –6 =0 |
Блок №5.
Указания учителя. Молодцы!!! Вы ребята освоили
решение уравнений высших степеней. Целью
дальнейшей вашей работы является применение
своих знаний и умений в более сложных ситуациях.
КАРТОЧКА №5
| 1. (х2 –1)(х2 +1) – 4(х2 – 11)
= 0 2. х5 + х4 – 6х2 – 6х2 + 5х +5 = 0 3. При каких с не имеет корней уравнение х4 – 12х2 +с = 0 |
Указания учителя: В случае затруднений воспользуйтесь подсказками, данными ниже.
Подсказки.
1. Воспользуйтесь формулой (а-в)(а+в)=а2-в2, преобразуйте данное уравнение в биквадратное.
2. Сгруппируйте первое слагаемое со вторым, третье с четвертым и пятое с шестым, примените способ группировки и разложите на множители.
3. Сделайте замену и запишите условие, при котором уравнение не имеет корней, решите получившееся неравенство.
ОТВЕТЫ: (только у учителя)
ОТВЕТЫ |
|||
| № таблицы | № задания |
вариант |
|
I |
II |
||
1 |
1 |
— 5; 2. |
|
2 |
0, -v6, v6. |
||
3 |
— 11/17 |
||
4 |
23/11 |
||
5 |
0; 2. |
||
2 |
1 |
— 3±v6; — 3 ± v17 |
±2, ± 1. |
2 |
±v2 |
2 |
|
3 |
1 |
±v3 |
± 3 |
2 |
Нет корней |
±v2, ± 2 |
|
3 |
± v2 |
± 0. |
|
4 |
1 |
— 1, 3. |
— 3, 4. |
2 |
±v3, ± v6. |
±v10 |
|
3 |
— 4, 5. |
-4,5; 1; (-7± v65)· 0,25 |
|
5 |
1 |
Нет корней |
|
2 |
±1, ±v5 |
||
3 |
с > 36 |
||
4.
 Урок-коррекция ЗУН.
Урок-коррекция ЗУН.На этом уроке разбираются у доски задания, которые вызвали затруднения на самостоятельной работе, вторая часть урока посвящена решению задач повышенного уровня, заданиям с параметрами. “Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы”,9 класс, издательство “Дрофа”. Л.В.Кузнецова и др.
5.
Урок контроля ЗУН.Проводится проверочная или контрольная работа. Предлагаю провести проверочную работу в форме ЕГЭ с целью подготовки учащихся 9-х классов к выпускным экзаменам в форме ЕГЭ.
Цель проверки: 1. Проверка ЗУН по основным разделам курса алгебры по теме “Уравнения”; 2. Корректировка учебной программы, с целью ликвидации пробелов в ЗУН учащихся.
Время проведения работы – 1 урок (40 минут).
Бланк для ответов: Часть А, часть В.
Ответы к тесту Ф.И. _______________________________________________ класс ______________
№ вопроса |
А1 |
А2 |
А3 |
А4 |
А5 |
В1 |
В2 |
Вариант ответа |
|
Для части С выдается двойной лист или
задание выполняется в тетради для контрольных
работ, куда обязательно вкладывается черновик и
бланк ответов частиА,В.
Приложение
Конспект урока по математике на тему «Уравнения с одной переменной»(9 класс)
Графический способ решения уравнений не обеспечивает …?
Каким способом можно решить уравнение х3+х-4=0?
Полное квадратное, старший коэффициент которого равен 1, называется … квадратным уравнением?
Задание 2. Выпишите буквы обозначенные цифрами в кружках.
Ученики получают фамилию известного математика Виета. После этого заслушивается сообщение ученика по теме «Великий математик Франсуа Виет».
Франсуа Виет (1540-1603)
Знаменитый математик Франсуа Виет родился в 1540 году в небольшом городке Фантанеле-Конт на юге Франции. Юрист по образованию, Виет служил при дворе Генриха IX. Математикой занимался в часы отдыха. Франсуа Виет обладал огромной трудоспособностью, он мог работать по трое суток без отдыха, многие его результаты и открытия достойны восхищения. Во время войны с Франции с Испанией Виет оказал большую услугу родине – он расшифровал весьма важное письмо испанского двора. Правители Испании, письмо которых было перехвачено, не допускали мысли, что такой сложный шифр может быть раскрыт. Впоследствии они приписали раскрытие их шифра волшебству чародея.
Во время войны с Франции с Испанией Виет оказал большую услугу родине – он расшифровал весьма важное письмо испанского двора. Правители Испании, письмо которых было перехвачено, не допускали мысли, что такой сложный шифр может быть раскрыт. Впоследствии они приписали раскрытие их шифра волшебству чародея.
Его знаменитой теоремой, которая известна под названием теорема Виета, люди пользуются уже пятое столетие.
Теорема Виета.
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого,
Умножишь ты корни – и дробь уж готова:
В числителе c, в знаменателе a,
И сумма корней тоже дроби равна.
Хоть с минусом дробь эта,
Что за беда –
В числителе b, в знаменателе а.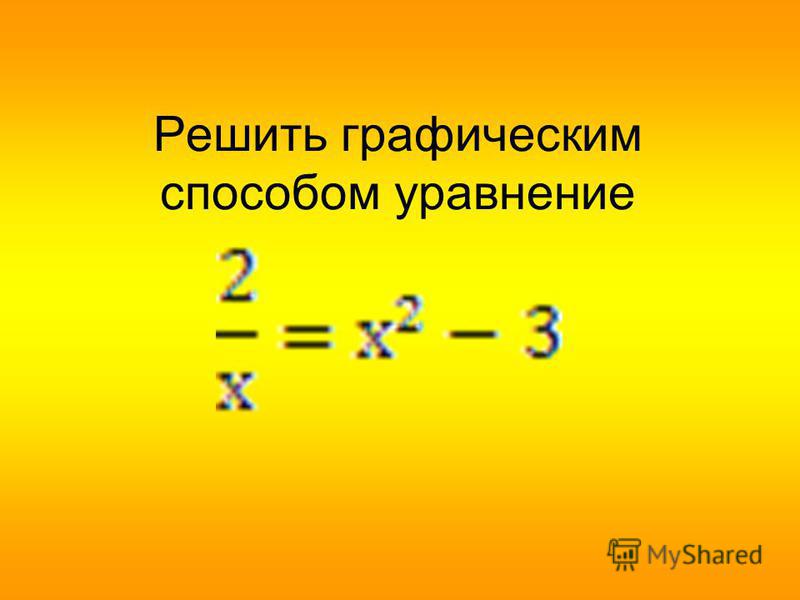
(На магнитной доске висит плакат).
— Сформулируйте теорему, обратную теореме Виета.
— Для решения каких квадратных уравнений ее удобно применять?
Задание 3. На доске висят 4 карточки.
x2-6x+5=0
3x2-4x+7=0
x2-10x+9=0
7x2-3x+5=0
Какие уравнения удобно решить по теореме, обратной теореме Виета?
Если вы найдете корни этих уравнений, пользуясь данной теоремой, то сможете узнать, в каком году Ф. Виет доказал ее. (Ответ: в 1591 г.)
Задание 4. Самостоятельно ответьте на вопросы теста, букву правильного ответа занесите в таблицу в конце теста.
Функция у=х2 задается графиком изображенным на рисунке.

Уравнение х2=а при а>0 имеет
у) 1 корень; а) 2 корня; т) нет корней.
Сколько точек пересечения имеют графики функций, изображенных на рисунке?
н) одну; а) две; т) три.
Чтобы построить график линейной функции, сколько точек достаточно отметить?
а) одну; ю) две; к) как можно больше, чтобы график был точнее.
Функция y=kx+b, если k>0
т) возрастает; у) убывает.
В каких четвертях расположен график функции у=2х2-3х+15 (D<0)?
а) III и IV четверти; у) I и II четверти.
График какой функции изображен на рисунке?
б) y=kx; р) у=1/х; и) у=√х.
В каких четвертях расположен график функции y=kx, если k<0?
и) I и III; д) II и IV.
Когда вершина параболы находится на оси Ох?
а) D<0; в) D=0; н) D>0.
Задание 5. Как бы Вы могли окончить фразу «Статую красит вид, а …»?
(«… человека его деяния.»)
— Чьи это слова? (Пифагора).
Пифагор (справка)
В Древней Греции жил ученый Пифагор. О жизни этого ученого известно немного, зато с его именем связано много легенд. Пифагор организовал кружок молодежи из представителей аристократии. В кружок принимали после долгих испытаний. Каждый вступивший в кружок отрекался от своего имущества. Ими было сделано множество открытий. В школе существовал обычай, по которому авторство всех работ приписывалось Пифагору. После его смерти ученики окружили имя своего учителя множеством легенд.
В кружок принимали после долгих испытаний. Каждый вступивший в кружок отрекался от своего имущества. Ими было сделано множество открытий. В школе существовал обычай, по которому авторство всех работ приписывалось Пифагору. После его смерти ученики окружили имя своего учителя множеством легенд.
Задание 6. Решите уравнения:
x3=4-3x;
.
На столах лежат таблицы. Назовите букву рисунка, на котором график соответствует графику функции y=x3. Назовите букву рисунка, на котором график соответствует графику функции y=4-3x.
Если мы изобразим графики данных функций в одной системе координат, то мы узнаем, есть ли точки пересечения, сколько их и какие у них абсциссы.
Решение задач.

Задание 7. На доске вывешиваются карточки с правильными и неправильными ответами, на которых с одной стороны варианты ответов, с другой обрывки фразы «Ты лучше голодай, чем что попало ешь». Ученикам предлагается решить шесть уравнений. Ученик, решивший уравнение, выходит к доске и переворачивает карточку с правильным ответом. В результате должна получиться фраза.
Уравнения, предлагаемые ученикам:
Решить уравнение
Ответ: 0;6.
Решить уравнение (6-х)(6+х)-х(х-11)=36.
Ответ: 0; 5,5.
Решить уравнение х3+4х=5х2.
Ответ: 0; 4; 1.
Решить уравнение 3х3-х2+18х-6=0.

Ответ: 1/3.
I Вариант. Решить уравнение х4-5х2-36=0.
Ответ: ±3.
II Вариант. Решить уравнение x4-7x2+12=0.
Ответ: , ±2.
№5 и №6 ученикам предлагается решить самостоятельно, с последующей проверкой при помощи плаката с правильными ответами.
— Получена строка из стихотворения поэта и математика Омара Хаяма.
Омар Хаям (справка)
Омар Хаям жил в Северной Персии. Он написал «Алгебру» (полное название «Трактат о документах алгебры и алмукабалы»), выдающееся произведение, так как в ней содержится систематическое исследование уравнений третьей степени.
Чтоб мудро жизнь прожить
Знать надобно не мало
Ты лучше голодай, чем что попало ешь
И лучше будь один, чем вместе с кем попало.
Человек — это истина мира, венец,
Знает это не каждый, а только мудрец.
Закрепление пройденного за урок в форме игры.
Задание. Ученик решил уравнения и получил следующие ответы. Вам нужно оставить только те карточки, на которых корни найдены правильно.
После выполнения задания учитель переворачивает оставшиеся карточки и если задание выполнено верно, то получится слово Фалес.
+4)=0
x = ±5
x = ±8
Сообщение
x = 5
x = ±3
x = 3, =4
x = 8
x=0, x = ±2
Фалес (справка)
Отцом греческой математики является милетский купец Фалес. Среди семи известных мудрецов, живших в VII—VI вв. до н. э. в Греции, он занимал первое место. Фалес ставил перед собой не только вопрос «как?», но и современный научный вопрос «почему?». Он разделил год на 365 дней, объяснил причину солнечных затмений. Одна из теорем геометрии носит его имя.
Среди семи известных мудрецов, живших в VII—VI вв. до н. э. в Греции, он занимал первое место. Фалес ставил перед собой не только вопрос «как?», но и современный научный вопрос «почему?». Он разделил год на 365 дней, объяснил причину солнечных затмений. Одна из теорем геометрии носит его имя.
VI. Подведение итогов урока.
VII. Домашнее задание. Повторить тему «Уравнения с одной переменной».
Линейное уравнение с одной переменной с примерами.
п.1. Количество корней линейного уравнения с одной переменной
Линейным уравнением с одной переменной x называют уравнение вида ax = b, где a и b — действительные числа.
a называют коэффициентом при переменной , а b — свободным членом .
При решении линейных уравнений возможны три случая.
a
b
x
Количество корней
$b \in \Bbb R$ — любой
$x = \frac{b}{a}$
$x \in \Bbb R$ — любой
Бесконечное множество корней
$x \in \Bbb \varnothing $
п.
 2. Примеры
2. ПримерыПример 1. Решите уравнение 6-5x = 8(3,5-2x)
Решение:
$ 6-5x = 8(3,5-2x) \iff 6-5x = 28-16x \iff -5x+16x = 28-6 \iff $
$ \iff 11x = 22 \iff x = 2 $
Ответ: x=2
Пример 2. Решите уравнение $\frac{2}{3} x-\frac{4}{5} = 0,6x$
Решение:
$ \frac{2}{3}x-\frac{4}{5} = 0,6x | ×15 \iff 2x∙5-4∙3 = 0,6x∙15 \iff 10x-12=9x \iff $
$ \iff 10x-9x = 12 \iff x = 12 $
Ответ: x = 12
Пример 3. Решите уравнение 8(x+7)-7(2x-3) = 2(5x-11)
Решение:
$ 8(x+7)-7(2x-3) = 2(5x-11) \iff 8x+56-14x+21 = 10x-22 \iff$
$ \iff -6x+77 = 10x-22 \iff -6x-10x = -22-77 \iff -16x=-99 \iff $
$ \iff x = \frac{-99}{-16} = 6\frac{3}{16}$
Ответ: x = $6\frac{3}{16}$
Пример 4. Найдите все значения коэффициента a, при которых корень уравнения ax=-6– целое число.
Решение:
$$ax = -6 \Rightarrow {\left\{ \begin{array}{c} a ≠ 0 \\ x=- \frac{6}{a} \end{array} \right. 2-3a)}{a} = \frac{a(a-3)}{a} = a-3 \end{array} \right.} \\ {\left\{ \begin{array}{c} a = 0 \\ 0x = 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a≠0 \\ x = a-3 \end{array} \right.} \\ {\left\{ \begin{array}{c} a = 0 \\ x \in \Bbb R \end{array} \right.} \end{array} \right. $$
2-3a)}{a} = \frac{a(a-3)}{a} = a-3 \end{array} \right.} \\ {\left\{ \begin{array}{c} a = 0 \\ 0x = 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a≠0 \\ x = a-3 \end{array} \right.} \\ {\left\{ \begin{array}{c} a = 0 \\ x \in \Bbb R \end{array} \right.} \end{array} \right. $$
Ответ: при a ≠ 0,x = a-3; при a = 0, $x \in \Bbb R$ — любой
Пример 6*. Решите уравнение (k+1)x = k
Решение:
$$ (k+1)x = k \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} k+1 ≠ 0 \\ x = \frac{k}{k+1} \end{array} \right.} \\ {\left\{ \begin{array}{c} k+1 = 0 \\ 0x = -1 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} k ≠ -1 \\ x = \frac{k}{k+1} \end{array} \right.} \\ {\left\{ \begin{array}{c} k = -1 \\ x \in \Bbb \varnothing — решений \quad нет \end{array} \right.} \end{array} \right. $$
Ответ: при k ≠ -1, $ x = \frac{k}{k+1} $, при k = -1 решений нет
Пример 7*. Решите уравнение ax+b = cx+d
Решите уравнение ax+b = cx+d
Решение:
$$ ax+b = cx+d \iff ax-cx = d-b \iff (a-c)x = d-b \iff $$
$$ \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a-c ≠ 0 \\ x = \frac{d-b}{a-c} \end{array} \right.} \\ {\left\{ \begin{array}{c} a-c = 0 \\ d-b = 0 \\ 0x = 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} a-c = 0 \\ d-b ≠ 0 \\ 0x ≠ 0 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a ≠ c \\ x = \frac{d-b}{a-c} \end{array} \right.} \\ {\left\{ \begin{array}{c} a = c \\ d = b \\ x \in \Bbb R — любой \end{array} \right.} \\ {\left\{ \begin{array}{c} a = c \\ d ≠ b \\ x \in \Bbb \varnothing — решений \quad нет \end{array} \right.} \end{array} \right. $$
Линейное уравнение с одной переменной
Нам известно, что решить уравнение — значит найти все его корни или показать, что их нет вообще. Также нам известно, что при решении уравнений используют следующие свойства:
- корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак;
- корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.

Уравнение вида , где — переменная, и — некоторые числа, называют линейным уравнением с одной переменной. |
Примеры линейных уравнений с одной переменной:
Выясним, сколько корней может иметь линейное уравнение .
1) Если в линейном уравнении коэффициент , то разделив обе части этого уравнения на , получим . Значит, линейное уравнение , в котором , имеет единственный корень, равный .
2) Если в линейном уравнении коэффициент и , то получим уравнение . Значит, линейное уравнение , в котором и , имеет бесконечного много корней, т.е. его корнем является любое число (т.к. при умножении любого числа на ноль всегда получится ноль).
3) Если в линейном уравнении коэффициент и , то при любом значении получим неверное равенство . Значит, линейное уравнение , в котором и , не имеет корней.
Значит, линейное уравнение , в котором и , не имеет корней.
Вывод:
Решение многих уравнений сводится к решению линейных уравнений.
Пример:
.
Раскроем скобки:
.
Перенесем слагаемое в левую часть уравнения, а слагаемое 28 в правую часть, изменив при этом их знаки:
.
Приведем подобные слагаемые:
.
Разделим обе части уравнения на 3:
.
При решении исходного уравнения мы применяли свойства уравнений и выполняли тождественные преобразования, последовательно заменяя одно уравнение другим, равносильным ему. Значит, корнем уравнения является число 11.
В рассматриваемом примере исходное уравнение свелось к равносильному линейному уравнению , в котором коэффициент при переменной отличен от нуля ( = 3).
Если при решении уравнения равносильное ему линейное уравнение получится вида , то исходное уравнение имеет бесконечно много корней.
Если при решении уравнения равносильное ему линейное уравнение получится вида , то исходное уравнение не имеет корней.
Уравнения с одной переменной
- Главная
- Справочник
- Алгебра
- Уравнения с одной переменной
На предыдущих занятиях мы знакомились с выражениями, а также учились их упрощать и вычислять. Теперь переходим к более сложному и интересному, а именно к уравнениям.
Уравнение и его корни
Равенство, содержащие переменную (-ые) называются уравнениями. Решить уравнение, значит найти значение переменной, при котором равенство будет верным. Значение переменной называют корнем уравнения.
Уравнения могут иметь, как один корень, так и несколько или вообще ни одного.
При решении уравнений используются следующие свойства:
- если в уравнении перенести слагаемое из одной части уравнения в другую, поменяв при этом знак на противоположный, то получится уравнение равносильное данному.
 2=10-3x \) являются числа -2 и 2.
2=10-3x \) являются числа -2 и 2.
Линейное уравнение с одной переменной
Линейное уравнение с одной переменной — это уравнения вида ax = b, где x — переменная, а a и b — некоторые числа.
Существует большое количество видов уравнений, но решение многих из них сводится именно к решению линейных уравнений, поэтому знание этой темы обязательно для дальнейшего обучения!
Пример №2 Решить уравнение: 4(x+7) = 3-x
Для решения данного уравнения, в первую очередь, нужно избавиться от скобки, а для этого домножим на 4 каждое из слагаемых в скобке, получаем:
4х + 28 = 3 — х
Теперь нужно перенести все значения с «х» в одну сторону, а все остальное в другую сторону (не забывая менять знак на противоположный), получаем:
4х + х = 3 — 28
Теперь вычитаем значение слева и справа:
5х = -25
Чтобы найти неизвестный множитель (х) нужно произведение (25) разделить на известный множитель (5):
х = -25:5
х = -5
Ответ х = -5
Если сомневаетесь в ответе можно проверить, подставив полученное значение в наше уравнение вместо х:
4(-5+7) = 3-(-5)
4*2 = 8
8 = 8 — уравнение решено верно!
Решить теперь что-нибудь по-сложнее:
Пример №3 Найти корни уравнения: \( (y+4)-(y-4)=6y \)
В первую очередь, также избавимся от скобок:
\( y+4-y+4=6y \)
Сразу видим в левой части y и -y, а значит их можно просто вычеркнуть, а полученные числа просто сложить, и записать выражение:
\( 8 = 6y \)
Теперь можно перенести значения с «y» в левую сторону, а значения с числами в правую.
 Но ведь это не обязательно, ведь не важно с какой стороны находятся переменные, главное, чтобы они были без чисел, а значит, ничего переносить не будем. Но для тех кто не понял, то сделаем, как гласит правило и разделим обе части на (-1), как гласит свойство:
Но ведь это не обязательно, ведь не важно с какой стороны находятся переменные, главное, чтобы они были без чисел, а значит, ничего переносить не будем. Но для тех кто не понял, то сделаем, как гласит правило и разделим обе части на (-1), как гласит свойство:\( 6y=8 \)
Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель:
\( y=\frac{8}{6} = \frac{4}{3} = 1\frac{1}{3} \)
Ответ: y = \( 1\frac{1}{3} \)
Также можно проверить ответ, но сделайте это самостоятельно.
Пример №4 \( (0,5x+1,2)-(3,6-4,5x)=(4,8-0,3x)+(10,5x+0,6) \)
Теперь я просто решу, без объяснений, а вы посмотрите на ход решения и правильную запись решения уравнений:
\( (0,5x+1,2)-(3,6-4,5x)=(4,8-0,3x)+(10,5x+0,6) \)
\( 0,5x+1,2-3,6+4,5x=4,8-0,3x+10,5x+0,6 \)
\( 0,5x+4,5x+0,3x-10,5x=4,8+0,6-1,2+3,6 \)
\( -5,2x=7,8 \)
\( x=\frac{7,8}{-5,2}=\frac{3}{-2} =-1,5 \)
Ответ: x = -1,5
Если что-то не понятно по ходу решения пишите в комментариях
Решение задач с помощью уравнений
Зная что такое уравнения и научившись их вычислять — вы также открываете себе доступ к решению множества задач, где для решения используются именно уравнения.

Не буду вдаваться в теорию, лучше показать все и сразу на примерах
Пример №5 В корзине было в 2 раза меньше яблок, чем в ящике. После того, как из корзины переложили в ящик 10 яблок, в ящике их стало в 5 раз больше, чем в корзине. Сколько яблок было в корзине, а сколько в ящике?
В первую очередь нужно определить, что мы примем за «х», в данной задаче можно принять и ящики, и корзины, но я возьму яблоки в корзине.
Значит, пусть в корзине было x яблок, так как в ящике яблок было в два раза больше, то возьмем это за 2х. После того, как из корзины яблоки переложили в ящик в корзине яблок стало: х — 10, а значит, в ящике стало — (2х + 10) яблок.
Теперь можно составить уравнение:
5(х-10) — в ящике стало в 5 раз больше яблок, чем в корзине.
Приравняем первое значение и второе:
2x+10 = 5(x-10) и решаем:
2х + 10 = 5х — 50
2х — 5х = -50 — 10
-3х = -60
х = -60/-3 = 20 (яблок) — в корзине
Теперь, зная сколько яблок было в корзине, найдем сколько яблок было в ящике — так как их было в два раза больше, то просто результат умножим на 2:
2*20 = 40 (яблок) — в ящике
Ответ: в ящике — 40 яблок, а в корзине — 20 яблок.

Я понимаю, что многие из вас, возможно, не до конца разобрались в решении задач, но уверяю к этой теме мы вернемся и еще не раз на наших уроках, а пока если у вас остались вопросы — задавайте их в комментариях.
Под конец еще несколько примеров на решения уравнений
Пример №6 \( 2x — 0,7x = 0 \)
\( 1,3x = 0 \)
\( x=0/1,3 \)
\( x = 0 \)
Пример №7 \( 3p — 1 -(p+3) = 1 \)
\( 3p-1-p-3=1 \)
\( 3p-p=1+1+3 \)
\( 2p=5 \)
\( p=5/2 \)
\( p=2,5 \)
Пример №8 \( 6y-(y-1) = 4+5y \)
\( 6y-y+1=4+5y \)
\( 6y-y-5y=4-1 \)
\( 0y=3 \) — корней нет, т.к. на ноль делить нельзя!
Всем спасибо за внимание. Если что-то непонятно спрашивайте в комментариях.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Источник
Больше интересного в телеграм @calcsboxNCERT Solutions for Class 9 Math Глава 4 Линейные уравнения с двумя переменными
Упражнение (4.
 1)
1)1: Постройте линейное уравнение с двумя переменными, чтобы выразить следующее утверждение.
Стоимость учебника вдвое превышает стоимость тетради.
Ответ. Пусть стоимость учебника $\text{x}$ рупий, а стоимость тетради $\text{y}$ рупий.
Данное утверждение: Стоимость учебника в два раза превышает стоимость тетради
Итак, чтобы составить линейное уравнение,
стоимость учебника $\text{=}\,\text{2 }\!\!\times\!\!\text{ }$ стоимость тетради.
$\Стрелка вправо \text{x=2y}$
$\Стрелка вправо \text{x-2y=0}$.
2: Определить значения $\text{a}$, $\text{b}$, $\text{c}$ из следующих линейных уравнений, представив каждое из них в стандартной форме \[\text{ топор+by+c=0}\].
(i) $\text{2x+3y=9}\text{.}\overline{\text{35}}$
Ответ. Заданное линейное уравнение имеет вид
$\text{2x+3y}-\text{9}\text{.
 }\overline{\text{35}}\text{=0}$
}\overline{\text{35}}\text{=0}$ Теперь, сравнивая приведенное выше уравнение со стандартной формой линейного уравнения $\text{ax+by+c=0}$, значения $\text{a,}\,\text{b,}$ и $\text{c}$ получаются как
$\text{a=2}$,
$\text{b=3 }$ и
$\text{c}=-\text{9}\text{.}\overline{\text{35}}$
(ii) $\text{x-}\frac{\ text{y}}{\text{5}}\text{-10=0}$
Ответ. Данное линейное уравнение равно
$\text{x-}\frac{\text{y}}{\text{5}}\text{-10}=\text{0}$
приведенное выше уравнение со стандартной формой линейного уравнения, $\text{ax+by+c=0}$, значениями $\text{a,}\,\text{b,}$ и $\text{c }$ получаются как
$\text{a}=\text{1}$,
$\text{b}=-\frac{\text{1}}{\text{5}}$, и
$\text{c}=-\text{10}$.
(iii) $\text{-2x+3y=6}$
Ответ. Данное линейное уравнение равно
$\text{-2x+3y=6}$
Вычитание $6$ из обеих частей уравнения дает
$-\text{2x+3y}-\text{6}=\ text{0}$
Теперь, сравнивая приведенное выше уравнение со стандартной формой линейного уравнения, $\text{ax+by+c=0}$, значения $\text{a,}\,\ text{b,}$ и $\text{c}$ получаются как
$\text{a}=-\text{2}$,
$\text{b}=\text{3}$, и
$\text{c}=-\text{6}$.

(iv) $\text{x=3y}$
Ответ. Данное линейное уравнение можно записать в виде
$\text{1x}=\text{3y}$
Вычитание $3y$ из обеих частей уравнения дает
$\text{1x-3y+0=0} $
Теперь, сравнивая приведенное выше уравнение со стандартной формой линейного уравнения $\text{ax+by+c=0}$, значения $\text{a,}\,\text{b,} $ и $\text{c}$ получаются как
$\text{a}=\text{1}$,
$\text{b}=-\text{3}$ и
$\ текст{с}=\текст{0}$.
(v) \[\text{2x}\mathbf{=-}\,\text{5y}\]
Ответ. Данное линейное уравнение имеет вид
\[\text{2x}=-\text{5y}\].
Добавление $5y$ к обеим частям уравнения дает
\[\text{2x+5y+0=0}\].
Теперь, сравнивая приведенное выше уравнение со стандартной формой линейного уравнения, $\text{ax+by+c=0}$, значения $\text{a,}\,\text{b,} $ и $\text{c}$ получаются как
$\text{a}=\text{2}$,
$\text{b}=\text{5}$ и
$\text {c}=\text{0}$.

(vi) $\text{3x+2=0}$
Ответ. Заданное линейное уравнение равно
$\text{3x+2=0}$.
Переписав уравнение, получим
$\text{3x+0y+2=0}$
Теперь, сравнив приведенное выше уравнение со стандартной формой линейного уравнения $\text{ax+by+c=0}$ , значения $\text{a,}\,\text{b,}$ и $\text{c}$ получаются как
$\text{a}=\text{3}$,
$ \text{b}=\text{0}$ и
$\text{c}=\text{2}$.
(vii) $\text{y-2=0}$
Ответ.Данным линейным уравнением является
$\text{y-2=0}$
Уравнение может быть выражено как
$\text{0x+1y-2}=\text{0}$
Теперь, сравнивая приведенное выше уравнение со стандартной формой линейного уравнения, $\text{ax+by+c=0}$, значениями $\text{a,}\,\text{b,}$ и $\text {c}$ получаются как
$\text{a}=\text{0}$,
$\text{b}=\text{1}$ и
$\text{c}=- \текст{2}$.

(viii) $\text{5=2x}$
Ответ: Данное линейное уравнение равно
$\text{5=2x}$.
Уравнение можно записать в виде
$\text{-2x+0y+5=0}$.
Теперь, сравнивая приведенное выше уравнение со стандартной формой линейного уравнения $\text{ax+by+c=0}$, значения $\text{a,}\,\text{b,}$ и $\text{c}$ получаются как
$\text{a}=-\text{2}$,
$\text{b}=\text{0}$ и
$\text {с}=\текст{5}$.
Упражнение (4.2)
1: Дополните следующее утверждение, выбрав соответствующий ответ, и объясните, почему именно его следует выбрать?
$\text{y=3x+5}$ имеет ___________.
(a) Единственное решение,
(b) Только два решения,
(c) Бесконечное множество решений.
Ответ: Обратите внимание, что $\text{y}=\text{3x+5}$ является линейным уравнением.
Теперь обратите внимание, что для $\text{x}=\text{0}$ $\text{y}=\text{0+5=5}$.

Итак, $\left( \text{0,5} \right)$ является решением данного уравнения.
Если $\text{x=1}$, то $\text{y}=\text{3 }\!\!\times\!\!\text{ 1+5}=\text{8}$ .
То есть $\left( \text{1,8} \right)$ — еще одно решение уравнения.
Опять же, когда $\text{y}=\text{0}$, $\text{x}=-\frac{5}{3}$ .
Следовательно, $\left( -\frac{5}{3},0 \right)$ является еще одним решением уравнения.
Таким образом, замечено, что при разных значениях $\text{x}$ и $\text{y}$ для данного уравнения получаются разные решения.
Итак, существует бесчисленное множество различных решений данного линейного уравнения с двумя переменными. Следовательно, линейное уравнение с двумя переменными имеет бесконечно много решений.
Следовательно, вариант (с) является правильным ответом.
2: Найдите любые четыре решения для каждого из приведенных ниже уравнений.
(i) $\mathbf{2x}+\mathbf{y}=\mathbf{7}$.

Ответ: Данное уравнение
$\text{2x+y}=\text{7}$ является линейным уравнением.
Решение уравнения относительно $y$ дает
$\text{y=7-2x}$.
Теперь последовательно подставьте $\text{x=0,1,2,3}$ в приведенное выше уравнение.
Для $\text{x=0}$,
$\text{2}\left( \text{0} \right)\text{+y=7}$
$\Rightarrow \text{y =7}$
Итак, одно из полученных решений есть $\left( \text{x,y} \right)\text{=}\left( \text{0,7} \right)$.
Для $\text{x=1}$,
$\text{2}\left( \text{1} \right)\text{+y=7}$
$\Rightarrow \text{y =5}$
Таким образом, другим полученным решением является $\left( \text{x,y} \right)\text{=}\left( \text{1,5} \right)$.
Для $\text{x=2}$,
$\text{2}\left( \text{2} \right)\text{+y=7}$
$\Rightarrow \text{y =3}$
То есть получено решение $\left( \text{x,y} \right)\text{=}\left( \text{3,1} \right)$.

Кроме того, для $\text{x=3}$
\[\text{2}\left( \text{3} \right)\text{+y=7}\]
$\Rightarrow \text{y=1}$
Итак, еще одно решение $\left( \text{x,y} \right)\text{=}\left( \text{3,1} \right)$.
Таким образом, для данных уравнений получены четыре решения: $\left( \text{0,7} \right)$ , $\left( 1,5 \right)$, $\left( 2,3 \right) $, $\влево( 3,1\вправо)$.
(ii) $\mathbf{\pi x}+\mathbf{y}=\mathbf{9}$.
Ответ.Данное уравнение
$\pi x+y=9$ …… (a)
90 уравнение является линейным.Путем транспонирования приведенное выше уравнение (a) можно записать как
$\text{y=9- }\!\!\pi\!\!\text{ x}$.
Теперь последовательно подставьте $\text{x=0,1,2,3}$ в приведенное выше уравнение.
Для $\text{x=0}$,
$\text{y=9- }\!\!\pi\!\!\text{ }\left( \text{0} \right)$
$\Rightarrow \text{y=9}$
Следовательно, одним из полученных решений является $\left( \text{x,y} \right)\text{=}\left( \text{0, 9} \справа)$.

Для $\text{x=1}$,
$\text{y}=\text{9}-\text{ }\!\!\pi\!\!\text{ }\left( \ text{1} \right)$
$\Rightarrow \text{y}=\text{9}-\text{ }\!\!\pi\!\!\text{ }$.
Таким образом, получено еще одно решение: $\left( \text{x,y} \right)\text{=}\left( \text{1,9- }\!\!\pi\!\!\text { } \справа)$.
Для $\text{x=2}$,
$\text{y}=\text{9}-\text{ }\!\!\pi\!\!\text{ }\left( \ text{2} \right)$
$\Rightarrow \text{y}=\text{9}-\text{2 }\!\!\pi\!\!\text{ }$
То есть, другое полученное решение: $\left( \text{x,y} \right)\text{=}\left( \text{2,}\,\text{9-2 }\!\!\pi\!\ !\text{ } \right)$.
Кроме того, для $\text{x=3}$
$\text{y}=\text{9}-\text{ }\!\!\pi\!\!\text{ }\left ( \text{3} \right)$
$\Rightarrow \text{y}=9-\text{3 }\!\!\pi\!\!\text{ }$.
Следовательно, еще одним решением является $\left( \text{x,y} \right)\text{=}\left( \text{3,}\,\text{9-3 }\!\!\ pi\!\!\text{ } \right)$.

Таким образом, для данных уравнений получены четыре решения: $\left( 0,9 \right)$, $\left( \text{1,9,- }\!\!\pi\!\!\text{ } \right)$, $\left( \text{2,9-2 }\!\!\pi\!\!\text{ } \right)$, $\left( \text{3,9-3 }\!\!\pi\!\!\text{ } \right)$.
(iii) $\mathbf{x}=\mathbf{4y}$.
Ответ. Данное уравнение
$\text{x=4y}$ является линейным уравнением с двумя переменными.
Путем транспонирования приведенное выше уравнение можно записать как
$\text{y=}\frac{\text{x}}{4}$ .
Теперь последовательно подставьте $\text{x=0,1,2,3}$ в приведенное выше уравнение.
Для $\text{x=0}$
$\text{y}=\frac{0}{4}=0$.
Следовательно, одним из решений является $\left( \text{x,y} \right)\text{=}\left( \text{0,0} \right)$.
Для $x=1$,
$\text{y}=\frac{1}{4}$.
Итак, другим решением данного уравнения является $\left( \text{x,y} \right)\text{=}\left( \text{1,}\frac{1}{4} \right) $.

Для $\text{x=2}$,
$\text{y}=\frac{2}{4}=\frac{1}{2}$.
То есть другое полученное решение $\left( \text{x,y} \right)\text{=}\left( \text{2,}\frac{1}{2} \right)$.
Кроме того, для $\text{x=3}$.,
$\text{y}=\frac{3}{4}$.
Следовательно, еще одним решением является $\left( \text{x,y} \right)=\left( 3,\frac{3}{4} \right)$.
Таким образом, для данных уравнений получены четыре решения: $\left( 0,0 \right)$, $\left( \text{1,}\frac{1}{4} \right)$, $\left ( \text{2,}\frac{1}{2} \right)$, $\left( 3,\frac{3}{4} \right)$.
3: Определите фактические решения линейного уравнения\[\text{ }\!\!~\!\!\text{ x-2y=4}\] из каждого из следующих решений.
(i) $\left( \mathbf{0},\mathbf{2} \right)$
Ответ: Подстановка $\text{x=0}$ и $\text{y=2}$ в Левая часть уравнения \[\text{ }\!\!~\!\!\text{ x-2y=4}\] дает
$\begin{align} & \text{x-2y}=0-2\влево( 2 \вправо) \\ &=-4\\ &\n 4.
 \end{align}$
\end{align}$Следовательно, левая часть не равна Правая часть данного уравнения для $\left( \text{x,y} \right)=\left( 0,2 \ правильно) $.
Следовательно, $\left( 0,2 \right)$ не является решением уравнения \[\text{x-2y=4}\].
(ii) $\left( \mathbf{2},\mathbf{0} \right)$
Ответ. Подставив $\text{x=2}$ и $\text{y=0}$ в левую часть уравнения \[\text{ }\!\!~\!\!\text{ x- 2y=4}\] дает
$\begin{align} & \text{x-2y}=2-2\влево( 0 \вправо) \\ & =2 \\ &\n 4. \end{align}$
Следовательно, левая часть не равна правой части данного уравнения для $\left( \text{x,y} \right)=\left( 2,0 \ правильно) $.
Следовательно, $\left( 2,0 \right)$ не является решением уравнения \[\text{x-2y=4}\].
(iii) $\left( \mathbf{4},\mathbf{0} \right)$
Ответ. Подставив $\text{x=4}$ и $\text{y=0}$ в левую часть уравнения\[\text{ }\!\!~\!\!\text{ x- 2y=4}\] дает
$\begin{align} & \text{x-2y}=4-2\влево( 0 \вправо) \\ & =4.
 \end{align}$
\end{align}$Следовательно, левая часть равна правой части данного уравнения для $\left( \text{x,y} \right)=\left( 4,0 \right )$.
Следовательно, $\left( 4,0 \right)$ является решением уравнения \[\text{x-2y=4}\].
(iv) $\left( \sqrt{\mathbf{2}}\mathbf{,4}\sqrt{\mathbf{2}} \right)$
Ответ. Подставив $\text{x=}\sqrt{2}$ и $\text{y=4}\sqrt{2}$ в левую часть уравнения\[\text{ }\!\!~ \!\!\text{x-2y=4}\] дает
$\begin{align} & \text{x-2y}=\sqrt{2}-2\left( 4\sqrt{2} \right) \\ & =\sqrt{2}-8\sqrt{2} \\ & =-7\sqrt{2} \\ &\n 4. \end{align}$
Следовательно, левая часть не равна правой части данного уравнения для $\left( \text{x,y} \right)=\left( \sqrt{2 },4\sqrt{2} \right)$.
Следовательно, $\left( \sqrt{2},4\sqrt{2} \right)$ не является решением уравнения \[\text{x-2y=4}\].
(v) $\left( \mathbf{1},\mathbf{1} \right)$
Ответ. Подставив $\text{x}=1$ и $\text{y}=1$ в левую часть уравнения\[\text{ }\!\!~\!\!\text{ x- 2y=4}\] дает
$\begin{align} & \text{x-2y}=1-2\влево( 1 \вправо) \\ &=1-2\\ & =-1 \\ &\n 4.
 \end{align}$
\end{align}$Следовательно, левая часть не равна Правая часть данного уравнения для $\left( \text{x,y} \right)=\left( 1,1 \ правильно) $.
Следовательно, $\left( 1,1 \right)$ не является решением уравнения \[\text{x-2y=4}\].
4: Если $\left( \mathbf{x},\mathbf{y} \right)=\left( \mathbf{2},\mathbf{1} \right)$ является решением уравнения \[ \text{2x+3y=k}\], то каково значение $\mathbf{k}$?
Ответ: Подстановка $\text{x}=2$, $\text{y}=1$ и в уравнение
\[\text{2x+3y=k}\] дает
$\text {2}\left( \text{2} \right)\text{+3}\left( \text{1} \right)\text{=k}$
$\Rightarrow \text{4+3= k}$
$\Rightarrow \text{k=7}$.
Следовательно, значение $\text{k}$ равно $7$.
Упражнение (4.3)
1: Нарисуйте график каждого из приведенных ниже линейных уравнений.
(i) \[\text{ }\!\!~\!\!\text{ x+y=4}\]
Ответ.
 Данное линейное уравнение
Данное линейное уравнение\ [\ Text {x + y = 4} \]
\ [\ prightarrow \ text {y = 4 — x} \] …… (a)
Замена $ \ text { x}=0$ в уравнение (a) дает
$\text{y}=4-0=4.$
Аналогично, последовательно подставляя $\text{x}=2,4$ в уравнение (a), получается следующая таблица $\text{y}$ -значений:
$ \ text {x} $
$ 0 $
$
$ 2 $
$
$ 4 $
$ \ Text {y} $
$ 4 $
$2$
$0$
Теперь нанесите точки $\left(0,4\right)$, $\left(2,2\right)$ и $\left(4 ,0 \right)$ на миллиметровке и соедините точки прямой линией.
Таким образом, следующий график прямой представляет искомый график линейного уравнения $\text{x+y}=4$.

(Изображение скоро будет загружено)
(ii) \[\text{x—y=2}\]
Ответ. Данное линейное уравнение составляет
\ [\ \ text {xy} = 2 \]
\ [\ \ priverarrow \ text {y} = \ text {x} -2 \] …… (a)
Замена $ \ text {x}=0$ в уравнение (a) дает
$\text{y}=0-2=-2.$
Аналогично, последовательно подставляя $\text{x}=2,4$ в уравнение (a), получается следующая таблица $\text{y}$ -значений:
$ \ Text {x} $
$ 0 $
$
$ 2 $
$ 4 $
$ \ Text {Y} $
$ -2 $
$0$
$2$
Теперь постройте точки $\left(0,-2 \right)$, $\left(2,0 \right)$ и $\ left( 4,2 \right)$ на миллиметровке и соедините точки прямой линией.

Таким образом, следующий график прямой представляет искомый график линейного уравнения $\text{x}-\text{y}=2$.
(Изображение скоро будет загружено)
(iii) \[\text{y=3x}\]
Ответ. Данное линейное уравнение составляет
\ [\ text {y} = 3 \ text {x} \] …… (a)
Заменение $ \ text {x} = 0 $ в уравнение (а) дает
$ \текст{у}=3\влево( 0 \вправо)=0.$
Аналогично, последовательно подставляя $\text{x}=2,-2$ в уравнение (a), получается следующая таблица $\text{y}$ -значений:
$ \ Text {x} $
$ 0 $
$ 2 $
$ -2 $
$ \ Text {y} $
$ 0 $
$6$
$-6$
Теперь постройте точки $\left( 0,0 \right)$, $\left( 2,6 \right)$ и $\left(-2,-6 \right)$ на миллиметровке и соедините точки прямой линией.

Таким образом, следующий график прямой представляет искомый график линейного уравнения $\text{y}=3\text{x}$.
(Изображение скоро будет загружено)
(iv) \[\text{3=2x+y}\]
Ответ. Данное линейное уравнение составляет
\ [3 = 2 \ text {x + y} \]
$ \ prightarrow \ text {y} = 3-2 \ text {x} $ …… (a)
Замена $ \text{x}=0$ в уравнение (a) дает
$\text{y}=3-2\left( 0 \right)=3$.
Аналогично, последовательно подставляя $\text{x}=1,\,3$ в уравнение (a), получается следующая таблица $\text{y}$ -значений:
$ \ Text {x} $
$ 0 $
$
$ 1 $
$ 3 $
$ \ Text {y} $
$ 3 $
$1$
$-3$
Теперь постройте точки $\left(0,3\right)$, $\left(1,1\right)$ и $\ left( 3,-3 \right)$ на миллиметровке и соедините точки прямой линией.

Таким образом, следующий график прямой представляет искомый график линейного уравнения $3=\text{2x}+\text{y}$.
(Изображение скоро будет загружено)
2: При условии, что уравнения двух прямых проходят через точку \[\left( \mathbf{2,14} \right)\]. Может ли существовать более двух уравнений такого типа? Если да, то укажите причину.
Ответ. При условии, что уравнения двух прямых проходят через \[\left( \text{2,14} \right)\].
Можно заметить, что точка \[\left( \text{2,14} \right)\] удовлетворяет уравнению \[\text{7x-y=0}\] и \[\text{x- у+12=0}\].
Итак, уравнения \[\text{7x-y=0}\] и \[\text{x-y+12=0}\] представляют собой две прямые, проходящие через точку \[\left( \text{ 2,14} \справа)\].
Теперь, поскольку мы знаем, что через любую точку может проходить бесконечное количество линий, значит, существует бесконечное количество таких типов линий, которые проходят через точку $\left( 2,14 \right)$.

Следовательно, существует более двух уравнений, график которых проходит через точку $\left( 2,14 \right)$.
3: Определить значение $\mathbf{a}$ в линейном уравнении \[\text{3y=ax+7}\], если точка \[\left( \mathbf{3,4} \right) \] лежит на графике уравнения.
Ответ. Учитывая, что \[\text{3y=ax+7}\] является линейным уравнением и точка \[\left( 3,4 \right)\] лежит на уравнении.
Подстановка $\text{x=3}$, \[\text{y=4}\] в уравнение дает
\[\text{3y=ax+7}\]
$\Rightarrow \text {3}\left( 4 \right)\text{=a}\left( 3 \right)\text{+7}$
$\Rightarrow \text{3a}=5$
$\Rightarrow \text {a}=\frac{5}{3}$.
Следовательно, значение $\text{a}$ равно $\frac{5}{3}$.
4: Выведите линейное уравнение для следующей ситуации:
За первый километр такси берет арендную плату в $\mathbf{8}$ рупиях, а за последующие расстояния она становится $\mathbf{5}$ рупий за километр.
 Предположим, что пройденное расстояние составляет $\mathbf{x}$ км, а общая арендная плата составляет $\mathbf{y}$ рупий. Итак, начертите график линейного уравнения.
Предположим, что пройденное расстояние составляет $\mathbf{x}$ км, а общая арендная плата составляет $\mathbf{y}$ рупий. Итак, начертите график линейного уравнения.Ответ. Пусть общее пройденное расстояние $=$ $\text{x}$ км
, а общая стоимость пройденного пути $=$$\text{y}$ рупий.
Дано, что арендная плата за 1-й километр составляет $8$ рупий, а за последующие км – $5$ рупий за километр.
Следовательно, аренда на оставшееся расстояние $=$ \[\left( \text{x-1} \right)\text{5}\] рупий.
Общая стоимость проезда $\text{x}$ км определяется как
\[\text{y=}\left[ \text{8+}\left( \text{x-1} \right)\ Текст {5} \ Right] \]
\ [\ \ priverarrow \ Text {y = 8 + 5x-5} \]
\ [\ \ priverarrow \ text {y = 5x + 3} \] …… (1)
\[\Rightarrow \text{5x-y+3=0}\],
, что является требуемым линейным уравнением.
Теперь подстановка $\text{x}=0$ в уравнение (1) дает
$\text{y}=5\left( 0 \right)+3=3$.

Аналогично, последовательно подставляя $\text{x}=1,\,-1$ в уравнение (1), получается следующая таблица $\text{y}$ -значений:
$ \ text {x} $
$ 0 $
$ 1 $
$ $ -1 $
$ \ Text {y y} $
$3$
$8$
$-2$
Теперь постройте точки $\left( 0,3 \right)$, $\left( 1,8 \right)$ и $\left(-1,-2 \right)$ на миллиметровке и соедините точки прямой линией.
Таким образом, следующий график прямой представляет искомый график линейного уравнения \[\text{5x-y+3=0}\].
(Изображение будет загружено в ближайшее время)
Из графика линейных уравнений можно сделать вывод, что переменные $\text{x}$ и $\text{y}$ представляют расстояние, пройденное автомобилем, и общее стоимость аренды за расстояние соответственно.
 Следовательно, $\text{x}$ и $\text{y}$ — неотрицательные величины.
Следовательно, $\text{x}$ и $\text{y}$ — неотрицательные величины.Таким образом, допустим только первый квадрант графика линейного уравнения \[\text{5x-y+3=0}\].
5: Выберите правильное линейное уравнение для данных графиков в (a) и (b).
(a) (i) $\mathbf{y}=\mathbf{x}$
(ii) $\mathbf{x}+\mathbf{y}=\mathbf{0}$
(iii) $\mathbf{y}=\mathbf{2x}$
(iv) $\mathbf{2}+\mathbf{3y}=\mathbf{7x}$
(изображение скоро будет загружено)
Ответ. На данном графике видно, что точки $\left(-1,1\right)$, $\left( 0,0 \right)$ и $\left( 1,-1 \right)$ лежат на прямая линия.Также координаты точек удовлетворяют уравнению \[\text{x+y=0}\].
Итак, \[\text{x+y=0}\] — это искомое линейное уравнение, соответствующее данному графику.
Следовательно, вариант (ii) является правильным ответом.
(b) (i) $\mathbf{y}=\mathbf{x}+\mathbf{2}$
(ii) $\mathbf{y}=\mathbf{x}-\mathbf{2} $
(iii) $\mathbf{y}=-\mathbf{x}+\mathbf{2}$
(iv) $\mathbf{x}+\mathbf{2y}=\mathbf{6}$
(Изображение скоро будет загружено)
Ответ.
 На данном графике видно, что точки $\left(-1,3\right)$, $\left( 0,2 \right)$ и $\left( 2,0 \right)$ лежат на прямая линия. Кроме того, координаты точек удовлетворяют уравнению \[\text{y}=-\text{x+2}\].
На данном графике видно, что точки $\left(-1,3\right)$, $\left( 0,2 \right)$ и $\left( 2,0 \right)$ лежат на прямая линия. Кроме того, координаты точек удовлетворяют уравнению \[\text{y}=-\text{x+2}\].Итак, \[\text{y}=-\text{x+2}\] — это искомое линейное уравнение, соответствующее данному графу.
Следовательно, вариант (iii) является правильным ответом.
6: Работа, совершаемая телом при приложении постоянной силы, пропорциональна расстоянию, пройденному телом.Сформулируйте это соотношение линейным уравнением и начертите его, используя постоянную силу в пять единиц. Отсюда по графику определите работу, совершенную при перемещении тела на расстояние, равное
(i) $\mathbf{2}$ единиц
(ii) $\mathbf{0}$ единиц.
Ответ: Пусть расстояние, пройденное телом, равно $\text{x}$ единицам, а выполненная работа — $\text{y}$ единицам.
Теперь, учитывая это, проделанная работа пропорциональна расстоянию.

Следовательно, \[\text{y}\propto \text{x}\].
\ [\ \ prightarrow \ text {y} = \ text {kx} \], …… (a)
, где $ \ text {k} $ — постоянная.
Учитывая постоянную силу в пять единиц, уравнение (а) принимает вид
$\text{y}=\text{5x}$. …… (b)
Теперь, подставляя $\text{x}=0$ в уравнение (b), получаем
$\text{y}=5\left( 0 \right)=0$.
Аналогично, последовательная подстановка $\text{x}=1,-1$ в уравнение (b) дает следующую таблицу значений $\text{y}$.
9000 $ Теперь постройте точки (1\$\left, $\left) ,5 \right)$ и $\left( -1,-5 \right)$ на миллиметровой бумаге и соедините точки прямой линией.$ \ Text {x} $
$
$ 0 $
$ 1 $
$ -1 $
$ \ Text {Y }$
$0$
$5$
$-5$

Таким образом, следующий график прямой представляет искомый график линейного уравнения $\text{y}=\text{5x}$.
(Изображение скоро будет загружено)
Наблюдая за графиком линейного уравнения, можно сделать вывод, что значение $\text{y}$, соответствующее \[\text{x=2}\], равно $10$ . Таким образом, если расстояние, пройденное телом, составляет $2$ единиц, то работа, совершенная им, составляет $10$ единиц.
Кроме того, значение $\text{y}$, соответствующее \[\text{x=0}\], равно $0$.Итак, если расстояние, пройденное телом, равно $0$ единице, то работа, совершенная им, равна $0$ единице.
7: Выведите линейное уравнение, удовлетворяющее следующим данным, и постройте его график.
Суджата и Сухана, учащиеся X класса школы, вместе пожертвовали $\mathbf{100}$ рупий в Фонд помощи премьер-министра для поддержки пострадавших от наводнения.
Ответ: Пусть Суджата и Сухана пожертвовали $\text{x}$ рупий и $\text{y}$ рупий соответственно в фонд помощи премьер-министру.

Учитывая это, общая сумма пожертвований Суджаты и Суханы составляет 100$ рупий.
Следовательно, $\text{x+y}=100$.
$\Rightarrow \text{y}=\text{100}-\text{x}$. …… (a)
Теперь, подставляя $\text{x}=0$ в уравнение (a), получаем
$\text{y}=100-0=100$.
Аналогично, последовательная подстановка $\text{x}=50,100$ в уравнение (a) дает следующую таблицу значений $\text{y}$.
$ 100 $ $ 100 $$ \ Text {x} $
$
$ 0 $
$ 50 $
$ 10004220
$ \ Text {y} $
$ 100 $
$ 50 $
$ 0
$ 0 $
Сюжет Участки очков $ \ Left (0,100 \ правильные) $, $ \ Left (50,50 \ верно) $ и $\left( 100,0 \right)$ на миллиметровке и соедините точки прямой линией.

Таким образом, следующий график прямой представляет искомый график линейного уравнения $\text{x+y}=100$.
(Изображение будет загружено в ближайшее время)
Наблюдение за графиком линейного уравнения позволяет сделать вывод, что переменные $\text{x}$ и $\text{y}$ показывают сумму, пожертвованную Суджатой и Суханой соответственно поэтому $\text{x}$ и $\text{y}$ — неотрицательные величины.
Следовательно, будут рассматриваться только значения $\text{x}$ и $\text{y}$, лежащие в первом квадранте.
8: Следующее линейное уравнение преобразует градусы Фаренгейта в градусы Цельсия:
$\mathbf{F=}\left( \frac{\mathbf{9}}{\mathbf{5}} \right)\mathbf{C+32 }$,
, где $\mathbf{F}$ обозначает измерение температуры в градусах Фаренгейта, а $\mathbf{C}$ в градусах Цельсия.
Затем выполните действия, указанные в следующих вопросах.
(i) Нарисуйте график приведенного выше линейного уравнения, приняв ось $\mathbf{x}$ за шкалу Цельсия и ось $\mathbf{y}$ за шкалу Фаренгейта.

Ответ. Заданное линейное уравнение имеет вид
$\text{F=}\left( \frac{\text{9}}{\text{5}} \right)\text{C+32}$ 0 …
Теперь подстановка $C=0$ в уравнение (a) дает
$\text{F}=\left( \frac{9}{5} \right)\left( 0 \right)+32=32 $.
Аналогично, последовательная подстановка $C=-40,10$ в уравнение (a) дает следующую таблицу значений $\text{F}$.
$ 32 $$ \ Text {C} $
$
$ 0 $
$ -40 $
$ 10 $
$ \ Text {F } $
$ 320421
$ 32 $
$ -40 $
$ 50 $
Теперь с участием пунктов $ \ Left (0,32 \ Right) $, $ \ Left (- 40,-40 \right)$ и $\left( 10,50 \right)$ на миллиметровой бумаге и соедините точки прямой линией.
 {\circ }}\text{C}\].{\ circ}} \ text {C} \].
{\circ }}\text{C}\].{\ circ}} \ text {C} \].(v) Существует ли температура, которая численно дает одно и то же значение как в градусах Фаренгейта, так и в градусах Цельсия? Если есть, то покажите.
Ответ: При условии, что
$\text{F=}\left( \frac{\text{9}}{\text{5}} \right)\text{c+32}$.
Предположим, что \[\text{F=C}\].
Тогда
$\text{F=}\left( \frac{\text{9}}{\text{5}} \right)\text{F+32}$
$\Rightarrow \left ( \frac{\text{9}}{\text{5}}-\text{1} \right)\text{F+32=0}$
$\Rightarrow \left( \frac{\text{ 4}}{\text{5}} \right)\text{F}=-\text{32}$
$ \Rightarrow \text{F}=-\text{40}$.\circ \], что дает численное одинаковое значение как в градусах Фаренгейта, так и в градусах Цельсия.
Упражнение (4.4)
1: Опишите геометрическое представление \[\text{y=3}\] в виде уравнения
(i) с одной переменной
Ответ.
 Данное уравнение имеет вид \[\text{y=3}\].
Данное уравнение имеет вид \[\text{y=3}\].Обратите внимание, что когда \[\text{y=3}\] рассматривается как уравнение с одной переменной, то на самом деле оно представляет собой число в одномерной числовой строке, как показано на следующем рисунке.
(изображение скоро будет загружено)
(ii) в двух переменных.
Ответ: Данное уравнение имеет вид \[\text{y=3}\].
Приведенное выше уравнение можно записать в виде \[\text{0}\text{.x+y=0}\].
Обратите внимание, что когда $\text{y=3}$ рассматривается в двух переменных, то она представляет собой прямую линию, проходящую через точку \[\left( 0,3 \right)\] и параллельную $\text{ x}$-ось. Следовательно, все точки графа, имеющие $\text{y}$-координату как $3$, содержатся в наборе.
Следовательно, at \[\text{x=0}\], \[\text{y=3}\];
в \[\text{x=2}\], \[\text{y=3}\]; и
at \[\text{x}=-2\], \[\text{y=3}\] являются решениями данного уравнения.

Теперь нанесите точки $\left( 0,3 \right)$, $\left( 2,3 \right)$ и $\left(-2,3 \right)$ на миллиметровую бумагу и соедините точки прямой линией. Графическое представление показано ниже:
(изображение скоро будет загружено)
2: Задайте геометрическое представление \[\text{2x+9=0}\] в виде уравнения
(i) с одной переменной
Ответ. Данное уравнение имеет вид \[\text{2x+9=0}\].
Теперь уравнение можно записать так:
\[\text{2x+9=0}\]
\[\Rightarrow \text{2x=(-9)}\]
$\Rightarrow \text {x=}\frac{\text{-9}}{2}=\text{-4}\text{.5}$
Следовательно, когда \[\text{2x+9=0}\] рассматривается как уравнение с одной переменной, то на самом деле оно представляет собой число $\text{x}=-4.5$ с одной- числовая линия, как показано на следующем рисунке
(изображение будет загружено в ближайшее время)
(ii) в двух переменных
Ответ: данное уравнение имеет вид \[\text{2x+9}=0\].

Приведенное выше уравнение можно записать в виде \[\text{2x+0y=}-\text{9}\].
Обратите внимание, что если \[\text{2x+9}=0\] рассматривается в двух переменных, то она представляет собой прямую линию, проходящую через точку \[\left( -4.5,0 \right)\] и параллельно оси $\text{y}$. Следовательно, все точки графа, имеющие $\text{x}$-координату $-4.5$, содержатся в наборе.
Следовательно, при \[\text{y=3}\], $\text{x}=-4.5$;
at \[\text{y}=-1\], $\text{x}=-4,5$; и
при \[\text{y}=1\], $\text{x}=-4.5$ — решения данного уравнения.
Теперь нарисуйте точки $\left(-4.5,3\right)$, $\left(-4.5,-1 \right)$ и $\left(-4.5,1\right)$ на миллиметровой бумаге. и соедините точки прямой линией.Графическое представление показано ниже:
(изображение будет загружено в ближайшее время)
Решения NCERT для класса 9 по математике. Глава 4. Линейные уравнения с двумя переменными — загрузка в формате PDF.
 для класса 9 по математике в формате PDF для предстоящих экзаменов, а также вы можете найти решения всех глав по математике ниже.
для класса 9 по математике в формате PDF для предстоящих экзаменов, а также вы можете найти решения всех глав по математике ниже.Решения NCERT для математики класса 9
Линейное уравнение с двумя переменными
Глава 4 Линейное уравнение с двумя переменными для класса 9 состоит из пяти разделов и четырех упражнений.Первый раздел представляет собой введение без упражнений. Во втором и третьем разделах обсуждается линейное уравнение и его решение, тогда как четвертый и пятый разделы представляют собой дополнительные темы, в которых мы узнаем о графике линейных уравнений с двумя переменными и уравнениях линий, параллельных оси x и оси y.
Список упражнений и тем, рассматриваемых в линейном уравнении с двумя переменными, класс 9:
Уравнения могут быть линейными — линейные уравнения
Уравнение включает знак равенства (=), который указывает, что члены в левой части равны слагаемым в правой части.
 Линейное уравнение — это уравнение прямой линии, содержащее переменные и константы в следующем виде:
Линейное уравнение — это уравнение прямой линии, содержащее переменные и константы в следующем виде:\[a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3} \]…… + b = 0
Где \[a_{1}, a_{2}, a_{3}\]… — коэффициенты, b — константа и \[x_{1}, x_{2}, x_{3}\]…. — переменные. Если значение любого коэффициента или переменной равно нулю, то термин, содержащий этот коэффициент или переменную, становится равным нулю. Это потому, что все, что умножается на ноль, равно нулю.
Линейное уравнение — это простое уравнение, содержащее коэффициенты, константы и одну или несколько переменных, но линейное уравнение не может иметь показателей и корней.
Один, два, три Какими могут быть переменные? Типы линейных уравнений
Линейное уравнение с одной переменной: Линейное уравнение, в котором есть только одна переменная (неизвестный термин), представленная буквами или символами, известно как линейное уравнение с одной переменной.
 Он представлен как ax+b = 0, где a — коэффициент переменной x, а b — константа. Коэффициент никогда не может быть равен нулю.
Он представлен как ax+b = 0, где a — коэффициент переменной x, а b — константа. Коэффициент никогда не может быть равен нулю.Примеры: 7x + 6 = 13
Линейное уравнение с двумя переменными: Линейное уравнение — это уравнение с двумя переменными (неизвестными терминами), представленное буквами или символами, известное как линейное уравнение с двумя переменными.Он представлен как ax+by+c = 0, где a и b — коэффициенты, x и y — переменные, а c — константа. Если какой-либо коэффициент становится равным нулю, то линейное уравнение с двумя переменными меняется на линейное уравнение с одной переменной.
Примеры: 2x +3y = 24
Линейные уравнения с тремя или более переменными: Линейное уравнение, содержащее более двух переменных, называется линейным уравнением с тремя или более переменными. Его можно представить в виде:
\[a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3}\]….. + b = 0.
Примеры: 5x+ 21y — 3z = -2
Линейное уравнение с двумя переменными
До сих пор, путешествуя по алгебраическим уравнениям, мы научились решать одиночные уравнения только с одной переменной.
 (неизвестный). Например, что-то вроде 9x + 4 = 22. Просто, не правда ли?
(неизвестный). Например, что-то вроде 9x + 4 = 22. Просто, не правда ли?Но что произойдет, если в уравнении есть более одного неизвестного, например, 5x + 3y = 15. Мы решаем это по-другому. Поэтому, прежде чем рассматривать решение линейного уравнения с двумя переменными, давайте разберемся с линейным уравнением с двумя переменными математически.
Определение
Уравнение типа ax+by+c = 0, где a,b,c — действительные числа, такие что a и b отличны от нуля, называется линейным уравнением с двумя переменными x и y .
Пример: x+y-5 = 0 представляет собой линейное уравнение с двумя переменными (неизвестными) x и y. Обратите внимание, что x=2 и y=3 удовлетворяют этому линейному уравнению.
Невозможно решить одно линейное уравнение с двумя переменными.
Никто не может на законных основаниях попросить вас решить одно уравнение с двумя переменными, потому что это даст вам бесконечное количество решений.
 Но можно решить два уравнения с двумя переменными в каждом, чтобы найти значения x и y одновременно. Группа из двух или более уравнений называется системой уравнений.
Но можно решить два уравнения с двумя переменными в каждом, чтобы найти значения x и y одновременно. Группа из двух или более уравнений называется системой уравнений.Каждое уравнение представляет собой прямую линию. Если взять две линии, то есть высокая вероятность того, что эти две линии пересекутся в уникальной точке, которая удовлетворяет обоим уравнениям. Чтобы найти точку пересечения, выберите две случайные линии и решите.
Решение линейного уравнения
Мы знаем, что каждое линейное уравнение с одной переменной имеет единственное решение.А как насчет решения линейного уравнения с двумя переменными? Всегда будет пара значений, одно для x, а другое для y, которые удовлетворяют данному уравнению. Также обратите внимание, что нет конца различным решениям линейного уравнения с двумя переменными. То есть линейное уравнение с двумя переменными имеет бесконечно много решений.
Существует множество способов решения системы линейных уравнений с двумя переменными.
 Ниже приведены два основных метода решения линейного уравнения с двумя переменными.
Ниже приведены два основных метода решения линейного уравнения с двумя переменными.1. Графический метод решения линейного уравнения
Вместо решения двух линейных уравнений по отдельности мы находим решение системы. Если мы начертим обе линии в одной системе координат, то точка пересечения двух линий будет решением системы.
Например: Чтобы решить систему уравнений, состоящую из двух уравнений —
2x+2 = y и x-1 = y, нам нужно рассмотреть значение x и найти соответствующее значение y для каждого уравнения.Для уравнений 2x+2 = y и x-1 = y берется случайное значение x и вычисляется соответствующее ему значение y. Точки будут (1,4), (2,6), (3,8) для уравнения 2x+2 = y. И точки (1,0), (2,1), (3,2) для уравнения x-1 = y. Точки должны быть нанесены на график. Точка пересечения этих двух прямых и будет решением системы.
2. Метод подстановки решения линейного уравнения
Другим способом решения системы линейных уравнений является метод подстановки.
 Эта система показывает, как легко решать линейные уравнения, находя значение одной переменной через другую переменную, используя одно уравнение, а затем заменяя это значение другим уравнением.
Эта система показывает, как легко решать линейные уравнения, находя значение одной переменной через другую переменную, используя одно уравнение, а затем заменяя это значение другим уравнением.Найдем решение той же системы линейных уравнений.
2x+2 = y
x-1 = y
Из уравнения (2) мы можем сказать, что y = x-1.
Подстановка значения y в уравнение (1).
2x+2 = x-1
2x-x = -2-1
x = -3
Таким образом, мы можем найти фактическое значение y, подставив значение x как -3 в уравнение (1 ).
2x + 2 = y
2(-3) + 2 = y
-6 + 2 = y
-4 = y
или, y= -4.
Следовательно, решение системы линейных уравнений равно (-3,-4).
Почему решения NCERT для математики класса 9?
У каждого экзамена есть образец для проверки знаний студентов и их способности работать в ближайшем будущем.
 Решение NCERT-решений линейных уравнений с двумя переменными Класс 9 после изучения главы поможет вам понять шаблон экзамена, вес каждой темы и обеспечит подготовку к экзамену.Практика по математике в классе 9, глава 4, увеличивает вашу скорость во время экзаменов, потому что многие ученики не успевают закончить работу вовремя. Практика тренирует в вас склонность думать о решении данного вопроса с бешеной скоростью. Кроме того, вы можете предсказать темы, которые могут появиться на экзамене, оценив частоту и интервал повторяющихся вопросов. Это может помочь вам разработать стратегию подготовки и получить хорошие оценки. С практикой вы также сможете решать неповторяющиеся или совершенно новые вопросы, потому что концепция вопросов в опросных листах обычно остается неизменной.Разница только в искаженных вопросах и измененных числах. Вы также привыкнете к уровню или стандарту экзаменационных вопросов. Так что поймите и узнайте концепцию при решении вопросов, и в итоге вы наберете более 90 процентов.
Решение NCERT-решений линейных уравнений с двумя переменными Класс 9 после изучения главы поможет вам понять шаблон экзамена, вес каждой темы и обеспечит подготовку к экзамену.Практика по математике в классе 9, глава 4, увеличивает вашу скорость во время экзаменов, потому что многие ученики не успевают закончить работу вовремя. Практика тренирует в вас склонность думать о решении данного вопроса с бешеной скоростью. Кроме того, вы можете предсказать темы, которые могут появиться на экзамене, оценив частоту и интервал повторяющихся вопросов. Это может помочь вам разработать стратегию подготовки и получить хорошие оценки. С практикой вы также сможете решать неповторяющиеся или совершенно новые вопросы, потому что концепция вопросов в опросных листах обычно остается неизменной.Разница только в искаженных вопросах и измененных числах. Вы также привыкнете к уровню или стандарту экзаменационных вопросов. Так что поймите и узнайте концепцию при решении вопросов, и в итоге вы наберете более 90 процентов. Хорошо известно, что некоторые из нас готовятся к тому, чтобы набрать максимум, но в итоге получают меньше из-за нашей небрежности или концептуальных ошибок. И это можно исправить правильной практикой. Решая математические задачи, вы не только улучшаете свои навыки решения задач, но и расширяете свои аналитические и логические способности, которые так необходимы современному поколению.Всем нам важно понимать и выявлять проблемы, логически мыслить, интерпретировать, принимать решения и решать проблемы.
Хорошо известно, что некоторые из нас готовятся к тому, чтобы набрать максимум, но в итоге получают меньше из-за нашей небрежности или концептуальных ошибок. И это можно исправить правильной практикой. Решая математические задачи, вы не только улучшаете свои навыки решения задач, но и расширяете свои аналитические и логические способности, которые так необходимы современному поколению.Всем нам важно понимать и выявлять проблемы, логически мыслить, интерпретировать, принимать решения и решать проблемы.Вы можете использовать решения NCERT для:
1. Проверьте свои навыки решения проблем.
2. Привыкайте к структурированным и стандартным вопросам.
3. Проверьте свои знания по главам.
4. Повысить уровень уверенности
5. Повысить скорость
6.Сделайте так, чтобы это также служило вашей заметкой о пересмотре.

Решения NCERT для математики класса 9 Глава 4 Линейные уравнения с двумя переменными Бесплатный PDF-файл, доступный на Vedantu, решается экспертами. Загрузите бесплатные учебные материалы для 9 класса, чтобы набрать больше баллов.
NCERT Solutions Chapter- 4 Class 9 Maths By Vedantu
Vedantu предлагает обучение в приятной и интересной форме, чтобы помочь вам разработать прочную концептуальную основу для каждой главы.Класс 9 Математика Глава 4 Решения предоставляются экспертами в предметной области, которые неустанно работают вместе над поиском точных, простых и пошаговых решений для каждого вопроса в учебниках NCERT. Численные задачи предназначены для того, чтобы помочь вам найти правильный подход к главе и улучшить ваше понимание важных понятий. Математика Глава 4 Решения подготовлены с целью охватить всю учебную программу в виде решений вопросов NCERT. Доказано, что это важный материал для студентов, стремящихся к эффективному обучению, чтобы сдать экзамены Совета и сложные конкурсные экзамены, такие как JEE (основной и продвинутый), AIM и т.
 Д.
Д.Vedantu, лучшая онлайн-репетиторская компания в Индии, делает все возможное, чтобы оказать вам реальную помощь, предоставляя решения NCERT для 9-го класса по математике, глава 4, линейные уравнения, и стремится предоставить достаточное количество задач и решений для практики и создания прочного фундамента на главе. Эксперты в предметной области предоставляют решения NCERT для математики класса 9 в простой и точной форме с подробным резюме, приведенным в конце главы.
Решения NCERT для класса 9 по математике. Глава 4. Линейные уравнения с двумя переменными — бесплатный PDF средний возраст учащихся.
Сложные решения разбиты на простые этапы, чтобы вам было проще понять суть за меньшее время.
Выделены основные факты, термины, принципы и приложения.
Растворы готовятся строго в соответствии с последними решениями NCERT.

Он охватывает всю программу и концепцию в виде решений.
Ответы систематизированы и интересны.
Содержание должно быть лаконичным, кратким и понятным.
Некоторые ответы содержат необходимые изображения для облегчения понимания концепции.
Он удобен и служит заметкой во время повторения экзамена.
Решения просты, чтобы вы могли решить максимальное количество вопросов и получить представление о главе. Кроме того, это повышает скорость решения задач
Углубление в упражнение — типы вопросов
NCERT 9 класс CBSE Глава 4 Линейные уравнения с двумя переменными относится к алгебре. Во введении описывается решение линейного уравнения с двумя переменными и то, как это решение выглядит на декартовой плоскости. Тема «Линейные уравнения» объясняет моменты, которые следует учитывать при решении линейной задачи. В этой главе вы получите решение линейного уравнения. В этом разделе объясняется решение линейного уравнения с двумя переменными с парой значений, одно для x и одно для y, которые удовлетворяют данному уравнению. Все эти концепции преподаются с помощью управляемых примеров, что делает процесс обучения более интерактивным.Решения, относящиеся к проблемам между главами, также помогают учащимся понять свой уровень обучения. Интересные темы, такие как график линейного уравнения с двумя переменными и уравнения линий, параллельных оси x и оси y, будут изучены в этой главе с помощью построения двух переменных линейного уравнения на листе графика. Решения, предлагаемые для всех этих тем, представлены шаг за шагом, чтобы учащийся мог шаг за шагом усваивать концепцию. Каждая из тем сопровождается компактными упражнениями.
Во введении описывается решение линейного уравнения с двумя переменными и то, как это решение выглядит на декартовой плоскости. Тема «Линейные уравнения» объясняет моменты, которые следует учитывать при решении линейной задачи. В этой главе вы получите решение линейного уравнения. В этом разделе объясняется решение линейного уравнения с двумя переменными с парой значений, одно для x и одно для y, которые удовлетворяют данному уравнению. Все эти концепции преподаются с помощью управляемых примеров, что делает процесс обучения более интерактивным.Решения, относящиеся к проблемам между главами, также помогают учащимся понять свой уровень обучения. Интересные темы, такие как график линейного уравнения с двумя переменными и уравнения линий, параллельных оси x и оси y, будут изучены в этой главе с помощью построения двух переменных линейного уравнения на листе графика. Решения, предлагаемые для всех этих тем, представлены шаг за шагом, чтобы учащийся мог шаг за шагом усваивать концепцию. Каждая из тем сопровождается компактными упражнениями. Упражнения направлены на проверку ваших знаний и глубины понимания различных теорем и понятий, представленных в этой главе. Несмотря на это, следует отметить, что числовые задачи этой главы в основном основаны на конкретных теоремах и других связанных концепциях.
Упражнения направлены на проверку ваших знаний и глубины понимания различных теорем и понятий, представленных в этой главе. Несмотря на это, следует отметить, что числовые задачи этой главы в основном основаны на конкретных теоремах и других связанных концепциях.
NCERT Solutions for Class 9 Math Глава 4 Линейные уравнения с двумя переменными — Скачать PDF
Все темы объясняются с помощью пошаговых решенных примеров в упражнениях.Решения, данные для задач в этой теме, помогут вам ознакомиться с основной концепцией линейных уравнений. Чтобы еще больше помочь вам лучше понять эти темы и связанные с ними концепции, также предлагается ряд решенных примеров числовых задач. Более того, для каждого решенного примера предоставляется подробное пошаговое объяснение. Это может помочь понять, какие методы следует использовать для подхода к различным типам вопросов для их точного решения. Команда Vedantu проверила, сколько упражнений и типов вопросов есть в главе 4 математики 9-го класса.
Раздел 1.2. Упражнение 1.1
Первое упражнение в этой главе состоит из 2 вопросов с вопросом номер два и восемью подвопросами в упражнении 1.2 решения NCERT для математики, класс 9, глава 4. Большинство вопросов этого упражнения основанный на стандартной форме линейного уравнения с двумя переменными, который является мощным методом для вычисления значения a, b и c любого заданного уравнения. В основном в этом разделе можно найти три типа вопросов:
Тип 1: Представление оператора в виде линейного уравнения с двумя переменными.
Тип 2: Выражение линейного уравнения в стандартной форме.
Тип 3: Идентификация a, b и c в линейном уравнении с двумя переменными.
Эти типы вопросов включают множество шагов для достижения решения и, следовательно, сопряжены с риском сделать много глупых ошибок. Убедитесь, что у вас есть четкое представление о линейных уравнениях и переменных. Кроме того, лучшее понимание необходимых шагов поможет им легко избавиться от затянувшихся сомнений. Проясните все свои сомнения и укрепите свои знания о различных концепциях, описанных в этой главе, обратившись к нашим решениям NCERT для математики 9-го класса, глава 4.Каждая числовая задача была объяснена шаг за шагом, чтобы вам было легко понять их и понять логику, стоящую за ними. Кроме того, вы также найдете много полезных советов и альтернативных методов для точного и более уверенного решения подобных задач.
Кроме того, лучшее понимание необходимых шагов поможет им легко избавиться от затянувшихся сомнений. Проясните все свои сомнения и укрепите свои знания о различных концепциях, описанных в этой главе, обратившись к нашим решениям NCERT для математики 9-го класса, глава 4.Каждая числовая задача была объяснена шаг за шагом, чтобы вам было легко понять их и понять логику, стоящую за ними. Кроме того, вы также найдете много полезных советов и альтернативных методов для точного и более уверенного решения подобных задач.
Раздел 1.3. Упражнение 1.2
Второе упражнение в главе 4 по математике для 9 класса состоит из 4 вопросов и в основном основано на решении линейных уравнений с двумя переменными. Как только вы поймете концепцию поиска решения, вы сможете идентифицировать уравнения, имеющие уникальные решения, два решения или множество решений.Математика 9 класс глава 4 нашла широкое применение как в области математики, так и за ее пределами. Ниже приведены типы найденных вопросов, связанных с темой:
Ниже приведены типы найденных вопросов, связанных с темой:
Тип 1: Определение количества решений данных уравнений.
Тип 2: Нахождение решения данного уравнения.
Тип 3: перекрестная проверка решений уравнения.
Тип 4: Нахождение значения неизвестного члена, если известно решение уравнения.
Это упражнение улучшит ваши знания в поиске решения уравнения.Поступая так, вы обретете больше уверенности в том, как найти неизвестные члены или как определить количество решений уравнения. Это также окажется полезным, помогая вам эффективно и за меньшее время решать аналогичные типы числовых задач. Изучите методы быстрого доступа с близкого расстояния, взглянув на pdf-файл NCERT Solutions for Class 9 Maths Chapter 4, который предлагается онлайн в формате PDF. Math Chapter 4 pdf в свой план пересмотра.Загрузите учебные решения Vedantu с его учебного портала одним щелчком мыши и улучшите свой учебный процесс без особых хлопот.
Раздел 1.4. Упражнение 1.3
Третье упражнение NCERT Solutions для главы 4 по математике, класс 9 состоит из максимального количества вопросов. Все упражнение разделено на восемь вопросов, все из которых основаны на графе линейных уравнений с двумя переменными.
Тип 1: Рисование графика линейного уравнения с двумя переменными.
Тип 2: Уравнение прямой, проходящей через точку (x,y).
Тип 3: Нахождение значения неизвестного члена, если задано решение.
Тип 4: Суммы задач.
Тип 5: Определение уравнения по графику.
Обычно числовые задачи включают в себя длительные шаги и сложные подходы, поэтому очень важно хорошо разбираться в основах концепций, на которых они основаны. Это упражнение состоит из важных и сложных вопросов в гл. 4, класс 9, математические решения. так вы усвоите основную концепцию этого раздела и начнете эффективно решать вопросы. Учебные пособия Vedantu, такие как NCERT Solutions for Class 9 Maths Chapter 4 pdf, были разработаны экспертами с учетом потребностей и требований как экзаменов совета CBSE, так и студентов.
Учебные пособия Vedantu, такие как NCERT Solutions for Class 9 Maths Chapter 4 pdf, были разработаны экспертами с учетом потребностей и требований как экзаменов совета CBSE, так и студентов.
Раздел 1.5 — Упражнение 1.4
Последнее упражнение Главы 4 Класс 9 Математика состоит из 2 вопросов с подразделами и в основном основано на понятиях геометрического представления уравнения прямой. Решение для 9-го класса математики, глава 4, подробно описывает каждую из этих концепций, чтобы помочь учащимся лучше понять их.Если у вас есть четкое понимание темы, вы сможете применить эту концепцию для решения различных числовых задач. На основании теорем упражнение можно разделить на следующие типы вопросов:
Тип 1: Геометрическое представление уравнения с одной и двумя переменными.
Рекомендуется решить упражнение и сопоставить свой ответ с нашими онлайн-решениями на основе глав, чтобы более эффективно оценить свое понимание тем. Настойчиво пересматривая NCERT Solutions for Class 9 Maths Chapter 4, вы сможете хорошо подготовиться к предстоящему экзамену на доске и оказаться полезным для получения хороших результатов.Это поможет вам эффективно решать числовые задачи такого типа точно и за меньшее время.
Настойчиво пересматривая NCERT Solutions for Class 9 Maths Chapter 4, вы сможете хорошо подготовиться к предстоящему экзамену на доске и оказаться полезным для получения хороших результатов.Это поможет вам эффективно решать числовые задачи такого типа точно и за меньшее время.
Загрузите решения NCERT для математики для 9-го класса от Vedantu, которые курируются ведущими учителями. Кроме того, вы можете пересмотреть и решить важные вопросы для экзамена по математике 9 класса 2019–2020, используя обновленные решения NCERT Book Solutions, предоставленные нами. Такие предметы, как естествознание, математика, английский язык, станут легкими для изучения, если у вас есть доступ к решению NCERT для естествознания класса 9, решениям по математике и решениям по другим предметам, которые доступны только на Vedantu.
Резюме
Уравнение вида ax + by + c = 0, где a, b и c — действительные числа, такое, что a и b оба не равны нулю, называется линейным уравнением с двумя переменными.
 .
.Линейное уравнение с двумя переменными имеет бесконечно много решений.
График любого линейного уравнения с двумя переменными представляет собой прямую линию.
x = 0 — уравнение оси y, а y = 0 — уравнение оси x.
График x = a представляет собой прямую линию, параллельную оси y.
График y = a представляет собой прямую линию, параллельную оси x.
Уравнение типа y = mx представляет прямую, проходящую через начало координат.
Каждая точка на графике линейного уравнения с двумя переменными является решением линейного уравнения.
 Более того, каждое решение линейного уравнения является точкой на графике линейного уравнения.
Более того, каждое решение линейного уравнения является точкой на графике линейного уравнения.
Математика Часть I (решения) для 9 класса Математика Глава 5
Страница № 86:
Вопрос 1:
Используя переменные x и y , составьте любые пять линейных уравнений с двумя переменными.
Ответ:
Линейные уравнения с двумя переменными x и y будут равны
x+y=12x+3y=8x-y=65x-2y=3x+2y=3
Страница № 86:
Вопрос 2:
Напишите пять решений уравнения x + y = 7.
Ответ:
Данное уравнение имеет вид x + y = 7.
Возможное решение:
Страница № 86:
Вопрос 3:
Решите следующие системы одновременных уравнений.
(i) х + y = 4; 2 91 506 х 91 507 — 5 91 506 у 91 507 = 1 91 505 (ii) 2 91 506 х 91 507 + 91 506 у 91 507 = 5; 3 x — y = 5
(iii) 3 x — 5 y =16; x — 3 y = 8
(iv) 2 y — х = 0; 10 х + 15 у = 105
(в) 2 х + 3 у + 4 = 0; x — 5 y = 11
(vi) 2 x -7 y = 7; 3 x + y = 22
Ответ:
(i) 91 506 x 91 507 + 91 506 y 91 507 = 4 …..(Я)2 x — 5 y = 1 …..(II)
Из (I) имеем
x=4-y
Поместив это значение x в (II)
24-y-5y=1⇒8-2y-5y=1⇒8-7y=1⇒8-1=7y⇒7=7y⇒y=1
Подставляя значение 91 506 y в (I), мы получаем
x+1=4⇒x=3
. Следовательно,
Складываем (I) и (II)
5x=10⇒x=105=2
Подставляя это значение в (I), получаем
2×2+y=5⇒4+y=5⇒y=1x,y= 2,1
(iii) 3 x — 5 y =16 . ….(I)
….(I)
x — 3 y = 8 …..(II)
Умножить (II) на 3
3x-9y=24 …..(III)
(I ) — (III)
4y=-8y=-2 Подставляя значение y в (II)x=2
10 x + 15 y = 105 …..(II)
Из (II)
2x+3y=21 …..(III)
Из (I) и (III)
22y+3y=21⇒4y+3y=21⇒7y=21⇒y=3x=2×3=6
(v) 2 x + 3 y + 4 = 0 ….. (i)
x — 5 y = 11 ….. (II)
от (i) у нас
2 x + 3 y = -4 …. .(III)
Умножить (II) на 2
2x-10y=22 …..(IV)
Из (III) и (IV) имеем
2 x + 3 y 9 1= -8 2x-10y=22
(III) — (IV)
13y=-26⇒y=-2
x = 11 + 5 y
x = 1
2 x
2 x
2 x
6 x 9150 6 7 г = 7 . …. (I)
…. (I)
3 x + y = 22 ….. (II)
Умножным (II) с 7
21 x + 7 y = 154 ….. (III)
(I) + (III)
23 x = 161
x = 7, y = 1
Страница № 90:
Вопрос 1:
В конверте лежат банкноты номиналом 5 и 10 рупий.Общая сумма этих банкнот вместе составляет 350 рупий. Количество банкнот в 5 рупий меньше на 10, чем количество банкнот в 10 рупий. Затем найдите количество банкнот номиналом 5 и 10 рупий.
Ответ:
Отказ от ответственности: В заданном вопросе ошибка. Вместо «Количество банкнот в 5 рупий меньше на 10, чем количество банкнот в 10 рупий»
, предложение должно быть таким: «Количество банкнот в 5 рупий больше на 10, чем количество банкнот в 10 рупий».
Пусть количество банкнот номиналом 5 рупий равно x , а количество банкнот номиналом 10 рупий равно y.
5x + 10y = 350⇒x + 2y = 70 ….. I
Количество 5 нот рупий превышает 10, чем 10 рупийных примечаний
Итак, xy = 10
⇒x = 10 + y .. …(II)
Из (I) и (II) имеем
10+y+2y=70⇒10+3y=70⇒3y=60⇒y=20
Таким образом, x = 10 + 20 = 30
Количество банкнот по 5 рупий = 30, количество банкнот по 10 рупий = 20
Страница № 90:
Вопрос 2:
Знаменатель дроби на 1 больше числителя.Если к числителю и знаменателю добавить 1 соответственно, отношение числителя к знаменателю будет 1 : 2. Найдите дробь.
Ответ:
Отказ от ответственности: В заданном вопросе ошибка. При данных утверждениях два сформированных линейных уравнения будут одинаковыми.
Страница № 90:
Вопрос 3:
Сумма возрастов Приянки и Дипики составляет 34 года. Приянка старше Дипики на 6 лет. Затем найдите их сегодняшний возраст.
Приянка старше Дипики на 6 лет. Затем найдите их сегодняшний возраст.
Ответ:
Пусть возраст Приянки будет х лет, а возраст Дипики х лет.
Сумма возрастов Приянки и Дипики составляет 34 года.
x+y=34 …..(I)
Приянка старше Дипики на 6 лет.
xy=6 …..(II)
Складывая (I) и (II), получаем
2x=40⇒x=20
. 14
Таким образом, возраст Приянки = 20 лет, а возраст Дипики = 14 лет.
Страница № 90:
Вопрос 4:
Общее количество львов и павлинов в определенном зоопарке равно 50. Общее количество их ног равно 140. Затем найдите количество львов и павлинов в зоопарке.
Ответ:
Пусть львов будет х , а павлинов х .
Общее количество львов и павлинов в определенном зоопарке равно 50.
Итак, x+y=50 …..(I)
Общее количество их ног равно 140.
У льва 4 ноги, а у павлина 2.
4x+2y=140⇒2x+y=70 ….. II
Вычитая (II) из (I), получаем
x=20y=30
Таким образом, число львов = 20 и количество павлинов = 30.
Страница № 90:
Вопрос 5:
Санджай получает фиксированный ежемесячный доход.Каждый год происходит определенная прибавка к его зарплате. Через 4 года его месячная зарплата составляла рупий. 4500, а через 10 лет его месячная зарплата стала 5400 рупий, затем найдите его первоначальную зарплату и ежегодную прибавку.
Ответ:
Пусть фиксированный месячный доход равен x рупий.
Годовой прирост составит и рупий.
Через 4 года его месячная зарплата составила рупий. 4500
Месячный оклад + ежегодная надбавка за 4 года = 4500
x+4y=4500 . ….(I)
….(I)
Через 10 лет его месячная зарплата стала 5400 рупий
Месячная зарплата + ежегодная надбавка за 10 лет = 5400
x+10y=5400 …..(II)
(II) — (I)
6 y = 900
y = 150
x = 4500 — 150 × 4 = 3900
Таким образом, месячная заработная плата = 3900
1 5018 1 500 1 годовая прибавка 0 рупий
Страница № 90:
Вопрос 6:
Цена 3 стульев и 2 столов 4500 рупий, а цена 5 стульев и 3 столов 7000 рупий, тогда найдите цену 2 стульев и 2 столов.
Ответ:
Пусть цена 1 стула х рупий, а цена 1 стола рупий у.
Цена за 3 стула и 2 стола 4500 рупий
3x+2y=4500 …..I
Цена за 5 стульев и 3 стола 7000 рупий
5x+3y=7000 …..II
Умножить (I) с 3 и (II) с 2
9x+6y=13500 . ….III10x+6y=14000 …..IVIV-IIIx=500. Подставим это значение x в I3×500+2y=4500⇒ 1500+2y=4500⇒2y=4500-1500=3000⇒y=1500
….III10x+6y=14000 …..IVIV-IIIx=500. Подставим это значение x в I3×500+2y=4500⇒ 1500+2y=4500⇒2y=4500-1500=3000⇒y=1500
Цена за 2 стула и 2 стола составит
=2x+2y=2x+y=2500+1500=2×2000=4000
Таким образом, цена за 2 стула и 2 стола 4000
Страница № 91:
Вопрос 7:
Сумма цифр двузначного числа равна 9.Число, полученное перестановкой цифр, больше исходного числа на 27. Найдите двузначное число.
Ответ:
Пусть число в разряде десятков будет x , а в разряде единиц y .
Полученное число = 10 x + y
Сумма цифр двузначного числа равна 9.
x+y=9 …..(I) исходный номер на 27.
10y+x-10x + y=27⇒10y+x-10x-y=27⇒9y-9x=27⇒yx=3 ….. II
Добавление (I) и (II)
2y= 12⇒y=6
x = 3
Таким образом, число равно 36.
Страница № 91:
Вопрос 8:
В ∆ABC мера угла A равна сумме мер ∠ B и ∠ C. Также отношение мер ∠ B и ∠ C равно 4 : 5. Затем найдите меры углов треугольника .
Ответ:
∠A = ∠B + ∠C …..(I)
∠B∠C=45⇒5∠B=4∠C ….. II ∠B + ∠C = 180°
Из (I)
∠B + ∠C +∠B + ∠C = 180°
⇒2∠B+∠C=180°⇒2∠B+5∠B4=180°⇒ ∠B+5∠B4=90°⇒4∠B+5∠B=360°⇒9∠B=360°⇒∠B=40°
5×40°=4∠C⇒∠C=50°
И ∠A = ∠B + ∠C = 40°+50°=90°.
Страница № 91:
Вопрос 9:
Разделите веревку длиной 560 см на 2 части так, чтобы удвоенная длина меньшей части равнялась 13 большей части.Затем найдите длину большей части.
Ответ:
Пусть меньшая часть будет х см, а большая х см.
x+y=560 …..(I)
Удвоенная длина меньшей части равна 13 большей части.
x=13y⇒3x=y
Подставив значение y в (I), мы получим
x+3x=560⇒4x=560⇒x=140
Таким образом, y=3×140=420
Таким образом, большая часть = 420 см, а меньшая часть 140 см.
Страница № 91:
Вопрос 10:
На конкурсном экзамене было 60 вопросов. За правильный ответ начисляется 2 балла, за неправильный ответ снимается 1 балл. Яшвант ответил на все вопросы и получил в общей сложности 90 баллов. Тогда в скольких вопросах он ошибся?
Ответ:
Пусть количество правильных ответов равно x , а количество неправильных ответов равно y.
Всего ответов = Количество правильных + количество неправильных = 60
x+y=60 …..(I)
Всего полученных баллов = 90
2x-y=90 . ….(II)
….(II)
Добавление (I) и (II) имеем
3x=150⇒x=50y=10
Количество вопросов, на которые он ответил неправильно, равно 10.
Страница № 91:
Вопрос 1:
Выберите правильные альтернативные ответы на следующие вопросы.
(i) Если 3 91 506 x 91 507 + 5 91 506 y 91 507 = 9 и 5 91 506 x 91 507 + 3 91 506 y 91 507 = 7, то каково значение 91 506 x 91 507 + 91 506 y 91 500?
(А) 2 (Б) 16 (В) 9 (Г) 7
(ii) «Если из длины и ширины прямоугольника вычесть 5, периметр станет равен 26». Какова математическая форма утверждения?
(а) x — y x + + + x + x + + = 8 (c) y + y = 23 (d) 2 x + y = 21
(iii) Аджай моложе Виджая на 5 лет.Сумма их возрастов 25 лет. Сколько лет Аджаю?
(А) 20 (Б) 15 (В) 10 (Г) 5
Ответ:
(i) 3 x + 5 y = 9 .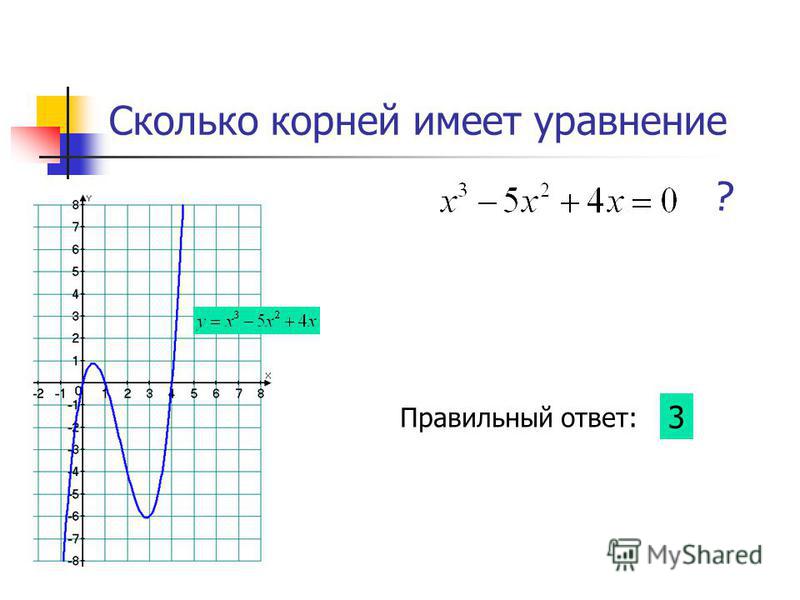 ….(I)
….(I)
5 x + 3 y = 7 II) имеем
8x+8y=16⇒x+y=2
Следовательно, правильный ответ – вариант (A).
(ii) Пусть длина будет x , а ширина y .
Периметр прямоугольника = 2( l + b ) = 26
2( l + b ) = 26
⇒2x-5+y-5=26⇒2x+y-10=26⇒2x+y-10=26 ⇒x+y=23
Следовательно, правильный ответ — вариант (C).
(iii) Пусть возраст Аджая будет х лет, а возраст Виджая х лет.
Аджай моложе Виджая на 5 лет.
y-x=5 …..I
Сумма их возрастов составляет 25 лет.
x+y=25 …..II
Складывая (I) и (II), мы получаем
2y=30⇒y=15x=10
Таким образом, возраст Аджая составляет 10 лет.
Следовательно, правильный ответ — вариант (С).
Страница № 91:
Вопрос 2:
Решите следующие одновременные уравнения.
(i) 2 х + у = 5 ; 3 x — y = 5
(ii) x -2 y = -1 ; 2 x — y = 7
(iii) 91 506 х 91 507 + 91 506 y 91 507 = 11; 2 x — 3 y = 7
(iv) 2 x + y = -2 ; 3 x — y = 7
(v) 2 91 506 х 91 507 — 91 506 у 91 507 = 5; 3 х + 2 у = 11
(vi) х — 2 у = -2 ; х + 2 у = 10
Ответ:
(i) 2 x + y = 5 …..(I)
3 x — y = 5 …..(II)
(I) + (II)
5x=10⇒x=2
Подставляя значение x в (I)
2×2+y=5⇒4+y=5⇒y=1
(ii) x -2 y = -1 ….. (I)
2 x — y = 7 ….. (II)
Умножьте (i) с 2
2x-4y=-2 . ….(III)
….(III)
Вычитая (III) из (II)
-3y=-9⇒y=3
Подставляя значение y в (I), получаем
x -2×3=-1⇒x-6=-1⇒x=5
(iii) x + y = 11 …..(Я)
2 x — 3 y = 7 …..(II)
Умножьте (I) на 3
3x+3y=33 …..(III)
Сложение (II) и (III)
5x=40⇒x=8
Подставляя значение x в (I)
8+y=11⇒y=3
(iv) 2 x + y = -2 7 …..(I)
3 — 3 y = 7 …..(II)
Сложение (I) с (II)
5x=5⇒x=1 2⇒2+у=-2⇒у=-4
(v) 2 x — y = 5 …..(Я)
3 x + 2 y = 11 …..(II)
Умножая (I) на 2, получаем
4x-2y=10 …..(III)
Складывая (II) с (III )
7x=21⇒x=3
Подставляя значение x в (I), получаем
2×3-y=5⇒6-y=5⇒y=1
(vi) x — 2 y = -2 . ….(I)
….(I)
x + 2 y = 10 …..(II)
Подставляя значение x в (I), мы получаем
4-2y=-2⇒-2y=-6⇒y=3
Страница № 91:
Вопрос 3:
Приравнивая коэффициенты при переменных, решите следующие уравнения.
(i) 3 91 506 x 91 507 — 4 91 506 y 91 507 = 7; 5 91 506 x 91 507 + 2 91 506 y 91 507 = 3 91 505 (ii) 5 91 506 x 91 507 + 7 91 506 y 91 507 = 17; 3 x -2 y = 4
(iii) 91 506 x 91 507 -2 91 506 y 91 507 = -10; 3 x — 5 y = -12
(iv) 4 x + y = 34 ; х + 4 у = 16
Ответ:
(i) 3 x — 4 y = 7 …..(I)
5 x + 2 y = 3 …..(II)
Умножьте (II) на 2
10 x + 4 y = 6 = 6 . (III)
(III)
Складываем (I) и (III)
13x=13⇒x=1
Подставляя значение x в (I), получаем
3×1-4y=7⇒3-4y=7⇒ y=-1
Таким образом, x = 1 и y=-1.
(ii) 5 x + 7 y = 17 …..(I)
3 x -2 y = 4 = 4 , (II)
Умножьте (i) с 3 и (ii) с 5
15 x + 21 y = 51 ….. (III)
15 x -10 y = 20. ….(IV)
Вычитая (IV) из (III), получаем
31y=31⇒y=1
Подставляя это значение y в (I), получаем
5x+7×1=17⇒5x =10⇒x=2
Таким образом, x=2, y=1.
(iii) 91 506 x -2 y = -10 …..(I)
3 x — 5 y = -12 …..(II)
Умножить (I) на 3
3x-6y=-30 …..(III)
Вычитая (II) из (III), получаем
-y=-18⇒y=18
Подставляя значение y в (I), получаем
x-2×18=-10⇒x=-10+36=26
Таким образом, x=26,y=18
(iv) 4 x + y = 34 . …. (i)
…. (i)
x + 4 y = 16 ….. (ii)
Добавление (i) и (ii) мы получаем
5x + 5Y = 50 ⇒x+y=10 …..I
Вычитая (II) из (I), мы получаем
3x-3y=18⇒xy=6 …..IV
(III) + (IV)
2x=16⇒x=8
Подставляя значение x в (I), получаем
48+y=34⇒y=34-32=2⇒ y=2
Таким образом, x=8,y=2
Страница № 91:
Вопрос 4:
Решите следующие одновременные уравнения.
(i) x3 + y4 = 4 ; x2 — y4= 1
(ii) x3 + 5y = 13 ; 2x + y2 = 19
(iii) 2x + 3y = 13 ; 5x — 4y = -2
Ответ:
(i) x3 + y4 = 4 …..(I)
x2 — y4= 1 …..(II)
Умножив (I) на НОК 3 и 4, что равно 12, мы получим
4x+3y=48 …..(III )
Умножая (II) на НОК 2 и 4, что равно 4, получаем
2x-y=4 . ….(IV)
….(IV)
Умножая (IV) на 2
4x-2y=8 …..( V)
Вычитая (V) из (III)
5y=40⇒y=8
Подставляя это значение y в (IV), мы получаем
2x-8=4⇒2x=12⇒x=6
( ii)
x3 + 5y = 13 …..I2x + y2 =19 …..II
⇒x+15y=39 …..III4x+y=38 …..IV
Умножая (III) на 4, получаем
4x+
4x 60y=156 …..(V)
Вычитая (IV) из (V)
59y=118⇒y=2
Подставляя значение y в (IV), получаем
4x+2=38⇒4x =36⇒x=9
(iii) 2x + 3y = 13 ; 5x — 4y = -2
Пусть 1x=u и 1y=v
Итак, получаем уравнения:….II ×210u+15v=65 …..III10u-8v=-4 …..IVВычитание IV из III23v=69⇒v=3Подстановка значения v в I2u+3×3=13⇒ 2u=4⇒u=21x=u⇒x=1u=121y=v⇒y=1v=13
Страница № 92:
Вопрос 5:
Двузначное число в 3 раза больше суммы своих цифр. Если к этому числу добавить 18, сумма будет равна числу, полученному путем перестановки цифр. Найдите число.
Если к этому числу добавить 18, сумма будет равна числу, полученному путем перестановки цифр. Найдите число.
Ответ:
Пусть двузначное число будет 10 х + у.
Двузначное число в 3 раза больше суммы своих цифр.
10x+y=4x+y+3⇒10x+y=4x+4y+3⇒2x-y=1 …..I
Если к этому числу добавить 18, сумма будет равна числу, полученному меняя местами цифры.
10x+y+18=10y+x⇒9x-9y=-18⇒xy=-2 …..II
(I) — (II)
x=3,y=5
Таким образом, полученное число 35.
Страница № 92:
Вопрос 6:
Общая стоимость 6 книг и 7 ручек 79 рупий, а общая стоимость 7 книг и 5 ручек 77 рупий. Найдите стоимость 1 книги и 2 ручек.
Ответ:
Отказ от ответственности: В заданном вопросе ошибка. Вместо 7 книг и 5 ручек должно быть 7 книг и 6 ручек.
Вместо 7 книг и 5 ручек должно быть 7 книг и 6 ручек.
Пусть стоимость 1 книги будет x , а стоимость 1 ручки y .
Общая стоимость 6 книг и 7 ручек 79 рупий.
6x+7y=79 …..I
Общая стоимость 7 книг и 6 ручек составляет 77 рупий.
7x+6y=77 …..II
Сложение (I) и (II)
13x+13y=156⇒x+y=12 …..III
Вычитание (II) из (I)
xy =-2 …..IV
Добавление (III) и (IV)
2x=10⇒x=5
y = 7
Стоимость 1 книги и 2 ручек составляет 5 + 14 = 19 рупий.
Страница № 92:
Вопрос 7:
Соотношение доходов двух человек 9 : 7. Соотношение их расходов 4 : 3. Каждый человек откладывает 200 рупий, найдите доход каждого.
Ответ:
Пусть доходы двух лиц равны x и y.
xy=97⇒7x=9y⇒7x-9y=0 . ….I
….I
Сбережения двух лиц = 200 рупий
Расходы = Доход — Сбережения
x-200y-200=43⇒3x-600=4y- 800⇒3x-4y=-200 …..II
Умножьте (I) на 3 и (II) на 7.
21x-27y=0 ….. III21x-28y=-1400 …..IVIV-III-y=-1400⇒ y=1400
Подставив значение y в (I), мы получим
x = 1800
. Таким образом, доход двух лиц составляет 1800 и 1400 рупий.
Страница № 92:
Вопрос 8:
Если длину прямоугольника уменьшить на 5 единиц, а ширину увеличить на 3 единицы, то площадь прямоугольника уменьшится на 8 квадратных единиц.Если длину уменьшить на 3 единицы, а ширину увеличить на 2 единицы, то площадь прямоугольника увеличится на 67 квадратных единиц. Затем найдите длину и ширину прямоугольника.
Ответ:
Пусть длина l , а ширина b .
Площадь прямоугольника = фунтов
Длина прямоугольника уменьшилась на 5 единиц, а ширина увеличилась на 3 единицы, тогда площадь прямоугольника уменьшилась на 8 квадратных единиц.
l-5b+3=lb-8⇒lb-5b+3l-15=lb-8⇒3l-5b=7 …..I
Если длина уменьшается на 3 единицы, а ширина увеличивается на 2 единицы, тогда площадь прямоугольника увеличится на 67 кв.
l-3b+2=lb+67⇒lb-3b+2l-6=lb+67⇒2l-3b=73 …..II
Умножьте (I) на 2 и (II) на 3
6l- 10b=14 …..III6l-9b=219 …..IV III-IVb=205
Подставляя это значение в (I), получаем
3l-5205=7⇒3l=7+1025=1032⇒l =344
Таким образом, длина = 344 единицы, а ширина = 205 единиц.
Страница № 92:
Вопрос 9:
Расстояние между двумя пунктами А и В по дороге равно 70 км. Одна машина отправляется из А, а другая из Б. Если они едут в одном направлении, то встретятся через 7 часов. Если они едут навстречу друг другу, то встретятся через 1 час, затем найдите их скорости.
Если они едут навстречу друг другу, то встретятся через 1 час, затем найдите их скорости.
Ответ:
Пусть скорость более быстрого автомобиля будет х км/ч, а скорость более медленного автомобиля будет х км/ч.
Общее расстояние между ними 70 км.
Speed=DistanceTime
Когда обе машины едут в одном направлении, они встретятся через 7 часов. I x+y=70 …..II
Сложение (I) и (II)
2x=80⇒x=40
Подстановка значения x в (I)
40-y=10⇒y=40 -10=30
Таким образом, скорость автомобилей 40 км/ч и 30 км/ч.
Страница № 92:
Вопрос 10:
Сумма двузначного числа и числа, полученного путем перестановки его цифр , равна 99. Найдите число.
Ответ:
Пусть двузначное число будет 10 x + y .
Число, полученное при перестановке цифр = 10 y + x .
Сумма двузначного числа и числа, полученного путем перестановки его цифр, равна 99.
10 x + y + 10 y + x = 99
⇒ 1xy=y+1 =9
С заданной информацией можно составить только одно уравнение. Таким образом, число может быть
18, 81, 54, 45, 27, 72, 36, 63.
Посмотреть решения NCERT для всех глав класса 9
Извините! — Страница не найдена
Пока разбираемся, возможно, поможет одна из ссылок ниже.
Домой Назад- Класс
- Онлайн-тесты
- Ускоренный онлайн-курс JEE
- Двухлетний курс для ЕГЭ 2021
- Класс
- Онлайн-курс NEET
- Серия онлайн-тестов
- Фонд CA
- CA Промежуточный
- Финал CA
- Программа CS
- Класс
- Серия испытаний
- Книги и материалы
- Тестовый зал
- Интеллектуальный взломщик BBA
- Обучение в классе
- Онлайн-коучинг
- Серия испытаний
- Интеллектуальный взломщик IPM
- Книги и материалы
- ГД-ПИ
- CBSE класс 8
- CBSE класс 9
- CBSE Класс 10
- CBSE Класс 11
- CBSE класс 12
- Обучение в классе
- Онлайн-классы CAT
- Серия тестов CAT
- MBA Жилой
- Интеллектуальный взломщик CAT
- Книги и материалы
- Онлайн-классы без CAT
- Серия испытаний без CAT
- Тестовый зал
- ГД-ПИ
- Обучение в классе
- Серия испытаний
- Гражданские интервью
- Класс
- Онлайн-классы
- Серия испытаний SSC
- Переписка
- Практические тесты
- Электронные книги SSC
- Пакет исследований SSC JE
- Класс
- RBI класс B
- Серия тестов банка
- Переписка
- Электронные книги по банковскому делу
- Банк ПДП
- Онлайн-коучинг
- Коучинг в классе
- Серия испытаний
- Книги и материалы
- Класс
- Программа моста GRE
- Онлайн-коучинг GMAT
- Консультации по приему
- Коучинг GMAT в классе
- Стажировка
- Корпоративные программы
- Студенты колледжа
- Работающие специалисты
- Колледжи
- Школы
Решения NCERT для математики класса 9, глава 4.
 Линейные уравнения с двумя переменными
Линейные уравнения с двумя переменнымиРешения NCERT для математики класса 9, глава 4. Линейные уравнения с двумя переменными Пример 4.1 являются частью решений NCERT для математики класса 9. Здесь мы дали решения NCERT для математики класса 9, глава 4, линейные уравнения с двумя переменными, пример 4.1.
Решения NCERT для класса 9 по математике Глава 4 Линейные уравнения с двумя переменными Пример 4.1
Упр. 4.1 Класс 9 Математика Вопрос 1.
Стоимость тетради в два раза превышает стоимость ручки. Напишите линейное уравнение с двумя переменными, чтобы представить это утверждение.
(Примите стоимость блокнота за X рупий, а стоимость ручки за рупий.г).
Решение:
Пусть стоимость ноутбука = рупий. х
и стоимость ручки = рупий. у
По условию имеем
[Стоимость тетради] =2 х [Стоимость ручки]
i. e„ (x) = 2 x (y) или, x = 2y
или, x – 2y = 0
Таким образом, искомое линейное уравнение имеет вид x – 2y = 0,
Упр. 4.1 Класс 9 Математика Вопрос 2
4.1 Класс 9 Математика Вопрос 2
Запишите следующие линейные уравнения в виде ax + by + c = 0 и укажите значения a, b и c в каждом случае:
(i) 2x + 3y = \( 9.3\overline { 5 }\)
(ii) \(x-\frac { y }{ 5 } -10\quad =\quad 0\)
(iii) – 2x + 3y = 6
(iv) x = 3y
(v) 2x = -5y
(vi) 3x + 2 = 0
(vii) y – 2 = 0
(viii) 5 = 2x
Решение:
(i) Имеем 2x + 3y = \(9.3 \overline { 5 }\)
или (2)x + (3)y + (\(-9.3\overline { 5 }\)) = 0
Сравнивая это с ax + by +c= 0, мы получаем = 2 ,
b = 3 и c= –\(9.3\overline { 5 }\) .
(ii) Имеем \(x-\frac { y }{ 5 } -10\quad =\quad 0\)
или x + (- \(\frac { 1 }{ 5 }\)) y + ( 10) = 0
Сравнивая его с ax + by + c = 0, получаем
a =1, b =- \(\frac { 1 }{ 5 }\) и c= -10
(iii) Имеем -2x + 3y = 6 или (-2)x + (3)y + (-6) = 0 б = 3 и с = -6.
(iv) Имеем x = 3y или (1)x + (-3)y + (0) = 0. Сравнивая это с ax + by + c = 0, получаем a = 1, b = -3 и c = 0.
(v) Имеем 2x = -5y или (2)x + (5)y + (0) = 0 Сравнивая с ax + by + c = 0, получаем a = 2, b = 5 и c = 0.
(vi) Имеем 3x + 2 = 0 или (3)x + (0)y + (2) = 0. Сравнивая это с ax + by + c = 0, получаем a = 3, b = 0 и c = 2.
(vii) Имеем y – 2 = 0 или (0)x + (1)y + (-2) = 0. Сравнивая это с ax + by + c = 0, получаем a = 0, б = 1 и с = -2.
(viii) Имеем 5 = 2x ⇒ 5 – 2x = 0
или -2x + 0y + 5 = 0
или (-2)x + (0)y + (5) = 0
Сравнивая это с ax + by + c = 0, мы получаем a = -2, b = 0 и c = 5.
NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables (दो चरों में रैखिक समीकरण) (Hindi Medium) Ex 4.1
Решения NCERT для класса 9 по математике Глава 4 Линейные уравнения с двумя переменными Пример 4.2
Вопрос 1
Какой из следующих вариантов верен и почему?
y = 3x + 5 имеет
(i) единственное решение,
(ii) только два решения,
(iii) бесконечно много решений
Решение:
Вариант (iii) верен, потому что для каждого значения x мы получаем соответствующее значение y и наоборот в данном уравнении.
Следовательно, данное линейное уравнение имеет бесконечно много решений.
Вопрос 2
Напишите четыре решения для каждого из следующих уравнений:
(i) 2x + y = 7
(ii) πx + y = 9
(iii) x = 4y
Решение:
(i) 2x + y = 7
Когда x = 0, 2(0) + y = 7 ⇒ y = 7
∴ Решение (0, 7)
Когда x = 1, 2(1) + y = 7 ⇒ y = 7 – 2 ⇒ y = 5
∴ Решение: (1, 5)
При x = 2, 2(2) + y =7y = 7 – 4 ⇒ y = 3
∴ Решение: (2, 3)
При x = 3, 2( 3) + y = 7y = 7 – 6 ⇒ y = 1
∴ Решение (3, 1).
(ii) πx + y = 9
Когда x = 0, π(0) + y = 9 ⇒ y = 9 – 0 ⇒ y = 9
∴ Решение (0, 9)
Когда x = 1, π( 1) + y = 9 ⇒ y = 9 – π
∴ Решение (1, (9 – π))
Когда x = 2, π(2) + y = 9 ⇒ y = 9 – 2π
∴ Решение ( 2, (9 – 2π))
Когда x = -1,π(-1) + y = 9 ⇒ y = 9 + π
∴ Решение: (-1, (9 + π))
(iii) x = 4y
Когда x = 0, 4y = 1 ⇒ y = 0
∴ Решение (0, 0)
Когда x = 1, 4y = 1 ⇒ y = \(\frac { 1 }{ 4 }\)
∴ Решение: (1,\(\frac { 1 }{ 4 }\))
Когда x = 4, 4y = 4 ⇒ y = 1
∴ Решение: (4, 1)
Когда x = 4 , 4y = 4 ⇒ y = -1
∴ Решение: (-4, -1)
Вопрос 3
Проверьте, какие из следующих решений являются решениями уравнения x – 2y = 4, а какие нет:
(i) (0,2)
(ii) (2,0)
(iii) (4, 0 )
(iv) (√2, 4√2)
(v) (1, 1)
Решение:
(i) (0,2) означает x = 0 и y = 2
Пыхтение x = 0 и y = 2 в х – 2у = 4, получаем
л. Х.С. = 0 – 2(2) = -4.
Х.С. = 0 – 2(2) = -4.
Но Р.Х.С. = 4
∴ Л.В.С. ≠ Р.Х.С.
∴ x =0, y =2 не является решением.
(ii) (2, 0) означает, что x = 2 и y = 0
Подставляя x = 2 и y = 0 в x – 2y = 4, мы получаем
L.H:S. 2 – 2(0) = 2 – 0 = 2.
Но Р.Х.С. = 4
∴ Л.В.С. ≠ Р.Х.С.
∴ (2,0) не является решением.
(iii) (4, 0) означает x = 4 и y = 0
Полагая x = 4 и y = o в x – 2y = 4, мы получаем
= 4 – 2(0) = 4 – 0 = 4 =R.H.S.
∴ Л.Х.С. = R.H.S.
∴ (4, 0) является решением.
(iv) (√2, 4√2) означает x = √2 и y = 4√2 = √2 – 2(4√2) = √2 – 8√2 = -7√2
Но R.H.S. = 4
∴ Л.В.С. ≠ Р.Х.С.
∴ (√2 , 4√2) не является решением.
(v) (1, 1) означает x =1 и y = 1
Подставляя x = 1 и y = 1 в x – 2y = 4, получаем
LH.S. = 1 – 2(1) = 1 – 2 = -1. Но R.H.S = 4
∴ LH.S. ≠ Р.Х.С.
∴ (1, 1) не является решением.
Вопрос 4
Найдите значение k, если x = 2, y = 1 – решение уравнения 2x + 3y = k.
Решение:
У нас есть 2x + 3y = k
. Положив x = 2 и y = 1 в 2x+3y = k, мы получим
Положив x = 2 и y = 1 в 2x+3y = k, мы получим
2(2) + 3(1) ⇒ k = 4 + 3 – k ⇒ 7 = k
Таким образом, искомое значение k равно 7.
Решения NCERT для класса 9 по математике Глава 4 Линейные уравнения с двумя переменными Пример 4.3
Вопрос 1
Нарисуйте график каждого из следующих линейных уравнений с двумя переменными:
(i) x + y = 4
(ii) x – y = 2
(iii) y = 3x
(iv) 3 = 2x + y
Решение:
(i) x + y = 4 ⇒ y = 4 – x
Если мы имеем x = 0, то y = 4 – 0 = 4
x = 1, тогда y =4 – 1 = 3
x = 2, тогда y = 4 – 2 = 2
∴ Получаем следующую таблицу:
Начертите на миллиметровке упорядоченные пары (0, 4), (1,3) и (2,2).Соединив эти точки, мы получим прямую линию AB, как показано на рисунке.
Таким образом, линия AB является искомым графиком x + y = 4
(ii) x – y = 2 ⇒ y = x – 2
Если x = 0, то y = 0 – 2 = -2
x = 1, тогда y = 1 – 2 = -1
x = 2 , тогда y = 2 – 2 = 0
∴ Получим следующую таблицу:
Начертите на миллиметровке упорядоченные пары (0, -2), (1, -1) и (2, 0). Соединив эти точки, мы получим прямую линию PQ, как показано на рисунке.
Соединив эти точки, мы получим прямую линию PQ, как показано на рисунке.
Таким образом, время есть искомый график x – y = 2
(iii) y = 3x
Если у нас есть x = 0,
, то y = 3(0) ⇒ y = 0
x = 1, тогда y = 3(1) = 3
x= -1, тогда y = 3(-1) = -3
∴ Получим следующую таблицу:
Начертите на миллиметровке упорядоченные пары (0, 0), (1, 3) и (-1, -3).Соединив эти точки, мы получим прямую линию LM, как показано на рисунке.
Таким образом, прямая LM является искомым графиком y = 3x.
(iv) 3 = 2x + y ⇒ y = 3 – 2x
Если у нас есть x = 0, то y = 3 – 2(0) = 3
x = 1, тогда y = 3 – 2(1) = 3 – 2 = 1
x = 2, тогда y = 3 – 2(2) = 3 – 4 = -1
∴ Получаем следующую таблицу:
Построим упорядоченные пары (0, 3), (1, 1) и (2, – 1) на миллиметровой бумаге. Соединив эти точки, мы получим прямую линию CD, как показано на рисунке.
Таким образом, линия CD является искомым графом 3 = 2x + y.
Вопрос 2
Приведите уравнения двух прямых, проходящих через (2, 14). Сколько еще таких строк и почему?
Сколько еще таких строк и почему?
Решение:
(2, 14) означает, что x = 2 и y = 14
Уравнения, решение которых (2,14): (i) x + y = 16, (ii) 7x – y = 0
Существуют бесконечное количество прямых, проходящих через точку (2, 14), потому что через точку можно провести бесконечное количество прямых.
Вопрос 3
Если точка (3, 4) лежит на графике уравнения 3y = ax + 7, найти значение a.
Решение:
Уравнение данной прямой 3y = ax + 7
∵ (3, 4) лежит на данной прямой.
∴ Он должен удовлетворять уравнению 3y = ax + 7
Имеем (3, 4) ⇒ x = 3 и y = 4.
Подставляя эти значения в данное уравнение, мы получаем
3 x 4 = ax 3 + 7
⇒ 12 = 3a + 7
⇒ 3a = 12 – 7 = 5 ⇒ a = \(\frac { 5 }{ 3 }\)
Таким образом, искомое значение a равно \(\frac { 5 }{ 3 }\ )
Вопрос 4
Стоимость проезда на такси В городе выглядит следующим образом: Первый километр стоит рупий.8, а на последующее расстояние – рупий. 5 за км. Приняв пройденное расстояние за x км и общую стоимость проезда за Rs. y, напишите линейное уравнение для этой информации и нарисуйте его график.
y, напишите линейное уравнение для этой информации и нарисуйте его график.
Решение:
Здесь общее пройденное расстояние = x км, а общая стоимость проезда на такси = рупий. y
Стоимость проезда за 1 км = рупий. 8
Оставшееся расстояние = (x – 1) км
∴ Стоимость проезда (x – 1) км = 5 рупий x(x – 1)
Общая стоимость такси = рупий. 8 + рупий. 5(x – 1)
Согласно вопросу,
y = 8 + 5(x – 1) = y = 8 + 5x – 5
⇒ y = 5x + 3,
, что является требуемым линейным уравнением, представляющим данную информацию.
График: имеем y = 5x + 3
Wben x = 0, тогда y = 5(0) + 3 ⇒ y = 3
x = -1, тогда y = 5(-1) + 3 ⇒ y = -2
x = -2, тогда y = 5(-2) + 3 ⇒ y = -7
∴ Получаем следующую таблицу:
Теперь наносим упорядоченные пары (0, 3), (-1, -2) и (-2, -7) на миллиметровке и соединив их, мы получим прямую линию PQ, как показано на рисунке.
Таким образом, линия PQ является искомым графиком линейного уравнения y = 5x + 3.
Вопрос 5
Из предложенных ниже вариантов выберите уравнение, графики которого представлены на рис. (1) и рис. (2).
(1) и рис. (2).
Для рис.
Для рис. (2)
(i) y = x + 2
(ii) y = x – 2
(iii) y = -x + 2
(iv) x + 2y = 6
Решение:
Для На рис. (1) правильное линейное уравнение x + y = 0
[Поскольку (-1, 1) = -1 + 1 = 0 и (1, -1) = 1 + (-1) = 0]
Для рис. (2) правильным линейным уравнением является y = -x + 2
[As (-1,3) 3 = -1 (-1) + 2 = 3 = 3 и (0,2)
⇒ 2 = -(0) + 2 ⇒ 2 = 2]
Вопрос 6
Если работа, совершаемая телом при приложении постоянной силы, прямо пропорциональна расстоянию, пройденному телом, выразить это в виде уравнения с двумя переменными и начертить его график, взяв постоянную сила 5 ед.Также прочтите из графика работу, выполненную, когда расстояние, пройденное телом, равно
(i) 2 единицы
(ii) 0 единиц
Решение:
Постоянная сила равна 5 единицам.
Пусть пройденный путь = x единиц, а проделанная работа = y единиц.
Проделанная работа = Сила x Расстояние
⇒ y = 5 xx ⇒ y = 5x
Для построения графика имеем y = 5x
Когда x = 0, тогда y = 5(0) = 0
x = 1, тогда y = 5(1) = 5
x = -1, тогда y = 5(-1) = -5
∴ Получаем следующую таблицу:
Разыгрывая упорядоченные пары (0, 0), (1, 5) и (-1, -5) на миллиметровке и соединив точки, мы получим прямую линию AB, как показано на рисунке.
Из графика получаем
(i) Пройденное расстояние = 2 единицы, т. е. x = 2
∴ Если x = 2, то y = 5(2) = 10
⇒ Проделанная работа = 10 единиц.
(ii) Пройденное расстояние = 0 единиц, т. е. x = 0
∴ Если x = 0 ⇒ y = 5(0) – 0
⇒ Выполненная работа = 0 единиц.
Вопрос 7
Ямини и Фатима, двое учащихся IX класса школы, вместе пожертвовали рупий. 100 в Фонд помощи премьер-министра для помощи пострадавшим от землетрясения. Напишите линейное уравнение, удовлетворяющее этим данным.(Вы можете принять их вклад как Rs.x и Rs.y.) Начертите тот же график.
Решение:
Пусть вклад Ямини = рупий. x
и взнос Фатимы рупий. y
∴ Имеем x + y = 100 ⇒ y = 100 – x
Теперь, когда x = 0, y = 100 – 0 = 100
x = 50, y = 100 – 50 = 50
x = 100, y = 100 – 100 = 0
∴ Получаем следующую таблицу:
Нанося упорядоченные пары (0,100), (50,50) и (100, 0) на миллиметровую бумагу в соответствующем масштабе и соединяя эти точки, получаем прямую линию PQ, как показано.
Таким образом, линия PQ является искомым графиком линейного уравнения x + y = 100.
Вопрос 8
В таких странах, как США и Канада, температура измеряется в градусах Фаренгейта, тогда как в таких странах, как Индия, она измеряется в градусах Цельсия. Вот линейное уравнение
, которое преобразует градусы Фаренгейта в градусы Цельсия:
F = (\(\frac { 9 }{ 5 }\) )C + 32
(i) Нарисуйте график линейного уравнения, приведенного выше, используя шкалу Цельсия для оси x. и градусы Фаренгейта для оси Y.
(ii) Если температура равна 30°C, какова температура в градусах Фаренгейта?
(iii) Если температура 95°F, какова температура в градусах Цельсия?
(iv) Если температура равна 0°C, какова температура в градусах Фаренгейта, а если температура равна 0°F, какова температура в градусах Цельсия?
(v) Существует ли температура, численно одинаковая как в градусах Фаренгейта, так и в градусах Цельсия? Если да, найдите Его.
Решение:
(i) Имеем
F = (\(\frac { 9 }{ 5 }\))C + 32
Когда C = 0 , F = (\(\frac { 9 }{ 5 }\) ) x 0 + 32 = 32
Когда C = 15, F = (\(\frac { 9 }{ 5 }\))(-15) + 32= -27 + 32 = 5
Когда C = -10, F = \(\frac { 9 }{ 5 }\) (-10)+32 = -18 + 32 = 14
У нас есть следующая таблица:
Построение упорядоченных пар (0, 32), (-15, 5 ) и (-10,14) на миллиметровой бумаге. Соединив эти точки, получим прямую АВ.
Соединив эти точки, получим прямую АВ.
(ii) Из графика видно, что 86°F соответствует 30°C.
(iii) Из графика видно, что 95°F соответствует 35°C.
(iv) Имеем C = 0
Из (1) получаем
F = (\(\frac { 9 }{ 5 }\))0 + 32 = 32
Также F = 0
Из (1 ), получаем
0 = (\(\frac { 9 }{ 5 }\))C + 32 ⇒ \(\frac { -32\times 5 }{ 9 } \) = C ⇒ C = -17,8
( V) Когда F = C (численно)
Из (1) получаем
F = \(\frac { 9 }{ 5 }\)F + 32 ⇒ F – \(\frac { 9 }{ 5 }\) F = 32
⇒ \(\frac { -4 }{ 5 }\)F = 32 ⇒ F = -40
∴ Температура – 40° как в F, так и в C.
Решения NCERT для класса 9 по математике Глава 4 Линейные уравнения с двумя переменными Пример 4.4
Вопрос 1
Дайте геометрическое представление y = 3 в виде уравнения
(i) с одной переменной
(ii) с двумя переменными
Решение:
(i) y = 3
∵ y = 3 является уравнением с одной переменной , т. е. только у.
∴ y = 3 является уникальным решением на числовой прямой, как показано ниже:
(ii) y = 3
Мы можем записать y = 3 в двух переменных как 0. x + y = 3
x + y = 3
Теперь, когда x = 1, y = 3
x = 2, y = 3
x = -1, y = 3
∴ Получаем следующую таблицу:
Нанося на миллиметровую бумагу упорядоченные пары (1, 3), (2, 3) и (-1, 3) и соединяя их, получаем линию AB как решение уравнения 0.х + у = 3,
т. е. у = 3.
Вопрос 2
Дайте геометрическое представление 2x + 9 = 0 в виде уравнения
(i) с одной переменной
(ii) с двумя переменными
Решение:
(i) 2x + 9 = 0
Имеем, 2x + 9 = 0 ⇒ 2x = – 9 ⇒ x = \(\ frac { -9 }{ 2 }\)
, что представляет собой линейное уравнение с одной переменной, т. е. только x.
Следовательно, x = \(-\frac { 9 }{ 2 }\) является единственным решением на числовой прямой, как показано ниже:
(ii) 2x +9=0
Мы можем записать 2x + 9 = 0 в двух переменных как 2x + 0, y + 9 = 0
или \(x=\frac { -9-0.y }{ 2 }\)
∴ Когда y = 1, x = \(x=\frac { -9-0(1) }{ 2 }\) = \(-\ frac { 9 }{ 2 }\)
Таким образом, мы получаем следующую таблицу:
Теперь, строя упорядоченные пары \((\frac { -9 }{ 2 } ,3)\) ,\((\frac { -9 }{ 2 } ,3 )\) и \((\frac { -9 }{ 2 } ,3)\) на миллиметровой бумаге и соединяя их, мы получаем прямую PQ как решение 2x + 9 = 0,
Мы надеемся, что решения NCERT для класса 9 по математике, глава 4, линейные уравнения с двумя переменными, пример 4. 1, помогут вам. Если у вас есть какие-либо вопросы относительно решений NCERT для математики класса 9, глава 4, линейные уравнения с двумя переменными, пример 4.1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
1, помогут вам. Если у вас есть какие-либо вопросы относительно решений NCERT для математики класса 9, глава 4, линейные уравнения с двумя переменными, пример 4.1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
Линейные уравнения с одной переменной
Линейные уравнения с одной переменной Равенство двух алгебраических выражений, включающих одну или несколько неизвестных величин, называется уравнением.
Линейное уравнение — это уравнение, содержащее линейные многочлены.
Значение переменной, при котором две части уравнения равны, называется решением уравнения.
К обеим частям уравнения можно прибавлять/вычитать одну и ту же величину без изменения равенства.
Обе части уравнения можно умножить/поделить на одно и то же ненулевое число без изменения равенства.
ОБЩАЯ ФОРМА ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ
ax + by + c = 0, a ≠ 0, b ≠ 0 или любой из a и b может быть равен нулю.
Подробнее:
Общая форма линейного уравнения с двумя переменными Пример Задачи с решениями Пример 1. .Решение:
Составьте линейное уравнение с помощью следующих утверждений:
Пример 2: Стоимость 2 кг яблок и 1 кг винограда в день составила 160. Через месяц стоимость 4 кг яблок и 2 кг винограда равно 300. Представьте ситуацию алгебраически.
Решение: Пусть стоимость килограмма яблок и винограда равна x и y соответственно, тогда по первому условию:
2x + y = 160 ……(i)
и по второму условию: 4x + 2y = 300 …..(ii)
Пример 3: Тренер крикетной команды покупает 3 биты и 6 мячей за 3900. Позже она покупает еще одну биту и еще 3 таких же мяча за 1300. Представьте эту ситуацию алгебраически.
Решение: Пусть стоимость биты и мяча равна x и y соответственно. Согласно вопросам
Согласно вопросам
3x + 6y = 3900 …..(i)
& x + 3y = 1300 …..(ii)
.Если девочек на 4 больше, чем мальчиков.
Решение: Пусть нет. мальчиков и девочек равны x и y, то согласно вопросу
x + y = 10 ……(i)
& y = x + 4 ……(ii)
Пример 5: Половина периметра прямоугольного сада, длина которого на 4 м больше ширины, составляет
36 м.
Решение: Пусть длина и ширина равны x м и y м.
∴ согласно вопросу 1/2 периметра = 36
1/2 [2(l + b)] = 36
⇒ x + y = 36 …..(i)
также длина = 4 + ширина
x = 4 + y ..…(ii)
Пример 6: Разница между двумя числами равна 26, и одно число в три раза больше другого.
Решение: Пусть числа равны x и y & x > y
∴ x – y = 26 ……(i)
и x = 3y ……(ii)
Пример 7: Большее из двух дополнительных углов превышает меньший на 18 градусов.
Решение: Sol. Пусть два дополнительных угла равны x и y & x > y
Тогда x + y = 180° ……(i)
и x = y + 18° ……(ii)
Пример 8: Дробь становится 9 /11, если 2 добавить и к числителю, и к знаменателю.Если к числителю и знаменателю прибавить 3, получится 5/6.
Решение: Пусть дробь равна x/y
Теперь согласно вопросу \(\frac{x+2}{y+2}=\frac{9}{11}\)
⇒ 11x + 22 = 9y + 18
⇒ 11x – 9y = – 4 ….. (i)
и
\(\frac{x+3}{y+3}=\frac{5}{6}\)
⇒ 6x + 18 = 5y + 15
⇒ 6x – 5y = –3 ….(ii)
Пример 9: Через пять лет Сачин будет в три раза старше своего сына. Пять лет назад Сачин был в семь раз старше своего сына.
Решение: Пусть настоящий возраст Сачина и его сына равен
x лет и y лет.
Через пять лет
возраст Сачина = (x + 5) лет и возраст его сына = (y + 5) лет
согласно вопросу (x + 5) = 3(y + 5)
⇒ x + 5 = 3y + 15
⇒ x – 3y = 10 ……(i)
и 5 лет назад возраст обоих был (x – 5) лет и (y – 5) лет соответственно
согласно вопросу (x – 5) = 7(y – 5)
⇒ x – 5 = 7y – 35
⇒ x – 7y = –30 . …(ii)
…(ii)
Linear Equations — Free Math Help
Простое определение линейного уравнения:
Уравнение, которое образует прямую линию на графике.
Точнее, линейное уравнение — это уравнение, зависящее только от констант и переменной, возведенной в первую степень. Например, \(y=6x+2\) является линейным, потому что в нем нет квадратов, кубов, квадратных корней, синусов и т. д. Линейные уравнения всегда можно изменить, чтобы они приняли следующую форму:
$$ топор+b=0 $$Вы не всегда увидите линейные уравнения, написанные именно так, но имейте в виду, что мы можем манипулировать уравнениями, чтобы придать им определенную форму, если это необходимо.
Линейные уравнения часто записываются с несколькими переменными, обычно x и y.Такие уравнения будут иметь много возможных комбинаций x и y, которые работают. Когда эти точки (известные как пары координат) нанесены на ось x-y, они образуют прямую линию. Давайте посмотрим на это графически ниже. Нарисованные два уравнения являются линейными. Обратите внимание, что одно уравнение имеет форму \(y=3\) (оно зависит только от константы, 3), а другое уравнение имеет вид \(y=0,75x — 0,5\) (линейный член и константа ).
Давайте посмотрим на это графически ниже. Нарисованные два уравнения являются линейными. Обратите внимание, что одно уравнение имеет форму \(y=3\) (оно зависит только от константы, 3), а другое уравнение имеет вид \(y=0,75x — 0,5\) (линейный член и константа ).
Как узнать, является ли уравнение линейным?
Включает ли уравнение (или функцию) какие-либо члены в квадрате? Как насчет других терминов с показателями, отличными от 1 (или, технически, нуля)? Если у функции нет членов с порядком выше 1 (причудливый способ сказать показатель степени), то она линейна!
Что делать, если у него есть функция журнала или триггера и т. д.?
Это нелинейные члены. Просто они не являются константами (обычными числами) или переменными с показателем степени 1, поэтому функция не является линейной. Если бы мы могли записать sin(x) или log(x) как что-то линейное, например \(2x+3\), то мы бы сделали это вместо использования сложных нелинейных функций, таких как синус и логарифм! Конечно, если вы еще не рассмотрели эти понятия в своем классе, даже не беспокойтесь об этом.
Итак, как мне решить линейное уравнение?
Некоторые линейные уравнения действительно легко решить.А вот этот:
$$ у=4 $$Это линейное уравнение, и оно уже решено относительно y! Это просто… ничего не поделаешь. Но этот довольно тривиальный пример показывает нам, что линейные уравнения могут быть довольно простыми, а также показывает нашу цель: переписать уравнение так, чтобы переменная, для которой мы решаем, находилась на одной стороне, а все остальное — на другой.
Маленький шаг вперед:
$$ у+2=4 $$В этом уравнении нам просто нужно вычесть 2 из обеих частей, чтобы представить наше уравнение в решенной форме с y=2.Решение любого линейного уравнения — это просто вопрос выполнения операций с обеих сторон знака равенства до тех пор, пока уравнение не примет желаемую форму (обычно решается для одной переменной, например X или Y). Шаги подробно показаны ниже:
$$ у+2=4 $$ $$ у+2-2=4-2 $$ $$ у+0=2 $$ $$ у=2 $$А как насчет более сложных уравнений?
К счастью, с линейными уравнениями шаги всегда относительно просты. Единого способа сделать это не существует, и со временем вы сможете думать с помощью линейного уравнения без необходимости записывать каждый шаг.Попробуйте следующий подход для решения уравнений и посмотрите, сработает ли он у вас:
Единого способа сделать это не существует, и со временем вы сможете думать с помощью линейного уравнения без необходимости записывать каждый шаг.Попробуйте следующий подход для решения уравнений и посмотрите, сработает ли он у вас:
- Собрать одинаковые термины — это значит собрать вместе все x, все y и все обычные числа (известные как константы) и сложить их по отдельности. Например, выражение \(4x+2y+3x-5+10\) становится \(7x+2y+5\). Помните, что вы можете складывать, вычитать, умножать или делить до тех пор, пока вы делаете это с 91 506 обеими 91 507 частями уравнения.
- Изолируйте переменную, для которой вы хотите найти — Если задача требует, чтобы вы решили для y, вам нужно получить y с одной стороны знака равенства, а все остальное с другой стороны.Здесь вы можете перейти от \(2y — 6 = 4\) к \(2y = 10\).
- Удалите все коэффициенты, оставшиеся для этой переменной. Если ваш ответ после шага 2 выглядит как \(5y = 7x — 10\), просто разделите обе части на 5, чтобы получить \(y=\frac{7x}{5} — \ дробь{10}{2}\).

- Проверьте свой ответ — кажется ли вам, что ваш ответ имеет смысл? Можете ли вы подставить свой ответ в исходное уравнение, и оно все равно сработает?
Рассмотрим несколько примеров решения линейных уравнений.
Следует иметь в виду, что вы не можете всегда решать уравнение до чего-то определенного, например y=5. Совершенно нормально иметь y=x+5, и это просто означает, что y зависит от x. На самом деле существует ровно одно значение y для каждого значения x, и все они образуют точки, лежащие на прямой линии (как я показал в начале).
Пример 1:
Найдите у: \(2y+5=9\)
Если вы замените y на 2 в исходной задаче, вы получите 9=9, так что все верно!
Пример 2:
Найдите у: \(2y-x=4+x+3x\)
Пример 3:
Найдите у: \(2x+7=\frac{y+6}{2}\)
Подведение итогов
Помните, что линейные уравнения по своей сути просты — не пытайтесь слишком много думать! Они состоят только из линейных членов (таких как 3x, 2y, y/2 и т. д.).) и константы. Если вы застряли, пытаясь упростить или решить проблему, просто не забывайте делать это шаг за шагом. Соберите одинаковые условия, объединив все ваши переменные по отдельности, затем изолируйте переменную, для которой вы хотите найти решение, и, наконец, выполните все необходимые дополнительные математические операции, чтобы у вас остались только «y =» или «x =» на одной стороне уравнения.
д.).) и константы. Если вы застряли, пытаясь упростить или решить проблему, просто не забывайте делать это шаг за шагом. Соберите одинаковые условия, объединив все ваши переменные по отдельности, затем изолируйте переменную, для которой вы хотите найти решение, и, наконец, выполните все необходимые дополнительные математические операции, чтобы у вас остались только «y =» или «x =» на одной стороне уравнения.
уравнений с более чем одной переменной
Показать мобильное уведомление Показать все примечания Скрыть все примечания Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-4: уравнения с более чем одной переменной
В этом разделе мы рассмотрим тему, которая часто не получает должного освещения на уроках алгебры.Вероятно, это связано с тем, что он используется не более чем в нескольких разделах курса алгебры. Тем не менее, это тема, которая может и часто широко используется на других занятиях.
Здесь мы будем решать уравнения, содержащие более одной переменной. Процесс, который мы пройдем здесь, очень похож на решение линейных уравнений, что является одной из причин, по которой это вводится на данном этапе. Однако есть одно исключение из этого. Иногда, как мы увидим, порядок процесса для некоторых задач будет другим.Вот процесс в стандартном порядке.
- Умножьте обе части на ЖК-дисплее, чтобы убрать любые дроби.
- Максимально упростите обе стороны. Это часто будет означать удаление скобок и т.
 п.
п. - Переместите все термины, содержащие искомую переменную, в одну сторону, а все термины, не содержащие переменную, в противоположную сторону.
- Получите один экземпляр переменной, которую мы ищем в уравнении.Для типов задач, которые мы здесь рассмотрим, это почти всегда будет выполняться путем простого вынесения переменной из каждого члена.
- Разделить на коэффициент переменной. Этот шаг будет иметь смысл, когда мы будем работать над проблемами. Заметьте также, что в этих задачах «коэффициент», вероятно, будет содержать не только числа, но и другие вещи.
Обычно проще всего увидеть, с чем мы будем работать и как они работают, на примере.Мы также дадим основной процесс для их решения в первом примере.
Пример 1. Решите \(A = P\left( {1 + rt} \right)\) для \(r\). Показать решениеЗдесь мы ищем выражение в форме
. \[r = \underline {{\mbox{Уравнение с числами,}}A,\,P,\,{\mbox{и}}t} \] Другими словами, единственное место, где мы хотим видеть \(r\), находится слева от знака равенства. В уравнении не должно быть других \(r\). Приведенный выше процесс должен сделать это за нас.
В уравнении не должно быть других \(r\). Приведенный выше процесс должен сделать это за нас.
Хорошо, давайте решим эту задачу. У нас нет дробей, поэтому нам не нужно об этом беспокоиться. Для упрощения умножим \(P\) через скобки. Выполнение этого дает,
\[А = Р + Прт\]Теперь нам нужно получить все члены с \(r\) на одной стороне. В этом уравнении уже есть то, что нам нужно, и это хорошо.Далее нам нужно перенести все термины, в которых нет \(r\), на другую сторону. Это означает вычитание \(P\) с обеих сторон.
\[А — Р = Прт\]В качестве последнего шага мы разделим обе части на коэффициент \(r\). Кроме того, как отмечалось в описанном выше процессе, «коэффициент» не является числом. В данном случае это Pt . На данном этапе коэффициент переменной — это просто то, на что умножается переменная.
\[\frac{{A — P}}{{Pt}} = r\hspace{0. 5in} \Rightarrow \hspace{0.5in}r = \frac{{A — P}}{{Pt}}\]
5in} \Rightarrow \hspace{0.5in}r = \frac{{A — P}}{{Pt}}\]Чтобы получить окончательный ответ, мы пошли дальше и перевернули порядок, чтобы получить ответ в более «стандартной» форме.
Чуть позже мы поработаем с другими примерами. Тем не менее, давайте сначала отметим пару вещей. Поначалу эти задачи кажутся довольно сложными, но если подумать, все, что мы на самом деле делали, это использовали точно такой же процесс, который мы использовали для решения линейных уравнений. Главное отличие, конечно, в том, что в этом процессе больше «бардака».Это подводит нас ко второму пункту. Не увлекайтесь бардаком в этих задачах. Иногда проблемы будут немного запутанными, но шаги, которые необходимо выполнить, — это шаги, которые вы можете сделать! Наконец, ответ не будет простым числом, но опять же он будет немного запутанным, часто более запутанным, чем исходное уравнение. Тот нормально и ожидаемо.
Давайте поработаем еще несколько примеров.
Этот пример очень похож на первый. Однако это работает немного по-другому. Помните из первого примера, что мы делали замечание, что иногда порядок шагов в процессе нужно менять? Ну, это то, что мы собираемся сделать здесь.
На первом этапе процесса нам нужно очистить дроби. Однако, поскольку дробь находится внутри скобок, давайте сначала умножим \(m\) на скобки.Заметьте также, что если мы умножим \(m\) на первое, мы фактически автоматически очистим одну из дробей. Это немного облегчит нам работу, когда мы будем убирать дроби.
\[V = \frac{m}{b} — 5aR\]Теперь очистите дроби, умножив обе части на \(b\). Мы также переместим все термины, в которых нет \(R\), на другую сторону.
\[\begin{align*}Vb & = m — 5abR\\ Vb — m & = — 5abR\end{align*}\] Будьте осторожны, не потеряйте знак минус перед цифрой 5! Потерять это из виду очень легко. Последним шагом является деление обеих частей на коэффициент \(R\), в данном случае -5ab .
Последним шагом является деление обеих частей на коэффициент \(R\), в данном случае -5ab .
Обратите также внимание, что мы немного поработали со знаком минус в знаменателе, чтобы несколько упростить ответ.
В предыдущем примере мы решили для \(R\), но нет причин не решать одну из других переменных в задачах.Например, рассмотрим следующий пример.
Пример 3 Решите \(\displaystyle V = m\left( {\frac{1}{b} — \frac{{5aR}}{m}} \right)\) для \(b\). Показать решениеПервые несколько шагов идентичны предыдущему примеру. Сначала мы умножим \(m\) через круглые скобки, а затем умножим обе части на \(b\), чтобы очистить дроби. Мы уже сделали эту работу, поэтому из предыдущего примера у нас есть
\[Vb — m = — 5abR\] В этом случае у нас есть \(b\) с обеих сторон знака равенства, и нам нужны все члены с \(b\) в них с одной стороны уравнения и все остальные члены с другой сторону уравнения. В этом случае мы можем убрать знаки минус, если соберем \(b\) слева, а остальные члены справа. Выполнение этого дает,
В этом случае мы можем убрать знаки минус, если соберем \(b\) слева, а остальные члены справа. Выполнение этого дает,
Теперь оба слагаемых в правой части содержат \(b\), поэтому, если мы выделим это из обоих слагаемых, мы получим
\[b\left( {V + 5aR} \right) = m\]Наконец, разделите на коэффициент \(b\). Напомним также, что «коэффициент» — это все то, на что умножается \(b\).Выполнение этого дает,
\[b = \frac{m}{{V + 5aR}}\] Пример 4. Решите \(\displaystyle \frac{1}{a} = \frac{1}{b} + \frac{1}{c}\) для \(c\). Показать решениеВо-первых, умножьте на LCD, что в этой задаче \(abc\).
\[\begin{align*}\frac{1}{a}\left( {abc} \right) & = \left( {\frac{1}{b} + \frac{1}{c}} \ вправо)\влево({abc} \right)\\ bc & = ac + ab\end{align*}\] Затем соберите все \(с\) с одной стороны (слева, вероятно, будет проще всего), вынесите \(с\) из слагаемых и разделите на коэффициент.
Во-первых, нам нужно очистить знаменатель. Для этого умножим обе части на \(5x — 9\). Мы также удалим все скобки в задаче после того, как выполним умножение.
\[\begin{align*}y\left( {5x — 9} \right) & = 4\\ 5xy — 9y & = 4\end{align*}\]Теперь мы хотим найти \(x\), так что это означает, что нам нужно получить все термины без \(y\) в них на другую сторону.Итак, прибавьте 9\(y\) к обеим частям и разделите на коэффициент при \(x\).
\[\begin{align*}5xy & = 9y + 4\\ x & = \frac{{9y + 4}}{{5y}}\end{align*}\] Пример 6. Решите \(\displaystyle y = \frac{{4 — 3x}}{{1 + 8x}}\) для \(x\). Показать решение Этот пример очень похож на предыдущий. Вот работа над этой проблемой.
Вот работа над этой проблемой.
Как упоминалось в начале этого раздела, мы не будем часто сталкиваться с такой проблемой в этом классе.Однако за пределами этого класса (например, класса Calculus) такого рода проблемы возникают с удивительной регулярностью.
.






 0.5х2— х2 = 0
0.5х2— х2 = 0
 5; ± 2.
5; ± 2.



 2=10-3x \) являются числа -2 и 2.
2=10-3x \) являются числа -2 и 2.
 Но ведь это не обязательно, ведь не важно с какой стороны находятся переменные, главное, чтобы они были без чисел, а значит, ничего переносить не будем. Но для тех кто не понял, то сделаем, как гласит правило и разделим обе части на (-1), как гласит свойство:
Но ведь это не обязательно, ведь не важно с какой стороны находятся переменные, главное, чтобы они были без чисел, а значит, ничего переносить не будем. Но для тех кто не понял, то сделаем, как гласит правило и разделим обе части на (-1), как гласит свойство:

 1)
1) }\overline{\text{35}}\text{=0}$
}\overline{\text{35}}\text{=0}$ 








 \end{align}$
\end{align}$ \end{align}$
\end{align}$ \end{align}$
\end{align}$ Данное линейное уравнение
Данное линейное уравнение




 Предположим, что пройденное расстояние составляет $\mathbf{x}$ км, а общая арендная плата составляет $\mathbf{y}$ рупий. Итак, начертите график линейного уравнения.
Предположим, что пройденное расстояние составляет $\mathbf{x}$ км, а общая арендная плата составляет $\mathbf{y}$ рупий. Итак, начертите график линейного уравнения.
 Следовательно, $\text{x}$ и $\text{y}$ — неотрицательные величины.
Следовательно, $\text{x}$ и $\text{y}$ — неотрицательные величины. На данном графике видно, что точки $\left(-1,3\right)$, $\left( 0,2 \right)$ и $\left( 2,0 \right)$ лежат на прямая линия. Кроме того, координаты точек удовлетворяют уравнению \[\text{y}=-\text{x+2}\].
На данном графике видно, что точки $\left(-1,3\right)$, $\left( 0,2 \right)$ и $\left( 2,0 \right)$ лежат на прямая линия. Кроме того, координаты точек удовлетворяют уравнению \[\text{y}=-\text{x+2}\].




 {\circ }}\text{C}\].{\ circ}} \ text {C} \].
{\circ }}\text{C}\].{\ circ}} \ text {C} \]. Данное уравнение имеет вид \[\text{y=3}\].
Данное уравнение имеет вид \[\text{y=3}\].

 для класса 9 по математике в формате PDF для предстоящих экзаменов, а также вы можете найти решения всех глав по математике ниже.
для класса 9 по математике в формате PDF для предстоящих экзаменов, а также вы можете найти решения всех глав по математике ниже. Линейное уравнение — это уравнение прямой линии, содержащее переменные и константы в следующем виде:
Линейное уравнение — это уравнение прямой линии, содержащее переменные и константы в следующем виде: Он представлен как ax+b = 0, где a — коэффициент переменной x, а b — константа. Коэффициент никогда не может быть равен нулю.
Он представлен как ax+b = 0, где a — коэффициент переменной x, а b — константа. Коэффициент никогда не может быть равен нулю. (неизвестный). Например, что-то вроде 9x + 4 = 22. Просто, не правда ли?
(неизвестный). Например, что-то вроде 9x + 4 = 22. Просто, не правда ли? Но можно решить два уравнения с двумя переменными в каждом, чтобы найти значения x и y одновременно. Группа из двух или более уравнений называется системой уравнений.
Но можно решить два уравнения с двумя переменными в каждом, чтобы найти значения x и y одновременно. Группа из двух или более уравнений называется системой уравнений. Ниже приведены два основных метода решения линейного уравнения с двумя переменными.
Ниже приведены два основных метода решения линейного уравнения с двумя переменными. Эта система показывает, как легко решать линейные уравнения, находя значение одной переменной через другую переменную, используя одно уравнение, а затем заменяя это значение другим уравнением.
Эта система показывает, как легко решать линейные уравнения, находя значение одной переменной через другую переменную, используя одно уравнение, а затем заменяя это значение другим уравнением. Решение NCERT-решений линейных уравнений с двумя переменными Класс 9 после изучения главы поможет вам понять шаблон экзамена, вес каждой темы и обеспечит подготовку к экзамену.Практика по математике в классе 9, глава 4, увеличивает вашу скорость во время экзаменов, потому что многие ученики не успевают закончить работу вовремя. Практика тренирует в вас склонность думать о решении данного вопроса с бешеной скоростью. Кроме того, вы можете предсказать темы, которые могут появиться на экзамене, оценив частоту и интервал повторяющихся вопросов. Это может помочь вам разработать стратегию подготовки и получить хорошие оценки. С практикой вы также сможете решать неповторяющиеся или совершенно новые вопросы, потому что концепция вопросов в опросных листах обычно остается неизменной.Разница только в искаженных вопросах и измененных числах. Вы также привыкнете к уровню или стандарту экзаменационных вопросов. Так что поймите и узнайте концепцию при решении вопросов, и в итоге вы наберете более 90 процентов.
Решение NCERT-решений линейных уравнений с двумя переменными Класс 9 после изучения главы поможет вам понять шаблон экзамена, вес каждой темы и обеспечит подготовку к экзамену.Практика по математике в классе 9, глава 4, увеличивает вашу скорость во время экзаменов, потому что многие ученики не успевают закончить работу вовремя. Практика тренирует в вас склонность думать о решении данного вопроса с бешеной скоростью. Кроме того, вы можете предсказать темы, которые могут появиться на экзамене, оценив частоту и интервал повторяющихся вопросов. Это может помочь вам разработать стратегию подготовки и получить хорошие оценки. С практикой вы также сможете решать неповторяющиеся или совершенно новые вопросы, потому что концепция вопросов в опросных листах обычно остается неизменной.Разница только в искаженных вопросах и измененных числах. Вы также привыкнете к уровню или стандарту экзаменационных вопросов. Так что поймите и узнайте концепцию при решении вопросов, и в итоге вы наберете более 90 процентов. Хорошо известно, что некоторые из нас готовятся к тому, чтобы набрать максимум, но в итоге получают меньше из-за нашей небрежности или концептуальных ошибок. И это можно исправить правильной практикой. Решая математические задачи, вы не только улучшаете свои навыки решения задач, но и расширяете свои аналитические и логические способности, которые так необходимы современному поколению.Всем нам важно понимать и выявлять проблемы, логически мыслить, интерпретировать, принимать решения и решать проблемы.
Хорошо известно, что некоторые из нас готовятся к тому, чтобы набрать максимум, но в итоге получают меньше из-за нашей небрежности или концептуальных ошибок. И это можно исправить правильной практикой. Решая математические задачи, вы не только улучшаете свои навыки решения задач, но и расширяете свои аналитические и логические способности, которые так необходимы современному поколению.Всем нам важно понимать и выявлять проблемы, логически мыслить, интерпретировать, принимать решения и решать проблемы.
 Д.
Д.
 .
. Более того, каждое решение линейного уравнения является точкой на графике линейного уравнения.
Более того, каждое решение линейного уравнения является точкой на графике линейного уравнения.
 п.
п.