Конспект урока «Движение тела по окружности. Решение задач», 9 класс

Тема урока: Движение тел по окружности. Решение задач.

Цели урока:

Образовательные:

• продолжить формирование представлений о движении тела;

• продолжить формирование умения описывать движение тела по окружности;

• повторить основные характеристики равномерного движения тела по окружности: линейная скорость, угловая скорость, ускорение, период и частота движения тела по окружности;

• формировать практические умения и навыки решения задач.

Развивающие:

• умение применять знания теории на практике;

• внимательность, самостоятельность;

• мышление учащихся посредством логических учебных действий.

Воспитательные:

Планируемые результаты:

Знать:

Уметь:

Можно считать, что цели урока достигнуты на уровне

воспроизведения, если учащиеся способны сформулировать основные характеристики движения тела по окружности;

понимания, если учащиеся способны объяснить практическую значимость изучения движения тела по окружности, описывать движение тела по окружности;

применения, если учащиеся применяют полученные знания для решения расчетных задач.

Тип урока: закрепление знаний.

Форма урока: комбинированный.

Комплексно-методическое обеспечение: мультимедийный проектор, компьютер, экран.

Методы обучения: словесные, наглядные.

Межпредметные связи: астрономия, литература.

Ход урока:

1. Организационный момент (мотивация учебной деятельности).

Актуализация опорных знаний. Фронтальная работа с классом.

1. Какие виды движения мы с вами изучили? Чем они отличаются?

2. Какой самый простой вид криволинейного движения? В чем значимость его изучения?

3. Какое движение называют равномерным движением по окружности?

4. Приведите примеры движения тел по окружности, встречающиеся в нашей жизни.

5. Какие физические величины вводятся для характеристики движения по окружности?

6. Что называют периодом обращения?

7. Что называют частотой обращения? Как связаны между собой период и частота обращения?

8. Что называют линейной скоростью? Как она направлена?

9. Что называют угловой скоростью? Что является единицей угловой скорости?

10. Как связаны угловая и линейная скорости движения тела?

11. Как направлено центростремительное ускорение? По какой формуле оно рассчитывается?

12. Как направлены относительно друг друга вектор скорости и вектор ускорения?

Мы повторили теоретический материал. Теперь необходимо научиться применять полученные знания при решении задач.

Цель: научиться применять полученные знания при решении задач. Тема нашего урока: «Движение тела по окружности. Решение задач.»

2. Решение задач.

Задача 1

На арене цирка лошадь скачет с такой скоростью, что за 1 минуту обегает 2 круга. Радиус арены равен 6,5 м. Определите период и частоту вращения , скорость и центростремительное ускорение.

Дано:

t = 1мин.=60с

N=2

R=6,5 м

Решение:

Т= ; T= = 30c. ν = ; ν = = 0.03 c^-1.

ϑ = ; ϑ= = 1,4м/с.

а_ц.с. = ; a_ц.с. = = 0,3 м/с².

T-? ν-? ϑ-? а_ц.с.-?

Ответ: T= 30c; ν = 0.03 c^-1; ϑ= 1,4м/с; a = 0,3 м/с² .

Задача 2.

Оцените, с какой скоростью движется Луна вокруг Земли. Радиус орбиты Луны примите равным 400000 км, а время одного полного оборота вокруг Земли 27 суток.

Дано:

Т = 27сут.=648ч

R=400000км

Решение:

ϑ = ; ϑ= = 3887км/ч.

ϑ = = 1077 м/с

ϑ-?

Ответ: ϑ= 1077 м/с.

Физкультминутка.

Задача 3.

С какой скоростью автомобиль должен проходить середину выпуклого моста радиусом 40 м, чтобы центростремительное ускорение было равно ускорению свободного падения?

Дано:

R = 40м

а_ц.с.=9,8 м/с

Решение:

а_ц.с. = ;

ϑ² = а_ц.с.·R; ϑ= ;

ϑ= = 20м/с

ϑ-?

Ответ: ϑ= 20м/с.

Задача 4.

А.С.Пушкин «Руслан и Людмила».

У лукоморья дуб зеленый,

Златая цепь на дубе том;

И днем и ночью кот ученый

Все ходит по цепи кругом…

Определите частоту его движения, если за 1 минуту он делает 3 «круга». Чему равен период? Определите угловую скорость кота.

Дано:

t = 1мин.=60с

N=3

Решение:

Т= ; T= = 20c. ν = ; ν = = 0,05 с^-1

= ; = = 0,1рад/с

T-? _.-?

Ответ: T= 20c; ν = 0,05 с^-1; = 0,1рад/с.

Задача 5.

В 1953 г. на главном здании Московского государственного университета имени М.В. Ломоносова были установлены самые большие башенные часы. Девятиметровый циферблат виден издалека, а длина минутной стрелки — 4,13 метра.

Определите линейную и угловую скорость конца минутной стрелки этих часов.

Дано:

Т = 3600с

R=4.13м

Решение:

= ; = = 0,0017рад/с

ϑ = ; ϑ = = 0,007м/с или

ϑ = R; ϑ = 0,0017 рад/с4,13 м = 0,007 м/с

ϑ -? _.-?

Ответ: ϑ = 0,007м/c; = 0,0017рад/с

Задача 6.

С какой скоростью движутся концы часовой, минутной и секундной стрелок настенных часов? Примите, что длина часовой стрелки 10 см, а длина минутной стрелки в 1,5 раза больше. Определите, во сколько раз скорость конца минутной стрелки превышает скорость конца часовой стрелки?

Дано:

Т_с = 60с

Т_м= 3600с

Т_ч =43200с

R_ч=10см=0,1 м

R_м=1,5 R_ч

Решение:

ϑ = ; ϑ_с = = 0,02м/с.

ϑ_м= =0,0003м/с

ϑ_ч = =0,00001м/с

= =30

ϑ_с-? ϑ_м-? ϑ_ч-?

-?

Ответ: ϑ_с = 0,02м/с; ϑ_м=0,0003м/с; ϑ_ч =0,00001м/с; =30.

4.Закрепление.

Ученикам предлагается ответить на вопросы теста. Затем осуществляется взаимоконтроль.

Тест №1

1. Примером криволинейного движения является…

а) падение камня;

б) бросок мяча под углом к горизонту;

в) движение спринтера на стометровке.

2. Минутная стрелка часов делает один полный оборот. Чему равен период обращения?

а) 60 с; б) 1/3600 с; в) 3600 с.

3. Колесо велосипеда делает один оборот за 2 с. Определите частоту вращения.

а) 0,5 с^-1; б) 2 с^-1; в) 1 с^-1.

4. Винт самолета Ан-2 делает 25 оборотов за 1 с. Чему равна угловая скорость винта?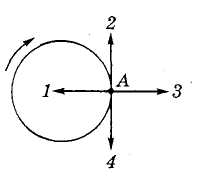

а) 25 рад/с; б) π/25 рад/с; в) 50π рад/с.

5. Тело движется по окружности с постоянной угловой

скоростью. Определите направление линейной

скорости движения в точке A.

а) 1; б) 2; в) 3; г) 4.

Тест №2

1. Примером криволинейного движения является…

а) движение лифта;

б) движение лыжников в слаломе;

в) спуск парашютиста в безветренную погоду.

2. Секундная стрелка часов делает один полный оборот. Чему равна её частота обращения?

а) 1/60 с; б) 60 с; в) 1 с.

3. Колесо велосипеда делает 10 оборотов за 5 с. Определите период вращения.

а) 5 с; б) 10 с; в) 0,5 с.

4. Ротор мощной паровой турбины делает 1 оборот за 0,02 с. Какова его угловая скорость?

а) 50π рад/с; б) π/50 рад/с; в) 100π рад/с.

5. Тело движется по окружности с постоянной угловой

скоростью. Определите направление ускорения движения в точке A.
а) 1; б) 2; в) 3; г) 4.

5. Подведение итогов.

6. Домашнее задание: повторить теорию, № 58.8; 58.15; 58.19.

infourok.ru

Задачи на движение по окружности (9-11 кл.)

Задачи на движение по окружности (9-11 кл.)

Вопрос 1. Точка движется с постоянной по модулю скоростью 2 м/с по окружности радиуса 2 м. Определите ее центростремительное ускорение (м/с²).

Вопрос 2. Шлифовальный камень радиусом 30 см совершает один оборот за 0,6 с. Где расположены точки, имеющие наибольшую линейную скорость, и чему они равны? Ответ указать с точностью до сотых, в м/с.

Вопрос 3. Угловая скорость лопастей вентилятора 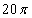 рад/с. Найдите число оборотов за 10 минут.

Вопрос 4. Точка движется по окружности с постоянной по модулю скоростью, равной 1,5 м/с. Определите центростремительное ускорение (см/с²) точки, если за время 2,5 с направление вектора ее скорости изменяется на 57⁰.

Вопрос 5. Колесо диаметром 50 см, двигаясь равномерно, проходит расстояние 2 м за 4 с. Какова угловая скорость (рад/с) вращения колеса?

Вопрос 6. Найти линейную скорость (км/c) Земли при ее орбитальном движении. Средний радиус земной орбиты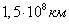 

Вопрос 7. Линейная скорость точек обода вращающегося колеса равна 50 см/с, а линейная скорость его точек, находящихся на 3 см ближе к оси вращения, равна 40 см/с. Определите радиус ( в см) колеса.

Вопрос 8. Минутная стрелка часов на 20% длиннее секундной. Во сколько раз линейная скорость конца секундной стрелки больше, чем конца минутной стрелки?

Вопрос 9. Точка движется по окружности с постоянной по модулю скоростью. За какую долю периода обращения она пройдет путь, равный радиусу окружности? Ответ указать с точностью до сотых.

Вопрос 10. Материальная точка движется по окружности с постоянной по модулю скоростью 2 м/с. Определить центростремительное ускорение движения точки, если за 1,6 с вектор скорости изменяет свое направление на противоположное.

Вопрос 11. Какую поступательную скорость (км/ч) имеют верхние точки обода велосипедного колеса, если велосипедист едет со скоростью 20 км/ч?

Вопрос 12. Во сколько раз линейная скорость точки поверхности Земли, лежащей на широте 60⁰, меньше линейной скорости точки, лежащей на экваторе?

Вопрос 13. Маленький шарик, подвешенный к нити длиной 1м, равномерно двигается по горизонтальной окружности, образуя с вертикалью угол равный 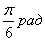. Определить линейную скорость (м/с) шарика, если его период 0,5с,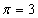 

Вопрос 14. Самолет летит со скоростью 360 км/ч. Пропеллер самолета диаметром 200 см вращается с частотой 1800 об/мин. Определить скорость (м/с) конца пропеллера относительно неподвижного наблюдателя на земле.

Вопрос 15. Волчок, вращающийся с угловой скоростью 62,8 рад/с, свободно падает со стола высотой 1 м. Какое число оборотов совершит волчок за время падения?

Вопрос 16. Мальчик вращает камень, привязанный к веревке длиной 0,5 м в вертикальной плоскости, так, что частота равна 3 об/с. На какую высоту (м) взлетел камень, если веревка оборвалась в тот момент, когда скорость была направлена вертикально вверх?

Вопрос 17. Первая в мире орбитальная космическая станция двигалась со скоростью 7,3 км/с и имела период обращения 88,85 мин. Считая ее орбиту круговой, найти высоту (км) станции над поверхностью Земли. Радиус Земли принять равным 6400 км.

Вопрос 18. Круглая горизонтальная платформа вращается вокруг своей оси с частотой 30 мин^-1. Шар катится в направлении АО со скоростью 7 м/с. Найти скорость (м/с) шара относительно платформы в момент, когда АО = 8 м.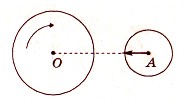

infourok.ru

Конспект урока «Решение задач по теме «Движение тела по окружности» 9 класс

Открытый урок решения задач по подготовке к ОГЭ в 9 классе “ Движение тела по окружности» 24 ноября 2016 г.

Цели урока: закрепить представление о криволинейном движении, основных характеристик частоты, периода, центростремительного ускорения и центростремительной силы.

Задачи.

Образовательные:

Повторить виды механического движения. Закрепить понятия: движение по окружности, центростремительное ускорение, период, частота.

Развивающие:

Развивать умения применять теоретические знания для решения конкретных задач, развивать культуру логического мышления, развивать интерес к предмету; познавательную деятельность при постановке и проведении эксперимента.

Воспитательные:

Формировать мировоззрение в процессе изучения физики и аргументировать свои выводы, воспитывать самостоятельность, аккуратность.

Воспитание коммуникативной и информационной культуры учащихся.

Оснащение урока: компьютер, проектор, экран, презентация к уроку « Решение задач на тему «Движение тела по окружности», распечатка карточек с заданиями. .

Форма организации обучения: фронтальная, индивидуальная, групповая.

Тип урока: повторение и обобщение знаний, умений решать задачи по теме.

Вид урока: комбинированный с элементами исследования

Ход урока

1. Организационный момент.

Мотивация к учебной деятельности

Учитель. Здравствуйте, ребята. Я очень рада вас видеть.

Позвольте начать наш сегодняшний урок с таких строк

«Незнающие
пусть научатся,
знающие –
вспомнят еще раз (слайд 2)

Но, прежде чем приступить разгадывать загадки, давайте немного повторим:

II. Актуализация опорных знаний.

Слайд 3.

Физический диктант:

1. Изменение положения тела в пространстве с течением времени. (Движение)

2. Физическая векторная величина, измеряемая в метрах. (Перемещение)

3. Физическая векторная величина, характеризующая быстроту движения. (Скорость)

4. Основная единица измерения длины в физике. (Метр)

5. Физическая величина, единицами измерения которой служат год, сутки, час. (Время)

6. Длина траектории. (Путь)

7. Единицы измерения ускорения (м/с²)

(Проведение диктанта с последующей проверкой, самооценка работ учениками) Работа в паре.

III. Чему сегодня посвящен наш урок?

Тема нашего урока (слайд 5) «Движение тела по окружности”

Учитель. Что характеризует движение тела по окружности (слайд 6)

Опрос детей

Учитель. Давайте вместе заполним таблицу основных характеристик движения тела по окружности (слайд 7)

Дети заполняют на карточках с последующей проверкой

Учитель; Настало время применить свои знания на практике

Слайд 8

Дети решают у доски задачи с подробным объяснением

1. Колесо делает 120 оборотов за 2 минуты. Какова частота вращения колеса и период вращения?

2. Точильный круг радиусом 10 см делает один оборот за 0,2 с. Найдите скорость точек, наиболее удаленных от оси вращения.

3. Автомобиль движется по закруглению дороги радиусом 100 м. Чему равно центростремительное ускорение автомобиля, если он движется со скоростью 54 км/ч?

4. Какова скорость движения автомобиля, если его колеса радиусом 30 см делают 600 оборотов в минуту?

5. Период обращения первого космического корабля — спутника Земли «Восток» равнялось 90 минут. Средняя высота спутника над Землей была равна 320 км. Радиус Земли 6400 км. Вычислить скорость корабля.

Учитель: Настало время отдохнуть

(слайд 9) – физкультминутка

Практикум по подготовке к ОГЭ слайд 10-11-12

Самостоятельная работа по 2-м вариантам с последующей проверкой

Домашнее задание слайд 13

2. Подведение итогов урока.

Выставление оценок.

Рефлексия. Слайд 14

Учитель. Сегодня на этом уроке мы решали задачи на движение тела по окружности. Данные задачи встречаются в экзаменационных материалах, я думаю, что сегодняшний урок для вас не прошел даром Слайд 15

infourok.ru

Решения задач по теме: «Движение тела по окружности»

Урок №________ Дата_________ Класс_9______ Учитель Физики Османова Л.М.

Тема урока: Решения задач по теме: «Движение тела по окружности»

Цели урока: закрепить представление о криволинейном движении, основных характеристик частоты, периода, центростремительного ускорения и центростремительной силы.

Задачи урока :

Образовательные:

Повторить виды механического движения. Закрепить понятия: движение по окружности, центростремительное ускорение, период, частота.

Развивающие:

Развивать умения применять теоретические знания для решения конкретных задач, развивать культуру логического мышления, развивать интерес к предмету; познавательную деятельность при постановке и проведении эксперимента.

Воспитательные:

Формировать мировоззрение в процессе изучения физики и аргументировать свои выводы, воспитывать самостоятельность, аккуратность.

Воспитание коммуникативной и информационной культуры учащихся.

Оборудование: компьютер, проектор, экран, презентация к уроку « Решение задач на тему «Движение тела по окружности», распечатка карточек с заданиями. .

Форма работы: фронтальная, индивидуальная, групповая.

Тип урока: повторение и обобщение знаний, умений решать задачи по теме.

Вид урока: комбинированный с элементами исследования

Ход урока

1. Организационный момент.

Мотивация к учебной деятельности

Учитель.

«Незнающие пусть научатся, знающие – вспомнят еще раз

II. Актуализация опорных знаний.

Физический диктант:

1. Изменение положения тела в пространстве с течением времени. (Движение)

2. Физическая векторная величина, измеряемая в метрах. (Перемещение)

3. Физическая векторная величина, характеризующая быстроту движения. (Скорость)

4. Основная единица измерения длины в физике. (Метр)

5. Физическая величина, единицами измерения которой служат год, сутки, час. (Время)

6. Длина траектории. (Путь)

7. Единицы измерения ускорения (м/с²)

(Проведение диктанта с последующей проверкой, самооценка работ учениками) Работа в паре.
Тема урока : Решения задач по теме: «Движение тела по окружности»

Учитель. Что характеризует движение тела по окружности

Опрос детей устно

Решение у доски задачи с подробным объяснением

1. Колесо делает 120 оборотов за 2 минуты. Какова частота вращения колеса и период вращения?

2. Точильный круг радиусом 10 см делает один оборот за 0,2 с. Найдите скорость точек, наиболее удаленных от оси вращения.

3. Автомобиль движется по закруглению дороги радиусом 100 м. Чему равно центростремительное ускорение автомобиля, если он движется со скоростью 54 км/ч?

4. Какова скорость движения автомобиля, если его колеса радиусом 30 см делают 600 оборотов в минуту?

5. Период обращения первого космического корабля — спутника Земли «Восток» равнялось 90 минут. Средняя высота спутника над Землей была равна 320 км. Радиус Земли 6400 км. Вычислить скорость корабля.

физкультминутка

Домашнее задание

2. Подведение итогов урока. Выставление оценок.

Рефлексия.

Вариант №1

З адача 1 C какой скоростью велосипедист проходит закругление с радиусом 25 метров, если центростремительная скорость его движения равна 4 м/с?

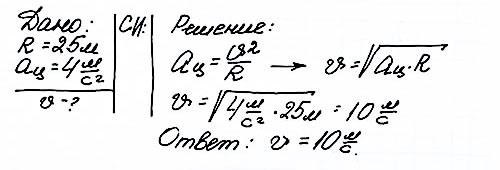
Задача 2 Колесо радиусом 40 см делает один оборот за 0,4 секунды. Найти скорость точек на ободе колеса.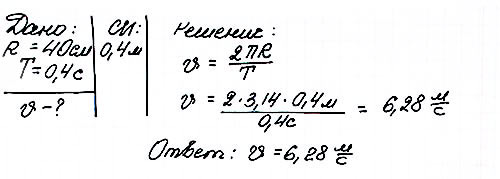

Задача 3 Колесо велосипедиста имеет радиус 40 см. С какой скоростью едет велосипедист, если колесо делает 4 оборота в секунду? Чему равен период вращения колеса?

Задача 4 С какой скоростью велосипедист должен проходить середину выпуклого моста радиусом 22,5 метра, чтобы его центростремительное ускорение было бы равно ускорению свободного падения?

Задача 5 Чему равно центростремительное ускорение тела, движущегося по окружности радиус ом 50 см при частоте вращения 5 оборотов в секунду?

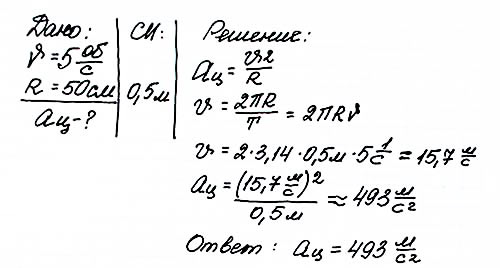
Вариант 2

задача1. Колесо радиусом 80 см делает один оборот за 0,8 секунды. Найти скорость точек на ободе колеса.

Задача 2 Скорость точек экватора Солнца при его вращении вокруг своей оси равно 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек его экватора.

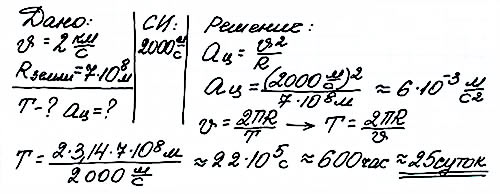
Задача 3 Какова скорость движения автомобиля, если его колесо радиусом 30 см делает 500 оборотов в минуту?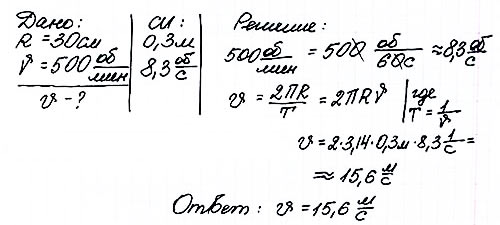

Задача 4 Чему равна центростремительная сила и центростремительное ускорение, действующие на пращу массой 800 г, вращающуюся на веревке длиной 60 сантиметров равномерно со скоростью 2 м/с?

Задача 5 Период обращения космического корабля вокруг Земли равен 90 минутам. Высота подъема корабля над поверхностью Земли составляет 300 км, радиус Земли равен 6400 км. Определить скорость корабля.

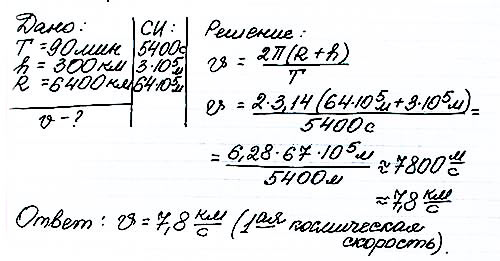
9кл.Самостоятельная работа по теме : «Движение тела по окружности»

Вариант№1

Задача 1 C какой скоростью велосипедист проходит закругление с радиусом 25 метров, если центростремительная скорость его движения равна 4 м/с?

Задача 2 Колесо радиусом 40 см делает один оборот за 0,4 секунды. Найти скорость точек на ободе колеса.

Задача 3 Колесо велосипедиста имеет радиус 40 см. С какой скоростью едет велосипедист, если колесо делает 4 оборота в секунду? Чему равен период вращения колеса?

Задача 4 С какой скоростью велосипедист должен проходить середину выпуклого моста радиусом 22,5 метра, чтобы его центростремительное ускорение было бы равно ускорению свободного падения?

Задача 5 Чему равно центростремительное ускорение тела, движущегося по окружности радиусом 50 см при частоте вращения 5 оборотов в секунду?

9 кл. Самостоятельная работа по теме : «Движение тела по окружности»

Вариант№2

задача1. Колесо радиусом 80 см делает один оборот за 0,8 секунды. Найти скорость точек на ободе колеса.

Задача 2 Скорость точек экватора Солнца при его вращении вокруг своей оси равно 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек его экватора.

Задача 3 Какова скорость движения автомобиля, если его колесо радиусом 30 см делает 500 оборотов в минуту?

Задача 4 Чему равна центростремительная сила и центростремительное ускорение, действующие на пращу массой 800 г, вращающуюся на веревке длиной 60 сантиметров равномерно со скоростью 2 м/с?

Задача 5 Период обращения космического корабля вокруг Земли равен 90 минутам. Высота подъема корабля над поверхностью Земли составляет 300 км, радиус Земли равен 6400 км. Определить скорость корабля.

infourok.ru

Задачи на движение по окружности

Анализ статистических данных результатов проведения ЕГЭ говорит о том, что процент решения заданий, содержащих текстовые задачи, из года в год составляет порядка 30%. Такие сведения позволяют сделать вывод, что большинство учащихся школ не владеют в полной мере техникой решения текстовых задач. За нетрадиционной формулировкой ученики с трудом распознают типовые задания, которые были хорошо изучены и отработаны на уроках математики в школе. По этой причине возникла необходимость более глубоко изучить этот раздел элементарной математики.

Остановимся на решении текстовых задач на движение по окружности.

Задача 1.

Двигаясь по окружности в одном направлении, две точки встречаются каждые 12 минут. Так же известно, что первая точка обходит всю окружности на 10 секунд быстрее, чем вторая. Определить, сколько времени потребуется второй точке, чтобы обойти всю окружность.

Решение.

Введем некоторые обозначения. Пусть точка А – место встречи двух точек, которые движутся по окружности со скоростями х м/с и у м/с соответственно. Длина окружности равна р м (рис. 1).

Можно сказать, что время, за которое первая точка обойдет один раз всю окружность будет равна р/x секунд, а время, необходимое второй точке для полного оборота – р/y с. В этом случае можно составить первое уравнение: р/y – р/x = 10.

Первая точка за 12 минут, а это значит за 720 секунд (12 · 60 секунд = 720 секунд) проходит 720х метров, а вторая точка – 720у м. Причем первая точка за 12 минут обходит окружность на один раз больше, чем вторая. В таком случае, имеем второе уравнение: 720х – 720у = р. Можно составить систему уравнений:

{р/у – р/х = 10,
{720х – 720у = р.

Разделим обе части второго уравнения на р:

{р/у – р/х = 10,
{720х/р – 720у/р = 1.

Пусть р/х = t₁, а р/у = t₂, тогда система примет вид:

{t₂ – t₁ = 10,
{720/t₁ – 720/t₂ = 1.

Перепишем следующим образом:

{t₂ – t₁ = 10,
{720(t₂ – t₁) = t₁ t₂.

Решим методом подстановки:

{t₂ = 10 + t₁,
{720 · 10 = t₁(10 + t₁).

Из второго уравнения имеем квадратное уравнение

t₁² + 10t₁ – 7200 = 0.

Корни t₁ = -90 или t₁ = 80.

По смыслу задачи t₁ = 80 секунд, тогда t₂ = 10 + 80 = 90 секунд.

Ответ: 90 секунд.

Задача 2.

На окружности взята некоторая точка А. Из этой точки одновременно выходят два тела, которые движутся по данной окружности равномерно в противоположных направлениях. В момент их встречи оказалось, что первое тело прошло на 10 метров больше второго. Кроме того, первое тело пришло в точку А через 10 секунд, а второе – через 16 секунд после встречи. Определить длину окружности в метрах.

Решение. 

Обозначим длину окружности р м, а скорости первого и второго тел за х м/с и у м/с соответственно. Кроме того, будем считать, что x > y (рис. 2).

Пусть t секунд – время, за которое тела прошли путь от точки А до пункта их встречи – точки В, тогда (хt) метров и (уt) метров – расстояние, которое прошло первое и второе тела от точки А до точки В соответственно. С другой стороны, (9х) метров и (16у) метров – это расстояние, которые прошли тела от В до А уже после встречи, то есть хt = 16y и yt = 9х.

Имеем: t = 16у/х и t = 9х/у,

значит, 16у/х = 9х/у или 16у² = 9х².

Извлечем корень из обеих частей равенства,

получим: 4х = 3у, х = 4у/3.

Так как, путь, пройденный первым телом до встречи, на 10 метров больше, чем путь, пройденный вторым телом до встречи, то 16у – 9х = 10.

Зная зависимость х = 4у/3, имеем:

16у – 9 · 4у/3 = 10;

16у – 12у = 10;

4у = 10;

у = 2,5.

Тогда х = 4/3 · 2,5 = 10/3.

Найдем длину окружности:

р = 16у + 9х = 16 · 2,5 + 9 · 10/3 = 8 · 5 + 3 · 10 = 40 + 30 = 70 (метров).

Ответ: 70 метров.

Чтобы научится успешно решать текстовые задачи, нужно постоянно практиковаться. Занимаясь несколько часов в неделю можно легко освоить основные методы решения текстовых задач. 

 Остались вопросы? Не знаете, как решать задачи на движение?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Движение по окружности, олимпиадная подготовка. 9 класс.

В этой статье представлены задачи на движение по кругу. Задачи предназначены для подготовки к олимпиадам по физике для ребят 9 класса.

 

Задача 1. Направление вращения Земли вокруг своей оси совпадает с направлением ее вращения вокруг Солнца. Каким было бы число дней в году , если бы Земля вращалась вокруг Солнца в противоположном направлении? Ответ дать в сутках, округлив до целых. Считать, что сейчас год длится ровно дней.

Решение.

Пусть центр Земли вращается с периодом вокруг Солнца год). Рассмотрим точку на экваторе Земли, которая в свою очередь вращается вокруг земной оси с угловой скоростью . Назовем земными сутками интервал времени между двумя последовательными положениями Солнца, например, в зените.

Если направления вращения не совпадают, то за сутки точке надо совершить поворот на угол, меньший, чем . Угол, на который сместилась Земля относительно Солнца, будет равен . В этом случае длительность суток будет

   

Аналогично в случае вращения в ту же сторону точке надо будет совершать за сутки (другой длительности, более длинные) полный оборот на и небольшой дополнительный поворот на угол, на который сместилась Земля относительно Солнца В этом случае длительность суток будет

   

Если разделить одно уравнение на другое, получим

   

   

, то есть число дней в «длинном» году станет 367.

Ответ: 367 суток.

 

Задача 2. Скорость точки вращающегося диска равна см/с, а скорость точки , находящейся на см ближе к оси диска, равна см/с. Определите период вращения диска. Ответ дать в секундах. Округлить до сотых.

Решение.

Обозначим расстояние от оси до точки за . Тогда можно записать линейные скорости точек через угловую скорость и радиусы:

   

и

   

Вычитая, получим . Подставив период , получаем

   

Ответ: 6,28 с.

Задача 3. Мальчик вращает камень, привязанный к веревке длиной м, в вертикальной плоскости с частотой Гц. На какую высоту взлетел камень, если веревка оборвалась в тот момент, когда скорость была направлена вертикально вверх? Ответ дать в метрах, округлив до десятых. Ускорение свободного падения м/c.

Решение.

Скорость камня в момент отрыва найдем по формуле

   

Высоту подъема тела определим из выражения

   

Учитывая, что в верхней точке подъема камня получаем

   

Ответ: 4,4 м.

 

Задача 4. Вентилятор вращается с частотой об/мин. После выключения вращение происходит равнозамедленно, причём вентилятор делает до остановки оборотов. Сколько времени прошло с момента выключения вентилятора до полной его остановки? Ответ дать в секундах, округлив до целых.

Решение.

Найдем среднюю частоту вращения. С одной стороны,

   

Но с другой ( – начальная скорость, – конечная скорость)

   

так как движение равнозамедленное, а частота линейно связана с угловой скоростью. Приравнивая уравнения и выражая , получим, что

   

Ответ: 10 с.

Задача 5. Три самолета выполняют разворот в горизонтальной плоскости» двигаясь равномерно по концентрическим окружностям на расстоянии м друг от друга. Ближайший к центру виража самолет движется по окружности м. Средний самолет движется со скоростью км/ч. Найти ускорение самолета, летящего по внешней траектории. Ответ дать в м/c, округлив до целых.

Решение.

Угловая скорость среднего самолета равна

   

Но угловая скорость всех самолетов одинакова, так как они движутся по концентрическим окружностям на одинаковых расстояниях друг от друга. Ускорение внешнего самолета можно найти через угловую скорость и радиус его траектории

   

Ответ: 15 м/c.

 

easy-physic.ru

Движение по окружности. 9 класс. Презентация.

Просмотр содержимого документа
«Движение по окружности. 9 класс. Презентация.»

Движение тела по окружности

Физика.

9 класс.

Равномерное движение по окружности

• Криволинейное движение с постоянной по модулю скоростью;
• Вектор скорости

при движении тела

по окружности направлен

по касательной к окружности.

v

v

v

v

R

Равномерное движение по окружности

• Движение с ускорением , т.к. скорость меняет направление.
• Ускорение при движении по окружности, которое направлено вдоль радиуса окружности к центру окружности, называется центростремительным
• При движении по окружности с постоянной скоростью ускорение по модулю имеет одно и то же значение.

а

v

Период и частота

• Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.
• Единица измерения периода — секунда

• Частота вращения n – число полных оборотов в единицу времени.
• Единица измерения частоты

[n ] = с -1 = Гц.

Угловая скорость

• Угловая скорость (циклическая частота)- число оборотов за единицу времени выраженное в радианах.



Кинематика движения по окружности

• Линейная скорость

• Угловая скорость

Центростремительная сила

• Сила, удерживающая вращающееся тело на окружности и направленная к центру вращения, называется центростремительной силой.

Величина

Определение

Период

Частота

Формулы связи

T=t/N

Единица измерения

Линейная скорость

n= N/t

T= 2  R/v

Угловая

Особенности

с

n= 1 / Т

T=1/n

скорость

 =  /t

Центростремительное ускорение

v=2  R/T

 

с -1

Меньше для больших скоростей

a=v 2 /R

 =2  /T

Обороты в секунду

v=  R

 

a=4  2 R/T 2

 

рад/с

Увеличивается с возрастанием частоты

м/с

Угол поворота

 

м/с 2

за 1 секунду

Больше при малых R и при больших v

 

Задача №1

• Автомобиль движется по закруглению дороги, радиус которой равен 20 м. Определите скорость автомобиля, если центростремительное ускорение равно 5 м/с 2 .

Задача №2

• Линейная скорость конца минутной стрелки Кремлевских курантов равна 6 мм/с. Определите длину минутной стрелки.

Найти : l-?

Решение :

длина минутной стрелки — это радиус окружности, которую

описывает эта стрелка при своем движении l=R

один оборот стрелка делает за время t=T=1ч=3600с

Ответ: 3,44 м

Задача №3

• Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?

• линейная скорость точки обода колеса радиусом 8 см в 1,6 раза больше точки, расположенной на 3 см ближе к оси вращения.
• Ответ : в 1,6 раза.

Задача №4

t=2мин=120с

N=2400

r=10см=0,01м

__________

n- ? Т-? V-?

Решение:

Ответ :  20 с 1 ; ≈0,05 с; 12,6 м/с.

• Вентилятор вращается с постоянной скоростью и за две минуты совершает 2400 оборотов. Определите частоту вращения вентилятора, период обращения и линейную скорость точки, расположенной на краю лопасти вентилятора на расстоянии 10 см от оси вращения.

Задача №5

•   Велосипедист ехал со скоростью 25,2 км/ч. Сколько оборотов совершило колесо диаметром 70 см за 10 мин?
• Ответ : 1910

• Решение: количество оборотов колеса находим как отношение расстояния, которое проехал велосипедист за 10 минут, к длине окружности колеса :

Самостоятельная работа

1 вариант

2 вариант

• С каким периодом должна вращаться карусель радиусом 6,4 м для того, чтобы центростремительное ускорение человека на карусели было равно 10 м/с 2 ?

• Частота обращения карусели 0,05 с -1 . Человек, вращающийся на карусели, находится на расстоянии 4 м от оси вращения. Определите центростремительное ускорение человека, период обращения и угловую скорость карусели.

• На арене цирка лошадь скачет с такой скоростью, что за 1 минуту обегает 2 круга. Радиус арены равен 6,5 м. Определите период и частоту вращения, скорость и центростремительное ускорение.

• Точка обода колеса велосипеда совершает один оборот за 2 с. Радиус колеса 35 см. Чему равно центростремительное ускорение точки обода колеса?

Использованные источники

• Сборник задач по физике 7-9, Лукашик В.И., Иванова Е.В..
• (задачи №161,162,163,165,167)

multiurok.ru