область определения, нули функции, четность функции и все остальные.
Функция — это одно из важнейших математических понятий. Функция — зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y), образуют область значений функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x, а по оси ординат откладываются значения переменной y. Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!
Для построения графика функции советуем использовать нашу программу — Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при
которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.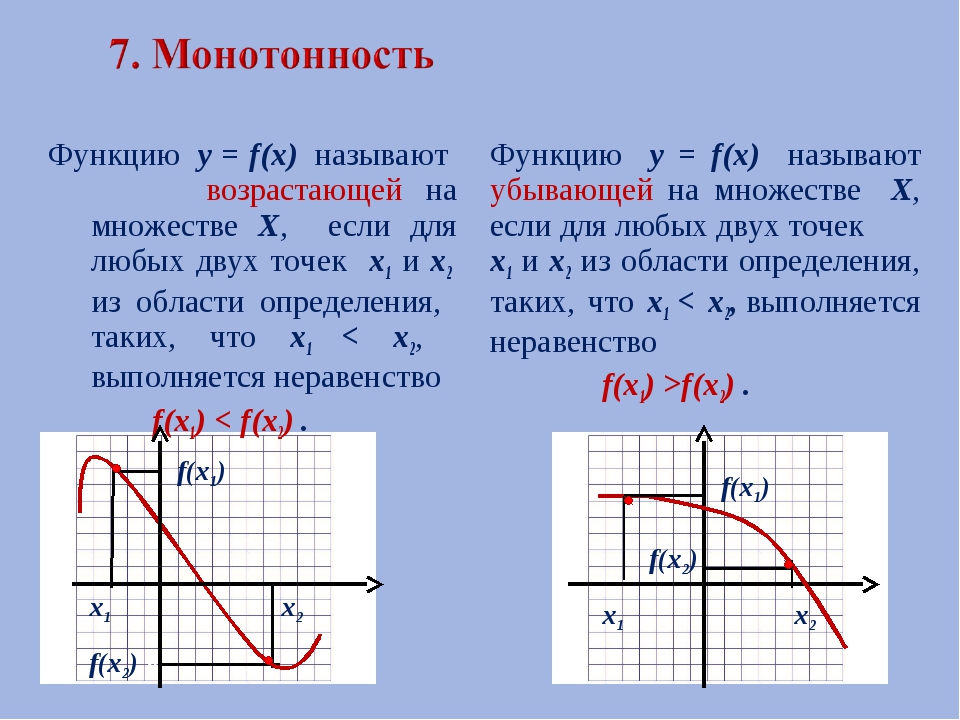
2) Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции.
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция — функция, у которой область определения симметрична относительно
начала координат и для любого х из области определения выполняется равенство
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.
7) Периодическость функции.
Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по
свойствам функции сможете построить график функции.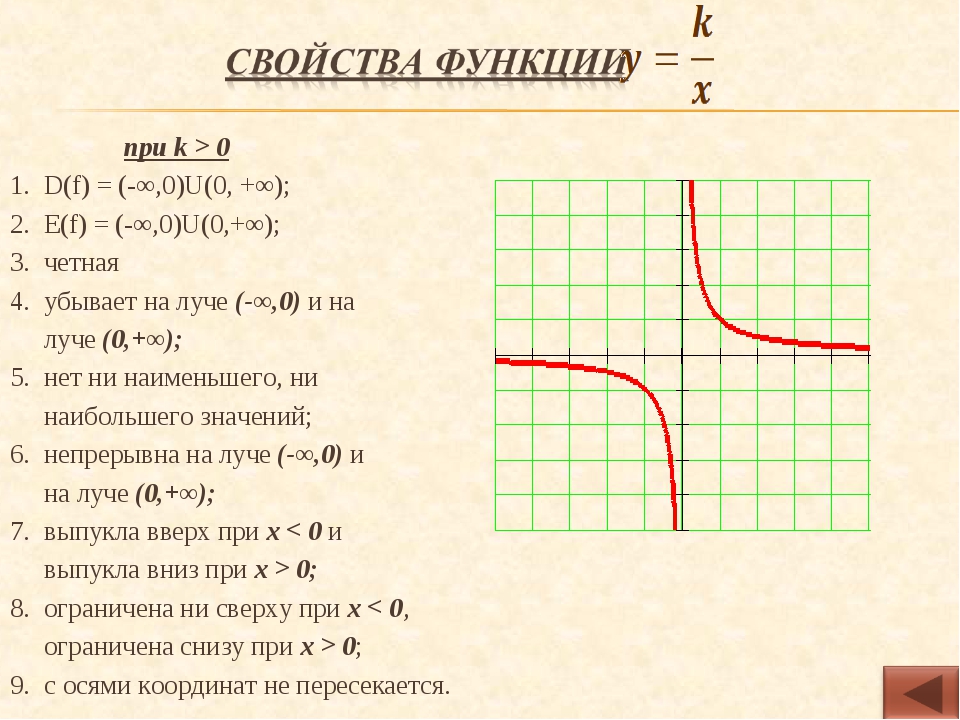 Также посмотрите материал про
таблицу истинности,
таблицу умножения,
таблицу Менделеева,
таблицу производных и
таблицу интегралов.
Также посмотрите материал про
таблицу истинности,
таблицу умножения,
таблицу Менделеева,
таблицу производных и
таблицу интегралов.
Слишком сложно?
Свойства функции не по зубам? Тебе ответит эксперт через 10 минут!
Нахождение свойств функции по её графику
Анализ урока в соответствии с ФГОС
Учитель: Улубиевой Нины Майрбековны
Предмет: математика
Класс: 9
Тема урока: Нахождение свойств функции по графику.
Тип урока: Урок усвоения новых знаний ( УУНЗ)
Цель урока: систематизировать и обобщить знания о свойствах функции. Способствовать выработке навыков и умений в прочтении графиков функций. Научить определять основные свойства функции, заданной графически.
Задачи: Образовательная — создать условия для: обобщения и систематизации знаний по выявлению основных свойств функции. Используя активные методы обучения, научить учащихся находить свойства функции по графику.
Развивающая — формирования умений логически обосновывать суждения. Ясно, точно и грамотно выражать свои мысли в устной и письменной речи. Использовать различные языки математики (словесный, символический, графический) .
Воспитательная – воспитание уверенности, внимания
Актуальность:
— задания по данной теме встречаются в ГИА по математике в 9 классе и в ЕГЭ — 11 класса;
— чтение графиков функций имеет большое практическое значение
Планируемые образовательные результаты:
Личностные: осознание цели деятельности (ожидаемый результат), анализ и оценивание полученного результата; оценка своих возможностей; положительное отношение к учению, к познавательной деятельности, желание совершенствовать имеющиеся знания и умения;
Регулятивные: принимать учебную задачу; целеполагание; планировать (в сотрудничестве с учителем и одноклассниками или самостоятельно) необходимые действия, операции, действовать по плану; контролировать процесс и результаты деятельности, вносить необходимые коррективы; адекватно оценивать свои достижения.

Познавательные: осознавать познавательную задачу; читать и слушать, извлекая нужную информацию, понимать информацию; осуществлять для решения учебных задач мыслительные операции; устанавливать причинно-следственные связи, делать выводы.
Коммуникативные: вступать в учебный диалог с учителем, одноклассниками, участвовать в общей беседе, соблюдая правила речевого поведения; задавать вопросы, слушать и отвечать на вопросы других, формулировать собственные
Используемые на уроке средства и ИКТ:
1.Соотвествие дидактической задачи урока отобранному содержанию.2.Результативность решения дидактической задачи
5
5
Содержание урока
Соответствие основного содержания содержанию программы и учебника
5
Методы обучения
Соответствие приёмов обучения (методов обучения) решению триединой образовательной цели.
5
Формы обучения
1.Соотвествие форм обучения (фронтальная, групповая, индивидуальная, коллективная) решению основной дидактической задачи урока.
2.Целесообразность предложенных заданий.
4
5Результативность урока
Достижение цели и решение основной дидактической задачи урока.
5
Практическая направленность урока
Практическая направленность вопросов, упражнений и задач, предлагаемых для выполнения обучающимся.
5
Самостоятельная работа школьников как форма организации учебной деятельности.
1.уровень самостоятельности школьников при решении дидактической задачи урока.
2.Характер самостоятельной учебной деятельности (репродуктивный, творческий).
3.Взаимопомощь.
4
5
5
Формирование универсальных учебных действий на каждом этапе урока
Личностные, познавательные, коммуникативные, регулятивные.
5
Формирование ИКТ компетентности
Применение ИКТ на уроке, уровень сформированности ИКТ компетентности учащихся
5
Структура урока
Соотвествие структуры урока основной дидактической задаче
5
Педагогический стиль
Соблюдение норм педагогической этики.
5
Использование современных образовательных технологий в процессе обучения преподаваемого предмета
Цель применения образовательной технологии
Формируемые компетентности
Эффекты, результативности использования образовательной технологии
5
5
5
Применение здоровьесберегающих технологий.
Использование здоровьесберегающих технологий, методик и приёмов оздоровления детей.
4
ИТОГО
95
Директор школы _______________________ /Тилибова Ж.Ш.
Зачет по алгебре и началам анализа по теме «Функция и её свойства», 10-й класс
Цели:
- Проверить знания о свойствах функции, знание всех определений.
- Уметь по графику определять свойства функций.
- Уметь, используя свойства функций, строить схематически её график.
- Показать умение работать в коллективе.
- Показать смекалку, сообразительность, быстроту
мышления.

Виды работ:
I. Диктант (на знание определений) — 25′
II. Лабораторно-практическая работа (исследование функции по графику) — 20′
III. Письменная работа — 25′ “Построить схематически график функции с предварительным исследованием по схеме”.
IV. Урок-соревнование — 45′
Ход зачёта
I. Оборудование зачёта:
- Проектор, экран.
- Индивидуальные карточки для лабораторно – практической работы.
- Модель координатной плоскости с индивидуальными заданиями.
- Графики, выполненные на компьютере и проецируемые на доску с помощью проектора.
II. Диктант. (25′)
- Дайте определение числовой функции.
- Что такое аргумент функции?
- Что называется областью определения функции?
- Что такое область значения функции?
- Что называется графиком функции?
- Какие преобразования графиков функций вы знаете? Перечислите.
- Дайте определение чётной функции.
- Какая функция называется нечётной?
- Назовите особенность графика чётной функции.
- Какова особенность графика нечётной функции?
- Какая функция называется периодической?
- Какая функция называется возрастающей на множестве Р?
- Какая функция называется убывающей на множестве Р?
- Какая точка называется точкой минимума функции?
- Какая точка называется точкой максимума функции?
- Как называются точки max и min?
III. Лабораторно-практическая работа. — (20′)
Каждому учащемуся выдаётся индивидуальная
карточка и листок бумаги для ответов. Карточки 8
вариантов (Приложение №1).
Карточки 8
вариантов (Приложение №1).
IV. Письменная работа.
Задание: “Построить схематически эскиз графика заданной функции, предварительно исследовав её по общей схеме”.
Карточки трёх видов
V. Урок-соревнование по теме “Функция”
Цели:
- Обобщить полученные знания по свойствам функции.
- Уметь определять по графику все свойства функции.
- Знать определения свойств функции.
- Уметь работать коллективно, уважая друг друга.
Класс разбит на две команды. Все задания подготовлены на доске. За каждый правильный ответ команда получает жетон.
Ход урока
I. Устные упражнения.
1. Найдите область определения функции:
| а) f (x) = 1/x | б) g (x) = v |
| в) h (x) = 1/ | г) f (x) = |
2. Найдите нули функции:
а) y = 3x + 1
б) y = x? — 9
3. Пусть f (x) = x + 1/x
Сравните
f (3) и f (-3)
f (-5) и -f (5)
4. Найдите множество значений функции:
| у = x? — 2 | f (x) = cos x |
5. Пусть f (3) = -5; f (-4) = 3;
Найдите f (-3) и f (4), если
а) f (x) – чётная
б) f (x) – нечётная
в) f (x) – периодическая, с периодом Т = 2.
Какое значение функция y = sin x принимает на [?; 2?] ровно один раз.
II. На рисунке изображена часть графика
функции с областью определения [-3; 3]. Постройте
график функции, если известно, что она а)
чётная б) нечётная
Постройте
график функции, если известно, что она а)
чётная б) нечётная
Ответы: Приложение №2
Учащиеся выполняют это задание в парах на отдельных листочках и сдают учителю.
III. На рисунке даны 4 графика функции и записаны 4 формулы.
| 1. | 2. |
| 3. | 4. |
2)y =2 – x
3) y = x2 + 4x + 3
4) y = |x – 1|
Вопросы:
- Какой формулой задаётся каждый из графиков?
- Как называется каждый из графиков?
- Назовите области определения и области значения этих графиков.
- Какие из этих графиков являются чётными, а какие нечётными?
Команды дают устные ответы в порядке поднятия руки.
IV. Даны графики функций: (проецируются на экран)
а) y = cos x
Постройте график функции y = cos x – 1
б) y = sin x
Постройте график функции y = sin x + 1
Команды выполняют данные задания на месте и отвечают на вопрос “Какой вид преобразования функции здесь используется?”
Листки с выполненными заданиями сдаются учителю.
V. Проявите смекалку.
Чтобы проиллюстрировать характерные свойства функций, можно обратиться к пословицам, ведь пословицы – это отражение устойчивых закономерностей, выверенных многовековым опытом народа.
На доске написаны пословицы:
- “Чем дальше в лес, тем больше дров”.

- “Выше меры конь не скачет”.
- “На пол упало, на половину пропало”.
Изобразите пословицы при помощи графика. Как вы её понимаете?
Ответы: Приложение №3.
Команды на листках выполняют задания и сдают их учителю.
VI. Отгадайте загадки и шараду.
1. Загадка. О какой кривой идёт речь?
Как утомительны вечные спуски,
Как утомительны вечные взлёты!…
В каждой ложбинке,
На каждой вершине –
Тщетна надежда – мечта о привале,
Об остановке и передышке. (синусоида)
2. Загадка. Какое свойство функции описывается в стихотворении?
“У попа была собака, он её любил.
Она съела кусок мяса, он её убил.
В землю закопал, надпись написал
…………………………………… ” (периодичность)
3. Шарада. Угадай функцию.
Привычное слово кудлатой наседки
Поставьте на первое место.
На месте втором, посмотрите-ка – нота,
Важна для любого оркестра.
На третьем – одна одинокая буква
Пятнадцатая в алфавите.
Один из волос на мордашке котёнка
На месте четвёртом прочтите. (косинус)
VII. Отгадайте кроссворд по теме “Функция”.
(Кроссворд прилагается) Приложение №4.
Кроссворд и вопросы к нему получают обе команды. Отгадывают командой.
VIII. Составьте существительные из слова “тригонометрическая”.
Лучше всех задание выполнили:
Ларионова Д. – 64 слова
Никонов Е. – 57 слов
Бандеров С. – 54 слова
Дурнева М. – 52 слова
Итоги урока.
Оценки выставляют каждому всей командой по %
участию каждого в выполнении заданий.
Тема 2.1 Числовые функции. Функция, ее свойства и график
Степенная функция. Функция вида y=x k, где k>0 постоянная, называется степенной функцией. Если k=1, то y=x линейная функция, ее график прямая линия.
Степенная функция Функция вида y=x k, где k>0 постоянная, называется степенной функцией. Если k=1, то y=x линейная функция, ее график прямая линия. Если k=2, то y=x 2 квадратичная функция, ее график парабола.
ПодробнееТема 1.4 Функции, их свойства и графики
Тема.4 Функции, их свойства и графики Автор: Переверзьева Н.С. Преподаватель математики Лицей 6 Цели урока: Ознакомиться с понятием «функция», закрепить его на примерах Усвоить новые термины Узнать методы
ПодробнееТема 9 «Функция. Свойства функций»
Тема 9 «Функция. Свойства функций» Пусть X некоторое непустое множество действительных чисел. И пусть указан закон f, по которому каждому числу х ϵ X ставится в соответствие единственное число y ϵ Y, обозначаемое
ПодробнееМатематический анализ
Математический анализ Понятие функции. Основные свойства функций Математический анализ (лекция 2) 28 / 64 Понятие функции. Основные свойства функций Если каждому элементу (значению) x множества X поставлен
Подробнееϕ называется ортогональной на [ a, b]
ТЕМА V РЯД ФУРЬЕ ЛЕКЦИЯ 6 Разложение периодической функции в ряд Фурье Многие процессы происходящие в природе и технике обладают свойствами повторяться через определенные промежутки времени Такие процессы
Подробнее4 Лекция Функция
Функция Понятие функции Способы задания функции Характеристики функции Обратная функция Предел функции Предел функции в точке Односторонние пределы Предел функции при x Бесконечно большая функция 4 Лекция
ПодробнееАЛГЕБРА И НАЧАЛА АНАЛИЗА
СОДЕРЖАНИЕ АЛГЕБРА И НАЧАЛА АНАЛИЗА ФУНКЦИИ. ..10 Основные свойства функций…11 Четность и нечетность…11 Периодичность…12 Нули функции…12 Монотонность (возрастание, убывание)…13 Экстремумы (максимумы
..10 Основные свойства функций…11 Четность и нечетность…11 Периодичность…12 Нули функции…12 Монотонность (возрастание, убывание)…13 Экстремумы (максимумы
Алгоритм решения квадратных неравенств
Алгоритм решения квадратных неравенств 1) Привести неравенство к стандартному виду : 2) Решить квадратное уравнение (т.е. найти точки пересечения параболы с осью Ох):,, если D > 0, то (две точки пересечения
ПодробнееГлава 11 ТЕСТОВЫЕ ЗАДАНИЯ
Глава ТЕСТОВЫЕ ЗАДАНИЯ Т-0 Исследование функции по графику Т-0 Соответствие между графиком рациональной функции и формулой Т-0 Построение графика по свойствам Т-04 Параллельный перенос графика Т-05 Симметричное
ПодробнееТема: Понятие функции
Математический анализ Раздел: Введение в анализ Тема: Понятие функции (основные определения, классификация, основные характеристики поведения) Лектор Рожкова С.В. 2012 г. Литература Пискунов Н.С. Дифференциальное
ПодробнееИррациональные неравенства
Иррациональные неравенства Неравенства, в которых переменная содержится под знаком корня, называются иррациональными Основным методом решения иррациональных неравенств является метод сведения исходного
ПодробнееФункция y = cos x. Ее свойства и график
Функция y = cos x Ее свойства и график 1 Сегодня мы рассмотрим Построение графика функции y = cos x; Свойства функции y = cos x; Изменение графика функции y = cos x в зависимости от изменения функции и
ПодробнееАлгебра. Программа. 9 класс
Алгебра. Программа. 9 класс Пояснительная записка. Изучение математики на ступени основного общего образования направлено на достижение следующих целей: овладение системой математических знаний и умений,
Изучение математики на ступени основного общего образования направлено на достижение следующих целей: овладение системой математических знаний и умений,
10 класс, Математика (профиль) уч.год Тема модуля 1 «Корни, степени, логарифмы»
0 класс, Математика (профиль) 0-08 учгод Тема модуля «Корни, степени, логарифмы» Знать Понятия действительного числа, множества чисел, свойства действительных чисел, делимость целых чисел****, свойства
ПодробнееМатематическая индустрия моды
Краевая научно-практическая конференция учебно-исследовательских и проектных работ учащихся 6-11 классов «Прикладные и фундаментальные вопросы математики» прикладные вопросы математики Математическая индустрия
ПодробнееЭлементы высшей математики
Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Теория пределов Составитель: доцент
ПодробнееЗадание 18. Задачи с параметром
Линейное уравнение a x = b имеет: единственное решение, при a 0; бесконечное множество решений, при a = 0, b = 0; не имеет решений, при a = 0, b 0. Квадратное уравнение ax 2 + bx + c = 0 имеет: два различных
ПодробнееДифференциальное исчисление
Дифференциальное исчисление Основные понятия и формулы Определение 1 Производной функции в точке называется предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента
ПодробнееОпределение 1. Функция y = ax + bx + c, где a, b, c — действительные числа, причем a 0, называется квадратичной.
 1) Область определения. ( f ) R.
1) Область определения. ( f ) R.СВОЙСТВА ФУНКЦИИ И ЕЕ ГРАФИК Определение. Функция, где,, — действительные числа, причем 0, называется квадратичной. Область определения. ( f R, так как выражение определено для любых. Область значений.
Подробнее1 Степень с целым показателем
Глава 9 Степени Степень с целым показателем. 0 = 0; 0 = ; 0 = 0. > 0 > 0 ; > >.. >. Если четно, то ( ) < ( ). Например, ( ) 0 = 0 < 0 = = ( ) 0. Если нечетно, то ( ) > ( ). Например, ( ) = > = = ( ), так
ПодробнееФункции одной переменной
Функции одной переменной. Действительные числа В нашем курсе мы постоянно будем иметь дело с действительными числами. Напомним основные сведения о действительных числах, известные и школьного курса математики.
Подробнее= 1 е) f(9) = 27; f(1) = 3
Глава 8 ФУНКЦИИ И ГРАФИКИ Алгоритмы А- Задание стандартных функций А- Понятие функции. График функции А-3 Каноническая запись зависимостей А- Задание стандартных функций. К стандартным функциям отнесем
ПодробнееКритерии оценки заданий 18
Задание 18 Критерии оценки заданий 18 Содержание критерия Балл ы Обоснованно получен правильный ответ. 4 С помощью верного рассуждения получено множество значений а, отличающееся от искомого конечным числом
ПодробнееУрок на тему: Построение графиков.
Урок на тему: Построение графиков. Ребята, мы с вами строили уже не мало графиков функций, например параболы, гиперболы, тригонометрических функций и другие. Давайте вспомним, как мы это делали? Мы выбирали
Подробнее6 Общая схема исследования функции
5 6 Общая схема исследования функции Исследование дважды дифференцируемой функции будем проводить по следующей схеме.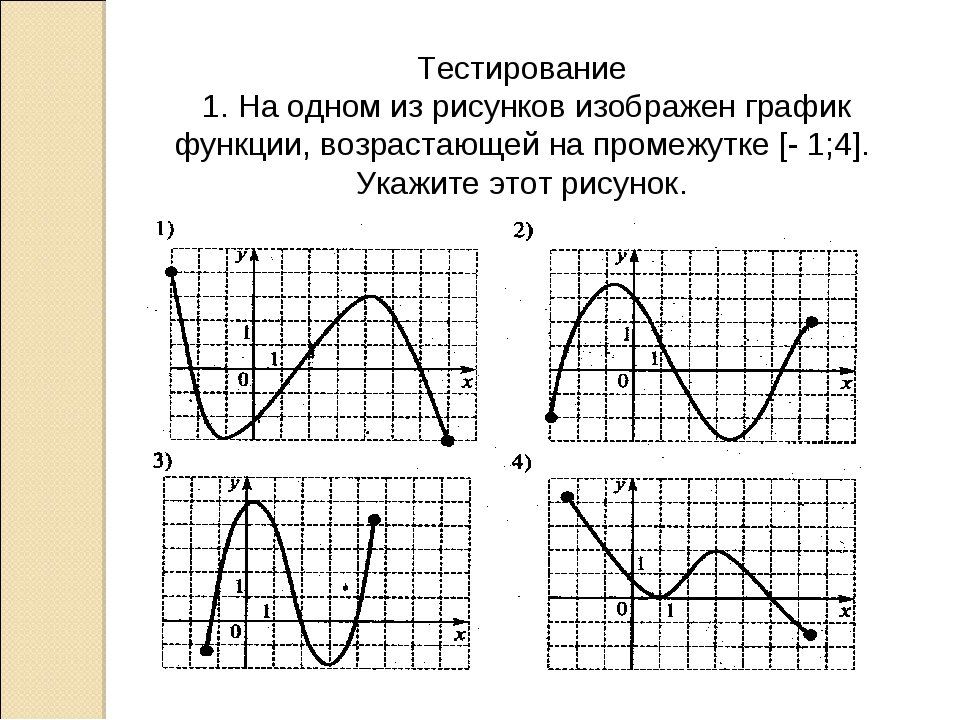 Находим область определения функции D( f.. Определяем точки разрыва функции.. Находим
Находим область определения функции D( f.. Определяем точки разрыва функции.. Находим
Пусть задано числовое множество D
Пусть задано числовое множество D R. Если каждому числу x D поставлено в соответствие единственное число y, то говорят, что на множестве D задана числовая функция: y = f (x), x D. Множество D, называется
ПодробнееГЛАВА II. Квадратный трехчлен
ГЛАВА II. Квадратный трехчлен Справочный материал Квадратным трехчленом называют выражение a + b + c, где abc,, и a 0. График квадратного трехчлена парабола. Прямая b = ее ось симметрии. Точка ( в; в)
ПодробнееИССЛЕДОВАНИЕ ФУНКЦИЙ
Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И.М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы ИССЛЕДОВАНИЕ ФУНКЦИЙ (для
ПодробнееТЕСТ Запишите координаты точек на координатной прямой, показанной на рисунке.
wwwaleeiivanovcom ДЗ Функции ТЕСТ 0 Запишите координаты точек на координатной прямой, показанной на рисунке ) G(-), C(-), K(-), A(4), J(0), M() ) G(-5), C(-6), K(-), A(9), J(0), M(5) ) G(-9), C(-5), K(-4),
ПодробнееЭлементы высшей математики
Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Дифференциальное исчисление Составитель:
Подробнее1. Понятие числовой последовательности
Понятие числовой последовательности В курсе математического анализа изучаются переменные величины и зависимость между ними Простейшими переменными величинами являются числовые последовательности Определение
ПодробнееМатематический анализ
Кафедра математики и информатики Математический анализ Учебно-методический комплекс для студентов ВПО, обучающихся с применением дистанционных технологий Модуль 4 Приложения производной Составитель: доцент
ПодробнееФУНКЦИЯ ПЕРЕМЕННАЯ ВЕЛИЧИНА
ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА понятия, которые можно описать, но нельзя строго определить, так как любая попытка дать строгое определение неизбежно сведётся к замене определяемого понятия ему
Подробнее«Чтение свойств функции по графику функции»
Конденко Любовь Николаевна
Учитель высшей квалификационной категории
Средней школы № 1 г. Елабуга
Елабуга
ТЕМА: «ЧТЕНИЕ СВОЙСТВ ФУНКЦИИ ПО ГРАФИКУ ФУНКЦИИ»
“График – это говорящая линия,
которая может о многом рассказать”
М.Б. Балк
Цели:
- Образовательные
Продолжить формирование у учащихся понятия, что функция- математическая модель, позволяющая описывать изучать разнообразные зависимости между реальными величинами. Обобщить и систематизировать систему функциональных понятий (функция, значение функции, график, аргумент, область определения и область значений функции, возрастание, убывание, монотонность, сохранение знака). Формирование свободного чтения графиков, формирование умений отражать свойства функций на графике.
Развитие всех познавательных процессов, в частности функционального стиля мышления. Развитие графической культуры.
- Воспитательные
Вырабатывать внимание, самостоятельность при работе на уроке. Воспитывать гордость за учёных, инженеров, конструкторов, создавших теорию графиков, применивших теорию к практической деятельности .Осуществлять профессиональную ориентацию учащихся.
1.Актуализация знаний
2. Формирование умений , навыков.
Функция – одно из основных математических общенаучных понятий, зависимость между переменными величинами. Математика рассматривает абстрактные переменные величины, изучает различные законы их взаимосвязи, не углубляясь в природу задачи. Например, в соотношении у = х2 геодезист или геометр увидит зависимость площади квадрата от его стороны, а физик, авиаконструктор или кораблестроитель может усмотреть в нем зависимость силы у сопротивления воздуха или воды от скорости х движения. Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение х в 2 раза приведет к увеличению у в 4 раза, и это заключение может применяться в любой конкретной ситуации. В школьном курсе изучается немало функций.
Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение х в 2 раза приведет к увеличению у в 4 раза, и это заключение может применяться в любой конкретной ситуации. В школьном курсе изучается немало функций.
Понятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их предметы взаимосвязаны. Они еще не умели считать , но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя не будет голодать; чем сильнее натянуть тетиву лука, тем дальше полетит стрела; чем дольше горит костер, тем теплее в пещере.
Оно сыграло и поныне играет большую роль в познании реального мира .Идея функциональной зависимости присутствует уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами.
Функция является одним из основных понятий математики, в частности математического анализа, так как математические модели реальных ситуаций, изучаемые на протяжении всего курса алгебра, напрямую связаны с функциями.
В технике и физике часто пользуются именно графическим способом задания функции. Более того , по- мере развития математики все активнее проникает графический метод в самые различные области жизни человека. В частности, использование функциональных зависимостей и построение графиков широко применяется в экономике.
Задание № 1.
Само слово «функция» (от латинского functio — совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673 году в письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати он его ввел с1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа». В восемнадцатом веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой.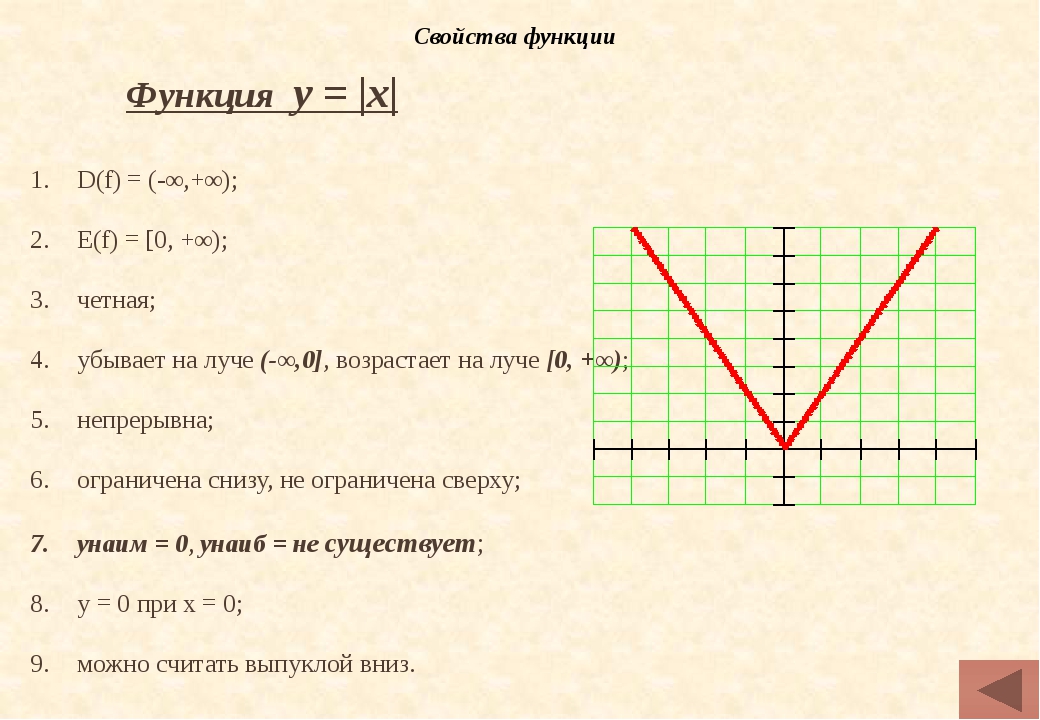 Это так называемая аналитическая точка зрения на понятие функции. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».
Это так называемая аналитическая точка зрения на понятие функции. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».
Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер (во «Введении в анализ бесконечного»): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего восемнадцатого века.
Как видно из представленных определений, само понятие функции фактически отождествлялось с аналитическим выражением. Новые шаги в развитии естествознания и математики вызвали и дальнейшее обобщение понятия функции.
Графиком функции — называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты- соответствующим значениям функции.
График функции у =f(x)) строиться по точкам; чем больше точек вида (х;f(Х)) мы возьмем, тем более точное представление о графике получим. Если этих точек взять достаточно много, то и представление о графике сложится более полное. Именно в этом случае интуиция и подсказывает нам, что график нужно изобразить в виде сплошной линии.
Находясь на выставке картин, мы рассматриваем произведения искусств и обращаем внимание на то, сумел ли художник предать глубину, завершенность образного содержания. Картина является итогом длительных наблюдений и размышлений художника над жизнью. График функции это своего рода «портрет» функции. Чтобы научиться видеть и создавать такие картины необходимо знать основные математические функции и их свойства.
Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством их решения.
По графику можно прочитать многие свойства функции, можно решать неравенства и уравнения.
Читая ,график функции мы можем делать выводы об :
-
Области определения
-
Области значений
-
Нулях функции
-
Знакопостоянстве
-
Монотонности
-
Четности
-
Периодичности
-
Экстремумах
-
Ограниченности
-
Непрерывности
Выполним задание:
Множество всех значений независимой переменной, которые она может принимать называют областью определения функции.
Если известен график функции, то область ее определения найти нетрудно. Для этого достаточно спроецировать график на ось абсцисс. То числовое множество, геометрическая модель которого получится на оси абсцисс в результате указанного проецирования, и будет представлять собой область определения функции.
Ответ: (-9;9]
Выполним задание:
Множество всех значений зависимой переменной называют областью значений функции.
Если известен график функции, то область значений найти сравнительно нетрудно. Для этого достаточно спроецировать график на ось ординат. То числовое множество, геометрическая модель которого получится на оси ординат в результате указанного проецирования, и будет представлять собой область значений функции.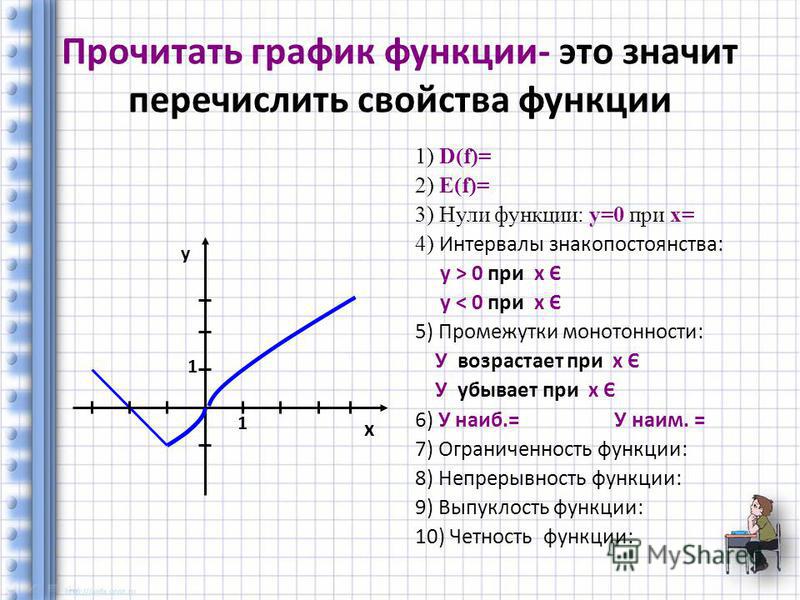
Ответ: [-4;6).
Выполним задание:
Функция у равное f(х) достигает на промежутке Х своего наибольшего значения, если существует такая точка х0 Î Х, что для всех х Î Х выполняется неравенство f(x) ≤ f(x0).
Из рисунка видим, что при х =-3, f(-3)=3 и это значение больше других значений функции.
Ответ: 3.
На практике удобнее пользоваться следующей формулировкой: функция возрастает, если большему значению аргумента соответствует большее значение функции. Или используя геометрическое истолкование понятий возрастания: двигаясь по графику возрастающей функции слева направо, мы как бы поднимаемся в гору.
Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Или используя геометрическое истолкование понятий убывания: двигаясь по графику убывающей функции слева направо, мы как бы спускаемся в горы.
Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.
Выполним задание:
Найти промежутки монотонности функции у=f (x), заданной графиком.
Для определения промежутков монотонности будем использовать геометрическое истолкование : двигаясь по графику убывающей функции слева направо, мы как бы спускаемся в горы ,а двигаясь по графику возрастающей функции слева направо, мы как бы поднимаемся в гору.
Функция возрастает на промежутках [-5;-2) и на (-2; 1]
Функция у=f(x ) убывает на промежутках (-9;- 5] и на [1; 9].
На слайде 13 представлено задание из единого государственного экзамена: На каком из следующих рисунков изображен график функции, возрастающей на промежутке [-1;2].
Функцию y=f(x) называют периодической с периодом Т, Т≠0, если для любого х из области определения функции выполняются равенства f(x-T) = f(x)= =f(x+T).
Число Т, удовлетворяющее указанному условию, называется периодом функции y= f (x).
Если функция у=f(x) имеет период Т, то для построения графика функции нужно сначала построить часть графика на любом промежутке длины Т, а затем сдвинуть эту часть по оси Ох вправо и влево на Т, 2Т, 3Т и так далее.
Обычно стараются, если это возможно, выделить наименьший положительный период, его и называют основным периодом.
Задание 1.
Функция у =f (x), имеющая период Т = 4 задана графиком на промежутке [-1; 3]. Найдите значение этой функции при х = 10.
Задание2.
Функция у=f(x) определена на всей числовой прямой и является периодической с периодом 4. На рисунке изображен график этой функции при -3≤х≤1. Найдите значение выражения f(-6)∙f(-3)∙f(13).
Выполнить эти задания можно двумя способами.
1 способ:
Используя определение периодической функции достраиваем график функции с учетом периода вдоль оси абсцисс. Затем по графику находим значение функции для указанных значений аргументов.
2 способ:
Используя равенство f(x-T)= f(x)= f(x+T).
Решение можно посмотреть в презентации на слайдах 15, 16.
Определение четной и нечетной функции.
Функция y= f(x) называется четной, если область ее определения симметрична относительно нуля и для любого значения х, из области определения верно равенство f(-х)=f(x).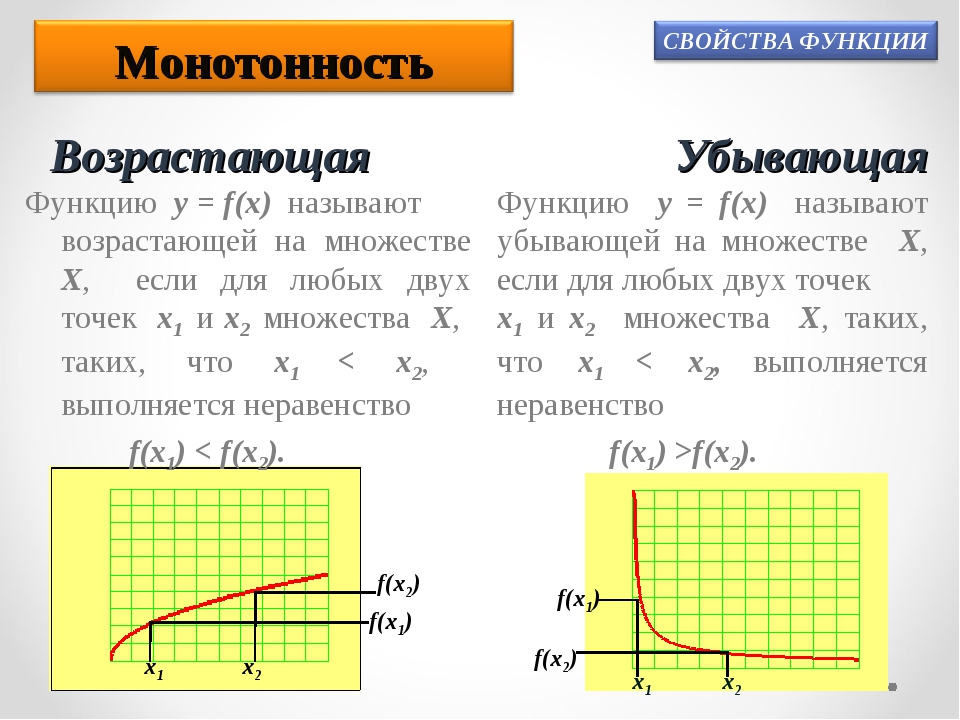 График четной функции симметричен относительно оси ординат.
График четной функции симметричен относительно оси ординат.
На слайде приведены примеры четных функций и примеры симметрии относительно прямой.
Функция y=f(x) называется нечетной, если ее область определения симметрична относительно нуля и для любого значения х из области определения верно равенство f(-х)=-f(x).
График нечетной функции симметричен относительно начала координат.
На слайде приведен пример симметрии относительно точки и на следующем слайде примеры графиков нечетных функций, изучаемых в школьном курсе алгебры. На графиках показана симметрия точек графика относительно начала координат. (Слайды 17-19).
На 20 слайде предложено задание:
Укажите график четной функции. (Решение можно посмотреть на слайде 20).
Определение промежутков знакопостоянства.
Решите неравенство f(x)≥0, если на рисунке изображен график функции у=f(x).
Решите неравенство f(x)≤0, если на рисунке изображен график функции у=f(x).
Другими словами нужно найти промежутки знакопостоянства функции у равное f(x).Функция принимает значение, равное нулю в тех точках, в которых график функции пересекает ось абсцисс. Функция принимает отрицательные значения на множестве тех значений аргумента, которым соответствуют части графика, расположенные ниже оси абсцисс, то есть f(x) меньше или равно нулю. Функция принимает положительные значения на множестве тех значений аргумента, которым соответствуют части графика, расположенные выше оси абсцисс, те есть f(x) больше или равно нуля.
f(x) ≥0 на промежутках хÎ (-9;-7,2]U(-1,8;5,8]
f(x)≤0 на промежутках хÎ [7,2;-1,8)U[5,8;9,2].
Раздел долгосрочного плана: 10. | Школа: НИШ ХБН г. Усть-Каменогорск | ||||||||||||||||||||||||
Дата: | Имя учителя: Тюлюбергенев РК | ||||||||||||||||||||||||
Класс: 10 | Количество присутствующих: | Количество отсутствующих: | |||||||||||||||||||||||
Тема урока | Свойства функции (1 урок) | ||||||||||||||||||||||||
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 10.4.1.4 уметь описывать по заданному графику функции её свойства: 1) область определения функции; 2) область значений функции; 3) нули функции; 4) периодичность функции; 5) промежутки монотонности функции; 6) промежутки знакопостоянства функции; | ||||||||||||||||||||||||
Цели урока | Учащиеся повторят и систематизируют материал по свойствам функции | ||||||||||||||||||||||||
Критерии оценивания | Учащийся: 1) По графику функции верно находит область определения функции; 2) По графику функции верно находит область значений функции; 3) По графику функции верно находит нули функции; 4) Верно указывает период функции; 5) Верно указывает промежутки монотонности функции; 6) Верно указывает промежутки знакопостоянства функции. | ||||||||||||||||||||||||
Языковые цели | Учащиеся будут Предметная лексика и терминология: — область определения/значения — периодичность — четность/нечетность | ||||||||||||||||||||||||
Привитие ценностей | Умение учиться, анализировать ситуацию, адаптироваться к новым ситуациям, ставить проблемы и принимать решения, отвечать за качество своей работы, умение организовывать свое время Привитие ценностей осуществляется посредством работ, запланированных на данном уроке. | ||||||||||||||||||||||||
Межпредметные связи | Графики широко используются в физике, химии и биологии для описания различных реальных процессов. | ||||||||||||||||||||||||
Навыки использования ИКТ | Использование интерактивной доски в качестве демонстрационного средства и средства записи. Программа Geogebra | ||||||||||||||||||||||||
Первоначальные знания | Учащиеся рассмотрели графики различных элементарных функций, изучили свойства функции | ||||||||||||||||||||||||
Ход урока | |||||||||||||||||||||||||
Этапы урока | Запланированная деятельность на уроке | Ресурсы | |||||||||||||||||||||||
Первый урок Начало (5 минут) | Постановка целей урока. (Стартер) Прежде чем сказать тему урока, посмотрите на слайд (слайд 1). И скажите, какой математический термин объединяет всё, что вы видите на этом слайде? | Презентация Слайды 1 –4 | |||||||||||||||||||||||
Середина урока (5 минут) (10 минут) (12 минут) (10 минут) | Закрепление раннее изученного материала. Фронтальная работа Совместно с учителем повторяют свойства функции. Область определения и область значения функции. Нули функции. Парная работа. Учащиеся самостоятельно выполняют задание с последующей взаимопроверкой в парах. №1. По данным рисункам определите: а) область определения функции; б) область значений функции; в) нули функции; г) промежутки знакопостоянства функции.
Монотонность функции. Групповая работа. Объедините учащихся в группы. Предложите карточки с графиками нескольких функций для закрепления понятия монотонности на промежутке. Попросите учащихся определить промежутки возрастания, убывания и постоянства функции. Является ли функция непрерывной? 1. Определите промежутки возрастания, убывания и постоянства функции. Является ли функция непрерывной? 2 3. Закончите утверждения, установив соответствия:
Ответ: 1-В, 2-С, 3-А Период функции. При объяснении материала рассмотреть различные виды периодических функций и их свойства. Например, функцию y = С, где С-const, периодом которой является любое число T ≠ 0 и функцию дробной части числа , где периодом будет T =1. Индивидуальная работа. Предложите выполнить следующее задание. 1. Функция, имеющая период Т = 4 задана графиком на промежутке (-3;1]. Найдите значение этой функции при х = 11. Проверку решения можно осуществить через взаимооценивания. Ученики обмениваются тетрадями. | Презентация Слайды 5 –9 https://videouroki.net/blog/matematika/ Приложение1 | |||||||||||||||||||||||
Конец урока 3 мин | Рефлексия Подведение итогов. Учащийся закрашивают человечка, который соответствует его положению в данной теме. По желанию некоторые могут прокоментировать. | Приложение 2 Слайд 15 | |||||||||||||||||||||||
Дополнительная информация | |||||||||||||||||||||||||
Дифференциация – как Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащихся? | Межпредметные связи | |||||||||||||||||||||||
Индивидуальная консультация со стороны учителя. Более сильные ученики возьмут на себя роль лидера | Формативное оценивание проводится через наблюдение работ учащихся и использование диалога. | Ценности: У них будет возможность для диалога, и с учителем и с сверстниками, развивая коммуникативные способности. Возможность сотрудничать при решении задач Весь урок проходит в активной деятельности учащихся | |||||||||||||||||||||||
Рефлексия Были ли реализованы цели урока/Ожидаемые результаты реалистичными? Чему сегодня научились учащиеся? Какова была атмосфера в классе? Сработала ли дифференциация? На все ли хватило времени? Какие изменения были внесены в план и почему? | Используйте данный раздел для рефлексии урока. Ответьте на вопросы о Вашем уроке из левой колонки. | ||||||||||||||||||||||||
Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об изучении)? 1: 2: Какие две вещи могли бы улучшить урок (подумайте как о преподавании, так и об изучении)? 1: 2: Что я узнал (а) за время урока о классе или отдельных учениках такого, что поможет мне подготовиться к следующему уроку? | |||||||||||||||||||||||||
Свойства функции распределения, график
Свойства функции распределения
Вначале напомним определение функции распределения вероятностей.
Определение 1
Функцией распределения называется функция $F(x)$ удовлетворяющая условию $F\left(x\right)=P(X
Введем свойства функции распределения:
1. Функция распределения является неубывающей функцией.
Доказательство: очевидно, что для любых событий $x_1 \[F\left(x_1\right)=P\left(Xч. т. д.
2. Существуют пределы ${\mathop{lim}_{x\to -\infty } F(x)\ }$ и ${\mathop{lim}_{x\to +\infty } F(x)\ }$, причем выполняются равенства:
Доказательство: Существование данных пределов следует из непрерывности и ограниченности функции $F(x)$. Докажем сначала, что:
Докажем сначала, что:
Рисунок 1.
Рассмотрим убывающую последовательность событий $A_n=(X
Лемма 1: Дана убывающая последовательность вложенных друг друга множеств ${\dots \subseteq A_n\subseteq A_{n-1}\subseteq \dots \subseteq A}_3\subseteq A_2\subseteq A_1$ удовлетворяющая условиям $A={\cap A}_n$ и $\mu \left(A_n\right)
Используя лемму 1, получим
Докажем теперь, что:
Рисунок 2.
Рассмотрим убывающую последовательность событий $B_n=(X\ge n)$, такую что$B_{n+1}=(X\ge (n+1))\subseteq B_n=(X\ge n)$ для всех $n\ge 1$. Очевидно, что пересечение всех событий $B_n$ $B={\cap B}_n=\emptyset $. Поэтому, по лемме 1, получим
ч. т. д.
3. $F(x)$ непрерывна слева любой точке, то есть:
Рисунок 3.
Доказательство. Существование предела следует из непрерывности и ограниченности функции $F(x)$. Рассмотрим следующую разность $F\left(x_0\right)-F\left(x_0-\frac{1}{n}\right)$. Очевидно, что
Следовательно, $F\left(x_0\right)-F\left(x_0-\frac{1}{n}\right)\to 0$. То есть:
Рисунок 4.
ч. т. д.
4. Для любых $x_0$ выполняется равенство: $F\left(x_0+0\right)-F\left(x_0\right)=P({X=x}_0)$.
Это свойство очевидно.
5. Для любых $X$ выполняется равенство: $P\left(a\le X
Доказательство. Очевидно, что $\left(X \[F\left(a\right)+P\left(a\le Xч. т. д.
Примечание 1
Если функция непрерывна во всех точках справа, то$P\left(a\le X\le b\right)=P\left(a
График функции распределения вероятностей
- Пусть случайная величина $X$ является дискретной. Тогда график функции распределения такой случайной величины всегда представляет собой ступенчатую функцию, скачки которой происходят в точках возможных значений случайной величины (рис. 1).
- Пусть случайная величина $X$ теперь является непрерывной.
 График функции распределения такой случайной величины всегда представляет собой неубывающую непрерывную функцию (рис. 2).
График функции распределения такой случайной величины всегда представляет собой неубывающую непрерывную функцию (рис. 2).
- Пусть случайная величина $X$ является смешанной. График функции распределения такой случайной величины всегда представляет собой неубывающую функцию, которая имеет минимальное значение в 0, максимальное значение в 1, но которая не на всей области определения является непрерывной функцией (имеет скачки в отдельных точках) (рис. 3).
Рисунок 7. Функция распределения смешанной случайной величины
Примеры задач с использованием понятия функции распределения
Пример 1
Приведен ряд распределений появления события $A$ в трех опытах
Рисунок 8.
Найти функцию распределения вероятностей и построить её график.
Решение.
При $x\le 1$, $F\left(x\right)=0$;
При $1
При $2
При $x>3$, $F\left(x\right)=0,2+0,1+0,3+0,4=1$;
Отсюда получаем следующую функцию распределения вероятностей:
Рисунок 9.
Пример 2
Случайная величина задана следующей функцией распределения:
Рисунок 10.
Найти вероятность, что величина $X$ будет принадлежать интервалу $\left(\frac{7}{6};;1,2\right)$.
Решение. Нам необходимо найти значение $P\left(\frac{7}{6} \[P\left(\frac{7}{6}\le XОтвет: 0,1.
Графики полиномиальных функций — Алгебра и тригонометрия
Цели обучения
В этом разделе вы:
- Распознавать характеристики графиков полиномиальных функций.
- Используйте факторизацию, чтобы найти нули полиномиальных функций.
- Определите нули и их кратности.
- Определите конечное поведение.
- Поймите взаимосвязь между градусом и поворотными точками.
- Граф полиномиальных функций.
- Используйте теорему о промежуточном значении.

Выручка в миллионах долларов вымышленной кабельной компании с 2006 по 2013 год показана на (Рисунок) .
| Год | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| Выручка | 52,4 | 52,8 | 51.2 | 49,5 | 48,6 | 48,6 | 48,7 | 47,1 |
Выручку можно смоделировать с помощью полиномиальной функции
, где представляет доход в миллионах долларов и представляет год, соответствующий 2006 году. В течение каких интервалов выручка компании увеличивается? Через какие промежутки времени выручка компании снижается? На эти вопросы, как и на многие другие, можно ответить, исследуя график полиномиальной функции.Мы уже исследовали локальное поведение квадратиков, частного случая многочленов. В этом разделе мы исследуем локальное поведение многочленов в целом.
Распознавание характеристик графов полиномиальных функций
Полиномиальные функции степени 2 или более имеют графики без острых углов; Напомним, что эти типы графиков называются гладкими кривыми. Полиномиальные функции также отображают графики без разрывов. Кривые без изломов называются непрерывными.(Рисунок) показывает график, представляющий полиномиальную функцию, и график, представляющий функцию, не являющуюся полиномом.
Рисунок 1.Распознавание полиномиальных функций
Какой из графиков на (Рисунок) представляет полиномиальную функцию?
Рисунок 2.
Все ли полиномиальные функции имеют в качестве своей области все действительные числа?
Да. Любое действительное число является допустимым вводом для полиномиальной функции.
Определение нулей и их кратностей
Графики ведут себя по-разному при разных интервалах x .Иногда график пересекает горизонтальную ось в точке пересечения. В других случаях график будет касаться горизонтальной оси и «отскочить» от нее.
Предположим, например, что мы построили график показанной функции.
Обратите внимание на (рисунок), что поведение функции на каждом из перехватов x отличается.
Рисунок 7. Идентификация поведения графика в точке пересечения с осью x путем изучения кратности нуля. Пересечение x
является решением уравнения График проходит непосредственно через точку пересечения x при Фактор является линейным (имеет степень 1), поэтому поведение вблизи точки пересечения похоже на поведение линии — он проходит прямо через перехват.Мы называем это одиночным нулем, потому что ноль соответствует единственному множителю функции.
Перехват x — это повторное решение уравнения График касается оси в точке пересечения и меняет направление. Коэффициент квадратичный (степень 2), поэтому поведение вблизи точки пересечения похоже на поведение квадратичного элемента — он отскакивает от горизонтальной оси в точке пересечения.
Фактор повторяется, то есть факт повторяется дважды. Количество раз, когда данный фактор появляется в факторизованной форме уравнения многочлена, называется кратностью.Нуль, связанный с этим фактором, имеет кратность 2, потому что фактор встречается дважды.
Перехват x — это повторное решение фактора График проходит через ось в точке пересечения, но сначала немного выравнивается. Этот коэффициент является кубическим (степень 3), поэтому поведение вблизи точки пересечения похоже на поведение кубической точки — с той же S-образной формой возле точки пересечения, что и функция инструментария. Мы называем это тройным нулем или нулем с кратностью 3.
Мы называем это тройным нулем или нулем с кратностью 3.
Для нулей с четной кратностью графики касаются или касаются оси x .Для нулей с нечетной кратностью графики пересекают или пересекают ось x . См. (Рисунок) примеры графиков полиномиальных функций с кратностью 1, 2 и 3.
Рисунок 8.Для более высоких четных степеней, таких как 4, 6 и 8, график по-прежнему будет касаться и отскакивать от горизонтальной оси, но при каждом увеличении четной мощности график будет казаться более плоским по мере приближения и выхода из x — ось.
Для более высоких нечетных степеней, таких как 5, 7 и 9, график по-прежнему будет пересекать горизонтальную ось, но для каждого увеличения нечетной степени график будет более плоским по мере приближения и покидания оси x .
Как записаться
Дан график полиномиальной функции степени идентифицируйте нули и их кратности.
- Если график пересекает ось x и выглядит почти линейным в точке пересечения, это единственный ноль.
- Если график касается оси x и отскакивает от оси, это ноль с четной кратностью.
- Если график пересекает ось x в нуле, это ноль с нечетной кратностью.
- Сумма кратностей равна .
Определение нулей и их кратностей
Используйте график функции степени 6 на (Рисунок), чтобы определить нули функции и их возможные кратности.
Рисунок 9. [show-answer q = ”fs-id1165135533053 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135533053 ″]
Полиномиальная функция имеет степень 6. Сумма кратностей должна быть 6.
Начиная слева, первый ноль встречается на графике, касающемся оси x , поэтому кратность нуля должна быть четной.Скорее всего, ноль имеет кратность
. Следующий ноль находится в точке График в этой точке выглядит почти линейным. Это единственный ноль кратности 1.
Это единственный ноль кратности 1.
Последний ноль находится на Графике пересекает ось x , поэтому кратность нуля должна быть нечетной. Мы знаем, что кратность, вероятно, равна 3, а сумма кратностей равна 6.
[/ hidden-answer]
Попробуйте
Используйте график функции степени 9 на (Рисунок), чтобы определить нули функции и их кратности.
Рисунок 10. [show-answer q = ”fs-id1165135255999 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135255999 ″]
На графике есть ноль –5 с кратностью 3, ноль -1 с кратностью 2 и ноль 3 с кратностью 4.
[/ hidden-answer]
Определение конечного поведения
Как мы уже узнали, поведение графика полиномиальной функции вида
в конечном итоге будет либо расти, либо падать по мере неограниченного увеличения
, и либо повышаться, либо падать по мере неограниченного уменьшения
.Это связано с тем, что для очень больших входных данных, скажем, 100 или 1000, главный член доминирует над размером выходных данных. То же самое верно и для очень маленьких входных данных, скажем, –100 или –1000.
Напомним, что мы называем это поведение конечным поведением функции. Как мы указывали при обсуждении квадратных уравнений, когда главный член полиномиальной функции является четной степенной функцией, неограниченно возрастающая или убывающая, неограниченно возрастающая. Когда главный член является нечетной степенной функцией, как неограниченно убывает, так и неограниченно убывает; как неограниченно возрастает, так и неограниченно увеличивается.Если ведущий член отрицательный, это изменит направление конечного поведения. (Рисунок) суммирует все четыре случая.
Рисунок 11.Понимание взаимосвязи между степенью и поворотными моментами
Напомним, что помимо конечного поведения мы можем анализировать локальное поведение полиномиальной функции. У него может быть поворотный момент, когда график изменяется от увеличения к уменьшению (рост к падению) или от падения к увеличению (падение к росту). Посмотрите на график полиномиальной функции в (рисунок).На графике есть три поворотные точки.
Посмотрите на график полиномиальной функции в (рисунок).На графике есть три поворотные точки.
Эта функция является полиномиальной функцией 4 th градусов и имеет 3 точки поворота. Максимальное количество точек поворота полиномиальной функции всегда на единицу меньше степени функции.
Устный перевод поворотных моментов
Точка поворота — это точка на графике, в которой график изменяется от увеличения к уменьшению (повышение к падению) или от убывания к увеличению (от падения к повышению).
Полином степени будет иметь не более точек поворота.
Нахождение максимального количества точек поворота с использованием степени полиномиальной функции
Найдите максимальное количество точек поворота для каждой полиномиальной функции.
[hidden-answer a = ”514289 ″]
Сначала перепишите полиномиальную функцию в порядке убывания:
Укажите степень полиномиальной функции. Эта полиномиальная функция имеет степень 5.
Максимальное количество точек поворота —
Сначала определите главный член полиномиальной функции, если функция была развернута.
Затем определите степень полиномиальной функции. Эта полиномиальная функция имеет степень 4.
Максимальное количество точек поворота —
[/ hidden-answer]
Графические полиномиальные функции
Мы можем использовать то, что мы узнали о множественности, конечном поведении и точках поворота, чтобы нарисовать графики полиномиальных функций.Давайте соберем все это вместе и рассмотрим шаги, необходимые для построения графика полиномиальных функций.
Как записаться
Для заданной полиномиальной функции нарисуйте график.
- Найдите перехватчики.
- Проверить симметрию.
 Если функция является четной функцией, ее график симметричен относительно оси, то есть
Если функция является четной функцией, ее график симметричен относительно оси, то есть
Если функция является нечетной функцией, ее график симметричен относительно начала координат, то есть - Используйте кратности нулей, чтобы определить поведение полинома в точках пересечения.
- Определите конечное поведение, исследуя начальный член.
- Используйте поведение конца и поведение на пересечениях, чтобы нарисовать график.
- Убедитесь, что количество точек поворота не превышает на единицу меньше степени полинома.
- При желании можно использовать технологию для проверки графика.
Построение графика полиномиальной функции
Нарисуйте график
[show-answer q = ”fs-id1165135237926 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135237926 ″]
На этом графике есть две точки пересечения x .Фактор возведен в квадрат, что указывает на кратность 2. График отскочит на этом пересечении x . Функция At имеет кратность, равную единице, что указывает на то, что график пересекает ось в этом месте пересечения.
Перехват y находится путем вычисления
Перехват y —
Кроме того, мы можем видеть, что главный член, если бы этот многочлен был умножен, был бы
, поэтому конечное поведение будет таким же, как у вертикально отраженной кубики, с выходными значениями, уменьшающимися по мере приближения входов к бесконечности, и выходами, увеличивающимися по мере приближения входов отрицательная бесконечность.См. (Рисунок).
Чтобы набросать это, мы считаем, что:
Рис. 14.Где-то после этой точки график должен повернуться вниз или начать убывание по направлению к горизонтальной оси, потому что график проходит через следующую точку пересечения в точке (см. Рисунок).
Рисунок 15. Как мы знаем, что график продолжает уменьшаться, и мы можем перестать рисовать график в четвертом квадранте.
Используя технологию, мы можем создать график для полиномиальной функции, показанный на (Рисунок), и убедиться, что полученный график выглядит так, как наш эскиз на (Рисунок).
Рисунок 16. Полный график полиномиальной функции[/ hidden-answer]
Попробуйте
Нарисуйте график
[show-answer q = ”fs-id1165135264689 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135264689 ″] [/ скрытый-ответ]
Использование теоремы о промежуточном значении
В некоторых ситуациях мы можем знать две точки на графике, но не нули. Если эти две точки находятся на противоположных сторонах оси x , мы можем подтвердить, что между ними есть ноль.Рассмотрим полиномиальную функцию, график которой гладкий и непрерывный. Теорема о промежуточном значении утверждает, что для двух чисел и в области, если и тогда функция принимает каждое значение между и (хотя теорема интуитивно понятна, доказательство на самом деле довольно сложно и требует высшей математики). Мы можем применить эту теорему к частному случаю, который полезен в построение графиков полиномиальных функций. Если точка на графике непрерывной функции находится выше оси, а другая точка находится ниже оси, должна существовать третья точка между тем местом, где график пересекает ось.Назовите этот пункт Это означает, что мы уверены, что есть решение, где
Другими словами, теорема о промежуточном значении говорит нам, что когда полиномиальная функция изменяется с отрицательного значения на положительное значение, функция должна пересекать ось. (Рисунок) показывает, что между
и
Попробуйте
Покажите, что функция имеет хотя бы один действительный ноль между
и.Написание формул для полиномиальных функций
Теперь, когда мы знаем, как находить нули полиномиальных функций, мы можем использовать их для написания формул на основе графиков. Поскольку полиномиальная функция, записанная в факторизованной форме, будет иметь перехват x , где каждый множитель равен нулю, мы можем сформировать функцию, которая будет проходить через набор перехватов x , введя соответствующий набор факторов.
Поскольку полиномиальная функция, записанная в факторизованной форме, будет иметь перехват x , где каждый множитель равен нулю, мы можем сформировать функцию, которая будет проходить через набор перехватов x , введя соответствующий набор факторов.
Как записаться
Дан график полиномиальной функции, напишите формулу для функции.
- Определите точки пересечения x графика, чтобы найти множители многочлена.
- Изучите поведение графика на пересечениях x , чтобы определить кратность каждого фактора.
- Найдите многочлен наименьшей степени, содержащий все множители, найденные на предыдущем шаге.
- Используйте любую другую точку на графике (интервал y может быть самым простым), чтобы определить коэффициент растяжения.
Написание формулы для полиномиальной функции из графика
Напишите формулу для полиномиальной функции, показанной на (Рисунок).
Рисунок 19.Попробуйте
Учитывая график, показанный на (Рисунок), напишите формулу для показанной функции.
Рисунок 20. [show-answer q = ”fs-id1165135559461 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135559461 ″]
[/ hidden-answer]
Использование локальных и глобальных экстремумов
С квадратиками мы смогли алгебраически найти максимальное или минимальное значение функции, найдя вершину. Для общих многочленов найти эти поворотные точки невозможно без более продвинутых методов исчисления. Даже в этом случае определение места возникновения экстремумов все еще может быть алгебраически сложной задачей.А пока мы оценим местоположения поворотных точек, используя технологию для построения графика.
Каждая поворотная точка представляет собой локальный минимум или максимум. Иногда точка поворота — это самая высокая или самая низкая точка на всем графике.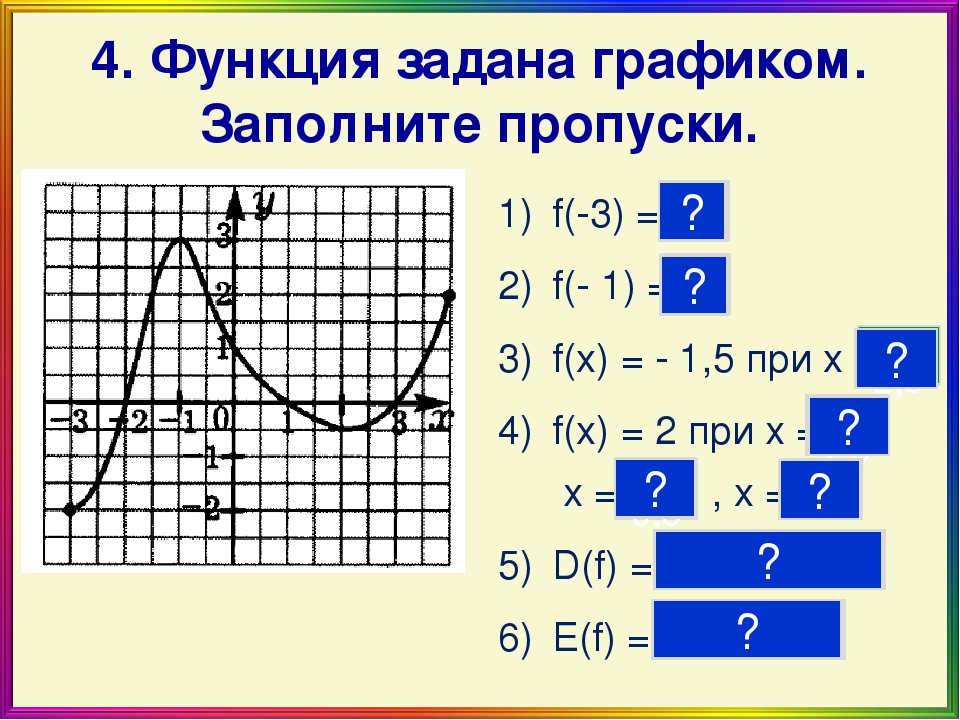 В этих случаях мы говорим, что поворотная точка — это глобальный максимум или глобальный минимум. Они также называются абсолютным максимальным и абсолютным минимальным значениями функции.
В этих случаях мы говорим, что поворотная точка — это глобальный максимум или глобальный минимум. Они также называются абсолютным максимальным и абсолютным минимальным значениями функции.
Все ли полиномиальные функции имеют глобальный минимум или максимум?
№Только полиномиальные функции четной степени имеют глобальный минимум или максимум. Например, не имеет ни глобального максимума, ни глобального минимума.
Использование локальных экстремумов для решения приложений
Ящик с открытым верхом должен быть изготовлен путем вырезания квадратов из каждого угла листа пластика размером 14 на 20 см и последующего складывания боковых сторон. Найдите размер квадратов, которые нужно вырезать, чтобы максимально увеличить объем, заключенный в коробке.
[show-answer q = ”fs-id1165135470058 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135470058 ″]
Мы начнем эту задачу, нарисовав картинку, подобную изображенной на (Рисунок), пометив ширину вырезанных квадратов переменной
. Рисунок 22.Обратите внимание, что после того, как квадрат вырезан с каждого конца, остается прямоугольник размером acm bycm для основания коробки, и коробка становится высотой. Это дает объем
Обратите внимание, поскольку множители равны [латекс] \, 20–2w \, [/ латекс], а три нуля — 10, 7 и 0 соответственно. Поскольку высота 0 см не является разумной, мы рассматриваем только нули 10 и 7. Самая короткая сторона равна 14, и мы отсекаем два квадрата, поэтому значения могут быть больше нуля или меньше 7. Это означает, что мы будем Ограничьте область действия этой функции до Используя технологию для создания эскиза графика в этой разумной области, мы получим график, подобный изображенному на (Рисунок).Мы можем использовать этот график для оценки максимального значения объема, ограниченного значениями, которые являются разумными для этой задачи — значениями от 0 до 7.
Рис. 23.
23. На этом графике мы сфокусируемся только на той части, которая находится в разумной области. Мы можем оценить максимальное значение примерно в 340 кубических см, что происходит, когда квадраты составляют примерно 2,75 см с каждой стороны. Чтобы улучшить эту оценку, мы могли бы использовать расширенные функции нашей технологии, если они доступны, или просто изменить наше окно, чтобы увеличить масштаб графика для получения результатов (рисунок).
Рис. 24.С этого увеличенного изображения мы можем уточнить нашу оценку максимального объема до примерно 339 кубических см, когда квадраты имеют размер примерно 2,7 см с каждой стороны.
[/ hidden-answer]
Попробуйте
Используйте технологию, чтобы найти максимальное и минимальное значения на интервале функции
[show-answer q = ”fs-id1165134559223 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134559223 ″]
Минимум происходит примерно в точке, а максимум — примерно в точке
.[/ hidden-answer]
Упражнения по разделам
Устный
Если полиномиальная функция степени имеет различные нули, что вы знаете о графике функции?
Объясните, как теорема о промежуточном значении может помочь нам найти нуль функции.
[show-answer q = ”fs-id1165135314696 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135314696 ″]
Если мы оценим функцию в точке и в точке и знак значения функции изменится, то мы узнаем, что ноль существует между и
.[/ hidden-answer]
Объясните, как факторизованная форма многочлена помогает нам в построении графика.
Если график полинома просто касается оси x , а затем меняет направление, какой мы можем сделать вывод о факторизованной форме полинома?
[show-answer q = ”fs-id1165135621855 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135621855 ″]
Будет множитель в равной степени.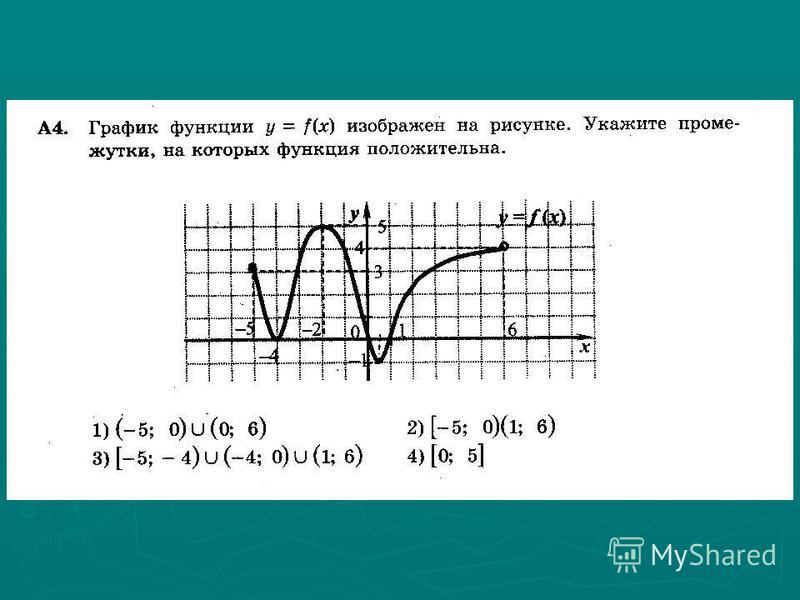
[/ hidden-answer]
Алгебраические
Для следующих упражнений найдите или t -перехваты полиномиальных функций.
[show-answer q = ”fs-id1165135347433 ″] Показать решение [/ show-answer][hidden-answer a = ”fs-id1165135347433 ″]
[/ hidden-answer] [show-answer q = ”fs-id1165132941732 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165132941732 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165134149980 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134149980 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165134331988 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134331988 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165134103103 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134103103 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165134478959 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134478959 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165134340053 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134340053 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165133104635 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133104635 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165135376471 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135376471 ″]
[/ hidden-answer]
В следующих упражнениях используйте теорему о промежуточном значении, чтобы убедиться, что данный многочлен имеет хотя бы один нуль в пределах данного интервала.
[show-answer q = ”fs-id1165135621876 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135621876 ″]
и
Подтверждение смены знака.
[/ hidden-answer]
[show-answer q = ”fs-id1165133073928 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133073928 ″]
и изменение знака подтверждает.
[/ hidden-answer]
[show-answer q = ”fs-id1165135524657 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135524657 ″]
и изменение знака подтверждает.
[/ hidden-answer]
В следующих упражнениях найдите нули и укажите кратность каждого.
[show-answer q = ”fs-id1165134534140 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134534140 ″]
0 с кратностью 2, с кратностью 5, 4 с кратностью 2
[/ hidden-answer]
[show-answer q = ”fs-id1165134357524 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134357524 ″]
0 с кратностью 2, –2 с кратностью 2
[/ hidden-answer]
[show-answer q = ”fs-id1165133277602 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133277602 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165135349287 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135349287 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165133035945 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133035945 ″]
с кратностью 2, 0 с кратностью 3
[/ hidden-answer]
[show-answer q = ”fs-id1165131857396 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165131857396 ″]
[/ hidden-answer]
Графический
Для следующих упражнений постройте график полиномиальных функций.Обратите внимание на перехват, множественность и конечное поведение.
Для следующих упражнений используйте графики, чтобы написать формулу полиномиальной функции наименьшей степени.
[скрытый-ответ a = ”fs-id1165134087659 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1165133104571 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133104571 ″]
[/ hidden-answer]
В следующих упражнениях используйте график для определения нулей и кратности.
[show-answer q = ”fs-id1165134156011 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134156011 ″]
–4, –2, 1, 3 с кратностью 1
[/ hidden-answer]
[show-answer q = ”fs-id1165134347476 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134347476 ″]
–2, по 3 с кратностью 2
[/ hidden-answer]
В следующих упражнениях используйте данную информацию о полиномиальном графе, чтобы написать уравнение.
Степень 3. Нули при и — перехват на
Степень 4. Корень кратности 2 at и корень кратности 1 at и y -пересечение на
Степень 5. Двойной ноль в точке и тройной ноль в точке проходит через точку
. [show-answer q = ”fs-id1165134277296 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134277296 ″]
[/ hidden-answer]
Степень 3. Нули в [latex] \, x = 3, [/ latex] и
Степень 5.Корень кратности 2 в точках
и
и корень кратности 1 в точках
y — перехват в
Двойной ноль в точке
и тройной ноль в точке
Проходит через точку
Технологии
Для следующих упражнений используйте калькулятор для аппроксимации локальных минимумов и максимумов или глобальных минимумов и максимумов.
[show-answer q = ”fs-id1165133348575 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165133348575 ″]
местный макс.
местный мин.
[/ hidden-answer]
[show-answer q = ”fs-id1165135314791 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165135314791 ″]
глобальный минимум
[/ hidden-answer]
[show-answer q = ”fs-id1165134402645 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1165134402645 ″]
глобальный минимум
[/ hidden-answer]
Расширения
Для следующих упражнений используйте графики, чтобы написать полиномиальную функцию наименьшей степени.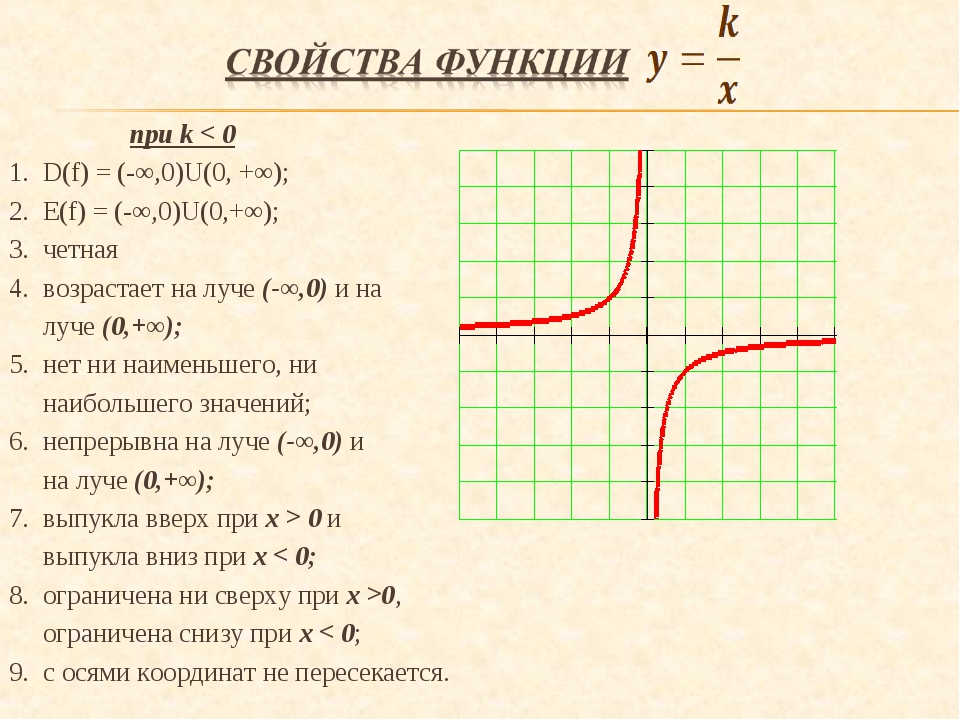
[скрытый-ответ a = ”fs-id1165134402716 ″]
[/ hidden-answer]
Функция «один к одному» — объяснение и примеры
Вы знаете, что изучаете функции, когда слышите «один к одному» чаще, чем когда-либо. Хотите узнать, что отличает от индивидуальных функций ? Эта статья поможет вам узнать об их свойствах и оценить эти функции. Давайте начнем с этого краткого определения индивидуальных функций:
Индивидуальные функции — это функции, которые возвращают уникальный диапазон для каждого элемента в своем домене.
Поскольку индивидуальные функции — это особые типы функций, лучше всего проверить наши знания о функциях, их предметной области и их диапазоне.
Эта статья поможет нам понять свойства взаимно однозначных функций . Мы также узнаем, как определять индивидуальные функции на основе их выражений и графиков.
Давайте продолжим и начнем с определения и свойств взаимно однозначных функций.
Что такое индивидуальная функция?
Чтобы легко вспомнить, что такое взаимно однозначные функции, попробуйте вспомнить следующее утверждение: «для каждого y существует уникальный x.Следующие два раздела покажут вам, почему эта фраза помогает нам запомнить основную концепцию, лежащую в основе индивидуальных функций.
Индивидуальное определение функции
Функция f (x), является функцией один к одному, когда один уникальный элемент из ее домена будет возвращать каждый элемент своего диапазона. Это означает, что для каждого значения x будет уникальное значение y или f (x).
Почему бы нам не визуализировать это, отображая две пары значений для сравнения функций, которые не находятся во взаимно однозначном соответствии?
Давайте сначала посмотрим на g (x), g (4) и g (-4) имеют общее значение y, равное 16. Это также верно для g (-2) и g (2). Вы правильно угадали; g (x) — функция, не имеющая взаимно однозначного соответствия.
Это также верно для g (-2) и g (2). Вы правильно угадали; g (x) — функция, не имеющая взаимно однозначного соответствия.
Теперь обратите внимание на f (x). Обратите внимание, как для каждого значения f (x) существует только одно уникальное значение x? Когда вы наблюдаете функции, имеющие это соответствие, мы вызываем эти функции один к одному.
График функции один к одному
Чтобы лучше понять концепцию функции один к одному, давайте изучим график функции один к одному. Помните, что для функций «один к одному» каждый x должен иметь уникальное значение y.
Так как каждый x будет иметь уникальное значение для y, функции один к одному никогда не будут иметь упорядоченных пар с одной и той же координатой y.
Теперь, когда мы изучили определение взаимно однозначных функций, понимаете ли вы, почему выражение «для каждого y есть уникальный x» полезно запомнить?
Индивидуальные свойства функций
Какие еще важные свойства однозначных функций мы должны помнить? Вот некоторые свойства, которые могут помочь вам понять различные типы функций с взаимно однозначным соответствием:
- Если две функции, f (x) и g (x), равны один к одному, то f ◦ g взаимно однозначно. функции.
- Если функция является взаимно однозначной, ее график будет либо всегда увеличиваться, либо всегда уменьшаться.
- Если g ◦ f взаимно однозначная функция, то f (x) также гарантированно будет взаимно однозначной функцией.
Попробуйте самостоятельно изучить две пары графиков и посмотреть, сможете ли вы подтвердить эти свойства. Конечно, прежде чем мы сможем применить эти свойства, нам будет важно узнать, как мы можем подтвердить, является ли данная функция взаимно однозначной функцией или нет.
Как определить, взаимно однозначна функция?
Следующие два раздела покажут вам, как мы можем протестировать однозначное соответствие функций.Иногда нам дают выражение или график функции, поэтому мы должны научиться определять однозначные функции алгебраически и геометрически. Давайте начнем с последнего!
Давайте начнем с последнего!
Тестирование функций один к одному геометрически
Помните, что функции должны быть взаимно однозначными. Каждая координата x должна иметь уникальную координату y? Мы можем проверить взаимно однозначные функции, используя тест горизонтальной линии .
- Когда задана функция, рисует горизонтальные линии вместе с системой координат.
- Проверьте, могут ли горизонтальные линии проходить через две точки.
- Если горизонтальные линии проходят только через одну точку на всем графике, функция является взаимно однозначной функцией .
Что делать, если он проходит две или более точки функции? Тогда, как вы уже догадались, они не считаются однозначными функциями.
Чтобы лучше понять процесс, давайте продолжим и изучим эти два графика, показанные ниже.
Известно, что обратная функция f (x) = 1 / x является взаимно однозначной функцией.Мы также можем проверить это, проведя горизонтальные линии на его графике.
Посмотрите, как каждая горизонтальная линия каждый раз проходит через уникальную упорядоченную пару? Когда это происходит, мы можем подтвердить, что данная функция является функцией один к одному.
Что происходит, если функция не является взаимно однозначной? Например, квадратичная функция f (x) = x 2 не является взаимно однозначной функцией. Давайте посмотрим на его график, показанный ниже, чтобы увидеть, как тест горизонтальной линии применяется к таким функциям.
Как видите, каждая горизонтальная линия, проведенная через график f (x) = x 2 , проходит через две упорядоченные пары. Это еще раз подтверждает, что квадратичная функция не является взаимно однозначной функцией.
Алгебраическое тестирование индивидуальных функций
Давайте освежим нашу память о том, как мы определяем индивидуальные функции. Напомним, что функции являются взаимно однозначными, если:
- f (x 1 ) = f (x 2 ) тогда и только тогда, когда x 1 = x 2
- f (x 1 ) ≠ f (x 2 ) тогда и только тогда, когда x 1 ≠ x 2
Мы будем использовать это алгебраическое определение, чтобы проверить, является ли функция взаимно однозначной. Как же тогда это сделать?
Как же тогда это сделать?
- Используйте заданную функцию и найдите выражение для f (x 1 ).
- Примените тот же процесс и найдите выражение для f (x 2 ).
- Приравняйте оба выражения и покажите, что x 1 = x 2 .
Почему бы нам не попробовать доказать, что f (x) = 1 / x является взаимно однозначной функцией, используя этот метод?
Давайте сначала подставим x 1 и x 2 в выражение. У нас будет f (x 1 ) = 1 / x 1 и f (x 2 ) = 1 / x 2 .Чтобы подтвердить взаимно однозначное соответствие функции, приравняем f (x 1 ) и f (x 2 ).
1 / x 1 = 1 / x 2
Перемножьте обе части уравнения, чтобы упростить уравнение.
x 2 = x 1
x 1 = x 2
Мы только что показали, что x 1 = x 2 , когда f (x 1 ) = f ( x 2 ), следовательно, обратная функция является взаимно однозначной.
Пример 1
Заполните пропуски иногда , всегда или никогда , чтобы следующие утверждения были верными.
- Отношения могут _______________ быть взаимно однозначными.
- Индивидуальные функции — это ______________ функции.
- Когда горизонтальная линия проходит через функцию, которая не является взаимно однозначной, она ____________ будет проходить через две упорядоченные пары.
Решение
Отвечая на подобные вопросы, всегда возвращайтесь к определениям и свойствам, которые мы только что изучили.
- Иногда отношения могут быть функциями и, следовательно, иногда может представлять функцию один к одному.
- Поскольку функции «один к одному» представляют собой особый тип функций, всегда будут , прежде всего, функциями.

- В нашем примере горизонтальные линии могут проходить через график f (x) = x 2 дважды, но горизонтальные линии могут проходить через большее количество точек. Следовательно, иногда проходит через две упорядоченные пары.
Пример 2
Пусть A = {2, 4, 8, 10} и B = {w, x, y, z}. Какой из следующих наборов упорядоченных пар представляет собой функцию один к одному?
- {(2, w), (2, x), (2, y), (2, z)}
- {(4, w), (2, x), (10, z), ( 8, y)}
- {(4, w), (2, x), (8, x), (10, y)}
Решение
Чтобы функция была взаимно однозначной функцией , каждый элемент из A должен объединяться с уникальным элементом из B.
- Первый вариант имеет одно и то же значение x для каждого значения y, поэтому это не функция и, следовательно, не взаимно однозначная функция. .
- Третий вариант имеет разные значения x для каждой упорядоченной пары, но 2 и 8 имеют один и тот же диапазон x. Следовательно, он не представляет собой функцию «один к одному».
- Второй вариант использует уникальный элемент из A для каждого уникального элемента из B, представляя функцию «один к одному».
Это означает, что {(4, w), (2, x), (10, z), (8, y)} представляют собой взаимно однозначную функцию .
Пример 3
Какой из следующих наборов значений представляет функцию один к одному?
Решение
Всегда возвращайтесь к утверждению «для каждого y есть уникальный x.»Для каждого набора давайте проверим, сочетается ли каждый элемент справа с уникальным значением слева.
- Для первого набора f (x) мы можем видеть, что каждый элемент с правой стороны объединен в пару с уникальным элементом слева. Следовательно, , f (x) является взаимно однозначной функцией .
- Набор g (x) показывает разное количество элементов с каждой стороны.
 Уже одно это скажет нам, что функция не является взаимно однозначной.
Уже одно это скажет нам, что функция не является взаимно однозначной. - Некоторые значения с левой стороны соответствуют одному и тому же элементу справа, поэтому m (x) также не является взаимно однозначной функцией.
- Каждый из элементов в первом наборе соответствует уникальному элементу в следующем, поэтому n (x) представляет собой взаимно однозначную функцию.
Пример 4
График f (x) = | x | + 1 и определить, является ли функция f (x) взаимно однозначной.
Решение
Создайте таблицу значений для f (x) и нанесите на график сгенерированные упорядоченные пары. Соединил эти точки с графиком f (x).
Уже сама таблица может дать вам ключ к разгадке того, является ли f (x) взаимно однозначной функцией [подсказка : f (1) = 2 и f (-1) = 2 ].Но давайте продолжим и построим эти точки на плоскости xy и на графике f (x).
После того, как мы построили график f (x) = | x | +1, проведите горизонтальные линии поперек графика и посмотрите, проходит ли он через одну или несколько точек.
На графике мы видим, что построенные нами горизонтальные линии проходят через две точки каждая, поэтому функция не является взаимно однозначной функцией .
Пример 5
Определите, является ли f (x) = -2x 3 -1 функцией один к одному, используя алгебраический подход.
Решение
Напомним, что для того, чтобы функция была взаимно однозначной, f (x 1 ) = f (x 2 ) тогда и только тогда, когда x 1 = x 2 . Чтобы проверить, является ли функция f (x) взаимно однозначной, давайте сначала найдем соответствующие выражения для x 1 и x 2 .
f (x 1 ) = -2 x 1 3 — 1
f (x 2 ) = -2 x 2 3 — 1
Приравняйте оба выражения и посмотрите, если он уменьшается до x 1 = x 2 .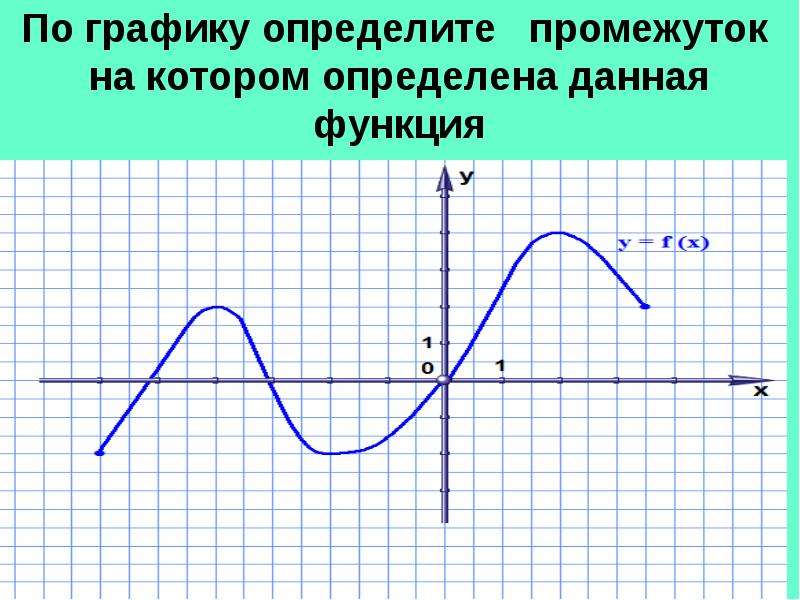
-2 x 1 3 — 1 = -2 x 2 3 — 1
-2 x 1 3 = -2 x 2 3
(x 1 ) 3 = (x 2 ) 3
Извлечение кубического корня из обеих частей уравнения приведет нас к x 1 = x 2 . Следовательно, f (x) = -2x 3 — 1 взаимно однозначная функция.
Пример 6
Покажите, что f (x) = -5x 2 + 1 не является взаимно однозначной функцией.
Решение
Еще одно важное свойство взаимно однозначных функций состоит в том, что при x 1 ≠ x 2 , f (x 1 ) не должно быть равно f (x 2 ).
Быстрый способ доказать, что f (x) не является взаимно однозначной функцией, — это подумать о контрпримере, показывающем два значения x, где они возвращают одно и то же значение для f (x).
Давайте посмотрим, что произойдет, если x 1 = -4 и x 2 = 4.
f (x 1 ) = -5 (-4) 2 + 1 = -80 + 1 = -79 | f (x 2 ) = -5 (4) 2 + 1 = -80 + 1 = -79 |
ср. можно видеть, что даже когда x 1 не равно x 2 , он все равно возвращает то же значение для f (x).Это показывает, что функция f (x) = -5x 2 + 1 не является взаимно однозначной функцией.
Пример 7
Учитывая, что a и b не равны 0, показывают, что все линейные функции являются взаимно однозначными функциями.
Решение
Помните, что общий вид линейных функций может быть выражен как ax + b, где a и b ненулевые константы.
Мы применяем тот же процесс, подставляя x 1 и x 2 в общее выражение для линейных функций.
f (x 1 ) = ax 1 + b
f (x 2 ) = ax 2 + b
Приравняйте оба уравнения и посмотрите, можно ли их уменьшить до x 1 = х 2 . Поскольку b представляет собой константу, мы можем вычесть b из обеих частей уравнения.
ax 1 + b = ax 2 + b
ax 1 = ax 2
Разделим обе части уравнения на a, и мы получим x 1 = x 2 .Из этого можно сделать вывод, что все линейные функции взаимно однозначны.
Практические вопросы- Заполните пропуски иногда , всегда или никогда сделайте следующие утверждения верными.
- Косинусные функции могут _______________ быть взаимно однозначными функциями.
- Если функция f (x) взаимно однозначна, ее домен ______________ будет иметь то же количество элементов, что и диапазон.
- Когда горизонтальная линия проходит через функцию, которая является функцией один к одному, она ____________ будет проходить через две упорядоченные пары.
- Пусть M = {3, 6, 9, 12} и N = {a, b, c, d}. Какой из следующих наборов упорядоченных пар представляет собой функцию один к одному?
- {(6, a), (6, b), (6, c), (6, d)}
- {(9, d), (12, b), (6, b), (3, c)}
- {(6, d), (9, c), (12, b), (3, a)}
- Какой из следующих наборов значений представляет собой взаимно однозначную функцию ?
- Изобразите следующие функции и определите, являются ли они взаимно однозначными или нет.
- f (x) = x 2 — 4
- g (x) = -4x + 1
- h (x) = e x
- Убедитесь, что следующие функции взаимно однозначны используя алгебраический подход.
- f (x) = 2x — 1
- g (x) = 1 / x 2
- h (x) = | x | + 4
- Покажите, что g (x) = | x | — 4 не является однозначной функцией.

- Покажите, что все квадратичные выражения не являются взаимно однозначными функциями.
Изображения / математические рисунки создаются с помощью GeoGebra.
Определение наилучшего метода построения графика функции
Лучший метод построения графиков
Знакомство с различными типами функций и их свойствами значительно упрощает определение наилучшего метода построения графиков.Есть много разных типов функций. Каждая из этих функций имеет разные свойства. Поскольку для объяснения каждого из этих типов функций и их свойств потребуется целый урок, мы просто рассмотрим несколько избранных примеров. Рекомендуется ознакомиться со многими различными типами функций и их графиками.
Вот несколько общих рекомендаций, которые можно использовать для определения наилучшего метода построения графика функции.
- Если вы хорошо знакомы с формой графика данной функции (например, линии), и функция довольно проста, то метод 1, вероятно, самый простой.
- Если вы знакомы со свойствами и характеристиками заданной функции и как они соотносятся с графиком функции, то метод 2 прост в использовании.
- Если функция достаточно сложная или представляет собой смесь функций разных типов, и вы не совсем уверены, какой будет форма функции, то графический калькулятор, вероятно, будет вашим лучшим выбором.
Примеры
Наш пример с бактериями был примером, в котором Метод 1 был лучшим методом для использования.Давайте рассмотрим метод 2, взглянув на квадратичную функцию и то, как построить график, используя ее свойства. Квадратичная функция — это полиномиальная функция со старшим показателем, равным 2, и она имеет следующий общий вид:
Квадратичные функции обладают многими свойствами. Вот некоторые из тех, которые мы можем использовать для построения графиков:
Вот некоторые из тех, которые мы можем использовать для построения графиков:
- Общая форма их графиков — U или перевернутая U.
- Их графики имеют точку максимума или минимума, называемую вершиной, в точке (- b / (2 a ), f (- b / (2 a ))).
- Их графики симметричны относительно линии x = — b / (2 a ), называемой осью симметрии.
- Для квадратичной функции вида f ( x ) = ax 2 + bx + c , точка пересечения y (или точка, где график пересекает ось y ) и где x = 0) всегда (0, c ).
Хорошо, давайте воспользуемся этими свойствами! Рассмотрим следующую квадратичную функцию:
Из наших свойств мы знаем общую форму ее графика и следующие факты:
- Его вершина находится в точке (- 4 / (2⋅1), g (- 4 / (2⋅1)) или (- 2, 0).
- График симметричен относительно прямой x = — 4 / (2⋅1), или x = — 2.
- График пересекает ось y в точке (0, 4).
Собрав все это вместе, мы можем легко построить график функции.
Мы видим, что, когда мы знакомы со свойствами данной функции, метод 2 часто оказывается лучшим путем для построения графика функции.
Еще один пример! Рассмотрим следующую функцию:
Хммм… у нее есть рациональное выражение и выражение в квадрате.Он представляет собой смесь различных типов функций, поэтому довольно сложно узнать его общую форму или какие-либо конкретные свойства, которым он может следовать. В таких случаях лучшим выбором будет графический калькулятор или Метод 3.
Резюме урока
Методы построения графиков — это методы построения графиков функции. Есть много способов сделать это, но три из наиболее распространенных:
- Постройте несколько случайных точек, удовлетворяющих функции, и соедините их соответствующей кривой.

- Используйте различные свойства и характеристики заданной функции для построения графика функции.
- Воспользуйтесь графическим калькулятором.
Определение лучшего метода может быть непростым делом, но в основном это сводится к определению того, что вы знаете о данной функции. Если вы знаете, что это линейная функция, то, вероятно, лучше всего подходит метод 1. Если вы знаете свойства данной функции и ее общую форму, то, вероятно, лучше всего подойдет метод 2. Наконец, если это сложная функция, то, вероятно, лучше всего подойдет метод 3.
Основная идея заключается в том, что чем больше вы знакомы с различными типами функций, их характеристиками и общими формами их графиков, тем легче будет построить график этих функций. Поэтому рекомендуется ознакомиться со многими различными типами функций, чтобы узнать лучший метод построения графиков каждого типа.
OpenAlgebra.com: обратные функции
Начнем с определения: Обратные функции — Функции f (x) и g (x) являются обратными, если обе
для всех x в домене g и f соответственно.Другими словами, если вы составите обратные функции, результат будет x .
Убедитесь, что указанные функции являются обратными .
Определить, являются ли данные функции инверсными .
Найдите время, чтобы просмотреть функции один-к-одному (1-1), потому что оказывается, что если функция 1-1, то у нее есть обратная функция. Следовательно, мы можем рассматривать тест горизонтальной линии как тест, который определяет, имеет ли функция инверсию или нет.
Далее мы очерчиваем процедуру для фактического нахождения обратных функций .
Шаг 1 : Замените f (x) на y .
Шаг 2 : поменять местами x и y .
Шаг 3 : Решите полученное уравнение относительно y .
Шаг 4 : Замените y обозначением, обратным f .
Шаг 5 : (Необязательно) Убедитесь, что функции инвертированы.
Найдите функцию, обратную заданной .
Теперь, когда вы знаете определение обратной функции и как ее найти, мы теперь обратим наше внимание на их графики.Для любой однозначной функции f , где
и мы имеем следующее свойство.
Симметрия обратных функций — Если ( a , b ) — точка на графике функции f , то ( b , a ) — точка на графике ее обратной функции. Кроме того, два графика будут симметричными относительно линии y = x .
На следующем графике видно, что функции
Обратите внимание, что (2, 3) — точка на f , а (3, 2) — точка на обратном. Другими словами, чтобы построить график обратного, все, что вам нужно сделать, это переключить координаты каждой упорядоченной пары. Мы использовали этот факт для поиска обратных значений, и он будет очень важен в следующей главе, когда мы разработаем определение логарифма.
Дан график функции 1-1, нарисуйте ее обратную и линию симметрии .
Видео на YouTube:
BioMath: функции
В этом разделе будут представлены несколько терминов для квалификации
функции.Понимание этих свойств пригодится, когда вы рисуете графики функций или смотрите, что происходит, когда заданное количество максимизируется или минимизируется.
Функции увеличения и уменьшения
Представьте, что вы наблюдаете, как определенное свойство биологической системы изменяется с течением времени. Математически вы будете смотреть, увеличивается или уменьшается функция, моделирующая свойство.
Чтобы определить, увеличивается или уменьшается функция, мы должны «прочитать» график функции слева направо.Вы можете думать об увеличении функция, при которой поднимается, слева направо, и функция убывания, когда падает на слева направо.
Большинство функций не увеличиваются / уменьшаются для всех x в домене, а наоборот, они увеличиваются одни интервалы и уменьшение на других. Мы говорим, что f увеличивается на некотором интервале, I , если для x 1 и x 2 в I ,
С другой стороны, мы говорим, что f уменьшается на I , если для x 1 и x 2 в I ,
Чтобы определить, увеличивается или уменьшается график функции за указанный интервале, читаем график слева направо и определяем, есть ли у него восходящий или нисходящий тренд, как показано ниже,
Если вы представите мяч, катящийся по графику, он будет катиться вниз по склону. части графика, которые уменьшаются, и он будет катиться вверх на частях графика график, который увеличивается.
Нечетные и четные функции
Некоторые функции обладают особым свойством быть четными или нечетными. Нечетные и четные функции обладают особой графической симметрией.
Определение Функция f ( x ) называется odd if, для всех x в домене f . |
Как узнать, что функция нечетная? Пример нечетной функции: f ( x ) = x . Мы можем продемонстрировать, что f ( x ) = x является нечетным, показывая, что f (- x ) = — f (x) путем замены — x на x as,
f (- x ) = — x = — f ( x ).
Если функция не является нечетной, она может быть (но не обязательно) четной.
Определение Функция f ( x ) называется , даже если , если, f (- x ) = f ( x ), для всех x в домене f . |
Пример четной функции: f ( x ) = x 2 .Мы может продемонстрировать, что f ( x ) = x 2 даже если показать, что f (- x ) = f ( x ) as,
f (- x ) = (- x 2 ) = (−1) 2 x 2 = x 2 = f ( x ) .
Как указано выше, графики нечетных и четных функций имеют особую симметрию.
График нечетной функции симметричен относительно начала координат. График симметричен относительно начала координат, если точка (- x , — y ) лежит на графике всякий раз, когда ( x , y ) находится. С другой стороны, график четной функции симметричен относительно
ось y . График симметричен относительно оси y , если точка ( -x , y ) лежит на
график всегда ( x , y ).
Не все функции классифицируются как четные или нечетные; функция, которая не является четной или нечетное называется ни .
Пример функции, которая не является ни четной, ни нечетной: f ( x ) = x + 1. Мы можем продемонстрировать это, найдя f (- x ) как,
f (- x ) = — x + 1.
Обратите внимание, что f (- x ) не равно — f ( x ), потому что
— f ( x ) = — ( x + 1) = — x −1;
и f (- x ) не равно f ( x ), потому что
f ( x ) = x + 1.
Полезен тот факт, что четные и нечетные функции обладают определенной графической симметрией. знать.В частности, если вы знаете, что какая-то функция f ( x ) является нечетной (четной) и знаете значение f ( a ), тогда вы также знаете, что значение f (- a ) равно — f ( a ) (f (a)). Точно так же, если вы знаете, что какая-то функция f ( x ) является четной, и знаете значение f ( a ), тогда вы также знаете, что значение f (- a ) — f ( a ).Это становится важным при изучении интегрального исчисления, поскольку интеграл нечетной или четной функции на симметричном интервале можно значительно упростить.
Максимумы и минимумы функций
Функция может достигать значений, которые можно классифицировать как максимумы и / или минимумы. В совокупности максимумы и минимумы называются экстремумами.
Графически вы можете думать о максимумах и минимумах как о функциональных значениях
пики и впадины. Экстремумы можно разделить на глобальные и локальные. Как следует из названий,
глобальный максимум — это максимальное значение функции
достигает, в то время как глобальный минимум — это минимальное значение, достигаемое функцией. Если функция
ограничен и имеет область, состоящую из всей действительной прямой, глобальный максимум равен
самый высокий пик и глобальный минимум — самая низкая долина.
Экстремумы можно разделить на глобальные и локальные. Как следует из названий,
глобальный максимум — это максимальное значение функции
достигает, в то время как глобальный минимум — это минимальное значение, достигаемое функцией. Если функция
ограничен и имеет область, состоящую из всей действительной прямой, глобальный максимум равен
самый высокий пик и глобальный минимум — самая низкая долина.
Максимум и минимум функции должны быть конечным числом.Следовательно, если функция увеличивается без связанная, эта функция не имеет глобального максимума. Точно так же, если функция неограниченно убывает, глобального минимума не существует. Однако эти неограниченные функции могут иметь локальные максимумы и минимумы, как показано на рисунке ниже,
Экстремумы, изображенные на приведенном выше графике, являются локальными, потому что функция увеличивается и неограниченно убывает, как показано стрелками на графике.
Функции подбарабанья вверх и вниз
Функция может быть классифицирована как вогнутая вверх или вогнутая вниз в интервале – на основе ее формы. Формально мы определяем термины вогнутый вверх и вогнутый вниз.
используя концепции исчисления. Однако мы можем понять эти термины, посмотрев на
следующие графики:
Может быть полезно думать о вогнутых функциях как о способности удерживать воду;
функции вогнутого вниз проливают воду.Функция не обязательно должна быть вогнутой или
вниз для всех x в домене; функция может изменить вогнутость. Точки, в которых
Изменения вогнутости называются точками перегиба. Мы обсудим эти концепции
при изучении дифференциального исчисления.
*****
В следующем разделе мы узнаем, как складывать, вычитать, умножать и делить функции.
Операции
Область и диапазон функции
Определения домена и диапазона
Домен
Домен а функция — это полный набор возможных значений независимой переменной.
На простом английском языке это определение означает:
Домен — это совокупность всех возможных x — значения, которые сделают функцию «работа» и выдаст реальные значения и .
При нахождении домена запомните:
- Знаменатель (внизу) дроби не может быть ноль
- Число под знаком квадратного корня должно быть положительный в этом разделе
Пример 1а
Вот график y = sqrt (x + 4):
12345-1-2-3-4123xyДомен: `x> = — 4`
Область определения этой функции — `x ≥ −4`, так как x не может быть меньше, чем` −4`.Чтобы понять, почему, попробуйте использовать в калькуляторе некоторые числа меньше, чем «−4» (например, «−5» или «−10»), и некоторые числа, превышающие «−4» (например, «−2» или «8»). Единственные, которые «работают» и дают нам ответ, — это те, которые больше или равны «−4». Это сделает число под квадратным корнем положительным.
Примечания:
- Закрашенный кружок в точке `(-4, 0)`. Это указывает на то, что домен «запускается» в этот момент.
- Мы видели, как рисовать подобные графики в разделе 4, График функции.2 = х — 2.
Как найти домен
В общем, мы определяем область каждой функции, ища те значения независимой переменной (обычно x ), которые разрешено использовать для . (Обычно нам нужно избегать 0 в нижней части дроби или отрицательных значений под знаком квадратного корня).
Диапазон
Серия из
функция — это полный набор всех возможных результирующих значений зависимой переменной ( y, обычно ) после того, как мы подставили домен.
На простом английском языке это определение означает:
Диапазон — это результат y- значений, которые мы получаем после подстановки всех возможных значений x .
Как найти диапазон
- Диапазон функции — это разброс возможных значений y (от минимального y -значения до максимального y -значения)
- Подставьте различные значения x в выражение для y на посмотреть, что происходит.(Спросите себя: всегда ли и положительны? Всегда отрицательны? Или, может быть, не равны определенным значениям?)
- Убедитесь, что вы ищете минимальные и максимальные значения y .
- Нарисуйте эскиз ! С точки зрения математики, картина стоит тысячи слов.
Вернемся к примеру выше, `y = sqrt (x + 4)`.
Мы замечаем, что кривая находится либо на горизонтальной оси, либо над ней.Независимо от того, какое значение x мы попробуем, мы всегда получим нулевое или положительное значение y . Мы говорим, что диапазон в данном случае равен y ≥ 0.
12345-1-2-3-4123xyДиапазон: `y> = 0`
Кривая всегда продолжается вертикально, за пределы того, что показано на графике, поэтому диапазон — это все неотрицательные значения `y`.
Пример 2
График кривой y = sin x показывает диапазон между -1 и 1.
12345-1-2-3-4-5-6-71-1xyДиапазон: `-1
Область y = sin x — это «все значения x », поскольку нет никаких ограничений на значения для x . (Введите любое число в функцию «sin» в вашем калькуляторе. Любое число должно работать и даст вам окончательный ответ от -1 до 1. )
)
Эксперимент с калькулятором и наблюдение кривой показывают, что диапазон составляет y между -1 и 1.Мы могли бы записать это как −1 ≤ y ≤ 1.
Откуда взялся этот график? Мы узнаем о графиках sin и cos позже в Графах греха x и cos x
Примечание 1: Поскольку мы предполагаем, что для значений x должны использоваться только действительные числа, числа, которые приводят к делению на ноль или к мнимым числам (которые возникают при нахождении квадратного корня из отрицательное число) не включаются.В главе «Комплексные числа» более подробно рассказывается о мнимых числах, но мы не включаем такие числа в эту главу.
Примечание 2: При выполнении примеров квадратного корня многие люди спрашивают: «Разве мы не получаем 2 ответа, один положительный и один отрицательный, когда мы находим квадратный корень?» Квадратный корень имеет не более одного значения, а не два. См. Это обсуждение: Квадратный корень 16 — сколько ответов?
Примечание 3: Мы говорим о домене и диапазоне функций , которые имеют не более одно y -значение для каждого x -значение, а не отношения (которые могут иметь более одного .).
Поиск домена и диапазона без использования графика
Всегда намного легче определить домен и диапазон, считывая его с графика (но мы должны убедиться, что мы увеличиваем и уменьшаем масштаб графика, чтобы убедиться, что мы видим все, что нам нужно увидеть). Однако у нас не всегда есть доступ к программному обеспечению для построения графиков, и для построения эскиза графика обычно в любом случае сначала требуется знать о разрывах и так далее.
Как упоминалось ранее, ключевые вещи, которые нужно проверить:
- Нет отрицательных значений под знаком квадратного корня
- В знаменателе (внизу) дроби нет нулевых значений
Пример 3
Найдите домен и диапазон функции `f (x) = sqrt (x + 2) / (x ^ 2-9),` без использования графика.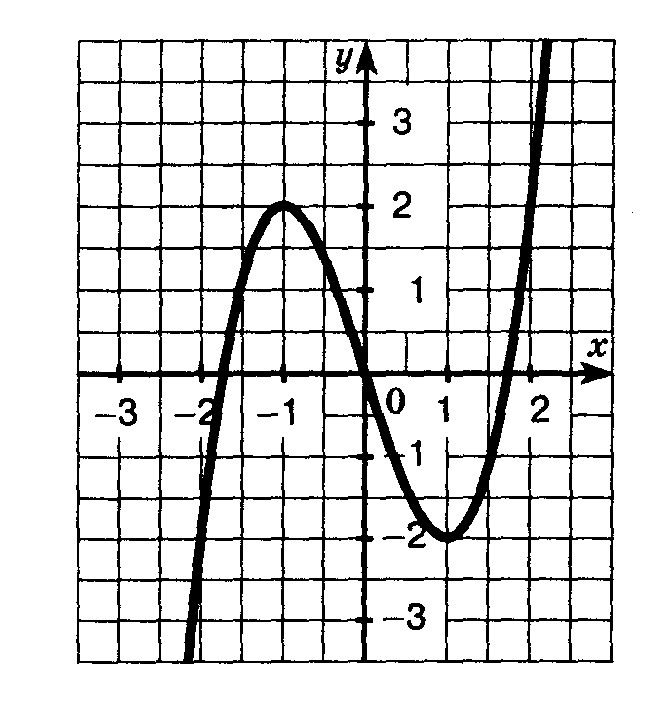 2-9`, которое, как мы понимаем, можно записать как `(x + 3) (x-3)`. Таким образом, наши значения для `x` не могут включать` -3` (из первой скобки) или `3` (из второй).
2-9`, которое, как мы понимаем, можно записать как `(x + 3) (x-3)`. Таким образом, наши значения для `x` не могут включать` -3` (из первой скобки) или `3` (из второй).
В любом случае нам не нужно беспокоиться о «-3», потому что на первом этапе мы решили, что «x> = -2».
Таким образом, домен для этого случая — `x> = -2, x! = 3`, который мы можем записать как` [-2,3) uu (3, oo) `.
Для определения диапазона мы рассматриваем верхнюю и нижнюю части дроби отдельно.
Числитель: Если `x = -2`, верхняя часть имеет значение` sqrt (2 + 2) = sqrt (0) = 0`.2-9) `приближается к` 0`, поэтому `f (x)` переходит в `-oo`, когда приближается к` x = 3`.
Для `x> 3`, когда` x` просто больше, чем `3`, значение дна чуть больше` 0`, поэтому `f (x)` будет очень большим положительным числом.
Для очень большого `x` верхний край большой, но нижний будет намного больше, поэтому в целом значение функции будет очень маленьким.
Итак, мы можем заключить, что диапазон равен `(-oo, 0] uu (oo, 0)`.
Посмотрите на график (который мы все равно рисуем, чтобы убедиться, что мы на правильном пути):
Показать график
Мы можем видеть на следующем графике, что действительно домен равен «[-2,3) uu (3, oo)» (который включает «-2», но не «3»), а диапазон — «все значения из `f (x)`, кроме `F (x) = 0`.2-9) `.
Резюме
В общем, мы определяем домен по ищем те значения независимой переменной (обычно x ), которые нам разрешено использовать . (Мы должны избегать 0 в нижней части дроби или отрицательных значений под знаком квадратного корня).
Диапазон находится путем нахождения результирующих значений y после того, как мы подставили возможные значения x .
Упражнение 1
Найдите домен и диапазон для каждого из следующих.2+ 2`.
Ответ
Домен: Функция
f ( x ) = x 2 + 2
определен
для всех реальных значений x (поскольку нет ограничений на значение x ).
Следовательно, домен `f (x)` равен
«все реальные значения x «.
Диапазон: Поскольку x 2 никогда не бывает отрицательным, x 2 + 2 никогда не меньше 2
Следовательно, диапазон `f (x)` равен
«все действительные числа` f (x) ≥ 2` «.
Мы видим, что x может принимать любое значение на графике, но результирующие значения y = f ( x ) больше или равны 2.
123-1-2-312345678910-1xf (x)Диапазон: `y> = 2`
Домен: Все `x`
Примечание
- При построении графиков важно обозначить оси как . Это помогает понять, что представляет собой график.
- Мы видели, как рисовать такие графики в Графике функции.
(б) `f (t) = 1 / (t + 2)`
Ответ
Домен: Функция
`f (t) = 1 / (t + 2)`
не определено для т = -2, так как это значение приведет к делению на ноль. (Внизу дроби будет 0.)
Следовательно, домен из f ( t ) равен
«все вещественные числа кроме -2 «
Диапазон: Независимо от того, насколько велик т , f ( t ) никогда не будет равно нулю.
[ Почему? Если мы попытаемся решить уравнение относительно 0, произойдет следующее:
`0 = 1 / (t + 2)`
Умножаем обе стороны на ( t + 2) и получаем
`0 = 1`
Это невозможно.]
Таким образом, диапазон для f ( t ) равен
«все вещественные числа кроме нуля ».
2 + 4` для `x> 2`
Ответ
Функция `f (x)` имеет область «все действительные числа,` x> 2` «, как определено в вопросе.(Здесь не используются квадратные корни из отрицательных чисел или деления на ноль.)
Чтобы найти диапазон :
- Когда `x = 2`,` f (2) = 8`
- Когда x увеличивается с `2`,` f (x) `становится больше, чем `8` (попробуйте подставить некоторые числа, чтобы понять, почему)
Следовательно, диапазон — «все действительные числа,` f (x)> 8` «
Вот график функции с открытым кружком в «(2, 8)», указывающим, что домен не включает «x = 2», а диапазон не включает «f (2) = 8».
123456510152025xf (x) (2, 8)Домен: Все `x> 2`
Диапазон:
Все `f (x)> 8`Функция является частью параболы. [Подробнее о параболе.]
Упражнение 2
Мы запускаем шар в воздух и находим высота h , в метрах, как функция времени т , в секундах, равно
ч = 20 т — 4,9 т 2
Найдите домен и диапазон для функции ч ( т ).
Ответ
Как правило, отрицательные значения времени не имеют имея в виду. Кроме того, нам нужно предположить, что снаряд попадает в землю, а затем останавливается — он не уходит под землю.
Итак, нам нужно рассчитать, когда он упадет на землю. Это будет, когда h = 0. Итак, решаем:
20 т — 4,9 т 2 = 0
Факторинг дает:
(20 — 4.9 т ) т = 0
Это верно, когда
`t = 0 \» s «`,
или
`t = 20/4.9 = 4.082 текст (ы) `
Следовательно, домен функции h равен
«все реально значения t такие, что `0 ≤ t ≤ 4.
082`»
Из выражения функции видно, что это парабола с вершиной вверх. (Это имеет смысл, если вы думаете о подбрасывании мяча вверх. Он поднимается на определенную высоту, а затем падает обратно.)
Какое максимальное значение ч ? Воспользуемся формулой максимума (или минимума) квадратичной функции.
Значение т. дает максимум
.`t = -b / (2a) = -20 / (2 xx (-4.9)) = 2.041 с`
Таким образом, максимальное значение —
.20 (2,041) — 4,9 (2,041) 2 = 20,408 м
Наблюдая за функцией h , мы видим, что по мере увеличения t , h сначала увеличивается до максимума. 20,408 м, затем ч снова уменьшается до нуля, как и ожидалось.
Следовательно, диапазон из h равен
«все реально числа, `0 ≤ h ≤ 20,408`»
Вот график функции h :
1234565101520-5-й (t)Домен: `0
Диапазон:
`0Функции, определяемые координатами
Иногда у нас нет непрерывных функций. Что нам делать в этом случае? Давайте посмотрим на пример.
Упражнение 3
Найдите область и диапазон функции, заданной координатами:
`{(−4, 1), (−2, 2.5), (2, −1), (3, 2)} `
Ответ
Домен — это просто следующие значения x : `x = {−4, −2, 2, 3}`
Диапазон состоит из следующих значений `f (x)`: `f (x) = {−1, 1, 2, 2.5}`
Вот график нашей разрывной функции.
1234-1-2-3-41234-1-2-3-е (т) (3, 2) (2, -1) (- 4, 1)(-2, 2,5)
Алгебра — рациональные функции
Показать мобильное уведомление Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-8: Рациональные функции
В этом последнем разделе нам нужно обсудить построение графиков рациональных функций.Вероятно, лучше всего начать с довольно простого, и мы можем обойтись без особых знаний о том, как они работают.
Давайте нарисуем график \ (f \ left (x \ right) = \ frac {1} {x} \). Во-первых, поскольку это рациональная функция, нам нужно быть осторожными с делением на ноль. Итак, из этого уравнения мы видим, что нам нужно избегать \ (x = 0 \), поскольку это даст деление на ноль.
Теперь давайте просто подставим некоторые значения \ (x \) и посмотрим, что мы получим.
\ (х \) \ (е (х) \) -4 -0,25 -2 -0,5 -1 -1 -0,1 -10 -0,01 -100 0.01 100 0,1 10 1 1 2 0,5 4 0,25 Итак, по мере увеличения \ (x \) (положительного и отрицательного) функция сохраняет знак \ (x \) и становится все меньше и меньше.
Точно так же, когда мы приближаемся к \ (x = 0 \), функция снова сохраняет тот же знак, что и \ (x \), но начинает становиться довольно большим.Вот набросок этого графика.
Во-первых, обратите внимание, что график состоит из двух частей. Почти все рациональные функции будут иметь графики, состоящие из нескольких частей, подобных этому.
Затем обратите внимание, что на этом графике нет никаких перехватов. Это достаточно легко проверить сами.
Напомним, что граф будет иметь \ (y \) — точку пересечения \ (\ left ({0, f \ left (0 \ right)} \ right) \). Однако в этом случае мы должны избегать \ (x = 0 \), и поэтому этот график никогда не пересечет ось \ (y \).Он действительно приближается к оси \ (y \), но никогда не пересечет и не коснется ее, и поэтому не будет пересекаться с \ (y \).
Затем напомним, что мы можем определить, где граф будет иметь \ (x \) — точки пересечения, решив \ (f \ left (x \ right) = 0 \). Для рациональных функций это может показаться беспорядком. Однако есть приятный факт о рациональных функциях, который мы можем здесь использовать. Рациональная функция будет равна нулю при определенном значении \ (x \), только если числитель равен нулю при этом \ (x \), а знаменатель не равен нулю при этом \ (x \).Другими словами, чтобы определить, равна ли когда-либо рациональная функция нулю, все, что нам нужно сделать, это установить числитель равным нулю и решить. Когда у нас есть эти решения, нам просто нужно убедитесь, что ни один из них не делает знаменатель равным нулю.
В нашем случае числитель равен единице и никогда не будет равен нулю, поэтому эта функция не будет иметь \ (x \) — перехватов. Опять же, график будет очень близко к оси \ (x \), но никогда не коснется и не пересечет ее.
Наконец, нам нужно обратить внимание на тот факт, что график очень близко подходит к осям \ (x \) и \ (y \), но никогда не пересекает их.
Поскольку в самой оси нет ничего особенного, мы будем использовать тот факт, что ось \ (x \) на самом деле является линией, заданной \ (y = 0 \), а ось \ (y \) — действительно строка, заданная \ (x = 0 \).
В нашем графике, когда значение \ (x \) приближается к \ (x = 0 \), график становится очень большим по обе стороны от линии, заданной \ (x = 0 \). Эта линия называется вертикальной асимптотой .
Кроме того, поскольку \ (x \) становится очень большим, как положительным, так и отрицательным, график приближается к линии, заданной \ (y = 0 \).Эта линия называется горизонтальной асимптотой .
Вот общие определения двух асимптот.
- Линия \ (x = a \) представляет собой вертикальную асимптоту , если график неограниченно увеличивается или уменьшается на одной или обеих сторонах линии по мере того, как \ (x \) приближается к \ (x = a \).
- Линия \ (y = b \) является горизонтальной асимптотой , если график приближается к \ (y = b \), когда \ (x \) неограниченно увеличивается или уменьшается.m} + \ cdots}} \]
, где \ (n \) — наибольший показатель степени в числителе, а \ (m \) — наибольший показатель степени в знаменателе.
Тогда мы имеем следующие факты об асимптотах.
- График будет иметь вертикальную асимптоту в точке \ (x = a \), если знаменатель равен нулю в точке \ (x = a \), а числитель не равен нулю в точке \ (x = a \).
- Если \ (n
- Если \ (n = m \), то линия \ (\ displaystyle y = \ frac {a} {b} \) является горизонтальной асимптотой.
- Если \ (n> m \) не будет горизонтальных асимптот.
Процесс построения графика рациональной функции довольно прост. Вот.
Процесс построения графика рациональной функции
- Найдите перехватчики, если они есть.
Помните, что \ (y \) — точка пересечения задается как \ (\ left ({0, f \ left (0 \ right)} \ right) \), и мы находим \ (x \) — точки пересечения, устанавливая числитель равен нулю и решает.
- Найдите вертикальные асимптоты, установив знаменатель равным нулю и решив.
- Найдите горизонтальную асимптоту, если она существует, используя вышеизложенный факт.
- Вертикальные асимптоты разделят числовую прямую на области. В каждом регионе на графике не менее одной точки в каждом регионе. Эта точка сообщит нам, будет ли график выше или ниже горизонтальной асимптоты, и, если нам нужно, мы должны получить несколько точек, чтобы определить общую форму графика.
- Сделайте набросок графика.
Обратите внимание, что набросок, который мы получим в процессе, будет довольно грубым, но это нормально. Это все, что нам действительно нужно — это базовое представление о том, на что будет смотреть график.
Давайте взглянем на пару примеров.
Пример 1 Нарисуйте график следующей функции. \ [f \ left (x \ right) = \ frac {{3x + 6}} {{x — 1}} \] Показать решениеИтак, начнем с перехвата.Перехватчик \ (y \) равен,
\ [f \ left (0 \ right) = \ frac {6} {{- 1}} = — 6 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ left ({0, — 6} \ right ) \]\ (x \) — перехватов будет,
\ [\ begin {align *} 3x + 6 & = 0 \\ x & = — 2 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ left ({- 2,0} \ right) \ end { выровнять*}\]Теперь нам нужно определить асимптоты. Давайте сначала найдем вертикальные асимптоты.
\ [x — 1 = 0 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} x = 1 \]Итак, у нас есть одна вертикальная асимптота. Это означает, что теперь есть две области \ (x \) ‘s. 2} — 9 = 0 \ hspace {0.25 дюймов} \ Rightarrow \ hspace {0,25 дюйма} x = \ pm 3 \]
Итак, в этом случае у нас будет три области нашего графа: \ (x <- 3 \), \ (- 3
3 \). Кроме того, наибольший показатель степени в знаменателе равен 2, а поскольку в числителе нет \ (x \), наибольший показатель степени равен 0, поэтому ось \ (x \) будет горизонтальной асимптотой.
Наконец, нам нужны очки. Здесь мы будем использовать следующие моменты.
\ [\ begin {align *} f \ left ({- 4} \ right) & = \ frac {9} {7} & \ hspace {0,25in} & \ left ({- 4, \ frac {9} { 7}} \ right) \\ f \ left ({- 2} \ right) & = — \ frac {9} {5} & \ hspace {0,25in} & \ left ({- 2, — \ frac {9 } {5}} \ right) \\ f \ left (2 \ right) & = — \ frac {9} {5} & \ hspace {0,25in} & \ left ({2, — \ frac {9} { 5}} \ right) \\ f \ left (4 \ right) & = \ frac {9} {7} & \ hspace {0,25 дюйма} & \ left ({4, \ frac {9} {7}} \ вправо) \ end {align *} \]Обратите внимание, что вместе с точкой пересечения \ (y \) у нас фактически есть три точки в средней области.2} — 4x = x \ left ({x — 4} \ right) = 0 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25in} x = 0, \, \, x = 4 \]
Итак, у нас снова две области, и мы получили три области: \ (x <0 \), \ (0
4 \). Далее, наибольший показатель как в числителе, так и в знаменателе равен 2, поэтому, поскольку на линии будет горизонтальная асимптота,
\ [y = \ frac {1} {1} = 1 \]Теперь одна из точек пересечения \ (x \) — находится в крайней левой области, поэтому нам не нужны там точки.Другой перехватчик \ (x \) находится в средней области. Итак, нам понадобится точка в крайней правой области, и, как отмечалось в предыдущем примере, мы захотим получить еще пару точек в средней области, чтобы полностью определить ее поведение.
\ [\ begin {align *} f \ left (1 \ right) & = 1 & \ hspace {0,25 дюйма} & \ left ({1,1} \ right) \\ f \ left (3 \ right) & = — \ frac {5} {3} & \ hspace {0,25 дюйма} & \ left ({3, — \ frac {5} {3}} \ right) \\ f \ left (5 \ right) & = \ frac {{21}} {5} & \ hspace {0.

 1А Функция, ее свойства и график
1А Функция, ее свойства и график
 Приходят к единому мнению по спорным вопросам. При необходимости получают консультацию учителя. Необходимо выполнить задание
Приходят к единому мнению по спорным вопросам. При необходимости получают консультацию учителя. Необходимо выполнить задание

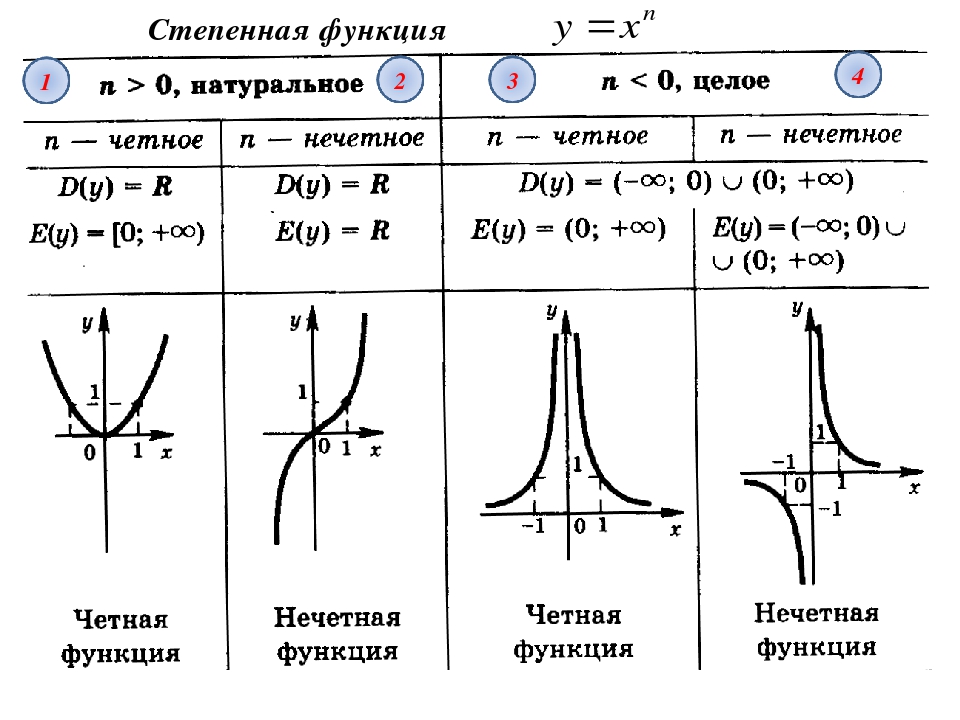 График функции распределения такой случайной величины всегда представляет собой неубывающую непрерывную функцию (рис. 2).
График функции распределения такой случайной величины всегда представляет собой неубывающую непрерывную функцию (рис. 2).
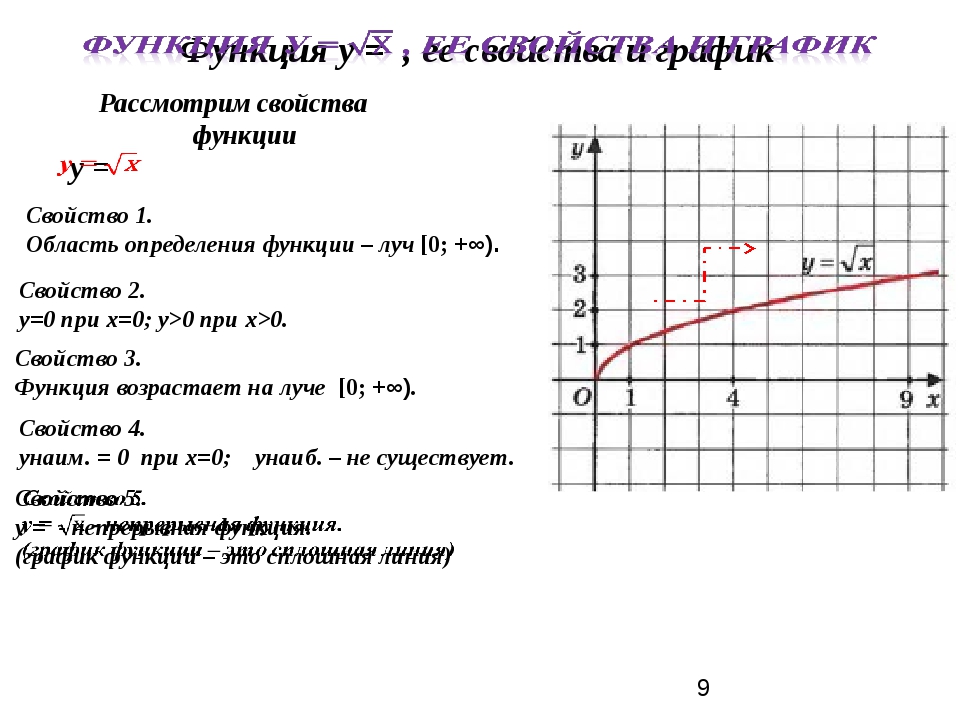 Если функция является четной функцией, ее график симметричен относительно оси, то есть
Если функция является четной функцией, ее график симметричен относительно оси, то есть 
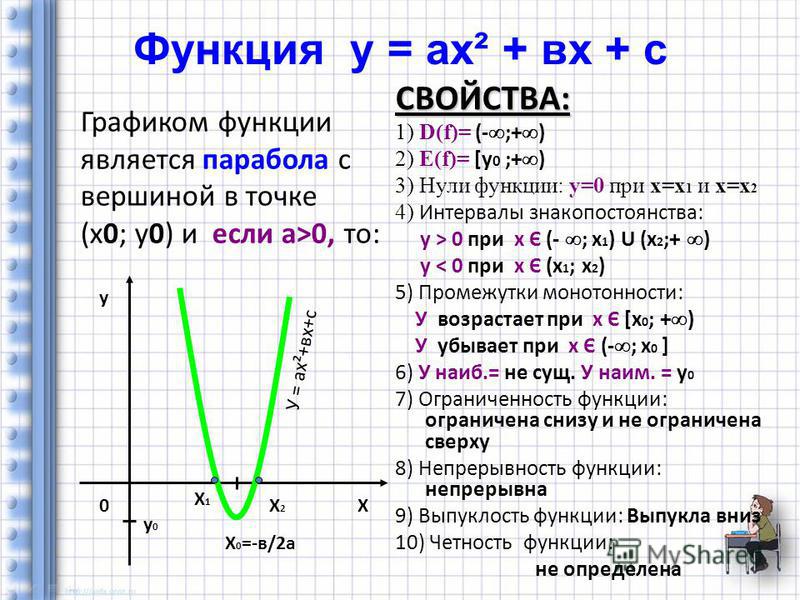 Уже одно это скажет нам, что функция не является взаимно однозначной.
Уже одно это скажет нам, что функция не является взаимно однозначной.

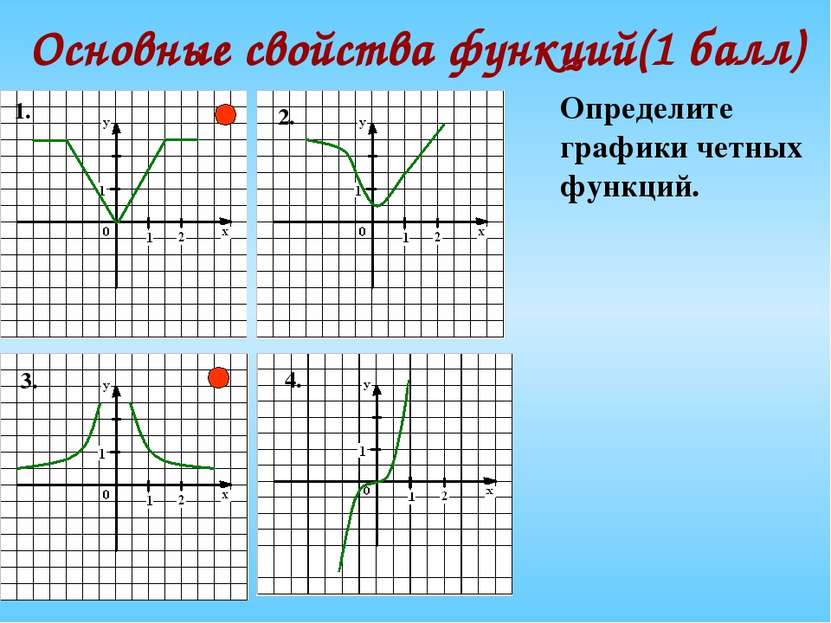
 2 + 4` для
`x> 2`
2 + 4` для
`x> 2` 082`»
082`»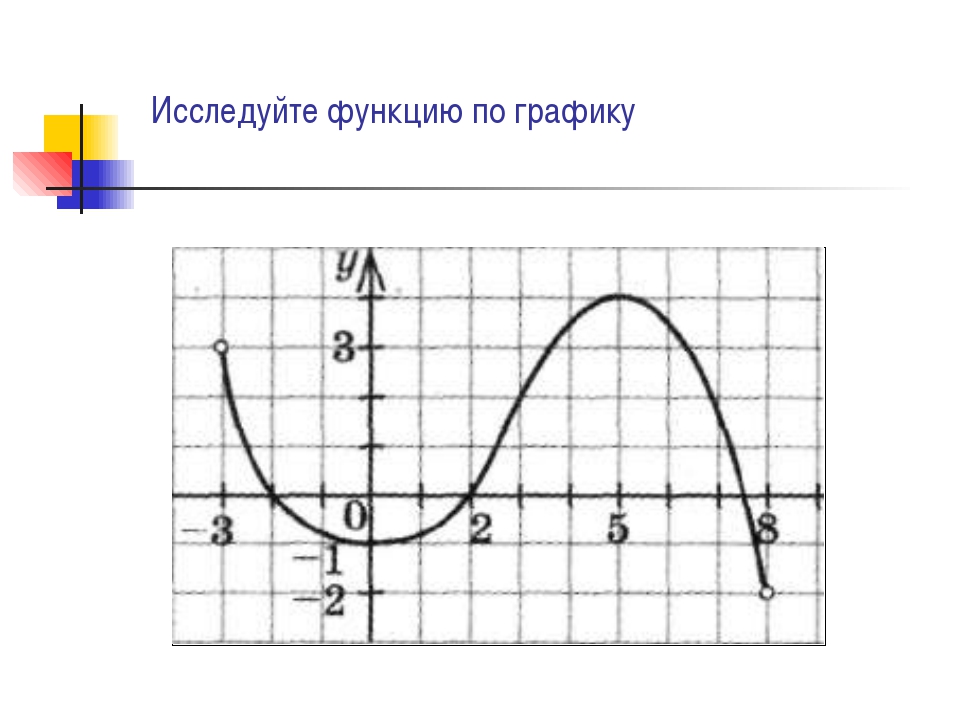 е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. Точно так же, когда мы приближаемся к \ (x = 0 \), функция снова сохраняет тот же знак, что и \ (x \), но начинает становиться довольно большим.Вот набросок этого графика.
Точно так же, когда мы приближаемся к \ (x = 0 \), функция снова сохраняет тот же знак, что и \ (x \), но начинает становиться довольно большим.Вот набросок этого графика. Поскольку в самой оси нет ничего особенного, мы будем использовать тот факт, что ось \ (x \) на самом деле является линией, заданной \ (y = 0 \), а ось \ (y \) — действительно строка, заданная \ (x = 0 \).
Поскольку в самой оси нет ничего особенного, мы будем использовать тот факт, что ось \ (x \) на самом деле является линией, заданной \ (y = 0 \), а ось \ (y \) — действительно строка, заданная \ (x = 0 \). Помните, что \ (y \) — точка пересечения задается как \ (\ left ({0, f \ left (0 \ right)} \ right) \), и мы находим \ (x \) — точки пересечения, устанавливая числитель равен нулю и решает.
Помните, что \ (y \) — точка пересечения задается как \ (\ left ({0, f \ left (0 \ right)} \ right) \), и мы находим \ (x \) — точки пересечения, устанавливая числитель равен нулю и решает.