Общий метод решения | 1) если а корней нет | 2) если а > 0, то возведем в квадрат обе части уравнения f (x) = a2 | возведем в квадрат обе части уравнения при условии, что g (x) ≥ 0 | возведем в квадрат обе части уравнения при условии, что g (x) ≥ 0 или f (x) ≥ 0 | Примеры – образцы решений | 1) решение: т.к. -3 Ответ: корней нет. 2) решение: возведем в квадрат обе части уравнения 2х – 5 = 9 решаем получившееся уравнение 2х = 9 + 5 2х = 14 х = 14 : 2 х = 7 Ответ: 7 |
решение: возведем в квадрат обе части уравнения 2х + 10 = х2 + 2х + 1 решаем получившееся уравнение при условии, что х + 1 ≥ 0 2х + 10 – х2 – 2х – 1 = 0 — х2 + 9 = 0 х2 – 9 = 0 (х — 3)(х + 3) = 0 х – 3 = 0 или х + 3 = 0 х = 3 х = — 3 проверка условия: х + 1 ≥ 0 если х = 3, то 3 + 1 ≥ 0 4 ≥ 0 — верно, значит 3 – корень уравнения если х = -3, то -3 + 1 ≥ 0 -2 ≥ 0 – неверно, значит -3 – не корень уравнения Ответ: 3 | 1) решение: возведем в квадрат обе части уравнения 2х + 10 = х + 1 решаем получившееся уравнение при условии, что х + 1 ≥ 0 2х – х = 1 – 10 х = -9 проверка условия: х + 1 ≥ 0 -9 + 1 ≥ 0 -8 ≥ 0 – неверно значит -9 – не корень уравнения Ответ: корней нет | 2) решение: возведем в квадрат обе части уравнения 3х — 10 = х + 2 решаем получившееся уравнение при условии, что х + 2 ≥ 0 3х – х = 2 + 10 2х = 12 х = 12 : 2 х = 6 проверка условия: х + 2 ≥ 0 6 + 1 ≥ 0 7 ≥ 0 – верно значит 6 – корень уравнения Ответ: 6 |
План-конспект урока по алгебре (10 класс) на тему: Урок по теме Иррациональные уравнения 10 класс
Тема. Методы решения иррациональных уравнений 10 класс
(с применением интерактивной доски)
Цель:
1.Познакомить учащихся с методами решения иррациональных уравнений, закрепить решение иррациональных уравнений при выполнении упражнений.
2. Развить умение сравнивать, анализировать.
3.Воспитывать уважение к мыслям своих товарищей, взаимовыручку, взаимоподддержку.
Ход урока:
1.Организационный момент
«Успешность реализации планов развития экономики и социальной сферы России зависит от того насколько выпускники школы смогут поддерживать свою конкурентно способность, важнейшими условиями которой являются такие качества личности, как инициатива, способность творчески мыслить и находить нестандартные решения». Президент РФ Д.А. Медведев
Мы согласны со словами Президента РФ, потому что способность творчески мыслить, быть инициативным вырабатывается именно в школьные годы, и во многом это заслуга математики.
Разные способы решения одной и той же задачи — разве это не творческий подход? А красивое решение – разве это не полет творческой мысли?
2.Актуализация знаний
Интеллектуальная разминка (устная работа)
Какие из предложенных уравнении являются иррациональными?
Ответ: 1, 4, 6.
На прошлом уроке мы познакомились с иррациональными уравнениями и было дано домашнее задание — самостоятельно найти методы решения иррациональных уравнений, т.е. провести небольшое исследование.
Запишите число, тему урока.
3.Изучение нового
Сейчас мы познакомимся с некоторыми методами решения иррациональных уравнений.
Презентация Саша Костюченко (возведение обеих частей уравнения в квадрат, введение новой переменной), презентация Лена Зебрева (графический способ, использование монотонности функции).
4.Физпауза для глаз
1.Перечислите все корни, которые вы видите на экране.
2.В какой геометрической фигуре расположен ?
3.Какого цвета эта фигура?
4.Какое число находится в квадрате?
5.Какого цвета фигура, в которой располагается ?
6.Как называется эта фигура?
«Мне приходится делить свое время между политикой и уравнениями. Однако, уравнения, по-моему, важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно».
А.Эйнштейн.
5.Закрепление изученного
А сейчас предлагаю вам для решения два уравнения, а способ решения вы должны выбрать сами.
Решить уравнение . Решить графическим способом. Ответ: x=3
Решить уравнение . Заменой переменной. Ответ:x=-1
А теперь Вам предлагается тест. Под музыку.
6.Домашнее задание: гл.V§ 5 № 56 (3), № 58 (2), № 65 (3)
7.Итог урока:
Сегодня мы познакомились с некоторыми способами решения иррациональных уравнений, которые вы нашли сами. В учебнике эти методы не озаглавлены и особенно радует, что вы сумели их увидеть и выделить используя учебник и дополнительную литературу. Мы продолжим знакомство с методами решения иррациональных уравнений на следующем уроке.
Сегодня урок помогли подготовить Саша Костюченко, Лена Зебрева, Женя Горелов, Настя Неяскина.
Оценки за урок
В 11-ом классе вы будете сдавать ЕГЭ и встретитесь с иррациональными уравнениями на экзамене
№ 1 Решить уравнение .
№ 2 Решить уравнение .
№ 3 Найдите все значения параметра , при каждом из которых уравнение имеет ровно 8 решений.
«О сколько нам открытий чудных готовит просвещенья дух!
И опыт – сын ошибок трудных,
И гений — парадоксов друг…»
А.С.Пушкин
План-конспект урока по алгебре (10, 11 класс) на тему: Методическая разработка урока по «Иррациональные уравнения»
Урок разноуровневого обобщающего повторения по теме:
«Иррациональные уравнения»
10, 11 класс
Цели урока.
Образовательные цели урока:
- Закрепить навыки решения квадратных уравнений, расширить и углубить знания по данной теме.
- Научить учащихся решать уравнения, используя метод введения новой переменной.
Воспитательные цели урока:
- Воспитывать самостоятельность и творчество.
- Способствовать выработке у школьников желания и потребности в применении изучаемых фактов.
Развивающие цели урока:
- Научить применять знакомые формулы в измененных условиях.
- Продолжить работу над развитием речи, умением анализировать, выделять главное, обобщать, доказывать.
Метод ведения урока:
- Беседа.
- Мини-диалог.
- Самостоятельная работа.
Оборудование:
- Мультимедийная установка. На уроке используется презентация: «Иррациональные уравнения»:
- при повторении теоретического материала на экране высвечиваются повторяемые формулы, примеры, иллюстрирующие основные определения и алгоритмы решения уравнений;
- при самопроверки самостоятельной работы на экране появляются эталонные ответы на соответствующие задания.
- На столах лежит дидактический материал, который используется на различных этапах урока.
I этап урока – организационный
Сообщается тема урока и для каждой группы определятся основная цель:
- для 1-й группы – развить умения решать задачи на базовом уровне;
- для 2-й группы – закрепить и развить умения решать задачи базового и повышенного уровня сложности;
- для 3-й группы – закрепить и развить умения решать задачи базового и повышенного уровня сложности;
II этап урока – повторение теоретического материала по теме (5мин.)
Учитель. Какое уравнение называется иррациональным?
Ученик. Даёт определение.
Уравнения, в которых под знаком корня содержится переменная, называют иррациональными.
Учитель. Выберите иррациональные уравнения (на экране высвечиваются примеры):
а) = 5; б) = 27; в) х= 3х + 8;
г) = х + 2; д) (3х – 8)=
Учитель. Какие уравнения называются равносильными?
Ученик. Два уравнения равносильны, если множества их корней совпадают.
Учитель. Какое уравнение называется следствием другого?
Ученик. Это уравнение, полученное в результате преобразования данного уравнения, при решении которого появляются посторонние корни.
Учитель. Равносильны ли уравнения (на экране высвечиваются примеры):
1) (х – 3)(х – 5) = 0 и х- 8х +15 = 0; (ответ: да)
2) 2х + 7 = 3х – 3 и –х = -10; ( ответ: да)
3) = и 3х – 2 =4х – 5; ( ответ: нет, так как второе уравнение – следствие первого, первое уравнение не имеет корней, а второе имеет корень х = 3)
Учитель: Теперь Вашему вниманию предлагается самостоятельная работа.
По окончании её, вы сможете сразу же проверить себя. У кого возникнут затруднения при решении работы, могут воспользоваться раздаточным материалом, лежащим на столах. (Текст работы, а потом и ответы высвечиваются на доске)
1 вариант | 2 вариант |
1. | 1. |
2. | 2. |
3. | 3. |
4. Дополнительное задание | 4. Дополнительное задание |
Учитель. Назовите два способа решения уравнения вида g (х).
Ученики. Первый способ: возвести обе части уравнения в квадрат, решить уравнение f (х) = g(х) и проверить, какой из полученных корней удовлетворяет уравнению g (х).
Второй способ: возвести обе части уравнения в квадрат, решить уравнение f (х) = g(х) и найти область допустимых значений переменной уравнения.
Учитель. Решите уравнение вида = g (х).
Ученик. Данное уравнение будет равносильно уравнению f (х) = g(х).
Учитель обобщает ответы учащихся и на экране высвечиваются алгоритмы решения иррациональных уравнений.
№ п/п | Уравнение вида | Решение | Проверка корней |
1 | =а | f(x)=a2 | f(x) 0 |
2 | = g(x) | f(x) = g2(x) | f(x) 0 |
3 | = | f(x) = g(x) | f(x) 0, g(x) 0 |
4 | =a | f(x) g2(x) = a2 | f(x) 0, g(x) 0 |
5 | = a | = a2 | f(x) 0, g(x) 0 |
6 | = a | f(x) + 2 + f(x) = a2 2 = a2 – f(x) –g(x) дальше, как в п.2 | f(x) 0, g(x) 0 |
7 | + = | f(x) + 2 + f(x) = h(x) 2 = h(x) – f(x) –g(x) дальше, как в п.2 | f(x) 0, g(x) 0, h(x) 0 |
III этап. Устная работа.
Учитель предлагает учащимся рассмотреть способы решения иррациональных уравнений, используя раздаточный материал.
Учитель. Решите устно уравнения (уравнения высвечиваются на экране):
1) = 7; (ответ: 49)
2) = 5; (ответ: 28)
3) 2 +3= 0; (ответ: нет решений, так как левая часть уравнения представляет собой сумму двух неотрицательных слагаемых)
4) = 4; (ответ: 64)
5) = — 2; (ответ: нет решений, так как левая часть уравнения принимает только неотрицательные значения)
6) = 25; (ответ: -25 и 25)
7) = -2; (ответ: нет решений, так как сумма двух
неотрицательных чисел не может быть отрицательной)
Учитель. Найди ошибку (решение уравнений высвечивается на экране):
1. Ошибка.
Не найдена область допустимых значений
Решение. переменной х.
х+ 3 = 3х + 11 х-3
-2х = 8
х = -4
Ответ: -4. Ответ: нет решений.
2.
Решение. Ошибка.
х = -6 – посторонний корень,
(х +6)(х – 4) = 0 так как х – 2
х = -6, х = 4
Ответ: -6; 4. Ответ: 4.
IV этап. Работа с разноуровневыми группами.
Учащиеся по группам решают уравнения.
Учащиеся 1 – ой группы.
1. Решите уравнение:
Решение:
х = -1.
Ответ: -1.
2. Решите уравнение: .
Решение:
Пусть =t, t. Тогда уравнение примет вид: t+ 6t – 7 = 0. Решив квадратное уравнение, получим: t = -7 или t = 1. t = -7 не удовлетворяет условию t.
= 1, х = 3.
Ответ: 3.
Далее учащиеся 1 – ой группы выполняют самостоятельную работу.
Ответы: 1 вариант. 1. 37. 2. 7. 3. 1,5. 4. -1.
2 вариант. 1. . 2. -1. 3. 15. 4. -4; 4.
Учащиеся 2 –ой группы.
1. Решите уравнение:
Решение:
Найдём ОДЗ:
6 х 9
Возведём обе части уравнения в квадрат:
(
10 – 2 = 2х – 12,
2 = 22 – 2х,
= 11 – х,
х-15х + 56 = 0,
х = 7 или х = 8. Ответ: 7; 8.
Далее учащиеся 2 – ой группы выполняют самостоятельную работу.
Ответы: 1 вариант. 1. 4. 2. -1. 2 вариант. 1. ; . 2. 2.
Учащиеся 3 – ей группы.
1. Решите уравнение: + 2 = .
Решение:
+ 2 = ,
+ 2 = ,
+ 2 = |2х — 1|.
Так как 1 – 4х , х , то |2х – 1| = 1 – 2х.
+ 2 = 1 – 2х,
= -1 – 2х, где -1 – 2х , х .
1 – 4х = 1 + 4х + 4х,
4х+ 8х = 0,
х = 0 или х = -2.
Ответ: -2.
Далее учащиеся 3 – ей группы выполняют самостоятельную работу.
1 вариант. 2 вариант. Решите уравнение: Решите уравнение: |
Ответы: 1 вариант. 5; 7.
2 вариант. 3; 4,5.
Ребята сдают самостоятельную работу.
V этап. Подведение итогов урока.
Учитель ещё раз обращает внимание учащихся на типы уравнений, которые вспомнили на уроке, отмечает успешную работу отдельных учащихся, выставляет оценки за ответы у доски, даёт и поясняет домашнее задание.
В качестве домашнего задания ребята обмениваются вариантами самостоятельной работы.
План-конспект урока по алгебре (10 класс) по теме: «Решение иррациональных уравнений — обобщение и систематизация знаний»
Санкт-Петербургская академия
постдипломного педагогического образования
Кафедра физико-математического образования
ГБОУ лицей №369 Красносельского района г. Санкт-Петербурга
Методическая разработка урока алгебры и начала анализа в 10 классе по теме:
«Решение иррациональных уравнений — обобщение и систематизация знаний»
Филиппова Ольга Константиновна
учитель математики
г. Санкт-Петербург
2013год
Методическая разработка урока алгебры и начала анализа в 10 классе по теме: «Решение иррациональных уравнений. Обобщение и систематизация знаний»
Пояснительная записка.
Этот урок является одним из последних по теме «Иррациональные уравнения».На этом уроке необходимо отработать алгоритм решения иррациональных уравнений доступных для каждого ученика, чтобы каждый ученик смог сделать шаг вперёд в процессе обучения.
Основные цели:
-обобщить и систематизировать знания и умения решать иррациональные уравнения различного вида и различными способами.
-развивать у учащихся внимание и аккуратность
-воспитывать усидчивость и трудолюбие
Одной из задач данного урока является повторение пройденного по теме «Иррарациональные уравнения» материала, подготовка учащихся к контрольной работе по данной теме.
Элементы технологий:
- развивающее обучение,
- дифференцированное обучение,
- индивидуализированное обучение,
- изучение алгоритма с последующим воспроизведением,
- обучающая беседа.
Оборудование, средства обучения:
- разноуровневые задачи
- карточки индивидуального обучения
- компьютер
- интерактивная доска.
1. Организационный момент.
2. Проверка домашнего задания:
а) Раздать карточки учащимся, которые садятся на первые парты, с индивидуальным заданием.
В этих карточках- часть домашней работы (для слабых учащихся).
Карточка №1 Карточка №2 Карточка №3
б) Вторая часть домашней работы проверяется на электронной доске. На доске выведены примеры с решением. Учащимся предлагается найти ошибку в решении, исправить её и объяснить.
№644(1) №644(3) №644(5)
Вызванные 3 ученика исправляют ошибки:
№644(1) №644(3) №644(5)
2х+7=(х+2)² 2х+3-2+(х+1)=1 2x²-х+10-x²-4х-4=0
2х+7=x²+4х+4 3х+4-2 =1 x²-5х+6=0
x²+2х-3=0 3х+3=2 х1=3 х2=2
Проверка показывает 9x²+18х+9=8x²+20х+12 с учётом проверки
что, х=-3 не является x²-12х-3=0 Ответ: 3; 2
корнем х1=3 х2=-1
Ответ: 1 Проверка показывает,
что оба корня подходят
Ответ: 3 ; -1
3.Объявление темы: сегодня мы повторим способы решения иррациональных уравнений и начнем с самых простых.
4.Устный счет: 1) Решить уравнения:
а) (0,125) Что общего в этих уравнениях?
(-32) (корни нечётной степени)
(-26) Что можно сказать про подкоренное выражение?
(может быть любым числом)
(31) Что можно сказать про значение этого корня?
(может быть любым действительным числом)
б) (81) Что общего в этих уравнениях?
(24) (корни чётной степени)
(+1 и -1) Что можно сказать про подкоренное выражение?
(корней нет) (положительное или 0)
(1) Что можно сказать про значение этого корня?
(положительное или 0)
2) Представить в виде квадрата следующие выражения:
5. Запись числа, темы урока: «Решение иррациональных уравнений».
Решение уравнений:
Ученик №1
С чего обычно начинают решать иррациональные уравнения?
( с возведения в квадрат) Удобно ли это здесь? (нет)
Почему? (останется корень)
Упростим:
Решение с пояснениями О.О.У х>-1 Д.У. х>5
х-5=Öх+1
х 2-10х+25=х+1
х 2 -11х+24=0
х1=8 х 2=3 — вне Д.У.
Ответ: 8
Ученик №2
Сразу от корней не избавиться.
15-х+2+3-х=36 Возведём в квадрат дважды.
2=18+2х
=х+9
-18х+45=+18х+81
-36х=36
х=-1
Проверка: Л.ч. Ö15+1+Ö3+1=4+2=6
Пр. ч. 6 ; Л.ч.=Пр.ч.
Ответ: -1
Данный способ можно использовать не только с квадратными корнями, но и с корнями других степеней.
Ученик №3
О.Д.З.
+15=8(х+3) (-∞; +∞)
+15=8х+24
+8х-9=0
х1=9 х2=-1
Ответ: 9 ; -1
Ученик№4
О.Д.З.
+4х=32 (-∞; +∞)
+4х-32=0
х1=-8 х2=4
Ответ: 4 ; -8
Ученик №5
О.Д.З.
-5+16х-5=-6+12х-8 (-∞; +∞)
+4х+3=0
х1=-3 х2=-1
Ответ: -3 ; -1
Ученик№6
-3х=0
3+3х=0
3х(х+1)=0
х1=0 х2=-1
Проверка: х=0
Л.ч. =0 Пр. 0
Л.ч. =Пр. ч.
Л.ч. = Пр.ч. — не существует.
Ответ: 0
7.)Возьмем уравнения посложнее
Ребята такие уравнения подготовили дома:
Ученик№7
а) Д.У. х >0
3-2=
+2-3=0
Пусть =t, t>0 , тогда t2+2t-3=0
t1=-3, но t>0 , t2=1
Т.к. t2=1, то х2=1
х1=1 х1=-1 — вне Д.У.
Ответ: 1
Ученик№8
б) О.Д.З. х >1
Пусть =t, t>0 то тогда
2+t-3=0
t1=1,5 ,но t>0 t2=1
Т.к. t=1 , то =1
х-1=1
х=2
Ответ: 2
Ученик№9
в)
Пусть =t, t>0
то тогда
+3t-4=0
t1=-4 , но t>0, t2=1
Значит,
-3=1
=4
х1=2 х2=-2
Проверка: х1,2=±2
Л.ч.
П.ч. 0 Л.ч.=Пр.ч.
Ответ: 2 ;-2
6. Запишем домашнее задание:
№168(5), №169(3), №644(2,4), №645(1).
Индивидуально раздать карточки с заданиями на следующий урок, который продолжает эту тему.
Карточка №1
Карточка №2
Карточка№3
Ö11х+3-Ö2-х-Ö9х+7+Öх-2=0
7. Подведение итогов:
1)Как же решаются иррациональные уравнения?
Какие способы мы повторили?
(возведение в квадрат, замена переменной)
При решении этих уравнений всегда ли мы делаем равносильные преобразования?
Как уберечься от ошибки?
(следить за равносильностью преобразований или делать проверку)
2)Выставить оценки учащимся.
Литература:
1.Алимом Ш. А., Колягин Ю.М. и др.
«Алгебра и начала анализа»-учебник для 10-11 классов «Просвешение» 2006 год.
2.Колягин Ю.М., Ткачева М.В. и др. «Алгебра и начала анализа 10» «Просвешение»
2011 год.
3.Михайлова Ш.М. «алгоритмы-ключ к решению задач по алгебре10-11 классы»
» Просвешение» 2009 год.
4.Карачинский Е.Я. «Самостоятельные и контрольные работы по Алгебре для 10 класса» «СМНОПресс» 2012год.
5.Шестаков С.А., Захаров П.И. «ЕГЭ 2013Математика» «МЦНМО» 2013 год.
6.СергеевИ.Н., Панфёров В.С. «ЕГЭ 2013 Математика» «МЦНМО» 2013 год.
7.
8.Сайт Гущина reshuege.ru
9.Сайт Александра Ларина alеxlarin.net
10. Сайт Савченко Елена Михайловна le-savchen.ucoz.ru
Решение иррациональных уравнений и неравенств .( 10 класс)
Решение иррациональных уравнений и неравенств (алгебра, 10 класс)
Тема урока: Решение иррациональных уравнений и неравенств.
Цели урока:
обобщить и систематизировать знания учащихся по данной теме;
повторить способы решения иррациональных уравнений и неравенств;
закрепить навыки и умения применения знаний по теме к решению упражнений;
формировать навыки самоконтроля;
воспитывать трудолюбие, аккуратность ведения записей, умение объективно оценивать результаты своей работы.
Тип урока – урок систематизации знаний.
План урока:
Организационный момент.
Сообщение темы, целей, формы проведения урока.
Актуализация прежних знаний.
Выполнение упражнений (применение знаний в различных ситуациях).
Подведение итогов работы на уроке.
Рефлексия.
Итог урока.
Ход урока
1. Организационный момент.
Приветствие учителем учащихся. Настрой на работу.
2. Сообщение темы, целей, формы проведения урока.
Итак, мы завершаем изучение темы «Иррациональные уравнения и неравенства», выходим на контрольную работу, поэтому цель нашего урока систематизировать знания по этой теме.
1)Вспоминаем определения, схемы решения.
Иррациональные уравнения
Иррациональным называется уравнение, в котором переменная содержится под знаком корня.
Решаются такие уравнения возведением обеих частей в степень. При возведении в четную степень возможно расширение области определения заданного уравнения. Поэтому при решении таких иррациональных уравнений обязательны проверка или нахождение области допустимых значений уравнений. При возведении в нечетную степень обеих частей иррационального уравнения область определения не меняется.
Иррациональные уравнения стандартного вида можно решить пользуясь следующим правилом:
Решение иррациональных уравнений стандартного вида:
а) Решить уравнение = x – 2,
Решение.
= x – 2,
2x – 1 = x2 – 4x + 4, Проверка:
x2 – 6x + 5 = 0, х = 5, = 5 – 2,
x1 = 5, 3 = 3
x2 = 1 – постор. корень х = 1, 1 – 2 ,
Ответ: 5 пост. к. 1 -1.
б) Решить уравнение = х + 4,
Решение.
Ответ: -1
Решение иррациональных неравенств стандартного вида:
Иррациональные неравенства
Неравенства называются иррациональными, если его неизвестное входит под знак корня (радикала).
Иррациональное неравенство вида равносильно системе неравенств:
Иррациональное неравенство вида равносильно совокупности двух систем неравенств:
и
а) Решить неравенство
Решение.
Данное неравенство равносильно системе неравенств:
+ – +
Ответ: [1; 2). 1 3 x
б) Решить неравенство
Решение.
Данное неравенство равносильно двум системам неравенств:
Ответ:
в) Решить неравенствоРешение.
Данное неравенство равносильно системе неравенств:
Ответ: нет решений
Самостоятельная работа
Решите уравнение:
а) 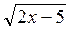 =
= 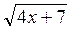 . (4 балла)
. (4 балла)
б) 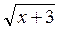 –
– 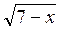 = 2. (4 балла)
= 2. (4 балла)
в) 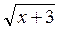
Вариант 2
Решите уравнение:
a) 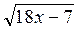 =
= 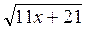 . (4 балла)
. (4 балла)
б) 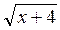 –
– 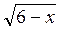 = 2. (4 балла)
= 2. (4 балла)
в) 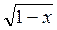 = х – 3. (4 балла)
= х – 3. (4 балла)
Ответ: В-1: а) корней нет; б) 6; в) корней нет.
В-2: а) 4; б) 5; в) корней нет.
Задания для сильных учащихся
Решение иррациональных неравенств нестандартного вида:
а) Решить неравенство
Решение.
Данное неравенство равносильно системе неравенств:
Ответ:
5. Подведение итогов работы на уроке.
6. Рефлексия.
Учащимся предлагается закончить одно из предложений
Закончите предложение:
Мне сегодня удалось (понять, разобраться, уяснить, осознать) …, теперь я …
Самым интересным (познавательным, удивительным, невероятным, необыкновенным ) сегодня было (стало) …
Труднее всего мне сегодня …, и все-таки …
7. Домашнее задание №189
Урок 20. иррациональные уравнения и неравенства — Алгебра и начала математического анализа — 10 класс
Урок Конспект Дополнительные материалыИррациональные уравнения
Решите уравнения:
ПодсказкаПрименить правила решения уравнений.
Иррациональные уравнения
Выберите иррациональные уравнения, неравенства:
ПодсказкаВспомните определение иррациональных уравнений и неравенств.
Иррациональные уравнения
Соотнесите уравнение и его корень.
ПодсказкаПрименить методы решения иррациональных уравнений.
Иррациональные уравнения
Укажите сколько корней имеет уравнение:
1) $\sqrt{x^2-4x-5}=0$
2) $\sqrt{x+15}=3$
3) $(x²+4)\sqrt{x+9}=0$
4) $\sqrt{x²-5x+8}=0$
5) $\sqrt{x}+5=-2$
6) $\sqrt{x-4}=2$
ПодсказкаПрименить методы решения иррациональных уравнений.
1) 1 корень 2 корня Нет корней
2) Нет корней 2 корня 1 корень
3) 1 корень 2 корня Нет корней
4) 1 корень 2 корня Нет корней
5) 2 корня 1 корень Нет корней
6) Нет корней 2 корня 1 корень
Иррациональные неравенства
Выделите решение неравенства $\sqrt{2х-3} > 4$
ПодсказкаПрименить метод решения иррационального неравенства.
- $[9,5; +∞)$
- $(-∞;9,5)$
- $(9,5; +∞)$
- $(-∞;9,5]$
Иррациональные уравнения
Подчеркните корни данного уравнения:$\sqrt[3]{1+x^{4}}=\sqrt[3]{1+x^{2}}$
Подсказкаприменить методы решения иррациональных уравнений, обратите внимание, что корни одинакового показателя.
Иррациональные уравнения
Решите уравнение (если корней несколько — впишите наибольший).
ПодсказкаПрименить методы решения иррациональных уравнений.
Иррациональные неравенства
Решите уравнения и найдите для каждого соответствующий ответ.
ПодсказкаОбратить внимание- строгое или нестрогое неравенство.
Иррациональные неравенства
Решите неравенства и соотнесите с ответом:
ПодсказкаОбратить внимание на обе части неравенства, применить методы решения иррациональных неравенств.
Иррациональные уравнения
Соотнесите уравнение и его корень.
ПодсказкаПрименить методы решения иррациональных уравнений.
Иррациональные уравнения
Найдите корни уравнений, если их больше одного, то напишите наибольший.
ПодсказкаПрименить методы решения иррациональных уравнений
Иррациональные уравнения
Найдите корни уравнений.
ПодсказкаПрименить методы решения иррациональных уравнений.
Иррациональные уравнения
Решите неравенство и соотнесите с ответом.
ПодсказкаПримените формулы сокращенного умножения, методы решения иррациональных неравенств.
Иррациональные неравенства
Решить неравенство:
$\sqrt{7} − x \lt \sqrt{x^{3}} − 6x^{2} + 14x − 7\sqrt{x} − 1$
ПодсказкаИзбавьтесь от знаменателя, помножив левую и правую части неравенства, применить методы решения иррациональных неравенств.
- (−2;1)∪(3;7]
- (1;2)∪(3;7]
- [1;2)∪(3;7)
Иррациональные уравнения 10 класс алгебра
Самостоятельная работа по алгебре и началам анализа в 10 классе по теме «Иррациональные уравнения»
Вариант 1
Решите уравнения:
 =4
=4 =x
=x +
+ =8
=8x+1=

 =2
=2
Вариант 1
Решите уравнения:
 =4
=4 =x
=x +
+ =8
=8x+1=

 =2
=2
Вариант 1
Решите уравнения:
 =4
=4 =x
=x +
+ =8
=8x+1=

 =2
=2
Вариант 1
Решите уравнения:
 =4
=4 =x
=x +
+ =8
=8x+1=

 =2
=2
Вариант 1
Решите уравнения:
 =4
=4 =x
=x +
+ =8
=8x+1=

 =2
=2
Вариант 1
Решите уравнения:
 =4
=4 =x
=x +
+ =8
=8x+1=

 =2
=2
Вариант 1
Решите уравнения:
 =4
=4 =x
=x +
+ =8
=8x+1=

 =2
=2
Вариант 1
Решите уравнения:
 =4
=4 =x
=x +
+ =8
=8x+1=

 =2
=2
Вариант 2
Решите уравнения:
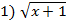 =6
=6
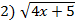 =x
=x
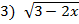 —
—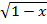 =1
=1
4) x=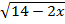 +3
+3
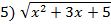 =3
=3
Вариант 2
Решите уравнения:
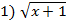 =6
=6
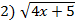 =x
=x
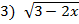 —
—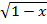 =1
=1
4) x=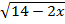 +3
+3
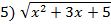
Вариант 2
Решите уравнения:
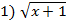 =6
=6
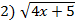 =x
=x
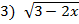 —
—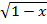 =1
=1
4) x=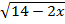 +3
+3
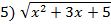 =3
=3
Вариант 2
Решите уравнения:
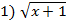 =6
=6
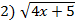 =x
=x
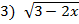 —
—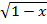 =1
=1
4) x=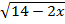 +3
+3
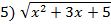 =3
=3
Вариант 2
Решите уравнения:
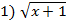 =6
=6
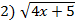 =x
=x
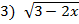 —
—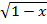 =1
=1
4) x=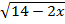 +3
+3
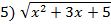 =3
=3
Вариант 2
Решите уравнения:
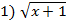 =6
=6
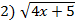 =x
=x
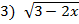 —
—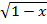 =1
=1
4) x=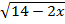 +3
+3
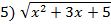 =3
=3
Вариант 2
Решите уравнения:
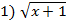 =6
=6
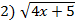 =x
=x
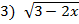 —
—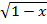 =1
=1
4) x=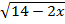 +3
+3
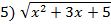 =3
=3
Вариант 2
Решите уравнения:
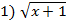 =6
=6
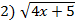 =x
=x
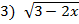 —
—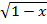 =1
=1
4) x=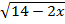 +3
+3
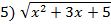 =3
=3
Вариант 3
Решите уравнения:
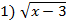 =4
=4
2)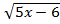 =x
=x
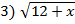 —
—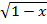 =1
=1
4) x-2=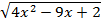
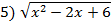 =3
=3
Вариант 3
Решите уравнения:
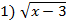 =4
=4
2)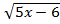 =x
=x
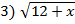 —
—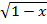 =1
=1
4) x-2=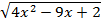
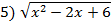 =3
=3
Вариант 3
Решите уравнения:
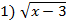 =4
=4
2)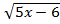 =x
=x
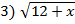 —
—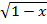 =1
=1
4) x-2=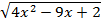
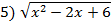 =3
=3
Вариант 3
Решите уравнения:
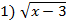 =4
=4
2)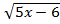 =x
=x
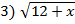 —
—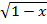 =1
=1
4) x-2=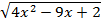
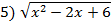 =3
=3
Вариант 3
Решите уравнения:
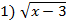 =4
=4
2)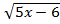 =x
=x
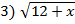 —
—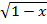 =1
=1
4) x-2=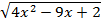
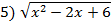 =3
=3
Вариант 3
Решите уравнения:
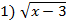 =4
=4
2)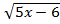 =x
=x
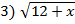 —
—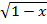 =1
=1
4) x-2=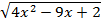
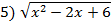 =3
=3
Вариант 3
Решите уравнения:
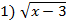 =4
=4
2)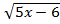 =x
=x
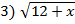 —
—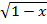 =1
=1
4) x-2=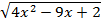
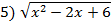 =3
=3
Вариант 3
Решите уравнения:
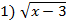 =4
=4
2)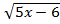 =x
=x
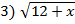 —
—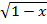 =1
=1
4) x-2=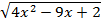
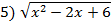 =3
=3
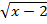 =4
=4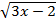 =x
=x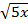 +
+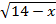 =8
=8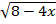
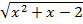 =2
=2