План-конспект урока по алгебре (10 класс) на тему: План-конспект урока в 10-м классе «Способы решения иррациональных уравнений»
План-конспект урока в 10-м классе по теме:
« Способы решения иррациональных уравнений»
Цель:
- обобщение знаний учеников по данной теме;
- демонстрация различных методов решения иррациональных уравнений;
- показ возможности решения иррациональных уравнений на основе исследования;
- формирование навыка самообразования, самоорганизации, умения анализировать, сравнивать, обобщать, делать выводы;
- воспитание самостоятельности, умения выслушивать других и умения общаться в группе;
- повышение интереса к предмету.
Форма проведения: семинарское занятие.
Оборудование: компьютер, мультимедийный проектор.
Ход занятия:
Учитель:
Сегодня мы поговорим об иррациональных уравнениях.
На доске приведены примеры уравнений иррациональных и не являющихся иррациональными.
1)
Назовите те уравнения, которые являются иррациональными.
Дайте определения иррационального уравнения.
Ответы учеников.(иррациональными являются уравнения 1), 3), 4), 6). Определение иррационального уравнения:
Иррациональным называют уравнение, в котором переменная содержится под знаком радикала или под знаком возведения в дробную степень.)
I. Учитель:
На предыдущих уроках мы рассматривали решение иррациональных уравнений методом возведения обеих частей уравнения в степень корня (в основном в квадрат). При возведении частей уравнения в чётную степень мы получаем уравнение-следствие, решение которого приводит иногда к появлению посторонних корней. И тогда обязательной частью решения уравнения является проверка корней или нахождение области определения уравнения.
Однако при решении иррациональных уравнений не всегда следует сразу приступать к «слепому» применению известного алгоритма решения.
В заданиях Единого государственного экзамена имеется довольно много уравнений, при решении которых необходимо выбрать такой способ решения, который позволяет решить уравнения проще, быстрее. Поэтому необходимо знать и другие методы решения иррациональных уравнений, с некоторыми из них мы сегодня познакомимся.
При подготовке к уроку некоторые ученики получили листы-рекомендации, в которых рассматриваются основные приёмы решения иррациональных уравнений. Ребята ознакомились с предложенными решениями и подобрали свои уравнения, решить которые предстоит нам на уроке.
II.Выступление учеников
1 ученик.
Решение иррационального уравнения методом возведения обеих частей уравнения в степень корня.
х + = 3х – 7
Решим данное уравнение традиционным способом – методом возведения обеих частей в квадрат. Слагаемое, содержащее квадратный корень оставим в левой части уравнения, а х перенесём в правую часть.
= 2х – 7
Возведём обе части уравнения в квадрат:
=
Получаем:
х + 4 = 4 – 28х + 49
Перенесём все члены уравнения в одну часть, получаем квадратное уравнение
4 – 29х + 45 = 0
Корни этого уравнения х = 5 и х = 2,25
Решая это уравнение мы возводили обе части уравнения в квадрат. При возведении обеих частей уравнения в любую четную степень получается уравнение, являющееся не равносильное данному, а являющееся следствием исходного, следовательно, при этом возможно появление посторонних корней. Поэтому необходимым условием решения является проверка корней.
Если х = 5, то = 10 — 7
3 = 3 – верно
х = 5 – корень уравнения
Если х = 2,25, то = 4,5 — 7
2,5 = — 2,5 – неверно
х = 2,25 посторонний корень
Ответ: х = 5
Предлагаю решить в классе уравнение:
2 ученик. Решение уравнения методом исследования области определения уравнения.
Пусть дано уравнение: — = –
Возведение обеих частей в квадрат приведёт нас к громоздким вычислениям и трате времени на экзамене.
Воспользуемся методом исследования области допустимых значений заданного уравнения.
Область допустимых значений данного уравнения определяется системой неравенств х=2
Данное уравнение определено только при х = 2.
Проверим, является ли число 2 корнем уравнения:
— = –
5 = 5 – верно.
Ответ: х = 2.
Попробуйте решить уравнение: = х — 2
3 ученик. Использование свойства монотонности функции.
Я хочу рассказать об уравнениях, решение которых основывается на свойстве монотонности функций. Существуют теоремы:
Теорема 1. Пусть уравнение имеет вид: f(x) = с, где f(x) –монотонно возрастающая (убывающая) функция, а с – число, входящее область значений функции f(x), тогда уравнение f(x) = с имеет единственный корень.
Теорема 2. Пусть уравнение имеет вид f(x)= g(x), где функции f(x) и g(x) «встречно монотонны», т.е. f(x) возрастает, а g(x) убывает или наоборот, то такое уравнение имеет не более одного корня.
Если удается заметить эти свойства функций в уравнении или привести уравнение к таким видам, и при этом нетрудно угадать корень уравнения, то он и будет единственным решением данного уравнения.
Пример для изучения
Пусть дано уравнение: + = 6
ОДЗ уравнения: х+60; х
Функции = и = являются возрастающими на промежутке [- 6; , поэтому функция у = + так же является возрастающей на этом промежутке, и следовательно принимает любое значение, в том числе и 6, только один раз. Значит, уравнение имеет единственный корень.
Найдём этот корень подбором.
х = 2.
Проверкой убеждаемся, что число 2 является корнем данного уравнения.
Ответ: х = 2.
Я предлагаю решить на уроке уравнение:
+ = 9 –
Это уравнение можно попытаться решить возведением обеих частей в квадрат (трижды!). Однако при этом получится уравнение четвертой степени.
Попробуйте использовать свойства монотонности функций, входящих в уравнение.
Ответ: х = 1
4 ученик Метод введения новой перменной.
Удобным средством решения иррациональных уравнений иногда является метод введения новой переменной, или «метод замены». Метод обычно применяется в случае, если в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины. Тогда имеет смысл обозначить это выражение какой-нибудь новой буквой и попытаться решить уравнение сначала относительно введенной неизвестной, а потом уже найти исходную неизвестную.
Пример для изучения:
Дано уравнение: + =
ОДЗ уравнения: х х
Пусть , тогда
Получаем уравнение t + =
= = 2
Тогда
или
Возведём обе части уравнения в 5-ю степень. При возведении обеих частей уравнения в нечётную степень получаем уравнение, равносильное данному, следовательно, не требуется проверка найденных корней. Получаем
; х = ; х = 2
Ответ: х = ; х = 2
В классе я предлагаю решить уравнение:
5 ученик Метод оценки частей уравнения.
Рассмотрим уравнение: + = 14х —
Запишем уравнение в виде + = -( +49)
+ = —
Так как левая часть данного уравнения неотрицательная, а
правая — неположительная при любых допустимых значениях x ,
то равенство возможно только в том случае, когда они обе части уравнения
равны нулю. Легко убедиться, что это возможно только при х = 7.
Для решения в классе предлагаю уравнение:
+ = 0
III. Работа учеников в группах.
После прослушивания выступающих начинается работа учеников в группах по решению предложенных уравнений.
Учитель контролирует работу групп, даёт консультации.
IV . Домашнее задание № 1712 – 1719 (а) стр 253 задачника
Урок в 10 классе по теме «Иррациональные уравнения»
Пояснительная записка
Чтобы обеспечить способность учащихся к саморазвитию, самосовершенствованию необходимо проводить такие уроки, которые бы способствовали формированию навыков самостоятельного подхода. Данный урок дает возможность учащимся получить навыки самостоятельной работы в плане отбора, поиска и решения нестандартных уравнений с помощью информационных средств. Самостоятельность, ответственность, организованность во время урока поможет учащимся совершенствовать умения и навыки решения иррациональных уравнений.
В заданиях ЕГЭ имеется довольно много уравнений, при решении которых необходимо выбрать такой способ решения, который позволяет решить его проще, быстрее, поэтому на этом уроке представлены различные методы решения иррациональных уравнений учащимися.
К концу урока учащиеся должны знать основные способы решения уравнений, уметь быстро определить метод решения; а в случаях, если способов решения несколько, найти альтернативный вариант. Также итогом совместной работы учителя и учеников должна явиться «копилка» интересных уравнений. И результатом этого урока может служить самостоятельная подборка иррациональных уравнений и из КИМов ЕГЭ по математике.
Все это поможет сделать шаг вперед по пути саморазвития, самосовершенствования учащихся.
Цель:
Образовательные:
— систематизировать знания учащихся по теме;
— создать содержательные и организационные условия для применения учащимися комплекса знаний и способов действий при решении нестандартных уравнений;
— формировать навыки самообразования, самоорганизации, работы в парах при выполнении домашнего задания, умения анализировать, сравнивать, обобщать, делать выводы, развитие логического мышления, алгоритмической культуры.
Развивающие:
— развивать личностно-смысловые отношения учащихся к изучаемому предмету;
— способствовать формированию навыков самостоятельного подхода к решению нестандартных уравнений с помощью информационных средств;
— развивать мышление и творческие способности учащихся;
— прививать учащимся интерес к предмету через совместную творческую работу;
— формировать умение аккуратно и грамотно выполнять математические записи.
Форма проведения: урок комплексного применения знаний и способов действий. Класс разбит на 3 группы.
Оборудование: компьютер, проектор, интерактивная доска.
Подготовительная работа:
Творческое задание №1. (За три недели до урока). Решить различные иррациональные уравнения, взятые из КИМов ЕГЭ из частей В,С.
Творческое задание №2. (За одну неделю до урока. Индивидуальная работа.) Решить уравнение
 различными способами. Оценить достоинства и недостатки каждого способа. Оформить запись выводов в виде таблицы.
различными способами. Оценить достоинства и недостатки каждого способа. Оформить запись выводов в виде таблицы.В течение выполнения творческого задания провести (по необходимости) консультации для учащихся, у которых возникают вопросы по заданию.
План проведения урока:
Сообщение темы и цели урока.
Презентация по теме «Методы решения иррациональных уравнений».
Анализ методов решения творческого задания № 2.(Каждая группа должна приготовить уравнение для учащихся других групп для домашнего задания).
Практическая часть.
Самостоятельная работа.
Итог урока.
Ход урока
1. Сообщение темы и цели урока.
2. Презентация по теме «Методы решения иррациональных уравнений».
3. Анализ методов решения творческого задания.
(Перед началом урока учащиеся групп №1 и №2 записали на доске предложенные ими способы решения, учащиеся группы №3 записали на интерактивной доске.)
Каждая группа анализирует один из способов решения, оценивает достоинства и недостатки, делает вывод. Учащиеся других групп делают дополнения, если это необходимо. Оценивается анализ и вывод какой группы будет наиболее четким и полным.
Способ I. Метод возведения обеих частей уравнения в одну и ту же степень с последующей проверкой
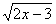
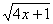 =4,
=4,возведем обе части уравнения в квадрат.
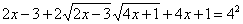 ,
,
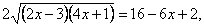
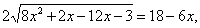
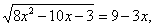
возведем обе части уравнения в квадрат.
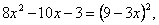
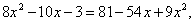
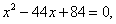
По теореме Виета:

Проверка:
1) Если х=42, то

Значит, число 42 не является корнем уравнения.
2) Если х=2, то
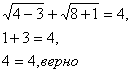
Значит, число 2 является корнем уравнения.
Ответ: 2
Достоинства
1. Понятно
1. Словесная запись
2. Доступно
2. Громоздкая проверка иногда занимает много времени и места
Вывод: При решении иррациональных уравнений методом возведения обеих частей уравнения в одну и туже степень необходимо вести словесную запись, что делает решение понятным и доступным. Однако обязательная проверка иногда бывает громоздкой и занимает много времени. Этот метод можно использовать для несложных иррациональных уравнений, содержащих 1-2 радикала.
Способ II. Метод равносильных преобразований
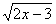 +
+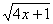
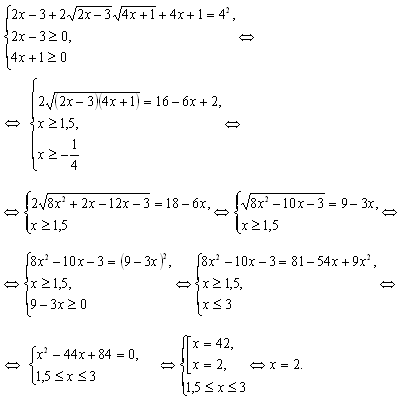
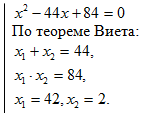
Ответ: 2.
Достоинства
Недостатки
1. Отсутствие словесного описания
1. Громоздкая запись
2. Нет проверки
2. Можно ошибиться при комбинации знаков системы и совокупности и получить неверный ответ
3. Четкая логическая запись
4. Последовательность равносильных переходов
Вывод: При решении иррациональных уравнений методом равносильных переходов нужно четко знать, когда ставить знак системы, а когда совокупности. Громоздкость записи, различные комбинации знаков системы и совокупности не редко приводят к ошибкам. Однако, последовательность равносильных переходов, четкая логическая запись без словесного описания, не требующая проверки, являются бесспорными плюсами данного способа.
Способ III. Метод введения новых переменных
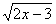 +
+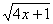 =4.
=4.
Введем новые переменные, обозначив 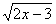 =а,
=а, 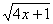
Получим первое уравнение системы: a+b=4.
Составим второе уравнение системы:

Получим систему двух рациональных уравнений, относительно а и b:
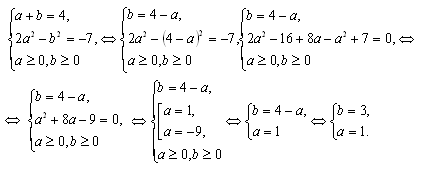
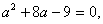
по теореме Виета:
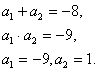
Вернемся к переменной х: 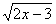 =1
=1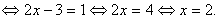
Ответ: 2.
Достоинства
Недостатки
1. Этот метод для данного уравнения
1.Словесное описание.
не рационален.
2. Громоздкое решение.
Вывод: Метод введения новых переменных и переход к системе рациональных уравнений для данного уравнения не рационален. Этот метод лучше применять для иррациональных уравнений, содержащих радикалы различных степеней, или одинаковые многочлены под знаком корня и за знаком корня, или взаимообратные выражения под знаками корня.
Итак, ребята, значит, для каждого иррационального уравнения необходимо выбирать наиболее рациональный способ решения: понятный, доступный, логически грамотно оформленный.
Ребята, поднимите руку, кто из вас при решении этого уравнения отдал бы предпочтение:
методу возведения обеих частей уравнения в одну и туже степень с проверкой;
методу равносильных переходов;
методу введения новых переменных?
4. Практическая часть урока
Работа в группах.
Каждая группа учащихся получает карточку с уравнением и решают его в тетради.
В это время учащийся из группы № 1 решает на центральной доске с комментарием, учащийся из группы № 2 решает на боковой доске молча, а затем комментирует решение.
Один из учащихся группы № 3 решает на интерактивной доске, а затем комментирует решение.
Учащиеся каждой группы решают тот пример, который решает член их группы, следят за правильностью решения на досках. Если решающий у доски допускает ошибки, то тот, кто их заметил, поднимает руку и помогает отвечающему исправить их.
Задание №2 на центральной доске решает учащийся из группы № 2, на боковой доске- из группы № 3, на интерактивной — из группы № 1 и так далее.
В ходе урока каждый учащийся помимо примеров, решаемых его группой, должен записать в тетрадь все примеры, предложенные другим группам и дома решить их.
Задание №1.
Рассмотрим и решим иррациональные уравнения, содержащие модуль:
Группа 1.
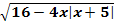 = x+4
= x+4
Группа 2.
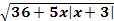 = x+6
= x+6
Группа 3. 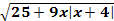 -5 = 2x
-5 = 2x
Задание №2.
Решить уравнения методом расщепления:
Группа 1.
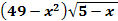 =0
=0
Группа 2.
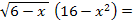 0
0
Группа 3.
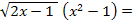 0
0
5. Самостоятельная работа
Решить уравнение, содержащее 3 радикала третьей степени, используя тождество 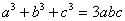 .
.
В каждой группе один учащийся решает на листе, чтобы затем проверить решение. В группах сначала идет обсуждение хода решения, а затем приступают к решению.
Кто решит раньше, тот назначается консультантом и помогает тем, кто затрудняется решить.
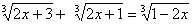
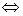
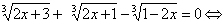
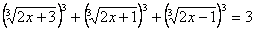
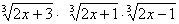
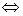
 2x+3+2x+1+2x-1=3
2x+3+2x+1+2x-1=3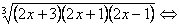 6x+3=3
6x+3=3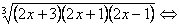

 2x+1=
2x+1=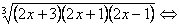
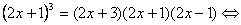
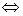 (2x+1)(
(2x+1)( =0
=0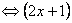
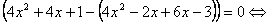
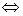 (2x+1)4=0
(2x+1)4=0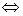 2x=-1
2x=-1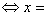 —
—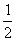
Ответ:-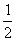 .
.
Проверка решения проводится с помощью проектора.
6.Выставление оценок
7. Итог урока
Решение иррациональных уравнений требует от учащихся хороших теоретических знаний, умений применять их на практике, требует внимания, трудолюбия, сообразительности.
Именно поэтому аналогичные уравнения предлагается решить в частях В и С КИМов для проведения ЕГЭ по математике.
План-конспект урока по алгебре (10 класс): Разработка урока «Иррациональные уравнения»
Урок в 10 классе по теме «Иррациональные уравнения»
Аннотация:
Урок алгебры и начала анализа в 10 общеобразовательном классе.
Цель урока: обобщение и систематизация знаний по теме «Иррациональные уравнения», рассмотреть практическое применение иррациональных уравнений. Подготовка учащихся к ЕГЭ. В заданиях Единого государственного экзамена имеется довольно много уравнений, при решении которых необходимо выбрать такой способ решения, который позволяет решить уравнения проще, быстрее. На уроках учащиеся анализируют различные методы решения иррациональных уравнений. Также среди заданий ЕГЭ есть задачки на практическое применение данной темы. Одна из целей урока – рассмотреть применение иррациональных уравнений при решении задач ЕГЭ на практическое применение в жизни.
Цель урока:
- Обобщение и систематизация знаний, умений и навыков по теме урока.
- Решение задач ЕГЭ по теме урока на практическое применение в жизни.
- Развивать умение обобщать, правильно отбирать способы решения иррациональных уравнений.
- Развивать самостоятельность, воспитывать грамотность речи.
Задачи урока:
1. Расширить и углубить представления учащихся о приемах и методах решения иррациональных уравнений.
2. Помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их использования.
3. Развить интерес и положительную мотивацию изучения математики.
Тип урока: урок-практикум с использованием на уроке ЭОР.
Форма урока: индивидуальная, групповая.
Оборудование: компьютеры, мультимедийный проектор.
Продолжительность: 45 минут.
Ход урока:
- Организационный момент
Альберт Эйнштейн сказал замечательные слова, вслушайтесь в них: “Ощущение тайны – наиболее прекрасное из доступных нам переживаний. Именно это чувство стоит у колыбели истинного искусства и настоящей науки”.
Вот и мы сегодня с вами в очередной раз попытаемся приоткрыть одну из тайн, которую дарит нам наука. Тема нашего сегодняшнего урока: учитель зачитывает тему и цель урока.
На предыдущих уроках мы с вами рассмотрели различные методы и способы решения иррациональных уравнений. На данном уроке мы рассмотрим практическое применение данной темы, поссмотрим задания из ЕГЭ на практическое применение иррациональных уравнений в жизни.
А начнём урок с проверки домашнего задания.
- Проверка домашнего задания
1 ученик:
Метод замены переменной или метод подстановки очень часто используется при решении иррациональных уравнений и неравенств. Он позволяет значительно упростить решение, разбить его на самостоятельные этапы. Решить уравнение. .
Решение.
Проверка:
Выполняем обратную подстановку
Ответ: -5; 2.
2 ученик:
Решить уравнение
Решение. Умножим обе части уравнения на .
Получим, .
Имеем,
Отсюда,
Проверкой убеждаемся, что х = 1 является корнем данного уравнения.
Ответ: 1.
Во время проверки домашнего задания трое учащихся работают за компьютерами, выполняют интерактивный тест, состоящий из 5 заданий по теме урока. (это учащиеся, которые по мнению учителя, наиболее хорошо усвоили тему)
Остальные учащиеся класса работают устно.
3.Устная работа.
Ребята, вы знаете, что учителя работают экспертами ЕГЭ, они проверяют ваши работы. Сегодня я вам предлагаю побыть экспертами.
Перед вами работы учащихся. Вам необходимо найти ошибки в их работе.
После выполнения устной работы учитель проверяет выполнение домашней работы и выполнение интерактивных тестов.
4.Решение задач.
Существует мнение, что математика, изучаемая в старших классах школы, не имеет практического применения в жизни. Но мне не хочется с этим соглашаться.
Оказывается, иррациональные уравнения применяются не только в математике, но и в фигурном катании(чтобы рассчитать длину шага при вращении, в биологии (для расчёта площади тела насекомого или плотности среды обитания), в физике (для вычисления скорости тела в специальной теории относительности Эйнштейна), а также в авиации (вычисление скорости горизонтального полёта самолёта).
Обсуждение решения практической задачи «Определение глубины ущелья».
В повседневной жизни человек решает много практических задач. Одну из таких задач я предлагаю решить тебе. Учитель открывает презентацию, выполненную в программе «Живая математика», делает Демонстрацию экрана. Ученик на своем экране видит презентацию.
После нажатия кнопки «Опредедление глубины ущелья» происходит переход по ссылке на сайт (http://mikahome.narod.ru/10a/), где выложен ролик, необходимый на уроке. В ролике смоделированна ситуация: определение глубины ущелья с помощью камешка. После запуска ролика и определения времени полета камешка, ученику задается вопрос: «Как определить по формуле, глубину ущелья?»
Нужно в формулу подставить вместо t время полета камня.
А сейчас мы посмотрим практическое применение иррациональных уравнений, рассмотрим это на примерах заданий ЕГЭ.
- Задание В 12
Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землeй, до наблюдаемой им линии горизонта вычисляется по формуле l=√2Rh, где R=6400 (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 4 километров? Ответ выразите в километрах.
Решение
Нам нужно найти такую высоту h, что
4=√2⋅6400⋅h
Решаем уравнение и получаем
h=1/800=0.00125 км
Ответ: 0.00125.
- Задание B12 (№ 28331)
Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной км с постоянным ускорением , вычисляется по формуле . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 110 км/ч. Ответ выразите в км/ч.
- Задание B12 (№ 28343)
При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону , где м — длина покоящейся ракеты, км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 21 м? Ответ выразите в км/с.
Ребята, подобные задания вы можете увидеть на моём персональном сайте сайте
http://bobrova-teacher.ucoz.ru
5.Подведение итогов урока.
Сегодня на уроке мы посмотрели практическое применение в жизни иррациональных уравнений. А закончить урок мне бы хотелось словами М.В.Ломоносова «Математику уже затем учить надо, что она ум в порядок приводит»
План-конспект урока по алгебре в 10 классе на тему «Решение иррациональных уравнений и неравенств»
Урок «Решение иррациональных уравнений и неравенств»
10 класс
Цели: совершенствовать навыки решения иррациональных уравнений и неравенств. Отрабатывать умение и навыки при решении иррациональных уравнений и неравенств для подготовки к ЕГЭ.
Задачи:
Образовательные: закрепить алгоритм решения уравнений методом возведения в степень, равную показателю корня, показать способы решения иррациональных неравенств всех возможных видов.
Развивающие: развитие операции мышления (обобщения, анализы, выделение существенного) , развитие внимания, развития навыков сотрудничества, развитие интеллектуальных способностей, умение переносить знания в новой ситуации.
Воспитательные: продолжить развитие культуры математической речи, способствовать формированию коммуникативной компетентности, способствовать развитию личностных качеств обучающихся: самостоятельность, адекватность самооценки, чувство ответственности за результат своего труда.
Тип урока: урок закрепления изученного материала.
Формы организации учебной деятельности: фронтальная, индивидуальная.
Методы: объяснительно-иллюстративный, частично-поисковый
Оборудование: индивидуальные конспекты, классная доска, рабочая тетрадь, учебник «Алгебра и начала анализа. 10-11 класс», Ш. А. Алимов и др.
Ход урока-
Организационный момент.
Проверка домашнего задания.
Повторение изученного материала.
Решение иррациональных уравнений по определению арифметического корня натуральной степени (работа учащихся на доске по вариантам).
Использование свойств монотонности функций при решении иррациональных уравнений:

Утверждение: Если на промежутке две функции имеют различные монотонности, то графики этих функций на данном промежутке имеют не более одной общей точки.
Т.о. уравнение , где и – функции разной монотонности, имеет не более одного корня
1) Решите уравнение: .
Решение: ; ОДЗ: ;
; .
.
Ответ: .
2) Решите уравнение: .
Решение: ;
;
.
Ответ: .
3) Решите уравнение: .
Решение: т.к. арифметическим корнем четной степени является неотрицательное число, то данное уравнение не имеет решений.
4) Решите уравнение: .
Решение: ; ОДЗ: ;
;
; либо ;
по теореме, обратной теореме Виета: ;
;
Доп. условие: ;
.
;
Ответ:
5) Решите уравнение: .
Решение: ОДЗ: .
Доп. условие: ;
.
решений нет
Ответ: нет решений.
Решение иррациональных неравенств. Повторение способов решения иррациональных неравенств с помощью схем.
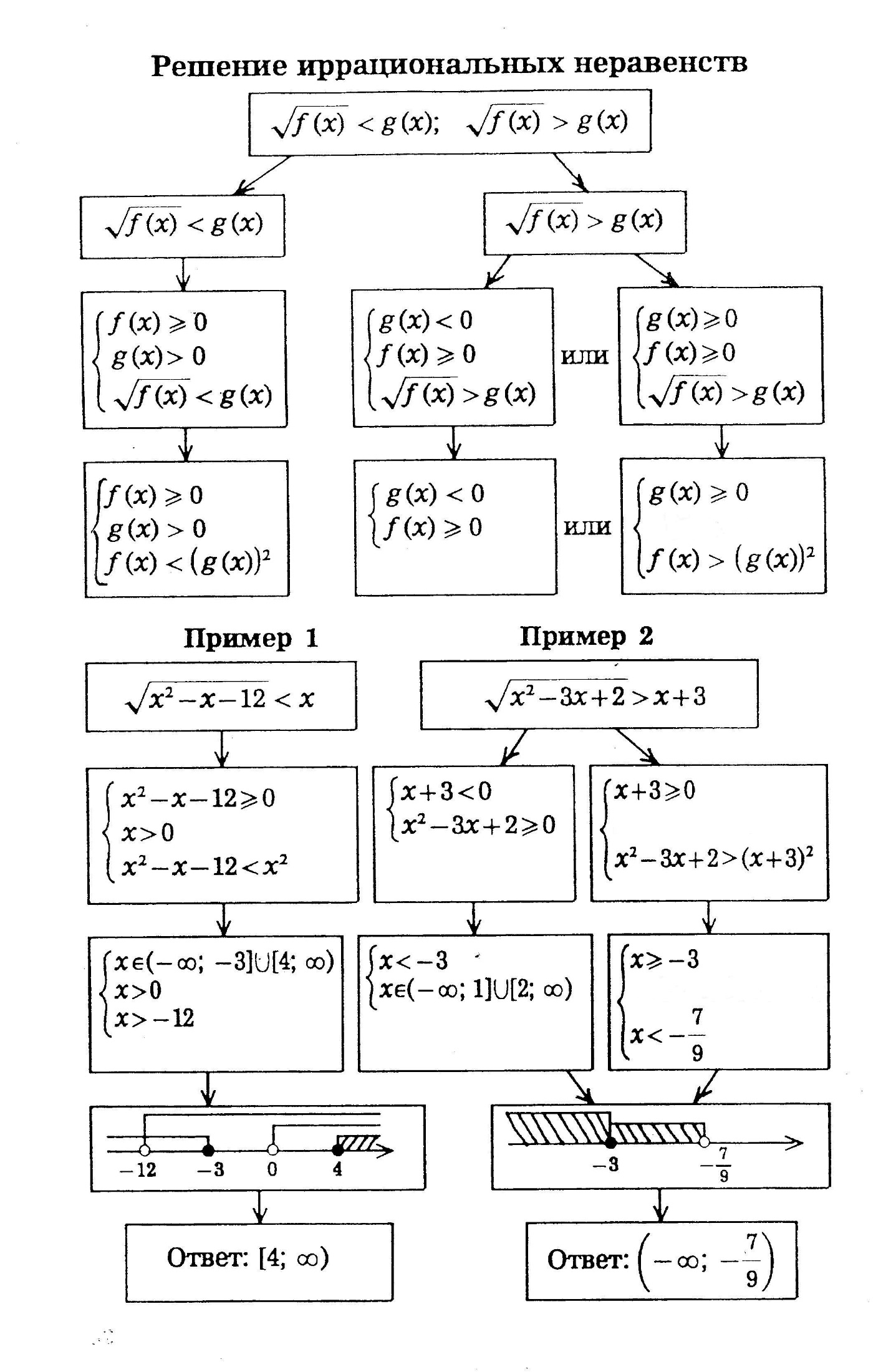
Решение иррациональных уравнений по группам с последующей проверкой.
Решите неравенство: .
Решение: ;
;
.
Ответ: .
2) Решите неравенство: .
Решение: ;
решим квадратное уравнение ;
;
по теореме, обратной теореме Виета:
Ответ: .
3) Решите неравенство: .
Решение:
Ответ:
4. Самостоятельное решение неравенств.
4) Решите неравенство: .
Решение: т.к. арифметическим корнем четной степени является неотрицательное число, то данное неравенство решений не имеет.
Ответ: неравенство решений не имеет.
5) Решите неравенство: .
Решение: ;
;
;
;
; .
Ответ: ; .
Подведение итогов
Домашнее задание: №169, №170
Методическая разработка по алгебре (10 класс): Проверочная работа «Иррациональные уравнения и неравенства»
По теме: методические разработки, презентации и конспекты
 Презентация по теме «Показательные и логарифмические функции, уравнения и неравенства», 10 класс
Презентация по теме «Показательные и логарифмические функции, уравнения и неравенства», 10 классПрезентация к уроку…
 обобщающий урок-игра «Логарифмическая функция, логарифмические уравнения и неравенства».
обобщающий урок-игра «Логарифмическая функция, логарифмические уравнения и неравенства».Методическая разработка+ презентация…
 Тема 15. ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 9-14: «Показательные уравнения. Показательно-степенные уравнения. Показательные неравенства. Преобразования и вычисления логарифмических выражений. Логарифмические уравнения. Логарифмические неравенства».
Тема 15. ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 9-14: «Показательные уравнения. Показательно-степенные уравнения. Показательные неравенства. Преобразования и вычисления логарифмических выражений. Логарифмические уравнения. Логарифмические неравенства».Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступител…
Рабочая программа элективного учебного предмета «Иррациональные уравнения . Трансцендентные уравнения и неравенства» для учащихся 10 классовРабочая программа элективного учебного предмета «Иррациональные уравнения . Трансцендентные уравнения и неравенства» для учащихся 10классов разработана на основе федерального государственн…
 Проверочная работа по теме « Показательная функция, показательные уравнения и неравенства » 11 класс
Проверочная работа по теме « Показательная функция, показательные уравнения и неравенства » 11 классПроверочная работа по теме « Показательная функция, показательные уравнения и неравенства » для учащихся 11 класса составлена в двух вариантах и содержит по 8 заданий. Работа может быть ис…
 Проверочная работа по теме: « Показательная и логарифмическая функции, уравнения и неравенства »
Проверочная работа по теме: « Показательная и логарифмическая функции, уравнения и неравенства »Проверочная работа по теме: «Показательная и логарифмическая функции, уравнения, неравенства» для учащихся 11 класса представлена в двух вариантах с выбором правильного ответа и предназначен…
Рабочая программа «Иррациональные уравнения . Трансцендентные уравнения и неравенства»Рабочая программа элективного учебного предмета «Иррациональные уравнения . Трансцендентные уравнения и неравенства» для учащихся 10классов разработана на основе федерального государственн…
Статья по алгебре (10 класс) по теме: Решение иррациональных уравнений
Урок математики в 10 классе.
Решение иррациональных уравнений.
Решение иррациональных уравнений изучается в теме « Степенная функция» в 10 классе, на тему отводится 20 часов, обучение ведется по учебнику Ш.А.Алимова, Ю.М.Колягина, Ю.В.Сидорова. Данный урок – третий урок по теме, учащиеся уже познакомились с иррациональными уравнениями, знают традиционные способы решения данных уравнений ( уединение радикала, возведение в степень и т.д.).
Для учащихся решение иррациональных уравнений оказывается сложнее, чем, например, решение показательных и логарифмических уравнений, поскольку здесь появление посторонних корней, как правило, не связано с областью определения уравнений, что создает у учащихся, которые не сталкивались с этим ранее, некоторый психологический дискомфорт. Иррациональные уравнения, включенные в задания ЕГЭ ( часть В ), являются уравнениями одного из трех типов: « корень нечетной степени равен числу», «корень четной степени равен числу», «арифметический квадратный корень равен линейному выражению». Задания С5 – одни из наиболее сложных экзаменационных задач. Их решение сводится к перебору и анализу различных вариантов в той или иной алгебраической ситуации. Иногда для облегчения решений заданий с параметрами удобно придать алгебраическим соотношениям геометрический смысл. На данном уроке уделяется внимание различным ситуациям: учет области определения уравнения, наложение дополнительных условий, использование равносильности преобразований, использование графоаналитического метода при решении задач с параметрами.
Цели урока:
-рассмотреть различные ситуации при решении иррациональных уравнений; перейти к решению уравнений с параметрами;
— формировать навыки самостоятельной работы;
— формировать умение действовать в нестандартной ситуации;
— формировать наблюдательность, логическое мышление.
Ход урока
- Учащимся предложено решить 9 уравнений, 10 минут отводится на решение.
Решить уравнения:
Учащиеся сдают ответы, затем ответы появляются на доске, учащиеся комментируют, полученные ответы.
сумма двух неотрицательных чисел равна нулю, когда каждое слагаемое равно нулю, следовательно, решением данного уравнения является решение системы:
- Нет решений.
данное уравнение не имеет решений, так как левая часть- число неотрицательное, а правая часть- число отрицательное
возвели уравнение в третью степень
следует обратить внимание на дополнительное условие для существования корней:
число -1 является посторонним корнем, несмотря на то, что удовлетворяет области определения уравнения, но не удовлетворяет дополнительны условия
область определения уравнения , поэтому 3 не является корнем уравнения.
- Нет решения.
область допустимых значений данного уравнения является пустым множеством, так как :
- Условие для существования корней
Уравнение может быть правильно решено даже при отсутствии
упоминания об области определения уравнения. Более того, верно найденная ООУ и отбор корней по ней не гарантирует появления посторонних корней, и сама задача нахождения ООУ оказывается сложной, ненужной.
ООУ задается системой: первое неравенство решить сложно,
В то же время исходное уравнение равносильно системе, которая решается устно.
ООУ состоит из двух чисел: . Проверкой убеждаемся, что корнем уравнения является только значение .
Вывод6 универсальных рекомендаций и рецептов, вообще говоря, нет. Например, нахождение ООУ, как правило, не нужно, но может оказаться полезным. Иногда удобнее пользоваться равносильными системами, иногда использовать следствия и проверку.
Обсудив решение уравнений аналитическими способами, переходим к графическому способу. Сначала вспомним графики некоторых уравнений.
- Поставить в соответствие графики уравнений и формулы, задающие эти графики, записать в таблицу:
- 2)
3) 4)
- Переходим к решению уравнений с параметрами. Решить уравнение:
нет решений
Графическая иллюстрация
а)
решений нет
b)
Ответ: при , ;
при , решений нет.
- Найти корни уравнения, для каждого значения параметра.
Ответ: при , ;
при
- При каких значениях параметра а уравнение имеет три корня:
Ответ: уравнение имеет три корня при
- При каких значениях параметра а уравнение имеет одно значение.
Рассмотрим графическое решение. Построим графики функций.
полуокружность, с центром в точке (0,0), радиуса 5
прямая
Одно решение при , кроме этого данное уравнение будет иметь одно решение, когда прямая является касательной к полуокружности.
Рассмотрев равнобедренный прямоугольный треугольник, находим значение а, при котором данная прямая будет касательной .
Ответ: уравнение имеет одно решение при
Подведем итоги:
Способы решений иррациональных уравнений | |||
аналитический | графический | ||
Возведение в степень | Введение новой переменной | Другие: анализ ОДЗ | Построение графиков функций их исследование |
На уроке были рассмотрены различные ситуации при решении иррациональных уравнений: учет области определения уравнения, наложения дополнительного условия, использование равносильных преобразований, использование графоаналитического метода, что позволяет решать задачи повышенного уровня- задачи с параметром.
Домашнее задание:
Решить уравнения:
5. при каких значениях параметра а, уравнение имеет два корня.
Ответы: 1.4; 2.2; 3.1; 4. ; 5.
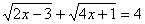 различными способами. Оценить достоинства и недостатки каждого способа. Оформить запись выводов в виде таблицы.
различными способами. Оценить достоинства и недостатки каждого способа. Оформить запись выводов в виде таблицы.