Наибольшее и наименьшее значение функции, формулы и примеры
Если функция $y=f(x)$ определена и непрерывна на отрезке $[a ; b]$ , то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение $M$ функция $f(x)$ принимает в точке $x_{0} \in[a ; b]$, то $M=f\left(x_{0}\right)$ будет локальным максимумом функции $f(x)$, так как в этом случае существует окрестность точки $x_{0}$, такая, что $f(x) \leq f\left(x_{0}\right)$ .
Однако свое наибольшее значение $M$ функция
$f(x)$ может принимать и на концах отрезка
$[a ; b]$ . Поэтому, чтобы найти наибольшее значение
$M$ непрерывной на отрезке
$[a ; b]$ функции
$f(x)$, надо найти все максимумы функции на интервале
$(a ; b)$ и значения
$f(x)$ на концах отрезка
$[a ; b]$, то есть
$f(a)$ и
$f(b)$, и выбрать среди них наибольшее. Вместо исследования
на максимум можно ограничиться нахождением значений функции в критических точках.
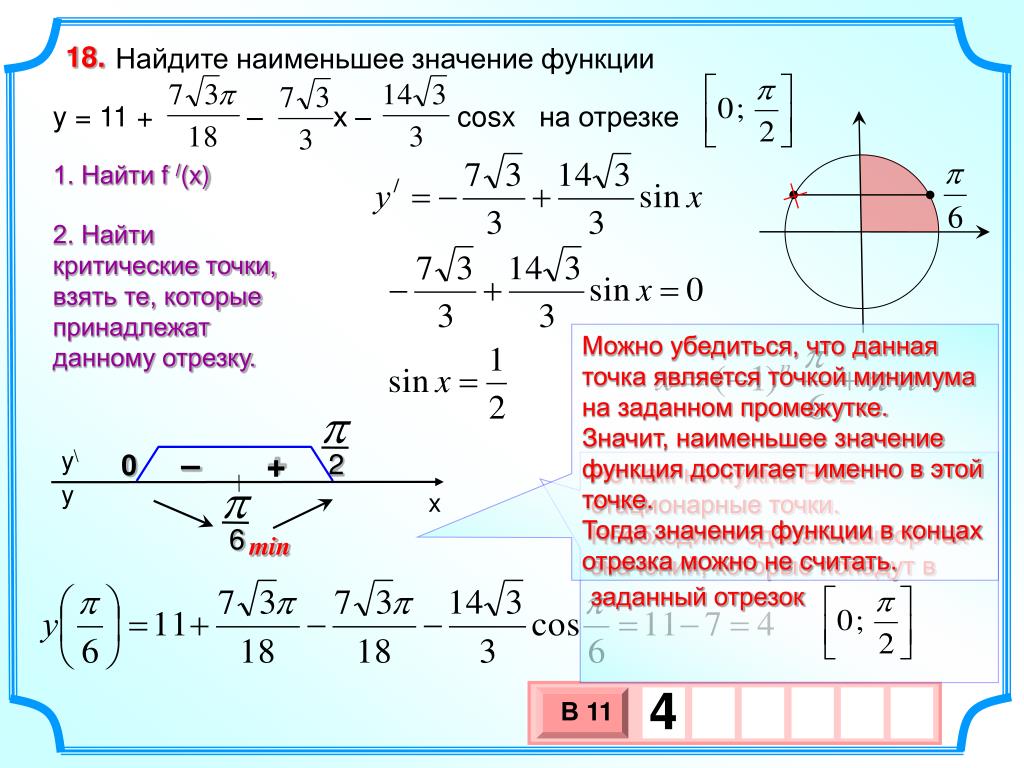
Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку $[0 ; 5]$ . Оба значения лежат в этом промежутке.
Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:
$y(0)=4 ; \quad y\left(\frac{1}{3}\right)=\frac{106}{27} \approx 3,92 ; y(5)=454$
Таким образом,
Ответ.
Читать дальше: выпуклость функции, точки перегиба.
Слишком сложно?
Наибольшее и наименьшее значение функции, непрерывной на отрезке не по зубам? Тебе ответит эксперт через 10 минут!
Наибольшее и наименьшее значение функции
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др.
Обычно мы определяем эти значения в рамках некоторого интервала x, который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [a; b], так и открытый интервал (a; b), (a; b], [a; b), бесконечный интервал (a; b), (a; b], [a; b) либо бесконечный промежуток -∞; a, (-∞; a], [a; +∞), (-∞; +∞).
В этом материале мы расскажем, как вычисляется наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x)y=f(x).
Основные определения
Начнем, как всегда, с формулировки основных определений.
Наибольшее значение функции y=f(x) на некотором промежутке x – это значение max y=f(x0)x∈X, которое при любом значении xx∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).
Определение 2Наименьшее значение функции y=f(x) на некотором промежутке x– это значение minx∈Xy=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(Xf(x)≥f(x0).
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее самое большое значение на известном интервале при абсциссе x0, а наименьшее – это самое маленькое принимаемое значение на том же интервале при x0.
Определение 3Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0.
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [-6;6].
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [-3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.
Наибольшее и наименьшее значение функции на открытом интервале
Теперь посмотрим на четвертый рисунок.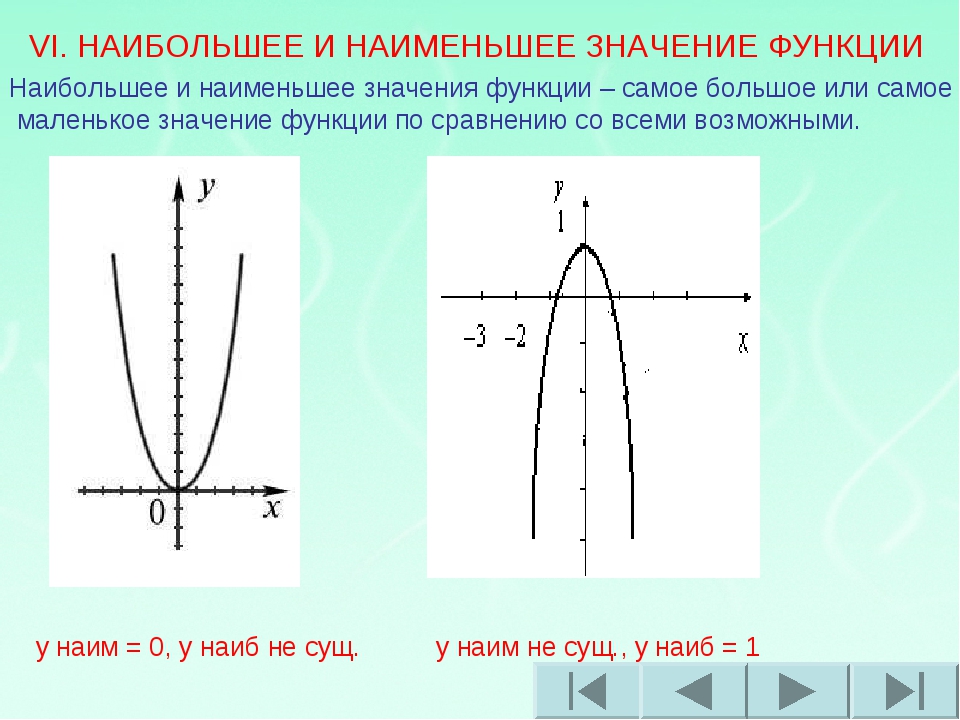 В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).
В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).
Если мы возьмем интервал [1;6), то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x, равном 6, если бы x=6 принадлежала интервалу. Именно этот случай нарисован на графике 5.
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (-3;2], а о наибольшем значении мы не можем сделать определенных выводов.
Наибольшее и наименьшее значение функции на бесконечности
На рисунке 7 мы видим, что функция будет иметь max y в стационарной точке, имеющей абсциссу, равную 1. Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y=3.
Если мы возьмем интервал x∈2; +∞, то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения.
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок.
 Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу. - Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x=a и x=b.
- 5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 1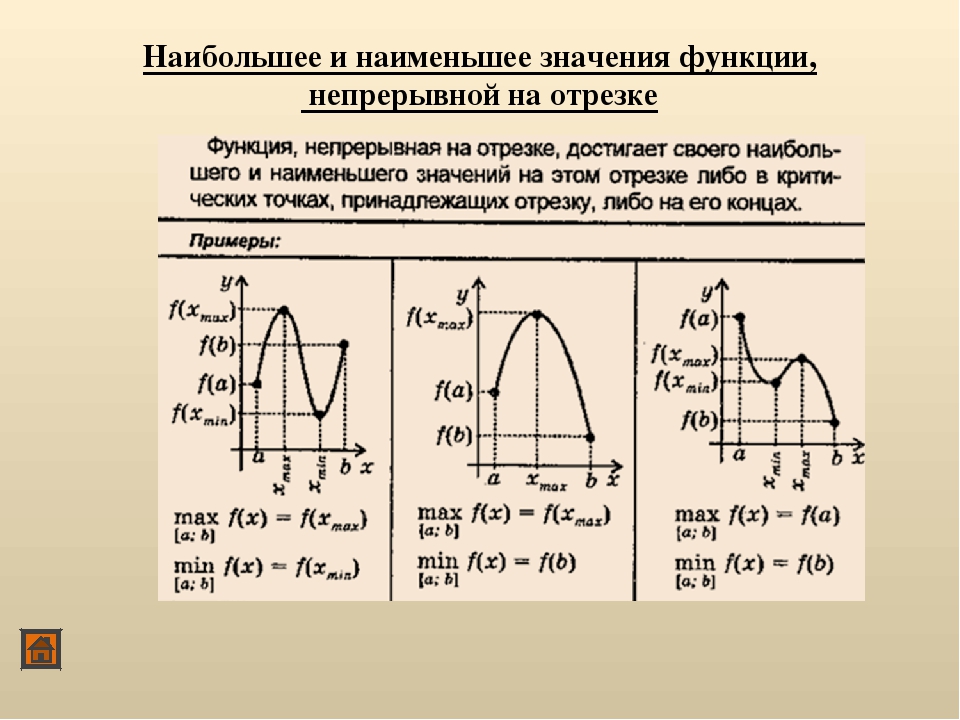
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0. Иными словами, D(y): x∈(-∞; 0)∪0; +∞. Оба отрезка, заданных в условии, будут находиться внутри области определения.
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y’=x3+4×2’=x3+4’·x2-x3+4·x2’x4==3×2·x2-(x3-4)·2xx4=x3-8×3
Мы узнали, что производная функции будет существовать во всех точках отрезков [1;4] и [-4;-1].
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x3-8×3=0. У него есть только один действительный корень, равный 2. Он будет стационарной точкой функции и попадет в первый отрезок [1;4].
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x=1, x=2 и x=4:
y(1)=13+412=5y(2)=23+422=3y(4)=43+442=414
Мы получили, что наибольшее значение функции max yx∈[1; 4]=y(2)=3 будет достигнуто при x=1, а наименьшее min yx∈[1; 4]=y(2)=3 – при x=2.
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y(-1)=(-1)3+4(-1)2=3
Значит, max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
Ответ: Для отрезка [1;4] — max yx∈[1; 4]=y(2)=3, min yx∈[1; 4]=y(2)=3, для отрезка [-4;-1] — max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
См. на рисунке:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.

- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0, решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.
- Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b-0f(x).
- Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+0f(x).
- Если интервал имеет вид (a;b), то нам надо вычислить односторонние пределы limx→b-0f(x),limx→a+0f(x).

- Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
- Если интервал выглядит как (-∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→-∞f(x).
- Если -∞; b, то считаем односторонний предел limx→b-0f(x) и предел на минус бесконечности limx→-∞f(x)
- Если же -∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x), limx→-∞f(x).
- В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4-8 в первой части материала.
Условие: дана функция y=3e1x2+x-6-4. Вычислите ее наибольшее и наименьшее значение в интервалах -∞; -4, -∞; -3, (-3;1], (-3;2), [1;2), 2; +∞, [4; +∞).
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0:
x2+x-6=0D=12-4·1·(-6)=25×1=-1-52=-3×2=-1+52=2⇒D(y): x∈(-∞; -3)∪(-3; 2)∪(2; +∞)
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
y’=3e1x2+x-6-4’=3·e1x2+x-6’=3·e1x2+x-6·1×2+x-6’==3·e1x2+x-6·1’·x2+x-6-1·x2+x-6′(x2+x-6)2=-3·(2x+1)·e1x2+x-6×2+x-62
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x=-12. Это стационарная точка, которая находится в интервалах (-3;1] и (-3;2).
Вычислим значение функции при x=-4 для промежутка (-∞; -4], а также предел на минус бесконечности:
y(-4)=3e1(-4)2+(-4)-6-4=3e16-4≈-0.456limx→-∞3e1x2+x-6=3e0-4=-1
Поскольку 3e16-4>-1, значит, max yx∈(-∞; -4]=y(-4)=3e16-4. Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:
limx→-3-03e1x2+x-6-4=limx→-3-03e1(x+3)(x-3)-4=3e1(-3-0+3)(-3-0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→-∞3e1x2+x-6-4=3e0-4=-1
Значит, значения функции будут расположены в интервале -1; +∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x=-12, если x=1. Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к -3 с правой стороны:
y-12=3e1-122+-12-6-4=3e425-4≈-1. 444y(1)=3e112+1-6-4≈-1.644limx→-3+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1-3+0+3(-3+0-2)-4==3e1(-0)-4=3e-∞-4=3·0-4=-4
444y(1)=3e112+1-6-4≈-1.644limx→-3+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1-3+0+3(-3+0-2)-4==3e1(-0)-4=3e-∞-4=3·0-4=-4
У нас получилось, что наибольшее значение функция примет в стационарной точке max yx∈(3; 1]=y-12=3e-425-4. Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до -4.
Для интервала (-3;2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y-12=3e1-122+-12-6-4=3e-425-4≈-1.444limx→-3+03e1x2+x-6-4=-4limx→2-03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2-0+3)(2-0-2)-4==3e1-0-4=3e-∞-4=3·0-4=-4
Значит, max yx∈(-3; 2)=y-12=3e-425-4, а наименьшее значение определить невозможно, и значения функции ограничены снизу числом -4.
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [1;2) наибольшее значение функция примет при x=1, а найти наименьшее невозможно.
На промежутке (2; +∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка -1; +∞.
limx→2+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2+0+3)(2+0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→+∞3e1x2+x-6-4=3e0-4=-1
Вычислив, чему будет равно значение функции при x=4, выясним, что max yx∈[4; +∞)=y(4)=3e114-4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y=-1.
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Урок 17. наибольшее и наименьшее значения функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №17. Наибольшее и наименьшее значения функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение наибольшего и наименьшего значения функции,
2)Определение алгоритма нахождения наибольшего и наименьшего значений функции на отрезке,
3) Рассмотреть прикладные задачи на нахождение наибольшего и наименьшего значений
Глоссарий по теме
Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти область определения функции D(f).
- Найти производную f‘ (x).
- Найти стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b).

- Среди полученных значений выбрать наибольшее и наименьшее.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Нахождение наибольшего и наименьшего значений функции на отрезке.
- Если функция непрерывна на отрезке, то она достигает на нем своего наибольшего и своего наименьшего значения.
- Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
- Если наибольшее (наименьшее) значение функции достигается внутри отрезка, то только в стационарной или критической точке.

Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти производную f‘ (x) стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b)и среди полученных значений выбрать наибольшее и наименьшее
Примеры и разбор решения заданий тренировочного модуля
№1.Найти наибольшее и наименьшее значения функции f (x) = 2x3 – 9x2 + 12x – 2 на отрезке [0; 3]
Решение. Действуем в соответствии с алгоритмом.
1) D(f) = (-∞; +∞).
2) f (x) = 6x2 – 18x + 12
3) Стационарные точки: х = 1; х = 2.
4) f(0) = -2
f(3) = 7
f(1) = 3
f(2) = 2
5) fнаим.=f(0) = -2
fнаиб.=f(3) = 7.
Ответ: fнаим= -2
fнаиб.= 7.
№2.Найдите два положительных числа, сумма которых равна 16, а произведение наибольшее.
Решение.
Пусть первое число равно х,
Тогда второе число —
Следовательно,
Произведение этих чисел равно х(16 – х).
Составим функцию:
f(x) = x(16 – x)
x = 8 – единственная стационарная точка на интервале (0; 16), она является точкой максимума.
Следовательно, в этой точке функция F(x) = x(16 – x) принимает наибольшее значение.
Следовательно, два положительных числа, сумма которых равна 16, а произведение наибольшее, это 8 и 8.
Ответ: 8 и 8
Наибольшее и наименьшее значение функции | ЕГЭ по математике (профильной)
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Проверить, какие стационарные точки входят в заданный отрезок.

- Вычислить значение функции на концах отрезка и в стационарных точках из п.3
- Выбрать из полученных результатов наибольшее или наименьшее значение.
Чтобы найти точки максимума или минимума необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Разложить производную функции на множители.
- Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
- Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.
Таблица производных некоторых элементарных функций:
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n, n∈N$ | $nx^{n-1}, n∈N$ |
| ${1}/{x}$ | $-{1}/{x^2}$ |
| ${1}/x{^n}, n∈N$ | $-{n}/{x^{n+1}}, n∈N$ |
| $√^n{x}, n∈N$ | ${1}/{n√^n{x^{n-1}}, n∈N$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | ${1}/{cos^2x}$ |
| $ctgx$ | $-{1}/{sin^2x}$ |
| $cos^2x$ | $-sin2x$ |
| $sin^2x$ | $sin2x$ |
| $e^x$ | $e^x$ |
| $a^x$ | $a^xlna$ |
| $lnx$ | ${1}/{x}$ |
| $log_{a}x$ | ${1}/{xlna}$ |
Основные правила дифференцирования
1. 2}$
2}$
4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))′=f′(g(x))∙g′(x)$
Пример:
$f(x)= cos(5x)$
$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$
Пример:
Найдите точку минимума функции $y=2x-ln(x+11)+4$
Решение:
1. Найдем ОДЗ функции: $х+11>0; х>-11$
2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$
3. Найдем стационарные точки, приравняв производную к нулю
${2x+21}/{x+11}=0$
Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю
$2x+21=0; x≠-11$
$2х=-21$
$х=-10,5$
4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.
$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$
5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума. 3-5=6-90-5= -89$
3-5=6-90-5= -89$
Наибольшее значение равно $967$
Ответ: $967$
Найти наибольшее и наименьшее значение функции на отрезке
Онлайн калькулятор поможет найти наибольшее и наименьшее значение функции на отрезке.
Наибольшее значение функции y=f(x) – это значение maxx∈X y=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).
Наименьшее значение функции y=f(x) – это значение minx∈X y=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(x)≥f(x0).
Наибольшее и наименьшее значение непрерывной функции f(x) на промежутке a,b достигаются в критических точках, то есть в точках в которых производная функции равна нулю f′(x)=0, бесконечности f′(x)=±∞, не существует, либо на концах отрезка a,b.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция «И» ∧: &&
дизъюнкция «ИЛИ» ∨: ||
отрицание «НЕ» ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
Смотрите также
Значения функции и точки максимума и минимума
Значения функции и точки максимума и минимума
Наибольшее значение функции
Наменьшее значение функции
Точки max
Точки min
Как говорил крестный отец: «Ничего личного». Только производные!
Только производные!
Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.
12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.
12 задание бывает двух видов:
- Найти точку максимума / минимума (просят найти значения «x»).
- Найти наибольшее / наименьшее значение функции (просят найти значения «y»).
Найти точку максимума / минимума
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный или найденные «х» и будут являться точками минимума или максимума.
- Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.
Задания с ЕГЭ:
Найдите точку максимума функции
- Берем производную:
- Приравняем ее к нулю:
- Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):
Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15
Найдите точку минимума функции
- Преобразуем и возьмем производную:
- Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.

- Отлично! Сначала функция убывает, затем возрасает — это точка минимума!
Найти наибольшее / наименьшее значение функции
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный «х» и будет являться точкой минимума или максимума.
- Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
- В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
- Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.
Задания с ЕГЭ:
Найдите наибольшее значение функции на отрезке [−4; −1]
- Преобразуем и возьмем производную:
- «3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?
- Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции.
 Остается только подставить в первоначальную функцию:
Остается только подставить в первоначальную функцию:
Ответ: −6
Найдите наибольшее значение функции на отрезке [0; 1,5π]
- Берем производную:
- Находим, чему равняется sin(x):
- Но такое невозможно! Sin(x)…
- Получается, что уравнение не имеет решения, и в таких ситуациях нужно подставлять крайние значения промежутка в первоначальное уравнение:
- Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».
Ответ: 11
Выводы:
- 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
- Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
- Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
- В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана.
 Получили одну точку — можно смело писать в ответ.
Получили одну точку — можно смело писать в ответ. - А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.
Будь в курсе новых статеек, видео и легкого математического юмора.
Исследование графика функции. Минимум и максимум
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции
- область значений функции
- нули функции
- промежутки возрастания и убывания
- точки максимума и минимума
- наибольшее и наименьшее значение функции на отрезке.
Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .
Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.
Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.
Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
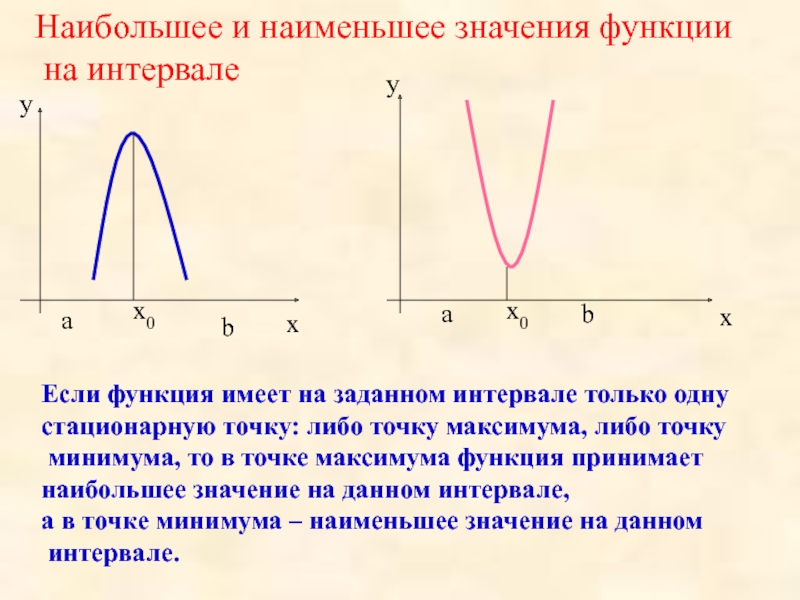
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .
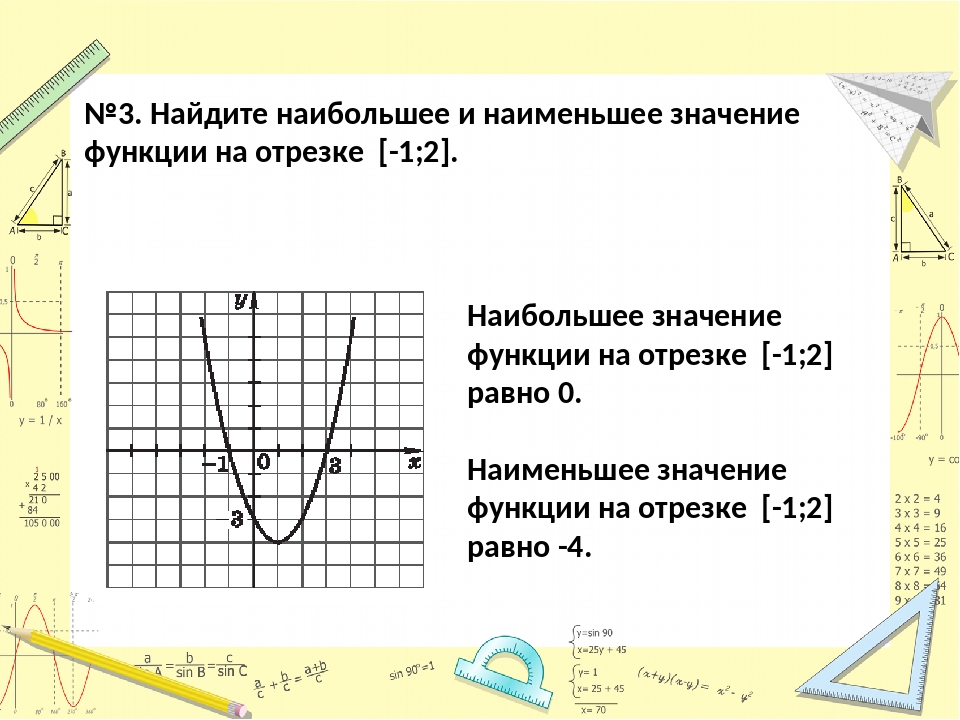
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .
Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Как использовать функцию НАИБОЛЬШИЙ в Excel
Функция НАИБОЛЬШИЙ полностью автоматическая — вам просто нужно указать диапазон и целое число для «nth», чтобы указать желаемое ранжированное значение. Проблема в этом случае заключается в том, что мы не хотим, чтобы LARGE работал с каждым значением в . ..
..
Функцию НАИБОЛЬШИЙ можно использовать для получения «n-го» наибольшего значения в числовых данных следующим образом: = НАИБОЛЬШИЙ (значения; n) В этом примере нам нужно включить только значения, связанные с группой B.Для этого мы используем функцию ЕСЛИ, чтобы …
Функция СРЗНАЧ будет вычислять среднее значение чисел, представленных в массиве, поэтому почти вся работа в этой формуле заключается в создании массива из трех последних числовых значений в диапазоне. Работая изнутри наружу, …
В простейшей форме LARGE вернет «N-е по величине» значение в диапазоне. Например, формула: = НАИБОЛЬШИЙ (B4: B13; 2) вернет 2-е по величине значение в диапазоне B4: B13, которое в приведенном выше примере является…
Функция НАИБОЛЬШИЙ — это простой способ получить n-е наибольшее значение в диапазоне: = НАИБОЛЬШИЙ (диапазон; 1) // 1-й по величине
= НАИБОЛЬШИЙ (диапазон; 2) // 2-й по величине
= НАИБОЛЬШИЙ (диапазон; 3) // 3-й по величине В этом примере мы можем использовать БОЛЬШОЙ . ..
..
Эта формула использует функцию ФИЛЬТР для извлечения данных на основе логического теста, построенного с помощью функции НАИБОЛЬШИЙ. Функция НАИБОЛЬШИЙ — это простой способ получить n-е по величине значение в диапазоне.Просто укажите диапазон …
Этот пример для ясности состоит из двух частей: (1) формула для определения трех верхних сумм за каждый месяц и (2) формула для получения имени клиента для каждой из трех верхних месячных сумм. Обратите внимание, что нет …
В простейшей форме LARGE возвращает «N-е по величине» значение в диапазоне с помощью этой конструкции: = НАИБОЛЬШИЙ (диапазон; N) Так, например: = НАИБОЛЬШИЙ (C5: C12,2) вернет 2-е по величине значение в диапазоне C5: C12, т.е…
Эта формула использует функцию ФИЛЬТР для извлечения данных на основе логического теста, построенного с помощью функций НАИБОЛЬШИЙ и ЕСЛИ. Результат — 3 лучших результата в группе B. Функция ФИЛЬТР применяет критерии с …
Результат — 3 лучших результата в группе B. Функция ФИЛЬТР применяет критерии с …
В этой формуле используются два именованных диапазона: данные (B4: G11) и входные (F2). Это сделано только для удобства чтения. Если вы не хотите использовать именованные диапазоны, убедитесь, что вы используете абсолютные ссылки для обоих этих диапазонов в…
Функция МАЛЕНЬКИЙ предназначена для извлечения «n-го» наименьшего значения из набора данных. Значение N предоставляется в качестве второго аргумента. Чтобы получить наименьшее значение с помощью SMALL, укажите 1, чтобы получить второе наименьшее значение, …
Функция НАИБОЛЬШИЙ предназначена для извлечения верхнего n-го значения из набора чисел. Так, например, НАИБОЛЬШИЙ (A1: A10,1) вернет наивысшее значение, НАИБОЛЬШИЙ (A1: A10,2) вернет второе по величине значение и так далее: БОЛЬШОЙ (диапазон…
Вкратце, эта формула использует функцию НАИБОЛЬШИЙ для нахождения n-го наибольшего значения в наборе данных. Получив это значение, мы вставляем его в стандартную формулу ИНДЕКС и ПОИСКПОЗ, чтобы получить связанное имя. В прочем …
Получив это значение, мы вставляем его в стандартную формулу ИНДЕКС и ПОИСКПОЗ, чтобы получить связанное имя. В прочем …
Функция НАИБОЛЬШИЙ полностью автоматическая — вам просто нужно указать диапазон и целое число для «nth», чтобы указать желаемое ранжированное значение. Официальные названия этих аргументов — «массив» и «k».Например, мы можем использовать …
Определение наибольших и наименьших значений в списке Excel — Accounting Advisors, Inc.
Дэвид Рингстром, CPA
Периодически вы можете захотеть ранжировать серию элементов в электронной таблице Excel. Многие пользователи часто полагаются на сортировку данных в порядке возрастания или убывания. Я опишу альтернативу, которая использует функции НАИБОЛЬШИЙ и МАЛЕНЬКИЙ для создания упорядоченного списка того, что вы хотите ранжировать.
Вы, вероятно, уже знакомы с функциями MIN и MAX в Excel, которые возвращают наименьшее или наибольшее значение в списке соответственно.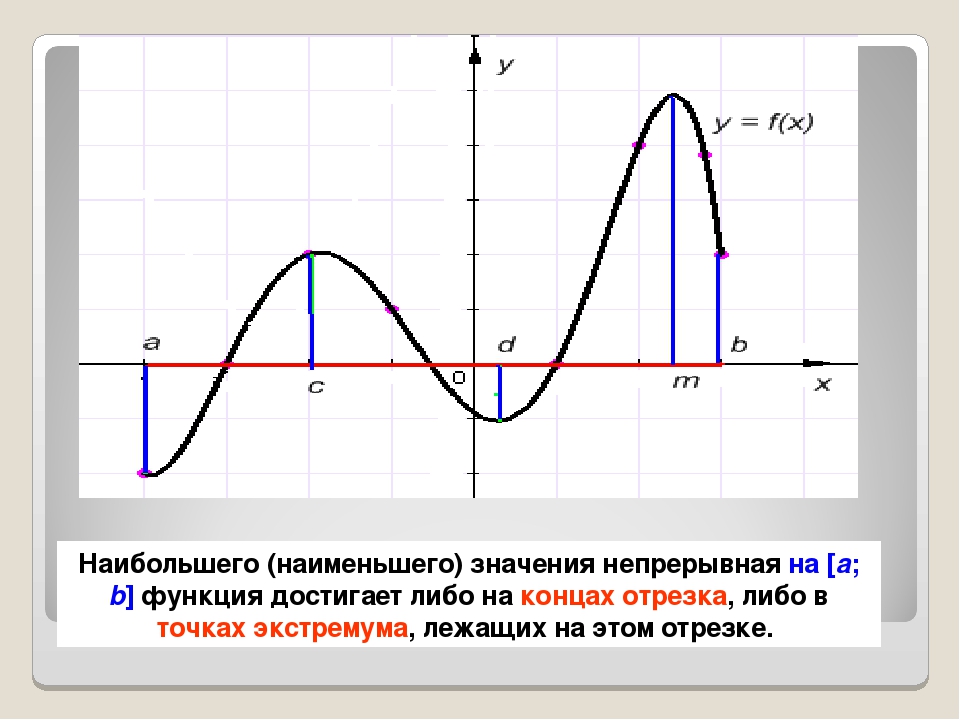 Как показано на рисунке 1, MIN указывает, что наименьшее значение — 191, а наибольшее — 958. MIN и MAX ограничены одним наименьшим или наибольшим значением соответственно, но LARGE и SMALL позволяют вам возвращать второе наибольшее или третье наименьшее значение. если вы выберете. Я объясню эти функции чуть позже, но сначала давайте рассмотрим MIN и MAX.
Как показано на рисунке 1, MIN указывает, что наименьшее значение — 191, а наибольшее — 958. MIN и MAX ограничены одним наименьшим или наибольшим значением соответственно, но LARGE и SMALL позволяют вам возвращать второе наибольшее или третье наименьшее значение. если вы выберете. Я объясню эти функции чуть позже, но сначала давайте рассмотрим MIN и MAX.
Рисунок 1: MIN и MAX возвращают наибольшее и наименьшее значения из списка соответственно.
Как показано на рисунке 1, функции MIN и MAX похожи по своей природе на известную функцию SUM, за исключением того, что они возвращают единственное наименьшее или наибольшее значение, соответственно, вместо того, чтобы складывать значения.Функции МАЛЕНЬКИЙ и НАИБОЛЬШИЙ работают аналогичным образом, но с дополнительным аргументом:
.= МАЛЕНЬКИЙ (массив, k)
= БОЛЬШОЙ (массив, k)
В этих функциях массив — это диапазон ячеек, а k — n-е значение, которое вы хотите вернуть. Как показано на рисунке 2, = LARGE (B2: B11,2) вернет 872 как второе по величине значение, а = SMALL (B2: B11,3) вернет 266 как третье наименьшее значение. Для сравнения, следующие формулы возвращают 958 и 191 для наибольшего и наименьшего значений соответственно:
Для сравнения, следующие формулы возвращают 958 и 191 для наибольшего и наименьшего значений соответственно:
= МИН (B2: B7)
= МАЛЕНЬКИЙ (B2: B7,1)
= МАКС (B2: B7)
= БОЛЬШОЙ (B2: B7,1)
Рисунок 2: LARGE и SMALL возвращают n-е значения из заданного списка.
Если вы создаете список из 10 верхних или нижних значений, может быть утомительно вручную редактировать каждую функцию НАИБОЛЬШИЙ или МАЛЕНЬКИЙ с правильным значением для аргумента k. Чтобы сэкономить время, я использую функцию СТРОКА, либо внутри функции НАИБОЛЬШИЙ или МАЛЕНЬКИЙ, либо в отдельном столбце. Функция СТРОКА возвращает номер строки для данной ячейки. Если вы введете это в ячейку D2, Excel вернет 2:
.= СТРОКА ()
На рисунке 3 вы можете видеть, что я ввел эту формулу в ячейку D2:
.= СТРОКА () — 1
В этом случае ROW () вернет 2, потому что он введен во второй строке, поэтому вычитание 1 изменяет результат на 1. В качестве альтернативы я мог бы указать адрес ячейки в строке 1 рабочего листа:
В качестве альтернативы я мог бы указать адрес ячейки в строке 1 рабочего листа:
= СТРОКА (D1)
Рисунок 3: Эти формулы являются основой для создания ранжированного списка без повторной сортировки исходных данных
В ячейке F2 я ввел эту формулу:
= БОЛЬШОЙ (2 B $: 11 B $, D2)
В зависимости от моих потребностей я мог бы использовать вместо этого эту формулу:
= БОЛЬШОЙ (B $ 2: B $ 11, СТРОКА () — 1)
Знаки доллара в формуле указывают Excel не изменять номера строк при копировании формулы вниз.Последняя часть информации, которую вы, вероятно, захотите, — это связать имя с выделенными вами значениями. Для этого вы можете использовать функции ПОИСКПОЗ и ИНДЕКС вместе в ячейке E2:
.= ИНДЕКС (A $ 2: A $ 11, ПОИСКПОЗ (F2, B $ 2: B $ 11,0))
Я объясню ПОИСКПОЗ и ИНДЕКС более подробно в следующей статье, но пока краткий ответ заключается в том, что в этом случае ПОИСКПОЗ определяет, в какой строке находится сумма продаж, а затем ИНДЕКС возвращает соответствующий текст из столбца А. Это похоже на VLOOKUP, но с гибкостью возможности искать данные слева, что не может сделать VLOOKUP без специальных условий.
Это похоже на VLOOKUP, но с гибкостью возможности искать данные слева, что не может сделать VLOOKUP без специальных условий.
У этого подхода есть одна оговорка, о которой вам следует знать. Если одно и то же значение присутствует в вашем списке дважды, то ПОИСКПОЗ / ИНДЕКС вернет соответствующее имя дважды. На следующей неделе я опишу, как вы можете использовать функцию СЧЁТЕСЛИ для создания разрешения конфликтов, которое даст вам уникальное значение, соответствующее каждому элементу в списке.
В любом случае, когда у меня есть формулы в ячейках с D2 по F2, я могу скопировать формулы вниз на столько строк, сколько необходимо, без каких-либо дополнительных изменений, как показано на рисунке 4.Помните, что если вы перетащите слишком далеко, БОЛЬШОЙ или МАЛЕНЬКИЙ вернет # ЧИСЛО !.
Рисунок 4: Если вы перетащите формулы в ячейках D2: F2 слишком далеко, НАИБОЛЬШИЙ вернет # ЧИСЛО !.
Об авторе:
Дэвид Х. Рингстром, CPA возглавляет компанию Accounting Advisors, Inc., базирующуюся в Атланте консалтинговую фирму по программному обеспечению и базам данных, предоставляющую услуги по обучению и консультированию по всей стране. Свяжитесь с Дэвидом по телефону [email protected] или подпишитесь на него в Twitter .Дэвид говорит на конференциях о Microsoft Excel и представляет веб-трансляции для нескольких поставщиков CPE, включая партнера AccountingWEB CPE Link
Рингстром, CPA возглавляет компанию Accounting Advisors, Inc., базирующуюся в Атланте консалтинговую фирму по программному обеспечению и базам данных, предоставляющую услуги по обучению и консультированию по всей стране. Свяжитесь с Дэвидом по телефону [email protected] или подпишитесь на него в Twitter .Дэвид говорит на конференциях о Microsoft Excel и представляет веб-трансляции для нескольких поставщиков CPE, включая партнера AccountingWEB CPE Link
Поиск наибольших и наименьших значений с помощью функций НАИБОЛЬШИЙ и МАЛЕНЬКИЙ
Обновлено
01.03.2016Выпущено
28.01.2016 Эксперт по Excel Деннис Тейлор демистифицирует некоторые из наиболее полезных из более чем 450 формул и функций Excel и показывает, как их можно использовать наилучшим образом.Деннис начинает с обзора основных функций (СУММ, СРЕДНЕЕ и МАКС) и нескольких важных сочетаний клавиш, которые позволяют находить и отображать ячейки формул и ускорять работу с формулами Excel — даже на нескольких листах. Затем он рассказывает, как находить и извлекать данные с помощью функций ВПР и ИНДЕКС, вычислять итоги с помощью счетных и статистических функций, извлекать данные с помощью текстовых функций и работать с функциями даты, времени, массива, математическими и информационными функциями. Курс посвящен практическим примерам, которые помогут зрителям легко перейти к использованию наиболее эффективных формул и функций Excel в реальных сценариях.Темы включают:
Затем он рассказывает, как находить и извлекать данные с помощью функций ВПР и ИНДЕКС, вычислять итоги с помощью счетных и статистических функций, извлекать данные с помощью текстовых функций и работать с функциями даты, времени, массива, математическими и информационными функциями. Курс посвящен практическим примерам, которые помогут зрителям легко перейти к использованию наиболее эффективных формул и функций Excel в реальных сценариях.Темы включают:- Отображение и выделение формул
- Преобразование формул в значения
- Табулирование данных с нескольких листов
- Понимание иерархии операций в формулах
- Использование абсолютных и относительных ссылок
- Создание и расширение вложенных операторов IF
- Поиск информации с помощью VLOOKUP, MATCH и INDEX
- Использование мощного семейства функций СЧЁТЕСЛИ
- Анализ данных с помощью статистических функций
- Расчет даты и времени
- Анализ данных с помощью формул и функций массива
- Извлечение данных с помощью текстовой функции
Уровень навыка
Продвинутый6ч 18м
Продолжительность
1 394 576
Просмотры
Показать больше Показывай меньше
Вопрос: Этот курс был обновлен 01.
 03.2016.Что изменилось?
03.2016.Что изменилось?A: Мы добавили одно руководство по новым формулам в Excel 2016.
Продолжить оценку
Вы начали эту оценку ранее, но не завершили ее. Вы можете продолжить с того места, на котором остановились, или начать заново.
Резюме Начать сначалаСамый быстрый способ найти минимальное и максимальное значения в массиве в JavaScript | автор Dr.Дерек Остин 🥳 | Кодирование на рассвете
Является ли оператор распространения медленнее, чем цикл
для в JavaScript?JavaScript предлагает несколько способов поиска наименьших и наибольших чисел в списке, включая встроенные математические функции и числовую сортировку массива. Сравниваю производительность 5 методов с использованием jsPerf — и оператор спреда проигрывает.
Фото Лейо Макларена (@leiomclaren) на UnsplashИногда, учитывая массив чисел в JavaScript, нужно определить наименьшее или наибольшее значение — и быстро!
Существует несколько встроенных способов нахождения минимального или максимального значения из массива в JavaScript, включая использование функций Math с оператором распространения (… ) и числовую сортировку массива с помощью .. Сортировка ()
Сортировка ()
В этой статье я объясняю, как работает каждый метод, а затем сравниваю производительность 5 различных методов нахождения минимального и максимального значений массива чисел в JavaScript.
Фото Готье Саллеса на Unsplash Встроенные математические функции Math.min () и Math.max () делают именно то, что и следовало ожидать — они возвращают наименьшее или наибольшее число из списка чисел, переданных в их как аргументы.
Начиная с Math.min () и Math.max () оба ожидают, что числа являются аргументами, а не массивом, они не кажутся на первый взгляд хорошими вариантами для получения наименьшего или наибольшего числа из массива:
Сначала взгляд, похоже, нужен другой подход. К счастью, использование синтаксиса расширения функций ES6 (… ) делает массивы легко совместимыми с этими функциями, как я объясню в следующем разделе.
«Оператор [Spread] заставляет значения в массиве расширяться или« распространяться »в аргументы функции.
”- Джоэл Ловера на jstips.co
Оператор распространения (…) в JavaScript может расширять массив чисел в список аргументов, например, с Math.min () и Math.max () :
Использование трех «волшебных точек» (… ) позволяет легко вызывать любую функцию, ожидающую аргументов, например эти встроенные математические функции, с использованием массива.
Если кто-то программирует для поддержки старых браузеров, таких как Internet Explorer, и не использует такой инструмент, как Babel, для компиляции кода JavaScript в старый синтаксис с помощью такого плагина, как babel-plugin-transform-spread, то оператор распространения не будет работать.
Вот текущая диаграмма совместимости браузера для оператора распространения:
Вызов функции Function.prototype.apply () будет иметь тот же эффект, что и синтаксис распространения:
Обратите внимание, что первый аргумент для . является целью для , а это , что в данном случае не имеет значения, поэтому я передал 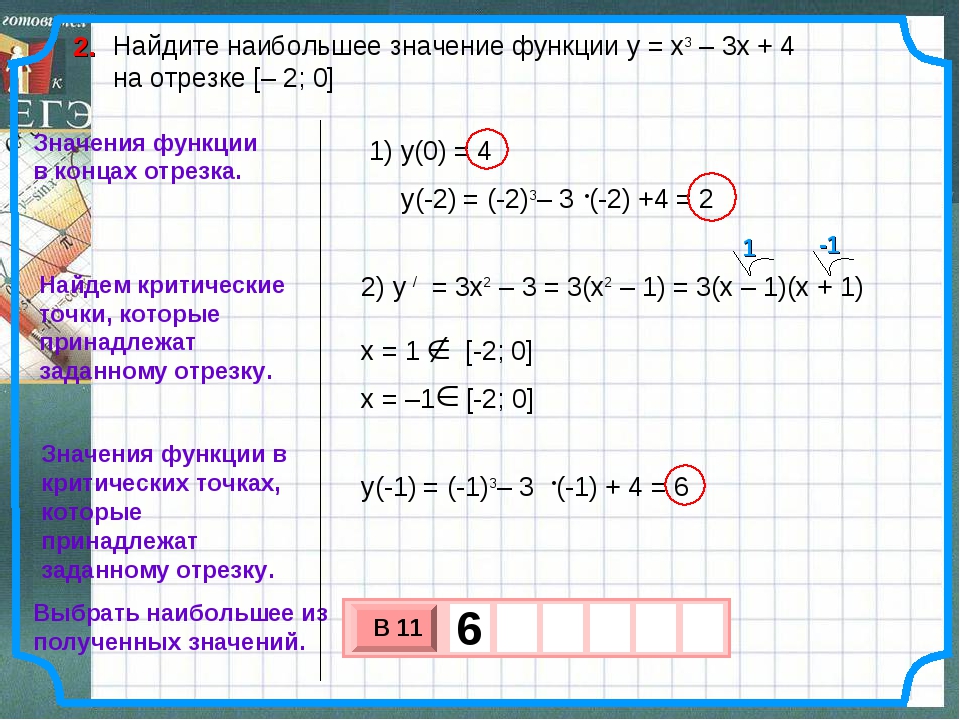 apply ( )
apply ( ) null в качестве первого аргумента.
По умолчанию в JavaScript используется лексикографическая (алфавитная) сортировка, при которой числа преобразуются в строки, а затем сортируются в алфавитном порядке.
Сортировка числового массива в JavaScript выполняется путем передачи функции Array.prototype.sort () «оператора сравнения».
Например, код .sort ((a, b) => a-b) отсортирует числа в порядке возрастания от наименьшего к наибольшему.
После сортировки первым номером будет мин. , а последним — макс. :
. Фото Фила Рида на Unsplash. Либо для цикла , либо массив .Метод prototype.reduce () можно использовать для поиска минимальных и максимальных чисел в массиве:
Брэндон Морелли ранее сообщил на Codeburst.io, что эти методы могут быть самыми быстрыми, поэтому я сравниваю производительность всех 5 методов.
Я провел несколько тестов с помощью jsPerf, бесплатного инструмента для проверки производительности кода JavaScript в браузере. Каждый образец кода находит минимум и максимум случайного массива из 40 чисел. Вот результаты:
Вау, ! По какой-то причине оператор распространения вдвое меньше скорости других методов.Поскольку использование .apply () работает быстро, похоже, что использование оператора распространения по 40 аргументам действительно замедляет работу.
Похоже, что это не вина самих функций Math.min () или Math.max () как таковых, поскольку цикл для , который избегает этих функций, имеет в основном такую же производительность для этого тестового примера. из 40 случайных предметов.
Я обновил набор тестов, чтобы сгенерировать массив из 4000 элементов, чтобы проверить, меняет ли он сравнительную производительность при нахождении минимума и максимума.
Действительно, это так, поскольку оператор распространения на 92% медленнее :
Это показывает, что падение производительности связано с оператором распространения таким образом, который масштабируется с количеством распространяемых аргументов.
С очень большими массивами для цикл является самым быстрым на данный момент , причем .apply () идет вторым, .sort () и .reduce () связано с третьим , и распространяться мертвым последним.
Стоит отметить, что использование Babel для компиляции кода может восстановить некоторую производительность для больших и очень больших массивов, поскольку он перенесет оператор распространения в .apply () с использованием babel-plugin-transform-spread.
Однако пока не стоит отказываться от оператора спреда — нет разницы в производительности, когда мы опускаемся до трех элементов:
Итак, для повседневного использования оператор спреда работает блестяще.
Между тем, итеративный для цикла на 3% медленнее , чем оператор распространения, когда работает только с массивом всего из 3 элементов.
Существует несколько способов найти наименьшее и наибольшее числа в массиве JavaScript, и производительность каждого метода зависит от количества значений в массиве.
Наиболее удобный способ — использовать синтаксис Math.min (... массив) и Math.max (... массив) — использовать оператор распространения ES6 (… ) для распределения массива по аргументам ожидается встроенными математическими функциями JavaScript.
Однако при работе с большими массивами из 40 элементов и более использование оператора распространения дает значительно худшую производительность по сравнению с другими методами поиска минимума и максимума.
Что делать для больших массивов
Для больших массивов, используя Math.min.apply (null, array) и Math. восстанавливает потерянную производительность от оператора распространения и позволяет продолжать использовать встроенные математические функции. max.apply (null, array)
max.apply (null, array)
Это именно то, что Babel делает с babel-plugin-transform-spread, поэтому компиляция вашего кода JavaScript поможет с массивами из 40 элементов.
Наконец, с очень большими массивами из 4000 элементов и более цикл для является самым быстрым методом, так что имейте это в виду. Это может быть некрасиво, но это работает.
А теперь найдите минимумы и максимумы! 😄
Фотография Ханны Рединг на Unsplash- GeeksforGeeks исследует использование
.map ()и.reduce (), чтобы найти min / max:
- Библиотека d3-array включает полезный
.minIndex ()&.maxIndex (), хотя циклдля, вероятно, будет быстрее для очень больших массивов:
- Предыдущее исследование очень больших массивов из 250 000 элементов, опубликованных в блоге разработчиков Microsoft, показало, что циклы for являются самым быстрым методом.
 far:
far:
Как использовать функцию малого и большого размера в Excel
Анализ широкого набора чисел требует времени, но Microsoft Excel упрощает его.Функции МАЛЕНЬКИЙ и НАИБОЛЬШИЙ в Excel могут помочь вам выбрать конкретные числа и значения в наборе данных. Вот как использовать эти функции.
Инструкции в этой статье относятся к Excel для Microsoft 365, Excel 2019, Excel 2016, Excel 2013 и Excel 2010.
Используйте функцию МАЛЕНЬКИЙ в Excel
Функция МАЛЕНЬКИЙ в Excel возвращает k-е наименьшее значение (где k — представляет положение значения, например первое, второе или пятое) в определяемом вами наборе данных.Возможно, вы захотите узнать первое, третье или пятое наименьшее значение. Цель этой функции — вернуть значения с определенным относительным положением в наборе данных.
Функция МАЛЕНЬКИЙ записывается как МАЛЫЙ (массив, k) , где массив — это диапазон данных, которые вы хотите исследовать, а k — определяемая пользователем точка (например, первая, вторая или четырнадцатая), которая функция ищет среди этого массива данных.
Выберите массив данных.Эти данные могут быть распределены по одному столбцу или строке или по нескольким строкам и столбцам. Вы определите этот массив в синтаксисе функции МАЛЕНЬКИЙ.
Если n — количество точек данных в массиве, МАЛЕНЬКИЙ (массив, 1) равняется наименьшему значению, а МАЛЕНЬКИЙ (массив, n) равно наибольшему значению.
Выберите ячейку в электронной таблице, чтобы ввести функцию МАЛЕНЬКИЙ. В примере, используемом в этом руководстве, выполняется поиск третьего наименьшего числа в наборе данных, поэтому k = 3 .
Введите = МАЛЕНЬКИЙ (, чтобы начать формулу.
Выберите массив данных. Excel позволяет выделить набор данных. Когда выбраны правильные значения, Excel называет массив (в данном случае это B2: D9 ).
После выбора массива данных введите запятую (, ), чтобы продолжить формулу.

Введите значение k. В этом примере используется 3. Введите 3 , а затем закройте скобки функции.Формула должна гласить:
= МАЛЕНЬКИЙ (B2: D9,3)
Перед вводом функции и параметров функции и формулы в Excel должны начинаться со знака равенства ( = ).
Нажмите Введите , чтобы вычислить результат функции.
Это возвращает значение 4 , что означает, что из этого массива данных 4 является третьим наименьшим значением.
Используйте функцию Excel НАИБОЛЬШИЙ
И наоборот, функция НАИБОЛЬШИЙ в Excel возвращает k-е наибольшее значение (где k- представляет положение значения, например, первое наибольшее или пятое наибольшее), которое вы определяете в наборе данных.
Функция НАИБОЛЬШИЙ записывается как НАИБОЛЬШИЙ (массив, k) , где массив — это диапазон данных, которые вы хотите исследовать, а k — определяемая пользователем точка (например, первая, вторая или четырнадцатая) функция ищет среди массива данных.
Выберите массив данных. Эти данные могут быть распределены по одному столбцу или строке или по нескольким строкам и столбцам. Вам нужно будет определить этот массив в синтаксисе функции НАИБОЛЬШИЙ.
Если n — количество точек данных в массиве, LARGE (массив, 1) равно наибольшему значению, а LARGE (массив, n) равно наибольшему значению.
Выберите ячейку в электронной таблице, чтобы ввести функцию НАИБОЛЬШИЙ. В примере выполняется поиск наибольшего числа в наборе данных, поэтому k = 1 .
Начните формулу, набрав = НАИБОЛЬШИЙ (
Выберите массив данных.Excel позволяет выделить набор данных. Когда выбраны правильные значения, Excel называет массив (в данном случае это B2: D9 ). Введите запятую (, ), чтобы продолжить формулу.
Введите значение k .
 В этом примере используется 1 . Введите 1 и закройте скобки функции. Формула должна гласить:
В этом примере используется 1 . Введите 1 и закройте скобки функции. Формула должна гласить:= БОЛЬШОЙ (B2: D9,1)
Нажмите клавишу Enter , чтобы вычислить результат функции.
В этом примере выполняется поиск самого большого числа в массиве, которое составляет 5111 .
Если массив большой, вам может потребоваться знать, сколько точек данных находится в наборе. Выделите массив, затем посмотрите на нижнюю часть экрана Excel. Count: XX указывает, сколько частей данных находится в массиве, где XX — это число.
Возможные ошибки в МАЛЫХ и БОЛЬШИХ функциях в Excel
Формулы Excel должны быть абсолютно правильными, чтобы работать.Если вы столкнулись с ошибкой, обратите внимание на следующие моменты:
- Если массив пуст, то есть вы не выбрали ячейки, содержащие данные, функции МАЛЕНЬКИЙ и НАИБОЛЬШИЙ возвращают # ЧИСЛО! ошибка.

- Если k ≤ 0 или k превышает количество точек данных в массиве, МАЛЫЙ и НАИБОЛЬШИЙ возвращают # ЧИСЛО! ошибка.
Спасибо, что сообщили нам об этом!
Расскажите, почему!
Другой Недостаточно подробностей Сложно понятьМаксимальные и минимальные значения — подход к исчислению
10
Поворотные точки графика
МЫ ГОВОРЯЕМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение при x = a ,
, если f ( a ) на больше , чем любое предшествующее или последующее значение.
Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше.
Мы говорим, что функция f ( x ) имеет относительное минимальное значение при x = b ,
, если f ( b ) на меньше , чем любое значение, непосредственно предшествующее или последующее.
Опять же, другие значения функции могут быть меньше. С таким пониманием мы откажемся от термина «относительный».
Значение функции, значение y , максимальное или минимальное, называется экстремальным значением.
Теперь, что характеризует график при экстремальном значении?
Касательная к кривой горизонтальна . Мы видим это в точках A и B . Наклон каждой касательной линии — производной при оценке на a или b — равен 0.
f ‘ ( x ) = 0,
Более того, в точках непосредственно к слева от максимума — в точке C — наклон касательной положительный: f ‘ ( x )> 0. В то время как в точках непосредственно к справа — в точке D — наклон отрицательный: f ‘ ( x )
Другими словами, максимум f ‘ ( x ) меняет знак с + на -.
Как минимум, f ‘ ( x ) меняет знак с — на +. Мы видим, что в точках E и F .
Также можно заметить, что максимум на A график вогнут вниз. (Тема 14 Precalculus.) Хотя, как минимум, на B , она вогнута вверх.
Значение x , при котором функция имеет максимум или минимум, называется критическим значением.На рисунке —
— критические значения x = a и x = b .
Критические значения определяют точки поворота, в которых касательная параллельна оси x . Критические значения — если таковые имеются — будут решениями от до f ‘ ( x ) = 0.
Пример 1. Пусть f ( x ) = x 2 — 6 x + 5.
Есть ли критические значения — какие-то поворотные моменты? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума?
Решение . f ‘ ( x ) = 2 x — 6 = 0 подразумевает x = 3. (Урок 9 алгебры.)
x = 3 — единственное критическое значение. Это x — координата поворотной точки.Чтобы определить y -координат, оцените f при этом критическом значении — оцените f (3):
| f ( x ) | = | x 2 -6 x + 5 |
| f (3) | = | 3 2 — 6 · 3 + 5 |
| = | −4. | |
Крайнее значение — 4. Чтобы увидеть, является ли он максимумом или минимумом, в этом случае мы можем просто посмотреть на график.
f ( x ) — парабола, и мы видим, что точка поворота минимальна.
Найдя значение x , где производная равна 0, мы обнаружили, что вершина параболы находится в точке (3, −4).
Но мы не всегда сможем посмотреть на график.Алгебраическим условием минимума является то, что f ‘ ( x ) меняет знак с — на +. Мы видим это в точках E , B , F выше. Величина наклона увеличивается.
Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (Урок 9), которая представляет собой скорость изменения наклона, равна положительному значению .
Опять же, вот f ( x ):
| f ( x ) | = | x 2 — 6 x + 5. |
| f ‘ ( x ) | = | 2 x — 6. |
| f ‘ ( x ) | = | 2. |
f » при критическом значении 3 — f » (3) = 2 — положительно. Это алгебраически говорит нам, что критическое значение 3 определяет минимум.
Достаточные условия
Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении a :
Функция имеет минимальное значение x = a , если f ‘ ( a ) = 0
и f’ ‘ ( a ) = положительное число.
Функция имеет максимальное значение в x = a , если f ‘ ( a ) = 0
и f’ ‘ ( a ) = отрицательное число.
В случае максимума наклон касательной составляет с уменьшением — он меняется от положительного к отрицательному. Мы видим, что в точках C , A , D .
Пример 2. Пусть f ( x ) = 2 x 3 — 9 x 2 + 12 x — 3.
Есть ли крайние значения? Во-первых, существуют ли какие-либо критические значения — решения для f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты?
| Раствор . f ‘ ( x ) = 6 x 2 -18 x + 12 | = | 6 ( x 2 -3 x + 2) |
| = | 6 ( x -1) ( x -2) | |
| = | 0 | |
подразумевает:
x = 1 или x = 2.
(Урок алгебры 37.)
Это критические значения. Каждый определяет максимум или минимум? Чтобы ответить, мы должны оценить вторую производную для каждого значения.
| f ‘ ( x ) | = | 6 x 2 -18 x + 12. |
| f ‘ ( x ) | = | 12 x — 18. |
| f ‘ (1) | = | 12-18 = −6. |
Вторая производная отрицательна. Таким образом, функция имеет максимум x = 1.
Чтобы найти y -coördinate — крайнее значение — на этом максимуме мы оцениваем f (1):
| f ( x ) | = | 2 x 3 — 9 x 2 + 12 x — 3 |
| f (1) | = | 2–9 + 12–3 |
| = | 2. | |
Максимум приходится на точку (1, 2).
Затем, x = 2 определяет максимум или минимум?
| f ‘ ( x ) | = | 12 x — 18. |
| f ‘ (2) | = | 24–18 = 6. |
Вторая производная положительна.Таким образом, функция имеет минимум x = 2.
Чтобы найти y -coördinate — крайнее значение — при этом минимуме, мы оцениваем f (2):
| f ( x ) | = | 2 x 3 — 9 x 2 + 12 x — 3. |
| f (2) | = | 16–36 + 24–3 |
| = | 1. | |
Минимум находится в точке (2, 1).
Вот собственно график f ( x ):
Решения для f » ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум. Пример: y = x 3 . y » = 6 x = 0 подразумевает x = 0. Но x = 0 является точкой перегиба на графике y = x 3 , а не максимум или минимум .
Другой пример: y = sin x . Решения для y » = 0 являются умножениями π, которые являются точками перегиба.
Задача 1. Найти координаты вершины параболы,
y = x 2 — 8 x + 1.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
y ‘ = 2 x — 8 = 0.
Это подразумевает x = 4. Это x -кординация вершины. Чтобы найти y -coördinate, оцените y при x = 4:
y = 4 2 -8 · 4 + 1 = −15.
Вершина находится в точке (4, −15).
Задача 2. Проверьте каждую функцию на наличие максимумов и минимумов.
a) y = x 3 — 3 x 2 + 2.
y ‘ = 3 x 2 — 6 x = 3 x ( x — 2) = 0 означает
x = 0 или x = 2.
y ‘ ( x ) = 6 x — 6.
у » (0) = −6.
Вторая производная отрицательна. Это означает, что существует максимум x = 0. Это максимальное значение составляет
.y (0) = 2.
Далее,
y ‘ (2) = 12 — 6 = 6.
Вторая производная положительна. Это означает, что существует минимум x = 2.Это минимальное значение —
.y (2) = 2 3 -3 · 2 2 + 2 = 8-12 + 2 = −2.
б) y = −2 x 3 -3 x 2 + 12 x + 10.
При x = 1 получается максимум y = 17.
При x = −2 минимум y = −10.
c) y = 2 x 3 + 3 x 2 + 12 x — 4.
Поскольку f ‘ ( x ) = 0 не имеет реальных решений, нет экстремальных значений.
d) y = 3 x 4 — 4 x 3 — 12 x 2 + 2.
При x = 0 максимум y = 2.
При x = −1 минимум y = −3.
При x = 2 минимум y = −30.
Следующий урок: Применение максимальных и минимальных значений
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Поиск наибольшего или наименьшего числа с помощью Excel — Office Mastery
Найти наибольшее число в диапазоне ячеек Excel очень просто.
То же самое для выбора наименьшего числа.
Есть много ситуаций, когда вам нужно найти наибольшее / наименьшее, наибольшее / наименьшее, наибольшее / наименьшее значение в наборе данных. Например,
- Какой сотрудник брал больше всего больничных дней в этом году?
- Какие самые большие расходы в этом году?
- Какова самая низкая стоимость лида в наших рекламных кампаниях?
Возьмите контрольный список :
7 шагов к совершенствованию формул
1.Как найти наибольшее число в Excel
Используйте функцию МАКС, чтобы найти наибольшее число в списке (или самое высокое, самое длинное, наибольшее и т. Д.)
= МАКС (число1, число 2…)
= MAX (A1, A2, A3)
= MAX (A1: A10)
= MAX (TestScores)
2. Как найти наименьшее число в Excel
Используйте функцию MIN для найти наименьшее число в списке (или наименьшее, наименьшее, наименьшее и т. д.))
= MIN (число1, число 2…)
= MIN (B1, B2, B3)
= MIN (B1: B10)
= MIN (DepartmentSpend)
Функции MAX и MIN можно выбрать в раскрывающемся меню Автосумма или введя их непосредственно в ячейку.
Допустим, у вас есть значения в ячейках от A1 до A10,
Чтобы использовать инструмент автосуммирования:
1. Выделите 10 ячеек.
2. Щелкните стрелку раскрывающегося списка на значке AutoSum .
3. Выберите MAX или MIN .
 Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.





 Остается только подставить в первоначальную функцию:
Остается только подставить в первоначальную функцию: Получили одну точку — можно смело писать в ответ.
Получили одну точку — можно смело писать в ответ.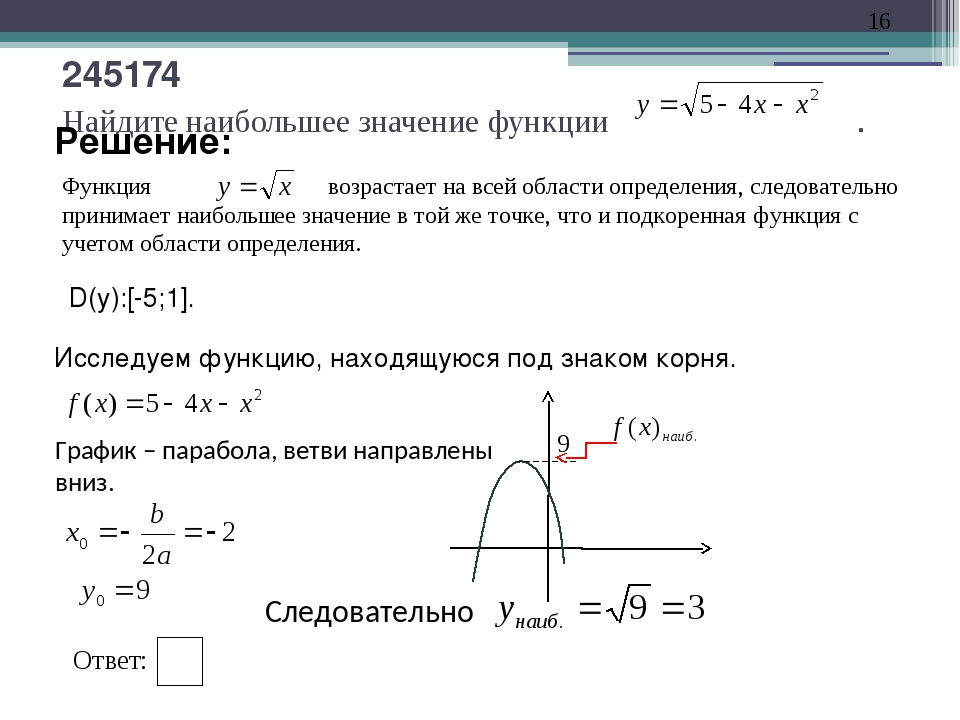 ”- Джоэл Ловера на jstips.co
”- Джоэл Ловера на jstips.co far:
far:
 В этом примере используется 1 . Введите 1 и закройте скобки функции. Формула должна гласить:
В этом примере используется 1 . Введите 1 и закройте скобки функции. Формула должна гласить: