Алгебра. Урок 4. Уравнения, системы уравнений

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Уравнения”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

 

Линейное уравнение – уравнение вида ax=b, где x – переменная, a и b некоторые числа, причем a≠0.

Примеры линейных уравнений:

Линейными уравнениями называют не только уравнения вида ax=b, но и любые уравнения, которые при помощи преобразований и упрощений сводятся к этому виду.

Как же решать уравнения, которые приведены к виду ax=b? Достаточно поделить левую и правую часть уравнения на величину a. В результате получим ответ: x=ba.

Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.

Для того, чтобы решить линейное уравнение, необходимо раскрыть скобки (если они есть), перенести «иксы» в левую часть, числа – в правую, привести подобные слагаемые. Получится уравнение вида ax=b. Решение данного линейного уравнения: x=ba.

Примеры решения линейных уравнений:

1. 2x+1=2(x−3)+8

Это линейное уравнение, так как переменная стоит в первое степени.

Попробуем преобразовать его к виду ax=b:

Для начала раскроем скобки:

2x+1=4x−6+8

В левую часть переносятся все слагаемые с x, в правую – числа:

2x−4x=2−1

−2x=1

Теперь поделим левую и правую часть на число (-2):

−2x−2=1−2=−12=−0,5

Ответ: x=−0,5

 

1. x2−1=0

Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.

 

1. x(x+3)−8=x−1

Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:

x2+3x−8=x−1

Это уравнение не является линейным уравнением.

 

Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)

Примеры:

1. 2x−4=2(x−2)

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

2x−4=2x−4

2x−2x=−4+4

0=0

И как же здесь искать x, если его нет? После выполнения преобразований мы получили верное равенство (тождество), которое не зависит от значения переменной x . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда получается верное равенство (тождество). Значит x может быть любым числом. Запишем ответ к данном линейному уравнению.

Ответ: x∈(−∞; +∞)

 

1. 2x−4=2(x−8)

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

2x−4=2x−16

2x−2x=−16+4

0=−12

В результате преобразований x сократился, но в итоге получилось неверное равенство, так как . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда будет неверное равенство. А это означает, что нет таких значений x, при которых равенство становилось бы верным. Запишем ответ к данному линейному уравнению.

Ответ: x∈∅

 

Квадратное уравнение – уравнение вида ax2+bx+c=0, где x – переменная, a,b и c – некоторые числа, причем a≠0.

Алгоритм решения квадратного уравнения:

1. Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: ax2+bx+c=0
2. Выписать, чему равны в числах коэффициенты: a=…b=…c=…
3. Вычислить дискриминант по формуле: D=b2−4ac
4. Если D>0, будет два различных корня, которые находятся по формуле: x1,2=−b±D2a
5. Если D=0, будет один корень, который находится по формуле: x=−b2a
6. Если D<0, решений нет: x∈∅

Примеры решения квадратного уравнения:

1. −x2+6x+7=0

a=−1,b=6,c=7

D=b2−4ac=62−4⋅(−1)⋅7=36+28=64

D>0 – будет два различных корня:

x1,2=−b±D2a=−6±642⋅(−1)=−6±8−2=[−6+8−2=2−2=−1−6−8−2=−14−2=7

Ответ: x1=−1,x2=7

 

1. −x2+4x−4=0

a=−1,b=4,c=−4

D=b2−4ac=42−4⋅(−1)⋅(−4)=16−16=0

D=0 – будет один корень:

x=−b2a=−42⋅(−1)=−4−2=2

Ответ: x=2

 

1. 2×2−7x+10=0

a=2,b=−7,c=10

D=b2−4ac=(−7)2−4⋅2⋅10=49−80=−31

D<0 – решений нет.

Ответ: x∈∅

Также существуют неполные квадратные уравнения (это квадратные уравнения, у которых либо b=0, либо с=0, либо b=с=0 ). Смотрите видео, как решать такие квадратные уравнения!

 

Квадратный трехчлен можно разложить на множители следующим образом:

ax2+bx+c=a⋅(x−x1)⋅(x−x2)

где a – число, коэффициент перед старшим коэффициентом,

x – переменная (то есть буква),

x1 и x2 – числа, корни квадратного уравнения ax2+bx+c=0, которые найдены через дискриминант.

Если квадратное уравнение имеет только один корень , то разложение выглядит так:

ax2+bx+c=a⋅(x−x0)2

Примеры разложения квадратного трехчлена на множители:

1. −x2+6x+7=0⇒x1=−1, x2=7

−x2+6x+7=(−1)⋅(x−(−1))(x−7)=−(x+1)(x−7)=(x+1)(7−x)

 

1. −x2+4x−4=0;⇒x0=2

−x2+4x−4=(−1)⋅(x−2)2=−(x−2)2

 

Если квадратный трехчлен является неполным, ( (b=0 или c=0) то его можно разложить на множители следующими способами:

 

Пусть f(x) и g(x) – некоторые функции, зависящие от переменной x.

Дробно рациональное уравнение – это уравнение вида f(x)g(x)=0.

Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.

ОДЗ – область допустимых значений переменной.

В выражении вида f(x)g(x)=0

ОДЗ: g(x)≠0 (знаменатель дроби не может быть равен нулю).

Алгоритм решения дробно рационального уравнения:

1. Привести выражение к виду f(x)g(x)=0.
2. Выписать ОДЗ: g(x)≠0.
3. Приравнять числитель дроби к нулю f(x)=0 и найти корни.
4. Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.

Пример решения дробного рационального уравнения:

Решить дробно рациональное уравнение x2−42−x=1.

Решение:

Будем действовать в соответствии с алгоритмом.

1. Привести выражение к виду f(x)g(x)=0.

Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:

x2−42−x−1\2−x=0

x2−42−x−2−x2−x=0

x2−4−(2−x)2−x=0

x2−4−2+x2−x=0

x2+x−62−x=0

Первый шаг алгоритма выполнен успешно.

1. Выписать ОДЗ:

g(x)≠0

2−x≠0

−x≠−2

x≠2

Обводим в рамочку ОДЗ, не забываем про него: x≠2

1. Приравнять числитель дроби к нулю f(x)=0 и найти корни:

x2+x−6=0 – Квадратное уравнение. Решаем через дискриминант.

a=1,b=1,c=−6

D=b2−4ac=12−4⋅1⋅(−6)=1+24=25

D>0 – будет два различных корня.

x1,2=−b±D2a=−1±252⋅1=−1±52=[−1+52=42=2−1−52=−62=−3

[x1=2×2=−3

 

1. Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.

Корни, полученные на предыдущем шаге:

[x1=2×2=−3

ОДЗ: x≠2

Значит, в ответ идет только один корень, x=−3.

Ответ: x=−3.

 

Системой уравнений называют два уравнения с двумя неизвестными (как правило, неизвестные обозначаются x и y), которые объединены в общую систему фигурной скобкой.

Пример системы уравнений

{x+2y=83x−y=−4

Решить систему уравнений – найти пару чисел x и y, которые при подстановке в систему уравнений образуют верное равенство в обоих уравнениях системы.

Существует два метода решений систем линейных уравнений:

1. Метод подстановки.
2. Метод сложения.

Алгоритм решения системы уравнений методом подстановки:

1. Выразить из любого уравнения одну переменную через другую.
2. Подставить в другое уравнение вместо выраженной переменной полученное значение.
3. Решить уравнение с одной неизвестной.
4. Найти оставшуюся неизвестную.

Пример:

Решить систему уравнений методом подстановки

{x+2y=83x−y=−4

Решение:

1. Выразить из любого уравнения одну переменную через другую.

{x=8−2y3x−y=−4

1. Подставить в другое уравнение вместо выраженной переменной полученное значение.

{x=8−2y3x−y=−4

{x=8−2y3(8−2y)−y=−4

1. Решить уравнение с одной неизвестной.

3(8−2y)−y=−4

24−6y−y=−4

−7y=−4−24

−7y=−28

y=−28−7=287=4

y=4

1. Найти оставшуюся неизвестную.

y=4

x=8−2y=8−2⋅4=8−8=0

Ответ можно записать одним из трех способов:

Ответ:

1. x=0,y=4
2. {x=0y=4
3. (0; 4)

 

Решение системы уравнений методом сложения.

Метод сложения основывается на следующем свойстве:

если

{a=bc=d

то

(a+c)=(b+d)

Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.

Пример:

Решить систему уравнений методом сложения

{x+2y=83x−y=−4

Давайте избавимся в данном примере от переменной x. Суть метода состоит в том, чтобы в первом и во втором уравнении перед переменной x стояли противоположные коэффициенты. Во втором уравнении перед x стоит коэффициент 3. Для того, чтобы метод сложения сработал, надо чтобы перед переменной x оказался коэффициент (−3). Для этого домножим левую и правую часть первого уравнения на (−3).

{x+2y=8 | ⋅(−3)3x−y=−4

{(−3)⋅(x+2y)=(−3)⋅83x−y=−4

{−3x−6y=−243x−y=−4

Теперь, когда перед переменной  в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.

{−3x−6y=−243x−y=−4⊕

(−3x−6y)+(3x−y)=(−24)+(−4)

−3x−6y+3x−y=−24−4

−7y=−28

y=−28−7=287=4

Осталось найти переменную x. Для этого подставим y=4 в любое из двух уравнений системы. Например, в первое.

x+2y=8

x+2⋅4=8

x+8=8

x=8−8=0

Ответ можно записать одним из трех способов:

Ответ:

1. x=0,y=4
2. {x=0y=4
3. (0; 4)

 

 

Скачать домашнее задание к уроку 4.

 

epmat.ru

определение, виды, примеры решения, что это такое

Статья знакомит с таким понятием, как определение системы уравнений и ее решением. Будут рассмотрены часто встречающиеся случаи решений систем. Приведенные примеры помогут подробно пояснить решение.

Определение системы уравнений

Чтобы перейти к определению системы уравнений, необходимо обратить внимание на два момента: вид записи и ее смысл. Чтобы понять это, нужно подробно остановиться на каждом из видов, тогда сможем прийти к определению систем уравнений.

Например, возьмем два уравнения 2·x+y=−3 и x=5, после чего объединим фигурной скобкой такого плана:

2·x+y=-3,x=5.

Уравнения, объединенные фигурной скобкой, считаются записями систем уравнений. Они задают множества решений уравнений данной системы. Каждое решение должно являться решением всех заданных уравнений.

Другими словами это означает, что любые решения первого уравнения будут решениями всех уравнений, объединенных системой.

Определение 1

Системы уравнений – это некоторое количество уравнений, объединенных фигурной скобкой, имеющих множество решений уравнений, которые одновременно являются решениями для всей системы.

Основные виды систем уравнений

Видов уравнений достаточно много, как систем уравнений. Для того, чтобы было удобно решать и изучать их, подразделяют на группы по определенным характеристикам. Это поможет в рассмотрении систем уравнений отдельных видов.

Для начала уравнения классифицируются по количеству уравнений. Если уравнение одно, то оно является обычным уравнением, если их более, тогда имеем дело с системой, состоящей из двух или более уравнений.

Другая классификация затрагивает число переменных. Когда количество переменных 1, говорят, что имеем дело с системой уравнений с одной неизвестной, когда 2 – с двумя переменными. Рассмотрим пример

x+y=5,2·x-3·y=1

Очевидно, что система уравнений включает в себя две переменные х и у.

При записи таких уравнений считается число всех переменных, имеющихся в записи. Их наличие в каждом уравнении необязательно. Хотя бы одно уравнение должно иметь одну переменную. Рассмотрим пример системы уравнений

2x=11,

zaochnik.com

Методы решения систем уравнений. Алгебра, 9 класс: уроки, тесты, задания.

1.	Метод сложения (линейные уравнения) Сложность: лёгкое
2.	Метод подстановки (линейные уравнения) Сложность: лёгкое
3.	Корни квадратного уравнения, теорема Виета Сложность: лёгкое
4.	Метод подстановки (линейное и квадратное) Сложность: лёгкое
5.	Метод алгебраического сложения Сложность: среднее
6.	Способ сложения Сложность: среднее
7.	Пары чисел, которые являются решением системы уравнений Сложность: среднее
8.	Графический метод (парабола и прямая) Сложность: среднее
9.	Графический метод (гипербола и прямая) Сложность: среднее
10.	Графический метод (элементарные функции) Сложность: среднее
11.	Система квадратных уравнений Сложность: среднее
12.	Система уравнений (линейное и квадратное) I Сложность: среднее
13.	Система уравнений (линейное и квадратное) II Сложность: среднее
14.	Система уравнений (линейное и квадратное) III Сложность: среднее
15.	Задача на составление системы уравнений Сложность: среднее
16.	Система рациональных уравнений Сложность: среднее
17.	Система, состоящая из рационального и квадратного уравнений Сложность: среднее
18.	Система, состоящая из рационального и линейного уравнений Сложность: среднее
19.	Система рациональных уравнений, вводится одна новая переменная Сложность: среднее
20.	Система, состоящая из рациональных уравнений Сложность: среднее
21.	Система, состоящая из квадратного и рационального уравнений Сложность: среднее
22.	Система линейных уравнений Сложность: среднее
23.	Система, состоящая из квадратного и рационального уравнений, метод умножения Сложность: среднее
24.	Пары чисел, которые являются решением системы уравнений Сложность: среднее
25.	Графический метод (окружность и парабола) Сложность: сложное

www.yaklass.ru

Основные определения, примеры системы двух уравнений. Видеоурок. Алгебра 9 Класс

На этом уроке мы начнем изучение решения систем из двух уравнений. Вначале дадим определение рационального уравнения, зависящего от двух переменных и его решения. Рассмотрим примеры таких уравнений и их графики. Дадим определение равносильных уравнений и правила равносильных преобразований. Рассмотрим построение графиков для некоторых типовых уравнений.
Далее дадим определение системы двух уравнений и рассмотрим решение систем графическим методом.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства»

Рациональным уравнением с двумя переменными называется уравнение вида 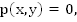 где 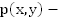 рациональное выражение (т.е. алгебраическое выражение, составленное из чисел и переменных  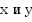 с помощью операций сложения, вычитания, умножения, деления и возведения в натуральную степень).

Например:

 

 

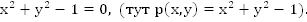
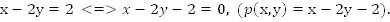
Решением уравнения с двумя переменными называется пара чисел, которая обращает уравнение в верное числовое равенство.

Ранее мы рассматривали линейное уравнение с двумя переменными 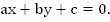 Линейное уравнение имеет бесчисленное множество решений, график линейного уравнения – прямая линия.

Рассмотрим пример:

Найти хотя бы одно решение уравнения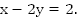

Зададим 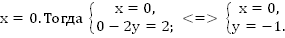 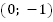  – решение уравнения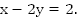

Если задана одна переменную, то вторую можно найти.

Итак, основные понятия сводятся к следующему:

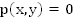 называется уравнением с двумя переменными. Частным решением такого уравнения называется любая пара чисел 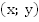, которая удовлетворяет уравнению. Но наша задача – найти все решения этого уравнения, т.е. множество всех пар чисел, которые удовлетворяют уравнению.

Мы рассмотрели линейное уравнение, теперь рассмотрим уравнение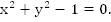

Вспомним, что 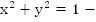 уравнение окружности с центром в т.(0;0) и радиусом 1 (Рис. 1).

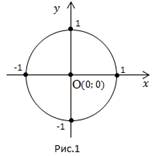
Любая точка на этой окружности имеет две координаты – x и y, и эти координаты удовлетворяют уравнени

interneturok.ru

Системы уравнений. Способы решения систем уравнений

Система уравнений – это группа уравнений, в которых одни и те же неизвестные подразумевают одни те же числа. Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:

	x — 4y = 2
	3x — 2y = 16

Решить систему уравнений – это значит, найти общие решения для всех уравнений системы или убедиться, что решения нет.

Чтобы решить систему уравнений, нужно исключить одно неизвестное, то есть из двух уравнений с двумя неизвестными составить одно уравнение с одним неизвестным. Исключить одно из неизвестных можно тремя способами: подстановкой, сравнением, сложением или вычитанием.

Способ подстановки

Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное. Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.

Рассмотрим решение системы уравнений:

	x — 4y = 2
	3x — 2y = 16

Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:

x — 4y = 2

x = 2 + 4y

Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:

3x	— 2y = 16
3(2 + 4y)	— 2y = 16

Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.

3(2 + 4y) — 2y = 16

6 + 12y — 2y = 16

6 + 10y = 16

10y = 16 — 6

10y = 10

y = 10 : 10

y = 1

Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:

x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6

Ответ: x = 6, y = 1.

Способ сравнения

Способ сравнения – это частный случай подстановки. Чтобы решить систему уравнений способом сравнения, нужно в обоих уравнениях найти, какому выражению будет равно одно и то же неизвестное и приравнять полученные выражения друг к другу. Получившееся в результате уравнение позволяет узнать значение одного неизвестного. С помощью этого значения затем вычисляется значение второго неизвестного.

Например, для решение системы:

	x — 4y = 2
	3x — 2y = 16

найдём в обоих уравнениях, чему равен y (можно сделать и наоборот – найти, чему равен x):

x — 4y = 2	3x — 2y = 16
-4y = 2 — x	-2y = 16 — 3x
y = (2 — x) : — 4	y = (16 — 3x) : -2

Составляем из полученных выражений уравнение:

Решаем уравнение, чтобы узнать значение x:

2 — x  · (-4) =  16 — 3x  · (-4) -4 -2

2 — x = 32 — 6x

2 — x + 6x = 32 — 2

5x = 30

x = 30 : 5

x = 6

Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:

x — 4y = 2	3x — 2y = 16
6 — 4y = 2	3 · 6 — 2y = 16
-4y = 2 — 6	-2y = 16 — 18
-4y = -4	-2y = -2
y = 1	y = 1

Ответ: x = 6, y = 1.

Способ сложения или вычитания

Чтобы решить систему уравнений способом сложения, нужно составить из двух уравнений одно, сложив левые и правые части, при этом одно из неизвестных должно быть исключено из полученного уравнения. Неизвестное можно исключить, уравняв при нём коэффициенты в обоих уравнениях.

Рассмотрим систему:

	x — 4y = 2
	3x — 2y = 16

Уравняем коэффициенты при неизвестном y, умножив все члены второго уравнения на -2:

(3x — 2y) · -2 = 16 · -2

-6x + 4y = -32

Получим:

	x — 4y = 2
	-6x + 4y = -32

Теперь сложим по частям оба уравнения, чтобы получить уравнение с одним неизвестным:

+	x  —  4y = 2
	-6x + 4y = -32
	-5x         = -30

Находим значение x (x = 6). Теперь, подставив значение x в любое уравнение системы, найдём y = 1.

Если уравнять коэффициенты у x, то, для исключения этого неизвестного, нужно было бы вычесть одно уравнение из другого.

Уравняем коэффициенты при неизвестном x, умножив все члены первого уравнения на 3:

(x — 4y) · 3 = 2 · 3

3x — 12y = 6

Получим:

	3x — 12y = 6
	3x — 2y = 16

Теперь вычтем по частям второе уравнение из первого, чтобы получить уравнение с одним неизвестным:

—	3x  —  12y = 6
	3x  —   2y = 16
	-10y = -10

Находим значение y (y = 1). Теперь, подставив значение y в любое уравнение системы, найдём x = 6:

3x — 2y = 16

3x — 2 · 1 = 16

3x — 2 = 16

3x = 16 + 2

3x = 18

x = 18 : 3

x = 6

Ответ: x = 6, y = 1.

Для решения системы уравнений, рассмотренной выше, был использован способ сложения, который основан на следующем свойстве:

Любое уравнение системы можно заменить на уравнение, получаемое путём сложения (или вычитания) уравнений, входящих в систему. При этом получается система уравнений, имеющая те же решения, что и исходная.

naobumium.info

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Нелинейные уравнения с двумя неизвестными

      Определение 1. Пусть   A   – некоторое множество пар чисел   (x ;  y) .   Говорят, что на множестве   A   задана числовая функция   z   от двух переменных   x   и   y ,   если указано правило, с помощью которого каждой паре чисел из множества   A   ставится в соответствие некоторое число.

      Задание числовой функции   z   от двух переменных   x   и   y   часто обозначают так:

причем в записи (1) числа   x   и   y   называют аргументами функции, а число   z   – значением функции, соответствующим паре аргументов   (x ; y) .

      Определение 2. Нелинейным уравнением с двумя неизвестными   x   и   y   называют уравнение вида

где   f (x , y)   – любая функция, отличная от функции

f (x , y) = ax +by + c ,

где   a ,  b ,  c   – заданные числа.

      Определение 3. Решением уравнения (2) называют пару чисел   (x ; y) ,   для которых формула (2) является верным равенством.

      Пример 1. Решить уравнение

x2 – 4xy + 6y2 – – 12 y +18 = 0 .

(3)

      Решение. Преобразуем левую часть уравнения (3):

x² – 4xy + 6y² – 12 y +18 =
= (x² – 4xy + 4y²) +
+ (2y²– 12y +18) =
= (x – 2y)² + 2(y – 3)² .

      Таким образом, уравнение (3) можно переписать в виде

(x – 2y)2 + 2(y – 3)2 = 0 .

(4)

      Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные   x   и   y   удовлетворяют системе уравнений

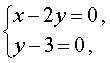
решением которой служит пара чисел   (6 ; 3) .

      Ответ:   (6 ; 3)

      Пример 2. Решить уравнение

      Решение. Из неравенства

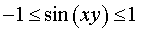
вытекает, что уравнение (5) решений не имеет.

      Ответ: Решений нет.

      Пример 3. Решить уравнение

      Решение. В соответствии с определением логарифма из формулы (6) получаем

      Следовательно, решением уравнения (6) является бесконечное множество пар чисел вида

(1 + y ; y) ,

где   y   – любое число.

Системы из двух уравнений, одно из которых линейное

      Определение 4. Решением системы уравнений

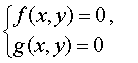
называют пару чисел   (x ; y) ,   при подстановке которых в каждое из уравнений этой системы получается верное равенство.

      Системы из двух уравнений, одно из которых линейное, имеют вид

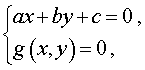
где   a ,  b ,  c   – заданные числа, а   g(x , y)   – функция двух переменных   x   и   y .  

      Пример 4. Решить систему уравнений

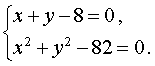(7)

      Решение. Выразим из первого уравнения системы (7) неизвестное   y   через неизвестное   x   и подставим полученное выражение во второе уравнение системы:

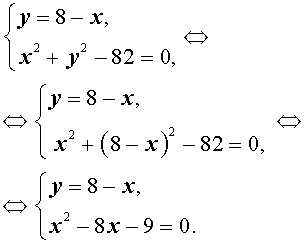
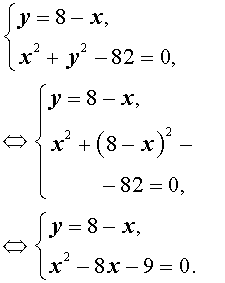
      Решая уравнение

x² – 8x – 9 = 0 ,

находим корни

x₁ = – 1 ,   x₂ = 9 .

      Следовательно,

y₁ = 8 – x₁ = 9 ,  
y₂ = 8 – x₂ = – 1 .

      Таким образом, решениями системы (7) являются две пары чисел

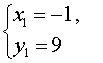и    

Ответ:   (– 1 ; 9) ,   (9 ; – 1)

Однородные уравнения второй степени с двумя неизвестными

      Определение 5. Однородным уравнением второй степени с двумя неизвестными   x   и   y   называют уравнение вида

ax² + bxy + cy² = 0 .

где   a ,  b ,  c   – заданные числа.

      Пример 5. Решить уравнение

3x2 – 8xy + 5y2 = 0 .

(8)

      Решение. Для каждого значения   y   рассмотрим уравнение (8) как квадратное уравнение относительно неизвестного   x .   Тогда дискриминант   D   квадратного уравнения (8) будет выражаться по формуле

D = (8y)² – 60y² = 4y² ,

откуда с помощью формулы для корней квадратного уравнения найдем корни уравнения (8):

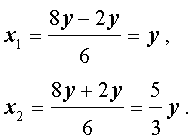
      Ответ. Решениями уравнения (8) являются все пары чисел вида

( y ; y)   или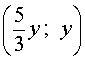    

где   y   – любое число.

      Следствие. Левую часть уравнения (8) можно разложить на множители

Системы из двух уравнений, одно из которых однородное

      Системы из двух уравнений, одно из которых однородное, имеют вид

где   a ,  b ,  c   – заданные числа, а   g(x , y)   – функция двух переменных   x   и   y .

      Пример 6. Решить систему уравнений

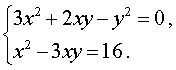(9)

      Решение. Решим однородное уравнение

3x² + 2xy – y² = 0 ,

рассматривая его как квадратное уравнение относительно неизвестного   x :

.

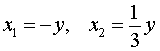      В случае, когда   x = – y ,   из второго уравнения системы (9) получаем уравнение

4y² = 16 ,

корнями которого служат числа   y₁ = 2 ,   y₂ = – 2 .  Находя для каждого из этих значений   y   соответствующее ему значение   x ,   получаем два решения системы:   (– 2 ; 2) ,   (2 ; – 2) .

      В случае, когда

,

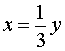из второго уравнения системы (9) получаем уравнение

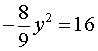
которое корней не имеет.

Ответ:   (– 2 ; 2) ,   (2 ; – 2)

Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное

      Пример 7. Решить систему уравнений

(10)

      Решение. Совершим над системой (10) следующие преобразования:

• второе уравнение системы оставим без изменений;
• к первому уравнению, умноженному на   5 ,   прибавим второе уравнение, умноженное на   3 ,   и запишем полученный результат вместо первого уравнения системы (10).

      В результате система (10) преобразуется в равносильную ей систему (11), в которой первое уравнение является однородным уравнением:

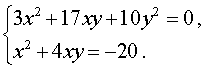(11)

     Решим однородное уравнение

3x² + 17xy + 10y² = 0 ,

рассматривая его как квадратное уравнение относительно неизвестного   x :

.

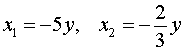      В случае, когда   x = – 5y ,   из второго уравнения системы (11) получаем уравнение

5y² = – 20 ,

которое корней не имеет.

      В случае, когда

,

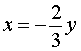из второго уравнения системы (11) получаем уравнение

,

корнями которого служат числа   y₁ = 3 ,   y₂ = – 3 .  Находя для каждого из этих значений   y   соответствующее ему значение   x ,   получаем два решения системы:   (– 2 ; 3) ,   (2 ; – 3) .

Ответ:   (– 2 ; 3) ,   (2 ; – 3)

Примеры решения систем уравнений других видов

      Пример 8. Решить систему уравнений (МФТИ)

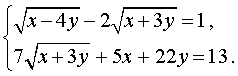(12)

      Решение. Введем новые неизвестные   u   и   v ,   которые выражаются через   x   и   y   по формулам:

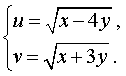(13)

      Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные   x   и   y   через   u   и   v .   Из системы (13) следует, что

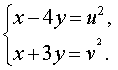(14)

      Решим линейную систему (14), исключив из второго уравнения этой системы переменную   x .   С этой целью совершим над системой (14) следующие преобразования:

• первое уравнение системы оставим без изменений;
• из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

      В результате система (14) преобразуется в равносильную ей систему

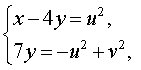
из которой находим

(15)

      Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде

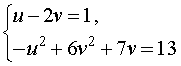(16)

      У системы (16) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное   u   через неизвестное   v   и подставить это выражение во второе уравнение системы:

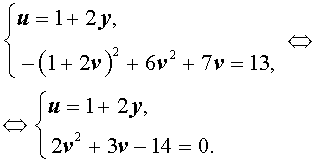
      Решая уравнение

2v² + 3v – 14 = 0 ,

находим корни

      Следовательно, решениями системы (16) являются две пары чисел

      Из формул (13) вытекает, что 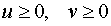  ,  поэтому первое решение должно быть отброшено. В случае   u₂ = 5,   v₂ = 2   из формул (15) находим значения   x   и   y :

x = 13,   y = – 3 .

      Ответ:   (13 ; – 3)

      Определение 6. Решением системы из двух уравнений с тремя неизвестными называют тройку чисел   (x ; y ; z) ,   при подстановке которых в каждое уравнение системы получается верное равенство.

      Пример 9. Решить систему из двух уравнений с тремя неизвестными

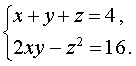(17)

      Решение. У системы (17) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное   z   через неизвестные   x   и   y   и подставить это выражение во второе уравнение системы:

(18)

      Перепишем второе уравнение системы (18) в другом виде:

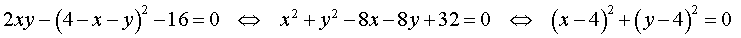
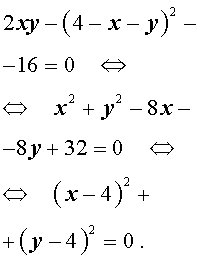
      Поскольку квадрат любого числа неотрицателен, то выполнение последнего равенства возможно лишь в случае   x = 4,   y = 4 .

      Следовательно,

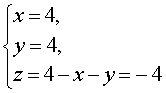
      Ответ:   (4 ; 4 ; – 4)

      Замечание. Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы линейных уравнений» и нашим учебным пособием «Системы уравнений».

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

www.resolventa.ru

Методы решения систем уравнений — методическая рекомендация. Алгебра, 9 класс.

1.	Метод сложения (линейные уравнения)	1 вид — рецептивный	лёгкое	2 Б.	Решение системы уравнений методом алгебраического сложения.
2.	Метод подстановки (линейные уравнения)	1 вид — рецептивный	лёгкое	2 Б.	Решение системы двух линейных уравнений.
3.	Корни квадратного уравнения, теорема Виета	1 вид — рецептивный	лёгкое	2 Б.	Составление квадратного уравнения.
4.	Метод подстановки (линейное и квадратное)	1 вид — рецептивный	лёгкое	2 Б.	Решение системы уравнений.
5.	Метод алгебраического сложения	2 вид — интерпретация	среднее	4 Б.	Решение системы уравнений методом алгебраического сложения.
6.	Способ сложения	2 вид — интерпретация	среднее	4 Б.	Решение системы методом сложения.
7.	Пары чисел, которые являются решением системы уравнений	2 вид — интерпретация	среднее	4 Б.	Выбор пар чисел, которые являются решением системы уравнений.
8.	Графический метод (парабола и прямая)	2 вид — интерпретация	среднее	4 Б.	Решение системы двух уравнений графическим методом.
9.	Графический метод (гипербола и прямая)	2 вид — интерпретация	среднее	4 Б.	Решение системы двух уравнений графическим методом.
10.	Графический метод (элементарные функции)	2 вид — интерпретация	среднее	3 Б.	Изобразив схематически графики уравнений, выяснить, сколько решений имеет система уравнений.
11.	Система квадратных уравнений	2 вид — интерпретация	среднее	4 Б.	Решение системы квадратных уравнений методом сложения.
12.	Система уравнений (линейное и квадратное) I	2 вид — интерпретация	среднее	4 Б.	Решение системы уравнений (линейное и квадратное) методом подстановки.
13.	Система уравнений (линейное и квадратное) II	2 вид — интерпретация	среднее	4 Б.	Решение системы уравнений (линейное и квадратное) методом подстановки.
14.	Система уравнений (линейное и квадратное) III	2 вид — интерпретация	среднее	3 Б.	Решение системы уравнений (линейное и квадратное) методом подстановки, использование формулы разности квадратов.
15.	Задача на составление системы уравнений	2 вид — интерпретация	среднее	4 Б.	Текстовая задача на составление системы уравнений, которая решается методом подстановки.
16.	Система рациональных уравнений	2 вид — интерпретация	среднее	4 Б.	Решение системы рациональных уравнений методом введения новых переменных.
17.	Система, состоящая из рационального и квадратного уравнений	2 вид — интерпретация	среднее	4 Б.	Решение системы, состоящей из квадратного и рационального уравнений, методом введения новой переменной.
18.	Система, состоящая из рационального и линейного уравнений	2 вид — интерпретация	среднее	3 Б.	Решение системы, состоящей из рационального и линейного уравнений, методом введения новой переменной.
19.	Система рациональных уравнений, вводится одна новая переменная	2 вид — интерпретация	среднее	4 Б.	Решение системы, состоящей из рациональных уравнений, методом введения новой переменной.
20.	Система, состоящая из рациональных уравнений	2 вид — интерпретация	среднее	4 Б.	Решение системы рациональных уравнений методом введения новой переменной.
21.	Система, состоящая из квадратного и рационального уравнений	2 вид — интерпретация	среднее	3 Б.	Решение системы, состоящей из квадратного и рационального уравнений, методом введения новой переменной.
22.	Система линейных уравнений	2 вид — интерпретация	среднее	4 Б.	Решение системы линейных уравнений графическим методом.
23.	Система, состоящая из квадратного и рационального уравнений, метод умножения	2 вид — интерпретация	среднее	3 Б.	Решение системы, состоящей из квадратного и рационального уравнений, методом введения новой переменной, также используется метод умножения.
24.	Пары чисел, которые являются решением системы уравнений	2 вид — интерпретация	среднее	6 Б.	Выбор пар чисел, которые являются решением системы уравнений.
25.	Графический метод (окружность и парабола)	3 вид — анализ	сложное	3 Б.	Выяснение, при каком значении параметра система уравнений имеет одно или три решения.

www.yaklass.ru