Системы уравнений. Способы решения систем уравнений
Система уравнений — это группа уравнений, в которых одни и те же неизвестные обозначают одни те же числа. Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:
| x — 4y = 2 | |
| 3x — 2y = 16 |
Решить систему уравнений — это значит, найти общие решения для всех уравнений системы или убедиться, что решения нет.
Чтобы решить систему уравнений, нужно исключить одно неизвестное, то есть из двух уравнений с двумя неизвестными составить одно уравнение с одним неизвестным. Исключить одно из неизвестных можно тремя способами: подстановкой, сравнением, сложением или вычитанием.
Способ подстановки
Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное.
Рассмотрим решение системы уравнений:
| x — 4y = 2 | |
| 3x — 2y = 16 |
Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:
x — 4y = 2;
x = 2 + 4y.
Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:
| 3x | — 2y = 16; |
| 3(2 + 4y) | — 2y = 16. |
Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.
| 3(2 + 4y) — 2y = 16; |
| 6 + 12y — 2y = 16; |
| 6 + 10y = 16; |
| 10y = 16 — 6; |
| 10y = 10; |
| y = 10 : 10; |
| y = 1. |
Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:
x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6.
Ответ: x = 6, y = 1.
Способ сравнения
Способ сравнения
 С помощью этого значения затем вычисляется значение второго неизвестного.
С помощью этого значения затем вычисляется значение второго неизвестного.Например, для решение системы:
| x — 4y = 2 | |
| 3x — 2y = 16 |
найдём в обоих уравнениях, чему равен y (можно сделать и наоборот — найти, чему равен x):
| x — 4y = 2 | 3x — 2y = 16 |
| -4y = 2 — x | -2y = 16 — 3x |
| y = (2 — x) : — 4 | y = (16 — 3x) : -2 |
Составляем из полученных выражений уравнение:
Решаем уравнение, чтобы узнать значение x:
| ||||||
| 2 — x = 32 — 6x | ||||||
| —x + 6x = 32 — 2 | ||||||
| 5x = 30 | ||||||
| x = 30 : 5 | ||||||
| x = 6 |
Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:
| x — 4y = 2 | 3x — 2y = 16 |
| 6 — 4y = 2 | 3 · 6 — 2y = 16 |
| -4y = 2 — 6 | -2y = 16 — 18 |
| -4y = -4 | -2y = -2 |
| y = 1 | y = 1 |
Ответ: x = 6, y = 1.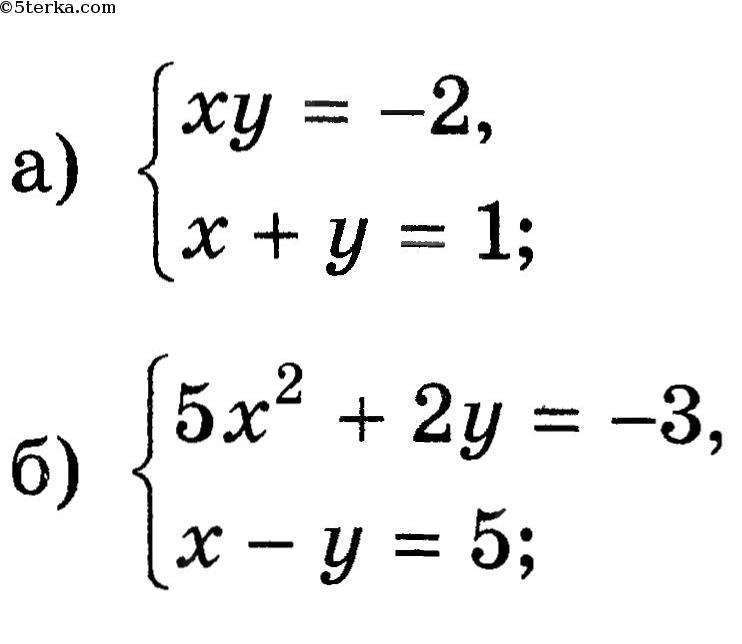
Способ сложения или вычитания
Чтобы решить систему уравнений способом сложения, нужно составить из двух уравнений одно, сложив левые и правые части, при этом одно из неизвестных должно быть исключено из полученного уравнения. Неизвестное можно исключить, уравняв при нём коэффициенты в обоих уравнениях.
Рассмотрим систему:
| x — 4y = 2 | |
| 3x — 2y = 16 |
Уравняем коэффициенты при неизвестном y, умножив все члены второго уравнения на -2:
(3x — 2y) · -2 = 16 · -2
-6x + 4y = -32
Получим:
| x — 4y = 2 | |
| -6x + 4y = -32 |
Теперь сложим по частям оба уравнения, чтобы получить уравнение с одним неизвестным:
| + | x — 4y = 2 |
| -6x + 4y = -32 | |
| -5x = -30 |
Находим значение x (x = 6). Теперь, подставив значение x в любое уравнение системы, найдём y = 1.
Теперь, подставив значение x в любое уравнение системы, найдём y = 1.
Если уравнять коэффициенты у x, то, для исключения этого неизвестного, нужно было бы вычесть одно уравнение из другого.
Уравняем коэффициенты при неизвестном x, умножив все члены первого уравнения на 3:
(x — 4y) · 3 = 2 · 3
3x — 12y = 6
Получим:
| 3x — 12y = 6 | |
| 3x — 2y = 16 |
Теперь вычтем по частям второе уравнение из первого, чтобы получить уравнение с одним неизвестным:
| — | 3x — 12y = 6 |
| 3x — 2y = 16 | |
| -10y = -10 |
Находим значение y (y = 1). Теперь, подставив значение y в любое уравнение системы, найдём x = 6:
| 3x — 2y = 16 |
| 3x — 2 · 1 = 16 |
| 3x — 2 = 16 |
| 3x = 16 + 2 |
| 3x = 18 |
| x = 18 : 3 |
| x = 6 |
Ответ: x = 6, y = 1.
Для решения системы уравнений, рассмотренной выше, был использован способ сложения, который основан на следующем свойстве:
Любое уравнение системы можно заменить на уравнение, получаемое путём сложения (или вычитания) уравнений, входящих в систему. При этом получается система уравнений, имеющая те же решения, что и исходная.
| 1. |
Метод сложения (линейные уравнения)
Сложность: лёгкое |
|
2.
|
Метод подстановки (линейные уравнения)
Сложность: лёгкое |
|
| 3. |
Корни квадратного уравнения, теорема Виета
Сложность: лёгкое |
|
4.
|
Метод подстановки (линейное и квадратное)
Сложность: лёгкое |
|
| 5. |
Метод алгебраического сложения
|
|
6.
|
Способ сложения
Сложность: среднее |
|
| 7. |
Пары чисел, которые являются решением системы уравнений
Сложность: среднее |
|
8.
|
Графический метод (парабола и прямая)
Сложность: среднее |
|
| 9. |
Графический метод (гипербола и прямая)
Сложность: среднее |
|
10.
|
Графический метод (элементарные функции)
Сложность: среднее |
|
| 11. |
Система квадратных уравнений
Сложность: среднее |
|
12.
|
Система уравнений (линейное и квадратное) I
Сложность: среднее |
|
| 13. |
Система уравнений (линейное и квадратное) II
Сложность: среднее |
|
14.
|
Система уравнений (линейное и квадратное) III
Сложность: среднее |
|
| 15. |
Задача на составление системы уравнений
Сложность: среднее |
|
16.
|
Система рациональных уравнений
Сложность: среднее |
|
| 17. |
Система, состоящая из рационального и квадратного уравнений
Сложность: среднее |
|
18.
|
Система, состоящая из рационального и линейного уравнений
Сложность: среднее |
|
| 19. |
Система рациональных уравнений, вводится одна новая переменная
Сложность: среднее |
|
20.
|
Система, состоящая из рациональных уравнений
Сложность: среднее |
|
| 21. |
Система, состоящая из квадратного и рационального уравнений
Сложность: среднее |
|
22.
|
Система линейных уравнений
Сложность: среднее |
|
| 23. |
Система, состоящая из квадратного и рационального уравнений, метод умножения
Сложность: среднее |
|
24.
|
Пары чисел, которые являются решением системы уравнений
Сложность: среднее |
|
| 25. |
Графический метод (окружность и парабола)
Сложность: сложное |
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1. Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
где a , b , c – заданные числа.
Определение 2. Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1. Найти решение уравнения
Решение. Выразим из равенства (2) переменную y через переменную x :
| (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание. Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Системы из двух линейных уравнений с двумя неизвестными
Определение 3. Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
| (4) |
где a1 , b1 , c1 , a2 , b2 , c2 – заданные числа.
Определение 4. В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных, а числа c1 , c2 – свободными членами.
Определение 5. Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6. Две системы уравнений называют равносильными (эквивалентными), если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «»
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных, который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
| (5) |
Решение. Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х.
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
| (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Ответ. (–2 ; 3) .
Пример 3. Найти все значения параметра p , при которых система уравнений
| (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение. Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
| (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если , то уравнение (9) имеет единственное решение
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда , система (7) имеет единственное решение
Если p = – 2 , то уравнение (9) принимает вид
,
и его решением является любое число . Поэтому решением системы (7) служит бесконечное множество всех пар чисел
Поэтому решением системы (7) служит бесконечное множество всех пар чисел
,
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Системы из трех линейных уравнений с тремя неизвестными
Определение 7. Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
| (10) |
где a1 , b1 , c1 , d1 , a2 , b2 , c2 , d2 , a3 , b3 , c3 , d3 – заданные числа.
Определение 8. В системе уравнений (10) числа a1 , b1 , c1 , a2 , b2 , c2 , a3 , b3 , c3 называют коэффициентами при неизвестных, а числа d1 , d2 , d3 – свободными членами.
Определение 9. Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
| (11) |
Решение. Будем решать систему (11) при помощи метода последовательного исключения неизвестных.
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
| (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
| (13) |
Из системы (13) последовательно находим
z = – 2 ; x = 1 ; y = 2 .
Ответ. (1 ; 2 ; –2) .
Пример 5. Решить систему уравнений
| (14) |
Решение. Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Ответ: (3 ; 0 ; –1) .
Замечание. Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Понятие системы уравнений. |
|||||
|
|||||
Свойства систем уравнений: |
|||||
Линейные системы уравнений с двумя неизвестными: |
|||||
|
Линейные системы уравнений с двумя переменными — это система вида: |
|||||
|
Прямые — графики уравнений системы пересекаются в одной точке. Система имеет единственное решение: |
|||||
| Прямые — графики уравнений системы — параллельны. Система не имеет решений. | |||||
|
Прямые — графики уравнений системы совпадают. Система имеет бесконечно много решений: |
|||||
Основные методы решения систем уравнений: |
|||||
| Графический метод: | |||||
| 1. Построить в одной системе координат графики обоих уравнений: | |||||
| 2. Найти координаты точек пересечения графиков. | |||||
| Метод подстановки: | |||||
| 1. Выразить одну переменную через другую в одном из уравнений. | |||||
| 2. Подставить это выражение в другое уравнение и получить уравнение с одной переменной. | |||||
| 3. Найти корни уравнения с одной переменной. | |||||
| 4. Подставить найденные корни в выражение для первой переменной и получить ее значение. | |||||
| Метод сложения (вычитания): | |||||
|
1. Сложить почленно уравнения системы, предварительно умножив каждое из уравнений на такой множитель: |
|||||
| 2. Найти корни уравнения с одной переменной. | |||||
| 3. Подставить найденные корни в любое из уравнений системы и получить уравнение с одной неизвестной. | |||||
| 4. Найти корни этого уравнения. | |||||
| Метод введения новых переменных: | |||||
|
1. Вместо исходных переменных x и y ввести такие новые переменные: чтобы система с ними стала проще. |
|||||
| 2. Решить систему с новыми переменными. | |||||
| 3. Найти значения исходных переменных. | |||||
7 класс. Алгебра. Системы двух уравнений с двумя переменными. — Способы решения систем уравнений с двумя неизвестными.
Комментарии преподавателяМетод подстановки.
Существует несколько методов решения систем. Один из них метод подстановки. Рассмотрим пример.
Пример 1:
Суть метода подстановки заключается в том, что в одном из уравнений нужно выразить одну переменную через вторую и подставить полученное выражение во второе уравнение.
В данном случае удобно выразить х во втором уравнении:
Подставим полученное выражение в первое уравнение:
Преобразуем первое уравнение:
,
,
,
Подставим полученное значение во второе уравнение:
, ,
Получаем следующее решение системы:
Пример 2:
В данном случае некоторая сложность заключается в том, что исходную систему нужно преобразовать, чтобы была возможность удобно и без ошибок применить метод подстановки. Для этого умножим оба уравнения на шесть:
Выразим у из первого уравнения:
Подставим полученное выражение во второе уравнение и выполним преобразования:
, ,
,
Подставим полученное значение в первое уравнение:
Получаем единственное решение системы, пара чисел:
Вывод:
на данном уроке мы ознакомились с понятием системы двух линейных уравнений с двумя неизвестными и одним из методов ее решения – способом подстановки. Мы решили примеры для понимания и закрепления данной техники.
Источник конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/osnovnye-ponyatiya-metod-podstanovki?konspekt&chapter_id=10
Метод сложения.Рассмотрим еще один способ решения систем двух линейных уравнений с двумя неизвестными – способ алгебраического сложения. Мы решим несколько различных примеров для закрепления техники.Метод алгебраического сложения, как и метод подстановки, заключается в том, что изначально из двух уравнений с двумя переменными нужно получить одно уравнение с одной переменной. Рассмотрим метод алгебраического сложения на примере:
Пример 1:
Задана система двух линейных уравнений с двумя неизвестными, и нужно найти такую пару х и у, чтобы при подстановке ее в уравнения получились верные числовые равенства.
Несложно заметить, что в первом уравнении у стоит с минусом, а во втором – с плюсом, и если сложить эти уравнения, то у уничтожится, и мы получим одно уравнение с одной неизвестной:
+
Получаем:
Найдем значение х:
,
Подставим значение х во второе уравнение и найдем у:
Ответ: (2,4; 2,2)
Обратим внимание на то, что мы рассматриваем метод алгебраического сложения, значит, уравнения можно не только складывать, но и вычитать. Рассмотрим пример:
Пример
При сложении уравнений получим:
,
Попробуем вычесть уравнения, причем, вычтем первое из второго:
,
Ответ: (5,5; 0,5)
Вывод:
на данном уроке мы рассмотрели новый метод решения систем двух линейных уравнений – метод алгебраического сложения. Мы решили несколько примеров для закрепления данной техники.
- Способ заключается в построении графика каждого уравнения, входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков. Координаты этой точки (x; y) и будут являться решением данной системы уравнений.
- Если прямые, являющиеся графиками уравнений системы, пересекаются, то система уравнений имеет единственное решение.
- Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет решений.
- Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений имеет бесконечное множество решений.
Примеры. Решить графическим способом систему уравнений.
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Ответ: (4; 5).
Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
Ответ: (-2; 5).
Источники конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/metod-algebraicheskogo-slozheniya?konspekt&chapter_id=10
http://www.mathematics-repetition.com/6-klass-mathematics/6-9-1-reshenie-sistem-lineynh-uravneniy-grafitcheskim-sposobom.html
Источник видео: https://www.youtube.com/watch?v=VltC62A-Tt4
Системы уравнений, урок по алгебре в 11 классе, презентация
Дата публикации: .
Темой сегодняшнего занятия будут системы уравнений. В курсе алгебры мы с вами научились решать многие системы уравнений с двумя переменными.
Мы знаем несколько методов решений систем уравнений:
- метод подстановки,
- метод сложения,
- метод введения новых переменных,
- графический метод.
Определение. Если поставлена задача: найти такую пару чисел $(х;y)$, причем эти числа удовлетворяют каждому уравнению $p(x;y)=0$ и $u(x;y)=0$, то эти уравнения образуют систему уравнений: $\begin {cases} p(x;y)=0, \\ u(x;y)=0. \end {cases}$.
Пара чисел $(x; y)$, удовлетворяющая каждому уравнению системы, называется решением системы уравнений. Решить систему уравнений – найти все пары чисел $(x; y)$, удовлетворяющие данной системе.
При решении систем уравнений мы руководствуемся теми же принципами, что и при решении обычных уравнений. Постепенно переходим к более простым уравнениям, выполняя равносильные преобразования. К уравнениям следствиям мы также можем переходить, но не стоит забывать, что в этом случае мы должны проверить все полученные корни.
Определение. Две системы уравнений называются равносильными, если они имеют одни и те же решения или если решений нет у каждой из систем.
Равносильными являются методы:
1. Метод подстановки.
2. Метод сложения.
3. Метод введения новой переменой.
Используя эти методы, мы заменяем исходную систему уравнений равносильной системой, как правило, получившуюся систему решить гораздо проще.
Методы, приводящие к уравнениям следствиям:
1. Возведение в квадрат обеих частей уравнения.
2. Умножение уравнений системы.
3. Преобразования, расширяющие область допустимых значений каждого уравнения.
При использовании данных методов проверку корней следует проводить всегда!
Система уравнений может состоять и из трех уравнений, и вообще, любого количества уравнений. В этом случае нужно найти такие числа, которые удовлетворяют каждому уравнению системы.5 == 0, x]
| Out[2]= |
Функция Reduce сводит системы неравенств к простой форме:
(Наберите <= для ввода символа≤.)| In[1]:= | ⨯Reduce[{0 < x < 2, 1 <= x <= 4}, x] |
| Out[1]= |
Упрощенная форма может состоять из нескольких интервалов:
| In[2]:= | ⨯Reduce[(x - 1) (x - 2) (x - 3) (x - 4) > 0, x] |
| Out[2]= |
Функция NumberLinePlot — это удобный способ визуализации этих результатов:
| In[3]:= | ⨯NumberLinePlot[x < 1 || 2 < x < 3 || x > 4, {x, -10, 10}] |
| Out[3]= |
Большое число уравнений и формул доступно через естественную форму ввода:
| In[1]:= | Xquadratic equation |
| Out[1]= |
Справочная информация: Полиномиальные уравнения »
Справочная информация: Решение уравнений »
Hands–on Start to
Wolfram Mathematica »
Полная документация »
Demonstrations Project »
Решение систем уравнений с двумя переменными (Алгебра 2, Как решить систему линейных уравнений) — Mathplanet
Система линейного уравнения состоит из двух или более уравнений, и одно ищет общее решение этих уравнений. В системе линейных уравнений каждому уравнению соответствует прямая линия, и каждый ищет точку, где две линии пересекаются.
Пример
Решите следующую систему линейных уравнений:
$$ \ left \ {\ begin {matrix} y = 2x + 4 \\ y = 3x + 2 \\ \ end {matrix} \ right.
$Поскольку мы ищем точку пересечения, мы можем изобразить уравнения:
Здесь мы видим, что линии пересекаются друг с другом в точке x = 2, y = 8. Это наше решение, и мы можем называть его графическим решением задачи.
Но как найти решение, если линии никогда не пересекаются? Нельзя, система уравнений не имеет решения.
Можно также прийти к правильному ответу с помощью метода исключения (также называемого методом сложения или методом линейной комбинации) или методом подстановки.
При использовании метода подстановки мы используем тот факт, что если два выражения y и x имеют равное значение x = y, то x может заменить y или наоборот в другом выражении без изменения значения выражения.
Пример
Решите системы уравнений методом подстановки
$$ \ left \ {\ begin {matrix} y = 2x + 4 \\ y = 3x + 2 \\ \ end {matrix} \ right. $$
Подставляем y в верхнем уравнении выражением для второго уравнения:
$$ \ begin {array} {lcl} 2x + 4 & = & 3x + 2 \\ 4-2 & = & 3x-2x \\ 2 & = & x \\ \ end {array} $$
Чтобы определить значение y , мы можем продолжить, вставив наше значение x в любое из уравнений.Выбираем первое уравнение:
$$ y = 2x + 4 $$
Подключаем x = 2 и получаем
$$ y = 2 \ cdot 2 + 4 = 8 $$
Таким образом, мы пришли к тому же ответу, что и в графическом решении.
Метод исключения требует, чтобы мы добавляли или вычитали уравнения, чтобы исключить x или y , часто нельзя приступить к сложению напрямую, не умножив сначала первое или второе уравнение на некоторое значение.
Пример
$$ 2x-2y = 8 $$
$$ x + y = 1 $$
Теперь мы хотим сложить два уравнения, но это не приведет к исключению x или y .Следовательно, мы должны умножить второе уравнение на 2 с обеих сторон и получить:
$$ 2x-2y = 8 $$
$$ 2x + 2y = 2 $$
Теперь мы пытаемся добавить нашу систему уравнений. Мы начинаем с терминов x слева, а затем с терминов y и, наконец, с цифр справа:
$$ (2x + 2x) + (- 2y + 2y) = 8 + 2 $$
Термины и теперь удалены, и теперь у нас есть уравнение только с одной переменной:
$$ 4x = 10 $$
$$ x = \ frac {10} {4} = 2.5 $$
После этого, чтобы определить значение y , мы вставляем x = 2,5 в одно из уравнений. Выбираем первое:
$$ \ begin {array} {lcl} 2 \ cdot 2.5-2y & = & 8 \\ 5-8 & = & 2y \\ -3 & = & 2y \\ \ frac {-3} {2} & = & y \\ y & = & -1,5 \\ \ end {array} $$
Видеоурок
Решите систему уравнений:
$$ \ left \ {\ begin {matrix} 2x-4y = 0 \\ -4x + 4y = -4 \ end {matrix} \ right.
$
Системы линейных уравнений
Линейное уравнение — это уравнение для линии .
Линейное уравнение не всегда имеет вид y = 3,5 — 0,5x ,
Это также может быть как y = 0,5 (7 — x)
Или как y + 0,5x = 3,5
Или как y + 0,5x — 3,5 = 0 и более.
(Примечание: это одно и то же линейное уравнение!)
A Система линейных уравнений — это когда у нас есть два или более линейных уравнения , работающих вместе.
Пример: Вот два линейных уравнения:
Вместе они представляют собой систему линейных уравнений.
Сможете ли вы сами определить значения x и y ? (Просто попробуйте, поиграйте с ними немного.)
Попробуем построить и решить реальный пример:
Пример: вы против лошади
Это гонка!
Вы можете бегать 0,2 км каждую минуту.
Лошадь может бежать 0.5 км каждую минуту. Но оседлать лошадь нужно за 6 минут.
Как далеко вы можете уйти, прежде чем лошадь вас поймает?
Мы можем составить два уравнения ( d = расстояние в км, t = время в минутах)
- Вы бежите со скоростью 0,2 км каждую минуту, поэтому d = 0,2t
- Лошадь бежит со скоростью 0,5 км в минуту, но мы берем на ее время 6: d = 0,5 (t − 6)
Итак, у нас есть система уравнений (это линейных ):
Решаем на графике:
Вы видите, как лошадь стартует через 6 минут, а потом бежит быстрее?
Кажется, тебя поймают через 10 минут… ты всего в 2 км.
В следующий раз беги быстрее.
Итак, теперь вы знаете, что такое система линейных уравнений.
Давайте продолжим узнавать о них больше ….
Решение
Существует множество способов решения линейных уравнений!
Давайте посмотрим на другой пример:
Пример: решите эти два уравнения:
На этом графике показаны два уравнения:
Наша задача — найти место пересечения двух линий.
Ну, мы видим, где они пересекаются, так что это уже решено графически.
А теперь давайте решим это с помощью алгебры!
Хммм … как это решить? Способов может быть много! В этом случае в обоих уравнениях есть «y», поэтому давайте попробуем вычесть все второе уравнение из первого:
x + y — (−3x + y) = 6 — 2
А теперь упростим:
х + у + 3х — у = 6-2
4x = 4
х = 1
Итак, теперь мы знаем, что линии пересекаются в точке x = 1 .
И мы можем найти совпадающее значение y , используя любое из двух исходных уравнений (потому что мы знаем, что они имеют одинаковое значение при x = 1). Воспользуемся первым (второй можете попробовать сами):
х + у = 6
1 + у = 6
г = 5
И решение:
x = 1 и y = 5
И график показывает, что мы правы!
Линейные уравнения
В линейных уравнениях допускаются только простые переменные. Нет x 2 , y 3 , √x и т. Д. :
Линейное против нелинейного
Размеры
| Линейное уравнение может быть в 2 измерениях … (например, x и y ) | ||
| … или в 3-х измерениях … (он делает самолет) | ||
| … или 4 размера … | ||
| … или больше! |
Общие переменные
Чтобы уравнения «работали вместе», они разделяют одну или несколько переменных:
Система уравнений состоит из двух или более уравнений в одной или нескольких переменных
Множество переменных
Таким образом, Система уравнений может иметь многих, уравнений и многих, переменных.
Пример: 3 уравнения с 3 переменными
| 2x | + | y | – | 2z | = | 3 |
| х | – | y | – | z | = | 0 |
| х | + | y | + | 3z | = | 12 |
Может быть любая комбинация:
- 2 уравнения с 3 переменными,
- 6 уравнений с 4 переменными,
- 9000 уравнений в 567 переменных,
- и др.
Решения
Когда количество уравнений равно , то же , что и количество переменных, , вероятно, будет решением. Не гарантировано, но вероятно.
На самом деле есть только три возможных случая:
- Нет раствор
- Одно решение
- Бесконечно много решений
Когда нет решения , уравнения называются «несовместимыми» .
Один или бесконечно много решения называются «согласованными»
Вот диаграмма для 2 уравнений с 2 переменными :
Независимая
«Независимый» означает, что каждое уравнение дает новую информацию.
В противном случае они «Зависимые» .
Также называется «линейная независимость» и «линейная зависимость»
Пример:
Эти уравнения «Зависимые» , потому что на самом деле это то же уравнение , только умноженное на 2.
Итак, второе уравнение не дало новой информации .
Истинные уравнения
Уловка состоит в том, чтобы найти, где все уравнения являются истинными одновременно .
Верно? Что это значит?
Пример: вы против лошади
Линия «ты» истинна по всей ее длине (но больше нигде).
В любом месте этой строки d равно 0.2т
- при t = 5 и d = 1 уравнение истинно (d = 0,2t? Да, поскольку 1 = 0,2 × 5 верно)
- при t = 5 и d = 3 уравнение не соответствует действительности (верно ли d = 0,2t? Нет, поскольку 3 = 0,2 × 5 неверно )
Точно так же линия «лошади» также истинна по всей своей длине (но больше нигде).
Но только в точке, где они пересекают (при t = 10, d = 2), они оба истинны .
Значит, они должны быть правдой одновременно …
… поэтому некоторые люди называют их «Одновременные линейные уравнения»
Решить с помощью алгебры
Для их решения принято использовать алгебру.
Вот пример «Лошади», решенный с помощью алгебры:
Пример: вы против лошади
Система уравнений:
В этом случае кажется, что проще всего установить их равными друг другу:
д = 0.2т = 0,5 (т − 6)
Начать с : 0,2t = 0,5 (t — 6)
Расширить 0,5 (t − 6) : 0,2t = 0,5t — 3
Вычтем 0,5t с обеих сторон: −0,3t = −3
Разделим обе части на −0,3 : t = −3 / −0,3 = 10 минута
Теперь мы знаем , когда тебя поймают!
Зная t , мы можем вычислить d : d = 0,2t = 0,2 × 10 = 2 км
И наше решение:
t = 10 минут и d = 2 км
Алгебра против графиков
Зачем использовать алгебру, если графики настолько просты? Потому что:
Более двух переменных невозможно решить с помощью простого графика.
Итак, алгебра приходит на помощь двумя популярными методами:
- Решение заменой
- Решение методом исключения
Мы увидим каждую с примерами по 2 переменным и 3 переменным. Вот и …
Решение заменой
Это шаги:
- Напишите одно из уравнений в стиле «переменная = …»
- Заменить (т.е. заменить) эту переменную в другое уравнение (а).
- Решите другое уравнение (я)
- (при необходимости повторить)
Вот пример с 2 уравнениями с 2 переменными :
Пример:
Мы можем начать с любого уравнения и любой переменной .
Воспользуемся вторым уравнением и переменной «y» (это выглядит как простейшее уравнение).
Напишите одно из уравнений в стиле «переменная =»… «:
Мы можем вычесть x из обеих частей x + y = 8, чтобы получить y = 8 — x . Теперь наши уравнения выглядят так:
Теперь замените «y» на «8 — x» в другом уравнении:
- 3x + 2 (8 — x) = 19
- у = 8 — х
Решите, используя обычные методы алгебры:
Развернуть 2 (8 − x) :
- 3x + 16 — 2x = 19
- у = 8 — х
Тогда 3x − 2x = x :
И на последок 19-16 = 3
Теперь мы знаем, что такое x , мы можем поместить его в уравнение y = 8 — x :
И ответ:
х = 3
у = 5
Примечание: поскольку — это решение , уравнения «непротиворечивы»
Проверка: почему бы вам не проверить, работают ли x = 3 и y = 5 в обоих уравнениях?
Решение подстановкой: 3 уравнения с 3 переменными
ОК! Давайте перейдем к более длинному примеру : 3 уравнения с 3 переменными .
Это несложно, сделать … просто нужно много времени !
Пример:
- х + г = 6
- г — 3у = 7
- 2x + y + 3z = 15
Мы должны аккуратно выровнять переменные, иначе мы потеряем из виду то, что делаем:
| x | + | z | = | 6 | |||||
| – | 3 года | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 |
WeI может начать с любого уравнения и любой переменной.Воспользуемся первым уравнением и переменной «x».
Напишите одно из уравнений в стиле «переменная = …»:
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 | |||
Теперь замените «x» на «6 — z» в других уравнениях:
(К счастью, есть только одно уравнение с x в нем)
| х | = | 6 — z | ||||||||
| – | 3 года | + | z | = | 7 | |||||
| 2 (6-z) | + | y | + | 3z | = | 15 | ||||
Решите, используя обычные методы алгебры:
2 (6 − z) + y + 3z = 15 упрощается до y + z = 3 :
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| y | + | z | = | 3 | |||||
Хорошо.Мы добились некоторого прогресса, но пока не достигли этого.
Теперь повторите процесс , но только для последних 2 уравнений.
Напишите одно из уравнений в стиле «переменная = …»:
Выберем последнее уравнение и переменную z:
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| z | = | 3 — х лет | |||||||
Теперь замените «z» на «3 — y» в другом уравнении:
| x | = | 6 — z | |||||||
| – | 3 года | + | 3 — х лет | = | 7 | ||||
| z | = | 3-х лет | |||||||
Решите, используя обычные методы алгебры:
−3y + (3 − y) = 7 упрощается до −4y = 4 , или другими словами y = −1
| x | = | 6 — z | |||||||
| y | = | -1 | |||||||
| z | = | 3-х лет | |||||||
Почти готово!
Зная, что y = −1 , мы можем вычислить, что z = 3 − y = 4 :
| x | = | 6 — z | |||||||
| y | = | -1 | |||||||
| z | = | 4 | |||||||
И зная, что z = 4 , мы можем вычислить, что x = 6 − z = 2 :
| x | = | 2 | |||||||
| y | = | -1 | |||||||
| z | = | 4 |
И ответ:
х = 2
у = -1
г = 4
Проверка: проверьте сами.
Мы можем использовать этот метод для 4 или более уравнений и переменных … просто повторяйте одни и те же шаги снова и снова, пока не решите проблему.
Заключение: Замена работает хорошо, но требует много времени.
Решение путем исключения
Уничтожение может быть быстрее … но должно быть аккуратным.
«Исключить» означает удалить : этот метод работает путем удаления переменных до тех пор, пока не останется только одна.
По идее, мы можем спокойно :
- умножить уравнение на константу (кроме нуля),
- прибавить (или вычесть) уравнение к другому уравнению
Как в этих примерах:
ПОЧЕМУ мы можем складывать уравнения друг в друга?
Представьте себе два действительно простых уравнения:
х — 5 = 3
5 = 5
Мы можем добавить «5 = 5» к «x — 5 = 3»:
х — 5 + 5 = 3 + 5
х = 8
Попробуйте сами, но используйте 5 = 3 + 2 в качестве второго уравнения
Он по-прежнему будет работать нормально, потому что обе стороны равны (для этого стоит знак =!)
Мы также можем поменять местами уравнения, чтобы первое могло стать вторым и т. Д., Если это поможет.
Хорошо, время для полного примера. Давайте использовать 2 уравнения с 2 переменными, пример из предыдущего:
Пример:
Очень важно, чтобы все было в порядке:
| 3x | + | 2 года | = | 19 | |||
| х | + | y | = | 8 |
Сейчас… наша цель — исключить переменную из уравнения.
Сначала мы видим, что есть «2y» и «y», так что давайте поработаем над этим.
Умножьте второе уравнение на 2:
| 3x | + | 2 года | = | 19 | |||
| 2 x | + | 2 y | = | 16 |
Вычтем второе уравнение из первого уравнения:
| x | = | 3 | |||||
| 2x | + | 2 года | = | 16 |
Ура! Теперь мы знаем, что такое x!
Затем мы видим, что во втором уравнении есть «2x», поэтому давайте уменьшим его вдвое, а затем вычтем «x»:
Умножьте второе уравнение на ½ (т. Е.е. разделить на 2):
| x | = | 3 | |||||
| x | + | y | = | 8 |
Вычтем первое уравнение из второго уравнения:
| x | = | 3 | |||||
| y | = | 5 |
Готово!
И ответ:
x = 3 и y = 5
А вот график:
Синяя линия — это место, где 3x + 2y = 19 истинно
Красная линия — это место, где x + y = 8 верно
При x = 3, y = 5 (где линии пересекаются) они равны , оба истинны. Этот и есть ответ.
Вот еще один пример:
Пример:
- 2х — у = 4
- 6x — 3y = 3
Разложите аккуратно:
| 2x | – | y | = | 4 | |||
| 6x | – | 3 года | = | 3 |
Умножьте первое уравнение на 3:
| 6x | – | 3 года | = | 12 | |||
| 6x | – | 3 года | = | 3 |
Вычтем второе уравнение из первого уравнения:
| 0 | – | 0 | = | 9 | |||
| 6x | – | 3 года | = | 3 |
0-0 = 9 ???
Что здесь происходит?
Проще говоря, решения нет.
| На самом деле это параллельные линии: |
И на последок:
Пример:
- 2х — у = 4
- 6x — 3y = 12
Аккуратно:
| 2x | – | y | = | 4 | |||
| 6x | – | 3 года | = | 12 |
Умножьте первое уравнение на 3:
| 6x | – | 3 года | = | 12 | |||
| 6x | – | 3 года | = | 12 |
Вычтем второе уравнение из первого уравнения:
| 0 | – | 0 | = | 0 | |||
| 6x | – | 3 года | = | 3 |
0 — 0 = 0
Ну, это на самом деле ИСТИНА! Ноль действительно равен нулю…
… это потому, что на самом деле это одно и то же уравнение …
… значит существует бесконечное количество решений
| Это та же строка: |
Итак, теперь мы рассмотрели пример каждого из трех возможных случаев:
- Нет раствор
- Одно решение
- Бесконечно много решений
Решение методом исключения: 3 уравнения с 3 переменными
Прежде чем мы начнем со следующего примера, давайте рассмотрим улучшенный способ решения задач.
Следуйте этому методу, и мы с меньшей вероятностью ошибемся.
Прежде всего удалите переменные в порядке :
.- Сначала удалите x с (из уравнений 2 и 3, по порядку)
- , затем исключите y (из уравнения 3)
Вот как мы их устраняем:
У нас есть «форма треугольника»:
Теперь начните снизу и вернитесь к исходному состоянию (так называемая «обратная подстановка»)
(введите z , чтобы найти y , затем z и y , чтобы найти x ):
И решаемся:
ТАКЖЕ, мы обнаружим, что проще выполнить примерно вычислений в уме или на бумаге для заметок, чем всегда работать в рамках системы уравнений:
Пример:
- х + у + г = 6
- 2y + 5z = −4
- 2х + 5у — г = 27
Аккуратно написано:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| 2x | + | 5 лет | – | z | = | 27 |
Сначала удалите x из 2-го и 3-го уравнения.
Во втором уравнении нет x … переходите к третьему уравнению:
Вычтите 2 раза 1-е уравнение из 3-го уравнения (просто проделайте это в уме или на бумаге для заметок):
И получаем:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| 3 года | – | 3z | = | 15 |
Затем удалите y из 3-го уравнения.
Мы, , могли бы вычесть 1½ раза 2-е уравнение из 3-го (потому что 1½, умноженное на 2, будет 3) …
… но мы можем избежать дробей , если мы:
- умножьте третье уравнение на 2 и
- умножьте второе уравнение на 3
и , затем выполняют вычитание … вот так:
И в итоге получаем:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| z | = | -2 |
Теперь у нас есть «треугольная форма»!
Теперь вернемся снова вверх «обратная замена»:
Мы знаем z , поэтому 2y + 5z = −4 становится 2y − 10 = −4 , затем 2y = 6 , поэтому y = 3 :
| x | + | y | + | z | = | 6 | |||
| y | = | 3 | |||||||
| z | = | −2 |
Тогда x + y + z = 6 становится x + 3−2 = 6 , поэтому x = 6−3 + 2 = 5
| x | = | 5 | |||||||
| y | = | 3 | |||||||
| z | = | −2 |
И ответ:
x = 5
y = 3
z = −2
Проверка: проверьте сами.
Общий совет
Когда вы привыкнете к методу исключения, он станет проще, чем замена, потому что вы просто выполняете шаги, и ответы появляются.
Но иногда замена может дать более быстрый результат.
- Замена часто проще для небольших случаев (например, 2 уравнения, а иногда и 3 уравнения)
- Удаление проще для больших ящиков
И всегда полезно сначала просмотреть уравнения, чтобы увидеть, есть ли простой ярлык… так что опыт помогает.
Алгебраические методы решения систем
Результаты обучения
- Используйте метод замены
- Решите систему уравнений, используя метод подстановки.
- Распознавать системы уравнений, не имеющие решения или бесконечное число решений
- Используйте метод исключения без умножения
- Решите систему уравнений, когда умножение не требуется для исключения переменной
- Используйте метод исключения с умножением
- Используйте умножение в сочетании с методом исключения для решения системы линейных уравнений
- Распознать, когда решение системы линейных уравнений подразумевает, что существует бесконечное число решений
Решите систему уравнений методом подстановки
В последних парах разделов мы проверили, что упорядоченные пары являются решениями систем, и использовали графики, чтобы классифицировать, сколько решений имеет система двух линейных уравнений.Что, если нам не дана точка пересечения или она не очевидна из графика? Можем ли мы еще найти решение этой системы? Конечно, можно, используя алгебру!
В этом разделе мы изучим метод подстановки для нахождения решения системы линейных уравнений с двумя переменными. На протяжении всего курса мы использовали подстановку по-разному, например, когда использовали формулы для вычисления площади треугольника и простого процента. Мы подставили значения, которые мы знали, в формулу, чтобы найти значения, которых мы не знали.Идея аналогична применительно к решению систем, в этом процессе всего несколько этапов. Сначала вы решите одну переменную, а затем подставите это выражение в другое уравнение. Чтобы понять, что это означает, давайте начнем с примера.
Пример
Найдите значение x для этой системы.
Уравнение A: [латекс] 4x + 3y = −14 [/ латекс]
Уравнение B: [латекс] y = 2 [/ латекс]
Показать решение Задачу просит решить для х .Уравнение B дает вам значение y , [latex] y = 2 [/ latex], поэтому вы можете заменить 2 в уравнение A для y.[латекс] \ begin {array} {r} 4x + 3y = −14 \\ y = 2 \, \, \, \, \, \, \, \ end {array} [/ latex]
Подставьте [латекс] y = 2 [/ латекс] в уравнение A.
[латекс] 4x + 3 \ влево (2 \ вправо) = — 14 [/ латекс]
Упростите и решите уравнение для x.
[латекс] \ begin {array} {r} 4x + 6 = −14 \\ 4x = −20 \ x = −5 \, \, \, \ end {array} [/ latex]
Ответ
[латекс] x = −5 [/ латекс]
Вы можете заменить значение переменной, даже если это выражение.Вот пример.
Пример
Решите относительно x и y .
Уравнение A: [латекс] y + x = 3 [/ латекс]
Уравнение B: [латекс] x = y + 5 [/ латекс]
Показать решение Цель метода подстановки — переписать одно из уравнений в терминах одной переменной. Уравнение B говорит нам, что [латекс] x = y + 5 [/ latex], поэтому имеет смысл заменить [latex] y + 5 [/ latex] в уравнение A для x .[латекс] \ begin {array} {l} y + x = 3 \\ x = y + 5 \ end {array} [/ latex]
Подставьте [латекс] y + 5 [/ латекс] в уравнение A для x .
[латекс] \ begin {array} {r} y + x = 3 \\ y + \ left (y + 5 \ right) = 3 \ end {array} [/ latex]
Упростите и решите уравнение для y.
[латекс] \ begin {array} {r} 2y + 5 = \, \, \, \, 3 \\\ подчеркивание {−5 \, \, \, \, \, — 5} \\ 2y = — 2 \\ y = −1 \ end {array} [/ latex]
Теперь найдите x , подставив это значение для y в любое уравнение, и решите относительно x . Здесь мы будем использовать уравнение A.
[латекс] \ begin {array} {r} y + x = 3 \\ — 1 + x = 3 \\\ подчеркивание {+1 \, \, \, \, \, \, \, \, \, +1} \\ x = 4 \ end {array} [/ latex]
Наконец, проверьте решение [latex] x = 4 [/ latex], [latex] y = −1 [/ latex], подставив эти значения в каждое из исходных уравнений.
[латекс] \ begin {array} {r} y + x = 3 \\ — 1 + 4 = 3 \\ 3 = 3 \\\ text {TRUE} \ end {array} [/ latex]
[латекс] \ begin {массив} {l} x = y + 5 \\ 4 = −1 + 5 \\ 4 = 4 \\\ text {TRUE} \ end {array} [/ latex]
Ответ
[латекс] x = 4 [/ латекс] и [латекс] y = -1 [/ латекс]
Решение — [латекс] (4, -1) [/ латекс].
Помните, решение системы уравнений должно быть решением каждого из уравнений внутри системы. Упорядоченная пара [latex] (4, −1) [/ latex] действительно работает для обоих уравнений, поэтому вы знаете, что это также решение системы.
Давайте посмотрим на другой пример, замена которого включает свойство распределения.
Пример
Решите относительно x и y .
[латекс] \ begin {array} {l} y = 3x + 6 \\ — 2x + 4y = 4 \ end {array} [/ latex]
Показать решение Выберите уравнение для замены.Первое уравнение говорит вам, как выразить y через x , поэтому имеет смысл подставить 3 x + 6 во второе уравнение для y .
[латекс] \ begin {array} {l} y = 3x + 6 \\ — 2x + 4y = 4 \ end {array} [/ latex]
Подставьте [латекс] 3x + 6 [/ latex] вместо y во второе уравнение.
[латекс] \ begin {array} {r} −2x + 4y = 4 \\ — 2x + 4 \ left (3x + 6 \ right) = 4 \ end {array} [/ latex]
Упростите и решите уравнение для x.
[латекс] \ begin {array} {r} −2x + 12x + 24 = 4 \, \, \, \, \, \, \, \\ 10x + 24 = 4 \, \, \, \, \ , \, \, \\\ подчеркивание {−24 \, \, — 24 \, \, \, \,} \\ 10x = −20 \\ x = −2 \, \, \, \ end {array} [/ латекс]
Чтобы найти y , подставьте это значение вместо x обратно в одно из исходных уравнений.
[латекс] \ begin {array} {l} y = 3x + 6 \\ y = 3 \ left (−2 \ right) +6 \\ y = −6 + 6 \\ y = 0 \ end {array} [/ латекс]
Проверьте решение [латекс] x = −2 [/ latex], [latex] y = 0 [/ latex], подставив их в каждое из исходных уравнений.
[латекс] \ begin {array} {l} y = 3x + 6 \\ 0 = 3 \ left (−2 \ right) +6 \\ 0 = −6 + 6 \\ 0 = 0 \\\ text { ИСТИНА} \ end {array} [/ latex]
[латекс] \ begin {array} {r} −2x + 4y = 4 \\ — 2 \ left (-2 \ right) +4 \ left (0 \ right) = 4 \\ 4 + 0 = 4 \\ 4 = 4 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Ответ
[латекс] x = -2 [/ латекс] и [латекс] y = 0 [/ латекс]
Решение (−2, 0).
В приведенных выше примерах одно из уравнений уже было дано нам в терминах переменной x или y . Это позволило нам быстро подставить это значение в другое уравнение и найти одно из неизвестных.
Иногда вам, возможно, придется сначала переписать одно из уравнений в терминах одной из переменных, прежде чем вы сможете произвести замену. В приведенном ниже примере вам сначала нужно изолировать одну из переменных, прежде чем вы сможете заменить ее в другое уравнение.
Пример
Решите относительно x и y .
[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 3x + y = 19 \ end {array} [/ latex]
Показать решение Выберите уравнение для замены. Второе уравнение,[латекс] 3x + y = 19 [/ latex], может быть легко переписан в терминах y , поэтому имеет смысл начать с этого.
[латекс] \ begin {array} 2x + 3y = 22 \\ 3x + y = 19 \ end {array} [/ latex]
Перепишите [латекс] 3x + y = 19 [/ latex] в виде y .
[латекс] \ begin {array} 3x + y = 19 \\ y = 19–3x \ end {array} [/ latex]
Замените [латекс] 19–3x [/ латекс] на y в другом уравнении.
[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 2x + 3 (19–3x) = 22 \ end {array} [/ latex]
Упростите и решите уравнение для x.
[латекс] \ begin {array} {r} 2x + 57–9x = 22 \, \, \, \, \\ — 7x + 57 = 22 \, \, \, \, \\ — 7x = −35 \\ x = 5 \, \, \, \, \, \, \, \ end {array} [/ latex]
Подставьте [latex] x = 5 [/ latex] обратно в одно из исходных уравнений, чтобы найти y.
[латекс] \ begin {array} {r} 3x + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ 3 \ left (5 \ right ) + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ 15 + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ y = 19−15 \\ y = 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
Проверьте оба решения, подставив их в каждое из исходных уравнений.
[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 2 (5) +3 \ left (4 \ right) = 22 \\ 10 + 12 = 22 \\ 22 = 22 \\\ текст {ИСТИНА} \\\\ 3x + y = 19 \\ 3 \ left (5 \ right) + 4 = 19 \\ 19 = 19 \\\ text {TRUE} \ end {array} [/ latex]
Ответ
[латекс] x = 5 [/ латекс] и [латекс] y = 4 [/ латекс]
Решение (5, 4).
В следующем видео вам будет показан пример решения системы двух уравнений с использованием метода подстановки.
Если бы вы выбрали другое уравнение для начала в предыдущем примере, вы все равно смогли бы найти такое же решение. Это действительно вопрос предпочтений, потому что иногда решение для переменной приводит к необходимости работать с дробями. По мере того, как вы приобретете больший опыт в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.
Распознавать системы уравнений, не имеющие решения или бесконечное число решений
Когда мы изучили методы решения линейных уравнений с одной переменной, мы обнаружили, что некоторые уравнения не имеют решений, а другие имеют бесконечное количество решений. Мы снова увидели это поведение, когда начали описывать решения систем уравнений с двумя переменными.
Вспомните этот пример из модуля 1 для решения линейных уравнений с одной переменной:
Решите относительно x .[латекс] 12 + 2x – 8 = 7x + 5–5x [/ латекс]
[латекс] \ displaystyle \ begin {array} {l} 12 + 2x-8 = 7x + 5-5x \\\, \, \, \, \, \, \, \, \, \, \, \ , \, \, 2x + 4 = 2x + 5 \ end {array} [/ latex]
[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, \, \, \, 2x + 4 = 2x + 5 \\\, \, \ , \, \, \, \, \, \ underline {-2x \, \, \, \, \, \, \, \, \, \, — 2x \, \, \, \, \, \, \, \,} \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, 4 = \, 5 \ end {array} [/ latex]
Это ложное утверждение подразумевает, что не существует решений этого уравнения. Точно так же вы можете увидеть такой результат, когда используете метод подстановки, чтобы найти решение системы линейных уравнений с двумя переменными.В следующем примере вы увидите пример системы двух уравнений, не имеющей решения.
Пример
Решите относительно x и y .
[латекс] \ begin {array} {l} y = 5x + 4 \\ 10x − 2y = 4 \ end {array} [/ latex]
Показать решение Поскольку первое уравнение [латекс] y = 5x + 4 [/ latex], вы можете заменить [латекс] 5x + 4 [/ latex] на y во втором уравнении.[латекс] \ begin {array} {r} y = 5x + 4 \\ 10x − 2y = 4 \, \, \, \, \, \, \, \, \, \, \, \, \\ 10x – 2 \ left (5x + 4 \ right) = 4 \, \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
Разверните выражение слева.
[латекс] 10x – 10x – 8 = 4 [/ латекс]
Объедините похожие члены в левой части уравнения.
[латекс] 10x – 10x = 0 [/ latex], поэтому у вас остается [latex] −8 = 4 [/ latex].
[латекс] \ begin {array} {r} 0–8 = 4 \\ — 8 = 4 \ end {array} [/ latex]
Ответ
Утверждение [latex] −8 = 4 [/ latex] неверно, поэтому решения нет.
Вы получаете ложное утверждение [латекс] −8 = 4 [/ латекс]. Что это значит? График этой системы проливает свет на то, что происходит.
Прямые параллельны, они никогда не пересекаются, и у этой системы линейных уравнений нет решения. Обратите внимание, что результат [latex] −8 = 4 [/ latex] — это , а не как решение. Это просто ложное утверждение, и оно указывает на то, что не существует решения .
Мы также видели линейные уравнения с одной переменной и системы уравнений с двумя переменными, которые имеют бесконечное количество решений. В следующем примере вы увидите, что происходит, когда вы применяете метод подстановки к системе с бесконечным числом решений.
Пример
Решите относительно x и y.
[латекс] \ begin {массив} {l} \, \, \, y = −0,5x \\ 9y = −4,5x \ end {array} [/ latex]
Показать решениеПодставляя -0,5 x вместо y во втором уравнении, вы получаете следующее:
[латекс] \ begin {array} {r} 9y = −4.5x \\ 9 (−0.5x) = — 4.5 \, \, \, \\ — 4.5x = −4.5x \ end {array} [/ латекс]
На этот раз вы получите верное утверждение: [латекс] −4,5x = −4,5x [/ latex]. Но что означает такой ответ? Опять же, построение графиков может помочь вам разобраться в этой системе.
Эта система состоит из двух уравнений, которые представляют одну и ту же линию; две линии коллинеарны. Каждая точка на линии будет решением системы, и поэтому метод подстановки дает верное утверждение. В этом случае существует бесконечное количество решений.
В следующем видео вы увидите пример решения системы, имеющей бесконечное количество решений.
В следующем видео вы увидите пример решения системы уравнений, не имеющей решений.
Решите систему уравнений методом исключения
Метод исключения для решения систем линейных уравнений использует добавочное свойство равенства. Вы можете добавить одно и то же значение к каждой стороне уравнения, чтобы исключить один из переменных членов. В этом методе вам может потребоваться, а может и не потребоваться сначала умножить члены в одном уравнении на число. Сначала мы рассмотрим примеры, в которых умножение не требуется для использования метода исключения.В следующем разделе вы увидите примеры использования умножения после того, как познакомитесь с идеей метода исключения.
С помощью этого метода легче показать, чем рассказать, поэтому давайте сразу же рассмотрим несколько примеров.
Если сложить два уравнения,
[латекс] x – y = −6 [/ latex] и [latex] x + y = 8 [/ latex] вместе, посмотрите, что произойдет.
[латекс] \ displaystyle \ begin {array} {l} \, \, \, \, \, xy = \, — 6 \\\ подчеркивание {+ \, x + y = \, \, \, 8} \\\, 2x + 0 \, = \, \, \, \, 2 \ end {array} [/ latex]
Вы исключили член y , и это уравнение можно решить, используя методы решения уравнений с одной переменной.
Давайте посмотрим, как эта система решается методом исключения.
Пример
Используйте устранение, чтобы решить систему.
[латекс] \ begin {array} {r} x – y = −6 \\ x + y = \, \, \, \, 8 \ end {array} [/ latex]
Показать решение Добавьте уравнения.[латекс] \ displaystyle \ begin {array} {r} xy = \, \, — 6 \\ + \ underline {\, \, x + y = \, \, \, \, \, 8} \\ \, \, \, \, \, \, 2x \, \, \, \, \, = \, \, \, \, \, \, 2 \ end {array} [/ latex]
Решите относительно x .
[латекс] \ begin {array} {r} 2x = 2 \\ x = 1 \ end {array} [/ latex]
Подставьте [latex] x = 1 [/ latex] в одно из исходных уравнений и решите относительно y .
[латекс] \ begin {array} {l} x + y = 8 \\ 1 + y = 8 \\\, \, \, \, \, \, \, \, \, \, y = 8– 1 \\\, \, \, \, \, \, \, \, \, \, y = 7 \ end {array} [/ latex]
Обязательно проверьте свой ответ в обоих уравнениях!
[латекс] \ begin {array} {r} x – y = −6 \\ 1–7 = −6 \\ — 6 = −6 \\\ text {TRUE} \\\\ x + y = 8 \ \ 1 + 7 = 8 \\ 8 = 8 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Проверяйте ответы.
Ответ
Решение (1, 7).
К сожалению, не все системы справляются с этим легко. Как насчет такой системы, как [латекс] 2x + y = 12 [/ latex] и [latex] −3x + y = 2 [/ latex].Если вы сложите эти два уравнения вместе, никакие переменные не будут исключены.
[латекс] \ displaystyle \ begin {array} {l} \, \, \, \, 2x + y = 12 \\\ подчеркивание {-3x + y = \, \, \, 2} \\ — x + 2y = 14 \ end {array} [/ latex]
Но вы хотите исключить переменную. Итак, давайте добавим противоположность одного из уравнений к другому уравнению. Это означает умножение каждого члена в одном из уравнений на -1, чтобы знак каждого члена был противоположным.
[латекс] \ begin {array} {l} \, \, \, \, 2x + \, \, y \, = 12 \ rightarrow2x + y = 12 \ rightarrow2x + y = 12 \\ — 3x + \, \, y \, = 2 \ rightarrow− \ left (−3x + y \ right) = — (2) \ rightarrow3x – y = −2 \\\, \, \, \, 5x + 0y = 10 \ end {array} [/ латекс]
Вы удалили переменную y , и теперь проблема может быть решена.
В следующем видео описывается аналогичная проблема, при которой можно исключить одну переменную, сложив два уравнения вместе.
Осторожность! Когда вы добавляете противоположность одного целого уравнения к другому, не забудьте изменить знак КАЖДОГО члена с обеих сторон уравнения. Это очень распространенная ошибка.
Пример
Используйте устранение, чтобы решить систему.
[латекс] \ begin {array} {r} 2x + y = 12 \\ — 3x + y = 2 \, \, \, \ end {array} [/ latex]
Показать решение Вы можете исключить переменную y , добавив противоположность одного из уравнений к другому уравнению.[латекс] \ begin {array} {r} 2x + y = 12 \\ — 3x + y = 2 \, \, \, \ end {array} [/ latex]
Перепишем второе уравнение как противоположное.
Доп. Решите относительно x .
[латекс] \ begin {array} {r} 2x + y = 12 \, \\ 3x – y = −2 \\ 5x = 10 \, \\ x = 2 \, \, \, \, \ end { array} [/ latex]
Подставьте [латекс] y = 2 [/ latex] в одно из исходных уравнений и решите относительно y .
[латекс] \ begin {array} {r} 2 \ left (2 \ right) + y = 12 \\ 4 + y = 12 \\ y = 8 \, \, \, \ end {array} [/ latex ]
Обязательно проверьте свой ответ в обоих уравнениях!
[латекс] \ begin {array} {r} 2x + y = 12 \\ 2 \ left (2 \ right) + 8 = 12 \\ 4 + 8 = 12 \\ 12 = 12 \\\ text {TRUE} \\\\ — 3x + y = 2 \\ — 3 \ left (2 \ right) + 8 = 2 \\ — 6 + 8 = 2 \\ 2 = 2 \\\ текст {ИСТИНА} \ end {array} [/ латекс]
Проверяйте ответы.
Ответ
Решение: (2, 8).
Ниже приведены еще два примера, показывающих, как решать линейные системы уравнений с использованием исключения.
Пример
Используйте устранение, чтобы решить систему.
[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = \, 25 \ end {array} [/ latex]
Показать решение Обратите внимание на коэффициенты каждой переменной в каждом уравнении. Если вы сложите эти два уравнения, член x будет удален, поскольку [латекс] −2x + 2x = 0 [/ latex].[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = \, 25 \ end {array} [/ latex]
Складываем и решаем относительно и .
[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = 25 \, \\ 8y = 24 \, \\ y = 3 \, \, \, \, \ end {array} [/ latex]
Подставьте [латекс] y = 3 [/ latex] в одно из исходных уравнений.
[латекс] \ begin {array} {r} 2x + 5y = 25 \\ 2x + 5 \ left (3 \ right) = 25 \\ 2x + 15 = 25 \\ 2x = 10 \ x = 5 \, \, \, \ end {array} [/ latex]
Проверить решения.
[латекс] \ begin {array} {r} −2x + 3y = −1 \\ — 2 \ left (5 \ right) +3 \ left (3 \ right) = — 1 \\ — 10 + 9 = — 1 \\ — 1 = −1 \\\ текст {ИСТИНА} \\\\ 2x + 5y = 25 \\ 2 \ left (5 \ right) +5 \ left (3 \ right) = 25 \\ 10 + 15 = 25 \\ 25 = 25 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Проверяйте ответы.
Ответ
Решение: (5, 3).
Пример
Используйте исключение, чтобы найти x и y.
[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 5x + 2y = 16 \ end {array} [/ latex]
Показать решение Обратите внимание на коэффициенты каждой переменной в каждом уравнении. Вам нужно будет добавить противоположное одному из уравнений, чтобы исключить переменную y , так как [latex] 2y + 2y = 4y [/ latex], но [latex] 2y + \ left (−2y \ right) = 0 [ /латекс].[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 5x + 2y = 16 \ end {array} [/ latex]
Замените одно из уравнений на противоположное, сложите и решите относительно x .
[латекс] \ begin {array} {r} 4x + 2y = 14 \, \, \, \, \\ — 5x – 2y = −16 \\ — x = −2 \, \, \, \\ x = 2 \, \, \, \, \, \, \, \ end {array} [/ latex]
Подставьте [латекс] x = 2 [/ latex] в одно из исходных уравнений и решите относительно y .
[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 4 \ left (2 \ right) + 2y = 14 \\ 8 + 2y = 14 \\ 2y = 6 \, \, \, \ \ y = 3 \, \, \, \ end {array} [/ latex]
Ответ
Решение: (2, 3).
Проверьте последний пример — подставьте (2, 3) в оба уравнения. Получается два верных утверждения: 14 = 14 и 16 = 16!
Обратите внимание, что вы могли бы использовать противоположное первому уравнению, а не второе уравнение, и получить тот же результат.
Распознавать системы, у которых нет решения или бесконечное количество решений
Как и в случае с методом подстановки, метод исключения иногда удаляет и v ariables, и вы получаете либо истинное, либо ложное утверждение. Напомним, ложное утверждение означает, что решения нет.
Давайте посмотрим на пример.
Пример
Решите относительно x и y.
[латекс] \ begin {array} {r} -x – y = -4 \\ x + y = 2 \, \, \, \, \ end {array} [/ latex]
Показать решение Добавьте уравнения, чтобы исключить член x .[латекс] \ begin {array} {r} -x – y = -4 \\\ подчеркивание {x + y = 2 \, \, \,} \\ 0 = −2 \ end {array} [/ latex ]
Ответ
Нет решения.
Построение этих линий показывает, что они параллельны и не имеют общих точек, что подтверждает отсутствие решения.
Если обе переменные исключены и у вас осталось истинное утверждение, это означает, что существует бесконечное количество упорядоченных пар, которые удовлетворяют обоим уравнениям. По сути, уравнения — это одна и та же линия.
Пример
Решите относительно x и y .
[латекс] \ begin {array} {r} x + y = 2 \, \, \, \, \\ — x − y = -2 \ end {array} [/ latex]
Показать решение Добавьте уравнения, чтобы исключить член x .[латекс] \ begin {array} {r} x + y = 2 \, \, \, \, \\\ underline {-x − y = -2} \\ 0 = 0 \, \, \, \ , \, \ end {array} [/ latex]
Ответ
Есть бесконечное количество решений.
Построение этих двух уравнений поможет проиллюстрировать, что происходит.
В следующем видео система уравнений, не имеющая решений, решается методом исключения.
Решите систему уравнений, когда необходимо умножение для исключения переменной
Многократное добавление уравнений или добавление противоположности одного из уравнений не приведет к удалению переменной. Посмотрите на систему ниже.
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Если вы сложите приведенные выше уравнения или добавите противоположное одному из уравнений, вы получите уравнение, в котором по-прежнему есть две переменные.Итак, давайте теперь сначала воспользуемся свойством умножения равенства. Вы можете умножить обе части одного уравнения на число, которое позволит вам исключить ту же переменную из другого уравнения.
Мы делаем это с умножением. Обратите внимание, что первое уравнение содержит член 4 y , а второе уравнение содержит член y . Если вы умножите второе уравнение на −4, когда вы сложите оба уравнения, переменные y в сумме дадут 0.
В следующем примере показаны все шаги по поиску решения для этой системы.
Пример
Решите относительно x и y .
Уравнение A: [латекс] 3x + 4y = 52 [/ латекс]
Уравнение B: [латекс] 5x + y = 30 [/ латекс]
Показать решение Ищите термины, которые можно исключить. В уравнениях нет членов x или y с одинаковыми коэффициентами.[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Умножьте второе уравнение на [латекс] −4 [/ латекс], чтобы получить одинаковый коэффициент.
[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, 3x + 4y = 52 \\ — 4 \ left (5x + y \ right) = — 4 \ влево (30 \ вправо) \ end {array} [/ latex]
Перепишите систему и добавьте уравнения.
[латекс] \ begin {array} {r} 3x + 4y = 52 \, \, \, \, \, \, \, \\ — 20x – 4y = −120 \ end {array} [/ latex]
Решите относительно x .
[латекс] \ begin {array} {l} −17x = -68 \\\, \, \, \, \, \, \, \, \, \, \, x = 4 \ end {array} [/ latex ]
Подставьте [латекс] x = 4 [/ latex] в одно из исходных уравнений, чтобы найти y .
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3 \ left (4 \ right) + 4y = 52 \\ 12 + 4y = 52 \\ 4y = 40 \\ y = 10 \ end {array} [/ latex]
Проверьте свой ответ.
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3 \ left (4 \ right) +4 \ left (10 \ right) = 52 \\ 12 + 40 = 52 \\ 52 = 52 \\\ текст {ИСТИНА} \\\\ 5x + y = 30 \\ 5 \ влево (4 \ вправо) + 10 = 30 \\ 20 + 10 = 30 \\ 30 = 30 \\\ текст {ИСТИНА} \ конец {array} [/ latex]
Проверяйте ответы.
Ответ
Решение: (4, 10).
Осторожность! Когда вы используете умножение для исключения переменной, вы должны умножить КАЖДЫЙ член в уравнении на выбранное вами число.Забыть умножить каждый член — распространенная ошибка.Есть и другие способы решить эту систему. Вместо умножения одного уравнения, чтобы исключить переменную при добавлении уравнений, вы могли бы умножить обоих уравнений на разные числа.
На этот раз удалим переменную x . Умножьте уравнение A на 5 и уравнение B на [латекс] -3 [/ латекс].
Пример
Решите для x и y .
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Показать решение Ищите термины, которые можно исключить.В уравнениях нет членов x или y с одним и тем же коэффициентом.[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Чтобы использовать метод исключения, вы должны создать переменные с одинаковым коэффициентом — тогда вы можете их исключить. Умножьте верхнее уравнение на 5.
[латекс] \ begin {array} {r} 5 \ left (3x + 4y \ right) = 5 \ left (52 \ right) \\ 5x + y = 30 \, \, \, \, \, \, \, \, \, \, \, \, \\ 15x + 20y = 260 \, \, \, \, \, \, \\ 5x + y = 30 \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
Теперь умножьте нижнее уравнение на −3.
[латекс] \ begin {array} {r} 15x + 20y = 260 \, \, \, \, \, \, \, \, \\ — 3 (5x + y) = — 3 (30) \\ 15x + 20y = 260 \, \, \, \, \, \, \, \, \\ — 15x – 3y = −90 \, \, \, \, \, \, \, \ end {array} [ / латекс]
Затем сложите уравнения и решите относительно y .
[латекс] \ begin {array} {r} 15x + 20y = 260 \\ — 15x – 3y = \, — 90 \\ 17y = 170 \\ y = \, \, \, 10 \ end {array} [ / латекс]
Подставьте [латекс] y = 10 [/ latex] в одно из исходных уравнений, чтобы найти x .
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3x + 4 \ left (10 \ right) = 52 \\ 3x + 40 = 52 \\ 3x = 12 \ x = 4 \, \, \, \ end {array} [/ latex]
Вы пришли к тому же решению, что и раньше.
Ответ
Решение: (4, 10).
Эти уравнения были умножены на 5 и [латекс] −3 [/ латекс] соответственно, потому что это дало вам члены, которые в сумме дают 0. Не забудьте умножить все члены уравнения.
В следующем видео вы увидите пример использования метода исключения для решения системы уравнений.
Можно использовать метод исключения с умножением и получить результат, который не указывает решений или бесконечно много решений, точно так же, как с другими методами, которые мы изучили для поиска решений систем.В следующем примере вы увидите систему, которая имеет бесконечно много решений.
Пример
Решите относительно x и y .
Уравнение A: [латекс] x-3y = -2 [/ латекс]
Уравнение B: [латекс] -2x + 6y = 4 [/ латекс]
Показать решение Ищите термины, которые можно исключить. В уравнениях нет членов x или y с одинаковыми коэффициентами.[латекс] \ begin {array} {r} x-3y = -2 \\ — 2x + 6y = 4 \ end {array} [/ latex]
Умножьте первое уравнение на [latex] 2 [/ latex] так, чтобы члены x уравнялись.
[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, 2 \ left (x-3y \ right) = 2 \ left (-2 \ right) \\ — 2x + 6y = 4 \ end {array} [/ latex]
Перепишите систему и добавьте уравнения.
[латекс] \ begin {array} {r} 2x-6y = -4 \\ — 2x + 6y = 4 \\ 0x + 0y = 0 \\\, \, \, \, \, \, \, \ , 0 = 0 \ end {array} [/ latex]
Вам знакомо такое решение? Это представляет собой решение всех действительных чисел для линейных уравнений, и это представляет то же самое, когда вы получаете такой результат с системами. Если мы решим оба этих уравнения относительно y, вы увидите, что это одно и то же уравнение.
Решите уравнение A относительно y:
[латекс] \ begin {array} {r} x-3y = -2 \\ — 3y = -x-2 \\ y = \ frac {1} {3} x + \ frac {2} {3} \ end {array} [/ latex]
Решите уравнение B относительно y:
[латекс] \ begin {array} -2x + 6y = 4 \\ 6y = 2x + 4 \\ y = \ frac {2} {6} x + \ frac {4} {6} \ end {array} [/ латекс]
Уменьшите дроби, разделив числитель и знаменатель обеих дробей на 2:
[латекс] y = \ frac {1} {3} + \ frac {2} {3} [/ latex]
Оба уравнения одинаковы, если записаны в форме пересечения наклона, и поэтому набором решений для системы являются все действительные числа.
Ответ
Решение: x и y могут быть действительными числами.
В следующем видео метод исключения используется для решения системы уравнений. Обратите внимание, что сначала нужно умножить одно из уравнений на отрицательное. Вдобавок у этой системы есть бесконечное количество решений.
Сводка
Метод подстановки — это один из способов решения систем уравнений. Чтобы использовать метод подстановки, используйте одно уравнение, чтобы найти выражение для одной из переменных в терминах другой переменной.Затем замените это выражение этой переменной во втором уравнении. Затем вы можете решить это уравнение, поскольку теперь оно будет иметь только одну переменную. Решение с использованием метода подстановки даст один из трех результатов: одно значение для каждой переменной в системе (с указанием одного решения), неверное утверждение (с указанием отсутствия решений) или истинное утверждение (с указанием бесконечного числа решений).
Объединение уравнений — мощный инструмент для решения системы уравнений.Сложение или вычитание двух уравнений для исключения общей переменной называется методом исключения (или добавления). Как только одна переменная исключена, становится намного проще найти другую.
Умножение можно использовать для создания условий совпадения в уравнениях перед их объединением, чтобы помочь в поиске решения системы. При использовании метода умножения важно умножить все члены с обеих сторон уравнения, а не только один член, который вы пытаетесь исключить.
Системы линейных уравнений: определения (стр. 1 из 7) Разделы: Определения, Решение путем построения графиков, подстановки, исключения / добавления, исключения Гаусса. А «система» уравнения — это набор или набор уравнений, с которыми вы работаете вместе сразу.Линейные уравнения (те, которые отображаются в виде прямых линий) проще чем нелинейные уравнения, и простейшая линейная система — это система с два уравнения и две переменные. Вспомните линейные уравнения. Например, рассмотрим линейное уравнение y = 3 x — 5. «Решение» к этому уравнению была любая точка x , y , которая «работала» в уравнении. Итак (2, 1) было решением, потому что, подключение 2 для x : С другой стороны, (1, 2) не было решением, потому что, подключение 1 для x : … что не равнялось y (что было 2, для этого пункта). Конечно, в практическом плане решений вы не нашли в уравнение, выбирая случайные точки, вставляя их и проверяя чтобы увидеть, «работают» ли они в уравнении. Вместо этого вы выбрали значения x . а затем вычислили соответствующие значения y . И вы использовали ту же процедуру для построения графика уравнение. Этот указывает на важный факт: каждая точка на графике была решением к уравнению, и любое решение уравнения отмечалось точкой на графике. Теперь рассмотрим следующее двухпараметрическая система линейных уравнений:
В частности, этот фиолетовый точка отмечает пересечение двух линий.Поскольку эта точка находится на обе строки, таким образом, он решает оба уравнения, поэтому он решает всю систему уравнения. И это соотношение всегда верно: для систем уравнений «решения» — это «пересечения». Вы можете подтвердить решение, подставив его в систему уравнений и подтвердив, что решение работает в каждом уравнении. Проверить данные возможные решения, я просто подключаю x — и y — координаты в уравнения и проверьте, работают ли они. Авторские права © Элизабет Стапель 2003-2011 Все права защищены Поскольку данная точка работает в каждом уравнении, это решение системы. Теперь проверю другой пункт (который мы уже знаем, глядя на график, это не решение): Итак, решение работает в одном из уравнений. Но чтобы решить систему, она должна работать в обоих уравнениях.Продолжая чек: Но –2 не равно –6, так что это «решение» не проверяет. Тогда ответ: только точка (–1, –5) — это решение системы Вверх | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Возвращаться к указателю Вперед >>
|
Введение в системы уравнений — Концепция
Система уравнений — это два или более уравнений, содержащих одни и те же переменные.Решения системы уравнений — это точка пересечения линий. Существует четыре метода решения систем уравнений : построение графиков, подстановка, исключение и матрицы. Решение систем уравнений — важная концепция, которая сначала появляется в алгебре I, но строится на математике верхнего уровня.
Решение систем уравнений — действительно важный навык на всех уроках математики.Он появляется на первом курсе по алгебре, но после этого продолжается практически во всех курсах. Так что это действительно важная идея, на которой вы захотите сосредоточиться в первый раз.
Система уравнений — это два или более уравнений, содержащих одни и те же переменные.
В классе алгебры вы, вероятно, увидите только две переменные, которые возведены в первую степень, но когда вы перейдете к продвинутой алгебре или к алгебре два, вы можете начать видеть вещи с x в квадрате, y в квадрате, иногда у вас есть три или даже четыре уравнения, не только x и y, но xyz и w или что-то в этом роде, но в алгебре большую часть времени мы просто говорим о двух уравнениях, в которых есть x и y.
Решение системы уравнений — это решение обоих или всех исходных уравнений. Это точка пересечения линий. Это означает, что если я возьму свои пары x и y, которые, как мне кажется, являются решением, и подставлю их в оба исходных уравнения, оба исходных уравнения окажутся верными, они выйдут как равенства, вот как я узнаю, будут ли мои работа правильная. Другой способ проверить свою работу — это построить график и посмотреть, находится ли моя точка решения там, где пересекаются линии. Вы усвоите это, когда начнете выполнять некоторые практические задания.Когда вас просят решить эти проблемы, обычно используются четыре метода.
Первый метод — построить график, вы нарисуете обе линии, увидите, где они пересекаются, и это ваша точка решения. Если вы не умеете рисовать, не волнуйтесь, у вас есть другие варианты. Подстановка — это когда вы выделяете одну переменную, а затем подставляете это выражение в другое уравнение. Вот как выглядит подстановка, и она действительно часто используется, когда у вас есть уравнения, оба в форме y = mx + b.
Третий метод называется «Исключение», и именно здесь вы смотрите на коэффициенты перед x и y и пытаетесь получить коэффициенты в ваших двух уравнениях, которые являются аддитивно обратными. Например, если мое уравнение 1 имеет 3x + 4y или что-то в этом роде, я хочу, чтобы мое уравнение 2 имело -3x, таким образом, когда я работаю с уравнениями вместе, мои положительные 3x и -3x будут удалены, когда я сложу их вместе. Вот что такое аддитивная инверсия.
Четвертый метод — это то, что вы не увидите, пока не станете более продвинутым в классах математики, вероятно, не раньше, чем вы продвинетесь в классе алгебры или алгебры 2.Так что я вычеркну это, мы не собираемся повторять это в одном курсе алгебры, но вы увидите это в будущем.
Так что, если вы хорошо умеете рисовать, это может быть ваш выбор, если вы хорошо используете алгебру, как будто вы довольно точны, когда выписываете все домашние задания по математике и не теряете отрицательных знаков Вы довольно хорошо разбираетесь в дробях и тому подобном. Замещение или исключение может быть вашим любимым методом. Тем не менее, лучше знать, как использовать все методы, чтобы в случае, если вы дойдете до своего теста по математике, и у вас будет как пердеть, и вы забудете, как выполнять подстановку, вы все равно могли использовать либо исключение, либо график.
Систем уравнений — Колледж алгебры
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Алгебра систем уравнений — Задачи | Системы уравнений
В алгебре система уравнений — это группа из двух или более уравнений, содержащих один и тот же набор переменных.Решение системы — это значения набора переменных, которые могут одновременно удовлетворять всем уравнениям системы. При графическом выражении, поскольку каждое уравнение системы можно изобразить в виде линии, когда мы ищем решение системы, мы фактически ищем пересечение этих линий. Также обратите внимание, что существуют как «линейные», так и «нелинейные» системы уравнений. Разница в том, что линейные уравнения дают прямые линии и содержат только переменные, коэффициенты и константы.Нелинейные уравнения могут содержать показатели степени, квадратные корни и т. Д. Это может показаться очевидным, но для осмысленного решения системы уравнений они должны разделять одну или несколько переменных. Например, мы можем решить такие уравнения, как\ (5 = x + y \)
и\ (2y + x = 7 \)
, потому что они разделяют переменные x и y. Как решить эти уравнения? Существует несколько методов, таких как подстановка, исключение, матрица и т. Д. Для этого урока давайте воспользуемся подстановкой, которая кажется наиболее интуитивно понятным методом для начинающих.Решите следующую систему уравнений:\ (5 = х + у \)
\ (2у + х = 7 \)
Начнем с первого уравнения\ (5 = x + y \)
. Вычитание y с обеих сторон дает нам\ (x \)
само по себе как\ (5-y = x \)
, которое можно переписать как\ (x = 5-y \)
. Затем мы подставляем\ (x = 5-y \)
во второе уравнение\ (2y + x = 7 \)
, что дает\ (2y + 5-y = 7 \)
. Мы можем упростить это до\ (y + 5 = 7 \)
, что говорит нам, что\ (y = 2 \)
.Затем мы заменяем\ (y = 2 \)
обратно на\ (x = 5-y \)
, что составляет\ (x = 5-2 \)
. Это упрощается до\ (x = 3 \)
. Мы сделали! Мы обнаружили, что\ (x = 3 \)
и\ (y = 2 \)
. Это решение этой системы уравнений. Вы можете более подробно ознакомиться с системами уравнений, используя практические задачи в верхней части этой страницы. Вы также можете попробовать другие темы на нашей странице практики. Готовы вывести свое обучение на новый уровень с помощью шагов «как» и «почему»? Подпишитесь на Cymath Plus сегодня.