Метод алгебраического сложения (В.А.Тарасов). Видеоурок. Алгебра 7 Класс
На данном уроке мы рассмотрим еще один способ решения систем двух линейных уравнений с двумя неизвестными – способ алгебраического сложения. Мы решим несколько различных примеров для закрепления техники.
Метод алгебраического сложения, как и метод подстановки, заключается в том, что изначально из двух уравнений с двумя переменными нужно получить одно уравнение с одной переменной. Рассмотрим метод алгебраического сложения на примере:
Пример 1:
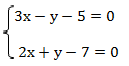
Задана система двух линейных уравнений с двумя неизвестными, и нужно найти такую пару х и у, чтобы при подстановке ее в уравнения получились верные числовые равенства.
Несложно заметить, что в первом уравнении у стоит с минусом, а во втором – с плюсом, и если сложить эти уравнения, то у уничтожится, и мы получим одно уравнение с одной неизвестной:
+
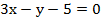
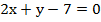
Получаем:
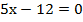
Найдем значение х:
, 
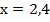
Подставим значение х во второе уравнение и найдем у:
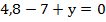
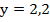
Ответ: (2,4; 2,2)
Пример 2:
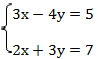
В данном случае если сразу применить метод алгебраического сложения, это ничего не даст и ни одна из переменных не уничтожится, так как ни одна из переменных не имеет противоположных коэффициентов, чтобы можно было применить данный метод, произведем некоторые преобразования:
Получаем:
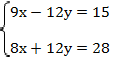
Теперь противоположные коэффициенты имеет переменная у, и при сложении уравнений переменная уничтожится:
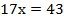
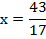
Подставим значение х во второе уравнение и найдем у:
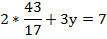
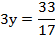
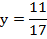
Ответ: (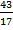
; 
)
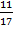Обратим внимание на то, что мы рассматриваем метод алгебраического сложения, значит, уравнения можно не только складывать, но и вычитать. Рассмотрим пример:
Пример 3:
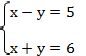
При сложении уравнений получим:
, 
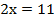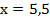
Попробуем вычесть уравнения, причем, вычтем первое из второго:
, 
Ответ: (5,5; 0,5)
Пример 4:
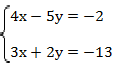
Хотелось бы сложить уравнения, чтобы избавиться, например, от переменной х, но для этого исходные уравнения необходимо преобразовать:
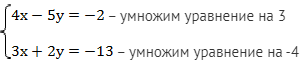
Получаем:
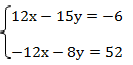
Выполним сложение, получим:
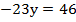
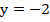
Подставим полученное значение у в первое уравнение:
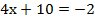
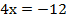
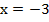
Ответ: (-3; -2)
Вывод: в данном уроке мы рассмотрели новый метод решения систем двух линейных уравнений – метод алгебраического сложения. Мы решили несколько примеров для закрепления данной техники.
Список литературы
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. – М.: Просвещение, 2010.
- Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. – М.: ВЕНТАНА-ГРАФ.
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Портал для всей семьи (Источник).
- Интернет-портал Nado5.ru (Источник).
- Интернет-портал Nado5.ru (Источник).
Домашнее задание
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, № 637, ст.228;
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, № 639, ст.228;
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, № 640, ст.229.
interneturok.ru
Метод алгебраического сложения. Видеоурок. Алгебра 9 Класс
На этом уроке мы продолжим изучение метод решения систем уравнений, а именно: метода алгебраического сложения. Вначале рассмотрим применение этого метода на примере линейных уравнений и его суть. Также вспомним, как уравнивать коэффициенты в уравнениях. И решим ряд задач на применение этого метода.
Рассмотрим метод алгебраического сложения на примере линейных систем.
Пример 1. Решить систему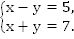 
Решение:
Если мы сложим эти два уравнения, то y взаимно уничтожатся, и останется уравнение относительно x.
Если же вычтем из первого уравнения второе, взаимно уничтожатся x, и мы получим уравнение относительно y. В этом и заключается смысл метода алгебраического сложения.
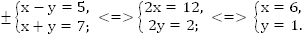
Ответ: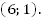 
Мы решили систему и вспомнили метод алгебраического сложения. Повторим его суть: мы можем складывать и вычитать уравнения, но при этом необходимо обеспечить, чтобы получилось уравнение только с одним неизвестным.
Пример 2. Решить систему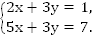 
Решение:
Член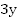 
присутствует в обоих уравнениях, поэтому удобен метод алгебраического сложения. Вычтем из первого уравнения второе.
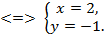
Ответ: (2; -1).
Таким образом, проанализировав систему уравнений, можно увидеть, что она удобна для метода алгебраического сложения, и применить его.
Рассмотрим еще одну линейную систему.
Пример 3. Решить систему 
Решение:
Мы хотим избавиться от y, но в двух уравнениях коэффициенты при y разные. Уравняем их, для этого умножим первое уравнение на 3, второе – на 4.
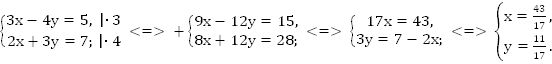
Ответ: 
Пример 4. Решить систему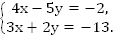 
Решение:
Уравняем коэффициенты при x
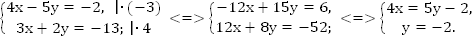
Можно сделать иначе – уравнять коэффициенты при y.
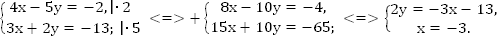
Ответ: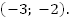 
Мы решили систему, дважды применив метод алгебраического сложения.
Метод алгебраического сложения применим и при решении нелинейных систем.
Пример 5. Решить систему 
Решение:
Сложим эти уравнения, и мы избавимся от y.
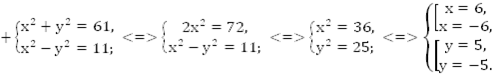
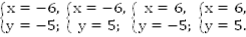
Эту же систему можно решить, дважды применив метод алгебраического сложения. Сложим и вычтем из одного уравнения другое.
Ответ: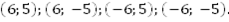
Пример 6. Решить систему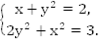 
Решение:
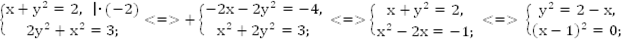
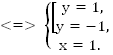
Ответ:
Пример 7. Решить систему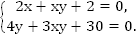 
Решение:
Методом алгебраического сложения избавимся от члена xy. Умножим первое уравнение на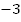 
.
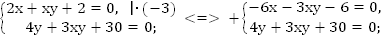
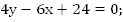
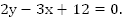
Первое уравнение остается без изменений, вместо второго записываем алгебраическую сумму.
Далее применяем метод подстановки.
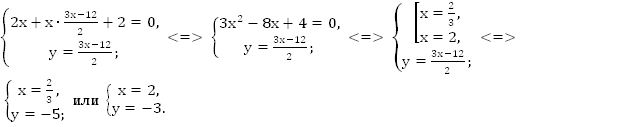
Ответ:
Пример 8. Решить систему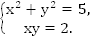 
Решение:
Умножим второе уравнение на 2, чтобы выделить полный квадрат.
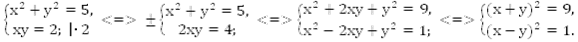
Наша задача свелась к решению четырех простейших систем.
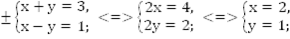
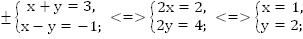
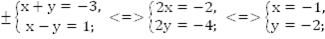
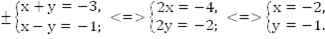
Ответ: 
Мы рассмотрели метод алгебраического сложения на примере решения линейных и нелинейных систем. На следующем уроке рассмотрим метод введения новых переменных.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 125 – 127.
interneturok.ru
Системы уравнений. Метод алгебраического сложения. Видеоурок. Алгебра 11 Класс
Тема: Уравнения и неравенства. Системы уравнений и неравенств
Урок: Системы уравнений. Метод алгебраического сложения
Рассмотрим системы двух уравнений с двумя неизвестными (1) и трех уравнений с тремя неизвестными (2).
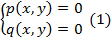
Здесь р и q – некоторые выражения, зависящие от пары переменных х и у.
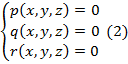
Здесь р, q и r – некоторые выражения, зависящие от тройки переменных х, у и z.
Частным решением системы 1 называется пара чисел (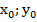
) такая, при подстановке которой в уравнения системы получим верные равенства.
Частным решением системы 2 называется тройка чисел (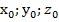
) такая, при подстановке которой в уравнения системы получим верные равенства.
Решить систему уравнений означает найти множество всех ее решений.
Чтобы найти множество всех решений системы, лучше всего пользоваться эквивалентными или равносильными преобразованиями, то есть такими, которые не искажают множество решений. В результате таких преобразований мы получаем равносильные системы, то есть имеющие одно и то же множество решений
Таким образом, процесс решения системы сводится к постепенному переходу от заданной сложной системы к все более простой и так до тех пор, пока не получим ответ.
При использовании эквивалентных преобразований проверка решений не является обязательной.
Методы решения систем с помощью эквивалентных преобразований:
-метод подстановки;
-метод алгебраического сложения;
-метод введения новых переменных;
Цель данного урока – метод алгебраического сложения, напомним его на простейшем примере. Рассмотрим систему двух линейных уравнений с двумя неизвестными:
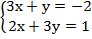
Несложно заметить, что если первое уравнение умножить на минус три и сложить со вторым, то мы избавимся от у. преобразуем:
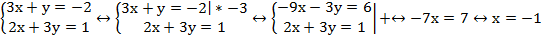
Теперь можно подставить значение х в любое уравнение и найти у, подставим во второе:
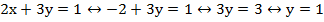
Ответ: (-1;1)
Мы получили единственное решение и это можно предвидеть. Оба уравнения системы линейны, геометрический образ каждого из них – прямая. коэффициенты перед х не пропорциональны, коэффициенты перед у непропорциональны, значит прямые пересекаются и мы имеем единственное решение системы.
Рассмотрим систему трех линейных уравнений с тремя неизвестными:
Первое уравнение оставим без изменений, в нем удобен коэффициент перед х, равный единице, это так называемый направляющий элемент.
Чтобы избавиться от х во втором уравнении умножим первое уравнение на минус два и сложим со вторым.
Чтобы избавиться от х в третьем уравнении умножим первое уравнение на минус единицу и сложим с третьим.
Преобразуем:
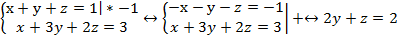
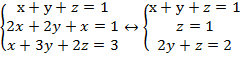
Так как мы легко нашли z, подставим его значение в первое и третье уравнения:
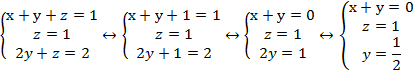
Подставим полученное значение у в первое уравнение и найдем х:
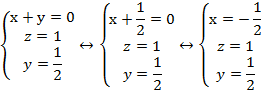
Ответ: (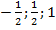
)
Мы получили единственное решение и это можно было предвидеть. Геометрическим образом каждого уравнения данной системы является плоскость. Все три плоскости могут пересечься в одной точке. Линия пересечения двух плоскостей пересекается с третьей плоскостью и в результате получается единственная точка пересечения – единственное решение системы трех линейных уравнений с тремя неизвестными.
Напомним, что системы линейных уравнений могут либо иметь единственное решение, либо бесчисленное множество решений, либо не иметь решений вовсе.
В данном случае система не имела бы решений, если бы плоскости были параллельны. Такова геометрическая интерпретация данной системы.
Пример 1 – решить систему методом алгебраического сложения:
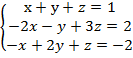
За направляющий элемент примем коэффициент единицу перед х в первом уравнении.
Оставим х в первом уравнении и исключим его из остальных уравнений.
Чтобы избавиться от х во втором уравнении умножим первое уравнение на два и сложим со вторым.
Чтобы избавиться от х в третьем уравнении сложим первое уравнение с третьим.
Преобразуем:
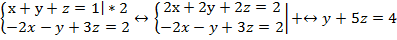
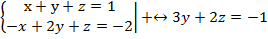
После преобразования получили систему:
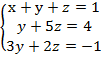
Теперь избавимся от у. за направляющий элемент выберем у с коэффициентом единица во втором уравнении.
Чтобы избавиться от у в первом уравнении умножим второе уравнение на минус единицу и сложим с первым.
Чтобы избавиться от у в третьем уравнении умножим второе уравнение на минус три и сложим с третьим.
Преобразуем:
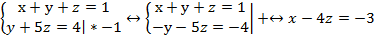
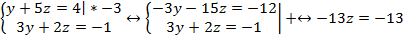
Получили систему:
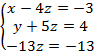
Теперь можем легко найти z:
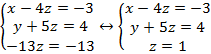
Подставим z в первое и второе уравнение:
Ответ: (1;-1;1)
Рассмотрим нелинейную систему.
Пример 2 – решить систему методом алгебраического сложения:
Несложно заметить, что можно исключить у. для этого умножим первое уравнение на минус два и сложим со вторым:
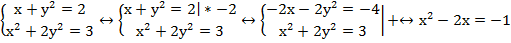
Решаем полученное квадратное уравнение любым способом и находим его корни:
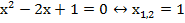
Находим у, подставив найденное значение в любое уравнение, например в первое:
Ответ: (1;1), (1;-1)
Рассмотрим систему с иррациональными выражениями.
Пример 3 – решить систему методом алгебраического сложения:
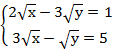
Несложно заметить, что можно исключить у. для этого умножим второе уравнение на минус три и сложим с первым:
Получили уравнение с одной неизвестной. Решаем его и находим х:
Находим соответствующее значение у:
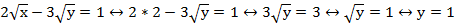
Поскольку в уравнениях присутствуют квадратные корни, проверяем ОДЗ и только после этого выписываем ответ.
Ответ: (4;1)
Пример 4 – решить систему методом алгебраического сложения:
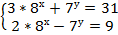
Очевидно, что здесь нужно избавиться от у, для этого сложим уравнения:
Получили уравнение с одной неизвестной. Решаем его и находим х:
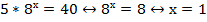
Находим соответствующее значение у:
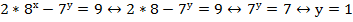
Ответ: (1;1)
Итак, мы рассмотрели метод алгебраического сложения при решении различных систем уравнений, далее рассмотрим метод введения новых переменных.
Список рекомендованной литературы
1. Мордкович А.Г. Алгебра и начала математического анализа. М.: Мнемозина
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. М.: Просвещение.
Рекомендованные ссылки на ресурсы интернет
1. Школьный помощник (Источник).
2. Xvatit.com (Источник).
3. Xvatit.com (Источник).
Рекомендованное домашнее задание
1. Алгебра и начала анализа, 10—11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, №186-188 ст.288;
2. Решить систему методом алгебраического сложения:
3. Решить систему методом алгебраического сложения:
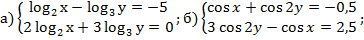
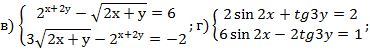
interneturok.ru
| 1. |
Неизвестная переменная x
Сложность: лёгкое |
2 |
| 2. |
Неизвестная переменная y
Сложность: лёгкое |
2 |
| 3. |
Система линейных уравнений
Сложность: лёгкое |
2 |
| 4. |
Система линейных уравнений
Сложность: лёгкое |
1 |
| 5. |
Система линейных уравнений (одинаковые коэффициенты при y)
Сложность: среднее |
4 |
| 6. |
Решение системы двух уравнений (обыкновенные дроби)
Сложность: среднее |
4 |
| 7. |
Система двух линейных уравнений (одинаковые коэффициенты при x)
Сложность: среднее |
4 |
| 8. |
Система линейных уравнений
Сложность: среднее |
4 |
| 9. |
Система линейных уравнений (смешанные числа и обыкновенные дроби)
Сложность: среднее |
4 |
| 10. |
Система линейных уравнений
Сложность: среднее |
1 |
| 11. |
Система линейных уравнений
Сложность: среднее |
4 |
| 12. |
Система линейных уравнений
Сложность: среднее |
4 |
| 13. |
Система линейных уравнений, одно из которых целое по сути, но дробное по виду
Сложность: среднее |
4 |
| 14. |
Решение системы линейных уравнений
Сложность: сложное |
6 |
| 15. |
Система линейных уравнений (сумма дробей)
Сложность: сложное |
5 |
| 16. |
Система двух уравнений
Сложность: сложное |
6 |
www.yaklass.ru
Решение систем уравнений способом сложения
Очень часто ученики затрудняются с выбором способа решения систем уравнений.
В данной статье мы рассмотрим один из способов решения систем – способ подстановки.
Если находят общее решение двух уравнений, то говорят, что эти уравнения образуют систему. В системе уравнений каждое неизвестное обозначает одно и то же число во всех уравнениях. Чтобы показать, что данные уравнения образуют систему, их обычно записывают одно под другим и объединяют фигурной скобкой, например
Замечаем, что при х = 15 , а у = 5 оба уравнения системы верны. Эта пара чисел и есть решение системы уравнений. Каждая пара значений неизвестных, которая одновременно удовлетворяет обоим уравнениям системы, называется решением системы.
Система может иметь одно решение (как в нашем примере), бесконечно много решений и не иметь решений.
Как же решать системы способом подстановки? Если коэффициенты при каком – нибудь неизвестном в обоих уравнениях равны по абсолютной величине (если же не равны , то уравниваем), то, складывая оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Затем решаем это уравнение. Определяем одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы ( в первое или во второе). Находим другое неизвестное. Давайте рассмотрим на примерах применение этого способа.
Пример 1. Решите систему уравнений
Здесь коэффициенты при у по абсолютному значению равны между собой, но противоположны по знаку. Давайте попробуем почленно сложить уравнения системы.
Полученное значение х=4, подставляем в какое–нибудь уравнение системы (например в первое) и находим значение у:
2 *4 +у = 11, у = 11 – 8, у = 3.
Наша система имеет решение х = 4, у = 3. Или же ответ можно записать в круглых скобках, как координаты точки, на первом месте х , на втором у.
Ответ: (4; 3)
Пример 2. Решить систему уравнений
Уравняем коэффициенты при переменной х, для этого умножим первое уравнение на 3, а второе на (-2), получим
Будьте внимательны при сложении уравнений
Тогда у = — 2. Подставим в первое уравнение вместо у число (-2), получим
4х + 3( -2) = — 4. Решаем это уравнение 4х = — 4 + 6, 4х = 2, х = ½.
Ответ: (1/2; — 2)
Пример 3. Решите систему уравнений
Умножим первое уравнение на (-2)
Решаем систему
получаем 0 = — 13.
Система решений не имеет, так ка 0 не равен (-13).
Ответ: решений нет.
Пример 4. Решите систему уравнений
Замечаем, что все коэффициенты второго уравнения делятся на 3,
давайте разделим второе уравнение на три и мы получаем систему, которая состоит из двух одинаковых уравнений.
Эта система имеет бесконечно много решений, так как первое и второе уравнения одинаковы (мы получили всего одно уравнение с двумя переменными). Как же представить решение этой системы? Давайте выразим переменную у из уравнения х + у = 5. Получим у = 5 – х.
Тогда ответ запишется так: (х; 5-х), х – любое число.
Мы рассмотрели решение систем уравнений способом сложения. Если остались вопросы или что – то непонятно запишитесь на урок и мы с вами устраним все проблемы.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
«Решение систем линейных уравнений способом сложения»
Цель:
1. Научить решать системы уравнений способом сложения;
2. Отработать алгоритм решения систем уравнений методом подстановки и сложения;
3. Воспитание внимания, точности, логики рассуждения.
Оборудование : учебник Ю.Н. Макарычев, Н.Г. Миндюк, Алгебра-7 класс, проверочный материал.
Ход урока
I. Организационный момент:
Сегодня на уроке мы должны научиться решать системы уравнений способом сложения.
II. Устный счет:
- Дано уравнение 4x-3y=-2. Укажите какое-либо решение (пару чисел (x;y)) этого уравнения.
- Выразите переменную y через x , если 3x-0.5y=1.
- Решите систему уравнений
- Является ли пара чисел (-2; -1) решением системы уравнений
- Четыре медвежонка тяжелее медведицы на 30 кг, а два таких медвежонка легче медведицы на 80 кг. Найдите массу медведицы.
III. Объяснение нового материала.
Составим систему уравнений для задачи с медвежатами. Пусть масса медведицы х кг, а одного медвежонка у кг.
Решим данную систему способом подстановки, при этом ответим на вопросы:
Метод подстановки
- Правильно ли выразили одно неизвестное через другое в одном из уравнений?
- Правильно ли вы подставили полученное выражение в другое уравнение?
- Правильно ли вы решили уравнение с одной неизвестной?
- Правильно ли вы подставили найденное значение для вычисления значения другой неизвестной?
В результате получаем: х=190, у=55.
А теперь подумаем, как решить эту систему методом сложения?
Умножить одно из уравнений системы или каждое из них на какое-либо число, чтобы коэффициенты при одной из переменных стали противоположными.
2у=110
у=55, а х=80+2*55 , х=190.
Какие можно поставить вопросы к методу сложения?
Метод сложения
- Каковы коэффициенты при х и y?
- При какой неизвестной вы делали коэффициенты противоположными?
- Для какого уравнения требуется дополнительный множитель, и какой именно?
- Все ли члены выбранного уравнения вы умножили на этот множитель?
- Правильно ли вы выполнили сложение левых и правых частей уравнений в полученной системе?
- Правильно ли вы решили уравнение с одной неизвестной?
- В какое уравнение вы подставили полученное значение неизвестной?
- Правильно ли вычислено значение другой неизвестной?
Подумайте, а можно ли решить данную систему графически?
Если да, то дома оформить решение графически.
IV. Закрепление изученного материала.
Решите систему уравнений методом сложения.
а)3
19у=76
у=4, 4х+3*4=6
4х=6-12
х=-1,5 Ответ: (-1,5; 4)
Закончите решение системы:
Ответ: (2;-3)
б)
Ответ: (13;-6).
Работа с учебником. Глава VI,§ 16 п 43 стр 203, алгоритм стр205- прочитать.
Выполнить у доски (парами) № 1147 (а;б)
а)Ответ:(2;1)
б) Ответ: (-8;-4).
Самостоятельная работа по учебнику: № 1147 (в;г)
в)
г)
Ответ: в) (60;30), г) (2; -1/4).
V. Домашняя работа:
выполнить графически систему уравнений, если сможете, рассмотреть примеры 1-3 учебника, решить №1148 (а), повторить №1162.
VI. Познакомимся с контрольным листом и домашней недельной проверочной работой.
Лист контроля
- Какое уравнение называется линейным уравнением с двумя неизвестными?
- Что значит решить линейное уравнение с двумя неизвестными?
- Что называется решением линейного уравнения с двумя неизвестными? Как записывается это решение?
- Что является графиком линейного уравнения с двумя неизвестными?
- Что называется системой двух линейных уравнений с двумя неизвестными?
- Что называется решение системы двух линейных уравнений с двумя неизвестными?
- Что значит решить систему двух линейных уравнений с двумя неизвестными?
- Какими методами можно решить систему двух линейных уравнений с двумя неизвестными? Каков алгоритм решения каждым методом?
- Как решается одно линейное уравнение с двумя неизвестными?
- Сколько решений имеет линейное уравнение с двумя неизвестными?
Как записывается общее решение линейного уравнения с двумя неизвестными?
Практикум
urok.1sept.ru
Примеры решения способом сложения | Алгебра
Рассмотрим конкретные примеры решения систем линейных уравнений способом сложения.
Ищем наибольший общий делитель коэффициентов при каждой из переменных (коэффициенты берем со знаком «+»).
Наибольший общий делитель коэффициентов при x — НОД(5;2)=10, при y — НОД(3;3)=3.
Проще работать с y, поскольку для получения перед y противоположных чисел достаточно умножить любое из уравнений на -1. Проще умножить на -1 второе уравнение системы (в этом случае после сложения уравнений коэффициент при x — положительное число).
Теперь подставим x=3 в любое из уравнений системы, например, во второе:
Решаем это уравнение:
6-3y=21
-3y=21-6
-3y=15
y= -5.
Ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.
Ответ: (3; -5).
НОД(6; 4)=12, НОД(13; 5)=65. Проще работать с коэффициентами перед x.
Чтобы получить перед иксами противоположные числа, первую систему умножим на -2, вторую — на 3
и сложим почленно левые и правые части уравнений:
Подставляем y= -1 в первое уравнение системы и находим x:
Ответ: (-2; -1).
НОД(3; 5)=15, НОД(5; 7)=35. Проще получить противоположные числа перед x.
Для этого умножим первое уравнение системы на 5, второе — на -3:
и сложим почленное левые и правые части полученных уравнений:
Подставляем y=2 в первое уравнение системы и находим x:
Ответ: (-7; 2).
Прежде чем применить способ сложения, данную систему следует упростить. Умножим первое уравнение на наименьший общий знаменатель дробей, во втором раскроем скобки:
Получили систему линейных уравнений с двумя переменными. Для решения её способом сложения достаточно умножить второе уравнение на -1 и сложить почленно левые и правые части уравнений:
Подставляем найденное значение b в первое уравнение системы (линейных уравнений):
Ответ: (-3; 10).
Систему линейных уравнений с тремя переменными можно решить, сначала исключив одно из неизвестных, а затем — другое.
В данной системе проще всего исключить переменную z.
К первому уравнению прибавим третье, умноженное на -3:
Ко второму уравнению прибавим третье, умноженное на 2:
Получили систему линейных уравнений с двумя переменными:
НОК(8;10)=40, НОК(13; 7)=91. Проще работать с x:
Подставив полученные значение y во второе уравнение системы с двумя переменными, найдём x:
Подставив значения y и x в третье уравнение системы с тремя переменными, найдём z:
Ответ: (2; 0; -1).
www.algebraclass.ru