Алгоритм извлечения квадратного корня столбиком — Алгебра — Математика — Каталог статей
Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью.
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Пусть извлекается корень из целого числа A. В отличие от деления снос производится группами по две цифры, причём группы следует отмечать, начиная с десятичной запятой (в обе стороны), дописывая необходимым количеством нулей.
Найти an, квадрат которого наиболее близко подходит к группе старших разрядов числа A, оставаясь меньше последнего.
Провести вычитание из старших разрядов A квадрата числа an.
Удвоить an.
Сдвинуть остаток от вычитания на 2 разряда влево, а величину 2an – на один разряд влево. Под сдвигом в данном алгоритме понимается умножение / деление на степени 10, что соответственно является сдвигом влево и вправо.
Приписать справа от остатка вычитания два следующих старших разряда числа A.
Сравнить полученное число с нулём.
Если полученное число не равно 0, то найти такое 2an − 1, которое, будучи умноженным на (2an10+an− 1), даст в результате число, меньшее полученного на четвёртом шаге, но наиболее близкое к нему по значению. Перейти к п. 3.
Если в п. 6 получено равенство, то перейти к п. 4, предварительно приписав справа от an нуль.
После получения количества цифр, равного n/2, прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой.
Описанная последовательность действий в математике получила название алгоритма извлечения квадратного корня.
1. Чтобы извлечь квадратный корень из данного целого числа, разбивают его справа налево на грани, по две цифры в каждой, кроме первой (крайней левой), в которой может быть и одна цифра.
2. Чтобы найти первую цифру корня, извлекают квадратный корень из первой грани.
3. Чтобы найти вторую цифру, из первой грани вычитают квадрат первой цифры корня, к остатку сносят вторую грань и число десятков получившегося числа делят на удвоенную первую цифру корня; полученное целое число снова подвергают испытанию.
4. Испытание проводится так: за вертикальной чертой (слева от остатка) пишут удвоенное, ранее найденное число корня, и к нему с правой стороны приписывают испытуемую цифру; получившееся после этой приписки число умножают на испытуемую цифру. Если после умножения получится число, больше остатка, то испытуемая цифра не годится и надо испытать следующую меньшую цифру.
5. Следующие цифры корня находят с помощью того же приёма.
6. Если после снесения грани число десятков получившегося числа окажется меньше делителя, т.е. меньше удвоенной найденной части корня, то в корне ставят 0, сносят следующую грань и продолжают действие дальше.
Пример. Извлечём корень√8649 .
1-й шаг. Число 8649 разбиваем на грани справа налево; каждая из которых должна содержать две цифры. Получаем две грани:
2-й шаг. Извлекаем квадратный корень из первой грани 86, получаем √86≈9 с недостатком. Цифра 9 – это первая цифра корня.
3-й шаг. Число 9 возводим в квадрат (92 = 81) и число 81 вычитаем из первой грани, получаем 86 – 81 = 5. Число 5 – первый остаток.
4-й шаг. К остатку 5 приписываем вторую грань 49, получаем число 549.
5-й шаг. Удваиваем первую цифру корня 9 и, записывая слева, получаем:
√86’49 = 9
¯ 81
18… ¯¯¯¯¯549¯¯¯¯¯
К числу 18 нужно приписать такую наибольшую цифру, чтобы произведение числа, которое мы получим, на эту цифру было бы либо равно числу 549, либо меньше, чем 549. Это цифра 3. Она находится путем подбора: количество десятков числа 549, то есть число 54 делится на 18, получаем 3, так как 183 ∙ 3 = 549. Цифра 3 – это вторая цифра корня.
6-й шаг. Находим остаток 549 – 549 = 0. Так как остаток равен нулю, то мы получили точное значение корня – 93. Процесс извлечения корня закончился. Число 93 – двузначное, так как подкоренное число 8649 содержит две грани. Корень из числа содержит столько цифр, сколько граней содержит это число.
Аналогично извлекают квадратный корень из десятичных дробей. Только подкоренное число разбивают на грани так, чтобы запятая была между гранями, т.е. от запятой влево и вправо. Если в крайней правой грани окажется одна цифра, то её дополняют дописыванием к числу нуля.
Извлечение кубического корня в столбик
Я уже писала здесь, как можно извлекать в столбик квадратный корень. Однако практически такой же алгоритм, напоминающий деление столбиком (или арабский способ деления) работает и для извлечения корней более высоких степеней. Рассмотрим, как извлекать кубический корень с произвольной точностью, определяя на каждом шаге по одной цифре этого корня. Как и для квадратных корней, буду описывать алгоритм пошагово, и каждый шаг будет сопровождаться примером.
Итак, давайте для примера будем извлекать кубический корень из .
1. Разобьем цифры исходного числа на группы по три цифры в каждой. При этом разбиение начинаем от десятичной запятой, двигаясь влево и вправо.
Пример. В нашем случае разбиение выглядит таким образом: .
2. Извлечем кубический корень из первой слева группы цифр. Разумеется, точно корень может не извлекаться, поэтому возьмем наибольшее число, куб которого меньше числа, образованного данной группой цифр.
Пример. В нашем случае первая слева группа цифр , поэтому первая цифра кубического корня — . Действительно, , а вот уже равно .
3. Возводим найденное число в куб и вычитаем из первой слева группы цифр, к разности приписываем справа следующие три цифры (т.е. цифры следующей группы).
Пример. В нашем случае получаем:
4. Теперь нужно подобрать следующую цифру корня. Для этого квадрат числа, образованного уже имеющимися цифрами, умножаем на и выбираем цифру, при умножении на которую получится число, меньшее, чем число, образованное всеми цифрами разности, кроме двух последних, но достаточно близкое к нему. Однако следует иметь в виду, что если при очередном вычитании получилось отрицательное число, нужно последнюю вычисленную цифру уменьшить на единицу.
Пример. Имеем: , поэтому выбираем цифру (в самом деле, , а ).
5. Умножаем полученное ранее произведение на выбранную цифру, потом еще на , прибавляем к полученному числу квадрат выбранной цифры, умноженный на число, образованное уже найденными цифрами корня, домноженное на , после чего прибавляем еще куб выбранной цифры.
Пример. У нас получится
.
6. Из полученной на шаге 3 разности вычитаем число, полученное на шаге
Пример. В нашем случае это будет .
7. Переходим к шагу 4.
Продолжаем данную последовательность шагов алгоритма до тех пор, пока корень не вычислен с требуемой точностью.
Пример. В нашем случае мы возводим в квадрат и умножаем его на : . Теперь подберем цифру, при умножении на которую числа получим близкое к , но меньшее его число. Эта цифра (). Теперь из числа (разность, полученная на предыдущем шаге и приписанная справа следующая группа цифр) нужно вычесть следующую сумму:
Тем самым, разность будет равна нулю, и корень, который оказался точным, извлечен — это .
Теперь приведу запись, которая при этом получается (разумеется, при реальных вычислениях все скорее всего будет не столь красиво и аккуратно ).
Алгоритм основан на формуле куба суммы: .
Для тех же, кому интересно извлечение корней высших степеней, даю ссылку (правда, материал на английском): http://en.wikipedia.org/wiki/Shifting_nth-root_algorithm.Как извлечь квадратный корень из многозначного числа?
такое на множители проще всего разложить, из которых корни известны типа 48400 = 4*4*25*121
такое на множители проще всего разложить, из которых корни известны типа 48400 = 4*4*25*121
Как извлечь корень из числа — видео
Как извлечь корень из числа. В этой статье мы будем учиться извлекать квадратный корень из четырехзначных и пятизначных чисел.
Давайте, для примера, извлечем квадратный корень из числа 1936.
, следовательно, 
.
Последняя цифра в числе 1936 — цифра 6. На 6 заканчивается квадрат числа 4 и числа 6. Следовательно, 1936 может быть квадратом числа 44 или числа 46. Осталось проверить с помощью умножения.
, значит, 
Извлечем квадратный корень из числа 15129.
, следовательно, 
.
Последняя цифра в числе 15129 — цифра 9. На 9 заканчивается квадрат числа 3 и числа 7. Следовательно, 15129 может быть квадратом числа 123 или числа 127. Проверим с помощью умножения.
, значит, 
Как извлечь корень — видео
А теперь предлагаю вам посмотреть видео Анны Денисовой — «Как извлечь корень«, автора сайта «Простая физика», в котором она рассказывает, как извлекать квадратные и кубические корни без калькулятора.
В видео рассматривается несколько способов извлечения корней:
1. Самый простой способ извлечения квадратного корня.
2. Подбором, используя квадрат суммы.
3. Вавилонский способ.
4. Способ извлечения квадратного корня в столбик.
5. Быстрый способ извлечения кубического корня.
6. Способ извлечения кубического корня в столбик.
И.В. Фельдман, репетитор по математике.
Способы извлечения квадратного корня
Нахождение приближённого значения арифметического квадратного корня.
Существует несколько способов извлечения арифметического квадратного корня. Рассмотрим некоторые из них.
I. Графический метод (очень грубое приближение).
Строим график функции 
. На оси Ох отмечаем необходимое число и находим соответствующее значение у.
Из рисунка видно, что 
.
II. Метод оценки (трудоёмкий метод):
Найдём, например, приближённое значение 
с тремя знаками после запятой. Так как 
, то 
. Дробная часть значения корня находится подбором. 
. Так как 
, то уточняем 
до сотых тем же способом: 
. Так как 
, то уточняем 4,12 до тысячных. 
. Так как 
, то делаем вывод, что приближённое значение равно 
. Таким же образом можно уточнить значение корня с любым количеством знаков после запятой.
III. Метод Герона. Древние вавилоняне пользовались следующим способом нахождения приближённого значения квадратного корня из числа х. Число х они представляли в виде суммы 
, где 
ближайший к числу х точный квадрат натурального числа а и пользовались формулой: 
. Приведём пример: 
.
IV. Арифметический метод (удобен для целых, не очень больших чисел).
Для квадратов чисел верны следующие равенства:
1 = 12
1 + 3 = 22
1 + 3 + 5 = 32
1 + 3 + 5 + 7 = 42
и так далее.
То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и посчитав количество выполненных действий. Например, так: вычислить
17 − 1 = 16
16 − 3 = 13
13 − 5 = 8
8 – 7 = 1
Выполнено 4 действия, целая часть квадратного корня из числа 17 равна 4.
Вычислить 
121 – 1 = 120
120 – 3 = 117
117 – 5 = 112
112 – 7 = 105
105 – 9 = 96
96 – 11 = 85
85 – 13 = 72
72 – 15 = 57
57 – 17 = 40
40 – 19 = 21
21 – 21 = 0
Выполнено 11 действий, значит 
.
V. Метод вычисления квадратного корня «столбиком» (удобен для любых чисел с любой точностью).
Вычислить 
.
Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41. Чтобы получить первую цифру извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани.
Затем из первой слева грани вычитаем 
, к остатку сносим всю вторую грань.
Слева от полученного числа 298 пишут удвоенную цифру корня (10), делят на неё число всех десятков раннее полученного числа (29/2 ≈ 2), проверяют частное (102 ∙2 = 204 должно быть не больше 298) и записывают (2) после первой цифры корня.
Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41).
Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня.
Получили ответ .
Только надо помнить, что если десятичная дробь имеет нечётное число десятичных знаков, из неё точно квадратный корень не извлекается.
Извлеките квадратный корень из числа:
32; 32,45; 249,5; 0,9511
а) с точностью до 0,1;
б) с точностью до 0,01;
в) с точностью до 0,001.
Извлеките квадратный корень из числа:
2; 3; 5
а) с точностью до 0,1;
б) с точностью до 0,01;
в) с точностью до 0,001.
Сравните числа:
а) ; б) ; в) ;
г) ; д) ; е) .
Вычислите с точностью до 0,01:
.
3
Конспект урока.Тема:» Алгоритм извлечения квадратного корня»
Тема: «Алгоритм извлечения квадратного корня»
Цели: обобщение и расширение знаний учащихся по данной теме, развитие умений обобщать и абстрагировать и конкретизировать свойства изучаемых объектов, воспитывать уважительное отношение к сверстникам.
Оборудование: проектор, раздаточный материал.
Структура урока
:
Сообщение темы урока и его целей.
Проверка домашнего задания.
Систематизация знаний и умений по пройденному материалу.
Контроль знаний (проведение тестовой работы).
Объяснение нового материала.
Постановка домашнего задания.
Подведение итогов урока.
Ход урока:
Сообщение темы урока и его целей.
Задаёт вопросы по пройденной теме:
Что называется арифметическим квадратным корнем?
Как называется число a в записи
?При каких значениях a данное выражение имеет смысл?
При каких значениях a уравнение вида x=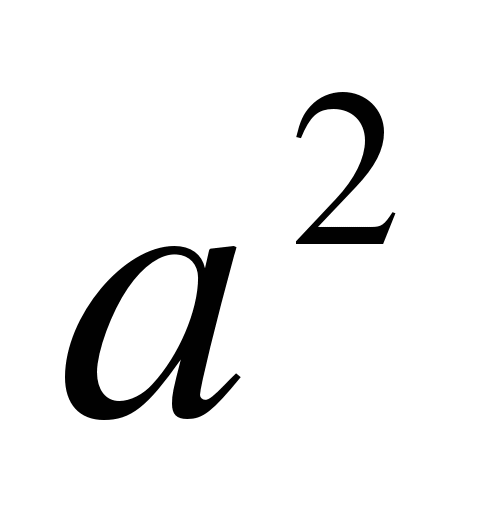
решения?
Читают план урока, который проектируется на экран через проектор.
Отвечают на заданные учителем вопросы.
2 .Проверка домашнего задания.
4. Контроль знаний (проведение тестовой работы).
1 вариант 2 вариант
1.Вычислите. 1. Вычислите
+
—
+
—
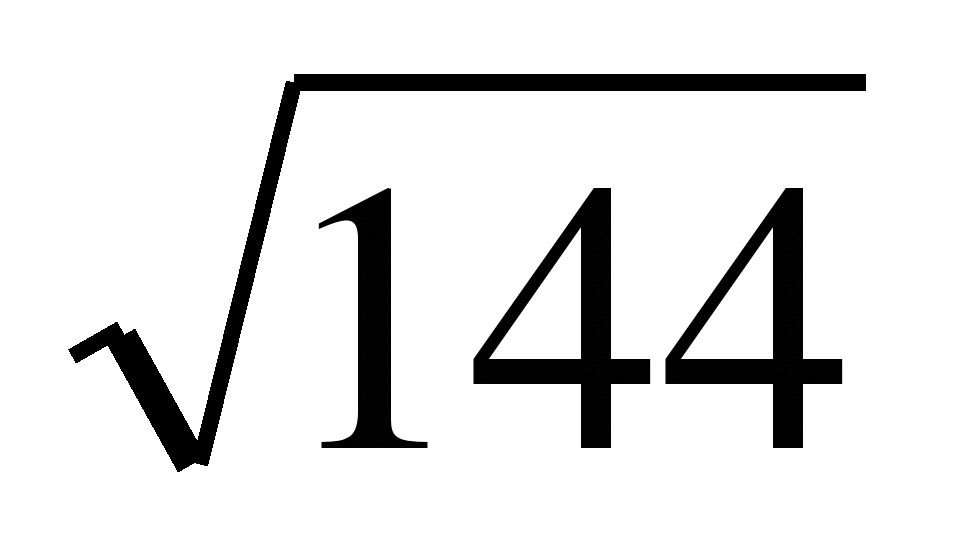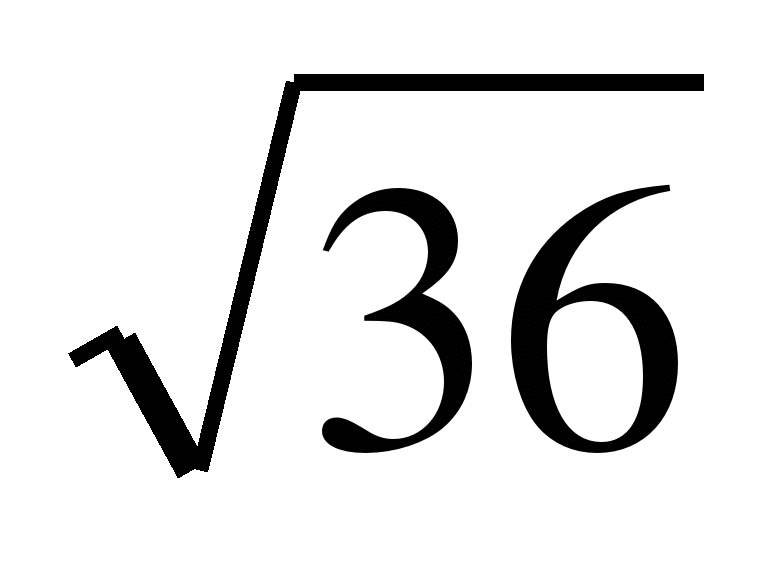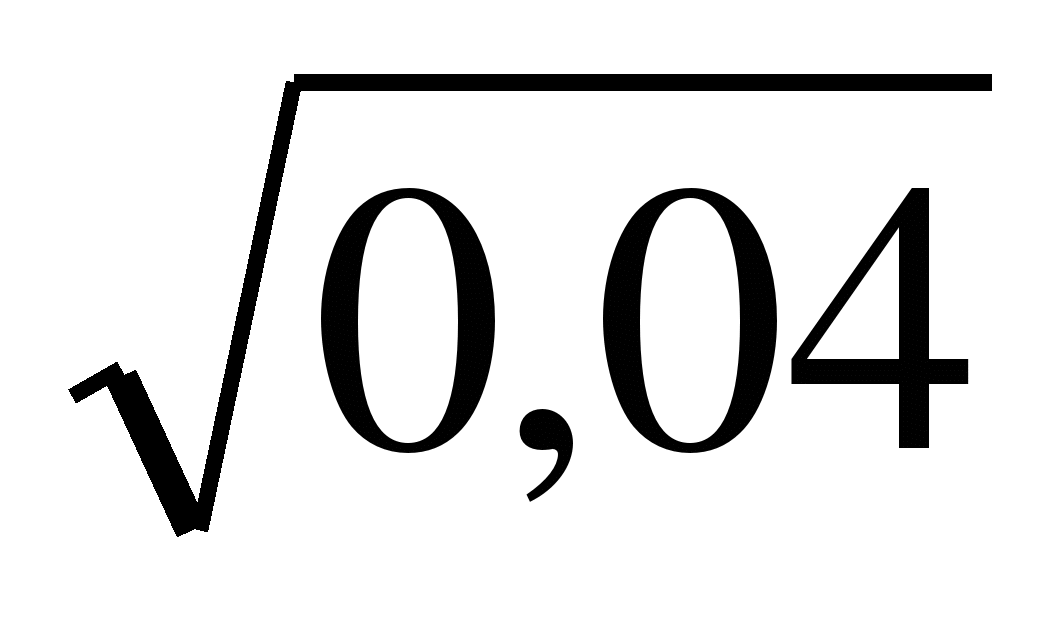
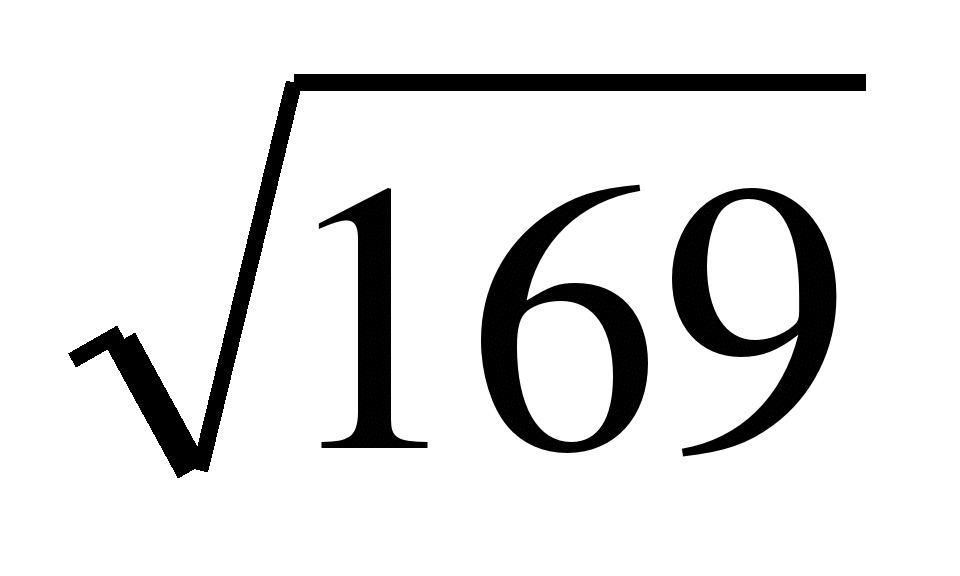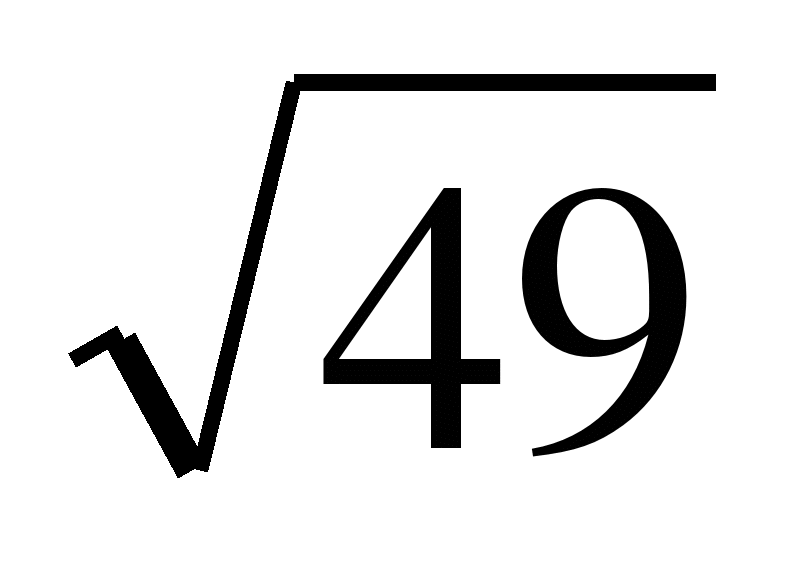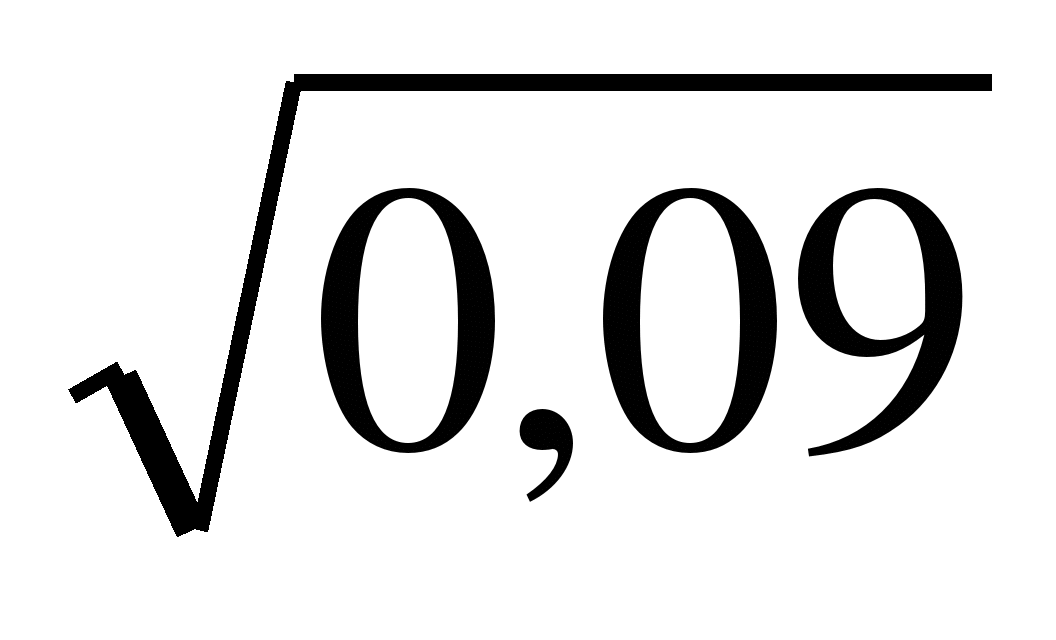
a)5 b)17,8 в)-3 a)19,7 b)6 в)-8
2.Найдите значения выражения.
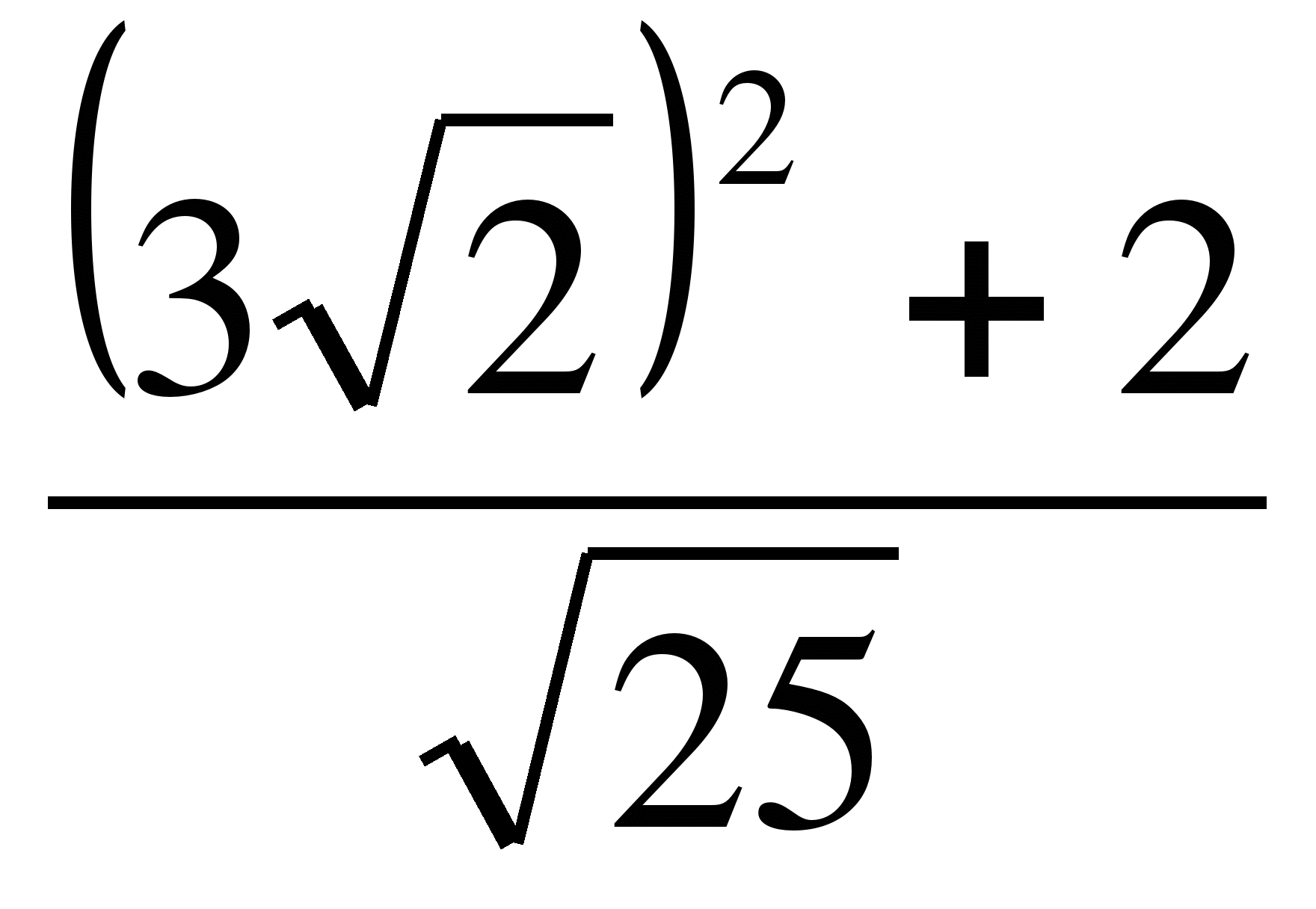
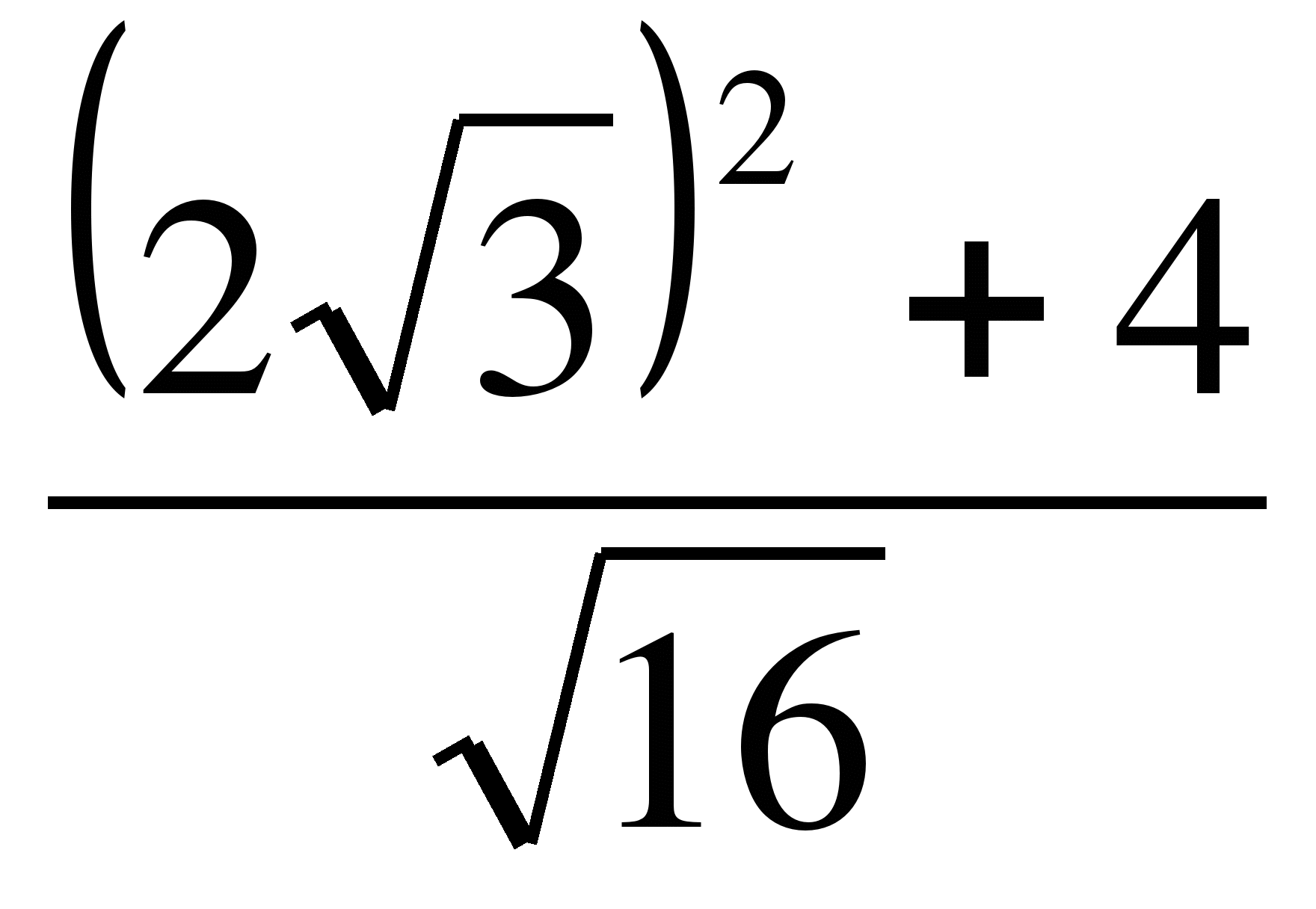
a)4 b)3,5 в)0,25 a)4 b)2,5 в)0,58
3.Решите уравнение.
2x2-8=0 4x2-16=0
a)3;-3 b)-2:2 в)корней нет a)4;-4 b)2;-2 в)корней нет
4. Решите уравнение.
1-3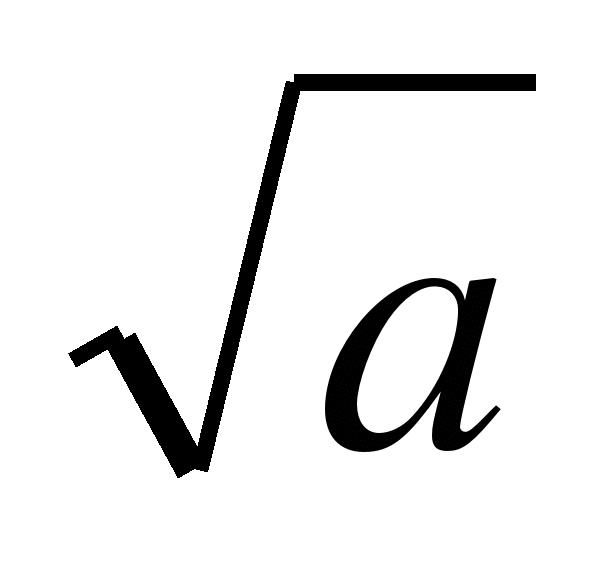
=0 2-5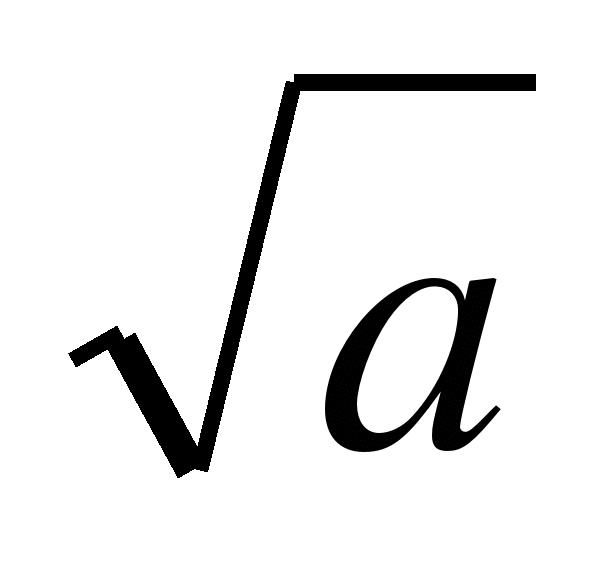=0
a)корней нет; b)4; в)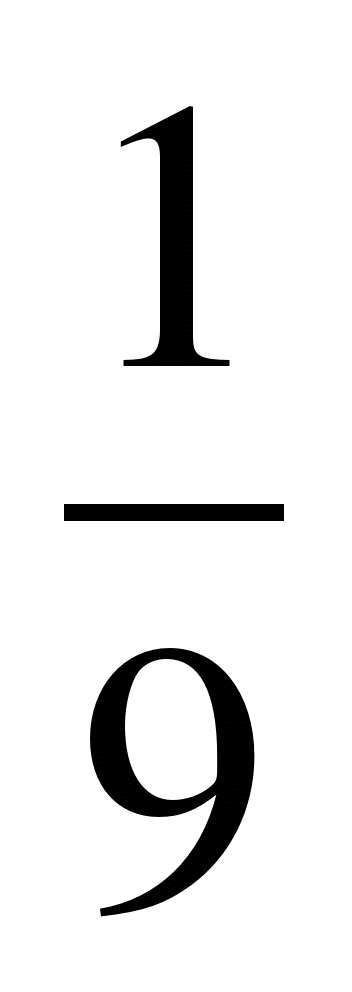
а)5; b)корней нет; в)
5.При каких значениях x выражение имеет смысл :
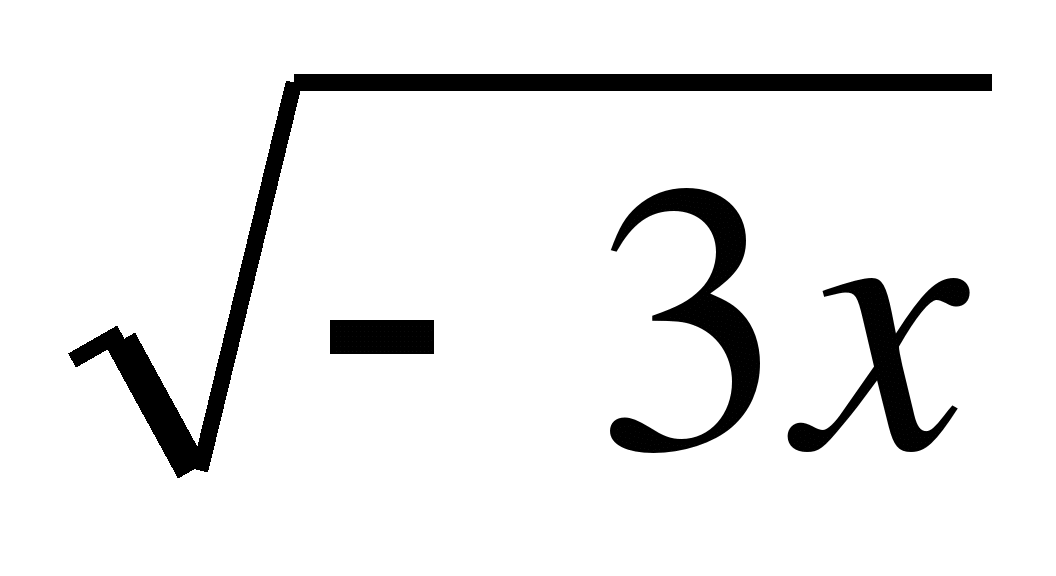
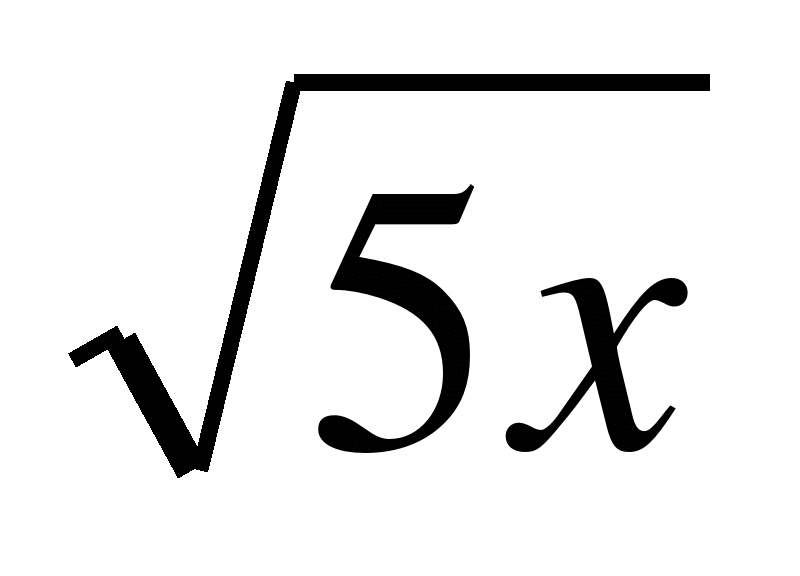
a) x
0 b)x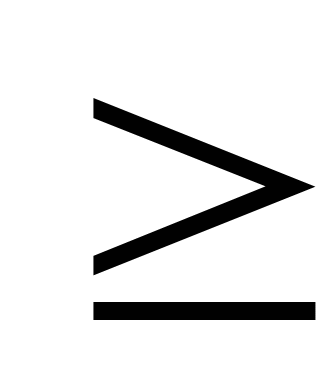
0 d)x>0 г)x<0
Выполняют работу
5.Объяснение нового материала.
Для того чтобы извлечь квадратный корень из многозначного числа надо:
Число разбить на грани. Грань – это группа из двух цифр, начиная с цифры единиц.
Найти наибольшее натуральное число, квадрат которого не превосходит числа 13, стоящего в первой грани. Этим числом является 3, возводим 3 в квадрат и вычитаем из первой грани, к остатку приписываем вторую грань.
3. Удваиваем имеющуюся цифру результата и приписываем к полученному числу справа и припишем к нему *.
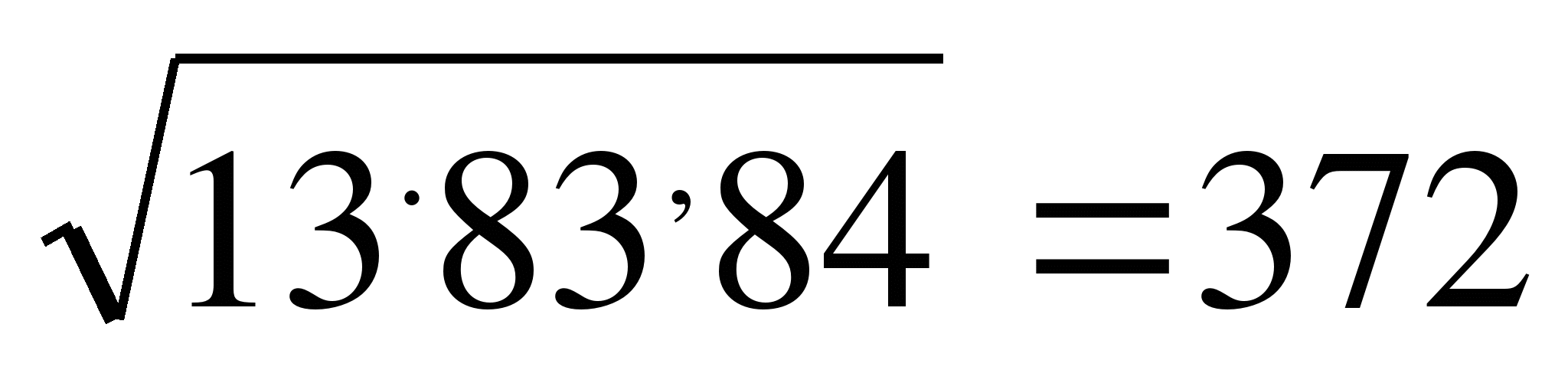4. Вместо звездочки надо придумать число такое
9 чтобы при умножении на число 6*, результат не превос
67 483 ходил 483. Таким числом является 7, значит вторая
7 469 цифра в ответе 7.
742 1484 5. К остатку приписываем следующую грань, затем
2 1484 удвоенное число результата приписываем к получен-
0 ному числу и приписываем следующую * и придумываем цифру : 74* умножить на * получим 1484. Это 2.
6. Постановка домашнего задания: учебник Мордкович стр.109 
№18.02; Галицкий №4,3; 4,6; 4,7; 4,8.
7 . Подведение итогов урока.
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа — количество единиц. Слева у нас 5 паль Оглавление.
Для того чтобы извлечь квадратный корень из многозначного числа надо:
Число разбить на грани. Грань – это группа из двух цифр, начиная с цифры единиц.
Найти наибольшее натуральное число, квадрат которого не превосходит числа 13, стоящего в первой грани. Этим числом является 3, возводим 3 в квадрат и вычитаем из первой грани, к остатку приписываем вторую грань.
138384=372
9 чтобы при умножении на число 6*, результат не превос
67 483 ходил 483. Таким числом является 7, значит вторая
7 469 цифра в ответе 7.
742 1484 К остатку приписываем следующую грань, затем
2 1484 удвоенное число результата приписываем к получен-
0 ному числу и приписываем следующую * и придумываем цифру : 74* умножить на * получим 1484. Это 2.
Оглавление.
1.Введение……………………………………………………………………….1
2.Умножение на пальцах………………………………………………………..2
3.Умножение на 11 и 111………………………………………………………..3
4.Возведение в квадрат числа оканчивающегося на 5………………………..3
5.Умножение методом Ферроля…………………………………………………4
6.Крестьянский способ умножения……………………………………………..4
7.Итальянский способ умножения «сеткой»……………………………………5
8.Нахождение числа по его квадрату……………………………………………6
9.Умножение на китайских палочках …………………………………………..7
10.Исследование………………………………………………………………….8
11.Заключение…………………………………………………………………….9
12.Литература…………………………………………………………………….10
1. Введениее.
« Счет и вычисления-основы порядка в голове»
Иоганн Генрих Пестолоцц
(1746-1827)
Математика является одной из важнейших наук на земле и именно с ней человек встречается каждый день .
Вычислять быстро, подчас на ходу – это требование времени. Без вычислений не обойтись как в повседневной жизни, так и во время учёбы в школе (не на одном экзамене по математике не разрешается пользоваться калькулятором).
Счет в уме является самым древним и простым способом вычисления.
Вычисления активизируют память, тренируют внимание, стремление к рациональной организации деятельности и прочие качества, оказывающие существенное влияние на развитие человека.
В той или иной степени устным счетом владеет каждый.
Кроме общих приемов устного счета имеются особые или специальные приемы, которые применимы только к некоторым числам. Такие приемы мы в этой работе и рассмотрим. Кроме этого мы постараемся найти способы, которые будут интересны и расширят наш кругозор.
Поэтому , цель нашей работы – показать лёгкие, быстрые и точные методы счёта, которые не только помогут во время каких-либо расчётах, сэкономить время, но вызовут немалое удивление у знакомых и товарищей, ведь свободное выполнение счётных операций в значительной степени может свидетельствовать о незаурядности вашего интеллекта.
.
1
2.Умножение на пальцах.
Начнем с самого простого. Таблица умножения. Что в ней самое трудное. Конечно умножение на 9. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).
цев не загнуто, справа — 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип «вычисления».
Слева у нас 5 пальцев не загнуто, справа — 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип «вычисления».
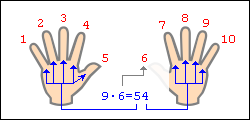
Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве «счетной машинки» не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа — 2 клеточки. Значит 9·8=72. Все очень просто.
2
3.Умножение на 11 и 111.
Теперь перейдем к более сложным приемам.
Например, займемся умножением на 11 и на 111.
Сначала, рассмотрим числа, которые состоят из цифр, сумма соседних в них не превышает 10:
Рассмотрим примеры,:
72*11= ? 792
324*111= ? 35964
Вычислить в столбик конечно можно, но давайте попробуем воспользоваться следующими правилами:
ав*11=а ( а + в ) в
авс*111=а ( а + в ) (а + в +с ) (в + с) в
Посчитаем примеры попроще:
56*11= 5 (11)6=616,если ( а + в )≥10,то количество единиц оставляем на месте,а количество десятков прибавляем к числу которое стоит впереди.
78*11= 7(7+8)8=858
4.Возведение в квадрат числа оканчивающегося на 5.
В этом году мы познакомились с понятием степени ,и у нас возникла необходимость возводить числа в квадрат. Некоторые значения мы знаем наизусть, но большую часть конечно не помним. Хотим рассказать вам , как возвести в квадрат числа оканчивающиеся пятеркой..
Оказывается, это очень просто:
Число, стоящее перед пятеркой, надо умножить на него же плюс единица и приписать 25.
752=5625
852=7225
1152=13225.
3
5.Умножение методом Ферроля.
Для умножения ,умножаем единицы множителей, для получения десятков, умножают десятки одного на единицы другого и наоборот и результаты складывают, для получения сотен умножают десятки. Методом Ферроля легко умножать устно двухзначные числа от 10 до 20.
Например: 12х14=168
а) 2х4=8, пишем 8
б) 1х4+2х1=6, пишем 6
в) 1х1=1, пишем 1.
Если в каком то пункте получаем двухзначное число , то десятки прибавляем к следующему разряду.
6. Крестьянский способ умножения.
Самым, на мой взгляд, «родным» и легким способом умножения является способ, который употребляли русские крестьяне. Этот прием вообще не требует знания таблицы умножения дальше числа 2. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат.
В случае нечетного числа надо откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением
37……….32
74……….16
148……….8
296……….4
592……….2
1184……….1
Произведение всех пар соответственных чисел одинаковое, поэтому
37 ∙ 32 = 1184 ∙ 1 = 1184
В случае, когда одно из чисел нечетное или оба числа нечетные, поступаем следующим образом:
24 ∙ 17
24 ∙ 16 =
= 48 ∙ 8 =
= 96 ∙ 4 =
= 192 ∙ 2 =
=384 ∙ 1 = 384
17 = 24∙(16+1)=24 ∙ 16 + 24 = 384 + 24 = 408
4
7.Итальянский способ умножения (“Сеткой”)
В Италии, а также во многих странах Востока, этот способ приобрел большую известность.
Использование приема:
Например, умножим 6827 на 345.
1. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.
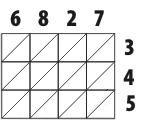
2. Умножаем число каждого ряда последовательно на числа каждой колонки.
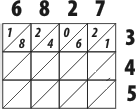
т.е.
6*3 = 18. Записываем 1 и 8
8*3 = 24. Записываем 2 и 4
Если при умножении получается однозначное число, записываем вверху 0, а внизу это число.
(Как у нас в примере,при умножении 2 на 3 получилось 6. Вверху мы записали 0, а внизу 6)
3. Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.
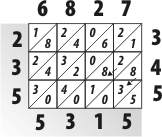
Ответ: 2355315.
5
8 .Нахождение числа по его квадрату.
Для того чтобы извлечь квадратный корень из многозначного числа надо:
1. Число разбить на грани. Грань – это группа из двух цифр, начиная с цифры единиц.
2. Найти наибольшее натуральное число, квадрат которого не превосходит числа 13, стоящего в первой грани. Этим числом является 3, возводим 3 в квадрат и вычитаем из первой грани, к остатку приписываем вторую грань.
3. Удваиваем имеющуюся цифру результата и приписываем к полученному числу справа и припишем к нему *.
4.Вместо звездочки надо придумать число такое
13 83 84= 3722
9
67 483
7 469
742 1484 .
2 1484 чтобы при умножении на число 6* на *, результат не превосходил 483. Таким числом является 7, значит вторая цифра в ответе 7. К остатку приписываем следующую грань, затем удвоенное число результата приписываем к полученному числу и приписываем следующую * и придумываем цифру: 74* умножить на * получим 1484. Это 2.
6
9.Умножение на китайских палочках.
Такой прием напоминает умножение столбиком, но проводится довольно долго.
Использование приема. Допустим, нам надо умножить 13 на 24. Начертим следующий рисунок:
Этот рисунок состоит из 10 линий (количество может быть любым)
Эти линии обозначают число 24 (2 линии, отступ, 4 линии)
А эти линии обозначают число 13 (1 линия, отступ, 3 линии)
Теперь нужно сосчитать пересечения линий на всех четырех концах следующим способом:
(пересечения на рисунке указаны точками)
Количество пересечений:
Верхний левый край: 2
Нижний левый край: 6
Верхний правый: 4
Нижний правый: 12
1) Пересечения в верхнем левом крае (2) – первое число ответа
2) Сумма пересечений нижнего левого и верхнего правого краев (6+4) – второе число ответа
3) Пересечения в нижнем правом крае (12) – третье число ответа.
Получается: 2; 10; 12.
Т.к. два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему.
3(2+1)1(0+1)2
Ответ: 312
7
10.Исследования.
Изучив изложенные выше приемы и методы быстрого и рационального счета, мы решили предложить одноклассникам, которые достаточно хорошо умеют считать ,выполнить следующие действия:
33 ∙ 24
352
Определить какое число при возведении в квадрат дает 625.
643 ∙ 123
567 ∙11
После этого мы выступили перед одноклассниками и рассказали им найденные приемы вычислений. Дали возможность потренироваться и снова провели диктант представленный выше.
При сравнении данных видно ,что абсолютно все учащиеся улучшали свои результаты. Все ученики класса высказали свое мнение и подтвердили, что предложенные нами методы являются интересными и очень помогают при вычислениях, в частности убыстряют процесс.
8
11.Заключение.
Работая над этой темой, мы узнали, что существует много различных, забавных и интересных способов устного счета. Используя некоторые из них на уроках или дома, можно развить скорость вычислений. Мы думаем, что данная работа может быть использована для занятий на кружках, дополнительных занятиях во внеурочное время. Думаем, что это привлечет внимание и интерес учащихся к математике.
Высказывание древнегреческого математика, философа, жившего в 4 веке д. н.э.- Пифагора — “Всё есть число!”.
Согласно философскому воззрению этого учёного и его последователей, числа управляют не только мерой и весом, но также всеми явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса.
Рассматривая различные методы вычислений мы попытались показать, что как в прошлом, так и в будущем , а так же в различных странах без математики, науки созданной разумом человека, не обойтись.
“Кто с детских лет занимается математикой, тот развивает внимание, тренирует мозг, свою волю, воспитывает настойчивость и упорство в достижении цели”. (А.Маркушевич)
А самое главное данные находки помогут нам при сдаче экзаменов, так как калькулятором пользоваться на ОГЭ и ЕГЭ нельзя.
9
Литература.
1.Энциклопедия для детей. “T.23”. Универсальный энциклопедический словарь \ ред. коллегия: М. Аксёнова, Е.Журавлёва, Д.Люри и др. – М.: Мир энциклопедий Аванта +, Астрель, 2008. – 688 с.
2.Ожегов С. И. Словарь русского языка : ок. 57000 слов/ Под ред. чл. – корр. АНСИР Н.Ю. Шведовой. – 20 – е изд.– М. : Просвещение, 2000. – 1012 с.
3.Xочу всё знать! Большая иллюстрированная энциклопедия интеллекта / Пер. с англ. А. Зыковой, К. Малькова, О.Озёровой. – М.: Изд-во ЭКМО, 2006. – 440 с.
4.Шейнина О.С., Соловьева Г.М. Математика. Занятия школьного кружка 5-6 кл./ О.С.Шейнина, Г.М. Соловьева – М.: Изд-во НЦЭНАС, 2007. – 208 с.
5.Кордемский Б. А., Ахадов А. А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986.
6.Минских Е. М. “От игры к знаниям”, М., “Просвещение” 1982г.
7.Свечников А. А. Числа, фигуры, задачи М., Просвещение, 1977г.
8.http://matsievsky. newmail. ru/sys-schi/file15.htm
9.http://sch69.narod. ru/mod/1/6506/hystory. Html
10
Нам известно высказывание древнегреческого математика, философа, жившего в IV веке до н.э.- Пифагора: «Всё есть число!». Согласно мнению этого учёного и его последователей, числа управляют не только мерой и весом, но также всеми явлениями в природе, и являются сущностью гармонии, царствующей в мире.
Научившись считать всеми представленными способами, я пришла к выводу: что самые простые способы это те, которые мы изучаем в школе, может быть они для нас более привычны.
Из всех найденных мною необычных способов счета более интересным показался способ умножение методом «ревность».
Самым простым мне показался метод «удвоения и раздвоения», который использовали русские крестьяне, очень удобно его использовать при умножении двузначных чисел.
Заинтересовал меня новый способ умножения, потому что он позволяет в уме «ворочать» огромными числами.
Старинные и современные способы вычислений показывают, что как в прошлом, так и в будущем, без математики, науки, созданной разумом человека, не обойтись.
Список литературы
Гейзер Г.И. История математики в школе, VII-VII классы. Пособие для учителя. — М.: Просвещение, 1982
http://matsievsky. newmail. ru/sys-schi/file15.htm
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 5»
с углубленным изучением отдельных предметов.
Реферат
Тема:
Нахождение кратчайшего расстояния на поверхности объемных тел
Выполнил ученик 9″А» класса
Щербатов Иван
Учитель: Бурмистрова Татьяна
Владимировна
Участник областного конкурса «Лучший учитель-предметник» 2016 в номинации учитель математики.
Бурмистрова Татьяна Владимировна учитель математики « Средней общеобразовательной школы No5» с углубленным изучением отдельных предметов города Ступино Мос. обл.
В 1994 году окончила Коломенский педагогический институт физико-математический факультет, и уже 22 года работает учителем в школе.
Т.В. учитель высшей квалификационной категории, имеет отличную подготовку, профессионально владеет методикой преподавания курса математики. Т.В. из числа тех ,кто не только знает предмет , но им дышит, через него она воспринимает мир и этому старается научить своих учеников.
Инициативный , творческий, талантливый педагог Т.В. разрабатывает уроки используя различные образовательные технологии, они позволяют ребятам каждый день делать свои маленькие открытия, проявлять свою индивидуальность. Каждый урок учителя это творчество , импровизация, поиск новых форм и методов , основанных на использовании передового педагогического опыта.
Вот уже в течении 18 лет она работает в классах с углубленным изучением математики. Т.В. чуткий педагог, преданный своему делу, знающий возможности каждого ребенка. Все её усилия направлены на пробуждение в ребенке любви к умственному труду и труду мысли. Вот поэтому все ученики Т.В. с удовольствием овладевают знаниями и умело ими пользуются на практике. С 2001 года Т.В. воспитала и выпустила 29 медалистов.
Высокий уровень обученности подтверждают стабильно высокие результаты ОГЭ и ЕГЭ, по итогам которых учащиеся имеют возможность поступать в престижные вузы страны.
Практически 100%учащися привлечены к внеурочной деятельности по предмету.Под руководством Т.В. ребята одерживают победы в различных конкурсах , конференциях ,круглых столах и других мероприятиях Международного, Всероссийского и муниципального уровня.
Ежегодно её ребята являются победителями и призерами муниципального этапа Всероссийской олимпиады школьников по математике, а также муниципального конкурса исследовательских работ.
Т.В. на протяжении 10 лет руководила школьным методическим объединением учителей математики. В настоящее время является руководителем районного методического объединения учителей математики Ступинского муниципального района.
Т.В. знающий опытный педагог , что позволяет ей быть членом жюри различных муниципальных конкурсов.
С 2009 года она является экспертом предметной комиссии по математике при проведении единого Государственного экзамена на территории Мос.обл.
Экспертом экзаменационной комиссии по проверке работ учащихся 9-ых классов Ступинского муниципального района.
Является членом ассоциации учителей математики и физики МО., членом ассоциации педагогических работников работающих с одаренными детьми; Член педагогического клуба «открытый урок».
Т.В. охотно делится накопленным опытом с коллегами , дает открытые уроки, проводит мастер мастер- классы:2012 урок в рамках межзонального семинара учительских клубов Чеховского и Ступинского муниципальных районов; выступление на заседании областного клуба «Педагог года Подмосковья»
2015 урок на региональном итоговом мероприятии предметной недели математики «Современный урок математики в свете концепции развития образования в России»
Публикации разработок и статей Т.В. можно найти на на сайтах «Инфоурок», «Вестник педагога», информационно-образовательном журнале «Радуга мастерства», «Первое сентября»
ЕЁ статьи вышли в сборниках научно-практических статей конференций города Таганрога., в сборниках «Первое сентября»
Татьяна Владимировна занимает призовые места в Международных, Всероссийских и муниципальных конкурсах.
Она является Победителем конкурсного отбора лучших учителей в рамках ПНПО 2011года и многих др. муниципальных конкурсов.
Её работа получила высокую оценку на муниципальном уровне ,свидельством чего являются многочисленные грамоты и благодарственные письма. А ТАК ЖЕ Т.В. награждена Почетной граматой Министерства образования Мос.обл.
Но самой большой наградой Т.В. считает успехи своих учеников ,их горящие глаза.
Является Председателем Участковой Избирательной комиссии 2009-2014гг,Принимала участие в переписи населения РФ в 2010г.Награждена ведомственным знаком отличия Федеральной службы государственной статистики-медали «За заслуги в проведении Всероссийской переписи населения 2010 года» No030881.
Членом аттестационной к…….
1. | Разобьем число от запятой вправо и влево по две цифры | 39.81.61 |
2. | Для числа, образованного крайней левой парой (39) ищем число, квадрат которого меньше. Это число 6. (36 6 – первая цифра искомого числа | 39.81.61 | 6 |
3. | К разности чисел 39 и 36 (число 3) припишем следующую пару (число 81). Получим новое число 381 Левее числа 381 запишем удвоенное значение первой цифры (6∙2=12) |
|
4. | К числу 12 припишем такое однозначное число, чтобы произведение полученного трехзначного числа на приписанное однозначное было меньше или равно 381. Это число 3. 3 – вторая цифра искомого числа |
|
5 | К разности чисел 389 и 369 (число 12) припишем следующую пару (число 61). Получим новое число 1261 Левее числа 1261 запишем удвоенное значение числа, образованного первой и второй цифрой искомого значения корня (63∙2=126) |
|
6 | К числу 126 припишем такое однозначное число, чтобы произведение полученного четырехзнач-ного числа на приписан-ное однозначное было меньше или равно 1261. Это число 1. 1 – третья цифра искомого числа. |
|
1. | Разобьем число от запятой вправо и влево по две цифры | 10.53.65.16 |
2. | Для числа, образованного крайней левой парой (10) ищем число, квадрат которого меньше. Это число 3. (9 3 – первая цифра искомого числа | 10.53.65.16 I 3 |
3. | К разности чисел 10 и 9 (число 1) припишем следующую пару (число 53). Получим новое число 153 Левее числа 153 запишем удвоенное значение первой цифры (3∙2=6) | 10.53.65.16 I 3 9 6 153 |
4. | К числу 6 припишем такое однозначное число, чтобы произведение полученного двухзначного числа на приписанное однозначное было меньше или равно 153. Это число 2. 2 – вторая цифра искомого числа | 10.53.65.16 I 32 9 62 153 2 124 |
5 | К разности чисел 153 и 124 (число 29) припишем следующую пару (число 65). Получим новое число 2965 Левее числа 2965 запишем удвоенное значение числа, образо-ванного первой и второй цифрой искомого значе-ния корня (32∙2=64) | 10.53.65.16 I 32 9 1 53 1 24 64 29 65 |
6 | К числу 64 припишем такое однозначное число, чтобы произведение полученного трехзнач-ного числа на приписан-ное однозначное было меньше или равно 2965. Это число 4. 4 – третья цифра искомого числа. | 10.53.65.16 I 324 9 1 53 1 24 644 29 65 4 25 76 |
7 | К разности чисел 2965 и 2576 (число 389) припишем следующую пару (число 16). Получим новое число 38916 Левее числа 38916 запишем удвоенное значение числа, образованного первой, второй и третьей цифрой искомого значения корня (324∙2=648) | 10.53.65.16 I 324 9 1 53 1 24 29 65 25 76 648 3 89 16 |
8 | К числу 648 припишем такое однозначное число, чтобы произведение полученного четырехзнач-ного числа на приписан-ное однозначное было меньше или равно 38916. Это число 6. 6 – третья цифра искомого числа. | 10.53.65.16I3246 9 1 53 1 24 29 65 25 76 6486 3 89 16 6 3 89 16 |
