Дискретное логарифмирование — Википедия
Дискретное логарифмирование (DLOG) — задача обращения функции gx{\displaystyle g^{x}} в некоторой конечной мультипликативной группе G{\displaystyle G}.
Наиболее часто задачу дискретного логарифмирования рассматривают в мультипликативной группе кольца вычетов или конечного поля, а также в группе точек эллиптической кривой над конечным полем. Эффективные алгоритмы для решения задачи дискретного логарифмирования в общем случае неизвестны.
Для заданных g и a решение x уравнения gx=a{\displaystyle g^{x}=a} называется дискретным логарифмом элемента a по основанию g. В случае, когда G является мультипликативной группой кольца вычетов по модулю m, решение называют также индексом числа a по основанию g. Индекс числа a по основанию g гарантированно существует, если g является первообразным корнем по модулю m.
Пусть в некоторой конечной мультипликативной абелевой группе G{\displaystyle G} задано уравнение
| gx=a{\displaystyle g^{x}=a}. | (1) |
Решение задачи дискретного логарифмирования состоит в нахождении некоторого целого неотрицательного числа x{\displaystyle x}, удовлетворяющего уравнению (1). Если оно разрешимо, у него должно быть хотя бы одно натуральное решение, не превышающее порядок группы. Это сразу даёт грубую оценку сложности алгоритма поиска решений сверху — алгоритм полного перебора нашел бы решение за число шагов не выше порядка данной группы.
Чаще всего рассматривается случай, когда G=⟨g⟩{\displaystyle G=\langle g\rangle }, то есть группа является циклической, порождённой элементом g{\displaystyle g}. В этом случае уравнение всегда имеет решение. В случае же произвольной группы вопрос о разрешимости задачи дискретного логарифмирования, то есть вопрос о существовании решений уравнения (1), требует отдельного рассмотрения.
Рассмотрим задачу дискретного логарифмирования в кольце вычетов по модулю простого числа. Пусть задано сравнение
| 3x≡13(mod17).{\displaystyle 3^{x}\equiv 13{\pmod {17}}.} |
Будем решать задачу методом перебора. Выпишем таблицу всех степеней числа 3. Каждый раз мы вычисляем остаток от деления на 17 (например, 33≡27 — остаток от деления на 17 равен 10).
| 31 ≡ 3 | 32 ≡ 9 | 33 ≡ 10 | 34 ≡ 13 | 35 ≡ 5 | 36 ≡ 15 | 37 ≡ 11 | 38 ≡ 16 |
| 39 ≡ 14 | 310 ≡ 8 | 311 ≡ 7 | 312 ≡ 4 | 313 ≡ 12 | 314 ≡ 2 | 315 ≡ 6 | 316 ≡ 1 |
Теперь легко увидеть, что решением рассматриваемого сравнения является x=4, поскольку 34≡13.
На практике модуль обычно является достаточно большим числом, и метод перебора является слишком медленным, поэтому возникает потребность в более быстрых алгоритмах.
В произвольной мультипликативной группе[править | править код]
Разрешимости и решению задачи дискретного логарифмирования в произвольной конечной абелевой группе посвящена статья J. Buchmann, M. J. Jacobson и E. Teske.[1] В алгоритме используется таблица, состоящая из O(|⟨g⟩|){\displaystyle O({\sqrt {|\langle g\rangle |}})} пар элементов и выполняется O(|⟨g⟩|){\displaystyle O({\sqrt {|\langle g\rangle |}})} умножений. Данный алгоритм медленный и не пригоден для практического использования. Для конкретных групп существуют свои, более эффективные, алгоритмы.
В кольце вычетов по простому модулю[править | править код]
Рассмотрим сравнение
| ax≡b(modp),{\displaystyle a^{x}\equiv b{\pmod {p}},} | (2) |
где p{\displaystyle p} — простое, b{\displaystyle b} не делится на p{\displaystyle p} без остатка. Если a{\displaystyle a} является образующим элементом группы Z/pZ{\displaystyle \mathbb {Z} /p\mathbb {Z} }, то уравнение (2) имеет решение при любых b{\displaystyle b}. Такие числа a{\displaystyle a} называются ещё первообразными корнями, и их количество равно ϕ(p−1){\displaystyle \phi (p-1)}, где ϕ{\displaystyle \phi } — функция Эйлера. Решение уравнения (2) можно находить по формуле:
| x≡∑i=1p−2(1−ai)−1bi(modp).{\displaystyle x\equiv \sum \limits _{i=1}^{p-2}(1-a^{i})^{-1}b^{i}{\pmod {p}}.} |
Однако, сложность вычисления по этой формуле хуже, чем сложность перебора.
Следующий алгоритм имеет сложность O(p⋅logp){\displaystyle O({\sqrt {p}}\cdot \log {p})}.
- Алгоритм (метод согласования)
- Присвоить H:=⌊p⌋+1{\displaystyle H:=\left\lfloor {\sqrt {p}}\right\rfloor +1}
- Вычислить c=aHmodp{\displaystyle c=a^{H}{\bmod {p}}}
- Составить таблицу значений cumodp{\displaystyle c^{u}{\bmod {p}}} для 1≤u≤H{\displaystyle 1\leq u\leq H} и отсортировать её.
- Составить таблицу значений b⋅avmodp{\displaystyle b\cdot a^{v}{\bmod {p}}} для 0≤v≤H{\displaystyle 0\leq v\leq H} и отсортировать её.
- Найти общие элементы в таблицах. Для них cu≡b⋅av(modp),{\displaystyle c^{u}\equiv b\cdot a^{v}{\pmod {p}},} откуда aHu−v≡b(modp).{\displaystyle a^{Hu-v}\equiv b{\pmod {p}}.}
- Выдать Hu−v{\displaystyle Hu-v}.
Существует также множество других алгоритмов для решения задачи дискретного логарифмирования в поле вычетов. Их принято разделять на экспоненциальные и субэкспоненциальные. Полиномиального алгоритма для решения этой задачи пока не существует.
Алгоритмы с экспоненциальной сложностью[править | править код]
- Алгоритм Шенкса (алгоритм больших и малых шагов, baby-step giant-step)
- Алгоритм Полига-Хеллмана — работает, если известно разложение числа p−1=∏i=1sqiαi{\displaystyle p-1=\prod \limits _{i=1}^{s}q_{i}^{\alpha _{i}}} на простые множители. Сложность: O(∑i=1sαi(logp+qi)){\displaystyle O(\sum \limits _{i=1}^{s}\alpha _{i}(\log {p}+q_{i}))}. Если множители, на которые раскладывается p−1{\displaystyle p-1}, достаточно маленькие, то алгоритм очень эффективен[2].
- ρ-метод Полларда имеет эвристическую оценку сложности O(p12){\displaystyle O(p^{\frac {1}{2}})}[3].
Субэкспоненциальные алгоритмы[править | править код]
В L-нотации вычислительная сложность данных алгоритмов оценивается как Lp[d,c]{\displaystyle L_{p}[d,c]} арифметических операций, где c{\displaystyle c} и 0≤d<1{\displaystyle 0\leq d<1} — некоторые константы. Эффективность алгоритма во многом зависит от близости величин c{\displaystyle c} и d{\displaystyle d} к 1 и 0, соответственно.
- Алгоритм Адлемана появился в 1979 году[4]. Это был первый субэкспоненциалный алгоритм дискретного логарифмирования. На практике он всё же недостаточно эффективен. В этом алгоритме d=12{\displaystyle d={\frac {1}{2}}}.
- Алгоритм COS был предложен в 1986 году математиками Копперсмитом (Don Coppersmith), Одлыжко (Andrew Odlyzko) и Шреппелем (Richard Schroeppel)[5]. В этом алгоритме константа c=1{\displaystyle c=1}, d=12{\displaystyle d={\frac {1}{2}}}. В 1991 году с помощью этого метода было проведено логарифмирование по модулю p≈1058{\displaystyle p\approx 10^{58}}. В 1997 году Вебер провел дискретное логарифмирование по модулю p≈1085{\displaystyle p\approx 10^{85}} с помощью некоторой версии данного алгоритма. Экспериментально показано, что при p≤1090{\displaystyle p\leq 10^{90}} алгоритм COS лучше решета числового поля.
- Дискретное логарифмирование при помощи решета числового поля было применено к дискретному логарифмированию позднее, чем к факторизации чисел. Первые идеи появились в 1990-х годах. Алгоритм, предложенный Д. Гордоном в 1993 году, имел эвристическую сложность Lp[13,33/2]{\displaystyle L_{p}\left[{\tfrac {1}{3}},3^{3/2}\right]}[6], но оказался достаточно непрактичным. Позднее было предложено множество различных улучшений данного алгоритма. Было показано, что при p≥10100{\displaystyle p\geq 10^{100}} решето числового поля быстрее, чем COS. Современные рекорды в дискретном логарифмировании получены именно с помощью этого метода.
Наилучшими параметрами в оценке сложности на данный момент является c=(92+2613)13/3≈1,902{\displaystyle c=(92+26{\sqrt {13}})^{\frac {1}{3}}/3\approx 1{,}902}, d=13{\displaystyle d={\frac {1}{3}}}[7].
Для чисел специального вида результат можно улучшить. В некоторых случаях можно построить алгоритм, для которого константы будут c≈1,00475{\displaystyle c\approx 1{,}00475}, d=25{\displaystyle d={\frac {2}{5}}}. За счёт того, что константа c{\displaystyle c} достаточно близка к 1, подобные алгоритмы могут обогнать алгоритм с d=13{\displaystyle d={\frac {1}{3}}}.
В произвольном конечном поле[править | править код]
Задача рассматривается в поле GF(q), где q=pn{\displaystyle q=p^{n}}, p{\displaystyle p} — простое.
- Алгоритм исчисления индексов (index-calculus) эффективен, если p{\displaystyle p} невелико. В этом случае он имеет эвристическую оценку сложности Lp[12,c]{\displaystyle L_{p}\left[{\tfrac {1}{2}},c\right]}.
- Алгоритм Эль-Гамаля, появившийся в 1985 году, применим при n=2{\displaystyle n=2} и имеет сложность Lp[12,c]{\displaystyle L_{p}\left[{\tfrac {1}{2}},c\right]} арифметических операций.
- Алгоритм Копперсмита дискретного логарифмирования в конечном поле характеристики 2 стал первым субэкспоненциальным алгоритмом дискретного логарифмирования с константой d=13{\displaystyle d={\frac {1}{3}}} в оценке сложности Lp[d,c]{\displaystyle L_{p}[d,c]}. Данный алгоритм появился в 1984 году — до изобретения решета числового поля[8].
В группе точек на эллиптической кривой[править | править код]
Рассматривается группа точек эллиптической кривой над конечным полем. В данной группе определена операция сложения двух точек. Тогда mP{\displaystyle mP} — это P+…+P⏟m{\displaystyle \underbrace {P+\ldots +P} \limits _{m}}. Решением задачи дискретного логарифмирования на эллиптической кривой является нахождение такого натурального числа m{\displaystyle m}, что mP=A{\displaystyle mP=A} для заданных точек P{\displaystyle P} и A.{\displaystyle A.}
До 1990 года не существовало алгоритмов дискретного логарифмирования, учитывающих особенностей строения группы точек эллиптической кривой. Впоследствии, Альфред Менезес[en]*, Окамото (Tatsuaki Okamoto) и Скотт Ванстоун[en]* предложили алгоритм, использующий спаривание Вейля[9]. Для эллиптической кривой, определённой над полем GF(q){\displaystyle GF(q)}, данный алгоритм сводит задачу дискретного логарифмирования к аналогичной задаче в поле GF(qk){\displaystyle GF(q^{k})}. Однако, данное сведение полезно, только если степень k{\displaystyle k} мала. Это условие выполняется, в основном, для суперсингулярных эллиптических кривых. В остальных случаях подобное сведение практически никогда не приводит к субэкспоненциальным алгоритмам.
Вычислительная сложность и приложения в криптографии[править | править код]
Задача дискретного логарифмирования является одной из основных задач, на которых базируется криптография с открытым ключом. Классическими криптографическими схемами на её основе являются схема выработки общего ключа Диффи-Хеллмана[10], схема электронной подписи Эль-Гамаля[11][12], криптосистема Мэсси-Омуры[13] для передачи сообщений. Их криптостойкость основывается на предположительно высокой вычислительной сложности обращения показательной функции. Хотя сама показательная функция вычисляется достаточно эффективно, даже самые современные алгоритмы вычисления дискретного логарифма имеют очень высокую сложность, которая сравнима со сложностью наиболее быстрых алгоритмов разложения чисел на множители.
Другая возможность эффективного решения задачи вычисления дискретного логарифма связана с квантовыми вычислениями. Теоретически доказано, что с помощью Алгоритма Шора дискретный логарифм можно вычислить за полиномиальное время[14][15][16]. В любом случае, если полиномиальный алгоритм вычисления дискретного логарифма будет реализован, это будет означать практическую непригодность криптосистем на его основе для долговременной защиты данных. Рассматривается ряд идей для создания новых алгоритмов с открытым ключом.
- ↑ Buchmann J., Jacobson M. J., Teske E. On some computational problems in finite abelian groups (англ.) // Mathematics of Computation (англ.)русск. : journal. — 1997. — Vol. 66. — P. 1663—1687. — DOI:10.1090/S0025-5718-97-00880-6.
- ↑ S. Pohlig, M. Hellman. An improved algorithm for computing logarithms over and its cryptographic significance (Corresp.) // IEEE Transactions on Information Theory. — 1978. — Январь (т. 24, вып. 1). — С. 106—110. — ISSN 0018-9448. — DOI:10.1109/TIT.1978.1055817.
- ↑ J. M. Pollard. Monte Carlo methods for index computation (mod p) // Mathematics of Computation. — 1978. — Январь (т. 32, вып. 143). — С. 918—924. — DOI:10.1090/S0025-5718-1978-0491431-9.
- ↑ L. Adleman. A subexponential algorithm for the discrete logarithm problem with applications to cryptography // 20th Annual Symposium on Foundations of Computer Science. — 1979. — Октябрь. — С. 55—60. — DOI:10.1109/SFCS.1979.2.
- ↑ Don Coppersmith, Andrew M. Odlzyko, Richard Schroeppel. Discrete logarithms inGF(p) (англ.) // Algorithmica. — 1986. — November (vol. 1, iss. 1—4). — P. 1—15. — DOI:10.1007/BF01840433.
- ↑ Daniel M. Gordon. Discrete Logarithms in GF(p) Using the Number Field Sieve // SIAM Journal on Discrete Mathematics. — 1993. — Т. 6, вып. 1. — С. 124—138. — DOI:10.1137/0406010.
- ↑
- ↑ D. Coppersmith. Fast evaluation of logarithms in fields of characteristic two // IEEE Transactions on Information Theory. — 1984. — Июль (т. 30, вып. 4). — С. 587—594. — ISSN 0018-9448. — DOI:10.1109/TIT.1984.1056941.
- ↑ A. J. Menezes, T. Okamoto, S. A. Vanstone. Reducing elliptic curve logarithms to logarithms in a finite field // IEEE Transactions on Information Theory. — 1993-09-01. — Т. 39, вып. 5. — С. 1639—1646. — ISSN 0018-9448. — DOI:10.1109/18.259647.
- ↑ Diffie, Hellman, 1976.
- ↑ Elgamal, 1984.
- ↑ Elgamal, 1985.
- ↑ James L. Massey, Jimmy K. Omura. Method and apparatus for maintaining the privacy of digital messages conveyed by public transmission (неопр.) (28 января 1986).
- ↑ Shor, 1994.
- ↑ Shor P. W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer // Foundations of Computer Science : Conference Publications. — 1997. — P. 1484–1509.
- ↑ CompuTerra Online #224 — Квантовые компьютеры и квантовые вычисления… Беседа с кандидатом физико-математических наук, специалистом по теории алгоритмов Михаилом Вялым (Вычислительный центр РАН)
- Diffie W., Hellman M. E. New Directions in Cryptography // IEEE Trans. Inf. Theory / F. Kschischang — IEEE, 1976. — Vol. 22, Iss. 6. — P. 644–654. — ISSN 0018-9448 — doi:10.1109/TIT.1976.1055638
- Elgamal T. A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms // Advances in Cryptology — CRYPTO ’84: 4th Annual International Cryptology Conference, Santa Barbara, 1984, Proceedings / George Robert Blakley Jr., D. Chaum — New York, NY, USA: Springer-Verlag New York, 1985. — P. 10–18. — 491 p. — (Lecture Notes in Computer Science; Vol. 196) — ISBN 978-0-387-15658-3 — ISSN 0302-9743 — doi:10.1007/3-540-39568-7_2
- Elgamal T. A Public-Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms // IEEE Trans. Inf. Theory / F. Kschischang — IEEE, 1985. — Vol. 31, Iss. 4. — P. 469–472. — ISSN 0018-9448 — doi:10.1109/TIT.1985.1057074
- Shor P. Algorithms for Quantum Computation: Discrete Logarithms and Factoring // Foundations of Computer Science, 1994 Proceedings., 35th Annual Symposium on — IEEE, 1994. — P. 124–134. — ISBN 0-8186-6580-7 — doi:10.1109/SFCS.1994.365700
- Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. — Москва: МЦНМО, 2003. — 328 с. — ISBN 5-94057-103-4. Архивная копия от 27 января 2007 на Wayback Machine
- Коблиц Н. Курс теории чисел и криптографии. — Москва: ТВПб, 2001. — 254 с. — ISBN 5-85484-014-6.
- Odlyzko A. M. Discrete logarithms in finite fields and their cryptographic significance // LNCS [en]. — 1984. — Т. 209. — С. 224—316.
- Ю. В. Нестеренко. Глава 4.8. Дискретное логарифмирование // Введение в криптографию / Под ред. В. В. Ященко. — Питер, 2001. — 288 с. — ISBN 5-318-00443-1.
- Обзор методов вычисления дискретного логарифма (англ.)
- Нечаев В.И. К вопросу о сложности детерминированного алгоритма для дискретного логарифма // Математические заметки. — 1994. — Февраль (т. 55, вып. 2). — С. 91—101.
Введение в анализ сложности алгоритмов (часть 3) / Habr
От переводчика: данный текст даётся с незначительными сокращениями по причине местами излишней «разжёванности» материала. Автор абсолютно справедливо предупреждает, что отдельные темы могут показаться читателю чересчур простыми или общеизвестными. Тем не менее, лично мне этот текст помог упорядочить имеющиеся знания по анализу сложности алгоритмов. Надеюсь, что он окажется полезен и кому-то ещё.Из-за большого объёма оригинальной статьи я разбила её на части, которых в общей сложности будет четыре.
Опубликовано ранее:
Часть 1
Часть 2
Логарифмы
Если вы знаете, что такое логарифмы, то можете спокойно пропустить этот раздел. Глава предназначается тем, кто незнаком с данным понятием или пользуется им настолько редко, что уже забыл что там к чему. Логарифмы важны, поскольку они очень часто встречаются при анализе сложности. Логарифм — это операция, которая при применении её к числу делает его гораздо меньше (подобно взятию квадратного корня). Итак, первая вещь, которую вы должны запомнить: логарифм возвращает число, меньшее, чем оригинал. На рисунке справа зелёный график — линейная функция
f(n) = n, красный — f(n) = sqrt(n), а наименее быстро возрастающий — f(n) = log(n). Далее: подобно тому, как взятие квадратного корня является операцией, обратной возведению в квадрат, логарифм — обратная операция возведению чего-либо в степень. Поясню на примере. Рассмотрим уравнение
2x = 1024
Чтобы найти из него x, спросим себя: в какую степень надо возвести 2, чтобы получить 1024? Ответ: в десятую. В самом деле, 210 = 1024, что легко проверить. Логарифмы помогают нам описать данную задачу, используя новую нотацию. В данном случае, 10 является логарифмом 1024 и записывается, как log( 1024 ). Читается: «логарифм 1024». Поскольку мы использовали 2 в качестве основания, то такие логарифмы называются «по основанию 2». Основанием может быть любое число, но в этой статье мы будем использовать только двойку. Если вы ученик-олимпиадник и не знакомы с логарифмами, то я рекомендую вам попрактиковаться после того, как закончите чтение этой статьи. В информатике логарифмы по основанию 2 распространены больше, чем какие-либо другие, поскольку часто мы имеем всего две сущности: 0 и 1. Также существует тенденция разбивать объёмные задачи пополам, а половин, как известно, тоже бывает всего две. Поэтому для дальнейшего чтения статьи вам достаточно иметь представление только о логарифмах по основанию 2.
- 2x = 64
- (22)x = 64
- 4x = 4
- 2x = 1
- 2x + 2x = 32
- (2x) * (2x) = 64
- Методом проб и ошибок, находим, что
x = 6. Таким образом,log( 64 ) = 6 - По свойству степеней (22)x можно записать как 22x. Таким образом, получим, что
2x = 6(потому чтоlog( 64 ) = 6из предыдущего примера) и, следовательно,x = 3 - Используя знания, полученные при решении предыдущего примера, запишем 4 как 22. Тогда наше уравнение превратится в (22)x = 4, что эквивалентно 22x. Заметим, что log( 4 ) = 2 (поскольку 22 = 4), так что мы получаем
2x = 2, откудаx = 1. Это легко заметить по исходному уравнению, поскольку степень 1 даёт основание в качестве результата - Вспомнив, что степень 0 даёт результатом 1 (т.е.
log( 1 ) = 0), получимx = 0 - Здесь мы имеем дело с суммой, поэтому непосредственно взять логарифм не получится. Однако, мы замечаем, что
2x+ 2x — это тоже самое, что и2 * (2x). Умножение на 2 даст2x + 1, и мы получим уравнение2x + 1= 32. Находим, чтоlog( 32 ) = 5x + 1 = 5иx = 4. - Мы перемножаем две степени двойки, следовательно, можем объединить их в 22x. Остаётся просто решить уравнение
22x= 64, что мы уже делали выше. Ответ:x = 3
Практическая рекомендация: на соревнованиях алгоритмы часто реализуются на С++. Как только вы проанализировали сложность вашего алгоритма, так сразу можете получить и грубую оценку того, как быстро он будет работать, приняв, что в секунду выполняется 1 000 000 команд. Их количество считается из полученной вами функции асимптотической оценки, описывающей алгоритм. Например, вычисление по алгоритму с Θ( n ) займёт около секунды при n = 1 000 000.
Рекурсивная сложность
А теперь давайте обратимся к рекурсивным функциям. Рекурсивная функция — это функция, которая вызывает сама себя. Можем ли мы проанализировать её сложность? Следующая функция, написанная на Python, вычисляет факториал заданного числа. Факториал целого положительного числа находится как произведение всех предыдущих положительных целых чисел. Например, факториал 5 — это
5 * 4 * 3 * 2 * 1. Обозначается он как «5!» и произносится «факториал пяти» (впрочем, некоторые предпочитают «ПЯТЬ!!!11»).def factorial( n ):
if n == 1:
return 1
return n * factorial( n - 1 )
Давайте проанализируем эту функцию. Она не содержит циклов, но её сложность всё равно не является константной. Что ж, придётся вновь заняться подсчётом инструкций. Очевидно, что если мы применим эту функцию к некоторому
n, то она будет вычисляться n раз. (Если вы в этом не уверены, то можете вручную расписать ход вычисления при n = 5, чтобы определить, как это на самом деле работает.) Таким образом, мы видим, что эта функция является Θ( n ).Если вы всё же не уверены в этом, то вы всегда можете найти точную сложность путём подсчёта количества инструкций. Примените этот метод к данной функции, чтобы найти её f( n ), и убедитесь, что она линейная (напомню, что линейность означает Θ( n )).
Логарифмическая сложность
Одной из известнейших задач в информатике является поиск значения в массиве. Мы уже решали её ранее для общего случая. Задача становится интереснее, если у нас есть отсортированный массив, в котором мы хотим найти заданное значение. Одним из способов сделать это является бинарный поиск. Мы берём средний элемент из нашего массива: если он совпадает с тем, что мы искали, то задача решена. В противном случае, если заданное значение больше этого элемента, то мы знаем, что оно должно лежать в правой части массива. А если меньше — то в левой. Мы будем разбивать эти подмассивы до тех пор, пока не получим искомое.
Вот реализация такого метода в псевдокоде:
def binarySearch( A, n, value ):
if n = 1:
if A[ 0 ] = value:
return true
else:
return false
if value < A[ n / 2 ]:
return binarySearch( A[ 0...( n / 2 - 1 ) ], n / 2 - 1, value )
else if value > A[ n / 2 ]:
return binarySearch( A[ ( n / 2 + 1 )...n ], n / 2 - 1, value )
else:
return true
Приведённый псевдокод — упрощение настоящей реализации. На практике этот метод описать проще, чем воплотить, поскольку программисту нужно решить некоторые дополнительные вопросы. Например, защиту от ошибок на одну позицию (off-by-one error, OBOE), да и деление на два не всегда может давать целое число, поэтому потребуется применять функции
floor() или ceil(). Однако, предположим, что в нашем случае деление всегда будет успешным, наш код защищён от ошибок off-by-one, и всё, что мы хотим — это проанализировать сложность данного метода. Если вы никогда раньше не реализовывали бинарный поиск, то можете сделать это на вашем любимом языке программирования. Такая задача по-настоящему поучительна.Если вы не уверены, что метод работает в принципе, то отвлекитесь и решите вручную какой-нибудь простой пример.
Теперь давайте попробуем проанализировать этот алгоритм. Ещё раз, в этом случае мы имеем рекурсивный алгоритм. Давайте для простоты предположим, что массив всегда разбивается ровно пополам, игнорируя +1 и -1 части в рекурсивном вызове. К этому моменту вы должны быть уверены, что такое небольшое изменение, как игнорирование +1 и -1, не повлияет на конечный результат оценки сложности. В принципе, обычно этот факт необходимо доказывать, если мы хотим проявить осторожность с математической точки зрения. Но на практике это очевидно на уровне интуиции. Также для простоты давайте предположим, что наш массив имеет размер одной из степеней двойки. Опять-таки, это предположение никоим образом не повлияет на конечный результат расчёта сложности алгоритма. Наихудшим сценарием для данной задачи будет вариант, когда массив в принципе не содержит искомое значение. В этом случае мы начинаем с массива размером n на первом рекурсивном вызове, n / 2 на втором, n / 4 на третьем и так далее. В общем, наш массив разбивается пополам на каждом вызове до тех пор, пока мы не достигнем единицы. Давайте запишем количество элементов в массиве на каждом вызове:
0-я итерация: n
1-я итерация: n / 2
2-я итерация: n / 4
3-я итерация: n / 8
…
i-я итерация: n / 2i
…
последняя итерация: 1
Заметьте, что на i-й итерации массив имеет n / 2i элементов. Мы каждый раз разбиваем его пополам, что подразумевает деление количества элементов на два (равноценно умножению знаменателя на два). Проделав это i раз, получим n / 2i. Процесс будет продолжаться, и из каждого большого i мы будем получать меньшее количество элементов до тех пор, пока не достигнем единицы. Если мы захотим узнать, на какой итерации это произошло, нам нужно будет просто решить следующее уравнение:
1 = n / 2i
Равенство будет истинным только тогда, когда мы достигнем конечного вызова функции binarySearch(), так что узнав из него i, мы будем знать номер последней рекурсивной итерации. Умножив обе части на 2i, получим:
2i = n
Если вы прочли раздел о логарифмах выше, то такое выражение будет для вас знакомым. Решив его, мы получим:
i = log( n )
Этот ответ говорит нам, что количество итераций, необходимых для бинарного поиска, равняется log( n ), где n — размер оригинального массива.
Если немного подумать, то это имеет смысл. Например, возьмём n = 32 (массив из 32-х элементов). Сколько раз нам потребуется разделить его, чтобы получить один элемент? Считаем: 32 → 16 → 8 → 4 → 2 → 1 — итого 5 раз, что является логарифмом 32. Таким образом, сложность бинарного поиска равна Θ( log( n ) ).
Последний результат позволяет нам сравнивать бинарный поиск с линейным (нашим предыдущим методом). Несомненно, log( n ) намного меньше n, из чего правомерно заключить, что первый намного быстрее второго. Так что имеет смысл хранить массивы в отсортированном виде, если мы собираемся часто искать в них значения.
Практическая рекомендация: улучшение асимптотического времени выполнения программы часто чрезвычайно повышает её производительность. Намного сильнее, чем небольшая «техническая» оптимизация в виде использования более быстрого языка программирования.
Рекурсивный алгоритм вычисления логарифма — PDF Free Download
Лекции 8,9. Глава 5. Непрерывность функции
 Лекции 89 Глава 5 Непрерывность функции 5 Непрерывность функции в точке Понятие непрерывности функции является одним из основных понятий высшей математики Очевидно графиком непрерывной функции является
Лекции 89 Глава 5 Непрерывность функции 5 Непрерывность функции в точке Понятие непрерывности функции является одним из основных понятий высшей математики Очевидно графиком непрерывной функции является
2. Решение нелинейных уравнений.
 Решение нелинейных уравнений Не всегда алгебраические или трансцендентные уравнения могут быть решены точно Понятие точности решения подразумевает: ) возможность написания «точной формулы», а точнее говоря
Решение нелинейных уравнений Не всегда алгебраические или трансцендентные уравнения могут быть решены точно Понятие точности решения подразумевает: ) возможность написания «точной формулы», а точнее говоря
1. Числовые последовательности
 ТЕОРИЯ ПРЕДЕЛОВ И НЕПРЕРЫВНОСТЬ 1. Числовые последовательности Определение 1. Отображение a: N R множества натуральных, принимающее свои значения в множестве действительных чисел, называется числовой последовательностью.
ТЕОРИЯ ПРЕДЕЛОВ И НЕПРЕРЫВНОСТЬ 1. Числовые последовательности Определение 1. Отображение a: N R множества натуральных, принимающее свои значения в множестве действительных чисел, называется числовой последовательностью.
12. Определенный интеграл
 58 Определенный интеграл Пусть на промежутке [] задана функция () Будем считать функцию непрерывной, хотя это не обязательно Выберем на промежутке [] произвольные числа,, 3,, n-, удовлетворяющие условию:
58 Определенный интеграл Пусть на промежутке [] задана функция () Будем считать функцию непрерывной, хотя это не обязательно Выберем на промежутке [] произвольные числа,, 3,, n-, удовлетворяющие условию:
1 Степень с целым показателем
 Глава 9 Степени Степень с целым показателем. 0 = 0; 0 = ; 0 = 0. > 0 > 0 ; > >.. >. Если четно, то ( ) < ( ). Например, ( ) 0 = 0 < 0 = = ( ) 0. Если нечетно, то ( ) > ( ). Например, ( ) = > = = ( ), так
Глава 9 Степени Степень с целым показателем. 0 = 0; 0 = ; 0 = 0. > 0 > 0 ; > >.. >. Если четно, то ( ) < ( ). Например, ( ) 0 = 0 < 0 = = ( ) 0. Если нечетно, то ( ) > ( ). Например, ( ) = > = = ( ), так
Тема 1. Элементы теории погрешностей
 — 1 — Тема 1 Элементы теории погрешностей 11 Источники и классификация погрешностей Численное решение любой задачи, как правило, осуществляется приближенно, те с некоторой точностью Это может быть обусловлено
— 1 — Тема 1 Элементы теории погрешностей 11 Источники и классификация погрешностей Численное решение любой задачи, как правило, осуществляется приближенно, те с некоторой точностью Это может быть обусловлено
Ряды. Числовые ряды.
 Ряды Числовые ряды Общие понятия Опр Если каждому натуральному числу ставится в соответствие по определенному закону некоторое число, то множество занумерованных чисел, называется числовой последовательностью,
Ряды Числовые ряды Общие понятия Опр Если каждому натуральному числу ставится в соответствие по определенному закону некоторое число, то множество занумерованных чисел, называется числовой последовательностью,
Coa Компьютерная алгебра
 6. Быстрые алгоритмы деления Деление чисел методом Ньютона Для определенности будем считать, что делимое a = ( a,, am) и делитель b = ( b,, b ) записаны в позиционной системе счисления по основанию ( ).
6. Быстрые алгоритмы деления Деление чисел методом Ньютона Для определенности будем считать, что делимое a = ( a,, am) и делитель b = ( b,, b ) записаны в позиционной системе счисления по основанию ( ).
Ariel University Center
 Ariel Uiversity Ceter Deprtmet of Computer Sciece d Mthemtics 68 E-mil: dom@rielcil F: PO Bo Ariel 87 ISRAEL 906669 69 Университетский Центр «Ариэль» государство Израиль Олимпиада по математике 008 Решения
Ariel Uiversity Ceter Deprtmet of Computer Sciece d Mthemtics 68 E-mil: dom@rielcil F: PO Bo Ariel 87 ISRAEL 906669 69 Университетский Центр «Ариэль» государство Израиль Олимпиада по математике 008 Решения
Лекции 15, Гамма-функция Эйлера
 Лекции 15,16-19. Гамма-функция Эйлера Здесь описываются свойства одной из самых важных неэлементарных функций анализа. Обычно ее название пишется так: Γ-функция. 1 Определение Γ-функции. Γ-функция определяется
Лекции 15,16-19. Гамма-функция Эйлера Здесь описываются свойства одной из самых важных неэлементарных функций анализа. Обычно ее название пишется так: Γ-функция. 1 Определение Γ-функции. Γ-функция определяется
Элементарный подход к вычислению ζ(2n)
 Элементарный подход к вычислению ζ(2n) Устинов А. В. Хорошо известно, что значения ζ функции Римана в четных положительных точках вычисляются явно: ( ) n π 2n 2 2n ζ(2n) = B 2n (n ), () где B n числа Бернулли,
Элементарный подход к вычислению ζ(2n) Устинов А. В. Хорошо известно, что значения ζ функции Римана в четных положительных точках вычисляются явно: ( ) n π 2n 2 2n ζ(2n) = B 2n (n ), () где B n числа Бернулли,
ПРЕДЕЛЫ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ
 Министерство образования Московской области Государственное бюджетное образовательное учреждение высшего профессионального образования Московской области «Международный университет природы, общества и
Министерство образования Московской области Государственное бюджетное образовательное учреждение высшего профессионального образования Московской области «Международный университет природы, общества и
Лекция 2. Последовательности
 Лекция 2 Последовательности Определение. Если каждому натуральному числу ставится в соответствие по определенному закону некоторое вещественное число x, то множество занумерованных чисел x, x2,…, x,…
Лекция 2 Последовательности Определение. Если каждому натуральному числу ставится в соответствие по определенному закону некоторое вещественное число x, то множество занумерованных чисел x, x2,…, x,…
Занятие 1 (2 часа) Ход занятия.
 Тема Целая и дробная части числа Занятие 1 ( часа) Цель занятия Дидактическая Познакомить учащихся с целой и дробной частью числа Установить их свойства и соотношения между ними Научить строить простейшие
Тема Целая и дробная части числа Занятие 1 ( часа) Цель занятия Дидактическая Познакомить учащихся с целой и дробной частью числа Установить их свойства и соотношения между ними Научить строить простейшие
В.В. Калинин, А.Н. Филиппов, Т.С. Филиппова
 Министерство образования и науки Российской Федерации РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА имени И.М. ГУБКИНА (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ) Кафедра высшей математики В.В.
Министерство образования и науки Российской Федерации РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА имени И.М. ГУБКИНА (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ) Кафедра высшей математики В.В.
Одно замечательное тождество для sin nx
 Одно замечательное тождество для x Г.И. Фалин д.ф.м.н., профессор кафедра теории вероятностей механико-математический факультет МГУ им.м.в.ломоносова А.И. Фалин к.ф.м.н., доцент кафедра общей математики
Одно замечательное тождество для x Г.И. Фалин д.ф.м.н., профессор кафедра теории вероятностей механико-математический факультет МГУ им.м.в.ломоносова А.И. Фалин к.ф.м.н., доцент кафедра общей математики
ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ
 ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ Основная задача теории погрешностей состоит в оценке погрешности результата вычислений при известных погрешностях исходных данных. Источники и классификация погрешностей результата
ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ Основная задача теории погрешностей состоит в оценке погрешности результата вычислений при известных погрешностях исходных данных. Источники и классификация погрешностей результата
0, если заданы приближения a
 1. ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА 3 курс 5 семестр 1. Отличия вычислительной математики от других математических наук.. Грубая (линейная) оценка абсолютной погрешности A ( u *). 3. Теор. задача. Вычислить относительную
1. ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА 3 курс 5 семестр 1. Отличия вычислительной математики от других математических наук.. Грубая (линейная) оценка абсолютной погрешности A ( u *). 3. Теор. задача. Вычислить относительную
Математический анализ в вопросах и задачах
 ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Нижегородский государственный университет им. Н.И. Лобачевского Национальный исследовательский университет Математический
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Нижегородский государственный университет им. Н.И. Лобачевского Национальный исследовательский университет Математический
, а всю числовую последовательность — y
Лекции Глава Числовые последовательности Основные понятия Числовую функцию y f N y R заданную на множестве N натуральных чисел называют числовой последовательностью Число f называют -м элементом последовательности
Подробнее8 Методы численного интегрирования.
 интеграла. 8 Методы численного интегрирования. В данной главе будут рассмотрены методы вычисления определенного Методы численного интегрирования находят широкое применение при автоматизации решения научных
интеграла. 8 Методы численного интегрирования. В данной главе будут рассмотрены методы вычисления определенного Методы численного интегрирования находят широкое применение при автоматизации решения научных
Делимость и модульная арифметика
 Лекция. Введение в теоретико-числовые алгоритмы Делимость и модульная арифметика, отношение сравнимости, бинарное возвещение в степень, простые числа, наименьшее общее кратное, наибольший общий делитель,
Лекция. Введение в теоретико-числовые алгоритмы Делимость и модульная арифметика, отношение сравнимости, бинарное возвещение в степень, простые числа, наименьшее общее кратное, наибольший общий делитель,
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
 СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ После изучения данной темы вы сможете: проводить численное решение задач линейной алгебры. К решению систем линейных уравнений сводятся многочисленные практические задачи, решение
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ После изучения данной темы вы сможете: проводить численное решение задач линейной алгебры. К решению систем линейных уравнений сводятся многочисленные практические задачи, решение
РГУ нефти и газа им. И.М. ГУБКИНА
 РГУ нефти и газа им. И.М. ГУБКИНА ЛЕКЦИИ ПО ФИЗИКЕ ДЛЯ СТУДЕНТОВ ФАКУЛЬТЕТА ЭКОНОМИКИ И УПРАВЛЕНИЯ Автор профессор Бекетов В.Г. ВВОДНАЯ ЧАСТЬ ТОЧНОСТЬ. ЗНАЧАЩИЕ ЦИФРЫ ЧИСЛА Результаты измерений и расчетов
РГУ нефти и газа им. И.М. ГУБКИНА ЛЕКЦИИ ПО ФИЗИКЕ ДЛЯ СТУДЕНТОВ ФАКУЛЬТЕТА ЭКОНОМИКИ И УПРАВЛЕНИЯ Автор профессор Бекетов В.Г. ВВОДНАЯ ЧАСТЬ ТОЧНОСТЬ. ЗНАЧАЩИЕ ЦИФРЫ ЧИСЛА Результаты измерений и расчетов
Разложение функции в ряд Тейлора
 82 4. Раздел 4. Функциональные и степенные ряды 4.2. Занятие 3 4.2. Занятие 3 4.2.. Разложение функции в ряд Тейлора ОПРЕДЕЛЕНИЕ 4.2.. Пусть функция y = f(x) бесконечно дифференцируема в некоторой окрестности
82 4. Раздел 4. Функциональные и степенные ряды 4.2. Занятие 3 4.2. Занятие 3 4.2.. Разложение функции в ряд Тейлора ОПРЕДЕЛЕНИЕ 4.2.. Пусть функция y = f(x) бесконечно дифференцируема в некоторой окрестности
Тема курса лекций: ЧИСЛОВЫЕ РЯДЫ.
 Тема курса лекций: ЧИСЛОВЫЕ РЯДЫ. Лекция 2. Абсолютно сходящиеся ряды, признаки сходимости. Свойства абсолютно сходящихся рядов. Условная сходимость. Признаки сходимости Лейбница, Дирихле, Абеля. Далее
Тема курса лекций: ЧИСЛОВЫЕ РЯДЫ. Лекция 2. Абсолютно сходящиеся ряды, признаки сходимости. Свойства абсолютно сходящихся рядов. Условная сходимость. Признаки сходимости Лейбница, Дирихле, Абеля. Далее
Элементы высшей математики
 Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Дифференциальное исчисление Составитель:
Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Дифференциальное исчисление Составитель:
10 класс, Математика (профиль) уч.год Тема модуля 1 «Корни, степени, логарифмы»
 0 класс, Математика (профиль) 0-08 учгод Тема модуля «Корни, степени, логарифмы» Знать Понятия действительного числа, множества чисел, свойства действительных чисел, делимость целых чисел****, свойства
0 класс, Математика (профиль) 0-08 учгод Тема модуля «Корни, степени, логарифмы» Знать Понятия действительного числа, множества чисел, свойства действительных чисел, делимость целых чисел****, свойства
{ z } { 1 2 3, 4,…, ( 1) n = ; ,, n,…}
 Тема Теория пределов Как мы понимаем слово «предел»? В повседневной жизни мы часто употребляем термин «предел», не углубляясь в его сущность В нашем представлении чаще всего предел отождествляется с понятием
Тема Теория пределов Как мы понимаем слово «предел»? В повседневной жизни мы часто употребляем термин «предел», не углубляясь в его сущность В нашем представлении чаще всего предел отождествляется с понятием
0.5 setgray0 0.5 setgray1
 0.5 setgray0 0.5 setgray1 1 Лекция 1 ОПРЕДЕЛИТЕЛИ. СИСТЕМЫ УРАВНЕНИЙ 0. План лекции 1. Определитель второго порядка. 1.1 Система двух уравнений. 1.2. Метод исключения переменных. 1.3. Матрица 2 2. 1.4.
0.5 setgray0 0.5 setgray1 1 Лекция 1 ОПРЕДЕЛИТЕЛИ. СИСТЕМЫ УРАВНЕНИЙ 0. План лекции 1. Определитель второго порядка. 1.1 Система двух уравнений. 1.2. Метод исключения переменных. 1.3. Матрица 2 2. 1.4.
Лекция 3. Интегральный признак
 С. А. Лавренченко www.lwreceko.ru Лекция Интегральный признак Перед прослушиванием этой лекции рекомендуется повторить несобственные интегралы (лекция 9 и практическое занятие 9 из модуля «Интегральное
С. А. Лавренченко www.lwreceko.ru Лекция Интегральный признак Перед прослушиванием этой лекции рекомендуется повторить несобственные интегралы (лекция 9 и практическое занятие 9 из модуля «Интегральное
Дискретная математика
 Дискретная математика Часть 5 В.Е. Алексеев 2014 Глава 9. Кодирование Кодирование преобразование информации, выполняемое с разнообразными целями: экономное представление (сжатие данных), защита от помех
Дискретная математика Часть 5 В.Е. Алексеев 2014 Глава 9. Кодирование Кодирование преобразование информации, выполняемое с разнообразными целями: экономное представление (сжатие данных), защита от помех
8. Свойства дифференцируемых функций
 8. Свойства дифференцируемых функций 8.. Производная функции в данной точке отражает локальные свойства функции, т. е. свойства, присущие функции в некоторой окрестности данной точки. Вместе с тем есть
8. Свойства дифференцируемых функций 8.. Производная функции в данной точке отражает локальные свойства функции, т. е. свойства, присущие функции в некоторой окрестности данной точки. Вместе с тем есть
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
 ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ. Интегральные суммы и определённый интеграл Пусть дана функция y = f (), определённая на отрезке [, b ], где < b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ. Интегральные суммы и определённый интеграл Пусть дана функция y = f (), определённая на отрезке [, b ], где < b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных
Александр Охотин. 25 марта 2019 г.
 Теоретическая информатика II Лекция 6. Дискретное преобразование Фурье в кольце. Быстрое преобразование Фурье, его рекурсивная и итеративная реализация Александр Охотин 25 марта 2019 г. Содержание 1 Быстрое
Теоретическая информатика II Лекция 6. Дискретное преобразование Фурье в кольце. Быстрое преобразование Фурье, его рекурсивная и итеративная реализация Александр Охотин 25 марта 2019 г. Содержание 1 Быстрое
Гл.1. Степенные ряды., постоянные, называемые коэффициентами ряда. Иногда рассматривают степенной ряд более
 Гл Степенные ряды a a a Ряд вида a a a a a () называется степенным, где,,,, a, постоянные, называемые коэффициентами ряда Иногда рассматривают степенной ряд более общего вида: a a( a) a( a) a( a) (), где
Гл Степенные ряды a a a Ряд вида a a a a a () называется степенным, где,,,, a, постоянные, называемые коэффициентами ряда Иногда рассматривают степенной ряд более общего вида: a a( a) a( a) a( a) (), где
Кодирование. В.Е. Алексеев
 http://vmcozet/ Кодирование ВЕ Алексеев Задача оптимального кодирования Побуквенное кодирование Пусть A a a a } и B b b b } два алфавита Побуквенное кодирование состоит в том что в кодируемом тексте слове
http://vmcozet/ Кодирование ВЕ Алексеев Задача оптимального кодирования Побуквенное кодирование Пусть A a a a } и B b b b } два алфавита Побуквенное кодирование состоит в том что в кодируемом тексте слове
РЯДЫ. Методические указания
 Металлургический факультет Кафедра высшей математики РЯДЫ Методические указания Новокузнецк 5 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
Металлургический факультет Кафедра высшей математики РЯДЫ Методические указания Новокузнецк 5 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ
 ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ Успех решения тригонометрических уравнений и неравенств, доказательства тригонометрических тождеств и решения вычислительных задач в значительной мере определяются знанием основных
ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ Успех решения тригонометрических уравнений и неравенств, доказательства тригонометрических тождеств и решения вычислительных задач в значительной мере определяются знанием основных
Вычисление дискретного логарифма
Определение. Пусть G = < G; •, 1 > — конечная группа, а и b —элементы группы G; r = ordb. Натуральное число l называют дискретнымлогарифмом элемента а при основании b, если
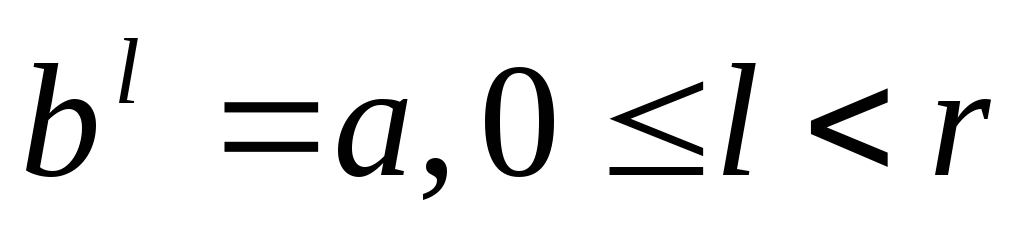 (1.1)
(1.1)
Замечания.
а) В
качестве группы G избираем мультипликативную
группу из ненулевых элементов конечного
поля Fr
б) Если q = р — простое число и b — первообразный корень по модулю р, то число l, определяемое условием (1.1), называют индексом числа а при основании b по модулю р.
в) Вместо термина «дискретный логарифм элемента а при основании b» употребляют также термин » индекс элемента а при основании b».
Обозначение. indba — дискретный логарифм элемента а при основании b. (Группа G обычно подразумевается из контекста.)
Задача определения дискретного логарифма элемента конечной группы может быть легко решена, если порядок группы не слишком велик и для этой группы составлена таблица индексов. При отыскании логарифма положительного действительного числа, если нет таблицы логарифмов или она недоступна, можно воспользоваться методом последовательного приближения. Он состоит в следующем. На каждом шаге применения этого метода интервал границ значения арифметического логарифма сужают вдвое. Так продолжая, легко определить значение этого логарифма с любой заранее объявленной точностью. Успех применения этого метода основан на использовании свойств неравенств. Ничего подобного нет в конечном поле. Точнее говоря, в конечном поле нельзя построить метод вычисления дискретного логарифма, подобный методу последовательного приближения. В самом деле, в конечном поле нельзя определить антисимметричное, транзитивное, связное бинарное отношение, согласованное с какой-нибудь операцией.
Алгоритм перебора — метод, который хотя бы теоретически может всегда привести к успеху. Он состоит в следующем. Пусть b —примитивный элемент данного конечного поля и a — другой какой-нибудь элемент того же поля. Чтобы найти indba, начиная, например, с п = 0, сравниваем элемент а с элементом bn, если a = bn, то indba = п, в противном случае находим bп+1 = bn • b и опять сравниваем элемент а с элементом bп+1 и т.д. Если число элементов поля 2100 или больше, то количество операций (умножений), необходимое для вычисления дискретною логарифма произвольного элемента конечного поля в приемлемое время, чрезвычайно велико и находится за пределами возможностей современных вычислительных машин.
Алгоритм согласования
Теорема 1. Пусть t, r — натуральные числа, r2 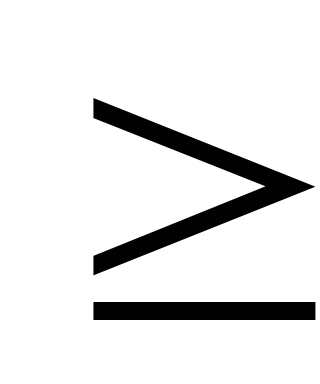 t . Для любого целого l можно указать целые числа х и у такие,
что
t . Для любого целого l можно указать целые числа х и у такие,
что

Доказательство. Можем предполагать,
что .
Полагаем
.
Полагаем
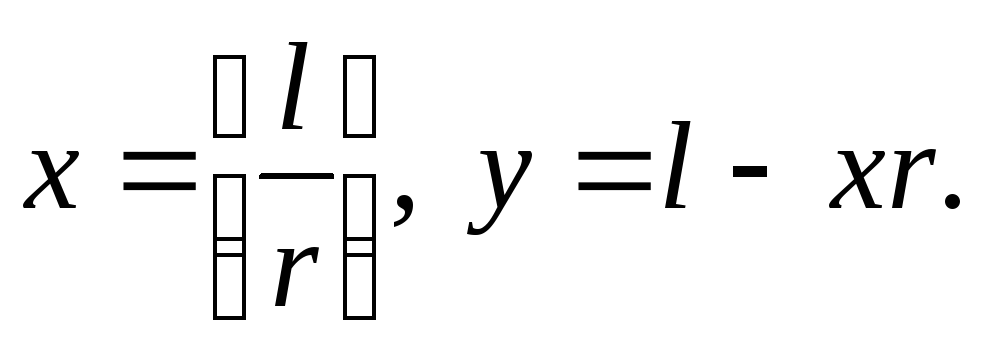
Имеем
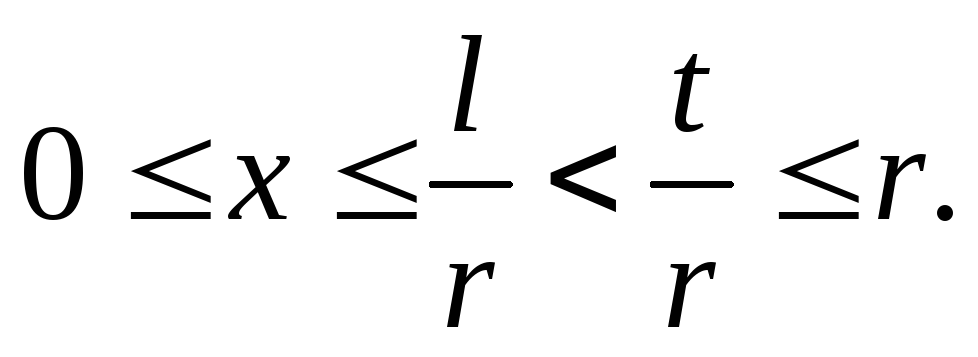
С другой стороны.

поэтому

или
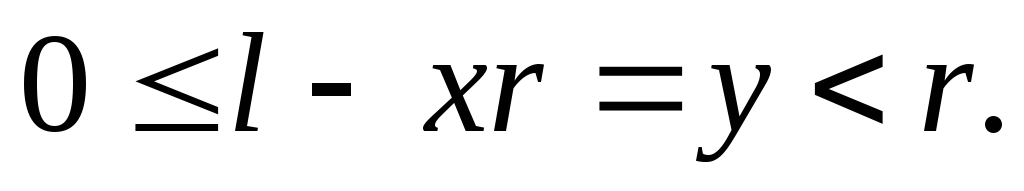
Теорема 2. Пусть G = < G,  ,
1 > —конечная группа;
а и b элементы группы G; t = ord b;
,
1 > —конечная группа;
а и b элементы группы G; t = ord b;
 (1.2)
(1.2)
Тогда число l можно найти, выполнив не более чем  операции
умножения на элементы группыG.
операции
умножения на элементы группыG.
Доказательство.
Полагаем  .
Рассмотрим ряды
.
Рассмотрим ряды
 (1.3)
(1.3)
 (1.4)
(1.4)
Если  разрешимо
относительно l, представим l ввиде
разрешимо
относительно l, представим l ввиде

Так как t = ord b, то b‘ = bxr+y = а в том и только в том случае, когда
 , (1.5)
, (1.5)
т.е. когда найдется элемент ряда (1.3), который совпадет с каким-нибудь членом ряда (1.4).
Нетрудно сосчитать число
операций, позволяющих установить
равенство (1.2). При вычислении элементов
ряда (1.3) потребуется выполнить не более
r-2
умножений. Для вычисления 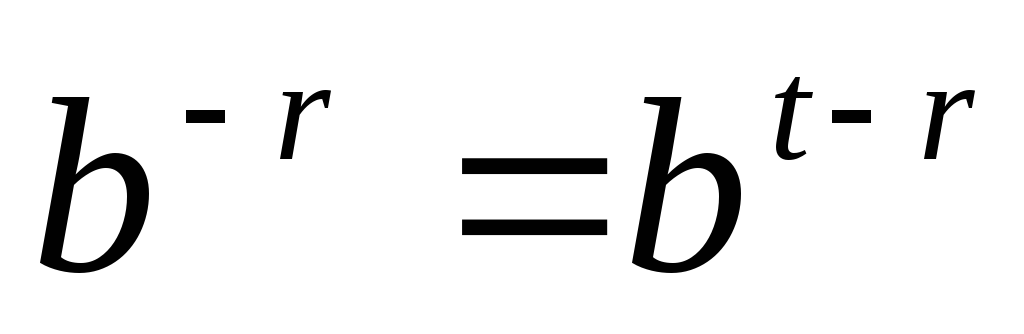 в силу следующей леммы
в силу следующей леммы
Дискретное логарифмирование | Контроль Разума
Дискретное логарифмирование (DLOG) – задача обращения функции $ g^x $ в некоторой конечной мультипликативной группе $ G $.
В основном данную задачу рассматривают в мультипликативной группе конечного поля или в группе точек на эллиптической кривой. На данный момент нет эффективных алгоритмов решения задачи в общем случае.
Решение данной задачи называется дискретным логарифмом. Если же рассматривается кольцо вычетов по простому модулю и g является первообразным элементом данного кольца, то решение называют также индексом числа a по основанию g.
Постановка задачиПравить
Пусть в некоторой конечной мультипликативной абелевой группе $ G $ задано уравнение
Решение задачи дискретного логарифмирования состоит в нахождении некоторо целого неотрицательного числа $ x $, удовлетворяющего уравнению (1). Если оно разрешимо, у него должно быть хотя бы одно натуральное решение, не превышающее порядок группы. Это сразу даёт грубую оценку сложности алгоритма поиска решений сверху — алгоритм полного перебора нашел бы решение за число шагов, не выше порядка данной группы.
Чаще всего рассматривается случай, когда $ G=\langle g\rangle $, то есть группа является циклической, порождённой элементом $ g $. В этом случае уравнение всегда имеет решение. В случае же произвольной группы, вопрос о разрешимости задачи дискретного логарифмирования, то есть вопрос о существовании решений уравнения (1), требует отдельного рассмотрения.
Проще всего рассмотреть задачу дискретного логарифмирования в кольце вычетов по модулю простого числа.
Пусть задано сравнение
| $ 3^x\equiv 13\mod{17}. $ |
Будем решать задачу методом перебора. Выпишем таблицу всех степеней числа 3. Каждый раз мы вычисляем остаток от деления на 17 (например, 33≡27 — остаток от деления на 17 равен 10).
| 31 ≡ 3 | 32 ≡ 9 | 33 ≡ 10 | 34 ≡ 13 | 35 ≡ 5 | 36 ≡ 15 | 37 ≡ 11 | 38 ≡ 16 |
| 39 ≡ 14 | 310 ≡ 8 | 311 ≡ 7 | 312 ≡ 4 | 313 ≡ 12 | 314 ≡ 2 | 315 ≡ 6 | 316 ≡ 1 |
Теперь легко увидеть, что решением рассматриваемого сравнения является x=4, поскольку 34≡13.
На практике модуль обычно является достаточно большим числом, и метод перебора является слишком медленным, поэтому возникает потребность в более быстрых алгоритмах.
Алгоритмы решенияПравить
В произвольной мультипликативной группе Править
Разрешимости и решению задачи дискретного логарифмирования в произвольной конечной абелевой группе посвящена статья BuchmannJ., Jacobson M.J., Teske E. On some computational problems in finite abelian groups[1]. В алгоритме используется таблица, состоящая из $ O(\sqrt{|\langle g\rangle|}) $ пар элементов и выполняется $ O(\sqrt{|\langle g\rangle|}) $ умножений. Данный алгоритм медленный и не пригоден для практического использования. Для конкретных групп существуют свои, более эффективные, алгоритмы.
В кольце вычетов по простому модулю Править
Рассмотрим уравнение
| $ a^x\equiv b\mod{p}, $ | (2) |
где $ p $ — простое, $ b $ не делится на $ p $. Если $ a $ является образующим элементом группы $ \mathbb{Z}/p\mathbb{Z} $, то уравнение (2) имеет решение при любых $ b $. Такие числа $ a $ называются ещё первообразными корнями, и их количество равно $ \phi(p-1) $, где $ \phi $ — функция Эйлера. Решение уравнения (2) можно находить по формуле:
| $ x=\sum\limits_{i=1}^{p-1}(1-a^i)^{-1}b^i\mod{p}. $ |
Однако, сложность вычисления по этой формуле хуже, чем сложность перебора.
Следующий алгоритм имеет сложность $ O(p^{\frac{1}{2}}\log{p}) $
Алгоритм
- Присвоить $ H:=[p^{\frac{1}{2}}]+1 $
- Найти $ c\equiv a^H\mod{p} $
- Составить таблицу значений $ c^u\mod{p}, 1\leq u\leq H, $ и упорядочить её.
- Составить таблицу значений $ b\cdot a^v\mod{p}, 0\leq v\leq H, $ и упорядочить её.
- Найти совпавшие элементы из первой и второй таблиц. Для них
$ c^u=b\cdot a^v\mod{p}, $
откуда $ a^{Hu-v}\equiv b\mod{p}. $ - Выдать $ x\equiv Hu-v\mod{p-1} $.
Конец алгоритма
Существует также множество других алгоритмов для решения задачи дискретного логарифмирования в поле вычетов. Их принято разделять на экспоненциальные и субэкспоненциальные. Полиномиального алгоритма для решения этой задачи пока не существует.
Алгоритмы с экспоненциальной сложностью Править
- Алгоритм Шенкса (алгоритм больших и малых шагов, baby-step giant-step)
- Алгоритм Полига-Хеллмана — работает, если известно разложение числа $ p-1=\prod\limits_{i=1}^{s}q_i^{\alpha_i} $ на простые множители. Сложность: $ O(\sum\limits_{i=0}^{s}\alpha_i(\log{p}+q_i)) $. Если множители, на которые раскладывается $ p-1 $, достаточно маленькие, то алгоритм очень эффективен.
- ρ-метод Полларда имеет эвристическую оценку сложности $ O(p^{\frac{1}{2}}) $.
Субэкспоненциальные алгоритмы Править
Данные алгоритмы имеют сложность $ O(\exp{(c(\log{p}\log{\log{p}})^{d})}) $ арифметических операций, где $ c $ и
Самый натуральный логарифм / Habr
Вдохновившись постом про вычисление pi, решил вычислить подобным образом число e. По пути получилась функция натурального логарифма.
Собственно,
#include <iostream>
#define I r=
#define l ;
#define o
#define x if(1+(d*2)*(1/(__*2))<=k)d++;
#define e p+=d;d=1;
#define h _++;
#define s __++;
double ln(double k){double p=0,n,y,r,d,_=0,__=0;
I 3.30 l o o o o o o
I 3.25 l o o o o o o
I 3.20 l o o o o o o
I 3.15 l o o o o o o
I 3.10 l o o o o o o
I 3.05 l o o o o o o
I 3.00 l o o o o o o
I 2.95 l o o o o o o
I 2.90 l o o o o o o
I 2.85 l o o o o o o
I 2.80 l o o o o o o
I 2.75 l o o o o o o o
I 2.70 l o o o o o o o
I 2.65 l o o o o o o o
I 2.60 l o o o o o o o
I 2.55 l o o o o o o o
I 2.50 l o o o o o o o
I 2.45 l o o o o o o o
I 2.40 l o o o o o o o o
I 2.35 l o o o o o o o o
I 2.30 l o o o o o o o o
I 2.25 l o o o o o o o o
I 2.20 l o o o o o o o o
I 2.15 l o o o o o o o o
I 2.10 l o o o o o o o o
I 2.05 l o o o o o o o o
I 2.00 l o o o o o o o o
I 1.95 l o o o o o o o o o
I 1.90 l o o o o o o o o o
I 1.85 l o o o o o o o o o
I 1.80 l o o o o o o o o o
I 1.75 l o o o o o o o o o
I 1.70 l o o o o o o o o o
I 1.65 l o o o o o o o o o
I 1.60 l o o o o o o o o o
I 1.55 l o o o o o o o o o o
I 1.50 l o o o o o o o o o o
I 1.45 l o o o o o o o o o o
I 1.40 l o o o o o o o o o o
I 1.35 l o o o o o o o o o o o
I 1.30 l o o o o o o o o o o o
I 1.25 l o o o o o o o o o o o
I 1.20 l o o o o o o o o o o o o
I 1.15 l o o o o o o o o o o o o
I 1.10 l o o o o o o o o o o o o
I 1.05 l o o s s s s s s s s s s o
I 1.00 l o o h h h h h h h h h h o
I 0.95 l o o h h h h h h h h h h e o
I 0.90 l o o h h h h h h h h h h e o
I 0.85 l o o h h h h h h h h h h e x o
I 0.80 l o o h h h h h h h h h h e x x o
I 0.75 l o o h h h h h h h h h h e x x x o
I 0.70 l o o h h h h h h h h h h e x x x x o
I 0.65 l o o h h h h h h h h h h e x x x x x o
I 0.60 l o o h h h h h h h h h h e x x x x x x o
I 0.55 l o o h h h h h h h h h h e x x x x x x x x o
I 0.50 l o o h h h h h h h h h h e x x x x x x x x x x o
I 0.45 l o o h h h h h h h h h h e x x x x x x x x x x x x x x o
I 0.40 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x o
I 0.35 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x o
I 0.30 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x o
I 0.25 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
I 0.20 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
I 0.15 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
I 0.10 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x e return p/_;
// 0 +1 +2 +3 +4 +5
}
Принцип прост — натуральный логарифм от a есть площадь под графиком 1/x от единицы до a.
Соответственно, чем точнее нарисован график, тем точнее будут вычисления. Немного о построении графика. Символами s обозначается единичный отрезок, h — квадрат единичной площади, e — функция f(x)=1, x — площадь под графиком 1/x на отрезке (1, +inf).
Имея функцию натурального логарифма и зная, что ln(e)=1 найти теперь e перебором не составляет труда.
for(double i = 0; i <= 3; i += 0.01)
if (ln(i) > 0.98)
{
std::cout << i << std::endl;
break;
}
Некоторые результаты:
| Выражение | Значение | Истинное значение |
| ln(2) | 0.721053 | 0.69315 |
| ln(2.7) | 1 | 0.99325 |
| ln(3) | 1.09474 | 1.09861 |
| ln(4) | 1.35263 | 1.38629 |
| ln(5) | 1.54211 | 1.60943 |
| e | 2.7 | 2.718281828 |
Ссылка на полный код.
Дискретный логарифм — это… Что такое Дискретный логарифм?
Дискретное логарифмирование (DLOG) – задача обращения функции gx в некоторой конечной мультипликативной группе G.
Наиболее часто задачу дискетного логарифмирования рассматривают в группе обратимых элементов кольца вычетов, в мультипликативной группе конечного поля, или в группе точек на эллиптической кривой над конечным полем. Эффективные алгоритмы для решения задачи дискетного логарифмирования в общем случае неизвестны.
Для заданных g и a решение x уравнения gx = a называется дискретным логарифмом элемента a по основанию g. В случае, когда G является группой обратимых элементов кольца вычетов по модулю m, решение называют также индексом числа a по основанию g. Индекс числа a по основанию g гарантированно существует, если g является первообразным корнем по модулю m.
Постановка задачи
Пусть в некоторой конечной мультипликативной абелевой группе G задано уравнение
Решение задачи дискретного логарифмирования состоит в нахождении некоторого целого неотрицательного числа x, удовлетворяющего уравнению (1). Если оно разрешимо, у него должно быть хотя бы одно натуральное решение, не превышающее порядок группы. Это сразу даёт грубую оценку сложности алгоритма поиска решений сверху — алгоритм полного перебора нашел бы решение за число шагов, не выше порядка данной группы.
Чаще всего рассматривается случай, когда 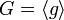 , то есть группа является циклической, порождённой элементом g. В этом случае уравнение всегда имеет решение. В случае же произвольной группы, вопрос о разрешимости задачи дискретного логарифмирования, то есть вопрос о существовании решений уравнения (1), требует отдельного рассмотрения.
, то есть группа является циклической, порождённой элементом g. В этом случае уравнение всегда имеет решение. В случае же произвольной группы, вопрос о разрешимости задачи дискретного логарифмирования, то есть вопрос о существовании решений уравнения (1), требует отдельного рассмотрения.
Пример
Проще всего рассмотреть задачу дискретного логарифмирования в кольце вычетов по модулю простого числа.
Пусть задано сравнение
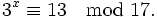 |
Будем решать задачу методом перебора. Выпишем таблицу всех степеней числа 3. Каждый раз мы вычисляем остаток от деления на 17 (например, 33≡27 — остаток от деления на 17 равен 10).
| 31 ≡ 3 | 32 ≡ 9 | 33 ≡ 10 | 34 ≡ 13 | 35 ≡ 5 | 36 ≡ 15 | 37 ≡ 11 | 38 ≡ 16 |
| 39 ≡ 14 | 310 ≡ 8 | 311 ≡ 7 | 312 ≡ 4 | 313 ≡ 12 | 314 ≡ 2 | 315 ≡ 6 | 316 ≡ 1 |
Теперь легко увидеть, что решением рассматриваемого сравнения является x=4, поскольку 34≡13.
На практике модуль обычно является достаточно большим числом, и метод перебора является слишком медленным, поэтому возникает потребность в более быстрых алгоритмах.
Алгоритмы решения
В произвольной мультипликативной группе
Разрешимости и решению задачи дискретного логарифмирования в произвольной конечной абелевой группе посвящена статья BuchmannJ., Jacobson M.J., Teske E. On some computational problems in finite abelian groups[1]. В алгоритме используется таблица, состоящая из 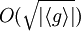 пар элементов и выполняется
пар элементов и выполняется 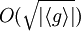 умножений. Данный алгоритм медленный и не пригоден для практического использования. Для конкретных групп существуют свои, более эффективные, алгоритмы.
умножений. Данный алгоритм медленный и не пригоден для практического использования. Для конкретных групп существуют свои, более эффективные, алгоритмы.
В кольце вычетов по простому модулю
Рассмотрим уравнение
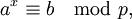 | (2) |
где p — простое, b не делится на p. Если a является образующим элементом группы 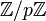 , то уравнение (2) имеет решение при любых b. Такие числа a называются ещё первообразными корнями, и их количество равно φ(p − 1), где φ — функция Эйлера. Решение уравнения (2) можно находить по формуле:
, то уравнение (2) имеет решение при любых b. Такие числа a называются ещё первообразными корнями, и их количество равно φ(p − 1), где φ — функция Эйлера. Решение уравнения (2) можно находить по формуле:
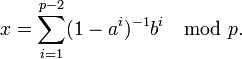 |
Однако, сложность вычисления по этой формуле хуже, чем сложность перебора.
Следующий алгоритм имеет сложность 
Алгоритм
- Присвоить
![H:=[p^{\frac{1}{2}}]+1](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
- Найти

- Составить таблицу значений
 и упорядочить её.
и упорядочить её. - Составить таблицу значений
 и упорядочить её.
и упорядочить её. - Найти совпавшие элементы из первой и второй таблиц. Для них

откуда
- Выдать
 .
.
Конец алгоритма
Существует также множество других алгоритмов для решения задачи дискретного логарифмирования в поле вычетов. Их принято разделять на экспоненциальные и субэкспоненциальные. Полиномиального алгоритма для решения этой задачи пока не существует.
Алгоритмы с экспоненциальной сложностью
- Алгоритм Шенкса (алгоритм больших и малых шагов, baby-step giant-step)
- Алгоритм Полига-Хеллмана — работает, если известно разложение числа
 на простые множители. Сложность:
на простые множители. Сложность:  . Если множители, на которые раскладывается p − 1, достаточно маленькие, то алгоритм очень эффективен.
. Если множители, на которые раскладывается p − 1, достаточно маленькие, то алгоритм очень эффективен. - ρ-метод Полларда имеет эвристическую оценку сложности
 .
.
Субэкспоненциальные алгоритмы
Данные алгоритмы имеют сложность 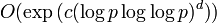 арифметических операций, где
арифметических операций, где  и
и 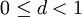 — некоторые константы. Эффективность алгоритма во многом зависит от близости c к 1 и d — к 0.
— некоторые константы. Эффективность алгоритма во многом зависит от близости c к 1 и d — к 0.
- Алгоритм Адлемана появился в 1979 году. Это был первый субэкспоненциалный алгоритм дискретного логарифмирования. На практике он всё же недостаточно эффективен. В этом алгоритме
 .
. - Алгоритм COS был предложен в 1986 году математиками Копперсмитом (Don Coppersmith), Одлыжко (Andrew Odlyzko) и Шреппелем (Richard Schroeppel). В этом алгоритме константа
 ,
,  . В 1991 году с помощью Этого метода было проведено логарифмирование по модулю
. В 1991 году с помощью Этого метода было проведено логарифмирование по модулю  . В 1997 году Вебер провел дискретное логарифмирование по модулю
. В 1997 году Вебер провел дискретное логарифмирование по модулю  с помощью некоторой версии данного алгоритма. Экспериментально показано, что при
с помощью некоторой версии данного алгоритма. Экспериментально показано, что при  алгоритм COS лучше решета числового поля.
алгоритм COS лучше решета числового поля. - Решето числового поля было применено к дискретному логарифмированию позднее, чем к факторизации чисел. Первые идеи появились в 1990-х годах. Алгоритм, предложенный Д. Гордоном в 1993 году, имел эвристическую сложность
 , но оказался достаточно непрактичным. Позднее было предложено множество различных улучшений данного алгоритма. Было показано, что при
, но оказался достаточно непрактичным. Позднее было предложено множество различных улучшений данного алгоритма. Было показано, что при  решето числового поля быстрее, чем COS. Современные рекорды в дискретном логарифмировании получены именно с помощью этого метода.
решето числового поля быстрее, чем COS. Современные рекорды в дискретном логарифмировании получены именно с помощью этого метода.
Наилучшими параметрами в оценке сложности на данный момент является 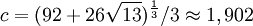 ,
, 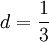 .
.
Для чисел специального вида результат можно улучшить. В некоторых случаях можно построить алгоритм, для которого константы будут 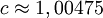 ,
, 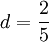 . За счёт того, что константа c достаточно близка к 1, подобные алгоритмы могут обогнать алгоритм с
. За счёт того, что константа c достаточно близка к 1, подобные алгоритмы могут обогнать алгоритм с 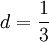 .
.
В произвольном конечном поле
Задача рассматривается в поле GF(q), где q = pn, p — простое.
- Алгоритм исчисления индексов (index-calculus) эффективен, если p невелико. В этом случае он имеет эвристическую оценку сложности
 .
. - Алгоритм Эль-Гамаля, появившийся в 1985 году, применим при n = 2 и имеет сложность
 арифметических операций.
арифметических операций. - Алгоритм Копперсмита дискретного логарифмирования в конечном поле характеристики 2 стал первым субэкспоненциальным алгоритмом дискретного логарифмирования с константой
 в оценки сложности. Данный алгоритм появился в 1984 году — до изобретения решета числового поля.
в оценки сложности. Данный алгоритм появился в 1984 году — до изобретения решета числового поля.
В группе точек на эллиптической кривой
Рассматривается группа точек эллиптической кривой над конечным полем. В данной группе определена операция сложения двух точек. Тогда mP — это 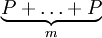 . Решением задачи дискретного логарифмирования на эллиптической кривой является нахождение такого натурального числа m, что
. Решением задачи дискретного логарифмирования на эллиптической кривой является нахождение такого натурального числа m, что
для заданных точек P и A.
До 1990 года не существовало алгоритмов дискретного логарифмирования, учитывающих особенностей строения группы точек элиптической кривой. Впоследствии, Менезес (Alfred J. Menezes), Окамото (Tatsuaki Okamoto) и Венстон (Scott A. Vanstone) предложили алгоритм, использующий спаривание Вейля. Для эллиптической кривой, определённой над полем GF(q), данный алгоритм сводит задачу дискретного логарифмирования к аналогичной задаче в поле GF(qk). Однако, данное сведение полезно, только если степень k мала. Это условие выполняется, в основном, для суперсингулярных эллиптических кривых. В остальных случаях подобное сведение практически никогда не приводит к субэкспоненциальным алгоритмам.
Вычислительная сложность и приложения в криптографии
Задача дискретного логарифмирования является одной из основных задач, на которых базируется криптография с открытым ключом. Идея, лежащая в основе подобных систем, опирается на высокую вычислительную сложность обращения некоторых числовых функций. В данном случае, операция дискретного логарифмирования является обратной к показательной функции. Последняя вычисляется достаточно просто, в то время как даже самые современные алгоритмы вычисления дискретного логарифма имеют очень высокую сложность, которая сравнима со сложностью наиболее быстрых алгоритмов разложения чисел на множители.
Другая возможность эффективного решения задачи вычисления дискретного логарифма связана с квантовыми вычислениями. Теоретически доказано, что, используя их, дискретный логарифм может быть вычислен за полиномиальное время[2]. В любом случае, если полиномиальный алгоритм вычисления дискретного логарифма будет реализован, это будет означать практическую непригодность криптосистем на его основе.
Классическими криптографическими схемами, базирующимися на сложности задачи дискретного логарифмирования, являются схема выработки общего ключа Диффи-Хеллмана, схема электронной подписи Эль-Гамаля, криптосистема Мэсси-Омуры для передачи сообщений.
Ссылки
- ↑ Электронную версию см. на http://citeseer.ist.psu.edu/716900.html
- ↑ http://cs.mipt.ru/docs/comp/rus/develop/other/quantum_comp
Wikimedia Foundation. 2010.
![H:=[p^{\frac{1}{2}}]+1](/800/600/https/dic.academic.ru/pictures/wiki/files/49/1e885aa87936d933ad1b70aaa3deebb2.png)

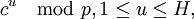 и упорядочить её.
и упорядочить её.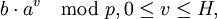 и упорядочить её.
и упорядочить её.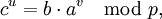
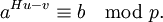
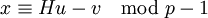 .
.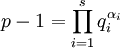 на простые множители. Сложность:
на простые множители. Сложность:  . Если множители, на которые раскладывается p − 1, достаточно маленькие, то алгоритм очень эффективен.
. Если множители, на которые раскладывается p − 1, достаточно маленькие, то алгоритм очень эффективен.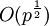 .
.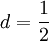 .
.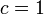 ,
, 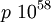 . В 1997 году Вебер провел дискретное логарифмирование по модулю
. В 1997 году Вебер провел дискретное логарифмирование по модулю 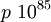 с помощью некоторой версии данного алгоритма. Экспериментально показано, что при
с помощью некоторой версии данного алгоритма. Экспериментально показано, что при 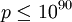 алгоритм COS лучше решета числового поля.
алгоритм COS лучше решета числового поля.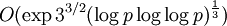 , но оказался достаточно непрактичным. Позднее было предложено множество различных улучшений данного алгоритма. Было показано, что при
, но оказался достаточно непрактичным. Позднее было предложено множество различных улучшений данного алгоритма. Было показано, что при 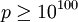 решето числового поля быстрее, чем COS. Современные рекорды в дискретном логарифмировании получены именно с помощью этого метода.
решето числового поля быстрее, чем COS. Современные рекорды в дискретном логарифмировании получены именно с помощью этого метода.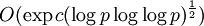 .
.