Арифметическая и геометрическая прогрессии. Примеры

Примеры на арифметическую и геометрическую прогрессию взяты из «Сборника задач для абитуриентов. Математика» изданного Волынским государственным университетом имени Леси Украинки в 2001 году. Внимательно ознакомьтесь с ответами и выберите для себя самое необходимое.

Группа А (уровень 1)

Пример 1. Вычислить шестой член арифметической прогрессии 21,3; 22,4; …,
Решение: Найдем разницу (шаг) прогрессии
d=a₂-a₁=22,4-21,3=1,1.
Далее вычисляем шестой член арифметической прогрессии
a₆=a₁+(6-1)d=21,3+5*1,1=26,8.

 

Пример 2. Вычислить шестой член геометрической прогрессии 5; 10; 20; …
Решение: Найдем знаменатель геометрической прогрессии
q=b₂/b₁=10/5=2.
Вычисляем шестой член геометрической прогрессии
b₆=b₁q^6-1=5*25=5*32=160.

 

Пример 3. В арифметической прогрессии a₁=2,1 a₁₀=12,9. Вычислить разницу прогрессии.
Решение: Представим десятый член прогрессии в виде формулы
a₁₀=a₁+(10-1)d= a₁+9d.
Подставим известные значения и решим
12,9=2,1+9d;
9d=12,9-2,1=10,8;
d=10,8/9=1,2.
Ответ: разница прогрессии d=1,2.

 

Пример 4. В геометрической прогрессии b₁=2,56; b₄=4,42368. Вычислить знаменатель прогрессии.
Решение: Находим знаменатель прогрессии
q=b₂/b₁=4,42368/2,56=1,728.
Без калькулятора здесь не обойтись.
Ответ: знаменатель прогрессии равен q=1,728.

 

Пример 5. В арифметической прогрессии a₁=20,1, d=1,3. Вычислить сумму первых восьми членов прогрессии.
Решение: Cуму арифметической прогрессии находим по формуле

Выполняем вычисления
S₈=(2*20,1+(8-1)*1,3)*8/2=197,2.
Ответ: S₈=197,2.

 

Пример 6. В геометрической прогрессии b₁=1,5; q=1,2. Вычислить сумму первых четырех членов прогрессии.
Решение: Cуму геометрической прогрессии вычисляем по формуле

Находим сумму прогрессии

Ответ: S₈=8,052.

 

Пример 7. В арифметической прогрессии a₁=1,35 d=-2,4. Вычислить номер члена прогрессии, равный -25,05.
Решение: Член арифметической прогрессии находят по формуле
a_n=a₁+(n-1)d.
По условию задано все кроме порядкового номера известно, найдем его
-25,05=1,35+(n-1)(-2,4);

Ответ: n=12.

 

Пример 8. Вычислить седьмой член прогрессии 23,5; 24,82; 26,14; …
Решение: Поскольку в условии не задано какая прогрессия задана, то сначала нужно ето установить . Получите, что арифметическая
d=a₂-a₁=24,82-23,5=1,32;
d=a₃-a₂=26,14-24,82=1,32.
Находим седьмой член прогрессии
a₇=a₁+(7-1)d=23,5+6*1,32=31,42.
Ответ: a₇= 31,42.

 

Пример 9. Вычислить номер члена прогрессии 2,1; 3,3; 4,5; … , равный 11,7.
Решение: Легко убедиться, что задана арифметическая прогрессия. Найдем разницу прогрессии
d=a₂-a₁=3,3-2,1=1,2.
По формуле члена прогрессии
a_n=a₁+(n-1)d
найдем номер
11,7=2,1+(n-1)*1,2;

Ответ: n= 9.

 

Пример 10. Вычислить четвертый член прогрессии 1,5; 1,8; 2,16; ….
Решение: Без проверки можно сказать, что прогрессия — геометрическая. Найдем ее знаменатель
q=b₂/b₁=1, 8/1,5=1,2.
Вычислим 4 член геометрической прогрессии по формуле
b₄=b₁q³=1,5*1,2³=2,592.
Ответ: b₄=2,592.

 

Пример 11. Вычислить номер члена прогрессии 1,2; 1,8; 2,16; … равный 4,05.
Решение: Имеем геометрическую прогрессию. Найдем знаменатель прогрессии
q=b₂/b₁=1, 8/1,2=1,5.
Найдем номер прогресии из зависимости
b_n=b₁q^n-1.
4,05=1,2*1,5^n-1;
1,5^n-1=4,05/1,2=3,375=1,5³;
n-1=3; n=4.
Ответ: n=4.

 

Пример 12. В арифметической прогрессии a₅=14,91 a₉=20,11. Вычислить a₁.
Решение: Выразим 9 член прогрессии через 5
a₉= a₅+(9-5)d
и найдем шаг прогрессии
20,11=14,91+4d;
4d=5,2; d=5,2/4=1,3.
Выразим 5 член прогрессии через 1 и вычислим первый
a₅= a₁+4d;
14,91= a₁+5,2;
a₁=14,91-5,2=9,71.
Ответ: a₁=9,71.

 

Пример 13. В арифметической прогрессии а₇=12,01; a₁₁=17,61. Вычислить разницу прогрессии.
Решение: Выразим 11 член прогрессии через 7
a₁₁= a₇+(11-7)d.
Отсюда вычислим шаг прогрессии
17,61=12,01+4d;
4d=5,6; d=5,6/4=1,4.
Ответ: d=1,4.

 

Пример 14. В геометрической прогрессии b₅=64; b₈=1. Вычислить b₃.
Решение: Выразим 8 член прогрессии через 5
b₈= b₅q^8-5.
Отсюда находим знаменатель прогрессии
1=64 q³;
q³=1/64=(1/4)³;
q=1/4.
Подобным образом находим

yukhym.com

Арифметическая и геометрическая прогрессии

Геометрическая прогрессия.

I. Легенда о шахматах.

Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен её остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, он приказал привести его, чтобы лично наградить за удачную выдумку.

Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.

– Я желаю достойно наградить вознаградить тебя за прекрасную игру, которую ты придумал – сказал царь.

Мудрец поклонился.

– Я достаточно богат, чтобы исполнить самое смелое твое пожелание, – продолжал царь. – Назови награду, которая тебя удовлетворит, и ты получишь её.

Сета молчал.

– Не робей, – ободрил его царь. – Выскажи свое желание. Я не пожалею ничего, чтобы исполнить его.

– Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра, по зрелом размышлении, я сообщу тебе мою просьбу.

Когда на следующий день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.

– Повелитель, – сказал Сета, – прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.

– Простое пшеничное зерно? – изумился царь.

– Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью – 4, за четвертую – 8, за пятую – 16, за шестую – 32…

– Довольно, – с раздражением прервал его царь. – Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше предыдущей. Но знай, что просьба твоя не достойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Поистине, как учитель ты мог бы показать лучший пример уважения к доброте своего государя. Ступай. Слуги мои вынесут тебе твой мешок с пшеницей.

Сета улыбнулся, покинул залу и стал дожидаться у ворот дворца.

За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.

– Повелитель, – был ответ, – приказание твое исполняется. Придворные математики исчисляют число следуемых зерен.

Царь нахмурился. Он не привык, чтобы повеления его исполнялись так медлительно. Вечером, отходя ко сну, царь ещё раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.

– Повелитель, – ответили ему, – математики твои трудятся без устали и надеются ещё до рассвета закончить подсчет.

– Почему медлят с этим делом? – гневно воскликнул царь. – Завтра, прежде чем я проснусь, все до последнего зерна должно быть выдано Сете. Я дважды не приказываю.

Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.

– Прежде чем скажешь о твоем деле, – объявил Шерам, – я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.

– Ради этого я и осмелился явиться перед тобой в столь ранний час, – ответил старик. – Мы добросовестно исчислили всё количество зерен, которое желает получить Сета. Число это так велико…

– Как бы велико оно не было – надменно перебил царь, – житницы мои не оскудеют. Награда обещана и должна быть выдана.

– Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерён, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зёрен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыни. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду.

С изумлением царь внимал словам старца.

– Назови же мне это чудовищное число, – сказал он в раздумье.

– 18 квинтильонов 446 квадрильонов 744 трилионна 073 биллиона 709 миллионов 551 тысяча 615, о, повелитель!

II.

Другой знаменитой задачей на геометрическую прогрессию является задача, известная еще в Древнем Египте, появившаяся в русском фольклоре в следующем виде:

“Шли семь старцев,
У каждого старца
По семи костылей,
На каждом костыле
По семи сучков,
На каждом сучке
По семи кошелей,
В каждом кошеле
По семи пирогов,
А в каждом пироге
По семи воробьев.

Сколько всего?”

Практическое применение геометрической прогрессии.

1. Вероятно, первая ситуация, в которой людям пришлось столкнуться с геометрической прогрессией – подсчет численности стада, проведенный несколько раз, через равные промежутки времени. Если не происходит никаких чрезвычайных ситуаций, количество новорожденных и умерших животных пропорционально числу всех животных. Значит, если за какой-то период времени количество овец у пастуха увеличилось с 10 голов до 20, то за следующий такой же период оно снова вырастит вдвое и станет равным 40.

2. В жизненной практике геометрическая прогрессия появляется в первую очередь в задаче об исчислении так называемых “сложных процентов”. Если положить деньги на срочный вклад в сберегательный банк, то через год вклад увеличится на 3% от исходной суммы, т.е. новая сумма будет равна вкладу, умноженному на 1,03. Ещё через год уже эта сумма увеличится на 3%, т.е. вновь умножится на 1,03. За 20 лет сумма на сберкнижке увеличится в (1,03)

20 1,8 раза.

Если процент будет больше, то и результат будет резко расти. Так при 50% годовом увеличении за 10 лет сумма увеличится в (1,5)¹⁰ 55,7 раза. Под такой процент давали деньги ростовщики в Англии в XIII веке. Это вызывало страшное недовольство. Издавались законы, ограничивающие процент. Король Генрих VII даже совсем отменил взимание процентов, что привело в упадок, как банковское дело, так и промышленность, лишившуюся возможности получения кредитов. В конце концов, взимание процентов было разрешено, но не должно было быть большим 10%.

3. Еще один пример геометрической прогрессии – изменение массы радиоактивного вещества со временем. Известно, что за единицу времени такое вещество теряет определенную часть своей массы (она переходит в другое вещество и энергию). Для каждого радиоактивного вещества определяется величина T – время периода полураспада. Массы нераспавшегося вещества в моменты 0, T, 2T, 3T,… будут образовывать бесконечно убывающую геометрическую прогрессию.

4. Прирост древесины в лесном массиве происходит по законам геометрической прогрессии. При этом у каждой породы дерева свой коэффициент годового роста объема. Учет этих изменений позволяет планировать вырубку части лесных массивов и одновременную работу по восстановлению лесов.

5. В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две.

6. Английский экономист епископ Мальтус использовал геометрическую и арифметическую прогрессии для оправдания войн: средства потребления (пища, одежда) растут по законам арифметической прогрессии, а люди размножаются по законам геометрической прогрессии. Чтоб избавиться от лишнего населения необходимы войны.

Почему геометрическая прогрессия названа “геометрической”? Видимо потому, что каждый её член равен среднему геометрическому, соседних с ним членов.

А такое среднее названо геометрическим, поскольку оно является стороной квадрата, равновеликого прямоугольнику, стороны которого имеют длины, равные тем величинам, от которых берется среднее.

Геометрические прогрессии удивляют своим чрезвычайно быстрым ростом. В жизни с растущими геометрическими прогрессиями надо обращаться осторожно. Если в геометрической прогрессии растет количество животных в стаде – скоро ему не хватит пастбища. Если число распадов в куче плутония – дело идет к атомному взрыву. А если вам обещают большие доходы – лучше не связываться с этими “благодетелями”.

Арифметическая прогрессия.

При изучении данной темы предлагается использовать ряд нестандартных задач, а также задач с практическим содержанием и совершить небольшой экскурс в историю.

1. Представьте, что вы учетчик на стройке. Привезли и выгрузили большое количество бревен строевого леса. Нужно быстро определить, сколько бревен привезли, чтобы закрыть наряд шоферу.

2. Известна интересная история о знаменитом немецком математике К. Гауссе (1777 – 1855), который еще в детстве обнаружил выдающиеся способности к математике. Учитель предложил учащимся сложить все натуральные числа от 1 до 100. Маленький Гаусс решил эту задачу за одну минуту, сообразив, что суммы 1+100, 2+99 и т.д равны, он умножил 101 на 50, т.е. на число таких сумм. Иначе говоря, он заметил закономерность, присущую арифметическим прогрессиям.

Задача очень непроста:

Как сделать, чтобы быстро
От единицы и до ста
Сложить в уме все числа?
Пять первых связок изучи.
Найдешь к решению ключи!
1+100? 2+99? 3+98?
4+97? 5+96?
Давным-давно один мудрец сказал,
Что прежде надо
Связать начало и конец
У численного ряда.

3. Представители точных наук во всем ищут математические закономерности и учат этому на своих уроках детей. Одна из форм демонстрации математических закономерностей – это математические фокусы. Например, фокусы с календарями.

Фокус 1. Таинственные квадраты.

На помесячном табель – календаре выберите любой месяц, отметьте на нем квадрат, содержащий 9 чисел. Теперь назовите наименьшее из них, а я объявлю сумму всех девяти чисел.

Ответ: (m+8)*9; (m – наименьшее число).

m;	m+7;	m+14;
m+1;	m+8;	m+15;
m+2;	m+9;	m+16.

9m+72= 9*(m+8)

Фокус 2. Предсказание.

На каком-нибудь листе помесячного календаря заключите в квадрат 16 чисел. Разрешите мне мельком взглянуть на ваши квадраты (предсказать число).

Обведите кружком любое число из этого квадрата. Затем зачеркните все числа, стоящие в той же строке и том же столбце, что и обведенное число. В качестве второго обведите любое число, оставшееся не зачеркнутым. Затем зачеркните все числа, оказавшиеся на одной строке и одном столбце с этим числом. Также выбирается и третье число.

В результате этих действий у вас осталось одно число, его тоже обведите кружочком. Найдите сумму чисел, обведенных кружочком. Эта сумма равна предсказанному числу.

Объяснение. Заметить два числа, находящихся на двух диагонально противоположных углах квадрата. Нужно сложить эти два числа и результат удвоить.

urok.1sept.ru

Арифметическая и геометрическая прогрессии. 9-й класс

Цель урока: повторение и обобщение изученного материала путём решения комбинированных задач; развитие познавательного интереса к математике.

Задачи урока:

Образовательные:

• совершенствовать навыки решения разнообразных задач по использованию формул арифметической и геометрической прогрессий; применять свои знания в практических ситуациях; расширять знания учащихся путём решения нестандартных задач;

Развивающие:

• развивать математический кругозор, мышление, математическую речь;

Воспитательные:

• воспитывать стремление к непрерывному совершенствованию; воспитывать чувство прекрасного; формировать отношения взаимной ответственности при совместной работе;

Ход урока

I. Организационный момент

Слайд №1 (Презентация)

Слова учителя:

Изучена данная тема,
Пройдена теории схема,
Вы много новых формул узнали,
Задачи с прогрессией решали.
И вот в последний урок
Нас поведет
Красивый лозунг
«ПРОГРЕССИО — ВПЕРЕД»

Сегодня пред последний урок по главе «Арифметическая и геометрическая прогрессии». Предстоит контрольная работа. Перед вами задача - показать, как вы знаете формулы прогрессии и умеете их применять при решении различных задач.

На столах лежат задания к уроку, ваша цель внимательно работать на уроке и по ходу урока заполнить таблицу:

1	2	3	4	5	6	7	8	9
Е	Р	О	Г	П	С	Д	И	В

 Задача 1 (На столе карточка №1) Приложение №1

Определите какая последовательность является арифметической или геометрической прогрессией, ответы запишите на листочках, найти разность и знаменатель, при проверке повторить определение прогрессий.

Слайд №2

1) 2; 5; 8; 11;14; 17;:

2) 3; 9; 27; 81; 243;:

3) 1; 6; 11; 20; 25;:

4) -4; -8; -16; -32;:

5) 5; 25; 35; 45; 55;:

6)-2; -4; — 6; — 8; — 10;:

Слайд №3 проверим решение

Ответ:

1) 2; 5; 8; 11;14; 17;: арифметическая прогрессия d = 3

2) 3; 9; 27; 81; 243;: геометрическая прогрессия q = 3

3) 1; 6; 11; 20; 25;: последовательность чисел

4) -4; -8; -16; -32; : геометрическая прогрессия q = 2

5) 5; 25; 35; 45; 55;: последовательность чисел

6) -2; -4; — 6; — 8; — 10;: арифметическая прогрессия d = — 2

Примерные вопросы

1. Что называется арифметической прогрессией?
2. Что называется геометрической прогрессией?
3. Как вычислить знаменатель геометрической прогрессии?
4. Как вычислить разность арифметической прогрессии?
5. Почему прогрессия называется арифметической?
6. Почему прогрессия называется геометрической? 7.К каком числам принадлежит n?

Историческая справка.

Слайд №4

Слова учителя: закончился ХХ век, а вот термин «прогрессия» был введен римским автором Боэцием еще в IV в. н.э. От латинского слова progressio - «движение вперед». Первые представления об арифметической прогрессии были еще у древних народов. В клинописных вавилонских табличках и египетских папирусах встречаются задачи на прогрессии и указания как их решать. Считалось, что в древнеегипетском папирусе Ахмеса находилась древнейшая задача на прогрессии о вознаграждении изобретателя шахмат, насчитывающая за собою двухтысячелетнюю давность. Но есть гораздо более старая задача о делении хлеба, которая записана в знаменитом египетском папирусе Ринда. Папирус этот, разысканный Риндом полвека назад, составлен около 2000 лет до нашей эры и является списком с другого, еще более древнего математического сочинения, относящегося, быть может, к третьему тысячелетию до нашей эры. В числе арифметических, алгебраических и геометрических задач этого документа имеется такая, которую мы приводим в вольной передаче. Прочитайте внимательно условие на листке №2. Откройте тетради, запишите число, тему урока. Приготовились слушать и записывать решение этой интереснейшей задачи, которую разобрала ескина Алёна .

Слайд №5

Задача 1: (задача из папируса Ринда) Приложение №2

Сто мер хлеба разделили между 5 людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых получили в 7 раз меньше трех остальных. Сколько нужно дать каждому?

Решение задачи: Очевидно, количество хлеба, полученные участниками раздела, составляют возрастающую арифметическую прогрессию. Пусть первый ее член x, разность y. Тогда:

а ₁-Доля первого — x,

а₂-Доля второго — x+y,

а₃-Доля третьего — x+2y,

а₄-Доля четвертого — x+3y,

а₅-Доля пятого — x+4у.

На основании условия задачи составляем следующие 2 уравнения:

После упрощений первое уравнение получает вид x+2y=20, а второе 11x=2y.

Решив эту систему, имеем:

Значит, хлеб должен быть разделен на следующие части:

Слайд № 6 Приложение №3

Устная работа

1) Дано: (а _n ) , а₁ = 5 d = 3 Найти: а₆ ; а_10.

2) Дано: (b _n ) ,b₁= 5 q = 3 Найти: b₃ ; b_5.

3) Дано: (а _n ) , а₄ = 11 d = 2 Найти: а₁ ;

4) Дано: (b _n ) , b₄= 40 q = 2 Найти: b₁ ;

Слайд № 7

Ответы

1) а₆ = а₁ +5 d = 5+ 53 = 20

а₁₀ = а₁ +9 d = 5+ 93 = 32

2) b₃ = b₁q² = 5 3² =59=45

b₅ = b₁q⁴ = 5 3⁴ =581=405

3) а₄= а₁ +3 d  а₁ = а₄ — 3 d = 11 — 32 = 5

4) b ₄= b₁ q³

b ₁ = b ₄ : q³ = 40 : 2³ = 5

Занимательное свойство арифметической прогрессии.

Слова учителя:

Слайд № 7

А теперь, рассмотрим еще одно свойство членов арифметической прогрессии. Оно, скорее всего, занимательное. Расскажет о нем Ученик 4.

Выступление Ученика 4.

На доске написана «стайка девяти чисел»

3, 5, 7, 9, 11, 13, 15,17, 19.

Она представляет собой арифметическую прогрессию. Кроме того, данная стайка чисел привлекательна способностью разместиться в девяти клетках квадрата 33 так, что образуется магический квадрат с константой, равной 33

Знаете ли вы, что такое магический квадрат? Квадрат, состоящий из 9 клеток, в него вписывают числа, так чтобы сумма чисел по вертикали, горизонтали диагонали была одним и тем же числом- constanta.

Замечание об арифметической прогрессии само по себе очень интересно. Дело в том, что из каждых девяти последовательных членов любой арифметической прогрессии натуральных чисел можно составить магический квадрат.

Слайд № 8

В самом деле, пусть дана арифметическая прогрессия: a, a+d, a+2d, a+3d, :, a+8d, где a и d натуральные. Расположим её члены в таблицу.

a+3d	a+8d	a+d
a+2d	a+4d	a+6d
a+7d	a	a+5d

Нетрудно видеть, что получился магический квадрат, константа C которого равна 3a+12d

Действительно, сумма чисел в каждой строке, в каждом столбце и по каждой диагонали квадрата равна 3a+12d.

А какие свойства арифметической или геометрической прогрессии вы уже знаете ?

Слайд № 9

1) Дано: (а _n ) , а₄=12,5; а₆=17,5 Найти: а₅

Решение: Используя свойство арифметической прогрессии

имеем: а₅

Ответ: 15( О)

1) Дано: (b _n ) , b₄=12,5; b₆=17,5 Найти: b₅

Решение: Используя свойство геометрической прогрессии

имеем: =

Ответ: 12( Д)

Слайд № 10 Приложение №4

«Карусель» — обучающая самостоятельная работа

Каждый ученик получает листок с задачами. если шесть человек, то и задач шесть (задачи элементарные).

1	Дано: (а n ), а1 = — 3, а2 = 4. Найти: а16 — ?	Фамилия, имя_________ Ответ:________
2	Дано: (b n ) , b 12 = — 32, b 13 = — 16. Найти: q — ?	Фамилия, имя_________ Ответ:________
3	Дано: (а n ), а21 = — 44, а22 = — 42. Найти: d — ?	Фамилия, имя_________ Ответ:________
4	Дано: (b n ) , bп > 0, b2 = 4, b4 = 9. Найти: b3 — ?	Фамилия, имя_________ Ответ:________
5	Дано: (а n ), а1 = 28, а21 = 4. Найти: d — ?	Фамилия, имя_________ Ответ:________
6	Дано: (b n ) , q = 2. Найти: b5 — ?	Фамилия, имя_________ Ответ:________
7	Дано: (а n ), а7 = 16, а9 = 30. Найти: а8 -?	Фамилия, имя_________ Ответ:________

Каждую одну-две минуты учитель говорит: «Меняемся», и ученики передают свой лист по кругу. «Карусель» останавливается, если к каждому вернется лист, на котором в задаче 1 стоит его фамилия. Таким образом, каждый ученик решает все задачи.

Ответы записываются на слайде. Ученики зачеркивают неправильные ответы и сдают работу учителю.

Ответы: 1) 102; ( П) 2) 0,5; ( В) 3)2; ( Р) 4)6; ( Г) 5) — 1,2; ( Е) 6) 8;( С),7) 23.

Задания из сборника предназначенного для подготовки к итоговой аттестации в новой форме по алгебре в 9 классе, предлагаются задания которые оцениваются в 2 балла: 3-5минут на выполнение заданий по группам, решение показать на доске.

6.1. 1) Пятый член арифметической прогрессии равен 8,4, а ее десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии.

6.2. 1) Число -3,8 является восьмым членом арифметической прогрессии (а_п), а число -11 является ее двенадцатым членом. Является ли членом этой прогрессии число -30,8?

6.5. 1) Между числами 6 и 17 вставьте четыре числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию.

6.8. 1) В геометрической прогрессии b₁₂ = З¹⁵ и b₁₄ = З¹⁷. Найдите b₁.

Ответы: 6.1 (20,4)( И) 6.2. (является), 6.5. (6;8,2;10’4;12’6;14’8;17.), 6.8. (b₁=3⁴ или b₁= -3⁴).

5	2	3	4	2	1	6	6	8	3
П	Р	О	Г	Р	Е	С	С	И	О

 

9	5	1	2	1	7
В	П	Е	Р	Ё	Д

Подведение итогов урока.

Вспомним начало нашего урока, ребята. Удалось ли за сегодняшний урок узнать что-то новое, сделать какие-то открытия? А какие цели урока мы ставили перед собой? Как Вы считаете, нам удалось достигнуть поставленных целей?

 За работу с формулами и тестом каждый учащийся получает оценки в журнал. Дополнительные оценки получают те, кто был активен на уроке.

Домашнее задание — творческое: составить 3 комбинированных задачи по теме «Прогрессии» и их решения оформить на альбомном листе.

Урок сегодня завершён,
Но каждый должен знать:
Познание, упорство, труд
К прогрессу в жизни приведут.

Спасибо за урок, ребята. Вы сегодня хорошо потрудились.

urok.1sept.ru

Арифметическая и геометрическая прогрессии

Урок-презентация «Арифметическая и геометрическая прогрессия»

Цель урока:

обобщение тем “Арифметическая прогрессия” и “Геометрическая прогрессия”.

Задачи урока:

обобщить и систематизировать теоретические знания учащихся;

проконтролировать и развивать умения и навыки применять формулы прогрессий при решении задач;

повысить интерес к предмету.

Ход урока

Организационный момент

Презентация Слайд №1

Слова учителя:

Изучена данная тема,

Пройдена теории схема,

Вы много новых формул узнали,

Задачи с прогрессией решали.

И вот в последний урок

Нас поведет

Красивый лозунг

“ПРОГРЕССИО — ВПЕРЕД”

Сегодня пред последний урок по главе “Арифметическая и геометрическая прогрессии”. Предстоит контрольная работа. Перед вами задача — показать, как вы знаете формулы прогрессии и умеете их применять при решении различных задач.

На столах лежат задания к уроку, ваша цель внимательно работать на уроке и по ходу урока заполнить таблицу:

Задача 1(На столе карточка №1)

Определите какая последовательность является арифметической или геометрической прогрессией, ответы запишите на листочках, найти разность и знаменатель, при проверке повторить определение прогрессий.

Слайд №2

1) 2; 5; 8; 11;14; 17;…

2) 3; 9; 27; 81; 243;…

3) 1; 6; 11; 20; 25;…

4) –4; –8; –16; –32;…

5) 5; 25; 35; 45; 55;…

6)–2; –4; – 6; – 8; – 10;…

Слайд №3 проверим решение

Ответ:

1) 2; 5; 8; 11;14; 17;…

арифметическая прогрессия d = 3

2) 3; 9; 27; 81; 243;…

геометрическая прогрессия q = 3

3) 1; 6; 11; 20; 25;…

последовательность чисел

4) –4; –8; –16; –32; …

геометрическая прогрессия q = 2

5) 5; 25; 35; 45; 55;…

последовательность чисел

6) –2; –4; – 6; – 8; – 10;…

арифметическая прогрессия d = – 2

Примерные вопросы

Что называется арифметической прогрессией?

Что называется геометрической прогрессией?

Как вычислить знаменатель геометрической прогрессии?

Как вычислить разность арифметической прогрессии?

Почему прогрессия называется арифметической?

Почему прогрессия называется геометрической?

К каком числам принадлежит n?

Историческая справка.

Слайд №4

Слова учителя:

Закончился ХХ век, а вот термин “прогрессия” был введен римским автором Боэцием еще в IV в. н.э. От латинского слова progressio – “движение вперед”.

Первые представления об арифметической прогрессии были еще у древних народов. В клинописных вавилонских табличках и египетских папирусах встречаются задачи на прогрессии и указания как их решать. Считалось, что в древнеегипетском папирусе Ахмеса находилась древнейшая задача на прогрессии о вознаграждении изобретателя шахмат, насчитывающая за собою двухтысячелетнюю давность. Но есть гораздо более старая задача о делении хлеба, которая записана в знаменитом египетском папирусе Ринда. Папирус этот, разысканный Риндом полвека назад, составлен около 2000 лет до нашей эры и является списком с другого, еще более древнего математического сочинения, относящегося, быть может, к третьему тысячелетию до нашей эры. В числе арифметических, алгебраических и геометрических задач этого документа имеется такая, которую мы приводим в вольной передаче.

Прочитайте внимательно условие на листке

Откройте тетради, запишите число, тему урока.

Приготовились слушать и записывать решение этой интереснейшей задачи.

Слайд №5

Задача 1: (задача из папируса Ринда)

Сто мер хлеба разделили между 5 людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых получили в 7 раз меньше трех остальных. Сколько нужно дать каждому?

Решение задачи: Очевидно, количество хлеба, полученные участниками раздела, составляют возрастающую арифметическую прогрессию. Пусть первый ее член x, разность y. Тогда:

а 1–Доля первого – x,

а2–Доля второго – x+y,

а3–Доля третьего – x+2y,

а4–Доля четвертого – x+3y,

а5–Доля пятого – x+4у.

На основании условия задачи составляем следующие 2 уравнения:

После упрощений первое уравнение получает вид x+2y=20, а второе 11x=2y.

Решив эту систему, имеем:

Значит, хлеб должен быть разделен на следующие части:

Слайд № 6

Устная работа

1) Дано: (а n ) , а1 = 5 d = 3 Найти: а6 ; а10.

2) Дано: (b n ) ,b1= 5 q = 3 Найти: b3 ; b5.

3) Дано: (а n ) , а4 = 11 d = 2 Найти: а1 ;

4) Дано: (b n ) , b4= 40 q = 2 Найти: b1 ;

Слайд № 7

Ответы

1) а6 = а1 +5 d = 5+ 53 = 20

а10 = а1 +9 d = 5+ 93 = 32

2) b3 = b1q2 = 5 32 =59=45

b5 = b1q4 = 5 34 =581=405

3) а4= а1 +3 d а1 = а4 – 3 d = 11 – 32 = 5

4) b 4= b1 q3 b 1 = b 4 : q3 = 40 : 23 = 5

Занимательное свойство арифметической прогрессии.

Слова учителя:

Слайд № 7

А теперь, рассмотрим еще одно свойство членов арифметической прогрессии. Оно, скорее всего, занимательное. Расскажет о нем Ученик 4.

Выступление Ученика 4.

На доске написана “стайка девяти чисел”

3, 5, 7, 9, 11, 13, 15,17, 19.

Она представляет собой арифметическую прогрессию. Кроме того, данная стайка чисел привлекательна способностью разместиться в девяти клетках квадрата 3х3 так, что образуется магический квадрат с константой, равной 33.

Знаете ли вы, что такое магический квадрат? Квадрат, состоящий из 9 клеток, в него вписывают числа, так чтобы сумма чисел по вертикали, горизонтали диагонали была одним и тем же числом- constanta.

Слайд № 8

В самом деле, пусть дана арифметическая прогрессия: a, a+d, a+2d, a+3d, …, a+8d, где a и d натуральные. Расположим её члены в таблицу.

Действительно, сумма чисел в каждой строке, в каждом столбце и по каждой диагонали квадрата равна 3a+12d.

А какие свойства арифметической или геометрической прогрессии вы уже знаете ?

Слайд № 9

1) Дано: (а n ) , а4=12,5; а6=17,5 Найти: а5

Решение: Используя свойство арифметической прогрессии

Имеем: а5

Ответ: 15( О)

1) Дано: (b n ) , b4=12,5; b6=17,5 Найти: b5

Решение: Используя свойство геометрической прогрессии

Имеем: =

Ответ: 12 (Д)

Слайд № 10

“Карусель” — обучающая самостоятельная работа

Каждый ученик получает листок с задачами. если шесть человек, то и задач шесть (задачи элементарные).

Дано: (а _n )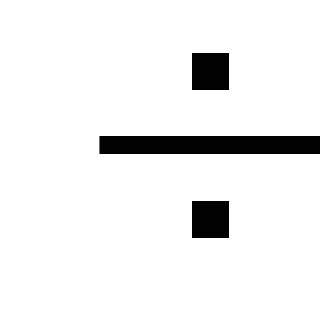, а₁ = – 3, а₂ = 4.

Найти: а₁₆ – ?

Фамилия, имя_________

Ответ:________

2

Дано: (b _n ) 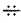, b ₁₂ = – 32, b ₁₃ = – 16.

Найти: q – ?

Фамилия, имя_________

Ответ:________

3

Дано: (а _n ), а₂₁ = – 44, а₂₂ = – 42.

Найти: d — ?

Фамилия, имя_________

Ответ:________

4

Дано: (b _n ) , b_п > 0, b₂ = 4, b₄ = 9.

Найти: b₃ – ?

Фамилия, имя_________

Ответ:________

5

Дано: (а _n ), а₁ = 28, а₂₁ = 4.

Найти: d — ?

Фамилия, имя_________

Ответ:________

6

Дано: (b _n ) , 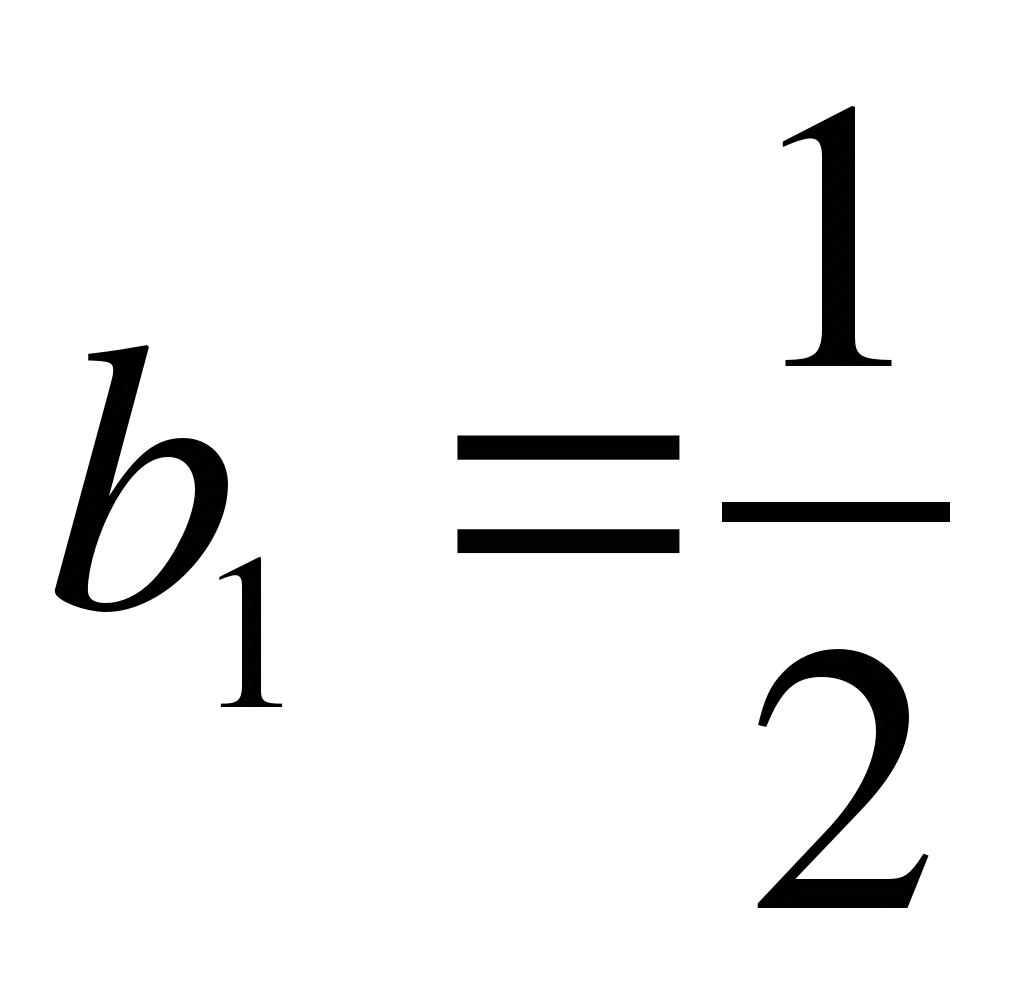q = 2.

Найти: b₅ – ?

Фамилия, имя_________

Ответ:________

7

Дано: (а _n ), а₇ = 16, а₉ = 30.

Найти: а₈ –?

Фамилия, имя_________

Ответ:________

Каждую одну-две минуты учитель говорит: “Меняемся”, и ученики передают свой лист по кругу. “Карусель” останавливается, если к каждому вернется лист, на котором в задаче 1 стоит его фамилия. Таким образом, каждый ученик решает все задачи.

Ответы записываются на слайде. Ученики зачеркивают неправильные ответы и сдают работу учителю.

Ответы: 1) 102; ( П) 2) 0,5; ( В) 3)2; ( Р) 4)6; ( Г) 5) – 1,2; ( Е) 6) 8;( С),7) 23.

Задания из сборника предназначенного для подготовки к итоговой аттестации в новой форме по алгебре в 9 классе, предлагаются задания которые оцениваются в 2 балла: 3-5минут на выполнение заданий по группам, решение показать на доске.

6.1. 1) Пятый член арифметической прогрессии равен 8,4, а ее десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии.

6.2. 1) Число –3,8 является восьмым членом арифметической прогрессии (ап), а число –11 является ее двенадцатым членом. Является ли членом этой прогрессии число –30,8?

6.5. 1) Между числами 6 и 17 вставьте четыре числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию.

6.8. 1) В геометрической прогрессии b12 = З15 и b14 = З17. Найдите b1.

Ответы:

6.1 (20,4)( И) 6.2. (является), 6.5. (6;8,2;10’4;12’6;14’8;17.), 6.8. (b1=34 или b1= –34).

Дружней вас не сыскать.

Но каждый должен знать:

Познание, упорство, труд

К прогрессу в жизни приведут.

Спасибо за урок!

infourok.ru

Алгебраическая и геометрическая прогрессии

Муниципальное общеобразовательное учреждение

«Ягельная средняя общеобразовательная школа»

Обобщение и систематизация по теме

«Алгебраическая и геометрическая прогрессии»

Учитель математики

Изекеева А.М.

2016/2017 учебный год

п. Ягельный

Обобщение и систематизация знаний по теме

«Арифметическая и геометрическая прогрессии»

Образовательные задачи:

• обобщить и систематизировать знания об арифметической и геометрической прогрессиях с целью подготовки к итоговой аттестации;

• контроль усвоения знаний и умений.

Развивающие задачи:

• способствовать развитию умений анализировать, обобщать, сравнивать, самостоятельно применять знания, умения и навыки по теме, осуществлять их перенос в новые условия; развитию памяти, внимания, логического мышления, правильной математической речи, познавательного интереса.

Воспитательная задача:

• способствовать воспитанию ответственности, активности, умения работать в группах, общей культуры.

План занятия:

1. Организационный момент.

2. Актуализация опорных знаний.

3. Фронтальная работа с классом.

4. Работа в группах.

5. Самостоятельная работа.

6. Подведение итогов урока.

Ход занятия

I. Организационный момент.

Цель:

Учитель: Тема нашего занятия «Обобщение и систематизация знаний по теме «Арифметическая и геометрическая прогрессии».

Для работы на занятии мы должны вспомнить: Демонстрируется слайд 1

определения АП и ГП, формулы п- го члена этих прогрессий и суммы n первых членов этих прогрессий.

II. Актуализация опорных знаний.

1. Устная фронтальная работа с классом с использованием мультимедийной

презентации.

Цель данного этапа урока: повторить известные учащимся сведения об

арифметической и геометрической прогрессиях.

Учитель: Даны две последовательности чисел (записаны на доске):

6; 8; 10;… (12; 14; 16;…)

3;6;12;…. (24; 48; 96;…)

Назовите следующие три члена первой последовательности.

Ученик:

12; 14; 16;…

Учитель:

Сформулируйте закономерность составления данной последовательности.

Ученик:

Каждый следующий член последовательности получен прибавлением числа 2 к

предшествующему числу.

Учитель:

Как называется такая последовательность чисел?

Ученик:

Такая последовательность чисел называется арифметической прогрессией.

Демонстрируется слайд 2.

Учитель: Устно решить задачу:

Назовите первые пять членов АП, если .

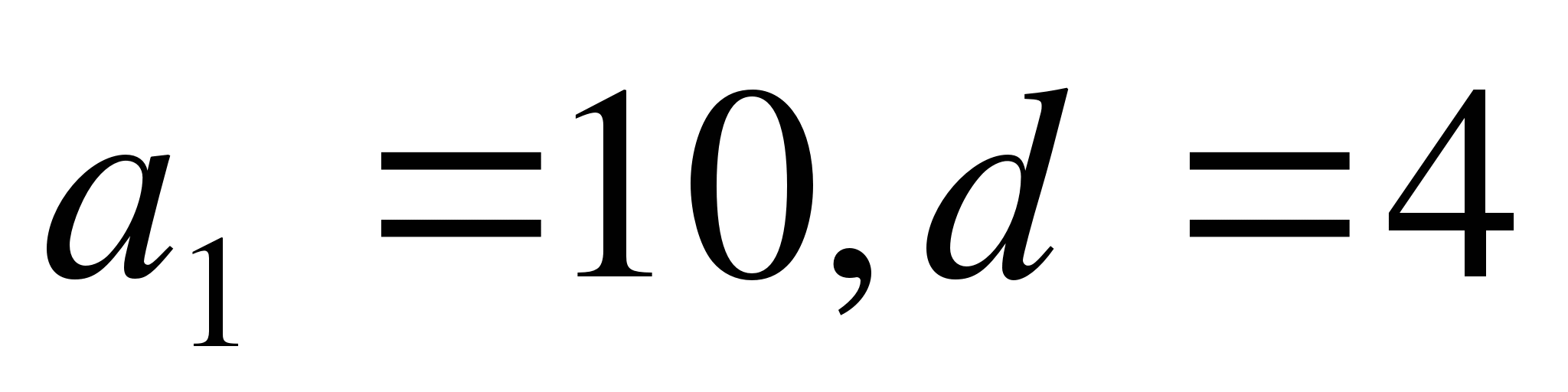Ученик: .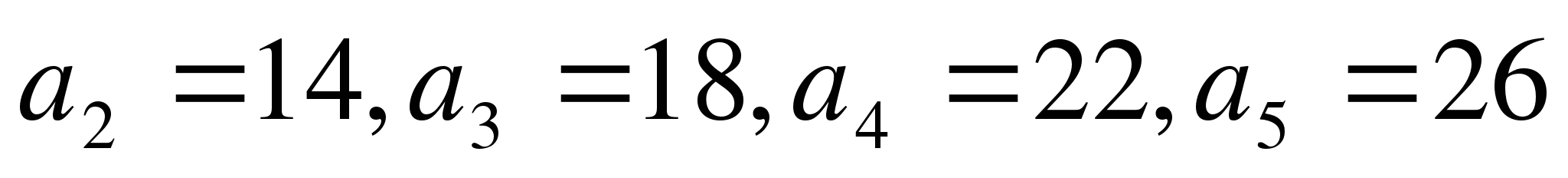

Учитель: Какую закономерность можно заметить в первой последовательности?

Ученик: .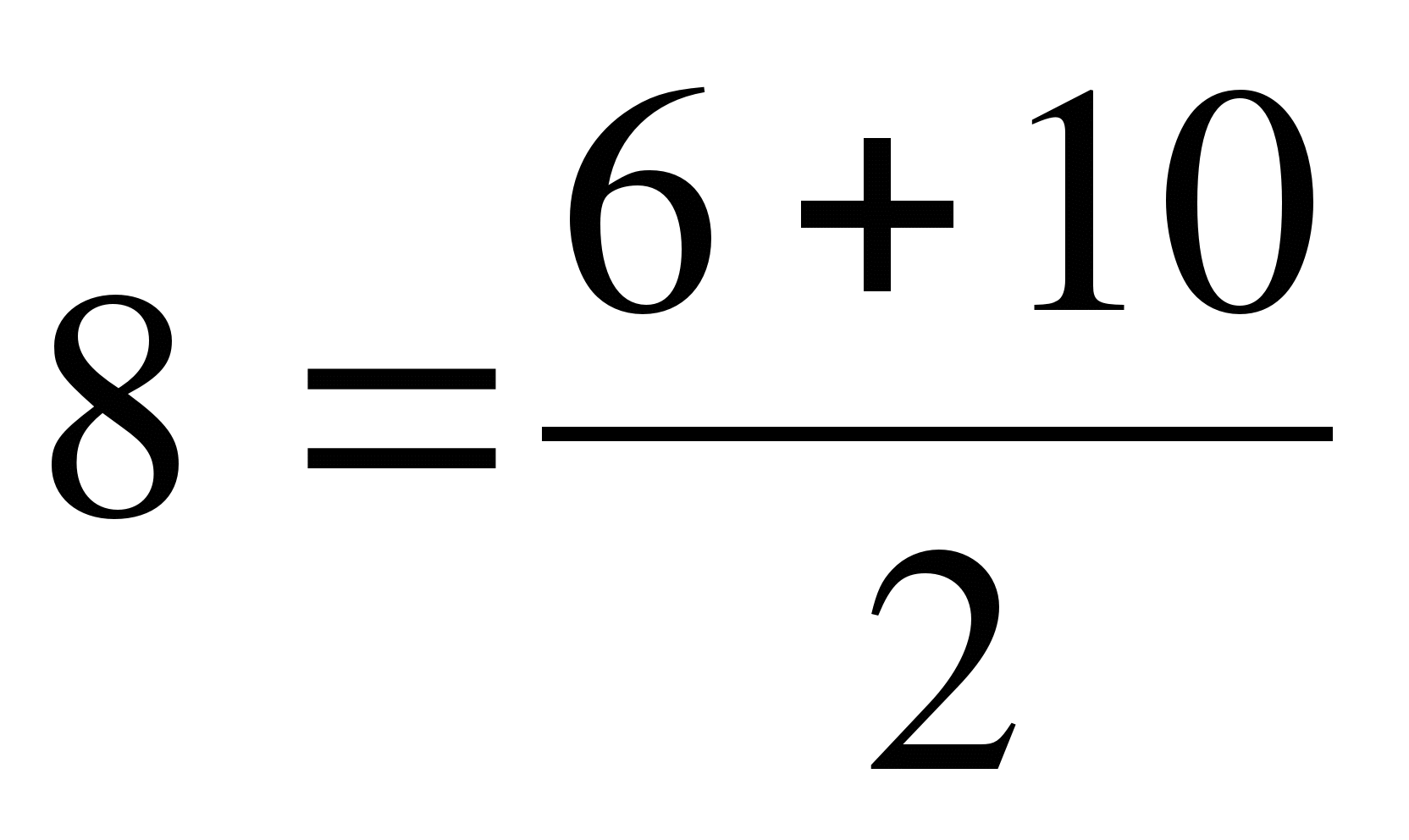

(Если затрудняются, задаем вопрос: Как получить 8, зная 6 и 10?)

Демонстрируется слайд 3 — характеристическое свойство АП

Учитель:

Рассмотрим вторую последовательность.

Назовите следующие три члена второй последовательности.

Ученик:

24; 48; 96;…

Учитель:

Сформулируйте закономерность составления данной последовательности.

Ученик:

Каждый следующий член последовательности получен умножением предшествующего числа на 2.

Учитель:

Как называется такая последовательность чисел?

Ученик:

Такая последовательность чисел называется геометрической прогрессией.

Демонстрируется слайд 4.

Учитель: Назовите первые пять членов ГП, если .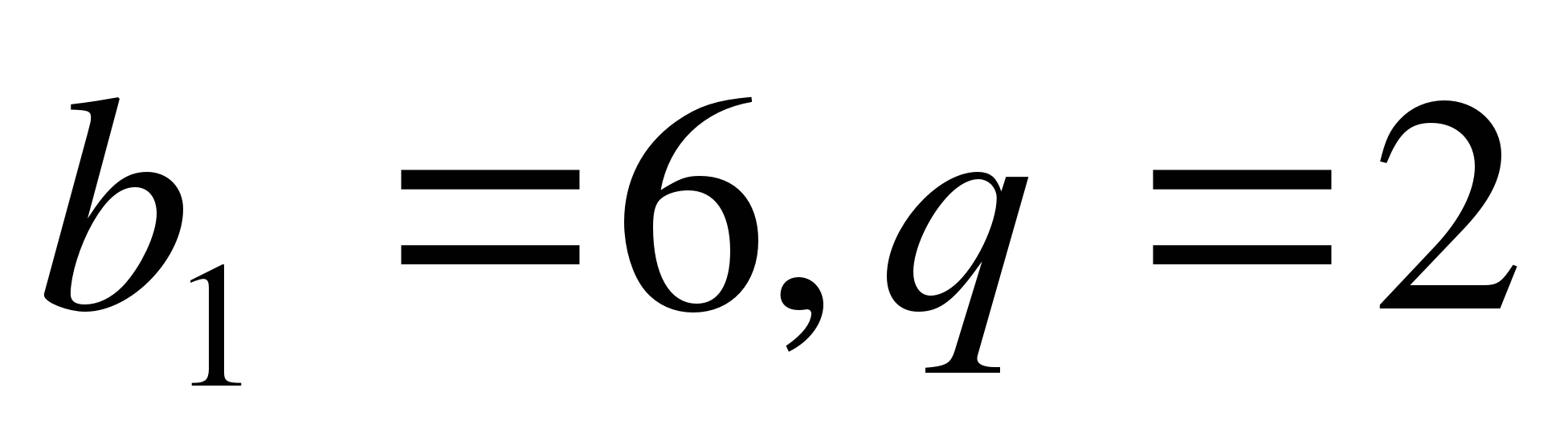

Ученик: .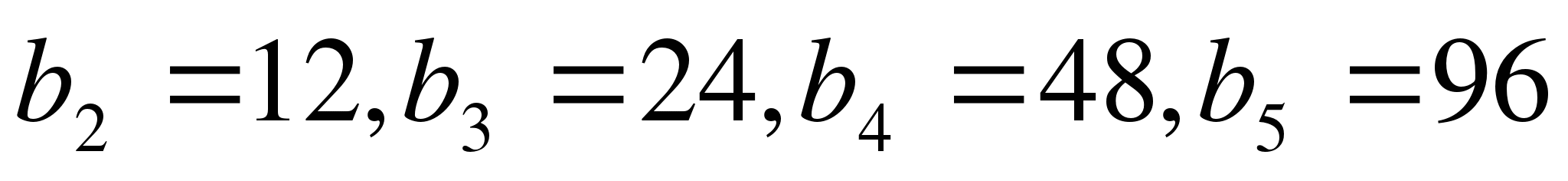

Учитель: Сформулируйте закономерность для второй последовательности.

Ученик: .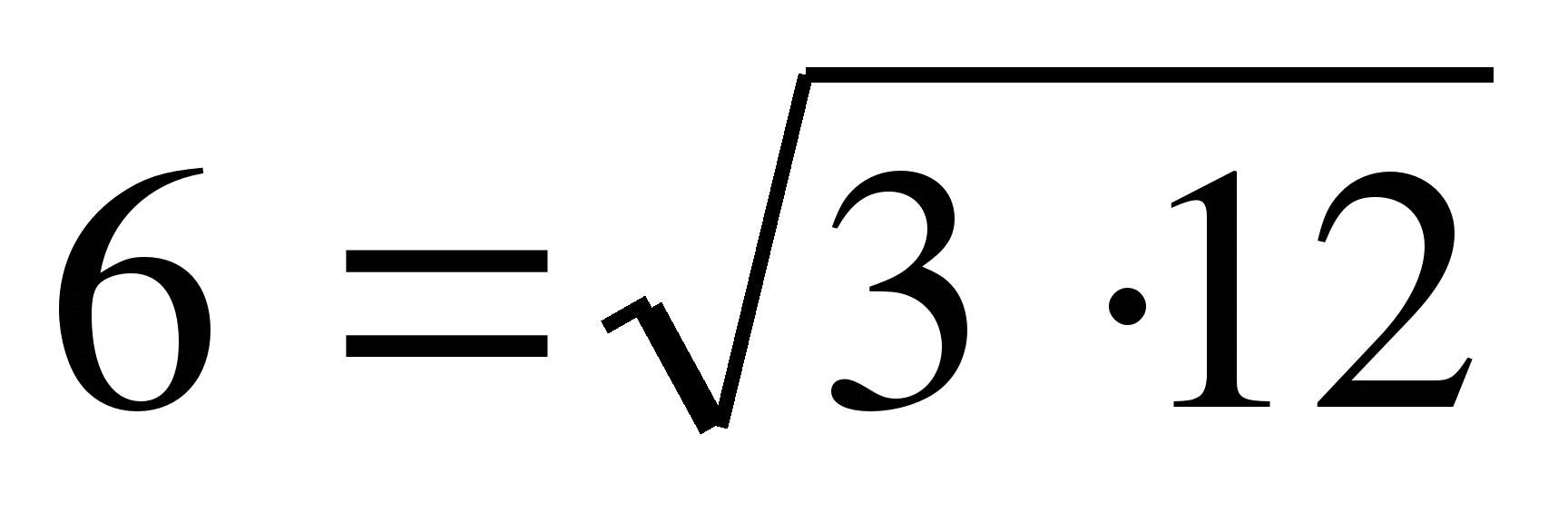

Демонстрируется слайд 5 — характеристическое свойство ГП.

Учитель: Зная первый член арифметической прогрессии и ее разность можно найти любой член этой прогрессии. Вспомните формулу.

Ученик: .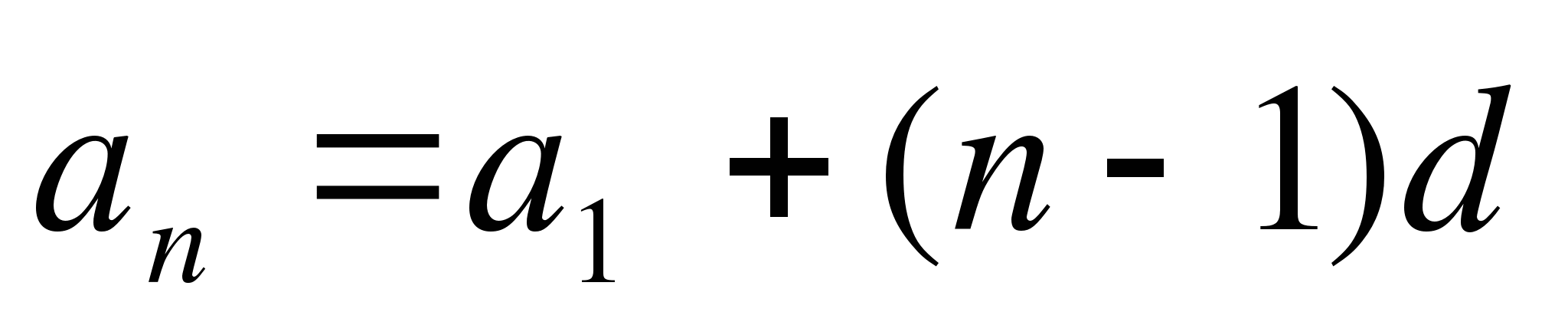

Демонстрируется слайд 6 — формула n-го члена АП.

Учитель: Вспомните формулу п — го члена геометрической прогрессии.

Ученик: .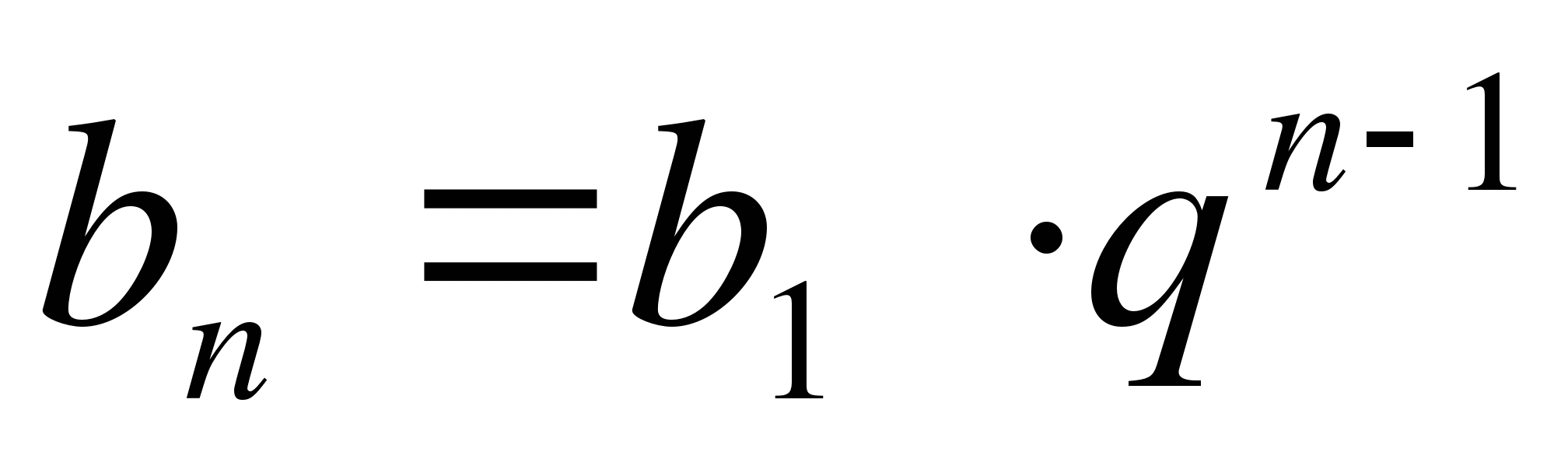

Демонстрируется слайд 7 – формула n – го члена ГП.

Учитель:

Решите задачу. (Два человека работают у доски – Чеботарев А — задача на АП, Ковтун Н — задача на ГП). (Для работающих у доски задача дается на листе). Класс делится на две группы.

Группа 1. Егоров А, Чеботарев А, Чанов С, Яценко М, Панкова Я. – решают задачу на АП.

Группа 2. Князькова Л, Гализянова Э, Ковтун Н, Чеботарева Е – решают задачу на ГП.

Между числами 4 и 9 вставьте положительное число так, чтобы получилось три последовательных члена арифметической прогрессии. Сформулируйте и решите аналогичную задачу для геометрической прогрессии.

Ученик: задача на АП.

Ученик: задача на ГП. (сформулировать).

Между числами 4 и 9 вставьте положительное число так, чтобы получилось три последовательных члена геометрической прогрессии.

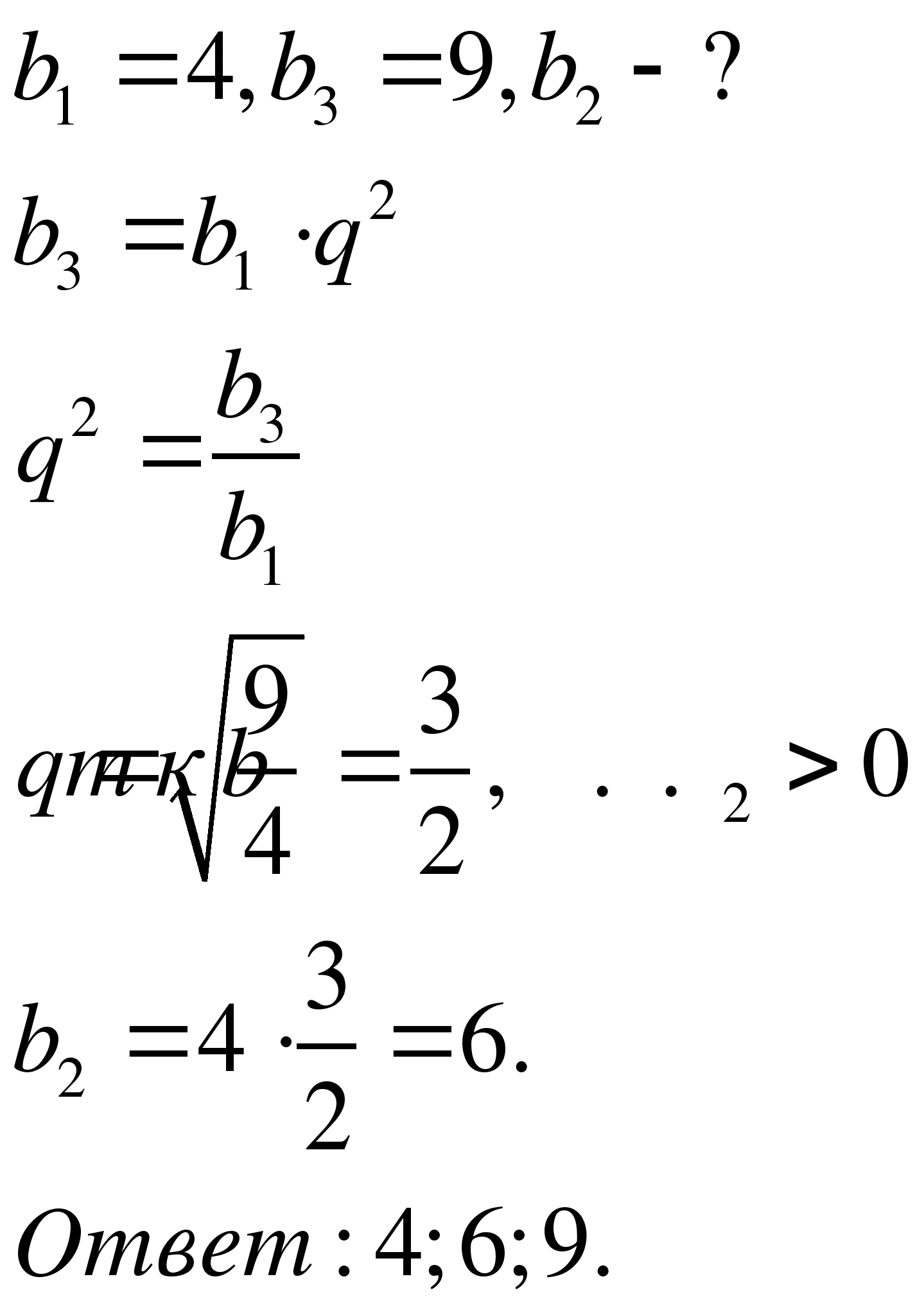
Учитель: Решите задачу. (Демонстрируется слайд 8)

Найдите сумму пятидесяти первых членов арифметической прогрессии, первый член

которой равен — 45,6, а пятнадцатый член равен 2.

Какую формулу нужно знать, чтобы решить эту задачу?

Ученик: Формулу суммы n первых членов АП.

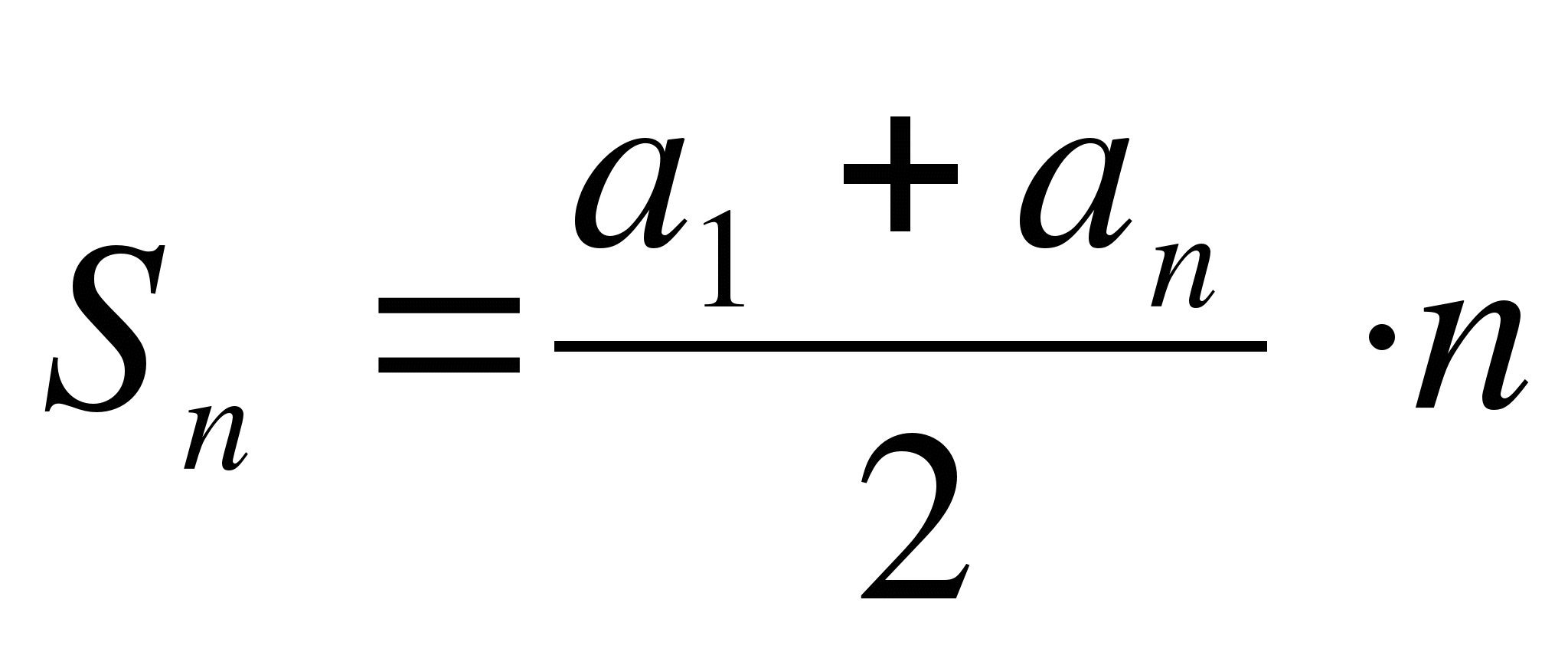
Демонстрируется слайд 9

Задачу решают самостоятельно с последующей самопроверкой. Самопроверка осуществляется с помощью мультимедийного проектора. Решение появляется поочередно по действиям.

Демонстрируется слайд 10.

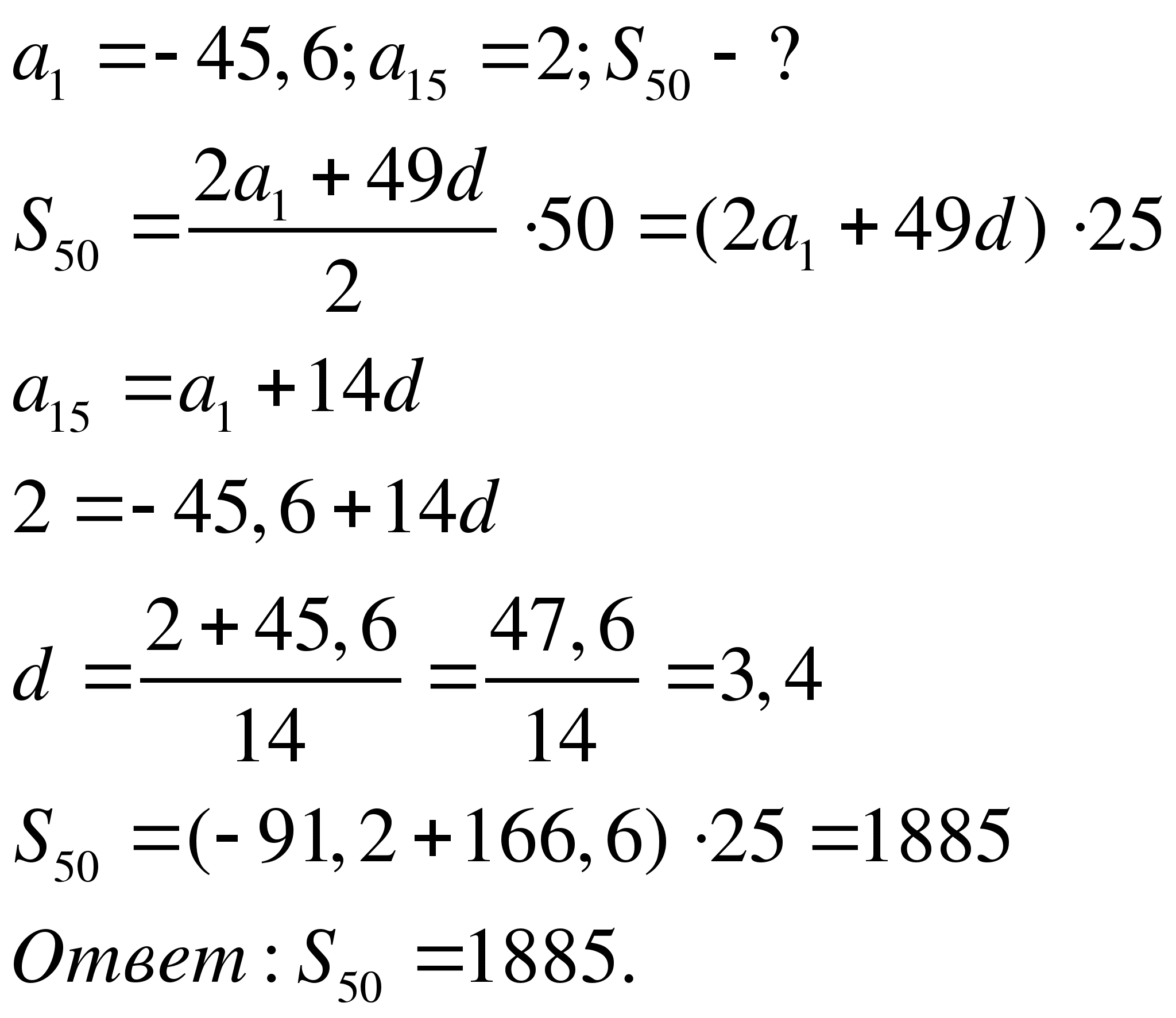
Учитель: Решите задачу: ( у доски работает Князькова Л)

В геометрической прогрессии найти число п членов, если 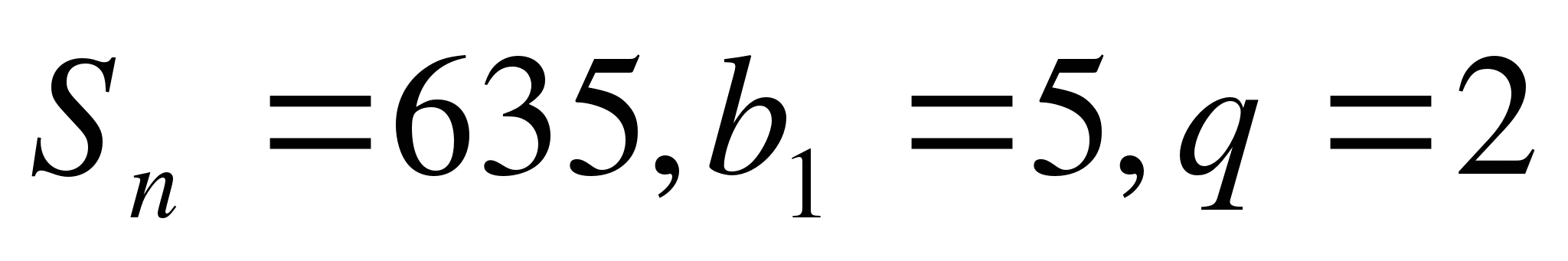. . Вспомните формулу суммы п первых членов геометрической прогрессии.

Ученик: .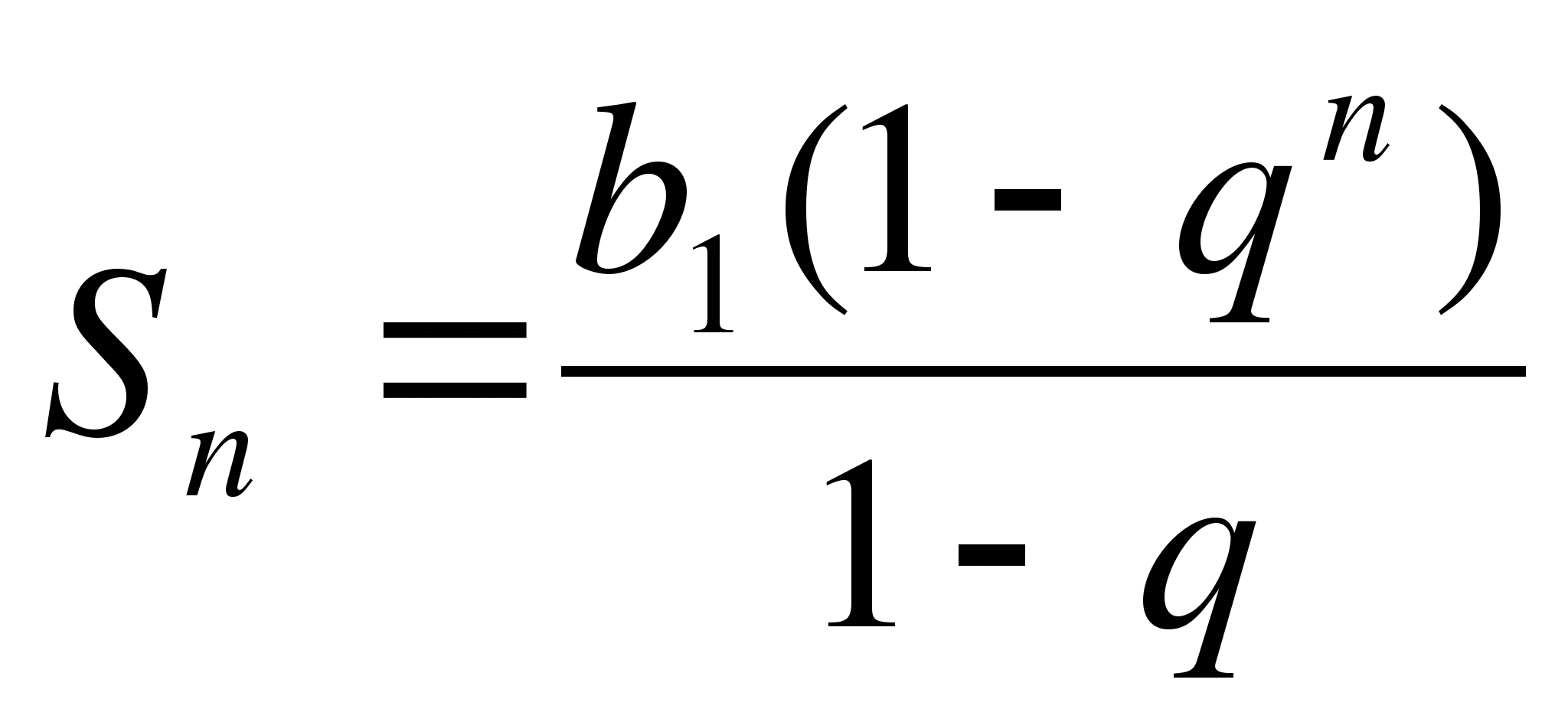

Демонстрируется слайд 11.

Решение задачи.

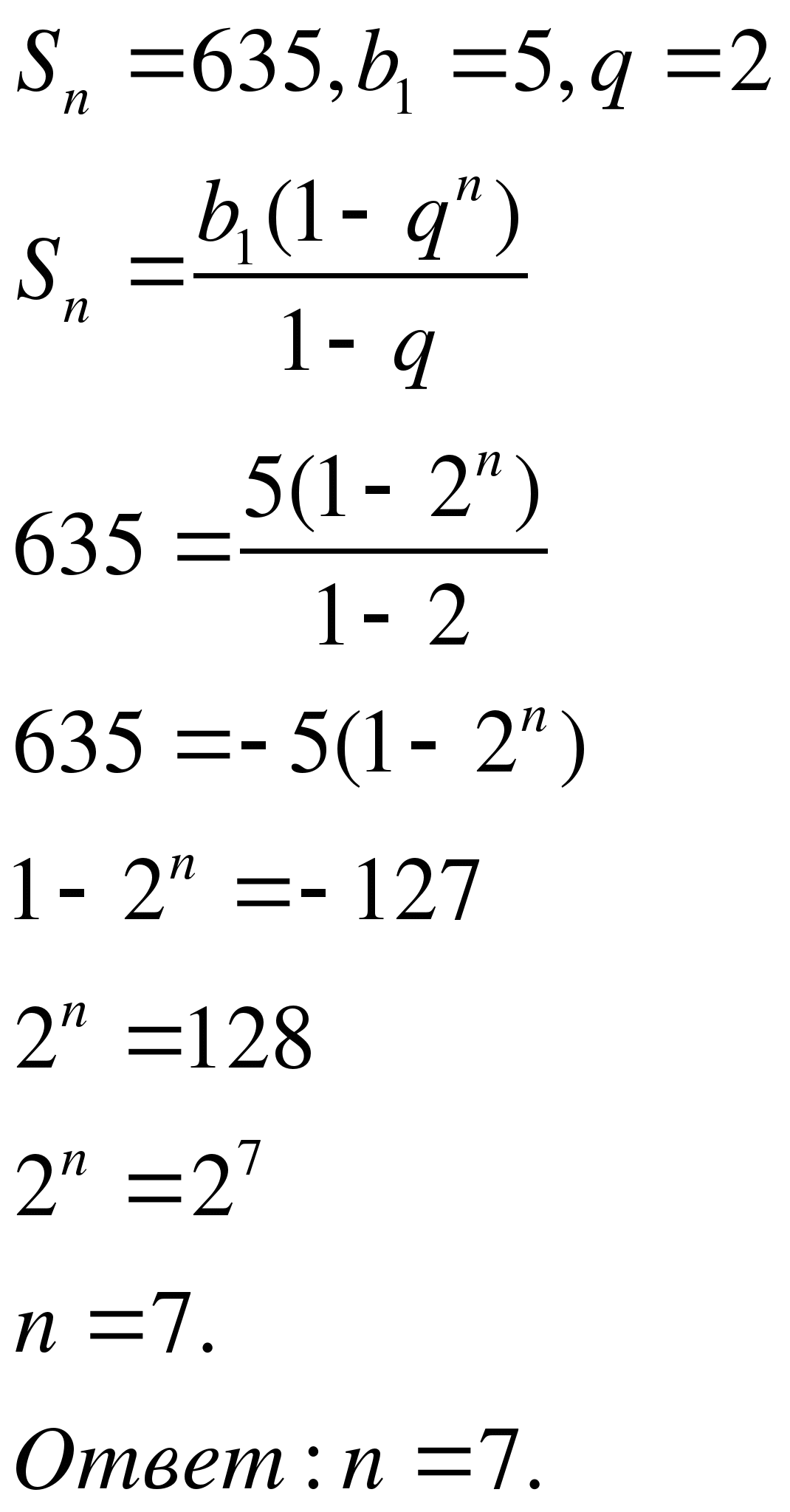
Учитель: Повторили основные формулы по данной теме, а дальше будем применять их при решении задач.

3. Работа в группах.

Цель: — закрепить знания основных формул и умения применять их в новой измененной ситуации.

Группа 1. Егоров А, Яценко М, Чеботарев А, Чанов С, Панкова Я. (работают с учителем).

Решите задачу:

Компьютерная игра состоит в последовательном прохождении нескольких уровней. За прохождение каждого уровня игрок получает 50 баллов. Кроме того, начисляются и премиальные баллы по следующей схеме: 10 баллов за второй уровень и за каждый следующий уровень на 10 баллов больше, чем за предыдущий. Сколько уровней надо пройти, чтобы набрать равно 1100 баллов?

Решение. (У доски работает Панкова Я)

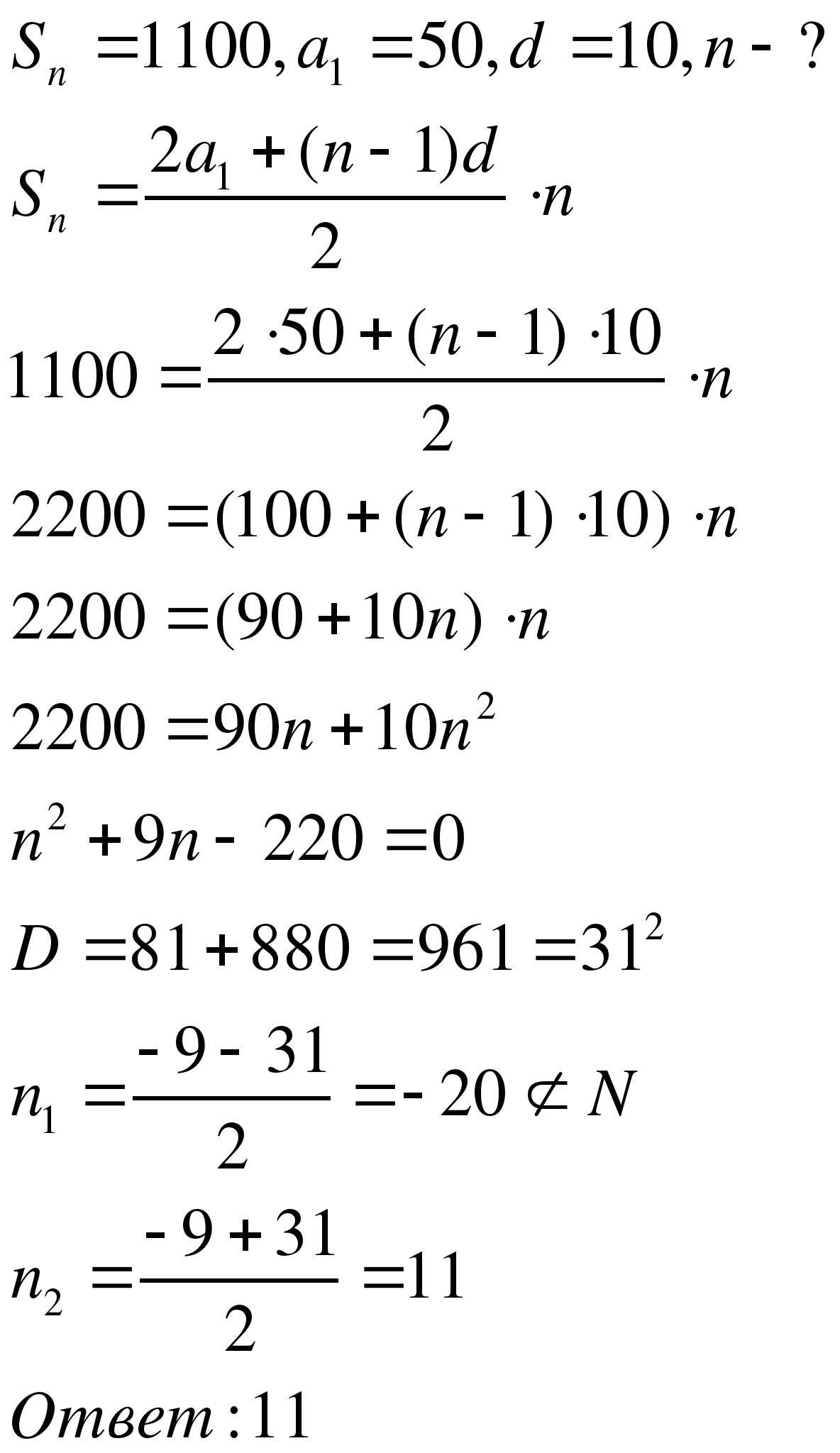
Задача 2.

Найдите сумму семи первых членов геометрической прогрессии, у которой первый член равен 32, а знаменатель равен .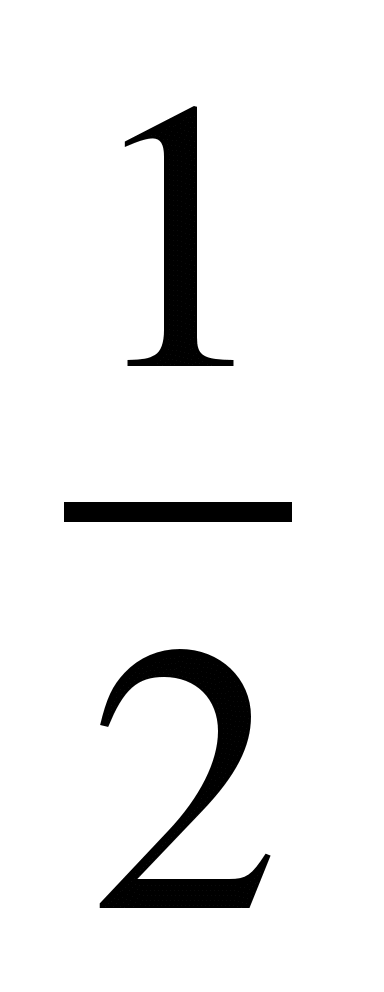

Решение.

(У доски работает Яценко М)

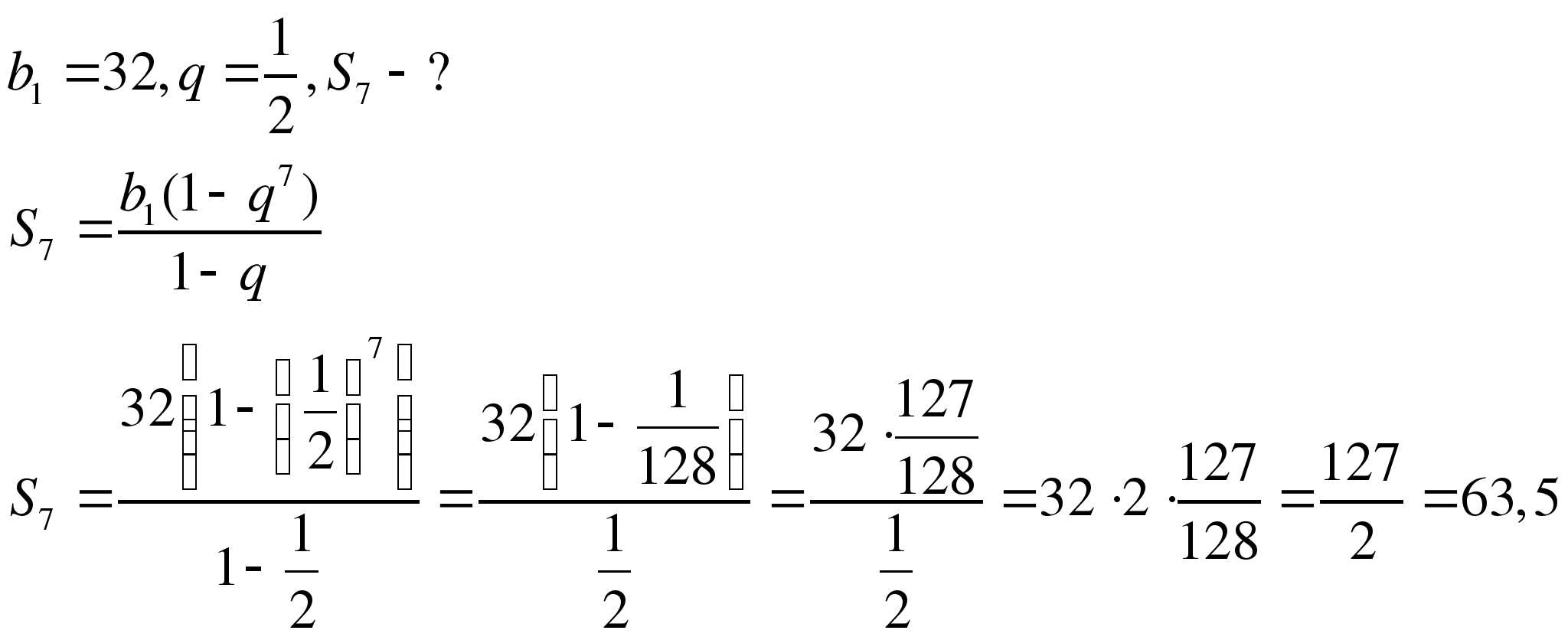
Ответ: 63,5.

Задачи для второй группы.

1. При свободном падении тело проходит в первую секунду 4,9 м, а в каждую следующую на 9,8 м больше. Найдите глубину шахты, если свободно падающее тело достигло ее дна через 5 с после начала падения.

Решение.

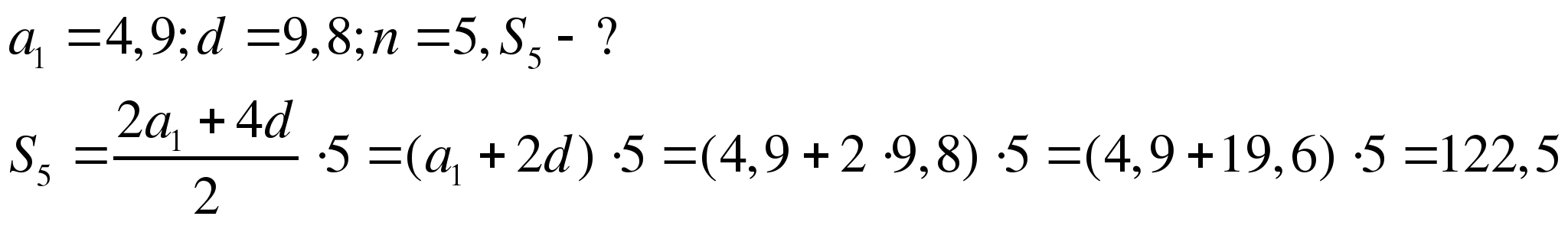
Ответ: 122,5 м.

2. В геометрической прогрессии Найти и сумму первых шести ее членов.

Решение.

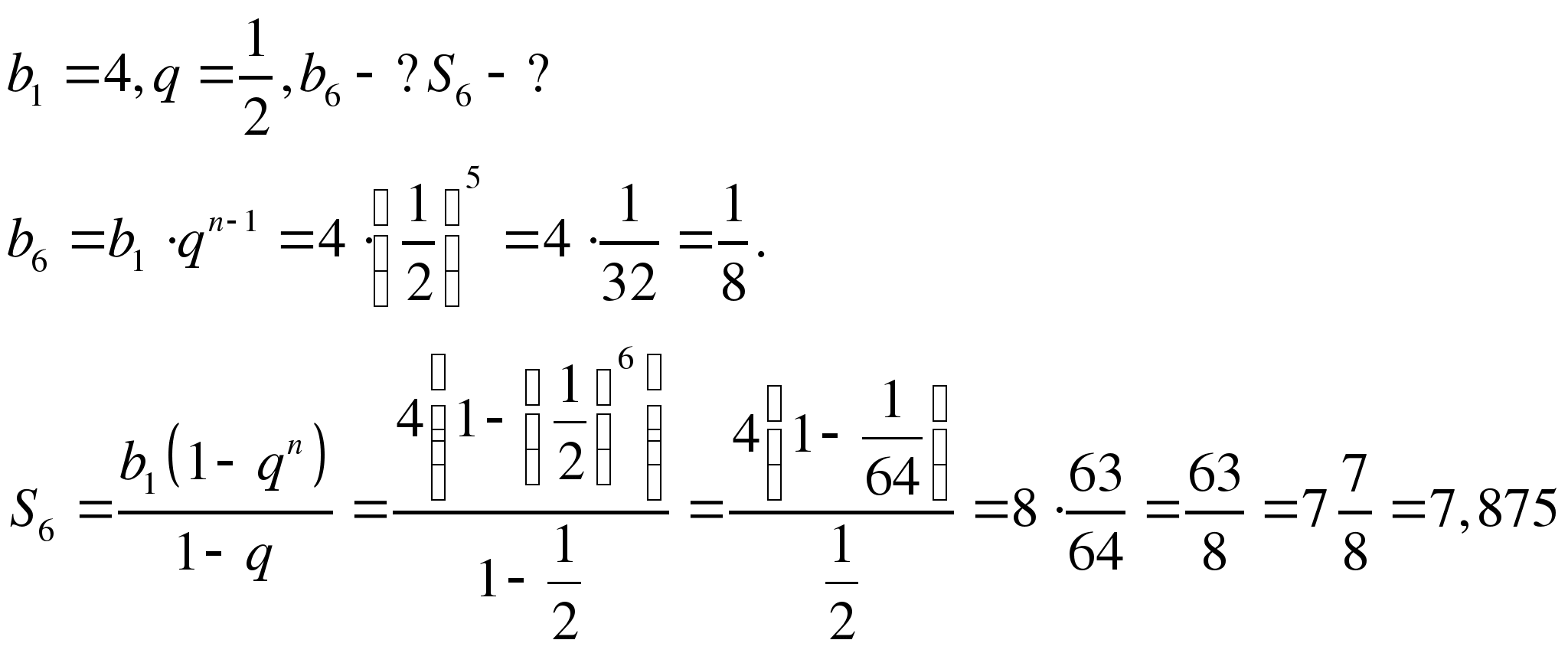
Ответ: 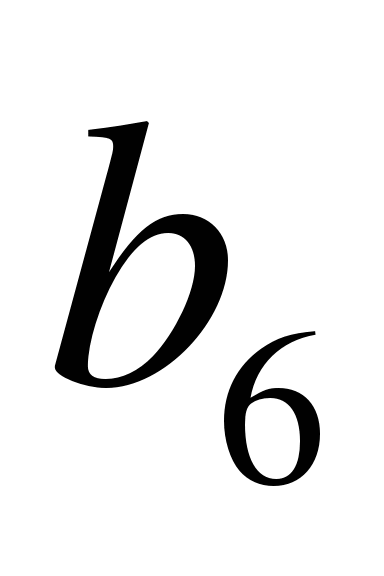=0,125;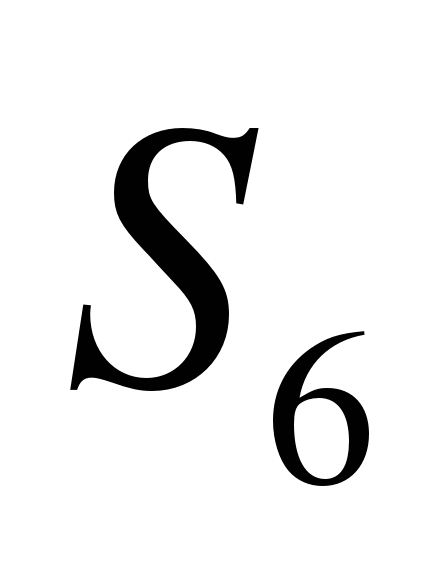=7,875.

3. Второй член арифметической прогрессии равен 18, а пятый член равен 9. Найти сумму первого и шестого членов этой прогрессии.

Решение.

1 способ:

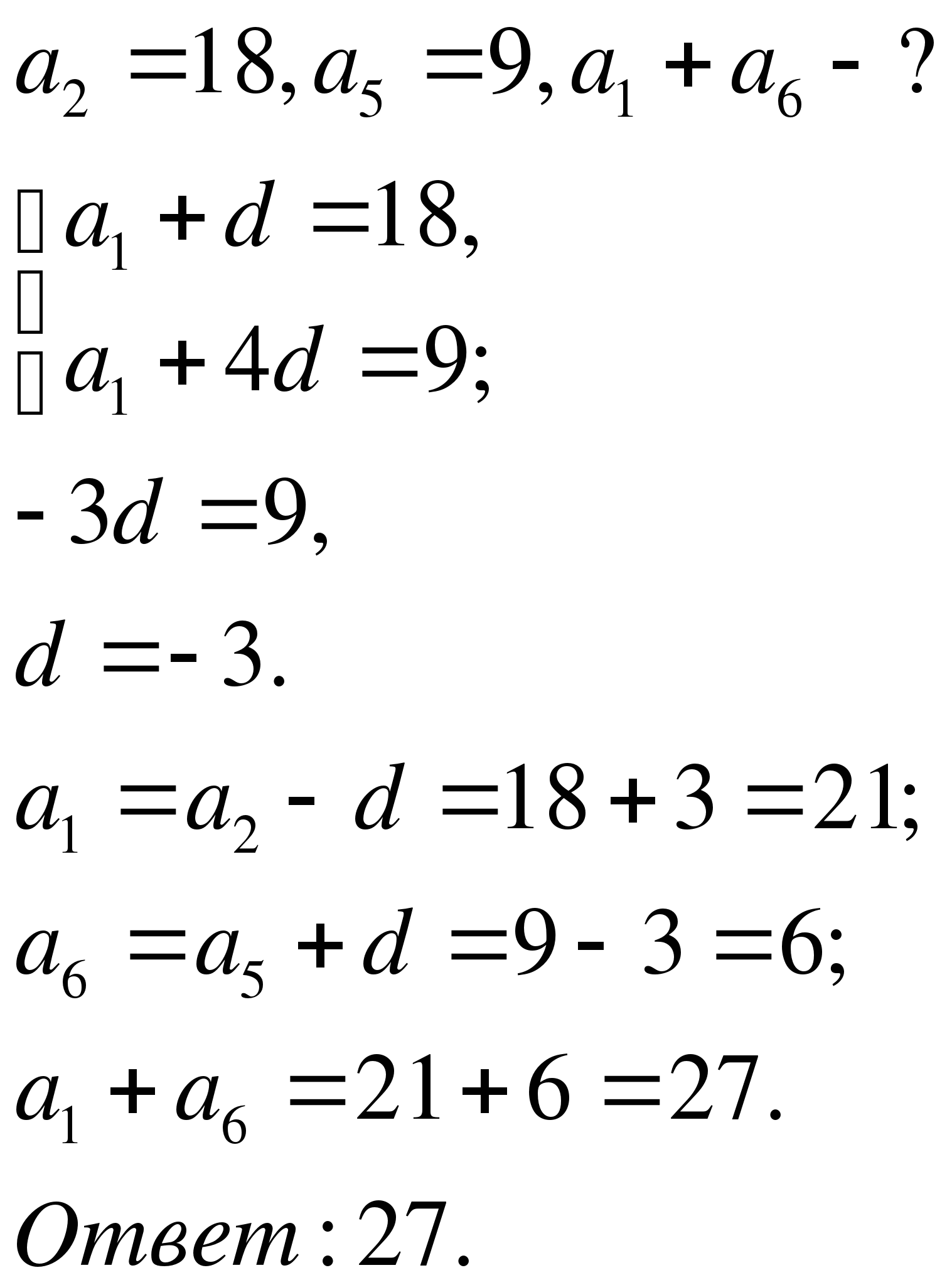
2 способ.

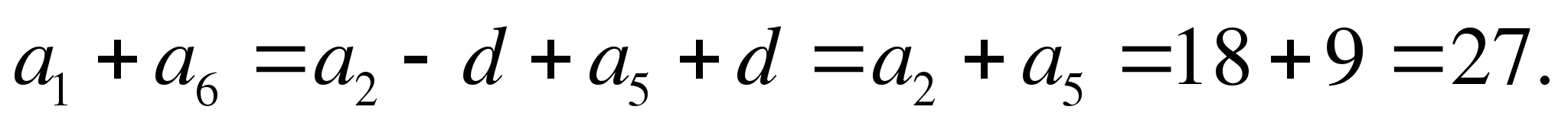
4. Сумма первых шести членов геометрической прогрессии равна 910, знаменатель прогрессии равен 3. Найти сумму первого и пятого членов этой прогрессии.

Решение.

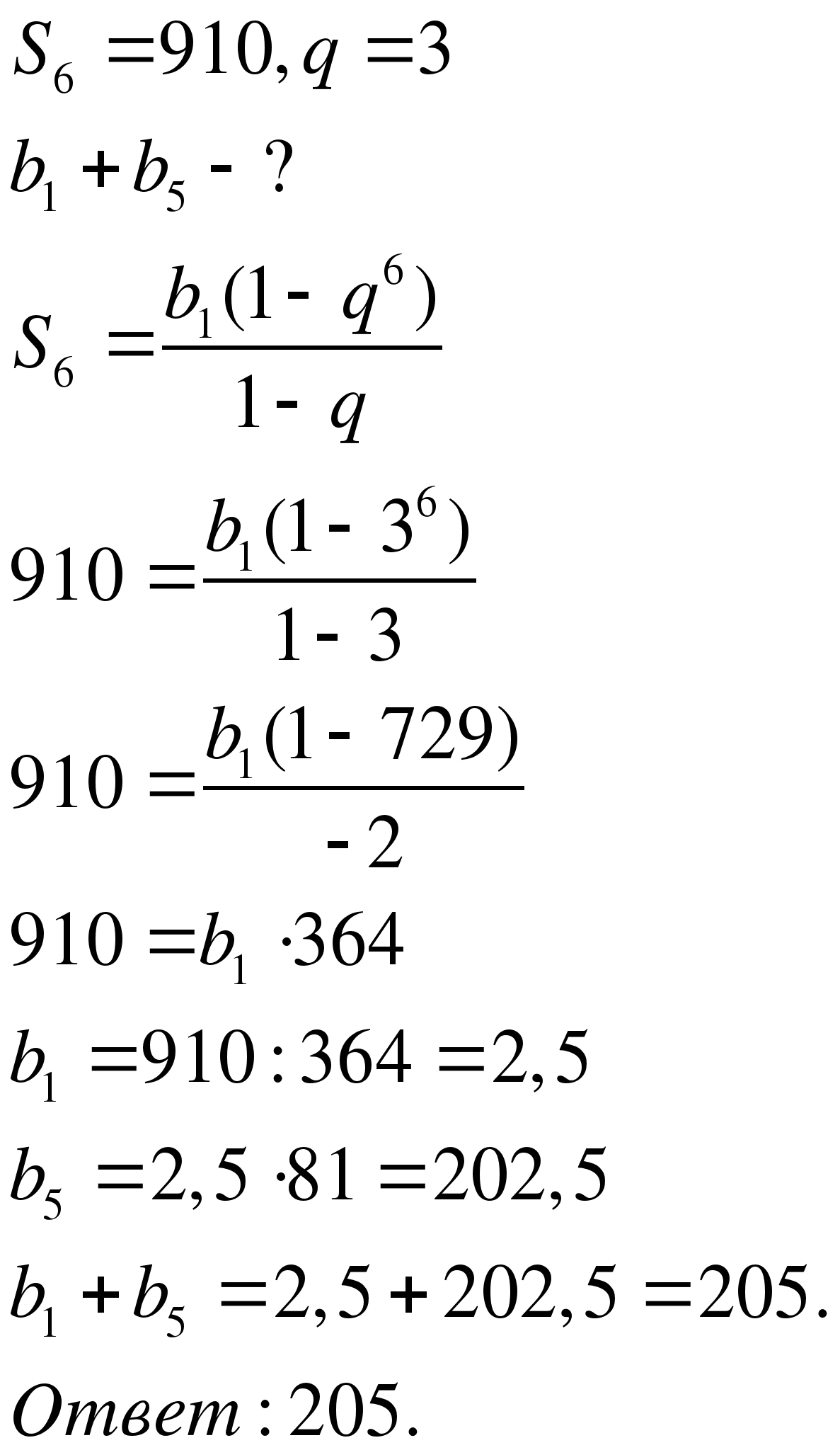
3. Проверочная работа (дифференцированная, в формате ЕГЭ 2010 г) – задания внесены в ноутбук, обучающиеся решают задачи в черновиках, ответы заносят в компьютер.

Задания для 1 группы.

1. Найдите номер члена арифметической прогрессии — 2; 3; 8;…, равного 28. Ответ: 7.

2. Известно, что в геометрической прогрессии первый член равен 4, а второй равен 2. Найдите шестой член прогрессии.

Ответ:0,125.

3. Найдите сумму первых двадцати членов арифметической прогрессии 5; 2; — 1; — 4; …

Ответ: — 470.

Задания для 2 группы.

1. Найдите первый член арифметической прогрессии, если известно, что сумма одиннадцати ее первых членов равна 165, а ее разность равна 7.

Ответ: — 20.

2. Найдите четвертый член геометрической прогрессии, если известно, что сумма пяти ее первых членов равна 713, а ее знаменатель равен 2.

Ответ: 184.

3. Пятый член арифметической прогрессии равен 14, а сумма первых десяти членов этой же арифметической прогрессии равна 155. Найдите произведение третьего и пятого членов этой прогрессии.

Ответ: 112.

V. Подведение итогов.

Ребята, мы с вами на этом занятии повторили арифметическую и геометрическую прогрессии, решали задачи по данной теме. Некоторые из вас показали хорошие результаты. Но с некоторыми из вас нам следует вернуться к этой теме на консультациях.

Задачи в ноутбуке.

Группа 1.

1. Между числами 4 и 9 вставьте положительное число так, чтобы получилось три последовательных члена арифметической прогрессии.

2. Найдите сумму пятидесяти первых членов арифметической прогрессии, первый член

которой равен — 45,6, а пятнадцатый член равен 2.

3. В геометрической прогрессии найти число п членов, если .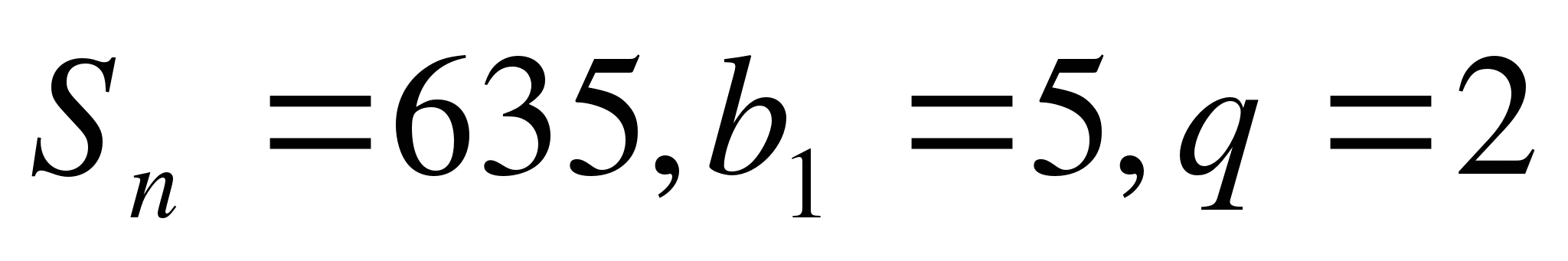

4. Компьютерная игра состоит в последовательном прохождении нескольких уровней. За прохождение каждого уровня игрок получает 50 баллов. Кроме того, начисляются и премиальные баллы по следующей схеме: 10 баллов за второй уровень и за каждый следующий уровень на 10 баллов больше, чем за предыдущий. Сколько уровней надо пройти, чтобы набрать равно 1100 баллов?

5. Найдите сумму семи первых членов геометрической прогрессии, у которой первый член равен 32, а знаменатель равен .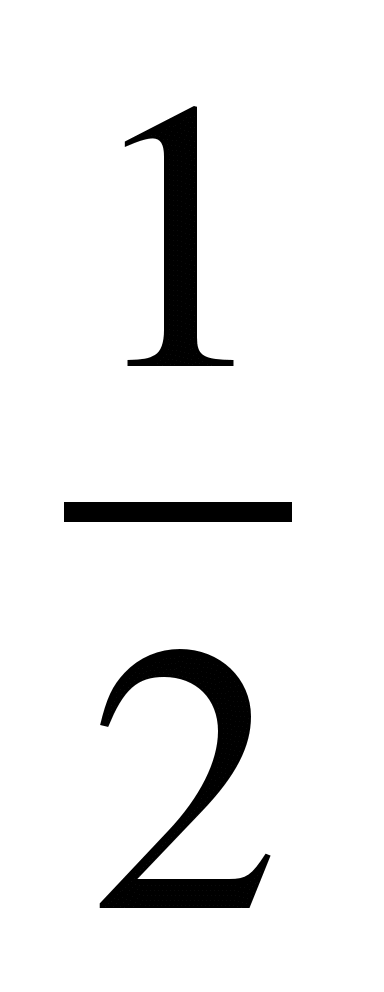

Группа 2.

1. Между числами 4 и 9 вставьте положительное число так, чтобы получилось три последовательных члена геометрической прогрессии.

2. Найдите сумму пятидесяти первых членов арифметической прогрессии, первый член

которой равен — 45,6, а пятнадцатый член равен 2.

3. В геометрической прогрессии найти число п членов, если .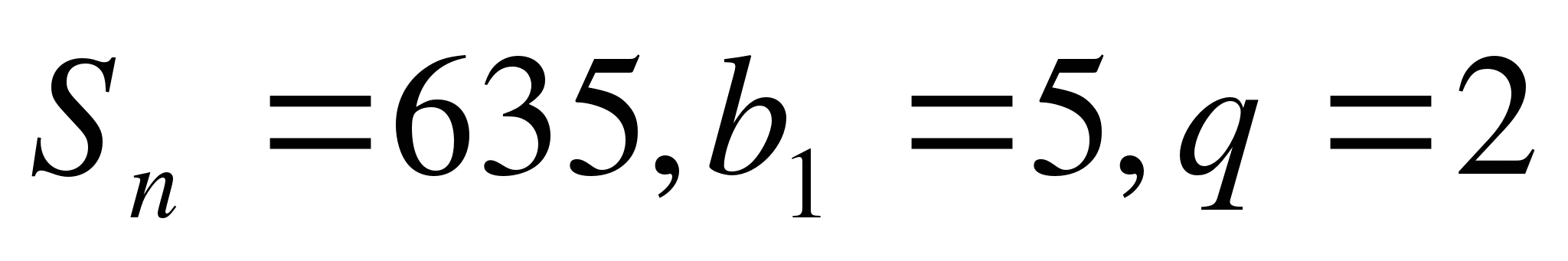

4. При свободном падении тело проходит в первую секунду 4,9 м, а в каждую следующую на 9,8 м больше. Найдите глубину шахты, если свободно падающее тело достигло ее дна через 5 с после начала падения.

5. В геометрической прогресси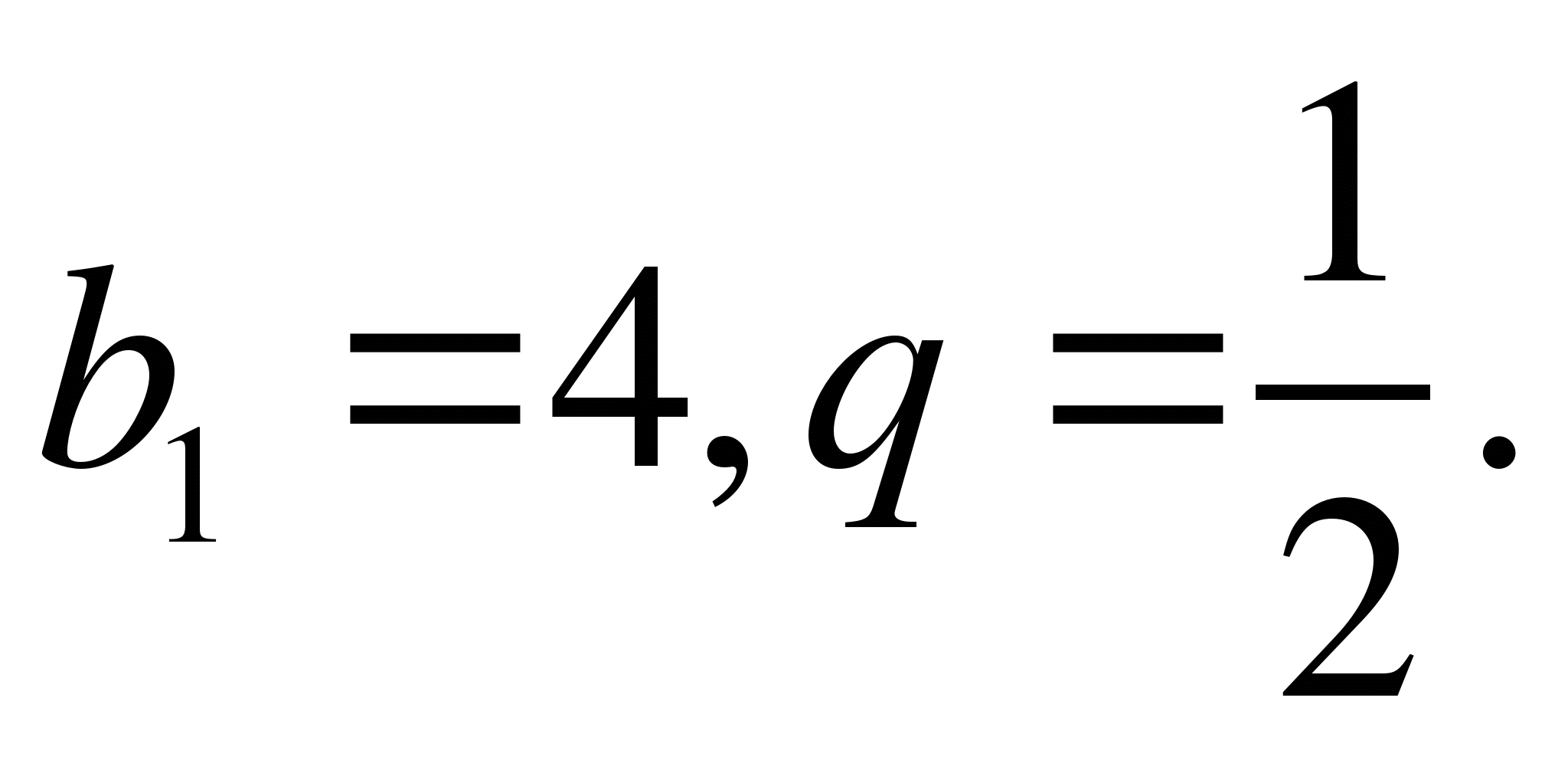и Найти 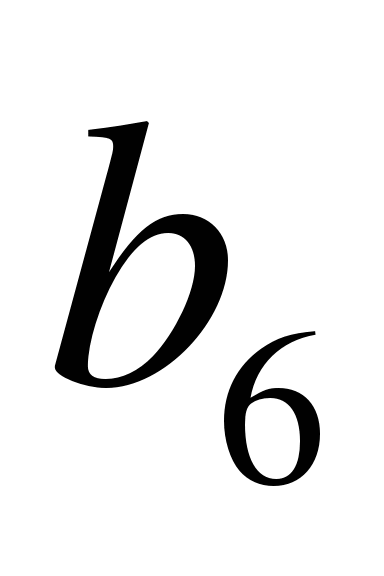и сумму первых шести ее членов.

6. Второй член арифметической прогрессии равен 18, а пятый член равен 9. Найти сумму первого и шестого членов этой прогрессии.

7. Сумма первых шести членов геометрической прогрессии равна 910, знаменатель прогрессии равен 3. Найти сумму первого и пятого членов этой прогрессии.

infourok.ru

Арифметическая прогрессия — это… Что такое Арифметическая прогрессия?

У этого термина существуют и другие значения, см. Прогрессия.

Арифмети́ческая прогре́ссия — числовая последовательность вида

,

то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа (шага или разности прогрессии):

Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:

Арифметическая прогрессия является монотонной последовательностью. При она является возрастающей, а при  — убывающей. Если , то последовательность будет стационарной. Эти утверждения следуют из соотношения для членов арифметической прогрессии.

Свойства

Общий член арифметической прогрессии

Член арифметической прогрессии с номером может быть найден по формуле

, где  — первый член прогрессии,  — ее разность.

Доказательство

Характеристическое свойство арифметической прогрессии

Последовательность есть арифметическая прогрессия для ее элементов выполняется условие .

Доказательство

Необходимость:

Поскольку — арифметическая прогрессия, то для выполняются соотношения:

.

Сложив эти равенства и разделив обе части на 2, получим .

Достаточность:

Имеем, что для каждого элемента последовательности, начиная со второго, выполняется . Следует показать, что эта последовательность есть арифметическая прогрессия. Преобразуем эту формулу к виду . Поскольку соотношения верны при всех , с помощью математической индукции покажем, что .

База индукции  :

— утверждение истинно.

Переход индукции:

Пусть наше утверждение верно при , то есть . Докажем истинность утверждения при :

Но по предположению индукции следует, что . Получаем, что .

Итак, утверждение верно и при . Это значит, что .

Обозначим эти разности через . Итак, , а отсюда имеем для . Поскольку для членов последовательности выполняется соотношение , то это есть арифметическая прогрессия.

Сумма первых членов арифметической прогрессии

Сумма первых членов арифметической прогрессии может быть найдена по формулам

, где  — первый член прогрессии,  — член с номером ,  — количество суммируемых членов.

, где  — первый член прогрессии,  — разность прогрессии,  — количество суммируемых членов.

Доказательство

Сходимость арифметической прогрессии

Арифметическая прогрессия расходится при и сходится при . Причем

Доказательство

Записав выражение для общего члена и исследуя предел , получаем искомый результат.

Связь между арифметической и геометрической прогрессиями

Пусть  — арифметическая прогрессия с разностью и число . Тогда последовательность вида есть геометрическая прогрессия со знаменателем .

Доказательство

Проверим характеристическое свойство для образованной геометрической прогрессии:

Воспользуемся выражением для общего члена арифметической прогрессии:

Итак, поскольку характеристическое свойство выполняется, то — геометрическая прогрессия. Ее знаменатель можно найти, например, из соотношения .

Арифметические прогрессии высших порядков

Арифметической прогрессией второго порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:

0, 1, 4, 9, 16, 25, 36…,

разности которых образуют простую арифметическую прогрессию с разностью 2:

1, 3, 5, 7, 9, 11…

Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.

Примеры

.

См. также

Ссылки

dik.academic.ru