Пропорции математика. Пропорция – это равенство двух отношений. Соотношение.
Пропорция – это равенство, утверждающее, что два отношения равны. Пропорциональный — значит находящийся в определенном отношении к какой-либо величине. Четыре величины \(4, 2, 8 \) и \(4\) находятся в отношении, если \(\frac{4}{2}=\frac{8}{4}\). Произведение крайних членов пропорции равно произведению средних.
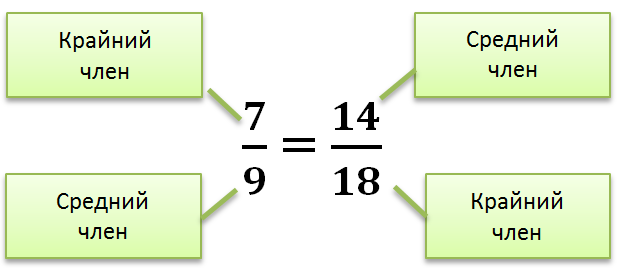
Пропорция всегда включает равные коэффициенты. Когда соотношение остается постоянным, это соотношение называется пропорциональным.
Если \(\frac{A}{B} = \frac{C}{D}\), то
Пропорция состоит из двух равных отношений. Однако если \(\frac{A}{B}\) не равно \(\frac{C}{D}\), то \(A, B, C, D \) не называются пропорцией.
Три величины считаются пропорциональными, если отношение первого ко второму равно соотношению второго и третьего.
\(A, B , C\) находятся в постоянной пропорции, если \(\frac{A}{B} =\frac{C}{D}\)
Если \(A, B ,C \) находятся в постоянном отношении, то \(B\) называется средней в пропорции.
В косвенной пропорции как одно значение увеличивается, так и другое значение уменьшается.
Задача 1. За \(5\) дней и \(12\) человек построили забор. Сколько дней это займет у \(6\) людей?
Решение.
- \(12\) человек → \(5\) дней
- \(6\) человек → \(x\) дней
- \(\frac{12}{6} = \frac{x}{5}\)
- умножаем крест на крест члены пропорции и сокращаем на \(6\):
\(12*5=6x\)
\(60=6x\)
\(x=10\)
Ответ: \(6\) людей будут работать \(10\) дней, чтобы закончить работу.
Задача 2. Найдите значение \(x\), если \(\frac{2}{5}=\frac{x}{15}\)
Решение:
- \(2*15=5x\)
- \(30 =5x\)
- Делим на 5 обе части равенства: \(\frac{30}{5}=x\), откуда находим
Задача 3. Что должно быть добавлено к каждому из четырех чисел 10, 18, 22, 38, чтобы сделать их пропорцией?
Решение:\(\)
- \((10+x)(18+x)=(22+x)(38+x)\)
- \(380+48x+2x=396+40x+2x\)
- \(8x=16\)
- \(x=2\)
Задача 4. Найти четвертый член пропорции \(6,10\) и \(12\)
Решение:
\(\frac{6}{10}=\frac{12}{x}\)
6×х = 120
x = 120/6
x = 20
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Пропорция (математика) — Википедия. Что такое Пропорция (математика)
Основные свойства пропорций
- ac=bd{\displaystyle \ {\frac {a}{c}}={\frac {b}{d}}} (перестановка средних членов пропорции),
- db=ca{\displaystyle \ {\frac {d}{b}}={\frac {c}{a}}} (перестановка крайних членов пропорции).
- Увеличение и уменьшение пропорции. Если ab=cd{\displaystyle \ {\frac {a}{b}}={\frac {c}{d}}}, то
- a+bb=c+dd{\displaystyle \ {\dfrac {a+b}{b}}={\dfrac {c+d}{d}}} (увеличение пропорции),
- a−bb=c−dd{\displaystyle \ {\dfrac {a-b}{b}}={\dfrac {c-d}{d}}} (уменьшение пропорции).
- Составление пропорции сложением и вычитанием. Если ab=cd{\displaystyle \ {\frac {a}{b}}={\frac {c}{d}}}, то
- a+cb+d=ab=cd{\displaystyle \ {\dfrac {a+c}{b+d}}={\frac {a}{b}}={\frac {c}{d}}} (составление пропорции сложением),
- a−cb−d=ab=cd{\displaystyle \ {\dfrac {a-c}{b-d}}={\frac {a}{b}}={\frac {c}{d}}} (составление пропорции вычитанием).
История
Первое известное определение равных пропорций было дано как равенство последовательных вычитаний[1], современным языком это можно выразить как равенство цепных дробей для отношений величин.[2] Позже Евдокс упростил определение, равенство пропорций a:b=c:d{\displaystyle a:b=c:d} им определялось как одновременное выполнение одной из трёх пар соотношений
для любой пары натуральных чисел m{\displaystyle m} и n{\displaystyle n}. Это определение даётся в «Началах» Евклида.
С появлением вещественных чисел отпала необходимость в специальной теории пропорций, древние математики не рассматривали пропорции длины как числа. Определение Евдокса, в несколько более абстрактном виде использовалось далее при определении вещественных чисел данное Дедекиндом через сечения.
Связанные определения
Арифметическая пропорция
Равенство двух разностей a−b=c−d{\displaystyle a-b=c-d} иногда называют арифметической пропорцией[3].
Гармоническая пропорция
Если у геометрической пропорции средние члены равны, а последний является разницей между первым и средним, такая пропорция называется гармонической: a:b=b:(a−b){\displaystyle a:b=b:(a-b)}. В этом случае, разложение a{\displaystyle a} на сумму двух слагаемых b{\displaystyle b} и a−b{\displaystyle a-b} называется гармоническим делением или золотым сечением [4].
Задачи на тройное правило
В содержание задачи на простое тройное правило входят две величины, связанные пропорциональной зависимостью, при этом даются два значения одной величины и одно из соответствующих значений другой величины, требуется же найти её второе значение.
Задачами на сложное тройное правило называют задачи, в которых по ряду нескольких (более двух) пропорциональных величин требуется найти значение одной из них, соответствующее другому ряду данных значений величин[5][6].
Литература
- Ван дер Варден, Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. / пер. с голл. И. Н. Веселовского. — М.: ГИФМЛ, 1959.
Примечания
См. также
Пропорция (математика) — это… Что такое Пропорция (математика)?
Пропо́рция (лат. proportio — соразмерность, выровненность частей), равенство двух отношений, т. е. равенство вида a : b = c : d, или, в других обозначениях, равенство (часто читается как: «a относится к b так же, как c относится к d»). Если a : b = c : d, то a и d называют крайними, а b и c — средними членами пропорции.
Основные свойства пропорций
- (перестановка средних членов пропорции),
- (перестановка крайних членов пропорции).
- Увеличение и уменьшение пропорции. Если , то
- (увеличение пропорции),
- (уменьшение пропорции).
- Составление пропорции сложением и вычитанием. Если , то
- (составление пропорции сложением),
- (составление пропорции вычитанием).
Литература
- ван дер Варден, Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. — пер. с голл. И. Н. Веселовского — М.: ГИФМЛ, 1959
См. также
dic.academic.ru
Пропорция (математика) — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Пропорция.Пропо́рция (лат. proportio — соразмерность, выравненность частей; определённое соотношение частей между собой), равенство отношений двух [и более] пар чисел a,b{\displaystyle a,b} и c,d{\displaystyle c,d}, т. е. равенство вида a:b=c:d{\displaystyle a:b=c:d}, или, в других обозначениях, равенство ab=cd{\displaystyle \ {\frac {a}{b}}={\frac {c}{d}}} (часто читается как: «a{\displaystyle a} относится к b{\displaystyle b} так же, как c{\displaystyle c} относится к d{\displaystyle d}»). В этом случае a{\displaystyle a} и d{\displaystyle d} называют
Основные свойства пропорций
- ac=bd{\displaystyle \ {\frac {a}{c}}={\frac {b}{d}}} (перестановка средних членов пропорции),
- db=ca{\displaystyle \ {\frac {d}{b}}={\frac {c}{a}}} (перестановка крайних членов пропорции).
- Увеличение и уменьшение пропорции. Если ab=cd{\displaystyle \ {\frac {a}{b}}={\frac {c}{d}}}, то
- a+bb=c+dd{\displaystyle \ {\dfrac {a+b}{b}}={\dfrac {c+d}{d}}} (увеличение пропорции),
- a−bb=c−dd{\displaystyle \ {\dfrac {a-b}{b}}={\dfrac {c-d}{d}}} (уменьшение пропорции).
- Составление пропорции сложением и вычитанием. Если ab=cd{\displaystyle \ {\frac {a}{b}}={\frac {c}{d}}}, то
- a+cb+d=ab=cd{\displaystyle \ {\dfrac {a+c}{b+d}}={\frac {a}{b}}={\frac {c}{d}}} (составление пропорции сложением),
- a−cb−d=ab=cd{\displaystyle \ {\dfrac {a-c}{b-d}}={\frac {a}{b}}={\frac {c}{d}}} (составление пропорции вычитанием).
История
Первое известное определение равных пропорций было дано как равенство последовательных вычитаний[1], современным языком это можно выразить как равенство цепных дробей для отношений величин.[2] Позже Евдокс упростил определение, равенство пропорций a:b=c:d{\displaystyle a:b=c:d} им определялось как одновременное выполнение одной из трёх пар соотношений
для любой пары натуральных чисел m{\displaystyle m} и n{\displaystyle n}. Это определение даётся в «Началах» Евклида.
С появлением вещественных чисел отпала необходимость в специальной теории пропорций, древние математики не рассматривали пропорции длины как числа. Определение Евдокса, в несколько более абстрактном виде использовалось далее при определении вещественных чисел данное Дедекиндом через сечения.
Связанные определения
Арифметическая пропорция
Равенство двух разностей a−b=c−d{\displaystyle a-b=c-d} иногда называют арифметической пропорцией[3].
Гармоническая пропорция
Если у геометрической пропорции средние члены равны, а последний является разницей между первым и средним, такая пропорция называется гармонической: a:b=b:(a−b){\displaystyle a:b=b:(a-b)}. В этом случае, разложение a{\displaystyle a} на сумму двух слагаемых b{\displaystyle b} и a−b{\displaystyle a-b} называется гармоническим делением или золотым сечением[4].
Задачи на тройное правило
В содержание задачи на простое тройное правило входят две величины, связанные пропорциональной зависимостью, при этом даются два значения одной величины и одно из соответствующих значений другой величины, требуется же найти её второе значение.
Задачами на сложное тройное правило называют задачи, в которых по ряду нескольких (более двух) пропорциональных величин требуется найти значение одной из них, соответствующее другому ряду данных значений величин[5][6].
Литература
- Ван дер Варден, Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. / пер. с голл. И. Н. Веселовского. — М.: ГИФМЛ, 1959.
Примечания
См. также
wikipedia.green
Пропорция — это… Что такое Пропорция?
ПРОПОРЦИЯ — (лат., от pro для, и portio часть, порция). 1) соразмерность, согласование. 2) отношение частей между собою и к их целому. Отношение величин между собою. 3) в архитектуре: удачные размеры. Словарь иностранных слов, вошедших в состав русского… … Словарь иностранных слов русского языка
ПРОПОРЦИЯ — ПРОПОРЦИЯ, пропорции, жен. (книжн.) (лат. proportio). 1. Соразмерность, определенное соотношение частей между собой. Правильные пропорции частей тела. Смешать сахар с желтком в такой пропорции: две ложки сахара на один желток. 2. Равенство двух… … Толковый словарь Ушакова
пропорция — отношение, соотношение; соразмерность. Ant. диспропорция Словарь русских синонимов. пропорция см. соотношение Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова … Словарь синонимов
ПРОПОРЦИЯ — жен., франц. соразмерность; величина или количество, отвечающее чему либо; | мат. равенство содержания, одинаковые отношения двойной четы цифры; арифметическая, если второе число на столько же более или менее, первого, на сколько четвертое против … Толковый словарь Даля
ПРОПОРЦИЯ — (лат. proportio) в математике равенство между двумя отношениями четырех величин: a/b =c/d … Большой Энциклопедический словарь
ПРОПОРЦИЯ — ПРОПОРЦИЯ, в математике равенство между двумя отношениями четырех величин: a/b=с/d. Непрерывной пропорцией называют группу из трех или более величин, каждая из которых имеет одно и то же отношение к последующей величине, как, например, в… … Научно-технический энциклопедический словарь
ПРОПОРЦИЯ — ПРОПОРЦИЯ, и, жен. 1. В математике: равенство двух отношений (в 3 знач.). 2. Определённое соотношение частей между собой, соразмерность. П. в частях здания. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ПРОПОРЦИЯ — англ. proportion; нем. Proportion. 1. Соразмерность, определенное соотношение частей целого между собой. 2. Равенство двух отношений. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
пропорция — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN ratedegreeDdegdrratio … Справочник технического переводчика
ПРОПОРЦИЯ — равенство двух (см.), т.е. а: b = с: d, где а, b, с, d члены пропорции, причём а и d крайние, b и с средине. Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних: ad = bс … Большая политехническая энциклопедия
пропорция — и; ж. [лат. proportio] 1. Соразмерное соотношение частей между собой. Соблюсти все архитектурные пропорции. Идеальная п. частей тела. 2. Определённое количественное соотношение между чем л. Нарушить пропорцию. Смешав ягоды с песком в пропорции… … Энциклопедический словарь
dic.academic.ru
ПРОПОРЦИЯ — это… Что такое ПРОПОРЦИЯ?
ПРОПОРЦИЯ — (лат., от pro для, и portio часть, порция). 1) соразмерность, согласование. 2) отношение частей между собою и к их целому. Отношение величин между собою. 3) в архитектуре: удачные размеры. Словарь иностранных слов, вошедших в состав русского… … Словарь иностранных слов русского языка
ПРОПОРЦИЯ — ПРОПОРЦИЯ, пропорции, жен. (книжн.) (лат. proportio). 1. Соразмерность, определенное соотношение частей между собой. Правильные пропорции частей тела. Смешать сахар с желтком в такой пропорции: две ложки сахара на один желток. 2. Равенство двух… … Толковый словарь Ушакова
пропорция — отношение, соотношение; соразмерность. Ant. диспропорция Словарь русских синонимов. пропорция см. соотношение Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова … Словарь синонимов
ПРОПОРЦИЯ — жен., франц. соразмерность; величина или количество, отвечающее чему либо; | мат. равенство содержания, одинаковые отношения двойной четы цифры; арифметическая, если второе число на столько же более или менее, первого, на сколько четвертое против … Толковый словарь Даля
ПРОПОРЦИЯ — (лат. proportio) в математике равенство между двумя отношениями четырех величин: a/b =c/d … Большой Энциклопедический словарь
ПРОПОРЦИЯ — ПРОПОРЦИЯ, и, жен. 1. В математике: равенство двух отношений (в 3 знач.). 2. Определённое соотношение частей между собой, соразмерность. П. в частях здания. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ПРОПОРЦИЯ — англ. proportion; нем. Proportion. 1. Соразмерность, определенное соотношение частей целого между собой. 2. Равенство двух отношений. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
пропорция — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN ratedegreeDdegdrratio … Справочник технического переводчика
ПРОПОРЦИЯ — равенство двух (см.), т.е. а: b = с: d, где а, b, с, d члены пропорции, причём а и d крайние, b и с средине. Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних: ad = bс … Большая политехническая энциклопедия
пропорция — и; ж. [лат. proportio] 1. Соразмерное соотношение частей между собой. Соблюсти все архитектурные пропорции. Идеальная п. частей тела. 2. Определённое количественное соотношение между чем л. Нарушить пропорцию. Смешав ягоды с песком в пропорции… … Энциклопедический словарь
dic.academic.ru
ПРОПОРЦИЯ — это… Что такое ПРОПОРЦИЯ?
ПРОПОРЦИЯ — (лат., от pro для, и portio часть, порция). 1) соразмерность, согласование. 2) отношение частей между собою и к их целому. Отношение величин между собою. 3) в архитектуре: удачные размеры. Словарь иностранных слов, вошедших в состав русского… … Словарь иностранных слов русского языка
ПРОПОРЦИЯ — ПРОПОРЦИЯ, пропорции, жен. (книжн.) (лат. proportio). 1. Соразмерность, определенное соотношение частей между собой. Правильные пропорции частей тела. Смешать сахар с желтком в такой пропорции: две ложки сахара на один желток. 2. Равенство двух… … Толковый словарь Ушакова
пропорция — отношение, соотношение; соразмерность. Ant. диспропорция Словарь русских синонимов. пропорция см. соотношение Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова … Словарь синонимов
ПРОПОРЦИЯ — жен., франц. соразмерность; величина или количество, отвечающее чему либо; | мат. равенство содержания, одинаковые отношения двойной четы цифры; арифметическая, если второе число на столько же более или менее, первого, на сколько четвертое против … Толковый словарь Даля
ПРОПОРЦИЯ — ПРОПОРЦИЯ, в математике равенство между двумя отношениями четырех величин: a/b=с/d. Непрерывной пропорцией называют группу из трех или более величин, каждая из которых имеет одно и то же отношение к последующей величине, как, например, в… … Научно-технический энциклопедический словарь
ПРОПОРЦИЯ — ПРОПОРЦИЯ, и, жен. 1. В математике: равенство двух отношений (в 3 знач.). 2. Определённое соотношение частей между собой, соразмерность. П. в частях здания. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ПРОПОРЦИЯ — англ. proportion; нем. Proportion. 1. Соразмерность, определенное соотношение частей целого между собой. 2. Равенство двух отношений. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
пропорция — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN ratedegreeDdegdrratio … Справочник технического переводчика
ПРОПОРЦИЯ — равенство двух (см.), т.е. а: b = с: d, где а, b, с, d члены пропорции, причём а и d крайние, b и с средине. Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних: ad = bс … Большая политехническая энциклопедия
пропорция — и; ж. [лат. proportio] 1. Соразмерное соотношение частей между собой. Соблюсти все архитектурные пропорции. Идеальная п. частей тела. 2. Определённое количественное соотношение между чем л. Нарушить пропорцию. Смешав ягоды с песком в пропорции… … Энциклопедический словарь
dic.academic.ru