Арифметическая прогрессия. 9-й класс
Тип урока: урок изучения нового материала.
Цель урока: Формирование понятия арифметической прогрессии как одного из видов последовательностей, вывод формулы n-го члена, знакомство с характеристическим свойством членов арифметической прогрессии. Решение задач.
Задачи урока:
- Образовательные — ввести понятия арифметической прогрессии; формулы n-го члена; характеристическое свойство, которым обладают члены арифметических прогрессий.
- Развивающие — вырабатывать умения сравнивать математические понятия, находить сходства и различия, умения наблюдать, подмечать закономерности, проводить рассуждения по аналогии; сформировать умение строить и интерпретировать математическую модель некоторой реальной ситуации.
- Воспитательные
Оборудование: компьютер, мультимедийный проектор, презентация (Приложение 1)
Учебные пособия: Алгебра 9, Ю.Н.Макарычев, Н.Г.Миндюк, К.Н.Нешков, С.Б.Суворова под редакцией С.А.Теляковского, ОАО «Московские учебники», 2010
План урока:
- Организационный момент , постановка задачи
- Актуализация знаний, устная работа
- Изучение нового материала
- Первичное закрепление
- Подведение итогов урока
- Домашнее задание
В целях повышения наглядности и удобства работы с материалом, урок идет в сопровождении презентации. Однако это не является обязательным условием, и тот же урок может быть проведен в классах, не оснащенных мультимедийным оборудованием. Для этого необходимые данные могут быть подготовлены на доске или в виде таблиц и плакатов.
Ход урока
I. Организационный момент, постановка задачи.
Приветствие.
Тема сегодняшнего урока — арифметическая прогрессия. На этом уроке мы узнаем, что такое арифметическая прогрессия, какой общий вид она имеет, выясним, как отличить арифметическую прогрессию от других последовательностей и решим задачи, где используются свойства арифметических прогрессий.
II. Актуализация знаний, устная работа.
Последовательность () задана формулой: =. Какой номер имеет член этой последовательности, если он равен 144? 225? 100? Являются ли членами этой последовательности числа 48? 49? 168?
О последовательности () известно, что , . Как называется такой способ задания последовательности? Найдите первые четыре члена этой последовательности.
О последовательности () известно, что . Как называется такой способ задания последовательности? Найдите , если?
III. Изучение нового материала.
Прогрессия — последовательность величин, каждая следующая из которых находится в некоей, общей для всей прогрессии, зависимости от предыдущей. Термин ныне во многом устарел и встречается только в сочетаниях «арифметическая прогрессия» и «геометрическая прогрессия».
Термин «прогрессия» имеет латинское происхождение (progression, что означает «движение вперед») и был введен римским автором Боэцием (VI в.). Этим термином в математике прежде именовали всякую последовательность чисел, построенную по такому закону, который позволяет неограниченно продолжать эту последовательность в одном направлении. В настоящее время термин «прогрессия» в первоначально широком смысле не употребляется. Два важных частных вида прогрессий — арифметическая и геометрическая - сохранили свои названия.
Рассмотрим последовательности чисел:
- 2, 6, 10, 14, 18, :.
- 11, 8, 5, 2, -1, :.
- 5, 5, 5, 5, 5, :.
Чему равен третий член первой последовательности? Последующий член? Предыдущий член? Чему равна разность между вторым и первым членами? Третьим и вторым членами? Четвертым и третьим?
Если последовательность построена по одному закону, сделайте вывод, какой будет разность между шестым и пятым членами первой последовательности? Между седьмым и шестым?
Назовите два последующих члена каждой последовательности. Почему Вы так считаете?
(Ответы учеников)
Каким общим свойством обладают эти последовательности? Сформулируйте это свойство.
(Ответы учеников)
Числовые последовательности, обладающие этим свойством, называются арифметическими прогрессиями. Предложить учащимся самим попробовать сформулировать определение.
Определение арифметической прогрессии: арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом:
( - арифметическая прогрессия, если , где некоторое число.
Число d, показывающее, на сколько следующий член последовательности отличается от предыдущего, называется разностью прогрессии: .
Давайте еще раз посмотрим на последовательности и поговорим о различиях. Какие особенности есть у каждой последовательности и с чем они связаны?
Если в арифметической прогрессии разность положительна , то прогрессия является возрастающей: 2, 6, 10, 14, 18, :. (
Если в арифметической прогрессии разность отрицательна ( , то прогрессия является убывающей: 11, 8, 5, 2, -1, :. (
В случае, если разность равна нулю () и все члены прогрессии равны одному и тому же числу, последовательность называется стационарной: 5, 5, 5, 5, :.
Как задать арифметическую прогрессию? Рассмотрим следующую задачу.
Задача. На складе 1 числа было 50 тонн угля. Каждый день в течение месяца на склад приходит машина с 3 тоннами угля. Сколько угля будет на складе 30 числа, если в течение этого времени уголь со склада не расходовался.
Если выписать количество угля, находящегося на складе каждого числа, получим арифметическую прогрессию. Как решить эту задачу? Неужели придется просчитывать количество угля в каждый из дней месяца? Можно ли как-то обойтись без этого? Замечаем, что до 30 числа на склад придет 29 машин с углем. Таким образом, 30 числа на складе будет 50+329=137 тонн угля.
Таким образом, зная только первый член арифметической прогрессии и разность, мы можем найти любой член последовательности. Всегда ли это так?
Проанализируем, как зависит каждый член последовательности от первого члена и разности:
:::::::::::::
Таким образом, мы получили формулу n-ого члена арифметической прогрессии.
Пример 1. Последовательность ()-арифметическая прогрессия. Найдите , если и .
Воспользуемся формулой n-ого члена ,
Ответ: 260.
Рассмотрим следующую задачу:
В арифметической прогрессии четные члены оказались затерты: 3, :, 7, :, 13: Можно ли восстановить утраченные числа?
Учащиеся, скорее всего, сначала вычислят разность прогрессии, а затем будут находить неизвестные члены прогрессии. Тогда можно предложить им найти зависимость между неизвестным членом последовательности, предыдущим и последующим.
Решение:
Воспользуемся тем, что в арифметической прогрессии разность между соседними членами постоянна. Пусть — искомый член последовательности. Тогда .Замечание. Данное свойство арифметической прогрессии является ее характеристическим свойством. Это означает, что в любой арифметической прогрессии каждый член, начиная со второго равен среднему арифметическому предыдущего и последующего ( . И, наоборот, любая последовательность, в которой каждый член, начиная со второго равен среднему арифметическому предыдущего и последующего, является арифметической прогрессией.
IV. Первичное закрепление.
- № 575 аб — устно
- № 576 авд — устно
- № 577б — самостоятельно с проверкой
Последовательность (- арифметическая прогрессия. Найдите , если и
Воспользуемся формулой n-ого члена ,
Ответ: -24,2.
№ 580 а
Найдите 23-й и n-ый члены арифметической прогрессии -8; -6,5; :
Решение: Первый член арифметической прогрессии равен -8. Найдем разность арифметической прогрессии, для этого надо из последующего члена последовательности вычесть предыдущий: -6,5-(-8)=1,5.
Воспользуемся формулой n-ого члена:
Ответ: 25.
№584 а
Найдите первый член арифметической прогрессии (), если
Решение. Воспользуемся формулой n-ого члена, записав ее для тридцатого члена последовательности:
Подставив известные значения, получаем: 128 =
, .Ответ: 12.
Задача. Числовая последовательность задана формулой
Является ли эта последовательность арифметической прогрессией?
Решение.
1-й способ. Поскольку , при всех значениях n, то последовательность является арифметической прогрессией по определению. Из полученной формулы разность этой прогрессии равна 5.
2-й способ. Если последовательность является арифметической прогрессией, то должно выполняться характеристическое свойство:.
, , . Выполнив преобразования в обратную сторону для любого n, получаем, что данная последовательность является арифметической прогрессией.Ответ: является.
Замечание. Любая арифметическая прогрессия может быть задана формулой где k и b - некоторые числа.
Задача. Седьмой член арифметической прогрессии равен 1 и равен разности между четвертым и вторым членами. Найти первый член прогрессии.
Решение. По условию , . Заметим, что , откуда .
По формуле n-ого члена , откуда
Ответ: -2.
V. Подведение итогов урока.
Вспомним начало нашего урока, ребята. Удалось ли за сегодняшний урок узнать что-то новое, сделать какие-то открытия? А какие цели урока мы ставили перед собой? Как Вы считаете, нам удалось достигнуть поставленных целей?
Домашнее задание.
Пункт 25, № 578а, № 580б, №582, №586а, №601а.
Творческое задание для сильных учеников: Докажите, что в арифметической прогрессии для любых номеров, таких что k<n, выполняются равенства и .
Спасибо за урок, ребята. Вы сегодня хорошо потрудились.
Презентация.
Арифметическая прогрессия — методическая рекомендация. Алгебра, 9 класс.
| 1. | Разность арифметической прогрессии | 2 вид — интерпретация | лёгкое | 1 Б. | Вычисление разности арифметической прогрессии, если даны последовательные члены прогрессии. |
| 2. | Нахождение члена и разности арифметической прогрессии | 2 вид — интерпретация | лёгкое | 1 Б. | Нахождение следующего члена арифметической прогрессии, если даны два предыдущих, разность прогрессии. |
| 3. | Нахождение членов арифметической прогрессии | 2 вид — интерпретация | лёгкое | 5 Б. | Нахождение первых четырёх и десятого членов арифметической прогрессии, если дана общая формула. |
| 4. | Сумма членов арифметической прогрессии | 2 вид — интерпретация | среднее | 1 Б. | Нахождение суммы первых n членов арифметической прогрессии, если известны первый член и разность. |
| 5. | Нахождение члена арифметической прогрессии, даны разность и первый член | 2 вид — интерпретация | среднее | 3 Б. | Вычисление n-ого члена арифметической прогрессии, если даны разность и первый член прогрессии. |
| 6. | Сумма первых членов арифметической прогрессии | 2 вид — интерпретация | среднее | 4 Б. | Вычислить сумму первых n членов арифметической прогрессии, если даны первые два члена. |
| 7. | Разность арифметической прогрессии | 2 вид — интерпретация | лёгкое | 2 Б. | Вычисление разности и третьего члена арифметической прогрессии. |
| 8. | Сумма членов арифметической прогрессии | 2 вид — интерпретация | среднее | 2 Б. | Вычисление суммы членов арифметической прогрессии, если даны два первых члена. |
| 9. | Прогрессия в текстовой задаче, вычисление высоты | 2 вид — интерпретация | среднее | 4 Б. | Использование прогрессии при вычислении высоты. |
| 10. | Сумма натуральных чисел | 3 вид — анализ | сложное | 4 Б. | В условии дан остаток деления. При решении используется неравенство. |
| 11. | Вычисление разности при наименьшем значении членов прогрессии | 3 вид — анализ | сложное | 4,5 Б. | При вычислении используются свойства квадратичной функции. |
| 12. | Арифметическая прогрессия и трапеция | 2 вид — интерпретация | сложное | 8 Б. | Трапеция и арифметическая прогрессия. |
Типовые задачи по теме «Арифметическая прогрессия». Видеоурок. Алгебра 9 Класс
Представляем вашему вниманию видеоурок по теме «Типовые задачи по теме “Арифметическая прогрессия”». В начале урока преподаватель систематизирует знания учащихся по пройденному ранее материалу «Арифметическая прогрессия»: дает определение, приводит формулы и определяет характеристики арифметической прогрессии. После краткого повторения теории преподаватель переходит к рассмотрению решений конкретных задач.
Тема: Прогрессии
Урок: Решение типовых задач по теме “Арифметическая прогрессия”
1. Числовая последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называется арифметической прогрессией, число d называется ее разностью.
 .
.
2.  – формула n-го члена арифметической прогрессии.
– формула n-го члена арифметической прогрессии.
 , т.е. n-й член арифметической прогрессии зависит от n, значит, является функцией натурального аргумента.
, т.е. n-й член арифметической прогрессии зависит от n, значит, является функцией натурального аргумента.
3.  – первая формула суммы первых n членов арифметической прогрессии.
– первая формула суммы первых n членов арифметической прогрессии.
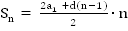 – вторая формула суммы первых n членов арифметической прогрессии.
– вторая формула суммы первых n членов арифметической прогрессии.
4. Характеристическое свойство арифметической прогрессии:

исловая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, кроме первого (и последнего в случае конечной последовательности), равен среднему арифметическому предшествующего и последующего членов.
5. Обобщение характеристического свойства арифметической прогрессии:
n-й член арифметической прогрессии равен среднему арифметическому равноотстоящих членов, т.е.  при допустимых значениях p (
при допустимых значениях p (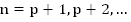 ).
).
6. Свойство членов арифметической прогрессии: 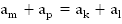 , если
, если  . Например,
. Например,  .
.
Задача 1.
Дано: n-й член последовательности задан формулой
а. 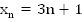 , б.
, б.  .
.
Доказать:  ,
,  .
.
Доказательство.
1-й способ. Поскольку 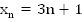 и
и
Арифметическая прогрессия. Алгебра, 9 класс: уроки, тесты, задания.
| 1. |
Разность арифметической прогрессии
Сложность: лёгкое |
1 |
| 2. |
Нахождение члена и разности арифметической прогрессии
Сложность: лёгкое |
1 |
| 3. |
Нахождение членов арифметической прогрессии
Сложность: лёгкое |
5 |
| 4. |
Сумма членов арифметической прогрессии
Сложность: среднее |
1 |
| 5. |
Нахождение члена арифметической прогрессии, даны разность и первый член
Сложность: среднее |
3 |
| 6. |
Сумма первых членов арифметической прогрессии
Сложность: среднее |
4 |
| 7. |
Разность арифметической прогрессии
Сложность: лёгкое |
2 |
| 8. |
Сумма членов арифметической прогрессии
Сложность: среднее |
2 |
| 9. |
Прогрессия в текстовой задаче, вычисление высоты
Сложность: среднее |
4 |
| 10. |
Сумма натуральных чисел
Сложность: сложное |
4 |
| 11. |
Вычисление разности при наименьшем значении членов прогрессии
Сложность: сложное |
4,5 |
| 12. |
Арифметическая прогрессия и трапеция
Сложность: сложное |
8 |
Обзорный урок по теме «Арифметическая прогрессия». Видеоурок. Алгебра 9 Класс
Данный видеоурок поможет пользователям получить представление о теме «Обзорный урок по теме «Арифметическая прогрессия»». На этом уроке учащиеся вспомнят теорию по упомянутой теме, а именно: повторят определение арифметической прогрессии, формулу n члена арифметической прогрессии, формулу суммы n первых членов арифметической прогрессии, суть свойств арифметической прогрессии. А также предлагает закрепить полученные знания в ходе решения задач.
Тема: Арифметическая прогрессия
Урок: Обзорный урок по теме “Арифметическая прогрессия”
Сегодня у нас обзорный урок по теме «Арифметическая прогрессия».
Наша цель – вспомнить теорию по теме «Арифметическая прогрессия», обсудить ее интересные свойства.
Числовая последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называется арифметической прогрессией, число d называется ее разностью.
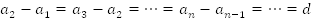 .
.
Задано  и d, тогда
и d, тогда 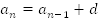 — рекуррентная формула для арифметической прогрессии для n=2,3,4,….
— рекуррентная формула для арифметической прогрессии для n=2,3,4,….
Пример.
 1; 3; 5; 7; …} – арифметическая прогрессия.
1; 3; 5; 7; …} – арифметическая прогрессия.
 ;
; 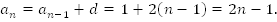

Получили формулу для обозначения нечетных чисел.
Из определения арифметической прогрессии следует истинность равенств:  . Тогда
. Тогда


 и т.д. Значит,
и т.д. Значит, 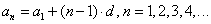
Т.е., зная первый член и разность арифметической прогрессии, можно найти любой ее член.
 – формула n-го члена арифметической прогрессии.
– формула n-го члена арифметической прогрессии.
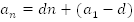 , т.е. n-й член арифметической прогрессии линейно зависит от n. Арифметическая прогрессия является функцией натурального аргумента:
, т.е. n-й член арифметической прогрессии линейно зависит от n. Арифметическая прогрессия является функцией натурального аргумента: , где
, где 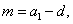
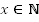 .
.
Открытый урок алгебра 9 класс «Арифметическая прогрессия »
Открытый урок алгебра 9 класс
«Арифметическая прогрессия »
Тип урока: обобщающий.
Задачи:
совершенствовать навыки нахождения п-го члена и суммы п — первых членов арифметической прогрессии с помощью формул; показать детям практическую значимость ЗУН по этой теме.
развивать грамотную математическую речь; самостоятельность, дисциплинированность, умение высказывать свои мысли последовательно.
Оборудование: мультимедийный проектор, интерактивная доска,
Раздаточный дидактический материал для учащихся.
Ход урока.
Орг.момент, приветствие, пожелания.
Здравствуйте ребята и наши гости. (садитесь) сядьте прямо.
Мы начинаем наш урок.
— Давайте улыбнемся друг другу . Пусть сегодняшний урок принесет нам всем радость общения и удачу.
А сейчас я бы хотела что бы вы ответили вот на этот вопрос.
Для чего вы пришли на урок? ( передают смайлик друг другу).
Сегодня на уроке, ребята, вас ожидает много интересных заданий, новых открытий, а помощниками вам будут: внимание, находчивость, смекалка.
А сейчас вы должны определить, какая сегодня тема урока.
Мотивационное начало
Открываем тетради с Д\з.
Учащимся предлагаются проверить домашнее задание. По ответам определяем слово прогрессия.
«Прогрессио» в переводе с греческого языка означает движение вперёд.
Закончился двадцатый век.
Куда стремится человек?
Изучен космос и моря,
Строенье звезд и вся земля.
Но математиков зовет
Известный лозунг

Вместе с вами мы будем двигаться только вперёд, т.к. слово «Прогрессио» в переводе с греческого языка означает движение вперёд.
С какой прогрессией вы уже знакомы?
Как можно сформулировать тему данного урока.
Учащиеся формулируют тему урока.
Тема нашего урока : «Арифметическая прогрессия»
(Открыли тетради и записали сегодняшнее число и тему урока.)
Давайте вместе с вами определим цели урока.
На уроке мы с вами повторим и обобщим все знания о арифметической прогрессии, повторим формулы, порешаем задачи на нахождение н-го члена и суммы н- первых членов арифметической прогрессии. Узнаем много интересного.
Работать вы будете в группах.
Ваша главная задача – быть внимательными, активными, находчивыми, а главное – трудолюбивыми и дисциплинированными и аккуратными.
Показать , что мы знаем и как умеем работать.
2.Устная работа. А теперь работаем устно.
Только ответьте , сразу на вопрос какую прогрессию называют арифметической?
1. А сейчас в качестве небольшой разминки выполним задание. «Бездонный сундучок»
Арифметическая не арифметическая
3;-1;-5;-9;-13;-17… 2;7;9;12…
10;9;8;7;6… -1;1;-1;1;-1;1..
3;5;7;9;11… 4;8;16;32..
2;4;6;8;10;12… -17;25;36;48…
2.В последовательности
(хn): 3; 0; -3; -6; -9; -12;… (3 ; -3; -12)
назовите первый, третий и шестой члены
3..Последовательность а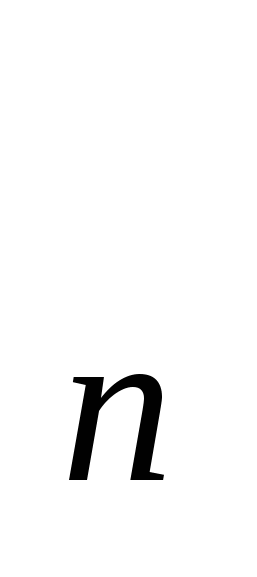 задана формулой а
задана формулой а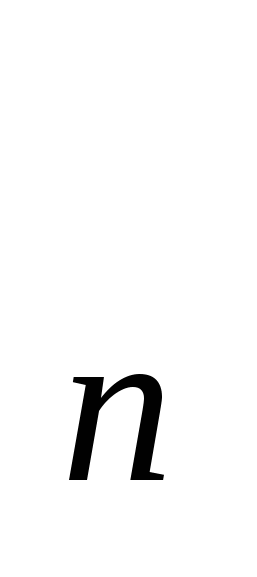 = 6n — 1.
= 6n — 1.
Найдите: a , а
, а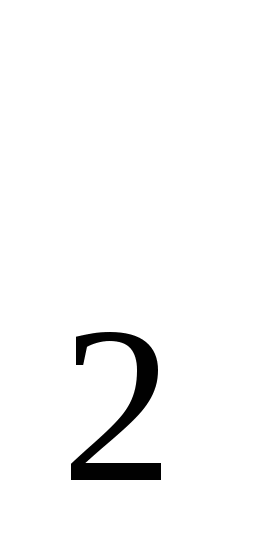 , a
, a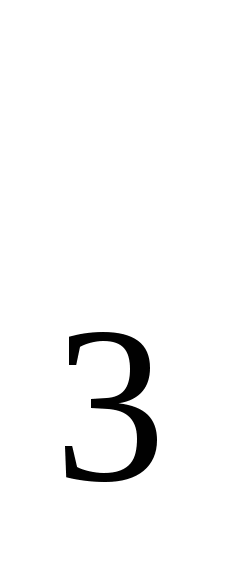 ; а
; а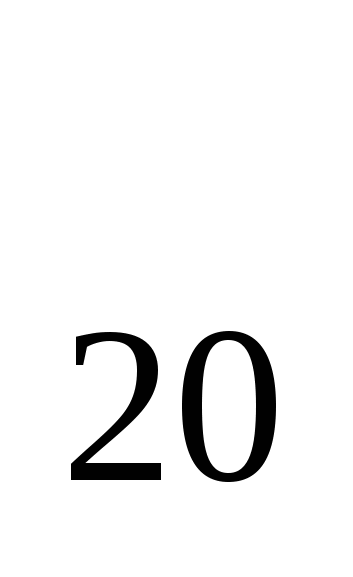 , (5; 11; 17; 119)
, (5; 11; 17; 119)
.
3..Продолжите данную последовательность: 5; 9; 13; 17;… (21; 25; 29; 33; 37).
4.А сейчас мы выясним, как вы знаете формулы по данной теме.
Составить из данных частей, формулы и назвать их.
5. Тренировочные упражнения. (Карусель)
Как вы думаете , а где ещё применяют арифметическую прогрессию? Проверим, используются ли формулы прогрессии другими науками.
А узнаем мы это ,решив задание.
Каждый уч-ся группы решает по одному заданию. Решив передаёт следующему. Когда я говорю: стоп. “Карусель” останавливается.
Проверяем ответы.
Под каждым числом зашифрованы предметы где используется арифметическая прогрессия.(мозаика) 102—литература, 16 –физика,6,5-биология, -1,2—химия, 23- прогрессия вокруг нас
Вам на дом было дано задание, подготовить сообщения , В каких науках встречается прогрессия. Сообщения детей .
Рассмотрим прогрессии в литературе.
Даже в литературе мы встречаемся с математическими понятиями!
Так, вспомним строки из «Евгения Онегина».
…Не мог он ямба от хорея,
Как мы не бились отличить…
Ямб — это стихотворный размер с ударением на чётных слогах 2; 4; 6; 8… Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и разностью прогрессии 2.
Ямб «Мой дЯдя сАмых чЕстных прАвил…»
Прогрессия: 2; 4; 6; 8…
Хорей — это стихотворный размер с ударением на нечётных слогах стиха. Номера ударных слогов образуют арифметическую прогрессию 1; 3; 5; 7… С первым членом 1 и разностью прогрессии 2.
Хорей «Я пропАл, как звЕрь в загОне» (Пастернак)
Прогрессия: 1; 3 ;5; 7…
Классический хорей:
Листья падают в саду…
В этот старый сад, бывало,
Ранним утром я уйду
И блуждаю, где попало. (И.Бунин)
Вот ещё хорей (тоже из Бунина):
Яблони и сизые дорожки,
Изумрудно-яркая трава
На берёзах — серые серёжки
И ветвей плакучих кружева.
В литературе:
Хорей: «Ветер по морю гуляет…»
Ямб: «Мой дядя самых честных правил…»
В биологии:
Высота саженца 60 см, первые полгода она увеличивается ежемесячно в среднем на 4 см.
В физике:
Брошенное с некоторой высоты тело в первую секунду падает на 5 м, а в каждую следующую на 9,8 м больше, чем в предыдущую.
В химии:
Заряды ядер атомов элементов, расположенных в таблице Менделеева друг за другом, отличаются на +1. Заряд ядра атома водорода (№1) равен +1.
Итак, арифметическая прогрессия вокруг нас
6.«Действительно ли прогрессии играют большую роль в повседневной жизни человека?»
Вообще, зная формулы арифметической прогрессии, можно решить много интересных задач литературного, исторического и практического содержания.
Рассмотрим прогрессии в жизни и быту. ( Работа в группах)
(Дети решают задачи, потом проверяем, и один уч-ся с каждой группы идёт в другие группы и расказывает как решена задача).
Задача 1: При свободном падении тело проходит в первую секунду 5 м, а в каждую следующую на 10 м больше. Найдите глубину шахты, если свободно падающее тело достигло ее дна через 5 с после начала падения.
Дано:
(аn) – арифм.прогрессия
а1=5, d = 10
Найти: S5 — ?
Решение:
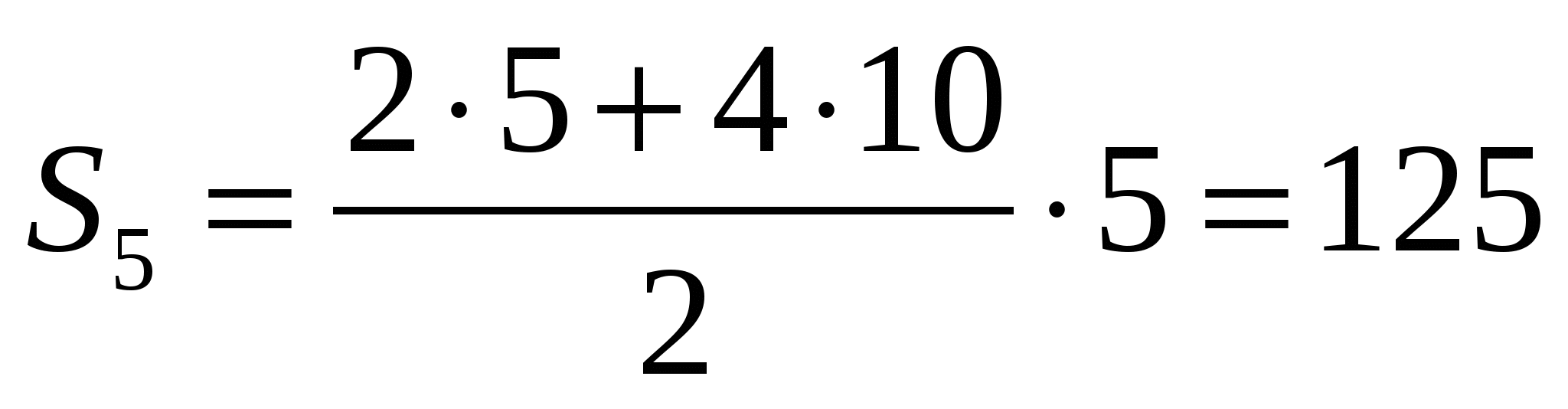
Ответ: 125 м
З адача 2: При хранении бревен строевого леса их укладывают как показано на рисунке. Сколько брёвен находится в одной кладке, если в ее основании положено 12 бревен?
адача 2: При хранении бревен строевого леса их укладывают как показано на рисунке. Сколько брёвен находится в одной кладке, если в ее основании положено 12 бревен?

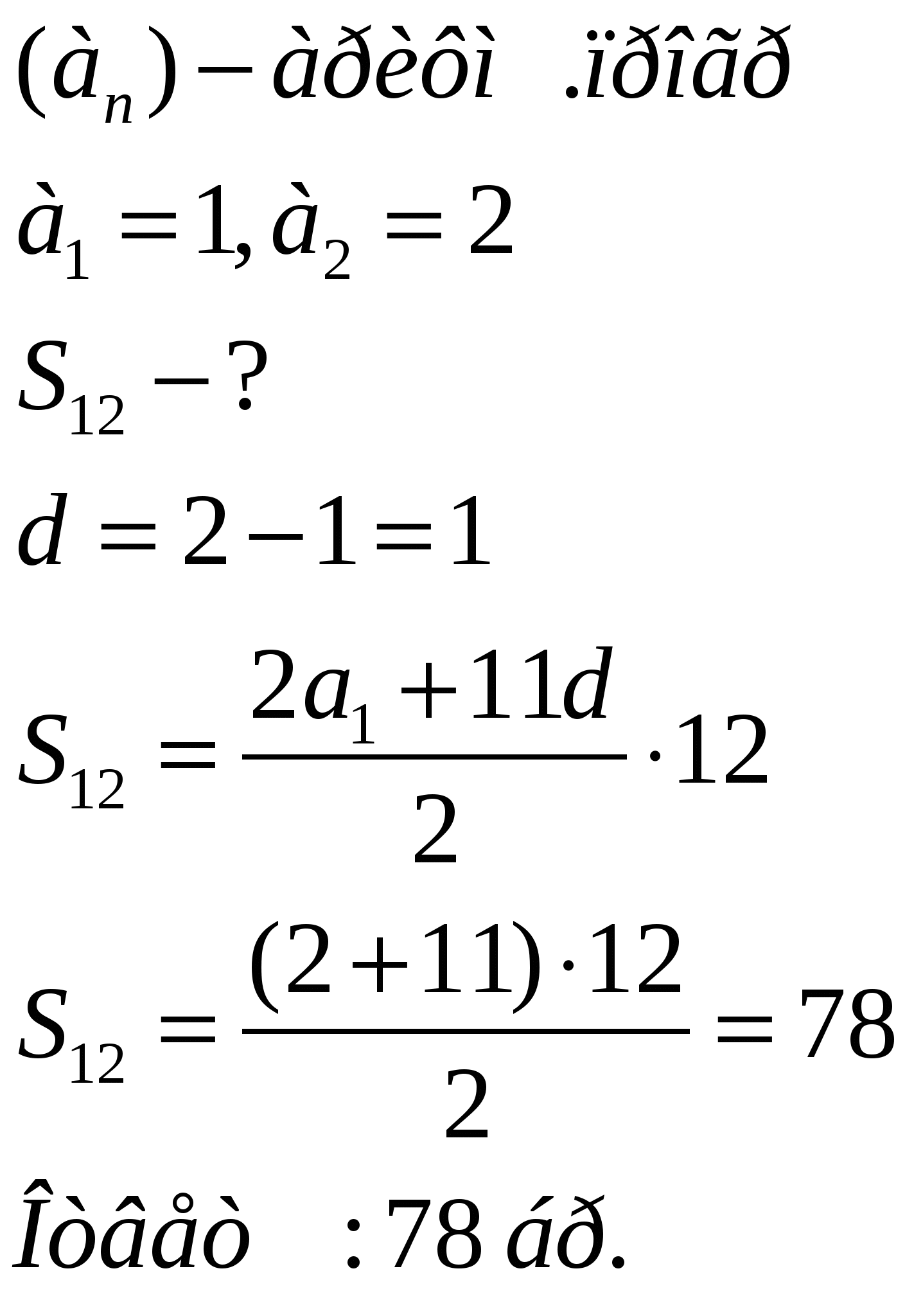
Задача 3.
Родители ко Дню рождения своего сына Андрея решили купить и обновить ему мобильный телефон. Для этого они в первый месяц отложили 1500 тысячи тенге , а в каждый последующий месяц они откладывали на 500 тенге больше, чем в предыдущий. Какая сумма будет у родителей Андрея через 10 месяцев?
Д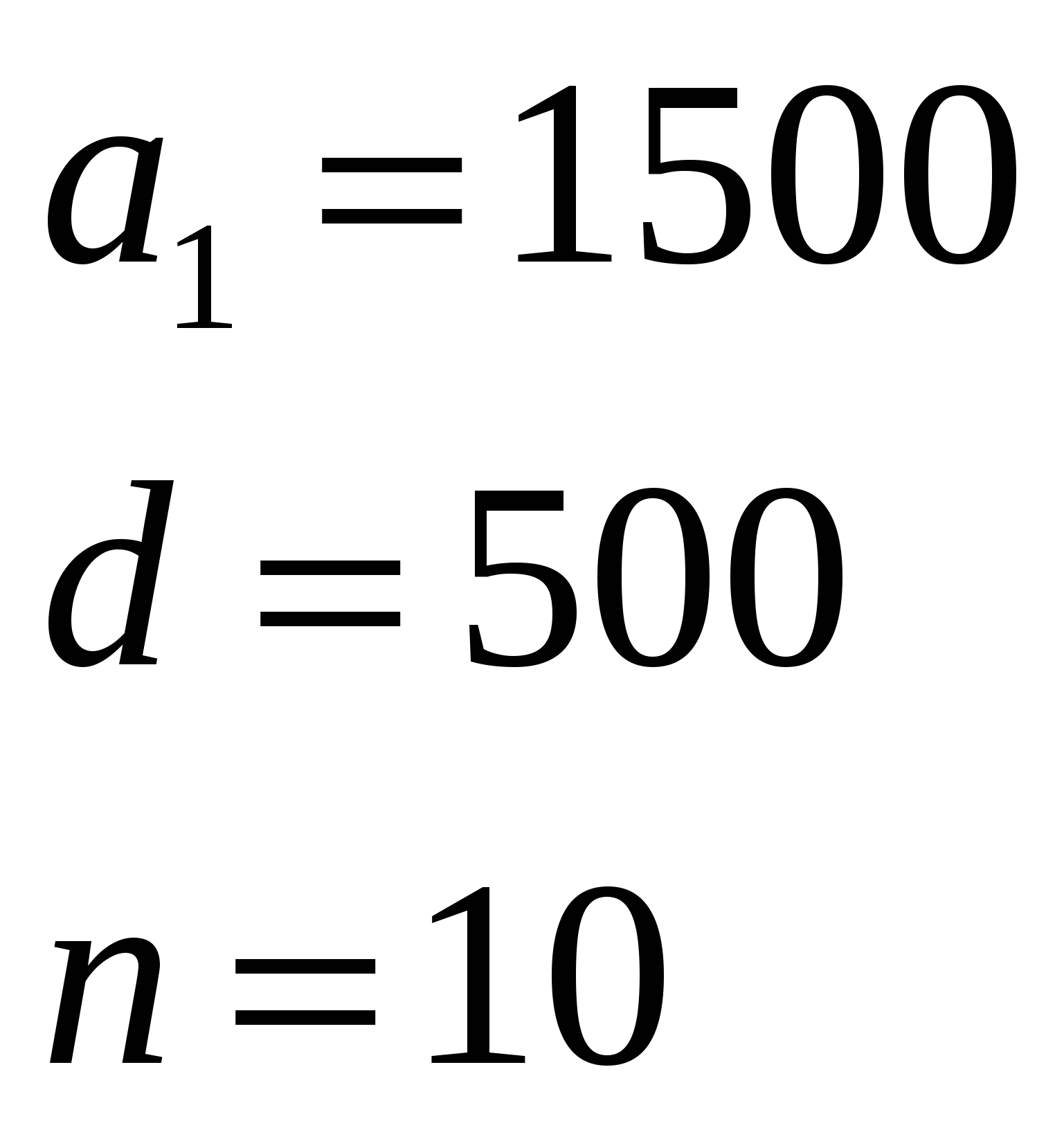 ано:
ано:
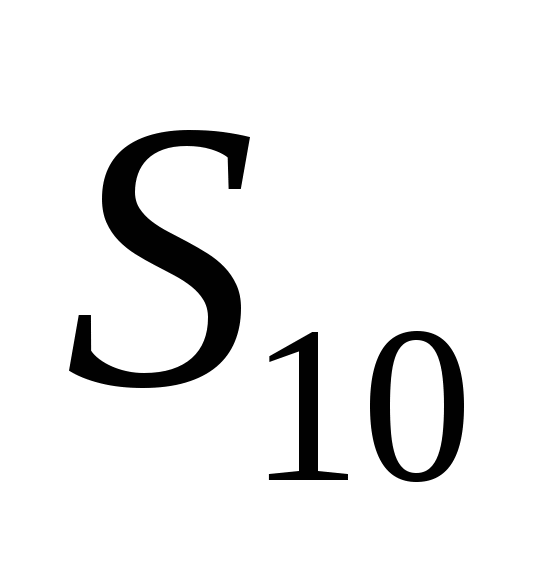
Найти:
Решение:
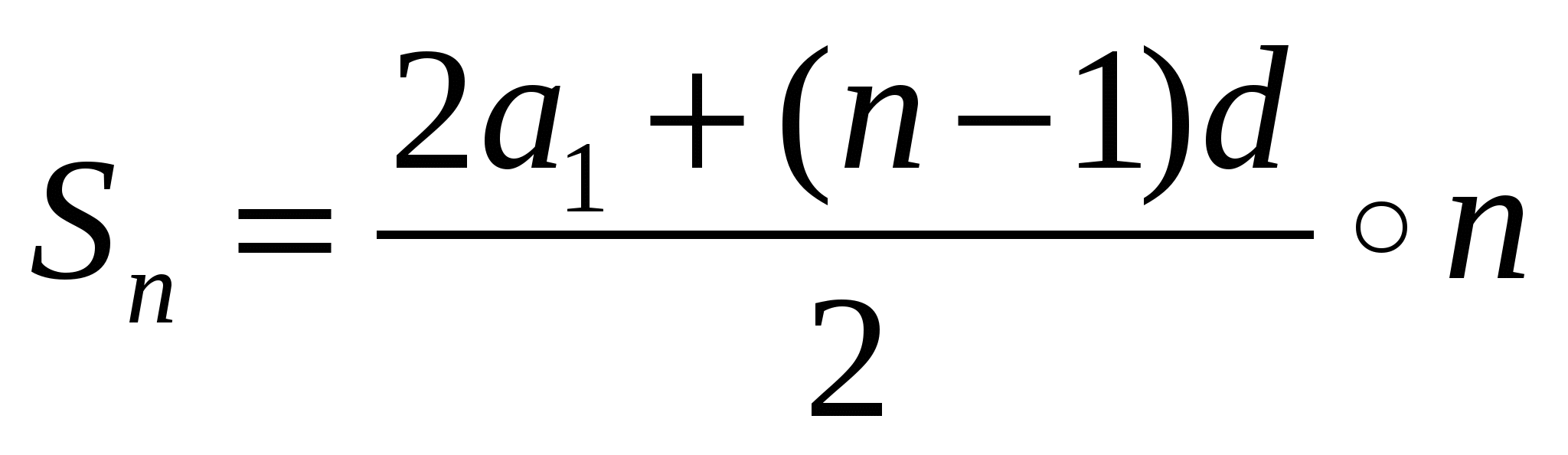
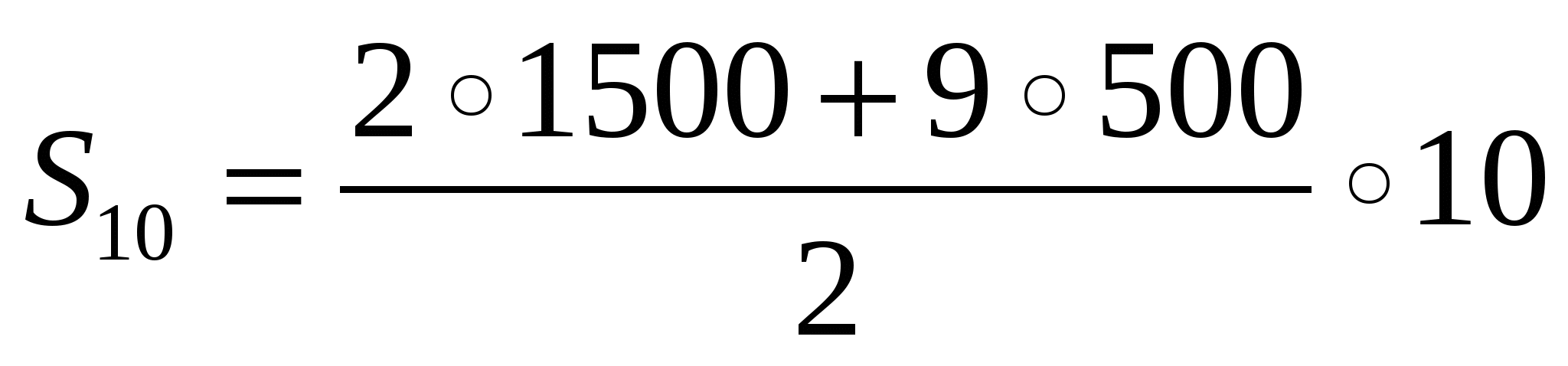
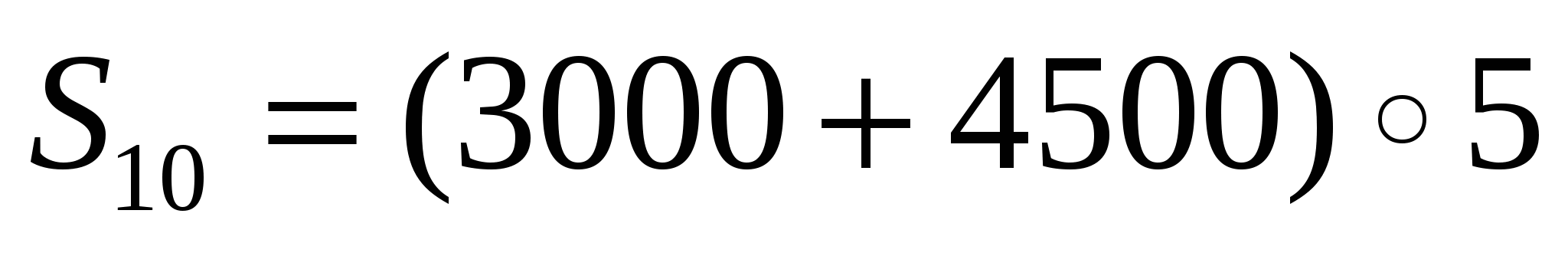
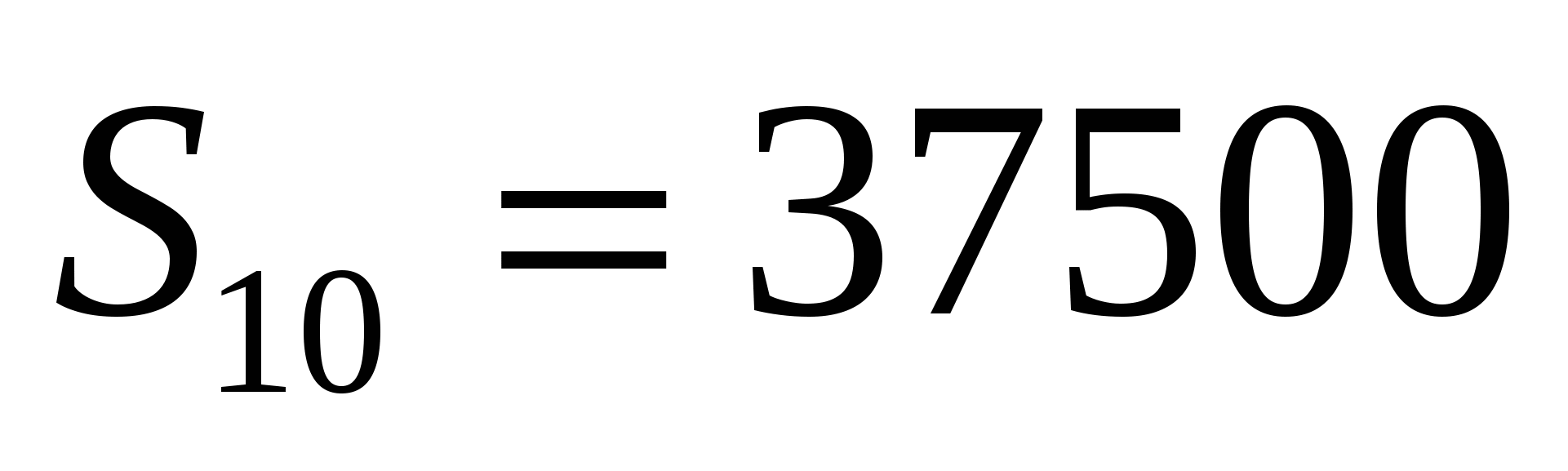
О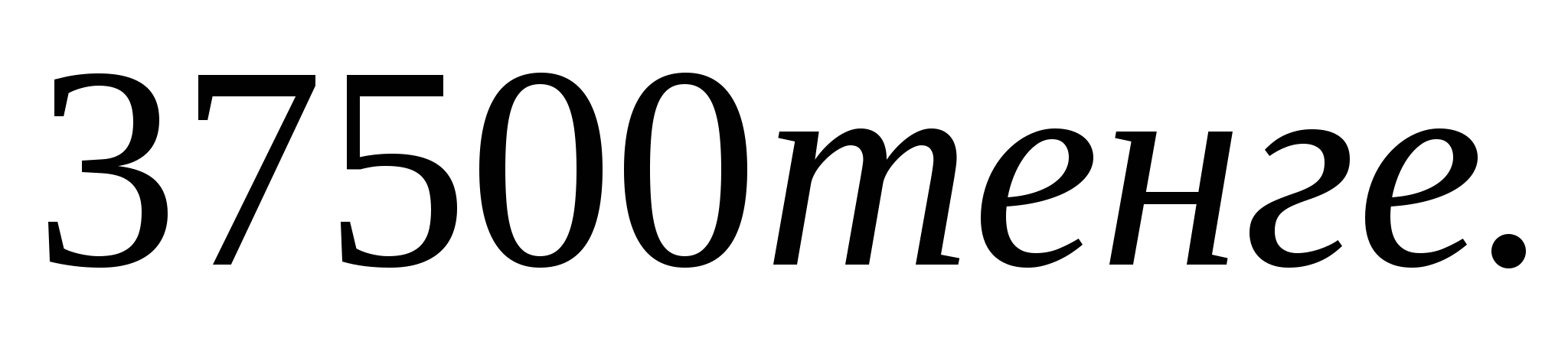 твет:
твет:
Задача 4
Курс воздушных ванн начинают с 15 мин. в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1 час 45 минут?
Дано: арифметическая прогрессия, 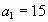 мин,
мин,  мин,
мин, 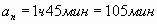
Найти: 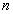
Решение:
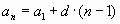
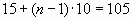
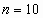
Ответ: 10 дней следует принимать ванны.
Когда задачи решены .Проверяем ответы. Потом один участник с каждой группы идёт в другую группу и объясняет решение задачи.
Молодцы ! Справились. Теперь вы знаете как можно с помощью прогрессии решить задачи практического содержания.
7. Сегодня вы работаете в группах. А какая группа лучше решает? Давайте определим? А сейчас с оревнование.
Работа в группах (РЕШЕНИЕ ЗАДАНИЙ) СОРЕВНОВАНИЕ. КНОПКА РОСТА.
Работа в группах
1группа
1. В арифметической прогрессии (аn): 15; 11; 7;… разность d=?
2. а1= — 4; d=3. Найдите а20.
3. а1= — 3; d=7. Найдите S7.
2 группа
1.а7=21; а9=29. Найдите d; а1.
2. а1= — 3; d=7. Найдите S7.
3. В арифметической прогрессии
(аn): 12; 9; 6;…разность d=?
3 группа
а1=5; d=-7. Найдите а30
а7=22; а9=32. Найдите d; а1.
а1= — 2; d=9. Найдите S7.
4 группа
1. а1= — 4; d=3. Найдите а20.
2. а1=5; d=-7. Найдите а30.
3. (аn): 5; 2; -1; -4;… арифметическая прогрессия. Найдите S20.
Ответы к тесту
№ п/п
1 группа
2 группа
3 группа
4 группа
1.
d= — 4
d= 4 а =-3
=-3
a30= — 198
a20=53
2.
a20=53
S7=126
d=5; a1= — 8
a30= — 198
3.
S7=126
d= — 3
S7=175
S20= — 470
Победила группа.
Гимнастика для глаз
Вертикальные движения глаз вверх-вниз.
Горизонтальное вправо-влево.
Вращение глазами по часовой стрелке и против.
Закрыть глаза и представить по очереди цвета радуги как можно отчётливее.
Глазами «нарисовать» кривую, несколько раз, сначала в одном, а затем в другом направлении.
8.Вы выпускной класс и вам в этом году сдавать гос. экзамены, поэтому давайте решим задание, которое встречается на экзаменах и ЕНТ.
Найдите сумму первых двадцати членов арифметической прогрессии (сn),если
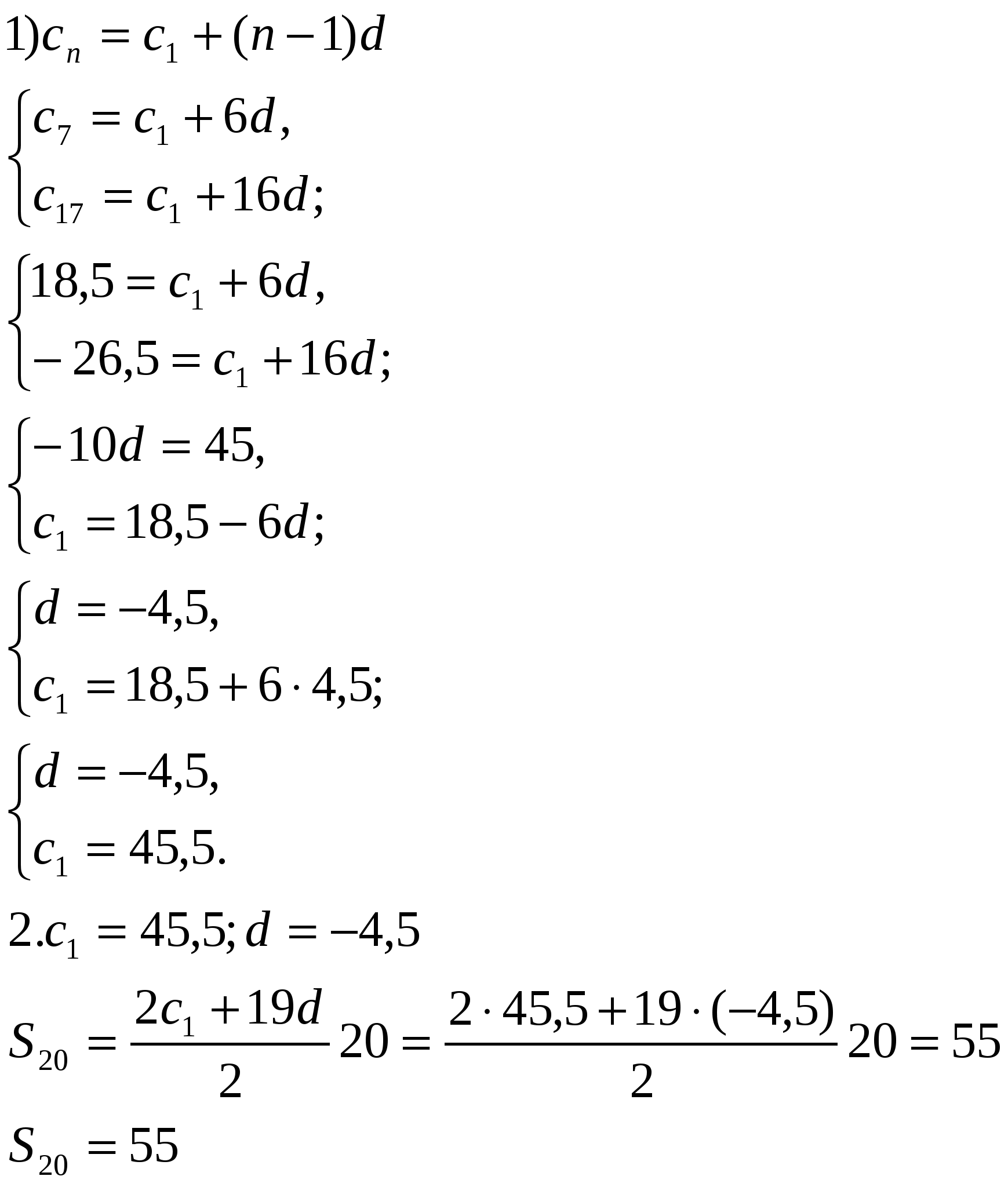
с7=18,5 и с17= — 26,5.
Решение:
Ответ: 55.
Итак, сегодня мы с вами говорили о прогрессии, которая называется арифметической. Посмотрите на эти прогрессии.
5; 10; 15; 20…
-1; -3; -5; -7…
2; 4; 8; 16…
-3;-9;-27;-81…
Какие это прогрессии?
2; 4; 8; 16… ув в 2
-3;-9;-27;-81… ув в 3
Каким способом получена эта прогрессия?
Но есть и другая прогрессия. А ответить на этот вопрос вы сможете, изучив другую прогрессию, которая называется геометрической .
А вот что это за прогрессия, мы узнаем на следующих уроках.
9. А подведением итога нашего урока будет тест. Проверим как вы усвоили эту тему.
Тест.
Обменяться тетрадями. Взаимопроверка.
10..Домашнее задание:
№258, №266(1)
Творческое: найти задачу по данной теме из
различных областей. И решить.
11.Рефлексия.
12.Итог урока.
Вот наш урок подошёл к концу. На уроке вы работали все хорошо, особенно хочется отметить …..
Дать словесную оценку тем кто хорошо работал.

Спасибо за внимание, благодарю за сотрудничество.
Задачи для ОГЭ. Арифметическая прогрессия
Задачи для ОГЭ с ответами и решениями
Арифметическая прогрессия
перейти к содержанию задачника
- Дана арифметическая прогрессия , разность которой равна , . Найдите .
- Дана арифметическая прогрессия , разность которой равна , . Найдите .
- Дана арифметическая прогрессия , разность которой равна , . Найдите сумму первых семи ее членов.
- Дана арифметическая прогрессия , разность которой равна , . Найдите сумму первых 15 ее членов.
- Арифметическая прогрессия задана условием . Найдите .
- Арифметическая прогрессия задана условиями , . Найдите .
- Арифметическая прогрессия задана условиями , . Найдите .
- Дана арифметическая прогрессия 11; 18; 25; … . Какое число стоит в этой последовательности на 6-м месте?
- Дана арифметическая прогрессия 7; 12; 17; … . Какое число стоит в этой последовательности на 7-м месте?
- Дана арифметическая прогрессия 10; 5; 0; … . Какое число стоит в этой последовательности на 61-м месте?
- Арифметическая прогрессия задана условиями , . Найдите сумму первых 17 ее членов.
- Дана арифметическая прогрессия 35; 32; 29; … . Найдите первый отрицательный член этой прогрессии.
- В первом ряду кинозала 40 мест, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в ряду с номером ?
- В первом ряду кинозала 30 мест, а в каждом следующем на 1 больше, чем в предыдущем. Сколько мест в ряду с номером ?
- Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 16-й строке?
- Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 4 квадратов больше, чем в предыдущей. Сколько квадратов в 12-й строке?
- В арифметической прогрессии , . Найдите разность арифметической прогрессии.
- В арифметической прогрессии , . Найдите разность арифметической прогрессии.
- Дана арифметическая прогрессия . Найдите сумму первых десяти ее членов.
- Арифметическая прогрессия задана условием . Найдите сумму первых шести членов прогрессии.
- Арифметическая прогрессия задана условием . Найдите сумму первых пяти членов прогрессии.
- Арифметическая прогрессия задана условием . Найдите сумму первых десяти членов прогрессии.
перейти к содержанию задачника
Ответы
- -39,5
- 20,6
- 105,7
- 453
- 73,9
- -7
- -9
- 46
- 37
- -290
- -2329
- -1
- 122
- 48
- -0,6
- 10
- 75
- -40,5
- 275
- -59,5
Метки ОГЭ. Смотреть запись.