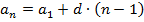Типовые задачи по теме «Арифметическая прогрессия» (продолжение)

В ходе урока все желающие смогут получить представление о теме «Типовые задачи по теме «Арифметическая прогрессия» (продолжение)». На данном уроке преподаватель повторяет ранее изученный материал касательно арифметической прогрессии. В процессе занятия у учащихся нарабатываются навыки решения типовых разноплановых задач по теме «Арифметическая прогрессия».

Тема: Прогрессии

 Урок: Решение типовых задач по теме “Арифметическая прогрессия”

1. Числовая последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называется арифметической прогрессией, число d называется ее разностью. 

.

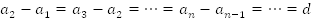2.

 – формула n-го члена арифметической прогрессии.

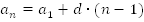
, т.е. n-й член арифметической прогрессии зависит от n, значит,  является функцией натурального аргумента.

3.  – первая формула суммы первых n членов арифметической прогрессии.

 – вторая формула суммы первых n членов арифметической прогрессии.

4. Характеристическое свойство арифметической прогрессии:

Числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, кроме первого (и последнего в случае конечной последовательности), равен среднему арифметическому предшествующего и последующего членов.

5. Обобщение характеристического свойства арифметической прогрессии:

n-й член арифметической прогрессии равен среднему арифметическому равноотстоящих членов, т.е. 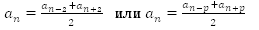при допустимых значениях p ().

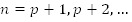6. Свойство членов арифметической прогрессии:  , если

. Например, .

Задача 1.

Дано: .

Найти: .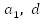

Решение.

Воспользуемся формулой n-го члена арифметической прогрессии

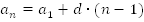 для выражения членов данной прогрессии (основной метод решения подобных  задач):

 

 Составим и решим систему:

Прогрессии. Арифметическая прогрессия. Видеоурок. Алгебра 9 Класс

Урок посвящен повторению понятия «арифметическая прогрессия». Рассматриваются определение и основные формулы. На конкретных примерах показаны основные приемы при решении типовых заданий.

Чтобы найти сумму, можно складывать числа не по порядку.

Заметим:

первое и последнее слагаемое дают в сумме 101;

второе и предпоследнее дают в сумме 101;

третье с начала и третье с конца – в сумме тоже 101.

Чисел всего 100, значит, подобным образом составленных сумм 50.

Этот пример иллюстрирует формулу суммы первых n членов арифметической прогрессии.

Арифметическая прогрессия – это такая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.

Это число d называется разностью арифметической прогрессии

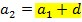
По определению арифметической прогрессии второй член равен предыдущему, т. е. первому, сложенному с d.

Аналогично, третий член равен второму, сложенному с d. Второй же член равен первому плюс d. Итак, мы выразили третий член через первый и разность арифметической прогрессии.

Любой член арифметической прогрессии можно выразить через . Поэтому арифметическую прогрессию можно задать, указав ее первый член и разность.

Слева и справа – разность арифметической прогрессии.

Поменяем в этом равенстве  местами.

Итак,  является средним арифметическим предшествующего и последующего члена.

Это справедливо для любого члена арифметической прогрессии, кроме первого и последнего. Более того, это критерий для определения, является ли данная последовательность арифметической прогрессией.

Задачи по теме «Арифметическая и геометрическая прогрессии»

Данный видеоурок поможет пользователям получить представление о теме «Задачи по теме “Арифметическая и геометрическая прогрессии”». Дается определение арифметической прогрессии, формулы n-го члена и суммы n-х членов, характеристическое свойство арифметической прогрессии, определение и основные свойства геометрической прогрессии. Рассматриваются примеры задач арифметической и геометрической прогрессии.

Здесь мы рассмотрим задачи на арифметическую и геометрическую прогрессии, начнем с краткого повторения теории.

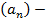 арифметическая прогрессия, если

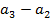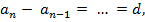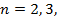= = … =  где  – разность прогрессии.  – формула го члена;  – сумма n членов;   , ,… — характеристическое свойство арифметической прогрессии; 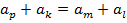, если

 

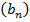 – геометрическая прогрессия, если , где – знаменатель прогрессии,

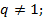
 – формула n-го члена;  – сумма n первых членов, ,  — характеристическое свойство; , если

Рассмотрим задачи

1.      Три числа составляют конечную геометрическую прогрессию. Если из последнего числа вычесть 16, то получится конечная арифметическая прогрессия. Найдите два последних числа, если первое равно 9. Обозначим искомые числа y и z. Дано:

» Арифметическая прогрессия» 9 класс

1. Задание 11 № 35

Дана арифметическая прогрессия: 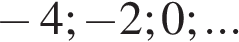 Найдите сумму первых десяти её членов.

2. Задание 11 № 113

Дана арифметическая прогрессия 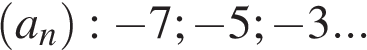  Найдите  .

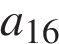3. Задание 11 № 165

Дана арифметическая прогрессия 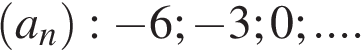  Найдите сумму первых десяти её членов.

4. Задание 11 № 137301

Выписаны первые несколько членов арифметической прогрессии: 3; 6; 9; 12;… Какое из следующих чисел есть среди членов этой прогрессии?

 

1) 83

2) 95

3) 100

4) 102

6. Задание 11 № 137303

В первом ряду кинозала 30 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в ряду с номером n?

 

1) 

2) 

3) 

4) 

8. Задание 11 № 137305

Арифметическая прогрессия задана условиями: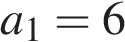, . Какое из данных чисел является членом этой прогрессии?

 

1) 80

2) 56

3) 48

4) 32

9. Задание 11 № 311254

Найдите сумму всех отрицательных членов арифметической прогрессии: −8,6; −8,4; …

10. Задание 11 № 311330

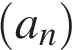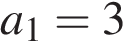Арифметическая прогрессия  задана формулой n-го члена  и известно, что . Найдите пятый член этой прогрессии.

11. Задание 11 № 311363

В арифметической прогрессии 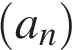   известно, что  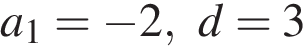. Найдите четвёртый член этой прогрессии.

12. Задание 11 № 311909

Арифметическая прогрессия задана условиями: 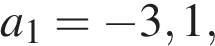 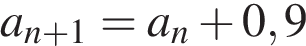. Найдите сумму первых 19 её членов.

14. Задание 11 № 314408

Найдите сумму всех положительных членов арифметической прогрессии 11,2; 10,8; …

16. Задание 11 № 314425

Найдите сумму всех отрицательных членов арифметической прогрессии –7,2; –6,9; …

17. Задание 11 № 314619

Арифметическая прогрессия (a_n) задана условиями: a₁ = 3, a_n + 1 = a_n + 4. Найдите a₁₀.

18. Задание 11 № 314628

Записаны первые три члена арифметической прогрессии: 20; 17; 14. Какое число стоит в этой арифметической прогрессии на 91-м месте?

19. Задание 11 № 314653

Дана арифметическая прогрессия (а_n): −6; −2; 2; … . Найдите a₁₆.

21. Задание 11 № 321384

В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?

Прогрессии. Алгебра, 9 класс: уроки, тесты, задания.

Вход Вход Регистрация Начало Поиск по сайту ТОПы Учебные заведения Предметы Проверочные работы Обновления Новости Переменка Отправить отзыв

• Предметы
• Алгебра
• 9 класс

1. Числовые последовательности

2. Арифметическая прогрессия

3. Геометрическая прогрессия

Отправить отзыв Нашёл ошибку? Сообщи нам! Copyright © 2020 ООО ЯКласс Контакты Пользовательское соглашение

Тестовые задания по теме «Арифметическая прогрессия», 9 класс

Тестовые задания по теме: «Арифметическая прогрессия»

Часть 1.

А1. Последовательность (а_n) задана формулой а_n = 2n — n². Найдите пятый член этой последовательности.

А2. Первый член и разность арифметической прогрессии (а_n) соответственно равны 2 и

-3. Найдите шестой член этой прогрессии.

А3. Второй член арифметической прогрессии (а_n) равен 4, а шестой равен 14. Найдите разность этой прогрессии.

А4. Найдите сумму десяти первых членов арифметической прогрессии, если первый член равен 2, а разность равна 4.

Часть 2.

В1. Дана арифметическая прогрессия 3; 2,8; 2,6 … Сколько в этой прогрессии положительных членов?

В2. В арифметической прогрессии (а_n), а₃ = 10, а₇ = 40. Найдите а₅?

В3. Найдите сумму всех четных натуральных чисел от 10 до 100 включительно.

Часть 3.

С1. Найдите сумму первых тридцати членов последовательности (х_n), заданной формулой

х_n = 4n – 1

Тестовые задания по теме: «Арифметическая прогрессия»

Часть 1.

А1. Последовательность (а_n) задана формулой а_n = 2n — n². Найдите пятый член этой последовательности.

А2. Первый член и разность арифметической прогрессии (а_n) соответственно равны 2 и

-3. Найдите шестой член этой прогрессии.

А3. Второй член арифметической прогрессии (а_n) равен 4, а шестой равен 14. Найдите разность этой прогрессии.

А4. Найдите сумму десяти первых членов арифметической прогрессии, если первый член равен 2, а разность равна 4.

Часть 2.

В1. Дана арифметическая прогрессия 3; 2,8; 2,6 … Сколько в этой прогрессии положительных членов?

В2. В арифметической прогрессии (а_n), а₃ = 10, а₇ = 40. Найдите а₅?

В3. Найдите сумму всех четных натуральных чисел от 10 до 100 включительно.

Часть 3.

С1. Найдите сумму первых тридцати членов последовательности (х_n), заданной формулой

х_n = 4n – 1