| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) ) |
|
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) ) |
|
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | sin(theta)^2+cos(theta)^2 | ||
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.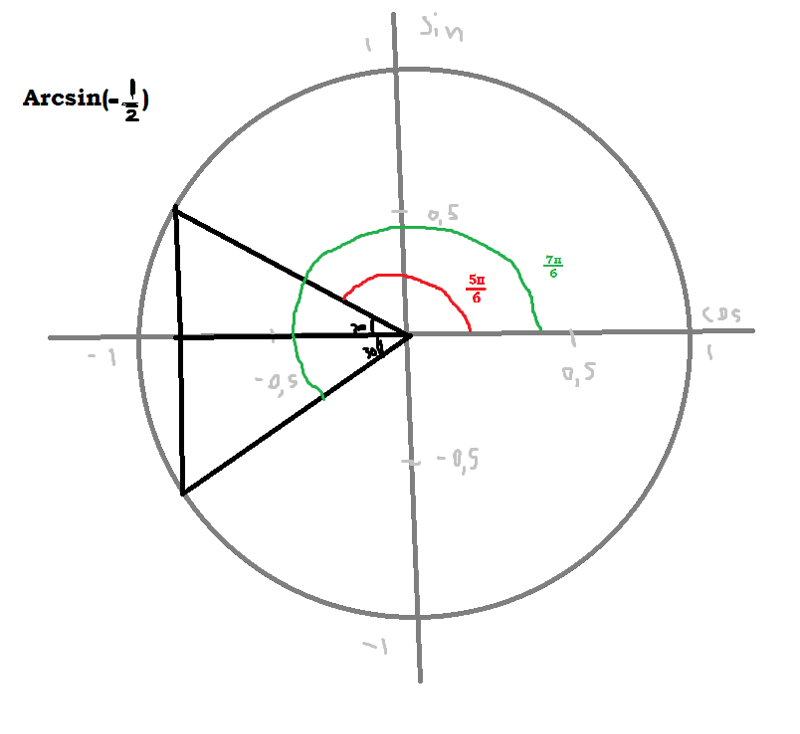 ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | ||
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Внеклассный урок — Арксинус
Арксинус
Арксинус в переводе с латинского означает дуга и синус. Это обратная функция.
При этом | a | ≤ 1. Обозначается так: arcsin a. |
Говоря иначе:
arcsin a = t, следовательно sin t = a. Условия: модуль а не больше 1; t в отрезке [-π/2; π/2] (| a | ≤ 1; –π/2 ≤ t ≤ π/2) |
Пример-пояснение:
Найдем arcsin 1/2.
Решение.
Выражение arcsin 1/2 показывает, что синус угла t равен 1/2 (sin t = 1/2).
Далее просто находим точку этого синуса на числовой окружности, что и является ответом:
точка 1/2, находящася на оси у, соответствует точке π/6 на числовой окружности.
Значит, arcsin 1/2 = π/6.
Обратите внимание:
если sin π/6 = 1/2, то arcsin 1/2 = π/6.
То есть в первом случае по точке на числовой окружности находим значение синуса, а во втором – наоборот, по значению синуса находим точку на числовой окружности. Движение в обратную сторону. Это и есть арксинус.
Формулы.
(1)
t = π – arcsin a + 2πk Эти две формулы можно объединить в одну: (k – любое целое число; n – любое целое число; | a | ≤ 1) Значение четного n: Значение нечетного n: Если n – четное число, то получается первая формула. Если n – нечетное число, то получается вторая формула. |
(2)
|
√2
Пример 1: Вычислить arcsin (– ——).
2
Решение.
Решая пример, следуем буквально по таблице над нашим примером.
Итак:
√2
а = – ——.
2
√2
Тогда sin t = – ——, при этом t входит в отрезок [–π/2; π/2]
2
π
Значит t = – —— (входит в отрезок [–π/2; π/2])
4
√2 π
Ответ: arcsin (– ——) = – —
2 4
Акцентируем ваше внимание: синусом числа –π/4 является -√2/2, а арксинусом -√2/2 является –π/4. Движение в обратном порядке. Cинусом числа является точка на оси координат, а арксинусом – точка на числовой окружности.
Движение в обратном порядке. Cинусом числа является точка на оси координат, а арксинусом – точка на числовой окружности.
√3
Пример 2: Вычислить arcsin ——
2
Решение.
√3
Пусть arcsin —— = t.
2
√3
Тогда sin t = ——.
2
Точка t находится в отрезке [–π/2; π/2]. Вычисляем значение t.
√3
Число —— соответствует значению sin π/3, при этом π/3 находится в отрезке [–π/2; π/2].
2
Значит:
t = π/3.
Итог:
√3
arcsin —— = π/3.
2
Пример решен.
Арксинус. Решение простейших уравнений с синусом. Часть 2
Арксинусом числа \(a\) (\(a∈[-1;1]\)) называют число \(x∈[-\frac{π}{2};\frac{π}{2}]\) синус которого равен \(a\) т. е.
е.
\(\arcsin a=x\) \(<=>\) \(\sin x=a\)
Примеры:
\(\arcsin{\frac{\sqrt{2}}{2}}=\frac{π}{4}\) потому что \(\sin \frac{π}{4}=\frac{\sqrt{2}}{2}\) и \(\frac{π}{4}∈[-\frac{π}{2}; \frac{π}{2}]\)
\(\arcsin 1=\frac{π}{2}\) потому что \(\sin\frac{π}{2}=1\) и \(\frac{π}{2}∈[-\frac{π}{2};\frac{π}{2}]\)
\(\arcsin 0=0\) потому что \(\sin 0=0\) и \(0∈[-\frac{π}{2};\frac{π}{2}] \)
Проще говоря, арксинус обратен синусу.
На круге это выглядит так:
Как вычислить арксинус?
Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от \(-\frac{π}{2}\) до \(\frac{π}{2}\) ) равен аргументу арксинуса?
Например, вычислите значение арксинуса:
а) \(\arcsin(-\frac{1}{2})\)
б) \(\arcsin(\frac{\sqrt{3}}{2})\)
в) \(\arcsin(-1)\)
а) Синус какого числа равен \(-\frac{1}{2}\)? Или в более точной формулировке можно спросить так: если \(\sin x=-\frac{1}{2}\), то чему равен \(x\)? Причем, обратите внимание, нам нужно такое значение, которое лежит между \(-\frac{π}{2}\) и \(\frac{π}{2}\). Ответ очевиден:
Ответ очевиден:
\(\arcsin(-\frac{1}{2})=-\frac{π}{6}\)
б) Синус какого числа равен \(\frac{\sqrt{3}}{2}\)? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ \(\frac{π}{3}\).
\(\arcsin(-\frac{\sqrt{3}}{2})=-\frac{π}{3}\)
в) Синус от чего равен \(-1\)?
Иначе говоря, \(\sin x=-1\), \(x=\) ?
\(\arcsin(-1)=-\frac{π}{2}\)
Тригонометрический круг со всеми стандартными арксинусами:
Зачем нужен арксинус? Решение уравнения \(\sin x=a\)
Чтобы понять зачем придумали арксинус, давайте решим уравнение: \(\sin x=\frac{1}{2}\).
Это не вызывает затруднений:
\( \left[ \begin{gathered}x=\frac{π}{6}+2πn, n∈Z\\ x=\frac{5π}{6}+2πl, l∈Z\end{gathered}\right.\)
Внимание! Если вдруг затруднения всё же были, то почитайте здесь о решении простейших уравнений с синусом.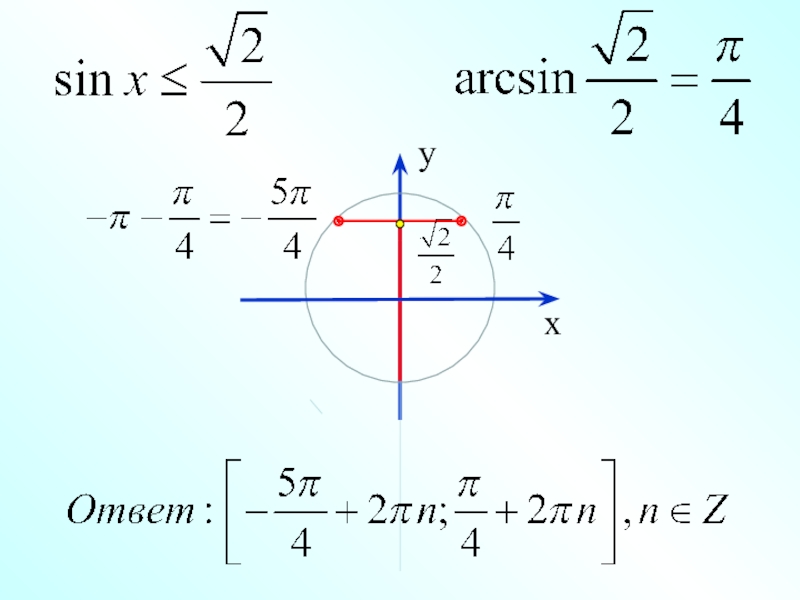
А теперь решите уравнение: \(\sin x=\frac{1}{3}\).
Что тут будет ответом? Не \(\frac{π}{6}\), не \(\frac{π}{4}\), даже не \(\frac{π}{7}\) — вообще никакие привычные числа не подходят, однако при этом очевидно, что решения есть. Но как их записать?
Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin\frac{1}{3}\), потому что известно, что синус равен \(\frac{1}{3}\). Длина дуги от \(0\) до правой точки тогда тоже будет равна \(\arcsin\frac{1}{3}\). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному \(\arcsin\frac{1}{3}\) от \(π\), то её значение составляет \(π- \arcsin\frac{1}{3}\).
Ок, значение этих двух точек нашли. Теперь запишем полный ответ: \( \left[ \begin{gathered}x=\arcsin \frac{1}{3}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{3}+2πl, l∈Z\end{gathered}\right.\) Без арксинусов решить уравнение \(\sin x=\frac{1}{3}\) не получилось бы. Как и уравнение \(\sin x=0,125\), \(\sin x=-\frac{1}{9}\), \(\sin x=\frac{1}{\sqrt{3}}\) и многие другие. Фактически без арксинуса мы можем решать только \(9\) простейших уравнений с синусом:
Как и уравнение \(\sin x=0,125\), \(\sin x=-\frac{1}{9}\), \(\sin x=\frac{1}{\sqrt{3}}\) и многие другие. Фактически без арксинуса мы можем решать только \(9\) простейших уравнений с синусом:
С арксинусом – бесконечное количество.
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{1}{\sqrt{3}}\).
Решение:
Ответ: \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{1}{\sqrt{2}}\).
Решение:
Кто поторопился написать ответ \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{2}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{2}}+2πl, l∈Z\end{gathered}\right.\), тот на ЕГЭ потеряет 2 балла. Дело в том, что в отличии от прошлых примеров \(\arcsin \frac{1}{\sqrt{2}}\) — вычислимое значение, но чтобы это стало очевидно нужно избавиться от иррациональности в знаменателе аргумента. Для этого умножим и числитель и знаменатель дробь на корень из двух \(\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}= \frac{\sqrt{2}}{2}\). Таким образом, получаем:
Для этого умножим и числитель и знаменатель дробь на корень из двух \(\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}= \frac{\sqrt{2}}{2}\). Таким образом, получаем:
\(\arcsin \frac{1}{\sqrt{2}} = \arcsin \frac{\sqrt{2}}{2}=\frac{π}{4}\)
Значит в ответе вместо арксинусов нужно написать \(\frac{π}{4}\).
Ответ: \( \left[ \begin{gathered}x=\frac{π}{4}+2πn, n∈Z\\ x=\frac{3π}{4}+2πl, l∈Z\end{gathered}\right.\)
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{7}{6}\).
Решение:
И вновь тот, кто поторопился написать \( \left[ \begin{gathered}x= \arcsin \frac{7}{6}+2πn, n∈Z\\ x=π- \arcsin\frac{7}{6}+2πl, l∈Z\end{gathered}\right.\) на ЕГЭ потеряет \(2\) балла. Что не так? – спросите вы. Ведь точно не табличное значение, почему нельзя написать \(\arcsin\frac{7}{6}\)? Пролистайте до самого верха, туда, где было определение арксинуса. Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен \(1\) и больше или равен \(-1\). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.
Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен \(1\) и больше или равен \(-1\). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.
Ответ: решений нет.
Думаю, вы уловили закономерность.
Если \(\sin x\) равен не табличному значению между \(1\) и \(-1\), то решения будут выглядеть как: \( \left[ \begin{gathered}x= \arcsin a +2πn, n∈Z\\ x=π- \arcsin a +2πl, l∈Z\end{gathered}\right.\)
Арксинус отрицательного числа
Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:
\(\arcsin({-a})=-\arcsin a\)
Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:
Примеры:
\(\arcsin(-0,7)=-\arcsin 0,7\)
\(\arcsin(-\frac{\sqrt{3}}{2})=-\arcsin\frac{\sqrt{3}}{2}=-\frac{π}{6}\)
\(\arcsin(-\frac{\sqrt{7}}{2}) \neq -\arcsin\frac{\sqrt{7}}{2}\)
Удивил последний пример? Почему в нем формула не работает? Потому что запись \(\arcsin(-\frac{\sqrt{7}}{2})\) в принципе неверна, ведь \(-\frac{\sqrt{7}}{2}<-1\), а значит арксинус от \(-\frac{\sqrt{7}}{2}\) взять нельзя – он не вычислим, не существует, точно также как \(\sqrt{-5}\) или \(\frac{3}{0}\).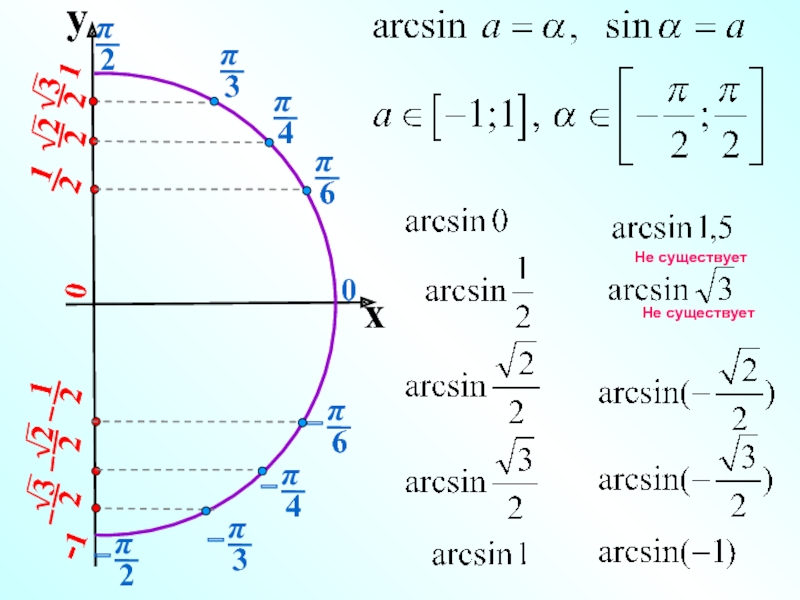
Пример. Решите тригонометрическое уравнение: \(\sin x=-\frac{1}{\sqrt{3}}\).
Решение:
Можно воспользоваться готовой формулой и написать:
\( \left[ \begin{gathered}x=\arcsin (-\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π-\arcsin (-\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)
\( \left[ \begin{gathered}x=-\arcsin (\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π+\arcsin (\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)
Но я фанатка круга, поэтому:
Ответ: \( \left[ \begin{gathered}x=-\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π+\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)
На всякий случай, уточню, что при решении уравнений написанное синим писать не обязательно – это скорее пояснения, как надо рассуждать.
Смотрите также:
Синус
Тригонометрические уравнения
Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом
Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg
Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.
Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.
Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.
Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса
Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.
для α∈-1, 1 sin(arccis α)=α, cos(arccos α)=α,для α∈(-∞, ∞) tg(arctg α)=α, ctg(arcctg α)=α
Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.
Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса
для -π2≤α≤π2 arcsin (sin α)=α,для 0≤α≤π arccos(cos α)=α,для -π2<α<π2 arctg (tg α)=α,для 0<α<π arcctg (ctg α)=α
Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.
Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел
В этом блоке мы сформулируем важное утверждение:
Определение 1Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.
для α∈-1, 1 arccis (-α)=-arcsin α, arccos (-α)=π-arccos α,для α∈(-∞, ∞) arctg (-α)=-arctg α, arcctg (-α)=π-arcctg α
Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.
Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс
Они выглядят следующим образом:
для α∈-1, 1 arccis α+arccos α=π2,для α∈(-∞, ∞) arctg α+arcctg α=π2
Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.
Формулы связи между прямыми и обратными тригонометрическими функциями
Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.
| -1≤α≤1,sin (arcsin α)=α | -1≤α≤1,sin (arccos α)=1-α2 | -∞≤α≤+∞,sin (arctg α)=α1+α2 | -∞≤α≤+∞, sin (arcctg α)=11+α2 |
| -1≤α≤1,cos (arcsin α)=1-α2 | -1≤α≤1,cos (arccos α)=α | -∞≤α≤+∞,cos (arctg α)=11+α2 | -∞≤α≤+∞, cos (arcctg α)=11+α2 |
| -1<α<1,tg (arcsin α) =α1-α2 | α∈(-1, 0)∪(0, 1),tg (arccos α) =1-α2α | -∞≤α≤+∞,tg (arctg α)=α | α≠0 ,tg (arcctg α)=1α |
| α∈(-1, 0)∪(0, 1),ctg (arcsin α)=1-α2α | -1<α<1,ctg (arccos α)=α1-α2 | α≠0,ctg (arctg α)=1α | -∞≤α≤+∞, ctg (arcctg α)=α |
Теперь разберем примеры, как они применяются в задачах.
Вычислите косинус арктангенса из 5.
Решение
У нас для этого есть подходящая формула следующего вида: cos(arctg α)=11+α2
Подставляем нужное значение: cos(arctg5)=11+(5)2=26
Пример 2Вычислить синус арккосинуса 12.
Решение
Для этого нам понадобится формула: sin (arccos α)=1-a2
Подставляем в нее значения и получаем: sin (arccos 12)=1-(12)2=32
Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin(arccos 12)=sin π3=32
Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.
Доказательства формул синусов арккосинуса, арккотангенса и арктангенса
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеДля того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций — косинуса арккосинуса и др. Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:
Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:
sin2α+cos2α=11+ctg2α=1sin2α
Вспомним, что tgα·ctgα=1. Из этого можно получить:
sinα=1-cos2α, 0≤α≤π sinα=tgα1+tg2α, -π2<α<π2sinα=11+ctg2α, 0<α<π
У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.
Теперь в первой формуле вместо a мы добавим arccos a. Итог — формула синуса арккосинуса.
Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.
Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.
Все наши расчеты можно сформулировать более емко:
- sinα=1-cos2α, 0≤α≤π
Следовательно, sin(arccosα)=1-cos2(arccosα)=1-a2
- sinα=tgα1+tgα, -π2<α<π2,
Следовательно, sin(arctgα)=tg(arctgα)1+tg2(arctgα)=α1+α2
- sinα=11+ctg2α, 0<α<π
Следовательно, sin(arctgα)=11+tg2(arctgα)=11+α2
Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.
Их мы выведем по имеющемуся шаблону:
- Из cosα=1-sin2α, -π2≤α≤π2 следует, что
cos(arcsin α)=1-sin2(arcsin α)=1-a2
- Из cosα=11+tg2α, -π2<α<π2 следует, что
- Из cosα=ctgα1+ctg2α, 0<α<πcos(arctgα)=11+tg2(arctgα)=11+α2
следует, что cos(arctgα)=ctg(arcctgα)1+ctg2(arcctgα)=α1+α2
Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса
- Исходим из tgα=sin α1-sin2α, -π2<α<π2. Получаем tg(arcsin α)=sin(arcsinα)1-sin2(arcsinα)=α1-α2 при условии, что -1<α<1.
- Исходим из tgα=1-cos2αcosα, α∈[0, π2)∪(π2, π], получаем
tg(arccosα)=1-cos2(arccosα)cos(arccosα)=1-α2α при условии α∈(-1, 0)∪(0, 1).
- Исходим из tgα=1ctgα, α∈(0, π2)∪(π2, π), получаем tg(arcctgα)=1ctg(arcctgα)=1α при условии, что α≠0.
Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:
ctgα=1tgα
Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.
Для этого понадобится поменять в них местами числитель и знаменатель.
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
arcsinα=arccos1-α2, 0≤α≤1-arccos1-a2, -1≤α<0arcsinα=arctgα1-α2, -1<α<1arcsinα=arcctg1-α2α, 0<α≤1arcctg1-α2α-π, -1≤α≤0
А так мы выразим арккосинус через остальные обратные функции:
arccosα=arcsin1-α2, 0≤α≤1π-arcsin1-α2, -1≤α<0arccosα=arctg1-α2α, 0<α≤1π+arctg1-α2α, -1<α<0arccosα=arcctgα1-α2, -1<α<1
Формула выражения арктангенса:
arctgα=arcsinα1+α2, -∞<α<+∞arctgα=arccos11+α2, α≥0-arccos11+α2, α<0arctgα=arcctg1α, α≠0
Последняя часть – выражение арккотангенса через другие обратные функции:
arcctgα=arcsin11+α2, α≥0π-arcsin11+α2, α<0arcctgα=arccosα1+α2, -∞<α<+∞arcctgα=arctg1α, α≠0
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Возьмём arcsinα=arctgα1-α2, -1<α<1 и постараемся вывести доказательство.
Мы знаем, что arctgα1-α2 — это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:
sin(arctgα1-α2)=α1-α21+(α1-α2)2=α1-α21+α21-α2=α1-α21+α21-α2=α1-α211-α2=α
Получается, что arctgα1-α2 при условии 1<a<1 – это и есть арксинус числа a.
Вывод: arcsina=arctga1-a2, -1<a<1
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Пример 3Условие Вычислить синус арккотангенса минус корня из 3.
Решение
Нам понадобится формула выражения арккотангенса через арксинус: arcctgα=arcsin11+a2, α≥0π-arcsin 11+a2, α<0
Подставим в нее α=-3 и получим ответ – 12. Непосредственное вычисление дало бы нам те же результаты: sin(arcctg(-3))=sin5π6=12 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sinα=11+ctg2α, 0<α<π
В итоге у нас бы вышло: sin(arcctg(-3))=11+ctg2(arcctg(-3))=11+(-3)2=12
Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin(arcctgα)=11+α2 sin(arcctg(-3))=11+(-3)2=12
Прочие формулы с обратными функциями
Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач.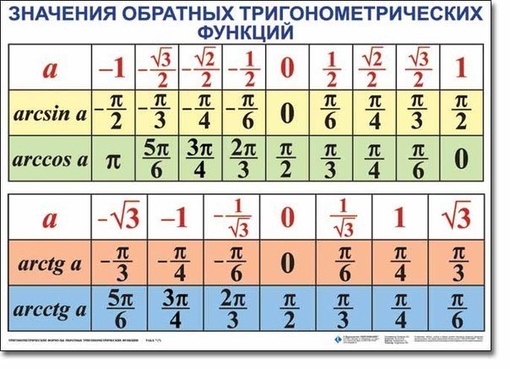 Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.
Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.
Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:
sin2α2=1-cosα2
Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:
sinα2=1-cosα2
Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:
sinarccosα2=1-cos(arccosα)2⇔sinarccosα2=1-α2
Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:
arccosα2=arcsin1-α2
Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.
В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
определение, формула, таблица, график, свойства
Определение
Арксинус (arcsin) – это обратная тригонометрическая функция.
Арксинус x определяется как функция, обратная к синусу x, при -1≤x≤1.
Если синус угла у равен х (sin y = x), значит арксинус x равняется y:
arcsin x = sin-1 x = y
Примечание: sin-1x означает обратный синус, а не синус в степени -1.
Например:
arcsin 1 = sin-1 1 = 90° (π/2 рад)
График арксинуса
Функция арксинуса пишется как y = arcsin (x).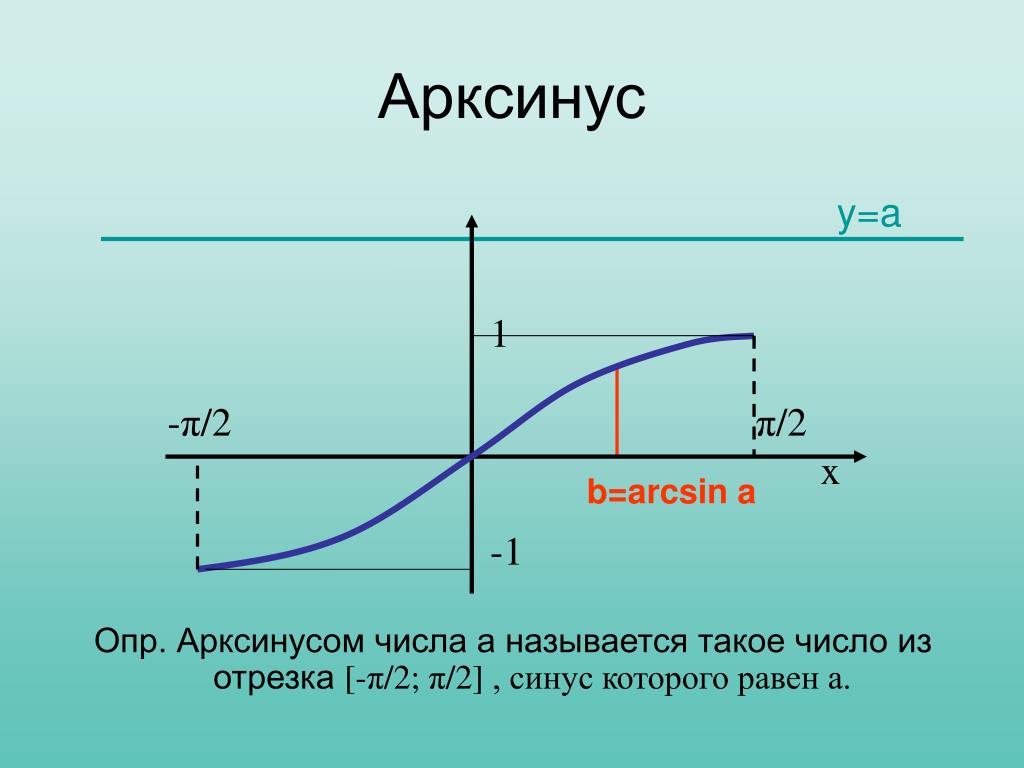 График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):
График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):
Свойства арксинуса
Ниже в табличном виде представлены основные свойства арксинуса с формулами.
Таблица арксинусов
| x | arcsin x (рад) | arcsin x (°) |
| -1 | -π/2 | -90° |
| -√3/2 | -π/3 | -60° |
| -√2/2 | -π/4 | -45° |
| -1/2 | -π/6 | -30° |
| 0 | 0 | 0° |
| 1/2 | π/6 | 30° |
| √2/2 | π/4 | 45° |
| √3/2 | π/3 | 60° |
| 1 | π/2 | 90° |
microexcel. ru
ru
Обратные тригонометрические функции.
Алгебра. 10 класс. Глава VI. Тест 1.
Вариант I.
1. Вычислите:
2. Вычислите: arcsin (-0,5).
3. Вычислите: 2 arccos(-1).
A) π; B) 3π; C) 4π; D) 2π.
4. Вычислите:
5. Найдите значение выражения:
A) 0,5; B) 1; C) 0; D) -1.
6. Найдите значение выражения:
7. Вычислите:
A) -1; B) 0; C) 1; D) π.
8. Вычислите:
Вычислите:
A) -1; B) 0; C) 1; D) 0,5.
9.Вычислите:
10. Найдите значение выражения: sin(arccos 0,6).
A) 0,8; B) 0,6; C) 1,25; D) 1.
11. Вычислить: sin(2arccos 0,8).
A) 0,8; B) 0,6; C) 0,96; D) 0,48.
12. Вычислить:
Вариант II.
1. Вычислите:
2. Вычислите:
3. Вычислите: 4 arcsin(-1).
A) -2π; B) 3π ; C) -4π ; D) 2π.
4. Вычислите:
5. Найдите значение выражения:
A) 0,5; B) 1; C) 0; D) -1.
6. Найдите значение выражения:
cos(arccos0,4).
A) 0,5; B) 0,4; C) 0,6; D) 0.
7. Вычислите:
A) -1; B) 0; C) 1; D) π.
8. Вычислите:
A) 3; B) 2; C) 1; D) 0.
9. Вычислите:
A) -1; B) 1; C) 0; D) π/3.
10. Найдите значение выражения: cos(arcsin 0,8).
A) 0,8; B) 0,6; C) 1,25; D) 1.
11. Вычислить: sin(2arccos 0,6).
Вычислить: sin(2arccos 0,6).
A) 0,8; B) 0,6; C) 0,96; D) 0,48.
12. Вычислить:
A) -5; B) 12; C) 5; D) π/6.
Сверить ответы.
СПРАВОЧНЫЕ МАТЕРИАЛЫ.
π = 180°; π/2 = 90°; π/3 = 60°; π/4 = 45°; π/6 = 30°.
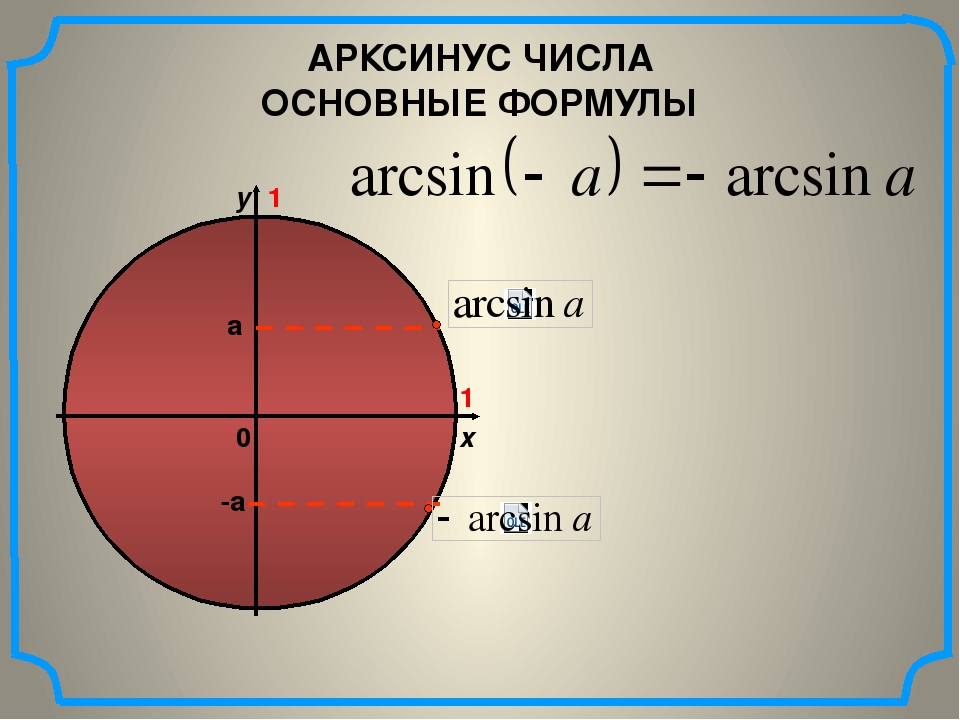
Обратные тригонометрические функции.
1) Арксинусом числа а (arcsin a) называется угол из промежутка [- π/2; π/2], синус которого равен а. Примеры:
а) arcsin ( 1/2) = π/6, так как sin(π/6) = 1/2;
б) arcsin(-1/2 ) =- π/6 , т. к. sin(-π/6 )= — sin(π/6) = — 1/2.
arcsin(-a)=- arcsin a.
2) Арккосинусом числа а (arccos a) называется угол из промежутка [0; π], косинус которого равен а. Примеры:
Примеры:
а) arccos( 1/2) = π/3, так как cos (π/3) = 1/2;
б) arccos(-1/2)= 2π/3, так как cos (2π/3) =cos(π — π/3) = — cos (π/3)=- 1/2.
arccos(-a) = π–arccosa.
3) Арктангенсом числа а (arctg a) называется угол из промежутка (- π/2; π/2), тангенс которого равен а.
Примеры: а) arctg 1 = π/4, так как tg π/4 = 1;
б) arctg(-1)= — π/4, так как tg(- π/4)= — tg π/4 = — 1.
arctg(-a)=- arctg a.
4) Арккотангенсом числа а (arcctg a) называется угол из промежутка (0; π), котангенс которого равен а.
Примеры: а) arcctg 1 = π/4, так как ctg (π/4) = 1;
б) arcctg(-1)= 3π/4, так как ctg (3π/4) = ctg(π – π/4) = — ctg (π/4)= -1.
arcctg(-a) = π–arcctg a.
Таблица значений тригонометрических функций некоторых углов.
Поделиться новостью в соцсетях Метки: алгебра 10 класс, тригонометрические формулы
Арксинус, формула, график функции арксинус, урок и презентация
Дата публикации: .
Урок и презентация на темы: «Арксинус. Таблица арксинусов. Формула y=arcsin(x)»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать: Тригонометрические уравнения. Арксинус (PPTX)
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Что будем изучать:
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.
5. Таблица значений арксинуса.
6. Примеры.
Что такое арксинус?
Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G. Эти точки и будут решением нашего уравнения. Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
Эти точки и будут решением нашего уравнения. Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
а x2= 2π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение
sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk,
где x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?
Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.
Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).
И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.
Немного истории арксинуса
История происхождения нашего символа совершенно такая же, как и у arccos. Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.
Определение арксинуса
Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.
Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и
x= π — arcsin(a) + 2πk
Перепишем:
x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1.
С учётом этого, запишем общую формула решения для уравнения sin(x)=a:
Есть три случая, в которых предпочитают записывать решения более простым способом:
sin(x)=0, то x= πk,
sin(x)=1, то x= π/2 + 2πk,
sin(x)=-1, то x= -π/2 + 2πk.
Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).
Таблица значений арксинуса
Таблица значений синуса
Таблица значений арксинуса
Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.
Примеры
1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.
2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.
3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
4. Решить уравнение: sin(x) = -√2/2.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2 ) + 2πk.
Посмотрим в таблице значение: arcsin (-√2/2 )= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.
5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk
6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1)n — arcsin(3/5) + πk.
7. Решить неравенство sin(x)
Решение: Синус — это ордината точки числовой окружности.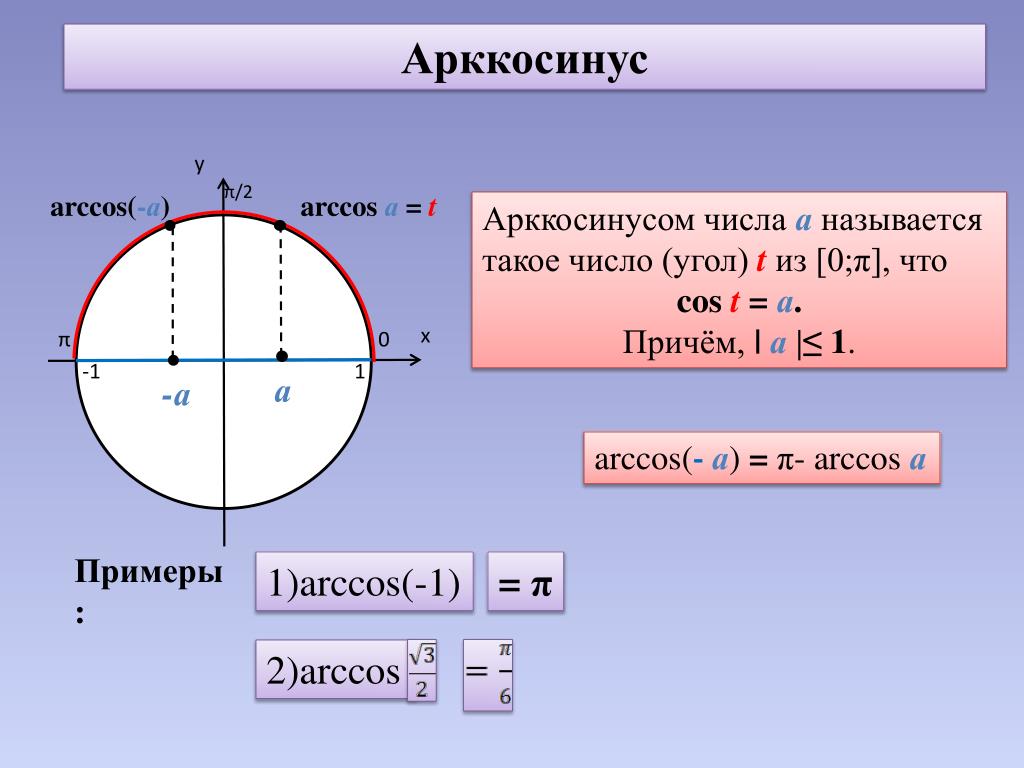 Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Задачи на арксинус для самостоятельного решения
1) Вычислить: а) arcsin(√2/2), б) arcsin(1/2), в) arcsin(1), г) arcsin(-0.8).
2) Решить уравнение: а) sin(x) = 1/2, б) sin(x) = 1, в) sin(x) = √3/2, г) sin(x) = 0.25,
д) sin(x) = -1.2.
3) Решить неравенство: а) sin (x)> 0.6, б) sin (x)≤ 1/2. Тригонометрия
— Решение $ \ arcsin (1-x) -2 \ arcsin (x) = \ pi / 2 $ — Обмен математическими стеками Тригонометрия
— Решение $ \ arcsin (1-x) -2 \ arcsin (x) = \ pi / 2 $ — Обмен стеками математикиСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 4к раз
$ \ begingroup $\ begin {eqnarray *} \ arcsin (1-x) -2 \ arcsin (x) & = & \ frac {\ pi} {2} \\ 1-x & = & \ sin \ left (\ frac {\ pi} {2} +2 \ arcsin (x) \ right) \\ & = & \ cos \ left (2 \ arcsin (x) \ right) \\ & = & 1-2 \ left (\ sin \ left (\ arcsin (x) \ right) \ right) ^ {2} \\ & = & 1-2x ^ {2} \\ х & = & 2x ^ {2} \\ x \ left (x- \ frac {1} {2} \ right) & = & 0 \ end {eqnarray *}
Итак, $ x = 0 $ или $ x = \ frac {1} {2} $
.
Но путтиг $ x = \ frac {1} {2} $ в исходном выражении дает $ — \ frac {\ pi} 4 \ ne \ frac \ pi 2 $
Итак, , почему мы получаем в качестве ответа $ x = -1 / 2 $?
Создан 27 фев.
пользователь8055154988 серебряных знаков1818 бронзовых знаков
$ \ endgroup $ $ \ begingroup $На первом этапе вы добавили дополнительное решение.
Так как $ \ arcsin x $ должно быть меньше $ \ pi / 2 $, первая строка гласит: $$ \ arcsin (1-x) = \ frac {\ pi} {2} +2 \ arcsin (x) \ le \ frac {\ pi} {2} $$ Таким образом, и $ x \ le 0 $.
Теперь, взяв $ \ sin $ с обеих сторон, вы взяли функцию, которая была определена только до $ x = 1 $ (например, $ \ arcsin (x-1) $), и расширили ее на все действительные числа (например, $ х-1 $). Здесь вы добавили дополнительное решение.
Здесь вы добавили дополнительное решение.
Создан 27 фев.
nbubisnbubis 31.2}} — \ frac {1} {\ sqrt {(2-x) x}} $$ всегда отрицательно (с бесконечными ветвями при $ x = 0 $ и $ x = 1 $). Для $ x = 0 $, $ f (0) = 0 $ и поскольку функция уменьшается, у вас не может быть никакого корня, кроме $ x = 0 $ (помните, что $ f (x) $ определен только для [$ 0 Создан 27 фев. 191k5151 золотой знак8181 серебряный знак173173 бронзовых знака как $ \ displaystyle \ sin \ left (\ frac \ pi2 \ pm A \ right) = \ cos A, $ $ \ displaystyle \ sin \ left (\ frac \ pi2 \ pm2 \ arcsin x \ right) = \ cos (2 \ arcsin x) = 1-2 \ left [\ sin (\ arcsin x) \ right] ^ 2 = 1-2x ^ 2 Итак, $ \ displaystyle x = \ frac12 $ соответствует $ \ displaystyle \ arcsin (1-x) +2 \ arcsin x = \ frac \ pi2 $ as $ \ displaystyle \ arcsin \ frac12 = \ frac \ pi6 $ Создан 27 фев. 265k1717 золотых знаков1 Ваша конфиденциальность Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie. Принимать все файлы cookie
Настроить параметры С помощью этого калькулятора арксинуса (или калькулятора обратного синуса) у вас не будет проблем с поиском арксинуса в вашей задаче.Просто введите значение синуса для треугольника, и появится нужный угол. Единственное, что вам нужно запомнить, это ограниченная область арксинуса (−1 ≤ sine ≤ 1). Если вам интересно, , что такое арксинус или , как выглядит график arcsin x , не ждите больше — прокрутите вниз, и вы найдете ответы ниже! Мы также включили короткий абзац об отношениях арксинусов, таких как отношения между интегралом арксинуса и производной. И так, чего же ты ждешь? Арксинус — это функция, обратная синусоиде. Синус — периодическая функция, поэтому существует несколько чисел, которые имеют одинаковое значение синуса. Например, sin (0) = 0, но также sin (π) = 0, sin (2π) = 0, sin (-π) = 0 и sin (-326π) = 0. Следовательно, если кто-то хочет вычислить arcsin ( 0), ответ может быть 0, 2π (360 °) или -π (-180 °), и это лишь некоторые из вариантов! Все они верны, но обычно мы даем только одно число, называемое основным значением . Arcsin (x) — наиболее распространенное обозначение, поскольку sin -1 x может привести к путанице (потому что sin -1 x ≠ 1 / sin (x)).Аббревиатура asin обычно используется в языках программирования. Поскольку синус основной функции не является взаимно однозначным, ее область должна быть ограничена, чтобы гарантировать, что арксинус также является функцией. Обычно выбирается область -π / 2 ≤ y ≤ π / 2. Это означает, что диапазон обратной функции будет равен диапазону основной функции; таким образом, диапазон функции arcsin равен [−π / 2, π / 2], а область arcsine находится между [−1,1]. Ниже вы можете найти график arcsin (x), а также некоторые часто используемые значения арксинуса: Хотите знать, откуда взялся этот граф arcsin x? Его можно найти, отразив график sin (x) в диапазоне [-π / 2 π / 2] через линию y = x: Связь между тригонометрическими функциями и арксинусом может помочь вам еще лучше понять тему. Прямоугольный треугольник с гипотенузой длины 1 — хорошая отправная точка. Просто быстрое напоминание: для прямоугольного треугольника функция синуса принимает угол θ и возвращает отношение противоположности / гипотенузы, которое равно x в нашем примерном треугольнике.Функция обратного синуса, арксинус, принимает отношение противоположности / гипотенузы (x) и возвращает угол θ. Итак, зная, что для нашего треугольника arcsin (x) = θ, мы также можем записать, что: Другие полезные отношения с арксинусом: Иногда также нужны интеграл и производная от arcsin: интеграл от arcsin: производная от arcsin: Арксинус — полезная функция e.грамм. в нахождении угла прямоугольного треугольника. Если вы ищете углы в прямоугольном треугольнике и знаете длины сторон, хорошо известная теорема Пифагора не будет столь полезной. Чтобы найти углы прямоугольного треугольника, нужно применить арксинус: Итак, предположим, что у нас есть два значения, заданные в прямоугольном треугольнике, a = 6 и c = 10, и мы хотели бы найти значение угла α: Отлично! Теперь, когда вы понимаете, что такое арксинус, может быть, вы захотите познакомиться с более продвинутыми приложениями тригонометрии? Например, закон синусов (тесно связанный с законом косинусов) является обязательным при решении задач треугольника. Используйте этот калькулятор арксинуса, чтобы легко вычислить арксинус числа. Онлайн-инструмент для вычисления арксинуса с выводом в градусах или радианах. Поддерживает ввод десятичных чисел (0,5, 6, -1 и т. Д.) И дробей (1/4, 2/3, 4/3, 1/3 и т. Д.). Арксинус является одной из обратных тригонометрических функций (антитригонометрических функций) и является обратной функцией синуса. Иногда его записывают как sin -1 (x), но этого обозначения следует избегать, так как его можно спутать с обозначением экспоненты (степень, возведенная в степень).Арксинус используется для получения угла из тригонометрического отношения синуса, которое представляет собой отношение между стороной, противоположной углу, и самой длинной стороной треугольника. Диапазон значений функции от -1 до 1, как и результаты нашего калькулятора arcsin. Диапазон значений угла обычно составляет от -90 ° до 90 °. Существует ряд правил arcsin, например sin (arcsin (x)) = x или arcsinα + arcsinβ = arcsin (α√ (1-β 2 ) + β√ (1-α 2 )) , а также косинус арксинуса: cos (arcsin (x)) = sin (arccos (x)) = √ (1-x 2 ), который может помочь вам в исчислении тригонометрии. Самый простой способ вычислить его — использовать наш калькулятор arcsin, описанный выше, который будет выводить результаты как в градусах, так и в радианах. Другие способы включают другую заданную информацию, такую как значения других тригонометрических функций для того же угла или других углов в том же треугольнике. Вот таблица общих значений arcsin: π — это, конечно, математическая константа, примерно равная 3.14159. Для прямоугольного треугольника на рисунке ниже с известной длиной стороны a = 52 и гипотенузы c = 60 можно использовать функцию обратного косинуса arcsin, чтобы найти угол α в точке A. Сначала вычислите синус α, разделив противоположную сторону на гипотенузу. Это приводит к sin (α) = a / c = 52/60 = 0,8666. Используйте обратную функцию с этим результатом, чтобы вычислить угол α = arcsin (0.8666) = 60 ° (1,05 радиана). В предыдущем разделе мы изучили производные шести основных тригонометрических функций: \ [{\ color {blue} {\ sin x, \;}} \ kern0pt \ color {red} {\ cos x, \;} \ kern0pt \ color {darkgreen} {\ tan x, \;} \ kern0pt \ color {magenta} {\ cot x, \;} \ kern0pt \ color {шоколад} {\ sec x, \;} \ kern0pt \ color {maroon} {\ csc x. \;} \] В этом разделе мы рассмотрим производные обратных тригонометрических функций, которые соответственно обозначаются как \ [{\ color {синий} {\ arcsin x, \;}} \ kern0pt \ color {red} {\ arccos x, \;} \ kern0pt \ color {darkgreen} {\ arctan x, \;} \ kern0pt \ color {magenta} {\ text {arccot} x, \;} \ kern0pt \ color {шоколад} {\ text {arcsec} x, \;} \ kern0pt \ color {maroon} {\ text {arccsc} x.\;} \] Обратные функции существуют, когда на область определения исходных функций накладываются соответствующие ограничения. Например, домен для \ (\ arcsin x \) составляет от \ (- 1 \) до \ (1. \) Диапазон или выход для \ (\ arcsin x \) — все углы от \ (- \ большие {\ frac {\ pi} {2}} \ normalsize \) в \ (\ large {\ frac {\ pi} {2}} \ normalsize \) радианы. Области других тригонометрических функций ограничены соответствующим образом, так что они становятся взаимно однозначными функциями, и их обратные функции могут быть определены.2} — 1}}}.} В последней формуле абсолютное значение \ (\ left | x \ right | \) в знаменателе появляется из-за того, что произведение \ ({\ tan y \ sec y} \) всегда должно быть положительным в диапазоне допустимых значений \ (y \), где \ (y \ in \ left ({0, {\ large \ frac {\ pi} {2} \ normalsize}} \ right) \ cup \ left ({{\ large \ frac {\ pi} {2} \ normalsize}, \ pi} \ right), \) то есть производная обратной секущей всегда положительна. 2} \] Темы | Дом 19 Диапазон y = arcsin x Диапазон y = arctan x Диапазон y = arccos x Диапазон y = arcsec x sin −1 x .Обратный синус Обратные отношения УГЛЫ в исчислении будут в радианах. Таким образом, если нам, например, задан радианный угол, мы можем вычислить его функцию. (Тема 13.) И наоборот, если нам дано, что значение синусоидальной функции равно
½, тогда задача состоит в том, чтобы назвать угол радиана x . sin x = ½. «Синус какого угла равен ½?» Однако мы пишем: Оценить arcsin ½ «Угол , синус которого равен & frac12.« Функция y = arcsin x называется функцией, обратной y = sin x . arcsin x — это угол , синус которого равен числу x . Строго говоря, arcsin x — это дуга arc , синус которой равен x . Потому что в единичном круге длина этой дуги является мерой в радианах.Тема 14. Итак, есть много углов, у которых синус равен ½. Это будет любой угол, которому соответствует острый угол. Следовательно, мы должны ограничить диапазон значений этого угла y = arcsin x — так, чтобы он фактически был функцией; так что он будет однозначным. Как мы это сделаем? Мы ограничим их теми углами, которые имеют наименьшее абсолютное значение. Они называются главными значениями y = arcsin x . Таким образом, arcsin ½ =. Угол первого квадранта — это угол с наименьшим абсолютным значением, синус которого равен ½. Пример 1. Вычислить arcsin (−½). Решение. Углы с отрицательными синусами попадают в 3-й и 4-й квадранты. Угол наименьшего абсолютного значения попадает в 4-й квадрант между 0 и -. Угол, синус которого равен — x , является просто отрицательной величиной угла, синус которого равен x . arcsin (−½) = −arcsin (½) = -. Тогда диапазон функции y = arcsin x будет углами, которые попадают в 1-й и 4-й квадранты, между — и. Углы с положительными синусами будут углами 1-го квадранта. Углы с отрицательными синусами попадут в 4-й квадрант. Ограничение диапазона arcsin x эквивалентно ограничению домена sin x теми же значениями.Так будет со всеми последующими ограниченными диапазонами. sin −1 x . Обратный синус Другое обозначение для arcsin x — sin −1 x . Прочтите: «Обратный синус x ». −1 здесь , а не показатель степени. (См. Тему 19 Precalculus.) Задача 1. Вычислите следующее в радианах. Чтобы увидеть ответ, наведите указатель мыши на цветную область. a) sin −1 0 = 0. (Тема 15.) б) sin −1 1 = π / 2. (Тема 15.) в) sin −1 (−1) = −π / 2. (Тема 15.) Каждой тригонометрической функции соответствует ее обратная функция. arcsin x , arccos x , арктан х , arccsc x , угловых секунды x , arccot x . В каждом из них нам дается значение x тригонометрической функции.Мы должны назвать угол радиана , который имеет это значение. В каждом случае мы должны ограничить его диапазон, чтобы функция была однозначной. Диапазон y = arctan x Как y = arcsin x , y = arctan x имеет наименьшие абсолютные значения в 1-м и 4-м квадрантах. Обратите внимание, что y — угол , тангенс которого равен x — должен быть больше — и меньше чем.Поскольку при этих углах квадранта касательная не существует. (Тема 15.) Углы, тангенсы которых положительны, будут углами 1-го квадранта. Углы с отрицательными касательными попадают в 4-й квадрант. То же самое, что и с arcsin (- x ). Угол, тангенс которого равен — x , является просто отрицательной величиной угла, тангенс которого равен x . Проблема 2. Оцените следующее. Диапазон y = arccos x Пример 2.Оцените arccos ½. Проблема 3. Почему это не так? arccos (−½) = -. — угол 4-го квадранта. А в 4-м квадранте косинус положительный. Урок 15. Угол с отрицательным косинусом попадет во 2-й квадрант, где он будет иметь наименьшее абсолютное значение. (Тема 15.) Косинус угла 2-го квадранта является отрицательной величиной косинуса соответствующего острого угла, который является его дополнением. Другими словами: Угол θ, косинус которого равен — x , является дополнением arccos (- x ) = π — arccos x . Пример 3. Вычислите arccos (−½). Решение . Мы видели: arccos ½ =. Следовательно, arccos (−½) является дополнением к углу, к которому мы должны прибавить π. + θ = π. Теперь это одна треть числа π. Следовательно, его добавка будет двух- третей числа π:. θ = arccos (−½) =. Тогда диапазон y = arccos x будет от 0 до π. Угол, косинус которого положителен, будет углом 1-го квадранта; угол с отрицательным косинусом попадет во 2-й угол. Будет дополнением угла 1-го квадранта. Проблема 4. Оцените следующее. * Обратное соотношение выглядит следующим образом: arccos x = θ тогда и только тогда, когда x = cos θ. Например, В общем, так и есть. Проблема 5. a) arctan t = β тогда и только тогда, когда t = tan β. б) arcsec u = α тогда и только тогда, когда u = sec α. c) arccos 1 = 0 тогда и только тогда, когда 1 = cos 0. Диапазон y = arcsec x В исчислении наиболее важными обратными тригонометрическими функциями являются sin −1 x , tan −1 x и cos −1 x .Тем не менее, вот диапазоны, делающие остальные однозначными. Если x положительно, то значение обратной функции всегда является углом первого квадранта, или 0. Если x отрицательно, значение обратной будет попадать в квадрант, в котором прямая функция отрицательна. Таким образом, если x отрицательно, arcsec x попадет во 2-й квадрант, потому что именно там sec x отрицательно. Единственная обратная функция ниже, в которой x может быть 0, — это arccot x .arccot 0 = π / 2. Опять же, мы ограничиваем значения y теми углами, которые имеют наименьшее абсолютное значение. Обратные отношения Если поставить f ( x ) = sin x и г ( x ) = arcsin x , , то согласно определению обратных функций (Тема 19 Precalculus): f ( g ( x )) = x и g ( f ( x )) = x . sin (arcsin x ) = x и arcsin (sin x ) = x . В частности, если Взяв обратную функцию обеих сторон, мы извлекли или освободили аргумент x . (См. Тему 19 Precalculus, Извлечение аргумента.) Это позволяет нам решать многие тригонометрические уравнения. Пример 4. Решите относительно x : Решение .Взяв обратную функцию — синус — с обеих сторон, мы можем освободить аргумент x — 1 и сразу записать — Следовательно, Задача 6. Решите для x : загар ( x + 2) = 1. Задача 7. Решите для x : cos x 2 = -1. x 2 = arccos −1 = π. х = ±. Задача 8. Решите для x : Теорема. Если y = arcsec x , , затем продукт сек y tan y никогда не бывает отрицательным. Например, если y = arcsec x , то угол y попадает либо в первый, либо во второй квадрант. Когда угол y попадает в первый квадрант, то значения sec y и tan y положительны.Следовательно, их продукт положительный. Когда угол y попадает во второй квадрант, sec y и tan y оба отрицательны, так что их произведение снова положительно. Если y = 0, то tan y = 0, следовательно, произведение sec y tan y равно 0. Следовательно, этот продукт никогда не бывает отрицательным. (Эта теорема упоминается в доказательстве производной от y = arcsec x .) Следующая тема: Тригонометрические идентификаторы Содержание | Дом Сделайте пожертвование, чтобы TheMathPage оставалась в сети. Авторские права © 2021 Лоуренс Спектор Вопросы или комментарии? Эл. Почта: [email protected] Функция arcsin — это функция, обратная синусоиде. Для каждой тригонометрической функции существует обратная функция, которая работает в обратном порядке.
Эти обратные функции имеют то же имя, но с дугой впереди.
(На некоторых калькуляторах кнопка arcsin может быть помечена как asin, а иногда
грех -1 .)
Итак, обратное к греху — это arcsin и т. Д. Когда мы видим «arcsin A», мы понимаем его как «угол, грех которого равен A». На рисунке выше нажмите «Сброс».
Нам известны длины сторон, но нам нужно найти величину угла C. Напомним, что мы можем применить
триггерные функции на любой угол, включая большие и отрицательные углы. Но когда мы
Рассмотрим обратную функцию, мы столкнемся с проблемой, потому что существует бесконечное количество углов, которые имеют один и тот же синус.
Например, 45 ° и 360 + 45 ° будут иметь одинаковый синус. Подробнее об этом см.
Обратные тригонометрические функции. Чтобы решить эту проблему,
диапазон
обратных триггерных функций ограничены
таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат. Напомним, что область определения функции — это набор допустимых входных данных для нее. Диапазон — это набор возможных выходов. По соглашению диапазон arcsin ограничен от -90 ° до + 90 °.
Итак, если вы используете калькулятор для решения, скажем, arcsin 0,55, из бесконечного числа возможностей он вернет 33,36 °,
тот, который находится в диапазоне функции. (C) Открытый справочник по математике, 2011 г. Обратный синус, поэлементно. y — координата на единичной окружности. Местоположение, в котором сохраняется результат. Если предусмотрено, он должен иметь
форма, которой транслируются входы. Если не указано или Нет,
возвращается только что выделенный массив.Кортеж (возможно только как
аргумент ключевого слова) должен иметь длину, равную количеству выходов. Это условие транслируется по входу. В местах, где
Условие равно True, массив out будет установлен на результат ufunc.
В другом месте массив из сохранит свое исходное значение.
Обратите внимание, что если неинициализированный массив из создается по умолчанию Другие аргументы, содержащие только ключевые слова, см.
ufunc docs. Обратный синус каждого элемента в x , в радианах и в
закрытый интервал Банкноты Для типов входных данных с действительным знаком arcsin всегда возвращает действительный вывод.
Для каждого значения, которое не может быть выражено действительным числом или бесконечностью,
он дает Для входных комплексных значений Список литературы Абрамовиц М., Стегун И. А., Справочник по математическим функциям ,
10-е издание, Нью-Йорк: Довер, 1964, стр. 79 и далее.
http://www.math.sfu.ca/~cbm/aands/ Примеры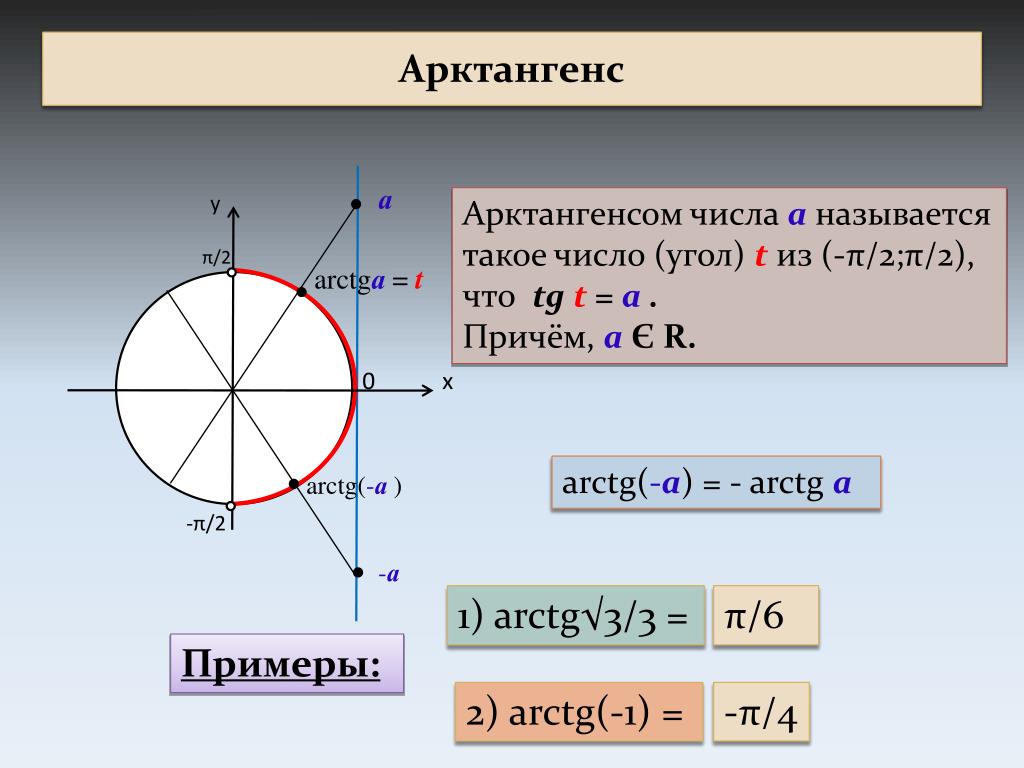
серебряных знаков304304 бронзовых знака $ \ endgroup $ 6 Mathematics Stack Exchange лучше всего работает с включенным JavaScript 
Arcsin. Нахождение обратной функции синуса.
Что такое арксинус?
 Другими словами, это помогает найти угол треугольника, который имеет известное значение синуса. Поскольку область синуса для действительных чисел равна [-1, 1], мы можем вычислить арксинус только для чисел в этом интервале.
Другими словами, это помогает найти угол треугольника, который имеет известное значение синуса. Поскольку область синуса для действительных чисел равна [-1, 1], мы можем вычислить арксинус только для чисел в этом интервале. Сокращение Определение Домен arcsin x
для реального результата Диапазон обычных
основных значений arcsin (x)
sin -1 x,
asin х = грех (у) -1 ≤ х ≤ 1 -π / 2 ≤ y ≤ π / 2
-90 ° ≤ y ≤ 90 ° График arcsin x
x arcsin (x) График ° рад -1 -90 ° -π / 2 Компьютерщик 3, CC BY-SA 4.0 через Wikimedia Commons -√3 / 2 -60 ° -π / 3 -√2 / 2 -45 ° -π / 4 -1/2 -30 ° -π / 6 0 0 ° 0 1/2 30 ° π / 6 √2 / 2 45 ° π / 4 √3 / 2 60 ° π / 3 1 90 ° π / 2 Обратный синус, тригонометрические функции и другие отношения
sin (arcsin (x)) = x cos (arcsin (x)) = √ (1-x²) tan (arcsin (x)) = x / √ (1-x²) arcsin (x) = π / 2 - arccos (x) arcsin (-x) = -arcsin (x) arcsin (x) dx = x arcsin (x) + √ (1 - x²) + C d / dx arcsin (x) = 1 / √ (1 - x²) где x ≠ -1, 1 Пример использования калькулятора arcsin
sin (α) = a / c, поэтому α = arcsin (a / c) sin (β) = b / c, поэтому β = arcsin (b / c) Калькулятор арксинуса — вычисляет арксинус (x)
Функция арксинуса
Как вычислить арксинус числа?
x arcsin (x) (°) arcsin (x) (рад.) -1 -90 ° -π / 2 -√3 / 2 -60 ° -π / 3 -√2 / 2 -45 ° -π / 4 -1/2 -30 ° -π / 6 0 0 ° 0 1/2 30 ° π / 6 √2 / 2 45 ° π / 4 √3 / 2 60 ° π / 3 1 90 ° π / 2 Использование арксинуса для нахождения угла
Производные обратных тригонометрических функций
Введение в обратные тригонометрические функции
\] Пример 4
\ [y = {\ frac {1} {a}} \ arctan {\ frac {x} {a}} \] Пример 5
\ [{y = \ arctan \ frac {{x + 1}} {{x — 1}} \; \;} \ kern-0.4}}}.} \] Обратные тригонометрические функции — Разделы тригонометрии
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами! −π / 3. −π / 6. = −θ. = θ. Следовательно, arctan (- x ) = −arctan x . а) арктангенс 1 = π
4 б) арктангенс (-1) = – π
4 в) загар -1 = π
3 г) загар −1 (-) = – π
3 д) арктангенс 0 = 0 е) = – π
6 Решение . arccos ½ = π
3. Угол в радианах, косинус которого равен ½, равен . π
3 (60 °).
к углу, косинус которого равен x . а) arccos 1 = 0 б) arccos (−1) = π в) cos -1
2 = π
4 г) cos −1 (-
2) = π — π
4 = 3π
4 e) = π
6 е) = π — π
6 = 5π
6 г) arccos 0 = π
2 arccos ½ = π
3 тогда и только тогда, когда ½ = cos π
3. г) arccot 1 = π
4 тогда и только тогда, когда 1 = детская кроватка π
4. arcsin x = y затем, взяв обратную функцию — синус — обеих сторон: x = sin y . arcsin ( x — 1) = . x — 1 = грех =
2 x = 1 +
2. х + 2 = арктан 1 = π
4. x = π
4 — 2. sin −1 ( x 2 -1) = 0. x 2 — 1 = arcsin 0 = 0 x 2 = 1 x = ± 1.
Даже 1 доллар поможет. Тригонометрическая функция arcsin () — обратный синус — определение математического слова
Тригонометрическая функция arcsin () — обратный синус — определение математического слова — Math Open Reference
Возвращает угол, синус которого является заданным числом.
Используйте arcsin, если вы знаете синус угла и хотите узнать фактический угол. sin30 = 0.5 Означает: синус 30 градусов равен 0,5 arcsin 0,5 = 30 Означает: Угол, грех которого равен 0,5, равен 30 градусам.
См. Также Обратные функции — тригонометрия Пример — использование arcsin для нахождения угла
Мы знаем, что поэтому нам нужно знать угол, грех которого равен 0.5, или формально: Используя калькулятор, чтобы найти arcsin 0,5, мы находим, что это 30 °. Большие и отрицательные углы
Диапазон и домен arcsin
Для y = arcsin x:
Что попробовать
Другие темы по тригонометрии
Уголки
Тригонометрические функции
Решение задач тригонометрии
Исчисление
Все права защищены. кол-во номеров.arcsin — NumPy v1.20 Manual
out = None , местоположения в нем, где условие False будет
оставаться неинициализированным. [-pi / 2, pi / 2] .
Это скаляр, если x — скаляр. arcsin — многозначная функция: на каждые x приходится бесконечно
много чисел z таких, что.Конвенция заключается в
вернуть угол z , действительная часть которого лежит в [-pi / 2, pi / 2]. нан и устанавливает флаг ошибки с плавающей запятой недопустимый . arcsin — это комплексная аналитическая функция, которая
по соглашению ветвь разрезает [-inf, -1] и [1, inf] и является
сплошной сверху на первом и снизу на втором.{-1}. >>> np.arcsin (1) # pi / 2
1,5707963267948966
>>> np.arcsin (-1) # -pi / 2
-1,5707963267948966
>>> np.arcsin (0)
0,0
.

