2.10.3. Всеобщий закон сохранения и превращения энергии
Изучение процесса превращения теплоты в работу и обратно и установление механического эквивалента теплоты сыграло основную роль в открытии всеобщего закона сохранения и превращения энергии. Все большее место в физических исследованиях занимали явления, в которых происходило превращение одних форм движения в другие. Исследования многих химических, тепловых, электрических, магнитных, механических, световых явлений постепенно способствовали возникновению и развитию идеи о взаимопревращении различных форм движения друг в друга в эквивалентных количественных отношениях.
А к середине XIX в. закон сохранения и превращения энергии был признан как общий закон природы, охватывающий все физические явления. Приоритет установления данного закона научная общественность того времени признала за тремя учеными. Из них двое немецких ученых –
То, что именно врачи Ю.Р. Майер и Г. Гельмгольц сделали решающий вклад в установление этого закона, не случаен, поскольку, изучая физиологию человека, обмен веществ в живом организме, они столкнулись с наиболее сложными комплексными процессами энергопревращения в различных органах и тканях. В частности, Ю.Р. Майер обнаружил, что в условиях разного теплообмена между человеком и окружающей средой в северных и южных районах в связи с неодинаковыми перепадами температур окислительно-восстановительные процессы в организме идут по-разному. В результате состав и цвет крови у южан и северян различный.
Развивая свои исследования, немецкие ученые осуществили ряд блестящих опытов и расчетов по выявлению связи между отдельными частными видами взаимопревращения энергии.
Так, Ю.Р. Майер также исследовал процессы перехода механического движения в теплоту и обратно и определил механический эквивалент теплоты (равный 365 кГм/ккал), процессы превращения механической энергии через трение в электричество и электричества в теплоту.Г. Гельмгольц изучал процессы превращения кинетической энергии в потенциальную и обратно, превращение механической энергии в теплоту, электрической энергии в теплоту и механическую энергию при производстве работы за счет электричества.
Третий из авторов закона сохранения и превращения энергии Дж. Джоуль основное внимание уделял изучению процессов выделения тепла электрическим током во всей электрической цепи, в том числе и в гальванических элементах, где происходят электролитические химические реакции. В результате им была установлена связь между тепловой, электрической и, что очень важно, одновременно химической энергией.
Он определил, что общее количество теплоты равно теплоте химических реакций, протекающих в гальванических элементах, за то же время. Таким образом, им было показано, что источником теплоты, выделенной в цепи электрического тока, являются химические процессы, проходящие в гальваническом элементе, а электрический ток как бы разносит эту теплоту по всей цепи. Он писал, что «электричество может рассматриваться как важный агент, который переносит, упорядочивает и изменяет химическое тепло».
В дальнейшем Дж. Джоуль проделал свой знаменитый опыт, в котором экспериментально более точно определил механический эквивалент теплоты. С помощью падающих грузов он заставлял ось с лопастями вращаться внутри калориметра, наполненного жидкостью. Измеряя совершаемую грузами работу и выделенную в калориметре теплоту, Дж. Джоуль получил механический эквивалент теплоты, равный 424 кГм/ккал.
Установление закона сохранения и превращения энергии сыграло в истории естествознания огромную роль. Его утверждение стало свое образным катализатором для понимания многих явлений, а также обоснования и открытия целого ряда других частных законов природы.
studfile.net
Мифы современной физики. Законы сохранения / Habr
Продолжение. Начало тут и тут:В этот раз мы замахнемся на святое: на законы сохранения, в том числе на закон сохранения энергии. Правда, вечного двигателя я вам не обещаю.
Закон сохранения энергии имеет такой ореол святости, что практически любой человек напрягается, услышав, что с ним не все хорошо. Между тем, энергия сохраняется в механике, в квантовой механике и даже в СТО – Специальной Теории Относительности. Но… не в ОТО – Общей Теории Относительности. Однако сказать, что энергия не сохраняется, тоже нельзя. Вначале разберемся,
Что же такое – сохраняться?
Вот мы положили в мешок два шара, синий и красный. Через какое-то время достали их. Ага, было два шара, и стало два шара, шары
Однако с количеством шаров все просто – все наблюдатели, как бы они ни двигались, согласятся с тем, что шаров – два. А как быть с энергией? Вот, например, я стою около дома весом 1000 тонн. Кинетическая энергия его в моей системе отсчета равна нулю. Теперь я пойду от дома со скоростью 1 метр в секунду. В моей системе отсчета дом приобрел огромную энергию! Как я, слабый человек, мог дать дому такую энергию всего одним шагом?
Если вы внимательно следили за руками, то, несомненно, заметили, что я совершил грязный хак. Считал энергию вначале в одной системе отсчёта, а потом нагло перескочил в другую. Так делать нельзя. Для энергии состояние до и состояние после должно быть привязано к одной и той же системе отсчета.
Для нашей картинки с шарами это означает, что дно и крышка цилиндра (в общем случае любой фигуры) должны быть параллельны
друг другу. А вот с этим в искривленном пространстве плохо: как вы помните, в искривленном пространстве могут быть много параллельных или не быть ни одной! Хуже того, пространство может быть таким кривым, что туда вообще не вписать такую фигуру!Или время закольцовано – и понятия до и после не вполне определены. Таким образом, в ОТО не то, чтобы энергия не сохраняется, а само понятие “сохраняться” плохо определено.
Канонический пример несохранения энергии
Мы все знаем, что Вселенная расширяется. Когда ее линейный размер увеличивается в 10 раз, то ее объем увеличивается в 1000 раз, и плотность обычного вещества (ведь атомы – это шарики, и все наблюдатели согласны с тем, сколько их) падает тоже в 1000 раз
А вот плотность излучения, в частности реликтового излучения, падает в 10000 раз – помимо того, что фотоны рассеялись в большем объеме, каждый из них еще и покраснел. То есть плотность вещества падает как третья степень, а излучения – как четвертая.
У этого есть интересное следствие – если мы будем двигаться в прошлое, то плотность излучения будет расти быстрее, чем плотность материи, и мы можем дойти до периода, когда плотностью и давлением обычной материи можно будет вообще пренебречь. Гравитация в основном создавалась давлением фотонного газа.
Следует заметить, что космологическая точка зрения – “вся вселенная в такое-то время”, несмотря на ее интуитивную понятность и полезность, для каждого времени после Большого Взрыва образует в пространстве-времени кривую поверхность, то есть не является валидной системой отсчета.
Можно ли поднять себя за волосы?
Спойлер: ДА. Импульс, как вы догадались, тоже не сохраняется. Вы можете погуглить по словам Swimming in space. Вот видео, как это выглядит. Конечно, практической ценности в этом почти нет, но все равно интересно.
habr.com
28. Закон сохранения энергии
В макроскопических процессах.
Способы передачи энергии от одного
Макроскопического тепа другому
XIX в. ознаменовался открытием одного из самых великих принципов современной науки, приведшему к объединению самых различных явлений природы. Принцип этот гласит, что существует определенная величина, называемая энергией, которая не меняется ни при каких превращениях, происходящих в природе. Энергия — единая мера различных форм движения материи.
На протяжении более четырех десятилетий формировался этот принцип в науке. Следует отметить, что процесс установления закона сохранения и превращения энергии — это одновременно процесс формирования таких дисциплин в физике, как статистическая физика и термодинамика, процесс установления I и II начал термодинамики, выработка понятий энергии, тепловой (внутренней) энергии, работы, энтропии.
Механическая энергия и внутренняя энергия — это только две из многих форм энергии. Все, что может быть превращено в какую-либо из этих форм, есть тоже форма энергии.
Возможны два качественно различных способа передачи энергии от одного макроскопического тела к другому — в форме работы и в форме теплоты (путем теплообмена). Первый закон термодинамики устанавливает эквивалентность этих двух способов передачи энергии, утверждая, что изменить внутреннюю энергию тела можно любым из этих способов.
Изменение энергии тела, осуществленное первым способом, называют работой, совершаемой над этим телом. Передача энергии в форме работы производится в процессе силового взаимодействия тел и всегда сопровождается макроперемещением. Работа, совершаемая над телом, может непосредственно пойти на увеличение любого вида энергии.
Передача энергии путем теплообмена между телами обусловлена различием температур этих тел. Энергия, получаемая телом в форме теплоты, может непосредственно пойти только на увеличение его внутренней энергии.
Невозможен вечный двигатель (перпетуум-мобиле) первого рода. Это является следствием начала термодинамики.
Всеми явлениями природы управляет закон сохранения и превращения энергии: «Энергия в природе не возникает из ничего и не исчезает: количество энергии неизменно, она только переходит из одной формы в другую».
29. Концепция вероятностного детерминизма в статистической физике
История открытия закона сохранения и превращения энергии привела к изучению тепловых явлений в двух направлениях: термодинамическом и молекулярно-кинетическом. С. Карно положил начало новому методу рассмотрения превращения теплоты и работы друг в друга в макроскопических системах, в первую очередь в тепловых машинах, и тем самым явился основателем науки, которая впоследствии была названа У. Томсоном «термодинамикой». Термодинамическое рассмотрение ограничивается в основном изучением особенностей превращения тепловой формы движения в другие формы, не интересуясь вопросом микроскопического движения частиц, составляющих вещество, то есть без учета молекулярного строения вещества.
Молекулярно-кинетическая теория явилась развитием кинетической теории вещества (альтернативной теплородной). Она характеризуется рассмотрением различных макропроявлений систем как результатов суммарного действия огромной совокупности хаотически движущихся молекул. При этом молекулярно-кинетическая теория использует
При
рассмотрении систем, состоящих из
огромного числа частиц,
состояние системы характеризуют не
полным набором
значений координат и импульсов всех
частиц, а вероятностью
того, что эти значения лежат внутри
определенных  интервалов.
Тогда состояние системы задается с
помощью функции
распределения, зависящей от координат,
импульсов всех
частиц системы и от времени. Функция
распределения интерпретируется
как плотность вероятности обнаружения
той или
иной физической величины (например, х. или Р) в
определенных
интервалах от х до X, + ∆х,
или от Р. до Р.
+ АР.. По
известной
функции распределения можно найти
средние значения
любой физической величины, зависящей
от координат и
импульсов, и вероятность того, что эта
величина принимает определенное значение
в заданных интервалах.
интервалов.
Тогда состояние системы задается с
помощью функции
распределения, зависящей от координат,
импульсов всех
частиц системы и от времени. Функция
распределения интерпретируется
как плотность вероятности обнаружения
той или
иной физической величины (например, х. или Р) в
определенных
интервалах от х до X, + ∆х,
или от Р. до Р.
+ АР.. По
известной
функции распределения можно найти
средние значения
любой физической величины, зависящей
от координат и
импульсов, и вероятность того, что эта
величина принимает определенное значение
в заданных интервалах.
Статистическая механика в некотором смысле нарушает традиции классического описания физической реальности. Ведь идеалом классического описания считалась динамическая детерминированная форма законов физики. Поэтому первоначально физики негативно относились к введению вероятности в статистические законы. Многие считали, что вероятность в законах свидетельствует о мере нашего незнания. Однако это не так. Статистические законы также выражают необходимые связи в природе. Действительно, во всех фундаментальных статистических теориях состояние представляет собой вероятностную характеристику системы, ее уравнения движения по-прежнему однозначно определяют состояние (статистическое распределение) в любой последующий момент времени по заданному распределению в начальный момент. Т.Я. Мякишев подчеркивает, что главное отличие статистических законов от динамических состоит в учете случайного (флуктуации). В философии давно выработано представление о диалектическом тождестве и различии противоположных сторон любого явления. В диалектике необходимое и случайное — это две противоположности единого явления, две стороны одной медали, которые взаимообуславливают друг друга, взаимопревращаются, не существуют друг без друга. Главное различие между динамическими и статистическими законами с философско-методологической точки зрения состоит в том, что в статистических законах необходимость выступает в диалектической связи со случайностью, а в динамических — как абсолютная противоположность случайного. А отсюда вывод: «Динамические законы представляют собой первый низший этап в процессе познания окружающего нас мира? статистические законы обеспечивают более современное отображение объективных связей в природе: они выражают следующий, более высокий этап познания».
studfile.net
§ 13. Закон сохранения энергии
Закон сохранения энергии — результат обобщения многих экспериментальных данных. Идея этого закона принадлежит М. В. Ломоносову (1711 —1765), изложившему закон сохранения материи и движения, а количественная формулировка закона сохранения энергии дана немецким врачом Ю. Майером (1814—1878) и немецким естествоиспытателем Г. Гельмгольцем (1821 — 1894).
Рассмотрим систему материальных точек массами m1, m2, …, mn, движущихся со скоростями v1, v2, …, vn. Пусть F‘1, F‘2, …, F‘n — равнодействующие внутренних консервативных сил, действующих на каждую из этих точек, a f1, F2, …, Fn— равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим f1, f2, …, fn. При v<<с массы материальных точек
25
постоянны и уравнения второго закона Ньютона для этих точек следующие:
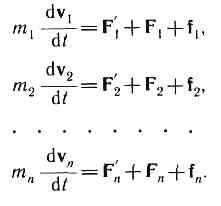
Двигаясь под действием сил, точки системы за интервал времени dt совершают перемещения, соответственно равные dr1, dr2, …, drn. Умножим каждое из уравнений скалярно на соответствующее перемещение и, учитывая, что dri = vidt, получим:
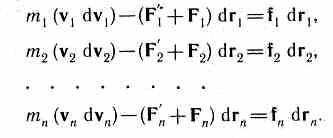
Сложив эти уравнения, получим
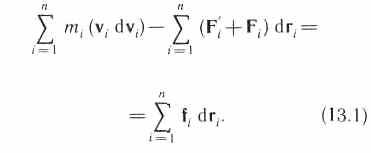
Первый член левой части равенства (13.1)
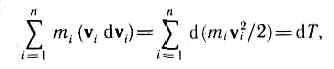
где dT есть приращение кинетической энергии системы. Второй член
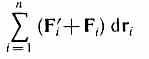
равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т. е. равен элементарному приращению потенциальной энергии dП системы (см. (12.2)).
Правая часть равенства (13.1) задает работу внешних неконсервативных сил,
действующих на систему. Таким образом, имеем
d(T+П)=dA. (13.2)
При переходе системы из состояния 1 в какое-либо состояние 2
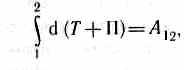
т. е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (13.2) следует, что
d(Т+П) = 0,
откуда
Т+П = E=const, (13.3)
т. е. полная механическая энергия системы сохраняется постоянной. Выражение (13.3) представляет собой закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем.
Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами. Закон сохранения механической энергии можно сформулировать так: в консервативных системах полная механическая энергия сохраняется.
Закон сохранения механической энергии связан с однородностью времени, т. е. инвариантностью физических законов относительно выбора начала отсчета времени. Например, при свободном падении тела в поле сил тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, когда тело начало падать.
Существует еще один вид систем — диссипативные системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие (немеха-
26
нические) формы энергии. Этот процесс получил название диссипации (или рассеяния) энергии. Строго говоря, все системы в природе являются диссипативными.
В консервативных системах полная механическая энергия остается постоянной. Могут происходить лишь превращения кинетической энергии в потенциальную и обратно в эквивалентных количествах, так что полная энергия остается неизменной. Поэтому, как указывает Ф. Энгельс, этот закон не есть просто закон количественного сохранения энергии, а закон сохранения и превращения энергии, выражающий и качественную сторону взаимного превращения различных форм движения друг в друга. Закон сохранения и превращения энергии — фундаментальный закон природы, он справедлив как для систем макроскопических тел, так и для систем микротел.
В системе, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии — сущность неуничтожимости материи и ее движения.
studfile.net
Кто открыл закон сохранения энергии?
Впервые его сформулировал Лейбниц в 1686 году (для механических систем) . Позднее понятие энергии было обобщено и на немеханические явления, и закон сохранения энергии в более общем виде был сформулирован в работах Ю. Р. Майера, Дж. Джоуля и Г. Гельмгольца уже в середине 19 века. Народ, не путайте божий дар с яичницей.. . Ломоносов сформулировал закон сохранения ВЕЩЕСТВА, а не энергии. Практически одновременно с Лавуазье, хотя и независимо от него. А Эйнштейн доказал эквивалентность массы и энергии и сформулировал закон сохранения энергии-массы в релятивистском случае.
Закон сохранения энергии. Закон сохранения энергии — физический закон, в соответствии с которым: Полная механическая энергия системы тел сохраняется в процессе их движения, если внешние и внутренние силы, действующие на систему тел, являются потенциальными. Общую оценку вновь открытому закону сохранения и превращения энергии дал Фридрих Энгельс Роберт Майер, открывший закон сохранения энергии, был врачом, который, как и один из создателей кибернетики У. Эшби не имел ни математического, ни физического образования
В начале сороковых годов XIX в. Майеру удалось сформулировать один из важнейших законов современной физики — закон сохранения энергии, согласно которому энергия в произвольной замкнутой системе при любых процессах, происходящих в системе, остается величиной постоянной и лишь переходит из одной формы в другую.
Лейбниц в 1686 год
Ломоносов-это гений в квадрате! Он сформулировал закон сохранения массы вещества. Фундаментальнейший закон природы! Он же сформулировал закон сохранения энергии. Ещё один фундаментальнейший закон природы! Исключений из них не бывает!!! Вы всё что угодно можете проверять этими законами. Действует всегда и во всех уголках вселенной. Во всех размерах. На всех уровнях организации материи (нано, микро, космических). Истинность ваших открытий, изобретений можете всегда проверить этими законами. Я думаю, что их вообще можно объединить. А если вас в какой-то степени смущают формулировки, то в законах главное смысл. Смысл выясненного. А формулировки с течением времени всегда изменяются из-за расширения (изменения) научной картины! Я не могу понять, почему Ломоносову до сих пор не отдают должного? Наши, как всегда боятся, подать голос. Ведь, чёрт возьми, можно стереть, забыть все остальные законы и мир сможет открыть их заново при помощи этих двух (одного)! Их можно принять за аксиому.
touch.otvet.mail.ru
Закон сохранения энергии в механике. Общефизический закон сохранения.
Рассмотрим систему материальных точек и обозначим:
 — результирующая
всех внешних сил, действующих на систему;
— результирующая
всех внешних сил, действующих на систему;
 — результирующая
всех внутренних консервативных сил;
— результирующая
всех внутренних консервативных сил;
 — результирующая
всех внутренних неконсервативных сил,
действующих на материальные точки.
— результирующая
всех внутренних неконсервативных сил,
действующих на материальные точки.
Тогда результирующая всех сил:
 (34)
(34)
Умножим (1) скалярно
на малое перемещение  :
:
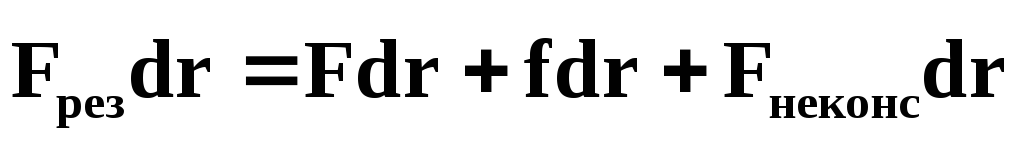 (35)
(35)
Выясним физический смысл:
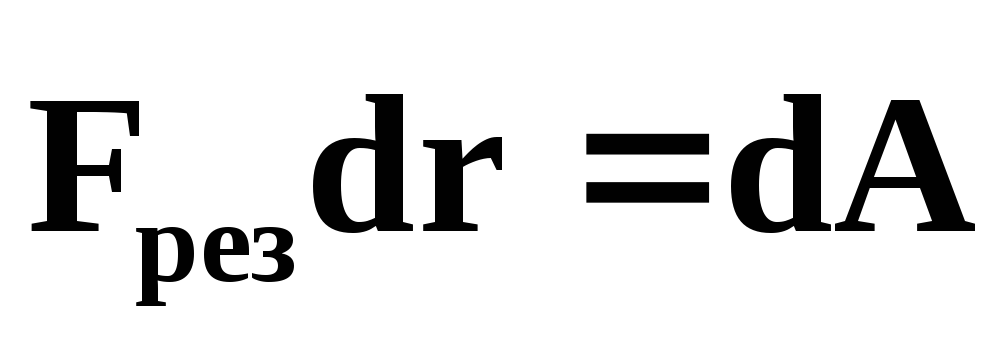 — работа результирующей
силы, которая, как было установлено
ранее, равна приращению
— работа результирующей
силы, которая, как было установлено
ранее, равна приращению 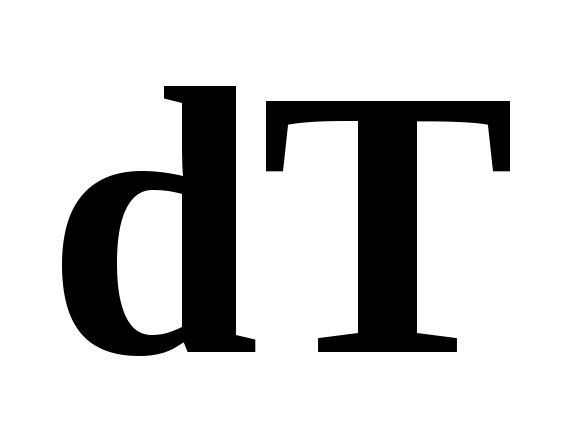 кинетической
энергии системы:
кинетической
энергии системы:
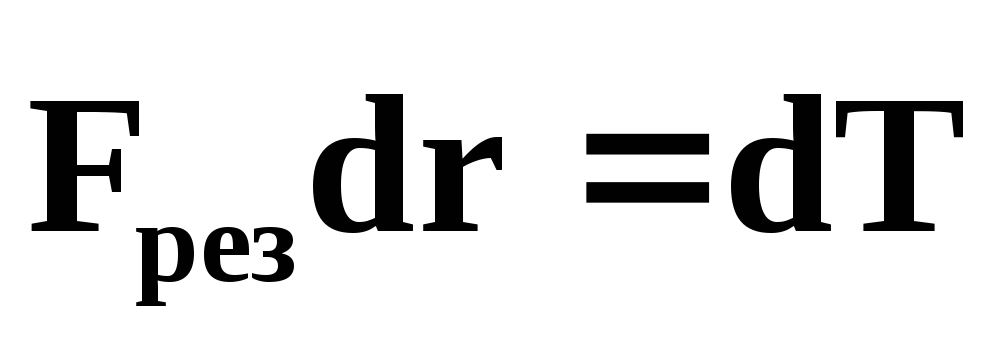
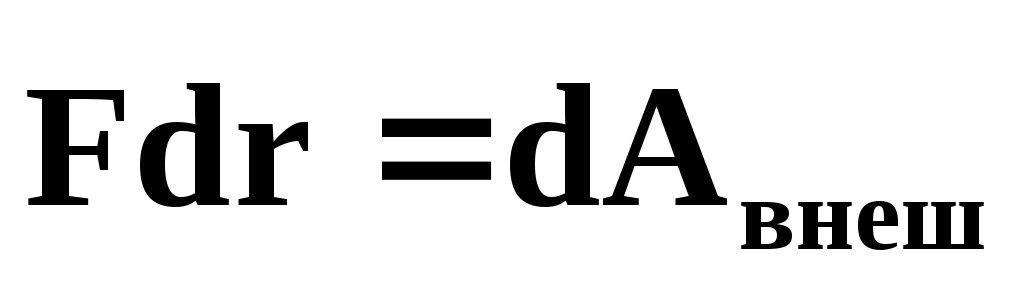 — работа внешних
сил;
— работа внешних
сил;
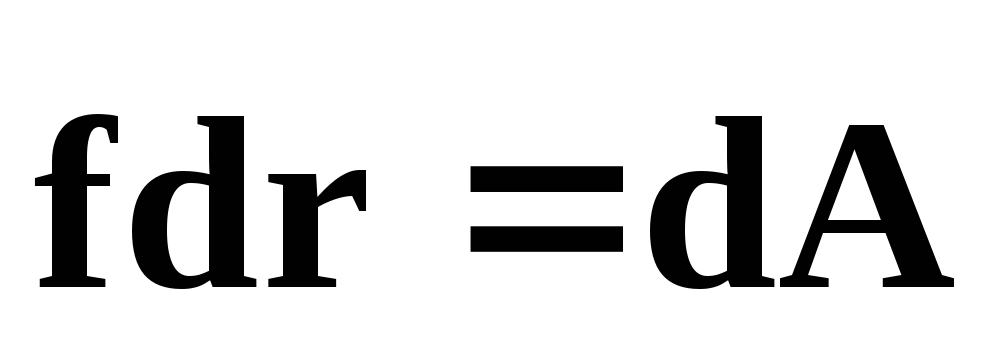 — работа консервативных
сил, равная убыли потенциальной энергии
системы:
— работа консервативных
сил, равная убыли потенциальной энергии
системы:
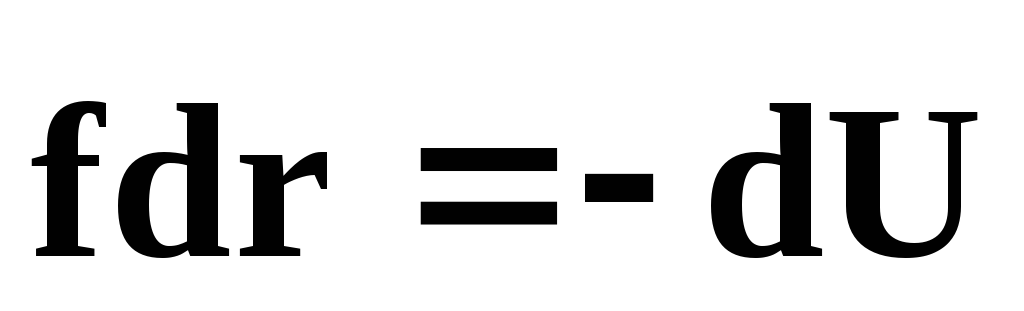
 — работа
неконсервативных сил.
— работа
неконсервативных сил.
Перепишем (35) в виде:

или  (36)
(36)
Принимая во
внимание, что  ,
где
,
где — полная энергия системы, получим:
— полная энергия системы, получим:

Если система
замкнута, то на нее внешние силы не
действуют и  ,
тогда:
,
тогда:
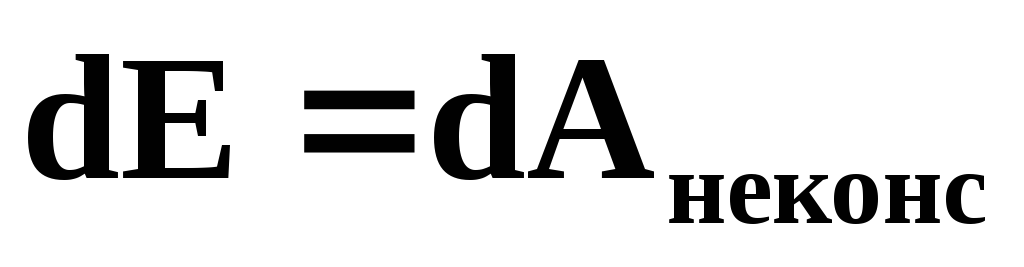
Если в системе не
действуют неконсервативные силы,
например силы трения, то  и
и
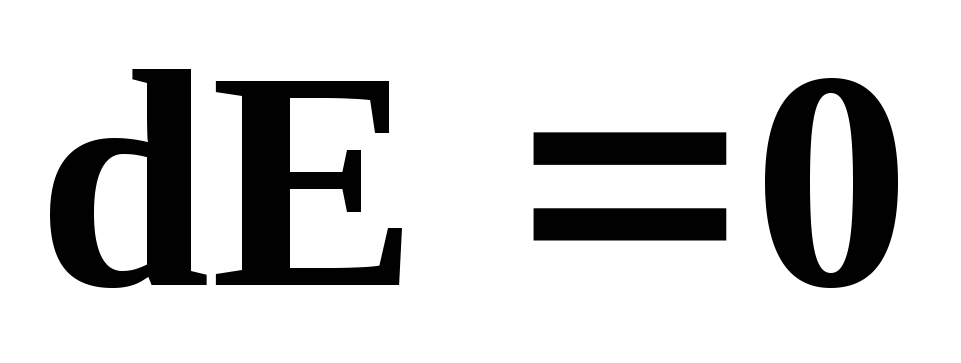 ,
т.е.
,
т.е.  (37)
(37)
(37) – математическая формулировка закона сохранения механической энергии:
— полная энергия замкнутой механической системы не меняется с течением времени.
Однако в реальных
системах механическая энергия, отдельно
взятая, не сохраняется. В любой реальной
системе при движении тел возникают силы
трения, которые являются неконсервативными
силами. В этом случае 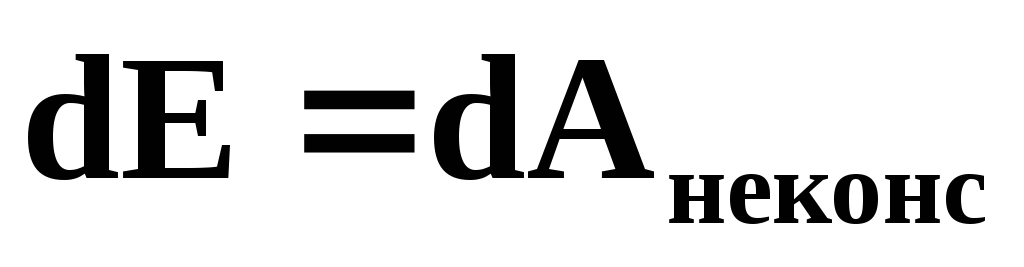 и полная механическая энергия такой
системы убывает. Но при этом механическая
энергия переходит в различные виды
немеханической энергии, например, в
энергию теплового движения, т.е. во
внутреннюю энергию среды, в которой
происходит движение.
и полная механическая энергия такой
системы убывает. Но при этом механическая
энергия переходит в различные виды
немеханической энергии, например, в
энергию теплового движения, т.е. во
внутреннюю энергию среды, в которой
происходит движение.
Поэтому рассмотренный нами закон сохранения и превращения механической энергии является частным случаем всеобщего физического закона сохранения и превращения энергии.
Абсолютно упругий и абсолютно неупругий центральные удары.
Абсолютно упругий центральный удар
подчиняется закону сохранения импульса и закону сохранения механической энергии:
ЗСИ: 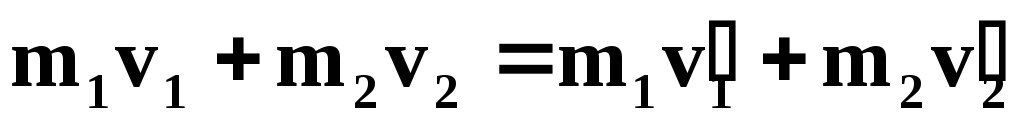
ЗСЭ: 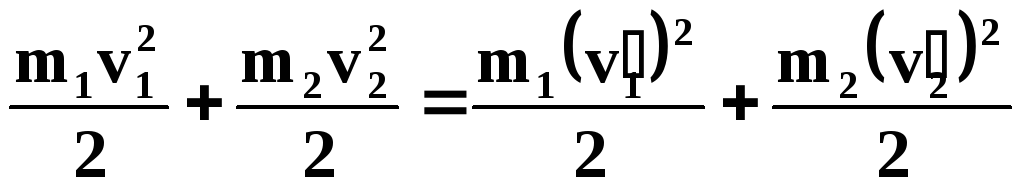
Абсолютно неупругий центральный удар
наличие общей скорости после соударения
ЗСИ: 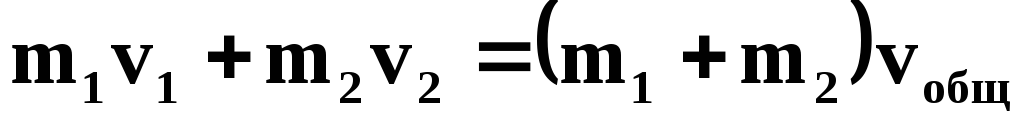
ЗСЭ: 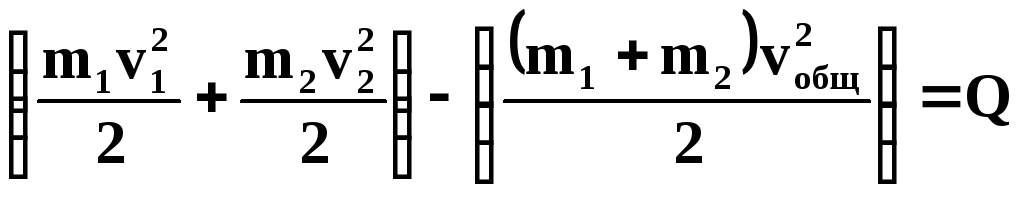
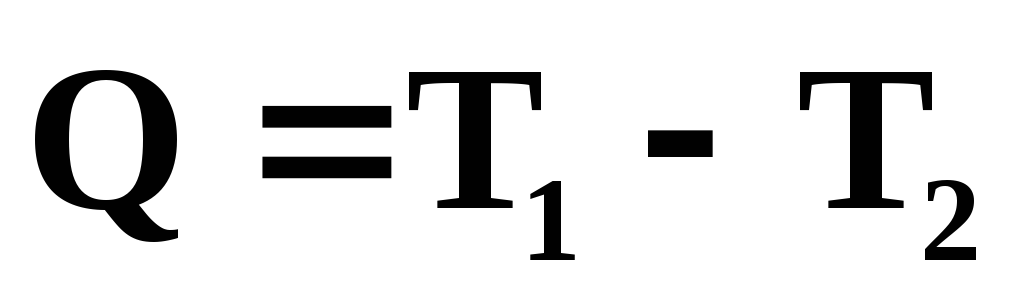
где  — выделившееся после соударения тепло;
— выделившееся после соударения тепло;
 — кинетическая
энергия тел до соударения;
— кинетическая
энергия тел до соударения;
 — кинетическая
энергия тел после соударения.
— кинетическая
энергия тел после соударения.
Твердое тело в механике. Уравнение вращательного движения твердого тела относительно точки.
| Будем рассматривать твердое тело, как систему n точек в системе координат xyz. Обозначим:
|
 — равнодействующая
всех внешних сил, действующих на i-тую
точку.
— равнодействующая
всех внешних сил, действующих на i-тую
точку.
Запишем для i-той материальной точки II закон Ньютона:
 (38)
(38)
Умножим слева обе
части (38) векторно на 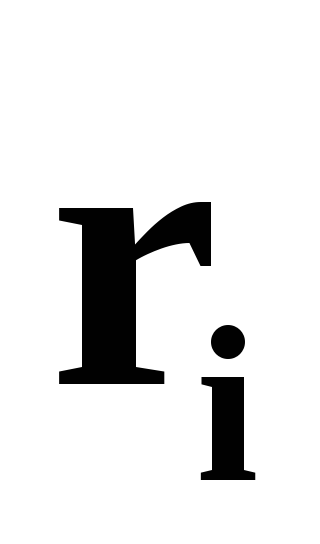 :
:
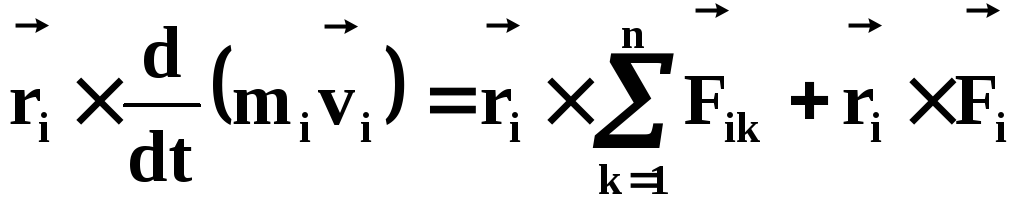 (39)
(39)
Видно, что
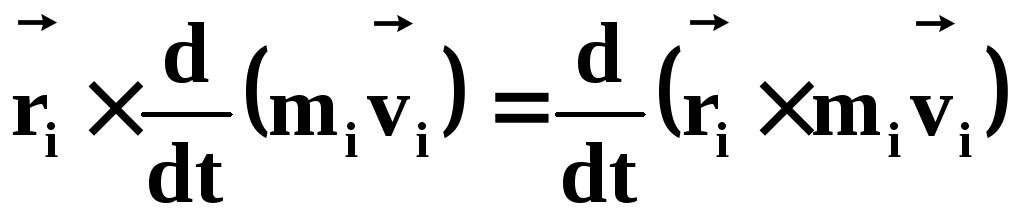 (40)
(40)
В самом деле:
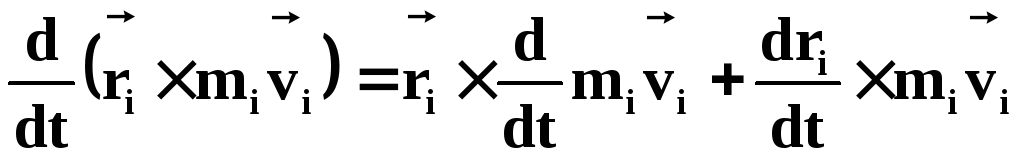
причем:
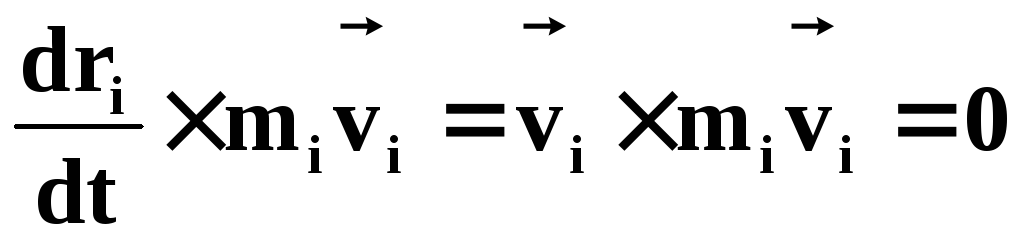
Перепишем уравнение (39) с учетом (40):
 (41)
(41)
Векторное произведение радиус-вектора точки на ее импульс называется моментом импульса точки относительно т. О:
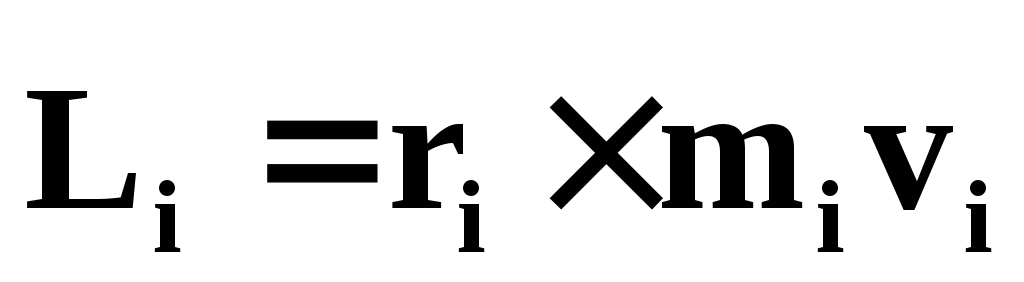 (42)
(42)
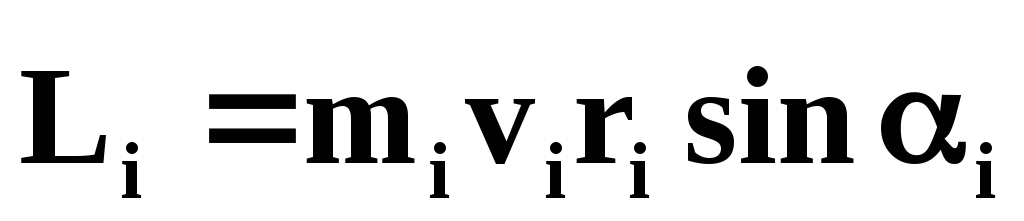 ,
,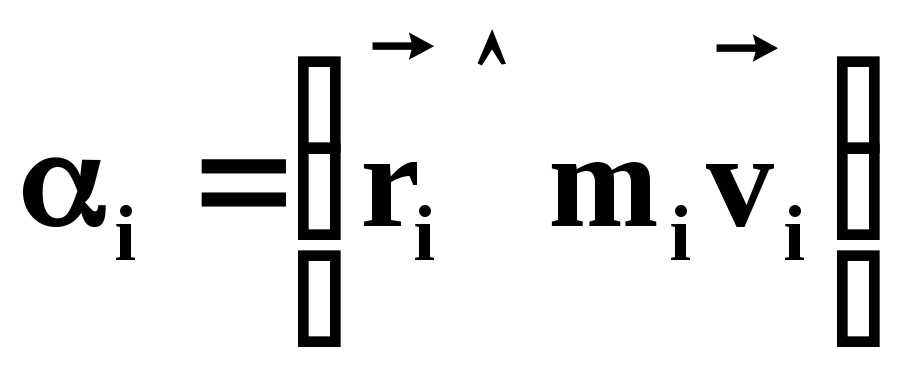 (43)
(43)
Векторное произведение радиус-вектора точки приложения силы на вектор этой силы называется моментом силы относительно т. О.
Перпендикуляр 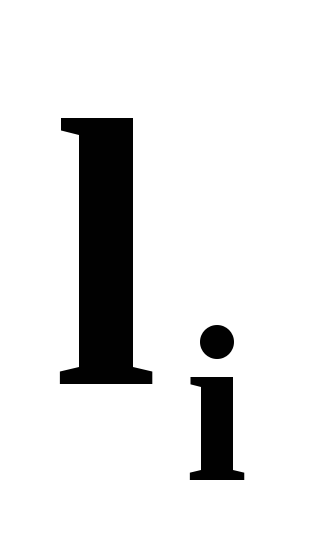 ,
опущенный из т.О на направление вектора
силы, называетсяплечом
этой силы.
,
опущенный из т.О на направление вектора
силы, называетсяплечом
этой силы.
С учетом (41) и (43) перепишем (40) в виде:
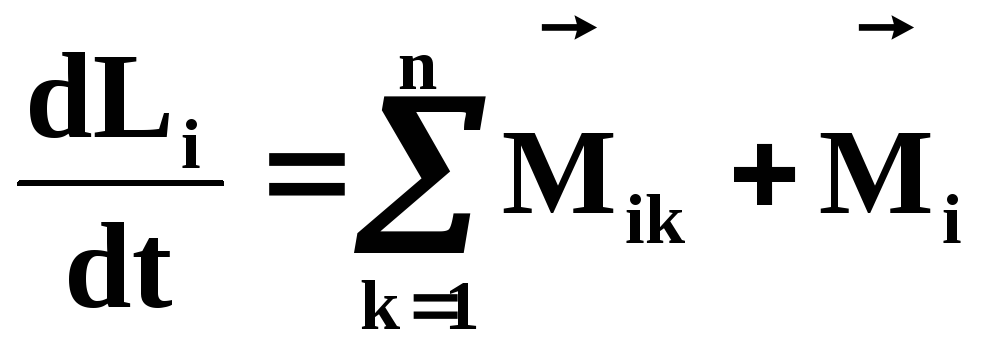 (45)
(45)
Записывая аналогичные уравнения для всех n точек твердого тела и суммируя их почленно, получим:
 (46)
(46)
Векторная сумма 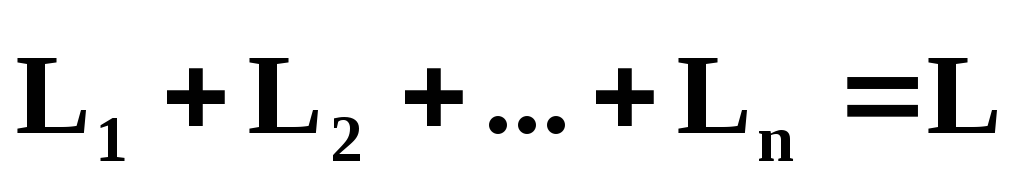 называетсямоментом
импульса тела относительно т. О.
называетсямоментом
импульса тела относительно т. О.
Векторная сумма моментов внешних сил, приложенных ко всем точкам системы, называется результирующим или главным моментом внешних сил относительно т. О:
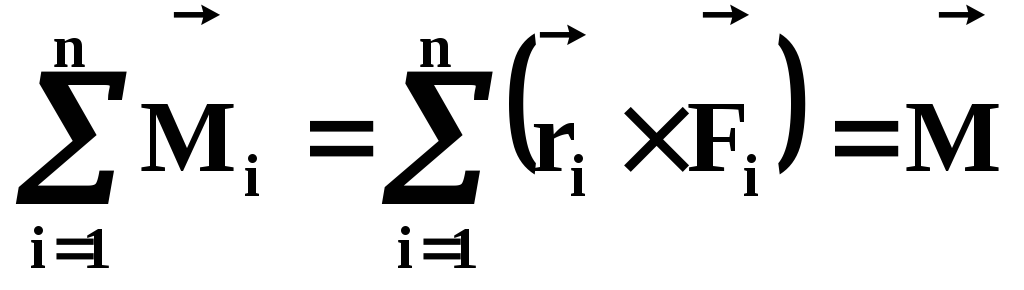
Наконец, векторная
сумма моментов всех внутренних сил
относительно т. О равна нулю: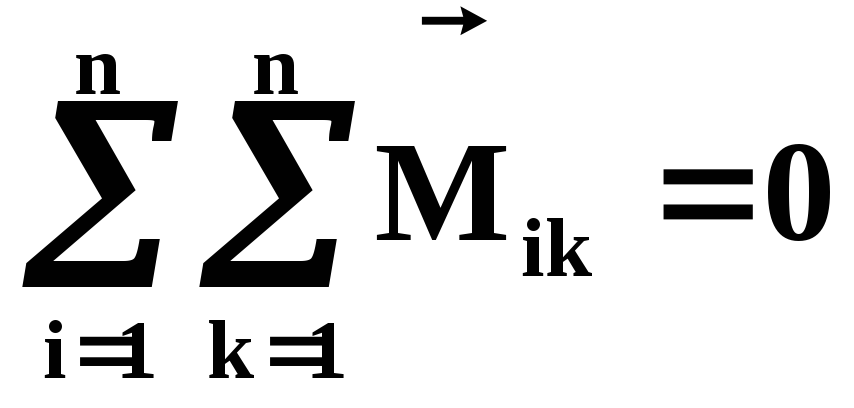 ,
т.к. момент каждой пары внутренних сил
,
т.к. момент каждой пары внутренних сил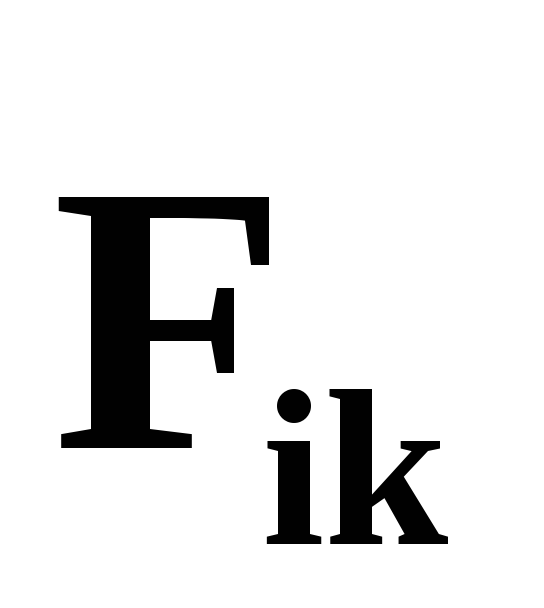 и
и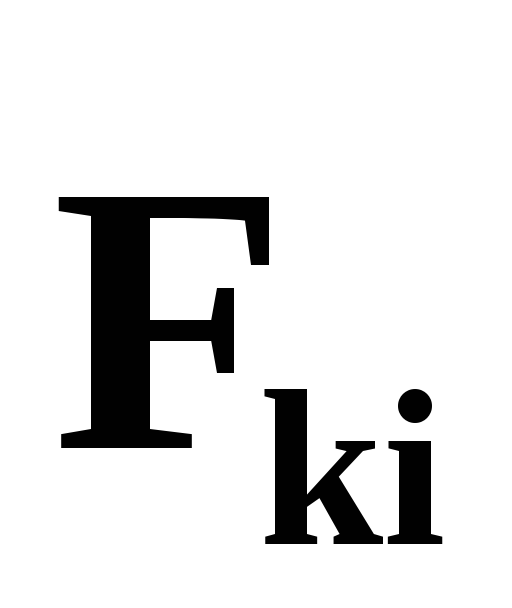
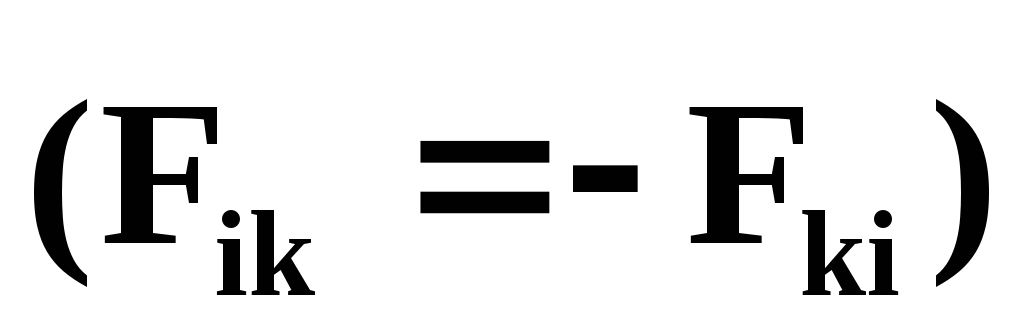 равен нулю. Тогда уравнение (40) примет
вид:
равен нулю. Тогда уравнение (40) примет
вид:
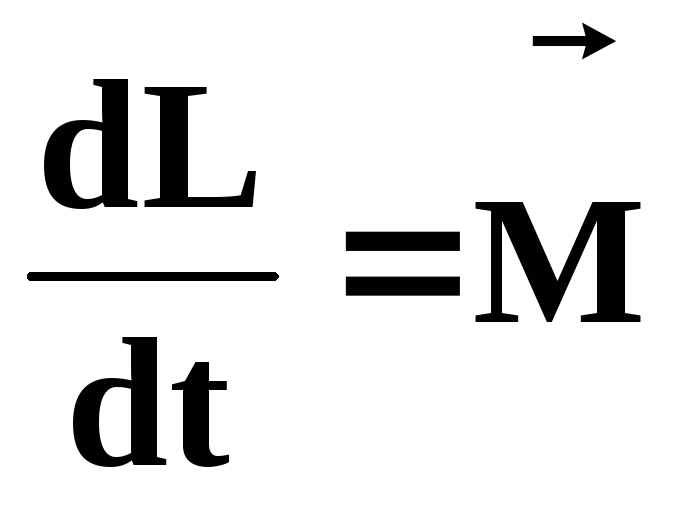 (47)
(47)
Это уравнение называется уравнением вращательного движения твердого тела относительно неподвижной точки.
studfile.net
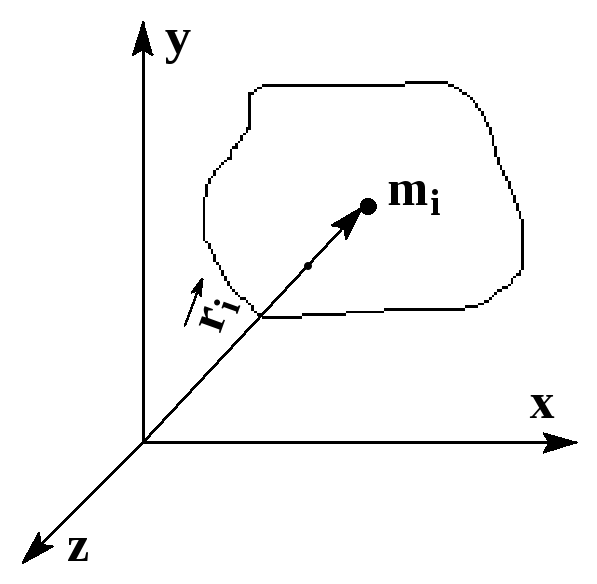
 ,
,  — масса и скоростьi-той
точки;
— масса и скоростьi-той
точки;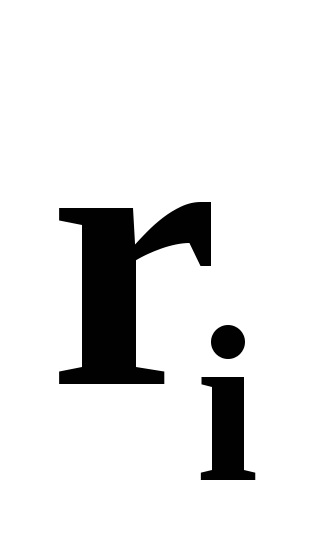 — ее радиус-вектор;
— ее радиус-вектор; — внутренняя
сила, действующая на i-тую
точку со стороны k-той;
— внутренняя
сила, действующая на i-тую
точку со стороны k-той;