Бесконечная убывающая геометрическая прогрессия и ее формулы — энциклопедический справочник и словарь для студента от А до Я
ОПРЕДЕЛЕНИЕ
Численная последовательность \(\ B=\left\{b_{1}, b_{2}, \dots, b_{n}, \dots\right\} \) , каждый член которой равен предыдущей, умноженной на постоянное число \(\ q \) для этой последовательности, называется геометрической прогрессией. Число q называется знаменателем прогрессии.
Если знаменатель \(\ |q|Количество бесконечно уменьшающейся геометрической прогрессии
Сумма бесконечно убывающей прогрессии — это число, к которому сумма первых n членов убывающей прогрессии приближается без ограничений, поскольку число n стремится к бесконечности. Сумма бесконечно уменьшающейся геометрической прогрессии рассчитывается по формуле:
\(\ S_{n}=\frac{b_{1}}{1-q} \)
Примеры решения проблем
ПРИМЕР 1
Чтобы найти сумму бесконечной геометрической прогрессии \(\ 1, \frac{1}{3}, \frac{1}{9}, \dots \)
Эта последовательность чисел будет бесконечно уменьшающейся прогрессией, поскольку
\(\ S_{n}=\frac{b_{1}}{1-q}=\frac{1}{1-\frac{1}{3}}=\frac{3}{2} \)
\(\ S_{n}=\frac{3}{2} \)
ПРИМЕР 2
Представить число \(\ 0 \) в виде обычной фракции, \(\ (6) \)
Написание числа как \(\ 0,(6) \) означает периодическую долю \(\ 0.6666 \dots \), которая может быть представлена в виде следующей суммы:
\(\ 0,(6)=0,6+0,06+0,006+\dots \)
Эта сумма представляет собой сумму бесконечной геометрической прогрессии с первым членом \(\ b_{1}=0,6 \) и знаменателем \(\ \mathrm{q}=\mathrm{O}_{.1} \). Найдите эту сумму по формуле
\(\ S_{n}=\frac{b_{1}}{1-q}=\frac{0,6}{1-0,1}=\frac{0,6}{0,9}=\frac{6}{9}=\frac{2}{3} \)
Поэтому \(\ 0,(6)=\frac{2}{3} \)
\(\ 0,(6)=\frac{2}{3} \)
sciterm.ru
Урок по теме “Бесконечно убывающая геометрическая прогрессия”
Урок по теме “Бесконечно убывающая геометрическая прогрессия”
Цель урока: ознакомление учащихся с новым видом последовательности – бесконечно убывающей геометрической прогрессией.
Задачи:
формулирование начального представления о пределе числовой последовательности; знакомство с ещё одним способом обращения бесконечных периодических дробей в обыкновенные с помощью формулы суммы бесконечно убывающей геометрической прогрессии;
развитие интеллектуальных качеств личности школьников такие, как логическое мышление, способность к оценочным действиям, обобщению;
воспитание активности, взаимопомощи, коллективизма, интереса к предмету.
Оборудование: компьютерный класс, проектор, экран.
Тип урока: урок – усвоение новой темы.
Ход урока
I. Орг. момент. Сообщение темы и цели урока.
II. Актуализация знаний учащихся. 1. Проверка домашнего задания.
1) Проверка основных формул, связанных с арифметической и геометрической прогрессиями. Два ученика готовят записи формул у доски.
2) Остальные учащиеся выполняют математический диктант по теме «Формулы суммы».
Задания:
№1. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен 6 (1-й вариант), -20 (2-й вариант), а пятый член -6 (1-й вариант), 20 (2-й вариант).
№2. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен -20(1-й вариант), 6 (2-й вариант), а разность равна 10(1-й вариант), -3(2-й вариант).
№3. Найдите сумму первых пяти членов геометрической прогрессии, если её первый член равен 1(1-й вариант), -1 (2-й вариант), а знаменатель равен -2(1-й вариант), 2(2-й вариант).
По окончании диктанта, выборочно, у двоих учеников работы проверяются на оценку, остальные выполняют самопроверку по готовым решениям, записанным на отворотах доски.
Решения:
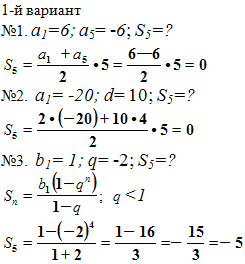
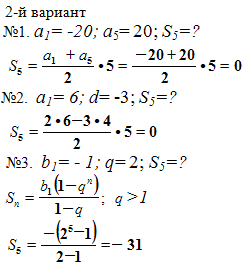
Задания
1. Арифметическая прогрессия задана формулой an = 7 – 4n. Найдите a10. (-33)
2. В арифметической прогрессии a3 = 7 и a5 = 1. Найдите a4. (4)
3. В арифметической прогрессии a3 = 7 и a5 = 1. Найдите a17
4. В арифметической прогрессии a3 = 7 и a5 = 1. Найдите S17. (-187)
5. Для геометрической прогрессии 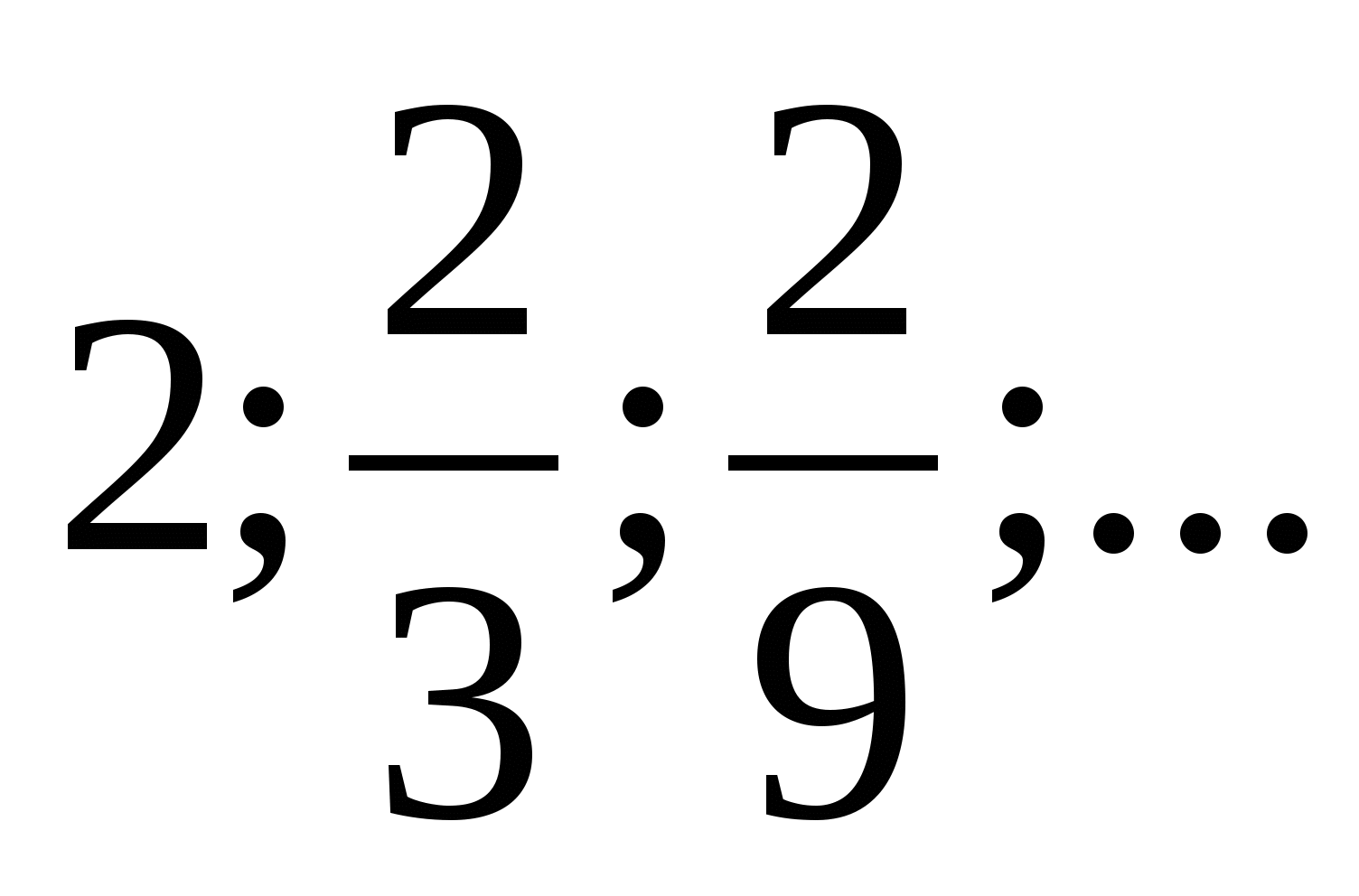 найдите пятый член.
найдите пятый член. 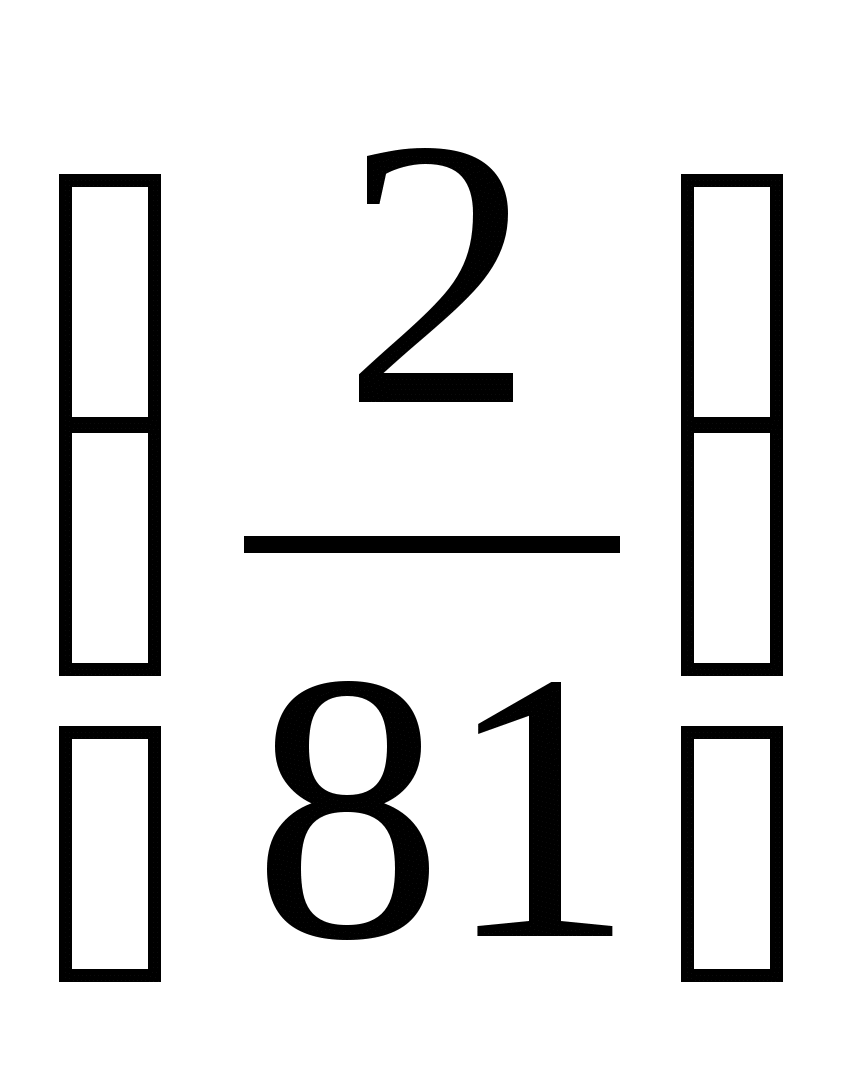
6. Для геометрической прогрессии 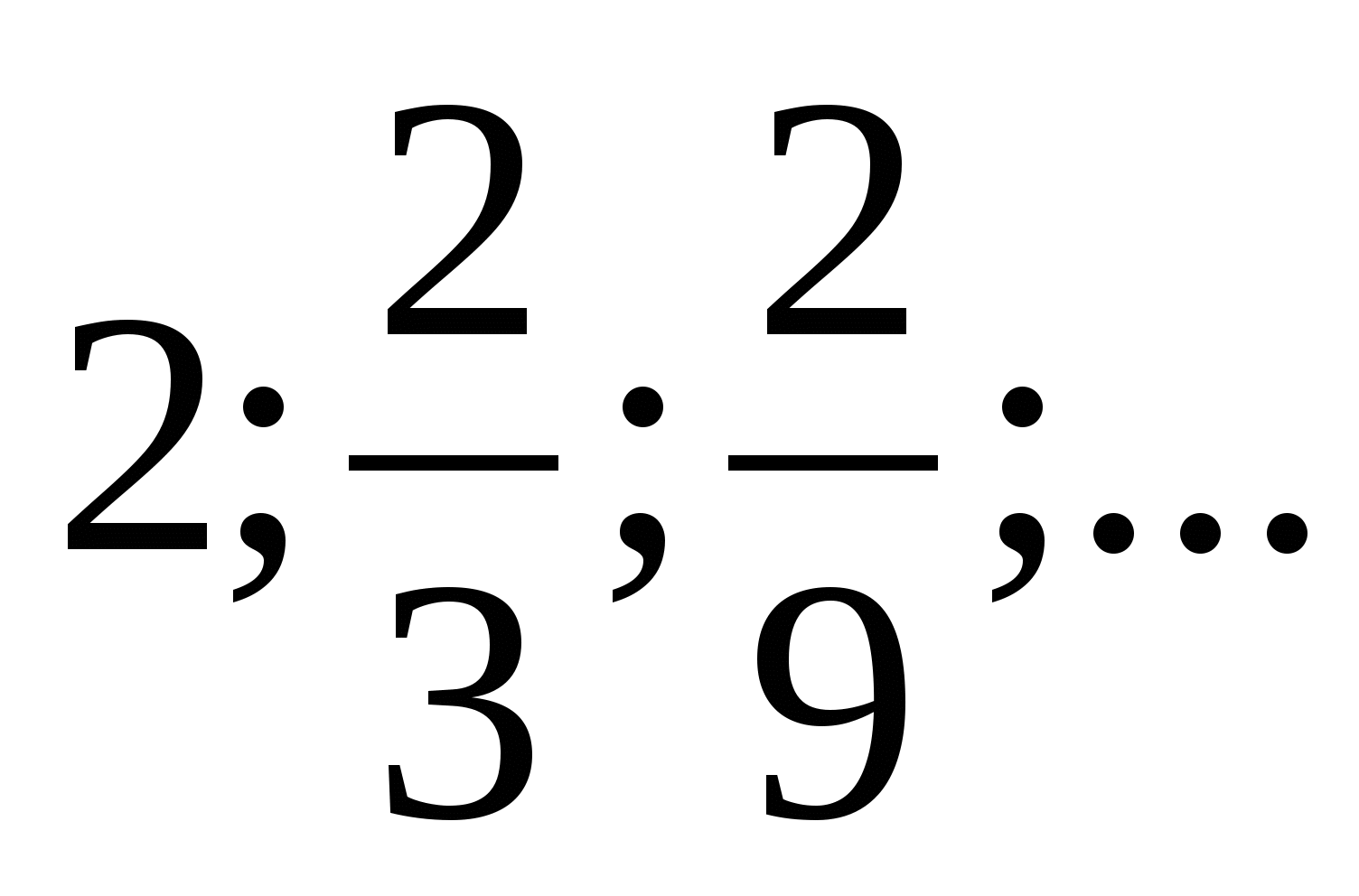 найдите n-й член.
найдите n-й член. 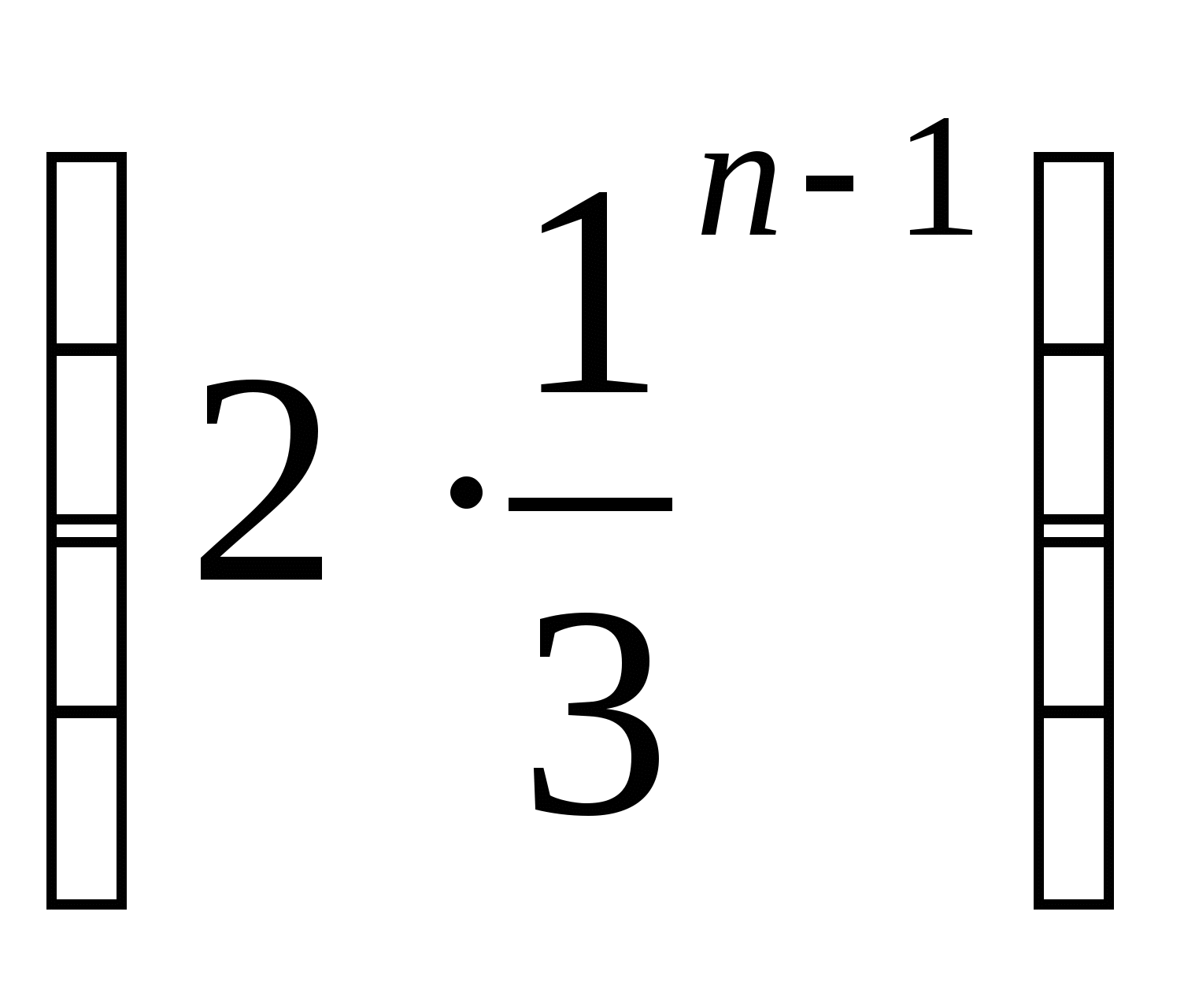
7. В геометрической прогрессии b3 = 8 и b5 = 2. Найдите b4. (4)
8. В геометрической прогрессии b3 = 8 и b5 = 2. Найдите b1 и q. 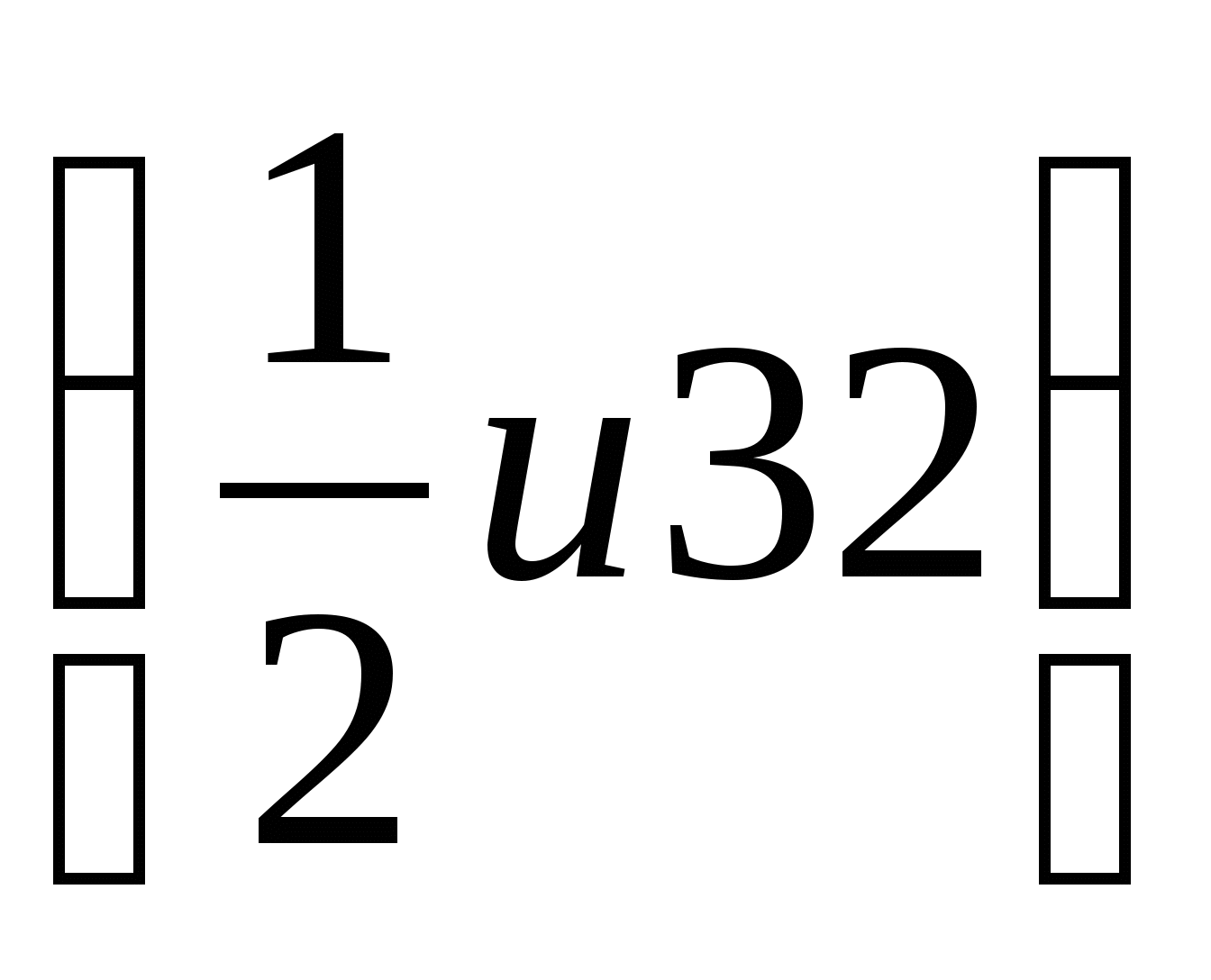
9. В геометрической прогрессии b3 = 8 и b5 = 2. Найдите S5. (62)
III. Изучение новой темы (демонстрация презентации).
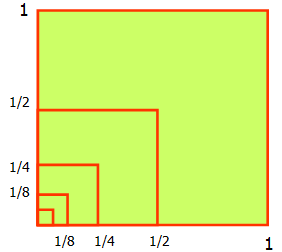
Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего.
В результате, мы получили последовательность сторон квадратов 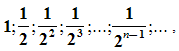
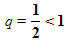 .
.И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,
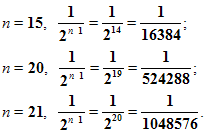
Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.
С помощью этого рисунка можно рассмотреть и ещё одну последовательность.

Например, последовательность площадей квадратов:
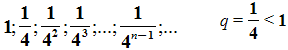
 . И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
. И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
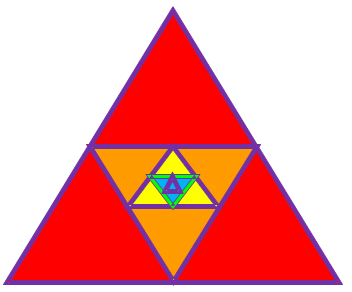
Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников.
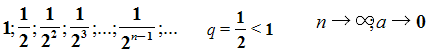
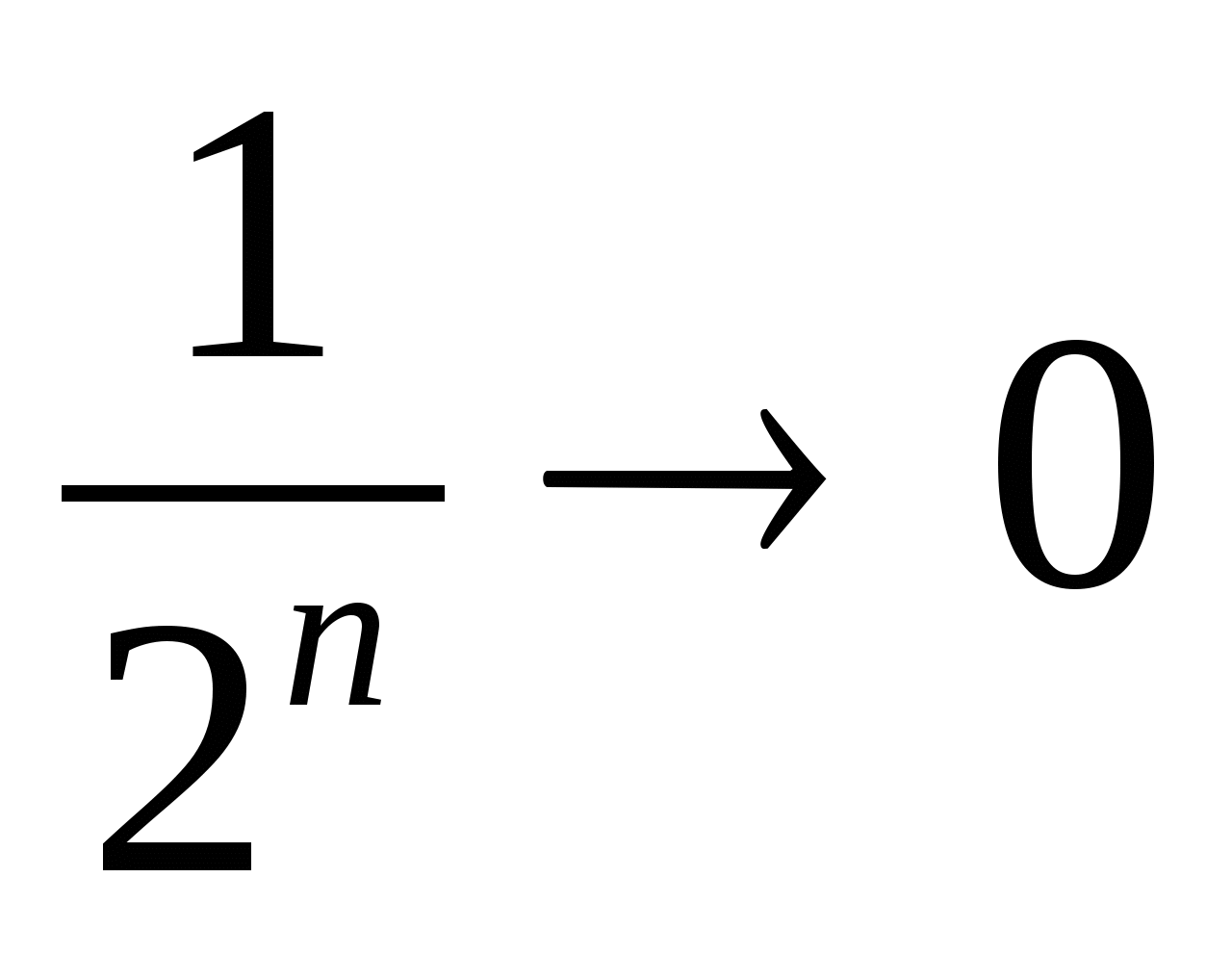
 .
.Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.
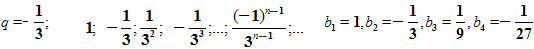
То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.
Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.
Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.
Фронтальная работа.
Определение:
Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы. 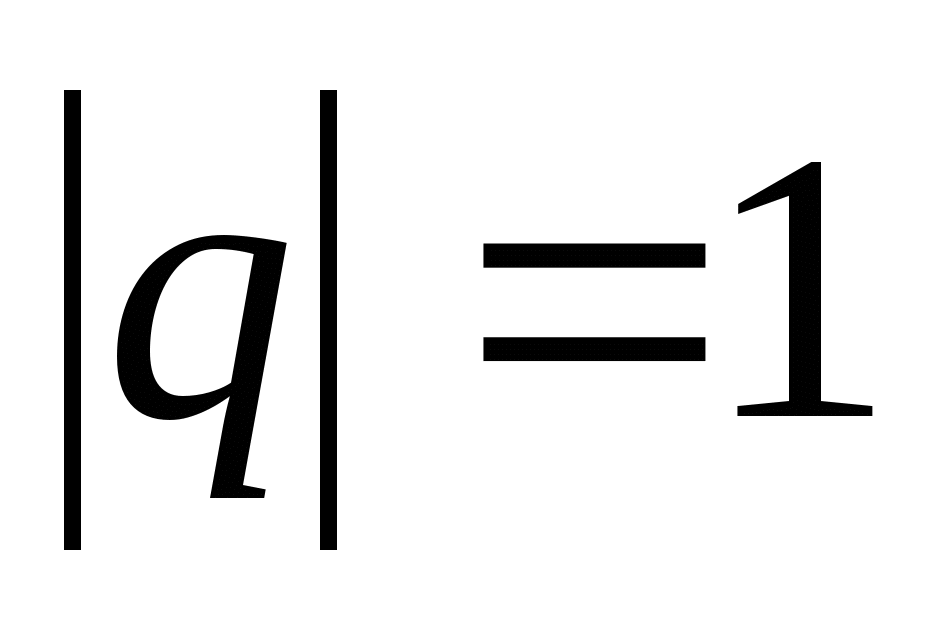
С помощью определения можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.
Задача
Является ли последовательность бесконечно убывающей геометрической прогрессией, если она заданна формулой:
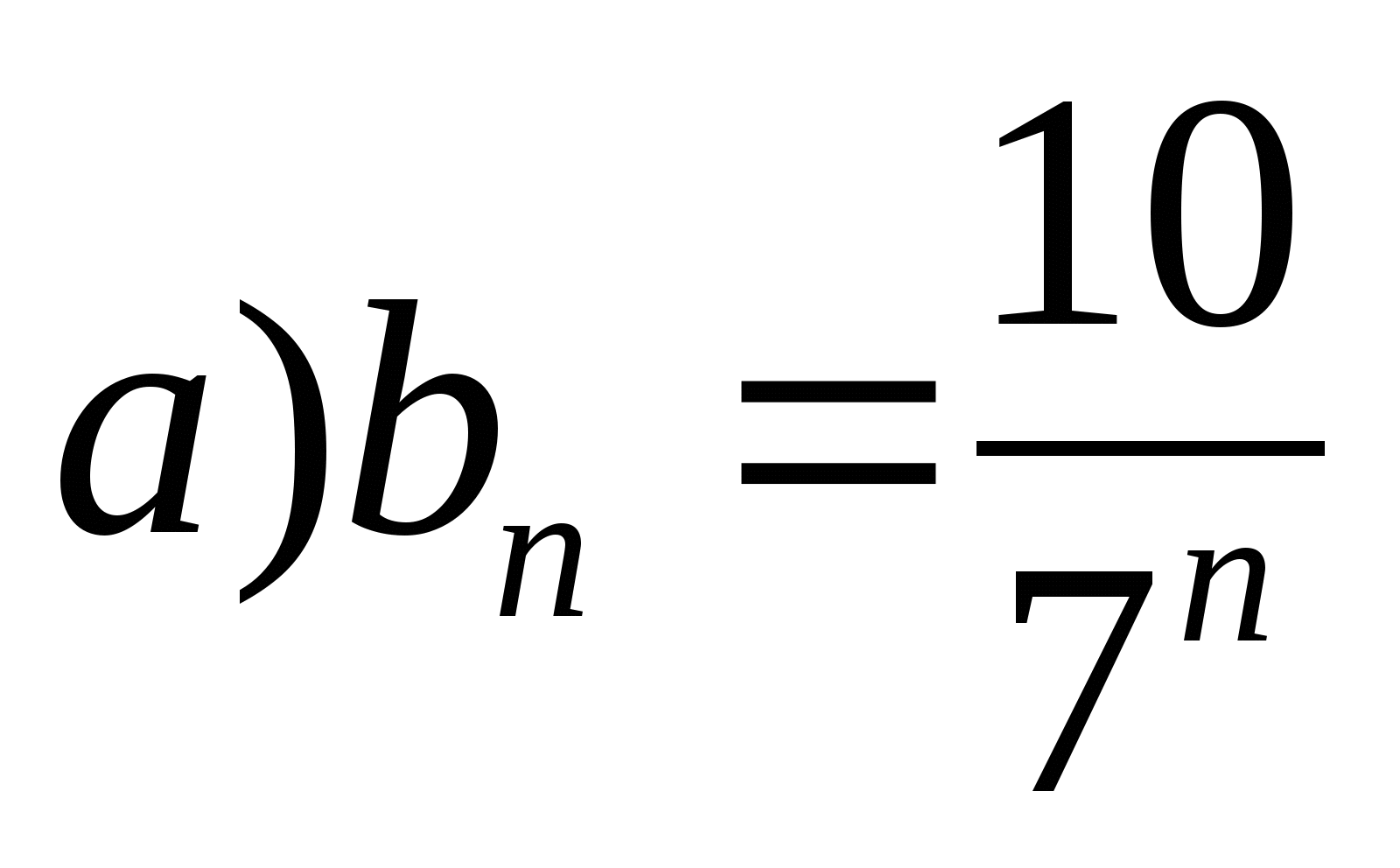 ;
; 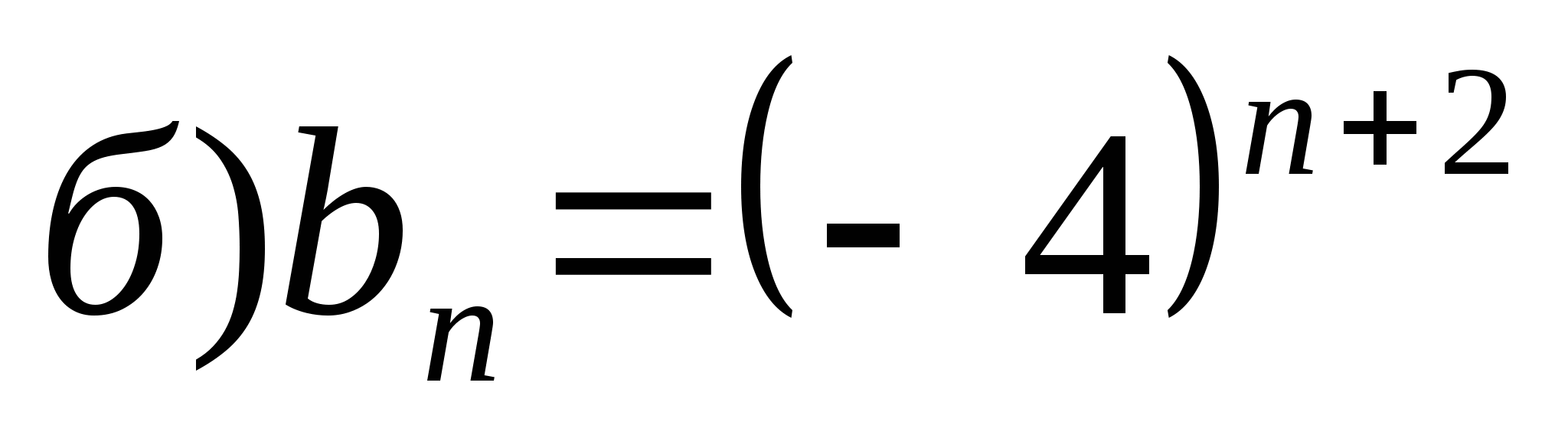 .
.
Решение:
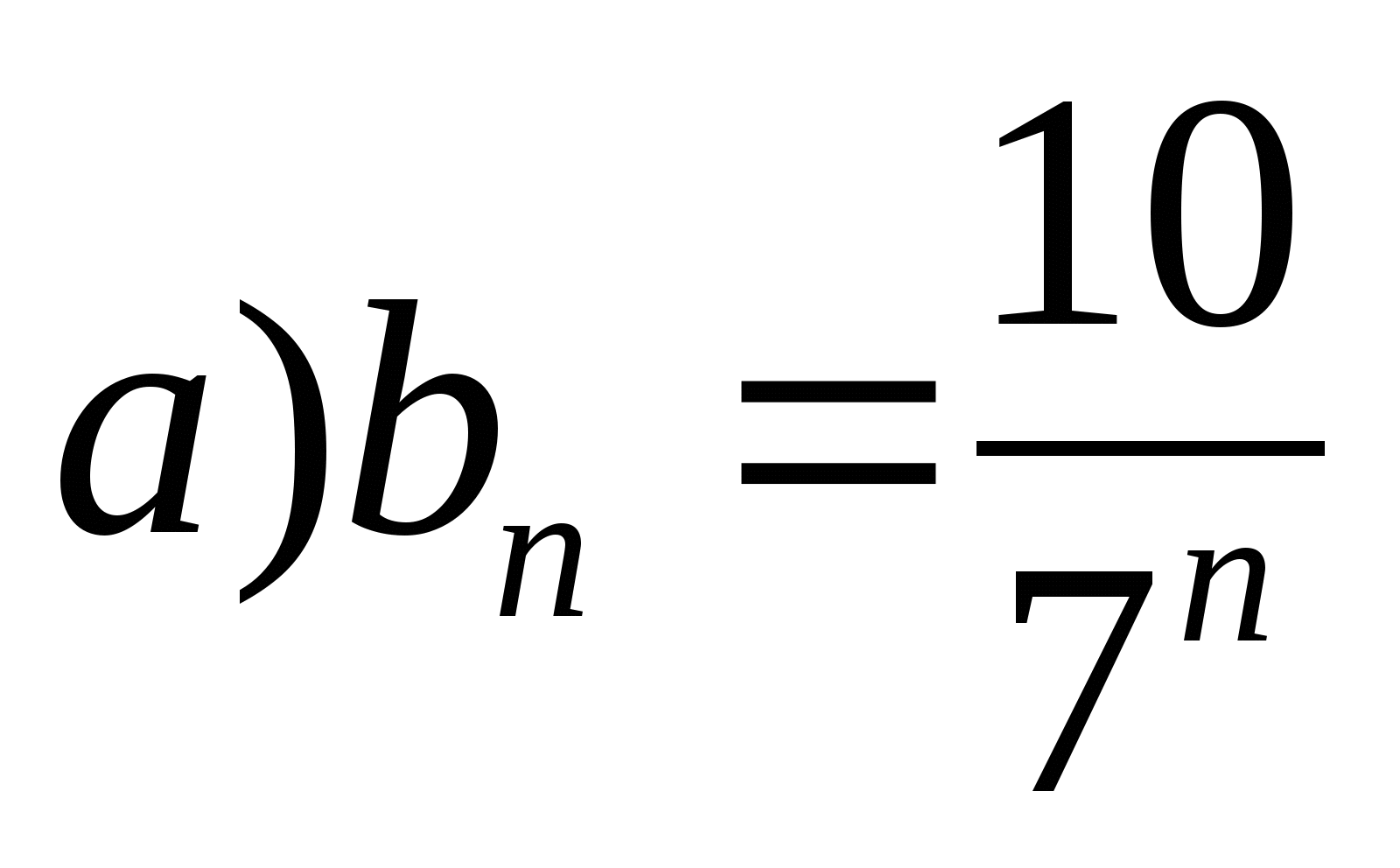 . Найдем q.
. Найдем q.
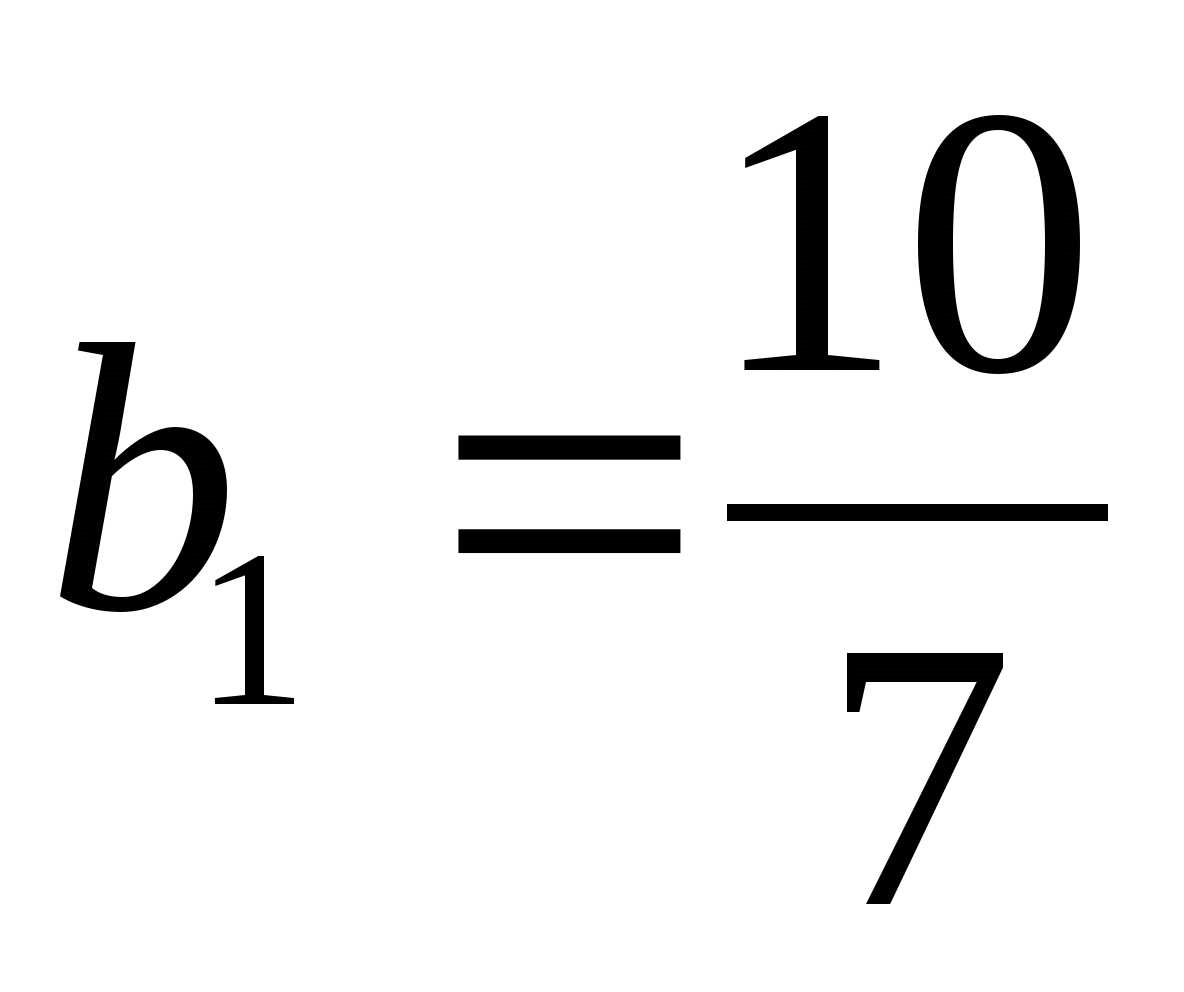
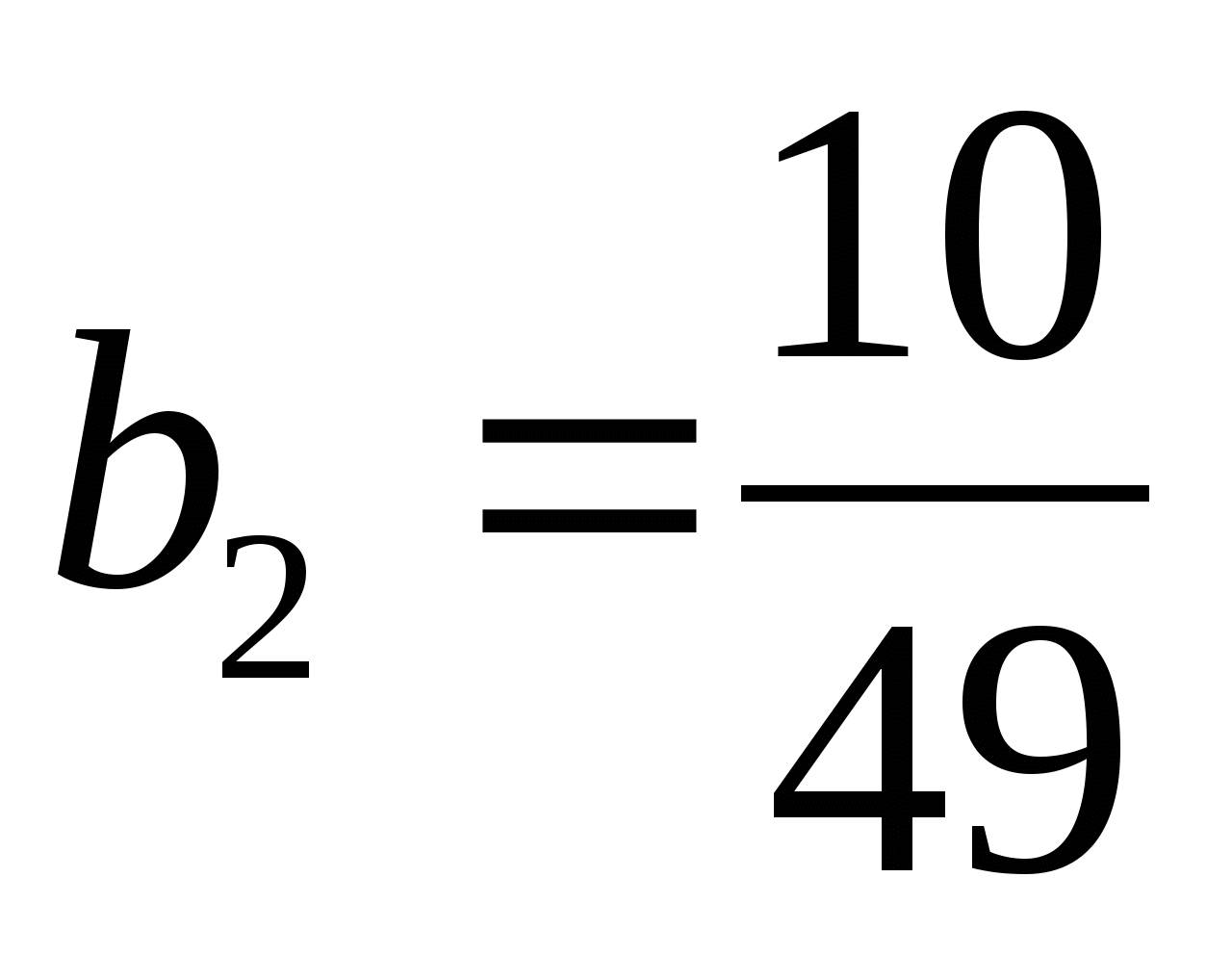 ;
; 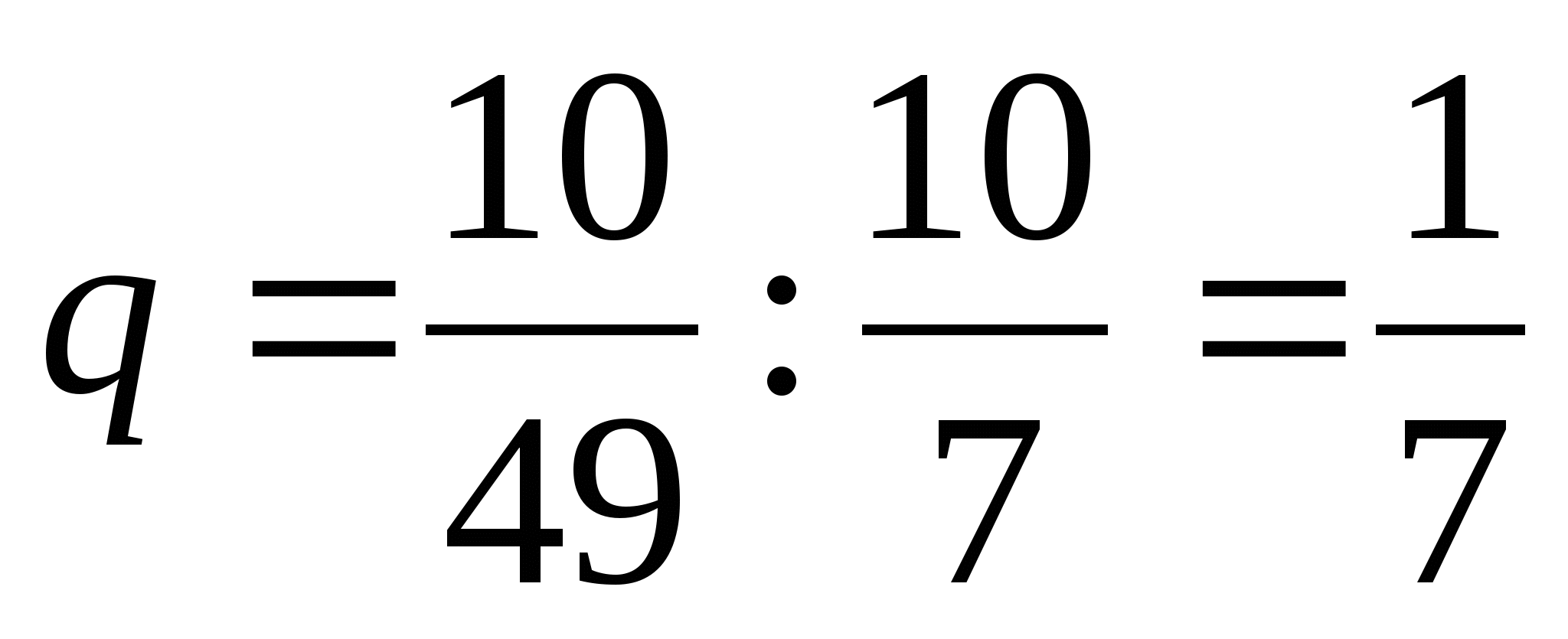 ;
; 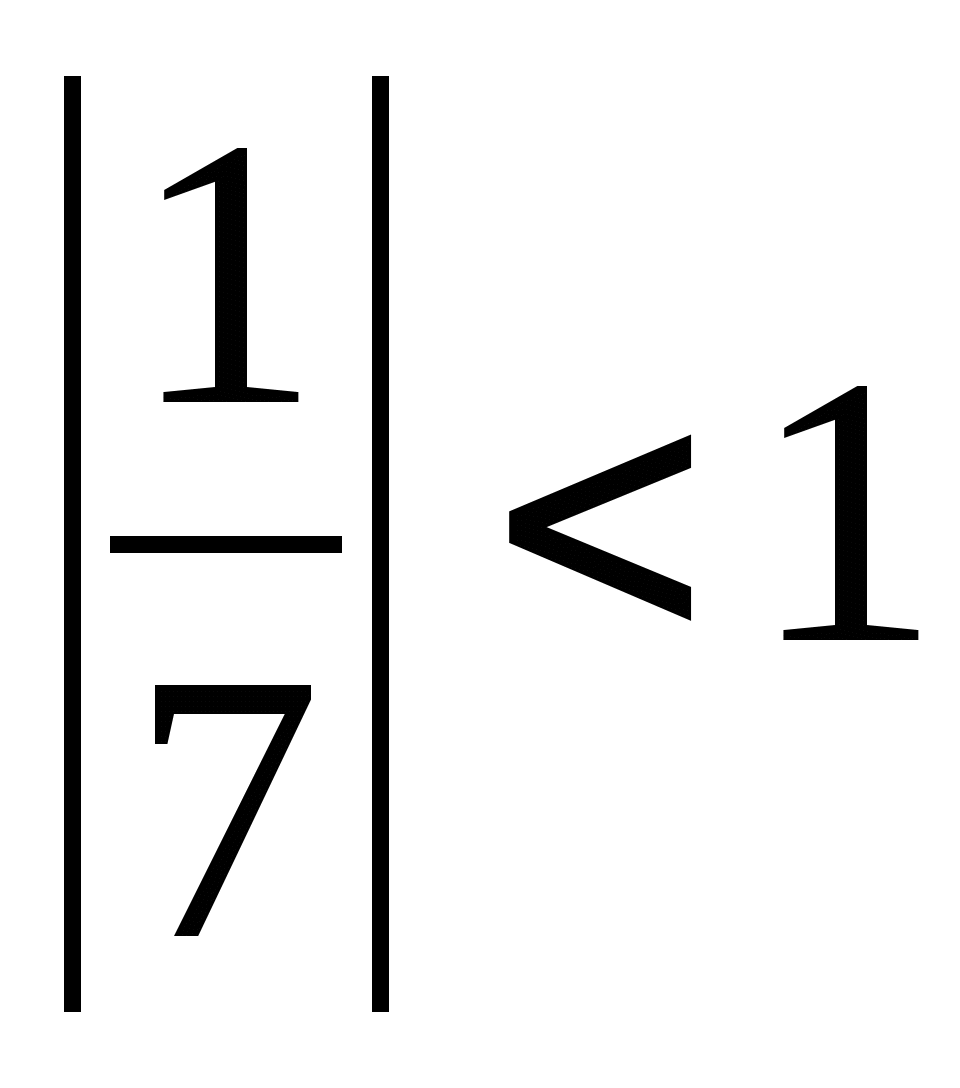 .
.данная геометрическая прогрессия является бесконечно убывающей.
б)  данная последовательность не является бесконечно убывающей геометрической прогрессией.
данная последовательность не является бесконечно убывающей геометрической прогрессией.

Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию: 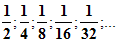
Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1. 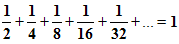
Но в левой части этого равенства – сумма бесконечного числа слагаемых.
Рассмотрим сумму n первых слагаемых.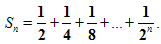
По формуле суммы n первых членов геометрической прогрессии, она равна 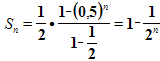 .
.
Если n неограниченно возрастает, то 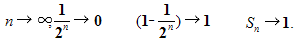
или 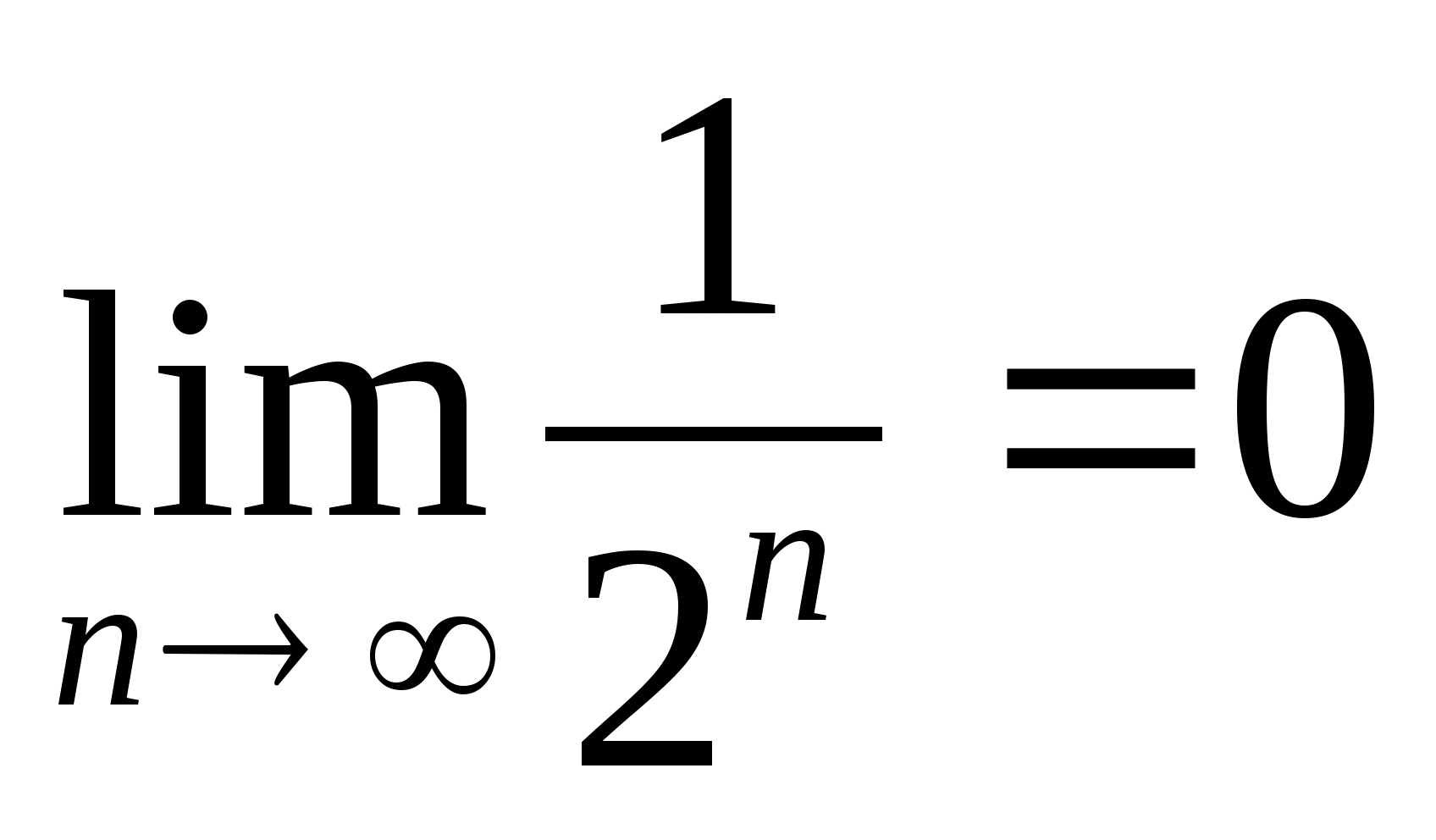 . Поэтому
. Поэтому 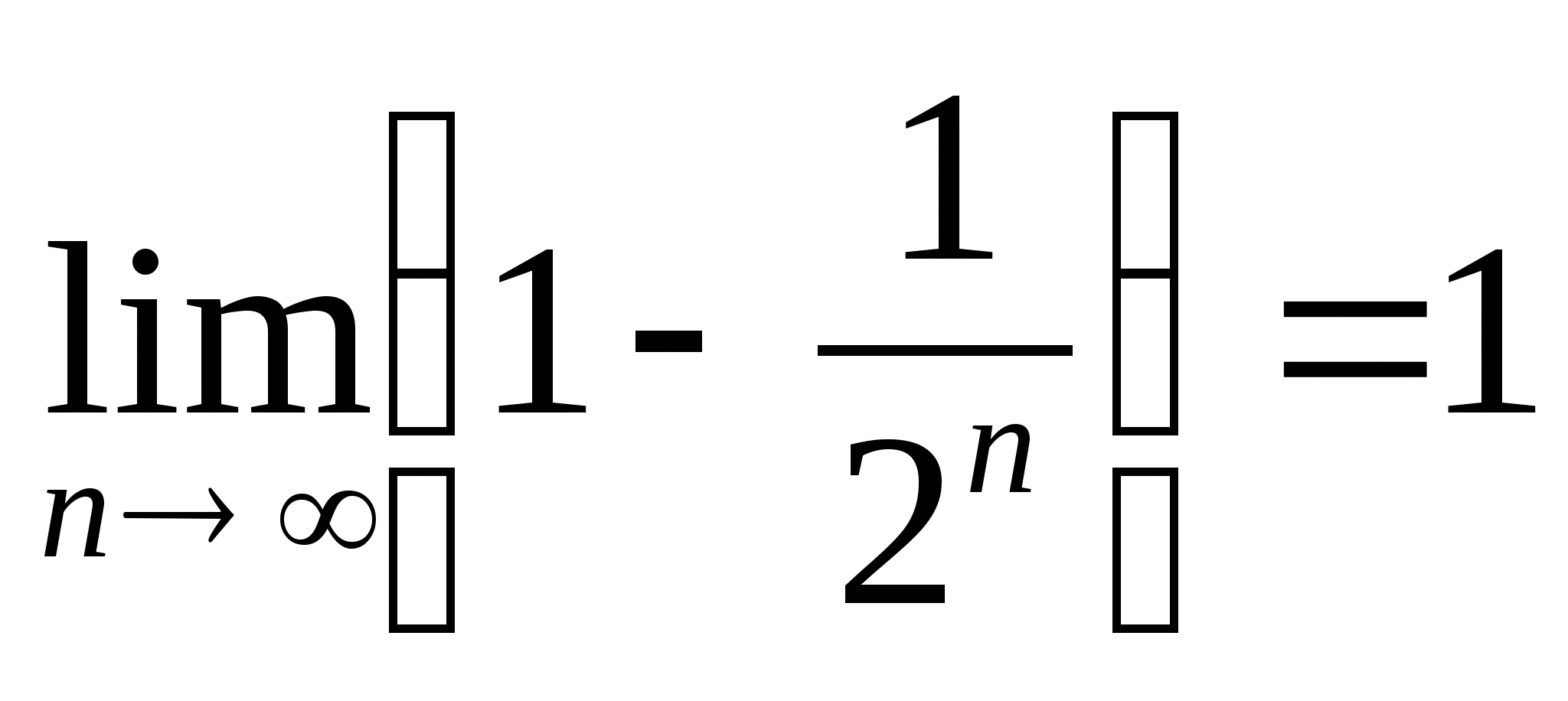 , т.е.
, т.е. 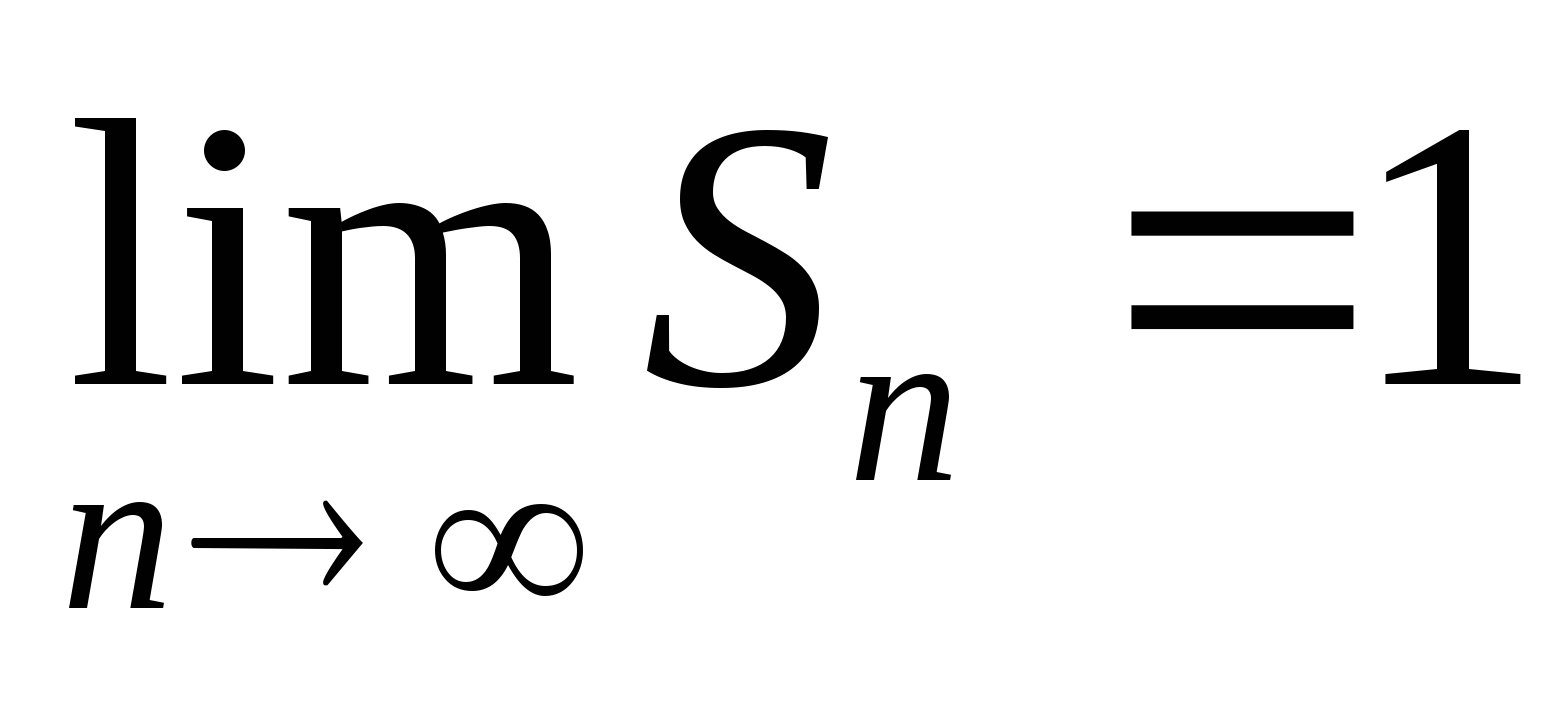 .
.
Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности S1, S2, S3, …, Sn, … .
Например, для прогрессии 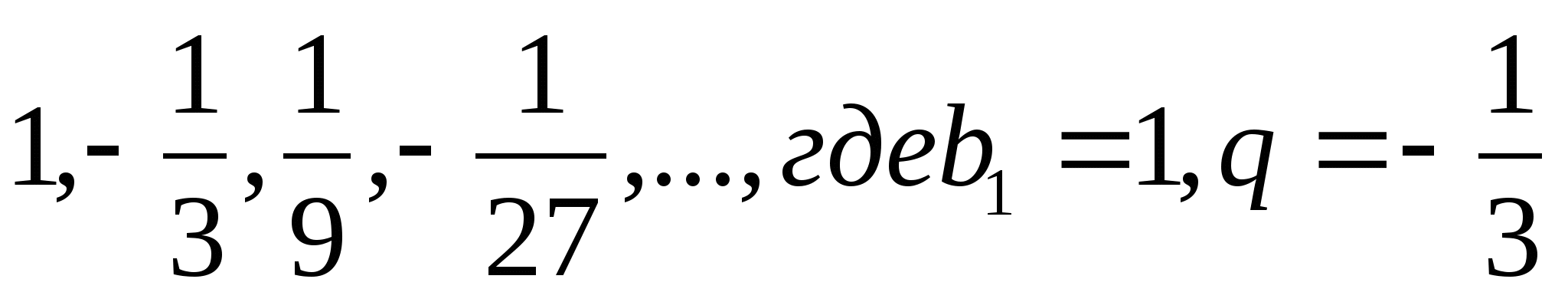 ,
,
имеем 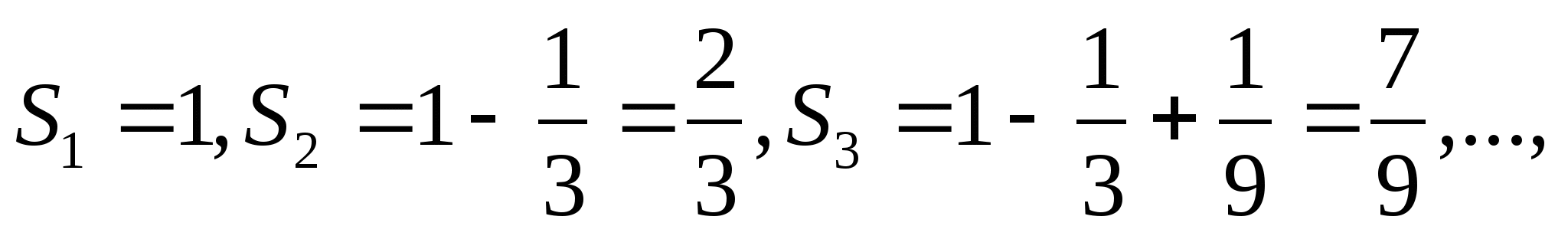
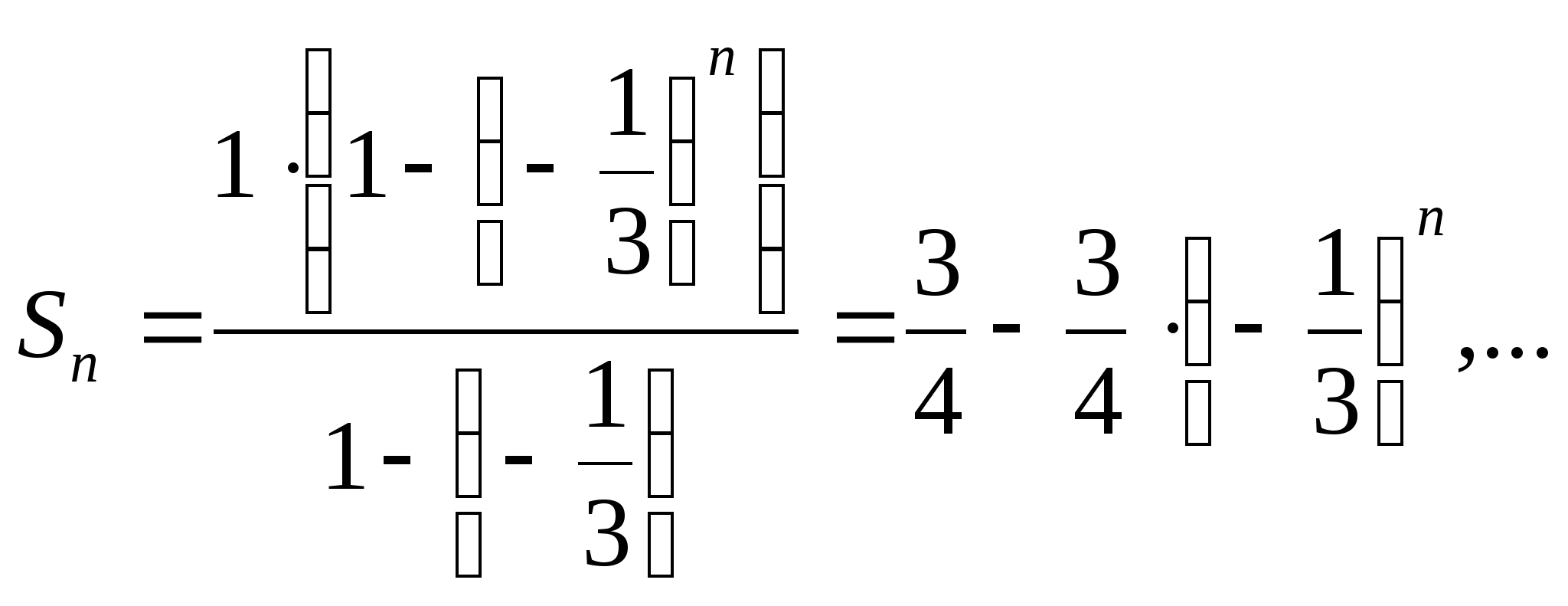 Так как
Так как 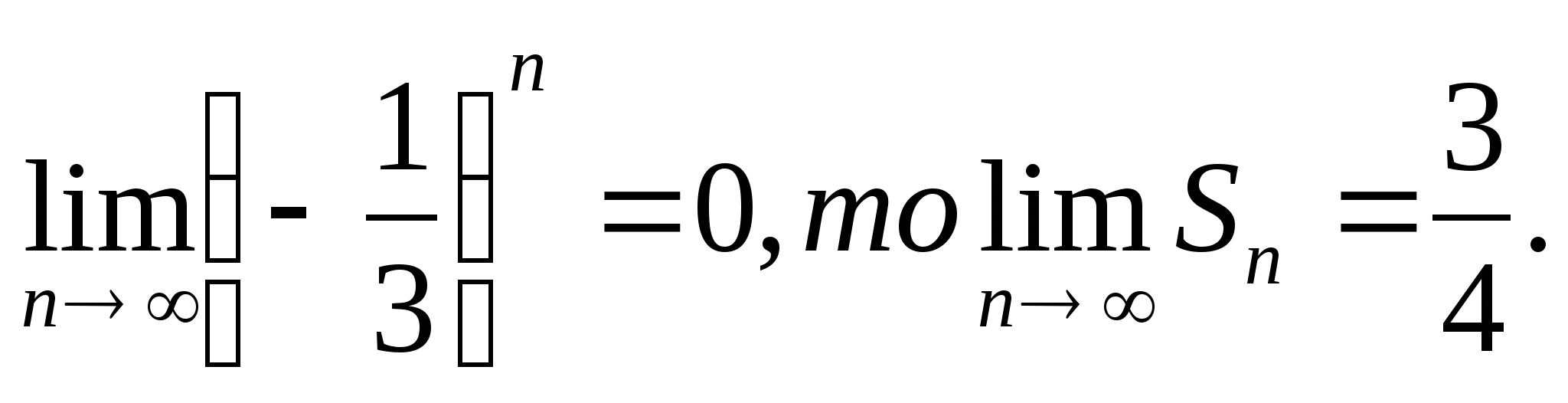
Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле 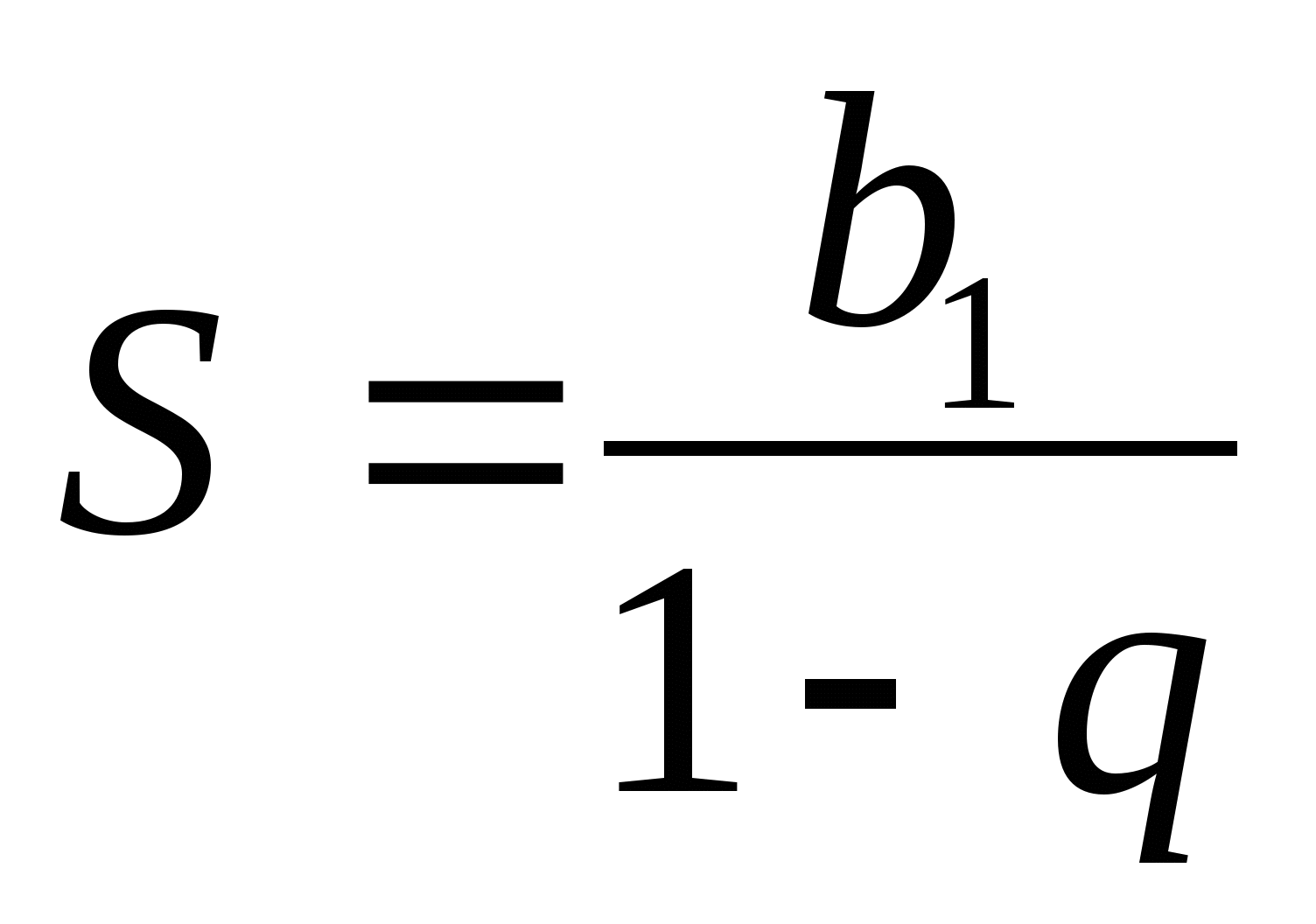 .
.
III. Осмысление и закрепление (выполнение заданий).
Задача №2. Найти сумму бесконечно убывающей геометрической прогрессии с первым членом 3,вторым 0,3.
Решение:
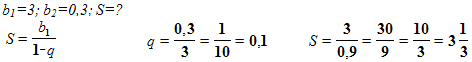
Задача №3. учебник [1], стр. 160, №433(1)
Найти сумму бесконечно убывающей геометрической прогрессии: 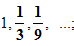
Решение:
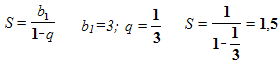
Задача №4. Записать бесконечную периодическую десятичную дробь 0,(5) в виде обыкновенной дроби.
1-й способ. Пусть х=0,(5)= 0,555… /•10 2-й способ. 0,(5)=0,555…=
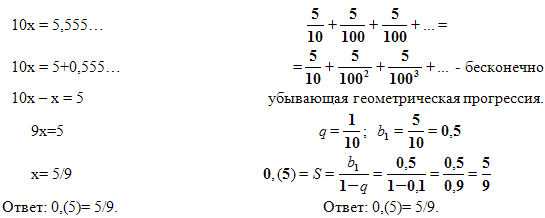
Задача №5. учебник [1], стр. 162, №445(3) (самостоятельное решение)
Записать бесконечную периодическую десятичную дробь 0,(12) в виде обыкновенной дроби.
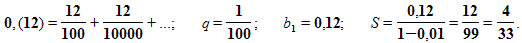
Ответ: 0,(12)= 4/33.
IV. Подведение итогов.
С какой последовательностью сегодня познакомились?
Дайте определение бесконечно убывающей геометрической прогрессии.
Как доказать, что геометрическая прогрессия является бесконечно убывающей?
Назовите формулу суммы бесконечно убывающей геометрической прогрессии.
V. Домашнее задание.
infourok.ru
Бесконечно убывающая геометрическая прогрессия
Напомним,
что геометрическая прогрессия – это числовая
последовательность ,
,
 ,
,
 ,
…,
,
…,  ,
…, где
,
…, где ,
что для всех натуральных
,
что для всех натуральных  выполняется
равенство
выполняется
равенство ,
где
,
где  .
Число
.
Число  называется
знаменателем геометрической последовательности, число
называется
знаменателем геометрической последовательности, число  –первым
её членом, а число
–первым
её членом, а число –
общим её членом.
–
общим её членом.
 ,
,
 ,
,
 ,
,
 ,
…,
,
…,  ,
…
,
… ,
,
 ,
,  ,
,  ,
,  , …,
, …,  , …
, … ,
,
Также
напомним, что  —ый
член геометрической прогрессии можно вычислить по формуле
—ый
член геометрической прогрессии можно вычислить по формуле 
А
сумму первых  членов
геометрической прогрессии можно вычислить по формуле
членов
геометрической прогрессии можно вычислить по формуле  , если
, если  ;
;
 , если
, если  .
.
Однако среди геометрических прогрессий особый интерес вызывают так называемые бесконечно убывающие геометрические прогрессии. Давайте познакомимся с такими прогрессиями.
Начнём с примера. Итак, перед вами изображены квадраты.

Сторона
первого, самого большого квадрата равна  ,
сторона второго равна
,
сторона второго равна  ,
сторона третьего квадрата –
,
сторона третьего квадрата –  ,
сторона четвёртого квадрата –
,
сторона четвёртого квадрата –  ,
сторона пятого квадрата –
,
сторона пятого квадрата –  и
так далее.
и
так далее.
Обратите
внимание! Стороны наших квадратов образуют геометрическую прогрессию:
 ,
,  ,
,  ,
,  ,
,  , …
, …
Перепишем
эту геометрическую прогрессию в таком виде:  ,
,  ,
,  ,
,  ,
,  , …,
, …,  , …
, …
Знаменатель
этой геометрической прогрессии равен  .
.
Заметим, что и площади этих квадратов также образуют геометрическую прогрессию:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
…
,
…
 ,
,
 ,
,
 ,
,
 ,
,
 ,
…,
,
…,  ,
…
,
…

Хотелось
бы отметить, что стороны квадратов и их площади с возрастанием номера  становятся
всё меньше и всё больше приближаются к
становятся
всё меньше и всё больше приближаются к .
Так вот, каждую из прогрессий, что мы с вами записали, называют бесконечно
убывающей геометрической прогрессией.
.
Так вот, каждую из прогрессий, что мы с вами записали, называют бесконечно
убывающей геометрической прогрессией.
А теперь давайте рассмотрим следующую геометрическую прогрессию:
 ,
,  ,
,  ,
,  , …,
, …,  , …
, …
Здесь ,
,  ,
,  ,
,  , … , знаменатель нашей
геометрической прогрессии
, … , знаменатель нашей
геометрической прогрессии  .
.
Видим,
что с возрастанием номера  члены
этой прогрессии приближаются к
члены
этой прогрессии приближаются к .
Значит, эта прогрессия является бесконечно убывающей геометрической
прогрессией. Обратите внимание!
.
Значит, эта прогрессия является бесконечно убывающей геометрической
прогрессией. Обратите внимание!  .
.
Запомните: геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.
А теперь давайте перейдём к выводу формулы суммы бесконечно убывающей геометрической прогрессии.

Итак,
на экране вы видите квадрат со стороной равной единице. Разделим этот квадрат
пополам. Заштрихуем обе части нашего квадрата, как показано на экране. Продолжим
делить пополам наши квадраты и штриховать их. Заметим, что площади
заштрихованных прямоугольников образуют бесконечно убывающую
геометрическую прогрессию:  ,
,  ,
,  ,
,  ,
,  , …
, …
Если
мы заштрихуем все получающиеся таким образом прямоугольники, то понятно, что
весь квадрат покроется штриховкой. Разумеется, сумма площадей всех
заштрихованных прямоугольников будет равна единице. То есть  …
…
Обратите внимание: в левой части нашего равенства стоит сумма бесконечного числа слагаемых.
Давайте
рассмотрим сумму первых  слагаемых.
Применяя формулу суммы
слагаемых.
Применяя формулу суммы  членов
геометрической прогрессии, имеем
членов
геометрической прогрессии, имеем  ….
Получим, что
….
Получим, что  .
.
Заметим,
что если  неограниченно
возрастает, то
неограниченно
возрастает, то  будет
как угодно близко приближаться к 0. Это выражение записывают следующим образом:
будет
как угодно близко приближаться к 0. Это выражение записывают следующим образом:
 при
при
 ,
а читают так: «единица делённая на два в степени эн стремится к нулю при эн
стремящемся к бесконечности, или предел единицы делённой на два в степени эн
при эн стремящемся к бесконечности равен нулю».
,
а читают так: «единица делённая на два в степени эн стремится к нулю при эн
стремящемся к бесконечности, или предел единицы делённой на два в степени эн
при эн стремящемся к бесконечности равен нулю».
Так
как  при
при
 ,
то
,
то  при
при
 ,
то есть
,
то есть  или
или
 .
Поэтому бесконечную сумму
.
Поэтому бесконечную сумму  …
… .
.
В
этом случае говорят, что сумма бесконечно убывающей геометрической прогрессии
есть предел последовательности  ,
,  ,
,  , …,
, …,  , …
, …
Например,
если мы возьмём бесконечно убывающую геометрическую прогрессию  ,
,  ,
,  ,
,  , …,
, …,  , …
, …
Где
 ,
, .
.
 ,
,
 ,
,
 ,
…,
,
…,
 ,
…
,
…
Так
как  ,
то
,
то  .
.
А теперь выведем формулу суммы бесконечно убывающей геометрической прогрессии.
Мы
помним, что сумму первых  членов
геометрической прогрессии можно вычислить по формуле
членов
геометрической прогрессии можно вычислить по формуле  .
.
Перепишем
эту формулу таким образом:  .
.
Так
как  ,
то
,
то  ,
, .
.
Следовательно,
 .
.
Таким
образом, сумму  бесконечно
убывающей геометрической прогрессии можно вычислить по формуле:
бесконечно
убывающей геометрической прогрессии можно вычислить по формуле:  .
.
Из
этой формулы при  имеем
имеем
 .
.
Это равенство обычно записывают следующим образом:
 …
… …
… .
.
Обратите
внимание: это равенство справедливо при  ,
в частности при
,
в частности при  .
.
Задание 1.
Докажите,
что геометрическая прогрессия:
 …
, является бесконечно убывающей.
…
, является бесконечно убывающей.
Решение.
 ,
,  .
.


Следовательно, данная геометрическая прогрессия является бесконечно убывающей.
Задание 2.
Найдите
сумму бесконечно убывающей геометрической прогрессии  …
…
Решение.
 ,
,
 .
.




Задание 3.
Найдите
сумму бесконечно убывающей геометрической прогрессии, если  ,
,  .
.
Решение.
По условию нам даны  и
и
 прогрессии.
прогрессии.
 ,
,
 .
.











videouroki.net
Урок математики в 9-м классе по теме «Бесконечно убывающая геометрическая прогрессия»
Цели урока:
- ознакомление учащихся с новым видом последовательности – бесконечно убывающей геометрической прогрессией;
- формулирование начального представления о пределе числовой последовательности;
- знакомство с ещё одним способом обращения бесконечных периодических дробей в обыкновенные с помощью формулы суммы бесконечно убывающей геометрической прогрессии.
Ход урока
1. Проверка домашнего задания.
1) Проверка основных формул, связанных с арифметической и геометрической прогрессиями. Два ученика готовят записи формул у доски.
2) Остальные учащиеся выполняют математический диктант по теме «Формулы суммы».
Задания:
№1. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен 6 (1-й вариант), -20 (2-й вариант), а пятый член -6 (1-й вариант), 20 (2-й вариант).
№2. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен -20(1-й вариант), 6 (2-й вариант), а разность равна 10(1-й вариант), -3(2-й вариант).
№3. Найдите сумму первых пяти членов геометрической прогрессии, если её первый член равен 1(1-й вариант), -1 (2-й вариант), а знаменатель равен -2(1-й вариант), 2(2-й вариант).
По окончании диктанта, выборочно, у двоих учеников работы проверяются на оценку, остальные выполняют самопроверку по готовым решениям, записанным на отворотах доски.
Решения:
2. Изучение новой темы. (демонстрация презентации. Приложение 1)
1) Слайд №2.
Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего.
В результате, мы получили последовательность сторон квадратов образующих геометрическую прогрессию со знаменателем .
И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,
Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.
С помощью этого рисунка можно рассмотреть и ещё одну последовательность. Например, последовательность площадей квадратов:
. И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
2) Слайд №3.
Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников.
Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.
То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.
Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.
Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.
Фронтальная работа.
Записать определение: геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.
С помощью определения можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.
Задача №1.
Является ли последовательность бесконечно убывающей геометрической прогрессией, если она заданна формулой:
а)
Решение:
а) (фронтальная работа, запись на доске)
данная геометрическая прогрессия является бесконечно убывающей.
б) (самостоятельно)
данная последовательность не является бесконечно убывающей геометрической прогрессией.
Продолжить работу с презентацией.
3) Слайд №4.
Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию:
Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1.
Но в левой части этого равенства – сумма бесконечного числа слагаемых.
Рассмотрим сумму n первых слагаемых.
По формуле суммы n первых членов геометрической прогрессии, она равна .
Если n неограниченно возрастает, то
4) Слайд №5.
Записать определение. Суммой бесконечно убывающей геометрической прогрессии называют число, к которому стремится сумма её первых n членов при n →. Теперь получим формулу, с помощью которой будем вычислять сумму бесконечно убывающей геометрической прогрессии.
Рассмотрим формулу n первых членов геометрической прогрессии.
Тренировочные упражнения.
Задача №2. Найти сумму бесконечно убывающей геометрической прогрессии с первым членом 3,вторым 0,3.
Решение:
Задача №3. учебник [1], стр. 160, №433(1)
Найти сумму бесконечно убывающей геометрической прогрессии:
Решение:
Задача №4. учебник [1], стр. 160, №434(1)
Найти сумму бесконечно убывающей геометрической прогрессии, если
Решение:
Пользуясь формулой суммы бесконечно убывающей геометрической прогрессии, можно записывать бесконечную периодическую десятичную дробь в виде обыкновенной дроби.
Задача №4. Записать бесконечную периодическую десятичную дробь 0,(5) в виде обыкновенной дроби.
1-й способ. Пусть х=0,(5)= 0,555… /•10 2-й способ. 0,(5)=0,555…=
Задача №5. учебник [1], стр. 162, №445(3) (самостоятельное решение)
Записать бесконечную периодическую десятичную дробь 0,(12) в виде обыкновенной дроби.
Ответ: 0,(12)= 4/33.
5) Слайд №6.
Подведение итогов.
- С какой последовательностью сегодня познакомились?
- Дайте определение бесконечно убывающей геометрической прогрессии.
- Как доказать, что геометрическая прогрессия является бесконечно убывающей?
- Назовите формулу суммы бесконечно убывающей геометрической прогрессии.
Самостоятельная работа. (выполняется в рабочих тетрадях с использованием копирок и чистых листов бумаги, по окончании работы, откопированные записи решений сдаются на проверку, а по записям в тетрадях учащиеся выполняют самопроверку по готовым решениям).
Задания (слайд №6):
- Является ли геометрическая прогрессия бесконечно убывающей, если: b7= -30; b6= 15?
- Найдите сумму бесконечно убывающей геометрической прогрессии: -25; -5; -1;…
- Записать бесконечную десятичную периодическую дробь 0,(9) в виде обыкновенной дроби.
Самопроверка (слайд №7).
Домашнее задание.
№435(1;3), 445(4), 436. [1]
Литература:
- Алимов Ш.А., Колягин Ю.М., Сидоров и др.- 8-е изд.-М.: Просвещение, 2002.
urok.1sept.ru
««Сумма бесконечно убывающей геометрической прогрессии»
Филиал Муниципального бюджетного общеобразовательного учреждения «Трудовская школа» при ГБУЗ РК «КПБ №5»
Урок в 9 классе на тему:
«Сумма бесконечно убывающей
геометрической прогрессии»

Павловская Светлана Фёдоровна,
учитель математики МБУО
«Трудовская школа» при ГБУЗ РК
«КПБ №5»
2016 год

ЦЕЛИ УРОКА.
Образовательные цели:
закрепить навыки решения задач по нахождению суммы n первых членов геометрической прогрессии; ввести понятие бесконечно убывающей геометрической прогрессии; вывести формулу суммы бесконечно убывающей геометрической прогрессии, сформировать умение в её применении.
Развивающие цели:
развивать познавательные процессы, память, воображение, мышление, сообразительность, речь учащихся.
Воспитательные цели:
повысить интерес к решению нестандартных задач, сформировать положительный мотив учения.
Образовательные технологи:
Тип урока: урок изучения и закрепления полученных знаний.
Оборудование: проектор, компьютер, экран, презентация, карточки с домашней контрольной работой.
ХОД УРОКА.
Организационный момент (2 минуты): приветствие, проверка готовности учащихся к уроку, определение личностных целей (приложение 1).
. Познакомить учащихся с порядком работы на уроке.
Математическая разминка (8 минут).
Сообщение исторического содержания (приложение 2).
Математический диктант.

с) Фронтальный опрос:
Какая последовательность называется геометрической прогрессией?
Что называется знаменателем геометрической прогрессии?
Какова формула n –го члена геометрической прогрессии?
Формулы суммы n первых членов геометрической прогрессии?
Такие геометрические прогрессии называются бесконечно убывающими.
Самостоятельная работа контролирующего характера (7 мин.). (Учащиеся выполняют работу по карточкам и сдают на проверку учителю)
Уровень 1.
b1 = -4, q = 2. Найдите сумму первых пяти членов геометрической прогрессии.
Найдите сумму первых 5 членов геометрической прогрессии: 2; 4; …
Уровень 2.
b1 = 8, q = 1/2. Найдите сумму пяти первых членов геометрической прогрессии.
Найдите сумму шести первых членов геометрической прогрессии: 3; — 6; ….
Найдите сумму четырех первых членов геометрической прогрессии (bn), в которой: b2 = 2, b4 = 18, q > 0.
Уровень 3.
Найдите сумму пяти первых членов геометрической прогрессии, если b1 = 2 , q = .
Найдите сумму четырех первых членов геометрической прогрессии (bn), в которой: b2 = 6, b4 = 24, q > 0.
Докажите, что последовательность (bn) является геометрической прогрессией, и найдите сумму n первых ее членов, если bn = 32n-1.
Изучение нового материала (8 мин.).
Устные упражнения:
Укажите знаменатель геометрической прогрессии сравните его модуль с 1:
1,
1; 0,1; 0,01; ……
25; — 5; 1; ……..
1; 0,25; ……….
Сделайте вывод. Предллагаю учащимся самостоятельно сформулировать определение бесконечно убывающей геометрической прогрессии. (определение записывают в тетрадь)
Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы.
а) Задача практического характера.
Один из учеников, вызванный к доске, должен идти от стола учителя к двери по прямой. Первый шаг он делает длиной 1 м., второй 1/2м, третий 1/4 м и т. д. так, что длина следующего шага в два раза меньше длины предыдущего.
Дойдет ли ученик до двери, если расстояние от стола до двери по прямой 5 м?
(после практического решения задачи делается вывод, что не дойдёт). Возникает вопрос: «А какое расстояние он пройдёт?»
Актуализация знаний учащихся, подготовка к восприятию нового. Устные упражнения (8 мин).
Сообщение темы и цели урока.
В результате, мы получили последовательность шагов: образующих геометрическую прогрессию со знаменателем .
Применяя формулу суммы первых членов геометрической прогрессии
Получим: = = — 2( -1) = 2, т.к. 0, при n
б) Вывод формулы суммы бесконечно убывающей геометрической прогрессии.
Суммой бесконечно убывающей геометрической прогрессии называют число, к которому стремится сумма её первых n членов при n →∞
Практическое применение нового материала (6 мин.). (приложения 2-3).
Задача №1 (самостоятельно на местах).
b1 = , b2 = , S — ?
q = : 1, то
S = = = Ответ:
Задача №2 (один учащийся у доски, остальные помогают и записывают в тетрадь).
Записать бесконечную периодическую десятичную дробь
а = 0,(15) = =0,151515 в виде обыкновенной дроби.
Решение этой задачи знакомит учащихся с ещё одним способом обращения бесконечных периодических дробей в обыкновенные с помощью формулы суммы бесконечно убывающей геометрической прогрессии.
0,(15) = 0,15 + 0,0015 + 0,000015 + …………
0,15; 0,0015; ……- бесконечно убывающая геометрическая прогрессия
b1 = 0,15
b2 = 0,0015
S — ?
Решение:
q = = 0,0015 : 0,15 = 0,01
S = = : = = =
Ответ: 0,(15) =
Самостоятельная работа на закрепление материала с последующей проверкой (4 мин).
Уровень 1.
Представьте бесконечную десятичную дробь 0,(5) в виде обыкновенной. Ответ:
Уровень 2.
Представьте бесконечную десятичную дробь 0,(18) в виде обыкновенной. Ответ:
Уровень 3.
Представьте бесконечную десятичную дробь 0,4(6) в виде обыкновенной. Ответ:
Итог урока. Рефлексия (2 мин.)
С каким видом геометрической прогрессии мы познакомились на уроке?
Какую последовательность чисел можно назвать геометрической прогрессией?
Какую геометрическую прогрессию называют бесконечно убывающей?
Как найти сумму бесконечно убывающей геометрической прогрессии?


Приложение 2.
ДЛЯ ЧЕГО НУЖНА ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
И ИСТОРИЯ ЕЕ ВОЗНИКНОВЕНИЯ.
Еще в древности итальянский математик монах Леонардо из Пизы (более известный под именем Фибоначчи) занимался решением практических нужд торговли. Перед монахом стояла задача определить, с помощью какого наименьшего количества гирь можно взвесить товар? В своих трудах Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16…Это одна из первых ситуаций, в которой людям пришлось столкнуться с геометрической прогрессией, о которой ты уже наверное слышал и имеешь хотя бы общее понятие. Как только полностью разберешься в теме, подумай, почему такая система является оптимальной?
В настоящее время, в жизненной практике, геометрическая прогрессия проявляется при вложении денежных средств в банк, когда сумма процентов начисляется на сумму, скопившуюся на счете за предыдущий период. Иными словами, если положить деньги на срочный вклад в сберегательный банк, то через год вклад увеличится на 7%, умноженному на 1,07. Ещё через год уже эта сумма увеличится на 7%, т.е. получившаяся в тот раз сумма вновь умножится на 1,07. Подобная ситуация описана в задачах на вычисление так называемых сложных процентов – процент берется каждый раз от суммы, которая есть на счете с учетом предыдущих процентов. Об этих задачах мы поговорим чуть позднее.
Есть еще много простых случаев, где применяется геометрическая прогрессия. Например, распространение гриппа: один человек заразил 4 человек, те в свою очередь заразили еще по 4 человека, и таким образом вторая волна заражения – 16 человек, а те в свою очередь, заразили еще 4… и так далее…
Кстати, финансовая пирамида, та же МММ – это простой и сухой расчет по свойствам геометрической прогрессии. Интересно? Давай разбираться.
Приложение 3.


Приложение 4.
ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА
Уровень 1.
Найдите седьмой член геометрической прогрессии (bn), если b1 = — 3, q = 2.
Первый член геометрической прогрессии (bn) равен 2, а знаменатель 3. Найдите сумму шести первых членов этой прогрессии.
Найдите сумму бесконечной геометрической прогрессии 24, 12, 6, ……
Представьте в виде обыкновенной дроби бесконечную дробь 0,(27).
Уровень 2.
Найдите шестой член геометрической прогрессии (bn), если b1 = 0,81, q = .
Второй член геометрической прогрессии (bn) равен 21 , а четвёртый равен 189. Найдите сумму шести первых членов этой прогрессии, если все члены прогрессии положительны.
Найдите сумму бесконечной геометрической прогрессии — 40, 20, — 10, ……
Представьте в виде обыкновенной дроби бесконечную дробь 0,5(6).
Уровень 3.
Найдите седьмой член геометрической прогрессии (bn), если b1 = 729, q = .
Третий член геометрической прогрессии (bn) равен 3,6, а пятый равен 32,4. Найдите сумму пяти первых членов этой прогрессии, если все члены прогрессии положительны.
Найдите сумму бесконечной геометрической прогрессии -54, 18, — 6, ……
Представьте в виде обыкновенной дроби бесконечную дробь 0,7(4).
infourok.ru
Урок по теме “Бесконечно убывающая геометрическая прогрессия” (алгебра, 10кл.)
Урок по теме “Бесконечно убывающая геометрическая прогрессия” (алгебра, 10кл.)
Цель урока: ознакомление учащихся с новым видом последовательности – бесконечно убывающей геометрической прогрессией.
Оборудование: проектор, экран.
Тип урока: урок – усвоение новой темы.
Ход урока
I. Орг. момент. Сообщение темы и цели урока.
II. Актуализация знаний учащихся.
В 9 классе вы изучали арифметическую и геометрическую прогрессии.
Вопросы
1. Определение арифметической прогрессии. (Арифметической прогрессией называется последовательность, каждый член которой,начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом).
2. Формула n-го члена арифметической прогрессии (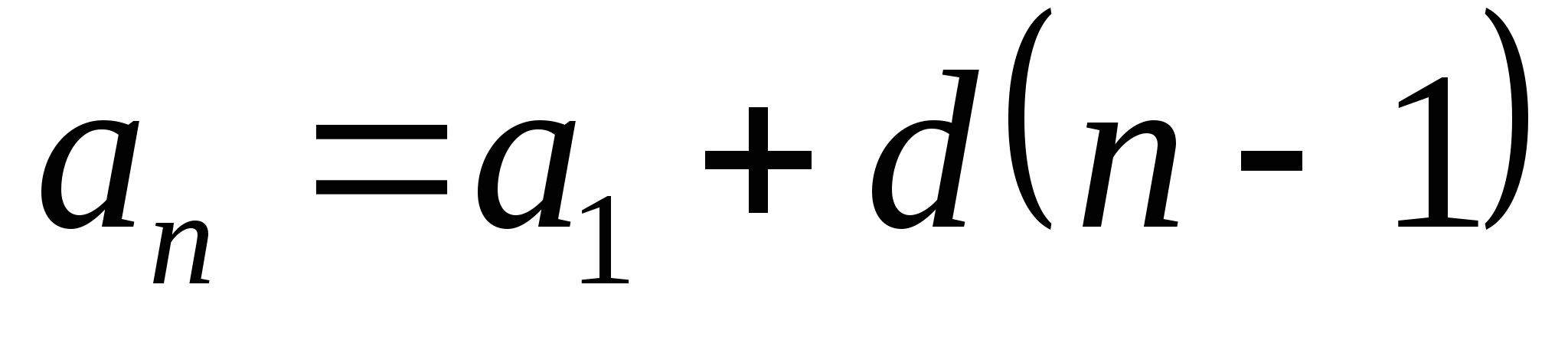
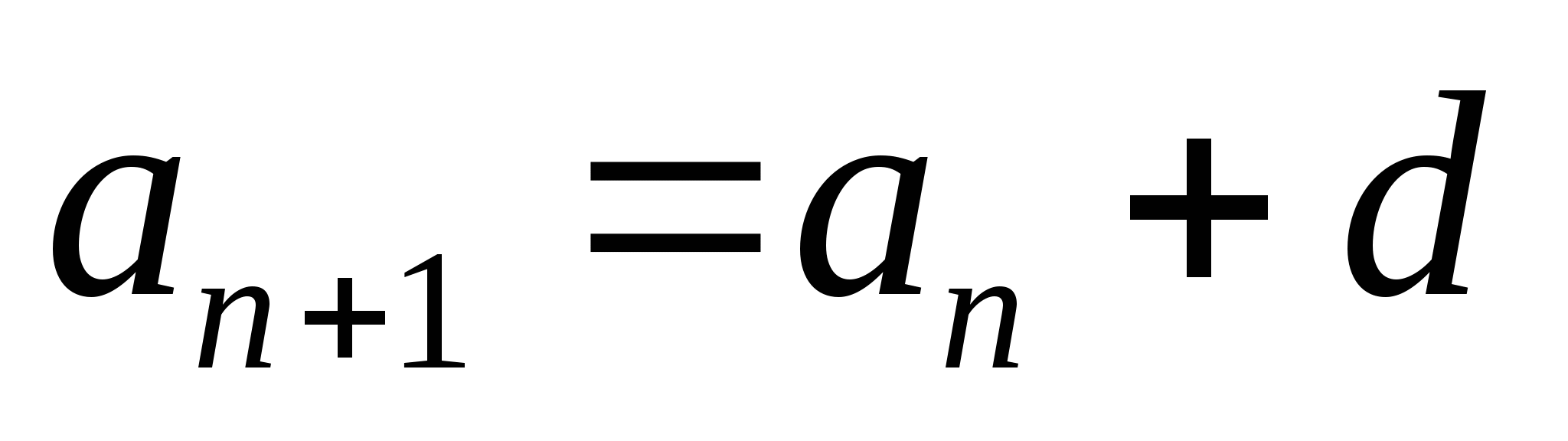 )
)
3. Формула суммы первых n членов арифметической прогрессии.
(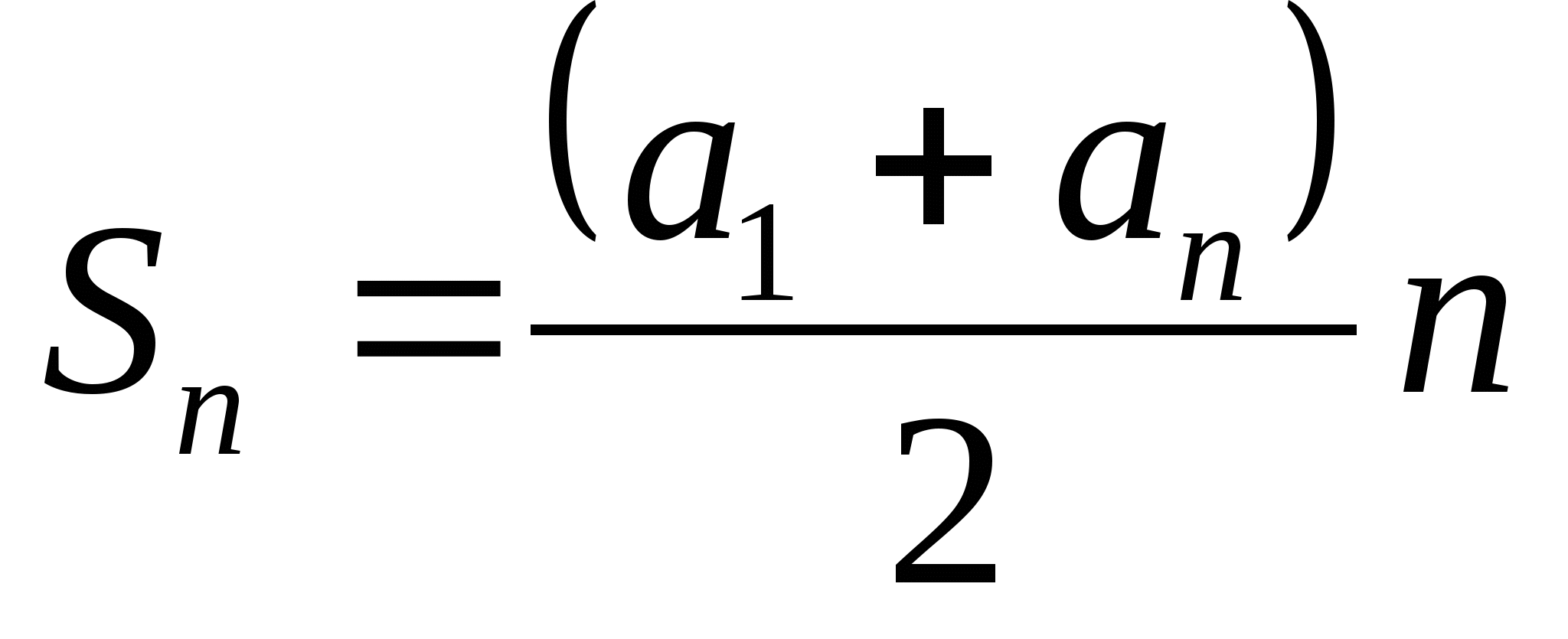 или
или 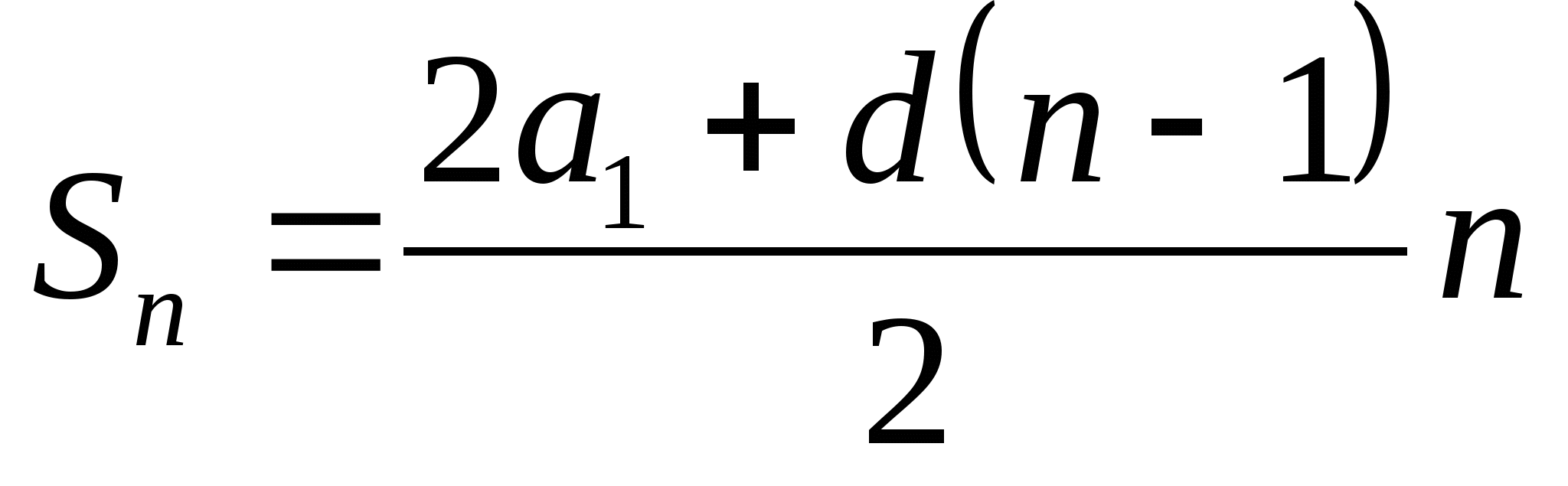 )
)
4. Определение геометрической прогрессии. (Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число).
5. Формула n-го члена геометрической прогрессии (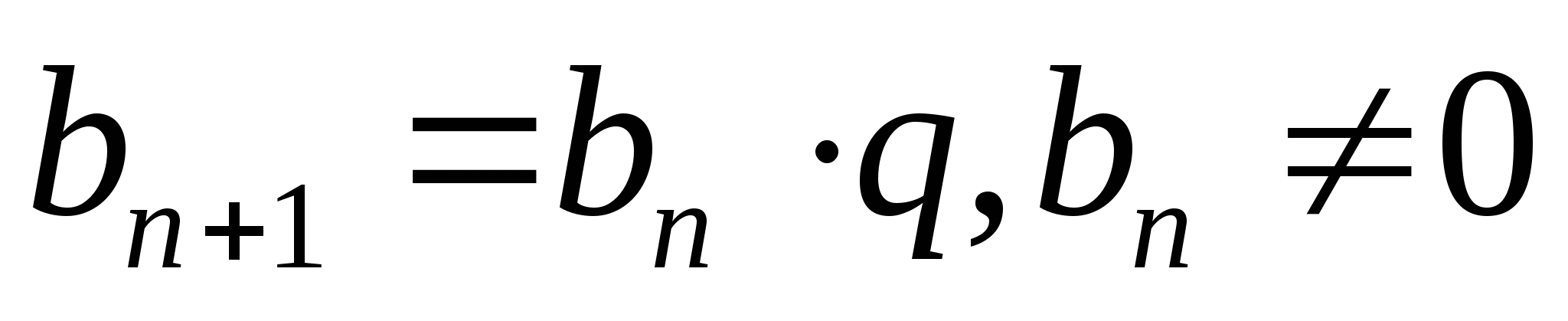
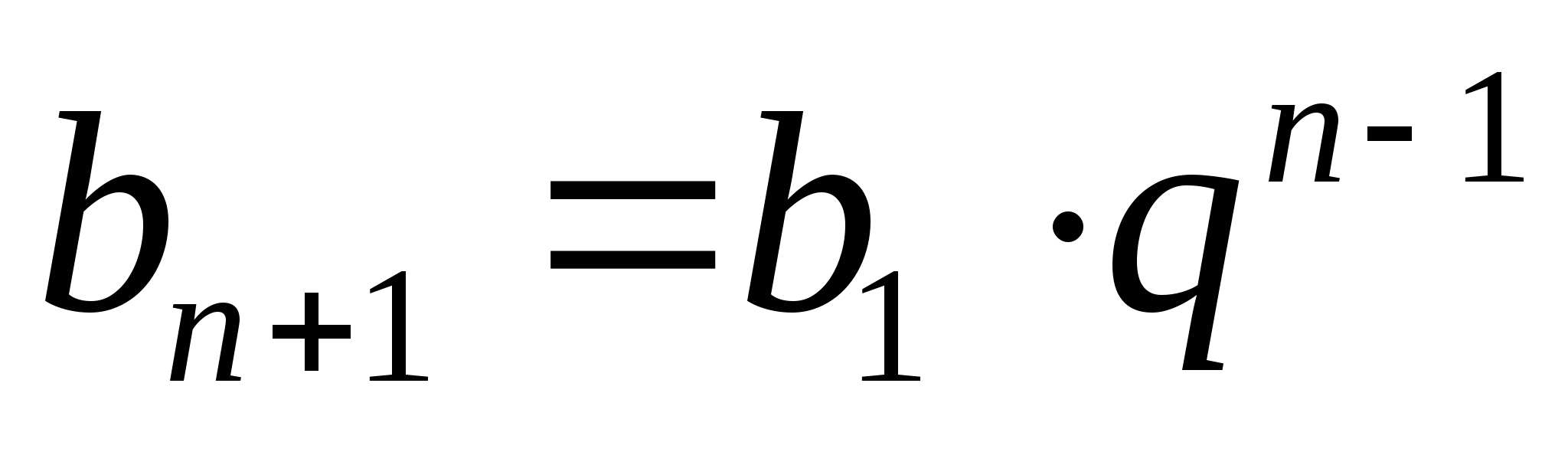 )
)
6. Формула суммы первых n членов геометрической прогрессии. (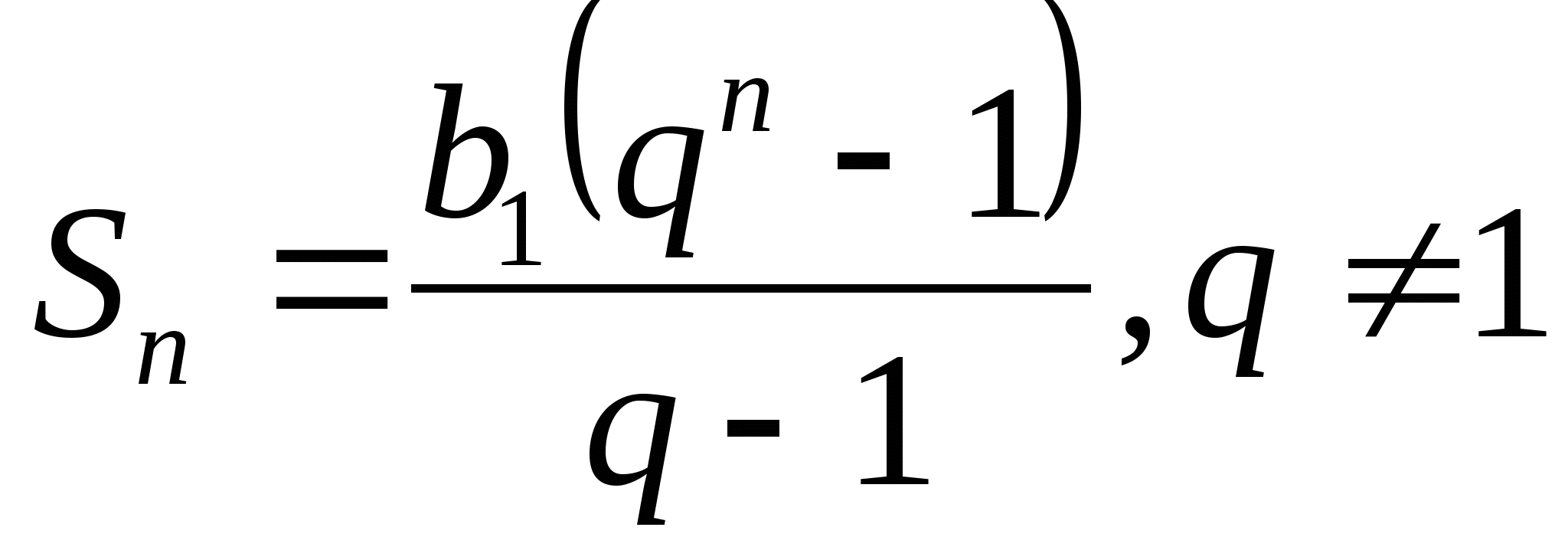 )
)
7. Какие формулы вы еще знаете?
(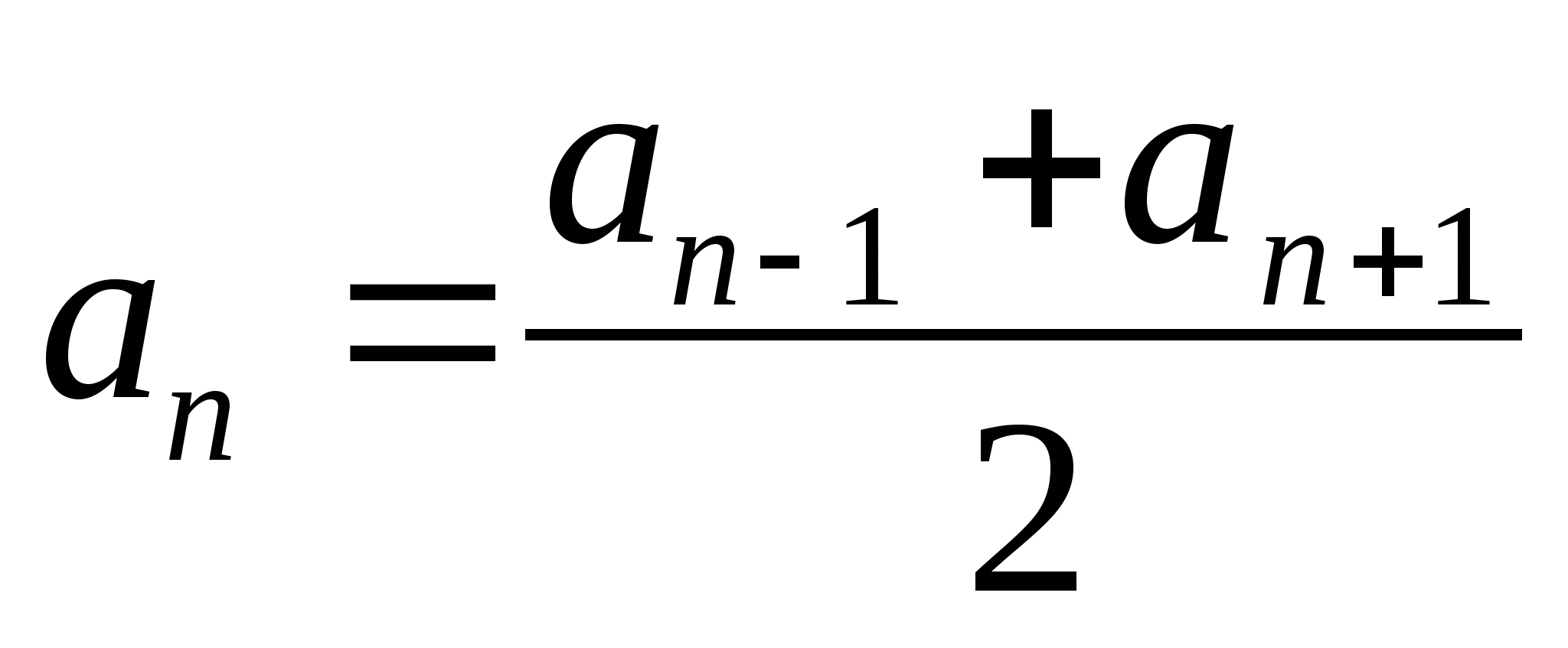 , где
, где 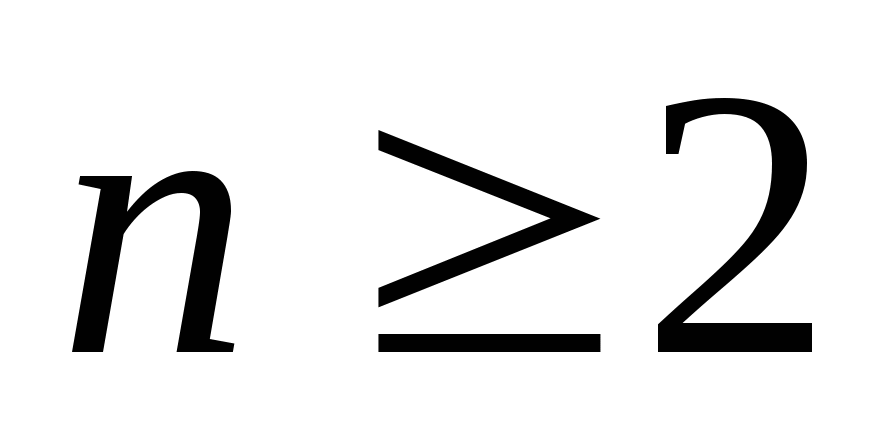 ;
; 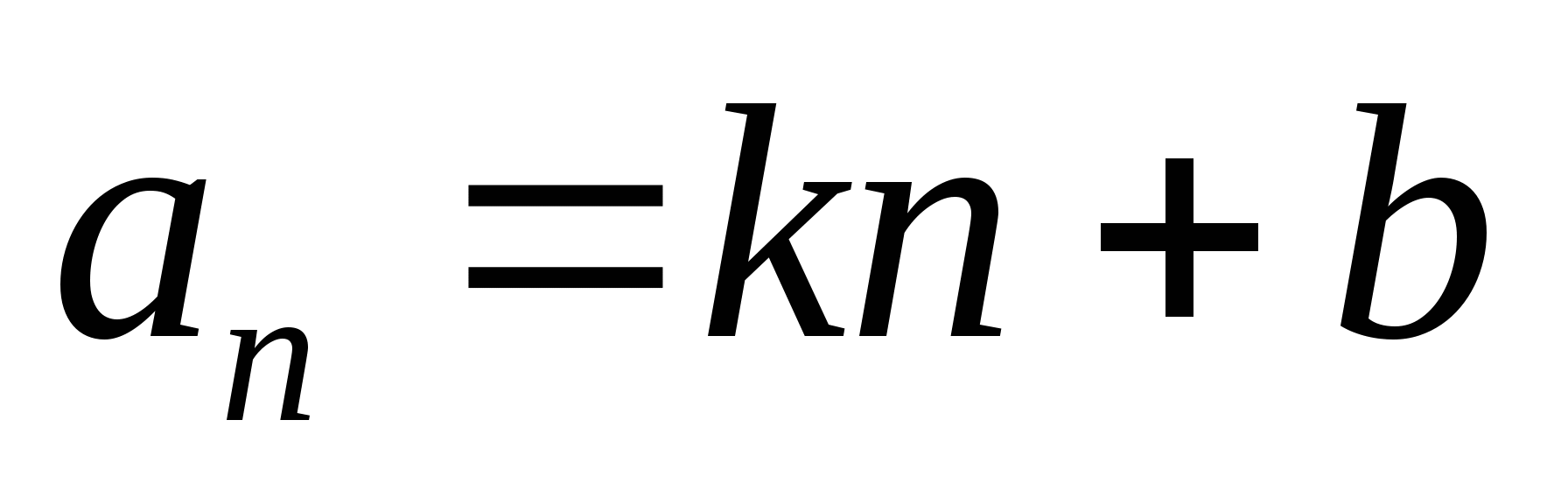 ;
; 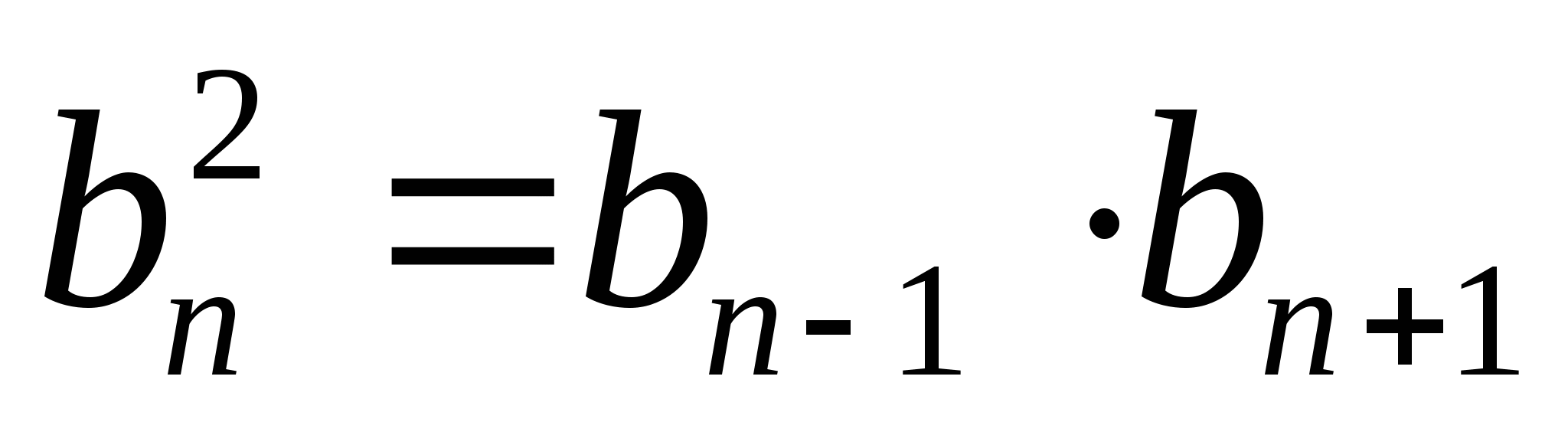 ;
; 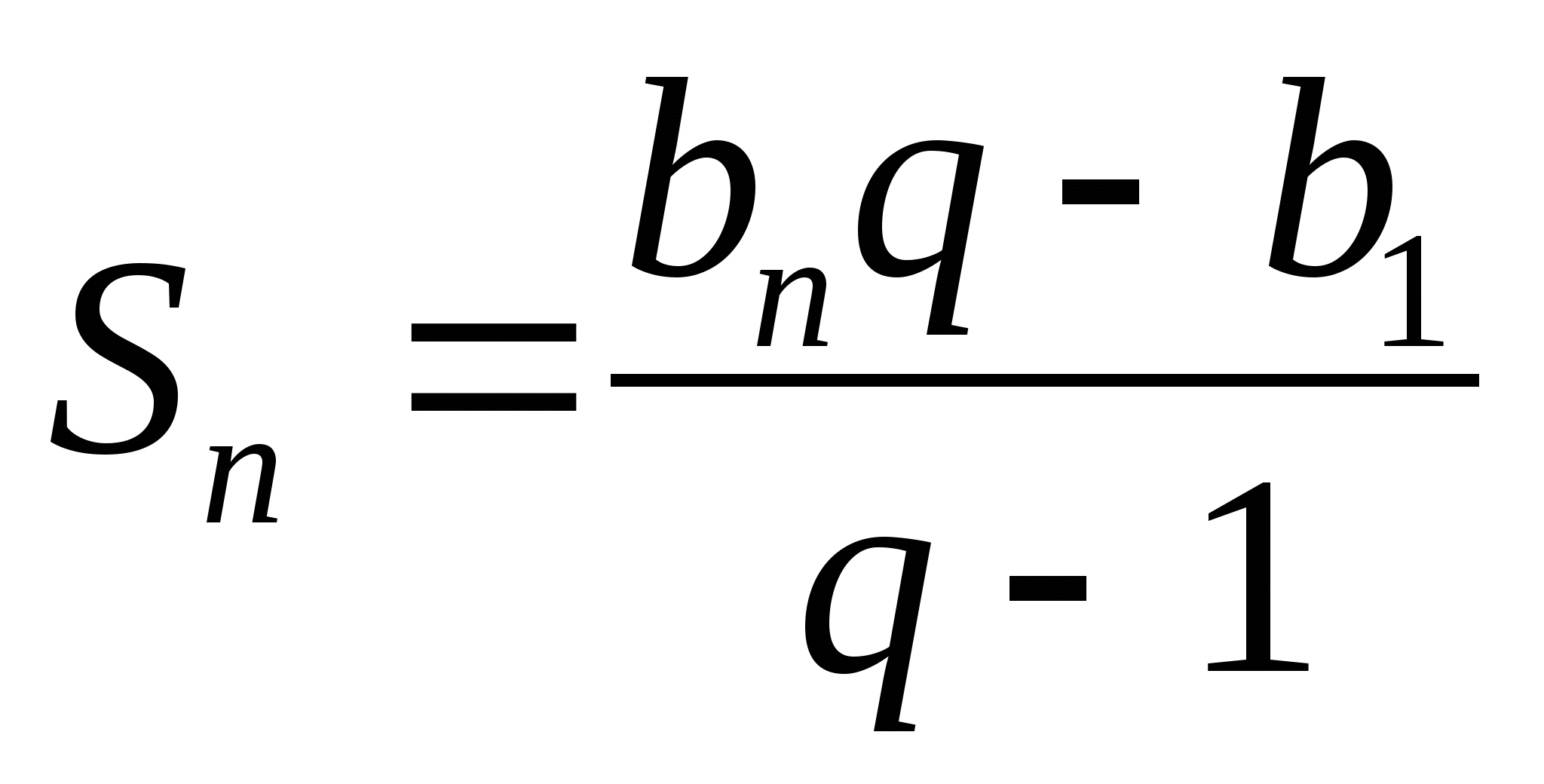 ,
, 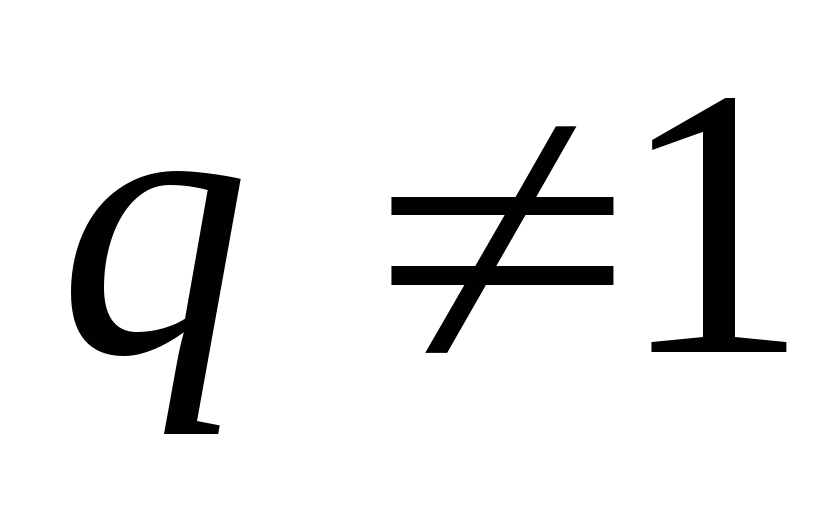 )
)
5. Для геометрической прогрессии 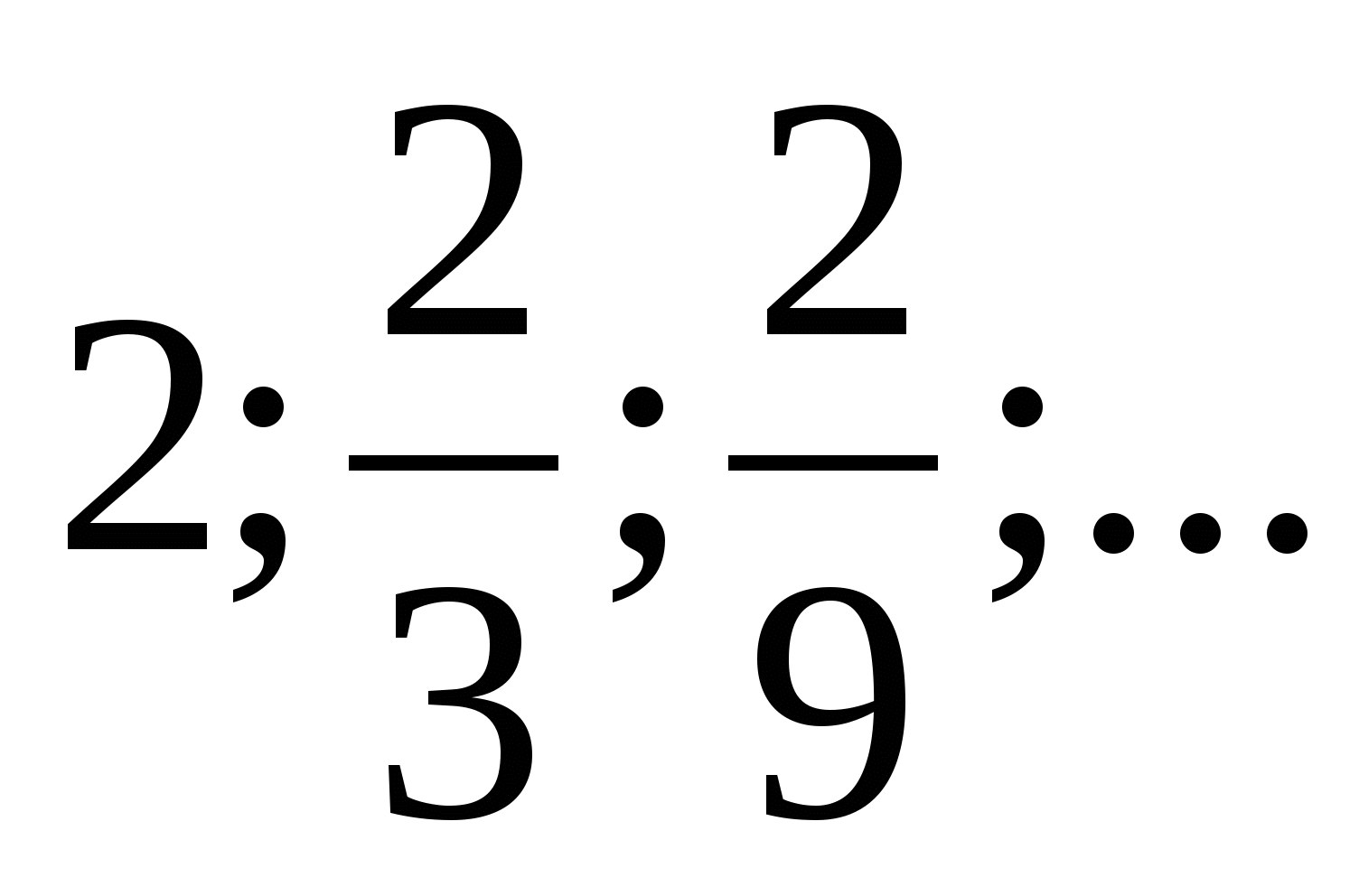 найдите пятый член.
найдите пятый член. 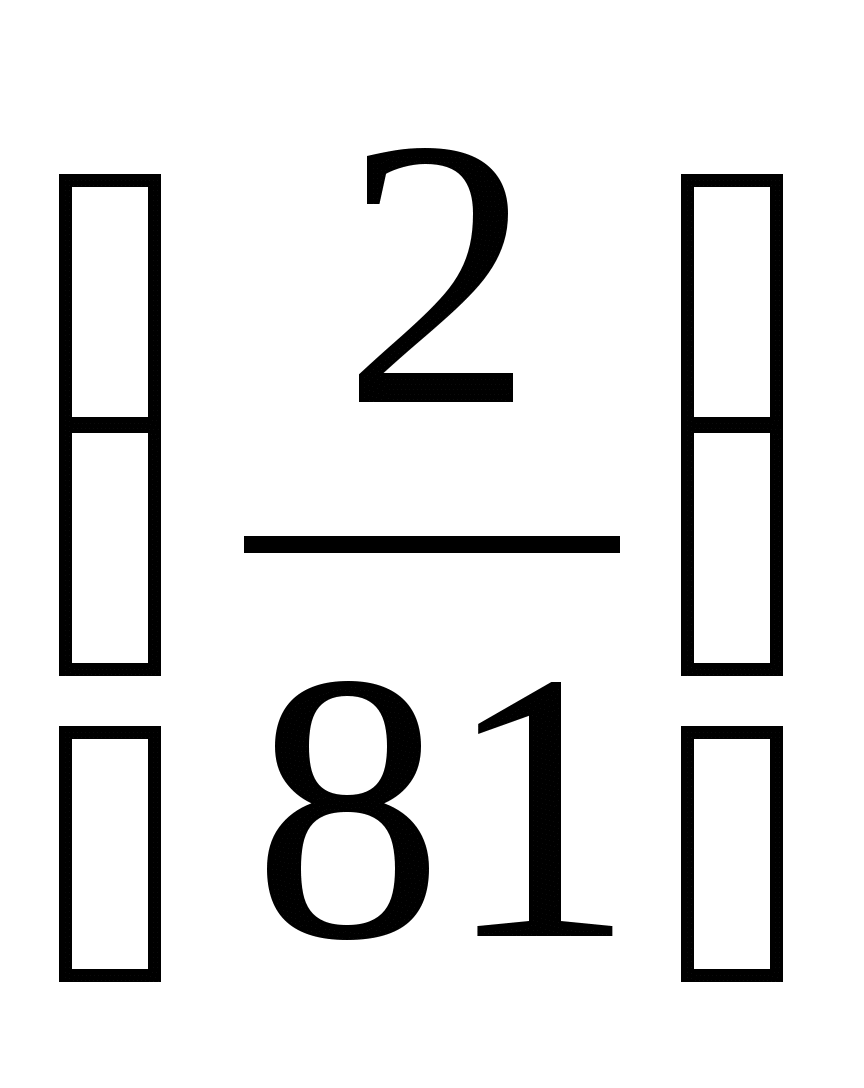
6. Для геометрической прогрессии 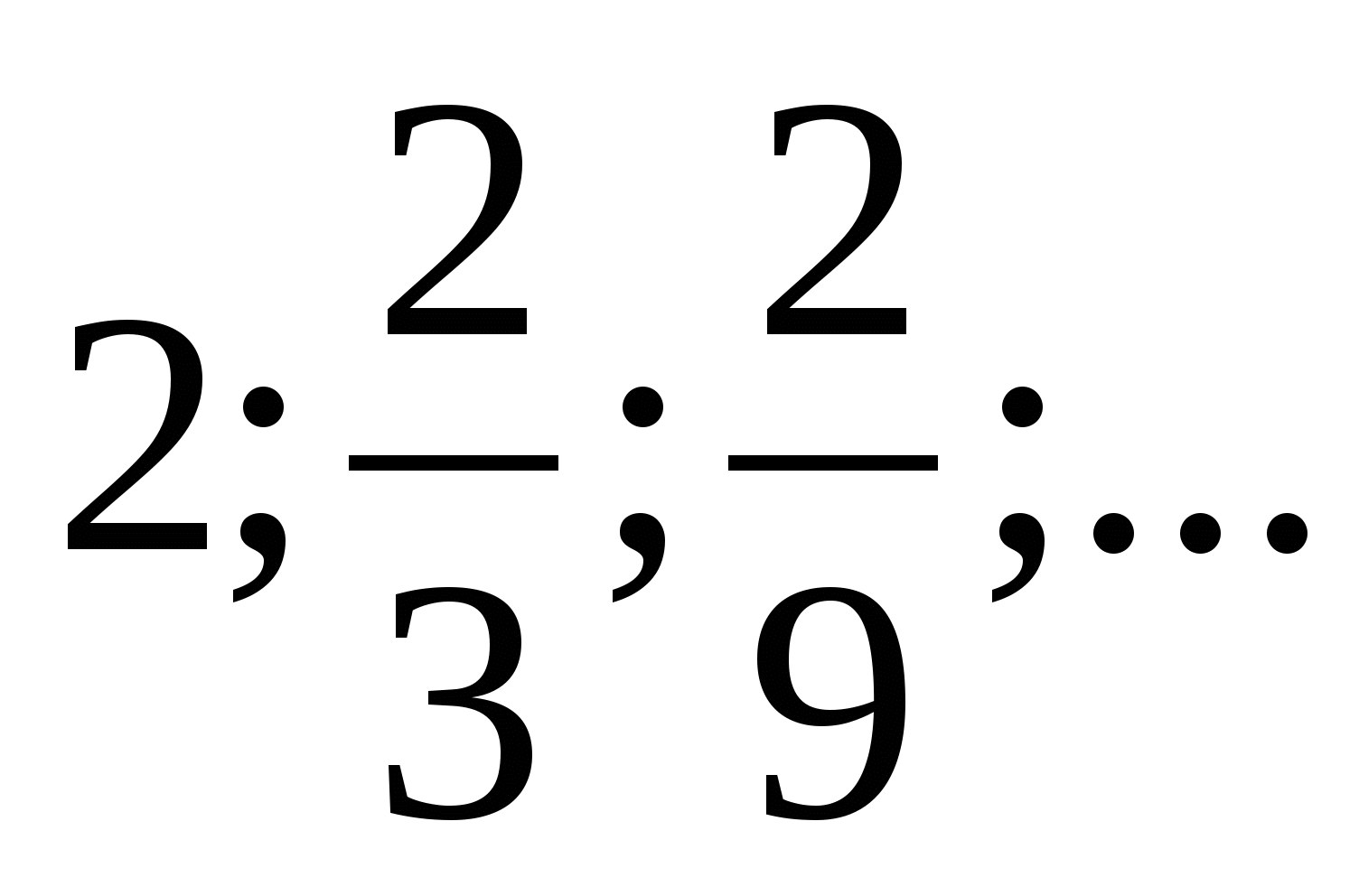 найдите n-й член.
найдите n-й член. 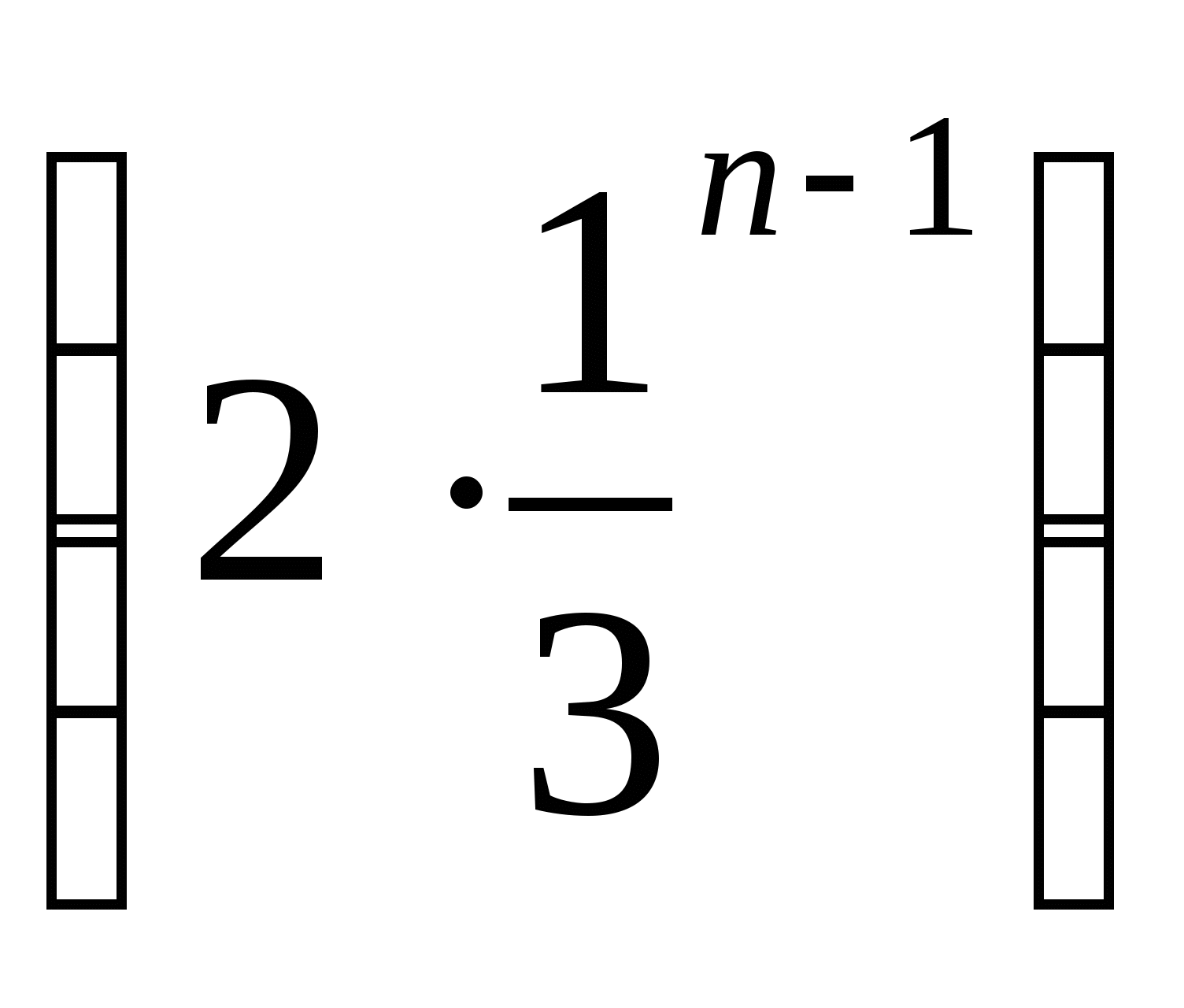
7. В геометрической прогрессии b3 = 8 и b5 = 2. Найдите b4. (4)
8. В геометрической прогрессии b3 = 8 и b5 = 2. Найдите b1 и q. 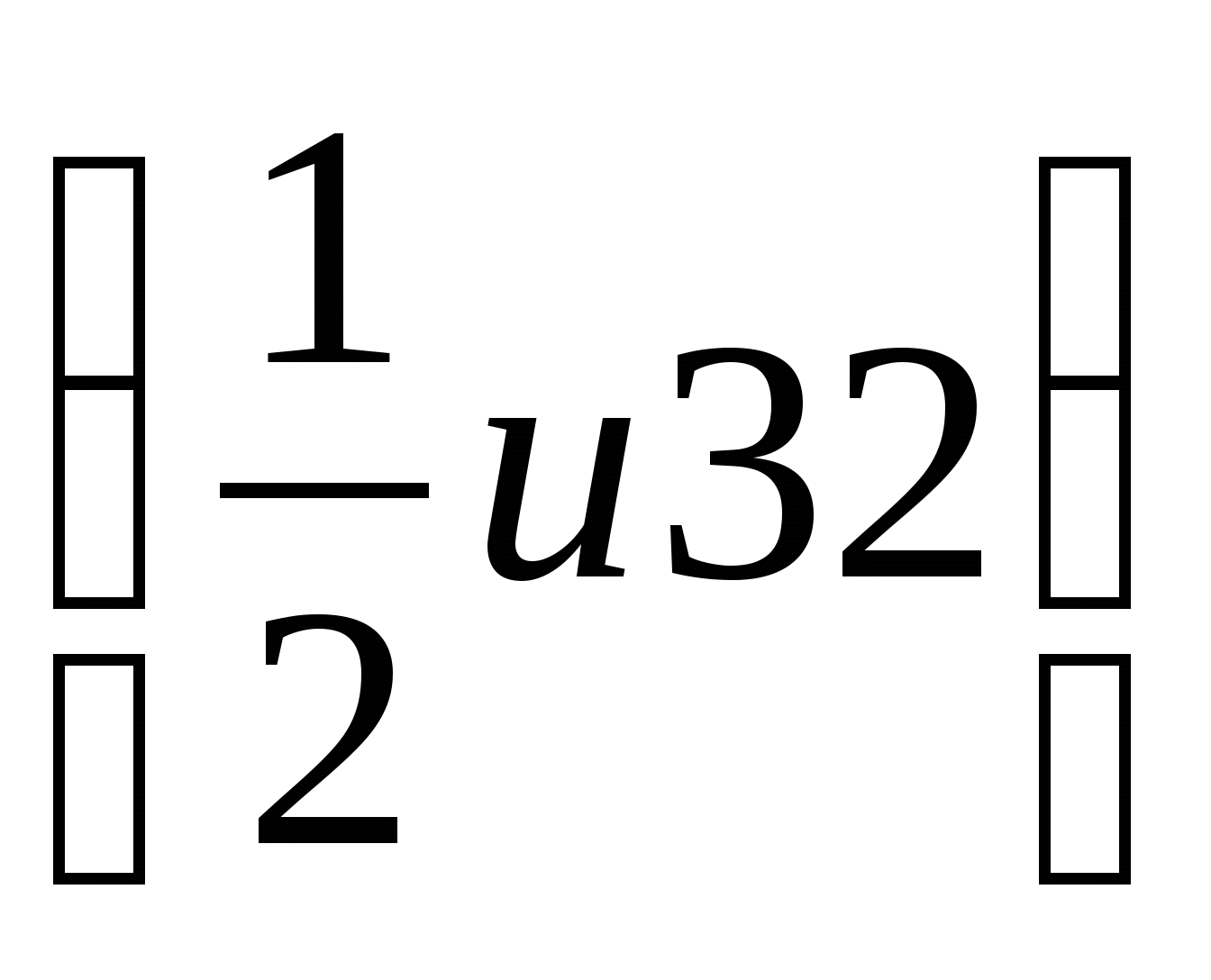
9. В геометрической прогрессии b3 = 8 и b5 = 2. Найдите S5. (62)
III. Изучение новой темы (демонстрация презентации).
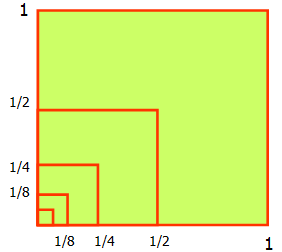
Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего.
В результате, мы получили последовательность сторон квадратов 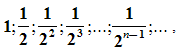 образующих геометрическую прогрессию со знаменателем
образующих геометрическую прогрессию со знаменателем 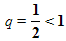 .
.
И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,
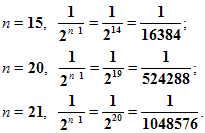
Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.
С помощью этого рисунка можно рассмотреть и ещё одну последовательность.

Например, последовательность площадей квадратов:
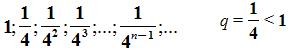
 . И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
. И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
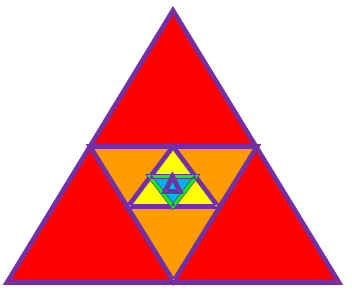
Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников.
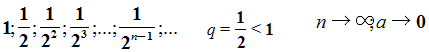
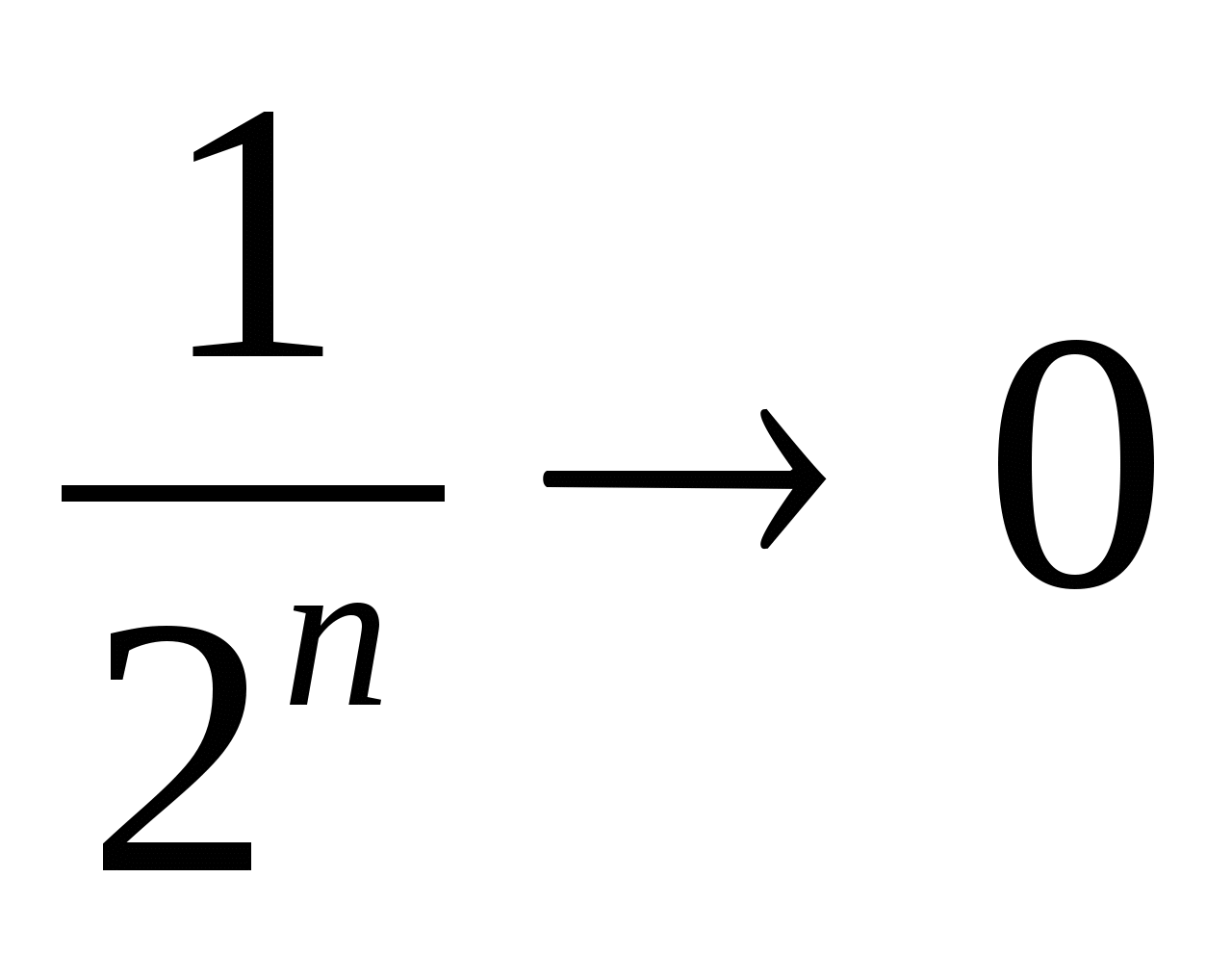 при
при  .
.
Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.
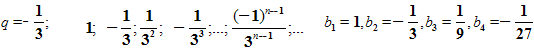
То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.
Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.
Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.
Определение:
Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы. 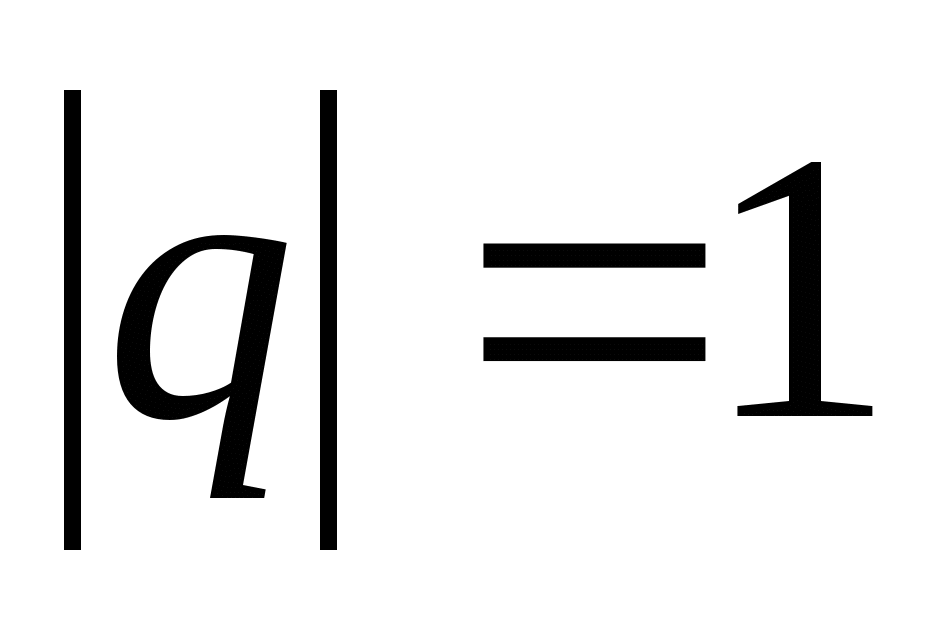 .
.
С помощью определения можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.
Задача
Является ли последовательность бесконечно убывающей геометрической прогрессией, если она заданна формулой:
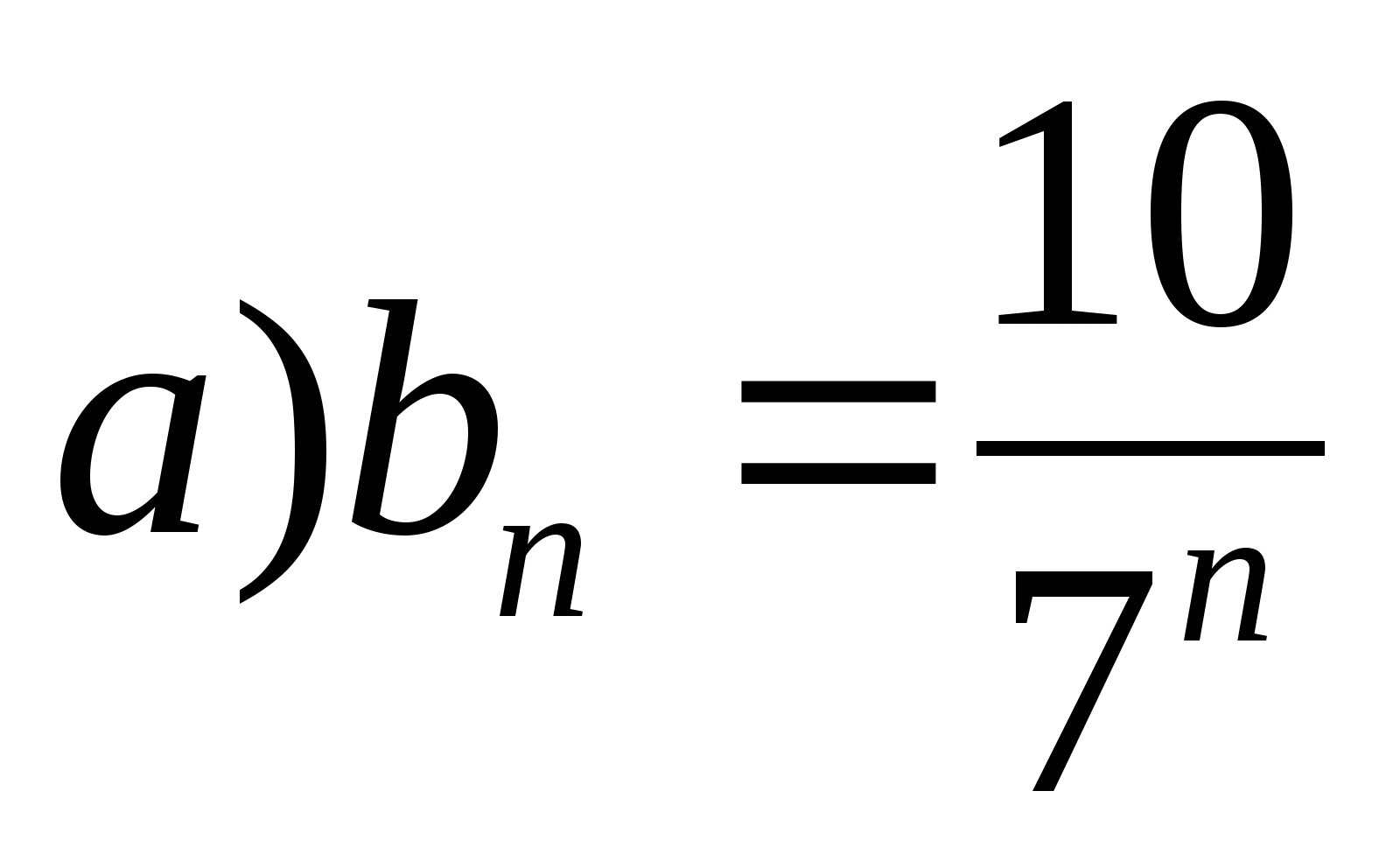 ;
; 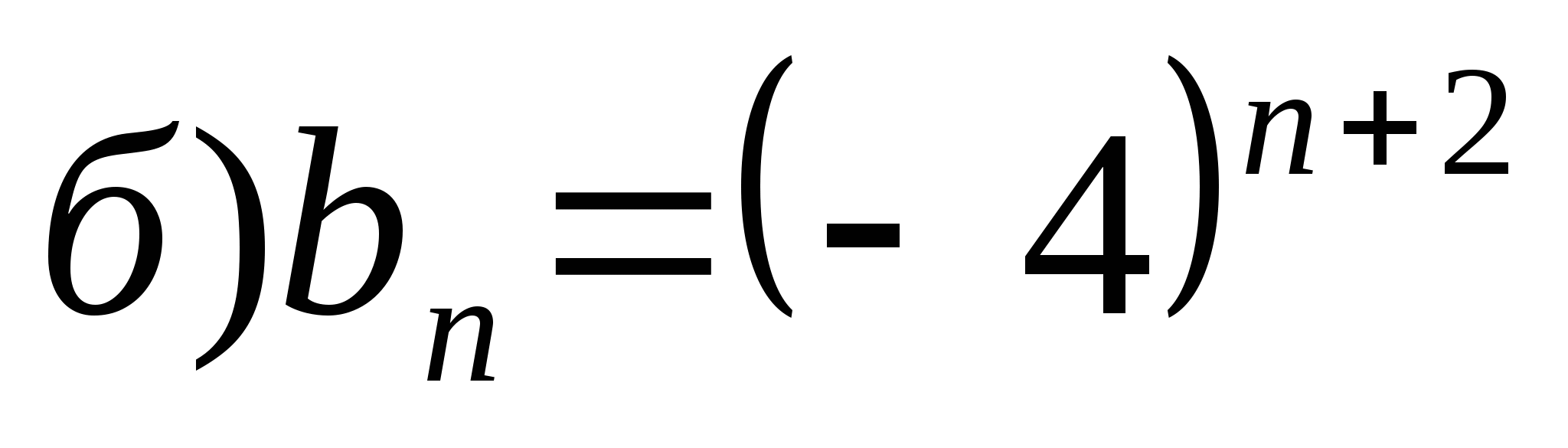 .
.
Решение:
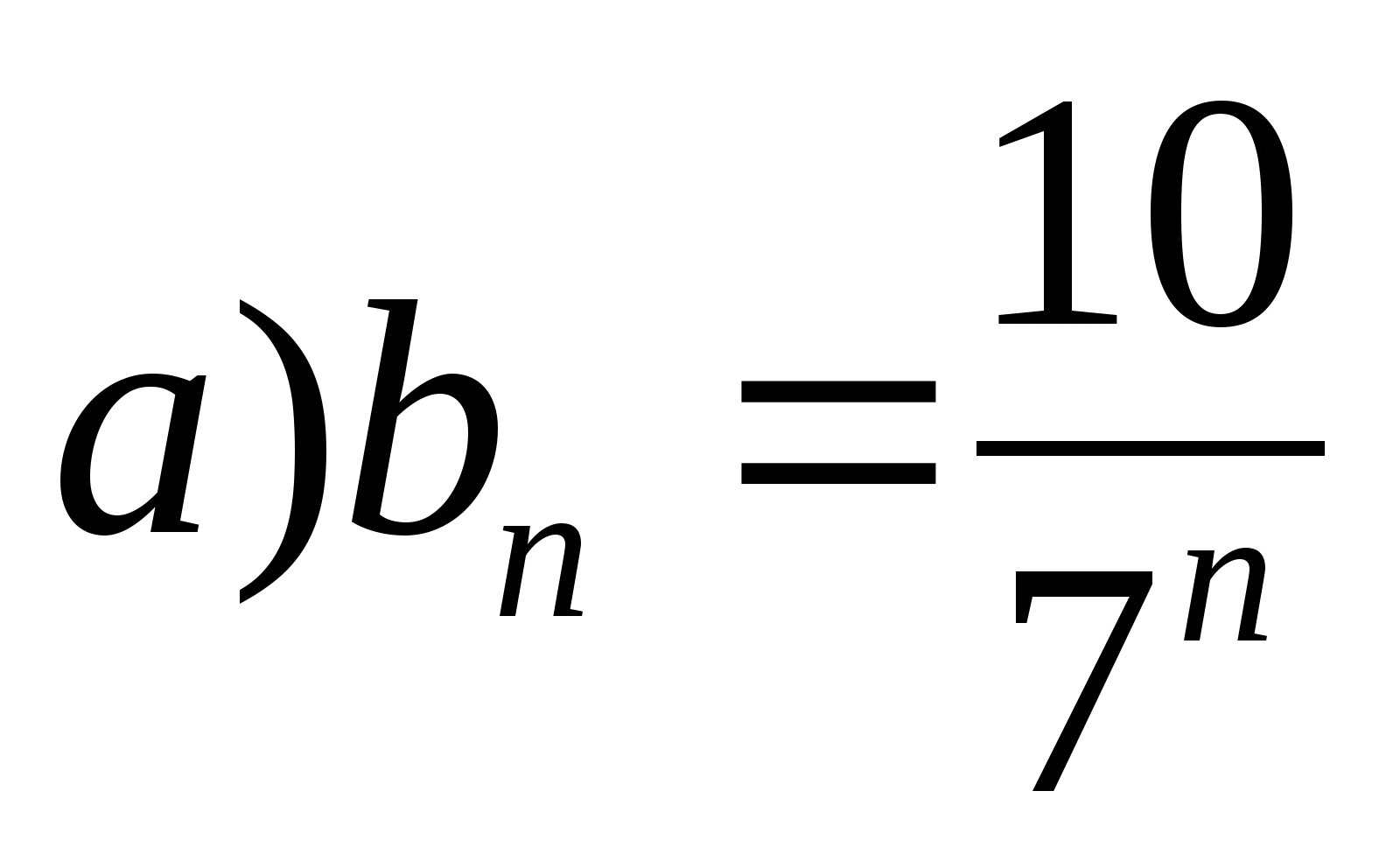 . Найдем q.
. Найдем q.
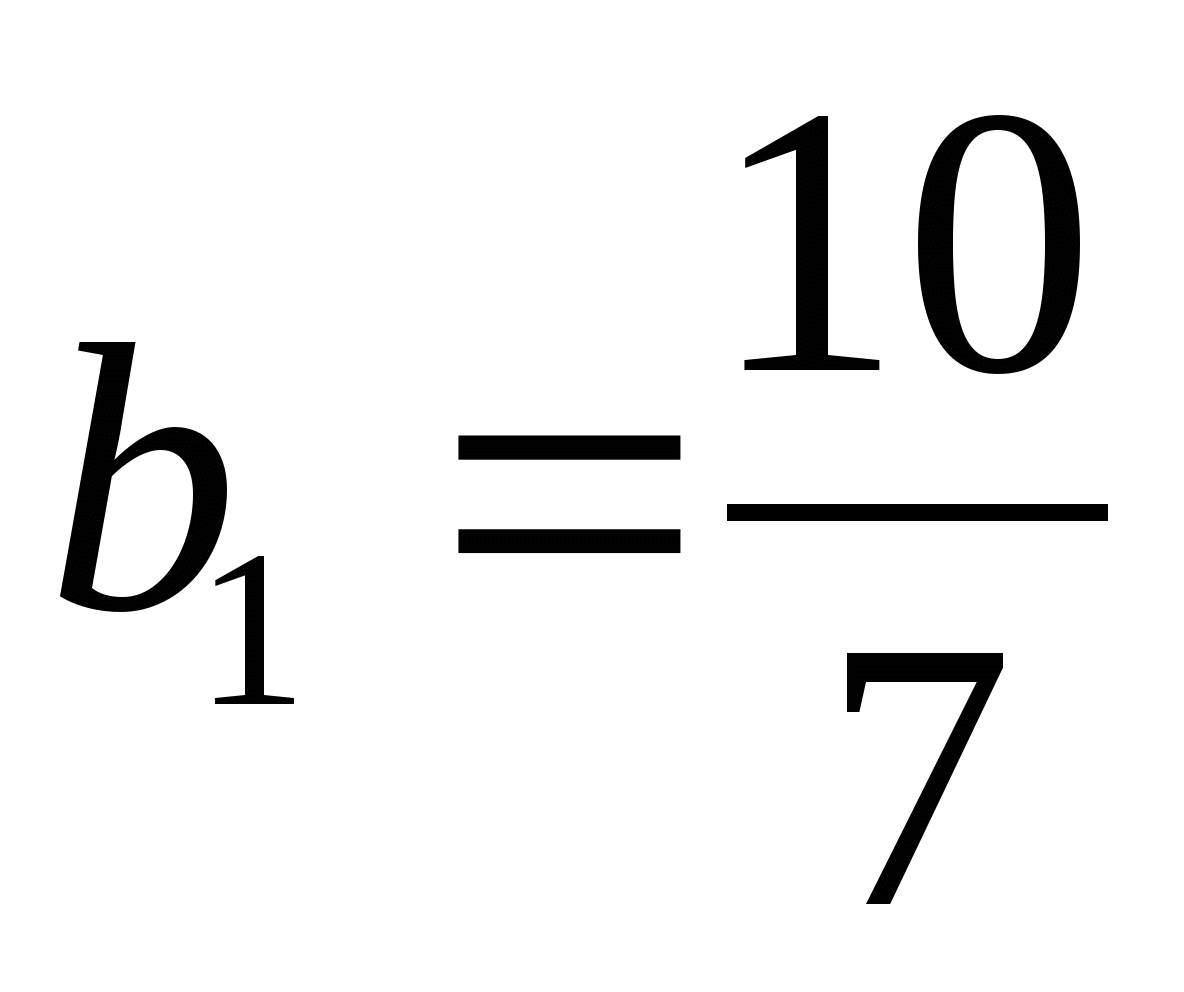 ;
; 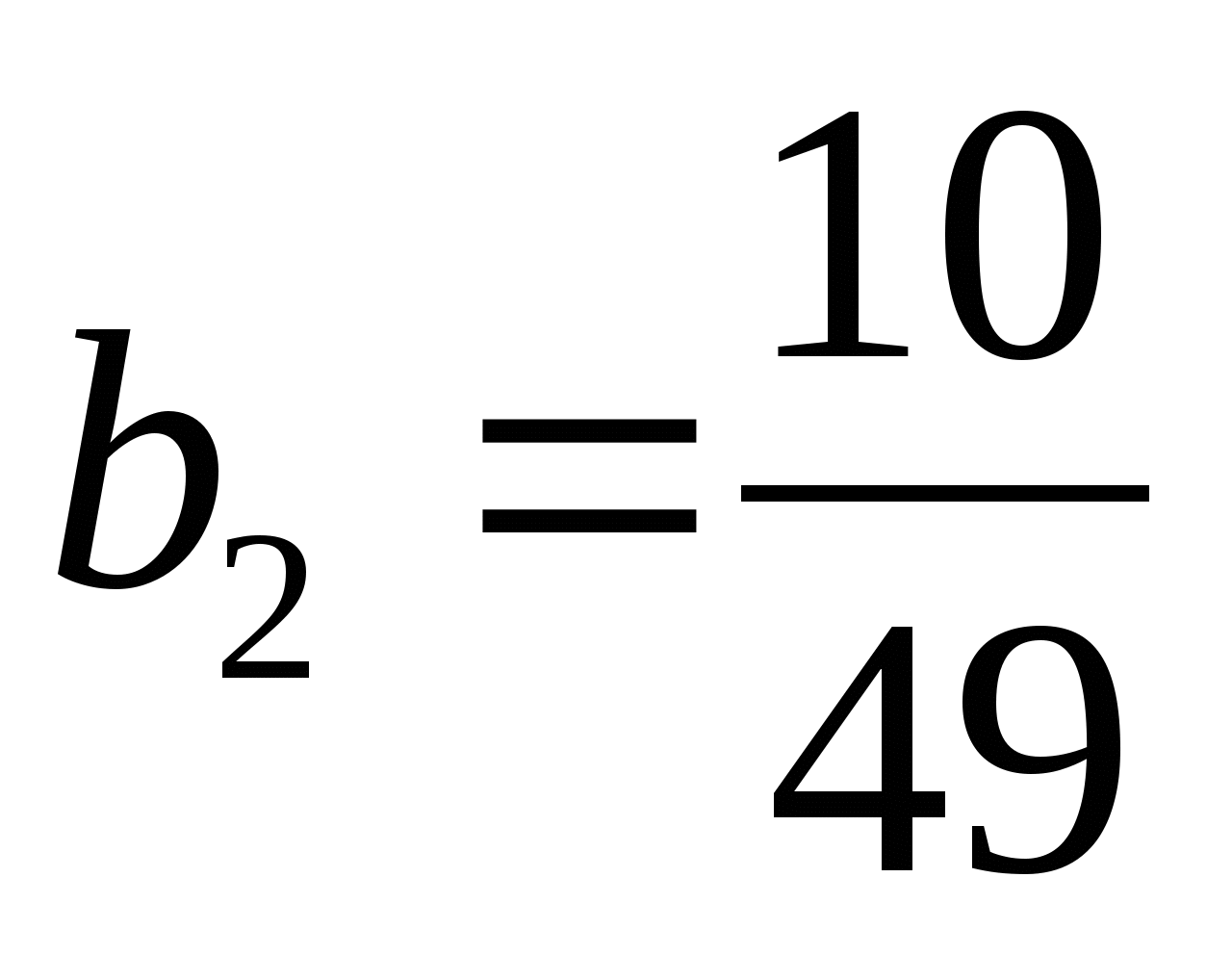 ;
; 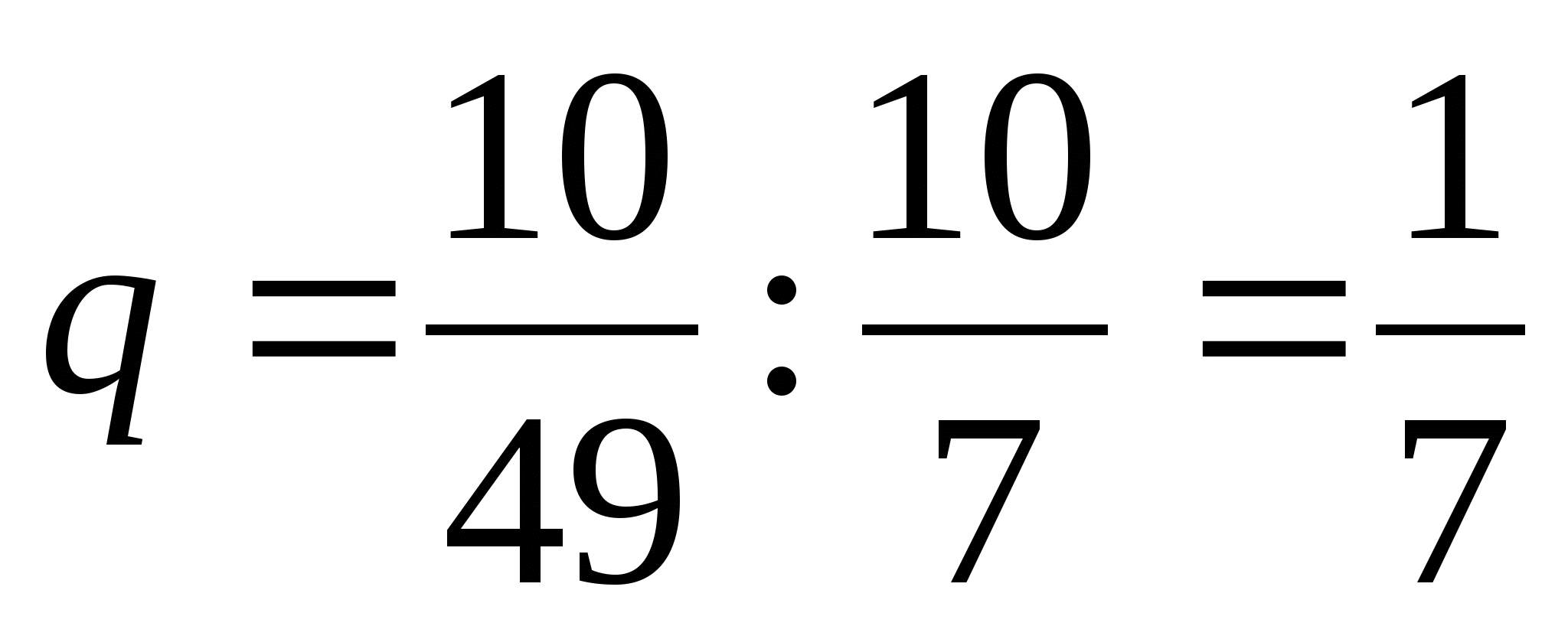 ;
; 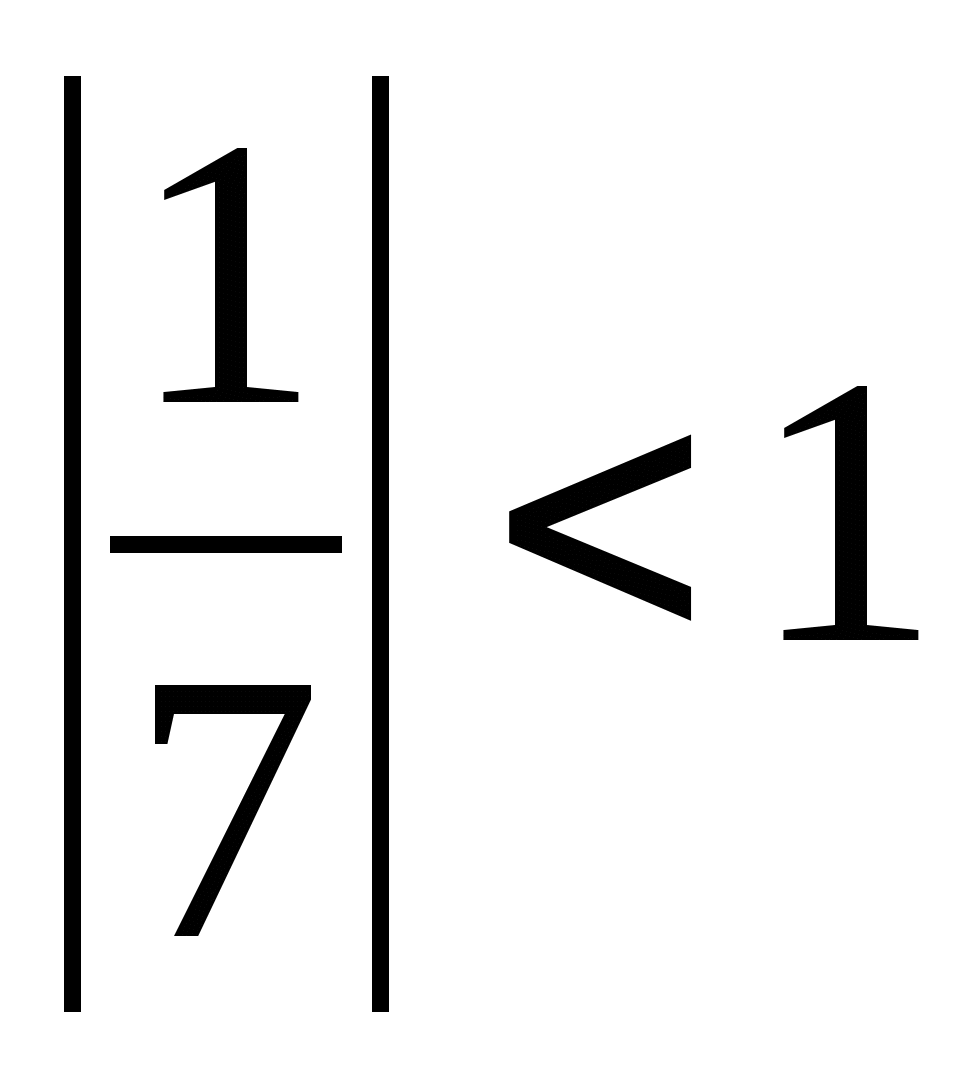 .
.
данная геометрическая прогрессия является бесконечно убывающей.
б) данная последовательность не является бесконечно убывающей геометрической прогрессией.
Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию: 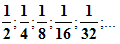
Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1. 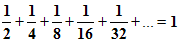
Но в левой части этого равенства – сумма бесконечного числа слагаемых.
Рассмотрим сумму n первых слагаемых.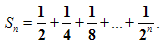
По формуле суммы n первых членов геометрической прогрессии, она равна 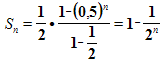 .
.
Если n неограниченно возрастает, то 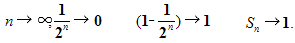
или 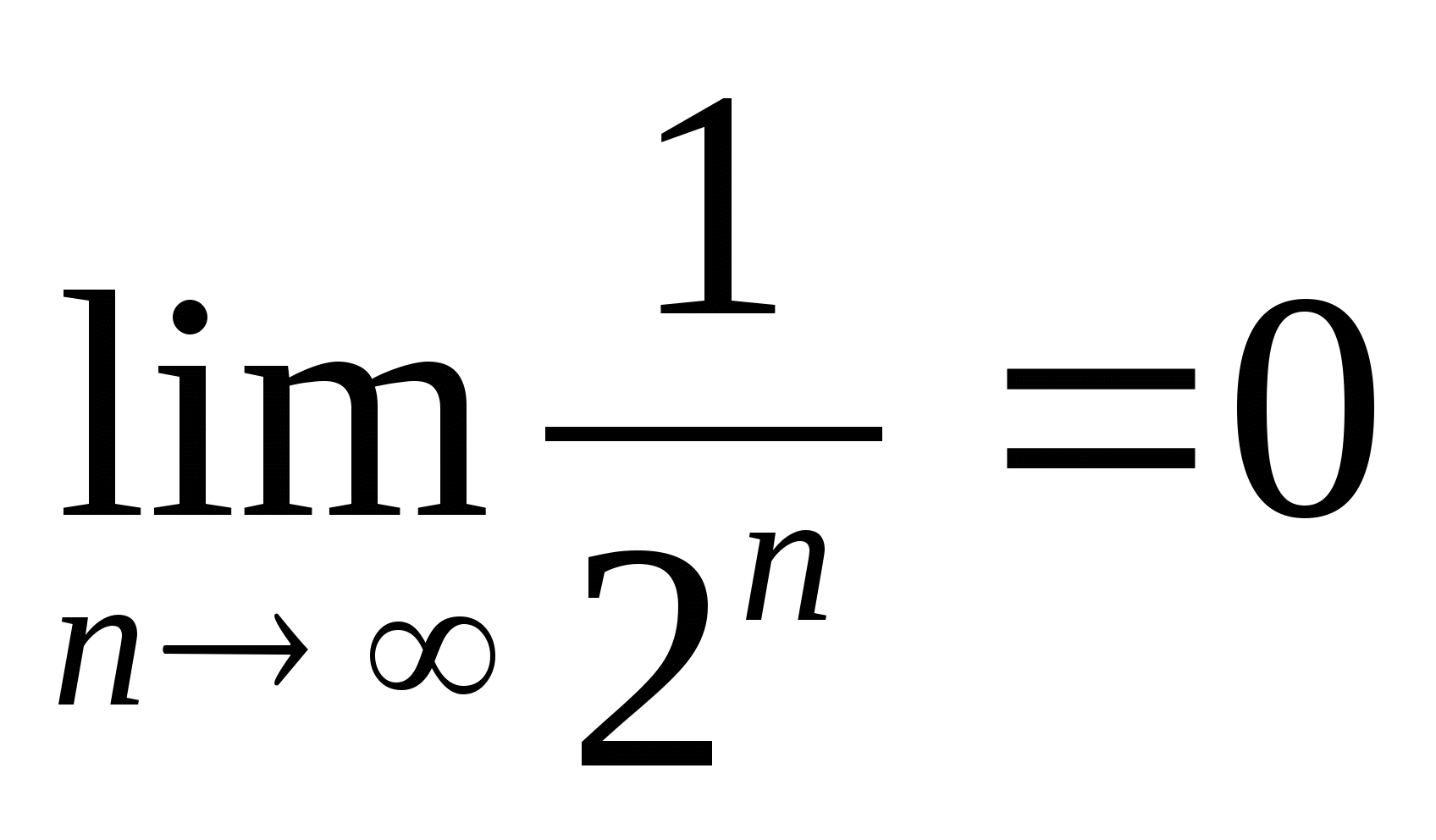 . Поэтому
. Поэтому 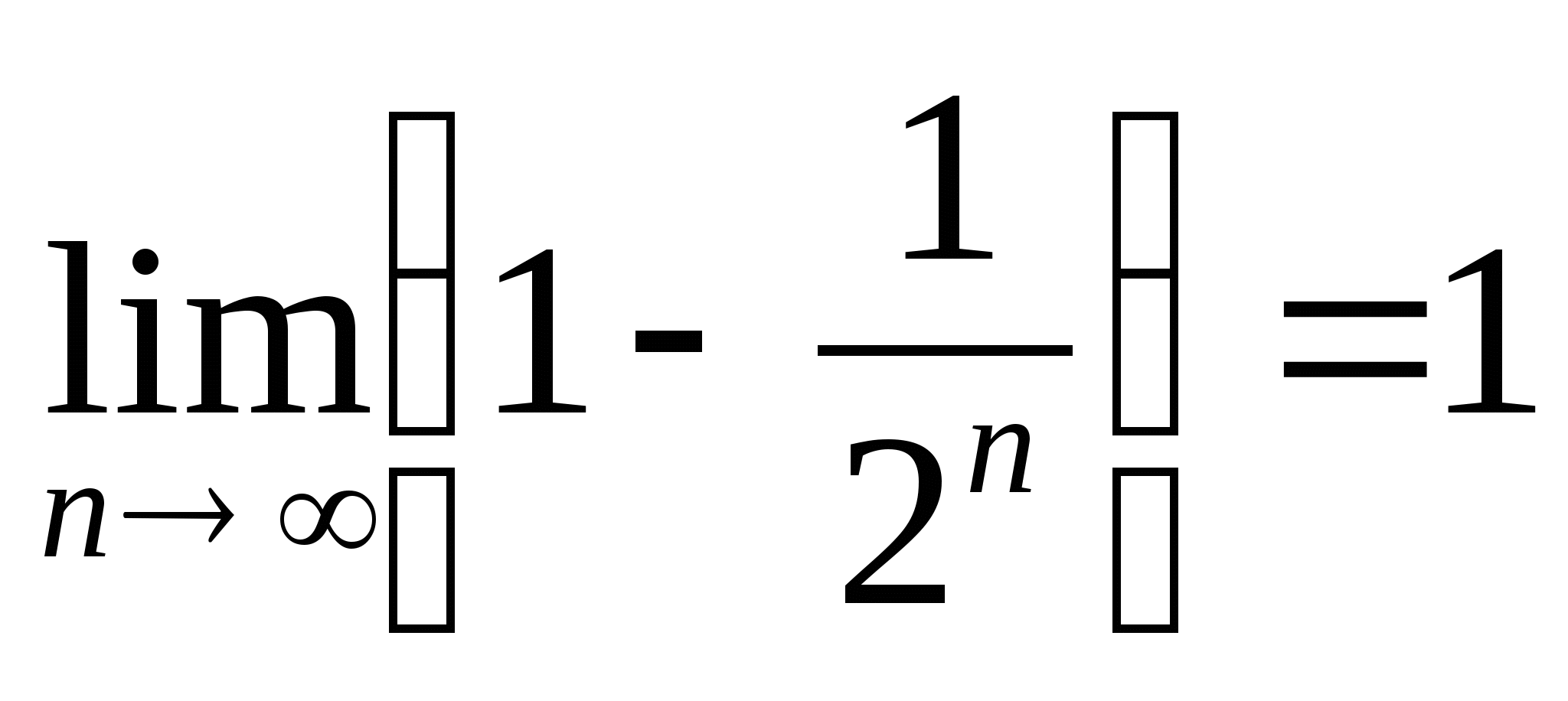 , т.е.
, т.е. 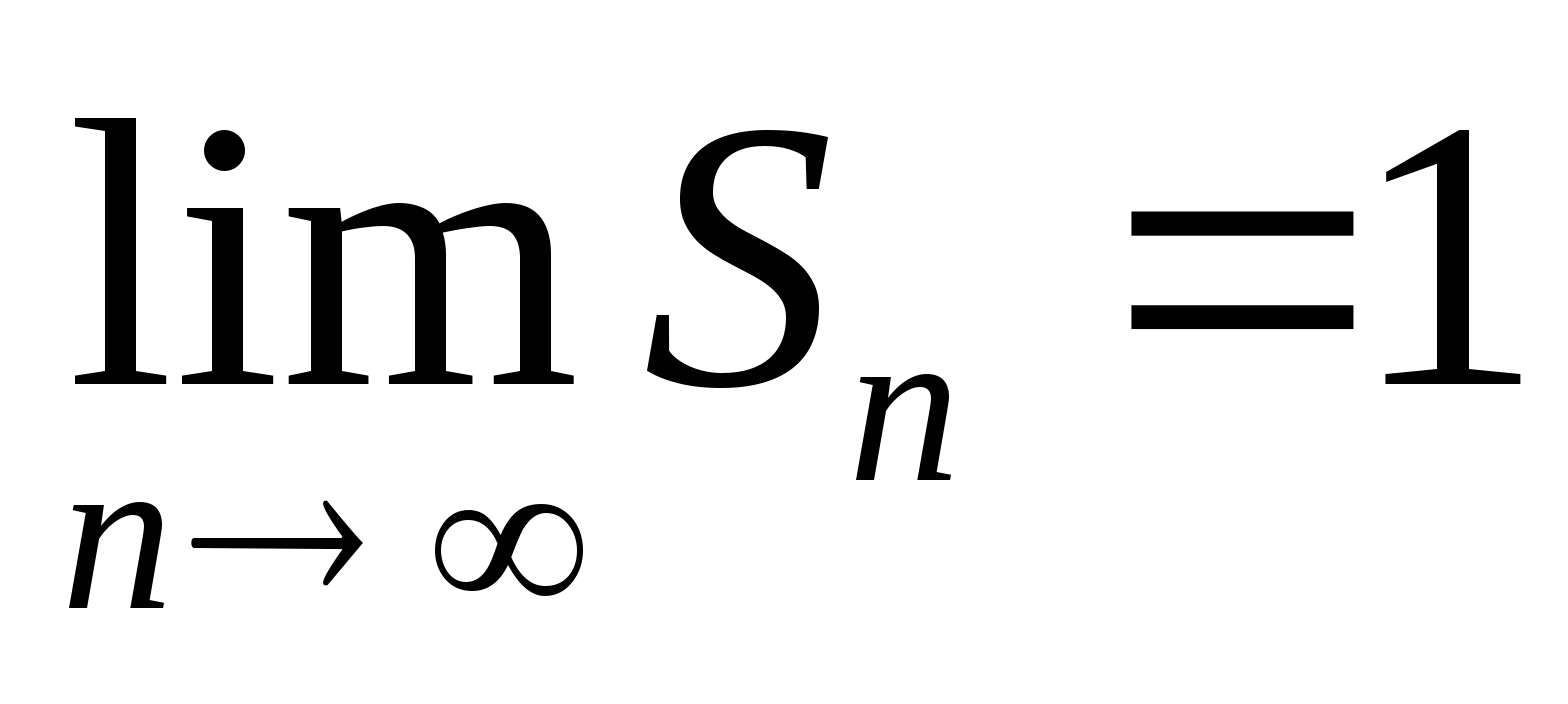 .
.
Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности S1, S2, S3, …, Sn, … .
Например, для прогрессии 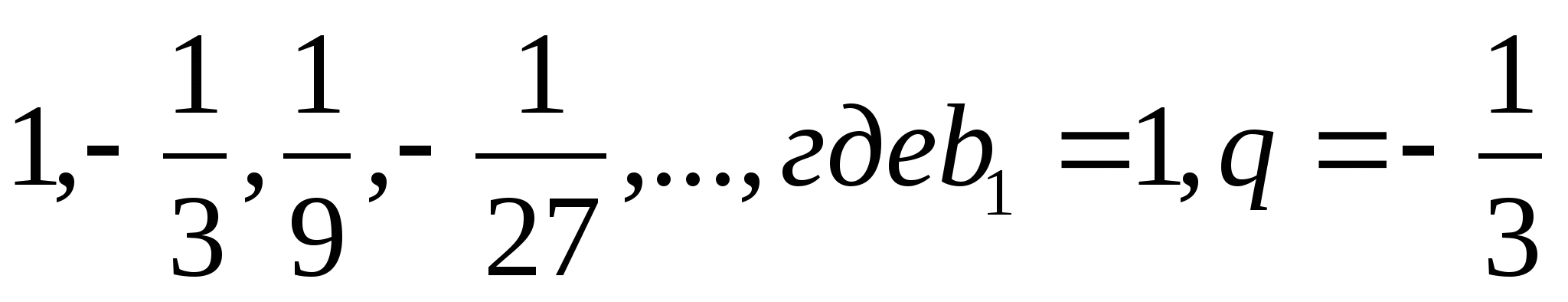 ,
,
имеем 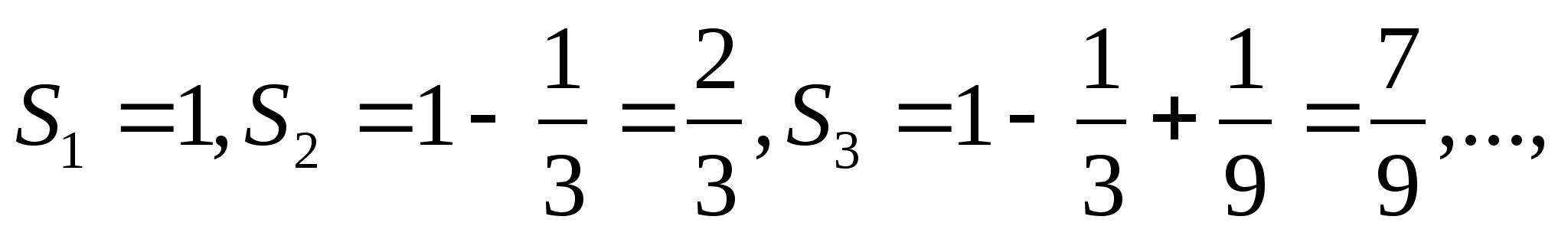
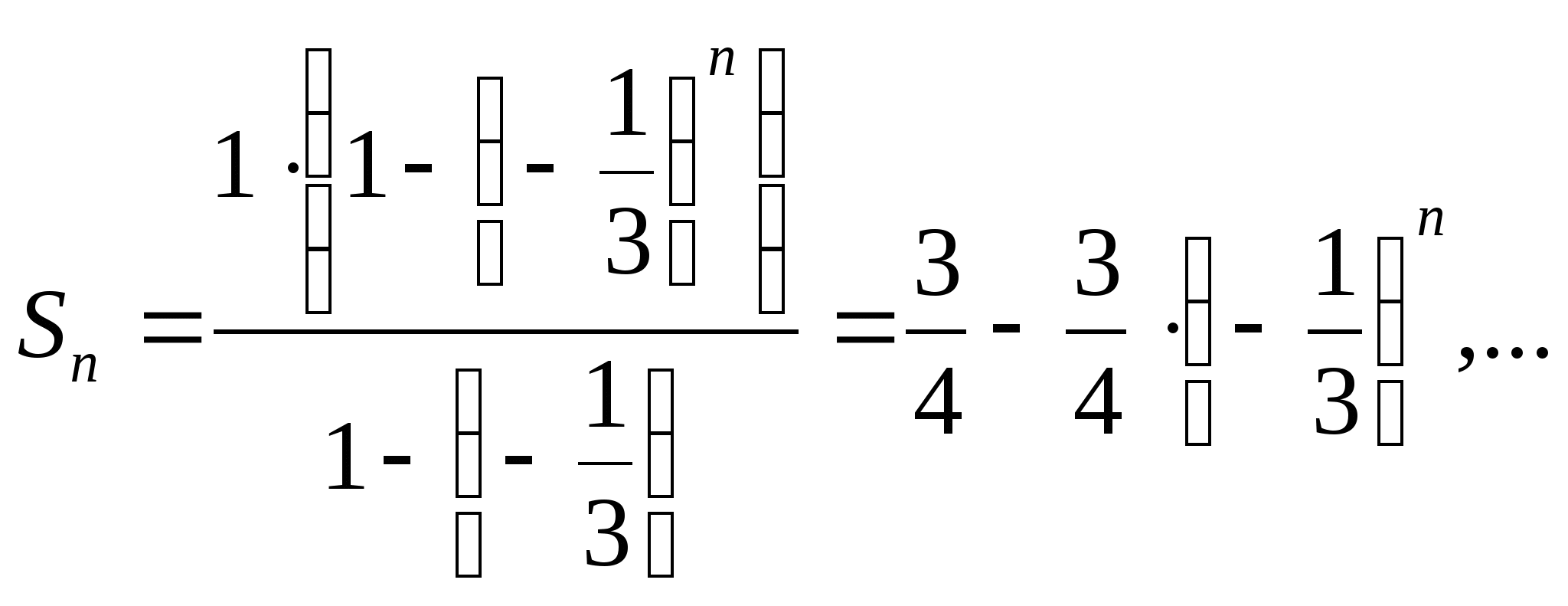 Так как
Так как 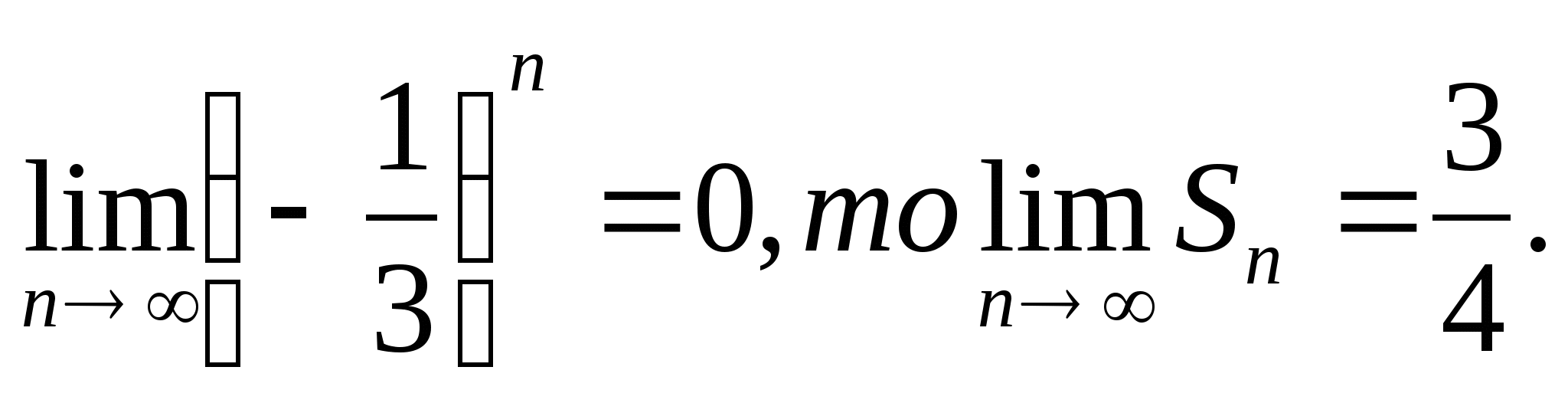
Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле 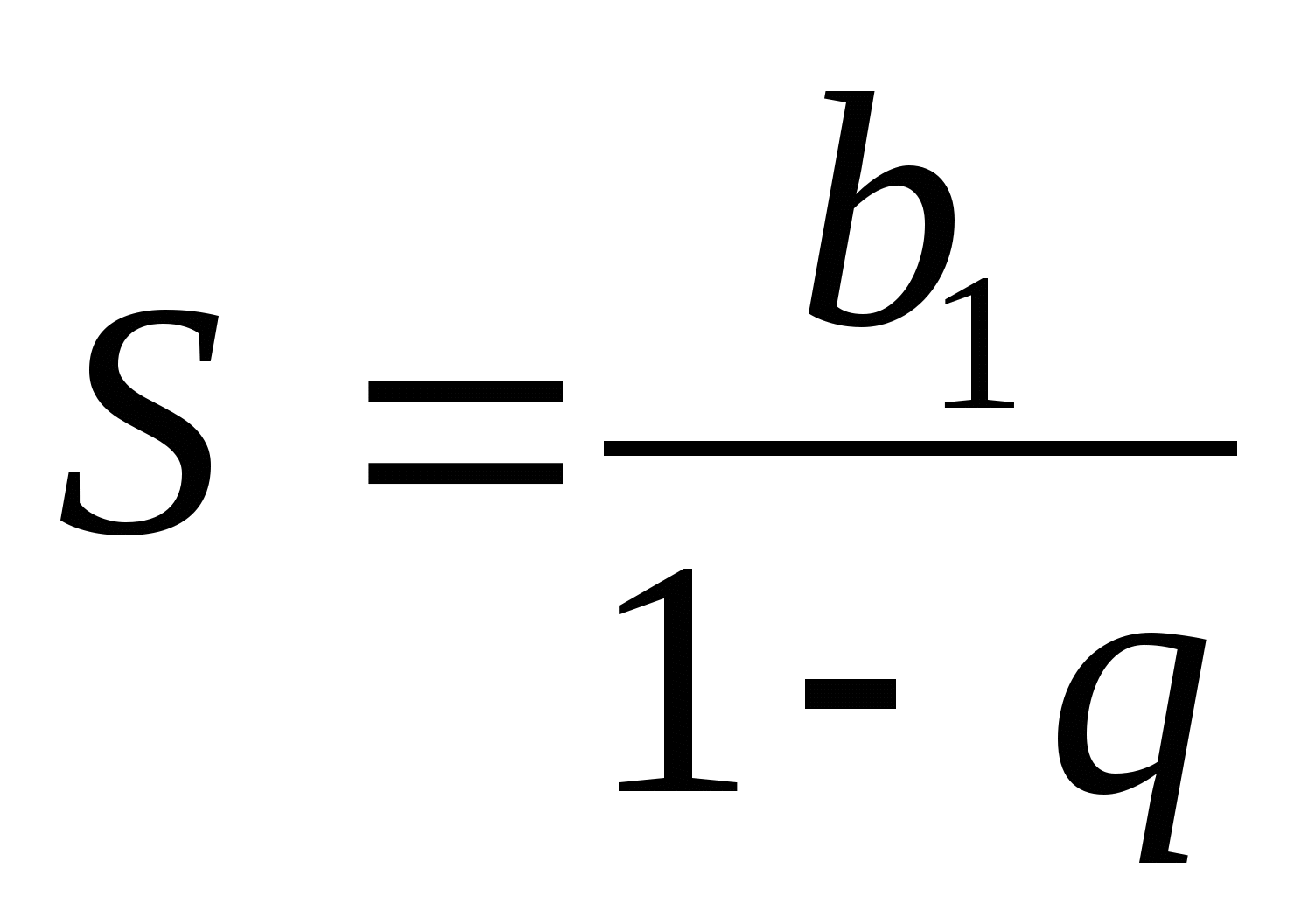 .
.
III. Осмысление и закрепление (выполнение заданий).№4.38
IV. Подведение итогов.
С какой последовательностью сегодня познакомились?
Дайте определение бесконечно убывающей геометрической прогрессии.
Как доказать, что геометрическая прогрессия является бесконечно убывающей?
Назовите формулу суммы бесконечно убывающей геометрической прогрессии.
V. Домашнее задание.
1. Читать п. 4.5. № 4.38
infourok.ru
Дата: | Предмет: алгебра | Учитель: Колодий О.В. | ||
Класс: 9 | Раздел: Числовые последовательности | № урока: 46 | ||
Тема: Бесконечно убывающая геометрическая прогрессия. | ||||
Цель урока | Ввести понятие бесконечной геометрической прогрессии, ознакомить с формулой суммы данной прогрессии | |||
Ожидаемый результат | Все: знают определение бесконечно убывающей геометрической прогрессии, формулу суммы этой прогрессии, применяют формулу при решении задач. Большинство: применяют формулу суммы бесконечно убывающей геометрической прогрессии для перевода периодической десятичной дроби в обыкновенную. Некоторые: выполняют более сложные задания на нахождение суммы бесконечно убывающей геометрической прогрессии, требующие дополнительных преобразований | |||
Первоначальные знания | Числовая последовательность, геометрическая прогрессия, формула n-го члена геометрической прогрессии, формулы суммы n-первых членов геометрической прогрессии, различия между геометрической и арифметической прогрессиями. | |||
Ресурсы | Учебник, раздаточный материал. | |||
Ход урока | ||||
Этап урока | t | Деятельность учителя | Деятельность учащихся | |
1.Организационный момент (психологический настрой на урок), проверка домашнего задания. | 5 | Психологический настрой на урок: с помощью метода «ассоциаций». — Какие ассоциации возникают у вас, когда вы слышите слово «успех»? (слова должны начинаться с букв данного слова) Проверка домашнего задания Взаимопроверка домашнего задания (комментирование). Выставление оценок в соответствии с критериями: «5»- 8 верно решенных заданий; «4»-7; «3»-5-6; «2»-0-4 верно решенных. | Настраиваются на урок. ФО -взаимопроверка домашнего задания с выставлением оценок на полях тетради в соответствии с критериями. | |
2.Вызов | 4 | Задача-проблема: Эпиграф: «Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью» Л.Н.Толстого Учитель вызывает к доске одного из учащихся и ставит перед ним задачу: — Дойдешь ли ты от стола до двери (расстояние примерно 3 метра), если каждый последующий шаг будешь делать в два раза меньше предыдущего? После предложенных вариантов решения ученик практически решает данную задачу и делает соответствующий вывод. — Сегодня на уроке с помощью математических расчетов мы дадим точный ответ на данную задачу. | Учащиеся делают предположение по решению проблемной задачи, затем практически решают её и делают соответствующие выводы. ФО- словесная оценка | |
3.Осмысление | 6 | Получили последовательность 1,1/2,1/4, 1/8,….Данная последовательность является бесконечной геометрической прогрессией со знаменателем g = — Сегодня на уроке мы рассмотрим данный вид геометрической прогрессии (записывают число и тему урока) Работа с учебником: Дать определение бесконечно убывающей геометрической прогрессии — Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии как число, к которому неограниченно приближается сумма Найдем сумму всех членов геометрической прогрессии, т.е. Sn = 1+ Sn = Ответ к проблемной задаче: ученик не сможет дойти до стола учителя. Совместно с учениками в ходе беседы дается вывод формулы суммы бесконечно убывающей геометрической прогрессии | g| Sn = Если | | Рассуждают, участвуют в объяснении нового материала | |
5 | Практическое применение формулы суммы бесконечно убывающей геометрической прогрессии: (Задание из сборника ВОУД) Представить в виде обыкновенной дроби 5,(17). Решение: 5,(17)= 5+0,17+0,0017+0,000017+0,00000017+… 0,17; 0,0017; 0,000017… — геометрическая прогрессия g = b2:b1= 0,0017:0,17=0,01 |g| = 0,01 Sn = | Записывают в тетрадь, задают вопросы по ходу выполнения задания | ||
6 | Решение упражнений: Эпиграф: «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!» (Д. Пойа) Дифференцированное задание: Уровень А — 236, уровень В — 239(а,б), уровень С — № 243 (а) | Выполняют задания в соответствии с выбранным уровнем, ФО -самопроверка с решением на доске | ||
Элективный (выборочный тест). Настрой на самостоятельную работу: Эпиграф: Кто воздвигнет тебя к небесам? Только сам. Кто низвергнет тебя с высоты? Только ты. Где куются ключи к твоей горькой судьбе? Лишь в тебе. Чем расплатишься ты за проигранный бой? Лишь собой. Раздает каждому ученику набор чисел от 1 до 4. Задает задание с четырьмя вариантами ответов (1,2,3,4). Через 20 секунд просит всех одновременно поднять карточку с номером правильного ответа. | Выполняют задания, через 20 секунд поднимают карточку с правильным номером ответа. Комментируют решение задания. ФО – элективный тест. | |||
4. Домашнее задание | 3 | Эпиграф: «Прежде чем решать задачу – прочитай условие». (Жак Адамар) № 237, 239(в), параграф 14 выучить | Слушают, делают карандашом пометки. | |
5. Подведение итогов урока | 5 | Прием «Кубик Блума» Эпиграф: «Незнающие пусть научатся, знающие — вспомнят еще раз» Одни учащиеся класса (по желанию) бросают «Кубик Блума» и задают вопрос в соответствии с выпавшим словом, другие учащиеся отвечают на вопросы. Грани кубика: Назови… Почему… Объясни… Предложи… Придумай… Поделись… | Определяют уровень усвоения материала и выявляют степень предметно-эмоционального погружения в тему ФО- словесная оценка | |
6. Рефлексия | 11 | Прием «Дневник обратной связи» Учащиеся заполняют дневник обратной связи, отвечая на 3 основных вопроса: 1.Я хорошо понял на уроке и могу выполнять…. 2.Я не понял…. 3.Для меня наиболее сложным является…. | Заполняют «Дневник обратной связи». Суммативное оценивание за урок. | |
Анализ и оценивание | Психологический настрой мобилизовал учащихся на дальнейшую работу на уроке. Время на каждый этап было распределено. Но урок был очень насыщенным из – за большого количества заданий. На протяжении всего урока внимание учащихся было сконцентрировано на выполнении заданий. Впервые был применен прием «Кубик Блума». Учащиеся учились составлять вопросы по теме в соответствии с выпавшим на грани кубика словом. «Дневник обратной связи» позволил во внеурочное время ознакомиться с тем, что написали ученики. Полученную информацию я использовала для планирования следующего урока. | |||
Изменения к последующим занятиям | Продолжить работу по применению рефлексии урока, психологического настроя. Провести уроки по обобщению материала по теме в нестандартной форме. | |||
multiurok.ru

 первых членов рассматриваемой прогрессии при неограниченном возрастании числа
первых членов рассматриваемой прогрессии при неограниченном возрастании числа  +
+  +…..+
+…..+ 
 Sn =
Sn =  = -2 * ( (
= -2 * ( ( стремиться к 2, т.к. при п стремящемся к ∞, вычитаемое стремится к нулю.
стремиться к 2, т.к. при п стремящемся к ∞, вычитаемое стремится к нулю.
 | множитель
| множитель  стремится к нулю, а значит разность
стремится к нулю, а значит разность  , т.е. стремится к единице. Поэтому при неограниченном увеличении
, т.е. стремится к единице. Поэтому при неограниченном увеличении сумма Snстремится к числу
сумма Snстремится к числу . Число
. Число 
 =
=  = , 5,(17)= 5+ = 5 Ответ: 5,(17) = 5
= , 5,(17)= 5+ = 5 Ответ: 5,(17) = 5