Часть окружности ограниченная двумя точками называется. Окружность. Форма и положение
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Это замкнутая плоская линия, всякая точки которой равноудалена от одной и той же точки (O ), называемой центром .
Прямые (OA , OB , OС. . .), соединяющие центр с точками окружности — это радиусы .
Из этого получаем:
1. Все радиусы одной окружности равны.
2. Два круга с одинаковыми радиусами будут равны.
3. Диаметр равен двум радиусам.
4. Точка , лежащая внутри круга, ближе к центру, а точка, лежащая вне круга, дальше от центра, чем точки окружности.
5. Диаметр , перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.
6. Дуги , заключенные между параллельными хордами , равны.
При работе с окружностями применяют следующие теоремы:
1. Теорема . Прямая и окружность не могут иметь более двух общих точек.
Из этой теоремы получаем два логично вытекающих следствия:
Никакая часть окружности не может совместиться с прямой, потому что в противном случае окружность с прямой имела бы более двух общих точек.
Линия, никакая часть которой не может совместиться с прямой, называется кривой .
Из предыдущего следует, что окружность есть кривая линия .
2. Теорема . Через всякие три точки, не лежащие на одной прямой, можно провести окружность и только одну.
Как следствие данной теоремы получаем:
Три перпендикуляра к сторонам треугольника вписанного в окружность проведенные через их середины, пересекаются в одной точке, которая является центром окружности.
Решим задачу. Требуется найти центр предложенной окружности .
Отметим на предложенной три любые точки A, B и С, начертим через них две хорды , например, AB и СB, и из середины этих хорд укажем перпендикуляры MN и PQ. Искомый центр, будучи одинаково удален от A, B и С, должен лежать и на MN, и на PQ, следовательно, он находится на пересечении этих перпендикуляров, т.е. в точке O.
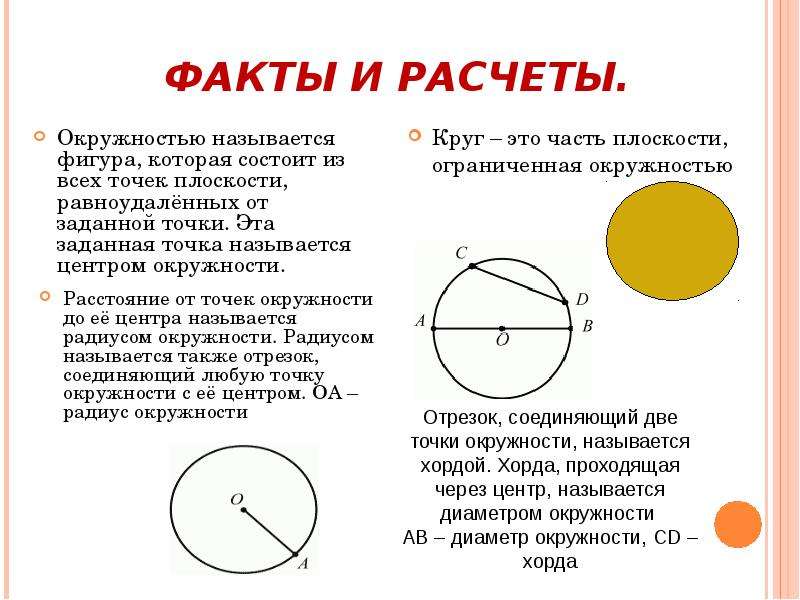
Окружность – это плоская замкнутая линия, все точки которой находятся на одинаковом расстоянии от некоторой точки (точки О), которая называется центром окружности.
(Окружность — геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. )
Круг – это часть плоскости, ограниченная окружностью.Точка О также называется центром круга.
Расстояние от точки окружности до её центра, а также отрезок, соединяющий центр окружности с её точкой, называется
радиусом
окружности/круга.
Посмотрите, как используется круг и окружность в нашей жизни, искусстве, дизайне.
Хорда — греческое — струна, стягивающая что-то
Диаметр
— «измерение через»
КРУГЛАЯ ФОРМА
Углы могут встречаться во все более возрастающем количестве, приобретать, соответственно, все больший разворот – пока не исчезнут окончательно и плоскость не станет кругом.
Это очень простой и одновременно очень сложный случай, о котором мне хотелось бы поговорить подробно. Здесь необходимо отметить, что как простота, так и сложность обусловлены отсутствием углов. Круг прост, поскольку давление его границ, в сравнении с прямоугольными формами, нивелировано – различия здесь не так велики. Он сложен, поскольку верх неощутимо перетекает в левое и правое, а левое и правое – в низ.
Он сложен, поскольку верх неощутимо перетекает в левое и правое, а левое и правое – в низ.
В. Кандинский
В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении.
В школе изучается много полезных свойств окружности. Одной из самых красивых теорем является следующая: проведем через заданную точку прямую, пересекающую заданную окружность, тогда произведение расстояний от этой точки до
точек пересечения окружности с прямой не зависит от того, как именно была проведена прямая. Этой теореме около двух тысяч лет.
На рис. 2 изображены две окружности и цепочка окружностей, каждая из которых касается этих двух окружностей и двух соседей по цепочке. Швейцарский геометр Якоб Штейнер около 150 лет назад доказал следующее утверждение: если при некотором выборе третьей окружности цепочка замкнется, то она замкнется и при любом другом выборе третьей окружности. Отсюда следует, что если однажды цепочка не замкнулась, то она не замкнется при любом выборе третьей окружности. Художнику, рисовавшему
изображенную цепочку, пришлось бы немало потрудиться, чтобы она получилась, или обратиться к математику для расчета расположения двух первых окружностей, при котором цепочка замыкается.
Отсюда следует, что если однажды цепочка не замкнулась, то она не замкнется при любом выборе третьей окружности. Художнику, рисовавшему
изображенную цепочку, пришлось бы немало потрудиться, чтобы она получилась, или обратиться к математику для расчета расположения двух первых окружностей, при котором цепочка замыкается.
Вначале мы упомянули о колесе, но еще до колеса люди использовали круглые бревна
— катки для перевозки тяжестей.
А можно ли использовать катки не круглой, а какой-нибудь другой формы? Немецкий
инженер Франц Рело обнаружил, что таким же свойством обладают катки, форма которых изображена на рис. 3. Эта фигура получается, если провести дуги окружностей с центрами в вершинах равностороннего треугольника, соединяющие две другие вершины. Если провести к этой фигуре две параллельные касательные, то расстояние между
ними будет равно длине стороны исходного равностороннего треугольника, так что такие катки ничем не хуже круглых. В дальнейшем были придуманы и другие фигуры, способные выполнять роль катков.
Энц. «Я познаю мир. Математика», 2006
У каждого треугольника имеется, и притом единственная, окружность девяти точек . Это
окружность, проходящая через следующие три тройки точек, положение которых определено для треугольника: основания его высот D1 D2 и D3, основания его медиан D4, D5 и D6
середины D7, D8 и D9 отрезков прямых от точки пересечения его высот Н до его вершин.
Эта окружность, найденная в XVIII в. великим ученым Л. Эйлером (поэтому ее часто также называют окружностью Эйлера), была заново открыта в следующем столетии учителем провинциальной гимназии в Германии. Звали этого учителя Карл Фейербах (он был родным братом известного философа Людвига Фейербаха).
Дополнительно К. Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это -точки ее касания с четырьмя окружностями специального вида. Одна из этих окружностей вписанная, остальные три — вневписанные. Они вписаны в углы треугольника и касаются внешним образом его сторон.
Окружность эту очень легко построить, если знать два ее свойства. Во-первых, центр окружности девяти точек лежит в середине отрезка, соединяющего центр описанной около треугольника окружности с точкой Н- его ортоцентром (точка пересечения его высот). Во-вторых, ее радиус для данного треугольника равен половине радиуса описанной около него окружности.
Энц. справочник юного математика, 1989
Окружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Данная точка (O) называется центром окружности .
Радиус окружности — это отрезок, соединяющий центр с какой-либо точкой окружности. Все радиусы имеют одну и ту же длину (по определению).
Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром . Центр окружности является серединой любого диаметра.
Хорда, проходящая через центр окружности, называется диаметром . Центр окружности является серединой любого диаметра.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности . Дуга называется полуокружностью , если отрезок, соединяющий её концы, является диаметром.
Длина единичной полуокружности обозначается через π .
Сумма градусных мер двух дуг окружности с общими концами равна 360º .
Часть плоскости, ограниченная окружностью, называется кругом .
Круговой сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Дуга, которая ограничивает сектор, называется дугой сектора .
Две окружности, имеющие общий центр, называются концентрическими .
Две окружности, пересекающиеся под прямым углом, называются ортогональными .
Взаимное расположение прямой и окружности
- Если расстояние от центра окружности до прямой меньше радиуса окружности (d), то прямая и окружность имеют две общие точки.
 В этом случае прямая называется секущей по отношению к окружности.
В этом случае прямая называется секущей по отношению к окружности. - Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку. Такая прямая называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности .
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .
Центральные и вписанные углы
Центральный угол — это угол с вершиной в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Вписанный угол измеряется половиной дуги, на которую он опирается.
- Следствие 1.
Вписанные углы, опирающиеся на одну и ту же дугу, равны. - Следствие 2.
Вписанный угол, опирающийся на полуокружность — прямой.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Основные формулы
- Длина окружности:
- Длина дуги окружности:
- Длина дуги окружности:
где α — градусная мера длины дуги окружности)
- Площадь круга:
- Площадь кругового сектора:
Уравнение окружности
- В прямоугольной системе координат уравнение окружности радиуса r с центром в точке C (x о;y о) имеет вид:
- Уравнение окружности радиуса r с центром в начале координат имеет вид:
Формы
круга, окружности мы встречаем повсюду: это и колесо машины, и линия горизонта,
и диск Луны. Математики стали заниматься геометрической фигурой — кругом на
плоскости — очень давно.
Математики стали заниматься геометрической фигурой — кругом на
плоскости — очень давно.
Кругом с центром и радиусом называется множество точек плоскости, удаленных от на расстояние, не большее . Круг ограничен окружностью, состоящей из точек, удаленных от центра в точности на расстояние . Отрезки, соединяющие центр с точками окружности, имеют длину и также называются радиусами (круга, окружности). Части круга, на которые он делится двумя радиусами, называются круговыми секторами (рис. 1). Хорда — отрезок, соединяющий две точки окружности, — делит круг на два сегмента, а окружность – на две дуги (рис. 2). Перпендикуляр, проведенный из центра к хорде, делит ее и стягиваемые ею дуги пополам. Хорда тем длиннее, чем ближе она расположена к центру; самые длинные хорды — хорды, проходящие через центр, — называются диаметрами (круга, окружности).
Если
прямая удалена от центра круга на расстояние , то при она не пересекается с кругом, при пересекается с
кругом по хорде и называется секущей, при имеет с кругом и окружностью
единственную общую точку и называется касательной. Касательная характеризуется
тем, что она перпендикулярна радиусу, проведенному в точку касания. К кругу из
точки, лежащей вне его, можно провести две касательные, причем их отрезки от
данной точки до точек касания равны.
Касательная характеризуется
тем, что она перпендикулярна радиусу, проведенному в точку касания. К кругу из
точки, лежащей вне его, можно провести две касательные, причем их отрезки от
данной точки до точек касания равны.
Дуги окружности, как и углы, можно измерять в градусах и его долях. За градус принимают часть всей окружности. Центральный угол (рис. 3) измеряется тем же числом градусов, что и дуга , на которую он опирается; вписанный угол измеряется половиной дуги . Если вершина угла лежит внутри круга, то этот угол в градусной мере равен полусумме дуг и (рис. 4,а). Угол с вершиной вне круга (рис. 4,б), высекающий на окружности дуги и , измеряется полуразностью дуг и . Наконец, угол между касательной и хордой равен половине заключенной между ними дуги окружности (рис. 4,в).
Круг и окружность имеют бесконечное множество осей симметрии.
Из
теорем об измерении углов и подобия треугольников следуют две теоремы о
пропорциональных отрезках в круге. Теорема о хордах говорит, что если точка лежит внутри
круга, то произведение длин отрезков проходящих через нее хорд постоянно. На рис. 5,a .
Теорема о секущей и касательной (имеются в виду длины отрезков частей этих
прямых) утверждает, что если точка лежит вне круга, то произведение
секущей на
ее внешнюю часть тоже
неизменно и равно квадрату касательной (рис. 5,б).
На рис. 5,a .
Теорема о секущей и касательной (имеются в виду длины отрезков частей этих
прямых) утверждает, что если точка лежит вне круга, то произведение
секущей на
ее внешнюю часть тоже
неизменно и равно квадрату касательной (рис. 5,б).
Еще в древности пытались решить задачи, связанные с кругом, — измерить длину окружности или ее дуги, площадь круга или сектора, сегмента. Первая из них имеет чисто «практическое» решение: можно уложить вдоль окружности нить, а потом развернуть ее и приложить к линейке или же отметить на окружности точку и «прокатить» ее вдоль линейки (можно, наоборот, «обкатить» линейкой окружность). Так или иначе измерения показывали, что отношение длины окружности к ее диаметру одно и то же для всех окружностей. Это отношение принято обозначать греческой буквой («пи» — начальная буква греческого слова perimetron, которое и означает «окружность»).
Однако
древнегреческих математиков такой эмпирический, опытный подход к определению
длины окружности не удовлетворял: окружность — это линия, т. е., по Евклиду,
«длина без ширины», а таких нитей не бывает. Если же мы катим окружность по
линейке, то возникает вопрос: почему при этом мы получим длину окружности, а не
какую-нибудь другую величину? К тому же такой подход не позволял определить
площадь круга.
е., по Евклиду,
«длина без ширины», а таких нитей не бывает. Если же мы катим окружность по
линейке, то возникает вопрос: почему при этом мы получим длину окружности, а не
какую-нибудь другую величину? К тому же такой подход не позволял определить
площадь круга.
Выход
был найден такой: если рассмотреть вписанные в круг правильные -угольники , то при , стремящемся к
бесконечности, в
пределе стремятся к . Поэтому естественно ввести
следующие, уже строгие, определения: длина окружности — это предел
последовательности периметров правильных вписанных в окружность -угольников, а
площадь круга —
предел последовательности их площадей. Такой подход принят и в
современной математике, причем по отношению не только к окружности и кругу, но
и к другим кривым или ограниченным криволинейными контурами областям: вместо
правильных многоугольников рассматривают последовательности ломаных с вершинами
на кривых или контурах областей, а предел берется при стремлении длины
наибольшего звена ломаной к нулю.
Аналогичным образом определяется длина дуги окружности: дуга делится на равных частей, точки деления соединяются ломаной и длина дуги полагается равной пределу периметров таких ломаных при , стремящемся к бесконечности. (Подобно древним грекам, мы не уточняем само понятие предела — оно относится уже не к геометрии и было вполне строго введено лишь в XIX в.)
Из самого определения числа следует формула для длины окружности:
Для длины дуги можно записать аналогичную формулу: поскольку для двух дуг и с общим центральным углом из соображений подобия вытекает пропорция , а из нее — пропорция , после перехода к пределу мы получаем независимость (от радиуса дуги) отношения . Это отношение определяется только центральным углом и называется радианной мерой этого угла и всех отвечающих ему дуг с центром в . Тем самым получается формула для длины дуги:
где — радианная мера дуги.
Записанные формулы для и — это всего лишь переписанные определения или обозначения, но с их помощью получаются уже далекие от просто обозначений формулы для площадей круга и сектора:
Для вывода первой формулы достаточно перейти к пределу в формуле для площади вписанного в круг правильного -угольника:
По определению левая часть стремится к площади круга , а правая — к числу
и , основания его
медиан и
,
середины и
отрезков
прямых от точки пересечения его высот до его вершин.
Эта окружность, найденная в XVIII в. великим ученым Л. Эйлером (поэтому ее часто также называют окружностью Эйлера), была заново открыта в следующем столетии учителем провинциальной гимназии в Германии. Звали этого учителя Карл Фейербах (он был родным братом известного философа Людвига Фейербаха). Дополнительно К. Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это — точки ее касания с четырьмя окружностями специального вида (рис. 2). Одна из этих окружностей вписанная, остальные три — вневписанные. Они вписаны в углы треугольника и касаются внешним образом его сторон. Точки касания этих окружностей с окружностью девяти точек и называются точками Фейербаха. Таким образом, окружность девяти точек является в действительности окружностью тринадцати точек.
Окружность
эту очень легко построить, если знать два ее свойства. Во-первых, центр
окружности девяти точек лежит в середине отрезка, соединяющего центр описанной
около треугольника окружности с точкой — его ортоцентром (точка пересечения
его высот). Во-вторых, ее радиус для данного треугольника равен половине
радиуса описанной около него окружности.
Во-вторых, ее радиус для данного треугольника равен половине
радиуса описанной около него окружности.
Тест «окружность и ее элементы»
Тест «Окружность и ее элементы»
Вычеркнуть ненужные слова текста в скобках:
а) Окружность – это (абстрактная, геометрическая, плоская) фигура, состоящая из (множества, всех) точек, расположенных на (одинаковом, заданном) расстоянии от (некоторой, центральной) точки.
б) Радиусом окружности называется (линия, прямая, отрезок), соединяющая центр окружности с (заданной, какой-либо) точкой окружности.
Выбрать правильный ответ
Диаметр окружности – это …
а) два радиуса, лежащие на одной прямой;
б) хорда, проходящая через центр окружности;
в) прямая, проходящая через две точки и центр окружности.
Центр окружности – это …
а) точка, куда ставится ножка циркуля при начертании окружности;
б) середина окружности;
в) точка, равноудаленная от всех точек
окружности.
Дуга окружности – это …
а) часть окружности, выделенная точками;
б) часть окружности, ограниченная двумя точками;
в) часть окружности, ограниченная хордой.
Определить, на сколько дуг делят окружность две точки, лежащие на окружности.
а) на одну; б) на две.
Как изображается хорда на чертеже окружности?
а) прямой линией; б) дугой окружности; в) отрезком с концами, лежащими на окружности.
Как называется отрезок, соединяющий центр окружности с любой точкой окружности?
а) длина окружности; б) радиус окружности; в) половина диаметра окружности.
Выбрать на рисунке хорду:
а) ОА; б) ВО; в) СD.
Выбрать на рисунке диаметр
а) MK; б) KN; в) OD.
Тест «Окружность и ее элементы»
Вычеркнуть ненужные слова текста в скобках:
а) Окружность – это (абстрактная, геометрическая, плоская) фигура, состоящая из (множества, всех) точек, расположенных на (одинаковом, заданном) расстоянии от (некоторой, центральной) точки.
б) Радиусом окружности называется (линия, прямая, отрезок), соединяющая центр окружности с (заданной, какой-либо) точкой окружности.
Выбрать правильный ответ
Диаметр окружности – это …
а) два радиуса, лежащие на одной прямой;
б) хорда, проходящая через центр окружности;
в) прямая, проходящая через две точки и центр окружности.
Центр окружности – это …
а) точка, куда ставится ножка циркуля при начертании окружности;
б) середина окружности;
в) точка, равноудаленная от всех точек
окружности.
Дуга окружности – это …
а) часть окружности, выделенная точками;
б) часть окружности, ограниченная двумя точками;
в) часть окружности, ограниченная хордой.
Определить, на сколько дуг делят окружность две точки, лежащие на окружности.
а) на одну; б) на две.
Как изображается хорда на чертеже окружности?
а) прямой линией; б) дугой окружности; в) отрезком с концами, лежащими на окружности.
Как называется отрезок, соединяющий центр окружности с любой точкой окружности?
а) длина окружности; б) радиус окружности; в) половина диаметра окружности.
Выбрать на рисунке хорду:
а) ОА; б) ВО; в) СD.
Выбрать на рисунке диаметр
а) MK; б) KN; в) OD.
Тест «Треугольники» — 4ЕГЭ
Обобщающий тест по геометрии для 7 класса.treugolnik.docx
А1. Треугольник — это геометрическая фигура, состоящая:
1) Из трех точек, не лежащих на одной прямой, и трех отрезков, их соединяющих
2) Из трех точек и трех отрезков, их соединяющих
3) Из трех отрезков
4) Из трех точек и трех отрезков
А2. В равных треугольниках:
1) Против равных углов лежат другие равные углы
2) Одноименные стороны и одноименные углы равны
3) Все углы и стороны равны
4) Против соответственно равных углов лежат равные стороны
А3. Высота треугольника — это:
1) Отрезок, перпендикулярный стороне треугольника
2) Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону
3) Отрезок, пересекающий сторону треугольника под прямым углом
4) Отрезок, соединяющий вершину треугольника с противолежащей стороной под прямым углом
А4. Треугольник называется равносторонним, если:
1) Две стороны равны
2) Его углы при основании равны
3) Его стороны равны
4) Два его угла равны
А5. В равнобедренном треугольнике:
В равнобедренном треугольнике:
1) Углы при основании равны
2) Любая из его медиан является высотой и биссектрисой
3) Биссектриса является медианой и высотой
4) Угол при основании может быть как острым, так и прямым или тупым
А6. Второй признак равенства треугольника гласит:
1) Если сторона и два прилежащих к ней угла одного треугольника равны стороне и двум углам другого треугольника, то такие треугольники равны
2) Если сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны
3) Если сторона и прилежащий к ней угол одного треугольника соответственно равны стороне и прилежащему к ней углу второго треугольника, то такие треугольники равны
4) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам второго треугольника, то такие треугольники равны.
А7. Два треугольника равны, если:
1) У них соответственные углы равны
2) Две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника
3) Два угла одного треугольника равны двум углам другого треугольника
4) Две стороны одного треугольника равны двум сторонам другого треугольника
А8. Диаметр окружности – это:
Диаметр окружности – это:
1) Отрезок, равный двум радиусам
2) Отрезок, соединяющий две точки окружности
3) Хорда, проходящая через центр окружности
4) Отрезок, проходящий через центр окружности
А9. Хорда окружности — это:
1) Отрезок, который меньше диаметра, но больше радиуса
2) Отрезок, который не проходит через центр окружности
3) Отрезок, соединяющий две точки окружности
4) Часть окружности, ограниченная двумя точками окружности
А10. Медианы треугольника:
1) попарно пересекаются
2) пересекаются в одной точке
3) Соединяют середины сторон треугольника
4) Являются высотами и биссектрисами
Ответы
1) 1
2) 4
3) 2
4) 3
5) 1
6) 4
7) 2
8) 3
9) 3
10) 2
Касательная к окружности — презентация онлайн
2. Разберем ошибки теста с прошлого урока
1.Выпиши нужное слово текста в скобках:
А) Окружность – это (абстрактная, геометрическая, плоская) фигура,
состоящая из (множества, всех) точек, расположенных на (одинаковом,
заданном) расстоянии от (некоторой, центральной) точки.

Б) Радиусом окружности называется (линия, прямая, отрезок), соединяющий
центр окружности с (заданной, какой-либо) точкой окружности.
2.Диаметр окружности – это…(закончить определение):
А) Два радиуса, лежащие на одной прямой;
Б) Хорда, проходящая через центр окружности;
В) Прямая, проходящая через две точки и центр окружности.
3.Центр окружности – это…(закончить определение):
А) Точка, куда ставится ножка циркуля при начертании окружности;
Б) Середина окружности;
В) Точка, равноудаленная от всех точек окружности.
4.Дуга окружности – это…(закончить определение):
А) Часть окружности, выделенная точками;
Б) Часть окружности, ограниченная двумя точками;
В) Часть окружности, ограниченная хордой.
5.Определить, на сколько дуг делят окружность две точки,
лежащие на окружности. Выбрать правильный ответ:
А) На одну;
Б) На две.
6.Как изображается хорда на чертеже окружности? Выбрать
правильный ответ:
А) Прямой линей;
Б) Дугой окружности;
В) Отрезком с концами, лежащими на окружности.

7.Как называется отрезок, соединяющий центр окружности с
любой точкой окружности? Выбрать правильный ответ:
А) Длина окружности;
Б) Радиус окружности;
В) Половина диаметра окружности.
4. ответы
вопросответ
1
А) геометрическая
множества
заданном
некоторой
б) отрезок
какой-либо
2
б
3
в
4
б
5
б
6
в
7
б
5. 09.04 Касательная к окружности
6. Заполнить таблицу в конце тетради
понятиеопределение
признак
свойства
Касательная к
окружности
Прямая,
имеющая с
окружность
только одну
общую
точку,
называется
касательной.
1.Если пряма. Проходящая
через точку окружности,
перпендикулярна радиусу,
проведённому в зту точку, то
эта прямая является
касательной к данной
окружности.
2. Если расстояние от центра
до некоторой прямой равно
радиусу окружности, то эта
прямая является касательной
к данной окружности.

1.Касательная к
окружности
перпендикулярна
радиусу проведённому
в точку касания.
2. Если через данную
точку к окружности
проведены две
касательные, то
отрезки касательных,
соединяющие данную
точку с точками
касания, равны
.
АВ=АС
7. Выучить: определение, признаки и свойства касательной к окружности.
• Учебник стр. 132-133 или тетрадь.дуга окружности
- дуга окружности
- apskritimo lankas statusas T sritis fizika atitikmenys: angl. circular arc vok. Kreisbogen, m rus. дуга окружности, f pranc. arc de cercle, m
Fizikos terminų žodynas : lietuvių, anglų, prancūzų, vokiečių ir rusų kalbomis. – Vilnius : Mokslo ir enciklopedijų leidybos institutas. Vilius Palenskis, Vytautas Valiukėnas, Valerijonas Žalkauskas, Pranas Juozas Žilinskas.
2007.
Vilius Palenskis, Vytautas Valiukėnas, Valerijonas Žalkauskas, Pranas Juozas Žilinskas.
2007.
- circular arc
- Kreisdiagramm
Look at other dictionaries:
Дуга окружности — Дуга одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки A и B окружности разбивают ее на две части; каждая из этих частей называется дугой. Если A и B – концы диаметра (т … Википедия
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками. Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
ДУГА — жен. согнутая линия, черта или вещь, образующая кривизну, погиб; часть окружности круга или другой кривой черты, и пр.
 элипса, параболы. | ·стар. и сев. радуга. | В оглобельной упряжи, деревянная, согнутая крутым лучком тугая распорка между… … Толковый словарь Даля
элипса, параболы. | ·стар. и сев. радуга. | В оглобельной упряжи, деревянная, согнутая крутым лучком тугая распорка между… … Толковый словарь ДаляДУГА НАБЛЮДЕНИЯ — наименьшее расстояние от Солнца, на котором планета видима, когда Солнце находится под горизонтом. Дневная дуга дуга, которую Солнце проходит от Восхода до Заката. В Равноденствие она составляет 180 градусов или 12 часов правого восхождения. С… … Астрологическая энциклопедия
дуга — и; мн. дуги; ж. 1. Часть окружности или какой л. другой кривой линии в виде полукруга. Ракета описала в небе дугу. Соединить дугой. // О том, что имеет форму кривой, изогнутой линии. Д. лука. Тёмные дуги бровей. Радуга дуга. На повороте река… … Энциклопедический словарь
ДУГА — ДУГА, дуги, мн. дуги, дугам, жен. 1. Принадлежность упряжи из круто изогнутого ствола тонкого дерева, концы которого вдеваются в гужи для скрепления оглобель с хомутом. «Дуги гнут с терпеньем и не вдруг.
 » Крылов. 2. Часть окружности круга или… … Толковый словарь Ушакова
» Крылов. 2. Часть окружности круга или… … Толковый словарь УшаковаДуга — I ж. 1. Изогнутая часть какого либо предмета. 2. Часть окружности или какой либо изогнутой линии. отт. устар. Название линии меридиана или параллели. 3. Часть конской упряжи из тонкого, круто изогнутого ствола дерева, служащая для прикрепления… … Современный толковый словарь русского языка Ефремовой
ДУГА БОЛЬШОГО КРУГА — часть окружности, получаемой при сечении шара плоскостью, проходящей через его центр. Под термином прямое направление жел. дор. линии понимают направление по Д. б. к. между конечными или промежуточными опорными точками жел. дор. линии. Для целей… … Технический железнодорожный словарь
Дуга (геометрия) — Дуга связное подмножество окружности.Свойства*Длина дуги L радиуса R с центральным углом alpha, измеренным в радианах, вычисляется по формуле: L=Ralpha … Википедия
дуга — ДУГА, и, мн дуги, ж Линия в виде полукруга, часть кривой, изогнутой линии или окружности, заключенная между двумя ее точками.
 Ракета описала в небе дугу … Толковый словарь русских существительных
Ракета описала в небе дугу … Толковый словарь русских существительных
Окружность. Математика. 5 класс.
Дисперсией ряда чисел называется среднее арифметическое Какая геометрическая фигура всегда привлекала внимание художников и архитекторов?
Дисперсией ряда чисел называется среднее арифметическое Внимание художников и архитекторов всегда привлекала окружность.
При использовании какой геометрической фигуры можно получать красивые узоры?
Красивые узоры можно получать при использовании окружности.
О К Р У Ж Н О С Т Ь
Окружность и круг
Окружность и круг Дисперсией ряда чисел называется среднее арифметическое Среди кривых линий важную роль играет окружность. В отличие от прямой окружность является замкнутой линией.
Окружность и круг
Дисперсией ряда чисел называется среднее арифметическое
Окружность разбивает плоскость на две области: внутреннюю и внешнюю. Фигура, ограниченная окружностью, − круг.
Фигура, ограниченная окружностью, − круг.
Окружность и круг Дисперсией ряда чисел называется среднее арифметическое Окружность удивительно гармоничная фигура, древние греки считали ее самой совершенной.
Окружность и круг Дисперсией ряда чисел называется среднее арифметическое Она обладает замечательным свойством: все точки окружности находятся на одинаковом расстоянии от одной точки − её центра.
Окружность и круг Дисперсией ряда чисел называется среднее арифметическое Это свойство окружности объясняет некоторые хорошо известные факты:
Окружность и круг Дисперсией ряда чисел называется среднее арифметическое Это свойство окружности объясняет некоторые хорошо известные факты: почему для вычерчивания окружности используют циркуль;
Окружность и круг Дисперсией ряда чисел называется среднее арифметическое Это свойство окружности объясняет некоторые хорошо известные факты: почему для вычерчивания окружности используют циркуль; почему колеса делают круглыми;
Окружность и круг
Дисперсией ряда чисел называется среднее арифметическое
Это свойство окружности объясняет некоторые
хорошо известные факты:
почему для вычерчивания
окружности используют циркуль;
почему колеса делают круглыми;
почему окружность может «скользить сама по себе».
Использование колеса Дисперсией ряда чисел называется среднее арифметическое Колесо используется не только в средствах передвижения: автомобилях, телегах, поездах, велосипедах, коньках …
Использование колеса Дисперсией ряда чисел называется среднее арифметическое Работает колесо и в различных станках: гончарном круге, точильном круге ….
Использование колеса Дисперсией ряда чисел называется среднее арифметическое Колесо используют для развлечений: в парке аттракционов можно покататься на «чёртовом колесе» и на карусели.
радиус и диаметр окружности
Радиус и диаметр окружности Дисперсией ряда чисел называется среднее арифметическое Как называются отрезки, соединяющие центр окружности с любой её точкой?
Радиус и диаметр окружности Дисперсией ряда чисел называется среднее арифметическое Как называются отрезки, соединяющие центр окружности с любой её точкой? ОА, ОВ, ОС, ОD − радиусы
Радиус и диаметр окружности
Дисперсией ряда чисел называется среднее арифметическое
Как называются отрезки, соединяющие
центр окружности с любой её точкой?
ОА, ОВ, ОС, ОD − радиусы
Радиус (лат. ) − «спица в колесе»
) − «спица в колесе»
Радиус и диаметр окружности Дисперсией ряда чисел называется среднее арифметическое Как называются отрезки, соединяющие центр окружности с любой её точкой? ОА, ОВ, ОС, ОD − радиусы Радиус (лат.) − «спица в колесе» ОА = ОВ = ОС = ОD
Радиус и диаметр окружности Дисперсией ряда чисел называется среднее арифметическое Как называется отрезок, соединяющий две точки окружности и проходящий через центр?
Радиус и диаметр окружности Дисперсией ряда чисел называется среднее арифметическое Как называется отрезок, соединяющий две точки окружности и проходящий через центр? АВ− диаметр
Радиус и диаметр окружности Дисперсией ряда чисел называется среднее арифметическое Как называется отрезок, соединяющий две точки окружности и проходящий через центр? АВ− диаметр Диаметр (лат.) − «поперечник»
Радиус и диаметр окружности
Дисперсией ряда чисел называется среднее арифметическое
Как называется отрезок, соединяющий две
точки окружности и проходящий через центр?
АВ− диаметр
Диаметр (лат. ) − «поперечник»
Диаметр состоит из двух радиусов
) − «поперечник»
Диаметр состоит из двух радиусов
Радиус и диаметр окружности Дисперсией ряда чисел называется среднее арифметическое Как называется часть окружности, ограниченная двумя точками?
Радиус и диаметр окружности Дисперсией ряда чисел называется среднее арифметическое Как называется часть окружности, ограниченная двумя точками?
Радиус и диаметр окружности Дисперсией ряда чисел называется среднее арифметическое Как называется часть окружности, ограниченная двумя точками? АВ − дуга
Вопросы
Как называется фигура на рисунке?
Как называется фигура на рисунке? Ответ: окружность.
Как называется фигура на рисунке?
Как называется фигура на рисунке? Ответ: круг.
Как называется отрезок ОС ?
Как называется отрезок ОС ? Ответ: ОС − радиус.
Как называется отрезок ВС ?
Как называется отрезок ВС ?
Ответ: ВС − диаметр.
Какова длина радиуса окружности?
Какова длина радиуса окружности?
Ответ: 1 см 5 мм.
Какова длина диаметра окружности?
Какова длина диаметра окружности?
Ответ: 3 см.
Окружность. Круг — Геометрические фигуры
В этом уроке Вы познакомитесь с такими понятиями, как окружность и круг, узнаете, что такое дуга, радиус, диаметр и хорда окружности.
Итак, начнем с определения, что же такое окружность?
Окружность – это геометрическая фигура на плоскости, все точки которой равноудалены от данной точки — центра окружности. Обычно центр окружности принято обозначать точкой О.
Как можно построить окружность? С помощью циркуля!
Ножку с иголкой устанавливают в точку О – центр окружности, а ножка с грифелем опишет замкнутую линию, которую и называют окружностью.
Любая окружность разделяет плоскость на 2 части. Ту часть плоскости, которая лежит внутри окружности вместе с самой окружностью, называют кругом. Точка О является как центром окружности, так и центром круга.
Таким образом, нетрудно заметить, что геометрическая фигура круг имеет площадь, а окружность нет, она имеет только длину, так как является замкнутой линией.
Как Вы догадались, точки могут лежать на окружности, т.е. мы будем говорить, принадлежать окружности, а могут и не лежать на ней, т.е. не принадлежать окружности. Например, точки А и В принадлежат окружности с центром в точке О; точки О, Е и D не принадлежат окружности с центром в точке О; точки О, Е, А, В принадлежат кругу с центром в точке О, а точка D не принадлежит этому кругу. Точки А и В делят окружность на две части, каждую из которых называют дугой окружности; ну а сами точки А и В – концами дуг. Значит, дуга – это часть окружности, ограниченная двумя точками.
Давайте выполним следующее задание: назовите дуги, на которые делят окружность точки А, В и С.
Решение: давайте сначала назовем дуги с концами в точках А и В: это дуга АВ, а вторая дуга АСВ, мы ее назвали по трем точкам, чтобы различать их, теперь назовем дуги с концами в точках В и С: дуга ВС, дуга ВАС, ну и остались дуги с концами в точках А и С: дуга АС, дуга АВС.
На рисунке вы видите, что отрезки ОА и ОВ соединяют центр окружности с точками, лежащими на окружности. Их называют радиусами. Таким образом, радиус – это отрезок, соединяющий центр окружности с одной из её точек. Радиусы принято обозначать латинской буквой R или r. В каждой окружности все радиусы равны между собой!
А как вы думаете, сколько радиусов можно провести в одной окружности? Бесконечное множество!
А теперь давайте выполним следующие построения: начертим окружность с центром в точке О и радиусом 3 см.
Это значит надо при помощи линейки раствор циркуля сделать равным трем сантиметрам, ножку с иголкой поместить в точку О, а ножкой с грифелем описать окружность.
Затем, отметим на данной окружности две точки – А и В. Соединим их отрезком, получили хорду АВ. То есть, отрезок, соединяющий две точки окружности, называют хордой. Кстати, самую большую хорду, ту, которая проходит через центр окружности, называют диаметром. Диаметр принято обозначать латинскими буквами d или D. Между прочим, диаметр равен удвоенному радиусу, пишут d = 2R. Диаметр делит круг на два полукруга, а окружность – на две полуокружности.
Диаметр принято обозначать латинскими буквами d или D. Между прочим, диаметр равен удвоенному радиусу, пишут d = 2R. Диаметр делит круг на два полукруга, а окружность – на две полуокружности.
Таким образом, в этом уроке Вы узнали, что такое окружность и круг, научились их строить, а также познакомились с таким понятиями как дуга, радиус, диаметр и хорда окружности.
Геометрия: Дуги
Дуги
Я знаю, что я только что бросил вам много новой терминологии, но я еще не закончил. Я соединил точки на окружности отрезками прямых линий. Также возможно соединить точки на окружности, используя извилистую часть окружности. Предположим, у вас есть две точки А и В на окружности, как показано на рис. 17.3. Точки между A и B образуют отрезок AB, а точки между A и B, лежащие на окружности, составляют дугу AB.Поскольку дуга AB кривая (она состоит из части окружности), ей дается аббревиатура ?AB.
Рисунок 17.2 AB и ?AB на окружности.
Есть только одна проблема с этой идеей. На самом деле две дуги, которые включают точки на окружности между A и B, и вам нужно уметь их различать. Вы можете сделать это, указав точку между A и B на правильной части круга. Таким образом, верхняя дуга — это ?ADB, а нижняя — ?AEB.Если A и B являются конечными точками диаметра, ?ADB и ?AEB называются полуокружностями. Дуга окружности представляет собой полуокружность, часть полуокружности (называемую малой дугой) или большую, чем полуокружность, но меньшую, чем весь круг (называемую большой дугой).
Эврика!
Разница между AB и ?AB заключается в том, что ?AB — это часть окружности, соединяющая A и B, а AB — отрезок прямой линии, соединяющий A и B.
Касательная
Если две дуги являются частью две окружности с разными радиусами, то они не могут иметь одинаковую кривизну (или быть конгруэнтными). Единственный способ, которым две дуги могут быть конгруэнтны, — это если окружности, на которых они находятся, конгруэнтны, а их длины дуг конгруэнтны.
Поскольку вы можете измерять длины отрезков, естественно задаться вопросом об измерении дуг. Дуги имеют длину и изгиб. Чтобы измерить длину дуги, представьте, что вы выпрямляете дугу и измеряете ее длину линейкой. Две дуги слева на рис. 17.3 имеют одинаковую длину, но разную кривизну. Дуги справа имеют одинаковую кривизну, но разную длину. Таким образом, при измерении длины дуги необходимо учитывать две характеристики: фактическую длину и кривизну.В окружности (или в конгруэнтных окружностях) конгруэнтных дуг дуг, которые совпадают как по длине, так и по кривизне.
Рисунок 17.3 Слева: две дуги одинаковой длины, но с разной кривой. Справа: две дуги с одинаковой кривой, но разной длины.
Кривизна дуги измеряется в градусах. Меру ?AB будем обозначать m?AB. Чтобы измерить дугу, мне нужно познакомить вас с центральным углом. Центральный угол окружности — это угол, вершина которого является центром окружности, а стороны — радиусами окружности. Причина, по которой центральные углы необходимы при измерении кривизны дуги ?AB, видна на рис. 17.4. Малая дуга AB и центральный угол ?ACB связаны друг с другом. С каждой дугой связан центральный угол, а с каждым центральным углом связана дуга. Если задан центральный угол, то его дуга пересечения определяется двумя точками пересечения угла с окружностью и всеми точками дуги внутри угла.
Причина, по которой центральные углы необходимы при измерении кривизны дуги ?AB, видна на рис. 17.4. Малая дуга AB и центральный угол ?ACB связаны друг с другом. С каждой дугой связан центральный угол, а с каждым центральным углом связана дуга. Если задан центральный угол, то его дуга пересечения определяется двумя точками пересечения угла с окружностью и всеми точками дуги внутри угла.
Рис. 17.4 Центральный угол и соответствующая ему малая дуга.
Соответствие между центральными углами и пересекаемыми дугами можно использовать для определения кривизны дуги (также известной как ее градусная мера). Чтобы закрепить эту идею, вам понадобится постулат.
- Постулат 17.1 : Постулат центрального угла. В окружности градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Этот постулат позволяет вам определить градусное измерение дуги путем определения измерения ее центрального угла. Поскольку вы уже подробно изучили углы, вы заложили основу для понимания градусного измерения дуги. Малая дуга имеет соответствующий центральный угол, мера которого меньше 180; у полукруга центральный угол прямой, поэтому его градусная мера равна 180; и большая дуга имеет градусную меру больше 180. Поскольку понятие градусного измерения дуги и измерения центрального угла объединены, допускается измерение центрального угла больше 180.А если вы добавите постулат сложения углов (постулат 4.2), вы увидите, что градусное измерение всего круга в два раза больше градусного измерения полукруга. Другими словами, градусная мера окружности равна 360. На рис. 17.5 показаны некоторые центральные углы и образующие их дуги.
Поскольку вы уже подробно изучили углы, вы заложили основу для понимания градусного измерения дуги. Малая дуга имеет соответствующий центральный угол, мера которого меньше 180; у полукруга центральный угол прямой, поэтому его градусная мера равна 180; и большая дуга имеет градусную меру больше 180. Поскольку понятие градусного измерения дуги и измерения центрального угла объединены, допускается измерение центрального угла больше 180.А если вы добавите постулат сложения углов (постулат 4.2), вы увидите, что градусное измерение всего круга в два раза больше градусного измерения полукруга. Другими словами, градусная мера окружности равна 360. На рис. 17.5 показаны некоторые центральные углы и образующие их дуги.
Рисунок 17.5 Центральные углы и образующие их дуги.
Последний термин, который мне нужно определить для вас, — это сектор круга. Представьте, что вы заказали кусок пиццы.Два прямых края пиццы можно рассматривать как радиусы круга (при условии, что она была разрезана правильно), а часть пиццы с корочкой — это дуга круга. Весь кусок пиццы является сектором круга. Сектор окружности — это область, ограниченная двумя радиусами окружности и дугой, на которой она пересекается.
Весь кусок пиццы является сектором круга. Сектор окружности — это область, ограниченная двумя радиусами окружности и дугой, на которой она пересекается.
Твердые факты
Дуга — это часть окружности, определяемая двумя точками и всеми точками между ними.
Конгруэнтные дуги — это дуги на окружностях с конгруэнтными радиусами, имеющими одинаковую градусную меру.
Малая дуга — это дуга, градусная мера которой находится в диапазоне от 0 до 180.
Полуокружность — это дуга, градусная мера которой точно равна 180 и 360.
Сектор окружности — это область, ограниченная двумя радиусами окружности и дугой, на которой она пересекается.
Вы уже видели постулат сложения сегментов и постулат сложения углов.Существует также Постулат Сложения Дуги, который говорит именно то, что вы ожидаете от него сказать.
- Постулат 17.2 : Постулат сложения дуги.
 Если B лежит между A и C на окружности, то m?AB + m?BC = m?AC.
Если B лежит между A и C на окружности, то m?AB + m?BC = m?AC.
Вы будете использовать этот постулат, когда будете комбинировать дуги окружностей.
Выдержки из The Complete Idiot’s Guide to Geometry 2004 Denise Szecsei, Ph.D. Все права защищены, включая право на полное или частичное воспроизведение в любой форме.Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
| A | B | |
|---|---|---|
| множество всех точек вне круга пересекает окружность ровно в одной точке | касательная окружности | |
| отрезок, концы которого лежат на окружности | хорда | |
| точка пересечения окружности или сферы с касательной прямой или плоскостью | 3 точка 90 Tangency | |
| линия, которая пересекает круг в двух точках | секунда | |
| линия, которая касается двух кружков | Common Tangent | |
| Набор всех точек внутри круга | окружность | |
| отрезок секущей, лежащий снаружи окружности с одним концом на окружности | внешний секущий отрезок | |
| угол, вершина которого лежит на окружности, а стороны содержат хорды окружности | вписанный угол | |
| где концы отрезка или дуги лежат на сторонах угла | стягиваемый | |
| угол, вершина которого находится в центре окружности | центральный угол | |
| дуга окружности, вершины которой лежат на центральном углу или вне его | большая дуга | |
| дуга | ||
| дуга окружности, точки которой лежат на или внутри центрального угла | малая дуга | |
| расстояние вдоль дуги, измеренное в линейных единицах | длина дуги | |
| две дуги одной и той же окружности, пересекающиеся ровно в одной точке 9 0113 | смежные дуги | |
| две дуги, лежащие в одной или конгруэнтной окружности и имеющие одинаковую меру | конгруэнтные дуги | |
| область внутри окружности, ограниченная хордой и дугой | ||
| Два кругов, которые имеют конгруэнтные радиусы | Connoguent Circles | |
| Два круга COPLANAR, которые пересекаются на ровно одна точка | касательные круги | |
| COPLANAR CORCES с одним и тем же центром | концентрические круги | |
| круга, концы которого лежат на диаметре | полуокружность | |
| область внутри круга, ограниченная двумя радиусами круга и дугой, пересекаемой с ними | сектором круга |
Часть окружности между двумя конечными точками называется дугой . Мерой дуги является угол, образованный линиями, проведенными из центра окружности к конечным точкам дуги.
Мерой дуги является угол, образованный линиями, проведенными из центра окружности к конечным точкам дуги.
Если размер дуги меньше 180°, это малая дуга . Если мера дуги ровно 180°, то это полуокружность . Если мера дуги больше 180°, это большая дуга .
Хорда — это отрезок, концы которого лежат на окружности, но не на самой окружности.Вместо того, чтобы быть изогнутой, как дуга, хорда представляет собой прямую линию. Касательная — это линия, которая касается только одной точки окружности.
Если взять только часть круга, это будет считаться дугой. Итак, здесь я нарисовал дугу ab, которую я могу записать как ab с дугой над ней, поэтому дуга — это непрерывная часть окружности между двумя конечными точками. Итак, если вы выберете две точки на окружности, дуга — это все точки, которые находятся между этими двумя конечными точками, и мы измеряем эту дугу, измеряя центральный угол. Что ж, центральный угол, как это, вероятно, звучит, находится в центре круга, поэтому, если я найду центр этого круга, содержащего эту дугу, и нарисую радиусы до конечных точек, это будет центральный угол мю. Таким образом, вершина центрального угла находится в центре окружности.
Что ж, центральный угол, как это, вероятно, звучит, находится в центре круга, поэтому, если я найду центр этого круга, содержащего эту дугу, и нарисую радиусы до конечных точек, это будет центральный угол мю. Таким образом, вершина центрального угла находится в центре окружности.
Теперь предположим, что если мера х, мера этой дуги. Если x меньше 180 градусов, мы называем это малой дугой. Если x равно точно 180 градусам, половине окружности, мы называем это полукругом, и, наконец, если x больше 180 градусов, мы называем это большой дугой.Поэтому, если вы возьмете только часть круга, она будет считаться дугой, и мы сможем различать их разные типы по степени измерения.
Теперь еще две ключевые особенности окружностей — касательные и хорды. Таким образом, хорда — это отрезок, концы которого находятся на окружности, и она соединяет эти две точки и не следует окружности, иначе это была бы дуга. Вот это и есть хорда, потому что ее концы лежат на окружности, и если она проходит через центр, то считается диаметром. Теперь последний ключевой термин — это касательная и что такое касательная; скажем, вы выбрали точку на этой окружности в любом месте этой окружности и нарисовали линию, которая пересекала эту касательную ровно один раз, или если вы нарисовали линию, которая пересекала эту окружность ровно один раз, это считается касательной. Итак, касательная по определению — это прямая, отрезок или луч, который пересекает окружность ровно в одной точке. Обратите внимание, что если я сдвину это чуть-чуть вверх, у нас будет часть хорды, потому что она пройдет через окружность, и у нас будет две точки пересечения.Теперь эта точка здесь, где ваша линия, касательная, пересекает ваш круг, называется точкой касания.
Теперь последний ключевой термин — это касательная и что такое касательная; скажем, вы выбрали точку на этой окружности в любом месте этой окружности и нарисовали линию, которая пересекала эту касательную ровно один раз, или если вы нарисовали линию, которая пересекала эту окружность ровно один раз, это считается касательной. Итак, касательная по определению — это прямая, отрезок или луч, который пересекает окружность ровно в одной точке. Обратите внимание, что если я сдвину это чуть-чуть вверх, у нас будет часть хорды, потому что она пройдет через окружность, и у нас будет две точки пересечения.Теперь эта точка здесь, где ваша линия, касательная, пересекает ваш круг, называется точкой касания.
Итак, это весь ключевой словарь, который вам нужно знать о кругах.
Счет, математика и статистика — Набор академических навыков
Геометрия круга
Определение
Расстояние вокруг границы круга называется окружностью .
Расстояние по окружности через центр называется диаметром .
Расстояние от центра круга до любой точки на границе называется радиусом . Радиус равен половине диаметра; $2r=d$.
Отрезок, соединяющий две точки окружности, представляет собой хорду . Каждый диаметр является хордой, но не каждая хорда является диаметром.
Область, которую отсекает хорда, называется сегментом .
Область внутри круга, ограниченная двумя радиусами, представляет собой сектор .
Длина между двумя точками по окружности равна дуге .
Окружность
Определение
Формула для вычисления длины окружности: \[C = \pi d \qquad\text{или } \qquad C = 2\pi r\], где $d$ — диаметр, а $r$ — радиус.
Примеры работы
Пример 1
Радиус данной окружности равен $r=4$см. Вычислите окружность.
Решение
\begin{align} C &= 2\pi r\\ &= 2 \times \pi \times 4\\ &= 8 \pi \\ &\приблизительно 25. 2\]
2\]
Примеры работы
Пример 1
Радиус данной окружности равен $2.2 &= \frac{50}{\pi}\\ r &= \sqrt{\frac{50}{\pi} }\\ r &\приблизительно 4,0 \text{см (до 1 знака после запятой)} \end {выравнивание}
Рабочая тетрадь
Эта рабочая тетрадь, созданная HELM, является хорошим пособием по повторению, содержащим ключевые моменты для исправления и множество рабочих примеров.
См. также
Внешние ресурсы
Проверь себя
Проверь себя: площадь геометрических фигур
кругов
Обзор
Окружность — это простая фигура, состоящая из точек, лежащих в двумерной плоскости на равном расстоянии от некоторой общей точки ( центра окружности) в этой плоскости.Окружности часто называют в честь точки, определяемой как центр окружности, поэтому в примере, показанном ниже, мы могли бы называть окружность окружностью A. На самом деле фигура является примером простой замкнутой кривой (иногда называемой ). Кривая Жордана , в честь французского математика Камиллы Жордана). Согласно теореме о кривой Жордана , простая замкнутая кривая делит плоскость, в которой она лежит, на две области — внутреннюю область, ограниченную кривой, и внешнюю область , содержащую все внешние точки, так что непрерывный путь, соединяющий любую точку одной области с любой точкой другой области, должен пересекать кривую в некоторой точке.Хотя это может показаться интуитивно очевидным, обеспечить математическое доказательство — далеко не простая задача.
На самом деле фигура является примером простой замкнутой кривой (иногда называемой ). Кривая Жордана , в честь французского математика Камиллы Жордана). Согласно теореме о кривой Жордана , простая замкнутая кривая делит плоскость, в которой она лежит, на две области — внутреннюю область, ограниченную кривой, и внешнюю область , содержащую все внешние точки, так что непрерывный путь, соединяющий любую точку одной области с любой точкой другой области, должен пересекать кривую в некоторой точке.Хотя это может показаться интуитивно очевидным, обеспечить математическое доказательство — далеко не простая задача.
Окружность является примером простой замкнутой кривой.
Человечество знало о круге как о геометрической форме с самого начала истории, и существует бесчисленное множество примеров кругов, встречающихся в мире природы. И солнце, и полная луна появляются на небе в виде круглых фигур.Глаза многих животных, птиц, рыб и насекомых имеют круглую форму, как и различные фрукты и ягоды. Вероятно, вы можете придумать еще много примеров, встречающихся в природе. Круг также является очень важной формой во многих областях человеческой деятельности, включая науку и технику. Например, одним из самых ранних и важных изобретений в истории цивилизации было колесо. Трубы, по которым текут наша вода и газ, и кабели, передающие электроэнергию и сигналы связи, имеют круглое поперечное сечение.Даже монеты, которые мы используем, и тарелки, из которых мы едим, чаще всего имеют круглую форму.
И солнце, и полная луна появляются на небе в виде круглых фигур.Глаза многих животных, птиц, рыб и насекомых имеют круглую форму, как и различные фрукты и ягоды. Вероятно, вы можете придумать еще много примеров, встречающихся в природе. Круг также является очень важной формой во многих областях человеческой деятельности, включая науку и технику. Например, одним из самых ранних и важных изобретений в истории цивилизации было колесо. Трубы, по которым текут наша вода и газ, и кабели, передающие электроэнергию и сигналы связи, имеют круглое поперечное сечение.Даже монеты, которые мы используем, и тарелки, из которых мы едим, чаще всего имеют круглую форму.
Общие свойства кругов
Общая длина замкнутой кривой называется ее окружностью . На самом деле, хотя слово окружность можно применить к длине любой замкнутой кривой, чаще всего оно ассоциируется в сознании людей с окружностью. Его также можно использовать для обозначения периметра, образованного замкнутой кривой, т.е.е. граница, отделяющая внутреннюю область круга от внешней области. На самом деле окружность заключает в себе наибольшую возможную площадь любой замкнутой кривой, имеющей данную длину окружности. Помимо создания двух отдельных областей, круг можно рассматривать как разделение всех точек на плоскости на три отдельные группы: те, что внутри круга, те, что снаружи круга, и те, которые лежат по периметру круга.
Его также можно использовать для обозначения периметра, образованного замкнутой кривой, т.е.е. граница, отделяющая внутреннюю область круга от внешней области. На самом деле окружность заключает в себе наибольшую возможную площадь любой замкнутой кривой, имеющей данную длину окружности. Помимо создания двух отдельных областей, круг можно рассматривать как разделение всех точек на плоскости на три отдельные группы: те, что внутри круга, те, что снаружи круга, и те, которые лежат по периметру круга.
У круга есть центр, радиус, диаметр и длина окружности
Расстояние между центром круга (иногда называемым началом координат ) и любой точкой на окружности называется радиусом .Длина отрезка между любыми двумя точками на окружности, делящей центр окружности пополам, называется диаметром . Диаметр всегда ровно в два раза больше длины радиуса и представляет собой наибольшее расстояние, которое может существовать между любыми двумя точками, лежащими на окружности. Помимо обозначения расстояния, термин радиус может также использоваться для обозначения определенного отрезка линии, соединяющего центр круга с некоторой точкой на окружности.Точно так же термин диаметр может использоваться для определенного отрезка линии, который соединяет две точки на окружности и пересекает центр окружности.
Помимо обозначения расстояния, термин радиус может также использоваться для обозначения определенного отрезка линии, соединяющего центр круга с некоторой точкой на окружности.Точно так же термин диаметр может использоваться для определенного отрезка линии, который соединяет две точки на окружности и пересекает центр окружности.
Круг и Пи
Пи (обычно пишется как греческая буква π в математических выражениях) — важная математическая константа, представляющая отношение длины окружности круга к его диаметру .Значение Пи очень приблизительно равно трем целых четыре десятых (3,14). Пи — это иррациональное число , а это значит, что его нельзя точно выразить как дробь, имеющую целые значения как в знаменателе, так и в числителе. В результате десятичное представление числа Пи равно без завершения (порядок чисел после запятой не повторяется, а количество знаков после запятой неопределенно). На самом деле поиск еще более точного значения числа Пи продолжается (значение числа Пи, включающее около десяти триллионов цифр, по-видимому, было рассчитано совсем недавно, в 2011 году).Для наших целей вполне приемлемо гораздо менее точное приближение. На самом деле, даже космологам нравится число Пи, состоящее всего из тридцати девяти цифр, что позволило бы им рассчитать диаметр Вселенной с точностью до одного атома!
На самом деле поиск еще более точного значения числа Пи продолжается (значение числа Пи, включающее около десяти триллионов цифр, по-видимому, было рассчитано совсем недавно, в 2011 году).Для наших целей вполне приемлемо гораздо менее точное приближение. На самом деле, даже космологам нравится число Пи, состоящее всего из тридцати девяти цифр, что позволило бы им рассчитать диаметр Вселенной с точностью до одного атома!
Для окружности окружности C и диаметра d число Пи можно выразить следующим образом:
Для удобства, поскольку нам чаще дают радиус окружности r , чем диаметр, формулу длины окружности обычно записывают так:
C = 2π r
Также можно показать, что площадь круга пропорциональна квадрату его радиуса.В третьем веке до нашей эры греческий математик Архимед доказал, что площадь, ограниченная кругом, равна площади треугольника с длиной основания, равной длине окружности, и высотой, равной радиусу круга. Мы уже установили, что длина окружности равна числу Пи, умноженному на диаметр окружности. Поскольку площадь треугольника равна половине произведения длины его основания на высоту, площадь круга должна быть равна Пи, умноженному на квадрат радиуса круга.Таким образом, отношение площади круга к площади квадрата его радиуса идентично отношению длины окружности к его диаметру, другими словами, Пи. Как показано на рисунке ниже, площадь круга, таким образом, равна площади заштрихованной области ( r 2 ), умноженной на число Пи.
Мы уже установили, что длина окружности равна числу Пи, умноженному на диаметр окружности. Поскольку площадь треугольника равна половине произведения длины его основания на высоту, площадь круга должна быть равна Пи, умноженному на квадрат радиуса круга.Таким образом, отношение площади круга к площади квадрата его радиуса идентично отношению длины окружности к его диаметру, другими словами, Пи. Как показано на рисунке ниже, площадь круга, таким образом, равна площади заштрихованной области ( r 2 ), умноженной на число Пи.
Площадь круга равна квадрату его радиуса, умноженному на число Пи.
Чтобы выразить это в виде формулы, площадь круга определяется как:
Площадь = π r 2
Дуги и сектора
дуга окружности является некоторой частью ее окружности. Сектор — это область внутри круга, окруженная двумя радиусами и дугой, соединяющей точки, в которых радиусы пересекаются с окружностью (по форме напоминает кусок пиццы). Угол, образованный пересечением двух радиусов, образующих сектор, называется центральным углом . Этот угол, по определению, представляет собой угол 90 287, стягиваемый 90 288 дугой, завершающей сектор. Диаграмма ниже иллюстрирует отношения между дугами и секторами (греческая буква θ используется для обозначения центрального угла).
Сектор — это область внутри круга, окруженная двумя радиусами и дугой, соединяющей точки, в которых радиусы пересекаются с окружностью (по форме напоминает кусок пиццы). Угол, образованный пересечением двух радиусов, образующих сектор, называется центральным углом . Этот угол, по определению, представляет собой угол 90 287, стягиваемый 90 288 дугой, завершающей сектор. Диаграмма ниже иллюстрирует отношения между дугами и секторами (греческая буква θ используется для обозначения центрального угла).
Сектор ограничен двумя радиусами и дугой
Для любой дуги, если известно значение угла θ , образуемого дугой, и длина радиуса r , можно найти длину дуги по следующей формуле:
| Длина дуги = | 2π r θ |
| 360 |
Или, альтернативно, вы можете использовать эту эквивалентную формулу:
| Длина дуги = | π r θ |
| 180 |
Обратите внимание, что если угол указан в радианах, формула становится простой:
Длина дуги = r θ
Также для любой дуги, где известно значение угла θ , образуемого дугой, и длина радиуса r , можно найти площадь сектора по следующей формуле:
| Область сектора = | θ π R 2
| 360 |
Обратите внимание, что если угол указан в радианах, формула становится простой:
| Площадь сектора = | θr 2 | |
| 2 | ||
| Площадь сектора ( A | 2) =θ R 2 |
| 360110 | |
| 360110 | |
| 360102 | |
| Область треугольника ABC ( A 2 ) = | левый |
| 2 |
Площадь сегмента = a 1 — a 2
Обратите внимание, что если известны только l и r , то h можно найти с помощью теоремы Пифагора:
ч = √((0. 5л) 2 + р 2 )
5л) 2 + р 2 )
Точно так же, если известны только 90 287 h 90 288 и 90 287 r 90 288, 90 287 l 90 288 можно найти с помощью теоремы Пифагора:
l = 2√( r 2 — h 2 )
Касательные
Касательная (в контексте окружностей) — это линия или сегмент линии, который касается окружности только в одной точке и перпендикулярен радиусу, соединяющему эту точку с центром окружности.Из этого определения также можно сделать вывод, что любая линия, перпендикулярная касательной, которая проходит через точку, в которой касательная касается окружности, также должна проходить через центр окружности. Кроме того, из любой точки P, внешней по отношению к окружности, можно провести ровно две касательные из этой точки к точкам на окружности (назовем их A и B). Длины отрезков линии AP и BP будут равны, как показано на диаграмме ниже.Если мы назовем центр окружности О, то углы АОВ и АРВ являются дополнительными (т.е. в сумме они составляют сто восемьдесят градусов).
Длины отрезков линии AP и BP будут равны, как показано на диаграмме ниже.Если мы назовем центр окружности О, то углы АОВ и АРВ являются дополнительными (т.е. в сумме они составляют сто восемьдесят градусов).
Отрезки линии AP и BP касаются окружности и имеют одинаковую длину.
На приведенной ниже диаграмме показана ситуация, в которой отрезок PQ является касательной к окружности в точке Q, а отрезок QR является хордой этой окружности.Можно показать, что величина угла PQR составляет ровно половину центрального угла, образуемого хордой QR (т. е. угол QOR ). Поскольку отрезок OS является серединным перпендикуляром к хорде QR , углы QOS и ROS равны. Углы QOS и OQS в сумме составляют девяносто градусов (поскольку они являются дополнительными углами в прямоугольном треугольнике OQS), как и углы PQS и OQS . Следовательно, углы PQS и QOS должны быть равны, а поскольку углы QOS и ROS также равны, угол QOR должен быть в два раза больше угла PQR .
Следовательно, углы PQS и QOS должны быть равны, а поскольку углы QOS и ROS также равны, угол QOR должен быть в два раза больше угла PQR .
Угол PQR равен половине величины угла QOR .
Если точка O имеет координаты x 0 , y 0 , а точка Q имеет координаты x 1 , y 1 9028
( x 1 — x 0 ) x + ( y y — y 0 ) y = ( x 1 — x 0 ) x 1 + ( у 1 — у 0 ) у 1 или альтернативно: ( x 1 — x 0 ) ( x — x x y 1 — y 0 ) ( y — Y 0 ) = r 2 Наклон касательной также часто представляет интерес. Треугольный символ (Δ) в уравнении представляет собой заглавную греческую букву Delta и используется для обозначения разницы между двумя значениями переменной (иногда этот символ заменяется строчной буквой d ) .Обратите внимание, что если y 1 равно y 0 , то радиус, перпендикулярный касательной, представляет собой отрезок горизонтальной линии, и поэтому касательная будет вертикальной линией с неопределенным наклоном. И наоборот, если x 1 равно x 0 , радиус, перпендикулярный касательной, представляет собой отрезок вертикальной линии, а касательная будет горизонтальной линией с нулевым наклоном. Сеанс — это линия, которая пересекает окружность в двух точках. Вы можете думать об этом как о хорде, которая выходит за пределы окружности в обоих направлениях. На приведенной ниже диаграмме две секущие пересекаются в точке А, внешней по отношению к окружности.Секущие, пересекающиеся в точке А, пересекают окружность в точках В, С, D и Е, как показано на рисунке. Величина угла, образованного пересечением секущих (угол BAC ), составляет половину разности углов, образуемых пересекаемыми дугами (дуга BC и дуга DE ), которые являются углами BOC и МЭ соответственно. Величина угла BAC составляет половину разницы между углами BOC и DOE . Также можно показать, что произведение длин отрезков AE и AB равно произведению отрезков AD и AC : AE · AB = AD · AC На приведенной ниже диаграмме отрезок прямой из точки A, внешней по отношению к окружности, касается окружности в точке B.Второй отрезок из точки А образует секущую, которая пересекает окружность в точках С и D. Произведение AC и AD равно AB 2 Можно показать, что длина отрезка AB в квадрате равна произведению длин отрезков AC и AD : AC · AD = AB 2 Две секущие также могут пересекаться внутри круга. Величина углов AEB и CED составляет половину суммы углов AOB и COD Вписанный угол — это угол, образованный при пересечении двух хорд в общей точке окружности, которой они обе принадлежат.В приведенном ниже примере вписанный угол ACB образован пересечением хорд AC и BC . Величина центрального угла AOB вдвое больше, чем вписанного угла ACB . Если вписанный угол ACB больше девяноста градусов, то центральный угол AOB будет рефлекторным углом , т.е. он будет иметь величину, превышающую сто восемьдесят градусов (обратите внимание, что если вписанный угол ACB равен ровно девяносто градусов, точка пересечения дуги AB будет полуокружностью, а центральный угол AOB будет равен ста восьмидесяти градусам). Если вписанный угол тупой, то соответствующий центральный угол является рефлекторным углом. Учитывая, что центральный угол, опирающийся на дугу, всегда будет иметь в точности двойную величину любого вписанного угла, пересекающего дугу, все вписанные углы, пересекающие ту же дугу и находящиеся на 90 287 одной и той же стороне 90 288 хорды, соединяющей конец точки дуги, будут иметь ту же величину, что и показанная ниже. Вписанные углы, опирающиеся на одну и ту же дугу, будут иметь одинаковую величину Если два вписанных угла пересекают одну и ту же дугу, но лежат на противоположных сторонах хорды, соединяющей концы дуги, то вписанные углы будут дополнительными (т.е. в сумме они будут составлять сто восемьдесят градусов). Вписанные уголки ABC и ADC являются дополнительными Если нам известны координаты a и b центра окружности и радиус окружности r , то для любой точки x , y на окружности окружности выполняется следующее уравнение ( называется уравнением окружности ) будет верным: ( x — a ) 2 + ( y — b ) 2 = r 2 9045 Справедливость этого уравнения можно продемонстрировать графически, как показано на иллюстрации ниже. Радиус r — это гипотенуза прямоугольного треугольника. Обратите внимание, что если центр круга имеет координаты a = 0, b = 0, то уравнение упрощается до: x 2 + y 2 = r 2 Можно показать, что для любых трех точек плоскости, не лежащих на одной прямой, существует единственная окружность. Сегмент окружности — это область, ограниченная дугой и хордой окружности. Когда что-то делится на части, каждая часть называется сегментом. Точно так же сегмент является частью круга. Но отрезок — это не какая-то случайная часть круга, а определенная часть круга, пересекаемая его хордой.Давайте узнаем об определении сегмента круга и формуле, чтобы найти площадь сегмента круга подробно здесь. Сегмент окружности — это область, ограниченная дугой и хордой окружности. Существует два типа сегментов, один из которых является второстепенным, а другой — основным. Малый сегмент образован малой дугой, а большой сегмент образован большой дугой окружности. Предполагая, что y 1 не равно y 0 , можно показать, что наклон касательной определяется следующим уравнением:
Предполагая, что y 1 не равно y 0 , можно показать, что наклон касательной определяется следующим уравнением: Δ Y Y = x 1 — x 1 0 9 x Y 1 — y 0  Обратите также внимание, что если центр круга является началом координат (т.е. x 0 = 0, y 0 = 0), то наклон касательной становится простым:
Обратите также внимание, что если центр круга является началом координат (т.е. x 0 = 0, y 0 = 0), то наклон касательной становится простым: секущие

 На приведенной ниже диаграмме две секущие пересекаются в точке Е, находящейся внутри круга. Секущие, пересекающиеся в точке E, пересекают окружность в точках A, B, C и D, как показано на рисунке. Величина обоих углов, образованных пересечением секущих (углы AEB и CED ), составляет половину суммы углов, образуемых пересекаемыми дугами (дуга AB и дуга CD ), которые представляют собой уголки AOB и COD соответственно.
На приведенной ниже диаграмме две секущие пересекаются в точке Е, находящейся внутри круга. Секущие, пересекающиеся в точке E, пересекают окружность в точках A, B, C и D, как показано на рисунке. Величина обоих углов, образованных пересечением секущих (углы AEB и CED ), составляет половину суммы углов, образуемых пересекаемыми дугами (дуга AB и дуга CD ), которые представляют собой уголки AOB и COD соответственно. Вписанные углы
 Центральный угол, образуемый дугой, соединяющей точки A и B (угол AOB ), ровно в два раза больше угла ACB . Это соотношение будет одинаковым для любого вписанного угла, даже если вписанный угол равен тупому (т.е. больше девяноста градусов). Дуга, соединяющая непересекающиеся концы двух хорд, образующих вписанный угол, называется дугой , охваченной дугой .
Центральный угол, образуемый дугой, соединяющей точки A и B (угол AOB ), ровно в два раза больше угла ACB . Это соотношение будет одинаковым для любого вписанного угла, даже если вписанный угол равен тупому (т.е. больше девяноста градусов). Дуга, соединяющая непересекающиеся концы двух хорд, образующих вписанный угол, называется дугой , охваченной дугой .
Уравнение окружности
 Радиус окружности r является гипотенузой прямоугольного треугольника, в котором длина горизонтального катета равна x — a , а длина вертикального катета равна y — б . Таким образом, уравнение является просто применением теоремы Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон.
Радиус окружности r является гипотенузой прямоугольного треугольника, в котором длина горизонтального катета равна x — a , а длина вертикального катета равна y — б . Таким образом, уравнение является просто применением теоремы Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Можно использовать уравнение окружности, чтобы найти как радиус окружности, так и координаты центра окружности, если известны координаты всех трех точек. Просто подставьте известные значения x и y для каждой точки в уравнение. Это даст вам три уравнения, каждое из которых будет иметь три переменные ( a , b и r ), значения которых неизвестны. Неизвестные значения можно найти, решая уравнения одновременно.
Можно использовать уравнение окружности, чтобы найти как радиус окружности, так и координаты центра окружности, если известны координаты всех трех точек. Просто подставьте известные значения x и y для каждой точки в уравнение. Это даст вам три уравнения, каждое из которых будет иметь три переменные ( a , b и r ), значения которых неизвестны. Неизвестные значения можно найти, решая уравнения одновременно. Сегмент круга — формула, площадь сегмента круга, свойства, примеры
Что такое сегмент круга?
 Напомним, что понимают под дугой и хордой окружности.
Напомним, что понимают под дугой и хордой окружности. Свойства сегмента окружности
Свойства сегмента круга:
- Это область, ограниченная хордой и дугой.
- Угол, образуемый сегментом в центре окружности, равен углу, образуемому соответствующей дугой.Этот угол обычно называют центральным углом.
- Малый сегмент получается удалением соответствующего большого сегмента из общей площади круга.
- Большой сегмент получается удалением соответствующего меньшего сегмента из общей площади круга.
- Полуокружность — это самый большой сегмент в любой окружности, образованной диаметром и соответствующей дугой.

Площадь сегмента круга
Дуга и два радиуса окружности образуют сектор.Эти два радиуса и хорда отрезка вместе образуют треугольник. Таким образом, площадь сегмента круга получается путем вычитания площади треугольника из площади сектора. то есть
Площадь сегмента круга = площадь сектора — площадь треугольника
Давайте воспользуемся этой логикой, чтобы вывести формулы для нахождения площади сегмента круга. Обратите внимание, что это площадь малого сегмента. Обычно сегмент круга относится к малому сегменту.
Примечание: Чтобы найти площадь большого сегмента круга, мы просто вычитаем соответствующую площадь меньшего сегмента из общей площади круга.
Площадь сегмента круга Формула
Давайте рассмотрим меньший сегмент вышеприведенного круга, который образован хордой PQ окружности радиуса «r» с центром в «O». Мы знаем, что каждая дуга окружности стягивает угол в центре, который называется центральным углом дуги. Угол, образуемый дугой PQ, равен θ. Из тригонометрии мы знаем, что площадь треугольника OPQ равна (1/2) r 2 sin θ. Также мы знаем, что площадь сектора OPQ составляет:
Угол, образуемый дугой PQ, равен θ. Из тригонометрии мы знаем, что площадь треугольника OPQ равна (1/2) r 2 sin θ. Также мы знаем, что площадь сектора OPQ составляет:
- (θ / 360 o ) × πr 2 , если ‘θ’ в градусах
- (1/2) × r 2 θ, если θ’ в радианах
Таким образом, площадь меньшего сегмента круга равна:
- (θ / 360 o ) × πr 2 — (1/2) r 2 sin θ (OR) r 2 [πθ/360 o — sin θ// θ’ в градусах
- (1/2) × r 2 θ — (1/2) r 2 sin θ (OR) (r 2 / 2) [θ — sin θ], если ‘θ’ в радианах
Периметр сегмента окружности
Мы знаем, что сегмент окружности состоит из дуги и хорды окружности.Рассмотрим тот же сегмент, что и на рисунке выше.
Периметр сегмента = длина дуги + длина хорды
Мы это знаем,
- длина дуги равна rθ, если ‘θ’ в радианах, и πrθ/180, если ‘θ’ в градусах.

- длина хорды = 2r sin (θ/2)
Таким образом, формула периметра отрезка:
- Периметр сегмента круга = rθ + 2r sin (θ/2), если ‘θ’ в радианах.
- Периметр сегмента круга = πrθ/180 + 2r sin (θ/2), если «θ» в радианах.
Теоремы об отрезке окружности
В основном существуют две теоремы, основанные на сегменте окружности.
- Теорема об углах одного отрезка
- Теорема об альтернативном сегменте
Углы в одном отрезке Теорема
Утверждается, что углы, образованные в одном сегменте окружности, всегда равны.
Теорема об альтернативном сегменте
Эта теорема утверждает, что угол, образованный касательной и хордой в точке касания, равен углу, образованному на альтернативном отрезке окружности через концы хорды.
Связанные темы
Вот несколько тем, связанных с сегментом круга, посмотрите.
Часто задаваемые вопросы о сегменте круга
Что такое сегмент круга?
Сегмент окружности — это область, ограниченная дугой и хордой окружности. Существует два типа сегментов: один — второстепенный сегмент (образованный малой дугой), а другой — большой сегмент (образованный большой дугой).
Существует два типа сегментов: один — второстепенный сегмент (образованный малой дугой), а другой — большой сегмент (образованный большой дугой).
В чем разница между хордой и сегментом окружности?
Хорда окружности — это отрезок, соединяющий любые две точки окружности, тогда как отрезок — это область, ограниченная хордой и дугой окружности.
В чем разница между дугой и сегментом окружности?
Дуга — это часть окружности окружности, тогда как сегмент окружности — это область, ограниченная дугой и хордой окружности.
В чем разница между сектором круга и сегментом круга?
Сектором окружности называется область, ограниченная двумя радиусами и соответствующей дугой, а сегментом окружности является область, ограниченная хордой и соответствующей дугой.
Какая формула площади сегмента круга?
Площадь сегмента окружности (или) малого сегмента окружности равна:
- (θ / 360 o ) × πr 2 — (1/2) r 2 sin θ (OR) r 2 [πθ/360 o — sin θ// θ’ в градусах
- (1/2) × r 2 θ — (1/2) r 2 sin θ (OR) (r 2 / 2) [θ — sin θ], если ‘θ’ в радианах
Здесь ‘r’ — радиус окружности, а ‘θ’ — угол, образуемый дугой сегмента.
Как найти площадь сегмента круга?
Вот шаги, чтобы найти площадь сегмента круга.
- Определите радиус круга и обозначьте его буквой «r».
- Определите центральный угол, образованный дугой сегмента, и обозначьте его ‘θ’.
- Найдите площадь треугольника по формуле (1/2) r 2 sin θ.
- Найдите площадь сектора по формуле
(θ / 360 o ) × πr 2 , если ‘θ’ в градусах (или)
(1/2) × r 2 θ, если θ’ в радианах - Вычтите площадь треугольника из площади сектора, чтобы найти площадь сегмента.
Как найти площадь большого сегмента круга?
Площадь большого сегмента круга находится путем вычитания площади соответствующего меньшего сегмента из общей площади круга.
Равны ли углы на одном отрезке окружности?
Да, углы, образованные одним и тем же отрезком окружности, равны. т. е. углы на окружности, образованной одной и той же дугой, равны.
Что такое альтернативная теорема сегмента круга?
Теорема о чередующихся сегментах утверждает, что угол, образованный касательной и хордой в точке касания, равен углу, образованному в альтернативном сегменте на окружности окружности через концы хорды.
Является ли полуокружность сегментом окружности?
Мы знаем, что диаметр окружности также является хордой окружности (фактически это самая длинная хорда окружности). Кроме того, мы знаем, что длина окружности полукруга является дугой окружности. Таким образом, полуокружность ограничена хордой и дугой и, следовательно, является сегментом окружности.
Геометрия окружностей
Определения и формулы радиуса окружности, диаметра окружности, длины окружности (периметра) окружности, площади окружности, хорды окружности, дуги и длины дуги круга, сектора и площади сектора круга
Просто прокрутите вниз или нажмите на то, что вы хотите, и я прокрутлю вниз для вас!
| Радиус окружности: | |
Радиус круга — это расстояние от центра круга до внешнего края. | |
| Диаметр круга: | |
| Диаметр круга — это наибольшее расстояние поперек круга. (Диаметр проходит через центр круга. Это делает его самым длинным расстоянием.) | |
| Длина окружности (периметр круга): | |
| Длина окружности — это периметр — расстояние вокруг внешнего края. Окружность = | |
| Хорда окружности: | |
Хорда окружности — это отрезок, соединяющий одну точку на краю окружности с другой точкой на окружности. | |
 В этом случае прямая называется секущей по отношению к окружности.
В этом случае прямая называется секущей по отношению к окружности. 
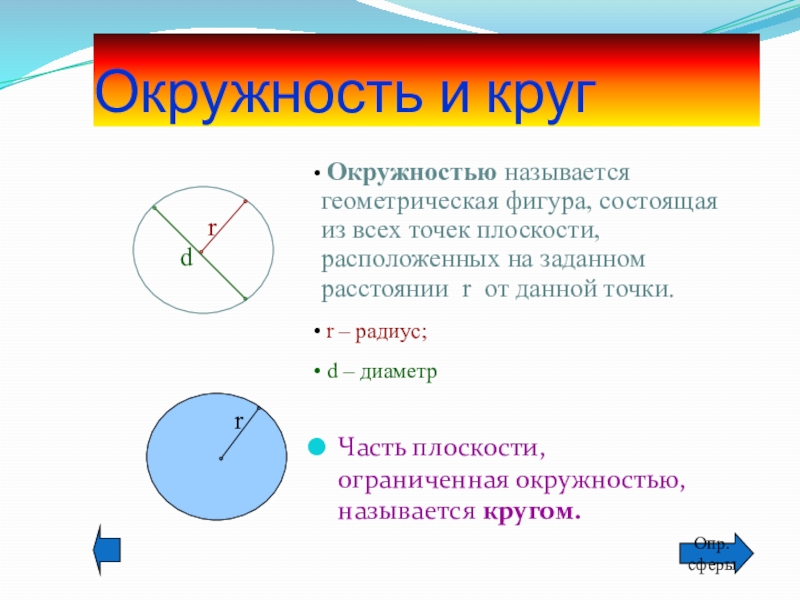 элипса, параболы. | ·стар. и сев. радуга. | В оглобельной упряжи, деревянная, согнутая крутым лучком тугая распорка между… … Толковый словарь Даля
элипса, параболы. | ·стар. и сев. радуга. | В оглобельной упряжи, деревянная, согнутая крутым лучком тугая распорка между… … Толковый словарь Даля » Крылов. 2. Часть окружности круга или… … Толковый словарь Ушакова
» Крылов. 2. Часть окружности круга или… … Толковый словарь Ушакова Ракета описала в небе дугу … Толковый словарь русских существительных
Ракета описала в небе дугу … Толковый словарь русских существительных Если B лежит между A и C на окружности, то m?AB + m?BC = m?AC.
Если B лежит между A и C на окружности, то m?AB + m?BC = m?AC. е. они имеют одинаковую форму и размер), если они содержат один и тот же центральный угол и образованы радиусами одинаковой длины. Таким образом, два сектора, содержащие один и тот же центральный угол, будут конгруэнтны, если они принадлежат одной и той же окружности (в этом случае радиусы, образующие центральный угол для обоих секторов, будут иметь одинаковую длину) или если они принадлежат разным окружностям, которые сами по себе равны. конгруэнтны (в этом случае радиусы, образующие центральный угол для обоих секторов, будут по-прежнему иметь одинаковую длину). Глядя на это с другой точки зрения, если два сектора имеют одинаковую длину дуги и принадлежат либо одному и тому же кругу , либо двум конгруэнтным кругам, обе дуги будут опираться на один и тот же угол, и сектора будут конгруэнтны.На приведенном ниже рисунке окружности A и B конгруэнтны, а центральный угол для каждого из секторов a, b и c равен θ , поэтому сектора a, b и c конгруэнтны.
е. они имеют одинаковую форму и размер), если они содержат один и тот же центральный угол и образованы радиусами одинаковой длины. Таким образом, два сектора, содержащие один и тот же центральный угол, будут конгруэнтны, если они принадлежат одной и той же окружности (в этом случае радиусы, образующие центральный угол для обоих секторов, будут иметь одинаковую длину) или если они принадлежат разным окружностям, которые сами по себе равны. конгруэнтны (в этом случае радиусы, образующие центральный угол для обоих секторов, будут по-прежнему иметь одинаковую длину). Глядя на это с другой точки зрения, если два сектора имеют одинаковую длину дуги и принадлежат либо одному и тому же кругу , либо двум конгруэнтным кругам, обе дуги будут опираться на один и тот же угол, и сектора будут конгруэнтны.На приведенном ниже рисунке окружности A и B конгруэнтны, а центральный угол для каждого из секторов a, b и c равен θ , поэтому сектора a, b и c конгруэнтны. 
 И наоборот, если радиус перпендикулярен хорде, то радиус делит эту хорду пополам. Фактически любая линия, перпендикулярная хорде, проходит через центр окружности, которой принадлежит эта хорда.На приведенной ниже диаграмме хорда AC перпендикулярна радиусу r , который пересекает его в точке B. Следовательно, радиус r делит хорду AC пополам, а отрезки AB и BC равны по длине.
И наоборот, если радиус перпендикулярен хорде, то радиус делит эту хорду пополам. Фактически любая линия, перпендикулярная хорде, проходит через центр окружности, которой принадлежит эта хорда.На приведенной ниже диаграмме хорда AC перпендикулярна радиусу r , который пересекает его в точке B. Следовательно, радиус r делит хорду AC пополам, а отрезки AB и BC равны по длине. На диаграмме ниже окружности C1 и C2 конгруэнтны. Хорды AB , CD и EF находятся на одинаковом перпендикулярном расстоянии от центра соответствующих окружностей. Следовательно, хорды AB , CD и EF конгруэнтны.
На диаграмме ниже окружности C1 и C2 конгруэнтны. Хорды AB , CD и EF находятся на одинаковом перпендикулярном расстоянии от центра соответствующих окружностей. Следовательно, хорды AB , CD и EF конгруэнтны. Эти отношения можно выразить алгебраически следующим образом:
Эти отношения можно выразить алгебраически следующим образом:
 е. дуга, лежащая между концами этой хорды). Если радиус окружности 90 287 r 90 288, длина хорды 90 287 l 90 288, перпендикулярное расстояние 90 287 h 90 288 от хорды до центра окружности и центральный угол 90 287 θ 90 288 известны, площадь сегмент можно найти. Сначала вычислите площадь сектора, связанного с сегментом (см. выше). Затем вычислите площадь треугольной части сектора и вычтите результат из общей площади сектора, чтобы оставить площадь сегмента.Обратите внимание, что если ни длина хорды, ни ее перпендикулярное расстояние от центра не известны, площадь сегмента все же можно рассчитать, но расчет будет включать тригонометрию. На приведенном ниже рисунке сегмент представляет собой область, заштрихованную бледно-голубым цветом.
е. дуга, лежащая между концами этой хорды). Если радиус окружности 90 287 r 90 288, длина хорды 90 287 l 90 288, перпендикулярное расстояние 90 287 h 90 288 от хорды до центра окружности и центральный угол 90 287 θ 90 288 известны, площадь сегмент можно найти. Сначала вычислите площадь сектора, связанного с сегментом (см. выше). Затем вычислите площадь треугольной части сектора и вычтите результат из общей площади сектора, чтобы оставить площадь сегмента.Обратите внимание, что если ни длина хорды, ни ее перпендикулярное расстояние от центра не известны, площадь сегмента все же можно рассчитать, но расчет будет включать тригонометрию. На приведенном ниже рисунке сегмент представляет собой область, заштрихованную бледно-голубым цветом.