Ответы на вопросы ‘ограниченная окружностью’

Сегмент	Часть круга, ограниченная дугой и ее хордой 7 букв
Шар	В математике: часть пространства, ограниченная сферой 3 буквы
Квартал	Часть городской застройки, ограниченная улицами 7 букв
Квартал	Городская застройка, ограниченная пересекающимися улицами 7 букв
Квартал	Часть города, ограниченная пересекающимися улицами 7 букв
Овал	Фигура, ограниченная кривой линией яйцеобразной формы 4 буквы
Геоид	Общая форма земли, ограниченная поверхностью океана 5 букв
Мирок	Узкая, ограниченная область жизни, явлений, интересов 5 букв

Задача о наименьшей окружности — Википедия

Материал из Википедии — свободной энциклопедии

Задача о наименьшей окружности или задача о минимальном покрывающем круге — задача о вычислении наименьшей окружности, содержащей все заданные точки из множества на евклидовой плоскости. Соответствующая задача в n-мерном пространстве, задача о наименьшей ограничивающей сфере, вычисляет наименьшую гиперсферу, содержащую все точки заданного множества^[1]. Задачу о наименьшей окружности первым поставил английский математик Джеймс Джозеф Сильвестр в 1857^[2].

Задача о наименьшей окружности на плоскости является примером задачи о размещении объектов (задача об 1-центре), в которой расположение новой организации нужно выбрать так, чтобы обслужить заданное множество клиентов с минимизацией максимального расстояния, которое должен преодолеть клиент, чтобы добраться до организации

[3]. Как задача о наименьшей окружности на плоскости, так и задача о наименьшей ограничивающей гиперсфере в более высоких размерностях разрешимы за линейное время.

Большинство геометрических подходов к задаче просматривают точки, лежащие на границе минимальной окружности и основываются на следующих простых фактах:

• Минимальный покрывающий круг единственен.
• Минимальный покрывающий круг множества S может быть определён максимум по трём точкам из S, которые лежат на границе круга. Если он определяется лишь двумя точками, то хорда, соединяющая эти точки, является диаметром минимальной окружности. Если окружность определяется тремя точками, то треугольник не может быть тупоугольным.

Как показал Нимрод Мегиддо^[4], минимальная ограничивающая окружность может быть найдена за линейное время, и то же самое верно для наименьшей ограничивающей сферы в евклидовых пространствах бо́льших размерностей.

Эмо Вельцль^[5] предложил простой рандомизированный алгоритм для задачи покрытия кругом, среднее время работы которого равно O(N){\displaystyle O(N)}, основанный на алгоритме линейного программирования Раймунда Зейделя. Алгоритм является рекурсивным и в качестве аргументов принимает два множества точек S и Q. Алгоритм вычисляет наименьшую окружность, ограничивающую объединение множеств S и Q, если любая точка множества Q является граничной точкой возможной ограничивающей окружности. Исходная задача о наименьшей ограничивающей окружности может быть решена, начав с S, равного полному множеству точек, и с Q, равного пустому множеству. Когда алгоритм вызывает себя рекурсивно, он увеличивает множество Q, пока в него не попадут все граничные точки.

Алгоритм обрабатывает точки множества S в случайном порядке, используя множество P обработанных точек и минимальную окружность, ограничивающую объединение

P и Q. На каждом шаге алгоритм проверяет, принадлежит ли обрабатываемая точка r этой окружности. Если не принадлежит, алгоритм заменяет ограничивающую окружность путём рекурсивного вызова алгоритма на множествах P и Q+r. В зависимости о того, окружность заменяется или нет, r включается в множество P. Обработка каждой точки, таким образом, заключается в проверке (за постоянное время), принадлежит ли точка окружности, и возможном рекурсивном вызове алгоритма. Можно показать, что i-я обрабатываемая точка имеет вероятность O(1/i){\displaystyle O(1/i)} рекурсивного вызова, а потому общее время линейно.

Позднее задача о наименьшей окружности была включена в общий класс задач LP-типа^[en], которые могут быть решены алгоритмами, подобными алгоритму Вельцля, основанному на линейном программировании. Как следствие принадлежности этому классу, было показано, что зависимость постоянного множителя от размерности в оценке времени O(N){\displaystyle O(N)}, которая была факториальной в методе Зейделя, может быть сведена к субэкспоненциальной, но оценка времени остаётся линейной по

N^[6].

До результата Мегиддо, показывающего, что задача о наименьшей окружности может быть решена за линейное время, в литературе появлялись алгоритмы большей сложности. Наивный алгоритм решает задачу за время O(n⁴) путём проверки окружностей, задаваемых всеми парами и тройками точек.

• Алгоритм Христала и Пирса использует стратегию локальной оптимизации. Алгоритм просматривает две точки на границе ограничивающей окружности и последовательно уменьшает окружность, заменяя пары ограничивающих точек, пока не будет найдена оптимальная окружность. Чакраборты и Чаудхури^[7] предложили метод с линейным временем работы для выбора подходящей начальной окружности и пары граничных точек на окружности. Каждый шаг алгоритма включает в качестве второй ограничивающей точки новую вершину выпуклой оболочки, так что, если выпуклая оболочка имеет h вершин, этот метод может работать за время O(nh).
• Элзинга и Хирн^[8] описали алгоритм, который рассматривает ограничивающие сферы для подмножества точек. На каждом шаге точка, лежащая вне сферы, используется для поиска большей сферы, включающей новое подмножество точек, в которое входит эта точка. Хотя наихудший случай работы алгоритма оценивается как O(h³n), авторы утверждают, что в их экспериментах алгоритм работал за линейное время. Сложность метода проанализировали Дрезнер и Шелах^[9]. В статье Хирна, Виджея и Никеля можно найти коды метода на Фортране и C^[10].
• Задачу о наименьшей сфере можно сформулировать как задачу квадратичного программирования^[1], определённую как систему линейных ограничений с выпуклой квадратичной целевой функцией. Таким образом, любой алгоритм возможных направлений может дать решение задачи
  [11]. Хирн и Виджей^[12] доказали, что подход на основе метода возможных направлений, выбранный Якобсеном, эквивалентен алгоритму Христала–Пирса.
• Двойственную задачу задаче квадратичного программирования можно сформулировать явно^[13]. Алгоритм Лоусона^[14] можно описать как алгоритм одновременного решения прямой и двойственной задач^[12].
• Шамос и Хауи ^[15] предложили алгоритм со временем решения O(n log n), основанный на наблюдении, что центр наименьшей ограничивающей окружности должен быть вершиной наиболее удалённой точки в диаграмме Вороного входного множества точек.

Взвешенная версия задачи о минимальном накрывающем круге берёт в качестве входных данных точки евклидова пространства с назначенным каждой точке весом. Целью задачи является поиск одной точки, минимизирующей максимальное взвешенное расстояние до любой точки. Исходную задачу покрытия кругом можно рассматривать как задачу с одинаковыми весами. Как и в случае задачи без весов, взвешенную задачу можно решить за линейное время в любом пространстве ограниченной размерности, если использовать подход, основанный на алгоритме линейного программирования ограниченной размерности, хотя в литературе постоянно встречаются более медленные алгоритмы

[12]^[16][17].

1. ↑ ^{1 2} Elzinga, Hearn, 1972, с. 96–104.
2. ↑ Sylvester, 1857, с. 79.
3. ↑ Francis, McGinnis, White, 1992.
4. ↑ Megiddo, 1983, с. 759–776.
5. ↑ Welzl, 1991, с. 359–370.
6. ↑ Matoušek, Sharir, Welzl, 1996, с. 498–516.
7. ↑ Chakraborty, Chaudhuri, 1981, с. 164–166.
8. ↑ Elzinga, Hearn, 1972, с. 379–394.
9. ↑ Drezner, Shelah, 1987, с. 255–261.
10. ↑ Hearn, Vijay, Nickel, 1995, с. 236–237.
11. ↑ Jacobsen, 1981, с. 144–148.
12. ↑ ^{1 2 3} Hearn, Vijay, 1982, с. 777–795.
13. ↑ Elzinga, Hearn, Randolph, 1976, с. 321–336.
14. ↑ Lawson, 1965, с. 415–417.
15. ↑ Shamos, Hoey, 1975, с. 151–162.
16. ↑ Megiddo, 1983, с. 498–504.
17. ↑ Megiddo, Zemel, 1986, с. 358–368.

• J. Elzinga, D. W. Hearn. The minimum covering sphere problem // Management Science. — 1972. — Т. 19. — DOI:10.1287/mnsc.19.1.96.
• J. J. Sylvester. A question in the geometry of situation // Quarterly Journal of Mathematics. — 1857. — Т. 1. — С. 79.
• R. L. Francis, L. F. McGinnis, J. A. White. Facility Layout and Location: An Analytical Approach. — 2nd. — Englewood Cliffs, N.J.: Prentice–Hall, Inc., 1992.
• Nimrod Megiddo. Linear-time algorithms for linear programming in R³ and related problems // SIAM Journal on Computing. — 1983. — Т. 12, вып. 4. — С. 759–776. — DOI:10.1137/0212052.
• Emo Welzl. New Results and New Trends in Computer Science / H. Maurer. — Springer-Verlag, 1991. — Т. 555. — С. 359–370. — (Lecture Notes in Computer Science). — DOI:10.1007/BFb0038202.
• Jiří Matoušek, Micha Sharir, Emo Welzl. A subexponential bound for linear programming // Algorithmica. — 1996. — Т. 16. — С. 498–516. — DOI:10.1007/BF01940877.
• R. K. Chakraborty, P. K. Chaudhuri. Note on geometrical solutions for some minimax location problems // Transportation Science. — 1981. — Т. 15. — DOI:10.1287/trsc.15.2.164.
• J. Elzinga, D. W. Hearn. Geometrical solutions for some minimax location problems // Transportation Science. — 1972. — Т. 6. — С. 379–394. — DOI:10.1287/trsc.6.4.379.
• Z. Drezner, S. Shelah. On the complexity of the Elzinga–Hearn algorithm for the 1-center problem // Mathematics of Operations Research. — 1987. — Т. 12, вып. 2. — С. 255–261. — DOI:10.1287/moor.12.2.255.
• D. W. Hearn, J. Vijay, S. Nickel. Codes of geometrical algorithms for the (weighted) minimum circle problem // European Journal of Operational Research. — 1995. — Т. 80. — DOI:10.1016/0377-2217(95)90075-6.
• S. K. Jacobsen. An algorithm for the minimax Weber problem // European Journal of Operational Research. — 1981. — Т. 6. — DOI:10.1016/0377-2217(81)90200-9.
• D. W. Hearn, J. Vijay. Efficient algorithms for the (weighted) minimum circle problem // Operations Research. — 1982. — Т. 30, вып. 4. — DOI:10.1287/opre.30.4.777.
• J. Elzinga, D. W. Hearn, W. D. Randolph. Minimax multifacility location with Euclidean distances // Transportation Science. — 1976. — Т. 10. — DOI:10.1287/trsc.10.4.321.
• C. L. Lawson. The smallest covering cone or sphere // SIAM Review. — 1965. — Т. 7, вып. 3. — DOI:10.1137/1007084.
• M. I. Shamos, D. Hoey. Proceedings of 16th Annual IEEE Symposium on Foundations of Computer Science. — 1975. — DOI:10.1109/SFCS.1975.8.
• N. Megiddo. The weighted Euclidean 1-center problem // Mathematics of Operations Research. — 1983. — Т. 8. — DOI:10.1287/moor.8.4.498.
• N. Megiddo, E. Zemel. An O(n log n) randomizing algorithm for the weighted Euclidean 1-center problem // Journal of Algorithms. — 1986. — Т. 7. — DOI:10.1016/0196-6774(86)90027-1.

Подскажите определения. НУЖНЫ ОПРЕДЕЛЕНИЯ СЛОВ:ОКРУЖНОСТЬ,КРУГ,РАДИУС,ДИАМЕТР,ХОРДА,ДУГА

Окружность — это замкнутая кривая линия, все точки которой находятся на равном расстоянии от данной точки плоскости, называемой центром окружности. Круг — это часть плоскости, ограниченная окружностью. Расстояние от любой точки круга до центра круга не превышает расстояния от центра круга до любой точки на окружности. Радиус — отрезок прямой линии, соединяющий центр с любой точкой окружности. Диаметр – отрезок прямой линии, соединяющии две точки окружности и проходящий через центр. Можно так — это наибольшая из хорд окружности. Дуга — часть окружности или другой кривой линии, заключенная между двумя точками. Хорда — прямая, соединяющая две точки кривой линии.

ОКР? УЖНОСТЬ, замкнутая плоская кривая, все точки которой одинаково удалены от ее центра КРУГ, часть плоскости, ограниченная окружностью (содержащая ее центр) . Р? АДИУС (лат. radius, букв. — спица колеса, луч) , отрезок, соединяющий какую-либо точку окружности или сферы с центром, а также длина этого отрезка. ДИ? АМЕТР (от греч. diametros — поперечник) окружности, отрезок прямой, соединяющий две точки окружности и проходящий через ее центр. Х? ОРДА (от греч. chorde — струна) , отрезок прямой, соединяющий две какие-либо точки кривой. ДУГ? А, часть кривой линии, заключенная между двумя какими-либо точками.

Окружность — множество точек на плоскости, расположенном на одинаковом расстоянии от центра. Круг — множество точек на плоскости, расположенных от центра на расстоянии не более заданного. Радиус — расстояние от центра до окружности (отрезок, соединяющий центр с окружностью) . Диаметр — отрезок, соединяющий две точки окружности и проходящий через ее центр. Хорда — отрезок, соединяющий две точки окружности и не проходящий через центр. Дуга — часть окружности, ограниченная концами хорды.

Окружность-это геометрическая фигура, состоящая из множества точек, находящихся на одинаковом расстоянии от точки, называемой центром окружности. Радиус- это отрезок, соединяющий центр окружности и любую точку окружности. Диаметр-это отрезок, соединяющий две точки окружности и проходящий через центр. Хорда- это отрезок, соединяющий две любые точки окружности.

всё правильно окужность, хорда, радиус, диамеетр

Степень точки относительно окружности — Википедия

У этого термина существуют и другие значения, см. Степень точки.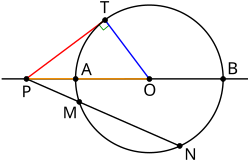 Степень внешней точки P{\displaystyle P} относительно окружности равна PO2−OT2={\displaystyle {\color {DarkOrange}PO}^{2}-{\color {blue}OT}^{2}=}PT2={\displaystyle {\color {red}PT}^{2}=}PA⋅PB={\displaystyle PA\cdot PB=}PM⋅PN{\displaystyle PM\cdot PN}

Степень точки относительно окружности — величина d2−R2{\displaystyle d^{2}-R^{2}}, где d{\displaystyle d} — расстояние от точки до центра окружности, a R{\displaystyle R} — радиус окружности. По этому определению точки внутри круга имеют отрицательные степени, точки вне круга имеют положительные степени, а точки на окружности имеют нулевую степень. Для точки, лежащей вне окружности, из теоремы Пифагора следует, что степень точки относительно окружности есть квадрат длины касательной, проведенных из данной точки к данной окружности. Степень точки также известна как степень окружности или степень круга относительно точки.

Содержание

• 1 Свойства
• 2 Связанные определения
• 3 История
• 4 Вариации и обобщения
• 5 Литература
• 6 Ссылки

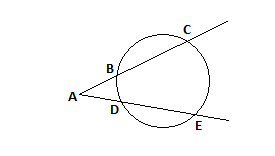
• Если прямая, проходящая через точку A{\displaystyle A}, пересекает окружность Γ{\displaystyle \Gamma } в точках B{\displaystyle B} и C{\displaystyle C}, то степень A{\displaystyle A} относительно Γ{\displaystyle \Gamma } равна ±AB⋅AC{\displaystyle \pm AB\cdot AC}; в этой формуле стоит «+» если A{\displaystyle A} лежит снаружи Γ{\displaystyle \Gamma } и «-» если внутри. В частности,
  • Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть.
  • Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной.

• Для двух не концентрических окружностей геометрическое место точек Р, для которых степени относительно обеих окружностей равны, является прямой, называемой радикальной осью окружностей.
• Для трёх окружностей, центры которых не лежат на одной прямой существует единственная точка, такая, что её степени относительно всех трёх окружностей равны. Эта точка называется радикальным центром трёх окружностей.
• Со степенью точки относительно окружности тесно связано понятие Инверсное расстояние.

Термин «степень» в этом значении был впервые употреблён Штейнером.

• Аналогично определяется степень точки относительно сферы в n{\displaystyle n}-мерном евклидовом пространстве.

• Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
• Я. П. Понарин. §3.1 Степень точки относительно сферы // Элементарная геометрия. — М.: МЦНМО, 2006. — Т. 2. — С. 146. — 256 с. — 2000 экз. — ISBN 5-94057-223-5.

• На Викискладе есть медиафайлы по теме Степень точки относительно окружности

Это заготовка статьи по математике. Вы можете помочь проекту, дополнив её.