Прямая содержащая высоту конуса: Образующая конуса. Длина образующей конуса – Высота конуса | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU — Детская игровая комната «Волшебный лес»

Posted on 05.11.202011.02.2020 by alexxlab

Содержание

Образующая конуса. Длина образующей конуса

Геометрия является разделом математики, изучающим структуры в пространстве и отношение между ними. В свою очередь она также состоит из разделов, и одним из них является стереометрия. Она предусматривает изучение свойств объемных фигур, находящихся в пространстве: куба, пирамиды, шара, конуса, цилиндра и др.

Конус – это тело в евклидовом пространстве, которое ограничивает коническая поверхность и плоскость, на которой лежат концы ее образующих. Его образование происходит в процессе вращения прямоугольного треугольника вокруг любого из его катетов, поэтому он относится к телам вращения.

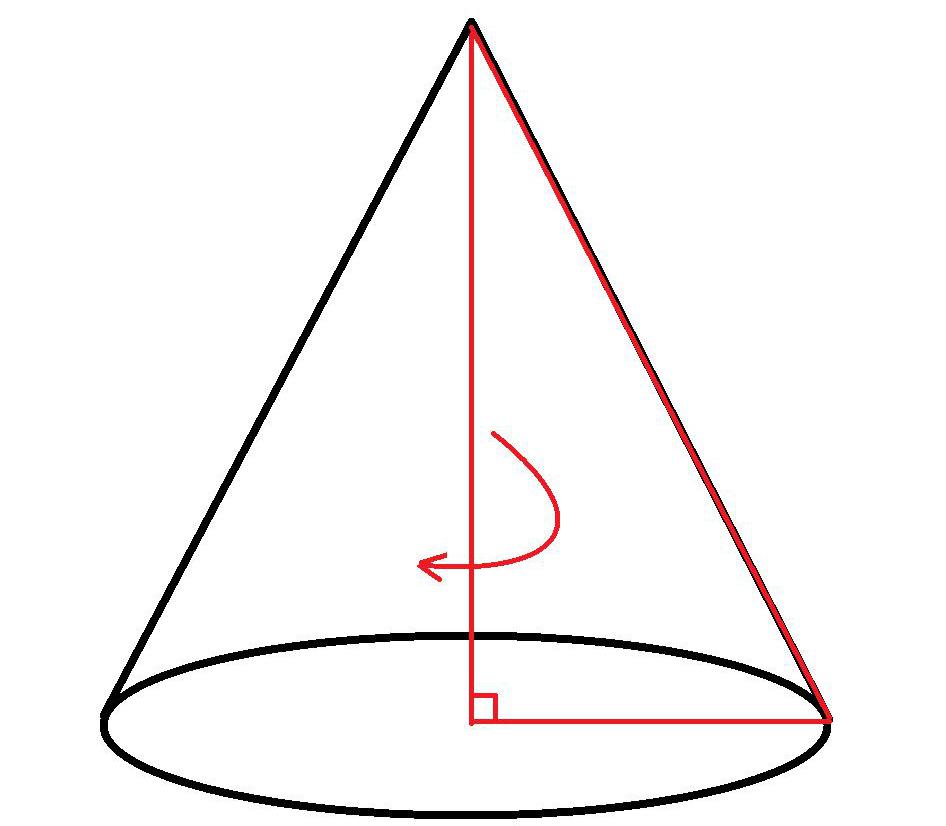
Составляющие конуса

Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.

Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.

Конус состоит из следующих элементов:

Круга, являющегося его основанием.
Боковой поверхности.
Точки, не лежащей в плоскости основания, называющейся вершиной конуса.
Отрезков, которые соединяют точки круга основания геометрического тела и его вершину.

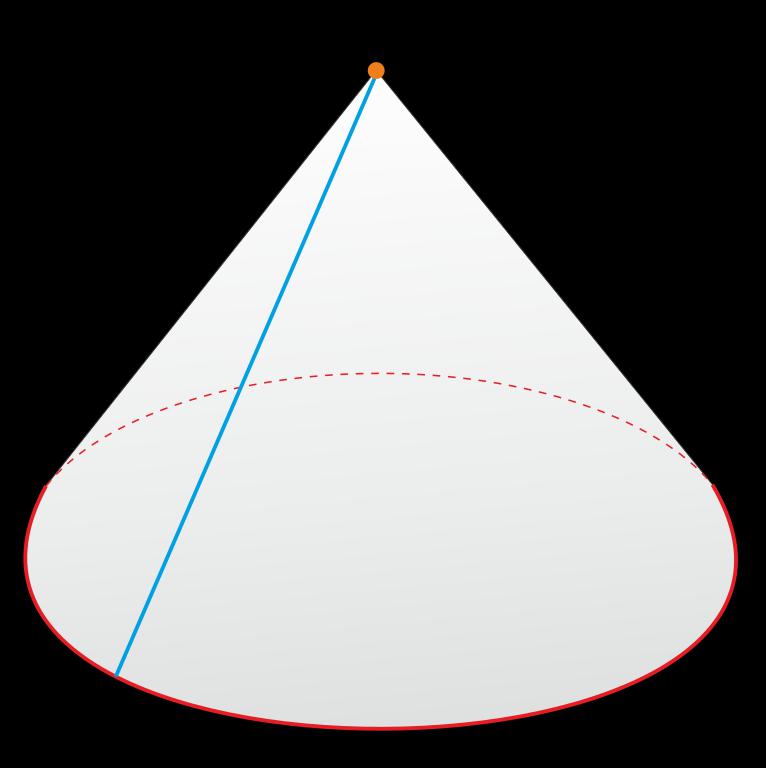
Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.

Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.

Длина образующих в прямом конусе

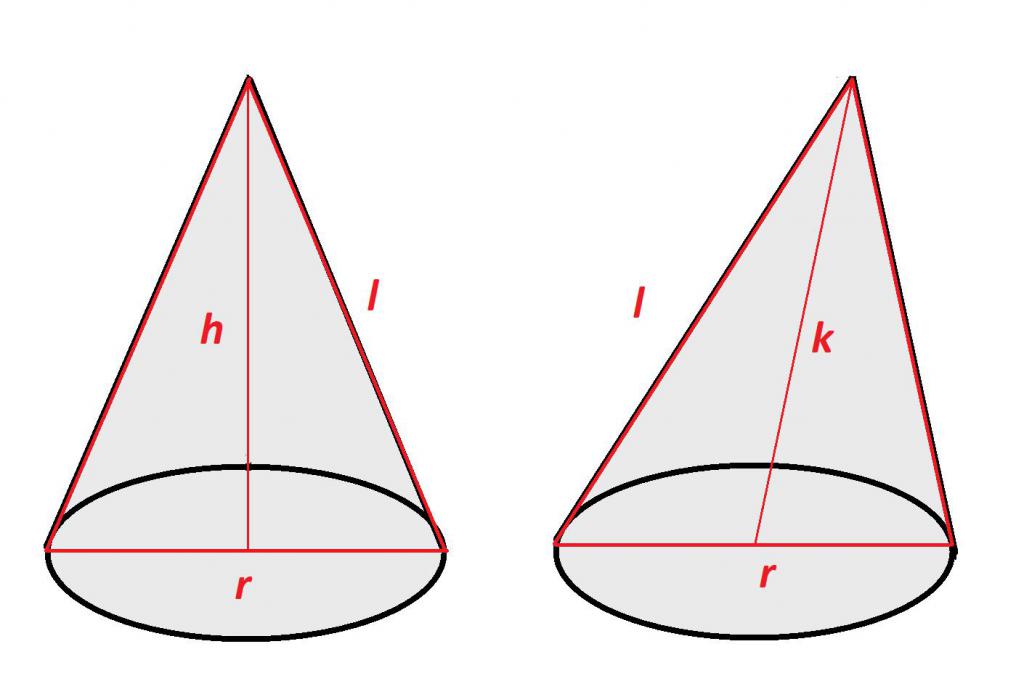
Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.

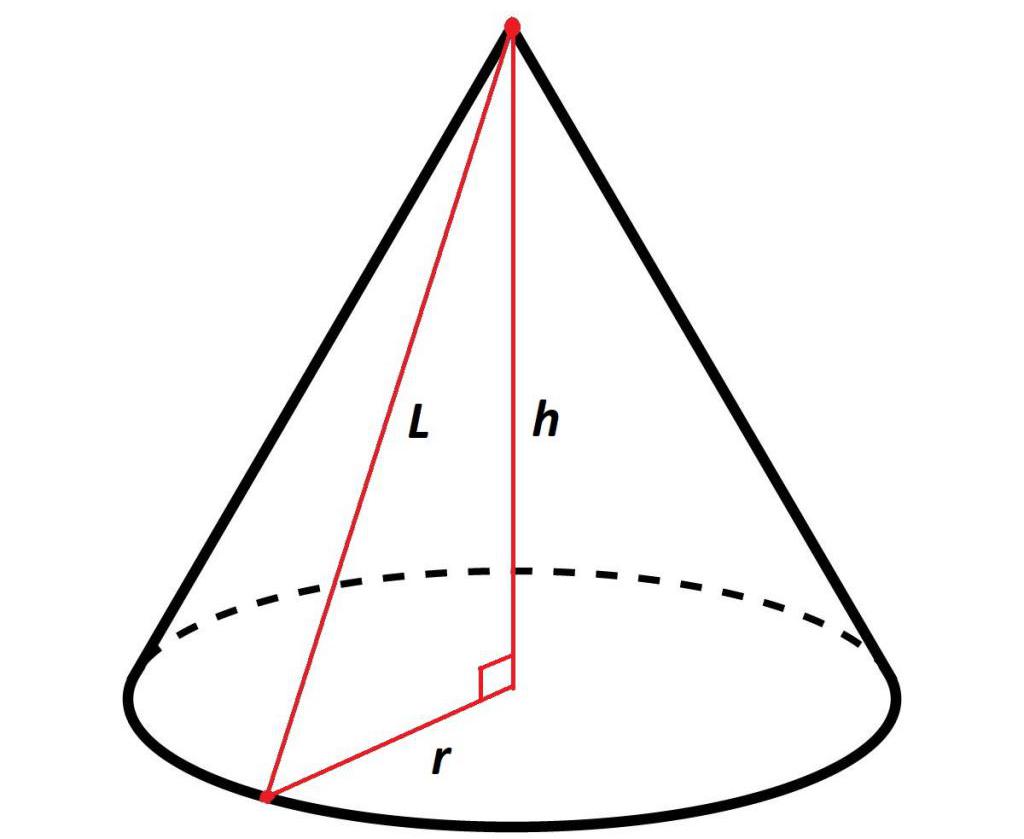
То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:

l²= r²+ h² или l = √r²+ h²

где l – образующая;

r – радиус;

h – высота.

Образующая в наклонном конусе

Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.

Прежде всего необходимо знать высоту, длину оси и радиус основания.

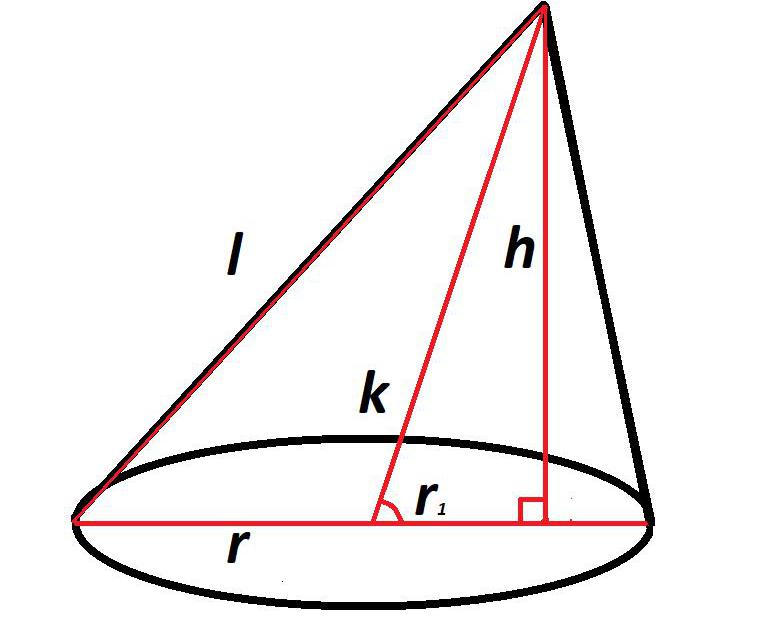
Имея эти данные, можно рассчитать часть радиуса, лежащую между осью и высотой, по формуле из теоремы Пифагора:

r₁= √k²— h²

где r₁ – это часть радиуса между осью и высотой;

k – длина оси;

h – высота.

В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r₁), можно узнать полную сторону прямоугольного треугольника, сформированного образующей конуса, его высотой и частью диаметра:

R = r + r₁

где R – катет треугольника, образованного высотой, образующей и частью диаметра основания;

r – радиус основания;

r₁ – часть радиуса между осью и высотой.

Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:

l = √h²+ R²

или, не производя отдельно расчет R, объединить две формулы в одну:

l = √h² + (r + r₁)².

Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу — использованию теоремы Пифагора.

Сечение конуса

Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.

Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.

Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие — оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.

Площадь сечения

Упомянутое ранее осевое сечение конуса представляет собой треугольник. Исходя из этого, его площадь можно рассчитать по формуле площади треугольника:

S = 1/2 * d * h или S = 1/2 * 2r * h

где S – это площадь сечения;

d – диаметр основания;

r – радиус;

h – высота.

В косом, или наклонном конусе сечение по оси также является треугольником, поэтому в нем площадь сечения рассчитывается аналогично.

Объем

Поскольку конус является объемной фигурой в трехмерном пространстве, то можно вычислить его объем. Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м³. Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.

Как указано ранее, образование прямого конуса происходит вследствие вращения прямоугольного треугольника по одному из его катетов. Наклонный же, или косой конус образуется иначе, поскольку его высота смещена в сторону от центра плоскости основания тела. Тем не менее такие отличия в строении не влияют на методику расчета его объема.

Расчет объема

Формула объема любого конуса выглядит следующим образом:

V = 1/3 * π * h * r²

где V – это объем конуса;

h – высота;

r – радиус;

π — константа, равная 3,14.

Для того чтобы рассчитать обьем конуса, необходимо иметь данные о высоте и радиусе основания тела.

Для расчета высоты тела необходимо знать радиус основания и длину его образующей. Поскольку радиус, высота и образующая объединяются в прямоугольный треугольник, то высоту можно рассчитать по формуле из теоремы Пифагора (a²+ b²= c² или в нашем случае h²+ r²= l², где l – образующая). Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:

a = √c²— b²

То есть высота конуса будет равна величине, полученной после извлечения квадратного корня из разности квадрата длины образующей и квадрата радиуса основания:

h = √l²— r²

Рассчитав таким методом высоту и зная радиус его основания, можно вычислить объем конуса. Образующая при этом играет важную роль, так как служит вспомогательным элементом в расчетах.

Аналогичным образом, если известна высота тела и длина его образующей, можно узнать радиус его основания, извлекая квадратный корень из разности квадрата образующей и квадрата высоты:

r = √l²— h²

После чего по той же формуле, что указана выше, рассчитать объем конуса.

Объем наклонного конуса

Так как формула объема конуса одинакова для всех видов тела вращения, отличие в его расчете составляет поиск высоты.

Для того чтобы узнать высоту наклонного конуса, вводные данные должны включать длину образующей, радиус основания и расстояние между центром основания и местом пересечения высоты тела с плоскостью его основания. Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.

Ответы@Mail.Ru: срочно!!! нужна помащь.

основание и вершина

Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга, — вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Поверхность конуса состоит из основания и боковой поверхности. конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом. Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту. Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конусаВ частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса

Конус — Тела вращения — Большой справочник школьника

Конус

Круговым конусом называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга, — вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называются созидательными конуса.
Конус называется прямым (далее просто «конус»), если прямая, соединяющая вершины конуса с центром основания, перпендикулярна к плоскости основания.

Прямой круговой конус можно рассматривать как тело, образованное в результате вращения прямоугольного треугольника вокруг его катета как оси.
Высота конуса — перпендикуляр, опущенный из его вершины на плоскость основания.
Осью прямого кругового конуса называется прямая, содержащая его высоту.
Обратите внимание на рисунок ниже. Так называемые «контурные образующие» SA и SB являются касательными к эллипсу, который изображает основание конуса, точки A и B не являются концами большой оси эллипса. Сечение конуса плоскостью, проходящей через его вершину — равнобедренный треугольник, у которого боковые стороны являются созидательными конуса, а основой является хорда основания.

Рассмотрим сечение CSD. Он пересекает основание конуса по хорде CD.
Хорду CD видно из центра основания под углом COD, а из вершины конуса — под углом CSD.
Сам сечение — равнобедренный с основанием CD, где — образующие конуса. Его ортогональной проекцией на плоскость основания конуса является равнобедренный с основанием CD и . Отрезок ОК является биссектрисой, медианой, высотой , расстоянием от точки O до хорды CD. Отрезок SK является биссектрисой, медианой, высотой и расстоянием от вершины конуса S до хорды CD. является линейным углом двугранного угла между плоскостью сечения и плоскостью основания. Следовательно, , — углы наклона образующей конуса к его основанию.
Площадь боковой поверхности конуса вычисляется по формуле , где Sосн — площадь основания, — угол наклона образующей конуса к его основанию.
Конус | Социальная сеть работников образования
Слайд 1
К о н у с
Слайд 2
Наглядно прямой круговой конус можно представить себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси.
Слайд 3
Конус – это тело, которое состоит из круга. Круг является основанием конуса . Вершиной конуса – являются точки не лежащие в плоскости этого круга и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса . Прямой конус – если прямая, соединяющая вершину конуса с центром основания, перпендикулярно плоскости основания. Высота конуса – перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Ось прямого кругового конуса – это прямая, содержащая его высоту.
Слайд 4
Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен r , его высота – h , а расстояние между прямой АВ и осью цилиндра равно d . Найдите h , если r = 10 дм, d = 8 дм, АВ = 13 дм. ЗАДАЧА Дано: Цилиндр, r = 10 дм – радиус основания, d = 8 дм – расстояние от ОО1 до АВ, АВ = 13 дм, h – высота. Найти: h . А 1 О О 1 В 1 K Решение: Построим секущую плоскость ВВ 1 АА 1 , параллельную оси цилиндра, в которой лежит прямая АВ. Получили прямоугольник с диагональю АВ. ВВ 1 АА 1 ║ОО 1 . ВВ 1 = АА 1 = h . ВАВ 1 – прямоугольный. По теореме Пифагора: ВВ 1 = √ АВ ² — АВ 1 ² Найдем АВ 1 : ∆ОАВ1 – равнобедренный (ОА = ОВ1 = r ). ОК = d т. к. ОК ┴ АВ1 (высота ∆ ОАВ1 ), то ОК – медиана (К – середина отрезка АВ1). ∆АОК – прямоугольный, по теореме Пифагора: КА = √ ОА ² — ОК ² , КА = √ 10 ² — 8 ² = 6 дм АВ1 = 2 · КА = 6 · 2 = 12 дм ВВ1 = √ 13 ² — 12 ² = √ (13 — 12)(13 + 12) = 5 дм, h = ВВ1 = 5 дм.
Слайд 5
Дано: цилиндр ABCD – сечение, квадрат дуга AD — 90 ° R = 4 см Найти: S ABCD Решение: S ABCD = AB · BC = BC 2 , т.к. ABCD – квадрат ВОС – прямоугольный, т.к. дуга AD — 90 ° ВОС = 90 ° ОС = ОВ = 4 (см), т.к. ОС и ОВ – радиусы основания ВС = ОВ 2 + ОС 2 = 4 2 + 4 2 = 32 = 4 2 (см) S ABCD = (4 2) 2 = 32 (см 2 ) Ответ: 32 см 2
Тела и поверхности вращения — урок. Геометрия, 9 класс.
Цилиндр можно получить вращением прямоугольника AA1O1O вокруг одной из его сторон OO1 или прямоугольника AA1B1B вокруг прямой OO1, которая проходит через серединные точки противолежащих сторон.

Прямая OO1 называется осью цилиндра, AA1 и BB1 — образующими.

Высота \(H\) цилиндра совпадает с любым из отрезков OO1 \(=\) AA1 \(=\) BB1.

Два круга, которые образовались при вращении, называют основаниями цилиндра.

Радиусом \(R\) \(=\) \(OA\) \(=\) \(OB\) цилиндра называется радиус его основания.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевым сечением цилиндра (прямого кругового цилиндра) является прямоугольник, на данном рисунке — прямоугольник AA1B1B.

Развёртка боковой поверхности цилиндра — тоже прямоугольник.

Боковая поверхность прямого кругового цилиндра равна произведению длины окружности основания на высоту:
Sбок.=2πRH.

Полная поверхность цилиндра вычисляется по формуле:
S=Sбок.+2Sосн.=2πRH+2πR2.

Для объёма прямого кругового цилиндра верно:
V=πR2H.
Конус можно получить вращением прямоугольного треугольника \(POA\) вокруг одного из его катетов \(PO\) или равнобедренного треугольника \(APB\) вокруг прямой \(PO\), проходящей через вершину \(P\) и середину \(O\) основания треугольника.

Осью прямого кругового конуса называется прямая \(PO\), содержащая его высоту \(H\).

Осевое сечение конуса, проходящее через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны \(PA\) и \(PB\) являются образующими \(l\) конуса.

Радиус конуса \(R\) \(=\) \(OA\) \(=\) \(OB\) — это радиус основания.

Развёртка боковой поверхности конуса представляет собой круговой сектор.

Радиус этого сектора равен образующей конуса, то есть равен \(l\), а длина дуги сектора равна длине окружности основания конуса, то есть равна \(2πr\).

Площадь боковой поверхности конуса определяется как площадь данного кругового сектора:
Sбок.=πl2⋅α°360°.

Если рассмотреть длину окружности основания конуса как длину дуги кругового сектора, получаем:
2πR=2πl⋅α°360°;2πR=πl⋅α°180°;α°=2πR⋅180°πl=R⋅360°l;Sбок.=πl2⋅α°360°=πl2⋅R⋅360°360°⋅l=πRl.

Sбок.=πRl — ещё одна формула для определения боковой поверхности конуса.

Полная поверхность конуса:
S=Sбок.+Sосн.=πRl+πR2.

Объём конуса находим по формуле:
V=13πR2H.
Шар и поверхность шара — сфера
Сфера получается при вращении полукруга или круга вокруг его диаметра \(AB\) как оси.

Граница шара называется шаровой поверхностью, или сферой.

Таким образом, точками сферы являются все точки шара, которые удалены от центра \(O\) на расстояние, равное радиусу \(R\).

Любой отрезок, такой как \(OA\), \(OB\) и \(OC\) или другие, соединяющие центр шара с точкой шаровой поверхности, также называется радиусом.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром, как \(AB\) на рисунке. Концы любого диаметра называются диаметрально противоположными точками шара.

Сечение шара плоскостью, проходящей через его центр, называется большим кругом, а сечение сферы — большой окружностью.
Поверхность сферы:
S=4πR2.

Объём шара:
V=43πR3.
Тест по математике для 11 класса » Конус»
Тест по математике для 10-11 классов
«Конус».

Тест – одна из самых популярных форм контроля знаний учащихся.
Он помогает учителю за сравнительно короткий промежуток времени определить уровень усвоения материала учащимися и корректировки процесса обучения в соответствии с требованиями образовательных стандартов.
Ученик получает возможность провести самоконтроль знаний.
Задания данного теста предназначены для проверки уровня знаний, умений и навыков по теме: «Конус».
Задания данного теста соответствуют теории в пределах учебного материала за 10-11 классы.
Тест позволяют оценить степень и качество усвоения материала по теме «Конус» и может помочь выпускникам при подготовке к ЕГЭ в 11 классе.
Тест может быть использован на уроке для фронтальной работы и работы в парах, самоконтроля.
В тесте представлены основные теоретические сведения, двадцать три задача и ответы к ним.
Тест разделён на три блока.
Все задачи средней степени сложности.
Для их решения требуется хорошо знать формулы по теме « Конус», теорему Пифагора, формулы площадей круга и треугольника.

Тщательной проработки эти задания требуют только со слабыми учениками.
Задачи теста сформированы из заданий, взятых из официальных источников:
— ЕГЭ портал 4ege.ru,
— http://math.reshuege.ru/ образовательный портал для подготовки к экзаменам Дмитрия Гущина ,
— тренировочные варианты от А.А. Ларина.
Конус.
Основные теоретические сведения.
Конус — это тело, получающееся при вращении прямоугольного треугольника вокруг одного из своих катетов.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.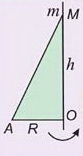

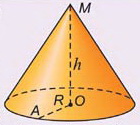
Полная поверхность конуса состоит из основания и боковой поверхности
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания.
У прямого конуса основание высоты совпадает с центром основания.
Осью прямого конуса называется прямая, содержащая его высоту.
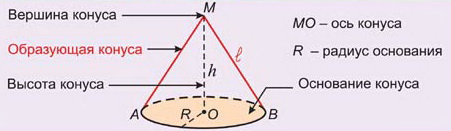
Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением.
Возможны четыре основных типа конических сечений: эллипс, парабола, круг, равнобедренный треугольник.
Площадь осевого сечения конуса
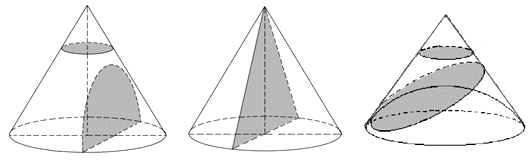
Осевое сечение — равнобедренный треугольник, с основания 2R и высотой h, где R — радиус основания, h — высота конуса.
Sосев = Rh.
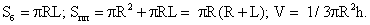
R — радиус основания, L — образующая, h — высота конуса.

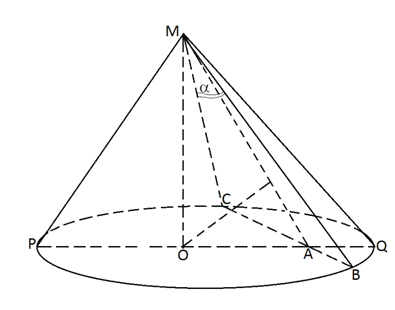
МР = МС = МВ = МQ – образующие.
РМQ и МСВ — равнобедренные треугольники.
Прямые РQ и СВ – взаимно перпендикулярны.
Тест «Конус».
1.

Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30. В ответе укажите .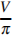
2.
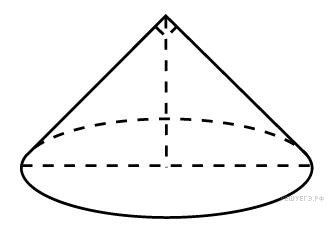
Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.
3

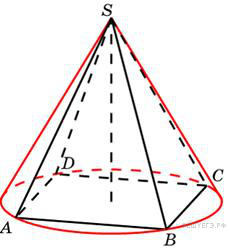
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на .
4

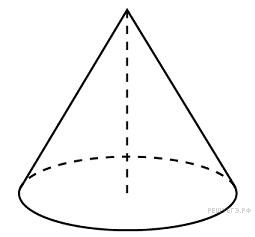
Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на .
5
Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на .
6

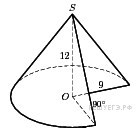
Найдите объем 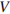 части конуса, изображенной на рисунке. В ответе укажите .
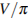7
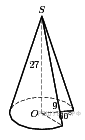
Найдите объем 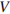 части конуса, изображенной на рисунке. В ответе укажите .
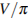Тест «Конус».
8
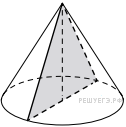
Площадь основания конуса равна 16π, высота — 6. Найдите площадь осевого сечения конуса.
9
Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
10
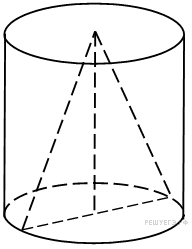
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 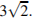Найдите площадь боковой поверхности конуса.
11
Во сколько раз уменьшится объём конуса, если его высоту уменьшить в 8 раз, а радиус основания оставить прежним?
12
Высота конуса равна 4, а диаметр основания равен 6. Найдите образующую конуса.
13
Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на .
14.
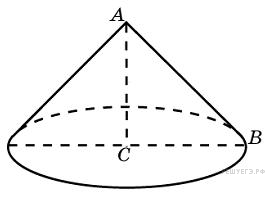
Конус получается при вращении равнобедренного прямоугольного треугольника 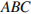 вокруг катета, равного 6. Найдите его объем, деленный на .
15
Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
Тест «Конус».
16.
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
17
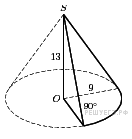
Найдите объем 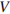 части конуса, изображенной на рисунке. В ответе укажите .
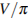18
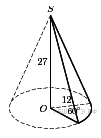
Найдите объем 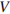 части конуса, изображенной на рисунке. В ответе укажите .
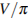19
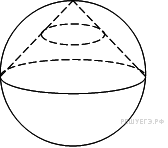
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
20
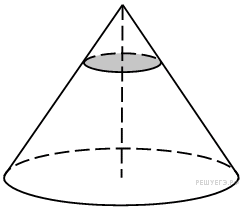
Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
21
Диаметр основания конуса равен 12, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
22
Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 5 раз, а радиус основания оставить прежним?
23
Высота конуса равна 12, а диаметр основания равен 10. Найдите образующую конуса.
Ответы «Конус».
1
2
3
4
5
6
7
1
9
16
144
24
243
607,5
8
9
10
11
12
13
14
15
24
48
3
8
5
128
72
3
16
17
18
19
20
21
22
23
60
87,75
216
7
2
48
5
13
5.4.2 Конус. Основание, высота, боковая поверхность, образующая, развертка
Видеоурок: Конус. Свойства конуса. Сечения конуса. Усеченный конус
Лекция: Конус. Основание, высота, боковая поверхность, образующая, развертка
Конус – это тело, которой состоит из окружности, которая находится в основании, из точки равноудаленной от всех точек на окружности, а также от прямых, соединяющих эту точку (вершину) со всеми точками, лежащими на окружности.
Несколькими вопросами ранее, мы рассматривали пирамиду. Так вот конус – это частный случай пирамиды, в основании которой лежит окружность. Практически все свойства пирамиды подходят и для конуса.
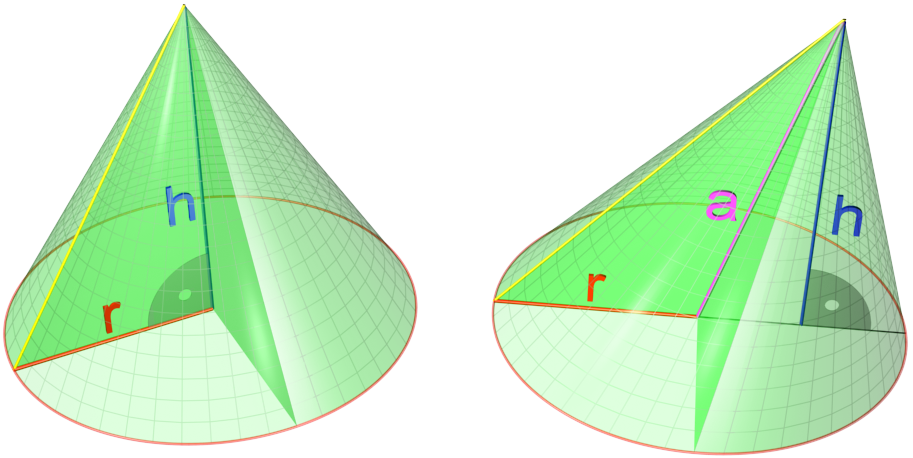
Каким образом можно получить конус? Вспомните прошлый вопрос и то, как мы получили цилиндр. Теперь возьмите равнобедренный треугольник и крутите его вокруг своей оси – Вы получите конус.

Образующие конуса – это отрезки, заключенные между точками окружности и вершиной конуса. Образующие конуса равны между собой.
Чтобы найти длину образующей, следует воспользоваться формулой:
Если все образующие соединить между собой, можно получить боковую поверхность конуса. Общая его поверхность состоит из боковой поверхности и основания в виде окружности.

Конус имеет высоту. Чтобы ее получить, достаточно опустить перпендикуляр из вершины, непосредственно, в центр основания.
Чтобы найти площадь боковой поверхности, следует воспользоваться формулой:
Для нахождения полной площади поверхности конуса воспользуйтесь следующей формулой:
Формула объема конуса похожа на объем цилиндра, но разделенная на «3»: