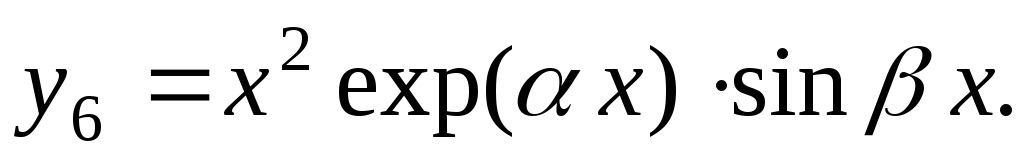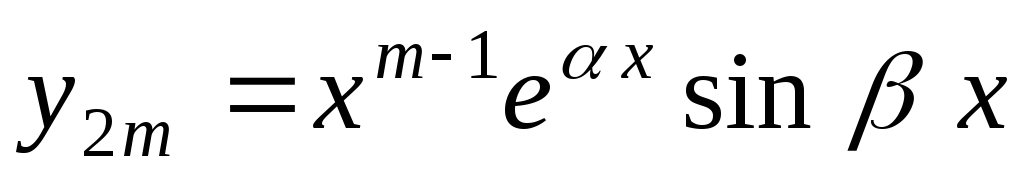1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
Уравнения, связывающие независимую переменную, неизвестную функцию и её производные называют дифференциальным. Если искомая функция зависит от одной переменной, то Д.У. называют обыкновенным.
Если искомая функция зависит от нескольких переменных, то Д.У. называют уравнение частных производных.
Наивысший
порядок производной, входящий в Д.У.
называют порядком этого уравнения. Д.У.
первого порядка называют выражение
вида F(x,y,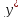 )=0(1).
Если это уравнение удаётся разрешить
относительно производной, то записывают
)=0(1).
Если это уравнение удаётся разрешить
относительно производной, то записывают 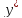 =
f(x,y)(2).
Решением уравнения (1) и (2) называют такую дифференцируемую функцию
y=
=
f(x,y)(2).
Решением уравнения (1) и (2) называют такую дифференцируемую функцию
y=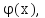
Задачей
Коши либо начальной задачей называют
задачу нахождения решения y=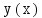 уравнения(2), удовлетворяющего
начальному условию y(xo)=yo (3).
уравнения(2), удовлетворяющего
начальному условию y(xo)=yo (3).
Общим
решением Д.У. (2) называется
функция y=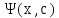 (4),
зависящая от переменной x и произвольной
постоянной c. Общее решение (4) удовлетворяет
условию уравнения (2) при
любых значениях константы с.
(4),
зависящая от переменной x и произвольной
постоянной c. Общее решение (4) удовлетворяет
условию уравнения (2) при
любых значениях константы с.
Каково
бы ни было начальное условие (3) можно
подобрать значение со константы с, так
чтобы функция y=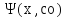 удовлетворяла заданному начальному
условию (3)(если
выполнены условия теоремы Коши).
удовлетворяла заданному начальному
условию (3)(если
выполнены условия теоремы Коши).
Частным решением Д.У. называют решение, полученное из общего решения (4) либо вида (4) при каком либо определённом значении постоянной произвольной с.
2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
Теорема
Коши (существования и единственности):
если функция f(x,y) непрерывна и имеет
непрерывную производную 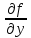 в областиD,
то решение Д.У.
в областиD,
то решение Д.У.  =
f(x,y) с начальным условием y(xo)=yo
, где точка с координатами (xo,yo) принадлежит
D, существует и единственно, то есть
через точку (xo,yo) принадлежащую области
D проходит единственная интегральная
кривая данного уравнения.
=
f(x,y) с начальным условием y(xo)=yo
, где точка с координатами (xo,yo) принадлежит
D, существует и единственно, то есть
через точку (xo,yo) принадлежащую области
D проходит единственная интегральная
кривая данного уравнения.
Если
во всех точках решения y = Ψ(x)
уравнения 
3.ДУ 1-го порядка,интегрируемые в квадратурах.
1.Ур-ия с разделяющимися переменними
P(xy)dx+Q(xy)dy=0 (1). Ур-е(1) наз. ур-ем,записанным в диф-лах.,где x-аргумент,y-искомая ф-я, dx,dy-диф-лы, P(xy), Q(xy)-заданные непрерывные в некот.области D ф-ии.
Пусть
P(xy)=p(x),а
Q(xy)=q(y),тогда
(1) примет вид (2): p(x)dx+q(y)dy=0.
(2)наз.ДУ с разделёнными переменнымы,
интегрируя которое мы получим: +
+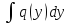 =C-общий
ин-л у-я(2). Если хотя бы один из интегралов
неберущ.,то ДУ(2) всё равно считается
решённым, при этом говорят, что решение
найдено в квадратурах.Пусть P(xy)=
=C-общий
ин-л у-я(2). Если хотя бы один из интегралов
неберущ.,то ДУ(2) всё равно считается
решённым, при этом говорят, что решение
найдено в квадратурах.Пусть P(xy)=
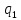 (y),
Q(xy)=
(y),
Q(xy)= (x)*
(x)*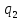 (y),
тогда (1) примет вид(3):
(y),
тогда (1) примет вид(3):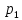 (x)*
(x)*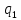 (y)dx+
(y)dx+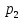 (x)*
(x)* (y)dy=0.У-е
(3)-ДУ с разделяющимися переменными.Разделив
(3) на
(y)dy=0.У-е
(3)-ДУ с разделяющимися переменными.Разделив
(3) на 
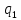 (y)
получаем:
(y)
получаем: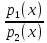 dx+
dx+ dy=0,которое
является ур-ем с разделёнными переменными:
dy=0,которое
является ур-ем с разделёнными переменными: 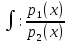 dx+
dx+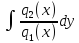 =C.
При таком решении могут быть потеряны
корни
=C.
При таком решении могут быть потеряны
корни 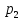 (x)=0
и
(x)=0
и  (y)=0,которые
необходимо рассматривать отдельно.
(y)=0,которые
необходимо рассматривать отдельно.Общее решение дифференциального уравнения — Википедия
Материал из Википедии — свободной энциклопедии
Общее решение дифференциального уравнения
— функция наиболее общего вида, которая при подстановке в дифференциальное уравнение видаF(x,y,y′,y″,…,y(n))=0,{\displaystyle F(x,\;y,\;y’,\;y»,\;\ldots ,\;y^{(n)})=0,}
обращает его в тождество.
Если каждое решение дифференциального уравнения представимо в виде:
y=φ(x,C10,C20,…,Cn0),{\displaystyle y=\varphi (x,\;C_{1}^{0},\;C_{2}^{0},\;\ldots ,\;C_{n}^{0}),}
где C10,C20,…,Cn0{\displaystyle C_{1}^{0},\;\;C_{2}^{0},\;\;\ldots ,\;\;C_{n}^{0}} — конкретные числа, то функция вида
y=φ(x,C1,C2,…,Cn){\displaystyle y=\varphi (x,\;C_{1},\;C_{2},\;\ldots ,\;C_{n})}
при всех допустимых значениях параметров (произвольных констант) C1,C2,…,Cn{\displaystyle C_{1},\;\;C_{2},\;\;\ldots ,\;\;C_{n}} называется общим решением дифференциального уравнения.
§ 2. Дифференциальные уравнения второго порядка
Линейное
однородное дифференциальное уравнение
второго порядка с постоянными
коэффициентами  имеет общее решение
имеет общее решение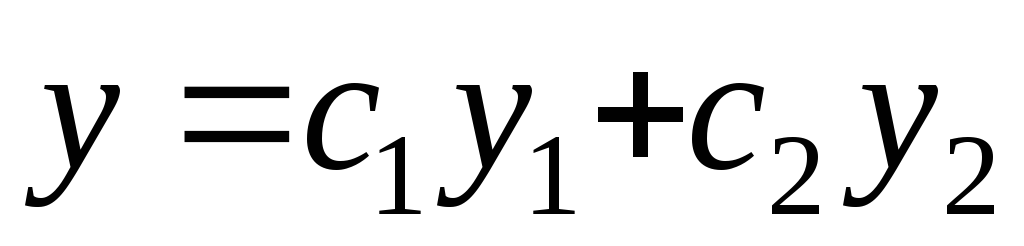 ,
где
,
где и
и линейно-независимые частные решения
этого уравнения.
линейно-независимые частные решения
этого уравнения.
Общий вид решений
однородного дифференциального уравнения
второго порядка с постоянными
коэффициентами  ,
зависит от корней характеристического
уравнения
,
зависит от корней характеристического
уравнения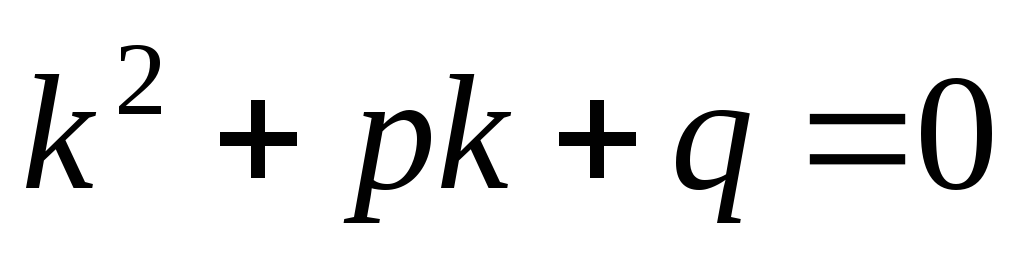 .
.
Корни характеристического уравнения | Вид общего решения |
Корни |
|
Корни действительные и одинаковые |
|
Корни
комплексные |
|
Пример
Найти общее решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
1) 
Решение: Составим
характеристическое уравнение:  .
.
Решив его, найдем
корни 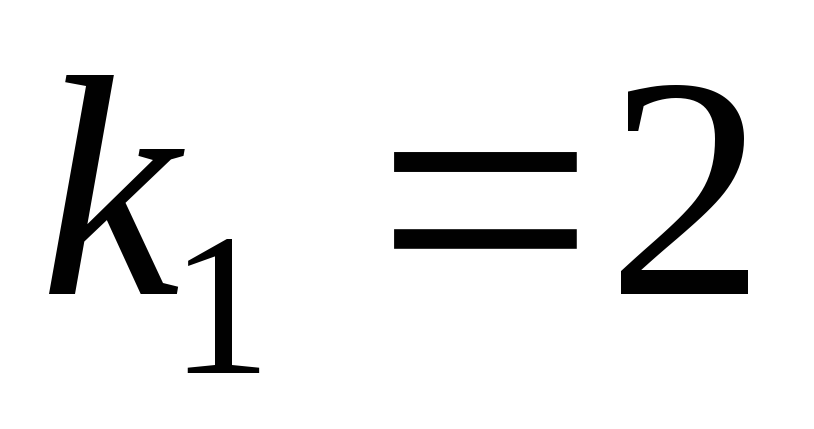 ,
, действительные и различные. Следовательно,
общее решение имеет вид:
действительные и различные. Следовательно,
общее решение имеет вид: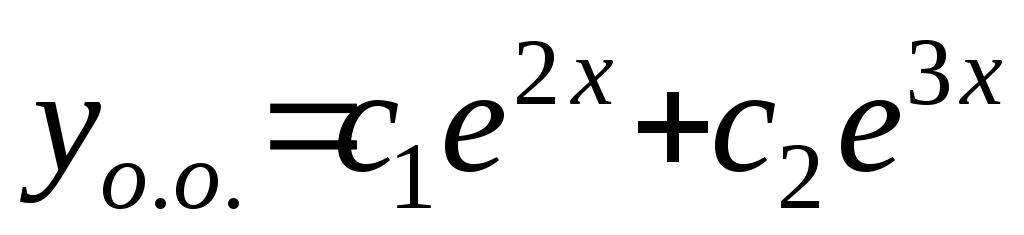 .
.
2) 
Решение: Составим
характеристическое уравнение: 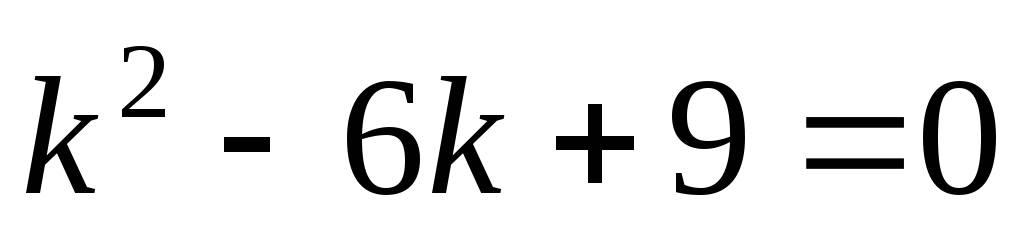 .
.
Решив его, найдем
корни 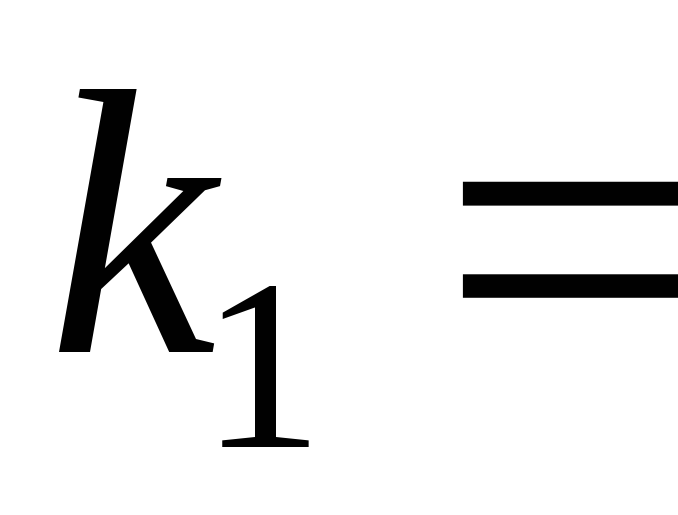
 действительные и одинаковые. Следовательно,
общее решение имеет вид:
действительные и одинаковые. Следовательно,
общее решение имеет вид: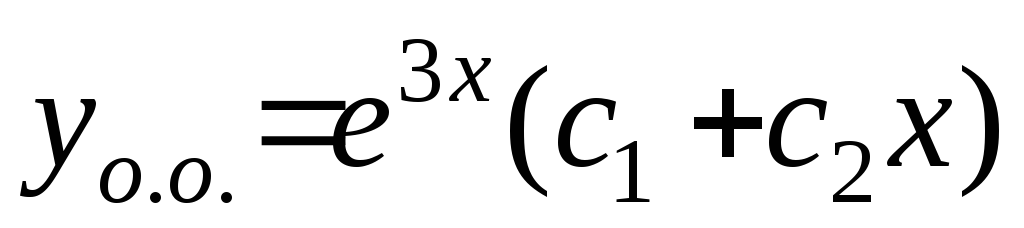 .
.
3) 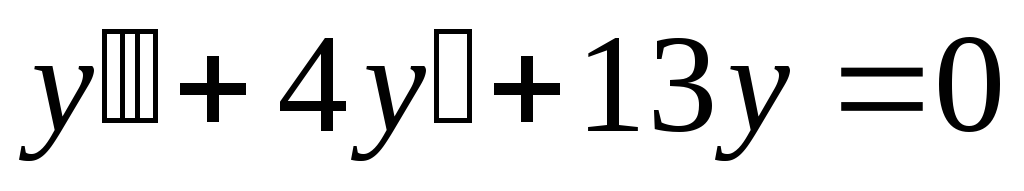
Решение: Составим
характеристическое уравнение: 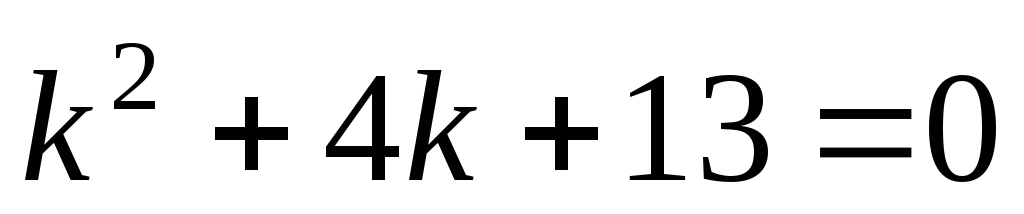 .
.
Решив его, найдем
корни 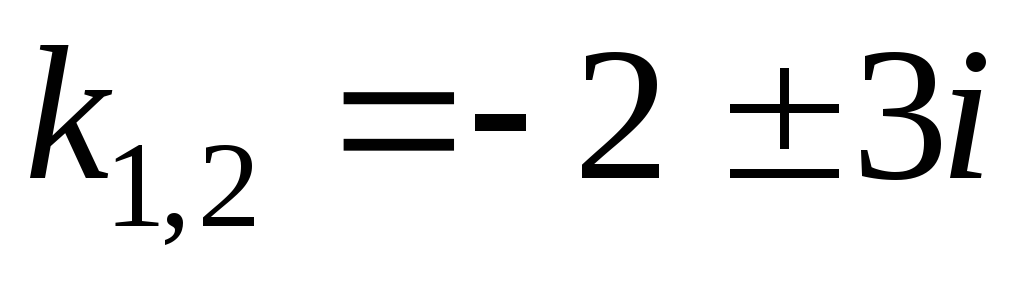 комплексные. Следовательно, общее
решение имеет вид:
комплексные. Следовательно, общее
решение имеет вид: .
.
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид
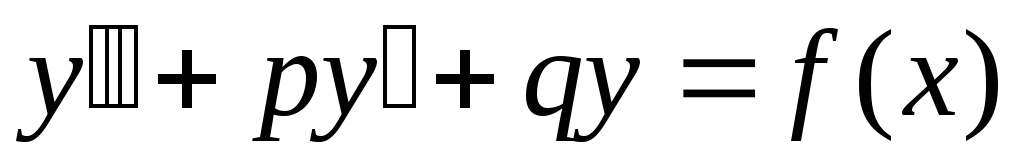 ,
где
,
где  . (1)
. (1)
Общее решение
линейного неоднородного дифференциального
уравнения второго порядка 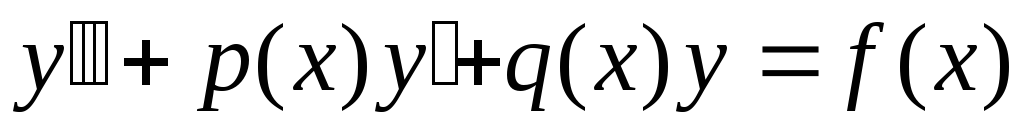 имеет вид
имеет вид ,
где
,
где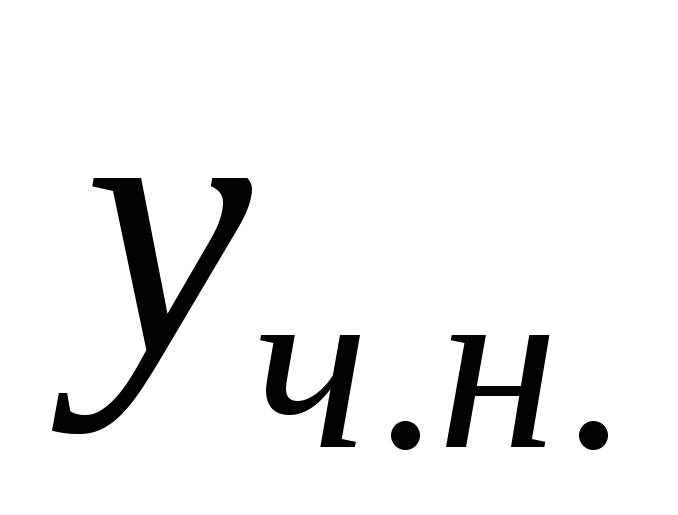 – частное решение этого уравнения,
– частное решение этого уравнения, – общее решение соответствующего
однородного уравнения, т.е. уравнения
– общее решение соответствующего
однородного уравнения, т.е. уравнения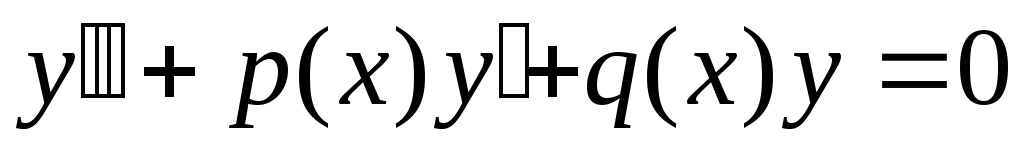 .
.
Вид частного
решения 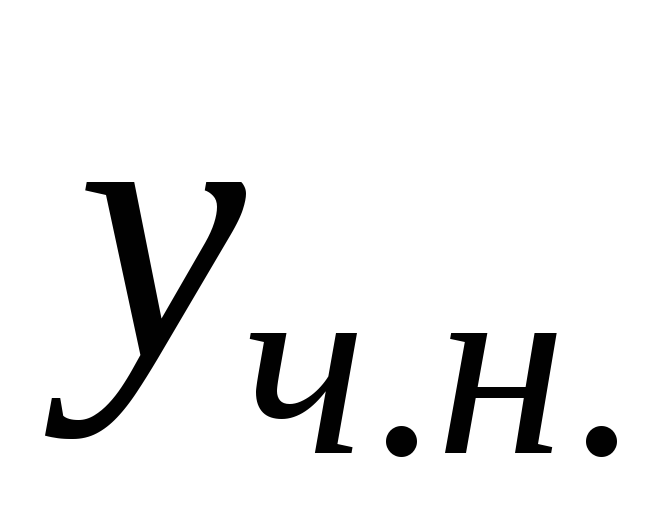 неоднородного уравнения (1) в зависимости
от правой части
неоднородного уравнения (1) в зависимости
от правой части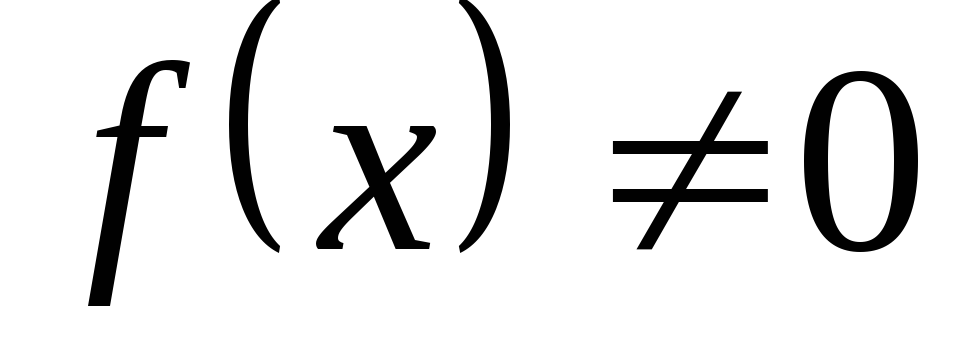 :
:
Рассмотрим различные
виды правых частей линейного неоднородного
дифференциального уравнения 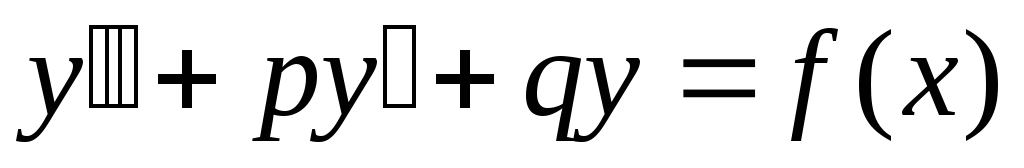 :
:
1. Пусть правая часть имеет вид 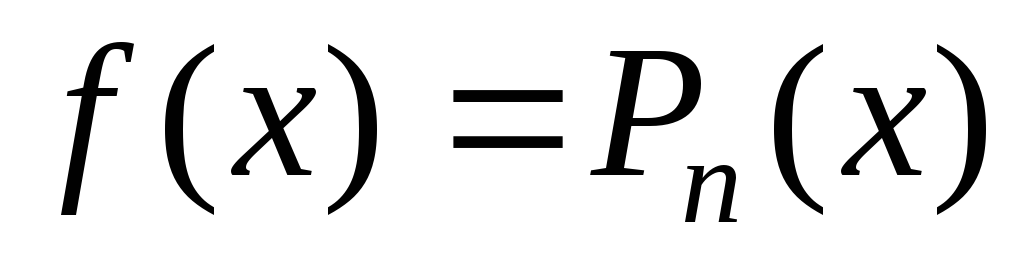 ,
где
,
где – многочлен степени
– многочлен степени .
Тогда частное решениеможно искать в виде
.
Тогда частное решениеможно искать в виде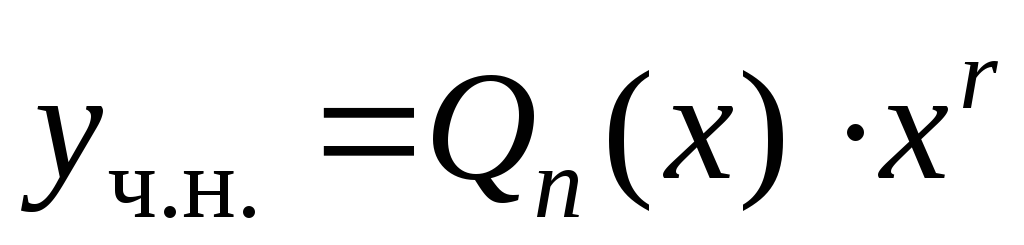
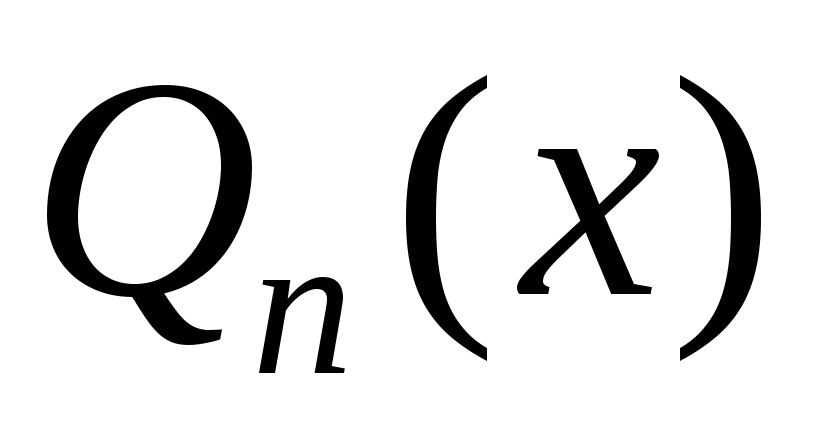 – многочлен той же степени, что и
– многочлен той же степени, что и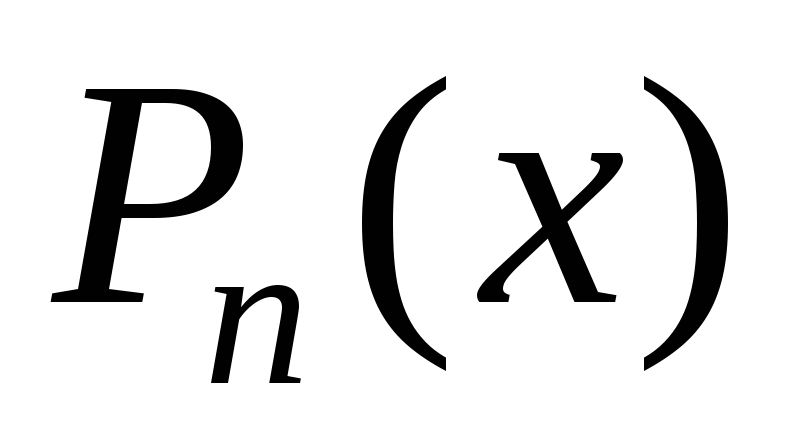 ,
а
,
а – число корней характеристического
уравнения, равных нулю.
– число корней характеристического
уравнения, равных нулю.Пример
Найти общее решение 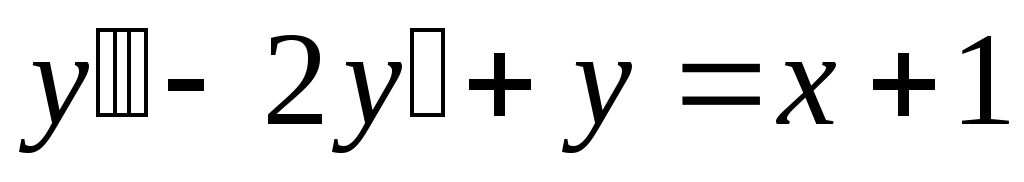 .
.
Решение:
А) Найдем общее
решение соответствующего однородного
уравнения 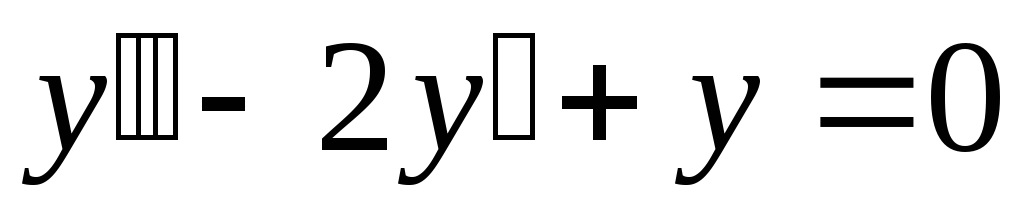 .
Для этого запишем характеристическое
уравнение
.
Для этого запишем характеристическое
уравнение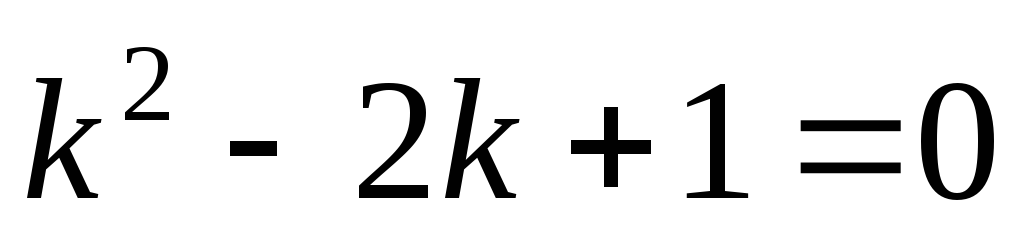
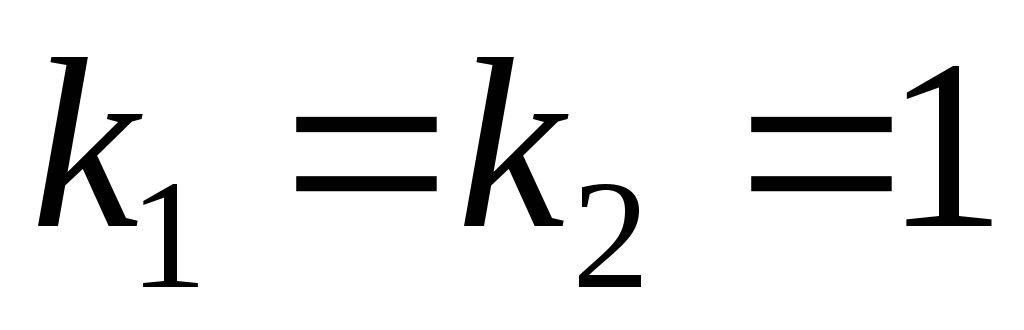 .
Следовательно, общее решение однородного
уравнения имеет вид
.
Следовательно, общее решение однородного
уравнения имеет вид .
. Б) Так как правая
часть уравнения является многочленом
первой степени и ни один из корней
характеристического уравнения 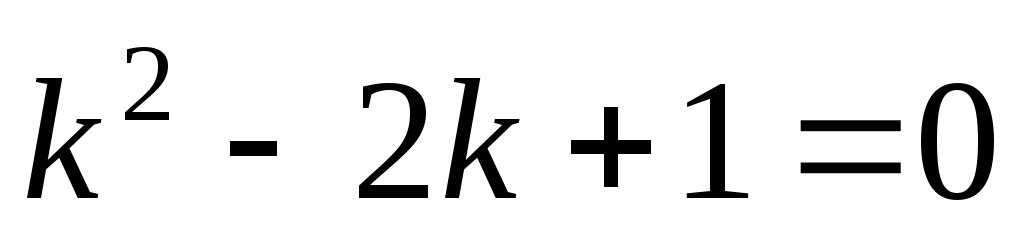 не равен нулю (
не равен нулю (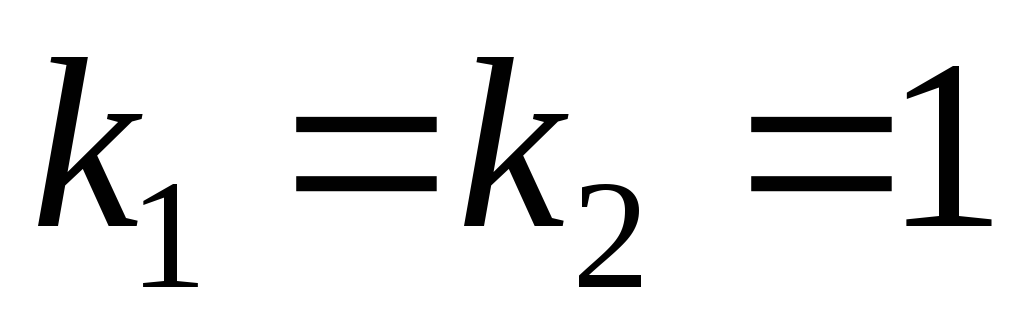 ),
то частное решение ищем в виде
),
то частное решение ищем в виде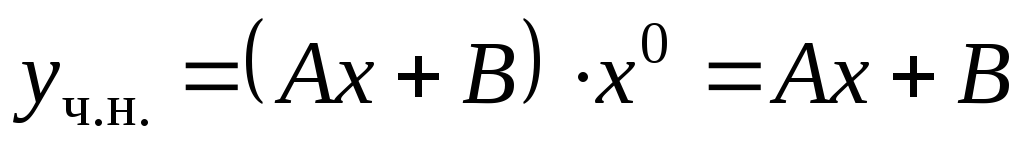 ,
где
,
где и
и – неизвестные коэффициенты. Дифференцируя
дважды
– неизвестные коэффициенты. Дифференцируя
дважды
 ,
, и
и в исходное уравнение, находим
в исходное уравнение, находим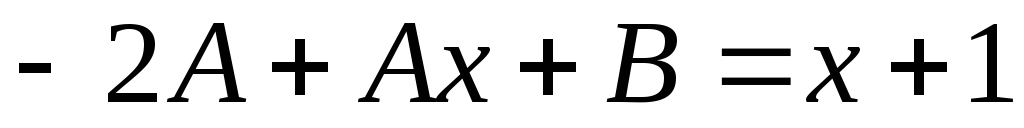 .
. Приравнивая
коэффициенты при одинаковых степенях 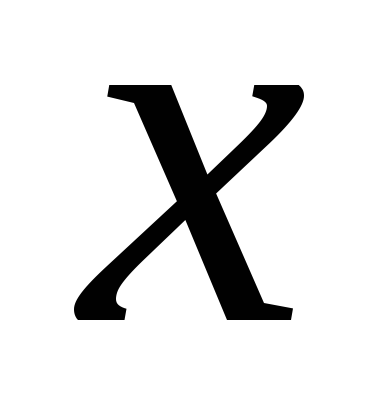 в обеих частях равенства
в обеих частях равенства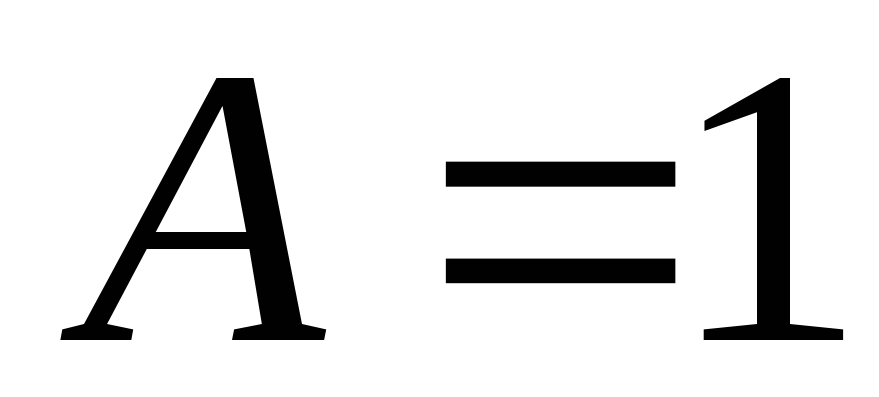 ,
,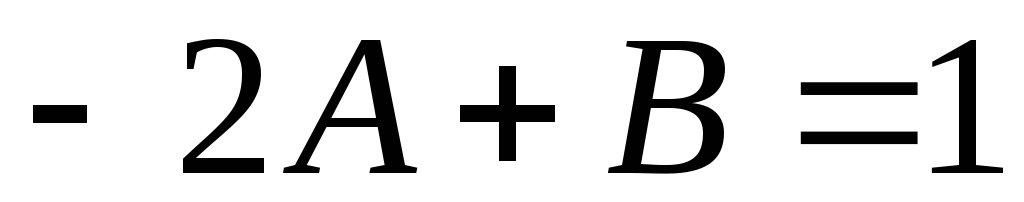 ,
находим
,
находим ,
,
 ,
а его общее решение
,
а его общее решение .
. 2. Пусть правая часть имеет вид 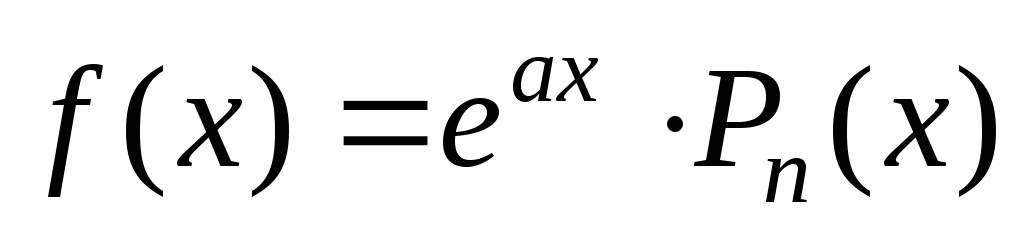 ,
где
,
где – многочлен степени
– многочлен степени .
Тогда частное решение
.
Тогда частное решение можно искать в виде
можно искать в виде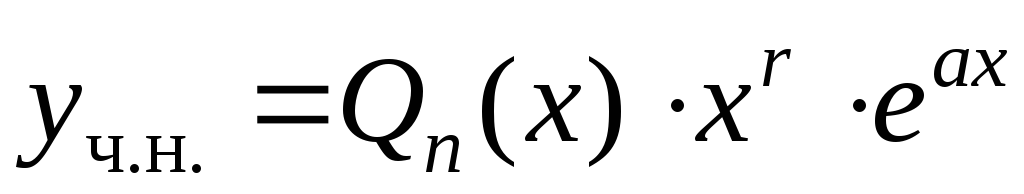 ,
где
,
где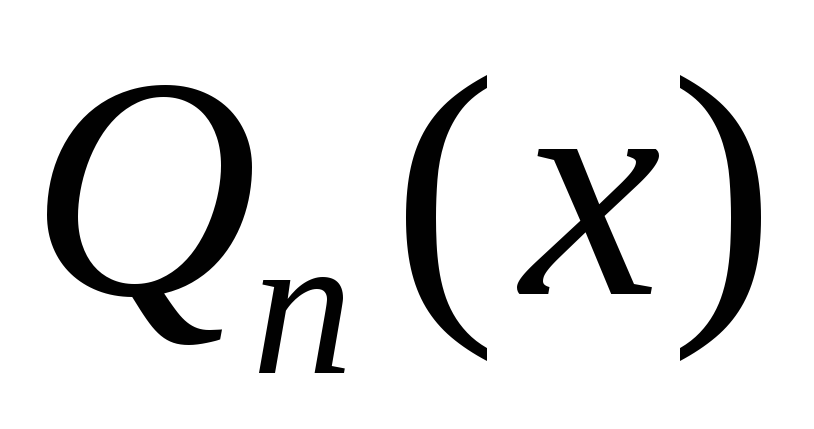
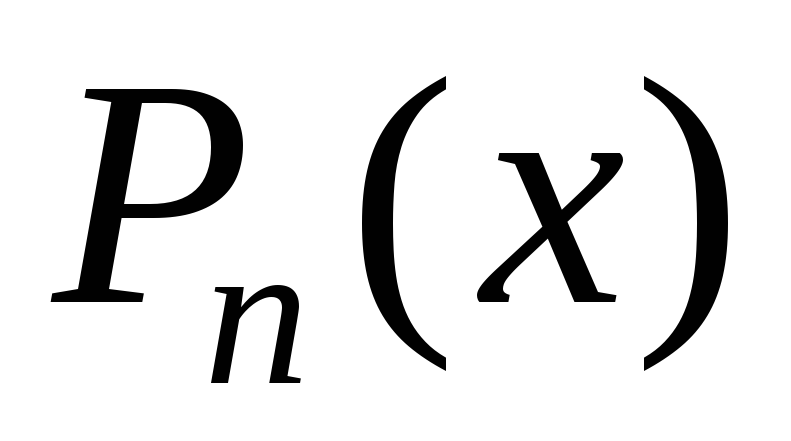 ,
а
,
а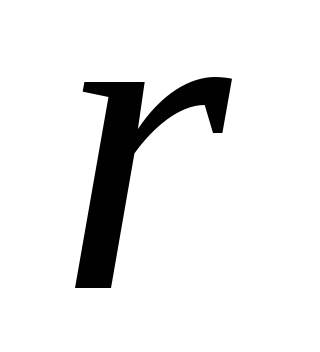 – число, показывающее, сколько раз
– число, показывающее, сколько раз является корнем характеристического
уравнения.
является корнем характеристического
уравнения.Пример
Найти общее решение 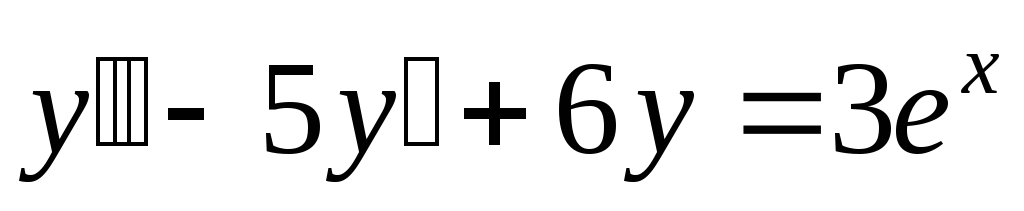 .
.
Решение:
А) Найдем общее
решение соответствующего однородного
уравнения 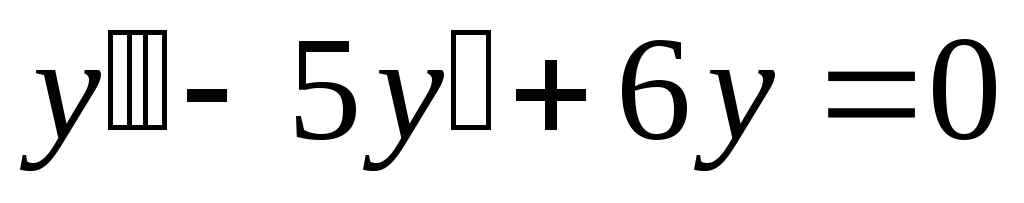 .
Для этого запишем характеристическое
уравнение
.
Для этого запишем характеристическое
уравнение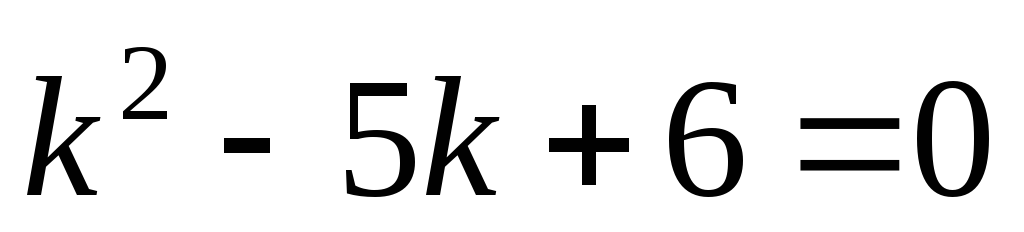 .
Найдем корни последнего уравнения
.
Найдем корни последнего уравнения .
Следовательно, общее решение однородного
уравнения имеет вид
.
Следовательно, общее решение однородного
уравнения имеет вид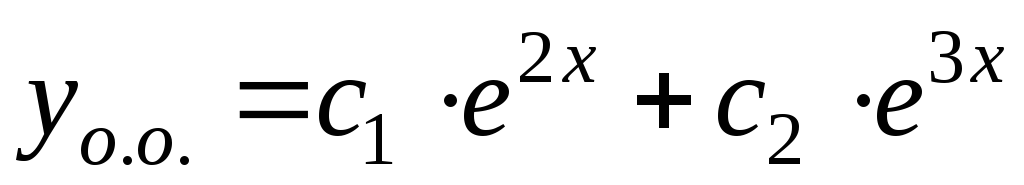 .
.
Б) Так как правая
часть уравнения есть функция 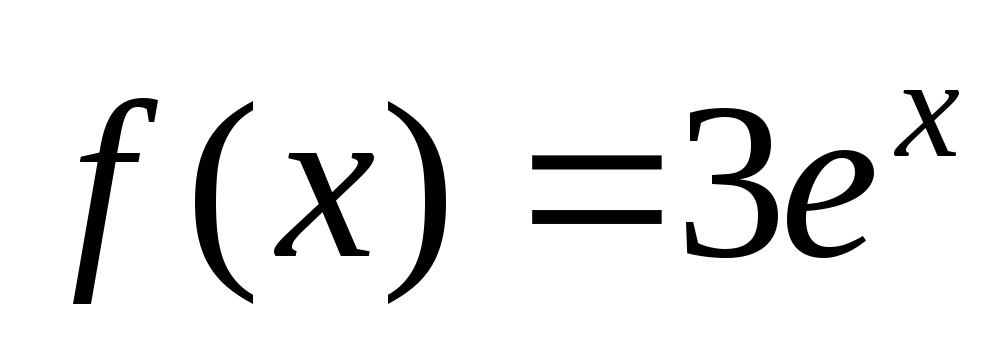 ,
то контрольное число данного уравнения
,
то контрольное число данного уравнения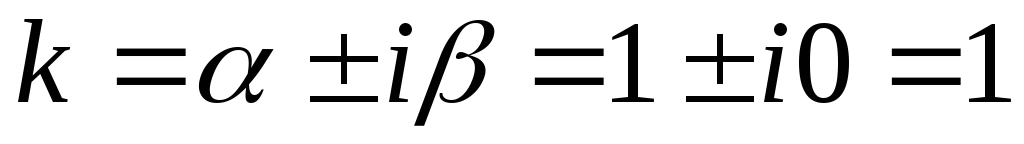 ,
оно не совпадает с корнями
,
оно не совпадает с корнями характеристического уравнения
характеристического уравнения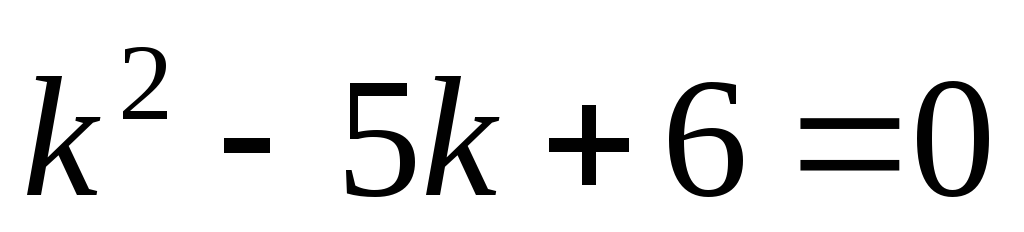 .
Тогда частное решение ищем в виде
.
Тогда частное решение ищем в виде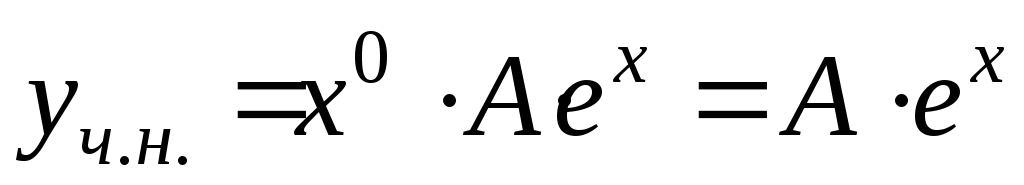 ,
где
,
где – неизвестный коэффициент. Дифференцируя
дважды
– неизвестный коэффициент. Дифференцируя
дважды и подставляя
и подставляя ,
, и
и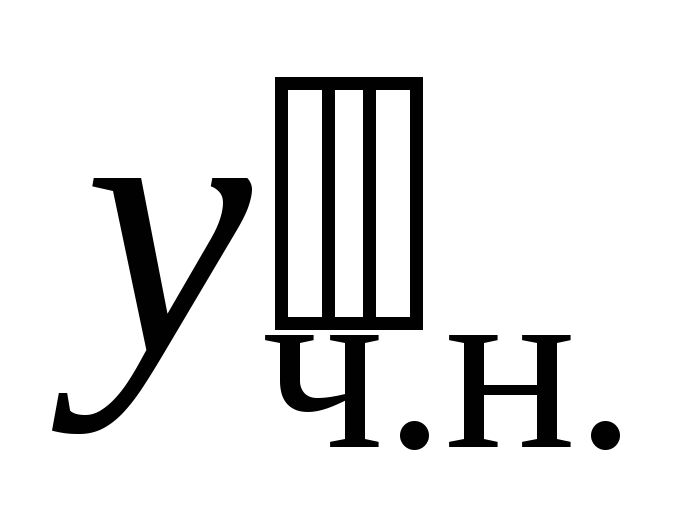 в исходное уравнение, находим
в исходное уравнение, находим .
Откуда
.
Откуда ,
то есть
,
то есть или
или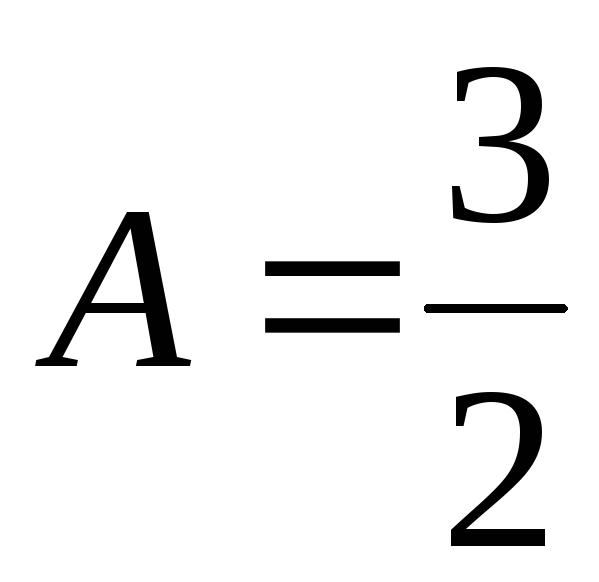 .
.
Итак, частное
решение данного уравнения имеет вид  ,
а его общее решение
,
а его общее решение .
.
3. Пусть правая часть имеет вид 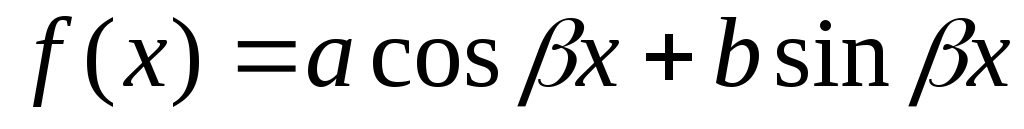 ,
где
,
где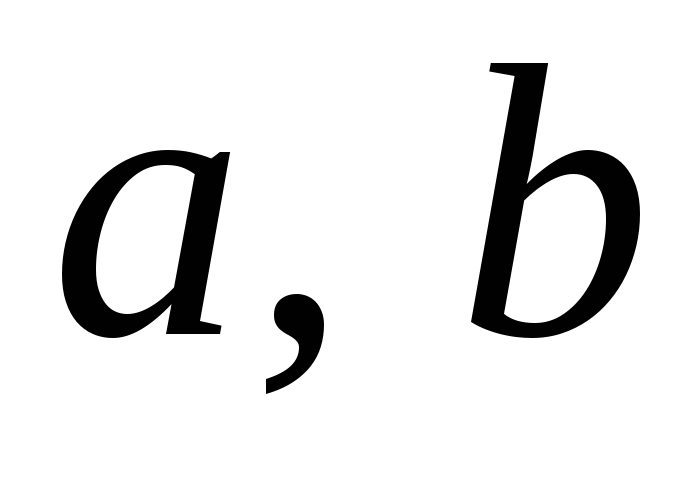 и
и – данные числа. Тогда частное решение
– данные числа. Тогда частное решение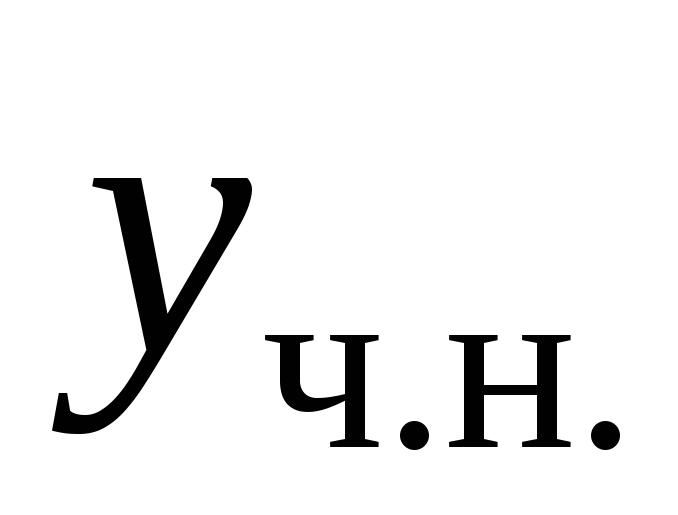 можно искать в виде
можно искать в виде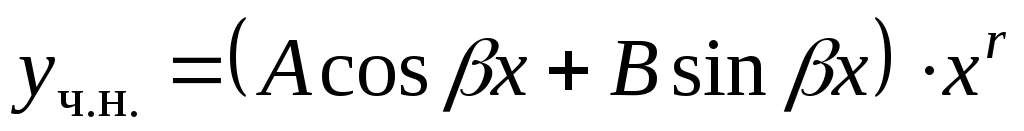 ,
где
,
где и
и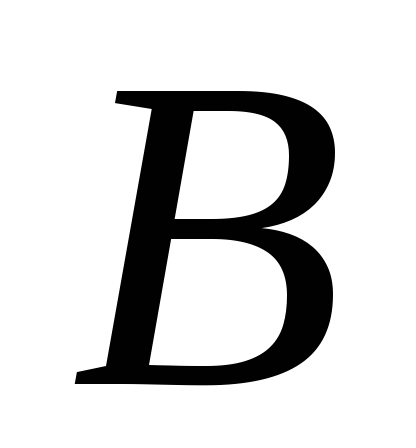 – неизвестные коэффициенты, а
– неизвестные коэффициенты, а – число, равное числу корней
характеристического уравнения,
совпадающих с
– число, равное числу корней
характеристического уравнения,
совпадающих с .
Если в выражение функции
.
Если в выражение функции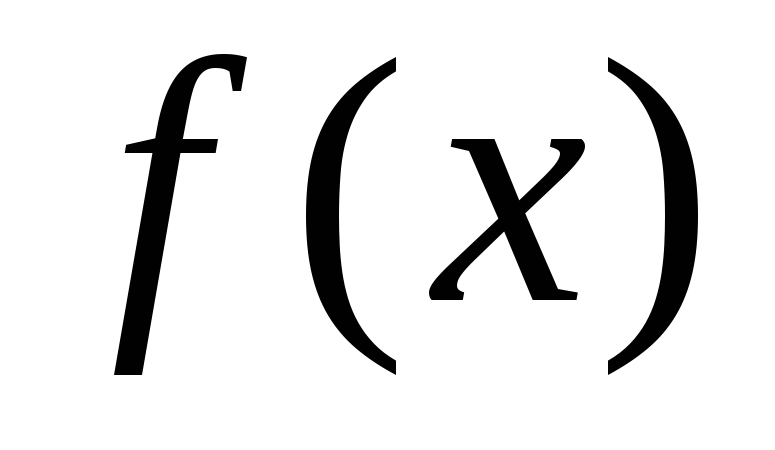 входит хотя бы одна из функций
входит хотя бы одна из функций или
или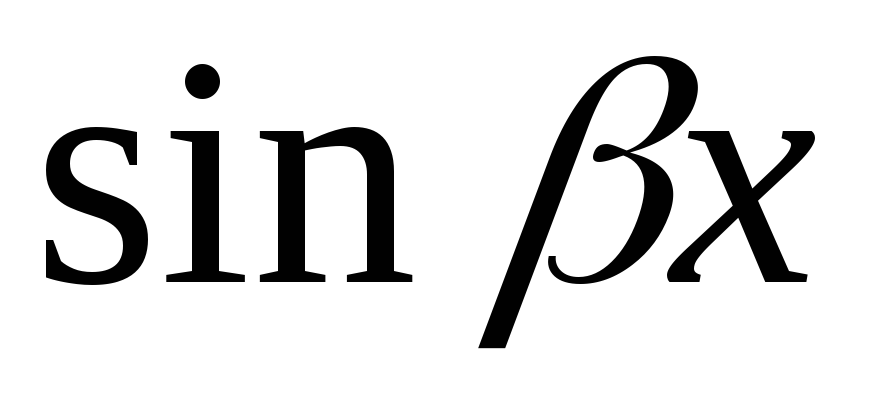 ,
то в
,
то в надо всегда вводитьобе функции.
надо всегда вводитьобе функции.
Пример
Найти общее решение 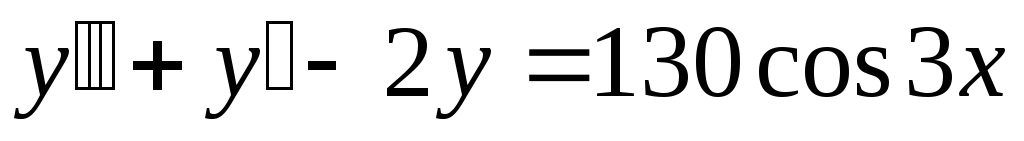 .
.
Решение:
А) Найдем общее
решение соответствующего однородного
уравнения 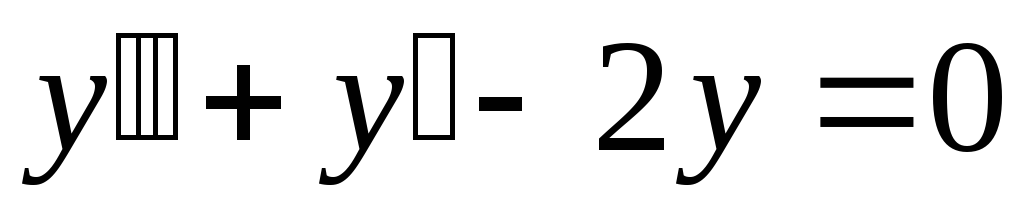 .
Для этого запишем характеристическое
уравнение
.
Для этого запишем характеристическое
уравнение .
Найдем корни последнего уравнения
.
Найдем корни последнего уравнения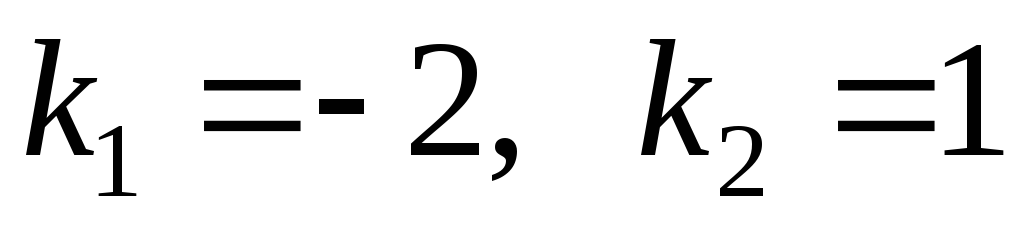 .
Следовательно, общее решение однородного
уравнения имеет вид
.
Следовательно, общее решение однородного
уравнения имеет вид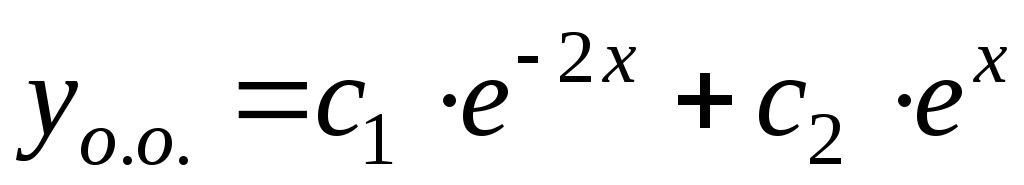 .
.
Б) Так как правая
часть уравнения есть функция 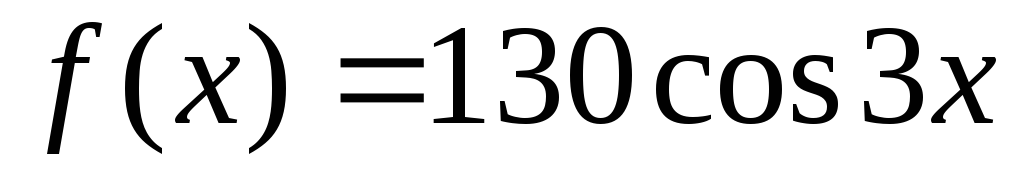 ,
то контрольное число данного уравнения
,
то контрольное число данного уравнения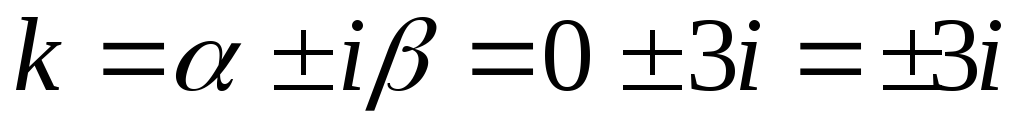 ,
оно не совпадает с корнями
,
оно не совпадает с корнями характеристического уравнения
характеристического уравнения .
Тогда частное решение ищем в виде
.
Тогда частное решение ищем в виде
,
где  и
и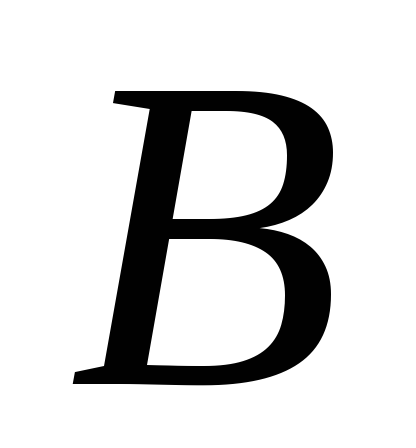 – неизвестные коэффициенты. Дифференцируя
дважды
– неизвестные коэффициенты. Дифференцируя
дважды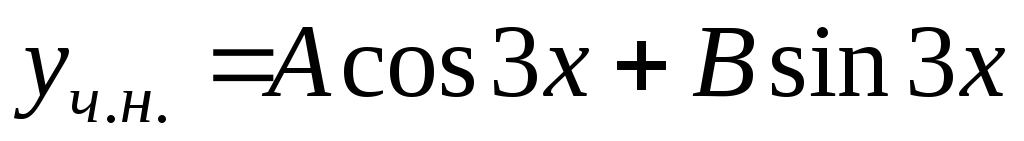 ,
получим
,
получим и
и .
Подставляя
.
Подставляя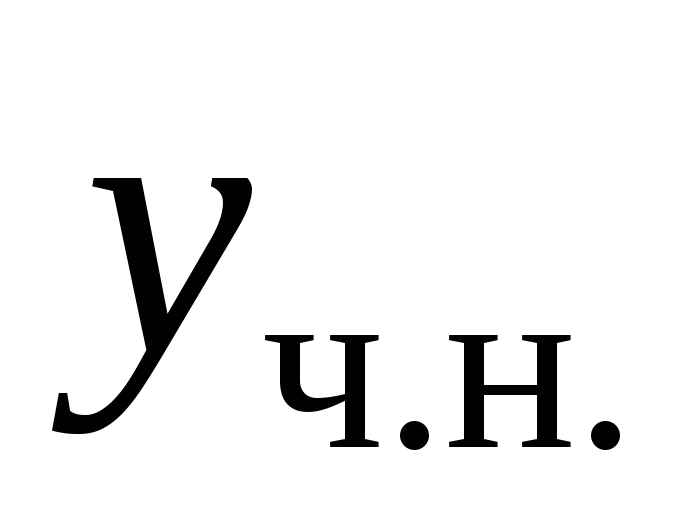 ,
,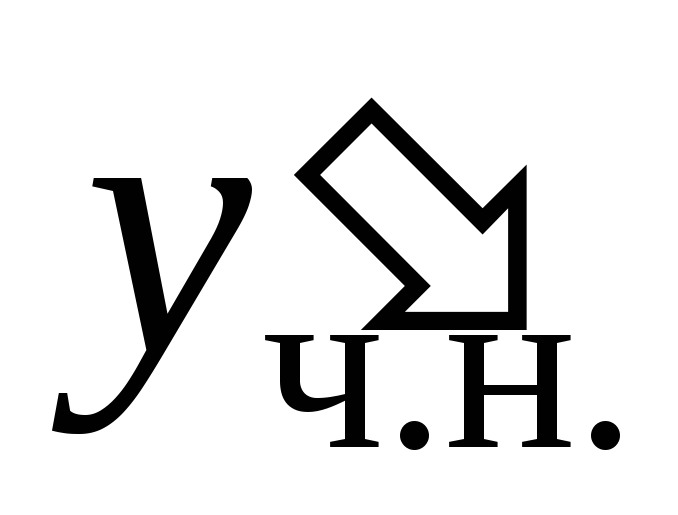 и
и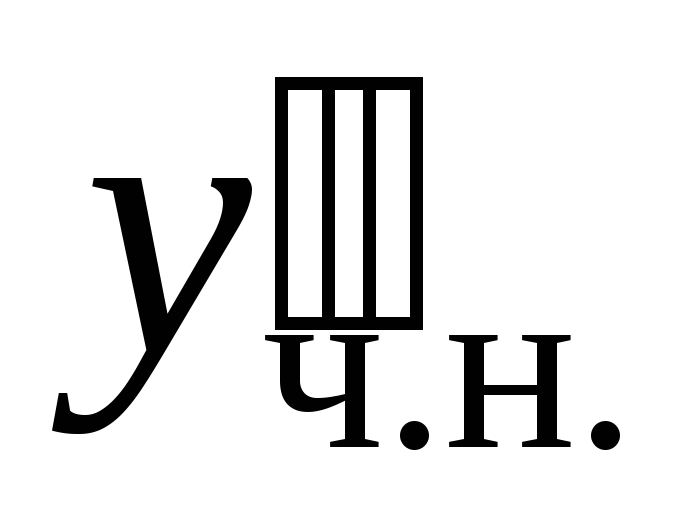 в исходное уравнение, находим
в исходное уравнение, находим



 .
.
Приводя подобные слагаемые, получим
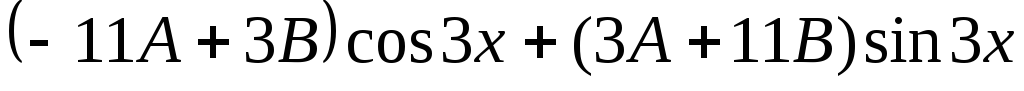
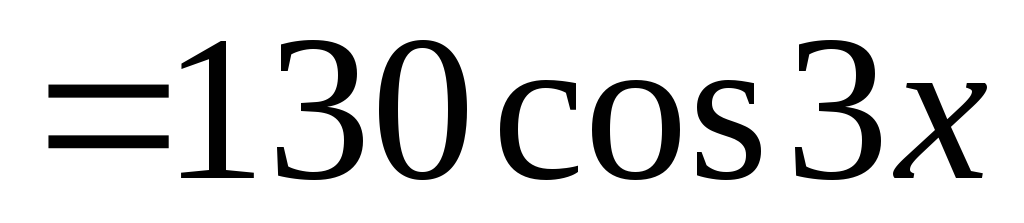 .
.
Приравниваем
коэффициенты при  и
и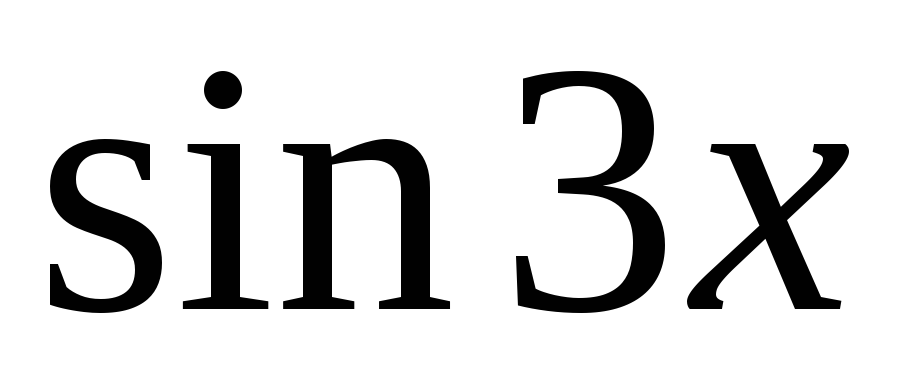 в правой и левой частях уравнения
соответственно. Получаем систему
в правой и левой частях уравнения
соответственно. Получаем систему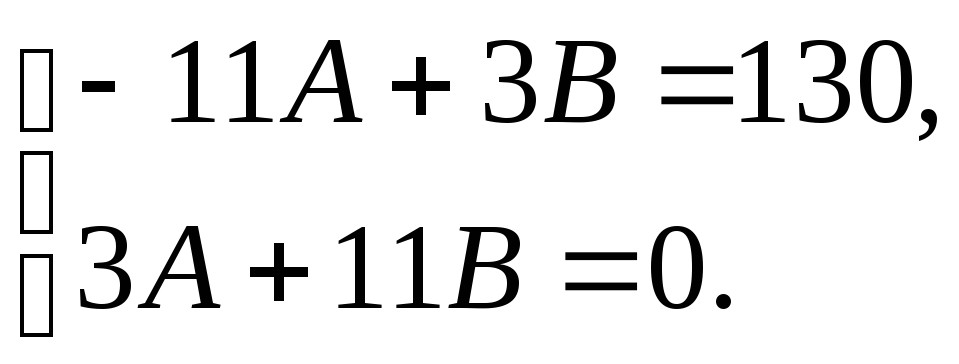 .
Решая ее, находим
.
Решая ее, находим ,
,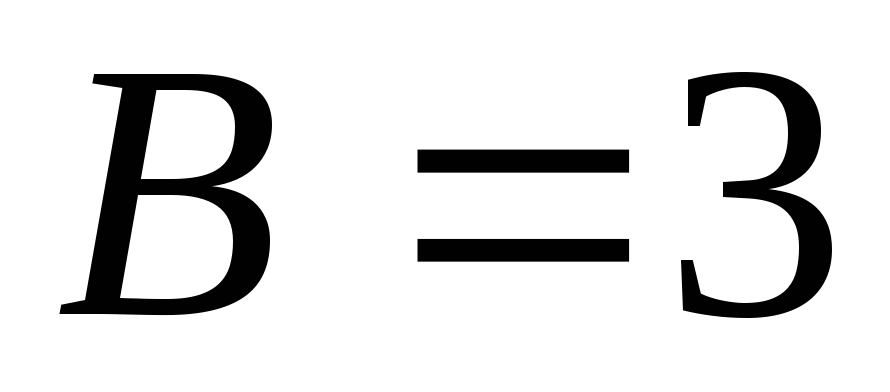 .
.
Итак, частное
решение исходного дифференциального
уравнения имеет вид  .
.
Общее решение
исходного дифференциального уравнения
имеет вид 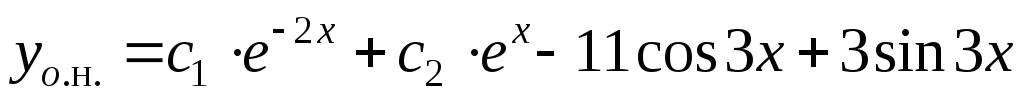 .
.
Дифференциальные уравнения с разделяющимися переменными
Одним из простейших видов дифференциальных уравнений является дифференциальное уравнение первого порядка, не содержащее искомой функции:
 .
(6)
.
(6)
Учитывая,
что  ,
запишем уравнение в виде
,
запишем уравнение в виде 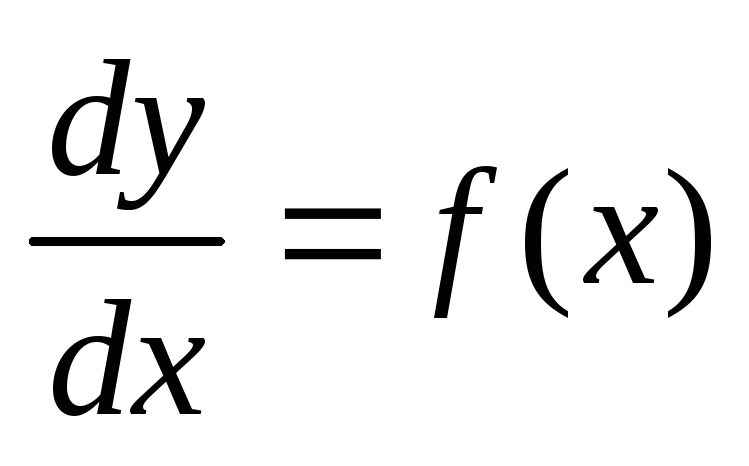 или
или 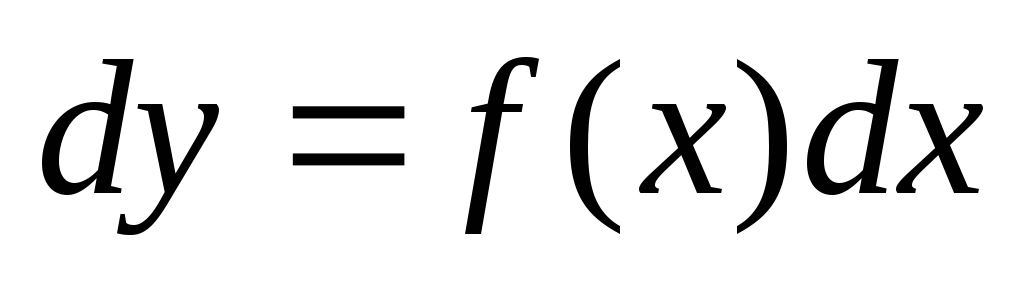 .
Интегрируя обе части последнего
уравнения, получим:
.
Интегрируя обе части последнего
уравнения, получим: 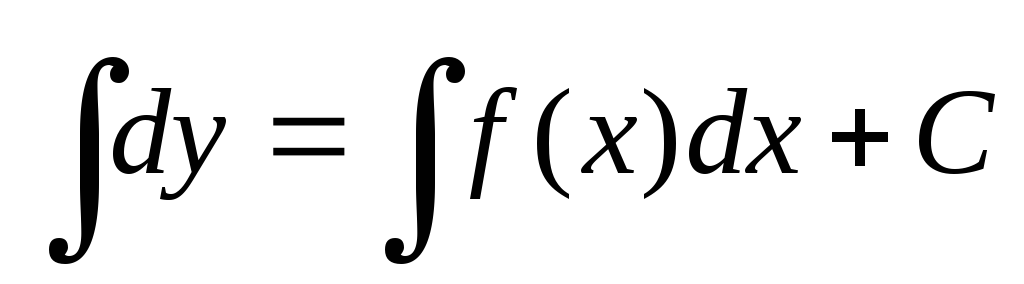 или
или
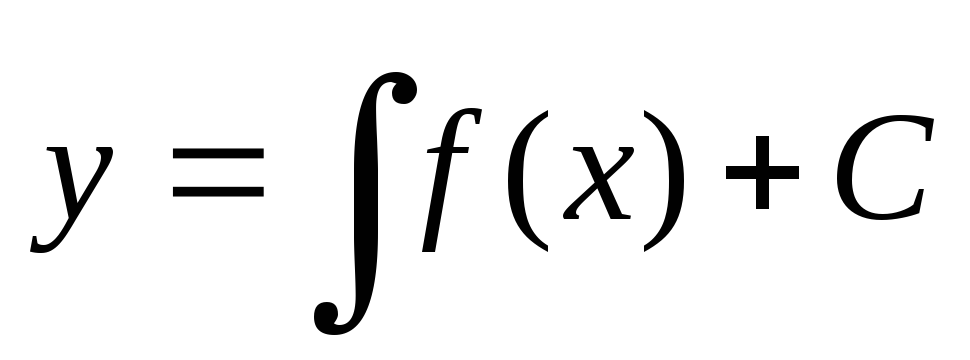 .
(7)
.
(7)
Таким образом, (7) является общим решением уравнения (6).
Пример
1.
Найти общее решение дифференциального
уравнения  .
.
Решение.
Запишем уравнение в виде  или
или  .
Проинтегрируем обе части полученного
уравнения:
.
Проинтегрируем обе части полученного
уравнения:  ,
,  .
Окончательно запишем
.
Окончательно запишем  .
.
Пример
2.
Найти решение уравнения 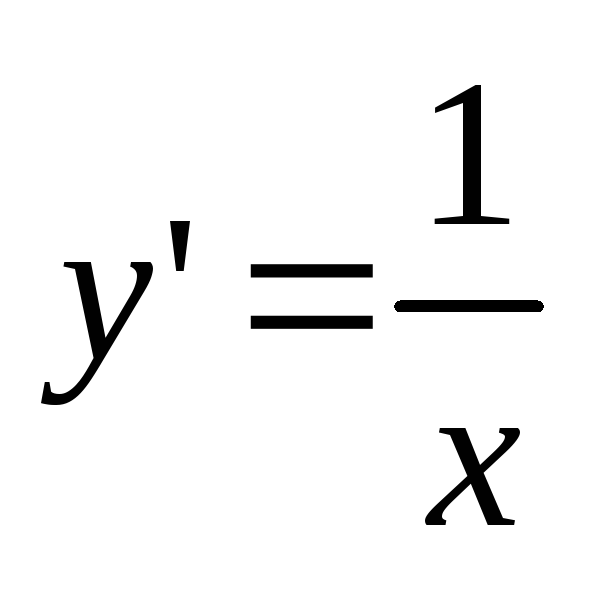 при условии
при условии 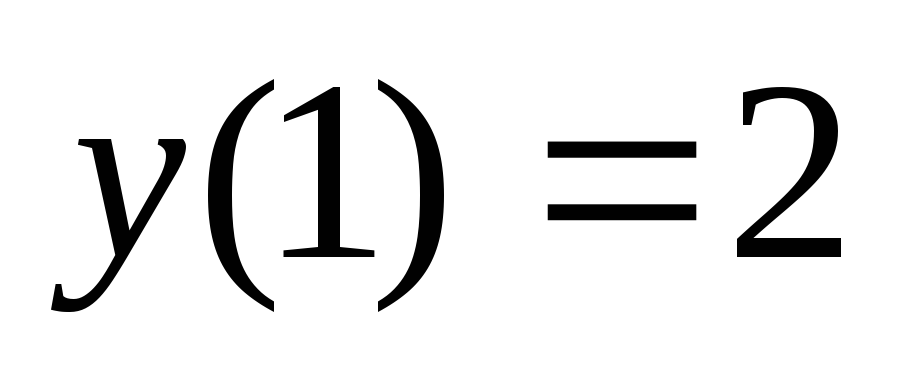 .
.
Решение.
Найдём общее решение уравнения: 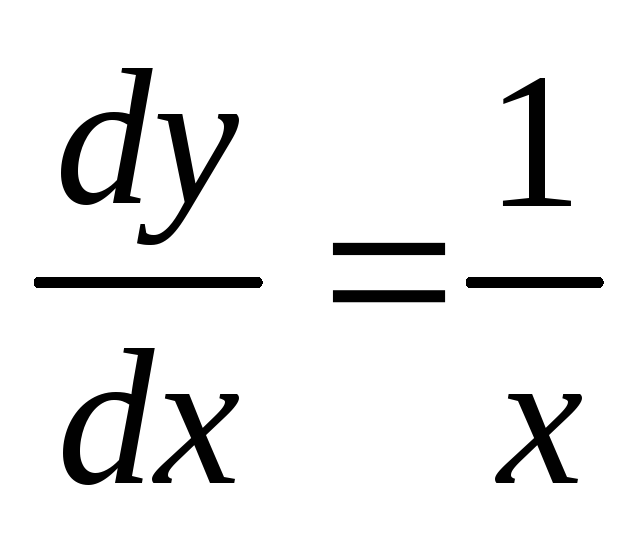 ,
, 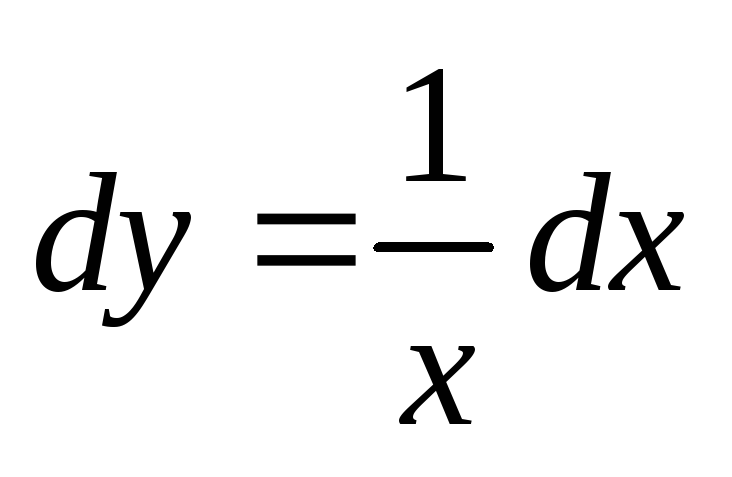 ,
,  ,
, 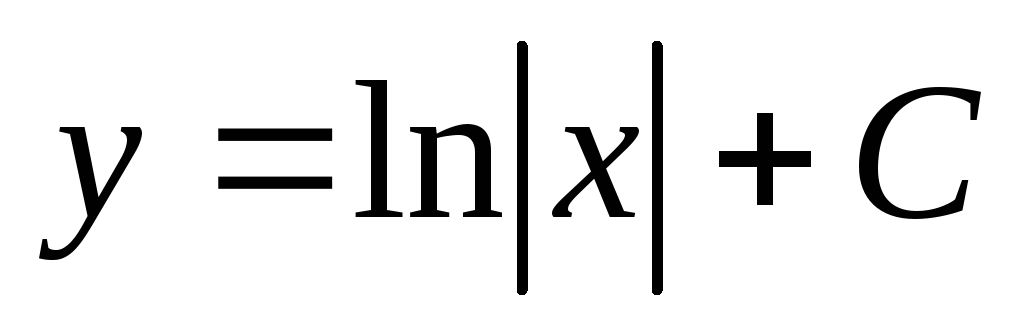 .
По условию
.
По условию 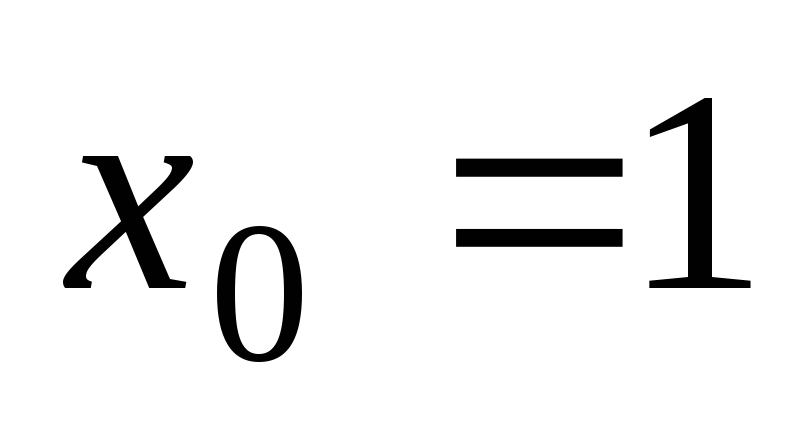 ,
,  .
Подставим в общее решение:
.
Подставим в общее решение:  или
или  .
Найденное значение произвольной
постоянной подставим в формулу общего
решения:
.
Найденное значение произвольной
постоянной подставим в формулу общего
решения:  .
Это и есть частное решение дифференциального
уравнения, удовлетворяющее заданному
условию.
.
Это и есть частное решение дифференциального
уравнения, удовлетворяющее заданному
условию.
Уравнение
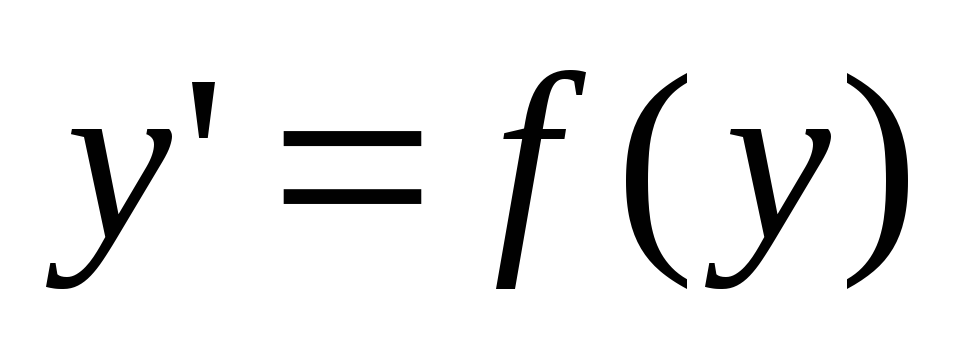 (8)
(8)
Называется дифференциальным
уравнением первого порядка, не содержащим
независимой переменной.
Запишем его в виде 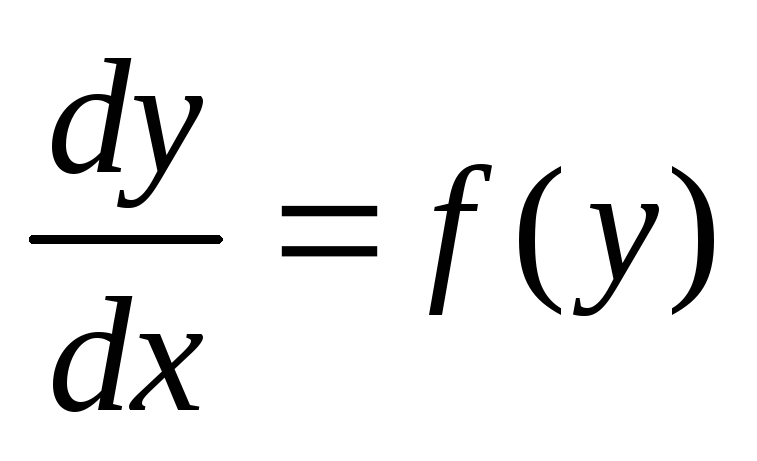 или
или 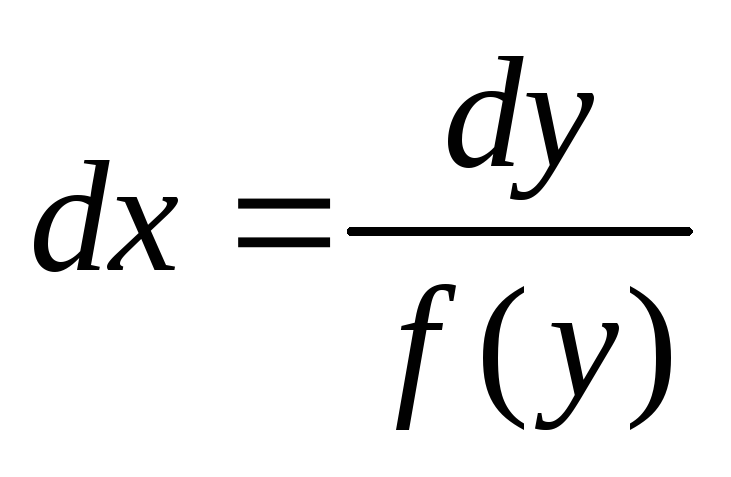 .
Проинтегрируем обе части последнего
уравнения:
.
Проинтегрируем обе части последнего
уравнения: 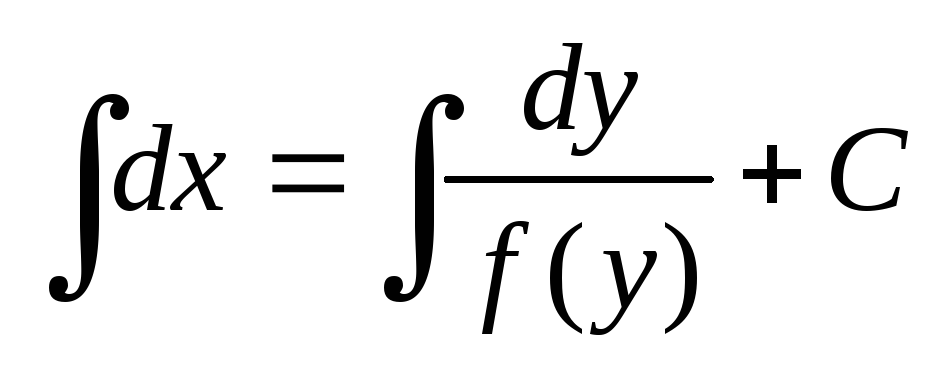 или
или  — общее решение уравнения (8).
— общее решение уравнения (8).
Пример.
Найти общее решение уравнения 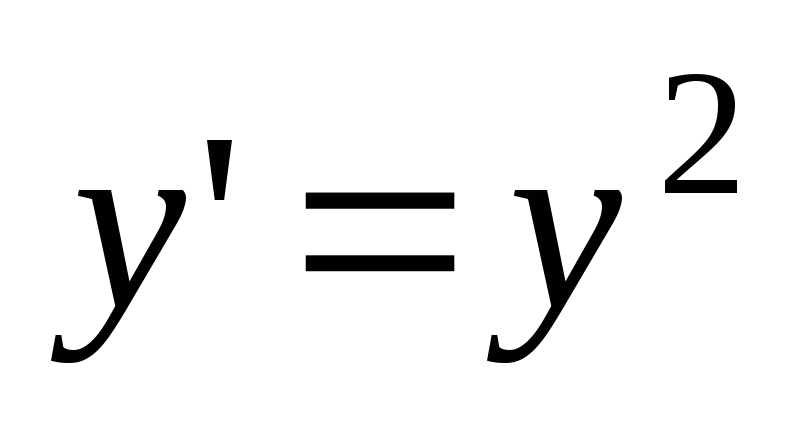 .
.
Решение.
Запишем это уравнение в виде: 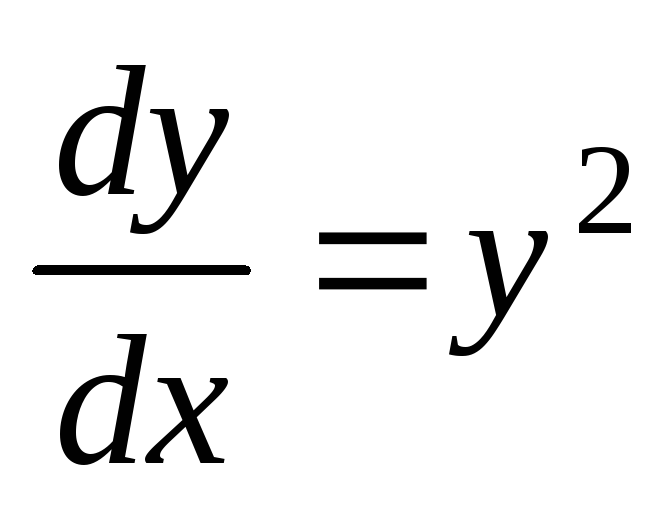 или
или 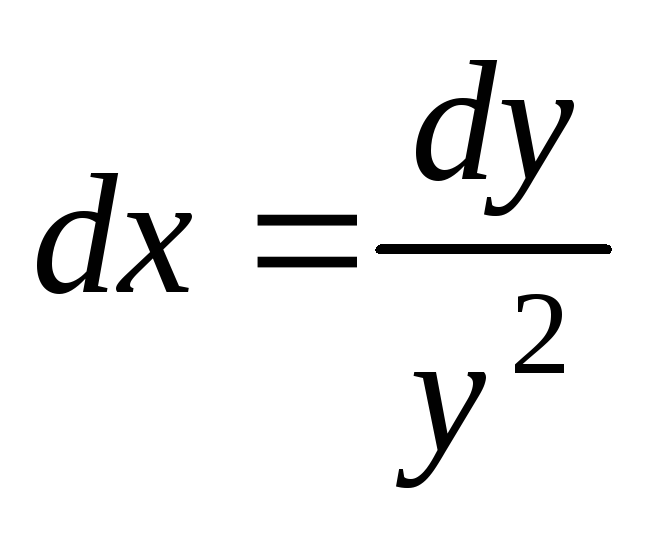 .
Тогда
.
Тогда  ,
, 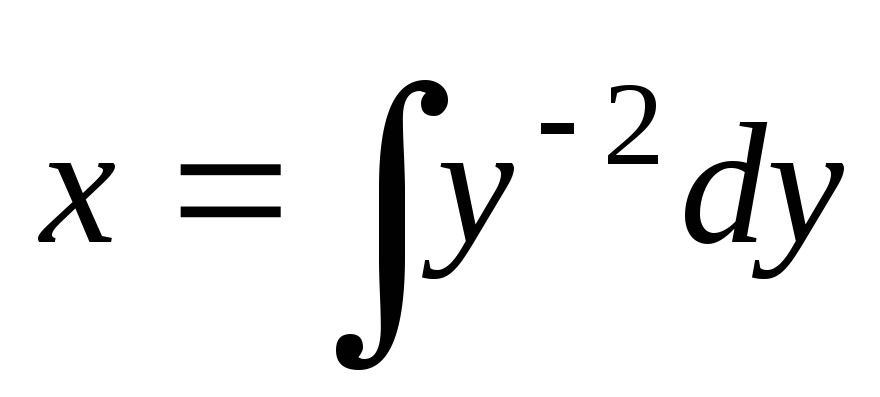 ,
, 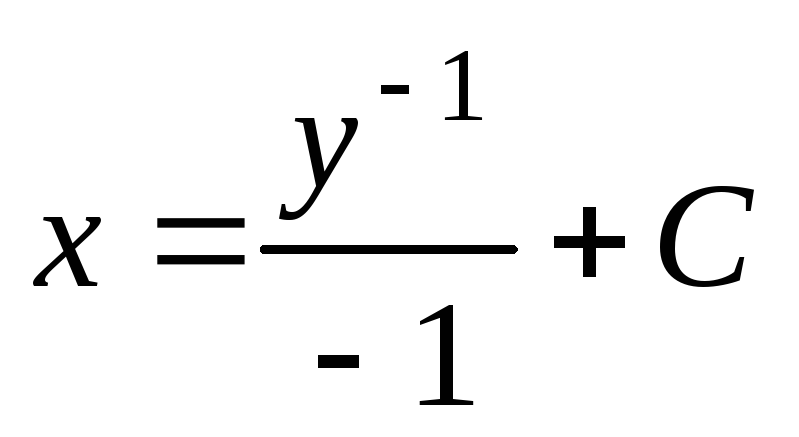 ,
, 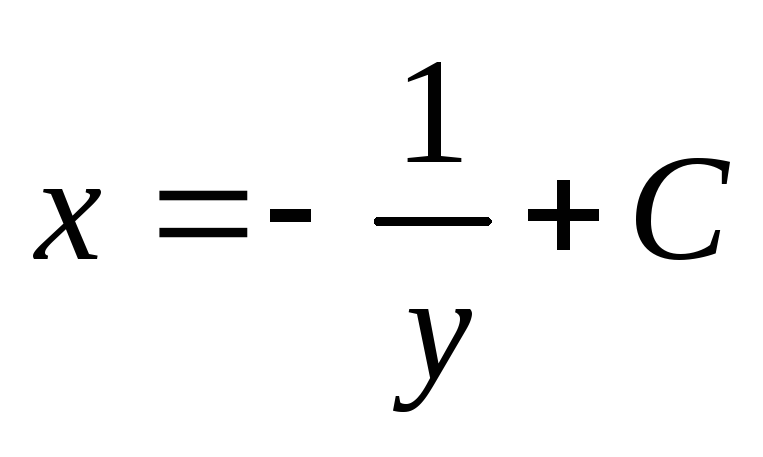 .
Таким образом,
.
Таким образом,  – общее решение данного уравнения.
– общее решение данного уравнения.
Уравнение вида
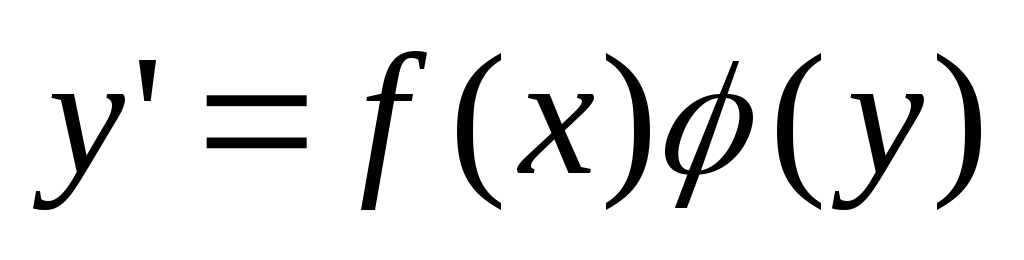 (9)
(9)
интегрируется
с помощью разделения переменных. Для
этого уравнение запишем в виде 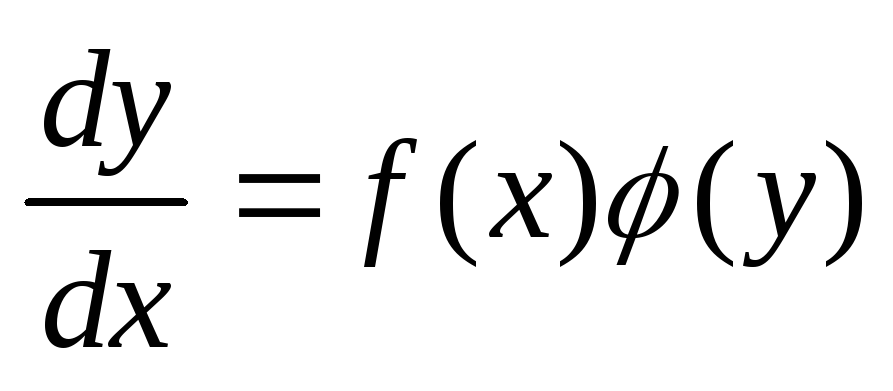 ,
а затем с помощью операций умножения и
деления приводим его к такой форме,
чтобы в одну часть входила только функция
от х и дифференциал dx,
а во вторую часть – функция от у и дифференциал dy.
Для этого обе части уравнения нужно
умножить на dx и разделить на
,
а затем с помощью операций умножения и
деления приводим его к такой форме,
чтобы в одну часть входила только функция
от х и дифференциал dx,
а во вторую часть – функция от у и дифференциал dy.
Для этого обе части уравнения нужно
умножить на dx и разделить на 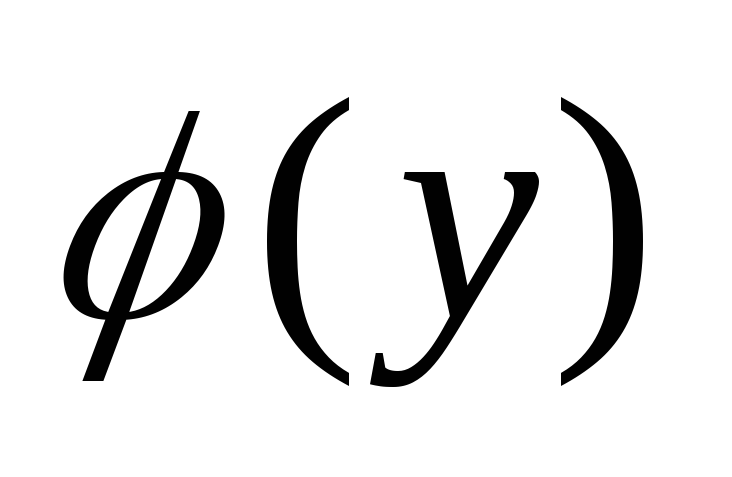 .
В результате получим уравнение
.
В результате получим уравнение
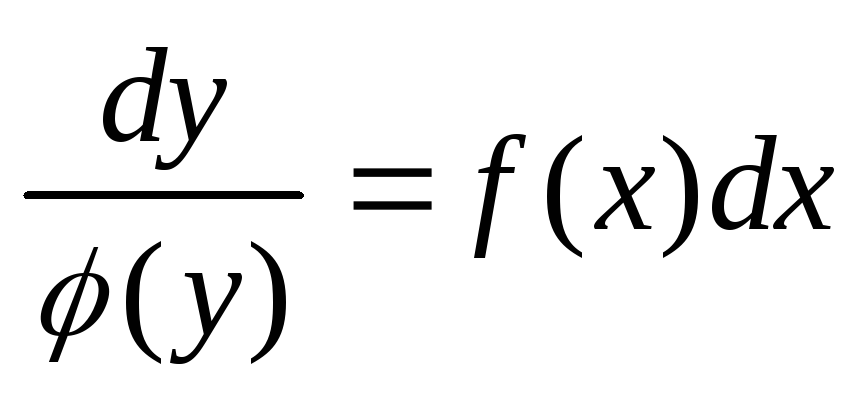 ,
(10)
,
(10)
в
котором переменные х и у разделены. Проинтегрируем обе части
уравнения (10): 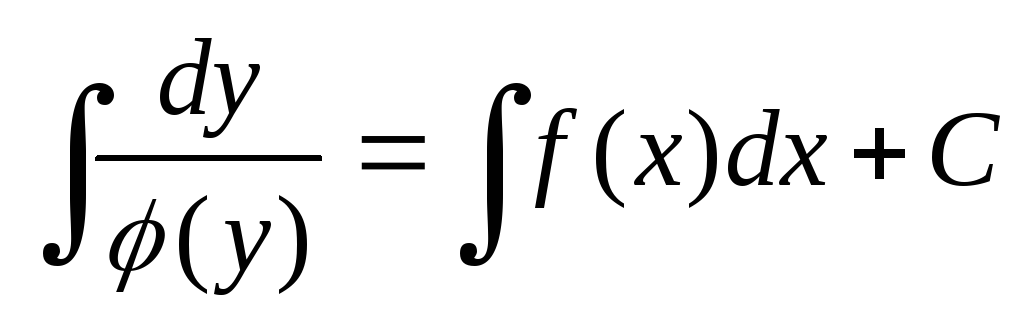 .
Полученное соотношение является общим
интегралом уравнения (9).
.
Полученное соотношение является общим
интегралом уравнения (9).
Пример
3.
Проинтегрировать
уравнение  .
.
Решение.
Преобразуем уравнение и разделим
переменные: 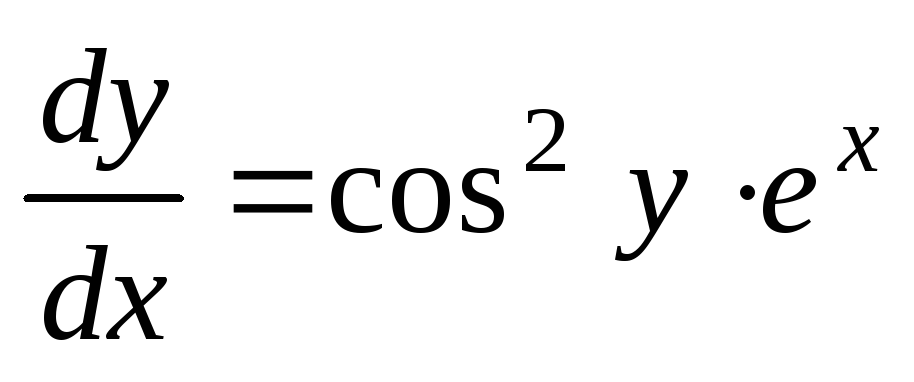 ,
, 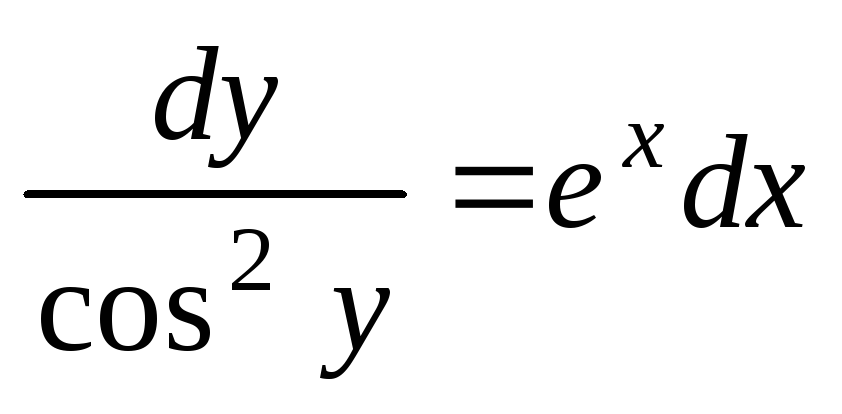 .
Проинтегрируем:
.
Проинтегрируем: 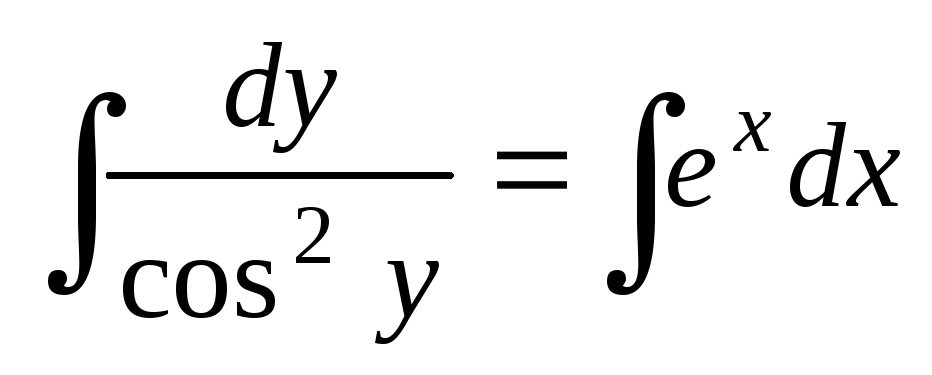 ,
,  или – общий интеграл данного уравнения.
или – общий интеграл данного уравнения.  .
.
Пусть уравнение задано в виде
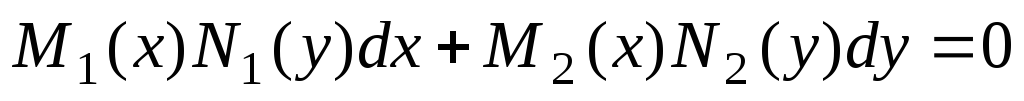 .
(11)
.
(11)
Такое уравнение называется дифференциальным уравнением первого порядка с разделяющимися переменными в симметрической форме.
Для
разделения переменных нужно обе части
уравнения разделить на 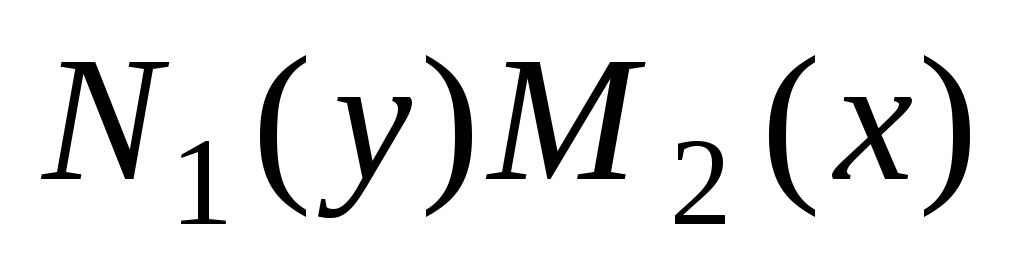 :
:
 .
(12)
.
(12)
Полученное уравнение называется дифференциальным уравнением с разделёнными переменными. Проинтегрируем уравнение (12):
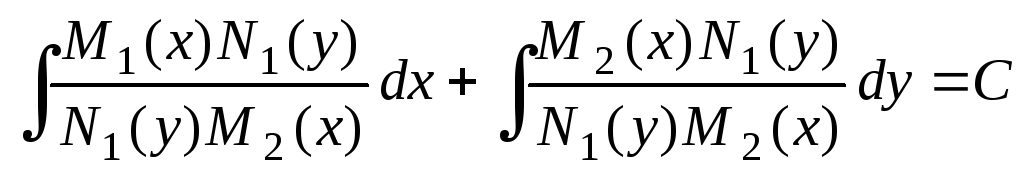 .
. (13)
(13)
Соотношение (13) является общим интегралом дифференциального уравнения (11).
Пример
4.
Проинтегрировать дифференциальное
уравнение  .
.
Решение. Запишем уравнение в виде
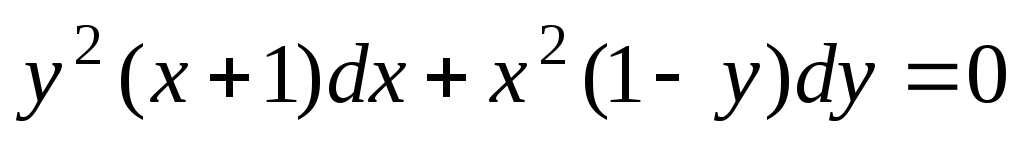 и
разделим обе его части на
и
разделим обе его части на 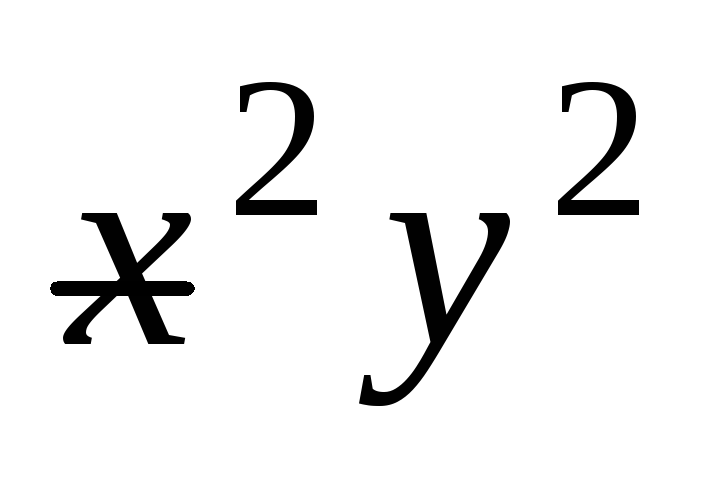 ,
,  .
Полученное уравнение:
.
Полученное уравнение: 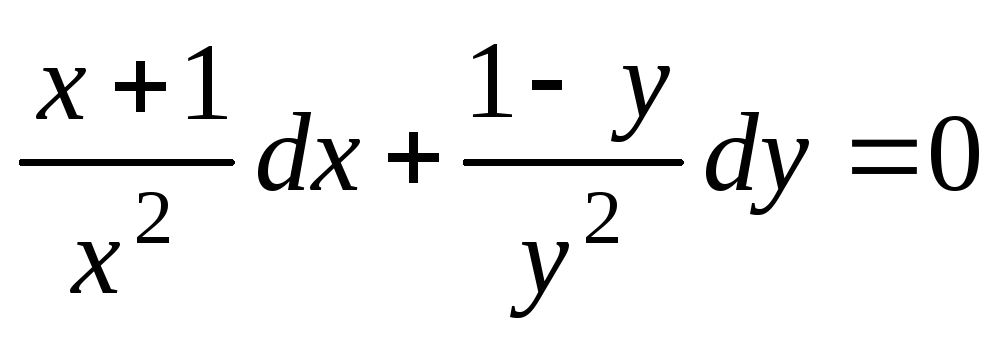 является уравнением с разделёнными
переменными. Проинтегрируем его:
является уравнением с разделёнными
переменными. Проинтегрируем его:
 ,
, 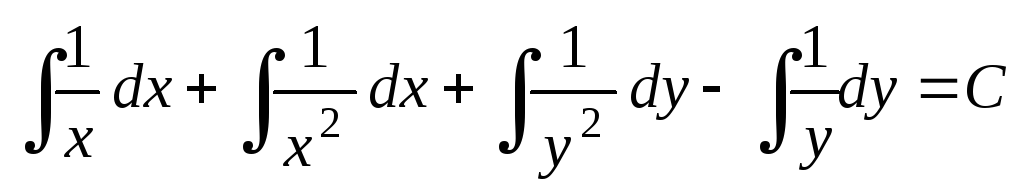 ,
,
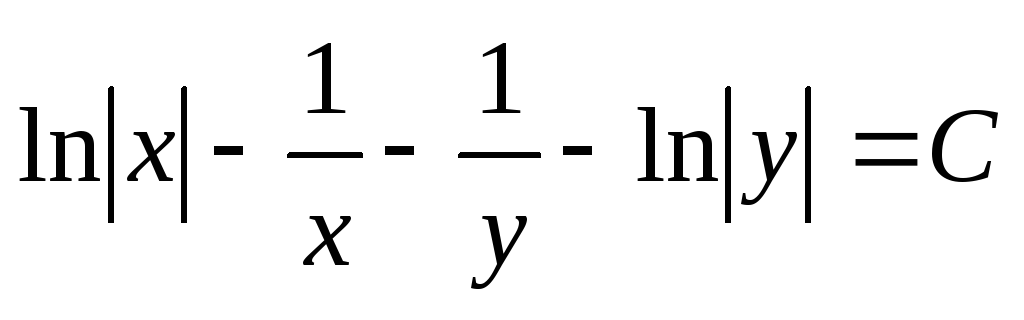 ,
, 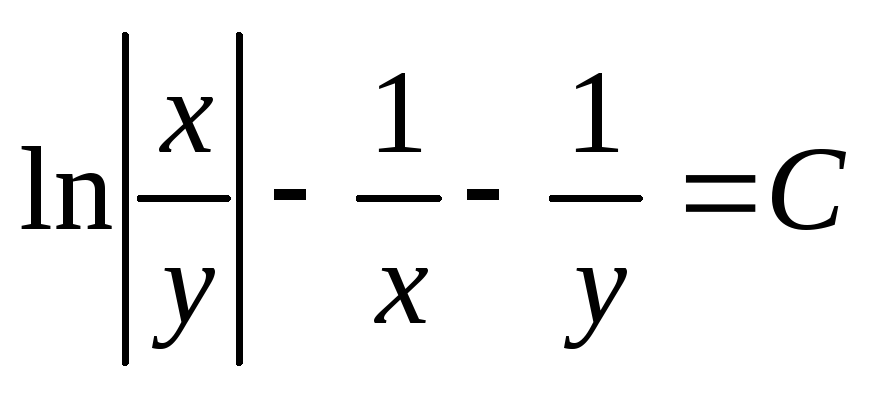 .
Последнее равенство является общим
интегралом данного дифференциального
уравнения.
.
Последнее равенство является общим
интегралом данного дифференциального
уравнения.
Пример
5.
Найти частное решение дифференциального
уравнения 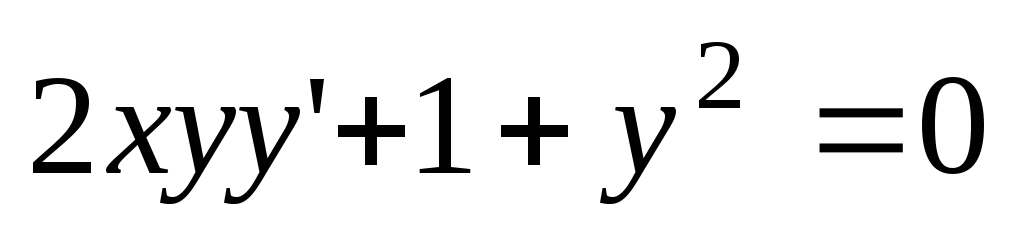 ,
удовлетворяющее условию
,
удовлетворяющее условию  .
.
Решение.
Учитывая, что  ,
запишем уравнение в виде
,
запишем уравнение в виде 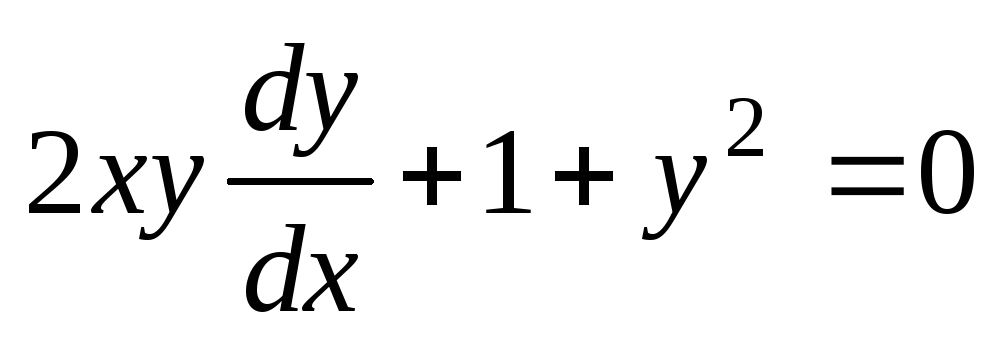 или
или 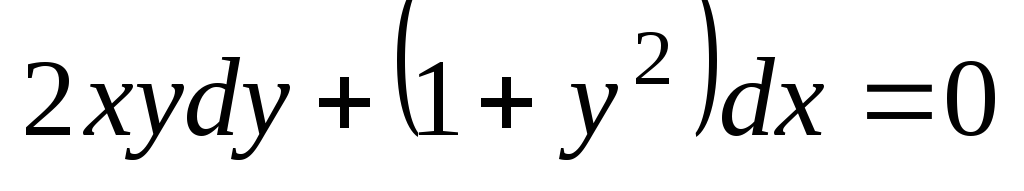 .
Разделим переменные:
.
Разделим переменные: 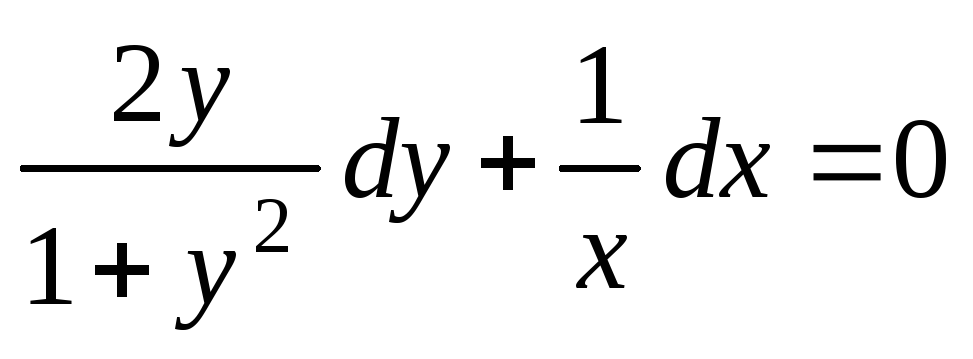 .
Проинтегрируем это уравнение:
.
Проинтегрируем это уравнение:  ,
,  ,
,  .
Полученное соотношение является общим
интегралом данного уравнения. По условию
.
Полученное соотношение является общим
интегралом данного уравнения. По условию  .
Подставим в общий интеграл и найдём С:
.
Подставим в общий интеграл и найдём С:  , С=1.
Тогда выражение
, С=1.
Тогда выражение 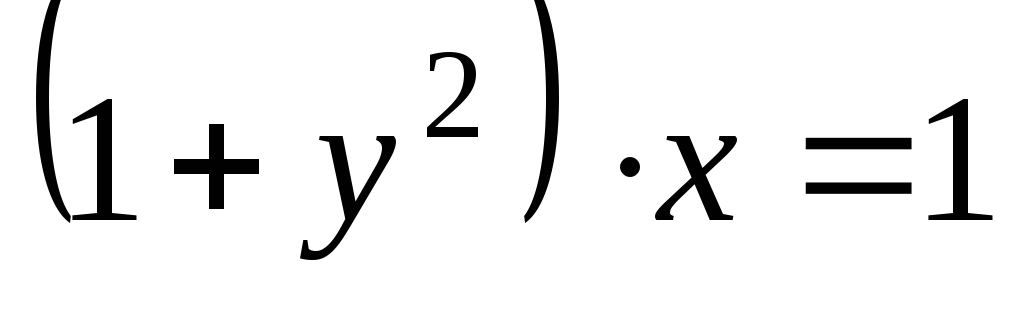 является частным решением данного
дифференциального уравнения, записанным
в виде частного интеграла.
является частным решением данного
дифференциального уравнения, записанным
в виде частного интеграла.
Lektsia_8
Введение.
На лекции изучаются ЛНДУ – линейные неоднородные дифференциальные уравнения. Рассматривается структура общего решения, решение ЛНДУ методом вариации произвольных постоянных, решение ЛНДУ с постоянными коэффициентами и правой частью специального вида. Рассматриваемые вопросы применяются при изучении вынужденных колебаний в физике, электротехнике и электронике, теории автоматического управления.
1. Структура общего решения линейного неоднородного дифференциального уравнения 2 порядка.
Рассмотрим
сначала линейное неоднородное уравнение
произвольного порядка: 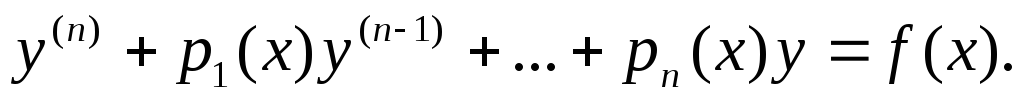
С
учетом обозначения  можно записать:
можно записать:
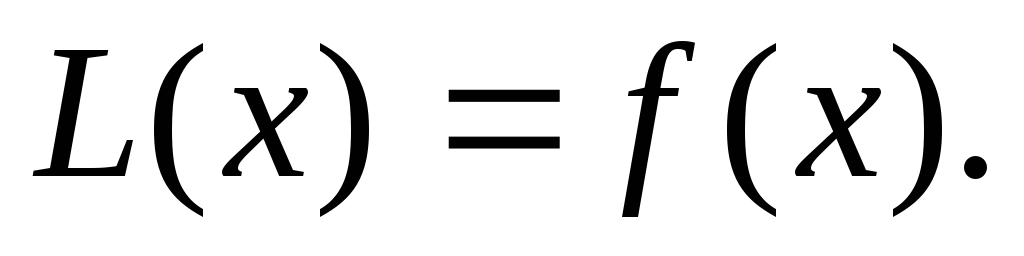
При этом будем полагать, что коэффициенты и правая часть этого уравнения непрерывны на некотором интервале.
Теорема. Общее
решение линейного неоднородного
дифференциального уравнения 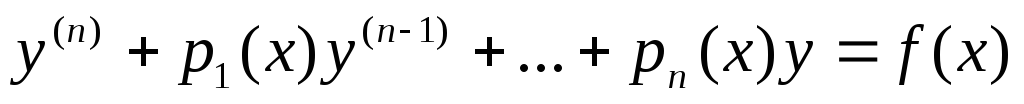 в
некоторой области есть сумма любого
его решения и общего решения соответствующего
линейного однородного дифференциального
уравнения.
в
некоторой области есть сумма любого
его решения и общего решения соответствующего
линейного однородного дифференциального
уравнения.
Доказательство. Пусть Y – некоторое решение неоднородного уравнения.
Тогда при подстановке этого решения в исходное уравнение получаем тождество:
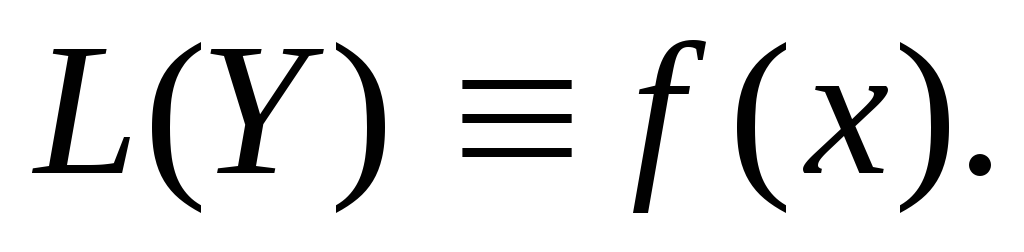
Пусть  — фундаментальная система решений
линейного однородного уравнения
— фундаментальная система решений
линейного однородного уравнения 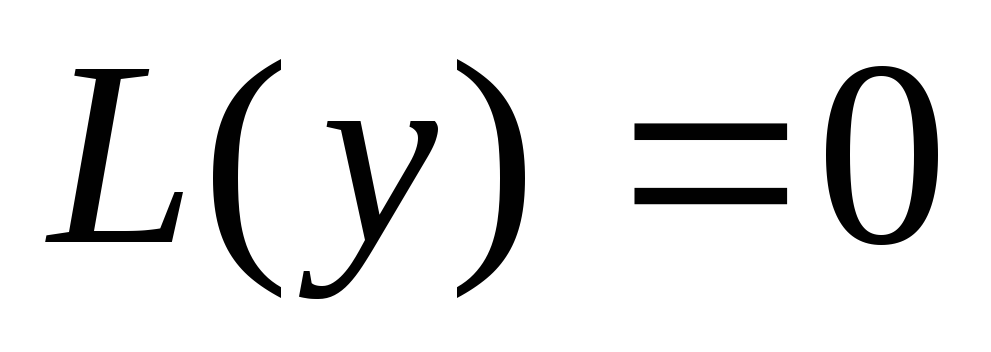 .
Тогда общее решение однородного уравнения
можно записать в виде:
.
Тогда общее решение однородного уравнения
можно записать в виде:

Далее,
сумма 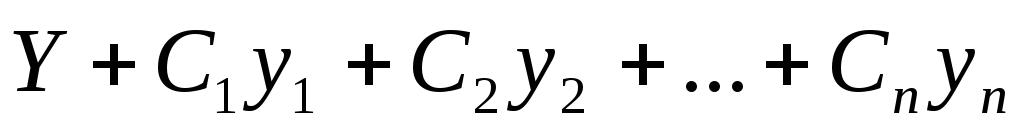 является
общим решением неоднородного уравнения.
является
общим решением неоднородного уравнения.


В частности, для линейного неоднородного дифференциального уравнения 2 порядка структура общего решения имеет вид:

где 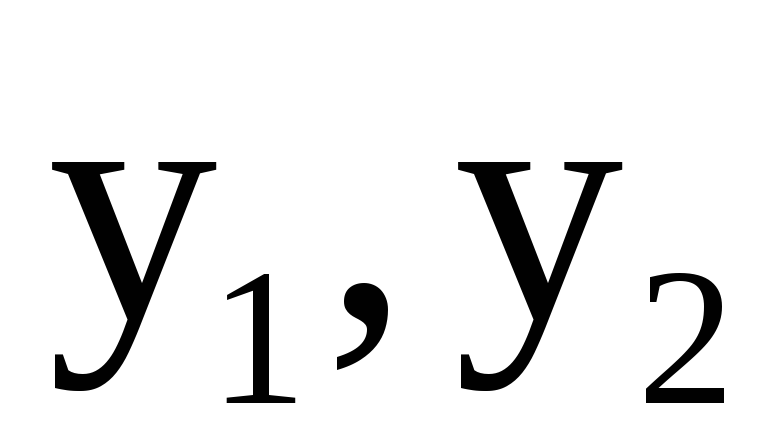 — фундаментальная система решений
соответствующего однородного уравнения,
а
— фундаментальная система решений
соответствующего однородного уравнения,
а  — какое-либо частное решение неоднородного
уравнения.
— какое-либо частное решение неоднородного
уравнения.
Таким образом, для решения линейного неоднородного дифференциального уравнения необходимо найти общее решение соответствующего однородного уравнения и каким- то образом отыскать одно частное решение неоднородного уравнения. Обычно оно находится подбором. Способы подбора частного решения рассмотрим в следующих вопросах.
2. Метод вариации
На практике удобно применять метод вариации произвольных постоянных.
Для этого сначала находят общее решение соответствующего однородного уравнения в виде:

Затем, полагая коэффициенты Ci функциями от х, ищется решение неоднородного уравнения:

Можно доказать, что для нахождения функций Ci(x) надо решить систему уравнений:

Пример. Решить уравнение 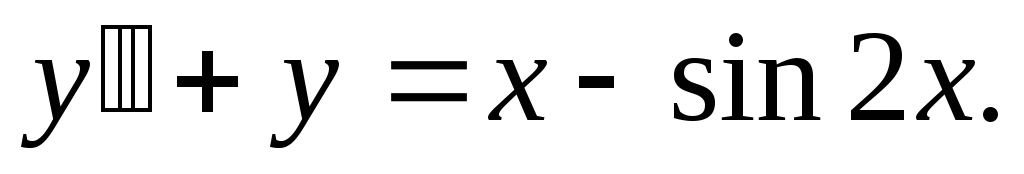
Решаем
линейное однородное уравнение 



Решение неоднородного уравнения будет иметь вид:
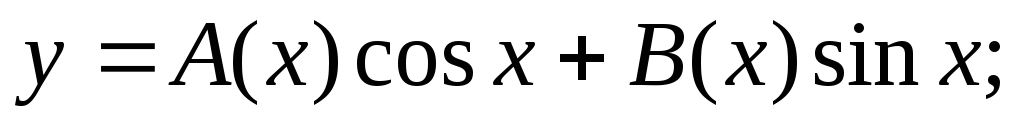
Составляем систему уравнений:

Решим эту систему:
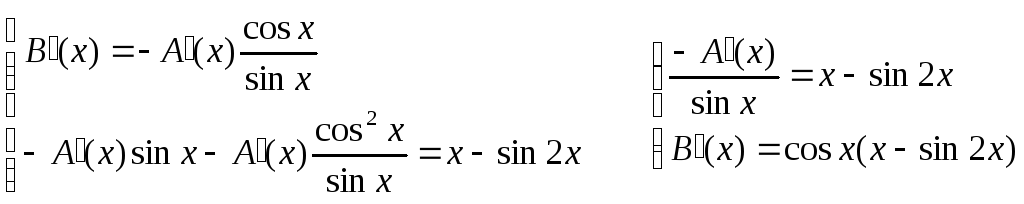
Из
соотношения  найдем функцию А(х).
найдем функцию А(х).
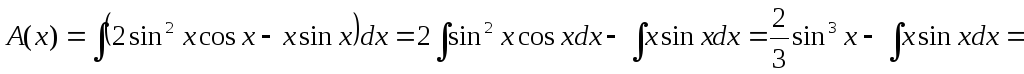
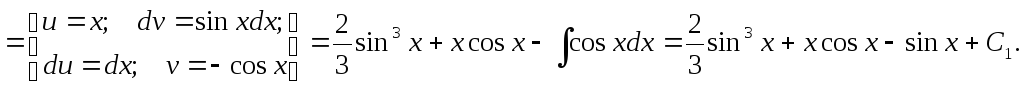
Теперь находим В(х).
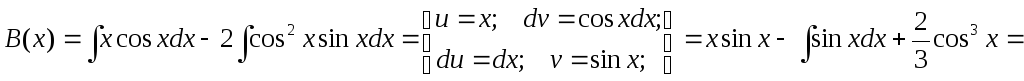
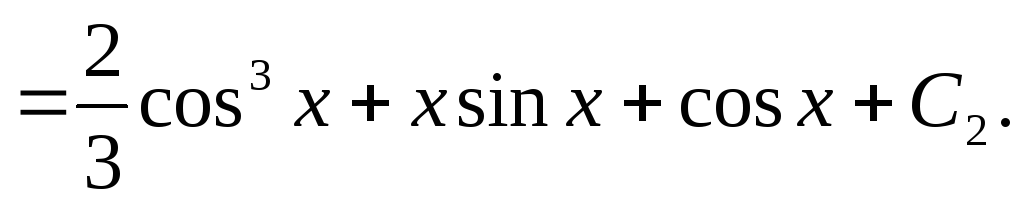
Подставляем полученные значения в формулу общего решения неоднородного уравнения:

Окончательный
ответ: 
Вообще говоря, метод вариации произвольных постоянных пригоден для нахождения решений любого линейного неоднородного уравнения. Но т.к. нахождение фундаментальной системы решений соответствующего однородного уравнения может быть достаточно сложной задачей, этот метод в основном применяется для неоднородных уравнений с постоянными коэффициентами.
3. Уравнения с правой частью специального вида
Представляется возможным представить вид частного решения в зависимости от вида правой части неоднородного уравнения.
Различают следующие случаи:
I. Правая часть линейного неоднородного дифференциального уравнения имеет вид:

где  —
многочлен степени m.
—
многочлен степени m.
Тогда частное решение ищется в виде:

Здесь Q(x)— многочлен той же степени, что и P(x), но с неопределенными коэффициентами, а r – число, показывающее сколько раз число является корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения.
Пример. Решить уравнение  .
.
Решим
соответствующее однородное уравнение: 
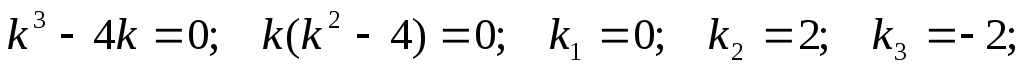

Теперь найдем частное решение исходного неоднородного уравнения.
Сопоставим правую часть уравнения с видом правой части, рассмотренным выше.
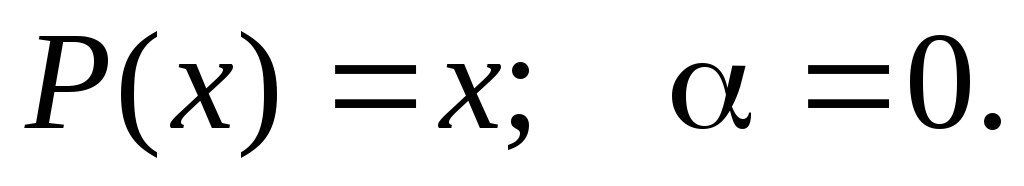
Частное
решение ищем в виде: 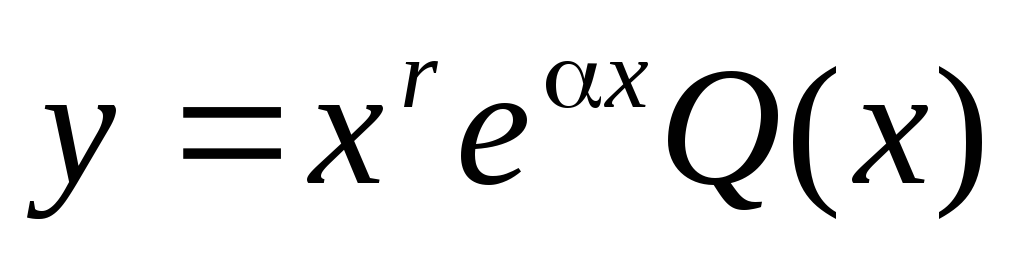 ,
где
,
где 
Т.е. 
Теперь определим неизвестные коэффициенты А и В.
Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение.

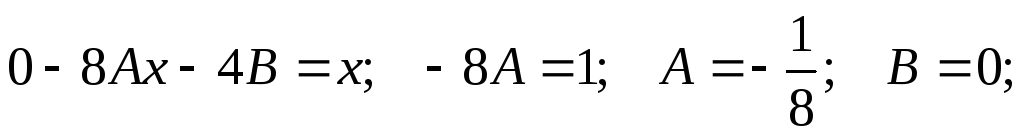
Итого,
частное решение: 
Тогда общее решение линейного неоднородного дифференциального уравнения:

II. Правая часть линейного неоднородного дифференциального уравнения имеет вид:
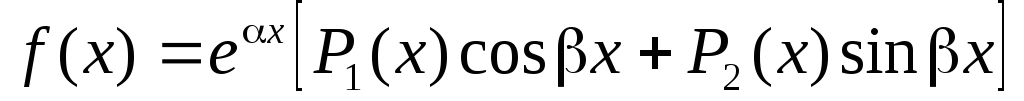
Здесь Р1(х) и Р2(х) – многочлены степени m1 и m2 соответственно.
Тогда частное решение неоднородного уравнения будет иметь вид:

где
число r показывает сколько раз число 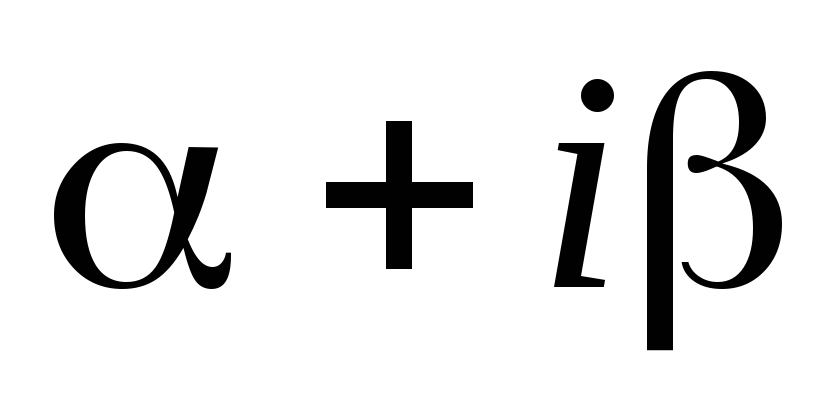 является корнем характеристического
уравнения для соответствующего
однородного уравнения, а Q1(x) и Q2(x) – многочлены степени не выше m,
где m—
большая из степеней m1 и m2.
является корнем характеристического
уравнения для соответствующего
однородного уравнения, а Q1(x) и Q2(x) – многочлены степени не выше m,
где m—
большая из степеней m1 и m2.
Сводная таблица видов частных решений
для различных видов правых частей
N | Правая часть дифф.уравнения | Корни характеристического уравнения | Виды частного решения |
I. |
| 1. Число не является корнем характеристического уравнения |
|
2.
Число – корень характеристического
уравнения кратности |
| ||
II. |
| 1.
Число |
|
2.
Число |
| ||
III. |
| 1.
Числа |
|
2.
Числа |
| ||
IV. |
| 1.
Числа |
|
2.
Числа |
|
Заметим, что если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию.
Т.е.
если уравнение имеет вид: 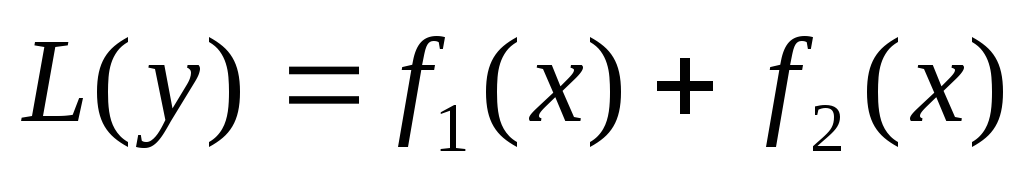 ,
то частное решение этого уравнения
будет
,
то частное решение этого уравнения
будет 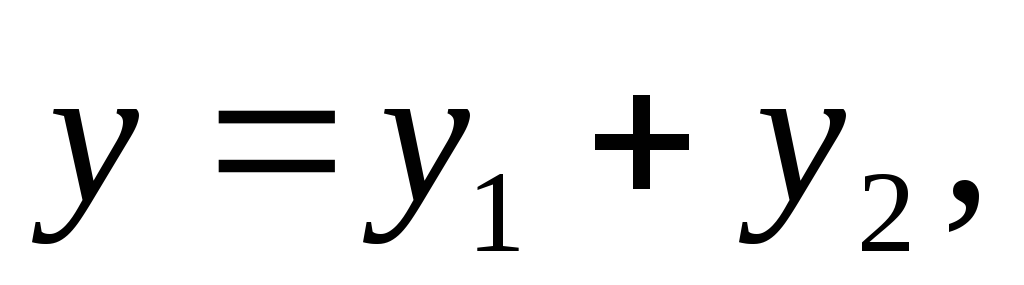 где у1 и у2 – частные решения вспомогательных
уравнений
где у1 и у2 – частные решения вспомогательных
уравнений
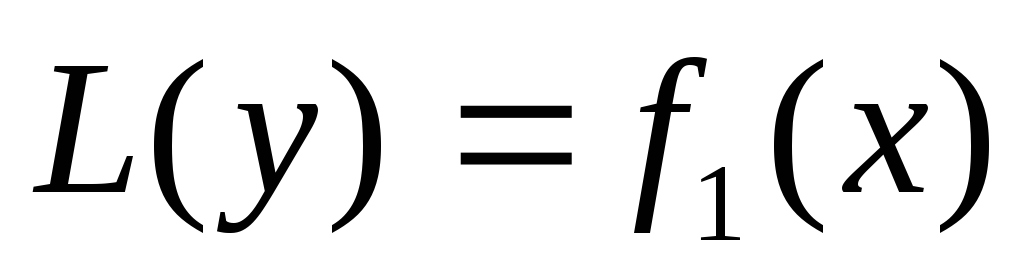 и
и 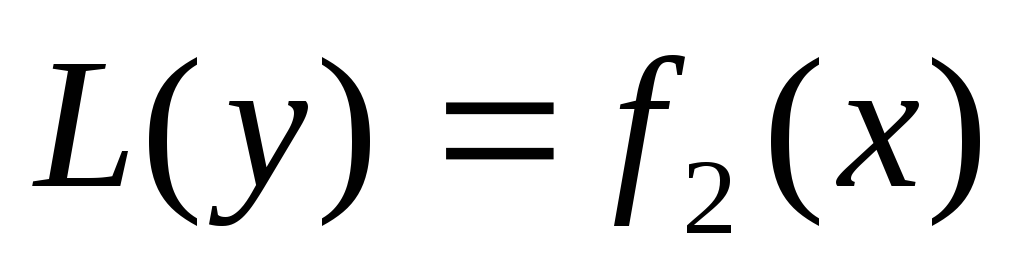
Для иллюстрации решим рассмотренный выше пример другим способом.
Пример. Решить уравнение 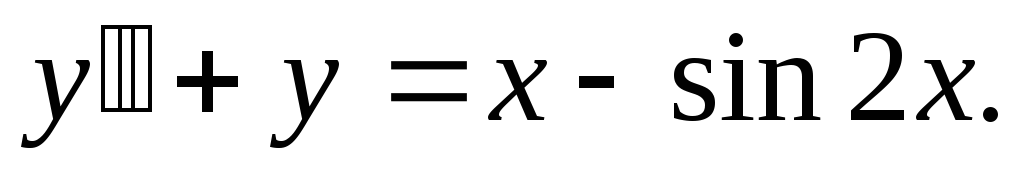
Правую часть дифференциального уравнения представим в виде суммы двух функций f1(x) + f2(x) = x + (—sinx).
Составим
и решим характеристическое уравнение: 
Для функции f1(x) решение ищем в виде
 .
.
Получаем:  Т.е.
Т.е. 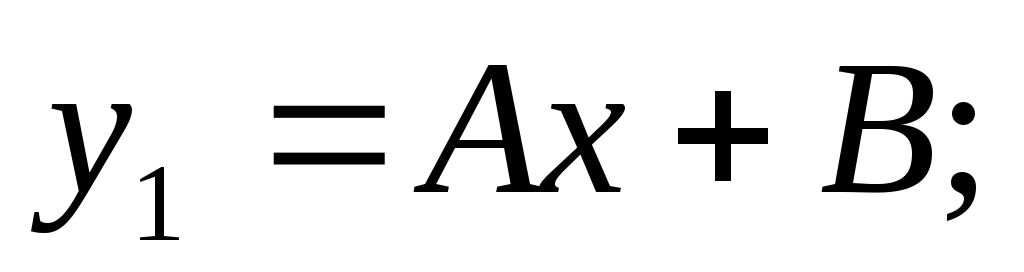
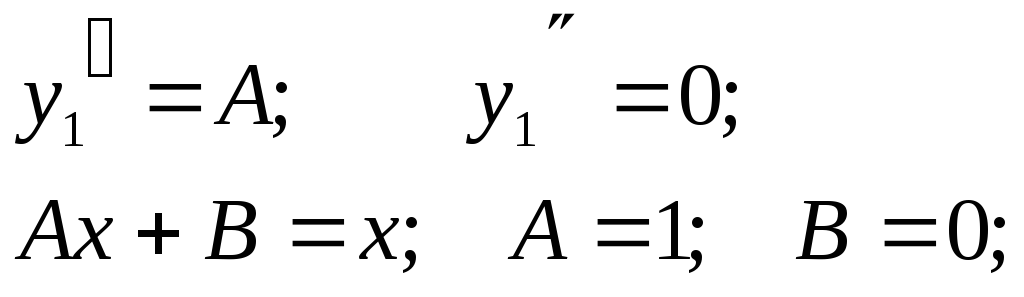
Итого: 
Т.е.
искомое частное решение имеет вид: 
Общее решение неоднородного дифференциального уравнения:
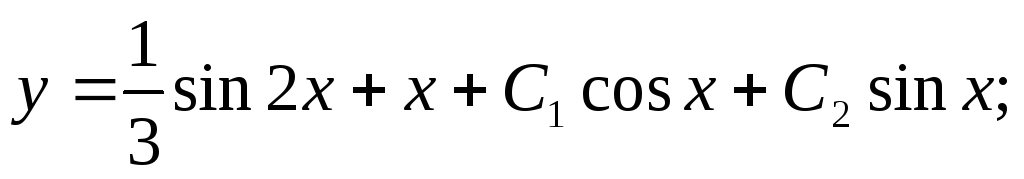
Рассмотрим примеры применения описанных методов.
Пример
1.. Решить уравнение 
Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:
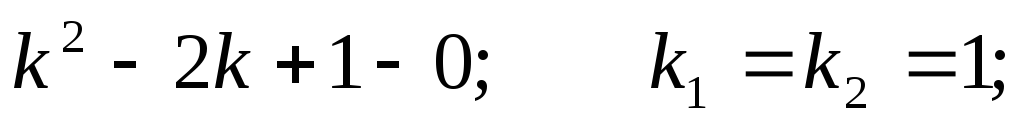
Общее
решение однородного уравнения: 
Теперь найдем частное решение неоднородного уравнения в виде:



Воспользуемся методом неопределенных коэффициентов.

Подставляя в исходное уравнение, получаем:
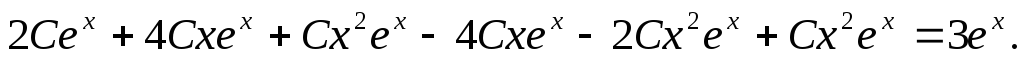

Частное
решение имеет вид: 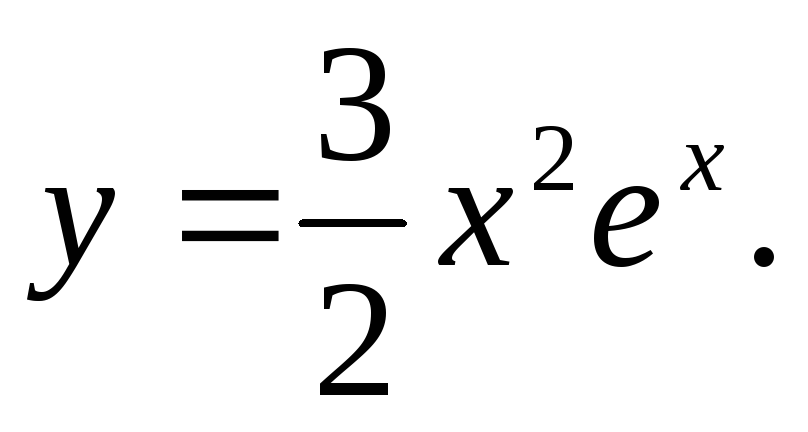
Общее
решение линейного неоднородного
уравнения: 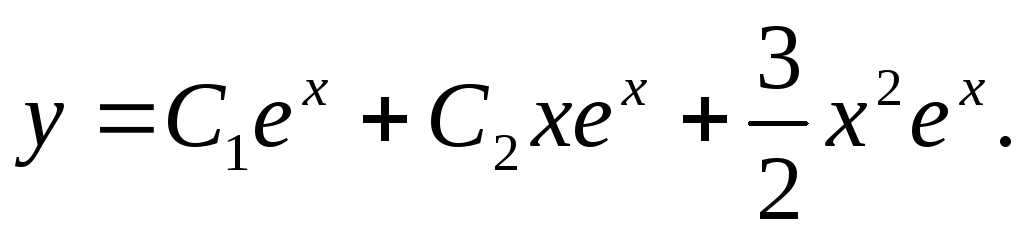
Пример. Решить уравнение 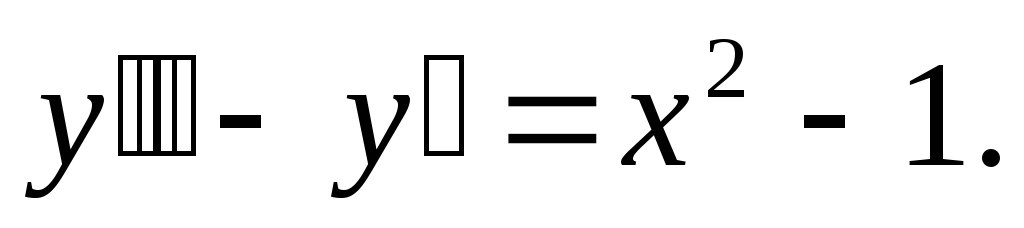
Характеристическое
уравнение: 
Общее
решение однородного уравнения: 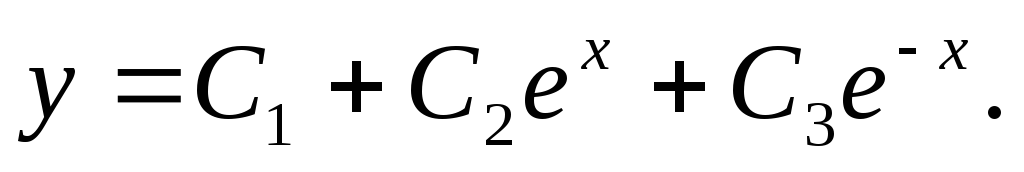
Частное
решение неоднородного уравнения: 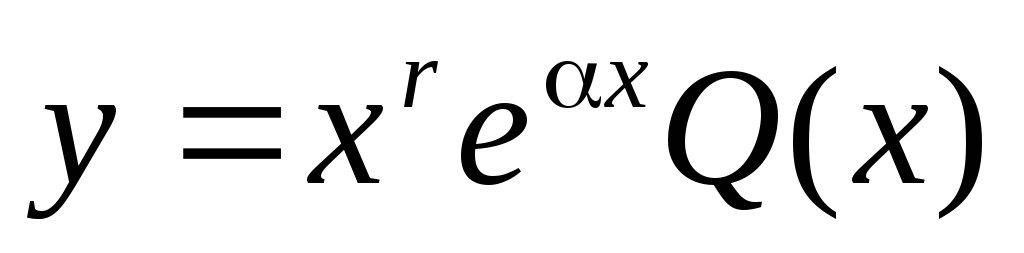 .
.


Находим производные и подставляем их в исходное неоднородное уравнение:


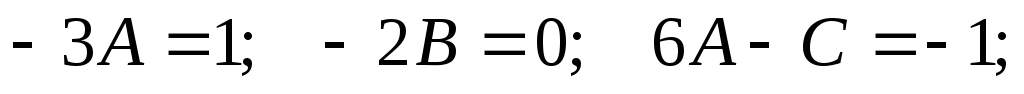
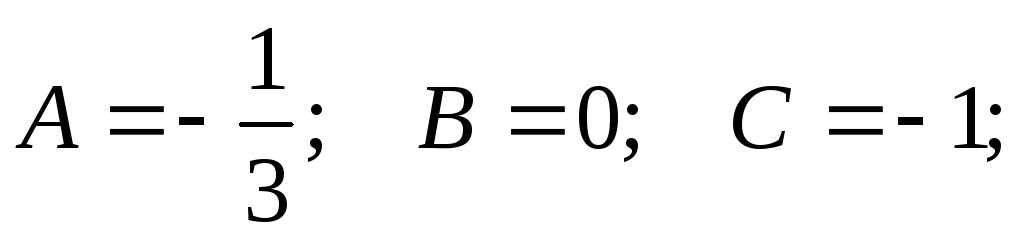
Получаем общее решение неоднородного дифференциального уравнения:

Дифференциальное уравнение в частных производных — Википедия
Дифференциальное уравнение в частных производных (частные случаи также известны как уравнения математической физики, УМФ) — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные.
Рассмотрим сравнительно простое уравнение в частных производных:
- ∂∂yu(x,y)=0.{\displaystyle {\frac {\partial }{\partial y}}u(x,y)=0\,.}
Из этого соотношения следует, что значение функции u(x,y){\displaystyle u(x,y)} не зависит от y{\displaystyle y}. Мы можем положить её равной произвольной функции от x{\displaystyle x}. Следовательно, общее решение уравнения следующее:
- u(x,y)=f(x),{\displaystyle u(x,y)=f(x),}
где f(x){\displaystyle f(x)} — произвольная функция переменной x{\displaystyle x}. Аналогичное обыкновенное дифференциальное уравнение имеет вид:
- dv(x)dx=0{\displaystyle {\frac {dv(x)}{dx}}=0}
и его решение
- v(x)=c,{\displaystyle v(x)=c,}
где c — произвольная константа (не зависящая от x{\displaystyle x}). Эти два примера показывают, что общее решение обыкновенного дифференциального уравнения содержит произвольные константы, но общее решение дифференциального уравнения в частных производных содержит произвольные функции. Решение дифференциального уравнения в частных производных, вообще говоря, не единственно. В общем случае на границе рассматриваемой области задаются дополнительные условия. Например, решение выше рассмотренного уравнения (функция f(x){\displaystyle f(x)}) определяется единственным образом, если u{\displaystyle u} определена на линии y=0{\displaystyle y=0}.
Первое уравнение в частных производных историки обнаружили в статьях Эйлера по теории поверхностей, относящихся к 1734—1735 годам (опубликованы в 1740 году). В современных обозначениях оно имело вид:
- ∂z∂x=f(x,y){\displaystyle {\frac {\partial z}{\partial x}}=f(x,y)}
Начиная с 1743 года к работам Эйлера присоединился Д’аламбер, открывший общее решение волнового уравнения для колебаний струны. В последующие годы Эйлер и Даламбер опубликовали ряд методов и приёмов для исследования и решения некоторых уравнений в частных производных. Эти работы ещё не создали сколько-нибудь завершённой теории.
Второй этап в развитии данной темы можно датировать 1770—1830 годами. К этому периоду относятся глубокие исследования Лагранжа, Коши и Якоби. Первые систематические исследования уравнений в частных производных начал проводить Фурье. Он применил новый метод к решению уравнения струны — метод разделения переменных, позднее получивший его имя.
Новый общий подход к теме, основанный на теории непрерывных групп преобразований, предложил в 1870-х годах Софус Ли.
Задачи доказательств существования и нахождения решений систем нелинейных дифференциальных уравнений в частных производных решаются с использованием теории гладких многообразий, дифференциальной геометрии, коммутативной и гомологической алгебры[1]. Эти методы применяются в физике при изучении лагранжева и гамильтонова формализма, исследовании высших симметрий и законов сохранения[1].
Размерность[править | править код]
Равна количеству независимых переменных. Должна быть не меньше 2 (при 1 получается обыкновенное дифференциальное уравнение).
Линейность[править | править код]
Есть линейные и нелинейные уравнения. Линейное уравнение представимо в виде линейной комбинации производных от неизвестных функций. Коэффициенты при этом могут быть либо постоянными, либо известными функциями.
Линейные уравнения хорошо исследованы, за решение отдельных видов нелинейных уравнений назначены миллионные премии (задачи тысячелетия).
Однородность[править | править код]
Уравнение является неоднородным, если есть слагаемое, не зависящее от неизвестных функций.
Порядок[править | править код]
Порядок уравнения определяется максимальным порядком производной. Имеют значение порядки по всем переменным.
Классификация линейных уравнений второго порядка[править | править код]
Линейные уравнения второго порядка в частных производных подразделяют на параболические, эллиптические и гиперболические.
Две независимые переменные[править | править код]
Линейное уравнение второго порядка, содержащее две независимые переменные, имеет вид:
- A∂2u∂x2+2B∂2u∂x∂y+C∂2u∂y2+…=0,{\displaystyle A{\frac {\partial ^{2}u}{\partial x^{2}}}+2B{\frac {\partial ^{2}u}{\partial x\partial y}}+C{\frac {\partial ^{2}u}{\partial y^{2}}}+…=0,}
где A,B,C{\displaystyle A,\;B,\;C} — коэффициенты, зависящие от переменных x{\displaystyle x} и y{\displaystyle y}, а многоточие означает члены, зависящие от x,y,u{\displaystyle x,\;y,\;u} и частных производных первого порядка: ∂u/∂x{\displaystyle {\partial u}/{\partial x}} и ∂u/∂y{\displaystyle {\partial u}/{\partial y}}. Это уравнение похоже на уравнение конического сечения:
- Ax2+2Bxy+Cy2+⋯=0.{\displaystyle Ax^{2}+2Bxy+Cy^{2}+\cdots =0.}
Так же, как конические сечения разделяются на эллипсы, параболы и гиперболы, в зависимости от знака дискриминанта D=B2−AC{\displaystyle D=B^{2}-AC}, классифицируются уравнения второго порядка в заданной точке:
- D=B2−AC>0{\displaystyle D=B^{2}-AC\,>0} — Гиперболическое уравнение,
- D=B2−AC<0{\displaystyle D=B^{2}-AC\,<0} — Эллиптическое уравнение,
- D=B2−AC=0{\displaystyle D=B^{2}-AC\,=0} — Параболическое уравнение (здесь предполагается, что в данной точке коэффициенты A,B,C{\displaystyle A,\;B,\;C}не обращаются в нуль одновременно).
В случае, когда все коэффициенты A,B,C{\displaystyle A,\;B,\;C} — постоянные, уравнение имеет один и тот же тип во всех точках плоскости переменных x{\displaystyle x} и y{\displaystyle y}. В случае, если коэффициенты A,B,C{\displaystyle A,\;B,\;C} непрерывно зависят от x{\displaystyle x} и y{\displaystyle y}, множество точек, в которых данное уравнение относится к гиперболическому (эллиптическому) типу, образует на плоскости открытую область, называемую гиперболической (эллиптической), а множество точек, в которых уравнение относится к параболическому типу, замкнуто. Уравнение называется смешанным (смешанного типа), если в некоторых точках плоскости оно гиперболическое, а в некоторых — эллиптическое. В этом случае параболические точки, как правило, образуют линию, называемую линией смены типа или линией вырождения.
Более двух независимых переменных[править | править код]
В общем случае, когда уравнение второго порядка зависит от многих независимых переменных:
- ∑i=1n∑j=1naij(x1,⋯,xn)∂2u∂xi∂xj+F(x1,⋯,xn,u,∂u∂x1,⋯,∂u∂xn)=0,{\displaystyle \sum _{i=1}^{n}\sum _{j=1}^{n}a_{ij}(x_{1},\cdots ,x_{n}){\frac {\partial ^{2}u}{\partial x_{i}\partial x_{j}}}+F\left(x_{1},\cdots ,x_{n},u,{\frac {\partial u}{\partial x_{1}}},\cdots ,{\frac {\partial u}{\partial x_{n}}}\right)=0,}
оно может быть классифицировано[2] в заданной точке M0(x10,⋯,xn0){\displaystyle M_{0}(x_{1}^{0},\cdots ,x_{n}^{0})} по аналогии с соответствующей квадратичной формой:
- ∑i=1n∑j=1naij(x10,⋯,xn0)titj.{\displaystyle \sum _{i=1}^{n}\sum _{j=1}^{n}a_{ij}(x_{1}^{0},\cdots ,x_{n}^{0})t_{i}t_{j}.}
Невырожденным линейным преобразованием
- si=∑j=1nAijtj,i=1,2⋯n,det‖Aij‖≠0{\displaystyle s_{i}=\sum _{j=1}^{n}A_{ij}t_{j},i=1,2\cdots n,\det \left\|A_{ij}\right\|\neq 0}
квадратичная форма всегда может быть приведена к каноническому виду:
- ∑i=1nλisi2.{\displaystyle \sum _{i=1}^{n}\lambda _{i}s_{i}^{2}.}
При этом согласно теореме инерции число положительных, отрицательных и равных нулю коэффициентов λi{\displaystyle \lambda _{i}} в каноническом виде квадратичной формы является инвариантом и не зависит от линейного преобразования. На основе этого и производится классификация (в точке M0{\displaystyle M_{0}}) рассматриваемого уравнения:
- Если в точке M0{\displaystyle M_{0}} квадратичная форма в каноническом виде имеет все коэффициенты одного знака, то уравнение в этой точке называется уравнением эллиптического типа.
- Если точке M0{\displaystyle M_{0}} квадратичная форма в каноническом виде имеет коэффициенты различных знаков, но при этом все они отличны от 0{\displaystyle 0}, то уравнение в этой точке называется уравнением гиперболического типа.
- Если точке M0{\displaystyle M_{0}} квадратичная форма в каноническом виде имеет хотя бы один коэффициент равный 0{\displaystyle 0}, то уравнение в этой точке называется уравнением параболического типа.
В случае многих независимых переменных может быть проведена и более подробная классификация (необходимость которой в случае двух независимых переменных не возникает):
- Гиперболический тип может быть дополнительно классифицирован на:
- Нормальный гиперболический тип, если один коэффициент одного знака, а остальные другого.
- Ультрагиперболический тип, если коэффициентов как одного знака так и другого более чем один.
- Параболический тип может быть дополнительно классифицирован на:
- Эллиптически-параболический тип, если только один коэффициент равен нулю, а остальные имеют один знак.
- Гиперболически-параболический тип, если только один коэффициент равен нулю, а остальные имеют различные знаки. Аналогично гиперболическому типу он может быть разделён на:
- Нормальный гиперболически-параболический тип
- Ультрагиперболически-параболический тип
- Ультрапараболический тип, если более чем один коэффициент равен нулю. Здесь также возможна дальнейшая классификация в зависимости от знаков не равных нулю коэффициентов.
Существование и единственность решения[править | править код]
Хотя ответ на вопрос о существовании и единственности решения обыкновенного дифференциального уравнения имеет вполне исчерпывающий ответ (теорема Пикара — Линделёфа), для уравнения в частных производных однозначного ответа на этот вопрос нет. Существует общая теорема (теорема Коши — Ковалевской), которая утверждает, что задача Коши для любого уравнения в частных производных, аналитического относительно неизвестных функций и их производных имеет единственное аналитическое решение[3]. Тем не менее, существуют примеры линейных уравнений в частных производных, коэффициенты которых имеют производные всех порядков и не имеющих решения (Леви[de], 1957). Даже если решение существует и единственно, оно может иметь нежелательные свойства.
Рассмотрим последовательность задач Коши (зависящую от n{\displaystyle n}) для уравнения Лапласа:
- ∂2u∂x2+∂2u∂y2=0,{\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=0,}
с начальными условиями:
- u(x,0)=0,{\displaystyle u(x,0)=0,}
- ∂u∂y(x,0)=sinnxn,{\displaystyle {\frac {\partial u}{\partial y}}(x,0)={\frac {\sin nx}{n}},}
где n{\displaystyle n} — целое. Производная от функции u{\displaystyle u} по переменной y{\displaystyle y} равномерно стремится к 0{\displaystyle 0} по x{\displaystyle x} при возрастании n{\displaystyle n}, однако решением уравнения является
- u(x,y)=(shny)(sinnx)n2.{\displaystyle u(x,y)={\frac {(\mathrm {sh} \,ny)(\sin nx)}{n^{2}}}.}
Решение стремится к бесконечности, если nx{\displaystyle nx} не кратно π{\displaystyle \pi } для любого ненулевого значения y{\displaystyle y}. Задача Коши для уравнения Лапласа называется плохо поставленной или некорректной, так как нет непрерывной зависимости решения от начальных данных.
Для систем нелинейных дифференциальных уравнений в частных производных доказательства существования решений и поиск многообразий всех решений проводятся с использованием теории гладких многообразий, дифференциальной геометрии, коммутативной и гомологической алгебры[1]. Эти методы применяются в физике при изучении лагранжева и гамильтонова формализма, исследовании высших симметрий и законов сохранения[1].
Одномерное уравнение теплопроводности[править | править код]
Уравнение, описывающее распространение тепла в однородном стержне относится к параболическому типу и имеет вид
- ∂u∂t=α2∂2u∂x2{\displaystyle {\frac {\partial u}{\partial t}}=\alpha ^{2}{\frac {\partial ^{2}u}{\partial x^{2}}}}
где u(t,x){\displaystyle u(t,x)} — температура, и α{\displaystyle \alpha } — положительная константа, описывающая скорость распространения тепла. Задача Коши ставится следующим образом:
u(0,x)=f(x){\displaystyle u(0,x)\,=f(x)},
где f(x){\displaystyle f(x)} — произвольная функция.
Уравнение колебания струны[править | править код]
- ∂2u∂t2=c2∂2u∂x2{\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}=c^{2}{\frac {\partial ^{2}u}{\partial x^{2}}}}
Уравнение относится к гиперболическому типу. Здесь u(t,x){\displaystyle u(t,x)} — смещение струны из положения равновесия, или избыточное давление воздуха в трубе, или магнитуда электромагнитного поля в трубе, а c{\displaystyle c} — скорость распространения волны. Для того, чтобы сформулировать задачу Коши в начальный момент времени, следует задать смещение и скорость струны в начальный момент времени:
- u(0,x)=f(x),{\displaystyle u(0,x)=f(x),}
- ∂u∂t(0,x)=g(x),{\displaystyle {\dfrac {\partial u}{\partial t}}(0,x)=g(x),}
Двумерное уравнение Лапласа[править | править код]
Уравнение Лапласа для неизвестной функции двух переменных имеет вид:
- ∂2u∂x2+∂2u∂y2=0{\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=0}
Уравнение эллиптического типа. Его решения называются гармоническими функциями.
Связь с аналитическими функциями[править | править код]
Вещественная и мнимая части любой голоморфной функции f{\displaystyle f} комплексной переменной z=x+iy{\displaystyle z=x+iy} являются сопряжённо гармоническими функциями: они обе удовлетворяют уравнению Лапласа и их градиенты ортогональны. Если f=u+iv{\displaystyle f=u+iv}, то условия Коши-Римана утверждают следующее:
- ∂u∂x=∂v∂y,∂v∂x=−∂u∂y,{\displaystyle {\frac {\partial u}{\partial x}}={\frac {\partial v}{\partial y}},\quad {\frac {\partial v}{\partial x}}=-{\frac {\partial u}{\partial y}},}
Складывая и вычитая уравнения друг из друга, получаем:
- ∂2u∂x2+∂2u∂y2=0,∂2v∂x2+∂2v∂y2=0.{\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=0,\quad {\frac {\partial ^{2}v}{\partial x^{2}}}+{\frac {\partial ^{2}v}{\partial y^{2}}}=0.}
Также можно показать, что любая гармоническая функция является вещественной частью некоторой аналитической функции.
Граничные задачи[править | править код]
Граничные задачи ставятся следующим образом: найти функцию u{\displaystyle u}, которая удовлетворяет уравнению Лапласа во всех внутренних точках области S{\displaystyle S}, а на границе области ∂S{\displaystyle \partial S} — некоторому условию. В зависимости от вида условия различают следующие краевые задачи:
- u|∂S=ψ(x,y),x,y∈∂S{\displaystyle u|_{\partial S}=\psi (x,y),\quad x,y\in \partial S} — задача Дирихле
- ∂u∂n|∂S=ψ(x,y),x,y∈∂S{\displaystyle {\frac {\partial u}{\partial n}}{\big |}_{\partial S}=\psi (x,y),\quad x,y\in \partial S} — задача Неймана
Решение уравнений математической физики[править | править код]
Существует два вида методов решения данного типа уравнений:
- аналитический, при котором результат выводится различными математическими преобразованиями;
- численный, при котором полученный результат соответствует действительному с заданной точностью, но который требует много рутинных вычислений и поэтому выполним только при помощи вычислительной техники (ЭВМ).
Аналитическое решение[править | править код]
Аналитические решения уравнений математической физики можно получить различными способами. Например:
Эти методы разработаны для различных типов уравнений и в некоторых простых случаях позволяют получить решение в виде некоторой формулы или сходящегося ряда, например для уравнения колебаний струны:
- Δu=a2∂2u∂t2{\displaystyle \Delta u=a^{2}{\frac {\partial ^{2}u}{\partial t^{2}}}}
- u(x,t)|x=0=u(x,t)|x=L=0{\displ
2.2. Решение линейных неоднородных дифференциальных уравнением n-го порядка с постоянными коэффициентами
Линейным дифференциальным уравнением n — го порядка с постоянными коэффициентами называется уравнение вида
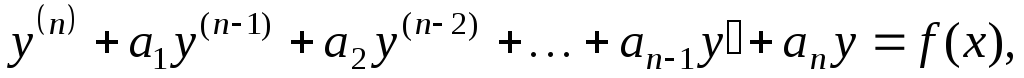 (2.28)
(2.28)
содержащее
неизвестную функцию и ее производные
в первой степени. В (2.28) 
Левая часть уравнения (2.28) называется линейным дифференциальным оператором и обозначается через
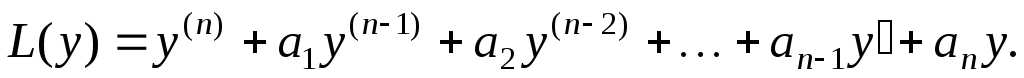
Поэтому в компактной форме уравнение (2.28) записывается так:

Если
правая часть уравнения 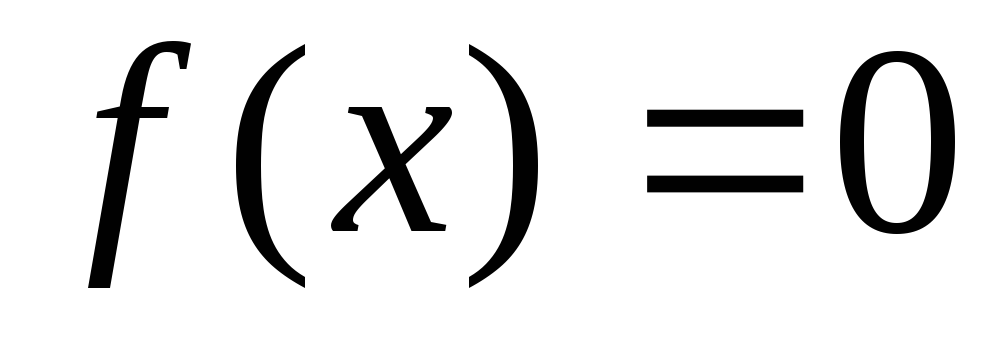 ,
то уравнение (2.28) принимает вид
,
то уравнение (2.28) принимает вид
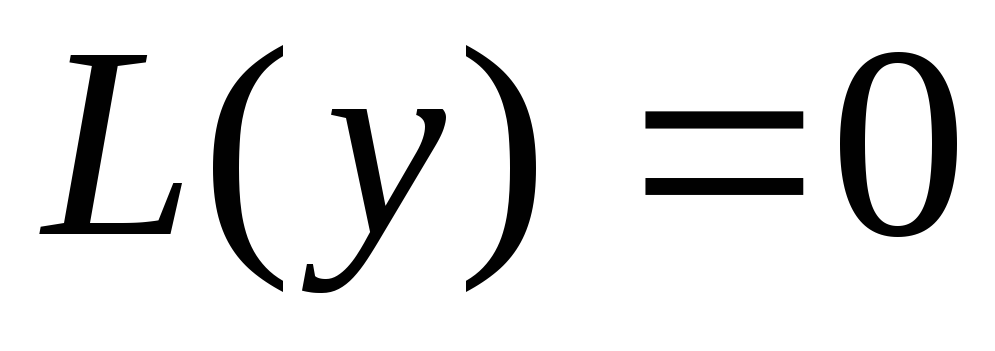 (2.29)
(2.29)
и называется линейным однородным дифференциальным уравнением, в противном случае — неоднородным.
Теорема (о структуре общего решения линейного неоднородного дифференциального уравнения n-го порядка).
Общее решение линейного неоднородного дифференциального уравнения n — го порядка представляется в виде суммы
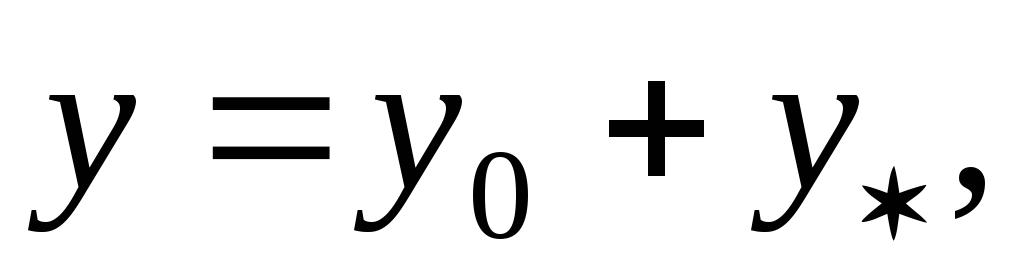 (2.30)
(2.30)
где 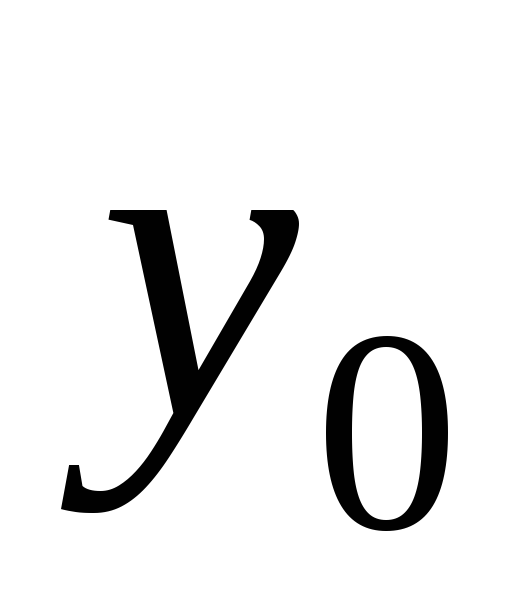 — общее решение соответствующего
линейного однородного уравнения
— общее решение соответствующего
линейного однородного уравнения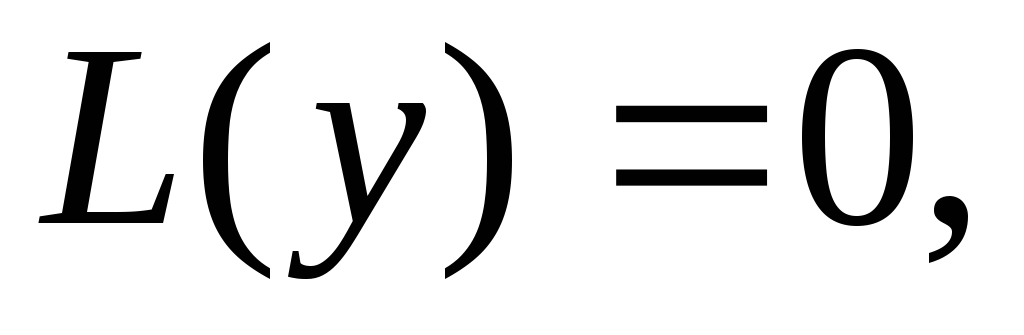 ,
,
 —
частное решение неоднородного уравнения
—
частное решение неоднородного уравнения 

Полезна также следующая теорема:
Общее решение линейного неоднородного дифференциального уравнения

может быть представлено в виде

где 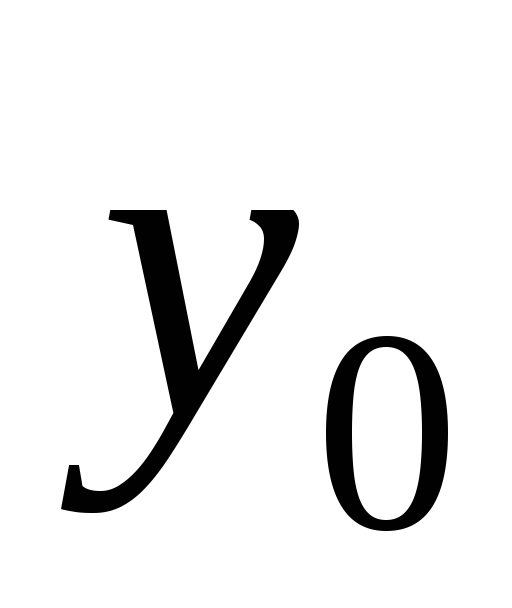 — общее решение соответствующего
однородного уравнения
— общее решение соответствующего
однородного уравнения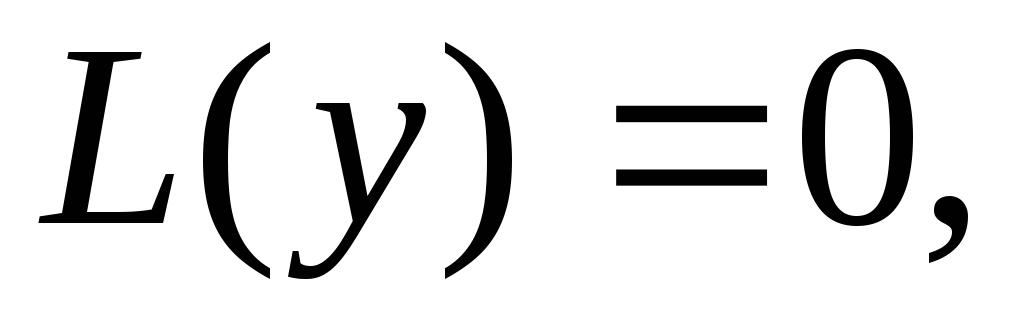
 — частные решения неоднородных уравнений
вида
— частные решения неоднородных уравнений
вида

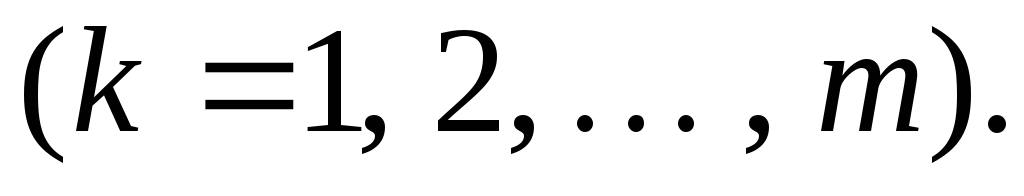
2.2.1. Построение общего решения линейного однородного дифференциального уравнения n -го порядка
Теорема (о структуре общего решения линейного однородного дифференциального уравнения n-го порядка).
Общее
решение линейного однородного
дифференциального уравнения n -го порядка 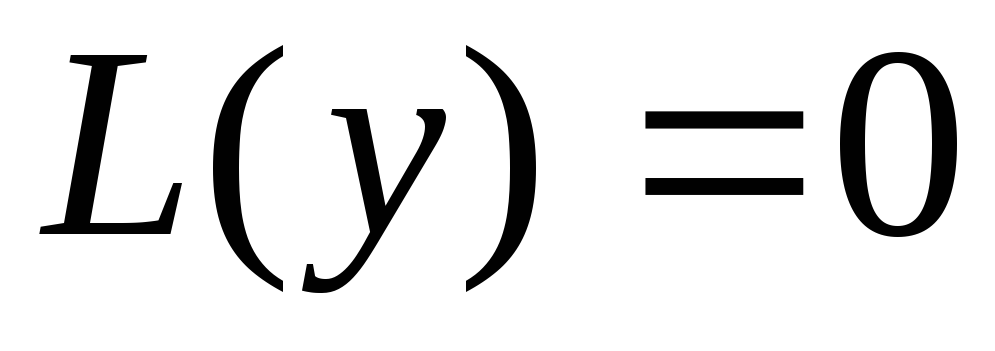 представляется в виде линейной комбинации
n линейно независимых частных решений
этого уравнения:
представляется в виде линейной комбинации
n линейно независимых частных решений
этого уравнения:
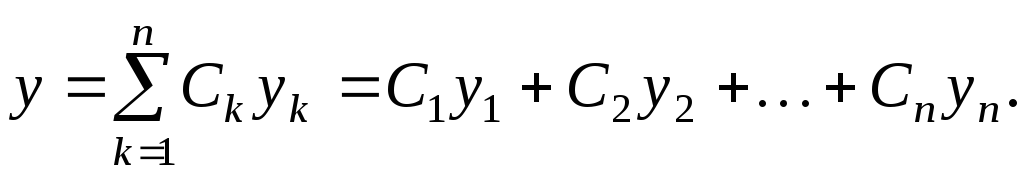 (2.31)
(2.31)
Здесь 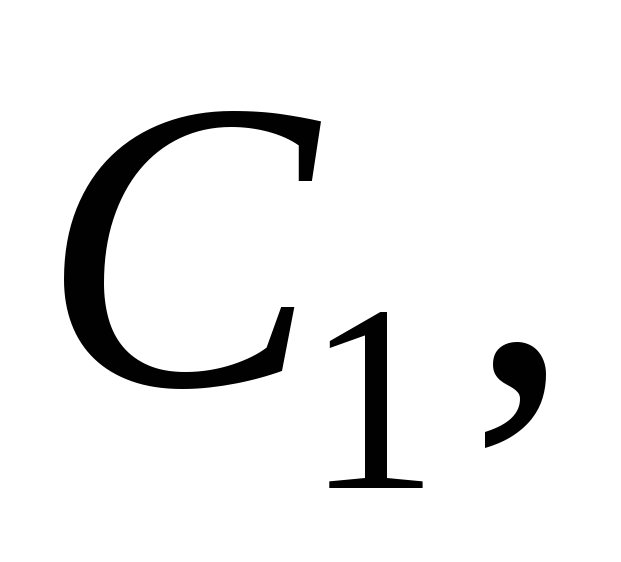
 — произвольные постоянные (заметим,
чтолинейной
комбинацией функций
называется сумма произведений функций
на различные постоянные числа, то есть
выражение вида
— произвольные постоянные (заметим,
чтолинейной
комбинацией функций
называется сумма произведений функций
на различные постоянные числа, то есть
выражение вида 

 —
частные линейно
независимые решения
уравнения
—
частные линейно
независимые решения
уравнения 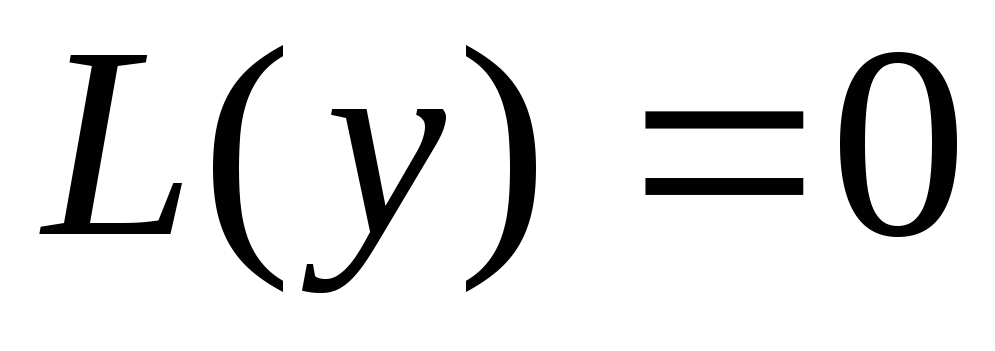 — такие решения, для которыхопределитель
Вронского
— такие решения, для которыхопределитель
Вронского

N линейно независимых частных решений линейного однородного дифференциального уравнения n-го порядка образуют фундаментальную систему решений этого уравнения.
Для
построения фундаментальной системы
решений уравнения 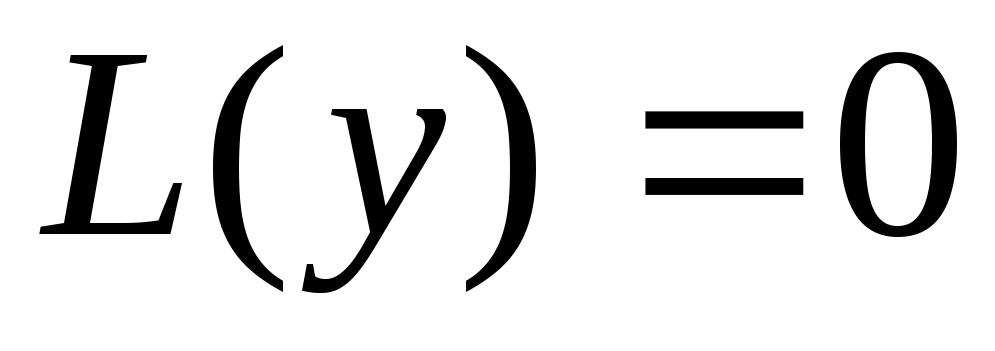 с постоянными коэффициентами его частные
решения ищутся в виде показательных
функций
с постоянными коэффициентами его частные
решения ищутся в виде показательных
функций
 (2.32)
(2.32)
где k — неизвестные постоянные числа. Подстановка (2.32) в дифференциальное уравнение (2.29) приводит к алгебраическому уравнению вида
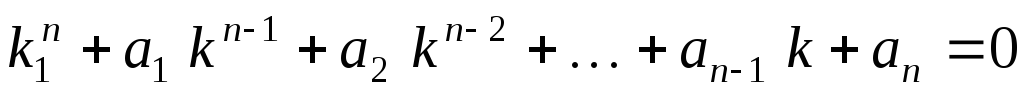 (2.33)
(2.33)
Алгебраическое уравнение (2.33) той же степени, что и порядок дифференциального уравнения (2.29) называется характеристическим уравнением.
Заметим,
что уравнение (2.33) получается из
уравнения (2.29) формальной заменой i — ой
производной  числом
числом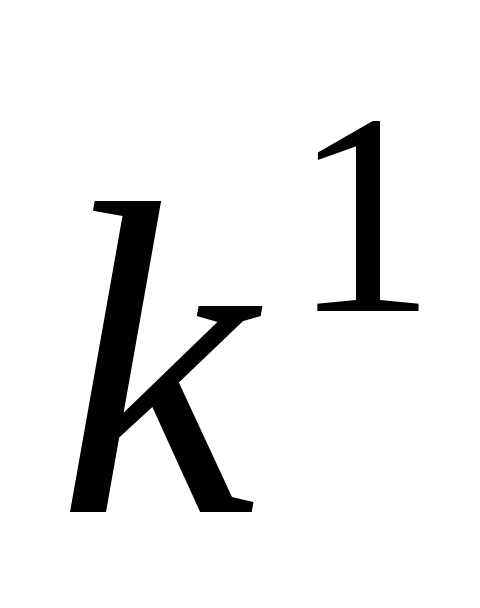 .
.
Характеристическое уравнение (2.33) имеет n корней (с учетом их кратности). В зависимости от вида корней соответствующие частные линейно независимые решения будут иметь различный вид (см. таблицу 1).
Вид частных решений линейного однородного уравнения L(y)=0 в зависимости от вида корней характеристического уравнения
Таблица 1
Вид корней | Вид частных решений | ||
1 | Корни
действительны и различны |
…………………………
| |
2a | Комплексные корни
|
| |
2б | Мнимые корни
|
| |
3а | Кратные действительные корни
|
……………………………… | |
3б | Кратные комплексные корни
кратности m,
кратности m |
……………………………………………
|
………………………………………
|
Частное
решение  неоднородного линейного дифференциального
уравнения n — го порядка может быть
получено или методом подбора ( методом
неопределенных коэффициентов ) или
методом вариации произвольных постоянных.
неоднородного линейного дифференциального
уравнения n — го порядка может быть
получено или методом подбора ( методом
неопределенных коэффициентов ) или
методом вариации произвольных постоянных.
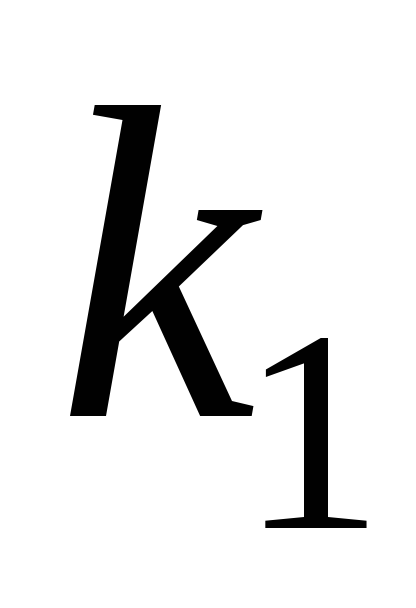 и
и действительные и различные
действительные и различные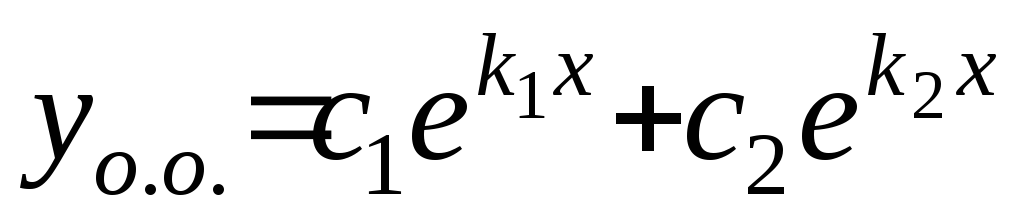
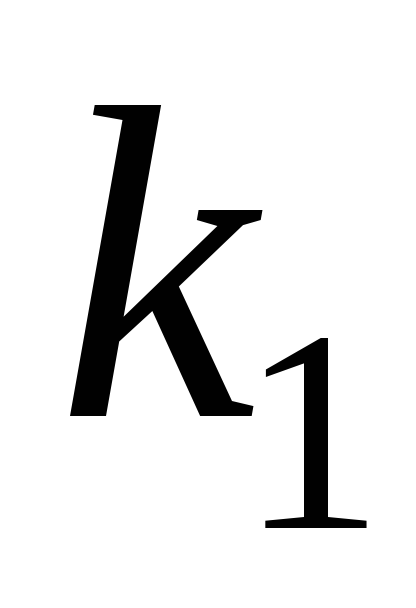 =
= =
=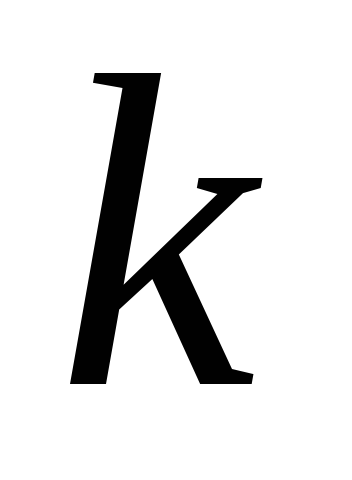

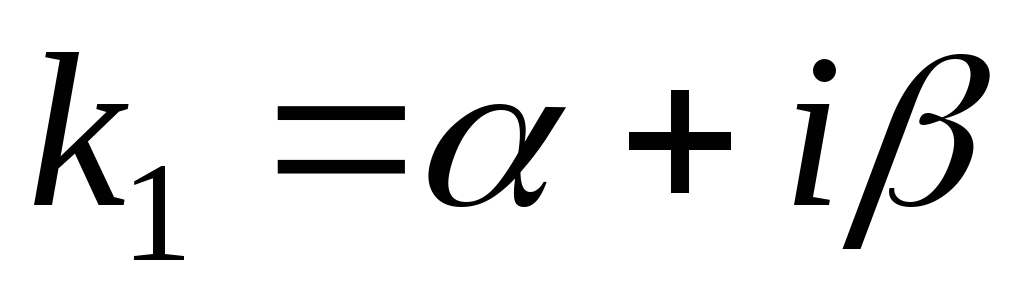 ,
,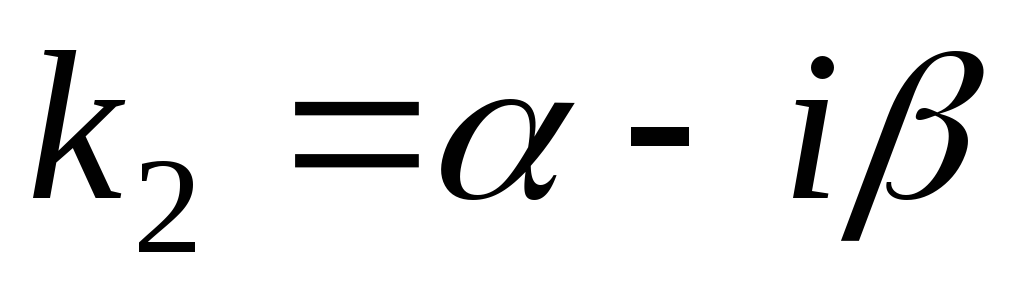


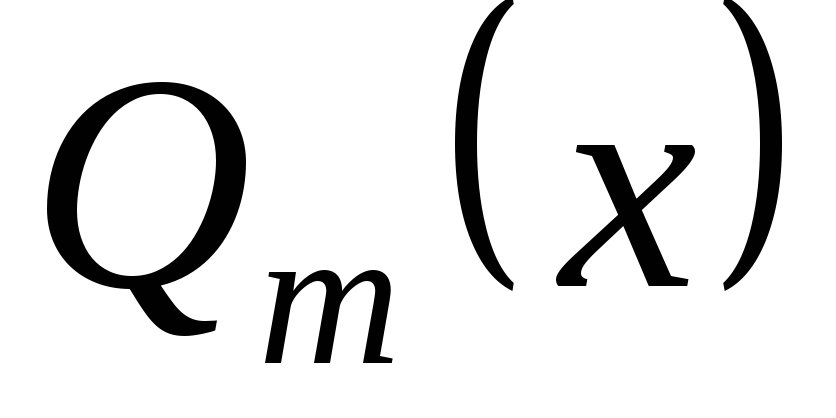


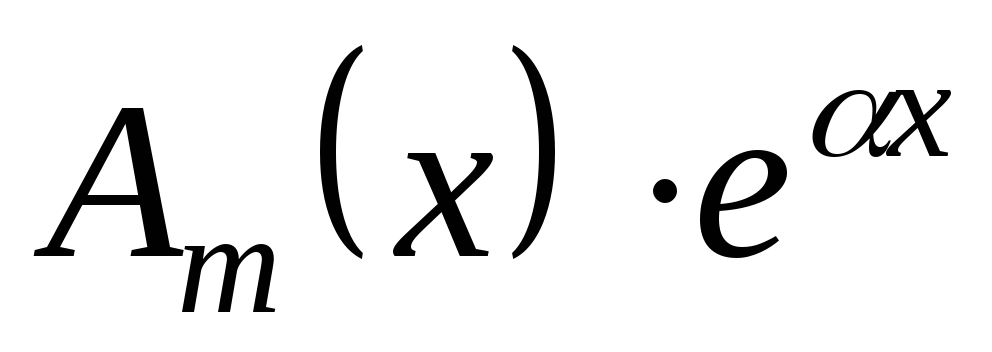

 не является корнем характеристического
уравнения
не является корнем характеристического
уравнения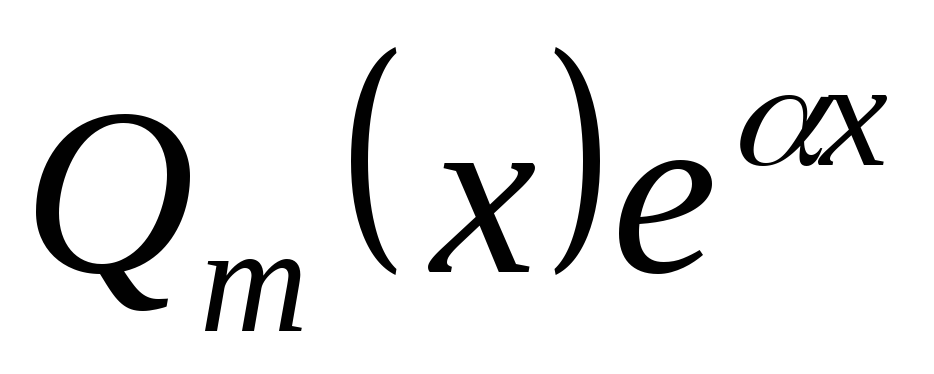
 является корнем характеристического
уравнения кратности
является корнем характеристического
уравнения кратности 
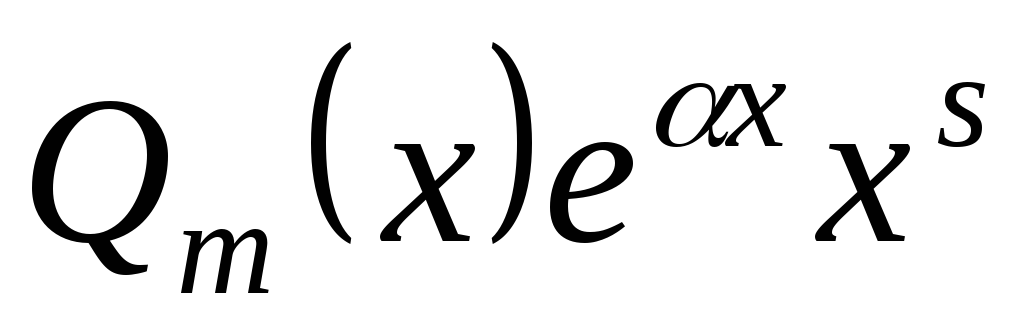
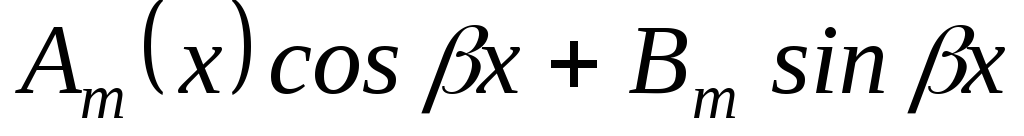
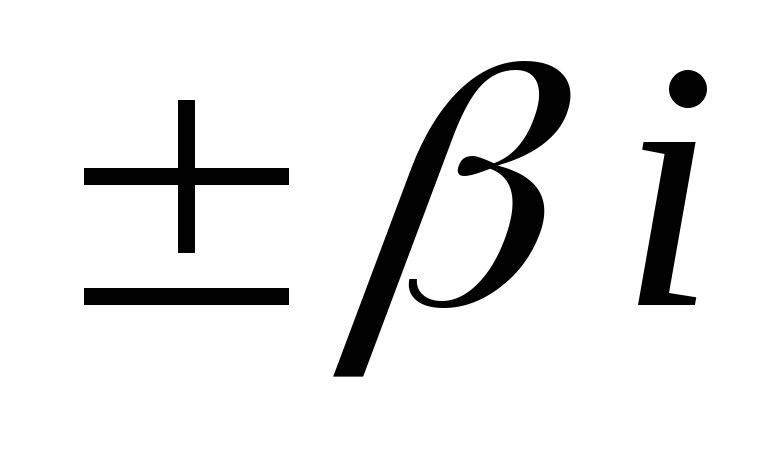 не являются корнями характеристического
уравнения кратности
не являются корнями характеристического
уравнения кратности 

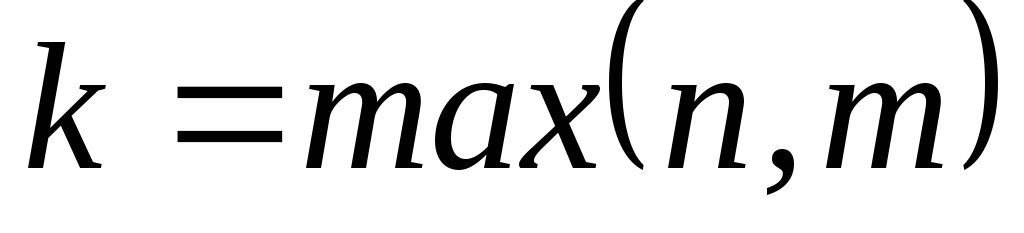
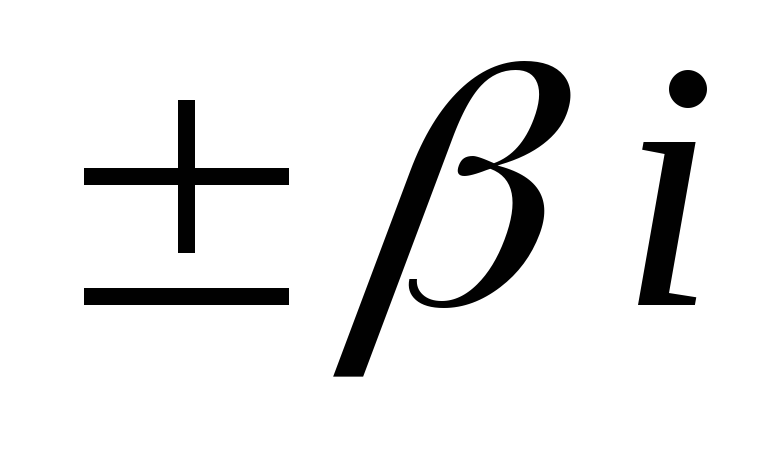 являются корнями характеристического
уравнения кратности
являются корнями характеристического
уравнения кратности 
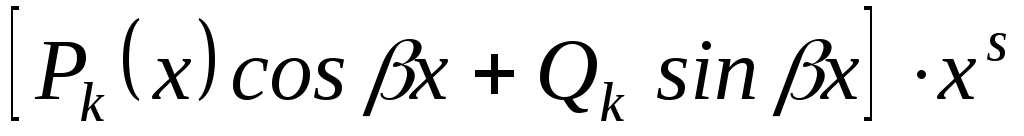

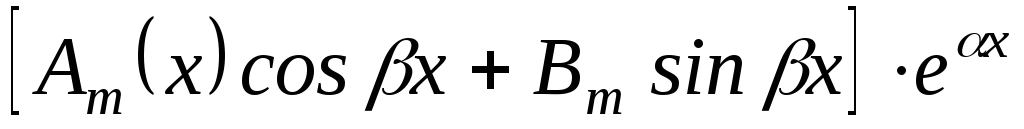
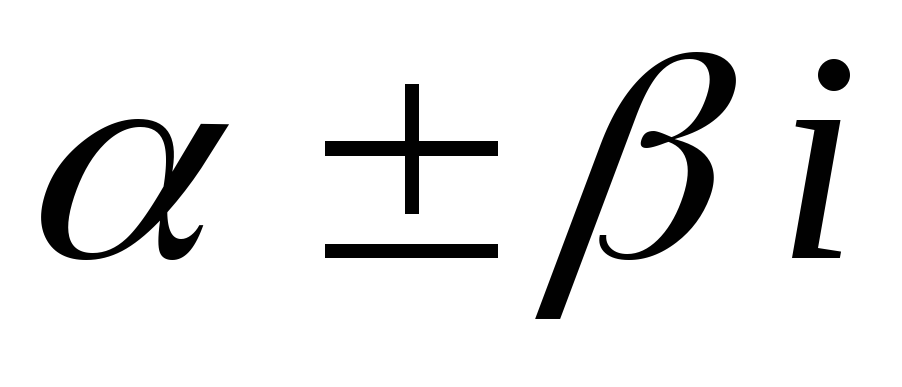 не являются корнями характеристического
уравнения кратности
не являются корнями характеристического
уравнения кратности 
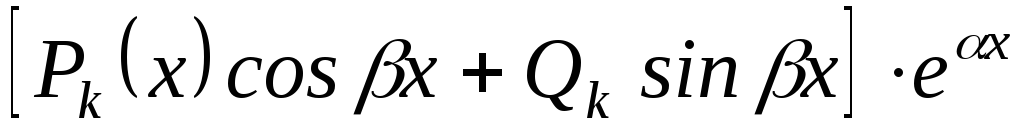
 являются корнями характеристического
уравнения кратности
являются корнями характеристического
уравнения кратности 
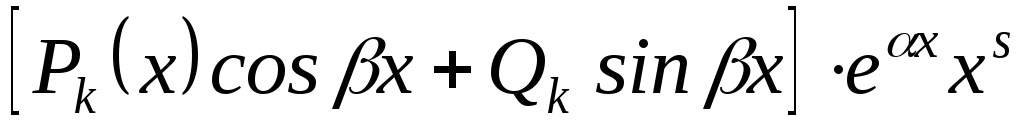
 .
.
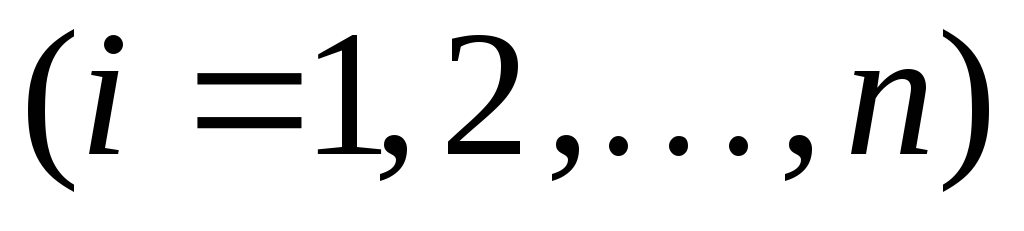



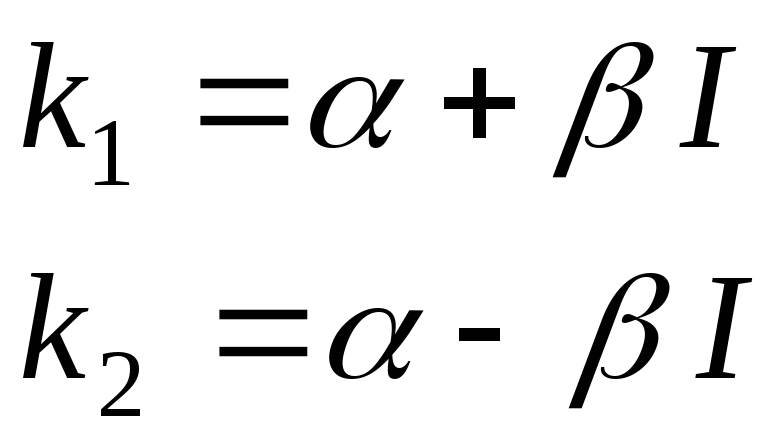
 ,
,


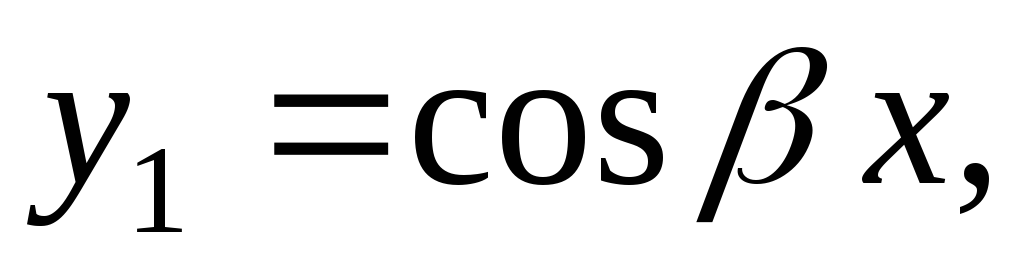
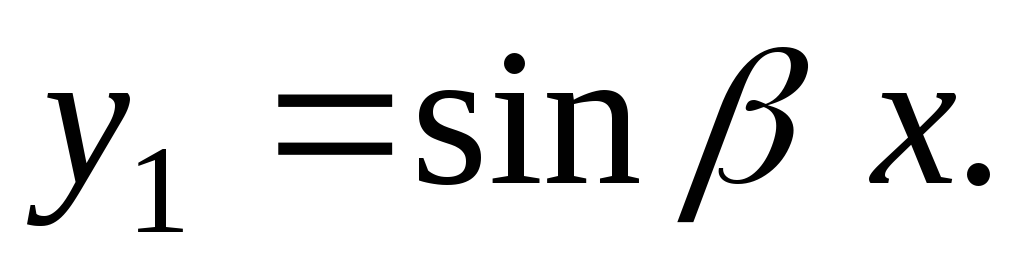






 ,
,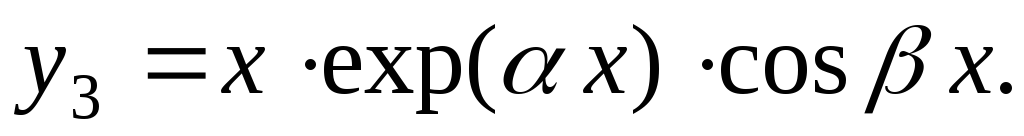
 ,
,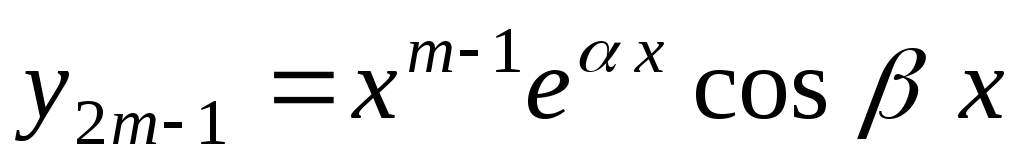
 ,
, ,
,