Оператор |
Опис |
Найпростіші математичні операції |
|
+ — * / () |
Додавання, віднімання, множення, ділення та групуючі символи: + — * / () . Знак множення * — необов’язковий: вираз 2sin(3x) еквівалентний 2*sin(3*x). Дужки використовуються для групування виразів. |
0.5 |
Десяткові дроби записуються через точку:
|
Елементарні функції |
|
xn |
Піднесення до степеню: x^n, наприклад, щоб ввести x2 використовується x^2 |
√x |
Квадратний корінь: \sqrt(x) або x^(1/2) |
3√x |
Кубічний корінь: x^(1/3) |
n√x |
Корінь n-того степеню з x: x^(1/n) |
ln(x) |
Натуральний логарифм (логарифм з основою e): log(x) |
logax |
Логарифм от x з основою a: log(x)/log(a) |
lg(x) |
Десятковий логарифм (логарифм з основою 10): log(x)/log(10) |
ex |
Експоненційна функція: exp(x) |
Тригонометричні функції |
|
sin(x) |
Синус від x: sin(x) |
cos(x) |
Косинус від x: cos(x) |
tg(x) |
Тангенс x: tan(x) |
ctg(x) |
Котангенс x: 1/tan(x) |
arcsin(x) |
Арксинус x: arcsin(x) |
arccos(x) |
Арккосинус x: arccos(x) |
| Арктангенс x: arctan(x) | |
arcctg(x) |
Арккотангенс x: \pi/2 — arctan(x) |
Деякі константи |
|
e |
Число Ейлера e: \e |
π |
Число π: \pi |
ua.onlinemschool.com
4. Основні методи інтегрування
4.1. Метод безпосереднього інтегрування (мбі)
Одним з найпростіших методів інтегрування є метод безпосереднього інтегрування, який полягає у використанні властивостей НІ та табличних інтегралів.
Приклад 2.
Обчислити невизначені інтеграли
а) 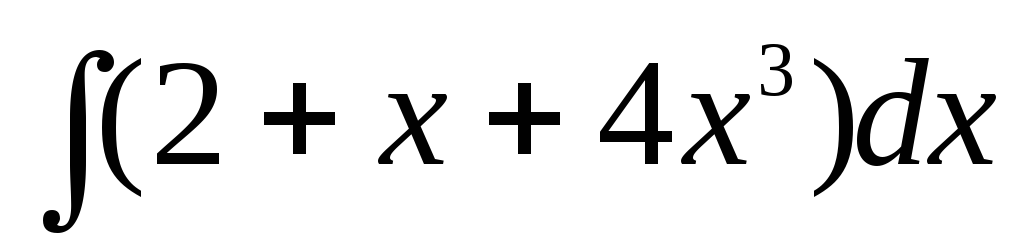
 ;
; в) 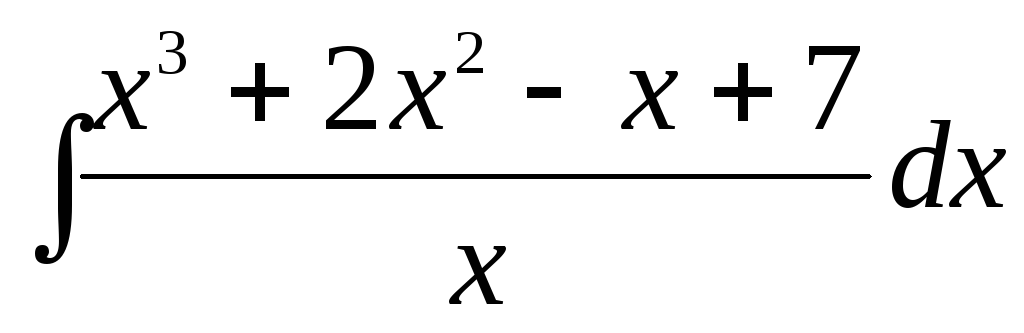 ;
г)
;
г)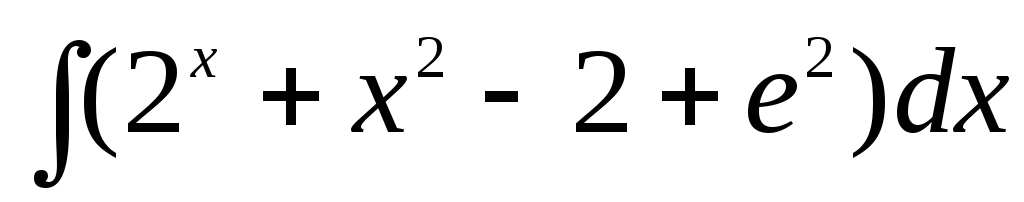 .
.
Розв’язання
а) 
б) 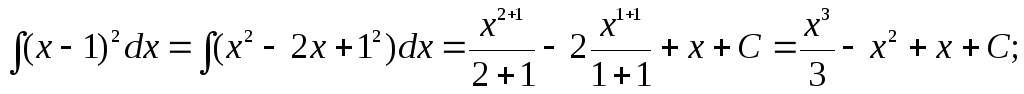
в) 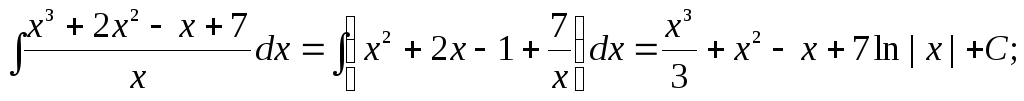
г) 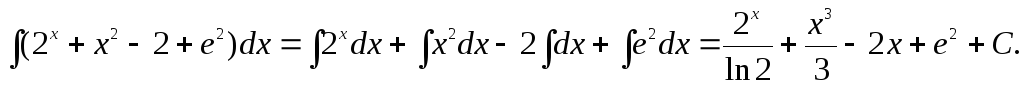
4.2. Метод заміни змінної (мзз)
Суть методу можна сформулювати в наступній теоремі
Теорема 1.1.
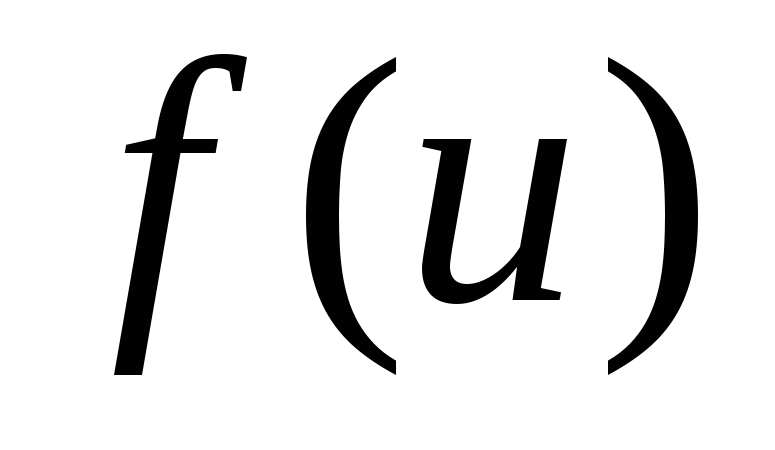 і
і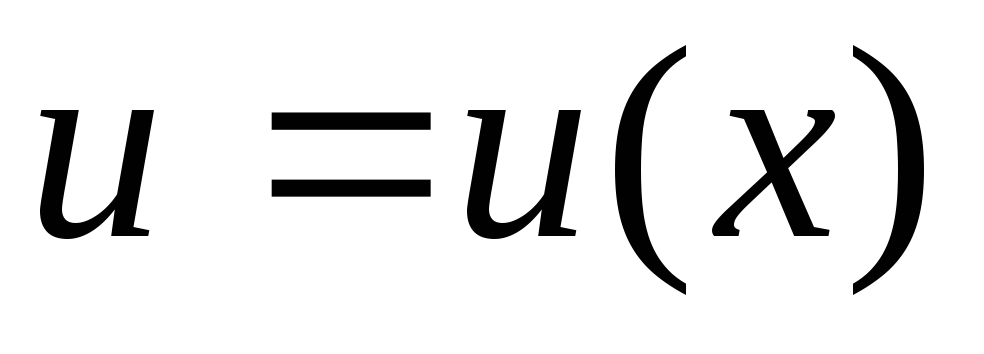 визначені на певних проміжках, причому
визначені на певних проміжках, причому диференційована.
Тоді, якщо
диференційована.
Тоді, якщо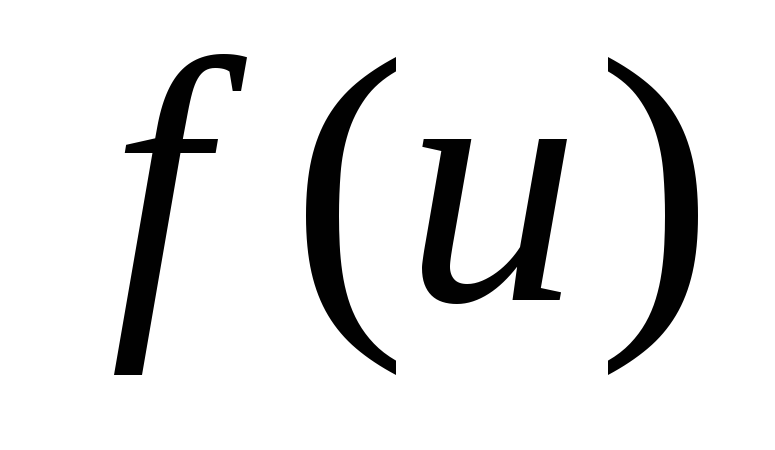 має первісну
має первісну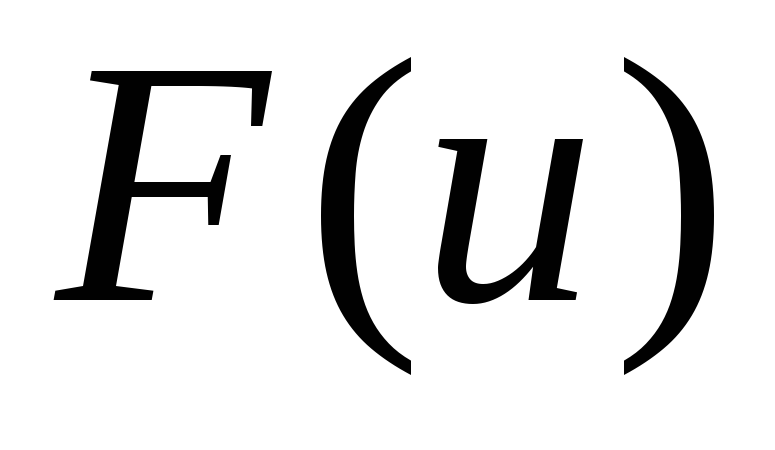 ,
то справедливо
,
то справедливо 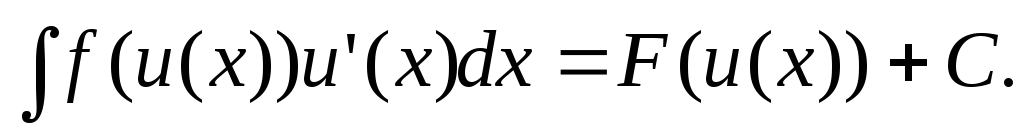 (*)
(*)
Доведення. Оскільки
функція 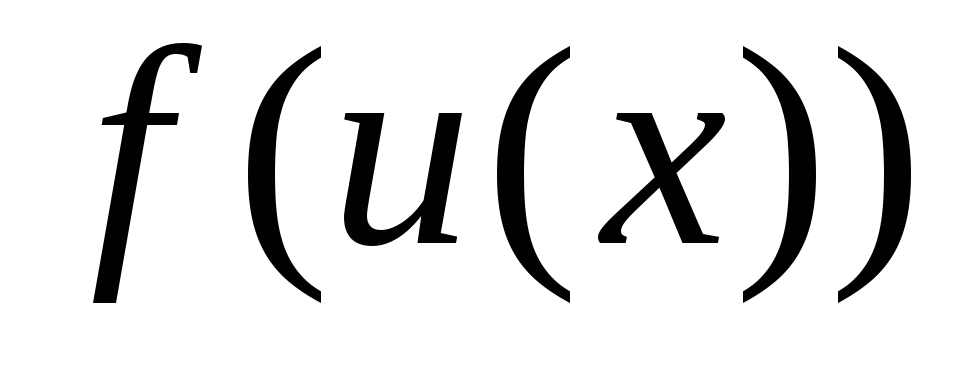 визначена, то буде визначеною і первісна
визначена, то буде визначеною і первісна

Таким чином, продиференціювавши (*), отримаємо


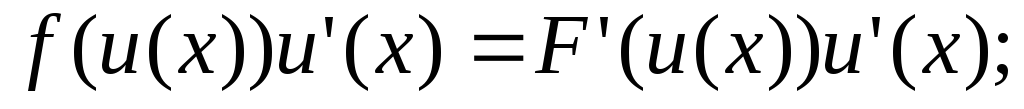
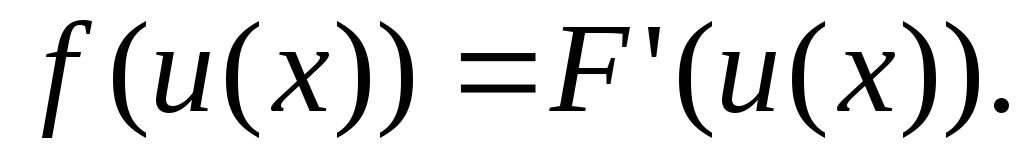
Остання рівність є правильною в силу означення первісної. Що й потрібно було довести.
Зауваження. На практиці не завжди підінтегральний вираз має класичний (для МЗЗ) вигляд
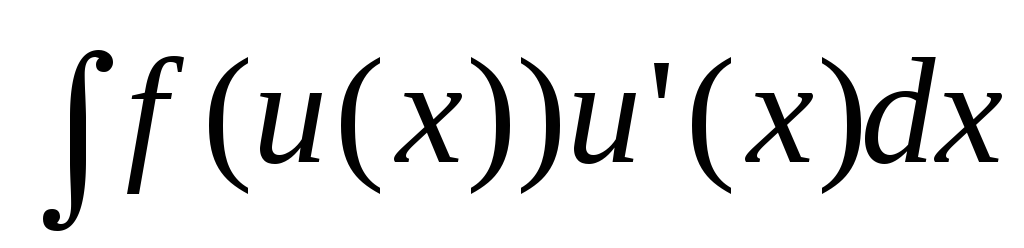 .
.В такому випадку потрібно вводити в розгляд штучну функцію.
Приклад 3.
Обчислити невизначені інтеграли
а) 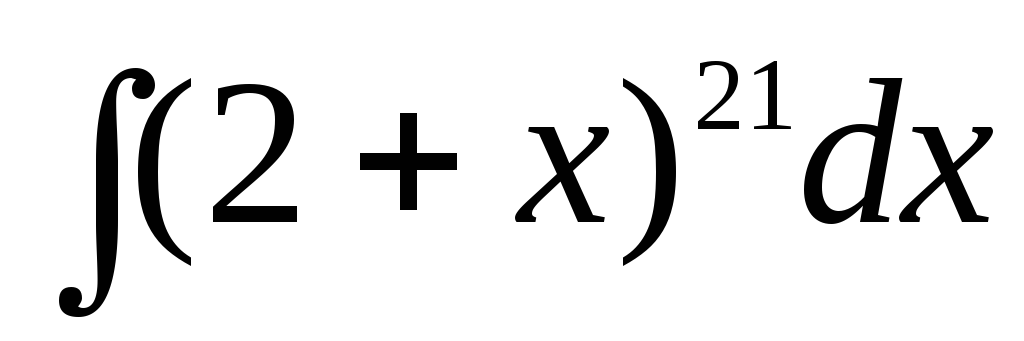 ;
б)
;
б)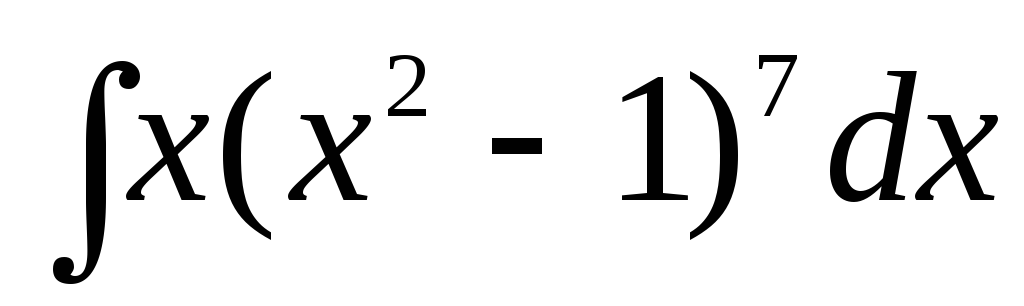 ;
;
в) 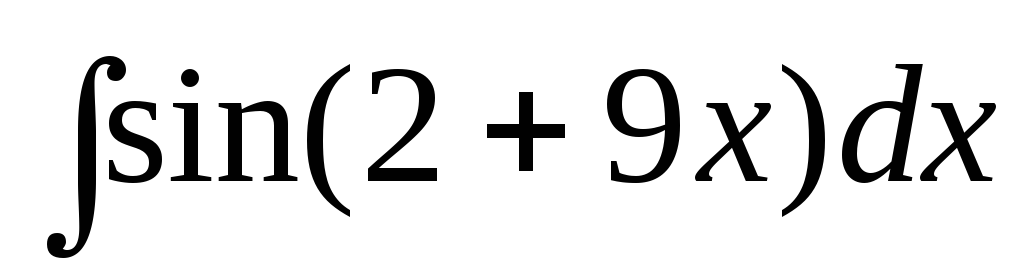 ;
г)
;
г) .
.
Розв’язання
а) 

б
)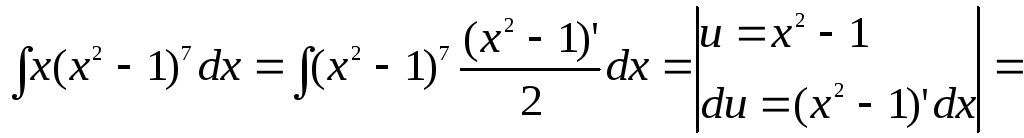
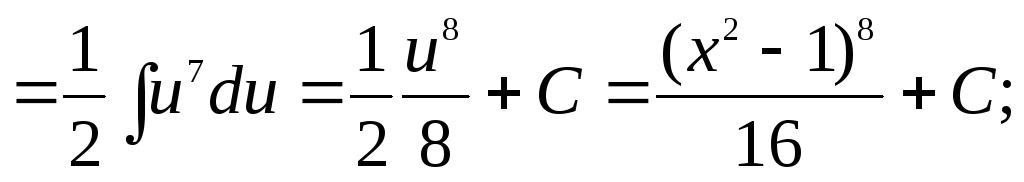
в) 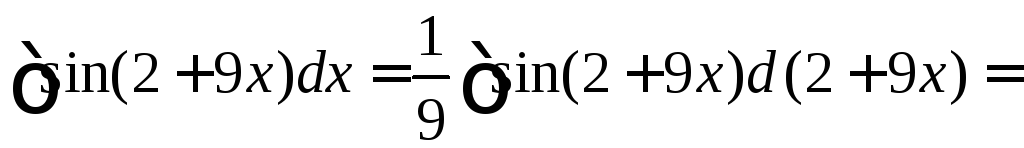
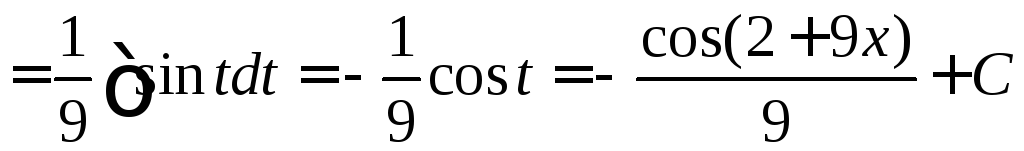 ;
;
г) 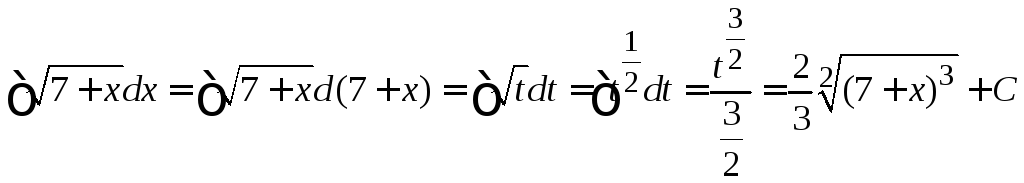 .
.
4.3. Метод інтегрування частинами (міч)
Формула
інтегрування частинами дає змогу звести
обчислення інтеграла 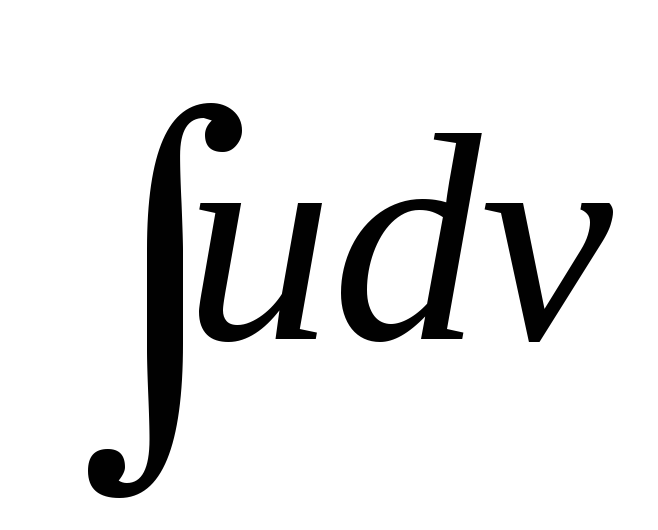 до обчислення більш простого інтеграла
до обчислення більш простого інтеграла використовуючи формулу
використовуючи формулу
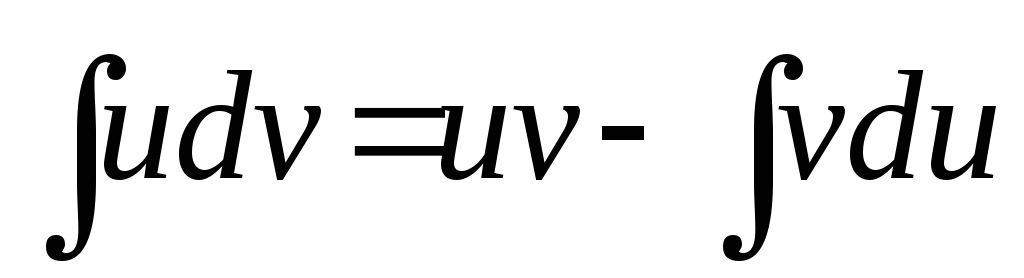 .
.Приклад 4.
Обчислити невизначені інтеграли
а)  ; б)
; б)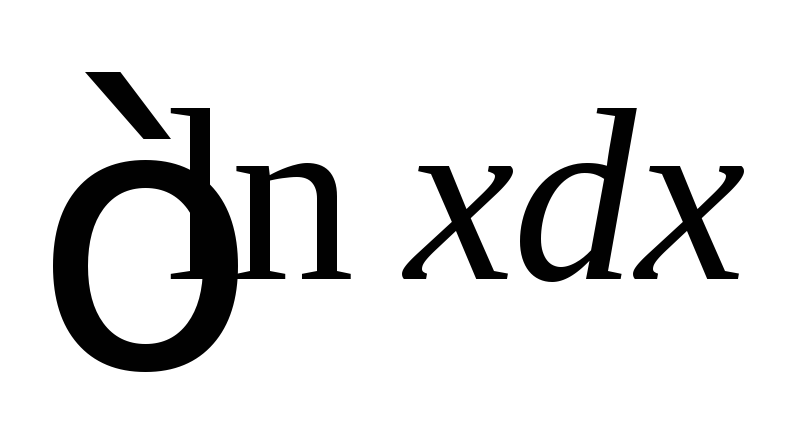 ; в)
; в) .
.
Розв’язання.
а) 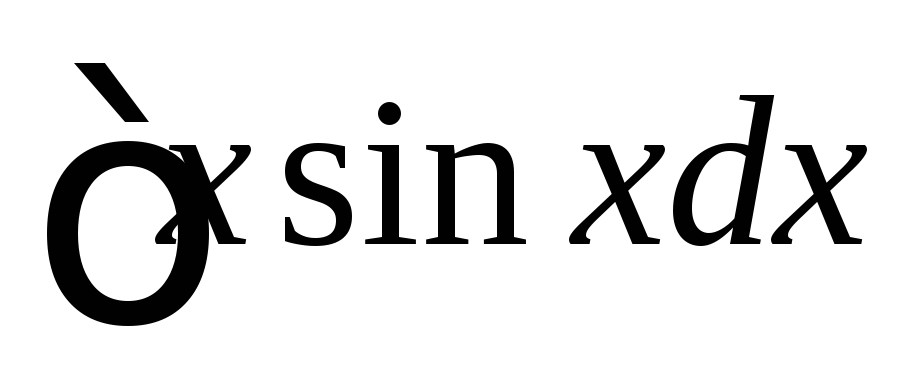 .
.
Для
інтеграла  покладемо
покладемо ,
,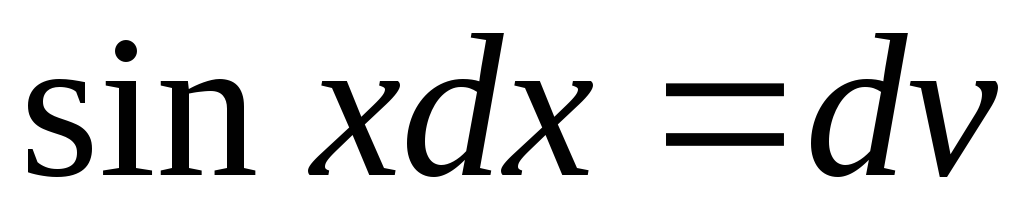 .
Тоді
.
Тоді
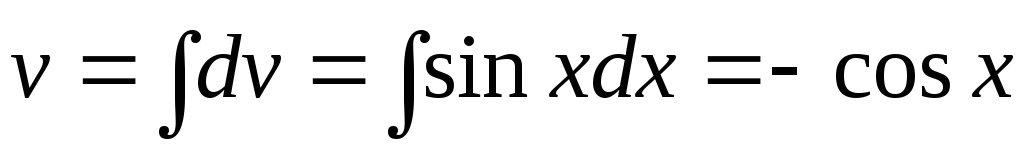 ,
маємо
,
маємо  .
.
Зауваження. Якщо змінна х буде в степені 2, 3, … , то стільки ж разів потрібно застосувати формулу інтегрування частинами.
б) 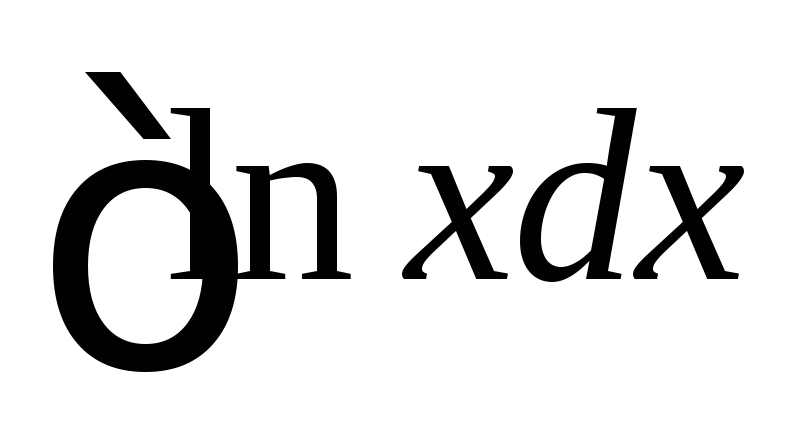 .
.
Для
інтеграла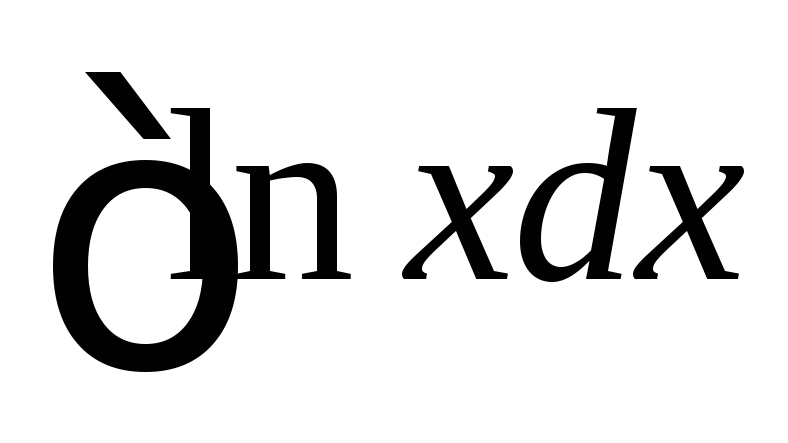 функція
функція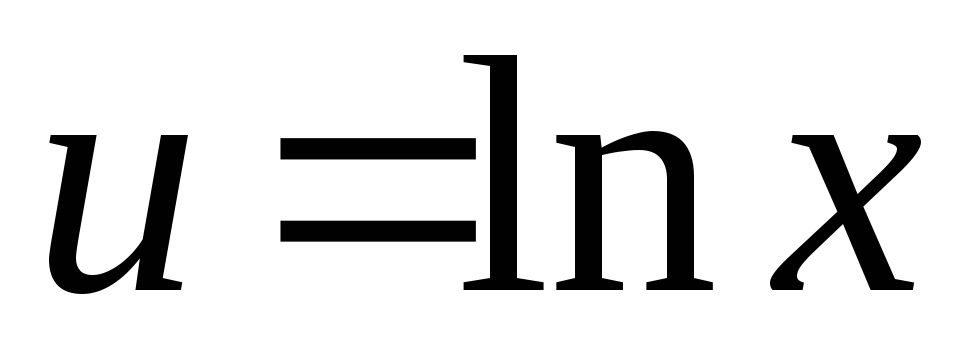 ,
тоді
,
тоді .
Звідси
.
Звідси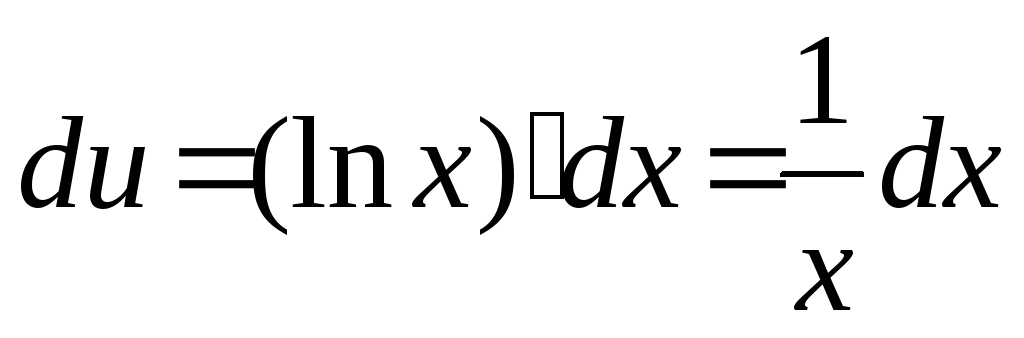 ,
а
,
а
Використовуючи
формулу інтегрування частинами  ,
одержимо
,
одержимо
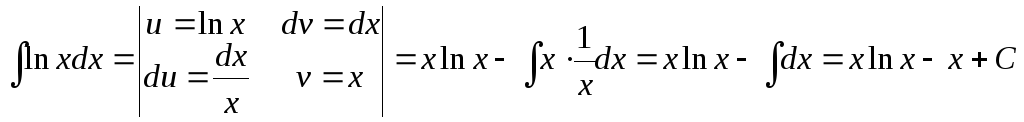 .
.
в) 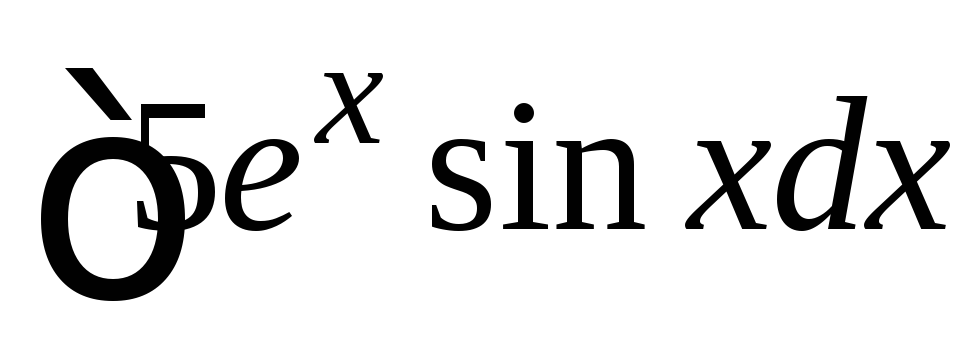 .
.
Інтеграли такого виду називають циклічними. Для них за и обирають тригонометричну функцію, а за v – експоненту, і інтегрують двічі. Маємо
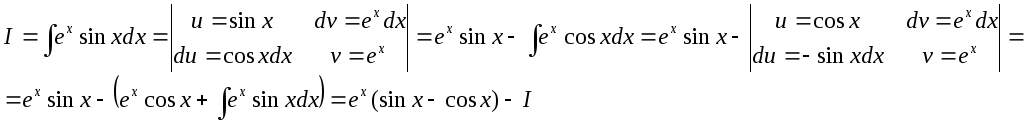 Отримаємо:
Отримаємо:
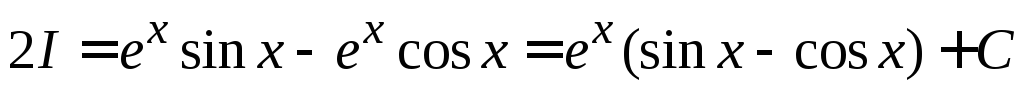
звідки
 .
.
Метод інтегрування раціональних дробів (МІРД)
Цей метод використовують під час обчислення інтегралів виду
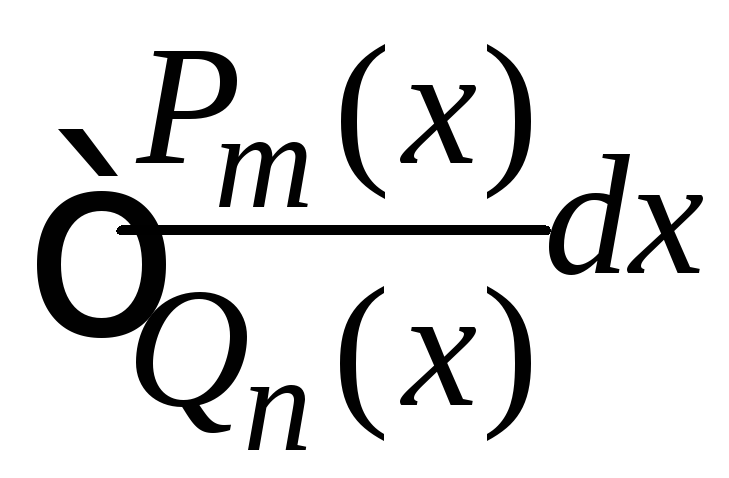 ,
,
де
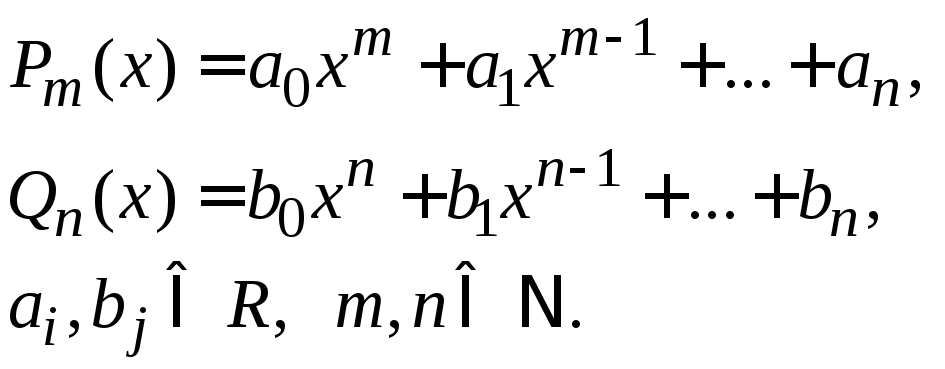
В залежності від вигляду підінтегральної функції розрізняють наступні способи обчислення інтегралів.
І. Метод внесення під диференціал або МЗЗ
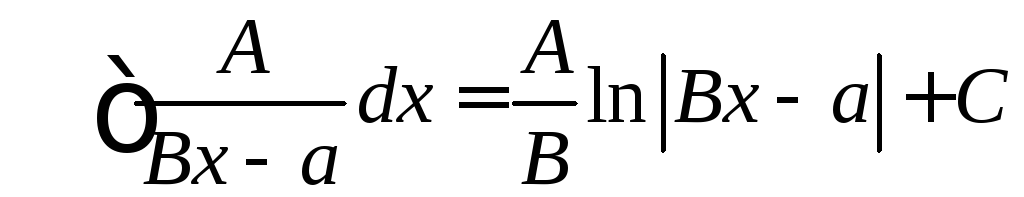 ,
,
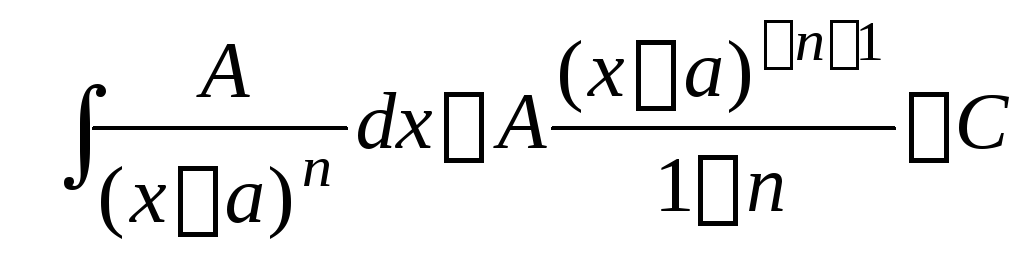
ІІ.
Використовуючи підстановку 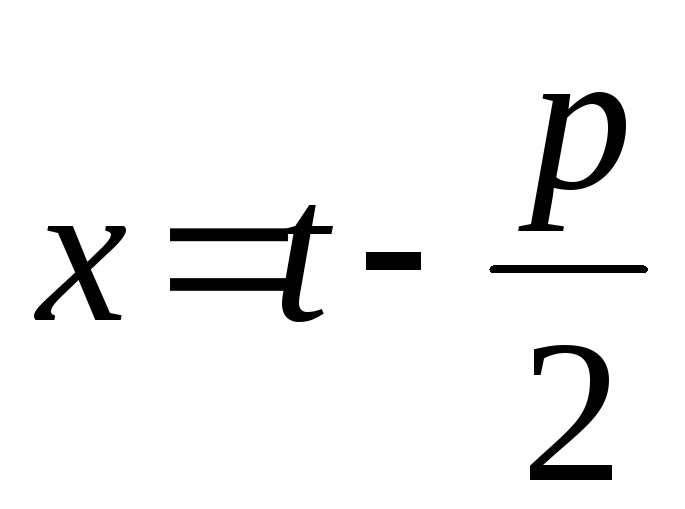 ;
;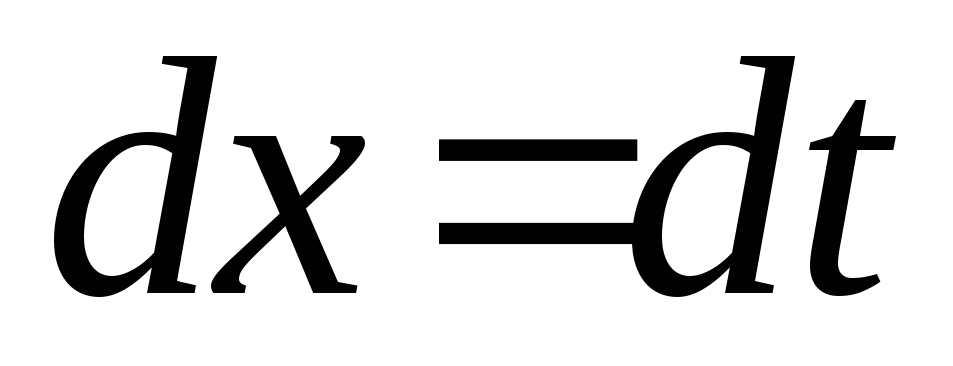 обчислюють інтеграли виду
обчислюють інтеграли виду
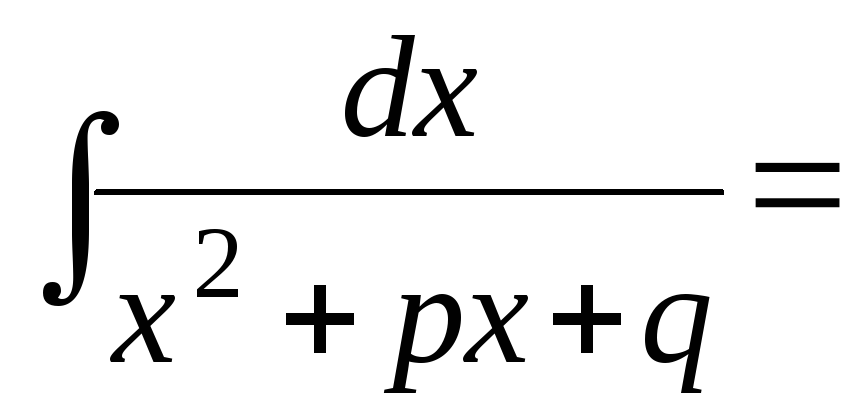
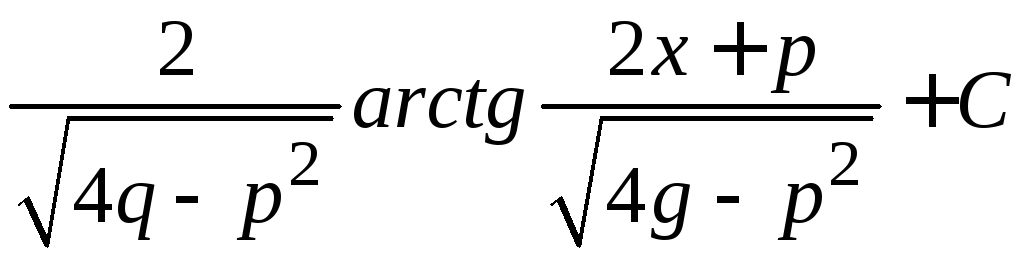 .
. 
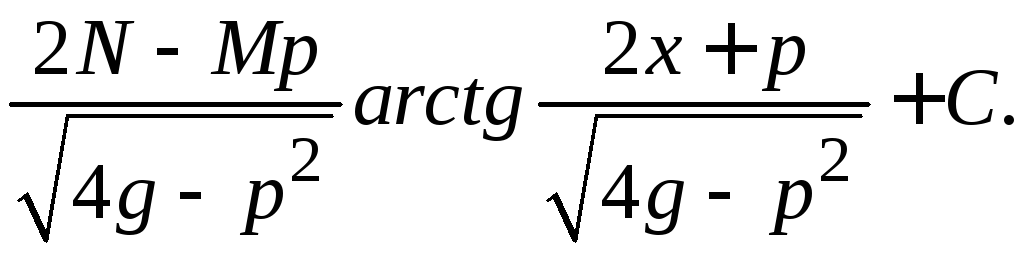
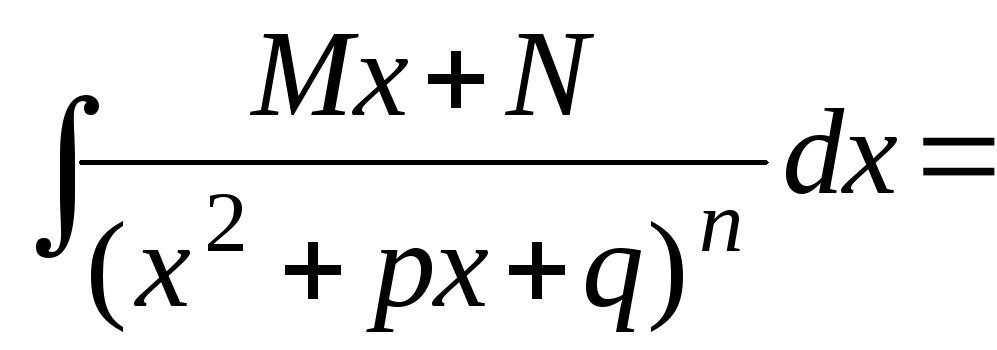
 ,
,
де 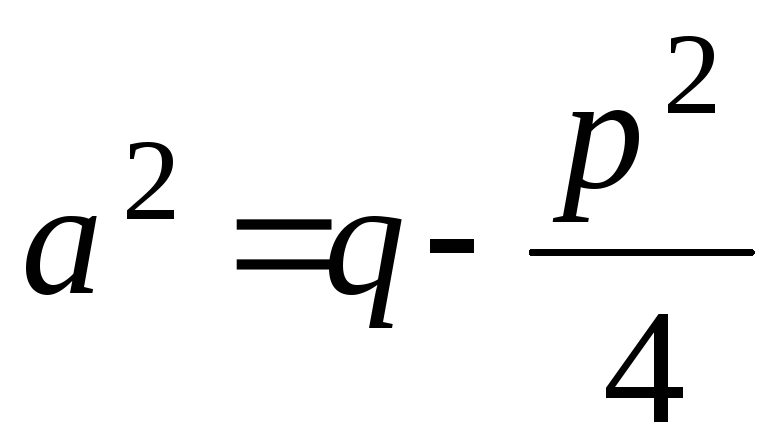 .
.
Перший інтеграл обчислюється безпосередньо, а другий за рекурентною формулою

 .
.
ІІІ. Використовується метод невизначених коефіцієнтів для інтегралів виду
І.
Якщо 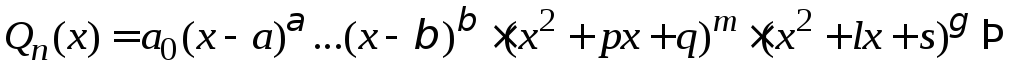
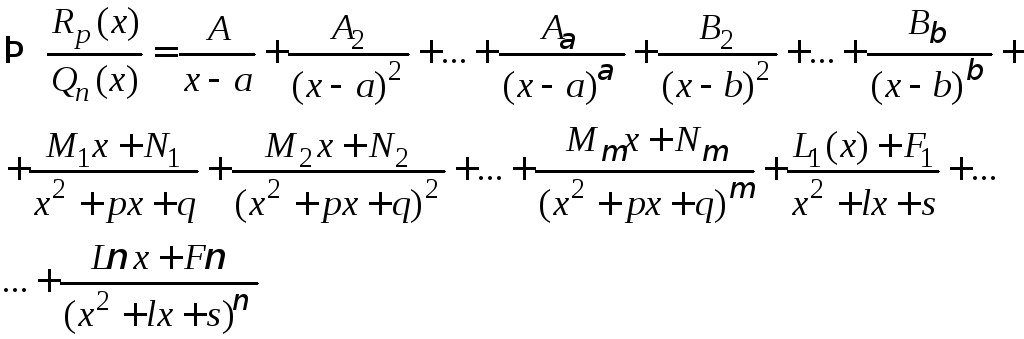
ІІ.
Якщо 
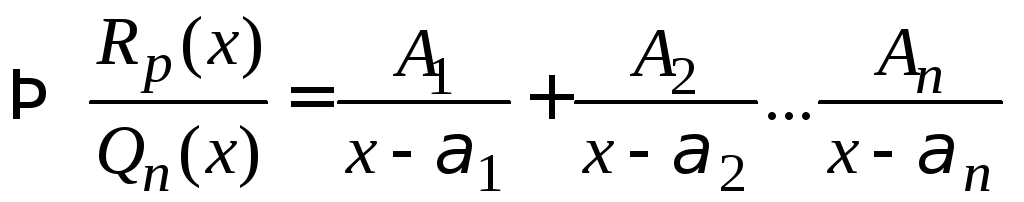
ІІІ.
Якщо 

IV.
Якщо 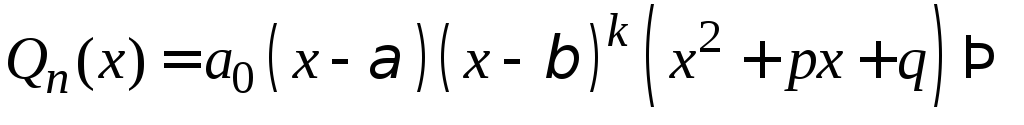
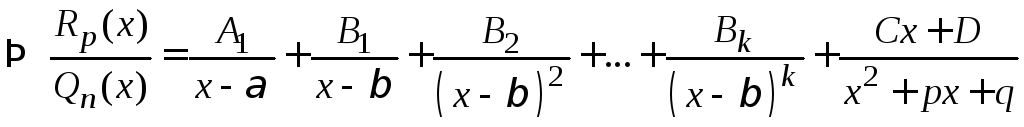 (*)
(*)
Для знаходження сталих Аі, Вj, Ck…, найчастіше користуються так званим методом невизначених коефіцієнтів. Так, наприклад, зводимо праву частину рівності (*) до спільного знаменника, який дорівнює многочлену Q(х). В результаті з рівності (*) дістанемо два рівні дроби з однаковими знаменниками. Отже, і чисельники цих дробів тотожно рівні. В лівій частині рівності чисельником є заданий многочлен R(х), а в правій частині — многочлен від змінної х, коефіцієнти якого містять невідомі Аі, Вj, Ck…. Прирівнюючи коефіцієнти при однакових степенях х, дістанемо систему к лінійних алгебраїчних рівнянь, з якої можна визначити шукані невідомі Аі, Вj, Ck…
studfile.net
3.2.2. Властивості визначеного інтегралу
1. Довільний постійний множник можна виносити за знак інтегралу:
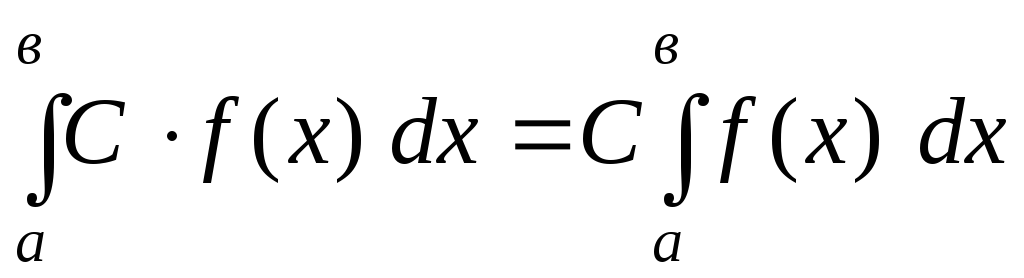 ,
де
,
де 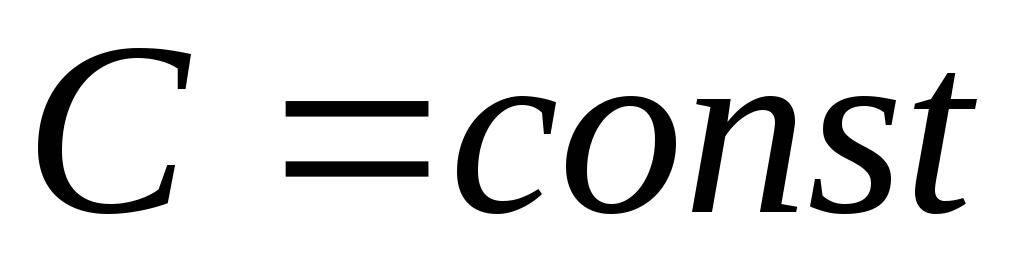 .
.
2. Інтеграл від алгебраїчної суми інтегрованих функцій дорівнює алгебраїчної сумі інтегралів від цих функцій:
 .
.
3. При перестановці меж інтегрування визначений інтеграл змінює свій знак на протилежний:
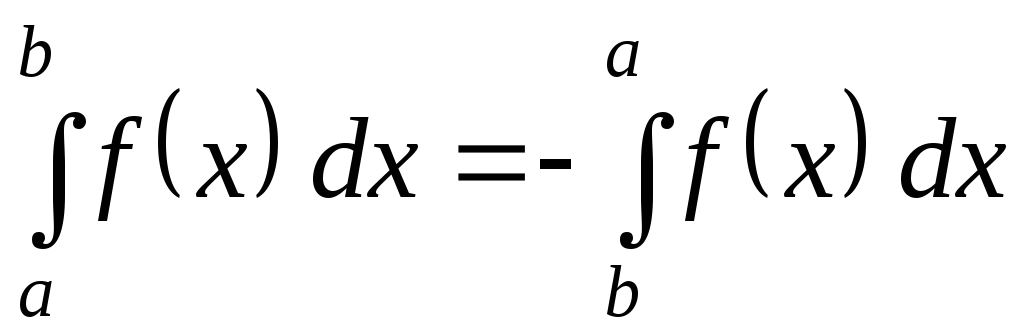 .
.
Зауваження. Якщо межі інтегрування рівні між собою 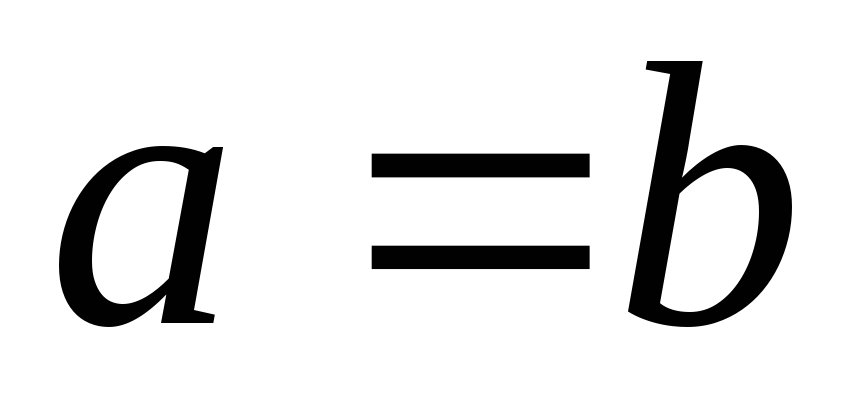 ,
то
,
то
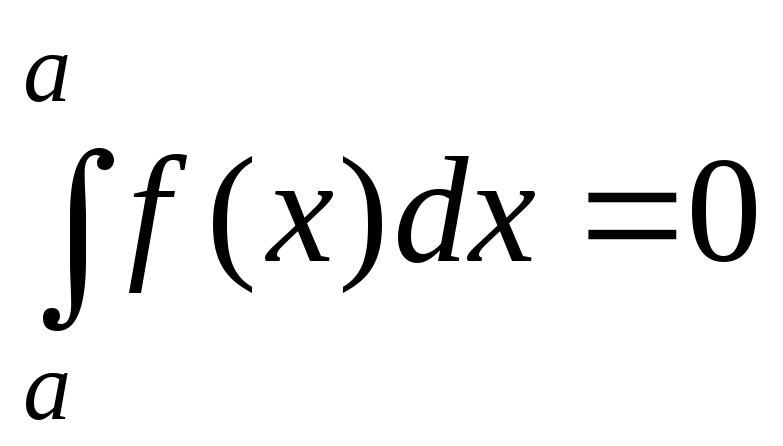 .
.
4. Інтеграл на всьому відрізку дорівнює сумі інтегралів на частинах цього відрізка:
 ,
, 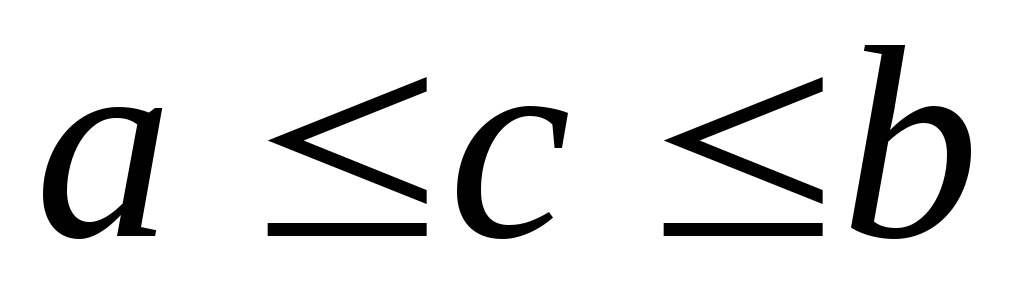
5. Значення визначеного інтеграла не залежить від позначення змінної інтегрування, тобто:
 .
.
6.
«Теорема про середнє»: Якщо функція 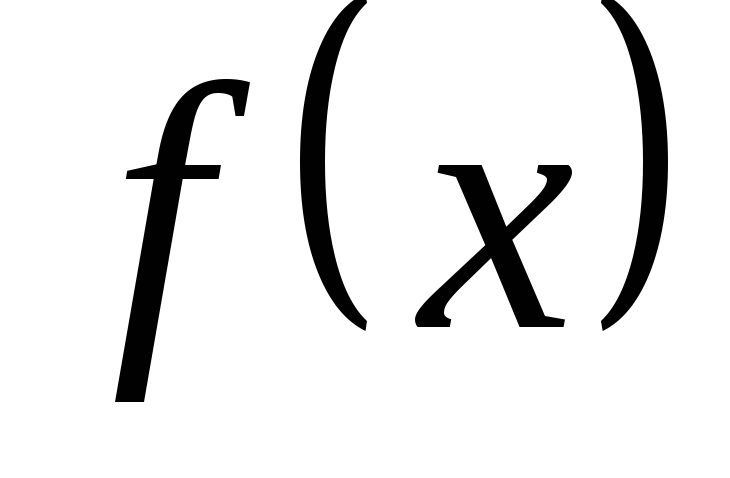 неперервна на відрізку
неперервна на відрізку  ,
то існує точка
,
то існує точка 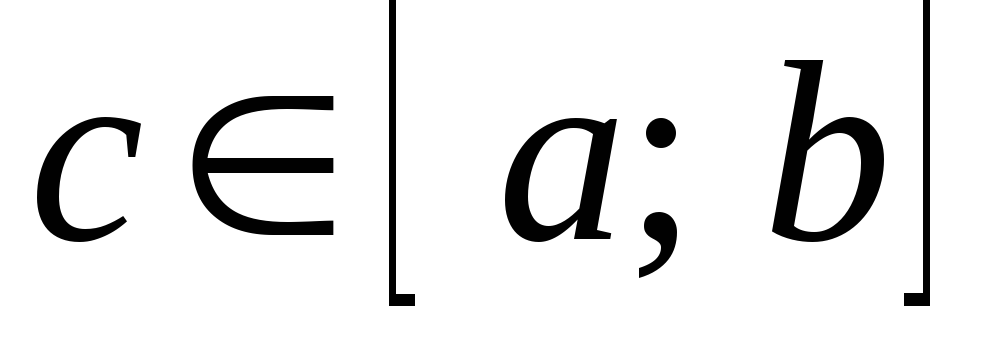 така, що
така, що
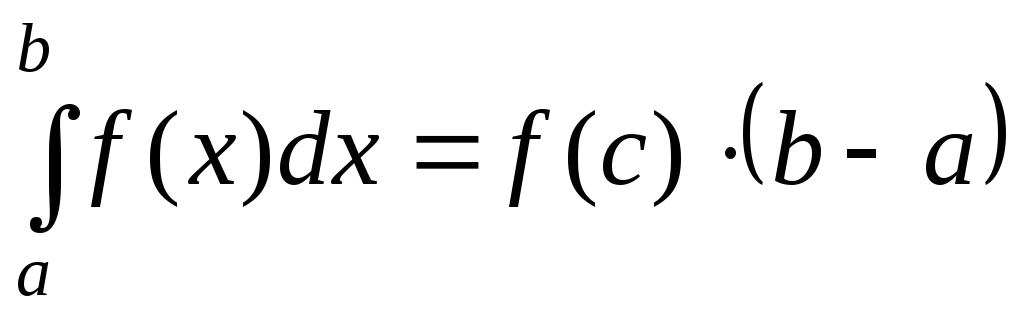 .
.
7.
Нерівність між неперервними на відрізку  функціями можна інтегрувати. Так, якщо
функціями можна інтегрувати. Так, якщо 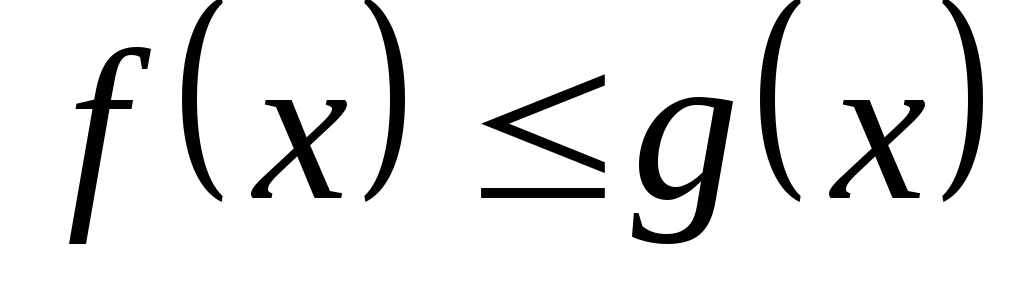 при
при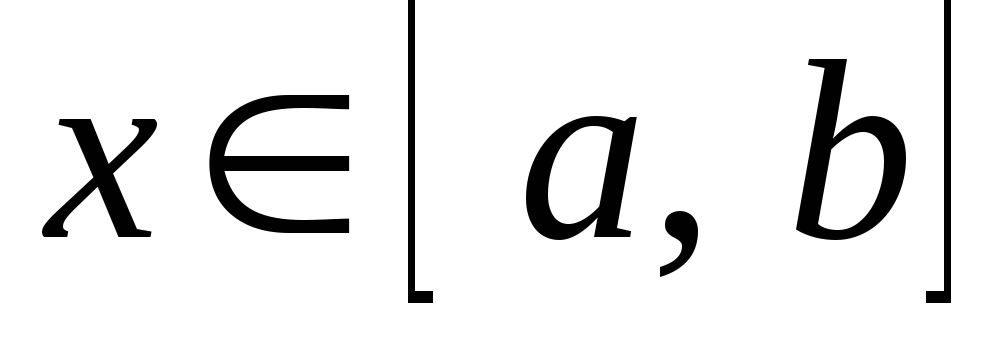 ,
то
,
то
 .
.
8.
Інтеграл можна оцінити найменшим
значенням функції  і найбільшим значенням функції
і найбільшим значенням функції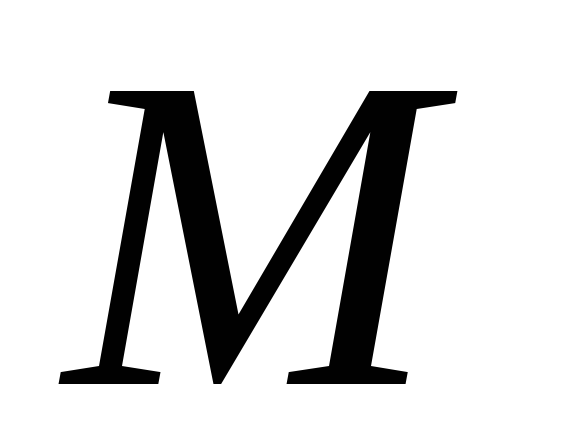 на відрізку
на відрізку 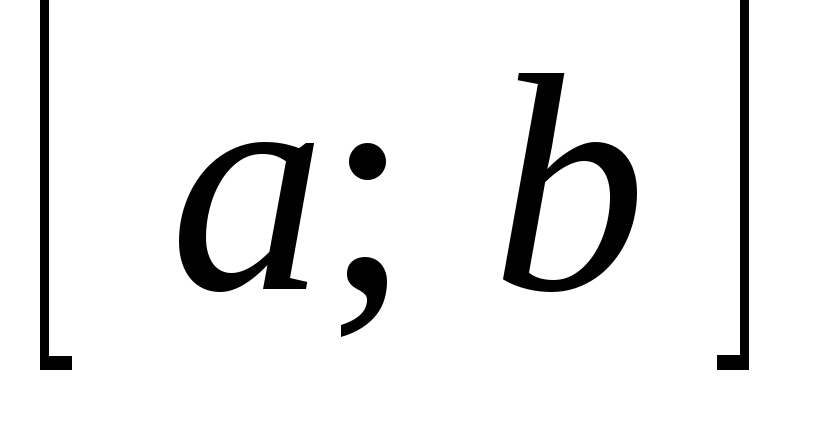 :
:
 .
.
3.2.3. Обчислення визначеного інтеграла
При обчисленні визначених інтегралів застосовують ті ж методи, що і для невизначених інтегралів, а саме: безпосереднє інтегрування, метод заміни змінної (метод підстановки) і метод інтегрування частинами.
Метод заміни змінної в визначеному інтегралі
Якщо
для неперервної підінтегральної функції 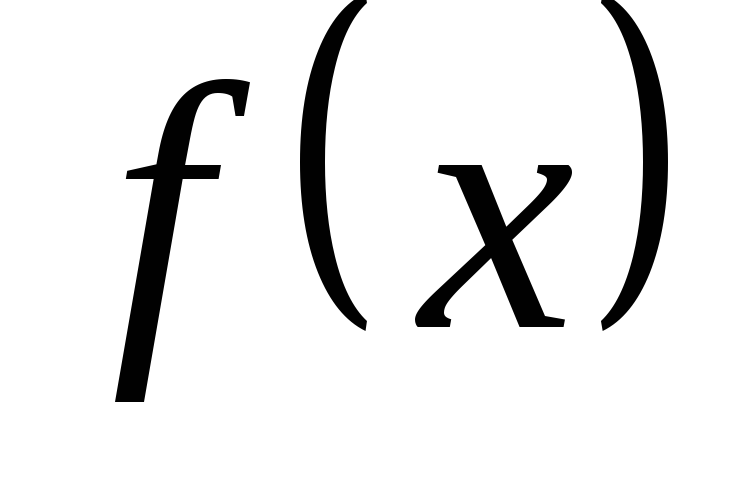 неможливо знайти первісну
неможливо знайти первісну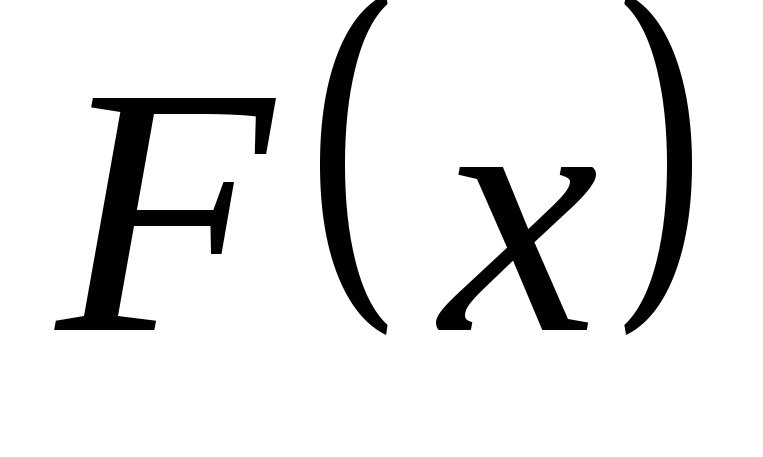 безпосереднім інтегруванням, то для
обчислення визначеного інтеграла
безпосереднім інтегруванням, то для
обчислення визначеного інтеграла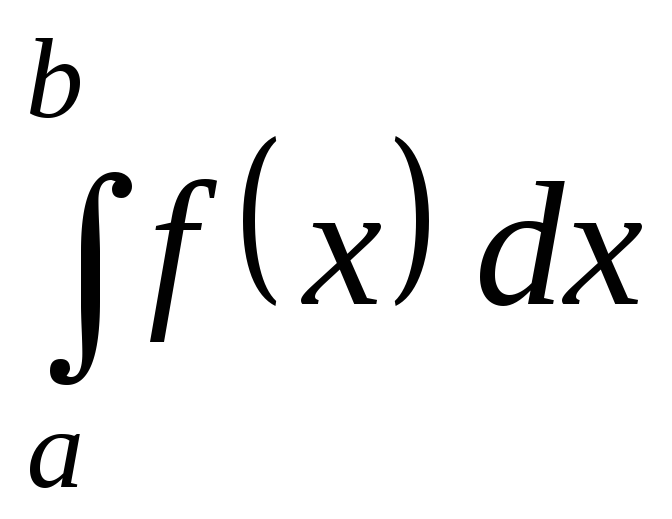 застосовують заміну змінної
застосовують заміну змінної .
У результаті інтеграл приводиться до
табличного і обчислюється за формулою
Ньютона-Лейбніца. Межі інтегрування
змінюються у відповідність із обраною
підстановкою.
.
У результаті інтеграл приводиться до
табличного і обчислюється за формулою
Ньютона-Лейбніца. Межі інтегрування
змінюються у відповідність із обраною
підстановкою.
Якщо
функція 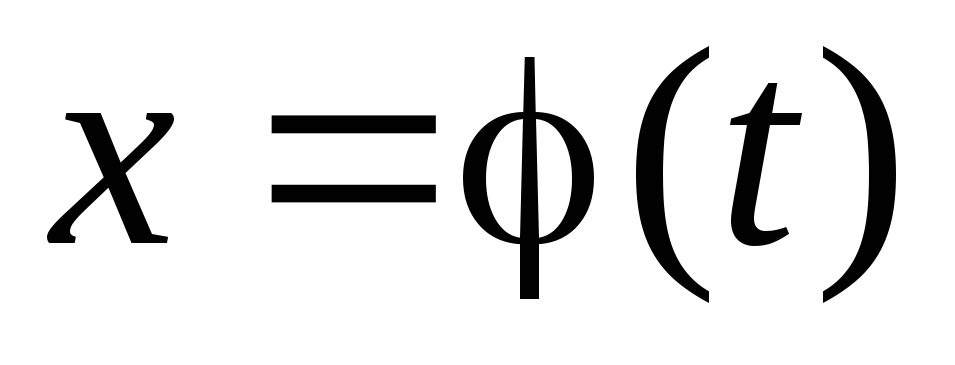 і
її похідна
і
її похідна  неперервні
на відрізку
неперервні
на відрізку  і при
цьому
і при
цьому  ,
, ,
то справедлива рівність:
,
то справедлива рівність:
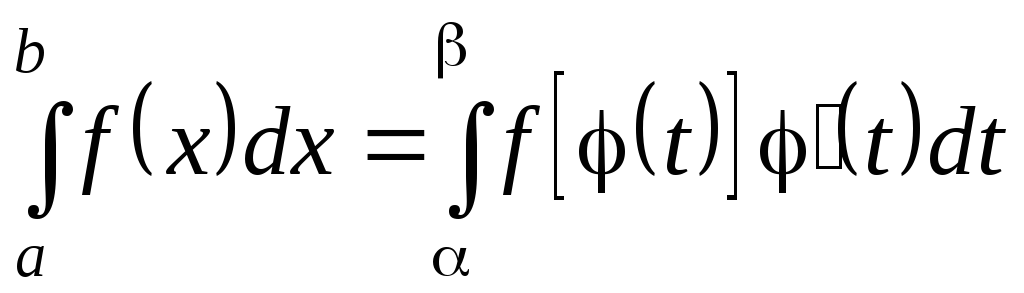 .
.
Дана формула описує метод підстановки в визначеному інтегралі.
Зауваження: При обчисленні визначеного інтеграла методом підстановки повертатися до старої змінної не потрібно, тому що межі інтегрування в визначеному інтегралі змінюються відповідно до нової змінної.
Приклад 39.
Обчислити визначені інтеграли методом підстановки:
а) 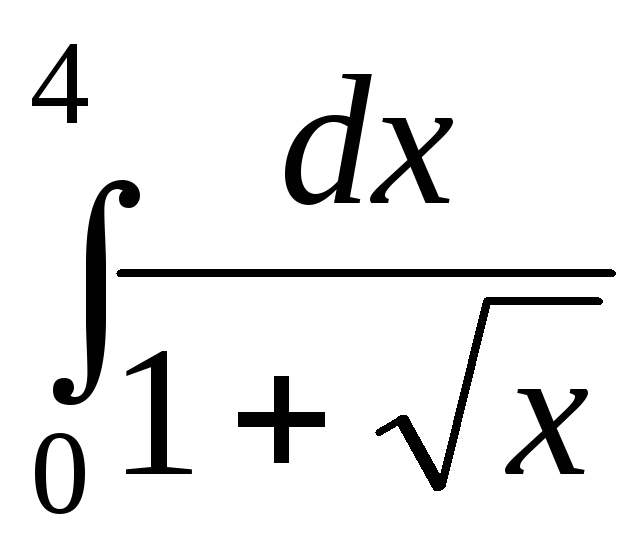 ;б)
;б) 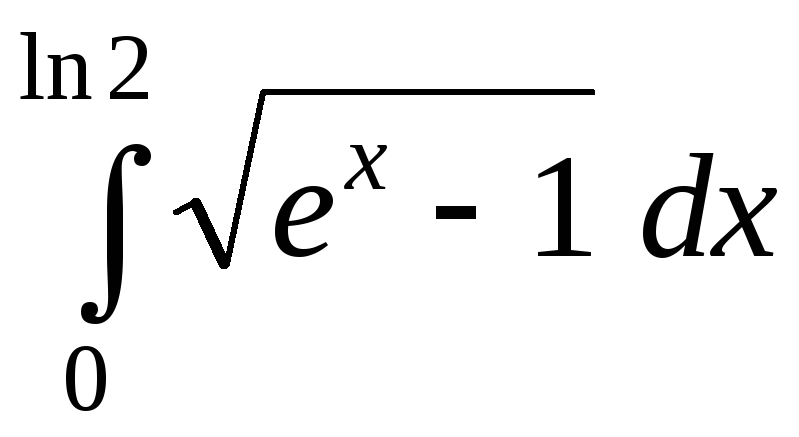 ;
в)
;
в)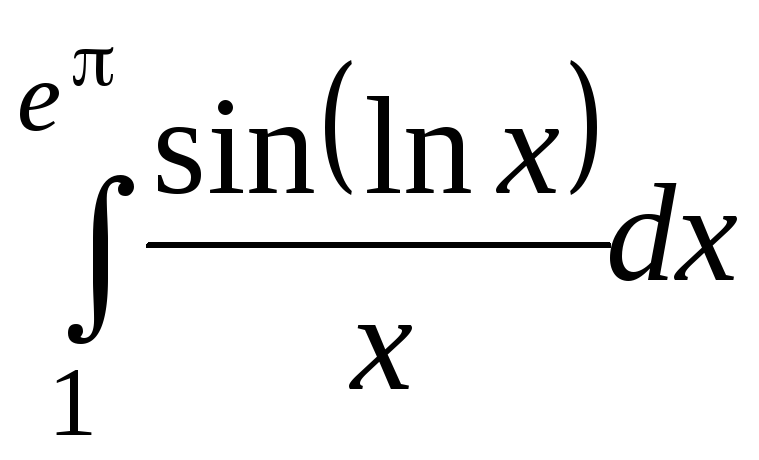 .
.
Розв’язок.
а)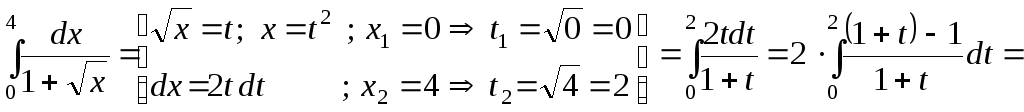
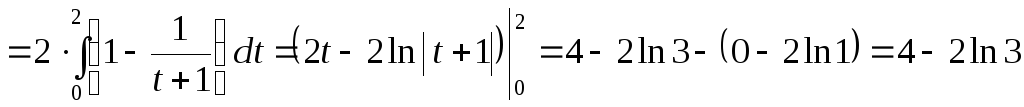 .
.
б) 

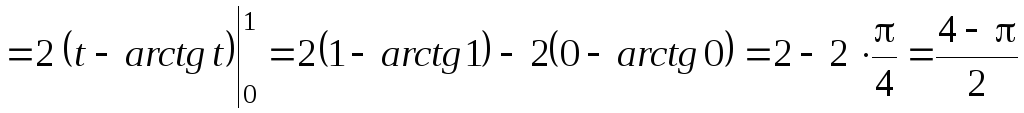 .
.
в) 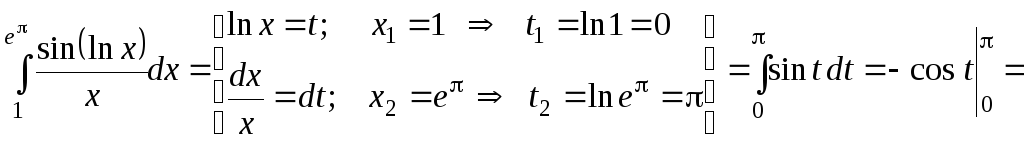
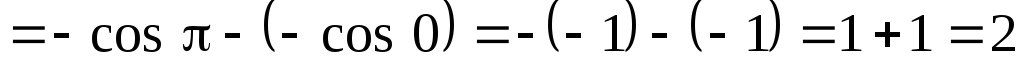 .
.
Метод інтегрування частинами у визначеному інтегралі
Якщо
функції 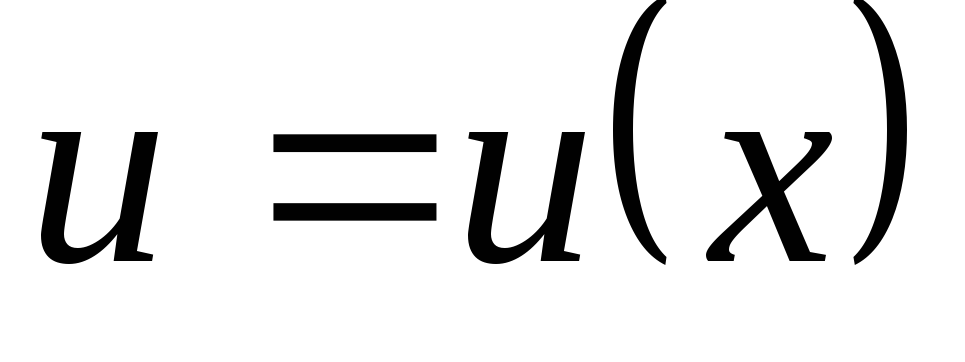 і
і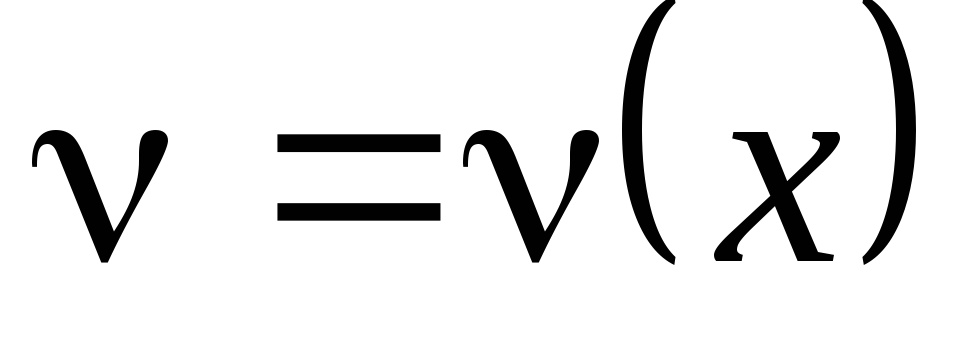 мають неперервні похідні на відрізку
мають неперервні похідні на відрізку  ,
то формула інтегрування частинами має
вигляд:
,
то формула інтегрування частинами має
вигляд:
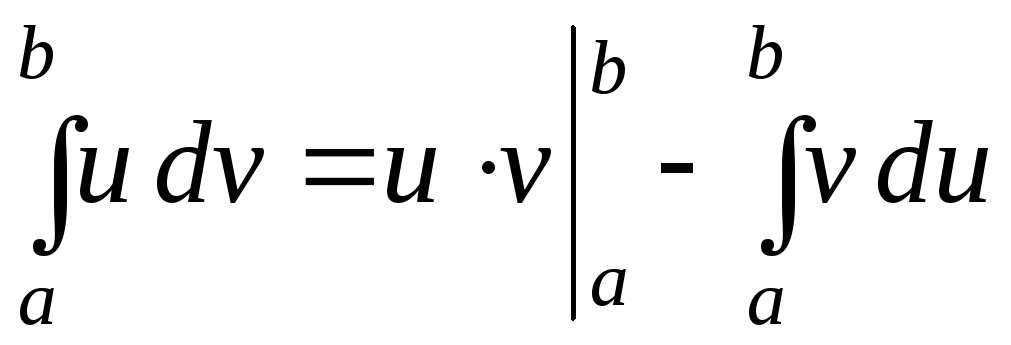 .
.
Приклад 40.
Обчислити визначені інтеграли методом інтегрування частинами:
а) 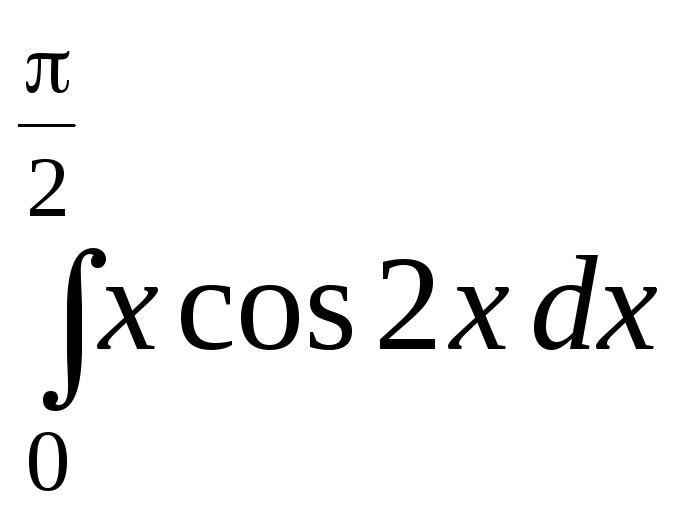 ;
б).
;
б).
Розв’язок.
а) 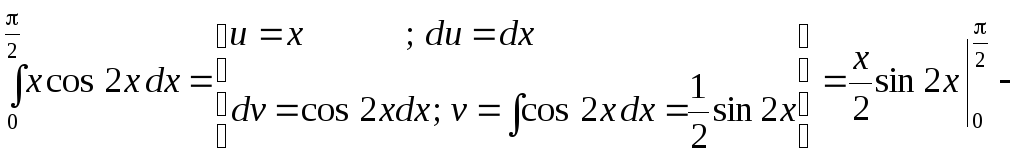
 .
.
б) 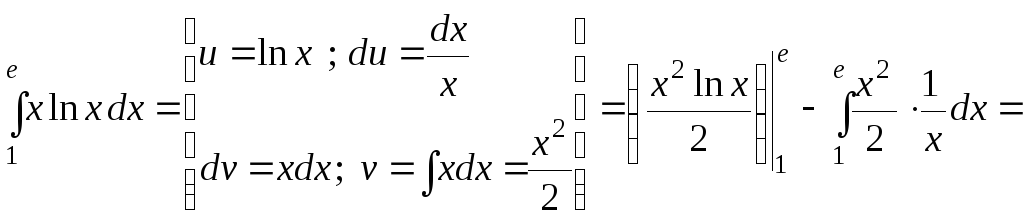
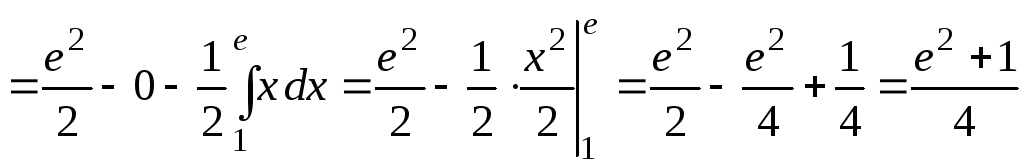 .
.
3.2.4. Невласні інтеграли
Визначений
інтеграл  ,
у якому проміжок інтегрування
,
у якому проміжок інтегрування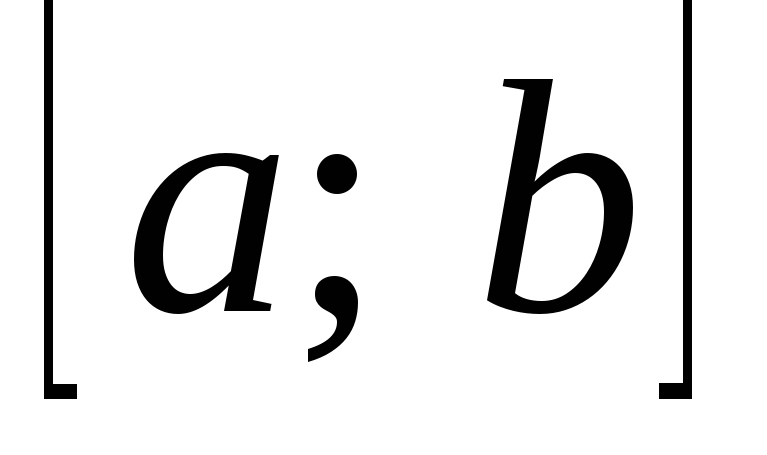 – скінченний, а підінтегральна функція
– скінченний, а підінтегральна функція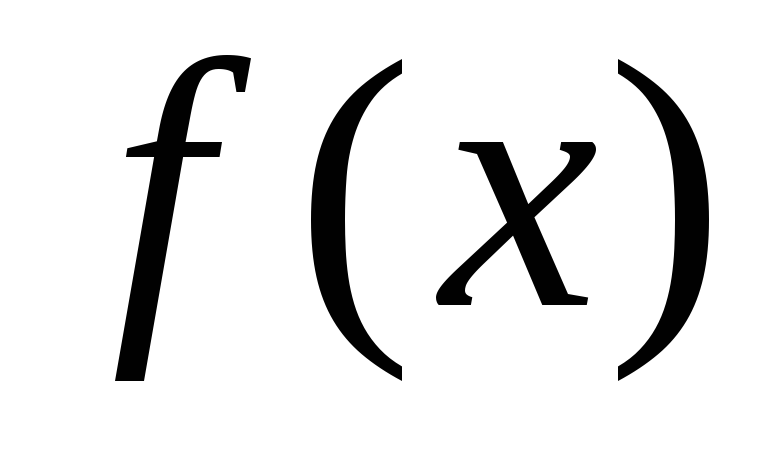 –
неперервна
на відрізку
–
неперервна
на відрізку 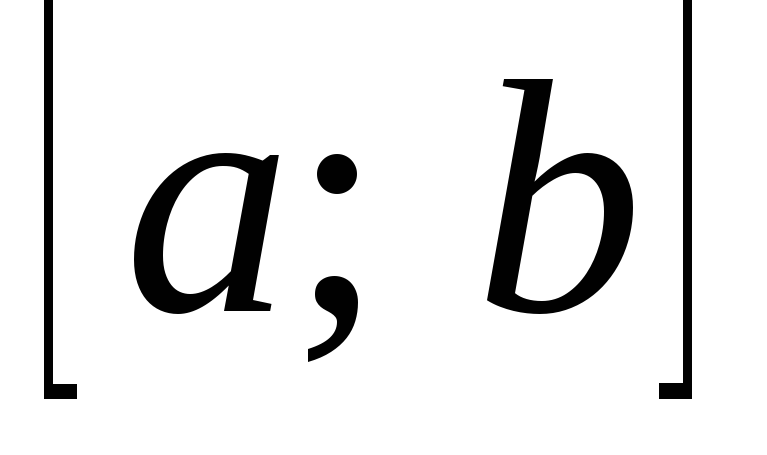 ,
називаєтьсявласним
інтегралом.
,
називаєтьсявласним
інтегралом.
Невласним інтегралом називається визначений інтеграл від неперервної функції, але з нескінченним проміжком інтегрування або визначений інтеграл з скінченним проміжком інтегрування, але від функції, що має на ньому нескінченний розрив. Відповідно, розрізняють невласні інтеграли I роду (з нескінченними межами) і II роду (інтеграл від розривної функції).
Невласним
інтегралом першого роду 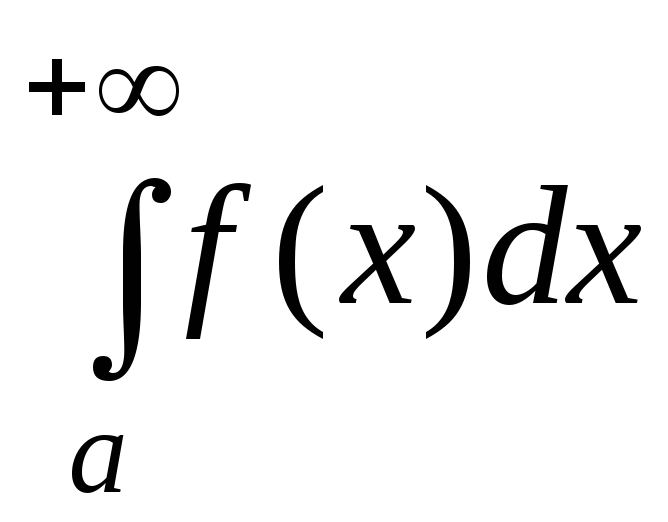 неперервної на інтервалі
неперервної на інтервалі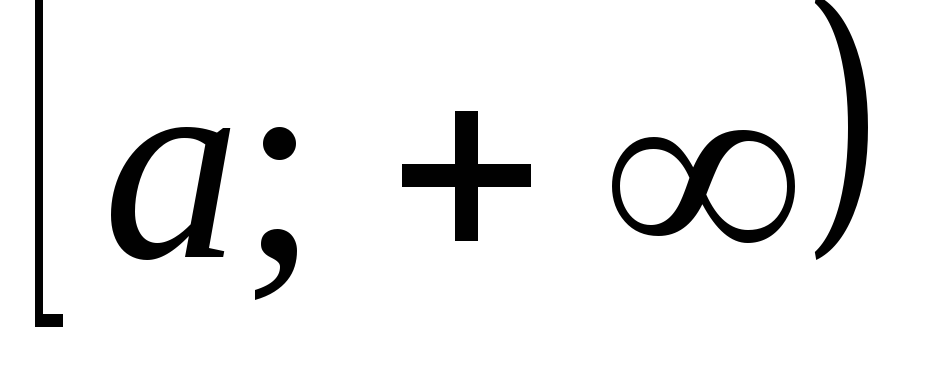 функції
функції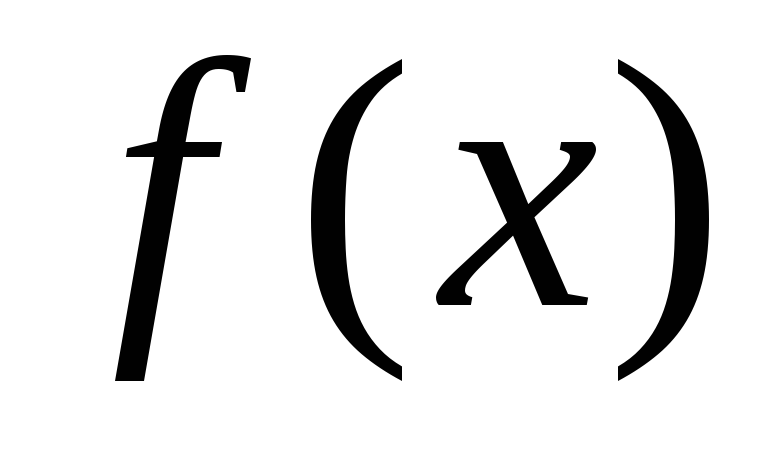 називається скінченна границя
називається скінченна границя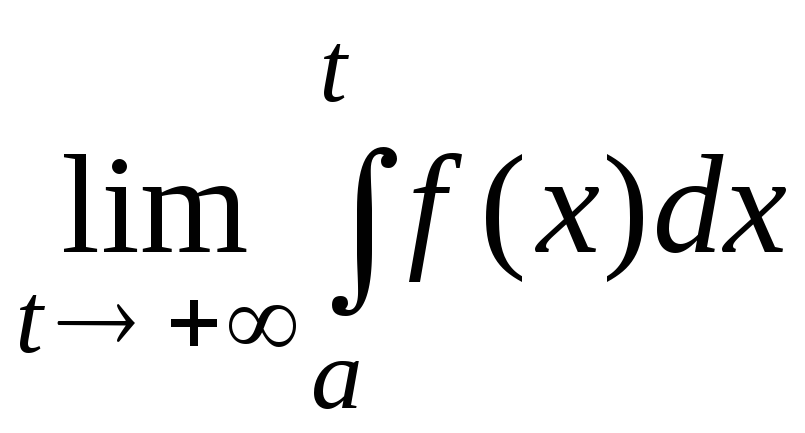 .
.
Таким чином, за визначенням:
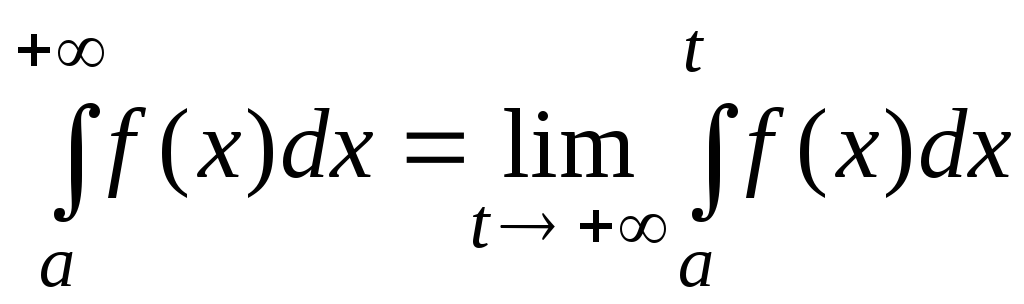 .
.
Якщо границя, яка знаходиться в правій частині рівності існує і скінченна, то невласний інтеграл збігається, у противному випадку – розбігається.
Аналогічно
визначається невласний інтеграл на
інтервалі  :
:
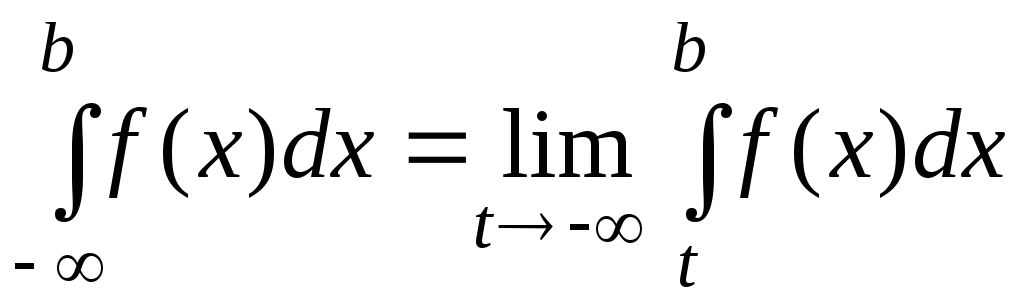 .
.
Невласний
інтеграл із двома нескінченними межами
(на інтервалі 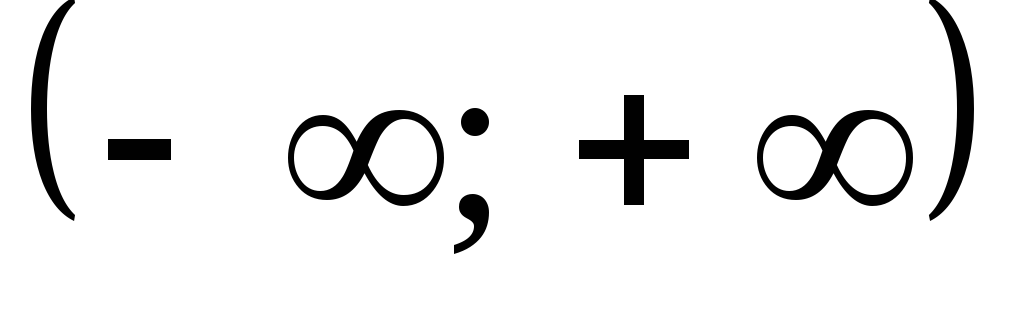 )
розбивається на два за формулою:
)
розбивається на два за формулою:
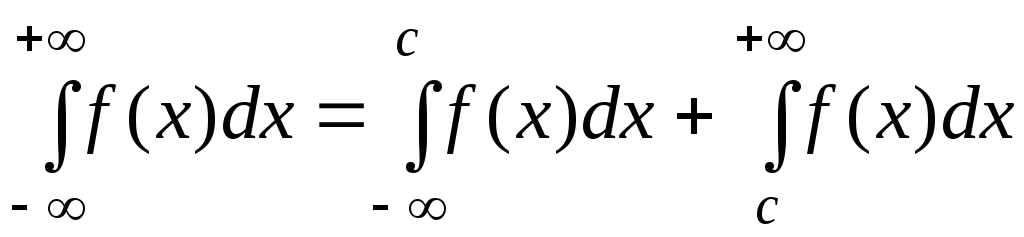 ,
де
,
де  – довільне число.
– довільне число.
Такий інтеграл збігається лише тоді, коли збігаються обидва інтеграли на які він розбивається.
Приклад 41.
Обчислити
невласні інтеграли І роду: а) 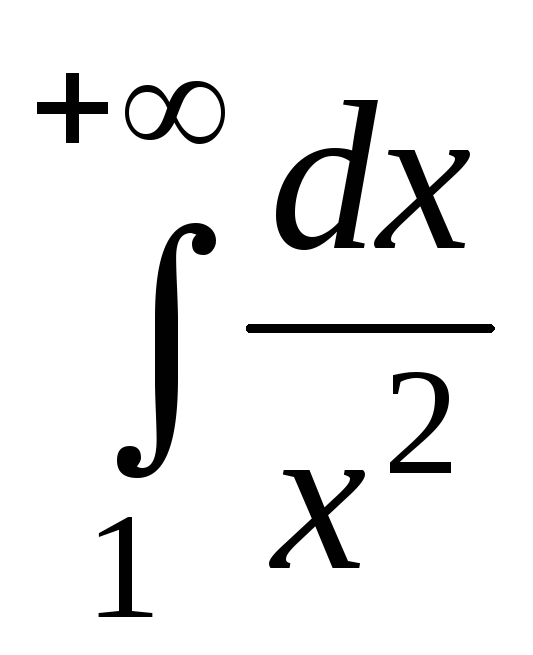 ;
б)
;
б)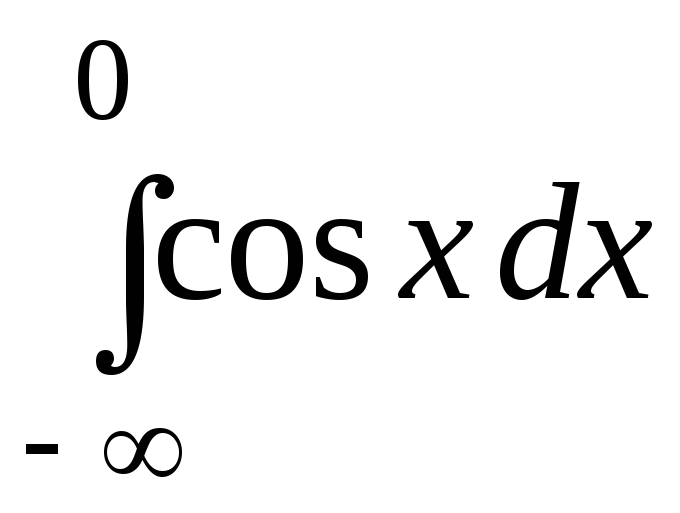 .
.
Розв’язок.
а) 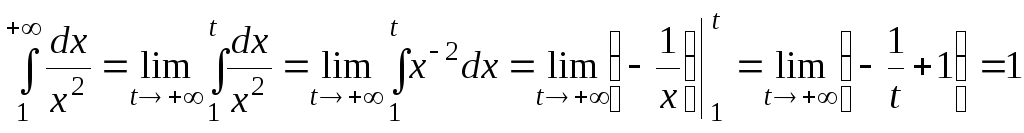 .
.
Оскільки границя – скінченна, то невласний інтеграл збігається.
б) 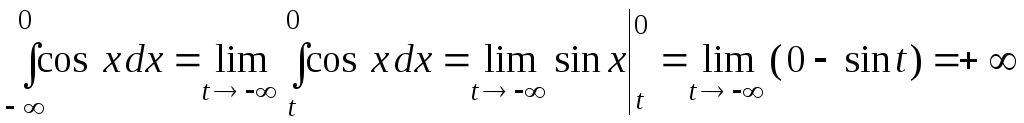 .
.
Оскільки границя — нескінченна, то невласний інтеграл розбігається.
Невласним
інтегралом другого роду 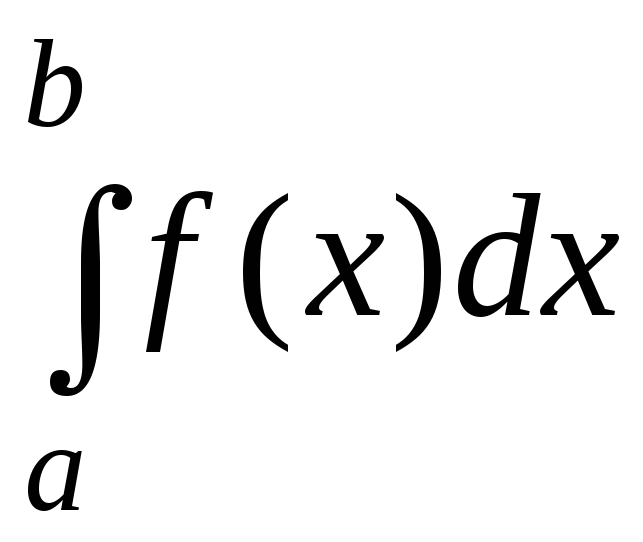 неперервної на інтервалі
неперервної на інтервалі функції
функції ,
що має нескінченний розрив при
,
що має нескінченний розрив при ,
називається скінченна границя
,
називається скінченна границя .
Таким чином, за визначенням:
.
Таким чином, за визначенням:
 .
.
Якщо границя, яка знаходиться в правій частині рівності існує і скінченна, то невласний інтеграл збігається, у противному випадку – розбігається.
Аналогічно,
якщо функція  ,
неперервна на інтервалі
,
неперервна на інтервалі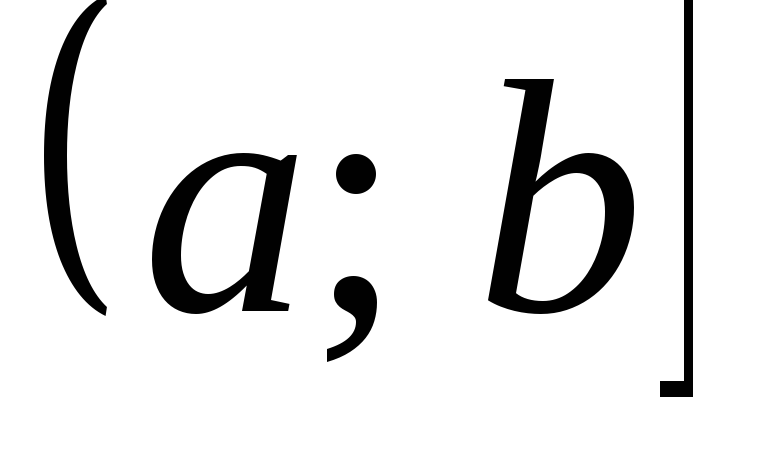 ,
має нескінченний розрив при
,
має нескінченний розрив при ,
то невласний інтеграл другого роду
визначається за формулою:
,
то невласний інтеграл другого роду
визначається за формулою:
 .
.
Якщо
функція  має нескінченний розрив у внутрішній
точці
має нескінченний розрив у внутрішній
точці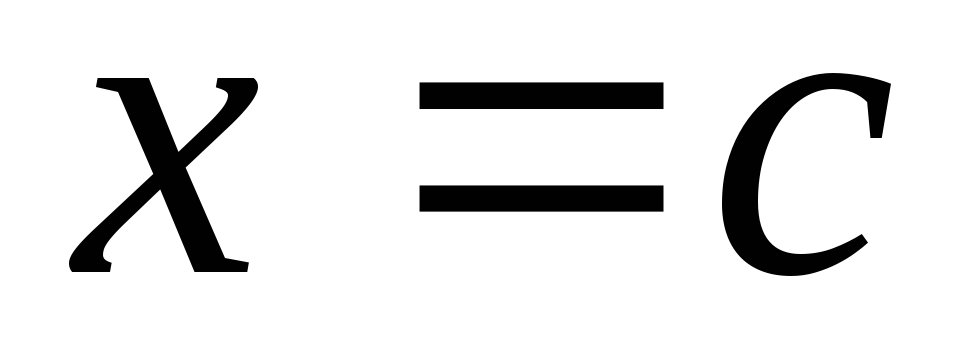 відрізка
відрізка ,
то невласний інтеграл другого роду
визначаєтьсяза
формулою:
,
то невласний інтеграл другого роду
визначаєтьсяза
формулою:
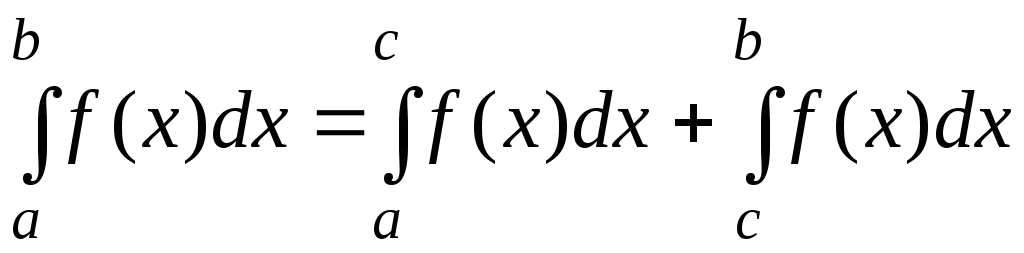 .
.
Такий інтеграл збігається лише тоді, коли збігаються обидва інтеграли на які він розбивається.
Приклад 42.
Обчислити
невласний інтеграл ІІ роду 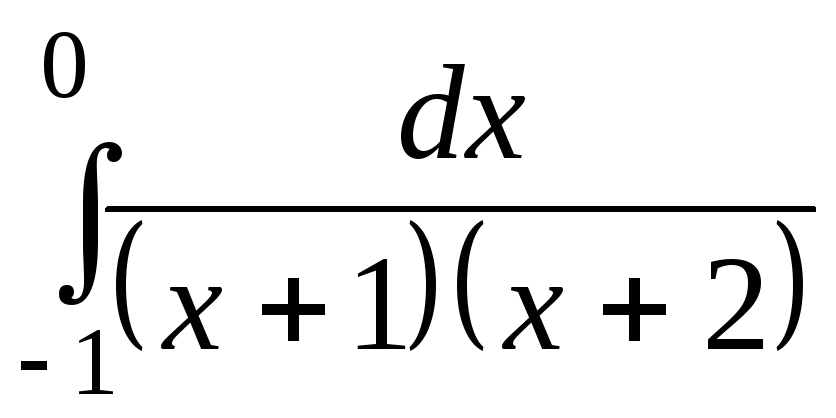 .
.
Розв’язок.
Підінтегральна
функція має нескінченний розрив на
лівій межі проміжку інтегрування 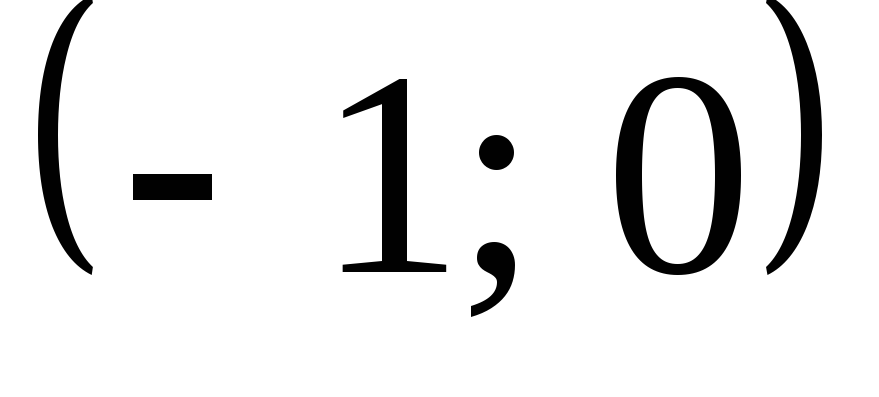 ,
оскільки дана функція не визначена при
,
оскільки дана функція не визначена при і
і .
Тоді:
.
Тоді:
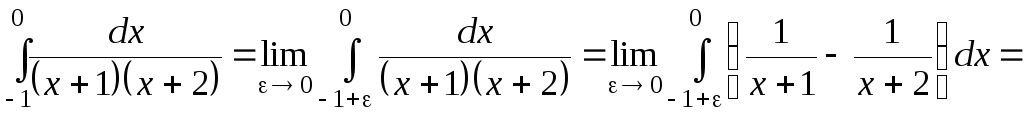

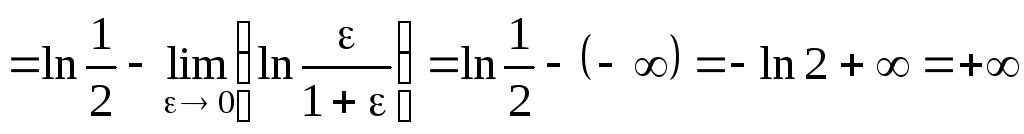 .
.
Оскільки границя – нескінченна, то невласний інтеграл розбігається.
studfile.net
Метод інтегрування частинами
Метод інтегрування частинами застосовується, в основному, коли підінтегральна функція складається з добутку двох множників певного виду. Формула інтегрування частинами має вигляд:
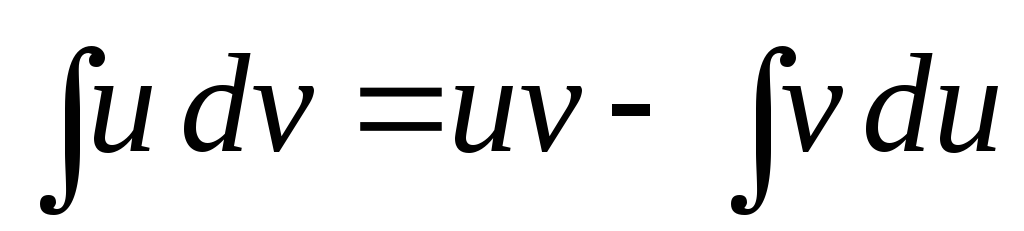 .
.
Вона
дає можливість звести обчислення
заданого інтеграла 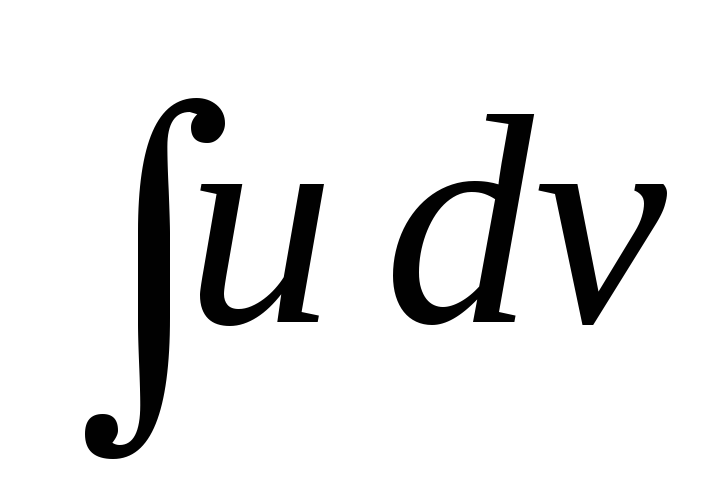 до обчислення інтеграла
до обчислення інтеграла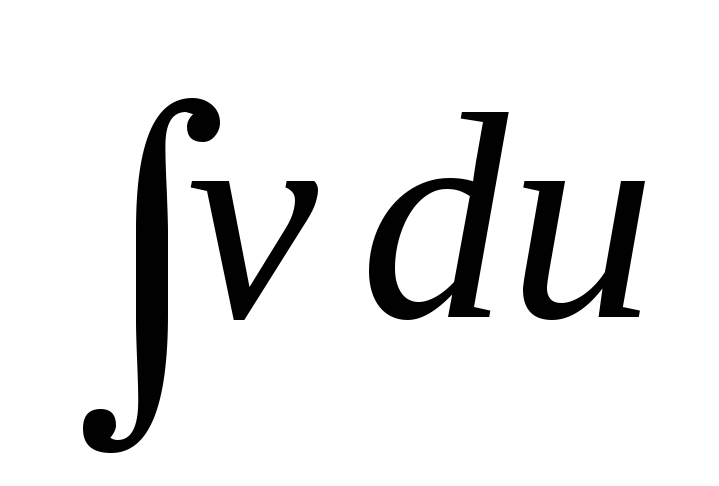 ,
який виявляється більш простим ніж
даний.
,
який виявляється більш простим ніж
даний.
Більшу частину інтегралів, що обчислюють методом інтегрування частинами, можна розбити на три групи:
1.
Інтеграли виду  ,
,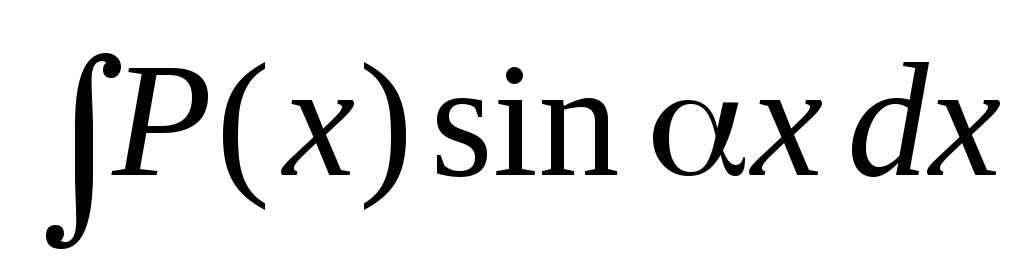 ,
, ,
де
,
де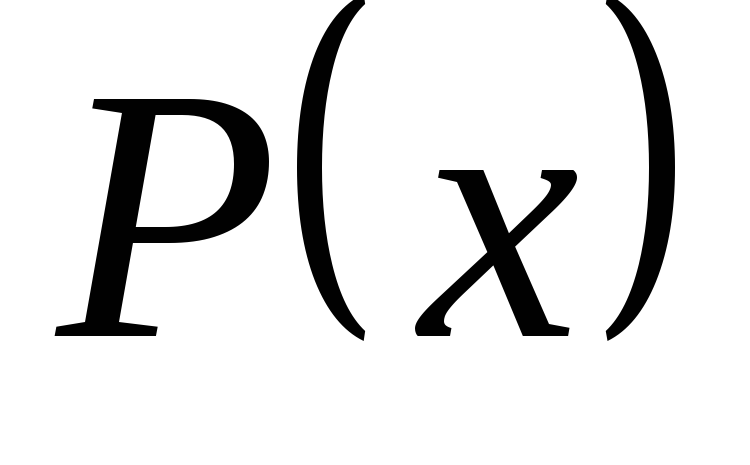 – многочлен,
– многочлен, – число, що не дорівнює нулю.
– число, що не дорівнює нулю.
У
цьому випадку через  позначають многочлен
позначають многочлен ,
а всю іншу частину підінтегрального
виразу через
,
а всю іншу частину підінтегрального
виразу через .
.
2.
Інтеграли виду 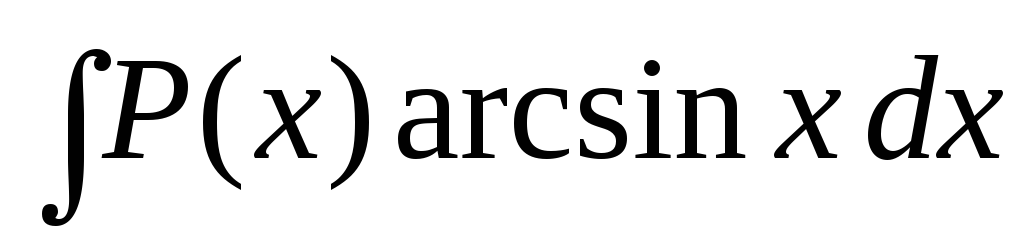 ,
,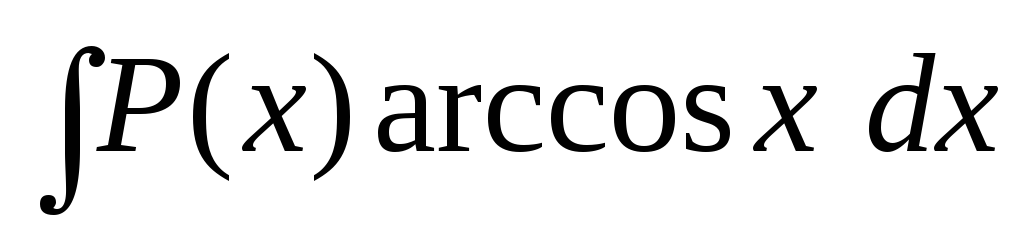 ,
, ,
, ,
,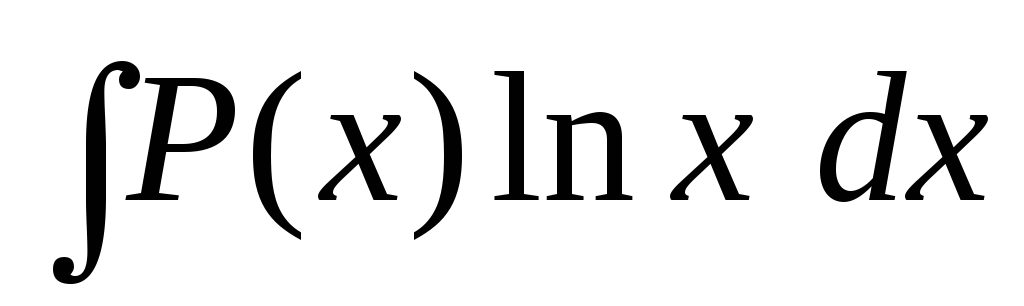 ,
де
,
де – многочлен.
– многочлен.
У
цьому випадку через  позначають
позначають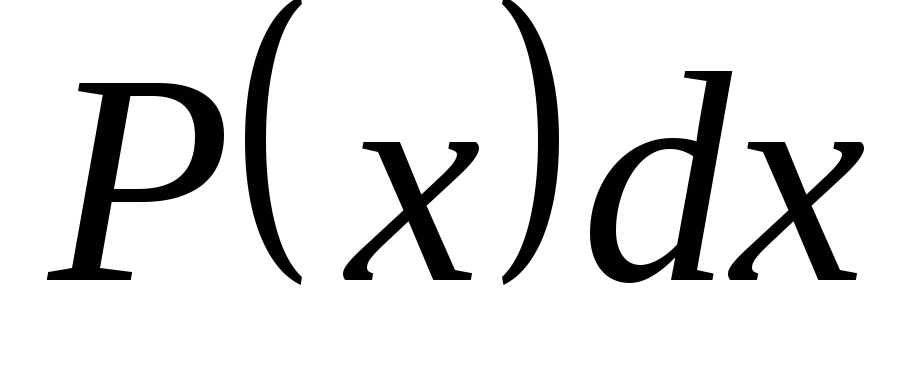 ,
а всю іншу частину підінтегрального
виразу через
,
а всю іншу частину підінтегрального
виразу через .
.
3.
Інтеграли виду 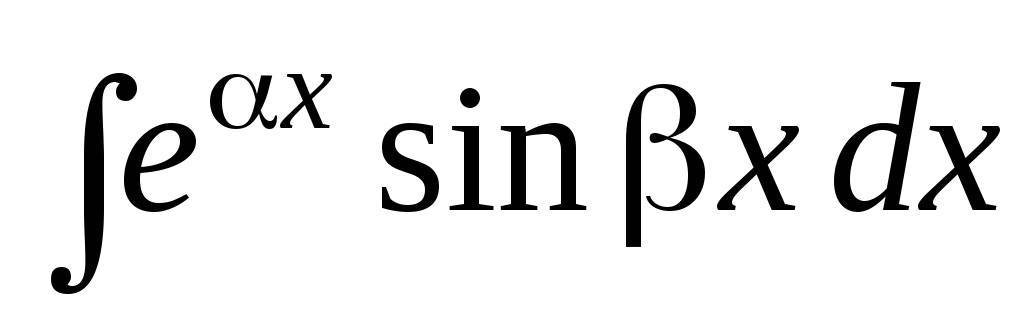 ,
, ,
де
,
де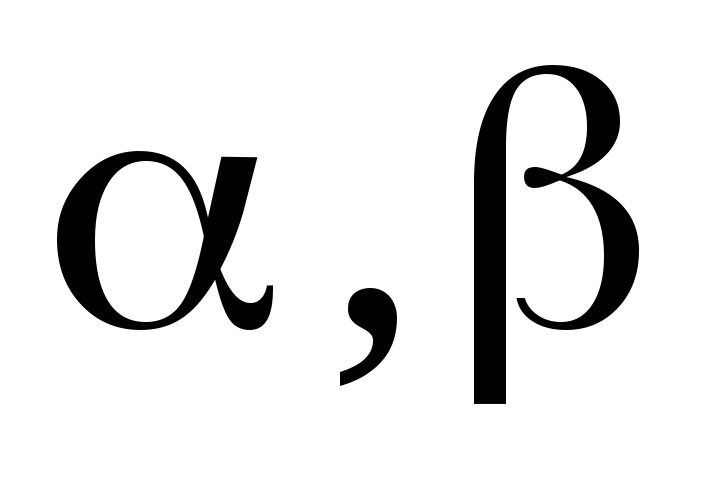 – числа.
– числа.
У
цьому випадку через  позначають
позначають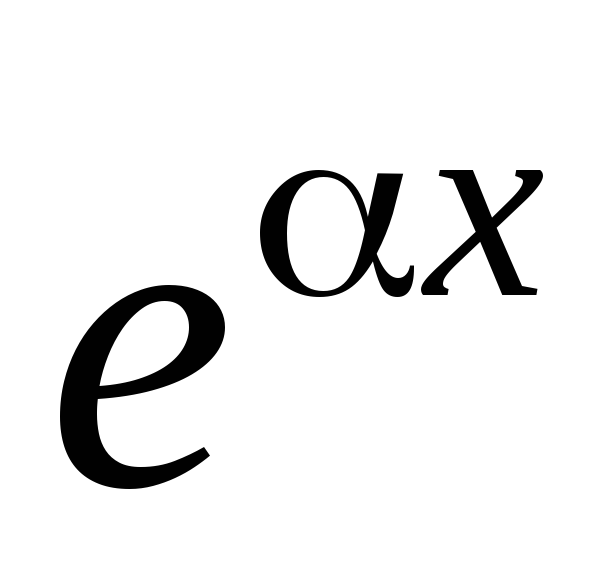 і застосовують формулу інтегрування
частинами двічі, повертаючись у результаті
до даного інтегралу, після чого даний
інтеграл виражається з рівності.
і застосовують формулу інтегрування
частинами двічі, повертаючись у результаті
до даного інтегралу, після чого даний
інтеграл виражається з рівності.
Зауваження: У деяких випадках для знаходження поданого інтегралу формулу інтегрування частинами необхідно застосовувати кілька разів. Також метод інтегрування частинами комбінують із іншими методами.
Приклад 26.
Знайти
інтеграли: а) 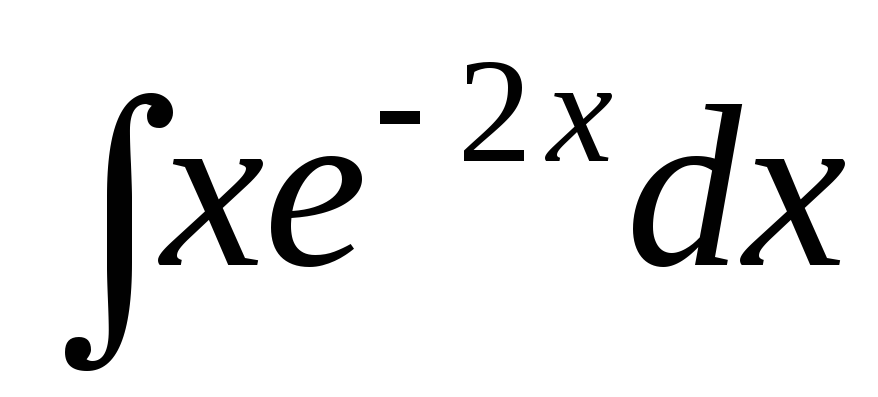 ;
б)
;
б) .
.
Розв’язок.
а)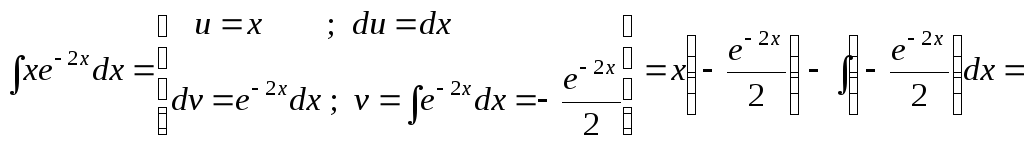
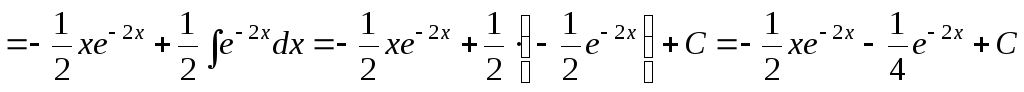 .
.
б) 

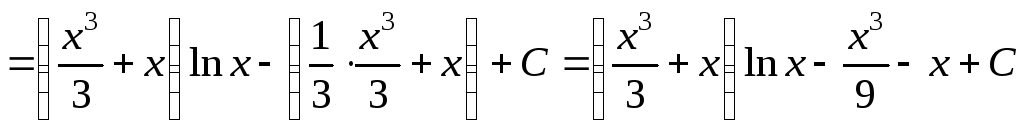 .
.
3.1.4. Інтегрування дрібно-раціональних функцій
Дробово-раціональною
функцією (раціональним
дробом) називається функція, що дорівнює
відношенню двох многочленів: 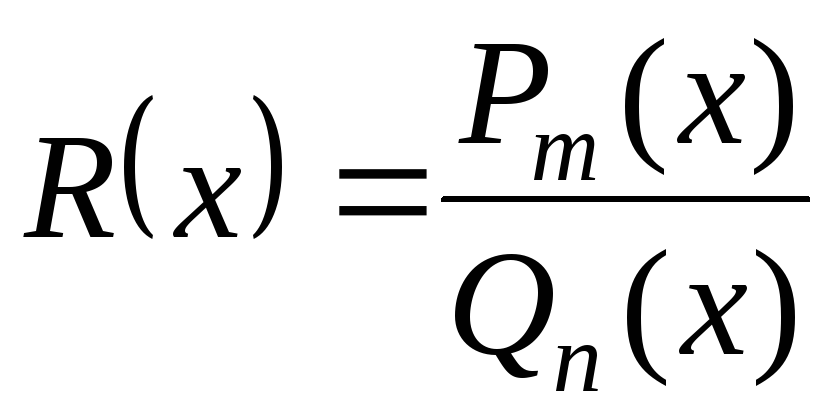 ,
де
,
де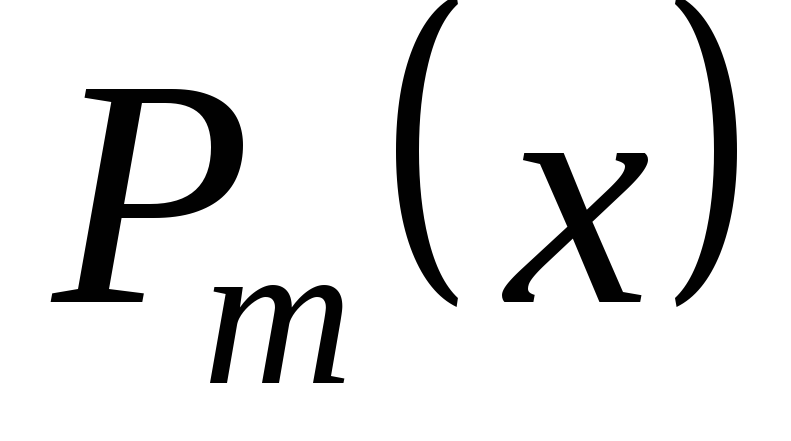 – многочлен степеня
– многочлен степеня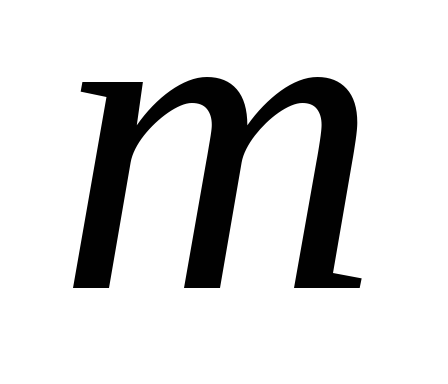 ,
,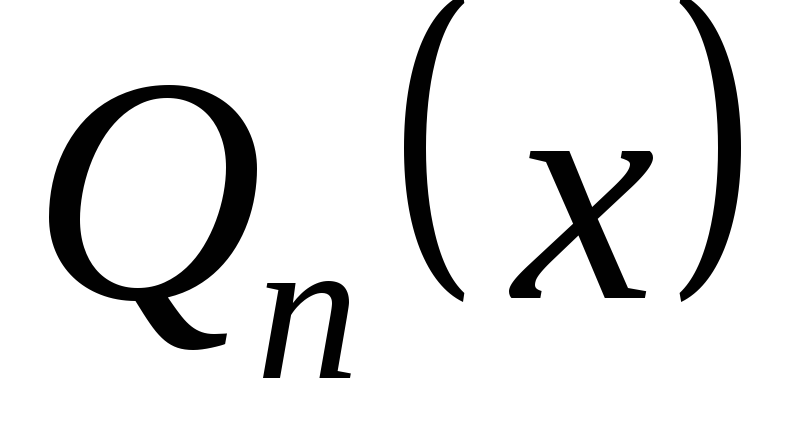 – многочлен степеня
– многочлен степеня 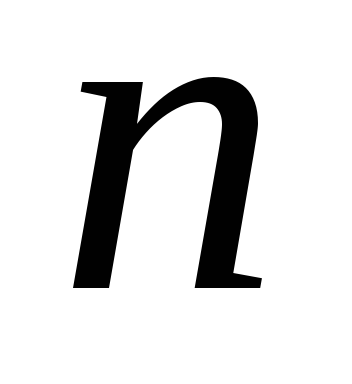 .
.
Раціональний
дріб
називається правильним,
якщо степінь многочлена в чисельнику
менше степеня многочлена в знаменнику,
тобто 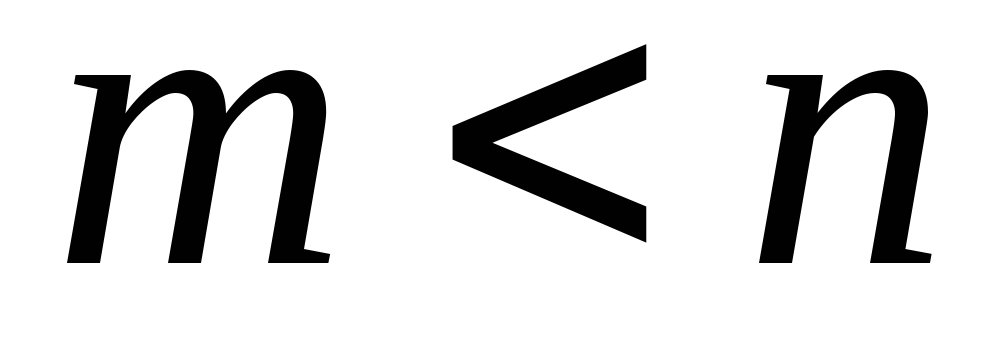 ,
у противному випадку (якщо
,
у противному випадку (якщо 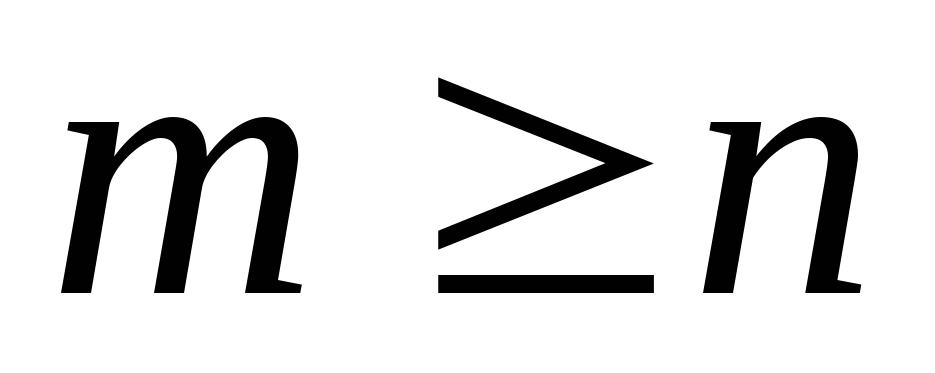 )
раціональний дріб називається неправильним.
)
раціональний дріб називається неправильним.
Будь-який неправильний раціональний дріб можна представити у вигляді суми многочлена і правильного раціонального дробу, розділивши чисельник на знаменник за правилом ділення многочленів:
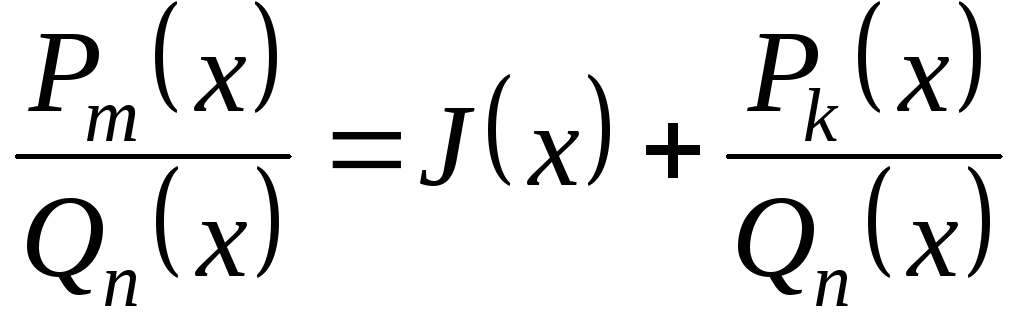 ,
,
де 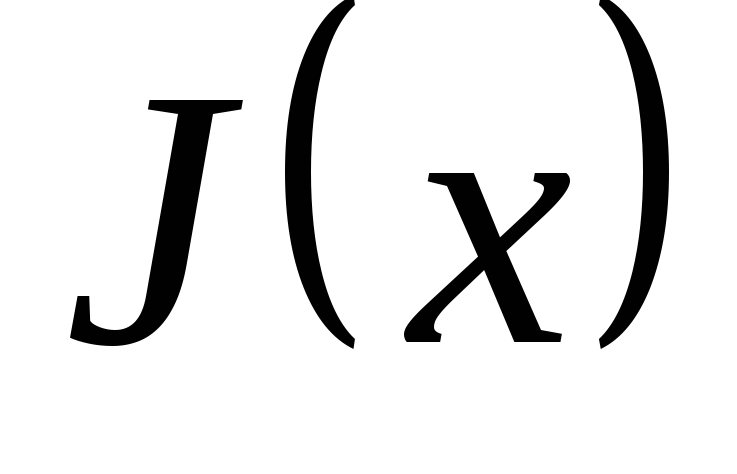 – ціла частина від ділення,
– ціла частина від ділення,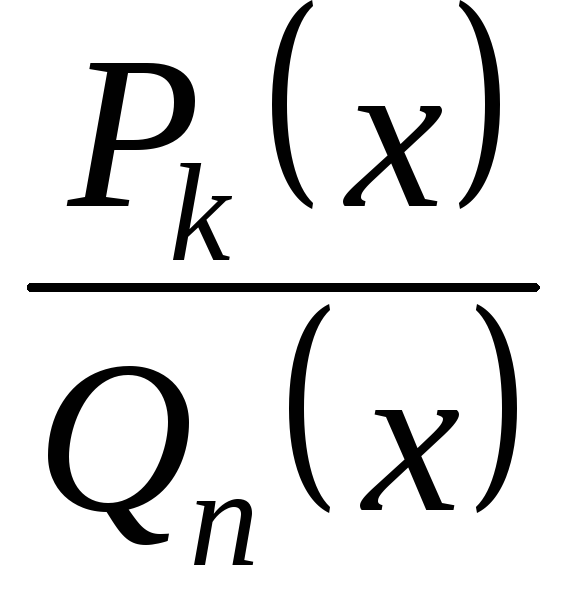 – правильний раціональний дріб,
– правильний раціональний дріб, – остача від ділення.
– остача від ділення.
Правильні раціональні дроби виду:
I. 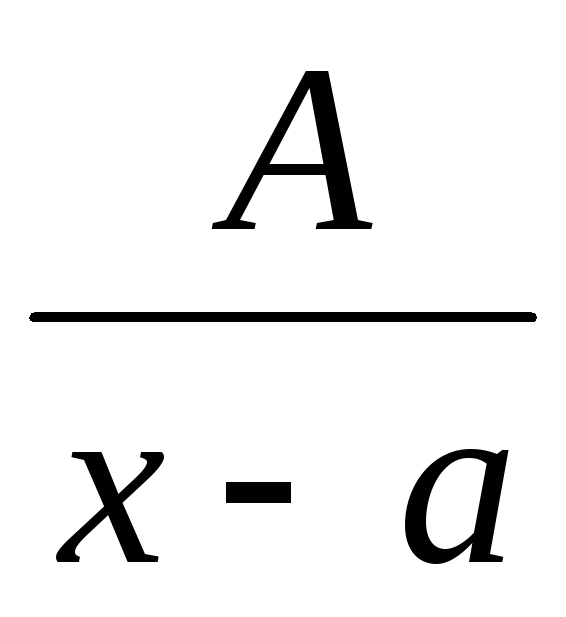 ;
;
II.  ;
;
III. 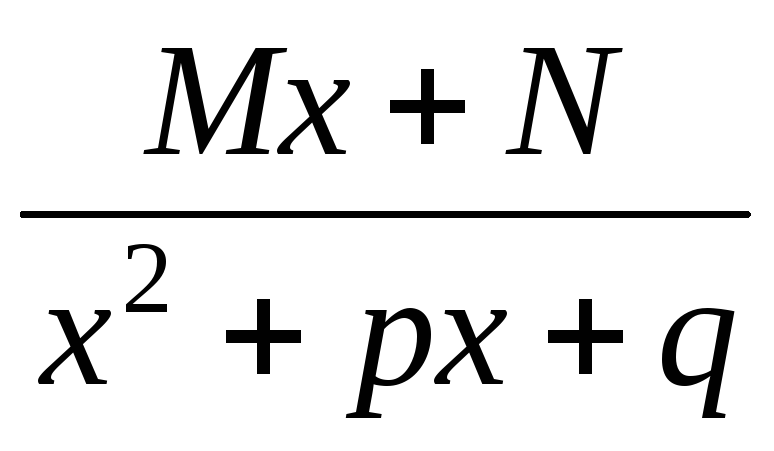 ;
;
IV. 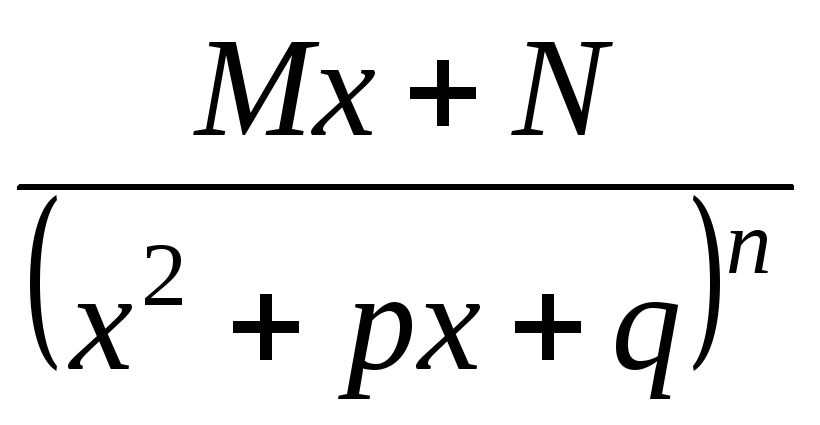 ,
,
де  ,
, ,
,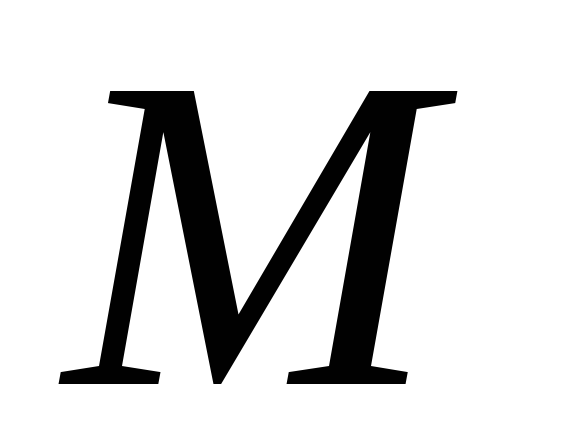 ,
, ,
, ,
, ,
, 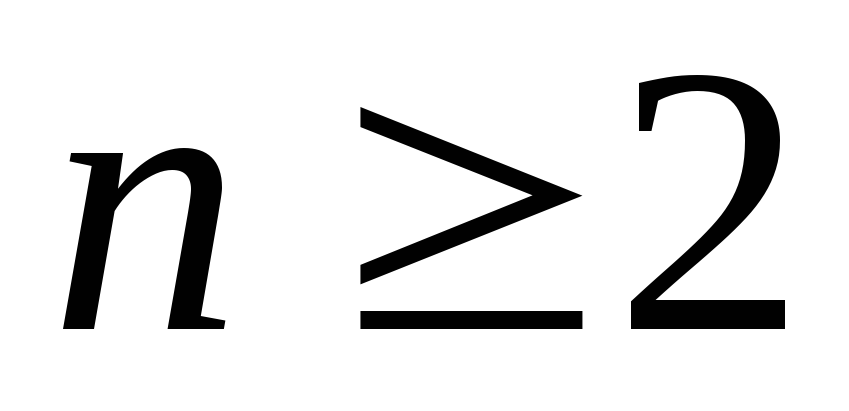 –
дійсні числа і
–
дійсні числа і  (тобто квадратний тричлен у знаменникуIII
і IV
дробів не має коренів – дискримінант
від’ємний) називаються найпростішими
раціональними дробами I, II, III і IV типів.
(тобто квадратний тричлен у знаменникуIII
і IV
дробів не має коренів – дискримінант
від’ємний) називаються найпростішими
раціональними дробами I, II, III і IV типів.
Інтегрування найпростіших дробів
Інтеграли від найпростіших дробів чотирьох типів обчислюються в такий спосіб.
I) 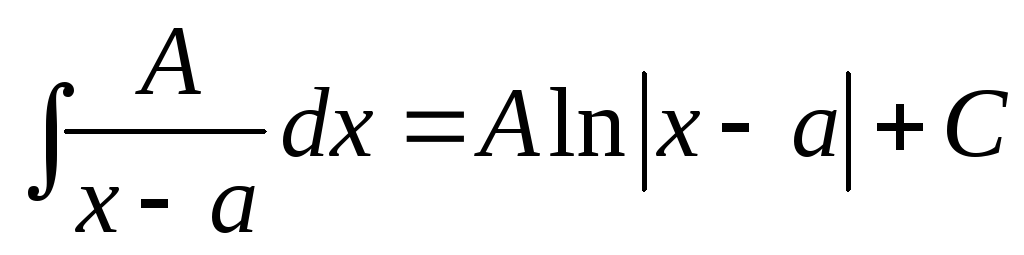 .
.
II) 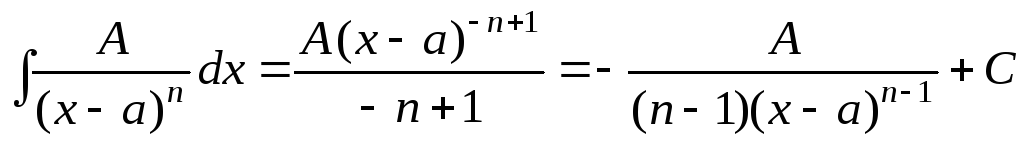 ,
, .
.
III)
Для інтегрування найпростішого дробу
III типу в знаменнику виділяють повний
квадрат, роблять заміну  .
Інтеграл після підстановки розбивають
на два інтеграли. Перший інтеграл
обчислюють виділенням у чисельнику
похідної знаменника, що дає табличний
інтеграл, а другий інтеграл перетворюють
до виду
.
Інтеграл після підстановки розбивають
на два інтеграли. Перший інтеграл
обчислюють виділенням у чисельнику
похідної знаменника, що дає табличний
інтеграл, а другий інтеграл перетворюють
до виду ,
оскільки
,
оскільки 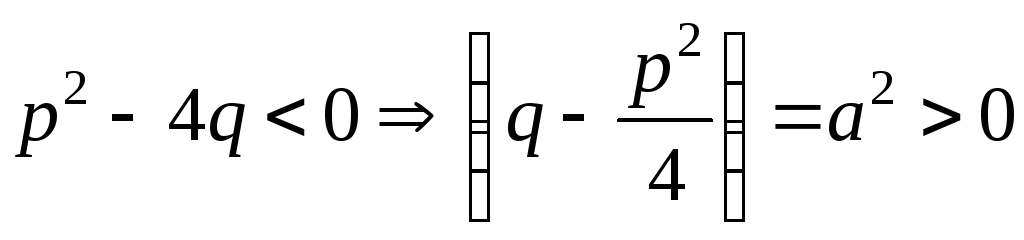 ,
що також дає табличний інтеграл.
,
що також дає табличний інтеграл.

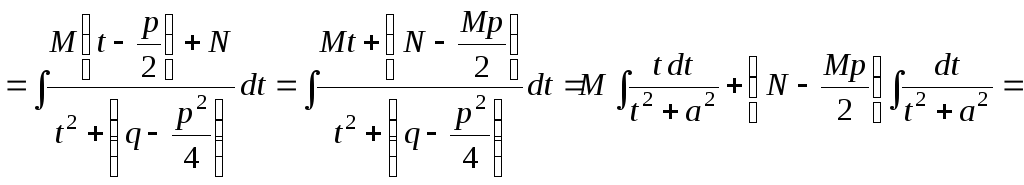
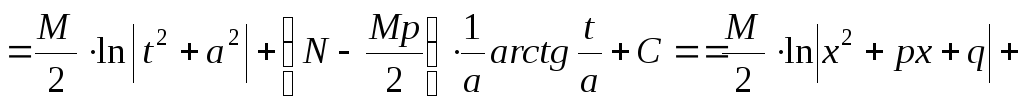
 ;
;
IV)
Для
інтегрування найпростішого дробу IV
типу в знаменнику виділяють повний
квадрат, роблять заміну 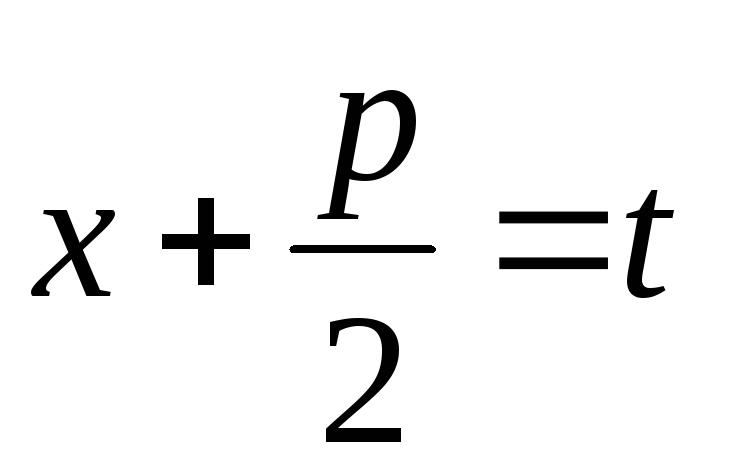 .
Інтеграл після підстановки розбивають
на два інтеграли. Перший інтеграл
обчислюють підстановкою
.
Інтеграл після підстановки розбивають
на два інтеграли. Перший інтеграл
обчислюють підстановкою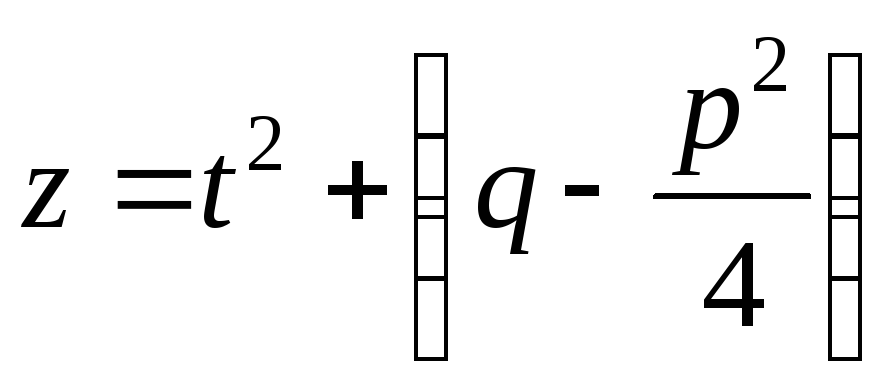 ,
а другий за допомогою рекурентних
співвідношень.
,
а другий за допомогою рекурентних
співвідношень.
Приклад 27.
Знайти інтеграли від найпростіших дробів:
а) 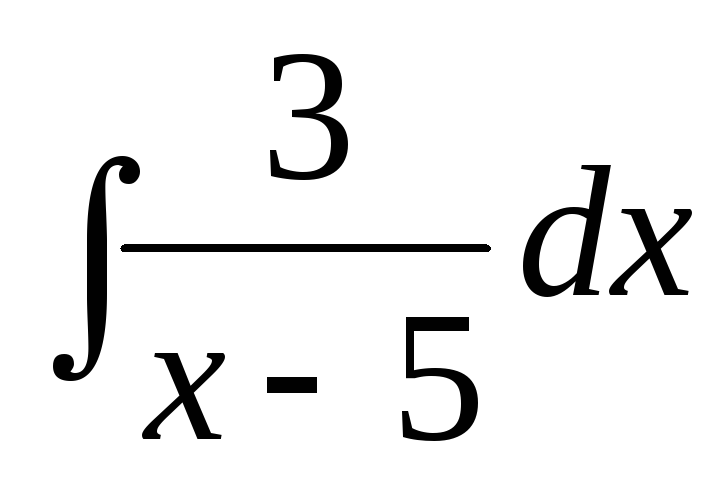 ;
б)
;
б)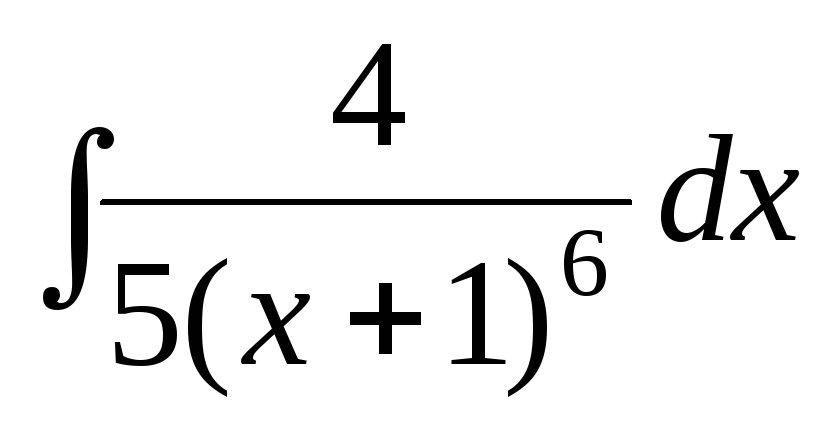 ;
в)
;
в) .
.
Розв’язок.
а) 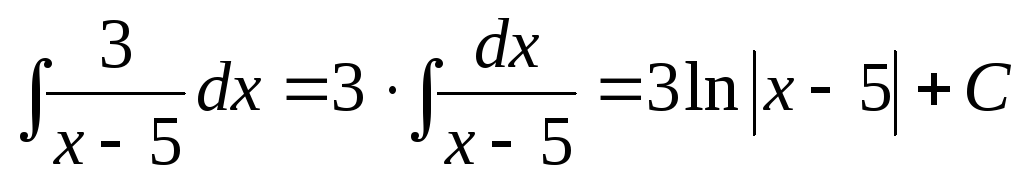 .
.
б) 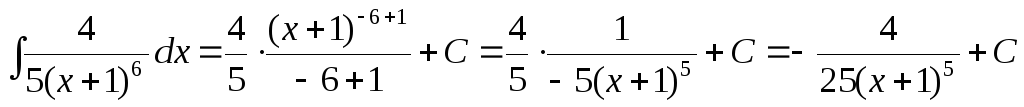 .
.
в) 


 .
.
Усякий правильний раціональний дріб, знаменник якого може бути розкладений на множники, можна представити у вигляді суми найпростіших дробів. Розкладання на суму найпростіших дробів здійснюють методом невизначених коефіцієнтів. Він полягає в наступному:
–
кожному
множнику знаменника  відповідає один дріб виду
відповідає один дріб виду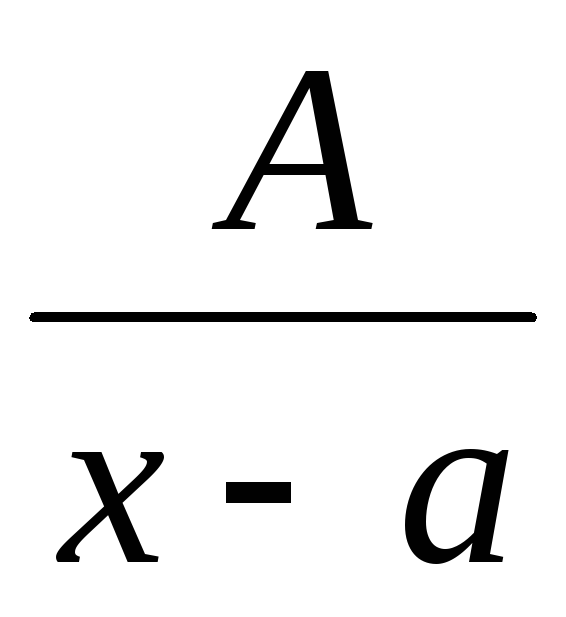 ;
;
–
кожному
множнику знаменника 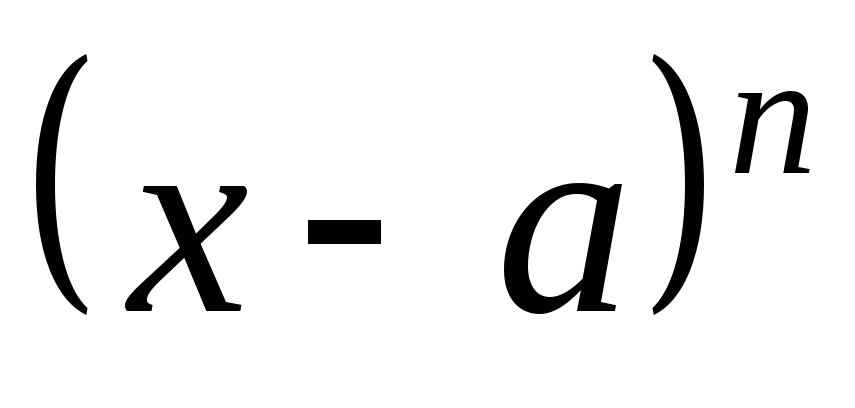 відповідає сума
відповідає сума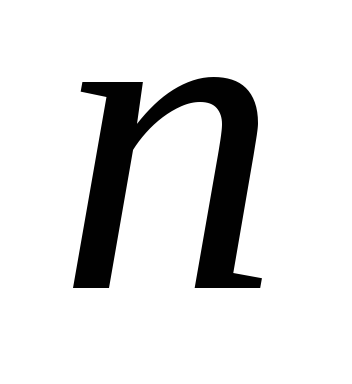 дробів
виду
дробів
виду
 ;
;
– кожному
квадратному множнику знаменника 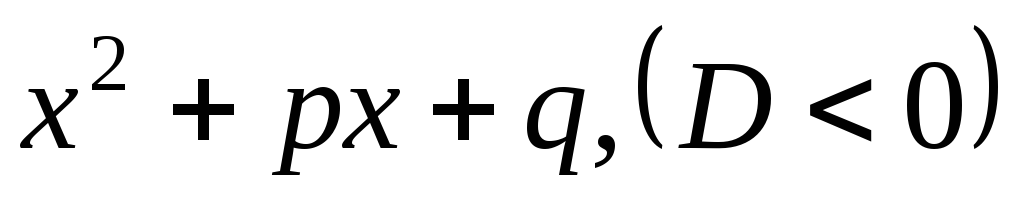 відповідає дріб виду
відповідає дріб виду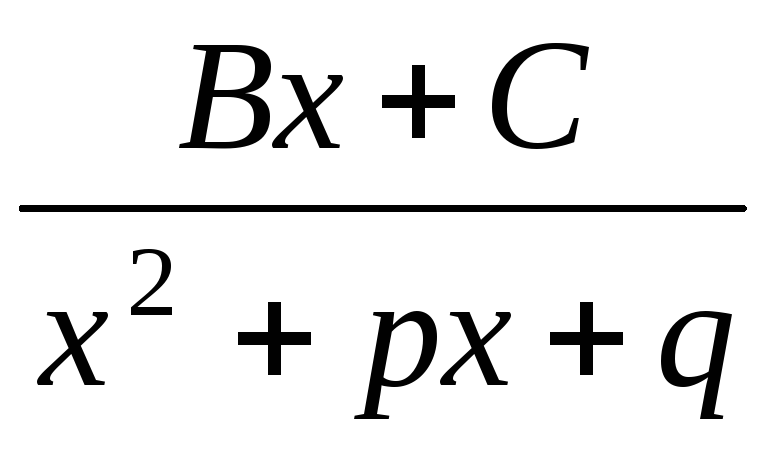 ;
;
– кожному
квадратному множнику знаменника  відповідає сума
відповідає сума дробів виду
дробів виду
 ,
,
де 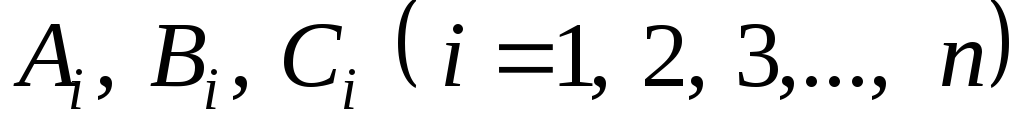 – невизначені коефіцієнти.
– невизначені коефіцієнти.
Для знаходження невизначених коефіцієнтів праву частину у вигляді суми найпростіших дробів приводять до загального знаменника і перетворюють. У результаті виходить дріб з тим же знаменником, що і у лівій частині рівності. Потім відкидають знаменники і дорівнюють чисельники. У результаті виходить тотожна рівність, у якій ліва частина – многочлен з відомими коефіцієнтами, а права частина – многочлен з невизначеними коефіцієнтами.
Існує два способи визначення невідомих коефіцієнтів: метод невизначених коефіцієнтів і метод часткових значень.
Метод невизначених коефіцієнтів.
Оскільки
многочлени тотожно рівні, то рівні
коефіцієнти при однакових степенях  .
Дорівнюючи коефіцієнти при однакових
степенях
.
Дорівнюючи коефіцієнти при однакових
степенях у многочленах лівої і правої частин,
одержимо систему лінійних рівнянь.
Розв’язуючи систему, визначаємо
невизначені коефіцієнти.
у многочленах лівої і правої частин,
одержимо систему лінійних рівнянь.
Розв’язуючи систему, визначаємо
невизначені коефіцієнти.
Метод часткових значень.
Оскільки
многочлени тотожно рівні, то, підставляючи
замість 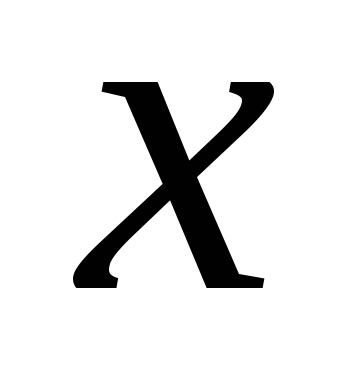 у ліву і праву частини будь-яке число,
одержимо вірну рівність, лінійну щодо
невідомих коефіцієнтів. Підставляючи
стільки значень
у ліву і праву частини будь-яке число,
одержимо вірну рівність, лінійну щодо
невідомих коефіцієнтів. Підставляючи
стільки значень ,
скільки є невідомих коефіцієнтів,
одержимо систему лінійних рівнянь.
Замість
,
скільки є невідомих коефіцієнтів,
одержимо систему лінійних рівнянь.
Замість у ліву і праву частини можна підставляти
будь-які числа, однак більш зручно
підставляти корені знаменників дробів.
у ліву і праву частини можна підставляти
будь-які числа, однак більш зручно
підставляти корені знаменників дробів.
Після знаходження значень невідомих коефіцієнтів, даний дріб записується у вигляді суми найпростіших дробів у підінтегральний вираз і здійснюється раніше розглянуте інтегрування по кожному найпростішому дробу.
Схема інтегрування раціональних дробів:
1. Якщо підінтегральний дріб неправильний, то необхідно представити його у вигляді суми многочлена і правильного раціонального дробу (тобто розділити многочлен чисельника на многочлен знаменника з остачею). Якщо підінтегральний дріб правильний відразу переходимо до другого пункту схеми.
2. Розкласти знаменник правильного раціонального дробу на множники, якщо це можливо.
3. Розкласти правильний раціональний дріб на суму найпростіших раціональних дробів, використовуючи метод невизначених коефіцієнтів.
4. Проінтегрувати отриману суму многочлена і найпростіших дробів.
Приклад 28.
Знайти інтеграли від раціональних дробів:
а)  ;
б)
;
б)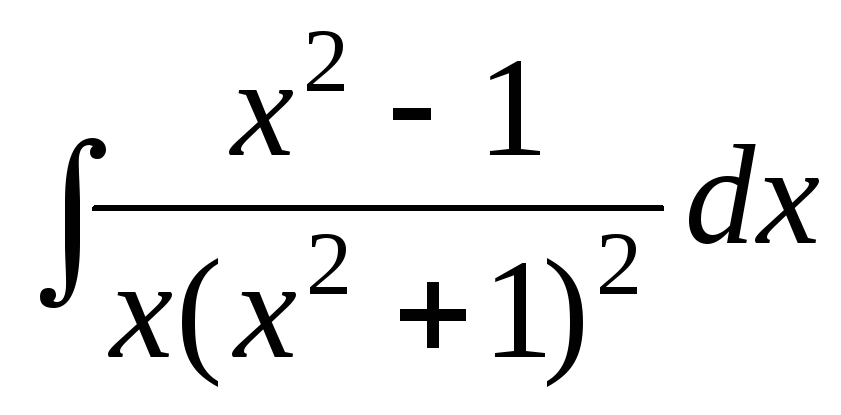 ;
в).
;
в).
Розв’язок.
а)  .
.
Оскільки підінтегральна функція є неправильним раціональним дробом, то виділимо з нього цілу частину, тобто представимо його у вигляді суми многочлена і правильного раціонального дробу. Розділимо многочлен у чисельнику на многочлен у знаменнику куточком.

Даний
інтеграл прийме вигляд: 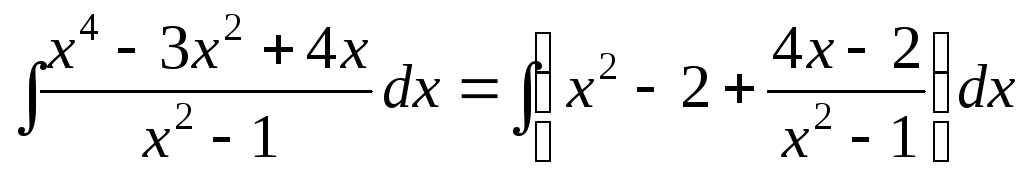 .
.
Розкладемо правильний раціональний дріб на суму найпростіших дробів за допомогою методу невизначених коефіцієнтів:
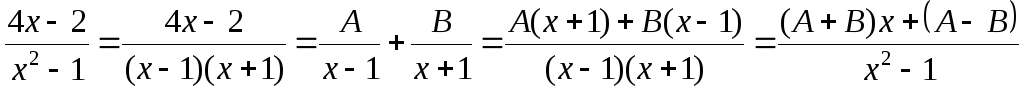 .
.
Відкинемо знаменники і дорівняємо ліву і праву частини:
 .
.
Дорівнюючи
коефіцієнти при однакових степенях 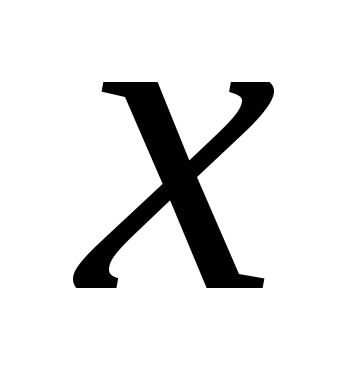 ,
одержуємо:
,
одержуємо:

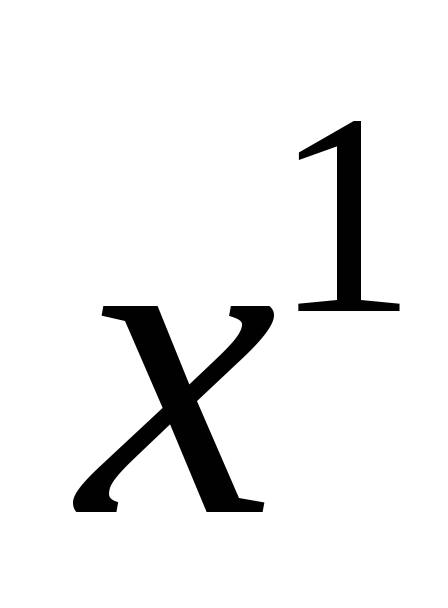

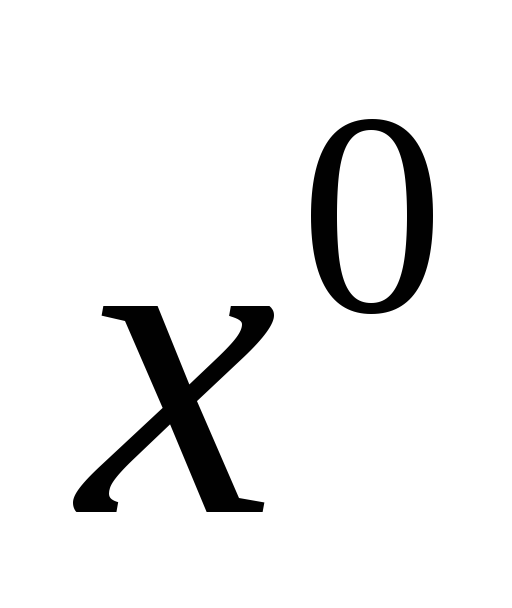
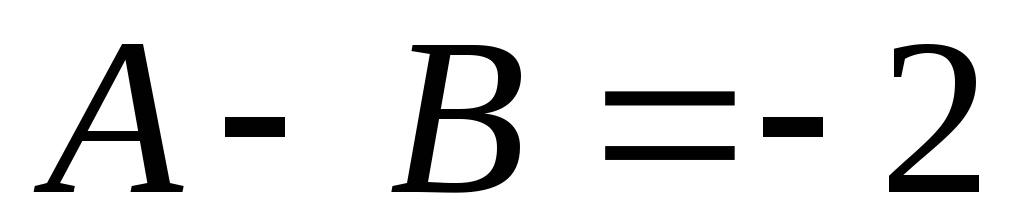
Вирішуючи систему лінійних рівнянь, одержимо значення невизначених коефіцієнтів: А = 1; В = 3.
Тоді
розкладання має вигляд: 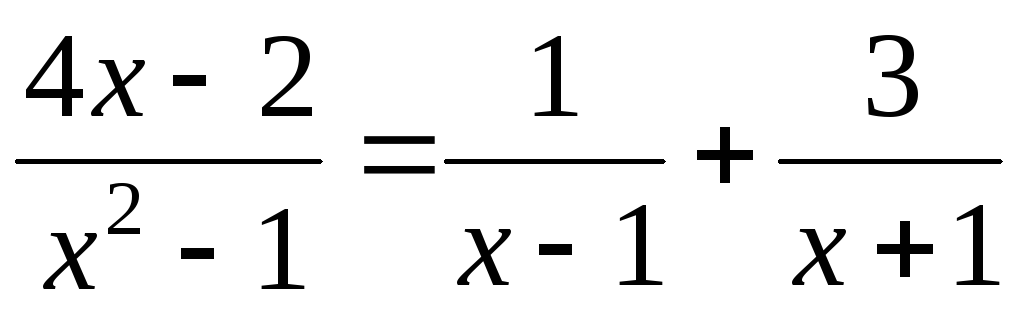 .
.
Знайдемо даний інтеграл, враховуючи отримане розкладання:
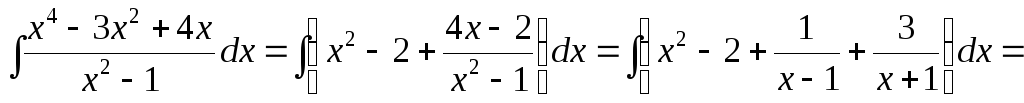
=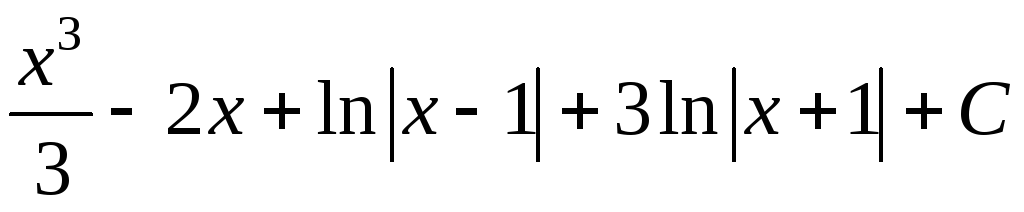 .
.
б) 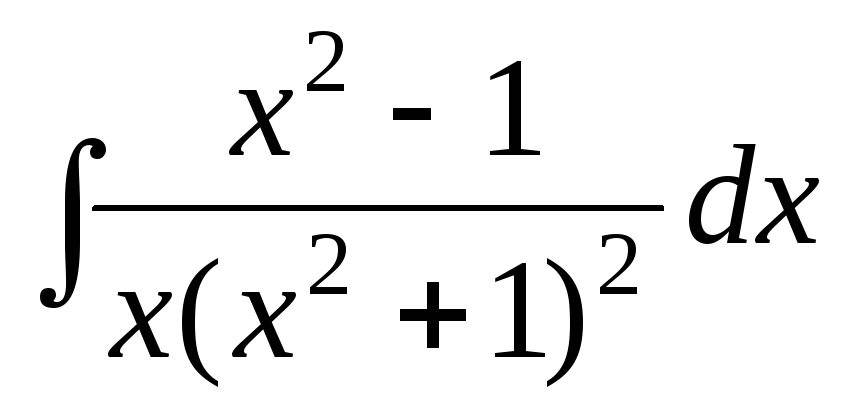 .
.
Розкладемо підінтегральну функцію (правильний раціональний дріб) на суму найпростіших дробів за допомогою методу невизначених коефіцієнтів. Розкладання шукаємо у вигляді:
 .
.
Привівши до загального знаменника, одержимо:
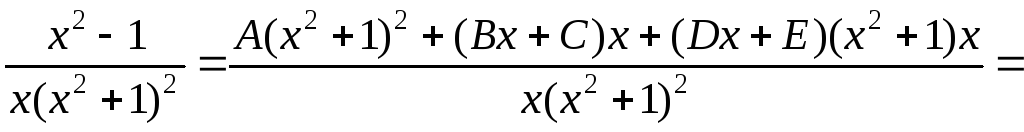

Відкинемо знаменники і дорівняємо ліву і праву частини:
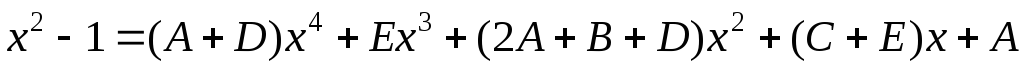 .
.
Дорівнюючи
коефіцієнти при однакових степенях  ,
одержуємо систему:
,
одержуємо систему:


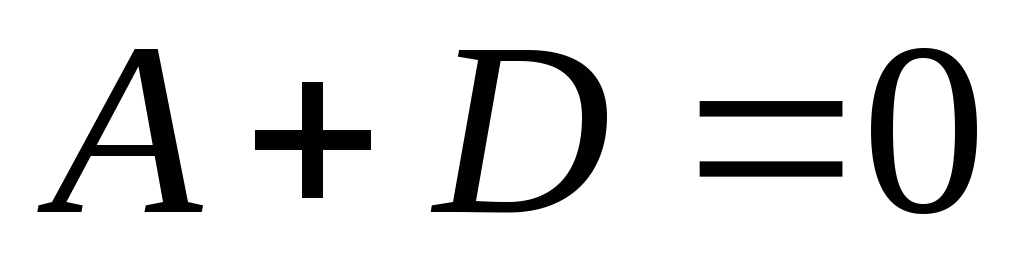
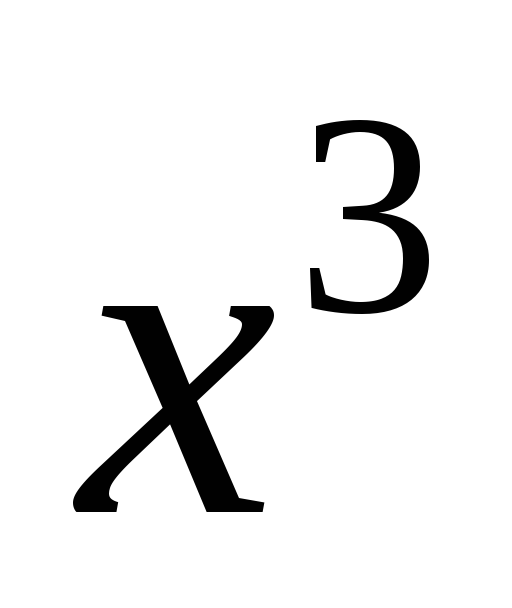

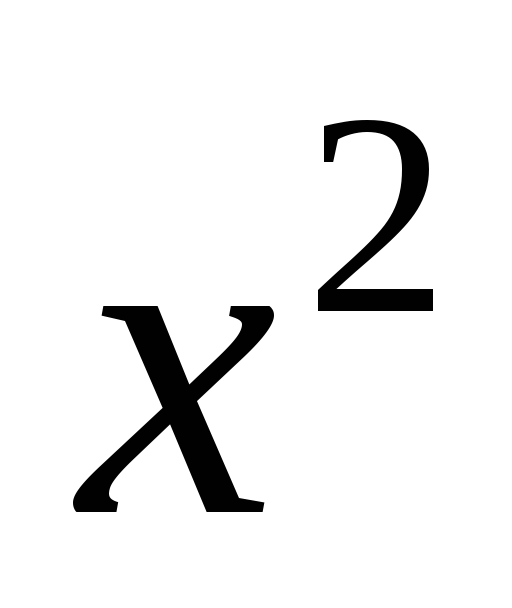
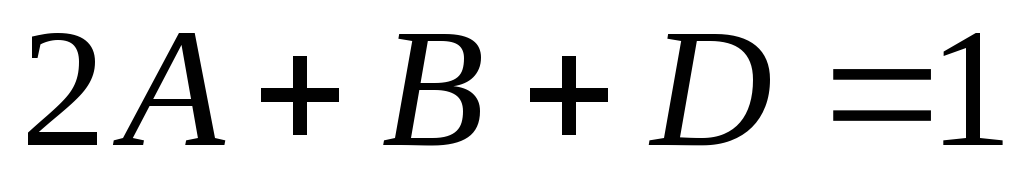


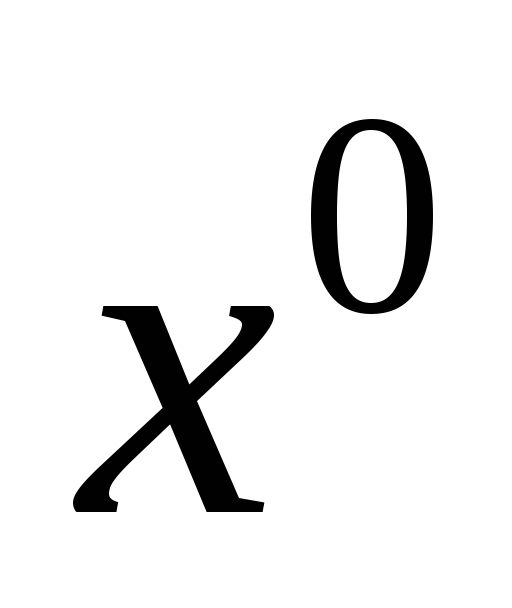

Вирішуючи систему з п’яти лінійних рівнянь, знаходимо невизначені коефіцієнти:
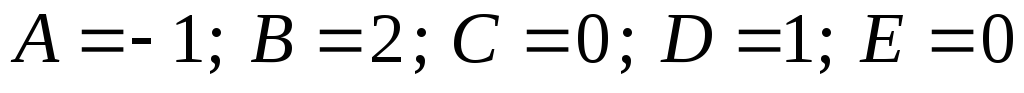 .
.
Тоді розкладання має вигляд:
 .
.
Знайдемо даний інтеграл, враховуючи отримане розкладання:
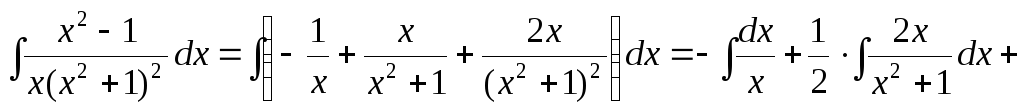
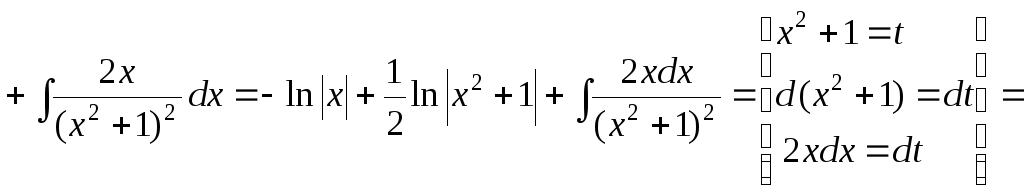

.
в)  .
.
Розкладемо підінтегральну функцію (правильний раціональний дріб) на суму найпростіших дробів за допомогою методу невизначених коефіцієнтів. Розкладання шукаємо у вигляді:
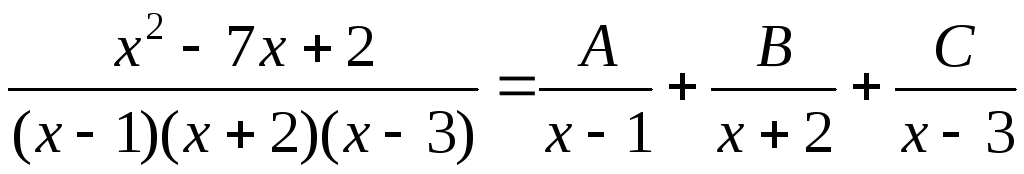 .
.
Привівши до загального знаменника, одержимо:
 .
.
Відкинемо знаменники і дорівняємо ліву і праву частини:
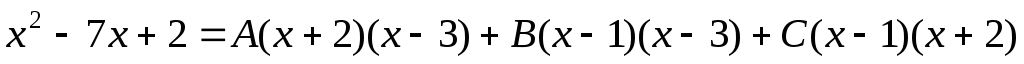 .
.
Для
знаходження невизначених коефіцієнтів
застосуємо метод часткових значень.
Надамо  часткові
значення
часткові
значення 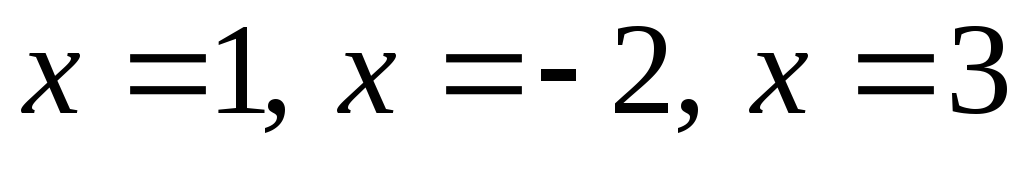 ,
при яких множники обертаються в нуль,
тобто підставимо ці значення в останній
вираз і одержимо три рівняння:
,
при яких множники обертаються в нуль,
тобто підставимо ці значення в останній
вираз і одержимо три рівняння:


 ;
; 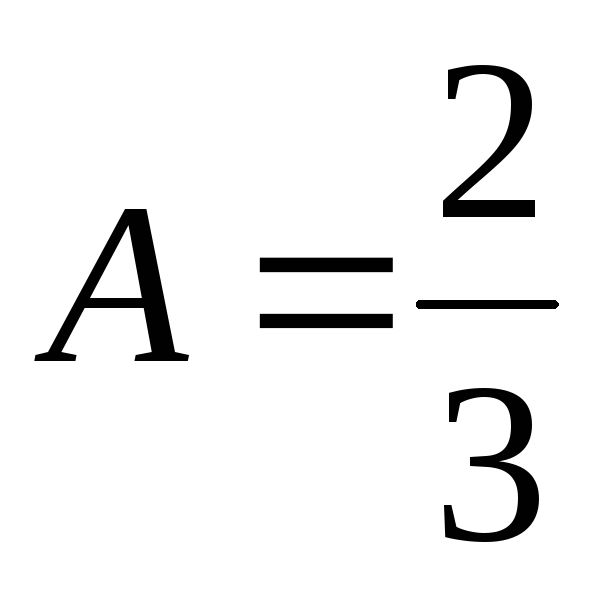 ;
;
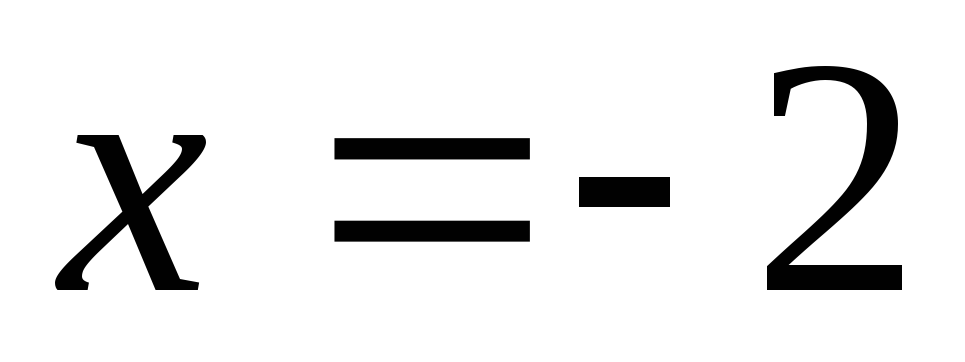
 ;
; 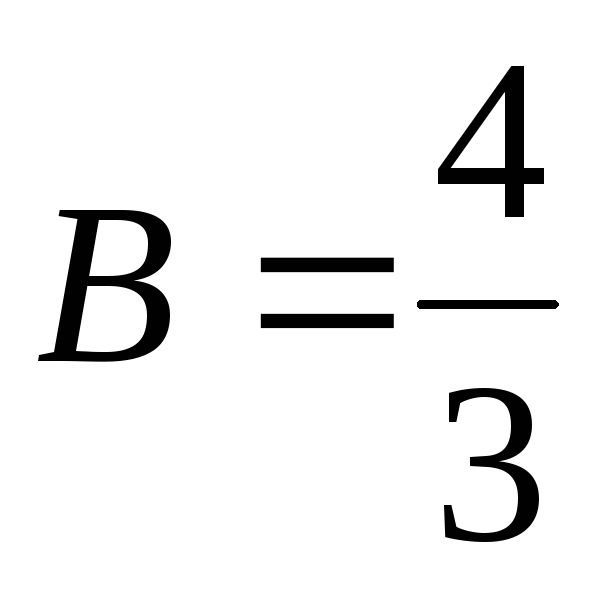 ;
;

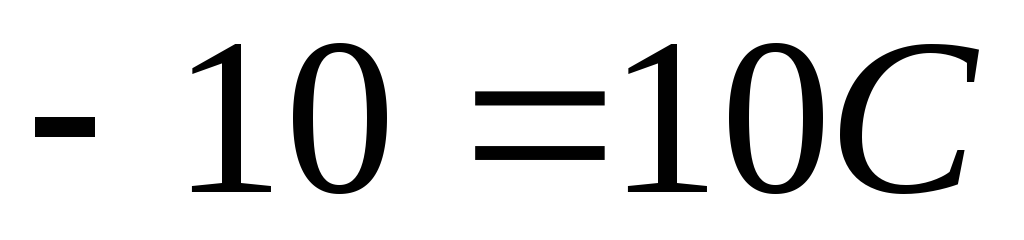 ;
;  .
.
Тоді розкладання має вигляд:
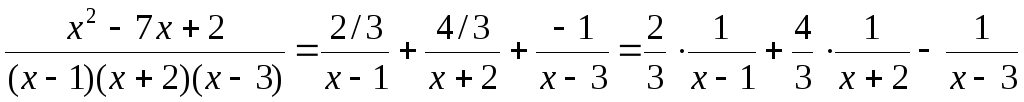 .
.
Знайдемо даний інтеграл, враховуючи отримане розкладання:

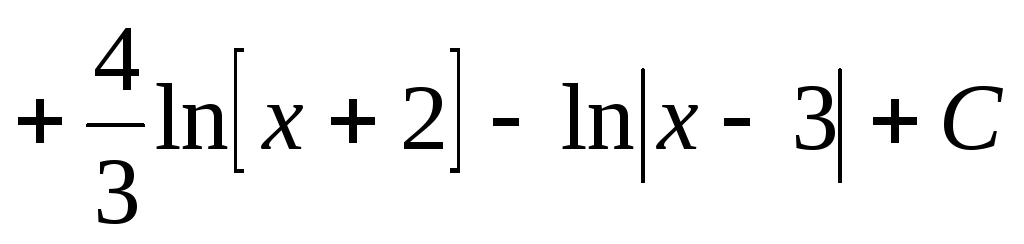 .
.
studfile.net
2.2. Обчислення визначеного інтеграла. Формула Ньютона-Лейбніца.
Нехай
функція  задана і неперервне на відрізку
задана і неперервне на відрізку де
де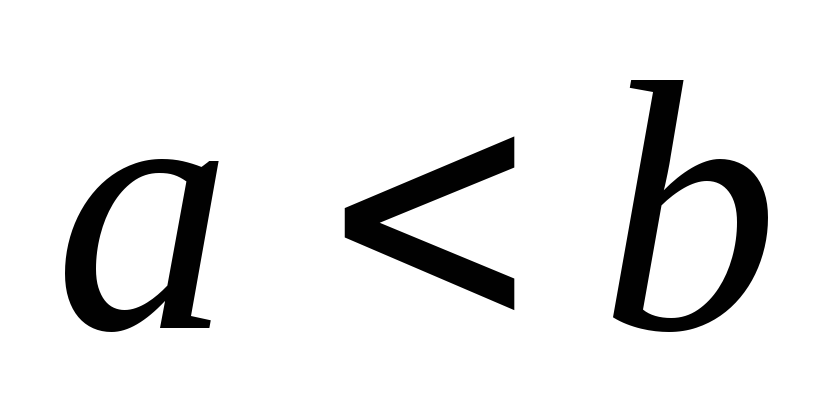 або
або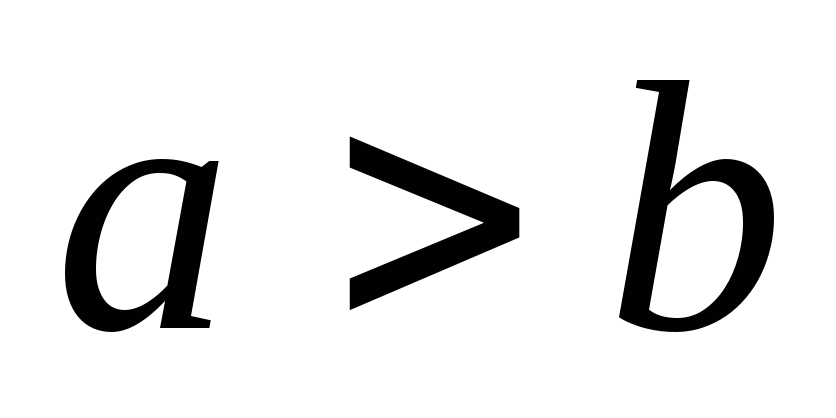 ,
а
,
а — деяка її первісна, тобто
— деяка її первісна, тобто при
при .
.
Теорема Якщо 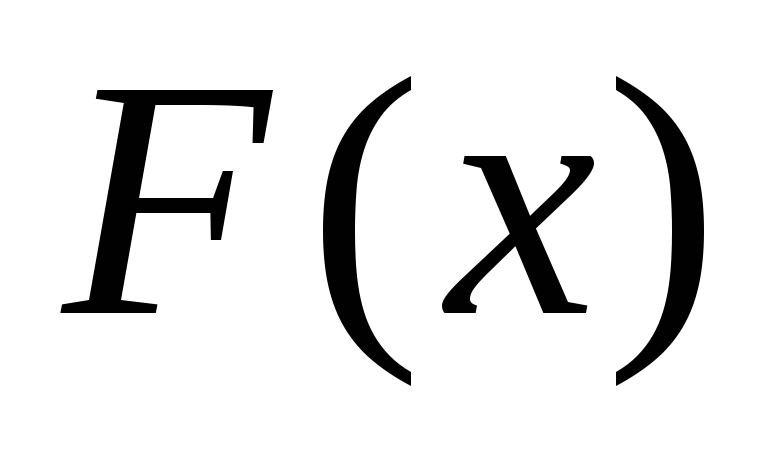 є якою-небудь первісною
є якою-небудь первісною ,
то справедлива формула
,
то справедлива формула
| (2.3) |
тобто
визначений інтеграл від від даної
неперервної функції 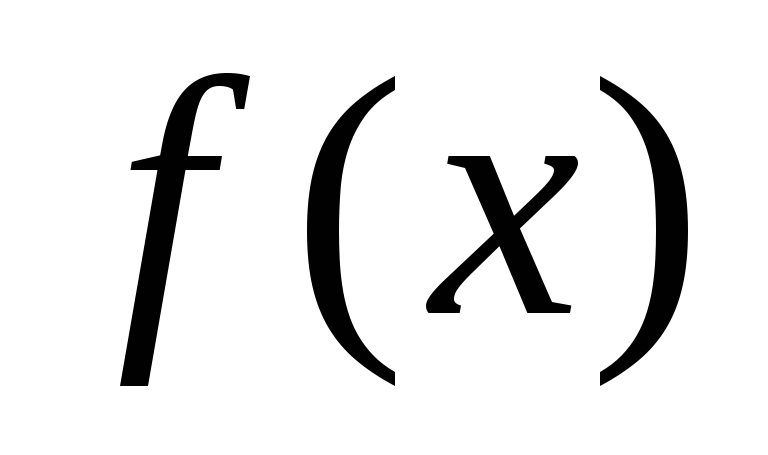 на даному відрізку
на даному відрізку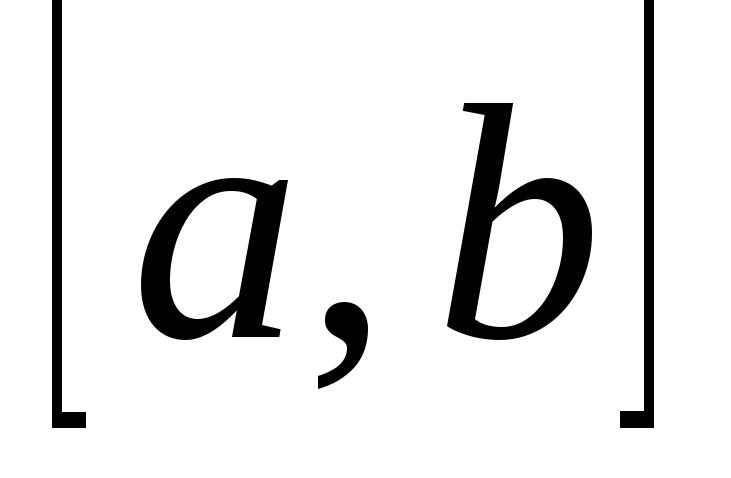 дорівнює приросту її первісної
дорівнює приросту її первісної
Ця формула називається формулою Ньютона-Лейбніца.
У виразі
(2.3) числа  і
і називаються межами інтегрування,
відповідно нижньою і верхньою,
називаються межами інтегрування,
відповідно нижньою і верхньою,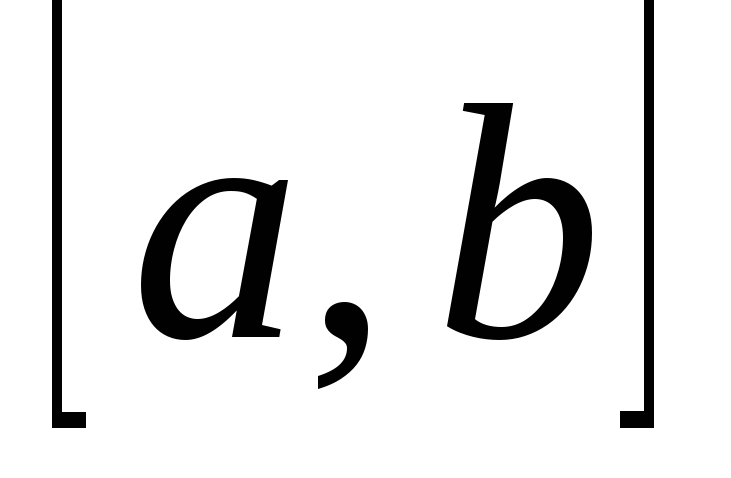 — проміжком інтегрування,
— проміжком інтегрування,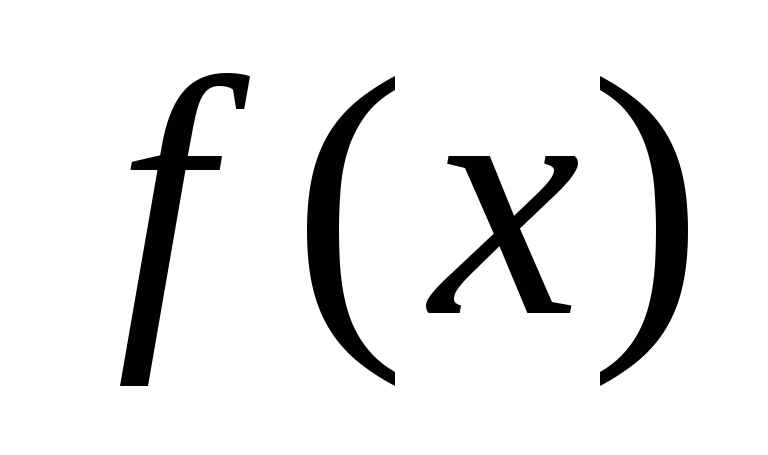 — підінтегральною функцією. Формулу
(2.3) можна подати як правило, а саме:
визначений інтеграл дорівнює різниці
значень первісної функції для верхньої
і нижньої меж інтегрування. Запишемо
це так:
— підінтегральною функцією. Формулу
(2.3) можна подати як правило, а саме:
визначений інтеграл дорівнює різниці
значень первісної функції для верхньої
і нижньої меж інтегрування. Запишемо
це так:
| (2.4) |
де
символ 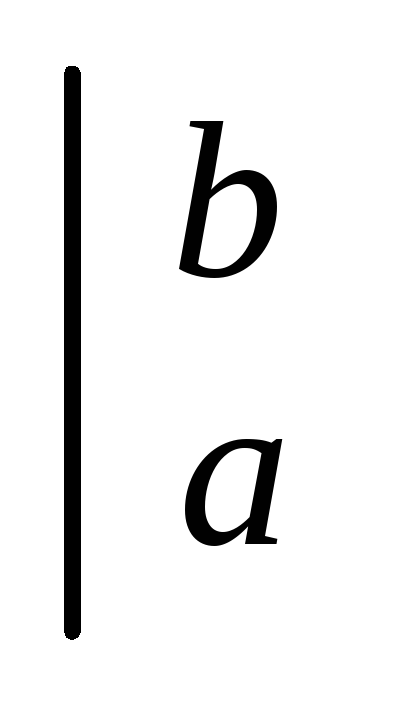 називається вставкою. Формула (2.4) дає
практичне правило обчислення визначеного
інтеграла. Воно означає знаходження
невизначеного інтеграла, тобто первісної
функції
називається вставкою. Формула (2.4) дає
практичне правило обчислення визначеного
інтеграла. Воно означає знаходження
невизначеного інтеграла, тобто первісної
функції із наступним обчисленням її значень
в точках
із наступним обчисленням її значень
в точках і
і .
.
Приклад. Обчислити інтеграл.
 .
.
2.3. Основні властивості визначеного інтеграла.
При
формулюванні основних властивостей
визначеного інтеграла будемо виходити
із формули (2.3), де  — неперервна на відрізку
— неперервна на відрізку , а
, а при
при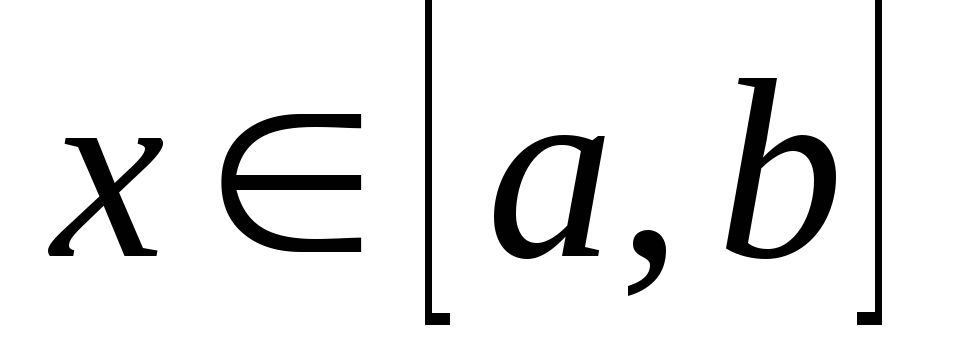 .
.
Величина визначеного інтеграла не залежить від позначення змінної інтегрування, тобто
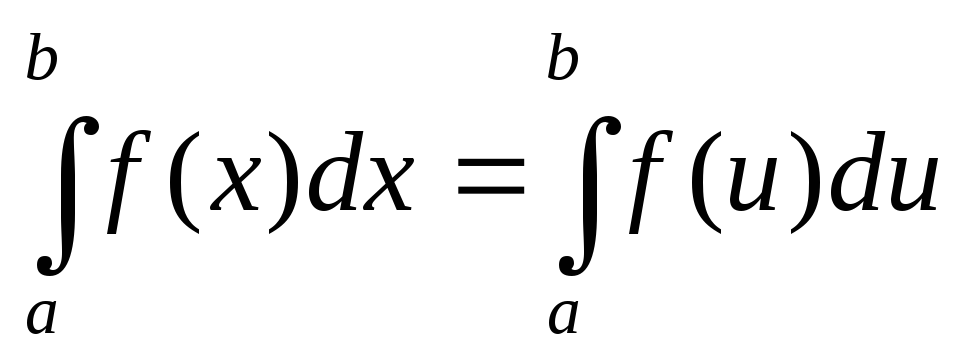
2. Визначений інтеграл з однаковими межами інтегрування дорівнює нулю, тобто
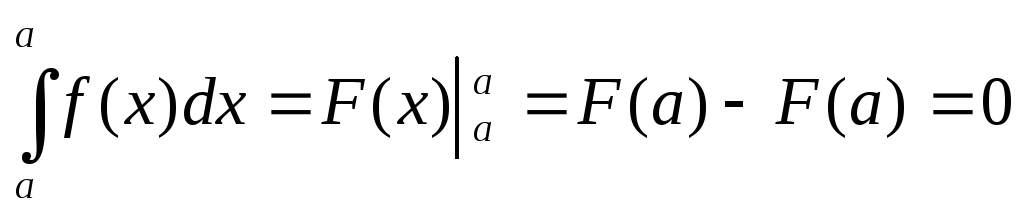 .
.
При перестановці меж інтегрування визначений інтеграл змінює свій знак на протилежний, тобто

Якщо відрізок
 точкоюс поділений на два відрізки
точкоюс поділений на два відрізки і
і ,
то має місце рівність
,
то має місце рівність

Сталий множник виноситься за знак визначеного інтеграла, тобто

6.
Визначений інтеграл від алгебраїчної
суми скінченого числа неперервних
функцій дорівнює такій же алгебраїчній
сумі визначених інтегралів від цих
функцій, тобто  .
.
7.
Якщо всюди на відрізку 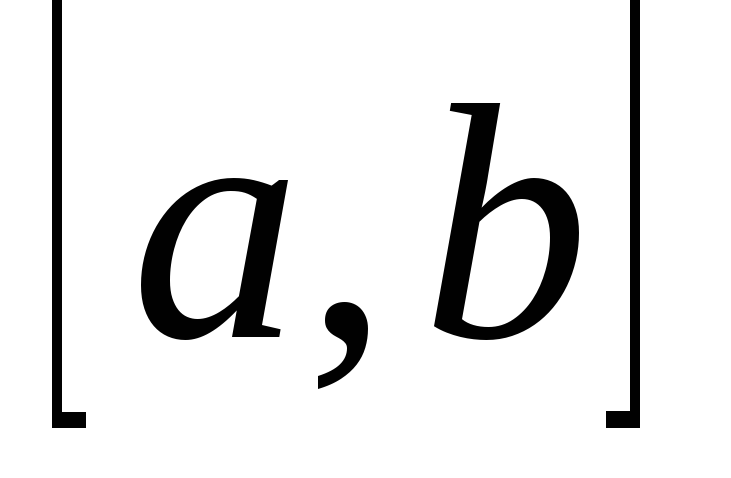 функція
функція
 ,
то
,
то
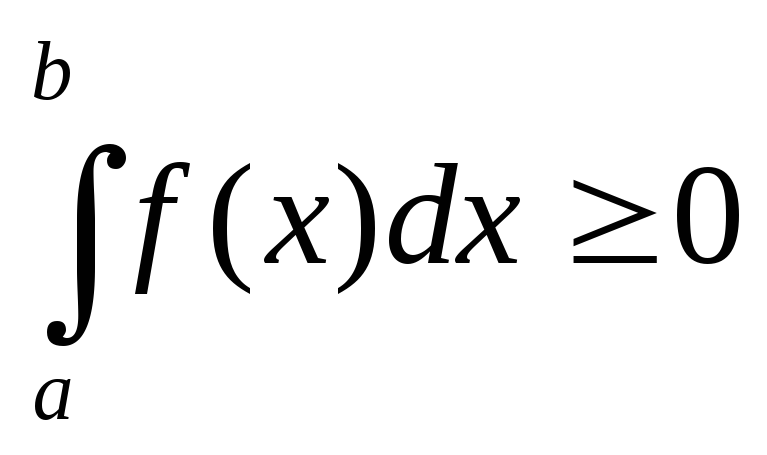
8. Якщо
всюди на відрізку  виконується умова
виконується умова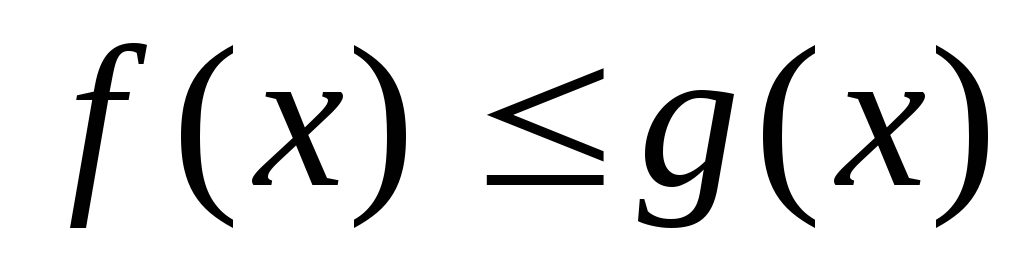
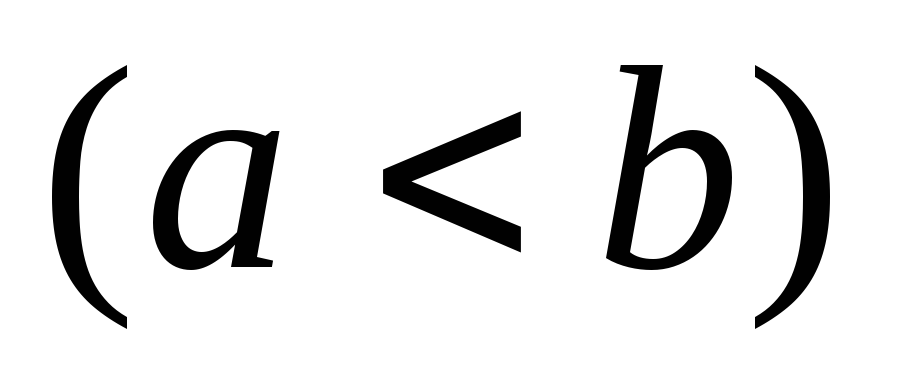 ,
то справедлива нерівність
,
то справедлива нерівність
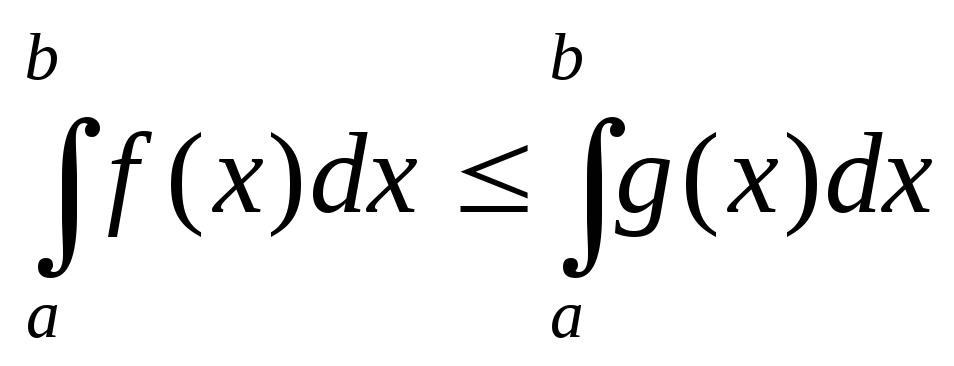 .
.
Якщо функція
 інтегровна на відрізку
інтегровна на відрізку
 ,
то
,
то

Якщо функція
 неперервна на відрізку
неперервна на відрізку , то на цьому відрізку знайдеться
така точкас ,
що
, то на цьому відрізку знайдеться
така точкас ,
що

11. Похідна визначеного інтеграла із змінною верхньою межою по цій межі дорівнює значенню підінтегральної функції для цієї межі, тобто
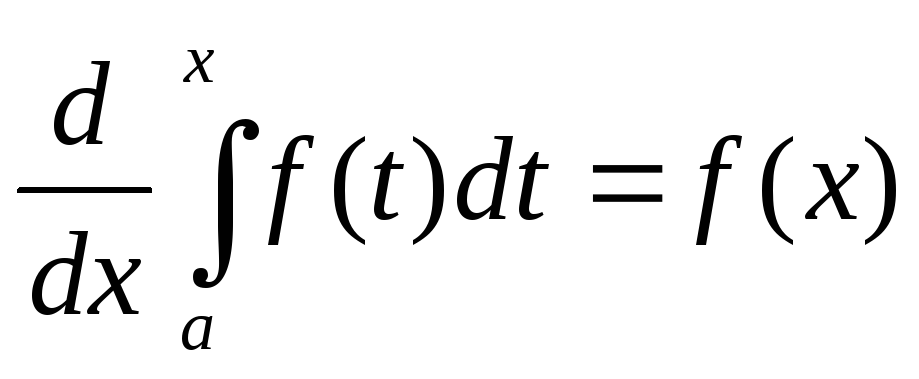
2.4. Методи обчислення визначених інтегралів
Обчислення визначених інтегралів здійснюється за формулами і правилами знаходження невизначених інтегралів із наступним використанням формули Ньютона-Лейбніца. Розглянемо деякі з них.
Інтегрування частинами у визначеному інтегралі.
Нехай
функції  і
і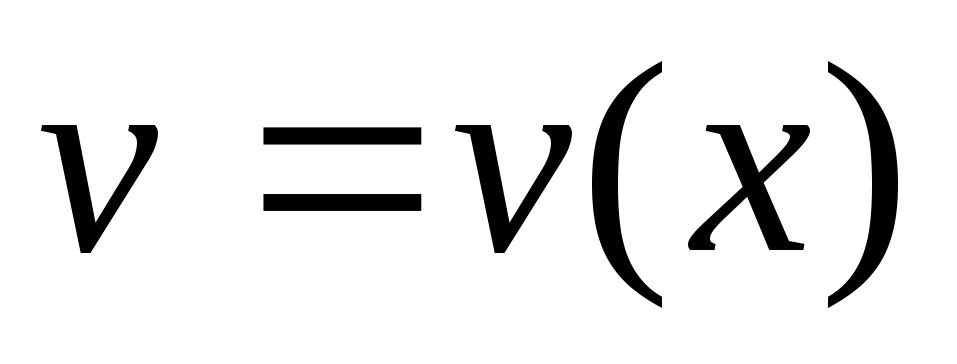 неперервно диференційовні на відрізку
неперервно диференційовні на відрізку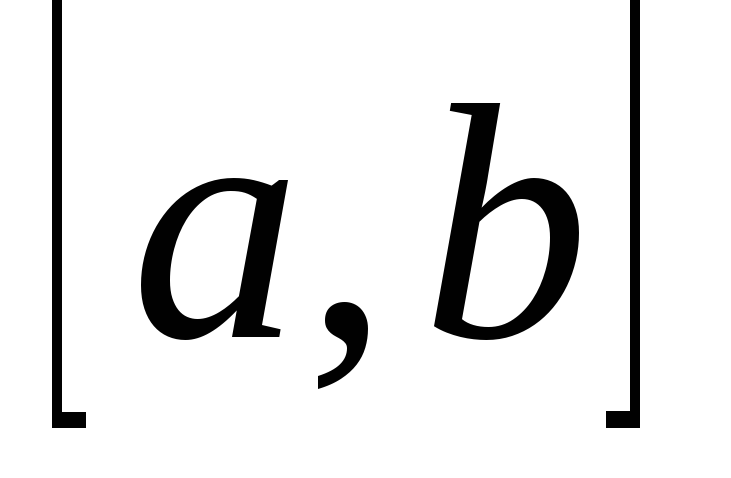 ,
тобтоі
,
тобтоі — неперервні функції. Тоді
— неперервні функції. Тоді
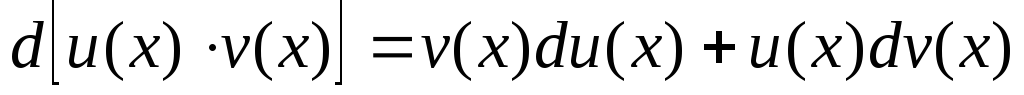
або
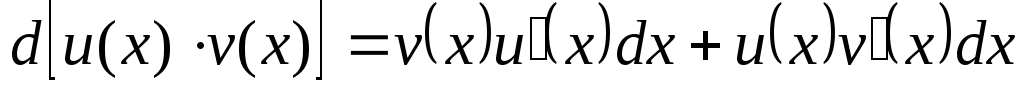
Інтегруючи
цю рівність в межах від  до
до ,
одержимо
,
одержимо

Звідси одержимо формулу інтегрування частинами
| (2.5) |
Приклад. Знайти інтеграл.
 .
.
Заміна змінної у визначеному інтегралі.
Заміна
змінної у визначеному інтегралі
здійснюється як і у випадку невизначеного
інтеграла з тим додатком, що із
підстановки 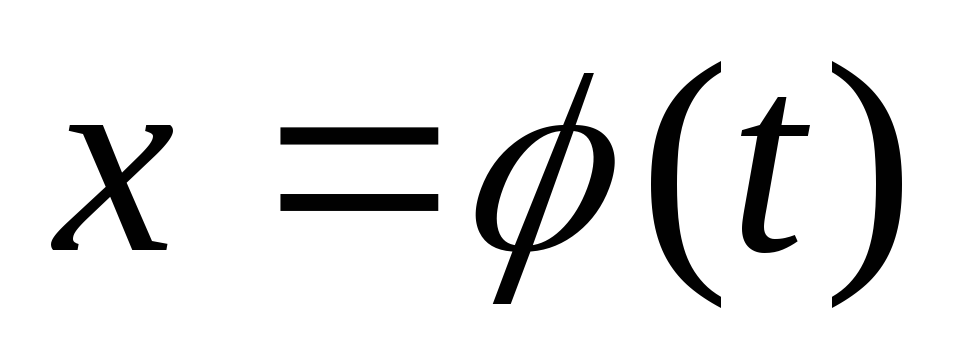 визначаються нові межі інтегрування.
Старі і нові межі інтегрування зв’язані
рівностями
визначаються нові межі інтегрування.
Старі і нові межі інтегрування зв’язані
рівностями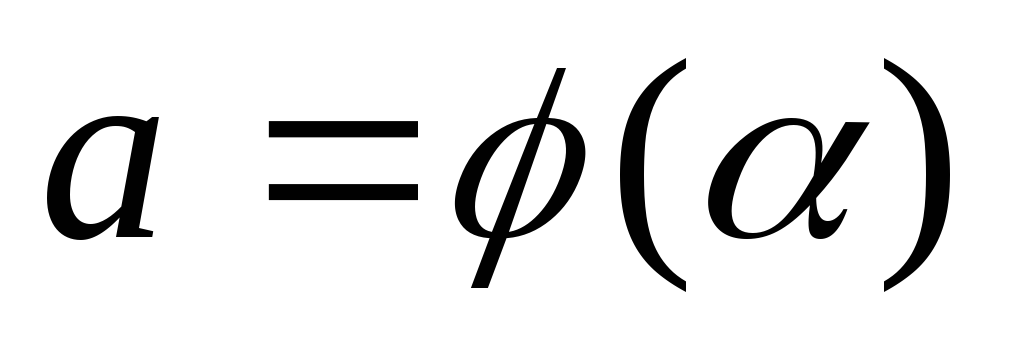 ,
, .
Формула (1.7) у даному випадку матиме
вигляд
.
Формула (1.7) у даному випадку матиме
вигляд

Приклад. Обчислити інтеграл.
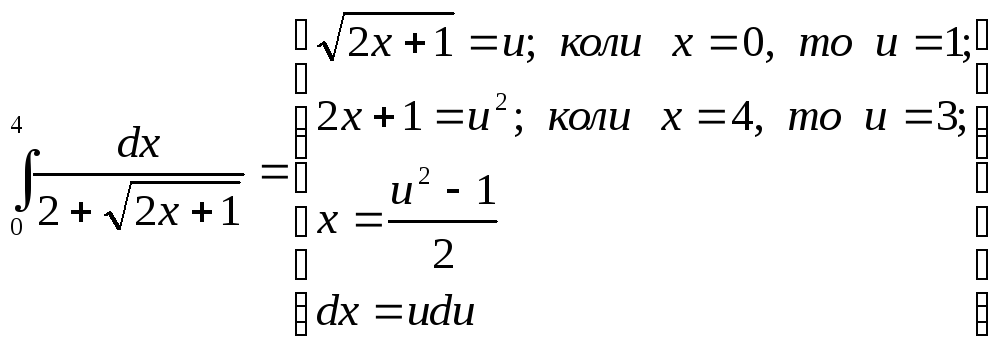 =
=
 ;
;
studfile.net
Невластиві інтеграли 1-го та 2-го роду
Невластивий інтеграл І роду
Якщо функція f(x) інтегровна за Ріманом на кожному кінцевому проміжку [a;b], тоді невластивий інтеграл знаходять через граничний перехід за формулою
і говорять, що невластивий інтеграл збіжний, якщо існує така скінченна границя. В протилежному разі (якщо границя нескінченна або не існує) говорять, що інтеграл розбігається.
Невластивий інтеграл ІІ роду
Якщо функція f(x) необмежена в околі точки B і інтегровна за Ріманом на кожному кінцевому проміжку , тоді невластивий інтеграл ІІ роду обчислюють за формулою
і говорять, що інтеграл збіжний, якщо існує його скінченна границя. В протилежному разі (якщо границя нескінченна або не існує) говорять, що інтеграл розбігається. Точка B називається особливою.
І. Обчислити інтеграли
Почнемо розгляд готових відповідей до невластивих інтегралів від простих до складних завдань.
Приклад 2.147 (2334) Знайти невластивий інтеграл
Маємо невластивий інтеграл І роду. Змінюємо безмежність на фіксовану точку з проміжку, обчислюємо інтеграл та після підстановки меж інтегрування знаходимо границю при прямуванні верхньої межі до безмежності
Приклад 2.148 ( 2335) Знайти інтеграл
Підінтегральна функція (логарифм) невизначена в нулі, що відповідає нижній границі інтегрування. Відповідно до наведених вище формул, маємо невластивий інтеграл другого роду. Для його знаходження переходимо до границі в нулі, також виконуємо інтегрування частинами
Сам по собі інтеграл не складний в плані обчислень.
Зауваження: надалі границю писати НЕ будемо, а при обчислення невластивих інтегралів розуміємо, що шукаємо значення границі в особливих точках (або в плюс мінус безмежності )!!!
Приклад 2.149 (2336) Обчислити інтеграл
Розбиваємо інтеграл на 2 та знаходимо невластиві інтеграли І роду
Приклад 2.150 (2337 ) Знайти інтеграл
Виконуємо маніпуляції ідентичні, як і в попередньому завданні та приходимо до невластивих інтегралів другого роду
Приклад 2.151 ( 2338) Знайти інтеграл
Верхня границя прямує до безмежності, отже маємо невластивий інтеграл першого роду. Для знаходження граничного значення знаходимо неозначений інтеграл і при підстановці меж виносимо змінну за дужки в чисельнику і знаменнику логарифму. В результаті вклад нескінченно малих величин (1/x) прямує до нуля при змінній прямуючій до безмежності. Таким чином знаходимо головне значення інтегралу
Приклад 2.152 (2339) Знайти інтеграл
Розв’язання: Обчислимо останній інтеграл методом Остроградського — метод не з простих, проте ефективний в подібних обчисленнях:
візьмемо похідну в кожній частині рівності (похідна від інтегралу рівна підінтегральній функції)
Зведемо дроби в правій частині рівності до спільного знаменника і прирівняємо коефіцієнти при відповідних степенях x кожної частини рівності
В результаті отримаємо систему із 4 лінійних рівнянь з якої знаходимо 4 константи
Таким чином можемо записати неозначений інтеграл у вигляді
Далі підставляємо межі та знаходимо границі дробу та арктангенсу при змінній прямуючій до плюс міну безмежності.
В кінцевій формулі можна ще позбутися ірраціональності в знаменнику, але це вже старайтеся робити самостійно.
Приклад 2.153 ( 2340)Знайти інтеграл
Обчислимо останній інтеграл методом невизначених коефіцієнтів:
Записуємо підінтегральні функції та, звівши їх під спільний знаменник, а далі
прирівняємо коефіцієнти при відповідних степенях x кожної частини рівності. В результаті розв’язуємо систему трьох рівнянь та визначаємо сталі
Підставимо їх в розклад та знайдемо неозначений інтеграл
після зведення під табличні формули інтегрування отри
yukhym.com
Оператор |
Опис |
Найпростіші математичні операції |
|
+ — * / () |
Додавання, віднімання, множення, ділення та групуючі символи: + — * / () . Знак множення * — необов’язковий: вираз 2sin(3x) еквівалентний 2*sin(3*x). Дужки використовуються для групування виразів. |
0.5 |
Десяткові дроби записуються через точку:
|
Елементарні функції |
|
xn |
Піднесення до степеню: x^n, наприклад, щоб ввести x2 використовується x^2 |
√x |
Квадратний корінь: \sqrt(x) або x^(1/2) |
3√x |
Кубічний корінь: x^(1/3) |
n√x |
Корінь n-того степеню з x: x^(1/n) |
ln(x) |
Натуральний логарифм (логарифм з основою e): log(x) |
logax |
Логарифм от x з основою a: log(x)/log(a) |
lg(x) |
Десятковий логарифм (логарифм з основою 10): log(x)/log(10) |
ex |
Експоненційна функція: exp(x) |
Тригонометричні функції |
|
sin(x) |
Синус від x: sin(x) |
cos(x) |
Косинус від x: cos(x) |
tg(x) |
Тангенс x: tan(x) |
ctg(x) |
Котангенс x: 1/tan(x) |
arcsin(x) |
Арксинус x: arcsin(x) |
arccos(x) |
Арккосинус x: arccos(x) |
arctan(x) |
Арктангенс x: arctan(x) |
arcctg(x) |
Арккотангенс x: \pi/2 — arctan(x) |
Деякі константи |
|
e |
Число Ейлера e: \e |
π |
Число π: \pi |
ua.onlinemschool.com
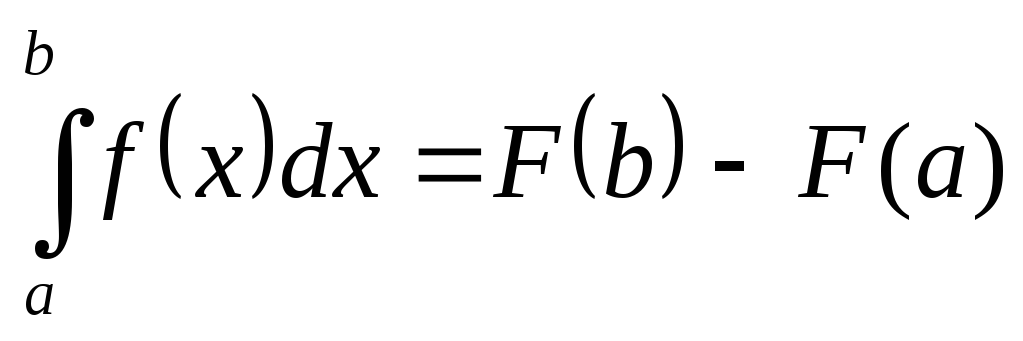 ,
,
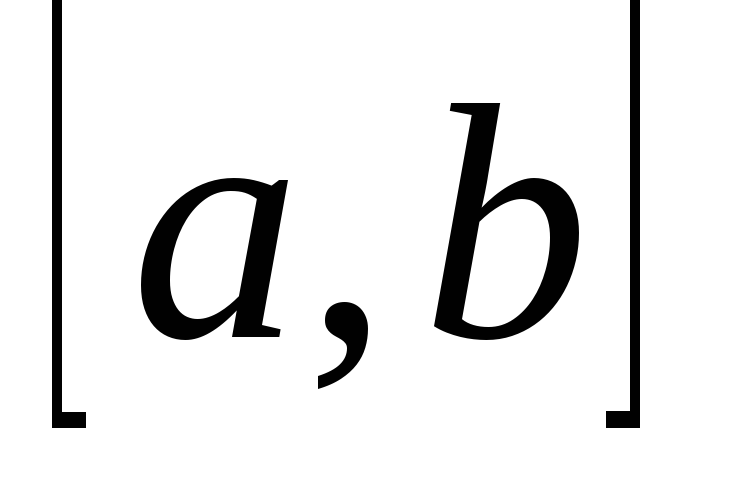 точкоюс поділений на два відрізки
точкоюс поділений на два відрізки і
і ,
то має місце рівність
,
то має місце рівність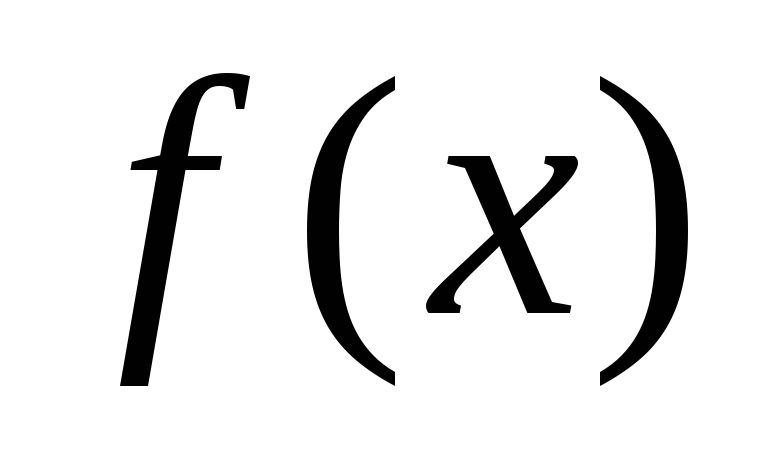 інтегровна на відрізку
інтегровна на відрізку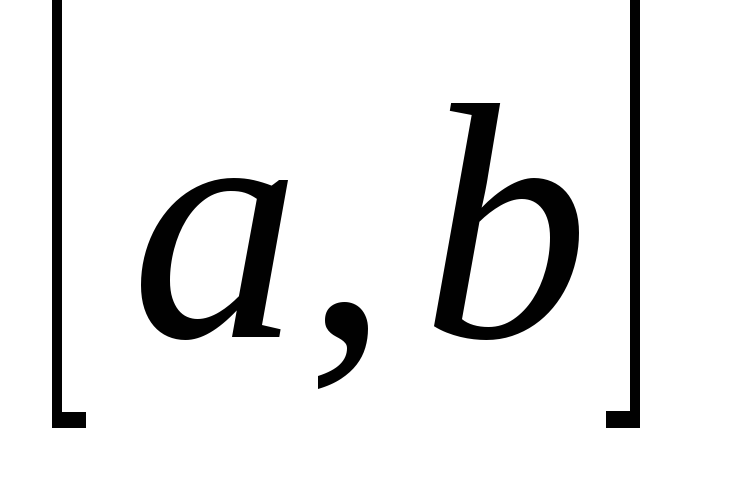
 ,
то
,
то неперервна на відрізку
неперервна на відрізку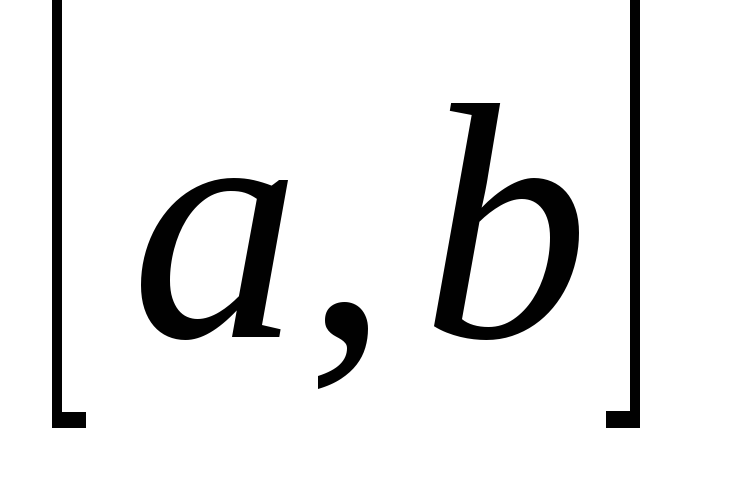 , то на цьому відрізку знайдеться
така точкас ,
що
, то на цьому відрізку знайдеться
така точкас ,
що