Разница между аксиомой и теоремой

Ключевое отличие: Аксиома и теорема — это утверждения, которые чаще всего используются в математике или физике. Аксиома — это утверждение, которое принимается за истину. Это не нужно доказывать. Теорема, с другой стороны, является утверждением, которое было доказано.

Аксиома и теорема — это утверждения, которые чаще всего используются в математике или физике. Аксиома — это утверждение, которое принимается за истину. Это не нужно доказывать. Теорема, с другой стороны, является утверждением, которое было доказано.

Согласно Dictionary.com, аксиома определяется как:

• Самоочевидная истина, не требующая доказательств.
• Общепризнанный принцип или правило.
• Логика, Математика. Утверждение, которое предполагается без доказательства ради изучения последствий, вытекающих из него.

По сути, аксиомы — это предположения, которые не нужно доказывать. Они обычно принимаются как истинные, либо потому, что в них нет противоречий, либо потому, что мы, очевидно, знаем, что это правда.

Аксиома слова происходит от греческого слова, которое означает «то, что считается достойным или подходящим» или «то, что оценивается как очевидное». Аксиома может иногда использоваться взаимозаменяемо с постулатом или предположением.

Теорема, с другой стороны, нуждается в доказательстве. Dictionary.com определяет теорему как:

• Математика. Теоретическое суждение, утверждение или формула, воплощающие что-то, что нужно доказать из других суждений или формул.
• Правило или закон, особенно тот, который выражается уравнением или формулой.
• Логика. Предложение, которое может быть выведено из предпосылок или предположений системы.
• Идея, убеждение, метод или утверждение обычно принимаются как истинные или стоящие без доказательств.

Теорема — это утверждение, которое было доказано путем тестирования или расчета. Это может быть доказано на основе теорем, которые были ранее доказаны или на основе аксиом. Теоремы состоят из двух частей: гипотезы и выводы.

Математик аксиома. Математик теорема. Доказательство в математике.

 Математика — это наука о количестве. 

Любая вещь, которую можно умножить, разделить или измерить, называется количеством. Таким образом, линия — это количество, потому что она может быть удвоена, утроена или уменьшена вдвое и может быть измерена.

Вес-это количество, которое можно измерить в  г, кг и тоннах.

Время — это вид количества, мера которого может быть выражена в часах, минутах и секундах.

Но цвет-это не количество. Нельзя сказать,  что один цвет вдвое больше, или наполовину больше, чем другой. Деятельность разума, как мысль, выбор, желание, ненависть не являются количествами. Их нельзя измерить.

 

Наиболее важные части математики: арифметикой, алгеброй и геометрией.

Арифметика — это наука о числах. Его помощь требуется для завершения и применения расчетов, почти в каждом другом отделении математики.

 

Алгебра — это метод вычисления буквами и другими символами. Флюксия или дифференциальное и интегральное исчисление, могут рассматриваться как принадлежащие к высшим разделам алгебры.

 

Геометрия-это та часть математики, которая относится к величине. Под величиной понимается тот вид количества, которое расширяется; то есть, который имеет одно или несколько из трех измерений, длину, ширину и толщину. Поверхность-это величина, имеющая длину и ширину. Твердое тело-это величина, имеющая длину, ширину и толщину. Но движение, хотя и количество, не является, строго говоря, величиной. Она не имеет ни длины, ни ширины, ни толщины. Тригонометрия и конические сечения являются ветвями математики, в которых принципы геометрии применяются к треугольникам и сечениям конуса.

 

Математика либо чистая, либо смешанная. В чистой математике количества рассматриваются независимо от фактически существующих веществ. Но, в смешанной математике отношения величин исследованы, в связи с некоторыми свойствами материи или бизнесом.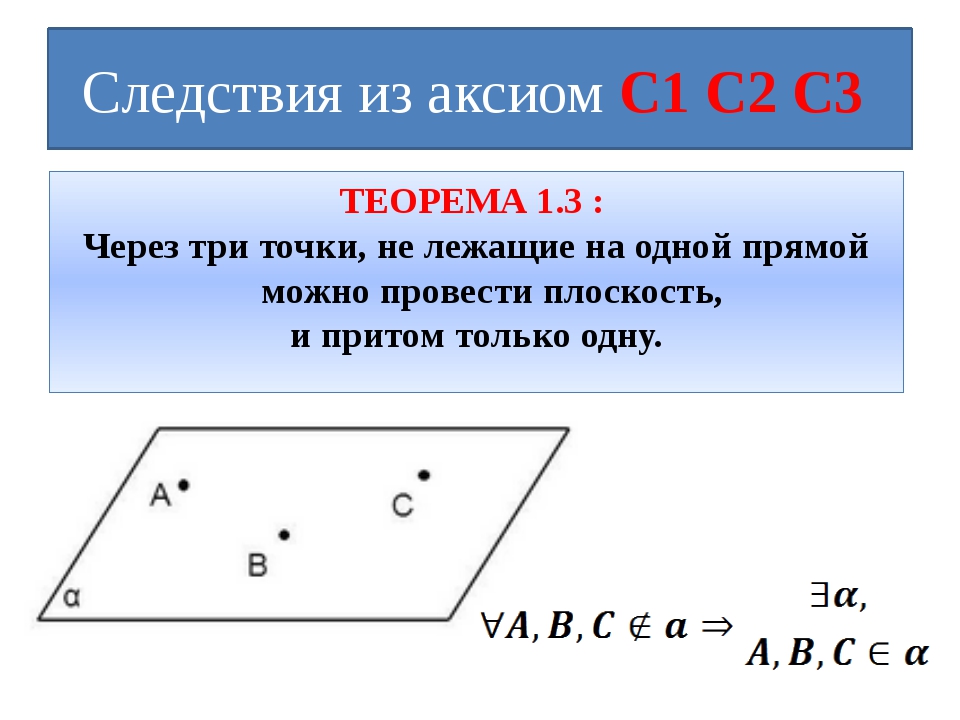 В геодезии математические принципы применяются к измерению земли, в оптике — к свойствам света и в астрономии — к движениям  небесных тел.

 

Наука о чистой математике издавна отличалась ясностью и отчетливостью своих принципов  и непреодолимой убежденностью, которую они несут в разуме каждого, кто когда-то познакомился с ними. Это должно быть объяснено, отчасти характером субъектов, а отчасти точностью определений, аксиом и доказательств.

Что такое определение?

Основа всех математических знаний должна быть заложена в определениях.

Определение — это объяснение того, что подразумевается под любым словом или фразой. Равносторонний треугольник определяется как  фигура, ограниченная тремя равными сторонами. Для полного определения важно, чтобы оно идеально отличало определенную вещь от любой другой. По многим темам трудно дать такую точность языку, чтобы он передавал каждому слушателю или читателю точно такие же идеи. Но, в математике, основные термины могут быть определены так, чтобы не оставить места для наименьшего различия сомнений, не теряя их значения , смысла.   Под заголовком определения могут быть включены пояснения к символам, которые используются для обозначения отношений величин. Символ √ означает квадратный корень.

Что такое теорема, аксиома, доказательство?

Следующим шагом, после ознакомления со значением математических терминов, является их объединение в виде предложений. Некоторые соотношения величин не требуют процесса рассуждения, чтобы сделать их очевидными. Чтобы их понять, их нужно только предложить. Квадрат-это фигура, отличная от круга; что вся вещь больше, чем одна из ее частей или что две прямые линии не могут заключать пространство, предложения являются настолько истинными, что никакие рассуждения не могут  сделать их более определенными. Поэтому их называют самоочевидными истинами или

аксиомами. Однако существует сравнительно мало математических истин, которые являются самоочевидными. Большинство из них должны быть доказаны цепочкой рассуждений. Предложения такого рода называются теоремами, а процесс, посредством которого они оказываются истинными, называется доказательством. Это способ объяснения, при котором каждый вывод немедленно выводится либо из определений, либо из принципов, которые были ранее продемонстрированы. 

Что такое лемма?

Помимо основных теорем в математике существуют также Леммы и следствия. Лемма — это предложение, которое демонстрируется с целью его использования в доказательстве некоторого другого предложения. 

 

Следствием этого является вывод из предыдущего предложения. Непосредственным объектом исследования в математике часто является не демонстрация общей истины, а метод выполнения какой-либо операции, такой как сокращение  дроби , извлечение корня Куба или вписывание круга в квадрат. Это называется решением проблемы. Теорема — это то, что нужно доказать. 

Что такое постулат?

Когда то, что требуется сделать, настолько легко, насколько это очевидно каждому, без объяснения причин, это называется постулатом. Например  прямая линия из одной точки в другую.

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа».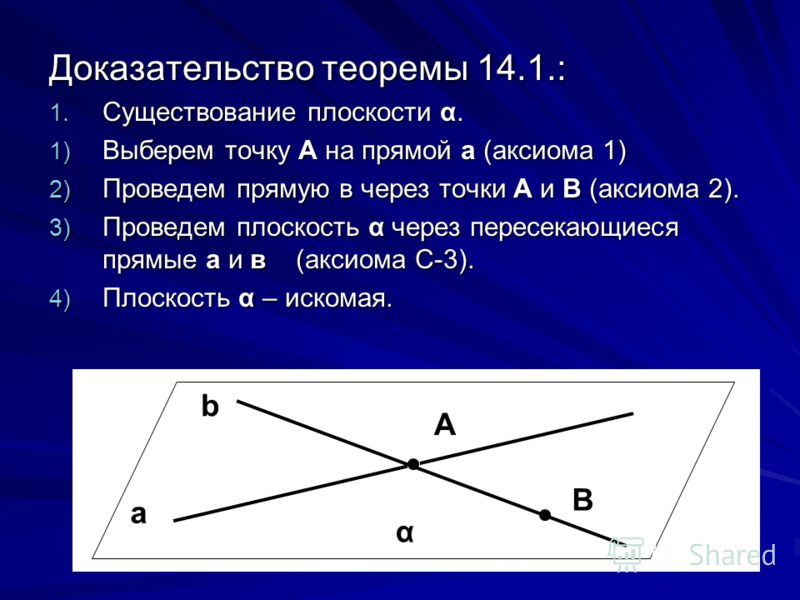

Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Наши преподаватели

Оставить заявку

Репетитор по математике

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 5-9 классов. Быстро нахожу контакт с учеником, заинтересовываю предметом. Рада помочь в развитии математического мышления, а главное – в получении удовольствия от занятий математикой!

Оставить заявку

Репетитор по математике

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 7-11 классов. Математика – это ясный и логичный мир, который откроется вам, когда вы узнаете его поближе. Надеюсь, вам он тоже понравится, как нравится мне. Я помогу вам понять законы и правила математики, справиться с трудными и опасными местами там. Мы сможем спокойно и уверенно подготовиться к любым контрольным и экзаменам. Ни ОГЭ, ни ЕГЭ не будут для вас препятствием.

Оставить заявку

Репетитор по математике

Южно-Уральский Государственный Гуманитарно Педагогичесий Университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике 8-11 классы.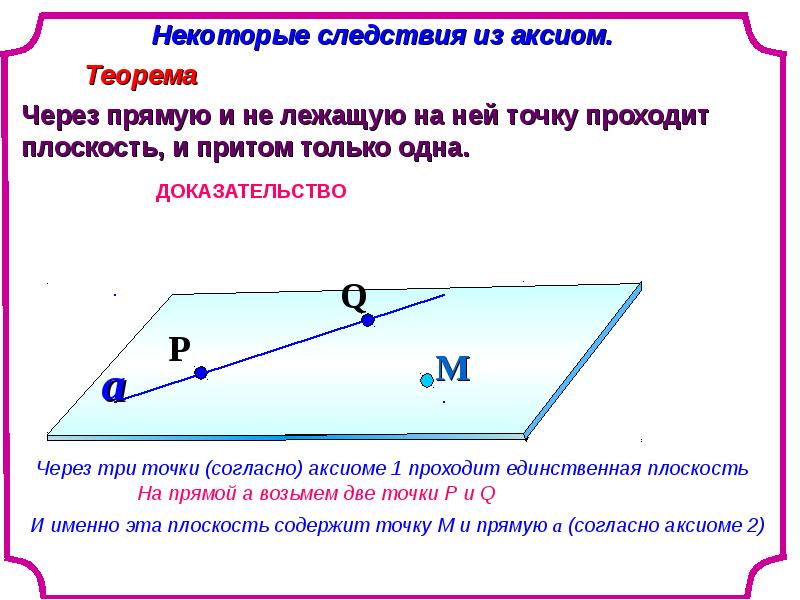 Веду подготовку к ОГЭ/ЕГЭ/ВПР Математика-царица точных наук, следовательно, она помогает в жизни выстраивать точные последовательности действий, организует, а также всегда может пригодится в быту. Работаю по принципу «пирамиды»: от простого к сложному. Всегда ищу индивидуальный подход к каждому ученику, разрабатываю индивидуальные планы осваивания материала. Люблю работать как с сильными, так и слабыми учениками. Нравится разбираться в задачах вместе с учеником, наводящими вопросами выстраивать логическую цепочку решений.

Геометрия с нуля

• — Индивидуальные занятия
• — В любое удобное для вас время
• — Бесплатное вводное занятие

Похожие статьи

Некоторые мысли о термине Аксиома

Систематизация и связи

Почитал тут дебаты вокруг термина «аксиома». Как то и у меня были дебаты с другом и одноклассником, который и здесь обитается. В общем широко распространенное представление об аксиоме как о положении, принимаемом без доказательств. Казалось бы все просто. Ан нет. Кем принимаемое? Достаточно одного человека, чтобы считать положение аксиомой? Десять, сто, тысяча, все? Если определенное количество, по какому критерию? Если все, кто же их всех опросить сможет по поводу этого положения? Если один, так этих аксиом наплодим столько, что переварить не сможем. Мало ли кто чего для себя принимает без доказательств.

Так может все-таки не принимаемое, а предлагаемое, даваемое без доказательств? Понятно, что дает один человек. Ну вот выдал он, например, дождик в четверг к удаче. Ну и теорию какую-нибудь из этой аксиомы. А другим с той аксиомы и теории ни холодно ни жарко. А ты, мил человек, может все-таки объяснишь, как ты до такой аксиомы додумался? А и правда, ведь пришла же в голову такая мысля. И ведь не послал ее подальше, взял на вооружение, да еще и вокруг нее чего то накрутил. И тут выясняется, что не просто так мысль появилась. Люди, мол, частенько обещают свои долги погасить после дождика в четверг. А возвращенный долг и есть какая-никакая, а удача. Т.е. человек сам для себя обоснование аксиоме все-таки дал. А потом может и другим это же обоснование предложить. И вот с обоснованием аксиома уже выглядит не как голословное утверждение, а имеющее под собой некоторый базис.  А это, между прочим, тоже какое то доказательство.

В общем, пришел я к такому определению. Аксиома (постулат) — утверждение, обобщающее некоторый человеческий опыт.

Опыт может быть одного человека. Тогда скорее всего только он сам этой аксиомой и будет пользоваться. Например, игрок, действующий по придуманной им схеме. А может обобщать опыт многих людей. Вот такой аксиоме доверие уже значительно больше. Хотя это не гарантирует истинность утверждения. Религиозным догматам верят множество людей, хотя много людей подвергает их сомнению.

Равно как опыт человеческий является доказательством (обоснованием) аксиомы, он же может являться и ее опровержением. Собственно, отсутствие опровержений и есть доказательство аксиомы. Взять, к примеру, хорошо известный гравитационный закон. Это ведь чистой воды аксиома. Она подтверждается всем известным человеческим опытом. И нет ни одного достоверного опыта его опровержения. Однако нет стопроцентной гарантии что в следующий миг, день, год, столетие такой опыт не появится. И если он появится, от этой аксиомы придется отказаться.

Доказательство-опровержение аксиом может быть не прямым, а опосредованным. На основе аксиом создается теория, с доказательством теорем и лемм, со своими выводами. Эти выводы также можно сравнивать с человеческим опытом. Если сравнение не в пользу выводов, а к логике выводов претензий нет, то можно ставить вопрос о верности, истинности аксиомы.  

в) Аксиомы и постулаты как основания доказательства

в) Аксиомы и постулаты как основания доказательства

Положения об удостоверенных фактах и определения входят в число оснований самых различных наук: естественных и общественных.

В математике, механике и теоретической физике кроме определений и удостоверенных фактов в число оснований доказательства входят ещё аксиомы, или постулаты. Так называются положения, которые предполагаются истинными, но в пределах каждой науки в качестве истинных не доказываются.

Так, доказательство теоремы евклидовой геометрии о равенстве суммы внутренних углов плоского треугольника двум прямым опирается не только на ранее доказанную теорему о равенстве суммы двух смежных углов двум прямым, но, кроме того, на теоремы о свойствах внутренних накрест лежащих и соответственных углов, которые в свою очередь опираются на положение, согласно которому через данную точку вне данной прямой в одной с ней плоскости можно провести одну — и притом только одну — прямую, которая ни при каком продолжении её в обе стороны от данной точки не пересечётся с данной прямой. Положение это уже не теорема, а аксиома (постулат). В «Началах» Евклида оно дано (в редакции, отличающейся от приведённой в тексте) в качестве 11-й аксиомы первой книги[16].

Аксиомой (постулатом) это положение является потому, что в «Началах» Евклида оно принимается без доказательства. И действительно: положение это утверждает, что возможно неограниченно продолжить прямую так, чтобы последняя нигде не пересекалась с данной прямой. Но совершенно очевидно, что утверждение это не может быть проверено или доказано: как бы далеко мы ни продолжали прямую, продолжение её будет для нашего наглядного представления ограниченным. В лучшем случае можно сказать, что в тех пределах, в каких прямая продолжена нами, она сохраняет параллельность данной прямой. Но сохранит ли она параллельность и при дальнейшем, ещё нами не воспринятом неограниченном её продолжении,— это остаётся недоказанным.

Аристотель, создавший не только науку логики в целом, но и разработавший, в частности, логическое учение о доказательстве, отличал аксиомы от другого вида недоказываемых наукой положений — от постулатов. Под аксиомами (???????) он разумел такие недоказываемые в данной науке положения, которые в сравнении с другими недоказываемыми положениями являются, во-первых, наиболее общими и, во-вторых, представляют необходимое условие доказательства.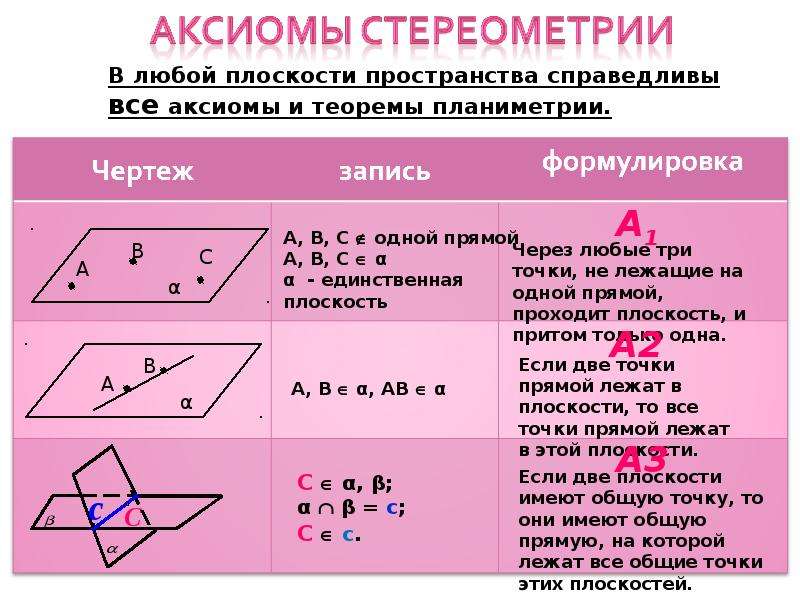 Так, в «Метафизике» (кн. III, гл. 2, 997а 5—13) Аристотель говорит, что «не может существовать доказательства для всего», что «все доказывающие науки применяют аксиомы» и что «аксиомы обладают наивысшей степенью общности и представляют начала всего» (??????? ??? ??????? ?? ?????? ????? ?? ???????? ?????).

Под постулатами (?? ????????, буквально — «требования») Аристотель понимал такие положения, которые, безотносительно к их доказуемости, вводятся в начала науки без доказательства, хотя бы они представлялись учащемуся противными его мнению[17]. Именно потому, что постулат может быть противным мнению учащегося, он вводится в качестве требования: это — положение, которое должно быть принято для того, чтобы были приняты все вытекающие из него выводы.

Постулаты Аристотель отличал от аксиом, но не противопоставлял их аксиомам.

В развитии античной математики после Аристотеля были выработаны три точки зрения по вопросу о различии между аксиомами и постулатами. Эти три точки зрения рассматривает математик и философ Прокл (V век н. э.) в своих «Комментариях» к «Началам» Евклида.

Согласно первой из этих точек зрения, аксиомы — не- доказываемые положения, на которые опираются доказательства теорем, а постулаты — недоказываемые положения, на которые опираются построения в геометрии.

Согласно второй точке зрения, аксиомы — допущения, общие для всех наук, а постулаты — специальные допущения, принятые в геометрии. Так, у Евклида в качестве аксиом рассматривались, например, такие положения: «равные одному и тому же равны и между собой», «если к равным прибавляются равные, то и целые будут равные» и т. д. В качестве постулатов у Евклида рассматриваются, например, такие положения: «от всякой точки до всякой точки <можно> провести прямую линию», «из всякого центра и всяким раствором <циркуля> <может быть> описан круг» и т. д.

Зачатки этого понимания различия между аксиомами и постулатами имелись уже у Аристотеля: «Из тех <на- чал>,— читаем у Аристотеля,— которые применяются в доказывающих науках, одни свойственны каждой науке в отдельности, другие — общи всем. ..»[18].

Согласно третьей точке зрения, постулаты — в отличие от аксиом — суть «требования», выдвигаемые преподающим науку или руководителем диспута. Постулаты должны быть приняты учащимися или участниками диспута, несмотря на то, что для них требования эти могут представляться не безусловно бесспорными[19].

Впоследствии возобладал взгляд, согласно которому аксиомами должны называться недоказываемые положения не специальные, имеющие силу для всех наук, постулатами же — недоказываемые положения более частные, относящиеся к области какой-нибудь особой специальной науки. Согласно этому взгляду, положение о том, что две величины, равные порознь третьей, равны между собой, рассматривалось в силу его всеобщности как типичная аксиома. Напротив, положение о параллельных вследствие его специально геометрического характера толковалось как типичный постулат.

Распределение аксиом и постулатов в «Началах» Евклида не вполне соответствует этому различению. Хотя ряд постулатов Евклида принадлежит к области геометрия, а ряд его аксиом — к области более общего учения о величинах, последовательное разграничение аксиом и постулатов по степени их специального характера оказывается невозможным. Так, 7-я аксиома первой книги «Начал», утверждающая, что «совмещающиеся друг с другом равны между собой», есть, конечно, аксиома геометрии. Положение о параллельных, принадлежащее к области геометрии, помещалось Евклидом в числе аксиом (11-я аксиома первой книги«Начал») и только позднейшими комментаторами и издателями стало рассматриваться как постулат (5-й постулат той же книги).

В философии и математике XVII века понимание логической природы аксиом и постулатов изменилось. Ряд математиков и логиков этого века сущность аксиом стал видеть в их будто бы безусловной очевидности или самоочевидности. Согласно этому новому взгляду, аксиомы — такие основания доказательства, которые не доказываются в науке не в силу своей общепринятости, а в силу своей полной и безусловной очевидности. Существуют будто бы такие положения, которые, как только на них направляется наш ум, представляются ему с ясностью и очевидностью, исключающими возможность какого бы то ни было сомнения. Будучи совершенно очевидными, положения эти будто не требуют доказательства, ниоткуда не выводятся, представляют истины, непосредственно постигаемые умом, или, другими словами, являются «интуициями», притом интуициями не чувств, а ума. Аксиомы—не просто недоказываемые истины, какими их считали древние математики. Это — истины будто бы недоказуемые. Не нуждаясь ни в каком доказательстве, они составляют последнюю основу всех доказываемых в науке истин. Доказать — значит вывести доказываемое положение или прямо из таких самоочевидных аксиом, или вывести его из положений, которые если не прямо, то в последней инстанции сами опираются на самоочевидные аксиомы и доказываются с их помощью.

В этом учении существенным признаком аксиом провозглашается их непосредственно постигаемая самоочевидность (интуитивность) и их недоказуемость. Напротив, их общепризнанность и более или менее общий для всех наук или специальный характер получает значение свойства, производного от указанных основных свойств.

В связи с этим характерное для античных логиков и математиков понимание различия между постулатами и аксиомами у логиков и математиков XVII века в значительной мере утрачивает прежнее значение. Возникает тенденция к сближению постулатов с аксиомами. Поскольку некоторые постулаты представляются не менее очевидными, чем аксиомы, и поскольку непосредственная очевидность аксиом рассматривается как основание их недоказуемости, такие постулаты по сути уже не отличаются от аксиом и вместе с аксиомами образуют совокупность последних оснований всякого доказательства.

В то же время, однако, некоторые постулаты не поддавались этому сближению с аксиомами по признаку безусловной очевидности. Таков был прежде всего постулат

Евклида о параллельных. Уже в самой своей формулировке он содержал понятие о неограниченном продолжении прямой — понятие, которое никак не могло быть признано ни самоочевидным, ни непосредственно постигаемым.

К этому присоединилось ещё и то, что целый ряд начальных положений (теорем и задач на построение) геометрии Евклида доказывался и решался вовсе без участия постулата о параллельных. Только в двадцать девятом предложении первой книги «Начал» постулат Евклида впервые использовался в качестве одного из оснований доказательства этого предложения.

Эта далеко не безусловная «очевидность» постулата о параллельных, а также «позднее» появление его в числе оснований, на которые опираются доказательства теорем геометрии Евклида, в сопоставлении со взглядом на аксиомы, как на истины самоочевидные, уже давно внушали математикам мысль — не является ли этот постулат теоремой, которая может быть доказана.

Попытки доказать 5-й постулат Евклида предпринимались ещё античными математиками и продолжались до Лобачевского. Великий русский математик во второй половине 20-х годов прошлого века пришёл к гениальному открытию, которое повлекло за собой коренную переработку взгляда логики на природу аксиом и на их значение для доказательства.

В начале своих исследований, посвящённых теории параллельных, Лобачевский пытался доказать постулат Евклида способом от противного. Предполагая, в противоречии с постулатом Евклида, что через точку вне данной прямой в одной с ней плоскости можно провести не одну единственную прямую, не пересекающуюся с данной, Лобачевский надеялся, что, развивая следствия из этого предположения, он придёт в конце концов к следствию, опровергающему это предположение и тем самым доказывающему истинность самого постулата Евклида.

Но никакие следствия, развиваемые из предположения, противоречащего постулату Евклида, не могли доказать абсурдность этого предположения. Никаких противоречий между теоремами, доказанными на основе предположения, противоречащего постулату Евклида, не получалось.

В конце концов Лобачевский убедился, что все старания ряда математиков доказать постулат Евклида, т. е. вывести его как следствие из других аксиом и постулатов

Евклида, были ошибочны не только по выполнению, но и по замыслу. Постулат о параллельных оказался независимым от остальных аксиом и постулатов Евклида. С другой стороны, как уже говорилось выше, постулат этот не обладает и безусловной очевидностью. Тем не менее постулат Евклида является одним из оснований классической системы геометрии, не заключающей нигде в своих доказываемых с помощью этого постулата положениях никаких противоречий.

Небезусловная очевидность постулата Евклида и отсутствие противоречий в системе теорем, доказываемых на основе постулата, противоречащего постулату о параллельных, даёт возможность поставить вопрос, каков будет результат, если вместо постулата Евклида в число оснований геометрии будет принят другой — тоже не безусловно очевидный — постулат. Согласно последнему, получившему название постулата Лобачевского, через данную точку С, лежащую вне данной прямой АВ, можно провести в одной с ней плоскости не . одну единственную не пересекающуюся с прямой АВ прямую, как это утверждает постулат Евклида, а целый пучок прямых, заключающийся между двумя прямыми KL и MN, проходящими через данную точку (см. рис.1) и называемыми параллельными относительно АВ[20].

Исследования Лобачевского показали, что замена постулата Евклида постулатом Лобачевского приводит к выявлению новой системы геометрии, получившей название геометрии Лобачевского и оказавшейся одним из видов так называемой неевклидовой геометрии. В геометрии Лобачевского сохраняются все определения, аксиомы и постулаты геометрии Евклида, кроме 5-го постулата, или 11-й аксиомы. Последний заменяется постулатом Лобачевского. Доказательства теорем развиваются безупречно строго в полную систему геометрии, которая нигде не приводит ни к каким противоречиям. По содержанию теоремы геометрии Лобачевского делятся на два класса: во-первых, теоремы, доказываемые без помощи постулата Лобачевского (так называемая абсолютная геометрия), и, во-вторых, теоремы, доказываемые с помощью этого постулата. Первые ничем не отличаются от соответствующих теорем Евклида. Вторые отличаются, а именно: разность в численных результатах этих теорем сравнительно с результатами теорем Евклида тем больше, чем больше масштаб соответствующего геометрического объекта. Например, по Евклиду, сумма внутренних углов плоского треугольника равна двум прямым. По Лобачевскому, эта сумма меньше двух прямых. При этом разность эта тем больше, чем больше данный треугольник.

Открытие Лобачевским неевклидовой геометрии означало эпоху не только в развитии математики, но также и в развитии логического учения об аксиомах как об основаниях доказательства. Это открытие Лобачевского нанесло смертельный удар идеалистическим теориям рационалистов и кантианцев. Логики этого направления сущность аксиом полагали в их интуитивной, т. е. непосредственной очевидности, в их априорной, т. е. будто бы предшествующей всякому опыту, безусловной и необходимой наглядности. Так как, по Канту, истины математики имеют, во-первых, всеобщий и необходимый характер, во- вторых, основываются на априорных формах чувственной интуиции, то ни о какой неевклидовой геометрии, разумеется, не может быть и речи.

Напротив, по Лобачевскому, вопрос о том, какие аксиомы или постулаты должны быть приняты в число оснований всей системы доказательств данной науки, определяется отнюдь не априорными формами интуиции. Такие положения геометрии, как постулат Евклида или постулат Лобачевского, отнюдь не безусловно самоочевидны.

Так как аксиомы не обладают безусловной очевидностью, то для решения вопроса о том, какие из небезусловно очевидных положений будут в данной науке доказываться, а какие будут приняты в ней без доказательства, т. е. в качестве аксиом,— необходимо некоторое основание.

Таким основанием не может быть произвол, условное соглашение, субъективная точка зрения. Если в числе оснований данной науки имеются аксиомы, то в такой науке основанием для выбора системы или группы аксиом, входящих в начальные основания науки, являются следующие требования:

1. Выбранная группа аксиом должна представлять группу допущений, между которыми нет противоречий. Другими словами, группа аксиом должна быть такова, чтобы, опираясь на неё, нельзя было доказать суждение и отрицание этого суждения.

2. Выбранная группа аксиом должна быть такова, чтобы из неё (а также из принятых наукой определений) могла быть последовательно выведена вся совокупность теорем данной науки. При этом число аксиом не должно превышать того, какое необходимо и достаточно, чтобы с помощью данной группы аксиом могли быть доказаны все теоремы данной науки.

3. Ни одна из принятых в данной науке аксиом не может быть получена как вывод ни из какой другой аксиомы или других аксиом той же науки, т. е. каждая аксиома должна быть предположением вполне независимым от предположений, выражаемых всеми другими аксиомами данной науки.

Последнее свойство аксиом нуждается в объяснении. Свойство это нельзя понимать так, будто аксиома вообще не может быть выводима ни из каких других положений. Аксиома не может быть выводима из других аксиом только в рамках данной системы науки. Так, 11-я аксиома Евклида (постулат о параллельных) не может быть выведена из других аксиом геометрии Евклида. Именно поэтому все попытки доказать эту аксиому в рамках геометрии Евклида с её аксиомами и постулатами потерпели неудачу.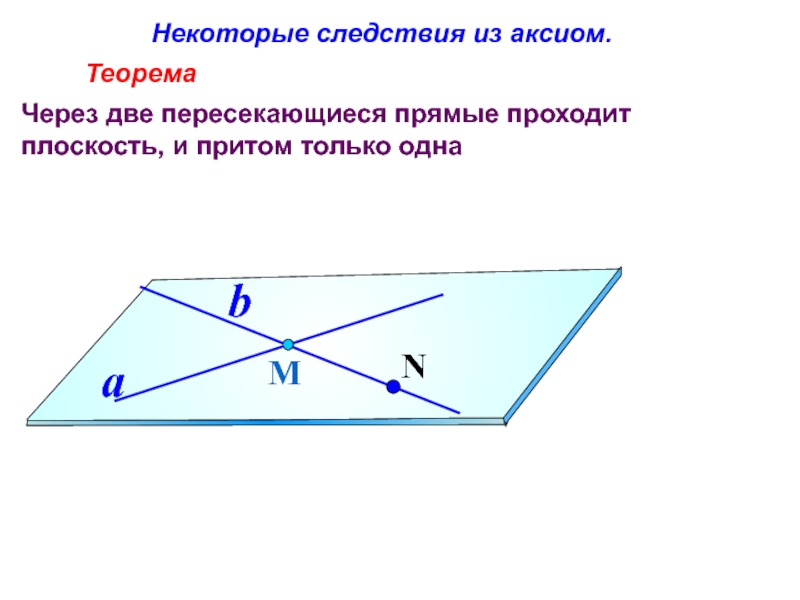

Но можно взять другую систему или группу аксиом геометрии. Можно выбрать такую группу аксиом, что постулат о параллельных, который в системе геометрии

Евклида является независимой аксиомой, будет в этой другой системе теоремой, выводимой из принятых в этой системе аксиом.

Таким образом, аксиоматическое значение некоторых положений науки не есть безусловное свойство этих положений. Разница между аксиомой и теоремой — не безусловная. Положение, которое в одной системе науки будет аксиомой, оказывается теоремой в системе науки с другой совокупностью аксиом. И наоборот: положение, доказываемое в данной системе науки как её теорема, не доказывается, а принимается в качестве аксиомы в системе науки с другой совокупностью аксиом.

В конечном счёте выбор той или другой группы аксиом (или постулатов) в качестве принятой в науке системы оснований её доказательств обусловливается и оправдывается не самоочевидностью этих оснований, а всей суммой результатов, к которым приводят доказательства науки, опирающиеся на принятые аксиомы и постулаты. Только содержательная плодотворность результатов, полученных с помощью принятой в данной системе науки группы аксиом, составляет основание для их выбора. Тем самым выбор оснований для всей системы доказательств науки — выбор аксиом или постулатов — связывается с проверкой этих оснований по их результатам, связывается с материальной практикой, с опытом.

Таким образом, с точки зрения современной логики, опирающейся на данные новейшей науки, аксиомами называются положения, не доказываемые в данной науке и играющие в ней — наряду с определениями основных понятий — роль допускаемых оснований всех доказываемых в науке истин. Роль эту аксиомы играют не в силу своей безусловной очевидности, хотя некоторые аксиомы представляются очевидными, и тем более не в силу своей априорности, так как никаких априорных положений нет ни в какой науке. Аксиомы данной науки выбираются в качестве аксиом. Однако основанием для выбора является не субъективный произвол, не «удобство», не «соглашение», а способность выбранной группы аксиом доказать всю совокупность известных истин науки, оправданных в своих результатах, т. е. в конечном счёте удостоверенных в своей истинности материальной практикой.

То, что в аксиомах не следует видеть истины безусловно недоказуемые, было не раз показано классиками марксизма-ленинизма. Энгельс говорит, что, например, аксиомы математики «доказуемы диалектически, поскольку они не чистые тавтологии»[21]. И точно также Ленин поясняет в конспекте «Науки логики» Гегеля, что фигуры силлогизма могли получить значение аксиом только после того, как значение это было доказано в миллиардах случаев опытом: «практическая деятельность человека миллиарды раз должна была приводить сознание человека к повторению разных логических фигур, дабы эти фигуры могли получить значение аксиом»[22].

Таким образом, и аксиомы как части оснований доказательства отнюдь не «возвышаются» над опытом, отнюдь не «предшествуют» опыту, а составляют результат материальной практики и опыта, лежащего в основе доказательства.

Все указанные выше требования, предъявляемые при выборе аксиом, имеют силу, разумеется, только в отношении тех наук, которые имеют в числе своих оснований аксиомы (постулаты) или, как говорят, допускают аксиоматическое построение. Таковы математика, теоретическая физика. Но существует обширный класс наук, в которых аксиоматическое построение неприменимо. В этих науках аксиомы (постулаты) не входят в число оснований науки» Такова, например, история.

г) Доказанные ранее положения науки как основания доказательства. Непосредственные и предшествующие основания доказательства. Начальные основания

В число оснований доказательств, кроме положений об удостоверенных фактах, на которые опирается доказываемый тезис, кроме определений основных понятий науки и аксиом, входят ещё доказанные ранее положения науки, необходимые для обоснования тезиса.

Так, при доказательстве теоремы евклидовой геометрии о сумме внутренних углов плоского треугольника в качестве оснований доказательства используют не только определения понятий, например понятий о параллельных, о смежных углах о внутренних накрест лежащих углах, о соответственных углах, и не только аксиомы, например аксиому (постулат) Евклида о параллельных. В качестве оснований доказательства этой теоремы используют также доказанную до неё теорему о равенстве суммы смежных углов двум прямым.

Рассматривая доказательство, нетрудно убедиться, что ранее доказанные положения, на которые опирается доказываемый тезис, используются в ходе доказательства либо непосредственным, либо опосредствованным образом.

Непосредственно используются те положения, на которые прямо ссылаются в ходе доказательства, как на положения, из истинности которых следует истинность доказываемого тезиса. Так, одним из положений, непосредственно используемых для доказательства теоремы Пифагора, будет 41-я теорема первой книги Евклида. Теорема эта утверждает, что если параллелограмм имеет с треугольником одно и то же основание и находится между теми же параллельными, то параллелограмм будет вдвое больше треугольника. Теорема эта принадлежит к непосредственным основаниям теоремы Пифагора, так как при доказательстве последней Евклид дважды ссылается в самом ходе доказательства на 41-ю теорему. Иными словами, 41-я теорема прямо входит в число оснований, истинность которых приводит к признанию истинности теоремы Пифагора.

Опосредствованным образом используются для доказательства те положения, на которые в самом ходе данного доказательства прямо не ссылаются, но при помощи которых были ранее доказаны непосредственные основания данного доказательства. Положения эти могут быть названы предшествующими основаниями доказательства. Так, для той же теоремы Пифагора одним из таких ранее доказанных, или предшествующих, оснований её доказательства будет 38-я теорема первой книги Евклида. Теорема эта утверждает, что треугольники, находящиеся на равных основаниях и между теми же параллельными, равны между собой. Эта теорема не входит в число непосредственных оснований доказательства теоремы Пифагора, так как в ходе этого доказательства Евклид на 38-ю теорему не ссылается. Но она входит в число оснований доказательства опосредствованным образом, будучи одним из оснований, при помощи которых была доказана 41-я теорема. А эта последняя есть, как мы уже знаем, одно из непосредственных оснований доказательства теоремы Пифагора.

Чем дальше развивает наука доказательства своих положений, тем большим становится число предшествующих оснований доказательства каждого нового положения. Если, рассматривая данный тезис науки, мы задались бы целью выяснить все основания, на которые опирается его доказательство, то оказалось бы, что непосредственные основания его доказательства опираются на некоторые предшествующие им основания, эти последние — в свою очередь на другие предшествующие основания и т. д. Однако, каким бы большим ни было число предшествующих оснований данного доказательства, оно не может быть бесконечным. Рано или поздно мы дойдём до таких предшествующих оснований, которые ни из каких предшествующих им оснований уже не могут быть выведены.

Основания доказательства, которые не могут быть выведены ни из каких предшествующих им оснований, называются начальными основаниями данной науки.

Начальными основаниями для данной науки являются: положения об удостоверенных единичных фактах, определения и аксиомы (постулаты). Теоремы не могут быть начальными основаниями, так как начальные основания ниоткуда не выводятся; напротив, всякая теорема — доказываемое положение, а все доказываемые положения выводятся из оснований непосредственных или предшествующих.

Все определения и аксиомы, которые могут встретиться в отдельных доказательствах в качестве непосредственных оснований или к которым доказательство может быть возведено как к своим предшествующим основаниям, входят в число начальных оснований науки. При этом, однако, в доказательства эти основания входят в каждом отдельном случае лишь частично. Так, доказательство, например, теоремы Пифагора опирается непосредственно не на все, а лишь на некоторые аксиомы, не на все, а лишь на некоторые определения, входящие в круг начальных аксиом и определений.

Напротив, в числе начальных оснований науки находится не часть аксиом, а все аксиомы данной науки, не часть определений, а все её определения.

Чем дальше отстоит доказываемое положение от начальных оснований данной науки, тем большим становится число предшествующих оснований доказательства. И действительно: каждое доказанное ранее положение, на которое в данном доказательстве наука ссылается, как на одно из непосредственных оснований доказываемого тезиса, обусловлено, в свою очередь, длинным рядом предшествующих ему положений. Ни на одно из них в пределах данного доказательства не ссылаются — иначе доказательство каждой теоремы было бы повторением всего предшествующего этой теореме содержания науки со всеми её доказательствами. В то же время все они могут быть найдены в соответствующем месте системы науки, где они полностью излагаются, иначе основание, на которое опирается доказываемое положение, само было бы -недоказанным.

Наличие в далеко продвинувшейся науке длинной цепи не непосредственных оснований, предполагаемых каждым непосредственным основанием любого доказательства, делает особенно важным условием состоятельности доказательства истинность всех оснований доказываемого тезиса.

В самом деле, непосредственное для данного доказательства основание есть только звено предшествующей ему цепи обусловливающих его оснований. Если эта цепь длинна и если какое-нибудь из её звеньев окажется ложным, то и заключительное звено — данное непосредственное основание доказательства — тоже может оказаться ложным. А в таком случае и доказываемый тезис, как опирающийся на ложное основание, может оказаться ложным.

Поэтому в качестве оснований доказательства должны быть принимаемы только истинные, строго доказанные, проверенные и удостоверенные в своей истинности положения. Любой вид оснований, вообще говоря, сказывается на истинности результата. Поэтому ни входящие в число оснований доказательства положения об удостоверенных фактах, ни определения основных понятий науки, ни аксиомы, ни уже ранее доказанные положения науки не должны быть ложными. Основания доказательства не должны быть даже сомнительными. Сомнительность основания есть по крайней мере возможность его ложности, а возможность ложности в основаниях доказательства делает возможным ложность самого доказываемого тезиса. Поэтому доказательство, опирающееся на сомнительные основания, не есть, строго говоря, подлинное доказательство. Только вполне удостоверенная истинность всех оснований, на которые опирается доказательство, делает доказательство (при соблюдении всех прочих условий и правил, о которых речь впереди) путём и средством к отысканию новой истины.

Определения, аксиомы, теоремы, рассуждение, утверждение и лемма

Определение:

Для краткого описания существенных признаков или из коннотации и расширения понятия вещи. Эквивалент установки неизвестных заданий по математике, например, «множество неизвестных, как известно, с тем, чтобы вычислить букву х, чтобы упрощать,» наделенный определенными словами или образами о значении имени, это поможет определить и обмен идентичность.

Аксиома:

В математике аксиома , что термин используется при два связанных , но различном смысле — логические аксиомы и не-логические аксиомы. В этих двух чувств, аксиомы используются для определения начальной точки других предложений. И теорема отличается, а аксиомы (если избыточный) не могут быть выведены из других аксиом, в противном случае она не будет сама отправной точкой, но может быть получена от начальной точки определенного результата — может просто быть классифицированы как теоремы.

Теорема:

Это подтверждается логикой ограничивается истинное утверждение. В общем, в области математики, теоремы только важное или интересное заявление называется. Доказательство теоремы является основным видом деятельности математики.

Следствие:

Из известного предложения или какой-либо мысли процесса или нарисовать новое мышление в виде предложений. Известно утверждение, которое является предпосылкой, то вывод предложения.

Предложение:

В современной философии, математике, логике, лингвистике, предложение ссылается на решение (заявление) семантики (фактическое выражение концепции), эта концепция может быть определена и наблюдается явление. Предложение не относится к суждению (заявление) сам по себе, а скорее выражению семантики. Когда разные суждения (заявление) с той же семантикой, они выражают то же самое предложение. В математике, общее суждение определенной вещи называют декларативное предложение.

Лемма:

Для доказательства леммы является теорема решения проблемы или использования в предложении. Лемма и теорема не существует четкого разграничения, если аргумент пропозиции, не существует прямой в соответствии с потребностями конкретных выводов еще не было доказано, предлагается доказать, так называемую конструкцию леммы.

Как работает доказательство Гёделя / Хабр

Его теоремы о неполноте разгромили поиск математической теории всего. Почти сто лет спустя мы всё ещё пытаемся осмыслить последствия этого.

В 1931 году австрийский логик Курт Гёдель провернул, вероятно, один из самых потрясающих интеллектуальных трюков в истории.

Математики той эпохи искали неколебимые основы математики: набор базовых фактов, аксиом, которые были бы непротиворечивыми и полными, играя роль строительных блоков всех математических истин.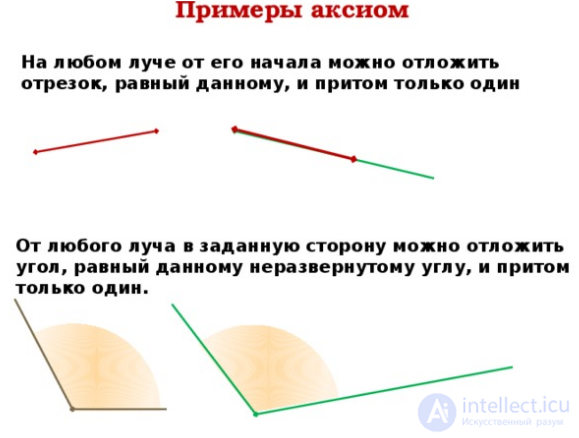

Однако шокирующие теоремы Гёделя о неполноте, опубликованные им всего лишь в 25-летнем возрасте, разбили эту мечту. Он доказал, что любой набор аксиом, который вы можете предложить на роль основы математики, неизбежно будет неполным. Всегда найдутся истинные утверждения, касающиеся чисел, которые невозможно будет доказать при помощи этих аксиом. Он также показал, что ни один набор аксиом нельзя использовать для доказательства их собственной непротиворечивости.

Его теоремы о неполноте означают, что математической теории всего быть не может, и нельзя объединить множество доказуемых утверждений со множеством истинных. То, что математики могут доказать, зависит от начальных предположений, а не от какой-то фундаментальной истины, из которой происходят все ответы.

За 89 лет, прошедших с открытия Гёделя, математики уже натыкались на подобные вопросы без ответов, существование которых предсказывали его теоремы. К примеру, сам Гёдель помог установить, что континуум-гипотеза, касающаяся мощностей бесконечностей, неразрешима – как и проблема остановки, в которой требуется определить, завершится ли когда-нибудь выполнение компьютерной программы с определёнными входными данными, или она будет работать вечно. Неразрешимые вопросы возникали даже и в физике, что говорит о том, что гёделева неполнота влияет не только на математику, но и в каком-то (не совсем понятном) смысле, на реальность.

Далее идёт краткая, упрощённая и неформальная сводка того, как Гёдель доказал свои теоремы.

Нумерация Гёделя

Главным ходом Гёделя стало сопоставление утверждений, касающихся системы аксиом, с утверждениями, сделанными в рамках этой системы – с утверждениями, касающимися чисел. Такое сопоставление позволяет системе аксиом спокойно рассуждать о себе самой.

Первый шаг – сопоставить любое возможное математическое утверждение, или последовательность утверждений, с уникальным номером, который называется номером Гёделя.

Немного исправленная версия нумерации Гёделя, представленная в книге 1958 года «Доказательство Гёделя» за авторством Эрнеста Нагеля и Джеймса Ньюмена, начинается с 12 элементарных символов, служащих словарём для выражения набора базовых аксиом. К примеру, утверждение о существовании чего-либо можно выразить символом ∃, а сложение – символом +. Символ s, обозначающий «следующий элемент», даёт возможность обозначать числа: к примеру, ss0 обозначает двойку.

Затем этим двенадцати символам назначаются номера Гёделя с 1 по 12.

Затем буквы, обозначающие переменные, начиная с x, y и z, сопоставляются с простыми числами, большими 12 (13, 17, 19,..).

Затем каждая из комбинаций этих символов и переменных – то есть, любая арифметическая формула или последовательность формул, которые только можно составить – получает свой номер Гёделя.

Рассмотрим, к примеру, утверждение 0 = 0. Три её символа соответствуют номерам Гёделя 6, 5 и 6. Гёделю нужно заменить эту последовательность из трёх номеров одним уникальным – номером, который не выдаст ни одна другая последовательность символов. Для этого он берёт три первых простых числа (2, 3 и 5), возводит каждое из них в степень, равную соответствующему номеру в последовательности, и перемножает их. Таким образом 0 = 0 превращается в 2⁶ × 3⁵ × 5⁶, или 243 000 000.

Эта разметка работает потому, что никакие две формулы не дадут один и тот же номер Гёделя. Номера Гёделя – целые числа, а числа можно разложить на простые множители единственным способом. Поэтому единственный способ разложить 243 000 000 на множители — это 2⁶ × 3⁵ × 5⁶, то есть, расшифровать этот номер Гёделя можно только одним способом: написав формулу 0 = 0.

Затем Гёдель пошёл ещё дальше. Математическое доказательство состоит из последовательности формул. Поэтому Гёдель назначил каждой последовательности формул свой номер Гёделя. В данном случае он также начинает с последовательности простых чисел – 2, 3, 5, и т.д. Затем он возводит каждое из них в степень, соответствующую номеру Гёделя для формулы, находящейся на том же порядковом месте в последовательности (допустим, 2^{243 000 000}, если первой идёт формула 0 = 0), и перемножает всё вместе.

Арифметизация математики

Замечательно, что даже утверждения, касающиеся арифметических формул, т. н.

метаматематические

утверждения, можно перевести в формулы, и назначить им собственные номера Гёделя.

Рассмотрим сначала формулу ~(0 = 0), означающую «ноль не равен нулю». Она явно ложная. Тем не менее, у неё есть номер Гёделя: 2 в степени 1 (номер Гёделя для символа ~), умноженное на 3 в степени 8 (номер Гёделя для символа «левая скобка»), и так далее, что в итоге даёт 2¹ × 3⁸ × 5⁶ × 7⁵ × 11⁶ × 13⁹.

Поскольку мы можем генерировать номера Гёделя для всех формул, даже ложных, мы можем осмысленно рассуждать о них, используя их номера Гёделя.

Рассмотрим утверждение «Первый символ формулы ~(0 = 0) это тильда». Это истинное метаматематическое утверждение, касающееся ~(0 = 0), превращается в утверждение о номере Гёделя конкретной формулы – а именно, что его первая степень равняется 1, то есть, номеру Гёделя для тильды. Иначе говоря, наше утверждение говорит о том, что в 2¹ × 3⁸ × 5⁶ × 7⁵ × 11⁶ × 13⁹ есть только один множитель «2». Если бы ~(0 = 0) начиналась с любого другого символа, кроме тильды, в её номере ГЁ было бы, по меньшей мере, два множителя 2. Так что, если сформулировать точнее, 2 является множителем 2¹ × 3⁸ × 5⁶ × 7⁵ × 11⁶ × 13⁹, а 2² — не является.

Мы можем преобразовать последнее предложение в точную математическую формулу, и записать её при помощи элементарных символов. У этой формулы, естественно, будет свой номер Гёделя, который мы сможем подсчитать, сопоставив её символы степеням простых чисел.

Если вам интересно, то формулировка получается такая: существует такое целое х, что х, помноженное на 2, будет равно 2¹ × 3⁸ × 5⁶ × 7⁵ × 11⁶ × 13⁹, но не существует такого целого х, чтобы оно, помноженное на 4, давало 2¹ × 3⁸ × 5⁶ × 7⁵ × 11⁶ × 13⁹. Соответствующая формула выглядит так:

(∃x)(x × ss0 = sss … sss0) ⋅ ~(∃x)(x × ssss0 = sss … sss0)

Где sss … sss0 обозначает 2¹ × 3⁸ × 5⁶ × 7⁵ × 11⁶ × 13⁹ копий символа следующего элемента s. Символ ⋅ означает «и», и представляет собой более краткую запись для фундаментального словаря: p ⋅ q означает ~(~p ∨ ~q).

Данный пример, как писали Нагель и Ньюмен, «иллюстрирует общую и глубокую идею, лежащую в основе открытия Гёделя: мы можем очень точно говорить о типографических свойствах длинных последовательностей символов, но не напрямую, а через свойства разложения на простые множители больших целых чисел.

Преобразовать в символы можно и метаматематические утверждения. „Существует некая последовательность формул с номером Гёделя х, доказывающая формулу с номером Гёделя k“ – или, короче говоря, „формула с номером Гёделя k доказуема“. Именно возможность „арифметизировать“ подобные заявления и заложила основы переворота.

G само по себе

Дополнительно Гёдель догадался о том, что можно подставить собственный номер Гёделя, обозначающий формулу, в саму формулу – а это уже ведёт к нескончаемым проблемам.

Чтобы понять, как работает эта подстановка, рассмотрим формулу (∃x)(x = sy). Она означает „существует переменная x, являющаяся следующим элементом для y“, или, проще говоря, „у »y» есть следующий элемент“. Как и у всех формул, у неё есть свой номер Гёделя – некое большое целое число, назовём его m.

Теперь введём число m в формулу вместо символа y. Получится новая формула (∃x)(x = sm), означающая „у m есть следующий элемент“. Как назвать номер Гёделя для этой формулы? Нам нужно передать три особенности: мы начали с формулы, имеющей номер Гёделя m. В ней мы заменили символ y на символ m. И, согласно ранее описанной схеме сопоставления, номер Гёделя у символа y равен 17. Давайте тогда обозначим номер Гёделя новой формулы sub(m, m, 17).

Подстановка формирует основу доказательства Гёделя.

Студент Курт Гёдель в Вене. Теоремы о неполноте он опубликовал в 1931 году, через год после получения диплома.

Он рассмотрел следующее математическое утверждение: „Формулу с номером Гёделя sub(y, y, 17) нельзя доказать“. Вспоминая только что принятые нами обозначения, мы знаем, что формулу с номером Гёделя sub(y, y, 17) мы получаем, взяв формулу с номером Гёделя y (некая неизвестная переменная) и подставив эту переменную y везде, где в формуле стоит символ с номером Гёделя, равным 17 (то есть, везде, где встречается y).

Голова уже начинает кружиться, но, тем не менее, мы определённо можем перевести наше метаматематическое утверждение, „формулу с номером Гёделя sub(y, y, 17) нельзя доказать“, в формулу с уникальным номером Гёделя. Назовём его n.

И последний этап подстановок: Гёдель создаёт новую формулу, подставляя число n везде, где в предыдущей формуле стоит y. Его новая формула получается следующей: „Формулу с номером Гёделя sub(n, n, 17) нельзя доказать“. Назовём эту формулу G.

У G, естественно, есть номер Гёделя. Каков этот номер? Вуаля – он должен равняться sub(n, n, 17). По определению, sub(n, n, 17) – это номер Гёделя для формулы, которая получается путём взятия формулы с номером Гёделя n и подстановки n везде, где в формуле встречается символ с номером Гёделя, равным 17. И G именно такая формула и есть! Поскольку целые числа раскладываются на простые множители уникальным способом, нам становится понятно, что формула G говорит нам только о самой формуле G, и более ни о какой другой.

G говорит о том, что её саму нельзя доказать.

Но можно ли доказать G? Если бы это было возможно, это означало бы, что существует некая последовательность формул, доказывающих формулу с номером Гёделя, равным sub(n, n, 17). Но это противоположность формулы G, утверждающей, что такого доказательства не существует. Противоположные утверждения, G и ~G, в непротиворечивой системе аксиом не могут быть одновременно истинными. Поэтому G должна быть недоказуемой.

Однако, несмотря на то, что G доказать нельзя, она определённо правдива. G говорит, что „формулу с номером Гёделя sub(n, n, 17) нельзя доказать“, а именно это мы и установили! Поскольку G – истинное, но недоказуемое утверждение, существующее в рамках аксиоматической системы, которую мы использовали для его построения, эта система неполна.

Можно подумать, что мы можем просто добавить некую дополнительную аксиому, использовать её для доказательства G, и разрешить этот парадокс. Но это невозможно. Гёдель показал, что дополненная система аксиом позволит создать новую истинную формулу G’ по той же схеме, что и ранее, которую нельзя будет доказать в рамках новой, дополненной системы. Пытаясь построить полную математическую систему, вы будете лишь безуспешно гоняться за собственным хвостом.

Отсутствие доказательства непротиворечивости

Теперь мы знаем, что если набор аксиом непротиворечив, он неполон. Это первая теорема Гёделя о неполноте. Из неё легко следует вторая – ни один набор аксиом не может доказать свою непротиворечивость.

Что означало бы, если бы набор аксиом мог доказать, что он никогда не вызовет противоречий? Это означало бы, что существует последовательность формул, построенных на этих аксиомах, доказывающих формулу, которая метаматематически означает „этот набор аксиом непротиворечив“. Но тогда, согласно первой теореме, этот набор аксиом обязательно был бы неполным.

Однако сказать, что „набор аксиом неполон“, это то же самое, что сказать „существует истинная формула, которую нельзя доказать“. А это равнозначно нашей формуле G. А мы знаем, что аксиомы не могут доказать G.

Так Гёдель построил доказательство от противного: если бы набор аксиом мог доказать собственную непротиворечивость, тогда мы могли бы доказать G. Но мы этого сделать не можем. Следовательно, ни один набор аксиом не доказывает собственную непротиворечивость.

Доказательство Гёделя убило поиски непротиворечивой и полной математической системы. Математики „не смогли осознать всю глубину“ неполноты, писали Нагель и Ньюмен в 1958. И сегодня это утверждение остаётся истинным.

См. также:

Аксиома Паша | Математика, которая мне нравится

Мориц Паш родился в 1843 году в Бреслау (Германия), ныне город Вроцлав в Польше. В 1860 году закончил гимназию в Бреслау и поступил там же в университет, где учился у Генриха Шрётера, Фердинанда Йоахимшталя и Рудольфа Липшица. В 1865 году он закончил университет, получив докторскую степень. После этого он учился в университете Берлина у Вейерштрасса и Кронекера. В 1866 году умер его отец, и Паш должен был оставить работу над диссертацией, чтобы помочь семье. Однако в 1870 году он представил свою диссертацию в университет Юстуса Либиха в Гессене. В 1873 году он стал там внештатным профессором, а через два года — профессором, после того как отверг аналогичное предложение в Бреслау. Работал Паш над основаниями геометрии. Он также принимал участие в управлении университетом. Уйдя в отставку в 1911 году, он продолжал жить в Гессене. Умер Мориц Паш в 1930 году.

А теперь сама аксиома Паша.

Если прямая пересекает одну сторону треугольника, тогда она пересекает и вторую его сторону, а также продолжение третьей стороны, если только прямая не проходит через вершину треугольника.

(В случае, если прямая параллельна стороне треугольника, то считается, что она пересекает продолжение этой стороны в бесконечности).

Две черные прямые пересекают две стороны треугольника и продолжение его третьей стороны.

Паш опубликовал свою аксиому в 1882 году. Он показал, что аксиомы Евклида являются неполными. Эта аксиома была им использована при введении порядка в геометрии на плоскости.

При использовании различных наборов аксиом элементарной геометрии аксиома Паша может быть доказана как теорема. Она является следствием аксиомы о делении плоскости, если ее рассматривать как одну из аксиом.

Давид Гильберт использовал аксиому Паша в своей книге “Основания геометрии’’, в которой он привел аксиоматический базис евклидовой геометрии.

Аксиому Паша не стоит путать с теоремой Паша о порядке четырех точек на прямой. Она также отличается от аксиомы проективной геометрии Веблен-Янга, которая формулируется следующим образом:

Если прямая пересекает две стороны треугольника, то она пересекает и его третью сторону.

Здесь нет различия в пересечении сторон треугольника или продолжений его сторон, важно только пересечение прямых.

Источники: http://www-gap.dcs.st-and.ac.uk/~history/Biographies/Pasch.html
http://en.wikipedia.org/wiki/Pasch’s_axiom?utm_medium=referral&utm_source=t.co

Разница между аксиомой и теоремой

Ключевое отличие: Аксиома и теорема — это утверждения, которые чаще всего используются в математике или физике. Аксиома – это утверждение, которое принимается за истинное. Это не нужно доказывать. Теорема, с другой стороны, является утверждением, истинность которого доказана.

Аксиома и теорема — это утверждения, наиболее часто используемые в математике или физике. Аксиома – это утверждение, которое принимается за истинное. Это не нужно доказывать.Теорема, с другой стороны, является утверждением, истинность которого доказана.

Согласно Dictionary.com, аксиома определяется как:

• Самоочевидная истина, не требующая доказательств.
• Общепринятый принцип или правило.
• Логика, Математика. Предложение, которое принимается без доказательства ради изучения следствий, вытекающих из него.

По сути, аксиомы — это предположения, которые не нужно доказывать. Они обычно принимаются как истинные либо потому, что в них нет противоречия, либо потому, что мы заведомо знаем, что они истинны.Слово аксиома происходит от греческого слова, обозначающего «то, что считается достойным или подходящим» или «то, что представляется очевидным». Аксиому иногда можно использовать как взаимозаменяемую с постулатом или предположением.

Теорема, с другой стороны, нуждается в доказательстве. Dictionary.com определяет теорему как:

.

• Математика. Теоретическое предложение, утверждение или формула, заключающая в себе что-то, что должно быть доказано из других предложений или формул.
• Правило или закон, особенно выраженный уравнением или формулой.
• Логика. Утверждение, которое может быть выведено из предпосылок или допущений системы.
• Идея, убеждение, метод или утверждение, обычно принимаемые как истинные или заслуживающие внимания без доказательства.

Теорема — это утверждение, подтвержденное тестированием или расчетом. Это может быть доказано на основе ранее доказанных теорем или на основе аксиом. Теоремы состоят из двух частей: гипотез и выводов.

%PDF-1.5 % 1 0 объект > эндообъект 2 0 объект > эндообъект 3 0 объект >поток 2013-10-03T17:03:27-04:00TeX2013-10-09T07:34:56-07:002013-10-09T07:34:56-07:00Это MiKTeX-pdfTeX 2. 9.4902 (1.40.14)MiKTeX pdfTeX-1.40.14; изменено с использованием iText 2.1.6 автором 1T3XTFalseapplication/pdfuuid:681d3637-9c96-4a9e-a4c7-60c2d45f97a6uuid:965cf784-1484-44d3-af1b-fd73ea2ae61b конечный поток эндообъект 4 0 объект > эндообъект 7 0 объект >>> эндообъект 6 0 объект >поток xڵXMo6W؋,Zt. vd-;lkk9Pd+r=qyo8`K&H/ף~

Что такое аксиома — Как обсуждать

Что такое аксиома

В чем разница между аксиомой и законом? Отличие аксиомы от закона в том, что аксиома (философия) — это явление, которое нельзя доказать или опровергнуть, тогда как закон (неисчислимый) — это свод правил и предписаний, издаваемых правительством или применяемых судами и т. д. или закон может быть (устаревшим) грудой камней.

Какие есть хорошие примеры аксиом?

Аксиома Теорема должна быть ясной.Это означает, что большинство людей думают, что это правда. Утверждение основано на законах физики, и ему легко следовать. Примером могут служить законы движения Ньютона. Заявление – это предложение. Аксиома здесь — это любое математическое утверждение, служащее отправной точкой, из которой логически выводятся другие утверждения.

Какое определение лучше всего подходит для слова аксиома?

В математике или логике аксиома — это недоказуемое правило или первый принцип, который принимается за истину, потому что он очевиден или особенно полезен. Ничто не может быть и не быть одновременно, и это тоже пример аксиомы.

Что означает слово аксиома?

Определение аксиомы. 1: утверждение, принятое как истинное в качестве основы для аргумента или вывода: значение постулата 1 одной из аксиом теории эволюции.

В чем разница между аксиомой и теорией?

Аксиома — это утверждение, которое считается истинным без доказательства, в то время как теория должна быть доказана, прежде чем она будет считаться истинной или ложной.Аксиома часто очевидна, в то время как теории часто требуют других утверждений, таких как другие теории и аксиомы, чтобы быть действительными.

Какое утверждение является производным от аксиомы?

Аксиомы служат отправной точкой для других математических утверждений. Эти утверждения, основанные на аксиомах, называются теоремами. По определению, предложение — это доказанное предложение, основанное на аксиомах, других теоремах и ряде логических связей.

Можно ли принять лемму за аксиому?

Обратите внимание, что традиции иногда мешают — вы можете принять девиз Цорна как аксиому, а также есть девизы, которые были превращены в предложения.Не всегда есть четкое различие! Поделись этим.

В чем разница между логической и нелогической аксиомой?

Аксиомы можно разделить на логические и нелогические. Логические аксиомы являются действительными и общепринятыми утверждениями, в то время как нелогические аксиомы обычно представляют собой логические выражения, используемые для построения математических теорий. В математике гораздо проще выделить аксиому.

В чем разница между аксиомой и законом движения

Разница между аксиомой и законом в том, что аксиома (философия) — явление, которое нельзя доказать или опровергнуть, а закон (неисчислимый) — это набор правил и положений выданные правительством или применяемые судами и т. д.или закон может быть (устаревшим) грудой камней. Действует закон междометий.

В чем разница между аксиомой и постулатом?

Логически аксиома или постулат — это самоочевидное утверждение. Аксиомы и постулаты считаются истинными без доказательств и доказательств. На самом деле то, что очевидно или считается истинным и принятым, но не имеет доказательств, называется аксиомой или постулатом.

Чем аксиомы похожи на правила игры?

Аксиомы — это всего лишь основные предположения, которые вы делаете.Лучшая аналогия, которую я знаю, состоит в том, что аксиомы — это правила игры, в геометрии Евклида основные аксиомы/постулаты таковы: если даны две разные точки, то существует линия, содержащая их. Каждый сегмент линии может быть расширен в бесконечную линию.

В чем разница между аксиомой и законом спроса

Важные моменты, которые следует помнить 1. Закон спроса устанавливает обратную зависимость между ценой и спросом. 2 Закон спроса предполагает, что все детерминанты спроса остаются неизменными, за исключением цены. 3 Спрос можно представить визуально в виде кривой спроса на графике, называемом планом спроса.

Чем отличается аксиома от постулата?

Аксиома — это общее, общее утверждение, имеющее меньшее значение и вес. Постулат – это утверждение с высшим смыслом, относящееся к определенной области. Поскольку аксиома является более общей, она обычно используется во многих научных и смежных областях.

Чем аксиома отличается от закона природы

Закон тоже аксиома.Разница между аксиомой и законом заключается в том, что аксиома (философия) — это явление, которое нельзя доказать или опровергнуть, а закон (неисчислимый) — это свод правил и положений, издаваемых правительством или применяемых судами и т. д. или закон может быть (устаревшим) грудой камней. Действует закон междометий.

Существуют ли законы природы в науке?

Наука включает в себя множество принципов, которые хотя бы когда-то считались законами природы: закон всемирного тяготения Ньютона, его три закона движения, идеальные законы газа, законы Менделя, законы спроса и предложения и т. д.Законы важны тем, что не имеют статуса науки.

Какие бывают виды аксиом?

Слабая аксиома выявленных предпочтений (WARP) Сильная аксиома выявленных предпочтений (SARP) Обобщенная аксиома выявленных предпочтений (GARP).

Что такое аксиомы равенства?

Равенство множеств по логике первого порядка с равенством Логическая аксиома: x = yz, (zx ⇔ z ∈ y) Логическая аксиома: x = y ⇒ ∀ z, (xz ⇔ y ∈ z) Аксиома теории множеств: (∀ z , (z ∈ x ⇔ z ∈ y)) ⇒ x = y.

Что такое аксиома в математике?

В математике или логике аксиома — это недоказуемое правило или первый принцип, который принимается за истину, потому что он самоочевиден или особенно полезен.

Каковы некоторые хорошие примеры аксиом книги

Давайте посмотрим на некоторые примеры аксиом повседневной жизни. Это натуральное число, которое принято всеми людьми на земле. Это утверждение не нуждается в подтверждении научными экспериментами или расчетами. 2. Солнце встает на востоке.

Какая аксиома верна без доказательства?

Каждый известный результат исходит из чего-то другого; это подтверждается и другими фактами. Единственными исключениями являются аксиомы: вещи, которые вы принимаете, не глядя на них. Математическое утверждение, которое вы считаете истинным без доказательства, называется аксиомой. Это общепринятые и общие истины.

Как аксиомы используются в формальной системе?

В формальной математической системе аксиомы представляют собой начальные условия или предположения, из которых выводятся другие утверждения.Но аксиомы не могут быть правильными или неправильными. Если кто-то решает изменить набор аксиом, возникает другая система.

Как аксиомы геометрии используются в геометрии?

Два прямых угла равны. Две или более прямых параллельны, если они никогда не пересекаются. Они имеют одинаковый наклон и расстояние между ними всегда постоянно. Каждая из этих аксиом кажется довольно очевидной и очевидной, но вместе они составляют основу геометрии и могут быть использованы для вывода почти любой другой.

Какой пример аксиомы в математике?

В математике или логике аксиома — это недоказуемое правило или первый принцип, который принимается за истину, потому что он самоочевиден или особенно полезен. «Ничто не может и не может быть одновременно и в одном смысле» — это пример аксиомы. Чем аксиома отличается от теоремы? Аксиома – это самоочевидное утверждение.

Речь идет о выборе правильного набора аксиом?

Математика заключается не в выборе правильных аксиом, а в построении фундамента из этих принципов.Если вы начнете с других аксиом, вы получите другую математику, но логические аргументы останутся прежними. Каждая область математики имеет свой набор основных аксиом.

Каковы пять основных аксиом алгебры?

Таким образом, пятью основными аксиомами алгебры являются рефлексивная аксиома, симметричная аксиома, транзитивная аксиома, аддитивная аксиома и мультипликативная аксиома. Что такое аксиомы Евклида? Вот некоторые из аксиом Евклида: (1) Подобные вещи одинаковы.

Сколько значений имеет слово аксиома?

Слово «аксиома» имеет как минимум четыре разных значения! общепринятый принцип или закон, который не является необходимой истиной: аксиомы политики.(Математика и математическая логика) Утверждение или формула, которые считаются верными для аргументации: основы формальной дедуктивной системы.

Является ли Книга аксиом математическим трактатом?

Хотя эта книга неизбежно включает некоторые аспекты математики и естественных наук, часто называемые «натурфилософией» или «математической философией», она не предназначена для использования в качестве математического или научного трактата.

Где Евклид опубликовал пять аксиом геометрии?

Евклид опубликовал пять аксиом в книге «Начала».Это первый пример системного подхода к математике, который на протяжении тысячелетий использовался в качестве учебника по математике.

Что означает аксиома в Притчах?

• Пословица – это популярная поговорка, обычно древнего или неизвестного происхождения (например, друг в беде на самом деле друг). • Аксиома – это очевидная истина, не требующая доказательств (например, кровь гуще воды).

Какое лучшее определение слова аксиома в Библии

1: утверждение, которое принимается за истину в качестве основы для аргументов или выводов: постулат Значение 1 является одной из аксиом теории эволюции 2: правило, установленный принцип или очевидная истина цитирует аксиому, на ошибочность которой никто не претендует.есть 3: общепризнанный принцип внутренней ценности, аксиомы мудрости.

В чем смысл аксиомы Гёделя?

Главный прием Гёделя состоял в том, чтобы сопоставить утверждения, использующие систему аксиом, с утверждениями внутри системы, то есть с утверждениями, использующими числа. Они узнали, что набор непротиворечивых аксиом неполон. Независимо от того, говорил ли Гиппократ «сначала не навреди», эта аксиома лежит в основе медицинской этики.

Когда была сделана первая версия аксиомы?

Несмотря на противоречивый характер, версии этой аксиомы существуют с середины XIX века: Роджер Дули, Forbes, 28 июня 2021 г.Со времен Коэна теоретики множеств пытались укрепить основы бесконечной математики, предоставив хотя бы одну новую аксиому.

В чем смысл аксиомы прощения?

Джейкс говорит, что верит в аксиому, согласно которой акт прощения на самом деле является подарком не другим, а самому себе. Его трюк иллюстрирует известную обратную аксиому: отныне вся политика национальна. Общепризнанной аксиомой является то, что общественный деятель не может позволить себе быть скромным в этом ■■■■.

Что означает аксиома, когда в сомнении ничего не значит?

Аксиома, указывающая на завершение мероприятия, визита или темы исследования. (Правило конца, Тезаурус NCI) Существует аксиома об обратном, которая гласит: «Если сомневаетесь, ничего не делайте», и она работает, когда ситуация разворачивается и вам нужна дополнительная информация.

Когда вы используете слово аксиоматический в предложении?

Термин аксиоматика обычно используется для обозначения утверждения, которое настолько очевидно, что не требует доказательства.Новый словарь художественного образования, третье издание Авторское право .

Каково точное значение этих похожих слов в математике: свойство, аксиома, постулат, теорема, правило, закон, принцип. Каковы различия между ними.

 

 

 

             Аксиома – это утверждение, которое считается самоочевидным истинным без доказательства.

 

 

 

             Постулат – это истинное утверждение, не требующее доказательств.

Подробнее о постулате
Постулат используется для получения других логических утверждений для решения проблемы.
Постулаты также называют аксиомами.

 

 

Результат, который был подтвержден (с использованием уже известных фактов).

Пример: «Теорема Пифагора» доказала, что для прямоугольного треугольника a2 + b2 = c2

 

Функции обычно представляются правилом функции, в котором зависимая переменная y выражается через независимую переменную x.Пара входного значения и соответствующего ему выходного значения называется упорядоченной парой и может быть записана как (a, b).

 

 

-2проголоса против
Теорема — это утверждение, доказываемое цепочкой рассуждений. Теорема не является самоочевидной. Он выводится после рассмотрения результатов нескольких логических утверждений (часто включающих другие теоремы). Известным примером этого является теорема Пифагора, имеющая около 400 доказательств.

Законы — это утверждения, которые выводятся путем наблюдения.Законы не доказаны. Законы демонстрируются на основе повторных наблюдений. Он выражает причинно-следственную связь между сущностями при определенных условиях и часто выражается математически. Законы термодинамики (которые так часто цитируются без математического контекста и именно по этой причине искажаются) являются хорошими примерами.

Теория – это установленное и уважаемое объяснение природного явления, полученное путем подтверждения его принципов с помощью научного метода – проверки, подтверждения, наблюдения и экспериментирования.

Факт — это истинное утверждение при заданных условиях. Дело в том, что это бесспорно. Как правило, факты можно воспроизвести для проверки. Единственный контрпример сразу же понизит факт до ложного утверждения.

Доказательство в науке успешная демонстрация изучаемой гипотезы с использованием доказательств и анализа. Во многом это заблуждение, поскольку наука на самом деле ничего не может доказать наверняка. В этом смысле «доказательство» — это упрощенный способ сказать «значительно повышенная уверенность».

Правило — это неформальная аксиома, выражающая философскую точку зрения. Правило определяет, как субъект ведет себя при определенных обстоятельствах. Правило указывает на повышенную вероятность определенного результата, когда субъект находится в определенном состоянии. Примерами могут служить «правила» Ньютона или бритва Оккама.

Гипотеза — это утверждение, которое (еще) не доказано, но которое интуитивно кажется верным или для которого автор имеет более сложные причины полагать, что оно может быть истинным. Некоторые из них, обманчиво простые, сопротивляются столетиям нападок ярчайших математиков.
поделиться|цитировать|улучшить этот ответ
ответил 12 мая 2015, в 3:08

 

 

основная сумма

основная сумма денег, заимствованная или инвестированная

 

В математике свойства демонстрируют общие правила, используемые в вычислениях. Наиболее часто используемые свойства в повседневной математике — это свойства сложения и умножения. Коммутативное свойство сложения, например, гласит, что независимо от того, как вы упорядочиваете числа при сложении, результат будет один и тот же.

 

 

 

 

 

 

      Ответы получены от Google в Интернете…

 

 

               Надеюсь, это поможет!

                       Оскар

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В чем разница между теоремой и аксиомой? – идвотер.ком

В чем разница между теоремой и аксиомой?

Аксиома — это математическое утверждение, которое считается истинным даже без доказательства. Теорема – это математическое утверждение, истинность которого логически установлена ​​и доказана.

Что такое постулат или аксиома в геометрии?

Утверждение, также известное как аксиома, которое считается истинным без доказательства. Постулаты являются базовой структурой, из которой выводятся леммы и теоремы. Вся евклидова геометрия, например, основана на пяти постулатах, известных как постулаты Евклида.

Что такое теорема постулатов?

Постулат – это утверждение, которое считается истинным без доказательства. Теорема – это истинное утверждение, которое можно доказать.

Что такое 4 аксиомы?

Группа — это особый вид набора, который должен следовать четырем основным аксиомам. Это аксиома замыкания, ассоциативная аксиома, аксиома тождества и обратная аксиома. Это может показаться знакомым, так как это некоторые из аксиом поля, однако группа шире, чем поле.

Может ли теорема быть аксиомой?

Математическое утверждение, истинность которого мы знаем и которое имеет доказательство, является теоремой. Итак, если утверждение всегда истинно и не нуждается в доказательстве, оно является аксиомой. Если нужно доказательство, то это предположение. Утверждение, которое было доказано логическими рассуждениями, основанными на аксиомах, является теоремой.

В чем разница между аксиомой и постулатом?

Первые два имеют много примеров. С точки зрения логики аксиома или постулат — это утверждение, которое считается самоочевидным.И аксиомы, и постулаты считаются истинными без каких-либо доказательств или доказательств. По сути, то, что очевидно или объявлено истинным и принятым, но не имеет доказательств этого, называется аксиомой или постулатом.

Какое утверждение является производным от аксиомы?

Аксиомы служат отправной точкой для других математических утверждений. Эти утверждения, выведенные из аксиом, называются теоремами. Теорема, по определению, является утверждением, доказанным на основе аксиом, других теорем и некоторого набора логических связок.

Каковы теоремы постулата 6?

Постулат 6: Если две плоскости пересекаются, то их пересечение есть прямая. Теорема 1: Если две прямые пересекаются, то они пересекаются ровно в одной точке. Теорема 2: Если точка лежит вне прямой, то ровно одна плоскость содержит и прямую, и точку. Теорема 3: Если две прямые пересекаются, то ровно одна плоскость содержит обе прямые.

В чем разница между аксиомой и теорией?

Аксиома — это утверждение, которое считается истинным без каких-либо доказательств, в то время как теория подлежит доказательству, прежде чем она будет считаться истинной или ложной.

Разница между аксиомой и теоремой

Далее мы можем объяснить это как ряд предположений (доказательств), которые в совокупности дают верный результат. Итак, если утверждение всегда истинно и не нуждается в доказательстве, это аксиома. Если нужно доказательство, то это предположение. Утверждение, которое было доказано логическими рассуждениями, основанными на аксиомах, является теоремой.

1. В чем разница между аксиомами, постулатами и теоремами?
2. Что такое 5 аксиом?
3. Что такое пример аксиомы?
4. В чем разница между теоремой и теорией?
5. Что такое 7 аксиом?
6. Нужны ли доказательства аксиомам?
7. Что такое аксиомы Евклида?
8. Сколько существует аксиом?
9. Могут ли аксиомы быть неверными?
10. Как вы используете слово аксиома?
11. Что такое аксиома в логике?

В чем разница между аксиомами, постулатами и теоремами?

Аксиома, как правило, верна для любой области науки, тогда как постулат может быть специфичен для конкретной области.Доказать из других аксиом невозможно, а постулаты доказуемы до аксиом. Затем теоремы выводятся из «первых принципов», то есть аксиом и постулатов.

Что такое 5 аксиом?

АКСИОМЫ

• Вещи, которые равны одной и той же вещи, также равны друг другу.
• Если равные прибавить к равным, то все станет равным.
• Если из равных вычесть равные, то остатки равны.
• Вещи, которые совпадают друг с другом, равны друг другу.
• Целое больше, чем часть.

Что такое пример аксиомы?

В математике или логике аксиома — это недоказуемое правило или первый принцип, принимаемый как истинный, поскольку он самоочевиден или особенно полезен. «Ничто не может быть и не быть одновременно и в одном и том же отношении» — пример аксиомы.

В чем разница между теоремой и теорией?

Теорема — это результат, истинность которого можно доказать на основе набора аксиом…. Теория — это набор идей, используемых для объяснения того, почему что-то верно, или набор правил, на которых основан предмет.

Что такое 7 аксиом?

Вот семь аксиом, данных Евклидом для геометрии.

• Вещи, равные одной и той же вещи, равны друг другу.
• Если равные прибавляются к равным, целые становятся равными.
• Если равные вычитаются из равных, остатки равны.
• Вещи, которые совпадают друг с другом, равны друг другу.

Нужны ли аксиомам доказательства?

К сожалению, ничего не докажешь. Для начала вам нужно хотя бы несколько строительных блоков, и они называются аксиомами. Математики предполагают, что аксиомы верны, но не могут их доказать. … Если аксиом слишком мало, можно очень мало доказать, и математика будет не очень интересна.

Что такое аксиомы Евклида?

Вот некоторые из аксиом Евклида: (1) Вещи, равные одной и той же вещи, равны друг другу.(2) Если равные добавляются к равным, целые равны. (3) Если равные вычитаются из равных, остатки равны. (4) Вещи, которые совпадают друг с другом, равны друг другу.

Сколько существует аксиом?

Ответ: Есть пять аксиом. Как вы знаете, это математическое утверждение, которое мы предполагаем верным. Таким образом, пятью основными аксиомами алгебры являются рефлексивная аксиома, симметричная аксиома, транзитивная аксиома, аддитивная аксиома и мультипликативная аксиома.

Могут ли аксиомы быть неверными?

К сожалению, не существует набора аксиом, который позволил бы вам доказать или опровергнуть каждое утверждение.Истинное и ложное не имеют особого значения, когда применяются к аксиомам.

Как вы используете слово аксиома?

Аксиома в предложении 🔉

1. Хотя вы продолжаете использовать эту аксиому в качестве основы для своей статьи, сама концепция неверна. …
2. Госпожа …
3. Согласно аксиоме, все люди имеют одинаковую ценность. …
4. Аксиома о том, что в десятки раз дешевле, неверна, когда речь идет о том, чтобы прокормить большую семью по сегодняшним рыночным ценам.

Что такое аксиома в логике?

Согласно определению классической философии, аксиома — это утверждение, которое настолько очевидно или хорошо установлено, что принимается без разногласий или вопросов.Как используется в современной логике, аксиома является предпосылкой или отправной точкой для рассуждений.

11. Аксиомы и вычисления — Доказательство теорем в документации Lean 3.23.0

Мы видели, что версия Конструктивного исчисления, которая была реализована в Lean, включает зависимые типы функций, индуктивные типы и иерархию вселенных, которая начинается с непредикативного, не относящегося к доказательству Prop внизу. В этой главе мы рассмотрим способы расширения CIC дополнительными аксиомами и правилами.Расширение базовой системы таким образом часто бывает удобным; это может позволить доказать больше теорем, а также упростить доказательство теорем, которые можно было бы доказать в противном случае. Но могут быть негативные последствия добавления дополнительных аксиом, последствия, которые могут выходить за рамки опасений по поводу их правильности. В частности, использование аксиом связано с вычислительным содержанием определений и теорем, что мы и рассмотрим здесь.

Lean предназначен для поддержки как вычислительных, так и классических рассуждений.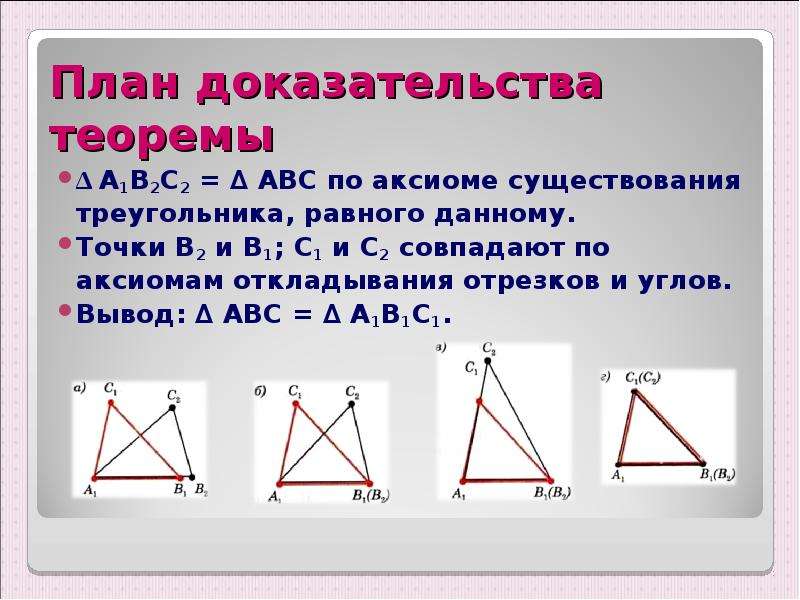 Пользователи, которые так склонны, могут придерживаться «вычислительно чистого» фрагмента, который гарантирует, что замкнутые выражения в системе оцениваются как канонические нормальные формы. В частности, любое замкнутое вычислительно чистое выражение типа ℕ , например, сведется к числу.

Стандартная библиотека Lean определяет дополнительную аксиому, пропозициональную экстенсиональность и частную конструкцию, которая, в свою очередь, подразумевает принцип экстенсиональности функции. Эти расширения используются, например, для разработки теорий множеств и конечных множеств.Ниже мы увидим, что использование этих теорем может заблокировать вычисление в ядре Lean, так что закрытые термы типа ℕ больше не будут оцениваться как числа. Но Lean стирает типы и пропозициональную информацию при компиляции определений в байт-код для своего оценщика виртуальной машины, и, поскольку эти аксиомы только добавляют новые пропозиции, они совместимы с этой вычислительной интерпретацией. Даже склонные к вычислениям пользователи могут захотеть использовать классический закон исключенного третьего, чтобы рассуждать о вычислениях.Это также блокирует оценку в ядре, но совместимо с компиляцией в байт-код.

Стандартная библиотека также определяет принцип выбора, который полностью противоположен вычислительной интерпретации, поскольку он волшебным образом производит «данные» из предложения, утверждающего его существование. Его использование необходимо для некоторых классических конструкций, и пользователи могут импортировать его при необходимости. Но выражения, использующие эту конструкцию для получения данных, не имеют вычислительного содержания, и в бережливом производстве мы обязаны помечать такие определения как невычислимое , чтобы отметить этот факт.

Используя хитрый прием (известный как теорема Диаконеску), можно использовать экстенсиональность высказываний, экстенсиональность функций и выбор, чтобы вывести закон исключенного третьего. Однако, как отмечалось выше, использование закона исключенного третьего по-прежнему совместимо с компиляцией байт-кода и извлечением кода, как и другие классические принципы, пока они не используются для производства данных.

Подводя итог, можно сказать, что помимо базовой структуры юниверсов, зависимых функциональных типов и индуктивных типов стандартная библиотека добавляет три дополнительных компонента:

• аксиома пропозициональной экстенсиональности

• факторная конструкция, из которой следует экстенсиональность функции

• принцип выбора, который производит данные из экзистенциального предложения.

Первые два из этих блоков нормализуются в рамках Lean, но совместимы с оценкой байт-кода, тогда как третий не поддается вычислительной интерпретации. Более точно мы распишем подробности ниже.

11.1. Исторический и философский контекст

На протяжении большей части своей истории математика была в основном вычислительной: геометрия имела дело с конструкциями геометрических объектов, алгебра занималась алгоритмическими решениями систем уравнений, а анализ предоставлял средства для вычисления будущего поведения систем, эволюционирующих во времени. Из доказательства теоремы о том, что «для каждых 90 492 x 90 493 существует 90 492 y 90 493 такое, что …», обычно было просто извлечь алгоритм для вычисления таких 90 492 y 90 493 при заданном 90 492 x 90 493 .

Однако в девятнадцатом веке рост сложности математических аргументов подтолкнул математиков к разработке новых стилей рассуждений, которые подавляют алгоритмическую информацию и вызывают описания математических объектов, которые абстрагируются от деталей того, как эти объекты представлены.Цель состояла в том, чтобы получить мощное «концептуальное» понимание, не увязая в вычислительных деталях, но это привело к признанию математических теорем, которые просто ложны при прямом расчетном прочтении.

Сегодня все еще существует довольно единодушное мнение, что вычисления важны для математики. Но существуют разные взгляды на то, как лучше всего решать вычислительные проблемы. С конструктивной точки зрения было бы ошибкой отделять математику от ее вычислительных корней; каждая осмысленная математическая теорема должна иметь прямую вычислительную интерпретацию. С классической точки зрения более плодотворно поддерживать разделение задач: мы можем использовать один язык и совокупность методов для написания компьютерных программ, сохраняя при этом свободу использования неконструктивных теорий и методов для их рассуждения. Lean предназначен для поддержки обоих этих подходов. Основные части библиотеки разработаны конструктивно, но система также обеспечивает поддержку проведения классических математических рассуждений.

В вычислительном отношении самая чистая часть теории зависимых типов полностью избегает использования Prop .Индуктивные типы и типы зависимых функций можно рассматривать как типы данных, а термины этих типов можно «оценивать», применяя правила редукции до тех пор, пока нельзя будет применить другие правила. В принципе, любой замкнутый терм (то есть терм без свободных переменных) типа ℕ должен оцениваться как число succ (... (succ zero)...) .

Введение нерелевантного доказательства Prop и пометка теорем как неприводимых представляет собой первый шаг к разделению задач. Намерение состоит в том, что элементы типа p : Prop не должны играть никакой роли в вычислениях, и поэтому конкретная конструкция терма t : p в этом смысле «неуместна».Можно по-прежнему определять вычислительные объекты, которые включают элементы типа Prop ; дело в том, что эти элементы могут помочь нам рассуждать о последствиях вычислений, но их можно игнорировать, когда мы извлекаем «код» из термина. Однако элементы типа Prop не совсем безобидны. Они включают уравнения s = t : α для любого типа α , и такие уравнения можно использовать в качестве слепков, чтобы ввести проверочные термины. Ниже мы увидим примеры того, как такие приведения могут блокировать вычисления в системе.Однако вычисления по-прежнему возможны при схеме оценки, которая стирает пропозициональное содержание, игнорирует промежуточные ограничения типизации и сокращает термины до тех пор, пока они не примут нормальную форму. Это именно то, что делает виртуальная машина Lean.

Приняв нерелевантную для доказательства Prop , можно было бы считать правомерным использовать, например, закон исключенного третьего p ∨ ¬p , где p — любая пропозиция. Конечно, это тоже может блокировать вычисления по правилам CIC, но не блокирует вычисление байт-кода, как описано выше.Только принципы выбора, обсуждавшиеся в разделе 11.5, полностью стирают различие между частями теории, не относящимися к доказательствам, и частями теории, относящимися к данным.

11.2. Пропозициональная экстенсиональность

Пропозициональная экстенсиональность есть следующая аксиома:

 аксиома propext {a b : Prop} : (a ↔ b) → a = b
 

Он утверждает, что когда два предложения предполагают друг друга, они фактически равны. Это согласуется с теоретико-множественными интерпретациями, в которых любой элемент a : Prop либо пуст, либо одноэлементный набор {*} для некоторого выделенного элемента * .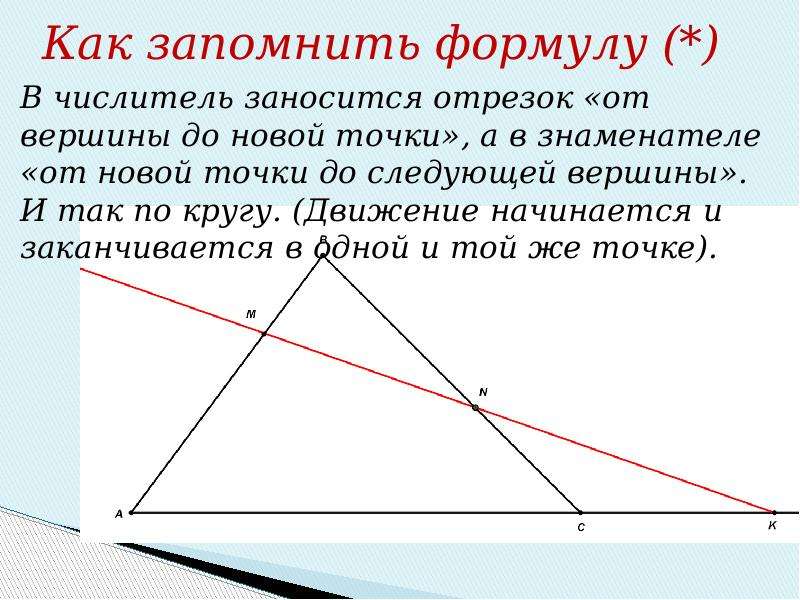 Аксиома приводит к тому, что эквивалентные предложения могут быть заменены друг другом в любом контексте:

 раздел
переменные a b c d e : Prop
переменная p : Prop → Prop

теорема thm₁ (h : a ↔ b) : (c ∧ a ∧ d → e) ↔ ​​(c ∧ b ∧ d → e) :=
пропекст h ▸ iff.refl _

теорема thm₂ (h : a ↔ b) (h₁ : p a) : p b :=
проспект ч ▸ ч₁
конец
 

Первый пример можно было бы доказать более трудоемко без протекста , используя тот факт, что пропозициональные связки соблюдают пропозициональную эквивалентность.Второй пример представляет собой более существенное использование propext . На самом деле, он эквивалентен самому proext , факт, который мы рекомендуем вам доказать.

Имея любое определение или теорему в Lean, вы можете использовать команду #print axioms для отображения аксиом, от которых она зависит.

 #print axioms thm₁ -- propext
#распечатать аксиомы thm₂ -- propext
 

11.3. Расширение функций

Подобно пропозициональной экстенсиональности, функциональная экстенсиональность утверждает, что любые две функции типа Π x : α, β x , которые согласуются по всем своим входам, равны.

 вселенных u₁ u₂

#check (@funext : ∀ {α : введите u₁} {β : α → введите u₂}
           {f₁ f₂ : Π (x : α), β x},
         (∀ (x : α), f₁ x = f₂ x) → f₁ = f₂)
 

С классической теоретико-множественной точки зрения именно это и означает равенство двух функций. Это известно как «расширенный» взгляд на функции. Однако с конструктивной точки зрения иногда более естественно думать о функциях как об алгоритмах или компьютерных программах, которые представлены в явном виде.Несомненно, две компьютерные программы могут вычислить один и тот же ответ для каждого ввода, несмотря на то, что они синтаксически весьма различны. Во многом таким же образом вы можете захотеть поддерживать представление функций, которое не вынуждает вас идентифицировать две функции, которые имеют одинаковое поведение ввода/вывода. Это известно как «интенсиональное» представление функций.

На самом деле экстенсиональность функции следует из существования частных, которые мы опишем в следующем разделе.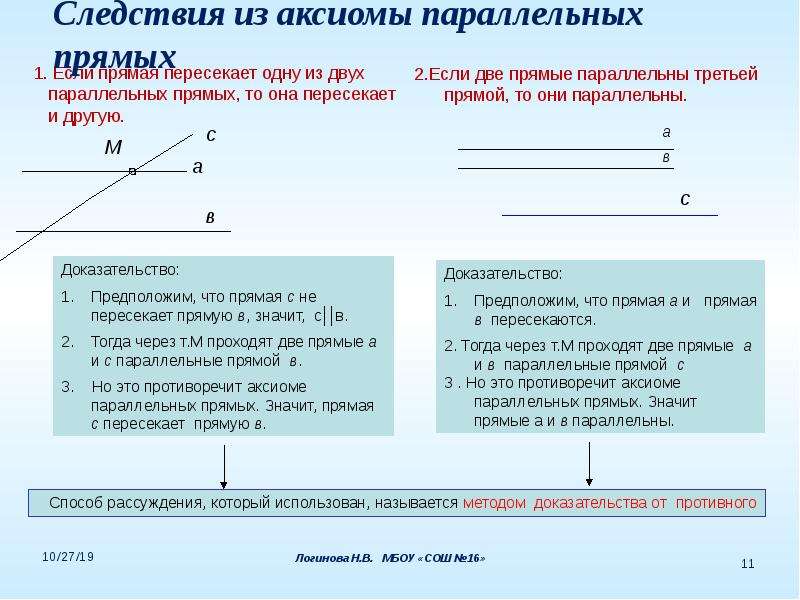 Таким образом, в стандартной библиотеке Lean funext доказывается из построения частного.

Предположим, что для α : Тип мы определяем множество α := α → Prop для обозначения типа подмножеств α , по существу идентифицируя подмножества с предикатами. Комбинируя funext и propext , мы получаем экстенсиональную теорию таких множеств:

 def set (α : Type*) := α → Prop

набор пространств имен

переменная {α : Тип*}

определение mem (x : α) (a : множество α) := a x
обозначение e ∈ a := mem e a

теорема setext {a b : множество α} (h : ∀ x, x ∈ a ↔ x ∈ b) : a = b :=
funext (предположим, x, proext (h x))

конечный набор
 

Затем мы можем приступить к определению пустого множества и его пересечения, например, и доказать тождество множества:

 определение пусто: установить α := λ x, ложь
локальная запись `∅` := пусто

определение inter (ab : множество α) : множество α := λ x, x ∈ a ∧ x ∈ b
обозначение a ∩ b := inter a b

теорема inter_self (a : множество α) : a ∩ a = a :=
setext (предположим, что x и_self _)

теорема inter_empty (a : множество α) : a ∩ ∅ = ∅ :=
setext (предположим, что x и_false _)

теорема empty_inter (a : множество α) : ∅ ∩ a = ∅ :=
setext (предположим, x, false_and _)

теорема меж. comm (a b : множество α) : a ∩ b = b ∩ a :=
setext (предположим, x, and_comm _ _)
 

Ниже приведен пример того, как расширенность функций блокирует вычисления внутри ядра Lean.

 импорт data.nat.basic

защита f₁ (х : ℕ) := х
Def f₂ (х: ℕ) = 0 + х

теорема feq : f₁ = f₂ := funext (предположим x, (zero_add x).symm)

def val : ℕ := eq.rec_on feq (0 : ℕ)

-- сложный!
#уменьшить значение

-- оценивается как 0
#оценка
 

Сначала мы покажем, что две функции f₁ и f₂ равны, используя экстенсиональность функции, а затем мы приведем 0 типа ℕ , заменив f₁ на f₂ типа .Конечно, состав пустой, потому что ℕ не зависит от f₁ . Но этого достаточно, чтобы причинить вред: по вычислительным правилам системы у нас теперь есть замкнутый член ℕ , который не сводится к числу. В этом случае у нас может возникнуть соблазн сократить выражение до 0 . Но в нетривиальных примерах устранение приведения меняет тип термина, что может сделать неверным тип внешнего выражения. Однако виртуальная машина без труда вычислит выражение до 0 .Вот похожий надуманный пример, показывающий, как propext может мешать.

 теорема tteq : (true ∧ true) = true := propext (and_true true)

def val : ℕ := eq.rec_on tteq 0

-- сложный!
#уменьшить значение

-- оценивается как 0
#оценка
 

Текущие исследовательские программы, в том числе работа над теорией наблюдаемых типов и теорией кубических типов , направлены на расширение теории типов таким образом, чтобы можно было сократить приведения типов, включая экстенсиональность функций, частные и т. д.Но решения не столь однозначны, и правила исчисления, лежащие в основе бережливого производства, не допускают таких сокращений.

Однако в некотором смысле приведение не меняет значения выражения. Скорее, это механизм рассуждений о типе выражения.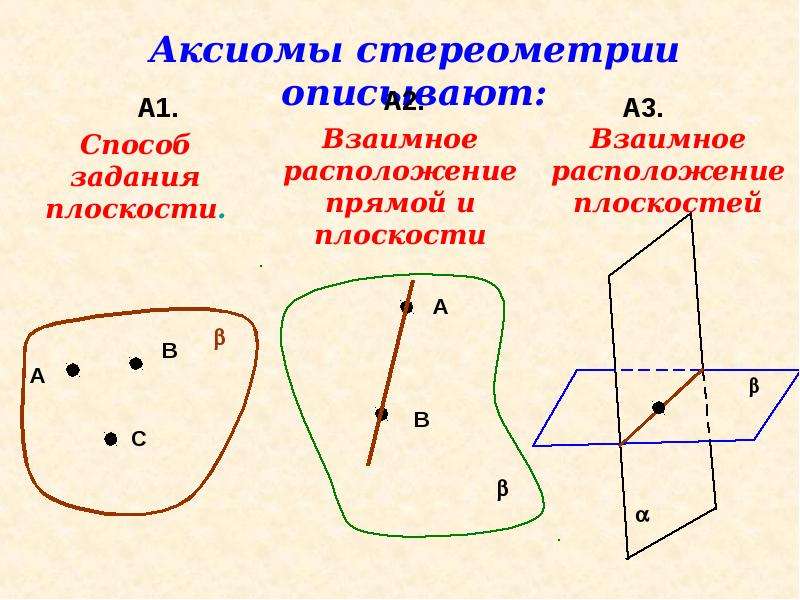 При соответствующей семантике имеет смысл сокращать термины таким образом, чтобы сохранить их значение, игнорируя промежуточные расчеты, необходимые для корректного типа сокращения. В этом случае добавление новых аксиом в Prop не имеет значения; из-за нерелевантности доказательства выражение в Prop не несет никакой информации и может быть безопасно проигнорировано процедурами редукции.

11.4. Коэффициенты

Пусть α — любой тип, и пусть r — отношение эквивалентности на α . Математически принято формировать «частное» α / r , то есть тип элементов α «по модулю» r . Теоретически можно рассматривать α / r как набор классов эквивалентности α по модулю r . Если f : α → β является любой функцией, которая соблюдает отношение эквивалентности в том смысле, что для каждого xy : α , rxy влечет fx = fy , то f «поднимает» к функции f ' : α / r → β определено на каждом классе эквивалентности ⟦x⟧ посредством f' ⟦x⟧ = fx . Стандартная библиотека Lean расширяет исчисление построений дополнительными константами, которые выполняют именно эти построения, и устанавливает это последнее уравнение в качестве правила редукции по определению.

В своей самой основной форме конструкция частного даже не требует, чтобы r было отношением эквивалентности. Следующие константы встроены в Lean:

 вселенных u v

константа quot : Π {α : Sort u}, (α → α → Prop) → Sort u

постоянная quot.мк :
  Π {α : Sort u} (r : α → α → Prop), α → quot r

аксиома цитата.инд :
  ∀ {α : Sort u} {r : α → α → Prop} {β : quot r → Prop},
    (∀ a, β (quot.mk r a)) → ∀ (q : quot r), β q

постоянный квот.подъем :
  Π {α : Сортировать u} {r : α → α → Prop} {β : Сортировать u} (f : α → β),
    (∀ a b, r a b → f a = f b) → quot r → β
 

Первый формирует тип quot r , заданный типом α любым бинарным отношением r на α . Второй отображает α в quot α , так что если r : α → α → Prop и a : α , то quot. mk r a является элементом quotr . Третий принцип, quot.ind , говорит, что каждый элемент quot.mk r a имеет эту форму. Что касается quot.lift , для данной функции f : α → β , если h является доказательством того, что f соблюдает соотношение r , то quot.lift fh является соответствующей функцией на quot р . Идея состоит в том, что для каждого элемента a в α функция quot.Лифт f h отображает quot.mk r a (класс r , содержащий a ) в f a , где h показывает, что эта функция хорошо определена. На самом деле, принцип вычисления объявляется правилом редукции, что ясно из приведенного ниже доказательства.

 переменных α β : Тип*
переменная r : α → α → Prop
переменная а : а

-- частный тип
#check (quot r : Type*)

-- класс а
#check(quot. mk r a :quot r)

переменная f : α → β
переменная h : ∀ a₁ a₂, r a₁ a₂ → f a₁ = f a₂

-- соответствующая функция на quot r
#проверить (цит.поднять f h : quot r → β)

-- принцип вычисления
теорема thm : quot.lift f h (quot.mk r a) = f a := rfl
 

Четыре константы, quot. , quot.mk , quot.ind и quot.lift сами по себе не очень сильны. Вы можете проверить, что quot.ind выполняется, если мы возьмем quot r просто α и возьмем quot.lift в качестве функции тождества (игнорируя h ). По этой причине эти четыре константы не рассматриваются как дополнительные аксиомы:

 #print axioms thm -- без аксиом
 

Они, подобно индуктивно определенным типам и связанным с ними конструкторам и рекурсорам, рассматриваются как часть логической структуры.

То, что превращает конструкцию quot в истинное частное, это следующая дополнительная аксиома:

 аксиома quot. sound :
  ∀ {α : Type*} {r : α → α → Prop} {ab : α},
    r a b → quot.mk r a = quot.mk r b
 

Это аксиома, утверждающая, что любые два элемента числа α , связанные соотношением r , отождествляются в частном. Если в теореме или определении используется quot.sound , это будет отображаться в команде #print axioms .

Конечно, конструкция частного чаще всего используется в ситуациях, когда r является отношением эквивалентности. Учитывая r , как указано выше, если мы определим r' в соответствии с правилом r' a b тогда и только тогда, когда quot.mk r a = quot.mk r b , тогда ясно, что r' является отношением эквивалентности. Действительно, r' есть -ядро функции a ↦ quot.mk r a . Аксиома quot.sound говорит, что r a b подразумевает r' a b .Используя quot. lift и quot.ind , мы можем показать, что r' является наименьшим отношением эквивалентности, содержащим r , в том смысле, что если r'' является любым отношением эквивалентности, содержащим r , тогда r' ab подразумевает r'' ab . В частности, если r изначально было отношением эквивалентности, то для всех a и b мы имеем r a b тогда и только тогда, когда r' a b .

Для поддержки этого распространенного варианта использования в стандартной библиотеке определено понятие setoid , которое представляет собой просто тип со связанным отношением эквивалентности:

Сетоид класса

 (α : Тип*) :=
(r : α → α → Prop) (iseqv : эквивалентность r)

setoid пространства имен
инфикс `≈` := setoid.р

переменная {α : Тип*}
переменная [s : setoid α]
включает в себя

теорема refl (a : α) : a ≈ a :=
(@setoid. iseqv α s).left a

теорема symm {a b : α} : a ≈ b → b ≈ a :=
λ h, (@setoid.iseqv α s).right.left h

теорема транс {a b c : α} : a ≈ b → b ≈ c → a ≈ c :=
λ h₁ h₂, (@setoid.iseqv α s).right.right h₁ h₂
конечный сетоид
 

Имея тип α , отношение r к α и доказательство p того, что r является отношением эквивалентности, мы можем определить setoid.mk p как экземпляр класса setoid.

 коэффициент по умолчанию {α : Тип*} (s : setoid α) :=
@quot α setoid.r
 

Константы quotient.mk , quotient.ind , quotient.lift и quotient.sound являются не более чем специализациями соответствующих элементов quot . Тот факт, что вывод класса типов может найти setoid, связанный с типом α , дает ряд преимуществ. Во-первых, мы можем использовать обозначение a ≈ b (вводится с \ приблизительно ) для setoid. r a b , где экземпляр setoid подразумевается в нотации setoid.r . Мы можем использовать общие теоремы setoid.refl , setoid.symm , setoid.trans , чтобы рассуждать об отношении. В частности, с частными мы можем использовать общее обозначение ⟦a⟧ для quot.mk setoid.r , где экземпляр setoid подразумевается в обозначении setoid.r , а также теорему quotient.exact :

 переменных {α : Тип*} [setoid α] (ab : α)

#проверить (частное.точно: ⟦a⟧ = ⟦b⟧ → a ≈ b)
 

Вместе с factor.sound это означает, что элементы частного точно соответствуют классам эквивалентности элементов в α .

Напомним, что в стандартной библиотеке α × β представляет декартово произведение типов α и β . Чтобы проиллюстрировать использование частных, определим тип неупорядоченных пар элементов типа α как частное типа α × α .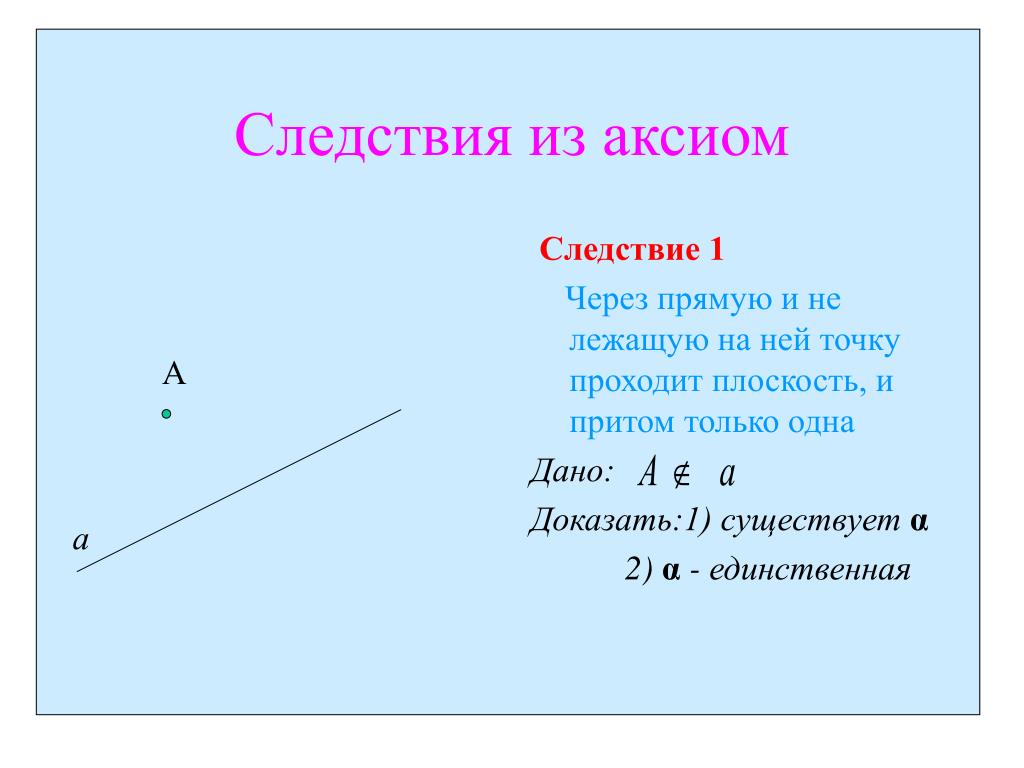 Во-первых, мы определяем соответствующее отношение эквивалентности:

 частное определение eqv {α : Type*} (p₁ p₂ : α × α) : Prop :=
(p₁,1 = p₂,1 ∧ p₁,2 = p₂,2) ∨ (p₁,1 = p₂,2 ∧ p₁,2 = p₂,1)

инфикс `~` := eqv
 

Следующий шаг — доказать, что eqv на самом деле является отношением эквивалентности, т. е. рефлексивным, симметричным и транзитивным. Мы можем доказать эти три факта удобным и удобочитаемым способом, используя зависимое сопоставление с образцом, чтобы выполнить анализ случаев и разбить гипотезы на части, которые затем повторно собираются для получения заключения.

 открытый или

частная теорема eqv.refl {α : Type*} :
  ∀ p : α × α, p ~ p :=
предположим, что p, inl ⟨rfl, rfl⟩

частная теорема eqv.symm {α : Type*} :
  ∀ p₁ p₂ : α × α, p₁ ~ p₂ → p₂ ~ p₁
| (a₁, a₂) (b₁, b₂) (inl ⟨a₁b₁, a₂b₂⟩) :=
    inl ⟨symm a₁b₁, symm a₂b₂⟩
| (a₁, a₂) (b₁, b₂) (inr ⟨a₁b₂, a₂b₁⟩) :=
    inr ⟨symm a₂b₁, symm a₁b₂⟩

частная теорема eqv.trans {α : Type*} :
  ∀ p₁ p₂ p₃ : α × α, p₁ ~ p₂ → p₂ ~ p₃ → p₁ ~ p₃
| (а₁, а₂) (б₁, б₂) (с₁, с₂)
    (inl ⟨a₁b₁, a₂b₂⟩) (inl ⟨b₁c₁, b₂c₂⟩) :=
  inl ⟨транс a₁b₁ b₁c₁, транс a₂b₂ b₂c₂⟩
| (а₁, а₂) (б₁, б₂) (с₁, с₂)
    (inl ⟨a₁b₁, a₂b₂⟩) (inr ⟨b₁c₂, b₂c₁⟩) :=
  инр ⟨транс а₁b₁ б₁с₂, транс а₂b₂ б₂с₁⟩
| (а₁, а₂) (б₁, б₂) (с₁, с₂)
    (inr ⟨a₁b₂, a₂b₁⟩) (inl ⟨b₁c₁, b₂c₂⟩) :=
  инр ⟨транс а₁b₂ б₂с₂, транс а₂b₁ б₁с₁⟩
| (а₁, а₂) (б₁, б₂) (с₁, с₂)
    (inr ⟨a₁b₂, a₂b₁⟩) (inr ⟨b₁c₂, b₂c₁⟩) :=
  inl ⟨транс a₁b₂ b₂c₁, транс a₂b₁ b₁c₂⟩

частная теорема is_equivalence (α : Type*) :
  эквивалентность (@eqv α) :=
mk_equivalence (@eqv α) (@eqv. refl α) (@eqv.symm α)
  (@eqv.trans α)
 

Мы открываем пространства имен или и eq , чтобы иметь возможность более удобно использовать or.inl , or.inr и eq.trans .

Теперь, когда мы доказали, что eqv является отношением эквивалентности, мы можем построить набор (α × α) и использовать его для определения типа upprod α неупорядоченных пар.

 instance uprod.setoid (α : Type*) : setoid (α × α) :=
сетоид.mk (@eqv α) (is_equivalence α)

определение upprod (α : Тип*) : Тип* :=
частное (упрод.сетоид α)

пространство имен
определение mk {α : Type*} (a₁ a₂ : α) : upprod α :=
⟦(а₁, а₂)⟧

локальная нотация `{` a₁ `,` a₂ `}` := mk a₁ a₂
конец вверх
 

Обратите внимание, что мы локально определяем обозначение {a₁, a₂} для упорядоченных пар как ⟦(a₁, a₂)⟧ . Это полезно для иллюстративных целей, но в целом это не очень хорошая идея, так как нотация затмит другие варианты использования фигурных скобок, например, для записей и наборов.

Мы можем легко доказать, что {a₁, a₂} = {a₂, a₁} , используя quot.sound , поскольку у нас есть (a₁, a₂) ~ (a₂, a₁) .

 теорема mk_eq_mk {α : Type*} (a₁ a₂ : α) :
  {а₁, а₂} = {а₂, а₁} :=
quot.звук (инр ⟨rfl, rfl⟩)
 

Чтобы завершить пример, учитывая a : α и u : uprod α , определим предложение a ∈ u , которое должно выполняться, если a является одним из элементов неупорядоченной пары u .Во-первых, мы определяем аналогичное предложение mem_fn a u на (упорядоченных) парах; затем мы показываем, что mem_fn соответствует отношению эквивалентности eqv с леммой mem_respects . Эта идиома широко используется в стандартной библиотеке Lean.

 частное определение mem_fn {α : Type*} (a : α) :
  α × α → Опора
| (а₁, а₂) := а = а₁ ∨ а = а₂

-- вспомогательная лемма для доказательства mem_respects
частная лемма mem_swap {α : Type*} {a : α} :
  ∀ {p : α × α}, mem_fn a p = mem_fn a (⟨стр. 2, стр.1⟩)
| (a₁, a₂) := протекст (iff.intro
    (λ l : а = а₁ ∨ а = а₂,
      or.elim l (λ h₁, inr h₁) (λ h₂, inl h₂))
    (λ r : а ​​= а₂ ∨ а = а₁,
      or.elim r (λ h₁, inr h₁) (λ h₂, inl h₂)))

частная лемма mem_respects {α : Type*} :
  ∀ {p₁ p₂ : α × α} (a : α),
    p₁ ~ p₂ → mem_fn a p₁ = mem_fn a p₂
| (a₁, a₂) (b₁, b₂) a (inl ⟨a₁b₁, a₂b₂⟩) :=
  by {dsimp при a₁b₁, dsimp при a₂b₂, rw [a₁b₁, a₂b₂]}
| (a₁, a₂) (b₁, b₂) a (inr ⟨a₁b₂, a₂b₁⟩) :=
  на { dsimp при a₁b₂, dsimp при a₂b₁, rw [a₁b₂, a₂b₁],
        применить mem_swap }

def mem {α : Type*} (a : α) (u : uprod α) : Prop :=
цитатаlift_on u (λ p, mem_fn a p) (λ p₁ p₂ e, mem_respects a e)

локальный инфикс `∈` := mem

теорема mem_mk_left {α : Type*} (ab : α) : a ∈ {a, b} :=
инл рфл

теорема mem_mk_right {α : Type*} (ab : α) : b ∈ {a, b} :=
вн рфл

теорема mem_or_mem_of_mem_mk {α : Type*} {a b c : α} :
  c ∈ {a, b} → c = a ∨ c = b :=
λ ч, ч
 

Для удобства стандартная библиотека также определяет quotient.lift₂ для поднятия бинарных функций и quotient. ind₂ для индукции по двум переменным.

Мы завершаем этот раздел некоторыми намеками на то, почему фактор-конструкция подразумевает экстенсиональность функции. Нетрудно показать, что экстенсиональное равенство на П х : а, р х является отношением эквивалентности, и поэтому мы можем рассматривать тип extfun а р функций «с точностью до эквивалентности». Конечно, приложение учитывает эту эквивалентность в том смысле, что если f₁ эквивалентно f₂ , то f₁ a равно f₂ a . Таким образом, приложение порождает функцию extfun_app : extfun α β → Π x : α, β x .Но для каждого f , extfun_app ⟦f⟧ по определению равно λ x, f x , что, в свою очередь, по определению равно f . Итак, когда f₁ и f₂ экстенсионально равны, мы имеем следующую цепочку равенств:

 f₁ = extfun_app ⟦f₁⟧ = extfun_app ⟦f₂⟧ = f₂
 

В итоге f₁ равно f₂ .

11.5. Выбор

Чтобы сформулировать окончательную аксиому, определенную в стандартной библиотеке, нам нужен непустой тип , который определяется следующим образом:

 класс индуктивный непустой (α : Sort*) : Prop
| введение: α → непустое
 

Поскольку непустой α имеет тип Prop , а его конструктор содержит данные, он может исключить только до Prop .На самом деле, непустых α эквивалентно ∃ x : α, истинное :

 пример (α : Тип*) : непусто α ↔ ∃ x : α, правда :=
iff.intro (λ ⟨a⟩, ⟨a, тривиальный⟩) (λ ⟨a, h⟩, ⟨a⟩)
 

Наша аксиома выбора теперь выражается просто следующим образом:

 выбор аксиомы {α : Сортировка*} : непусто α → α
 

Учитывая только утверждение h о том, что α не пусто, выбор h волшебным образом производит элемент α . Конечно, это блокирует любые осмысленные вычисления: согласно интерпретации Prop , h вообще не содержит информации о том, как найти такой элемент.

Это находится в пространстве имен classic , поэтому полное название теоремы classic.choice . Принцип выбора эквивалентен принципу неопределенного описания , который можно выразить с помощью подтипов следующим образом:

 невычислимая теорема indefinite_description
    {α: Сортировка*} (p: α → Prop):
  (∃ x, p x) → {x // p x} :=
λ h, выбор (пусть ⟨x, px⟩ := h в ⟨⟨x, px⟩⟩)
 

Поскольку это зависит от выбора , Lean не может сгенерировать байт-код для indefinite_description , и поэтому требует, чтобы мы пометили определение как невычислимое .Также в классическом пространстве имен функция some и свойство some_spec разлагают две части вывода indefinite_description :

.

 невычислимое определение некоторого {a : Sort*} {p : a → Prop}
  (ч : ∃ х, р х) : а :=
subtype.val (indefinite_description p h)

теорема some_spec {a : Sort*} {p : a → Prop}
  (h : ∃ x, p x) : p (некоторое h) :=
subtype. property (indefinite_description p h)
 

Принцип выбора также стирает различие между свойством быть непустым и более конструктивным свойством быть обитаемым :

 невычислимая теорема inhabited_of_nonempty {α : Type*} :
  непустое α → обитаемое α :=
λ h, выбор (пусть ⟨a⟩ := h в ⟨⟨a⟩⟩)
 

В следующем разделе мы увидим, что propext , funext и selection , взятые вместе, влекут за собой закон исключенного третьего и разрешимость всех предложений.Используя их, можно усилить принцип неопределенного описания следующим образом:

 #check (@strong_indefinite_description :
        Π {α : Sort*} (p : α → Prop),
          непусто α → {x // (∃ (y : α), p y) → p x})
 

Предполагая, что объемлющий тип α непустой, strong_indefinite_description p создает элемент α , удовлетворяющий p , если он есть. Компонент данных этого определения обычно известен как эпсилон-функция Гильберта :

.

 #check (@epsilon : Π {α : Sort*} [непустое α],
                     (α → Опора) → α)

#check (@epsilon_spec : ∀ {a : Sort*} {p : a → Prop}
           (hex : ∃ (y : a), p y),
         p (@epsilon _ (nonempty_of_exists hex) p))
 

11.6. Закон исключенного третьего 90 041

Закон исключенного третьего следующий

 #check (@em : ∀ (p : Prop), p ∨ ¬p)
 

Теорема Диаконеску утверждает, что аксиомы выбора достаточно, чтобы вывести закон исключенного третьего. Точнее, он показывает, что закон исключенного третьего следует из classic.choice , propext и funext . Мы набросаем доказательство, которое можно найти в стандартной библиотеке.

Сначала мы импортируем необходимые аксиомы, фиксируем параметр p и определяем два предиката U и V :

 открытый классический

секция диаконеску
параметр p : Опора

def U (x : Prop) : Prop := x = true ∨ p
def V (x : Prop) : Prop := x = false ∨ p

лемма exU : ∃ x, U x := ⟨true, или. инл рфл⟩
лемма exV : ∃ x, V x := ⟨false, или.inl rfl⟩

конец диаконеску
 

Если p истинно, то каждый элемент Prop находится как в U , так и в V . Если p ложно, то U является одноэлементным истинным , а V является одноэлементным ложным .

Затем мы используем и , чтобы выбрать элемент из каждого из U и V :

 невычислимое def u := некоторый exU
невычислимое def v := некоторое exV

лемма u_def : U u := some_spec exU
лемма v_def : V v := some_spec exV
 

Каждый из U и V является дизъюнкцией, поэтому u_def и v_def представляют четыре случая.В одном из этих случаев u = true и v = false , а во всех остальных случаях p верно. Таким образом имеем:

Лемма

 not_uv_or_p : u ≠ v ∨ p :=
или. elim u_def
  (предположим хижина: u = true,
    или.elim v_def
      (предположим, что hvf : v = ложь,
        есть hne : u ≠ v,
          от eq.symm hvf ▸ eq.symm hut ▸ true_ne_false,
        или.inl hne)
      (предполагается, что hp : p или.inr hp))
  (предполагается, что л.с. : p или.inr л.с.)
 

С другой стороны, если p истинно, то в силу экстенсиональности функции и пропозициональная экстенсиональность, U и V равны.Посредством определения u и v , это означает, что они также равны.

 лемма p_implies_uv : p → u = v :=
предположим, hp : p,
иметь hпред : U = V, из
  funext (предположим, что x : Prop,
    имеем hl : (x = true ∨ p) → (x = false ∨ p), из
      предположим a, или.inr л.с.,
    имеют hr : (x = false ∨ p) → (x = true ∨ p), из
      предположим a, или.inr л.с.,
    показать (x = истина ∨ p) = (x = ложь ∨ p), из
      протекст (iff.intro hl hr)),
имеем h₀ : ∀ exU exV,
    @classical. some _ U exU = @classical.какой-то _ V exV,
  от hpred ▸ λ exU exV, rfl,
показать u = v, из h₀ _ _
 

Сопоставление этих двух последних фактов дает желаемый вывод:

 теорема em : p ∨ ¬p :=
имеем h : ¬(u = v) → ¬p, из mt p_implies_uv,
  or.elim не_uv_or_p
    (предположим, что hne : ¬(u = v), или.inr (h hne))
    (предполагается, что hp : p или.inl hp)
 

Последствия исключения третьего включают устранение двойного отрицания, доказательство по случаям и доказательство от противного, все из которых описаны в разделе 3.5. Закон исключенного третьего и пропозициональная экстенсиональность влекут за собой пропозициональную полноту:

 теорема prop_complete (a : Prop): a = true ∨ a = false :=
or.elim (эм а)
  (λ t, or.inl (propext (iff.intro (λ h, тривиальный) (λ h, t))))
  (λ f, or.inr (propext (iff.intro (λ h, absurd h f)
                                   (λ ч, лжеэлим ч))))
 

Вместе с выбором мы также получаем более сильный принцип, что каждое предложение разрешимо. Напомним, что класс из разрешимых предложений определяется следующим образом:

Индуктивная разрешимость класса

 (p : Prop)
| is_false : ¬p → разрешимый
| is_true : p → разрешимый
 

В отличие от p ∨ ¬ p , который может исключить только до Prop , разрешимый тип p эквивалентен типу суммы p ⊕ ¬ p , который может исключить до любого типа.Именно эти данные нужны для написания выражения if-then-else.

В качестве примера классического рассуждения мы используем вместо , чтобы показать, что если f : α → β инъективно и α обитаемо, то f имеет левую инверсию. Чтобы определить левую обратную linv , мы используем зависимое выражение if-then-else. Напомним, что , если h : c, то t, иначе e — это обозначение дит c (λ h : c, t) (λ h : ¬c, e) . В определении linv выбор используется дважды: во-первых, чтобы показать, что (∃ a : A, fa = b) является «разрешимым», а затем чтобы выбрать a так, что fa = b . Обратите внимание, что мы делаем prop_decidable локальным экземпляром, чтобы оправдать выражение if-then-else. (См. также обсуждение в Разделе 10.4.)

 открыть классическую функцию
локальный атрибут [экземпляр] prop_decidable

невычислимое определение linv {α β : Type*} [h : обитаемый α]
  (f : α → β) : β → α :=
λ b : β, если ex : (∃ a : α, f a = b), то некоторое ex иначе произвольное α

теорема linv_comp_self {α β : Type*} {f : α → β}
    [обитаемый α] (inj: инъективное f):
  linv f ∘ f = id :=
funext (предположим,
  есть ex : ∃ a₁ : α, f a₁ = f a, из существует.интро рфл,
  have feq : f (some ex) = f a, from some_spec ex,
  calc linv f (fa) = some ex : dif_pos ex
             ... = a : inj feq)
 

С классической точки зрения linv — это функция. С конструктивной точки зрения это неприемлемо; потому что нет возможности реализовать такую ​​функцию вообще конструкция не информативна.

.