| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | ||
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град.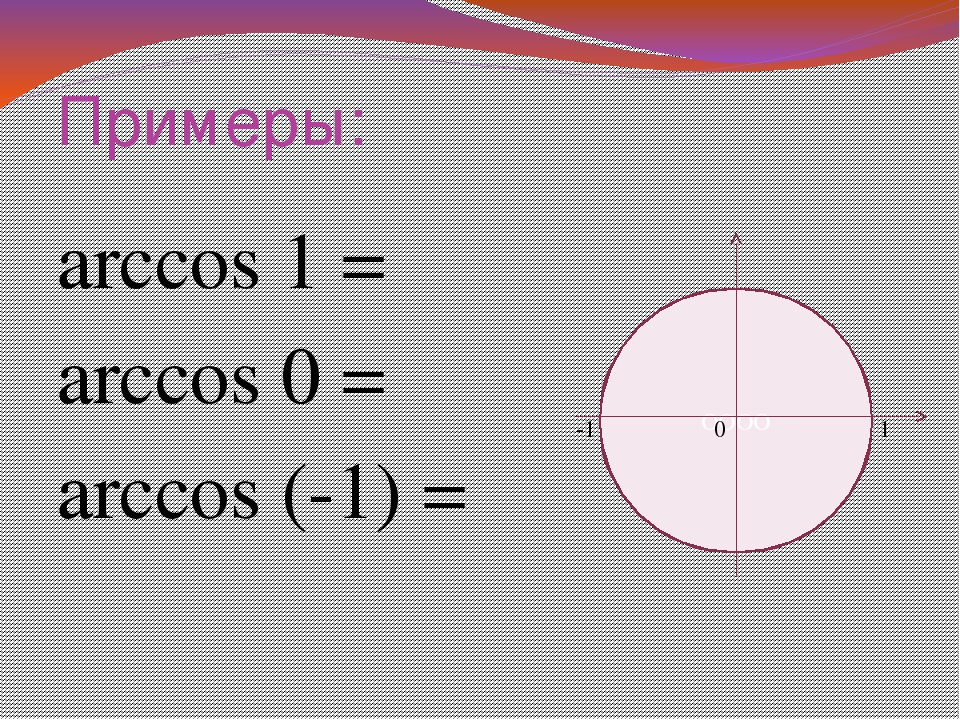 ) ) |
|
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | sin(60) | ||
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) ) |
|
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.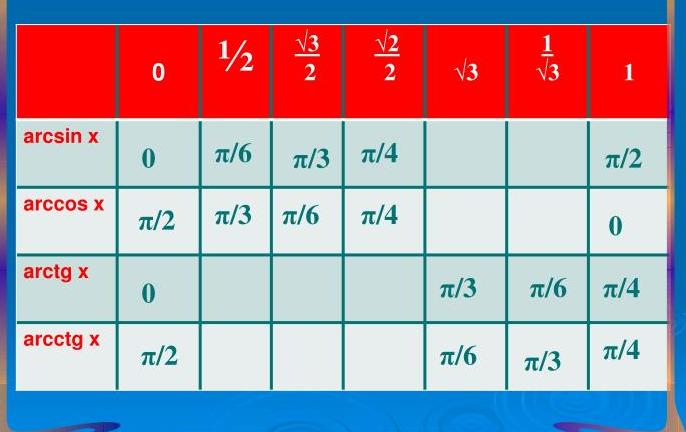 ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.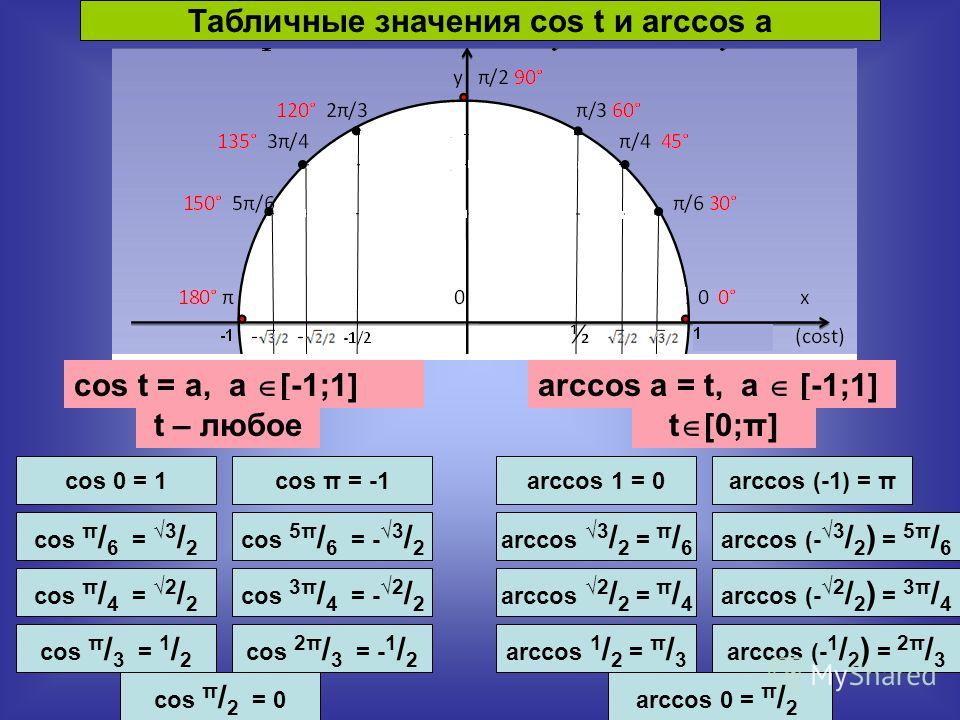 ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | arcsin(-1/2) | ||
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Функция ACOS
В этой статье описаны синтаксис формулы и использование функции ACOS в Microsoft Excel.
Описание
Возвращает арккосинус числа. Арккосинус числа — это угол, косинус которого равен числу. Угол определяется в радианах в интервале от 0 до «пи».
Арккосинус числа — это угол, косинус которого равен числу. Угол определяется в радианах в интервале от 0 до «пи».
Синтаксис
ACOS(число)
Аргументы функции ACOS описаны ниже.
Замечания
Если нужно преобразовать результат из радиан в градусы, умножьте его на 180/ПИ() или используйте функцию ГРАДУСЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ACOS(-0,5) |
Арккосинус числа -0,5 в радианах, 2*ПИ/3 (2,094395) |
2,094395102 |
|
=ACOS(-0,5)*180/ПИ() |
Арккосинус -0,5 в градусах |
120 |
|
=ГРАДУСЫ(ACOS(-0,5)) |
Арккосинус -0,5 в градусах |
120 |
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс? Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса.

Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус. .. Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
.. Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
И не только по тригонометрии. Очень помогает.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса ».
Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты. Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a , arccos(−a)=π−arccos a , arctg(−a)=−arctg a и arcctg(−a)=π−arcctg a .
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.
Пусть нам требуется найти значение арксинуса 0,2857
. Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже). Ему соответствует синус 16
градусов 36
минут. Следовательно, искомым значением арксинуса числа 0,2857
является угол 16
градусов 36
минут.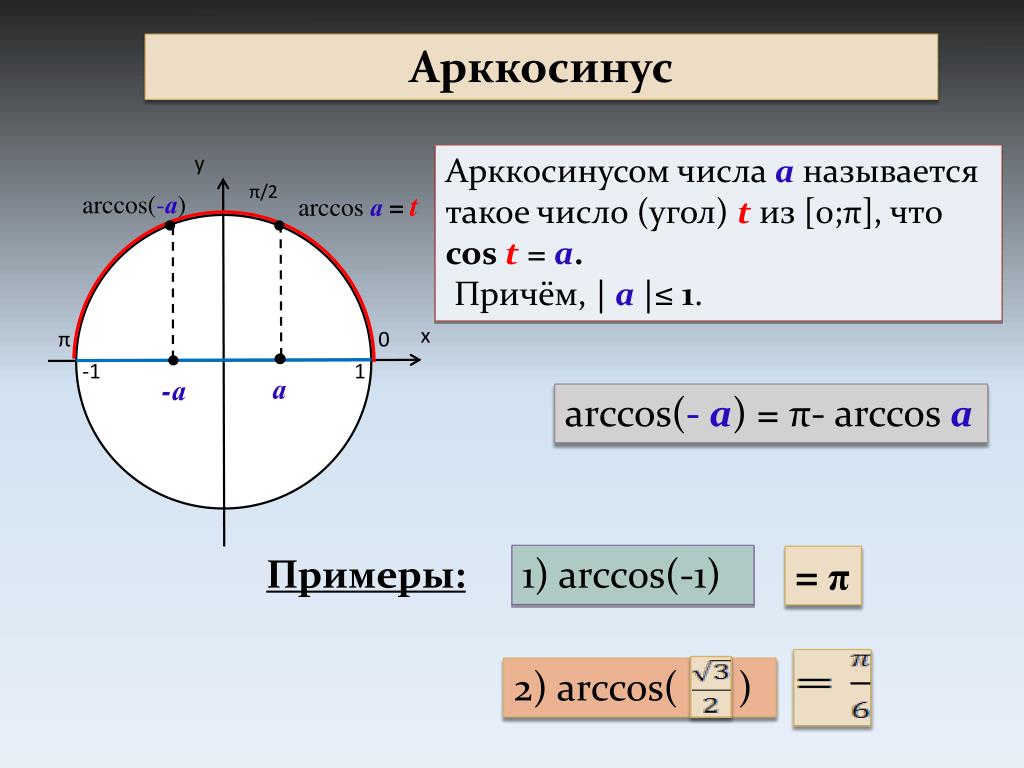
Часто приходится учитывать и поправки из трех справа столбцов таблицы. К примеру, если нам нужно найти арксинус 0,2863
. По таблице синусов это значение получается как 0,2857
плюс поправка 0,0006
, то есть, значению 0,2863
соответствует синус 16
градусов 38
минут (16
градусов 36
минут плюс 2
минуты поправки).
Если же число, арксинус которого нас интересует, отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно отыскать два наиболее близких к нему значения синусов, между которыми данное число заключено. Например, мы ищем значение арксинуса числа 0,2861573
. Этого числа нет в таблице, с помощью поправок это число тоже не получить. Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.п.
Например, пусть нам известно, что arcsin a=−π/12 , а нужно найти значение arccos a . Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12 .
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Пусть нам известно, что арккосинус числа a
равен π/10
, и нужно вычислить значение арктангенса этого числа a
. Решить поставленную задачу можно так: по известному значению арккосинуса найти число a
, после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.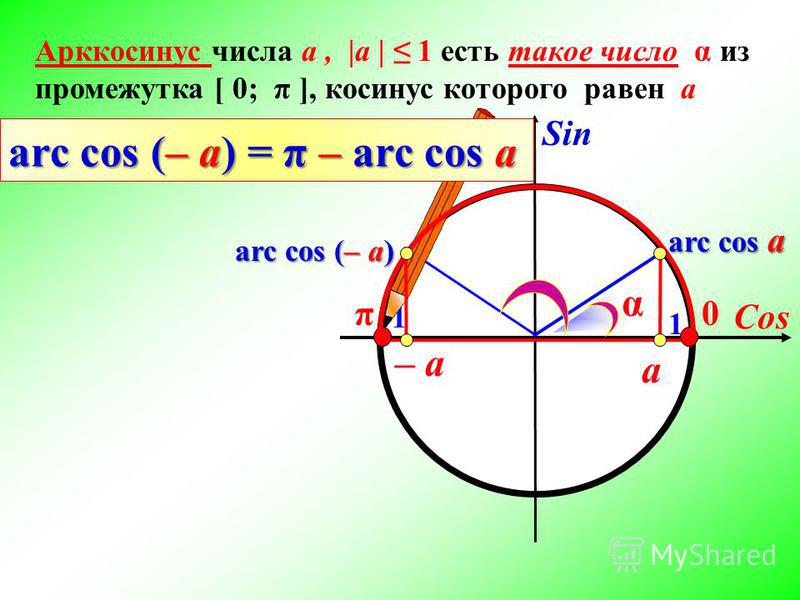
Угол π/10
радиан – это угол 18
градусов, по таблице косинусов находим, что косинус 18
градусов приближенно равен 0,9511
, тогда число a
в нашем примере есть 0,9511
.
Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511
, оно приближенно равно 43
градусам 34
минутам.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg .
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П.
 Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3. - И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Урок и презентация на темы: «Арккосинус. Таблица арккосинусов. arccos(0), arccos(1), arccos(2)»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Что такое арккосинус?
2. Обозначение арккосинуса.
3. Немного истории.
4. Определение.
5. Таблица значений арккосинуса.
6. Примеры.
Что такое арккосинус?
Ребята, мы с вами уже изучили функцию Y=cos(X), построили ее график и решали некоторые уравнения, например cos(x)= 1/2. Для решения этого уравнения требовалось провести прямую x= 1/2 и посмотреть, в каких точках она пересекает числовую окружность.
Видно что прямая пересекает окружность в двух точках F и G. Эти точки и являются решением уравнения. Переобозначим F как x1, а G — как x2. Решение уравнения мы нашли довольно легко и определили, что x1 = π/3 + 2πk, а x2 = -π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение cos(x)=4/7. Очевидно, что решением уравнения будут две точки, но какие значения будут соответствовать решению на числовой окружности?
Обозначение арккосинуса
Давайте внимательно посмотрим на уравнение cos(x)=4/7.
Как мы и говорили, решениями нашего уравнения будут две точки: F=x1+2πk и G=x2+2πk, но, что это за точки? Много лет назад столкнувшись с этой проблемой математики решили, что надо придумать некоторый способ описания решения на математическом языке. И был придуман новый символ – arccos(x). Будем читать как арккосинус.
И был придуман новый символ – arccos(x). Будем читать как арккосинус.
Тогда решения нашего уравнения запишутся как: x1=arccos(4/7) и x2=-arccos(4/7). И решение в общем виде: x=arccos(4/7) + 2πk и x=-arccos(4/7) + 2πk. Арккосинус — это угол (длина дуги AF, AG), косинус которого равен 4/7.
Немного истории
Символ arccos появляется впервые в 18 веке в работах математика Шерфера и известного французского ученого Жозефа Луи Лагранжа, портрет которого вы видите на этой странице. Несколько ранее понятие арккосинус уже рассматривал Д. Бернули, но записывал его совсем другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга), что вполне согласуется со смыслом понятия:
arccos x — это угол (можно сказать и дуга), косинус которого равен x.
Определение арккосинуса.
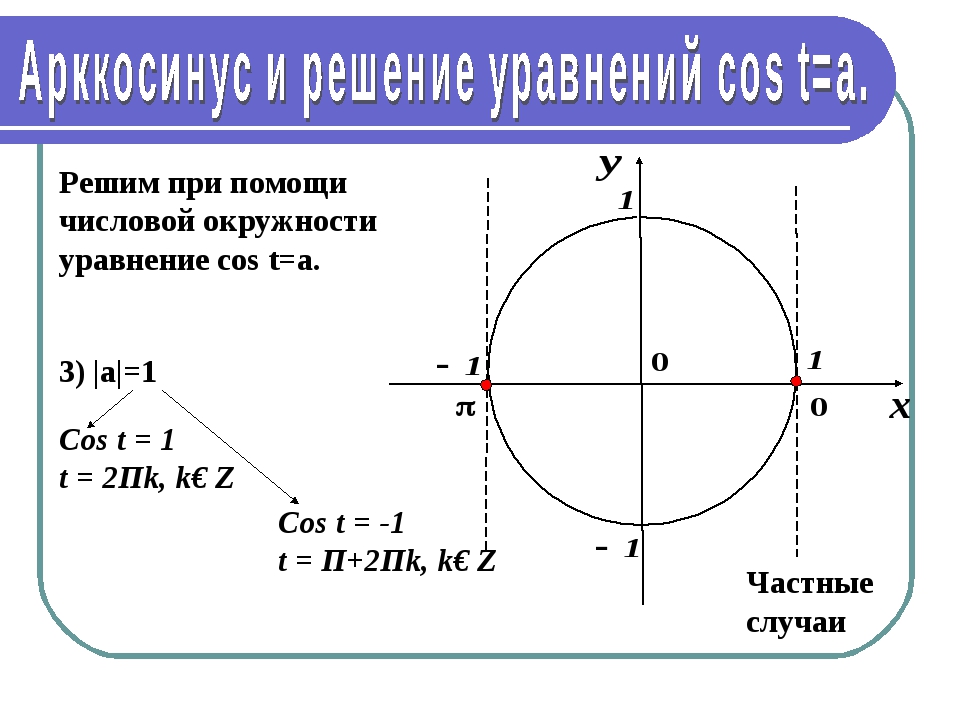
Если |а|≤ 1, то arccos(a) – это такое число из отрезка , косинус которого равен а.
Если |а|≤ 1, то уравнение cos(x)=a имеет решение: x=±arccos(a) + 2πk
Есть три случая, в которых предпочитают записывать решения более простым способом:
cos(x)=0, то x= π/2 + πk
cos(x)=1, то x= 2πk
cos(x)=-1, то x= π + 2πk
Также стоит записать важное равенство:
Для любого -1 ≤ а ≤ 1 выполняется равенство: arccos(a) + arccos(-a) = π ; при решение заданий удобнее использовать: arccos(-a) = π — arccos(a), где -1 ≤ а ≤ 1
Таблица значений арккосинуса
Напишем таблицу значений косинуса наоборот и получим таблицу для арккосинуса
Примеры
1. Найти значение функции arccos(-√3/2).
Найти значение функции arccos(-√3/2).
Решение: Пусть arccos(-√3/2)=x, тогда cos(x)=-√3/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=5π/6, т.к. cos(5π/6)= -√3/2 и 0 ≤ 5π/6 ≤ π.
Ответ: arccos(-√3/2)=5π/6
2. Найти значение функции arccos(√2/2).
Решение: Пусть arccos(√2/2) = x, тогда cos(x)= √2/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=π/4, т.к. cos(π/4)= √2/2 и 0 ≤ π/4 ≤ π.
Ответ: arccos(√2/2)=π/4
3. Найти значение функции arccos(1).
Решение: Пусть arccos(1) = x, тогда cos(x)= 1 и по определению 0≤ x ≤ π. Посмотрим значения косинуса в таблице: значит x=0, т.к. cos(0)= 1 и 0 ≤ 0 ≤ π.
Ответ: arccos(1)=0
4. Решить неравенство cos(x)> -0.3.
Решение: Косинус — это абсцисса точки числовой окружности. Значит необходимо найти такие точки, абсциссы которых больше -0.3. Нарисуем прямую x=-0.3. Она пересекает числовую окружность в двух точках: F и G. Неравенству x>-0.3 соответствуют точки дуги GF. Точкам F и G соответствуют абсциссы:
±arccos(-0.3)= ±(π — arccos(0.3)). Запишем аналитическую запись дуги GF: -π + arccos(0.3)
Ответ: -π + arccos(0.3)
Точкам F и G соответствуют абсциссы:
±arccos(-0.3)= ±(π — arccos(0.3)). Запишем аналитическую запись дуги GF: -π + arccos(0.3)
Ответ: -π + arccos(0.3)
Задачи для самостоятельного решения
1)Вычислить:а) $arccos(\frac{\sqrt{3}}{2})$,
б) $arccos(-\frac{1}{2})$,
в) $arccos(0)$,
г) $arccos(-0,5)$.
2) Решить уравнения:
а) $cos(x)=-\frac{1}{2}$,
б) $cos(x)=1$,
в) $cos(x)=\frac{\sqrt{3}}{2}$,
г) $cos(x)=0,25$,
д) $cos(x)=-1,2$.
3) Решить неравенства:
а) $cos(x)>0,6$,
б) $cos(x)≤0,2$.
Таблица КОСИНУСОВ для углов от 0° до 360° градусов
КОСИНУС (COS α) острого угла в прямоугольном треугольнике равен отношению прилежащего катета к его гипотенузе…
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cos α (Косинус) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
…
| Угол в градусах | Cos (Косинус) |
|---|---|
| 0° | 1 |
| 1° | 0.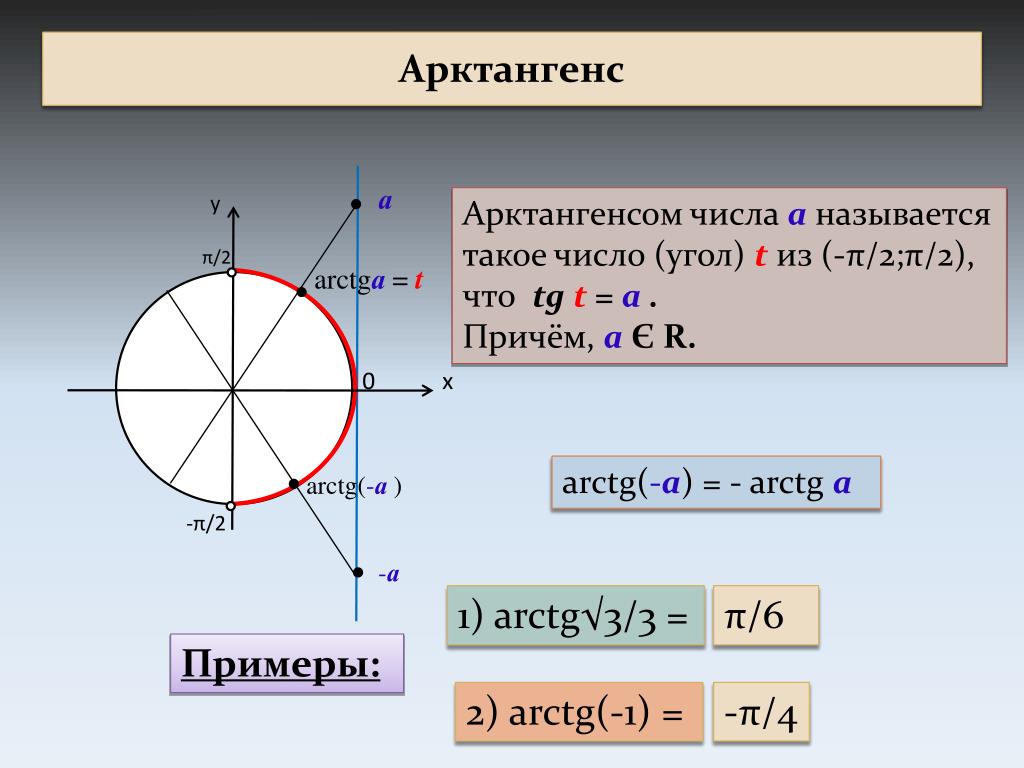 9998 9998 |
| 2° | 0.9994 |
| 3° | 0.9986 |
| 4° | 0.9976 |
| 5° | 0.9962 |
| 6° | 0.9945 |
| 7° | 0.9925 |
| 8° | 0.9903 |
| 9° | 0.9877 |
| 10° | 0.9848 |
| 11° | 0.9816 |
| 12° | 0.9781 |
| 13° | 0.9744 |
| 14° | 0.9703 |
| 15° | 0.9659 |
| 16° | 0.9613 |
| 17° | 0.9563 |
| 18° | 0.9511 |
| 19° | 0.9455 |
| 20° | 0.9397 |
| 21° | 0.9336 |
| 22° | 0.9272 |
| 23° | 0.9205 |
| 24° | 0.9135 |
| 25° | 0.9063 |
| 26° | 0.8988 |
| 27° | 0.891 |
| 28° | 0. 8829 8829 |
| 29° | 0.8746 |
| 30° | 0.866 |
| 31° | 0.8572 |
| 32° | 0.848 |
| 33° | 0.8387 |
| 34° | 0.829 |
| 35° | 0.8192 |
| 36° | 0.809 |
| 37° | 0.7986 |
| 38° | 0.788 |
| 39° | 0.7771 |
| 40° | 0.766 |
| 41° | 0.7547 |
| 42° | 0.7431 |
| 43° | 0.7314 |
| 44° | 0.7193 |
| 45° | 0.7071 |
| 46° | 0.6947 |
| 47° | 0.682 |
| 48° | 0.6691 |
| 49° | 0.6561 |
| 50° | 0.6428 |
| 51° | 0.6293 |
| 52° | 0.6157 |
| 53° | 0.6018 |
| 54° | 0.5878 |
| 55° | 0. 5736 5736 |
| 56° | 0.5592 |
| 57° | 0.5446 |
| 58° | 0.5299 |
| 59° | 0.515 |
| 60° | 0.5 |
| 61° | 0.4848 |
| 62° | 0.4695 |
| 63° | 0.454 |
| 64° | 0.4384 |
| 65° | 0.4226 |
| 66° | 0.4067 |
| 67° | 0.3907 |
| 68° | 0.3746 |
| 69° | 0.3584 |
| 70° | 0.342 |
| 71° | 0.3256 |
| 72° | 0.309 |
| 73° | 0.2924 |
| 74° | 0.2756 |
| 75° | 0.2588 |
| 76° | 0.2419 |
| 77° | 0.225 |
| 78° | 0.2079 |
| 79° | 0.1908 |
| 80° | 0.1736 |
| 81° | 0.1564 |
| 82° | 0. 1392 1392 |
| 83° | 0.1219 |
| 84° | 0.1045 |
| 85° | 0.0872 |
| 86° | 0.0698 |
| 87° | 0.0523 |
| 88° | 0.0349 |
| 89° | 0.0175 |
| 90° | 0 |
…
| Угол | cos (Косинус) |
|---|---|
| 91° | -0.0175 |
| 92° | -0.0349 |
| 93° | -0.0523 |
| 94° | -0.0698 |
| 95° | -0.0872 |
| 96° | -0.1045 |
| 97° | -0.1219 |
| 98° | -0.1392 |
| 99° | -0.1564 |
| 100° | -0.1736 |
| 101° | -0.1908 |
| 102° | -0.2079 |
| 103° | -0.225 |
| 104° | -0.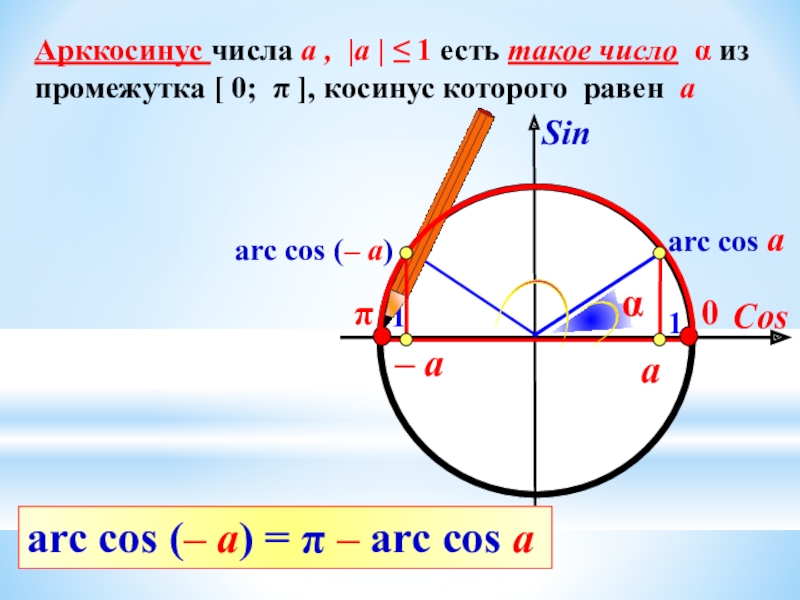 2419 2419 |
| 105° | -0.2588 |
| 106° | -0.2756 |
| 107° | -0.2924 |
| 108° | -0.309 |
| 109° | -0.3256 |
| 110° | -0.342 |
| 111° | -0.3584 |
| 112° | -0.3746 |
| 113° | -0.3907 |
| 114° | -0.4067 |
| 115° | -0.4226 |
| 116° | -0.4384 |
| 117° | -0.454 |
| 118° | -0.4695 |
| 119° | -0.4848 |
| 120° | -0.5 |
| 121° | -0.515 |
| 122° | -0.5299 |
| 123° | -0.5446 |
| 124° | -0.5592 |
| 125° | -0.5736 |
| 126° | -0.5878 |
| 127° | -0.6018 |
| 128° | -0.6157 |
| 129° | -0.6293 |
| 130° | -0. 6428 6428 |
| 131° | -0.6561 |
| 132° | -0.6691 |
| 133° | -0.682 |
| 134° | -0.6947 |
| 135° | -0.7071 |
| 136° | -0.7193 |
| 137° | -0.7314 |
| 138° | -0.7431 |
| 139° | -0.7547 |
| 140° | -0.766 |
| 141° | -0.7771 |
| 142° | -0.788 |
| 143° | -0.7986 |
| 144° | -0.809 |
| 145° | -0.8192 |
| 146° | -0.829 |
| 147° | -0.8387 |
| 148° | -0.848 |
| 149° | -0.8572 |
| 150° | -0.866 |
| 151° | -0.8746 |
| 152° | -0.8829 |
| 153° | -0.891 |
| 154° | -0.8988 |
| 155° | -0.9063 |
| 156° | -0. 9135 9135 |
| 157° | -0.9205 |
| 158° | -0.9272 |
| 159° | -0.9336 |
| 160° | -0.9397 |
| 161° | -0.9455 |
| 162° | -0.9511 |
| 163° | -0.9563 |
| 164° | -0.9613 |
| 165° | -0.9659 |
| 166° | -0.9703 |
| 167° | -0.9744 |
| 168° | -0.9781 |
| 169° | -0.9816 |
| 170° | -0.9848 |
| 171° | -0.9877 |
| 172° | -0.9903 |
| 173° | -0.9925 |
| 174° | -0.9945 |
| 175° | -0.9962 |
| 176° | -0.9976 |
| 177° | -0.9986 |
| 178° | -0.9994 |
| 179° | -0.9998 |
| 180° | -1 |
…
| Угол | cos (косинус) |
|---|---|
| 181° | -0. 9998 9998 |
| 182° | -0.9994 |
| 183° | -0.9986 |
| 184° | -0.9976 |
| 185° | -0.9962 |
| 186° | -0.9945 |
| 187° | -0.9925 |
| 188° | -0.9903 |
| 189° | -0.9877 |
| 190° | -0.9848 |
| 191° | -0.9816 |
| 192° | -0.9781 |
| 193° | -0.9744 |
| 194° | -0.9703 |
| 195° | -0.9659 |
| 196° | -0.9613 |
| 197° | -0.9563 |
| 198° | -0.9511 |
| 199° | -0.9455 |
| 200° | -0.9397 |
| 201° | -0.9336 |
| 202° | -0.9272 |
| 203° | -0.9205 |
| 204° | -0.9135 |
| 205° | -0.9063 |
| 206° | -0.8988 |
| 207° | -0.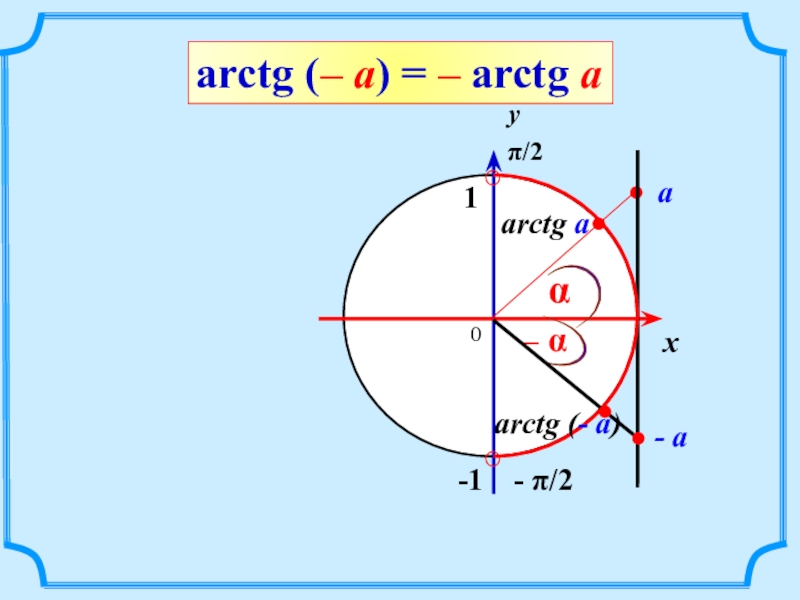 891 891 |
| 208° | -0.8829 |
| 209° | -0.8746 |
| 210° | -0.866 |
| 211° | -0.8572 |
| 212° | -0.848 |
| 213° | -0.8387 |
| 214° | -0.829 |
| 215° | -0.8192 |
| 216° | -0.809 |
| 217° | -0.7986 |
| 218° | -0.788 |
| 219° | -0.7771 |
| 220° | -0.766 |
| 221° | -0.7547 |
| 222° | -0.7431 |
| 223° | -0.7314 |
| 224° | -0.7193 |
| 225° | -0.7071 |
| 226° | -0.6947 |
| 227° | -0.682 |
| 228° | -0.6691 |
| 229° | -0.6561 |
| 230° | -0.6428 |
| 231° | -0.6293 |
| 232° | -0.6157 |
| 233° | -0.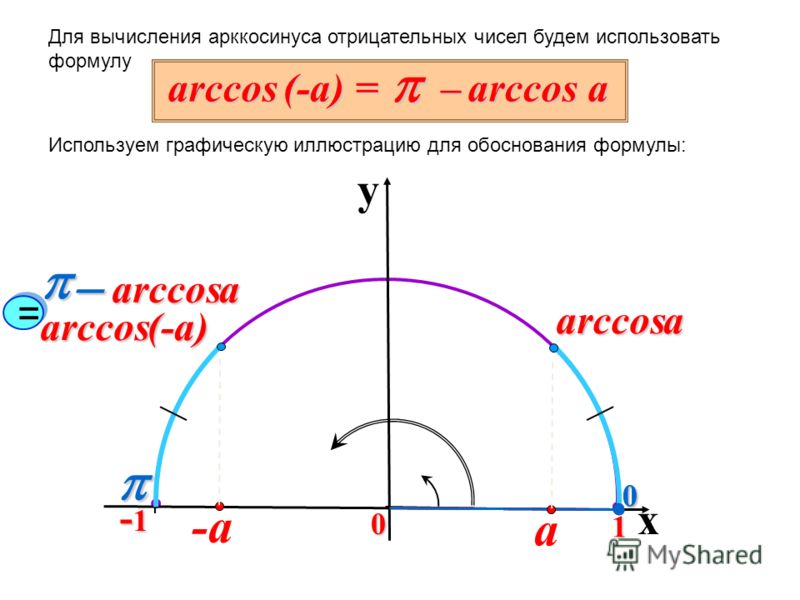 6018 6018 |
| 234° | -0.5878 |
| 235° | -0.5736 |
| 236° | -0.5592 |
| 237° | -0.5446 |
| 238° | -0.5299 |
| 239° | -0.515 |
| 240° | -0.5 |
| 241° | -0.4848 |
| 242° | -0.4695 |
| 243° | -0.454 |
| 244° | -0.4384 |
| 245° | -0.4226 |
| 246° | -0.4067 |
| 247° | -0.3907 |
| 248° | -0.3746 |
| 249° | -0.3584 |
| 250° | -0.342 |
| 251° | -0.3256 |
| 252° | -0.309 |
| 253° | -0.2924 |
| 254° | -0.2756 |
| 255° | -0.2588 |
| 256° | -0.2419 |
| 257° | -0.225 |
| 258° | -0.2079 |
| 259° | -0. 1908 1908 |
| 260° | -0.1736 |
| 261° | -0.1564 |
| 262° | -0.1392 |
| 263° | -0.1219 |
| 264° | -0.1045 |
| 265° | -0.0872 |
| 266° | -0.0698 |
| 267° | -0.0523 |
| 268° | -0.0349 |
| 269° | -0.0175 |
| 270° | 0 |
…
| Угол | Cos (Косинус) |
|---|---|
| 271° | 0.0175 |
| 272° | 0.0349 |
| 273° | 0.0523 |
| 274° | 0.0698 |
| 275° | 0.0872 |
| 276° | 0.1045 |
| 277° | 0.1219 |
| 278° | 0.1392 |
| 279° | 0.1564 |
| 280° | 0.1736 |
| 281° | 0. 1908 1908 |
| 282° | 0.2079 |
| 283° | 0.225 |
| 284° | 0.2419 |
| 285° | 0.2588 |
| 286° | 0.2756 |
| 287° | 0.2924 |
| 288° | 0.309 |
| 289° | 0.3256 |
| 290° | 0.342 |
| 291° | 0.3584 |
| 292° | 0.3746 |
| 293° | 0.3907 |
| 294° | 0.4067 |
| 295° | 0.4226 |
| 296° | 0.4384 |
| 297° | 0.454 |
| 298° | 0.4695 |
| 299° | 0.4848 |
| 300° | 0.5 |
| 301° | 0.515 |
| 302° | 0.5299 |
| 303° | 0.5446 |
| 304° | 0.5592 |
| 305° | 0.5736 |
| 306° | 0.5878 |
| 307° | 0. 6018 6018 |
| 308° | 0.6157 |
| 309° | 0.6293 |
| 310° | 0.6428 |
| 311° | 0.6561 |
| 312° | 0.6691 |
| 313° | 0.682 |
| 314° | 0.6947 |
| 315° | 0.7071 |
| 316° | 0.7193 |
| 317° | 0.7314 |
| 318° | 0.7431 |
| 319° | 0.7547 |
| 320° | 0.766 |
| 321° | 0.7771 |
| 322° | 0.788 |
| 323° | 0.7986 |
| 324° | 0.809 |
| 325° | 0.8192 |
| 326° | 0.829 |
| 327° | 0.8387 |
| 328° | 0.848 |
| 329° | 0.8572 |
| 330° | 0.866 |
| 331° | 0.8746 |
| 332° | 0.8829 |
| 333° | 0. 891 891 |
| 334° | 0.8988 |
| 335° | 0.9063 |
| 336° | 0.9135 |
| 337° | 0.9205 |
| 338° | 0.9272 |
| 339° | 0.9336 |
| 340° | 0.9397 |
| 341° | 0.9455 |
| 342° | 0.9511 |
| 343° | 0.9563 |
| 344° | 0.9613 |
| 345° | 0.9659 |
| 346° | 0.9703 |
| 347° | 0.9744 |
| 348° | 0.9781 |
| 349° | 0.9816 |
| 350° | 0.9848 |
| 351° | 0.9877 |
| 352° | 0.9903 |
| 353° | 0.9925 |
| 354° | 0.9945 |
| 355° | 0.9962 |
| 356° | 0.9976 |
| 357° | 0.9986 |
| 358° | 0.9994 |
| 359° | 0. 9998 9998 |
| 360° | 1 |
…
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Пример
Чему равен косинус 30? …
— Ищем в таблице соответствующее значение. Правильный ответ: 0.866
Автор: Bill4iam
Алгебра – 10 класс. Арккосинус, arccos (x)
Дата публикации: .
Урок и презентация на темы: «Арккосинус. Таблица арккосинусов. arccos(0), arccos(1), arccos(2)»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать: Тригонометрические уравнения.
 Арккосинус (PPTX)
Арккосинус (PPTX)Что будем изучать:
1. Что такое арккосинус?
2. Обозначение арккосинуса.
3. Немного истории.
4. Определение.
5. Таблица значений арккосинуса.
6. Примеры.
Что такое арккосинус?
Ребята, мы с вами уже изучили функцию Y=cos(X), построили ее график и решали некоторые уравнения, например cos(x)= 1/2. Для решения этого уравнения требовалось провести прямую x= 1/2 и посмотреть, в каких точках она пересекает числовую окружность.
Видно что прямая пересекает окружность в двух точках F и G. Эти точки и являются решением уравнения. Переобозначим F как x1, а G — как x2. Решение уравнения мы нашли довольно легко и определили, что x1 = π/3 + 2πk, а x2 = -π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение cos(x)=4/7. Очевидно, что решением уравнения будут две точки, но какие значения будут соответствовать решению на числовой окружности?
Обозначение арккосинуса
Давайте внимательно посмотрим на уравнение cos(x)=4/7.
Как мы и говорили, решениями нашего уравнения будут две точки: F=x1+2πk и G=x2+2πk, но, что это за точки? Много лет назад столкнувшись с этой проблемой математики решили, что надо придумать некоторый способ описания решения на математическом языке. И был придуман новый символ – arccos(x). Будем читать как арккосинус.
Тогда решения нашего уравнения запишутся как: x1=arccos(4/7) и x2=-arccos(4/7). И решение в общем виде: x=arccos(4/7) + 2πk и x=-arccos(4/7) + 2πk. Арккосинус — это угол (длина дуги AF, AG), косинус которого равен 4/7.
Немного истории
Символ arccos появляется впервые в 18 веке в работах математика Шерфера и известного французского ученого Жозефа Луи Лагранжа, портрет которого вы видите на этой странице. Несколько ранее понятие арккосинус уже рассматривал Д. Бернули, но записывал его совсем другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга), что вполне согласуется со смыслом понятия:
arccos x — это угол (можно сказать и дуга), косинус которого равен x.
Определение арккосинуса.
Если |а|≤ 1, то arccos(a) – это такое число из отрезка [0; π], косинус которого равен а.
Если |а|≤ 1, то уравнение cos(x)=a имеет решение: x=±arccos(a) + 2πk
Есть три случая, в которых предпочитают записывать решения более простым способом:
cos(x)=0, то x= π/2 + πk
cos(x)=1, то x= 2πk
cos(x)=-1, то x= π + 2πk
Также стоит записать важное равенство:
Для любого -1 ≤ а ≤ 1 выполняется равенство: arccos(a) + arccos(-a) = π; при решение заданий удобнее использовать: arccos(-a) = π — arccos(a), где -1 ≤ а ≤ 1
Таблица значений косинуса
Таблица значений арккосинуса
Напишем таблицу значений косинуса наоборот и получим таблицу для арккосинуса
Примеры
1. Найти значение функции arccos(-√3/2).
Решение: Пусть arccos(-√3/2)=x, тогда cos(x)=-√3/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=5π/6, т. к. cos(5π/6)= -√3/2 и 0 ≤ 5π/6 ≤ π.
к. cos(5π/6)= -√3/2 и 0 ≤ 5π/6 ≤ π.
Ответ: arccos(-√3/2)=5π/6
2. Найти значение функции arccos(√2/2).
Решение: Пусть arccos(√2/2) = x, тогда cos(x)= √2/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=π/4, т.к. cos(π/4)= √2/2 и 0 ≤ π/4 ≤ π.
Ответ: arccos(√2/2)=π/4
3. Найти значение функции arccos(1).
Решение: Пусть arccos(1) = x, тогда cos(x)= 1 и по определению 0≤ x ≤ π. Посмотрим значения косинуса в таблице: значит x=0, т.к. cos(0)= 1 и 0 ≤ 0 ≤ π.
Ответ: arccos(1)=0
4. Решить неравенство cos(x)> -0.3.
Решение: Косинус — это абсцисса точки числовой окружности. Значит необходимо найти такие точки, абсциссы которых больше -0.3. Нарисуем прямую x=-0.3. Она пересекает числовую окружность в двух точках: F и G. Неравенству x>-0.3 соответствуют точки дуги GF. Точкам F и G соответствуют абсциссы:
±arccos(-0.3)= ±(π — arccos(0.3)). Запишем аналитическую запись дуги GF: -π + arccos(0.3)
Ответ: -π + arccos(0.3)
Задачи для самостоятельного решения
1)Вычислить:
а) $arccos(\frac{\sqrt{3}}{2})$,
б) $arccos(-\frac{1}{2})$,
в) $arccos(0)$,
г) $arccos(-0,5)$.

2) Решить уравнения:
а) $cos(x)=-\frac{1}{2}$,
б) $cos(x)=1$,
в) $cos(x)=\frac{\sqrt{3}}{2}$,
г) $cos(x)=0,25$,
д) $cos(x)=-1,2$.
3) Решить неравенства:
а) $cos(x)>0,6$,
б) $cos(x)≤0,2$.
Информио
×Неверный логин или пароль
×Все поля являются обязательными для заполнения
×Сервис «Комментарии» — это возможность для всех наших читателей дополнить опубликованный на сайте материал фактами или выразить свое мнение по затрагиваемой материалом теме.
Редакция Информио.ру оставляет за собой право удалить комментарий пользователя без предупреждения и объяснения причин. Однако этого, скорее всего, не произойдет, если Вы будете придерживаться следующих правил:
- Не стоит размещать бессодержательные сообщения, не несущие смысловой нагрузки.
- Не разрешается публикация комментариев, написанных полностью или частично в режиме Caps Lock (Заглавными буквами). Запрещается использование нецензурных выражений и ругательств, способных оскорбить честь и достоинство, а также национальные и религиозные чувства людей (на любом языке, в любой кодировке, в любой части сообщения — заголовке, тексте, подписи и пр.
 )
) - Запрещается пропаганда употребления наркотиков и спиртных напитков. Например, обсуждать преимущества употребления того или иного вида наркотиков; утверждать, что они якобы безвредны для здоровья.
- Запрещается обсуждать способы изготовления, а также места и способы распространения наркотиков, оружия и взрывчатых веществ.
- Запрещается размещение сообщений, направленных на разжигание социальной, национальной, половой и религиозной ненависти и нетерпимости в любых формах.
- Запрещается размещение сообщений, прямо либо косвенно призывающих к нарушению законодательства РФ. Например: не платить налоги, не служить в армии, саботировать работу городских служб и т.д.
- Запрещается использование в качестве аватара фотографии эротического характера, изображения с зарегистрированным товарным знаком и фотоснимки с узнаваемым изображением известных людей. Редакция оставляет за собой право удалять аватары без предупреждения и объяснения причин.

- Запрещается публикация комментариев, содержащих личные оскорбления собеседника по форуму, комментатора, чье мнение приводится в статье, а также журналиста.
Претензии к качеству материалов, заголовкам, работе журналистов и СМИ в целом присылайте на адрес
×Информация доступна только для зарегистрированных пользователей.
×Уважаемые коллеги. Убедительная просьба быть внимательнее при оформлении заявки. На основании заполненной формы оформляется электронное свидетельство. В случае неверно указанных данных организация ответственности не несёт.
Arccos
Арккосинус, записываемый как arccos или cos-1 (не путать с ), является функцией арккосинуса. Косинус имеет обратный только в ограниченной области, 0≤x≤π. На рисунке ниже часть графика, выделенная красным цветом, показывает часть графика cos(x), которая имеет обратную.
Домен должен быть ограничен, поскольку для того, чтобы у функции была обратная функция, она должна быть взаимно однозначной, то есть никакая горизонтальная линия не может пересекать график функции более одного раза.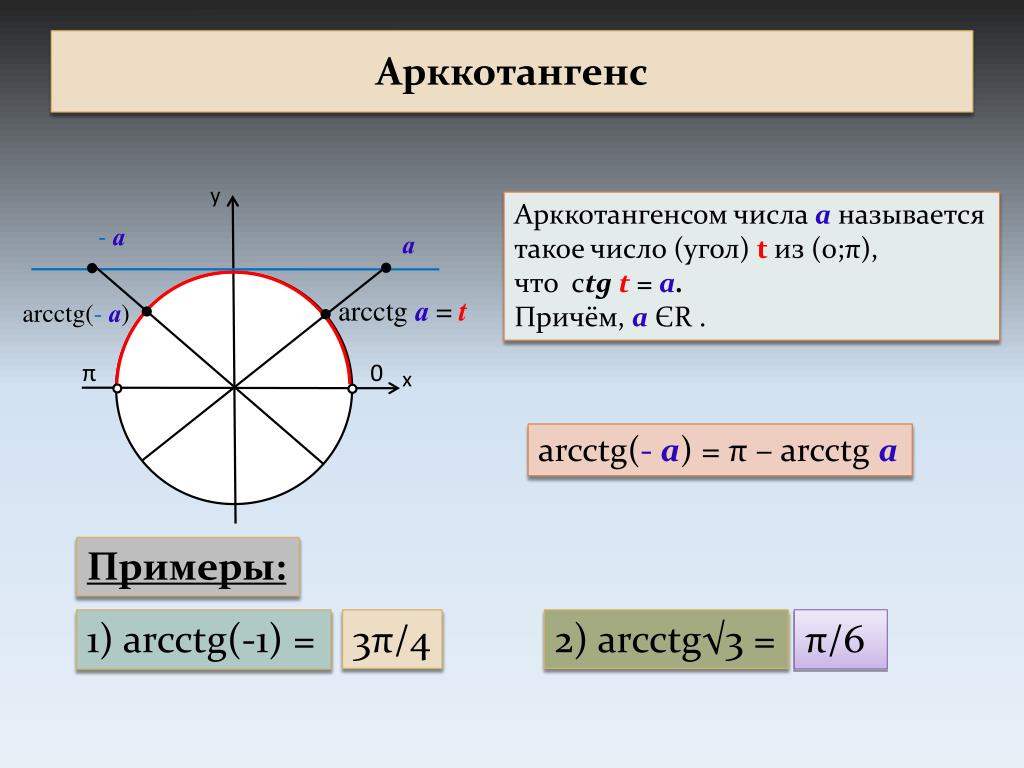 Поскольку косинус является периодической функцией, без ограничения области определения горизонтальная линия будет периодически пересекать функцию бесконечно много раз.
Поскольку косинус является периодической функцией, без ограничения области определения горизонтальная линия будет периодически пересекать функцию бесконечно много раз.
Одно из свойств обратных функций состоит в том, что если точка (a, b) находится на графике функции f, то точка (b, a) находится на графике обратной функции. Это фактически означает, что график обратной функции является отражением графика функции через прямую y = x.
График y = arccos(x) показан ниже.
Как видно из рисунка, y = arccos(x) является отражением cos(x) для ограниченной области 0≤x≤π через прямую y = x.Домен arccos(x), -1≤x≤1, является диапазоном cos(x), а его диапазон, 0≤x≤π, является доменом cos(x).
Калькулятор Arccos
Ниже приведен калькулятор для определения либо значения арккоса числа от -1 до 1, либо значения косинуса угла.
Использование специальных углов для поиска arccos
Хотя мы можем найти значение арккосинуса для любого значения x в интервале [-1, 1], существуют определенные углы, которые часто используются в тригонометрии (0°, 30°, 45°, 60°, 90° и их кратные и эквиваленты в радианах), значения косинуса и арккосинуса которых стоит запомнить. Ниже приведена таблица, показывающая эти углы (θ) в градусах и их соответствующие значения косинуса, cos(θ).
Ниже приведена таблица, показывающая эти углы (θ) в градусах и их соответствующие значения косинуса, cos(θ).
Один из методов, который может помочь в запоминании этих значений, заключается в выражении всех значений cos(θ) в виде дробей, содержащих квадратный корень. Начиная с 0° и увеличивая до 90°, cos(0°)=1=. Последующие значения cos(30°), cos(45°), cos(60°) и cos(90°) следуют шаблону, так что используя значение cos(0°) в качестве эталона, чтобы найти значения косинуса для последующих углов, мы просто уменьшаем число под знаком радикала в числителе на 1, как показано ниже:
| θ | 0° | 30° | 45° | 60° | 90° |
| соз(θ) | 0 |
От 90° до 180° вместо этого мы увеличиваем число под радикалом на 1, но также должны учитывать квадрант, в котором находится угол.Косинус отрицателен в квадрантах II и III, поэтому значения будут равными, но отрицательными.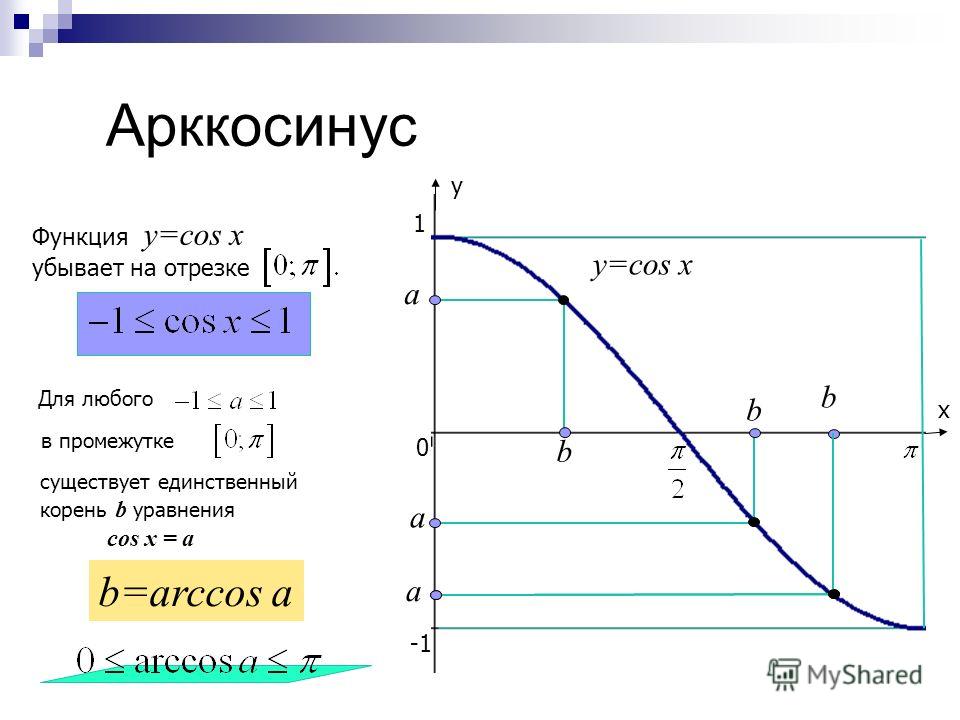 В квадрантах I и IV значения будут положительными. Этот шаблон периодически повторяется для соответствующих угловых измерений.
В квадрантах I и IV значения будут положительными. Этот шаблон периодически повторяется для соответствующих угловых измерений.
После того, как мы запомнили значения, или если у нас есть какая-то ссылка, становится относительно просто распознавать и определять значения косинуса или арккосинуса для специальных углов.
Обратные свойства
Как правило, функции и их обратные функции демонстрируют отношение
f(f -1 (x)) = x и f -1 (f(x)) = x
при условии, что x находится в области определения функции.То же самое верно для cos(x) и arccos(x) в пределах их соответствующих ограниченных доменов:
cos(arccos(x)) = x, для всех x в [-1, 1]
и
arccos(cos(x)) = x, для всех x в [0, π]
Эти свойства позволяют оценить состав тригонометрических функций.
Состав арккосинуса и косинуса
Если x находится в пределах домена, вычисление композиции арккосинуса и косинуса относительно просто.
Примеры:
1.
2.
Если x не входит в область, нам нужно определить опорный угол, а также соответствующий квадрант. Учитывая arccos(cos()), мы не можем оценить это, как мы сделали выше, потому что x не находится в пределах [0, π], поэтому решение не может быть . Чтобы оценить это, нам нужно сначала определить cos() перед использованием arccos:
.3.
В приведенном выше примере опорный угол равен , а cos() равен , но, поскольку он лежит в квадранте III, его косинус отрицателен, и единственный угол, косинус которого равен , который находится в области определения arccos(x), равен .
Состав других тригонометрических функций
Мы также можем составлять композиции, используя все остальные тригонометрические функции: синус, тангенс, косеканс, секанс и котангенс.
Пример:
Найти sin(arccos()).
Так как это не одно из соотношений для специальных углов, мы можем использовать прямоугольный треугольник, чтобы найти значение этой композиции. Учитывая arccos() = θ, мы можем найти, что cos(θ) = . Прямоугольный треугольник ниже показывает θ и отношение его смежной стороны к гипотенузе треугольника.
Учитывая arccos() = θ, мы можем найти, что cos(θ) = . Прямоугольный треугольник ниже показывает θ и отношение его смежной стороны к гипотенузе треугольника.
Чтобы найти синус, нам нужно найти противоположную сторону, так как sin(θ)=. Пусть а — длина противоположной стороны. Используя теорему Пифагора,
a 2 + 12 2 = 13 2
а 2 + 144 = 169
а 2 = 25
а = 5
и
грех (arccos()) = грех (θ) =
Тот же процесс можно использовать с переменным выражением.
Пример:
Найдите загар(arccos(4x)).
Учитывая arccos(4x) = θ, мы можем найти, что cos(θ)= и построить следующий прямоугольный треугольник:
Чтобы найти касательную, нам нужно найти противоположную сторону, так как tan(θ)=. Пусть b — длина противоположной стороны. Используя теорему Пифагора,
(4x) 2 + b 2 = 1 2
16x 2 + б 2 = 1
б 2 = 1 — 16x 2
б =
и
tan(arccos(4x)) = tan(θ) = , где — Арккосинус можно также использовать для решения тригонометрических уравнений, включающих функцию косинуса. Пример: Решите следующие тригонометрические уравнения относительно x, где 0≤x<2π. 1. 2cos(x) = 2cos(x) = соз(х) = х = arccos() Косинус отрицателен в квадрантах II и III, поэтому есть два решения: x= и x=. Это единственные два угла в пределах 0≤x<2π, значение косинуса которых равно . 2. 6cos 2 (x) + 9cos(x) — 36 = 0 6cos 2 (х) + 9sin(х) — 6 = 0 (6cos(x) — 3)(cos(x) + 2) = 0 6cos(x) — 3 = 0 или cos(x) + 2 = 0 cos(x) = или cos(x) = -2 x = arccos() или x = arccos(-2) Решение для x = arccos(), х = или Мы не можем решить для x = arccos(-2), потому что он не определен, поэтому x= или являются единственными решениями. Арккосинус является одной из обратных тригонометрических функций и также записывается как cos -1 . Поскольку cos -1 (x) является обратной функцией cos(x), арккосинус (x) является обратной функцией cos x. Здесь мы подробно изучим обратную функцию косинуса (арккосинус), а также ее график, область значений, диапазон, формулы, производную и интеграл, а также несколько решенных примеров. Использование арккосинуса для решения тригонометрических уравнений

Свойства, Домен, Диапазон, График, Производная, Интеграл
 У нас есть 6 обратных тригонометрических функций, таких как
У нас есть 6 обратных тригонометрических функций, таких как Что такое арккосинус?
Арккосинус является обратной функцией косинуса и, таким образом, является одной из обратных тригонометрических функций. Арккосинус произносится как «арккосинус». Арккосинус x также может быть записан как «acosx» (или) «cos -1 x» или «arccos». Если f и f -1 являются обратными функциями друг друга, то f(x) = y ⇒ x = f -1 (y).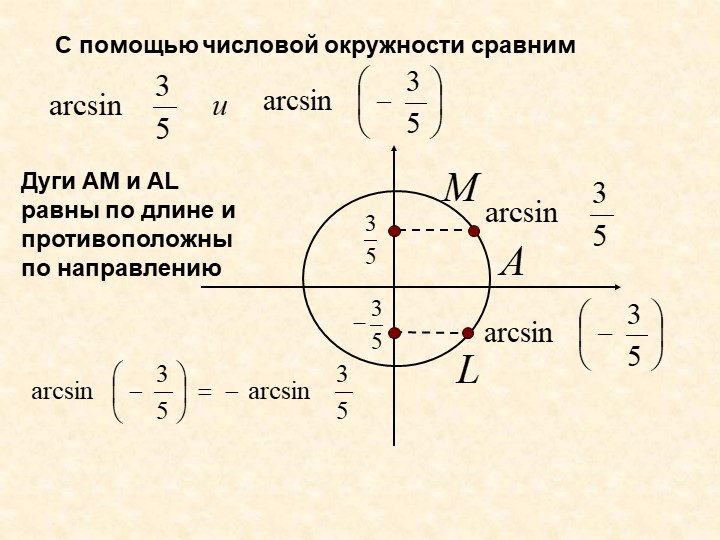 Итак, y = cos x ⇒ x = cos -1 (y) . В этом смысл арккосинуса.Давайте рассмотрим несколько примеров, чтобы увидеть, как работает функция арккосинуса.
Итак, y = cos x ⇒ x = cos -1 (y) . В этом смысл арккосинуса.Давайте рассмотрим несколько примеров, чтобы увидеть, как работает функция арккосинуса.
Примеры арккосинуса
- cos 0 = 1 ⇒ 0 = arccos (1)
- потому что π/2 = 0 ⇒ π/2 = arccos (0)
- потому что π = -1 ⇒ π = arccos (-1)
Определение арккосинуса
В прямоугольном треугольнике косинус угла (θ) равен отношению прилежащего катета к гипотенузе. т. е. cos θ = (прилежащая сторона) / (гипотенуза). Тогда по определению арккосинуса θ = cos -1 [(прилегающая сторона) / (гипотенуза)] .
Таким образом, функция арккосинуса используется для нахождения неизвестных углов в прямоугольном треугольнике. Кроме того, его можно использовать для нахождения неизвестных углов в любом треугольнике, используя закон косинусов. Например, в треугольнике ABC, если AB = c, BC = a и CA = b, то по закону косинусов
a 2 = b 2 + c 2 — 2bc cos A
Используя это,
cos A = (b 2 + c 2 — a 2 ) / (2bc)
A = cos -1 [(b 2 + c 2 — a 2 ) / (2bc)] (или) арккосинус [(b 2 + c 2 — a 9 2 — a 9 ) / (2bc)].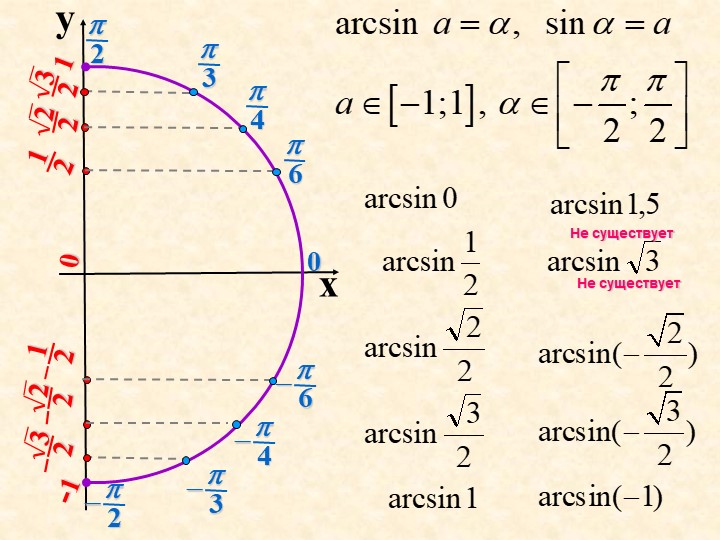
Точно так же мы можем найти другие углы треугольника, зная длины его сторон.
Домен, диапазон и график арккосинуса
В этом разделе давайте посмотрим, как можно найти область определения и диапазон функции арккосинуса. Кроме того, мы увидим, как изобразить его в его основной области.
Домен и диапазон арккосинуса
Мы знаем, что функция косинуса является функцией из R → [-1, 1]. Но функция косинуса НЕ является биекцией (поскольку она НЕ является взаимно однозначной) в области R.Следовательно, она не может иметь обратной, если ее область определения равна R. Чтобы функция косинуса была взаимно однозначной, ее область определения может быть ограничена одним из интервалов [-π, 0], [0, π], [π, 2π] и т. д. Каждому из этих интервалов соответствует ветвь арккосинуса. Ветвь арккосинуса с диапазоном [0, π] называется главной ветвью. Таким образом, область определения косинуса обычно ограничивается значением [0, π], а его диапазон — [-1, 1].
Мы знаем, что область определения и область значений функции будут соответственно областью значений и областью значений обратной функции.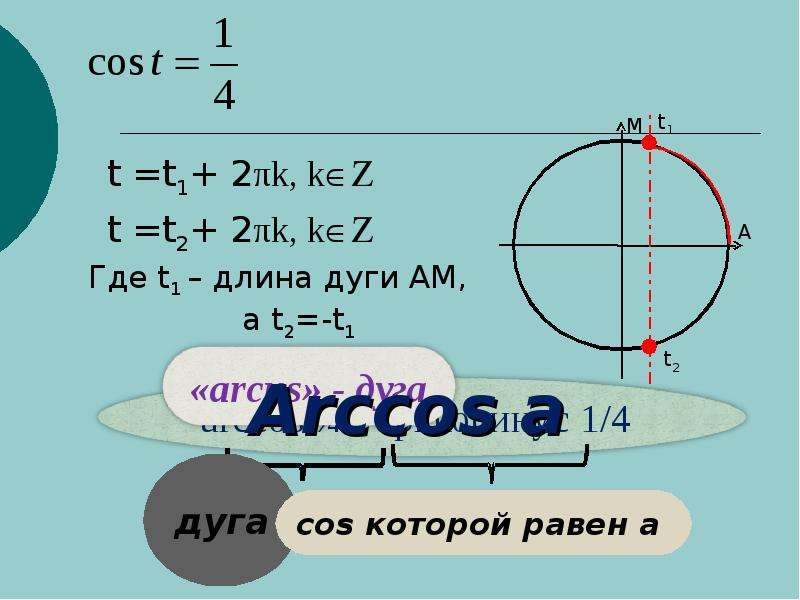 Следовательно, область обратной величины косинуса, которая является арккосинусом, равна [-1, 1], а ее диапазон равен [0, π] . то есть
Следовательно, область обратной величины косинуса, которая является арккосинусом, равна [-1, 1], а ее диапазон равен [0, π] . то есть
arccos x (или) cos -1 x : [-1, 1] → [0, π]
График арккосинуса
График функции арккосинуса, областью значений которой является главная ветвь [0, π], можно построить с помощью следующей таблицы. Здесь мы выбрали случайные значения для x в области арккосинуса, которая равна [-1, 1].
| х | у = cos -1 х |
|---|---|
| -1 | потому что -1 (-1) = π — 0 = π |
| -0.5 | потому что -1 (-0,5) = π — π/3 = 2π/3 |
| 0 | потому что -1 (0) = π/2 |
| 0,5 | потому что -1 (0,5) = π/3 |
| 1 | потому что -1 (1) = 0 |
Нанеся эти точки на график, мы получим график arccos.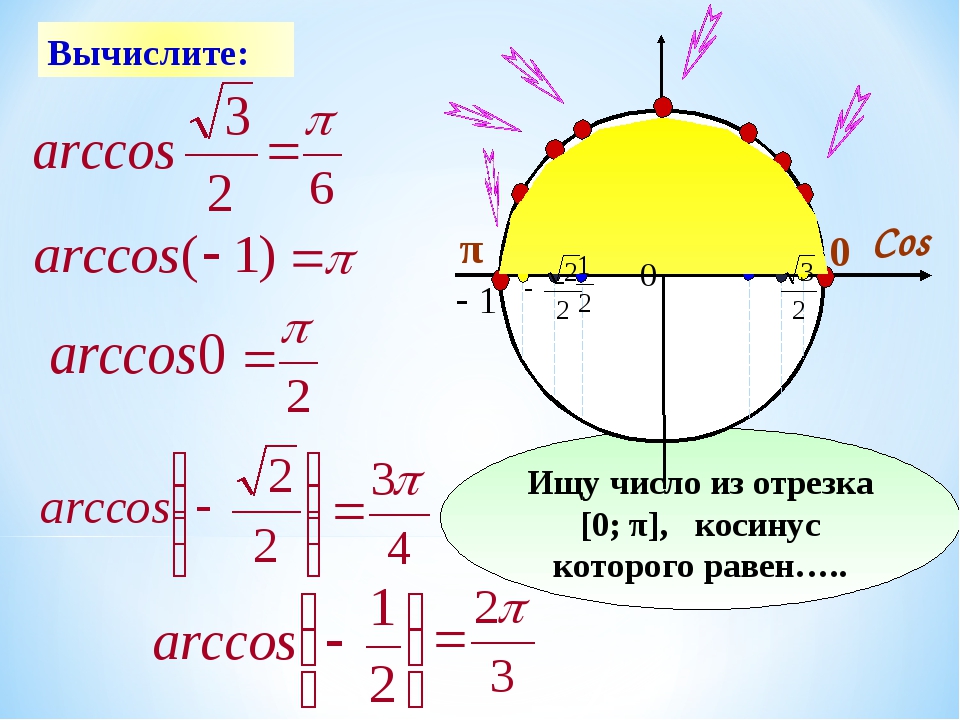
Свойства арккосинуса
Вот некоторые свойства/формулы арккосинуса.Они очень полезны при решении задач, связанных с обратными косами в тригонометрии.
- cos(cos -1 x) = x только тогда, когда x ∈ [-1, 1]
([Когда x ∉ [-1, 1], cos(cos -1 x) НЕ определено) - cos -1 (cos x) = x, только когда x ∈ [0, π]
(Когда x ∉ [0, π], либо найдите котерминальный угол x, либо примените тригонометрические тождества, чтобы найти эквивалентный угол x, лежащий в [0, π] ) - , потому что -1 (-x) = π — потому что -1 x
- cos -1 (1/x) = сек -1 x, когда |x| ≥ 1
- sin -1 x + cos -1 x = π/2, когда x ∈ [-1, 1]
Производная арккосинуса
Найдем производную от y = cos -1 x.По определению арккосинуса y = cos -1 x можно записать как cos y = x. Дифференцируя это с обеих сторон по x с использованием цепного правила,
Дифференцируя это с обеих сторон по x с использованием цепного правила,
— sin y (dy/dx) = 1
dy/dx = -1/sin y … (1)
Теперь у нас есть sin 2 y + cos 2 y = 1 ⇒ sin 2 y = 1 — cos 2 y ⇒ sin y = √(1 — cos²y) = √1 — x².
Подставив это в (1),
dy/dx = -1/√1 — x²
Таким образом, производная арккосинуса (или) производная от cos -1 x равна -1/√(1 — x²).
Интеграл арккосинуса
Найдем ∫cos -1 x dx, используя интегрирование по частям. Для этого запишем приведенный выше интеграл в виде
∫cos -1 x · 1 dx
Используя LIATE, f(x) = cos -1 x и g(x) = 1.
Интегрированием по частям,
∫f(x) . g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) ∫g(x) dx) dx + C
∫cos -1 x · 1 dx = cos -1 x ∫1 dx — ∫ [d/dx(cos -1 x) ∫x dx] + C
∫cos -1 x dx = cos -1 x (x) — ∫ [-1/√1 — x²] x dx + C
Мы вычислим этот интеграл с помощью u-подстановки. Для этого пусть 1-х 2 = u. Тогда -2x dx = du (или) x dx = -1/2 du.
Для этого пусть 1-х 2 = u. Тогда -2x dx = du (или) x dx = -1/2 du.
∫cos -1 x dx = x cos -1 x — ∫(-1/√u) (-1/2) du + C
= x cos -1 x — 1/2 ∫u -1/2 du + C
= x cos -1 x — (1/2) (u 1/2 /(1/2)) + C
= х cos -1 х — √u + C
= x cos -1 x — √1 — x² + C
Следовательно, ∫cos -1 x dx = x cos -1 x — √(1 — x²) + C.
Важные примечания:
Вот несколько важных замечаний, связанных с функцией арккосинуса.
- арккосинус можно записать как cos -1 (или) arccos (или) acos, и это функция с областью определения [-1, 1] и диапазоном [0, π].
- арккосинус НЕ совпадает с (cos x) -1 как (cos x) -1 = 1/(cos x) = sec x.
- cos -1 (-x) НЕ -cos -1 (x), а cos -1 (-x) = π — cos -1 x.

- cos(cos -1 x) НЕ всегда x. cos(cos -1 x) = x только тогда, когда x ∈ [-1, 1].
- cos -1 (cos x) НЕ всегда x. cos -1 (cos x) = x только тогда, когда x ∈ [0, π].
Связанные темы:
Вот некоторые темы, которые могут вас заинтересовать при чтении об арккосинусе.
Часто задаваемые вопросы по Arccosine
Что означает арккосинус?
Арккосинус является обратной функцией тригонометрической функции cos x и, следовательно, является обратной тригонометрической функцией.По определению обратной функции y = cos x ⇒ x = cos -1 (y).
Что такое определение арккосинуса?
В прямоугольном треугольнике, если θ — один из острых углов, то cos θ = (прилежащий)/(гипотенуза). Тогда θ = arccos((смежный)/(гипотенуза).
Является ли арккосинус x таким же, как cos⁻¹x?
Арккосинус является обратным cos x, поэтому да, арккосинус x равен cos⁻¹x.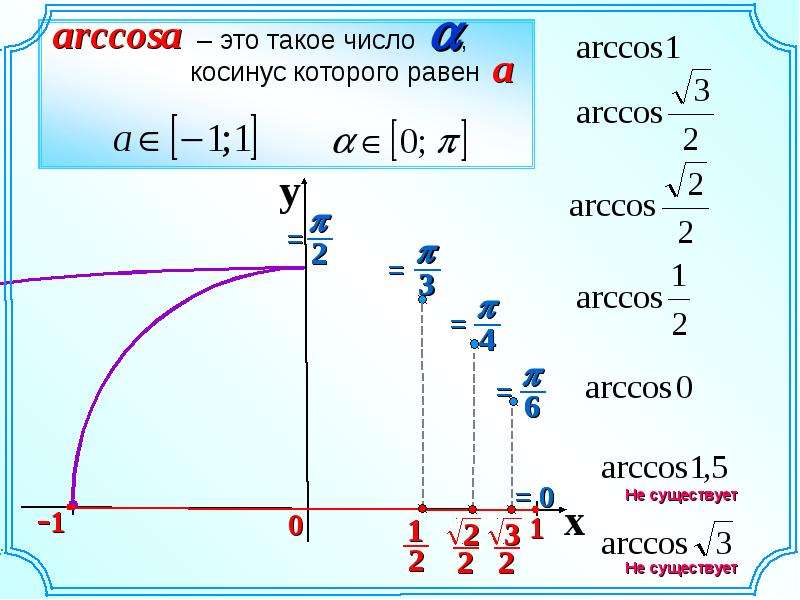
Является ли арккосинус таким же, как (cos x)⁻¹?
Нет. Арккосинус является обратной функцией косинуса, т.е.е., arccos x = cos -1 x. Но оно НЕ равно (cos x) -1 , так как (cos x) -1 = 1/cos x = sec x.
Что такое произношение арккосинуса?
«Арккосинус» является одной из обратных тригонометрических функций и может произноситься как «арккосинус» или «арккосинус».
Что такое область арккосинуса?
Область определения арккосинуса (или) cos -1 x равна [-1, 1], поскольку диапазон его обратной функции (которой является функция косинуса) равен [-1, 1].
Что такое диапазон арккосинуса?
Диапазон арккосинуса (или) cos -1 x равен [0, π], поскольку ограниченная область его обратной функции (которая является функцией косинуса) равна [0, π], чтобы сделать функцию косинуса единицей.
Что такое арккосинус Cos x?
Арккосинус cos x равен x (или) cos -1 (cos x) = x, если x ∈ [0, π]. Если x ∉ [0, π], то либо найдите котерминальный угол x, либо примените тригонометрические тождества, чтобы найти эквивалентный угол x, лежащий в [0, π], а затем примените cos -1 (cos x) = x .
Если x ∉ [0, π], то либо найдите котерминальный угол x, либо примените тригонометрические тождества, чтобы найти эквивалентный угол x, лежащий в [0, π], а затем примените cos -1 (cos x) = x .
Что такое Косинус арккосинуса x?
Cos арккосинуса x равно x (или) cos(cos -1 x) = x, если x ∈ [-1, 1]. Если x ∉ [-1, 1], то cos(cos -1 x) НЕ определен.
Функции арксинуса, арккосинуса и арктангенса
Функции арксинуса, арккосинуса и арктангенсаФункция арксинуса
Исходная информация: Функция арксинуса является обратной функцией синуса. (пока функция синуса ограничена определенной областью).Щелкните здесь для обзора обратных функций.Напомним, что функция синуса принимает угол x в качестве входных данных и возвращает синус этого угла в качестве выходных данных:
Например, если 30° — это вход, то 0,5 — это выход. Здесь мы хотим создать обратную функцию, которая будет принимать 0,5 в качестве входных данных и возврат 30° в качестве выхода.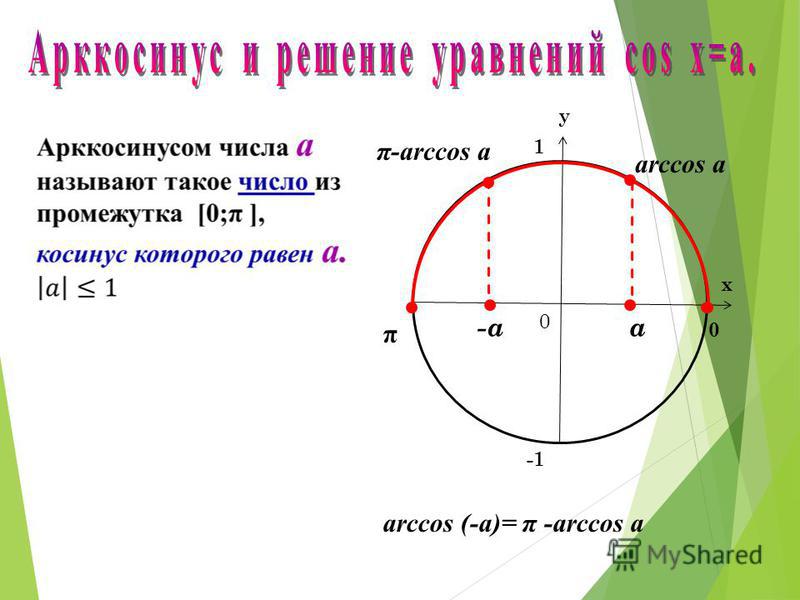 Но есть проблема. Обратите внимание, что существует много углов, синус которых равен 0,5: Мы говорим, что это отображение много к одному .Это означает, что обратная
отображение было бы один-ко-многим и, следовательно, не удовлетворяло бы
Требование «одно значение диапазона»
чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется арксинусом (с большой буквы и сокращением арксинус), а функция называется арксинусом
(со строчной буквой «а» и аббревиатурой arcsin). Вот как они определяются.Это отношение один ко многим . Вот пример: Определение: Арксинус x , обозначаемый arcsin( x ), определяется как определяется как
‘ один угол между −π/2 и +π/2 радиан
(или между −90° и +90°), чей синус равен 90 663 x 90 664’.
Это функция один к одному . Вот пример: Определение: Из всех значений, возвращаемых отношением арксинуса,
тот, который совпадает со значением, возвращаемым функцией арксинуса
называется главным значением отношения арксинуса.
Но есть проблема. Обратите внимание, что существует много углов, синус которых равен 0,5: Мы говорим, что это отображение много к одному .Это означает, что обратная
отображение было бы один-ко-многим и, следовательно, не удовлетворяло бы
Требование «одно значение диапазона»
чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется арксинусом (с большой буквы и сокращением арксинус), а функция называется арксинусом
(со строчной буквой «а» и аббревиатурой arcsin). Вот как они определяются.Это отношение один ко многим . Вот пример: Определение: Арксинус x , обозначаемый arcsin( x ), определяется как определяется как
‘ один угол между −π/2 и +π/2 радиан
(или между −90° и +90°), чей синус равен 90 663 x 90 664’.
Это функция один к одному . Вот пример: Определение: Из всех значений, возвращаемых отношением арксинуса,
тот, который совпадает со значением, возвращаемым функцией арксинуса
называется главным значением отношения арксинуса. (Примером может служить значение 30°, показанное выше красным.)
(Примером может служить значение 30°, показанное выше красным.)График: Красная кривая на графике справа — функция арксинуса. Обратите внимание, что для любого x между −1 и +1 он возвращает один значение между -π/2 и +π/2 радиан.
Если мы добавим серую кривую к красной кривой, мы получим график Отношение арксинуса. Вертикальная линия, нарисованная в любом месте между x = −1 и +1 касались бы этой кривой во многих местах, а это означает, что отношение арксинуса вернет много значений.
На этом графике угол y измерен в радианах. Если вы хотите измерить y в градусах , то просто измените масштаб по вертикали так что и проходят от −360 ° до 360 °, а не от от -2π до 2π радиан; в остальном форма графика не меняется.
Если сравнить график арксинуса с графиком синуса тогда вы видите, что одно можно получить из другого, поменяв местами горизонтальная и вертикальная оси.
Домен и диапазон: Область определения функции арксинуса составляет от −1 до +1 включительно, а диапазон — от
от −π/2 до π/2 радиан включительно (или от −90° до 90°).
Функция арксинуса может быть распространяется на комплексные числа, в которых случай домен все комплексные числа.
Специальные значения функции арксинуса (Нажмите здесь для более подробной информации)
Решение уравнения sin( θ ) = c для θ с помощью арксинуса и арксинуса e
Предположим, что угол θ неизвестен, но известен его синус быть c .Тогда нахождение этого угла требует решения этого уравнения для θ :
sin ( θ ) = сЕсли это, скажем, простая задача о прямоугольном треугольнике и мы знаем , что угол θ должен быть где-то между 0 и 90°, тогда решение является единственным значением:
θ = арксинус ( c )С другой стороны, если это более сложная задача и нам нужно найти все возможные углы у которых синус равен c тогда решение это весь набор значений:
θ = арксинус ( c )Решения в этих двух случаях следуют непосредственно из определения функции арксинуса и отношения арксинуса.
 Обратите внимание, что если c больше 1 или меньше -1, то существуют
нет реальных решений. Однако есть комплексные решения.
Обратите внимание, что если c больше 1 или меньше -1, то существуют
нет реальных решений. Однако есть комплексные решения.Оценка Arcsin( c )
Если c число, то весь набор значений Arcsin( c ) можно найти с помощью следующей процедуры. Обратитесь к графику справа где точки — желаемые значения.
- Первое значение (главное значение), обозначенное как θ PV , находится по формуле вычисление arcsin( c ) с помощью калькулятора или с помощью тренера по алгебре.
- Второе значение, называемое θ 2 , находится по формуле
используя симметрию кривой арксинуса. Обратите внимание, что две синие стрелки в
графы имеют одинаковую длину. Это означает, что 90 663 θ 90 664 90 804 2 90 805 находится настолько ниже π, насколько θ PV больше нуля. В виде формулы:
θ 2 = π − θ PV
(Нажмите здесь, чтобы увидеть метод CAST для поиска θ 2 . )
) - Все остальные значения выше и ниже этих двух значений можно найти из этих двух значений, добавив или вычитание кратных 2π. Если мы используем целое число n для подсчета которое кратно другим значениям, можно получить по этой формуле: Например, если мы допустим n = −1, тогда мы получим значения для две нижние точки на графике.
- Если вы используете градусы вместо радианов, используйте следующие формулы вместо предыдущих:
Как использовать функцию арксинуса в Algebra Coach
- Введите arcsin(x) в текстовое поле, где x — аргумент.Аргумент должен быть заключен в скобки.
- Установите соответствующие параметры:
- Установите параметр arcsin, arccos и arctan .
(Настройка возврата основного значения возвращает одно значение;
параметр не оценивать полезен, если вам нужны все значения
отношения Arc — но вам придется их вычислить самостоятельно.
 )
) - Установите параметр точная / с плавающей запятой.(Точный режим позволяет использовать специальные значения.)
- Установите параметр режима градусов/радиан.
- Установите параметр p, который соответствует или не соответствует параметру π. (Если вы хотите, чтобы арксинус возвращал специальные значения в радианном режиме затем включите это.)
- Включите комплексные числа , если вы хотите иметь возможность оценивать арксинус комплексного числа или числа больше 1.
- Установите параметр arcsin, arccos и arctan .
(Настройка возврата основного значения возвращает одно значение;
параметр не оценивать полезен, если вам нужны все значения
отношения Arc — но вам придется их вычислить самостоятельно.
- Нажмите кнопку «Упростить».
Алгоритм для функции арксинуса
Нажмите здесь чтобы увидеть алгоритм, который компьютеры используют для вычисления функции арксинуса.
Функция арккосинуса
Исходная информация: Функция арккосинуса является обратной функцией косинуса . (пока функция косинуса ограничена определенной областью). Щелкните здесь для обзора обратных функций.
Щелкните здесь для обзора обратных функций.Напомним, что функция косинуса принимает угол x в качестве входных данных и возвращает косинус этого угла в качестве выходных данных:
Например, если 60° — вход, то 0,5 — выход. Здесь мы хотим создать обратную функцию, которая будет принимать 0,5 в качестве входных данных и вернуть 60 ° в качестве вывода. Но есть проблема. Обратите внимание, что существует много углов, косинус которых равен 0,5: Мы говорим, что это отображение много к одному .Это означает, что обратная отображение было бы один-ко-многим и, следовательно, не удовлетворяло бы Требование «одно значение диапазона» чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется арккосинусом (с большой буквы и аббревиатурой Arccos) и функцией , называемой арккосинусом (со строчной буквой «а» и аббревиатурой arccos). Вот как они определяются:Определение: Арккосинус x , обозначаемый Arccos ( x ), определяется как ‘ множество всех углов , косинус которых равен х ’.
 Это отношение один ко многим . Вот пример: Определение: Арккосинус x , обозначаемый как arccos( x ), определяется как
‘ один угол между 0 и π радиан
(или от 0° до 180°), косинус которого равен x ’.
Это функция один к одному . Вот пример: Определение: Из всех значений, возвращаемых отношением арккосинуса,
тот, который совпадает со значением, возвращаемым функцией арккосинуса
называется главным значением отношения арккосинуса.(Примером может служить значение 60°, показанное выше красным.)
Это отношение один ко многим . Вот пример: Определение: Арккосинус x , обозначаемый как arccos( x ), определяется как
‘ один угол между 0 и π радиан
(или от 0° до 180°), косинус которого равен x ’.
Это функция один к одному . Вот пример: Определение: Из всех значений, возвращаемых отношением арккосинуса,
тот, который совпадает со значением, возвращаемым функцией арккосинуса
называется главным значением отношения арккосинуса.(Примером может служить значение 60°, показанное выше красным.)График: Красная кривая на графике справа — функция арккосинуса. Обратите внимание, что для любого x между −1 и +1 он возвращает один значение между 0 и +π радиан.
Если мы добавим серую кривую к красной кривой, мы получим график
Отношение арккосинуса. Вертикальная линия, нарисованная в любом месте между x =
−1 и +1 касались бы этой кривой во многих местах, а это означает, что
отношение арккосинуса вернет много значений.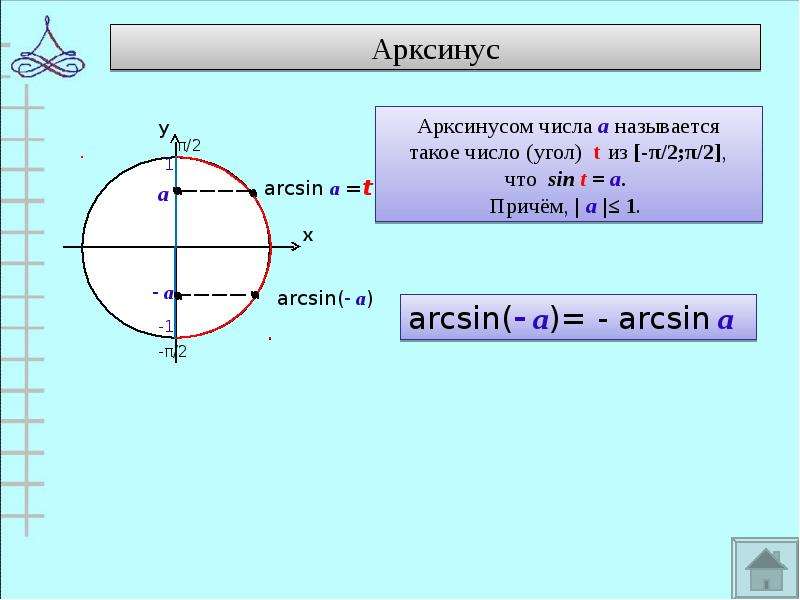
На этом графике угол y измерен в радианах. Если вы хотите измерить y в градусах , то просто измените масштаб по вертикали так что и проходят от −360 ° до 360 °, а не от от -2π до 2π радиан; в остальном форма графика не меняется.
Если сравнить график арккосинуса с графиком косинуса тогда вы видите, что одно можно получить из другого, поменяв местами горизонтальная и вертикальная оси.
Домен и диапазон: Область определения функции арккосинуса составляет от −1 до +1 включительно, а диапазон — от От 0 до π радиан включительно (или от 0° до 180°).
Функция арккосинуса может быть распространяется на комплексные числа, в которых случай домен все комплексные числа.
Специальные значения функции арккосинуса (Нажмите здесь для более подробной информации)
Решение уравнения cos( θ ) = c для θ с помощью арккосинуса и Arccos ine
Предположим, что угол θ неизвестен, но известен его косинус
быть c .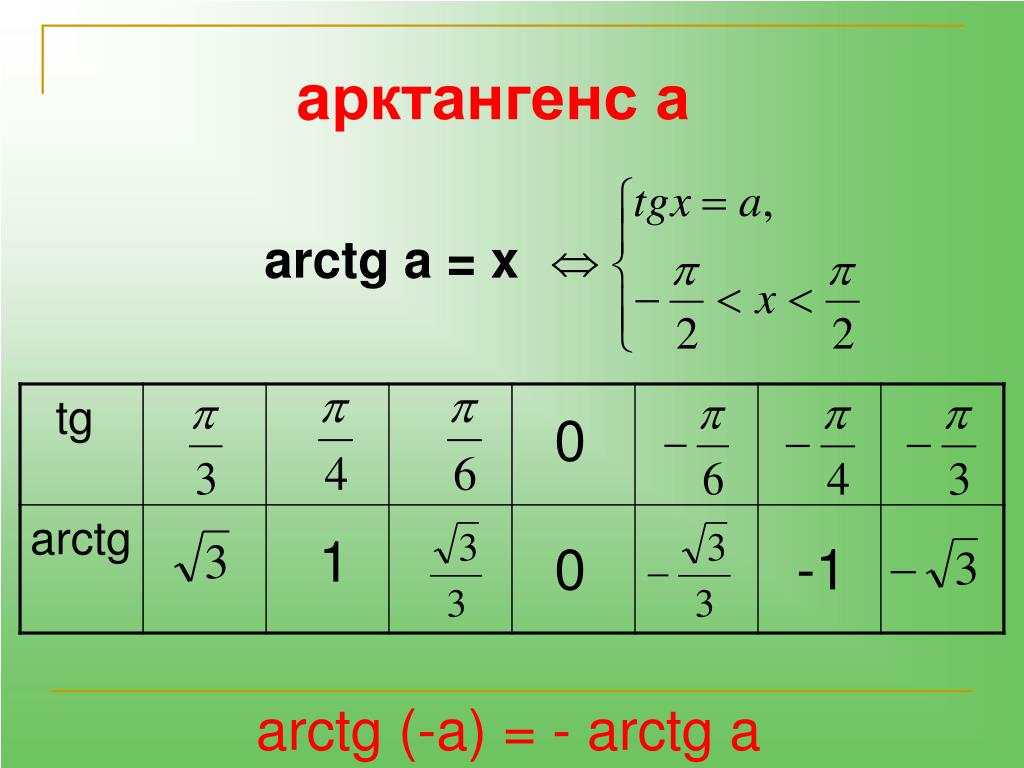 Тогда нахождение этого угла требует решения этого уравнения
для θ :
Тогда нахождение этого угла требует решения этого уравнения
для θ :
потому что ( θ ) = сЕсли это, скажем, простая задача о прямоугольном треугольнике и мы знаем , что угол θ должен быть где-то между 0 и 90°, тогда решение является единственным значением:
θ = arccos ( c )С другой стороны, если это более сложная задача и нам нужно найти все возможные углы косинус которых равен c тогда решение это весь набор значений:
θ = Arccos ( c )Решения в этих двух случаях следуют непосредственно из определения функции арккосинуса и соотношения арккосинуса.Обратите внимание, что если c больше 1 или меньше -1, то существуют нет реальных решений. Однако есть комплексные решения.
Оценка Arccos( c )
Если c число, то весь набор значений Arccos( c ) можно найти с помощью следующей процедуры.
 Обратитесь к графику справа
где точки — желаемые значения.
Обратитесь к графику справа
где точки — желаемые значения.- Первое значение (главное значение), обозначенное как θ PV , находится по формуле оценка arccos( c ) с помощью калькулятора или с помощью тренера по алгебре.
- Второе значение, называемое θ 2 , находится по формуле
используя симметрию кривой арккосинуса. Обратите внимание, что две синие стрелки в
графы имеют одинаковую длину. Это означает, что θ 2 настолько меньше 2π, насколько θ PV больше нуля. В виде формулы:
θ 2 = 2 π − θ PV
(Нажмите здесь, чтобы увидеть метод CAST для поиска θ 2 .) - Все остальные значения выше и ниже этих двух значений
можно найти из этих двух значений, добавив или
вычитание кратных 2π. Если мы используем целое число n для подсчета
которое кратно другим значениям, можно получить по этой формуле: Например, если мы допустим n = −1, тогда мы получим значения для
две нижние точки на графике.

- Если вы используете градусы вместо радианов, используйте следующие формулы вместо предыдущих:
Как использовать функцию арккосинуса в Algebra Coach
- Введите arccos(x) в текстовое поле, где x — аргумент.Аргумент должен быть заключен в скобки.
- Установите соответствующие параметры:
- Установите параметр arcsin, arccos и arctan . (Настройка возврата основного значения возвращает одно значение; параметр не оценивать полезен, если вам нужны все значения отношения Arc — но вам придется их вычислить самостоятельно.)
- Установите параметр точная / с плавающей запятой.(Точный режим позволяет использовать специальные значения.)
- Установите параметр режима градусов/радиан.
- Установите параметр p, который соответствует или не соответствует параметру π.
 (Если вы хотите, чтобы арккосинус возвращал специальные значения в радианном режиме
затем включите это.)
(Если вы хотите, чтобы арккосинус возвращал специальные значения в радианном режиме
затем включите это.) - Включите комплексные числа , если вы хотите иметь возможность оценивать арккосинус комплексного числа или числа больше 1.
- Нажмите кнопку «Упростить».
Алгоритм для функции арккосинуса
Нажмите здесь чтобы увидеть алгоритм, который компьютеры используют для вычисления функции арккосинуса.
Функция арктангенса
Исходная информация: Функция арктангенса является обратной функцией тангенса (пока функция тангенса ограничена определенной областью).Щелкните здесь для обзора обратных функций.Напомним, что функция тангенса принимает угол x в качестве входных данных и возвращает тангенс этого угла в качестве выходных данных:
Например, если 45° — вход, то 1.0 — выход.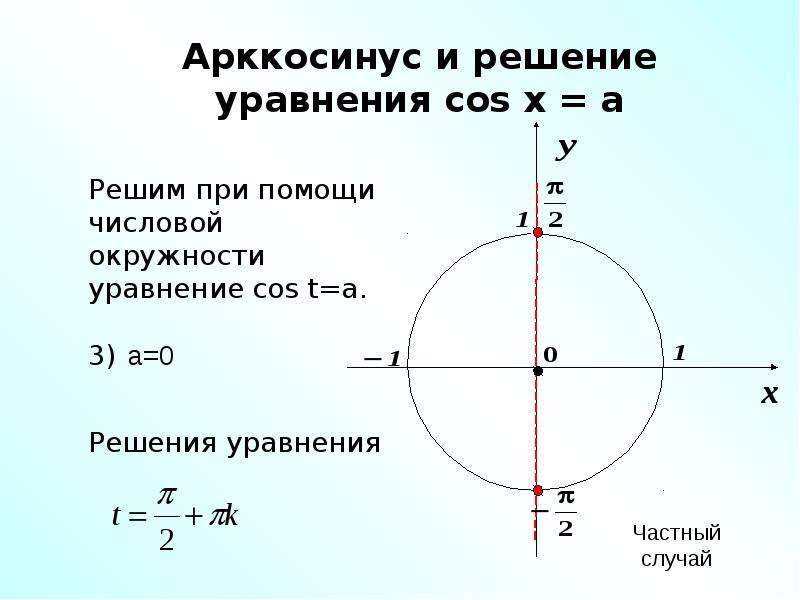 Здесь мы хотим создать обратную функцию, которая будет принимать 1.0 в качестве входных данных и
возврат 45° в качестве вывода.
Но есть проблема. Обратите внимание, что существует множество углов, тангенс которых равен 1,0: Мы говорим, что это отображение много к одному .Это означает, что обратная
отображение было бы один-ко-многим и, следовательно, не удовлетворяло бы
Требование «одно значение диапазона»
чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется арктангенс (с большой буквы и сокращением арктангенс) и функция называется арктангенс
(со строчной буквой «а» и аббревиатурой arctan). Вот как они определяются:
Здесь мы хотим создать обратную функцию, которая будет принимать 1.0 в качестве входных данных и
возврат 45° в качестве вывода.
Но есть проблема. Обратите внимание, что существует множество углов, тангенс которых равен 1,0: Мы говорим, что это отображение много к одному .Это означает, что обратная
отображение было бы один-ко-многим и, следовательно, не удовлетворяло бы
Требование «одно значение диапазона»
чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется арктангенс (с большой буквы и сокращением арктангенс) и функция называется арктангенс
(со строчной буквой «а» и аббревиатурой arctan). Вот как они определяются:Определение: Арктангенс x , обозначаемый как Arctan( x ), определяется как ‘ множество всех углов , тангенс которых равен х ’.Это отношение один ко многим . Вот пример: Определение: Арктангенс x , обозначаемый как arctan( x ), определяется как ‘ один угол между −π/2 и +π/2 радиан (или между −90° и +90°), тангенс которого равен x ’.
 Это функция один к одному . Вот пример: Определение: Из всех значений, возвращаемых отношением арктангенс,
тот, который совпадает со значением, возвращаемым функцией арктангенса
называется главным значением отношения арктангенса.(Примером является значение 45°, показанное выше красным.)
Это функция один к одному . Вот пример: Определение: Из всех значений, возвращаемых отношением арктангенс,
тот, который совпадает со значением, возвращаемым функцией арктангенса
называется главным значением отношения арктангенса.(Примером является значение 45°, показанное выше красным.)График: Красная кривая на графике справа — функция арктангенса. Обратите внимание, что для любого разрешения x он возвращает один значение между -π/2 и +π/2 радиан.
Если мы добавим серые кривые к красной кривой, то мы получим график Арктангенс отношения. Вертикальная линия, проведенная в любом месте будет касаться этого набора кривых во многих местах, а это означает, что отношение арктангенса вернет много значений.
На этом графике угол y измерен в радианах.
Если вы хотите измерить y в градусах , то
просто измените масштаб по вертикали так
что и проходят от −180 ° до 180 °, а не от
от -π до π радиан;
в остальном форма графика не меняется.
Если сравнить график арктангенса с графиком касательной тогда вы видите, что одно можно получить из другого, поменяв местами горизонтальная и вертикальная оси.
Домен и диапазон: Область определения функции арктангенса — это все действительные числа, а диапазон — от От −π/2 до π/2 радиан без учета (или от −90° до 90°).
Функцию арктангенса можно распространяется на комплексные числа, в которых случай домен все комплексные числа.
Специальные значения функции арктангенса (Нажмите здесь для более подробной информации)
Решение уравнения tan( θ ) = c для θ с помощью арктангенса и арктангенса
Предположим, что угол θ неизвестен, но известен его тангенс быть c .Тогда нахождение этого угла требует решения этого уравнения для θ :
тангенс ( θ ) = сЕсли это, скажем, простая задача о прямоугольном треугольнике и мы знаем , что угол θ должен быть где-то между 0 и 90°, тогда решение является единственным значением:
θ = арктангенс ( c )С другой стороны, если это более сложная задача и нам нужно найти все возможные углы , тангенс которых равен c тогда решение это весь набор значений:
θ = арктан ( c )Решения в этих двух случаях следуют непосредственно из определений функции арктангенса и отношения арктангенса.

Оценка Arctan( c )
Если c число, то весь набор значений Arctan( c ) можно найти с помощью следующей процедуры. Обратитесь к графику справа где точки — желаемые значения.
- Первое значение (главное значение), обозначенное как θ PV , находится по формуле оценка arctan( c ) с помощью калькулятора или с помощью тренера по алгебре.
- Все остальные значения выше и ниже этого значения можно найти с помощью
используя тот факт, что соседние значения удалены друг от друга на расстояние π.Если мы используем целое число n для подсчета кратных π, то другое число
значения можно получить по этой формуле:
θ = θ PV + π n
(Нажмите здесь, чтобы увидеть метод CAST для поиска θ 2 .) - Если вы используете градусы вместо радианов, используйте следующие формулы
вместо предыдущих:
θ = θ PV + 180° · n
Как использовать функцию арктангенса в Algebra Coach
- Введите arctan(x) в текстовое поле, где x — аргумент.
 Аргумент должен быть заключен в скобки.
Аргумент должен быть заключен в скобки. - Установите соответствующие параметры:
- Установите параметр arcsin, arccos и arctan . (Настройка возврата основного значения возвращает одно значение; параметр не оценивать полезен, если вам нужны все значения отношения Arc — но вам придется их вычислить самостоятельно.)
- Установите параметр точная / с плавающей запятой.(Точный режим позволяет использовать специальные значения.)
- Установите параметр режима градусов/радиан.
- Установите параметр p, который соответствует или не соответствует параметру π. (Если вы хотите, чтобы арктангенс возвращал специальные значения в радианном режиме затем включите это.)
- Включите комплексные числа , если вы хотите иметь возможность оценивать арктангенс комплексного числа.
- Нажмите кнопку «Упростить».

Алгоритм для функции арктангенса
Нажмите здесь чтобы увидеть алгоритм, который компьютеры используют для вычисления функции арктангенса.
Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
Арккосинус — математический способ
Арккосинус (обозначение: arccos или cos -1 ) является обратной функцией косинуса.То есть:
Поскольку арксинус и синус являются обратными функциями, их композиция тождественна. То есть:
Свойства арккосинуса
- Домен ( x ): домен для arcsin x находится в диапазоне от −1 до 1, .
- Диапазон (θ): диапазон или вывод для угловых синусов x — это все углы от 0 до π радиан.

Чтобы определить обратную функцию функции, она обязательно должна быть биективной (или однозначной).Функция косинуса не является инъективной в множестве вещественных чисел. По соглашению кодовый домен ограничен интервалом
, чтобы сделать функцию косинуса биективной.То есть, поскольку ни одна из шести тригонометрических функций не является взаимно однозначной, они должны иметь обратные функции. Таким образом, области определения тригонометрических функций ограничиваются соответствующим образом, так что они становятся взаимно однозначными функциями, и их обратные могут быть определены.
- Симметрия : нет.
- Возрастание-убывание : убывание.
- Непрерывность : непрерывно для всех разрешений x в домене.
- Производная функции арккосинуса :
- Интеграл функции арккосинуса :
- Конечное поведение : Пределы при приближении x к ±∞ не существуют.

Таблица арккосинуса
Арккосинус из наиболее распространенных значений :
Графическое представление функции арккосинуса
Чтобы лучше понять график арккосинуса , давайте сначала посмотрим на графическое представление функции косинуса:
Как мы видим на графике выше, косинус является периодическим, он не является взаимно однозначным, и график функции косинуса не проходит тест горизонтальной линии.Следовательно, у косинуса нет обратного, если мы не ограничим его область определения. Итак, по соглашению область определения косинуса обычно ограничивается интервалом (0, π).
График функции арккосинуса симметричен графику функции косинуса относительно биссектрисы первого и третьего квадрантов ( y = x ).
numpy.arccos — Руководство NumPy v1.22
Тригонометрический арккосинус, поэлементно.
Инверсия , потому что , так что если y = cos(x) , то x = arccos(y) .
- Параметры
- x array_like
x -координата на единичной окружности. Для реальных аргументов доменом является [-1, 1].
- out ndarray, None или кортеж ndarray и None, необязательный
Местоположение, в котором сохраняется результат. Если он предусмотрен, он должен иметь форма, на которую транслируются входные данные. Если не указано или Нет, возвращается только что выделенный массив. Кортеж (возможен только как аргумент ключевого слова) должен иметь длину, равную количеству выходов.
- где array_like, необязательный
Это условие передается по входу. В местах, где условие равно True, массив из будет установлен в результат ufunc. В другом месте массив из сохранит исходное значение. Обратите внимание, что если неинициализированный массив из создается по умолчанию
out=None, места внутри него, где условие равно False, будут остаются неинициализированными.
- **kwargs
Другие аргументы, содержащие только ключевые слова, см. документы ufunc.
- Возвращает
- угол ndarray
Угол луча, пересекающего единичную окружность при данной x -координата в радианах [0, пи]. Это скаляр, если x является скаляром.
Примечания
arccos — многозначная функция: для каждого x существует бесконечное число
много чисел z таких, что cos(z) = x .Конвенция заключается в том, чтобы вернуться
угол z , действительная часть которого лежит в [0, pi] .
Для типов входных данных с действительным знаком arccos всегда возвращает действительные выходные данные.
Для каждого значения, которое не может быть выражено как действительное число или бесконечность,
это дает nan и устанавливает недопустимый флаг ошибки с плавающей запятой .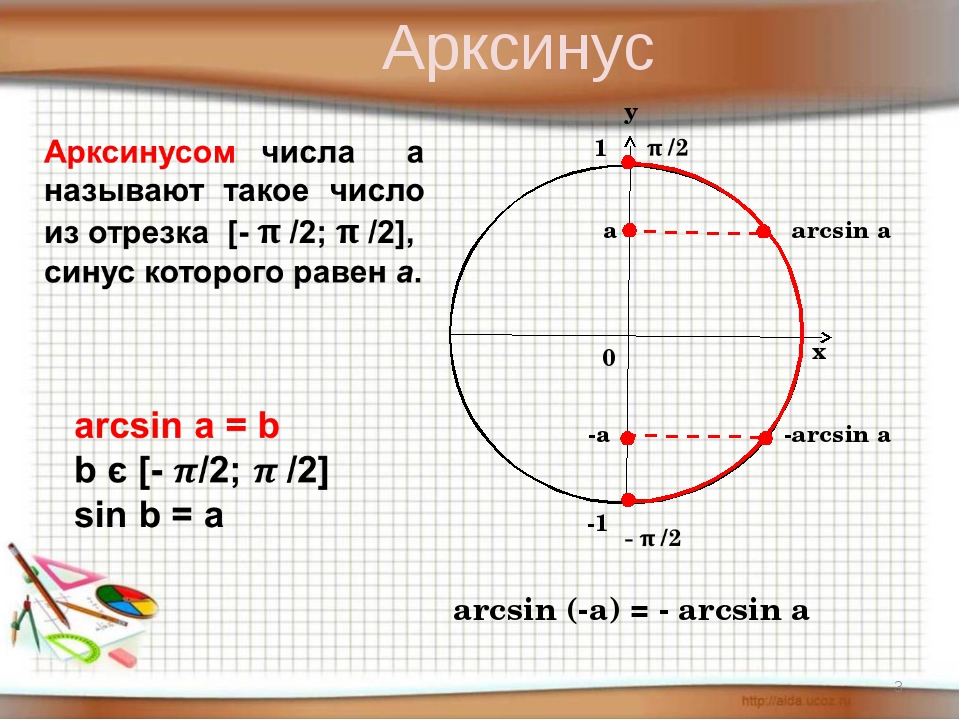
Для входных данных с комплексным знаком arccos представляет собой комплексную аналитическую функцию, которая
имеет ответвления [-inf, -1] и [1, inf] и является непрерывным от
сверху на первых и снизу на вторых.-1.
Ссылки
М. Абрамовиц и И.А. Стегун, «Справочник по математическим функциям», 10-е издание, 1964, стр. 79. https://personal.math.ubc.ca/~cbm/aands/page_79.htm
Примеры
Мы ожидаем, что arccos 1 будет равен 0, а -1 будет равен pi:
>>> np.arccos([1, -1]) массив([ 0. , 3.14159265])
Участок arccos:
>>> импортировать matplotlib.pyplot как plt
>>> x = np.linspace(-1, 1, число=100)
>>> пл.график (х, np.arccos (х))
>>> plt.axis('плотно')
>>> plt.show()
Каково точное значение Arccos 0? — Ответы на все
Каково точное значение Arccos 0?
№2
Какой косинус обратный 0?
арккос
Что такое решение Arccos 0.
 5?
5?Стол Arccos
| х | арккос(х) | |
|---|---|---|
| градусов | радиан | |
| -0.5 | 120° | 2π/3 |
| 0 | 90° | №/2 |
| 0,5 | 60° | №/3 |
Что такое cos 0 в радианах?
Синусы и косинусы для особых общих углов
| Градусы | Радиан | косинус |
|---|---|---|
| 60° | №/3 | 1/2 |
| 45° | №/4 | √2 / 2 |
| 30° | №/6 | √3 / 2 |
| 0° | 0 | 1 |
Параболы функционируют один к одному?
Функция f(x)=x2 не является взаимно однозначной, поскольку f(2) = f(-2).Его график представляет собой параболу, и множество горизонтальных линий дважды пересекают параболу.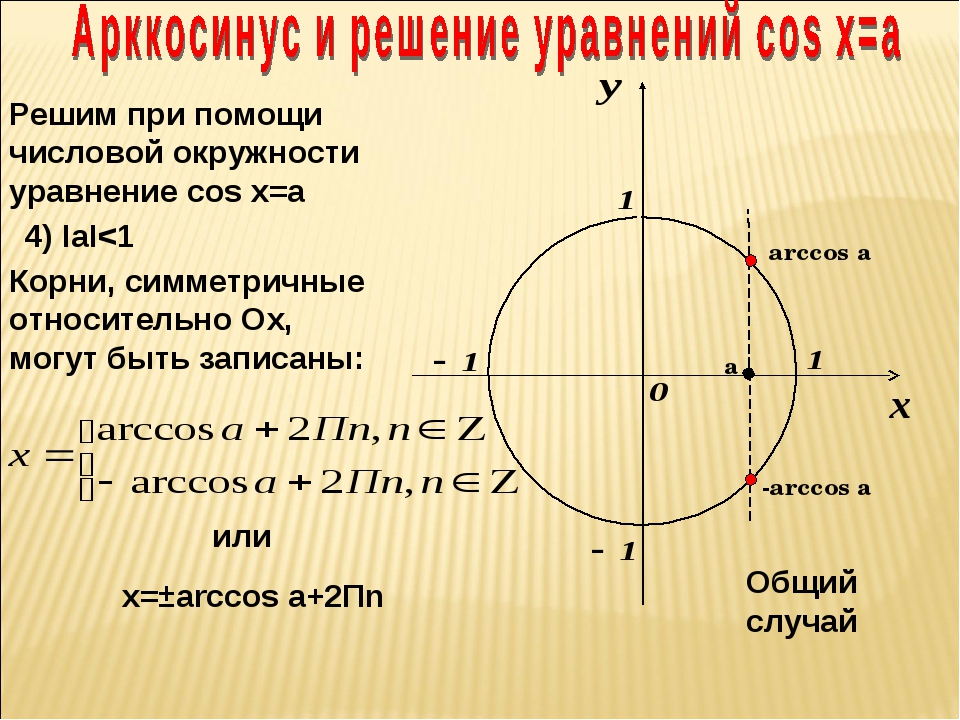 С другой стороны, функция f(x)=x 3 является взаимно однозначной. Если два действительных числа имеют одинаковый куб, то они равны.
С другой стороны, функция f(x)=x 3 является взаимно однозначной. Если два действительных числа имеют одинаковый куб, то они равны.
Как узнать, является ли функция взаимно однозначной, без построения графика?
Используйте тест горизонтальной линии. Если ни одна горизонтальная линия не пересекает график функции f более чем в одной точке, то функция является 1-к-1. Функция f имеет обратную функцию f−1 (читай обратную f) тогда и только тогда, когда функция является 1-к-1.
Как узнать, является ли функция взаимно однозначной?
Простой способ определить, является ли функция взаимно однозначной функцией, — использовать тест горизонтальной линии на графике функции. Для этого проведите через график горизонтальные линии. Если любая горизонтальная линия пересекает график более одного раза, то график не представляет однозначной функции.
Может ли граф быть непрерывным, но не дифференцируемым?
Непрерывный. Но функция может быть непрерывной, но не дифференцируемой.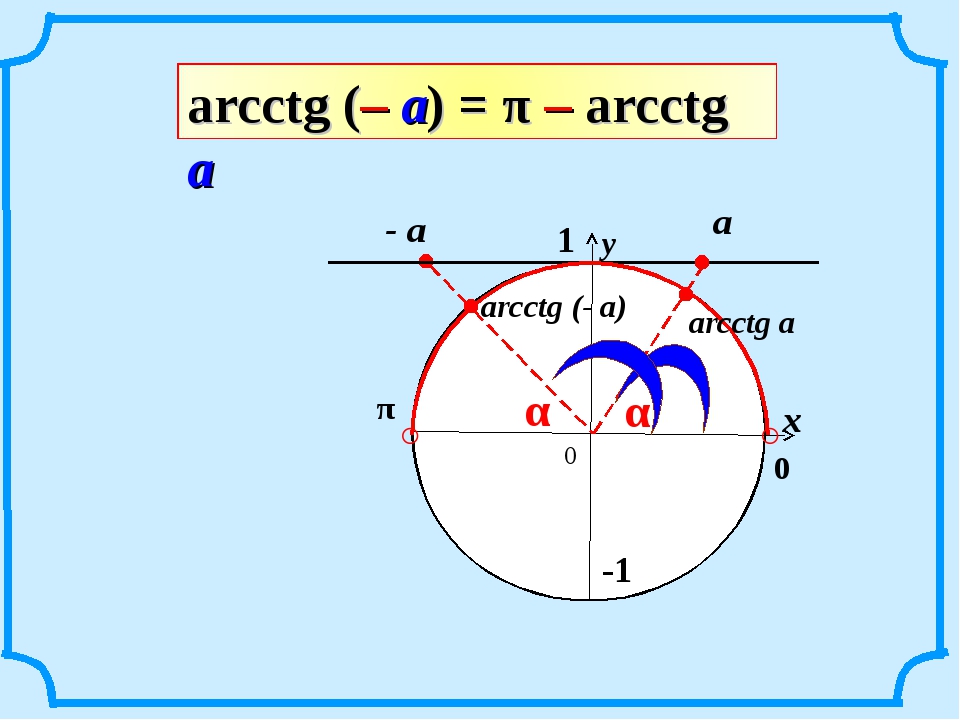 Например, функция абсолютного значения фактически непрерывна (хотя и не дифференцируема) при x=0.
Например, функция абсолютного значения фактически непрерывна (хотя и не дифференцируема) при x=0.
Как узнать, непрерывна ли функция в точке?
Сказать, что функция f непрерывна при x=c, то же самое, что сказать, что двусторонний предел функции при x=c существует и равен f(c).
Как определить, является функция непрерывной или дифференцируемой?
- Урок 2.6: Дифференцируемость: Функция дифференцируема в точке, если она имеет там производную.
- Пример 1:
- Если f(x) дифференцируема в точке x = a, то f(x) также непрерывна в точке x = a.
- е(х) — е(а)
- (f(x) − f(a)) = lim.
- (x − a) · f(x) − f(a) x − a Это нормально, поскольку x − a = 0 для предела в точке a.
- (х — а) предел.
- е(х) — е(а)
Как узнать, дифференцируема ли точка?
Кусочная функция дифференцируема в точке, если обе части имеют производные в этой точке, и производные в этой точке равны.
Всякая ли непрерывная функция дифференцируема?
В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. Обратное неверно: непрерывная функция не обязана быть дифференцируемой. Например, функция с изгибом, каспом или вертикальной касательной может быть непрерывной, но не дифференцируемой в месте аномалии.
Обратное неверно: непрерывная функция не обязана быть дифференцируемой. Например, функция с изгибом, каспом или вертикальной касательной может быть непрерывной, но не дифференцируемой в месте аномалии.
Обратные тригонометрические функции — Разделы по тригонометрии
Темы | Дом
19
Диапазон y = arcsin x
Диапазон y = арктангенс x
Диапазон y = arccos x
Диапазон y = угловых секунд x
sin −1 x .Обратный синус
Обратные отношения
УГЛЫ в исчислении будут измеряться в радианах. Таким образом, если нам дан, например, угол в радианах, мы можем оценить его функцию.
(Тема 13.)
Обратно, если нам дано, что значение функции синуса равно ½, то задача состоит в том, чтобы назвать угол x в радианах.
грех х = ½.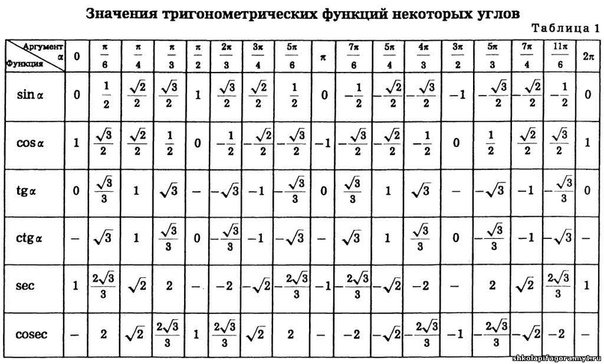
«Синус какого угла равен ½?»
Пишем однако: Оценить
угловой синус ½
« угол , синус которого равен ½.»
Функция
y = арксинус x
называется обратной функцией
.у = грех х .
дуги в x — это угла , синус которого равен числу x .
Строго говоря, угловых синусов x — это угловых синусов , синус которых равен x . Потому что в единичном круге длина этой дуги измеряется в радианах.Тема 14.
Теперь есть много углов, у которых синус равен ½. Это будет любой угол, соответствующий острый угол которого равен . Следовательно, мы должны ограничить диапазон 90 663 y 90 664 = arcsin 90 663 x 90 664 — значения этого угла — так, чтобы он действительно был функцией; чтобы оно было однозначным.
Как мы это сделаем? Мы ограничим их теми углами, которые имеют наименьшее абсолютное значение.
Они называются главными значениями y = arcsin x .
Так
угловых синусов ½ = .
Первый квадрант угла — это угол с наименьшим абсолютным значением, синус которого равен ½.
Пример 1. Вычислите arcsin (−½).
Раствор. Углы, синусы которых отрицательны, попадают в 3-й и 4-й квадранты. Угол наименьшего абсолютного значения находится в 4-м квадранте между 0 и -.
Угол, синус которого равен − x , является просто отрицательным значением угла, синус которого равен x .
дугового синуса (−½) = −arcsin (½) = −.
Таким образом, диапазоном функции y = arcsin x будут углы, попадающие в 1-й и 4-й квадранты, между — и .
Углы, синусы которых положительны, будут углами 1-го квадранта. Углы, синусы которых отрицательны, попадают в четвертую четверть.
Ограничение диапазона arcsin x эквивалентно ограничению домена sin x теми же значениями. Это будет иметь место со всеми ограниченными диапазонами, которые следуют.
Это будет иметь место со всеми ограниченными диапазонами, которые следуют.
sin −1 x . Обратный синус
Другим обозначением для arcsin x является sin −1 x . Прочтите: «Обратный синус x «. −1 здесь , а не показатель степени. (См. Тему 19 Предварительного исчисления.)
Задача 1. Оцените следующее в радианах.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
а) sin −1 0 = 0. (Тема 15.)
б) sin −1 1 = π/2. (Тема 15.)
c) sin −1 (−1) = −π/2. (Тема 15.)
| -π/3. |
| -π/6. |
Каждой тригонометрической функции соответствует обратная ей функция.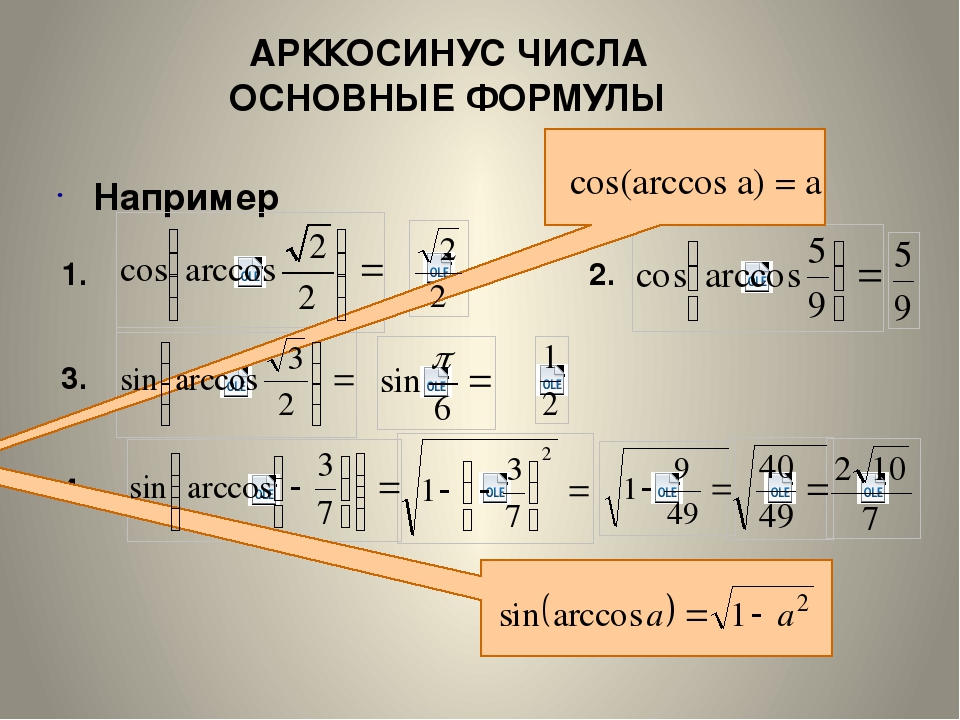
угловых синусов x ,
arccos x ,
арктан x ,
arccsc x ,
угловых секунды x ,
арккот x .
В каждом из них нам дано значение x тригонометрической функции.Мы должны назвать радиан углом , который имеет это значение.
В каждом случае мы должны ограничить его диапазон, чтобы функция была однозначной.
Диапазон y = арктангенс x
Как y = arcsin x , y = arctan x имеет наименьшие абсолютные значения в 1-м и 4-м квадрантах.
Обратите внимание, что y — угол , тангенс которого равен x — должен быть больше — и меньше .Ибо при этих квадрантных углах касательная не существует. (Тема 15.)
Углы, касательные которых положительны, будут углами 1-го квадранта. Углы, тангенсы которых отрицательны, попадут в четвертую четверть.
То же самое, что и с arcsin (− x ).
Угол, тангенс которого равен − x , является просто отрицательным значением угла, тангенс которого равен x .
| = | -θ. | |
| = | θ. | |
| Следовательно, | ||
| арктангенс (− x ) | = | −арктан x . |
Проблема 2. Оцените следующее.
| а) арктан 1 = | № 4 | б) арктан (−1) = | — | № 4 |
| c) tan −1 | = | № 3 | d) tan −1 (−) | = | — | № 3 |
| e) арктан 0 = | 0 | е) | = | — | № 6 |
Диапазон y = arccos x
Пример 2. Оцените arccos ½.
Оцените arccos ½.
| Решение . | arccos ½ = | № 3 | . |
| Угол в радианах, косинус которого равен ½, равен | № 3 | (60°). |
Проблема 3. Почему это не так?
arccos (−½) = −.
— угол 4-го квадранта. А в четвертом квадранте косинус положительный.
Урок 15.
Угол, косинус которого отрицательный, попадет во 2-й квадрант, где он будет иметь наименьшее абсолютное значение. (Тема 15.)
Косинус 2-го квадрантного угла равен отрицательной величине косинуса соответствующего ему острого угла, являющегося дополнением к нему.
Другими словами:
Угол θ, косинус которого равен − x , является дополнением
к углу, косинус которого равен x .
arccos (− x ) = π − arccos x .
Пример 3. Вычислите arccos (−½).
Решение . Мы видели:
arccos ½ = .
Таким образом, arccos (−½) является дополнением к углу, к которому мы должны прибавить, чтобы получить π.
+ θ = π.
Теперь это одна треть числа π. Следовательно, его дополнение составит два-
трети числа π: .
θ = arccos (−½) = .
Таким образом, диапазон y = arccos x будет от 0 до π.
Угол, косинус которого положителен, будет углом 1-го квадранта; угол, косинус которого отрицательный, попадет во 2-ю. Он будет дополнением угла 1-го квадранта.
Проблема 4. Оцените следующее.
| а) arccos 1 = | 0 | б) arccos (−1) = | № |
| c) cos −1 | 2 | = | № 4 | d) cos −1 (− | 2 | ) = | π − | № 4 | = | 3π 4 |
| д) | = | № 6 | е) | = | π − | № 6 | = | 5π 6 |
| g) arccos 0 = | № 2 |
*
Обратная зависимость выглядит следующим образом:
arccos x = θ тогда и только тогда, когда x = cos θ.
Например,
| arccos ½ = | № 3 | если и только если ½ = cos | № 3 | . |
В общем так и есть.
Задача 5.
а) арктан t = β тогда и только тогда, когда t = тангенс β.
b) угл.сек u = α тогда и только тогда, когда u = сек α.
c) arccos 1 = 0 тогда и только тогда, когда 1 = cos 0.
| d) arccot 1 = | № 4 | тогда и только тогда | 1 | = кроватка | № 4 | . |
Диапазон y = угловых секунд x
В математическом анализе sin -1 x , tan -1 x и cos -1 x являются наиболее важными обратными тригонометрическими функциями.Тем не менее, вот диапазоны, которые делают остальные однозначными.
Если x положительное значение, то значение обратной функции всегда равно первому квадранту угла или 0. Если x отрицательное, значение обратной функции попадет в квадрант, в котором прямая функция отрицательна. Таким образом, если 90 663 x 90 664 – отрицательное значение, то 90 663 x 90 664 угловых секунд попадет во 2-й квадрант, потому что именно там значение sec x отрицательно.
Единственная обратная функция ниже, в которой x может быть 0, это arccot x .аркот 0 = π/2.
Опять же, мы ограничиваем значения y теми углами, которые имеют наименьшее абсолютное значение.
Обратные отношения
Если поставить
f ( х ) = грех х
и
г ( x ) = arcsin x ,
, то по определению обратных функций (тема 19 предварительного исчисления):
f ( г ( x )) = x и г ( f ( x )) = x 9
sin(arcsin x ) = x и arcsin(sin x ) = x .
В частности, если
| arcsin x | = | г | |
| , тогда, взяв обратную функцию — синус — обеих сторон: | |||
| x | = | грех и . | |
Взяв обратную функцию обеих частей, мы извлекли или освободили аргумент x . (См. Тему 19 предварительного исчисления, Извлечение аргумента.) Это позволяет нам решать многие тригонометрические уравнения.
Пример 4. Решите для x :
| arcsin ( x — 1) = | . |
Решение .Взяв обратную функцию — синус — обеих сторон, мы можем освободить аргумент x − 1 и сразу записать —
.| х − 1 | = грех | = | 2 |
Следовательно,
| х | = 1 + | 2 | .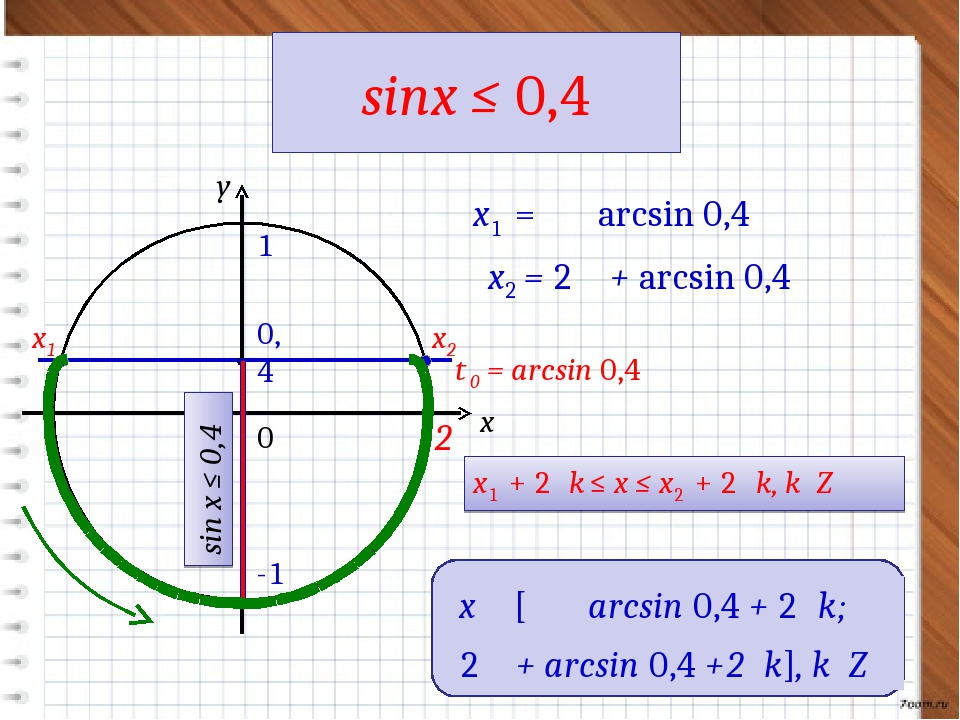 |
Задача 6. Решите для x :
тангенс ( х + 2) = 1.
| х + 2 | = | арктангенс 1 = | № 4 | . |
| х | = | № 4 | – 2. |
Задача 7. Решите для x :
, потому что x 2 = −1.
x 2 = arccos −1 = π.
х = ±.
Задача 8. Решите для x :
| sin −1 ( x 2 − 1) | = | 0. | |
| x 2 − 1 | = | угловой синус 0 | = 0 |
| x 2 | = | 1 | |
| x | = | ±1. | |
Теорема. Если
y = угловая секунда x ,
затем товар
sec y tan y никогда не бывает отрицательным.
Действительно, если y = угловые секунды x , то угол y попадает либо в первый, либо во второй квадрант. Когда угол y попадает в первый квадрант, тогда как sec y , так и тангенс y положительны.Следовательно, их произведение положительно.
Когда угол y попадает во второй квадрант, sec y и тангенс y оба отрицательны, так что их произведение снова положительно.
Если y = 0, то tan y = 0, следовательно, произведение sec y tan y равно 0,
Следовательно, это произведение никогда не бывает отрицательным.
(Эта теорема упоминается в доказательстве производной y = arcsec x .
 Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.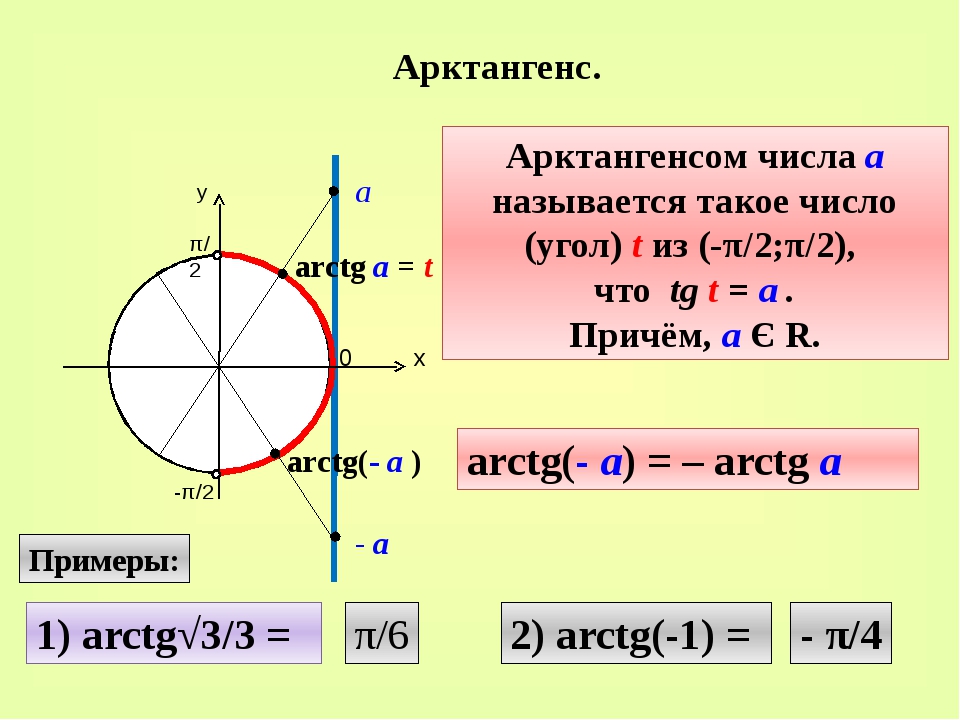 )
)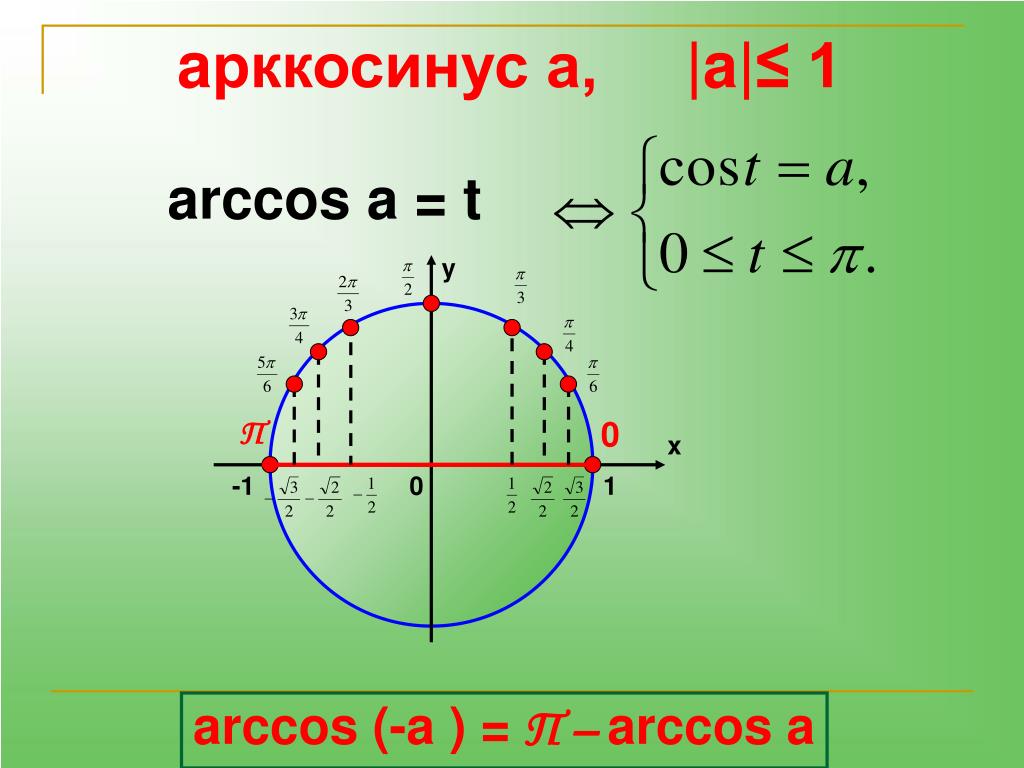

 )
)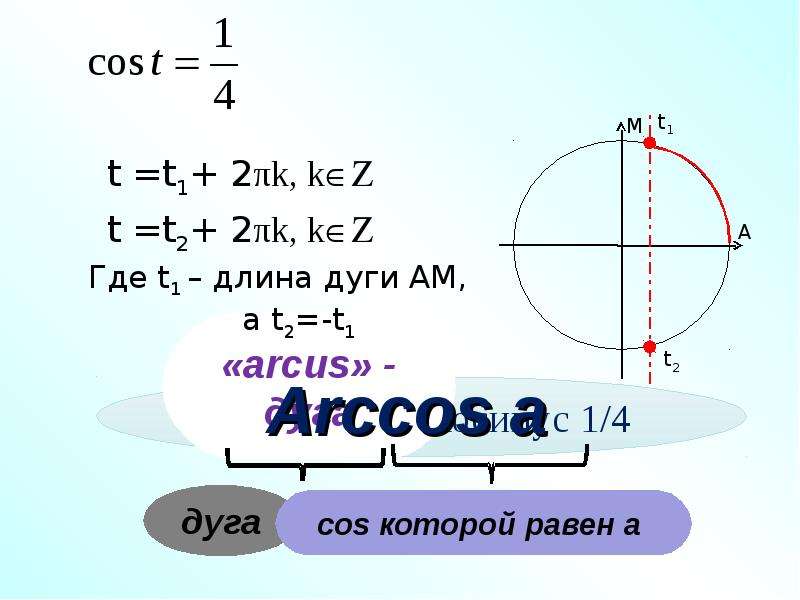 )
)
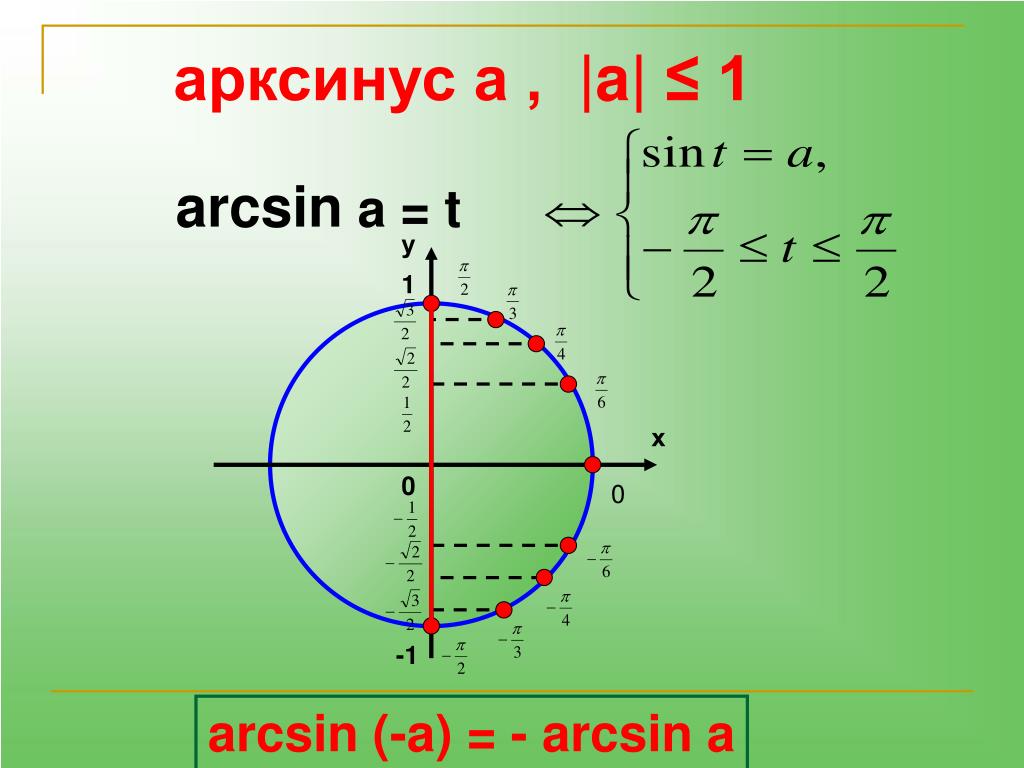 (Если вы хотите, чтобы арккосинус возвращал специальные значения в радианном режиме
затем включите это.)
(Если вы хотите, чтобы арккосинус возвращал специальные значения в радианном режиме
затем включите это.) Аргумент должен быть заключен в скобки.
Аргумент должен быть заключен в скобки.


