Синус, косинус и тангенс угла. Основное тригонометрическое тождество

Как измерить высоту дерева ? Как найти расстояние  до недоступной точки , вершины дерева (рис. 1)?

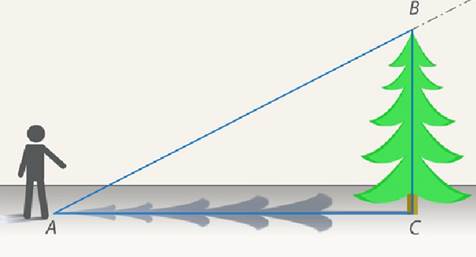
Рис. 1. Наглядный пример из 8 класса о введении тригонометрических функций острого угла

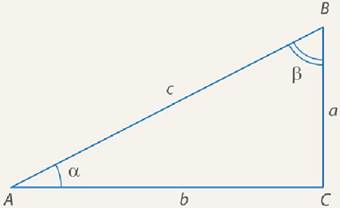
Рис. 2. Прямоугольный треугольник АВС

Пусть задан треугольник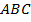

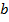 (рис. 2), a;  – катеты,  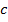– гипотенуза,  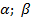– угол.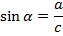

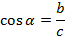
Поместим единичную полуокружность в координатную плоскость (рис. 3).

1. Рассмотрим 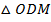, в нем , где 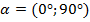, т. е. это прямоугольный треугольник, угол  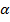– острый.

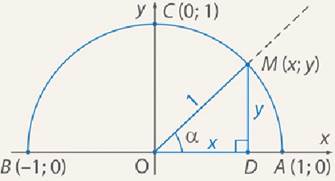
Рис. 3. Единичная окружность в координатной плоскости

Синусом угла 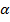 называется отношение противолежащего катета

 гипотенузе :

Но гипотенуза 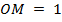, поэтому:

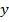 – ордината точки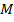

:

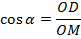
но 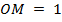, значит:

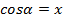
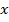 – абсцисса точки  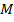единичной полуокружности.

Синус острого угла – это ордината, а косинус – это абсцисса точки 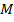 первой четверти.

Точка 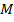 имеет единственную пару координат 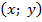, 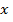– это косинус 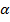,  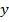– синус .

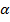Но абсциссу и ординату имеют все точки полуокружности.

2. Рассмотрим любой 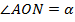 (рисунок 4), из отрезка .

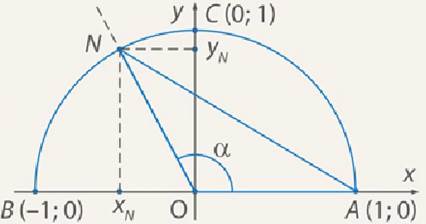
Рис. 4. 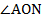 единичной окружности в координатной плоскости

Его луч  определяет единственную точку

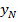 на полуокружности, ординату  назовем синусом 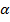, а абсциссу  – его косинусом.

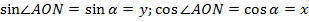
примем, что 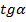 – это отношение  к

:

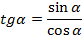
Дано: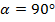

Найти: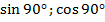

Решение

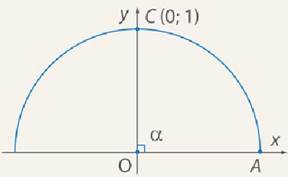
Рис. 5. Единичная окружность в координатной плоскости

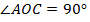(рис. 5)

По определению, точка

 с координатами (0;1) есть точка  с координатами :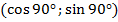

Примечание: т. к.  есть 0, то  не существует:

Ответ: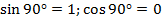

.

Задача решена.

Дано: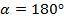

Найти: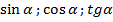

Решение

Рис. 6. Единичная окружность в координатной плоскости

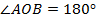(рис. 6)

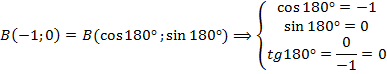
Ответ: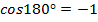

; ; .

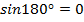Задача решена.

Рассмотрим некоторые свойства единичной полуокружности (рис. 7).

Она проецируется на ось 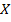 в отрезок 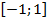, а на ось  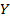в отрезок , отсюда вывод:

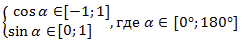
Рис. 7. Единичная полуокружность в координатной плоскости

В частности, косинус тупого угла отрицателен.

Уравнение единичной окружности с центром в точке 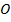 и :

Для

interneturok.ru

Замечательные отношения в прямоугольном треугольнике

Категория: ПланиметрияСправочные материалы

Елена Репина 2013-05-22 2013-08-04

  На всякий случай, уточним, что гипотенузой называется та сторона треугольника, что лежит против угла в 90 градусов, две оставшиеся стороны называются катетами прямоугольного треугольника.

Подробнее про прямоугольный треугольник здесь.

Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.

Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.

Тангенсом угла в прямоугольном треугольнике  называется отношение  противолежащего катета к прилежащему.

Котангенсом угла в прямоугольном треугольнике  называется отношение  прилежащего катета к противолежащему.

Бывает (и на ЕГЭ, ГИА), что приходится иметь дело с косинусами, синусами и тангенсами внешних углов треугольника.  Формулы приведения  позволяют увидеть, что есть еще и вот такая связь между смежными углами (помимо того, что их сумма равна 180):

 Смотрите подборку задач на применение указанных соотношений в статье «Прямоугольный треугольник. Вычисление длин и углов» часть I, часть II.

Автор: egeMax | комментариев 8 | Метки: шпаргалки-таблицы

egemaximum.ru

Свойства синуса, косинуса, тангенса и котангенса

В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.

Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α. Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и -α.

Знаки тригонометрических функций по четвертям

Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?

Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A0(1, 0) и, поворачивая ее вокруг точки O на угол α, попадем в точку A1(x, y). В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно. 

Для наглядности приведем иллюстрацию.

                                     

Угол α=30° лежит в первой четверти. Угол -210° является углом второй четверти. Угол 585° — угол третьей четверти. Угол -45° —  это угол четвертой четверти.

При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на координатных осях.

Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.

Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A1(x, y). Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.

Косинус — это абсцисса точки A1(x, y). В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.

                                  

zaochnik.com

1.2.1 Синус, косинус, тангенс, котангенс произвольного угла

Видеоурок: Синус, косинус, тангенс и котангенс угла

Лекция: Синус, косинус, тангенс, котангенс произвольного угла

Синус, косинус произвольного угла

Чтобы понять, что такое тригонометрические функции, обратимся к окружности с единичным радиусом. Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР, который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ. Так как окружность имеет радиус, равный единице, то ОР = R = 1.

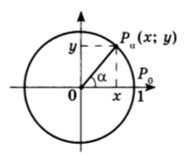
Если с точки Р опустить перпендикуляр на ось ОХ, то получим прямоугольный треугольник с гипотенузой, равной единице.

Если радиус-вектор двигается по часовой стрелке, то данное направление называется отрицательным, если же он двигается против движения часовой стрелки — положительным.

   

Синусом угла данной окружности, образованного радиусом-вектором ОР, является ордината точки Р вектора на окружности. 

То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.

Как данное значение было получено? Так как мы знаем, что синус произвольного угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе, получим, что

А так как R = 1, то sin(α) = y₀.

В единичной окружности значение ординаты не может быть меньше -1 и больше 1, значит,

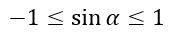
Синус принимает положительное значение в первой и второй четверти единичной окружности, а в третьей и четвертой — отрицательное.

Косинусом угла данной окружности, образованного радиусом-вектором ОР, является абсцисса точки Р вектора на окружности.

 

То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.

Косинус произвольного угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе, получим, что

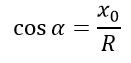
А так как R = 1, то cos(α) = x₀.

В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит,

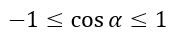
Косинус принимает положительное значение в первой и четвертой четверти единичной окружности, а во второй и в третьей — отрицательное.

Тангенсом произвольного угла считается отношение синуса к косинусу. 

Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.

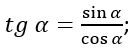
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов. Все остальные значения тангенс принимать может.

Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.

Котангенсом произвольного угла называется отношение косинуса к синусу.

 

Рассматривая прямоугольный треугольник — отношение прилежащего катета к противолежащему, то есть абсциссы к ординате.

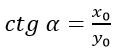
Так как ордината находится в знаменателе дроби, то котангенс не может существовать при угле альфа, равном нулю градусов.

Котангенс принимает те же значения в четвертях единичной окружности, что и тангенс.

Все перечисленные функции являются периодичными. Косинус и синус имеют период 360 градусов, то есть 2Пи, а тангенс и котангенс 180 градусов, то есть Пи.

cknow.ru

1.2.3 Синус, косинус, тангенс и котангенс числа

Итак, напоминаем, что при рассмотрении тригонометрических функций мы рассматриваем окружность, которая имеет единичный радиус. Данное упрощение используется для удобства. Все отношения справедливы для произвольных окружностей, с произвольным радиусом.

Пример. Давайте построим точки на единичной окружности, которые будут соответствовать повороту радиус-вектора на угол  

Решение. За начало отсчета принимаем точку Р₀. Угол, равный нулю радиан совпадает с данной точкой.

Мы знаем, что граничными считаются углы 0, π/2, π, 3π/2, 2π. Если использовать угол π/2 и разделить первую четверть на 3 равных части, то первое от начала отсчета разделение будет соответствовать углу π/6. На графике данная точка имеет место Р_π/6.

Чтобы получить угол π/4, необходимо прямой угол разделить на две части. Если необходимо отметить угол с отрицательным аргументом, необходимо пойти по часовой стрелке от начальной точки. Например, точка — π/4 будет находиться симметрично относительно оси ОХ в 4 четверти.

Давайте теперь вспомним, каким образом исчисляются углы, выраженные в радианной мере. Чему, например, соответствует в радианах π/4? Чтобы это узнать, следует числовое значение числа π разделить на 4.

3,14 : 4 = 0,78, если углу π/2 соответствует 3,14 : 2 = 1,57. Следовательно, на окружности угол, равный единице будет лежать выше π/4, но ниже π/2. Отрицательное значение угла симметрично положительному относительно оси ОХ.

Таким же образом следует найти и местонахождение угла, равного 2. Так как граничному прямому углу соответствует значение 1,57, то угол, равный двум, будет находиться во второй четверти.

Можно убедиться, что каждому числу соответствует своя ордината и абсцисса на плоскости.

Отсюда можно сделать вывод, что: 

Синус некоторого числа — это значение ординаты на плоскости, которая соответствует точке этого числа на единичной окружности.

Косинус некоторого числа — это значение абсциссы на плоскости, которая соответствует точке этого числа на единичной окружности.

Тангенс некоторого числа — это значение, полученное в результате отношения синуса к косинусу, иначе говоря, отношение ординаты к абсциссе.

Котангенс некоторого числа — это значение, полученное в результате отношения косинуса к синусу, иначе говоря, отношение абсциссы к ординате.

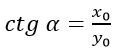
Синус и косинус имеют период, равный 6,28. Тангенс и котангенс имеет период, равный 3,14.

cknow.ru

Синус, косинус, тангенс, котангенс

В курсе геометрии 8 класса, мы с вами уже знакомились с понятиями синуса, косинуса, тангенса и котангенса для углов прямоугольного треугольника. Давайте вспомним их.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

 

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

 

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

;  

 

Еще мы с вами учили таблицу синусов, косинусов для углов в 30, 45 и 60 градусов. Давайте вспомним ее.

Сегодня на уроке мы познакомимся с понятиями синуса, косинуса, тангенса и котангенса произвольного угла из промежутка от 0 до 180º.

Построим в прямоугольной системе координат полуокружность радиус которой равен 1 так, чтобы центр этой полуокружности совпадал с началом координат.

Такую полуокружность мы назовем единичной полуокружностью. Из точки О давайте проведем произвольный луч h. Этот луч пересекает полуокружность с точке М (0;0). Угол между лучом h и положительным направлением оси Ox обозначим за α. Если луч h совпадает с положительным направлением оси Ox, то угол α равен 90º. Если луч h совпадает с осью Oy, то угол α= 90º. Если луч h совпадает с отрицательным направлением оси Ox, то угол α= 180º. Опустим из точки М перпендикуляр на ось Ox и рассмотрим прямоугольный треугольник ОМD.

Запишем элементы этого треугольника. Поскольку радиус полуокружности равен 1, значит, ОM=1. Так как координаты точки М равны x и y, то, очевидно, что МD=y, а ОD=x. Тогда , . Мы получили, что синус острого угла равен ординате точки М, а косинус угла α равен абсциссе точки М. По этим же формулам вычисляются синус и косинус для углов в 90º и 180º.

Для любого угла  синусом угла  называется ордината  точки , а косинусом угла  абсцисса  точки  

Поскольку речь у нас идет о единичной полуокружности, то ордината точки может изменятся от 0 до 1, значит, и синус угла α может принимать значения от 0 до 1. Абсцисса точки М может изменятся от -1 до 1, то есть и косинус угла α из промежутка от 0 до 180º может изменятся от -1 до 1.

Задача. Может ли:

а) абсцисса точки единичной полуокружности быть равна ?

б) ордината точки единичной полуокружности быть равна ?

Решение.

а) Поскольку полуокружность единичная, значит абсцисса точки должны принадлежать промежутку от -1 до 1, то есть абсцисса точки может быть равна , но не может быть равна 4 и 5.

б) Поскольку полуокружность располагается выше оси Ox, то ординаты точек могут быть только из промежутка от 0 до 1, то есть ордината точки может быть равна но не может быть равна .

Дополним известную нам таблицу синусов косинусов:

Для определения sin 0º и cos 0º давайте рассмотрим луч ОА. На единичной полуокружности точка А имеет координаты (1;0), значит , а .

Найдем теперь значение sin90 º и cos 90º. Этот угол задается лучом ОB. Координаты точки B равны (0;1), значит, , .

Проводя аналогичные рассуждения, получим , .

Задача. Определить координаты точки , если:

а) ;   б) ;   в) .

Решение.

а)

 

 

б)

 

 

в)

 

 

Ответ: ; ; .

Решим теперь обратную задачу.

Задача. Определить , , если:

а) ;   б) ;   в) .

Решение.

а)

 

б)

 

в)

 

Тангенсом острого угла мы называли отношение
. Эта же формула справедлива для произвольного угла от 0º до 180º. Однако, если угол равен  90º, то его cos 90º=0, а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить нельзя, поэтому для угла в 90º тангенс не существует. Таким образом, мы немного уточнили определение тангенса.

Тангенсом угла , называется .

Котангенсом острого угла мы называли отношение . Эта же формула справедлива для произвольного угла от 0º до 180º. Однако, если угол равен 0º или 180º, то sin равен 0, а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить нельзя, поэтому
,  –  не существует. Таким образом, мы немного уточнили определение котангенса.

Котангенсом угла , называется .

Задача. Определить , , если:

а) ;   б) ;   в) ;   г) ;   д) .

Решение.

 

а)

 

 

б)

 

 

в)

 

 

г)

 

 

д)

 

    

Давайте занесем полученные данные в таблицу и составим таблицу синусов, косинусов, тангенсов и котангенсов для углов 0º, 30º, 45º, 60º, 90º, 180º.

Подведем итоги урока. Сегодня на уроке мы определили, что Для любого угла  синусом угла  называется ордината  точки , а косинусом угла  абсцисса  точки  

Тангенсом угла ,  называется .

Котангенсом угла , называется .

Также мы дополнили известную нам таблицу значений синуса, косинуса и тангенсов для некоторых углов.

 

videouroki.net

Внеклассный урок — Синус, косинус, тангенс, котангенс

Синус, косинус, тангенс, котангенс

Прежде чем перейти к этому разделу, напомним определения синуса и косинуса, изложенные в учебнике геометрии 7-9 классов.

— Синус острого угла t прямоугольного треугольника равен отношению противолежащего катета к гипотенузе (рис.1):

sin t = b/c.

— Косинус острого угла t прямоугольного треугольника равен отношению прилежащего катета к гипотенузе (рис.1):

cos t = a/c.

Эти определения относятся к прямоугольному треугольнику и являются частными случаями тех определений, которые представлены в данном разделе.

Поместим тот же прямоугольный треугольник в числовую окружность (рис.2).

 

Мы видим, что катет b равен определенной величине y на оси Y (оси ординат), катет а равен определенной величине x на оси X (оси абсцисс). А гипотенуза с равна радиусу окружности (R).

Таким образом, наши формулы обретают иной вид.

Так как b = y, a = x, c = R, то:

              y                    x
sin t = —— , cos t = ——.
             R                    R

Кстати, тогда иной вид обретают, естественно, и формулы тангенса и котангенса.

Так как tg t = b/a,  ctg t = a/b, то, верны и другие уравнения:

tg t = y/x,

ctg = x/y.

Но вернемся к синусу и косинусу. Мы имеем дело с числовой окружностью, в которой радиус равен 1. Значит, получается:

              y
sin t = —— = y,
              1

               x
cos t = —— = x.
               1

Так мы приходим к третьему, более простому виду тригонометрических формул.

Эти формулы применимы не только к острому, но и к любому другому углу (тупому или развернутому).

 

Определения и формулы cos t, sin t, tg t, ctg t.

Косинусом числа t числовой окружности называют абсциссу этого числа:  cos t = x Синус числа t – это его ордината: sin t = y Тангенс числа t – это отношение синуса к косинусу:                                                                                      sin t                    π                                                                          tg t = ———,  где t  ≠  —  +  πk                                                                                      cos t                    2 Котангенс числа t – это отношение косинуса к синусу:                                                                                       cos t                                                                          ctg t = ———,  где t  ≠  πk                                                                                       sin t

 

Из формул тангенса и котангенса следует еще одна формула:

sin t        cos t                          πk                                                          tg t · ctg t = ——— · ——— = 1, при t ≠ ——                                                                                cos t        sin t                           2

 

Уравнения числовой окружности.

Из предыдущего раздела мы знаем одно уравнение числовой окружности: x2 + y2 = 1 Но поскольку x = cos t, а y = sin t, то получается новое уравнение: cos2 t + sin2 t = 1

 

Знаки синуса, косинуса, тангенса и котангенса в четвертях окружности:

	1-я четверть	2-я четверть	3-я четверть	4-я четверть
cos t	+	–	–	+
sin t	+	+	–	–
tg t, ctg t	+	–	+	–

 

Косинус и синус основных точек числовой окружности:

 

Как запомнить значения косинусов и синусов основных точек числовой окружности.

Прежде всего надо знать, что в каждой паре чисел значения косинуса стоят первыми, значения синуса – вторыми.

1) Обратите внимание: при всем множестве точек числовой окружности мы имеем дело лишь с пятью числами (в модуле):

      1      √2      √3
0;  —;  ——; ——;  1.
      2       2        2

Сделайте для себя это «открытие» — и вы снимете психологический страх перед обилием чисел: их на самом деле всего-то пять.

2) Начнем с целых чисел 0 и 1. Они находятся только на осях координат.

Не надо учить наизусть, где, к примеру, косинус в модуле имеет единицу, а где 0.

На концах оси косинусов (оси х), разумеется, косинусы равны модулю 1, а синусы равны 0.

На концах оси синусов (оси у) синусы равны модулю 1, а косинусы равны 0.

Теперь о знаках. Ноль знака не имеет. Что касается 1 – тут просто надо вспомнить самую простую вещь: из курса  7 класса вы знаете, что на оси х справа от центра координатной плоскости – положительные числа, слева – отрицательные; на оси у вверх от центра идут положительные числа, вниз – отрицательные. И тогда вы не ошибетесь со знаком 1.

3) Теперь перейдем к дробным значениям.

— Во всех знаменателях дробей – одно и то же число 2. Уже не ошибемся, что писать в знаменателе.

— В серединах четвертей косинус и синус имеют абсолютно одинаковое значение по модулю: √2/2. В каком случае они со знаком плюс или минус – см.таблицу выше. Но вряд ли вам нужна такая таблица: вы знаете это из того же курса 7 класса.

— Все ближайшие к оси х точки имеют абсолютно одинаковые по модулю значения косинуса и синуса: (√3/2; 1/2).

— Значения всех ближайших к оси у точек тоже абсолютно идентичны по модулю – причем в них те же числа, только они «поменялись» местами: (1/2; √3/2).

Теперь о знаках – тут свое интересное чередование (хотя со знаками, полагаем, вы должны легко разобраться и так).

Если в первой четверти значения и косинуса, и синуса со знаком плюс, то в диаметрально противоположной (третьей) они со знаком минус.

Если во второй четверти со знаком минус только косинусы, то в диаметрально противоположной (четвертой) – только синусы.

Осталось только напомнить, что в каждом сочетании значений косинуса и синуса первое число – это значение косинуса, второе число – значение синуса.

— Обратите внимание еще на одну закономерность: синус и косинус всех диаметрально противоположных точек окружности абсолютно равны по модулю. Возьмем, к примеру, противоположные точки π/3 и 4π/3:

cos π/3 = 1/2,       sin π/3 = √3/2
cos 4π/3 = -1/2,    sin 4π/3 = -√3/2

Различаются значения косинусов и синусов двух противоположных точек только по знаку. Но и здесь есть своя закономерность: синусы и косинусы диаметрально противоположных точек всегда имеют противоположные знаки.

Важно знать:

Значения косинусов и синусов точек числовой окружности последовательно возрастают или убывают в строго определенном порядке: от самого малого значения до самого большого и наоборот (см. раздел «Возрастание и убывание тригонометрических функций» — впрочем, в этом легко убедиться, лишь просто посмотрев на числовую окружность выше).

В порядке убывания получается такое чередование значений:

       √3      √2      1              1         √2          √3
1;  ——;  ——; —;  0;   – —;  – ——;  – ——; –1
        2        2       2              2          2             2

Возрастают они строго в обратном порядке.

Поняв эту простую закономерность, вы научитесь довольно легко определять значения синуса и косинуса.

 

Тангенс и котангенс основных точек числовой окружности.

Зная косинус и синус точек числовой окружности, легко можно вычислить их тангенс и котангенс. Делим синус на косинус — получаем тангенс. Делим косинус на синус — получаем котангенс. Результаты этого деления — на рисунке.

ПРИМЕЧАНИЕ: В некоторых таблицах значения тангенса и котангенса, равные модулю √3/3, указаны как 1/√3. Ошибки тут нет, так как это равнозначные числа. Если числитель и знаменатель числа 1/√3 умножить на √3, то получим √3/3.

Как запомнить значение тангенсов и котангенсов основных точек числовой окружности.

Здесь такие же закономерности, что и с синусами и косинусами. И чисел тут всего четыре (в модуле): 0, √3/3, 1, √3.

На концах осей координат – прочерки и нули. Прочерки означают, что в данных точках тангенс или котангенс не имеют смысла.

Как запомнить, где прочерки, а где нули? Поможет правило.

Тангенс – это отношение синуса к косинусу. На концах оси синусов (ось у) тангенс не существует.

Котангенс – это отношение косинуса к синусу. На концах оси косинусов (ось х) котангенс не существует.

В остальных точках идет чередование всего лишь трех чисел: 1, √3 и √3/3 со знаками плюс или минус. Как с ними разобраться? Запомните (а лучше представьте) три обстоятельства:

1) тангенсы и котангенсы всех середин четвертей имеют в модуле 1.

2) тангенсы и котангенсы ближайших к оси х точек имеют в модуле √3/3; √3.

3) тангенсы и котангенсы ближайших к оси у точек имеют в модуле √3; √3/3.

Не ошибитесь со знаками – и вы большой знаток.

Нелишне будет запомнить, как возрастают и убывают тангенс и котангенс на числовой окружности (см.числовую окружность выше или раздел «Возрастание и убывание тригонометрических функций»). Тогда еще лучше будет понятен и порядок чередования значений тангенса и котангенса.

 

Тригонометрические свойства чисел числовой окружности.

Представим, что определенная точка М имеет значение t.

Свойство 1:

sin (–t) = –sin t

cos (–t) = cos t

tg (–t) = –tg t

ctg (–t) = –ctg t

Пояснение. Пусть t = –60º  и  t = –210º.

cos –60º равен 1/2. Но cos 60º тоже равен 1/2. То есть косинусы –60º  и 60º  равны как по модулю, так и по знаку: cos –60º = cos 60º.

cos –210º равен –√3/2. Но cos 210º тоже равен –√3/2. То есть: cos –210º = cos 210º.

Таким образом, мы доказали, что cos (–t) = cos t.

sin –60º равен –√3/2. А sin 60º равен √3/2. То есть sin –60º и sin 60º равны по модулю, но противоположны по знаку.

sin –210º равен 1/2. А sin 210º равен –1/2. То есть sin –210º и sin 210º равны по модулю, но противоположны по знаку.

Таким образом, мы доказали, что sin (–t) = –sin t.

Посмотрите, что происходит с тангенсами и котангенсами этих углов – и вы сами легко докажете себе верность двух других тождеств, приведенных в таблице.

Вывод: косинус – четная функция, синус, тангенс и котангенс – нечетные функции.

Свойство 2: Так как t = t + 2πk, то:

sin (t + 2πk) = sin t

cos (t + 2πk) = cos t

Пояснение: t и t + 2πk – это одна и та же точка на числовой окружности. Просто в случае с 2πk  мы совершаем определенное количество полных оборотов по окружности, прежде чем приходим к точке t. Значит, и равенства, изложенные в этой таблице, очевидны.

 

Свойство 3: Если две точки окружности находятся друг против друга относительно центра О, то их синусы и косинусы равны по модулю, но противоположны по знаку, а их тангенсы и котангенсы одинаковы как по модулю, так и по знаку.

sin (t + π) = –sin t

cos (t + π) = –cos t

tg (t + π) = tg t

ctg (t + π) = ctg t

Пояснение: Пусть точка М находится в первой четверти. Она имеет положительное значение синуса и косинуса. Проведем от этой точки диаметр – то есть отрезок, проходящий через центр оси координат и заканчивающийся  в точке окружности напротив. Обозначим эту точку буквой N. Как видите, дуга MN равна половине окружности. Вы уже знаете, что половина окружности – это величина, равная π. Значит, точка N находится на расстоянии π от точки М. Говоря иначе, если к точке М прибавить расстояние π, то мы получим точку N, находящуюся напротив. Она находится в третьей четверти. Проверьте, и увидите: косинус и синус точки N – со знаком «минус» (x и y имеют отрицательные значения).

Тангенс и котангенс точки М имеют положительное значение. А тангенс и котангенс точки N? Ответ простой: ведь тангенс и котангенс – это отношение синуса и косинуса. В нашем примере синус и косинус точки N – со знаком «минус». Значит:

                     –sin t
tg (t + π) = ———— = tg t
                    –cos t

 

                      –cos t
ctg (t + π) = ———— = ctg t
                      –sin t

Мы доказали, что тангенс и котангенс диаметрально противоположных точек окружности имеют не только одинаковое значение, но и одинаковый знак.

 

Свойство 4: Если две точки окружности находятся в соседних четвертях, а расстояние между точками равно одной четверти окружности, то синус одной точки равен косинусу другой с тем же знаком, а косинус одной точки равен синусу второй с противоположным знаком.

π                         sin (t + —) = cos t                                      2

π                       cos (t + —) = –sin t                                     2

 

raal100.narod.ru