виды пирамид, формулы объема и площади поверхности, апофема, высота — Колпаков Александр Николаевич

Здесь собраны основные сведения о пирамидах и связанных с ней формулах и понятиях. Все они изучаются с репетитором по математике при подготовке к ЕГЭ.

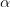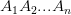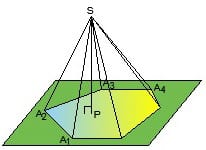Рассмотрим плоскость , многоугольник , лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой. Отрезки называются боковыми ребрами. Многоугольник называется основанием, а точка S — вершиной пирамиды. В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), птяиугольной (n=5) и так далее. Альтернативное название треугольной пирамиды –

тетраэдр. Высотой пирамиды называется перпендикуляр, опущенный из ее вершины к плоскости основания.

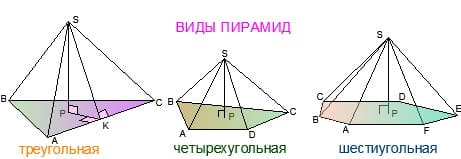
Пирамида называется правильной, если 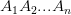правильный многоугольник, а основание высоты пирамиды (основание перпендикуляра) является его центром.

Комментарий репетитора:
Не путайте понятие «правильная пирамида» и «правильный тетраэдр». У правильной пирамиды боковые ребра совсем не обязательно равны ребрам основания, а в правильном тетраэдре все 6 ребер ребра равные. Это его определение. Легко доказать, что из равенства

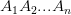следует совпадение центра P многоугольника с основанием высоты, поэтому правильный тетраэдр является правильной пирамидой.

Что такое апофема?
Апофемой пирамиды называется высота ее боковой грани. Если пирамида правильная, то все ее апофемы равны. Обратное неверно.

Репетитор по математике о своей терминологии: работа с пирамидами на 80% строится через два вида треугольников:
1) Содержащий апофему SK и высоту SP

2) Содержащий боковое ребро SA и его проекцию PA

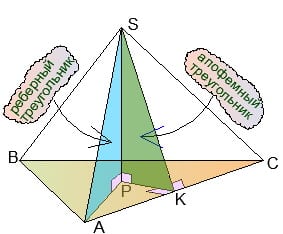
Чтобы упростить ссылки на эти треугольники репетитору по математике удобнее называть первый из них апофемным, а второй реберным. К сожалению, этой терминологии вы не встретите ни в одном из учебников, и преподавателю приходится вводить ее в одностороннем порядке.

Формула объема пирамиды:
1) 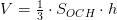, где 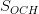– площадь основания пирамиды, а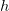

-высота пирамиды
2) , где – радиус вписанного шара, а 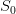– площадь полной поверхности пирамиды.
3) 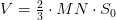, где MN – расстояние любыми двумя скрещивающимися ребрами, а – площадь параллелограмма, образованного серединами четырех оставшихся ребер.

Свойство основания высоты пирамиды:

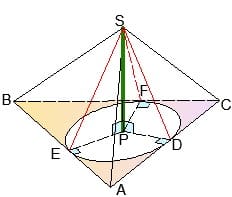Точка P (смотри рисунок) совпадает с центром вписанной окружности в основание пирамиды, если выполняется одно из следующих условий:
1) Все апофемы равны
2) Все боковые грани одинаково наклонены к основанию
3) Все апофемы одинаково наклонены к высоте пирамиды
4) Высота пирамиды одинаково наклонена ко всем боковым граням

Комментарий репетитора по математике: обратите внимание, что все пункты объединяет одно общее свойство: так или иначе везде участвуют боковые грани (апофемы — это их элементы). Поэтому репетитор может предложить менее точную, но более удобную для заучивания формулировку: точка P совпадает с центром вписанной окружности основание пирамиды, если имеется любая равная информация о ее боковых гранях. Для доказательства достаточно показать, что все апофемные треугольники равны.

Точка P совпадает с центром описанной около основания пирамиды окружностью, если верно одно их трех условий:
1) Все боковые ребра равны
2) Все боковые ребра одинаково наклонены к основанию
3) Все боковые ребра одинаково наклонены к высоте

Комментарий репетитора. Аналогично предыдущему пункту текст можно упростить и вместо этих условий произнести : «если имеется любая равная информация о боковых ребрах». При этом все апофемные треугольники будут равны

все проекции боковых ребер будет равны P будет равноудалена от всех вершин основания и поэтому окажется центром описанной окружности.

Площадь полной поверхности пирамиды:
Полощадью поверности пирамиды называется сумма площадей всех ее граней .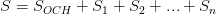
Площадь боковой поверхностии — сумма площадей всех боковых граней .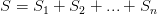
Если все апофемы равны (например в правильной пирамиде), то площадь ее боковой поверхности вычисляется по формуле

, где p — полупериметр основания, а SK-апофема.

Правильная треугольная пирамида однозначно определяется двумя параметрами: один плоский, а другой пространственный: к плоскому я отношу любой элемент правильного треугольника (кроме угла), а к пространственному любой связующий параметр между основанием и точкой S: апофема, высота, углы наклона ребер, граней, объем, площадь поверхности и др. При наличие в условии задачи этих двух начальных данных репетитор с учеником может найти у такой пирамиды все что угодно.

Пирамида — обязательный пункт подготовки к ЕГЭ по математике. Програмный минимум по стереометрии включает в себя все вышеуказанные сведения, кроме третьей формулы вычисления объема пирамиды.

Колпаков Александр,
репетитор по математике в Москве. Строгино

ankolpakov.ru

Правильная шестиугольная пирамида | Банк ЕГЭ

Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник.

Обозначения

• $SABCDEF$ — правильная шестиугольная пирамида
• $O$ — центр основания пирамиды
• $a$ — длина стороны основания пирамиды
• $h$ — длина бокового ребра пирамиды
• $S_{\text{осн.}}$ — площадь основания пирамиды
• $V_{\text{пирамиды}}$ — объем пирамиды

Площадь основания пирамиды

В основаниях пирамиды находится правильный шестиугольник со стороной $a$. По свойствам правильного шестиугольника, площадь основания пирамиды равна $$ S_{\text{осн.}}=\frac{3\sqrt{3}}{2}\cdot a^2 $$

Правильный шестиугольник в основании пирамиды

По свойствам правильного шестиугольника, треугольники AOB, BOC, COD, DOE, EOF, FOA являются правильными треугольниками. Отсюда следует, что $$ AO=OD=EO=OB=CO=OF=a $$ Проводим отрезок AE, пересекающийся с отрезком CF в точке M. Треугольник AEO равнобедренный, в нём $AO=OE=a,\ \angle EOA=120^{\circ}$. По свойствам равнобедренного треугольника $$ AE=a\cdot\sqrt{2(1-\cos EOA)}=\sqrt{3}\cdot a $$ Аналогичным образом приходим к заключению, что $ AC=CE=\sqrt{3}\cdot a $, $FM=MO=\frac{1}{2}\cdot a$.

Находим $SO$

Прямая $SO$ является высотой пирамиды, поэтому $\angle SOF=90^{\circ}$. Треугольник $SOF$ прямоугольный, в нем $FO=a,\ FS=h$. По свойствам прямоугольного треугольника $$ SO=\sqrt{FS^2-FO^2}=\sqrt{h^2-a^2} $$

Объем пирамиды

Объем пирамиды вычисляется как треть произведения площади ее основания на ее высоту. Высотой правильной пирамиды является отрезок $SO$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{\text{пирамиды}}=\frac{1}{3}\cdot S_{\text{осн.}}\cdot SO=\frac{\sqrt{3}}{2}\cdot a^2 \cdot \sqrt{h^2-a^2} $$

Находим $ST$ и $TO$

Пусть точка $T$ является серединой ребра $AF$. Треугольник $AOF$ правильный, поэтому, по свойствам правильного треугольника $$ TO=\frac{\sqrt{3}}{2}\cdot a $$ Треугольник $STO$ прямоугольный, высота $SO$ равна $\sqrt{h^2-a^2}$. По теореме Пифагора $$ ST=\sqrt{SO^2+TO^2}=\sqrt{h^2-\frac{1}{4}\cdot a^2} $$

bankege.ru

Пирамида с равными боковыми рёбрами — урок. Геометрия, 10 класс.

Чтобы было легче запомнить, можно представить вид пирамиды сверху

Проекции рёбер равны, через их концы можно провести окружность.

У пирамиды могут быть равны боковые рёбра тогда, когда около многоугольника основания можно описать окружность.

    

Главные зависимости для многоугольников, около которых можно описать окружность

Многоугольник, около которого можно описать окружность	Центр описанной окружности	Формулы
произвольный треугольник	точка пересечения серединных перпендикуляров	R=abc4S;asinα=2R, где \(a, b, c\) — стороны треугольника
равнобедренный треугольник	точка пересечения серединных перпендикуляров находится на высоте, проведённой к основанию	R=abc4S;asinα=2R,
прямоугольный треугольник	середина гипотенузы	\(R\) — половина гипотенузы
прямоугольник	точка пересечения диагоналей	\(R\) — половина диагонали

 

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для таких пирамид нельзя использовать формулы правильной пирамиды для вычисления площади боковой поверхности, площадь боковой поверхности находят, сложив площади всех боковых граней пирамиды.

Ss=S1+S2+…

 

Если основание — правильный многоугольник и все боковые грани равны, то пирамида является правильной.

www.yaklass.ru

Правильная треугольная пирамида (правильная пирамида с треугольником в основании). Тетраэдр

В этом уроке приведены определение и свойства правильной треугольной пирамиды и ее частного случая — тетраэдра (см. ниже). Ссылки на примеры решения задач приведены в конце урока.

Определение

Правильная треугольная пирамида — это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.

На рисунке обозначены:
ABC — Основание пирамиды
OS — Высота
KS — Апофема
OK — радиус окружности, вписанной в основание
AO — радиус окружности, описанной вокруг основания правильной треугольной пирамиды
SKO — двугранный угол между основанием и гранью пирамиды (в правильной пирамиде они равны)

Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC). Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже).

Свойства правильной треугольной пирамиды:

• боковые ребра правильной пирамиды равны
• все боковые грани правильной пирамиды являются равнобедренными треугольниками
• в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу
• если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3  (пи делить на 3 или 60 градусов ).
• площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
• вершина пирамиды проецируется на основание в центр правильного равностороннего треугольника,, который является центром вписанной окружности и точкой пересечения медиан

Формулы для правильной треугольной пирамиды

Формула объема правильной треугольной пирамиды:

где

V — объем правильной пирамиды, имеющей в основании правильный (равносторонний) треугольник
h — высота пирамиды
a — длина стороны основания пирамиды
R — радиус описанной окружности
r — радиус вписанной окружности

Поскольку правильная треугольная пирамида является частным случаем правильной пирамиды, то формулы, которые верны для правильной пирамиды, верны и для правильной треугольной — см. формулы для правильной пирамиды.

Примеры решения задач:

Тетраэдр

Частным случаем правильной треугольной пирамиды является тетраэдр.

Тетраэдр — это правильный многогранник (правильная треугольная пирамида) у которой все грани являются правильными треугольниками.

У тетраэдра:

• Все грани равны
• 4 грани, 4 вершины и 6 ребер
• Все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны

Медиана тетраэдра — это отрезок, соединяющий вершину с точкой пересечения медиан противоположной грани (медиан равностороннего треугольника, противолежащего вершине)

Бимедиана тетраэдра — это отрезок, соединяющий середины скрещивающихся рёбер (соединяющий середины сторон треугольника, являющегося одной из граней тетраэдра)

Высота тетраэдра — это отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани (то есть является высотой, проведенной от любой грани, также совпадает с центром описанной окружности).

Тетраэдр обладает следующими свойствами:

• Все медианы и бимедианы тетраэдра пересекаются в одной точке
• Эта точка делит медианы в отношении 3:1, считая от вершины
• Эта точка делит бимедианы пополам

Площадь, объем, высота, радиус вписанной и описанной окружности и другие формулы для тетраэдра

См. пример задачи: формулы и свойства тетраэдра.

Содержание главы:
 Пирамида с равнобедренным треугольником в основании | Описание курса | Периметр основания правильной треугольной пирамиды 

   

profmeter.com.ua

Пирамида

Нам хорошо известны великие египетские пирамиды, каждый может представить себе, как они выглядят. Это представление и поможет нам разобраться в особенностях такой геометрической фигуры, как пирамида.

Пирамида – это многогранник, состоящий из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, – вершины пирамиды и всех отрезков, соединяющих вершину с точками основания. Отрезки, которые соединяют вершину пирамиды с вершинами основания, называются боковыми рёбрами. На рис. 1 изображена пирамида SABCD. Четырёхугольник ABCD – основание пирамиды, точка S – вершина пирамиды, отрезки SA, SB, SC и SD –  рёбра пирамиды.

Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания. На рис. 1 SO – высота пирамиды.

Пирамида называется n-угольной, если её основанием является n-угольник. На рисунке 1 изображена четырёхугольная пирамида. Треугольная пирамида называется тетраэдром.

Пирамида называется правильной, если её основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника. Боковые рёбра у правильной пирамиды равны, а, следовательно, боковые грани являются равнобедренными треугольниками. В правильной пирамиде высота боковой грани, проведённая из вершины пирамиды, называется апофемой.

Пирамида обладает рядом свойств.

Все диагонали пирамиды принадлежат её граням.

Если все боковые ребра равны, то:

• около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;
• боковые ребра образуют с плоскостью основания равные углы, и, наоборот, если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

Если боковые грани наклонены к плоскости основания под одним углом, то:

• в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
• высоты боковых граней равны;
• площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.

Рассмотрим формулы для нахождения объёма, площади поверхности пирамиды.

Объём пирамиды можно вычислить по следующей формуле:

V = 1/3 Sh,

где S – площадь основания, а h – высота.

Чтобы найти площадь полной поверхности пирамиды, необходимо воспользоваться формулой:

S_p = S_b + S_o,

где S_p  – площадь полной поверхности, S_b – площадь боковой поверхности, S_o – площадь основания.

Усечённой пирамида – это многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию. Грани усечённой пирамиды, лежащие в параллельных плоскостях, называются основаниями усечённой пирамиды, остальные грани называются боковыми гранями. Основаниями усечённой пирамиды являются подобные многоугольники, боковыми гранями – трапеции. Усечённая пирамида, которая получается из правильной пирамиды, называется правильной усечённой пирамидой. Боковые грани правильной усечённой трапеции представляют собой равные равнобокие трапеции, их высоты называются апофемами.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Помогите!!! что лежит в основании правильной четырёхугольной пирамиды? квадрат или треугольник? если можно по скорее

нухно уметь инетом пользоваться, вот: Материал из Википедии — свободной энциклопедии Пирами́да (др. -греч. πυραμίς, род. п. πυραμίδος) — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д..

ошиблась, квадрат

Пирамида четырехугольная — значит, в основании 4 угла, то есть у правильной основание — это квадрат.

квадрат!! квадрат!! квадрат!!

Раз 4 угольная, значит квадрат.

раз четыре угла следовательно прямоугольник.

а вдруг ромб???

touch.otvet.mail.ru

Четырехугольная пирамида в задаче C2

9 марта 2012

Решая задачу C2 методом координат, многие ученики сталкиваются с одной и той же проблемой. Они не могут рассчитать координаты точек, входящих в формулу скалярного произведения. Наибольшие трудности вызывают пирамиды. И если точки основания считаются более-менее нормально, то вершины — настоящий ад.

Сегодня мы займемся правильной четырехугольной пирамидой. Есть еще треугольная пирамида (она же — тетраэдр). Это более сложная конструкция, поэтому ей будет посвящен отдельный урок.

Для начала вспомним определение:

Правильная пирамида — это такая пирамида, у которой:

1. В основании лежит правильный многоугольник: треугольник, квадрат и т.д.;
2. Высота, проведенная к основанию, проходит через его центр.

В частности, основанием четырехугольной пирамиды является квадрат. Прямо как у Хеопса, только чуть поменьше.

Ниже приведены расчеты для пирамиды, у которой все ребра равны 1. Если в вашей задаче это не так, выкладки не меняются — просто числа будут другими.

Вершины четырехугольной пирамиды

Итак, пусть дана правильная четырехугольная пирамида SABCD,где S — вершина, основание ABCD — квадрат. Все ребра равны 1. Требуется ввести систему координат и найти координаты всех точек. Имеем:

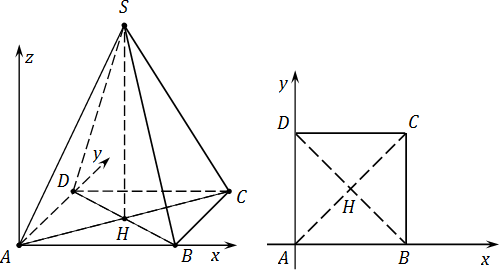
Вводим систему координат с началом в точке A:

1. Ось OX направлена параллельно ребру AB;
2. Ось OY — параллельно AD. Поскольку ABCD — квадрат, AB ⊥ AD;
3. Наконец, ось OZ направим вверх, перпендикулярно плоскости ABCD.

Теперь считаем координаты. Дополнительное построение: SH — высота, проведенная к основанию. Для удобства вынесем основание пирамиды на отдельный рисунок. Поскольку точки A, B, C и D лежат в плоскости OXY, их координата z = 0. Имеем:

1. A = (0; 0; 0) — совпадает с началом координат;
2. B = (1; 0; 0) — шаг на 1 по оси OX от начала координат;
3. C = (1; 1; 0) — шаг на 1 по оси OX и на 1 по оси OY;
4. D = (0; 1; 0) — шаг только по оси OY.
5. H = (0,5; 0,5; 0) — центр квадрата, середина отрезка AC.

Осталось найти координаты точки S. Заметим, что координаты x и y точек S и H совпадают, поскольку они лежат на прямой, параллельной оси OZ. Осталось найти координату zдля точки S.

Рассмотрим треугольники ASH и ABH:

1. AS = AB = 1 по условию;
2. Угол AHS = AHB = 90°, поскольку SH — высота, а AH ⊥ HB как диагонали квадрата;
3. Сторона AH — общая.

Следовательно, прямоугольные треугольники ASH и ABHравны по одному катету и гипотенузе. Значит, SH = BH = 0,5 · BD.Но BD — диагональ квадрата со стороной 1. Поэтому имеем:

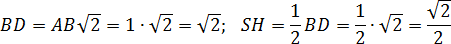
Итого координаты точки S:

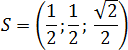
В заключение, выпишем координаты всех вершин правильной прямоугольной пирамиды:

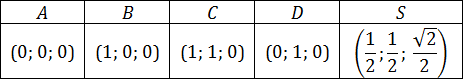
Что делать, когда ребра разные

А что, если боковые ребра пирамиды не равны ребрам основания? В этом случае рассмотрим треугольник AHS:

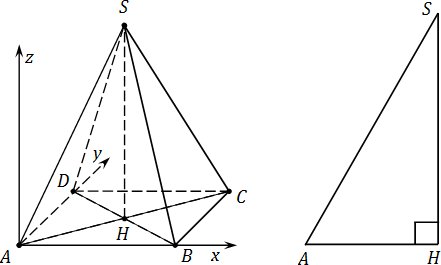
Треугольник AHS —прямоугольный, причем гипотенуза AS — это одновременно и боковое ребро исходной пирамиды SABCD.Катет AH легко считается: AH = 0,5 · AC. Оставшийся катет SH найдем по теореме Пифагора. Это и будет координата zдля точки S.

Задача. Дана правильная четырехугольная пирамида SABCD, в основании которой лежит квадрат со стороной 1. Боковое ребро BS = 3. Найдите координаты точки S.

Координаты x и y этой точки мы уже знаем: x = y = 0,5. Это следует из двух фактов:

1. Проекция точки S на плоскость OXY — это точка H;
2. Одновременно точка H — центр квадрата ABCD, все стороны которого равны 1.

Осталось найти координату точки S. Рассмотрим треугольник AHS. Он прямоугольный, причем гипотенуза AS = BS = 3,катет AH — половина диагонали. Для дальнейших вычислений нам потребуется его длина:

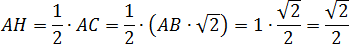
Теорема Пифагора для треугольника AHS:AH ² + SH ² = AS². Имеем:

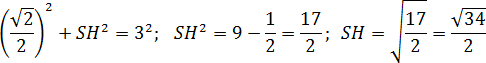
Итак, координаты точки S:

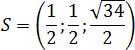
Смотрите также:

1. Четырехугольная пирамида: как найти координаты вершин
2. Введение системы координат
3. Тест к уроку «Что такое логарифм» (средний)
4. Основное тригонометрическое тождество
5. Тригонометрические функции
6. Тест по задачам B14: средний уровень, 2 вариант

www.berdov.com