Дифференциальные уравнения Основные понятия
Уравнения, связывающие независимую переменную, искомую функцию и ее производные, называются дифференциальными.
Общий вид дифференциальных уравнений: F (x,y,y’,y’’..y’’’) = 0
Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Наивысший порядок производной, входящей в ДУ, называется порядкомэтого уравнения.
Процесс отыскания решения ДУ называется его интегрированием.
Дифференциальные уравнения первого порядка
Обыкновенным
дифференциальным уравнением первого
порядка называется уравнение вида F(x,
y, y‘
)=0, где F — известная функция трех переменных, x —
независимая переменная, y(
Уравнение y‘=f(x, y) устанавливает связь между координатами точки (x, y) и угловым коэффициентом y‘ касательной к интегральной кривой, проходящей через эту точку.
Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:
P(x;y)dx+Q(x;y)dy=0,
Где P(x;y) и Q(x;y) – известные функции. Уравнение P(x;y)dx+Q(x;
y)dy=0 удобно тем, что переменные в нем равноправны, т.е. любую из них можно рассматривать как функцию другой.
Если дифференциальное уравнение первого порядка y‘=f(x, y), имеет решение, то решений у него, вообще говоря, бесконечно много и эти решения могут быть записаны в виде y=φ(x,C), где C — произвольная константа.
Функция y=φ(x,C) называется общим решением дифференциального уравнения 1-го порядка. Она содержит одну произвольную постоянную и удовлетворяет условиям:
Функция y=φ(x,C) является решением ДУ при каждом фиксированном значении С.
Каково бы ни было начальное условие y(x0)= y0, можно найти такое значение постоянной С=С0 , что
Частным решением ДУ первого порядка называется любая функция y=φ(x,C0), полученная из общего решения y=φ(x,C) при конкретном значении постоянной С=С0.
Задача отыскания решения ДУ первого порядка P(x;y)dx+Q(x;y)dy=0, удовлетворяющего заданному начальному условию y(x0)= y0 , называется задачей Коши.
Теорема(существования и единственности решения задачи Коши).
Если в уравнении y‘=f(x, y) функция f(x, y) и ее частная производная f‘y( x, y) непрерывны в некоторой области D, содержащей точку (x0 ; y0 ), то существует единственное решение y=φ(x) этого уравнения, удовлетворяющее начальному условию y(x0)= y0 . (без доказательства)
Уравнения с разделяющимися переменными
Наиболее простым ДУ первого порядка является уравнение вида
P(x)dx+Q(y)dy=0.
В нем одно слагаемое зависит только от x, а другое — от y. Иногда такие ДУ называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получаем:
∫ P(x)dx+∫Q(y)dy=с – его общий интеграл.
P1(x) . Q1(y) . dx+ P2(x) . Q2(y) . dy=0.
Особенность этого уравнения в том, что коэффициенты представляют собой произведения двух функций, одна из которых зависит только от х другая – только от у.
Уравнение P1(x) . Q1(y) . dx+ P2(x) . Q2(y) . dy=0 легко сводится к уравнению P(x)dx+Q
(y)dy=0. путем почленного деления его на Q1(y) . P2(x)≠0. Получаем: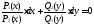 ,
,  —
общий интеграл.
—
общий интеграл.
studfile.net
Обыкновенные дифференциальные уравнения.
Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.
Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:
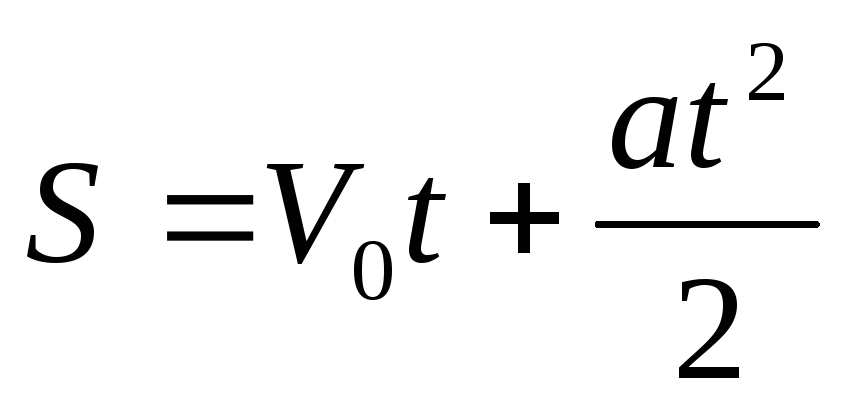
В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.
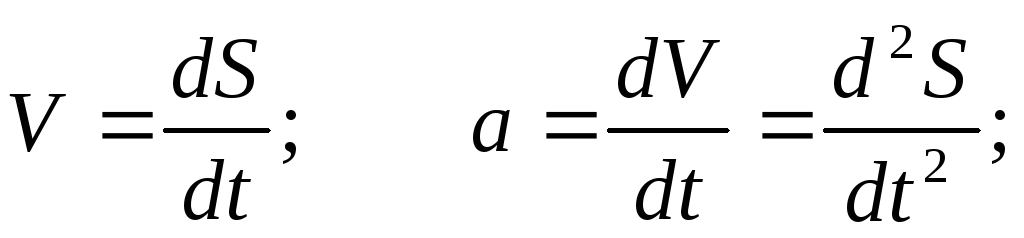
Тогда
получаем:  — уравнение связывает функцию f(t)
с независимой переменной t
и производной второго порядка функции
f(t).
— уравнение связывает функцию f(t)
с независимой переменной t
и производной второго порядка функции
f(t).
Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Пример.
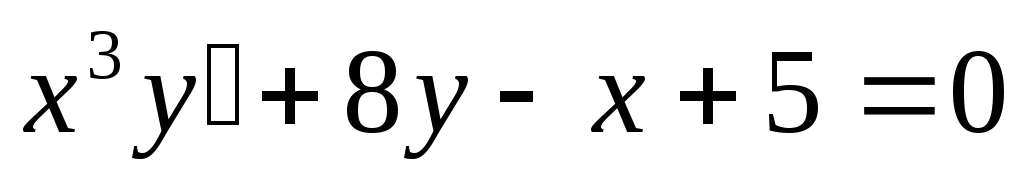 — обыкновенное
дифференциальное уравнение 1 – го
порядка. В общем виде записывается
— обыкновенное
дифференциальное уравнение 1 – го
порядка. В общем виде записывается 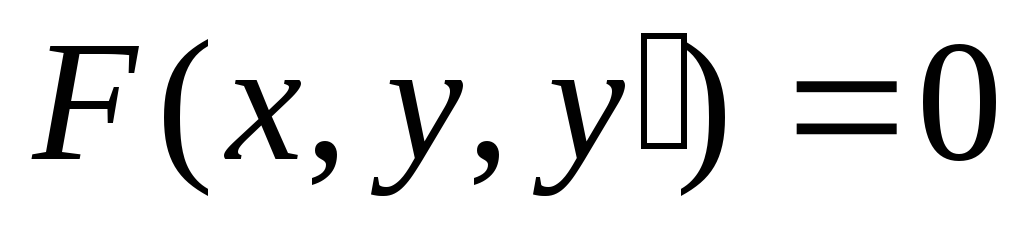
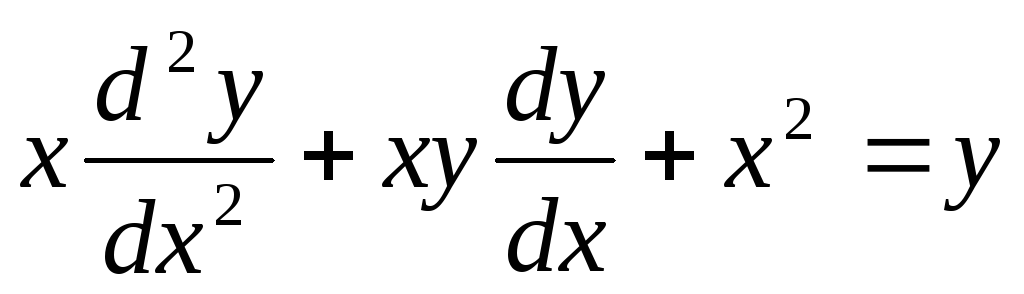 — обыкновенное
дифференциальное уравнение 2 – го
порядка. В общем виде записывается
— обыкновенное
дифференциальное уравнение 2 – го
порядка. В общем виде записывается 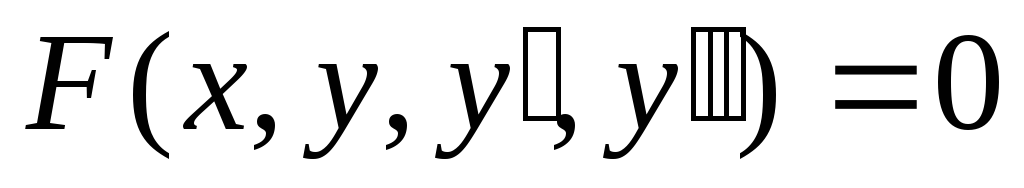
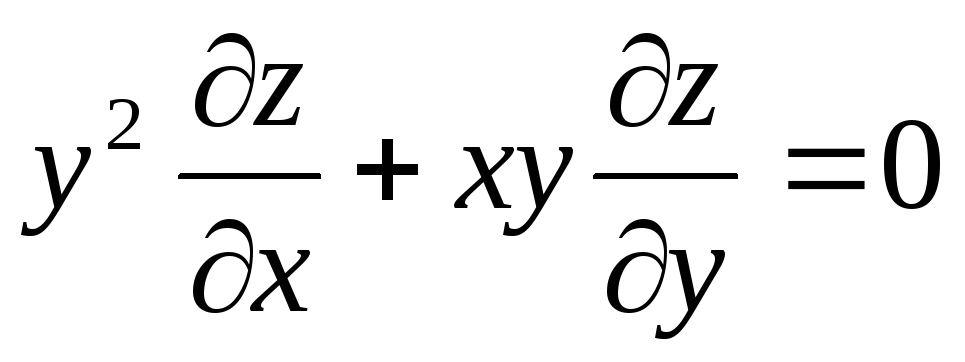 — дифференциальное
уравнение в частных производных первого
порядка.
— дифференциальное
уравнение в частных производных первого
порядка.
Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = (x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество
Свойства общего решения.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х 0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = (х, С0).
Определение. Решение вида у = (х, С0) называется частным решением дифференциального уравнения.
Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = (х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если
функция f(x, y)
непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную
частную производную 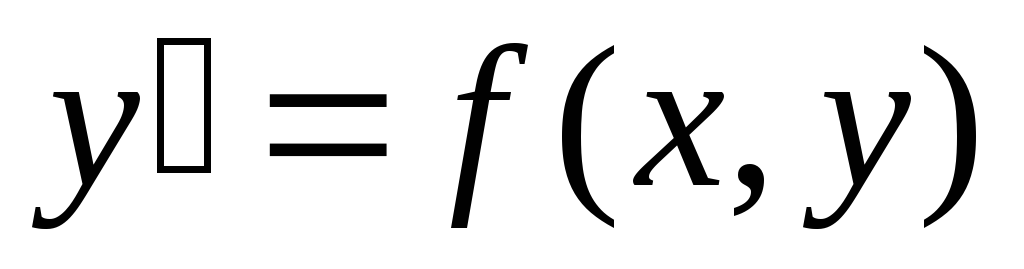
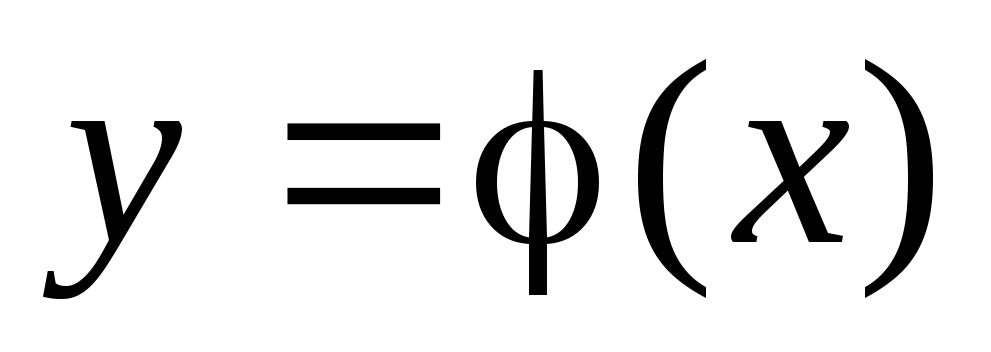 уравнения
уравнения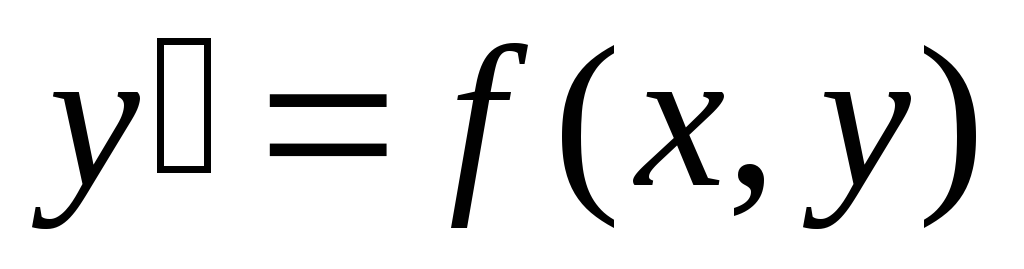 ,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения. Определение. Интегралом дифференциального
уравнения называется любое уравнение,
не содержащее производных, для которого
данное дифференциальное уравнение
является следствием.
Пример. Найти общее решение дифференциального
уравнения 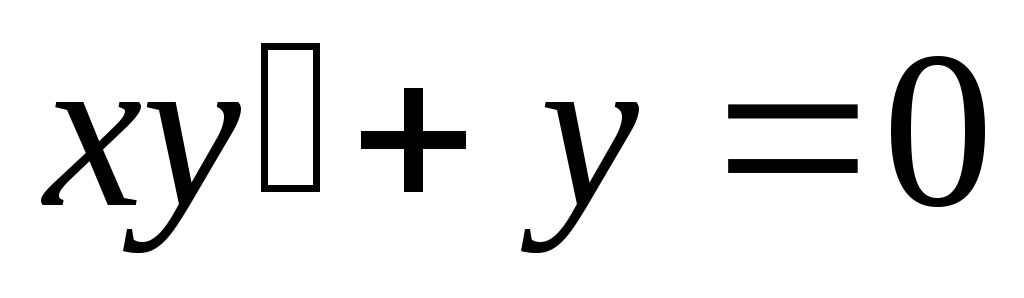 .
.
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:

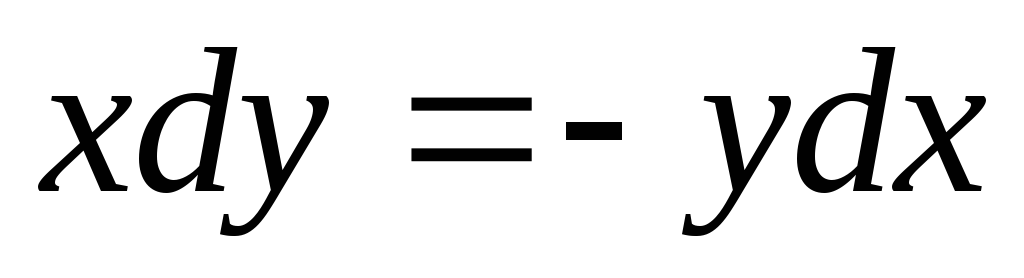
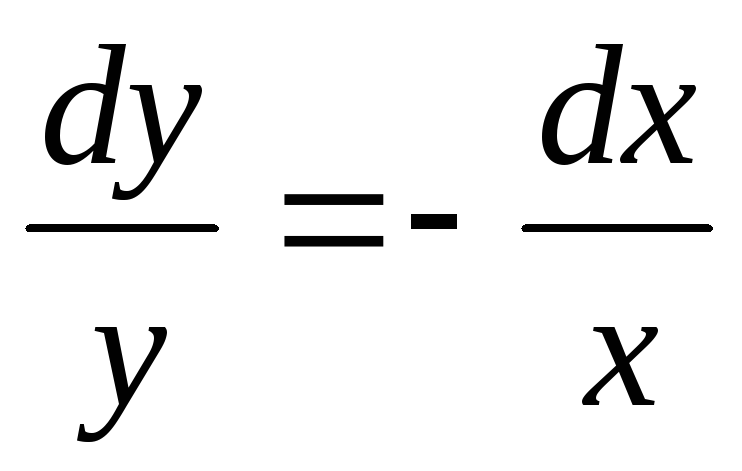
Теперь
интегрируем: 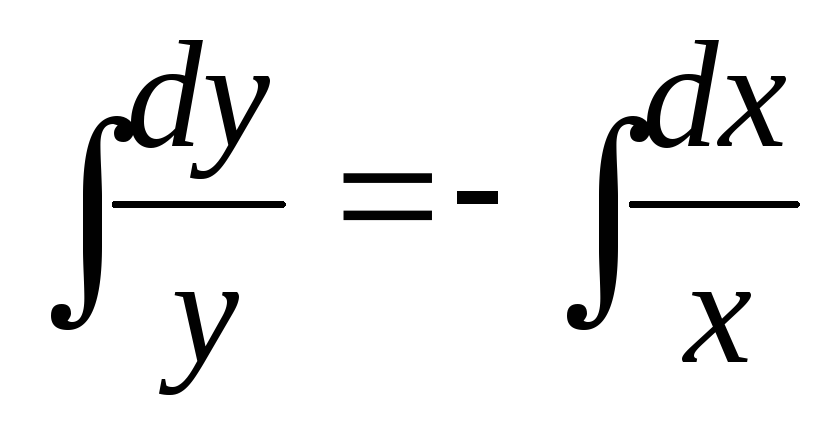
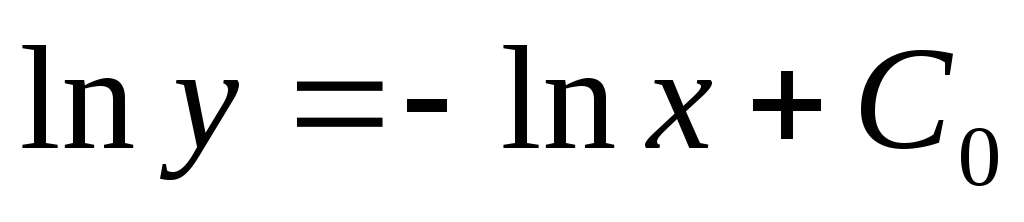

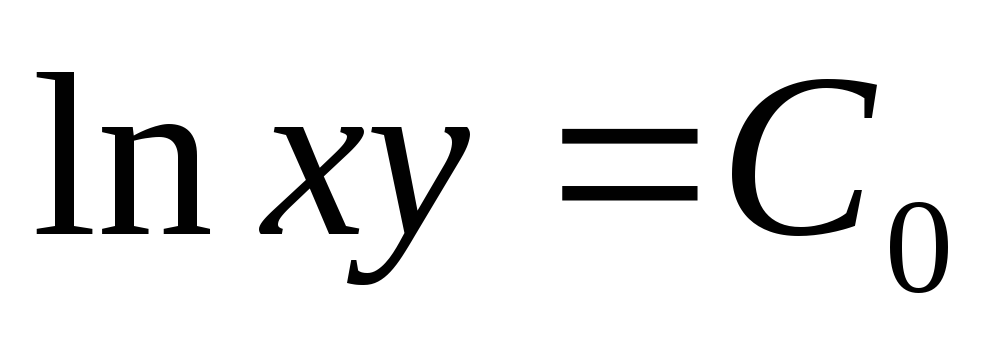
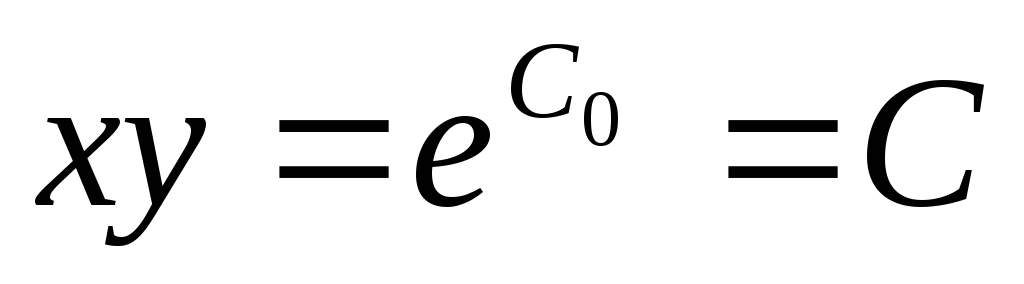
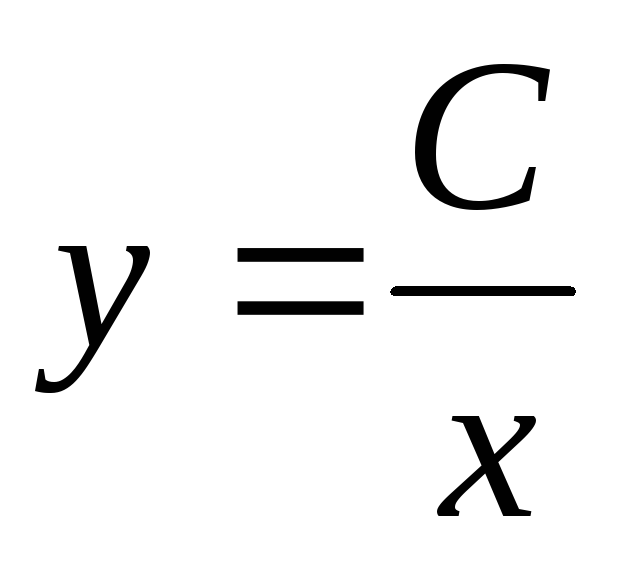 — это общее решение
исходного дифференциального уравнения.
— это общее решение
исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
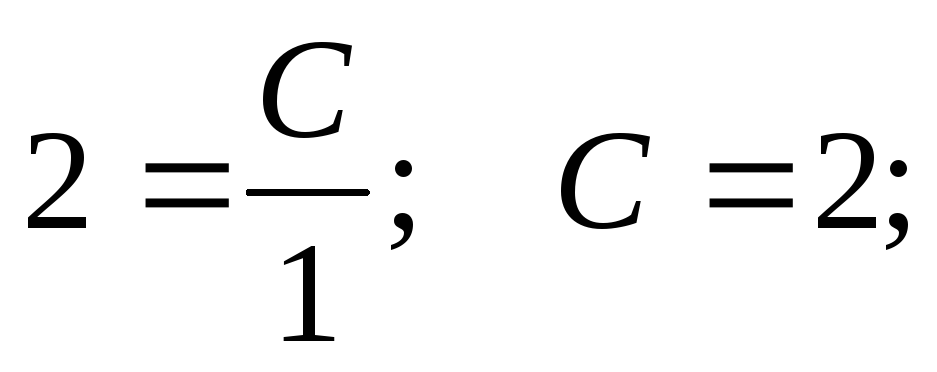
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
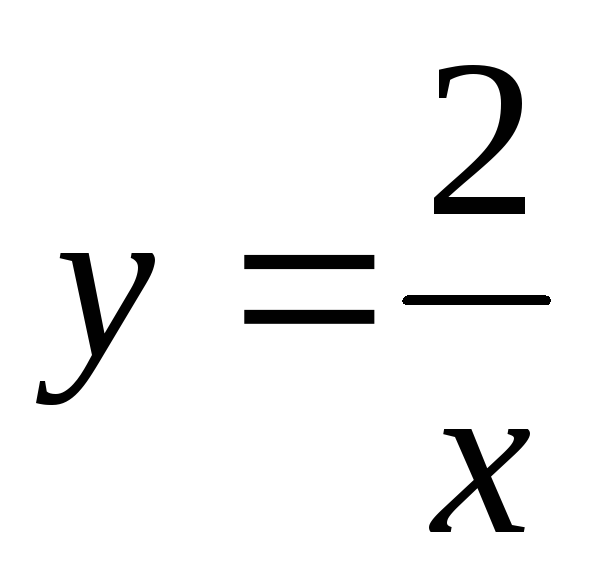
Определение. Интегральной кривой называется график y = (x) решения дифференциального уравнения на плоскости ХОY.
Определение. Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши (см. Теорема Коши. ) не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Пример. Найти общее решение дифференциального
уравнения: 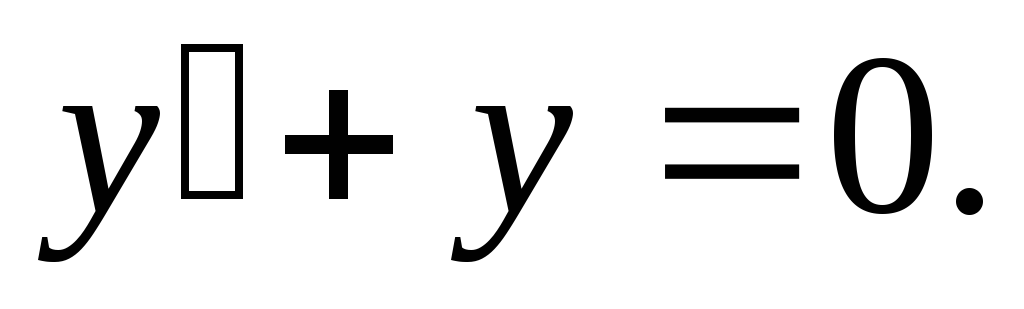 Найти особое решение, если оно существует.
Найти особое решение, если оно существует.
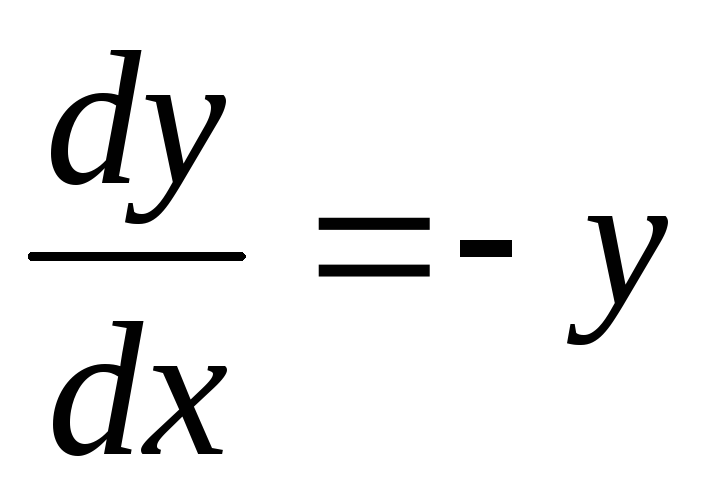
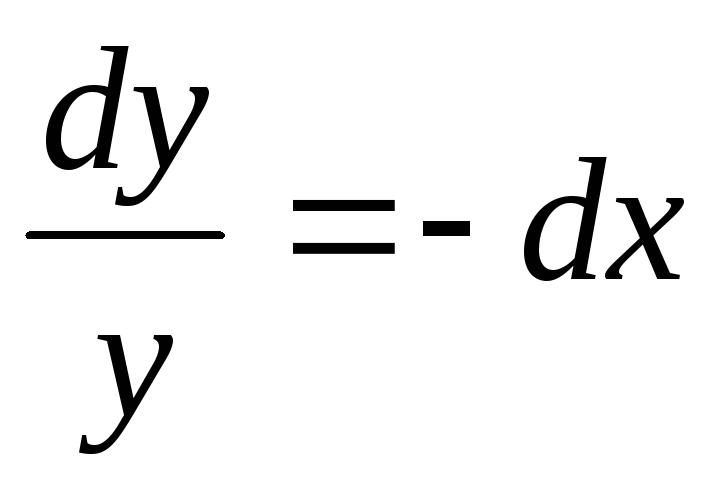
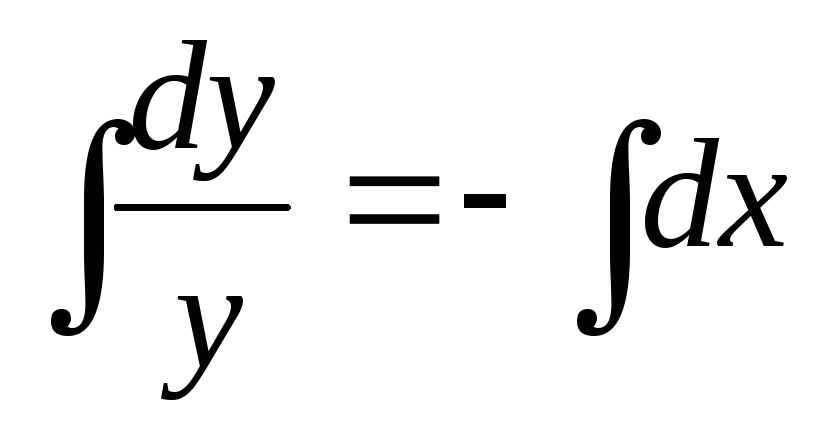

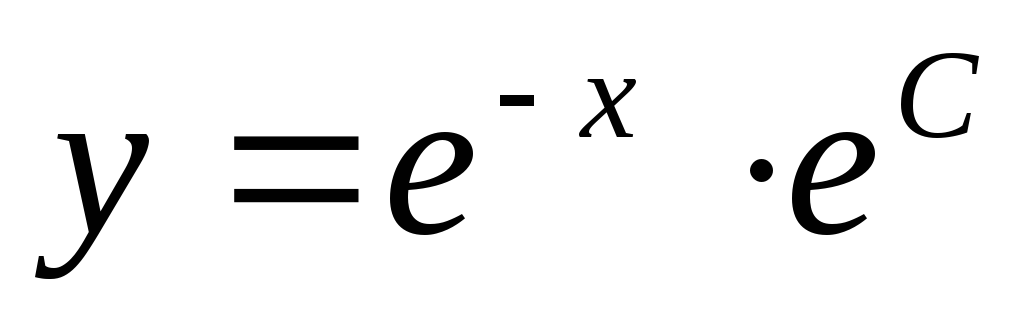

Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0 можно получить из общего решения при С1 = 0 ошибочно, ведь C1 = eC 0.
Далее рассмотрим подробнее приемы и методы, которые используются при решении дифференциальных уравнений различных типов.
studfile.net
22. Дифференциальные уравнения
22.1. Дифференциальные уравнения первого
порядка. Дифференциальные уравнения
с разделяющимися переменными
Пусть x– независимая переменная,y(x) – функция от переменнойx, заданная на некотором промежутке.
Дифференциальным уравнением(обыкновенным дифференциальным уравнением) называется уравнение, связывающее независимую переменнуюx, функциюy(x) и ее производные.
Порядкомдифференциального уравнения называется наивысший порядок производной, входящей в него.
Дифференциальное уравнение 1-го порядка имеет вид:
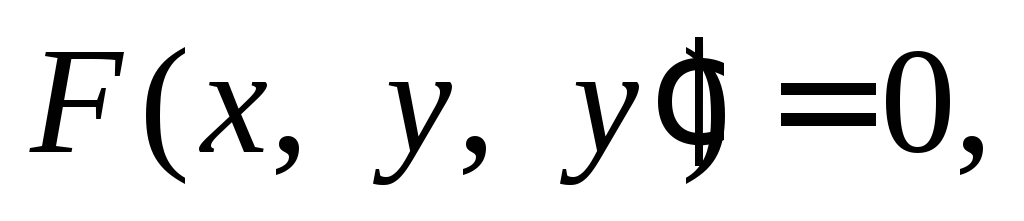 (22.1)
(22.1)
где F– некоторое выражение относительноx,
искомой функцииy(x)
и ее производной, заданное в области 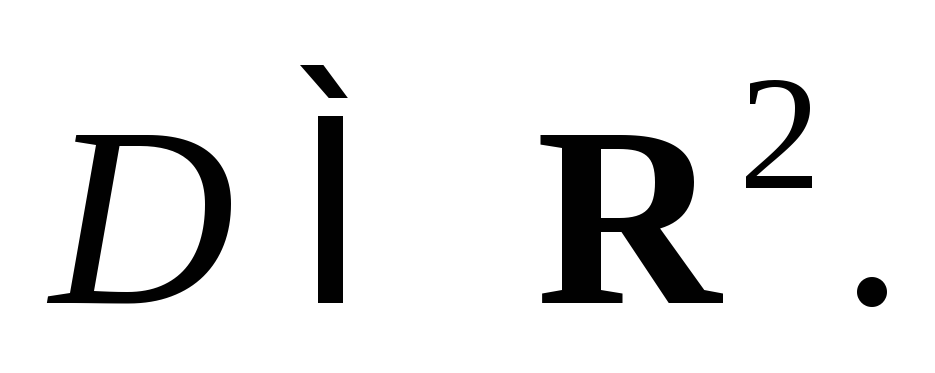
Если дифференциальное уравнение разрешено относительно производной функции, то его общий вид:
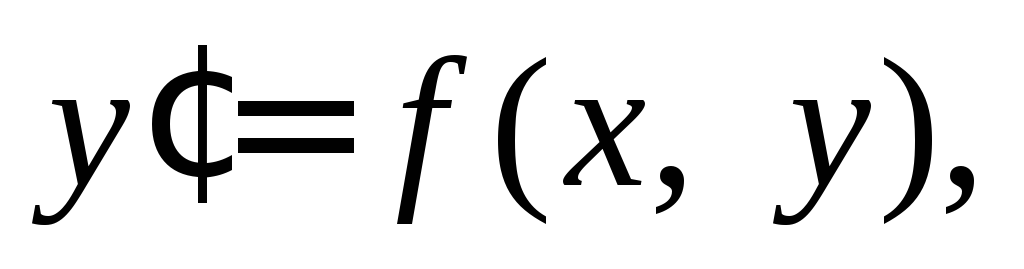 (22.2)
(22.2)
где f– некоторое выражение относительноxиy,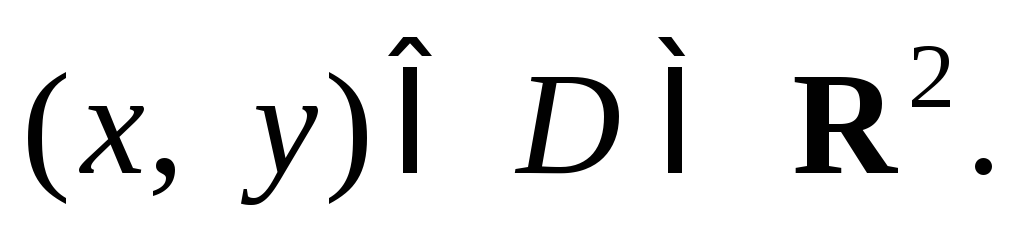 В таком случае говорят, что дифференциальное
уравнение записано внормальном виде.
В таком случае говорят, что дифференциальное
уравнение записано внормальном виде.
Решениемдифференциального уравнения называется
такая дифференцируемая функция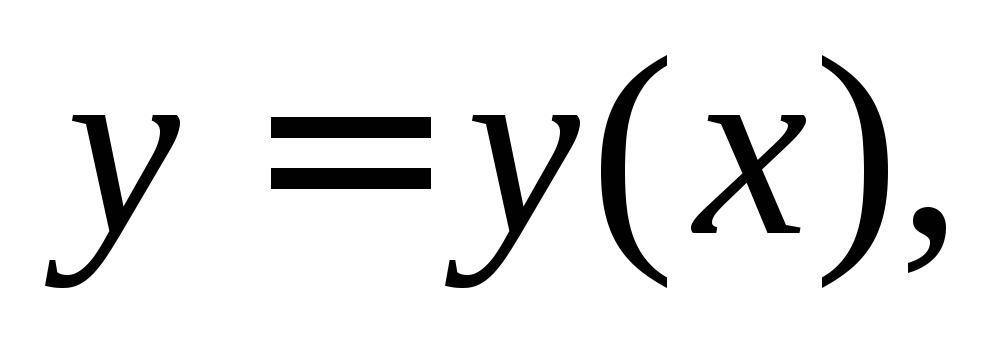 которая обращает это уравнение в
тождество.
которая обращает это уравнение в
тождество.
Поиск решения дифференциального уравнения называется интегрированием дифференциального уравнения, а график этого решения –интегральной кривой.
Начальным
условием(условием Коши)
называется условие
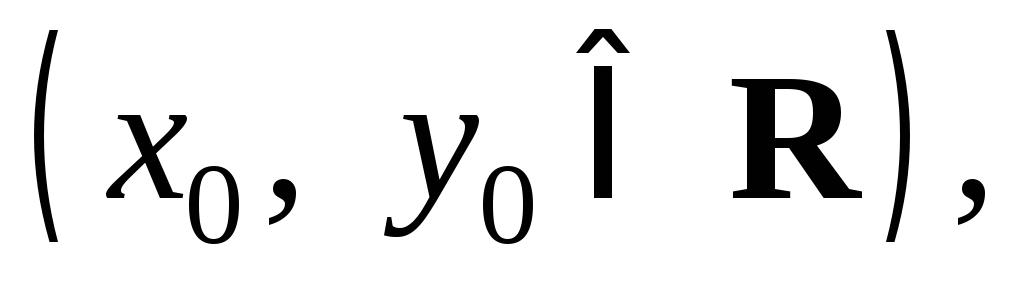 которым задается дополнительное
требование на решениеy(x)
дифференциального уравнения.
которым задается дополнительное
требование на решениеy(x)
дифференциального уравнения.
Общим решениемдифференциального уравнения (22.2) в
области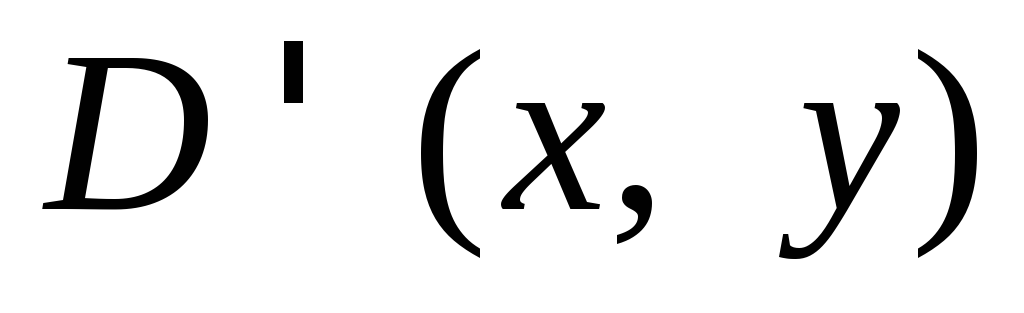 называется функция
называется функция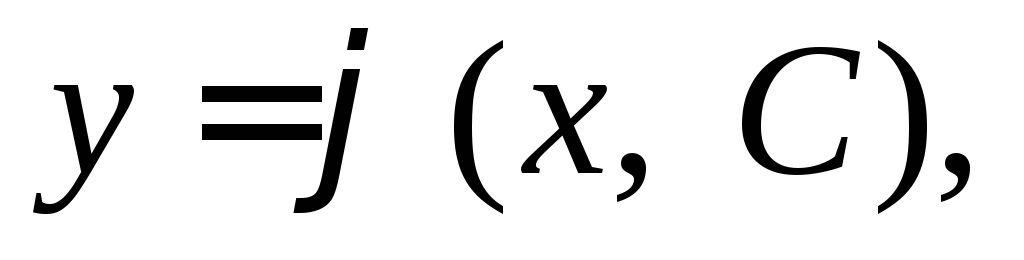 удовлетворяющая условиям:
удовлетворяющая условиям:
1)  является решением данного дифференциального
уравнения при любом значении произвольной
постояннойС;
является решением данного дифференциального
уравнения при любом значении произвольной
постояннойС;
2) для любого
начального условия  такого, что
такого, что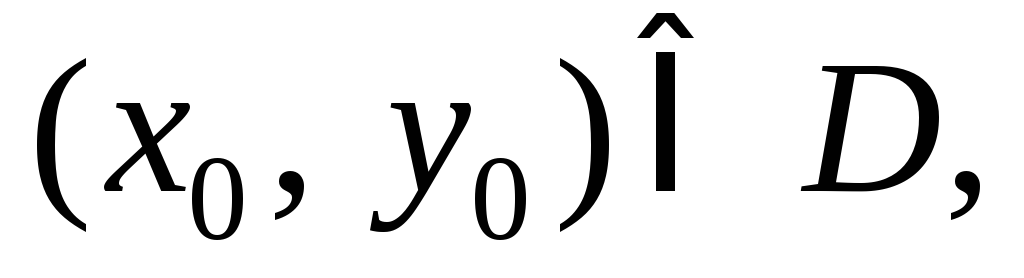 существует единственное значение
существует единственное значение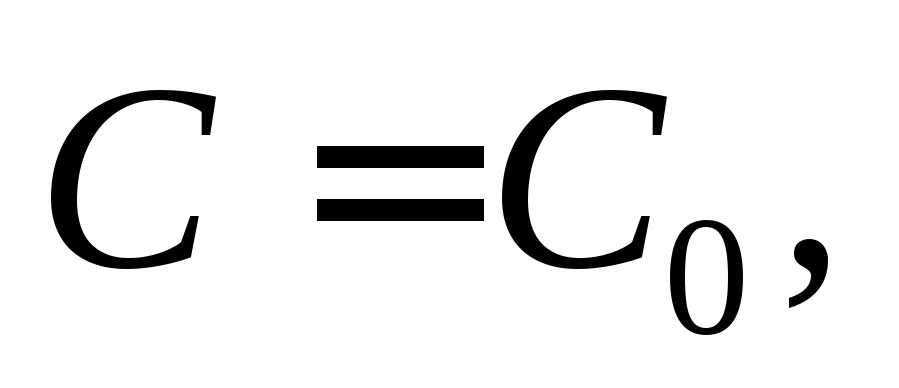 при котором решение
при котором решение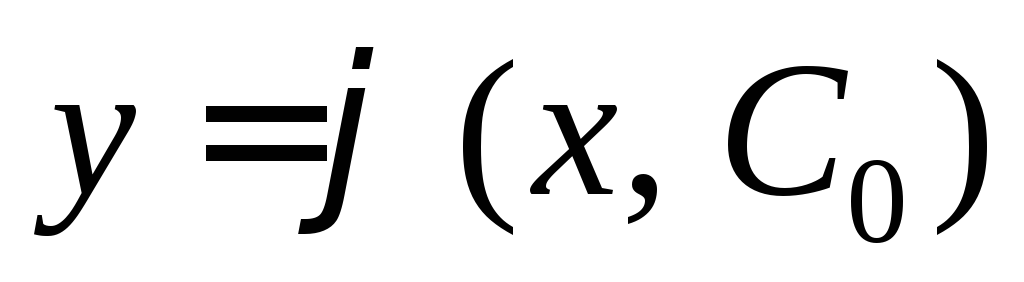 удовлетворяет начальному условию.
удовлетворяет начальному условию.
Общее решение 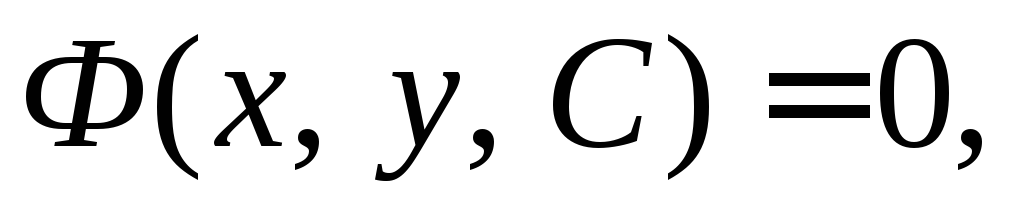 заданное в неявном виде, называетсяобщим интегралом дифференциального
уравнения.
заданное в неявном виде, называетсяобщим интегралом дифференциального
уравнения.
Частным решением дифференциального уравнения
называется всякое решение, полученное
из общего при конкретном значении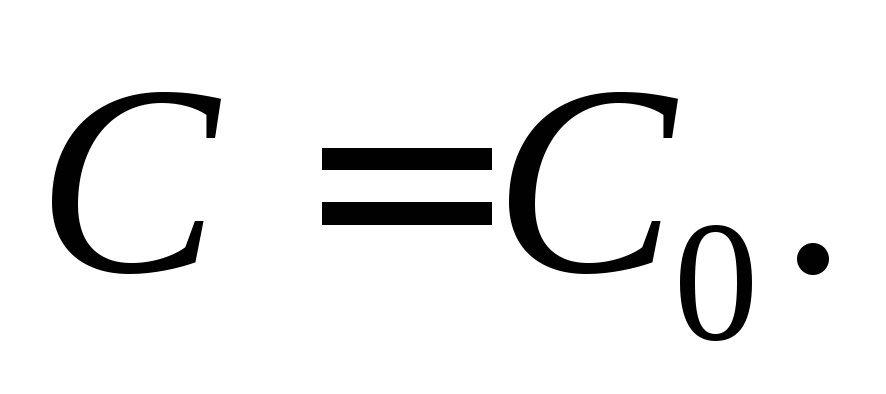
Задачей Кошиназывается задача отыскания частного
решения дифференциального уравнения,
удовлетворяющего заданному начальному
условию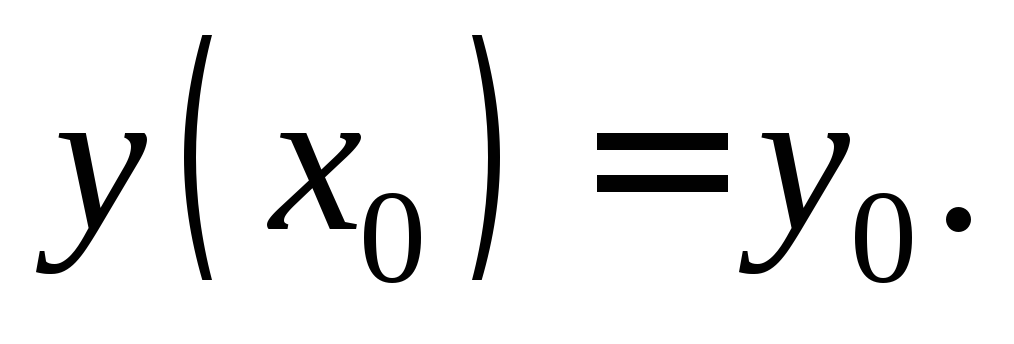 Геометрически общему решению на
координатной плоскости соответствует
семейство интегральных кривых
Геометрически общему решению на
координатной плоскости соответствует
семейство интегральных кривых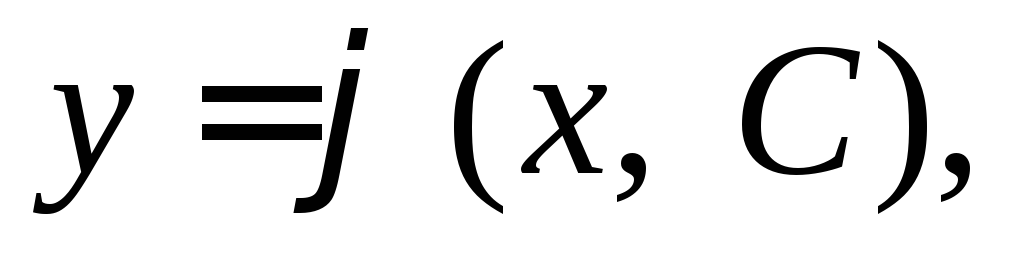 зависящее от числового параметраС,
а частному решению – определенная
интегральная кривая, проходящая через
точку
зависящее от числового параметраС,
а частному решению – определенная
интегральная кривая, проходящая через
точку
Теорема Коши.
Если функцияf(x, y)
непрерывна и имеет непрерывную производную в областиD, то решение
дифференциального уравнения (22.2) при
начальном условии
в областиD, то решение
дифференциального уравнения (22.2) при
начальном условии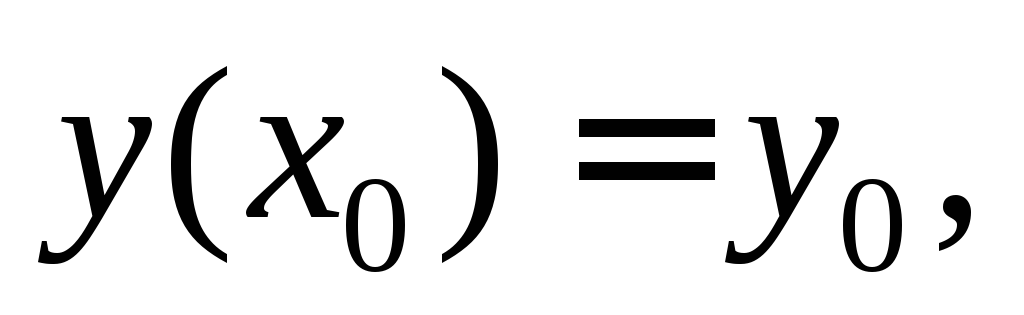
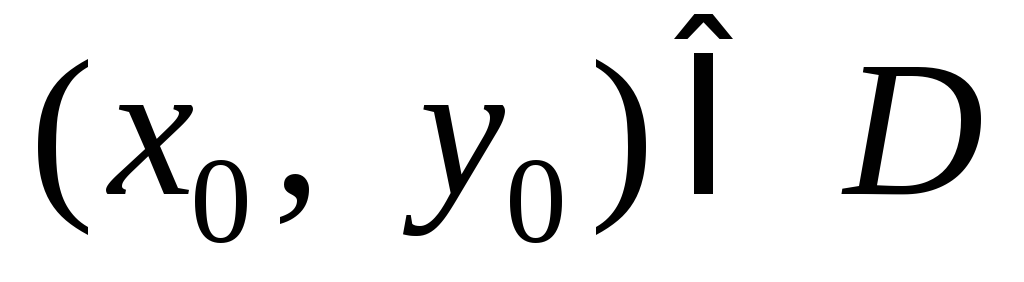 существует и единственно.
существует и единственно.
Решение дифференциального уравнения, во всех точках которого не выполняется условие единственности, называется особым решением. Особое решение не может быть получено из общего решения дифференциального уравнения ни при каком значении произвольной постояннойC.
Дифференциальное уравнение вида
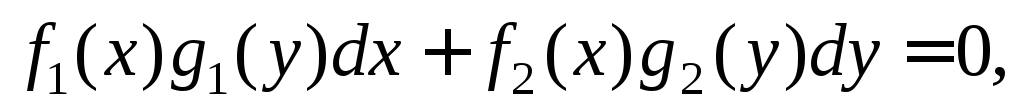 (22.3)
(22.3)
где  – функции
переменной x,
– функции
переменной x,  – функции переменнойy,
называется уравнением
с разделяющимися переменными.
– функции переменнойy,
называется уравнением
с разделяющимися переменными.
Для решения
уравнения (22.3) предполагают 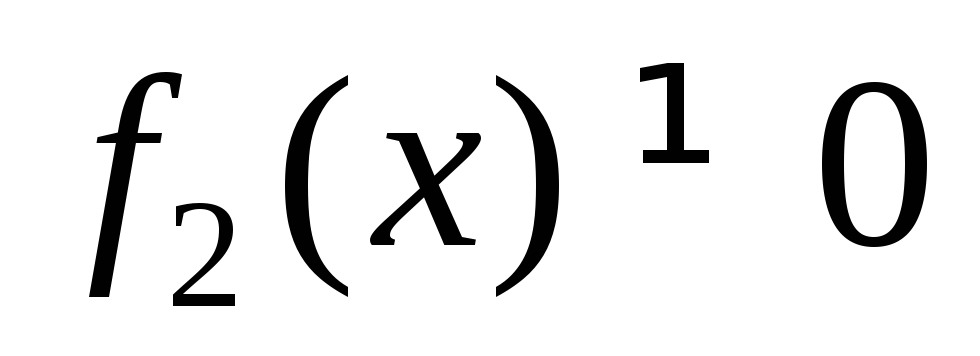 и
и Почленным делением уравнения (22.3) на
Почленным делением уравнения (22.3) на его сводят к уравнению
его сводят к уравнению
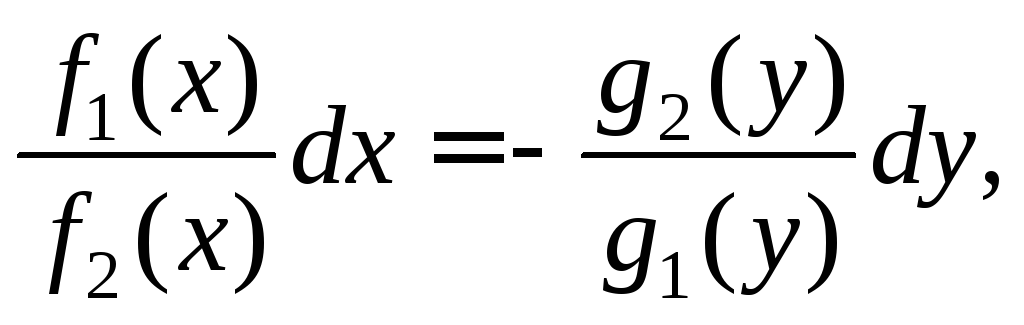 (22.4)
(22.4)
которое в левой части содержит выражение только от переменной x, а в правой – только от переменнойy(этим объясняется название данного типа дифференциальных уравнений). Далее интегрируют равенство (22.4) (слева – по переменнойx, а справа – поy) и получают общее решение.
Ограничения 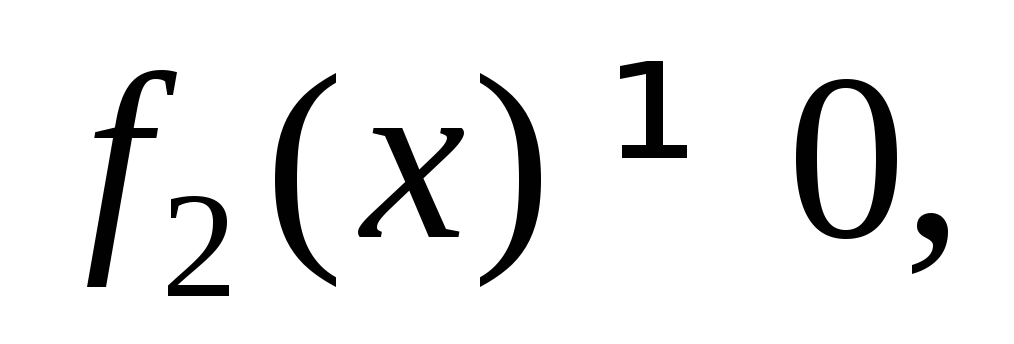
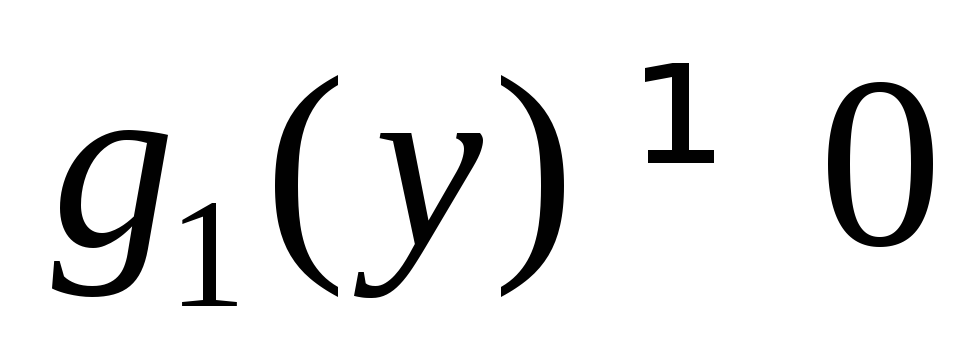 могут привести к потере решений, поэтому
следует решить уравнения
могут привести к потере решений, поэтому
следует решить уравнения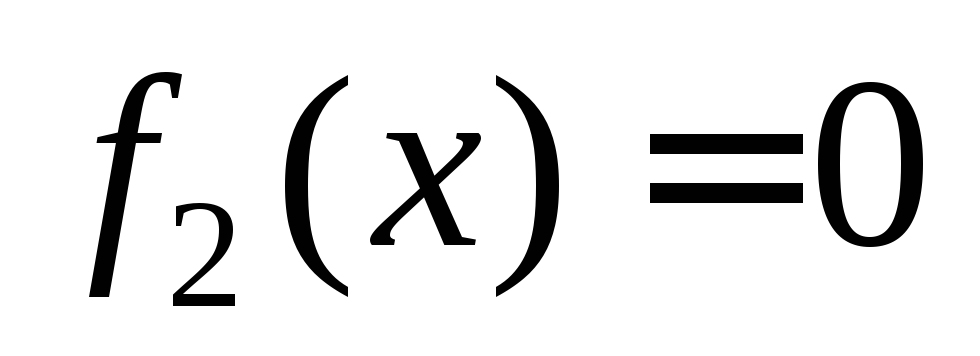 и
и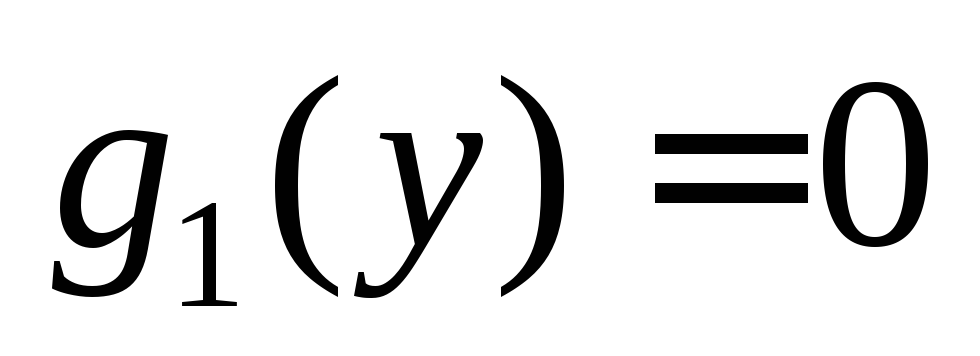 и установить подстановкой в заданное
дифференциальное уравнение, являются
ли они решением дифференциального
уравнения. Затем необходимо определить,
входят ли они в общее решение (или
являются особыми).
и установить подстановкой в заданное
дифференциальное уравнение, являются
ли они решением дифференциального
уравнения. Затем необходимо определить,
входят ли они в общее решение (или
являются особыми).
Пример
1. Доказать,
что функция  является решением дифференциального
уравнения
является решением дифференциального
уравнения
Решение. Продифференцируем функцию: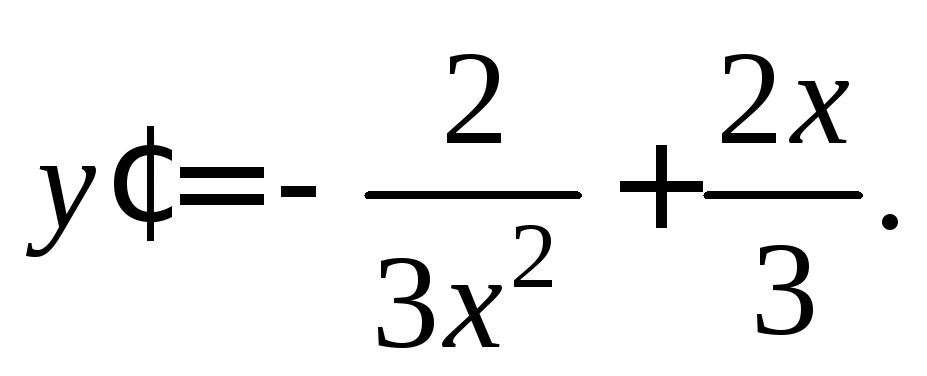 Подставим ее в заданное дифференциальное
уравнение:
Подставим ее в заданное дифференциальное
уравнение:
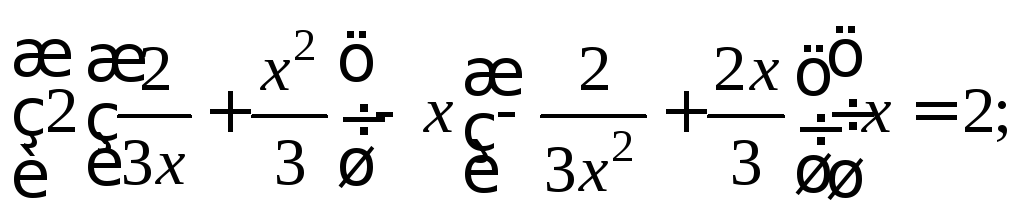

В итоге получаем тождество
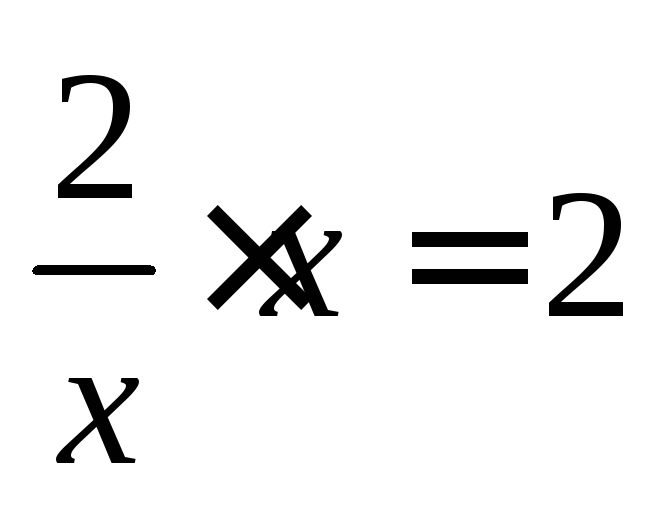 или
или 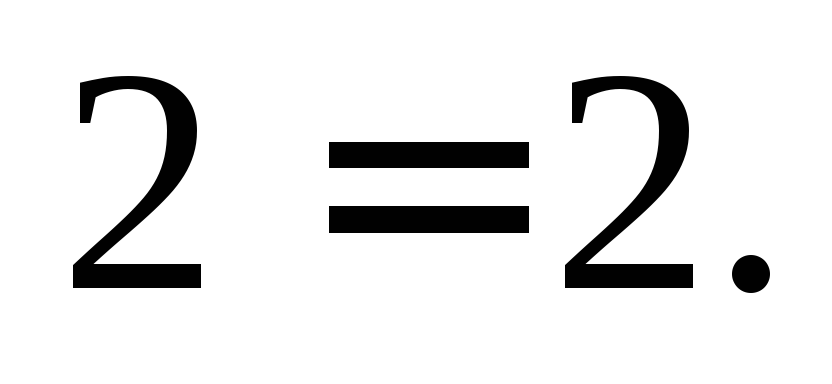
Это
доказывает, что функция  является решением заданного
дифференциального уравнения.
является решением заданного
дифференциального уравнения.
Пример
2. Доказать,
что равенство  является общим интегралом дифференциального
уравнения
является общим интегралом дифференциального
уравнения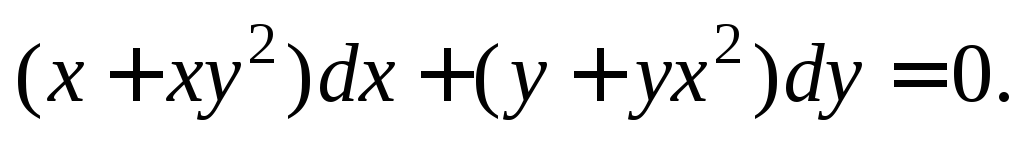
Решение. Вычислим производную неявной функции  по формуле
по формуле
поскольку 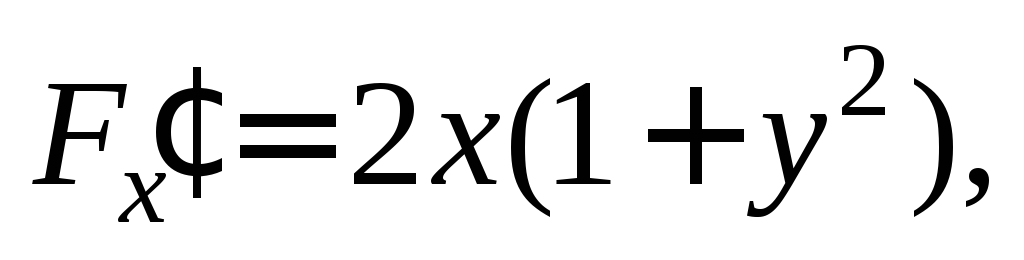
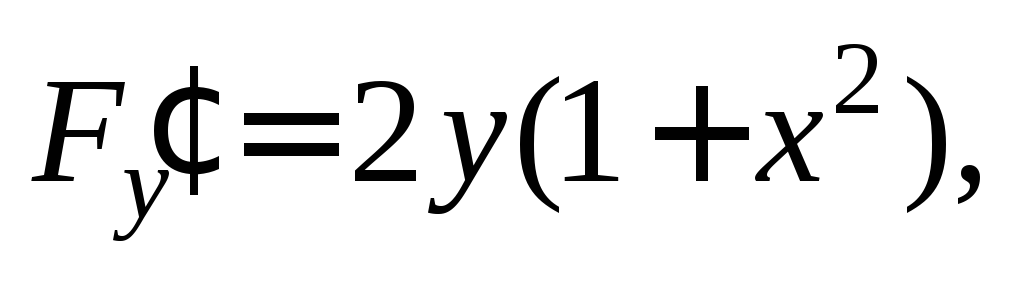 то
то
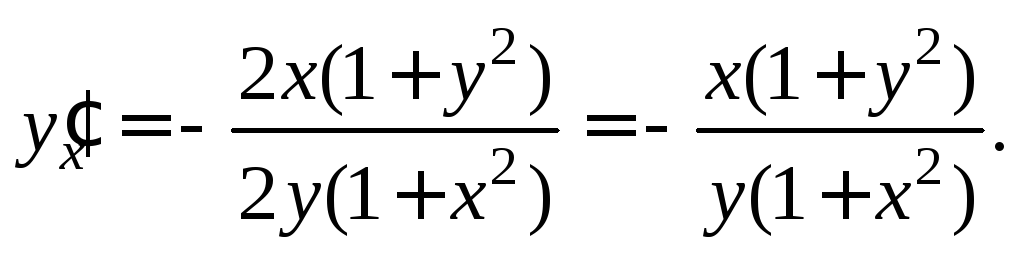
Подставим 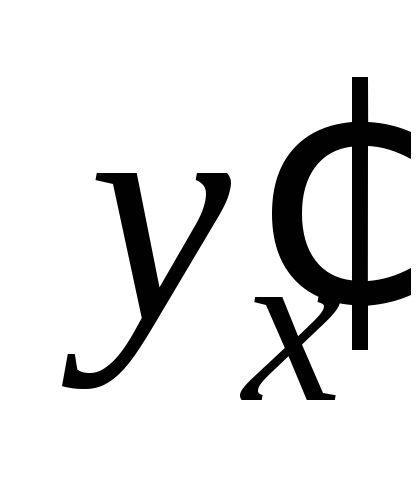 и
и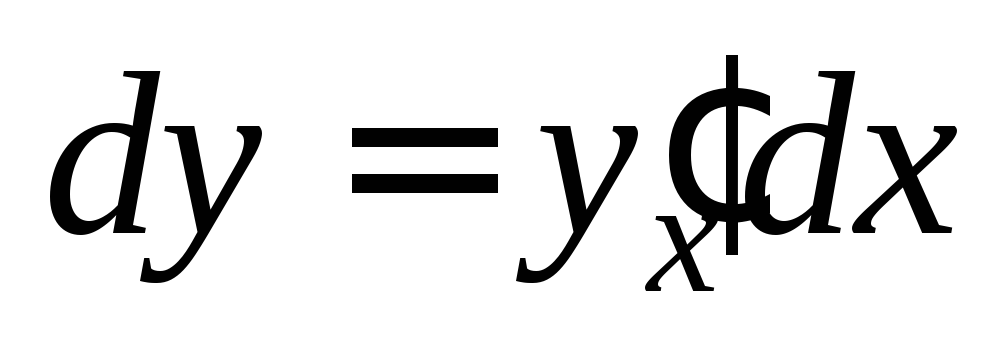 в заданное дифференциальное уравнение:
в заданное дифференциальное уравнение:
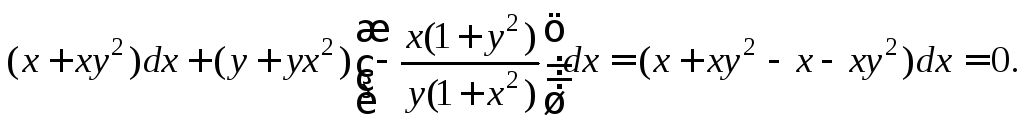
Получили
тождество  что и доказывает требуемое.
что и доказывает требуемое.
Пример 3. Найти общее решение дифференциального уравнения:
1) 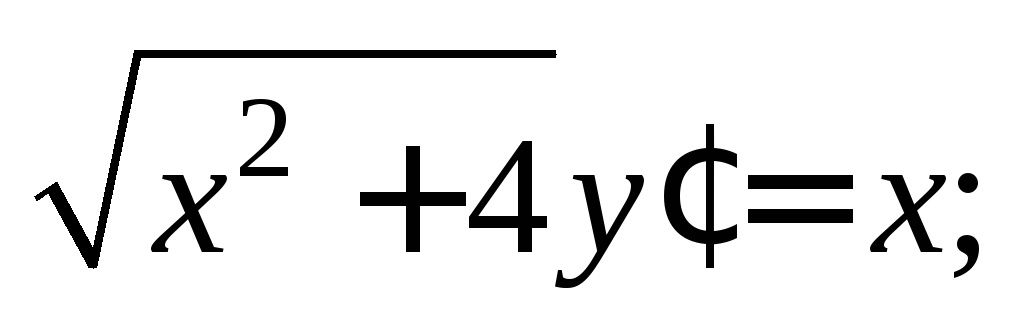 2)
2)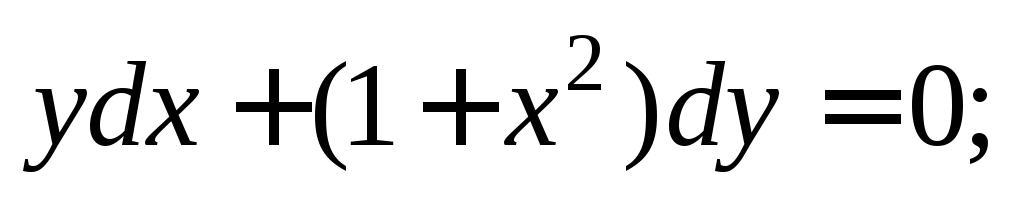 3)
3)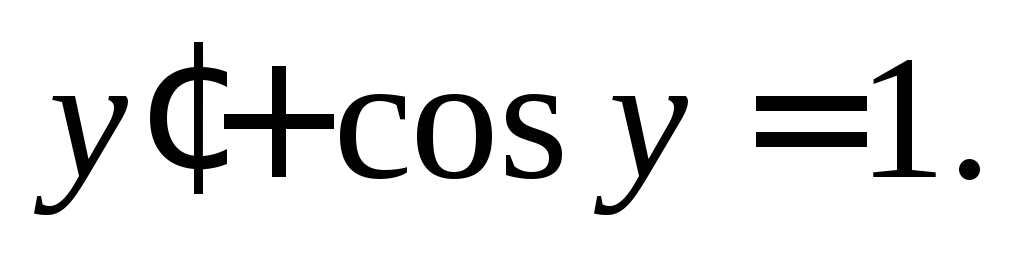
Решение. 1) Используем то, что 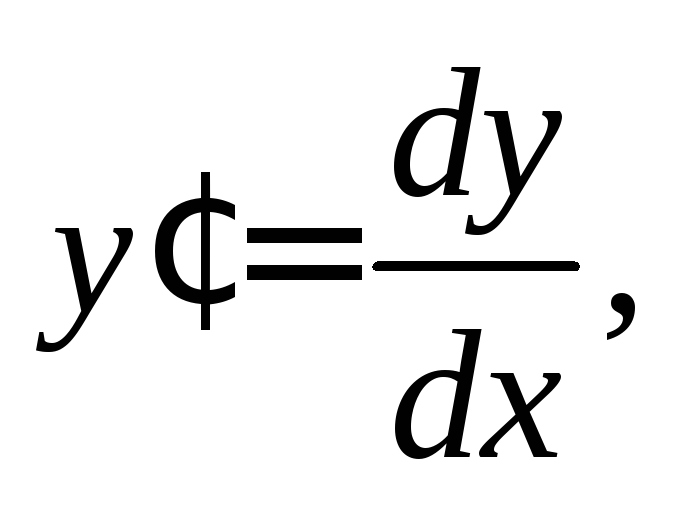 и запишем исходное дифференциальное
уравнение в виде
и запишем исходное дифференциальное
уравнение в виде
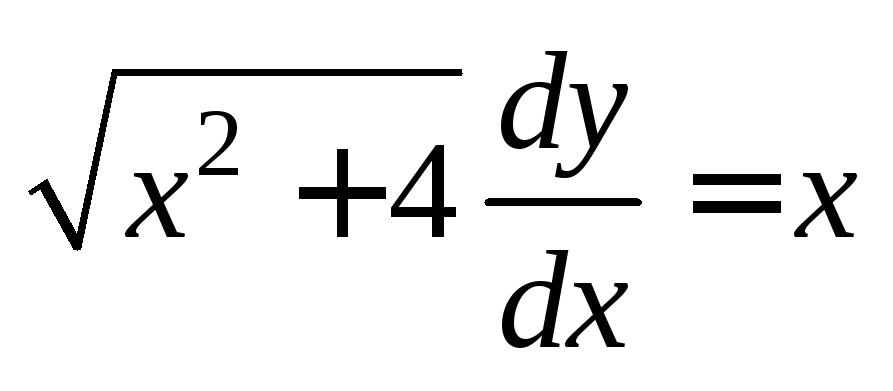 или
или 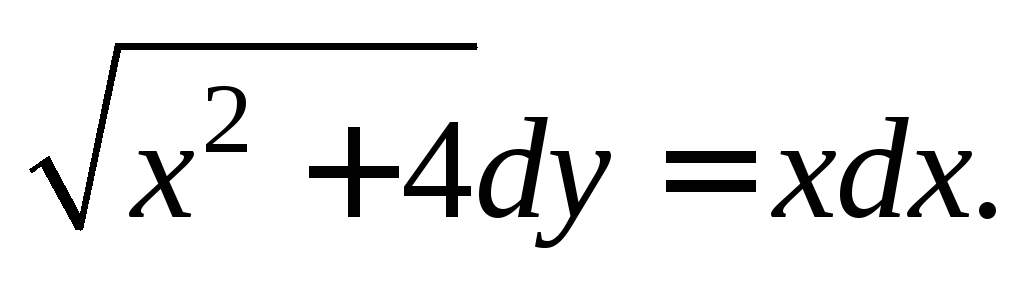
Так
как  для всех
для всех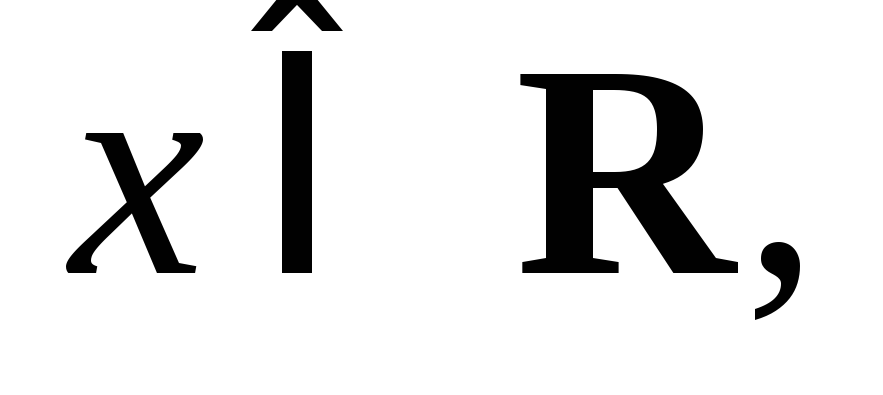 то преобразуем уравнение к виду
то преобразуем уравнение к виду
Интегрируем
последнее равенство: 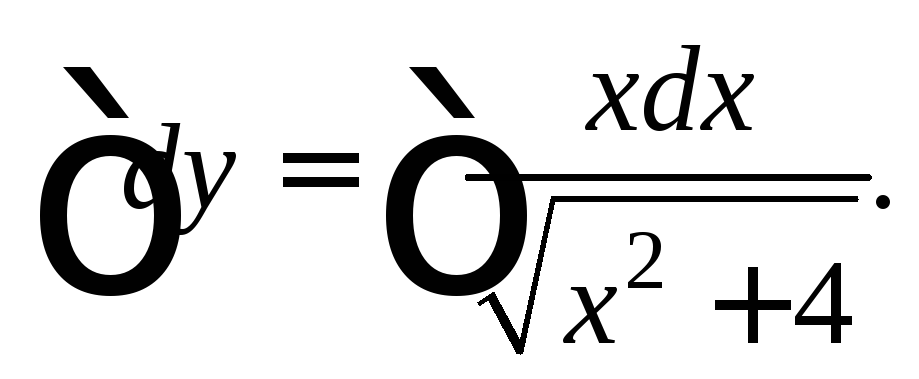 Получаем
Получаем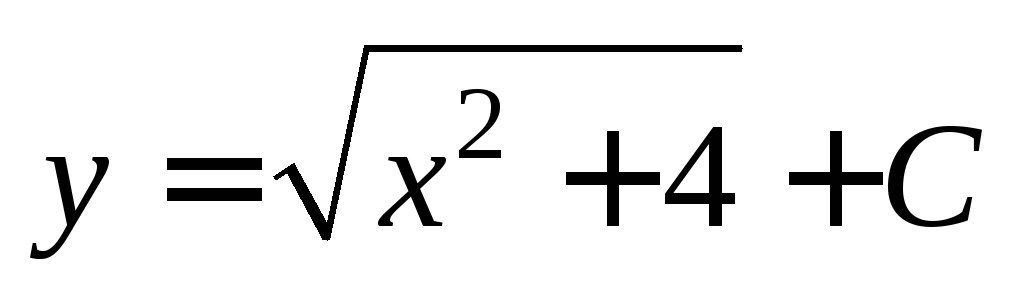 – общее решение заданного дифференциального
уравнения.
– общее решение заданного дифференциального
уравнения.
2)
Предполагаем, что  а так как
а так как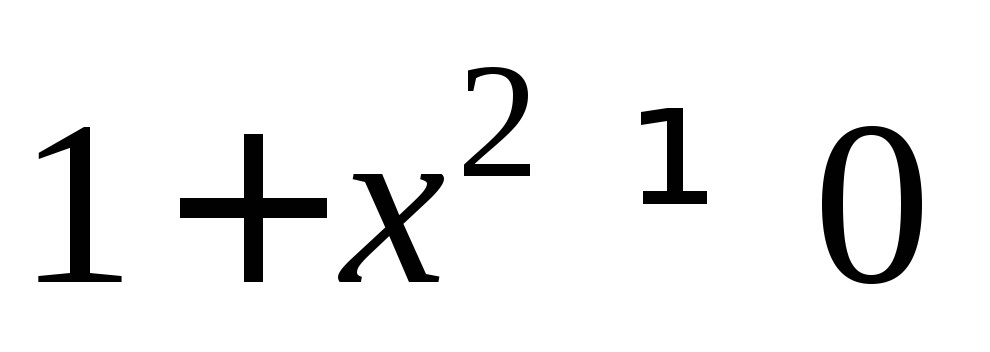 для всех
для всех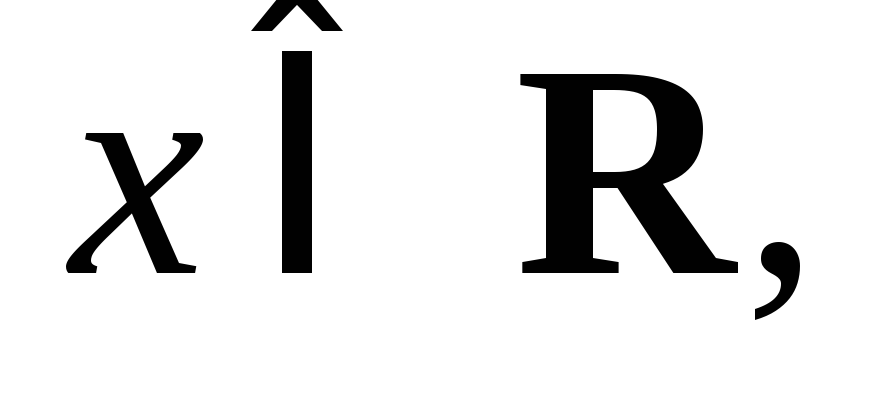 то преобразуем заданное дифференциальное
уравнение к виду
то преобразуем заданное дифференциальное
уравнение к виду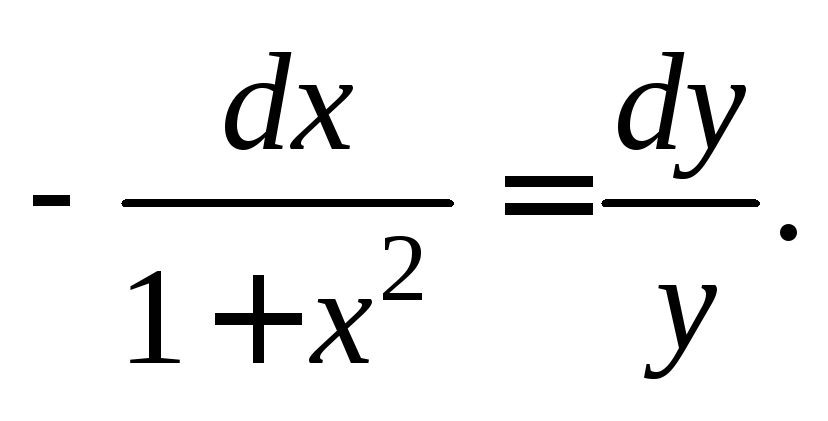
Интегрируем
последнее равенство: 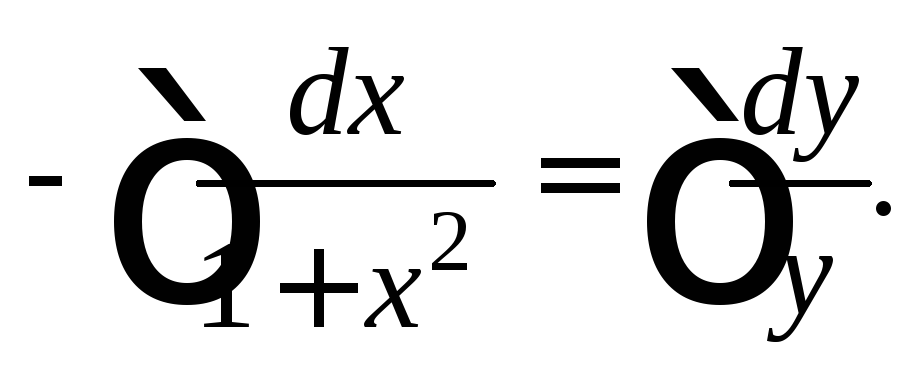
Получаем:

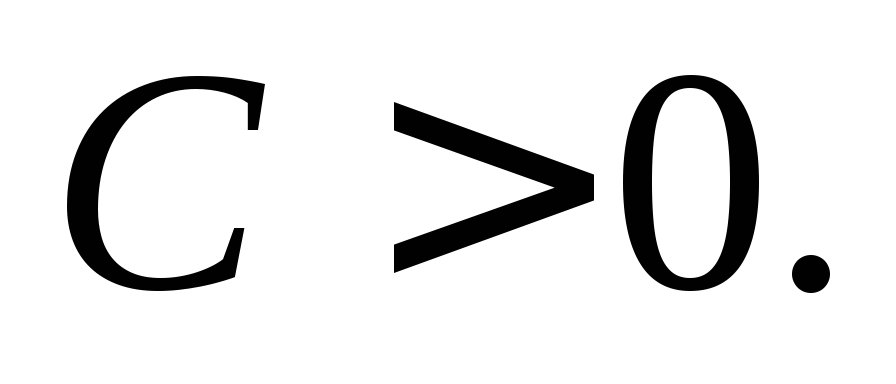
Произвольную константу записали в форме lnC для удобства дальнейших преобразований:
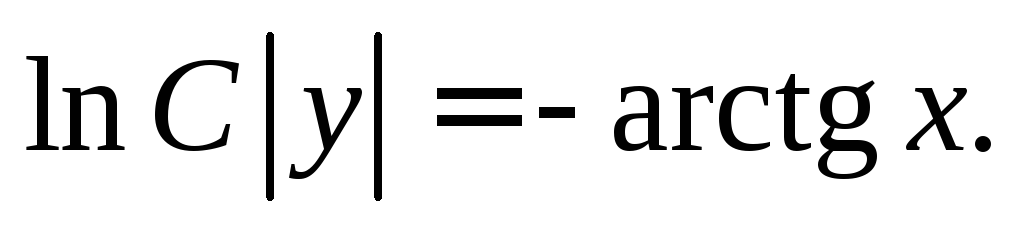
 т. е.
т. е. 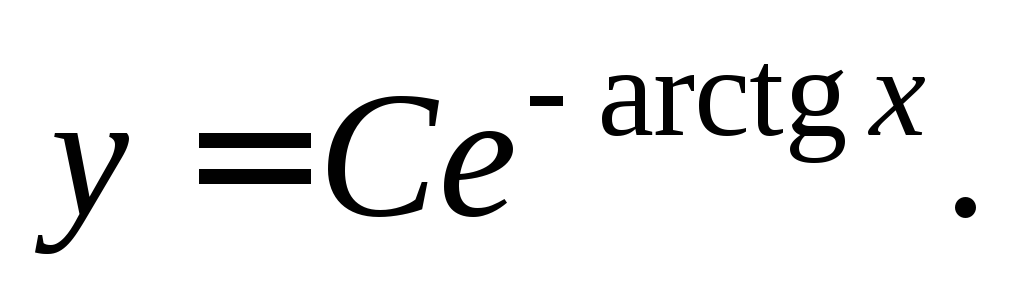
Заметим, что преобразования аналитических выражений производятся с точностью до константы C.
Таким
образом,  – общее решение исходного дифференциального
уравнения.
– общее решение исходного дифференциального
уравнения.
Проверяем,
является ли решением 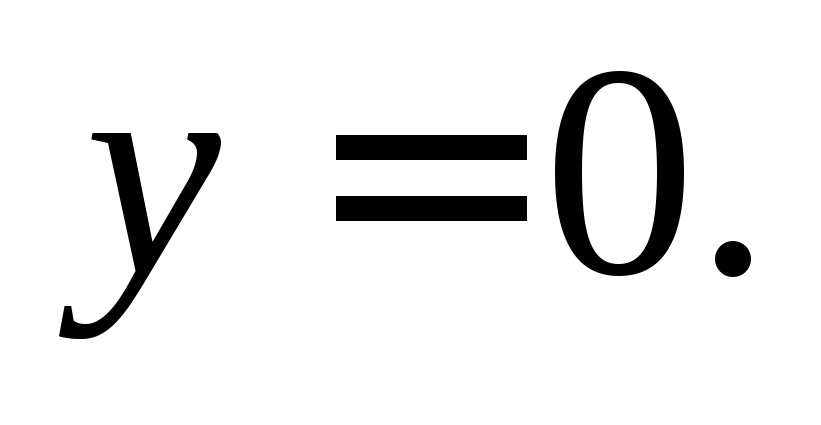 Подставляем в заданное дифференциальное
уравнение и видим, что
Подставляем в заданное дифференциальное
уравнение и видим, что является решением дифференциального
уравнения. Однако оно не является особым,
так как получается из общего решения
при
является решением дифференциального
уравнения. Однако оно не является особым,
так как получается из общего решения
при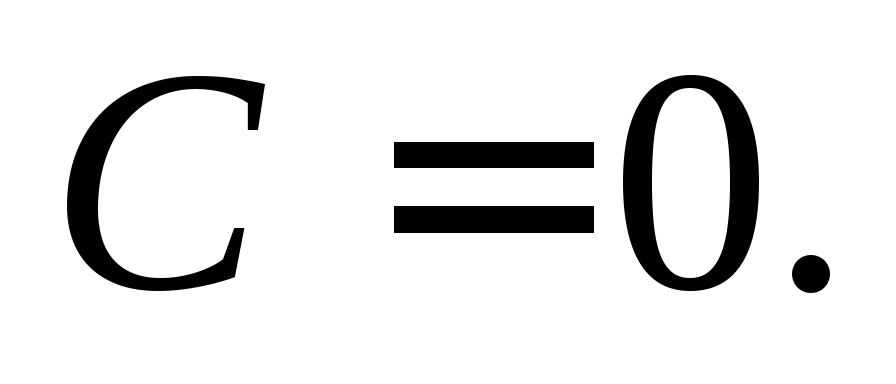
Приходим к ответу:
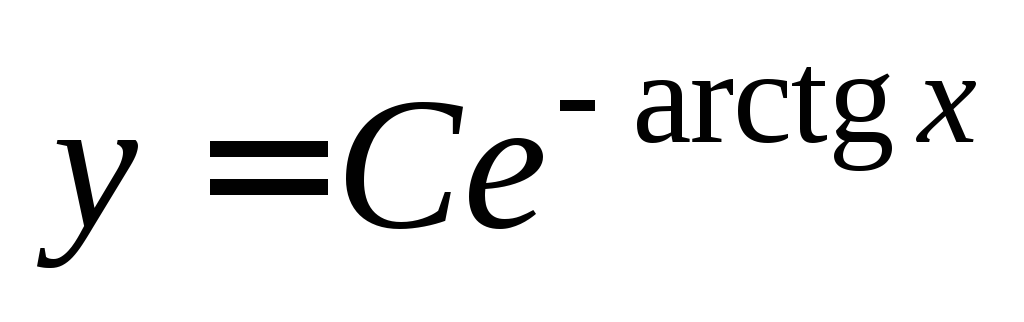 –общее
решение, С = const.
–общее
решение, С = const.
3)
Используя то, что  запишем уравнение в виде
запишем уравнение в виде
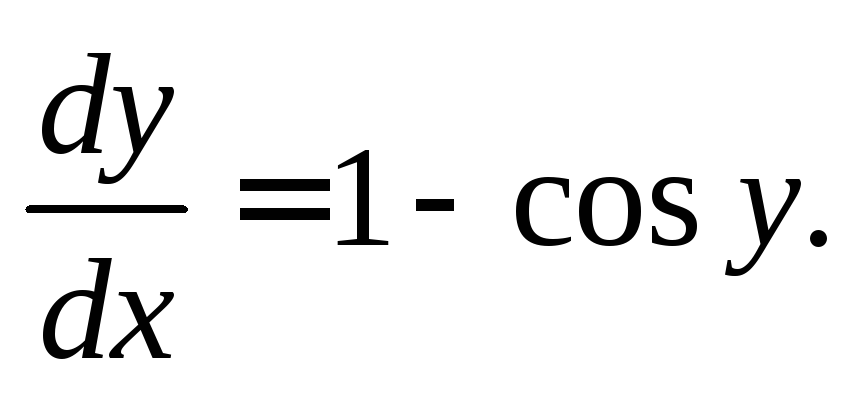
Предполагаем,
что  и преобразуем уравнение к виду
и преобразуем уравнение к виду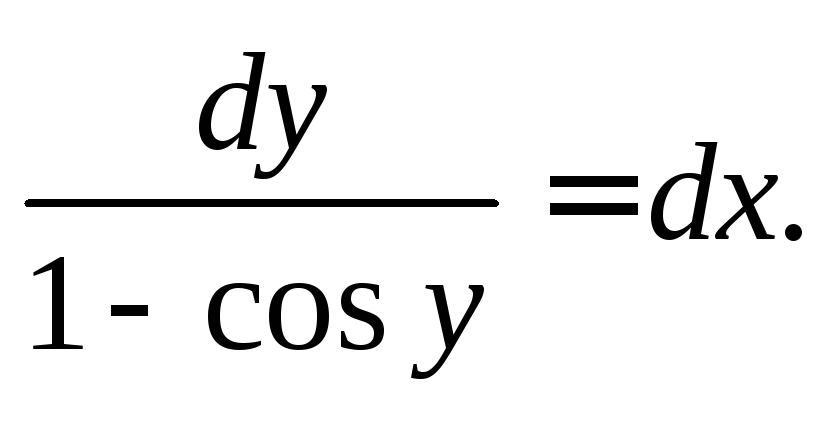 Используя формулу тригонометрии
Используя формулу тригонометрии интегрируем последнее равенство:
интегрируем последнее равенство:
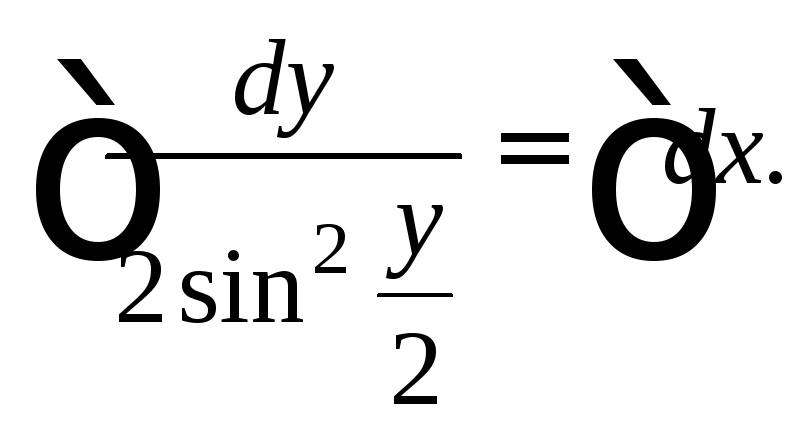
Имеем:
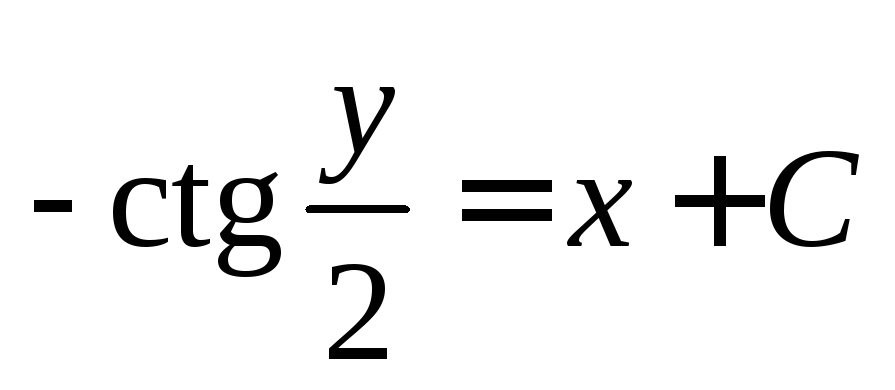 или
или 
Таким
образом, получаем 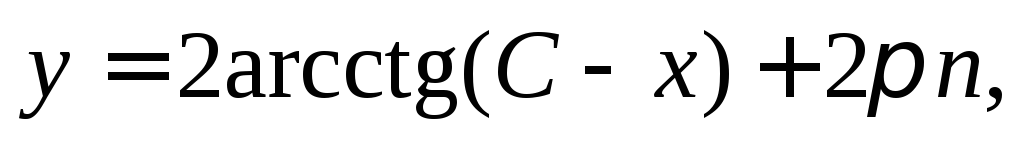
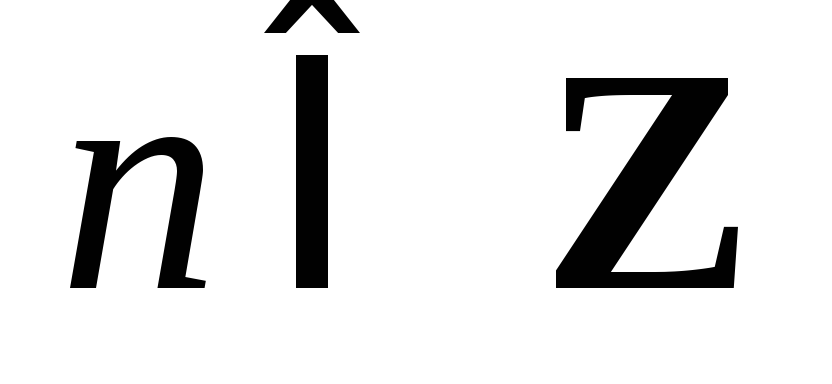 – общее решение исходного дифференциального
уравнения.
– общее решение исходного дифференциального
уравнения.
Проверяем,
дает ли равенство 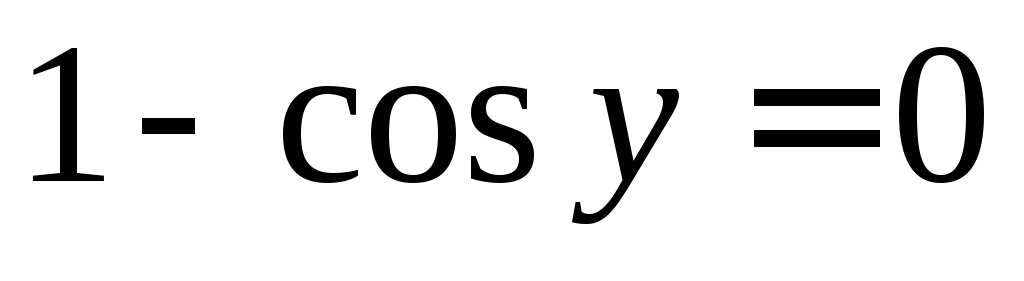 особые решения. Получаем,
особые решения. Получаем,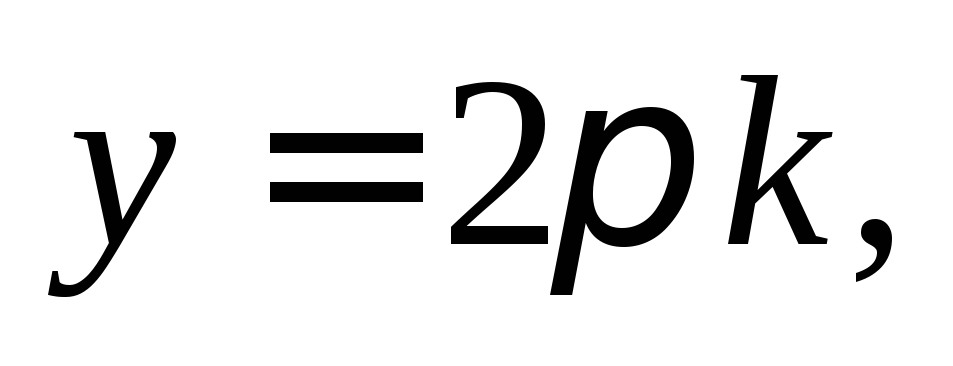
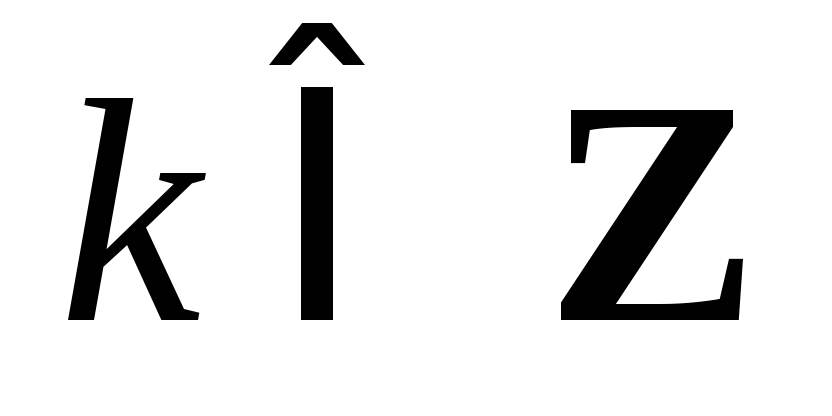 – это есть особые решения исходного
дифференциального уравнения. Таким
образом, решение заданного дифференциального
уравнения:
– это есть особые решения исходного
дифференциального уравнения. Таким
образом, решение заданного дифференциального
уравнения:
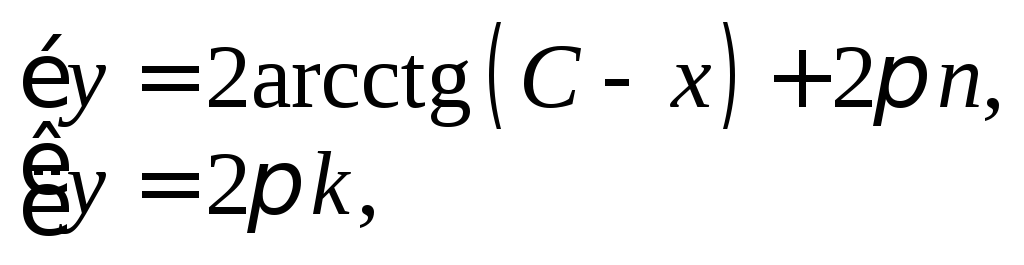
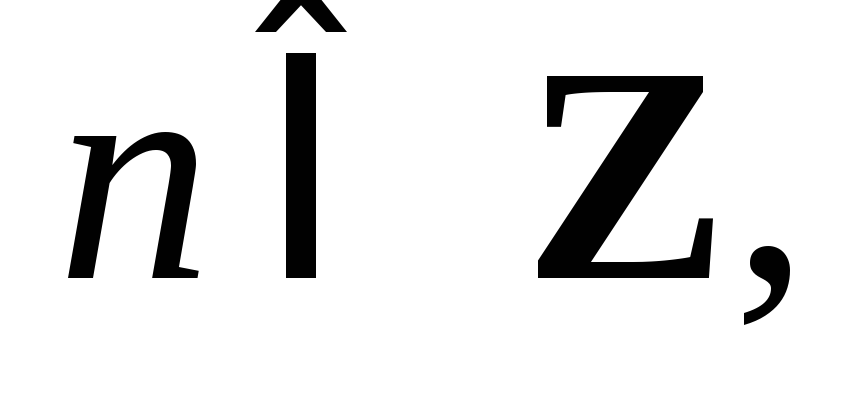
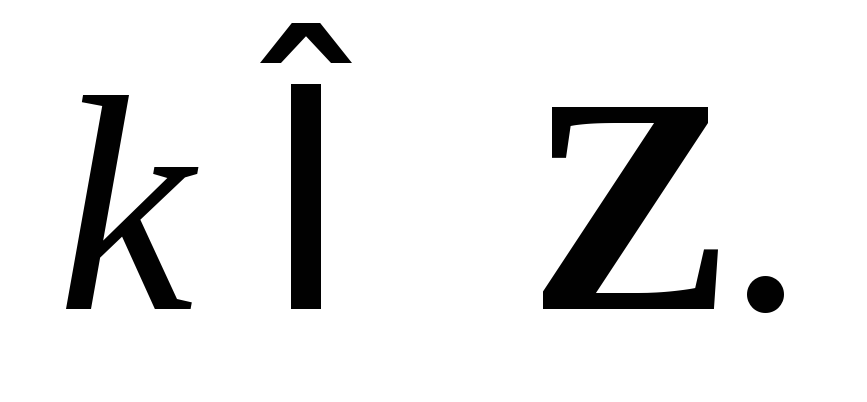
Пример
4. Известно,
что решением некоторого дифференциального
уравнения является семейство парабол 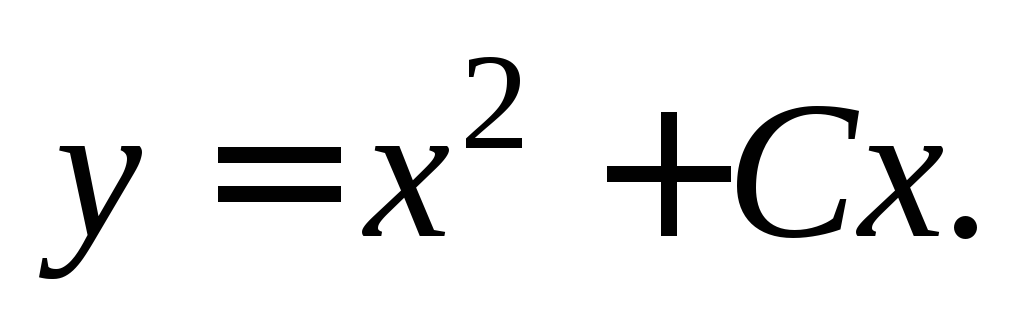 Определить это дифференциальное
уравнение.
Определить это дифференциальное
уравнение.
Решение. Дифференцируя равенство 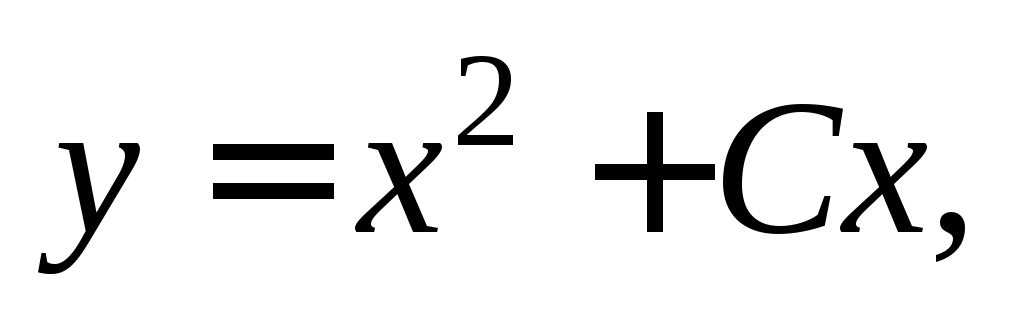 имеем
имеем
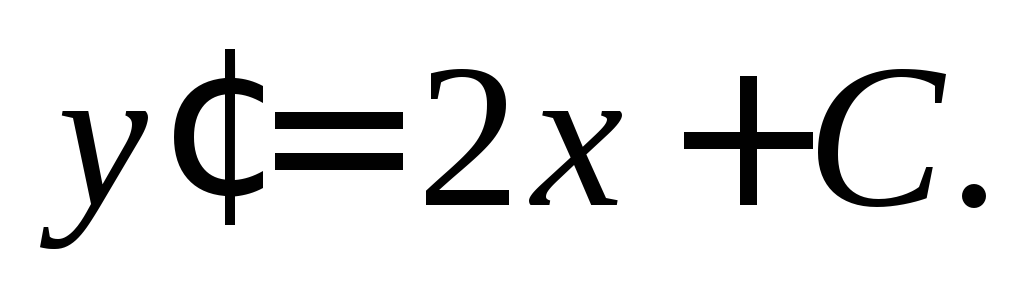 (22.5)
(22.5)
Выразим C из уравнения параболы: 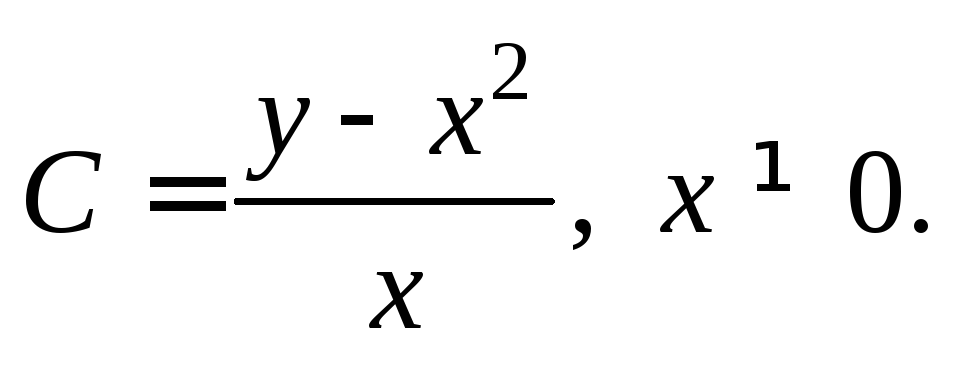 Подставив найденное значениеС в уравнение (22.5), получим
Подставив найденное значениеС в уравнение (22.5), получим 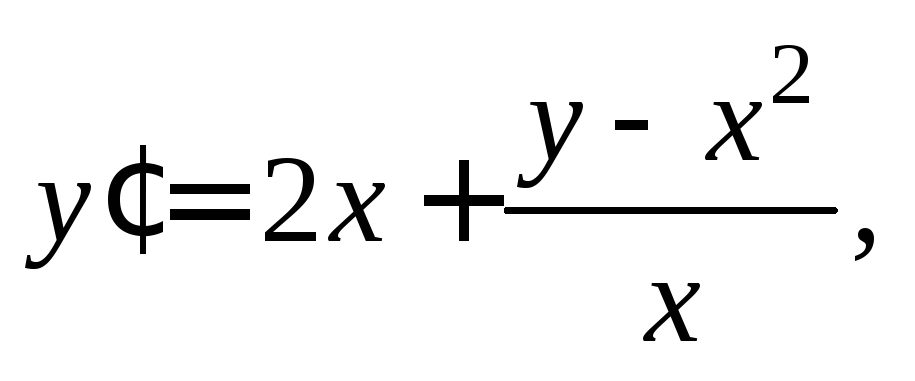 т. е.
т. е.
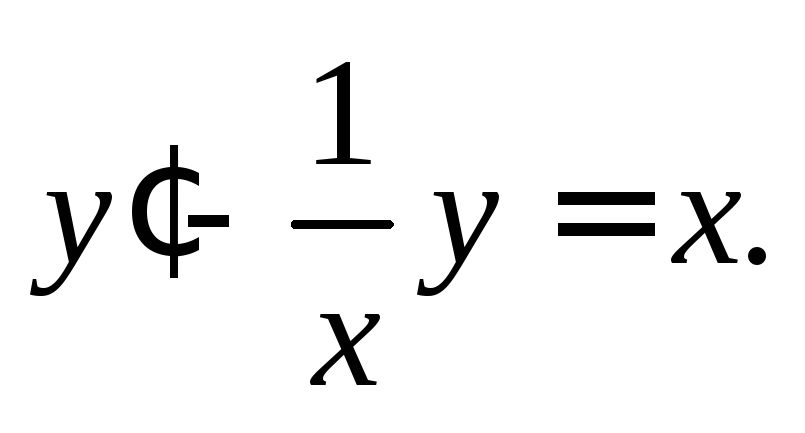 (22.6)
(22.6)
Заданное семейство парабол является решением дифференциального уравнения (22.6).
Пример
5. Доказать,
что 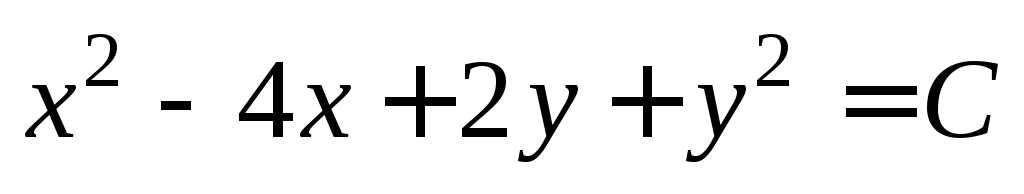 является общим интегралом дифференциального
уравнения
является общим интегралом дифференциального
уравнения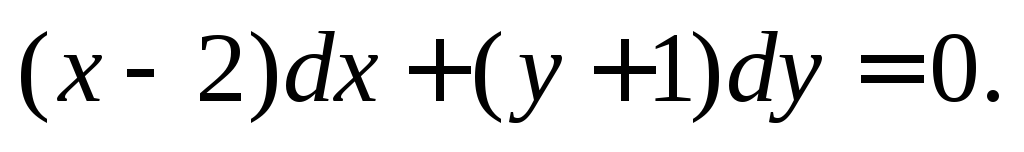 Определить частные интегралы, если
известно, что интегральные кривые
проходят соответственно через точки
(0, – 1) и (2, 0), построить эти
кривые.
Определить частные интегралы, если
известно, что интегральные кривые
проходят соответственно через точки
(0, – 1) и (2, 0), построить эти
кривые.
Решение. Вычислим производную неявной функции по формуле
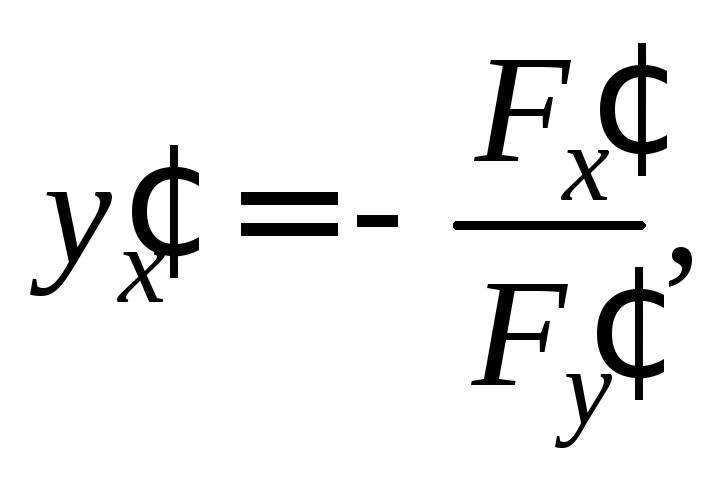 где
где 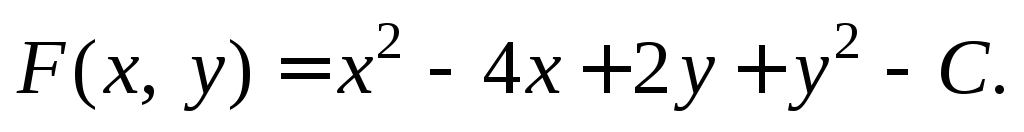
Тогда 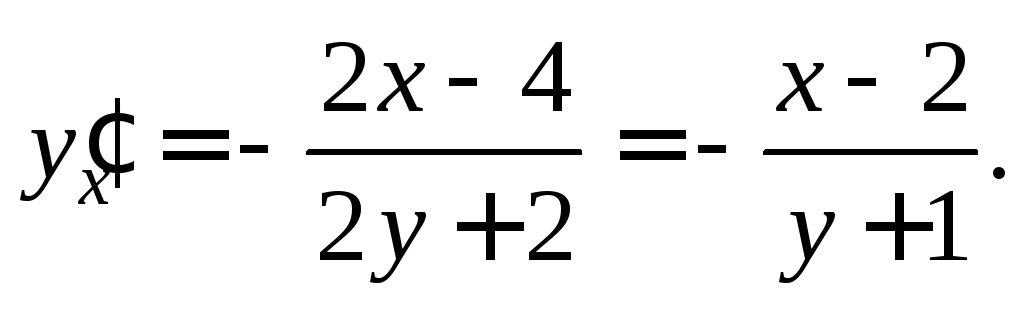 Подставим
Подставим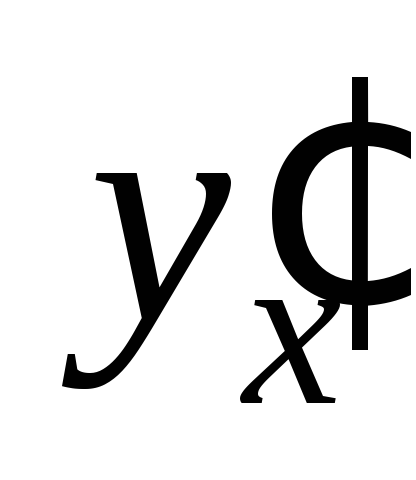 и
и  в заданное дифференциальное уравнение:
в заданное дифференциальное уравнение:
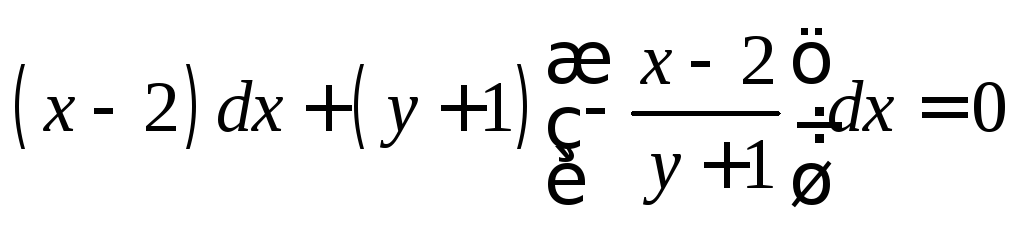 или
или
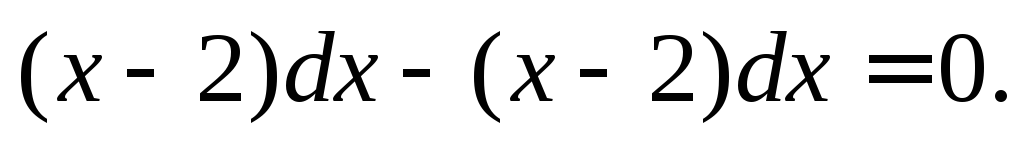
Получили
тождество 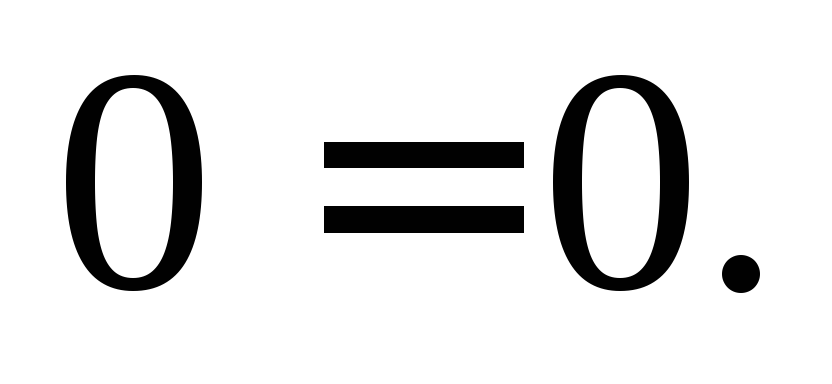 Это доказывает, что заданная неявно
функция является общим интегралом
исходного дифференциального уравнения.
Для нахождения частных интегралов и
проходящих через заданные точки
интегральных кривых подставляем
координаты этих точек в общий интеграл
и определяем соответствующие константы.
Это доказывает, что заданная неявно
функция является общим интегралом
исходного дифференциального уравнения.
Для нахождения частных интегралов и
проходящих через заданные точки
интегральных кривых подставляем
координаты этих точек в общий интеграл
и определяем соответствующие константы.
Для
точки (0, – 1) получаем: 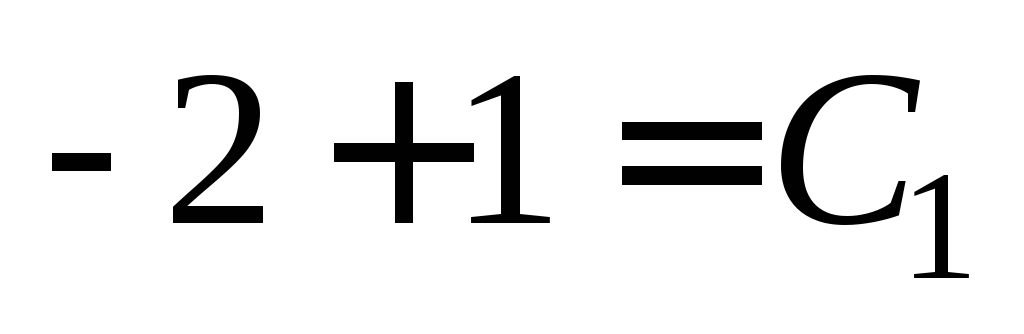 или
или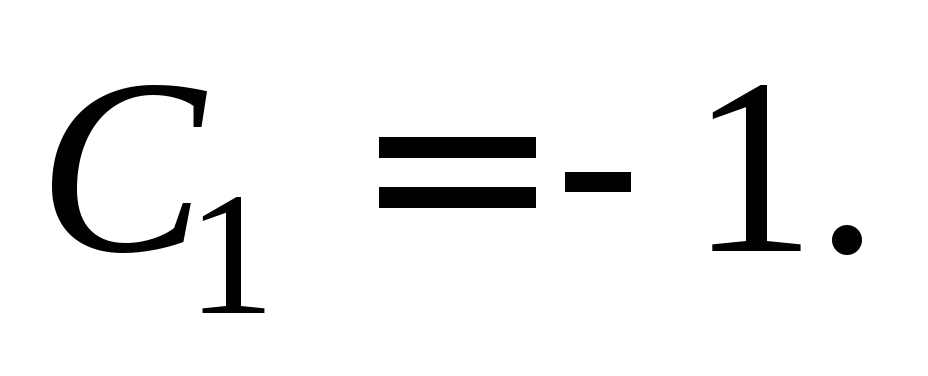 Для точки (2, 0) получаем:
Для точки (2, 0) получаем: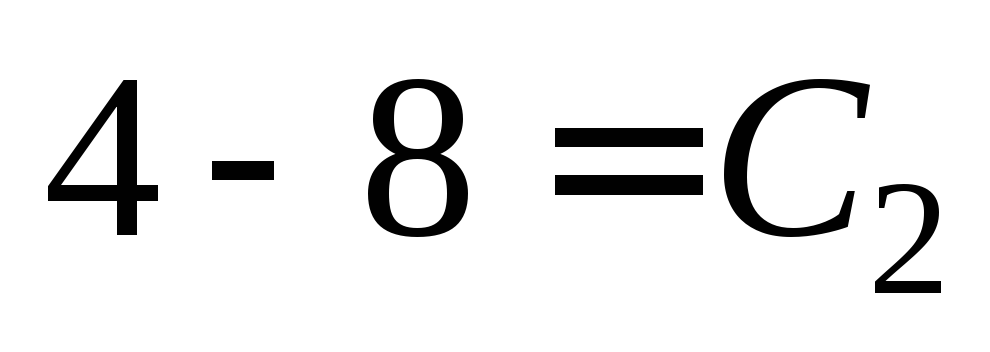 или
или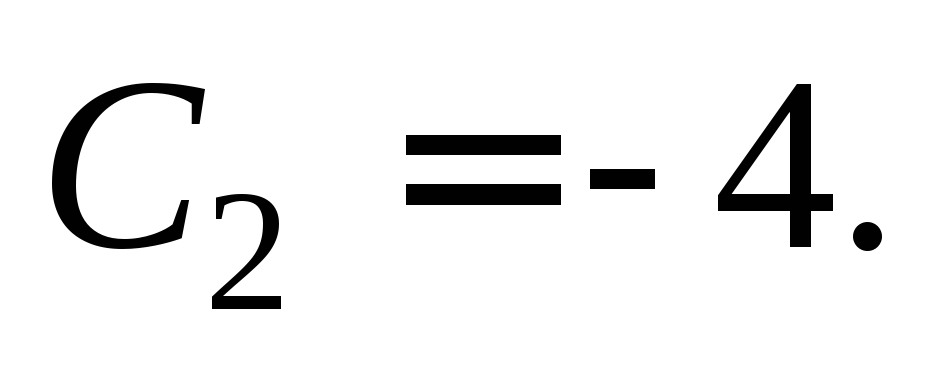 Тогда частными интегралами будут:
Тогда частными интегралами будут:
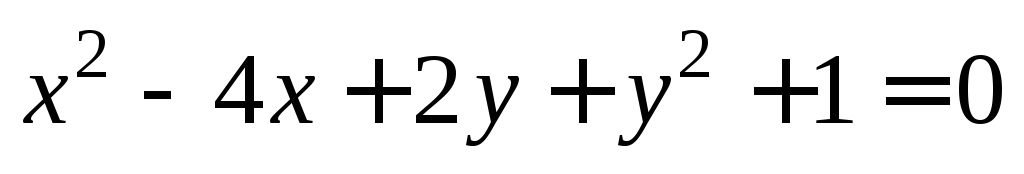 и
и 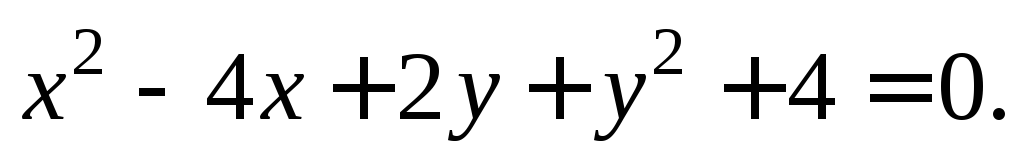
Интегральными
кривыми являются концентрические
окружности с центром в точке 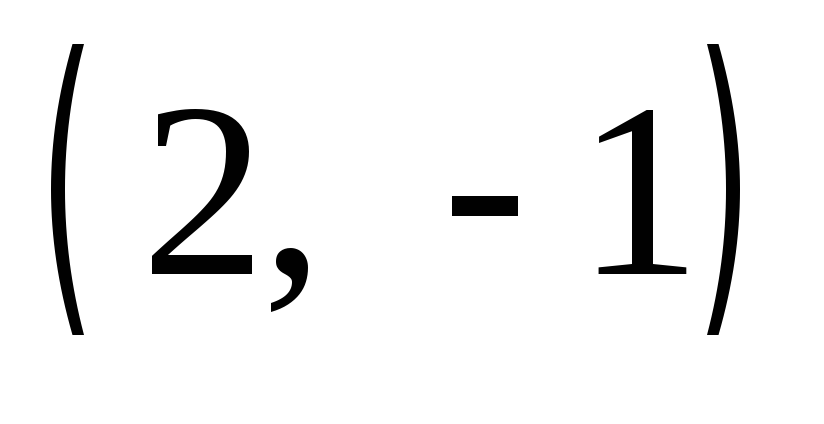 и радиусами 2 и 1 соответственно. Это
видно, если в полученных частных
интегралах выделить полный квадрат поx и по y:
и радиусами 2 и 1 соответственно. Это
видно, если в полученных частных
интегралах выделить полный квадрат поx и по y:
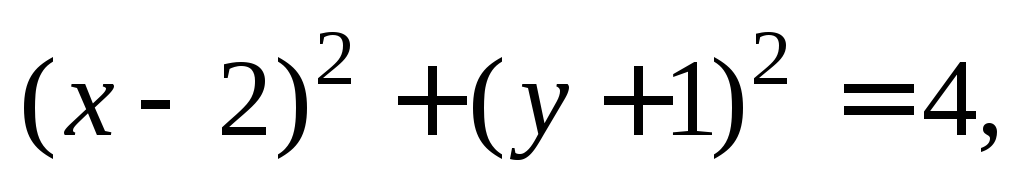
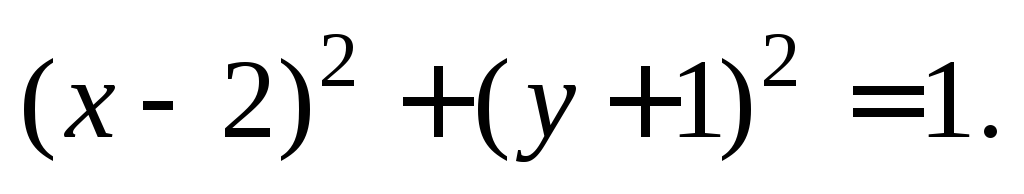
Графики интегральных кривых изображены на рис. 22.1.

Рис. 22.1
Пример 6. Найти частное решение дифференциального уравнения:
1) 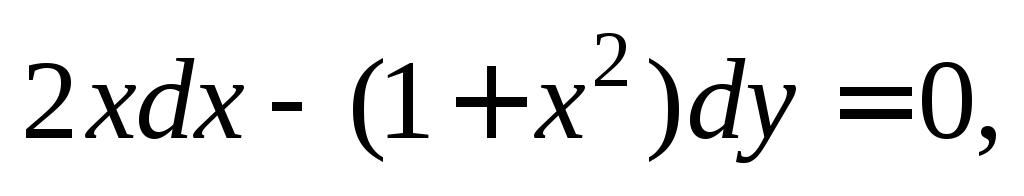
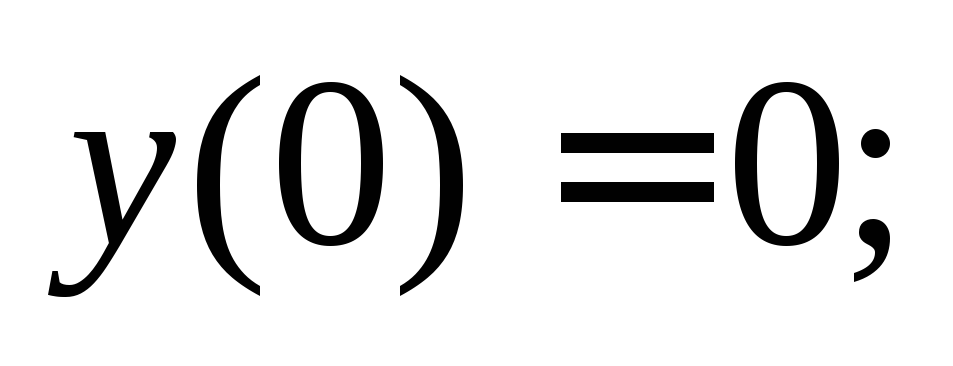 2)
2)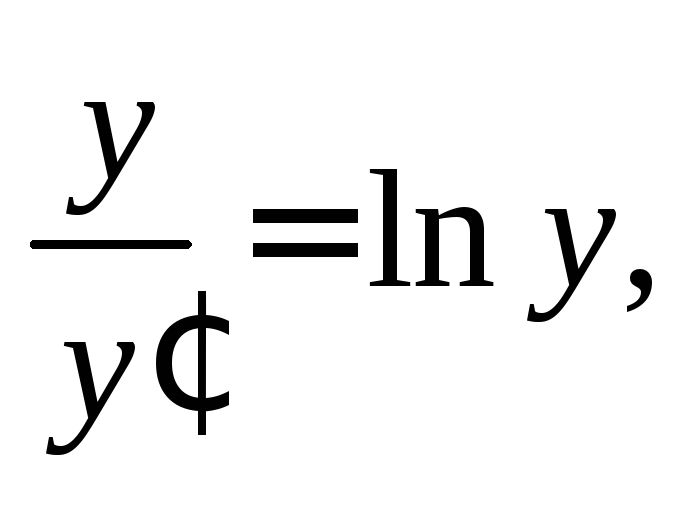

3) 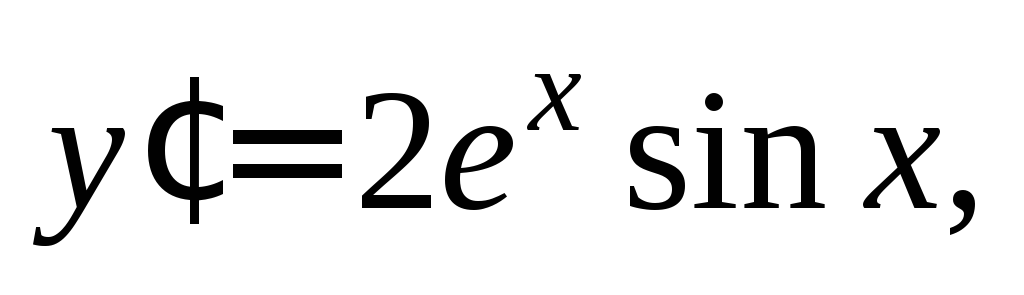
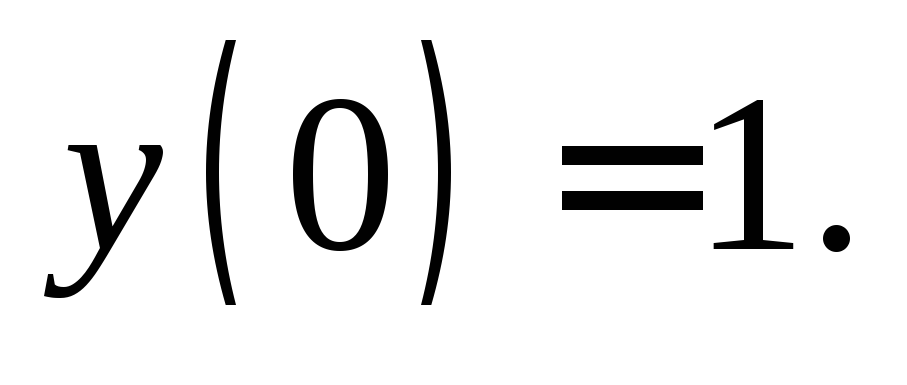
Решение. 1) Разделив уравнение на  получим:
получим:
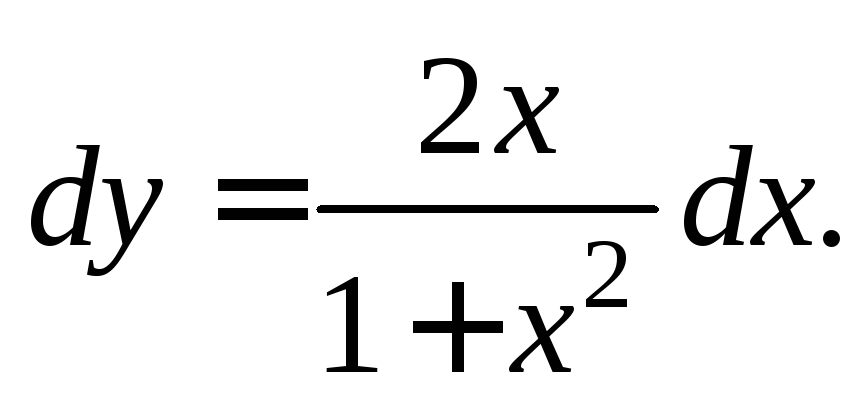
Интегрируем левую и правую части:
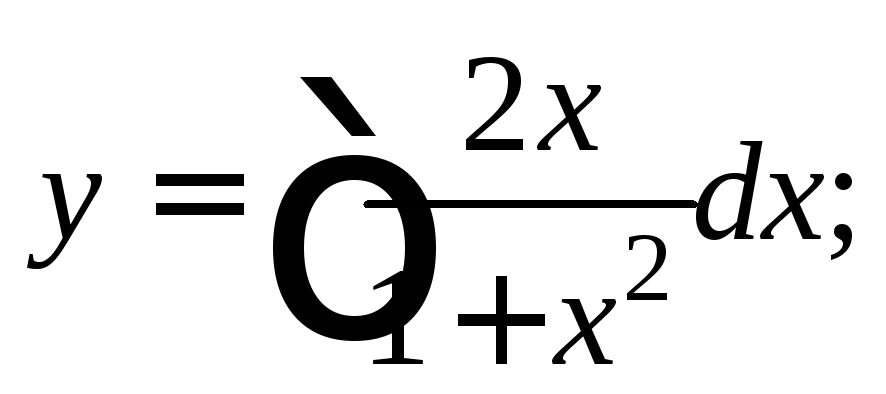
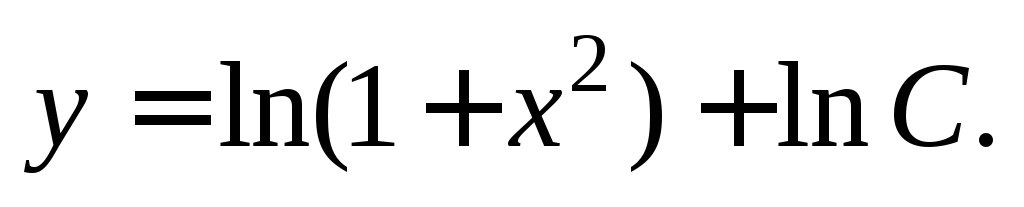
Получаем 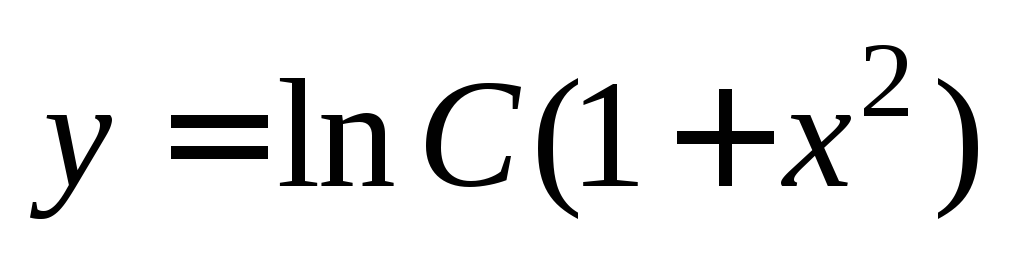 – общее решение исходного дифференциального
уравнения. Подставляем начальное условие
– общее решение исходного дифференциального
уравнения. Подставляем начальное условие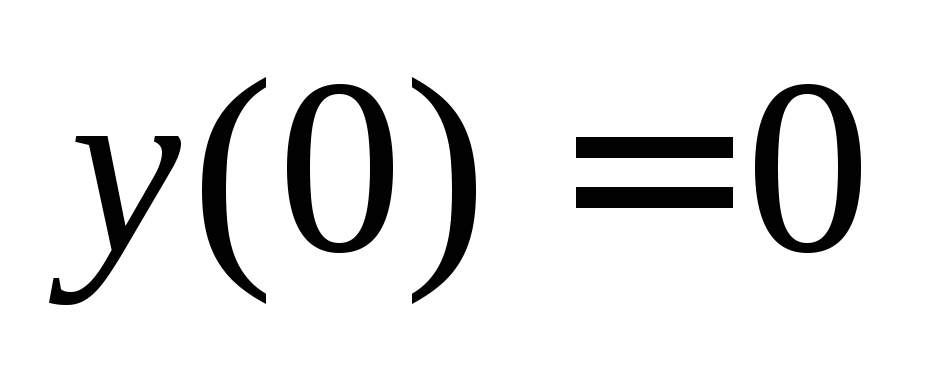 и находим константуС:
и находим константуС:
 или
или 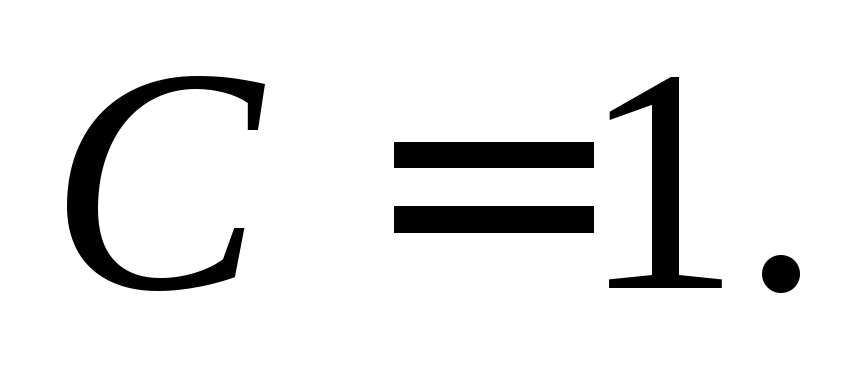
Нашли
частное решение 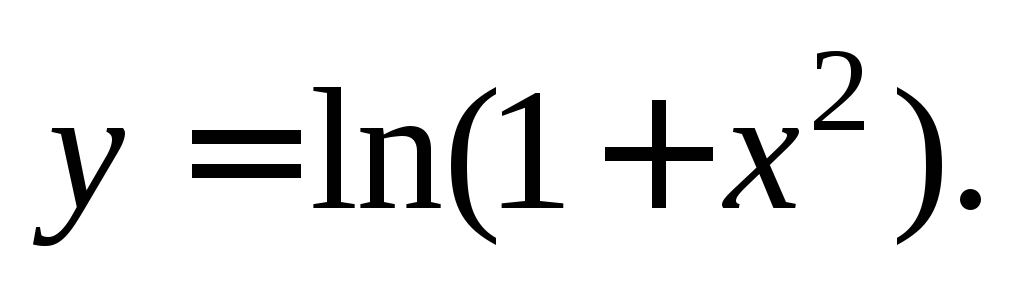
2)
Преобразуя заданное уравнение с учетом
того, что 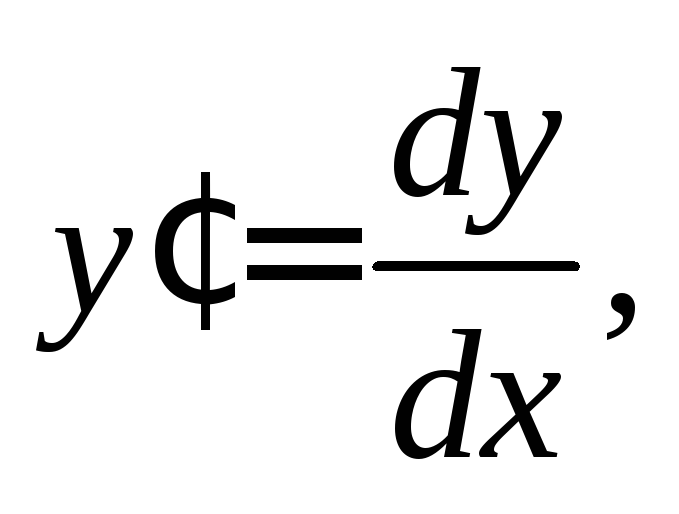 получаем
получаем Далее интегрируем:
Далее интегрируем:
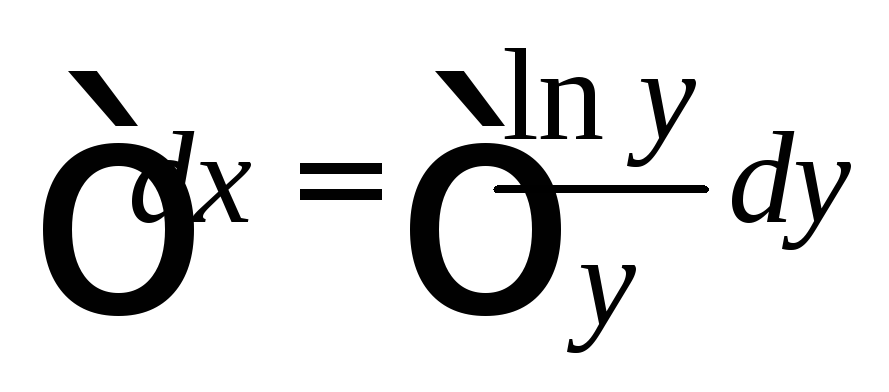 или
или 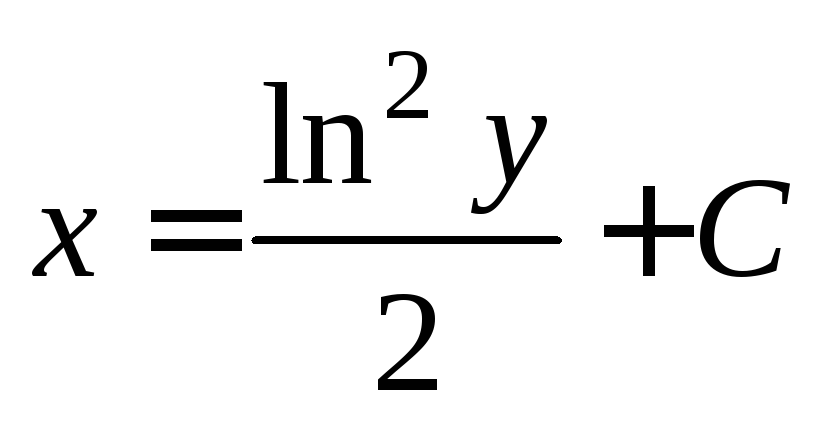 – это общий интеграл исходного уравнения.
– это общий интеграл исходного уравнения.
Используем
начальное условие: в полученное решение
подставляем  и
и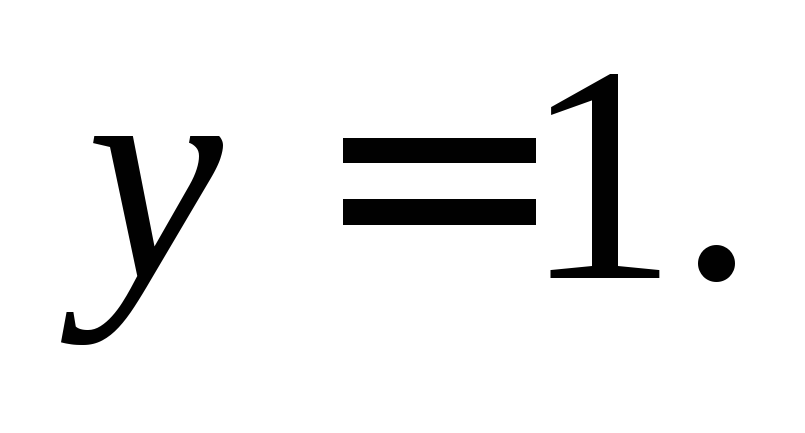 Находим константуС:
Находим константуС:
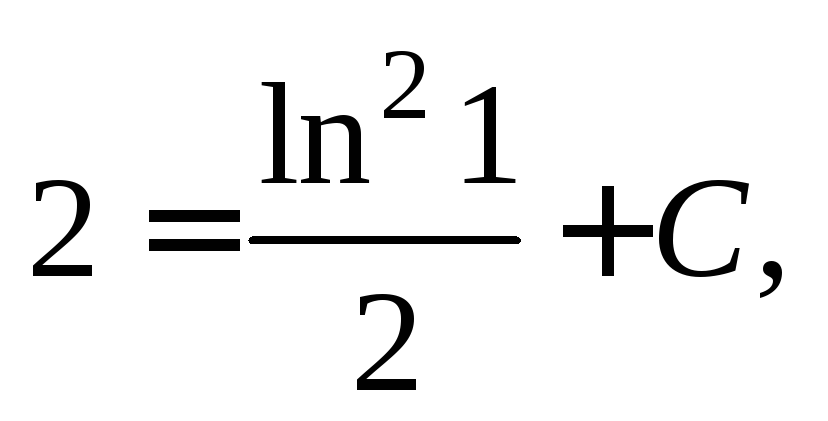 т.
е.
т.
е. 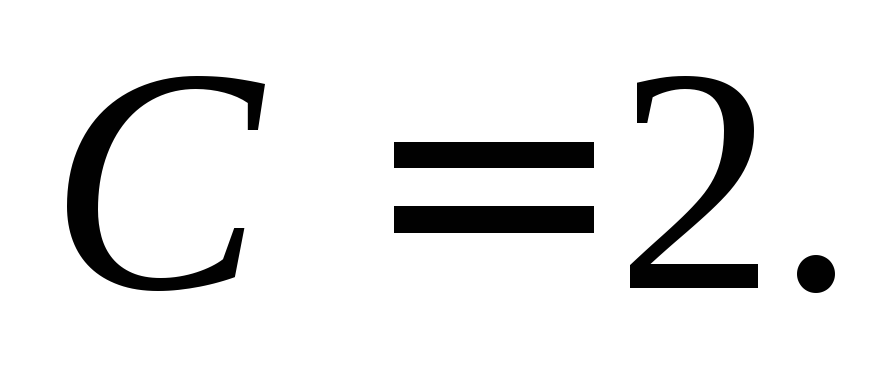 Значит,
Значит,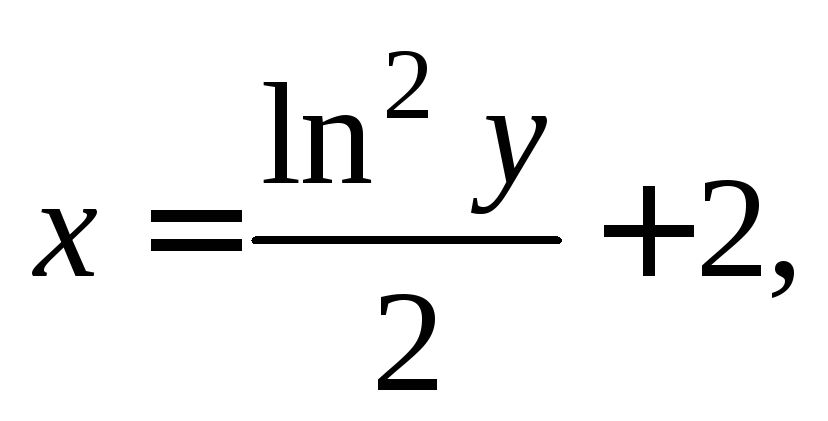 откуда получаем:
откуда получаем:
 –искомое
частное решение (частный интеграл).
–искомое
частное решение (частный интеграл).
3)
С учетом равенства 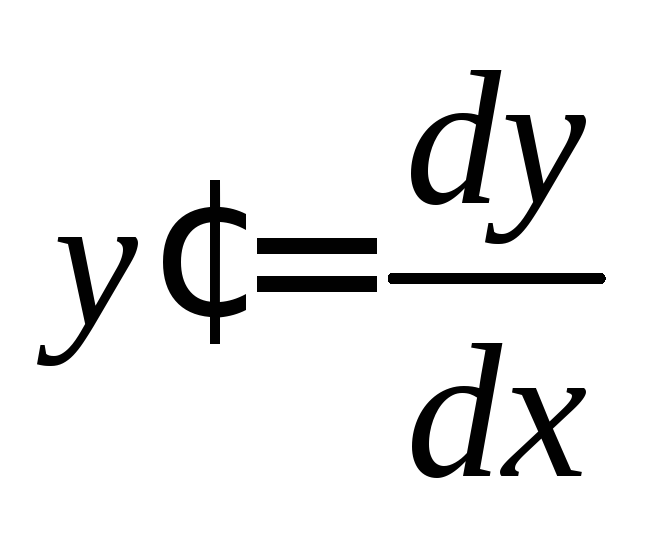 получаем
получаем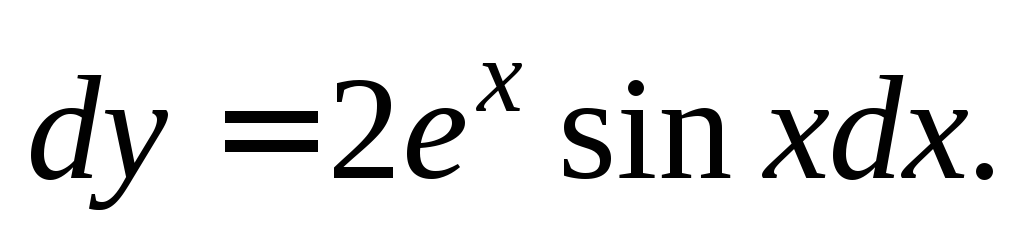 Интегрируем:
Интегрируем: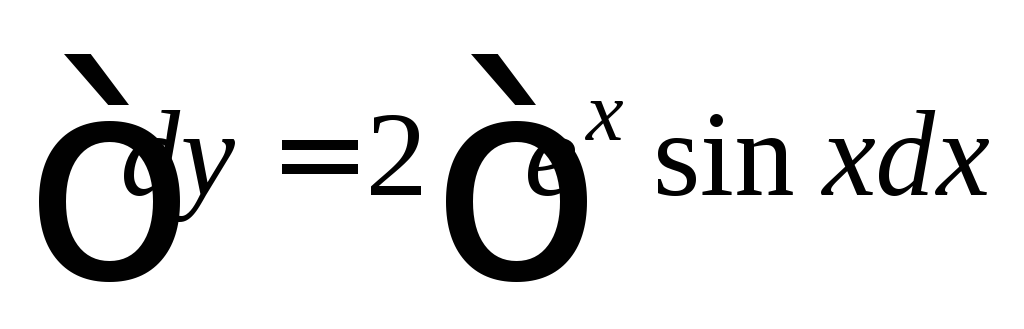 или
или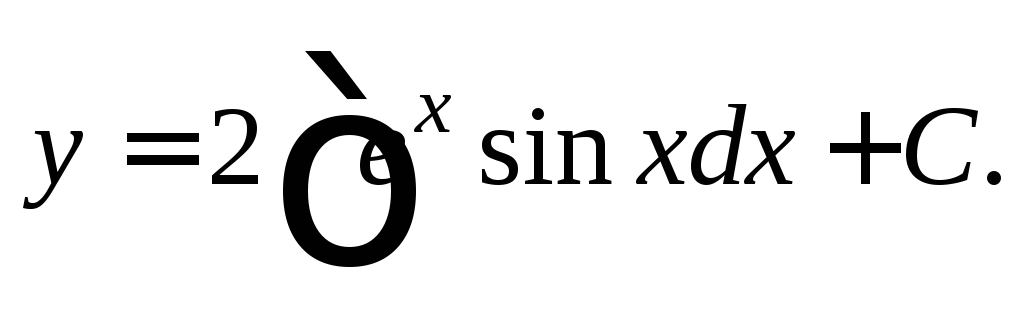 Вычисляем последний интеграл, дважды
интегрируя по частям:
Вычисляем последний интеграл, дважды
интегрируя по частям:
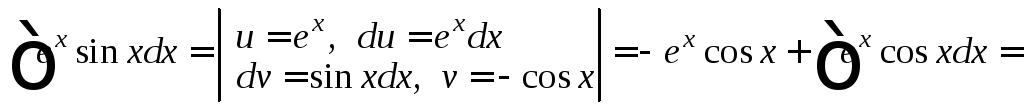
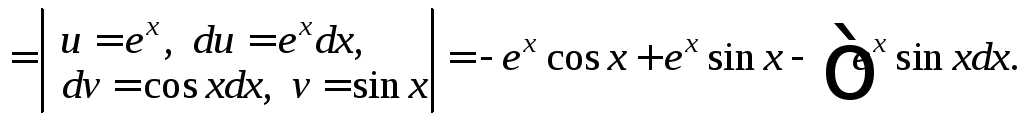
Отсюда
получаем 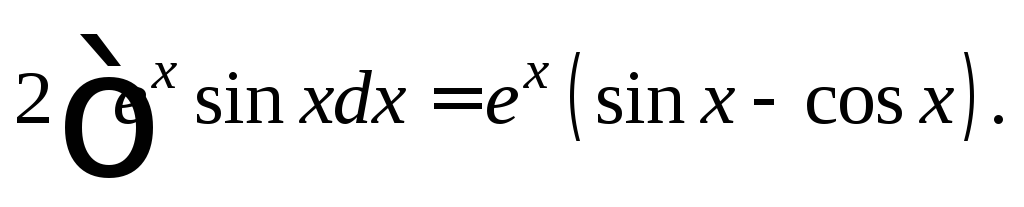
Таким
образом, 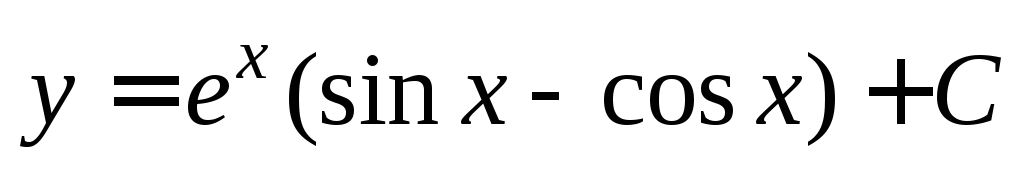 – общее решение исходного дифференциального
уравнения. Подставляя в него
– общее решение исходного дифференциального
уравнения. Подставляя в него
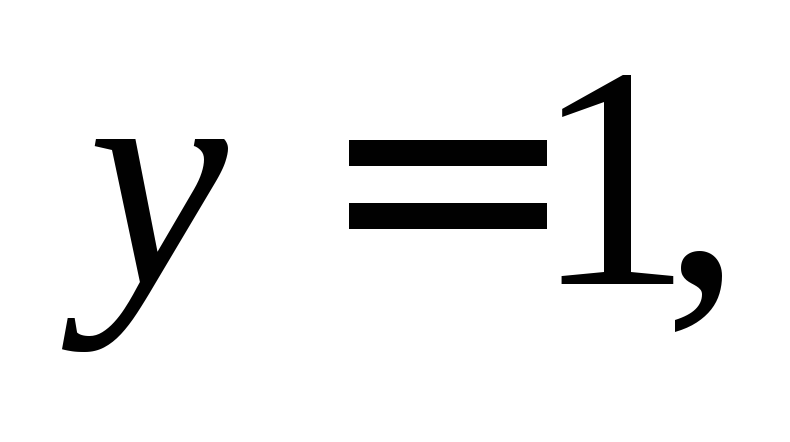 находимС:
находимС:  т. е.
т. е.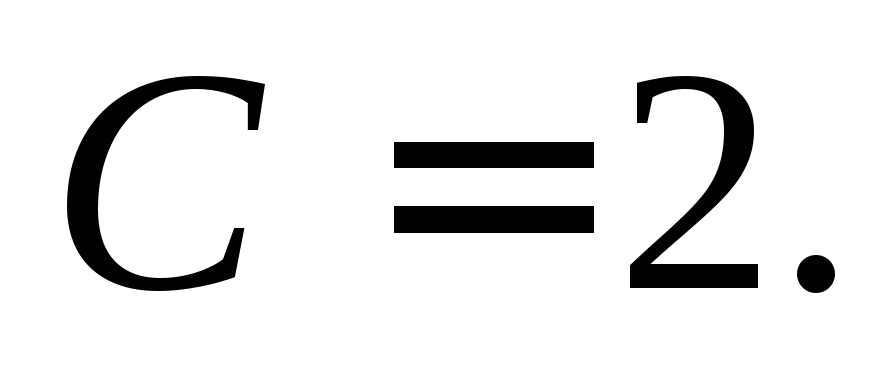 Частным решением является
Частным решением является
Задания
studfile.net
Дифференциальные уравнения.
Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких – то уравнением в частных производных.
Дифференциальное
уравнение можно записать в виде:  ,
где
,
где – некоторая функция
– некоторая функция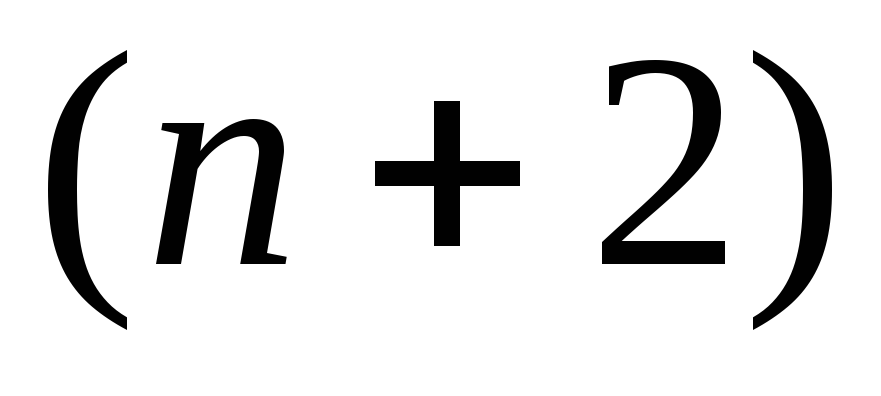 переменных
переменных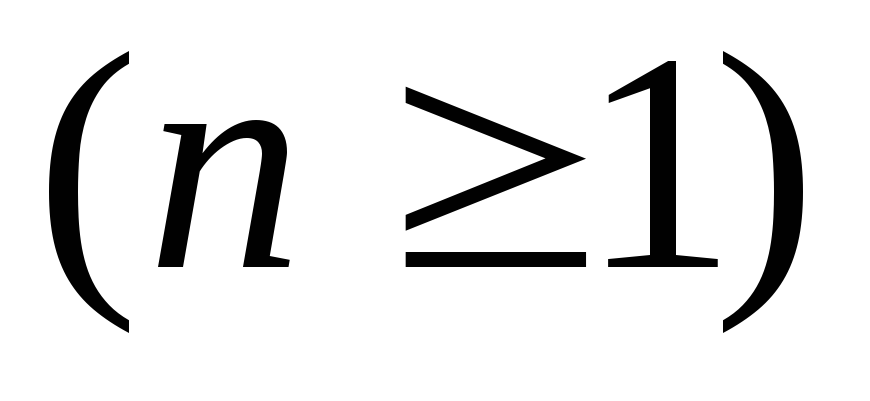 .
.
Порядок 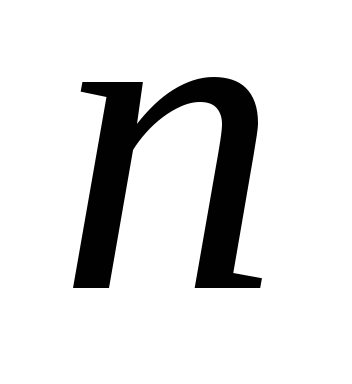 старшей производной называетсяпорядком
дифференциального уравнения.
старшей производной называетсяпорядком
дифференциального уравнения.
Дифференциальное
уравнение  -го
порядка называетсяразрешенным относительно старшей производной, если
оно имеет вид:
-го
порядка называетсяразрешенным относительно старшей производной, если
оно имеет вид: 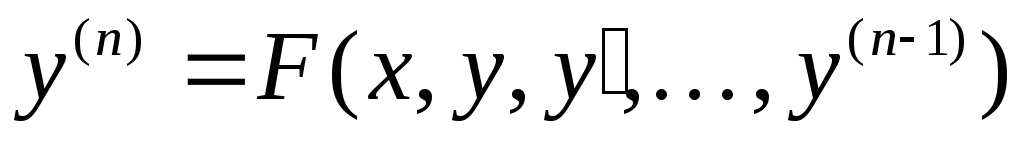 ,
где
,
где
некоторая функция от
некоторая функция от  переменной.
переменной.
Решением
дифференциального уравнения  называется функция
называется функция ,
которая при подстановке ее в это уравнение
обращает его в тождество.
,
которая при подстановке ее в это уравнение
обращает его в тождество.
Пример. Найти решение дифференциального
уравнения 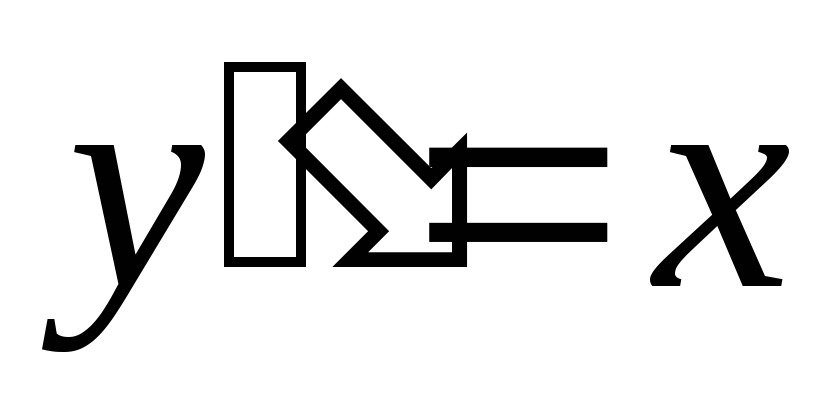 .
.
Решение:
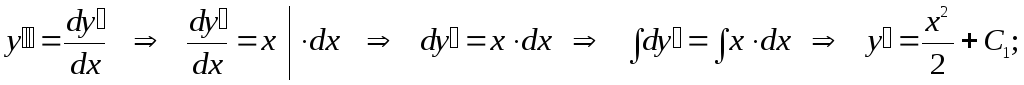

Ответ: 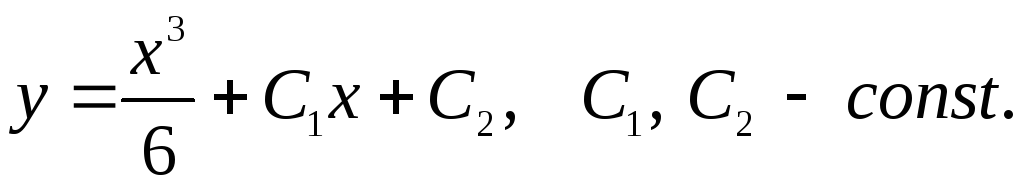
Общим
решением дифференциального уравнения 
 -го
порядка называется такое его решение
-го
порядка называется такое его решение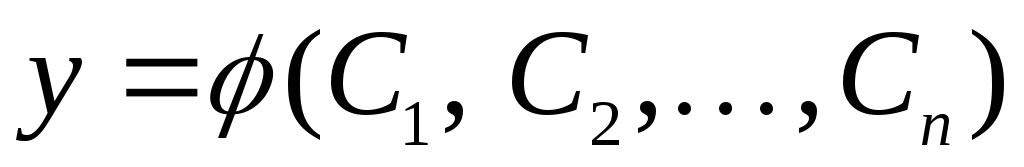 ,
которое является функцией переменной
,
которое является функцией переменной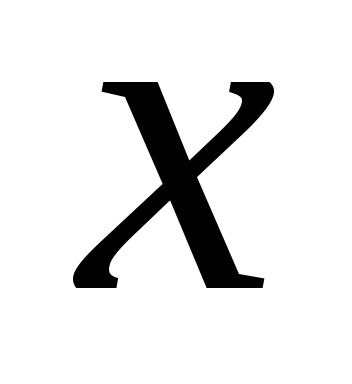 и
и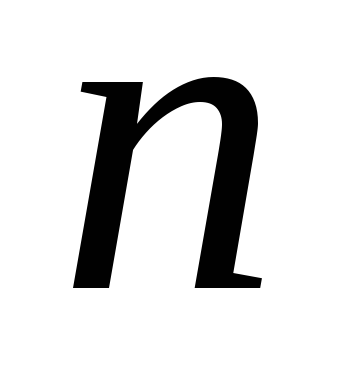 произвольных постоянных
произвольных постоянных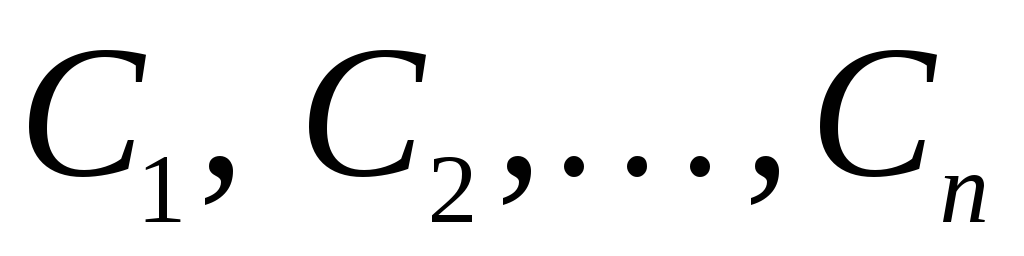 .
.
Частным
решением дифференциального уравнения  называется решение, получаемое из общего
решения при некоторых конкретных
числовых значениях
называется решение, получаемое из общего
решения при некоторых конкретных
числовых значениях .
.
Пример. Рассмотрим дифференциальное уравнение
из предыдущего примера  .
Тогда общим решением будет
.
Тогда общим решением будет
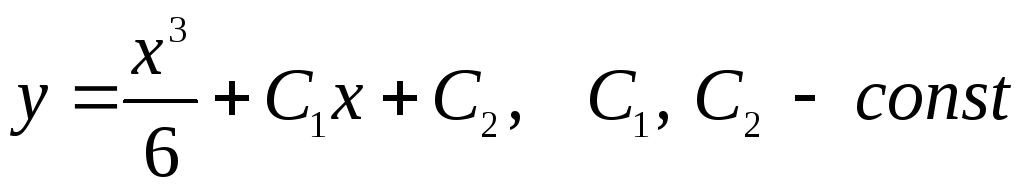 ,
,
а
частным решением: 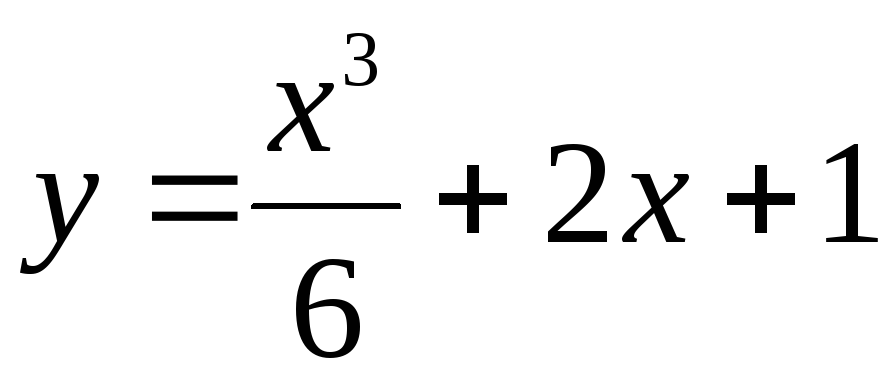 или
или .
.
Дифференциальные уравнения первого порядка.
Дифференциальное
уравнение первого порядка имеет вид: 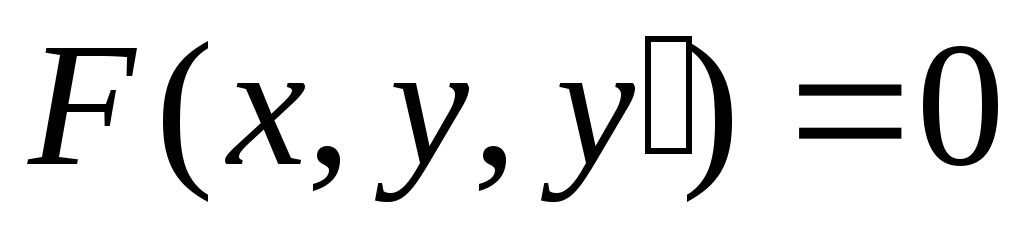 или
или ,
где
,
где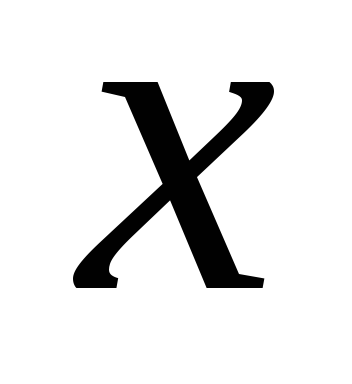 – независимая переменная;
– независимая переменная;
неизвестная функция и ее производная.
неизвестная функция и ее производная.
Учитывая,
что  уравнение первого порядка можно записать
в форме:
уравнение первого порядка можно записать
в форме: .
.
Общим
решением дифференциального уравнения первого
порядка называется функция вида 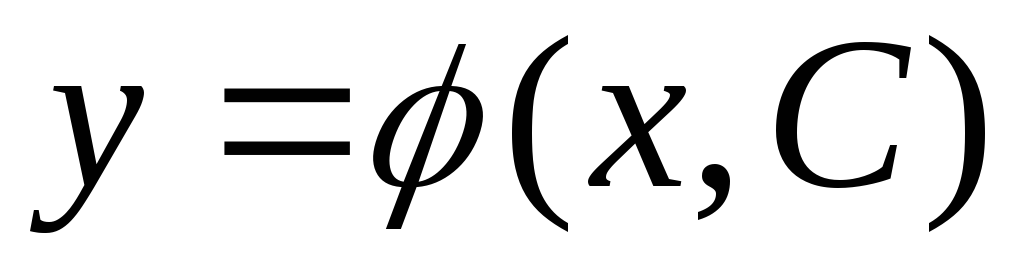 ,
где
,
где – произвольная постоянная, удовлетворяющая
условиям:
– произвольная постоянная, удовлетворяющая
условиям:
Для любого значения
 она является решением уравнения;
она является решением уравнения;При любом допустимом начальном условии
 найдется такое значение
найдется такое значение ,
что
,
что .
.
Если общее решение не представлено в явном виде, то оно называется общим интегралом.
Задача
нахождения частного решения,
удовлетворяющего заданному начальному
условию 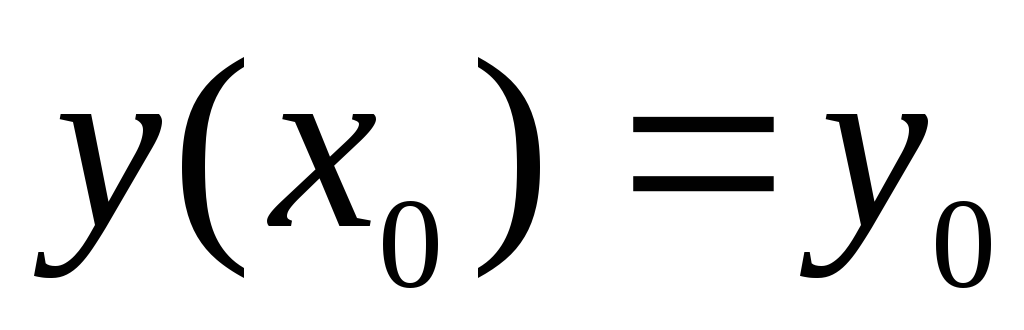 ,
называетсязадачей
Коши.
,
называетсязадачей
Коши.
Пример. Дана задача Коши 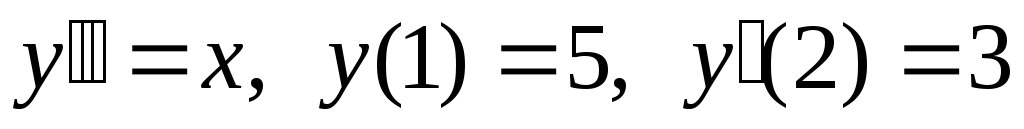 .
Найти частное решение.
.
Найти частное решение.
Решение: Общее решение имеет вид
 ,
, 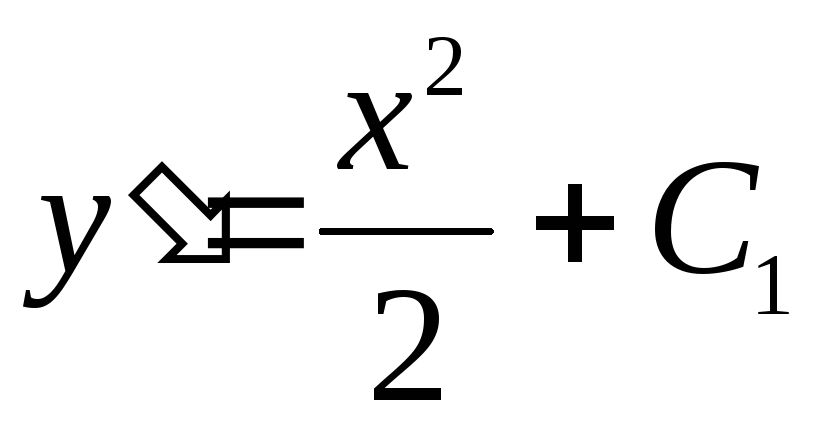 .
.
Подставляем начальные условия:
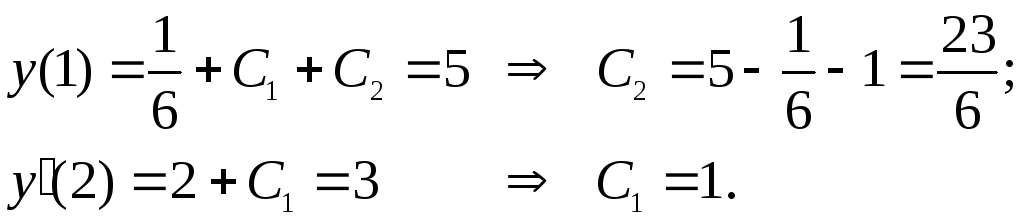
Получим,
что частное решение данной задачи Коши 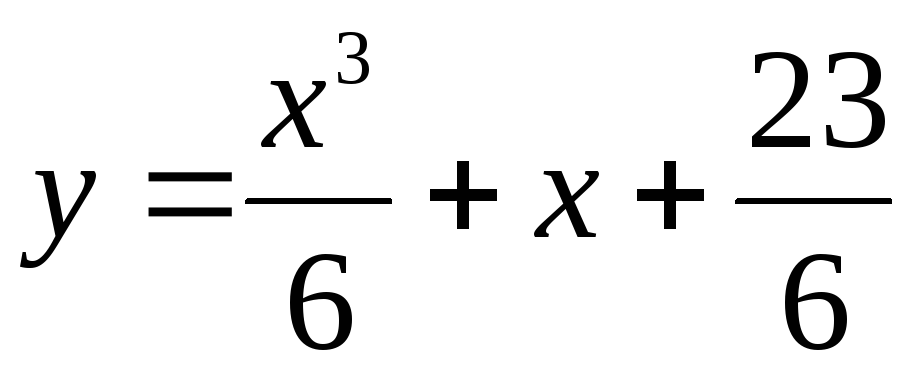 .
.
Ответ:  .
.
Теорема
Коши о существовании и единственности
решения. Пусть дано дифференциальное уравнение 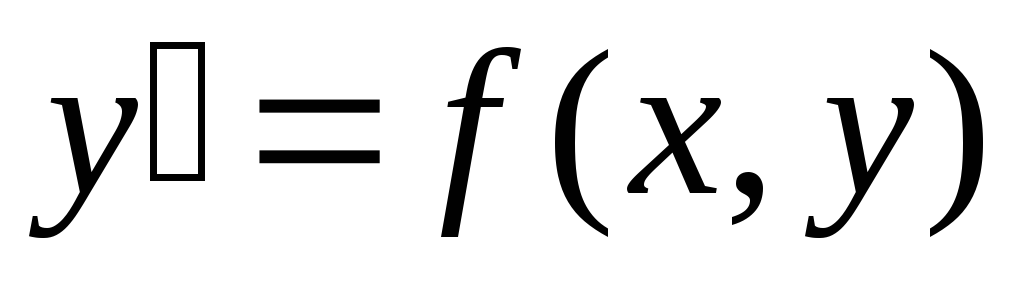 .
Если функция
.
Если функция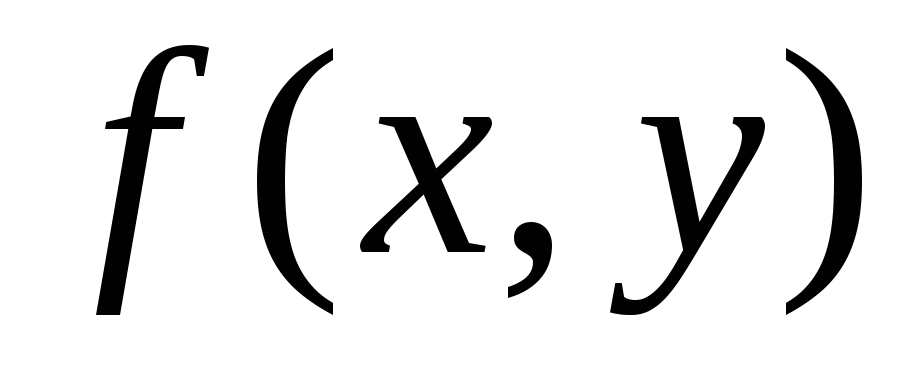 и ее частная производная
и ее частная производная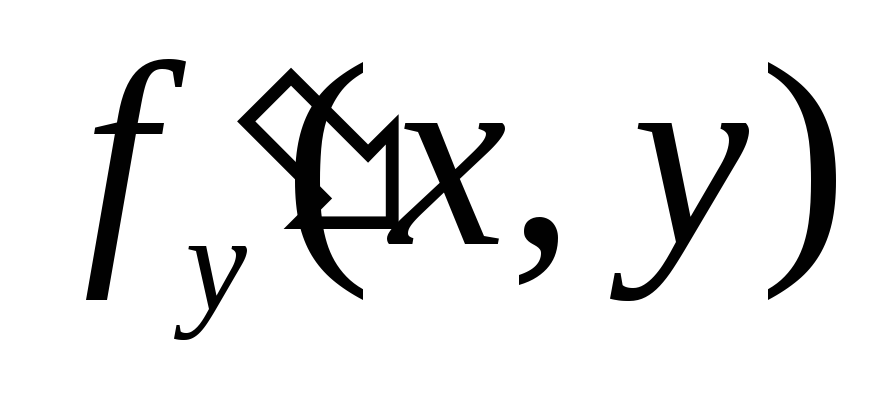 непрерывны в некоторой области
непрерывны в некоторой области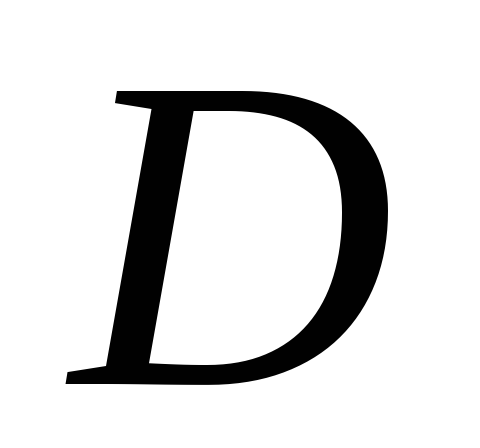 плоскости
плоскости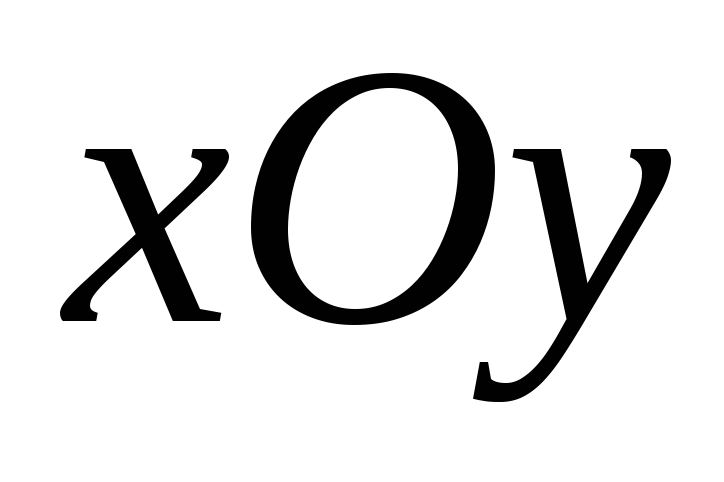 ,
то в некоторой окрестности любой
внутренней точки
,
то в некоторой окрестности любой
внутренней точки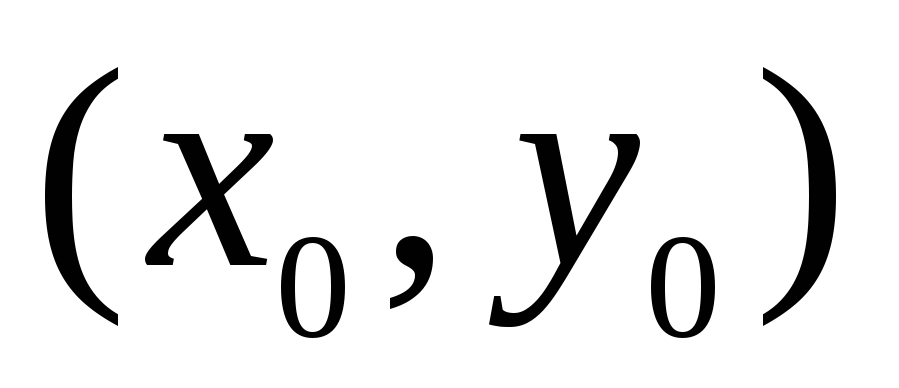 этой области существует единственное
решение уравнения
этой области существует единственное
решение уравнения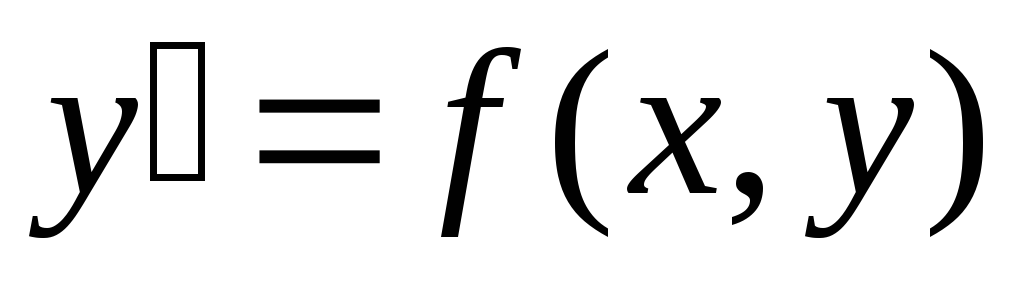 ,
удовлетворяющее условию
,
удовлетворяющее условию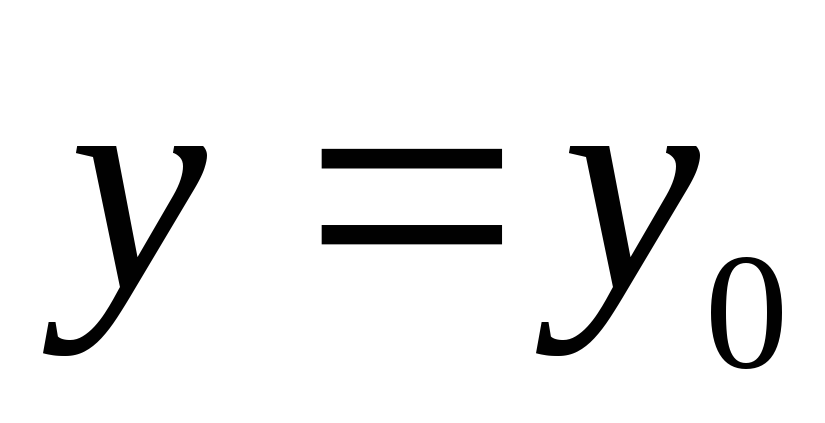 при
при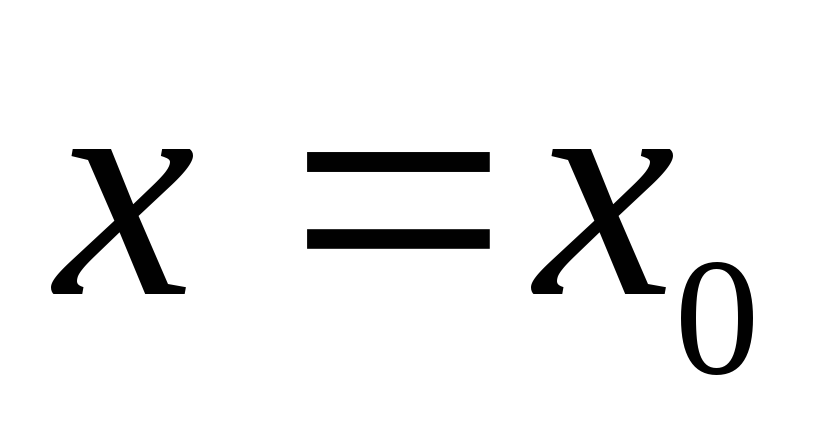 .
.
Геометрически общее решение представляет собой
однопараметрическое семейство
интегральных кривых на плоскости  .
Частное решение – одна из кривых этого
семейства, проходящая через точку
.
Частное решение – одна из кривых этого
семейства, проходящая через точку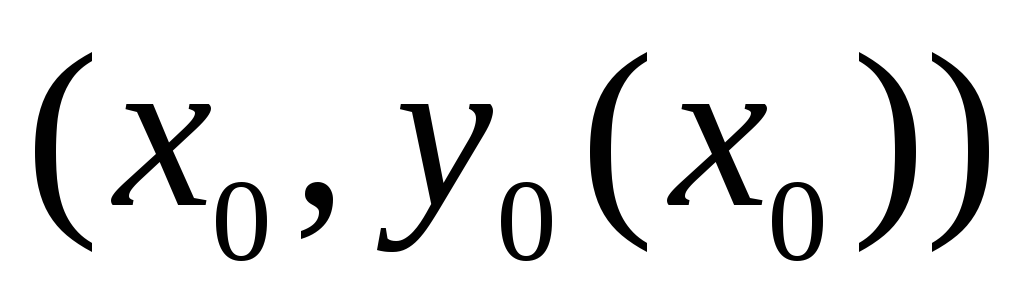 .
.
Типы дифференциальных уравнений первого порядка:
Дифференциальное уравнение с разделяющимися переменными имеет вид:
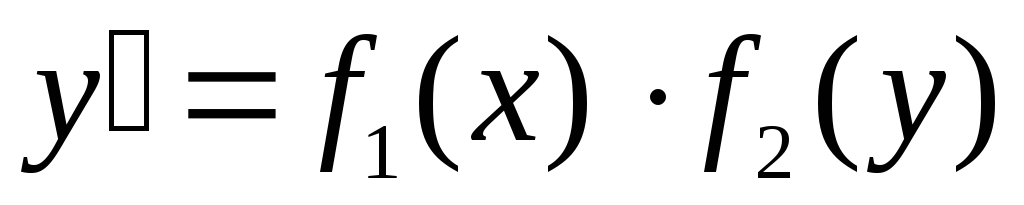 или
или  ,
,
где 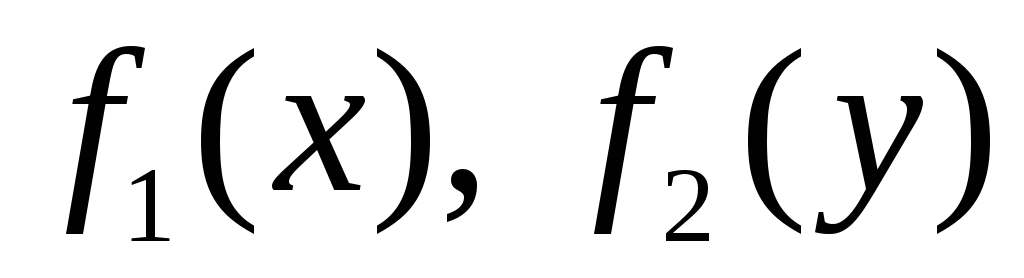 – непрерывные функции.
– непрерывные функции.
Разделив
обе части уравнения на 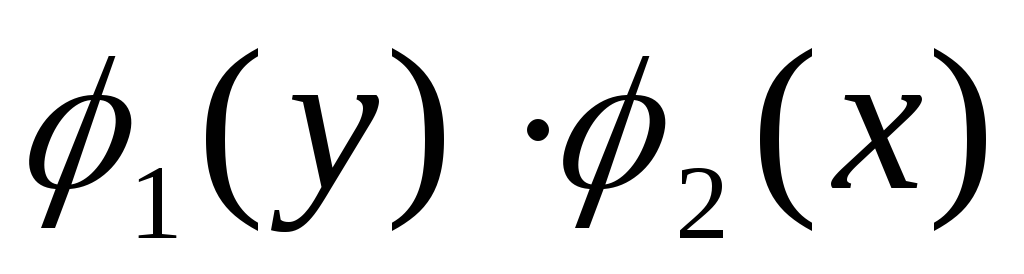 ,
получим уравнение:
,
получим уравнение:
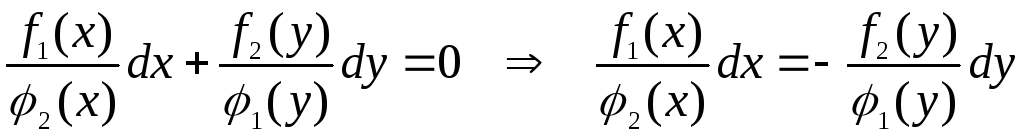 ,
,
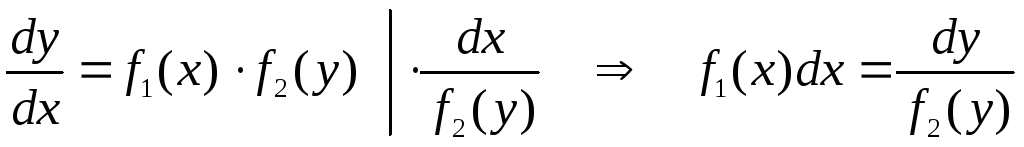 .
.
В
полученных уравнениях левая часть
зависит только от  ,
а правая часть только от
,
а правая часть только от ,
т.е. переменные разделены.
,
т.е. переменные разделены.
Поскольку
дифференциалы равны, то их неопределенные
интегралы различаются на постоянную
величину. Интегрируя слева по переменной  ,
а справа по переменной
,
а справа по переменной ,
получаем:
,
получаем:
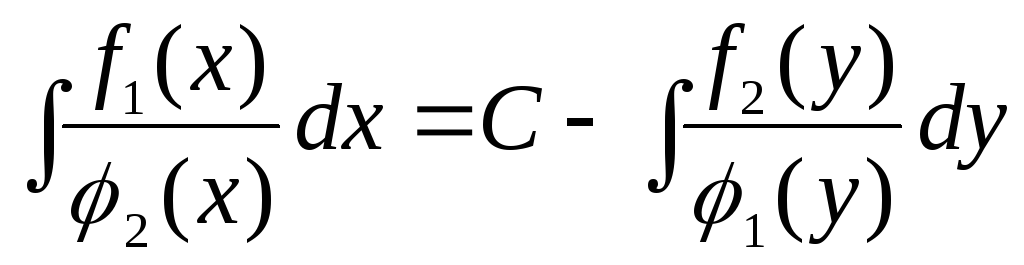 или
или 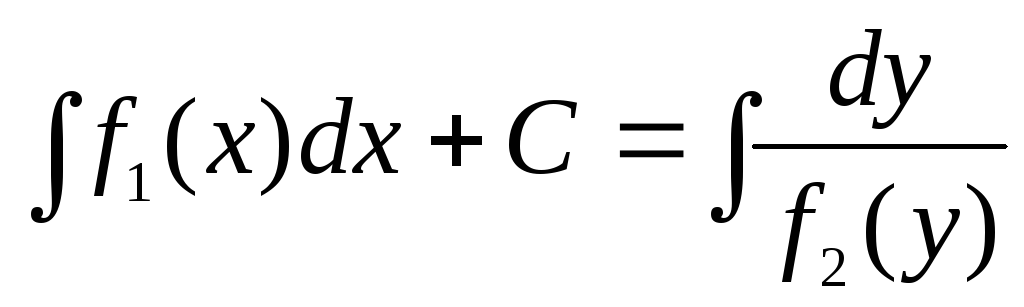 .
.
Пример. Найти частное решение дифференциального
уравнения 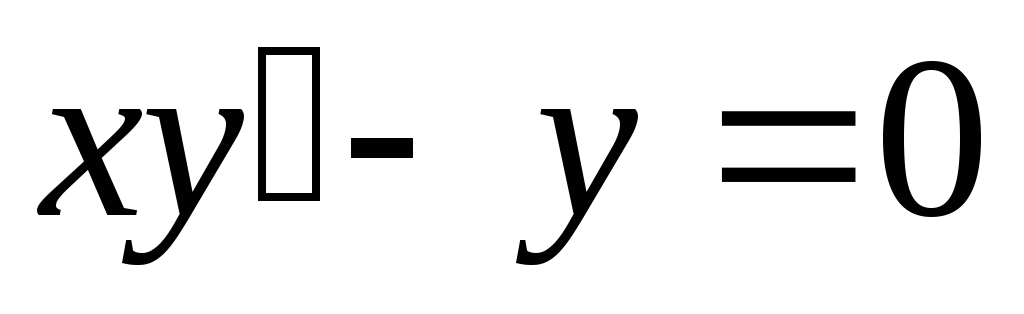 при начальных условиях
при начальных условиях .
.
Решение:

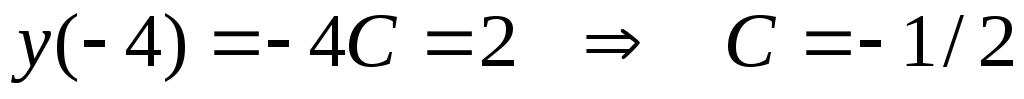 .
.
Ответ: 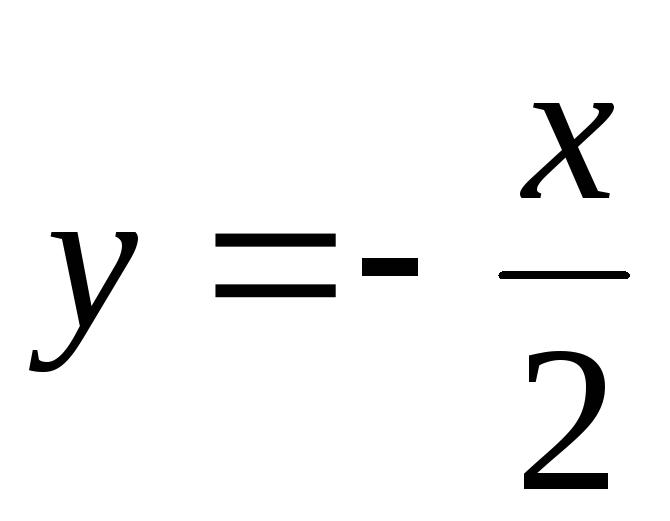 .
.
Пример. Найти решение дифференциального
уравнения  .
.
Решение: 
Ответ:  .
.
Неполные дифференциальные уравнения первого порядка
 – это дифференциальные уравнения, в
которых функция
– это дифференциальные уравнения, в
которых функция явно зависит только от одной переменной:
явно зависит только от одной переменной:
А)
Пусть 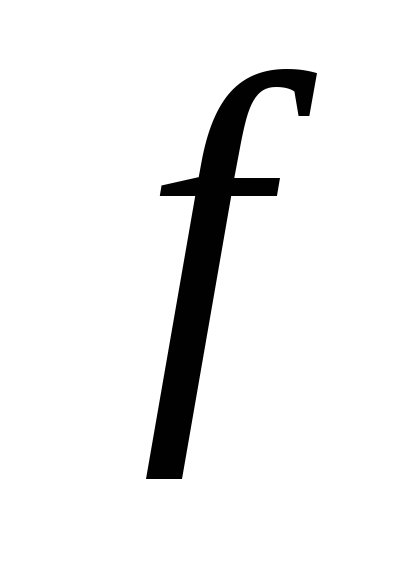 зависит только от
зависит только от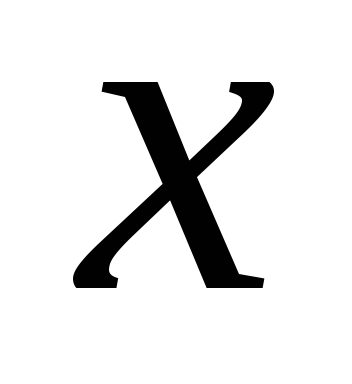 ,
тогда
,
тогда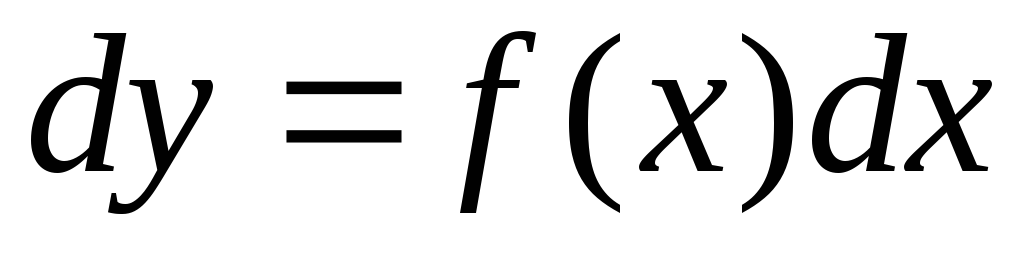 ,
откуда получаем:
,
откуда получаем: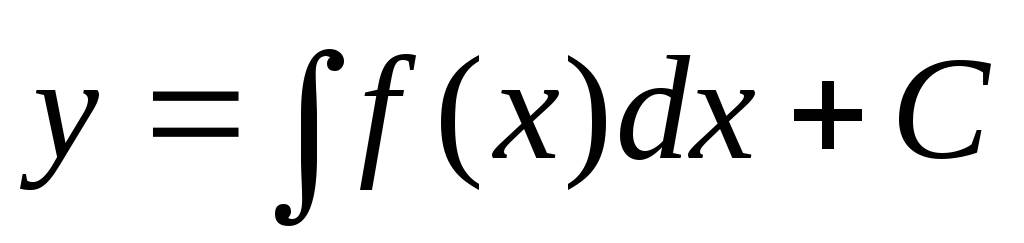 .
.
Б)
Пусть 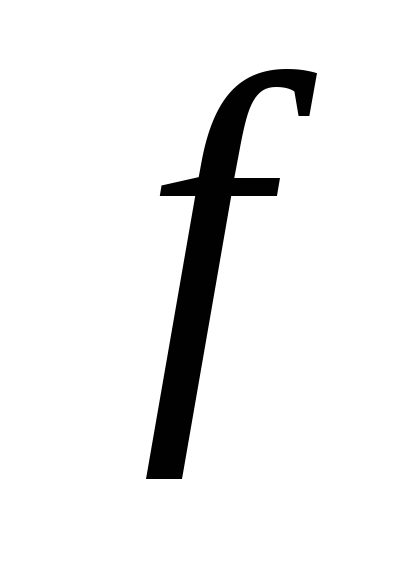 зависит только от
зависит только от ,
т.е.
,
т.е. – это уравнение называетсяавтономным.
Откуда получаем:
– это уравнение называетсяавтономным.
Откуда получаем: 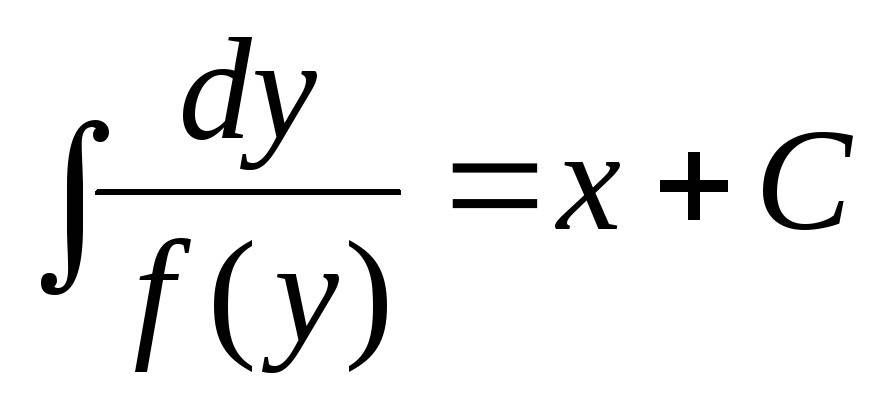 .
.
Линейные дифференциальные уравнения первого порядка имеют вид:
 .
.
Если 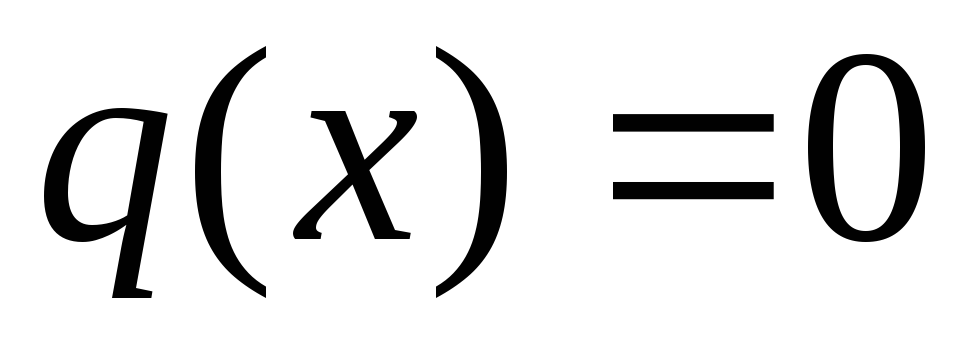 ,
то уравнение
,
то уравнение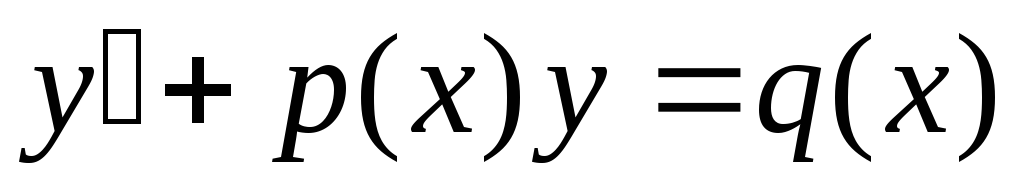 называетсялинейным
однородным уравнением,
если
называетсялинейным
однородным уравнением,
если 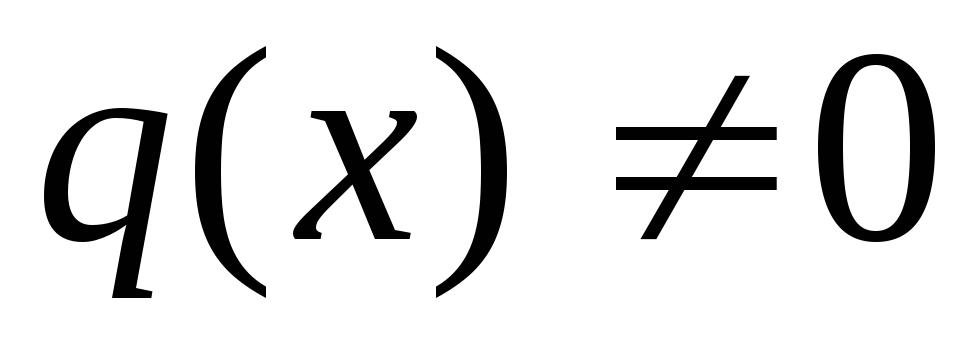 ,
то –линейным
неоднородным уравнением.
,
то –линейным
неоднородным уравнением.
А) Однородное
уравнение – это уравнение, приводящееся к виду: 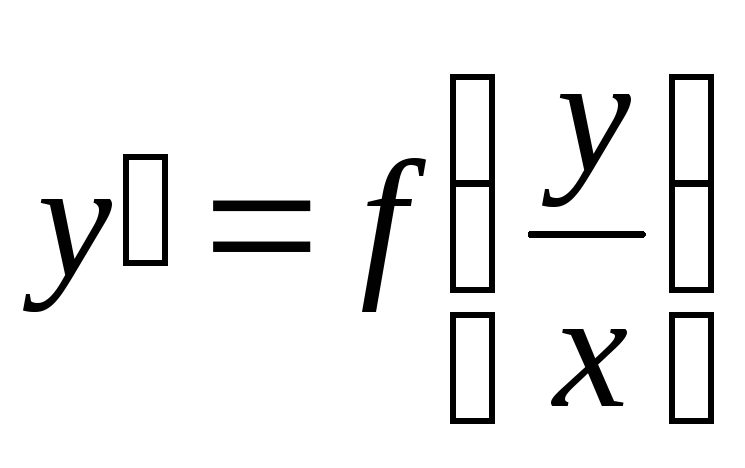 .
Подстановкой
.
Подстановкой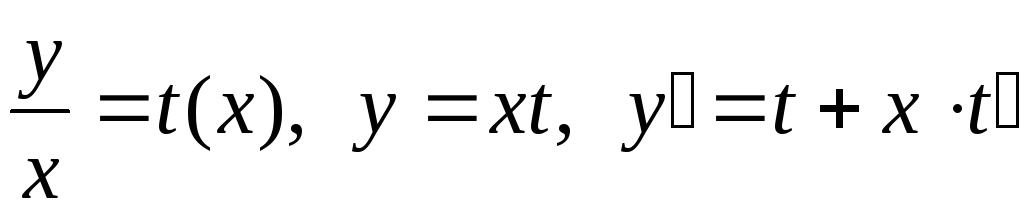 однородное уравнение сводится к уравнению
с разделяющимися переменными.
однородное уравнение сводится к уравнению
с разделяющимися переменными.
Пример. Найти решение дифференциального
уравнения  .
.
Решение: Воспользуемся подстановкой, приводящей исходное уравнение к уравнению с разделяющимися переменными, и решим его:
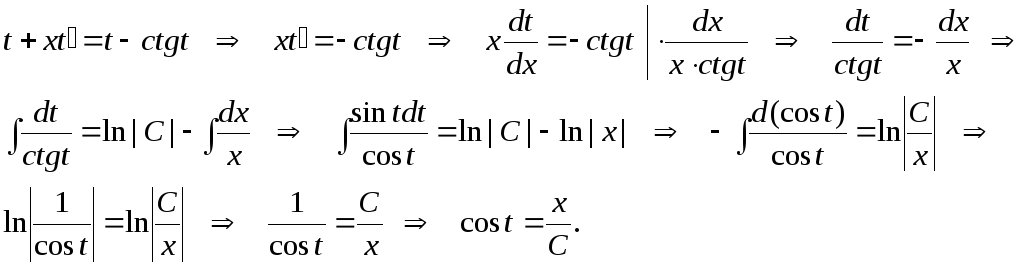 Выполним
обратную замену и получим искомое
решение:
Выполним
обратную замену и получим искомое
решение:
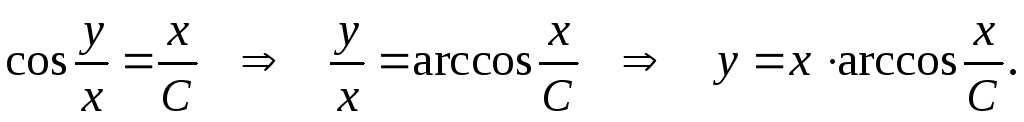
Ответ: 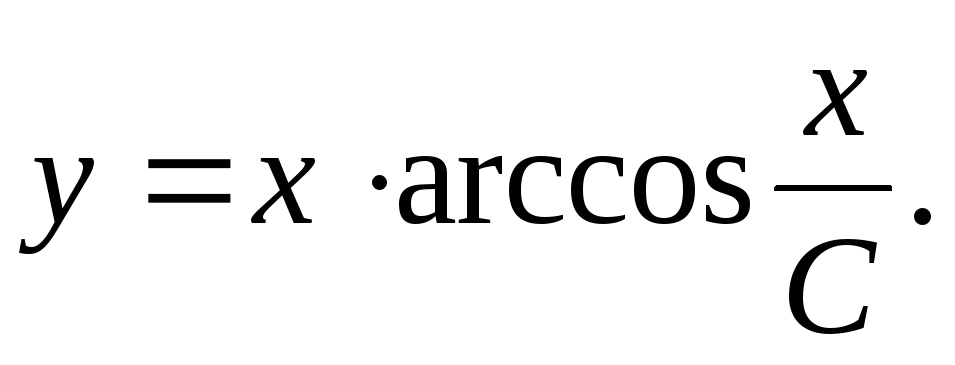 .
.
Б) Линейное
неоднородное дифференциальное уравнение 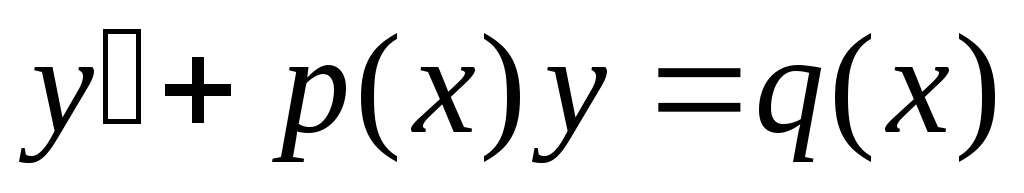 подстановкой
подстановкой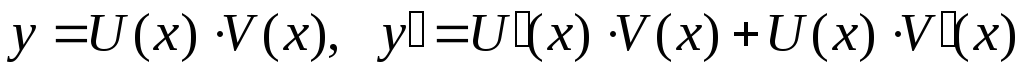 сводится
к уравнению
сводится
к уравнению .
Далее требуется, чтобы
.
Далее требуется, чтобы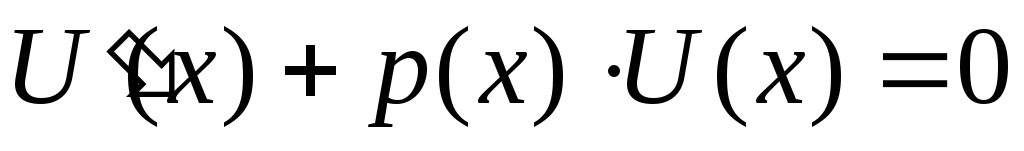 ,
тогда из этого уравнения можно найти
,
тогда из этого уравнения можно найти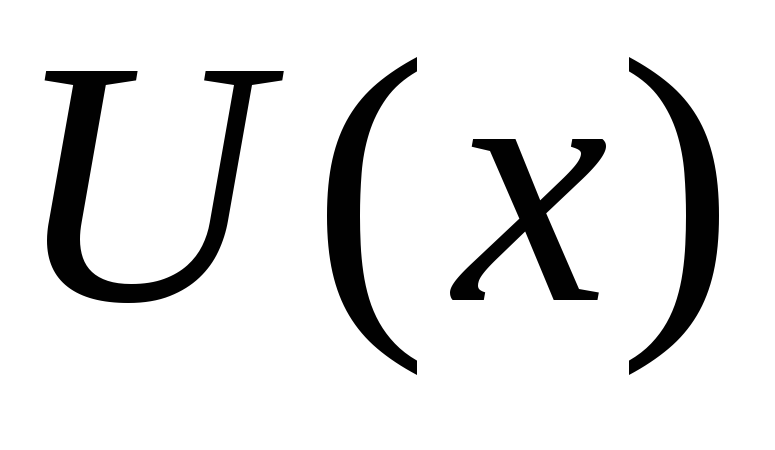 ,
а из предыдущего зная
,
а из предыдущего зная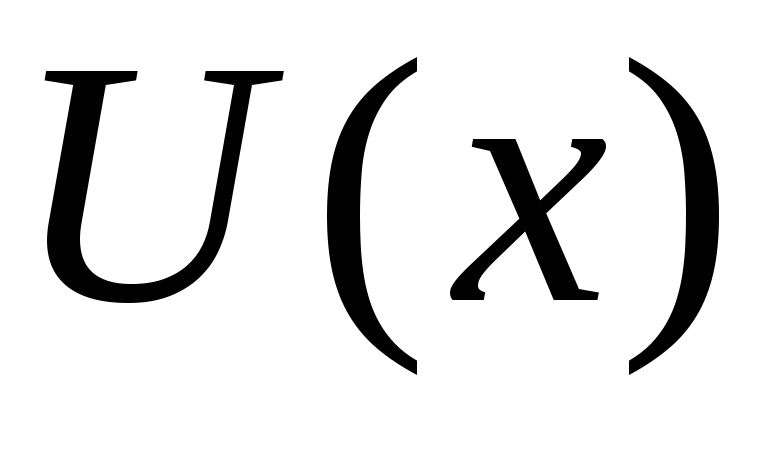 ,
находят
,
находят .
Зная
.
Зная и
и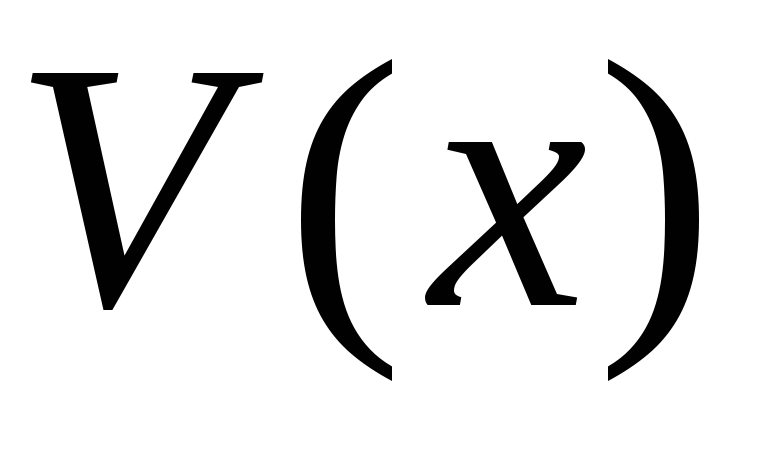 ,
находят
,
находят .
.
Для
решения неоднородного линейного
уравнения также можно использовать метод
вариации произвольных постоянных.
Этот метод состоит в том, что сначала
находят общее решение соответствующего
однородного линейного уравнения, т.е. 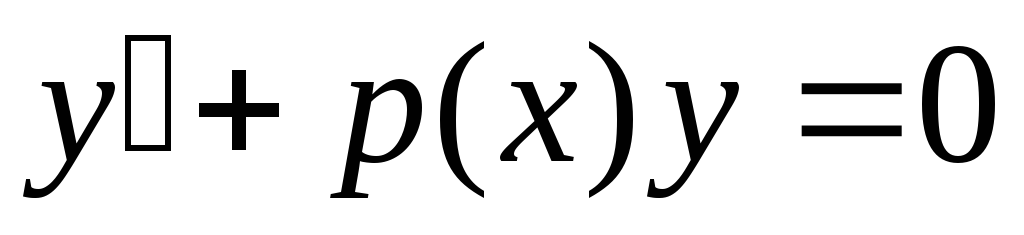 .
Затем, полагают в решении однородного
уравнения
.
Затем, полагают в решении однородного
уравнения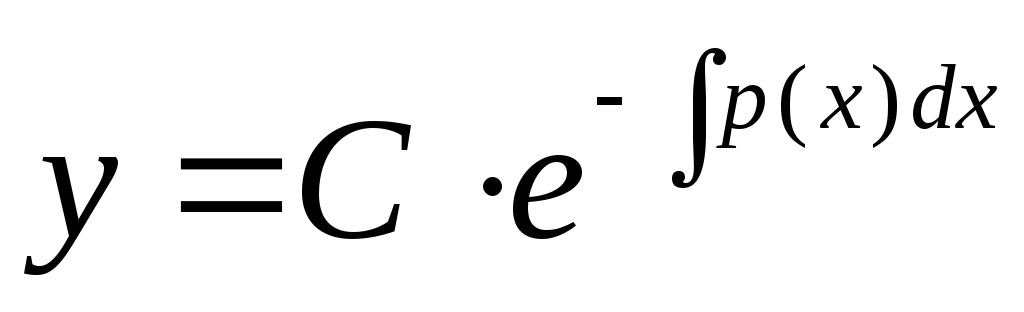 величину
величину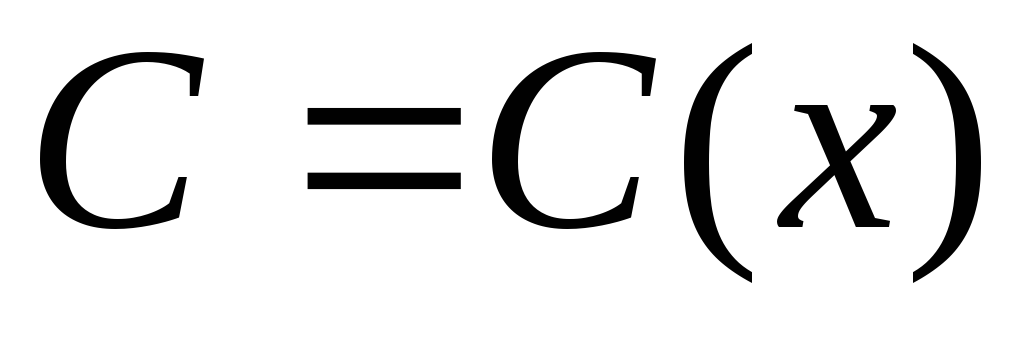 ищут решение неоднородного уравнения.
Для этого подставляют в неоднородное
уравнение
ищут решение неоднородного уравнения.
Для этого подставляют в неоднородное
уравнение и
и ,
и из полученного дифференциального
уравнения определяют функцию
,
и из полученного дифференциального
уравнения определяют функцию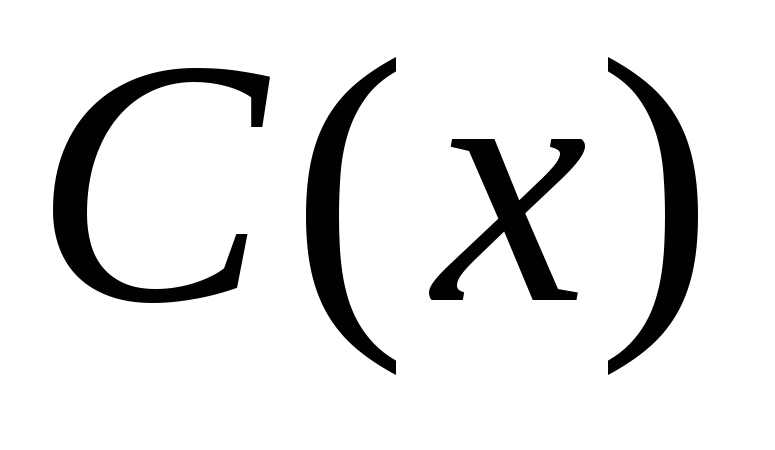 .
Таким образом, общее решение неоднородного
уравнения имеет вид:
.
Таким образом, общее решение неоднородного
уравнения имеет вид: .
.
Пример. Найти решение дифференциального уравнения
.
Решение: 1 способ.
Используя
подстановку 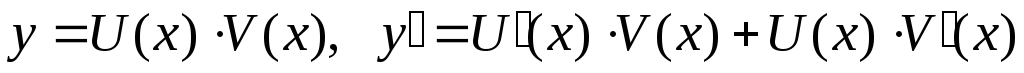 ,
уравнение примет вид
,
уравнение примет вид

Приравнивая
скобку к нулю, находим 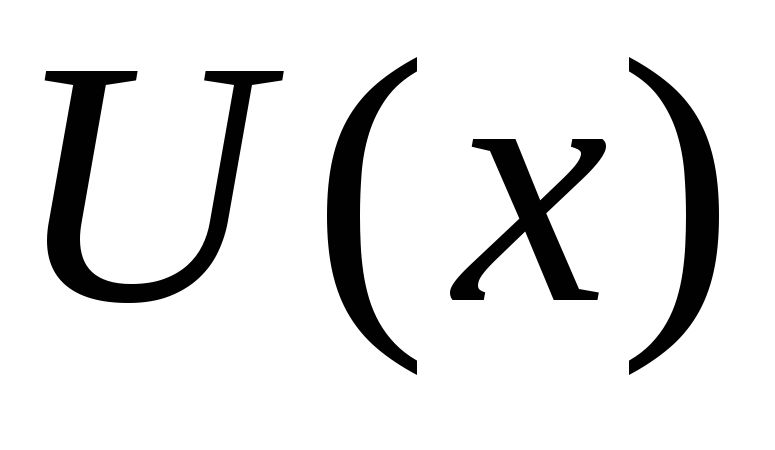 :
:

Зная  ,
можно посчитать
,
можно посчитать :
:

Ответ: 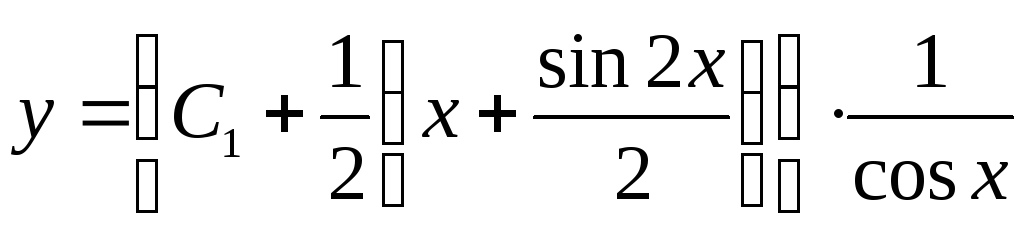 .
.
2способ. Находим общее решение соответствующего однородного линейного уравнения

Пусть
в решении однородного уравнения величина 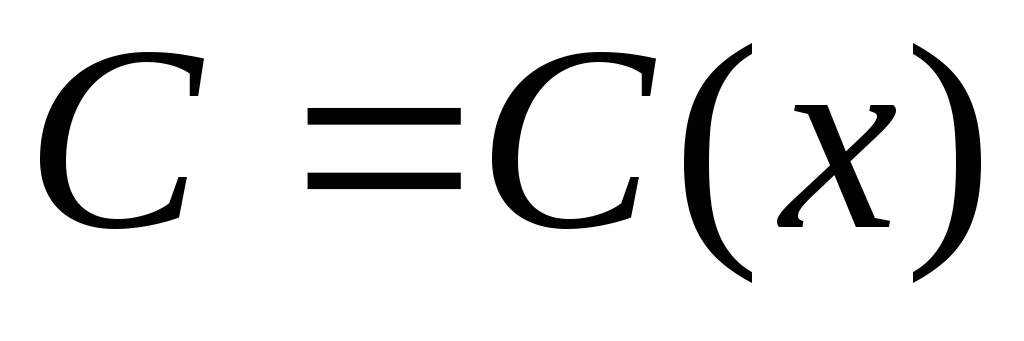 ,
получим решение неоднородного уравнения
,
получим решение неоднородного уравнения
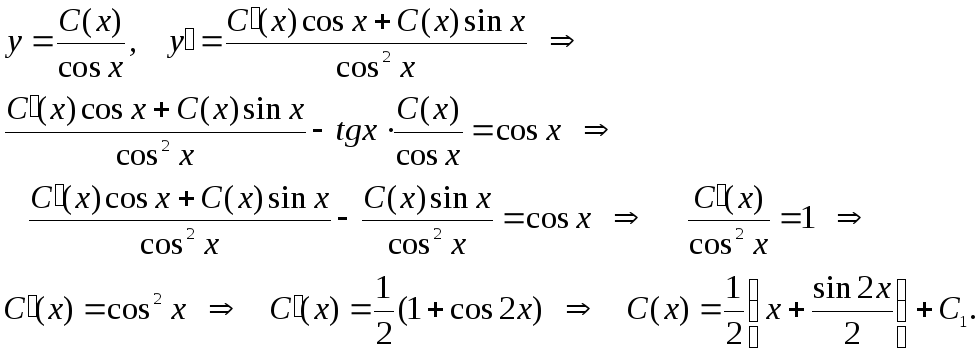
Ответ: 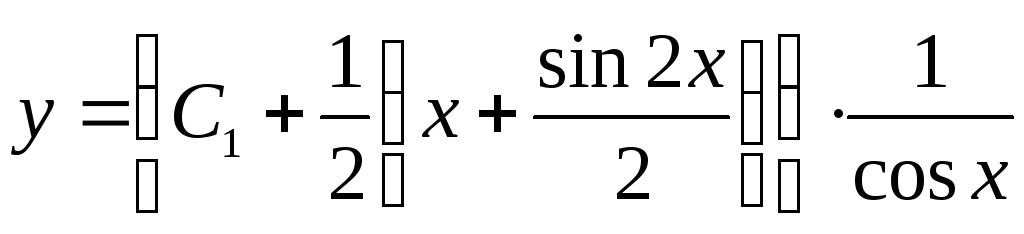 .
.
Уравнение Бернулли – это нелинейное уравнение, которое можно привести к линейному соответствующей заменой неизвестной функции
 .
Уравнение Бернулли имеет вид:
.
Уравнение Бернулли имеет вид: ,
где
,
где и
и – непрерывные функции;
– непрерывные функции;
постоянное число,
постоянное число,  .
Данное уравнение приводится к линейному
заменой
.
Данное уравнение приводится к линейному
заменой тогда
тогда .
Разделим обе части уравнения Бернулли
на
.
Разделим обе части уравнения Бернулли
на :
: .
Умножим обе части на
.
Умножим обе части на :
: .
Переходим к
.
Переходим к :
: .
.
Пример. Найти решение дифференциального
уравнения 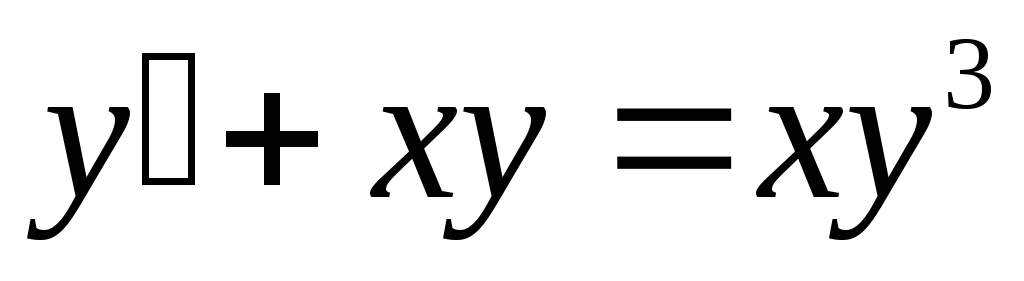 .
.
Решение: Разделим обе части уравнения на  и умножим на
и умножим на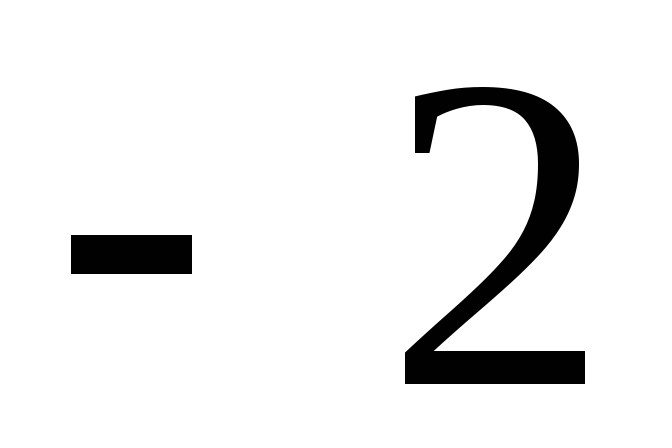 ,
получим
,
получим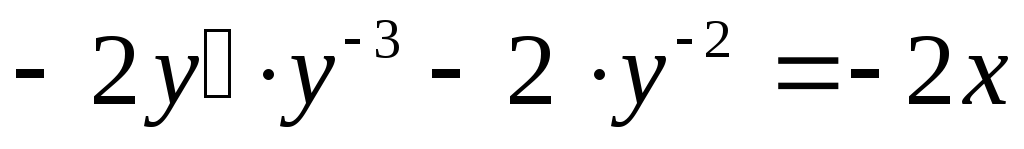 .
Используя замену
.
Используя замену ,
наше уравнение примет вид
,
наше уравнение примет вид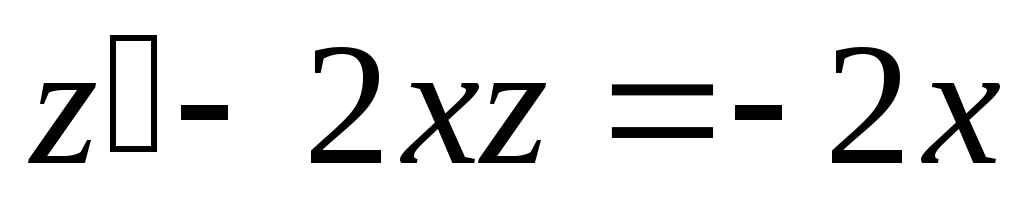 ,
а это линейное неоднородное дифференциальное
уравнение.
,
а это линейное неоднородное дифференциальное
уравнение.
Найдем
сначала решение однородного уравнения: 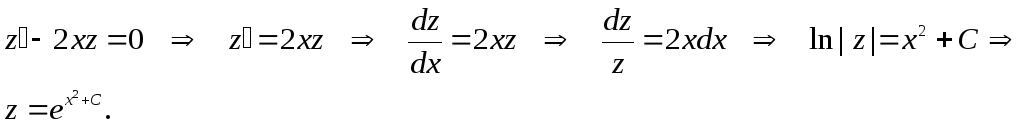
Принимаем 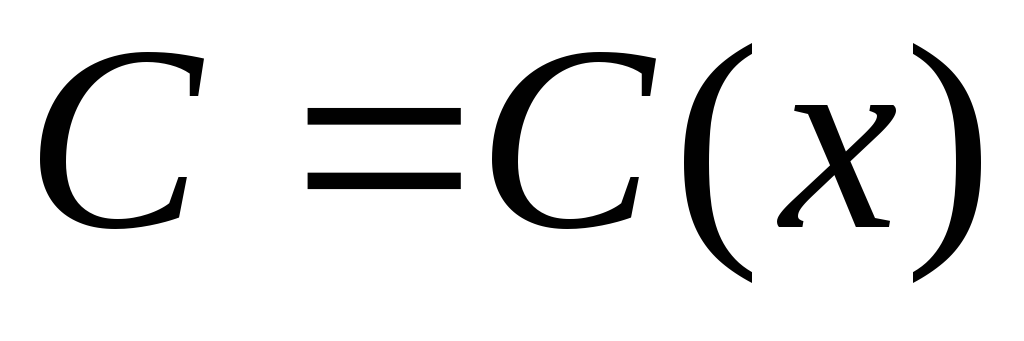 и находим решение неоднородного
уравнения:
и находим решение неоднородного
уравнения:
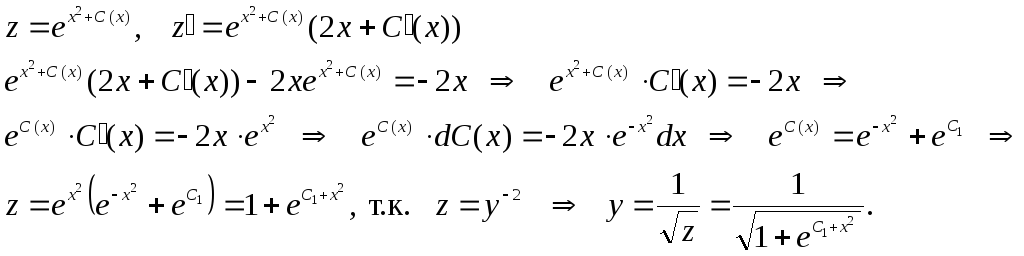
Ответ:  .
.
studfile.net
Лекция тема: дифференциальные уравнения.
Опр. Дифференциальным называется уравнение содержащее независимые переменные, функцию этих переменных и ее производные.
Опр. Если диф уравнение относительно функции одной независимой переменной, то уравнение называется обыкновенным диф. уравнением.
Опр. Если функция зависит от одной, двух и более переменных, то его называют уравнением частных производных.
Опр. Порядком диф. уравнения называют порядок старшей производной, входящей в это уравнение.
Примеры:
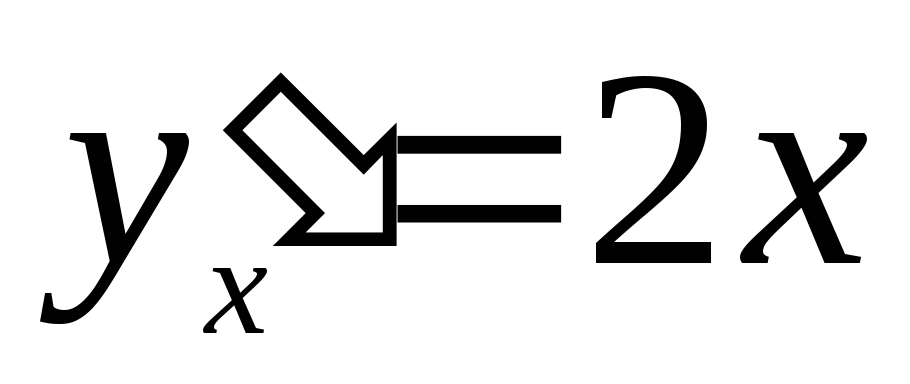 –обыкновенное
диф.уравнение 1-го порядка.
–обыкновенное
диф.уравнение 1-го порядка.
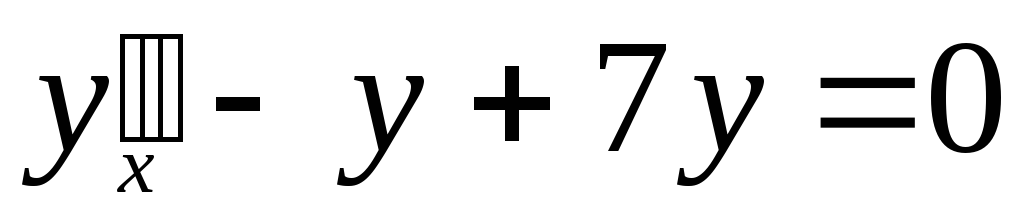 –обыкновенное
диф. уравнение 2-го порядка.
–обыкновенное
диф. уравнение 2-го порядка.
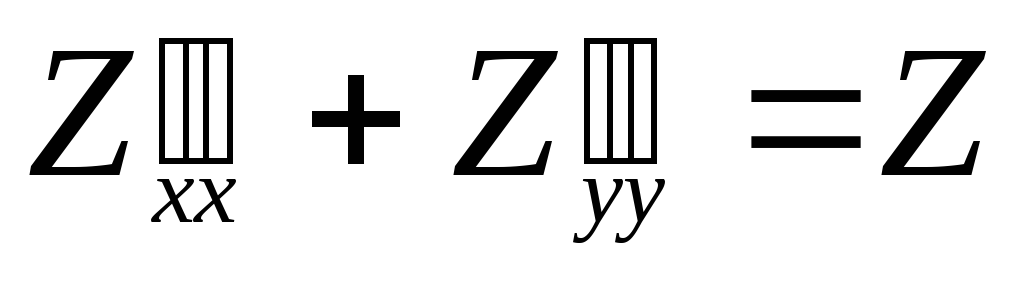 ,
где z=f(x,y)
– уравнение 2-го порядка в частных
производных.
,
где z=f(x,y)
– уравнение 2-го порядка в частных
производных.
Диф. уравнение можно записывать в производных и дифференциалах:
заменив 
Пример: 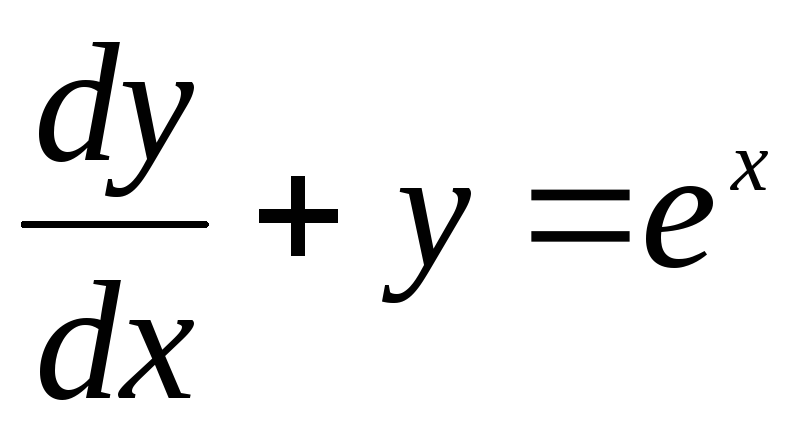 -диф
уравнение в дифференциалах.
-диф
уравнение в дифференциалах.
Опр. Решением дифференциального уравнения называется функция, которая будучи подставленной в уравнение, обращает его в верное тождество.
График решения дифференциального уравнения называется интегральной кривой диф. ур.
Пример:
Проверим является
ли функция 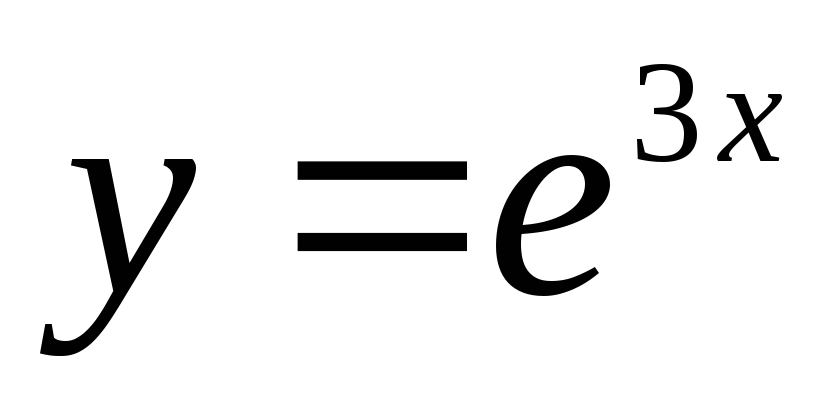 решением диф уравнения
решением диф уравнения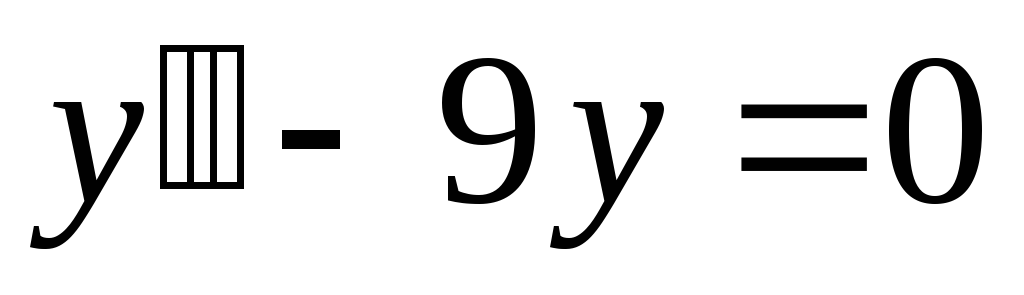
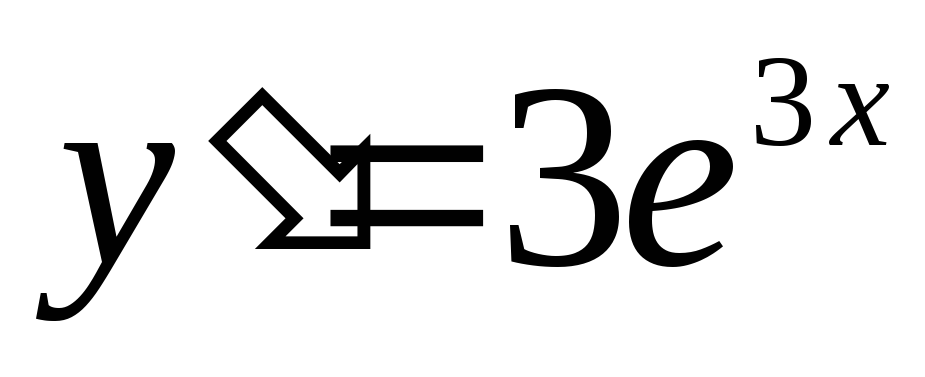
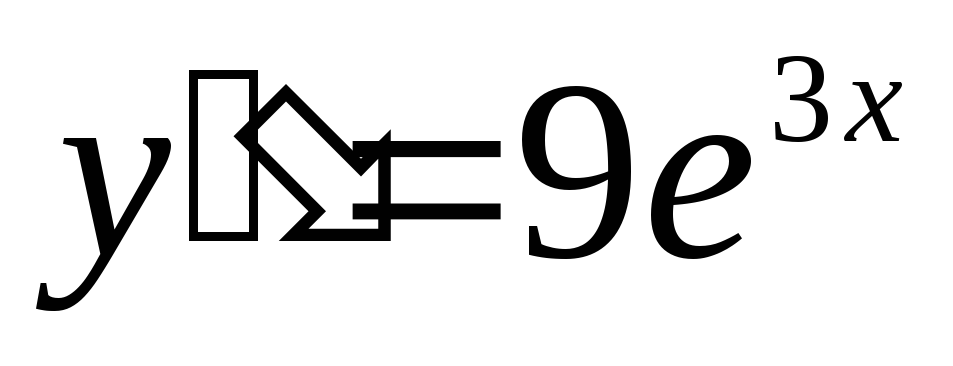
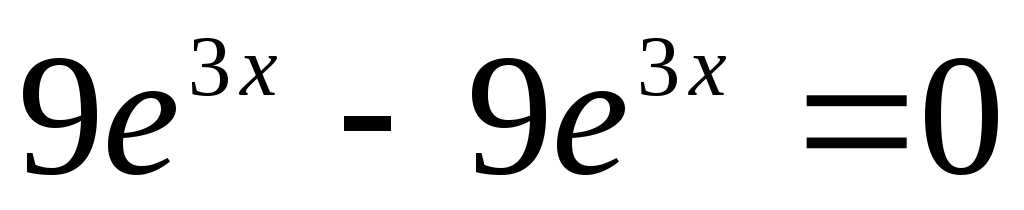
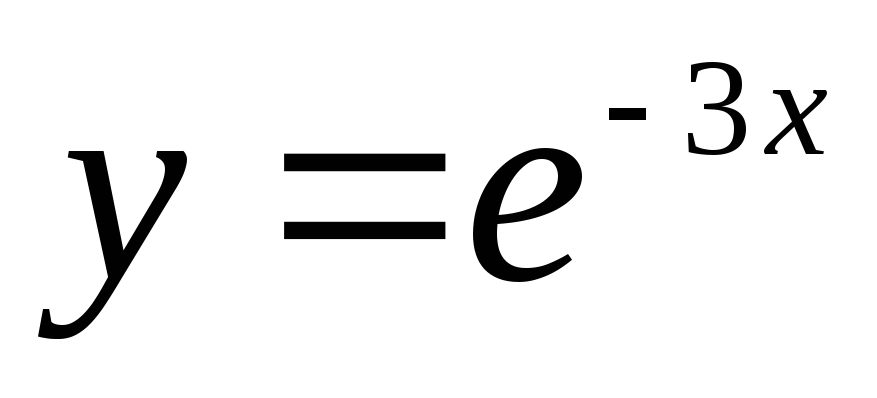 тоже
решение (
тоже
решение (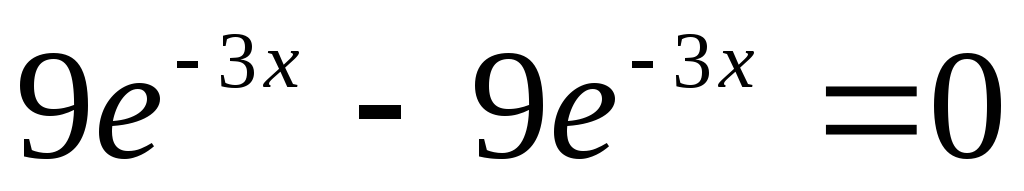 )
)
 тоже
решение диф уравнения (проверить
самостоятельно дома)
тоже
решение диф уравнения (проверить
самостоятельно дома)
Для диф уравнения
второго порядка 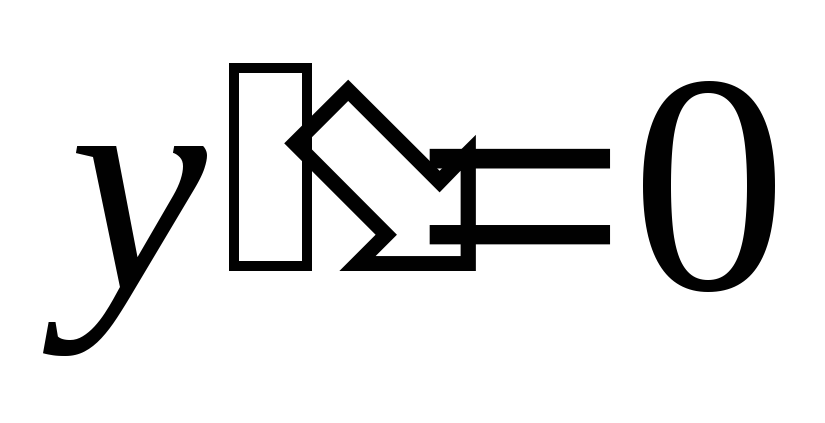 ,
легко заметить решением является
,
легко заметить решением является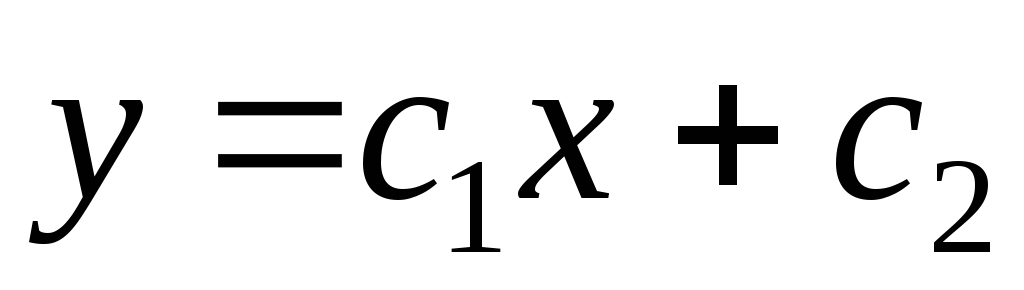 .
.
Таким образом для диф уравнения существует бесконечное множество решений.
Опр. Общим
решением диф.ур. называется
функция вида 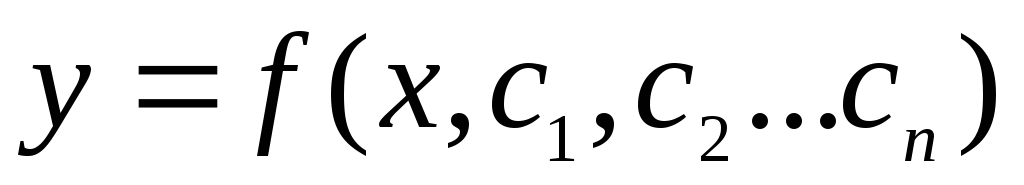
Т.е. для диф.ур.
1-го порядка 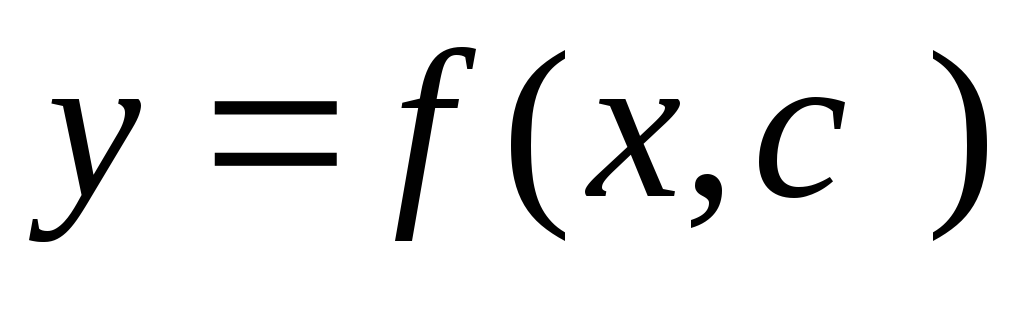
для диф.ур. 2-го
порядка 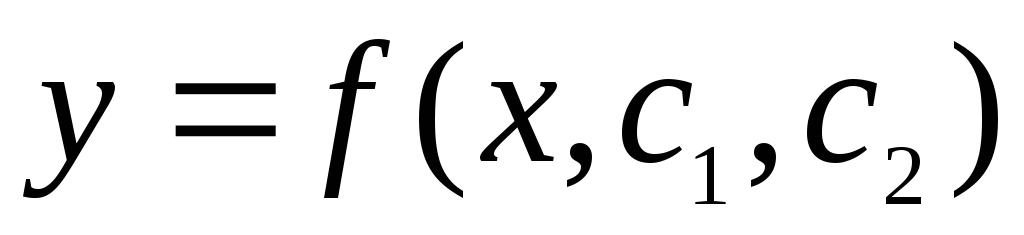
для диф.ур. n-го
порядка 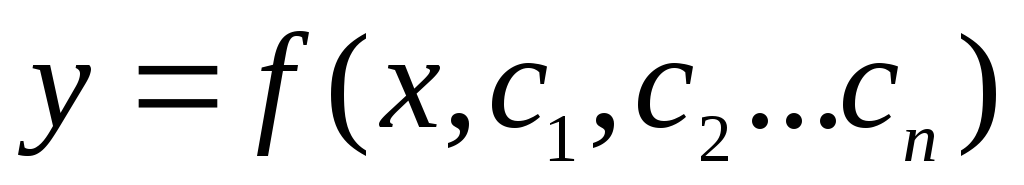
Если вместо постоянных подставить конкретные значения, то полученная функция будет называться частным решением.
Опр. Решить диф. ур. значит найти его общее решение.
Очень часто решение
диф.ур. получается в неявном виде. Т.е.
неявно заданное решение диф.ур. 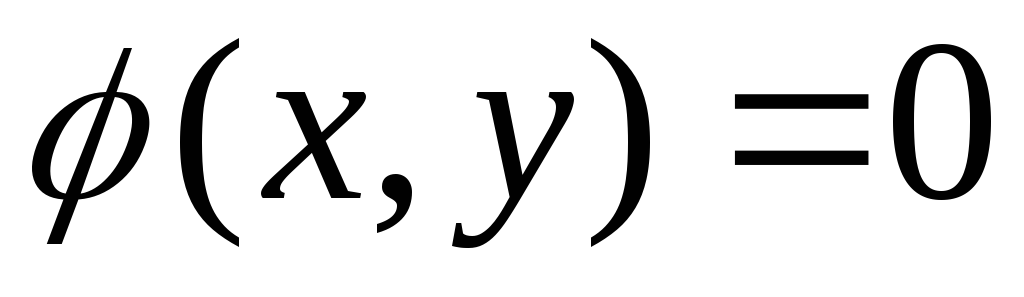 –
называется интегралом уравнения.
–
называется интегралом уравнения.
Некоторые типы диф.ур. первого порядка
1. Диф.Уравнения с разделенными и разделяющимися переменными.
Опр. Уравнения вида 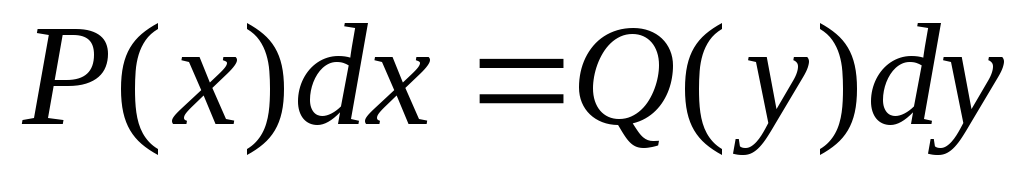 ,
называются уравнениями сразделенными
переменными.
,
называются уравнениями сразделенными
переменными.
Решение таких уравнений находится непосредственным интегрированием.
Пример: 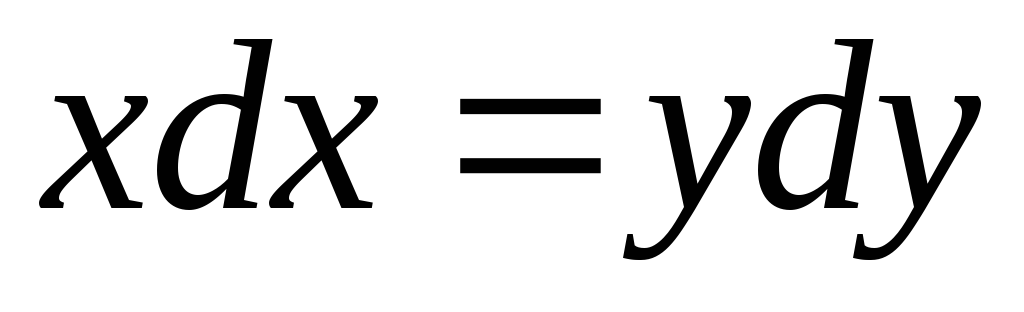
На первый взгляд кажется что решение у=х, но это только частное решение

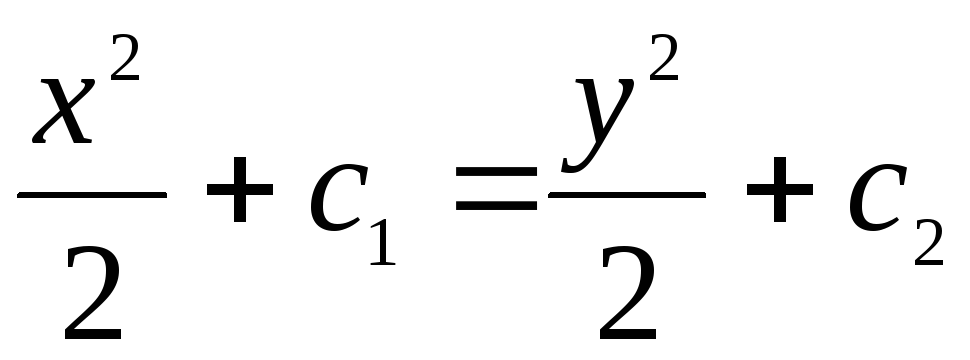
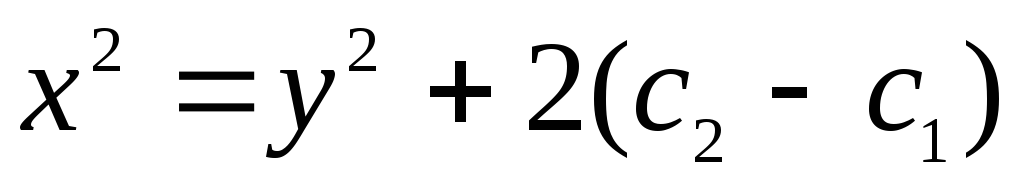

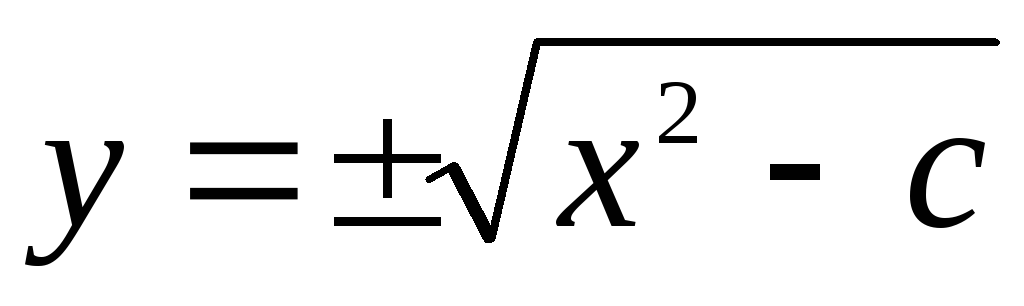
Опр. Уравнения вида 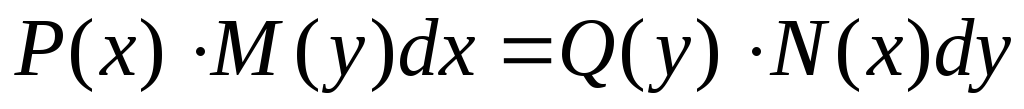 ,
называются уравнениями сразделяющимися
переменными.
,
называются уравнениями сразделяющимися
переменными.
Сводится к уравнению
с разделенными переменными путем деления
обеих частей уравнения на 
Пример:

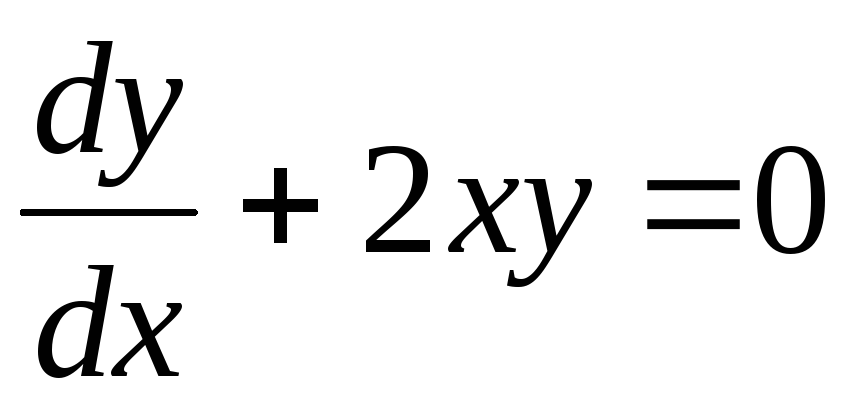
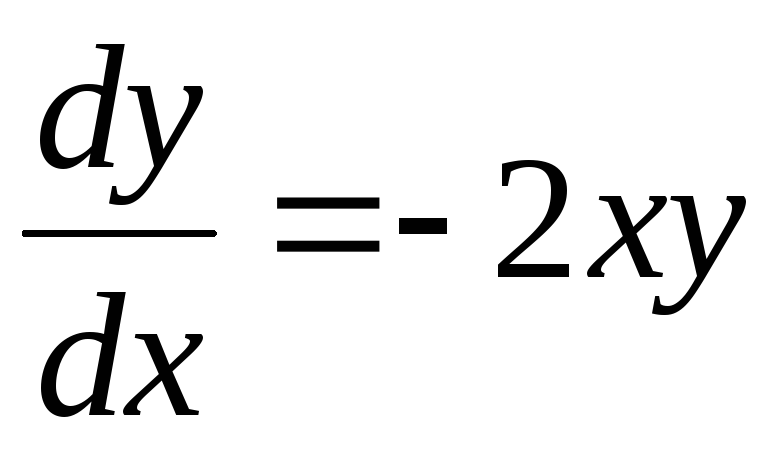

2. Однородные уравнения.
Функция 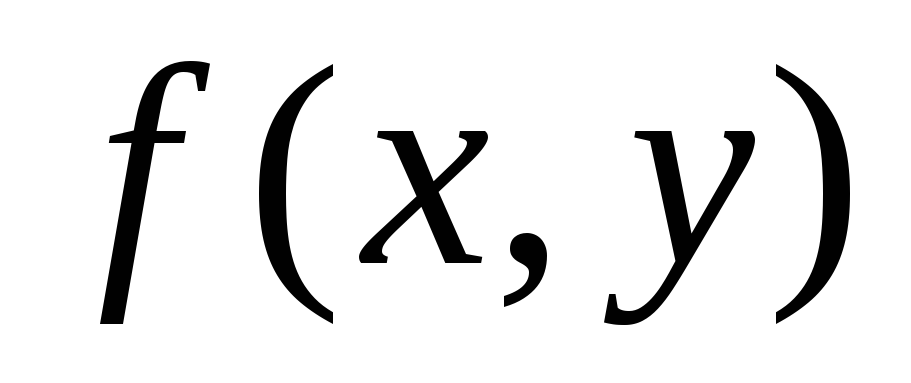 называется
однородной степениm,
если имеет место тождество:
называется
однородной степениm,
если имеет место тождество: 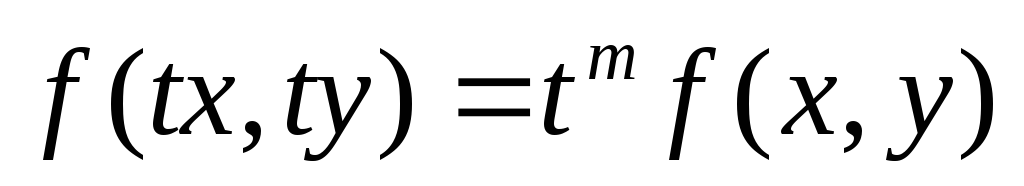
Уравнение 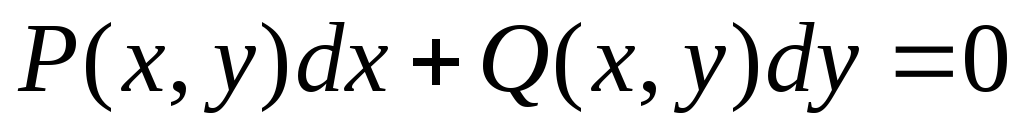 называется однородным дифференциальным
уравнением, если функции
называется однородным дифференциальным
уравнением, если функции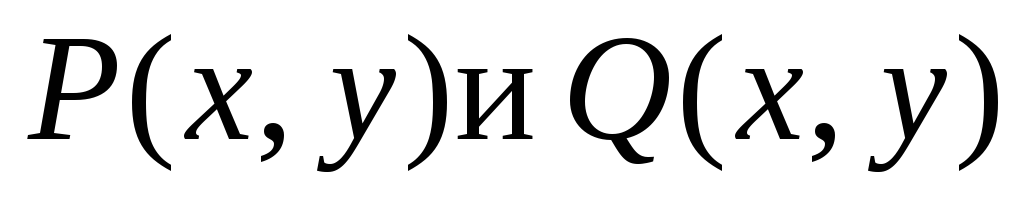 однородные
функции одной оной и той же степени.
однородные
функции одной оной и той же степени.
Решаются путем
подстановки 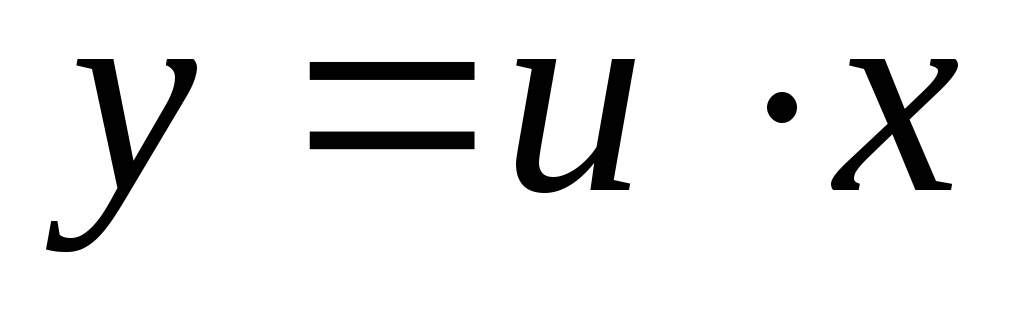
Пример:
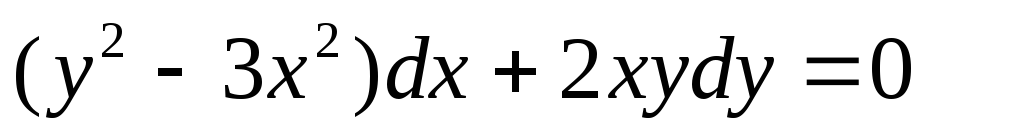
Функция 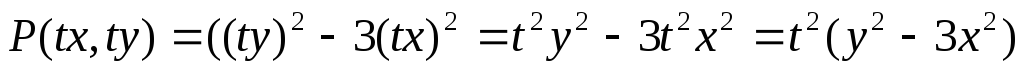 однородная
второй степени
однородная
второй степени
Функция  однородная
второй степени
однородная
второй степени
Следовательно, это однородное дифференциальное уравнение.
Применим подстановку ,
,



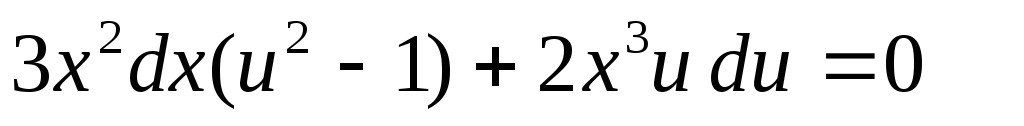
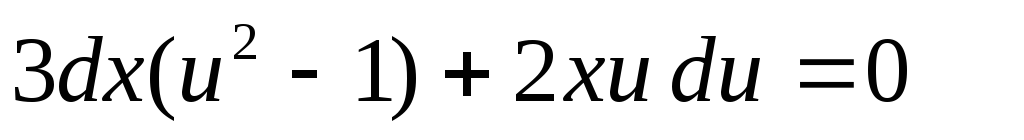

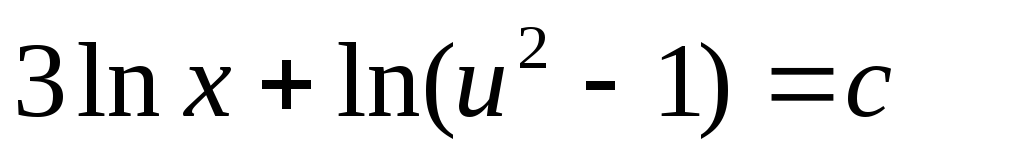
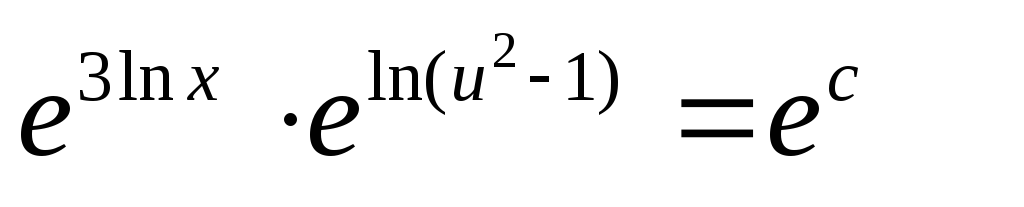
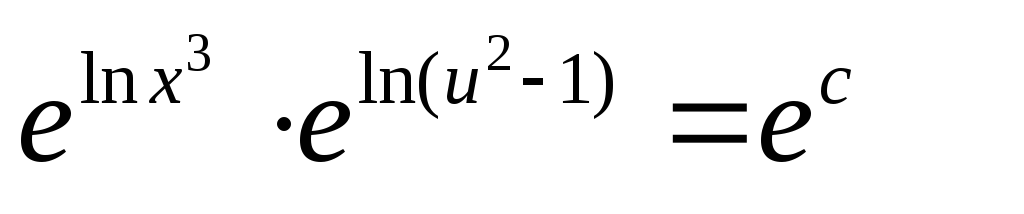
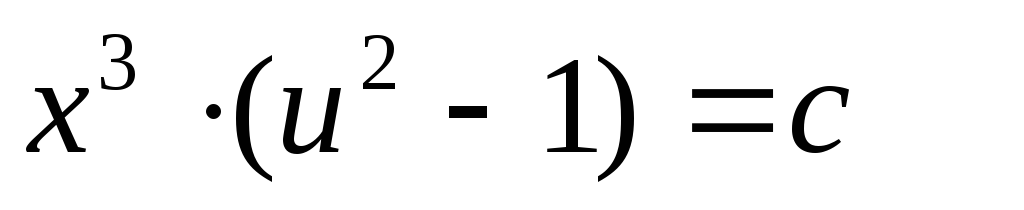
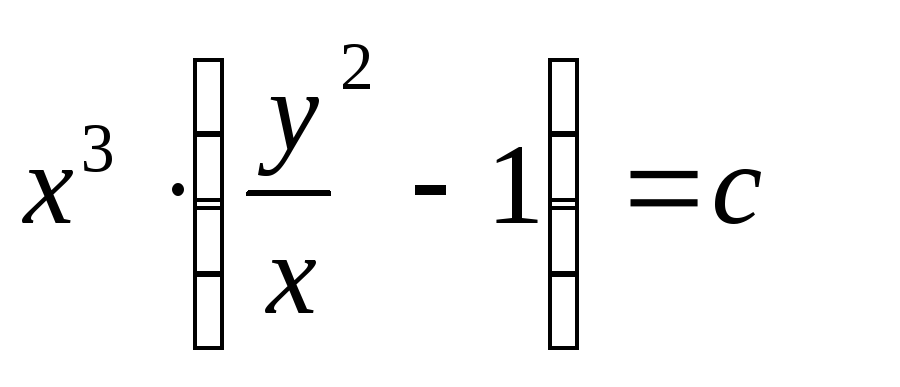
3. Линейные дифференциальные уравнения.
Опр. Диф.ур. называется линейным первого порядка, если его можно представить в виде.
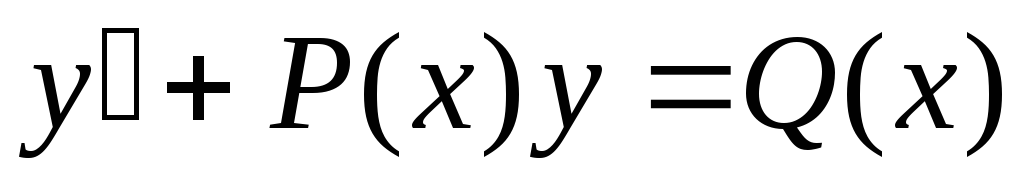 ,
Р(х) и Q(x)–функции
от х и могут быть постоянными.
,
Р(х) и Q(x)–функции
от х и могут быть постоянными.
Решаются такие уравнения с помощью подстановки у= UVвместо функции у, которую нужно найти.
1. Подставим вместо
у и у’ у= UV, 

2. Сгруппируем 1-е или 2-е слагаемое с третьим
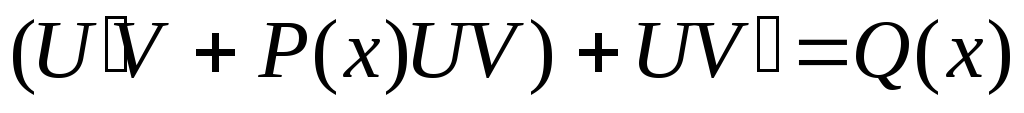
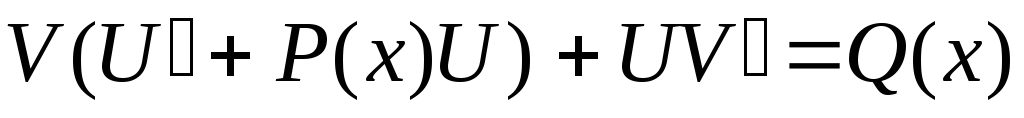
3. введем условие,
что выражение в скобках было равно нулю  –
ЛОДУ 1-го порядка которое мы решали выше
и его решением будет
–
ЛОДУ 1-го порядка которое мы решали выше
и его решением будет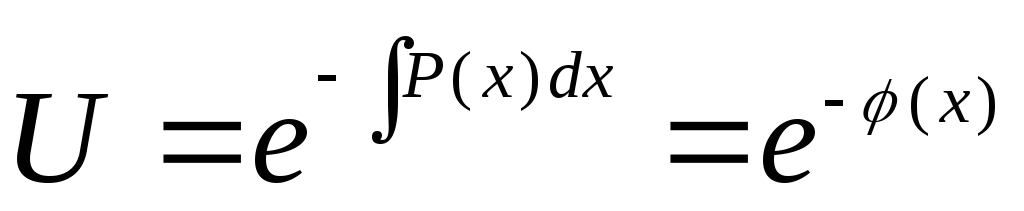
4. Вернемся к брошенному уравнению (в пункте 2). Подставим в уравнение:
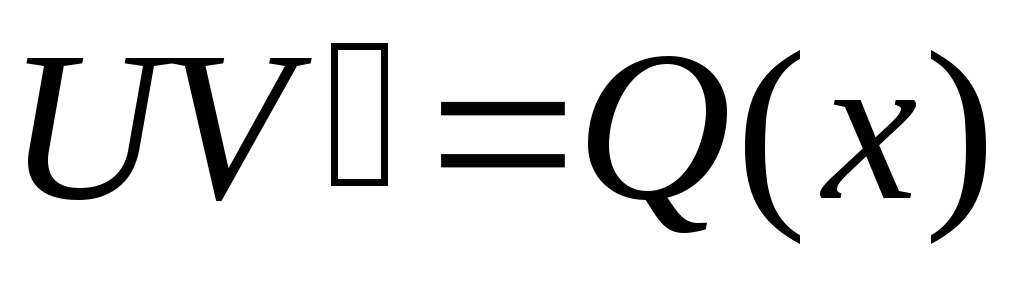


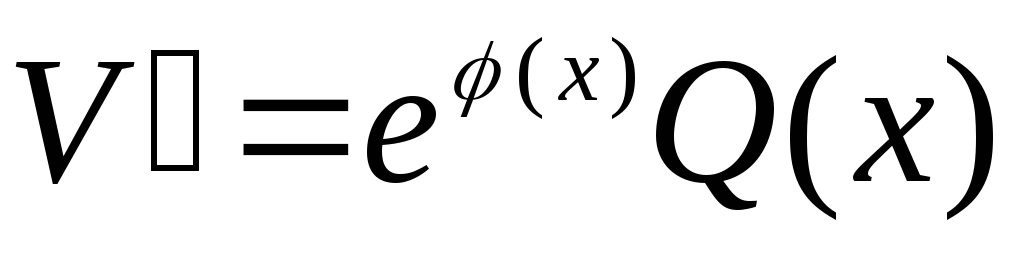
решим полученное диф.уравнение:
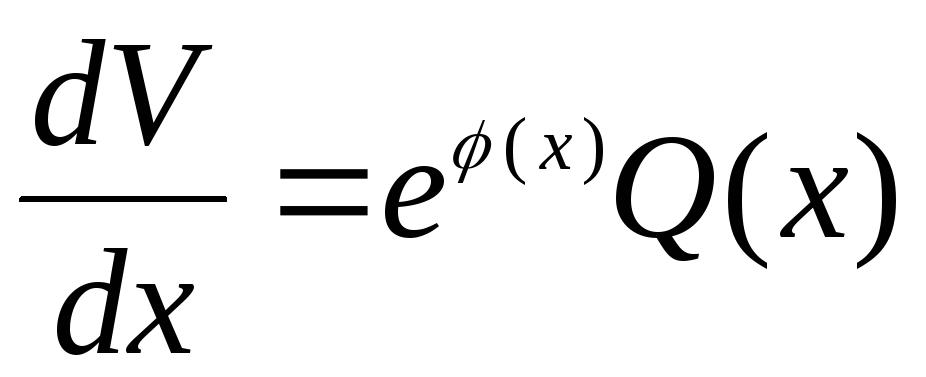 /dx
/dx

получим
5.  – решение уравнения в общем виде.
– решение уравнения в общем виде.
Пример: Решить уравнение вида 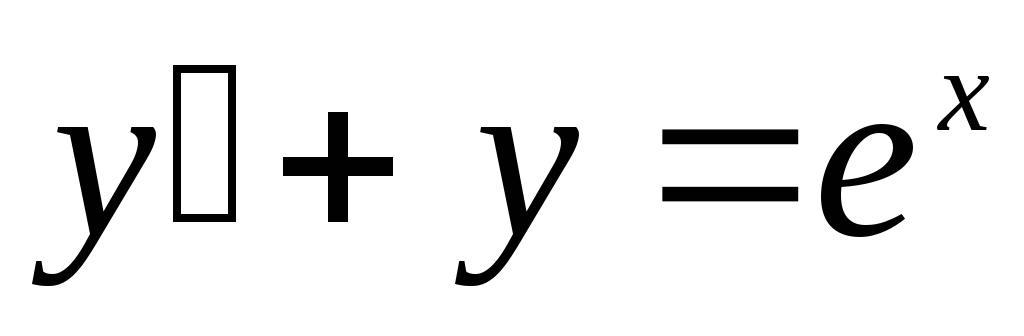
Это уравнение линейное, т.к. у и у’ входят в него в первой степени и нет члена с произведением уу’
Положим у=UV,
тогда 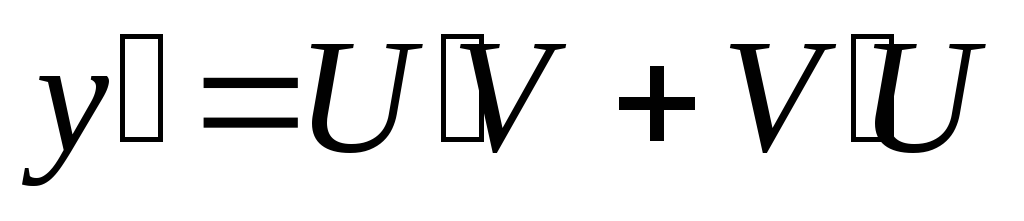 наше уравнение примет вид:
наше уравнение примет вид:
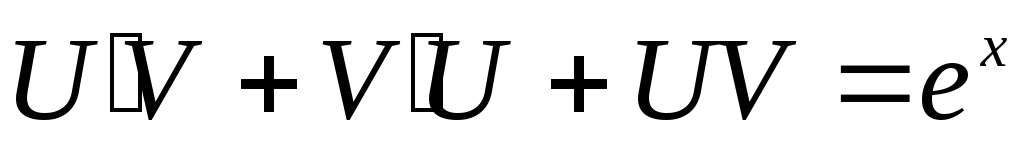 сгруппируем второе
и третье слагаемое
сгруппируем второе
и третье слагаемое

Приравняем выражение стоящее в скобках к нулю получим ЛОДУ 1-го порядка.



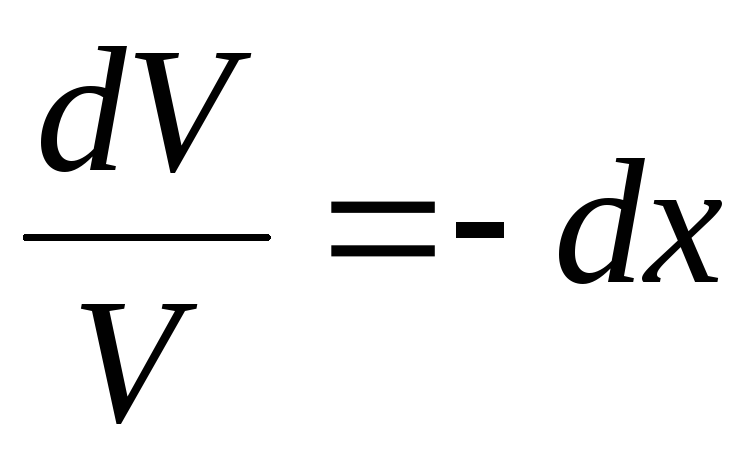 , проинтегрируем
обе части
, проинтегрируем
обе части
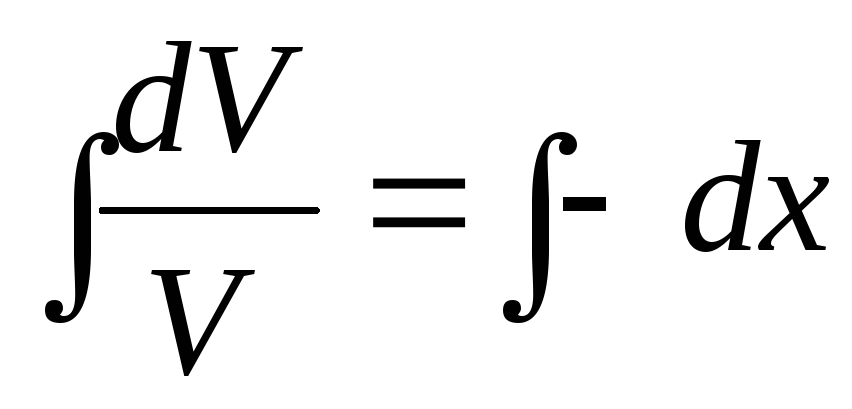
 положим с=0
положим с=0
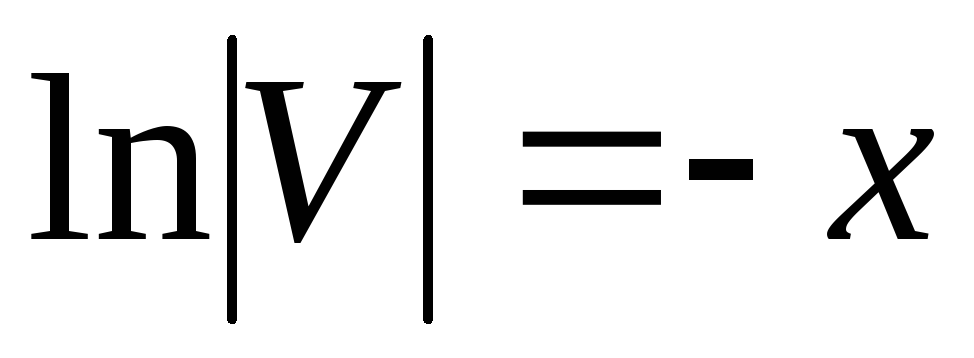
потенцируем обе части


От первоначального уравнения осталось
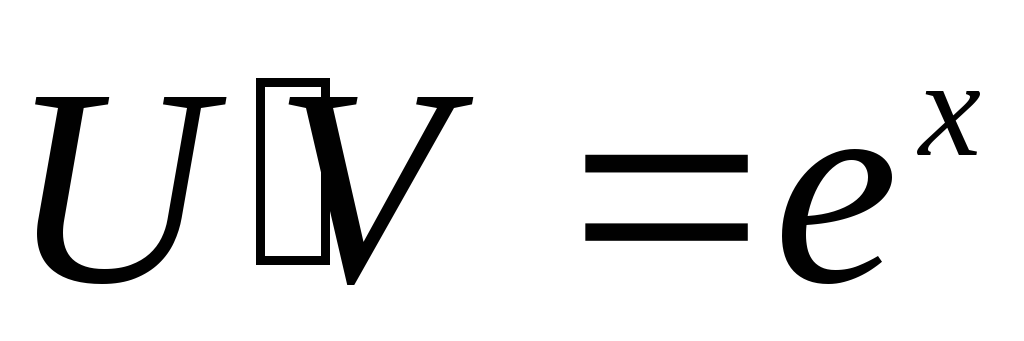
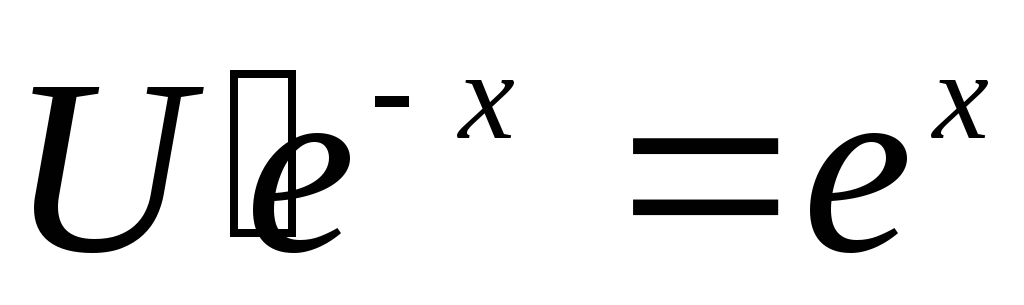
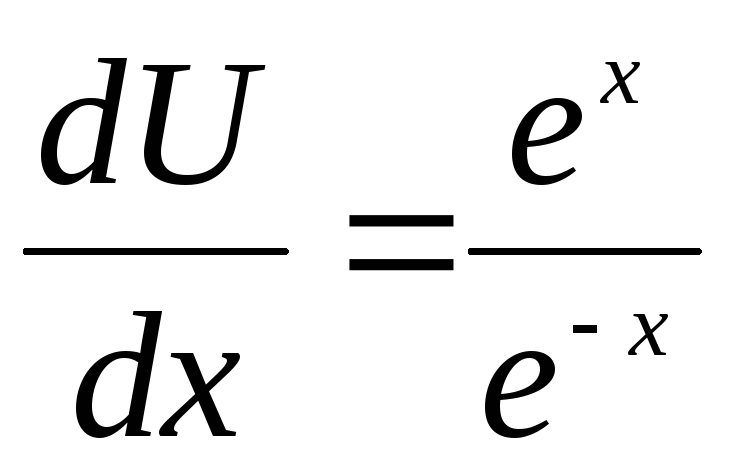
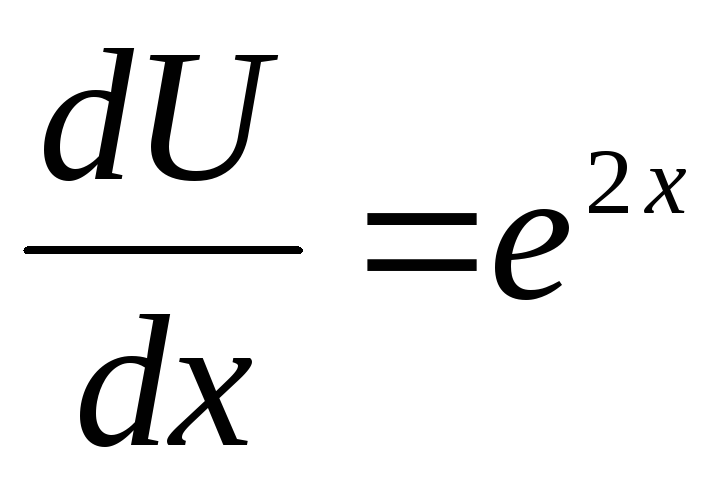
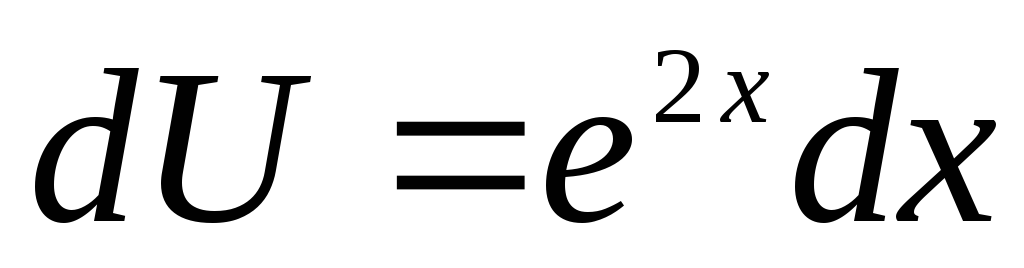

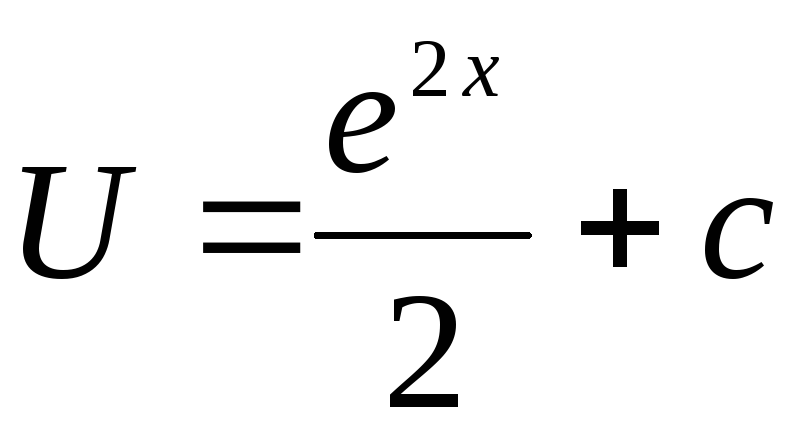
запишем решение уравнения у=UV=
studfile.net
1. Основные понятия и определения теории дифференциальных уравнений
85
Лекция 7.
При решении многих задач физики, химии, биологии, других наук не всегда удаётся непосредственно установить прямую зависимость между величинами, описывающими тот или иной процесс. Однако, в большинстве случаев можно установить связь между функциями и скоростями их изменения относительно независимых переменных, то есть найти уравнения, в которых неизвестные функции входят под знак производной.
Определение 1. Уравнение, содержащее независимую переменнуюx, искомую функциюy и её производныеy ‘,y», …,y(n)или дифференциалы называется дифференциальным.
Символически дифференциальное уравнение записывается так:
F (x, y, y’, y»,…,y(n)) = 0 | (1.1) |
или
| (1,1а) |
Определение 2.Если искомая функцияy=(x) есть функция одного независимого переменного, то дифференциальное уравнение называется обыкновенным.
Определение 3. Порядком дифференциального уравнения называется порядок наивысшей производной искомой функции, входящей в это уравнение.
Например, уравнение xy‘ + y —8 =0 является уравнением первого порядка, а уравнениеy»’+ 7y‘– 3y= 0 – уравнением третьего порядка. Уравнение (1.1) является уравнениемn-ого порядка, записанным в общем виде.
Всякая функция y=(x), которая, будучи подставлена в уравнение (1.1) обращает его в тождество, называется решением этого уравнения. Решить, или проинтегрировать данное дифференциальное уравнение – значит, найти все его решения в заданной области. График решения называется интегральной кривой.
При интегрировании дифференциальных уравнений высших порядков появляется несколько произвольных постоянных.
Определение 4.Общим решением дифференциального уравненияn-ого порядка называется функция
y = ( x, C1, C2, …,C n ), | (1.2) |
зависящая от nпроизвольных постоянныхС1,С2,…,Сnи удовлетворяющая данному уравнению при любых значениях этих постоянных.
Определение 5. Частным решением дифференциального уравнения называется решение, полученное из общего решения при фиксированных значениях произвольных постоянных.
Чтобы из бесконечного числа решений
дифференциального уравнения, определяемых
его общим решением, выделить одно частное
решение, требуется ввести начальные
условия. Задать начальные условия
дифференциального уравнения n—ого
порядка означает задать некоторое
фиксированное значение аргументаx=x0и соответствующие
значения функцииy(x0)
=y0и её
производных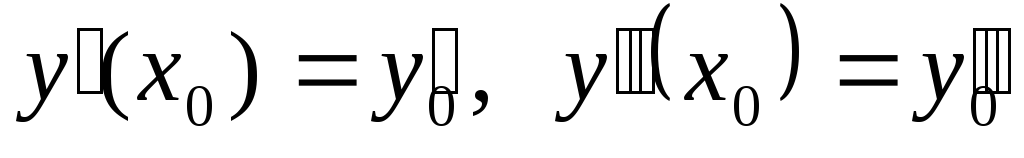 ,
…,y(n-1)
,
…,y(n-1)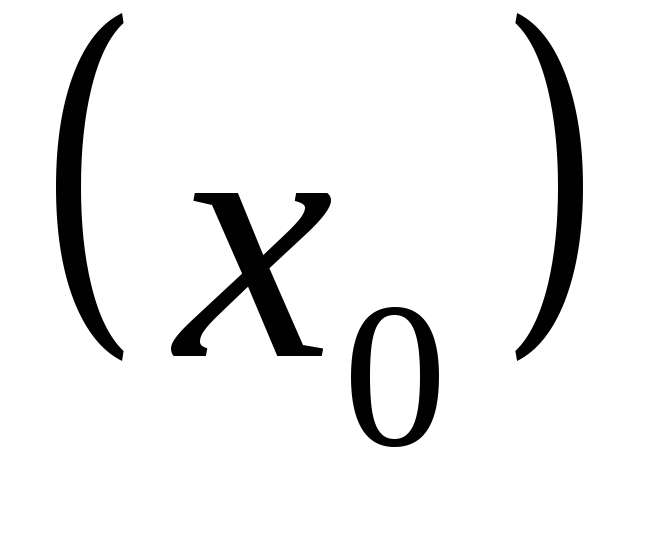 =
= (n-1).
Задача нахождения частного решенияy=y(x),
удовлетворяющего начальным условиям,
называется задачей Коши.
(n-1).
Задача нахождения частного решенияy=y(x),
удовлетворяющего начальным условиям,
называется задачей Коши.
Дифференциальное уравнение первого порядка в общем виде записывается так:
В простейших случаях оно может быть разрешено относительно производной y‘:
Общее решение уравнения (1.4) имеет вид:
где С – постоянная. Например, общим
решением уравненияy‘
= —  является всякая функция видаy =
является всякая функция видаy =  ,
обращающая данное уравнение в тождество.
,
обращающая данное уравнение в тождество.
В случае дифференциального уравнения
первого порядка задача Коши ставится
так: найти частное решение y = y(x)
уравненияy‘ = (x,y), удовлетворяющее
условиюy(x0)
=y0. Возвращаясь
к уравнениюy‘ = — ,
найдём его частное решение, удовлетворяющее
условиюy(2) = 4. Подставляя
в общее решение начальные условияx=2,y=4, найдём 4 =
,
найдём его частное решение, удовлетворяющее
условиюy(2) = 4. Подставляя
в общее решение начальные условияx=2,y=4, найдём 4 = ,
то естьС =8. Таким образом, искомым
частным решением является функцияy=
,
то естьС =8. Таким образом, искомым
частным решением является функцияy= .
.
 у
у



 4
4

 2х
2х
Общее решение y =  уравненияy‘ =—
уравненияy‘ =—  определяет
семейство равносторонних гипербол,
асимптотами которых являются оси
координат, а также прямуюy=0 (приС=0). Частное решение определяет
гиперболу, проходящую через точку (2;4).
определяет
семейство равносторонних гипербол,
асимптотами которых являются оси
координат, а также прямуюy=0 (приС=0). Частное решение определяет
гиперболу, проходящую через точку (2;4).
Сделаем ещё одно замечание относительно уравнений вида (1.4). Умножив обе его части на дифференциал независимой переменной dx, получим уравнение, содержащее дифференциалы:
Уравнение (1.6) также называется дифференциальным уравнением первого порядка. Из определения дифференциала следует, что уравнение (1.6) равносильно уравнению (1.4).
studfile.net
3.1. Понятие обыкновенного дифференциального уравнения n-го порядка и его решения
Определение 3.3. Решением дифференциального уравнения (3.1) называется всякая действительная функция y = y(x), опреде-
ленная на интервале (a,b) такая, что:
1)y(x) n раз непрерывно дифференцируема на интервале (a,b) ;
2)точка (x, y(x), y′(x),…, y(n) (x)) D Rn+2 , для всех x (a,b),
где D − область определения функции F ;
3)F(x, y(x), y′(x),…, y(n) (x)) ≡ 0 для всех x (a,b) .
Всякому решению дифференциального уравнения (3.1) на плоскости отвечает некоторая кривая y = y(x) , x (a,b) , которая называется
интегральной кривой дифференциального уравнения (3.1).
Одна из основных задач в теории дифференциальных уравнений является нахождение его решений. В простейших случаях эта задача в конечном итоге сводится к вычислению интегралов. Поэтому процесс нахождения решения дифференциального уравне-
ния называется интегрированием | этого уравнения. |
| ||||||||||||||
|
| Например, |
|
| решением | дифференциального | уравнения | |||||||||
| ′′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y | = | 1 | ′′ 2 |
|
| является функция | y = −sin x + 2x +C, так как при | |||||||||
| −(y ) |
| ||||||||||||||
x | (− | π | π | y | ′ | = −cos x + 2, |
| y | ′′ | = sin x, y | ′′′ | = cos x | и | |||
2 | ; 2 ), |
|
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||

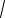 1−sin2 x = cos x, если x (−π2 ; π2 ).
1−sin2 x = cos x, если x (−π2 ; π2 ).
Уже простейшие примеры показывают, что дифференциальные уравнения, как правило, имеют бесчисленное множество решений. В связи с этим, общим решением дифференциального уравнения (3.1) (или (3.2)) обычно называют такое его решение
y =φ(x,C1,C2 ,…,Cn ) , которое содержит столько независимых произвольных постоянных C1,C2 ,…,Cn , каков порядок этого уравне-
ния. Заметим, что понятие общего решения будет уточнено позже. Общее решение, заданное в неявной форме Φ(x, y,C1,…,Cn ) = 0
называют общим интегралом уравнения. Чтобы выделить одно ка- кое-то решение, задают некоторые дополнительные условия.
studfile.net
 она является решением уравнения;
она является решением уравнения; найдется такое значение
найдется такое значение ,
что
,
что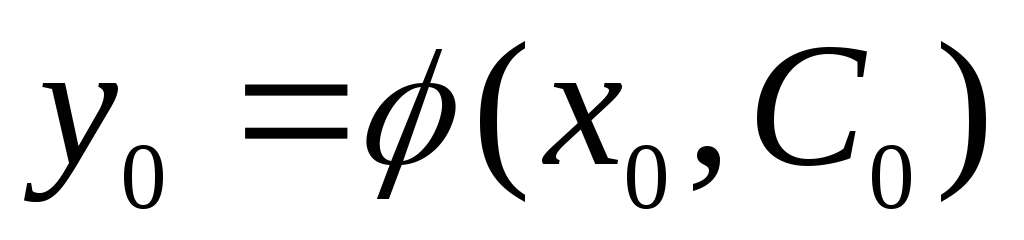 .
.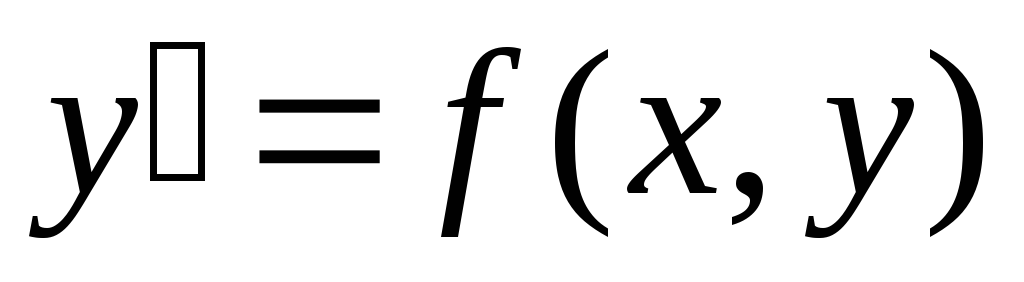 – это дифференциальные уравнения, в
которых функция
– это дифференциальные уравнения, в
которых функция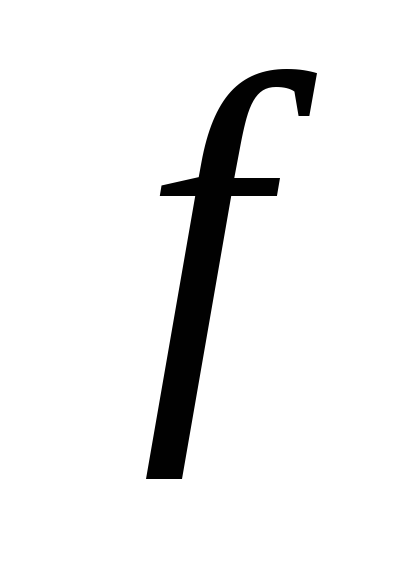 явно зависит только от одной переменной:
явно зависит только от одной переменной: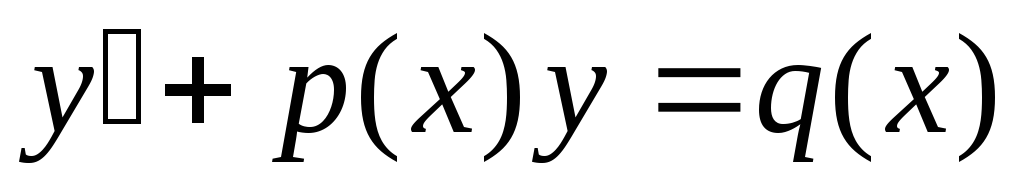 .
.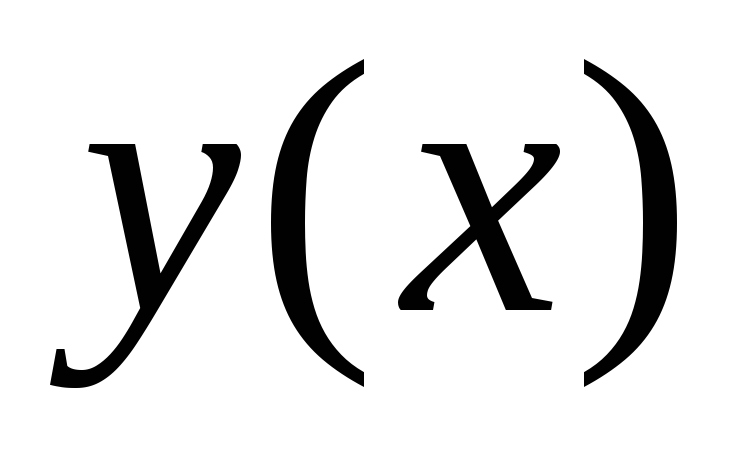 .
Уравнение Бернулли имеет вид:
.
Уравнение Бернулли имеет вид: ,
где
,
где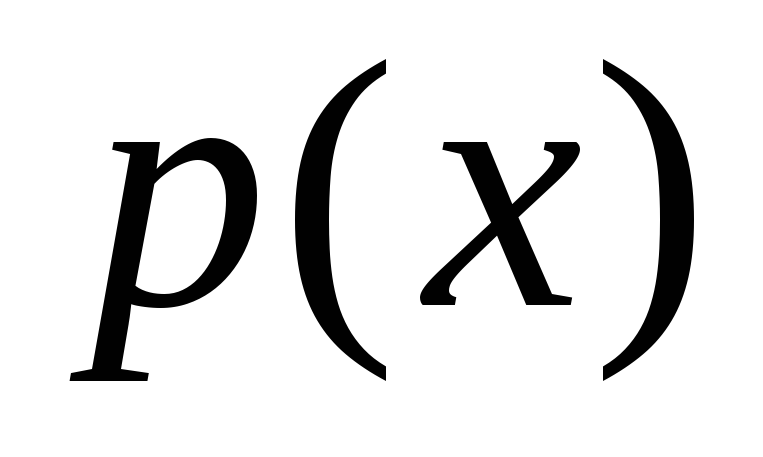 и
и – непрерывные функции;
– непрерывные функции;
постоянное число,
постоянное число,  .
Данное уравнение приводится к линейному
заменой
.
Данное уравнение приводится к линейному
заменой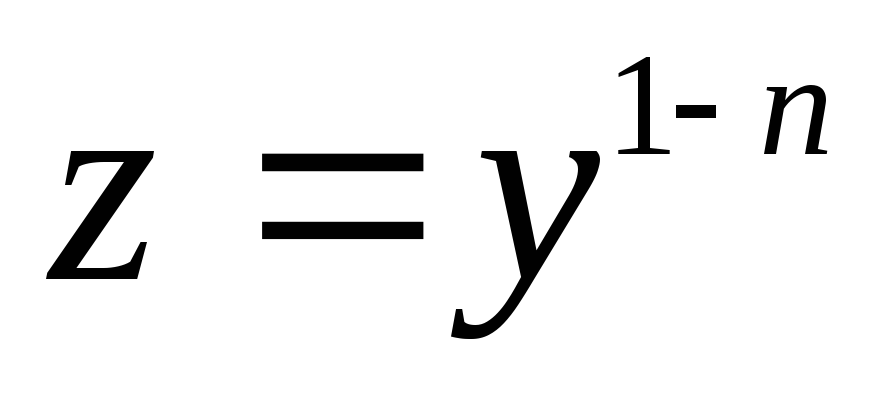 тогда
тогда .
Разделим обе части уравнения Бернулли
на
.
Разделим обе части уравнения Бернулли
на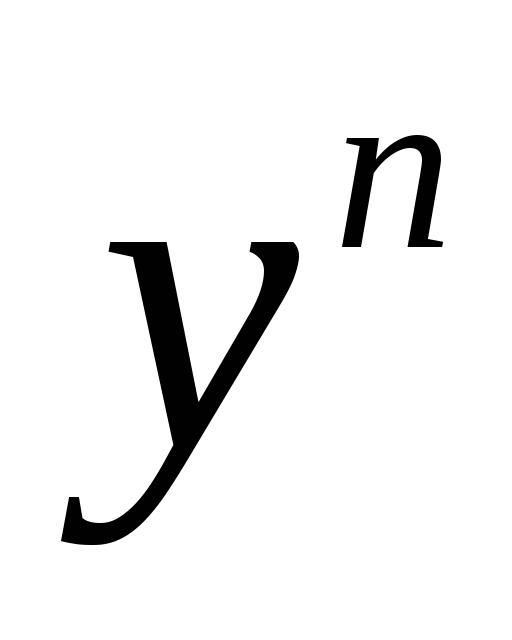 :
: .
Умножим обе части на
.
Умножим обе части на :
: .
Переходим к
.
Переходим к :
: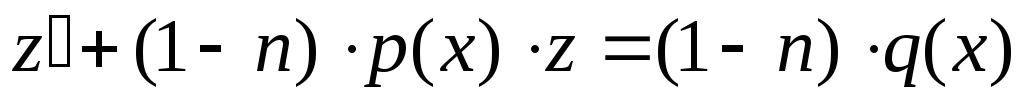 .
.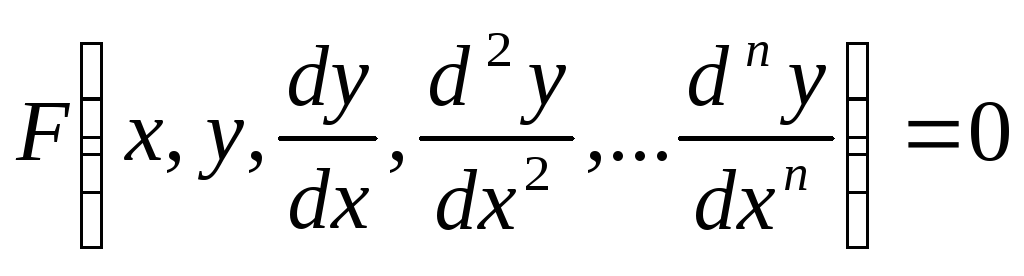 .
.