Задать вопрос репетитору по математике — Колпаков Александр Николаевич
Вам нужен виртуальный репетитор по математике для отдельных он-лайн консультаций? Возникают затруднения в решении задач школьного курса? Предлагаю свою помощь по различным разделам школьной и высшей математики. На этой странице Вы можете задать любой интересующий Вас вопрос по предмету и через какое-то время прочесть указания, подсказки или посмотреть решение задачи полностью.Ваш запрос будет обработан в течение одного — двух дней. Пока вопросы можно задавать только одному репетитору по математике — мне лично. По мере сил и имеющихся временных возможностей я постараюсь помочь Вам справиться с проблемой и опубликую на данной странице свой ответ как можно быстрее. Если решение окажется не слишком длинным, я покажу его полностью.
Заполните специальную форму, приведенную ниже. Желательно указать Ваш возраст, школу и класс (математический или обычный) и учебники, по которым вы учитесь. В таком случае услуга «он-лайн репетитор по математике» будет оказана в соответствии с содержанием школьной или ВУЗовской программы. Пожалуйста, постарайтесь максимально точно формулировать тексты вопросов и условия задач. Непонятные, неполные или некорректные формы рассматриваться не будут. Например, если Вы хотите узнать о том, как построить график функции или как сократить дробь — указывайте соответствующее аналитическое выражение (лучше всего через прикрепленный к вопросу сканер задания).
Реально оценивайте возможности репетитора. Например, бесполезно спрашивать доказательство великой теоремы Ферма. Автор сайта — всего лишь репетитор по математике, а не специалист по решению сложнейших научных проблем. Помните об этом.Возможно, в будущем на сайте появится страница вопросов посетителей другим преподавателям (отдельно репетиторам по школьной математике и отдельно по высшей), прошедшим регистрацию на портале. Прикрепляйте фотографии или сканеры заданий, уравнений и неравенств, любых математических объектов, с которыми у вас возникли затруднения. Желательно, чтобы фотографии не были слишком большими.
Репетитор по математике он-лайн. Решения ваших задач.
Внимание! Короткие ответы на вопросы и решения элементарных номеров публикуются здесь.
Открыты отдельные страницы для задач:
по тригонометрии
по планиметрии
по математике для 5-го и 6 класса
по функциям и графикам
на неравенства (алгебраические и иррациональные)
на квадратные корни и корни n-ных степеней
на числа и последовательности
по высшей математике
по теории вероятностей
по стереометрииB1-B12 подготовки к ЕГЭ
c олимпиад по математике 9 — 11 класс
Кроме этого я активно оформляю для Вас решения на страницах:
Помощь репетитора по математике в исследовании функций
Олимпиадные задачи по математике 4 — 5 класс
Олимпиадные задачи по математике 5 — 6 класс
Виртуальный репетитор по математическому анализуВыпускные экзамены в 9 и 11 классе:
Подготовка к ЕГЭ по математике:
Репетитор по математике решает задачи С3 на логарифмы
Подготовка к ГИА по математике (7 — 9 класс)
Если Вам понравилась страница — будьте так добры нажать на кнопку +1 в верхней части странички. Это поможет найти мои материалы в интернете другим ученикам и репетиторам.
Вопрос от Анны: Здравствуйте! Помогите пожалуйста, для функции 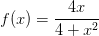 найти область определения, точки экстремума и т.д. У меня получается, что точки экстремума — комплексные числа. По графику интервалы возрастания и убывания можно определить, а если рассматривать поведение производной, то на всем промежутке она больше нуля, т.е. функция возрастает. Никогда не сталкивалась с таким. Заранее спасибо.
найти область определения, точки экстремума и т.д. У меня получается, что точки экстремума — комплексные числа. По графику интервалы возрастания и убывания можно определить, а если рассматривать поведение производной, то на всем промежутке она больше нуля, т.е. функция возрастает. Никогда не сталкивалась с таким. Заранее спасибо.
Репетитор по математике о построении графика. Внимательнее находите первую производную: 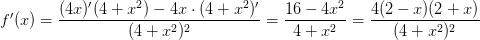 Нули вовсе не комплексные, а самые самые обычные действительные
Нули вовсе не комплексные, а самые самые обычные действительные 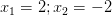 . Расставляя знаки производной методом интервалов получим следующую картину поведения функции:
. Расставляя знаки производной методом интервалов получим следующую картину поведения функции: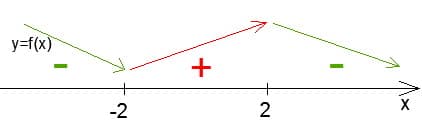 Вторая производная получилась такой:
Вторая производная получилась такой: 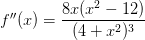 . Ее нули (точки перегиба)
. Ее нули (точки перегиба) 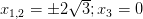 . Асимптоты: вертикальных нет (так как функция непрерывна на всей оси), для нахождения наклонных асимптот вида y=kx+b определяем коэффициенты k и b:
. Асимптоты: вертикальных нет (так как функция непрерывна на всей оси), для нахождения наклонных асимптот вида y=kx+b определяем коэффициенты k и b: 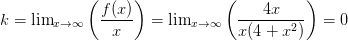 ,
, 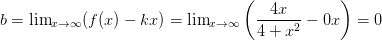 Делаем вывод, что y=0x+0 — горизонтальная асимптота (ось Ox). Пользуясь этой информацией уже можно строить график.
Делаем вывод, что y=0x+0 — горизонтальная асимптота (ось Ox). Пользуясь этой информацией уже можно строить график.
Вопрос репетитору от Михаила: Нужно найти V (t) в момент времени 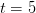 секунд, если точка движется по закону
секунд, если точка движется по закону 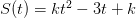 Если можно, подробно. Заранее, большое спасибо!
Если можно, подробно. Заранее, большое спасибо!
Репетитор по математике. Помощь ученику 10 класса. Подробно не получится, потому что задача решается в две строчки 🙂 Насколько я понял — нужно определить скорость точки при t=5, а число k-произвольный параметр .Тогда ответ можно выразить через k. Для этого воспользуемся законом, связывающим зависимость между скоростью V (t) и пройденным расстоянием S (t). Как известно, 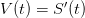 , поэтому вам необходимо найти производную от функции расстояния и подставить в нее временной момент t=5. Этим и займемся. Считаем производную
, поэтому вам необходимо найти производную от функции расстояния и подставить в нее временной момент t=5. Этим и займемся. Считаем производную 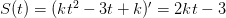 . Подставляя в нее t=5, получим:
. Подставляя в нее t=5, получим: 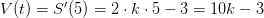 . Подробнее некуда 🙂
. Подробнее некуда 🙂
Вопрос от Марии:Здравствуйте! Помогите пожалуйста решить задачу С2 c ЕГЭ:дан цилиндр с радиусом основания 6 и высотой 10. Отрезки AB и CD -диаметры одного из оснований, а отрезок 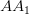 — образующая цилиндра. Найдите тангенс угла между прямыми
— образующая цилиндра. Найдите тангенс угла между прямыми 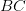 и
и 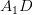 , если
, если 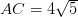 .
.
Репетитор по математике. Решение задачи.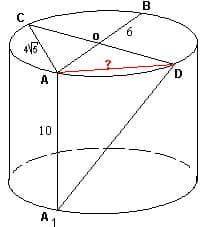 Углом между прямыми называется угол между любыми пересекающимися прямыми, параллельными исходным. Так как
Углом между прямыми называется угол между любыми пересекающимися прямыми, параллельными исходным. Так как 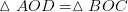 (по первому признаку), то
(по первому признаку), то 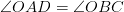 и поэтому
и поэтому 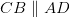 .Следовательно
.Следовательно 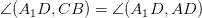 . Из прямоугольного треугольника CAD по теореме Пифагора находим
. Из прямоугольного треугольника CAD по теореме Пифагора находим 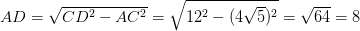 . Так как образующая
. Так как образующая 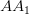 перпендикулярна основанию цилиндра, то она перпендикулярна и любой прямой в нем лежащей и поэтому
перпендикулярна основанию цилиндра, то она перпендикулярна и любой прямой в нем лежащей и поэтому 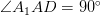 . Находим
. Находим 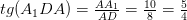
Вопрос от Веры:Как решить тригонометрическое уравнение 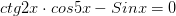 ?
?
Репетитор по математике. Решение задачи.Можно воспользоваться формулами, выражающими котангенс угла 2х через синус и косинус того же угла, затем привести дроби к общему знаменателю и применить формулы, преобразующие произведение тригонометрических функций в сумму. После этого уничтожить в числители два слагаемых и разложить оставшееся на множители. Вот решение: Обратите внимание на то, что углы вида
Обратите внимание на то, что углы вида 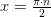 необходимо удалить из ответа. Для этого нужно изобразить нули числителя (
необходимо удалить из ответа. Для этого нужно изобразить нули числителя (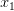 и
и 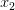 )изобразить на тригонометрическом круге. В первой серии
)изобразить на тригонометрическом круге. В первой серии 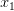 ни одного запрещенного угла нет, а из второй серии углов выбрасываются верхняя и нижняя точка круга. От нее остается множество вида
ни одного запрещенного угла нет, а из второй серии углов выбрасываются верхняя и нижняя точка круга. От нее остается множество вида 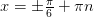 .
.
Вопрос репетитору от Веры:Подскажите, пожалуйста, как решить такое уравнения, как 7cos3x-3cosx=0
Решение репетитора: так углы под знаками тригонометрических функций отличаются в 3 раза, то лучше всего применить формулу тройного угла 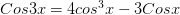 . Получим
. Получим 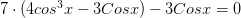 . Далее можно сделать замену
. Далее можно сделать замену 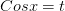 и решить полученное кубическое уравнение элементарным разложением его левой части на множители. Вниманию учеников! Пожалуйста присылайте отдельные (штучные) вопросы. За год существования сайта на мой e-mail пришло более 10 писем с целыми списками номеров по математике из всевозможных контрольных. Трижды я получал комплекты экзаменационных билетов переводных текущих экзаменов и зачетов. Я не занимаюсь помощью в масштабном решении задач. Я не являюсь полноценным он-лайн репетитором, чтобы сидеть целыми днями и решать объемные задания. Свободного времени не так много. Помогаю по мере сил. Оформление вопроса на сайте занимает от 20 до 50 минут. Умножьте на количество задач. Интересны задания, с которыми вы сами пытались биться, но у вас не получилось. Поймите, я помогаю, но отнюдь не заменяю вас полностью. Пробуйте решить сначала самостоятельно и присылайте вопросы в случае затруднений.
и решить полученное кубическое уравнение элементарным разложением его левой части на множители. Вниманию учеников! Пожалуйста присылайте отдельные (штучные) вопросы. За год существования сайта на мой e-mail пришло более 10 писем с целыми списками номеров по математике из всевозможных контрольных. Трижды я получал комплекты экзаменационных билетов переводных текущих экзаменов и зачетов. Я не занимаюсь помощью в масштабном решении задач. Я не являюсь полноценным он-лайн репетитором, чтобы сидеть целыми днями и решать объемные задания. Свободного времени не так много. Помогаю по мере сил. Оформление вопроса на сайте занимает от 20 до 50 минут. Умножьте на количество задач. Интересны задания, с которыми вы сами пытались биться, но у вас не получилось. Поймите, я помогаю, но отнюдь не заменяю вас полностью. Пробуйте решить сначала самостоятельно и присылайте вопросы в случае затруднений.
Александр Николаевич, репетитор по математике в Москве.Для просмотра перейдите на следующую страницу
Pages: 1 2 3 4
ankolpakov.ru
Насколько программисту нужно знать математику? Что думают в Яндексе
Почти в каждой школе в кабинете математики висит табличка с высказыванием Ломоносова: «Математику уже затем учить надо, что она ум в порядок приводит». Многим из тех, кто не понимает, что такое программирование, кажется, что писать код — это то же самое, что решать математические задачи, а все программисты — обязательно математики. Но как все обстоит на самом деле? Насколько помогает знание математики в решении практических задач?Наконец-то мы добрались до одной из самых острых тем и задали нашим коллегам в Яндексе вопрос: «Нужно ли программисту знать математику?»
Под катом, как всегда, полная текстовая версия.
Михаил Парахин
Москва. Программирует 24 года. В Яндексе — 9 месяцев.
После окончания МИФИ начал работать в ЗАО НТЦ «Модуль». В 90-х это было почти единственное место в Москве, где занимались системами автоматического обучения. Потом ушел в компанию Parascript, которая фактически является монополистом в области распознавания рукописного и печатного текста. Долгие годы работал в США. Последние семь лет — в Microsoft, пять из которых возглавлял в Bing подразделение мультимедийных поисковых сервисов. Весной пришёл в Яндекс директором по поисковым технологиям.
Математику приходится знать. И обязательно надо знать хотя бы базовую часть в рамках первых двух курсов института. Мне как-то выпало в жизни узнать очень много статистики и, поскольку я системно занимался автоматическим обучением, пришлось много учить специализированной математики. В целом если ты не знаешь математики в рамках школьно-институтского курса, то жизнь программиста тебе не очень понравится.
Григорий bobuk Бакунов
Москва. Программирует 25 лет. В Яндексе — 10 лет.
Когда-то пришёл работать системным администратором, а сейчас — директор по распространению технологий.
Как ты думаешь, нужно ли водителю автомобиля знать, как он ездит? Мне кажется, что необходимо. Это реальная человеческая потребность. Нужно достаточно глубоко понимать, как работают даже такие банальные вещи, как системная библиотека. И, как ни странно, для этого до сих пор нужна математика. Есть определенный класс программистов, которым действительно это, наверное, не нужно. Можно привести простое сравнение. Есть люди, которые рисуют картины — их называют художники. Есть люди, которые красят заборы, — это маляры. Вот так же и с программистами: есть некоторый класс программистов, которые творят что-то высокое, а есть люди, которые красят заборы. И в конечном итоге их во многом отличает знание математики, умение тонко и детально понимать что же они все-таки пишут. Дальше выбор за человеком. Или ты начинаешь заниматься математикой, и тогда у тебя появляется шанс стать художником. Или красишь заборы — это тоже хорошая профессия.
Антон pg83 Самохвалов
Москва. Программирует 18 лет. В Яндексе — 9 лет.
Пришёл в Маркет программистом на C++. Работал над самыми разными задачами сервиса. Через несколько лет перешёл в поиск, где занялся надежностью и производительностью runtime поиска. Сейчас занимается системой сборки, которая позволит собирать всю нашу кодовую базу за несколько минут на большом распределенном кластере.
Вопрос в том, для чего ему знать математику? Для того чтобы объяснить компьютеру, что ему надо делать, математику знать не надо — надо знать язык и уметь им пользоваться. Но есть какие-то предметные области, где математику знать необходимо. Если бы я, например, писал Матрикснет или работал с ДНК, вполне возможно, что какую-то математику мне нужно было бы знать. Но вот в программировании — нет. Я не могу вспомнить, когда мои знания матанализа пригодились мне в написании кода. Но само знание математики заставляет людей писать лучший код. Все самые лучшие программисты, которых я знаю, обычно заканчивали какой-нибудь механико-математический факультет, а не ВМК. Видимо, обучение математике как-то так правильно вправляет мозг, что ты начинаешь лучше программировать.
Андрей styskin Стыскин
Москва. Программирует 18 лет. В Яндексе — 9 лет.
Пришёл в Яндекс разработчиком на Java в группу поиска Маркета. Занимался классификацией товарных текстов и извлечением фактов из товарных описаний. Так началось его увлечение поиском и машинным обучением. Вне работы Андрей делал различные IR-игрушки: генератор стихов на языковых моделях, робота для прокачки социальных сетей. Сейчас Андрей руководит отделом ранжирования, в котором работает команда почти из 200 человек.
Человеку нужно хорошо знать математику, чтобы быть программистом в Яндексе. Можно сказать, это часть нашего корпоративного духа. Если кто-то не может решить сложную задачку с собеседования, то его просто всерьез никто не будет воспринимать в Яндексе. По крайне мере в поиске точно так. Мне кажется, это самоидентификация, механизм, с помощью которого можно понять, что человек мыслит теми же категориями, говорит на том же языке, что и ты, поэтому ты сможешь работать с ним в команде. Я знаю много хороших разработчиков, которые не смогли бы в Яндексе выполнить ни один проект, но с аналогичными в других структурах справились бы прекрасно. Например, в Яндексе тоже делаются инфраструктурные проекты, которые могут делаться в том же Luxoft, но просто этих людей мы бы никогда не наняли.
Анатолий anatolix Орлов
Программирует 25 лет. В Яндексе — 9 лет.
Первые два года писал Маркет. Долгое время занимался поиском — в основном его производительностью, а потом и всем остальным. Сейчас занимается разными проектами в области скорости, архитектуры и т.д. Заместитель руководителя направления поисковых сервисов. Входит в 2% людей, которые заканчивают курсы на Coursera.
Математика — это большая область знаний, где есть части, которые в программировании нужны и не нужны. Если вопрос в том, существует ли что-то в математике, что нужно знать программисту, то да, конечно. А если он звучит как: «Есть ли что-то в математике, что программисту знать необязательно?» — то ответ будет тоже: «Да, такого много»… Например, дискретка очень нужна программисту, а матан за много лет мне в программировании ни разу не пригодился.
Степан Кольцов
Москва. Программирует 10 лет. В Яндексе — 7 лет.
Старший разработчик в службе разработки систем хранения и обработки данных. Стёпа из тех сотрудников Яндекса, которые уходили, но потом возвращались. Сейчас работает над системами мониторинга в поиске.
Зависит от того, чем человек занимается. Если он пишет что-то высокотехнологичное, то ему математику надо знать прям суперобязательно. Чем ближе человек, условно говоря, к поиску Яндекса, в котором у нас самые высокотехнологичные задачи, тем лучше нужно знать математику. Если он ближе к совсем прикладным задачам (например, пишет программы для банка, чтобы оптимизировать работу бухгалтерии), то математику, конечно, можно не знать. Мне очень нравится Яндекс тем, что у нас гораздо больше таких мест, где она все же нужна.
Андрей Мищенко
Москва. Программирует 24 года. В Яндексе — 9 лет.
Пришёл в Яндекс разработчиком на C++, долго был руководителем разработки Поиска по блогам и писал на Perl. Андрей — кандидат физико-математических наук. Сейчас работает с Андреем Гулиным над улучшением алгоритмов машинного обучения в поиске.
Смотря какие у программиста цели. Для решения некоторых задач нужно знать математику лучше, чем некоторые ученые, а для других она совершенно не нужна. Если ты занимаешься инфраструктурными, инженерными задачами, то тебе нужны совсем другие умения. Есть задачи, в которых гуманитарное образование тебе даже больше поможет, чем фундаментальное математическое. Особенно там, где ты больше всего работаешь с пользователями. Если ты разрабатываешь интерфейс, который должен быть удобен среднестатистическому пользователю, глубокое математическое образование будет тебе только мешать. Интерфейс будет очень стройнымм, но при этом совершенно неудобным. Ты должен уметь срезать углы, делать его не таким стройным и более гладким, чтобы он был более интуитивный.Нужна математика в системном программировании на нижнем уровне, в каких-то хайтечных задачах. В том же машинное обучении, конечно, сплошная математика и статистика. Наверняка в криптографии тоже нужна очень глубокая математика. Таких областей хватает.
Александр sadovsky Садовский
Москва. В Яндексе — 10 лет.
Пришёл в Яндекс работать над проектами, связанными с поиском. Под его руководством были созданы поиск по блогам, Яндекс.XML, запущены новый алгоритм ранжирования и робот для оперативного индексирования свежей информации, создана служба асессоров и начато измерение качества поиска. Саша — автор множества публикаций в научных и популярных СМИ об алгоритмах поисковых систем и продвижении сайтов в интернете.
На мой взгляд, математика — очень мощная штука, которая может облегчать решение многих задач в программировании. И пусть программист не знает её на уровне математиков, но базовые знания высшей математики у него должны быть, чтобы общаться с теми, кто ее понимает, и уметь воспринимать ту информацию, которую передает собственно математик. Когда я работал в лаборатории, у нас был человек, который очень хорошо разбирался в математике, алгоритмах, оптимизации и мог построить хорошую математическую модель. Но если программист всего этого не понимает и тупо программирует один в один, как ему рассказали, результат получается не очень. Хорошо, когда два человека находят точки пересечения. Математика позволяет прикидывать в голове эффективность алгоритмов, то, за какое время они будут выполняться, позволяет лучше описывать объекты реального мира. В нашей области без математики невозможно создать такие алгоритмы, как Матрикснет.
Артём breqwas Киреев
Программирует 12 лет. В Яндексе — 8 лет.
В Яндекс позвали за то, что парсил данные из Поиска по блогам. Позвали не только поругать, но и на работу. Много лет делал Поиск по блогам, в частности был основным разработчиком подсервиса Яндекс.Пульс. Сейчас разрабатывает Рекламную сеть, один из самых критичных в смысле отказоустойчивости сервисов.
Я математику не знаю вообще. Причем это очень странная ситуация, потому что все, кто сидят вокруг меня, знают ее очень хорошо. Так что когда они начинают говорить какие-то умные вещи или когда у них на столах валяются бумажки, исписанные страшным даже не знаю чем, мне становится очень совестно. Но вот я математики не знаю, и ничего. Совершенно ничего хорошего, но без математики есть много задач, в которых её, серьёзную Computer Science, алгоритмы и все такое знать необязательно. Есть много прикладных задач, в которых это не нужно.
Сергей svv Вавинов
Москва. Программирует 27 лет. В Яндексе — 6 лет.
Пришёл в Яндекс разработчиком в Яндекс.Видео. Был главным в разработке Музыки, потом — в службе медиасервисов. Сделал несколько проектов для Яндекс.Диска. Сейчас — руководитель группы технологий работы с большими данными. Одна из задач, над которой работает Сергей, — проекты Яндекса для ЦЕРНа.
Программисту знать математику нужно обязательно. Конечно, бывает разное программирование, разные проекты, в некоторых математики нужно больше, в некоторых — меньше, в некоторых нужна специальная какая-то математика. Но базовое образование, базовое понимание математики необходимо просто потому, что она выстраивает мозги. У человека развивается абстрактное мышление, он может лучше смотреть на задачу, разбивать ее на какие-то части, понимать, как подходить к ней, искать какие-то новые подходы к решению – это в любом программировании важно. Еще есть некоторые совершенно базовые вещи. Например, оценка сложности алгоритмов. Её нужно уметь проводить в любой ситуации — какую бы программу вы ни писали, вам надо уметь ее оценить. Причем заранее, до того, как вы напишите код, чтобы просто понимать, нужно этот алгоритм использовать или вообще взять какой-то другой, чтобы он был более эффективным.
Роман Кашицын
Нижний Новгород. Программирует — 11 лет. В Яндексе — год.
Как и многие наши коллеги в Нижнем Новгороде, окончил ННГУ им. Н.И. Лобачевского. До Яндекса разрабатывал системы страхования, информационной безопасности, управления медиасерверами. Работал над ПО в телекоммуникациях, автоматизированными рабочими местами, порталами. У нас участвует в модернизации бэкофиса справочника организаций.
Такие вопросы часто задают известным хорошим программистам. Я считаю, что математика полезна, но необязательна. Ее очень полезно знать, особенно, если ты пишешь, например, на Haskell. Многие известные программисты не имели профессионального образования в области математики и писали очень хорошие программы. Скорее, программирование — это даже иногда такая лингвистическая работа; многие программисты были лингвистами, например. Но, с другой стороны, математика иногда очень помогает. Особенно если писать какие-то приложения, связанные с графикой. Там без высоких математических абстракций очень плохо. Матрицы, преобразования, кватернионы и всякие такие штуки очень нужны.
Елена Бунина
Москва. В Яндексе — 7 лет.
Директор отделения computer science в Школе анализа данных, HR-директор Яндекса, профессор кафедры высшей алгебры механико-математического факультета МГУ им. М.В. Ломоносова, заместитель заведующего кафедрой «Анализ данных» МФТИ. Доктор физико-математических наук. Тема её докторской диссертации «Автоморфизмы и элементарная эквивалентность групп Шевалле и других производных структур».
С моей точки зрения, есть разные программисты: те, кто просто по заданным алгоритмам что-то кодирует и может обойтись без математики, и все те, кто занимается анализом больших данных и теми вещами, которые есть у нас в Яндексе, — им математика нужна. Причем разные аспекты. Иногда даже нельзя представить заранее, какая математика им понадобится. Но уж точно те, кто имеет дело с машинным обучением, должен знать математику, должны хорошо владеть алгоритмами, и для них очень важны знания статистики.
Алексей Волохович
Нижний Новгород. Программирует — 25 лет. В Яндексе — 8 месяцев.
Лёша — руководитель нижегородского офиса разработки Яндекса. Окончил Нижегородский технический университет им Р. Е. Алексеева. Сейчас преподаёт там дискретную математику. Кандидат технических наук. До Яндекса занимался разработкой и программным менеджментом мобильных устройств.
Программисту знать математику в принципе важно, потому что те задачи, которые он решает, очень часто связаны со знаниями основным математических понятий. Писать код не означает ставить какие-то буковки, использовать какие-то операторы, функции и т.д., которые описаны в KPI. Можно написать такой код, который потом не сможет взлететь или, если полетит, то после этого упадет так, что развалится все, что под ним находилось. Поэтому закладывать красивые решения в самом начале проектирования системы — это основа основ. Для того чтобы получить это красивое решение, ты должен иметь базовые фундаментальные знания, понимать, в чем красота, в чем не красота, как посмотреть что данное решение оптимально для конкретного круга задач, которые решает твое программное обеспечение.
Михаил mlevin Левин
Москва. Программирует 18 лет. В Яндексе — 5 лет.
Вы могли видеть лекцию Миши о том, как математика помогает Яндексу зарабатывать. Очень большая часть его деятельности — работа в наших академических программах. Он преподает в Школе анализа данных, участвует в создании программы обучения на факультете Computer Science Вышки и Яндекса. Дважды завоевывал медали на ACM ICPC в составе команды МГУ им. М.В. Ломоносова.
Если хочется заниматься интересной работой, то математику нужно знать довольно хорошо. Есть определенные разделы (такие, как алгоритмы), которые требуют довольно глубокого знания математики и в общем-то отчасти математикой и являются. Мы все-таки считаем, что алгоритмы на каком-то базовом уровне должны знать все уважающие себя разработчики, и в общем-то в Яндексе на собеседованиях, по-моему, всех спрашивают алгоритмические задачки. Дальше уже зависит от направления деятельности. Если человек разрабатывает что-то инфраструктурное, то он может углубляться уже в системные вещи. Там своя математика тоже есть, но я про нее не очень много понимаю. Функциональные языки — это вообще то, над чем человек, не знающий математику, ломает голову, а какие-нибудь алгебраисты просто схватывают все на лету. Ну, и понятно, новые области машинного обучения — это вообще сплошная математика и там, конечно, можно просто применять инструменты, ничего в них не понимая, но тогда риск сделать глобальную ошибку, из-за которой вообще ничего не получается, очень большой.
Андрей Гулин
Программирует 25 лет. В Яндексе — 9 лет.
Пришёл в Яндекс программистом на C++. Первой задачей было переделать формат инвертированного индекса, чтобы записать в него информацию о точной форме слова в документах (до этого хранилась только лемма). Один из главных создателей Матрикснета, нашей технологии машинного обучения. Сейчас руководит службой ранжирования. Если бы Кнут не написал свой трехтомник, эту работу стоило бы отдать Андрею. Сам Андрей на вопрос, чем он занимается в Яндексе, ответил: «Я работаю за компьютером и делаю всякие штуки, чтобы всем было хорошо».
Конечно, знать математику необходимо. Тут коллеги смеются, настолько несуразный вопрос вы задаете. Но не очень понятно, можно ли не знать математику с нашей системой общего образования. Уже в первом классе всех обучают складывать, и это навык, который необходим и которым мы пользуемся постоянно. Математика не исчерпывается, как мы знаем, арифметикой — в ней есть много разделов с большей или меньшей полезностью. Некоторые изучают дифференциальную геометрию. Другие — сложные разделы математики, которые редко бывают полезны. В то же время есть разделы математики, которые считаются нетривиальными. Например, теория вероятностей, и хотелось бы, чтобы её знало как можно больше людей. Потому что она примерно так же полезна, как и обычная арифметика. Первая дает всем возможность посчитать, сколько денег нужно заплатить за обед и хватит ли их до конца месяца, а вторая позволит нам посчитать гораздо более интересные вещи. Например, какие у нас шансы на то, что нам удастся устроиться на новое место работы с большей зарплатой, что не отменят визы и мы сможем уехать в отпуск в этом году. Для в общем-то насущных решений вполне себе можно применять теорию вероятностей в полном объеме. Соответственно знать математику необходимо, и вообще, как мы знаем, математика — царица наук. И одна из самых абстрактных наук, которая вообще бывает.Машинное обучение — всего лишь другое название статистики. Если вы занимаетесь статистикой, но с применением компьютеров, то вы занимаетесь машинным обучением. Математику вам придется ее знать, и даже если вы ее не знаете, вы ее изучите. Единственное, что необходимо, — уметь изучать новые области. Без этого навыка говорить, что вы хотите заниматься чем-то новым в своей жизни, невозможно. Машинное обучение было новым недавно, поэтому все, кто им занимался, имели этот навык. Прямо сейчас изучать машинное обучение намного проще, чем это было 10 лет назад, потому что написали много книжек, есть много курсов. Соответственно, если вы хотите заниматься не машинным обучением, которым занимаются уже примерно все, а чем-то совершенно новым, нужно уметь изучать новые области и выбирать те области, которые действительно нужны.
Мнений по поводу математики и программирования в Яндексе, на самом деле, гораздо больше. Здесь мы постарались показать, что в принципе они разные. И даже когда кто-то в одной части Яндекса считает, что без глубоких математических знаний невозможно работать, в другой свои задачи решают и те, у кого их нет. А что думаете вы? Мешало ли вам когда-нибудь то, что вы прогуливали матан? Или же математика вам каждый день помогает?
habr.com
А что там по-математике задали?
Фига Вам! Мне в школу не надо 🙂
контрольную работу на дом составить таблицу матчей кубка УЕФА
уложиться в одну зарплату
Эти, как их там, многочлены какие-то, или членистоногие…)
Сколько осталось яблок, когда их съели.
touch.otvet.mail.ru
провокационные задачи по математике
Провоцирующие задачи.
К задачам провоцирующего характера будем относить все задачи, условия которых содержат упоминания, указания, намёки и другие побудители, подталкивающие учащихся к выбору ошибочного пути решения.
Достоинства и недостатки:
Главное достоинство провоцирующих задач заключается в том, что совершая ошибку на глазах учителя или учащихся ученик испытывает сильнейшее впечатление и надолго запоминает ошибочные действия.
А главный недостаток кроется в малой изученности феномена провоцирующих задач и отсутствие целостного описания задач и побудителей, подталкивающих к выбору неправильного ответа.
Виды провоцирующих задач.
Полезно выделить следующие разновидности задач провоцирующего характера:
I. Задачи, условия которых навязывают неверный ответ.
II. Задачи, условия которых подсказывают неверный путь решения.
III. Задачи, вынуждающие придумывать невозможные при заданных условиях математические объекты.
IV. Задачи, вводящие в заблуждение неоднозначной трактовкой терминов, словесных оборотов и выражений.
V. Задачи, условия которых допускают возможность опровержения семантически верного решения.
1. Задачи, навязывающие неверный ответ.
Их полезно делить на четыре группы, назовём их IА, IБ, IВ,IГ.
А: Задачи, навязывающие один определённый ответ.
Б: Задачи, побуждающие сделать выбор из предложенных неверных ответов.
В: Задачи, побуждающие сделать выбор из предложенных верных и неверных ответов.
Г: Задачи, указывающие на неверный ответ.
Задачи IA
Сколько граней имеет новый шестигранный карандаш?
Навязывается ответ: «6 граней», но он неверный, так как у карандаша ещё 2 торцевые грани. Ответ: «8 граней»
2. Сколько цифр требуется, чтобы записать двенадцатизначное число?
Навязывается ответ: «12 цифр», но десятичная сиситема счисления обходится десятью цифрами. Ответ: «Двенадцатизначное число можно записать одной, двумя, тремя, четырьмя, пятью, шестью, семью, восемью, девятью, десятью цифрами»
Задачи IБ
Какое из чисел 205, 206, 207, 208, 209 является простым?
Чаще всего учащиеся называют ответы 207 или 209, но все записанные числа являются составными. Ответ: «Никакое».
2. Какое из следующих утверждений истинно:
А) Четырёхугольник, диагонали которого делятся точкой пересечения пополам и взаимно перпендикулярны , является прямоугольником.
Б) Четырёхугольник, диагонали которого взаимно перпендикулярны и равны является ромбом.
Чаще всего учащиеся выбирают утверждение б, но оба варианта ложны. Ответ: «Никакое».
Задачи IГ
Какое простое число следует за числом 200?
Напрашивается ответ: 201, но это число составное. Ответ: 211
Какое число больше: а или 2а?
Напрашивается ответ: 2а, ведь оно в два раза больше чем а. Но число а может быть в отрицательном значении, соответственно ответ: неизвестно.
II. Задачи, навязывающие неверный путь решения.
Их тоже полезно делить на четыре группы: IIА, IIБ, IIВ, IIГ.
А: Задачи, подталкивающие к выполнению ненужных действий.
Б: Задачи, подталкивающие к выполнению неправильных действий.
В: Задачи, подталкивающие к решению действий неверным образом.
Г: Задачи, подталкивающие к выполнению невозможных действий.
Задачи IIА
Тройка лошадей проскакала 15 км. Сколько проскакала каждая лошадь?
Хочется выполнить действие 15:3=5 (км), но выполнять деление не требуется. Ответ: 15км.
2. Лупа даёт четырёхкратное увеличение. Каким будет угол величиной 2,5 рассматриваемый через лупу?
Хочется выполнить действие 2,5*4=10, но выполнять умножение не требуется. Ответ: 2,5
Задачи IIБ
У палки два конца. Если один из них отпилить, сколько концов получится?
Кажется, нужно выполнить вычитание 2-1=1. На самом же деле нужно находить сумму 2+2. Ответ: 4 конца
2. Стол имеет 4 угла. Если один из них отпилить сколько углов получиться?
Кажется, нужно выполнить вычитание 4-1=3. На самом деле нужно находить сумму 3+2. Ответ: 5 углов.
Задачи IIВ
На руках 10 пальцев. Сколько пальцев на 10-ти руках?
Чаще всего учащийся выполняет умножение: 10*10. Но правильное решение: 10*(10:2)=50
2. Стальной брус весит 40кг. Сколько будет весить брус если его размер уменьшить в три раза?
Чаще всего учащиеся выполняют деление: 40:10. Но правильное решение 40: (4*4*4)=0, 625
Задачи IIГ
Двое пошли, три гриба нашли. Четверо пойдут сколько грибов найдут?
Напрашивается последовательность действий: 4:2=2, 3*2=6. Но они могут вообще ничего не найти, правильный ответ: неизвестно.
III. Задачи, вынуждающие придумывать несуществующие объекты.
Придумайте простое трёхзначное число, в записи которого Употребляются только цифры 1 и 4.
Придумать такое число нельзя, так как по условию задачи оно кратно трём.
IV. Задачи, приводящие в заблуждение.
Чему равен угол в квадрате?
В квадрате все углы прямые!
2. На бумаге написано число 606. Какое действие следует выполнить, чтобы увеличить его в полтора раза?
Если перевернуть лист с такой надписью, то увидишь число 909, которое в полтора раза больше, чем число 606!
V. Задачи, допускающие опровержение верного ответа.
Три спички выложили на столе так, что получилось четыре. Могло ли такое быть? (других предметов на столе не было).
Напрашивающийся отрицательный ответ опровергается записью:
Ещё задачи…
Сколько распилов нужно сделать в 7-ми метровом бревне, чтобы получить столбики длиной 1м? (шесть)
2. Сколько углов в квадратной комнате? (восемь)
3. Двое играли в шашки 4 часа. Сколько играл каждый из них? (четыре)
4. Книга стоит 1 руб, и ещё половину стоимости. Сколько стоит книга? (2 руб)
infourok.ru