Линейное уравнение с одной переменной. 7-й класс
Урок № 1.
Тип урока: закрепление пройденного материала.
Цели урока:
Образовательные:
- формирование навыка решения уравнения с одним неизвестным сведением его к линейному уравнению с помощью свойств равносильности.
Развивающие:
- формирование ясности и точности мысли, логического мышления, элементов алгоритмической культуры;
- развитие математической речи;
- развитие внимания, памяти;
- формирование навыков само и взаимопроверки.
Воспитательные:
- формирование волевые качества;
- формирование коммуникабельность;
- выработка объективной оценки своих достижений;
- формирование ответственности.
Оборудование: интерактивная доска, доска для фломастеров, карточки с заданиями для самостоятельной работы, карточки для коррекции знаний для слабоуспевающих учащихся, учебник, рабочая тетрадь, тетрадь для домашних работ, тетрадь для самостоятельных работ.
Ход урока
1. Организационный момент – 1мин.
Поприветствовать учащихся, проверить их готовность к уроку, объявить тему урока и цель урока.
2. Проверка домашнего задания – 4 мин.
Учащиеся проверяют домашнюю работу, решение которой выведено с обратной стороны доски одним из учащихся.
3. Устная работа– 6 мин.
(1) Пока идет устный счет, слабоуспевающие учащиеся получают карточку для коррекции знаний и выполняют 1), 2), 4) и 6) задания по образцу. (См. Приложение 1.)
Карточка для коррекции знаний.
(2) Для остальных учащихся задания проецируются на интерактивную доску: (См. Презентацию: Слайд 2)
- Вместо звездочки поставь знак “+” или “–”, а вместо точек – числа:
а) (*5)+(*7) = 2;
б) (*8) – (*8) = (*4)–12;
в) (*9) + (*4) = –5;
г) (–15) – (*…) = 0;
д) (*8) + (*…) = –12;
е) (*10) – (*…) = 12. - Составь уравнения, равносильные уравнению:
а) х – 7 = 5;
б) 2х – 4 = 0;
в) х –11 = х – 7;
г) 2(х –12) = 2х – 24.
3. Логическая задача: Вика, Наташа и Лена в магазине купили капусту, яблоки и морковь. Все купили разные продукты. Вика купила овощ, Наташа – яблоки или морковь, Лена купила не овощ. Кто что купил? (Один из учащихся, выполнивший задание выходит к доске и заполняет таблицу.) (Слайд 3)
| Вика | Наташа | Лена | |
| К | |||
| Я | |||
| М |
Заполнить таблицу
| Вика | Наташа | Лена | |
| К | + | – | – |
| Я | – | – | + |
| М | – | + | – |
Ответ
(Учащиеся используют пластиковые листы и фломастеры.)
4. Обобщение умения решать уравнения сведением их к линейному уравнению –9 мин.
Коллективная работа с классом. (Слайд 4)
Решим уравнение
12 – (4х – 18) = (36 + 5х) + (28 – 6х). (1)
для этого выполним следующие преобразования:
1. Раскроем скобки. Если перед скобками стоит знак “плюс”, то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки. Если перед скобками стоит знак “минус”, то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки:
12 – 4х + 18 = 36 + 5х + 28 – 6х. (2)
Уравнения (2) и (1) равносильны:
2. Перенесем с противоположными знаками неизвестные члены так, чтобы они были только в одной части уравнения (или в левой, или в правой). Одновременно перенесем известные члены с противоположными знаками так, чтобы они были только в другой части уравнения.
Например, перенесем с противоположными знаками неизвестные члены в левую, а известные – в правую часть уравнения, тогда получим уравнение
– 4х – 5х + 6х = 36 + 28 – 18 — 12, (3)
равносильное уравнению (2), а следовательно, и уравнению (1).
3. Приведем подобные слагаемые:
–3х = 34. (4)
Уравнение (4) равносильно уравнению (3), а следовательно, и уравнению (1).
4. Разделим обе части уравнения (4) на коэффициент при неизвестном.
Полученное уравнение х = будет равносильно уравнению (4), а следовательно, и уравнениям (3), (2), (1)
Поэтому корнем уравнения (1) будет число
По этой схеме (алгоритму) решаем уравнения на сегодняшнем уроке:
- Раскрыть скобки.
- Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.
- Привести подобные члены.
- Разделить обе части уравнения на коэффициент при неизвестном.
Примечание: следует отметить, что приведенная схема не является обязательной, так как часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. При решении же других уравнений бывает проще отступить от этой схемы, как, например, в уравнении:
7(х – 2) = 42.
5. Тренировочные упражнения – 8 мин.
№ № 132(а, г), 135(а, г), 138(б, г) – с комментарием и записью на доске.
6. Самостоятельная работа – 14 мин. (выполняется в тетрадях для самостоятельных работ с последующей взаимопроверкой проверкой; ответы будут отображены на интерактивной доске)
Перед самостоятельной работой
Не отрывая карандаша от бумаги и не проходя дважды по одному и тому же участку линии, начертите распечатанное письмо. (Слайд 5)
(Учащиеся используют пластиковые листы и фломастеры.)
1. Решить уравнения (на карточках) (См. Приложение 2)
Дополнительное задание № 135 (б, в).
7. Подведение итогов урока – 1 мин.
Алгоритм сведения уравнения к линейному уравнению.
8. Сообщение домашнего задания – 2 мин.
п.6, № № 136 (а-г), 240 (а), 243(а, б), 224 (Разъяснить содержание домашнего задания).
Урок № 2.
Цели урока:
Образовательные:
- повторение правил, систематизация, углубление и расширение ЗУНов учащихся по решению линейных уравнений;
- формирование умения применять полученные знания при решении уравнений различными способами.
Развивающие:
- развитие интеллектуальных умений: анализа алгоритма решения уравнения, логического мышления при построении алгоритма решения уравнения, вариативности выбора способа решения, систематизации уравнений по способам решения;
- развитие математической речи;
- развитие зрительной памяти.
Воспитательные:
- воспитание познавательной активности;
- формирование навыков самоконтроля, взаимоконтроля и самооценки;
- воспитание чувства ответственности, взаимопомощи;
- привитие аккуратности, математической грамотности;
- воспитание чувства товарищества, вежливости, дисциплинированности, ответственности;
- Здоровьесбережение.
а) образовательная: повторение правил, систематизация, углубление и расширение ЗУНов учащихся по решению линейных уравнений;
б) развивающая: развитие гибкости мышления, памяти, внимания и сообразительности;
в) воспитательная: привитие интереса к предмету и к истории родного края.
Оборудование: интерактивная доска, сигнальные карточки (зеленая и красная), листы с тестовой работой, учебник, рабочая тетрадь, тетрадь для домашних работ, тетрадь для самостоятельных работ.
Форма работы: индивидуальная, коллективная.
Ход урока
1. Организационный момент – 1мин.
Поприветствовать учащихся, проверить их готовность к уроку, объявить тему урока и цель урока.
2. Устная работа – 10 мин.
(Задания для устного счета выводятся на интерактивную доску.) (Слайд 6)
1) Решите задачи:
а) Мама старше дочери на 22 года. Сколько лет маме, если им вместе 46 лет
б) В семье трое братьев и каждый следующий младше предыдущего в два раза. Вместе
всем братьям 21 год. Сколько лет каждому?
2) Решите уравнения: (Пояснить)
| ;
|
Какие из данных уравнений являются линейными?
(Во время устного счета учащиеся используют сигнальные карточки: зеленую и красную)
3) Проверьте, правильно ли решено уравнение, если нет, то найди ошибки. (Слайд 7)
| 4 · (х – 5) = 12 – х 4х – 5 = 12 – х 4х + х = 12 – 5 5х = 7 /:5 х = 1,4 |
Желающий выходит к интерактивной доске исправить ошибки
|
4) Пояснить задания из домашней работы, вызвавшие затруднение.
3. Выполнение упражнений – 10 мин. (Слайд 8)
(1) Какому неравенству удовлетворяет корень уравнения:
4 – 5х = 5
а) x > 1;
б) x < 0;
в) x > 0;
г) x < –1.
(2) При каком значении выражении у значение выражения 2у – 4 в 5 раз меньше значения выражения 5у – 10?
(3) При каком значении k уравнение kx – 9 = 0 имеет корень равный – 2?
Посмотри и запомни (7 секунд). (Слайд 9)
Через 30 секунд учащиеся воспроизводят рисунок на пластиковых листах.
4. Физкультминутка – 1,5 мин.
Упражнение для глаз и для рук
(Учащиеся смотрят и повторяют упражнения, которые проецируются на интерактивную доску.)
5. Самостоятельная тестовая работа – 15 мин.
(Учащиеся выполняют тестовую работу в тетрадях для самостоятельных работ, дублируя ответы в рабочих тетрадях. Сдав тесты, учащиеся сверяют ответы с ответами, отображенными на доске)
Учащиеся, справившиеся с работой раньше всех, помогают слабоуспевающим учащимся.
(См. Приложение 3)
6. Подведение итогов урока – 2 мин.
– Какое уравнение с одной переменной называется линейным?
– Что называется корнем уравнения?
– Что значит “решить уравнение”?
– Сколько корней может иметь уравнение?
7. Сообщение домашнего задания. – 1 мин.
п.6, № № 294(а, б),244, 241(а, в), 240(г) – Уровень А, В
п.6, № № 244, 241(б, в), 243(в),239, 237– Уровень С
(Разъяснить содержание домашнего задания.)
8. Рефлексия – 0,5 мин.
– Вы довольны своей работой на уроке?
– Какой вид деятельности вам понравился больше всего на уроке.
Литература:
- Алгебра 7. / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Пешков, С.В. Суворова. Под редакцией С.А. Теляковского. / М.: Просвещение, 1989 – 2006.
- Сборник тестовых заданий для тематического и итогового контроля. Алгебра 7 класс/ Гусева И.Л., Пушкин С.А., Рыбакова Н.В.. Общая ред.: Татур А.О. – М.: “Интеллект-Центр” 2009 – 160 с.
- Поурочное планирование по алгебре. / Т.Н.Ерина. Пособие для учителей /М: Изд. “Экзамен”, 2008. – 302,[2] с.
- Карточки для коррекции знаний по математике для 7 класса./ Левитас Г.Г. /М.: Илекса, 2000. – 56 с.
urok.1sept.ru
| 1. |
Корень линейного уравнения
Сложность: лёгкое |
1 |
| 2. |
Решение линейного уравнения
Сложность: лёгкое |
1 |
| 3. |
Линейное уравнение, схема решения
Сложность: лёгкое |
1 |
| 4. |
Линейное уравнение (коэффициент при x дробный)
Сложность: лёгкое |
1 |
| 5. |
Составление и решение линейного уравнения
Сложность: лёгкое |
2 |
| 6. |
Линейное уравнение вида x + a = b
Сложность: лёгкое |
1 |
| 7. |
Линейное уравнение вида x + a = 0
Сложность: лёгкое |
1 |
| 8. |
Линейное уравнение вида ax + b = 0
Сложность: лёгкое |
1 |
| 9. |
Линейное уравнение (с дробями)
Сложность: среднее |
2 |
| 10. |
Линейное уравнение вида a — kx = c
Сложность: среднее |
3 |
| 11. |
Линейное уравнение вида a — b + kx = c + d — mx
Сложность: среднее |
4 |
| 12. |
Задача на движение
Сложность: среднее |
3 |
| 13. |
Задача на движение, скорость по течению и против течения
Сложность: среднее |
4 |
| 14. |
Задача на движение, две лодки
Сложность: среднее |
4 |
| 15. |
Задача на движение в одном направлении
Сложность: среднее |
4 |
| 16. |
Задача на движение, скорость течения реки
Сложность: сложное |
5 |
| 17. |
Решение уравнения, записанного в виде пропорции
Сложность: сложное |
3 |
| 18. |
Определение книг на полках
Сложность: сложное |
6 |
www.yaklass.ru
Линейное уравнение с одной переменной. Алгебра ч.1
1. Решение линейного уравнения с одной переменной
Одним из самых простых и в то же время очень важных видов математических моделей реальных ситуаций являются известные вам из курса математики 5—6-го классов линейные уравнения с одной переменной. Приведём примеры линейных уравнений: 3х = 12, 5у — 10 = 0, 2а + 7 = 0 и т. д. Решить линейное уравнение — это значит найти все те значения переменной, при каждом из которых уравнение обращается в верное числовое равенство. Каждое такое значение переменной называют корнем уравнения. Так, уравнение 3х = 12 имеет корень х = 4, поскольку 3 • 4 = 12 — верное равенство, причём других корней нет; уравнение 5у — 10 = 0 имеет корень у = 2, поскольку 5 • 2 — 10 = 0 — верное равенство, причём других корней нет; уравнение 2а + 7 = 0 имеет корень а = -3,5, поскольку 2 • (-3,5) + 7 = 0 — верное равенство, причём других корней нет.
Вообще линейным уравнением с одной переменной х называют уравнение вида ах + b = 0, где а и b — любые числа (коэффициенты). Если а = 0 и b = 0, т. е. уравнение имеет вид 0 • х + 0 = 0, то корнем уравнения является любое число (бесконечное множество корней). Если а = 0 и b ≠ 0, т. е. уравнение имеет вид 0 • х + b = 0, то ни одно число этому уравнению не удовлетворяет; говорят, что уравнение не имеет корней.
Рассмотрим наиболее часто встречающийся случай, когда а ≠ 0. Рассуждаем так:
1) ах + b = 0, значит, ах = -b; фактически слагаемое b перенесли из левой части уравнения в правую с противоположным знаком;
2) ах = -b, т. е. произведение чисел а и х равно -b; но тогда множитель х равен частному от деления произведения -b на второй множитель. Значит, х = (-b) : а. Вместо знака деления можно использовать черту дроби: х = -b/a.
Фактически мы выработали определённую программу действий, определённый порядок ходов — в математике в таких случаях используется термин алгоритм — для решения линейного уравнения.
Алгоритм решения линейного уравнения ах + b = 0 в случае, когда а ≠ 0.
1. Преобразовать уравнение к виду ах = -b.
2. Записать корень уравнения в виде х = (-b) : а, или, что то же самое, х = -b/a.
А как быть, если уравнение записано в более сложном виде, например 2х — 2 = 10 — х?
Рассуждаем так. Два выражения равны тогда и только тогда, когда их разность равна нулю: (2х — 2) — (10 — х) = 0. Воспользуемся известными из курса математики 5—6-го классов правилами раскрытия скобок и приведения подобных членов:
2х — 2 — 10 + х = 0;
3х — 12 = 0;
3х = 12;
х = 4.
Такие уравнения вы уже решали в курсе математики 5—6-го классов. Обобщим проведённые рассуждения, оформив их в виде ещё одного полезного алгоритма.
Алгоритм решения уравнения ах + b = сх + d (а ≠ с)
1. Перенести все члены уравнения из правой части в левую с противоположными знаками.
2. Привести в левой части подобные слагаемые, в результате чего получится уравнение вида kx + m = 0, где k ≠ 0.
3. Преобразовать уравнение к виду kx = -m и записать его корень: х = —m/k.
Именно так было решено уравнение, которое получилось в предыдущем параграфе в примере 1.
2. Решение примеров
Решить уравнение 2у/3 + 7/8 = 5у/6 — 1/4.
Первый способ. Воспользуемся алгоритмом:
Второй способ. Прежде чем применять алгоритм, умножим обе части уравнения на 24 — это наименьший общий знаменатель имеющихся дробей. При этом мы пользуемся тем, что если А = В, то 24А = 24В, и обратно. Получим:
16у + 21 = 20у — 6.
А далее воспользуемся алгоритмом:
Ответ: y = 6 3/4.
ПРИМЕР 2. Решить уравнение.
Решение. Воспользовавшись основным свойством пропорции (произведение крайних членов пропорции равно произведению средних
членов), получим:
2(3z — 4) = 5(2z + 1).
Дальнейший ход решения, надеемся, уже не требует комментариев:
Ответ: z = -3 1/4.
ПРИМЕР 3. Решить уравнение:
Решение а) Наименьшим общим кратным для знаменателей 3, 6, 4, 12 является число 12. Умножив обе части уравнения на 12, получим:
Получили неверное числовое равенство. Что это означает для данного уравнения? То, что оно не имеет корней: ни при каком значении х уравнение не обращается в верное числовое равенство.
б) Умножив обе части уравнения на 10, получим:
Получили верное числовое равенство. Что это означает для данного уравнения? То, что оно обращается в верное числовое равенство при любом значении х.
Ответ: а) Корней нет; б) корнем является любое число.
3. Линейные уравнения как математические модели реальных ситуаций.
ПРИМЕР 4. Купили некоторое количество книг для библиотеки и пытаются разместить их на одинаковых полках стеллажа. Сначала поставили по 20 книг на каждую полку. В результате две полки оказались пустыми, а остальные заполненными (по 20 книг).
Затем решили ставить по 15 книг на полку. Попытка оказалась удачной: все полки заполнились (по 15 книг на каждой). Сколько книг было куплено?
Решение. I ЭТАП. Составление математической модели.
Обозначим буквой х число полок в стеллаже. Когда на каждую полку поставили по 20 книг, то заполненными оказались (х — 2) полки. Значит, общее число купленных книг выражается формулой 20(х — 2). Далее в задаче сказано, что когда на каждую полку поставили по 15 книг, то все х полок оказались заполненными сплошь. Значит, общее число купленных книг выражается формулой 15х. Остаётся приравнять два полученных выражения числа купленных книг:
20(х — 2) = 15х.
Это уравнение — математическая модель задачи.
II ЭТАП. Работа с составленной моделью. Решаем уравнение:
20(х — 2) — 15х = 0;
20х — 40 — 15х = 0;
5х — 40 = 0;
5х = 40;
х = 8.
III ЭТАП. Ответ на вопрос задачи. Мы выяснили, что в стеллаже 8 полок. Все купленные книги разместили на этих полках по 15 штук на каждой. Значит, всего было куплено 15 • 8 = 120 книг.
Ответ Всего было куплено 120 книг.
Вопросы для самопроверки
1. Что называют корнем уравнения с одной переменной?
2. Приведите пример уравнения, у которого нет корней.
3. Что такое линейное уравнение с одной переменной?
4. Что означает фраза: «Решить линейное уравнение»?
5. Как вы думаете, может ли корнем линейного уравнения с одной переменной быть отрицательное число? Если да, то приведите пример.
6. Найдите корень уравнения 2х + 7 = 11.
7. Приведите пример линейного уравнения с одной переменной, имеющего своим корнем число:
а) 0; б) 2; в) -1.
8. Сформулируйте алгоритм решения линейного уравнения ах + b = 0 в случае, когда а ≠ 0.
9. Сформулируйте алгоритм решения линейного уравнения ах + b = сх + d (а ≠ с).
10. Приведите пример таких значений а и Ь, при которых уравнение ах = b:
а) не имеет корней;
б) имеет бесконечное множество корней.
xn--7-8sb3ae5aa.xn--p1ai
Мини- пособие по теме «Линейные уравнения» (7 класс)
Линейные уравнения
Изучение данной темы мы начнем с определения уравнения вообще
1. Уравнения — это равенства, которые содержат неизвестные числа, обозначенные буквами. Неизвестные числа в уравнении называются переменными.
Например.: 6x + 12 = 2x — 4
2. Рассмотрим некоторые понятия, определение которых позволит понять, с помощью чего и каким образом решаются уравнения:
Корнем уравнения с одним неизвестным называется число, при подстановке которого в уравнение получается верное числовое равенство.
Решить уравнение — это значит найти все его корни или доказать, что уравнение корней не имеет.
При решении уравнений иногда используются различные способы приведения их к более простому и понятному виду, в результате чего возможна потеря или приобретение лишних корней данного уравнения. Вследствие чего уравнение необходимо приводить к равносильному виду.
3. Два уравнения называются равносильными, если совпадают множества их корней или оба уравнения корней не имеют.
Если же в процессе преобразования появились новые корни или были утеряны существующие, то данные уравнения не будут являться равносильными.
Уравнение g(x) = 0 называется следствием уравнения f(x) = 0, если каждое решение второго уравнения является решением первого уравнения.
4. Теперь перейдем непосредственно к определению линейных уравнений.
Уравнение вида ax = b, где a и b — данные числа, называется линейным уравнением с переменной x. Числа а и b — коэффициенты данного уравнения. а — коэффициент данного уравнения, b — свободный член.
Например.: 5x + 10 = 0
5. Если a <> 0, то уравнение ax = b называется уравнением первой степени с одной переменной. Его корень: x = b/a.
Каждое уравнение первой степени с одной переменной имеет 1 корень.
Линейное уравнение может не иметь корней или иметь один или множество корней.
Теперь попробуйте пройти тест-коррекцию!
1. Корнем уравнения называется:
Число, которое является решением этого уравнения.
Число, при подстановке которого в уравнение получается верное числовое равенство.
Число, при подстановке которого в уравнение всегда получается числовое равенство.
2 Решить уравнение — это значит:
Найти все его корни;
Найти все его корни или доказать, что корней нет;
Найти хотя бы один из корней;
Найти столько корней, сколько переменных в уравнении.
3 Два уравнения называются равносильными, если:
Совпадают множества их корней или оба уравнения корней не имеют;
Каждое из этих уравнений является следствием другого;
Каждый корень первого является корнем второго;
Если они имеют одинаковые правые и левые части.
4. Укажите уравнение, неравносильное уравнению 3x = 15:
6х = 30;
3х — 15 = 0;
9х = 45;
3х + 15 = 18.
5. Одно уравнение является следствием другого, если:
Совпадают множества их корней или оба уравнения корней не имеют;
Каждое из этих уравнений является следствием другого;
Каждый корень первого является корнем второго;
Если они имеют одинаковые правые и левые части.
6. Какое уравнение является следствием:
(х — 5)(х + 1) = 0 и х — 5 = 0;
5 + (х — 4) = 5 и х — 4 = 0;
х + 3 = 5 — х и x = 1;
7. Линейным уравнением называется:
Уравнение вида ах = b, где а и b — данные числа;
Уравнение вида ах = b, где а и b — данные числа, и а<>0;
Уравнение с одним неизвестным;
Уравнение с несколькими неизвестными, где а и b — данные числа.
8. Какое из приведенных уравнений является уравнением первой степени:
0y = 5;
0х = 0;
6х = 24;
2х = 0.
9. Сколько решений имеет уравнение 3(х — 5) + х = 4х — 18:
4
1;
2;
0;
не знаю.
10.Уравнение ах = b имеет один корень, если:
а <> 0;
а = b = 0;
а = 0, b <> 0;
а <> 0, b <> 0.
11.Сколько корней может иметь уравнение первой степени:
Один;
Много;
Задача
В одном баке было вдвое больше бензина, чем во втором. Когда из первого перелили во второй 25 л бензина, в обоих баках стало бензина поровну. Сколько бензина было в каждом баке первоначально?
Алгоритм решения
Подробно запиши свое решение: составление уравнения, решение уравнения, ответ задачи.
Надо быть внимательнее. Ведь из первого бака вылили 25 л, после чего осталось x л. Значит, до переливания в первом баке было не x л, а на 25 л больше.
Теперь подумай, что примешь за неизвестное x?
Итак, в первом баке после переливания стало x л, а до переливания в нем было (x+25)л. Сколько же было во втором баке до переливания? Теперь тебе, конечно, ясно, что до переливания во втором баке было не x л, а на 25л меньше, т. е. было (x-25)л.
Надо подумать, во сколько вопросов решается эта задача и какой первый вопрос
Принять за x л количество бензина, которое получилось после переливания в первом баке (по условию, столько же стало после переливания и во втором баке). Что же было до переливания?
В условии задачи сказано, что после переливания в обоих баках стало бензина одинаково. Получается соотношение 2x-25=x+25
В первом баке было 100 л, во втором — 50 л. Сказано, что в первом было в два раза больше: 100/50=2 (верно). Затем из первого перелили во второй бак 25 л. В первом стало 100-25=75 (л), во втором стало 50+25=75 . Сказано, что стало одинаково 75=75 (верно).
Данную задачу можно решить 3 способами. Подумай, что еще можно принять за неизвестное, составь новое уравнение и, вернувшись назад, проверь правильность своего нового выбора.
Мини- пособие по теме «Линейные уравнения»
Содержание
1. Актуализация знаний
2. Теоретические сведения
3. Задача-метод
4. Задача-софизм
5. Эвристики и поиск решения
6. Из истории линейных уравнений
Данную обучающую программу можно считать пособием по изучению темы «Линейные уравнения» школьного курса математики. Она предназначена для формирования приемов эвристического мышления у учащихся и абитуриентов.
Следование инструкциям и рекомендациям, а так же сознательное и добросовестное выполнение заданий предложенных в работе поможет учащимся углубить и расширить знания обязательного уровня, а также поможет сформировать у них приемы эвристического мышления.
Для эффективной работы с программой необходимо изучить структуру предложенных материалов и приемы работы с ними:
Первый этап (актуализация знаний). В тесте №1 обсуждаются вопросы, связанные с пониманием тех основ, которые входят в содержание данной темы на обязательном уровне их усвоения. Обучаемый имеет возможность самостоятельно проработать тест, при этом проанализировать и сравнить предлагаемое решение со своим личным. В случае большого количества допущенных ошибок ученик должен ознакомиться с теоретическим материалом обязательного уровня, предлагаемом его вниманию тут же. Затем он имеет возможность повторного тестирования при помощи теста №2, в котором обсуждаются те же идеи, что и в первом тесте. Такая работа позволяет ученику сосредоточить свое внимание на главных моментах в излагаемой теме и подготовиться к осознанному выполнению последующих задач.
Второй этап (ознакомление с теоретическими сведениями углубленного характера). Знакомство с этими материалами позволяет обучаемому систематизировать свои знания, обобщить представления об основных положениях, связанных с решением уравнений различных видов, сформировать у себя некоторые алгоритмы и эвристические правила-ориентиры решения уравнений.
Третий этап («задача-метод»). На этом этапе работы ученику необходимо к предложенной задаче или набору нескольких задач, с предложенными методами решения выбрать наиболее рациональный и правильный на его взгляд вариант.
Четвертый этап («задача-софизм»). При прохождении четвертого этапа ученику необходимо найти ошибку в рассуждении, когда предложенная задача представляет собой цепочку выполненных действий по ее решению, в которой на одном из звеньев допущена ошибка.
Пятый этап (эвристики и поиск решения задачи). Этот этап представляет из себя систему задач, к каждой из которых даны эвристические подсказки. Такие подсказки способствует осмысленному подходу к поиску решения задачи.
Шестой этап (некоторые исторические сведения по данной теме).
Когда все этапы пройдены можно переходить к изучению следующей темы.
Желаем успехов!
Задание
Проработайте тест. При этом можно пользоваться подсказками. По окончании тестирования, если допущено большое количество ошибок, ознакомтесь с теоретическим материалом обязательного уровня. Затем пройдите повторное тестирование при помощи теста №2, в котором обсуждаются те же идеи, что и в первом тесте.
Тест №1
(актуализация знаний)
1. Какое уравнение не является линейным?
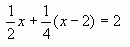
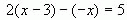
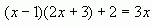
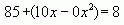
2. Какая пара уравнений не является равносильной:
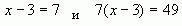
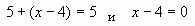
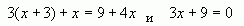
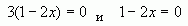
3. Сколько решений имеет уравнение 0х=-5?
Один корень
Не имеет решений
Бесконечно много
Ответ отличен от приведенных
4. Среди данных уравнений выберите то, которое имеет такой же корень, что и уравнение
2х-5=5х+5.
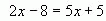
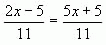
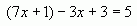
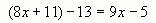
5. При каком значении у значение выражения 4(у-0,9) будет равно значению выражения 1,2+2у?
-2,4
1,2
2,4
-1,2
6. Найдите значение выражения 5k-(3k-8p), если k+4p=17.
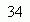
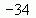
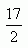
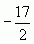
7. Если 0,75x=-1, то чему равно х+0,75?
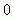
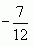
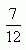
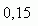
8. Найдите число, четверть которого меньше от его третьей части на два.
24
-24
12
6
9. При каком значении а уравнение ах=8 имеет отрицательный корень?
0
2
-2
4
10. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в два раза младше дедушки?
48 и 63
64 и 47
37 и 64
37 и 74
Линейные уравнения с модулем
Определение: Уравнение, содержащее неизвестное под знаком модуля, называется уравнением с модулем . Из определения модуля (абсолютной величины) числа следует, что:

При решении уравнений с модулями чаще всего применяется метод раскрытия модуля по определению. Рассмотрим этот метод на примерах.
Решим уравнение:
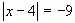
Решение: Данное уравнение не имеет решений так как модуль любого числа есть неотрицательное число.
Найдем корни уравнения:
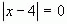
Решение: Уравнение 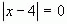 равносильно уравнению
равносильно уравнению 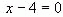 . Откуда
. Откуда 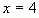
Теперь решим уравнение:
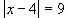
Решение:Данное уравнение равносильно совокупности уравнений:
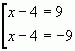
Откуда получаем два корня:
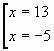
Еще один способ решения уравнений с модулями — это использование геометрического смысла модуля. Известно, что 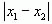 — это расстояние между двумя точками на оси с координатами
— это расстояние между двумя точками на оси с координатами 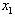 и
и 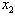 .
.
Например, решим уравнение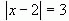 , используя геометрический смысл модуля. Найдем точки на числовой оси, которые удалены от точки 2 на расстояние равное 3
, используя геометрический смысл модуля. Найдем точки на числовой оси, которые удалены от точки 2 на расстояние равное 3

Это точки 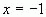 и
и 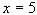 . Таким образом, корнями уравнения являются числа –1 и 5.
. Таким образом, корнями уравнения являются числа –1 и 5.
Уравнения с параметрами
Определение: Уравнением с параметрами называется уравнение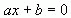 , в котором коэффициенты
, в котором коэффициенты 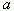 и
и 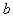 неопределены (т.е. вместо
неопределены (т.е. вместо 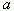 и
и 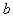 можно подставить любые числа).
можно подставить любые числа).
При решении уравнений с параметрами рассматривают все возможные случаи (в зависимости от параметров 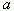 и
и 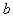 ).
).
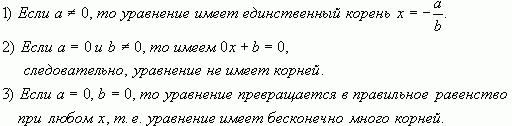
Графический метод решения уравнений с двумя переменными
Со времен Рене Декарта общий вид уравнений первой степени с одним неизвестным записывается следующим образом:
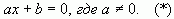
До Декарта уравнения с положительными коэффициентами записывали по обе стороны от знака равенства. Декарт впервые стал систематически представлять уравнения в канонической форме (т.е. с правой частью, равной нулю). Благодаря методу координат, разработанному Декартом, между алгеброй и геометрией была установлена тесная связь. Декарт стал рассматривать уравнения как зависимость между 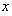 и
и 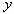 , определяющую положение точек на плоскости. Так например, корень уравнения (*)
, определяющую положение точек на плоскости. Так например, корень уравнения (*)
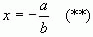
можно геометрически изобразить точкой M пересечения прямой 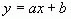 с прямой
с прямой 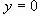 (т.е. с осью Ox).
(т.е. с осью Ox).
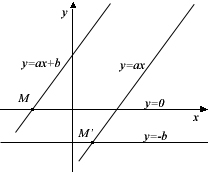
Таким образом, вводя второе неизвестное 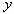 , Декарт разбил одно уравнение на два, каждое из которых представляет некоторое геометрическое место точек. Так, уравнение (*) можно представить и в виде
, Декарт разбил одно уравнение на два, каждое из которых представляет некоторое геометрическое место точек. Так, уравнение (*) можно представить и в виде 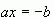 , тогда его корень (**) можно найти как абсциссу точки M’ пересечения прямых
, тогда его корень (**) можно найти как абсциссу точки M’ пересечения прямых 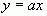 и
и 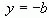 .
.
«Задача-метод»
Задание
В этом разделе вам будут предлагать задачу и несколько способов ее решения.
Вы должны выбрать наиболее рациональный на ваш взгляд способ.
1.Даны уравнения 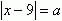 и
и 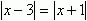 являются ли они равносильными?
являются ли они равносильными?
Среди предложенных ниже способов решения выберите наиболее рациональный. Решить оба уравнения и сравнить корни.
Привести оба уравнения к одинаковому виду.
2. При каких значениях х графики уравнений 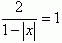 и
и 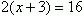 пересекаются?
пересекаются?
Среди предложенных ниже способов решения выберите наиболее рациональный. Построить графики уравнений и найти точку их пересечения.
Приравнять правые части и решить уравнение.
3. Сколько решений имеет уравнение 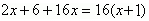 ?
?
Среди предложенных ниже способов решения выберите наиболее рациональный. Воспользоваться определением модуля.
Решить задачу графическим методом.
Воспользоваться геометрическим смыслом модуля.
4. Решите уравнение 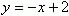 .
.
Среди предложенных ниже способов решения выберите наиболее рациональный. Воспользоваться определением модуля.
Решить задачу графическим методом.
Воспользоваться геометрическим смыслом модуля.
5. Решите уравнение 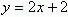 .
.
Среди предложенных ниже способов решения выберите наиболее рациональный. Воспользоваться определением модуля.
Решить задачу графическим методом.
Воспользоваться геометрическим смыслом модуля.
«Задача-софизм»
Задание
Ученики 7-го класса решали линейные уравнения. Предлагаем Вам попробовать себя в роли учителя.
Укажите каким из учеников, и на каком шаге, при решении уравнения, допущена ошибка.
Первый ученик решил уравнение 0,71х+1,98=0,37х-1,76 так:
0,71х-0,37х=1,98-1,76,
0,34х=0,22,
х=22/34;
Второй ученик решил уравнение 0,71х+1,98=0,37х-1,76 так:
0,71х-0,37х=-1,76-1,98,
0,34х=-3,74,
х =-11;
Третий ученик решил уравнение 3(4х-13)=12х-39 так
12х-39=12х-39,
12х-12х=39-39,
0=0.
Уравнение не имеет корней
Четвертый ученик решил уравнение 3(4х-13)=12х+5 так:
12х-39=12х+5,
12х-12х=39+5,
0х=44,
х=0.
Пятый ученик решил уравнение 3(4х-13)=12х-39 так:
12х-39=12х-39,
12х-12х=0,
х0=0,
Уравнение имеет бесконечно много корней.
Шестой ученик решил уравнение 3(4х-13)=10х-39 так:
12х-39=10х-39,
12х-10х=39-39,
2х=0,
х — любое число.
Седьмой ученик решил уравнение 12+7х-28=3х так:
12-3х=28-7х,
3(4-х)=7(4-х),
3=7,
Уравнение не имеет корней.
«Эвристики и поиск решения»
Задание
В этом разделе необходимо решить задачу самостоятельно. Можно пользоваться подсказками.
1. Решите уравнение 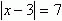
Используйте геометрический смысл модуля.
Найдите точки на оси, которые удалены от точки 3 на расстояние, равное 7.
Корнями уравнения являются числа –4 и 10.
2.Найдите все целые значения а, при которых корень уравнения 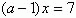 является натуральным числом.
является натуральным числом.
Сделайте перебор вариантов.
Перебирая значения, получаем, что а может равняться только 2 или 8.
3. Решите уравнение 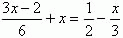
Умножьте каждый член уравнения на 6
Ответ: 6.
4.На доске написано уравнение 5(…+3х)(х+1)-4(1+2х)2=-36. Найдите случайно вытертое число в скобках, если х=-2
Обозначьте искомое число через у и решите уравнение относительно у.
Ответ: 6.
5. Найдите три последовательных нечетных натуральных числа, сумма которых равняется 6003.
Составьте и решите уравнение.
Первое число равно 1999, второе 2001, третье 2003.
Из истории линейных уравнений
Решение задач методом составления уравнения зародилось давно. Еще 4000 лет назад в древнем Египте решали задачи способом, который очень напоминает составление уравнения. Недостатком всей математики древних было отсутствие единой математической символики. Этот недостаток затруднял действия, мешал их наглядности. Поэтому и условие, и решение любой задачи приводилось полностью в словесной форме. Правда, у древних египтян были некоторые условные сокращения. Неизвестное, как полагают, они называли «куча». Так в папирусе Ринда уравнениe 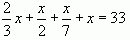 записано в такой форме:
записано в такой форме: 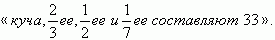
Эти частичные сокращения были впоследствии забыты другими учеными. Отсутствие единой формы записи уравнений задерживало создание общих правил их решения. Каждая задача решалась по своему, каждое уравнение требовало особого подхода. Отсутствие же общих правил решения приводило к кустарщине. Каждый решал как мог. Все это тормозило развитие алгебры в целом.
Первым, кто дал наиболее полное изложение способов решения уравнений, был узбекский ученый Мухаммед бен Муса ал-Хорезми. Свою книгу «Хисаб алджебр вал-Мукабала» он целиком посвятил составлению уравнений по условиям задачи и решению этих уравнений.
В первое время алгебру понимали как науку об уравнениях, впоследствии же этот взгляд несколько изменился. Кроме уравнений 1-й степени, в школе изучаются некоторые другие виды уравнений. Но ни один из этих видов нельзя усвоить, не усвоив хорошо решение уравнений 1-й степени.
Некоторые старинные задачи
Около 2500 лет назад в Греции уже умели довольно хорошо решать уравнения с одним неизвестным и систему уравнений с несколькими неизвестными. Независимо от греков этими приемами овладели и китайцы, а позднее и индийцы. Вот несколько старинных задач.
Задача в стихах из так называемой «Греческой Антологии»:
-Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?
-Вот сколько, — ответил философ, — половина изучает математику, четверть — музыку, седьмая часть пребывает в молчании и, кроме того, есть еще три женщины.
Решение: Если обозначить число учеников Пифагора через х, то можно составить такое уравнение: 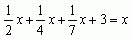 откуда x=28.
откуда x=28.
Древняя китайская задача: В клетке находится неизвестное число фазанов и кроликов. Известно только, что вся клетка содержит 35 голов и 94 ноги. Требуется узнать число фазанов и число кроликов.
Древняя индусская задача: Два лица имеют равные капиталы, причем каждый состоит из известного числа вещей одинаковой ценности и известного числа монет. Но как число вещей, так и суммы денег у каждого различны. Какова ценность вещи?
Решение:Пусть у первого будет «а» вещей и «m» монет, а у второго «b» вещей и «p» монет. Если х — ценность вещи, то 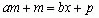 : откуда:
: откуда: 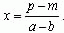
infourok.ru
Конспект урока алгебры в 7 классе по теме «Линейное уравнение с одной переменной»
Урок
Дата:
Класс: 7
Тема: Линейное уравнение с одной переменной
Цель урока:
1. Познакомить учащихся с тем, что такое линейное уравнение с одной переменной, что называется корнем уравнения, как решать уравнения с помощью алгоритма решения уравнений с одной переменной;
2.Способствовать развитию памяти, речи, логического мышления, внимания.
3. Способствовать воспитанию интереса к математике, упорства в достижении поставленной цели, трудолюбия, аккуратности.
Предметные: знать понятие линейного уравнения, равносильности уравнений, корней уравнения; уметь применять полученные знания при решении упражнений
Метапредметные: уметь устанавливать причинно – следственные связи, строить логическое рассуждение, умозаключение. Умение действовать в соответствии с предложенным алгоритмом.
Личностные: готовность к жизненному и личностному самоопределению, знания моральных норм, умения выделять нравственный аспект поведения и соотносить поступки и события с принятыми этическими нормами, ориентация в жизненных ролях и межличностных отношениях (формируются во время выполнения заданий, в которых школьникам предлагается дать собственную оценку)
Регулятивные: уметь поставить учебную цель, задачу на основе того, что уже известно и усвоено; уметь планировать последовательность своих действий для достижения конечного результата.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками; постановка вопросов.
Оборудование: учебник алгебры 7 кл., конспект, мел, доска, указка.
Ход урока.
I Организационный момент.
Здравствуйте, ребята! Садитесь! Проверьте свою готовность к уроку, проверьте принадлежности ,чтоб на парте у каждого были учебник ,тетрадь ,дневник, письменные принадлежности.
II Актуализация знаний.
Д.з к доске два человека, остальные работают на повторении. Прежде чем перейдём к изучению нового материала, давайте с вами немного повторим ( привидение подобных слагаемых, раскрытие скобок) . Посмотрите на доску, по очереди раскроем скобки, приведём подобные слагаемые:
a-(3+b)=
c-b(3c-c+2b)=
3d+4(c-3b+d)=
— Молодцы ребята!
III Сообщение темы и цели урока.
А сейчас запишите число, 8.09.11. на полях, классная работа и тему урока « Линейное уравнение с одной переменной». Мы познакомимся с вами: Что называется л.у. с одной переменной, что называется корнем уравнения, познакомимся с алгоритмом решения уравнения.
IV Изучение нового материала.
-Давайте приведём примеры линейных уравнений с одной переменной. ( учащиеся говорят, записываю на доске) 3x=12, 5y=10, 2a+7=0….
_ Как вы думаете, что значит решить уравнение? (ответ уч-ся: решить уравнение значит найти все те значения переменных, при которых уравнение обращается в верное равенство) Молодцы! Так вот каждое значение переменной называют корнем уравнения. Так какие корни имеют ,написанные нами на доске уравнения? (ответ учащихся: 3x=12, имеет корень x=4,т.к. 3*4=12 и т.д.)
_ на доску вешаю плакат. Посмотрите, ребята, давайте дадим определение линейному уравнению с одной переменной: Линейным уравнением с одной переменной x наз-ся уравнение вида ax+b=0 ,где a и b любые числа( коэффициенты). Если a=0 , b=0 , т.е. уравнение имеет вид 0x+0=0 , то корнем уравнения является любое число (бесконечное множество ) . Если a=0 ,b=0, уравнение имеет вид 0x+b=0., то ни одно число этому уравнению не удовлетворяет, т.е. корней нет.
Рассмотрим наиболее распространённый вид уравнения, когда a=0 ,
1) ax+b=0 = ax=-b (слагаемое перенесли вправо с противоположным знаком)
2) x=- b/a.
Фактически мы выработали определённый порядок действий, т.е. алгоритм .( стр. 20 учебника )
Алгоритм решения линейного уравнения ax+b=0 в случае, когда a=01. Преобразовать уравнение к виду ax=-b.
2. Записать корень уравнения в виде x=( — b) : a , или , что тоже самое , x=-b/a.
А как же быть ,если уравнение имеет такой вид, например: 2x-2=10-x? (пробуют ответить уч-ся) . Рассуждаем так: Два выражения равны тогда и только тогда, когда их разность равна 0. т.е. ( 2x-2)- (10-x)=0. Что делам дальше?(ответ уч-ся: Раскрываем скобки, приводим подобные слагаемые) К доске идёт ученик, остальные записывают в тетрадях.
Нашли x=4. А можем мы всё это решение обобщить в алгоритм? Конечно. ( стр.21 учебника)
Алгоритм решения уравнения ax+b=cx=d ( a=c)1. Перенести все члены уравнения из правой части в левую с противоположными знаками.
2. Привести в левой части подобные слагаемые , в результате чего получится уравнение вида kx+m=0, где k=0.
3. Преобразовать уравнение к виду kx=-m и записать его корень : x=-m/k.
Попробуем решить такое уравнение: (3x-4)/5=( 2x+1)/ 2. Давайте вспомним основное свойство пропорции? ( ответ уч-ся: произведение крайних членов равно произведению средних членов). После преобразований можем решить уравнение по алгоритму? (да) К доске вызываю ученика. Остальные работают самостоятельно в тетрадях. Не забывайте, ребята писать каждый раз с новой строчки, ставить запятые, записать ответ. Молодцы!
V Первичное закрепление.
Откройте задачник на стр.22 устно по цепочке решаем № 4.1, 4.2(письменно, на доске )
VI Подведение итогов урока.
Итак, ребята, что на уроке вы узнали нового? ( что наз-ся уравнением с одной переменной) , А что называется коэффициентом?( число при неизвестном ,или переменной)Что есть корень уравнения? ( Значение переменной, при котором уравнение переходит в верное равенство) Чему научились ? ( решать линейные уравнения с помощью алгоритма). Оценки за урок…Молодцы, ребята!
VII Дача домашнего задания.
Откройте дневники, запишите задание на дом. С. 20-21 учебника, выучить алгоритмы , В задачнике № 4.5,№4.7.
Спасибо за урок, все свободны!
infourok.ru
Линейное уравнение с одной переменной [7 класс]
Линейные уравнения — одна из самых простых тем в математике, которую проходят в 7 классе. Хотя бы раз с линейными уравнениями сталкивался каждый, не существует никаких трудностей в их решении, и подчиняются такие уравнения всего паре базовых правил.
Для того, чтобы разобраться в теме, необходимо в первую очередь вспомнить, какие же уравнения называют линейными.
Простые уравнения с одной переменной
Как гласит определение, линейным уравнением с одной переменной называют равенство, состоящее из букв и чисел и содержащее только одну переменную. Так, примерами могут служить:
- х – 4 = 8;
- х + 5 = 13;
- х : 3 = 3;
- 6х = 12.
Для того, чтобы решить уравнение, нужно просто найти его корень — иными словами, установить, при каком числовом значении переменной приведенное равенство будет правильным. Существуют и ситуации, когда равенство не может быть правильным ни при каких обстоятельствах — в таких случаях говорят, что корней у уравнения нет. И это также считается решением.
Согласно каким правилам решают линейные уравнения?
Существуют два правила, или свойства, которые делают работу с линейными уравнениями более простой и быстрой.
- Первое свойство гласит, что часть уравнения, или слагаемое, допустимо перенести на другую сторону уравнения, при этом изменив знак. Равенство в этом случае останется верным. Например, уравнение х – 6 = 12 можно записать следующим образом: х = 12 + 6. В ответе получится число 18, и простая проверка покажет, что решение совершенно правильное, поскольку 18 – 6 = 12.
- Второе свойство гласит, что можно взять некоторое число, не равное нулю, и разделить или умножить на него две части уравнения. В таком случае, при соблюдении всех условий, равенство останется верным. Например, это можно продемонстрировать в уравнении 3х = 9. Выражение записывается следующим образом: 3х : 3 = 9 : 3. Таким образом, 3х : 3 = 3, и в данном выражении х = 3.
Простейшие линейные уравнения, приведенные в примерах, вряд ли могут вызвать какие-то затруднения. Но в задачниках встречаются и более сложные, многосоставные выражения с одной переменной — и для их решения свойства окажутся очень полезными, поскольку помогут сэкономить время и силы.
Как правило, найти корни уравнения невозможно, если в буквенно-числовой записи присутствует число 0. Например, уравнение вида 0 * х = 5 верного решения не имеет, поскольку любое число при умножении или делении на ноль может давать только ноль. В таком случае пишут, что корней у уравнения нет.
infoogle.ru
План-конспект урока по алгебре (7 класс) на тему: Конспект урока алгебры в 7 классе по теме «Линейное уравнение с одной переменной»
Урок
Дата:
Класс: 7
Тема: Линейное уравнение с одной переменной
Цель урока:
1. Познакомить учащихся с тем, что такое линейное уравнение с одной переменной, что называется корнем уравнения, как решать уравнения с помощью алгоритма решения уравнений с одной переменной;
2.Способствовать развитию памяти, речи, логического мышления, внимания.
3. Способствовать воспитанию интереса к математике, упорства в достижении поставленной цели, трудолюбия, аккуратности.
Предметные: знать понятие линейного уравнения, равносильности уравнений, корней уравнения; уметь применять полученные знания при решении упражнений
Метапредметные: уметь устанавливать причинно – следственные связи, строить логическое рассуждение, умозаключение. Умение действовать в соответствии с предложенным алгоритмом.
Личностные: готовность к жизненному и личностному самоопределению, знания моральных норм, умения выделять нравственный аспект поведения и соотносить поступки и события с принятыми этическими нормами, ориентация в жизненных ролях и межличностных отношениях (формируются во время выполнения заданий, в которых школьникам предлагается дать собственную оценку)
Регулятивные: уметь поставить учебную цель, задачу на основе того, что уже известно и усвоено; уметь планировать последовательность своих действий для достижения конечного результата.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками; постановка вопросов.
Оборудование: учебник алгебры 7 кл., конспект, мел, доска, указка.
Ход урока.
I Организационный момент.
Здравствуйте, ребята! Садитесь! Проверьте свою готовность к уроку, проверьте принадлежности ,чтоб на парте у каждого были учебник ,тетрадь ,дневник, письменные принадлежности.
II Актуализация знаний.
Д.з к доске два человека, остальные работают на повторении. Прежде чем перейдём к изучению нового материала, давайте с вами немного повторим ( привидение подобных слагаемых, раскрытие скобок) . Посмотрите на доску, по очереди раскроем скобки, приведём подобные слагаемые:
a-(3+b)=
c-b(3c-c+2b)=
3d+4(c-3b+d)=
— Молодцы ребята!
III Сообщение темы и цели урока.
А сейчас запишите число, 8.09.11. на полях, классная работа и тему урока « Линейное уравнение с одной переменной». Мы познакомимся с вами: Что называется л.у. с одной переменной, что называется корнем уравнения, познакомимся с алгоритмом решения уравнения.
IV Изучение нового материала.
-Давайте приведём примеры линейных уравнений с одной переменной. ( учащиеся говорят, записываю на доске) 3x=12, 5y=10, 2a+7=0….
_ Как вы думаете, что значит решить уравнение? (ответ уч-ся: решить уравнение значит найти все те значения переменных, при которых уравнение обращается в верное равенство) Молодцы! Так вот каждое значение переменной называют корнем уравнения. Так какие корни имеют ,написанные нами на доске уравнения? (ответ учащихся: 3x=12, имеет корень x=4,т.к. 3*4=12 и т.д.)
_ на доску вешаю плакат. Посмотрите, ребята, давайте дадим определение линейному уравнению с одной переменной: Линейным уравнением с одной переменной x наз-ся уравнение вида ax+b=0 ,где a и b любые числа( коэффициенты). Если a=0 , b=0 , т.е. уравнение имеет вид 0x+0=0 , то корнем уравнения является любое число (бесконечное множество ) . Если a=0 ,b=0, уравнение имеет вид 0x+b=0., то ни одно число этому уравнению не удовлетворяет, т.е. корней нет.
Рассмотрим наиболее распространённый вид уравнения, когда a=0 ,
1) ax+b=0 = ax=-b (слагаемое перенесли вправо с противоположным знаком)
2) x=- b/a.
Фактически мы выработали определённый порядок действий, т.е. алгоритм .( стр. 20 учебника )
Алгоритм решения линейного уравнения ax+b=0 в случае, когда a=0 |
1. Преобразовать уравнение к виду ax=-b. 2. Записать корень уравнения в виде x=( — b) : a , или , что тоже самое , x=-b/a. |
А как же быть ,если уравнение имеет такой вид, например: 2x-2=10-x? (пробуют ответить уч-ся) . Рассуждаем так: Два выражения равны тогда и только тогда, когда их разность равна 0. т.е. ( 2x-2)- (10-x)=0. Что делам дальше?(ответ уч-ся: Раскрываем скобки, приводим подобные слагаемые) К доске идёт ученик, остальные записывают в тетрадях.
Нашли x=4. А можем мы всё это решение обобщить в алгоритм? Конечно. ( стр.21 учебника)
Алгоритм решения уравнения ax+b=cx=d ( a=c) |
1. Перенести все члены уравнения из правой части в левую с противоположными знаками. 2. Привести в левой части подобные слагаемые , в результате чего получится уравнение вида kx+m=0, где k=0. 3. Преобразовать уравнение к виду kx=-m и записать его корень : x=-m/k. |
Попробуем решить такое уравнение: (3x-4)/5=( 2x+1)/ 2. Давайте вспомним основное свойство пропорции? ( ответ уч-ся: произведение крайних членов равно произведению средних членов). После преобразований можем решить уравнение по алгоритму? (да) К доске вызываю ученика. Остальные работают самостоятельно в тетрадях. Не забывайте, ребята писать каждый раз с новой строчки, ставить запятые, записать ответ. Молодцы!
V Первичное закрепление.
Откройте задачник на стр.22 устно по цепочке решаем № 4.1, 4.2(письменно, на доске )
VI Подведение итогов урока.
Итак, ребята, что на уроке вы узнали нового? ( что наз-ся уравнением с одной переменной) , А что называется коэффициентом?( число при неизвестном ,или переменной)Что есть корень уравнения? ( Значение переменной, при котором уравнение переходит в верное равенство) Чему научились ? ( решать линейные уравнения с помощью алгоритма). Оценки за урок…Молодцы, ребята!
VII Дача домашнего задания.
Откройте дневники, запишите задание на дом. С. 20-21 учебника, выучить алгоритмы , В задачнике № 4.5,№4.7.
Спасибо за урок, все свободны!
nsportal.ru