Урок 51. обобщение и систематизация знаний по теме «линейные уравнения» — Алгебра — 7 класс

Алгебра

7 класс

Урок № 51

Обобщение и систематизация знаний по теме: «Линейные уравнения»

Перечень вопросов, рассматриваемых в теме:

Связь понятий: «линейное уравнение», система линейных уравнений», «линейная функция», «решение линейного уравнения», «решение системы линейных уравнений».

Способы решения систем линейных уравнений.

Тезаурус:

Уравнение вида ax = b, (где x – переменная, a, b – некоторые числа), называется линейным уравнением с одной переменной.

Система вида

(где x, y – переменные, a_i, b_i, c_i – некоторые числа) называется системой линейных уравнений с двумя переменными.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения

Уравнение вида (где x – переменная, a, b – некоторые числа) называется линейным уравнением с одной переменной.

a и b – коэффициенты линейного уравнения.

К уравнению такого вида можно привести уравнение, которое включает в себя переменную в первой степени.

Пример:

Для того, чтобы привести уравнение к виду ax = b, нужно его преобразовать.

Пример.

Рассмотрим уравнение.

Раскроем скобки и приведём подобные слагаемые:

В зависимости от значения коэффициентов, линейное уравнение может иметь либо один корень, либо ни одного корня, либо бесконечно много корней.

Если уравнение включает в себя две переменные в первой степени, получаем линейное уравнение с двумя переменными:

Можно из данного равенства выразить переменную y.

Получим уравнение линейной функции:

Её графиком является прямая. Таким образом, графиком линейного уравнения с двумя переменными является прямая, угловой коэффициент которой равен:

На прямой лежит бесконечно много точек, поэтому линейное уравнение с двумя переменными имеет бесконечно много решений. Все пары точек, координаты которых удовлетворяют уравнению:

Или координаты точек, лежащих на прямой, соответствующей уравнению.

Рассмотрим два линейных уравнения с двумя переменными и составим из них систему.

Геометрической интерпретацией решения системы двух уравнений с двумя переменными является точка пересечения прямых (если она есть).

Две прямые:

1) могут пересекаться (иметь одну общую точку), если их угловые коэффициенты не равны. В этом случае система имеет единственное решение.

Две прямые пересекаются, если:

– система имеет единственное решение;

2) могут быть параллельными (не иметь ни одной общей точки), если их угловые коэффициенты равны, а свободные коэффициенты не равны. В этом случае система не имеет решений.

Две прямые параллельны, если:

– система не имеет решений.

3) могут совпадать (иметь бесконечно много общих точек), если их угловые коэффициенты и свободные коэффициенты равны. В этом случае система имеет бесконечно много решений.

Две прямые совпадают, если:

Система имеет бесконечно много решений.

Для системы линейных уравнений могут быть использованы разные способы решения: алгебраический, в рамках которого рассматривается способ подстановки и способ алгебраического сложения. Или графический метод.

Рассмотрим пример.

Заметим, что и первое, и второе уравнения включают в себя выражение (5x – 2y)

Во втором уравнении оно выражено. Его и подставим в первое уравнение:

Теперь первое уравнение зависит только от одной переменной x.

Подставим найденное значение во второе уравнение и найдём значение y:

Ответ:

Текст для углублённого изучения.

Одним из простейших уравнений с параметром является линейное уравнение.

Рассмотрим уравнение с параметром:

a(a — 2)x = a²

— 4

Решение:

Рассмотрим коэффициент при переменной x.

Если: a(a – 2) ≠ 0, то есть уравнение имеет единственное решение.

Рассмотрим те значения параметра a, при которых a(a – 2) = 0

Пусть a = 0, тогда получим уравнение: 0 · x = –4. Это уравнение решений не имеет.

Пусть a = 2, тогда получим уравнение: 0 · x = 0. Это уравнение имеет бесконечно много решений.

Запишем ответ:

При a = 0 уравнение решений не имеет.

При a = 2 уравнение имеет бесконечно много решений.

Разбор решения заданий тренировочного модуля

Задача 1.

Рассортируйте уравнения по количеству их корней:

3x – 2(x + 5) = 6x – 12(2 – x)

15(1 – x) + 3 = 7 – 4x – 11(x – 1)

-5(2x + 4) = 5 – 10x

Решение.

Рассмотрим первое уравнение. Раскроем скобки:

3x – 2(x + 5) = 6x – 12(2 – x)

3х – 2х – 10 = 6х – 24 + 12х

Коэффициент при переменной не обратится в 0. Поэтому уравнение имеет единственное решение.

Рассмотрим второе уравнение. Раскроем скобки:

15(1 – x) + 3 = 7 – 4x – 11(x – 1)

15 – 15х + 3 = 7 – 4х – 11х + 11

18 – 15х = 18 – 15х

После преобразований получим уравнение 0x = 0, которое имеет бесконечно много корней.

Рассмотрим третье уравнение. Раскроем скобки:

-5(2x + 4) = 5 – 10x

-10х – 20 = 5 – 10х

Получим уравнение 0х = 25, которое не имеет решений.

Задача 2.

Выберите значения параметра, при каждом из которых уравнение не имеет решений:

Решение.

Количество решений линейного уравнения зависит от коэффициента при переменной. Рассмотрим его.

Приравняем его к нулю: a(a² – 9) = 0

Найдем значения параметра:

a = 0

a = 3

a = –3

При каждом из этих значений параметра уравнение имеет вид:

0 · x = k, где k ≠ 0

Поэтому при каждом из этих значений параметра уравнение решений не имеет.

Линейное уравнение с двумя переменными: решение и свойства

 

Линейное уравнение с двумя переменными — любое уравнение, которое имеет следующий вид: a*x + b*y =с. Здесь x и y есть две переменные, a,b,c – некоторые числа.

Ниже представлены несколько примеров линейных уравнений.

1. 10*x + 25*y = 150;

2. x-y=5;

3. -7*x +y = 5;

Как и уравнения с одним неизвестным, линейное уравнение с двумя переменными (неизвестными) тоже имеет решение. Например, линейное уравнение x-y=5, при x=8 и y=3 превращается в верное тождество 8-3=5. В таком случае говорят, что пара чисел x=8 и y=3 является решением линейного уравнения x-y=5. Еще можно говорить, что пара чисел x=8 и y=3 удовлетворяет линейному уравнению x-y=5.

Решение линейного уравнения

Таким образом, решением линейного уравнения a*x + b*y = с , называется, любая пара чисел (x,y) которая удовлетворяет этому уравнению, то есть обращает уравнение с переменными x и y в верное числовое равенство. Обратите внимание, как здесь записана пара чисел х и у. Такая запись короче и удобнее. Следует только помнить, что на первом месте в такой записи стоит значение переменной х, а на втором – значение переменной у.

Обратите внимание на то, что числа x=11 и y=8, x=205 и y=200 x= 4.5 и y= -0.5 тоже удовлетворяют линейному уравнению х-у=5, а следовательно являются решениями этого линейного уравнения. 

Решение линейного уравнения с двумя неизвестными не является единственным.

Каждое линейное уравнение с двумя неизвестными имеет бесконечно много различных решений. То есть существует бесконечно много различных двух чисел х и у, которые обращают линейное уравнение в верное тождество.

Если несколько уравнений с двумя переменными имеют одинаковые решения, то такие уравнения называются равносильными уравнениями. Следует отметить, что если уравнения с двумя неизвестными не имеют решений, то их тоже считают равносильными.

Основные свойства линейных уравнений с двумя неизвестными

1. Любое из слагаемых в уравнении можно перенести из одной части в другую, при этом необходимо изменить его знак на противоположный. Полученное уравнение будет равносильно исходному.

2. Обе части уравнения можно разделить на любое число, которое не равно нулю. В результате получим уравнение равносильное исходному.

Нужна помощь в учебе?

Предыдущая тема: Применение различных способов для разложения на множители
Следующая тема:&nbsp&nbsp&nbspГрафик линейного уравнения с двумя переменными: алгоритм построения

Как решать линейные уравнения? | О математике понятно

        Линейные уравнения — довольно безобидная и понятная тема школьной математики. Но, как это ни странно, количество ошибок на ровном месте при решении линейных уравнений лишь немногим меньше, чем в других темах — квадратных уравнениях, логарифмах, тригонометрии и прочих. Причины большинства ошибок — банальные тождественные преобразования уравнений. В первую очередь, это путаница в знаках при переносе слагаемых из одной части уравнения в другую, а также ошибки при работе с дробями и дробными коэффициентами. Да-да! Дроби в линейных уравнениях тоже встречаются! Сплошь и рядом. Чуть ниже такие злые уравнения мы с вами тоже обязательно разберём.)

        Ну что, не будем тянуть кота за хвост и начнём разбираться, пожалуй? Тогда читаем и вникаем.)

Что такое линейное уравнение? Примеры.

Обычно линейное уравнение имеет следующий вид:

ax + b = 0,

       где a и b — любые числа. Какие угодно: целые, дробные, отрицательные, иррациональные — всякие могут быть!

Например:

7х + 1 = 0 (здесь a = 7, b = 1)

x — 3 = 0 (здесь a = 1, b = -3)

x/2 — 1,1 = 0 (здесь a = 1/2, b = -1,1)

       В общем, вы поняли, я надеюсь.) Всё просто, как в сказке. До поры до времени… А если присмотреться к общей записи ax+b=0 более пристально, да немного призадуматься? Ведь a и b — любые числа! А если у нас, скажем, a = 0 и b = 0 (любые же числа можно брать!), то что у нас тогда получится?

0 = 0

       Но и это ещё не все приколы! А если, допустим, a = 0, b = -10? Тогда уже совсем какая-то ахинея получается:

0 = 10.

       Что весьма и весьма напрягает и подрывает завоёвываемое потом и кровью доверие к математике… Особенно на контрольных и экзаменах. А ведь из этих непонятных и странных равенств ещё и икс найти нужно! Которого нету вообще! И вот тут даже хорошо подготовленные ученики, порой, могут впасть, что называется, в ступор… Но не переживайте! В данном уроке все такие сюрпризы мы тоже рассмотрим. И икс из таких равенств тоже обязательно отыщем.) Причём этот самый икс ищется очень и очень просто. Да-да! Удивительно, но факт.)

       Ну хорошо, это понятно. Но как же можно узнать по внешнему виду задания, что перед нами именно линейное уравнение, а не какое-либо ещё? К сожалению, только по внешнему виду распознать тип уравнения возможно далеко не всегда. Дело всё в том, что линейными называются не только уравнения вида ax+b=0, но и любые другие уравнения, которые тождественными преобразованиями, так или иначе, сводятся к такому виду. А как тут узнаешь, сводится оно или нет? Пока пример почти не решишь — почти никак. Это огорчает. Но для некоторых типов уравнений можно при одном беглом взгляде сразу с уверенностью сказать, линейное оно или нет.

Для этого ещё разок обратимся к общей структуре любого линейного уравнения:

ax + b = 0

       Обратите внимание: в линейном уравнении всегда присутствует только переменная икс в первой степени и какие-то числа! И всё! Больше ничего. При этом нету иксов в квадрате, в кубе, под корнем, под логарифмом и прочей экзотики. И (что особенно важно!) нет дробей с иксом в знаменателях! А вот дроби с числами в знаменателях или деление на число — запросто!

Например:

       Это линейное уравнение. В уравнении присутствуют только иксы в первой степени да числа. И нету иксов в более высоких степенях — в квадрате, в кубе и так далее. Да, здесь есть дроби, но при этом в знаменателях дробей сидят только числа. А именно — двойка и тройка. Иными словами, в уравнении нету деления на икс.

       А вот уравнение

       

       уже нельзя назвать линейным, хотя здесь тоже присутствуют только числа и иксы в первой степени. Ибо, помимо всего прочего, здесь есть ещё и дроби с иксами в знаменателях. И после упрощений и преобразований такое уравнение может стать каким угодно: и линейным, и квадратным — всяким.

Как решать линейные уравнения? Примеры.

        Так как же решать линейные уравнения? Читайте дальше и удивляйтесь.) Всё решение линейных уравнений базируется всего на двух основных вещах. Перечислим их.

        1) Набор элементарных действий и правил математики.

        Это использование скобок, раскрытие скобок, работа с дробями, работа с отрицательными числами, таблица умножения и так далее. Эти знания и умения необходимы не только для решения линейных уравнений, а для всей математики вообще. И, если с этим проблемы, вспоминайте младшие классы. Иначе несладко вам придётся…

        2) Базовые тождественные преобразования уравнений.

        Их всего два. Да-да! Более того, эти самые базовые тождественные преобразования лежат в основе решения не только линейных, а вообще любых уравнений математики! Одним словом, решение любого другого уравнения — квадратного, логарифмического, тригонометрического, иррационального и т.д. — как правило, начинается с этих самых базовых преобразований. А вот решение именно линейных уравнений, собственно, на них же (преобразованиях) и заканчивается. Готовым ответом.) Так что не поленитесь и прогуляетесь по ссылке.) Тем более, что там линейные уравнения тоже детально разбираются.

        Что ж, я думаю, пора приступать к разбору примеров.

        Для начала, в качестве разминки, рассмотрим какую-нибудь элементарщину. Безо всяких дробей и прочих наворотов. Например, такое уравнение:

        х — 2 = 4 — 5х

        Это классическое линейное уравнение. Все иксы максимум в первой степени и деления на икс нигде нету. Схема решения в таких уравнениях всегда едина и проста до ужаса: все члены с иксами надо собрать слева, а все члены без иксов (т.е. числа) собрать справа. Вот и приступаем к сбору.

        Для этого запускаем в ход первое тождественное преобразование. Нам нужно перенести -5х влево, а -2 перенести вправо. Со сменой знака, ясное дело.) Вот и переносим:

        х + 5х = 4 + 2

        Ну вот. Полдела сделано: иксы собрали в кучку, числа — тоже. Теперь слева приводим подобные, а справа — считаем. Получаем:

        6х = 6

        Чего теперь нам не хватает для полного счастья? Да чтобы слева чистый икс остался! А шестёрка — мешает. Как от неё избавиться? Запускаем теперь второе тождественное преобразование — делим обе части уравнения на 6. И — вуаля! Ответ готов.)

        х = 1

        Разумеется, пример совсем примитивный. Чтобы общую идею уловить. Что ж, решим что-нибудь посущественнее. Например, разберём вот такое уравнение:

        Детально разберём.) Это тоже линейное уравнение, хотя, казалось бы, тут есть дроби. Но в дробях есть деление на двойку и есть деление на тройку, а вот деления на выражение с иксом — нету! Так что — решаем. Используя всё те же тождественные преобразования, да.)

        Что вначале делать будем? С иксами — влево, без иксов — вправо? В принципе, можно и так. Лететь в Сочи через Владивосток.) А можно пойти по кратчайшему пути, сразу воспользовавшись универсальным и мощным способом. Если знать тождественные преобразования, разумеется.)

        Для начала задаю ключевой вопрос: что вам сильнее всего бросается в глаза и больше всего не нравится в этом уравнении? 99 человек из 100 скажут: дроби! И будут правы.) Вот и избавимся сначала от них. Безопасно для самого уравнения.) Поэтому начнём сразу со второго тождественного преобразования — с домножения. На что надо помножить левую часть, чтобы знаменатель благополучно сократился? Правильно, на двойку. А правую часть? На тройку! Но… Математика — дама капризная. Она, понимаешь, требует умножать обе части только на одно и то же число! Каждую часть помножать на своё число — не катит… Что делать будем? Что-что… Искать компромисс. Чтобы и наши хотелки удовлетворить (избавиться от дробей) и математику не обидеть.) А помножим-ка обе части на шестёрку!) То есть, на общий знаменатель всех дробей, входящих в уравнение. Тогда одним махом и двойка сократится, и тройка!)

        Вот и домножаем. Всю левую часть и всю правую часть целиком! Посему используем скобочки. Вот так выглядит сама процедура:

        Теперь раскрываем эти самые скобочки:

        Теперь, представив 6 как 6/1, помножим шестёрку на каждую из дробей слева и справа. Это обычное умножение дробей, но, так уж и быть, распишу детально:

        

        

        А вот здесь — внимание! Числитель (х-3) я взял в скобки! Это всё потому, что при умножении дробей числитель умножается весь, целиком и полностью! И с выражением х-3 надо работать как с одной цельной конструкцией.  А вот если вы запишете числитель вот так:

        6х — 3,

        то это будет ошибкой. Дальше можно уже не решать, да…

        Но у нас всё правильно и надо дорешивать. Что дальше делать? Раскрывать скобки в числителе слева? Ни в коем случае! Мы с вами домножали обе части на 6, чтобы от дробей избавиться, а не для того чтобы париться с раскрытием скобок. На данном этапе нам надо сократить наши дроби. С чувством глубокого удовлетворения сокращаем все знаменатели и получаем уравнение безо всяких дробей, в линеечку:

        3(х-3) + 6х = 30 — 4х

        А вот теперь и оставшиеся скобки можно раскрыть:

        3х — 9 + 6х = 30 — 4х

        Уравнение становится всё лучше и лучше! Вот теперь вновь вспоминаем про первое тождественное преобразование. С каменным лицом повторяем заклинание из младших классов: с иксами — влево, без иксов — вправо. И применяем это преобразование:

        3х + 6х + 4х = 30 + 9

        Приводим подобные слева и считаем справа:

        13х = 39

        Осталось поделить обе части на 13. То есть, вновь применить второе преобразование. Делим и получаем ответ:

        х = 3

        Готово дело. Как вы видите, в данном уравнении нам пришлось один раз применить первое преобразование (перенос слагаемых) и дважды — второе: в начале решения мы использовали домножение (на 6) с целью избавиться от дробей, а в конце решения использовали деление (на 13), чтобы избавиться от коэффициента перед иксом. И решение любого (да-да, любого!) линейного уравнения состоит из комбинации этих самых преобразований в той или иной последовательности. С чего именно начинать — от конкретного уравнения зависит. Где-то выгоднее начинать с переноса, а где-то (как в этом примере) — с домножения (или деления).

        Работаем от простого — к сложному. Рассмотрим теперь откровенную жесть. С кучей дробей и скобок. А я уж подскажу, как не надорваться.)

        Например, вот такое уравнение:

        Минуту смотрим на уравнение, ужасаемся, но всё-таки берём себя в руки! Основная проблема — с чего начинать? Можно сложить дроби в правой части. Можно выполнить вычитание дробей в скобках. Можно обе части на что-нибудь домножить. Или поделить… Так что же всё-таки можно? Ответ: всё можно! Ни одно из перечисленных действий математика не запрещает. И какую бы последовательность действий и преобразований вы бы ни выбрали, ответ получится всегда один — правильный. Если, конечно, на каком-то шаге не нарушить тождественность ваших преобразований и, тем самым, не наляпать ошибок…

        А, чтобы не наляпать ошибок, в таких навороченных примерах, как этот, всегда полезнее всего оценить его внешний вид и в уме прикинуть: что можно такое сделать в примере, чтобы максимально упростить его за один шаг?

        Вот и прикидываем. Слева стоят шестёрки в знаменателях. Лично мне они не нравятся, а убрать их очень легко. Домножу-ка я обе части уравнения на 6! Тогда шестёрки слева благополучно сократятся, дроби в скобках пока никуда не денутся. Ну и ничего страшного. С ними чуток позже расправимся.) А вот справа у нас сократятся знаменатели 2 и 3. Именно при этом действии (умножении на 6) у нас за один шаг достигаются максимальные упрощения!

        После умножения всё наше злое уравнение станет вот таким:

        Кто не понял, как именно получилось это уравнение, значит, вы плохо усвоили разбор предыдущего примера. А я старался, между прочим…

        Что дальше можно сделать? Дальше удобнее всего раскрыть все скобки справа. Причём правильно раскрыть, соблюдая основы! В правой части перед обеими скобками стоит знак плюс, поэтому все знаки при раскрытии сохраняются.

        Итак, раскрываем:

        Теперь самым логичным шагом было бы уединить дроби слева, а 5х отправить в правую часть. Заодно и подобные в правой части приведём. Получим:

        Уже гораздо лучше. Теперь левая часть сама собой подготовилась к умножению. На что надо домножить левую часть, чтобы сразу и пятёрка сократилась, и четвёрка? На 20! Но ещё у нас присутствуют минусы в обеих частях уравнения. Поэтому удобнее всего будет умножать обе части уравнения не на 20, а на -20. Тогда одним махом и минусы исчезнут, и дроби.

        Вот и умножаем:

        Кому до сих пор непонятен этот шаг — значит, проблемы не в уравнениях. Проблемы — в основах! Вновь вспоминаем золотое правило раскрытия скобок:

        Если число умножается на какое-то выражение в скобках, то это число надо последовательно умножить на каждое слагаемое этого самого выражения. При этом если число положительно, то знаки выражений после раскрытия сохраняются. Если отрицательно — меняются на противоположные:

         a(b+c) = ab+ac

         -a(b+c) = -ab-ac

         Минусы у нас исчезли после домножения обеих частей на -20. И теперь скобки с дробями слева мы умножаем на вполне себе положительное число 20. Стало быть, при раскрытии этих скобок все знаки, что были внутри них, сохраняются. А вот откуда взялись скобки в числителях дробей, я уже подробно объяснял в предыдущем примере.

А вот теперь дроби и сократить можно:

        4(3-5х)-5(3х-2) = 20

        Раскрываем оставшиеся скобки. Опять же, правильно раскрываем. Первые скобки умножаются на положительное число 4 и, стало быть, все знаки при их раскрытии сохраняются. А вот вторые скобки умножаются на отрицательное число -5 и, поэтому, все знаки меняются на противоположные:

        12 — 20х — 15х + 10 = 20

        Остались сущие пустяки. С иксами влево, без иксов — вправо:

        -20х — 15х = 20 — 10 — 12

        -35х = -2

        Вот почти и всё. Слева нужен чистый икс, а число -35 мешает. Вот и делим обе части на (-35). Напоминаю, что второе тождественное преобразование разрешает нам умножать и делить обе части на какое угодно число. В том числе и на отрицательное.) Лишь бы не на ноль! Смело делим и получаем ответ:

        x = 2/35

        На сей раз икс получился дробным. Ничего страшного. Такой уж пример.)

        Как мы видим, принцип решения линейных уравнений (даже самых накрученных) довольно простой: берём исходное уравнение и тождественными преобразованиями последовательно упрощаем его прямо до получения ответа. С соблюдением основ, разумеется! Главные проблемы здесь именно в несоблюдении основ (скажем, перед скобками стоит минус, а знаки при раскрытии поменять забыли), а также в банальной арифметике. Так что не пренебрегайте основами! Они — фундамент всей остальной математики!

 

Некоторые приколы при решении линейных уравнений. Или особые случаи.

        Всё бы ничего. Однако… Попадаются среди линейных уравнений и такие забавные перлы, которые в процессе их решения могут и в сильный ступор вогнать. Даже отличника.)

        Например, вот такое безобидное с виду уравнение:

        7х + 3 = 4х + 5 + 3х — 2

        Широко позёвывая и слегка скучая, собираем все иксы слева, а все числа справа:

        7х-4х-3х = 5-2-3

        Приводим подобные, считаем и получаем:

        0 = 0

        Вот-те раз! Выдал примерчик фокус! Само по себе это равенство возражений не вызывает: ноль действительно равен нулю. Но икс-то пропал! Бесследно! А мы обязаны записать в ответе, чему равен икс. Иначе решение не считается, да.) Что же делать?

        Без паники! В таких нестандартных случаях спасают самые общие понятия и принципы математики. Что такое уравнение? Как решать уравнения? Что значит решить уравнение?

        Решить уравнение — это значит, найти все значения переменной икс, которые при подстановке в исходное уравнение дадут нам верное равенство (тождество)!

        Но верное равенство у нас уже получилось! 0=0, вернее некуда!) Остаётся догадаться, при каких именно иксах у нас получается это равенство. Какие же такие иксы можно подставлять в исходное уравнение, если при подстановке все они всё равно посокращаются в полный ноль? Неужели ещё не догадались?

        Ну, конечно же! Иксы можно подставлять любые!!! Совершенно любые. Какие хотите, такие и подставляйте. Хоть 1, хоть -23, хоть 2,7 — какие угодно! Они всё равно сократятся и в результате останется чистая правда.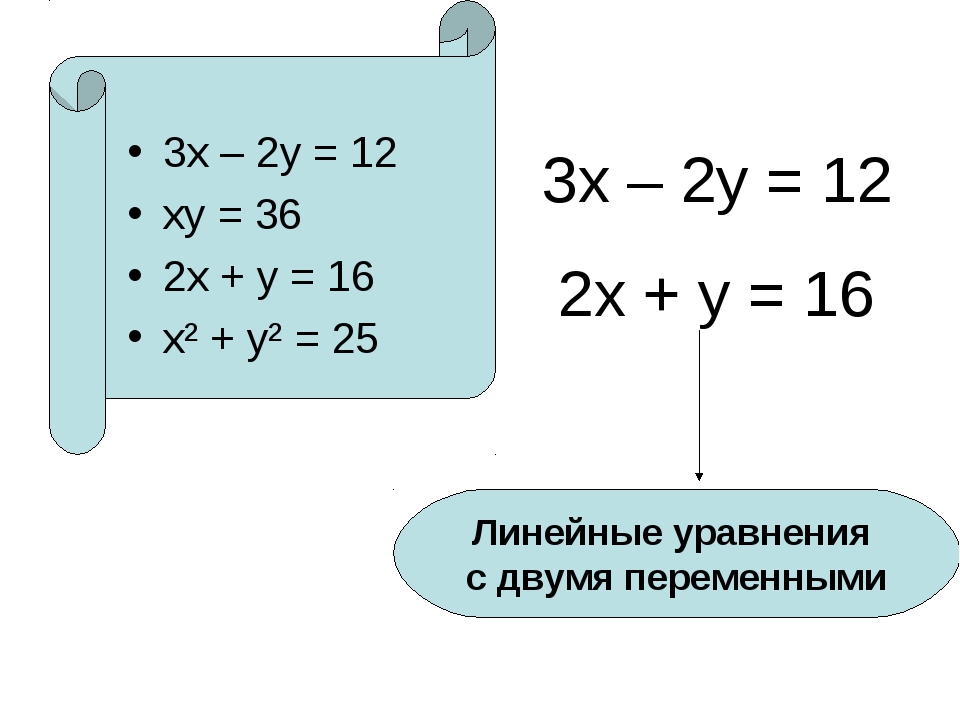 Попробуйте, поподставляйте и убедитесь лично.)

        Вот вам и ответ:

        х — любое число.

        В научной записи это равенство пишется так:

        

        Читается эта запись так: «Икс — любое действительное число.»

        Или в другой форме, через промежутки:

        

        Как вам больше нравится, так и оформляйте. Это верный и совершенно полноценный ответ!

        А теперь я изменю в нашем исходном уравнении всего одно число. Вот такое уравнение теперь решим:

        7х + 2 = 4х + 5 + 3х — 2

        Опять переносим слагаемые, считаем и получаем:

        7х — 4х — 3х = 5 — 2 — 2

        0 = 1

        И как вам этот прикол? Было обычное линейное уравнение, а стало непонятное равенство

        0 = 1…

        Говоря научным языком, мы получили неверное равенство. А по-русски неправда это. Бред сивой кобылы. Ахинея. ) Ибо ноль никак не равен единице!

        А теперь опять соображаем, какие же иксы при подстановке в исходное уравнение дадут нам верное равенство? Какие? А никакие! Какой икс ни подставляй, всё равно всё посокращается и останется лажа.)

        Вот и ответ: решений нет.

        В математической записи такой ответ оформляется вот так:

        

        Читается: «Икс принадлежит пустому множеству.»

        Такие ответы в математике тоже встречаются довольно часто: далеко не всегда у какого-либо уравнения имеются корни в принципе. Какие-то уравнения могут и вовсе не иметь корней. Совсем.

        Вот такие вот два сюрприза. Надеюсь, что теперь внезапная пропажа иксов в уравнении не поставит вас навечно в тупик. Дело вполне знакомое.)

        И тут слышу закономерный вопрос: а в ОГЭ или ЕГЭ они будут? На ЕГЭ сами по себе в качестве задания — нет. Слишком уж простенькие. А вот в ОГЭ или в текстовых задачках — запросто! Так что теперь — тренируемся и решаем:

        

        Ответы (в беспорядке): -2; -1; любое число; 2; нет решений; 7/13.

        Всё получилось? Отлично! У вас неплохие шансы на экзамене.

        Что-то не сходится? Гм… Печалька, конечно. Значит, где-то пока есть пробелы. Либо в основах, либо в тождественных преобразованиях. Либо же дело в банальной невнимательности. Перечитайте урок ещё раз. Ибо не та это тема, без которой можно вот так легко обойтись в математике…

        Удачи! Она вам обязательно улыбнётся, поверьте!)

        

Разработка урока «Линейное уравнение с двумя переменными» 7 класс

библиотека
материалов

Содержание слайдов

Номер слайда 1

Урок на тему Линейное уравнение с двумя переменными и его график

Номер слайда 2

Назвать уравнения:3х+7=14 14-у;2у-4=8 5(х-1) + 4(7-х) =02х+6; 0,5у +4,5 у-7;5у -2 +6у; 14-х =5

Номер слайда 3

Что называют уравнением?Что значит решить уравнение?Является ли корнем уравнения 2,5 х +5 =10 число 4? Число 2? -2?Решите уравнение: 5х -3 =12

Номер слайда 4

Рассмотрим задачу. Из городов А И В , расстояние между которыми 500км, навстречу друг другу вышли два поезда, каждый со своей скоростью. Известно, что первый вышел на 2 часа раньше второго. Через три часа после выхода второго, они встретились. Чему равны скорости поездов?

Номер слайда 5

Составим математическую модель. Х км/час – скорость 1 поезда. У км /час – скорость второго поезда. 5 Х + 3 У = 500 Можно ли это назвать уравнением? Чем оно отличается от предыдущих?

Номер слайда 6

Уравнение вида ах + ву +с = 0 называют линейным с двумя переменными. А, в – коэффициенты; с – свободный член.

Номер слайда 7

Решить уравнение Значит найти пару чисел(х; у), удовлетворяющую данному равенству, то есть обращает данное уравнение в верное равенство. 5х +3у = 500 Если х =40, у =100 , то 5 *40 + 3*100 = 500(40; 100) – решение данного уравнения.

Номер слайда 8

Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной. Если в уравнении перенести любой член из одной части в другую, изменив его знак, то получится уравнение, равносильное данному. Если обе части уравнения умножить или разделить на одно и то же (не равное нулю), то получится уравнение, равносильное данному.

Номер слайда 9

Номер слайда 10

Номер слайда 11

Номер слайда 12

Алгоритм построения графика уравнения ах+ву+с = 01. Придать переменной х =0; найти значение у.2. Придать переменной х еще какое – то значение и снова находят у.( можно у приравнять 0 и найти значение х)3. Построить точки на плоскости, и провести прямую

Номер слайда 13

Итак: Что такое уравнение с двумя переменными?Что значит решить линейное уравнение с двумя переменными?Что является графиком линейного уравнения? Как построить график?

Номер слайда 14

Построить по алгоритму. 4х+2у-4=03х –у+ 6 =0

Линейное уравнение с одной переменной

Слайды и текст этой онлайн презентации

Слайд 1

Линейное уравнение с одной переменной.
7 класс Подготовила учитель математики: Арнаутова Оксана Юрьевна.

Слайд 2

Линейным уравнением с одной переменной называется уравнение вида aх + b = с, где а, в, с – числа, х – переменная. Например: 3х + 8 = 0, 14 – 2х =9; – 4х = 10.
Определение

Слайд 3

— Решить уравнение – это значит найти все его корни или доказать, что корней нет. - Корнем уравнения с одной переменной называется значение переменной, при котором уравнение обращается в верное равенство.

Слайд 4

При решении уравнений с одной переменной используются следующие свойства: — Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному; — Если обе части уравнения умножить или разделить на одно и то же число, то получится уравнение, равносильное данному.

Слайд 5

Алгоритм решения уравнения
1.Раскрыть скобки. 2.Перенести слагаемые, содержащие переменную, в одну часть уравнения, а числа без переменной – в другую часть. 3.Упростить, привести подобные слагаемые. 4.Найти корень уравнения. 5.Сделать проверку.

Слайд 6

Раскрытие скобок
1)Если перед скобками стоит знак « +», то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки. (2 –3,5х) + (–2,4х + 6,75) = 2 – 3,5х – 2,4х + 6,75 = = 8,75 – 5,9х 2) Если перед скобками стоит знак « -», то скобки можно опустить, изменив на противоположный знак каждого слагаемого, заключенного в скобки. ( 4,2х – 3) – ( 1,3 – 2х) = 4,2х – 3 –1,3 + 2х = = 6,2х – 4,3

Слайд 7

Распределительное свойство умножения
а(в + с) = ав +ас а(в – с) = ав – ас Примеры: 6 ( 7 – 5х) = 42 – 30х; – 8,1 ( а + 3) = – 8,1а –24,3.

Слайд 8

Примеры решения уравнений
Пример1. 3(х + 7) = 12 3х + 21 = 12 3х =12 – 21; 3х = — 9 х = — 9 : 3 х = — 3

Слайд 9

Пример 2
2 (у + 8) + 4 = 6 – ( 6у + 2) 2у + 16 + 4 = 6 – 6у – 2 2у + 6у = 6 – 2 — 16 — 4 8у = — 16 у = — 16 : 8 у = — 2

Слайд 10

Задания для самостоятельного решения
Решить уравнения: 1) 2х + 5 = 2 (- х + 1) + 11 2) 6у – 3(у – 1) = 4 + 5у 3) 4 ( х – 1) – 3 = — (х + 7) + 8 4) – 2(5 у – 9) + 2 = 15 + 7(- х + 2) 5).12 + 4(х – 3) – 2х = (5 – 3х) + 9

Слайд 11

СПАСИБО ЗА ВНИМАНИЕ

ученикам помогут вспомнить школьную программу / Новости города / Сайт Москвы

Городской методический центр приглашает юных москвичей освежить свои знания по школьным предметам накануне начала учебного года, восполнить пробелы и узнать что-то новое. Для ребят подготовили мастер-классы по математике, биологии, английскому языку, обществознанию, информатике, химии и географии.

Школьники смогут изучить творчество Рэя Брэдбери, познакомиться со свойствами антисептиков, узнать, как разместить карту города на листе бумаги, и многое другое. Все занятия пройдут в режиме онлайн.

18 августа в 11:00 начнется мастер-класс по математике «Бесподобное подобие». Школьникам расскажут о том, как греческий математик Фалес определил высоту египетской пирамиды, что предпринимали в подобных случаях герои известных литературных произведений и в какой момент поднимающийся объект перестает отбрасывать тень на поверхность Земли.

В этот же день в 13:00 стартует мастер-класс «Кодирование графической и звуковой информации». Юные программисты рассмотрят основные принципы кодирования и декодирования графической и звуковой информации.

О том, как не забыть иностранный язык за время каникул, расскажут 19 августа в 11:00 на вебинаре «Английский язык вокруг нас». Школьники узнают о том, как практиковаться в иностранном языке, если нет возможности побывать за границей.

В этот же день в 13:00 начнется онлайн-занятие по математике «Применение систем линейных уравнений для решения прикладных задач». Ученикам напомнят об основных способах решения систем линейных уравнений, а также объяснят, как можно использовать эти системы на практике.

На мастер-классе «Учим английский с научной фантастикой» школьники узнают, как чтение художественной литературы помогает расширить словарный запас, и поймут, как работает грамматика языка, а также познакомятся с творчеством Рэя Брэдбери. Кстати, в этом году исполняется 100 лет со дня рождения американского писателя. Начало занятия — 20 августа в 11:00.

А в 13:00 стартует вебинар по биологии «Каково быть человеком?», на котором учащиеся изучат основные направления и факторы эволюции, а также обсудят родословное древо наших предков и наиболее важные культурные достижения человечества.

21 августа в 11:00 пройдет мастер-класс «Как можно измерить информацию». На нем обсудят, какие подходы к измерению информации существуют и как посчитать, какое количество информации содержит полученное сообщение. Во время занятия ребята вспомнят единицы измерения, повторят формулы и рассмотрят задачи, связанные с объемом информации различных сообщений.

В этот же день в 13:00 начнется онлайн-лекция по обществознанию «Когнитивные искажения и их роль в процессе познания». Школьникам объяснят, в чем заключается феномен когнитивных искажений и почему человек, находящийся в таком состоянии, не способен адекватно и объективно воспринимать окружающий мир и самого себя.

22 августа в 11:00 стартует онлайн-встреча по географии «Как изобразить школу на листе бумаги?». На ней расскажут, как изображаются неровности земной поверхности и зачем нужно уметь строить план местности.

В этот же день в 13:00 на мастер-классе «Как мыслит компьютер» ребята рассмотрят основные системы счисления в информатике, а также принципы машинных вычислений.

24 августа в 10:00 пройдет вебинар по химии «Рекомендованные ВОЗ рецептуры антисептиков для рук». На нем расскажут, в чем заключается эффективность антисептиков и какие компоненты могут нанести вред кожному покрову.

Линейные уравнения (ЕГЭ — 2021)

Начнем сразу же с примера

\( \displaystyle 4x=16\)

Смотрим и соображаем: что нам не нравится в этом примере? Неизвестное все в одной части, известные – в другой, но что-то нам мешает… И это что-то – четверка, так как если бы ее не было, все было бы идеально – икс равен числу – именно так, как нам и нужно!

Как можно от неё избавиться? Перенести вправо мы не можем, так как тогда нам нужно переносить весь множитель (мы же не можем ее взять и оторвать от \( \displaystyle x\)), а переносить весь множитель тоже не имеет смысла…

Пришло время вспомнить про деление, в связи с чем разделим все как раз на \( \displaystyle 4\)! Все – это означает и левую, и правую часть. Так и только так! Что у нас получается?

\( \displaystyle x=4\)

Вот и ответ.

Посмотрим теперь другой пример:

\( \displaystyle \frac{1}{2}x=3\)

Догадываешься, что нужно сделать в этом случае? Правильно, умножить левую и правую части на \( \displaystyle 2\)! Какой ты получил ответ? Правильно. {2}}-12x+6x+36+9=0\\-6x=-45\end{array}\)

Как ты видишь, иксы в квадрате исчезли, и здесь совершенно обычное линейное уравнение. Осталось только найти \( \displaystyle x\)!

\( \displaystyle x=\frac{-45}{-6}=7,5\)

И напоследок скажу еще одну очень важную вещь про тождественные преобразования.

Линейное уравнение | Britannica

Линейное уравнение , утверждение, что многочлен первой степени, то есть сумма набора членов, каждый из которых является произведением константы и первой степени переменной, равен константе. В частности, линейное уравнение в n переменных имеет вид a ₀ + a ₁ x ₁ +… + a _n x _n = c , в котором x ₁ ,…, x _n — переменные, коэффициенты a ₀ ,…, a _n — константы , а c — постоянная. Если существует более одной переменной, уравнение может быть линейным по некоторым переменным, но не по другим. Таким образом, уравнение x + y = 3 линейно как для x , так и для y, , тогда как x + y ² = 0 линейно для x , но не для y. Любое уравнение двух переменных, линейных по каждой, представляет собой прямую линию в декартовых координатах; если постоянный член c = 0, прямая проходит через начало координат.

Подробнее по этой теме

Восточноазиатская математика: Решение систем одновременных линейных уравнений

Девять глав посвящает главу решению одновременных линейных уравнений, то есть совокупности отношений между …

Система уравнений, имеющая общее решение, называется системой одновременных уравнений. Например, в системе

оба уравнения удовлетворяются решением x = 2, y = 3. Точка (2, 3) является пересечением прямых линий, представленных двумя уравнениями. См. Также правило Крамера.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Линейное дифференциальное уравнение первой степени относительно зависимой переменной (или переменных) и ее (или их) производных. В качестве простого примера, примечание dy / dx + Py = Q , в котором P и Q могут быть константами или могут быть функциями независимой переменной, x, , но не задействовать зависимую переменную, лет. В особом случае, когда P является константой и Q = 0, это представляет собой очень важное уравнение для экспоненциального роста или распада (например, радиоактивного распада), решение которого: y = k e ^{— Px} , где e — основание натурального логарифма.

Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) — Mathplanet

Линейное уравнение — это уравнение с двумя переменными, график которого представляет собой линию. График линейного уравнения — это набор точек на координатной плоскости, которые все являются решениями уравнения. Если все переменные представляют собой действительные числа, можно изобразить уравнение, нанеся на график достаточно точек, чтобы распознать шаблон, а затем соединить точки, чтобы включить все точки.

Если вы хотите построить график линейного уравнения, у вас должно быть как минимум две точки, но обычно рекомендуется использовать более двух точек. При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.

---

Пример

Постройте функцию y = x + 2

Начните с выбора пары значений для x, например -2, -1, 0, 1 и 2 и вычислите соответствующие значения y.

х	Y = х + 2	Заказанная пара
-2	-2 + 2 = 0	(-2, 0)
-1	-1 + 2 = 1	(-1, 1)
0	0 + 2 = 2	(0, 2)
1	1 + 2 = 3	(1, 3)
2	2 + 2 = 4	(2, 4)

Теперь вы можете просто построить пять упорядоченных пар в координатной плоскости

На данный момент это пример дискретной функции.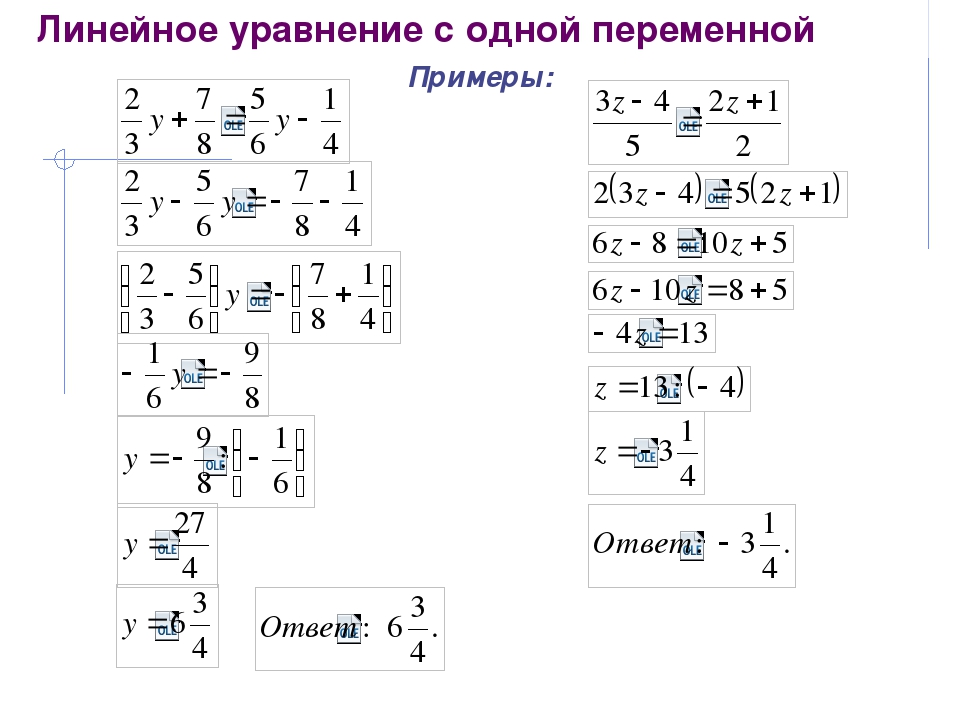 Дискретная функция состоит из изолированных точек.

Проведя линию через все точки и продолжая линию в обоих направлениях, мы получаем противоположность дискретной функции, непрерывную функцию, которая имеет непрерывный график.

Если вы хотите использовать только две точки для определения вашей линии, вы можете использовать две точки, где график пересекает оси. Точка, в которой график пересекает ось x, называется отрезком x, а точка, в которой график пересекает ось y, называется отрезком y.Пересечение по оси x находится путем нахождения значения x, когда y = 0, (x, 0), а точка пересечения по оси y находится путем нахождения значения y, когда x = 0, (0, y).

Стандартная форма линейного уравнения —

$$ Ax + By = C, \: \: A, B \ neq 0 $$

Прежде чем вы сможете построить линейное уравнение в его стандартной форме, вы сначала должны решить уравнение относительно y.

$$ 2y-4x = 8 $$

$$ 2y-4x \, {\ color {green} {+ \, 4x}} = 8 \, {\ color {green} {+ \, 4x}} $$

$$ 2y = 4x + 8 $$

$$ \ frac {2y} {{\ color {green} 2}} = \ frac {4x} {{\ color {green} 2}} + \ frac {8} {{\ color {green} 2}} $

$$ y = 2x + 4 $$

Отсюда вы можете построить уравнение, как в примере выше.

График y = a представляет собой горизонтальную линию, где прямая проходит через точку (0, a)

В то время как график x = a представляет собой вертикальную линию, проходящую через точку (a, 0)

---

Видеоурок

Постройте график линейного уравнения y = 3x — 2

Решение линейных уравнений: все типы

An уравнение должен иметь знак равенства, как в 3 Икс + 5 знак равно 11 .

А линейное уравнение — это переменная, в которой переменные умножаются на числа или добавляются к числам, и ничего более сложного, чем это (без экспонентов, квадратных корней, 1 Икс , или любой другой забавный бизнес).

А решение к уравнению это число который можно подключить к переменной, чтобы получить истинное числовое выражение.

Например, подставив 2 для Икс в 3 Икс + 5 знак равно 11 дает

3 ( 2 ) + 5 знак равно 11 , что говорит 6 + 5 знак равно 11 ; это правда! Так 2 это решение.

Но как начать с уравнения и получить (не догадываться) решение?

Одношаговые линейные уравнения

Некоторые линейные уравнения можно решить за одну операцию. Для этого типа уравнения используйте обратный операция решать.

Пример 1:

Решить для п .

п + 8 знак равно 10

Обратной операцией сложения является вычитание. Итак, вычтите 8 с обеих сторон.

п + 8 — 8 знак равно 10 — 8 п знак равно 2

Пример 2:

Решить для y .

3 4 y знак равно 15

Обратная операция умножения — это деление.Итак, разделите обе стороны на 3 4 ( что то же самое, что умножение на 4 3 ) .

4 3 ⋅ 3 4 y знак равно 4 3 ⋅ 15

y знак равно 20

Двухступенчатые линейные уравнения

Чаще всего нам нужны две операции для решения линейного уравнение.

Пример 3:

Решить для Икс .

3 Икс + 5 знак равно 11

3 Икс + 5 знак равно 11	Данный уравнение.
3 Икс + 5 — 5 знак равно 11 — 5	Чтобы изолировать переменную, мы следуем порядку операций в обратном порядке.Мы отменяем сложение перед отменой умножения. Вычесть 5 с обеих сторон.
3 Икс знак равно 6	Мы отменили одну операцию. Еще один.
3 Икс 3 знак равно 6 3	Разделите обе стороны на 3 .
Икс знак равно 2	Мы решили уравнение!

То, что делает эти уравнения линейный является что высшая сила Икс является Икс 1 (нет Икс 2 или другой полномочия; для тех, см. квадратные уравнения а также многочлены ).

Другие линейные уравнения имеют более одной переменной: например, y знак равно 3 Икс + 2 . Это уравнение имеет не одно, а бесконечное множество решений; решения могут быть нарисованный как линия на плоскости.

линейных уравнений | Введение в статистику

Результаты обучения

• Обсудить основные идеи линейной регрессии и корреляции

Линейная регрессия для двух переменных основана на линейном уравнении с одной независимой переменной.Уравнение имеет вид:

, где a и b — постоянные числа.

Переменная x — независимая переменная, а y — зависимая переменная. Обычно вы выбираете значение для замены независимой переменной, а затем решаете зависимую переменную.

Следующие ниже примеры представляют собой линейные уравнения.

попробуйте

Следующий пример является линейным уравнением?

y = –0.125 — 3,5 x

График линейного уравнения вида y = a + bx представляет собой прямую . Любая линия, которая не является вертикальной, может быть описана этим уравнением.

Изобразите уравнение y = –1 + 2 x .

попробуйте

1. Следующий пример является линейным уравнением? Почему или почему нет?

Служба обработки текстов Аарона (AWPS) занимается обработкой текста.Стоимость услуг составляет 32 доллара в час плюс единовременная оплата в размере 31,50 доллара. Общая стоимость для клиента зависит от количества часов, необходимых для выполнения работы.

Найдите уравнение, которое выражает общих затрат через количество часов , необходимых для выполнения работы.

попробуйте

Emma’s Extreme Sports нанимает инструкторов по дельтапланеризму и платит им гонорар в размере 50 долларов за класс, а также 20 долларов за каждого ученика в классе.Общая стоимость, которую платит Эмма, зависит от количества студентов в классе. Найдите уравнение, которое выражает общую стоимость через количество учеников в классе.

Для линейного уравнения y = a + bx , b = наклон и a = y — перехват. Из алгебры напомним, что наклон — это число, которое описывает крутизну линии, а точка пересечения y — это координата y точки (0, a ), где линия пересекает ось y . .

Три возможных графика y = a + bx . (a) Если b > 0, линия наклоняется вверх вправо. (b) Если b = 0, линия горизонтальная. (c) Если b <0, линия наклоняется вниз вправо. Светлана занимается репетитором, чтобы подзаработать в колледже. За каждую сессию репетиторства она взимает единовременную плату в размере 25 долларов плюс 15 долларов за час репетиторства. Линейное уравнение, которое выражает общую сумму денег, которую Светлана зарабатывает за каждое занятие, которое она проводит, составляет y = 25 + 15 x .

Какие бывают независимые и зависимые переменные? Что такое перехват y и какой угол наклона? Интерпретируйте их, используя полные предложения.

попробуйте

Итан ремонтирует бытовую технику, такую ​​как посудомоечные машины и холодильники. За каждое посещение он берет 25 долларов плюс 20 долларов за час работы. Линейное уравнение, которое выражает общую сумму денег, которую Итан зарабатывает за посещение, составляет y = 25 + 20 x .

Какие бывают независимые и зависимые переменные? Что такое перехват y и какой угол наклона? Интерпретируйте их, используя полные предложения.

Данные Центров по контролю и профилактике заболеваний.

Данные Национального центра профилактики ВИЧ, ИППП и ТБ.

Самый простой тип ассоциации — это линейная ассоциация. Этот тип взаимосвязи может быть определен алгебраически с помощью используемых уравнений, численно с фактическими или прогнозируемыми значениями данных или графически по построенной кривой. (Линии классифицируются как прямые кривые.) Алгебраически линейное уравнение обычно принимает форму y = mx + b , где m и b — константы, x — независимая переменная, y — зависимая переменная.В статистическом контексте линейное уравнение записывается в виде y = a + bx , где a и b — константы. Эта форма используется, чтобы помочь читателям отличить статистический контекст от алгебраического. В уравнении y = a + bx константа b , которая умножает переменную x ( b называется коэффициентом), называется наклоном .Наклон описывает скорость изменения между независимыми и зависимыми переменными; другими словами, скорость изменения описывает изменение, которое происходит в зависимой переменной при изменении независимой переменной. В уравнении y = a + bx константа a называется перехватом y . Графически пересечение y — это координата y точки, где график линии пересекает ось y . На данный момент x = 0.

Наклон линии — это значение, которое описывает скорость изменения между независимыми и зависимыми переменными. Наклон сообщает нам, как в среднем изменяется зависимая переменная ( y ) на каждую единицу увеличения независимой ( x ) переменной. Перехват y используется для описания зависимой переменной, когда независимая переменная равна нулю. Графически наклон представлен тремя типами линий в элементарной статистике.

y = a + bx , где a — пересечение y , а b — наклон. Переменная x является независимой переменной, а y — зависимой переменной.

Линейные уравнения — Введение в бизнес-статистику

Линейная регрессия и корреляция

Линейная регрессия для двух переменных основана на линейном уравнении с одной независимой переменной. Уравнение имеет вид:

, где a и b — постоянные числа.

Переменная x — независимая переменная, а y — зависимая переменная. Еще один способ подумать об этом уравнении — это причинно-следственная связь. Переменная X является причиной, а переменная Y — предполагаемым следствием. Обычно вы выбираете значение для замены независимой переменной, а затем решаете зависимую переменную.

Следующие ниже примеры представляют собой линейные уравнения.

График линейного уравнения вида y = a + bx представляет собой прямую . Любая линия, которая не является вертикальной, может быть описана этим уравнением.

Изобразите уравнение y = –1 + 2 x .

Попробуйте

Следующий пример является линейным уравнением? Почему или почему нет?

Нет, график не прямая линия; следовательно, это не линейное уравнение.

Служба обработки текстов Аарона (AWPS) занимается обработкой текста. Тариф на услуги составляет 32 евро в час плюс единовременная оплата в размере 31,50 евро. Общая стоимость для клиента зависит от количества часов, необходимых для выполнения работы.

Найдите уравнение, которое выражает общих затрат через количество часов , необходимых для выполнения работы.

Пусть x = количество часов, необходимое для выполнения работы.
Пусть y = общая стоимость для покупателя.

31,50 фунтов стерлингов — это фиксированная стоимость. Если для выполнения задания требуется x часов, то (32) ( x ) — это стоимость только обработки текста. Итоговая стоимость: y = 31,50 + 32 x

Наклон

и

Y — пересечение линейного уравнения

Для линейного уравнения y = a + bx , b = наклон и a = y — перехват. Из алгебры напомним, что наклон — это число, которое описывает крутизну линии, а точка пересечения y — это координата y точки (0, a ), где линия пересекает ось y . .Из расчетов наклон — это первая производная функции. Для линейной функции наклон составляет dy / dx = b , где мы можем прочитать математическое выражение как «изменение y ( dy ), которое является результатом изменения x ( dx ) = b * dx “.

Три возможных графика y = a + bx . (a) Если b > 0, линия наклоняется вверх вправо.(b) Если b = 0, линия горизонтальная. (c) Если b <0, линия наклоняется вниз вправо.

Светлана — репетиторы, чтобы подзаработать в колледже. За каждую сессию репетиторства она взимает единовременную плату в размере 25 фунтов стерлингов плюс 15 фунтов стерлингов за час репетиторства. Линейное уравнение, которое выражает общую сумму денег, которую Светлана зарабатывает за каждое занятие, которое она проводит, составляет y = 25 + 15 x .

Какие бывают независимые и зависимые переменные? Что такое перехват y и какой угол наклона? Интерпретируйте их, используя полные предложения.

Независимая переменная ( x ) — это количество часов, в течение которых Светлана занимается с репетитором на каждой сессии. Зависимая переменная ( y ) — это сумма в долларах, которую Светлана зарабатывает за каждую сессию.

Перехват y равен 25 ( a = 25). В начале репетиторства Светлана взимает единовременную плату в размере 25 евро (это когда x = 0). Наклон равен 15 ( b = 15). За каждое занятие Светлана зарабатывает 15 евро за каждый час репетиторства.

Верно или неверно: более безопасно интерпретировать коэффициенты корреляции как меры ассоциации, а не причинно-следственной связи, из-за возможности ложной корреляции.

Мы заинтересованы в поиске линейной зависимости между количеством виджетов, приобретаемых за один раз, и стоимостью одного виджета. Получены следующие данные:

X: количество купленных виджетов — 1, 3, 6, 10, 15

Y: Стоимость виджета (в долларах) — 55, 52, 46, 32, 25

Предположим, что линия регрессии. Мы вычисляем среднюю цену за виджет при покупке 30 и наблюдаем, что из следующего?

1. ; очевидно, мы ошибаемся; прогноз на самом деле +15 долларов.
2. , что, судя по имеющимся данным, кажется разумным.
3. , что явная чушь. Линия регрессии должна быть неправильной.
4. , что явная чушь. Это напоминает нам, что прогнозирование Y за пределами диапазона значений X в наших данных — очень плохая практика.

Кратко обсудите различие между корреляцией и причинностью.

Некоторые переменные кажутся связанными, поэтому знание статуса одной переменной позволяет нам предсказать статус другой. Эта взаимосвязь может быть измерена и называется корреляцией. Однако высокая корреляция между двумя переменными никоим образом не доказывает, что между ними существует причинно-следственная связь. Вполне возможно, что третий фактор заставляет обе переменные изменяться вместе.

Верно или неверно: Если r близко к + или -1, мы скажем, что существует сильная корреляция с молчаливым пониманием того, что мы имеем в виду линейную зависимость и ни о чем другом.

Обзор главы

Самый простой тип ассоциации — это линейная ассоциация. Этот тип взаимосвязи может быть определен алгебраически с помощью используемых уравнений, численно с фактическими или прогнозируемыми значениями данных или графически по построенной кривой. (Линии классифицируются как прямые кривые.) Алгебраически линейное уравнение обычно принимает форму y = mx + b , где m и b — константы, x — независимая переменная, y — зависимая переменная.В статистическом контексте линейное уравнение записывается в виде y = a + bx , где a и b — константы. Эта форма используется, чтобы помочь читателям отличить статистический контекст от алгебраического. В уравнении y = a + bx константа b , которая умножает переменную x ( b называется коэффициентом), называется наклоном .Наклон описывает скорость изменения между независимыми и зависимыми переменными; другими словами, скорость изменения описывает изменение, которое происходит в зависимой переменной при изменении независимой переменной. В уравнении y = a + bx константа a называется перехватом y . Графически пересечение y — это координата y точки, где график линии пересекает ось y . На данный момент x = 0.

Наклон линии — это значение, которое описывает скорость изменения между независимыми и зависимыми переменными. Наклон сообщает нам, как в среднем изменяется зависимая переменная ( y ) на каждую единицу увеличения независимой ( x ) переменной. Перехват y используется для описания зависимой переменной, когда независимая переменная равна нулю. Графически наклон представлен тремя типами линий в элементарной статистике.

линейных уравнений | Блестящая вики по математике и науке

Формула пересечения угла наклона прямой задается следующим образом: y = mx + b, y = mx + b, y = mx + b, где mmm и bbb — фиксированные числа. Множество точек, удовлетворяющих этому уравнению, описывает прямую линию в плоскости xyxyxy.

Наклон линии — это соотношение между изменением yyy и изменением xxx. Например, для двух разных точек на прямой p1 = (x1, y1) p_1 = (x_1, y_1) p1 = (x1, y1) и p2 = (x2, y2) p_2 = (x_2, y_2) p2 = (x2, y2), наклон равен отношению y2 − y1x2 − x1 \ frac {y_2 — y_1} {x_2 — x_1} x2 −x1 y2 −y1. Это также известно как скорость изменения yyy по отношению к xxx.

Наклон

иногда выражается как нарастание по сравнению с пробегом . Студенты, которые забывают, какой компонент является числителем, могут захотеть визуализировать определение уклона как подъем по лестнице. Сначала идет вертикальное изменение (числитель), а затем горизонтальное изменение (знаменатель).

Для прямой y = mx + by = mx + by = mx + b скорость изменения yyy по отношению к xxx всегда равна наклону mmm для любой пары различных точек на прямой, который можно вычислить как следующее:

y2 − y1x2 − x1 = (mx2 + b) — (mx1 + b) x2 − x1 = m (x2 − x1) x2 − x1 = m.\ frac {y_2 — y_1} {x_2 — x_1} = \ frac {(mx_2 + b) — (mx_1 + b)} {x_2 — x_1} = \ frac {m (x_2 — x_1)} {x_2 — x_1} = м. x2 −x1 y2 −y1 = x2 −x1 (mx2 + b) — (mx1 + b) = x2 −x1 m (x2 −x1) = m.

Примечание: Исключение из этого правила возникает для строк формы:

• x = k x = k x = k для некоторой постоянной kkk. В этом случае наклон не определен.
• y = k y = k y = k для некоторой постоянной kkk. В данном случае наклон равен 0,0,0.

Решая уравнение прямой, когда x = 0x = 0x = 0, получаем y = m⋅0 + b, y = m \ cdot 0 + b, y = m⋅0 + b, поэтому (0, b ) (0, b) (0, b) — точка на прямой.Поскольку эта точка лежит на оси yyy, это точка пересечения линии yyy. Это объясняет название форма пересечения наклона для линии y = mx + b, y = mx + b, y = mx + b, где mmm — наклон, а bbb — точка пересечения yyy.

Найдите наклон и точку пересечения yyy прямой x = 2y + 6. х = 2 у + 6. х = 2у + 6.

Отвечать

На первый взгляд, у вас может возникнуть соблазн сказать, что наклон линии равен 2.2.2. Однако данное уравнение не имеет формы пересечения наклона.\ circ, \ quad b-5 = -2 \\ а & = 4, \ quad b = 3 \\ \ Rightarrow a-b & = 4-3 \\ & = 1. \ _\квадратный \ end {align} (a − 3) x − y + b − 5ya − 3a⇒a − b = 0 = (a − 3) x + (b − 5) = tan45∘, b − 5 = −2 = 4 , b = 3 = 4−3 = 1. □

Что такое линейное уравнение? — Видео и стенограмма урока

Построение линейного уравнения

В чем смысл? Почему меня волнует линейное уравнение? Что ж, линейные уравнения — это наиболее распространенные модели чисел, которые мы видим, и их можно использовать для описания всевозможных ситуаций, которые вы видите вокруг себя.

Один из примеров связан с первой купленной мной машиной. Когда мне исполнилось 16 лет, родители помогли мне купить подержанную машину. Когда я получил свою машину, на ней было 27000 миль, и я владел ею уже некоторое время. Каждый год я проезжаю на нем еще около 12 000 миль. В конечном итоге мы получаем линейное уравнение, представляющее ситуацию, которая выглядит как y = 12 000x + 27 000, потому что я проезжаю на нем еще 12 000 миль каждый год, и именно столько движется схема. И картина началась на 27 000 км, когда я впервые купил машину.Итак, после первого года у него было 39 000; через год — 51 000; а после третьего года — 63 000. И так далее.

Построение графика

Построение графика этого линейного уравнения может помочь нам сделать много прогнозов относительно того, что этот паттерн будет делать в будущем, а также может дать нам лучшее представление о паттерне, которое может быть нелегко увидеть, просто взглянув на цифры. Когда я хочу изобразить линейное уравнение, я использую точку пересечения y, значение b в качестве начального значения на моем графике.Итак, до того, как я проехал на машине хоть один день, на ней уже было 27000 миль, потому что я привык. Спустя год я ехал на нем, а после этого года я проехал до 39 000 миль. Я продолжал ездить на нем и ездить на нем, так что через два года я проехал 51 000 миль. Итак, каждый раз, когда я проезжаю больше года, я поднимаюсь на 12 000 миль.

В итоге мы получаем набор точек, которые находятся ровно в ряд, и эти точки образуют линию. На графике все линейные уравнения выглядят как линии, что имеет смысл, поскольку линейный и линейный — это почти одно и то же слово. Когда я рисовал график, вы, возможно, заметили треугольник, который я нарисовал под ним, где я проехал за год и поднялся на 12 000 миль. Этот треугольник называется треугольником наклона, и он помогает нам определить и нарисовать наклон графика. Опять же, наклон — это еще одно название того, насколько сильно движется паттерн. Наклон — это также то, что мы называем подъемом над бегом; это в основном означает, как он идет вверх и вниз, разделенный на то, насколько он идет влево и вправо.

График линейного уравнения

Этот график действительно хорош, потому что он показывает мне, сколько миль будет на моей машине в любой момент на одной картинке, но на самом деле это только приблизительные оценки.Если бы я хотел узнать, сколько миль было на моей машине через 1 год, 7 месяцев и 6 дней, мне пришлось бы подойти к этому моменту и перечитать его. Мы могли догадаться, что их около 50, но точно не знаем. И здесь на помощь приходит алгебра.

Решение линейного уравнения

Итак, насколько я понимаю, большинство автомобилей служат около 250 000 миль; Думаю, я был бы счастлив, если бы моя машина доехала так далеко. У меня вопрос, сколько еще у меня осталось? Прослужит ли моя машина столько, сколько я думаю, или мне скоро придется покупать другую машину? Мы можем использовать уравнение, чтобы ответить на этот вопрос, где y — количество миль, а x — количество прошедших лет: 250 000 = 12 000x + 27 000.

На этом этапе я могу отменить то, что было сделано с x, чтобы изолировать x и получить количество лет, которое даст мой ответ. Я знаю, что x сначала умножается на 12000, а затем к нему прибавляется 27000, поэтому мне нужно отменить эти вещи в обратном порядке. Первое, что мне нужно сделать, это вычесть по 27000 с обеих сторон. Затем мне нужно разделить обе стороны на 12000. Итак, я отменяю умножение делением; Я делю обе стороны на 12000. И я узнаю, что x около 18 лет.

Шаги к решению линейного уравнения

Сводка

Линейные уравнения представляют собой шаблоны чисел, которые либо увеличиваются, либо уменьшаются на одну и ту же величину на каждом этапе пути.