Что такое линейное уравнение | Алгебра
Что такое линейное уравнение? Что называется корнем линейного уравнения? Сколько корней имеет линейное уравнение? Что значить решить линейное уравнение?
В курсе алгебры 7 класса линейное уравнение определяется следующим образом.
Определение.
Линейное уравнение с одной переменной — это уравнение вида ax=b, где a и b — числа, x — переменная.
Корнем линейного уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство.
Например, корень уравнения 5x=40 равен 8, так как при x=8 это уравнение превращается в верное числовое равенство:
5∙8=40
40=40.
Количество корней линейного уравнения зависит от значения a (коэффициента перед x).
При a≠0 линейное уравнение имеет единственное решение.
Чтобы найти x, обе части уравнения нужно разделить на число, стоящее перед иксом:
Любое число можно разделить на 2, 5 и числа, которые могут быть представлены в виде произведения только двоек и пятёрок ( например, любое число можно разделить на 10, так как 10=2∙5; на 40, так как 40=2∙2∙2∙5).
В остальных случаях ответ записывают в виде обыкновенной дроби (если дробь неправильная, следует выделить из нее целую часть).
При a=0, b≠0 линейное уравнение
не имеет решений.
При любом значении x левая часть уравнения равна нулю, а правая — отлична от нуля. То есть нет ни одного значения x, при котором уравнение обратилось бы в верное числовое равенство.
При a=0, b=0 линейное уравнение
имеет бесконечное множество решений.
При любом значении x левая часть уравнения 0x=0 обращается в нуль, в правой части также стоит нуль. Значит, любое число является корнем этого уравнения, то есть, при любом значении x это уравнение обращается в верное числовое равенство.
Возможные решения линейных уравнений можно изобразить в виде схемы.
Решить линейное уравнение — значит, найти корень (корни) уравнения, либо убедиться, что уравнение не имеет корней.
Решение многих уравнений сводится к решению линейных уравнений.
www.algebraclass.ru
Линейное уравнение — Википедия. Что такое Линейное уравнение
Материал из Википедии — свободной энциклопедииЛинейное уравнение — это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна 1. Линейное уравнение можно представить:
- в общей форме: a1x1+a2x2+⋯+anxn+b=0{\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}+b=0};
- в канонической форме: a1x1+a2x2+⋯+anxn=−b{\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}=-b}.
Линейное уравнение одной переменной
Линейное уравнение от одной переменной можно привести к виду:
- ax+b=0{\displaystyle ax+b=0}.
Количество решений зависит от параметров a и b.
Если a=b=0{\displaystyle a=b=0}, то уравнение имеет бесконечное множество решений, поскольку ∀x∈R:x⋅0=0{\displaystyle \forall x\in \mathbb {R} :x\cdot 0=0}.
Если a=0,b≠0{\displaystyle a=0,b\neq 0}, то уравнение не имеет решений, поскольку ∄x∈R:0⋅x=−b≠0{\displaystyle \not \exists x\in \mathbb {R} :0\cdot x=-b\neq 0}.
Если a≠0{\displaystyle a\neq 0}, то уравнение имеет единственное решение x=−ba{\displaystyle x=-{\frac {b}{a}}}.
Линейное уравнение двух переменных
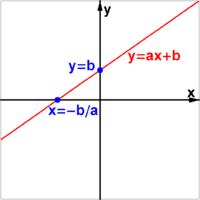 Геометрическое место точек линейного уравнения от двух переменных вида:
Геометрическое место точек линейного уравнения от двух переменных вида:y = ax + b
Линейное уравнение двух переменных можно представить:
- в общей форме: ax+by+c=0{\displaystyle ax+by+c=0};
- в канонической форме: ax+by=−c{\displaystyle ax+by=-c};
- в форме линейной функции: y=kx+m{\displaystyle y=kx+m}, где k=−ab; m=−cb{\displaystyle k=-{\frac {a}{b}};\ m=-{\frac {c}{b}}}.
Решением, или корнями, такого уравнения называют такую пару значений переменных (x;y){\displaystyle (x;y)}, которая обращает его в тождество. Таких решений (корней) линейное уравнение с двумя переменными имеет бесконечное множество. Геометрической моделью (графиком) такого уравнения является прямая y=kx+m{\displaystyle y=kx+m}.
См. также
Ссылки
wiki.sc
Линейное дифференциальное уравнение — это… Что такое Линейное дифференциальное уравнение?
В математике линейное дифференциальное уравнение имеет вид
где дифференциальный оператор L линеен, y — неизвестная функция , а правая часть — функция от той же переменной, что и y.
Линейный оператор L можно рассматривать в форме
Уравнения с переменными коэффициентами
Линейное дифференциальное уравнение порядка n с переменными коэффициентами имеет общий вид
Пример
Уравнение Коши — Эйлера, используемое в инженерии, является простым примером линейного дифференциального уравнения с переменными коэффициентами
Уравнение первого порядка
| Пример |
|---|
Решение уравнения с начальными условиями Имеем решение в общем виде Решение неопределённого интеграла Можно упростить до где 4/3, после подстановки начальных условий в решение. |
Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид
Уравнения в такой форме могут быть решены путём умножения на интегрирующий множитель
получим
используем правило дифференцирования произведения
что, после интегрирования обеих частей, дает нам
Таким образом, решение линейного дифференциального уравнения первого порядка
(в частности, с постоянными коэффициентами) имеет вид
где является константой интегрирования.
Пример
Возьмём дифференциальное уравнение первого порядка с постоянными коэффициентами:
Это уравнение имеет особое значение для систем первого порядка, таким как RC-схемы и масс-демпфер[неизвестный термин] системы.
В этом случае, p(x) = b, r(x) = 1.
Следовательно, решение будет:
dik.academic.ru
Линейные уравнения
Сперва необходимо понять, что же это такое.
Есть простое определение линейного уравнения, которое дают в обычной школе: «уравнение, в котором переменная встречается только в первой степени». Но оно не совсем верно: уравнение не является линейным, оно даже не приводится к такому, оно приводится к квадратичному.
Более точное определение таково: линейное уравнение – это уравнение, которое с помощью эквивалентных преобразований можно привести к виду , где . На деле мы будем приводить это уравнение к виду путём переноса в правую часть и деления обеих частей уравнения на . Осталось разъяснить, какие уравнения и как мы можем привести к такому виду, и, самое главное, что дальше делать с ними, чтобы решить его.
На самом деле, чтобы понять, является ли уравнение линейным или нет, его необходимо сперва упростить, то есть привести к виду, где его классификация будет однозначна. Запомните, с уравнением можно делать всё, что угодно, что не изменит его корней — это и есть эквивалентное преобразование. Из самых простых эквивалентных преобразований можно выделить:
- раскрытие скобок
- приведение подобных
- умножение и/или деление обеих частей уравнения на ненулевое число
- прибавление и/или вычитание из обеих частей одного и того же числа или выражения*
*Частной интерпретацией последнего преобразования является «перенос» слагаемых из одной части в другую со сменой знака.
Пример 1:
(раскроем скобки)
(прибавим к обеим частям и вычитание /перенесём со сменой знака числа влево, а переменные вправо)
(приведём подобные)
(разделим на 3 обе части уравнения)
Вот мы и получили уравнение, которое имеет такие же корни, как и исходное. Напомним читателю, что «решить уравнение» — значит найти все его корни и доказать, что других нет, а
Пример 2:
(умножим обе части уравнения на , предварительно убедившись, что мы не умножаем на : и . То есть если такие корни получатся, то мы их обязаны будем выкинуть.)
(раскроем скобки)
(перенесём слагаемые)
(приведём подобные)
(разделим обе части на )
Примерно так и решаются все линейные уравнения. Для читателей помладше, скорее всего, данное объяснение показалось сложным, поэтому предлагаем версию «линейные уравнения для 5 класса»
geniusmath.ru
Линейное дифференциальное уравнение — Википедия. Что такое Линейное дифференциальное уравнение
В математике линейное дифференциальное уравнение имеет вид- Ly=f{\displaystyle Ly=f}
где дифференциальный оператор L линеен, y — неизвестная функция y=y(t){\displaystyle y=y(t)}, а правая часть f=f(t){\displaystyle f=f(t)} — функция от той же переменной, что и y.
Линейный оператор L можно рассматривать в форме
- Ln(y)≡dnydtn+A1(t)dn−1ydtn−1+⋯+An−1(t)dydt+An(t)y{\displaystyle L_{n}(y)\equiv {\frac {d^{n}y}{dt^{n}}}+A_{1}(t){\frac {d^{n-1}y}{dt^{n-1}}}+\cdots +A_{n-1}(t){\frac {dy}{dt}}+A_{n}(t)y}
При этом, если f(t)≡0{\displaystyle f(t)\equiv 0}, то такое уравнение называется линейным однородным уравнением, иначе — линейным неоднородным уравнением.
Уравнения с переменными коэффициентами
Линейное дифференциальное уравнение порядка n с переменными коэффициентами имеет общий вид
- pn(x)y(n)(x)+pn−1(x)y(n−1)(x)+⋯+p0(x)y(x)=r(x){\displaystyle p_{n}(x)y^{(n)}(x)+p_{n-1}(x)y^{(n-1)}(x)+\cdots +p_{0}(x)y(x)=r(x)}
Пример
Уравнение Коши — Эйлера, используемое в инженерии, является простым примером линейного дифференциального уравнения с переменными коэффициентами
- xny(n)(x)+an−1xn−1y(n−1)(x)+⋯+a0y(x)=0{\displaystyle x^{n}y^{(n)}(x)+a_{n-1}x^{n-1}y^{(n-1)}(x)+\cdots +a_{0}y(x)=0}
Уравнение первого порядка
Пример
Решение уравнения
- y′(x)+3(y)=2{\displaystyle y’\left(x\right)+3\left(y\right)=2}
с начальными условиями
- y(0)=2{\displaystyle y\left(0\right)=2}
Имеем решение в общем виде
- y=e−3x(∫2e3xdx+κ){\displaystyle y=e^{-3x}\left(\int 2e^{3x}\,dx+\kappa \right)}
Решение неопределённого интеграла
- y=e−3x(2/3e3x+κ){\displaystyle y=e^{-3x}\left(2/3e^{3x}+\kappa \right)}
Можно упростить до
- y=2/3+κe−3x{\displaystyle y=2/3+\kappa e^{-3x}}
где κ={\displaystyle \kappa =} 4/3, после подстановки начальных условий в решение.
Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид
- y′(x)+f(x)y(x)=g(x){\displaystyle y'(x)+f(x)y(x)=g(x)}
Уравнения в такой форме могут быть решены путём умножения на интегрирующий множитель
- e∫f(x)dx{\displaystyle e^{\int f(x)\,dx}}
получим
- y′(x)e∫f(x)dx+f(x)y(x)e∫f(x)dx=g(x)e∫f(x)dx,{\displaystyle y'(x)e^{\int f(x)\,dx}+f(x)y(x)e^{\int f(x)\,dx}=g(x)e^{\int f(x)\,dx},}
используем правило дифференцирования произведения
- (y(x)e∫f(x)dx)′=g(x)e∫f(x)dx{\displaystyle \left(y(x)e^{\int f(x)\,dx}\right)’=g(x)e^{\int f(x)\,dx}}
что, после интегрирования обеих частей, дает нам
- y(x)e∫f(x)dx=∫g(x)e∫f(x)dxdx+C ,{\displaystyle y(x)e^{\int f(x)\,dx}=\int g(x)e^{\int f(x)\,dx}\,dx+C~,}
- y(x)=∫g(x)e∫f(x)dxdx+Ce∫f(x)dx .{\displaystyle y(x)={\dfrac {\int g(x)e^{\int f(x)\,dx}\,dx+C}{e^{\int f(x)\,dx}}}~.}
Таким образом, решение линейного дифференциального уравнения первого порядка
- y′(x)+f(x)y(x)=g(x),{\displaystyle y'(x)+f(x)y(x)=g(x),}
(в частности, с постоянными коэффициентами) имеет вид
- y(x)=e−∫f(x)dx(∫g(x)e∫f(x)dxdx+C){\displaystyle y(x)=e^{-{\int {f(x)\,dx}}}\left(\int g(x)e^{\int {f(x)\,dx}}\,dx+C\right)}
где C{\displaystyle C} является константой интегрирования.
Пример
Возьмём дифференциальное уравнение первого порядка с постоянными коэффициентами:
- dydx+by=1.{\displaystyle {\frac {dy}{dx}}+by=1.}
Это уравнение имеет особое значение для систем первого порядка, таким как RC-схемы и масс-демпфер[неизвестный термин] системы.
В этом случае p(x) = b, r(x) = 1.
Следовательно, решение будет:
- y(x)=e−bx(ebx/b+C)=1/b+Ce−bx.{\displaystyle y(x)=e^{-bx}\left(e^{bx}/b+C\right)=1/b+Ce^{-bx}.}
Уравнения с постоянными коэффициентами
wiki.sc
НЕЛИНЕЙНОЕ УРАВНЕНИЕ — это… Что такое НЕЛИНЕЙНОЕ УРАВНЕНИЕ?
численные методы решения — итерационные методы решения нелинейных уравнений.
Под нелинейными уравнениями понимаются (см. [1] — [3]) алгебраические и трансцендентные уравнения вида  где х- действительное число,
где х- действительное число,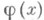 — нелинейная функция, а под системой нелинейных уравнений — система вида
— нелинейная функция, а под системой нелинейных уравнений — система вида
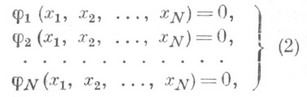
не являющаяся системой линейных алгебраич. уравнений; решением системы (2) является N-мерный вектор 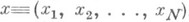 . Уравнение (1) и система (2) могут трактоваться как нелинейное операторное уравнение
. Уравнение (1) и система (2) могут трактоваться как нелинейное операторное уравнение

с нелинейным оператором L, действующим из векторного конечномерного пространства 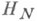 в
в 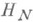 . Численными методами решения Н. у. (3) наз. итерационные методы, определяемые переходом от уже известного приближения
. Численными методами решения Н. у. (3) наз. итерационные методы, определяемые переходом от уже известного приближения 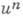 на n-й итерации к новому приближению
на n-й итерации к новому приближению 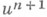 и позволяющие при достаточно большом числе итераций найти решение уравнения (3) с нужной точностью е.
Важнейшие итерационные методы приближенного решения уравнения (3) как относительно общего вида, так и специального вида, характерного для дискретных (сеточных) методов решения краевых задач для уравнений и систем уравнений с частными производными сильно эллиптич. типа, и являются предметом рассмотрения настоящей статьи. Нелинейные операторные уравнения, связанные с рассмотрением бесконечномерных пространств (см., напр., [4] — [8]), являются весьма широким математич. понятием, содержащим в себе как частные случаи, напр., нелинейные интегральные уравнения и нелинейные краевые задачи. Численные методы их приближенного решения включают в себя также методы их аппроксимации конечномерными уравнениями; эти методы рассматриваются отдельно.
и позволяющие при достаточно большом числе итераций найти решение уравнения (3) с нужной точностью е.
Важнейшие итерационные методы приближенного решения уравнения (3) как относительно общего вида, так и специального вида, характерного для дискретных (сеточных) методов решения краевых задач для уравнений и систем уравнений с частными производными сильно эллиптич. типа, и являются предметом рассмотрения настоящей статьи. Нелинейные операторные уравнения, связанные с рассмотрением бесконечномерных пространств (см., напр., [4] — [8]), являются весьма широким математич. понятием, содержащим в себе как частные случаи, напр., нелинейные интегральные уравнения и нелинейные краевые задачи. Численные методы их приближенного решения включают в себя также методы их аппроксимации конечномерными уравнениями; эти методы рассматриваются отдельно.
Одним из важнейших методов решения уравнения (3) является метод простой итерации, предполагающий возможность замены уравнения (3) эквивалентной системой

где 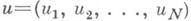 — элемент конечномерного нормированного пространства
— элемент конечномерного нормированного пространства 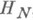 , а оператор Р, отображающий
, а оператор Р, отображающий 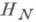 в
в 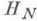 , является оператором сжатия:
, является оператором сжатия:
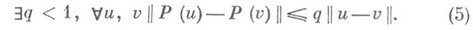
Тогда в силу общего принципа сжатых отображений (см. [1] — [4]) уравнение (1) имеет единственное решение, итерационный метод простой итерации
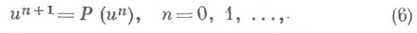
сходится при любом начальном приближении 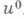 , и для погрешности
, и для погрешности 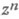 на n-й итерации справедлива оценка
на n-й итерации справедлива оценка

Пусть нек-рое решение  системы (3) удается окружить шаром
системы (3) удается окружить шаром 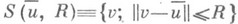 , и система (3), рассматриваемая вместе с дополнительным условием
, и система (3), рассматриваемая вместе с дополнительным условием

эквивалентна системе (4), рассматриваемой вместе с условием (7), причем неравенство (5) справедливо для 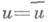 и любого
и любого 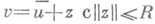 . Тогда при выборе начального приближения
. Тогда при выборе начального приближения  из
из 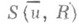 в методе (6) тоже
в методе (6) тоже
гарантируется сходимость 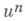 к
к 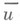 с оценкой погрешности
с оценкой погрешности
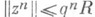
Для дважды непрерывно дифференцируемых функций 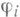 при наличии хорошего начального приближения к решению системы (2) часто эффективным методом повышения точности является метод Ньютон а- Канторовича. В этом методе уравнение
при наличии хорошего начального приближения к решению системы (2) часто эффективным методом повышения точности является метод Ньютон а- Канторовича. В этом методе уравнение 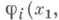
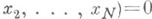 из (2), определяющее нек-рую поверхность
из (2), определяющее нек-рую поверхность 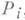 , заменяется уравнением касательной плоскости к
, заменяется уравнением касательной плоскости к 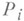 , проводимой через точку
, проводимой через точку 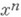 , где
, где 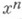 — ранее полученное приближение к решению (2) (см. [1] — [5]). При нек-рых дополнительных условиях метод Ньютона — Канторовича приводит к оценке погрешности типа
— ранее полученное приближение к решению (2) (см. [1] — [5]). При нек-рых дополнительных условиях метод Ньютона — Канторовича приводит к оценке погрешности типа

где  и
и 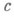 — нек-рые константы. На каждой итерации этого метода необходимо решать систему линейных алгебраич. уравнений с матрицей
— нек-рые константы. На каждой итерации этого метода необходимо решать систему линейных алгебраич. уравнений с матрицей 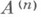 при неизвестных
при неизвестных

Иногда эту матрицу сохраняют на нескольких итерациях, иногда производные  заменяют разностными аппроксимациями.
заменяют разностными аппроксимациями.
Метод Ньютона — Канторовича относится к группе методов линеаризации (3). Другим методом из этой группы является метод секущих (см. [3]).
Большое число итерационных методов (так наз. методов спуска) (см. [1] — [3], [9], [10]) основано на замене задачи решения уравнения (3) задачей минимизации нек-рого функционала I(и). Напр., в качестве I(и)можно взять

В ряде случаев, когда исходные Н. у. сами являлись уравнениями Эйлера для задачи минимизации нек-рого функционала I(и), такая вариационная формулировка задачи является еще более естественной; операторы Lв подобных ситуациях являются градиентами функционалов I(и)и наз. потенциальными операторами (см. [5], [6]). Среди различных вариантов методов спуска можно назвать метод покоординатного спуска, различные градиентные методы и, в частности, метод наискорейшего спуска, метод сопряженных градиентов и др., а также и их модификации (см. [2] , [9], [10] и др.). Ряд итерационных методов для решения уравнений (3), описывающих нек-рое стационарное состояние, можно трактовать как дискретизации соответствующих нестационарных задач. Поэтому методы из этого класса называют установления методами (см., напр., [2]). Примером таких нестационарных задач являются задачи, описываемые системой обыкновенных дифференциальных уравнении:
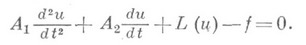
Введение дополнительной независимой переменной характерно и для метода дифференцирования по параметру (см. [5], [11]). Его суть состоит во введении вспомогательного параметра 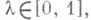 выборе непрерывно дифференцируемых функций
выборе непрерывно дифференцируемых функций 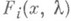 и замене системы (2) на систему
и замене системы (2) на систему
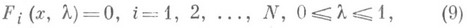
при 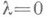 система (9) должна легко решаться, а функции
система (9) должна легко решаться, а функции 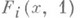 должны совпадать с
должны совпадать с 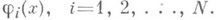 Система (9), вообще говоря, определяет
Система (9), вообще говоря, определяет 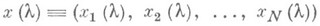 как функцию от
как функцию от 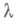 , и искомое решение системы (2) совпадает с
, и искомое решение системы (2) совпадает с 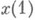 . Если систему (9) продифференцировать по
. Если систему (9) продифференцировать по  , то получится система обыкновенных дифференциальных уравнений
, то получится система обыкновенных дифференциальных уравнений
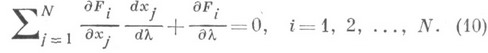
Если на отрезке 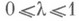 решить для нее задачу Коти с начальным условием, являющимся решением системы
решить для нее задачу Коти с начальным условием, являющимся решением системы
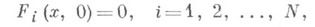
то будет найдено и нек-рое решение системы (2). Дискретизация (10) по 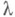 и приводит к численному методу для решения системы (2).
и приводит к численному методу для решения системы (2).
В методе продолжения по парапетру система (9) решается при 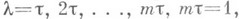 причем при каждом указанном значении
причем при каждом указанном значении 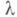
 . Оба названных метода по сути дела являются итерационными методами решения системы (2) со специальной процедурой нахождения хорошего начального приближения.
. Оба названных метода по сути дела являются итерационными методами решения системы (2) со специальной процедурой нахождения хорошего начального приближения.Для случая систем большую трудность представляет задача локализации решения. Так как большинство итерационных методов сходится лишь при наличии достаточно хорошего приближения к решению, описанные выше два метода часто позволяют избавиться от необходимости непосредственной локализации решения. Для локализации также часто используются теоремы, основанные на топологич. принципах и монотонности операторов (см. [4] — [8]).
Для решения уравнений (1), являющихся простейшими частными случаями (3), число известных и применяемых на практике итерационных методов очень велико (см., напр., [1] — [3], [12]). Помимо уже рассмотренных можно указать, напр., итерационные методы высших порядков (см. [1]), включающие в себя метод Ньютона как частный случай, и большое число итерационных методов, специально ориентированных на нахождение действительных или комплексных корней многочленов
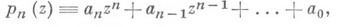
где  — действительные или комплексные числа (см. [1], [12]).
— действительные или комплексные числа (см. [1], [12]).
Проблема локализации решения уравнения (1) сводится к отысканию интервала, на концах к-рого непрерывная функция  принимает значения разных знаков. Для случая, когда
принимает значения разных знаков. Для случая, когда  является многочленом, она теряет свою остроту, т. к. известны теоретич. оценки (см. [1]) и имеются методы нахождения всех корней с нужной точностью без задания хороших приближений к ним (см. [12]).
является многочленом, она теряет свою остроту, т. к. известны теоретич. оценки (см. [1]) и имеются методы нахождения всех корней с нужной точностью без задания хороших приближений к ним (см. [12]).
Итерационные методы для решения уравнений (3), возникающих в сеточных аналогах нелинейных краевых задач для уравнений с частными производными, являются частными случаями методов решения сеточных систем (см., напр., [3], [13] — [18]). Одним из наиболее интенсивно применяемых методов решения уравнения (3), вероятно, является модифицированный метод простой итерации, записываемый в виде

Где уравнение (3) рассматривается как операторное уравнение в N-мерном евклидовом пространстве  ;
;
 , где S- обозначение множества линейных симметричных и положительных операторов, отображающих H в Н. Целесообразно изучение таких методов проводить не в пространстве H, а в пространстве Н B с новым скалярным произведением:
, где S- обозначение множества линейных симметричных и положительных операторов, отображающих H в Н. Целесообразно изучение таких методов проводить не в пространстве H, а в пространстве Н B с новым скалярным произведением:
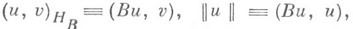
где 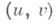 — скалярное произведение в Н.
— скалярное произведение в Н.
Если оператор Lтаков, что для него выполнены условия строгой монотонности и Липшиц-непрерывности
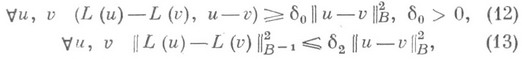
то уравнение (3) имеет единственное решение, метод (11) при подходящем выборе  сходится при любом
сходится при любом 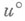 с оценкой погрешности:
с оценкой погрешности:

где  (см. [13], [15]).
(см. [13], [15]).
В более общем варианте этой теоремы достаточно требовать выполнения (12), (13) для решения м и всех v, принадлежащих шару 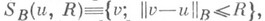 и принадлежности
и принадлежности 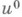 этому шару (см. [13]). В этом случае и константы
этому шару (см. [13]). В этом случае и константы 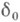 ,
, 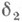 могут зависеть от R. Для проверки таких условий достаточно, напр., с помощью априорных оценок локализовать и, получая
могут зависеть от R. Для проверки таких условий достаточно, напр., с помощью априорных оценок локализовать и, получая 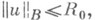 а затем, если (12) и (13) выполнены для любых ии vиз
а затем, если (12) и (13) выполнены для любых ии vиз
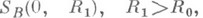 взять
взять 
В (14) константу qможно уменьшить, если оператор Lдифференцируем и для его производной  , представленной в виде суммы симметрия, части
, представленной в виде суммы симметрия, части 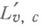 и кососимметрич. va известны неравенства
и кососимметрич. va известны неравенства
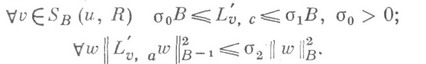
Тогда 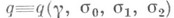 (см. [11], [13], [15]). Иногда при рассмотрении некоторых типов нелинейностей вместо (12) и (13) целесообразно использовать неравенства типа
(см. [11], [13], [15]). Иногда при рассмотрении некоторых типов нелинейностей вместо (12) и (13) целесообразно использовать неравенства типа

(см. [13]). В качестве операторов В в (11) используются, напр., расщепляющиеся разностные операторы (метод переменных направлений) и факторизуемые разностные операторы (попеременно-треугольный метод, метод неполной матричной факторизации) и др. Наиболее привлекательно с асимитотич. точки зрения использование операторов Втаких, что константы 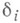 или
или 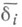 не зависят от размерности пространства HN (см. [13]), а сами операторы Вдостаточно просты. На этом пути удалось в ряде случаев строить итерационные методы, позволяющие находить решение уравнения (3) с точностью
не зависят от размерности пространства HN (см. [13]), а сами операторы Вдостаточно просты. На этом пути удалось в ряде случаев строить итерационные методы, позволяющие находить решение уравнения (3) с точностью  при затрате всего
при затрате всего 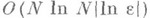 (или даже
(или даже 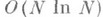 ) арифметич. действий при
) арифметич. действий при 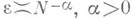 (см. [13], [14]), если затраты вычислительной работы на вычисление
(см. [13], [14]), если затраты вычислительной работы на вычисление 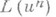 при заданном
при заданном  можно оценить как О (N). При проверке указанных условий типа (12), (13) во многих случаях большую помощь оказывают сеточные (разностные) аналоги теорем вложения С. Л. Соболева (см. [19]). Важно учитывать и специфику нелинейности. Так, напр., для случая, когда
можно оценить как О (N). При проверке указанных условий типа (12), (13) во многих случаях большую помощь оказывают сеточные (разностные) аналоги теорем вложения С. Л. Соболева (см. [19]). Важно учитывать и специфику нелинейности. Так, напр., для случая, когда 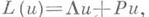 где
где 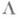 — линейный положительный оператор, а Р- квадратически нелинейный, обладающий свойством «кососимметрич»
— линейный положительный оператор, а Р- квадратически нелинейный, обладающий свойством «кососимметрич» удается часто получить константу
удается часто получить константу  в любом шаре
в любом шаре 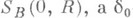 — зависящую только от
— зависящую только от 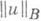 ; тогда сходимость (11) имеет место для любого
; тогда сходимость (11) имеет место для любого 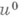 (см. [20]). В ряде случаев на основе априорных оценок можно заменить исходную задачу ей эквивалентной, для к-рой нужные условия уже выполняются во всем пространстве (см. [21] ).
(см. [20]). В ряде случаев на основе априорных оценок можно заменить исходную задачу ей эквивалентной, для к-рой нужные условия уже выполняются во всем пространстве (см. [21] ).
Лит.:[1] Березин И. С, Жидков Н. П., Методы вычислений, 3 изд., т. 1, М., 1966; [2] Бахвалов Н. С, Численные методы, 2 изд., М., 1975; [3] Ортега Дж., Рейнболдт В., Итерационные методы решения нелинейных систем уравнений со многими неизвестными, пер. с англ., М., 1975; [4] Красносельский М. А. [и др.]. Приближенное решение операторных уравнений, М., 1969; [5] Михлин С. Г., Численная реализация вариационных методов, М., 1966; [6] Вайнберг М. М., Вариационный метод и метод монотонных операторов, М., 1972; [7] Гаевский X., Грёгер К., Захариас К., Нелинейные операторные уравнения и операторные дифференциальные уравнения, пер. с нем., М., 1978; [8] Лионе Ж.-Л., Некоторые методы решения нелинейных краевых задач, пер. с франц., М., 1972; [9] Васильев Ф. П., Лекции по методам решения экстремальных задач, М., 1974; [10] Пшеничный Б. Н., Данилин Ю. М., Численные методы в экстремальных задачах, М., 1975; [11] Яковлев М. Н., «Тр. Матем. ин-та АН СССР», 1965, т. 84, с. 8-40; [12] Воеводин В. В., Численные методы алгебры. Теория и алгорифмы, М., 1966; [13] Дьяконов Е. Г., в кн.: Численные методы механики сплошной среды, т. 7, № 5, Новосиб., 1976, с. 14-78; [14] его же, в кн.: Вариационно-разностные методы в математической физике. Материалы Всесоюзной конференции, Новосиб., 1978, с. 149-64; [15] Самарский А. А., Николаев Е. С., Методы решения сеточных уравнений, М., 1978; [16] Гловински Р., Лионе Ж.-Л, Тремольер Р., Численное исследование вариационных неравенств, пер. с франц., М., 1979; [17] Келлер Г., в кн.: Разностные и вариационно-разностные методы, Новосиб., 1977, с. 8-36; [18] Кобельков Г. М., «Докл. АН СССР», 1978, т. 243, № 4, с. 843-46; [19] Дьяконов Е. Г., в кн.: Применение функциональных методов к краевым задачам математической физики, Новосиб., 1972, с. 55-62; [20] его ж е, «Acta Univ. Carolinae. Math, et Phys.», 1974, v. 15, № 1-2, p. 11 — 15; [21] Ривкинд В. Я., Уральцев а Н. Н., в кн.: Проблемы математического анализа, в. 3, Л., 1972, с. 69- 111.
Е. Г. Дьяконов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru