Решение математических уравнений с помощью помощника по преобразованию в математические выражения в OneNote
Типы проблем, поддерживаемые помощником по математическим вычислениям
При использовании помощникапо OneNote в формуле вы заметите, что в зависимости от выбранного уравнения изменяется в dropdown Select an action (Выбрать действие) под формулой. Вот некоторые из типов проблем, которые поддерживаются в зависимости от формулы, которая вы пытаетесь решить.
|
Массивы |
Для списка реальных чисел поддерживаются все ниже.
|
|
Выражения |
Для любого выражения доступны такие действия:
|
|
Уравнения и уравнения |
Для уравнений и уравнений доступны следующие действия:
|
|
Системы |
Важно иметь одинаковое количество формул и переменных, чтобы обеспечить доступ к правильным функциям. Системы можно писать двумя способами:
|
|
Производные и интегралы |
Производные могут быть записаны перед функцией с помощью d/dx или с помощью первой метки.
|
|
Матриц |
Матрицы можно в квадратных или круглых скобках. Для матриц поддерживаются следующие действия:
|
|
График в координатах |
Для графизации функции в координатах координаты r должны быть выражены как функцияta.
|
|
Сложный режим |
Примечание. Выберите Для сложных выражений и чисел, содержащих мнимую единицу i, доступны следующие действия:
|
Подробнее
Создание математического теста в Microsoft Forms
Создание математического теста для практики в OneNote с использованием помощника по преобразованию в математические выражения
Решение математических уравнений с помощью помощника по преобразованию в математические выражения в OneNote
Урок 21.
 задача. структура задачи — Математика — 1 класс
задача. структура задачи — Математика — 1 классМатематика, 1 класс
Урок 21. Задача. Структура задачи.
Перечень вопросов, рассматриваемых на уроке:
- Решение текстовых задач арифметическим способом.
- Структура задачи: условие, вопрос, решение, ответ.
- Решение задач в одно действие на увеличение (уменьшение) числа на несколько единиц.
- Задачи, содержащие отношения «больше (меньше) на..», «больше (меньше) в…».
- Дополнение условий задач недостающими данными или вопросом.
Глоссарий по теме
Компоненты задачи – условие, вопрос, решение, ответ.
Задачи на сложение и вычитание.
Взаимосвязь между условием и вопросом задачи.
Элементы задачи:
1. Условие (что известно в задаче).
2. Вопрос (что нужно узнать).
3. Решение (действие, нахождение неизвестного).
4. Ответ задачи (ответ на вопрос задачи).
Ключевые слова
Текстовая задача; условие задачи; вопрос задачи; решение задачи.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Волкова С. И., Степанова С. В. Математика. Учебник. 1 кл. В 2 ч. Ч. 1.– М.: Просвещение, 2017.– с. 88 – 89.
2. Моро М. И., Волкова С. И. Математика рабочая тетрадь. 1 кл. 1 ч.– М.: Просвещение, — с. 33 – 34.
На уроке мы узнаем, как построена задача и как называются структурные элементы задачи. Научимся решать задачи, записывать решение задачи и ответ. Сможем выделять задачи из предложенных текстов.
Основное содержание урока
Рассмотрите картинку.
Составьте задачу.
Послушайте два рассказа и сравните их:
1. В магазине мама купила 3 перца и 4 морковки. Сколько всего овощей купила мама?
2. В магазине мама купила 3 перца и 4 морковки. В овощах очень много витаминов, они очень полезные.
Какой из этих текстов мы будем изучать на уроке математики, а какой на уроке окружающего мира?
Первый текст на уроке математики, так как в нём есть вопрос, для ответа на который нужно выполнить вычисления, а второй на уроке окружающего мира.
Как называется текст с вопросом, для ответа на который нужны математические вычисления?
Такой текст называется «Задача».
Сегодня на уроке мы узнаем, какой текст называется задачей и из каких частей она состоит.
Тема нашего урока: «Задача. Структура задачи».
Посмотрите ещё раз на текст знакомой нам задачи и ответьте на вопрос.
Что в ней известно?
В магазине мама купила 3 перца и 4 морковки. Сколько всего овощей купила мама?
Что мама купила 3 перца и 4 морковки.
Это называется — условие задачи, другими словами, это то, что в задаче известно.
Что в задаче нужно узнать?
Сколько всего овощей купила мама.
Это вопрос задачи. Это о чём спрашивают в задаче, то, что нужно узнать.
Что нужно сделать, чтобы сосчитать, сколько мама купила овощей?
Нужно к трём прибавить четыре, получится семь овощей.
Это решение задачи.
Ещё раз прочитайте вопрос задачи и ответьте на него.
Мама купила семь овощей.
Это ответ задачи.
На уроке мы поймём, как построена задача – в ней есть условие и вопрос.
Будем учиться решать задачи, записывать решение задачи и ответ.
Составьте условие задачи по рисунку.
В корзинке четыре луковицы, ещё две луковицы лежат рядом.
Задайте вопрос.
Сколько всего луковиц?
Как решить такую задачу? Сложением или вычитанием?
Четыре да ещё две, задача решается сложением.
Запишем решение. К четырём прибавить два получится шесть.
Осталось записать ответ задачи. Ответим на вопрос задачи: всего шесть луковиц.
Ещё раз посмотрите внимательно на этот же рисунок:
Составьте другую задачу, которая будет решаться вычитанием:
В корзине было четыре луковицы, из неё взяли две луковицы.
Задайте вопрос.
Сколько луковиц осталось в корзине?
Как записать решение?
Из четырёх вычесть два, получится две луковицы.
Осталось записать ответ задачи.
Разбор тренировочных заданий.
Рассмотрите рисунок, дополните условие и решите задачу.
Ответ:
На огороде с одного куста сорвали 2 кабачка, а с другого куста 6 кабачков. Сколько кабачков собрали с двух кустов?
2 + 6 = 8 (к.)
Ответ: 8 кабачков.
Выберите только те тексты, которые являются математическими задачами.
Ответ:
Верные равенства обозначьте синим цветом, а неверные красным.
Ответ:
Прочитайте задачу и установите соответствия между её компонентами.
Ответ:
Попробуйте заменить овощи соответствующей цифрой.
Подсказка: у каждой цифры своя маска. На одинаковых цифрах — одинаковые маски.
Ответ:
Ответь на вопросы с помощью таблицы.
Ответ:
Покажите разным цветом, как можно получить число 6.
Ответ:
Урок 50.
 решение задач в 2 действия — Математика — 1 класс
решение задач в 2 действия — Математика — 1 классМатематика
1 класс
Урок №50
Решение задач в 2 действия
Перечень вопросов, рассматриваемых в теме:
Глоссарий по теме:
Задача – это математический рассказ, в котором есть условие и вопрос. Чтобы ответить на вопрос задачи, ее нужно решить.
Части задачи – условие, вопрос, решение, ответ.
Список литературы:
1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др.Математика. 1 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ –6-е изд. – М.: Просвещение, 2015. – с.62, 63
2. Волкова С. И. Математика. Проверочные работы. 1 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2014.- с.50, №2, с.51, №2
3. Волкова С. И. Математика. Рабочая тетрадь. 1 кл. 2 часть: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2016.-с.33
Теоретический материал для самостоятельного изучения
Решим задачу.
В одной коробке 6 карандашей, во второй на 2 карандаша меньше. Сколько карандашей в двух коробках?
О чём говорится в задаче? Правильно, о коробках и карандашах.
Что нам известно в задаче? Что в одной коробке было 6 карандашей.
Что сказано о количестве карандашей во второй коробке? Их на 2 меньше, чем в первой коробке.
Что нужно узнать в задаче? Сколько карандашей в двух коробках? Сразу можно ответить на вопрос задачи? Сразу ответить на вопрос задачи нельзя, потому что не сказано, сколько карандашей во второй коробке. Как это можно узнать? От шести отнять два. Теперь можно узнать, сколько всего карандашей в двух коробках? Да.
Составим план решения задачи:
1) Сначала надо узнать, сколько карандашей во второй коробке.
2) Потом можно узнать, сколько всего карандашей в двух коробках.
Решение:
1) 6 – 2 = 4 (к.)
2) 6 + 4 = 10 (к.)
Ответ: всего 10 карандашей.
Рассуждая так же, решим следующую задачу.
На верхней полке 6 книг, а на нижней – на 4 книги больше. Сколько книг на двух полках?
О чём говорится в задаче? О полках и книгах.
Сколько книг на верхней полке? Шесть.
Сколько книг на второй полке? Неизвестно, но сказано, что на 4 книги больше. Т.е. их столько же, сколько на верхней полке, и ещё четыре.
Что нужно узнать в задаче? Сколько книг на двух полках.
Можно ли сразу узнать, сколько книг на двух полках? Нет.
Почему? Мы не знаем, сколько книг на второй полке.
Как найти, сколько книг на второй полке?
Нужно к шести прибавить четыре,получится десять книг.
Теперь можем узнать, сколько книг на двух полках? Да.
Составим план решения задачи:
1) Сначала надо узнать, сколько книг на нижней полке.
2) Потом можно узнать, сколько книг на двух полках.
Решение:
1) 6 + 4 = 10 (кн.)
2) 6 + 10 = 16 (кн.)
Ответ: 16 книг на двух полках.
Тренировочные задания.
1. Выберите задачу, которая решается два действия
Выберите задачу, которая решается два действия
Варианты ответов:
1. На одной полке стоят 4 книги, на другой — на 3 книги больше. Сколько книг на второй полке?
2. На одной клумбе распустилось 6 тюльпанов, а на другой — на 3 тюльпана меньше. Сколько тюльпанов распустилось на двух клумбах?
3. На первой проволоке 5 шариков, на второй — на 4 шарика больше. Сколько шариков на второй проволоке?
Правильный ответ:
2.На одной клумбе распустилось 6 тюльпанов, а на другой — на 3 тюльпана меньше. Сколько тюльпанов распустилось на двух клумбах?
2. Решите задачу и выделите цветом правильное решение.
В одной вазе лежало 6 яблок, в другой на 3 яблока меньше. Сколько яблок в двух вазах?
Варианты ответов:
Первый вариант: 6 – 3 = 3 (яб.)
Второй вариант: 6 + 3 = 9 (яб.)
Третий вариант:
1) 6-3=3 (яб.)
2) 6+3=9 (яб.)
Вспомним, что эта задача решается в 2 действия, следовательно, верным будет третий вариант.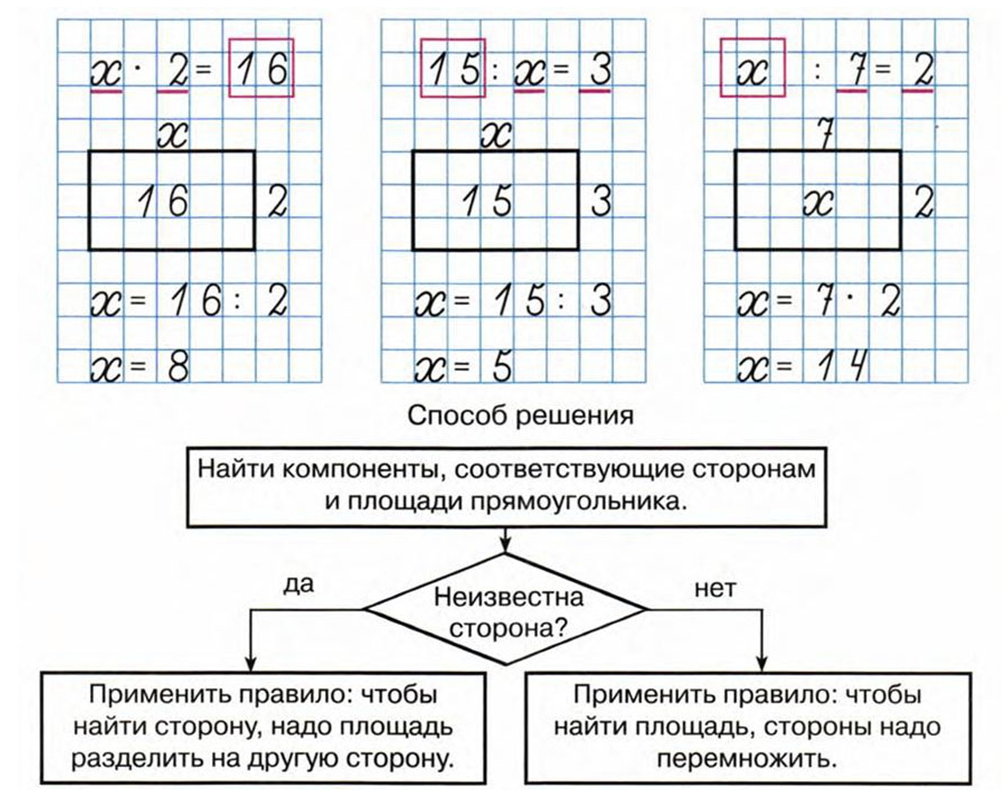
Правильный ответ:
1) 6-3=3 (яб.)
2) 6+3=9 (яб.)
Задачи и примеры
В трёх посёлках живут 18200 чел. В первом 4570 чел, во втором на 1635 чел больше, чем в первом. Сколько человек живёт в третьем посёлке?
На компе 2 диска. Диск c и диск d. Если с диска d на диск c перенести 24 мб, то на обоих дисках будет поровну. А если с диска c на диск d перенести 27 мб, то на диске d будет в 2 раза больше.
Сплав олова содержит 6 процентов. Сколько килограммов олова содержится в 520 кг сплава?
На трех клумбах растёт 320 кустов. На второй растёт на 40кустов больше, чем на первой, а на третей в трижды больше, чем на второй. Сколько кустов растёт на первой грядке?
Один гончар заработал 1300 тенге, а другой, изготавливая такие же изделия, 1950 тенге. Сколько изделий изготовил каждый из них, если первый изготовил на 2 изделия меньше второй?
Было 36м. ткани. Израсходовали на костюм 16м., на брюки 14м. Сколько метров ткани осталось?
ткани. Израсходовали на костюм 16м., на брюки 14м. Сколько метров ткани осталось?
Поезд вышел в восемь часов утра и прибыл на конечную станцию в одиннадцать часов утра следующих суток. Сколько часов он был в пути?
В двух экскурсионных катерах могут разместиться 300 пассажиров. В первом катере мест в 3 раза больше, чем во втором. Сколько мест в каждом катере.
Кирилл разделил задуманное им натуральное число на 4, потом разделил задуманное число 6, а затем разделил задуманное число на 7, получил в каждом из случаев некоторый остаток. Сумма этих остатков равна 14. Какой остаток дает задуманное Кириллом число при делении на 21?
Найдите второй корень уравнения х²–19х+18=0, если х=1
Не решая следующего уравнения, определите знаки их корней х²+4х–5=0
В магазин привезли 9 ящиков с апельсинами по 12 кг в каждом, и несколько ящиков с мандаринами. Всего привезли 188 кг апельсинов и мандаринов. Сколько кг мандаринов привезли в магазин.
Всего привезли 188 кг апельсинов и мандаринов. Сколько кг мандаринов привезли в магазин.
Сумма внутренних углов выпуклого многоугольника в 2 раза больше суммы его внешних углов. Найдите количество сторон такого многоугольника.
В классе 26 пятиклассников, из них 18 умеют танцевать, 11 умеют петь, 7 учеников умеют и то, и другое. Сколько учеников не умеют ни петь, ни танцевать?
Из треугольника со сторонами 39см, 34 см, 27см. вырезали треугольник со сторонами 9см, 7см, 4см. Определите периметр полученный формы.
Взяли 320000т, на 14 дней, под 15 процентов. Сколько будет переплата?
Если 4725 умножить на натуральное число а, то получится квадрат целого числа, а если 4725 умножить на натуральное число b, то получится куб целого числа. Найти наименьшее возможное значение a + b.
Найдите сумму всех нечетных чисел от 11 до 65 включительно арифметической прогрессии.
Первая труба пропускает на 4 л воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 221 литров она заполняет на 8 минут дольше, чем вторая труба заполняет резервуар объёмом 153 литра?
Гномы собрали подарки детям на новый год. В каждый подарок они сложили 150г шоколадных конфет и 300г карамельных. На складе имелось 2 ящика шоколадных и 5 ящиков карамельных конфет по 10кг. Какое наибольшее количество подарков собрали гномы?
App Store: Mathway — решатель задач
Mathway — мировой лидер среди программ для решения задач, в арсенале которого миллиарды решенных задач и которому доверяют миллионы пользователей. От элементарной алгебры до комплексных расчетов, Mathway мгновенно решает самые сложные математические задачи — просто введите условия задачи (или наведите камеру и сделайте фото!) и вы немедленно получите бесплатный ответ. Необходимы подробные, пошаговые решения? Mathway — как карманный частный репетитор, который без промедления помогает в решении домашних заданий в любом месте и в любое время.
Необходимы подробные, пошаговые решения? Mathway — как карманный частный репетитор, который без промедления помогает в решении домашних заданий в любом месте и в любое время.
Mathway охватывает все уровни математики, в том числе:
Начальную математику (арифметика, целые числа, дроби, десятичные числа, корни, коэффициенты и многое другое)
Алгебру (линейные уравнения/неравенства, квадратные уравнения/неравенства, абсолютные уравнения/неравенства, системы уравнений, логарифмы, функции, матрицы, графики и многое другое)
Тригонометрию / начало анализа (тригонометрические функции, тождества, конические сечения, векторы, матрицы, комплексные числа, последовательности и ряды и многое другое)
Математический анализ (пределы, производные, интегралы и многое другое)
Статистику (вероятность, перестановки, комбинации и многое другое)
Есть математическая задача? Обратитесь к Mathway.
«Простая в использовании и эффективная программа Mathway понравится любому, кому приходится решать математические задачи, от учеников старших классов до студентов институтов», — Yahoo! News
«Если вам нужно решить математические задачи, обратитесь к Mathway. Это приложение продемонстрирует весь процесс решения, чтобы вы могли параллельно учиться сами», — CNET
Это приложение продемонстрирует весь процесс решения, чтобы вы могли параллельно учиться сами», — CNET
«Mathway — незаменимый инструмент в тех случаях, когда нужно решить задачу. Это приложение помогает с домашними заданиями по математике. Оно не просто выполняет за вас задания, но и обучает правильному порядку решения. Все, что нужно сделать, — это ввести уравнение и нажать на кнопку Enter», — Lifehack
Mathway предоставляет ответы на задачи совершенно бесплатно. Для пошаговых решений доступна дополнительная ежемесячная или годовая подписка. Кроме того, Mathway предлагает дополнительную подписку на онлайн-обучение для связи с преподавателем в любое время, когда требуется дополнительная помощь. Если выбран вариант премиум-подписки:
Оплата будет списана с учетной записи iTunes при подтверждении покупки
Подписка автоматически продлевается, если автоматическое продление не будет отключено минимум за 24 часа до окончания текущего периода
С учетной записи будет снята плата за продление в течение 24 часов до окончания текущего периода подписки по тому же месячному или годовому тарифу, выбранному при ее оформлении
Подписками может управлять пользователь, а автоматическое продление можно отключить, перейдя в настройки учетной записи пользователя после покупки
Условия использования: https://www. mathway.com/terms
mathway.com/terms
Политика конфиденциальности: https://www.mathway.com/privacy
Решение развивающих задач по математике для 5-8 классов
Содержание (5 класс).
1. Математика – царица наук.
2. Приемы устного счета.
3. Решение занимательных задач.
4. Упражнения с многозначными числами.
5 .Загадки- смекалки.
6. Игры.
Решение в игровой форме заданий на знание разрядов и классов.
Формирование числовых и пространственных представлений у детей.
Закрепление знаний о классах и разрядах.
Закрепление знаний нумерации чисел.
7. Проектная деятельность «Газета любознательных».
Создание проектов. Самостоятельный поиск информации для газеты.
8. Решение нестандартных задач.
9. Наглядная алгебра.
10. Знакомьтесь: Архимед! Знакомьтесь: Пифагор!
11. Учимся комбинировать элементы знаковых систем.
12 Математический КВН.
Систематизация знаний по изученным разделам.
13-14. Круглый стол «Подведем итоги».
Систематизация знаний по изученным разделам.
Содержание (6 класс).
1. Математические аттракционы и истории.
2.Новый знак деления. Признаки делимости.
3.Алгоритм Евклида. НОД, НОК и калькулятор.
4. Использование принципа Дирихле при решении задач на делимость Рассмотреть суть принципа Дирихле; показать, как он применяется при решении задач на делимость.
5. Круги Эйлера.
6. Пифагорейский союз.
Число – это некоторые символ, определяющий многое в жизни человека.
7. Числовые ребусы (криптограмма).
Развитие логического мышления и терпения.
8. Центральная и зеркальная симметрии.
9. Денежные расчёты.
10. Житейские истории.
Решение задач различными методами.
11. Решение задач «обратным ходом».
Решение задач графическим способом. Задачи на совместную работу, связанные с задачами на движение.
12. Возраст и математика.
В молодом возрасте можно достичь многого и хорошими делами прославить своё имя.
13. Олимпиадные задачи.
14. Круглый стол «Подведем итоги».
Систематизация знаний по изученным разделам.
Содержание (7 класс).
1. Элементы истории математики.
Язык алгебры. Задача Диофанта. Старинные задачи. Листы Мебиуса. Историческая справка «Кто это, Эйлер?».
2. Действительные числа.
Числовые выражения. Вычисление значения числового выражения. Сравнение числовых выражений. Числовая прямая, сравнение и упорядочивание чисел. Пропорции. Решение задач на пропорции. Проценты. Основные задачи на проценты. Практическое применение процентов.
3. Уравнения с одной переменной.
Линейное уравнение с одной переменной. Корень уравнения. Решение линейных уравнений с одной переменной. Модуль числа. Геометрический смысл модуля. Решение уравнений, содержащих неизвестное под знаком модуля. Линейные уравнения с параметром. Решение линейных уравнений с параметром. Решение текстовых задач с помощью уравнений.
4. Комбинаторика. Описательная статистика.
Комбинаторика. Решение комбинаторных задач перебором вариантов. Графы. Решение комбинаторных задач с помощью графов. Комбинаторное правило умножения Перестановки. Факториал. Определение числа перестановок. Статистические характеристики набора данных: среднее арифметическое, мода, медиана, наибольшее и наименьшее значение. Практическое применение статистики.
5. Буквенные выражения. Многочлены.
Преобразование буквенных выражений. Деление многочлена на многочлен «уголком». Возведение двучлена в степень. Треугольник Паскаля.
6. Олимпиадные задачи.
Задачи о «мудрецах и лжецах». Логические задачи в сказочных сюжетах. Решение задач «методом дерева». Решение логических задач с помощью «спичек». Комбинации и расположения. Комбинаторика на шахматной доске. Задачи на движения. Задачи повышенной сложности. Старинные задачи. Познавательные задачи.
7. Уравнения с двумя переменными.
Системы линейных уравнений с двумя переменными. Решение систем уравнений различными способами.
Содержание (8 класс).
1.Решение текстовых задач.
Общие сведения о задачах и их решении, общие методы анализа задачи и поиска решения. Задачи на проценты. Задачи на «движение», на «концентрацию», на «смеси и сплавы». на «работу».
2.Уравнения и системы уравнений.
Способы решения различных уравнений. Различные методы решения систем уравнений (графический, метод подстановки, метод сложения). Применение специальных приёмов при решении систем уравнений.
3.Введение в теорию вероятности.
Решение задач по теории вероятности: «События и их вероятности», «Комбинаторные задачи».
4.Повторение.
Колягин Ю. М. Решение задач по математике с ответами и советами. — 2002 // Библиотека Mathedu.Ru
Колягин Ю. М. Решение задач по математике с ответами и советами. — 2002
ПодготовкатекстаПодготовка
текста
Содержание
Загрузкаструктуры
Информация
Загрузкаописаний
Справка
Загрузкасправки
Поиск
Страниц найдено: 1
Если строка в кавычках «. ..», то найдутся страницы со словосочетанием в точно такой форме.
..», то найдутся страницы со словосочетанием в точно такой форме.
Если слова указаны через пробел или оператор «&», то найдутся страницы, содержащие все введенные слова в одном предложении.
Если указано несколько слов через оператор «|», то найдутся страницы, содержащие любое из введенных слов.
Если указано два слова через оператор «~», то найдутся страницы, содержащие первое, но не содержащие второе слово в одном предложении.
По вашему запросу ничего не найдено.
Убедитесь, что слова написаны без ошибок или попробуйте выбрать другие значения.
null
Подождите,пожалуйста…
Печать
Обложка123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128Обложка (с. 4)
Подготовка [0%]…
Отмена
{«root»:»text»,»url»:»kolyagin_reshenie_zadach_po_matematike_2002″,»surl-package»:»\/text\/%PACKAGE%\/?query=%QUERY%»,»surl-page»:»\/text\/%PACKAGE%\/p%PAGE%\/?query=%QUERY%»,»query»:»\»\»»,»section»:»library»,»mode-gfx»:true,»mode-html»:true,»mode-prefer»:»gfx»,»layout-prefer»:»1×1″,»zoom»:{«1×1»:{«level»:100,»_w»:false,»_h»:true},»2×1″:{«level»:100,»_w»:true,»_h»:false},»html»:{«level»:100}},»textsize-prefer»:»2″,»textfont-prefer»:»a»,»tree-type»:»ajax»,»tree-state»:»visible»,»printbox-state»:»hidden»,»print-allowed»:»1″,»searchbox-state»:»hidden»,»searchbox-type»:»inline»,»goto-pageno»:null,»goto-page»:-1,»defw»:»800″,»defh»:»1370″,»minh»:1370,»maxh»:1370,»fixeven»:null,»package»:»left»,»sitemode»:»live»,»user»:{«uuid»:»»}}
Удерживайте правую кнопку мыши для выделения группы страниц.
Удерживайте клавишу Shift для выделения диапазона страниц.
Удерживайте клавишу Ctrl для перехода к странице без её выделения.
Позволяет находить заданные слова и словосочетания в тексте публикации.
Поиск поддерживает кириллический и латинский алфавиты.
Переключайте вид списка результатов поиска кнопками «Список» и «Карта».
Функция печати/скачивания доступна только зарегистрированным пользователям.
Пожалуйста, зарегистрируйтесь или авторизуйтесь.
Выбор оформления (светлое/тёмное) доступен только зарегистрированным пользователям.
Пожалуйста, зарегистрируйтесь или авторизуйтесь.
Какое решение по математике
Какое решение по математике
Какое решение по математике? Математический термин для решения. Решение — это значение или набор значений, которые могут удовлетворять одному или нескольким уравнениям. В зависимости от степени уравнения численные решения равны степени уравнения. Пример: (i) Для линейного уравнения количество решений равно одному.
В зависимости от степени уравнения численные решения равны степени уравнения. Пример: (i) Для линейного уравнения количество решений равно одному.
Что представляет собой пример уравнения с одним решением в математике?
Линейные уравнения с решением Пример 1. Рассмотрим уравнение 7 x 35 = 0.При решении они имеют 7 x = 35 или x = 5. Вышеупомянутое линейное уравнение верно, только если x = 5, и, следовательно, данное линейное уравнение имеет разрешение только x = 5.
Как найти набор решений уравнения?
Чтобы найти набор решений для набора подстановки, вставьте каждое значение в набор подстановки и оцените обе стороны уравнения. Если обе стороны равны, то уравнение правильное и, следовательно, значение является решением. Пример 1. Найдите набор решений 11 5w = 1 набора перестановок {0, 2, 4}.
Что означает набор решений в математике?
В математике набор решений — это набор значений, которые удовлетворяют определенному набору уравнений или неравенств.
Что означает в математике термин «решить»?
Решить (глагол) Найдите значения переменных, которые удовлетворяют системе уравнений и / или неравенств. решить (глагол) Алгебраически манипулирует уравнением или неравенством таким образом, чтобы изолировать выбранную переменную с одной стороны так, чтобы другая сторона состояла из выражения, которое можно использовать для генерации решений.
Что такое уравнение и решение в математике?
Уравнение — это алгебраическое выражение, которое связывает обычно неизвестные переменные с другими переменными или константами. Например, x + 2 = 15 — это уравнение, как и y 2 = 4. Решение или квадратный корень уравнения — это значение или набор значений, которые можно вставить в уравнение, чтобы сделать утверждение.
Что такое «набор решений» в математике?
Ряд решений. Любое значение переменных, удовлетворяющее уравнению, неравенству, системе уравнений или системе неравенств.В системе уравнений или системе неравенств набор решений — это набор, содержащий значение (значения) переменной (переменных), которые удовлетворяют всем уравнениям и / или неравенствам в системе.
Какое определение решения в математике?
Решение — это значение или набор значений, которые могут удовлетворять одному или нескольким уравнениям. В зависимости от степени уравнения численные решения равны степени уравнения. Пример: (i) Для линейного уравнения количество решений равно одному.
Что значит иметь решение в математической формуле
Решение — это значение или набор значений, которые могут удовлетворять одному или нескольким уравнениям. В зависимости от степени уравнения численные решения равны степени уравнения.
Что такое определение бесконечных решений?
Бесконечные решения будут означать, что каждое значение переменной делает уравнение истинным. Давайте посмотрим на следующее уравнение: Обратите внимание, что у вас есть переменные с обеих сторон уравнения.Итак, мы собираемся вычесть обе части, чтобы исключить правую часть уравнения.
Какое решение?
Раствор — это смесь одного вещества, растворенного в другом, поэтому его свойства везде одинаковы.
Раствор состоит из растворенного вещества и растворителя. Растворенное вещество — это вещество, которое растворяется, а растворитель — это часть раствора, которая растворяется.
Что значит иметь решение в математическом примере
Решение — это значение или набор значений, которые могут удовлетворять одному или нескольким уравнениям.В зависимости от степени уравнения численные решения равны степени уравнения. Пример: (i) Для линейного уравнения количество решений равно одному. (ii) Для квадратного уравнения численное решение равно двум и так далее.
Что означает набор решений в математических примерах
Определение набора решений уравнения обычно включает три шага: сначала вы решаете уравнение одной переменной для другой, соглашение заключается в том, чтобы найти y относительно x.Затем определите, какие значения x могут быть частью вашего набора решений. Наконец, подставьте значения x в уравнение, чтобы найти соответствующие значения y.
Как рассчитывается решение?
Расчет концентрации раствора Метод 1 из 3: Использование уравнения массы к объему. Найдите массу растворенного вещества, смешанного с растворителем. Метод 2/3: Найдите концентрацию в процентах или частях на миллион. Найдите массу растворенного вещества в граммах. Метод 3 из 3: Рассчитайте молярность.Сложите атомные массы растворенного вещества, чтобы найти молярную массу.
Каково определение решения уравнения?
Решение уравнения. Решение уравнения — это набор всех значений, которые при замене неизвестными делают уравнение истинным. Для уравнений неизвестной мощности используются два основных правила алгебры для определения их решений, включая свойство аддитивности и свойство мультипликативности.
Что значит иметь решение в математических задачах
Во-первых, решение уравнения или неравенства — это любое число, которое, когда оно связано с уравнением / неравенством, удовлетворяет уравнению / неравенству.
Что вы имеете в виду под удовлетворением? Давайте рассмотрим два примера, чтобы проиллюстрировать это.
Как создать линейное уравнение?
Шаги Убедитесь, что линейное уравнение имеет вид y = mx + b. Представьте себе число b на оси Y. Преобразуйте m в дроби. Продолжайте линию от точки b, начиная на склоне или в гору. Продолжайте вытягивать линию с помощью линейки, не забывая использовать наклон m в качестве ориентира.
Как найти значение переменной?
Для большинства простых событий используйте формулу ожидания для биномиальной случайной величины или формулу ожидания для нескольких событий.Формула математического ожидания для биномиальной случайной величины: P (x) * X. X — количество попыток, а P (x) — вероятность успеха.
Каково математическое определение решения?
Математический термин для решения. Решение — это значение или набор значений, которые могут удовлетворять одному или нескольким уравнениям. В зависимости от степени уравнения численные решения равны степени уравнения.
Пример: (i) Для линейного уравнения количество решений равно одному.(ii) Для квадратного уравнения численное решение равно двум и так далее.
Каково определение одного решения в математике?
Решение. Уравнение выкупа возникает, когда уравнение имеет только одно решение. Это означает, что при решении уравнения переменную можно заменить всего ОДНОЙ цифрой.
Что представляет собой пример уравнения с одним решением в математических десятичных дробях
Давайте рассмотрим несколько примеров добавления десятичных знаков. Пример 1: Сложение + Пример 2: Сложение + 5.Пример 3: Добавление ,, Решение: Пусть ,, y.
Как решить уравнение с десятичными знаками?
Итак, для уравнения с десятичными числами вы можете использовать тот же метод, который вы использовали для очистки дробей: умножьте обе части уравнения на наименьший общий делитель. Принимать решение:. Посмотрите на десятичные дроби и подумайте о соответствующих дробях.
Обратите внимание, что на ЖК-дисплее 100.
Есть ли только одно решение уравнения x?
Итак, есть только одно решение — ВРЕМЯ.x = 8. a Укажите в линейном уравнении ниже, имеет ли уравнение ровно одно решение, бесконечное количество решений или нет решений. Используйте свойство распределения. найти одинаковый коэффициент для x с обеих сторон.
Как решить уравнение с дробью?
КАК: Решите уравнения с дробными коэффициентами, исключив дроби. Найдите наименьший общий делитель всех дробей в уравнении. Умножьте обе части уравнения на этот ЖК-дисплей. Это исключит дроби.
Как найти количество решений линейного уравнения?
Следующая таблица помогает им найти количество решений линейного уравнения с одной переменной. В приведенном ниже линейном уравнении укажите, имеет ли уравнение решение, бесконечное количество решений или нет решения. Добавьте по 3 с обеих сторон. Оттянитесь по 2 раза с каждой стороны. Разделите каждую сторону на 2. Подставим в это уравнение x = 8.
Разделите каждую сторону на 2. Подставим в это уравнение x = 8.
Что такое уравнение решения
Решение уравнения — это значение переменной, которая делает утверждение истинным при включении в уравнение.Нахождение решения уравнения называется решением уравнения. Найти решение уравнения — это значит найти значение переменной, которая делает уравнение истинным. Что такое калькулятор переменных?
Что значит найти решение уравнения?
В математике решение уравнения означает нахождение его решений, которые являются значениями (числами, функциями, величинами и т. Д.), Удовлетворяющими условию, заданному уравнением, которое обычно состоит из двух выражений, связанных равными подписать.При поиске решения одна или несколько свободных переменных идентифицируются как неизвестные.
Как найти решение уравнения?
Чтобы решить эту проблему, сначала необходимо объединить s в правой части уравнения. Это даст вам.
Затем вычтите y из обеих частей уравнения, чтобы получить. Наконец, разделите обе части на числа, чтобы получить ответ.
Каково решение уравнения с двумя переменными?
Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо.В этом примере упорядоченная пара (4.7) (4, 7) является решением линейной системы уравнений. Вы можете проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.
Как рассчитать систему уравнений?
Решение умножением Запишите одно уравнение поверх другого. Умножайте одно или оба уравнения до тех пор, пока одна из переменных в двух членах не будет иметь равные коэффициенты. Сложите или вычтите уравнения. Решайте до конца срока.Вставьте член обратно в уравнение, чтобы найти значение первого члена. Проверьте свой ответ.
Что представляет собой пример уравнения с одним решением в листах математики
Линейные уравнения с примером решения 1: Рассмотрим уравнение 7x — 35 = 0. При решении они имеют 7 x = 35 или x = 5. Приведенное выше линейное уравнение верно только если x = 5 и, следовательно, данное линейное уравнение имеет разрешение только x = 5.
При решении они имеют 7 x = 35 или x = 5. Приведенное выше линейное уравнение верно только если x = 5 и, следовательно, данное линейное уравнение имеет разрешение только x = 5.
Имеет ли уравнение одно истинное решение?
Однако возможно, что уравнение не может иметь более одного решения, или бесконечное число решений, или вообще не иметь решения.Отсутствие решения означает, что уравнение не имеет ответа, а бесконечные решения уравнения означают, что любое значение переменной делает уравнение истинным.
Когда системы уравнений имеют одно решение?
Решение Уравнение выкупа — это когда уравнение имеет только одно решение. Когда уравнение имеет бесконечное количество решений, это означает, что если бы переменная была преобразована в число, уравнение было бы либо истинным, либо истинным, независимо от числа или значения.Уравнение без решения — это когда, несмотря ни на что, никакое число не делает уравнение истинным.
Как вы решаете уравнения?
Решение уравнений с одной переменной Напишите задачу. Определите, хотите ли вы выделить переменный член путем сложения или вычитания. Добавление или вычитание константы из обеих частей уравнения. Исключите коэффициент переменной делением или умножением. Найдите переменную.
Определите, хотите ли вы выделить переменный член путем сложения или вычитания. Добавление или вычитание константы из обеих частей уравнения. Исключите коэффициент переменной делением или умножением. Найдите переменную.
Каково решение уравнений?
Решение уравнения — это набор всех значений, которые при замене неизвестными делают уравнение истинным.Для уравнений с неизвестной в единственной степени для определения их решений используются два основных правила алгебры, включая свойство сложения и свойство мультипликативности.
Ситуационное уравнение
Ситуационное уравнение — это уравнение, которое представляет ситуацию повествовательной задачи. Уравнение решения — это уравнение, которое представляет операцию, необходимую для решения переменных. Переменная представляет собой букву, представляющую неизвестное число.
Какие примеры уравнений?
Уравнение — это утверждение, которое выражает равенство двух математических выражений.
У уравнения есть знак равенства, выражение справа и выражение слева. Примеры уравнений. 3x + 3 = 2x + 4: левая часть уравнения равна 3x + 3, а правая часть — 2x + 4.
Какой пример уравнения?
Уравнение определяется как состояние равенства и часто представляется как математическое выражение с равными значениями с обеих сторон или относится к проблеме, требующей учета множества факторов.Пример уравнения: 2 + 2 = 3 + 1.
Что такое среднее уравнение?
Уравнение — это математическое утверждение, что две вещи равны. Он состоит из двух выражений, по одному с каждой стороны от знака равенства.
Какое определение ситуации?
Определение ситуации. общее состояние стечения обстоятельств в любой момент времени, сложившаяся международная ситуация опасна; кто-то задается вопросом, как возникло это состояние; Вечные истины не являются истинными или вечными, если они не приводят к новому настроению Франклина для каждой новой социальной ситуации.
Что представляет собой пример уравнения с одним решением в математике, который показывает
Существует только одно решение для одной переменной. Например, уравнение x + 2 = 0 имеет только одно решение, такое как x = 2. Но в случае линейного уравнения с двумя переменными решения вычисляются как декартовы координаты точки на евклидовой плоскости.
Что такое ситуационное уравнение
Ситуационное уравнение — это уравнение, которое представляет ситуацию повествовательной задачи.Уравнение решения — это уравнение, которое представляет операцию, необходимую для решения переменных. Переменная представляет собой букву, представляющую неизвестное число.
Что представляет собой пример уравнения с одним решением в математическом определении
В случае переменной существует только одно решение, поэтому x + 2 = 0. Однако в случае линейного уравнения с двумя переменными решения вычисляются как декартовы координаты точки на евклидовой плоскости.
Что такое определение линейных уравнений и примеров? Уравнение с максимальным порядком 1 называется линейным уравнением.
Сколько решений имеет уравнение?
Система двух линейных уравнений может иметь одно решение, бесконечное число решений или не иметь решения. Системы уравнений можно классифицировать по количеству решений.
Какие примеры нелинейных уравнений?
Примерами нелинейных дифференциальных уравнений являются уравнения Навье-Стокса в гидродинамике и уравнения Лотки-Вольтерра в биологии. Одна из самых больших проблем с нелинейными задачами состоит в том, что обычно невозможно объединить известные решения в новые решения.
Какие есть три метода решения системы уравнений?
Три наиболее часто используемых метода решения систем уравнений — это подстановка, исключение и расширенные матрицы.
Как вы проверяете решение системы уравнений?
Чтобы проверить систему уравнений с помощью подстановки, замените значения x и y в исходных уравнениях. Если оба упрощенных выражения верны, ваш ответ правильный. Например: Чтобы проверить, было ли (2, −3) правильным решением для системы уравнений: y = −2x + 1 и y = x — 5, замените x на 2 и y на 3 в каждом уравнении.
Если оба упрощенных выражения верны, ваш ответ правильный. Например: Чтобы проверить, было ли (2, −3) правильным решением для системы уравнений: y = −2x + 1 и y = x — 5, замените x на 2 и y на 3 в каждом уравнении.
Каковы этапы решения уравнения?
Решение линейного уравнения: пять шагов к успеху.
Шаг 1 : Найдите распределение для ().
Шаг 2 : Объедините одинаковые термины с каждой стороны знака =.
Шаг 3 : Сложите или вычтите термины из переменных, чтобы все переменные находились по одну сторону от знака =.
Как правильно решить уравнение?
Чтобы решить уравнение, используйте свойство суммирования тяги, чтобы преобразовать данное уравнение в эквивалентное уравнение формы x = a, из которого вы можете проверить, чтобы найти решение.Пример 3 Решите 2x + 1 = x 2.
Каковы шаги для решения уравнения?
Используйте следующую процедуру для решения уравнений. Этапы решения уравнений
Шаг 1 : Очистите дробные и десятичные дроби путем умножения каждого члена в уравнении с помощью дисплея наименьшего общего делителя (ЖКД).
Шаг 2 : Снимите скобы при электромонтаже.
Шаг 3 : объединяет все похожие термины на одной странице.
Как решить уравнение со ступенями?
ШАГИ ДЛЯ РАЗРЕШЕНИЯ УРАВНЕНИЙ В НЕСКОЛЬКО ШАГОВ.
Шаг 1 Используйте свойство распределения.
Шаг 2 Выровняйте одинаковые элементы с каждой стороны.
Шаг 3 Переместите переменные в одну часть уравнения.
Шаг 4 Отменить сложение или вычитание.
Шаг 5 Отмените умножение или деление.
Как вы решаете уравнения с помощью подстановки?
Замена — это метод решения системы уравнений путем исключения всех переменных, кроме одной, в одном из уравнений и последующего решения этого уравнения.Это достигается путем выделения другой переменной в одно уравнение и последующей подстановки значений этих переменных в другое уравнение.
Какое решение системы уравнений?
Решение системы уравнений — это набор значений одной переменной, которым одновременно удовлетворяют все уравнения. Чтобы решить систему уравнений, вы должны найти все наборы значений переменных, которые представляют решения системы.
Чтобы решить систему уравнений, вы должны найти все наборы значений переменных, которые представляют решения системы.
Как найти решение уравнения на два
1) Сначала сложите обе части линейного уравнения с одинаковым числом.2) Во-вторых, умножьте или разделите обе части линейного уравнения на одно и то же число. 3) * вместо
step # 2 всегда умножайте обе части уравнения на обратную величину коэффициента переменной. Пример 1. Решите следующее уравнение в два этапа.
Что такое решение системы уравнений?
Система уравнений — это набор из двух или более уравнений с одним и тем же набором неизвестных. Решая систему уравнений, они пытаются найти значения для каждой из неизвестных, которые удовлетворяют всем уравнениям в системе.Уравнения системы могут быть линейными или нелинейными.
Что такое два линейных уравнения?
- Убедитесь, что линейное уравнение имеет вид y = mx + b.
- Нарисуйте число b на оси Y.
 Ваш b всегда будет рациональным числом.
Ваш b всегда будет рациональным числом. - Преобразовать м в дроби.
- Начните удлинение линии от точки b вверх по склону или вверх по склону.
- Продолжайте вытягивать линию с помощью линейки, не забывая использовать наклон m в качестве ориентира.
Какое уравнение не имеет решения?
Иногда уравнения не имеют решения.Это означает, что независимо от того, какое значение вставлено перед переменной, вы всегда будете получать противоречие. Ознакомьтесь с этим руководством, чтобы узнать, что нужно сделать, чтобы ваше уравнение оставалось неразрешенным.
Как найти решение уравнения на основе
Вы можете решить систему уравнений, заменив значение y второго уравнения первым. Пересечение первых двух прямых равно (1,1). Теперь вы можете найти пересечение второй и третьей линий.
Какой пример набора решений?
Ряд решений.Фамилия. Определение набора решений — это группа чисел, которая может удовлетворять уравнению.
Примерный диапазон решений: 0, 1 и 2 для 4×4. <4.
Какое решение задается в математике?
В математике набор решений — это набор значений, которые удовлетворяют определенному набору уравнений или неравенств.
Что означает одно решение в математике?
Решение Уравнение выкупа — это когда уравнение имеет только одно решение. Это означает, что при решении уравнения переменную можно заменить всего ОДНОЙ цифрой.
Каково определение решения в математике?
Ряд решений. Любое значение переменной или переменных, которые удовлетворяют уравнению, неравенству, системе уравнений или системе неравенств. В системе уравнений или системе неравенств набор решений — это набор, содержащий значение (значения) переменной (переменных), которые удовлетворяют всем уравнениям и / или неравенствам в системе.
Значение приостановки в науке
Что такое приостановка? Суспензия определяется как гетерогенная смесь, в которой твердые частицы распределены в жидкости, но не растворяются в ней. Суспензия определяется как гомогенная смесь частиц диаметром более 1000 нм, так что частицы видны невооруженным глазом.
Суспензия определяется как гомогенная смесь частиц диаметром более 1000 нм, так что частицы видны невооруженным глазом.
Что означает отстранение с точки зрения науки?
Суспензия — это смесь, в которой мелкие частицы взвешены в жидкости, где они переносятся плавучестью (химическим составом), веществом, состоящим из двух или более веществ, смешанных вместе (не в твердых телах и без химической связи).
Что означает «приостановлено» с точки зрения науки?
В науке суспензия — это смесь, в которой мелкие частицы вещества диспергированы в газе или жидкости.
Что такое приостановка в науке?
Определение подвески. В химии суспензия — это гетерогенная смесь твердых и жидких частиц. Чтобы быть суспензией, частицы не должны растворяться в жидкости.
Какой пример суспензии в химии?
Частицы и жидкость смешиваются так, что частицы диспергируются в жидкости. Они взвешены в жидкости. Важной характеристикой раствора является то, что твердые частицы со временем оседают и оседают, если их оставить в покое.Примером затирки является смесь воды и песка.
Они взвешены в жидкости. Важной характеристикой раствора является то, что твердые частицы со временем оседают и оседают, если их оставить в покое.Примером затирки является смесь воды и песка.
Что означает набор решений в математических неравенствах
Набор решений — это набор значений, удовлетворяющих заданному неравенству. Это означает, что каждое значение в наборе решений удовлетворяет неравенству, и никакое другое значение не удовлетворяет неравенству. Как найти набор решений? Набор замены — это набор значений, которые можно заменить переменной.
Каково решение этого неравенства?
Набор решений — это набор значений, удовлетворяющих заданному неравенству.Это означает, что каждое значение в наборе решений удовлетворяет неравенству, и никакое другое значение не удовлетворяет неравенству.
Какое множество решений уравнения x = 0?
Набор решений единственного уравнения x = {displaystyle x = 0} — это набор {0}. 2. Для любого ненулевого многочлена f {стиль отображения f} над комплексными числами в переменной множество решений состоит из конечного числа точек.
Как решить систему неравенства?
Система неравенств очень похожа, за исключением того, что вы работаете с неравенствами вместо уравнений! Чтобы решить такую систему, вы должны найти значения переменных, которые делают каждое неравенство одновременно истинным.Это руководство познакомит вас с системами неравенства.
Какой пример решения в науке?
Раствор представляет собой гомогенную смесь двух или более компонентов с размером частиц менее 1 нм. Распространенными примерами растворов являются растворы сахара в воде и соли в воде, газированной воде и т. Д. В растворе все компоненты имеют форму ступени. Есть однородность частиц. Частицы распределены равномерно.
Каковы характеристики решения в науке?
- Раствор — это однородная смесь двух или более веществ.
- Растворенные в растворе частицы не видны невооруженным глазом.
- Раствор не рассеивает световые лучи.
- Решение стабильное.
- Вещество, растворенное в растворе, не может быть отделено фильтрованием (или механическим способом).

- Состоит из фазы.
Какое простое решение в науке?
Simple Solutions Science предлагает мини-классы обучения и основана на стандартах академического содержания, общих в большинстве штатов.Эта серия поддерживает получение степени магистра в четырех областях: научные исследования, науки о Земле и космосе, науки о жизни и физика. Долгосрочная лояльность — это цель ежедневной распределенной практики, основанной на подходе простых решений.
В чем научный смысл решения?
В химии раствор — это особый вид гомогенной смеси двух или более веществ.
Как найти набор решений?
Чтобы найти набор решений уравнения с определенным диапазоном, необходимо сначала вставить каждое значение диапазона в уравнение, чтобы получить соответствующие значения диапазона.Составьте упорядоченные пары этих значений и запишите их как набор. Этот набор — ваш ответ!
Какие есть примеры решений в химии?
- Вода
- Этанол
- Метанол
- Н-пропанал
- Бутанол
- Эфир
- Дихлорметан
- сероуглерод
- глицерин
- Ацетон
Какие бывают типы растворов в химии?
Растворы, в которых растворителем является жидкость, а растворенное вещество — газ, жидкость или твердое вещество, широко используются.
Есть три типа растворов: газообразные растворы, жидкие растворы и твердые растворы. газообразные растворы.
Какое значение имеют растворы в химии?
Растворы играют очень важную роль во многих биологических, лабораторных и промышленных химикатах. Особый интерес представляют растворы с веществами, растворенными в воде или водных растворах. Решения — это системы равновесия, и выводы предыдущей главы снова будут представлять особый интерес.
Что означает в химии слово раствор?
Раствор: в химии однородная смесь двух или более веществ в относительных количествах, которые могут непрерывно изменяться до так называемого предела растворимости. Термин «раствор» часто используется для обозначения жидкого состояния, но также возможны растворы газов и твердых веществ.
Что такое решение по математической алгебре
Чувство. Решение. плюс Одно или несколько значений, которые можно использовать для замены переменной (например, x), которая делает сравнение истинным. Пример: x + 2 = 7. Если вы замените 5 на x, вы получите: 5 + 2 = 7,5 + 2 = 7 истинно, тогда x = 5 — решение. См .: переменная.
Пример: x + 2 = 7. Если вы замените 5 на x, вы получите: 5 + 2 = 7,5 + 2 = 7 истинно, тогда x = 5 — решение. См .: переменная.
Как мне решать алгебру?
Решите двухэтапное уравнение, умножая вместо деления в конце. Принцип решения этого типа уравнения тот же: используйте арифметику для соединения констант, изолировать переменную-член, а затем изолировать переменную, не являющуюся членом. Предположим, вы работаете с уравнением x / 5 + 7 = 3.
Что такое подстановка в алгебре?
Подстановка — это фундаментальная операция в алгебре.В системах компьютерной алгебры это часто называют pod или pod. Распространенным случаем подстановки являются полиномы, когда замена числового значения неопределенным (одномерным) полиномом сводится к вычислению полинома на этом значении.
Какое решение в математическом построении графиков
Иллюстрированное определение решения: значение или значения, заменяющие переменную (например, x), которая делает уравнение истинным.
Что такое решение в математическом определении
Определение решения (иллюстрированный математический словарь) Иллюстрированное определение решения: значение или значения, которые можно заменить переменной (например, x), которая делает уравнение истинным.
Есть ли решение для каждой математической задачи?
У каждой проблемы есть решение, но не совсем. Вы должны решить проблему и принять реальность. Математика не может научить их, как добавить любви или уменьшить ненависть. Но это дает им все основания надеяться, что для каждой проблемы есть решение.
Что такое решение в математике
Другими словами, решение — это значение или набор значений (по одному для каждого неизвестного), так что когда уравнение заменяется неизвестными, оно становится равенством.Решение уравнения часто называют корнем уравнения, особенно, но не только для полиномиальных уравнений.
Что такое решение в математических терминах
Определение решения (иллюстрированный математический словарь) Иллюстрированное определение решения: значение или значения, которые вы можете подставить вместо переменной (например, x), которая делает уравнение истинным.
Mathematical Solution — обзор
5.8. Неравновесные жидкостные системы и наш космологический «двигатель»
С другой стороны, мы можем посмотреть на «тепловое ощущение» наших планетных экосистем, которое, в целом, зависит от расположения в межзвездном пространстве [9, 191].Ни одна планета не является замкнутой системой и не находится в контакте с двумя или более термальными ваннами. Каждая планета находится в контакте с горячим излучателем (солнце ∼ 5800 K) и стоками холодного излучения (космическое пространство ∼ 2,75 K). Таким образом, каждая планета реализует своего рода «особый космологический двигатель». Сфера имеет решающее значение из-за ее режимов вращения и вращения с наклонной осью, которые ответственны за богатство и сложность поведения, вызванного солнечным притоком. Движение атмосферной жидкости добавляет изюминку хаоса, так что термодинамические события, происходящие на планете, поддерживаются неравновесными потоками, которые должны подчиняться фундаментальным законам неравновесной термодинамики.
Если бы наша атмосфера была жесткой, ее термодинамика не содержала бы никаких хаотических явлений. Если бы Земля была жесткой однородной сферой без атмосферы и, следовательно, без альбедо или нисходящей диффузии, прямой приток Солнца можно было бы рассчитать без каких-либо специальных экспериментальных измерений. В каждую точку поверхности приток солнечного света будет равен тригонометрическому коэффициенту, умноженному на солнечную постоянную, строго изменяющемуся вдоль открытой поверхности. Соседняя планета Марс активна таким образом, поэтому, если бы мы ее колонизировали, нам нужно было бы сначала создать ее альбедо, создав ретроактивно отражающую атмосферу при введении CO 2 из минеральных источников или просто доставив «земной тип». загрязнение »(как в нашей атмосфере), необходимое для повышения температуры поверхности и обеспечения возможности таяния и испарения воды, погребенной в почве.Этот процесс может быть относительно коротким по сравнению со следующим этапом, которым должно быть создание пригодной для жизни среды с помощью соответствующего процесса (посадки) для введения кислорода. Однако есть много других препятствий, которые необходимо преодолеть, например, слишком высокий уровень опасной радиации (которая экранируется от Земли ее экраном из магнитного поля). Поверхность планеты Венера, напротив, чрезвычайно горячая, потому что ее атмосфера плотная и непрозрачная из-за высокой концентрации отражающих назад компонентов и частиц (содержащих даже капли H 2 SO 4 ), которые, следовательно, демонстрируют: чрезвычайно сильное атмосферное движение.Из-за очень особого характера внешнего космологического состояния граничные условия для планет определяют возможность существования экосистемы, а именно диссипативной системы с устойчиво поддерживаемой жизнеспособностью. Мы можем ожидать очень сложную циркуляцию доступности по планете. Мы можем определить глобальную физическую экосистему как систему, которая удовлетворяет следующим свойствам: она замкнута в отношении массообмена (занимает конечную область), но открыта в отношении энергии (исходящий поток соответствует полученному) и является в глобальном устойчивом состоянии в течение более длительного периода (энергетический баланс).
Однако есть много других препятствий, которые необходимо преодолеть, например, слишком высокий уровень опасной радиации (которая экранируется от Земли ее экраном из магнитного поля). Поверхность планеты Венера, напротив, чрезвычайно горячая, потому что ее атмосфера плотная и непрозрачная из-за высокой концентрации отражающих назад компонентов и частиц (содержащих даже капли H 2 SO 4 ), которые, следовательно, демонстрируют: чрезвычайно сильное атмосферное движение.Из-за очень особого характера внешнего космологического состояния граничные условия для планет определяют возможность существования экосистемы, а именно диссипативной системы с устойчиво поддерживаемой жизнеспособностью. Мы можем ожидать очень сложную циркуляцию доступности по планете. Мы можем определить глобальную физическую экосистему как систему, которая удовлетворяет следующим свойствам: она замкнута в отношении массообмена (занимает конечную область), но открыта в отношении энергии (исходящий поток соответствует полученному) и является в глобальном устойчивом состоянии в течение более длительного периода (энергетический баланс).
Пока что космическая экосистема предлагает только один пример, Землю, и это может быть ее только одна реализация . Земля развивалась как гетерогенная термодинамическая система, состоящая из многих компонентов во всех трех фазах — газа, жидкости и твердого тела, и с их межфазными границами сложного характера. Его математическое решение, даже категорически сокращенное, бесконечно сложно: либо простейшее, использующее только один компонент и одну фазу в однородном виде, либо другое, с двумя несмешивающимися компонентами, предполагая гетерогенную концепцию, или многие другие, включая химические реакции и сложные оценки с помощью конечных элементов, решеток и т. д.. Дополнительное разнообразие биохимических циклов стало таким же сложным, как определение самой жизни. Проблемы предсказуемости со все более сложными нелинейными моделями всегда чрезвычайно раздуваются.
Рис. 28. Слева показано соотношение энтропии между Солнцем и Землей, в то время как правый эскиз предлагает проблемы с энтропией, которые приводят к тому, что наш мир находится в постепенном, но повторяющемся спиралевидном развитии. В центре показано глобальное представление энергии, получаемой от Солнца, в сравнении с одноразовыми капитальными ресурсами энергии, доступными на Земле, как схематично показано кубами, связанными друг с другом (на вставке показан исходный спектр, запускаемый Солнцем и его ступенчатые изменения при достижении внешней атмосферы и в конечном итоге собираются на уровне моря).
В центре показано глобальное представление энергии, получаемой от Солнца, в сравнении с одноразовыми капитальными ресурсами энергии, доступными на Земле, как схематично показано кубами, связанными друг с другом (на вставке показан исходный спектр, запускаемый Солнцем и его ступенчатые изменения при достижении внешней атмосферы и в конечном итоге собираются на уровне моря).
Например, давайте посмотрим на температурное поле и его уменьшение и проследим за температурой в данном пространственном элементе. Мы ожидаем, что после периода в один год или в среднем за десять лет или около того, эта температура повторится с определенной точностью. Нарушения его ожидания можно отнести к локальным хаотическим взаимодействиям (быстрые неоднородности), глобальным хаотическим взаимодействиям (медленные неоднородности) и, наконец, к антропогенным модификациям энергетического баланса, таким как введение избыточного CO 2 на земную поверхность. .Теперь, учитывая поле плотности других компонентов (SO 2 , аэрозоли) и его уменьшение методом конечных элементов, мы снова ожидаем лишь небольших изменений; в противном случае Земля стала бы термически или химически отравленной. Конечно, это может стать результатом внезапного извержения вулкана или внезапного удара метеорита, но в последнее время стабильно обеспечивается человеком, который, таким образом, является странным обитателем Экосистемы и, в то же время, наиболее гибким и очень уязвимым. . Он не переносит перепадов давления, химического состава окружающей среды и особенно температуры.Разница в температуре здорового тела составляет около одного градуса, поэтому человеку нужна сложная система контроля тела, а также укрытие — дом и одежда. Существует очевидная разница между живым существом (саморазвитая система управления) и всей экосистемой Земли (определяется солнечным излучением).
Конечно, это может стать результатом внезапного извержения вулкана или внезапного удара метеорита, но в последнее время стабильно обеспечивается человеком, который, таким образом, является странным обитателем Экосистемы и, в то же время, наиболее гибким и очень уязвимым. . Он не переносит перепадов давления, химического состава окружающей среды и особенно температуры.Разница в температуре здорового тела составляет около одного градуса, поэтому человеку нужна сложная система контроля тела, а также укрытие — дом и одежда. Существует очевидная разница между живым существом (саморазвитая система управления) и всей экосистемой Земли (определяется солнечным излучением).
Мощность на квадратный метр поверхности Земли — не большая цифра, но этот скромный дар — то, что дала нам природа. Любое особенно стабильное общество могло уживаться; поколения динозавров жили в равновесии с этим числом в течение ста миллионов лет, человечество также управляло в течение нескольких тысячелетий, пока не начало увеличивать свою популяцию и продвигать свои технологии. Наконец, в последнее столетие, страдающее от жажды, мгновение относительно истории, небольшой процент человечества развил тенденцию к потреблению ископаемой энергии, которая не соответствует естественным порядкам величины мощности, которые, вероятно, решила космическая эволюция. дать нам. Иногда трудно поверить, что мы недостаточно умны, действуем без научной совести, а просто движимы соблазном ускоряющегося роста.
Наконец, в последнее столетие, страдающее от жажды, мгновение относительно истории, небольшой процент человечества развил тенденцию к потреблению ископаемой энергии, которая не соответствует естественным порядкам величины мощности, которые, вероятно, решила космическая эволюция. дать нам. Иногда трудно поверить, что мы недостаточно умны, действуем без научной совести, а просто движимы соблазном ускоряющегося роста.
В первом приближении рассмотрим Солнце как стабильный источник распределенных Планка фотонов при температуре T s = 5800 K на его внешнем радиусе R s .Фотоны, которые покидают Солнце, движутся во всех направлениях и без взаимодействия опускаются на бесконечность или, лучше сказать, приходят в равновесие с ископаемым источником при температуре около 2,7 К. Мы можем определить температуру T d , на расстоянии d, которое составляет T d = T s √ (d / R s ) > 1. Для излучения энтропии Солнца выполняется аналогичное соотношение: S d ./S s . = √ (d / R s ) > 1.Если бы твердая Земля была черной жесткой сферой с радиусом R E и с прозрачной атмосферой, потоки внутрь и наружу задавались бы простыми граничными условиями T и R. Относительное движение Земли и Солнца создает периодическую функцию f с периодом p, которая воплощает непрерывность массы, уравнение Навье-Стокса и соотношения энергетического баланса для атмосферы, которые все еще очень далеки от достоверности. Стационарное распределение устойчивых равновесий соответствует мощности механической мощности, которая может быть выражена распределением бесконечного числа двигателей Карно, глобальная эффективность которых может быть сформулирована в общих терминах с помощью математики.Он аппроксимируется соотношением, η global = ∫ [λ (T 1 -T 2 ) 2 / max (T 1 .
Для излучения энтропии Солнца выполняется аналогичное соотношение: S d ./S s . = √ (d / R s ) > 1.Если бы твердая Земля была черной жесткой сферой с радиусом R E и с прозрачной атмосферой, потоки внутрь и наружу задавались бы простыми граничными условиями T и R. Относительное движение Земли и Солнца создает периодическую функцию f с периодом p, которая воплощает непрерывность массы, уравнение Навье-Стокса и соотношения энергетического баланса для атмосферы, которые все еще очень далеки от достоверности. Стационарное распределение устойчивых равновесий соответствует мощности механической мощности, которая может быть выражена распределением бесконечного числа двигателей Карно, глобальная эффективность которых может быть сформулирована в общих терминах с помощью математики.Он аппроксимируется соотношением, η global = ∫ [λ (T 1 -T 2 ) 2 / max (T 1 . T 2 )] dS / R 2 δT 4 , где λ и δ — соответственно общая теплопроводность Ньютона (фиксированная как 8 Вт / м 2 K) и константы излучения Стефана-Больцмана (обеспечивая δT 4 ≈ 1384 Вт / м 2 ). Вычисленные значения η global находятся в районе сотых.
T 2 )] dS / R 2 δT 4 , где λ и δ — соответственно общая теплопроводность Ньютона (фиксированная как 8 Вт / м 2 K) и константы излучения Стефана-Больцмана (обеспечивая δT 4 ≈ 1384 Вт / м 2 ). Вычисленные значения η global находятся в районе сотых.
Биологическая сеть взаимодействует с термодинамической экосистемой (фактически является «термодинамически живой»), так что это не пассивная стадия, а архитектура жизнеобеспечения. Глобальный подход способствует лучшему пониманию концепции глобальной устойчивости, регулирующей распределение локальных неравновесий. Если бы у Земли была нерегулярная орбита, проблема не допускала бы глобального устойчивого решения, и если бы, помимо суточной и годовой периодичности, были бы дополнительные нерегулярные движения, не было бы ни глобальной устойчивости, ни менее ограничивающего свойства глобального периодичность.Серьезным осложнением является изменение либо солнечного излучения, либо геометрии взаимной орбиты, что подразумевает изменения входных условий для экосистемы Земли и, как известно, происходит в определенные часто повторяющиеся короткие (30, 70 или 150 лет) или длительные ( тысячи и миллионы лет) интервалы, зависящие в основном от Солнца, но также имеющие много хаотических компонентов (извержений).
Отметим, что орбита Земли, к счастью, близка к круговой, но не полностью. Его эллиптичность меняется в течение года, но его влияние слишком слабое (3%), чтобы вызывать мгновенные сезоны, но достаточно сильное по своей строгости, регрессируя примерно на один полный день каждые 58 лет.Земля достигает перигелия (ближайшей точки к Солнцу) в начале января, но эта дата не остается фиксированной, а медленно регрессирует. Тропический год измеряется между двумя весенними равноденствиями (это основа нашего григорианского календаря), а между двумя перигелиями лежит аномальный год (примерно на 25 минут дольше), который полностью проходит через тропический год примерно за 21000 лет. Большая часть этой разницы связана с небольшим изменением направления оси вращения Земли в космосе, называемым прецессией, которая наклонена от нормали к плоскости орбиты под углом 23 градуса и прецессирует каждые 23000 лет.Эксцентриситет земной орбиты периодически меняется с временной шкалой около 100 000 лет, так что климатологически он может стать императивным, если положительно модулировать вместе с 21 000 циклом перигелия. Еще одна вариация за 41 000 лет — наклон, отличный от прецессии. Эти астрономические фазы часто называют циклами Миланковича и циклами (по теории сербского инженера-строителя), но их истинное влияние на климатические изменения еще не ясно.
Еще одна вариация за 41 000 лет — наклон, отличный от прецессии. Эти астрономические фазы часто называют циклами Миланковича и циклами (по теории сербского инженера-строителя), но их истинное влияние на климатические изменения еще не ясно.
Однако в космологическом масштабе концепция изолированной системы становится неосуществимой, потому что определение даже границ нашего соседства сложно (поскольку Солнце окружено далеко идущим дисперсным слоем, полным водоворотов и ужасных струй и нашей земной атмосферы. диффузный и полный движения, содержащий разреженные ионы со сверхбыстрыми потоками наружу), и уравнения движения жидкости не выполняются.Эти изменения входных условий вызывают еще один динамический режим атмосферных и океанических движений (помимо изменений в составе, структуре и т. Д.). Поскольку эти модификации снова являются нелинейными, никто не может предсказать или знать, каким может быть результирующий эффект по отношению к тому, что мы испытали или можем решить из истории.
Перейдем к примеру возобновляемого двигателя, а для этого рассмотрим термодинамику Земли. Это система, находящаяся примерно в глобальном устойчивом неравновесном состоянии, что означает, что более или менее уравновешиваются входящие и исходящие потоки излучения.Мы можем вспомнить стандартный термодинамический подход для рассмотрения пространственной области, Ом, с элементарным объемом d 3 v → с координатами, v → (x, y, z), граница, Ω B , и время t, принимая плотность, ρ (v → , t), скорость жидкости , v ( v → , t), и температуру, T ( v → , t), , которые не все локально стационарны.Диссипация энергии w (необратимость или производство энтропии) происходит от теплопроводности (∇T) и вязкого сдвига (тензор, σ ij ) и содержит сложный поддерживаемый поток неравновесий, которому соответствует рассеиваемая доступность для естественная система , w d n = σ ij ∂v i / ∂x (k) + λ (∇T) 2 / T (указано в [ Вт / м 3 ]). Плотность мощности постоянно создается и рассеивается, и это мощность, заключенная в естественном движении.Если мы знаем решение естественной динамики, мы могли бы построить величину w, вычислить ее численно, и это будет оценка рассеиваемой мощности Земли. Его интеграл по объему был бы фундаментальным глобальным числом, определяющим стационарные глобальные условия планеты, так сказать, ее «здоровье». На самом деле это продолжение истории классического двигателя, который производит механическую работу, и эта работа немедленно превращается в тепло. Бензин — это солнечное излучение, и окружающая среда совпадает с двигателем, потому что нет «внешнего» для глобального окружения.Правую часть вышеупомянутого уравнения можно разделить на две части, первая — это доступность сдвига, а вторая — доступность Карно. Для активной системы (обычно называемой «доступностью ветряной мельницы») второй термин объединяется с термином «механическая мощность», что дает Вт a = λ (∇T) 2 / T + v → ∇ P, , который технически является источником энергии подходящих плотин, ветряных мельниц и т.
Плотность мощности постоянно создается и рассеивается, и это мощность, заключенная в естественном движении.Если мы знаем решение естественной динамики, мы могли бы построить величину w, вычислить ее численно, и это будет оценка рассеиваемой мощности Земли. Его интеграл по объему был бы фундаментальным глобальным числом, определяющим стационарные глобальные условия планеты, так сказать, ее «здоровье». На самом деле это продолжение истории классического двигателя, который производит механическую работу, и эта работа немедленно превращается в тепло. Бензин — это солнечное излучение, и окружающая среда совпадает с двигателем, потому что нет «внешнего» для глобального окружения.Правую часть вышеупомянутого уравнения можно разделить на две части, первая — это доступность сдвига, а вторая — доступность Карно. Для активной системы (обычно называемой «доступностью ветряной мельницы») второй термин объединяется с термином «механическая мощность», что дает Вт a = λ (∇T) 2 / T + v → ∇ P, , который технически является источником энергии подходящих плотин, ветряных мельниц и т. Д., Построенных человеком, в то время как остаточное рассеивание, σ ij ∂v i / ∂x (k) , кроме незначительная задержка ничего не меняет в естественном кровообращении.Таким образом, мы можем рассматривать естественные движения как петлю, питаемую доступностью, которая создает движение, которое, в свою очередь, создает доступность, которая, в свою очередь, рассеивается и снова создает движение, и так далее. Естественная и активная системы действительно разные.
Д., Построенных человеком, в то время как остаточное рассеивание, σ ij ∂v i / ∂x (k) , кроме незначительная задержка ничего не меняет в естественном кровообращении.Таким образом, мы можем рассматривать естественные движения как петлю, питаемую доступностью, которая создает движение, которое, в свою очередь, создает доступность, которая, в свою очередь, рассеивается и снова создает движение, и так далее. Естественная и активная системы действительно разные.
Их совместное рассмотрение эквивалентно рассмотрению сжигания определенного количества бензина в природе, и посмотреть, что произойдет, если мы сожжем его внутри двигателя. Эти движения могут быть периодическими (или, лучше сказать, хаотическими) в зависимости от температурных градиентов.В тех местах, где (λ (∇T) 2 / T) и (v → ∇ P ) особенно велики, может произойти выброс механической энергии, обычно в виде пузырьков роста в горшок с горячей вулканической магмой. Он многому нас учит. Мы узнали, что в растянутый период солнечное излучение непостоянно, а его диаграмма излучения частично периодична, а частично хаотична. Конечным результатом является то, что экосистема Земли имеет чрезвычайно сложную термодинамическую конфигурацию [191, 192] с наличием хаоса, перекрывающего преобладающую периодичность.Это показывает физический факт, что фундаментальные числа возникли в результате чистого использования глобальной формулировки; в общем, это в основном температура Солнца, разделительное расстояние и сфероидичность Земли. Данная доступность на самом деле является оболочкой или, лучше сказать, явлением интерфейса, особенно при введении в модель изучения химических реакций и детального движения жидкости, которые обязательно сходятся вместе, потому что подавляющее большинство процессов происходит в жидком состоянии.Непонятно, какое количество химических реакций следует брать в описание, по крайней мере, биофизический цикл CO 2 (рост → 6CO 2 + 6H 2 O = C 6 H 12 O 6 + 6O 2 ← горение) является наиболее важным.
Он многому нас учит. Мы узнали, что в растянутый период солнечное излучение непостоянно, а его диаграмма излучения частично периодична, а частично хаотична. Конечным результатом является то, что экосистема Земли имеет чрезвычайно сложную термодинамическую конфигурацию [191, 192] с наличием хаоса, перекрывающего преобладающую периодичность.Это показывает физический факт, что фундаментальные числа возникли в результате чистого использования глобальной формулировки; в общем, это в основном температура Солнца, разделительное расстояние и сфероидичность Земли. Данная доступность на самом деле является оболочкой или, лучше сказать, явлением интерфейса, особенно при введении в модель изучения химических реакций и детального движения жидкости, которые обязательно сходятся вместе, потому что подавляющее большинство процессов происходит в жидком состоянии.Непонятно, какое количество химических реакций следует брать в описание, по крайней мере, биофизический цикл CO 2 (рост → 6CO 2 + 6H 2 O = C 6 H 12 O 6 + 6O 2 ← горение) является наиболее важным. Фактически сама природа изобрела сверхсложные химические циклы, и теперь человек в своей богатой империи пытается развить какие-то невежественные и аналогичные нарушения.
Фактически сама природа изобрела сверхсложные химические циклы, и теперь человек в своей богатой империи пытается развить какие-то невежественные и аналогичные нарушения.
Понятно, что хорошие идеи для теории экологического укрытия человека могут возникнуть в результате изучения диссипативных обучающих систем, т.е.е. такие адаптивные системы, которые пригодны для выживания. Земля обладает необходимой жизнеспособностью, сложностью и равновесной стабильностью, что является предпосылкой для ее выживания. Иерархия взаимодействий может помочь сформулировать концепцию, согласно которой человек — это не детерминированная система, а скорее финалистическая система или, лучше сказать, система контроля. Таким образом, экосистема видов имеет более простое внешнее взаимодействие, а экосистема, как гигантский двигатель, очень сложный внутри, имеет довольно упрощенное и почти ничтожное взаимодействие с самой Вселенной, что позволяет рассматривать ее как все же детерминированный мир.Следовательно, увидеть существование островов порядка, которые питают возможность разумной жизни, является глубокой тайной. Изучение и более широкое применение истинно неравновесной термодинамики и теории хаоса имеет смысл, но есть большая, неизученная область, помимо той, которая касается, в частности, неравновесной термодинамики самой среды Земли.
Изучение и более широкое применение истинно неравновесной термодинамики и теории хаоса имеет смысл, но есть большая, неизученная область, помимо той, которая касается, в частности, неравновесной термодинамики самой среды Земли.
Алгебра — Решения и наборы решений
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-1: Решения и наборы решений
Мы начнем эту главу с довольно короткого раздела с некоторой базовой терминологией, которую мы довольно регулярно используем при решении уравнений и неравенств.? 0 \\ 9–9 & = 0 \\ 0 & = 0 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
Итак, мы спрашиваем, равна ли правая сторона левой стороне после того, как мы подключим предложенное решение. В этом смысл символа «?» над знаком равенства в первой строке.
Поскольку правая и левая части совпадают, мы говорим, что \ (x = 3 \) удовлетворяет уравнению.
b \ (y = 8 \) in \ (3 \ left ({y + 1} \ right) = 4y — 5 \) Показать решение
Итак, мы хотим увидеть, удовлетворяет ли \ (y = 8 \) уравнению.? 4 \ left (8 \ right) — 5 \\ 27 & = 27 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
Итак, \ (y = 8 \) удовлетворяет уравнению и, следовательно, является решением.
c \ (z = 1 \) in \ (2 \ left ({z — 5} \ right) \ le 4z \) Показать решение
В этом случае мы имеем неравенство, и в этом случае «удовлетворить» означает что-то немного другое. В этом случае мы будем говорить, что число будет удовлетворять неравенству, если после его подключения мы получим в результате истинное неравенство.
Давайте проверим \ (z = 1 \).? 4 \ left (1 \ right) \\ — 8 & \ le 4 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
Итак, -8 меньше или равно 4 (на самом деле меньше), и мы имеем истинное неравенство. Следовательно, \ (z = 1 \) будет удовлетворять неравенству и, следовательно, является решением
d \ (z = — 5 \) in \ (2 \ left ({z — 5} \ right) \ le 4z \) Показать решение
Это то же неравенство с другим значением, давайте это проверим.
\ [\ begin {align *} 2 \ left ({- 5 — 5} \ right) & \ mathop \ le \ limits ^? 4 \ left ({- 5} \ right) \\ — 20 & \ le — 20 \, \, \, \, {\ mbox {OK}} \ end {align *} \]В этом случае -20 меньше или равно -20 (в данном случае оно равно), и поэтому мы снова получаем истинное неравенство, и поэтому \ (z = — 5 \) удовлетворяет неравенству и поэтому будет решением.
Мы также должны сделать быстрый пример чисел, которые не являются решением, чтобы мы могли увидеть, как они будут работать.
Пример 2 Покажите, что следующие числа не являются решениями данного уравнения или неравенства.- \ (y = — 2 \) в \ (3 \ left ({y + 1} \ right) = 4y — 5 \)
- \ (z = — 12 \) в \ (2 \ left ({z — 5} \ right) \ le 4z \)
В этом случае мы делаем то же самое, что и в предыдущем примере.? 4 \ left ({- 2} \ right) — 5 \\ — 3 & \ ne — 13 \, \, \, \, {\ mbox {НЕ ОК}} \ end {align *} \]
Итак, -3 — это не то же самое, что -13, и поэтому уравнение не выполняется. Следовательно, \ (y = — 2 \) не является решением уравнения.
b \ (z = — 12 \) in \ (2 \ left ({z — 5} \ right) \ le 4z \) Показать решение
На этот раз неравенство.? 4 \ left ({- 12} \ right) \\ — 34 \ require {cancel} & \ bcancel {\ le} — 48 \, \, \, \, {\ mbox {NOT OK}} \ end {align * } \]
В этом случае -34 НЕ меньше или равно -48, поэтому неравенство не выполняется.2} — 9 = 0 \). В этом случае \ (x = — 3 \) также является решением.
Мы называем полный набор всех решений набором решений для уравнения или неравенства. Есть также некоторые формальные обозначения для наборов решений, хотя мы не будем часто их использовать в этом курсе. Несмотря на это, мы все равно должны это признать.
Для уравнений мы обозначаем множество решений, заключая все решения в фигурные скобки \ (\ left \ {{} \ right \} \). Вот наборы решений для двух уравнений, которые мы рассмотрели выше.2} — 9 & = 0 & \ hspace {0,25 дюйма} & {\ mbox {Набор решений}}: \, \, \, \ left \ {{- 3,3} \ right \} \ end {align *} \]
Для неравенств используются аналогичные обозначения. В зависимости от сложности неравенства набор решений может быть одним числом или диапазоном чисел. Если это одно число, мы используем те же обозначения, что и для уравнений. Если набор решений представляет собой диапазон чисел, как тот, который мы рассмотрели выше, мы будем использовать так называемую нотацию конструктора наборов .Вот набор решений для неравенства, которое мы рассмотрели выше.
\ [\ left \ {{z | z \ ge — 5} \ right \} \]Это читается как: «Множество всех \ (z \) таких, что \ (z \) больше или равно -5».
Большинство неравенств, которые мы будем рассматривать, будут иметь достаточно простые наборы решений, которые мы часто сокращаем как
\ [z \ ge — 5 \]Есть еще одна последняя тема, которую мы должны затронуть в отношении наборов решений, прежде чем покинуть этот раздел.2} &
Если мы ограничимся только реальными решениями (что мы не всегда будем делать), тогда у уравнения не будет решения. Возведение в квадрат \ (x \) делает \ (x \) больше нуля, затем добавление 1 к этому означает, что левая часть гарантированно будет не меньше 1. Другими словами, у этого уравнения нет реального решения. По той же основной причине нет решения неравенства. Возведение любого вещественного \ (x \) в квадрат делает его положительным или нулевым, и поэтому никогда не будет отрицательным.
Нам нужен способ обозначить тот факт, что здесь нет решений.В обозначении набора решений мы говорим, что набор решений пустой , и обозначаем его символом: \ (\ emptyset \). Этот символ часто называют пустым набором .
Теперь нам нужно сделать пару заключительных замечаний, прежде чем покинуть этот раздел.
В приведенном выше обсуждении пустых множеств мы предполагали, что ищем только реальные решения. Хотя это то, что мы будем делать с неравенствами, мы не будем ограничиваться реальными решениями с уравнениями.2} + 1 = 0 \) действительно имеет сложные решения.
Наконец, как отмечалось выше, мы не будем часто использовать нотацию набора решений в этом курсе. Это хорошее обозначение, которое иногда может использоваться, особенно для сложных решений. Однако для подавляющего большинства уравнений и неравенств, которые мы будем рассматривать, будут достаточно простые наборы решений, так что их будет проще записать и отпустить. Следовательно, это то, что мы не будем использовать для обозначений наших наборов решений.Однако вы должны знать обозначения и понимать, что они означают.
Руководство по математическим задачам и решениям | K Squared Publishing
Нетехническая книга, которая объясняет математику от счета до исчисления. Темы основываются друг на друге, предоставляя читателю полный обзор математики. Эта книга разделена на три раздела — элементарный (числа, сложение, вычитание, умножение, деление, дроби, проценты, отрицательные числа, показатели, предалгебра), промежуточный (решение одного алгебраического уравнения, решение системы уравнений, задачи со словами. , функции, построение графиков, геометрия, измерение геометрических фигур, тригонометрия) и расширенный (логарифмы, комплексные числа, нахождение геометрии, использование алгебры, введение в исчисление, производная, интеграл).Это не текст, а обсуждение, включающее множество отработанных примеров. Для родителей, студентов или всех, кто хочет разбираться в математике. Также полезен как исчерпывающий справочник по математике. Нет смысла иметь текст без практики концепций. Учащиеся читают содержание основного текста «Понимание математики», затем заполняют соответствующий раздел в руководстве по решениям (сопутствующем). Первая половина руководства предлагает советы, примеры, объяснения, упражнения и задачи для практики.Содержание каждой главы основывается на предыдущей главе, а начальные задачи включают новую концепцию, представленную в основном тексте, и более сложные задачи с несколькими концепциями к концу главы. Во второй половине книги даются решения всех проблем книги. Резюме главы из 20 вопросов завершает каждую главу. Текст вместе с руководством по решениям обеспечивает дополнительную практику в определенных областях навыков, позволяет учащимся работать с опережением учебного плана для дополнительной задачи или может использоваться для всестороннего обзора перед прохождением стандартизированного теста.sc. ~ Ан / ДоннаВековые, вековые математические затруднения находят новые решения
Ряд нерешенных загадок теории чисел, называемых диофантовыми проблемами, появился 3700 лет назад. За прошедшие годы математики отказались от них, и недавние работы позволили добиться значительного прогресса в некоторых областях, а другие показали, что они столь же непоколебимы, как и прежде.
Исследователи использовали инструменты геометрии для решения проблем, названных в честь Диофанта, греческого математика третьего века. Они включают определение того, какие решения существуют для полиномиальных уравнений, таких как x n + y n = z n . Математики стремятся выяснить, есть ли у уравнений целочисленные или рациональные решения. Например, для x 2 + y 2 = z 2 , таких решений существует бесконечно много.
Диофантова геометрия — это область математики, сфокусированная на взаимосвязи между свойствами теории чисел уравнения, такими как его рациональные или целочисленные решения, и «геометрическими свойствами, такими как топология множества комплексных решений уравнения», — говорится в сообщении. Дэвид Корвин, математик из Университета Бен-Гуриона в Негеве в Израиле.
Удивительно, «как мало мы знаем о диофантовой геометрии по сравнению с другими областями математики», — говорит Бьорн Пунен, математик из Массачусетского технологического института.Например, он отмечает, что, хотя математики знают, что число 20 можно записать как сумму трех кубов, например, 3 3 + 1 3 + (–2) 3 = 20, может ли число 114 быть выраженным суммой трех кубиков остается открытой проблемой.
«Темная сторона»
Для некоторых диофантовых задач фокус математиков может показаться чрезмерно узким. Зачем тратить значительные усилия на то, чтобы определить, можно ли 114 записать в виде суммы трех кубов? Киран Кедлая, математик из Калифорнийского университета в Сан-Диего, говорит, что для многих диофантовых головоломок, которые легко сформулировать, «сама проблема не так важна … но методы, необходимые для ее решения, очень важны.”
Это свойство не редкость в математике. Знаменитая проблема, известная как Великая теорема Ферма, например, также более важна из-за методов, разработанных для ее решения, чем для самой проблемы, говорит Кедлая, «что не имеет особых прямых последствий для теории чисел. ” Однако инструменты, используемые для его атаки, включают ключевые достижения в теории алгебраических чисел в конце 19-го века, а также модульные формы в начале 20-го века. «Эти [разработки] невероятно важны для решения множества проблем современной теории чисел», — говорит он, включая вопросы, связанные с криптографией.
«Самые простые проблемы, как правило, являются мотивацией, которая побуждает нас разрабатывать методы, которые мы затем можем использовать для решения проблем, которые действительно говорят нам о многом», — говорит он. Например, проблема однородности Серра, относящаяся к исследованиям Кедлая, касается особого типа математической кривой, называемой модульной кривой. Однако, как отмечает Кедлая, «последствия этого довольно глубоки, и методы, которые мы используем для его применения» в различных случаях уходят корнями в более раннюю работу над проблемой Ферма.
Тем не менее, некоторые диофантовы проблемы более трудноразрешимы, чем другие. «Многие исследователи в этой области пытаются разработать новые методы решения диофантовых уравнений, — говорит Пунен, — но я работаю также над« темной стороной », пытаясь доказать, что некоторые классы проблем неразрешимы».
Новые инструменты для старых проблем
Вместо того, чтобы использовать инструменты из геометрии и других областей для решения конкретных диофантовых проблем, можно было бы разработать компьютерные программы для решения общего случая таких проблем.Но математики Мартин Дэвис, Юрий Матиясевич, Хилари Патнэм и Джулия Робинсон показали, что найти полные решения этих проблем не так просто, как поручить компьютеру поиск их. Их работа завершилась теоремой 1970 года, которая ответила на знаменитую 10-ю проблему немецкого математика Давида Гильберта. Эта проблема была сосредоточена на поиске алгоритма для определения того, существует ли для некоторой системы полиномиальных уравнений с целыми коэффициентами решение в целых числах, отмечает Кедлая.Думая, что такой алгоритм может быть найден, «Гильберт был оптимистом», — говорит Кедлая. «Гильберт был большим старанием, пытаясь решить общие классы проблем».
Но теорема Матиясевича, которую также называют теоремой DPRM или теоремой MRDP, показала, что такого алгоритма не существует. Это открытие означает, что «общая проблема такого типа, конечно, неразрешима», а отдельные примеры этих проблем могут быть «очень трудно решить», — говорит Кедлая.
Любопытно, что Корвин отмечает, что для полиномиальных уравнений (или систем таких уравнений) от нескольких переменных никто не знает, можно ли найти алгоритм для определения существования рациональных решений.«Это можно только догадываться», — говорит он. Пунен работал над тем, чтобы показать, что такой общий метод поиска решений в рациональных числах невозможен.
Что касается некоторых из этих древних вопросов, в том числе вопросов, заданных самим Диофантом, «мы только сейчас разрабатываем методы, которые могут помочь ответить на них», — говорит Дженнифер Балакришнан, математик из Бостонского университета. Например, проблема из книги Диофанта Arithmetica касается того, существуют ли положительные рациональные решения для x и y , такие, что уравнение y 2 = x 8 + x 4 + х 2 доволен.Хотя Диофант предоставил решение, которое составляет x = ½ и y = 9 ⁄ 16 , Балакришнан говорит, что до 1998 года было неизвестно, сколько других решений существовало. В докторской диссертации в Калифорнийском университете в Беркли Джозеф Ветерелл представил методы ответа на этот вопрос.
Совсем недавно Балакришнан и ее сотрудники разрабатывали новые методы для поиска аналогичных решений. По ее словам, недавним впечатляющим результатом стало новое доказательство Брайаном Лоуренсом и Акшаем Венкатешем того, что называется гипотезой Морделла.Хотя Герд Фалтингс впервые доказал гипотезу Морделла в 1983 году, работа Лоуренса и Венкатеша «дает другой взгляд на проблему, которой почти 100 лет», — говорит Балакришнан. Эти и другие достижения показывают, что интерес к диофантовой геометрии в последние годы растет, говорит Корвин, «особенно с появлением новых методов».
Обучение математике с использованием нескольких методов решения: влияние типов решений и активности учащихся
Эйнсворт, С. (2006).DeFT: концептуальная основа для рассмотрения обучения с несколькими представлениями. Обучение и инструктаж, 16 , 183–198. DOI: 10.1016 / j.learninstruc.2006.03.001.
Артикул Google Scholar
Эйнсворт, С., Бибби, П., и Вуд, Д. (2002). Изучение эффектов различных множественных репрезентативных систем в изучении начальной математики. Журнал обучающих наук, 11 , 25–61.
Артикул Google Scholar
Anghileri, J., Beishuizen, M., & Van Putten, K. (2002). От неформальных стратегий к структурированным процедурам: помните о пробелах! Образовательные занятия по математике, 49 , 149–170.
Артикул Google Scholar
Аткинсон, Р. К., Дерри, С. Дж., Ренкл, А., и Уортэм, Д. У. (2000).Учимся на примерах: обучающие принципы на основе исследования отработанных примеров. Обзор исследований в области образования, 70 , 181–214. DOI: 10.3102 / 00346543070002181.
Артикул Google Scholar
Аткинсон, Р. К., Ренкл, А., & Меррилл, М. М. (2003). Переход от изучения примеров к решению проблем: сочетание угасания с подсказками способствует обучению. Журнал педагогической психологии, 95 , 774–783.DOI: 10.1037 / 0022-0663.95.4.774.
Артикул Google Scholar
Бандура, А., и Локк, Э. А. (2003). Еще раз об отрицательной самоэффективности и целевых эффектах. Журнал прикладной психологии, 88 , 87–99. DOI: 10.1037 / 0021-9010.88.1.87.
Артикул Google Scholar
Бергер Р. (1989). Prozent — und Zinsrechnen in der Hauptschule — Didaktische Analysen und empirische Ergebnisse zu Schwierigkeiten, Lösungsverfahren und Selbstkorrekturverhalten der Schüler am Didde Calzeciten, анализируя процентное соотношение результатов средней школы и результатов расчета 259, а также процентное отношение к результатам средней школы25 и процентное решение проблем в средней школе25 [25] методы и самокоррекция поведения учащихся по окончании общеобразовательной школы.Регенсбург: С. Родерер.
Bortz, J. (1993). Statistik für Sozialwissenschaftler [Статистика для социологов] . Берлин: Springer.
Google Scholar
Коллинз А., Браун Дж. С. и Ньюман С. Е. (1989). Познавательное обучение. Обучение чтению, письму и математике. В Л. Б. Резник (ред.), Знание, обучение и обучение, (стр. 453–493). Хиллсдейл, Нью-Джерси: Эрлбаум.
Google Scholar
Инициатива Common Core State. (2012). Математика . Получено 21 января 2014 г. с сайта http://www.corestandards.org/Math.
Деци, Э. Л., и Райан, Р. М. (1993). Die Selbstbestimmungstheorie der Motivation und ihre Bedeutung für die Pädagogik [Теория самоопределения мотивации и ее значение для педагогики]. Zeitschrift für Pädagogik, 39 , 223–238.
Google Scholar
Gigerenzer, G., & Hoffrage, U. (1995). Как улучшить байесовские рассуждения без инструкции: частотные форматы. Психологическое обозрение, 102 , 684–704.
Артикул Google Scholar
Große, C. S. (2005). Lernen mit multiplen Lösungswegen [Обучение с использованием нескольких методов решения] .Мюнстер: Waxmann.
Google Scholar
Große, C. S., & Renkl, A. (2006). Эффекты множественных методов решения в обучении математике. Обучение и инструктаж, 16 , 122–138. DOI: 10.1016 / j.learninstruc.2006.02.001.
Артикул Google Scholar
Хэтти, Дж. И Тимперли, Х. (2007). Сила обратной связи. Обзор исследований в области образования, 77 , 81–112. DOI: 10.3102 / 003465430298487.
Артикул Google Scholar
Йоханнинг Д. И. (2004). Поддержка развития алгебраического мышления в средней школе: более пристальный взгляд на неформальные стратегии учащихся. Журнал математического поведения, 23 , 371–388.
Артикул Google Scholar
Калюга, С., Эйрес, П., Чендлер, П., и Свеллер, Дж. (2003). Эффект отмены экспертизы. Психолог-педагог, 38 , 23–31.
Артикул Google Scholar
Кёдингер, К. Р. и Натан, М. Дж. (2004). Реальная история проблем истории: влияние представлений на количественные рассуждения. Журнал обучающих наук, 13 , 129–164.DOI: 10.1207 / s15327809jls1302_1.
Артикул Google Scholar
Koedinger, K. R., & Tabachneck, H. J. M. (1994). Две стратегии лучше, чем одна: Использование нескольких стратегий для решения словесных задач. Представлено на ежегодном собрании Американской ассоциации исследований в области образования , Новый Орлеан, Луизиана.
Math Warehouse. (нет данных). Система линейных уравнений с 2-мя переменными. Получено 21 января 2014 г. с http: // www.mathwarehouse.com/algebra/linear_equation/systems-of-equation/index.php.
Мец, М. Л. (2010). Использование стандартов GAISE и NCTM в качестве основы для обучения теории вероятностей и статистики учителям математики начальных и средних школ. Journal of Statistics Education [онлайн], 18. Получено 20 января 2014 г. с http://www.amstat.org/publications/jse/v18n3/metz.pdf.
NCTM. (2014). Принципы и стандарты школьной математики. Получено 21 января 2014 г. с сайта http://www.nctm.org/standards/content.aspx?id=312.
Нойбранд, Дж., И Нойбранд, М. (2000). Эффект мультипликатора Lösungsmöglichkeiten: Beispiele aus einer japanischen Mathematikstunde [Эффекты нескольких решений: примеры урока японской математики]. В C. Selter & G. Walther (Eds.), Mathematikdidaktik als design science (стр. 148–158). Лейпциг: Клетт.
Google Scholar
Паас, Ф., Ренкл А. и Свеллер Дж. (2003). Теория когнитивной нагрузки и учебный дизайн: последние разработки. Психолог-педагог, 38 , 1–4.
Артикул Google Scholar
Предигер, С. (2004). «Darf man denn das so rechnen?» — Vielfalt im Mathematikunterricht [«Можно ли использовать этот метод решения?» — Разнообразие в математическом образовании]. Фридрих Ярешефт, 22 , 86–89.
Google Scholar
Ренкл А. (1997). Учимся на отработанных примерах: исследование индивидуальных различий. Когнитивная наука, 21 , 1-29.
Артикул Google Scholar
Ренкл, А. (1999). Изучение математики на основе разработанных примеров: анализ и содействие самооценкам. Европейский журнал психологии образования, 14 , 477–488.
Артикул Google Scholar
Ренкл А., Аткинсон Р. К. и Гроссе К. С. (2004). Как работает постепенное исчезновение шагов решения — перспектива когнитивной нагрузки. Instructional Science, 32 , 59–82.
Артикул Google Scholar
Ренкл А., Аткинсон Р. К. и Майер У. Х. (2000). От изучения примеров до решения проблем: постепенное исчезновение проработанных шагов решения помогает учиться.В Л. Глейтман и А. К. Джоши (ред.), Труды 22-й ежегодной конференции Общества когнитивных наук (стр. 393–398). Махва, Нью-Джерси: Эрлбаум.
Ренкл А., Аткинсон Р. К., Майер У. Х. и Стейли Р. (2002). От учебного примера к решению проблем: плавные переходы помогают обучению. Журнал экспериментального образования, 70 , 293–315.
Артикул Google Scholar
Райнберг, Ф.(2004). Motivationsdiagnostik [Диагностика мотивации] . Геттинген: Hogrefe.
Google Scholar
Риттл-Джонсон, Б., & Стар, Дж. Р. (2007). Облегчает ли сравнение методов решения концептуальные и процедурные знания? Экспериментальное исследование по обучению решению уравнений. Журнал педагогической психологии, 99 , 561–574. DOI: 10.1037 / 0022-0663.99.3.561.
Артикул Google Scholar
Риттл-Джонсон, Б., & Стар, Дж. Р. (2009). По сравнению с чем? Влияние различных сравнений на концептуальные знания и процедурную гибкость при решении уравнений. Журнал педагогической психологии, 101 , 529–544. DOI: 10.1037 / a0014224.
Артикул Google Scholar
Риттл-Джонсон, Б., Стар, Дж. Р., и Дуркин, К. (2009). Важность предварительных знаний при сравнении примеров: влияет на концептуальные и процедурные знания о решении уравнений. Журнал педагогической психологии, 101 , 836–852. DOI: 10.1037 / a0016026.
Артикул Google Scholar
Риттл-Джонсон, Б., Стар, Дж. Р., и Дуркин, К. (2012). Развитие процедурной гибкости: готовы ли новички учиться на сравнении процедур? Британский журнал педагогической психологии, 82 , 436–455. DOI: 10.1111 / j.2044-8279.2011.02037.x.
Артикул Google Scholar
Sedlmeier, P. (1999). Улучшение статистических рассуждений — теоретические модели и практическое применение . Махва, Нью-Джерси: Эрлбаум.
Google Scholar
Sedlmeier, P., & Gigerenzer, G. (2001). Обучение байесовскому мышлению менее чем за два часа. Журнал экспериментальной психологии: Общие, 130 , 380–400.DOI: 10.1037 / 0096-3445.130.3.380.
Артикул Google Scholar
Сютс, Дж. (2002). Unterschiedliche mentale Konstruktionen beim Aufgabenlösen — Eine Fallstudie zur Ma-tematik als Werkzeug zur Wissenspräsentation [Различные мысленные конструкции для решения проблем — Пример использования математики как инструмента для представления знаний]. Journal für Mathematik-Didaktik, 23 , 106–128.
Артикул Google Scholar
Спиро, Р.Дж., Фельтович, П. Дж., Якобсон, М. Дж., И Коулсон, Р. Л. (1991). Когнитивная гибкость, конструктивизм и гипертекст: инструкция произвольного доступа для получения дополнительных знаний в плохо структурированных областях. Образовательные технологии, 31 , 24–33.
Google Scholar
Спиро, Р. Дж., И Дженг, Дж. К. (1990). Когнитивная гибкость и гипертекст: теория и технология нелинейного и многомерного обхода сложных предметов.В Д. Никсе и Р. Дж. Спиро (редакторы), Познание, образование и мультимедиа: изучение идей в области высоких технологий, (стр. 163–205). Хиллсдейл, Нью-Джерси: Эрлбаум.
Google Scholar
Стар, Дж. Р. и Риттл-Джонсон, Б. (2008). Гибкость в решении проблем: случай решения уравнений. Обучение и инструктаж, 18 , 565–579. DOI: 10.1016 / j.learninstruc.2007.09.018.
Артикул Google Scholar
Стар, Дж.Р., и Риттл-Джонсон, Б. (2009). Стоит сравнивать: экспериментальное исследование вычислительной оценки. Журнал экспериментальной детской психологии, 102 , 408–426. DOI: 10.1016 / j.jecp.2008.11.004.
Артикул Google Scholar
Старк Р. (1999). Lernen mit Lösungsbeispielen. Der Einfluss unvollständiger Lösungsschritte auf Beispiel-development, Motivation und Lernerfolg [Обучение на рабочих примерах.Влияние неполных примеров на разработку примеров, мотивацию и результаты обучения] . Геттинген: Hogrefe.
Google Scholar
Старк Р., Грубер Х., Ренкл А. и Мандл Х. (2000). Instruktionale Effekte einer kombinierten Lernme-thode: Zahlt sich die Kombination von Lösungsbeispielen und Problemlöseaufgaben aus? [Учебные эффекты комбинированного метода обучения: окупается ли комбинация проработанных примеров и задач?]. Zeitschrift für Pädagogische Psychologie, 14 , 206–218.
Артикул Google Scholar
Staub, F. C., & Reusser, K. (1995). Роль презентационных структур в понимании и решении математических текстовых задач. В C. A. Weaver, S. Mannes, & C. R. Fletcher (Eds.), Понимание дискурса. Очерки в честь Вальтера Кинча (стр. 285–305). Хиллсдейл, Нью-Джерси: Лоуренс Эрлбаум Ассошиэйтс.
Google Scholar
Стерн, Э. (1993). Что делает некоторые арифметические задачи, связанные со сравнением наборов, такими трудными для детей? Журнал педагогической психологии, 85 , 7–23.
Артикул Google Scholar
Табачнек, Х. Дж. М., Кёдингер, К. Р., и Натан, М. Дж. (1994). К теоретическому учету использования стратегии и осмысления решения математических задач. Труды 16-й ежегодной конференции Общества когнитивных наук (стр. 836–841). Хиллсдейл, Нью-Джерси: Эрлбаум.
Trafton, J. G., & Reiser, B.J. (1993). Вклад изучения примеров и решения проблем в приобретение навыков. В М. Полсоне (ред.), Труды 15-й ежегодной конференции Общества когнитивных наук . Хиллсдейл, Нью-Джерси: Эрлбаум.
Ван Амером Б.А. (2003). Сосредоточение внимания на неформальных стратегиях при увязке арифметики с ранней алгеброй. Образовательные занятия по математике, 54 , 63–75.
Артикул Google Scholar
Ван Мерриенбоер, Дж. Дж. Г. (1990). Стратегии обучения программированию в средней школе: завершение программы по сравнению с генерацией программы. Журнал образовательных компьютерных исследований, 6 , 265–285.
Артикул Google Scholar
Ван Мерриенбор, Дж.Дж. Г. и де Крук, М. Б. М. (1992). Стратегии для обучения программированию на компьютере: завершение программы по сравнению с генерацией программы. Журнал образовательных компьютерных исследований, 8 , 365–394.
Google Scholar
решение [математика] синоним | Словарь синонимов английского языка
1. «Я думал, что я был глуп, провалив экзамен, но, по крайней мере, я попытался», 2. «Ты так не делаешь, тупица!» 3. «Я устал от этого дурацкого компьютера!»
образовался в результате обморока от дневной работы. Арендаторам выплачивается дарг (или дневная работа) за каждый акр.
Пр.1: Я думаю, что его источники ненадежны, и мне придется их изучить.Пример 2: Ваши тормоза немного странные, и вам следует их заменить
2. это значение популяризировано в сериале «Как я встретил вашу маму
».Пр.1: инспектор принимает во внимание предположение, что жертва могла быть дефенастрированный.Пример 2: Из-за отсутствия результатов было принято решение «дефенестрировать» менеджера.
1.Отряды тренировались, стреляли холостыми 2. Мы пытались завести ребенка целую вечность, пока серия тестов на фертильность не показала, что я стреляю холостыми.
может использоваться как существительное, так и прилагательное: подключи и работай; подключи и работай сотруднику или просто подключи и работай (существительное)
«почти» даже сильнее в соответствии с устаревшим, даже библейским стилем. «Конец света близок»
Пример: Его описывали как женоненавистника, гомофоба, ненавистника женщин / Этот сайт стал особенно язвительной питательной средой для ненавистников
большое спасибо команде за отличную работу
Пример: лектор подчеркнул необходимость целостного подхода к рыболовству
Пример: Эта клиника предлагает целостный медицинский подход к лечению лечите и тело, и разум, иногда даже используя практики восточных традиций, такие как медитация или иглоукалывание.
безумно успешным / большим / реалистичным
1. Она очень любит рассказы о жизни в ла-ла-стране 2. Он нереалистичен в этих вопросах и выглядит так, будто находится в ла-ла земля все время
Пример: у него есть неудачная и довольно опасная привычка показывать палец автомобилистам, которые режут перед ним.

 Вы также можете выбрать Graph двухуголовые диаграммы, чтобы просмотреть графики всех функций.
Вы также можете выбрать Graph двухуголовые диаграммы, чтобы просмотреть графики всех функций. Каждая сторона равенства или разнояренного права является отдельной функцией.
Каждая сторона равенства или разнояренного права является отдельной функцией.
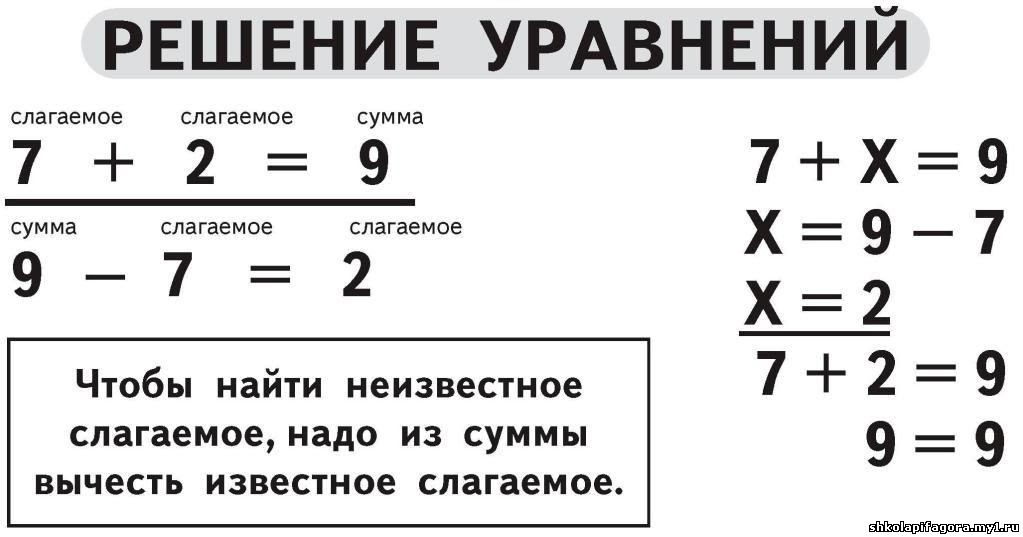
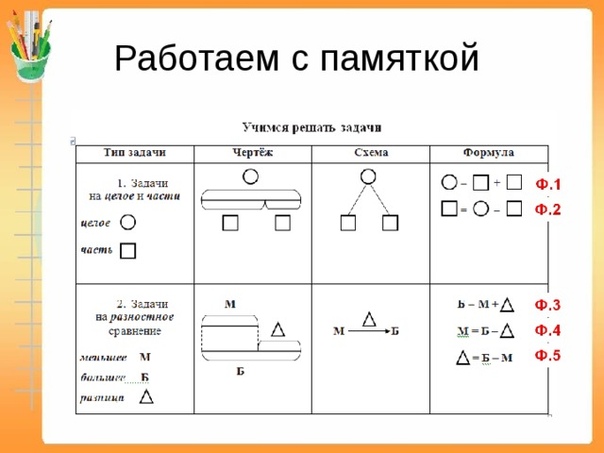
 Раствор состоит из растворенного вещества и растворителя. Растворенное вещество — это вещество, которое растворяется, а растворитель — это часть раствора, которая растворяется.
Раствор состоит из растворенного вещества и растворителя. Растворенное вещество — это вещество, которое растворяется, а растворитель — это часть раствора, которая растворяется.
 Что вы имеете в виду под удовлетворением? Давайте рассмотрим два примера, чтобы проиллюстрировать это.
Что вы имеете в виду под удовлетворением? Давайте рассмотрим два примера, чтобы проиллюстрировать это. Пример: (i) Для линейного уравнения количество решений равно одному.(ii) Для квадратного уравнения численное решение равно двум и так далее.
Пример: (i) Для линейного уравнения количество решений равно одному.(ii) Для квадратного уравнения численное решение равно двум и так далее. Обратите внимание, что на ЖК-дисплее 100.
Обратите внимание, что на ЖК-дисплее 100. Затем вычтите y из обеих частей уравнения, чтобы получить. Наконец, разделите обе части на числа, чтобы получить ответ.
Затем вычтите y из обеих частей уравнения, чтобы получить. Наконец, разделите обе части на числа, чтобы получить ответ. У уравнения есть знак равенства, выражение справа и выражение слева. Примеры уравнений. 3x + 3 = 2x + 4: левая часть уравнения равна 3x + 3, а правая часть — 2x + 4.
У уравнения есть знак равенства, выражение справа и выражение слева. Примеры уравнений. 3x + 3 = 2x + 4: левая часть уравнения равна 3x + 3, а правая часть — 2x + 4.
 Что такое определение линейных уравнений и примеров? Уравнение с максимальным порядком 1 называется линейным уравнением.
Что такое определение линейных уравнений и примеров? Уравнение с максимальным порядком 1 называется линейным уравнением. Ваш b всегда будет рациональным числом.
Ваш b всегда будет рациональным числом. Примерный диапазон решений: 0, 1 и 2 для 4×4. <4.
Примерный диапазон решений: 0, 1 и 2 для 4×4. <4.

 Есть три типа растворов: газообразные растворы, жидкие растворы и твердые растворы. газообразные растворы.
Есть три типа растворов: газообразные растворы, жидкие растворы и твердые растворы. газообразные растворы.