Треугольник / Треугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Треугольник
Треугольник — это геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, последовательно соединяющих эти точки. Указанные точки называются вершинами треугольника, а отрезки — сторонами.
Пример: Отметим точки A, B и C, которые не лежат на одной прямой.

Соединим данные точки отрезками

Получившаяся фигура называется треугольником, обозначается  ABC (читается: «треугольник ABC«). Данный треугольник также можно обозначить
ABC (читается: «треугольник ABC«). Данный треугольник также можно обозначить  BCA,
BCA,  CBA и т.д.
CBA и т.д.
Вершины треугольника: A, B, C.
Углы треугольника: 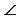 BAC,
BAC, 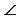 CBA,
CBA, 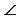 ACB (или их можно обозначать одной буквой
ACB (или их можно обозначать одной буквой 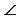
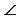 B,
B, 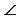 C — соответственно)
C — соответственно)Стороны треугольника: AB, BC, CA.
Периметр треугольника
Периметр треугольника — это сумма длин трех его сторон.
В нашем примере: 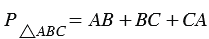 .
.
Если AB = 14 см, BC = 13 см, CA = 23 см, тогда периметр будет равен:  .
.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 7, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 254, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 309, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 540, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 676, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 807, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 887, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 996, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1098, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1152, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Основные свойства прямоугольных треугольников. Видеоурок. Геометрия 7 Класс
По определению, прямоугольный треугольник – это треугольник, в котором есть прямой угол (см. Рис. 1).
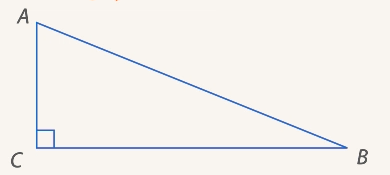
Рис. 1. Прямоугольный треугольник 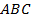 (
(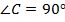 )
)
В прямоугольном треугольнике только один прямой угол. Если бы их было два, то тогда сумма этих двух углов уже была бы равна 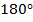
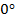 , чего в треугольнике быть не может (см. Рис. 2), т. к. по теореме о сумме углов треугольника
, чего в треугольнике быть не может (см. Рис. 2), т. к. по теореме о сумме углов треугольника 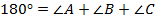 .
.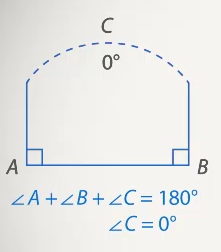
Рис. 2. Не существует треугольника с двумя прямыми углами.
Так что можно говорить только о треугольнике, в котором один прямой угол. Вспомним, что стороны, заключающие прямой угол – катеты, а третья сторона – напротив прямого угла – гипотенуза (см. Рис. 3).

Рис. 3. Катеты и гипотенуза
Теперь вспомним, что такое «свойство». Когда объект нам уже известен и мы пытаемся найти его характеристики, то обнаруженные характеристики и являются свойствами данного объекта. Таким образом, нам будет дан треугольник с прямым углом, а мы будем из этого делать какие-то выводы.
Сумма двух острых углов прямоугольного треугольника равна 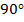 (см. Рис. 4).
(см. Рис. 4).
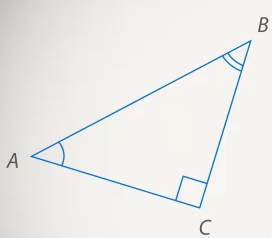
Рис. 4. 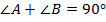
Разберемся, почему речь идет именно об острых углах. Рассмотрим 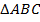 (см. Рис. 5).
(см. Рис. 5).
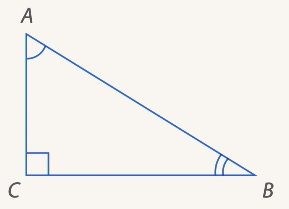
Рис. 5. Прямоугольный 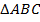
Сумма всех трех углов треугольника 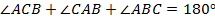 . Как мы знаем, один из углов прямоугольного треугольника
. Как мы знаем, один из углов прямоугольного треугольника 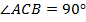 , значит, сумма оставшихся
, значит, сумма оставшихся 
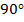 , то каждый из них меньше
, то каждый из них меньше 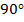 . Получили, что
. Получили, что  , то есть свойство доказано.
, то есть свойство доказано.Если в прямоугольном треугольнике один из углов равен 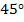 , то такой треугольник – равнобедренный.
, то такой треугольник – равнобедренный.
Доказательство. Пусть  (см. Рис. 6).
(см. Рис. 6).
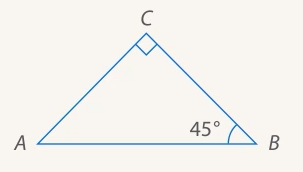
Рис. 6. Прямоугольный треугольник с углом 
Исходя из первого свойства, 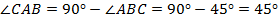 . Получаем, что
. Получаем, что  . Тогда треугольник равнобедренный по признаку – углы при основании равны (см. Рис. 7). Значит, катеты равны
. Тогда треугольник равнобедренный по признаку – углы при основании равны (см. Рис. 7). Значит, катеты равны 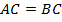 .
.
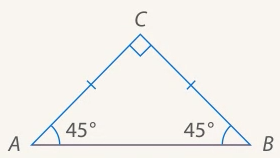
Рис. 7. Углы при основании равны – треугольник равнобедренный
Катет прямоугольного треугольника, лежащий против угла 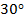 , равен половине гипотенузы (см. Рис. 8).
, равен половине гипотенузы (см. Рис. 8).

Рис. 8. Иллюстрация свойства 3
Доказательство. Рассмотрим прямоугольный 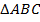 . Пусть
. Пусть 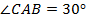 и
и 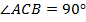 . Нужно доказать, что
. Нужно доказать, что 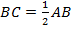 (см. Рис. 9).
(см. Рис. 9).

Рис. 9. Иллюстрация к доказательству
Отразим зеркально 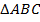 относительно катета
относительно катета 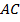 , полученную вершину назовем
, полученную вершину назовем  (см. Рис. 10).
(см. Рис. 10).
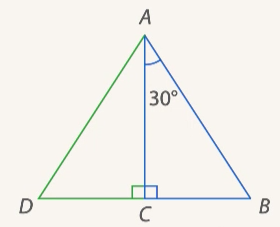
Рис. 10. Отражение 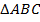 относительно катета
относительно катета 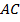
Раз треугольник полностью «скопирован», то  ,
, 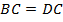 . Также заметим, что
. Также заметим, что 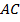 – высота и медиана образованного
– высота и медиана образованного 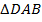 . Раз высота совпала с медианой, значит,
. Раз высота совпала с медианой, значит, 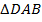 – равнобедренный (
– равнобедренный ( ) (см. Рис. 11).
) (см. Рис. 11).
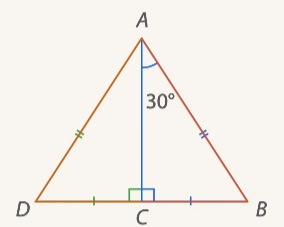
Рис. 11. 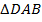 – равнобедренный
– равнобедренный
Поскольку 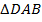 – равнобедренный, то
– равнобедренный, то  . Получили, что в
. Получили, что в 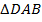 все углы равны, а значит,
все углы равны, а значит, 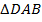 – равносторонний (см. Рис. 12).
– равносторонний (см. Рис. 12).
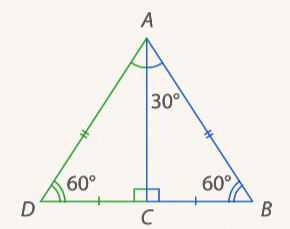
Рис. 12. 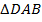 – равносторонний
– равносторонний
Тогда 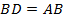 , а, в свою очередь,
, а, в свою очередь, 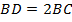 , то есть
, то есть  , откуда
, откуда 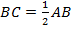 . Что и требовалось доказать.
. Что и требовалось доказать.
Если катет прямоугольного треугольника равен половине гипотенузы, то угол напротив этого катета равен 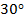 .
.
Доказательство. Рассмотрим прямоугольный 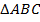 . Пусть
. Пусть 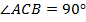 и
и 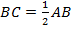 . Нужно доказать, что
. Нужно доказать, что 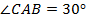 (см. Рис. 13).
(см. Рис. 13).
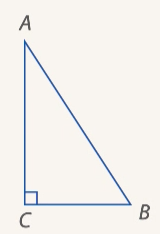
Рис. 13. Прямоугольный 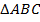
Отразим зеркально 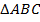 относительно катета
относительно катета 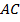 , полученную вершину назовем
, полученную вершину назовем  . Образовался
. Образовался 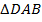 (см. Рис. 14).
(см. Рис. 14).
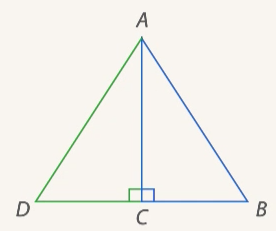
Рис. 14. Полученный 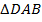
В 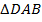 известно, что
известно, что  ,
, 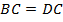 , значит,
, значит, 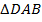 – равнобедренный. Кроме того, из третьего свойства известно, что
– равнобедренный. Кроме того, из третьего свойства известно, что 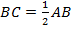 . Значит,
. Значит,  , а
, а  , отсюда
, отсюда 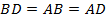 . Тогда
. Тогда 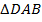 – равносторонний (см. Рис. 15).
– равносторонний (см. Рис. 15).
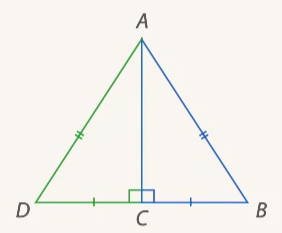
Рис. 15. 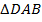 – равносторонний
– равносторонний
Из этого следует, что 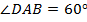 , а тогда
, а тогда 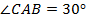 , т. к.
, т. к. 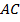 – высота, медиана и биссектриса
– высота, медиана и биссектриса 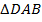 . Что и требовалось доказать.
. Что и требовалось доказать.
Доказательство (медиана, проведенная к гипотенузе, равна ее половине).
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине (см. Рис. 16).
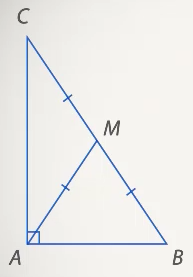
Рис. 16. Иллюстрация к свойству прямоугольного треугольника
Доказательство. Рассмотрим прямоугольный 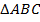
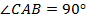 ,
, 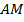 – медиана. Нужно доказать, что
– медиана. Нужно доказать, что  . Удвоим отрезок
. Удвоим отрезок 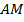 – получим точку
– получим точку  (
(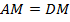 ) (см. Рис. 17).
) (см. Рис. 17).
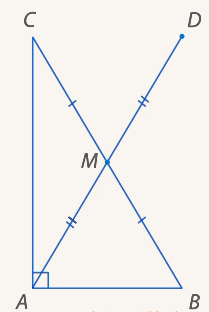
Рис. 17. 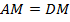
Соединим точку  с точками
с точками 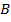 и
и  . Тогда несложно доказать, что
. Тогда несложно доказать, что 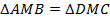 равны по 1 признаку (соответствующие стороны попарно равны, а углы между сторонами равны как вертикальные) (см. Рис. 18).
равны по 1 признаку (соответствующие стороны попарно равны, а углы между сторонами равны как вертикальные) (см. Рис. 18).
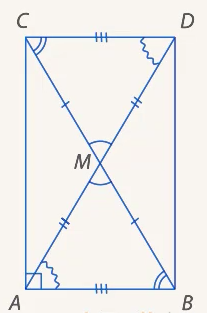
Рис. 18. Равенство 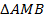 и
и , и равенство соответствующих элементов
, и равенство соответствующих элементов
Рассмотрим 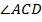 .
.  .
.
Теперь рассмотрим 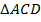 и
и 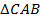 .
. 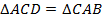 (т. к.
(т. к.  ,
, 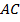 – общая,
– общая, 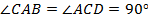 – треугольники равны по первому признаку). Отсюда следует, что
– треугольники равны по первому признаку). Отсюда следует, что 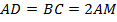 , тогда
, тогда  . Что и требовалось доказать.
. Что и требовалось доказать.
Обратное тоже верно: если медиана в треугольнике равна половине стороны, к которой она проведена, то треугольник – прямоугольный.
1. В прямоугольном 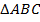 :
: 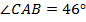 и
и 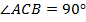 . Найти угол
. Найти угол 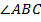 (см. Рис. 19).
(см. Рис. 19).
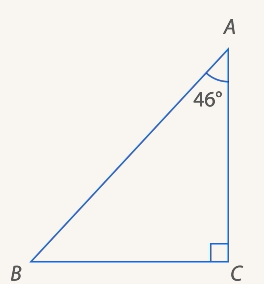
Рис. 19. Иллюстрация к примеру 1
Решение. По свойству  сумма острых углов прямоугольного треугольника равна
сумма острых углов прямоугольного треугольника равна 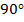 , значит,
, значит,  .
.
Ответ: 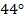 .
.
2. Один из углов прямоугольного 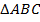 (
(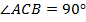 ) втрое меньше другого (
) втрое меньше другого ( ). Найти острые углы треугольника
). Найти острые углы треугольника 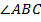 и
и 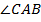 (см. Рис. 20).
(см. Рис. 20).
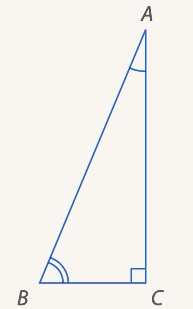
Рис. 20. Иллюстрация к примеру 2
Решение. Ясно, что искомый угол – один из острых. Тогда он может быть меньше либо другого острого, либо меньше прямого, то есть нужно рассмотреть два варианта.
1. Вариант первый – острый угол втрое меньше прямого. Пусть искомый угол 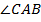 . Тогда
. Тогда 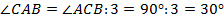 . Значит, по свойству 1
. Значит, по свойству 1 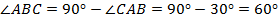 .
.
2. Вариант второй – один острый угол втрое меньше другого острого угла. Пусть  , тогда
, тогда  . По свойству 1
. По свойству 1 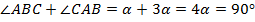 . Значит,
. Значит, 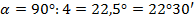 , а тогда
, а тогда 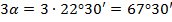 .
.
Ответ: 1. 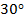 и
и 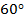 ; 2.
; 2. 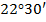 и
и 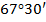 .
.
3. В прямоугольном треугольнике 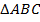
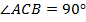 катет
катет 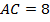 см,
см, 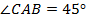 . Найти катет
. Найти катет 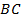 (см. Рис. 21).
(см. Рис. 21).
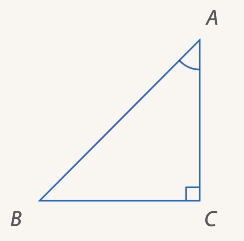
Рис. 21. Иллюстрация к примеру 3
Решение. По свойству
Первый признак равенства треугольников — урок. Геометрия, 7 класс.
Треугольники. Равенство треугольников

Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки.
Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника.
Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла.

Обозначение треугольника:
ΔABC, или ΔBCA, или буквы вершин в любом другом порядке.
Обозначение угла:
∡A, ∡BAC или ∡CAB.
Обозначение стороны:
AB или BA.
Сторону, которая лежит напротив угла, называют противолежащей углу, и угол называют противолежащим стороне.
Углы, которые имеет одну общую сторону, называют прилежащими этой стороне.
Сумма сторон треугольника называется периметром.
Если два треугольника можно совместить наложением, их называют равными.
 При этом совпадают все стороны и все углы.
При этом совпадают все стороны и все углы.Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
То есть, противолежащие стороны соответственно равных углов тоже равны, и противолежащие углы соответственно равных сторон равны.
Обозначение равных треугольников:
ΔABC=ΔA1B1C1, ΔBCA=ΔB1C1A1 или буквы вершин в любом другом порядке, но соблюдая следующее правило.
Обрати внимание!
В каком порядке названы вершины одного треугольника, в таком же порядке называют соответствующие вершины равного треугольника.
На практике не всегда можно применить наложение для сравнивания фигур. Чаще необходимо ограничиться измерением некоторых элементов фигур и по этим измерениям судить о равенстве фигур.
Докажем, что для равенства двух треугольников достаточно двух равных сторон и угла, который образован этими сторонами.
Первый признак равенства треугольников
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

MN=PR;KN=TR;∡N=∡R.
Достаточно ли этого для равенства треугольников, можно ли их полностью совместить?
1. Так как ∡N=∡R, то треугольник ΔMNK можно наложить на треугольник ΔPRT так, что вершина \(N\) совместится с вершиной \(R\), а стороны \(NM\) и \(NK\) наложатся соответственно на лучи \(RP\) и \(RT\).
2. Поскольку MN=PR,KN=TR, то сторона \(MN\) совместится со
стороной \(PR\), а сторона \(KN\) — со стороной \(TR\), в частности совместятся точки \(M\) и \(P\), \(K\) и \(T\).
3. Следовательно, совместятся стороны \(MK\) и \(PT\). Итак, ΔMNK и ΔPRT полностью совместятся, значит, они равны.
Сумма углов треугольника — урок. Геометрия, 7 класс.
Сумма углов треугольника равна \(180°\).

Доказательство
Рассмотрим произвольный треугольник \(KLM\) и докажем, что ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(M =\) 180°.
Проведём через вершину \(L\) прямую \(a\), параллельную стороне \(KM\).
Углы, обозначенные \(1\), являются накрест лежащими углами при пересечении параллельных прямых \(a\) и \(KM\) секущей \(KL\), а углы, обозначенные \(2\) — накрест лежащими углами при пересечении тех же параллельных прямых секущей \(ML\).
Очевидно, сумма углов \(1\), \(2\) и \(3\) равна развёрнутому углу с вершиной \(L\), т. е.
∡ \(1\) \(+\) ∡ \(2\) \(+\) ∡ \(3 =\) 180°, или ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(M =\) 180°.
Теорема доказана.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна 90°.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
Следствие 3. В равностороннем треугольнике каждый угол равен 60°.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Доказательство
Из равенств ∡ \(KML\) \(+\) ∡ \(BML=\) 180° и ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(KML =\) 180° получаем, что ∡ \(BML =\) ∡ \(K\) \(+\) ∡ \(L\).
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.

У треугольника \(KLM\) все углы острые.

У треугольника \(KMN\) угол \(K = 90\)°.
У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.
На рисунке \(MN\) — гипотенуза, \(MK\) и \(KN\) — катеты.

У треугольника \(KLM\) один угол тупой.
Определения, теоремы (Геометрия I четверть 7 класс) — Сайт учителя математики Косыхиной Н.В.
Определения
1. Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).
2.В планиметрии изучаются свойства фигур на плоскости. В стереометрии изучаются свойства фигур в пространстве.
3. Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.
4. Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а точка — вершиной угла.
5. Угол называется развёрнутым, если обе его стороны лежат на одной прямой. ( Развёрнутый угол равен 180°).
6. Две геометрические фигуры называются равными, если их можно совместить наложением.
7. Середина отрезка — это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
8. Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
9.Угол называется прямым, если он равен 90°.
10. Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
11. Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).
12. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.
13. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
14. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
15 Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами треугольника.
16. Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
17. Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы.
18.Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
19.Треугольник называется равносторонним, если все его стороны равны.
20.Аксиомы – это утверждения о свойствах геометрических фигур, которые принимаются в качестве исходных положений, на основе которых доказываются теоремы и строится вся геометрия.
21.(Аксиома) Через любые две точки проходит прямая, и притом только одна.
22. Если все три угла треугольника острые, то треугольник называется остроугольным.
23. Если один из углов треугольника тупой, то треугольник называется тупоугольным.
24. Если один из углов треугольника прямой, то треугольник называется прямоугольным.
Теоремы
Теорема 1: Две прямые, перпендикулярные к третьей, не пересекаются.
Доказательство от противного. Есть две прямые АА1 и ВВ1 перпендикулярны к прямой PQ одновременно. Предположим, что, продолжая прямые, можно достичь некоторой точки M, в которой они пересекаются. Перегнем плоскость вдоль прямой PQ. В этом случае углы при данных прямых накладываются друг на друга, а наложенные лучи совпадают. При этом точка М, получит проекцию некоторой точки M1 (при пересечения АА1 и ВВ1 в нижней полуплоскости) . Это будет означать, что две прямые АА1 и ВВ1 пересекаются в двух точках М и М1. Но через любые две точки на плоскости можно провести только одну прямую! Таким образом, предположение о том, что данные прямые пересекаются неверно. Следовательно, две прямые, перпендикулярные к третьей, не пересекаются. Что и требовалось доказать.
Теорема 2
Первый признак равенства треугольников ( по двум сторонам и углу между ними)
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство:
Так как ∠A=∠A1, то можно треугольник A1B1C1 наложить на треугольник ABC так, чтобы
точка A1 совместилась с точкой A,
луч A1C1 наложился на луч AC,
луч A1B1 — на луч AB.
Так как AB=A1B1, то при таком наложении сторона A1B1 совместится со стороной AB, а значит, точка B1 совместится с точкой B.
Аналогично, сторона A1C1 совместится со стороной AC, а точка C1 — с точкой C.
Следовательно, сторона B1C1 совместится со стороной BC.
Значит, при наложении треугольники полностью совместятся, поэтому ΔABC= ΔA1B1C1 (по определению).
Что и требовалось доказать.
Теорема 3
Теорема единственности перпендикуляра, проведенного из произвольной точки к заданной прямой
Из любой точки А, не лежащей на данной прямой, можно провести перпендикуляр к прямой. К тому же этот перпендикуляр единственный.
Дано: точка А не принадлежит прямой a.
Доказать: существует единственный отрезок АН, где АН- перпендикуляр к a из точки A.
Доказательство:
1. Построим 2 равных угла. ∠АВС =∠МВС или ∠1 = ∠2.
2. Равные углы можно совместить наложением. При этом точка А перейдет в точку A1. ВА = ВA1(перегибание по прямой ВС).
3. Соединим точки А и A1. Получим точку Н. Углы ∠ВНА = ∠3, ∠ВНA1 = ∠4.
4. Так как ∠1 = ∠2,ВА = ВA1, BC- общая,то треугольники ВНА = ВНA1 по первому признаку равенства треугольников, то есть по углу и двум прилежащим сторонам. Из равенства треугольников следует равенство всех элементов. А значит, ∠3 = ∠4. Эти углы лежат против равных сторон. Два смежных равны только в случае, если каждый из них равен по 90°. А значит, АН ⊥ ВС. Мы доказали, что из точки А можно провести перпендикуляр к прямой a.
Единственность перпендикуляра, проведенного из точки А к прямой, докажем методом «от противного».
5. Предположим, что из точки А можно провести к прямой a два разных перпендикуляра.
АН ⊥ a, Аh2 ⊥ a.

Это невозможно, поскольку из разных точек прямой a проведены 2 перпендикуляра, которые имеют общую точку А. Мы получили противоречие, значит, наше предположение неверно. Из точки А можно провести лишь один перпендикуляр к прямой a. Теорема доказана.
Задачи
Из учебника «Геометрия», под редакцией Атанасян Л.С. и др
стр. 26 №74,78, стр. 31 №96
Высоты треугольника / Треугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Высоты треугольника
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 133, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 154, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 212, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 350, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 505, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 668, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 727, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 820, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1143, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1251, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
что такое треугольник определение в геометрии 7 класс
Скрытый текст
Дорогие друзья, Огромное Спасибо, за то, что посетили наш скромный ресурс! Единственный доход, который имеет наш сайт Zmeinogorsk.RU – это реклама на сайте, поэтому убедительно Вас просим: ПОСЕТИТЕ рекламодателей нашего сайта!Здесь вы можете найти много полезной информации. Вы пришли к нам в поисках полезной информации (видео) по теме: (видео) по теме: что такое треугольник определение в геометрии 7 класс.
На сайте, автоматически производится сборка самой новой и актуальный информации, которая соответствует Вашим релевантным запросам. Информация становится доступной Вам при помощи функции . На сайте Вы сможете найти много уникального контента! Целью публикаций данных подборок на сайте ZmeinoGorsk.RU «Град обреченный» (он же «Змеиногорск» или «Zmeinogorsk») является обсуждение информации без каких-либо личностных предубеждений!
Геометрия 7. Урок 8 — Признаки равенства треугольников.
Изучается понятие равных треугольников; объясняются три признака равенства треугольников. Будет полезно…
Геометрия 7 Первый признак равенства треугольников
Наши репетиторы https://znaika.ru/teachers Школьная ярмарка: экономия родителям кэшбэк https://znaika.ru/market ✓ Официальный…
Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.
Основные свойства равнобедренного треугольника. Теория необходимая для решения задач.
7 класс, 17 урок, Медианы, биссектрисы и высоты треугольника
Если Вам понравился данный видеоурок, пожалуйста поддержите наш проект — https://qiwi.me/videokursy и мы будем старатьс…
7 класс, 18 урок, Свойства равнобедренного треугольника
Если Вам понравился данный видеоурок, пожалуйста поддержите наш проект — https://qiwi.me/videokursy и мы будем старатьс…
Математика| Признаки равенства треугольников
ЗАПИШИСЬ на онлайн-уроки по математике к репетитору: http://bit.ly/2tsuT5p Математика, геометрия, матан… Наша Ольга…
Равнобедренный треугольник
Равнобедренный треугольник, свойства.
Геометрия 7 класс. Свойства равнобедренного треугольника
Наши репетиторы https://znaika.ru/teachers Школьная ярмарка: экономия родителям кэшбэк https://znaika.ru/market ✓ Официальный…
треугольник. Равные треугольники. Определения. Обозначения. геометрия 7
что такое треугольник. Почему треугольники равны. Как обозначают треугольники.
Медиана биссектриса и высота треугольника . Геометрия 7 класс.
геометрия особенно подробно изучает #треугольник. #медиана, #биссектриса и #высота очень много могут расска…
No tags for this post.