ВЫЧИСЛЕНИЕ — это… Что такое ВЫЧИСЛЕНИЕ?

вычисление — подсчёт, расчёт, счёт, итог, калькуляция, подсчитывание, высчитывание, отсчёт; калькулирование, расчет, прикидка, исчисление, просчитывание, подсчет Словарь русских синонимов. вычисление см. подсчёт Словарь синонимов русского языка. Практический… …   Словарь синонимов

вычисление — ВШЫЧИСЛИТЬ, лю, лишь; ленный; сов. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

вычисление — вычисления Процесс выполнения арифметических и логических операций, а также обработки данных с помощью компьютера или других вычислительных средств. См. RISC. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь… …   Справочник технического переводчика

ВЫЧИСЛЕНИЕ — получение числового результата некоторым алгоритмом из исходных данных …   Большая политехническая энциклопедия

Вычисление

— математическое преобразование, позволяющее преобразовывать входящий поток информации в выходной, с отличной от первого структурой. Если смотреть с точки зрения теории информации, вычисление это получение из входных данных нового знания. Этот… …   Википедия

вычисление — ▲ определение (неявного) ↑ величина вычисление определение величины (произвести #). вычислять. счет (устный #). считать (# в уме). высчитать. счетный. расчет. расчетчик. рассчитать. подсчет. подсчитать. просчитать. насчитать. выкладки. прикинуть …   Идеографический словарь русского языка

вычисление — skaičiavimas statusas T sritis automatika atitikmenys: angl. calculation; calculus; computation vok. Berechnung, f; Kalkulation, f; Rechnung, f; Zählung, f rus. вычисление, n; исчисление, n; расчёт, m; счёт, m pranc. calcul, m; compte, m …   Automatikos terminų žodynas

вычисление — skaičiavimas statusas T sritis Standartizacija ir metrologija apibrėžtis Tam tikro uždavinio sprendimas remiantis kiekybiniais duomenimis. atitikmenys: angl. calculation; counting vok. Rechnen, f; Rechnung, f rus. вычисление, n pranc. calcul, m …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

вычисление — apskaičiavimas statusas T sritis chemija apibrėžtis Matematinio uždavinio sprendimas remiantis kiekybiniais duomenimis. atitikmenys: angl. calculation; computation rus. вычисление; исчисление; расчет …   Chemijos terminų aiškinamasis žodynas

вычисление — skaičiavimas statusas T sritis fizika atitikmenys: angl. calculation; computation; counting vok. Rechnen, n; Rechnung, f; Zählung, f rus. вычисление, n; расчёт, m; счёт, m pranc. calcul, m …   Fizikos terminų žodynas

dic.academic.ru

Что такое вычислительная математика — Викиучебник

• Исходный вариант статьи (И. Б. Петров, Что такое вычислительная математика?) опубликован в журнале «Потенциал».

В статье рассказывается о том, что это за наука — вычислительная математика, с помощью которой решаются задачи физики, которая проникла в химию, биологию, экономику, медицину, социологию и другие науки. Оказывается, что эта наука использует как математику, так и информатику, а иногда и знания рассматриваемой предметной области. Подходы и методы вычислительной математики своеобразны и красивы, а сама эта наука давно уже стала самостоятельной дисциплиной, изучаемой во всех университетах мира.

На первый взгляд кажется, что вычислительная математика — это та же математика, только с вычислениями конкретных величин в формулах. Иногда приходится слышать иную позицию: «Вычислительная математика? Это, кажется, что-то от информатики?» Однако и первая, и вторая точка зрения верны лишь отчасти. Да, у вычислительной математики много общего с математическими дисциплинами; порой говорят о том, что это одна из математических дисциплин.

Вычислительная математика — это наука о методах решения вычислительных задач на компьютере. Она появилась от необходимости решать практические задачи, такие, как управление сложными технологическими процессами, управление полётом ракет, моделирование физических процессов (процесса ядерного распада, химических реакций, роста кристаллов и др.), а не только создание всё более реалистичных и ярких компьютерных игрушек, как ныне думают многие школьники.

Задачами вычислительной математики занимались такие выдающиеся учёные, как Эйлер, Лагранж, Чебышёв, Якоби, Лежандр, фон Нейман и многие другие. Они, часто занимаясь сложными вычислениями вручную на бумаге, невольно заложили основы науки об эффективных безошибочных вычислениях на компьютерах.

Всем известно, что компьютеры имеют дело с числами с ограниченным количеством знаков после запятой^[1]. Казалось бы, какая мелочь! Однако именно эти «мелочи» могут сильно исказить результаты численных расчётов. Появился важнейший раздел вычислительной математики — теория устойчивости вычислительных методов, то есть таких методов, которые позволяют на компьютере с «неточной» арифметикой получать точные (правдивые) результаты.

Как вычислительная математика решает прикладные задачи[править]

Во многих прикладных задачах искомым результатом является не одно число, а целая функция на отрезке. А как описать произвольную функцию на компьютере? Самый простой способ — это хранить значения функции в нескольких точках и «в уме» соединять их гладкой кривой. Таким образом, отрезок может рассматриваться как система нескольких выбранных точек {xk}k=0K{\displaystyle \left\{{x_{k}}\right\}_{k=0}^{K}\,\!}, а непрерывная функция — как набор {fk}k=0K{\displaystyle \left\{{f_{k}}\right\}_{k=0}^{K}\,\!} значений функции в этих точках. Очень важный объект f′(x){\displaystyle f'(x)\,\!} — производная функции в точке x{\displaystyle x} — характеризует угол наклона прямой, касающейся графика функции. Вместо него приходится использовать отношение fk+1−fkxk+1−xk{\displaystyle {{f_{k+1}-f_{k}} \over {x_{k+1}-x_{k}}}\,\!}, где xk{\displaystyle x_{k}\,\!} и xk+1{\displaystyle x_{k+1}\,\!} ближайшие к x{\displaystyle x\,\!} выбранные точки. При решении задач на компьютерах приходится приближать не только числа, но и сами задачи несколько «округлять» и вместо идеальных непрерывных объектов рассматривать их дискретные приближения. Этот вынужденный шаг называется аппроксимацией задачи.

Как узнать, насколько адекватные результаты даёт компьютерная модель, которую вы построили, или, как принято говорить у вычислительных математиков, имеется ли сходимость решения модели к решению исходной «непрерывной» задачи? Кроме ряда сложных и красивых теорем, есть несколько простых хитростей, которые позволяют определить адекватность вашей модели:

1. Точность вычислений. В машинных вычислениях всегда присутствует машинная погрешность, о чём уже упоминалось. И прежде чем верить результатам, полученным на компьютере, попробуйте увеличить точность всех расчетов на пару разрядов. Если это изменит результат в предыдущих знаках, значит, вычисления проводились с недостаточной точностью и нужно использовать более точные типы для представления чисел (например, в языке Си float заменить на double, а в языке Паскаль тип real заменить на extended).
2. Обусловленность. В вычислительной практике большое значение имеет чувствительность решения к малым изменениям входных данных. Задача называется плохо обусловленной, если малые изменения входных данных приводят к заметным изменениям решения. Измерить эту обусловленность на практике очень просто. Нужно просто попробовать чуть-чуть поменять входные данные и посмотреть, как меняется результат. Собственно, нужно выяснить, с какой погрешностью заданы входные данные, и экспериментально проверить в каких пределах меняется результат при варьировании входных данных в пределах их погрешности.
3. Зависимость от алгоритма и модели. Есть ещё один источник неадекватности численных результатов, полученных на компьютере. Это неточность выбранной модели и алгоритма вычисления. Здесь всё несколько сложнее, нежели в предыдущих пунктах. Но для богатых заказчиков можно предложить надёжное решение — следует дать одну и ту же задачу нескольким группам прикладных математиков. Они, скорее всего, построят разные модели и будут пользоваться разными алгоритмами. Если все выдадут один и тот же результат, значит задача хорошая — она устойчива к выбору модели и алгоритма, и не так важно каким способом её решать. Конечно, бывают и такие случаи, когда все делают одну и ту же ошибку. У начинающих вычислительных математиков есть несколько таких излюбленных ошибок.
   

Разумеется, если есть возможность сравнить результаты расчета с экспериментальными, то такие сравнения являются поводом для подтверждения верности расчетов. Что же касается исследования численных методов на аппроксимацию — то эта теория достаточно хорошо разработана, однако без вычислительных ошибок численных решений не бывает. Вопрос заключается в том, значительны ли они или незначительны, что, впрочем, также можно оценить.

Приведём некоторые примеры, демонстрирующие что «шутки с погрешностью плохи».

Пример 1: корни многочлена[править]

Есть множество программ, позволяющие численно вычислять корни многочленов. Давайте рассмотрим уравнение x4−4×3+8×2−16x+15.9…9⏟8=(x−2)4−10−8=0;{\displaystyle x^{4}-4x^{3}+8x^{2}-16x+15.\underbrace {9…9} _{8}=(x-2)^{4}-10^{-8}=0;\,\!}

Это уравнение просто решить аналитически:(x−2)2=10−4{\displaystyle (x-2)^{2}=10^{-4}\,\!} , x1,2=2±0.01;x3,4=2±0,01i.{\displaystyle x_{1,2}=2\pm 0.01;{\rm {}}x_{3,4}=2\pm 0,01i.\,\!}

Предположим, что мы проводим вычисления на компьютере, имеющем точность δM>10−8{\displaystyle \delta _{M}>10^{-8}\,\!} . В этом случае последнее слагаемое в уравнение будет округлено до 16.0, и с позиции компьютера будет решаться уравнение (x−2)4=0{\displaystyle \left({x-2}\right)^{4}=0\,\!} , у которого один корень 2. Таким образом, малые погрешности в задании числа порядка 10−8{\displaystyle 10^{-8}\,\!} привели к появлению погрешностей в определении корней уравнения порядка 10−2{\displaystyle 10^{-2}\,\!}. Более того, вместо двух действительных и двух комплексных корней у нас получился лишь один действительный. Такие плохо обусловленные многочлены не редкость. Например, если в многочлене (x−1)(x−2)…(x−20)=x20−210×19+…{\displaystyle \left({x-1}\right)\left({x-2}\right)\ldots \left({x-20}\right)=x^{20}-210x^{19}+\ldots \,\!}

коэффициент при x19{\displaystyle x^{19}\,\!} изменить на малую величину порядка 10−7{\displaystyle 10^{-7}\,\!} , то вместо максимального корня x20=20{\displaystyle x_{20}=20\,\!} получим корень x20≈20,8{\displaystyle x_{20}\approx 20,8\,\!}

Пример 2: cистема уравнений[править]

Другой пример плохо обусловленной задачи — это система двух линейных уравнений: {u+10v=11,100u+1001v=1101.{\displaystyle \left\{{\begin{matrix}u+10v=11,\\100u+1001v=1101.\end{matrix}}\right.\,\!}

Решением является пара чисел {1;1}.{\displaystyle \left\{{1;1}\right\}.\,\!}

«Возмутим» правую часть первого уравнения на 0,01 (вместо 11 напишем 11,01) и получим новую, «возмущенную» систему, решением которой является пара чисел {11,01; 0,00}, не имеющая ничего общего с решением невозмущенной системы. Здесь изменение значения одного параметра на 0,1%{\displaystyle 0,1\%\,\!} привело к совсем другому решению.

Пример 3: вычисление sin x[править]

В математическом анализе показывается, что функция sin⁡x{\displaystyle \sin x\,\!} может быть представлена в виде ряда sin⁡x=x−x33!+x55!−x77!+…{\displaystyle \sin x=x-{{x^{3}} \over {3!}}+{{x^{5}} \over {5!}}-{{x^{7}} \over {7!}}+…\,\!}, причём этот ряд будет сходиться к значению sin⁡x{\displaystyle \sin x\,\!} при любых значениях x. После вычисления значения нашей функции при x=0,5236{\displaystyle x{\rm {=0}}{\rm {,5236}}\,\!} (x≈30∘{\displaystyle x\approx 30^{\circ }\,\!}) с четырьмя значащими цифрами и с учётом лишь членов ряда, больших 10−4{\displaystyle {10^{-4}}\,\!}, получим значение sin⁡x{\displaystyle \sin x\,\!} с той же точностью: sin⁡(0,5236)=0,5000.{\displaystyle \sin(0,5236)=0,5000.\,\!}

Теперь положим, что x=25,66{\displaystyle x{\rm {=25}}{\rm {,66}}\,\!} (x≈1470∘{\displaystyle x\approx 1470^{\circ }\,\!}). Если мы проведём вычисления с восемью значащими цифрами с учётом членов ряда, больших 10−8{\displaystyle {10^{-8}}\,\!}, то получим ошеломляющий результат; sin⁡(25,66)=24,…{\displaystyle \sin(25,66)=24,…\,\!}

Впрочем, в данном случае выход из положения достаточно прост — необходимо использовать формулы приведения: sin⁡1470∘=sin⁡30∘{\displaystyle \sin 1470^{\circ }=\sin 30^{\circ }\,\!}. А что делать, если нам необходимо вычислить экспоненту, представленную в виде ряда ex=1+x+x22!+x33!+…{\displaystyle e^{x}=1+x+{{x^{2}} \over {2!}}+{{x^{3}} \over {3!}}+…\,\!}? Очевидно, что нас и в этом случае ждут подобные сюрпризы. Однако и здесь существует выход: будем вычислять экспоненту с отрицательным показателем e−x=1−x+x22!−x33!+…{\displaystyle e^{-x}=1-x+{{x^{2}} \over {2!}}-{{x^{3}} \over {3!}}+…\,\!} , а затем вычислим обратную величину: ex=1e−x=11−x+x22!−x33!+…{\displaystyle e^{x}={1 \over {e^{-x}}}={1 \over {1-x+{{x^{2}} \over {2!}}-{{x^{3}} \over {3!}}+…}}\,\!} . Дело в том, что e−x{\displaystyle e^{-x}\,\!} вычисляется как сумма знакопеременного ряда. После того, когда каждое следующее слагаемое в этой сумме станет меньше, чем предыдущее, по модулю, мы будем чётко представлять верхнюю и нижнюю оценку вычисляемого значения и будем знать, на каком слагаемом следует оборвать суммируемый ряд.

Пример 4: корень из двойки[править]

Мы говорили о том, что на результат вычисления может оказать влияние выбор алгоритма решения задачи. Действительно, пусть нам нужно вычислить значение выражения A=(2−12+1)3.{\displaystyle A=\left({{{\sqrt {2}}-1} \over {{\sqrt {2}}+1}}\right)^{3}.\,\!} После избавления от иррациональности в знаменателе, получим: A=(2−1)6{\displaystyle A=\left({{\sqrt {2}}-1}\right)^{6}\,\!} или A=(3−22)3{\displaystyle A=\left({3-2{\sqrt {2}}}\right)^{3}\,\!} или A=99−702.{\displaystyle A=99-70{\sqrt {2}}.\,\!} Эти три формулы и будут нашими тремя алгоритмами вычисления числа A. Выберем два разных приближения корня из двойки. 2≈75=1,4{\displaystyle {\sqrt {2}}\approx {7 \over 5}=1,4\,\!} и 2=1712≈1,416666…{\displaystyle {\sqrt {2}}={{17} \over {12}}\approx 1,416666…\,\!}

Проведём вычисления A по трём формулам для двух приближенных значений 2{\displaystyle {\sqrt {2}}\,\!} . Результаты вычислений представим в виде таблицы:

	2{\displaystyle {\sqrt {2}}\,\!}	(2−1)6{\displaystyle \left({{\sqrt {2}}-1}\right)^{6}\,\!}	(3−22)3{\displaystyle \left({3-2{\sqrt {2}}}\right)^{3}\,\!}	99−702{\displaystyle 99-70{\sqrt {2}}\,\!}
1-й способ	7/5	0,004096	0,008000	1
2-й способ	17/12	0,005233	0,004630	-0,1(6)

Видно, что первый «алгоритм» A=(2−1)6{\displaystyle A=\left({{\sqrt {2}}-1}\right)^{6}\,\!} является более устойчивым к погрешностям входных данных.

Задачи для самостоятельного решения[править]

Читателю предлагается добраться до компьютера и компилятора какого-нибудь языка программирования (Си или Pascal) и провести несколько незатейливых численных экспериментов.

Задача 1 (частичная сумма гармонического ряда).[править]

Напишите программу, которая суммирует первые миллион слагаемых гармонического ряда сначала с первого по последний элемент, а потом наоборот — с последнего по первый: A=11+12+13+…+1106=1106+…13+12+11{\displaystyle A={1 \over 1}+{1 \over 2}+{1 \over 3}+\ldots +{1 \over {10^{6}}}={1 \over {10^{6}}}+\ldots {1 \over 3}+{1 \over 2}+{1 \over 1}\,\!}. Убедитесь, что ассоциативный закон «(a+b)+c=a+(b+c){\displaystyle (a+b)+c=a+(b+c)\,\!}» при вычислении на компьютере с конечной точностью не выполняется, что может привести к довольно сильному расхождению между результатом вычислений и реальным значением выражения.

Задача 2 («страшный» предел).[править]

Найдите с помощью компьютера значение выражения sin⁡(tan⁡(x))−tan⁡(sin⁡(x))arcsin⁡(arctan⁡(x))−arctan⁡(arcsin⁡(x)){\displaystyle {\frac {\sin(\tan(x))-\tan(\sin(x))}{\arcsin(\arctan(x))-\arctan(\arcsin(x))}}\,\!}

при x, равном 1, 1/2, 1/4, 1/8, 1/10, 1/100, … (x измеряется в радианах). Как вы думаете, к чему это выражение на самом деле стремится по мере того, как x стремится к 0? дайте решение пожалуйста.

Задача 3 («башня» из степеней).[править]

Рассмотрим функцию f(x)=xxx⋅⋅⋅{\displaystyle f(x)=x^{x^{x^{\cdot ^{\cdot ^{\cdot }}}}}\,\!}. Эта функция представляет собой бесконечную башню степеней. При некоторых x{\displaystyle x} такая бесконечная конструкция имеет смысл. Видно, что f(x)=xf(x){\displaystyle f(x)=x^{f(x)}\,\!}. Это значит, что при f(x)=a{\displaystyle f(x)=a\,\!} имеем a=xa{\displaystyle a=x^{a}\,\!} и x=a1/a{\displaystyle x=a^{1/a}\,\!} . Из этого можно ошибочно вывести, что при x=31/3=33{\displaystyle x=3^{1/3}={\sqrt[{3}]{3}}\,\!} имеем f(x)=3{\displaystyle f(x)=3\,\!} . Это не так. Убедитесь в этом сами. Мы предлагаем вам изучить функцию f(x){\displaystyle f(x)\,\!} , приблизив её «башней» степеней конечной высоты. А именно, рассмотрите и запрограммируйте рекурсивную функцию Fn(x)=xFn−1(x){\displaystyle F_{n}(x)=x^{F_{n-1}(x)}\,\!} , F1(x)=x{\displaystyle F_{1}(x)=x\,\!} . Напишите программу (или используйте GnuPlot, Mathematica, Maple или другие подобные инструменты), которая рисует график четырёх функций F1000(x){\displaystyle F_{1000}(x)\,\!}, F1001(x){\displaystyle F_{1001}(x)\,\!}, F1002(x){\displaystyle F_{1002}(x)\,\!}, F1003(x){\displaystyle F_{1003}(x)\,\!} на интервале (0;3). Из вида этих графиков сделайте выводы. При каких x{\displaystyle x} определена функция f(x){\displaystyle f(x)\,\!}, то есть при каких x{\displaystyle x} значения Fn(x){\displaystyle F_{n}(x)\,\!} при увеличении n{\displaystyle n} становятся все ближе и ближе друг к другу и к некоторому фиксированному числу? Когда числа из последовательности a1,a2,…,an,…{\displaystyle a_{1},\;a_{2},\;\;\ldots ,\;a_{n},\;\ldots \,\!} приближаются к некоторому числу A{\displaystyle A}, то говорят, что последовательность ai{\displaystyle a_{i}\,\!} имеет предел A{\displaystyle A} и пишут an→A{\displaystyle a_{n}\to A\,\!} при n→∞{\displaystyle n\to \infty \,\!}.

Уточним это понятие: какое бы маленькое положительное число ε{\displaystyle \varepsilon \,\!} мы ни выбрали, всегда найдется такой элемент последовательности aM{\displaystyle a_{M}\,\!}, что он сам и все элементы последовательности после него оказываются удалены от числа A не более чем на ε{\displaystyle \varepsilon \,\!}

|aM−A|<ε,|aM+1−A|<ε,|aM+2−A|<ε,|aM

ru.wikibooks.org

вычисление — это… Что такое вычисление?

ВЫЧИСЛЕНИЕ — ВЫЧИСЛЕНИЕ, вычисления, ср. (книжн. научн.). 1. только ед. Действие по гл. вычислить вычислять. Произвести вычисление. 2. Результат этого действия, то, что получено посредством этого действия. Опубликовать свои вычисления. Толковый словарь… …   Толковый словарь Ушакова

вычисление — ВШЫЧИСЛИТЬ, лю, лишь; ленный; сов. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

вычисление — вычисления Процесс выполнения арифметических и логических операций, а также обработки данных с помощью компьютера или других вычислительных средств. См. RISC. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь… …   Справочник технического переводчика

ВЫЧИСЛЕНИЕ — получение числового результата некоторым алгоритмом из исходных данных …   Большая политехническая энциклопедия

Вычисление — математическое преобразование, позволяющее преобразовывать входящий поток информации в выходной, с отличной от первого структурой. Если смотреть с точки зрения теории информации, вычисление это получение из входных данных нового знания. Этот… …   Википедия

вычисление — ▲ определение (неявного) ↑ величина вычисление определение величины (произвести #). вычислять. счет (устный #). считать (# в уме). высчитать. счетный. расчет. расчетчик. рассчитать. подсчет. подсчитать. просчитать. насчитать. выкладки. прикинуть …   Идеографический словарь русского языка

вычисление — skaičiavimas statusas T sritis automatika atitikmenys: angl. calculation; calculus; computation vok. Berechnung, f; Kalkulation, f; Rechnung, f; Zählung, f rus. вычисление, n; исчисление, n; расчёт, m; счёт, m pranc. calcul, m; compte, m …   Automatikos terminų žodynas

вычисление — skaičiavimas statusas T sritis Standartizacija ir metrologija apibrėžtis Tam tikro uždavinio sprendimas remiantis kiekybiniais duomenimis. atitikmenys: angl. calculation; counting vok. Rechnen, f; Rechnung, f rus. вычисление, n pranc. calcul, m …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

вычисление — apskaičiavimas statusas T sritis chemija apibrėžtis Matematinio uždavinio sprendimas remiantis kiekybiniais duomenimis. atitikmenys: angl. calculation; computation rus. вычисление; исчисление; расчет …   Chemijos terminų aiškinamasis žodynas

вычисление — skaičiavimas statusas T sritis fizika atitikmenys: angl. calculation; computation; counting vok. Rechnen, n; Rechnung, f; Zählung, f rus. вычисление, n; расчёт, m; счёт, m pranc. calcul, m …   Fizikos terminų žodynas

dic.academic.ru

вычислить — это… Что такое вычислить?

вычислить — сделать подсчет, сосчитать, посчитать, расчислить, догадаться, подсчитать, выкопать, подытожить, высчитать, исчислить, скалькулировать, просчитать, разгадать, произвести выкладки, сделать выкладки, произвести подсчет, раскалькулировать,… …   Словарь синонимов

ВЫЧИСЛИТЬ — ВЫЧИСЛИТЬ, вычислю, вычислишь, совер. (к вычислять), что. Посредством действий над числами найти искомое, высчитать. Вычислить квартирную плату сообразно с заработком жильца. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 …   Толковый словарь Ушакова

ВЫЧИСЛИТЬ — ВЫЧИСЛИТЬ, лю, лишь; ленный; совер. 1. что. Установить, подсчитывая; высчитать. В. стоимость постройки. 2. Обработать числовую информацию ручным или машинным способом. В. с помощью ЭВМ. 3. перен., кого (что). Верно рассчитать, что кто н. будет… …   Толковый словарь Ожегова

вычислить — ВЫЧИСЛИТЬ, лю, лишь; сов., кого. Встретить, найти кого л. Вовремя я тебя вычислил …   Словарь русского арго

Вычислить — сов. перех. см. вычислять Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 …   Современный толковый словарь русского языка Ефремовой

вычислить — вычислить, вычислю, вычислим, вычислишь, вычислите, вычислит, вычислят, вычисля, вычислил, вычислила, вычислило, вычислили, вычисли, вычислите, вычисливший, вычислившая, вычислившее, вычислившие, вычислившего, вычислившей, вычислившего,… …   Формы слов

вычислить — в ычислить, лю, лит …   Русский орфографический словарь

вычислить — Syn: подсчитать, высчитать …   Тезаурус русской деловой лексики

вычислить — лю, лишь; св. 1. что. Произведя действие над числами, найти искомое; установить, подсчитывая. В. скорость и направление ветра. В. широту и долготу. В. стоимость постройки. 2. что. Обработать числовую информацию ручным или машинным способом. В. с… …   Энциклопедический словарь

вычислить — лю, лишь; св. см. тж. вычислять, вычисляться, вычисление 1) что Произведя действие над числами, найти искомое; установить, подсчитывая. Вы/числить скорость и направление ветра. Вы/ …   Словарь многих выражений

orthographic.academic.ru

Урок 1: Что такое математика?

План урока:

Что такое математика? 

Понятие числа. Виды чисел

Классы и разряды чисел

Математические действия

Порядок выполнения математических действий в выражениях со скобками и без скобок

Правила нахождения неизвестного компонента при выполнении математических действий

Основные законы выполнения действий (переместительный, сочетательный, распределительный)

Интересные сведения из истории возникновения математики

 

Что такое математика?

Часто можно услышать высказывание «Математика-царица наук». А существует ли история математики, и что же это за наука? Так ли она необходима в современном мире?

Любой из нас ежедневно выполняет множество действий, которые неразрывно связаны с математикой, но даже не догадывается об этом. Посмотрите вокруг — компьютеры, телефоны, кондиционеры, телевизоры, но для правильного использования домашней техники необходимы знания, связанные с математикой. Идем дальше — магазины, спортивные секции, танцевальные занятия, увлечение литературой также нельзя представить без использования математики. Математические знания облегчают жизнь и делают её насыщенной.

Давайте разберемся, что такое математика:            

Дословный перевод с греческого утверждает, что математика — это наука или изучение. Более точное определение поясняет, что это наука, изучающая величины, числовые отношения и формы.

В школьном курсе изучения представлены такие разделы математики:

 

В основе изучения математики лежит ряд математических понятий и действий, без понимания которых невозможно выполнять простейшие вычисления.

 

Понятие числа. Виды чисел

В понятие числа входит обозначение количественного состава чего-либо.Это одно из главных определений в математике. Каждый вид числа появлялся в результате необходимости выполнения человеком тех или иных расчетов. В связи с необходимостью владеть информацией о количестве предметов, появилось понятие натурального числа и бесконечности ряда натуральных чисел. Необходимость измерения площадей, длин, объемов — породила рациональное число. Для решения сложных уравнений ввели комплексные числа.

 

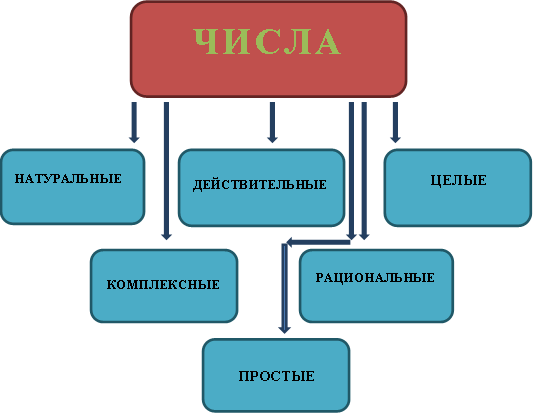
• Натуральные числа — это числа, получаемые при определении количества 1,2,3. Множество таких чисел принято обозначать буквой N. Например: 1,2,3 …..
• Целые числа. Определение понятия формулируется так: множество натуральных, отрицательных чисел и нуль. Их принято обозначать буквой Z. Например: -2,-1,0,1,2,3,4…..
• Рациональные числа. В понятие рационального числа входят дроби m/n, где n≠0, при этом m — целое число, а n — натуральное. Обозначаются буквой Q. Например: 2/3, -4/5
• Действительные. В понятие действительного числа включены рациональные и иррациональные числа, которые могут записываться в виде обычной и десятичной конечной и бесконечной дробей, а также нуль. Обозначаются буквой R. Например: 1245, 5⅔, -648,35
• Простыми называют натуральные числа, которые можно представить в виде двух множителей — единицы и самого этого числа. Обозначается буквой Р. Например: 1,3,7,11….
• Также существуют Иррациональные числа – это числа, не являющиеся рациональными, то есть нельзя представить в виде дроби m/n, где n≠0, при этом m — целое число, а n — натуральное. Например, число  пи=3,1415926535, число e=2.718281828, квадратный корень из 3 и так далее.

 

Классы и разряды чисел

Если число представлено в виде одной цифры (5,9), то оно называется однозначным, в виде двух (24,31), трех (211,984) цифр — двузначным, трехзначным, а далее (1893,100561) просто многозначными.

Все существующие цифры сгруппированы по классам и разрядам натуральных чисел. Место цифры в записи числа называют разрядом. Самый маленький разряд – разряд единиц, за ним следует разряд десятков, сотен, тысяч.

Например:

 

При этом число разрядов в классе равняется 3. Самым большим числом класса единиц является 9, а самым большим числом класса тысяч 999999.

 

Математические действия

Существование математики невозможно без выполнения математических действий. Всего существует 4 вида арифметических действий:

 

Порядок выполнения математических действий в выражениях со скобками и без скобок

Так же имеется определенный порядок математических действий, запомнив который с легкостью можно решать задания любой сложности. Этот порядок зависит от наличия скобок и предложенных действий:

При отсутствии скобок, действия выполняются в обычном порядке. Вот правильный порядок математических действий в примере без скобок:

 24+16-5=35

1 действие: 24+16=40

2 действие: 40-5=35

 

В любом выражении первыми необходимо выполнить умножение или деление в порядке очереди. Вот правильный порядок арифметических действий без скобок:

 40-4×5+50=70

1 действие: 4×5=20

2 действие: 40-20=20

3 действие: 20+50=70 

 

Когда выражение содержит скобки, первыми вычисляются действия в скобках, а потом по порядку все остальные. Вот необходимый порядок математических действий в примере со скобками:

5+(20-10):2=10

1действие: 20-10=10

2 действие: 10:2=5

3 действие: 5+5=10

Все очень просто. Если сразу запомнить не получается, то можно пользоваться этим уроком, как шпаргалкой!

 

Следующий интересный момент заключается в том, что любой компонент математического действия имеет свое название:

 

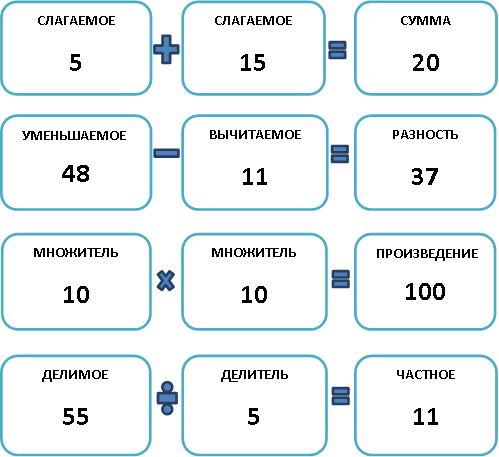
Правила нахождения неизвестного компонента при выполнении математических действий

Для того, чтобы максимально упростить решение задач и уравнений, существуют специальные правила нахождения неизвестного компонента:

1) Сложение:

— для нахождения одного из слагаемых необходимо от суммы отнять второе слагаемое:

                                                                                                                              

Например:

?+48=50;

?=50-48=2.

 

2) Вычитание:

-для нахождения уменьшаемого достаточно найти сумму разности и вычитаемого:

 

Например:

?-25=50;

?=50+25+75.

 

-для нахождения вычитаемого, нужно от уменьшаемого отнять разность

 

Например:

44-?=10;

?=44-10=34.

 

3) Умножение:

— для нахождения множителя, необходимо найти частное произведения и второго множителя

 

Например:

?×6=48;

?=48:6=8.

 

4) Деление:

— для нахождения неизвестного делимого, необходимо найти произведение делителя и частного

 

Например:

?:11=3;

?=11×3=33.

                

— для нахождения неизвестного делителя, необходимо делимое разделить на частное

 

Например:                                                 

95:?=19;

?=95:19=5.

 

Основные законы выполнения действий (перместительный, сочетательный, распределительный)

Чтобы правильно и быстро выполнять любые арифметические действия всегда нужно помнить их основные законы, которые упрощают даже самый сложный процесс вычислений:

Переместительный закон для действий сложения и умножения.

Сформулируем переместительный закон сложения: при перестановке слагаемых сумма остается прежней.

Запишем равенство, выражающее переместительный закон сложения a+b=b+a

Например:

21+39=60 или 39+21=6015×3=45 или 3×15=45

           60=60                                45=45

 

Использование переместительного закона умножения.

Давайте сформулируем переместительный закон умножения: в случае перестановки множителей произведение остается прежним.

Запишем равенство, выражающее переместительный закон умножения a*b=b*a

Например:

11×8=88 или 8×11=88

             88=88

 

Применение  сочетательного закона в сложении.

Давайте сформулируем сочетательный закон сложения: чтобы сложить число и сумму чисел достаточно найти сумму этого числа и любого слагаемого, и к ней прибавить второе слагаемое.

Запишем равенство, выражающее сочетательный закон сложения a+(b+c)=(a+b)+c=a+b+c

Примеры сочетательного закона сложения:

20+(60+10)=90 или 20+(60+10)=90 или 20+(60+10)=20+60+10=90

1 действие: 60+10=70   1 действие: 20+60=80

2 действие: 20+70=90   2 действие: 80+10=90

 

Использование сочетательного закона умножения.

Этот закон также распространяется и на действие умножение. Давайте сформулируем сочетательный закон умножения: если необходимо, выполнить умножение числа на произведение чисел, то можно любые два множителя заменить их произведением a×(b×c)=(a×b)×c=a×b×c

Например:

10×(5×2)=(10×5)×2=10×5×2=100

 

Применение распределительного закона.

Давайте разберемся, что такое распределительный закон и как он формулируется. Вот формулировка распределительного закона сложения: для умножения числа на сумму, необходимо найти произведения этого числа с одними вторым слагаемыми, а результаты сложить.

Запишем равенство, выражающее распределительный закон a×(b+c)=ab+ac

Например:

4×(5+10)=4×5+4×10=20+40=60

В случае, когда вычитаемое меньше или равно уменьшаемому, можно использовать распределительный закон для нахождения произведения числа и разности чисел. Для умножения числа на разность, необходимо сначала умножить на уменьшаемое, после на вычитаемое и найти разность полученных произведений. В буквенном виде записывается так: a×(b-c)=a×b-a×c, если b≥c

Например:                                                                                                   

9×(10-6)=9×10-9×6=90-54=36.

Достаточно понять или запомнить эти простые законы и тогда любые задачи или уравнения будут казаться очень простыми и интересными, а уроки математики станут любимыми.

 

Интересные сведения из истории возникновения математики

Откуда же взялась математика? Куда же уходит корнями история развития математики? Самым первым источником появления простейшей математики ученые считают пальцы на руках и ногах, а также различные части тела. Об этом свидетельствует множество наскальных рисунков, дошедших до нашего времени. Учеными установлено, что 6 тысяч лет назад древние вавилоняне уже использовали простые математические действия: для бытовых нужд, учета скота, подсчета количества урожая, размера прибыли и расходов, при совершении купли или продажи различных товаров. Позже они же первые упоминают о решении математических задач и уравнений повышенной сложности. К самым первым математическим открытиям относят возникновение математических действий, которые известны нам как сложение, вычитание, умножение и деление.

Ученые-историки до сих пор спорят о точной дате появления этой науки и о месте, где впервые она появилась. Конкурентами в этом споре выступают древний Вавилон и Египет. Самые первые подтверждения математической деятельности принадлежат Свазиленду. Там найдены кости бабуинов с нанесенными черточками, которые явно говорят о первых математических операциях, выполненных 40000 лет назад.

(Источник)

 

А когда же появились дроби? Упоминания о дробях возникли гораздо позже, но уже достоверно известно, что жители древнего Египта совершали операции с дробями, у которых числителем являлась единица.

А вот представление о десятичных дробях появилось всего лишь пять столетий назад, а в Европу попало только через 200 лет после появления.

 

 (Источник)

 

Невероятные факты, связанные с математикой:

• Всю математическую науку возможно записать в сто тысяч томов;
• Центилион — самое большое известное число, содержащее шестьсот нулей;
• Наименьшее число используется только в астрономии. Названия не имеет. Записывается дробью; после запятой имеет сто миллионов триллионов нулей, а в конце единицу;
• Самая магическая цифра, которая таит множество суеверий — 666. В Европейской палате все время пустует только одно кресло под номером 666. Во всем мире люди стараются не использовать это число. Такой номер не присваивается телефонным кодам, автобусам,трассам или поездам;
• В Китае самым суеверным числом считают число 4. При этом, такой номер не присваивается домам, квартирам, нет даже 4 этажа.

Математика очень дружна со всеми существующими науками, видами деятельности и профессиями. Одно мудрое выражение гласит «Математика-язык других наук». Поспорить с этим очень сложно, ведь она является основой для развития таких дисциплин:

• Химия;
• Физика;
• Астрономия;
• Биология;
• История;
• Экономика;
• География;
• Информатика;
• Политология;
• Музыка;
• Литература.

Теперь мы можем с уверенностью сказать, что знание математики — залог вашей успешности и развития не только в будущем, а уже сегодня!

100urokov.ru

вычисление — это… Что такое вычисление?

вычисление — подсчёт, расчёт, счёт, итог, калькуляция, подсчитывание, высчитывание, отсчёт; калькулирование, расчет, прикидка, исчисление, просчитывание, подсчет Словарь русских синонимов. вычисление см. подсчёт Словарь синонимов русского языка. Практический… …   Словарь синонимов

ВЫЧИСЛЕНИЕ — ВЫЧИСЛЕНИЕ, вычисления, ср. (книжн. научн.). 1. только ед. Действие по гл. вычислить вычислять. Произвести вычисление. 2. Результат этого действия, то, что получено посредством этого действия. Опубликовать свои вычисления. Толковый словарь… …   Толковый словарь Ушакова

вычисление — ВШЫЧИСЛИТЬ, лю, лишь; ленный; сов. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

ВЫЧИСЛЕНИЕ — получение числового результата некоторым алгоритмом из исходных данных …   Большая политехническая энциклопедия

Вычисление — математическое преобразование, позволяющее преобразовывать входящий поток информации в выходной, с отличной от первого структурой. Если смотреть с точки зрения теории информации, вычисление это получение из входных данных нового знания. Этот… …   Википедия

вычисление — ▲ определение (неявного) ↑ величина вычисление определение величины (произвести #). вычислять. счет (устный #). считать (# в уме). высчитать. счетный. расчет. расчетчик. рассчитать. подсчет. подсчитать. просчитать. насчитать. выкладки. прикинуть …   Идеографический словарь русского языка

вычисление — skaičiavimas statusas T sritis automatika atitikmenys: angl. calculation; calculus; computation vok. Berechnung, f; Kalkulation, f; Rechnung, f; Zählung, f rus. вычисление, n; исчисление, n; расчёт, m; счёт, m pranc. calcul, m; compte, m …   Automatikos terminų žodynas

вычисление — skaičiavimas statusas T sritis Standartizacija ir metrologija apibrėžtis Tam tikro uždavinio sprendimas remiantis kiekybiniais duomenimis. atitikmenys: angl. calculation; counting vok. Rechnen, f; Rechnung, f rus. вычисление, n pranc. calcul, m …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

вычисление — apskaičiavimas statusas T sritis chemija apibrėžtis Matematinio uždavinio sprendimas remiantis kiekybiniais duomenimis. atitikmenys: angl. calculation; computation rus. вычисление; исчисление; расчет …   Chemijos terminų aiškinamasis žodynas

вычисление — skaičiavimas statusas T sritis fizika atitikmenys: angl. calculation; computation; counting vok. Rechnen, n; Rechnung, f; Zählung, f rus. вычисление, n; расчёт, m; счёт, m pranc. calcul, m …   Fizikos terminų žodynas

technical_translator_dictionary.academic.ru

вычислять — Викисловарь

Морфологические и синтаксические свойства[править]

вы-чис-ля́ть

Глагол, несовершенный вид, переходный, тип спряжения по классификации А. Зализняка — 1a. Соответствующий глагол совершенного вида — вычислить.

Приставка: вы-; корень: -числ-; суффикс: -я; глагольное окончание: -ть ^{[Тихонов, 1996]}.

Произношение[править]

• МФА: [vɨt͡ɕɪˈslʲætʲ]

Семантические свойства[править]

Значение[править]

1. находить искомое число, производя математические действия с исходными числами ◆ Немец уже взялся было за карман, где у него был карандаш в книжечке, в которой он всё вычислял, но, вспомнив, что он сидит за обедом, и заметив холодный взгляд Вронского, воздержался. Л. Н. Толстой, «Анна Каренина», 1876 г.
2. перен. оценивать, взвешивать что-либо ◆ Он вычислял, какие уже перемерли, какие живут ещё. Н. В. Гоголь, «Тарас Бульба» ◆ Когда кто-нибудь из нас собирался подраться, он долго примеривался, вычислял шансы, взвешивал и, даже всё взвесив, долго колебался, как Кутузов перед Бородино. А. Т. Аверченко, «Страшный Мальчик»

Синонимы[править]

1. высчитывать
2. оценивать, взвешивать

Антонимы[править]

Гиперонимы[править]

Гипонимы[править]

Родственные слова[править]

Список всех слов с корнем «числ»
имена собственные: Книга Чисел пр.  существительные: число, числитель, числительное, численность, счисление, исчисление, вычисление, начисление, отчисление, перечисление, вычислимость, вычисляемость; вычислитель, вычислительница; многочисленность, малочисленность прилагательные: числовой, нечисловой, численный, вычислительный, бесчисленный, неисчислимый, многочисленный, малочисленный, исчисляемый, неисчисляемый глаголы: числить, числиться, вычислять, вычислить, вычисляться, исчислять, исчислить, исчисляться, начислять, начислить, начисляться, расчислить; отчислять, отчисляться, отчислить, отчислиться; перечислять, перечисляться, перечислить, перечислиться причастия: вычисленный, начисленный; отчислявший, отчисляющий, отчисленный, отчисляемый наречия: численно

Этимология[править]

Происходит от ??

Фразеологизмы и устойчивые сочетания[править]

Перевод[править]

Список переводов

Библиография[править]

ru.wiktionary.org