Как нарисовать цилиндр поэтапно? :: SYL.ru
Каждый художник, становясь на путь профессионального развития, стремится овладеть навыком академического и линейно-конструктивного рисунка: построение предметов насквозь с привлечением знаний по физике и геометрии дает художнику возможность набить руку и сделать рисунок твердым и убедительным, а правильное наложение штриховки поверх рисунка позволяет подчеркнуть форму объекта и сделать графику более выразительной.
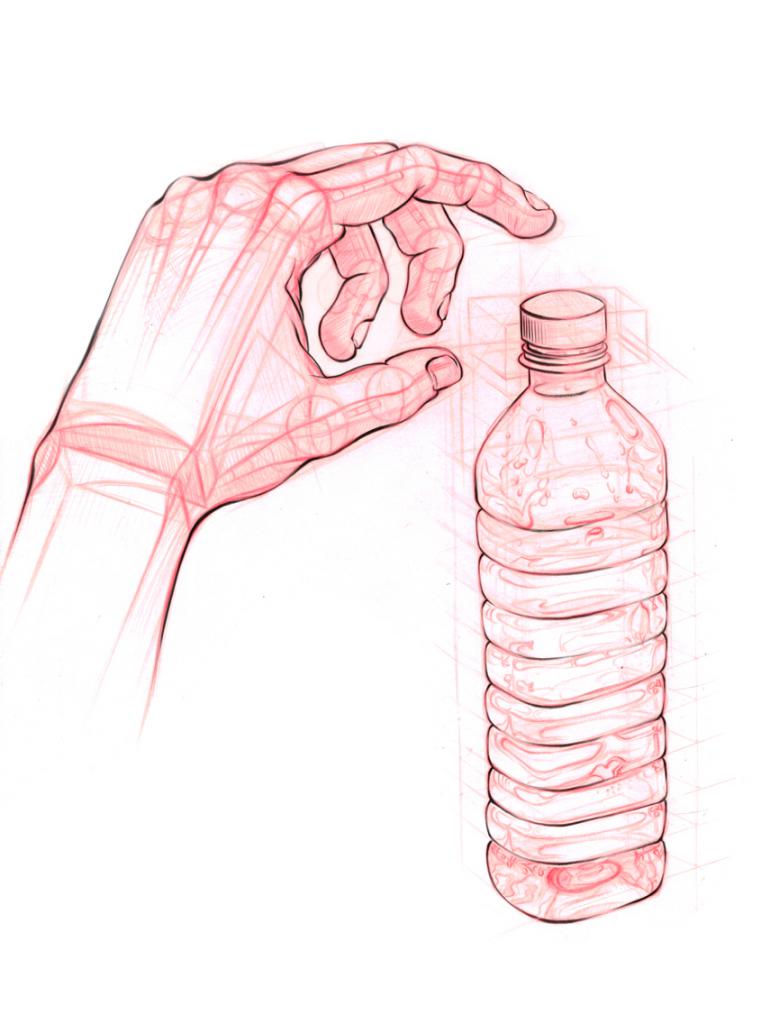
Изучение академического рисунка начинают с построения основных геометрических объектов, с помощью которых в будущем можно упростить более сложные конструкции и формы, например, кисть руки человека разбивается на параллелепипеды и цилиндры, и лишь потом ее изгибам придаются плавные формы. Сегодня мы рассмотрим вопрос о том, как нарисовать цилиндр карандашом поэтапно.
Подготовка инструментов
Прежде чем приступать к началу работы, необходимо остро заточить простые карандаши, что сделает ваш рисунок точнее. Для начального построения предметов используют твердые или твердо-мягкие карандаши (маркировка Т, ТМ или H, HB).
Бумагу выбирают достаточно плотную, чертежную — это позволит выдержать ей несколько десятков исправлений работы без потери качества. Предпочтительно выбирать мягкую стирательную резинку, которая бережна к фактуре бумаги. Если позволяют обстоятельства, можно приобрести в художественном магазине формопласт — маленький отрезок силикона, который дает возможность равномерно облегчить тон и линию рисунка. Теперь вы вооружились всем необходимым и готовы узнать, как нарисовать цилиндр.
Предварительные измерения
Если вы рисуете с натуры, то измерьте высоту цилиндра (расстояние между верхней и нижней границами) при помощи простого карандаша, держа его на вытянутой руке, выпрямленной в локте. Кончик карандаша с грифелем — ваша начальная точка отсчета.
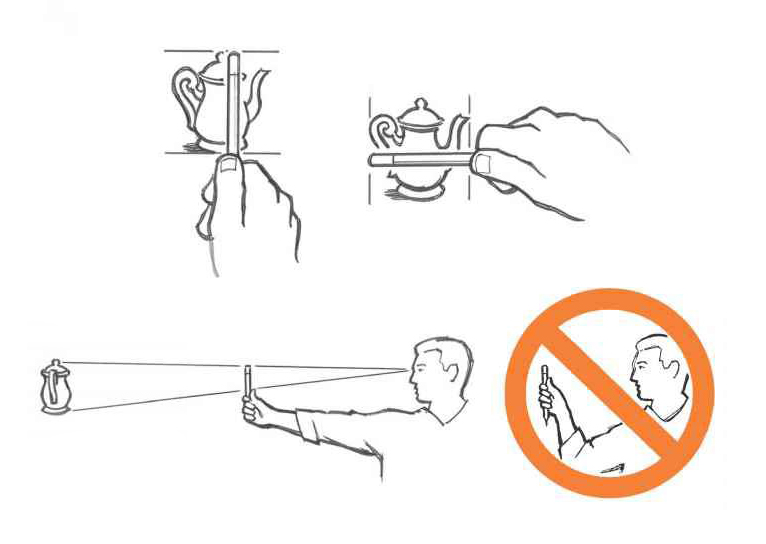
Большим пальцем зафиксируйте отметку, которая соответствует нижней части цилиндра. Затем проделайте ту же самую процедуру с шириной цилиндра: такое сопоставление двух величин поможет вам правильно определить пропорции, чтобы понять, как нарисовать цилиндр.
Каркас
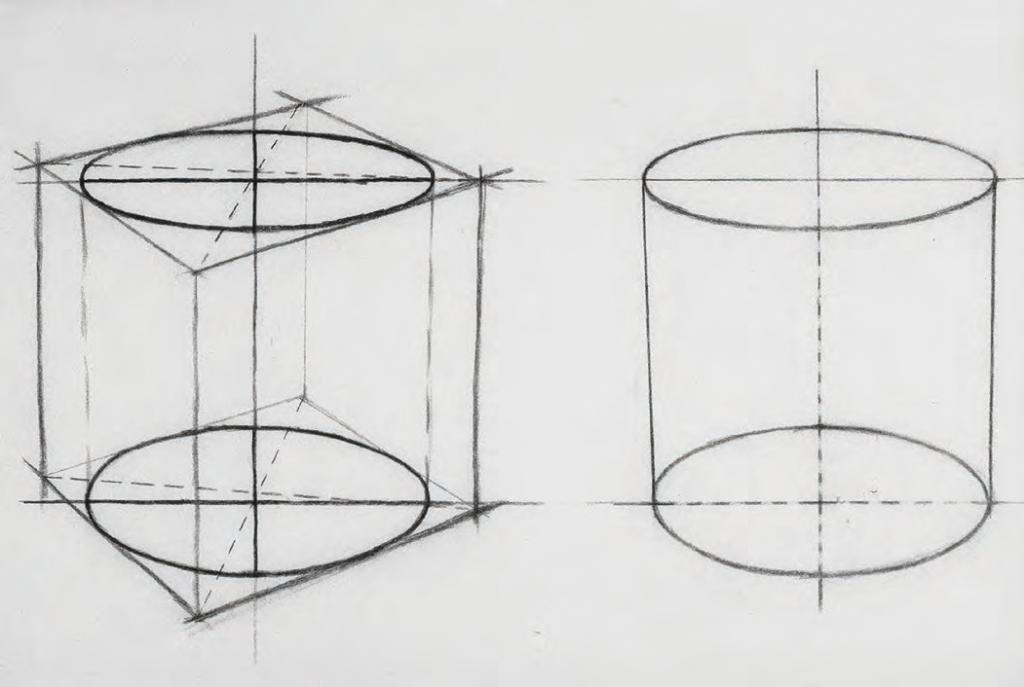
Представим, что вы находитесь прямо напротив цилиндра — это самый простой случай перспективы (пространственного искажения форм и размеров) для получения первого опыта по вопросу о том, как нарисовать цилиндр карандашом.
Проведите длинную вертикаль — линию, которая соответствует высоте цилиндра и будет делить его пополам. Ее название — осевая линия.
Затем добавьте две группы парных горизонтальных линий на некотором расстоянии друг от друга. Верхняя пара отвечает за одну плоскость, и расстояние между этими линиями будет немного меньше, чем между нижними линиями: нижняя грань шире вследствие перспективных искажений.
Затем добавьте две вертикальные линии по бокам будущего цилиндра, которые являются его шириной. Эти линии равно удалены от осевой линии. Итак, первый шаг к тому, как нарисовать цилиндр поэтапно, сделан.
Эллипсы
Мы подготовили каркас. В каждом из маленьких прямоугольников необходимо поставить крест: провести диагонали, а также разделить прямоугольники горизонтальной линией пополам. Эти действия упростят процесс создания эллипсов, которые следует вписать в прямоугольники. Эллипсы можно условно представить двумя дугами, которые плотно прилегают к каркасу и плавно переходят друг в друга. На первых порах будет сложно создать ровные и мягкие эллипсы, но при должной сноровке в будущем вы сможете обходиться без дополнительных линий-подсказок и не задаваться вопросом о том, как нарисовать цилиндр — вы научитесь делать это практически машинально.
Выделение граней
Прежде чем приступить к этому этапу, вам следует слегка ослабить сделанный рисунок мягкой резинкой в том случае, если вы рисовали мягким карандашом.
Как нарисовать цилиндр реалистично? В графике и живописи есть такие понятия, как разделение на передний и задний план. Все логично: то, что ближе к зрителю, относится к переднему плану, остальное — к заднему. Поэтому передний план необходимо выделить более толстыми линиями, чем основные, а именно боковые стороны цилиндра, нижнюю дугу лежащего в основании эллипса, а также ближайшую к зрителю дугу верхнего эллипса, а самую верхнюю дугу выделить четкой, но тонкой линией.
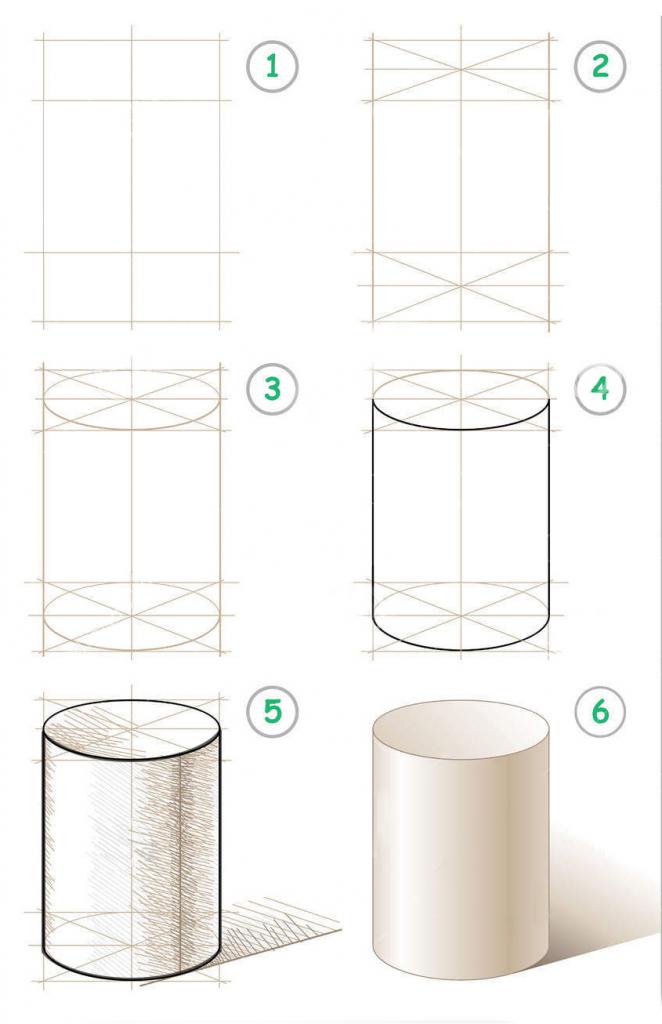
В целом на данном этапе у вас появится разделение на 3 линии по толщине: самые внушительные линии переднего плана, обычная по толщине линия заднего плана и едва видимые, но все же заметные линии построения каркаса.
Наложение штриховки
Теперь вы можете вооружиться мягким карандашом и начать накладывать штриховку на цилиндр. Существует множество техник штриховки, попробуйте начать с диагональной, накладывайте штрихи по форме цилиндра. Как нарисовать цилиндр с тенью? Начинайте с самых темных участков — это важно, потому что если начать штриховать со светлых участков, вам может не хватить тона карандаша для разбора рисунка по светлоте.
Блик, свет, полутень, собственная тень, рефлекс и падающая тень — все это элементы светотени, которые составляют тональный разбор цилиндра. Самым светлым из них является блик — его оставляют нетронутым, затем едва проходятся штрихом по свету, полутень — основной тон предмета, собственная тень — самый темный участок предмета, и рефлекс — отражение пространства на цилиндре (практически равен полутени, находится в районе кромки объекта). Падающая тень — самый темный и густой по наложению штриха участок. Она всегда противоположна источнику света.
На картинке ниже представлен подробный тональный разбор цилиндра. Руководствуйтесь им при наложении штриховки.
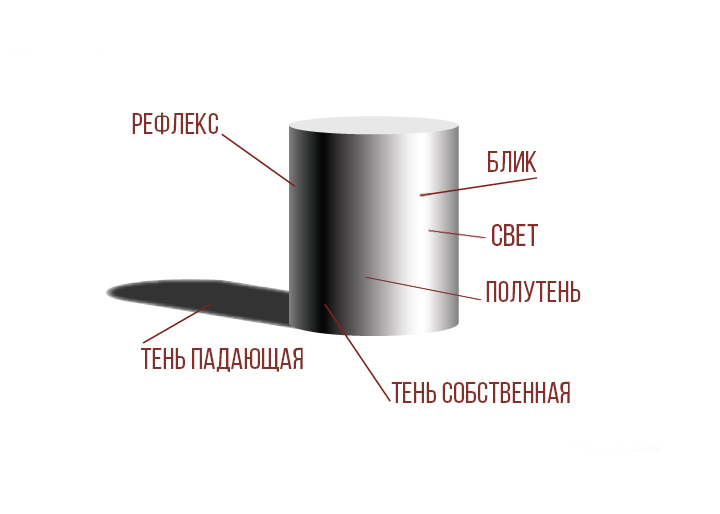
Старайтесь работать равномерно, чтобы на каждом этапе штриховки ваша работа выглядела законченной и была готовой к демонстрации. Поздравляем! Теперь вы знаете, как нарисовать цилиндр карандашом поэтапно с тенью.
Перспектива
Как только вы освоили построение цилиндра с прямого ракурса, вы можете экспериментировать и развиваться дальше. Изучите воздушную перспективу и правило точки схода, выходите за границы своих навыков!
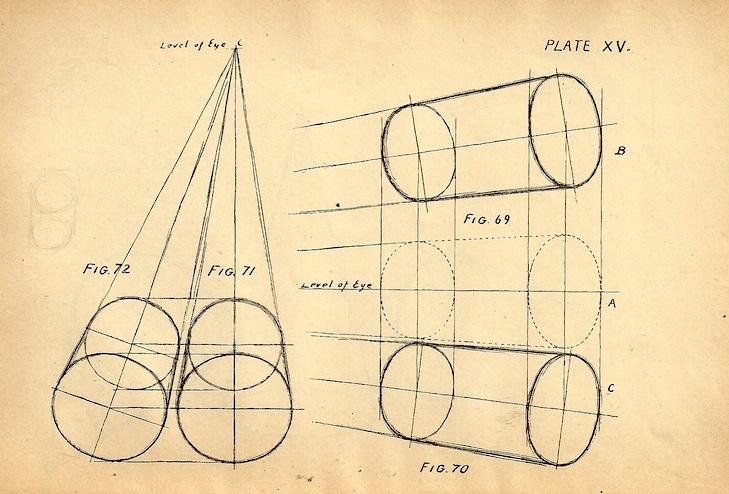
Вывод
Сегодня вы познакомились с линейно-конструктивным рисунком и узнали, как нарисовать цилиндр карандашом с тенью. Пусть это знание станет основой для ваших работ на пути к вершине творческого Олимпа.
Успехов и вдохновения!
www.syl.ru
Перспектива цилиндра в уроке рисунка на блоге «Иллюзион»
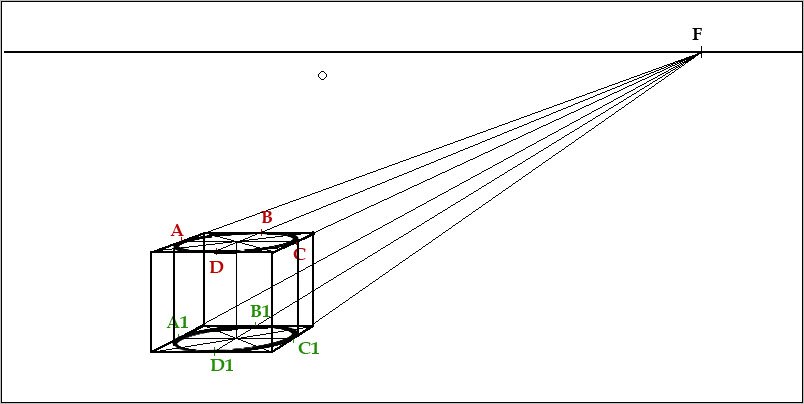
Давайте перейдем от перспективы куба к обзору — перспектива цилиндра, или скажем к фигуре цилиндрической формы. Это так же простое, не сложное задание.
Если рассмотреть мир вокруг нас — то эту форму имеют разные предметы это столб цилиндр, это труба цилиндр, это ваза цилиндр и даже шляпа цилиндр и т. д. А рисунок это умение строить, и тут уже не далеко и до гениальности, как написано в начале сайта.
Что бы правильно изобразить эту фигуру, нам необходимо будет вписать ее в прямоугольный параллелепипед.
Основа построения такая же, как и в уроке, перспектива куба.
Перспектива цилиндра
Вначале произвольно рисуем на листе линию горизонта, это прямая линия вдоль листа. Линия горизонта всегда находится на уровне глаз художника. На предметы выше этой линии художник смотрит снизу, на предметы ниже этой линии художник смотрит сверху. В данном уроке предмет у нас будет ниже линии горизонта, поэтому мы на него смотрим сверху. Все картинки кликабельны:
Дальше рисуем произвольно квадрат. В данном случае нарисуем фигуру ниже линии горизонта:
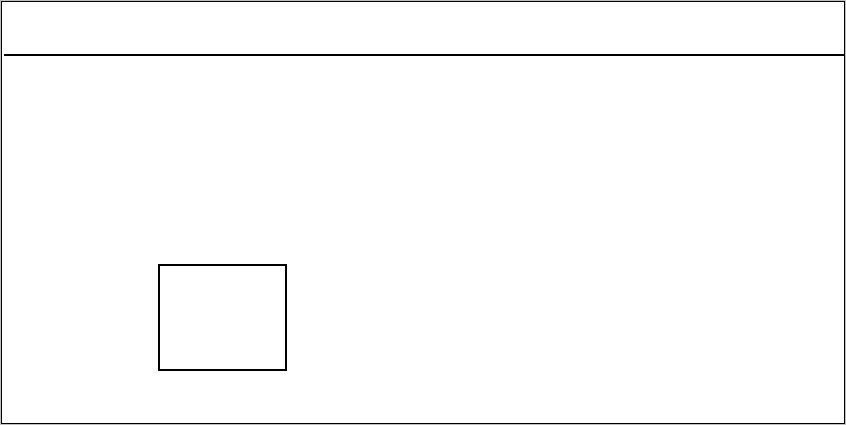
Потом на линии горизонта произвольно находим точку схода F , и луч соединяет углы нашего квадрата. Смотрим ниже:
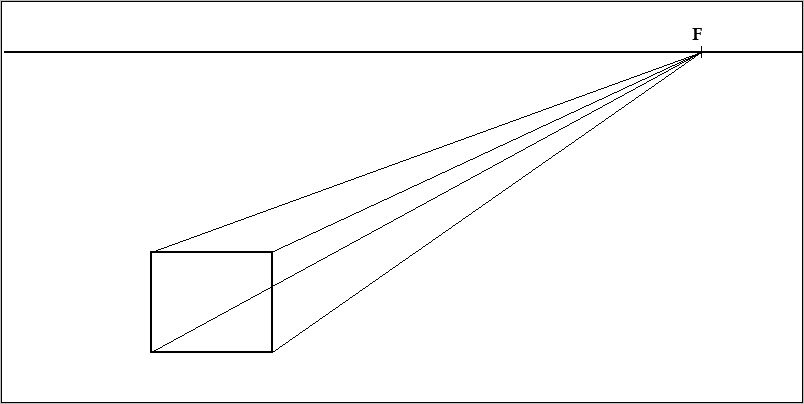
Теперь прорисовываем квадрат сзади, и соединяем линиями углы заднего квадрата и переднего. Смотрим вниз:
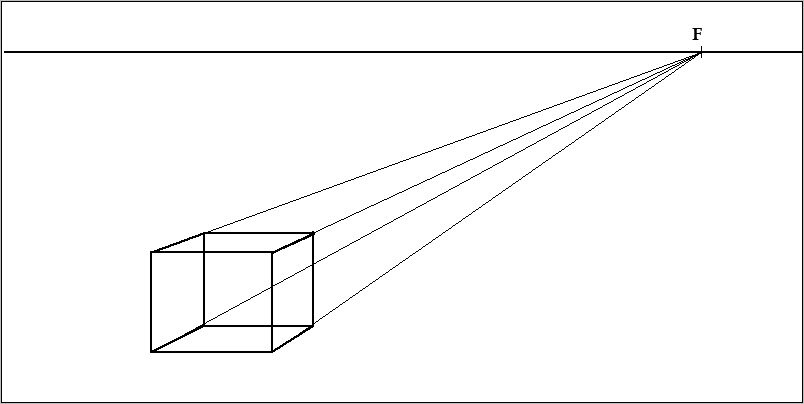
Теперь необходимо найти центр верхней и нижней плоскости параллелепипеда. Для этого проводим новые линии с углов плоскостей, крест — накрест. В пересечении крестов будут центры плоскостей. Теперь прямая линия делит верхнюю и нижнюю плоскости пополам. Смотрим на нижнюю картинку:
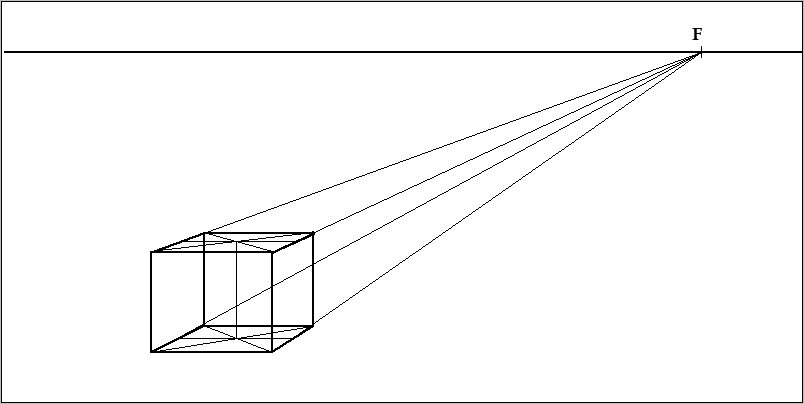
Мы поделили параллелепипед вдоль. Необходимо поделить его поперек. Для этого проводим линию от точки схода F через центр плоскостей параллелепипеда.
Смотрим вниз:
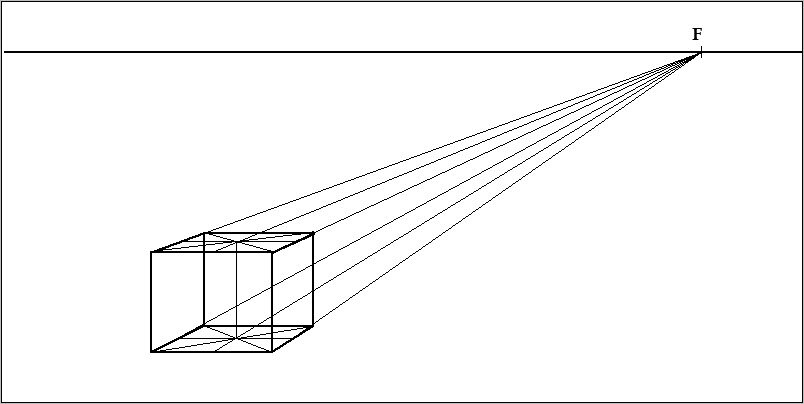
Итак, мы нашли необходимые нам точки верхней плоскости A, B, C, D, и нижней плоскости цилиндра A1, B1, C1, D1.
Рисунок внизу:
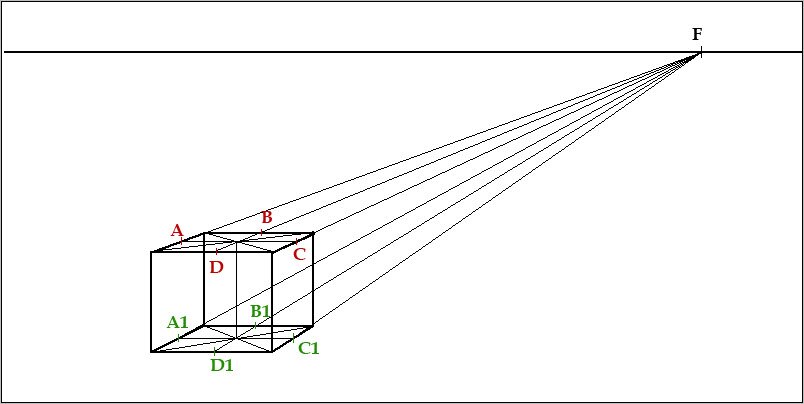
Теперь наша задача плавно вписать эллипс, соприкасаясь с точками верхней плоскости A, B, C, D .
Смотрим на рисунок ниже:
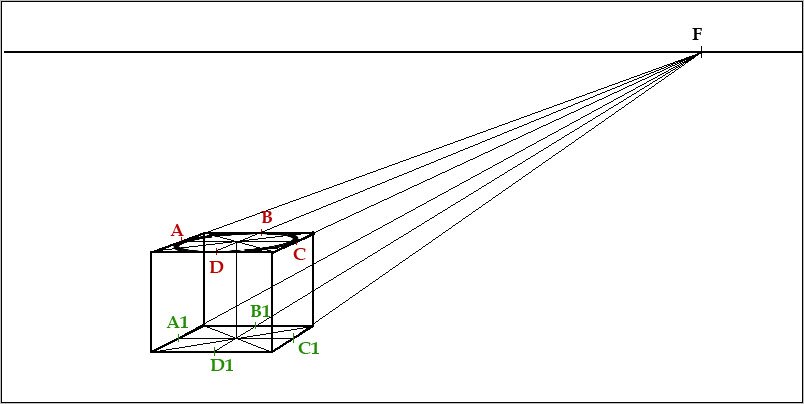
И так же поступаем с точками нижней плоскости цилиндра A1, B1, C1, D1. Таким образом мы очертим основание цилиндра :
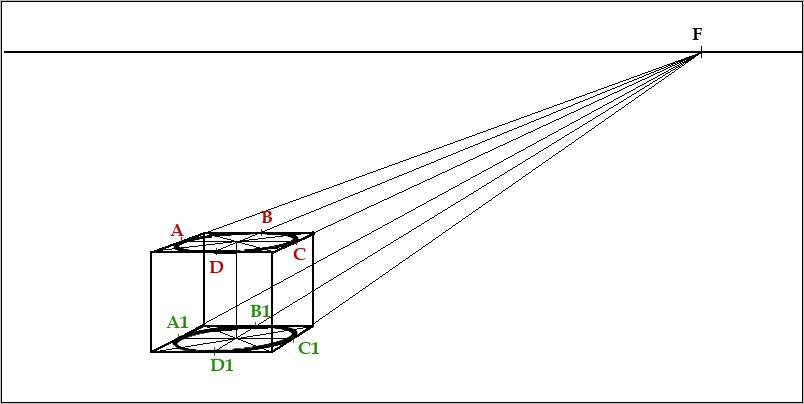
Теперь соединяем два эллипса, верхнее и нижнее основание цилиндра :
Убираем все вспомогательные линии, и получаем цилиндрическую форму :
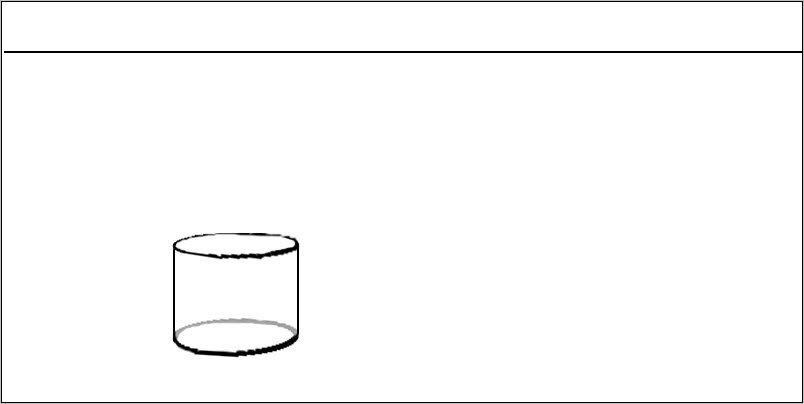
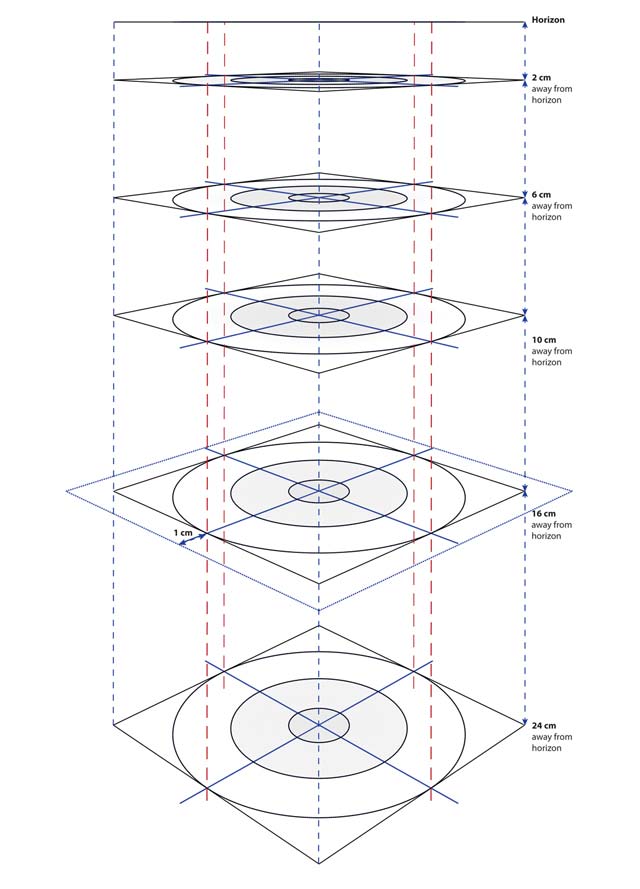
Причем чем выше линия горизонта, тем плоскость эллипса будет больше и больше стремится к кругу. Или к форме — окружность.
artatac.ru
Учебно-методическое пособие (8 класс) на тему: Методическое пособие для 8-го класса «Построение горизонтально лежащего цилиндра в перспективе» для обучающихся в ДХШ.
МЕТОДИЧЕСКОЕ ПОСОБИЕ ДЛЯ 8-9 КЛАССОВ ПО ПРЕДМЕТУ «РИСУНОК»
ПОСТРОЕНИЕ ГОРИЗОНТАЛЬНО ЛЕЖАЩЕГО ЦИЛИНДРА
СПб ГБОУ ДОД ДХШ№ 3 Шустров И.В.
Цель пособия: Приобретение теоретических и практических навыков построения цилиндра с горизонтально ориентированной осью вращения, которые являются базовыми для построения любых фигур вращения, лежащих на горизонтальной плоскости
Задача: Продемонстрировать последовательность этапов построения цилиндра в перспективе.
Практической работе предшествует объяснение особенностей построения вертикальных овалов, т.е. отсутствие строго горизонтальной оси, уже привычной для учащихся.
Далее определяем линию горизонта и положение цилиндра относительно угла зрения.
Определяем видимое отношение высоты основания и длины цилиндра.
1. Строим параллелепипед с учетом перспективного сокращения. Построение параллелепипеда начинаем с построения его основания, лежащего на плоскости.
2. Проводим диагонали из противоположных углов квадрата (ромба) основания цилиндра. Через точки их пересечения проводим ось цилиндра.
3. Под прямым углом к продольной оси цилиндра проводим большие оси овалов. Меньшими осями овалов будут служить продолжения продольной оси цилиндра.
4. Вписываем в квадраты (ромбы) окружности (овалы) основания цилиндра, где большая ось определяет больший диаметр цилиндра, а малая – меньший. По законам перспективы дальнее основание цилиндра всегда несколько шире по малой оси, чем ближнее. Вписываемые окружности (овалы) касаются сторон квадрата (ромба) в точках пересечения сторон вертикальным и горизонтальным перпендикулярами, пересекающихся в центре окружности и делящих стороны квадрата пополам.
5. Соединяем овалы касательными по большим осям. Придаем рисунку большую объемность, усиливая ближние и ослабляя дальние линии.
6. Решаем цилиндр в тоне, помня о тональной последовательности:
— падающая тень
— рефлекс
— собственная тень
— полутень
— свет (блик)
Усиливаем тон на границе света и тени.
nsportal.ru
Дайте определение цилиндра как геометрического тела.
Цилиндром называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра. а отрезки, соединяющие соответствующие точки окружностей кругов, — образующими цилиндра. Основания цилиндра равны и лежат в параллельных плоскостях. У цилиндра образующие параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих. Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра Призмой, вписанной в цилиндр, называется такая призма, основания которой — равные многоугольники, вписанные в основание цилиндра. Ее боковые ребра являются образующими цилиндра. Призма называется описанной около цилиндра. если ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости ее граней касаются боковой поверхности цилиндра. <img src=»//otvet.imgsmail.ru/download/b2cf36e91f7106e56bdf3d081dc1f1f6_i-70.gif» >
Цили́ндр (греч. kýlindros, валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра) ; причём если оснований два, то одно получено из другого параллельным переносом вдоль образующей боковой поверхности цилиндра; и основание пересекает каждую образующую боковой поверхности ровно один раз.
touch.otvet.mail.ru
Тела вращения. Цилиндр | Подготовка к ЕГЭ по математике
Цилиндром называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Круги, указанные в определении, называются основаниями цилиндра. Основания цилиндра равны и лежат в параллельных плоскостях.
Отрезки, соединяющие соответствующие точки окружностей кругов, называются образующими цилиндра. У цилиндра образующие параллельны и равны.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
Высотой цилиндра называется расстояние между плоскостями оснований.
Осью цилиндра называется прямая, проходящая через центры оснований.
Сечения цилидра
Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Сечение цилиндра плоскостью, паралелльной оси цилиндра, — прямоугольник.
Сечение цилиндра плоскостью, перпендикулярной оси цилиндра, — круг.
Развертка цилиндра
Вписанные и описанные призмы
Призма называется описанной около цилиндра, если ее основания – равные многоугольники, описанные около оснований цилиндра. Плоскости ее граней касаются боковой поверхности цилиндра.
Призмой, вписанной в цилиндр, называется призма, основания которой – равные многоугольники, вписанные в основание цилиндра. Ее боковые ребра являются образующими цилиндра.
Смотрите также таблицу «Тела вращения. Объем. Площадь поверхности».
egemaximum.ru
Понятие цилиндра
На этом уроке мы вспомним понятие цилиндра. Дадим его определение. Рассмотрим, какими элементами обладает цилиндр.
Вокруг нас существует множество объектов, которые являются физическими моделями цилиндра, или проще говоря, имеют форму цилиндра.
Например, кружки и стаканы имеют форму цилиндра. Карандаши, шляпы, пуфики, барабан также имеют форму цилиндра.
Некоторые архитектурные сооружения.
Колонны храмов и соборов, выполненные в форме цилиндра, подчеркивают их гармонию и красоту.
Итак, перейдём к самому цилиндру. Рассмотрим
произвольную плоскость 
и окружность 
с центром О
радиуса 
, лежащую в этой
плоскости. Через каждую точку окружности проведем прямую,
перпендикулярную к плоскости .
Определение:
Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые – образующими цилиндрической поверхности.
Прямая, проходящая через точку О перпендикулярно к
плоскости , называется осью
цилиндрической поверхности. Поскольку все образующие и ось
перпендикулярны к плоскости , то они
параллельны друг другу.
Рассмотрим теперь плоскость 
, параллельную
плоскости . Отрезки
образующих, заключённые между плоскостями и , параллельны и
равны друг другу. По построению концы этих отрезков, расположенные в плоскости , заполняют
окружность . Концы же,
расположенные в плоскости , заполняют
окружность 
с центром 
радиуса , где – точка
пересечения плоскости с осью
цилиндрической поверхности. Справедливость этого утверждения следует из того,
что множество концов образующих, лежащих в плоскости , получается из
окружности параллельным
переносом на вектор 
. Параллельный
перенос является движением и, значит, наложением, а при наложении любая фигура
переходит в равную ей фигуру. Следовательно, при параллельном переносе на
вектор . окружность перейдёт в равную
ей окружность радиуса с центром в точке
.
Определение:
Тело, ограниченное цилиндрической поверхностью и двумя
равными кругами с границами и , называется цилиндром.
Можно ещё услышать и такое определение: прямым
круговым цилиндром или просто цилиндром называется
геометрическое тело, ограниченное цилиндрической поверхностью и двумя
параллельными плоскостями и , которые
перпендикулярны образующим цилиндрической поверхности.
Назовём элементы цилиндра.
Круги называются основаниями цилиндра.
Отрезки образующих, заключенные между основаниями, — образующими цилиндра.
А образованная ими часть цилиндрической поверхности это есть боковая поверхность цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Как уже отмечалось ранее, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Цилиндр называется равносторонним, если его высота равна диаметру основания.
Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между основаниями цилиндра.
Цилиндр можно получить вращением прямоугольника вокруг
одной из его сторон на 
. Итак, если взять
некоторый прямоугольник 
и вращать его
вокруг одной из сторон, например, вокруг стороны 
, то в результате
получим тело, которое и называется цилиндром.
В этом случае основания цилиндра
образуются вращением сторон 
и 
, а боковая
поверхность цилиндра образуется вращении стороны 
.
Теперь рассмотрим сечения цилиндра различными плоскостями.
Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.
Определение:
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось.
Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие цилиндра, а две другие – хорды оснований цилиндра.
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.
В самом деле, такая секущая плоскость отсекает от данного цилиндра тело, которое также является цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.
Замечание. На практике очень часто встречаются предметы, которые имеют форму сложных цилиндров.
На экране, на первом рисунке вы видите цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком. На втором рисунке изображен цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскостям оснований, такой цилиндр называют еще наклонным цилиндром. Однако в дальнейшем мы будем рассматривать только прямые круговые цилиндры.
Задача: точка
– середина образующей цилиндра,
центрами оснований которого являются точки 
и 
. Верно ли, что 
?
Решение: рассмотрим
и 
.
Образующая перпендикулярна
плоскостям, в которых лежат основания цилиндра. Следовательно, она
перпендикулярна любой прямой лежащей в этих плоскостях. Прямые 
и 
являются
радиусами цилиндра и лежат в плоскостях оснований. Значит, прямая 
и 
. Отсюда получаем,
что и – прямоугольные.
Так как основаниями цилиндра являются равные круги, то
, как радиусы.
Так как по условию задачи точка – середина
образующей цилиндра, то
отрезки 
. Значит, 
равны по двум катетам.
Отсюда вытекает, что .
Ответ: .
Задача: точка
– центр основания
цилиндра. Отрезок – диаметр другого
его основания. Вычислите площадь 
, если радиус
цилиндра равен 
см, а его высота
– 
см.
Решение: напомним,
что площадь треугольника находится по формуле 
. Заметим, что
высота цилиндра является и высотой нашего и равна 
. А основание
треугольника есть диаметр цилиндра и равно оно двум радиусам, т.е. 
(см).
Подставим в формулу площади треугольника высоту и
длину основания треугольника. Посчитаем. Получим, что площадь треугольника
равна 
. Не забудем
записать ответ.
Задача: радиус
цилиндра 
см, а его высота
– 
см. Вычислите
площадь осевого сечения.
Решение: напомним, что осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.
Высота цилиндра – это есть длина образующей 
. Следовательно,
ширина осевого сечения равна 
. Длина сечения
равна диаметру основания цилиндра. И значит, равна 
(см).
Теперь вычислим площадь осевого сечения. Она равна 
(
).
Запишем ответ.
Итоги:
На этом уроке мы вспомнили понятие цилиндра. Узнали,
что тело, ограниченное цилиндрической поверхностью и двумя кругами с границами и , называется
цилиндром. Или прямым круговым цилиндром или просто цилиндром называется
геометрическое тело, ограниченное цилиндрической поверхностью и двумя
параллельными плоскостями и , которые
перпендикулярны образующим цилиндрической поверхности. Назвали элементы
цилиндра. А также рассмотрели сечения цилиндра различными плоскостями.
videouroki.net
Цилиндр
Понятие цилиндра
Определение 1
Геометрическая фигура, образованная двумя равными кругами, лежащими в параллельных плоскостях, все точки которых соединены между параллельными прямыми, так что никакая точка не остается несоединенной, называется цилиндром (рис. 1).
Рисунок 1. Цилиндр
Круги при этом называются основаниями цилиндра, а прямые их соединяющие — образующими. Прямая, которая проходит через центры окружностей оснований называется осью цилиндра, а совокупность всех образующих — боковой поверхностью цилиндра.
Виды цилиндров
Определение 2
Цилиндр, у которого все образующие перпендикулярны к плоскостям, проходящим через основания, называется прямым. В противном же случае он является наклонным (рис. 2).
Рисунок 2. Прямой и наклонный цилиндры
Площадь поверхности цилиндра
Площадь поверхности цилиндра определяется следующим образом:
Найдем теперь формулы для вычисления площадь боковой поверхности и основания.
Так как в основании лежат круги, то очевидно, что
Теорема 1
Площадь боковой поверхности цилиндра определяется как произведение длины окружности, ограничивающей основание цилиндра на его высоту.
Доказательство.
Для доказательства этой теоремы нам необходимо найти площадь развертки боковой поверхности цилиндра (рис. 3).
Рисунок 3.
Видим, что разверткой боковой поверхности цилиндра является прямоугольник. Высота прямоугольника равняется высоте цилиндра $h$, а длина равняется длине окружности, ограничивающей основание цилиндра, то есть
Теорема доказана.
Объем цилиндра
Теорема 2
Объем цилиндра определяется как произведение площади основания цилиндра на его высоту.
Доказательство.
Рассмотрим цилиндр с радиусом $r$ и высотой $h$. Найдем ее объем $V$. Для этого сначала впишем в нее правильную $n-$угольную призму, в которую впишем еще один цилиндр. Пусть радиус второго цилиндра равняется $r’$, а её объем равен $V’$ (рис. 4).
Рисунок 4.
Как мы знаем, объем призмы будет равен $S_{осн.пр.}h$. Следовательно, получим следующую оценку
Тогда из оценки, получим
Теорема доказана.
Пример задачи
Пример 1
Найти площадь полной поверхности цилиндра и его объем, если радиус его основания равняется $7$ см, а высота в два раза больше диаметра основания.
Решение.
Найдем вначале высоту цилиндра. Так как высота в два раза больше диаметра, получим
\[h=2\cdot 2r=4r=28\ см\]Как мы знаем
\[S_{осн}=\pi r^2=49\pi \]По теореме 1
\[S_{бок}=2\pi rh=392\pi \]Тогда
\[S_{полн}=S_{бок}+2S_{осн}=392\pi +98\pi =490\pi \]По теореме 2
\[V=\pi r^2h=49\pi \cdot 28=1372\pi \]Ответ: $490\pi ,\ 1372\pi $
spravochnick.ru