Cos равен 0 – Почему косинус 0 равен единице. Если он равен п/2. ))) Я чето голову сломал. Я не люблю математику. ПОМГОГИТТТЕЕ! — Детская игровая комната «Волшебный лес»

Posted on 22.02.202013.01.2020 by alexxlab

Содержание

cos x 0

Вы искали cos x 0? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и cos x 0 решение, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «cos x 0».

cos x 0

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как cos x 0,cos x 0 решение,cos x a,cosx 0,cosx 0 решение,кос х равен 0,косинус x равен 0,косинус икс равен 0,косинус икс равен 0 икс равен,косинус х 0,косинус х равен 0,решение cos x 0. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и cos x 0. Просто введите задачу в окошко и нажмите «решить» здесь (например, cos x a).

Где можно решить любую задачу по математике, а так же cos x 0 Онлайн?

Решить задачу cos x 0 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Таблица косинусов | umath.ru

cos(271°) = 0,017452
cos(272°) = 0,034899
cos(273°) = 0,052336
cos(274°) = 0,069756
cos(275°) = 0,087156
cos(276°) = 0,104528
cos(277°) = 0,121869
cos(278°) = 0,139173
cos(279°) = 0,156434
cos(280°) = 0,173648
cos(281°) = 0,190809
cos(282°) = 0,207912
cos(283°) = 0,224951
cos(284°) = 0,241922
cos(285°) = 0,258819
cos(286°) = 0,275637
cos(287°) = 0,292372
cos(288°) = 0,309017
cos(289°) = 0,325568
cos(290°) = 0,342020
cos(291°) = 0,358368
cos(292°) = 0,374607
cos(293°) = 0,390731
cos(294°) = 0,406737
cos(295°) = 0,422618
cos(296°) = 0,438371
cos(297°) = 0,453990
cos(298°) = 0,469472
cos(299°) = 0,484810
cos(300°) = 0,5

cos(301°) = 0,515038
cos(302°) = 0,529919
cos(303°) = 0,544639
cos(304°) = 0,559193
cos(305°) = 0,573576
cos(306°) = 0,587785
cos(307°) = 0,601815
cos(308°) = 0,615661
cos(309°) = 0,629320
cos(310°) = 0,642788
cos(311°) = 0,656059
cos(312°) = 0,669131
cos(313°) = 0,681998
cos(314°) = 0,694658
cos(315°) = 0,707107
cos(316°) = 0,719340
cos(317°) = 0,731354
cos(318°) = 0,743145
cos(319°) = 0,754710
cos(320°) = 0,766044
cos(321°) = 0,777146
cos(322°) = 0,788011
cos(323°) = 0,798636
cos(324°) = 0,809017
cos(325°) = 0,819152
cos(326°) = 0,829038
cos(327°) = 0,838671
cos(328°) = 0,848048
cos(329°) = 0,857167
cos(330°) = 0,866025

cos(331°) = 0,874620
cos(332°) = 0,882948
cos(333°) = 0,891007
cos(334°) = 0,898794
cos(335°) = 0,906308
cos(336°) = 0,913545
cos(337°) = 0,920505
cos(338°) = 0,927184
cos(339°) = 0,933580
cos(340°) = 0,939693
cos(341°) = 0,945519
cos(342°) = 0,951057
cos(343°) = 0,956305
cos(344°) = 0,961262

cos(345°) = 0,965926
cos(346°) = 0,970296
cos(347°) = 0,974370
cos(348°) = 0,978148
cos(349°) = 0,981627
cos(350°) = 0,984808
cos(351°) = 0,987688
cos(352°) = 0,990268
cos(353°) = 0,992546
cos(354°) = 0,994522
cos(355°) = 0,996195
cos(356°) = 0,997564
cos(357°) = 0,998630
cos(358°) = 0,999391
cos(359°) = 0,999848
cos(360°) = 1,0

Косинус

Примеры:

$\cos{⁡30^°}=$$\frac{\sqrt{3}}{2}$
$\cos⁡$$\frac{π}{3}$$=$$\frac{1}{2}$
$\cos⁡2=-0,416…$

Содержание:

Аргумент и значение

Косинус острого угла

Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.

Пример:

1) Пусть дан угол и нужно определить косинус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить косинус.

Косинус острого угла больше $0$ и меньше $1$

Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.

Косинус числа

Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи: $\frac{π}{2}$, $\frac{3π}{4}$, $-2π$.

Например, для числа $\frac{π}{6}$ — косинус будет равен $\frac{\sqrt{3}}{2}$. А для числа $-$$\frac{3π}{4}$ он будет равен $-$$\frac{\sqrt{2}}{2}$ (приблизительно $-0,71$).

Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице.

Значение косинуса всегда лежит в пределах от $-1$ до $1$. При этом вычислен косинус может быть для абсолютно любого угла и числа.

Косинус любого угла

Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем $360°$ (полный оборот). Как это делать — проще один раз увидеть, чем $100$ раз услышать, поэтому смотрите картинку.

Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в $150°$. Совмещаем точку О с центром окружности, а сторону ОК – с осью $x$. После этого откладываем $150°$ против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.

Если же нас интересует угол с градусной мерой, например, в $-60°$ (угол КОВ), делаем также, но $60°$ откладываем по часовой стрелке.

И, наконец, угол больше $360°$ (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол $405°$ отложен как $360° + 45°$.

Несложно догадаться, что для откладывания угла, например, в $960°$, надо сделать уже два оборота ($360°+360°+240°$), а для угла в $2640°$ — целых семь.

Стоит запомнить, что:

Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.

Знаки косинуса по четвертям

С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:

— там, где значения на оси от $0$ до $1$, косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от $0$ до $-1$, косинус будет иметь знак минус (II и III четверти – фиолетовая область).

Пример. Определите знак $\cos 1$.
Решение: Найдем $1$ на тригонометрическом круге. Будем отталкиваться от того, что $π=3,14$. Значит единица, примерно, в три раза ближе к нулю (точке «старта»).

Если провести перпендикуляр к оси косинусов, то станет очевидно, что $\cos⁡1$ – положителен.
Ответ: плюс.

Связь с другими тригонометрическими функциями:

— синусом того же угла (или числа): основным тригонометрическим тождеством $\sin^2⁡x+\cos^2⁡x=1$
— тангенсом того же угла (или числа): формулой $1+tg^2⁡x=$$\frac{1}{\cos^2⁡x}$
— котангенсом и синусом того же угла (или числа): формулой $ctgx=$$\frac{\cos{x}}{\sin⁡x}$
Другие наиболее часто применяемые формулы смотри здесь.

Функция $y=\cos{x}$

Если отложить по оси $x$ углы в радианах, а по оси $y$ — соответствующие этим углам значения косинуса, мы получим следующий график:

График данной функции называется косинусоида и обладает следующими свойствами:

— область определения – любое значение икса: $D(\cos{⁡x} )=R$
— область значений – от $-1$ до $1$ включительно: $E(\cos{x} )=[-1;1]$
— четная: $\cos⁡(-x)=\cos{x}$
— периодическая с периодом $2π$: $\cos⁡(x+2π)=\cos{x}$
— точки пересечения с осями координат:
ось абсцисс: $($$\frac{π}{2}$$+πn$,$;0)$, где $n ϵ Z$
ось ординат: $(0;1)$
— промежутки знакопостоянства:
функция положительна на интервалах: $(-$$\frac{π}{2}$$+2πn;$ $\frac{π}{2}$$+2πn)$, где $n ϵ Z$
функция отрицательна на интервалах: $($$\frac{π}{2}$$+2πn;$$\frac{3π}{2}$$+2πn)$, где $n ϵ Z$
— промежутки возрастания и убывания:
функция возрастает на интервалах: $(π+2πn;2π+2πn)$, где $n ϵ Z$
функция убывает на интервалах: $(2πn;π+2πn)$, где $n ϵ Z$
— максимумы и минимумы функции:
функция имеет максимальное значение $y=1$ в точках $x=2πn$, где $n ϵ Z$
функция имеет минимальное значение $y=-1$ в точках $x=π+2πn$, где $n ϵ Z$.

Смотрите также:

Синус
Тангенс
Котангенс
Решение уравнения $\cos⁡x=a$

Скачать статью

Коэффициент мощности — Википедия

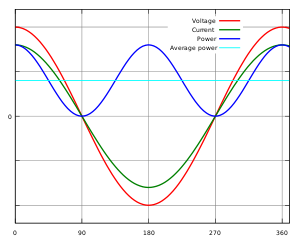Синусоидальное напряжение (красная линия) и ток (зелёная линия) синфазны — между ними нет фазового сдвига (φ=0∘{\displaystyle \varphi =0^{\circ }}, cos⁡φ=1{\displaystyle \cos \varphi =1}) — нагрузка полностью активная, нет реактивной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 1. Как видно, синяя линия (график мгновенной мощности) находится полностью над осью абсцисс (в положительной полуплоскости), вся подводимая энергия преобразуется в работу: переходит в активную мощность, потребляемую нагрузкой. 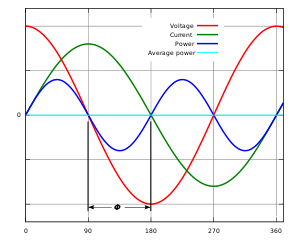$\cos \varphi =1$ Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг φ=90∘{\displaystyle \varphi =90^{\circ }} (cos⁡φ=0{\displaystyle \cos \varphi =0}) — нагрузка полностью реактивная, нет активной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 0. Расположение синей линии (графика мгновенной мощности) на оси абсцисс показывает, что в течение первой четверти цикла вся подводимая мощность временно сохраняется в нагрузке, а во второй четверти цикла возвращается в сеть, и так далее, то есть никакой активной мощности не потребляется, полезной работы в нагрузке не совершается. 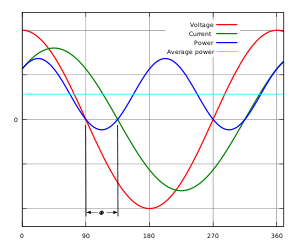$\cos \varphi =0$ Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг φ=45∘{\displaystyle \varphi =45^{\circ }} (cos⁡φ=0,71{\displaystyle \cos \varphi =0{,}71}) — нагрузка имеет и активную, и реактивную составляющие. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны из переменного напряжения и тока с коэффициентом мощности, равным 0,71. Расположение синей линии (графика мгновенной мощности) под осью абсцисс показывает, что некоторая часть подводимой мощности всё же возвращается в сеть в течение части цикла, отмеченного φ.

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей и мощности искажения (собирательное название — неактивная мощность). Следует отличать понятие «коэффициент мощности» от понятия «косинус фи», который равен косинусу сдвига фазы переменного тока, протекающего через нагрузку, относительно приложенного к ней напряжения. Второе понятие используют в случае синусоидальных тока и напряжения, и только в этом случае оба понятия эквивалентны.

Коэффициент мощности равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. В случае синусоидальных тока и напряжения полная мощность представляет собой геометрическую сумму активной и реактивной мощностей. Иными словами, она равна корню квадратному из суммы квадратов активной и реактивной мощностей. В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт).

В электроэнергетике для коэффициента мощности приняты обозначения cos⁡φ{\displaystyle \operatorname {cos} \varphi } (где φ{\displaystyle \varphi } — сдвиг фаз между силой тока и напряжением) либо λ{\displaystyle \lambda }. Когда для обозначения коэффициента мощности используется λ{\displaystyle \lambda }, его величину обычно выражают в процентах.

Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (или от 0 до 100 %).

Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения (в общем случае бесконечномерных). Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстоят соответствующие фазы.

В случае синусоидального напряжения, но несинусоидального тока, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой.

При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим.

Можно показать, что если к источнику синусоидального напряжения (например, розетка ~230 В, 50 Гц) подключить нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку с реактивной составляющей от электростанции требуется больше отвода тепла, чем при работе на активную нагрузку; избыток передаваемой энергии выделяется в виде тепла в проводах, и в масштабах, например, предприятия потери могут быть довольно значительными.

Не следует путать коэффициент мощности и коэффициент полезного действия (КПД) нагрузки. Коэффициент мощности практически не влияет на энергопотребление самого устройства, включённого в сеть, но влияет на потери энергии в идущих к нему проводах, а также в местах выработки или преобразования энергии (например, на подстанциях). Т.е. счётчик электроэнергии в квартире практически не будет реагировать на коэффициент мощности устройств, поскольку оплате подлежит лишь электроэнергия, совершающая работу (активная составляющая нагрузки). В то же время от КПД непосредственно зависит потребляемая электроприбором активная мощность. Например, компактная люминесцентная («энергосберегающая») лампа потребляет примерно в 1,5 раза больше энергии, чем аналогичная по яркости светодиодная лампа. Это связано с более высоким КПД последней. Однако независимо от этого каждая из этих ламп может иметь как низкий, так и высокий коэффициент мощности, который определяется используемыми схемотехническими решениями.

Треугольник мощностей

Коэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Если его снижение вызвано нелинейным, и особенно импульсным характером нагрузки, это дополнительно приводит к искажениям формы напряжения в сети. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПД электрооборудования, питающегося от данной сети.

Для расчётов в случае гармонических переменных U{\displaystyle U} (напряжение) и I{\displaystyle I} (сила тока) используются следующие математические формулы:

χ=PS{\displaystyle \chi ={\frac {P}{S}}}
P=U×I×cos⁡φ{\displaystyle P=U\times I\times \cos \varphi }
Q=U×I×sin⁡φ{\displaystyle Q=U\times I\times \sin \varphi }
S=∑k=1∞(U)×I=P2+Q2+T2{\displaystyle S=\textstyle \sum _{k=1}^{\infty }\displaystyle (U)\times I={\sqrt {P^{2}+Q^{2}+T^{2}}}}

Здесь P{\displaystyle P} — активная мощность, S{\displaystyle S} — полная мощность, Q{\displaystyle Q} — реактивная мощность, T — мощность искажения.

Типовые оценки качества электропотребления[править | править код]

При одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.


Значение коэффициента мощности	Высокое	Хорошее	Удовлетворительное	Низкое	Неудовлетворительное
cos⁡φ{\displaystyle \operatorname {cos} \varphi }	0,95…1	0,8…0,95	0,65…0,8	0,5…0,65	0…0,5
λ{\displaystyle \lambda }	95…100 %	80…95 %	65…80 %	50…65 %	0…50 %

Например, большинство старых светильников с люминесцентными лампами для зажигания и поддержания горения используют электромагнитные балласты (ЭмПРА), характеризующиеся низким значением коэффициента мощности, то есть неэффективным электропотреблением. Многие компактные люминесцентные («энергосберегающие») лампы, имеющие ЭПРА, тоже характеризуются низким коэффициентом мощности (0,5…0,65). Но аналогичные изделия известных производителей, как и большинство современных светильников, содержат схемы коррекции коэффициента мощности, и для них значение cos⁡φ{\displaystyle \operatorname {cos} \varphi } близко к 1, то есть к идеальному значению.

Несинусоидальность[править | править код]

Низкое качество потребителей электроэнергии, связанное с наличием в нагрузке мощности искажения, то есть нелинейная нагрузка (особенно при импульсном её характере), приводит к искажению синусоидальной формы питающего напряжения. Несинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях.

Источниками высших гармоник тока и напряжения являются электроприёмники с нелинейными нагрузками. Например, мощные выпрямители переменного тока, применяемые в металлургической промышленности и на железнодорожном транспорте, газоразрядные лампы, импульсные источники питания и др.

Коррекция коэффициента мощности при помощи конденсаторов

Коррекция коэффициента мощности (англ. power factor correction (PFC)) — процесс приведения потребления конечного устройства, обладающего низким коэффициентом мощности при питании от силовой сети переменного тока, к состоянию, при котором коэффициент мощности соответствует принятым стандартам.

К ухудшению коэффициента мощности (изменению потребляемого тока непропорционально приложенному напряжению) приводят нерезистивные нагрузки: реактивная и нелинейная. Реактивные нагрузки корректируются внешними реактивностями, именно для них определена величина cos⁡φ{\displaystyle \cos \varphi }. Коррекция нелинейной нагрузки технически реализуется в виде той или иной дополнительной схемы на входе устройства.

Данная процедура необходима для равномерного использования мощности фазы и исключения перегрузки нейтрального провода трёхфазной сети. Так, она обязательна для импульсных источников питания мощностью в 100 и более ватт^{[источник не указан 3159 дней]}. Компенсация обеспечивает отсутствие всплесков тока потребления на вершине синусоиды питающего напряжения и равномерную нагрузку на силовую линию.

Разновидности коррекции коэффициента мощности[править | править код]

Коррекция реактивной составляющей полной мощности потребления устройства. Выполняется путём включения в цепь реактивного элемента, производящего обратное действие. Например, для компенсации действия электродвигателя переменного тока, обладающего высокой индуктивной реактивной составляющей полной мощности, параллельно цепи питания включается конденсатор. В масштабах предприятия для компенсации реактивной мощности применяются батареи конденсаторов и других компенсирующих устройств.
Коррекция нелинейности потребления тока в течение периода колебаний питающего напряжения. Если нагрузка потребляет ток непропорционально приложенному напряжению, для повышения коэффициента мощности требуется схема пассивного (PPFC) или активного корректора коэффициента мощности (APFC). Простейшим пассивным корректором коэффициента мощности является дроссель с большой индуктивностью, включённый последовательно с питаемой нагрузкой. Дроссель выполняет сглаживание импульсного потребления нагрузки и выделение низшей, то есть основной, гармоники потребления тока, что и требуется (правда, это достигается в ущерб форме напряжения, поступающего на вход устройства). Активная коррекция коэффициента мощности ценой некоторого усложнения схемы устройства способна обеспечивать наилучшее качество коррекции, приближая коэффициент мощности к 1.

чему равен sin0 и cos0?

Да ты в таблицу посмотри!

косинус 0=1, синус 0=0

можно просто представить график, и все станет ясно, кос в нуле 1, син 0

Ольга, спасибо, что посоветовала <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&st.cmd=logExternal&st.link=http://mail.yandex.ru/r?url=http://fond2019.ru/&https://mail.ru &st.name=externalLinkRedirect&st» target=»_blank»>fond2019.ru</a> Выплатили 28 тысяч за 20 минут как ты и написала. Жаль что раньше не знала про такие фонды, на работу бы ходить не пришлось:)

Чему равен cos 1 в градусах?

в таблице брадиса кос 57.2957 градусов будет нужное значение

Косинус даёт единицу только при нуле градусов

единица — это аргумент? косинус одного градуса? мой Ситизен показывает 0,999876632 То есть очень близко в косинусу нуля, а это — единица 🙂

соs 1= 0градус59градус59.45 это калькулятор так показал

Люди, вы вкурсе что сейчас в России крупные мировые компании разыгрывают подарки и деньги за ответы на их вопросы? На www.fond2019.ru можете почитать подробнее. Может ещё успеете пока у них призы не кончились:)

Ольга, спасибо, что посоветовала <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&st.cmd=logExternal&st.link=http://mail.yandex.ru/r?url=http://aoru.ru/&https://mail.ru &st.name=externalLinkRedirect&st» target=»_blank»>aoru.ru</a> Выплатили 38 тысяч за 20 минут как ты и написала. Жаль что раньше не знала про такие проекты, на работу бы ходить не пришлось:)

Косинус фи (cos φ) или Коэффициент мощности

На шильдиках двигателей и некоторых других устройств можно видеть непонятный параметр косинус фи (cos φ). Что этот параметр означает, в данной статье коротко объясняется, что это такое.
Косинус фи (cos φ) часто называют «Коэффициент мощности». Это почти одно и то же при правильной синусоидальной форме тока.
Иногда для обозначения коэффициента мощности используется λ, эту величину выражают в процентах, или PF.

Условные обозначения

P — активная мощность S — полная мощность Q — реактивная мощность, U — напряжение I — ток.

Что такое Косинус фи (cos φ) — «Коэффициент мощности»

Косинус фи (cos φ) это косинус угла между фазой напряжения и фазой тока.
При активной нагрузке фаза напряжения совпадает с фазой тока, φ (между фазами) равен 0 (нулю). А как мы знаем cos0=1. То есть при активной нагрузке коэффициент мощности равен 1 или 100%.

Активная нагрузка

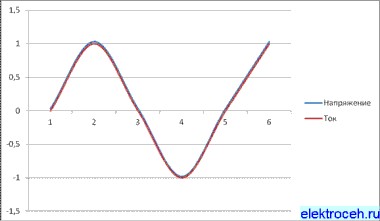
При емкостной или индуктивной нагрузке фаза тока не совпадает с фазой напряжения. Получается «сдвиг фаз».
При индуктивной или активно-индуктивной нагрузке (с катушками: двигатели, дросселя, трансформаторы) фаза тока отстает от фазы напряжения.
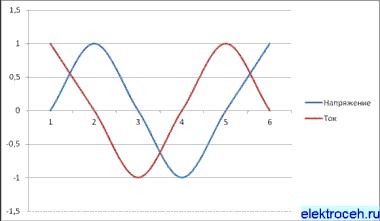
При емкостной нагрузке (конденсатор) фаза тока опережает фазу напряжения
А почему тогда косинус фи (cos φ) это тоже самое что коэффициент мощности, да потому что S=U*I.
Посмотрите на графики ниже. Здесь φ равно 90 косинус фи (cosφ)=0(нулю).

Емкостная нагрузка

Индуктивная нагрузка

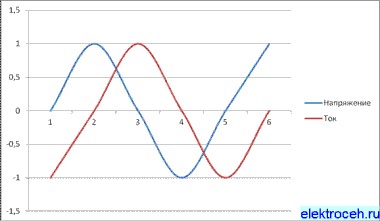
Попытаемся вычислить мощность для простоты возьмем максимальное значение напряжения равное 1(100%) в этот момент ток равен 0(нулю) соответственно их произведение, то есть мощность равны 0(нулю). И наоборот когда ток максимальный напряжение равно нулю.
Получается что полезная, активная мощность равна 0(нулю).

Коэффициент мощности это соотношение полезной активной мощности к полной мощности, то есть cosφ=P/S.

Треугольник мощностей

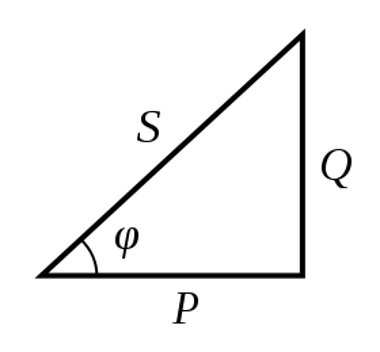
Посмотрите на треугольник мощностей. Вспомним тригонометрию (это что то из математики) вот здесь то она нам и пригодится.

P=U x I x cos φ

Q =U x I x sin φ

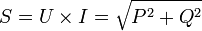
На практике. Если подключить асинхронный двигатель в сеть без нагрузки, в холостую. Напряжение вроде как есть, ток, если замерить тоже есть, при этом ни какой полезной работы не совершается. Соответственно активная мощность минимальна.
Если на двигателе увеличить нагрузку то сдвиг фаз начнет уменьшаться и соответственно косинус фи (cos φ) будет увеличиваться, а с ним и активная мощность.

К счастью счетчики активной мощности фиксируют соответственно только активную мощность. И нам не приходится переплачивать за полную мощность.

Однако у реактивной мощности есть большой минус она создает бесполезную нагрузку на электрическую сеть из-за этого образуются потери.