Практикум по решению линейных уравнений (7 класс)
а) 6х – 12 = 4х – 8 б) 5у – 8 = 2у – 5
в) г)
д) (2х – 5) – (3х — 7) = 4 е) (2 + 3х) – (4х — 7) = 10
ж) 5(х – 1,2) – 3х = 2 з) 2(х – 1,5) + х = 6
и) 0,3х + 8 = 2 к) 0,4х – 6 = -12
л) 4 – х = 1 + 4х м) х + 6 = 5 + 4х
н) 7 – 2(х + 3) = 9 – 6х о) 13 – 3(х + 1) = 4 – 5х
п) 0,9х + 1 = 0,2х — 6 р) 1,3х – 2 = 2,6х + 11
с) т) 
у) 4 = -1 – (11х – 5) ф) –6 = -2 – (4 + 9х)
х) 0,5(8х – 3) = -4(2,5 – х) ц) 1,2(5 – 4х) = -6(0,8 + 1)
а) 6х – 12 = 4х – 8 б) 5у – 8 = 2у – 5
в) г)
д) (2
ж) 5(х – 1,2) – 3х = 2 з) 2(х – 1,5) + х = 6
и) 0,3х + 8 = 2 к) 0,4х – 6 = -12
л) 4 – х = 1 + 4х м) х + 6 = 5 + 4х
н) 7 – 2(х + 3) = 9 – 6х о) 13 – 3(х + 1) = 4 – 5х
п) 0,9х + 1 = 0,2х — 6 р) 1,3х – 2 = 2,6х + 11
с) т) 
у) 4 = -1 – (11х – 5) ф) –6 = -2 – (4 + 9х)
х) 0,5(8х – 3) = -4(2,5 – х) ц) 1,2(5 – 4х) = -6(0,8 + 1)
а) 6х – 12 = 4х – 8 б) 5у – 8 = 2у – 5
в) г)
д) (2х – 5) – (3х — 7) = 4 е) (2 + 3х) – (4х — 7) = 10
ж) 5(х – 1,2) – 3х = 2 з) 2(х – 1,5) + х
= 6и) 0,3х + 8 = 2 к) 0,4х – 6 = -12
л) 4 – х = 1 + 4х м) х + 6 = 5 + 4х
н) 7 – 2(х + 3) = 9 – 6х о) 13 – 3(х + 1) = 4 – 5х
п) 0,9х + 1 = 0,2х — 6 р) 1,3х – 2 = 2,6х + 11
с) т) 
у) 4 = -1 – (11х – 5) ф) –6 = -2 – (4 + 9х)
х) 0,5(8х – 3) = -4(2,5 – х) ц) 1,2(5 – 4х) = -6(0,8 + 1)
План-конспект урока (алгебра, 7 класс) по теме: Задания для самоподготовки по теме: «Системы линейных уравнений с двумя неизвестными» 7 класс
Задания для самоподготовки по теме: «Системы линейных уравнений с двумя неизвестными»
- 3х-у=3, 2. 2х-3у=1, 3. 2х+у=1, 4. х+у=6,
3х-2у=0. 3х+у=7. 5х+2у=0. 5х-2у=9.
5. х+5у=7, 6. х+у=7, 7. 4х-3у=-1, 8. х+2у=-2,
3х+2у=-5. 5х-7у=11. х-5у =4. 3х-у=8.
9. 2х-5у=-7, 10. х-у=3, 11. 3х-5у=16, 12. 2х+3у=-7,
х-3у=-5. 3х+4у=2. 2х+у=2. х-у=4.
13. 2х+5у=-7, 14. х-3у=8, 15. 2х-3у=5, 16. х-4у=-1,
3х-у=15. 2х-у=6. х-6у=-2. 3х-у=8.
17. 5х-4у=12, 18. 6х+у=5, 19. 2х-3у=11, 20. х-6у=-2,
х-5у=-6. 2х-3у=-5. 5х+у=2. 2х+3у=11.
21. 3х-2у=16, 22. 2х+3у=3, 23. 4х-2у=-6, 24. 3х+2у=8,
4х+у=3. 5х+6у=9. 6х+у==11. 2х+6у=10.
25. 5х+у==14, 26. 3х-2у=5, 27. х+4у=7, 28. 2х-3у=5,
3х-2у=-2. 2х+5у=16. х-2у=-5. 3х+2у=14.
29. х-2у=7, 30. 4х-6у=26, 31. х+3у=7, 32. 8х+3у=-21,
х+2у=-1. 5х+3у=1. х+2у=5. 4х+5у=-7.
33. х-2у=8, 34. 8х+2у=11, 35. 2х-у=13, 36. 7х+3у=1,
х-3у=6. 6х-4у=11. 2х+3у=9. 2х-6у=-10.
37. 2х+3у=10, 38. 3х-2у=5, 39. 2х+у=-5, 40. 2х+3у=1,
х-2у=-9. 5х+4у=1. х-3у=-6. 6х-2у=14.
Задания для самоподготовки по теме: «Системы уравнений второй степени с двумя неизвестными»
- 2ху=5, 2. х+у=5, 3. х-2у=2, 4. х-у=1,
2х+у=6. ху=-14. 2ху=3. х2+2у=33.
5. 3ху=1, 6. у-х=2, 7. 4у-х=1, 8. х-у=1,
6х+у=3. 4х+у2=13. 2ху =1. х2-у=3.
9. х2-у=-2, 10 . х+у=4, 11. 3х-у=-10, 12. х+у=5,
2х+у=2. х2-у=2. х2+у=10. ху=6.
13. х-у=7, 14. ху=8, 15. х-у=7, 16. х+у=1,
ху=-10. х+у=6. ху=-12. х2+у2=25.
17. х+у=10, 18. х+у=3, 19. х-у=4, 20. 2х+у2=6,
х2-у2=40. х2+у2=29. х2-у2=40. х+у=3.
21. х-у=4, 22. х-у=2, 23. х-у=4, 24. х-у=6,
ху=5. 3х-у2=6. ху==12. х2+у2=20.
25. х2-3у==22, 26. х-у=4, 27. х+у=4, 28. х-у=2,
х+у=2. х2+у2=10. х2-4у=5. х-у2=2.
29. х+у=2, 30. х2-у=-1, 31. у-х=2, 32. х2+2у=12,
ху=-15. х+у=1. у2-4х=13. 2х-у=10.
33 . х2-3у=1, 34. х-2у=2, 35 . х-у=-6, 36. х+у=-2,
х+у=3. 3х-у2=11. ху=40. у2-3х=6.
37. х-у=4, 38. х2+ху=12, 39. 2х+у=-5, 40. 2х+3у=1,
ху+у2=6. у-х=2. х-3у=-6. 6х-2у=14.
41. х-у=5, 42. х+у=3, 43. у2-3ху+х2-х+у+9=0,
х2+2ху-у2=-7. х2+2ху+2у2=18. у-х=2.
44. ху=-8, 45. (х-у)(х+у)=12, 46. + = ,
(х-4)(у-2)=-12. х+у=3(х-у) х+у=12.
47. х-у=7, 48. — =-2, 49. + =4,
—=. + =8. — =10.
Ответы к теме: ««Системы линейных уравнений с двумя неизвестными»
- (2;3)
- (2;1)
- (-2;5)
- (3;3)
- (-3;2)
- (5;2)
- (-1;-1)
- (2;-2)
- (4;3)
- (2;-1)
- (2;-2)
- (1;-3)
- (4;-3)
- (2;-2)
- (4;1)
- (3;1)
- (4;2)
- (0,5;2)
- (1;-3)
- (4;1)
- (2;-5)
- (3;-1)
- (1;5)
- (2;1)
- (2;4)
- (3;2)
- (-1;2)
- (4;1)
- (3;-2)
- (2;-3)
- (1;2)
- (-3;1)
- (12;2)
- (1,5;-0,5)
- (6;-1)
- (-0,5;1,5)
- (-1;4)
- (1;-1)
- (-3;1)
- (2;-1)
Ответы к теме: «Системы уравнений второй степени с двумя неизвестными»
- (0,5;5) (2,5;1)
- (-2;7) (7;-2)
- (-1;-1,5) (3;0,5)
- (-7;-8) (5;4)
- (⅙;2) (⅓;1)
- (-9;-7) (1;3)
- (-2;-0,25) (1;0,5)
- (-1;-2) (2;1)
- (0;2) (-2;6)
- (2;2) (-3;7)
- (0;10) (-3;1)
- (2;3) (3;2)
- (2;-5) (5;-2)
- (4;2) (2;4)
- (3;-4) (4;-3)
- (-3;4) (4;-3)
- (7;3)
- (-2;5) (5;-2)
- (7;3)
- (3;0) (1;2)
- (-1;-5) (5;1)
- (2;0) (5;3)
- (-2;-6) (6;2)
- (2;-4) (4;-2)
- (-7;9) (4;-2)
- (3;-1) (1;-3)
- (3;1) (-7;11)
- (3;1) (2;0)
- (5;-3) (-3;5)
- (-1;2) (0;1)
- (-3;-1) (3;5)
- (-8;-26) (4;-2)
- (2;1) (-5;8)
- (4;1) (12;5)
- (-10;-4) (4;10)
- (-2;0) (1;-3)
- (1;5) (-3;1)
- (-3;-1) (2;4)
- (-3;1)
- (2;-1)
- (-3;-8) (3;-2)
- (0;3) (6;-3)
- (-5;-3) (3;5)
- (8;-1) (-2;4)
- (4;2) (-4;-2)
- (8;4) (4;8)
Решение задач с помощью линейных уравнений. 7-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока: Обеспечить повторение и обобщение ЗУН учащихся по решению линейных уравнений и задач с их помощью.
Задачи урока.
- Обеспечить в ходе урока повторение алгоритма решения линейных уравнений, основных типов текстовых задач, способов их оформления и решения. Закрепить умения по составлению и решению линейных уравнений в ходе решения задач.
- Продолжить развивать умения: анализировать, сопоставлять, сравнивать, выделять главное, приводить примеры. Формировать умение работать с таблицами, схемами. Развивать коммуникативные навыки при работе в группах.
- Воспитывать у учащихся ответственность за свою работу перед товарищами, поощрять взаимопомощь во время работы в группах. Воспитывать культуру учебного труда, экономного расходования времени.
Средства (оборудование):
- компьютер, проектор, экран;
- презентация: “Решение задач с помощью линейных уравнений”;
- раздаточный материал: карточки для устной работы (3 штуки), карты для практической работы в группах (по количеству групп), опорные конспекты для каждого учащихся.
Ход урока
I. Организационный момент. (2 минуты)
Учащимся сообщается тема урока, его цель и задачи, ход урока (основные этапы). Учащиеся записывают в тетрадь дату и тему урока.
Начинается демонстрация презентации “Решение задач с помощью линейных уравнений” (Презентация) – 1 слайд.
II. Актуализация опорных знаний. (10 минут)
1 этап. Устная работа – 2 слайд.
Каждый ряд получает карточку для устной работы (Приложение 1). Учащиеся решают линейные уравнения “по цепочке”, вписывают буквы в соответствующий столбец.
По окончании работы проверяются её результаты. Учитель объясняет, что получившиеся слова (
2 этап. “Найди ошибку” – 3 слайд.
Фронтальная работа с классом. Учащиеся находят ошибки в решении уравнений, объясняют как их исправить, обосновывают свои предложения, опираясь на алгоритм решения линейных уравнений.
По окончании работы алгоритм повторяется полностью наиболее слабыми учащимися.
III. Повторение материала. (8 минут)
Повторяются и обсуждаются основные этапы решения текстовой задачи – 4 слайд.
Повторяются основные типы задач – 5-8 слайды: учащиеся читают условие, вспоминают и называют тип задачи и способ оформления её условия (вид таблицы), основные соотношения и формулы для данного типа.
По окончании обсуждения каждому учащемуся выдаётся опорный конспект (Приложение 2).
IV. Практическая работа. (15 минут)
Учащиеся разбиваются на группы по 4 человека (2 соседних парты). Каждая группа получает карту для практической работы (Приложение 3). Группа совместно обсуждает условие задач №№1-4, заполняет таблицы для кратких условий, составляет уравнения (решать их не нужно).
По окончании работы производится фронтальная проверка и обсуждение задач и составленных уравнений – 10-13 слайды. Уравнения записываются в тетрадь.
— Ребята, мы вспомнили основные, наиболее часто встречающиеся типы текстовых задач. Однако вы знаете, что существует великое множество задач других типов. В частности, задачи с геометрическим, физическим содержанием и другие.
14 слайд
Способы оформления задач также различны. Составление таблиц – это наиболее удобный способ во многих случаях, хотя совсем не обязательный. Например, при решении задач с геометрическим содержанием зачастую более удобен рисунок –
И условия задач основных типов также могут оформляться по-разному. Например, задача № 1 может быть оформлена так: 16 слайд.
То есть рассмотренные нами схемы – это вовсе не догма, выбор оформления и способа решения задачи остаётся за вами. Он зависит как от условия задачи, так и от ваших личных предпочтений.
Задачу № 5 вы решите полностью так, как сочтёте наиболее удобным и правильным, а затем мы обсудим ваши варианты оформления.
Работа в группах, решение задачи № 5 в карте для практической работы.
По окончании решения обсуждаются варианты групп, учащимся демонстрируется 17 слайд как один из возможных вариантов оформления, проверяется правильность составления уравнении и полученного ответа.
V. Подведение итогов урока. (3 минуты)
Фронтальная работа с классом:
- Какие типы задач можно назвать основными?
- Каковы их характерные особенности?
- В чём их сходство, отличие?
- Как можно оформить условие задачи?
- Что необходимо проверить, прежде чем записывать ответ? (Соответствие ответа смыслу задачи).
Наиболее активным учащимся выставляются оценки за урок.
VI. Домашнее задание. (2 минуты)
- Решить уравнения, составленные по задачам № 1-4.
- Придумать и решить задачу одного из основных типов, оформив её в соответствии с опорным конспектом.
Конспект урока по алгебре в 7 классе «Решение задач с помощью систем линейных уравнений»
Конспект урока по алгебре в 7 классе «Решение задач с помощью систем линейных уравнений»
Автор учебника А.Г. Мерзляк, В.Б. Полонский, М.С. Якир – М.: Вентана- Граф, 2017.
Тема «Решение задач с помощью систем линейных уравнений»
Тип урока: урок обобщения и систематизации знаний
Формируемые результаты:
Предметные: обобщить и систематизировать навык решения текстовых задач, в которых используют системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций.
Личностные: формировать интерес к изучению темы и желание применять приобретённые знания и умения.
Метапредметные: формировать умение использовать приобретённые знания в практической деятельности.
Планируемые результаты:
Учащийся научится решать текстовые задачи, в которых используют системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций.
Основные понятия
:Задачи, в которых используют системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций.
Ход урока.
Организационный этап.
Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Проверка домашнего задания.
Актуализация знаний.
Устно. На доске записали число. Когда из него вычли 9 и полученный результат уменьшили в 7 раз, то получили 14. Какое число записали на доске?
Обобщение и систематизация знаний.
Решить задачи по учебнику № 1092, 1096, 1098, 1110, 1111, 1122
Информация о домашнем задании.
Изучить § 29,( базовый уровень) — № 1097, 1099, (повышенный уровень) №1112
Решение задач
№ 1092. Пусть в первом бидоне х л молока, а во II бидоне у л.
Тогда 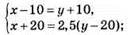
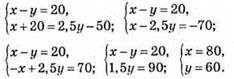
Ответ: в 1 бидоне 80 л молока, а во II бидоне 60 л.
№1096. Пусть ослик нес х мешков, а мул — у мешков.
Тогда:
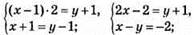
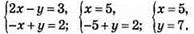
Ответ: ослик нес 5 мешков, мул — 7 мешков.
№ 1098. Пусть отцу х лет, сыну у лет.
Тогда:
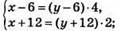
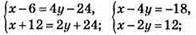
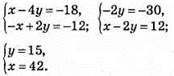
Ответ: отцу-42 года, сыну 15 лет.
№ 1110. Пусть 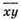 — искомое число.
— искомое число.
Тогда 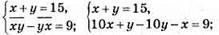
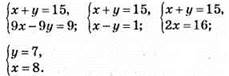
Следовательно, искомое число 87.
№ 1111. Пусть х и у — стороны прямоугольника.
Тогда х + у = 14, (х + 6)(y — 2) — ху = 24, или xy + 6y — 2х — 12 — ху = 24.
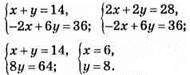
Ответ: стороны данного прямоугольника 6 см и 8 см.
№ 1122. Пусть 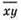 — данное число.
— данное число.
Тогда х + y = 9 и 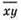 = (х — y) ∙ 14 + 2.
= (х — y) ∙ 14 + 2.
Имеем систему уравнений:
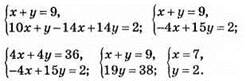
Ответ: 72 — искомое число.
Домашнее задание
№ 1097. Пусть у первого было х рупий, а у второго у рупий.
Тогда: 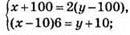
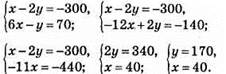
Ответ: у первого 40 рупий, у второго 170 рупий.
№ 1099. Пусть бабушки х лет, внучке у лет.
Тогда:
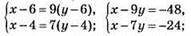
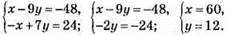
Ответ: бабушке 60 лет, внучке 12 лет.
№ 1112. Пусть х и у — стороны данного прямоугольника.
Тогда 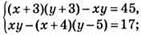
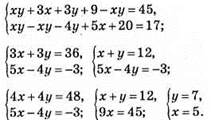
Ответ: 5 см и 7 см.