Действия над физическими величинами | Универсальный образовательный портал UniverFiles.com
План-конспект урока по теме «Действия над физическими величинами. Решение задач»
Дата:
Тема: «Действия над физическими величинами. Решение задач»
Цели:
Образовательная: формирование практических умений по выполнению действий над физическими величинами;
Развивающая: совершенствовать интеллектуальные умения (наблюдать, сравнивать, размышлять, применять знания, делать выводы), развивать познавательный интерес;Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.
Тип урока: обобщение и систематизация знаний
Оборудование и источники информации:
Исаченкова, Л. А. Физика : учеб. для 7 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский ; под ред.

мультимедийное оборудование.
Структура урока:
Организационный момент(4 мин)
Актуализация опорных знаний(3 мин)
Изучение нового материала (13 мин)
Первичная проверка понимания (12 мин)
Закрепление полученных знаний (8 мин)
Итоги урока(5 мин)
Содержание урока
Организационный момент (проверка присутствующих в классе, озвучивание темы и основных целей урока )Актуализация опорных знаний
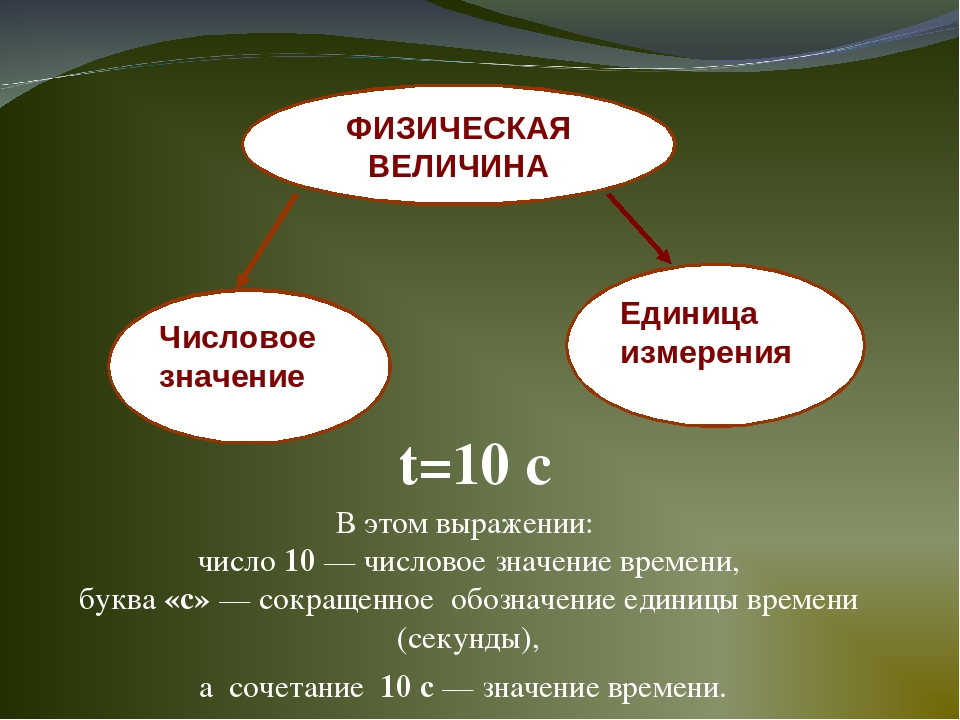
В математике можно складывать, вычитать и сравнивать любые числа. А какие же действия можно производить над физическими величинами?
Изучение нового материала
Действия сложения, вычитания и сравнения над физическими величинами можно производить только в том случае, если они однородны, т. е. представляют одну и ту же физическую величину.
Например:
4 м + 3 м = 7 м; 9 кг — 5 кг = 4 кг; 30 с > 10 с.

Во всех трех случаях мы производили действия над однородными физическими величинами. Складывали длину с длиной, вычитали из массы массу, сравнивали промежуток времени с промежутком времени. Смешно и нелепо было бы складывать 4 м и 5 кг или вычитать 30 с из 9 кг!
А вот умножать и делить можно не только однородные, но и разные физические величины. Например:
10 кг ÷2 кг = 5. Здесь делятся не только числовые значения (10 ÷ 2 = 5), но и единицы физических величин (кг ÷ кг = 1). Результат показывает, во сколько раз одна физическая величина (масса) больше другой.
2 м • 4 м = 8 м2. Умножаются числовые значения (2 • 4 = 8) и единицы физических величин (м • м = м2). В результате умножения двух физических величин — длин l1 = 2 м и l2 = 4 м — получилась новая физическая величина — площадь S = 8 м2.
10 м ÷ 2 с = 5 м/с. В результате деления двух разных физических величин — длины l = 10 м на промежуток времени t = 2 с, получилась новая физическая величина 5 м/c. Ее числовое значение равно 5, а единица новой физической величины — м/c.

10 м ÷ 2 с = 20 м ÷ 4 с. Знак равенства относится не только к числовым значениям, но и к единицам. Знак равенства поставить нельзя, если сравнить 10 м ÷ 2 с и 20 м ÷ 4 мин. Здесь м/с ≠ м/мин.
Первичная поверка понимания
Что необходимо учитывать при сложении и вычитании физических величин? Каким будет результат их сложения и вычитания?
Какие физические величины можно сравнивать между собой? Приведите примеры.
Можно ли делить и умножать разные физические величины? Что получится в результате?
Определите, значение какой физической величины получится в результате:
40 с — 10 с;
40 c ÷ 10 c;
3 м • 4 м • 2 м;
120 км ÷ 2 ч.
Далее рассматриваются примеры решения задач из учебника
Закрепление знаний
Решение задач из упражнения 2
Итоги урока
Итак, подведем итоги. Что нового вы сегодня узнали на уроке?
Какие сложности у вас возникли?
Организация домашнего задания
§6,ответить на контрольные вопросы; упр.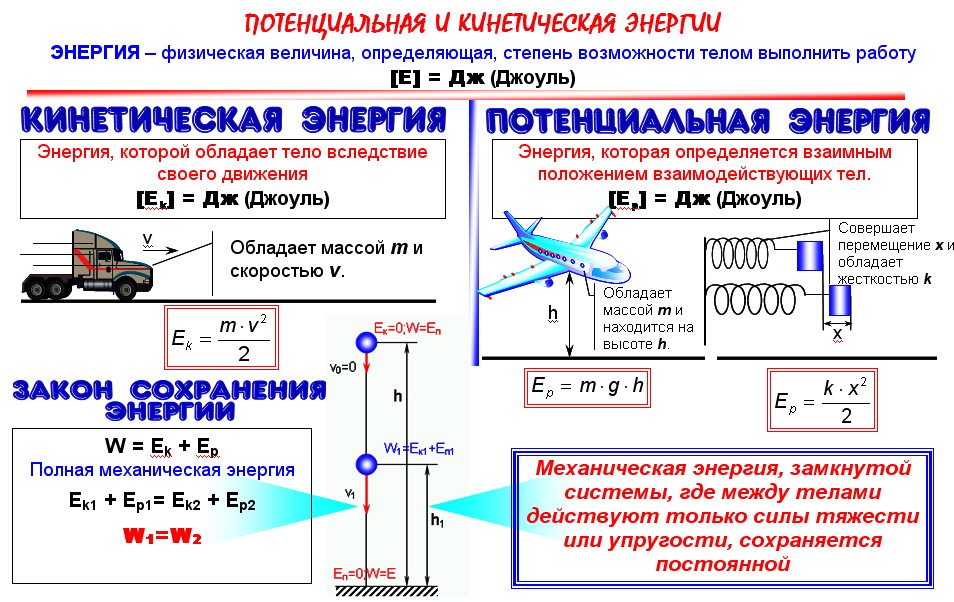 2(4 задание).
2(4 задание).
Рефлексия.
Продолжите фразы:
Сегодня на уроке я узнал…
Было интересно…
Знания, которые я получил на уроке, пригодятся
Школа №10 г. Североморск — Заякина Оксана Николаевна
Категория: UncategorisedЗаякина Оксана Николаевна
Расписание уроков
Перевод набранных процентов в оценку на платформе «ЯКласс».
| Баллы | Оценка |
| 87 %-100 % | 5 |
| 66 % — 86 % | 4 |
| 42 % — 65 % | 3 |
| 2 % — 41 % | 2 |
| 1 % — 0 % | 1 |
Факультатив по физике 6 класс
Уважаемые ребята, предлагаю вашему внимание фильм, посмотрите его пожалуйста:
https://www. youtube.com/watch?v=BSszjZVJPQA
youtube.com/watch?v=BSszjZVJPQA
Ответы присылать на Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.
Библиотека
7 класс
1. Задачник по физике 7 класс Генденштейн Л.Э., Кирик Л.А., Гельфгат И.М.
2. Сборник задач по физике 7-9 классов Лукашик В.И., Иванова Е.В.
10-11 класс
1. Сборник задач по физике Рымкевич А.П.
| Задачник по физике 7 класс Генденштейн | [ ] | 19855 Кб |
| Качественные задачи по физике 7-9 класс Кирик | [ ] | 37235 Кб |
| Кирик Сборник задач по физике 9 класс | [Кирик Сборник задач по физике 9 класс] | 38348 Кб |
| Гельфгат Сборник задач по физике 11 класс | [Гельфгат Сборник задач по физике 11 класс] | 19796 Кб |
| Сборник задач по физике 10 класс Гельфгат | [ ] | 31010 Кб |
- Назад
- Вперёд
|
Доп. материал |
Упражнения №1, №2 |
||
|
4 |
Действия над физическими величинами. Решение задач по теме «Действия над физическими величинами» |
||
|
5 |
|||
|
Доп. материал |
Упражнения №1, №2 |
||
|
6 |
Измерительные приборы. Цена деления. Точность измерений. |
||
|
Доп. материал |
Упражнения |
||
|
7 |
Решение задач по теме «Измерительные приборы. |
||
|
Упражнения №1, №2 |
|||
|
2. Строение вещества |
|||
|
8 |
Дискретное строение вещества. Тепловое движение частиц |
||
|
Доп. материал |
Упражнения №1, №2 |
||
|
9 |
Взаимодействие частиц вещества. Твердое, жидкое и газообразное состояния вещества |
||
|
Доп. материал |
Упражнения №1, №2 |
||
|
10 |
Тепловое расширение |
||
|
Доп. |
Упражнения |
||
|
11 |
Температура. Измерение температуры. Термометры |
||
|
Доп. материал |
Упражнения |
||
|
12 |
Научно-практическая конференция «Зачем нужны в науке измерения?» |
||
|
Доп. материал |
Упражнения |
||
|
3. Движение и силы |
|||
|
13 |
Механическое движение. Относительность покоя и движения. |
||
|
Доп. материал |
Упражнения |
||
|
14 |
Равномерное движение. Скорость. Единицы скорости |
||
|
Доп. материал |
Упражения |
||
|
|
Графики пути и скорости при равномерном прямолинейном движении |
||
|
Доп. материал |
Упражнения |
||
|
16 |
Неравномерное (переменное) движение. |
||
|
Доп. материал |
Упражения |
||
|
17 |
Решение задач по теме «Равномерное и неравномерное движение. Средняя скорость» |
||
|
мммм |
Упражнения |
||
|
18 |
Масса тела. Плотность вещества. Единицы плотности |
||
|
Доп. материал |
Упражнения |
||
|
19 |
Решение задач по теме «Масса тела. Плотность вещества» |
||
|
Упражнения |
|||
|
20 |
Сила |
||
|
Доп. |
|||
|
21 |
Явление тяготения. Сила тяжести |
||
|
Доп. материал |
Упражнения |
||
|
22 |
Сила упругости. |
||
|
Доп. материал |
Упражнения |
||
|
23 |
Вес тела |
||
|
Доп. материал |
Упражнения |
||
|
24 |
Единица силы. |
||
|
Доп. материал |
|||
|
25 |
Сложение сил. Равнодействующая сила |
||
|
Доп. материал |
Упражнения |
||
|
26 |
Трение. Сила трения |
||
|
Доп. материал |
Упражнения |
||
|
4. Давление |
|||
|
27 |
Давление. Единицы давления |
||
|
Доп. |
Упражнения |
||
|
28 |
Решение задач по теме «Давление твёрдых тел» |
||
|
Упражнения |
|||
|
29 |
Давление газа |
||
|
Доп. материал |
Упражнения |
||
|
30 |
Давление жидкости, обусловленное её весом |
||
|
Доп. материал |
Упражнения |
||
|
31 |
Решение задач по теме «Давление жидкости» |
||
|
Упражнения |
|||
|
32 |
Сообщающиеся сосуды |
||
|
Доп. |
Упражнения |
||
|
33 |
Решение задач по теме «Сообщающиеся сосуды» |
||
|
Упражнения |
|||
|
34 |
Газы и их вес. Атмосферное давление |
||
|
Доп. материал |
|||
|
35 |
Измерение атмосферного давления. Барометры и манометры |
||
|
Доп. материал |
|||
|
36 |
Решение задач по теме «Атмосферное давление» |
||
|
Упражнения |
|||
|
5. |
|||
|
37 |
Решение задач по теме «Мощность» |
||
|
Упражнения |
|||
|
38 |
Кинетическая энергия. Решение задач по теме «Кинетическая энергия» |
||
(PDF) Торсорная теория физических величин и их измерение
ОБЗОР ИЗМЕРЕНИЙ НАУКИ, 17, (2017), № 4, 152–177
пространств, и они известны как высокоэффективные инструменты
в алгебраической геометрии и современная физика. Как оказалось,
торсоров также являются фундаментальными для моделирования относительных физических
геометрических величин, таких как положение, время, температура, разность потенциалов, разность энергий и многие другие количественные связи, которые зависят от понятие различия между двумя состояниями
целевой количественно-несущей системы.
Как мы увидим в следующем разделе, с формальной точки зрения —
, отправной точкой для торсоров величин является фиксированная
коммутативная группа преобразований шкалы или состояний, т. Е. Непустое множество
G, снабженное двоичная операция, которая является изменчивой, ассоциативной, обратимой и имеет единицу измерения. Для группы
G торсор над G представляет собой непустое множество Q, снабженное свободным
и транзитивным «динамическим» действием Gon Q, которое является частным случаем известного преобразования изменения координат.
Одним из основных аргументов в пользу выбора рамы торсора —
работы является тот факт, что фундаментальная структура
физических величин данного вида в пространстве Q может быть получена из действия
группы масштабного преобразования. Например, для
любой пары физических величин Q и Q ‘одного вида в
Q мы всегда можем найти эталонную величину U и уникальный масштаб
преобразований α и α ′ в G, таких, что Q = α · U и Q ′ =
.
α ′ · U.Их сложение дается выражением Q + Q ′ = df (α + α ′) · U.
Одним из основных достоинств использования торсоров в количественном исчислении
является то, что все ранее обсуждавшиеся синтаксически данные операции
имеют естественные семантические аналоги, сформулированные в терминах
операций над торсорами величин. Дополнительные обоснования
будут представлены в следующем разделе после того, как мы вспомним набор математических инструментов rel-
evant и сделаем торсорную структуру из
физических величин из бетона.
Во-вторых, мы должны иметь возможность провести тщательное различие
между физической величиной Q
Q
Q как таковой и ее потенциальным значением
ед. Q, Q ‘, … уравнение. В этом наборе
нужно установить отдельное пространство значений для каждого физического
количества Q
Q
Q вместе с соответствующими алгебраическими операциями над ним.
Кроме того, необходимо также обеспечить произведение и возведение в степень
операций над абстрактно предоставленными величинами.Чтобы ответить на этот вопрос
, нам нужны конкретные определения этих операций.
И, наконец, в классической теории нет строгой характеристики
того, как абстрактно задуманные величины приобретают
своих значений. Сразу видно, что эти значения
не являются результатом стандартной операции оценки формы
Q
Q
Q (f), примененной к полю f, поскольку такое значение величины —
ед. на выбранном блоке, а также, возможно, на пространственной
отсчета.В дополнение к целевому полюсу, значения количества
также зависят от физико-геометрического состояния поляризада
, учитываемого во время измерения. Итак,
большой вопрос: какова точная связь между
абстрактно заданным количеством Q
Q
Q и его возможными значениями?
Чтобы продолжить, нам нужна точная характеристика
того, как физические величины приобретают свои значения, когда
инстанциируются обычными реальными системами. Кроме того, чтобы
Кроме того, чтобы
было совместимо с динамическими законами современных физических теорий, чрезвычайно важно иметь возможность строить повторяющиеся
(полные и частные) производные величин и их (время,
пространство,
). и т. д.) зависимые и случайные или стохастические альтернативы.
Непонятно, как эти конструкции новых количеств из
старых вписываются в классические рамки. Подробнее о
каждой из этих проблем будет сказано позже.
До сих пор мы представили краткое изложение
классического подхода к количеству и их измерению.
Мы также изложили наши оговорки в отношении синтаксической формулировки и интерпретации классов
и их значений, а также количественного исчисления в целом. Мы рассматриваем
этих критических замечаний как веские основания для разработки альтернативной собственной метрологической основы
, которая позволяет обойти ранее обсуждавшиеся
подводные камни и трудности интерпретации, связанные с расчетом и измерением количества
.
2. Масштабные преобразования и торсоры единичных величин
В этом разделе мы вводим четыре основных ингредиента теории единичных величин: физико-геометрические состояния величин. единичных величин
и групп преобразования шкалы и состояния не-
торсоров. Наша основная цель — привести концептуальную структуру количеств
в соответствие с требованиями современных физических теорий и связанных с ними методов измерения, а также обойти проблемы, обсуждавшиеся ранее.
Современная теоретическая физика использует чрезвычайно эффективную структуру для математического описания классических, квантовых и статистических физических систем, в которых базовыми понятиями
являются состояния и количества (также известные как наблюдаемые).
Эти в высшей степени плодотворные понятия находятся в соотношении двойственности —
корабль, что означает, что существует пара, в которой количества оцениваются по состояниям
, а совокупные количественные значения отдельных
состояний. Теория единичных величин, которую мы представляем в этом разделе
Теория единичных величин, которую мы представляем в этом разделе
, органично вписывается в принятую физическую основу.7
Единственное отличие заключается в геометрической размерности пространств состояний
. В то время как в моделях теоретической физики и системной науки базовые пространства состояний обычно являются многомерными, в теории детерминированных скалярных величин (в отличие от
векторных или тензорных) единичных величин эти пространства исключаются. Одномерные, характеризующие системы с одной степенью свободы
.По математическим причинам, не относящимся к
здесь, одномерное (непрерывная линия или полулиния) con-
деформация оказывается решающей для построения продукта
и обратных величин, необходимых для определения объема, скорости,
. Плотностьи многие другие производные величины.
В классическом подходе физическая величина рассматривается как
как количественно измеримый атрибут физических сущностей (то есть тела
лет, полей, частиц и пространственно-временных событий), которая приходит с
с внешне присоединенной единицей. Сами по себе
Сами по себе
являются абстрактными и теоретическими по своей природе и подлежат син-
тактически представленному продукту и рациональным силовым операциям.
К сожалению, это представление непрактично и противоречит
большинству приложений, потому что прикладные ученые и инженеры,
, которые заинтересованы в прогнозировании и выполнении
7Потому что измерительный прибор может различать только ограниченное соседство
Из-за большого количества альтернатив вокруг фактического состояния измеряемой системы, измерения измеряемой величины, кодирующей состояние, могут предоставить только
ограниченного количества информации о существующем состоянии измеряемой системы.
155 Без аутентификации
Дата загрузки | 9/10/17 14:30
«Физические величины — это не что иное, как количественные метафоры» ›Университет Фридриха Александра, Эрланген-Нюрнберг
Профессор доктор Клаус Меке (Изображение: Дэвид Хартфил) 5 июня 2015 г.
Физик-теоретик Клаус Меке объясняет, до какой степени мы должны полагаться на лингвистические изобретения, пытаясь сделать естественные явления понятными.
Отчет: Ральф Грёткер
Литература может превосходно представить актуальность и разнообразие физики.
Меня давно интересовало, как мой предмет, физика, отражается в литературе. За эти годы я создал аннотированную библиографию по этой теме и даже читал лекции по ней. Меня всегда спрашивают, что я получаю от изучения литературы как физика. В течение многих лет я отвечал «ничего особенного». Физика в основном занимается экспериментами и математическими моделями. Художественная литература тут ни при чем.
Однако все изменилось, когда четыре года назад мы начали интенсивную междисциплинарную дискуссию между литературой и физикой здесь, в Эрлангене.В том числе интервью с писателями, которые скоро будут опубликованы. Одно из наших интервью было с австрийским поэтом и писателем Раулем Шроттом. Он спросил меня, как я подхожу к метафорам как физик. Это побудило меня более глубоко взглянуть на тему метафор в физике.
Он спросил меня, как я подхожу к метафорам как физик. Это побудило меня более глубоко взглянуть на тему метафор в физике.
Сегодня общепризнано, что метафоры — это не только форма литературного выражения, но и помогают нам понимать вещи. Хорошо известен пример великого химика Августа Кекуле, которому, как говорят, приснилась змея, кусающая свой хвост, что дало ему представление о том, как может выглядеть атомная структура бензола, открытие, сделавшее его знаменитым.
Однако я считаю, что метафоры играют роль в естественных науках и, в частности, в физике на гораздо более фундаментальном уровне. При ближайшем рассмотрении многие физические величины — не более чем количественные метафоры. Например, мы теперь привыкли к идее электромагнитных полей. Эти «поля» были изобретены физиками в 19 веке. В своей лаборатории физик-экспериментатор Майкл Фарадей, сделавший это открытие, борется с проблемой того, на каком языке описать то, что он наблюдал, и какие дальнейшие эксперименты необходимы, чтобы закрепить свои наблюдения. Только когда он нашел конкретные процедуры измерения, которые позволили ему уловить то, что он описал с помощью выбранной им метафоры «поле» количественно — по шкале, по которой может быть прочитана концентрация железных опилок, — появился новый физический объект, возникло электромагнитное поле. Между прочим, я считаю, что эти процессы, которые мы можем проследить на протяжении истории науки, являются наиболее почетной задачей из всех в физике: расширять сферу нашего восприятия и открывать разнообразие природных явлений.
Только когда он нашел конкретные процедуры измерения, которые позволили ему уловить то, что он описал с помощью выбранной им метафоры «поле» количественно — по шкале, по которой может быть прочитана концентрация железных опилок, — появился новый физический объект, возникло электромагнитное поле. Между прочим, я считаю, что эти процессы, которые мы можем проследить на протяжении истории науки, являются наиболее почетной задачей из всех в физике: расширять сферу нашего восприятия и открывать разнообразие природных явлений.
Перенос метафор в ценности
Но продолжим. В частности, на этапе исследования физики, когда кто-то вводит новую величину, становится ясно, что речь идет не столько об открытии чего-то нового, сколько о создании новой метафоры. Мы знаем, что такое «поле» из нашего повседневного опыта, и можем переносить это метафорически на явления электромагнетизма. Однако здесь очень важно, чтобы мы постарались сделать так, чтобы это оставалось независимым от контекста. Физики стремятся четко назвать все возможные условия, которые влияют на явление, чтобы гарантировать, что требуемый эксперимент, который приводит к созданию или наблюдению явления, может быть воспроизведен в других контекстах. Для этого нам нужны измеряемые величины или шкалы — равенство измеренных значений показывает, была ли успешной попытка найти явления, не зависящие от контекста.
Физики стремятся четко назвать все возможные условия, которые влияют на явление, чтобы гарантировать, что требуемый эксперимент, который приводит к созданию или наблюдению явления, может быть воспроизведен в других контекстах. Для этого нам нужны измеряемые величины или шкалы — равенство измеренных значений показывает, была ли успешной попытка найти явления, не зависящие от контекста.
Физик, любящий слова: профессор д-р Клаус Меке, кафедра теоретической физики.(Изображение: Дэвид Хартфил)
Однако есть еще одна причина, по которой перенос метафор в ценности важен в физике. Например, Георг Симон Ом, родившийся в Эрлангене, обнаружил, что ток и напряжение связаны. Причина, по которой никто не мог увидеть это раньше, заключается в том, что ток и напряжение — это разные повествования об измерениях, результаты которых зависят от деталей эксперимента. Все, что Ом сделал, — это изменил стандартную схему эксперимента, использовав в качестве источника напряжения термопару вместо гальванической батареи. Как следствие, он сразу смог увидеть, что существует простая пропорциональная зависимость между током и напряжением. Ему даже не потребовалась математическая модель, чтобы понять, что ток есть напряжение. Этот пример ясно показывает, как шкалы измерений не только позволяют наблюдениям быть объективными, но также позволяют переносить одну величину или концепцию в другую. Чтобы эта передача произошла, значения должны быть равны. Эйнштейн никогда не смог бы объяснить, что энергия похожа на кривую без равных значений — значений инертной и гравитационной массы.По нашему непосредственному опыту, эти две концепции слишком далеки друг от друга, чтобы объединить их.
Как следствие, он сразу смог увидеть, что существует простая пропорциональная зависимость между током и напряжением. Ему даже не потребовалась математическая модель, чтобы понять, что ток есть напряжение. Этот пример ясно показывает, как шкалы измерений не только позволяют наблюдениям быть объективными, но также позволяют переносить одну величину или концепцию в другую. Чтобы эта передача произошла, значения должны быть равны. Эйнштейн никогда не смог бы объяснить, что энергия похожа на кривую без равных значений — значений инертной и гравитационной массы.По нашему непосредственному опыту, эти две концепции слишком далеки друг от друга, чтобы объединить их.
Ни вещей, ни имущества
Но это не конец истории. То, что мы можем так ясно увидеть на примере электромагнитного поля, на самом деле применимо ко всем физическим величинам. Температура также определяется описанием измерений: температура — это то, что мы измеряем термометром. Конечно, в некоторых учебниках физики сказано иное. Согласно определениям, данным в этих книгах, температура — это кинетическая энергия.Например, статистическая физика может показать, что для идеального газа температура по существу пропорциональна кинетической энергии, содержащейся в отдельных частицах газа. Однако это определение уже содержит целый ряд допущений при моделировании материала. Я сомневаюсь, почему все эти предположения необходимы для определения температуры. В конце концов, с исторической точки зрения, этот термин существовал как физическая величина задолго до появления каких-либо представлений об атомах в газах или жидкостях и кинетической энергии.Термин «температура» полностью от этого не зависит.
Согласно определениям, данным в этих книгах, температура — это кинетическая энергия.Например, статистическая физика может показать, что для идеального газа температура по существу пропорциональна кинетической энергии, содержащейся в отдельных частицах газа. Однако это определение уже содержит целый ряд допущений при моделировании материала. Я сомневаюсь, почему все эти предположения необходимы для определения температуры. В конце концов, с исторической точки зрения, этот термин существовал как физическая величина задолго до появления каких-либо представлений об атомах в газах или жидкостях и кинетической энергии.Термин «температура» полностью от этого не зависит.
Более общий момент, который я хотел бы высказать, можно очень хорошо продемонстрировать на примере научной истории света. Кстати, о свете часто говорят в превосходной степени. Это древнейшее явление, которое мы можем измерить как космическое фоновое излучение. Это единственный объект без массы. Через свет мы узнаем о самых далеких вещах, но также и о самых старых — просто подумайте о свете давно умерших звезд. Что такое свет? В 17 веке Ньютон понимал свет как движение частиц — корпускул — подобных шарам, которые движутся по воздуху по прямой линии с определенной скоростью. Используя эту теорию, можно было очень хорошо описать явление преломления света. Однако такие явления, как размытые края теней или интерференция лучей света в знаменитом эксперименте с двумя щелями, объяснить труднее. В этом эксперименте свет проходит через две щели, расположенные рядом друг с другом.Однако на экране наблюдения, на который проецируются лучи света, наблюдаются не две отдельные световые линии, а узор из линий. Объяснение этого эффекта заключается в том, что свет ведет себя как волны на поверхности воды, которые иногда усиливают друг друга, а иногда гасят друг друга. По этой причине теория света как волны также была разработана в 17 веке такими физиками, как Роберт Хук и Христиан Гюйгенс. С открытиями Фарадея и введением концепции электромагнитного поля ученые смогли распознать, что колеблется в свете: не вода, а электромагнитные поля.
Что такое свет? В 17 веке Ньютон понимал свет как движение частиц — корпускул — подобных шарам, которые движутся по воздуху по прямой линии с определенной скоростью. Используя эту теорию, можно было очень хорошо описать явление преломления света. Однако такие явления, как размытые края теней или интерференция лучей света в знаменитом эксперименте с двумя щелями, объяснить труднее. В этом эксперименте свет проходит через две щели, расположенные рядом друг с другом.Однако на экране наблюдения, на который проецируются лучи света, наблюдаются не две отдельные световые линии, а узор из линий. Объяснение этого эффекта заключается в том, что свет ведет себя как волны на поверхности воды, которые иногда усиливают друг друга, а иногда гасят друг друга. По этой причине теория света как волны также была разработана в 17 веке такими физиками, как Роберт Хук и Христиан Гюйгенс. С открытиями Фарадея и введением концепции электромагнитного поля ученые смогли распознать, что колеблется в свете: не вода, а электромагнитные поля.
Доминирующая теория снова изменилась с открытием квантовых эффектов. Внезапно появилась возможность измерить корпускулярные свойства света, предсказанные Ньютоном и его современниками в своих моделях! Исследователи неожиданно смогли наблюдать корпускулярные явления! Это можно сделать, например, направив свет на кусок металла и измерив количество электронов, выбитых из него светом. Это называется фотоэлектрическим эффектом. На основании этого эффекта Эйнштейн пришел к выводу, что свет — это частица.Однако в то же время волновая модель все еще требовалась для объяснения интерференционного эффекта, показанного в эксперименте с двумя щелями. Эйнштейн создал новую метафору того факта, что свет ведет себя как частица и волна. Свет — это «квант» — ограниченная, пространственно локализованная величина, дальнейшая форма которой, однако, определяется свойствами волн.
Квантовая теория прояснила, что в определенной степени то, что мы видим как материальную реальность — мир вещей со своими собственными свойствами, — это вымысел, образцовый нарратив. Это то, что мы создаем на наших условиях, но это не предусмотрено как таковое в природе. Споры вокруг света и частиц также показывают нам, насколько сложно использовать язык для визуализации физического мира, который состоит не из вещей и их свойств, а из физических величин, которые не являются ни вещами, ни свойствами. Пытаясь сделать это понятным, мы неизбежно вынуждены использовать метафоры.
Это то, что мы создаем на наших условиях, но это не предусмотрено как таковое в природе. Споры вокруг света и частиц также показывают нам, насколько сложно использовать язык для визуализации физического мира, который состоит не из вещей и их свойств, а из физических величин, которые не являются ни вещами, ни свойствами. Пытаясь сделать это понятным, мы неизбежно вынуждены использовать метафоры.
Видеть мир как рассказанный опыт природы
На мой взгляд, существует нечто большее, чем просто тонкая разница между тем, понимаем ли мы мир как рассказанный опыт природы, как предполагает квантовая теория, или, как это обычно бывает, предполагаем, что мир состоит из вещей и свойств.Понимание физики как речевого акта позволяет объединить объективные законы природы с явлениями свободы слова и действия, а также с историчностью и культурными явлениями. Законы природы просто создают основу для того, что происходит, и поэтому определяют, как что-то произойдет, только если это произойдет. Все остальное — происходит ли что-то, но также и то, что вызывает это, — остается открытым.
Все остальное — происходит ли что-то, но также и то, что вызывает это, — остается открытым.
Детерминист, утверждающий, что все события предопределены законами физики, полагает, что если бы мы знали начальные координаты всех точечных частиц, из которых состоит мир, то мы могли бы предсказать, как они будут взаимодействовать друг с другом.Тот факт, что мы не можем делать такие прогнозы на практике, объясняется только тем фактом, что мир настолько невероятно сложен, что мы не можем определить координаты всех частиц даже в крошечной его части. Однако это ограничение, которое накладывается на нас, не меняет того факта, что будущее состояние мира уже определено начальными координатами.
Я считаю эту форму детерминизма проблематичной, потому что она переносит математическую концепцию мира, состоящего из точечных частиц, обратно в природу.Поступая так, математические объекты физики внезапно становятся вещами в реальном мире — как, например, случилось с популярным пониманием теории струн. Пока что фактически никто не мог наблюдать «струны», и вопрос о том, разумно ли предполагать существование струн, является предметом больших споров. Так или иначе, на самом деле такие термины, как «струны» и «точечные частицы» — всего лишь метафоры, которые помогают нам приблизиться к природным явлениям.
Пока что фактически никто не мог наблюдать «струны», и вопрос о том, разумно ли предполагать существование струн, является предметом больших споров. Так или иначе, на самом деле такие термины, как «струны» и «точечные частицы» — всего лишь метафоры, которые помогают нам приблизиться к природным явлениям.
Эта статья основана на эссе Клауса Меке «Zahl und Erzählung.Метаферна в Erkenntnisprozessen der Physik ‘(Числа и повествование. Метафоры в когнитивных процессах в физике), опубликованная в A. Heydenreich и K. Mecke (ред.), Quarks and Letters: Naturwissenschaften in der Literatur und Kultur der Gegenwart (Quarks and Letters: естественные науки в современной литературе и культуре, 2014.
Вы заинтригованы?
Эта статья была первоначально опубликована в нашем исследовательском журнале Friedrich в выпуске, посвященном свету. Узнайте, что такое свет, откуда он исходит, почему мы его видим и что он делает с нами, во фридрихе no.114. (немецкий)
физическое количество | Примеры предложений
физической величины еще нет в Кембриджском словаре. Вы можете помочь!
Вы можете помочь!
 Датчики вращения и некоторые другие датчики выдают последовательности импульсов, ширина импульса которых пропорциональна измеренному физическому количеству .Это говорит о том, что с учетом того факта, что количество физических доступной листовой стали увеличилось, что-то произошло.
Аналоговый компьютер представляет данные как напряжение, расстояние, положение или другую физическую величину .
Из
Датчики вращения и некоторые другие датчики выдают последовательности импульсов, ширина импульса которых пропорциональна измеренному физическому количеству .Это говорит о том, что с учетом того факта, что количество физических доступной листовой стали увеличилось, что-то произошло.
Аналоговый компьютер представляет данные как напряжение, расстояние, положение или другую физическую величину .
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Собственные значения этих операторов являются возможными результатами измерения соответствующей физической величины . ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. В таком контексте конкретная физическая величина называется измеренной величиной.
Из
В таком контексте конкретная физическая величина называется измеренной величиной.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Интенсивность звука не такая же физическая количество как звуковое давление. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Формальное доказательство теоремы использует условие инвариантности, чтобы получить выражение для тока, связанного с сохраняющейся физической величиной . ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Единица измерения физического количества и ее размер связаны, но не идентичны.
Из
Единица измерения физического количества и ее размер связаны, но не идентичны.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Поскольку электрический ток «i» — это физическая величина , он должен быть действительным. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Световая энергия не то же самое, что лучистая энергия, соответствующий объектив физический количество . ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Чтобы отличить физическое количество от квантовомеханического оператора, используемого для его описания, над символами операторов используется шляпа.
Из
Чтобы отличить физическое количество от квантовомеханического оператора, используемого для его описания, над символами операторов используется шляпа.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Термин « физическое количество » не подразумевает физически «неизменное количество». ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Эти величины представляют собой комплексное средневзвешенное значение поглощенной дозы, которое представляет собой четкое физическое количество , измеренное в рад. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Несколько других критических показателей — ,,, и — определены, исследуя поведение степенного закона измеримой физической величины вблизи фазового перехода.
Из
Несколько других критических показателей — ,,, и — определены, исследуя поведение степенного закона измеримой физической величины вблизи фазового перехода.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.
физических величин еще нет в Кембриджском словаре.сообщение}}
Выберите часть речи и введите свое предложение в поле «Определение».
{{/сообщение}} Часть речи Выберите существительное, глагол и т. Д. Прилагательноеприлагательноерекламабъявление существительноечислопрефикссуффиксглагол
Д. Прилагательноеприлагательноерекламабъявление существительноечислопрефикссуффиксглагол
Определение
Представлять на рассмотрение Отмена
Введение • Элементарные величины и единицы измерения, используемые в механике
Биомеханика описывает движение человека и его причины количественно.Если свойство поддается количественной оценке, это означает, что определенные аспекты такого свойства измеримы и могут быть выражены числом. Таким образом, мы наблюдаем в предметах и явлениях их количественные свойства, преобладание которых выражается множеством выбранных единиц этого свойства.
Некоторые свойства и способности, используемые в биомеханике, могут быть выражены такими понятиями, как скорость, инерция, мощность, импульс, сила, масса, вес, расстояние, ускорение и т. Д.
Длина
Элементарная величина, которую мы хотим измерить, — это длина.Длина используется для описания пространства, в котором происходит движение. Длина является прямым выражением спортивных результатов в таких спортивных соревнованиях, как толкание ядра, прыжки в длину, прыжки в высоту и т. Д. В некоторых видах спорта длина имеет косвенное влияние на спортивные результаты. Например, длина бегового шага является важным показателем техники движения как на короткие, так и на длинные дистанции. Он также может быть частью оценки спортивных результатов, как в случае с прыжками с трамплина. В системе СИ 3 единицей измерения длины является метр (м).Используемое обозначение — l .
Время
Время — еще одна элементарная измеримая величина. Время является важным фактором практически во всех спортивных мероприятиях. В видах спорта, которые включают соревнования, время часто используется как мера спортивных результатов. Время реакции вратарей в различных коллективных видах спорта определяет успех команды в целом. Аналогичная ситуация наблюдается и в таких видах спорта, как теннис или сквош, где время реакции игрока оказывает сильное влияние на возвращение мяча обратно на сторону соперника.Время можно измерять в секундах, минутах, часах, днях, неделях, месяцах или годах. В системе СИ единицей измерения времени является секунда (с). Используемое обозначение — t .
Время является важным фактором практически во всех спортивных мероприятиях. В видах спорта, которые включают соревнования, время часто используется как мера спортивных результатов. Время реакции вратарей в различных коллективных видах спорта определяет успех команды в целом. Аналогичная ситуация наблюдается и в таких видах спорта, как теннис или сквош, где время реакции игрока оказывает сильное влияние на возвращение мяча обратно на сторону соперника.Время можно измерять в секундах, минутах, часах, днях, неделях, месяцах или годах. В системе СИ единицей измерения времени является секунда (с). Используемое обозначение — t .
Теперь мы знакомы с двумя элементарными величинами для описания движения в пространстве и времени. Многие величины, описывающие движения человека во время занятий спортом, основаны на знании положения тела относительно времени. Хорошие примеры — скорость и ускорение.
Масса
Какое свойство представляет собой серьезное препятствие для игроков американского футбола, когда они пытаются изменить направление движения? А какое свойство, с другой стороны, помогает им сломать оборону соперника? Это инерция.
Инерция — это сопротивление любого физического объекта изменению его состояния движения.
Масса — количественная мера инерции 4 .
Насколько важна масса в спорте и физических упражнениях? Спортсмены должны изменить направление своего снаряжения, например, теннисной ракетки, или направление тела другого человека, например, в дзюдо. Поскольку масса является мерой инерции, она определяет количество усилий, которые спортсмены должны приложить, чтобы изменить движение частей своего тела или оборудования, которое они используют.В системе СИ единицей массы является килограмм (кг). Используемое обозначение — м .
Итак, мы определили три элементарных единицы: массу, время и длину. Все остальные единицы механических величин могут быть производными от этих трех.
3 Система СИ (Le Système International d’Unités) — это международная система единиц физических величин.
4 Понятие массы часто путают с понятием веса.Вес будет определен в следующей главе.
Physical Quantities> Editors> Options
Dewesoft предлагает редактор, который позволяет пользователю добавлять или изменять физические количества. Редактор физических величин можно найти в списке редакторов в параметрах.
При входе в редактор появляется следующее окно:
- Добавьте физическое количество (если физическое количество отсутствует, здесь можно добавить дополнительное)
- Удалить физическое количество (с помощью этой опции можно удалить дополнительно добавленные физические количества)
- Сохранить (сохраняет изменения в PhysicalQuantitiesX.xml)
- Добавить единицы (дополнительные единицы могут быть добавлены к любому физическому количеству)
- Удалить юниты (дополнительно добавленные юниты могут быть удалены)
- Выход (закрыть редактор физических величин)
Добавить индивидуальное физическое количество
Чтобы добавить новое физическое количество, нажмите кнопку + над физическими количествами.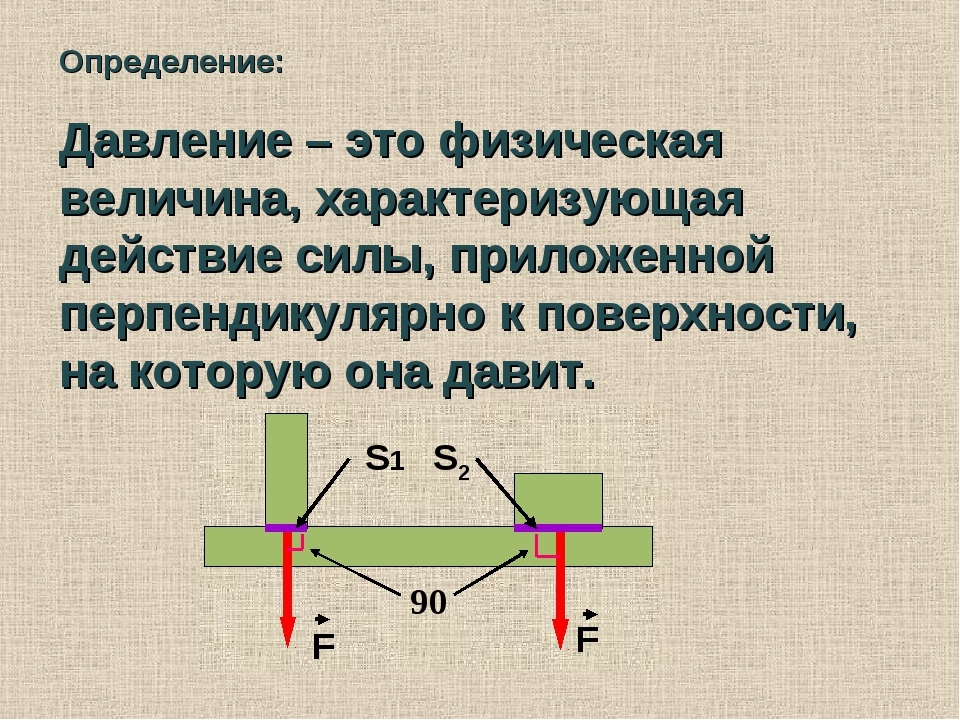
Существуют различные поля, которые необходимо заполнить, чтобы добавить новое количество:
- Дескриптор и имя (укажите имя новой физической величины)
- Единицы СИ (напишите правильную экспоненту рядом с единицей СИ)
М / с описывается показателем степени 1 рядом с единицей «m» и показателем -1 рядом с единицей «s».
В нашем примере мы использовали показатель электропроводности, который имеет следующие показатели SI:
| Единица СИ | Показатель |
|---|---|
| м | -2 |
| кг | 1 |
| с | 3 |
| А | 2 |
- Используется для измерения (этот параметр позволяет отображать пользовательские единицы только в некоторых типах измерений в настройке канала)
Каждая физическая величина требует также единиц, которые задаются в правой части редактора.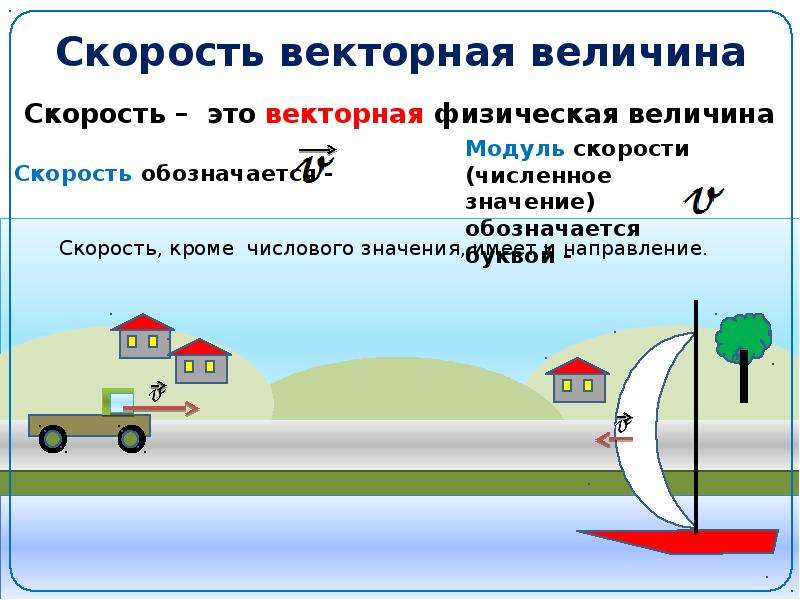
Для каждого устройства нам необходимо определить масштаб, оператора и смещение, которые позволяют Dewesoft передавать данные между модулями:
- Шкала (определяет отношение новой единицы к тоннам
- Оператор (определяет тип смещения: сложение, коэффициент, лог. Исх.)
- Смещение (определяет смещение между единицей измерения по умолчанию и новой единицей)
Отличный пример, где используются масштаб, оператор и смещение, его температура:
Как только будет добавлено новое физическое количество, мы также сможем увидеть его в настройке канала:
Физические величины, защитные величины и рабочие величины [MOE]
Чтобы контролировать воздействие радиации на человеческое тело, необходимо принимать во внимание воздействие облучения на несколько частей тела и последствия предыдущего облучения.Для этого были придуманы эквивалентная доза и эффективная доза.
Эквивалентная доза получается путем взвешивания воздействия на отдельные органы и ткани в соответствии с типами излучения.
Эффективная доза получается путем преобразования воздействия на отдельные ткани в значение для всего тела. Это не просто среднее значение эквивалентных доз для отдельных органов, а результат взвешивания в зависимости от различий в чувствительности органов к радиации.
Фактор для взвешивания радиационного воздействия на отдельные органы называется весовым коэффициентом ткани.
Таким образом, защитные величины рассчитываются на основе доз для органов и тканей человеческого тела. Поэтому они отличаются от физических величин, таких как интенсивность излучения (единица: беккерель) и поглощенная доза (единица: серый), и не могут быть измерены непосредственно с помощью инструментов. Для обозначения воздействия на человеческий организм определены рабочие количества.
Некоторые геодезические счетчики используют зиверты для снятия показаний.Они не измеряют непосредственно величину защиты, но показывают приблизительные значения, определенные на основе измеренных физических величин, т. Е. Рабочих величин. Рабочие величины включают эквивалент амбиентной дозы, используемый при мониторинге окружающей среды, и эквивалент индивидуальной дозы, используемый при индивидуальном мониторинге.
Е. Рабочих величин. Рабочие величины включают эквивалент амбиентной дозы, используемый при мониторинге окружающей среды, и эквивалент индивидуальной дозы, используемый при индивидуальном мониторинге.
(стр. 40 тома 1, «Дозовые эквиваленты: измеряемые рабочие величины для определения эффективных доз»).
Для обеспечения консервативных (на всякий случай) оценок защитных величин, рабочие величины определены так, чтобы в большинстве случаев принимать немного большие числовые значения, чем значения защитных величин.
- Включено в этот справочный материал 31 марта 2013 г.
- Обновлено 31 марта 2017 г.
Измерение в науке (Стэнфордская энциклопедия философии)
Современные философские дискуссии об измерении — начиная с
с конца девятнадцатого века до наших дней — можно разделить
по нескольким направлениям обучения. Эти пряди отражают разные
взгляды на природу измерения и условия, которые делают
измерения возможны и надежны.Основные нити математические
теории измерения, операционализм, конвенционализм, реализм,
теоретико-информационные счета и счета на основе моделей. Эти пряди
стипендий по большей части не составляют непосредственно
конкурирующие взгляды. Вместо этого их лучше всего понимать как выделение
различные и дополнительные аспекты измерения. Ниже приводится
очень приблизительный обзор этих перспектив:
Эти пряди
стипендий по большей части не составляют непосредственно
конкурирующие взгляды. Вместо этого их лучше всего понимать как выделение
различные и дополнительные аспекты измерения. Ниже приводится
очень приблизительный обзор этих перспектив:
- Математические теории измерение рассматривать измерение как отображение качественного эмпирические отношения к отношениям между числами (или другими математическими сущностей).
- Операционалисты и конвенционалисты просмотр измерение как набор операций, формирующих смысл и / или регулировать использование количественного термина.
- Реалисты рассматривают измерение как оценку независимые от разума свойства и / или отношения.
- Теоретико-информационные счета просмотр измерений как сбор и интерпретация информации о система.
- Счета на основе моделей рассматривают измерение как
согласованное присвоение значений параметрам в теоретической и / или
статистическая модель процесса.

Эти точки зрения в принципе согласуются друг с другом. Пока математические теории измерения имеют дело с математическими основы измерительных шкал, операционализм и конвенционализм в первую очередь связаны с семантикой количественных терминов, реализмом занимается метафизическим статусом измеримых величин, теоретико-информационные и модельные счета связаны с эпистемологические аспекты измерения. Тем не менее, предмет домен не так аккуратно разделен, как следует из приведенного выше списка.вопросы по метафизике, эпистемологии, семантике и математике основы измерения взаимосвязаны и часто опираются на одну Другой. Отсюда, например, операционалисты и конвенционалисты часто придерживался антиреалистических взглядов, а сторонники модельного счета выступили против преобладающей эмпирической интерпретации математических теорий измерения. Эти тонкости станут ясно в следующем обсуждении.
Список направлений стипендии не является исчерпывающим и неисключительным.
исчерпывающий. Он отражает историческую траекторию философского
обсуждение до сих пор, а не какое-либо принципиальное различие между
разные уровни анализа измерений. Некоторые философские работы
по замерам относятся к более чем одной нити, в то время как многие другие работы
тоже не подходят прямо. Это особенно актуально, поскольку
начале 2000-х, когда измерение вернулось на первый план
философская дискуссия после нескольких десятилетий относительного пренебрежения.
Эту недавнюю стипендию иногда называют «
эпистемология измерения », и включает в себя богатый набор работ
которые пока не могут быть разделены на отдельные школы мысли.В
последний раздел этой записи будет посвящен обзору некоторых из
эти события.
Он отражает историческую траекторию философского
обсуждение до сих пор, а не какое-либо принципиальное различие между
разные уровни анализа измерений. Некоторые философские работы
по замерам относятся к более чем одной нити, в то время как многие другие работы
тоже не подходят прямо. Это особенно актуально, поскольку
начале 2000-х, когда измерение вернулось на первый план
философская дискуссия после нескольких десятилетий относительного пренебрежения.
Эту недавнюю стипендию иногда называют «
эпистемология измерения », и включает в себя богатый набор работ
которые пока не могут быть разделены на отдельные школы мысли.В
последний раздел этой записи будет посвящен обзору некоторых из
эти события.
Хотя философия измерения сформировалась как отдельная область
исследование только во второй половине девятнадцатого века,
фундаментальные концепции измерения, такие как величина и количество
обсуждаются с древних времен. Согласно Евклиду Элементы , величина, например линия, поверхность или
твердый — измеряет другое, когда последнее является целым кратным
первое (Книга V, опр. 1 и 2). Две величины имеют общую
измерять, когда они оба целые кратные некоторой величины, и
несоизмеримым в противном случае (Книга X, определение 1). Открытие
несоизмеримые величины позволили Евклиду и его современникам
развивать понятие отношения величин. Соотношения могут быть
либо рациональным, либо иррациональным, поэтому понятие отношения
более общий, чем мера (Michell 2003, 2004a;
Grattan-Guinness 1996).
1 и 2). Две величины имеют общую
измерять, когда они оба целые кратные некоторой величины, и
несоизмеримым в противном случае (Книга X, определение 1). Открытие
несоизмеримые величины позволили Евклиду и его современникам
развивать понятие отношения величин. Соотношения могут быть
либо рациональным, либо иррациональным, поэтому понятие отношения
более общий, чем мера (Michell 2003, 2004a;
Grattan-Guinness 1996).
Аристотель различал количество и качество.Примеры
количества — это числа, линии, поверхности, тела, время и место,
а примерами качеств являются справедливость, здоровье, горячность и
бледность ( Категории §6 и §8). В соответствии с
Аристотеля, количества допускают равенство и неравенство, но не допускают
градусов, так как «одна вещь не более четырех футов, чем другая»
(Там же 6.6a19). Качества, наоборот, не допускают равенства или
неравенство, но допускают степени, «потому что одно называется
более бледный или менее бледный, чем другой »(там же 8. 10b26).Аристотель
не уточняет, являются ли степени таких качеств, как бледность
соответствуют различным качествам или одинаковому качеству,
бледность, была способна к разной интенсивности. Эта тема была на
центр продолжающихся дебатов в тринадцатом и четырнадцатом веках
(Юнг 2011). Дунс Скот поддержал «теорию сложения»,
согласно которому изменение степени качества может быть
объясняется сложением или вычитанием меньших степеней этого
качество (2011: 553). Позже эта теория была уточнена Николь Орем,
которые использовали геометрические фигуры для представления изменений интенсивности
такие качества, как скорость (Clagett 1968; Sylla 1971).Oresme’s
геометрические представления установили подмножество качеств, которые
поддаются количественной обработке, что ставит под сомнение
строгая аристотелевская дихотомия количества и качества. Эти
развития сделали возможным формулировку количественных законов
движение в течение шестнадцатого и семнадцатого веков (Грант
1996).
10b26).Аристотель
не уточняет, являются ли степени таких качеств, как бледность
соответствуют различным качествам или одинаковому качеству,
бледность, была способна к разной интенсивности. Эта тема была на
центр продолжающихся дебатов в тринадцатом и четырнадцатом веках
(Юнг 2011). Дунс Скот поддержал «теорию сложения»,
согласно которому изменение степени качества может быть
объясняется сложением или вычитанием меньших степеней этого
качество (2011: 553). Позже эта теория была уточнена Николь Орем,
которые использовали геометрические фигуры для представления изменений интенсивности
такие качества, как скорость (Clagett 1968; Sylla 1971).Oresme’s
геометрические представления установили подмножество качеств, которые
поддаются количественной обработке, что ставит под сомнение
строгая аристотелевская дихотомия количества и качества. Эти
развития сделали возможным формулировку количественных законов
движение в течение шестнадцатого и семнадцатого веков (Грант
1996).
Концепция качественной интенсивности была развита Лейбницем. и Канта. «Принцип непрерывности» Лейбница заявил
что все естественные изменения происходят постепенно.Лейбниц утверждал, что
этот принцип применим не только к изменениям в расширенных величинах, таких как
длины и продолжительности, но также и интенсивности репрезентативных
состояния сознания, такие как звуки (Jorgensen 2009; Diehl 2012).
Считается, что Кант опирался на принцип Лейбница
преемственности, чтобы сформулировать различие между экстенсивным и
интенсивные величины. Согласно Канту, экстенсивные величины
те, «в которых представление частей делает возможным
представление целого »(1787: A162 / B203).Пример
это длина: линия может быть мысленно представлена только последовательным
синтез, в котором части линии соединяются, образуя целое. Для Канта
возможность такого синтеза обосновывалась в формах
интуиция, а именно пространство и время. Интенсивные величины, такие как тепло или
цвета, также бывают в непрерывной степени, но их восприятие требует
место в мгновение ока, а не путем последовательного синтеза
части.
и Канта. «Принцип непрерывности» Лейбница заявил
что все естественные изменения происходят постепенно.Лейбниц утверждал, что
этот принцип применим не только к изменениям в расширенных величинах, таких как
длины и продолжительности, но также и интенсивности репрезентативных
состояния сознания, такие как звуки (Jorgensen 2009; Diehl 2012).
Считается, что Кант опирался на принцип Лейбница
преемственности, чтобы сформулировать различие между экстенсивным и
интенсивные величины. Согласно Канту, экстенсивные величины
те, «в которых представление частей делает возможным
представление целого »(1787: A162 / B203).Пример
это длина: линия может быть мысленно представлена только последовательным
синтез, в котором части линии соединяются, образуя целое. Для Канта
возможность такого синтеза обосновывалась в формах
интуиция, а именно пространство и время. Интенсивные величины, такие как тепло или
цвета, также бывают в непрерывной степени, но их восприятие требует
место в мгновение ока, а не путем последовательного синтеза
части. Степени интенсивных величин «могут быть только
представлен через приближение к отрицанию »(1787: A
168 / B210), то есть воображая их постепенное уменьшение до тех пор, пока
полное отсутствие.
Степени интенсивных величин «могут быть только
представлен через приближение к отрицанию »(1787: A
168 / B210), то есть воображая их постепенное уменьшение до тех пор, пока
полное отсутствие.
Научные разработки девятнадцатого века бросили вызов
различие между экстенсивными и интенсивными величинами. Термодинамика
и волновая оптика показала, что разница в температуре и оттенке
соответствовали различиям в пространственно-временных величинах, таких как
скорость и длина волны. Электрические величины, такие как сопротивление и
было показано, что проводимость может складываться и делиться, несмотря на
не является обширным в кантовском смысле, т.е. не синтезируется из
пространственные или временные части.Более того, ранние эксперименты в
психофизики предположили, что интенсивности ощущений, такие как
яркость и громкость можно представить как сумму «всего
заметные различия »между стимулами и, следовательно, могут быть
мыслится как состоящие из частей (см.
Раздел 3.3).
Эти результаты, наряду с достижениями в аксиоматизации ветвей
математики, мотивировала некоторых ведущих ученых конца
девятнадцатого века, чтобы попытаться прояснить математические основы
измерения (Максвелл 1873; фон Крис 1882; Гельмгольц 1887; Мах
1896; Poincaré 1898; Hölder 1901; для исторических обзоров
см. Darrigol 2003; Michell 1993, 2003; Канту и Шлаудт 2013;
Бьяджоли 2016: гл.4, 2018). Эти работы сегодня рассматриваются как
предшественники научной стипендии, известной как «измерение
теория ».
Darrigol 2003; Michell 1993, 2003; Канту и Шлаудт 2013;
Бьяджоли 2016: гл.4, 2018). Эти работы сегодня рассматриваются как
предшественники научной стипендии, известной как «измерение
теория ».
Математические теории измерения (часто называемые собирательно
как «теория измерения») относятся к условиям при
какие отношения между числами (и другими математическими объектами) могут быть
используется для выражения отношений между
объекты. [2] Чтобы понять необходимость математических теорий
измерения, учтите тот факт, что отношения, выставленные
числа, такие как равенство, сумма, разница и соотношение, не
всегда соответствуют отношениям между объектами, измеряемыми этими
числа.Например, 60 — это дважды 30, но можно ошибиться в
думая, что объект, измеренный при 60 градусах Цельсия, в два раза горячее
как объект при 30 градусах Цельсия. Это потому, что нулевая точка
шкала Цельсия произвольна и не соответствует отсутствию
из
температура. [3] Точно так же числовые интервалы не всегда несут эмпирические данные. Информация. Когда испытуемых просят оценить по шкале от 1 до 7
насколько сильно они согласны с данным утверждением, нет прима
facie причина думать, что интервалы между 5 и 6 и
от 6 до 7 соответствует равному приросту силы мнения.В качестве третьего примера: равенство чисел транзитивно [если
(a = b & b = c), затем a = c], но эмпирические сравнения физических
величины обнаруживают лишь приблизительное равенство, которое не является переходным
связь. Эти примеры показывают, что не все математические
отношения между числами, используемыми в измерениях, эмпирически
значительный, и что различные виды шкалы измерения передают
различные виды эмпирически значимой информации.
Информация. Когда испытуемых просят оценить по шкале от 1 до 7
насколько сильно они согласны с данным утверждением, нет прима
facie причина думать, что интервалы между 5 и 6 и
от 6 до 7 соответствует равному приросту силы мнения.В качестве третьего примера: равенство чисел транзитивно [если
(a = b & b = c), затем a = c], но эмпирические сравнения физических
величины обнаруживают лишь приблизительное равенство, которое не является переходным
связь. Эти примеры показывают, что не все математические
отношения между числами, используемыми в измерениях, эмпирически
значительный, и что различные виды шкалы измерения передают
различные виды эмпирически значимой информации.
Изучение шкал измерений и эмпирической информации в них Передача — это основная задача математических теорий измерения.В его основополагающее эссе 1887 года «Подсчет и измерение», Германн фон Гельмгольц сформулировал ключевой вопрос теории измерений как следует:
[W] hat — это объективный смысл выражения через деноминацию нумерует отношения реальных объектов как величины, а под каким условия мы можем это сделать? (1887: 4)
Вообще говоря, теория измерений направлена на: (i) выявление предположения, лежащие в основе использования различных математических структур для описывать аспекты эмпирического мира и (ii) извлекать уроки из адекватность и пределы использования этих математических структур для описание аспектов эмпирического мира.По следам Отто Гёльдера (1901), теоретики измерения часто достигают этих целей через формальные доказательства, с предположениями в (i), служащими аксиомами и уроками в (ii) следующее как теоремы. Ключевое понимание теории измерений: что эмпирически значимые аспекты данной математической структура — это те, которые отражают релевантные отношения среди объекты измерения. Например, отношение «больше чем »среди чисел является эмпирически значимым для измерения длина, поскольку она отражает отношение «длиннее, чем» среди объектов.Это отражение или отображение отношений между объекты и математические объекты составляют шкалу измерения. В виде будет пояснено ниже, шкалы измерений обычно понимаются как изоморфизмы или гомоморфизмы между объектами и математическими сущности.
Помимо этих общих целей и заявлений, теория измерений — это весьма неоднородный корпус ученых. В него входят произведения, охватывающие с конца девятнадцатого века до наших дней и поддерживают широкую множество взглядов на онтологию, эпистемологию и семантику измерение.Два основных различия между математическими теориями Особого упоминания заслуживают измерения. Первый касается характер relata , или «объекты», чьи номера отношений должны быть зеркальными. Эти relata могут быть понимается как минимум четырьмя разными способами: как конкретный человек объекты, как качественные наблюдения за конкретными отдельными объектами, как абстрактные представления отдельных объектов или как универсальные свойства объектов. Какая интерпретация будет принята, зависит от большая часть авторского метафизического и эпистемологического обязательства.Этот вопрос будет особенно актуален для обсуждения. реалистичных счетов измерения (Раздел 5). Во-вторых, разные теоретики измерения занимают разные позиции. на вид эмпирических данных, необходимых для установления сопоставления между объектами и числами. В результате измерения теоретики расходятся во мнениях относительно необходимых условий для установление измеримости атрибутов, в частности, о измеримы ли психологические атрибуты. Споры о измеримость оказались очень плодотворными для развития теории измерений, и в следующих подразделах будут представлены некоторые этих дебатов и разработанных в них центральных концепций.
3.1 Фундаментальные и производные измерения
В конце девятнадцатого и начале двадцатого веков несколько Были предприняты попытки дать универсальное определение измерения. Хотя способы измерения различались, единодушное мнение заключалось в том, что измерение — это метод присвоения чисел величине . Например, Гельмгольц (1887: 17) определил измерение как процедуру по которому можно найти номинальное число, которое выражает значение величина, где «номинальное число» — это число вместе с агрегатом, эл.г., 5 метров, а величина — качество объекты, которые можно упорядочить от меньшего к большему, например, длина. Бертран Рассел так же заявил, что измерение равно
.любой метод, с помощью которого устанавливается уникальное взаимное соответствие. установленный между всеми или некоторыми величинами вида и всеми или некоторые числа, целые, рациональные или действительные. (1903: 176)
Норман Кэмпбелл определил измерение просто как «процесс присвоение чисел для представления качеств », где качество — это свойство, допускающее непроизвольный порядок (1920: 267).
Определение измерения как числового присвоения поднимает вопрос: какие задания подходят и при каких условиях? Рано теоретики измерения, такие как Гельмгольц (1887 г.), Гельдер (1901 г.) и Кэмпбелл (1920) утверждал, что числа подходят для выражения величины, поскольку алгебраические операции между числами отражают эмпирические отношения между величинами. Например, качественный отношение «длиннее чем» среди жестких стержней (примерно) переходные и асимметричные, и в этом отношении разделяет структурные функции с отношением «больше чем» среди чисел.Кроме того, сквозное соединение жестких стержней разделяет конструктивные функции, такие как ассоциативность и коммутативность, с математическая операция сложения. Аналогичная ситуация имеет место для измерение веса с помощью равноблочных весов. Здесь отклонение оружие обеспечивает упорядочивание весов и наложение гирь на одна кастрюля представляет собой соединение.
Ранние теоретики измерения сформулировали аксиомы, описывающие эти качественных эмпирических структур, и использовал эти аксиомы для доказательства теоремы об адекватности приписывания чисел величинам, которые выставлять такие конструкции.В частности, они доказали, что заказывая и конкатенации вместе достаточно для построения аддитивный числовое представление соответствующих величин. Аддитивное представление — это такое представление, в котором сложение эмпирически осмысленное, а значит, и умножение, деление и т. д. Кэмпбелл так называемые процедуры измерения, которые удовлетворяют условиям аддитивность «фундаментальная», потому что они не включают измерение любой другой величины (1920: 277). Виды величин для которого была применена фундаментальная процедура измерения. найдено — например, длина, площадь, объем, продолжительность, вес и электрическое сопротивление — Кэмпбелл назвал «фундаментальным величины ».Отличительной чертой таких масштабов является то, что это их можно сгенерировать, объединив стандартную последовательность равные единицы, как в примере с серией одинаковых отметок на линейка.
Хотя они считали аддитивность отличительной чертой измерения, большинство ранние теоретики измерения признали, что аддитивность не необходимо для измерения. Существуют и другие величины, допускающие упорядочение. от меньшего к большему, но чьи соотношения и / или различия не могут в настоящее время быть определенными, кроме как через их отношения с другими, фундаментально измеримые величины.Примеры: температура, которая может быть измерен путем определения объема ртутного столба, и плотность, которая может быть измерена как отношение массы к объему. Такой косвенное определение стало называться «производным» измерения и соответствующие величины «производные величины »(Кэмпбелл 1920: 275–77).
На первый взгляд, различие между фундаментальным и производным измерение может показаться напоминанием о различии между обширными и интенсивные величины, и действительно фундаментальное измерение иногда называют «обширным».Тем не менее важно отметить, что эти два различия основаны на существенно разных критерии измеримости. Как обсуждалось в Раздел 2, экстенсивно-интенсивное различие сосредоточено на внутреннем структура рассматриваемой величины, т. е. является ли она состоит из пространственно-временных частей. Основополагающий различие, напротив, сосредотачивается на свойствах измерения операций . Принципиально измеримая величина — это величина в котором была найдена фундаментальная измерительная операция.Следовательно, фундаментальность не является внутренним свойством величина: полученная величина может стать фундаментальной с открытие новых операций по его измерению. Более того, в фундаментальное измерение, числовое присвоение не должно отражать структура пространственно-временной части. Электрическое сопротивление, для Например, можно принципиально измерить, подключив резисторы в серия (Кэмпбелл 1920: 293). Это считается фундаментальным операция измерения, потому что она имеет общую структуру с числовым кроме того, даже если объекты с одинаковым сопротивлением обычно не равные по размеру.
Различие между фундаментальным и производным измерением было отредактировано последующими авторами. Брайан Эллис (1966: гл. 5–8) различают три типа измерения: фундаментальный, ассоциативное и производное. Фундаментальные измерения требуют заказа и операции конкатенации, удовлетворяющие тем же условиям, указанным в Кэмпбелл. Процедуры ассоциативных измерений основаны на корреляция двух отношений порядка, например, корреляция между объемом ртутного столба и его температурой.Полученный процедуры измерения заключаются в определении значения константа в физическом законе. Константа может быть локальной, как в определение удельной плотности воды по массе и объему, или универсальный, как в определении ньютоновского гравитационного постоянная от силы, массы и расстояния. Генри Кибург (1984: гл. 5–7) предложил несколько иное тройное различие между прямое, косвенное и систематическое измерение, которое не полностью перекрываются с тем из Эллис. [4] Более радикальный пересмотр различия между фундаментальным и производное измерение было предложено Р. Дунканом Люсом и Джоном Тьюки. (1964) в своей работе по совместному измерению, которая будет обсуждаться в Раздел 3.4.
3.2 Классификация весов
В предыдущем подразделе обсуждалась аксиоматизация эмпирических структуры, линия расследования, которая восходит к ранним дням теория измерений. Дополнительная информация в рамках измерения Теория касается классификации шкал измерений.В психофизик С.С.Стивенс (1946, 1951) выделил четыре виды шкал: именные, порядковые, интервальные и передаточные. Номинальные шкалы представлять объекты как принадлежащие к классам, не имеющим конкретных порядок, например, мужской и женский. Порядковые шкалы представляют порядок, но не дальнейшая алгебраическая структура. Например, минеральная шкала Мооса твердость представляет собой минералы с номерами от 1 (самый мягкий) до 10 (самый сложный), но нет никакого эмпирического значения равенства между интервалы или отношения тех числа. [5] Цельсия и Фаренгейта являются примерами интервальных шкал: они представляют равенство или неравенство между интервалами температуры, но не отношения температур, потому что их нулевые точки произвольны. Шкала Кельвина, напротив, представляет собой шкалу отношений, как и знакомые шкалы, отображающие массу в килограммах, длину в метрах и продолжительность в секундах. Позже Стивенс уточнил эту классификацию и различают линейные и логарифмические интервальные шкалы (1959: 31–34) и между шкалами отношений с натуральной единицей и без нее. (1959: 34).Шкалы соотношений с естественными единицами измерения, например, используемые для подсчета дискретных объектов и представления вероятностей, были названы «абсолютными» шкалами.
Как отмечает Стивенс, типы гамм индивидуализируются по семействам трансформации, которые они могут претерпеть без потери эмпирических Информация. Эмпирические зависимости, представленные на шкалах отношений, для например, инвариантны относительно умножения на положительное число, например, умножение на 2,54 преобразует дюймы в сантиметры. Линейные интервальные шкалы допускают как умножение на положительное число и постоянный сдвиг, e.g., преобразование из Цельсия в Фаренгейт в соответствии с формулой ° C × 9/5 + 32 = ° F. Порядковые шкалы допускают любую функцию преобразования, пока она монотонно-возрастающие, а номинальные шкалы допускают любые взаимно однозначные подмена. Абсолютные шкалы не допускают никаких преобразований, кроме личность. Классификация весов Стивенса была позже обобщено Луи Наренсом (1981, 1985: гл. 2) и Люс и др. (1990: Гл. 20) с точки зрения однородности и уникальности соответствующих группы трансформации.
В то время как классификация шкал Стивенса встретила общие одобрение в научных и философских кругах, его шире последствия для теории измерений стали темой значительных дебаты. Особо оспаривались два вопроса. Во-первых, было ли операции классификации и упорядочивания заслуживают того, чтобы называться «Измерительные» операции и, соответственно, представление величин на номинальной и порядковой шкалах должно считать как измерение. Несколько физиков, в том числе Кэмпбелл, утверждали, что что операции классификации и упорядочивания не обеспечили достаточно богатая структура, чтобы гарантировать использование чисел, и, следовательно, не должны считаться измерительными операциями.Второй оспариваемый вопрос нужно ли было найти операцию конкатенации для величины прежде, чем это можно было фундаментально измерить по шкале отношений. Дебаты стал особенно горячим, когда снова разгорелся более длительный спор окружающая измеримость интенсивности ощущений. Это чтобы мы переходим к этой дискуссии.
3,3 Измеримость ощущений
Один из главных катализаторов развития математических теорий. измерения были продолжающимися дебатами об измеримости в психология.Эти дебаты часто восходят к работе Густава Фехнера. (1860) Elements of Psychophysics , в котором он описал метод измерения интенсивности ощущений. Метод Фехнера был основан на записи «едва заметных различия »между ощущениями, связанными с парами стимулы, например, два звука разной интенсивности. Эти различия были приняты равные приращения интенсивности ощущения. В виде Фехнер показал, что при этом предположении устойчивая линейная зависимость между интенсивностью ощущений и логарифмом интенсивность стимула, отношение, которое стало известно как «Закон Фехнера» (Heidelberger 1993a: 203; Luce and Суппес 2004: 11–2).Этот закон, в свою очередь, предоставляет метод для косвенно измеряя интенсивность ощущений путем измерения интенсивность стимула и, следовательно, утверждал Фехнер, обеспечивает обоснование измерения интенсивности ощущений на реальном числа.
Утверждения Фехнера об измеримости ощущений стал предметом серии дебатов, которые длились почти столетие и оказался чрезвычайно плодотворным для философии измерения, с участием таких ключевых фигур, как Мах, Гельмгольц, Кэмпбелл и Стивенс (Heidelberger 1993a: Ch.6 и 1993b; Мичелл 1999: гл. 6). Те возражая против измеримости ощущений, например, Кэмпбелл, подчеркнул необходимость эмпирической операции конкатенации для фундаментальное измерение. Поскольку интенсивности ощущений не могут быть соединены друг с другом способом, обеспечиваемым длинами и веса, фундаментального измерения ощущений быть не может. интенсивность. Более того, Кэмпбелл утверждал, что ни одно из психофизических обнаруженные к настоящему времени закономерности достаточно универсальны, чтобы как законы в том смысле, который требуется для производных измерений (Кэмпбелл в Ferguson et al.1940: 347). Все, что показали психофизики, что интенсивности ощущений можно последовательно упорядочить, но упорядочить сам по себе еще не гарантирует использование числовых соотношений, таких как суммы и соотношения для выражения эмпирических результатов.
Центральным оппонентом Кэмпбелла в этой дискуссии был Стивенс, чей Различие между типами шкалы измерений обсуждалось выше. Стивенс определил измерение как «присвоение цифр объекты или события в соответствии с правилами »(1951: 1) и утверждал, что любое последовательное и неслучайное назначение считается измерением в в широком смысле (1975: 47).В полезных случаях научного исследования Стивенс заявлено, измерение может быть истолковано несколько более узко как числовое присвоение, основанное на результатах сопоставления операции, такие как связь температуры с объемом ртути или соответствие ощущений друг другу. Стивенс выступал против считают, что отношения между числами должны отражать качественные эмпирические структур, утверждая вместо этого, что шкалы измерений должны быть рассматриваются как произвольные формальные схемы и принимаются в соответствии с их полезность для описания эмпирических данных.Например, приняв шкала соотношения для измерения ощущений громкости, громкости и плотность звуков приводит к формулировке простого линейного соотношения среди отчетов подопытных: громкость = громкость × плотность (1975: 57–8). Такое присвоение чисел ощущениям считается измерением, потому что оно непротиворечиво и неслучайно, потому что он основан на операциях согласования, выполняемых экспериментальными субъектов, и потому что он фиксирует закономерности в экспериментальных полученные результаты. По словам Стивенса, эти условия совпадают. достаточно, чтобы оправдать использование шкалы отношений для измерения ощущения, несмотря на то, что «ощущения не могут быть разделены на составные части или уложены встык, как измерения палки »(1975: 38; см. также Hempel 1952: 68–9).
3.4 Репрезентативная теория измерения
В середине двадцатого века два основных направления исследований в теория измерения, посвященная эмпирическим условиям количественная оценка и классификация шкал, сошлись в работах Патрика Суппеса (1951; Скотт и Суппс, 1958); для исторических обзоров см. Savage and Ehrlich 1992; Diez 1997a, b). Работа Суппеса заложила основу репрезентативной теории Измерение (RTM), которое остается наиболее влиятельным математическим теория измерений на сегодняшний день (Krantz et al.1971; Suppes et al. 1989; Luce et al. 1990). RTM определяет измерение как построение отображения эмпирических реляционных структур в числовые реляционные структуры (Krantz et al. 1971: 9). Эмпирический реляционный конструкция состоит из набора эмпирических объектов (например, жестких стержней) наряду с определенными качественными отношениями между ними (например, упорядочивание, конкатенация), а числовая реляционная структура состоит из набор чисел (например, действительные числа) и конкретные математические отношения между ними (e.g., «равно или больше», добавление). Проще говоря, шкала измерения — это соотношение «многие к одному». отображение — гомоморфизм — от эмпирического к числовому реляционная структура, а измерение — это построение напольные весы. [6] RTM очень подробно описывает предположения, лежащие в основе построение различных типов измерительных шкал. Каждый тип масштаба связана с набором предположений о качественном отношения между объектами, представленными на этом типе шкалы.Из этих предположений или аксиом авторы RTM выводят репрезентативная адекватность каждого типа шкалы, а также семейства допустимые преобразования, делающие этот тип шкалы уникальным. В этом способ RTM обеспечивает концептуальную связь между эмпирической базой измерение и типология напольные весы. [7]
Что касается измеримости, Репрезентативная теория принимает средний путь между либеральным подходом Стивенса и Строгий упор на операции конкатенации, поддерживаемый Кэмпбеллом.Нравиться Кэмпбелл, RTM признает, что правила количественной оценки должны быть основаны на известные эмпирические структуры и не должны выбираться произвольно, чтобы соответствовать данные. Однако RTM отвергает идею о том, что аддитивные шкалы адекватно только тогда, когда доступны операции конкатенации (Luce и Суппес 2004: 15). Вместо этого RTM отстаивает существование фундаментальных операции измерения, не связанные с конкатенацией. Центральный пример этого типа операции известен как «аддитивный конджойнт измерения »(Люс и Тьюки, 1964; Кранц и др.1971: 17–21 и гл. 6–7). Здесь измерения двух или более различные типы атрибутов, такие как температура и давление газа, получаются путем наблюдения за их совместным действием, таким как объем газа. Люси и Тьюки показали это, установив определенные качественные отношения между объемами при изменении температуры и давления, можно построить аддитивные представления температуры и давления, без использования каких-либо предшествующих методов объем измерения. Подобная процедура может быть обобщена на любой случай. соответствующим образом связанный триплет атрибутов, таких как громкость, интенсивность и частота чистых тонов или предпочтение награды, размер и задержка в получении (Люс и Суппес 2004: 17).В открытие аддитивного совместного измерения привело авторов RTM к разделить фундаментальные измерения на два вида: традиционные измерения процедуры, основанные на операциях конкатенации, которые они назвали «Обширное измерение» и совместное или «Неэкстенсивное» фундаментальное измерение. Под этим новым концепция фундаментальности, все традиционные физические атрибуты можно измерить фундаментально, как и многие психологические атрибуты (Кранц и др. 1971: 502–3).
Выше мы видели, что математические теории измерения в первую очередь связаны с математическими свойствами измерительных шкал и условия их применения.Родственная, но отличная нить стипендия касается значения и использования количественных терминов. Научный теории и модели обычно выражаются в терминах количественных отношения между параметрами, имеющими имена, такие как «Продолжительность», «уровень безработицы» и «Интроверсия». Реалист по поводу одного из этих терминов мог бы утверждают, что это относится к набору свойств или отношений, которые существуют независимо от измерения. Операционалист или конвенционалист будет утверждать, что способ применения таких количественных терминов к бетону детали зависят от нетривиального выбора, сделанного людьми, и конкретно о вариантах, которые связаны с тем, как соответствующие количество измеряется.Обратите внимание, что в соответствии с этой широкой концепцией реализм совместим с операционализмом и конвенционализмом. То есть это возможно, что выбор метода измерения регулирует использование количество-член и что при правильном выборе этот термин преуспевает в ссылке на независимое от разума свойство или отношение. Тем не менее многие операционалисты и конвенционалисты приняли более сильные взгляды, согласно которым нет фактов по делу как какая из нескольких и нетривиально разных операций верна для применения данного количественного термина.Эти более сильные варианты несовместимо с реализмом об измерениях. Этот раздел будет посвященный операционализму и конвенционализму, а следующий реализм об измерении.
Операционализм (или «операционизм») в отношении измерения — это точка зрения, что значение количественных понятий определяется набор операций, используемых для их измерения. Самое сильное выражение операционализма появляется в ранних работах Перси Бриджмена (1927), кто утверждал, что
под любым понятием мы понимаем не что иное, как набор операций; то понятие является синонимом соответствующего набора операций.(1927: 5)
Например, длина будет определяться как результат операции сцепления жестких стержней. Согласно этой крайней версии операционализм, разные операции измеряют разные величины. Длина измеряется линейками и синхронизацией электромагнитных импульсов. строго говоря, следует различать на два различных количественные понятия, помеченные как «длина-1» и «Длина-2» соответственно. Этот вывод привел Бриджмена к утверждают, что принятые в настоящее время количественные концепции имеют «Суставы», в которых различные операции пересекаются в своих область применения.Он предостерег от догматической веры в единство количественных концепций в этих «суставах», вместо этого это единство проверяется экспериментами всякий раз, когда применение количественное понятие должно быть расширено в новую область. Тем не менее, Бриджмен признал, что до тех пор, пока результаты различных операций согласен в пределах экспериментальной ошибки, прагматически оправдано маркировать соответствующие величины с таким же названием (1927: 16). [8]
Операционализм стал влиятельным в психологии, где он был хорошо принят бихевиористами, такими как Эдвин Боринг (1945) и Б.Ф. Скиннер (1945). В самом деле, Скиннер утверждал, что бихевиоризм «Не более чем тщательный оперативный анализ традиционные менталистские концепции »(1945: 271). Стивенс, который был Ученик Скуки был одним из главных пропагандистов операционализма в психологии, и утверждал, что психологические концепции имеют эмпирические имея в виду, только если они означают определенные и конкретные операции (1935: 517; см. также Isaac 2017). Идея о том, что концепции определяются операции измерения согласуются с либеральными взглядами Стивенса по измеримости, о которых говорилось выше (Раздел 3.3). Поскольку присвоение номеров объектам выполняется в в соответствии с конкретными и последовательными правилами, Стивенс утверждал, что такое присвоение имеет эмпирическое значение и не должно удовлетворять никаким дополнительные ограничения. Тем не менее Стивенс, вероятно, не принял антиреалистический взгляд на психологические атрибуты. Вместо этого там веские причины думать, что он понимал операционализм как методологический подход, который был ценен в той мере, в которой он позволили психологам обосновать выводы, которые они сделали из эксперименты (Feest 2005).Например, Стивенс не лечил операционные определения как априори , но как поддающиеся улучшение в свете эмпирических открытий, подразумевая, что он взял психологические атрибуты существуют независимо от таких определений (Стивенс 1935: 527). Это говорит о том, что операционализм Стивенса было более умеренным разнообразием, чем то, что было обнаружено в ранних произведениях из Бриджмен. [9]
Операционализм с первоначальным энтузиазмом встретил логические позитивисты, которые рассматривал это как сродни верификации.Тем не менее, это было скоро показали, что любая попытка основать теорию значения на операционалистские принципы были полны проблем. Среди таких проблемы были автоматическим операционализмом надежности измерения, неясности, связанные с понятием эксплуатации, чрезмерно ограничительный эксплуатационный критерий осмысленность и тот факт, что многие полезные теоретические концепции не хватает четких операционных определений (Чанг 2009 г.). [10] В частности, Карл Хемпель (1956, 1966) критиковал операционалистов. за неспособность дать определение диспозиционных терминов, таких как «Растворимость в воде», и для умножения количества научные концепции в манере, которая противоречит необходимости систематические и простые теории.Соответственно, большинство авторов семантика количественных терминов избегает поддержки операционного анализ. [11]
Более широко пропагандируемый подход допускал традиционный элемент в использование количественных терминов, сопротивляясь попыткам уменьшить значение количественных терминов в операциях измерения. Эти аккаунты классифицируются под общей рубрикой «Конвенционализм», хотя они различаются аспекты измерения, которые они считают общепринятыми, и в степени произвол они приписывают таким условности. [12] Первым предшественником конвенционализма был Эрнст Мах, исследовавший понятие равенства температурных интервалов (1896: 52). Мах отметил, что разные типы термометрической жидкости расширяются при разных (и нелинейно связанные) скорости при нагревании, в связи с чем возникает вопрос: какая жидкость расширяется наиболее равномерно с температурой? В соответствии с Мах, неважно, какая жидкость расширяется больше. равномерно, поскольку само понятие равенства температур интервалы не имеют определенного применения до обычного выбор стандартной термометрической жидкости.Мах придумал термин «Принцип согласования» для такого рода условно выбранный принцип применения количества концепция. Понятия об однородности времени и пространства получили аналогичные обработки Анри Пуанкаре (1898, 1902: Часть 2). Пуанкаре утверждал, что процедуры, используемые для определения равенства среди длительностей проистекает из бессознательного предпочтения ученых описательная простота, а не из каких-либо фактов о природе. Точно так же выбор ученых представить пространство либо Евклидова или неевклидова геометрия не определяется опытом но по соображениям удобства.
Конвенционализм в отношении измерения достиг своего максимума. сложное выражение в логическом позитивизме. Логические позитивисты как Ганс Райхенбах и Рудольф Карнап предложили «координационный определения »или« правила соответствия »в качестве семантическая связь между теоретическими и наблюдательными терминами. Эти a priori , утверждения, подобные определениям, предназначались для регулирования использование теоретических терминов, связав их с эмпирическими процедурами (Reichenbach 1927: 14–19; Carnap 1966: Ch.24). Пример координирующим определением является утверждение: «мерный стержень сохраняет свою длину при транспортировке ». По словам Райхенбаха, это утверждение не может быть проверено эмпирически, потому что универсальный и могла существовать экспериментально необнаруживаемая сила, которая в равной степени искажает длина каждого объекта при транспортировке. В соответствии с верификационизм, утверждения, которые не поддаются проверке, не являются ни правдой, ни ложный. Вместо этого Райхенбах использовал это заявление, чтобы выразить произвольное правило, регулирующее использование понятия равенства length, а именно для определения того, являются ли конкретные экземпляры length равны (Reichenbach 1927: 16).В то же время координационные определения не рассматривались как замена, а скорее как необходимые дополнения к знакомому типу теоретических определений понятий с точки зрения других концепций (1927: 14). Под условным точки зрения, то спецификация измерительных операций не исчерпать значение таких понятий, как длина или равенство длины, тем самым избегая многих проблем, связанных с операционализм. [13]
Реалисты в области измерения утверждают, что измерение лучше всего понимается как эмпирическая оценка объективного свойства или связь.Сделаем несколько пояснительных замечаний в отношении это характеристика измерения. Во-первых, термин «Объективный» не предназначен для исключения ментальных свойств или отношения, которые являются объектами психологического измерения. Скорее, измеримые свойства или отношения считаются объективными, поскольку поскольку они не зависят от верований и обычаев людей выполнение измерения и методы, используемые для измерения. Для Например, реалист будет утверждать, что отношение длины данного сплошная штанга к стандартному счетчику имеет объективное значение независимо от измеряется ли и как.Во-вторых, срок «Оценка» используется реалистами, чтобы подчеркнуть факт что результаты измерений являются всего лишь приближениями истинных ценности (Trout 1998: 46). В-третьих, по мнению реалистов, измерение направленных на получение знаний о свойствах и отношениях, скорее чем при присвоении значений непосредственно отдельным объектам. Это значимы, потому что наблюдаемые объекты (например, рычаги, химические решения, люди) часто определяют измеримые свойства и отношения, которые не наблюдаются напрямую (например,г., количество механических работа, кислая, интеллект). Знания о таких свойства и отношения должны предполагать некоторую фоновую теорию. От перенос акцента с объектов на свойства и отношения, реалисты подчеркивают теоретический характер измерений.
Реализм в отношении измерения не следует путать с реализмом в отношении сущности (например, электроны). Реализм в измерении обязательно влечет за собой реализм в отношении свойств (например, температуры), поскольку в принципе можно было принять только реальность отношений (напр.грамм., соотношения между количествами), не принимая во внимание реальность лежащих в основе характеристики. Тем не менее, большинство философов, защищавших реализм, об измерении сделали это, аргументируя это тем, что придерживаются некоторой формы реализма о собственности (Байерли и Лазара 1973; Свойер 1987; Манди 1987; Форель 1998, 2000). Эти реалисты утверждают, что по крайней мере некоторые измеримые свойства существуют независимо от убеждений и соглашений люди, которые их измеряют, и что существование и структура этих properties наилучшим образом объясняет ключевые особенности измерения, включая полезность чисел при выражении результаты измерений и надежность средств измерений.
Например, типичный реалист по поводу измерения длины будет утверждать, что что эмпирические закономерности, отображаемые отдельными объектами » длины, когда они упорядочены и объединены, лучше всего объясняются предполагая, что длина является объективным свойством, имеющим обширную структура (Swoyer 1987: 271–4). То есть отношения между длинами такие как «дольше чем» и «сумма» существуют независимо от того, заказываются ли какие-либо объекты и соединены людьми, и действительно независимо от того, являются ли объекты какая-то конкретная длина вообще существует.Существование обширная структура собственности означает, что длины разделяют большую часть их структура с положительными действительными числами, и это объясняет полезность положительных вещественных чисел в представлении длин. Более того, если измеримые свойства анализируются с точки зрения диспозиции, становится Легко объяснить, почему некоторые измерительные приборы надежны. Для Например, если предположить, что определенное количество электрического тока в проволока влечет за собой склонность отклонять стрелку амперметра определенным угла, следует, что показания амперметра контрфактически зависят от количества электрического тока в проводе, и поэтому амперметр надежен (Trout 1998: 65).
Другой аргумент в пользу реализма в отношении измерения принадлежит Джоэлю. Мичелл (1994, 2005), который предлагает реалистичную теорию чисел, основанную на евклидова концепция соотношения. По словам Мичелла, цифры соотношения между величинами и, следовательно, существуют в пространстве и времени. В частности, реальных чисел — это отношения между парами бесконечные стандартные последовательности, например, последовательность длин обычно обозначается «1 метр», «2 метра» и т. д., а последовательность целых кратных длины, которую мы пытаемся измерить.Измерение — это открытие и оценка таких соотношений. An Интересным следствием этого эмпирического реализма в отношении чисел является это измерение — не репрезентативная деятельность, а скорее деятельность по приближению независимых от разума чисел (Michell 1994: 400).
Реалистические представления об измерениях в основном формулируются противоположно к сильным версиям операционализма и конвенционализма, которые доминировали философские дискуссии об измерениях с 1930-х годов до 1960-х гг.Помимо недостатков операционализма уже обсуждалось в предыдущем разделе, реалисты отмечают, что антиреализм в отношении измеримых величин не может понять научная практика. Если бы количества не имели реальных значений независимо от выбор методики измерения, было бы трудно объясните, что ученые подразумевают под «точностью измерения» и «Ошибка измерения» и почему они пытаются повысить точность и уменьшить ошибку. Напротив, реалисты могут легко понять смысл понятия точности и ошибки с точки зрения расстояния между реальными и измеренные значения (Byerly and Lazara 1973: 17–8; Swoyer 1987: 239; Форель 1998: 57).С этим тесно связан тот факт, что более новые процедуры измерения имеют тенденцию к повышению точности по сравнению с более старыми. Если бы выбор процедуры измерения был просто обычным, он бы трудно разобраться в таком прогрессе. Кроме того, реализм дает интуитивно понятное объяснение того, почему разные измерения процедуры часто дают аналогичные результаты, а именно потому, что они чувствительны к тем же фактам (Swoyer 1987: 239; Trout 1998: 56). Наконец, реалисты отмечают, что конструкция измерительной аппаратуры и при анализе результатов измерений руководствуемся теоретическими предположения о причинно-следственных связях между величинами.В способность таких причинно-следственных предположений направлять измерения предполагает, что количества онтологически предшествуют процедурам измерения их. [14]
Хотя их позиция по отношению к операционализму и конвенционализму в значительной степени критичны, реалисты более снисходительны в своих оценках математические теории измерения. Брент Манди (1987) и Крис Swoyer (1987) оба принимают аксиоматическую трактовку измерения. шкалы, но возражают против эмпирической интерпретации, данной аксиомы выдающихся теоретиков измерений, таких как Кэмпбелл (1920) и Эрнест Нагель (1931; Коэн и Нагель 1934: гл.15). Скорее, чем интерпретация аксиом как относящихся к конкретным объектам или к наблюдаемые отношения между такими объектами, Манди и Свойер переосмысливают аксиомы, относящиеся к универсальным величинам, например, к универсальное свойство быть длиной 5 метров, а не бетоном экземпляры этого свойства. Эта конструкция сохраняет интуиция, что утверждения типа «размер x в два раза больше размером y ”- это в первую очередь около двух размеров , и только производно об объектах x и и сами (Манди 1987: 34). [15] Манди и Свойер утверждают, что их интерпретация является более общей, потому что это логически влечет за собой все последствия первого порядка эмпирическая интерпретация наряду с дополнительными утверждениями второго порядка о всемирных величинах. Более того, согласно их интерпретации теория измерения становится подлинной научной теорией с объяснительные гипотезы и проверяемые прогнозы. Основываясь на этом работы, Джо Вольф (2020a) недавно предложила новую реалистичную версию величин, которая опирается на репрезентативную теорию Измерение.Согласно структуралистской теории Вольфа количество, количественные атрибуты — это реляционные структуры. В частности, атрибут является количественным, если его структура имеет переводы, образующие архимедову упорядоченную группу. Вольфа сосредоточиться на переводах, а не на конкретных отношениях, таких как конкатенация и упорядочение, означает, что количественность может быть реализуется несколькими способами и не ограничивается обширными конструкции. Это также означает, что быть количеством ничего не значит. специально для чисел, как числовых, так и нечисловых структуры могут быть количественными.
Теоретико-информационные отчеты об измерениях основаны на аналогии между измерительными системами и системами связи. В простом система связи, сообщение (вход) кодируется в сигнал на конец передатчика, отправленный на конец приемника, и затем декодируется обратно (вывод). Точность передачи зависит от об особенностях системы связи, а также об особенностях окружающая среда, т. е. уровень фонового шума. Аналогичным образом, измеряя инструменты можно рассматривать как «информационные машины» (Финкельштейн 1977), которые взаимодействуют с объектом в заданном состоянии (ввод), кодируйте это состояние во внутренний сигнал и преобразуйте это сигнал в считывание (вывод).Точность измерения аналогично зависит от инструмента, а также от уровня шума в его среде. Задуманный как особый вид информации передачи, измерение становится анализируемым с точки зрения концептуальный аппарат теории информации (Hartley 1928; Shannon 1948; Шеннон и Уивер 1949). Например, информация о том, что чтение \ (y_i \) сообщает о возникновении состояния \ (x_k \) объект можно количественно оценить как \ (\ log \ left [\ frac {p (x_k \ mid y_i)} {p (x_k)} \ right] \), а именно как функция уменьшения неопределенность в отношении состояния объекта (Finkelstein 1975: 222; для альтернативные формулировки см. Brillouin 1962: Ch.15; Кирпатовский 1974; и Мари 1999: 185).
Людвик Финкельштейн (1975, 1977) и Лука Мари (1999) предложили возможность синтеза теории информации Шеннона-Уивера и теория измерений. По их мнению, обе теории апеллируют к центру. к идее отображения: теория информации касается отображения между символами во входных и выходных сообщениях, при измерении теория касается отображения между объектами и числами. Если измерение аналогично манипулированию символами, тогда Теория Шеннона-Уивера могла бы обеспечить формализацию синтаксиса измерения, в то время как теория измерений могла бы обеспечить формализацию его семантика.Тем не менее, Мари (1999: 185) также предупреждает, что аналогия между системами связи и измерения ограничена. В то время как сообщение отправителя может быть известно с произвольной точностью. независимо от его передачи состояние объекта не может быть известно с произвольной точностью независимо от его измерения.
Изначально теоретико-информационные отчеты об измерениях были разработаны метрологами — специалистами в области физических измерений и стандартизация — с небольшим участием философов.Независимо от достижений в метрологии, Бас ван Фраассен (2008: 141–185) недавно предложил концепцию измерения в какая информация играет ключевую роль. Он считает измерение составленным двух уровней: на физическом уровне измерительная аппаратура взаимодействует с объектом и производит чтение, например, указатель должность. [16] На абстрактном уровне фоновая теория представляет собой возможные состояния объекта в пространстве параметров. Измерение находит объект в подобласти этого абстрактного пространства параметров, тем самым сокращая диапазон возможных состояний (2008: 164 и 172).Это сокращение возможностей сводится к сбору информация об измеряемом объекте. Анализ ван Фраассена измерения отличается от теоретико-информационных счетов, разработанных в метрологии в ее явной апелляции к фоновой теории, и в тот факт, что он не ссылается на символическую концепцию информации разработан Шеннон и Уивер.
С начала 2000-х годов нахлынула новая волна философских исследований. появилось то, что подчеркивает взаимосвязь между измерением и теоретическое и статистическое моделирование (Morgan 2001; Boumans 2005a, 2015; Mari 2005b; Мари и Джордани 2013; Таль 2016, 2017; Паркер 2017; Мияке 2017).Согласно расчетам, основанным на модели, измерение состоит из двух уровней: (i) конкретный процесс, включающий взаимодействие между интересующий объект, инструмент и окружение; и (ii) a теоретическая и / или статистическая модель этого процесса, где «Модель» означает абстрактное и локальное представление построены на основе упрощающих предположений. Центральная цель измерение в соответствии с этой точкой зрения заключается в присвоении значений одному или нескольким интересующих параметров модели таким образом, чтобы Eptemic desiderata, в частности согласованность и последовательность.
Счета на основе моделей были разработаны на основе изучения измерений практики в науке, и особенно в метрологии. Метрология, официально определяется как «наука об измерениях и ее приложение »(JCGM 2012: 2.2), является предметом изучения с разработкой, обслуживанием и усовершенствованием средств измерений в естественных и технических науках. Метрологи обычно работают в бюро стандартизации или в специализированных лабораториях, которые ответственный за калибровку измерительного оборудования, сравнение стандартов и оценка измерений неопределенности, среди других задач.Только недавно философы начали заниматься богатыми концептуальными проблемами лежащей в основе метрологической практики, и особенно с выводами участвует в оценке и повышении точности измерений стандарты (Chang 2004; Boumans 2005a: Chap. 5, 2005b, 2007a; Frigerio и другие. 2010; Teller 2013, 2018; Риордан 2015; Шлаудт и Хубер 2015; Tal 2016a, 2018; Mitchell et al. 2017; Месснер и Нордманн 2017; de Courtenay et al. 2019).
Основной мотивацией для разработки модельных счетов является попытка прояснить эпистемологические принципы, лежащие в основе аспекты измерительной практики.Например, метрологи используют разнообразие методов калибровки средств измерений, стандартизация и отслеживание единиц и оценка неопределенности (обсуждение метрологии см. в предыдущем раздел). Традиционные философские учения, такие как математические теории измерения не основываются на предположениях, умозаключениях закономерности, доказательные основания или критерии успеха, связанные с такими методы. Как отмечает Frigerio et al. (2010) утверждают, что теория измерений плохо подходит для разъяснения этих аспектов измерения, потому что он абстрагируется от процесса измерения и сосредотачивается исключительно на математические свойства весов.Напротив, модельные бухгалтеры считают построение шкалы лишь одной из нескольких задач участвует в измерении, наряду с определением измеряемого параметры, конструкция и калибровка прибора, отбор образцов и подготовка, обнаружение ошибок и оценка неопределенности, среди прочего (2010: 145–7).
7.1 Роль моделей в измерении
Согласно модельным расчетам, измерение предполагает взаимодействие между интересующим объектом («система под измерение »), инструмент (« измерение система ») и среду, которая включает в себя измерения предметы.Другие, вторичные взаимодействия также могут иметь отношение к определение результата измерения, например, взаимодействие между измерительным прибором и эталонами, используемыми для его калибровка и цепочка сравнений, которые отслеживают эталон эталон обратно к первичным эталонам (Mari 2003: 25). Измерение продолжается путем представления этих взаимодействий с набором параметры и присвоение значений подмножеству этих параметров (известные как «измеряемые величины») на основе результатов взаимодействия.Когда измеряемые параметры являются числовыми, их называют «Количества». Хотя измеряемые величины не обязательно должны быть количествами, будет предложен сценарий количественного измерения, в котором следует.
Два типа результатов измерений различаются по моделям. счета [JCGM 2012: 2.9 и 4.1; Джордани и Мари 2012: 2146; Таль 2013]:
- Показания прибора (или «Показания»): это свойства измерительного прибор в конечном состоянии после того, как процесс измерения полный.Примеры: цифры на дисплее, отметки при множественном выборе. анкета и биты, хранящиеся в памяти устройства. Показания могут быть представлены числами, но такие числа описывают состояния инструмент, и его не следует путать с результатами измерения, которые касаются состояний измеряемого объекта.
- Результаты измерений (или «результаты»): это заявления о знании значений одной или нескольких величин приписываются измеряемому объекту и обычно сопровождаются указанием единицы измерения и шкалы и сметы неопределенности измерения.Например, результат измерения может быть следующим: выражается предложением «масса объекта a составляет 20 ± 1 грамм с вероятностью 68% ».
Сторонники теории, основанной на моделях, подчеркивают, что выводы из показания приборов к результатам измерений нетривиальны и зависят от множества теоретических и статистических предположений о измеряемый объект, прибор, окружающая среда и процесс калибровки. Результаты измерений часто достигаются через статистический анализ нескольких показаний, тем самым вовлекая предположения о форме распределения показаний и случайность воздействия окружающей среды (Боген и Вудворд 1988: 307–310).Результаты измерений также включают поправки на систематические эффекты, и такие поправки основаны на теоретических предположения относительно работы прибора и его взаимодействия с объектом и окружающей средой. Например, длина измерения должны быть скорректированы для изменения измерения длина стержня с температурой, поправка, которая выводится из теоретического уравнения теплового расширения. Систематический исправления связаны с собственными неопределенностями, например, в определение значений констант, и эти неопределенности оценивается посредством вторичных экспериментов, включающих дальнейшие и статистические допущения.Более того, неопределенность, связанная с результат измерения зависит от методов, используемых для калибровка прибора. Калибровка включает дополнительные предположения о приборе, калибрующем аппарате, измеряемая величина и свойства эталонов (Ротбарт и Слейден 1994; Франклин 1997; Бэрд 2004: Глава 4; Солер и др. al. 2013). Еще один компонент неопределенности проистекает из неопределенности. в определении измеряемой величины и известен как «Неопределенность определений» (Мари и Джордани, 2013; Греги 2015).Наконец, измерение включает в себя фон предположения о типе весов и системе единиц измерения, и эти предположения часто связаны с более широкими теоретическими и технологическими соображения, касающиеся определения и реализации весов и единицы.
Эти различные теоретические и статистические предположения составляют основу для построения одной или нескольких моделей измерительного процесса. В отличие от математических теорий измерения, где термин «Модель» обозначает теоретико-множественную структуру, которая интерпретирует формальный язык, здесь термин «модель» обозначает абстрактное и локальное представление целевой системы, которая построен на упрощении предположения. [17] Соответствующей целевой системой в этом случае является процесс измерения, то есть система, состоящая из измерительного прибора, объектов или события, подлежащие измерению, окружающая среда (включая людей-операторов), вторичные инструменты и эталоны, эволюция во времени эти компоненты и их различные взаимодействия друг с другом. Измерение рассматривается как набор процедур, цель которых — согласованно присваивать значения параметрам модели на основе прибора показания. Поэтому модели рассматриваются как необходимые предварительные условия для возможность вывода результатов измерения из прибора показания, и как решающее значение для определения содержания измерения результаты.Как подчеркивают сторонники модельных расчетов, показания, полученные в результате одного и того же процесса измерения, могут использоваться для установить разные результаты измерения в зависимости от того, как процесс измерения моделируется, например, в зависимости от того, в какой среде учитываются влияния, статистические допущения используются для анализа шума, и какие приближения используются при применении фоновая теория. Как выразился Лука Мари,
любой результат измерения содержит информацию, имеющую значение только в контекст метрологической модели, такая модель требуется для включить спецификацию для всех сущностей, которые явно или неявно фигурируют в выражении результата измерения.(2003: 25)
Точно так же говорят, что модели обеспечивают необходимый контекст для оценка различных аспектов качества результатов измерений, включая точность, прецизионность, погрешность и неопределенность (Boumans 2006, 2007a, 2009, 2012b; Мари 2005b).
Основанные на моделях описания расходятся с эмпирическими интерпретациями теории измерений в том, что они не требуют отношений между результаты измерения должны быть изоморфны или гомоморфны наблюдаемым отношения между объектами измерения (Mari 2000).Действительно, согласно модельным расчетам отношения между измеряемыми объектами вовсе не обязательно быть наблюдаемыми до их измерения (Frigerio et al. al. 2010: 125). Вместо этого ключевое нормативное требование основанной на моделях учетных записей заключается в том, что значения присваиваются параметрам модели в согласованном манера. Критерий согласованности можно рассматривать как сочетание двух подкритерии: (i) согласованность допущений модели с соответствующими фоновые теории или другие существенные предположения о измеряемая величина; и (ii) объективность, i.е. взаимное согласованность результатов измерений по разным измерениям инструменты, окружающая среда и модели [18] (Frigerio et al.2010; Tal 2017a; Teller 2018). Первое подкритерий предназначен для обеспечения того, чтобы предполагаемое количество измеряется, в то время как второй подкритерий предназначен для обеспечения что результаты измерения могут быть разумно отнесены к измеряемым объект , а не какой-то артефакт измерения инструмент, среда или модель.Взятые вместе, эти двое требования гарантируют, что результаты измерений остаются действительными независимо от конкретных допущений, связанных с их производства, и, следовательно, контекстная зависимость измерения результаты не угрожают их общей применимости.
7.2 Модели и измерения в экономике
Помимо их применимости к физическим измерениям, основанные на моделях Анализ также проливает свет на измерения в экономике. Как физический количества, значения экономических переменных часто невозможно наблюдать непосредственно и должны выводиться из наблюдений, основанных на абстрактных и идеализированные модели.Экономист девятнадцатого века Уильям Джевонс за Например, измерять изменения в стоимости золота, постулируя определенные причинно-следственные связи между стоимостью золота, предложением золота и общий уровень цен (Hoover and Dowell 2001: 155–159; Morgan 2001: 239). Как показывает Джулиан Рейсс (2001), Джевонс измерения стали возможны благодаря использованию двух моделей: причинно-теоретическая модель экономики, в основе которой предположение, что количество золота может увеличиваться или снижать цены; и статистическая модель данных, основанная на предположение, что местные колебания цен взаимно независимы и поэтому компенсируют друг друга при усреднении.Взятый вместе эти модели позволили Джевонсу сделать вывод об изменении значения золота из данных об исторических ценах различных товары. [19]
Способы, которыми модели функционируют в экономических измерениях, привели к некоторые философы считают определенные экономические модели инструменты сами по себе, аналогично линейкам и весам (Boumans 1999, 2005c, 2006, 2007a, 2009, 2012a, 2015; Morgan 2001). Марсель Буманс объясняет, как макроэкономисты могут изолировать переменная, представляющая интерес от внешних воздействий, путем настройки параметров в модель макроэкономической системы.Этот прием освобождает экономистов от невозможной задачи управления реальной системой. Как Боуманс утверждает, что макроэкономические модели функционируют как инструменты измерения, поскольку поскольку они создают инвариантные отношения между входами (показаниями) и выходов (результатов), и насколько эта инвариантность может быть проверена с помощью калибровка по известным и стабильным фактам. Когда такие модельные процедуры сочетаются с экспертной оценкой, они могут производить надежные измерения экономических явлений даже вне контроля лабораторные настройки (Boumans 2015: гл.5).
7.3 Психометрические модели и конструктивная валидность
Еще одна область, в которой модели играют центральную роль в измерениях, — это психология. Измерение большинства психологических атрибутов, таких как интеллект, тревога и депрессия, не полагаются на гомоморфные отображения типа, поддерживаемого Репрезентативной теорией Измерение (Уилсон 2013: 3766). Вместо этого психометрическая теория полагается преимущественно на разработке абстрактных моделей, предназначенных для прогнозировать производительность испытуемых в определенных задачах.Эти модели построены на основе существенных и статистических предположений о измеряемый психологический атрибут и его отношение к каждому задача измерения. Например, Теория отклика предмета, популярная подход к психологическому измерению, использует различные модели для оценить надежность и валидность анкет. Рассмотрим анкета, предназначенная для оценки понимания английского языка («способность»), предлагая испытуемым серию да / нет вопросы («предметы»).Одна из самых простых моделей Для калибровки таких вопросников используется модель Раша (Rasch 1960). Эта модель предполагает простое алгебраическое соотношение — известное как «журнал шансов» — между вероятностями что испытуемый ответит на заданный вопрос правильно, сложность этот конкретный предмет и способности субъекта. Новый анкеты калибруются путем проверки соответствия между их указания и прогнозы модели Раша и назначение уровни сложности для каждого элемента соответственно.Затем модель используется в в сочетании с анкетой для определения уровня владения английским языком понимание (результаты) из исходных баллов анкеты (показания) (Уилсон 2013; Мари и Уилсон 2014).
Своего рода статистическая калибровка (или «масштабирование») модели Раша дает повторяемые результаты, но часто только первый шаг к полноценному психологическому измерению. Психологов обычно интересуют результаты какой-либо меры. ради самого себя, но ради оценки некоторых основных и латентный психологический признак, e.г., понимание английского языка. Хорошего соответствия между ответами на вопросы и статистической моделью пока нет. определить, что измеряет анкета. Процесс установление того, что процедура измеряет предполагаемый психологический атрибут известен как «проверка». Один из способов проверки психометрический инструмент предназначен для проверки того, могут ли различные процедуры, предназначены для измерения одного и того же скрытого атрибута. полученные результаты. Такое тестирование относится к семейству методов валидации. известная как «проверка конструкции».Конструкция — это абстрактное представление скрытого атрибута, предназначенного для измерено, и
отражает гипотезу […] о том, что различные виды поведения коррелируют друг с другом в исследованиях индивидуальных различий и / или аналогично будут затронуты экспериментальные манипуляции. (Nunnally И Бернштейн 1994: 85)
Конструкции обозначаются переменными в модели, которая предсказывает, какие корреляции будут наблюдаться между показаниями различных меры, если они действительно являются показателями одного и того же атрибута.Такой модели включают существенные предположения об атрибуте, в том числе его внутренняя структура и его отношения с другими атрибутами, и статистические допущения о корреляции между различными показателями (Campbell & Fiske 1959; Nunnally & Bernstein 1994: Ch. 3; Angner 2008).
В последние годы философы науки все больше становятся интересуется психометрикой и концепцией валидности. Одна дискуссия касается онтологического статуса скрытых психологических атрибутов.Денни Борсбум выступил против операционализма по поводу латентного атрибуты, и в пользу определения действительности таким образом, чтобы охватывает реализм: «тест действителен для измерения атрибута, если и только если а) атрибут существует, и б) вариации в атрибута причинно порождают вариации в результатах методика измерения »(2005: 150; см. также Hood 2009, 2013; Праздник 2020). Элина Вессонен защищала умеренную форму операционализм о психологических атрибутах и утверждал, что умеренный операционализм совместим с осторожным реализмом (2019).Еще одна недавняя дискуссия посвящена обоснованию разработать процедуры проверки. По словам Анны Александровой, проверка конструкции в принципе является оправданной методологией, поскольку поскольку он устанавливает согласованность с теоретическими предположениями и фоновые знания о скрытом атрибуте. Однако Александрова отмечает, что на практике врачи-психометристы, намеревающиеся измерить счастье и благополучие часто избегают теоретических рассуждений об этих конструирует, а вместо этого апеллирует к народным верованиям респондентов.Это сводит на нет цель проверки конструкции и превращает ее в узкое, техническое упражнение (Александрова, Хайброн, 2016; Александрова 2017; см. также McClimans et al. 2017).
Более фундаментальная критика психометрии заключается в том, что она догматически предполагает, что психологические атрибуты могут быть количественно. Мичелл (2000, 2004b) утверждает, что психометристы не предпринимали серьезных попыток проверить, являются ли атрибуты, которые они подразумевают для измерения имеют количественную структуру, и вместо этого расплывчатая концепция измерения, скрывающая это пренебрежение.В ответ, Борсбум и Мелленберг (2004) утверждают, что ответ на предмет Теория обеспечивает вероятностные тесты количественной оценки атрибуты. Психометристы, строящие статистическую модель сначала предположить, что атрибут является количественным, а затем подвергнуть модель эмпирическим испытаниям. В случае успеха такие испытания обеспечивают косвенное подтверждение исходной гипотезы, например от показывая, что атрибут имеет аддитивную объединенную структуру (см. также Vessonen 2020).
Несколько ученых указали на сходство способов моделирования используются для стандартизации измеряемых величин в натуральных и социальные науки.Например, Марк Уилсон (2013) утверждает, что психометрические модели можно рассматривать как инструменты для построения эталоны в том же смысле слова «измерение эталон », применяемый метрологами. Другие вызвали сомнения по поводу целесообразность и желательность принятия примера естественные науки при стандартизации конструкций в социальных науках. Нэнси Картрайт и Роза Рунхардт (2014) обсуждают «Баллунг» — термин, заимствованный у Отто Нейрата. для обозначения концепций с нечеткой и контекстно-зависимой областью действия.Примеры понятий Баллунга — это раса, бедность, социальная изоляция и качество программ докторантуры. Такие концепции слишком многогранны, чтобы их измеряется по одной метрике без потери смысла и должен быть представлен либо матрицей индексов, либо несколькими разными меры в зависимости от целей и ценностей (см. также Брэдберн, Картрайт и Фуллер, 2016 г., Другие интернет-ресурсы). Александрова (2008) отмечает, что этические соображения влияют на вопросы об обоснованности мер благосостояния не менее соображения воспроизводимости.Такие этические соображения контекстно-зависимый и может применяться только по частям. В аналогичном vein, Лия МакКлиманс (2010) утверждает, что единообразие не всегда подходящая цель для разработки анкет, поскольку открытость вопросов часто неизбежны и желательны для получения соответствующая информация от предметы. [20] Переплетение этических и эпистемологических соображений особенно наглядно, когда психометрические анкеты используются в медицинских контексты для оценки благополучия и психического здоровья пациентов.В таком случаи, небольшие изменения в дизайне анкеты или анализа его результатов могут нанести значительный вред пациентам или принести им пользу. (McClimans 2017; Stegenga 2018, глава 8). Эти идеи подчеркивают ценностный и контекстуальный характер измерения умственных и социальные явления.
Разработка модельных счетов обсуждалась в предыдущем раздел является частью более крупного «эпистемологического поворота» в философия измерения, возникшая в начале 2000-х гг.Скорее чем упор на математические основы, метафизику или семантика измерения, философские работы последних лет имеют тенденцию к сосредоточиться на предпосылках и шаблонах вывода, участвующих в конкретные практики измерения, а также исторические, социальные и материальные размеры измерения. Философское изучение этих темы называют «эпистемологией измерение »(Mari 2003, 2005a; Leplège 2003; Tal 2017a). В самом широком смысле эпистемология измерения — это изучение отношения между измерением и знанием.Центральные темы которые подпадают под сферу эпистемологии измерения, включают условия, при которых измерения производят знания; в содержание, объем, обоснование и пределы таких знаний; в причины, по которым определенные методологии измерения и стандартизация успешна или не поддерживает определенные знания претензии и отношения между измерениями и другими познавательная деятельность, такая как наблюдение, теоретизирование, экспериментирование, моделирование и расчет.Следуя этим цели, философы опираются на работы историков и социологи науки, занимающиеся измерением практики в течение более длительного периода (Wise and Smith 1986; Latour 1987: Ch. 6; Schaffer 1992; Портер 1995, 2007; Wise 1995; Ольха 2002; Галисон 2003; Gooday 2004; Crease 2011), а также по истории и философия научных экспериментов (Harré 1981; Hacking 1983; Франклин 1986; Картрайт 1999). Следующие подразделы изучите некоторые из тем, обсуждаемых в этом быстрорастущем корпусе литература.
8.1 Стандартизация и научный прогресс
Тема, которая привлекла значительное внимание философов в последние годы — это выбор и совершенствование измерений стандарты. Вообще говоря, стандартизация количественной концепции означает: предписать определенный способ применения этой концепции к конкретный подробности. [21] Стандартизация измерительного прибора — это оценка того, насколько хорошо результаты измерений этим прибором соответствуют предписанному режиму применение соответствующей концепции. [22] Соответственно, термин «эталон» имеет не менее два значения: с одной стороны, он обычно используется для обозначения абстрактные правила и определения, регулирующие использование количества понятия, такие как определение счетчика. С другой стороны, термин «эталон» также обычно используется для обозначения к конкретным артефактам и процедурам, которые считаются образцовыми применение количественной концепции, такой как металлический стержень, который служил эталонным счетчиком до 1960 г.Эта двойственность смысла отражает двойственную природу стандартизации, которая включает в себя как абстрактные и конкретные аспекты.
В Раздел 4 было отмечено, что стандартизация предполагает выбор среди нетривиальных альтернативы, такие как выбор между различными термометрическими жидкостями или среди разных способов обозначения одинаковой продолжительности. Эти варианты нетривиальные в том смысле, что они влияют на то, температурные (или временные) интервалы считаются равными и, следовательно, влияют на содержат ли утверждения естественного права термин «Температура» (или «время») оказываются верными.Обращение к теории, чтобы решить, какой стандарт более точен, было бы круговой, поскольку теория не может быть однозначно применена к подробные сведения перед выбором эталона. Этот округлость по-разному называли «проблемой координации »(van Fraassen 2008: Ch. 5) и« проблема номических измерений »(Chang 2004: Ch. 2). Как уже упоминалось, конвенционалисты попытались уйти от округлости, положив априори утверждений, известных как «координационные определения », которые должны были связать количественные термины с специфические измерительные операции.Недостатком этого решения является то, что предполагается, что выбор эталона произвольный и статичны, тогда как на практике эталоны обычно выбираются на основе эмпирических соображений и в конечном итоге улучшаются или заменены стандартами, которые считаются более точными.
Новое направление работ по проблеме координации появилось в последние годы, в первую очередь из работ Хасока Чанга (2001, 2004, 2007; Барвич и Чанг, 2015) и Бас ван Фраассен (2008: Гл.5; 2009, 2012; см. также Padovani 2015, 2017; Мишель 2019). Эти Работы используют исторический и последовательный подход к проблеме. Вместо того, чтобы пытаться полностью избежать проблемы округлости, как и их предшественники, они намеревались показать, что округлость не порочный. Чанг утверждает, что построение количественной концепции и Стандартизация его измерения — взаимозависимые и повторяющиеся задачи. Каждая «эпистемическая итерация» в истории стандартизация уважает существующие традиции и в то же время исправляя их (Chang 2004: Ch.5). Донаучная концепция температура, например, была связана с грубым и неоднозначным методы упорядочивания предметов от горячего к холодному. Термоскопы и в конечном итоге термометры помогли изменить первоначальную концепцию и сделали это точнее. С каждой такой итерацией количественное понятие было пересмотрены на более стабильный набор стандартов, которые, в свою очередь, позволил более точно проверить теоретические предсказания, облегчение последующего развития теории и построения более стабильных стандартов и т. д.
Как этот процесс избегает порочной замкнутости, становится ясно, когда мы посмотрим. при этом либо «сверху», т. е. в ретроспективе с учетом наших текущие научные знания, или «изнутри», глядя в исторических событиях в их первоначальном контексте (ван Фраассен 2008: 122). С любой точки зрения координация успешна, потому что это увеличивает согласованность между элементами теории и инструментария. На вопросы «что считать количественным измерением X ? » и «какое количество X ?», хотя и не имеют ответа независимо друг от друга, адресованы вместе в процессе взаимного совершенствования.Только когда человек принимает фундаменталистской точки зрения и пытается найти отправную точку для координация, свободная от предположений, что этот исторический процесс ошибочно, кажется, не имеет эпистемологического обоснования (2008: 137).
В новой литературе по координации смещается акцент обсуждение от определений количественных терминов к реализаций этих определений. На метрологическом жаргоне «Реализация» — это физический инструмент или процедура, приблизительно удовлетворяет данному определению (ср.JCGM 2012: 5.1). Примеры метрологических реализаций — официальные прототипы килограмм и часы с цезиевым фонтаном, используемые для стандартизации второй. Недавние исследования показывают, что методы, используемые для проектирования, поддерживать и сравнивать реализации имеют прямое отношение к практическое применение понятий количества, единицы и масштаба, не менее чем определения этих понятий (Riordan 2015; Tal 2016). В связь между определением и реализацией единицы становится особенно сложно, когда определение сформулировано теоретически.Некоторые из основных единиц Международной системы (СИ) — включая метр, килограмм, ампер, кельвин и моль — нет больше определяется ссылкой на какой-либо конкретный вид физической системы, но фиксируя численное значение фундаментальной физической постоянной. Килограмм, например, был переопределен в 2019 году как единица массы. такое, что числовое значение постоянной Планка точно равно 6,62607015 × 10 -34 кг м 2 с -1 (BIPM 2019: 131). Понимание килограмма под этим определением — это в высшей степени теоретическая задача.Изучение практической реализации такие подразделения пролили новый свет на развивающиеся отношения между измерения и теория (Tal 2018; de Courtenay et al 2019; Wolff 2020b).
8.2 Теоретическая основа измерения
Как уже обсуждалось выше (разделы 7 а также 8.1), теория и измерение взаимозависимы как исторически, так и концептуально. С исторической стороны развитие теории и измерение происходит через итерационные и взаимные уточнения. На концептуальная сторона, спецификация форм процедур измерения эмпирическое содержание теоретических концепций, в то время как теория дает систематическая интерпретация показаний измерений инструменты.Эта взаимозависимость измерения и теории может показаться как угроза доказательной роли, которую измерение должно играть в научном предприятии. В конце концов, результаты измерений думал, что может проверить теоретические гипотезы, и это, кажется, требуют некоторой степени независимости измерения от теории. Этот угроза особенно очевидна, когда теоретическая гипотеза испытанный уже предполагается как часть модели измерения инструмент. Чтобы процитировать пример из работы Франклина и др.(1989: 230):
На первый взгляд может показаться замкнутым кругом, если кто-то должны были использовать ртутный термометр для измерения температуры объекты как часть эксперимента, чтобы проверить, расширяются ли объекты по мере повышения их температуры.
Тем не менее Франклин и др. сделать вывод, что округлость не беспощадный. Ртутный термометр можно откалибровать по другому термометр, принцип действия которого не предполагает закона теплового расширения, например, газовый термометр постоянного объема, тем самым подтверждая надежность ртутного термометра на независимые основания.Говоря шире, в контексте локальной проверки гипотез угроза замкнутости обычно может быть избегать обращения к другим видам инструментов и другим частям теория.
Другой вид беспокойства по поводу доказательной функции измерения возникает в глобальном масштабе, когда проводится проверка всех теорий. обеспокоенный. Как утверждает Томас Кун (1961), научные теории обычно принимаются задолго до количественных методов их тестирования становятся доступными. Надежность недавно введенного измерения методы обычно проверяются на соответствие предсказаниям теории а не наоборот.По словам Куна, « путь от научного закона к научному измерению редко бывает ехал в обратном направлении »(1961: 189). Например, Закон Дальтона, который гласит, что веса элементов в химические соединения связаны друг с другом целиком пропорции, изначально противоречащие некоторым из наиболее известных мерки таких пропорций. Только предполагая Закон Дальтона, который последующие химики-экспериментаторы смогли исправить и улучшить свои методы измерения (1961: 173).Следовательно, Кун утверждает, что функция измерения в физических науках не для проверки теории, а для ее применения во все большем объеме и точность, и, в конечном итоге, позволить стойким аномалиям выйти на поверхность это ускорит следующий кризис и научную революцию. Примечание что Кун не утверждает, что измерение не имеет доказательной роли для играть в науку. Вместо этого он утверждает, что измерения не могут проверить теория изолирована, но только в сравнении с альтернативной теорией это предлагается в попытке объяснить обнаруженные аномалии за счет все более точных измерений (для яркого обсуждения о диссертации Куна см. Hacking 1983: 243–5).
Традиционные дискуссии о теоретической нагруженности, как и у Куна, были проводится на фоне логических позитивистов различие между теоретическим и наблюдательным языком. В теоретическая нагруженность измерения правильно воспринималась как угроза возможность четкого разграничения между двумя языками. Современные дискуссии, напротив, больше не ведутся. теоретическая нагруженность как эпистемологическая угроза, но воспринимается как должное что некоторый уровень теоретической нагруженности является предпосылкой для измерений иметь какую-либо доказательную силу.Без какого-то минимального существенного предположения об измеряемой величине, например о ее приемлемости манипулированию и его отношениям к другим величинам, это было бы невозможно интерпретировать показания средств измерений и следовательно, невозможно установить доказательную релевантность этих показания. Об этом уже говорил Пьер Дюгем (1906: 153–6; см. также Carrier 1994: 9–19). Более того, современные авторы подчеркивают, что теоретические предположения играют важные роли в исправлении ошибок измерения и оценке неопределенности измерения.Действительно, физические процедуры измерения становятся на точнее на , когда лежащая в их основе модель деидеализованный, процесс, который включает в себя увеличение теоретических богатство модели (Tal 2011).
Признание того, что теория имеет решающее значение для гарантии Доказательная надежность измерений обращает внимание на «Проблема обоснования наблюдений», которая является обратной вызов традиционной угрозе теоретической нагруженности (Tal 2016b). Задача состоит в том, чтобы указать, какую роль наблюдение играет в измерения, и в частности, какая связь с наблюдением необходимо и / или достаточно для того, чтобы измерения могли сыграть доказательная роль в науках.Эта проблема особенно очевидна, когда одна попытка объяснить растущее использование вычислительных методы выполнения задач, которые традиционно решались измерительные приборы. В роли Маргарет Моррисон (2009) и Венди Паркер (2017) утверждают, есть случаи, когда достоверная количественная информация собирается о целевой системе с помощью компьютера моделирование, но таким образом, чтобы удовлетворить некоторые из основных Desiderata для измерения, такого как эмпирическое обоснование и ретроспективный (см. также Lusk 2016).На такую информацию не полагается по сигналам, передаваемым от конкретного объекта, представляющего интерес, к инструмента, но на использовании теоретических и статистических моделей для обрабатывать эмпирические данные о связанных объектах. Например, данные методы ассимиляции обычно используются для оценки прошлых атмосферных температуры в регионах, где нет показаний термометра. Некоторые методы делают это, подбирая вычислительную модель поведение атмосферы на комбинацию доступных данных из близлежащие регионы и модельный прогноз условий на момент наблюдение (Parker 2017).Эти оценки затем используются в различных способов, в том числе в качестве данных для оценки перспективных климатических моделей. Независимо от того, называют ли эти оценки «Измерения», они ставят под сомнение идею о том, что производство надежные количественные данные о состоянии объекта требуют наблюдая за этим объектом, как бы слабо он ни понимал термин «Наблюдение». [23]
8,3 Точность и прецизионность
Два ключевых аспекта надежности результатов измерений: тщательность и точность.Рассмотрим серию повторяющихся весов измерения, выполненные на конкретном объекте с равными руками остаток средств. С реалистической, «ошибочной» точки зрения, результаты этих измерений точные , если они близки истинному значению измеряемой величины — в нашем случае истинное соотношение веса объекта к выбранному unit — и , точный , если они расположены близко друг к другу. An аналогия, которую часто цитируют, чтобы прояснить основанное на ошибках различие, заключается в том, что стрелы стреляют в цель с точностью, аналогичной близости попадания в яблочко и точность, аналогичная плотности распространения хитов (ср.JCGM 2012: 2.13 и 2.15, Teller 2013: 192). Хотя интуитивно понятный, основанный на ошибках способ выделения различий вызывает эпистемологическую трудность. Принято считать, что точные истинные значения большинства величин, представляющих интерес для науки, непознаваемым, по крайней мере, когда эти количества измеряются в непрерывном напольные весы. Если это предположение выполнено, то точность, с которой такие измеряемые величины не могут быть известны с точностью, а только оценивается путем сравнения неточных измерений друг с другом.И все еще неясно, почему сходимость между неточными измерениями должна быть воспринимается как указание на истину. Ведь измерения могли быть страдают от общей предвзятости, которая предотвращает их индивидуальные неточности от компенсации друг друга при усреднении. В отсутствии когнитивный доступ к истинным ценностям, как оценка измерения точность возможна?
Отвечая на этот вопрос, философы извлекли пользу из изучения различные значения термина «точность измерения» как используется практикующими учеными.По крайней мере, пять разных чувств определены: метафизические, эпистемологические, операционные, сравнительные и прагматичный (Tal 2011: 1084–5). В частности, эпистемологические или «Основанный на неопределенности» смысл этого термина метафизически нейтрален и не предполагает существования истинных ценностей. Вместо, за точность результата измерения принимается близость согласие между ценностями, разумно отнесенными к данному количеству доступные эмпирические данные и базовые знания (см. JCGM 2012: 2.13 Заметка 3; Джордани и Мари 2012; де Куртенэ и Греги 2017).Таким образом, точность измерения может быть оценена следующим образом: установление устойчивости среди последствий моделей, представляющих различные измерительные процессы (Basso 2017; Tal 2017b; Bokulich 2020; Стейли 2020).
Согласно концепции, основанной на неопределенности, неточность — это особый вид. неточности. Например, неточность измерения веса составляет широта разброса ценностей, которые обоснованно приписываются вес объекта с учетом показаний весов и доступные базовые знания о том, как работает баланс, и используются стандартные веса.Неточность этих измерений заключается в компонент неточности, возникающий из-за неконтролируемых изменений показания баланса при повторных испытаниях. Другие источники неточности, помимо неточности, включают несовершенные исправления систематические ошибки, неточно известные физические константы и неопределенные определения измеряемых величин, среди прочего (см. Раздел 7.1).
Пол Теллер (2018) выдвигает другое возражение против ошибочного понятие точности измерения. Он возражает против предположения, что он называет «реализмом точности измерений», согласно которому в действительности измеримые величины имеют определенные значения.Теллер утверждает что это предположение неверно в том, что касается величин обычно измеряется в физике, потому что любое уточнение определенного значения (или диапазоны значений) для таких величин предполагает идеализацию и следовательно, не может относиться ни к чему в действительности. Например, концепция обычно понимается под фразой «скорость звука в воздух »включает в себя множество неявных идеализаций, касающихся однородность химического состава воздуха, температуры и давление, а также стабильность единиц измерения.Удаление эти идеализации полностью потребуют добавления бесконечного количества детали к каждой спецификации. Как утверждает Теллер, точность измерения следует понимать как полезную идеализацию, а именно как концепция, которая позволяет ученым оценивать согласованность и согласованность среди результатов измерения как будто лингвистическое выражение эти результаты зацепились за все в мире. Точность аналогично идеализированная концепция, основанная на неограниченном и неопределенное определение того, что считается повторением измерения при «тех же» обстоятельствах (Teller 2013: 194).
.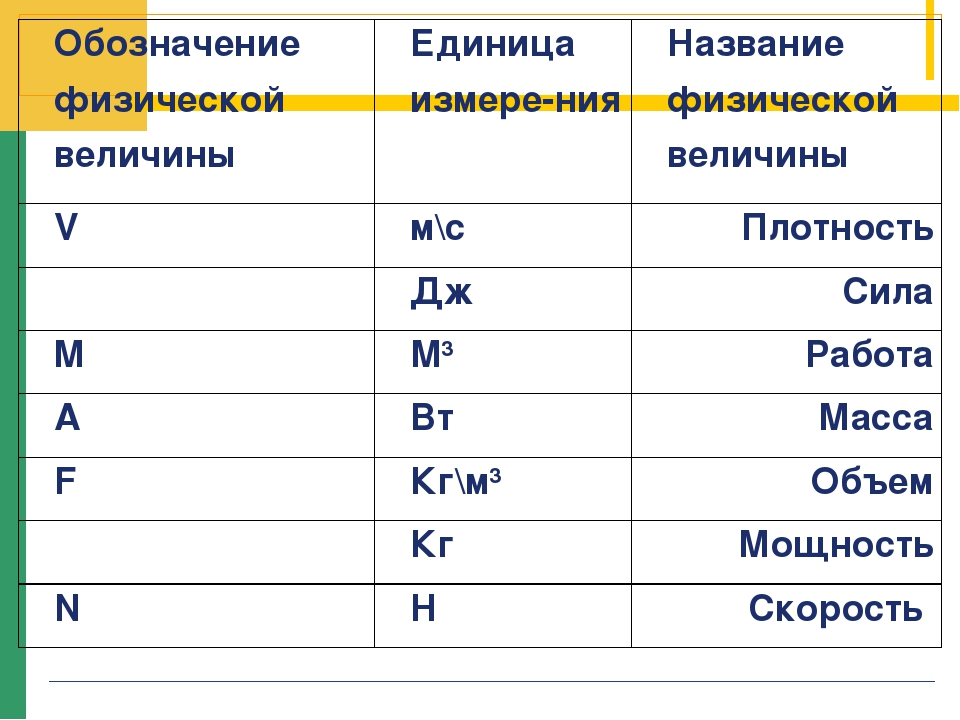 Филиал Плещеницкой средней школы
Филиал Плещеницкой средней школы
 материал
материал Траектория, путь, время. Единицы пути и времени
Траектория, путь, время. Единицы пути и времени Средняя скорость.
Средняя скорость.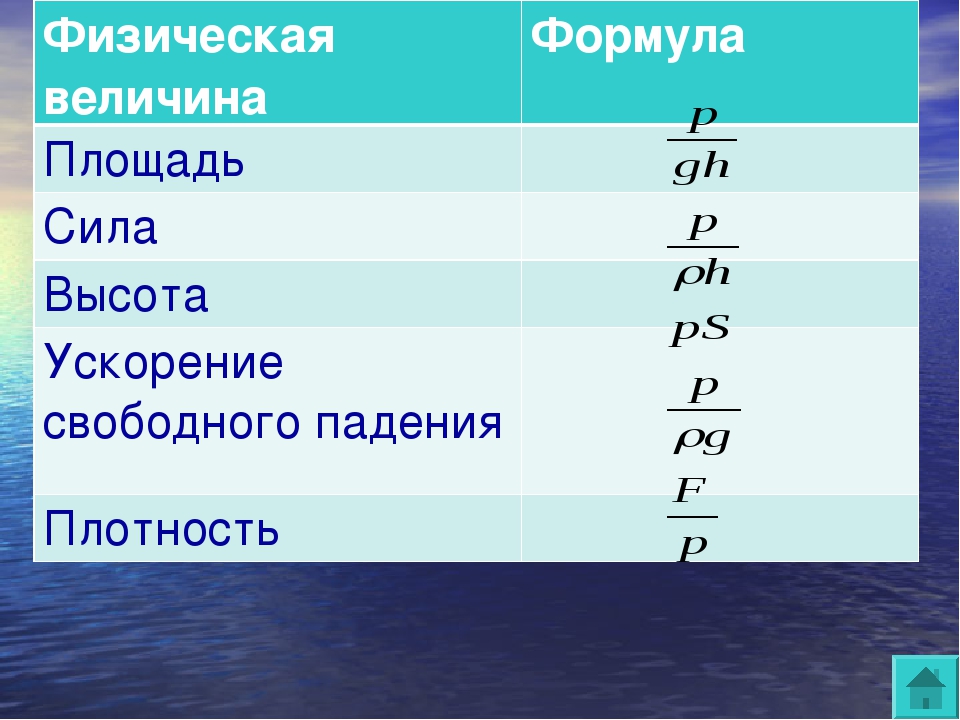 материал
материал Измерение силы. Динамометр
Измерение силы. Динамометр материал
материал материал
материал Работа. Мощность. Энергия
Работа. Мощность. Энергия