Где применяются дифференциальные уравнения 🚩 андреев а с дифференциальные уравнения 🚩 Культура и общество 🚩 Другое

Начнем с определения дифференциального уравнения. Итак, дифференциальное уравнение — это уравнение, которое связывает значение производной функции с самой функцией, значениями независимой переменной и некоторыми числами (параметрами).
Самая распространенная область, в которой применяются дифференциальные уравнения — математическое описание природных явлений. Также их применяют при решении задач, где невозможно установить прямую связь между некоторыми значениями, описывающими какой-либо процесс. Такие задачи возникают в биологии, физике, экономике.

Первой содержательной математической моделью, описывающей биологические сообщества была модель Лотки — Вольтерры. Она описывает популяцию, состоящую из двух взаимодействующих видов. Первый из них, именуемый хищниками, при отсутствии второго вымирает по закону x′ = –ax (a > 0), а второй — жертвы — при отсутствии хищников неограниченно размножается в соответствии с законом Мальтуса. Взаимодействие двух этих видов моделируется так. Жертвы вымирают со скоростью, равной числу встреч хищников и жертв, которое в данной модели предполагается пропорциональным численности обеих популяций, т. е. равной dxy (d > 0). Поэтому y′ = by – dxy. Хищники же размножаются со скоростью, пропорциональной числу съеденных жертв: x′ = –ax + cxy (c > 0). Система уравнений
x′ = –ax + cxy, (1)
y′ = by – dxy, (2)
описывающая такую популяцию хищник — жертва и называется системой (или моделью) Лотки — Вольтерры.

Второй закон Ньютона можно записать в форме дифференциального уравнения
m((d^2)x)/(dt^2) = F(x,t),
где m — масса тела, x — его координата, F(x, t) — сила, действующая на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы.

Модель естественного роста выпуска
Будем полагать, что некоторая продукция продается по фиксированной цене Р. Обозначим через Q(t) количество продукции, реализованной на момент времени t; тогда на этот момент времени получен доход, равный PQ(t). Пусть часть указанного дохода расходуется на инвестиции в производство реализуемой продукции, т.е.
I(t)=mPQ(t), (1)

где m — норма инвестиции — постоянное число, причем 0

www.kakprosto.ru

Методическая разработка по теме: Методическая разработка занятия по предмету Элементы высшей математики по теме: «Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными».

Методическая разработка

по предмету ЕН.01

ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ

по теме:

«Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными»

Преподаватель математики:

Т.Н. Рудзина

Москва

2015 г.

ОТКРЫТЫЙ УРОК по теме:

Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными.

«Великая книга природы написана на языке математики»

Галилей

Тип занятия: комбинированный, с элементами игры.

Формы занятия: индивидуальная, групповая, фронтальная.

Технология – игровая.

Оборудование: Кинофильм «Дифференциальные уравнения в науке и технике» (фрагменты), проектор, компьютер, доска, рабочие тетради.

Наглядные пособия. Таблица «Геометрическая интерпретация множества решений дифференциального уравнения».

Продолжительность занятия: 90 мин.

Цели занятия: 

Дидактическая цель. Дать понятие о дифференциальном уравнении, его общем, частном решении. Показать геометрическую интерпретацию множества решений дифференциального уравнения. Учить решать дифференциальные уравнения с разделенными переменными.

Воспитательная цель. Формировать мировоззрение учащихся, раскрыв основные идеи математического моделирования, в котором дифференциальные уравнения играют большую роль. Активизировать учебную деятельность учащихся, рассказав о широком применении дифференциальных уравнений во многих отраслях науки и техники. Развивать любознательность и интерес к изучению математики, раскрывая прикладную направленность дифференциальных уравнений и приводя исторические сведения.

Методическая цель: Организация деятельностного подхода обучающихся на уроке.

Основные знания и умения. З н а т ь определения: дифференциального уравнения, его порядка, общего и частного решения. Иметь понятие о задаче Коши. У м е т ь геометрически иллюстрировать дифференциальные уравнения в простейших случаях; отличать дифференциальные уравнения от алгебраических.

Учебно-методическое обеспечение: тест, презентация преподавателя к открытому уроку (Приложение 1), задания для группового решения, задания для самостоятельной работы, кроссворд, лист оценки знаний студента

ПЛАН УРОКА.

1. Организационный момент (5 мин).
2. Сообщение темы и целей урока.

 Мотивационная беседа с последующей постановкой цели (5 мин).

3. Актуализация опорных знаний:

1. Проверочная работа. (8 мин)

2. Отгадать имя ученого. (10 мин)

3. Историческая справка. (5 мин)

4. Просмотр научно-популярного фильма о применении дифференциальных уравнений. (6 мин)

4. Изучение нового материала. (20 мин)
5. Закрепление. (15 мин)
6. Домашнее задание. (2 мин)
7. Итог. (Решение кроссворда). (8 мин)
8. Рефлексия. (5 мин)

ХОД УРОКА.

I. Организационный момент.

Приветствие. Проверка готовности группы к уроку.

II. Сообщение темы и целей урока.

Тема нашего урока: Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными.

Цель нашего занятия: познакомиться с понятием дифференциального уравнения, его общим и частным решением, знать, как определяется порядок ДУ, иметь понятие о задаче Коши. Понимать какое уравнение называется уравнением с разделенными переменными и учиться его решать.

Для достижения этой цели мы проведем проверочную работу с взаимопроверкой, чтобы быть готовыми воспринимать новый материал; решим задания, с помощью которых узнаем кто ввел термин «Дифференциальные уравнения» и это все будет у нас проходить в духе соревнования (поэтому мы разделились с вами на 3 группы). Посмотрим фильм советских времен о применении ДУ в науке и технике. Разберем новый материал, закрепим его и в заключении разгадаем кроссворд, который подведет итог нашего урока. Результаты оценивания знаний на разных этапах заносятся в лист оценки знаний каждого студента. В процессе занятия учитывается и индивидуальная, и групповая формы работы.

1.  Мотивационная беседа с последующей постановкой цели.

Теория дифференциальных уравнений является заключительной темой после изучения дифференциально–интегрального исчисления. Тема эта очень сложная. Она является важной для получения фундаментального естественно – научного образования.

Для формирования представлений о математике, как о необходимой для каждого человека составляющей общих знаний о мире и понимания значимости этой науки для общественного прогресса.

«Математика – это то, посредством чего люди управляют природой и собой», – писал А.Н.Колмогоров (выдающийся математик современности).

III. Актуализация опорных знаний.

1. Проверочная работа. (8 мин)

(Слайд 2)

Найти производную.

I вариант                                         II вариант

          а) ;                         а)

б)                    б)

в)              в)

г)               г)

д)                  д) .

После решения нужно обменяться тетрадями и провести взаимопроверку по слайду. За каждый правильный ответ записываем себе 1 балл.

Ответы:                                                                                                  (Слайд 3)

           I вариант                                             II вариант

     а) ;                               а)    ;          

б) ;                                   б)   ;          

в) ;                               в)     

г)                      г)

д)                  д) .

2.   Отгадать фамилию ученого. 

(Слайд 4)

Кто ввел термин «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ»?

Для этого решаете примеры на вычисление определенного интеграла, а затем по полученным результатам прочитаем слово (фамилию ученного).

Задание.

Вычислить определенный интеграл:

 

1.                               2.

3.  ;                          4.

5.               6.      7. .

Проверим правильность решения примеров. С помощью таблицы определим, какой ответ решения определенного интеграла соответствует букве алфавита. С помощью полученных букв составим фамилию ученого, впервые применившего термин «Дифференциальные уравнения».

За каждый правильно вычисленный интеграл — 2 балла.

За составления фамилии ученого из полученных букв – 1 балл.

(Слайд 5)

Соответствие найденных значений определенных интегралов буквам алфавита.

7	6		8	0	1	2
Е	Н	Б	Ц	Й	Л	И

3. Историческая справка по применению дифференциальных уравнений.

Студенты группы подготовили свои сообщения по нашей теме. (Послушае        м их).

При изучении тех или иных физических, биологических процессов, механических явлений, ученым удается составить дифференциальные уравнения этого процесса или явления. А затем, решая это уравнение, удается вывести функциональный закон описания изучаемого вопроса. Дифференциальные уравнения играют большую роль в деле изучения природы и различных физических, химических и других процессов.

Существует много процессов в природе, которые описываются дифференциальными уравнениями. Например, процесс размножения бактерий, явление органического роста, изменение давления при подъеме над уровнем моря, ток самоиндукции, протекающий в катушке после выключения постоянного напряжения.

Можно так же написать дифференциальные уравнение движения планеты вокруг Солнца, искусственного спутника вокруг земли. Решая дифференциальные уравнения движения планет и их спутников (эти уравнения весьма сложны, т.к. планеты притягиваются не только к Солнцу, но и друг к другу), ученые предсказывают их будущее движение, узнают моменты солнечного и лунного затмений. Когда однажды оказалось, что планета Уран отклоняется от заранее вычисленной орбиты, ученые нисколько не сомневались в «правильности» математики. В середине 19 века французский астроном Леверье и английский астроном Джон Адамс одновременно и независимо один от другого сделали смелое предположение, что отклонение Урана вызывается притяжением к нему новой, до сих пор неизвестной планеты. С помощью дифференциальных уравнений они вычислили положение этой новой планеты и указали, где нужно искать ее на небе. Точно в указанном месте эта планета (её назвали НЕПТУН) была затем обнаружена. О ней говорят, что она открыта «на кончике пера» (путем вычислений).

Возникнув в XVI в. на базе задач математики и физики, теория дифференциальных уравнений как самостоятельная дисциплина сложилась к концу XVIII в. В настоящее время теория дифференциальных уравнений продолжает развиваться и является одной из важнейших частей математики.

Тот факт, что самые различные явления описываются одинаковыми дифференциальными уравнениями, часто используется на практике.

4. Просмотр научно-популярного фильма советских времен о применении дифференциальных уравнений. (Cлайд 6)

IV. Объяснение нового материала:

Мотивация: в школьном курсе встречались с различными уравнениями: алгебраическими, показательными, тригонометрическими и т.д. Во всех этих уравнениях неизвестными являются числа.

В математике и ее приложениях иногда приходиться рассматривать функциональные уравнения, решениями которых служат неизвестные функции (или семейство функций). (Вспомним, что же такое функция? Ответ: Это зависимость, когда каждому значению переменной x ставится в соответствие единственное значение y).

К функциональным уравнениям относятся дифференциальные уравнения.

        Рассмотрим некоторую функцию  . Обозначим через   ее первую производную,     — вторую и т.д., а дифференциалы функций и аргумента обозначим соответственно   и  .

        В дифференциальных уравнениях всегда присутствует производные или дифференциалы функции и аргумента. Это отличительный признак дифференциальных уравнений.

Например,   ,      – дифференциальные уравнения.

Выполним задание. (Слайд 7)

1. Установить, какое из указанных уравнений являются дифференциальными:

а) ;           б) ;               в) ;      

      г) ;           д) ;             е) .

  Ответ: а), г), е) — дифференциальные уравнения.

Определение:

(Слайд 8)

Дифференциальным уравнением называется уравнение, содержащее производные искомой функции или ее дифференциалы.

(Слайд 9)

        Решить дифференциальное уравнение — значит найти такую функцию, подстановка которой в это уравнение обращает его в тождество. Эта функция называется решением дифференциального уравнения.

2. Даны функции:  ,    ,    .  Какие из них являются решениями дифференциального уравнения      ? (Слайд 10)

Ответ:  .

(Слайд 11)

Решение, содержащее постоянную C, называется общим решением дифференциального уравнения.

Решение, в которое подставлено числовое значение C, называется частным решением дифференциального уравнения.

     Значение С вычисляется при подстановке начальных данных в общее решение. Геометрически частное решение представляется одной интегральной кривой, общее решение – совокупностью интегральных кривых.   

(Слайд 12)

3. Зная, что функция      является общим решением уравнения  , определить его частное решение, если  .

Решение:

Подставив в общее решение      заданные начальные условия   ,      , получим   , откуда    . Теперь подставим значение    

в общее решение и найдем искомое частное решение .

Таким образом, при решении дифференциальных уравнений сначала получается общее решение. Затем, если известны начальные данные, то можно получить частное решение.

(Слайд 13)

Для этого нужно:

1. подставить начальные данные в общее решение и вычислить С;
2. полученное числовое значение С подставить в общее решение.

(Слайд 14)

Задача нахождения частного решения дифференциального уравнения по начальным данным называется задачей Коши.

     При вычислении неопределенных интегралов мы имеем дело с дифференциальным уравнением. Нахождение неопределенного интеграла по заданному дифференциалу некоторой функции сводиться к решению дифференциального уравнения.

4. Найти решение    дифференциального уравнения   ,   удовлетворяющего условию   .

Общее решение этого уравнения находим интегрированием:  

 .

Подставив начальные данные и определив    , найдем частное решение (решение задачи Коши)   .

(Слайд 15)

Символически дифференциальное уравнение записывается так:

,             ,          .

(Слайд 16)

Определение:

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

(Слайд 17)

Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение. 

 – дифференциальное уравнение I порядка, т.к. наивысший порядок производной – I.

 – дифференциальное уравнение II-го порядка.

 – дифференциальное уравнение III-го порядка.

, где    – дифференциальное уравнение II-го порядка. (Определить порядок — на слайде 17)

К дифференциальным уравнениям I-го порядка относятся уравнения, в которые входят производные (или дифференциалы) не выше первого порядка.

Общий вид дифференциального уравнения I-го порядка  

(Слайд 18)

Если это уравнение можно разрешить относительно   , то оно примет вид                        .

Дифференциальные уравнения I порядка с разделенными переменными.

(Слайд 19)

Определение:

Уравнение вида     ,  где      и       – данные функции, называется уравнением с разделенными переменными.

Это уравнение можно переписать в виде:

и рассмотреть, как равенство двух дифференциалов.

Каждая часть уравнения с разделенными переменными представляет собой произведение некоторого выражения, зависящего от одной переменной, на дифференциал этой переменной.

(Слайд 20)

Пример: 

                                          

                                         

— уравнения с разделенными переменными. Решение таких уравнений выполняется непосредственным интегрированием.

5. Решить уравнение:    .

Здесь переменные разделены.

Интегрируя, получим:

,    

       

Так как    – произвольно, то    обозначим через   ,  тогда

  — общее решение или общий интеграл данного дифференциального уравнения.

С геометрической точки зрения получим семейство концентрических окружностей с центром в начале координат и радиусом равным   C.

(Слайд 21)

V. Закрепление. 

6. Решить уравнение   

Здесь    ,     .

,  интегрируя обе части

 

 – общее решение, его можно записать в явной форме:

.

7. Решить уравнение  

                                                 

                                                          

       

   

8. Решить уравнение  

                                               

 ,

  — общее решение.

9. Найти частное решение дифференциального уравнения                       , если , .

  Имеем:

 ,

         ,

          ,  

          ,

 – частное решение.

10.  Решить уравнение     , если   , при

                                                     

,      

  ,

 

   — частное решение.

(Слайд 22)

VI. Домашнее задание:

1.  ;

2. ;

3. ;

4. .

Ответы: 1)             3)

                 2)             4) .

                   

         VII. Итог.

(Слайд 23)

Решение кроссворда.

КРОССВОРД

По горизонтали:

1. Решение дифференциального уравнения, которое можно получить, если известны начальные данные.
2. Что показывает старшая производная дифференциального уравнения?
3. Действие нахождения общего решения ДУ.

     7. Нахождение конкретного частного решения по начальным данным – это задача … .

По вертикали:

4. Найти решение ДУ, значит, найти … .

5. Ученый, который ввел термин «Дифференциальные уравнения».

6. Дифференциальным уравнением называется уравнение, содержащее … .

8. Название ДУ, если искомая функция зависит от одного независимого переменного.

Теперь необходимо подсчитать количество баллов (индивидуально и по командам) соответственно таблице.

Таблица баллов

№ п/п	За что начисляются баллы	Количество	Максимальное количество баллов за данный пункт	Мои БАЛЛЫ
1	Решение проверочной работы	По 1 баллу за каждый правильно решенный пример	5
2	Решение заданий «Отгадай фамилию»	По 2 баллу за каждый правильно решенный пример	14
3	За составление фамилии ученого	1 балл	1
4	Историческая справка	1 балл	1
5	Участие в объяснении нового материала	По 1 баллу за каждый правильный ответ	1
6	Решение примеров на закрепление материала	3-5 баллов	5
7	Ответы на кроссворд	За каждое отгаданное слово – 1 балл	8

(Слайд 25).

КРИТЕРИИ ОЦЕНОК

Количество баллов	Оценка
18-20	5
13-17	4
8-12	3

VIII. Рефлексия.                                                                                  (Слайд 26)

1. «Я узнал много нового» —

2. «Мне это пригодится в жизни» —

3. «На уроке было над чем подумать» —

4. «На все вопросы, возникающие в ходе урока, я получил ответы» —

5. «На уроке я работал добросовестно и цели урока достиг» —

Поднимите руки, кто поставил 5 плюсов, а затем те, кто поставил 4 и три плюса.

5 –

4 –

3 –

2 –

nsportal.ru

Дифференциальные уравнения — ИСТОРИЯ

Дифференциальные уравнения — раздел математики, изучающий теорию и способы решения уравнений, содержащих искомую функцию и ее производные различных порядков одного аргумента (обыкновенные дифференциальные) или нескольких аргументов (дифференциальные уравнения в частных производных). Дифференциальные уравнения широко используются на практике, в частности для описания переходных процессов.

Теория дифференциальных уравнений — раздел математики, занимающийся изучением дифференциальных уравнений и связанных с ними задач. Их результаты применяются во многих естественных науках, особенно широко — в физике.

Проще говоря, дифференциальное уравнение — это уравнение, в котором неизвестной величиной является некоторая функция.При этом, в самом уравнении участвует не только неизвестная функция, но и различные ее производные. Дифференциальным уравнением описывается связь между неизвестной функцией и ее производными. Такие связи отыскиваются в различных областях знаний: в механике, физике, химии, биологии, экономике и др.

Различают обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных. Более сложными являются интегро-дифференциальные уравнения.

Сначала дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции от времени.

Дифференциальное уравнение называется интегрируемых в квадратурах, если задачу нахождения всех развязок связей можно свести к вычислению конечного числа интегралов от известных функций и простых алгебраических операций.
История

                       Леонард Эйлер                                          Жозеф-Луи Лагранж
                                                                             

Дифференциальные уравнения изобретены Ньютоном (1642-1727). Ньютон считал это свое изобретение настолько важным, что зашифровал его в виде анаграммы, смысл которой в современных терминах можно свободно передать так: «законы природы выражаются дифференциальными уравнениями».

Основным аналитическим достижением Ньютона было разложение всевозможных функций в степенные ряды (смысл второй, длинной анаграммы Ньютона в том, что для решения любого уравнения нужно подставить в уравнение ряд и приравнять члены одинакового степени). Особое значение имела здесь открытая им формула бинома Ньютона (разумеется, не только с целыми показателями, для которых формулу знал, например, Виет (1540-1603), но и, что особенно важно, с дробными и отрицательными показателями). Ньютон разложил в «ряды Тейлора» все основные элементарные функции Это, вместе с составленной им таблице первобытных (которая перешла в почти неизменном виде в современные учебники анализа ), позволяло ему, по его словам, сравнивать площади любых фигур «за половину четверти часа».

Ньютон указывал, что коэффициенты его рядов пропорциональны последовательным производным функции, но не останавливался на этом подробно, поскольку он справедливо считал, что все вычисления в анализе удобнее проводить не с помощью кратных дифференцировок, а путем вычисления первых членов ряда. Для Ньютона связь между коэффициентами ряда и производными был скорее средством вычисления производных, чем средством составления ряда. Одним из важнейших достижений Ньютона является его теория солнечной системы, изложенная в «Математических принципах натуральной философии» («Principia») без помощи математического анализа. Обычно считают, что Ньютон открыл с помощью своего анализа закон всемирного тяготения. На самом деле Ньютону (1680) принадлежит лишь доказательство эллиптичности орбит в поле притяжения по закону обратных квадратов: сам этот закон был указан Ньютону Гуком (1635-1703) и, пожалуй, угадывался еще несколькими учеными.

Пьер-Симон Лаплас
      

                                                           Из огромного числа работ XVIII века по дифференциальным уравнениям выделяются работы Эйлера (1707-1783)  и Лагранжа(1736-1813). В этих работах была прежде развита теория малых колебаний, а следовательно —   теория линейных систем дифференциальных уравнений; попутно возникли основные понятия линейной алгебры (собственные числа и векторы в n-мерном случае). Характеристическое уравнение линейного оператора долго называли секулярным, поскольку именно из такого уравнения определяются секулярные (возрастные, т.е. медленные по сравнению с годовым движением) возмущения планетных орбит согласно теории малых колебаний Лагранжа. Вслед за Ньютоном Лаплас и Лагранж, а позже Гаусс (1777-1855) развивают также методы теории возмущений.

Жозеф Лиувилль
     

                                                   Когда была доказана неразрешимость алгебраических уравнений в радикалах, Жозеф Лиувилль                        (1809-1882) построил аналогичную теорию для дифференциальных уравнений, установив невозможность решения ряда уравнений (в частности таких классических, как линейные уравнения второго порядка) в элементарных функциях и квадратурах. Позже Софус Ли (1842-1899), анализируя вопрос об интегрировании уравнений в квадратурах, пришел к необходимости детально исследовать группы дифеоморфизмив (получившие впоследствии имя групп Ли ) — так по теории дифференциальных уравнений возникла одна из самых плодотворных областей современной математики, дальнейшее развитие которой было тесно связано совсем с другими вопросами ( алгебры Ли еще раньше рассматривали Симеон-Дени Пуассон (1781-1840) и, особенно, Карл Густав Якоб Якоби (1804-1851)).

Анри Пуанкаре
              

                                              Новый этап развития теории дифференциальных уравнений начинается с работ Анри Пуанкаре (1854-1912),     созданная им «качественная теория дифференциальных уравнений» вместе с теорией функций комплексных  переменных привела к основанию современной топологии. Качественная теория дифференциальных уравнений, или, как теперь ее чаще называют, теория динамических систем, сейчас развивается наиболее активно и имеет наиболее важные применения теории дифференциальных уравнений в естествознании.

diffur.ucoz.ru

Дифференциальные уравнения в естествознании

Дифференциальные уравнения в естествознании

«Великая книга природы написана на языке математики»

Галилей

Тема «Дифференциальные уравнения» — составляет один из основных разделов высшей математики, через который она реализует себя в решении практических задачах. Эта тема является очень значимой для получения естественно – научного образования. Для создания представлений о науке математики, как о необходимой для освоения каждым человеком, а также понимания важности этой науки для дальнейшего развития технического и общественного прогресса.

Выдающийся математик современности А.Н. Колмогоров писал «Математика – это то, посредством чего люди управляют природой и собой».

Для изучения достаточно многих химических, физических ,биологических технических и экономических явлений учёным удалось составить дифференциальные уравнения того или иного процесса, т.е. перевести реальную задачу на язык математики , не теряя при этом основных свойств оригинала. В дальнейшем, решая эти уравнение, выводится функциональный закон описания изучаемой темы.

Дифференциальные уравнения играют огромную роль и в описании множества природных явлений. Они уникальные по содержанию и универсальные по применению в познания мира, повышая достоверность получаемых результатов.

Решение первых задач, приводящим к дифференциальным уравнениям, встречаются уде в 17 веке. К ним относится исследование Р. Декарта плоской кривой с применением свойств касательной, создание Дж. Неппером логарифмической таблицы.

Математические модели позволяют установить любые характеристики состояния процесса, качественные и количественные .

Например, скорость размножения бактерий, процесс самоиндукции, текущий в катушке после выключения постоянного напряжения, разность давлений при подъеме над уровнем моря.

С помощью дифференциальных уравнений можно вычислить движение планет солнечной системы вокруг Солнца. Решая такие , довольно сложные дифференциальные уравнения (т.к. планеты притягиваются не только к Солнцу, но и друг к другу), ученые могут достаточно точно предсказать моменты лунного и солнечного затмений.

И так мы убедились, что различных областях человеческой деятельности есть задачи, решение которых сводится с к дифференциальным уравнениям. Вот как можно описать методику их решения. При изучении какого-нибудь процесса нас всегда интересует изменение характеристик этого явление во времени, то есть некоторой величины (температуры, давления, массы и т. п.). Имея достаточное количество сведений о протекании этого процесса, мы сумеем построить его математическую модель. Получая информацию из экспериментальных данных или научных законов можно получить данные о скорости изменения любой величины у = у(t) в зависимости от времени t, то есть от производной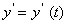

. Далее можно записать полученную информацию в виде дифференциального уравнения с неизвестной функцией у = у(t). Это уравнение и описывает наш изучаемый процесс с точки зрения его характеристики у. Решив его мы находим все возможные варианты изменения величины у.

Как показывает опыт развития различных наук, многие далёкие друг от друга по содержанию задачи приводят к решению одинаковых дифференциальных уравнений. Допустим, решение какой-то задачи сводится к дифференциальному уравнению, способы решения которого мы знаем, тогда задачу можно считать решённой. Творческий этап решения данной задачи состоит в составление дифференциального уравнения, следующий же этап – решений уравнения – имеет чисто техническую задачу.

Рассмотрим пример :

Чем выше над уровнем моря, тем становится разряжённее воздух , т.е. атмосферное давление уменьшается с высотой . Определить зависимость давления от высоты h. (p = p(h))

Решение задачи приводит к дифференциальному уравнению

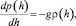
где ρ(h) – плотность воздуха на высоте h; g – ускорение свободного падения.

А вот пример радиоактивного распада: скорость уменьшения массы радиоактивного вещества пропорциональна количеству этого вещества. Следовательно, атмосферное давление 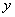 как функция высоты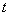 

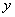 над уровнем моря и масса радиоактивного вещества  как функция времени  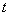удовлетворяют уравнению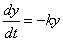

Эти примеры наглядно демонстрируют, что одно и то же дифференциальное уравнение может быть математической моделью совершенно различных природных процессов.

Итак, мы видим, что в изучении теории дифференциальных уравнений математика, конечно прежде всего, связана с другими разделами математики, но также выступает как неотъемлемая часть естествознания, на которой основывается вывод и понимание любых закономерностей, составляющих содержание наук о природе.

Список литературы

Интернет http://festival.1september.ru/articles/534688/

1.Половинкина Ю.С. методичка «Приложения дифференциальных уравнений»:Архангельск,2007.

2.Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика: Учебное пособие: В кн. – М.: ООО «Издательство Новая волна», 2004.

3.Б.В. Соболь, Н.Т. Мишняков, В.М. Поркшеян «Практикум по высшей математике». – Ростов-на-Дону, Феникс, 2004.

4.Н.В. Богомолов. Практические занятия по математике. – Москва, Высшая школа, 1990.

infourok.ru

Дифференциальные уравнения!

При решении различных задач физики, химии, математики и других точных наук часто пользуются математическими моделями в виде уравнений, связывающих одну или несколько независимых переменных, неизвестную функцию этих переменных и производные (или дифференциалы) этой функции. Такого сорта уравнения называют дифференциальными.
Если независимая переменная одна, то уравнение называется обыкновенным; если независимых переменных две или более, то уравнение называется дифференциальным уравнением в частных производных. С целью получить високовалифицированих специалистов во всех ВУЗах где изучают точные дисциплины обязательно курс дифференциальных уравнений. Для одних студентов теория дается тяжело, практика еще с горем пополам, для других тяжелая и теория, и практика. Если анализировать дифференциальные уравнения с практической стороны, то для их вычислений Вам нужно только хорошо уметь интегрировать и брать производные. Все остальные преобразования сводятся к нескольким схемам которые можно понять и изучить. Ниже изучем основные определения и метод решения простых ДР.

Теория дифференциальных уравнений

Определение: Обычным дифференциальным уравнением называют уравнение, которое в себе связывает независимую переменную х, функцию у(х) , ее производные у'(х), уⁿ(х) и имеет общий вид F(x,y(x),y’ (x), …, yⁿ(x))=0
Дифференциальным уравнением (ДР) называется или обычное дифференциальное уравнение, или дифференциальное уравнение в частных производных. Порядок дифференциального уравнения определяется порядком старшей производной (n), которая входит в данное дифференциальное уравнение.

Общим решением дифференциального уравнения называется функция, которая содержит столько постоянных, каков порядок дифференциального уравнения, и подстановка которой в данное дифференциальное уравнение превращает его в тождество, то есть имеет вид y=f(x, C₁, C₂, …, C_n).
Общее решение, которое не разрешено относительно у(х) и имеет вид F(x,y,C₁,C₂, …, C_n)=0 называется общим интегралом дифференциального уравнения.
Решение найденное из общего при фиксированных значениях постоянных C₁,C₂, …, C_n называется частным решением дифференциального уравнения.
Одновременное задания дифференциального уравнения и соответствующего количества начальных условий называется задачей Коши.
F(x,y,C₁,C₂, …, C_n)=0
y(x0)=y0;
….
yⁿ(x0)=yⁿ(0)
Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида
F(x, y, y’)=0. (1)
Интегралом уравнения (1) называется cоотношение вида Ф (x,y)=0, если каждая неявно заданная им непрерывно-дифференциированая функция является решением уравнения (1).
Уравнение которое имеет вид (1) и не может быть сведено к простому виду называется уравнением, неразрешимим относительно производной. Если его можно записать в виде
y’ = f(x,y), то оно называется решенным уравнением относительно производной.
Задача Коши для уравнения первого порядка содержит только одну начальную условие и имеет вид:
F(x,y,y’)=0
y(x₀)=y₀.
Уравнения вида
M(x,y)dx+N(x,y)dx=0 (2)
где переменные x i y является «симметричными»: можно предполагать, что x — независимая, а y — зависимая переменная, или наоборот, y — независимая, а x — зависимая переменная, называется уравнением в симметричной форме.
Геометрический смысл дифференциального уравнения первого порядка
y’=f(x,y) (3)
заключается в следующем.
Данное уравнение устанавливает связь (зависимость) между координатами точки (x;y) и угловым коэффициентом y’ касательной к интегральной кривой, проходящей через эту точку. Таким образом, уравнение y’= f(x,y) представляет собой совокупность направлений (поле направлений) на декартовой плоскости Oxy.
Кривая построенная на точках в которых направление поля одинаково называется изоклиной. Изоклины можно использовать для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить производную равную постоянной y’=С
f(x, y)=С — уравнение изоклины..
Интегральной линией уравнения (3) называется график решения этого уравнения.
Обычные дифференциальные уравнения, решения которых можно задать аналитически y=g(x), называются интегрируемыми уравнениями.
Уравнения вида
M₀(x)dx+N₀(y)dy=0 (3)
называются уравнениями с раздельными сменными.
Из них и начнем знакомство с дифференциальными уравнениями. Процесс нахождения решений ДР называют интегрированием дифференциального уравнения.

Уравнения с разделенными переменными

Пример 1. Найти решение уравнения y’=x .
Выполнить проверку решения.
Решени

yukhym.com

Дифференциальные уравнения, формулы и примеры

Понятие дифференциального уравнения

Например.

Толчком к развитию теории дифференциальных уравнений послужили различного рода механические задачи, в которых находились координаты тел, их скорости и ускорения. Названные величины зависели от времени при различных воздействиях.

Основой теории дифференциальных уравнений стало дифференциальное исчисление, которое было предложено немецким философом, логиком, математиком, механиком, физиком, юристом, историком, дипломатом, изобретателем и языковедом Готфридом Вильгельмом Лейбницем (1646-1716) и английским физиком, математиком, механиком и астрономом сэром Исааком Ньютоном (1642-1727). Термин «дифференциальное уравнение» предложил Готфрид Лейбниц в 1676 г.

18 век стал вправе переломным для развития теории дифференциальных уравнений. Появилось огромное количество работ, среди которых особо выделялись труды швейцарского, немецкого и российского математика и механика Леонардо Эйлера (1707-1783) и французского математика, астронома и механика Жозефа Луи Лагранжа (1736-1813). В их работах получила свое развитие теория малых колебаний, которая основывалась на теории линейных систем дифференциальных уравнений. Методы теории возмущения были разработаны французским математиком, механиком, физиком и астрономом Пьером-Симоном, маркизом де Лапласом (1749-1827), Ж. Лагранжем и немецким математиком, механиком, физиком, астрономом и геодезистом Иоганном Карлом Фридрихом Гауссом (1777-1855).

Французский математик Жозеф Лиувиль (1809-1882) установил неразрешимость ряда дифференциальных уравнений в элементарных функциях и квадратурах. «Качественная теория дифференциальных уравнений» (или теория динамических систем), предложенная французским математиком, механиком, физиком, астрономом и философом Жюлем Анри Пуанкаре (1854-1912), стала новой вехой в развитии теории дифференциальных уравнений.

От истории развития дифференциальных уравнений вернемся к ее основным определениям и понятиям.

Если неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной, то такое уравнение называется обыкновенным дифференциальным уравнением.

Например. .

Порядок дифференциального уравнения

Например. Уравнение – дифференциальное уравнение третьего порядка, поскольку старший порядок производной, входящей в него, равен трем (данная производная подчеркнута).

Обыкновенное дифференциальное уравнение n-го порядка имеет вид:

   

Обыкновенное дифференциальное уравнение первого порядка – или, если оно разрешимо относительно производной, – .

Решение дифференциального уравнения

Решением или общим интегралом дифференциального уравнения называется функция , удовлетворяющая указанному уравнению.

Кривая , соответствующая решению дифференциального уравнения, называется интегральной кривой этого уравнения.

Общее и частное решение дифференциального уравнения

Общим решением дифференциального уравнения называется соотношение

   

или

   

здесь C – произвольная постоянная или константа интегрирования. Это решение обладает следующим свойством: если разрешить выражение (или ) относительно y, то в результате получим функцию , являющуюся решением рассматриваемого дифференциального уравнения.

Уравнения (2) задают семейство интегральных кривых дифференциального уравнения (1).

Частное решение дифференциального уравнения – это решение, полученное из общего решения вида (2) при некотором значении произвольной постоянной C.

Например. Для дифференциального уравнения функция является общим решением, а при получаем частное решение .

Произвольную постоянную C можно определить из начальных условий – это такие условия, при которых ищется решение дифференциального уравнения, чтобы оно (решение) принимало значение при некотором заданном значении независимой переменной , то есть выполняется равенство

   

Если задано дифференциальное уравнение (1) с начальными условиями (3), то такая задача называется задачей Коши.

Например. .

ru.solverbook.com