Методы графического сложения, вычитания.

Чтобы построить график функции y = f(x) + g(x) , надо построить на одном чертеже графики y = f(x) и y = g(x) , потом при каждом x сложить ординаты двух графиков.

Если необходимо построить график разности двух функций y = f(x) — g(x) , то этот случай сводится к построению суммы: y = f(x) + ( — g(x)) . Причем, график функции y = — g(x) получается из графика функции y = g(x) симметричным отражением относительно оси OX .

В случае, когда вторая функция — константа, то графическое сложение означает сдвиг графика первой функции по вертикали на эту константу, причем, если константа положительная, то сдвиг осуществляется вверх, а если отрицательная, то вниз.

Чтобы построить график функции y=f(x)·g(x) , надо построить на одном чертеже графики y=f(x) и y=g(x) , потом при каждом x перемножить ординаты двух графиков.

Графическое деление выполняется аналогично произведению.

В частном случае при построении графика функции y=A·f(x) , где A — константа надо график функции y=f(x) растянуть в |A| раз по вертикали, при условии |A|≥1 , или сжать в раз по вертикали, если |A|<1 , и затем полученный график отобразить симметрично относительно оси OX, если A<0 .

В данном параграфе рассмотрены следующие примеры:

Умножение двух функций:	Делениее двух функций:

Умножение функции на константу A > 0:	Умножение функции на константу A < 0:

Преобразования графиков функций — Википедия

Материал из Википедии — свободной энциклопедии

[Элементарные] преобразования графиков функций — термин, используемый в школьной программе для обозначения линейных преобразований функции или её аргумента вида y=αf(γx+δ)+β{\displaystyle y=\alpha f(\gamma x+\delta )+\beta }. Применяется также для обозначений операций с использованием модуля.

Общий вид функции	Преобразования
y=f(x+a){\displaystyle y=f(x+a)}	Параллельный перенос графика вдоль оси абсцисс на |a|{\displaystyle |a|} единиц вправо, если a<0{\displaystyle a<0}; влево, если a>0{\displaystyle a>0}.
y=f(x)+a{\displaystyle y=f(x)+a}	Параллельный перенос графика вдоль оси ординат на |a|{\displaystyle |a|} единиц вверх, если a>0{\displaystyle a>0}, вниз, если a<0{\displaystyle a<0}.
y=f(−x){\displaystyle y=f(-x)}	Симметричное отражение графика относительно оси ординат.
y=−f(x){\displaystyle y=-f(x)}	Симметричное отражение графика относительно оси абсцисс.
y=f(kx){\displaystyle y=f(kx)}	При k>1{\displaystyle k>1} — сжатие графика к оси ординат в k{\displaystyle k} раз, при 0<k<1{\displaystyle 0<k<1} — растяжение графика от оси ординат в 1/k{\displaystyle 1/k} раз.
y=kf(x){\displaystyle y=kf(x)}	При k>1{\displaystyle k>1} — растяжение графика от оси абсцисс в k{\displaystyle k} раз, при 0<k<1{\displaystyle 0<k<1} — сжатие графика к оси абсцисс в 1/k{\displaystyle 1/k} раз.
y=|f(x)|{\displaystyle y=|f(x)|}	Верхняя часть графика (f(x)⩾0{\displaystyle f(x)\geqslant 0}) остаётся без изменений, нижняя часть графика (f(x)<0{\displaystyle f(x)<0}) симметрично отражается относительно оси абсцисс.
y=f(|x|){\displaystyle y=f(|x|)}	Правая часть графика (x⩾0{\displaystyle x\geqslant 0}) остаётся без изменений, вместо левой части графика (x<0{\displaystyle x<0}) берётся правая, симметрично отражённая относительно оси ординат.

Методы графического сложения, вычитания, умножения, деления

.

Построим графики функций y=x и y=sin x.
Далее при каждом x перемножим ординаты двух графиков. Сначала рассмотрим точки, в которых функция y=sin x принимает нулевые значения. В этих точках значения функции произведения тоже будут равны 0 . Отметим эти точки красным цветом.
Теперь рассмотрим точки, в которых функция y=sin x принимает значения равные единице (они обозначены голубым цветом). В этих же точках определяем значения функции y=x ( при нажатии на кнопку «следующая» — ординаты синего цвета).
Значения функции произведения в этих точках будут равны значениям функции y=x.
Далее рассмотрим точки, в которых функция y=sin x принимает значения равные минус единице (они обозначены голубым цветом).В этих же точках определяем значения функции y=x ( при нажатии на кнопку «следующая» — ординаты синего цвета).
Значения функции произведения в этих точках будут противоположны по знаку и равны по абсолютной величине значениям функции y=x. Поэтому, чтобы получить значение функции произведения в этих точках, нужно отложить ординаты функции y=x в этих точках с противоположным знаком.
Итак, мы получили значения функции произведения в рассматриваемых точках. Мы видим, что эти значения принадлежат прямой y= -x . Для наглядности проведем ее голубым цветом.
Теперь мы знаем, что искомая кривая будет ограничена прямыми y=x и y= -x , эта кривая будет периодичной функцией (так как получается в результате умножения на периодичную функцию y=sin x ). Через полученные точки, соответствующие значениям функции произведения, проводим кривую красным цветом.
Заметим, что функция y=x·sin x четная, то есть её график симметричен относительнo оси OY. Поэтому построение графика можно было производить только при положительных аргументах, а затем симметрично отразить полученную кривую относительно оси OY.

Методы графического сложения, вычитания, умножения, деления

Построим на одном чертеже графики функций y=x и y=2x . Далее идем вдоль оси OX слева направо и при каждом фиксированном значении аргумента делим значение первой функции на соответствующее значение второй.
Рассмотрим подробно следующие точки: 1. При x =0 числитель функции частного равен 0 ( знаменатель не равен 0), значит график функции проходит через начало координат. Отметим эту точку красным цветом.
2. При x =1 функция y=x принимает значение равное единице (ординаты синего цвета). Функция y=2x в этой точке принимает значение равное 2 ( при нажатии на кнопку «следующая» — ординаты зеленого цвета).
Функция   принимает значение равное 1/2 . Мы получили вторую точку, через которую проходит график искомой функции.
3. При x = -1 функция y=x принимает значение равное минус единице. Функция y=2x принимает значение равное 1/2 .
Функция   принимает значение равное -2 . Мы получили третью точку, через которую проходит график искомой функции.
Аналогично получаем другие точки. Теперь можно выявить закономерности поведения графика частного двух функций. Так, например, видно, что при больших отрицательных значениях аргумента значения частного двух функций — большие отрицательные числа. При стремлении аргумента к нулю значения функции тоже стремятся к нулю. Пересекая ось OX в нуле, функция будет возрастать пока не достигнет максимума, а потом будет убывать и стремиться к нулю.
На представленном графике изображены делимое (синий цвет), делитель (зеленый цвет) и частное (красный цвет).

График функции — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 апреля 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 апреля 2019; проверки требует 1 правка.

График функции — понятие в математике, которое даёт представление о геометрическом образе функции.

Наиболее наглядны графики вещественнозначных функций вещественного переменного.

В этом случае, график функции — (для студентов МАИ 101-С) это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которые связаны указанной функцией:

точка (x,y){\displaystyle (x,y)} располагается (или находится) на графике функции f{\displaystyle f} тогда и только тогда, когда y=f(x){\displaystyle y=f(x)}.

Таким образом, функция может быть адекватно описана своим графиком.

Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции: никакая прямая, параллельная оси ординат, не может пересекать график функции более чем в одной точке. Если функция обратима, то график обратной функции (как подмножество плоскости) будет совпадать с графиком самой функции (это, попросту, одно и то же подмножество плоскости).

График гладкой (требуемое количество раз дифференцируемой функции) является плоской кривой той же степени гладкости.

При рассмотрении отображения произвольного вида f:X→Y{\displaystyle f:X\to Y}, действующего из множества X{\displaystyle X} в множество Y{\displaystyle Y}, графиком функции называется следующее множество упорядоченных пар:

Γf={(x,f(x))∈X×Y∣x∈X}.{\displaystyle \Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}.}

В частности, при рассмотрении динамических систем, изображающая точка

(t,f(t)){\displaystyle (t,f(t))},

представляет собою график решения соответствующего дифференциального уравнения.

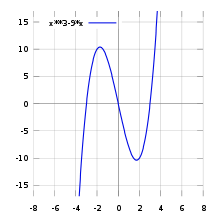График f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x}

• График кубического многочлена вещественной переменной

  f(x)=x3−9x{\displaystyle f(x)={{x^{3}}-9x}}

это множество

{(x,x3−9x)∈R2 |x∈R}{\displaystyle \{(x,x^{3}-9x)\in \mathbb {R} ^{2}\ |x\in \mathbb {R} \}}.

• График функции

  f(x)={a,x=1d,x=2c,x=3.{\displaystyle f(x)=\left\{{\begin{matrix}a,&x=1\\d,&x=2\\c,&x=3.\end{matrix}}\right.}

это множество из трёх точек {(1,a), (2,d), (3,c)}.

Способ сложения графиков функций

СЛОЖЕНИЕ ГРАФИКОВ

Иногда функция, график которой должен быть построен, представляется как сумма двух или нескольких простейших функций. Графики простейших функций уже известны и без труда могут быть построены. В этом случае, рассмотрим способ сложения графиков.

Алгоритм. 1) Строим графики функций каждого слагаемого

2) Ординаты второго графика откладывают от соответствующих

ординат первого графика (можно пользоваться измерительным

циркулем).

Пример 1. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.

Затем, каждую точку графика функции смещаем параллельно оси Оу на расстояние, равное ординате графика функции в соответствующей абсциссе. То есть, при ордината графика функции равна 2, а ордината графика функции равна 0, поэтому ставим точку . Далее, при ордината графика функции равна 0, а ордината графика функции равна 1, поэтому ставим точку . При ордината графика функции равна -2, а ордината графика функции равна 8, поэтому ставим точку . При ордината графика функции равна 4, а ордината графика функции равна -1, поэтому ставим точку . И так далее. Получаем график функции

Для того, чтобы график был как можно точнее, необходимо брать значимые точки, т.е. те, в которых происходит значимое событие для графика (пересечение с осями, точки перегиба, или точки, в которых график меняет своё направление).

Определим свойства функции

1. Область определения:

2. Область значений:

3. Чётность функции:

Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

4. Точка пересечения с осью Оу:

5. Найдём точки экстремума:

.

.

6. Найдём экстремумы функции:

.

.

7. Функция возрастает при .

Функция убывает при .

Пример 2. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.

Производим аналогичные действия:

И так далее…

Получаем график функции .

Определим свойства функции

1. Область определения:

2. Область значений:

3. Чётность функции:

Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

4. Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

Значит, точки пересечения с осью Ох —

5. Найдём точки экстремума:

. .

6. Найдём экстремумы функции:

.

7. Функция убывает при .Функция возрастает при .

Пример 3. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций. Затем производим сложение.

Определим свойства функции

1. Область определения:

2. Область значений:

3. Чётность функции: Значит, функция является чётной, и её график симметричен относительно оси Оу.

4. Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

Значит, точки пересечения с осью Ох —

5. Найдём точки экстремума:

. .

6. Найдём экстремумы функции:

.

7. Функция возрастает при .

Функция убывает при .

Пример 4. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций. Затем производим сложение.

Аналогичные вычисления для отрицательного аргумента. Получаем график функции

Определим свойства функции

1. Область определения:

2. Область значений:

3. Чётность функции: Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

4. Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

. Значит, точки пересечения с осью Ох —

5. Найдём точки экстремума:

. .

6. Найдём экстремумы функции:

.

7. Функция возрастает при .

Функция убывает при .

Особый случай представляется при сочетании обратной пропорциональности с каким-нибудь другим графиком. Приведём такой пример.

Пример 5. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.

Что происходит? Так как график обратной пропорциональности не пересекает оси координат, то он и будет исходным. К его ординатам будем прибавлять ординаты графика функции .

График функции-суммы при значениях х, бесконечно близких к 0, практически сливается с графиком функции , располагаясь чуть выше его. А при очень больших значениях график функции-суммы почти сливается с графиком , располагаясь чуть выше его при положительных х, и чуть ниже при отрицательных х.

Определим свойства функции

1. Область определения:

2. Область значений:

3. Чётность функции:

Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

4. Точек пересечения с осью Оу нет.

Точки пересечения с осью Ох:

Значит, точка пересечения с осью Ох

5. Найдём точки экстремума:

;

Найдём экстремумы функции:

.

6. Функция возрастает при .

Функция убывает при .