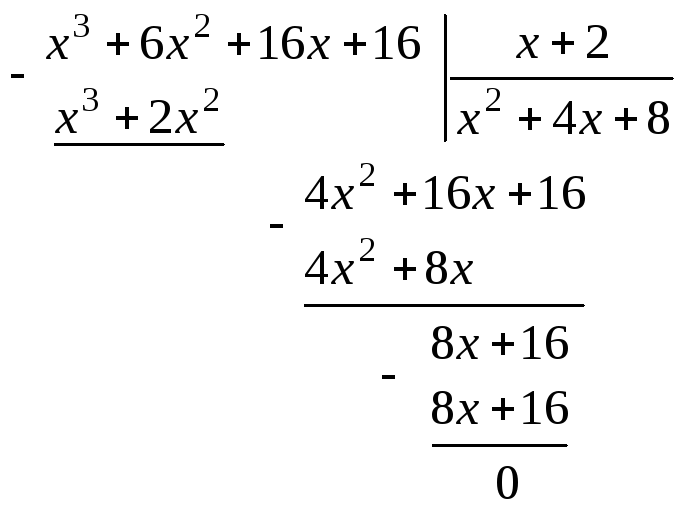Деление уравнения на уравнение: Кубические уравнения. Метод деления в столбик. Примеры * — Детская игровая комната «Волшебный лес»

Posted on 08.03.197314.01.2022 by alexxlab

{n-1}+\dots+a_1x+a_0\). Таким образом, сокращенно уравнение $(1)$ можно записать в виде $P_n(x)=0$.

Замечание

Заметим, что квадратное уравнение — это алгебраическое уравнение, степень которого равна $2$, а линейное — степень которого равна $1$.
Таким образом, все свойства алгебраических уравнений верны и для квадратных уравнений, и для линейных.

Теорема

Если уравнение $(1)$ имеет корень $x=x_0$, то оно равносильно уравнению

\[(x-x_0)\cdot P_{n-1}(x)=0\]

где $P_{n-1}(x)$ – некоторый многочлен степени $n-1$.

Для того, чтобы найти $P_{n-1}(x)$, необходимо найти частное от деления многочлена $P_n(x)$ на $(x-x_0)$
(т.к. $P_n(x)=(x-x_0)\cdot P_{n-1}(x)$).

Следствие: количество корней уравнения

Любое алгебраическое уравнение степени $n$ может иметь не более $n$ корней.

Замечание

В частности, квадратное уравнение действительно имеет всегда не более двух корней: два, один (или два совпадающих) или ни одного корня. 2-5x-3=0\).

В данном случае $a_0=-3, a_n=2$. Делители числа $-3$ — это $\pm 1, \pm 3$. Делители числа $2$ – это $\pm 1, \pm 2$. Комбинируя из полученных делителей дроби, получаем все возможные варианты рациональных корней:

\[\pm 1, \ \pm \dfrac12, \ \pm 3, \ \pm\dfrac32\]

По предыдущим теоремам можно быстро понять, что $\pm1$ не являются корнями. Подставив $x=-\dfrac12$ в уравнение, получим:

\[2\cdot \dfrac1{16}+5\cdot \dfrac18-\dfrac 14+5\cdot \dfrac12-3=0 \quad \Leftrightarrow \quad 0=0\]

Значит, число $x=-\frac12$ является корнем уравнения.

Можно перебрать остальные варианты: таким образом мы найдем еще один рациональный корень уравнения $x=3$. Значит, уравнение можно представить в виде

\[\left(x+\frac12\right)(x-3)\cdot Q_2(x)=0 \quad \text{или}\quad (2x+1)(x-3)\cdot P_2(x)=0\] (тогда $P_2(x)=\frac12 Q_2(x)$). Заметим, что второй вид записи уравнения более удобный, т.к. нам не придется при делении в столбик работать с дробями. 2-5x+9$.

Содержание

Деление многочленов

Продолжаем изучать многочлены. В данном уроке мы научимся их делить.

Предварительные навыки

Деление многочлена на одночлен

Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.

Например, разделим многочлен 15x²y³+ 10xy²+ 5xy³ на одночлен xy. Запишем это деление в виде дроби:

Теперь делим каждый член многочлена 15x²y³+ 10xy²+ 5

xy³ на одночлен xy. Получающиеся частные будем складывать:

Получили привычное для нас деление одночленов. Выполним это деление:

Таким образом, при делении многочлена 15x²y³+ 10xy²+ 5xy³ на одночлен xy получается многочлен 15xy²+ 10y + 5y².

При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.

В нашем примере произведение полученного многочлена 15xy²+ 10y + 5y² и делителя xy должно быть равно многочлену 15x²y³+ 10xy²+ 5xy³, то есть исходному делимому. Проверим так ли это:

(15xy²+ 10y + 5y²)xy = 15x²y³+ 10xy²+ 5xy³

Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.

Например, чтобы сложить дроби , и нужно записать следующее выражение:

Если мы вычислим выражение , то получим дробь , значение которой равно 1,5.

При этом выражение мы можем вернуть в исходное состояние , и вычислить по отдельности каждую дробь, затем сложить полученные частные. Результат по прежнему будет равен 1,5

Тоже самое происходит при делении многочлена на одночлен. Одночлен берёт на себя роль общего знаменателя для всех членов многочлена. Например, при делении многочлена

ax + bx + cx на многочлен x, образуется три дроби с общим знаменателем x

Вычисление каждой дроби даст в результате многочлен a + b + c

Пример 2. Разделить многочлен 8m³n + 24m²n² на одночлен 8m²n

Пример 3. Разделить многочлен 4c²d − 12c⁴d³ на одночлен −4c²d

Деление одночлена на многочлен

Не существует тождественного преобразования, позволяющего разделить одночлен на многочлен.

Допустим, мы захотели разделить одночлен 2xy на многочлен 5x + 3y + 5.

Результатом этого деления должен быть многочлен, перемножение которого с многочленом 5x + 3y + 5 даёт одночлен 2xy. Но не существует многочлена, перемножение которого с многочленом 5x + 3y + 5 давало бы в результате одночлен 2xy, поскольку перемножение многочленов даёт в результате многочлен, а не одночлен.

Но в учебниках можно встретить задания на нахождение значения выражения при заданных значениях переменных. В исходных выражениях таких заданий бывает выполнено деление одночлена на многочлен. В этом случае никаких преобразований выполнять не нужно. Достаточно подставить значения переменных в исходное выражение и вычислить получившееся числовое выражение.

Например, найдём значение выражения при x = 2.

Выражение представляет собой деление одночлена на многочлен. В данном случае мы не сможем выполнить какие-либо преобразования.

Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:

Деление многочлена на многочлен

Если первый многочлен умножить на второй многочлен, получается третий многочлен. Например, если умножить многочлен x + 5 на многочлен x + 3, получается многочлен x²+ 8x + 15

(x + 5)(x + 3) = x² + 5x + 3x + 15 = x² + 8x + 15

(x + 5)(x + 3) = x² + 8x + 15

Если произведение разделить на множитель, то получится множимое. Это правило распространяется не только для чисел, но и для многочленов.

Тогда согласно этому правилу, деление полученного нами многочлена x²+ 8x + 15 на многочлен x + 3 должно давать в результате многочлен x + 5.

Деление многочлена на многочлен выполняется уголком.

Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.

Выполним уголком деление многочлена x²+ 8x + 15 на многочлен x + 3. Так мы поэтапно увидим, как получается многочлен x + 5.

В данном случае результат нам известен заранее. Это будет многочлен x + 5. Но чаще всего результат бывает неизвестным. Поэтому решение будем комментировать так, будто результат нам неизвестен.

Результатом деления должен быть новый многочлен. Члены этого многочлена будут появляться один за другим в процессе деления.

Сейчас наша задача найти первый член нового многочлена. Как это сделать?

Когда мы изначально перемножали многочлены x + 5 и x + 3, мы сначала умножили первый член первого многочлена на первый член второго многочлена. Тем самым мы получили первый член третьего многочлена:

Если мы обратно разделим первый член третьего многочлена на первый член второго многочлена, то получим первый член первого многочлена. А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5.

Этот же принцип нахождения первого члена будет выполняться и при решении других задач на деление многочленов.

Итак, чтобы найти первый член нового многочлена, нужно первый член делимого разделить на первый член делителя.

Если первый член делимого (в нашем случае это x²) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:

Теперь, как и при делении обычных чисел, умножаем x на делитель x + 3. На этом этапе нужно суметь умножить одночлен на многочлен. При умножении

x на x + 3, получается x²+ 3x. Записываем этот многочлен под делимым x²+ 8x+ 15 так, чтобы подобные члены располагались друг под другом:

Теперь из делимого x²+ 8x + 15 вычитаем x²+ 3x. Подобные члены вычитаем из подобных им членов. Если из x² вычесть x², получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8x

Теперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:

Теперь делим многочлен 5x + 15 на x + 3. Для этого нужно найти второй член нового многочлена. Чтобы его найти, нужно первый член делимого (сейчас это член 5

x) разделить на первый член делителя (это член x). Если 5x разделить на x, получится 5. То есть вторым членом нового многочлена является 5. Записываем его под правым углом, вместе со своим знаком (член 5 в данном случае положителен)

Теперь умножаем 5 на делитель x + 3. При умножении 5 на x + 3, получается 5x + 15. Записываем этот многочлен под делимым 5x + 15

Теперь из делимого 5x + 15 вычитаем 5x + 15. Если из 5x + 15 вычесть 5x + 15 получится 0.

На этом деление завершено.

После выполнения деления можно выполнить проверку, умножив частное на делитель. В нашем случае, если частное x + 5 умножить на делитель x + 3, должен получаться многочлен x²+ 8x + 15

(x + 5)(x + 3) = x² + 5x + 3x + 15 = x² + 8x + 15

Пример 2. Разделить многочлен x²− 8x + 7 на многочлен x − 7

Записываем уголком данное деление:

Находим первый член частного. Разделим первый член делимого на первый член делителя, получим x. Записываем x под правым углом:

Умножаем x на x − 7, получаем x²− 7x. Записываем этот многочлен под делимым x²− 8x + 7 так, чтобы подобные члены располагались друг под другом:

Вычитаем из x²− 8x + 7 многочлен x²− 7x. При вычитании x² из x² получается 0. Ноль не записываем. А при вычитании −7x из −8x получается −x, поскольку −8x − (−7x) = −8x + 7x = −x. Записываем −x под членами −7x и −8x. Далее сносим следующий член 7

Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое. Давайте воспользуемся этим методом:

Вернёмся к нашей задаче. Разделим многочлен −x + 7 на x − 7. Для этого нужно найти второй член частного. Чтобы его найти, нужно первый член делимого (сейчас это член −x) разделить на первый член делителя (это член x). Если −x разделить на x, получится −1. Записываем −1 под правым углом вместе со своим знаком:

Умножаем −1 на x − 7, получаем −x + 7. Записываем этот многочлен под делимым −x + 7

Теперь из −x + 7 вычитаем −x + 7. Если из −x + 7 вычесть −x + 7 получится 0

Деление завершено. Таким образом, частное от деления многочлена x²− 8x + 7 на многочлен x − 7 равно x − 1

Выполним проверку. Умножим частное x − 1 на делитель x − 7. У нас должен получиться многочлен x²− 8x + 7

(x − 1)(x − 7) = x² − x − 7x + 7 = x² − 8x + 7

Пример 3. Разделить многочлен x⁶+ 2x⁴+ x⁷+ 2x⁵ на многочлен x²+ x³

Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x⁴

Умножаем x⁴ на делитель x²+ x³ и полученный результат записываем под делимым. Если x⁴ умножить на x²+ x³ получится x⁶+ x⁷. Члены этого многочлена записываем под делимым так, чтобы подобные члены располагались друг под другом:

Теперь из делимого вычитаем многочлен x⁶+ x⁷. Вычитание x⁶ из x⁶ даст в результате 0. Вычитание x⁷ из x⁷ тоже даст в результате 0. Оставшиеся члены 2x⁴ и 2x⁵ снесём:

Получилось новое делимое 2x⁴+ 2x⁵. Это же делимое можно было получить, выписав отдельно многочлен x⁶+ 2x⁴+ x⁷+ 2x⁵ и вычтя из него многочлен x⁶+ x⁷

Разделим многочлен 2x⁴+ 2x⁵ на делитель x²+ x³. Как и раньше сначала делим первый член делимого на первый член делителя, получим 2x². Записываем этот член в частном:

Умножаем 2x² на делитель x²+ x³ и полученный результат записываем под делимым. Если 2x² умножить на x²+ x³ получится 2x⁴+ 2x⁵. Записываем члены этого многочлена под делимым так, чтобы подобные члены располагались друг под другом. Затем выполним вычитание:

Вычитание многочлена 2x⁴+ 2x⁵ из многочлена 2x⁴+ 2x⁵ дало в результате 0, поэтому деление успешно завершилось.

В промежуточных вычислениях члены нового делимого располагались друг от друга, образуя большие расстояния. Это было по причине того, что при умножении частного на делитель, результаты были записаны так, чтобы подобные члены располагались друг под другом.

Эти расстояния между членами нового делимого образуются тогда, когда члены исходных многочленов расположены беспорядочно. Поэтому перед делением желательно упорядочить члены исходных многочленов в порядке убывания степеней. Тогда решение примет более аккуратный и понятный вид.

Решим предыдущий пример, упорядочив члены исходных многочленов в порядке убывания степеней. Если члены многочлена x⁶+ 2x⁴+ x⁷+ 2x⁵ упорядочить в порядке убывания степеней, то получим многочлен x⁷+ x⁶+ 2x⁵+ 2x⁴. А если члены многочлена x²+ x³ упорядочить в порядке убывания степеней, то получим многочлен x³+ x²

Тогда деление уголком многочлена x⁶+ 2x⁴+ x⁷+ 2x⁵ на многочлен x²+ x³ примет следующий вид:

Деление завершено. Таким образом, частное от деления многочлена x⁶+ 2x⁴+ x⁷+ 2x⁵ на многочлен x²+ x³ равно x⁴+ 2x²

Выполним проверку. Умножим частное x⁴+ 2x² на делитель x²+ x³. У нас должен получиться многочлен x⁶+ 2x⁴+ x⁷+ 2x⁵

(x⁴+ 2x²)(x²+ x³) = x⁴(x²+ x³) + 2x²(x²+ x³) = x⁶+ 2x⁴+ x⁷+ 2x⁵

При перемножении многочленов члены исходных многочленов тоже желательно упорядочивать в порядке убывания степеней. Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.

Перепишем умножение (x⁴+ 2x²)(x²+ x³) упорядочив члены многочленов в порядке убывания степеней.

(x⁴+ 2x²)(x³+ x²) = x⁴(x³+ x²) + 2x²(x³+ x²) = x⁷+ x⁶+ 2x⁵+ 2x⁴

Пример 4. Разделить многочлен 17x²− 6x⁴+ 5x³− 23x + 7 на многочлен 7 − 3x²− 2x

Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:

Значит,

Пример 5. Разделить многочлен 4a⁴− 14a³b − 24a²b²− 54b⁴ на многочлен a²− 3ab − 9b²

Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 4a². Записываем 4a² в частном:

Умножим 4a² на делитель a²− 3ab − 9b² и полученный результат запишем под делимым:

Вычтем из делимого полученный многочлен 4a⁴− 12a³b − 36a²b²

Теперь делим −2a³b + 12a²b²− 54b⁴ на делитель a²− 3ab − 9b². Разделим первый член делимого на первый член делителя, получим −2ab. Записываем −2ab в частном:

Умножим −2ab на делитель a²− 3ab − 9b² и полученный результат запишем под делимым −2a³b + 12a²b²− 54b⁴

Вычтем из многочлена −2a³b + 12a²b²− 54b⁴ многочлен −2a³b + 12a²b²− 18ab³. При вычитании подобных членов обнаруживаем, что члены −54b⁴ и 18ab³ не являются подобными, а значит их вычитание не даст никакого преобразования. В этом случае выполняем вычитание там где это можно, а именно вычтем −2a³b из −2a³b и 6a²b² из 12a²b², а вычитание 18ab³ из −54b⁴ запишем в виде разности −54b⁴− (+18ab³) или −54b⁴− 18ab³

Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:

Вернёмся к нашей задаче. Разделим 6a²b²− 54b⁴− 18ab³ на делитель a²− 3ab − 9b². Делим первый член делимого на первый член делителя, получим 6b². Записываем 6b² в частном:

Умножим 6b² на делитель a²− 3ab − 9b² и полученный результат запишем под делимым 6a²b²− 54b⁴− 18ab³. Сразу вычтем этот полученный результат из делимого 6a²b²− 54b⁴− 18ab³

Деление завершено. Таким образом, частное от деления многочлена 4a⁴− 14a³b − 24a²b²− 54b⁴ на многочлен a²− 3ab − 9b² равно 4a²− 2ab + 6b².

Выполним проверку. Умножим частное 4a²− 2ab + 6b² на делитель a²− 3ab − 9b². У нас должен получиться многочлен 4a⁴− 14a³b − 24a²b²− 54b⁴

Деление многочлена на многочлен с остатком

Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.

Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:

То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:

Рациональное число читается как семь целых плюс одна вторая. Знак «плюс» по традиции не записывают. Но если при делении многочлена на многочлен образуется остаток, то этот плюс записывать нужно.

Например, если при делении многочлена a на многочлен b получится частное c, да еще останется остаток q, то ответ будет записан так:

Например, разделим многочлен 2x³− x²− 5x + 4 на многочлен x − 3

Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 2x². Записываем 2x² в частном:

Умножим 2x² на делитель x − 3 и полученный результат запишем под делимым:

Вычтем из делимого полученный многочлен 2x³− 6x²

Теперь делим 5x²− 5x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 5x. Записываем 5x в частном:

Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x²− 5x + 4

Вычтем из многочлена 5x²− 5x + 4 многочлен 5x²− 15x

Теперь делим 10x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 10. Записываем 10 в частном:

Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4. Сразу вычтем этот полученный результат из делимого 10x + 4

Число 34, полученное в результате вычитания многочлена 10x − 30 из многочлена 10x + 4, является остатком. Мы не сможем найти следующий член частного, который при умножении с делителем x − 3 дал бы нам в результате 34.

Поэтому при делении многочлена 2x³− 2x²− 5x + 4 на многочлен x − 3 получается 2x²+ 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:

Когда деление многочленов невозможно

Деление многочлена на многочлен невозможно в случае, если степень делимого окажется меньше степени делителя.

Например, нельзя разделить многочлен x³+ x на многочлен x⁴ + x², поскольку делимое является многочленом третьей степени, а делитель — многочленом четвёртой степени.

Вопреки этому запрету можно попробовать разделить многочлен x³+ x на многочлен x⁴ + x², и даже получить частное x⁻¹, которое при перемножении с делителем будет давать делимое:

Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x⁻¹ многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x⁻¹ это дробь , которая не является произведением.

Пусть имеется прямоугольник со сторонами 4 и 2

Площадь этого прямоугольника будет равна 4 × 2 = 8 кв. ед.

Увеличим длину и ширину этого прямоугольника на x

Достроим отсутствующие стороны:

Теперь прямоугольник имеет длину x + 4 и ширину x + 2. Площадь этого прямоугольника будет равна произведению (x + 4)(x + 2) и выражаться многочленом x²+ 6x + 8

(x + 4)(x + 2) = x²+ 4x + 2x + 8 = x²+ 6x + 8

При этом мы можем выполнить обратную операцию, а именно разделить площадь x²+ 6x + 8 на ширину x + 2 и получить длину x + 4.

Степень многочлена x²+ 6x + 8 равна сумме степеней многочленов-сомножителей x + 4 и x + 2, а значит ни одна из степеней многочленов-сомножителей не может превосходить степень многочлена-произведения. Следовательно, чтобы обратное деление было возможным, степень делителя должна быть меньше степени делимого.

Задания для самостоятельного решения

Задание 1. Выполните деление:

Решение:

Задание 2. Выполните деление:

Решение:

Задание 3. Выполните деление:

Решение:

Задание 4. Выполните деление:

Решение:

Задание 5. Выполните деление:

Решение:

Задание 6. Выполните деление:

Решение:

Задание 7. Выполните деление:

Решение:

Задание 8. Выполните деление:

Решение:

Задание 9. Выполните деление:

Решение:

Задание 10. Выполните деление:

Решение:

Задание 11. Выполните деление:

Решение:

Задание 12. Выполните деление:

Решение:

Задание 13. Выполните деление:

Решение:

Задание 14. Выполните деление:

Решение:

Задание 15. Выполните деление:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Деление уравнения 2–5 степеней | BBF.

Деление уравнения 2–5 степени на полином — это метод разложения многочлена на множители. Такое разложение необходимо для упрощения алгебраических выражений, решения уравнений 3-ей и выше степени, а также для разложения дробно-рациональных функций на простейшие дроби.

Теоретическая основа

В целом разложение полиномов на множители требуется для решения уравнений третьей степени и выше. Алгебраическая теория позволяет это сделать следующим способом. Основная теорема алгебры гласит, что любой полином n-ной степени имеет по крайней мере один действительный или комплексный корень. Мы можем легко найти этот корень, если полином является линейным или квадратным, однако если выражение имеет большую степень, то задача значительно усложняется.

В некоторых удачных случаях мы можем использовать формулы сокращенного умножения, однако такая удача — это скорее исключение, ведь данные формулы не применимы для многочленов выше третьей степени. В таких ситуациях нам на помощь приходит теорема Безу.

Теорема Безу гласит, что при делении полинома P(x) на двучлен Q(x) = x − b остаток от деления s = P(a). Простыми словами это означает, что при делении некоторого полинома на многочлен вида x − b, остаток от этого деления равен значению функции в точке b. Однако для разложения полинома на множители используется не сама теорема, а следствие из нее. Если P(x) делится на Q(x) без остатка, то число bявляется корнем выражения.

Если мы поделим полином на бином без остатка, то сможем разложить выражение на множители. Следовательно, для этого нам надо найти хотя бы один корень полинома b и разделить выражение на бином x − b. После этого мы получим произведение полиномов низшей степени. При желании операцию можно повторить и разложить полином на несколько многочленов, что значительно упростит поиск корней.

Таким образом, для разложения полинома на множители требуется найти один из корней b, выразить двучлен Q(x) = x − b и разделить многочлен на Q(x).

Поиск корня b

Мы можем предположить любое значение корня, однако на практике первым делом проверяют значения 1 и -1. Для этого нам помогут два простых правила:

если сумма коэффициентов полинома равна нулю, то один из корней равен 1;
если сумма коэффициентов при четных степенях икса равна сумме коэффициентов при нечетных, то один из корней полинома равен -1.

Давайте проверим на примере. Пусть есть многочлен вида:

3x⁴ + 2x³ − 8x² + 2x + 1

Вычислим сумму коэффициентов: 3 + 2 − 8 + 2 + 1 = 0. Очевидно, что если вместо иксов подставить единицу, то мы получим аналогичное равенство.

Проверим второе правило. Возьмем полином вида:

3x⁴ + 4x³ + 2x² + 2x + 1

Коэффициенты при четных степенях дают в сумме 3 + 2 + 1 = 6. Коэффициенты при нечетных: 4 + 2 = 6. Если вместо иксов подставить -1, то шестерки взаимно уничтожатся и превратятся в ноль. Очевидно, что -1 является корнем данного полинома. Обратите внимание, что в данном случае 1 – это все равно что 1x⁰, поэтому свободный член учитывается как коэффициент икса в четной степени.

Если же 1 и -1 не подходят, то используем теорему Виета, которая в данном случае звучит следующим образом: если корни многочлена являются целыми числами, то они одновременно являются и делителями его свободного члена. Это означает, что целочисленный корень полинома без остатка делит его свободный член, то есть коэффициент без икса.

Таким образом, для поиска целочисленного корня требуется разложить свободный член на множители и поочередно подставлять найденные значения вместо иксов. Если при подстановке коэффициента значение полинома станет равно нулю, то данное значение и есть корень уравнения. Рассмотрим следующий полином:

x⁴ + x³ − 11x² − 5x + 30

Свободный член 30 имеет следующие делители: ±1, ±2, ±3, ±5, ±6, ±10, ±15, ±30. Теперь постепенно подставляем данные числа вместо иксов. В итоге уравнение превращается в ноль при значениях 2, ±3 и 5, которые и являются корнями данного уравнения. Из теоремы Безу вытекает, что данный многочлен без остатка делится на выражения типа x − 2 или x + 3.

Деление многочлена на Q(x)

Деление многочлена на бином Q(x) проще всего осуществить в столбик. Рассмотрим схему деления в столбик на простом примере. Возьмем полином

2x³ − 3x² + 5x − 14

и разделим его на бином x − 2.

Деление в столбик происходит в три этапа:

разделим самый первый элемент многочлена на старший член бинома, то есть 2x³ / x = 2x², запишем 2x² как первый член частного;
умножим результат на бином, то есть 2x² × (x − 2) = 2x³ − 4x²;
вычтем полученное выражение из многочлена (2x³ − 3x² + 5x − 14) − (2x³ − 4x²) = x² + 5x − 14.

Теперь требуется повторить предыдущие пункты, но уже для полинома x² + 5x − 14:

разделим x² на x, в результате получим x как второй член частного;
умножим x на бином и получим x × (x − 2) = x² − 2x;
вычислим разницу (x² + 5x − 14) − (x² − 2x) = 7x − 14.

Еще раз повторим этот круг, но для полинома 7x − 14:

разделим 7x на x, получим 7 как третий элемент частного;
умножим 7 на делитель, получим 7x − 14;
вычислим разницу (7x − 14) − (7x − 14) = 0.

На этом цикл деления окончен. Выпишем наши элементы в строчку и получим частное без остатка 2x² + x+ 7. Это означает, что полином вида 2x³ − 3x² + 5x − 14 мы можем представить как произведение (x − 2) × (2x² + x + 7).

Мы все вычисления провели вручную, однако разделить многочлен на бином можно и в режиме онлайн. Наша программа позволяет делить многочлены от 2 до 5 степени на биномы вида ax + b. Для этого требуется выбрать степень полинома, ввести коэффициенты в соответствующие ячейки и сделать один клик мышкой. Важно указать коэффициенты с соответствующими знаками, так как в программе по умолчанию установлены плюсы. В результате калькулятор выдаст ответ вида

R(x) = P(x) / Q(x) – s,

где s — остаток от деления.

Заключение

Наш калькулятор позволяет быстро и без проблем разделить многочлен на бином для разложения выражения на множители. Такая операция может понадобиться школьникам и студентам при решении уравнений 3-5 степени или для разложения дробно-рациональных функций в сумму простых дробей.

Пример решения иррационального уравнения путем деления его обеих частей на одно и то же выражение

Решите иррациональное уравнение

Несомненно, сразу можно пробовать уединить радикал, после чего решать иррациональное уравнение методом возведения обеих частей уравнения в квадрат. Такой подход вполне имеет право на существование. Однако видно, что он приведет нас к необходимости решать уравнение четвертой степени. В нашем случае это уравнение имеет два рациональных корня, что позволяет найти все его корни и в итоге получить интересующее нас решение. Однако в общем случае решение уравнений четвертой степени сопряжено со значительными сложностями. Аналогично, к уравнению четвертой степени приводит и введение новой переменной . Так что пока оставим эти пути решения и посмотрим, нет ли альтернативной возможности.

Попробуем решить иррациональное уравнение через проведение преобразований. Перепишем уравнение в виде . Проделанное преобразование является равносильным преобразованием уравнения, так как состоит в замене выражения 1+x тождественно равным ему выражением , и при такой замене не изменяется область допустимых значений (она определяется условием 1+x≥0 как для исходного уравнения, так и для полученного). Мы провели это преобразование для того, чтобы отчетливо увидеть, что левая часть уравнения представляет собой некоторый аналог однородного многочлена 4·x²+12·x·y−27·y². Типичным прием работы с такими многочленами состоит во введении новой переменной . По аналогии будем стремиться ввести новую переменную . Для этого нам нужно обе части иррационального уравнения разделить на одно и то же выражение , то есть, перейти к уравнению . И здесь возникает вопрос, а имеем ли мы право проводить такое деление? Мы знаем, что деление обеих частей уравнения на одно и то же выражение является равносильным преобразованием уравнения, если при этом не изменяется ОДЗ и это выражение не обращается на ней в нуль. Посмотрим, как у нас обстоят дела с этими условиями. При таком переходе у нас сужается ОДЗ: из нее пропадет число −1. А при каких значениях переменной выражение обращается в нуль на ОДЗ переменной x для исходного уравнения? При x=−1. Итак, все наши планы рушит минус единица. Другими словами, если бы область допустимых значений для исходного уравнения была бы не множеством [−1, +∞), а множеством (−1, +∞), то никаких проблем с намеченным делением у нас не было бы. Как же нам быть? Выход такой: отдельно проверить число −1, а дальше работать на множестве (−1, +∞).

Проверим, является ли x=−1 корнем исходного уравнения. Для этого осуществим проверку подстановкой. Имеем

Подстановка дала неверное числовое равенство, следовательно, x=−1 не является корнем решаемого уравнения.

Для остальных значений переменной из ОДЗ, то есть, на множестве (−1, +∞) мы можем проводить намеченное деление, то есть, переходить к уравнению и дальше

Теперь можно обращаться к методу введения новой переменной для решения иррационального уравнения. Принимаем , это дает квадратное уравнение 4·t²+12·t−27=0. Решаем его:

Возврат к старой переменной дает два уравнения: и . Решим их по очереди методом возведения обеих частей уравнений в квадрат:

Уравнение решено, осталось решить уравнение .

Таким образом, исходное иррациональное уравнение имеет два корня и 3.

Уравнения на умножение и деление

В контексте тем:				Традиции и фольклор
Раздел 3С				Числовые и буквенные выражения. Уравнения. Задачи
Школа: осш №23 им.А.Бокейханова
Дата: « 26 » 02 2019 г .					ФИО учителя: Кочкурова Ирина Викторовн
Класс: 2 «А» класс.					Количество присутствующих: отсутствующих:
Лексическая тема:					Народные музыкальные инструменты
Тема урока:					Уравнения на умножение и деление
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу):
2.2.2.2. Решать простейшие уравнения на умножение и деление;
Критерии успеха (Предполагаемый результат):		Все учащиеся будут: решать простейшие уравнения на умножение и деление. Многие учащиеся будут: объяснять, как найти неизвестный компонент умножения и деления. Некоторые учащиеся будут: самостоятельно составлять простейшие уравнения на умножение и деление.
Языковая цель		Учащиеся могут: объяснить, как найти неизвестный компонент при делении и умножении. Предметная лексика и терминология: Уравнение, корень уравнения, названия компонентов действий умножения и деления. Серия полезных фраз для диалога/письма Обсуждение: Как найти неизвестный компонент действия? Как связаны действия умножения и деления? Как связаны действия сложения и вычитания? Письмо: Запись уравнений. Решение уравнений.
Привитие ценностей		Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество. .
Навыки использования ИКТ		ИКТ — просмотр видеоролика, презентация урока.
Предварительные знания		Уравнения, взаимосвязь умножения и деления, названия компонентов действий.
Ход урока
Этапы урока, t	Запланированная деятельность на уроке						Ресурсы
Начало урока 0-3	Мотивация. На уроке будь старательным, Будь спокойным и внимательным. Все пиши, не отставая, Слушай, не перебивая. Говорите четко, внятно, Чтобы было все понятно. Если друг стал отвечать, Не спеши перебивать. Деление на группы. (Карточки)						Карточки с изображениями музыкальных инструментов.
4-6 Критерии успеха	Актуализация. – Чем вы любите заниматься в свободное время? – Любите ли вы слушать музыку, играть на инструментах? — Сегодня у нас необычный урок, к нам в гости спешат сказочные герои, которые помогут нам узнать много нового, и повторить ранее изученные темы. (На доске изображения сказочных героев) — Кто это? — Правильно, это Алдар-Косе, Емеля и Тостик. — Где встречали мы этих героев? (В народных сказках) — К какому разделу относятся народные сказки? (Традиции и фольклор) — Наши сказочные герои приготовили для вас задания, преодолев которые вы узнаете много нового и интересного. — С чего мы начнем наш урок? (Составим план работы на уроке) На доске таблица 1: Повторение таблицы умножения и деления. Изучение нового материала. Работа с учебником. Работа в тетради. — Первое задание мы выполним и узнаем, на каких музыкальных инструментах любят играть наши герои, а еще мы повторим таблицу умножения и деления. ( выполнение №2 с 61) – Как проверить умножение? – Как проверить деление? — На музыкальных инструментах записаны значения выражений, послушайте, что наши герои расскажут о них.						Презентация. Карточки с выражениями. Презентация Слайд 1 Слайд 2 Слайд 3,4,5,6,7
	Учащиеся решают примеры, составляют равенства и неравенства.
Середина урока 7-11	Постановка цели (проблемная ситуация). Игра: «Я беру тебя с собой». – Угадайте, по какому признаку я собираю объекты. Для этого предлагайте мне математические записи, чем-то похожие на то, что я выбрала, а я буду говорить, могу ли я взять их с собой. Итак, я беру с собой выражение х + 14 = 45. А что у вас? Д: Я беру с собой выражение 25 + у. У: Я не беру тебя с собой. Д: Я беру уравнение х : 6 = 3. У: Я беру тебя с собой. Д: Я беру выражение х · 3 = 12 У: Я беру тебя с собой. Д: Вы берете с собой уравнения? У: Да! Итак, по какому признаку мы собирали объекты? Это уравнения. Рассмотрите пары уравнений в каждом столбике. В чем сходство и отличие? 2 + х = 18 15 – у = 3 2 · х = 18 15 : у = 3 – Какого вида уравнения мы будем учиться решать на этом уроке? (Уравнения на умножение и деление)						Карточки с выражениями. Наборное полотно.
Критерии успеха	Учащиеся формулируют цель урока при помощи учителя.
12-22	Работа по учебнику. Открытие нового Предлагает выполнить задание №1 в учебнике.(Устно) Рассмотрите рисунки и записи уравнений. – Какой компонент неизвестен? – Как его можно найти? Дети формулируют правило и сверяют с правилом в учебнике. Первичное закрепление с проговариванием. Детям предлагает работать с комментированием по плану: 1. Какой компонент неизвестен? 2. Как найти неизвестный множитель (делимое, делитель)? 3. Запись уравнения. 4. Решение уравнения. 5. Проверка решения. Применение нового. Самостоятельная работа. Предлагает выполнить задание №4 в рабочей тетради с критериями оценивания. ФО (самооценивание) Педагог определяет, кто из детей усвоил материал и на каком уровне. Дети, которые не справились с заданием, возвращаются к №1 в учебнике и повторяют, как найти неизвестный компонент в уравнениях на умножение и деление.						Учебник. Слайд 9 Рабочая тетрадь.
Критерии успеха	Учащиеся формулируют цель урока при помощи учителя.
23-24	Физминутка
24-38	Работа в группах. Планируем работу: выделим этапы работы над задачей. 1. Прочитаем задачу. 2. Выделим условие, вопрос. 3. Решим задачу. 4. Напишем ответ. Выполнение №3 (а) в учебнике и тетради с проверкой по образцу. Взаимопроверка ФО (Критерии оценивания на доске) Работа над ранее изученным¹ Решение задач №5. Работа в парах. Дети записывают выражения по задачам. Обсуждают о числовых данных, которые можно использовать, записывают решения задач и выполняют взаимопроверку. (ФО) Взаимооценивание. (звездочка, квадратик, треугольник) -Скажем спасибо нашим героям за их интересные задания! — И давайте скажем, что нового мы узнали на уроке?						Тетрадь, учебник. Слайд 10 Слайд 12 Слайд 13
Критерии успеха	Учащиеся самостоятельно решают задачи на умножение.
39-40	Рефлексия. – Понравился ли вам урок? – Какие задания вы выполнили с удовольствием? – А есть ли задания, при выполнении которых вы испытывали трудности? — Кого бы вы похвалили за работу на уроке? Предлагает оценить свою работу при помощи «Дерева знаний»						Дерево знаний Слайд 14
Критерии успеха	Учащиеся оценивают себя при помощи «Дерева знаний».
Дифференциация			Оценивание			Здоровье и соблюдение ТБ
Способные учащиеся строят свои высказывания самостоятельно, а менее способным учитель оказывает поддержку, задавая наводящие вопросы.			Учитель проводит формативное оценивание выполненной работы.			Физкультминутка Под музыку выполняем движения.

Деление обыкновенных дробей. Продолжаем решать уравнения. | Успешный ученик

Ранее в статье мы с тобой затронули тему решения уравнений, при которым так или иначе используется деление обыкновенных дробей. В этой статье продолжим заниматься делением, а также решим несколько уравнений.

рисунок из открытых источников

Для начала решим пару примеров на все действия с обыкновенными дробями. Правила все помнишь? Нет? Не переживай. Держи карту с правилами.

Уже ждёшь пример? Держи.

Что сделаешь в первую очередь? Правильно! Нужно расставить порядок действий.

Вычислим результат первого действия. Есть проблемы? Иди по стрелкам.

Переходим ко второму действию. Вычисли, а потом проверь себя. Не знаешь как, иди по алгоритму.

Пришло время выполнить третье действие.

Осталось выполнить четвёртое действие. Давай, решай)

Осталось записать ответ.

Теперь реши ещё один пример. Если нужны подсказки, пользуйся на здоровье. Только не списывай — сначала реши, потом проверь

С примерами разобрались. Теперь возьмёмся за уравнения. Чтобы успешно решать уравнения, нужно знать компоненты и правила. Чтобы вспомнить их, можешь воспользоваться схемой.

Поскольку в прошлом материале (на уроке) мы разбирали с тобой решение более сложных уравнений, сейчас предлагаю решить уравнения самостоятельно, а потом выполнить проверку.

Решишь и сразу проверяй!

Разберём ещё одно уравнение.

Расставлять порядок действий здесь бессмысленно. А почему? Да потому что переменная присутствует в данном уравнении не один раз. Надо что-то делать. А именно сделать так, чтобы участвовала переменная х в уравнении только один раз.

Здесь на помощь нам приходит распределительное свойство умножения:

ac + bc = (a+b)c

Попросту одинаковый множитель можно вынести за скобки. Ты же помнишь, что между дробью и переменной спрятался знак умножения? Значит х — это тот самый общий множитель, который нужно вынести за скобки.

Дальше уравнение решается просто. Выполни необходимые вычисления, а потом проверь своё решение.

На этом мы с тобой остановимся. Здорово, что ты смог(ла) одолеть эту статью до конца. Успехов тебе в изучении математики.

А для тех, кто любит смотреть, а не читать ниже урок на видео.

Решение уравнений с использованием свойств деления и умножения равенства — Элементарная алгебра

Цели обучения

К концу этого раздела вы сможете:

Решите уравнения, используя свойства деления и умножения равенства
Решите уравнения, требующие упрощения
Перевести в уравнение и решить
Перевод и решение приложений

Решение уравнений с использованием свойств деления и умножения равенства

Возможно, вы заметили, что все уравнения, которые мы до сих пор решали, имели форму или .Мы смогли изолировать переменную, добавив или вычтя постоянный член на стороне уравнения с переменной. Теперь мы увидим, как решать уравнения, в которых переменная умножается на константу, и поэтому потребуется деление, чтобы изолировать переменную.

Давайте еще раз посмотрим на нашу головоломку с конвертами и жетонами (рисунок).

На рисунке показана модель уравнения с одной переменной, умноженной на константу. В левой части рабочей области находятся два экземпляра неизвестного (конверт), а в правой части рабочей области — шесть счетчиков.

На рисунке два одинаковых конверта с одинаковым количеством счетчиков. Помните, что левая сторона рабочего пространства должна равняться правой стороне, но счетчики с левой стороны «спрятаны» в конвертах. Итак, сколько фишек в каждом конверте?

Как определить число? Мы должны разделить жетоны с правой стороны на две группы одинакового размера, чтобы они соответствовали двум конвертам с левой стороны. 6 счетчиков, разделенных на 2 равные группы, дают по 3 счетчика в каждой группе (начиная с ).

Какое уравнение моделирует ситуацию, показанную на (рис.)? Есть два конверта, и каждый содержит жетоны. Вместе два конверта должны содержать в общей сложности 6 жетонов.

На иллюстрации показана модель уравнения.

At the top of the figure on the right is the equation 2 x equals 6. One line down on the left, the instructions say: “If we divide both sides of the equation by 2, as we did with the envelopes and counters, we get”. To the right of this phrase is the same equation divided by 2 on both sides: 2 x over 2 equals 6 over 2, with divided by 2 written in red on both sides. Another line down to the right is the answer to the equation: x equals 3.» data-label=»»>


Если мы разделим обе части уравнения на 2, как мы сделали с конвертами и счетчиками,
получаем:

Мы обнаружили, что каждый конверт содержит 3 фишки.Это проверяет? Мы знаем, так это работает! Три жетона в каждом из двух конвертов равняются шести!

Этот пример ведет к свойству разделения на равенство.

Отдел имущества равенства

Для любых чисел a , b и c , и ,

Когда вы делите обе части уравнения на любое ненулевое число, вы все равно получаете равенство.

Выполнение задания по манипулятивной математике «Свойство равенства деления» поможет вам лучше понять, как решать уравнения с помощью свойства равенства деления.

Цель решения уравнения — «отменить» операцию над переменной. В следующем примере переменная умножается на 5, поэтому мы разделим обе части на 5, чтобы «отменить» умножение.

Решить:

Рассмотрим уравнение . Мы хотим знать, какое число, деленное на 4, дает 3. Итак, чтобы «отменить» деление, нам нужно будет умножить на 4. Свойство равенства умножения позволит нам это сделать.Это свойство говорит о том, что если мы начнем с двух равных величин и умножим их на одно и то же число, результаты будут равны.

Свойство равенства умножения

Для любых номеров a , b и c ,

Если вы умножите обе части уравнения на одно и то же число, вы все равно получите равенство.

Решить:

Решение

Поскольку произведение числа и его обратной величины равно 1, наша стратегия будет состоять в том, чтобы изолировать путем умножения на обратную величину .

Решить:

В следующем примере все переменные члены находятся в правой части уравнения. Как всегда, наша цель при решении уравнения состоит в том, чтобы изолировать переменную.

Решить:

Решение уравнений, требующих упрощения

Многие уравнения начинаются сложнее, чем те, с которыми мы работали.

При работе с этими более сложными уравнениями первым шагом является максимальное упрощение обеих частей уравнения. Обычно это включает в себя объединение подобных терминов или использование распределительного свойства.

Решить:

Решение

Начните с упрощения каждой части уравнения.

Решить:

Решение

Здесь мы упростим каждую часть уравнения, используя сначала свойство распределения.

Решить:

Теперь мы рассмотрели все четыре свойства равенства — вычитание, сложение, деление и умножение. Мы перечислим их все вместе здесь для удобства.

Свойства равенства

Когда вы складываете, вычитаете, умножаете или делите одну и ту же величину из обеих частей уравнения, вы все равно получаете равенство.

Практика делает совершенным

Решение уравнений с использованием свойств деления и умножения равенства

В следующих упражнениях решите каждое уравнение, используя свойства равенства деления и умножения, и проверьте решение.

Решение уравнений, требующих упрощения

В следующих упражнениях решите каждое уравнение, требующее упрощения.

Смешанная практика

В следующих упражнениях решите каждое уравнение.

Преобразование в уравнение и решение

В следующих упражнениях переведите уравнение в уравнение, а затем решите его.

187 является произведением м .

133 является произведением и .

является произведением 23 и р .

является произведением 8 и q .

u разделить на 7 равно .

r разделить на 12 равно .

h разделить на равно .

j разделить на равно .

Частное и равно 38.

Частное от и равно 18.

Частное от и 26 равно .

Сумма девяти десятых и г равна двум третям.

Сумма двух пятых и f равна половине.

Разница p и одна шестая составляет две трети.

Разница между и и одной восьмой составляет три четверти.

Перевод и решение приложений

В следующих упражнениях преобразуйте в уравнение и решите.

Детский сад В детском саду Конни 24 ребенка. Она хочет, чтобы они разделились на 4 равные группы. Сколько детей она поместит в каждую группу?

Воздушные шары Рамона купила 18 воздушных шаров для вечеринки. Она хочет сделать 3 одинаковых пучка. Сколько воздушных шаров она использовала в каждой связке?

Билеты Молли заплатила 36 фунтов стерлингов.25 за 5 билетов в кино. Сколько стоил каждый билет?

Покупки Серена заплатила 12,96 фунтов стерлингов за упаковку из 12 пар спортивных носков. Сколько стоила пара спортивных носков?

Шитье Нэнси использовала 14 ярдов ткани, чтобы сшить флаги для одной трети тренировочной бригады. Сколько ткани потребуется Нэнси, чтобы сшить флаги для всей команды?

MPG Внедорожник Джона расходует 18 миль на галлон (миль на галлон). Это вдвое меньше, чем у гибридной машины его жены.Сколько миль на галлон расходует гибридный автомобиль?

Рост Рост Эйдена 27 дюймов. Он такой же высокий, как его отец. Какой рост у его отца?

Недвижимость Би заработала комиссионные в размере 11 700 фунтов стерлингов за продажу дома, исходя из продажной цены. Какова была цена продажи дома?

Математика на каждый день

Комиссия Каждую неделю Перри получает 150 фунтов плюс 12% от общей суммы продаж. Решите уравнение для a , чтобы найти общую сумму, которую Перри должен продать, чтобы получить 840 фунтов за неделю.

Марки Трэвис купил на 9,45 фунтов марок по 49 и 21 центов. Количество марок номиналом 21 цент было на 5 меньше, чем количество марок номиналом 49 центов. Решите уравнение для s , чтобы найти количество 49-центовых марок, купленных Трэвисом.

Письменные упражнения

Фрида начала решать уравнение, прибавив по 3 к обеим частям. Объясните, почему метод Фриды не решит уравнение.

Эмилиано думает, что это решение уравнения.Объясните, почему он не прав.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.

ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?

Разделить два многочлена — WebMath

Быстрый! Мне нужна помощь с: Выберите элемент справки по математике …Исчисление, Вычисление производных, Вычисление интеграции, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Расчет с комплексными числами, Умножение комплексных чисел, Полномочия комплексных чисел, Вычитание, преобразование площади, преобразование длины, преобразование массы, преобразование мощности, преобразование скорости, преобразование температуры, анализ объемных данных, поиск Анализ средних данных, Нахождение стандартного отклонения Анализ данных, ГистограммыДесятичные числа, Преобразование в дробьЭлектричество, Стоимость факторинга, Целочисленные коэффициенты, Наибольшие общие коэффициенты, Наименьшие общие дроби, Сложение дробей, Сравнение дробей, Преобразование дробей, Преобразование в десятичные дроби, Деление дробей, Умножение дробей, Сокращение дробей, Вычитание дробей, Что такое геометрия , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Any functionGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x,y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Уравнение из точки и наклонных линий, Уравнение из наклона и y-intLines, Уравнение из двух точек. Практика ПолиномовМатематика, Практика ОсновыМетрической системы, ПреобразованиеЧисел, СложениеЧисел, Вычисление сЧислами, Вычисление с переменнымиЧислами, ДелениеЧисел, УмножениеЧисел, Сравнение Чисел в строке, Числовая строкаЧисла, Поместите ЗначениеЧисла, ПроизношениеЧисла, ОкруглениеЧисла, ВычитаниеПараболы, ГрафикиПолиномов, Сложение/ВычитаниеМногочленов, , Разложение на множители Разность квадратовПолиномы, Разложение на множители трехчленовПолиномы, Разложение на множители с GCFПолиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Что это такоеКвадратные уравнения, Квадратная формулаКвадратное уравнение ns, Решить с помощью факторингаРадикалы, Другие корниРадикалы, Соотношения квадратных корней, Что они представляют собойВыход на пенсию, Сбережение для продажной цены, Расчет научной записи, Преобразование научной записи, Разделение научной записи, Умножение фигур, Прямоугольники, Упрощение, Все, что угодно, Упрощение экспоненты, Как термины, Упрощение, Продукты, Время, Размышление о совете, Вычисление тригонометрии, Выражения Прямоугольные треугольникиWindchill, фигура

Многочлены — длинное деление

Многочлен выглядит так:

пример многочлена
этот имеет 3 термина

Разделительный

Полиномы иногда можно разделить с помощью простых методов, показанных в разделе «Многочлены деления».

Но иногда лучше использовать «Долгое деление» (метод, аналогичный «Долгому делению» для чисел)

Числитель и знаменатель

Мы можем дать каждому многочлену имя:

верхний многочлен является числителем
нижний полином является знаменателем

Если у вас проблемы с запоминанием, считайте, что в знаменателе — это в нисходящем направлении — в знаменателе.

Метод

Аккуратно запишите:

знаменатель идет первым,
, затем «)»,
, то числитель со строкой выше

Оба полинома должны сначала иметь члены «высшего порядка» (с наибольшими показателями степени, например «2» в x ² ).

Тогда:

	Разделите первый член числителя на первый член знаменателя и подставьте это в ответ. Умножьте знаменатель на этот ответ, поместите его под числителем Вычесть, чтобы создать новый многочлен
	Повторить , используя новый многочлен

Легче показать на примере!

Пример:

Аккуратно запишите, как показано ниже, а затем решите шаг за шагом (нажмите кнопку воспроизведения):

Проверьте ответ:

Умножаем ответ на нижний полином, должен получиться верхний полином:

Остатки

Предыдущий пример работал отлично, но это не всегда так! Попробуйте этот:

После деления осталось «2», это «остаток».

Остаток — это то, что осталось после деления.

Но у нас все еще есть ответ: поместите остаток , разделенный на нижний многочлен , как часть ответа, например:

«Отсутствующие» термины

Могут быть «отсутствующие термины» (пример: может быть x ³ , но не может быть x ² ). В этом случае либо оставляйте пробелы, либо включайте недостающие члены с нулевым коэффициентом.

Пример:

Запишите его с коэффициентами «0» для пропущенных членов, затем решите его обычным образом (нажмите кнопку воспроизведения):

Видите, как нам нужно место для «3x ³» ?

Более одной переменной

До сих пор мы делили многочлены только с одной переменной ( x ), но мы можем обрабатывать многочлены с двумя или более переменными (например, x и y ), используя тот же метод.

Пример:

Решение уравнений с умножением/делением

Чтобы переместить число, которое умножается или делится на переменную, вы должны сделать обратное действие с обеих сторон. Это означает, что если число умножается, вы должны разделить его на обе части. Если оно разделено, вы должны умножить его на обе стороны.

1) 3x=10 Даже если вы можете сделать это в уме, вам нужно выучить

шага, чтобы применять их к более сложным задачам.Наша цель — получить x сам по себе, поэтому сначала нам нужно выяснить, что нужно переместить. 3 находится на той же стороне, что и x, так что это то, что нам нужно для перемещения. Оно умножается, поэтому мы собираемся разделить обе части на 3. Самый простой способ сделать это — разделить их на дроби и поставить 3 в знаменателе.

Теперь поработаем с каждой стороной. С левой стороны,
, тройки компенсируются и исчезают (3/3 = 1 и 1x = x).
У нас есть переменная сама по себе, так что это наш ответ.

Мы могли бы записать это как смешанное число, если бы захотели, но обычно допустима неправильная дробь.

3x = 10 Мы можем проверить ответ, подставив 10/3 обратно в истинное исходное уравнение
вместо x.

Окончательный ответ: Это правда, поэтому мы знаем, что у нас есть правильный ответ.

2)Даже если вы можете сделать это в уме, вам нужно выучить

шаги, чтобы вы могли применить их к более сложным задачам. Наша цель — получить y сам по себе, поэтому сначала нам нужно выяснить, что нужно переместить.5 находится на той же стороне, что и y, так что это то, что нам нужно для перемещения. Это деление, поэтому мы собираемся умножить

с обеих сторон на 5.
Теперь будем работать с каждой стороной. С левой стороны,
y = -10, пятерки сокращаются и исчезают. Справа
-2(5) = -10

У нас есть переменная сама по себе, так что это наш ответ. Мы можем проверить ответ, подставив -10 обратно в число

. исходное уравнение вместо y.

верно

Окончательный ответ: y = -10 Это правда, поэтому мы знаем, что у нас есть правильный ответ.

3) Дробь 2/3 находится на той же стороне, что и x, так что это

то, что нам нужно для перемещения. Оно умножается, поэтому мы собираемся разделить обе части на 2/3. Помните, что

Вы делите дробь, переворачивая ее и умножая на

(так называемое обратное число). Итак, мы перевернем 2/3 вверх ногами и умножим обе части на 3/2.

x = -9 Теперь поработаем с каждой стороной. С левой стороны,
, 3/2 и 2/3 компенсируются и исчезают. Справа, У нас есть переменная сама по себе, так что это наш ответ.
Мы можем проверить ответ, подставив обратно -9 в исходное уравнение
вместо x.

Окончательный ответ: x = -9 Это правда, поэтому мы знаем, что у нас есть правильный ответ.

Практика: Решите уравнение и проверьте свой ответ

1) 8х = -2

4) -11 = 6а

Ответы: 1) 2) у = 32 3) 4) 5) y = -20

2.2 Решать уравнения, используя свойства деления и умножения равенства — Элементарная алгебра 2e

Цели обучения

К концу этого раздела вы сможете:

Решите уравнения, используя свойства деления и умножения равенства
Решите уравнения, требующие упрощения
Перевести в уравнение и решить
Перевод и решение приложений

Будьте готовы 2. 5

Прежде чем начать, пройдите этот тест на готовность.

Упростить: −7(1−7).−7(1−7).
Если вы пропустили эту проблему, просмотрите пример 1.68.

Будьте готовы 2.6

Вычислите 9x+29x+2, когда x=−3x=−3.
Если вы пропустили эту проблему, просмотрите пример 1.57.

Решите уравнения, используя свойства деления и умножения равенства

Возможно, вы заметили, что все уравнения, которые мы решали до сих пор, имели вид x+a=bx+a=b или x−a=bx−a= б.Мы смогли изолировать переменную, добавив или вычтя постоянный член на стороне уравнения с переменной. Теперь мы увидим, как решать уравнения, в которых переменная умножается на константу, и поэтому потребуется деление, чтобы изолировать переменную.

Давайте еще раз посмотрим на нашу головоломку с конвертами и фишками на рис. 2.5.

Рисунок 2.5 На рисунке показана модель уравнения с одной переменной, умноженной на константу. В левой части рабочей области находятся два экземпляра неизвестного (конверт), а в правой части рабочей области — шесть счетчиков.

Какое уравнение моделирует ситуацию, показанную на рис. 2.6? Есть два конверта, и каждый содержит xx счетчиков. Вместе два конверта должны содержать в общей сложности 6 жетонов.

Рисунок 2.6 На иллюстрации показана модель уравнения 2x=62x=6.


Если мы разделим обе части уравнения на 2, как мы сделали с конвертами и счетчиками,
получаем:

Мы обнаружили, что каждый конверт содержит 3 счетчика. Это проверяет? Мы знаем, что 2·3=62·3=6, так что это работает! Три жетона в каждом из двух конвертов равняются шести!

Этот пример ведет к свойству разделения на равенство.

Отдел имущества равенства

Для любых чисел a , b и c , и c≠0c≠0,

Если a=b, то ac=bc, если fa=b, то ac=bc

Когда вы делите обе части уравнения на любое ненулевое число, вы все равно получаете равенство.

Манипулятивная математика

Выполнение упражнения по манипулятивной математике «Свойство равенства деления» поможет вам лучше понять, как решать уравнения с помощью свойства равенства деления.

Пример 2.13

Решите: 5x=-27,5x=-27.

Попробуйте 2. 25

Решите: 3y=-41.3y=-41.

Попробуйте 2.26

Решите: 4z=-55,4z=-55.

Рассмотрим уравнение x4=3×4=3. Мы хотим знать, какое число разделить на 4 дает 3.Итак, чтобы «отменить» деление, нам нужно будет умножить на 4. Свойство равенства умножения позволит нам это сделать. Это свойство говорит о том, что если мы начнем с двух равных величин и умножим их на одно и то же число, результаты будут равны.

Свойство равенства умножения

Для любых номеров a , b и c ,

Если a=b, то ac=bc, если fa=b, то ac=bc

Если вы умножите обе части уравнения на одно и то же число, вы все равно получите равенство.

Пример 2.14

Решите: y-7=-14.y-7=-14.

Решение

Здесь yy делится на −7−7. Мы должны умножить на −7−7, чтобы выделить yy.

Попробуйте 2. 27

Решите: a−7=−42.a−7=−42.

Попробуйте 2.28

Решите: b−6=−24.b−6=−24.

Пример 2.16

Решение

Поскольку произведение числа и его обратного числа равно 1, наша стратегия будет состоять в том, чтобы изолировать xx путем умножения на обратное число 3434.

Пример 2.17

Решите: 815=-45x.815=-45x.

Попробуйте 2.33

Решите: 925=-45z.925=-45z.

Попробуйте 2.34

Решите: 56=-83r.56=-83r.

Решение уравнений, требующих упрощения

Многие уравнения начинаются сложнее, чем те, с которыми мы работали.

Пример 2.18

Решите: 14−23=12y−4y−5y.14−23=12y−4y−5y.

Решение

Начните с упрощения каждой части уравнения.

Попробуйте 2.35

Решите: 18−27=15c−9c−3c.18−27=15c−9c−3c.

Попробуйте 2.36

Решите:18−22=12x−x−4x.18−22=12x−x−4x.

Пример 2.19

Решите: −4(a−3)−7=25.−4(a−3)−7=25.

Решение

Здесь мы упростим каждую часть уравнения, используя сначала свойство распределения.

Попробуйте 2.37

Решите: −4(q−2)−8=24.−4(q−2)−8=24.

Попробуйте 2.38

Решите: −6(r−2)−12=30.−6(r−2)−12=30.

Теперь мы рассмотрели все четыре свойства равенства — вычитание, сложение, деление и умножение.Мы перечислим их все вместе здесь для удобства.

Свойства равенства

Свойство вычитания равенстваСложение свойства равенстваДля любых действительных чиселa,b,andc,Для любых действительных чиселa,b,andc,ifa=b,thena-c=b-c.

ifa=b,thena+c=b+c.Свойство деления равенстваСвойство умножения равенстваДля любых чиселa,b,andc,andc≠0,Для любых чиселa,b,andc,ifa=b,thenac=bc.ifa=b,thenac=bc.Свойство вычитания равенстваСложение свойства равенстваДля любых действительных чиселa ,b, и c, Для любых действительных чисел a, b и c, если fa=b, то na-c=b-c.ifa=b,thena+c=b+c.Свойство равенства деленияСвойство равенства умноженияДля любых чиселa,b,andc,andc≠0,Для любых чиселa,b,andc,ifa=b,thenac=bc.ifa=b, тогда ас = до н.э.

Перевести в уравнение и решить

В следующих нескольких примерах мы будем переводить предложения в уравнения, а затем решать уравнения. Возможно, вы захотите просмотреть таблицу перевода в предыдущей главе.

Пример 2.20

Переведите и решите: Число 143 есть произведение −11−11 и y .

Решение

Начните с перевода предложения в уравнение.

Перевести.
Разделить на −11−11.
Упрощение.
Чек: 143=-11y143=?-11(-13)143=143✓143=-11y143=?-11(-13)143=143✓

Попробуйте 2.39

Переведите и решите: Число 132 есть произведение −12 и y .

Попробуйте 2.40

Переведите и решите: Число 117 есть произведение −13 и z .

Пример 2.21

Переведите и решите: nn разделить на 8 равно −32−32.

Решение

2 » data-label=»»>

Начните с перевода предложения в уравнение. Перевести.
Умножьте обе стороны на 8.
Упрощение.
Чек:	Является ли число nn, деленное на 8, равным −32?
Пусть n=−256n=−256.	-256-256 разделить на 88 равно -32-32?
Перевести.	-2568=?-32-2568=?-32
Упрощение.	−32=−32✓−32=−32✓

Попробуйте 2.41

Переведите и решите: nn разделить на 7 равно −21−21.

Попробуйте 2.42

Переведите и решите: nn разделить на 8 равно −56−56.

Пример 2.22

Переведите и решите: Частное yy и −4−4 равно 6868.

Решение

Начните с перевода предложения в уравнение.

Перевод.


Умножьте обе части на −4−4.
Упрощение.
Чек:	Является ли частное yy и −4−4 равным 6868?
Пусть y=−272y=−272.	Является ли частное −272−272 и −4−4 равным 6868?
Перевести.	−272−4=?68−272−4=?68
Упрощение.	68=68✓68=68✓

Попробуйте 2.43

Переведите и решите: Частное qq и −8−8 равно 72.

Попробуйте 2.44

Переведите и решите: Частное pp и −9−9 равно 81.

Пример 2.23

Переведи и реши: Три четверти pp равно 18.

Решение

Начните с перевода предложения в уравнение. Помните, что «из» переводится как умножение.

Перевести.
Умножьте обе стороны на 43.43.
Упрощение.
Чек:	Три четверти от p равны 18?
Пусть p=24.p=24.	Три четверти от 24 равны 18?
Перевести.	34·24=?1834·24=?18
Упрощение.	18=18✓18=18✓

Попробуйте 2.45

Переведите и решите: две пятых от ff равно 16.

Попробуйте 2.46

Переведите и решите: Три четверти ff равно 21.

Пример 2.24

Переведите и решите: Сумма трех восьмых и xx равна половине.

Решение

Начните с перевода предложения в уравнение.

Перевести.
Вычтите 3838 с каждой стороны.
Упростите и перепишите дроби с общим знаменателем.
Упрощение.
Чек:		Является ли сумма трех восьмых и xx равной половине?
Пустьx=18.Letx=18.		Является ли сумма трех восьмых и одной восьмой равной половине?
Перевести.		38+18=?1238+18=?12
Упрощение.		48=?1248=?12
Упрощение.		12=12✓12=12✓

Попробуйте 2. 47

Переведите и решите: Сумма пяти восьмых и x равна одной четвертой.

Попробуйте 2.48

Переведите и решите: Сумма трех четвертых и x равна пяти шестым.

Перевести и решить приложения

Чтобы решить приложения, использующие свойства равенства деления и умножения, мы будем следовать тем же шагам, что и в предыдущем разделе.Мы переформулируем задачу всего в одном предложении, назначим переменную, а затем переведем предложение в уравнение, которое нужно решить.

Пример 2.25

Дена купила 6 фунтов винограда за 10,74 доллара. Сколько стоил один фунт винограда?

Решение

Что вас просят найти?	Стоимость 1 фунта винограда
Назначить переменную.	Пусть cc = стоимость одного фунта.
Напишите предложение, которое дает информацию, чтобы найти его.	Стоимость 6 фунтов составляет 10,74 доллара США.
Преобразовать в уравнение.	6с=10,746с=10,74
Решить.	6с6=10,746с=1,796с6=10,746с=1,79
	Виноград стоит 1,79 доллара за фунт.
Проверить: если один фунт стоит 1,79 доллара, значит, 6 фунтов стоят 10,74 доллара? 6(1.79)=?10,7410,74=10,74✓6(1,79)=?10,7410,74=10,74✓

Таблица 2.3

Попробуйте 2.49

Переведи и реши:

Арианна купила упаковку из 24 бутылок с водой за 9,36 доллара. Сколько стоила одна бутылка воды?

Попробуйте 2.50

Переведи и реши:

В боулинг-клубе JB на одной дорожке могут играть 6 человек за 34,98 доллара. Какова стоимость для каждого человека?

Пример 2.

Андреас купил подержанную машину за 12 000 долларов.Поскольку машине было 4 года, ее цена была 3434 от первоначальной цены, когда машина была новой. Какова была первоначальная цена автомобиля?

Решение

Что вас просят найти?	Первоначальная цена автомобиля
Назначить переменную.	Пусть pp = исходная цена.
Напишите предложение, которое дает информацию, чтобы найти его.	12 000 долларов — это 3434 от первоначальной цены.
Преобразовать в уравнение.	12 000=34 пенса12 000=34 пенса
Решить.	43(12 000)=43·34p16 000=p43(12 000)=43·34p16 000=p
	Первоначальная стоимость автомобиля составляла 16 000 долларов.
Проверка: равно ли 3434 из 16 000 долларов 12 000 долларов? 34·16 000=?12 00012 000=12 000✓34·16 000=?12 00012 000=12 000✓

Таблица 2. 4

Попробуйте 2.51

Переведи и реши:

Годовой налог на недвижимость дома Мехты составляет 1800 долларов США, рассчитанный как 151 000 151 000 оценочной стоимости дома. Какова оценочная стоимость дома Мехты?

Попробуйте 2.52

Переведи и реши:

Стелла посадила 14 квартир цветов в 2323 своем саду. Сколько квартир цветов ей понадобится, чтобы заполнить весь сад?

Раздел 2.2 Упражнения

Практика ведет к совершенству

Решение уравнений с использованием свойств деления и умножения равенства

83.

−37p=−541−37p=−541

84.

−19м=−586−19м=−586

107.

−710x=−143−710x=−143

111.

−518=−109u−518=−109u

112.

−720=−74v−720=−74v

Решение уравнений, требующих упрощения

В следующих упражнениях решите каждое уравнение, требующее упрощения.

113.

100−16=4p−10p−p100−16=4p−10p−p

114.

−18−7=5t−9t−6t−18−7=5t−9t−6t

115.

78n−34n=9+278n−34n=9+2

116.

512q+12q=25−3512q+12q=25−3

117.

0,25d+0,10d=6−0,750,25d+0,10d=6−0,75

118.

0,05р-0,01р=2+0,240,05р-0,01р=2+0,24

119.

−10(q−4)−57=93−10(q−4)−57=93

120.

−12(d−5)−29=43−12(d−5)−29=43

121.

−10(x+4)−19=85−10(x+4)−19=85

122.

−15(z+9)−11=75−15(z+9)−11=75

Смешанная практика

В следующих упражнениях решите каждое уравнение.

136.

−15x=−120−15x=−120

138.

19,36=х-0,2х19,36=х-0,2х

139.

с-0,3с=35,70с-0,3с=35,70

Преобразование в уравнение и решение

В следующих упражнениях переведите уравнение в уравнение, а затем решите его.

142.

187 является произведением −17−17 и m .

143.

133 является произведением −19−19 и n .

144.

−184−184 является произведением 23 и p .

145.

−152−152 является произведением 8 и q .

146.

u разделить на 7 равно −49−49.

147.

r разделить на 12 равно −48−48.

148.

ч разделить на -13-13 равно -65-65.

149.

j разделить на -20-20 равно -80-80.

150.

Частное cc и −19−19 равно 38.

151.

Частное bb и −6−6 равно 18.

152.

Частное чч и 26 равно −52−52.

153.

Частное kk и 22 равно −66−66.

158.

Сумма девяти десятых и г равна двум третям.

159.

Сумма двух пятых и f равна половине.

160.

Разница p и одна шестая составляет две трети.

161.

Разница между и и одной восьмой составляет три четверти.

Перевод и решение приложений

В следующих упражнениях преобразуйте в уравнение и решите.

162.

163.

164.

Билеты Молли заплатила 36,25 долларов за 5 билетов в кино. Сколько стоил каждый билет?

165.

Покупки Серена заплатила 12 долларов.96 за упаковку из 12 пар спортивных носков. Сколько стоила пара спортивных носков?

166.

167.

MPG Внедорожник Джона расходует 18 миль на галлон (миль на галлон). Это вдвое меньше, чем у гибридной машины его жены. Сколько миль на галлон расходует гибридный автомобиль?

168.

Рост Рост Эйдена 27 дюймов.Он на 3838 выше своего отца. Какой рост у его отца?

169.

Недвижимость Беа заработала комиссионные в размере 11 700 долларов за продажу дома, что составляет 6 100 6100 продажной цены. Какова была цена продажи дома?

Математика на каждый день

170.

Комиссия Каждую неделю Перри получает 150 долларов плюс 12% от общей суммы продаж свыше 1250 долларов. Решите уравнение 840=150+0,12(a−1250)840=150+0,12(a−1250) для a , чтобы найти общую сумму, которую Перри должен продать, чтобы получить 840 долларов за неделю.

171.

Марки Трэвис купил марок номиналом 49 и 21 цент на сумму 9,45 доллара. Количество марок номиналом 21 цент было на 5 меньше, чем количество марок номиналом 49 центов. Решите уравнение 0,49s+0,21(s−5)=9,450,49s+0,21(s−5)=9,45 для s , чтобы найти количество 49-центовых марок, купленных Трэвисом.

Письменные упражнения

172.

Фрида начала решать уравнение −3x=36−3x=36, добавляя 3 к обеим частям. Объясните, почему метод Фриды не решит уравнение.

173.

Эмилиано считает, что x=40x=40 является решением уравнения 12x=8012x=80. Объясните, почему он не прав.

Самопроверка

Умножение и деление неравенств — GMAT Math Study Guide

Определения

Неравенство сравнивает два значения.

Неравенство — сравнение двух значений или выражений.
Например, 10x < 50 — это неравенство, а x = 5 — уравнение.
Уравнение — оператор, объявляющий равенство двух выражений.
Например, 4x = 8 — это уравнение, тогда как 10x > 20 — это неравенство.

Работа с неравенствами: умножение и деление

Выполнение умножения или деления с неравенством почти идентично умножению или делению частей традиционных уравнений (за одним исключением, описанным ниже).

Рассмотрим следующие примеры:

10x + 15 < 25 + 5x
10x + 15 — 15 < 25 - 15 + 5x
10x < 10 + 5x
10x — 5x < 10 + 5x - 5x
5x < 10
x < 2

10x — 5x < 10 + 5x - 5x

Исключение: отрицательные числа

Существует одно очень важное исключение из правила, согласно которому умножение или деление неравенства равносильно умножению или делению уравнения.

Всякий раз, когда вы умножаете или делите неравенство на отрицательное число, вы должны перевернуть знак неравенства.

В следующем примере обратите внимание, как знак < становится знаком >, когда неравенство делится на -2

-2x — 10 < 2
-2x — 10 + 10 < 2 + 10
-2x < 12
x > -6 [Для деления на -2 необходимо перевернуть знак неравенства]

В следующем примере обратите внимание, как знак < становится знаком >, когда неравенство делится на -2

-2x + 15 < 3
-2x + 15 — 15 < 3 - 15
-2x < -12
x > 6 [Для деления на -2 необходимо перевернуть знак неравенства]

Предупреждение. Будьте осторожны при умножении или делении переменных

Одно очень важное следствие этого правила: Вы не можете делить на неизвестное (т.е., переменная), если вы не уверены в ее знаке , поскольку вы не знаете, нужно ли менять знак неравенства. Есть много случаев, когда вы знаете знак переменной, и в результате вы можете умножать или делить и точно знать, нужно ли переворачивать знак неравенства. Однако вы всегда должны спрашивать себя, знаете ли вы наверняка знак переменной перед делением или умножением при работе с неравенством.

Если 2x5y < 10y, каков диапазон возможных значений x?
Вы не можете делить на y или 5y, так как вы не знаете, является ли y отрицательным или положительным, и, следовательно, вы не знаете, следует ли изменить неравенство.

Множественные неравенства

Как можно одновременно решить два уравнения, так можно решить и два неравенства (или три, или четыре и т. д.). При решении нескольких одновременных неравенств с помощью умножения или деления наиболее важной частью является решение каждого неравенства по отдельности, а затем их объединение.

Если 2x < 150, каков диапазон возможных значений x?

1.) Решите каждое неравенство отдельно.
2x < 10
x < 5 [Примечание: неравенство не переворачивается, так как мы делим на 2, что является положительным]

-5x < -10
x > 2 [Поскольку мы делим на -5, отрицательное число, переворачиваем знак неравенства]

15x < 150
x < 10

2.) Объедините каждое неравенство и найдите пересечение (т. е. области, в которых выполняется каждое неравенство — эта область является решением).
x < 5
x > 2
x < 10

Площадь перекрытия, т. е. решение системы неравенств, находится там, где x < 5 и x > 2

Многим учащимся приведенный выше набор неравенств лучше всего понять графически. Решением набора неравенств является перекрывающаяся графическая область.

3 простых шага для деления дробей с примерами, рабочими листами и другими материалами

Научить ваших учеников делить дроби может быть так же просто, как научить их умножению… как только вы узнаете все маленькие хитрости, чтобы получить правильный ответ.

Но, как и в случае с любой математической концепцией, когда вы обучаете делению, вы не хотите, чтобы ваши ученики просто решили задачу. Вы хотите, чтобы они понимали смысл каждого вопроса.

Но в том-то и дело. Трудно заставить их понять деление дробей, если вы сами этого не понимаете. Мы тоже немного запутались в этом вопросе. Вот почему мы рассмотрели лучшие инструменты и самые простые способы убедиться, что ваш класс понимает ключевые понятия деления дробей .Будьте внимательны, и к концу этой статьи вы станете полностью экипированным, сверхуверенным мастером фракционного деления.

Как работает деление дробей

Обучение учащихся делению дробей является частью Стандартов штата Common Core для математической практики. Одна из самых ценных вещей, которым следует научить своих учеников при делении дробей, — это то, что означает ответ. Взгляните на пример ниже:

½ ÷ ⅙ = 3

Почему число в решении больше, чем задействованные дроби?

Когда вы делите дробь, вы спрашиваете, сколько групп делителя (второй дроби) можно найти в делимом (первой дроби).

В приведенном выше уравнении мы спрашиваем, сколько ⅙ встречается в ½. Представьте пример уравнения в виде торта. У вас осталась половина торта. Если каждая порция торта составляет ⅙ целого, сколько порций у вас осталось? Как видите, у вас осталось три порции торта!

Как видите, у вас осталось три порции торта!

Как разделить дроби за 3 простых шага

Если бы вы просто делили дроби, как при делении обычной математической задачи, вы, скорее всего, создали бы несколько сложных дробей и получили бы что-то похожее на это:

Кредит: Математический клуб Майка

Это не совсем простой процесс.

К счастью, есть ярлык, который значительно упрощает деление дробей. Вы можете решить большинство задач на деление, выполнив следующие три шага:

Перевернуть (или инвертировать) делитель в обратное
Заменить знак деления на символ умножения и умножить
Упростить

По сути, при умножении дробей вы умножаете первую дробь на обратную вторую дробь.

Но в этом руководстве мы рассмотрим это более подробно, чтобы упростить разделение дробей и помочь вам избежать сложных дробей.

Шаг 1. Превратите делитель в обратное число

Обратное число — это то, на что нужно умножить число, чтобы получить значение единицы. Если вы хотите превратить два в один с помощью умножения, вам нужно умножить его на 0,5. В виде дроби это выглядит так:

²⁄₁ × ½ = 1

Чтобы найти обратную дробь, нужно просто перевернуть числа.Знаменатель становится числителем и наоборот.

Еще раз взгляните на пример уравнения:

½ ÷ ⅙ = ?

Первый шаг к решению задачи — превратить наш делитель ⅙ в обратное число.

⅙ → ⁶⁄₁

Шаг 2: Замените знак деления на символ умножения и умножьте

Деление и умножение противоположны друг другу. Когда вы создаете обратное число, вы также создаете его противоположность. В задаче на деление, когда вы превращаете делитель в обратное, вам также нужно изменить уравнение с деления на умножение.

Теперь, когда вы нашли величину, обратную вашему делителю, вы можете изменить уравнение с деления на умножение.

½ ÷ ⅙ = ? → ½ × ⁶⁄₁ = ?

У нас есть подробное руководство по умножению дробей, но вот краткое руководство:

Умножьте числители, чтобы получить новый числитель
Умножьте знаменатели, чтобы получить новый знаменатель
Упростите конечную дробь, если возможно

Для примера уравнения вам нужно решить две задачи:

1 × 6 = 6 2 × 1 = 2 ½ × ⁶⁄₁ = ⁶⁄₂

Теперь вы готовы упростить, чтобы получить окончательный ответ !

Шаг 3: Упростите свой ответ, если возможно

Дроби символизируют часть целого.Это означает, что многие дроби представляют одно и то же значение, так почему бы не сделать дробь максимально простой?

Например, вы почти никогда не говорите пять десятых или ⁵⁄₁₀. Вместо этого вы упрощаете это до половины или ½.

Чтобы привести дробь к ее простейшей форме, вы делите числитель и знаменатель на их наибольший общий делитель . Наибольший общий делитель в ⁵⁄₁₀ равен пяти. Разделив оба числа на пять, вы получите ½.

В примере вопроса наибольший общий делитель ⁶⁄₂ равен двум.Это превратит ваше решение из ⁶⁄₂ в ³⁄₁, что равносильно тому, чтобы сказать три.

Следовательно:

½ ÷ ⅙ = ? → ½ × ⁶⁄₁ = ⁶⁄₂ → ³⁄₁ → 3

Создание обратной величины и умножение уравнения вместо деления позволяет пропустить несколько шагов в уравнении. Это ярлык, который сделает жизнь ваших учеников намного проще!

Примеры деления дробей

Трехшаговая стратегия отлично подходит для простых задач с дробями, но что происходит, когда вы сталкиваетесь с целыми числами, смешанными дробями, неправильными дробями и задачами на слова?

По большей части процесс остается таким же, но в зависимости от типа проблемы может быть еще несколько шагов.

Давайте рассмотрим несколько примеров различных типов задач:

Как делить неправильные дроби

Кредит: edgalaxy

Неправильная дробь — это когда у вас есть числитель, значение которого в больше знаменателя . Увидев эти дроби, можно запутаться, но порядок операций не изменится.

Пример 1 :

⅓ ÷ ⁶⁄₅ = ? → ⅓ × ⅚ = ⁵⁄₁₈

Пример 2 :

⁷⁄₆ ÷ ¾ = ? →⁷⁄₆ × ⁴⁄₃ = ²⁸⁄₁₈ → ¹⁴⁄₉ → 1 ⁵⁄₉

Независимо от того, где стоит неправильная дробь, вы все равно превращаете делитель в обратную, а затем умножаете две дроби.

Как делить смешанные дроби

Credit: Fabulous Finch Facts

Смешанная дробь — это когда у вас есть целое число вместе с дробью. Например, 2 ½ будет считаться смешанной дробью. Как разделить смешанную дробь?

Замените смешанную дробь на неправильную, а затем приступайте к трехэтапной стратегии. Для этого умножьте свое целое число на знаменатель. Затем возьмите это значение и добавьте его к числителю.2 ½ изменится на ⁵⁄₂.

Пример 1:

3 ⅓ ÷ ⅖ = ? → ¹⁰⁄₃ ÷ ⅖ = ? → ¹⁰⁄₃ × ⁵⁄₂ = ⁵⁰⁄₆ → ²⁵⁄₃ → 8 ⅓

Пример 2:

¼ ÷ 2 ⅙ = ? → ¼ ÷ ¹³⁄₆ = ? → ¼ × ⁶⁄₁₃ = ⁶⁄₅₂ → ³⁄₂₆

Пример 3:

2 ½ ÷ 1 ⅓ = ? → ⁵⁄₂ ÷ ⁴⁄₃= ? → ⁵⁄₂ × ¾ = ¹⁵⁄₈ → 1 ⅞

Как делить дроби с целыми числами

Предоставлено: PBS LearningMedia

Вопросы с целыми числами аналогичны задачам со смешанными дробями. Прежде чем приступить к делению, нужно преобразовать целое число в дробь.

Чтобы превратить целое число в дробь, сделайте числитель целым числом, а знаменатель — единицей.

3 → ³⁄₁

Как только целое число будет преобразовано в дробь, вы можете продолжить решение задачи с помощью трехшаговой стратегии.

Пример:

⅓ ÷ 3 = ? → ⅓ ÷ ³⁄₁= ? → ⅓ × ⅓ = ⅑

Как делить дроби с одинаковыми знаменателями

Когда у вас одинаковые знаменатели, нет необходимости находить обратную или умножать.Вы можете просто разделить свои дроби, чтобы получить ответ. Знаменатели компенсируют друг друга и дадут вам единицу.

Любую дробь со знаменателем, равным единице, можно упростить до числителя.

Пример 1:

⅘ ÷ ⅖ = ²/₁ → 2

Пример 2:

⅓ ÷ ⅔ = ½ / 1 → ½

Разделение фракций Проблемы слова

Слово Проблемы могут быть сложными, потому что вы должны научить своих учеников понимать, какое значение становится дивидендом, а какое — делителем.

Как и во всех задачах на деление, в задаче на слова вы пытаетесь выяснить, сколько групп одного числа можно найти в другом.

Лучший способ понять, какое число есть какое, — это посмотреть на пример.

Необходимо отремонтировать 25,5-километровый участок дороги. Строительная бригада может отремонтировать 4 ¼ километра дороги в неделю. Сколько недель потребуется, чтобы отремонтировать шоссе?

В этом уравнении вы ищете количество недель, которое требуется для ремонта шоссе.

Чтобы получить этот ответ, вам нужно посмотреть, сколько групп из 4 ¼ (количество шоссе, которое можно отремонтировать за неделю) может вписаться в 25 ½ (общая длина шоссе, которое необходимо отремонтировать). Следовательно, 25 ½ будет вашим делимым, а 4 ¼ — вашим делителем!

После того, как вы вставите цифры в нужные места, вы обнаружите, что ремонт шоссе займет шесть недель.

Чтобы убедиться, что ваши учащиеся следуют вашим указаниям, вы можете вместе решить текстовые задачи, а затем попросить их поднять руку, если они считают, что одно число является дивидендом. Затем спросите еще раз, считают ли они другое число дивидендом.

Затем выберите учащегося, который объяснит, почему одно число является делимым, а другое — делителем. Это не только вовлечет студентов, но и даст вам возможность увидеть, как студенты обрабатывают материал, который вы преподаете!

Как Prodigy может помочь вам научить делить дроби

Prodigy Math поможет вам научить делить дроби, отслеживать успехи ваших учеников и задавать конкретные вопросы для подготовки вашего класса к стандартизированному тестированию — и учетные записи учителей бесплатны !

Математическая игра воодушевляет ваших учеников, и в большинстве случаев они даже не осознают, что их тестируют.У вас есть несколько вариантов, в том числе возможность сосредоточить внутриигровые вопросы на темах, которые вы преподаете, актуальную статистику и отчеты о прогрессе.

Вот как вы можете использовать Prodigy в своем классе, чтобы:

Prodigy работает быстрее, чем рабочие листы, поскольку все «оценки» делаются за вас — и в режиме реального времени. Вы можете просматривать отчеты по всему классу и видеть, с какими темами борются разные ученики!

Вы также можете создавать задания для каждого учащегося с учетом его конкретных потребностей и стиля обучения.Всем вашим ученикам будет предоставлена возможность попрактиковаться в вопросах, с которыми у них возникают проблемы, и улучшить свои общие математические навыки.

Когда время экзамена не за горами, вы можете создать тренировочный тест в игре, чтобы узнать, нужно ли более подробно осветить какие-либо темы в классе.

Prodigy Math бесплатна для учителей.

Рабочие листы, которые могут помочь в делении дробей

Чтобы убедиться, что основные понятия понятны при обучении делению дробей, вы также можете использовать рабочие листы для своего класса.Вы можете поместить в рабочий лист множество различных вопросов, чтобы увидеть, что учащиеся понимают и с чем они борются.

Единственным недостатком рабочих листов является то, что на их пометки может уйти много времени. Чем больше времени требуется для выставления оценок, тем больше времени потребуется, чтобы увидеть, в чем вашим ученикам нужна помощь.

Вот несколько веб-сайтов, на которых можно получить рабочие листы, которые вы можете попробовать в своем классе:

1. DadsWorksheets.com

DadsWorksheets.com предлагает широкий выбор рабочих листов в зависимости от темы, над которой вы работаете. .Все рабочие листы снабжены ключом для ответов, чтобы упростить задачу. Все, что они предлагают, можно загрузить и распечатать прямо с веб-сайта.

2. Common Core Sheets

Common Core Sheets выводит ваши рабочие листы на новый уровень, позволяя настраивать уроки. Вы можете выбрать типы вопросов, которые должны отображаться на ваших рабочих листах. Вы также можете выбрать, хотите ли вы, чтобы дроби были упрощены или превращены в смешанные числа для ответов.

В конечном продукте вы получите два рабочих листа.В первом есть только вопросы, а во втором — все ответы, включая процесс получения решения.

3. K5 Learning

K5 Learning предоставляет рабочие листы для классов от детского сада до пятого класса. Они охватывают многие темы, встречающиеся в учебной программе, и по каждому предмету есть несколько рабочих листов для использования. PDF-файл, который вы можете скачать с их веб-сайта, включает рабочие листы и ключ ответа.

Калькулятор деления дробей

Когда ваши ученики учатся делить дроби, вы можете показать им калькуляторы дробей.Это онлайн-инструменты для быстрого решения задач на дроби. Они отлично подходят для проверки ваших ответов, но будьте осторожны, показывая эти инструменты своему классу.

Калькуляторы дробей можно использовать, когда учащиеся делают домашнее задание, но вы не хотите, чтобы они полагались на них при решении вопросов, иначе они ничего не узнают. Если вы используете Calculator.net, они покажут вам всех различных шагов, которые необходимо предпринять для решения проблемы!

Заключительные мысли о том, как делить дроби

При обучении делению дробей скажите своим ученикам, что они пытаются найти, сколько делителей можно найти в делимом.