Диагональ трапеции делит среднюю линию трапеции: Диагональ трапеции делит среднюю линию на отрезки

Posted on by alexxlab

Содержание

Контролная работа 1 2 | Образовательный портал EduContest.Net — библиотека учебно-методических материалов


ВАРИАНТ А11.В равностороннем треугольнике АВС со стороной равной 10см, точки К и М – середины сторон АВ и ВС соответственно.
А) Докажите. Что АКМС – трапеция.
Б) Найдите периметр АКМС.
2. Средняя линия трапеции равна 16см. Найдите основания трапеции, если они относятся как 3:5.
3. Диагональ трапеции делит среднюю на отрезки 4см и 9см. Найдите основание трапеции. ВАРИАНТ А21.В равнобедренном треугольнике АВС с основанием АС равным 12см, и боковой стороной, равной 10см, точки D и Е – середины сторон АВ и ВС соответственно.
А) Докажите. Что АDЕС – трапеция.
Б) Найдите периметр АDЕС.
2. Средняя линия трапеции равна 20см. Найдите основания трапеции, если они относятся как 3:7.
3. Основания трапеции равны 8см и 14см. Найдите отрезки, на которые диагональ трапеции делит среднюю линию.
ВАРИАНТ Б11.В равнобедренном треугольнике АВС АВ=ВС= 10см, точки К ,N и D – середины сторон АВ, ВС и АС соответственно.
Определите вид четырехугольника КВND и найдите его периметр.
2.Биссектрисы острых углов равнобокой трапеции пересекаются в точке, лежащей на меньшем основании трапеции. Большее основание трапеции равно 18см. а боковая сторона равна 4см. Найдите среднюю линию трапеции.
3.Докажите, что если диагонали четырехугольника перпендикулярны, то середины его сторон являются вершинами
прямоугольника. ВАРИАНТ Б21.В равностороннем треугольнике АВС, АВС со стороной равной 6см,точки D ,E и F – середины сторон АВ, ВС и АС соответственно. Определите вид четырехугольника ADEF и найдите его периметр.
2.Биссектрисы тупых углов равнобокой трапеции пересекаются в точке, лежащей на большем основании трапеции. Меньшее основание трапеции равно 8см. а боковая сторона равна 9см. Найдите среднюю линию трапеции.
3.Докажите, что если диагонали четырехугольника, то середины его сторон являются вершинами
ромба.
ВАРИАНТ В11.Диагонали трапеции делят среднюю линию на три отрезка, два из которых равны 5см и 7см. Найдите основания трапеции. Сколько решений имеет задача?
2. Средняя линия данной трапеции делит ее на две трапеции. Средние линии которых равны 10см и 18см. Найдите основания данной трапеции.
3. Докажите, что если в равнобокой трапеции взаимно перпендикулярны, то ее высота равна средней линии. ВАРИАНТ В21.Диагонали трапеции делят среднюю линию на три отрезка, один из которых равен 3см. Найдите среднюю линию трапеции, если большее основание равно 14см. Сколько решений имеет задача?
2. Средняя линия данной трапеции длиной 21см делит ее на две трапеции. Средние линии которых относятся как 2:5. Найдите среднюю линию данной трапеции.
3. Докажите, что если в равнобокой трапеции высота равна средней линии, то диагонали взаимно перпендикулярны .
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ «СРЕДНИЕ ЛИНИИ ТРЕУГОЛЬНИКА И ТРАПЕЦИИ. ТРАПЕЦИЯ»

Приложенные файлы

Средняя линия — трапеция — Большая Энциклопедия Нефти и Газа, статья, страница 1

Средняя линия — трапеция

Cтраница 1

Средняя линия трапеции параллельна основаниям, а длина ее равна полусумме длин оснований.  [1]

Средняя линия трапеции параллельна основаниям и равна их полусумме.  [2]

Средняя линия трапеции равна полусумме оснований и параллельна им. Трапеция, у которой боковые стороны равны, называется равнобочной. В равнобочной трапеции углы при основании равны. Трапеция, у которой хотя бы один угол прямой, называется прямоугольной.  [3]

Средняя линия трапеции делит высоту трапеции на два равных отрезка.  [4]

Средняя линия трапеции равна 8 дм и делится диагональю на два отрезка, разность между которыми 2 дм.  [5]

Средняя линия трапеции параллельна ее основаниям и делит высоту пополам.  [6]

Средняя линия трапеции равна 8 дм и делится диагональю на два отрезка, разность между которыми равча 2 дм.  [7]

Средняя линия трапеции параллельна ее основаниям и равна их полусумме.  [8]

Средняя линия трапеции параллельна основаниям трапеции и длина ее равна полусумме длин оснований.  [9]

Средняя линия трапеции

равна 21 4, а биссектриса большего угла параллельна боковой стороне.  [10]

Средняя линия трапеции параллельна основаниям и равна их полусумме.  [11]

Средняя линия трапеции параллельна основаниям, а длина ее равна полусумме оснований.  [12]

Средняя линия трапеции равна 7 см, а одно из оснований больше другого на 4 см. Найти основания трапеции.  [13]

Средняя линия трапеции равна 56 дм.  [14]

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.  [15]

Страницы:      1    2    3    4

Подготовка школьников к ЕГЭ и ОГЭ Справочник по математике — Планиметрия

Средние линии треугольника

      Определение. Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

Рис.1

      На рисунке 1 средней линией является отрезок DE.

      Утверждение 1. Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

      Доказательство.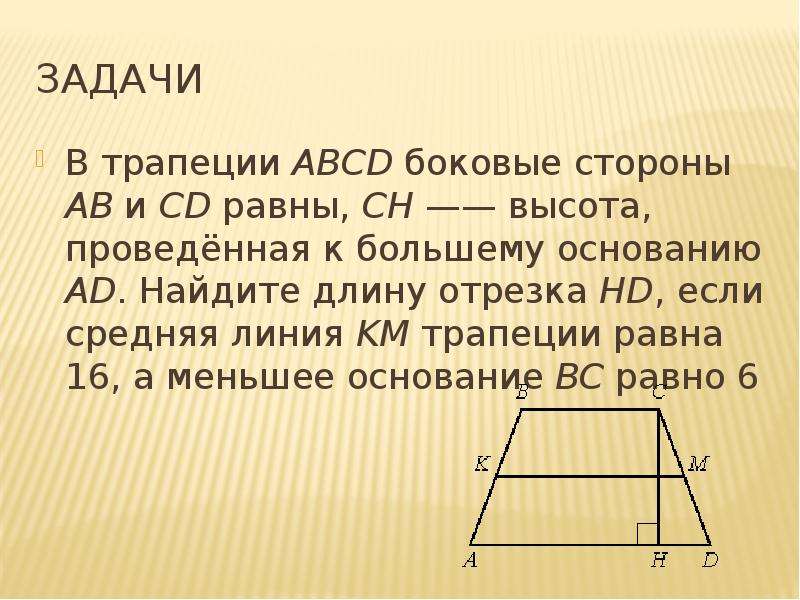 Рассмотрим произвольный треугольник   ABC   и обозначим буквой   D   середину стороны   AB   (рис. 2). Проведем через точку   D   до пересечения с прямой   BC   прямую, параллельную прямой   AC .   Обозначим буквой   E   точку пересечения прямых   DE   и   BC .

Рис.2

      Поскольку   AD = DB ,   а прямые   AC   и   DE   параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство:   CE = EB .   Отсюда вытекает, что точка   E   является серединой стороны   CB ,   а отрезок   DE   является средней линией треугольника.

      Первую часть утверждения 1 мы доказали.

      Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки   DE , EF   и   FD   (рис.3).

Рис.3

      Поскольку

DE | | FC ,       DF | | EC ,

то четырёхугольник DECF – параллелограммчетырёхугольник DECF – параллелограмм, следовательно,   DE = FC .

      Поскольку

DE | | AF ,       AD | | FE ,

то четырёхугольник   DEFA   – параллелограммчетырёхугольник   DEFA   – параллелограмм, следовательно,   DE = AF .

      Но поскольку   AF = FC ,   то отсюда вытекает равенство

что и требуется доказать.

      Доказательство утверждения 1 закончено.

      Следствие.

Рис.4

Средняя линия трапеции

      Напомним, что трапециейтрапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.

      Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции.

      Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.

      Определение. Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).

Рис.5

      На рисунке 5 средней линией трапеции является отрезок   EF .

      Утверждение 2. Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.

Рис.6

      Доказательство. Проведем через вершину   B   и середину боковой стороны   F   трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых   BF   и   AD   буквой   G .   Рассмотрим треугольники   BCF   и   FDG .   У этих треугольников стороны   CF   и   FD   равны, поскольку точка   F   – середина стороны   CD .   Углы   BCF   и   FDG   равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых   BC   и   AD   с секущей   CD .   Углы   BFC   и   DFG   равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники   BCF   и   FDG   равны. Из равенства треугольников   BCF   и   FDG   следует равенство отрезков   BF   и   FG ,   откуда вытекает, что отрезок   EF   является средней линией треугольника   ABG .   Поэтому

что и требовалось доказать.

      Задача 1. Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

Рис.7

      Решение. Пусть   ABCD   – трапеция,   EF   –  её средняя линия,   LM   – указанный отрезок (рис.7). Поскольку   AE = EB ,   то, в силу теоремы Фалеса, выполнено равенство:   LN = NM ,   что и требовалось доказать.

      Задача 2. Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

Рис. 8

      Решение. Пусть   ABCD   – трапеция,   EF   – её средняя линия,   KL   – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка   K   – середина отрезка   AC ,   а точка   L   – середина отрезка   BD .   Поэтому отрезок   EK   – средняя линия треугольника   BAC ,   а отрезок   EL   – средняя линия треугольника   ABD .   В силу утверждения 1 выполнены равенства:

      Следовательно,

что и требовалось доказать.

      Утверждение 3. Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

Рис.9

      Доказательство. Пусть   K   и   L   – середины оснований   BC   и   AD   трапеции   ABCD   соответственно (рис.9). Обозначим буквой   M   точку пересечения боковых сторон   AB   и   CD .   Проведем через точки   M   и   K   прямую и обозначим точку пересечения этой прямой с основанием   AD   символом   N .   Докажем, что точки   N   и   L   совпадают. Для этого заметим, что треугольник   BMK   подобен треугольнику   AMN .   Следовательно, выполнено равенство:

      Заметим также, что треугольник   KMC   подобен треугольнику   NMD .   Поэтому

      Из этих соотношений получаем:

откуда вытекает, что точки   N   и   L   совпадают. Доказательство завершено.

      Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

      Утверждение 4. Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

      Следствие. Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.

Средние линии четырехугольника.

Теорема Вариньона

      Определение. Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

      Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).

Рис.10

      На рисунке 10 средние линии – это отрезки   EF   и   GH .

      Замечание 1. Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

Рис.11

      На рисунке 11 изображен «пространственный четырёхугольник»   ABCD ,   средними линиями которого являются отрезки   EF   и   GH .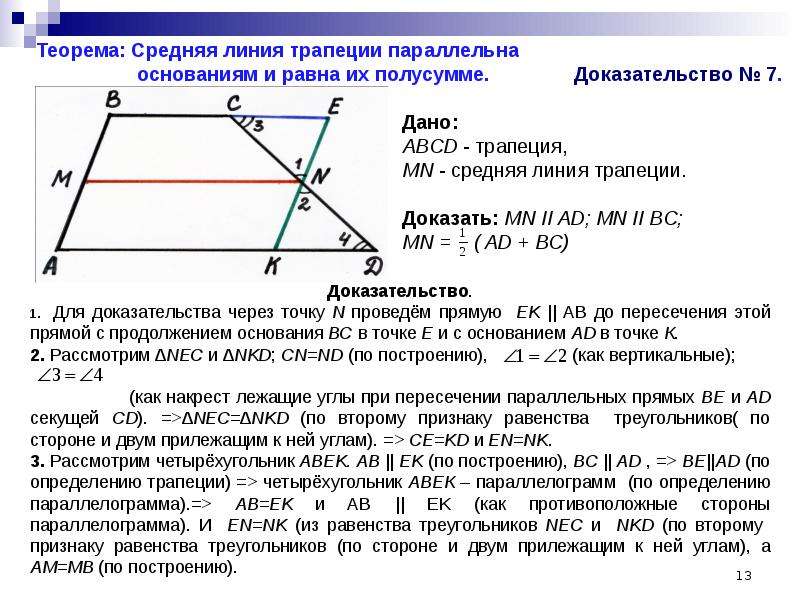

      Замечание 2. Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.

      Замечание 3. В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.

      Теорема Вариньона. Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограммапараллелограмма.

      Доказательство. Рассмотрим плоский четырёхугольник   ABCD ,   изображенный на рисунке 12. Точки   E, G, F, H   – середины сторон, отрезок   AC   – диагональ четырёхугольника.

Рис.12

      Поскольку отрезок   EG   – средняя линия треугольника   ABC ,   то отрезок   EG   параллелен диагонали   AC   и равен её половине.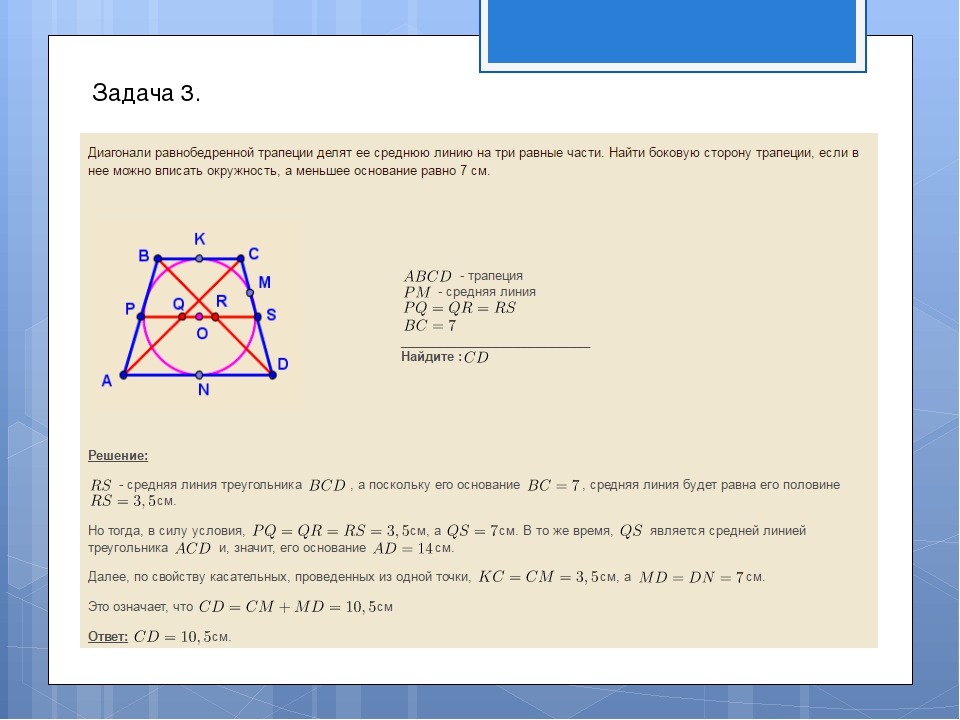 Поскольку отрезок   FH   – средняя линия треугольника   CDA ,   то отрезок   FH   параллелен диагонали   AC   и равен её половине. Таким образом, в четырёхугольнике   EGFH   противоположные стороны   EG   и   FH   равны и параллельны. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма отсюда вытекает, что четырёхугольник   EGFH   – параллелограмм, что и требовалось доказать.

      Замечание 4 . В случае «пространственного четырёхугольника»   ABCD   доказательство остаётся тем же (рис. 13).

Рис.13

      Поскольку диагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополам, то справедливо следующее утверждение, непосредственно вытекающее из теоремы Вариньона.

      Утверждение 5. Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).

Рис.14

      Утверждение 6. Рассмотрим произвольный плоский или «пространственный» четырёхугольник   ABCD ,   у которого отрезок   EF   является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:

Рис.15

      Доказательство. Рассмотрим в пространстве или на плоскости произвольную декартову систему координат с началом в некоторой точке   O   (рис. 16).

Рис.16

      В соответствии со свойствами векторов справедливы следующие равенства:

что и требовалось доказать.

      Следствие. Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.

      Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапециейтрапецией, а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.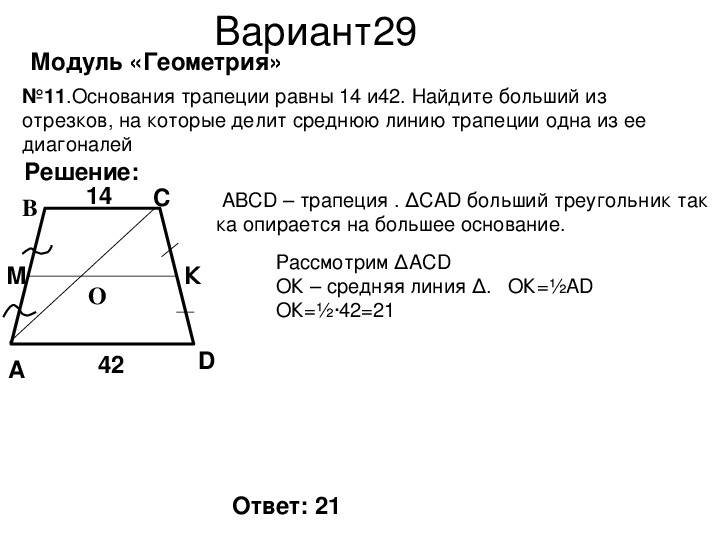

Средние линии тетраэдра

      Тетраэдром называют произвольную треугольную пирамиду (рис.17).

Рис.17

      У каждого тетраэдра имеется   4   вершины,   4   грани и   6   рёбер, причем все рёбра делятся на   3   пары непересекающихся рёбер. На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых.

      Определение. Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

Рис.18

      У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок   EF   является одной из средних линий тетраэдра.

      Утверждение 7. Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.

      Доказательство. Выберем какую-нибудь среднюю линию тетраэдра, например,   EF   и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка   EF .   Для этого рассмотрим, например, среднюю линию   GH ,   соединяющую середины рёбер   AC   и   BD ,   и соединим отрезками точки   E, H, F, G   (рис.19).

Рис.19

      Заметим, что отрезок   EH   является средней линией треугольника   ADB ,   поэтому

      Отрезок GF является средней линией треугольника   ACB ,   поэтому

      Отсюда вытекает, что отрезки   EH   и   GF   равны и параллельны, следовательно, четырёхугольник   EHFG   – параллелограммследовательно, четырёхугольник   EHFG   – параллелограммследовательно, четырёхугольник   EHFG   – параллелограмм.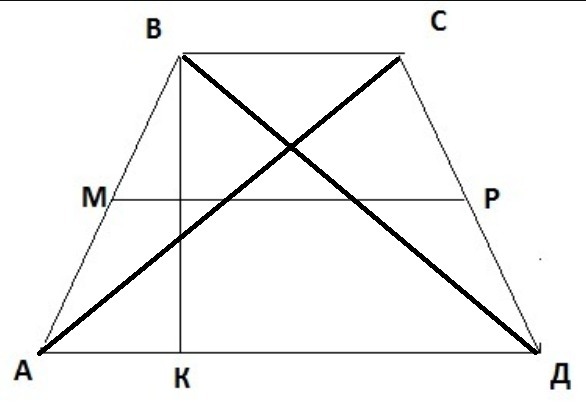 Поскольку средние линии тетраэдра   EF   и   GH   являются диагоналями этого параллелограмма, то в точке пересечения они делятся пополамв точке пересечения они делятся пополамв точке пересечения они делятся пополам, что и требовалось доказать.

      Определение. Точку пересечения средних линий тетраэдра называют центроидом тетраэдра.

      Утверждение 8. Рассмотрим в пространстве декартову систему координат с началом в точке   O   и произвольный тетраэдр   ABCD .   Если обозначить буквой   M   центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:

Рис.20

      Доказательство. По свойствам векторов

что и требовалось доказать.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Покажите, что диагонали трапеции делят ее на четыре треугольника, два из которых имеют одинаковую площадь? «Equi-extension»

Обычно трапеция определяется как четырехугольник с двумя параллельными сторонами. Равнобедренная трапеция — это особый случай трапеции, которая имеет боковую симметрию, что означает, что одна сторона будет зеркалом другой.

На изображении выше изображена равнобедренная трапеция, # «ABCD» #. Должно быть очевидно, что треугольники # «ABE» # и # «DCE» # имеют равные площади, поскольку они являются зеркальным отображением друг друга.Поэтому давайте сосредоточимся на попытке доказать, что эти два треугольника должны иметь одинаковую площадь для всех трапеций.

Площадь треугольника можно определить по тождеству:

#A = 1/2 (B xx H) #

Где # B # — основание треугольника, а # H # — высота. Треугольники # «ABE» # и # «DCE» # не имеют общих сторон, которые мы могли бы рассматривать как общую основу, однако треугольники # «ACD» # и # «DBA» # имеют общую сторону, основание трапеции. .

Если мы рассматриваем сторону # «AD» # как основание для обоих треугольников, то высота для обоих — это расстояние между линией # «AD» # и # «BC» #. Поскольку основание и высота у обоих треугольников равны, площадь обоих треугольников также должна быть одинаковой.

#A_ «ABD» = A_ «DCA» #

Теперь мы также можем видеть, что треугольник # «ABD» # состоит из треугольников # «ABE» # и # «AED» #. Кроме того, треугольник # «DCA» # состоит из треугольников # «DCE» # и # «AED» #.

#A_ «ABD» = A_ «ABE» + A_ «AED» #
#A_ «DCA» = A_ «DCE» + A_ «AED» #

Если мы вычтем площадь AED из ABD и DCA, мы увидим, что площади ABE и DCE действительно равны.

#A_ «ABD» = A_ «DCA» #
#A_ «ABE» + цвет (красный) отмена (цвет (черный) (A_ «AED»)) = A_ «DCE» + цвет (красный) отмена (цвет ( черный) (A_ «AED»)) #

#A_ «ABE» = A_ «DCE» #

Хотя я проиллюстрировал это доказательство с помощью равнобедренной трапеции, ни одна из работ не относилась конкретно к правильной трапеции. Следовательно, боковые треугольники любой трапеции можно показать равными, используя те же рассуждения.

Параллельно через пересечение диагоналей.

Параллель через пересечение диагоналей.

Необязательно, чтобы трапеция была равнобедренной. Возьми любую трапецию ABCD с диагоналями AC и BD , пересекающимися в точке E . Пусть a = AB и b = CD . Пусть c будет длиной отрезка FG параллельно двум основаниям трапеции. Наш проблема состоит в том, чтобы выразить c через a и b .

———————————

Вытяните стороны DA и CB так, чтобы они встретились в точке H. Постройте линию A, параллельную стороне. DA через G и продолжается до места пересечения AB в точке J (внешней по отношению к AB) и CD в K (внутренний для CD).

Это дает следующие похожих треугольника : HAB, HDC, GJB, GKC. Обратите внимание, что в терминах a , b и c , BJ = c — a и CK = b — c

Следовательно, учитывая треугольники GJB и HAB, отношение подобия есть и учитывая треугольники GKC и HDC, отношение подобия.Следовательно, у нас есть отношение, включающее a, b и c, которое мы можем решить для c.

Если три числа таковы, что по любой части наибольшее срок превышает средний срок, а средний срок превышает третий срок та же часть третьего, а затем среднего члена — это среднее гармоническое

первого и третьего. Это соотношение показано в этом уравнении. Обычно отношение записывается в одной из следующих форм, чтобы показать, что c — гармоническое среднее положительных чисел a и b :

или же

Таким образом, длина отрезка параллельной прямой через точку пересечения диагоналей — это гармоническое среднее оснований трапеции.

Возврат

Теорема о срединном отрезке трапеции | Справка по геометрии

На сегодняшнем уроке геометрии мы докажем теорему о среднем сегменте трапеции, опираясь на ранее доказанную теорему о среднем сегменте треугольника.

Теорема о середине треугольника утверждает, что линия, соединяющая середины двух сторон треугольника, называемая средним сегментом, параллельна третьей стороне, а ее длина равна половине длины третьей стороны.

Аналогичная теорема существует и для трапеций: линия, соединяющая середины двух сторон трапеции, параллельна основаниям, а ее длина равна половине суммы длин оснований.

Задача

ABCD — трапеция, AB || CD . EF — это линия, соединяющая середины ветвей AD и BC , AE = ED и BF = FC .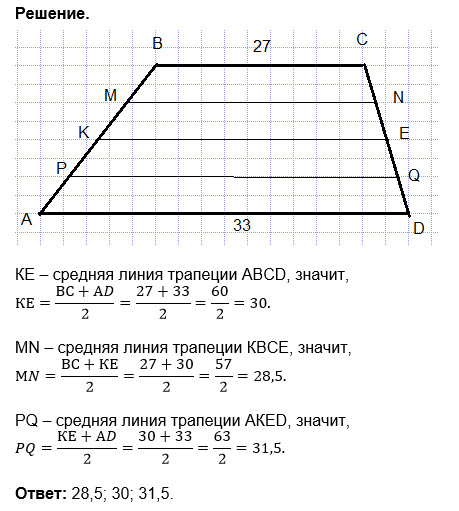 Докажите, что EF || DC и что EF = ½ ( AB + DC )

Стратегия

Поскольку мы имеем дело с серединами сегментов, мы будем использовать то, что мы уже доказали для средних сегментов треугольника.Давайте создадим такие треугольники, проведя линию от вершины A через среднюю точку F, пока она не пересечет продолжение базового DC в точке G:

Мы можем легко показать, что ΔABF и ΔGCF совпадают, используя Angle-Side -Угловой постулат. Отсюда мы можем показать, что EF — это средний сегмент треугольника ΔADG. Таким образом, согласно теореме треугольника о среднем сегменте, он параллелен DG и равен половине DG .

Но DG — это DC + CG , а поскольку ΔABF и ΔGCF совпадают, CG = AB , поэтому EF равно половине DC + AB .Другими словами, длина EF — это среднее арифметическое (среднее) длин оснований.

Доказательство

Вот как доказать теорему о среднем сегменте трапеции:

(1) AB || DG // Учитывая, что ABCD — это трапеция
(2) ∠BAF ≅ ∠CGF // Теорема об альтернативных внутренних углах
(3) ∠AED ≅ ∠CEF // Вертикальные углы
(4) BF = FC // Дано
(5) ΔABF ≅ ΔGCF // (2), (3), (4), Угол-боковой-угол
(6) AF = FG // (5), соответствующие стороны равных треугольников
(7) EF — мидсегмент // (6), определение мидсегмента
(8) EF || DG // (7), теорема о мидсегменте треугольника
(9) EF = ½DG // (7), Теорема о промежуточном сегменте треугольника
(10) DG = DC + CG
(11) CG = AB // (5), соответствующие стороны совпадающих треугольников
(12) EF = ½ (DC + CG ) // (9), (10), переходное свойство равенства
(13) EF = ½ (DC + AB ) // (11) , (12), Транзитивное свойство равенства

Верно и обратное утверждение этой теоремы — прямая, параллельная одной из траекторий Основание апезоида и пересекает одну из середин ноги, также пересекает середину другой ноги, и ее длина равна половине суммы длин оснований.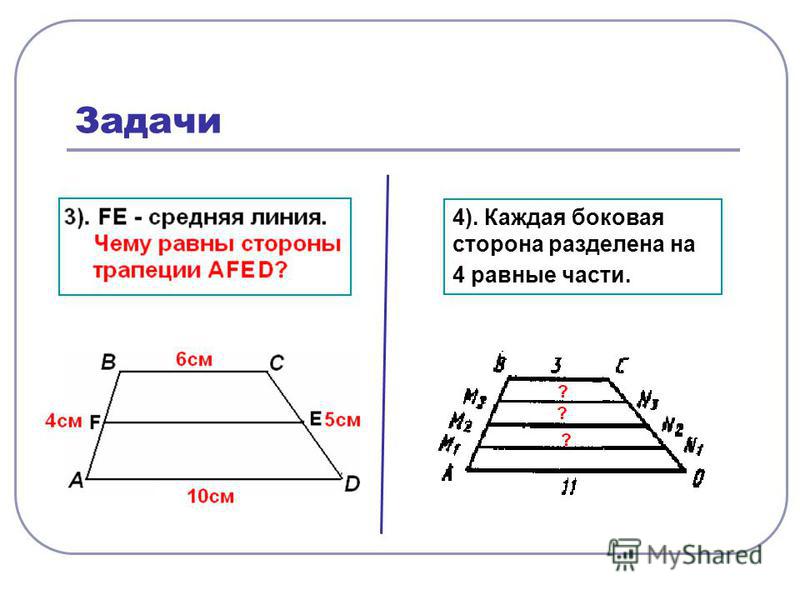

Основания трапеции, ножки, углы и площадь, правила и формулы

Трапеция — это четырехугольник с одной парой параллельных линий

Основания — две параллельные линии называются основаниями.

Ноги — две непараллельные линии — это ноги.

Недвижимость
  • Свойство №1) Углы на одной стороне ножки называются смежными углами и являются дополнительными (еще )
  • Свойство № 2) Площадь трапеции = $$ Площадь = высота \ cdot \ left (\ frac {\ text {sum base}} {2} \ right) $$ (еще )
  • Свойство № 3) Трапеции имеют средний сегмент, который соединяет мипоинты ног (еще )

Смежные углы трапеции

Углы на одной стороне ножки называются смежными углами, например $$ \ angle A $$ и $$ \ angle D $$ являются дополнительными. По той же причине $$ \ angle B $$ и $$ \ angle C $$ являются дополнительными.

Задача 1

$$ \ angle ZWX = 180 — 44 = 136 ° $$

Задача 2

Используйте теорему о смежных углах для вычисления m $$ \ angle MLO $$.

Покажи ответ

$$ \ angle MLO = 180-124 = 56 ° $$

Задача 3

Найдите значение x на трапеции ниже, затем определите меру углов $$ \ angle WXY $$ и $$ \ angle XYZ $$.

Покажи ответ
Задача 4

Что не так с трапецией LMNO, изображенной ниже? (Объясните, почему LMNO не может быть трапецией, основываясь на предоставленной информации) .

Покажи ответ

Если LMNO — трапеция, и ее основания LO и MN параллельны, то $$ \ angle MNO $$ и $$ \ angle NOL $$, которые должны быть дополнительными, сумма этих углов не равна 180 111 + 68 ≠ 180.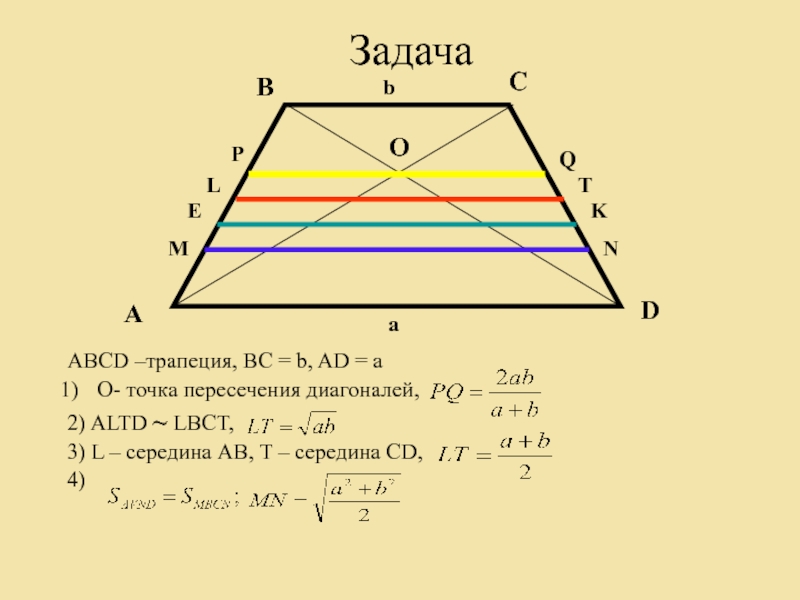 2 $

Средняя часть трапеции:

Задача 6

Используйте теорему о среднем сегменте, чтобы определить длину включения среднего сегмента.

Длина мидсегмента

Чтобы вычислить длину среднего сегмента, найдите среднее значение длины оснований среднего сегмента = (6 + 4) / 2 = 5.

Быстрый обзор Midpoint

Самая важная вещь, о которой нужно помнить, — это то, что средняя точка делит линию пополам (разрезает линию на две равные половины).

Показать среднюю точку

Средняя точка красного сегмента, изображенного ниже, — это точка $$ (A, 2b) $$ (нажмите кнопку ниже, чтобы увидеть).

Средний сегмент трапеции — это сегмент, соединяющий середины непараллельных сторон трапеции.

На трапеции ниже середины непараллельных сторон — это точки S и V. Средний сегмент — это красный отрезок линии от S до V.

Пример среднего сегмента
Трапеция # 10 Шаг 1 Расчет длины оснований. Верхняя база:

$$ 35–16 = 9 $$

Шаг 2

Расчет низкой базы:

$$ 45 — 0 = 45 $$

Шаг 3

Расчет суммы оснований

$$ 9 + 45 = 54 $$

Шаг 4

Разделите сумму на 2

$$ \ frac {54} {2} = \ boxed {27} $$

Задача 8

Какова длина среднего сегмента SV трапеции ниже?

Покажи ответ Шаг 1 Расчет длины оснований.Верхняя база:

$$ 17–8 = 9 $$

Шаг 2

Расчет низкой базы:

$$ 20 — 0 = 20 $$

Шаг 3

Расчет суммы оснований

$$ 9 + 20 = 29 $$

Шаг 4

Разделите сумму на 2

$$ \ frac {29} {2} = \ boxed {14.5} $$

Задача 9

Красный сегмент ниже среднего сегмента?

Покажи ответ

Это не настоящий средний сегмент, потому что его длина не равна половине суммы длин оснований.

Как найти площадь трапеции без длины одной из параллельных сторон

Трапеция — это четырехугольная геометрическая форма, имеющая две параллельные и две непараллельные стороны. Площадь трапеции можно рассчитать как произведение высоты и среднего значения двух параллельных сторон, также известных как основания.Есть несколько свойств трапеций, которые позволяют определять неизвестные параметры на основе известных факторов, включая меру параллельных сторон, меру непараллельных сторон и меру различных углов. Площадь трапеции, в частности, может быть получена с использованием этих различных свойств, несмотря на то, что известна только длина одного основания, если известны длина диагонали, высота трапеции и одна непараллельная сторона.

    Определите заданную длину одного основания, высоту трапеции и длину одной непараллельной стороны.Например, предположим, что высота трапеции составляет 4 дюйма, одно основание — 6 дюймов, а непараллельная сторона — 5 дюймов.

    Определите длину диагонали. Диагональ — это линия, которая проходит от одного угла до противоположного угла в пределах трапеции. У равнобедренной трапеции обе диагонали равны по длине. Однако для расчета площади потребуется только одна длина. В этом примере предположим, что длина диагонали трапеции составляет 8 дюймов.

    Используйте теорему Пифагора, чтобы определить длину неизвестного основания. 2 Длина неизвестной стороны = sqrt (39) или приблизительно 6 дюймов Длина неизвестного основания = 6 дюймов + 3 дюйма = 9 дюймов

    Используйте площадь формулы трапеции, чтобы найти площадь.2

    Поймите, что решить эти проблемы можно, разделив трапецию на прямоугольные треугольники, чтобы определить длину неизвестного основания. Этот тип проблемы может быть решен только при наличии достаточной информации о трапеции.

9.7: Использование свойств прямоугольников, треугольников и трапеций (часть 2)

Использование свойств треугольников

Теперь мы знаем, как найти площадь прямоугольника. Мы можем использовать этот факт, чтобы визуализировать формулу площади треугольника.В прямоугольнике на рисунке \ (\ PageIndex {9} \) мы обозначили длину b и ширину h, так что это площадь bh.

Рисунок \ (\ PageIndex {9} \) — Площадь прямоугольника равна основанию b, умноженному на высоту h.

Мы можем разделить этот прямоугольник на два равных треугольников (рисунок \ (\ PageIndex {10} \)). Конгруэнтные треугольники имеют одинаковую длину сторон и углы, поэтому их площади равны. Площадь каждого треугольника равна половине площади прямоугольника или \ (\ dfrac {1} {2} \) bh.Этот пример помогает нам понять, почему формула для вычисления площади треугольника имеет вид A = \ (\ dfrac {1} {2} \) bh.

Рисунок \ (\ PageIndex {10} \) — прямоугольник можно разделить на два треугольника равной площади. Площадь каждого треугольника составляет половину площади прямоугольника.

Формула площади треугольника: A = \ (\ dfrac {1} {2} \) bh, где b — основание, а h — высота. Чтобы найти площадь треугольника, нужно знать его основание и высоту. Основание — это длина одной стороны треугольника, обычно стороны внизу.Высота — это длина линии, которая соединяет основание с противоположной вершиной и составляет с основанием угол 90 °. На рисунке \ (\ PageIndex {11} \) показаны три треугольника с отмеченными основанием и высотой каждого.

Рисунок \ (\ PageIndex {11} \) — Высота h треугольника — это длина отрезка линии, соединяющего основание с противоположной вершиной и образующего угол 90 ° с основанием.

Определение: Свойства треугольника

Для любого треугольника ΔABC сумма углов равна 180 °.$$ m \ angle A + m \ angle B + m \ angle C = 180 ° $$ Периметр треугольника равен сумме длин сторон. $$ P = a + b + c $$ Площадь треугольник равен половине основания b, умноженной на высоту h. $$ A = \ dfrac {1} {2} bh \]

Пример \ (\ PageIndex {9} \):

Найдите площадь треугольника с основанием 11 дюймов и высотой 8 дюймов.

Раствор

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.
Шаг 2. Определите то, что вы ищете. площадь треугольника
Шаг 3. Имя . Выберите переменную для ее представления. пусть A = площадь треугольника
Шаг 4. Перевести . Напишите соответствующую формулу. Заменять.
Шаг 5. Решите уравнение. A = 44 квадратных дюйма
Шаг 6. Проверьте . $$ \ begin {split} A & = \ dfrac {1} {2} bh \\ 44 & \ stackrel {?} {=} \ Dfrac {1} {2} (11) 8 \\ 44 & = 44 \; \ checkmark \ end {split} $$
Шаг 7. Ответьте на вопрос. Площадь составляет 44 квадратных дюйма.

Упражнение \ (\ PageIndex {17} \):

Найдите площадь треугольника с основанием 13 дюймов и высотой 2 дюйма.

Ответ

13 кв. Дюймов

Упражнение \ (\ PageIndex {18} \):

Найдите площадь треугольника с основанием 14 дюймов и высотой 7 дюймов.

Ответ

49 кв. Дюймов

Пример \ (\ PageIndex {10} \):

Периметр треугольного сада составляет 24 фута. Длина двух сторон составляет 4 фута и 9 футов. Какова длина третьей стороны?

Раствор

Шаг 1. Прочтите задачу. Нарисуйте фигуру и напишите на ней указанную информацию.
Шаг 2. Определите то, что вы ищете. длина третьей стороны треугольника
Шаг 3. Имя . Выберите переменную для ее представления. Пусть c = третья сторона
Шаг 4. Перевести . Напишите соответствующую формулу.Подставьте в данную информацию.
Шаг 5. Решите уравнение. $$ \ begin {split} 24 & = 13 + c \\ 11 & = c \ end {split} $$
Шаг 6. Проверьте . $$ \ begin {split} P & = a + b + c \\ 24 & \ stackrel {?} {=} 4 + 9 + 11 \\ 24 & = 24 \; \ checkmark \ end {split} $$
Шаг 7. Ответьте на вопрос. Третья сторона имеет длину 11 футов.

Упражнение \ (\ PageIndex {19} \):

Периметр треугольного сада составляет 48 футов. Длина двух сторон 18 футов и 22 фута. Какова длина третьей стороны?

Ответ

8 футов

Упражнение \ (\ PageIndex {20} \):

Длина двух сторон треугольного окна составляет 7 футов 5 футов. По периметру 18 футов.Какова длина третьей стороны?

Ответ

6 футов

Пример \ (\ PageIndex {11} \):

Площадь треугольного церковного окна — 90 квадратных метров. База окна 15 метров. Какая высота окна?

Раствор

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.
Шаг 2. Определите то, что вы ищете. высота треугольника
Шаг 3. Имя . Выберите переменную для ее представления. Пусть h = высота
Шаг 4. Перевести . Напишите соответствующую формулу. Подставьте в данную информацию.
Шаг 5. Решите уравнение. $$ \ begin {split} 90 & = \ dfrac {15} {2} h \\ 12 & = h \ end {split} $$
Шаг 6. Чек . $$ \ begin {split} A & = \ dfrac {1} {2} bh \\ 90 & \ stackrel {?} {=} \ Dfrac {1} {2} \ cdot 15 \ cdot 12 \\ 90 & = 90 \; \ checkmark \ end {split} $$
Шаг 7. Ответьте на вопрос. Высота треугольника 12 метров.

Упражнение \ (\ PageIndex {21} \):

Площадь треугольной картины составляет 126 квадратных дюймов. База 18 дюймов.Какая высота?

Ответ

14 дюймов

Упражнение \ (\ PageIndex {22} \):

Треугольная дверь палатки имеет площадь 15 квадратных футов. Высота 5 футов. Что такое база?

Ответ

6 футов

Равнобедренные и равносторонние треугольники

Помимо прямоугольного треугольника, некоторые другие треугольники имеют особые имена. Треугольник с двумя сторонами равной длины называется равнобедренным треугольником .Треугольник, у которого три стороны равной длины, называется равносторонним треугольником . На рисунке \ (\ PageIndex {12} \) показаны оба типа треугольников.

Рисунок \ (\ PageIndex {12} \) — В равнобедренном треугольнике две стороны имеют одинаковую длину, а третья сторона является основанием. В равностороннем треугольнике все три стороны имеют одинаковую длину.

Определение: равнобедренные и равносторонние треугольники

У равнобедренного треугольника две стороны одинаковой длины.

Равносторонний треугольник имеет три стороны равной длины.

Пример \ (\ PageIndex {12} \):

Периметр равностороннего треугольника составляет 93 дюйма. Найдите длину каждой стороны.

Раствор

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.

Периметр = 93 дюйма

Шаг 2. Определите то, что вы ищете. длина сторон равностороннего треугольника
Шаг 3. Имя . Выберите переменную для ее представления. Пусть s = длина каждой стороны
Шаг 4. Перевести . Напишите соответствующую формулу. Заменять.
Шаг 5. Решите уравнение. $$ \ begin {split} 93 & = 3s \\ 31 & = s \ end {split} $$
Шаг 6. Чек . $$ \ begin {split} 93 & = 31 + 31 + 31 \\ 93 & = 93 \; \ checkmark \ end {split} $$
Шаг 7. Ответьте на вопрос. Каждая сторона 31 дюйм.

Упражнение \ (\ PageIndex {23} \):

Найдите длину каждой стороны равностороннего треугольника с периметром 39 дюймов.

Ответ

13 дюймов

Упражнение \ (\ PageIndex {24} \):

Найдите длину каждой стороны равностороннего треугольника с периметром 51 сантиметр.

Ответ

17 см

Пример \ (\ PageIndex {13} \):

У Арианны есть 156 дюймов бисера, которые можно использовать для обрезки шарфа. Платок будет представлять собой равнобедренный треугольник с основанием 60 дюймов. Как долго она сможет сделать две равные стороны?

Раствор

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.

P = 156 дюймов

Шаг 2. Определите то, что вы ищете. длины двух равных сторон
Шаг 3. Имя . Выберите переменную для ее представления. Пусть s = длина каждой стороны
Шаг 4. Перевести . Напишите соответствующую формулу. Подставьте в данную информацию.
Шаг 5. Решите уравнение. $$ \ begin {split} 156 & = 2s + 60 \\ 96 & = 2s \\ 48 & = s \ end {split} $$
Шаг 6. Проверьте . $$ \ begin {split} p & = a + b + c \\ 156 & \ stackrel {?} {=} 48 + 60 + 48 \\ 156 & = 156 \; \ checkmark \ end {split} $$
Шаг 7. Ответьте на вопрос. Арианна может сделать каждую из двух равных сторон по 48 дюймов в длину.

Упражнение \ (\ PageIndex {25} \):

Палуба заднего двора имеет форму равнобедренного треугольника с основанием 20 футов. Периметр палубы 48 футов. Какова длина каждой из равных сторон колоды?

Ответ

14 футов

Упражнение \ (\ PageIndex {26} \):

Парус лодки представляет собой равнобедренный треугольник с основанием 8 метров. Периметр — 22 метра. Какова длина каждой из равных сторон паруса?

Ответ

7 м

Используйте свойства трапеций

Трапеция — это четырехсторонняя фигура, четырехугольник , с двумя сторонами, которые параллельны, и двумя сторонами, которые не параллельны.Параллельные стороны называются основаниями. Мы называем длину меньшего основания b и длину большего основания B. Высота h трапеции — это расстояние между двумя основаниями, как показано на рисунке \ (\ PageIndex {13} \).

Рисунок \ (\ PageIndex {13} \) — Трапеция имеет большее основание, B, и меньшее основание, b. Высота h — это расстояние между основаниями.

Формула площади трапеции:

\ [Area_ {trapezoid} = \ dfrac {1} {2} h (b + B) \]

Разделение трапеции на два треугольника может помочь нам понять формулу.Площадь трапеции — это сумма площадей двух треугольников. См. Рисунок \ (\ PageIndex {14} \).

Рисунок \ (\ PageIndex {14} \) — Разделение трапеции на два треугольника может помочь вам понять формулу для ее площади.

Высота трапеции — это также высота каждого из двух треугольников. См. Рисунок \ (\ PageIndex {15} \).

Рисунок \ (\ PageIndex {15} \)

Формула площади трапеции

\ [Area_ {trapezoid} = \ dfrac {1} {2} h (\ textcolor {blue} {b} + \ textcolor {red} {B}) \]

Если раздадим, то получим,

Определение: Свойства трапеций

  • Трапеция имеет четыре стороны.См. Рисунок 9.25.
  • Две его стороны параллельны, а две — нет.
  • Площадь A трапеции равна A = \ (\ dfrac {1} {2} \) h (b + B).

Пример \ (\ PageIndex {14} \):

Найдите площадь трапеции, высота которой 6 дюймов, а основания 14 и 11 дюймов.

Раствор

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.
Шаг 2. Определите то, что вы ищете. площадь трапеции
Шаг 3. Имя . Выберите переменную для ее представления. Пусть A = площадь
Шаг 4. Перевести . Напишите соответствующую формулу. Заменять.
Шаг 5. Решите уравнение. $$ \ begin {split} A & = \ dfrac {1} {2} \ cdot 6 (25) \\ A & = 3 (25) \\ A & = 75 \; квадратный\; дюймы \ end {split} $$
Шаг 6. Проверка : разумен ли этот ответ?

Если мы нарисуем прямоугольник вокруг трапеции с таким же большим основанием B и высотой h, его площадь должна быть больше, чем у трапеции.

Если мы нарисуем прямоугольник внутри трапеции, имеющий такое же маленькое основание b и высоту h, его площадь должна быть меньше, чем у трапеции.

Площадь большего прямоугольника составляет 84 квадратных дюйма, а площадь меньшего прямоугольника — 66 квадратных дюймов.Таким образом, имеет смысл, что площадь трапеции составляет от 84 до 66 квадратных дюймов

.
Шаг 7. Ответьте на вопрос. Площадь трапеции составляет 75 квадратных дюймов.

Упражнение \ (\ PageIndex {27} \):

Высота трапеции 14 ярдов, а оснований 7 и 16 ярдов. Какой район?

Ответ

161 кв. Ярд

Упражнение \ (\ PageIndex {28} \):

Высота трапеции 18 сантиметров, основания 17 и 8 сантиметров.Какой район?

Ответ

255 кв. См

Пример \ (\ PageIndex {15} \):

Найдите площадь трапеции высотой 5 футов и основаниями 10,3 и 13,7 футов.

Раствор

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.
Шаг 2. Определите то, что вы ищете. площадь трапеции
Шаг 3. Имя . Выберите переменную для ее представления. Пусть A = площадь
Шаг 4. Перевести . Напишите соответствующую формулу. Заменять.
Шаг 5. Решите уравнение. $$ \ begin {split} A & = \ dfrac {1} {2} \ cdot 5 (24) \\ A & = 12 \ cdot 5 \\ A & = 60 \; квадратный\; футов \ end {split} $$
Шаг 6. Проверка : разумен ли этот ответ? Площадь трапеции должна быть меньше площади прямоугольника с основанием 13,7 и высотой 5, но больше площади прямоугольника с основанием 10,3 и высотой 5.
Шаг 7. Ответьте на вопрос. Площадь трапеции составляет 60 квадратных футов.

Упражнение \ (\ PageIndex {29} \):

Высота трапеции 7 сантиметров, оснований 4.6 и 7,4 сантиметра. Какой район?

Ответ

42 кв. См

Упражнение \ (\ PageIndex {30} \):

Высота трапеции 9 метров, оснований 6,2 и 7,8 метра. Какой район?

Ответ

63 кв.м

Пример \ (\ PageIndex {16} \):

У Винни есть сад в форме трапеции. Трапеция имеет высоту 3.4 ярда, а основания — 8,2 и 5,6 ярда. Сколько квадратных ярдов будет доступно для посадки?

Раствор

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.
Шаг 2. Определите то, что вы ищете. площадь трапеции
Шаг 3. Имя .Выберите переменную для ее представления. Пусть A = площадь
Шаг 4. Перевести . Напишите соответствующую формулу. Заменять.
Шаг 5. Решите уравнение. $$ \ begin {split} A & = \ dfrac {1} {2} \ cdot (3.4) (13.8) \\ A & = 23.46 \; квадратный\; ярдов \ end {split} $$

Шаг 6. Проверить : Разумен ли этот ответ? Да.Площадь трапеции меньше площади прямоугольника с основанием 8,2 ярда и высотой 3,4 ярда, но больше площади прямоугольника с основанием 5,6 ярда и высотой 3,4 ярда.

Шаг 7. Ответьте на вопрос. У Винни 23,46 квадратных ярда, на которых он может сажать растения.

Упражнение \ (\ PageIndex {31} \):

Линь хочет подстричь лужайку, имеющую форму трапеции.Основания составляют 10,8 ярда и 6,7 ярда, а высота — 4,6 ярда. Сколько квадратных ярдов дерна ему нужно?

Ответ

40,25 кв. Ярда

Упражнение \ (\ PageIndex {32} \):

Кира хочет покрыть свой внутренний двор бетонной брусчаткой. Если внутренний дворик имеет форму трапеции с основанием 18 футов 14 футов и высотой 15 футов, сколько квадратных футов брусчатки ему понадобится?

Ответ

240 кв.фут

Практика ведет к совершенству

Использование свойств прямоугольников

В следующих упражнениях найдите (а) периметр и (б) площадь каждого прямоугольника.

  1. Длина прямоугольника составляет 85 футов, а ширина — 45 футов.
  2. Длина прямоугольника составляет 26 дюймов, а ширина — 58 дюймов.
  3. Прямоугольная комната 15 футов шириной и 14 футов длиной.
  4. Подъездная дорога имеет форму прямоугольника 20 футов шириной и 35 футов длиной.

В следующих упражнениях решите.

  1. Найдите длину прямоугольника с периметром 124 дюйма и шириной 38 дюймов.
  2. Найдите длину прямоугольника с периметром 20,2 ярда и шириной 7,8 ярда.
  3. Найдите ширину прямоугольника с периметром 92 метра и длиной 19 метров.
  4. Найдите ширину прямоугольника с периметром 16,2 метра и длиной 3,2 метра.
  5. Площадь прямоугольника 414 квадратных метров.Длина 18 метров. Какая ширина?
  6. Площадь прямоугольника 782 квадратных сантиметра. Ширина 17 сантиметров. Какая длина?
  7. Длина прямоугольника на 9 дюймов больше ширины. По периметру 46 дюймов. Найдите длину и ширину.
  8. Ширина прямоугольника на 8 дюймов больше его длины. По периметру 52 дюйма. Найдите длину и ширину.
  9. Периметр прямоугольника 58 метров. Ширина прямоугольника на 5 метров меньше длины.Найдите длину и ширину прямоугольника.
  10. Периметр прямоугольника 62 фута. Ширина на 7 футов меньше длины. Найдите длину и ширину.
  11. Ширина прямоугольника на 0,7 метра меньше длины. Периметр прямоугольника 52,6 метра. Найдите размеры прямоугольника.
  12. Длина прямоугольника на 1,1 метра меньше ширины. Периметр прямоугольника 49,4 метра. Найдите размеры прямоугольника.
  13. Периметр прямоугольника 150 футов. Длина прямоугольника в два раза больше ширины. Найдите длину и ширину прямоугольника.
  14. Длина прямоугольника в три раза больше ширины. Периметр 72 фута. Найдите длину и ширину прямоугольника.
  15. Длина прямоугольника на 3 метра меньше двойной ширины. Периметр — 36 метров. Найдите длину и ширину.
  16. Длина прямоугольника на 5 дюймов больше, чем в два раза ширины.По периметру 34 дюйма. Найдите длину и ширину.
  17. Ширина прямоугольного окна 24 дюйма. Площадь — 624 квадратных дюйма. Какая длина?
  18. Длина прямоугольного плаката составляет 28 дюймов. Площадь составляет 1316 квадратных дюймов. Какая ширина?
  19. Площадь прямоугольной крыши — 2310 квадратных метров. Длина 42 метра. Какая ширина?
  20. Площадь прямоугольного брезента составляет 132 квадратных фута. Ширина 12 футов. Какая длина?
  21. Периметр прямоугольного двора составляет 160 футов.Длина на 10 футов больше ширины. Найдите длину и ширину.
  22. Периметр прямоугольной картины 306 сантиметров. Длина на 17 сантиметров больше ширины. Найдите длину и ширину.
  23. Ширина прямоугольного окна на 40 дюймов меньше высоты. Периметр дверного проема — 224 дюйма. Найдите длину и ширину.
  24. Ширина прямоугольной площадки на 7 метров меньше длины. Периметр детской площадки 46 метров.Найдите длину и ширину.

Используйте свойства треугольников

В следующих упражнениях решайте задачи, используя свойства треугольников.

  1. Найдите площадь треугольника с основанием 12 дюймов и высотой 5 дюймов.
  2. Найдите площадь треугольника с основанием 45 см и высотой 30 см.
  3. Найдите площадь треугольника с основанием 8,3 метра и высотой 6,1 метра.
  4. Найдите площадь треугольника с основанием 24.2 фута и высота 20,5 футов.
  5. Треугольный флаг имеет основание 1 фут и высоту 1,5 фута. Какая у него площадь?
  6. Треугольное окно имеет основание 8 футов и высоту 6 футов. Какая у него площадь?
  7. Если треугольник имеет стороны 6 футов и 9 футов, а периметр равен 23 футам, какова длина третьей стороны?
  8. Если треугольник имеет стороны 14 и 18 см, а периметр равен 49 см, какова длина третьей стороны?
  9. Что такое основание треугольника площадью 207 квадратных дюймов и высотой 18 дюймов?
  10. Какова высота треугольника площадью 893 квадратных дюйма и основанием 38 дюймов?
  11. Периметр треугольного отражающего бассейна составляет 36 ярдов.Длина двух сторон составляет 10 ярдов и 15 ярдов. Какова длина третьей стороны?
  12. Треугольный двор имеет периметр 120 метров. Длина двух сторон 30 метров и 50 метров. Какова длина третьей стороны?
  13. Равнобедренный треугольник имеет основание 20 сантиметров. Если периметр равен 76 сантиметрам, найдите длину каждой из других сторон.
  14. Равнобедренный треугольник имеет основание 25 дюймов. Если периметр составляет 95 дюймов, найдите длину каждой из других сторон.
  15. Найдите длину каждой стороны равностороннего треугольника с периметром 51 ярд.
  16. Найдите длину каждой стороны равностороннего треугольника с периметром 54 метра.
  17. Периметр равностороннего треугольника 18 метров. Найдите длину каждой стороны.
  18. Периметр равностороннего треугольника составляет 42 мили. Найдите длину каждой стороны.
  19. Периметр равнобедренного треугольника составляет 42 фута. Длина самой короткой стороны — 12 футов.Найдите длину двух других сторон.
  20. Периметр равнобедренного треугольника составляет 83 дюйма. Длина самой короткой стороны — 24 дюйма. Найдите длину двух других сторон.
  21. Блюдо имеет форму равностороннего треугольника. Каждая сторона 8 дюймов в длину. Найдите периметр.
  22. Плитка для пола имеет форму равностороннего треугольника. Каждая сторона 1,5 фута в длину. Найдите периметр.
  23. Дорожный знак в форме равнобедренного треугольника имеет основание 36 дюймов.Если периметр составляет 91 дюйм, найдите длину каждой из других сторон.
  24. Платок в форме равнобедренного треугольника имеет основу 0,75 метра. Если периметр составляет 2 метра, найдите длину каждой из других сторон.
  25. Периметр треугольника составляет 39 футов. Одна сторона треугольника на 1 фут длиннее второй. Третья сторона на 2 фута длиннее второй. Найдите длину каждой стороны.
  26. Периметр треугольника составляет 35 футов.Одна сторона треугольника на 5 футов длиннее второй. Третья сторона на 3 фута длиннее второй. Найдите длину каждой стороны.
  27. Одна сторона треугольника в два раза меньше наименьшей стороны. Третья сторона на 5 футов больше самой короткой. Периметр — 17 футов. Найдите длины всех трех сторон.
  28. Одна сторона треугольника в три раза больше наименьшей стороны. Третья сторона на 3 фута больше самой короткой. Периметр — 13 футов. Найдите длины всех трех сторон.

Использование свойств трапеций

В следующих упражнениях решайте, используя свойства трапеций.

  1. Высота трапеции составляет 12 футов, а основание — 9 и 15 футов. Какой район?
  2. Высота трапеции 24 ярда, а основания 18 и 30 ярдов. Какой район?
  3. Найдите площадь трапеции высотой 51 метр и основаниями 43 и 67 метров.
  4. Найдите площадь трапеции высотой 62 дюйма и основаниями 58 и 75 дюймов.
  5. Высота трапеции составляет 15 сантиметров, а основания — 12,5 и 18,3 сантиметра. Какой район?
  6. Высота трапеции составляет 48 футов, а основание — 38,6 и 60,2 фута. Какой район?
  7. Найдите площадь трапеции высотой 4,2 метра и основанием 8,1 и 5,5 метра.
  8. Найдите площадь трапеции высотой 32,5 см и основаниями 54,6 и 41,4 см.
  9. Лорел делает знамя в форме трапеции.Высота баннера составляет 3 фута, а основания — 4 и 5 футов. Какая площадь у баннера?
  10. Нико хочет выложить плиткой пол в ванной. Пол имеет форму трапеции шириной 5 футов и длиной 5 и 8 футов. Какая площадь этажа?
  11. Терезе нужна новая столешница для кухонной стойки. Счетчик имеет форму трапеции шириной 18,5 дюйма и длиной 62 и 50 дюймов. Какая площадь прилавка?
  12. Елена вяжет шарф.Шарф будет иметь форму трапеции шириной 8 дюймов и длиной 48,2 дюйма и 56,2 дюйма. Какая площадь у шарфа?

Где средняя линия трапеции. Диагонали трапеции. Треугольники-трапеции равной площади

  1. Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований
  2. Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения, подобны
  3. Треугольники, образованные сегментами диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равны (имеют одинаковую площадь)
  4. Если вы продлите боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой линией, соединяющей средние точки оснований
  5. Отрезок, соединяющий основания трапеции и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в ​​пропорции, равной отношению длин оснований трапеции
  6. Отрезок, параллельный основаниям трапеции и проведенный через точку пересечения диагоналей, делится этой точкой пополам, и его длина составляет 2ab / (a ​​+ b), где a и b — основания трапеции

Свойства отрезка прямой, соединяющего середины диагоналей трапеции

Соединяем середины диагоналей трапеции ABCD, в результате чего получаем отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .

Этот отрезок параллелен основаниям трапеции .

Длина отрезка, соединяющего середины диагоналей трапеции, равна половине разности ее оснований.

LM = (AD — BC) / 2
или
ЛМ = (а-б) / 2

Свойства треугольников, образованных диагоналями трапеции


Треугольники, образованные основанием трапеции и точкой пересечения диагоналей трапеции — , аналогичны .
Треугольники BOC и AOD похожи. Поскольку углы BOC и AOD вертикальные, они равны.
Углы OCB и OAD являются внутренними крестообразно с параллельными линиями AD и BC (основания трапеции параллельны друг другу) и секущей AC, следовательно, они равны.
Углы OBC и ODA равны по той же причине (внутреннее пересечение).

Поскольку все три угла одного треугольника равны соответствующим углам другого треугольника, эти треугольники подобны.

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если мы знаем значения длин двух соответствующих элементов одинаковых треугольников, то находим коэффициент подобия (делим один на другой). Следовательно, длины всех других элементов относятся друг к другу с одинаковым значением.

Свойства боковых треугольников и диагоналей трапеции


Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD.Это треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон этих треугольников могут быть совершенно разными, но площади треугольников, образованных сторонами и точкой пересечения диагоналей трапеции, равны , то есть треугольники равны по площади. размер.


Если вы продлите стороны трапеции к меньшему основанию, то точка пересечения сторон будет , выровненная с прямой линией, проходящей через средние точки оснований .

Таким образом, любую трапецию можно продолжить до треугольника. Где:

  • Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения вытянутых боковых сторон, аналогичны
  • Прямая линия, соединяющая середины оснований трапеции, является одновременно и серединой построенного треугольника

Свойства линии, соединяющей основания трапеции


Если провести отрезок, концы которого лежат на основаниях трапеции, лежащей в точке пересечения диагоналей трапеции (KN), то отношение составляющих его отрезков со стороны основания к точка пересечения диагоналей (KO / ON) будет равна отношению оснований трапеции (BC / AD).

КО / ОН = ВС / АД

Это свойство следует из подобия соответствующих треугольников (см. Выше).

Свойства линий, параллельных основанию трапеции


Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет иметь следующие свойства:

  • Предустановленное расстояние (км) делит точку пересечения диагоналей трапеции пополам
  • Длина сегмента , проходящего через точку пересечения диагоналей трапеции и параллельно основанию, равна КМ = 2ab / (a ​​+ b)

Формулы нахождения диагоналей трапеции


а, б — основание трапеции

c, d — боковые стороны трапеции

d1 d2 — диагонали трапеции

α β — уголки с большим основанием трапеции

Формулы для нахождения диагоналей трапеции через основания, стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1. Сумма квадратов диагоналей трапеции равна сумме квадратов сторон плюс удвоенное произведение ее оснований. Это свойство диагоналей трапеции можно доказать в виде отдельной теоремы

.

2 … Эта формула получается преобразованием предыдущей формулы. Квадрат второй диагонали перебрасывается через знак равенства, после чего извлекается квадратный корень из левой и правой частей выражения.

3 … Эта формула для определения длины диагонали трапеции аналогична предыдущей, с той разницей, что другая диагональ остается слева от выражения

Следующая группа формул (4-5) аналогична по значению и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна сторона и угол при основании.

Формулы для определения диагоналей трапеции по высоте


Примечание … Этот урок дает решение геометрических задач о трапеции. Если вы не нашли решение геометрической задачи интересующего вас типа — задайте вопрос на форуме .

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке O. Найти длину основания ВС трапеции, если основание АD = 24 см, длина AO = 9 см, длина ОС = 6 см.

Решение .
Идеологически решение этой проблемы абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC похожи по трем углам — AOD и BOC вертикальны, а остальные углы равны попарно, так как они образованы пересечением одной прямой и двух параллельных линий.

Поскольку треугольники подобны, все их геометрические размеры связаны друг с другом, как известные нам из постановки задачи геометрические размеры отрезков AO и OC. Т.е.

AO / OC = AD / BC
9/6 = 24 / BC
BC = 24 * 6/9 = 16

Ответ : 16 см

Задача.
В трапеции ABCD известно, что AD = 24, BC = 8, AC = 13, BD = 5√17. Найдите площадь трапеции.

Решение.
Чтобы найти высоту трапеции от вершин меньшего основания B и C, мы понижаем две высоты до большего основания. Поскольку трапеция неравная, обозначим длину AM = a, длину KD = b (не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, и мы опустили две высоты, перпендикулярные большему основанию, то MBCK представляет собой прямоугольник.

Средство
AD = AM + BC + KD
a + 8 + b = 24
a = 16 — b

Треугольники DBM и ACK прямоугольные, так как их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2

Учтем, что a = 16 — b, тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2

Подставим значение квадрата высоты в второе уравнение, полученное по теореме Пифагора.Получаем:
425 — (8 + b) 2 + (24 — b) 2 = 169
— (64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12

Итак, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5

Найдите площадь трапеции по ее высоте и половину суммы оснований
, где ab — основание трапеции, h — высота трапеции
S = (24 + 8) * 5/2 = 80 см 2

Ответ : площадь трапеции 80 см 2.

средняя линия фигуры в планиметрии — отрезок, соединяющий середины двух сторон этой фигуры. Понятие использовано для следующих фигур: треугольник, четырехугольник, трапеция.

Энциклопедический YouTube

    1 / 3

    ✪ 8 класс, 25 урок, Средняя линия треугольника

    ✪ геометрия СРЕДНИЙ ТРЕУГОЛЬНИК Атанасян 8 сорт

    ✪ Средняя линия треугольника | Геометрия 7-9 класс №62 | Инфо-урок

    Субтитры

Средняя линия треугольника

Свойства

  • средняя линия треугольника параллельна основанию и равна его половине.
  • , когда все три средние линии пересекаются, образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
  • средняя линия отсекает похожий на этот треугольник, а его площадь равна одной четвертой площади исходного треугольника.
  • Три средние линии треугольника делят его на 4 равных (одинаковых) треугольника, подобных исходному треугольнику. Все четыре одинаковых треугольника называются средними треугольниками.Центр этих 4 одинаковых треугольников называется дополнительным треугольником.

Знаки

  • если сегмент параллелен одной из сторон треугольника и соединяет среднюю точку одной стороны треугольника с точкой на другой стороне треугольника, то это средняя линия.

Средняя линия четырехугольника

Средняя линия четырехугольника — отрезок, соединяющий середины противоположных сторон четырехугольника.

Недвижимость

Первая линия соединяет 2 противоположные стороны. Второй соединяет 2 другие противоположные стороны. Третий соединяет центры двух диагоналей (не все четырехугольники имеют точку пересечения, которая делит диагонали пополам).

  • Если в выпуклом четырехугольнике средняя линия составляет равные углы с диагоналями четырехугольника, то диагонали равны.
  • Длина центральной линии четырехугольника меньше половины суммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
  • Середины сторон произвольного четырехугольника — это вершины параллелограмма. Его площадь составляет половину площади четырехугольника, а центр лежит на пересечении срединных линий. Этот параллелограмм называется параллелограммом Вариньона;
  • Последняя точка означает следующее: В выпуклом четырехугольнике четыре средних линий второго рода . Средние линии второго рода — четыре отрезка внутри четырехугольника, проходящие через середины его соседних сторон параллельно диагоналям.Четыре средних линий второго вида выпуклый четырехугольник, разрежьте его на четыре треугольника и один центральный четырехугольник. Этот центральный четырехугольник — параллелограмм Вариньона.
  • Точка пересечения срединных линий четырехугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она

Четырехугольник с параллельными только двумя сторонами называется трапецией .

Параллельные стороны трапеции называются основаниями , а те стороны, которые не параллельны, называются боковыми сторонами … Если стороны равны, то такая трапеция равнобедренная. Расстояние между основаниями называется высотой трапеции.

Средняя линия трапеции

Средняя линия — это отрезок прямой, соединяющий середины сторон трапеции. Средняя линия трапеции параллельна ее основаниям.

Теорема:

Если прямая линия, пересекающая середину одной стороны, параллельна основанию трапеции, то она делит пополам вторую сторону трапеции.

Теорема:

Длина средней линии равна среднему арифметическому длин ее оснований

MN || AB || DC
AM = MD; BN = NC

MN средняя линия, AB и CD — основания, AD и BC — стороны

МН = (AB + DC) / 2

Теорема:

Длина средней линии трапеции равна среднему арифметическому длин ее оснований.

Основная задача : Докажите, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине основания трапеции.

Центральная линия треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Он параллелен третьей стороне и составляет половину длины третьей стороны.
Теорема : Если линия, пересекающая середину одной стороны треугольника, параллельна другой стороне этого треугольника, то она делит третью сторону пополам.

AM = MC и BN = NC =>

Применить свойства осевой линии треугольника и трапеции

Разделение отрезка на определенное количество равных частей.
Задача: разделить отрезок AB на 5 равных частей.
Решение:
Пусть p — случайный луч с началом в точке A, не лежащий на прямой AB. Накладываем последовательно 5 равных отрезков на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 ​​A 5
Соединяем A 5 с B и проводим такие линии через A 4, A 3, A 2 и A 1, которые параллельны A 5 B. Они пересекают AB, соответственно, в точках B 4, B 3, B 2 и B 1. Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3.Таким же образом из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2

При этом из трапеции B 3 B 1 A 1 A 3, B 3 B 2 = B 2 B 1.
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключение получаем :
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Понятно, что чтобы разделить отрезок AB на другое количество равных частей, нам нужно спроецировать такое же число равных отрезков на луч p. А затем продолжайте, как описано выше.

В этой статье мы постараемся максимально полно отразить свойства трапеции. В частности, мы поговорим об общих чертах и ​​свойствах трапеции, а также о свойствах вписанной трапеции и о круге, вписанном в трапецию. Мы коснемся свойств равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет разобраться в местах в голове и лучше запомнить материал.

Трапеция и все-все

Для начала кратко напомним, что такое трапеция и какие еще понятия с ней связаны.

Итак, трапеция — это четырехугольная фигура, две стороны которой параллельны друг другу (это основания). И две не параллельны — это стороны.

У трапеции высота может быть уменьшена — перпендикулярно основанию. Рисуются средняя линия и диагонали. А также с любого угла трапеции можно провести биссектрису.

Теперь мы поговорим о различных свойствах, связанных со всеми этими элементами и их комбинациями.

Свойства диагоналей трапеции

Для большей ясности при чтении нарисуйте на листе бумаги трапецию AKME и нарисуйте на ней диагонали.

  1. Если вы найдете середины каждой из диагоналей (обозначим эти точки как X и T) и соедините их, вы получите сегмент. Одним из свойств диагоналей трапеции является то, что сегмент XT лежит на средней линии.А его длину можно получить, разделив разность баз на два: XT = (a — b) / 2 .
  2. Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке O. Рассмотрим треугольники AOE и MOC, образованные отрезками прямых вместе с основаниями трапеции. Эти треугольники похожи. Коэффициент подобия k треугольников выражается через соотношение оснований трапеции: k = AE / KM.
    Соотношение площадей треугольников AOE и MOC описывается коэффициентом k 2.
  3. Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только на этот раз мы рассмотрим треугольники, которые составляли отрезки диагоналей вместе с боковыми сторонами трапеции. Площади треугольников AKO и EMO равны — их площади одинаковы.
  4. Еще одно свойство трапеции — построение диагоналей. Итак, если мы продолжим боковые стороны АК и МЕ в сторону меньшего основания, то рано или поздно они пересекутся в какую-то точку.Далее через середину основ трапеции проведите прямую линию. Она пересекает основания в точках X и T.
    Если мы теперь продолжим линию XT, то она соединит вместе точку пересечения диагоналей трапеции O, точку, в которой продолжаются боковые стороны и середины трапеции. основания X и T пересекаются.
  5. Через точку пересечения диагоналей проведите отрезок, соединяющий основания трапеции (T лежит на меньшем основании CM, X — на большем AE).Точка пересечения диагоналей делит этот отрезок в следующем соотношении: TO / OX = KM / AE .
  6. А теперь через точку пересечения диагоналей проведите отрезок, параллельный основаниям трапеции (а и б). Перекресток разделит его на две равные части. Длину отрезка можно найти по формуле 2ab / (a ​​+ b) .

Свойства осевой линии трапеции

Проведите среднюю линию трапеции параллельно ее основаниям.

  1. Длину средней линии трапеции можно рассчитать, сложив длины оснований и разделив их пополам: м = (a + b) / 2 .
  2. Если вы проведете какой-либо сегмент (например, высоту) через оба основания трапеции, средняя линия разделит его на две равные части.

Свойство биссектрисы трапеции

Выберите любой угол трапеции и проведите биссектрису. Возьмем, к примеру, угол KAE нашей трапеции AKME.Завершив конструкцию самостоятельно, вы легко можете убедиться, что биссектриса отрезает от основания (или ее продолжения по прямой вне самой фигуры) отрезок такой же длины, как и сторона.

Свойства угла трапеции

  1. Какую бы из двух пар углов, примыкающих к боковой стороне, вы не выбрали, сумма углов в паре всегда будет 180 0: α + β = 180 0 и γ + δ = 180 0.
  2. Соедините середину основания трапеции с сегментом TX.Теперь посмотрим на углы у основания трапеции. Если сумма углов на любом из них равна 90 0, длину сегмента TX легко рассчитать исходя из разницы длин оснований, разделенной пополам: TX = (AE — KM) / 2 .
  3. Если провести параллельные прямые линии через стороны угла трапеции, они разделят стороны угла на пропорциональные сегменты.

Свойства равнобедренной (равнобедренной) трапеции

  1. У равнобедренной трапеции углы равны при любом из оснований.
  2. Теперь нарисуйте трапецию еще раз, чтобы было легче представить, о чем она. Посмотрите внимательно на основание AE — вершина противоположного основания M проецируется на точку на линии, которая содержит AE. Расстояние от вершины A до точки проекции вершины M и средней линии равнобедренной трапеции равны.
  3. Несколько слов о свойстве диагоналей равнобедренных трапеций — их длины равны. А также углы наклона этих диагоналей к основанию трапеции такие же.
  4. Окружность может быть описана только около равнобедренной трапеции, так как сумма противоположных углов четырехугольника 180 0 является предпосылкой для этого.
  5. Свойство равнобедренной трапеции следует из предыдущего абзаца — если окружность можно описать около трапеции, то она равнобедренная.
  6. Из особенностей равнобедренной трапеции следует свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b ) / 2 .
  7. Снова проведите сегмент TX через середины основания трапеции — у равнобедренной трапеции он перпендикулярен основаниям. И в то же время TX является осью симметрии равнобедренной трапеции.
  8. На этот раз уменьшите до большего основания (обозначьте его a) высоту от противоположной вершины трапеции. Будет два сегмента. Длину одного можно найти, если сложить длины оснований и разделить пополам: (a + b) / 2 … Второй получается, когда мы вычитаем меньшее из большего основания и делим полученное разница в два раза: (а — б) / 2 .

Свойства трапеции, вписанной в круг

Поскольку мы уже говорили о трапеции, вписанной в круг, остановимся на этом вопросе более подробно. В частности, где центр круга находится по отношению к трапеции. Здесь тоже рекомендуется не полениться взять в руки карандаш и нарисовать то, о чем пойдет речь ниже. Так вы быстрее поймете и лучше запомните.

  1. Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне.Например, диагональ может проходить от вершины трапеции под прямым углом к ​​стороне. В этом случае большее основание пересекает центр описанной окружности ровно посередине (R = ½AE).
  2. Диагональ и сторона также могут пересекаться под острым углом — тогда центр круга находится внутри трапеции.
  3. Центр описанной окружности может находиться за пределами трапеции, за ее большим основанием, если между диагональю трапеции и боковой стороной имеется тупой угол.
  4. Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол), составляет половину соответствующего ей центрального угла: MAE = ½MOE .
  5. Вкратце о двух способах определения радиуса описанной окружности. Метод первый: внимательно посмотрите на свой рисунок — что вы видите? Вы легко заметите, что диагональ делит трапецию на два треугольника. Радиус можно найти как отношение стороны треугольника к синусу противоположного угла, умноженное на два.Например, R = AE / 2 * sinAME … Аналогично формулу можно записать для любой стороны обоих треугольников.
  6. Метод второй: найти радиус описанной окружности через площадь треугольника, образованного диагональю, стороной и основанием трапеции: R = AM * ME * AE / 4 * S AME .

Свойства трапеции, описанной вокруг окружности

Можно вписать круг в трапецию, если выполнено одно условие.Подробнее об этом ниже. В совокупности это сочетание форм обладает рядом интересных свойств.

  1. Если в трапецию вписан круг, длину его средней линии можно легко найти, сложив длины боковых сторон и разделив полученную сумму пополам: м = (c + d) / 2 .
  2. В трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин сторон: АК + МЕ = КМ + АЕ .
  3. Из этого свойства оснований трапеции следует противоположное утверждение: в эту трапецию можно вписать круг, сумма оснований которого равна сумме боковых сторон.
  4. Точка касания окружности радиуса r, вписанной в трапецию, разделяет сторону на два сегмента, назовем их a и b. Радиус круга можно рассчитать по формуле: r = √ab .
  5. И еще одно свойство. Чтобы не запутаться, нарисуйте этот пример самостоятельно.У нас есть старая добрая трапеция АКМЕ, описанная по окружности. На нем нанесены диагонали, пересекающиеся в точке O. Треугольники AOK и EOM, образованные отрезками диагоналей и сторонами, имеют прямоугольную форму.
    Высоты этих треугольников, опущенных на гипотенузы (т. Е. Боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции совпадает с диаметром вписанной окружности.

Прямоугольная трапеция Свойства

Называется прямоугольная трапеция, один из углов которой правый.И его свойства проистекают из этого обстоятельства.

  1. У прямоугольной трапеции одна из боковых сторон перпендикулярна основанию.
  2. Высота и боковая сторона трапеции, прилегающая к прямому углу, равны. Это позволяет рассчитать площадь прямоугольной трапеции (общая формула S = (a + b) * h / 2 ) не только по высоте, но и через прилегающую к прямому углу сторону.
  3. Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.

Доказательства некоторых свойств трапеции

Равенство углов у основания равнобедренной трапеции:

  • Вы, наверное, уже догадались, что здесь нам снова понадобится трапеция АКМЕ — нарисуйте равнобедренную трапецию. Нарисуйте сверху M прямую линию MT, параллельную стороне AK (MT || AK).

Получившийся четырехугольник AKMT представляет собой параллелограмм (AK || MT, KM || AT). Поскольку ME = KA = MT, ∆ MTE — равнобедренный, а MET = MTE.

АК || MT, поэтому MTE = KAE, MET = MTE = KAE.

Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЭ = КМЕ.

Q.E.D.

Теперь, основываясь на свойстве равнобедренной трапеции (равенство диагоналей), мы доказываем, что трапеция AKME равнобедренная :

  • Для начала проведем прямую MX — MX || KE. Получаем параллелограмм KMXE (основание — MX || KE и KM || EX).

∆AMX — равнобедренный, так как AM = KE = MX, а MAX = MEA.

MX || KE, KEA = MXE, поэтому MAE = MXE.

Оказалось, что треугольники AKE и EMA равны между собой, потому что AM = KE и AE являются общей стороной двух треугольников. А также MAE = MXE. Можно сделать вывод, что АК = МЕ, а из этого следует, что трапеция АКМЕ равнобедренная.

Повторяющееся задание

Основания трапеции АКМЕ 9 см и 21 см, борт КА, равный 8 см, образует угол 150 0 с меньшим основанием.Требуется найти площадь трапеции.

Решение: От вершины K мы уменьшаем высоту до большего основания трапеции. И начнем с углов трапеции.

Уголки AEM и KAN односторонние. Это значит, что в сумме они дают 180 0. Следовательно, КАН = 30 0 (исходя из свойства угла трапеции).

Рассмотрим теперь прямоугольную ∆ANK (я думаю, этот момент очевиден для читателей без дополнительных доказательств). Из него находим высоту трапеции KN — в треугольнике это ножка, лежащая напротив угла 30 0.Следовательно, KH = ½AB = 4 см.

Площадь трапеции находится по формуле: S АКМЕ = (КМ + АЕ) * КН / 2 = (9 + 21) * 4/2 = 60 см 2.

Послесловие

Если вы внимательно и вдумчиво изучили эту статью, не поленились нарисовать карандашом в руке трапеции для всех вышеперечисленных свойств и разобрать их на практике, то материал должен был быть вам хорошо понят.

Конечно, здесь очень много информации, разнообразной и порой даже запутанной: спутать свойства описанной трапеции со свойствами вписанной не так уж и сложно.Но вы сами убедились, что разница огромна.

Теперь у вас есть подробный план всех общих свойств трапеции.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *