| Решение | Пусть . Отрезок соединяет середины диагоналей и лежит на средней линии :
Так как – середина диагонали, то
Треугольники и – подобные, а значит , откуда см. Следовательно,
Найдем среднюю линию трапеции
|
ru.solverbook.com
Все формулы диагоналей трапеции
Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны

a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:


Формулы диагоналей трапеции через четыре стороны:


2. Формула длины диагоналей трапеции через высоту

a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β
h — высота трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции через высоту:






3. Формула длины диагонали трапеции через другую диагональ

a — нижнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции :


Справедливо для данного случая :
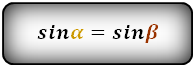
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей

a — нижнее основание
b — верхнее основание
c , d — боковые стороны
d1 , d2 — диагонали трапеции
Формула суммы квадратов диагоналей :

Формулы диагоналей трапеции :


Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
www-formula.ru
Диагональ трапеции
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:
Формулы диагоналей трапеции через четыре стороны:
2. Формула длины диагоналей трапеции через высоту
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции через высоту:
3. Формула длины диагонали трапеции через другую диагональ
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции :
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
d1 , d2 — диагонали трапеции
Формула суммы квадратов диагоналей :
Формулы диагоналей трапеции :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
zdesformula.ru
Прямоугольная трапеция
См. также: трапеция и ее свойства. Прямоугольная трапеция — это трапеция, у которой хотя бы один из углов прямой (классическое определение)Примечание. На самом деле, у прямоугольной трапеции, как минимум, два прямых угла (см. ниже — свойства)
Другие определения:
- Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
Формулы для прямоугольной трапеции
Обозначения формул даны на чертеже выше.Соответственно:
a и b — основания трапеции
с — боковая сторона прямоугольной трапеции, перпендикулярная основаниям
d — боковая сторона трапеции, не являющаяся перпендикулярной основаниям
α — острый угол при большем основании трапеции
m — средняя линия трапеции
Интерпретация формул:
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна высоте трапеции (Формула 1)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна произведению синуса острого угла при большем основании на длину второй боковой стороны. (Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)Боковая сторона, перпендикулярная основаниям, равна произведению разности оснований на тангенс острого угла при большем основании. (Треугольник CKD — прямоугольный. Поскольку трапеция — прямоугольная, то длина KD — это и есть разность оснований, а h/KD=tgα по определению тангенса, а c=h, откуда с/KD=tgα) (Формула 3)
Боковая сторона, которая не перпендикулярна основаниям, равна частному разности оснований к косинусу острого угла при большем основании или частному высоты трапеции и синуса острого угла при большем основании. (разность оснований равна KD. В прямоугольном треугольнике CKD по определению косинуса cos α = KD / d, откуда и проистекает искомая формула) (Формула 4)
Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна корню квадратному из разности квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна корню квадратному из суммы квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, прямоугольный, далее — следствие из теоремы Пифагора — находим сумму квадратов катетов и извлекаем из полученного выражения квадратный корень) (Формула 6)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна частному от деления двойной площади трапеции на сумму ее оснований. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 7)
Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна частному от деления двойной площади трапеции на произведение суммы ее оснований и синуса острого угла при основании. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
Так как прямоугольная трапеция — это частный случай трапеции, то остальные формулы и свойства можно посмотреть в разделе «Трапеция».Свойства прямоугольной трапеции
- У прямоугольной трапеции два угла обязательно прямые
- Оба прямых угла прямоугольной трапеции обязательно принадлежат смежным вершинам
- Оба прямых угла в прямоугольной трапеции обязательно прилежат к одной и той же боковой стороне
- Диагонали прямоугольной трапеции образуют с одной из боковых сторон прямоугольный треугольник
- Длина боковой стороны трапеции, перпендикулярной основаниям равна ее высоте
- У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям
- У прямоугольной трапеции два угла прямые, а два других – острый и тупой
Задача
В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см. Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.Решение.
Обозначим трапецию как ABCD. Обозначим длины оснований трапеции как a (большее основание AD) и b (меньшее основание BC). Пусть прямым углом будет
Площадь прямоугольника, стороны которого равны основаниям трапеции, будет равна
S = ab
Из вершины C верхнего основания трапеции ABCD опустим на нижнее основание высоту CK. Высота трапеции известна по условию задачи. Тогда, по теореме Пифагора
CK2 + KD
Поскольку большая боковая сторона трапеции по условию равна сумме оснований, то CD = a + b
Поскольку трапеция прямоугольная, то высота, проведенная из верхнего основания трапеции разбивает нижнее основание на два отрезка
то есть
122 + (a — b)2 = (a + b)2
откуда
144 + a2 — 2ab + b2 = a2+ 2ab + b2
144 = 4ab
Поскольку площадь прямоугольника S = ab (см. выше), то
144 = 4S
S = 144 / 4 = 36
Ответ: 36 см
2 .profmeter.com.ua
Все формулы сторон трапеции
1. Формула длины основания трапеции через среднюю линию

a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :


2. Формулы длины сторон через высоту и углы при нижнем основании

a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:






3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями

a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:


Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
www-formula.ru
Прямоугольная трапеция | Треугольники
Что такое прямоугольная трапеция и какими свойствами она обладает?
Определение.
Прямоугольная трапеция — это трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Рисунок прямоугольной трапеции
ABCD- прямоугольная трапеция,
AD ∥ BC — основания трапеции,
AB и CD — ее боковые стороны,
Свойства прямоугольной трапеции:
1) Высота прямоугольной трапеции равна ее меньшей боковой стороне.
AB — высота трапеции ABCD.
2) У прямоугольной трапеции два угла — прямые, один — острый и один — тупой.
∠A и ∠B — прямые, ∠D — острый, ∠C — тупой.
3) Высота, проведенная из вершины тупого угла, делит прямоугольную трапецию на прямоугольник и прямоугольный треугольник.
ABCD — прямоугольник (так как у него все углы — прямые). Следовательно, AF=BC, CF=AB.
FCD — прямоугольный треугольник. FD=AD-AF,
отсюда FD=AD-BC. Если AD=a, BC=b, CF=AB=h, то
и по теореме Пифагора
4) Квадрат меньшей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и меньшего основания.
Треугольник ABC — прямоугольный.
По теореме Пифагора,
5) Квадрат большей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и большего основания.
Треугольник ABD — прямоугольный.
По теореме Пифагора,
www.treugolniki.ru
Все формулы высоты трапеции
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
1. Формула высоты трапеции через стороны и углы при основании

a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы длины высоты, (h ):


2. Формула высоты трапеции через диагонали и углы между ними

d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):


3. Формула высоты трапеции через площадь

S — площадь трапеции
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):

Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
www-formula.ru