Дифференциальные уравнения 2-го порядка
§1. Методы понижения порядка уравнения.
Дифференциальное уравнение 2-го порядка имеет вид:
 .
(1.1)
.
(1.1)
Общим
решением уравнения является семейство
функций, зависящее от двух произвольных
постоянных  и
и  :
:  (или
(или  – общий интеграл дифференциального
уравнения 2-го порядка). Задача Коши для
дифференциального уравнения 2-го порядка
(1.1) состоит в отыскании частного решения
уравнения, удовлетворяющего начальным
условиям: при
– общий интеграл дифференциального
уравнения 2-го порядка). Задача Коши для
дифференциального уравнения 2-го порядка
(1.1) состоит в отыскании частного решения
уравнения, удовлетворяющего начальным
условиям: при
 :
:  ,
,  .
Необходимо заметить, что графики решений
уравнения 2-го порядка могут пересекаться
в отличие от графиков решений уравнения
1-го порядка. Однако решение задачи Коши
для уравнений 2-го порядка (1.1) при довольно
широких предположениях для функций,
входящих в уравнение, единственно, т.е.
всякие два решения с общим начальным
условием
.
Необходимо заметить, что графики решений
уравнения 2-го порядка могут пересекаться
в отличие от графиков решений уравнения
1-го порядка. Однако решение задачи Коши
для уравнений 2-го порядка (1.1) при довольно
широких предположениях для функций,
входящих в уравнение, единственно, т.е.
всякие два решения с общим начальным
условием  ,
,  совпадают на пересечении интервалов
определения.
совпадают на пересечении интервалов
определения. Получить общее решение или решить задачу Коши для дифференциального уравнения 2-го порядка аналитически удается далеко не всегда. Однако в некоторых случаях удается понизить порядок уравнения с помощью введения различных подстановок. Разберем эти случаи.
Уравнения, не содержащие явно независимой переменной
 .
.
Пусть
дифференциальное уравнение 2-го порядка
имеет вид:  ,
т.е. в уравнении (1.1) явно не присутствует
независимая переменная
,
т.е. в уравнении (1.1) явно не присутствует
независимая переменная 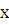 .
Это позволяет принять
.
Это позволяет принять  за новый аргумент, а производную 1-го
порядка
за новый аргумент, а производную 1-го
порядка
 принять за новую функцию
принять за новую функцию  .
Тогда
.
Тогда  .
. Таким
образом, уравнение 2-го порядка  для функции
для функции  ,
не содержащее явно
,
не содержащее явно  ,
свелось к уравнению 1-го порядка
,
свелось к уравнению 1-го порядка  для функции
для функции 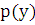
 или
или  ,
а это есть дифференциальное уравнение
1-го порядка для функции
,
а это есть дифференциальное уравнение
1-го порядка для функции  .
Решая его, получаем общий интеграл
исходного дифференциального уравнения,
зависящий от двух произвольных постоянных:
.
Решая его, получаем общий интеграл
исходного дифференциального уравнения,
зависящий от двух произвольных постоянных:  .
. Пример
1. Решить дифференциальное уравнение  при заданных начальных условиях:
при заданных начальных условиях:  ,
, 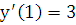
Решение.
Так
как в исходном уравнении в явном виде
отсутствует аргумент  ,
то примем
,
то примем  за новую независимую переменную, а
за новую независимую переменную, а  – за
– за  .
Тогда
.
Тогда  и уравнение приобретает следующий вид
для функции
и уравнение приобретает следующий вид
для функции  :
: 
Это
дифференциальное уравнение с разделяющимися
переменными:  . Откуда следует
. Откуда следует 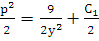 ,
т.е.
,
т.е.  .
.
Так
как при  и
и  ,
то подставляя начальные условия в
последнее равенство, получаем, что
,
то подставляя начальные условия в
последнее равенство, получаем, что  и
и 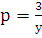 ,
что равносильно
,
что равносильно 
 имеем уравнение с разделяющимися
переменными, решая которое, получаем
имеем уравнение с разделяющимися
переменными, решая которое, получаем 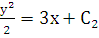 .
Используя начальные условия, получаем,
что
.
Используя начальные условия, получаем,
что  .
Следовательно, частный интеграл
уравнения, удовлетворяющий начальным
условиям, имеет вид:
.
Следовательно, частный интеграл
уравнения, удовлетворяющий начальным
условиям, имеет вид:  .
.Уравнения, не содержащие явно искомой функции
 .
.
Пусть дифференциальное уравнение 2-го порядка имеет вид:
 ,
т.е. в уравнение явно не входит искомая
функция
,
т.е. в уравнение явно не входит искомая
функция  .
В этом случае вводят постановку
.
В этом случае вводят постановку  .
Тогда
.
Тогда  и уравнение 2-го порядка
и уравнение 2-го порядка  для функции
для функции  переходит в уравнение 1-го порядка
переходит в уравнение 1-го порядка  для функции
для функции 
 :
:  .
Решая последнее уравнение, получаем
общий интеграл заданного дифференциального
уравнения
.
Решая последнее уравнение, получаем
общий интеграл заданного дифференциального
уравнения  ,
зависящий от двух произвольных постоянных:
,
зависящий от двух произвольных постоянных:  .
. Пример
2. Найти общее решение уравнения: 
Решение.
В
данное уравнение 2-го порядка явно не
входит искомая функция 
 и
и  .
В результате чего получаем дифференциальное
уравнение 1-го порядка для функции
.
В результате чего получаем дифференциальное
уравнение 1-го порядка для функции  : или
: или  ,
являющееся линейным уравнением. Решая
его, получаем:
,
являющееся линейным уравнением. Решая
его, получаем:  или
или 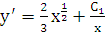 .
Итак, для функции
.
Итак, для функции  получили дифференциальное уравнение
с разделяющимися переменными:
получили дифференциальное уравнение
с разделяющимися переменными:  ,
откуда следует общее решение исходного
уравнения:
,
откуда следует общее решение исходного
уравнения:  .
.Порядок степени понижается, если удается преобразовать его к такому виду, что обе части уравнения становятся полными производными по
 от каких-нибудь функций. Например, пусть
дано уравнение
от каких-нибудь функций. Например, пусть
дано уравнение  .
Деля обе части на
.
Деля обе части на  ,
получаем
,
получаем  ;
;  ;
;  ;
;  – порядок уравнения понижен.
– порядок уравнения понижен.
Дифференциальные уравнения — ДУ 2-го порядка I
| В общем случае дифференциальное уравнение второго порядка можно записать в виде
где F − заданная функция указанных аргументов. Если дифференциальное уравнение можно разрешить относительно второй производной y», то его можно представить в следующем явном виде: В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такиенеполные уравнения включают в себя 5 различных типов: С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка.В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7):
Случай 1. Уравнение вида y»= f (x) Если дано уравнение y» = f(x), то его порядок можно понизить введением новой функции p(x), такой, чтоy’ = p(x). В результате мы получим дифференциальное уравнение первого порядка Решая его, находим функцию p(x). Затем решаем второе уравнение и получаем общее решение исходного уравнения.Случай 2. Уравнение вида y»= f (y) Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию p(y), полагаяy’ = p(y). Тогда можно записать: и уравнение принимает вид: Решая его, находим функцию p(y). Затем находим решение уравнения y’ = p(y), то есть функцию y(x).Случай 3. Уравнение вида y»= f (y’ ) В данном случае для понижения порядка вводим функцию y’ = p(x) и получаем уравнение которое является уравнением первого порядка с разделяющимися переменными p и x. Интегрируя, находим функцию p(x) и затем функцию y(x).Случай 4. Уравнение вида y»= f (x,y’ ) Используем подстановку y’ = p(x), где p(x) − новая неизвестная функция, и получаем уравнение первого порядка Интегрируя, определяем функцию p(x). Далее решаем еще одно уравнение 1-го порядка и находим общее решение y(x).Случай 5. Уравнение вида y»= f (y,y’ ) Для решения такого уравнения, также как и в случае 2, вводим новую функцию p(y), полагая y’ = p(y). Дифференцирование этого равенства по x приводит к уравнению В результате наше исходное уравнение записывается в виде уравнения 1-го порядка Решая его, находим функцию p(y). Затем решаем еще одно уравнение первого порядка и определяем общее решение y(x).Рассмотренные 5 случаев понижения порядка не являются независимыми. Исходя из структуры уравнений, ясно, что случай 2 следует из случая 5, а случай 3 вытекает из более общего случая 4. Случай 6. Функция F(x, y, y’, y») является однородной функцией аргументов y, y’, y» Если левая часть дифференциального уравнения удовлетворяет условию однородности, т.е. для любого k справедливо соотношение то порядок уравнения можно понизить с помощью подстановки После нахождения функции z(x) исходная функция y(x) находится интегрированием по формуле где C2 − постоянная интегрирования.Случай 7. Функция F(x, y, y’, y») является точной производной Если удается найти такую функцию Ф(x, y, y’), не содержащую второй производной y» и удовлетворяющую равенству то решение исходного уравнения представляется интегралом Таким образом уравнение второго порядка можно привести к уравнению первого порядка.В некоторых случаях левую часть исходного уравнения можно преобразовать в точную производную, используя интегрирующий множитель. |
Линейные неоднородные ДУ второго порядка
Определение и формулы линейных неоднородных ДУ 2-ого порядка
Соответствующее ему однородное уравнение:
Решение дифференциальные уравнения второго порядка
Решение уравнения (2) ищется в виде:
После подстановки этого решения в уравнение (2) получаем алгебраическое уравнение
Это квадратное уравнение называется характеристическим уравнением, соответствующим однородному дифференциальному уравнению (2).
В результате решения характеристического уравнения, возможны следующие варианты:
1) корни характеристического уравнения – различные действительные числа, тогда решение уравнения (2) записывается в виде:
2) корни характеристического уравнения – равные действительные числа, тогда решение уравнения (2) записывается в виде:
3) корни характеристического уравнения – комплексно сопряженные числа, тогда решение уравнения (2) записывается в виде:
Примеры решения задач
К уравнениям вида (1) чаще всего применяются два метода решения: метод вариации произвольных постоянных и метод неопределенных коэффициентов.
Метод вариации постоянных или метод Лагранжа
Если известно общее решение соответствующего однородного уравнения (2), то общее решение неоднородного уравнения (1) можно найти, используя метод вариации произвольных постоянных.
Пусть общее решение однородного дифференциального уравнения второго порядка (1) имеет вид:
Далее варьируем произвольные постоянные, то есть считаем, что в указанном решении величины и – это не постоянные, а функции переменной x:
То есть решение неоднородного уравнения тогда ищется в виде:
Искомые функции и находятся из системы
Определитель этой системы
называется определителем Вронского.
Решая систему (5) относительно пока неизвестных функций и (а точнее относительно их производных и ), будем иметь:
Интегрируя последние равенства, получаем:
Подставляя полученные в результате функции в решение (4), будем иметь:
или, после упрощения
Метод неопределенных коэффициентов
Если правая часть неоднородного дифференциального уравнения (1) представляет собой многочлен, экспоненциальную или тригонометрическую функцию (или комбинацию указанных функций):
то тогда решение удобнее искать с помощью метода неопределенных коэффициентов.
В любом из случаев вид частного решения соответствует структуре правой части исходного неоднородного дифференциального уравнения.
1) Если правая часть уравнения (1) имеет вид (7), то частное решение ищем в виде:
где – многочлен степени n с неопределенными коэффициентами и s=0 при , которое не является корнем характеристического многочлена, или s кратности , где — корень характеристического многочлена.
2) Если правая часть уравнения (1) имеет вид (8), то частное решение будем искать следующим образом:
Здесь – многочлены степени k с неопределенными коэффициентами и s=0 ( не является корнем характеристического многочлена), или s кратности — корень характеристического многочлена.
Неизвестные коэффициенты многочленов определяются подстановкой выражения для частного решения в исходное неоднородное дифференциальное уравнение (1).
Решение дифференциальных уравнений второго порядка
Решение простых дифференциальных уравнений второго порядка
Дифференциальные уравнения второго порядка вида
решаются двукратным интегрированием.
Решение линейных дифференциальных уравнений второго порядка
Рассмотрим линейное однородное дифференциальное уравнение второго порядка
Здесь коэффициенты – постоянные действительные числа. Решение этого уравнения будем искать в виде
Подставим эту функцию в уравнение (1):
Поскольку , то функция (2) будет решением линейного однородного уравнения тогда и только тогда, когда будет выполняться равенство
Уравнение (3) называется характеристическим уравнением линейного однородного дифференциального уравнения с постоянными коэффициентами (1). А многочлен n-й степени называется характеристическим многочленом этого уравнения.
Замечание. Корни характеристического уравнения линейного однородного дифференциального уравнения с постоянными коэффициентами могут быть как действительными, так и комплексными (простыми и кратными) числами.
Утверждение 1. Если числа – различные действительные корни характеристического уравнения (3) линейного однородного дифференциального уравнения с постоянными коэффициентами (1), то функции образуют фундаментальную систему решений этого уравнения и общее решение уравнения имеет вид:
Утверждение 2. Если – действительный корень характеристического уравнения кратности два, то функции – фундаментальная система решений уравнения (1), общее решение этого уравнения имеет вид:
Утверждение 3. Если – комплексно сопряженные корни характеристического уравнения (3), которое соответствует однородному дифференциальному уравнению второго порядка (1), то функции образуют фундаментальную систему решений этого уравнение и общее решение записывается в виде:
Решение линейных неоднородных ДУ второго порядка
Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка
Коэффициенты – некоторые действительные числа, – непрерывная на отрезке функция, называемая правой частью неоднородного дифференциального уравнения (4).
Общее решение этого уравнения имеет вид
где – произвольные постоянные, – фундаментальная система решений соответствующего однородного уравнения (1), – частное решение неоднородного уравнения (4).
Частное решение можно найти методом подбора (или методом неопределенных коэффициентов) в случае, если правая часть уравнения есть одной из функций вида
или
Здесь – заданные многочлены степени n, – известный многочлен степени m, – некоторые действительные числа.
Метод подбора нахождения частного решения линейного неоднородного уравнения (4) с функцией вида (5), (6) в правой части состоит в том, что частное решение уравнения ищут в виде
– многочлен степени n с неопределенными коэффициентами, s=0 при , которое не является корнем характеристического многочлена, или s кратности , где — корень характеристического многочлена.
или
– многочлены степени k с неопределенными коэффициентами, s=0 ( не является корнем характеристического многочлена), или s кратности — корень характеристического многочлена.
соответственно.
Принцип суперпозиции. Если функция – решение линейного дифференциального уравнения
то тогда функция
есть решением уравнения
или
Дифференциальные уравнения второго порядка
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒
Определение 10. Дифференциальным уравнением второго порядка называется уравнение, содержащее неизвестную функцию и её вторую производную, то есть уравнение вида
 ,
,
где  – независимая переменная,
– независимая переменная,  – искомая функция,
– искомая функция,  – её первая производная,
– её первая производная,  – вторая производная функции
– вторая производная функции  .
.
Линейные однородные дифференциальные уравнения
Второго порядка с постоянными коэффициентами
Определение 11.Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется дифференциальное уравнение, имеющее вид
 , (11)
, (11)
где  – искомая функция, а
– искомая функция, а  и
и  – числа.
– числа.
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами может иметь множество решений. Однако среди них выделяют два базисных решения, по которым строится общее решение уравнения.
Будем искать решение уравнения (11) в виде
 ,
,
где  – некоторое число. Подставляя эту функцию в само уравнение (11), получаем
– некоторое число. Подставляя эту функцию в само уравнение (11), получаем
 .
.
Деля обе части уравнения на  , имеем квадратное уравнение относительно
, имеем квадратное уравнение относительно  :
:
 . (12)
. (12)
Уравнение (12) называется характеристическим уравнением для дифференциального уравнения (11). Обозначим корни характеристического уравнения (12) через  ,
, 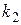 .
.
Справедлива следующая теорема:
Теорема.1)Если корни характеристического уравнения вещественные и различны:  ,
, 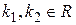 , то общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами (11) имеет вид
, то общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами (11) имеет вид
 ,
, 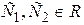 .
.
2) В случае, когда корни характеристического уравнения вещественные и равные:  , общим решением линейного однородного дифференциального уравнения с постоянными коэффициентами (11) является функция
, общим решением линейного однородного дифференциального уравнения с постоянными коэффициентами (11) является функция
 ,
, 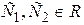 .
.
3) Если корни характеристического уравнения комплексно сопряженные:  ,
,  ,
,  , то общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами (11) имеет вид
, то общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами (11) имеет вид
 ,
, 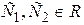 .
.
Примеры. Решим следующие дифференциальные уравнения:
1) 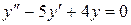 .
.
Данное уравнение является линейным однородным дифференциальным уравнением с постоянными коэффициентами. Составим характеристическое уравнение:  . Его корни вещественны и различны:
. Его корни вещественны и различны:  ,
,  . Следовательно, общее решение заданного уравнения имеет вид
. Следовательно, общее решение заданного уравнения имеет вид  ,
, 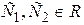 .
.
Ответ:  ,
,  .
.
2)  .
.
Это линейное однородное дифференциальное уравнение с постоянными коэффициентами. Корни характеристического уравнения  вещественны и совпадают:
вещественны и совпадают:  . Поэтому общее решение исходного уравнения таково
. Поэтому общее решение исходного уравнения таково  .
.
Ответ:  ,
,  .
.
3)  .
.
Корни характеристического уравнения  заданного линейного однородного дифференциального уравнения с постоянными коэффициентами комплексно сопряжены:
заданного линейного однородного дифференциального уравнения с постоянными коэффициентами комплексно сопряжены:  ,
,  . Следовательно, общее решение имеет вид
. Следовательно, общее решение имеет вид 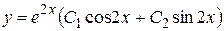 .
.
Ответ: 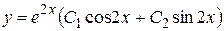 ,
, 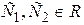 .
.
Тема 2. РЯДЫ
Понятие числового ряда
Определение 12.Пусть дана числовая последовательность 
 тогда выражение вида
тогда выражение вида
 (13)
(13)
называется числовым рядом или просто рядом.
Числа  называются членами ряда, первым, вторым и так далее,
называются членами ряда, первым, вторым и так далее,  – общим или
– общим или  -ым членом ряда.
-ым членом ряда.
Суммы конечного числа членов ряда
 ,
,
 ,
,
 ,
,
……………………

носят название частичных сумм ряда (13).
Числовой ряд (13) называется сходящимся, если предел его частичных сумм  конечен, то есть
конечен, то есть  . Число
. Число  называется суммой ряда (13):
называется суммой ряда (13):  . Если последовательность частичных сумм
. Если последовательность частичных сумм  не имеет конечного предела, то ряд (13) называется расходящимся.
не имеет конечного предела, то ряд (13) называется расходящимся.
Пример. Покажем, что ряд  сходится.
сходится.
Составим частичную сумму  первых
первых  членов ряда:
членов ряда:
 .
.
Чтобы упростить выражение для  , разложим
, разложим  на элементарные дроби. Имеем
на элементарные дроби. Имеем
 ,
,
 .
.
Приравнивая коэффициенты при одинаковых степенях  в числителях дробей, получаем
в числителях дробей, получаем
 ,
,  ;
;
 ,
,  ,
,
поэтому
 .
.
Следовательно,
 .
.
Переходя к пределу, находим
 .
.
Таким образом, ряд сходится и его сумма равна 1.
Важное место в теории рядов имеет теорема, отражающая необходимое условие сходимости ряда.
1.2. Необходимое условие сходимости ряда
Если ряд  сходится, то его общий член стремится к нулю, то есть
сходится, то его общий член стремится к нулю, то есть  .
.
Ряд из предыдущего примера сходится, и его общий член действительно стремится к нулю. Условие  является необходимым, но не достаточным для сходимости ряда.
является необходимым, но не достаточным для сходимости ряда.
Пример.Докажем, что ряд
 ,
,
который называется гармоническим рядом, расходится.
 , то есть для гармонического ряда необходимое условие сходимости выполнено. Докажем, что это ряд расходится методом от противного. Действительно, если бы этот ряд сходился, то обозначая его сумму через
, то есть для гармонического ряда необходимое условие сходимости выполнено. Докажем, что это ряд расходится методом от противного. Действительно, если бы этот ряд сходился, то обозначая его сумму через  , мы бы имели
, мы бы имели

Но  , то есть
, то есть  . Отсюда следует, что равенство
. Отсюда следует, что равенство  невозможно, то есть гармонический ряд расходится.
невозможно, то есть гармонический ряд расходится.
Но, если для некоторого ряда его общий член не стремится к нулю, то необходимый признак сходимости ряда позволяет сразу сказать, что такой ряд расходится.
1.2. Свойства сходящихся рядов
1) На сходимость ряда не влияет отбрасывание, добавление или изменение конечного числа его членов.
2) Пусть даны два сходящихся ряда  и
и  , тогда ряд
, тогда ряд  сходится и
сходится и  .
.
3) Пусть дан сходящийся ряд  и постоянная
и постоянная  , тогда ряд
, тогда ряд  сходится и
сходится и  .
.
Рекомендуемые страницы:
Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами [wiki.eduVdom.com]
Пример 1. $$
\frac{d^{2}y}{dx^{2}}+\frac{dy}{dx}-2y=3x-1$$ Решение:
Пример 2.
Решить уравнение $$ {Y}»+{y}’=4x^{2}e^{x} $$
Решение. Характеристическое уравнение
$$
k^{2}+k=0
\\
k(k+1)=0
\;;\;
k_{1}=0
\;;\;
k_{2}=-1
$$
Общее решение однородных уравнений имеет вид: $y=C_{1}+C_{2}e^{-x}$
Правая часть уравнения $ f(x)=4x^{2}e^{x} \,,\, \alpha=1 $ , т.к. $\alpha=1$ не является корнем характеристического уравнения, то частное решение неоднородного уравнения имеет вид (см. табл. Случай 2/1)
$$ \overline{y}=( A_{1}x^{2}+A_{2}x+A_{3} )e^{x} $$
Подставляя его в исходное уравнение и сокращая обе части уравнения на $e^{x}$ , будем иметь $$ 2A_{1}x^{2} + (6A_{1}+2A_{2})x + 2A_{1} + 3A_{2} + 2A_{3} = 4x^{2} $$
Приравнивая коэффициенты при одинаковых степенях в левой и правой частях равенства, получаем линейную систему уравнений для нахождения коэффициентов $A_{1} \,,\, A_{2} \text{ и } A_{3}$: $$ \left\{\begin{matrix} 2A_{1}=4 &;& A_{1}=2 \\ 6A_{1}+2A_{2}=0 &;& A_{2}=-6 \\ 2A_{1}+3A_{2}+2A_{3}=0 &;& A_{3}=7 \end{matrix}\right. $$ $$ \overline{y}=( 2x^{2}-6x+7 )e^{x} $$
Общее решение данного уравнения $$ y(x)=C_{1}+C_{2}e^{-x}+( 2x^{2}-6x+7 )e^{x} $$
Пример 3.
Найти общее решение уравнения $$ {y}»+{10y}’+25y=4e^{-5x} $$
Решение: характеристическое уравнение $k^{2}+10k+25=0$ имеет двукратный корень $k_{1}=k_{2}=-5$, поэтому $y=( C_{1}+C_{2}x )e^{-5x}$ .
Т.к. $к=-5$ является корнем характеристического уравнения кратности $S=2$, то частное решение неоднородного уравнения ищем в виде ( см. табл., случай 2(2) ):
$$
\overline{y}=Ax^{2}e^{-5x}
\;;\;
{\overline{y}}’=A( 2x-5x^{2} )e^{-5x}
\;;\;
{\overline{y}}»=A( 2-20x+25x^{2} )e^{-5x}
$$
Подставляя выражения для $ y \,,\, {y}’ \,,\, {y}» $ в исходное уравнение, получаем $ 2Ae^{-5x}=4e^{-5x} \,,\, A=2 \,,\, y=2x^{2}e^{-5x} $ . Общее решение данного уравнения $$ y=( C_{1}+C_{2}x )e^{-5x} + 2x^{2}e^{-5x} $$
Пример 4
Найти частное решение уравнения (решить задачу Коши) $$ {y}»+{y}’-2y=\cos{x}-3\sin{x} $$ Начальные условия: $ y(0)=1 \;;\; {y}'(0)=2 \;; $
Решение:
Характеристическое уравнение: $ k^{2}+k-2=0 $;
Корни характеристического уравнения: $ k_{1}=1 \;;\; k_{2}=-2 $;
Общее решение однородного уравнения: $ y=C_{1}e^{-2x}+C_{2}e^{x} $
Частное решение неоднородного дифференциального уравнения будем искать в виде (см.таблицу):
$$
\overline{y}=A\cos{x} + B\sin{x}
\;;\; \\
\overline{{y}’}=-A\sin{x}+B\cos{x}
\;;\; \\
{\overline{y}}»=-A\cos{x}-B\sin{x}
$$
Подставляя выражения для $ y \,,\, {y}’ \,,\, {y}» $ в исходное уравнение, получаем: $(B-3A)\cos{x}+(-3B-A)\sin{x}=\cos{x}–3\sin{x}$ $$ \left\{\begin{matrix} B-3A=1 \\ &\Rightarrow &A=0 &, &B=1 &; \\ -(3B+A)=-3 \end{matrix}\right. $$ Тогда общее решение заданного уравнения будет иметь вид: $$ y=C_{1}e^{-2x}+C_{2}e^{x}+\sin{x} $$
Найдем $С_1$ и $С_2$ , используя начальные условия ( $ y(0)=1 \;;\; {y}'(0)=2 $ ): $$ \left\{\begin{matrix} C_{1}e^{0}-C_{2}e^{0}+\sin{0}=1 \\ 2C_{1}e^{0}+C_{2}e^{0}+\cos{0}=2 \end{matrix}\right. \\ \left\{ \begin{matrix} C_{1}+C_{2}=1 \\ -2C_{1}+c_{2}=1 \end{matrix}\right. \\ C_{1}=0 \;;\; C_{2}=1 \;;\; $$ Задача Коши решена: $y=e^{x}+\sin{x}$
Пример 5.
Решить уравнение: $$ {y}»’+{y}»-{2y}’=x-e^{x} $$
Решение: $$
k^{3}+k^{2}-2k=0
\;;\;
k_{1}=0
\;;\;
k_{2}=1
\;;\;
k_{3}=-2
\;;\;
y=C_{1}+C_{2}e^{x}+C_{3}e^{-2x}
$$
т.к. $k_{1}=0$ – простой корень характеристического уравнения, т.е. S_{1}=1 , то частное решение ищем в виде:
$$
\overline{y}=x(Ax+B)+Cxe^{x}
\;;\; \\
{\overline{y}}’=2Ax+B+Ce^{x}+Cxe^{x}
\;;\; \\
{\overline{y}}»=2A+2Ce^{x}+Cxe^{x}
\;;\; \\
{\overline{y}}»’= 3Ce^{x}+Cxe^{x}
\\ \\
-4Ax+( 2A-3B )+3Ce^{x}=x-e^{x}
\;;\;
A=-\frac{1}{4}
\;;\;
B=-\frac{1}{4}
\;;\;
C=-\frac{1}{3}
$$
Ответ:
$$ y=C_{1}+C_{2}e^{x}+C_{3}e^{-2x}-\frac{1}{4}x( x+1 )-\frac{1}{3}xe^{x} $$
Неоднородные дифференциальные уравнения 2ого порядка
Определение и формулы неоднородных ДУ второго порядка
Нахождение решения однородного уравнения (2) можно посмотреть тут — решение дифференциальных уравнений второго порядка и линейные неоднородные дифференциальные уравнения второго порядка.
Методы нахождения частного решения неоднородных ДУ второго порядка
Существует несколько методов нахождения частного решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами (1). Эти методы выбираются в зависимости от вида правой части – функции .
1) Если функция представляет собой многочлен n-ой степени
то частное решение уравнения (1) ищется в виде
Здесь – многочлен степени n с неопределенными коэффициентами (которые подлежат определению), а s – кратность корня характеристического уравнения однородного уравнения (2) (или то есть количество корней характеристического уравнения, равных нулю).
Так как – частное решение уравнения (1), то коэффициенты, определяющие многочлен , можно найти методом неопределенных коэффициентов из равенства
использовав тот факт, что два многочлена равны, если равны коэффициенты при соответствующих степенях независимой переменной.
2) Если функция , стоящая в правой части уравнения (1), имеет вид
то есть представляет собой произведение многочлена степени n и экспоненты, то частное решение этого уравнения ищется в виде
где – многочлен степени n с неопределенными коэффициентами, а s – кратность корня в характеристическом уравнении соответствующего однородного уравнения (2) (или то есть количество корней характеристического уравнения, равных a). Коэффициенты многочлена определяются подстановкой частного решения в исходное уравнение (так как является решением, то оно должно удовлетворять уравнению). Таким образом, должно выполняться равенство (3).
3) Если правая часть неоднородного дифференциального уравнения (1) имеет вид:
то частное решение в этом случае ищем в виде:
Здесь s – число комплексно сопряженных пар корней характеристического уравнения – многочлены степени k с неизвестными коэффициентами. Коэффициенты этих многочленов определяются из равенства (3).
Если правая часть имеет отличную, от описанных выше, структуру, то для нахождение решения уравнения (1) применяют метод вариации произвольной постоянной:
1) находится общее решение соответствующего линейного однородного уравнения (2) в виде
где – линейно независимые частные решения линейного однородного дифференциального уравнения (2), – некоторые произвольные постоянные;
2) варьируются произвольные постоянные, то есть считается, что они являются функциями независимой переменной x:
А в качестве общего решения исходного дифференциального уравнения (1) рассматривается функция
Функции (точнее их производные ) являются решением системы
Тогда сами неизвестные функции находятся с помощью интегрирования.
 .
. .
. от каких-нибудь функций. Например, пусть
дано уравнение
от каких-нибудь функций. Например, пусть
дано уравнение 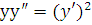 .
Деля обе части на
.
Деля обе части на  ,
получаем
,
получаем  ;
;  ;
;  ;
;  – порядок уравнения понижен.
– порядок уравнения понижен.