Контрольная работа № 4
Пример 1. Найти общее решение уравнения
Решение. Сначала определим вид дифференциального уравнения. Данное уравнение не является уравнением с разделенными переменными, так как коэффициенты при и зависят каждый от двух переменных. Но, разделив обе части уравнения на произведение (считая, что ), приведем его к виду
Это уравнение с разделенными переменными.
Находим общее решение
Или
.
Умножив обе части на (-1), включим знак “-“ в постоянную С. Решение примет вид
.
Таким образом, нами получено общее решение заданного уравнения.
3. Однородные уравнения первого порядка
[2, гл. ХIII, § 5, упр. 39-46].
Пример 2. Найти общее решение уравнения
. (1)
Решение. Определим вид этого уравнения. Это – однородное уравнение, поскольку его правая часть есть .
Поделив почленно правую часть на , получим
Делаем подстановку или . Тогда и уравнение примет вид
. (2)
Разделяем переменные
И интегрируем
Или после потенцирования
.
Нами получено общее решение уравнения (2).
Чтобы найти общее решение уравнения (1), вернемся к старой переменной Y. Подставим , тогда будем иметь
или .
4. Линейные уравнения первого порядка
[2, гл. ХIII, § 7, упр. 57-65].
Пример 3. Найти общее решение уравнения первого порядка
Решение. Определим вид этого уравнения. Уравнение вида Называется линейным. Полагаем ; и подставляем это в данное уравнение
Группируем члены
И полагаем
(3)
Остается
. (4)
Находим сначала V из (3)
Заметим, что V не содержит никаких произвольных постоянных.
Подставляем V в (4) и получаем
Окончательно получаем искомое общее решение
.
5. Дифференциальные уравнения высших порядков. Основные понятия.
[2, гл. ХIII, § 16, 17, упр. 118-124].
6.Линейные однородные уравнения второго порядка
Пример 4. Найти общее решение уравнения .
Решение. Ищем решение уравнения в виде тогда и, подставляя в исходное уравнение получим Так как то на него можно сократить и мы получим
Находим его корни
Корни характеристического уравнения вещественные, различные, значит, общее решение дифференциального уравнения имеет вид
Или
Пример 5. Найти общее решение уравнения
Решение. Составляем характеристическое уравнение (см. пример 9)
Решаем его
Корни характеристического уравнения вещественные равные. Общее решение дифференциального уравнения имеет вид
Или
Пример 6. Найти общее решение уравнения
Решение. Составляем характеристическое уравнение (см. пример 9)
Корни характеристического уравнения комплексные сопряженные, значит, общее решение дифференциального уравнения имеет вид
Или
7. Линейные, неоднородные уравнения второго порядка
Пример 7. Найти общее решение уравнения
Решение. Находим сначала общее решение соответствующего однородного уравнения
Характеристическое уравнение Его корни
Общее решение однородного уравнения
Теперь следует найти частное решение неоднородного уравнения. Правая часть значит ищем в форме , т. к. не является корнем характеристического уравнения.
Требуется найти неизвестные коэффициенты А и В. Для определения А и В дифференцируем дважды
И подставляем это в данное неоднородное уравнение:
Так как то сократив , получим тождественное равенство двух полиномов
Значения А и В найдем, приравнивая коэффициенты при одинаковых степенях в левой и правой частях
При Х :
При Х0:
Подставляем найденные А и В в
Общее решение неоднородного уравнения
Пример 8. Найти общее решение уравнения
Решение. Соответствующее однородное уравнение
Решаем его
Правая часть данного неоднородного уравнения
Следовательно, частное решение разыскиваем в виде
,
Т. к. не является решением характеристического уравнения.
Дифференцируем и подставляем это решение в неоднородное уравнение
Приравниваем коэффициенты при одинаковых тригонометрических функциях в левой и правой частях тождества
При
При
Из этой системы находим А и В
Общее решение
Пример 9. Найти частное решение уравнения удовлетворяющее начальным условиям
Решение. Чтобы найти частное решение, удовлетворяющее заданным начальным условиям, необходимо получить сначала общее решение данного неоднородного уравнения. Находим его (см. пример 8)
Подставляем в уравнение
Искомое частное решение будем находить из общего. Общее решение неоднородного уравнения
Подставляем начальные условия. При имеем
Найденные постоянные подставляем в общее решение неоднородного уравнения
• искомое частное решение.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме «Дифференциальные уравнения»
I. Обыкновенные дифференциальные уравнения
1.1. Основные понятия и определения
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.
Символически дифференциальное уравнение записывается так:
F(x,y,y’)=0, F(x,y,y»)=0, F(x,y,y’,y»,.., y(n))=0
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Решением дифференциального уравнения называется такая функция , которая обращает это уравнение в тождество.
Порядком дифференциального уравнения
Примеры.
1. Рассмотрим дифференциальное уравнение первого порядка
Решением этого уравнения является функция y = 5 ln x. Действительно, , подставляя y’ в уравнение, получим – тождество.
А это и значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения.
2. Рассмотрим дифференциальное уравнение второго порядка y» — 5y’ +6y = 0. Функция – решение этого уравнения.
Действительно, .
Подставляя эти выражения в уравнение, получим: , – тождество.
А это и значит, что функция – есть решение этого дифференциального уравнения.
Интегрированием дифференциальных уравнений называется процесс нахождения решений дифференциальных уравнений.
Общим решением дифференциального уравнения называется функция вида ,в которую входит столько независимых произвольных постоянных, каков порядок уравнения.
Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.
График частного решения дифференциального уравнения называется интегральной кривой.
Примеры
1.Найти частное решение дифференциального уравнения первого порядка
xdx + ydy = 0, если y = 4 при x = 3.
Решение. Интегрируя обе части уравнения, получим
Замечание. Произвольную постоянную С, полученную в результате интегрирования, можно представлять в любой форме, удобной для дальнейших преобразований. В данном случае, с учётом канонического уравнения окружности произвольную постоянную С удобно представить в виде .
— общее решение дифференциального уравнения.
Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 32 + 42= C2; C=5.
Подставляя С=5 в общее решение, получим x2 +y2 = 52.
Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях.
2. Найти общее решение дифференциального уравнения
Решением этого уравнения является всякая функция вида , где С – произвольная постоянная. Действительно, подставляя в уравнения , получим: , .
Следовательно, данное дифференциальное уравнение имеет бесконечное множество решений, так как при различных значениях постоянной С равенство определяет различные решения уравнения .
Например, непосредственной подстановкой можно убедиться, что функции являются решениями уравнения .
Задача, в которой требуется найти частное решение уравнения y’ = f(x,y) удовлетворяющее начальному условию y(x0) = y0, называется задачей Коши.
Решение уравнения y’ = f(x,y), удовлетворяющее начальному условию, y(x0) = y0, называется решением задачи Коши.
Решение задачи Коши имеет простой
геометрический смысл. Действительно,
согласно данным определениям, решить
задачу Коши y’ = f(x,y) при условии y(x
II. Дифференциальные уравнения первого порядка
2.1. Основные понятия
Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y’) = 0.
В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.
Уравнение y’ = f(x,y) называется уравнением первого порядка, разрешённым относительно производной.
Общим решением дифференциального уравнения первого порядка называется функция вида , которая содержит одну произвольную постоянную.
Пример. Рассмотрим дифференциальное уравнение первого порядка .
Решением этого уравнения является функция .
Действительно, заменив в данном уравнении, его значением, получим
то есть 3x=3x
Следовательно, функция является общим решением уравнения при любом постоянном С.
Найти частное решение данного уравнения, удовлетворяющее начальному условию y(1)=1 Подставляя начальные условия x = 1, y =1 в общее решение уравнения , получим откуда C = 0.
Таким образом, частное решение получим из общего подставив в это уравнение, полученное значение C = 0 – частное решение.
2.2. Дифференциальные уравнения с разделяющимися переменными
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y’=f(x)g(y) или через дифференциалы , где f(x) и g(y)– заданные функции.
Для тех y, для которых , уравнение y’=f(x)g(y) равносильно уравнению, в котором переменная y присутствует лишь в левой части, а переменная x- лишь в правой части. Говорят, «в уравнении y’=f(x)g(y разделим переменные».
Уравнение вида называется уравнением с разделёнными переменными.
Проинтегрировав обе части уравнения по x, получим G(y) = F(x) + C– общее решение уравнения, где G(y) и F(x) – некоторые первообразные соответственно функций и f(x), C произвольная постоянная.
Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными
- Производную функции переписать через её дифференциалы
- Разделить переменные.
- Проинтегрировать обе части равенства, найти общее решение.
- Если заданы начальные условия, найти частное решение.
Пример 1
Решить уравнение y’ = xy
Решение. Производную функции y’ заменим на
разделим переменные
проинтегрируем обе части равенства:
Ответ:
Пример 2
Найти частное решение уравнения
2yy’ = 1- 3x2, если y0 = 3 при x0 = 1
Это—уравнение с разделенными переменными. Представим его в дифференциалах. Для этого перепишем данное уравнение в виде Отсюда
Интегрируя обе части последнего равенства, найдем
Подставив начальные значения x0 = 1, y0 = 3 найдем С 9=1-1+C, т.е. С = 9.
Следовательно, искомый частный интеграл будет или
Пример 3
Составить уравнение кривой, проходящей через точку M(2;-3) и имеющей касательную с угловым коэффициентом
Решение. Согласно условию
Это уравнение с разделяющимися переменными. Разделив переменные, получим:
Проинтегрировав обе части уравнения, получим:
Используя начальные условия, x = 2 и y = — 3 найдем C:
Следовательно, искомое уравнение имеет вид
2.3. Линейные дифференциальные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка называется уравнение вида y’ = f(x)y + g(x)
где f(x) и g(x) — некоторые заданные функции.
Если g(x)=0 то линейное дифференциальное уравнение называется однородным и имеет вид: y’ = f(x)y
Если то уравнение y’ = f(x)y + g(x) называется неоднородным.
Общее решение линейного однородного дифференциального уравнения y’ = f(x)y задается формулой: где С – произвольная постоянная.
В частности, если С =0, то решением является y = 0 Если линейное однородное уравнение имеет вид y’ = ky где k — некоторая постоянная, то его общее решение имеет вид: .
Общее решение линейного неоднородного дифференциального уравнения y’ = f(x)y + g(x) задается формулой ,
т.е. равно сумме общего решения соответствующего линейного однородного уравнения и частного решения данного уравнения.
Для линейного неоднородного уравнения вида y’ = kx + b,
где k и b— некоторые числа и частным решением будет являться постоянная функция . Поэтому общее решение имеет вид .
Пример. Решить уравнение y’ + 2y +3 = 0
Решение. Представим уравнение в виде y’ = -2y — 3 где k = -2, b= -3 Общее решение задается формулой .
Следовательно, где С – произвольная постоянная.
Ответ:
2.4. Решение линейных дифференциальных уравнений первого порядка методом Бернулли
Нахождение общего решения линейного дифференциального уравнения первого порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных уравнений с разделенными переменными с помощью подстановки y=uv, где u и v — неизвестные функции от x. Этот метод решения называется методом Бернулли.
Алгоритм решения линейного дифференциального уравнения первого порядка
y’ = f(x)y + g(x)
1. Ввести подстановку y=uv.
2. Продифференцировать это равенство y’ = u’v + uv’
3. Подставить y и y’ в данное уравнение: u’v + uv’ = f(x)uv + g(x) или u’v + uv’ + f(x)uv = g(x).
4. Сгруппировать члены уравнения так, чтобы u вынести за скобки:
5. Из скобки, приравняв ее к нулю, найти функцию
Это уравнение с разделяющимися переменными:
Разделим переменные и получим:
Откуда . .
6. Подставить полученное значение v в уравнение (из п.4):
и найти функцию Это уравнение с разделяющимися переменными:
7. Записать общее решение в виде: , т.е. .
Пример 1
Найти частное решение уравнения y’ = -2y +3 = 0 если y =1 при x = 0
Решение. Решим его с помощью подстановки y=uv, .y’ = u’v + uv’
Подставляя y и y’ в данное уравнение, получим
Сгруппировав второе и третье слагаемое левой части уравнения, вынесем общий множитель u за скобки
Выражение в скобках приравниваем к нулю и, решив полученное уравнение, найдем функцию v = v(x)
Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения: Найдем функцию v:
Подставим полученное значение v в уравнение Получим:
Это уравнение с разделенными переменными. Проинтегрируем обе части уравнения: Найдем функцию u = u(x,c) Найдем общее решение: Найдем частное решение уравнения, удовлетворяющее начальным условиям y = 1 при x = 0:
Ответ:
III. Дифференциальные уравнения высших порядков
3.1. Основные понятия и определения
Дифференциальным уравнением второго порядка называется уравнение, содержащее производные не выше второго порядка. В общем случае дифференциальное уравнение второго порядка записывается в виде: F(x,y,y’,y») = 0
Общим решением дифференциального уравнения второго порядка называ
urok.1sept.ru
Обыкновенные дифференциальные уравнения.
Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.
В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.
Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:
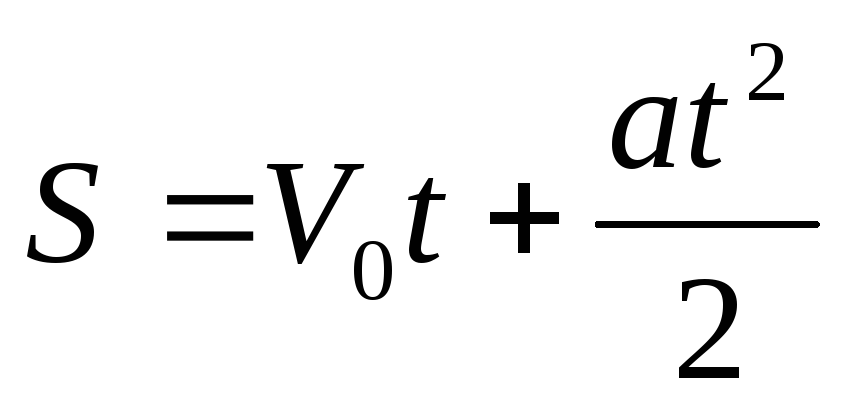
В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.
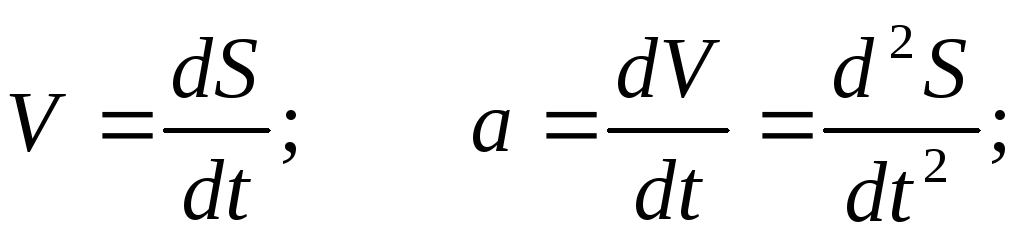
Тогда
получаем:  — уравнение связывает функцию f(t)
с независимой переменной t
и производной второго порядка функции
f(t).
— уравнение связывает функцию f(t)
с независимой переменной t
и производной второго порядка функции
f(t).
Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Пример.
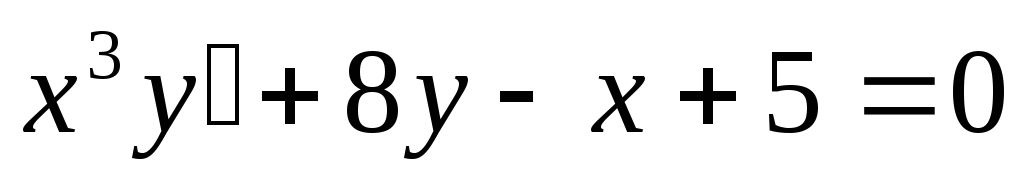 — обыкновенное
дифференциальное уравнение 1 – го
порядка. В общем виде записывается
— обыкновенное
дифференциальное уравнение 1 – го
порядка. В общем виде записывается 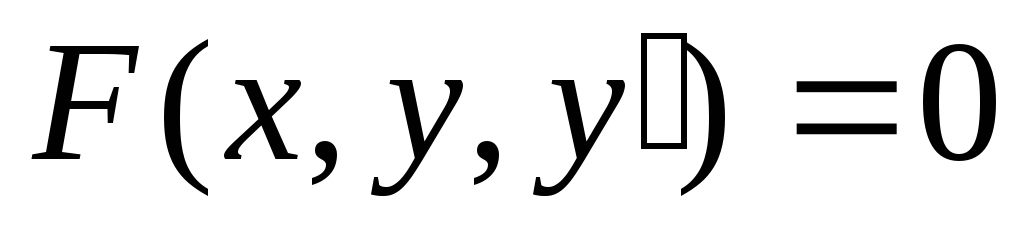 .
.
 — обыкновенное
дифференциальное уравнение 2 – го
порядка. В общем виде записывается
— обыкновенное
дифференциальное уравнение 2 – го
порядка. В общем виде записывается 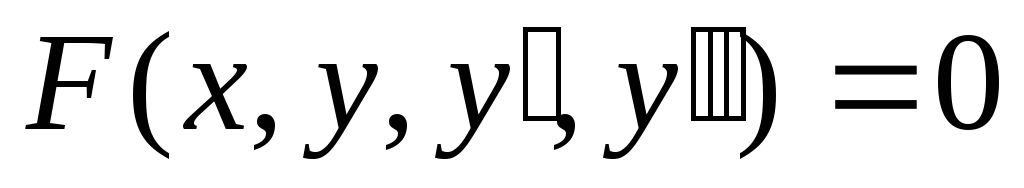
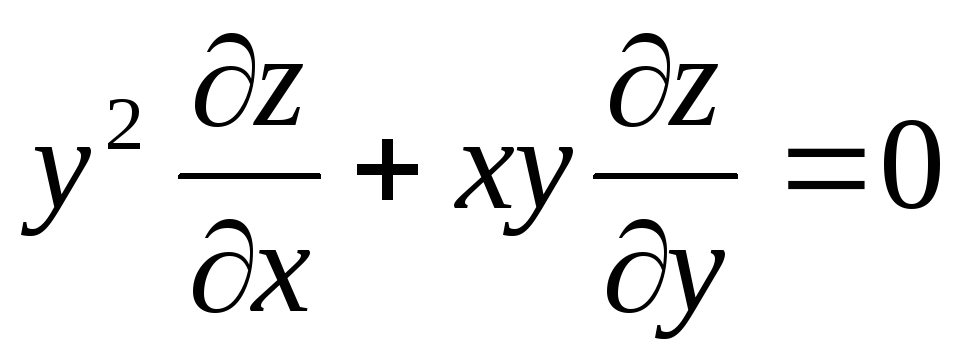 — дифференциальное
уравнение в частных производных первого
порядка.
— дифференциальное
уравнение в частных производных первого
порядка.
Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = (x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество
Свойства общего решения.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = (х, С0).
Определение. Решение вида у = (х, С0) называется частным решением дифференциального уравнения.
Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = (х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если
функция f(x, y)
непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную
частную производную 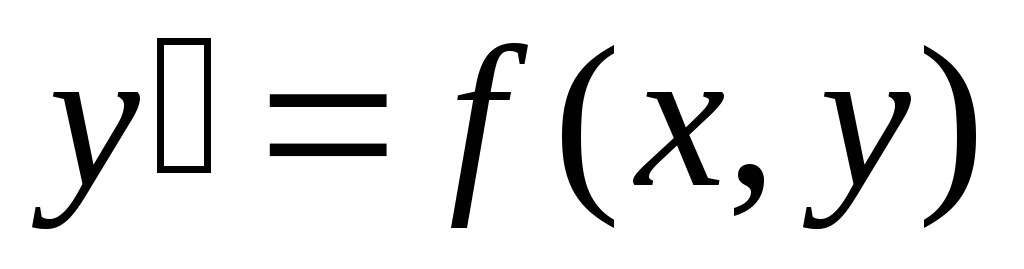 ,
то какова бы не была точка (х0,
у0)
в области D,
существует единственное решение
,
то какова бы не была точка (х0,
у0)
в области D,
существует единственное решение 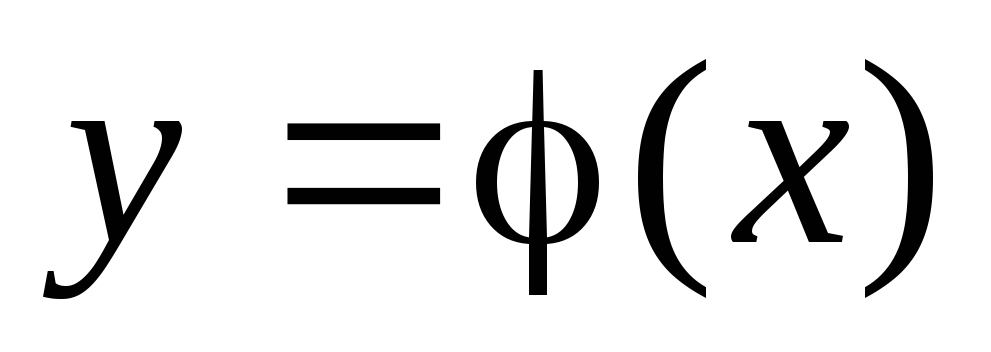 уравнения
уравнения ,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
Определение. Интегралом дифференциального
уравнения называется любое уравнение,
не содержащее производных, для которого
данное дифференциальное уравнение
является следствием.
Пример. Найти общее решение дифференциального
уравнения 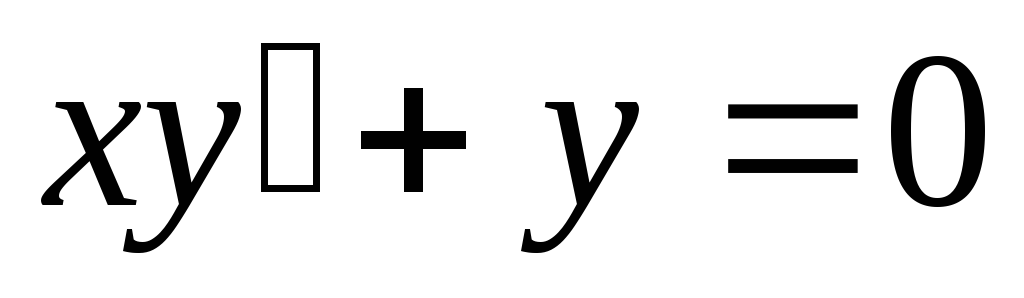 .
.
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
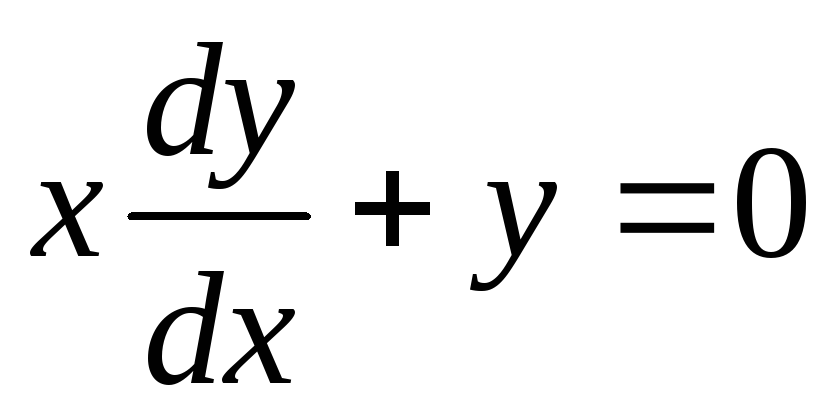
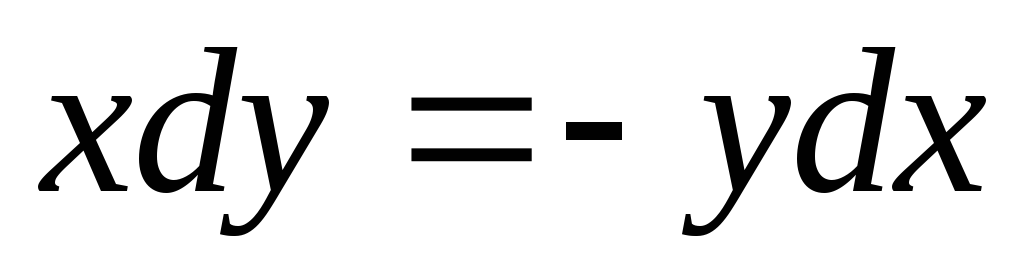
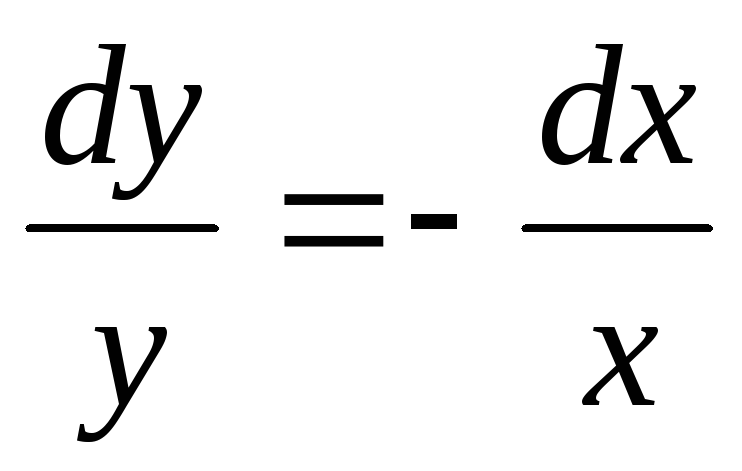
Теперь
интегрируем: 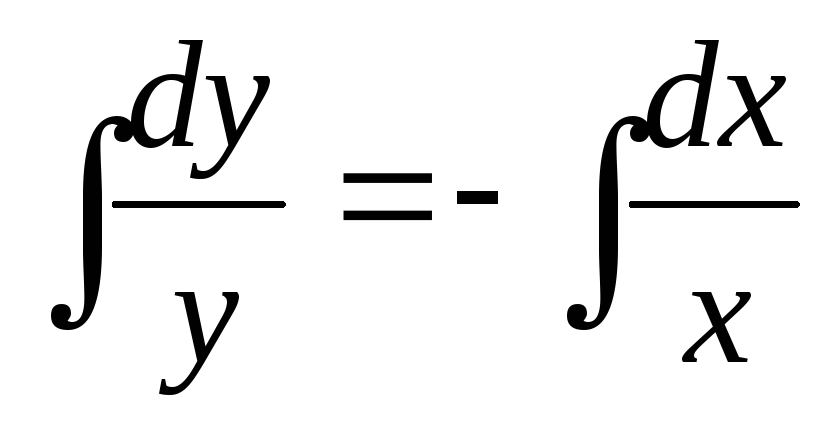
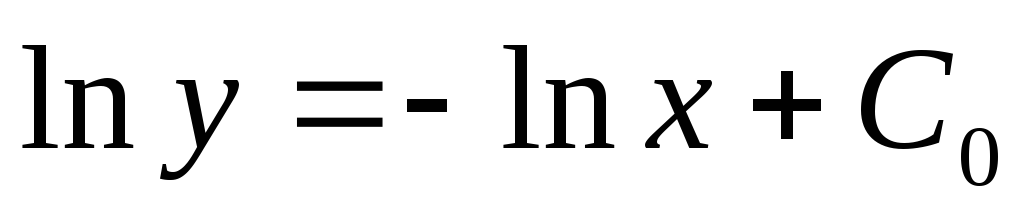

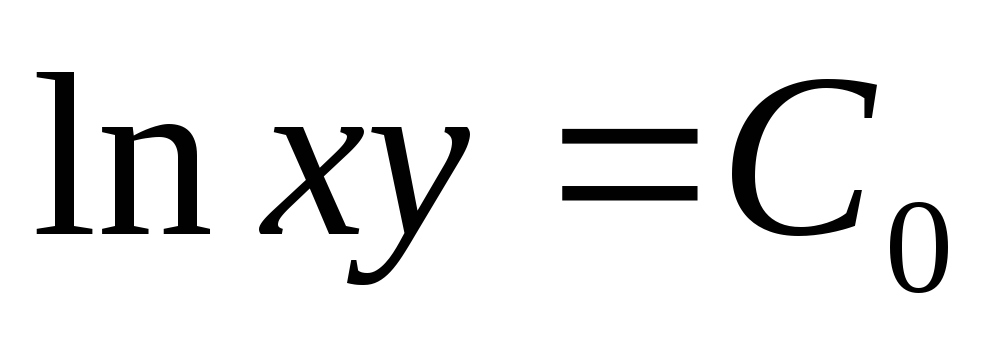
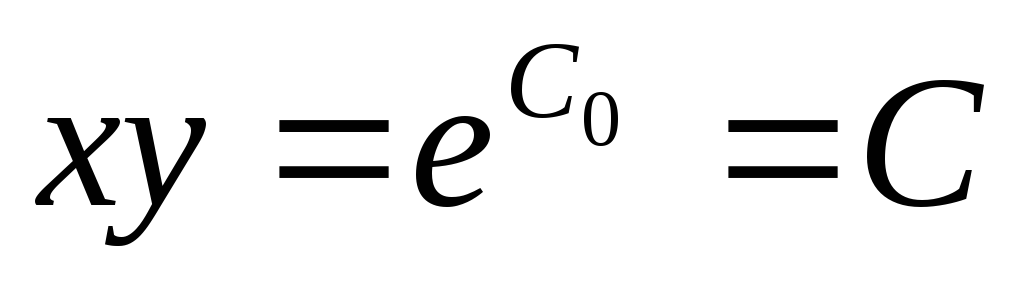
 — это общее решение
исходного дифференциального уравнения.
— это общее решение
исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
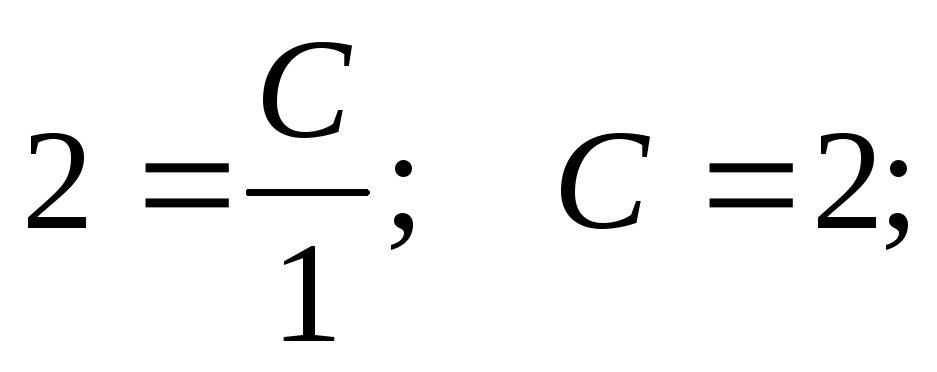
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).

Определение. Интегральной кривой называется график y = (x) решения дифференциального уравнения на плоскости ХОY.
Определение. Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши (см. Теорема Коши. ) не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Пример. Найти общее решение дифференциального
уравнения: 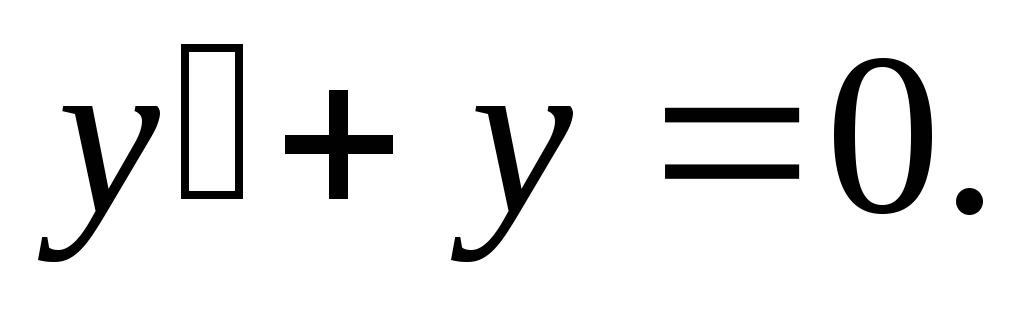 Найти особое решение, если оно существует.
Найти особое решение, если оно существует.




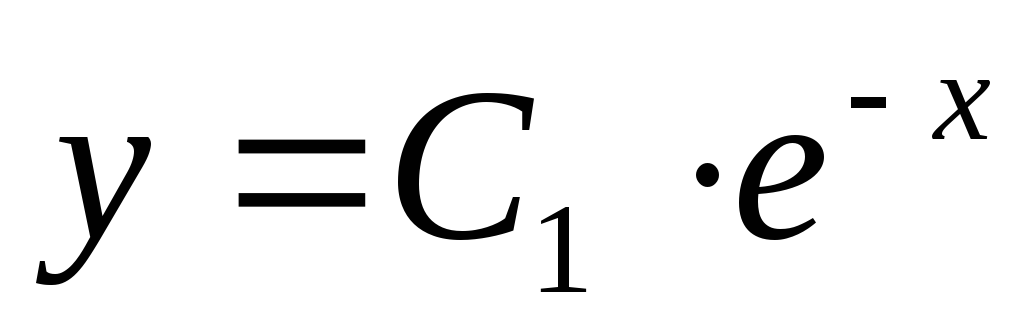
Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0 можно получить из общего решения при С1 = 0 ошибочно, ведь C1 = eC 0.
Далее рассмотрим подробнее приемы и методы, которые используются при решении дифференциальных уравнений различных типов.
studfile.net
Порядок дифференциального уравнения и его решения, задача Коши
Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию этой переменной и её производные (или дифференциалы) различных порядков.
Порядком дифференциального уравнения называется порядок старшей производной, содержащейся в нём.
Кроме обыкновенных изучаются также дифференциальные уравнения с частными производными. Это уравнения,
связывающие независимые переменные 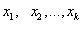 ,
неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только
обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово «обыкновенные».
,
неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только
обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово «обыкновенные».
Примеры дифференциальных уравнений:
(1)  ;
;
(2) 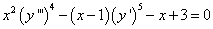 ;
;
(3) 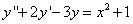 ;
;
(4) 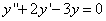 ;
;
(5)  .
.
Уравнение (1) — четвёртого порядка, уравнение (2) — третьего порядка, уравнения (3) и (4) — второго порядка, уравнение (5) — первого порядка.
Дифференциальное уравнение n-го порядка не обязательно должно содержать явно функцию, все её производные от первого до n-го порядка и независимую переменную. В нём могут не содержаться явно производные некоторых порядков, функция, независимая переменная.
Например, в уравнении (1) явно нет производных третьего и второго порядков, а также функции; в уравнении (2) — производной второго порядка и функции; в уравнении (4) — независимой переменной; в уравнении (5) — функции. Только в уравнении (3) содержатся явно все производные, функция и независимая переменная.
Решением дифференциального уравнения называется всякая функция y = f(x), при подстановке которой в уравнение оно обращается в тождество.
Процесс нахождения решения дифференциального уравнения называется его интегрированием.
Пример 1. Найти решение дифференциального уравнения  .
.
Решение. Запишем данное уравнение в виде 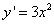 .
Решение состоит в нахождении функции по её производной. Изначальная функция, как известно из интегрального исчисления, есть
первообразная для
.
Решение состоит в нахождении функции по её производной. Изначальная функция, как известно из интегрального исчисления, есть
первообразная для  , т. е.
, т. е.
 .
.
Это и есть решение данного дифференциального уравнения. Меняя в нём C, будем получать различные решения. Мы выяснили, что существует бесконечное множество решений дифференциального уравнения первого порядка.
Общим решением дифференциального уравнения n-го порядка называется его решение, выраженное явно относительно неизвестной функции и содержащее n независимых произвольных постоянных, т. е.
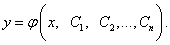
Решение дифференциального уравнения в примере 1 является общим.
Частным решением дифференциального уравнения называется такое его решение, в котором произвольным постоянным придаются конкретные числовые значения.
Пример 2. Найти общее решение дифференциального уравнения 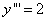 и частное решение при
и частное решение при 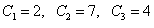 .
.
Решение. Проинтегрируем обе части уравнения такое число раз, которому равен порядок дифференциального уравнения.
 ,
,
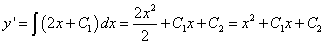 ,
,
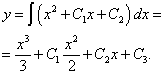 .
.
В результате мы получили общее решение —
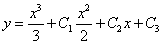
данного дифференциального уравнения третьего порядка.
Теперь найдём частное решение при указанных условиях. Для этого подставим вместо произвольных коэффициентов их значения и получим
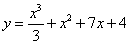 .
.
Если кроме дифференциального уравнения задано начальное условие в виде 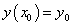 ,
то такая задача называется задачей Коши. В общее решение уравнения подставляют значения
,
то такая задача называется задачей Коши. В общее решение уравнения подставляют значения 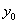 и
и
 и находят значение произвольной постоянной C,
а затем частное решение уравнения при найденном значении C. Это и есть решение задачи Коши.
и находят значение произвольной постоянной C,
а затем частное решение уравнения при найденном значении C. Это и есть решение задачи Коши.
Пример 3. Решить задачу Коши для дифференциального уравнения из примера 1
при условии 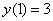 .
.
Решение. Подставим в общее решение  значения из начального условия y = 3, x = 1. Получаем
значения из начального условия y = 3, x = 1. Получаем
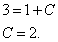 .
.
Записываем решение задачи Коши для данного дифференциального уравнения первого порядка:
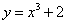 .
.
При решении дифференциальных уравнений, даже самых простых, требуются хорошие навыки интегрирования и взятия производных, в том числе сложных функций. Это видно на следующем примере.
Пример 4. Найти общее решение дифференциального уравнения 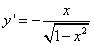 .
.
Решение. Уравнение записано в такой форме, что можно сразу же интегрировать обе его части.
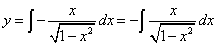 .
.
Применяем метод интегрирования заменой переменной (подстановкой). Пусть 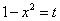 ,
тогда
,
тогда  .
.
Требуется взять dx и теперь — внимание — делаем это по правилам дифференцирования сложной функции, так как x и есть сложная функция («яблоко» — извлечение квадратного корня или, что то же самое — возведение в степень «одна вторая», а «фарш» — самое выражение под корнем):
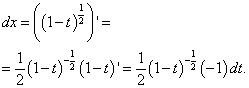
Находим интеграл:

Возвращаясь к переменной x, получаем:
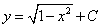 .
.
Это и есть общее решение данного дифференциального уравнения первой степени.
Не только навыки из предыдущих разделов высшей математики потребуются в решении дифференциальных уравнений, но и навыки из элементарной, то есть школьной математики. Как уже говорилось, в дифференциальном уравнении любого порядка может и не быть независимой переменной, то есть, переменной x. Помогут решить эту проблему не забытые (впрочем, у кого как) со школьной скамьи знания о пропорции. Таков следующий пример.
Пример 5. Найти общее решение дифференциального уравнения 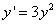 .
.
Решение. Как видим, переменная x в уравнении отсутствует. Вспоминаем из курса дифференциального
исчисления, что производная может быть записана также в виде 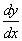 .
В результате уравнение приобретает вид
.
В результате уравнение приобретает вид
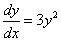 ,
,
то есть, в нём в некотором виде появился x.
Теперь вспомнаем одно из свойств пропорции: из пропорции 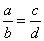 выткают следующие пропорции:
выткают следующие пропорции:
 ,
,
то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.
Применяя это свойство, преобразуем уравнение к виду
 ,
,
после чего интегрируем обе части уравнения:
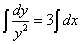 .
.
Оба интеграла — табличные, находим их:
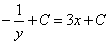
и получаем решение данного дифференциалного уравнения первого порядка:
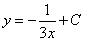 .
.
Эта статья представила необходимый минимум сведений о дифференциальных уравнениях и их решениях и должна помочь вам уверенно и увлечённо перейти к изучению различных видов дифференциальных уравнений.

Всё по теме «Дифференциальные уравнения»
Поделиться с друзьями
function-x.ru
Дифференциальные уравнения первого порядка
Далее в тексте – функции своих аргументов. Штрих ′ означает производную по аргументу. – постоянные.
Дифференциальные уравнения первого порядка, разрешенные относительно производной
Как решать дифференциальные уравнения первого порядка
Пусть мы имеем дифференциальное уравнение первого порядка, разрешенное относительно производной:
.
Разделив это уравнение на , при , мы получим уравнение вида:
,
где .
Далее смотрим, не относятся ли эти уравнения к одному из перечисленных ниже типов. Если нет, то перепишем уравнение в форме дифференциалов. Для этого пишем и умножаем уравнение на . Получаем уравнение в форме дифференциалов:
.
Если это уравнение не является уравнением в полных дифференциалах, то считаем, что в этом уравнении – независимая переменная, а – это функция от . Разделим уравнение на :
.
Далее смотрим, не относится ли это уравнение к одному из, перечисленных ниже типов учитывая, что и поменялись местами.
Если и для этого уравнения не найден тип, то смотрим, нельзя ли упростить уравнение простой подстановкой. Например, если уравнение имеет вид:
,
то замечаем, что . Тогда делаем подстановку . После этого уравнение примет более простой вид:
.
Если и это не помогает, то пытаемся найти интегрирующий множитель ⇓.
Уравнения с разделяющимися переменными
;
.
Делим на и интегрируем. При получаем:
.
Подробнее >>>
Уравнения, приводящиеся к уравнениям с разделяющимися переменными
Делаем подстановку . Тогда
;
.
Далее разделяем переменные и интегрируем.
Подробнее >>>
Однородные уравнения
Решаем подстановкой:
,
где – функция от . Тогда
;
.
Разделяем переменные и интегрируем.
Подробнее >>>
Уравнения, приводящиеся к однородным
Вводим переменные и :
;
.
Постоянные и выбираем так, чтобы свободные члены обратились в нуль:
;
.
В результате получаем однородное уравнение в переменных и .
Подробнее >>>
Обобщенные однородные уравнения
Делаем подстановку . Получаем однородное уравнение в переменных и .
Подробнее >>>
Линейные дифференциальные уравнения
Есть три метода решения линейных уравнений.
1) Метод интегрирующего множителя.
Умножаем уравнение на интегрирующий множитель :
;
.
Далее интегрируем.
Подробнее >>>
2) Метод Бернулли.
Ищем решение в виде произведения двух функций и от переменной :
.
;
.
Одну из этих функций мы можем выбрать произвольным образом. Поэтому в качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>
3) Метод вариации постоянной (Лагранжа).
Здесь мы сначала решаем однородное уравнение:
Общее решение однородного уравнения имеет вид:
,
где – постоянная. Далее мы заменяем постоянную на функцию , зависящую от переменной :
.
Подставляем в исходное уравнение. В результате получаем уравнение, из которого определяем .
Подробнее >>>
Уравнения Бернулли
Подстановкой уравнение Бернулли приводится к линейному уравнению.
Также это уравнение можно решать методом Бернулли. То есть ищем решение в виде произведения двух функций, зависящих от переменной :
.
Подставляем в исходное уравнение:
;
.
В качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>
Уравнения Риккати
Оно не решается в общем виде. Подстановкой
уравнение Риккати приводится к виду:
,
где – постоянная; ; .
Далее, подстановкой:
оно приводится к виду:
,
где .
Свойства уравнения Риккати и некоторые частные случаи его решения представлены на странице
Дифференциальное уравнение Риккати >>>
Уравнения Якоби
Решается подстановкой:
.
Подробнее >>>
Уравнения в полных дифференциалах
При условии
.
При выполнении этого условия, выражение в левой части равенства является дифференциалом некоторой функции:
.
Тогда
.
Отсюда получаем интеграл дифференциального уравнения:
.
Для нахождения функции , наиболее удобным способом является метод последовательного выделения дифференциала. Для этого используют формулы:
;
;
;
.
Подробнее >>>
Интегрирующий множитель
Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то можно попытаться найти интегрирующий множитель . Интегрирующий множитель – это такая функция, при умножении на которую, дифференциальное уравнение становится уравнением в полных дифференциалах. Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей. Однако, общих методов для нахождения интегрирующего множителя нет.
Подробнее >>>
Уравнения, не решенные относительно производной y’
Уравнения, допускающие решение относительно производной y’
Сначала нужно попытаться разрешить уравнение относительно производной . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.
Уравнения, допускающие разложение на множители
Если удастся уравнение разложить на множители:
,
то задача сводится к последовательному решению более простых уравнений:
;
;
;
Подробнее >>>
Уравнения, не содержащие x и y
Здесь – постоянная:
,
где – корень уравнения
.
Подробнее >>>
Уравнения, не содержащие x или y
или
Ищем решение в параметрическом виде. Вводим параметр . Полагаем . Тогда
или .
Далее интегрируем уравнение:
;
.
В результате получаем выражение второй переменной через параметр .
Более общие уравнения:
или
также решаются в параметрическом виде. Для этого нужно подобрать такую функцию , чтобы из исходного уравнения можно было выразить или через параметр .
Чтобы выразить вторую переменную через параметр , интегрируем уравнение:
;
.
Подробнее >>>
Уравнения, разрешенные относительно y
Уравнения Клеро
Такое уравнение имеет общее решение
Подробнее >>>
Уравнения Лагранжа
Решение ищем в параметрическом виде. Полагаем , где – параметр.
Подробнее >>>
Уравнения, приводящиеся к уравнению Бернулли
Эти уравнения приводятся к уравнению Бернулли, если искать их решения в параметрическом виде, введя параметр и делая подстановку .
Подробнее >>>
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Дифференциальные уравнения в полных дифференциалах
Дифференциальным уравнением в полных дифференциалах называется уравнение вида
P(x,y)dx + Q(x,y)dy = 0,
где левая часть является полным дифференциалом какой-либо функции двух переменных.
Обозначим неизвестную функцию двух переменных (её-то и требуется найти при решении уравнений в полных дифференциалах) через F и скоро вернёмся к ней.
Первое, на что следует обратить внимание: в правой части уравнения обязательно должен быть нуль, а знак, соединяющий два члена в левой части, должен быть плюсом.
Второе — должно соблюдаться некоторое равенство, которое является подтверждением того, что данное дифференциальное уравнение является уравнением в полных дифференциалах. Эта проверка является обязательной частью алгоритма решения уравнений в полных дифференциалах (он во втором параграфе этого урока), так процесс поиска функции F достаточно трудоёмкий и важно на начальном этапе убедиться в том, что мы не потратим время зря.
Итак, неизвестную функцию, которую требуется найти, обозначили через F. Сумма частных дифференциалов по всем независимым переменным даёт полный дифференциал. Следовательно, если уравнение является уравнением в полных дифференциалах, левая часть уравнения представляет собой сумму частных дифференциалов. Тогда по определению
dF = P(x,y)dx + Q(x,y)dy.
Вспоминаем формулу вычисления полного дифференциала функции двух переменных:
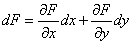 .
.
Решая два последних равенства, можем записать
 .
.
Первое равенство дифференцируем по переменной «игрек», второе — по переменной «икс»:
 .
.
Так как
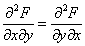 ,
,
получим
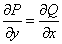 ,
,
что является условием того, что данное дифференциальное уравнение действительно представляет собой уравнение в полных дифференциалах.
Шаг 1. Убедиться, что уравнение является уравнением в полных дифференциалах. Для
того, чтобы выражение 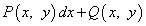 было
полным дифференциалом некоторой функции F(x, y), необходимо и достаточно, чтобы
было
полным дифференциалом некоторой функции F(x, y), необходимо и достаточно, чтобы  .
Иными словами, нужно взять частную производную по x одного слагаемого в левой части выражения и частную
производную по y другого слагаемого и, если эти производные равны, то уравнение является уравнением в полных дифференциалах.
.
Иными словами, нужно взять частную производную по x одного слагаемого в левой части выражения и частную
производную по y другого слагаемого и, если эти производные равны, то уравнение является уравнением в полных дифференциалах.
Шаг 2. Записать систему уравнений из частных производных, составляющих функцию F:

Шаг 3. Проинтегрировать первое уравнение системы — 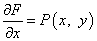 по x (y остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F:
по x (y остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F:
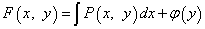 ,
,
где 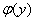 — пока неизвестная функция от y.
— пока неизвестная функция от y.
Альтернативный вариант (если так интеграл найти проще) — проинтегрировать второе уравнение системы
—  по y (x остаётся константой и выносится за знак интеграла).
Таким образом так же восстанавливается функция F:
по y (x остаётся константой и выносится за знак интеграла).
Таким образом так же восстанавливается функция F:
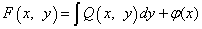 ,
,
где 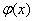 — пока неизвестная функция от х.
— пока неизвестная функция от х.
Шаг 4. Результат шага 3 (найденный общий интеграл) продифференцировать по y (в альтернативном варианте — по x) и приравнять ко второму уравнению системы:
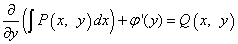 ,
,
а в альтернативном варианте — к первому уравнению системы:
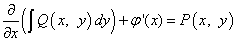 .
.
Из полученного уравнения определяем 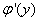 (в альтернативном варианте
(в альтернативном варианте 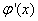 )
)
Шаг 5. Результат шага 4 интегрировать и найти  (в альтернативном варианте найти
(в альтернативном варианте найти 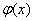 ).
).
Шаг 6. Результат шага 5 подставить в результат шага 3 — в восстановленную частным интегрированием функцию F. Произвольную постоянную C чаще записывают после знака равенства — в правой части уравнения. Таким образом получаем общее решение дифференциального уравнения в полных дифференциалах. Оно, как уже говорилось, имеет вид F(x, y) = C.
Какая ошибка возможна здесь с наибольшей вероятностью? Самые распространённые ошибки — принять частный интеграл по одной из переменных за обычный интеграл произведения функций и пытаться интегрировать по частям или заменной переменной а также принять частную производную двух сомножителей за производную произведения функций и искать производную по соответствующей формуле.
Это надо запомнить: при вычислении частного интеграла по одной из переменной другая является константой и выносится за знак интеграла, а при вычислении частной производной по одной из переменной другая также является константой и производная выражения находится как производная «действующей» переменной, умноженной на константу.
Среди уравнений в полных дифференциалах не редкость — примеры с экспонентой. Таков следующий пример. Он же примечателен и тем, что в его решении используется альтернативный вариант.
В следующем примере возвращаемся от альтернативного варианта к основному.

Всё по теме «Дифференциальные уравнения»
Поделиться с друзьями
function-x.ru