Динамика (физика) — Википедия

У этого термина существуют и другие значения, см. Динамика.

Дина́мика (греч. δύναμις «сила, мощь») — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, момент импульса, энергия^[1].

Также динамикой нередко называют, применительно к другим областям физики (например, к теории поля), ту часть рассматриваемой теории, которая более или менее прямо аналогична динамике в механике, противопоставляясь обычно кинематике (к кинематике в таких теориях обычно относят, например, соотношения, получающиеся из преобразований величин при смене системы отсчёта).

Иногда слово динамика применяется в физике и не в описанном смысле, а в более общелитературном: для обозначения просто процессов, развивающихся во времени, зависимости от времени каких-то величин, не обязательно имея в виду конкретный механизм или причину этой зависимости.

Динамика, базирующаяся на законах Ньютона, называется

классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.

Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.

С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.

В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.

Эрнст Мах считал, что основы динамики были заложены Галилеем^[2].

Исторически деление на прямую и обратную задачу динамики сложилось следующим образом^[3].

Классическая динамика основана на трёх основных законах Ньютона:

• 1-й: Существуют такие системы отсчёта, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.

∑i=1nFi→=0⇒v→=const{\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}=0\Rightarrow {\vec {v}}=const}

a→=∑i=1nFi→m,{\displaystyle {\vec {a}}={\frac {\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}}{m}},}

где a→{\displaystyle {\vec {a}}} — ускорение тела, Fi→{\displaystyle {\vec {F_{i}}}} — силы, приложенные к материальной точке, а  m{\displaystyle \ m} — её масса, или

ma→=∑i=1nFi→.{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}.}

В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами^[4][5].

Второй закона Ньютона можно также сформулировать с использованием понятия импульса:

В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на него силе^[6].

dp→dt=∑i=1nFi→,{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}},}

где p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} — импульс (количество движения) точки, v→{\displaystyle {\vec {v}}} — её скорость, а t{\displaystyle t} — время. При такой формулировке, как и ранее, полагают, что масса материальной точки неизменна во времени^[7][8][9].

• 3-й: Силы, с которыми тела действуют друг на друга, лежат на одной прямой, имеют противоположные направления и равные модули

|F1→|=|F2→|{\displaystyle |{\vec {F_{1}}}|=|{\vec {F_{2}}}|}

F1→=−F2→{\displaystyle {\vec {F_{1}}}={\vec {-F_{2}}}}

Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса

Законы Ньютона в неинерциальных системах отсчёта[править | править код]

Существование инерциальных систем отсчёта лишь постулируется первым законом Ньютона. Реальные системы отсчёта, связанные, например, с Землёй или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчёта, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса. Эти «силы» не обусловлены взаимодействием тел, то есть по своей природе не являются силами и вводятся лишь для сохранения формы второго закона Ньютона:

∑i=1nFi→+∑j=1nFfj→=ma→{\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}+\sum _{j=1}^{n}{\vec {F_{f_{j}}}}=m{\vec {a}}},

где ∑j=1nFfj→{\displaystyle \sum _{j=1}^{n}{\vec {F_{f_{j}}}}} — сумма всех фиктивных сил, возникающих в неинерциальной системе отсчёта.

Многие законы динамики могут быть описаны исходя не из законов Исаака Ньютона, а из принципа наименьшего действия.

Формулы некоторых сил, действующих на тело[править | править код]

• Сила всемирного тяготения:

FT=Gm1m2r2{\displaystyle F_{T}={Gm_{1}m_{2} \over r^{2}}}

или в векторной форме:

FT→(r1→)=Gm1m2|r2→−r1→|3(r2→−r1→){\displaystyle {\overrightarrow {F_{T}}}({\vec {r_{1}}})=G{\frac {m_{1}m_{2}}{|{\vec {r_{2}}}-{\vec {r_{1}}}|^{3}}}{({\vec {r_{2}}}-{\vec {r_{1}}})}}

вблизи земной поверхности:

FT→=mg→{\displaystyle {\overrightarrow {F_{T}}}=m{\vec {g}}}

Ff=μN{\displaystyle F_{f}=\mu N}

• Сила Архимеда:

FA=ρgV{\displaystyle F_{A}=\rho gV}

1. ↑ Тарг С. М. Динамика // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 616-617. — 707 с. — 100 000 экз.
2. ↑ Мах Э.  Механика. Историко-критический очерк её развития. — Ижевск: Ижевская республиканская типография, 2000. — С. 105. — 456 с. — ISBN 5-89806-023-5.
3. ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 183. — 416 с. — ISBN 5-06-003117-9.
4. ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
5. ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 287. — 416 с. — ISBN 5-06-003117-9. «В классической механике масса каждой точки или частицы системы считается при движении величиной постоянной»
6. ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; изд-во МФТИ, 2005. — Т. I. Механика. — С. 76. — 560 с. — ISBN 5-9221-0225-7.
7. ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
8. ↑ Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с.«В ньютоновской механике… m=const и dp/dt=ma».
9. ↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».

• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
• Матвеев А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
• Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
• Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
• Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие. М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-2

Динамика

Основным свойством материи является движение. Именно движение — в широком смысле этого слова — является предметом изучения науки физики.

Классическая механика изучает механическое движение с досветовыми скоростями. При этом составляющие её науки изучают разные аспекты механического движения. Так, кинематика изучает законы движения безотносительно к порождающим это движение причинам. Статика изучает силы, действующие на тело, их взаимодействие, и условия равновесия этих сил, при которых тело не будет двигаться.

Однако центральным разделом механики является динамика, исследующая причины изменений в движении тела. Причинами таких изменений являются силы, действующие на тело.

Сила $( \overrightarrow{F)}$ — векторная физическая величина, являющаяся количественной характеристикой действия одного тела на другое (или частей одного и того же тела).

Определение

Динамика — раздел механики, в котором изучаются законы и характер движения тел под действием приложенных к ним сил, порождающих это движение, и их инертности (массы).

Движение тел в данной системе отсчета начинаются и прекращаются, они становятся более быстрыми или более медленными, изменяются напрявления движений. Во всех этих случаях мы имеем дело с изменением скорости, то есть появлением ускорения. Понятно, насколько важно знать, при каких условиях возникают ускорения, а при каких условиях тела движутся без ускорений, как определять ускорения (их абсолютные значения и направления). Без этого нельзя решать задачи механики, без этого нельзя управлять движением. На все эти вопросы дает ответ динамика. Поэтому справедливо и такое определение предмета изучения динамики:

Определение

Часть механики, в которой изучаются причины появления ускорения и рассматриваются способы его вычисления, называется динамикой.

Вопрос о причинах механического движения имеет долгую историю. Аристотель в своём трактате, который назывался «Физика», утверждал, что всякому движению есть движущая сила, поэтому все учёные-физики до XVI века искали силу, которая движет. Например, в трактате XIII века причины движения пущенной стрелы со скоростью были описаны следующим образом: сдвинувшись, стрела разрезает воздух, который находится впереди, но за оперением остаётся пустое пространство, в него входит воздух из окружающей среды и подталкивает эту стрелу (Рис. 1). Из этого объяснения выходит, что воздух является движущей силой и в разряжённом воздухе стрела будет лететь меньшее расстояние, что совершенно неверно.

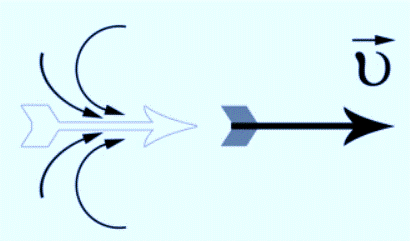
Рис. 1. Движение стрелы

Утверждения Аристотеля считались абсолютной истиной до трудов Галилея. Он сформулировал закон инерции: если на тело не действуют никакие силы или действие этих сил скомпенсировано, тело сохраняет состояние покоя или равномерного прямолинейного движения.

Следующим этапом развития динамики были труды И. Ньютона. Он сформулировал систему законов (3 закона Ньютона), которые являются основными законами классической механики. В механике Ньютона силы могут иметь различную физическую природу: сила трения, сила тяжести, упругая сила и др.

Динамика Галилея — Ньютона называется классической (нерелятивистской) динамикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света с в вакууме (с = 3$.$108 м/с). Макроскопическими называют тела, состоящие из множества молекул; макроскопические тела не всегда можно принимать за материальные точки.

С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.

В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.

Основные понятия классической механики:

Мамсса — скалярная физическая величина, являющаяся количественной мерой инертности тела, а также характеризующая количество вещества в теле;

Симла — векторная физическая величина, являющаяся мерой взаимодействия тел и приводящая к появлению у тела ускорения или к деформации тела. Сила характеризуется величиной, направлением и точкой приложения;

Линия действия силы — это линия, вдоль которой действует сила. Если тело является абсолютно твердым, то точку приложения силы можно перемещать вдоль линии действия силы в пределах тела;

Импульс — векторная физическая величина, равная произведению массы тела на его скорость: $\overrightarrow{р}=m\overrightarrow{v}$;

Энергия — количественная характеристика движения и взаимодействия тел, их способности совершать изменения во внешнем мире.

Алгоритм решения задач по теме «Динамика»

1. Сделать чертеж по плану:

• Опора (если есть)
• Тело
• Силы
• Ускорение (если есть)
• Оси координат (х вдоль $\overrightarrow{a}$)
• Проанализировать состояние объекта: покой, равномерное прямолинейное движение или равноускоренное движение. Записать I или II закон Ньютона, описывающий условие данной задачи в векторной форме.
• Сделать проекции этого выражения на оси.
• Записать систему уравнений, добавив в неё при необходимости формулу силы трения или уравнения кинематики.
• Решить систему уравнений относительно неизвестной.

Вопрос 1

Что изучает динамика?

1. Причины возникновения движения макроскопических тел
2. Причины возникновения движения микроскопических тел
3. Причины возникновения движения любых тел
4. Причины изменения движения любых тел

Ответ: правильным является четвёртый ответ.

Вопрос 2

Что такое инертная масса тела?

1. То же самое, что и количество вещества в этом теле
2. Свойство тела, проявляющееся в его стремлении сохранить данную скорость движения
3. Свойство тела, проявляющееся в его способности притягиваться к другим телам, а также притягивать к себе другие тела
4. То же самое, что и вес тела

Ответ: правильным является второй ответ.

Динамика — это… Что такое Динамика?

Содержание

1. Динамика в разных науках

— В физике

— В астрономии

— В науках о Земле

— В биологии

— В технике

— В музыке

2. Динамика в физике

3. Ряды динамики

4. Газовая динамика

Динамика – это состояние движения, ход развития, изменение какого-либо явления под влиянием действующих на него факторов.

Динамика в разных науках

В физике

Динамика

Аэрогазодинамика

Гидродинамика

Молекулярная динамика

Термодинамика

Нелинейная динамика

В астрономии

Звёздная динамика

В науках о Земле

Геодинамика

Динамика подземных вод

Динамика русловых потоков

В биологии

Популяционная динамика

Популяционная динамика старения

Динамика растительности (синдинамика) — процесс постепенной трансформации растительных сообществ под действием внешних и внутренних факторов.

В технике

Динамика машин и механизмов

Динамика сооружений

В музыке

Динамика в музыке — совокупность понятий и нотных обозначений, связанных с оттенками громкости звучания.

Динамика в физике

Динамика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия.

Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.

Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.

С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.

В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.

Основная задача динамики

Прямая задача динамики: по заданным силам определить характер движения тела.

Обратная задача динамики: по заданному характеру движения определить действующие на тело силы.

Законы Ньютона

Классическая динамика основана на трёх основных законах Ньютона:

1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.

2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).

3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению

Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса

Законы Ньютона в неинерциальных системах отсчета

Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса.

Ряды динамики

Ряды динамики, статистические ряды, характеризующие изменение (развитие) социально-экономических явлений во времени. Например, данные о производстве электричества в СССР за период 1928—73 представляют Ряды динамики

Производство электричества в СССР, млрд. кетЧч

1928 5.0

1932 13.5

1937 36.2

1940 48.3

1950 91.2

1960 292

1970 741

1973 915

Последовательно расположенные во времени статистические данные называются уровнями Ряды динамики Они должны быть сопоставимы между собой, особенно в территориальном разрезе, по кругу охватываемых объектов, методике расчёта, критической дате, структуре. Уровни Ряды динамики могут характеризовать величину явлении за некоторые отрезки времени (интегральные Ряды динамики) или на определённую дату (моментные Ряды динамики). Анализ Ряды динамики состоит в определении скорости и интенсивности развития рассматриваемого явления, нахождении основные тенденции его развития (тренда), измерении колеблемости уровней, установлении связи с развитием др. явлений, проведении сравнительного анализа развития разных стран или районов. Для анализа Ряды динамики определяются статистические показатели: абсолютные приросты, темпы роста и прироста, средние уровни ряда, средние абсолютные приросты, средние темпы роста и прироста. Абсолютным приростом называют разность между последующим и предыдущим уровнями, а темпом роста — их отношение. Темп прироста составит разность между темпом роста и 1 (в коэффициенте) или 100%. Средний уровень ряда для интервальных рядов определяется как средняя арифметическая, а для моментных рядов — по формуле:

где — средний уровень, y1. — начальный, а уп — конечный, n — число уровней. Средний абсолютный прирост определяется как частное от деления абсолютного прироста за весь период на число единиц времени в периоде. Средний темп роста вычисляется как средняя геометрическая темпов роста за отдельные отрезки времени или как корень, степень которого определяется числом периодов, а под корнем берётся темп роста за весь период.

Определение тренда ведётся выравниванием статистическим. Колеблемость уровней Ряды динамики измеряется средней из квадратов отклонений фактических уровней от тренда. Для установления связи развития данного явления с другими пользуются методом корреляции Ряды динамики, отличающимся от обычного возможностью автокорреляции, авторегрессии, переменной корреляции и временного лага. Для сравнительного анализа разных стран (районов) часто используется приведение к одному основанию, состоящее в определении темпов роста для двух или более стран за одинаковые отрезки времени. Сравнительный анализ развития лучше вести с расчётом показателей на душу населения. Всесторонний анализ Ряды динамики позволяет выявить закономерности развития отражаемых в них явлений.

Газовая динамика

Газовая динамика, раздел гидро-аэромеханики, в котором изучается движение сжимаемых газообразных и жидких сред и их взаимодействие с твёрдыми телами. Как часть физики, Газовая динамика связана с термодинамикой и акустикой.

Свойство сжимаемости состоит в способности вещества изменять свой первоначальный объём под действием перепада давления или при изменении температуры. Поэтому сжимаемость становится существенной лишь при больших скоростях движения среды, соизмеримых со скоростью распространения звука в этой среде и превосходящих её, когда в среде возникают большие перепады давления и большие градиенты температуры. Современная газовая динамика изучает также течения газов при высоких температурах, сопровождающиеся химическими (диссоциация, горение и др. химические реакции) и физическими (ионизация, излучение) процессами. Изучение движения газов при таких условиях, когда газ нельзя считать сплошной средой, а необходимо рассматривать взаимодействие составляющих его молекул между собой и с твёрдыми телами, относится к области аэродинамики разреженных газов, основанной на молекулярно-кинетической теории газов. Динамика сжимаемого газа при малых скоростях движения больших воздушных масс в атмосфере составляет основу динамической метеорологии. Газовая динамика исторически возникла как дальнейшее развитие и обобщение аэродинамики, поэтому часто говорят о единой науке — аэрогазодинамике.

Теоретическую основу газовая динамика составляет применение основных законов механики и термодинамики к движущемуся объёму сжимаемого газа. Навье — Стокса уравнения, описывающие движение вязкого сжимаемого газа, были получены в 1-й половине 19 в. Немецкий учёный Б.Риман (1860), английский — У. Ранкин (1870), французский -А. Гюгоньо (1887) исследовали распространение в газе ударных волн, которые возникают только в сжимаемых средах и движутся со скоростью, превышающей скорость распространения в них звуковых волн. Риман создал также основы теории неустановившихся движений газа, т. е. таких движений, когда параметры газового потока в каждой его точке изменяются с течением времени.

Фундаментальную роль в формировании Газовая динамика как самостоятельной науки сыграла опубликована в 1902 работа С. А. Чаплыгина «О газовых струях». Развитые в ней методы решения газодинамических задач получили впоследствии широкое распространение и обобщение. Плодотворный метод решения задач Газовая динамика предложили в 1908 нем. учёные Л. Прандтль и Т. Майер, исследовавшие частный случай течения газа с непрерывным увеличением скорости. В 1922 в работе «Опыт гидромеханики сжимаемой жидкости» советский учёный А. А. Фридман заложил основы динамической метеорологии. В 1929 нем. учёными Л. Прандтлем и А. Буземаном был разработан эффективный численно-графический метод решения широкого класса газодинамических задач, распространённый в 1934 сов. учёным Ф. И. Франклем на более сложные случаи течения газа. Эти методы широко применяются при решении задач Газовая динамика с помощью ЭВМ. В 1921 в СССР была создана, а в 1927 оформилась как научное учреждение газодинамическая лаборатория, деятельность которой совместно с Группой изучения реактивного движения (1932) заложила основы сов. ракетной техники.

Как самостоятельный раздел гидроаэромеханики Газовая динамика существует с 1930, когда рост скоростей в авиации потребовал серьёзного исследования влияния сжимаемости при изучении движения воздуха. В 1935 в Риме состоялся 1-й международный конгресс по Газовая динамика Интенсивное развитие Газовая динамика началось во время и особенно после окончания 2-й мировой войны 1939-45 в связи с широким использованием Газовая динамика в технике: применение реактивной авиации, ракетного оружия, ракетных и воздушно-реактивных двигателей; полёты самолётов и снарядов со сверхзвуковыми скоростями; создание атомных бомб, взрыв которых влечёт за собой распространение сильных взрывных и ударных волн. В этот период Газовая динамика выдающуюся роль сыграли исследования советских учёных С. А. Христиановича, А. А. Дородницына, Л. И. Седова, Г. И. Петрова, Г. Г. Чёрного и др., немецких учёных Прандтля, Буземана, английских учёных Дж. Тейлора, Дж. Лайтхилла, американских учёных Т. Кармана, А. Ферри, У. Хейса, китайского учёного Цянь Сюэ-сэня, а также учёных др. Стран.

Задачи газовой динамики при проектировании разнообразных аппаратов, двигателей и газовых машин состоят в определении сил давления и трения, температуры и теплового потока в любой точке поверхности тела или канала, омываемых газом, в любой момент времени. При исследовании распространения газовых струй, взрывных и ударных волн, горения и детонации методами Газовая динамика определяются давление, температура и др. параметры газа во всей области распространения. Изучение поставленных техникой сложных задач превратило современную газовою динамику в науку о движении произвольных смесей газов, которые могут содержать также твёрдые и жидкие частицы (например, выхлопные газы ракетных двигателей на жидком или твёрдом топливе), причём параметры, характеризующие состояние этих газов (давление, температура, плотность, электропроводность и др.), могут изменяться в широких пределах.

Для развития совресенной газовой динамики характерно неразрывное сочетание теоретических методов, использования ЭВМ и постановки сложных аэродинамических и физических экспериментов. Теоретические представления, частично опирающиеся на экспериментальные данные, позволяют описать с помощью уравнений движение газовых смесей сложного состава, в том числе многофазных смесей при наличии физико-химических превращений. Методами прикладной математики разрабатываются эффективные способы решения этих уравнений на ЭВМ. Наконец, из экспериментальных данных определяются необходимые значения физических и химических характеристик, свойственных изучаемой среде и рассматриваемым процессам (коэффициент вязкости и теплопроводности, скорости химических реакций, времена релаксации и др.).

Многие задачи, поставленные современной техникой перед газовой динамикой, пока не могут быть решены расчётно-теоретическими методами, в этих случаях широко пользуются газодинамическими экспериментами, поставленными на основе подобия теории и законов гидродинамического и аэродинамического моделирования. Газодинамические эксперименты в аэрогазодинамических лабораториях проводятся в сверхзвуковых и гиперзвуковых аэродинамических трубах, на баллистических установках, в ударных и импульсных трубах и на др. газодинамических установках специального назначения.

Законами газовой динамике широко пользуются во внешней и внутренней баллистике, при изучении таких явлений, как взрыв, горение, детонация, конденсация в движущемся потоке. Прикладная газовая динамика, в которой обычно применяются упрощённые теоретические представления об осреднённых по поперечному сечению параметрах газового потока и основные закономерности движения, найденные экспериментальным путём, используется при расчёте компрессоров и турбин, сопел и диффузоров, ракетных двигателей, аэродинамических труб, эжекторов, газопроводов и многих др. технических устройств.

Газодинамические исследования ведутся в тех же научных учреждениях, что и исследования по аэродинамике, а результаты их публикуются в тех же научных журналах и сборниках.

Источники

ru.wikipedia.org Википедия – свободная энциклопедия

bse.sci-lib.com Большая Советская энциклопедия

Конспект по физике на тему «Механика. Динамика» (подготовка к ЕГЭ)

Раздел 1.2. Динамика.

Тема 1. Три закона Ньютона.

Динамика изучает причины движения тел и способы определения ускорения.

Инерция – явление, при котором тело сохраняет состояние покоя или равномерного прямолинейного движения (т.е. в этих случаях отсутствует ускорение). Иначе говоря, инертность – это явление сохранения скорости тела.

Инерциальные системы отсчета (ИСО) – это системы отсчета, относительно которых наблюдается инерция, а также те, которые движутся равномерно и прямолинейно относительно ИСО.

ИСО – системы, ускорение которых равно нулю.

Инертность – физическое свойство, заключающееся в том, что любое тело оказывает сопротивление изменению его скорости (как по модулю, так и по направлению).

Проявление инертности чаще всего наблюдается в движущемся транспорте. Например, при резком увеличении скорости все пассажиры отклоняются назад, при резком торможении – вперед, при повороте направо все отклоняются влево и т.д.

Масса m (кг) – физическая величина, являющаяся мерой инертности тела. Измерительный прибор – весы.

Сила F (Н) – количественная характеристика воздействия одного тела на другое.

Сила – векторная величина, которая имеет числовое значение, направление в пространстве, точку приложения.

Точкой приложения всех сил (кроме веса) является центр тяжести тела. Измерительный прибор – динамометр.

Законы Ньютона

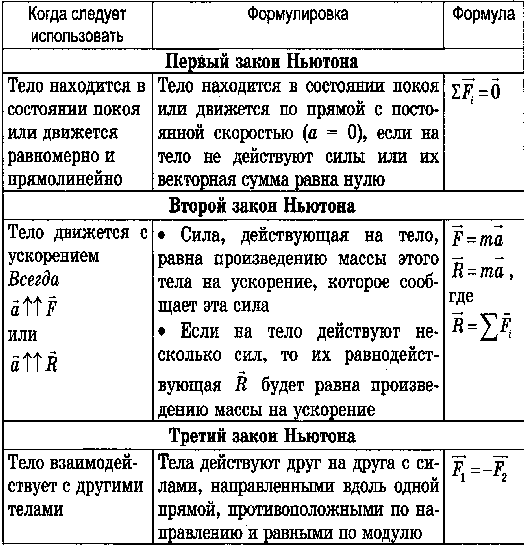
Законы Ньютона справедливы только в ИСО.

Равнодействующая сила – векторная сумма всех сил, действующих на тело:

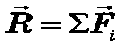
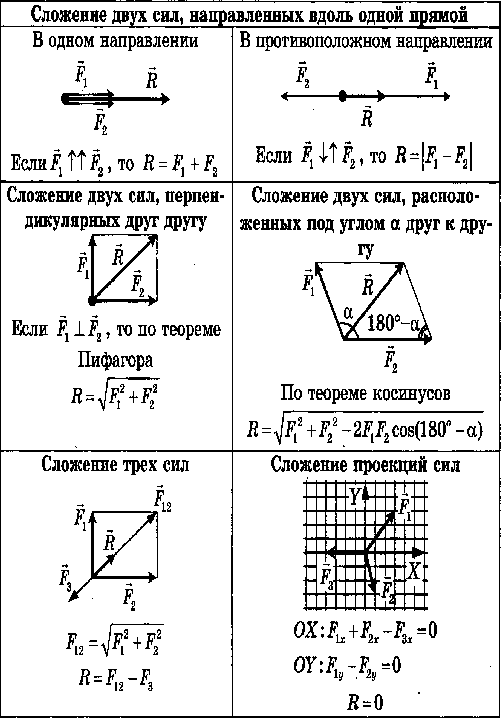
Тема 2. Сила всемирного тяготения.

Сила всемирного тяготения – это сила, с которой тела притягиваются к друг другу. Это сила наиболее заметно проявляется при взаимодействии массивных тел (звезд, планет, их спутников).

Закон всемирного тяготения: все тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними:

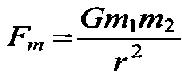, где

G=6,67*10^-11 Hм²/кг² – гравитационная постоянная, численно равная силе гравитационного притяжения двух тел массой по 1 кг каждое , находящихся на расстоянии 1м одно от другого;

r – расстояние между центрами тел.

Сила всемирного тяготения направлена по линии, соединяющей центры тел:

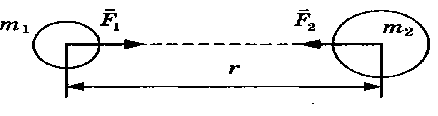
Тема 3. Сила тяжести

Сила тяжести – это сила, с которой планета (Земля) притягивает к себе окружающие тела. Сила тяжести имеет гравитационную природу. Направление силы тяжести – вертикально вниз:

Искусственный спутник планеты (ИСЗ) – это тело, которое обращается вокруг планеты. Движение искусственных спутников происходит по эллипсам, но для удобства рассматривают упрощенный случай – движение по окружности. Линейную скорость такого движения называют первой космической скоростью.

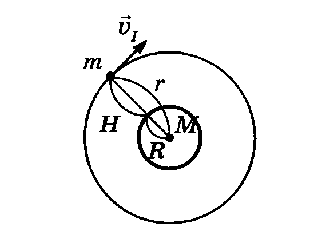
М – масса планеты,

m – масса спутника,

R –радиус планеты,

H –высота спутника над поверхностью планеты,

r – расстояние от центра планеты до спутника (r=R+H – радиус орбиты),

v_I – первая космическая скорость спутника.

Закон движения ИСЗ – второй закон Ньютона:

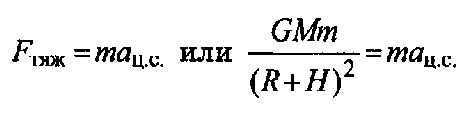
Тема 4. Сила упругости

Сила упругости – это сила, возникающая при деформации тел, как ответная реакция на внешнее воздействие. Сила упругости имеет электромагнитную природу.

Деформация – изменение формы или объема тела.

Виды деформации:

Растяжение –это вид деформации, при котором нагрузка прикладывается продольно от тела, то есть соосно или параллельно точкам крепления тела.

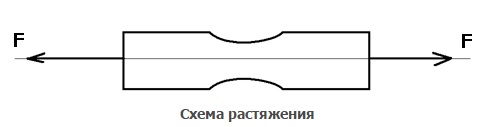
Сжатие –это вид деформации, аналогичный растяжению, с одним отличием в способе приложения нагрузки, ее прикладывают соосно, но по направлению к телу.

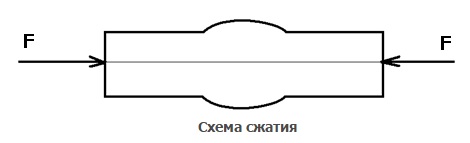
Изгиб – это вид деформации, при котором нарушается прямолинейность главной оси тела.

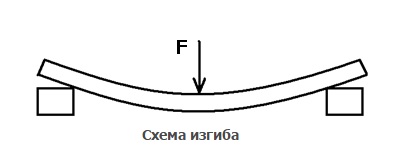
Сдвиг – это вид деформации, при котором нагрузка прикладывается параллельно основанию тела. В ходе деформации сдвига одна плоскость тела смещается в пространстве относительно другой.

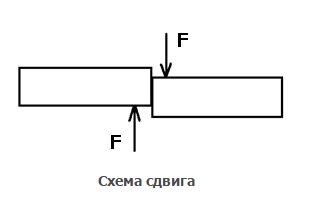
Кручение – это вид деформации, при котором к телу приложен крутящий момент, вызванный парой сил, действующих в перпендикулярной плоскости оси тела.

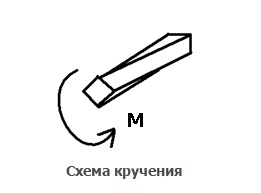
Упругие деформации исчезают после снятия нагрузки.

Пластические деформации остаются после снятия нагрузки.

Закон Гука: модуль силы упругости , возникающей при деформации тела, пропорционален его удлинению

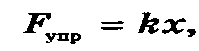где:

k – жесткость пружины, зависящая от его размеров, формы и материала. Единица измерения (H/m).

Закон Гука выполняется только для упругих деформаций.

Сила упругости направлена противоположно перемещению частиц при деформации.

Сила реакции опоры (N) всегда перпендикулярна опоре.

Сила натяжения нити (T) всегда направлена вдоль оси подвеса.

Архимедова сила (F_A) всегда противоположна силе тяжести.

Основные понятия и величины, характеризующие деформацию.

Деформация или абсолютное удлинение тела х (м):

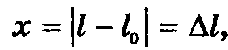где:

l₀ – начальная длина тела, l – длина деформированного тела.

Относительное удлинение тела :

.

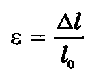Механическое напряжение (Н/м²):

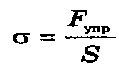
Жесткость пружины k (H/м):

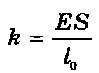, где:

E – модуль упругости (модуль Юнга).

Тема 5. Силы трения.

Сила трения возникает при движений тел или при попытке сдвинуть их с места.

Она действует на поверхности тел и затрудняет их перемещение относительно друг друга.

Относится к силам электромагнитной природы.

Трение бывает сухое и жидкое.

Сухое делится на три вида: трение покоя, трение скольжения и трение качения.

Трение скольжения возникает при скольжении одного тела по поверхности другого.

Направление трения скольжения противоположно скорости движения :

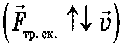
Трение скольжения находится по формуле:

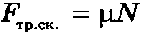,где:

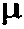– коэффициент трения.

Если движение происходит по гладкой поверхности, то силу трения учитывать не надо. Если тело преодолевает границу между гладкой и шероховатой поверхностью, то сила трения равна:

.

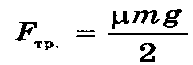Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно приложенной силе или направлению возможного движения.

Жидкое трение (сила сопротивления) возникает при движении в жидкостях и газах. Направление жидкого трения противоположно скорости движения:

.

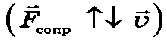Жидкое трение зависит от формы тел.

При малых скоростях :

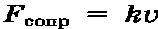
При больших скоростях:

.

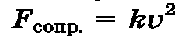Тема 6. Вес тела

Вес тела – это сила, с которой тело вследствие притяжения к Земле, действует на опору или подвес (сила, с которой тело давит на опору или растягивает подвес).

Относится к силам электромагнитной природы.

Измеряется динамометром.

Единица измерения – ньютон (Н).

Вес тела, опускающегося с ускорением или поднимающегося с замедлением:

Р = m(g – a).

Вес тела, поднимающегося с ускорением или опускающегося с замедлением:

Р = m(g + a).

Перегрузка при подъеме с ускорением или спуске с замедлением:

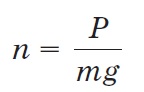,где :

n — перегрузка (безразмерная),

Р — вес (Н),

m — масса (кг),

g — ускорение свободного падения (м/с²).

Тема 7. Импульс тела

Импульс тела р (кг*м/с) – это векторная физическая величина, равная произведению массы тела на его скорость.

.

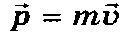Направление импульса совпадает с направлением скорости, так как масса есть величина положительная:

.

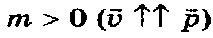Импульс равен нулю, если тело не движется (v=0).

Суммарный (полный) импульс системы тел – это векторная сумма импульсов всех тел:

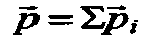
Изменение импульса тела – векторная разность между конечным и начальным импульсом тела:

.

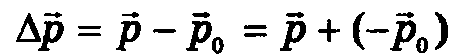Второй закон Ньютона:

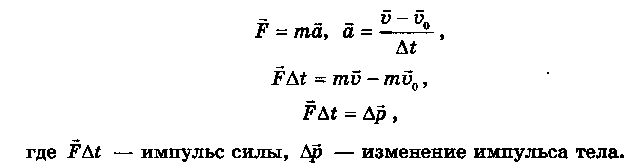
Закон сохранения импульса: полный импульс замкнутой системы сохраняется.

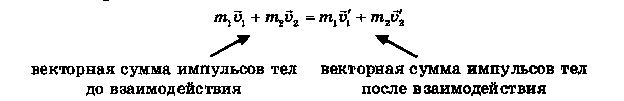
Систему называют замкнутой, если тела, входящие в нее, взаимодействуют только друг с другом, а влиянием внешних сил можно пренебречь.

Кинематика, динамика и статика в физике. Что это такое?

Одним из основополагающих разделов физики является механика – дисциплина, изучающая законы, согласно которым происходит движение тел, а также изменение параметров движения в результате влияния тел друг на друга.

Основными направлениями механики является изучение динамики, кинематики и статики. Подробному изучению этих наук специалисты посвящают всю жизнь, так как их положения лежат в основе наиболее важных общеинженерных дисциплин – теории механизмов, сопромата, деталей машин и др.

Что изучает теоретическая механика?

Движение и взаимодействие физических тел подчиняются строгим законам, по которым существует наша Вселенная. Описанию и обоснованию этих законов посвящена механика – раздел физики, позволяющий рассчитывать и предсказывать движение физических тел, исходя из их основных параметров и действующих на эти тела сил. В механике рассматриваются идеальные объекты:

• материальная точка – объект, основной характеристикой которого является масса, но размеры не учитываются;
• абсолютно твёрдое тело – заполненный веществом определённый объём, форма которого не изменяется ни при каких воздействиях, а между любыми двумя точками внутри этого объёма всегда сохраняется одно и то же расстояние;
• сплошная деформируемая среда – состояние вещества в конечном объёме либо в неограниченном пространстве, в котором расстояния между произвольно взятыми точками могут изменяться в результате внешних воздействий.

Механика рассматривает законы движения, когда с течением времени изменяется либо положение одного тела относительно другого, либо взаимное расположение частей одного тела. Время, масса и расстояние для механики являются базовыми величинами.

Кинематика

Раздел механики, изучающий законы движения, его геометрические свойства, законы скоростей и ускорений, называется кинематикой. Название дисциплины образовано от греческого слова «κινειν», означающего движение. Кинематика изучает чистое движение с точки зрения пространства и времени, не учитывая массы физических тел и действующие на них силы.

Движение в кинематике описывается исключительно математическими средствами, для чего используются алгебраические и геометрические методы, матанализ и т.д. При этом в классической кинематике не рассматриваются причины, по которым происходит механическое движение тел, а характеристики, присущие движению, считаются абсолютными, т.е. на них не влияет выбор системы отсчёта. Помимо классической, существует релятивистская механика, которая рассматривает общее понятие пространства-времени с инвариантными интервалами.

Динамика

Ещё один раздел механики, который рассматривает причины, порождающие механическое движение тел, называется динамикой. Это наименование образовано от греческого слова «δύναμις», означающего силу. Основными понятиями динамики являются масса тела, сила, которая на него воздействует, энергия, импульс и момент импульса. Основными задачами – определение силы, действующей на физическое тело, по характеру его движения, и определение характера движения, исходя из заданных сил воздействия.

Значительный вклад в развитие динамики внёс британский учёный Исаак Ньютон, сформулировавший три своих знаменитых закона, которые описывают взаимодействия сил, и фактически ставший родоначальником классической динамики. Эта дисциплина изучает закономерности движения при скоростях, ограниченных интервалом от долей одного миллиметра в секунду до десятков километров в секунду. Однако при рассмотрении движения сверхмалых объектов (элементарных частиц) и сверхвысоких скоростей, приближающихся к скорости света, законы классической динамики перестают действовать.

Статика

Законы пребывания тел и систем в равновесии при приложении к ним различных сил и моментов, изучает статика – ещё одно направление механики. Название дисциплины происходит от греческого слова «στατός», означающего неподвижность. Для статики сформулированы шесть аксиом, описывающих условия нахождения тела или системы физических тел в состоянии равновесия, а также два следствия из этих аксиом.

Основным объектом в статике является тело или материальная точка, находящаяся в состоянии равновесия, т.е. неподвижно либо движется в рассматриваемой инерциальной системе координат равномерно и по прямой линии. Ограничивающими факторами для тела, находящегося в равновесии, служат внешние силы, которые на него воздействуют, а также другие тела, называемые связями.

Газодинамика — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 марта 2017; проверки требуют 10 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 марта 2017; проверки требуют 10 правок. Конденсация пара в сверхзвуковых областях с пониженной температурой при околозвуковом полете. В задней части облака (на фотографии не видна) образуются ударные волны, в которых поток тормозится (эффект Прандтля — Глауэрта)

Газодина́мика (или га́зовая дина́мика) — раздел механики, изучающий законы движения газообразной среды и её взаимодействия с движущимися в ней твёрдыми телами. Чаще встречается под названием аэродина́мика (от др.-греч. ἀηρ — воздух и δύναμις — сила), но включает в себя не только аэродинамику, но и собственно газовую динамику. Последняя исторически возникла как дальнейшее развитие и обобщение аэродинамики, и именно поэтому часто говорят о единой науке — аэрогазодинамике. Как часть физики, аэрогазодинамика тесно связана с термодинамикой и акустикой.

Формальное исследование аэродинамики в современном смысле началось в восемнадцатом веке, хотя наблюдения фундаментальных понятий, таких как аэродинамическое сопротивление были описаны гораздо раньше. Большинство первых исследований в аэродинамике были направлены на достижение полета воздушного судна, что было впервые продемонстрировано Отто Лилиенталем в 1891 году^[1]. С тех пор использование аэродинамики посредством математического анализа, эмпирических приближений, экспериментов в аэродинамической трубе и компьютерное моделирование сформировало рациональную основу для развития полета воздушных судов и ряда других технологий. Последние работы в области аэродинамики были сосредоточены на проблемах, связанных со сжимаемым потоком, турбулентностью и пограничными слоями.

Раздел гидроаэромеханики, в котором изучаются законы движения воздуха и силы, возникающие на поверхности тел, относительно которых происходит его движение. В аэродинамике рассматривают движение с дозвуковыми скоростями, то есть в нормальных условиях до 340 м/с (1200 км/ч).

Прикладные задачи аэродинамики:

• распределение давления на поверхности тела;
• определение сил и моментов, действующих на обтекаемое газом тело;
• распределение скоростей в воздушном потоке, обтекающем тело;
• расчёт вентиляции;
• расчёт пневмотранспорта.

Специальный раздел аэродинамики — аэродинамика самолёта — занимается разработкой методов аэродинамического расчёта и определением аэродинамических сил и моментов, действующих на самолёт в целом и на его части — крыло, фюзеляж, оперение и т. д. К аэродинамике самолёта относят: расчёт устойчивости, балансировки самолёта, теорию воздушных винтов, теорию крыла. Вопросы, связанные с изменяющимся нестационарным режимом движения летательных аппаратов, рассматриваются в специальном разделе — динамике полёта.

Результаты аэродинамики находят многообразные применения в самолётостроении, авиастроении, автомобилестроении и в различных летательных аппаратах.

Основателем современной аэродинамики и аэрогидродинамики считается великий русский учёный Николай Егорович Жуковский.^[2] В 1902 году он руководил сооружением аэродинамической трубы всасывающего типа при механическом кабинете Московского университета, в которой осевым вентилятором создавался воздушный поток со скоростью до 9 м/с.^[3] В 1904 году возглавил первый в Европе аэродинамический институт, созданный на средства Д. П. Рябушинского в посёлке Кучино под Москвой. В 1905-м году 15-го ноября Николай Егорович Жуковский дал формулу для расчёта подъёмной силы, являющейся основой всех аэродинамических расчётов самолёта.^[4] С 1918 года возглавлял ЦАГИ (Центральный аэрогидродинамический институт).^[5]

Газовая динамика возникла как дальнейшее развитие аэродинамики и имеет дело с ситуациями, в которых условия существенно отличаются от нормальных.

В отличие от классической аэродинамики, газовая динамика имеет дело с такими задачами, в которых сжимаемость газа становится существенным фактором, влияющим на его поведение. В первую очередь, это — задачи о движении газовых потоков со скоростями, близкими или превышающими скорость звука в газе, что приводит к появлению значительных перепадов давления и ударных волн. Другим примером служат те процессы в газовых средах, которые сопровождают экзотермическими (горение, взрыв) или эндотермическими (диссоциация) химическими реакциями: в этих случаях из-за изменения средней молекулярной массы газа и процессов энерговыделения модель идеального газа неприменима.

Возникновение газовой динамики относится к середине и второй половине XIX века и связано с основополагающими работами К. Доплера, Г. Римана, Э. Маха, У. Дж. Ранкина и П.-А. Гюгонио^[6]. Бурное развитие данный раздел механики переживает в XX веке; среди многих имён учёных, внёсших значительный вклад в развитие газовой динамики, следует назвать С. А. Чаплыгина, Дж. Тейлора, Л. И. Седова, Я. Б. Зельдовича.

• Годунов С. К., Забродин А. В., Иванов М. Я., Крайко А. Н., Прокопов Г. П.  Численное решение многомерных задач газовой динамики. — М.: Наука, 1976. — 400 с.
• Дейч М. Е.  Техническая газодинамика. — М.: Энергия, 1974.
• Дейч М. Е., Филиппов Г. А.  Газодинамика двухфазных сред. — М.: Энергоатомиздат, 1981.
• Дейч М. Е., Зарянкин А. Е.  Гидрогазодинамика. — М.: Энергоатомиздат, 1984.
• Киреев В. И., Войновский А. С.  Численное моделирование газодинамических течений. — М.: Изд-во МАИ, 1991. — 254 с. — ISBN 5-7035-0148-2.
• Крайко А. Н.  Вариационные задачи газовой динамики. — М.: Наука, 1979. — 447 с.
• Мизес Р.  Математическая теория течений сжимаемой жидкости. — М.: ИИЛ, 1961. — 588 с.
• Соу С.  Гидродинамика многофазных сред. — М.: Мир, 1971.
• Falkovich, G. Fluid Mechanics, a short course for physicists (англ.). — Cambridge University Press, 2011. — ISBN 978-1-107-00575-4.

Что изучает динамика

☰

Динамика изучает причины изменения характера движения тел (в том числе возникновение движения), часто рассматривая их движение в инерциальных системах отсчета.

Динамика — это раздел механики, в котором в том числе изучаются три закона Ньютона. Они лежат в основе классической динамики, которая оказывается неприменимой для элементарных частиц и скоростей, близких к скорости света.

Динамика решает такие задачи, как по движению тел определить действующие на них силы, так и как по действующим на тело силам определить характер его движения.

Первый закон Ньютона. Существуют системы отсчета, относительно которых свободное точечное тело покоится или движется равномерно и прямолинейно. Эти системы отсчета называют инерциальными.

Обычно при решении задач все системы отсчета, связанные с Землей или с телами, движущимися относительно Земли равномерно прямолинейно, считают инерциальными.

Динамика изучает различные механические силы. Сила в механике — это физическая величина, характеризующая действие одного тела на второе, в результате которого второе тело получает ускорение в инерциальной системе отсчета.

Под инертностью тела понимают его свойство препятствовать приобретению ускорения (изменению своей скорости) под действием приложенной силы.

С понятием инерции в динамике связано понятие массы. Масса — это физическая величина, количественно характеризующая инертность тела.

В СИ массу измеряют в килограммах, а силу — в ньютонах.

Под действием силы, модуль которой равен 1 Н, первоначально покоившееся в инерциальной системе отсчета точечное тело массой 1 кг получает ускорение, модуль которого равен 1 м/с².

Второй закон Ньютона. Ускорение (a), приобретаемое точечным телом в инерциальной системе отсчета, равно отношению суммы всех действующих на это тело сил (F) к его массе (m). Формула второго закона Ньютона: a = F/m.

Третий закон Ньютона. Два тела взаимодействуют друг с другом с силами равными по модулю, противоположными по направлению, лежащими на одной прямой. При этом силы взаимодействия двух тел приложены к разным телам, следовательно, они не могут уравновесить друг друга. Хотя являются силами одной природы.

Динамика изучает следующие силы:

• Сила тяжести. Эта сила возникает под действием Земли (или других космических тел), действует на тело, находящееся близко к поверхности Земли, направлена вертикально вниз, т. е. притягивает тело к земле. Сила тяжести по модулю равна mg, где g — ускорение свободного падения.
• Сила упругости (F_упр). Эту силу вызывает деформированное тело, а действует сила упругости на тело, вызвавшее деформацию. Сила упругости направлена в сторону противоположную деформации, при этом стремится сдвинуть деформирующее тело. Сила упругости пропорциональна деформации: чем больше деформация, тем больше сила.
• Сила реакции горизонтальной опоры на свободно лежащее на ней тело (N). Силу вызывает горизонтальная опора, сила действует на тело, лежащее на этой опоре. По модулю сила реакции равна силе тяжести, но противоположна ей по направлению, так как направлена вверх. В результате она уравновешивает силу тяжести, прижимая тело к опоре.
• Вес тела (P), лежащего на опоре или висящего на подвесе. Силу вызывает само тело, и в первом случае сила (вес) действует на опору, во втором — на подвес. В первом случае вес по модулю равен силе реакции опоры, во втором — силе упругости подвеса. Вес направлен вертикально вниз и деформирует опору или растягивает подвес.
• Силы трения. Существует несколько типов сил трения. Силу сухого трения скольжения (F_тр) вызывает поверхность, по которой скользит тело. Сила действует на тело, скользящее по поверхности. Сила трения направлена в сторону, противоположную движению тела и препятствует движение тела по поверхности, т. е. тормозит его.