Динамика. Основные понятия и модели. Видеоурок. Физика 11 Класс
Этот урок посвящён разделу физики, который называется динамика. Мы узнаем, что изучает динамика, основные понятия и физические величины этого раздела. Также совершим небольшой экскурс в историю, чтобы узнать о первых научных работах, легших в основу современной динамики. На этом уроке будут подробно показаны решения трёх типовых задач различной сложности, которые взяты из сборника задач для подготовки к единому государственному экзамену
Динамика выясняет основные причины механического движения. Вопрос о причинах механического движения имеет долгую историю. Аристотель в своём трактате, который назывался «Физика», утверждал, что всякому движению есть движущая сила, поэтому все учёные-физики до XVI века искали силу, которая движет. Например, в трактате XIII века причины движения пущенной стрелы со скоростью 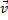 были описаны следующим образом: сдвинувшись, стрела разрезает воздух, который находится впереди, но за оперением остаётся пустое пространство, в него входит воздух из окружающей среды и подталкивает эту стрелу (см. Рис. 1). Из этого объяснения выходит, что воздух является движущей силой и в разряжённом воздухе стрела будет лететь меньшее расстояние, что совершенно неверно.
были описаны следующим образом: сдвинувшись, стрела разрезает воздух, который находится впереди, но за оперением остаётся пустое пространство, в него входит воздух из окружающей среды и подталкивает эту стрелу (см. Рис. 1). Из этого объяснения выходит, что воздух является движущей силой и в разряжённом воздухе стрела будет лететь меньшее расстояние, что совершенно неверно.
Рис. 1. Движение стрелы
Утверждения Аристотеля считались абсолютной истиной до трудов Галилея. Он сформулировал закон инерции: если на тело не действуют никакие силы или действие этих сил скомпенсировано, тело сохраняет состояние покоя или равномерного прямолинейного движения.
Следующим этапом развития динамики были труды И. Ньютона. Он сформулировал систему законов (3 закона Ньютона), которые являются основными законами механики.
Ньютон выяснил, что ответ на основной вопрос динамики оказывается разным в двух классах систем отсчёта – это инерциальные и неинерциальные системы отсчёта, и сформулировал первый закон, который является уточнённым вариантом закона инерции Галилея. Первый закон Ньютона: существуют инерциальные системы отсчёта, в которых единственной причиной изменения состояния движения является воздействие какого-нибудь другого тела или поля.
Система отсчёта является инерциальной, если она связана со свободным телом или движется относительно свободного тела без ускорения. Свободным является тело, на которое ничто не действует. Понятие свободного тела – это абстрактное понятие. Таких тел в природе нет. Поэтому об инерциальной системе отсчёта можно говорить как об относительном понятии. Например, системы отсчета, жестко связанные с поверхностью Земли, строго говоря, не являются инерциальными, так как Земля движется по орбите вокруг Солнца и при этом вращается вокруг своей оси, однако при описании движений, не имеющих глобального (т. е. всемирного) масштаба, системы отсчета, связанные с Землей, можно с достаточной точностью считать инерциальными.
Динамика по Ньютону оперирует следующими физическими величинами:
1. Сила – это мера механического воздействия на данное тело со стороны какого-либо другого тела или поля (F).
Механическое воздействие – это воздействие, приводящее к изменению скорости тела или к его деформации.
1 Ньютон – это сила, которая придаёт телу массой 1 килограмм ускорение 1 метр в секунду за секунду.
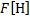
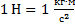
2. Масса – это мера инертности тела. Чем больше масса тела, тем труднее изменить его скорость.
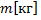
Для однородного тела масса определяется через его плотность:
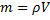
где 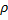 – плотность тела;
– плотность тела; 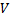 – объём тела.
– объём тела.
Немецкий физик В. Кауфман в своих опытах обнаружил, что масса, как мера инертности тела, не является постоянной величиной. Он экспериментально нашёл зависимость массы электрона от его скорости.
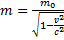 ,
,
где m – масса движущегося тела; 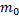 – масса покоящегося тела; v – скорость тела; c
– масса покоящегося тела; v – скорость тела; c
Задача 1
Прямоугольный брусок массой 32 г имеет размеры: длину 5 см, ширину 2 см и высоту 16 мм. Найти его плотность. Варианты ответа: 1. 500 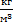 ; 2.
; 2. 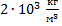 ; 3.
; 3. 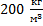 ; 4.
; 4. 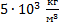 .
.
Дано: 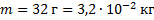 ;
; 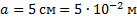
 ;
; 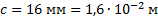
Найти: 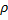
Решение
Из формулы массы выразим плотность:
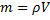
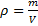
Объём найдём по формуле:
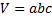
Следовательно:
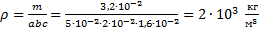
Ответ: 2. 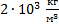
3. Импульс – это физическая векторная величина, равная произведению массы тела на его скорость.
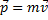
Задача 2
Найти импульс тела массой 1,2 кг при скорости 18 км/ч. Варианты ответа: 1. 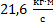 ; 2.
; 2. 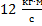 ; 3.
; 3. 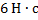 ; 4.
; 4. 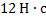 .
.
Дано: 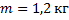 ;
; 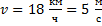
Найти: 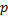
Решение
Импульс равен:

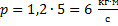
Ответ: 3) 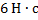
При выяснениях причин механического движения необходимо учитывать, что на рассматриваемое тело действует много различных тел и полей. В таком случае необходимо уметь находить результирующую сил, приложенных к телу.
Предположим к точке приложено три силы –  (см. Рис. 2). Для нахождения результирующей воспользуемся элементами векторной алгебры.
(см. Рис. 2). Для нахождения результирующей воспользуемся элементами векторной алгебры.
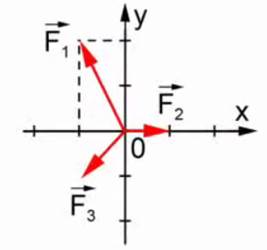
Рис. 2. Силы, приложенные к точке
Каждый вектор силы можно выразить через составляющие по координатным осям:
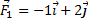
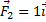
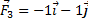
Результирующая находится таким образом:
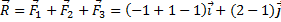
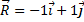
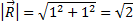
Мяч массой 400 г, двигаясь со скоростью 20 м/с, ударился о стенку и упруго отскочил от неё под углом 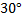 к её поверхности. Найти изменение импульса мяча при ударе.
к её поверхности. Найти изменение импульса мяча при ударе.
Дано: 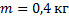 ;
; 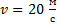 ;
; 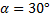
Найти: 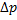
Решение
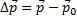
На рисунке 3 изображён схематический чертёж к задаче.
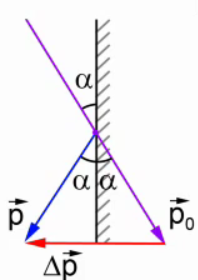
Рис. 3. Иллюстрация к задаче
При упругом соударении со стенкой угол, под которым падает тело, равен углу после отскока. В точке, которой мячик коснулся стены, нужно построить два вектора – вектор начального импульса 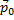 (совпадает с направлением первоначального движения мяча), вектор импульса после отскока
(совпадает с направлением первоначального движения мяча), вектор импульса после отскока 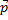 . Разность этих векторов – это вектор, который соединяет концы этих векторов и направлен в сторону уменьшаемого.
. Разность этих векторов – это вектор, который соединяет концы этих векторов и направлен в сторону уменьшаемого.
Три вектора 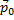 ,
, 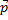 и
и 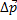 составляют равнобедренный треугольник с углом при вершине
составляют равнобедренный треугольник с углом при вершине 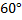 (удар упругий и
(удар упругий и 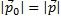 ). Следовательно, этот треугольник равносторонний, поэтому изменение импульса равно первоначальному импульсу:
). Следовательно, этот треугольник равносторонний, поэтому изменение импульса равно первоначальному импульсу:
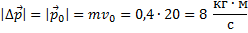
Ответ: 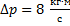 .
.
Домашнее задание
- Вопросы в конце параграфа 20 (стр. 57) – Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10 (см. список рекомендованной литературы)
- Под действием некоторой силы материальная точка приобретает ускорение
 . Каким будет ускорение этой точки, если ее масса увеличится в 1,5 раза, а сила увеличится в 3 раза?
. Каким будет ускорение этой точки, если ее масса увеличится в 1,5 раза, а сила увеличится в 3 раза? - Бильярдный шар с массой m и скоростью
 летит перпендикулярно гладкой неподвижной стенке и испытывает с ней абсолютно упругий удар. Найти изменение импульса шара, модуль этого изменения и изменение модуля импульса шара.
летит перпендикулярно гладкой неподвижной стенке и испытывает с ней абсолютно упругий удар. Найти изменение импульса шара, модуль этого изменения и изменение модуля импульса шара. - Граната, летящая со скоростью, равной по величине
 , разорвалась на два осколка. Больший осколок, масса которого
, разорвалась на два осколка. Больший осколок, масса которого  составляла 0,6 массы m всей гранаты, продолжал двигаться в прежнем направлении, но с большей по модулю скоростью
составляла 0,6 массы m всей гранаты, продолжал двигаться в прежнем направлении, но с большей по модулю скоростью  . Найти величину скорости
. Найти величину скорости  меньшего осколка.
меньшего осколка.
Список литературы
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
- А.П. Рымкевич. Физика. Задачник 10–11. – М.: Дрофа, 2006.
- О.Я. Савченко. Задачи по физике. – М.: Наука, 1988.
- А.В. Пёрышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
- Орлов В.А., Демидова М.Ю., Никифоров Г.Г., Ханнанов Н.К. Оптимальный банк заданий для подготовки к ЕГЭ. Единый государственный экзамен 2015. Физика. Учебное пособие. – М.: Интеллект-Центр, 2015.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Physics.ru (Источник).
- Интернет-портал Calc.ru (Источник).
- Интернет-портал Exir.ru (Источник).
interneturok.ru
Динамика (физика) — Википедия. Что такое Динамика (физика)
Дина́мика (греч. δύναμις «сила, мощь») — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, момент импульса, энергия[1].
Также динамикой нередко называют, применительно к другим областям физики (например, к теории поля), ту часть рассматриваемой теории, которая более или менее прямо аналогична динамике в механике, противопоставляясь обычно кинематике (к кинематике в таких теориях обычно относят, например, соотношения, получающиеся из преобразований величин при смене системы отсчета).
Иногда слово динамика применяется в физике и не в описанном смысле, а в более общелитературном: для обозначения просто процессов, развивающихся во времени, зависимости от времени каких-то величин, не обязательно имея в виду конкретный механизм или причину этой зависимости.
Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.
Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Эрнст Мах считал, что основы динамики были заложены Галилеем[2].
Основная задача динамики
Исторически деление на прямую и обратную задачу динамики сложилось следующим образом[3].
Классическая динамика основана на трёх основных законах Ньютона:
- 1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
- ∑i=1nFi→=0⇒v→=const{\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}=0\Rightarrow {\vec {v}}=const}
- a→=∑i=1nFi→m,{\displaystyle {\vec {a}}={\frac {\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}}{m}},}
где a→{\displaystyle {\vec {a}}} — ускорение тела, Fi→{\displaystyle {\vec {F_{i}}}} — силы, приложенные к материальной точке, а m{\displaystyle \ m} — её масса, или
- ma→=∑i=1nFi→.{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}.}
В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами[4][5].
Второй закона Ньютона можно также сформулировать с использованием понятия импульса:
В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на него силе[6].
- dp→dt=∑i=1nFi→,{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}},}
где p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} — импульс (количество движения) точки, v→{\displaystyle {\vec {v}}} — её скорость, а t{\displaystyle t} — время. При такой формулировке, как и ранее, полагают, что масса материальной точки неизменна во времени[7][8][9].
- 3-й: Силы, с которыми тела действуют друг на друга, лежат на одной прямой, имеют противоположные направления и равные модули
- |F1→|=|F2→|{\displaystyle |{\vec {F_{1}}}|=|{\vec {F_{2}}}|}
- F1→=−F2→{\displaystyle {\vec {F_{1}}}={\vec {-F_{2}}}}
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса
Законы Ньютона в неинерциальных системах отсчета
Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса. Эти «силы» не обусловлены взаимодействием тел, то есть по своей природе не являются силами и вводятся лишь для сохранения формы второго закона Ньютона:
- ∑i=1nFi→+∑j=1nFfj→=ma→{\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}+\sum _{j=1}^{n}{\vec {F_{f_{j}}}}=m{\vec {a}}},
где ∑j=1nFfj→{\displaystyle \sum _{j=1}^{n}{\vec {F_{f_{j}}}}} — сумма всех фиктивных сил, возникающих в неинерциальной системе отсчета.
Многие законы динамики могут быть описаны исходя не из законов Исаака Ньютона, а из принципа наименьшего действия.
Формулы некоторых сил, действующих на тело
- Сила всемирного тяготения:
- FT=Gm1m2r2{\displaystyle F_{T}={Gm_{1}m_{2} \over r^{2}}}
или в векторной форме:
- FT→(r1→)=Gm1m2|r2→−r1→|3(r2→−r1→){\displaystyle {\overrightarrow {F_{T}}}({\vec {r_{1}}})=G{\frac {m_{1}m_{2}}{|{\vec {r_{2}}}-{\vec {r_{1}}}|^{3}}}{({\vec {r_{2}}}-{\vec {r_{1}}})}}
вблизи земной поверхности:
- FT→=mg→{\displaystyle {\overrightarrow {F_{T}}}=m{\vec {g}}}
- Ff=μN{\displaystyle F_{f}=\mu N}
- Сила Архимеда:
- FA=ρgV{\displaystyle F_{A}=\rho gV}
См. также
Примечания
- ↑ Тарг С. М. Динамика // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 616-617. — 707 с. — 100 000 экз.
- ↑ Мах Э. Механика. Историко-критический очерк её развития. — Ижевск: Ижевская республиканская типография, 2000. — С. 105. — 456 с. — ISBN 5-89806-023-5.
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 183. — 416 с. — ISBN 5-06-003117-9.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 287. — 416 с. — ISBN 5-06-003117-9. «В классической механике масса каждой точки или частицы системы считается при движении величиной постоянной»
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; изд-во МФТИ, 2005. — Т. I. Механика. — С. 76. — 560 с. — ISBN 5-9221-0225-7.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
- ↑ Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с.«В ньютоновской механике… m=const и dp/dt=ma».
- ↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
Литература
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
- Матвеев А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие. М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-2
Ссылки
wiki.sc
Динамика (физика) — Википедия
У этого термина существуют и другие значения, см. Динамика.Дина́мика (греч. δύναμις «сила, мощь») — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, момент импульса, энергия[1].
Также динамикой нередко называют, применительно к другим областям физики (например, к теории поля), ту часть рассматриваемой теории, которая более или менее прямо аналогична динамике в механике, противопоставляясь обычно кинематике (к кинематике в таких теориях обычно относят, например, соотношения, получающиеся из преобразований величин при смене системы отсчета).
Иногда слово динамика применяется в физике и не в описанном смысле, а в более общелитературном: для обозначения просто процессов, развивающихся во времени, зависимости от времени каких-то величин, не обязательно имея в виду конкретный механизм или причину этой зависимости.
Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.
Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Эрнст Мах считал, что основы динамики были заложены Галилеем[2].
Основная задача динамики
Исторически деление на прямую и обратную задачу динамики сложилось следующим образом[3].
Классическая динамика основана на трёх основных законах Ньютона:
- 1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
- ∑i=1nFi→=0⇒v→=const{\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}=0\Rightarrow {\vec {v}}=const}
- a→=∑i=1nFi→m,{\displaystyle {\vec {a}}={\frac {\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}}{m}},}
где a→{\displaystyle {\vec {a}}} — ускорение тела, Fi→{\displaystyle {\vec {F_{i}}}} — силы, приложенные к материальной точке, а m{\displaystyle \ m} — её масса, или
- ma→=∑i=1nFi→.{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}.}
В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами[4][5].
Второй закона Ньютона можно также сформулировать с использованием понятия импульса:
В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на него силе[6].
- dp→dt=∑i=1nFi→,{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}},}
где p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} — импульс (количество движения) точки, v→{\displaystyle {\vec {v}}} — её скорость, а t{\displaystyle t} — время. При такой формулировке, как и ранее, полагают, что масса материальной точки неизменна во времени[7][8][9].
- 3-й: Силы, с которыми тела действуют друг на друга, лежат на одной прямой, имеют противоположные направления и равные модули
- |F1→|=|F2→|{\displaystyle |{\vec {F_{1}}}|=|{\vec {F_{2}}}|}
- F1→=−F2→{\displaystyle {\vec {F_{1}}}={\vec {-F_{2}}}}
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса
Законы Ньютона в неинерциальных системах отсчета
Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса. Эти «силы» не обусловлены взаимодействием тел, то есть по своей природе не являются силами и вводятся лишь для сохранения формы второго закона Ньютона:
- ∑i=1nFi→+∑j=1nFfj→=ma→{\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}+\sum _{j=1}^{n}{\vec {F_{f_{j}}}}=m{\vec {a}}},
где ∑j=1nFfj→{\displaystyle \sum _{j=1}^{n}{\vec {F_{f_{j}}}}} — сумма всех фиктивных сил, возникающих в неинерциальной системе отсчета.
Многие законы динамики могут быть описаны исходя не из законов Исаака Ньютона, а из принципа наименьшего действия.
Формулы некоторых сил, действующих на тело
- Сила всемирного тяготения:
- FT=Gm1m2r2{\displaystyle F_{T}={Gm_{1}m_{2} \over r^{2}}}
или в векторной форме:
- FT→(r1→)=Gm1m2|r2→−r1→|3(r2→−r1→){\displaystyle {\overrightarrow {F_{T}}}({\vec {r_{1}}})=G{\frac {m_{1}m_{2}}{|{\vec {r_{2}}}-{\vec {r_{1}}}|^{3}}}{({\vec {r_{2}}}-{\vec {r_{1}}})}}
вблизи земной поверхности:
- FT→=mg→{\displaystyle {\overrightarrow {F_{T}}}=m{\vec {g}}}
- Ff=μN{\displaystyle F_{f}=\mu N}
- Сила Архимеда:
- FA=ρgV{\displaystyle F_{A}=\rho gV}
См. также
Примечания
- ↑ Тарг С. М. Динамика // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 616-617. — 707 с. — 100 000 экз.
- ↑ Мах Э. Механика. Историко-критический очерк её развития. — Ижевск: Ижевская республиканская типография, 2000. — С. 105. — 456 с. — ISBN 5-89806-023-5.
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 183. — 416 с. — ISBN 5-06-003117-9.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 287. — 416 с. — ISBN 5-06-003117-9. «В классической механике масса каждой точки или частицы системы считается при движении величиной постоянной»
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; изд-во МФТИ, 2005. — Т. I. Механика. — С. 76. — 560 с. — ISBN 5-9221-0225-7.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
- ↑ Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с.«В ньютоновской механике… m=const и dp/dt=ma».
- ↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
Литература
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
- Матвеев А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие. М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-2
Ссылки
wikipedia.green
Динамика (физика) — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Динамика.Дина́мика (греч. δύναμις «сила, мощь») — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, момент импульса, энергия[1].
Также динамикой нередко называют, применительно к другим областям физики (например, к теории поля), ту часть рассматриваемой теории, которая более или менее прямо аналогична динамике в механике, противопоставляясь обычно кинематике (к кинематике в таких теориях обычно относят, например, соотношения, получающиеся из преобразований величин при смене системы отсчета).
Иногда слово динамика применяется в физике и не в описанном смысле, а в более общелитературном: для обозначения просто процессов, развивающихся во времени, зависимости от времени каких-то величин, не обязательно имея в виду конкретный механизм или причину этой зависимости.
Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.
Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Эрнст Мах считал, что основы динамики были заложены Галилеем[2].
Основная задача динамики
Исторически деление на прямую и обратную задачу динамики сложилось следующим образом[3].
Видео по теме
Классическая динамика основана на трёх основных законах Ньютона:
- 1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
- ∑i=1nFi→=0⇒v→=const{\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}=0\Rightarrow {\vec {v}}=const}
wiki2.red
Динамика (физика) — WiKi
У этого термина существуют и другие значения, см. Динамика.Дина́мика (греч. δύναμις «сила, мощь») — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, момент импульса, энергия[1].
Также динамикой нередко называют, применительно к другим областям физики (например, к теории поля), ту часть рассматриваемой теории, которая более или менее прямо аналогична динамике в механике, противопоставляясь обычно кинематике (к кинематике в таких теориях обычно относят, например, соотношения, получающиеся из преобразований величин при смене системы отсчёта).
Иногда слово динамика применяется в физике и не в описанном смысле, а в более общелитературном: для обозначения просто процессов, развивающихся во времени, зависимости от времени каких-то величин, не обязательно имея в виду конкретный механизм или причину этой зависимости.
Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.
Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Эрнст Мах считал, что основы динамики были заложены Галилеем[2].
Основная задача динамики
Исторически деление на прямую и обратную задачу динамики сложилось следующим образом[3].
Классическая динамика основана на трёх основных законах Ньютона:
- 1-й: Существуют такие системы отсчёта, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
- ∑i=1nFi→=0⇒v→=const{\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}=0\Rightarrow {\vec {v}}=const}
- a→=∑i=1nFi→m,{\displaystyle {\vec {a}}={\frac {\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}}{m}},}
где a→{\displaystyle {\vec {a}}} — ускорение тела, Fi→{\displaystyle {\vec {F_{i}}}} — силы, приложенные к материальной точке, а m{\displaystyle \ m} — её масса, или
- ma→=∑i=1nFi→.{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}.}
В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами[4][5].
Второй закона Ньютона можно также сформулировать с использованием понятия импульса:
В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на него силе[6].
- dp→dt=∑i=1nFi→,{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}},}
где p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} — импульс (количество движения) точки, v→{\displaystyle {\vec {v}}} — её скорость, а t{\displaystyle t} — время. При такой формулировке, как и ранее, полагают, что масса материальной точки неизменна во времени[7][8][9].
- 3-й: Силы, с которыми тела действуют друг на друга, лежат на одной прямой, имеют противоположные направления и равные модули
- |F1→|=|F2→|{\displaystyle |{\vec {F_{1}}}|=|{\vec {F_{2}}}|}
- F1→=−F2→{\displaystyle {\vec {F_{1}}}={\vec {-F_{2}}}}
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса
Законы Ньютона в неинерциальных системах отсчёта
Существование инерциальных систем отсчёта лишь постулируется первым законом Ньютона. Реальные системы отсчёта, связанные, например, с Землёй или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчёта, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса. Эти «силы» не обусловлены взаимодействием тел, то есть по своей природе не являются силами и вводятся лишь для сохранения формы второго закона Ньютона:
- ∑i=1nFi→+∑j=1nFfj→=ma→{\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}+\sum _{j=1}^{n}{\vec {F_{f_{j}}}}=m{\vec {a}}} ,
где ∑j=1nFfj→{\displaystyle \sum _{j=1}^{n}{\vec {F_{f_{j}}}}} — сумма всех фиктивных сил, возникающих в неинерциальной системе отсчёта.
Многие законы динамики могут быть описаны исходя не из законов Исаака Ньютона, а из принципа наименьшего действия.
Формулы некоторых сил, действующих на тело
См. также
Примечания
- ↑ Тарг С. М. Динамика // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 616-617. — 707 с. — 100 000 экз.
- ↑ Мах Э. Механика. Историко-критический очерк её развития. — Ижевск: Ижевская республиканская типография, 2000. — С. 105. — 456 с. — ISBN 5-89806-023-5.
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 183. — 416 с. — ISBN 5-06-003117-9.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 287. — 416 с. — ISBN 5-06-003117-9. «В классической механике масса каждой точки или частицы системы считается при движении величиной постоянной»
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; изд-во МФТИ, 2005. — Т. I. Механика. — С. 76. — 560 с. — ISBN 5-9221-0225-7.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
- ↑ Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с.«В ньютоновской механике… m=const и dp/dt=ma».
- ↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
Литература
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
- Матвеев А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие. М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-2
Ссылки
ru-wiki.org
Основы динамики
34. Динамика — это раздел механики, в котором изучаются связи между различными видами движений и причинами их вызывающими.
35. Первый закон Ньютона: существуют такие системы отсчёта, относительно которых тела движутся равномерно и прямолинейно, если на них не действуют другие тела или действие этих тел скомпенсировано.
36. Инерция — это свойство тела сохранять скорость своего движения неизменной по величине и направлению.
37. Инерциальная система отсчета — система отсчета, относительно которой свободная материальная точка, не подверженная воздействию других тел, движется равномерно и прямолинейно (по инерции).
38. Масса — это физическая величина, характеризующая инерционные и гравитационные свойства тел. Масса численно равна отношению ускорения a0 эталона массы m0=1 кг к ускорению a тела при их взаимодействии.

39. Плотность тела — это физическая величина, равная отношению массы тела к его объёму.

Измеряется в кг/м3.
40. Сила — это физическая величина, характеризующая действие на тело других тел или полей, в результате которого тело изменяет скорость своего движения или подвергается деформации. Сила измеряется в ньютонах. 1 Н= кг.м/с2. Сила — величина векторная. Она характеризуется числовым значением, направлением в пространстве и точкой приложения.
41. Второй закон Ньютона: ускорение, с которым движется тело, прямо пропорционально силе, приложенной к телу, и обратно пропорционально массе тела.

42. 1 ньютон — это сила, под действием которой тело массой 1 кг движется с ускорением 1 м/с2.
43. Третий закон Ньютона: Тела действуют друг на друга с силами равными по модулю, противоположными по направлению и одинаковыми по природе.
44. Закон всемирного тяготения: тела притягиваются друг к другу с силой прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

где G — гравитационная постоянная.
45. Гравитационная постоянная G численно равна силе, с которой притягиваются тела массами по 1 кг на расстоянии 1 м друг от друга.
46. Сила тяжести — это сила, с которой тело притягивается Землёй.
47. Вес тела — это сила, с которой тело давит на опору или растягивает подвес.
48. Силы трения — это силы, препятствующие перемещению одного тела по поверхности другого. Они возникают в результате зацепления друг за друга мелких выступов, находящихся на поверхностях тел. При шлифовке выступы и впадины уменьшаются, что приводит к уменьшению сил трения. Но, если поверхности отшлифовать очень хорошо, силы трения вновь начинают увеличиваться из-за действия межмолекулярных сил трущихся поверхностей. Для уменьшения сил трения кроме шлифовки применяют смазку и замену трения скольжения трением качения, которое обычно на порядок меньше сил трения скольжения.
49. Сила трения покоя — это сила, возникающая на границе соприкосновения тел при отсутствии относительного движения тел. Она численно равна силе, приложенной к телу, и может изменяться от нуля до максимального значения внешней силы, при котором тело начинает перемещаться. Сила трения покоя в некоторых случаях может быть больше силы трения скольжения.
50. Коэффициент трения — это число, показывающее долю силы трения от силы, прижимающей поверхности друг к другу.

Коэффициент трения зависит от рода трущихся поверхностей и от чистоты обработки поверхностей.
studfile.net
Динамика (физика) Википедия
У этого термина существуют и другие значения, см. Динамика.Дина́мика (греч. δύναμις «сила, мощь») — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, момент импульса, энергия[1].
Также динамикой нередко называют, применительно к другим областям физики (например, к теории поля), ту часть рассматриваемой теории, которая более или менее прямо аналогична динамике в механике, противопоставляясь обычно кинематике (к кинематике в таких теориях обычно относят, например, соотношения, получающиеся из преобразований величин при смене системы отсчёта).
Иногда слово динамика применяется в физике и не в описанном смысле, а в более общелитературном: для обозначения просто процессов, развивающихся во времени, зависимости от времени каких-то величин, не обязательно имея в виду конкретный механизм или причину этой зависимости.
Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.
Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Эрнст Мах считал, что основы динамики были заложены Галилеем[2].
Основная задача динамики
Исторически деление на прямую и обратную задачу динамики сложилось следующим образом[3].
Классическая динамика основана на трёх основных законах Ньютона:
- 1-й: Существуют такие системы отсчёта, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
- ∑i=1nFi→=0⇒v→=const{\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}=0\Rightarrow {\vec {v}}=const}
- a→=∑i=1nFi→m,{\displaystyle {\vec {a}}={\frac {\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}}{m}},}
где a→{\displaystyle {\vec {a}}} — ускорение тела, Fi→{\displaystyle {\vec {F_{i}}}} — силы, приложенные к материальной точке, а m{\displaystyle \ m} — её масса, или
- ma→=∑i=1nFi→.{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}.}
В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами[4][5].
Второй закона Ньютона можно также сформулировать с использованием понятия импульса:
В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на него силе[6].
- dp→dt=∑i=1nFi→,{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}},}
где p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} — импульс (количество движения) точки, v→{\displaystyle {\vec {v}}} — её скорость, а t{\displaystyle t} — время. При такой формулировке, как и ранее, полагают, что масса материальной точки неизменна во времени[7][8][9].
- 3-й: Силы, с которыми тела действуют друг на друга, лежат на одной прямой, имеют противоположные направления и равные модули
- |F1→|=|F2→|{\displaystyle |{\vec {F_{1}}}|=|{\vec {F_{2}}}|}
- F1→=−F2→{\displaystyle {\vec {F_{1}}}={\vec {-F_{2}}}}
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса
Законы Ньютона в неинерциальных системах отсчёта
Существование инерциальных систем отсчёта лишь постулируется первым законом Ньютона. Реальные системы отсчёта, связанные, например, с Землёй или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчёта, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса. Эти «силы» не обусловлены взаимодействием тел, то есть по своей природе не являются силами и вводятся лишь для сохранения формы второго закона Ньютона:
- ∑i=1nFi→+∑j=1nFfj→=ma→{\displaystyle \sum _{i=1}^{n}{\vec {F_{i}}}+\sum _{j=1}^{n}{\vec {F_{f_{j}}}}=m{\vec {a}}},
где ∑j=1nFfj→{\displaystyle \sum _{j=1}^{n}{\vec {F_{f_{j}}}}} — сумма всех фиктивных сил, возникающих в неинерциальной системе отсчёта.
Многие законы динамики могут быть описаны исходя не из законов Исаака Ньютона, а из принципа наименьшего действия.
Формулы некоторых сил, действующих на тело
- Сила всемирного тяготения:
- FT=Gm1m2r2{\displaystyle F_{T}={Gm_{1}m_{2} \over r^{2}}}
или в векторной форме:
- FT→(r1→)=Gm1m2|r2→−r1→|3(r2→−r1→){\displaystyle {\overrightarrow {F_{T}}}({\vec {r_{1}}})=G{\frac {m_{1}m_{2}}{|{\vec {r_{2}}}-{\vec {r_{1}}}|^{3}}}{({\vec {r_{2}}}-{\vec {r_{1}}})}}
вблизи земной поверхности:
- FT→=mg→{\displaystyle {\overrightarrow {F_{T}}}=m{\vec {g}}}
- Ff=μN{\displaystyle F_{f}=\mu N}
- Сила Архимеда:
- FA=ρgV{\displaystyle F_{A}=\rho gV}
См. также
Примечания
- ↑ Тарг С. М. Динамика // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 616-617. — 707 с. — 100 000 экз.
- ↑ Мах Э. Механика. Историко-критический очерк её развития. — Ижевск: Ижевская республиканская типография, 2000. — С. 105. — 456 с. — ISBN 5-89806-023-5.
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 183. — 416 с. — ISBN 5-06-003117-9.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 287. — 416 с. — ISBN 5-06-003117-9. «В классической механике масса каждой точки или частицы системы считается при движении величиной постоянной»
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; изд-во МФТИ, 2005. — Т. I. Механика. — С. 76. — 560 с. — ISBN 5-9221-0225-7.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
- ↑ Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с.«В ньютоновской механике… m=const и dp/dt=ma».
- ↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
Литература
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
- Матвеев А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие. М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-2
Ссылки
wikiredia.ru
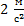 . Каким будет ускорение этой точки, если ее масса увеличится в 1,5 раза, а сила увеличится в 3 раза?
. Каким будет ускорение этой точки, если ее масса увеличится в 1,5 раза, а сила увеличится в 3 раза?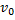 летит перпендикулярно гладкой неподвижной стенке и испытывает с ней абсолютно упругий удар. Найти изменение импульса шара, модуль этого изменения и изменение модуля импульса шара.
летит перпендикулярно гладкой неподвижной стенке и испытывает с ней абсолютно упругий удар. Найти изменение импульса шара, модуль этого изменения и изменение модуля импульса шара. 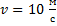 , разорвалась на два осколка. Больший осколок, масса которого
, разорвалась на два осколка. Больший осколок, масса которого 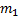 составляла 0,6 массы m всей гранаты, продолжал двигаться в прежнем направлении, но с большей по модулю скоростью
составляла 0,6 массы m всей гранаты, продолжал двигаться в прежнем направлении, но с большей по модулю скоростью 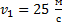 . Найти величину скорости
. Найти величину скорости 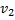 меньшего осколка.
меньшего осколка.