Лекции по динамике — Законы Ньютона

 

Динамика

 

Динамика – это раздел физики, который изучает причины возникновения ускорений и методы их определения.

 

I. Законы Ньютона.

 

1. Первый закон Ньютона

Существуют системы отсчета, называемые инерциальными, относительно которых тела (материальные точки), на которые не действуют другие тела или действие этих тел скомпенсировано, движутся прямолинейно и равномерно или остаются в покое.

Первый закон Ньютона также называют «законом инерции».

Определение: Инерция – это свойство тел сохранять свою скорость по величине и направлению, при отсутствии действия других тел.

2. Второй закон Ньютона

Определение: Сила – это векторная величина, характеризующая взаимодействия тел, мера действия тел друг на друга и различных полей на тела.

Действие силы приводит к возникновению ускорений или деформаций и напряжений в массивных телах.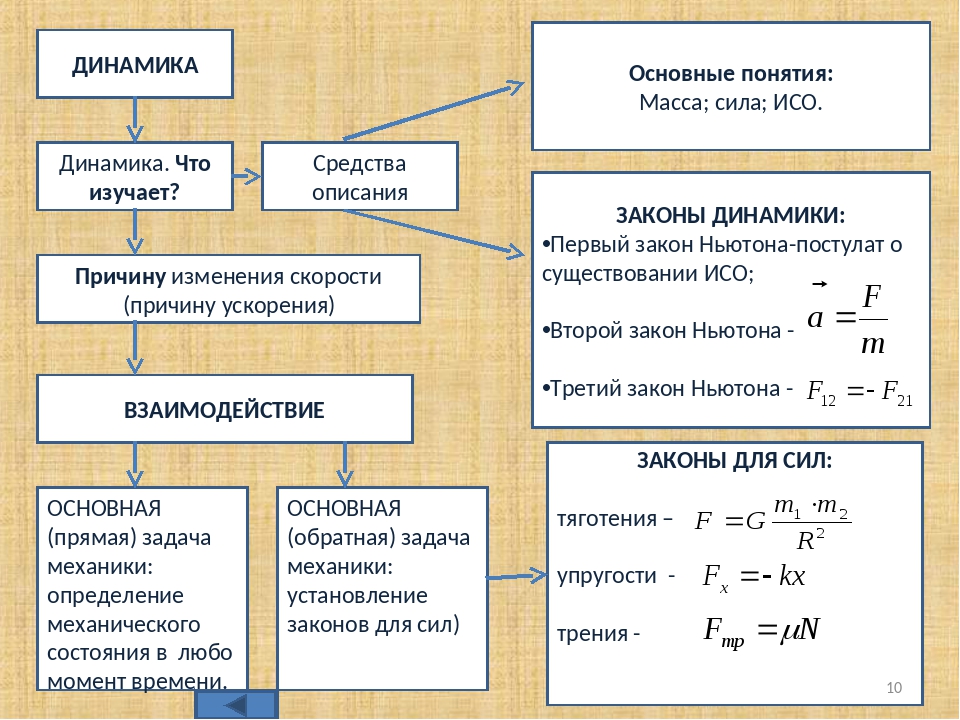

Второй закон Ньютона:

Векторная сумма всех сил, действующих на тело, равна произведению массы тела на его ускорение:

\buildrel n \over\sum_{i=1}\vec{F}_{i}=\vec{F}_{1}+\vec{F}_{2}+\cdots+\vec{F}_{n}=m\vec{a}

Или (так называемая «физическая формулировка»):

Ускорение тела равно сумме всех сил, действующих на тело, деленную на его массу:

\vec{a}=\frac{\buildrel n \over\sum_{i=1}\vec{F}_{i}}{m}

Второй закон Ньютона в проекциях:

\cases{O_{x}:F_{1x}+F_{2x}+\cdots+F_{nx}=ma_{x}\cr O_{y}:F_{1y}+F_{2y}+\cdots+F_{ny}=ma_{y}\cr O_{z}:F_{1z}+F_{2z}+\cdots+F_{nz}=ma_{z} }

3. Третий закон Ньютона

Два тела (материальные точки) действуют друг на друга с силами, имеющими одинаковую природу, лежащими на одной прямой, равными по величине и противоположными по направлению.

 

\vec{F}_{21}=-\vec{F}_{12}

\vec{F}_{12} – сила,действующая со стороны первого тела на второе;

\vec{F}_{21} – сила,действующая со стороны второго тела на первое;

Замечание: Эти силы приложены к разным телам и поэтому не компенсируют друг друга.

 

Движение, его причина и направление. Динамика – раздел механики, изучающий причины движения тел Примеры решения задач

Нелегко найти взрослого человека, который ни разу в жизни не слыхал крылатой фразы «Движение — это жизнь».

Существует и другая формулировка данного высказывания, звучащая несколько иначе: «Жизнь — это движение». Авторство данного афоризма принято приписывать Аристотелю — древнегреческому ученому и мыслителю, который считается основоположником всей «западной» философии и науки.

Сегодня трудно сказать с полной уверенностью, действительно ли великий древнегреческий философ когда-либо произносил подобную фразу, и как именно она звучала в те далекие времена, но, взглянув на вещи непредвзято, следует признать, что приведенное выше определение движения является хотя и звучным, но довольно расплывчатым и метафоричным. Попробуем разобраться, что же представляет собой движение с научной точки зрения.

Понятие движения в физике

Физика дает понятию «движение» вполне конкретное и однозначное определение. Раздел физики, изучающий движение материальных тел и взаимодействие между ними, называют механикой.

Раздел механики, изучающий и описывающий свойства движения без учета его конкретных причин, называется кинематика. С точки зрения механики и кинематики движением считается происходящее с течением времени изменение положения физического тела относительно других физических тел.

Что такое броуновское движение?

В задачи физики входит наблюдение и изучение любых проявлений движения, которые происходят или могли бы происходить в природе.

Одним из видов движения является так называемое броуновское движение, известное большинству читателей данной статьи из школьного курса физики. Для тех, кто по каким-то причинам не присутствовал при изучении данной темы или успел основательно ее подзабыть, поясним: броуновским движением называют беспорядочное движение мельчайших частиц вещества.


Броуновское движение происходит везде, где присутствует какая-либо материя, температура которой превышает абсолютный нуль. Абсолютным нулем называют температуру, при которой броуновское движение частиц вещества должно прекращаться. По шкале Цельсия, которой мы привыкли пользоваться в повседневной жизни для определения температуры воздуха и воды, температура абсолютного нуля составляет 273,15 °C со знаком минус.

Создать условия, вызывающие такое состояние вещества, ученым пока не удалось, более того, существует мнение, что абсолютный нуль является чисто теоретическим допущением, но на практике он недостижим, так как полностью остановить колебания частиц вещества невозможно.

Движение с точки зрения биологии

Поскольку биология тесно связана с физикой и в широком смысле совершенно от нее неотделима, в этой статье мы рассмотрим движение также и с точки зрения биологии. В биологии движение рассматривается как одно из проявлений жизнедеятельности организма. С этой точки зрения движение является результатом взаимодействия сил, внешних по отношению к отдельно взятому организму, с внутренними силами самого организма.

Другими словами, внешние раздражители вызывают определенную реакцию организма, которая проявляется в движении.

Следует отметить, что хотя формулировки понятия «движение», принятые в физике и биологии, несколько отличаются друг от друга, по своей сути они не вступают ни в малейшее противоречие, являясь просто различными определениями одного и того же научного понятия.


Таким образом мы убеждаемся в том, что крылатое выражение, о котором шла речь в начале данной статьи, вполне согласуется с определением движения с точки зрения физики, поэтому нам остается лишь еще раз повторить прописную истину: движение — это жизнь, а жизнь — это движение.

В чем причина движения? Аристотель – движение возможно только под действием силы; при отсутствии сил тело будет покоится. Галилей – тело может сохранять движение и в отсутствии сил. Сила необходима для того чтобы уравновесить другие силы, например, силу трения Ньютон – сформулировал законы движения.

Слайд 4 из презентации «Взаимодействие тел, законы Ньютона» . Размер архива с презентацией 304 КБ.

Физика 10 класс

краткое содержание других презентаций

««Сила трения» 10 класс» — Причины силы трения. Виды трения. Таблица для запоминания формул. Меч – это костяной отросток верхней челюсти рыбы. Сила трения. Трущиеся материелы. Как уменьшают и увеличивают трение. Определение коэффициента трения скольжения. Какую силу необходимо приложить к саням. Как можно увеличить силу трения. Речь пойдет о многократном победителе. Сила, которая возникает при движении одного тела по поверхности.

««Тепловые двигатели» 10 класс» — Охрана окружающей среды. Тепловые двигатели и охрана окружающей среды. Основные компоненты двигателя. История создания. Физика как наука предполагает не только изучение теории. Дизельные двигатели. Ракетные двигатели. Немного о создателе. Дени Папен. Применение. Гамфри Поттер. Пионеры ракетно-космической техники. Двухтактный двигатель. Огненное сердце. Профилактические меры. Как решить проблему. Охрана природы.

«Виды лазеров» — Жидкостный лазер. Полупроводниковый лазер. Источник электромагнитного излучения. Классификация лазеров. Свойства лазерного излучения. Химический лазер. Усилители и генераторы. Газовый лазер. Твердотельные лазеры. Применение лазера. Ультрафиолетовый лазер. Лазер.

«Законы постоянного электрического тока» — Виды соединения проводников. Общее сопротивление цепи. Последовательное и параллельное соединения. Знания основных законов постоянного тока. Действия электрического тока. Закон Ома для участка цепи. «Минусы» соединений. Преобразование цепей. Схемы соединений. Ошибки. Электрический ток. Сопротивления. Сила тока. Вольтметр. «Плюсы» соединений. Основные формулы темы. Общее сопротивление. Законы постоянного тока.

«Насыщенный и ненасыщенный пар» — Конденсационный гигрометр. Зависимость давления насыщенного пара от температуры. Абсолютная влажность воздуха. Приступаем к решению задач. Относительная влажность воздуха. Интересные явления. Изотермы реального газа. Испарение жидкости. Зона комфорта для человека. Роса. Определение влажности воздуха. Иней. Волосной гигрометр. Научимся пользоваться таблицей. Кипение. Процессы, происходящие в закрытом сосуде.

«Определение поверхностного натяжения» — Коэффициент поверхностного натяжения. Результаты исследования. Отношение к материалу урока. Виртуальная лабораторная работа. Длина проволоки. Сферическая поверхность. Поверхностное натяжение. Проблемный опыт. Как соединяются мыльные пузыри. Коррекция знаний. Процесс образования мыльных пузырей. Выдуть мыльные пузыри. Мыльные пузыри различного размера. Какие силы действуют вдоль поверхности жидкости.

Движение – это изменение чего-либо. Уже на эмпирическом уровне видно, что природа как множество естественных явлений – это не нечто застывшее и неизменное, а, наоборот, то, что находится в процессе постоянного движения. Смена дня на ночь и времен года, течение воды в реках и осадки, вращение планет вокруг Солнца и возникновение новых звезд – вот только некоторые факты, на основании которых можно говорить, что в природе все время происходят изменения.

Констатация факта постоянного изменения всего нашло свое выражение уже в античности в известном изречении Гераклита о том, что «все течет, подобно реке». Эмпирическое наблюдение требует соответствующего теоретического объяснения, главным содержанием которого являются ответы на следующие вопросы: 1) Почему происходит движение? 2) Как связаны между собой разные виды движения? 3) Существует ли общее направление изменений?

Со времен античности и до Нового времени объяснение движения строилось, с одной стороны, на основе обыденных наблюдений, а с другой, – на основе таких антропоморфных предпосылок, как представление о целесообразности всего и об идеальном как объективно-субстанциональном.

В частности, согласно тому же Гераклиту, «все возникает в силу противоположности. … Космос … рождается из огня и снова сгорает дотла через определенные периоды времени, попеременно в течение совокупной вечности, происходит же это согласно судьбе. Та из противоположностей, которая ведет к возникновению космоса, называется войной и распрей, а та, что – к сгоранию – согласием и миром, изменение – путем вверх-вниз, по которому и возникает космос.

Сгущаясь, огонь увлажняется и, сплачиваясь, становится водой; вода, затвердевая, превращается в землю: это путь вниз. Земля, в свою очередь, снова тает, из нее возникает вода, а из воды все остальное».

Cогласно физическим представлениям Аристотеля (сохранявшим свое значение до конца эпохи Возрождения), каждое тело стремится к своему месту, причем направление и скорость движения последнего зависят от того материала, из которого оно состоит. «Легкие» тела (например, огонь) стремятся к верху, а «тяжелые» (например, камни) – к низу. Достигнув своего «естественного» места, тело приходит в состояние покоя, поэтому для того, чтобы оно вновь стало двигаться, нужен движитель. Все на Земле движется, в конечном итоге, в результате действия некоего космического перводвигателя, который, сам, будучи идеальным, вечно вращается по кругу. Логика этого рассуждения такова: круговое движение – зримый символ бесконечного, т.е. вечного; перводвигатель идеален, а идеальное – вечно; значит, вечный идеальный перводвигатель вечно движется по кругу, как бы передавая силу своего движения на Землю; земное движется также и потому, что оно стремится к перводвигателю как к совершенству.

Физические представления о «естественности» покоя и «насильственности» движения в Средние века часто использовались в рамках т.н. «естественной теологии», где на их основе пытались строить естественнонаучное доказательство бытия бога (перводвигатель это и есть бог).

В Новое время антропоморфизм в физике был преодолен, и в результате теоретических и экспериментальных исследований стало понятно, что покой – не естественное и не абсолютное состояние тел, а движение не всегда насильственно. В частности, согласно первому закону классической механики Ньютона движение и покой есть равновероятные состояния и любое тело вечно движется или покоится до тех пор, пока не испытает противодействия со стороны других сил.

Открытие гравитационного взаимодействия как притяжения (закон всемирного тяготения, XVII в.) и электромагнитного взаимодействия как притяжения и отталкивания (закон Кулона о взаимодействии точечных электрических зарядов, XVIII в.) в значительной мере способствовало утверждению общего представления о том, что движение – это внутреннее свойство материи, т. е. идеи о том, что движение – это самодвижение материи. Французский философ Поль Анри Гольбах (1723 – 1789) выразил эту характерную для XVIII в. мысль следующим образом: «Спросят нас: откуда эта природа получила свое движение? Мы ответим, что от самой себя, ибо она есть великое целое, вне которого ничего не может существовать. Мы скажем, что движение – это способ существования, необходимым образом вытекающий из сущности материи; что материя движется благодаря собственной энергии; что она обязана своим движением внутренне присущим ей силам».

Согласно современным физическим представлениям, все множество наблюдаемых движений физических объектов в действительности представляет собой проявление четырех видов фундаментальных взаимодействий: гравитационного, электромагнитного, сильного и слабого ядерных.

Гравитационное взаимодействие обусловлено наличием у тел массы, и оно доминирует в мегамире. Закон всемирного тяготения является формальным выражением условий и величины этого взаимодействия. Электромагнитное взаимодействие обусловлено специфическим свойством ряда элементарных частиц, которое называется электрическим зарядом. Оно играет ведущую роль в макро- и микромире вплоть до расстояний, превосходящих размеры атомных ядер. Благодаря электромагнитному взаимодействию существуют атомы и молекулы и происходят химические превращения вещества. Ядерные взаимодействия проявляются лишь на расстояниях, сравнимых с размером атомного ядра. Все четыре типа фундаментальных взаимодействий весьма несхожи между собой (в частности, гравитационное взаимодействие – это только притяжение, а электромагнитное существует как притяжение и отталкивание) и обусловлены существенно разными механизмами. Тем не менее, в рамках теоретической физики существует вопрос о возможности построения единой теории всех фундаментальных взаимодействий. Тем более что в результате экспериментальных исследований взаимодействий элементарных частиц в 1983 г. было обнаружено, что при больших энергиях столкновения элементарных частиц слабое и электромагнитные взаимодействия не различаются и их можно рассматривать как единое электрослабое взаимодействие.

В современных естественных науках, а также в философии принято говорить об уровнях организации материи (выделяют физический, химический, биологический уровни организации), классификация которых основана на выделении соответствующих видов движения материи. В частности, движение материи на физическом уровне ее организации – это рассмотренные нами 4 фундаментальных взаимодействия; движение на химическом уровне – превращения веществ; на биологическом – обмен веществ внутри живого организма. Названные уровни организации материи представляют собой последовательные формы усложнения последней, при этом каждый следующий уровень не отделен от предыдущего непроходимой гранью, а является результатом его естественного развития. В частности, органические вещества могут возникать не только вследствие жизнедеятельности биологических организмов, но также и без них – в результате синтеза неорганических. В 1953 г. американский химик С. Миллер экспериментально доказал возможность абиогенного синтеза органических соединений из неорганических. Пропуская электрический разряд через смесь неорганических соединений, он получил органические кислоты.

Проблема направления движения, понятая в предельно общем смысле, может быть интерпретирована как теория тепловой смерти Вселенной (регресс) и как теория самоорганизации (прогресс).

Гипотеза о тепловой смерти Вселенной – это следствие второго начала термодинамики. Одним из первых эту гипотезу в середине XIX века высказал немецкий физик Рудольф Клаузиус (1822 – 1888) на основе толкования им второго начала термодинамики. Из второго начала следует, что на макроскопическом уровне существуют направленные и необратимые физические процессы. Для того чтобы это понять, рассмотрим следующий пример. Допустим, мы приносим в комнату только что вскипевший чайник и наливаем из него в стакан воду. Понятно, что температура воды в чайнике значительно выше температуры окружающей среды. Пусть температура воды 100 градусов, а температура в комнате 18 градусов. Что произойдет потом? Очевидно, вода постепенно остынет, а воздух немного нагреется. В конечном итоге температура воды и воздуха сравняется и будет, допустим, 18,5 градусов, то есть наступит термодинамическое равновесие. Возможно ли развитие событий в обратном направлении, когда чайник с водой начнет отбирать тепло из воздуха и в результате опять нагреется, а воздух, соответственно, остынет? Чисто теоретически да, но реальная вероятность этого близка к нулю.

Наш мир можно рассматривать как гигантскую термодинамическую систему, которая находится в неравновесном состоянии. Энергия сконцентрирована главным образом в горячих звездах и постепенно мигрирует в гораздо более холодное межзвездное пространство. Все имеющиеся двигатели оказываются работоспособными, в конечном итоге, за счет существования указанной глобальной неравновесности. Поэтому вполне естественными является вопрос о перспективах, связанных со стремлением глобальной системы к термодинамическому равновесию.

Согласно Клаузиусу, энтропия Вселенной стремиться к максимуму. Из этого следует, что во Вселенной, в конце концов, все виды энергии должны перейти в энергию теплового движения, которая равномерно распределится по всему веществу Вселенной. После чего в ней прекратятся все макроскопические процессы или наступит «тепловая смерть» .

Солнечная система, например, может рассматриваться как замкнутая неравновесная термодинамическая система. Энергия здесь главным образом сосредоточена на Солнце. Более 95% используемой человеком энергии – это энергия Солнца . Очевидно, если оно перестанет снабжать нас энергией, и мы израсходуем все ее запасы, то никакая работа окажется невозможной .

Таким образом, если и весь окружающий мир действительно считать замкнутой системой, к которой применимы выводы классической термодинамики, то при достижении равновесия он должен представлять собой однородное тело с постоянной температурой, плотностью вещества и излучения, в котором не будет возможно никакое направленное преобразование энергии.

Основные возражения против гипотезы тепловой смерти Вселенной следующие: 1) Вселенная не является изолированной системой. 2) Почему Вселенная, существующая неограниченный период времени, до сих пор не достигла состояния термодинамического равновесия?

Долгое время существовало представление, что способностью к самоорганизации обладают только биологические объекты и системы. После появления компьютеров, самообучающихся программ и возникновения робототехники стало понятно, что искусственные объекты тоже могут эволюционировать. Относительно недавно выяснилось, что способностью к самоорганизации могут обладать и объекты неживой природы, возникшие естественным путем без участия человека. В частности, в физике известны феномены образования устойчивых вихрей в нестационарных потоках жидкостей и газов; возникновение упорядоченного излучения в лазерах; образование и рост кристаллов. В химии – концентрационные колебания в реакции Белоусова – Жаботинского.

Необходимость и законы самоорганизации изучает синергетика. Термин «синергетика» предложил в начале 70-х гг. XX в. немецкий физик Герман Хакен (род. 1927 г.). Большой вклад в развитие теории самоорганизации внес бельгийский и американский физик Илья Пригожин (1917 – 2003). В настоящее время синергетика – это междисциплинарное направление научных исследований, предмет которого – общие закономерности самоорганизации в природных и социальных системах.

Для самопроизвольного возникновения более упорядоченных структур из структур менее упорядоченных необходимо сочетание следующих условий:

Они могут образовываться только в открытых системах . Для их возникновения обязателен приток энергии извне, компенсирующий потери и обеспечивающий существование упорядоченных состояний;

Упорядоченные структуры возникают в макроскопических системах, то есть системах, состоящих из большого числа атомов, молекул, клеток и т.д. Упорядоченное движение в таких системах всегда носит кооперативный характер, так как в него вовлекается большое число объектов.

Следует особо подчеркнуть, что самоорганизация не связана с каким-либо особым классом веществ. Она существует лишь при особых внутренних и внешних условиях системы и окружающей среды.

Рассмотрим простейший пример самоорганизации – ячейки Бенара . Структурирование (т.е. организацию) первоначально однородной жидкости можно наблюдать при возникновении конвекции (перемешивании ее слоев). Пусть в начальный момент жидкость находится в покое при некоторой постоянной температуре. Далее начнем подогревать ее снизу. По мере повышения интенсивности нагрева возникает явление конвекции: нагретый нижний слой жидкости расширяется, становится более легким и поэтому стремиться всплыть вверх. На смену ему, сверху вниз, опускается более холодный и плотный слой. Сначала это происходит спорадически: восходящие потоки возникают то в одном, то в другом месте и существуют недолго. То есть конвекция идет в хаотическом режиме. Когда разность температур между верхним и нижним слоем жидкости достигает некоторого критического значения, картина меняется принципиальным образом. Весь объем жидкости разделяется на одинаковые ячейки, в каждой из которых происходят уже незатухающие конвекционные движения частиц жидкости по замкнутым траекториям. Характерные размеры ячеек Бенара в случае экспериментов с жидкостью находятся в миллиметровом диапазоне (10 -3 м), в то время как характерный пространственный масштаб межмолекулярных сил приходится на существенно меньший диапазон: 10 -10 м. Иначе говоря, отдельная ячейка Бенара содержит около 10 21 молекул. Таким образом, огромное число частиц может демонстрировать когерентное (согласованное) поведение.

Ячейки Бенара могут образовываться при соответствующих условиях в любых жидкостях. Такие ячейки обнаружены на поверхности Солнца и предположительно существуют в мантии Земли. Более того, согласно современным астрономическим представлениям, наблюдаемая часть Вселенной также состоит из ячеистых структур – скоплений галактик.

Кроме самоорганизации, другим важным понятием синергетики является понятие бифуркации. Термин «бифуркация» – развилка или разделение надвое – в современной научной терминологии служит для описания особенности поведения сложных систем, которые подвержены воздействиям и напряжениям. В определенный момент такие системы должны сделать критический выбор: пойти либо по одной, либо по другой ветви развития. Простейший пример системы, находящейся в точке бифуркации – это неустойчивое равновесие шарика на поверхности выпуклой сферы большого диаметра. Шарик может скатиться с поверхности сферы в любую сторону и практически в любой момент времени. В рассмотренном примере с ячейками Бенара точкой бифуркации является случайное возникновение право- или левовращательных ячеек в жидкости. Подобная картина наблюдается и при биологической эволюции: случайная мутация, которая приведет к качественной необратимой перестройке организма, есть, говоря языком синергетики, точка бифуркации. Таким образом, понятие бифуркации может использоваться для описания изменений в самых разных системах, в том числе экологических и социальных.

Важнейшими особенностями точки бифуркации является то, что, во-первых, прохождение через нее переводит систему в качественно новое состояние, во-вторых, нельзя заранее знать, по какому именно направлению пойдет развитие системы, то есть бифуркация не детерминирована однозначно.

Следует четко представлять, что основная идея синергетики заключается в том, чтобы описать возможность самопроизвольного (без вмешательства человеческого разума) возникновения упорядочены структур из неупорядоченных или, говоря словами И. Пригожина, «порядка из хаоса» .

Причиной того, что тело начинает двигаться, является действие на это тело других тел. Мяч покатится только, если ударить его. Человек подпрыгнет, если оттолкнётся от пола. Некоторые тела действуют на расстоянии. Так, Земля притягивает всё вокруг, поэтому, если выпустить из рук мяч, то он сразу начнёт двигаться вниз. Скорость движения тела тоже может изменяться только при действии на это тело других тел. Например, мяч резко изменяет скорость движения, наталкиваясь на стену, а птица делает крутой вираж, отталкивая воздух своими крыльями и хвостовым опереньем.

Все вышеперечисленные примеры и множество других, с которыми мы встречаемся на каждом шагу, говорят о том, что тело может изменить свою скорость только тогда, когда на него подействуют другие тела. И наоборот, если на тело не действуют никакие другие тела, то тело будет находиться в покое или двигаться равномерно и прямолинейно. Впервые к такому выводу пришёл Г. Галилей в начале XVII века, а век спустя И. Ньютон назвал это одним из основных законов механики.

Способность тела сохранять свою скорость называют его инерцией. Поэтому закон, открытый Г. Галилеем и сформулированный И. Ньютоном, называют законом инерции или первым законом Ньютона.

Закон инерции справедлив далеко не во всех системах отсчёта. Например, в системе отсчёта, связанной с движущимся автомобилем, его водитель при резком торможении начинает двигаться вперёд, хотя никакие тела на него не действуют. Стоя на диске, который начинает вращаться вокруг своей оси, мы чувствуем, как какая-то неведомая сила заставляет двигаться нас от центра этого диска. Очевидно, что в этих двух системах отсчёта – тормозящий автомобиль и вращающийся диск, закон инерции не выполняется.

Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта. Систему отсчёта, связанную с Землёй, можно считать инерциальной, хотя, как известно, Земля (как диск в одном из предыдущих примеров) вращается вокруг своей оси, но так медленно, что только очень точные измерения показывают несоблюдение закона инерции в этой системе отсчёта.

Если тело отсчёта движется равномерно, прямолинейно и поступательно относительно инерциальной системы отсчёта, то система отсчёта, связанная с этим телом тоже является инерциальной. Докажем это, используя правило преобразования скоростей при переходе от одной системы отсчёта к другой (см. § 2). Пусть скорость тела М (см. рис.7), измеренная в системе отсчёта С 1 равна v 1 , тогда скорость v2 того же тела, но измеренная в системе отсчёта С 2 , движущейся относительно С 1 со скоростью v, равна:

v 2 = v 1 — v (7.1)

Из (7.1) следует, что изменения скоростей Dv 1 и Dv 2 за промежуток времени Dt должны быть одинаковы, так как скорость v остаётся неизменной. Поэтому величины ускорения тела М, измеренные в обеих системах, отсчёта тоже будут одинаковы. В частности, если тело М, на которое не действуют другие тела, движется без ускорения, т.е равномерно, в системе отсчёта С 1 , то его движение относительно системы С2 тоже будет равномерным, а значит систему отсчёта С 2 тоже можно считать инерциальной. Так, например, если считать Землю инерциальной системой отсчёта, то вагон поезда, движущийся равномерно, прямолинейно и поступательно, можно тоже считать инерциальной системой отсчёта.

Вопросы для повторения:

· Что изучает динамика?

· Что является причиной ускорения тела?

· Дайте определение инерции тела и сформулируйте закон инерции.

· Какие системы отсчёта называют инерциальными?

· Приведите примеры инерциальных систем отсчёта и тех, в которых закон инерции не соблюдается.

Рис. 7. Система отсчёта С2 является инерциальной, так как движется относительно инерциальной системы С1 поступательно, равномерно и прямолинейно со скоростью v. Показан способ вычисления скорости v2 тела М относительно системы С2 по известной скорости v1 этого тела в системе С1 .

§ 8. СИЛА – МЕРА ВЗАИМОДЕЙСТВИЯ ТЕЛ: ВИДЫ СИЛ И ИХ ИЗМЕРЕНИЕ

«) примерно в V в. до н. э. Видимо, одним из первых объектов ее исследования была механе-подъёмная машина, применявшаяся в театре для подъема и опускания актеров, изображавших богов. Отсюда и произошло название науки.

Люди уже давно заметили, что они живут в мире Движущихся предметов — качаются деревья, летят птицы, плывут корабли, поражают цели стрелы, выпущенные из лука. Причины подобных загадочных тогда явлений занимали умы древних и средневековых ученых.

В 1638 г. Галилео Галилей писал: «В природе нет ничего древнее движения, и о нем философы написали томов немало и немалых». Древние и особенно ученые средневековья и эпохи Возрождения ( , Н. Коперник, Г. Галилей, И. Кеплер, Р. Декарт и др.) уже правильно толковали отдельные вопросы движения, однако в целом ясного понимания законов движения во времена Галилея не было.

Учение о движении тел впервые предстает как строгая, последовательная наука, построенная, как и геометрия Евклида, на истинах, не требующих доказательств (аксиомах), в фундаментальном труде Исаака Ньютона «Математические начала натуральной философии», изданном в 1687 г. Оценивая вклад в науку ученых-предшественников, великий Ньютон сказал: «Если мы видели дальше других, то это потому, что стояли на плечах гигантов».

Движения вообще, движения, безотносительного к чему-либо, нет и быть не может. Движение тел может происходить только относительно других тел и связанных с ними пространств. Поэтому в начале своего труда Ньютон решает принципиально важный вопрос о пространстве, относительно которого будет изучаться движение тел.

Чтобы придать конкретность этому пространству, Ньютон связывает с ним систему координат, состоящую из трех взаимно перпендикулярных осей.

Ньютон вводит понятие абсолютное пространство, которое определяет так: «Абсолютное пространство по самой своей сущности безотносительно к чему бы то ни было внешнему остается всегда одинаковым и неподвижным». Определение пространства как неподвижного тождественно предположению о существовании абсолютно неподвижной системы координат, относительно которой рассматривается движение материальных точек и твердых тел.

В качестве такой системы координат Ньютон принимал гелиоцентрическую систему , начало которой он помещал в центр , а три воображаемых взаимно перпендикулярных оси направлял к трем «неподвижным» звездам. Но сегодня известно, что в мире нет ничего абсолютно неподвижного — вращается вокруг своей оси и вокруг Солнца, Солнце движется относительно центра Галактики, Галактика — относительно центра мира и т. д.

Таким образом, если говорить строго, то абсолютно неподвижной системы координат не существует. Однако движение «неподвижных» звезд относительно Земли настолько медленное, что для большинства задач, решаемых людьми на Земле, этим движением можно пренебречь и считать «неподвижные» звезды действительно неподвижными, а абсолютно неподвижную систему координат, предложенную Ньютоном, действительно существующей.

По отношению к абсолютно неподвижной системе координат Ньютон сформулировал свой первый закон (аксиому): «Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного прямолинейного движения, пока и поскольку оно не понуждается приложенными изменять это состояние».

С тех пор предпринимались и предпринимаются попытки редакционно улучшить формулировку Ньютона. Один из вариантов формулировок звучит так: «Тело, движущееся в пространстве, стремится сохранить величину и направление своей скорости» (имеется в виду, что покой — это движение со скоростью, равной нулю). Здесь уже вводится понятие одной из важнейших характеристик движения — поступательной, или линейной, скорости. Обычно линейная скорость обозначается V.

Обратим внимание на то, что в первом законе Ньютона говорится только о поступательном (прямолинейном) движении. Однако всем известно, что в мире существует и другое, более сложное движение тел — криволинейное, но о нем позже…

Стремление тел «удерживаться в своем состоянии» и «сохранять величину и направление своей скорости» называется инертностью , или инерцией , тел. Слово «инерция» латинское, в переводе на русский оно означает «покой», «бездействие». Интересно отметить, что инерция — органическое свойство материи вообще, «врожденная сила материи», как говорил Ньютон. Она свойственна не только механическому движению, но и другим явлениям природы, например электрическим, магнитным, тепловым. Инерция проявляется и в жизни общества, и в поведении отдельных людей. Но вернемся к механике.

Мерой инерции тела при его поступательном движении является масса тела, обозначаемая обычно m. Установлено, что при поступательном движении на величину инерции не влияет распределение массы внутри объема, занимаемого телом. Это дает основание при решении многих задач механики отвлечься от конкретных размеров тела и заменить его материальной точкой, масса которой равна массе тела.

Местоположение этой условной точки в объеме, занимаемом телом, называется центром масс тела , или, что почти то же самое, но более знакомо, центром тяжести .

Мерой механического прямолинейного движения, предложенной еще Р. Декартом в 1644 г., является количество движения, определяемое как произведение массы тела на его линейную скорость: mV.

Как правило, движущиеся тела не могут продолжительное время сохранять неизменным величину количества своего движения: расходуются в полете запасы топлива, уменьшая массу летательных аппаратов, тормозят и разгоняются поезда, изменяя свою скорость. Какая же причина вызывает изменение количества движения? Ответ па этот вопрос дает второй закон (аксиома) Ньютона, который в современной формулировке звучит так: скорость изменения количества движения материальной точки равна силе, действующей на эту точку.

Итак, причиной, вызывающей движение тел (если вначале mV=0) или изменяющей их количество движения (если вначале mV не равно О) относительно абсолютного пространства (других пространств Ньютон не рассматривал), являются силы. Эти силы позже получили уточняющие названия — физические , или Ньютоновы , силы. Они обычно обозначаются F.

Сам Ньютон дал следующее определение физическим силам: «Приложенная сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного прямолинейного движения». Существует много других определений силы. Л. Купер и Э. Роджерс — авторы замечательных популярных книг по физике, избегая скучноватых строгих определений силы, с известной долей лукавства вводят свое определение: «Силы — это то, что тянет и толкает». До конца не ясно, но какое-то представление о том, что такое сила, появляется.

К физическим силам относятся: силы , магнитные (см. статью « «), силы упругости и пластичности, силы сопротивления среды, света и многие другие.

Если во время движения тела его масса не меняется (только этот случай будет рассматриваться в дальнейшем), то формулировка второго закона Ньютона значительно упрощается: «Действующая на материальную точку сила равна произведению массы точки на изменение ее скорости».

Изменение линейной скорости тела или точки (по величине или направлению — запомним это) называется линейным ускорением тела или точки и обозначается обычно а.

Ускорения и скорости, с которыми тела движутся относительно абсолютного пространства, называются абсолютными ускорениями и скоростями .

Кроме абсолютной системы координат, можно представить себе (конечно, с какими-то допущениями) другие системы координат, которые движутся относительно абсолютной прямолинейно и равномерно. Поскольку (согласно первому закону Ньютона) покой и равномерное прямолинейное движение эквивалентны, то в таких системах справедливы законы Ньютона, в частности первый закон — закон инерции . По этой причине системы координат, движущиеся равномерно и прямолинейно относительно абсолютной системы, получили название инерциальных систем координат .

Однако в большинстве практических задач людей интересует движение тел не относительно далекого и неосязаемого абсолютного пространства и даже не относительно инерциальных пространств, а относительно других более близких и вполне материальных тел, например пассажира относительно кузова автомобиля. Но эти другие тела (и связанные с ними пространства и системы координат) сами движутся относительно абсолютного пространства непрямолинейно и неравномерно. Системы координат, связанные с такими телами, получили название подвижных . Впервые подвижные системы координат использовал для решения сложных задач механики Л. Эйлер (1707-1783).

С примерами движения тел относительно других подвижных тел мы постоянно встречаемся в нашей жизни. Плывут по морям и океанам корабли, перемещаясь относительно поверхности Земли, вращающейся в абсолютном пространстве; движется относительно стен мчащегося пассажирского вагона проводник, разносящий чай по купе; выплескивается чай из стакана при резких толчках вагона и т. д.

Для описания и изучения столь сложных явлений вводятся понятия переносного движения и относительного движения и соответствующих им переносных и относительных скоростей и ускорений.

В первом из приведенных примеров вращение Земли относительно абсолютного пространства будет переносным движением, а перемещение корабля относительно поверхности Земли — относительным движением.

Чтобы изучить движение проводника относительно стен вагона, нужно прежде принять, что вращение Земли существенного влияния на движение проводника не оказывает и поэтому Землю в данной задаче можно считать неподвижной. Тогда движение пассажирского вагона — движение переносное , а движение проводника относительно вагона — движение относительное . При относительном движении тела воздействуют друг на друга или непосредственно (соприкасаясь), или на расстоянии (например, магнитные и гравитационные взаимодействия).

Характер этих воздействий определяется третьим законом (аксиомой) Ньютона. Если вспомнить, что физические силы, приложенные к телам, Ньютон назвал действием, то третий закон может быть сформулирован так: «Действие равно противодействию». Следует отметить, что действие приложено к одному, а противодействие — к другому из двух взаимодействующих тел. Действие и противодействие не уравновешиваются, а вызывают ускорения взаимодействущих тел, причем с большим ускорением движется то тело, масса которого меньше.

Напомним также, что третий закон Ньютона в отличие от первых двух справедлив в любой системе координат, а не только в абсолютной или инерциальных.

Кроме прямолинейного движения, в природе широко распространено криволинейное движение, простейшим случаем которого является движение по окружности.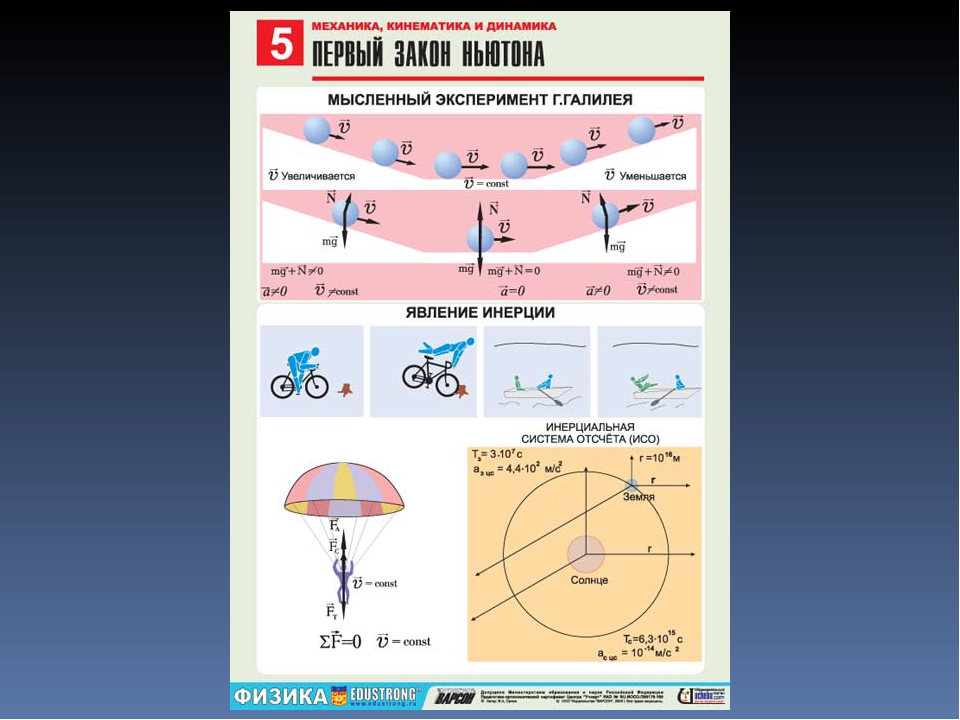 Только этот случай мы и будем рассматривать в дальнейшем, называя движение по окружности круговым движением. Примеры кругового движения: вращение Земли вокруг своей оси, движение дверей и качелей, вращение бесчисленных колес.

Круговое движение тел и материальных точек может происходить либо вокруг осей, либо вокруг точек.

Круговое движение (так же, как и прямолинейное) может быть абсолютным, переносным и относительным.

Как и прямолинейное, круговое движение характеризуется скоростью, ускорением, силовым фактором, мерой инерции, мерой движения. Количественно все эти характеристики в очень сильной степени зависят от того, на каком расстоянии от оси вращения находится вращающаяся материальная точка. Это расстояние называется радиусом вращения и обозначается r .

В гироскопической технике момент количества движения принято называть кинетическим моментом и выражать его через характеристики кругового движения. Таким образом, кинетический момент есть произведение момента инерции тела (относительно оси вращения) на его угловую скорость.

Естественно, законы Ньютона справедливы и для кругового движения. В применении к круговому движению эти законы несколько упрощенно могли бы быть сформулированы так.

• Первый закон: вращающееся тело стремится сохранить относительно абсолютного пространства величину и направление своего момента количества движения (т. е. величину и направление своего кинетического момента).
• Второй закон: изменение во времени момента количества движения (кинетического момента) равно приложенному моменту сил.
• Третий закон: момент действия равен моменту противодействия.

Изучение темы «Динамика» — Docsity

Содержание ВВЕДЕНИЕ………………………………………………………………..2 ГЛАВА 1. ЧТО ИЗУЧАЕТ ДИНАМИКА?………………………………… 4 1.1.Законы механики Ньютона……………………………………………………. 6 1.2. Силы в механике……………………………………………………………… 10 ГЛАВА 2.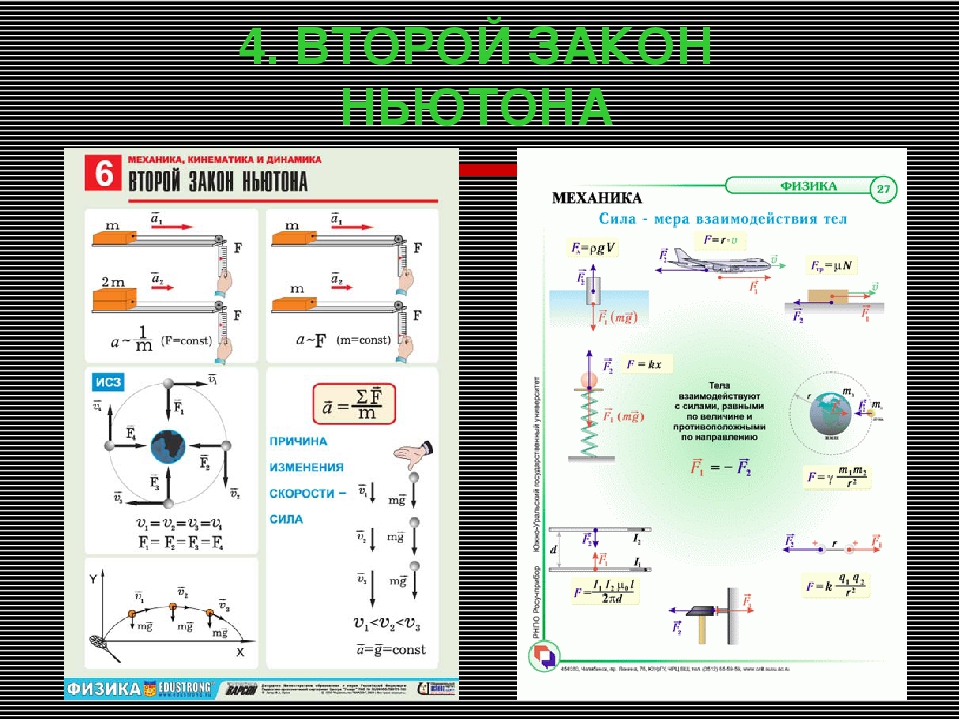 МЕТОДИКА ИЗУЧЕНИЯ ТЕМЫ «ДИНАМИКА» В ШКОЛЬНОМ КУРСЕ ФИЗИКИ……………………………………….. 16 ЗАКЛЮЧЕНИЕ……………………………………………………….. 17 СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ………………………. 18 1 ВВЕДЕНИЕ Одной из главных особенностей современного периода реформирования школьного образования является ориентация школьного образования на широкую дифференциацию обучения, позволяющую удовлетворить потребности каждого учащегося, в том числе и тех, кто проявляет особый интерес и способности к предмету. В настоящий момент эта тенденция углубляется переходом старшей ступени средней школы на профильное обучение, что позволяет обеспечить восстановление преемственности среднего и высшего образования. Концепция профильного обучения определила его целью «повышение качества образования и установление равного доступа к полноценному образованию различных категорий учащихся в соответствии с их индивидуальными склонностями и потребностями». В данном курсовом проекте мы будем изучать динамику. Динамика — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия. Также динамикой нередко называют, применительно к другим областям физики (например, к теории поля), ту часть рассматриваемой теории, которая более или менее прямо аналогична динамике в механике, противопоставляясь обычно кинематике (к кинематике в таких теориях обычно относят, например, соотношения, получающиеся из преобразований величин при смене системы отсчета). Иногда слово динамика применяется в физике и не в описанном смысле, а в более общелитературном: для обозначения просто процессов, развивающихся во времени, зависимости от времени каких-то величин, не обязательно имея в виду конкретный механизм или причину этой зависимости. 2 Инертность представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Если, например, при действии одинаковых сил изменение скорости первого тела происходит медленнее, чем второго, то говорят, что первое тело является более инертным и наоборот. Большая или меньшая степень инертности данного тела зависит от количества заключенного в нем вещества (материи). Величина, зависящая от количества вещества данного тела и определяющая меру его инертности, называется массой тела. В механике масса т рассматривается как величина скалярная, положительная и постоянная для каждого данного тела. В общем случае движение тела зависит не только от его суммарной массы и приложенных сил; характер движения может еще зависеть от геометрических размеров тела и от взаимного расположения образующих его частиц (т. е. от распределения масс). Чтобы при первоначальном изучении динамики иметь возможность отвлечься от учета влияния размеров тел и распределения масс, вводится понятие о материальной точке. Материальной точкой называется материальное тело (тело, имеющее массу), размерами которого при изучении его движения можно пренебречь. Практически данное тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела при его движении, очень велики по сравнению с размерами самого тела. Кроме того, как будет показано в динамике системы, поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе всего тела. Наконец, материальными точками можно считать частицы, на которые мы будем мысленно разбивать любое тело при определении тех или иных его динамических характеристик. Естественно, что изучение движения одной материальной точки должно предшествовать изучению движения системы точек и, в частности, твердого тела. Поэтому курс динамики принято обычно разделять на динамику точки и динамику системы материальных точек. 5 1.1.Законы механики Ньютона Законы механики, как и все основные законы физики, имеет точную количественную форму. Но вначале мы постараемся качественно сформулировать основное утверждение механике. Так будет проще уловить главное содержание механики Ньютона. После этого перейдем к количественной формулировке законов механики. В главном разделе механики – динамике – рассматриваются взаимодействие тел, являющиеся причиной изменения движения этих тел, т. е изменения их скоростей. Первый закон Ньютона. Первый закон механики, или закон инерции, как его часто называют, был, по существу, установлен еще Галилеем. Но общую формулировку этого закона дал Ньютон и включил этот закон в число основных законов механики. Движение свободного тела. И Закон инерции относится к самому простому случаю движения – движению – тела, которое не взаимодействует с другими телами. Такие тела мы будем называть свободными телами. Закон инерции и относительность движения. Движение относительно, и имеет смысл говорить лишь о движении тела по отношению к системе отсчета, связанной с другими телами. Формулировка первого закона Ньютона. Таким образом, наблюдения за движением тел и размышления о характере этого движения проводят нас к постоянной скоростью по отношению к определенным телам и связанным с ними системам отсчета, например по отношению к Земле. В этот состоит главное содержание закона инерции. Поэтому первый закон динамики может быть сформулирован так: Существуют системы отсчета, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно, если на него движется 6 прямолинейно и равномерно, если на него не действуют другие тела или действие этих тел скомпенсировано. Этот закон, с одной стороны, содержит определение инерциальной системы отсчета. С другой стороны, он содержит утверждение( которое с той или иной степенью точности можно проверить на опыте) о том, что инерциальные системы отсчета существуют в действительности. Первый закон механики ставит в особое, привилегированное положение инерциальные системы отсчета. Второй закон Ньютона. Масса Второй закон Ньютона. Ускорение (a), приобретаемое точечным телом в инерциальной системе отсчета, равно отношению суммы всех действующих на это тело сил (F) к его массе (m). Формула второго закона Ньютона: a = F/m. Масса. Прямая пропорциональность между модулями ускорения и силы означает, что отношение модуля силы к модулю ускорения является постоянной величиной, не зависящей от силы: 7

Методическая разработка учебного модуля по физике. «Динамика материальной точки»»

10 класс учебник Касьянов

Автор: Шипкина Е.А.

 

Динамика материальной точки – (10 часов)

Структурно-логическая схема:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Условные обозначения

1.        m-масса тела (кг)
2.        F-сила (Н)
3.        g-ускорение свободного падения (м/с)
4.        k-коэффициент жесткости (Н/м)
5.        N-сила реакции опоры (Н)
6.        G-гравитационная постоянная, G=6,67*10^-11 ()
7.        P-вес тела (Н)
8.        a-ускорение м/с²
9.        u-коэффициент трения
10. x-смещение тела от положения равновесия.

 

Глоссарий

1.Динамика-раздел механики, который отвечает на вопрос: ”Почему тело движется так, а не иначе?”

2.Движение по инерции — движение, происходящие без внешних воздействий.(Прочитать параграф №19 и ответить на вопросы 1 и 2 стр. 89)

3.Инерциальные системы отсчёта – системы отсчёта, в которых тело, не взаимодействующее с другими телами, сохраняет состояние покоя, или равномерного прямолинейного движения.(ответить на вопрос 3 стр. 89)

4.Инерция – явление сохранения скорости.(Привести три примера движения по инерции)

5.Масса – мера инертности.(Доказать утверждение примерами субъективного опыта).

6. Сила – Мера взаимодействия между телами, в результате которого тело приобретает ускорение. Сила векторная величина. (Прочитать параграф 21 и решить задачи на стр. 95 учебника)

7.Сила тяжести – сила, с которой Земля притягивает к себе все тела.

 

 

Направлена вертикально вниз.

(Прочитать параграф 26 учебника

И решить задачи на стр. 114.)

 

8.Сила упругости – сила, возникающая в результате деформации тела, и направлена в сторону, противоположную деформирующей силе.(Перечертить в тетрадь и проанализировать схему на стр. 101 учебника.)

F= — kx

 

 

                    F_упр.

 

 

 

9.Сила реакции опоры – сила, действующая на тело со стороны опоры перпендикулярно её поверхности.(Привести примеры действия силы реакции опоры).

10.Сила натяжения – упругая сила, действующая на тела со стороны нити или пружины.(Решить задачу 1 на стр. 102 учебника)

 

 

 

 

 

 

11.Сила трения – сила, возникающая при движении или попытке движения одного тела по поверхности другого, и направленная вдоль поверхности их контакта в сторону, противоположную движении..                                                                         F_тр=uN

 

 

 

                                         (Прочитать параграф 24 учебника и решить задачи на стр. 107)

 

 

 

 

12.Вес – это сила, действующая на опору или подвес.

                                              

 

 

 

 

(Как оказаться в невесомости?)

 

 

 

 

УТВЕРЖДЕНИЯ

1. Принцип инерции Галилея:

• Если на тело не действует сила, оно сохраняет состояние покоя или равномерного прямолинейного движения.

2.  Принцип относительности Галилея:

• Во всех инерциальных системах отсчета законы механики имеют одинаковый вид.

3. Закон всемирного тяготения:

• Гравитационная сила притяжения материальных точек пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.

F=G

(Прочитать параграф 25 учебника и решить задачи на стр. 111)

4. I Закон Ньютона:

• Тело сохраняет состояние покоя или прямолинейно равномерно движется, если на него не влияют другие тела, или их влияние скомпенсировано.

5. II Закон Ньютона:

• В инерциальных системах отсчета ускорение тела прямо пропорционально векторной сумме всех действующих на него сил и обратно пропорционально массе тела:

 

 

                                           a =

     6.   III Закон Ньютона:

• Тела взаимодействуют друг с другом с силами одной природы, направленными вдоль одной прямой, равными по модулю и противоположными по направлению:

 

F₁ = —F₂

(Провести анализ задач, приведенных в качестве примера в параграфе 27. Решить задачи на стр 120 учебника)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Примеры решения задач.

.1.Найти величину тормозящей силы, действующей на автомобиль массой 3 тонны, если при скорости 20 м/с тормозной путь составляет 40 метров.

 

 

2. Какую скорость должен иметь искусственный спутник Земли, чтобы вращаться по круговой орбите на высоте 900 км над Землёй? Каков период его обращения.

 

 

 

 

 

 

 

 

3. Троллейбус массой 10 тонн, трогаясь с места, на пути 50 метров приобрёл скорость 10 м/с. Найти коэффициент трения , если сила тяги 14 кН.

4. тело массой 0.6 кг падает с ускорением 9,4м/с². Найти силу сопротивления воздуха.

 

 

 

 

5.Деревянный брусок массой 3 кг тянут по горизонтальной деревянной доске с помощью пружины, М=0.3. Найти удлинение пружины, если к=10 кН/м.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Контроль знаний учащихся

 

1. Мяч массой 0,5кг после удара, длящегося 0,02 с приобретает скорость 10 м/с. Найти силу удара.
2. Определите массу удара, если при ударе о шар массой 2 кг он получает ускорение 0,2 м/с² , ускорение движущегося шара 0,1 м/с².
3. Какой груз нужно подвесить к пружине жесткостью 40 Н/м, чтобы растянуть её на 5см.
4. (П) Лыжник массой 50 кг движется со скоростью 20м/с по вогнутому, а затем по выпуклому участку дороги с радиусом кривизны 10м. Определите вес лыжника на каждом участке дороги в средней точке.
5. (П) Грузовик взял на буксир «Волгу» массой 2т и двигаясь равноускоренно, за 50сек проехал путь 400м. На сколько удлинился трос, соединяющий автомобили если k=2*10⁶H/m. Трением пренебречь.
6. (П) Скорость обращения Земли вокруг солнца 30км/с. Радиус Земной орбиты 1,5*10¹¹м. Определите массу солнца.

7*.   Тело массой 100кг движется вертикально  вниз со

       скоростью 6м/с , тормозит в течении 4с. Определите силу

        натяжения каната, к которому прикреплено это тело.

8*    Шофёр грузовика, движущегося со скоростью 72км/ч,  

        заметил на дороге знак. Сможет ли он, не сбавляя скорости, 

        проехать поворот если его радиус 25м, u=0.4.

9**.        Страница 120, (учебник) № 5.

10**.      Страница 95 , (учебник) №5.

«Основы динамики»

Цели урока:

1. Академическая: обеспечить формирование у школьников целостной системы ведущих знаний и способов деятельности по разделу “Основы динамики”, установлению внутрипредметных и межпредметных связей.
2. Развивающая: формирование аналитико-синтетического мышления при построении структурно-логических обобщающих схем по изученному материалу. Формирование навыков самоконтроля, взаимоконтроля рефлексии.
3. Воспитательная: Содействовать формированию мировоззренческой идеи познаваемости явлений и свойств окружающего мира.

Условия выполнения целей урока:

• Построение структурно-логических обобщающих схем по изученному материалу.
• Обобщение и систематизация на различных уровнях: понятийном, межпонятийном, тематическом, межпредметном.
• Обращение к субъективному опыту учащихся.
• Использование заданий, предусматривающих постепенное нарастание сложности упражнений и самостоятельности деятельности учащихся.
• Использование ИКТ.
• Использование справочного и контрольно измерительного материала.

Педагогическая технология : адаптивная система обучения.

Педагогические техники:

• выполнение заданий по специальным алгоритмам.
• Вопросно-ответное общение.
• Построение дерева темы.
• Элементы кооперативной деятельности.
• Лист обратной связи.

Оборудование урока:

• компьютер с проектором, презентация к уроку, выполненная в Power Point.
• Дидактический материал.
• Лист обратной связи.
• Алгоритм решения задач по динамике.
• Шаблоны для построения дерева темы.

План урока:

1. Оргмомент. 2 мин.
2. Мотивация на деятельность. Целеполагание. 5 мин.
3. Актуализация комплекса знаний и способов деятельности. 23мин

• Анализ содержания изученного материала и выделение главного.
• Установление внутрипредметных и межпредметных связей.
• Обобщение и систематизация комплекса знаний.

1. Самостоятельное применение знаний и способов деятельности в сходной и новой ситуации. 30мин.
2. Применение знаний и способов деятельности в комплексе.20мин
3. Рефлексия деятельности. 5 мин
4. Итог урока. 3мин.
5. Домашнее задание. 2мин.

Ход урока

1. Приветствие учащихся, гостей, жюри. Контроль готовности учащихся к уроку. Выяснение отсутствующих на уроке учащихся.
2. Без знаний физики науки-науки

Сегодня жизнь была бы пресной,
И был бы быт подобен муке,
Совсем бы был неинтересный…
Ни телевизор не включался,
Ни шла б FM волна в эфир,
По рельсам поезд бы не мчался,
И скучен сразу стал бы мир!
Познать, чтоб физики явленья,
Себя прославить и страну,
Должны вы быть полны стремленья
Учить и вширь и в глубину.
И будут в этом вам подмогой
Законы Ньютона, друзья!
Начнем урок! И будь вам в помощь
ГОСПОДЬ, соседи, ну и я!

Первый слайд презентации учителя знакомит учащихся с темой и типом урока.

Перед вами на столах находятся папки с материалами урока. Начнем работу со знакомства с картой деятельности на уроке (лист 1) .

Второй слайд презентации.

Постановка целей урока. Этапы урока. Оценка деятельности на уроке (самооценка: качественная и количественная, взаимооценка, итоговая оценка)

3. Обратимся в начале к литературному произведению — басня И.А. Крылова .

….Лебедь рвется в облака,
Рак пятится назад,
А щука тянет в воду.

С литературной точки зрения все понятно с исторической тоже: в басне выражено скептическое отношение к Александру I, она высмеивает неурядицы в Государственном Совете 1816 г. реформы и комитеты, затеваемые Александром I не в силах были стронуть с места глубоко увязший воз самодержавия.

Слайд №4

 

А как же объяснить с физической точки зрения ситуацию : а воз и ныне там?

Какой раздел механики в этом нам поможет?

Кто основоположник этого раздела?

Дети отвечают на поставленные вопросы.

Слай№5

Перед вами выдающийся математик, физик и астроном Исаак Ньютон.

Дата рождения: 4 января 1643

Место рождения: Вулсторп (графство Линкольншир)

Дата смерти: 31 марта 1727

Место смерти: Лондон, Англия

Научная сфера: физика, математика, астрономия

Слайд №5

Надпись на могиле Ньютона гласит:

Здесь покоится сэр Исаак Ньютон, дворянин, который почти божественным разумом первый доказал с факелом математики движение планет, пути комет и приливы океанов.
Он исследовал различие световых лучей и появляющиеся при этом различные свойства цветов, чего ранее никто не подозревал. Прилежный, мудрый и верный истолкователь природы, древности и Св. писания, он утверждал своей философией величие Всемогущего Бога, а нравом выражал евангельскую простоту.
Пусть смертные радуются, что существовало такое украшение рода человеческого.

Слайд №6

Статуя Ньютона в Тринити-колледже

На статуе, воздвигнутой Ньютону в 1755 г. в Тринити-колледже, высечены стихи из Лукреция:

Qui genus humanum ingenio superavit (Разумом он превосходил род человеческий)

Ребята, давайте вместе вспомним теоретический материал по разделу “Основы динамики ”, и приведем его в систему, построив дерево темы, т.е. структурную схему на основе обобщенного плана “что надо знать о теории”.

Учащиеся после диалога с учителем заполняют структурную схему (Учитель контролирует деятельность учащихся).

Далее учащимся предлагается оценить самостоятельно первый этап их деятельности в карте урока.

Второе задание

Самоанализ открытого урока школьного этапа конкурса

Презентация

границ | Коллективная динамика в квазиодномерной системе жестких дисков

1.

Введение

Твердые сферы и жесткие диски широко используются в качестве приближения первого выбора для моделирования различных объектов из мягкой конденсированной материи [1]. Несмотря на достаточно простое представление о веществе, модельные системы на основе твердого ядра все же способны восстановить ряд основных свойств и эффектов, связанных со структурой, термодинамикой (например, фазовые переходы) и динамикой реальных систем.В последнее время возродился интерес к свойствам жидкости твердых сфер, ограниченной узким каналом шириной, не превышающей двух диаметров твердого ядра. В такой системе, обычно называемой квазиодномерной (квазиодномерной) системой [2], твердые частицы не могут пройти через ближайших соседей, и их движение ограничено соседями. Особый интерес представляет так называемая однофайловая квазиодномерная система с шириной, не превышающей (1+3/2) диаметра диска [3], так как тогда диск не может касаться более одного соседа с каждой стороны.Это существенное упрощение позволяет установить контакт с точным решением Тонкса для чисто одномерной системы жестких стержней [4]. Причины интереса к этой системе как основные, так и прикладные. Фундаментальный интерес связан с существованием аналитического матричного подхода для изобарной статистической суммы [5–9] и точной канонической статистической суммы этой системы, полученной недавно в [10]. В настоящее время теоретические исследования в этой области в основном связаны с попытками (i) понять механизм трансформации свойств систем с твердым ядром по мере приближения их размерности к 2 и 3 [5, 11] и 2) рассматривать эти системы как стеклообразующие, см. [7–9, 12–14] и обзор [15].Практический интерес представляет возможность использования такой простой модели для фиксации свойств более сложных систем, например, для объяснения диффузии в цеолитных и углеродных каналах [16–18], микрофлюидных устройств [19], в технологии биоинтегрированных наноустройства [3] и т. д., рассматривая ось конечной длины квазиодномерной системы как ширину поры.

Замкнутые многочастичные системы очень универсальны и сложны, и компьютерное моделирование является идеальным и в большинстве случаев единственным доступным инструментом для изучения их структуры и динамики. Он широко применяется для изучения структуры и одночастичной динамики в квазиодномерных системах с различными модельными гладкими/непрерывными потенциалами взаимодействия частица-частица и частица-стенка. Но даже квазиодномерные системы, частично содержащие частицы с твердым ядром, и квазиодномерные системы с чисто твердыми частицами (которые являются основным предметом настоящего исследования) могут быть настолько различны по своей физике, что часто приходится сравнивать внешне сходные эффекты в таких системах. не имеет большого физического смысла. Например, в квазиодномерной системе частиц с твердым ядром, взвешенных в вязкоупругом жидком растворителе, их эффективные взаимодействия носят в основном гидродинамический характер, и роль удерживающих стенок заключается не столько в ограничении движения частиц, сколько в постановке граничного условия на поток жидкого растворителя.В то же время в квазиодномерной системе чисто твердых частиц все взаимодействия носят энтропийный характер. Другой пример касается зигзагообразного расположения частиц, которое очень часто представляет собой объект фундаментального интереса для различных квазиодномерных систем. Однако из-за различия потенциалов взаимодействия общее представление о зигзагообразной геометрии часто является единственным общим. Например, зигзагообразная структура может возникать как в квазиодномерной системе с чрезвычайно короткодействующим взаимодействием, таким как отталкивание жесткого ядра (т.g., см. [9]) и в квазиодномерной системе с дальнодействующим взаимодействием типа экранированного электростатического отталкивания в пылевой плазме (см., например, обзор [20]). Известно, что различие между этими двумя взаимодействиями принципиально даже в чисто одномерной геометрии, в которой фазовый переход существует только при дальнодействующем межчастичном отталкивании [21]. В то же время компьютерное моделирование динамических свойств квазиодномерных систем, содержащих только частицы с твердым ядром, т. е. квазиодномерных систем с твердым ядром, в основном проводилось в рамках стеклообразной динамики.В основном они были сосредоточены на проблемах, специфичных для динамики одиночных частиц, таких как время перескока диска между различными квазиравновесными состояниями и динамика дефектов [7, 9, 12], а также временная зависимость смещения частиц [9, 13]. Стеклообразное поведение жидкости жесткого диска, ограниченной узким каналом с жесткой стенкой, было также теоретически изучено в [7–9] путем анализа поперечных и продольных равновесных статических парных корреляционных функций с использованием подхода матрицы переноса [5].

Наши недавние исследования по компьютерному моделированию [22, 23] были посвящены корреляционным функциям коллективного времени в объемных двухмерных и трехмерных системах жесткого ядра.То, что в дальнейшем называется коллективной динамикой, означает корреляции в кооперативном движении системы многих частиц. Такой подход к пониманию динамических процессов является общим для изучения распространяющихся волн (звуковых, сдвиговых, тепловых) и процессов релаксации (тепловая релаксация, структурная релаксация, релаксация напряжений и т. д.). Соответствующие коллективные динамические переменные определяются через флуктуации сохраняющихся величин: числа частиц, продольной и поперечной составляющих полного импульса и энергии. Все эти коллективные динамические переменные известны из гидродинамического подхода и могут быть использованы для теоретического описания длинноволновых процессов. Для теоретического описания коллективной динамики за пределами гидродинамического режима набор коллективных переменных расширяется за счет ортогональных (ортогональных гидродинамическим переменным), которые представляют собой продольную и поперечную компоненты тензора напряжений, потока энергии и т. д. Точнее, компьютер Моделирование [22, 23] использовалось, чтобы выяснить, как коллективная динамика объемных твердых сфер и объемных жестких дисков ведет себя в разных пространственных масштабах.Достаточно неожиданно коротковолновые поперечные волны были обнаружены в обоих случаях по хорошо выраженным пикам спектральных функций поперечных течений. Хотя природа поперечных волн в системах с твердой сердцевиной оказывается в основном такой же, как и в простых жидкостях [24], т. е. они возникают как коротковолновые возбуждения за счет связи поперечного тока и поперечной компоненты тензора напряжений, жесткая -керновые жидкости известны отсутствием вязкоупругих эффектов. Интересно, что хотя коротковолновые поперечные волны отсутствуют в двумерной жидкости жесткого диска при низких плотностях частиц, они наблюдались в диапазоне более высоких плотностей, демонстрируя определенные особенности непосредственно перед переходом к замерзанию.

Настоящая статья посвящена квазиодномерной системе жестких дисков. Существенное отличие методов исследования коллективной динамики в твердотельных системах от методов для моделей, основанных на аналитических/непрерывных двухчастичных потенциалах, связано с отсутствием в первом случае локальных минимумов энергии. Даже в случае твердых тел, состоящих из твердых сфер или жестких дисков, частицы не колеблются вокруг минимума потенциальной ямы, а баллистически движутся в клетке, образованной ближайшими соседями.Это различие порождает интересный специфический аспект коллективной динамики в системе с твердым ядром, а именно наличие сильных корреляций между возникновением коротковолновых поперечных волн и явлением кеглинга [25, 26], которое было замечено в случай двумерной системы жестких дисков [22]. Поскольку в системе жестких дисков при квазиодномерном удержании неизбежно возникает каркас, вполне естественно ожидать существования коротковолновых поперечных волн и в этом случае. Тогда неясно, как ведут себя коллективные моды при дополнительном удержании, как отражения от границ канала влияют на продольные и поперечные возбуждения, возникающие в результате столкновений частиц, как суммируются одночастичные баллистические движения, образуя коллективные моды колебаний. .Случай поперечных возбуждений представляет особый интерес, поскольку последние отсутствуют в одномерном прототипе квазиодномерной системы жесткого диска. Все эти вопросы остаются неизученными. Поэтому наша цель — выполнить молекулярно-динамическое моделирование квазиодномерной системы жестких дисков, рассчитать ее статические структурные свойства и установить связь с коллективной динамикой системы. Оставшаяся часть теста организована следующим образом. В следующем разделе мы представляем информацию о моделировании молекулярной динамики; раздел 3 содержит результаты статических и динамических свойств исследуемых систем. В последнем разделе мы обсуждаем наши выводы.

2. Детали моделирования и симуляции

Квазиодномерная система моделируется размещением N жестких дисков диаметром σ в вытянутой прямоугольной коробке, образованной двумя стенками (линиями) длиной L _x ≡ L , разделенными расстоянием L _y ≡ H = σ + h с h < σ таким образом, что диски не могут проходить друг мимо друга.Взаимодействие двух тел диск-диск задается выражением

. u(rij)={∞, rij<σ0, rij≥σ,    (1)

где r _ij = | r _j − r _i | — расстояние между центрами дисков. Кроме того, обе ограничивающие стены непроницаемы,

uw(ri)={0, σ/2, образуя таким образом жесткостенный канал (или пору) шириной H = σ + h и длиной L .Концы канала открыты, и используются периодические граничные условия в направлении x .

Учитывая, что ширина H = σ соответствует одномерному случаю, диапазон ширин канала σ < H < 2σ можно рассматривать как мост между 1D и более высокими измерениями. Среди непрерывного многообразия ширины квазиодномерной системы в этом диапазоне σ < H < 2σ есть два, H /σ = 1,5 и H/σ=1+3/2, когда дисковое упорядочение при плотной упаковке соизмеримо с 2D треугольной решеткой, как вехи на пути от 1D к 2D.Для иллюстрации на рисунке 1 представлены два треугольных массива жестких дисков, которые соответствуют наиболее распространенным горизонтальным (рисунок 1А) и вертикальным (рисунок 1В) ориентациям двумерной треугольной решетки, которые отличаются на угол 30 градусов. Квазиодномерные системы, соответствующие H /σ = 1,5 и H/σ=1+3/2, показаны полыми дисками, которые при плотной упаковке образуют два очень отчетливых кристаллических зигзага. Основное различие касается числа ближайших соседей, взаимодействующих с каждым диском, т. е. двух для H /σ = 1. 5 и четыре в случае H/σ=1+3/2. Более узкая квазиодномерная система более близка к одномерной системе, а более широкая квазиодномерная система более близка к двумерной системе. В настоящем исследовании мы рассматриваем более узкую квазиодномерную систему с фиксированной шириной H /σ = 1,5.

Рисунок 1 . Зигзагообразный порядок диска в вертикальной (A) и горизонтальной (B) двумерной треугольной решетке при плотной упаковке диска. В настоящем исследовании мы используем квазиодномерную систему жестких дисков шириной H = σ + h с h /σ = 0.5 видно, что плотная упаковка диска напоминает зигзагообразный порядок, показанный в части (A) . Движущей силой такого зигзагообразного упорядочения является энтропия, которая в случае системы жестких дисков, ограниченной жесткими стенками, однозначно определяется исключенным объемом, как это показано в (C,D) . В случае 1D- или 2D-дисковых систем исключенный объем (область узора шириной σ/2 вокруг дисков и у стенок) зависит от расстояния между дисками, т.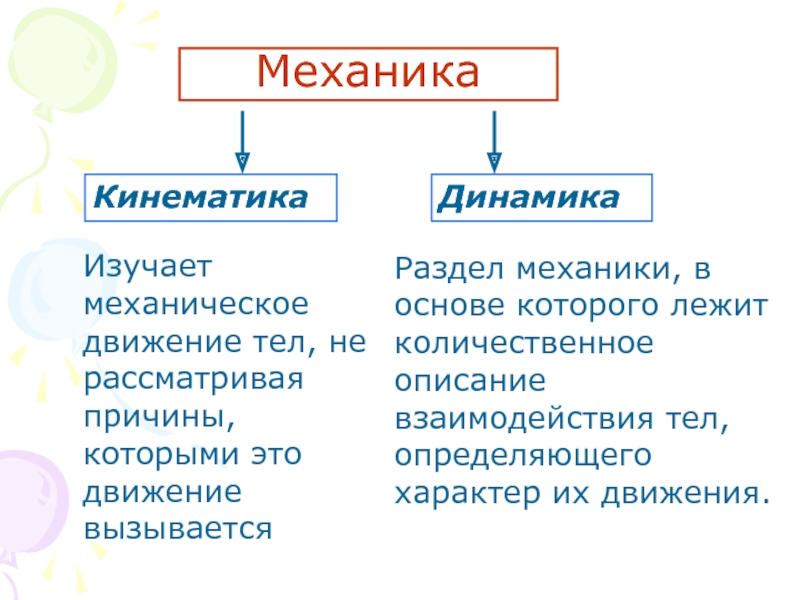 е. только от плотности дисков. Для системного жесткого диска квази-1D большое значение имеет расстояние между дисками и стеной.В части (D) мы иллюстрируем, как площадь (в некоторых относительных единицах), доступная для центров других дисков (площадь канала, закрашенного синим цветом), зависит от поперечного положения y ₀ = y _i − h центра одного отдельного диска. Видно, что такая площадь увеличивается при движении диска к стенкам канала и минимальна для его положения в середине канала.

Основная часть моделирования, в частности, касающаяся коллективной динамики, была выполнена с использованием набора из N = 200 жестких дисков при фиксированной ширине канала H с h /σ = 0.5 и различной длины L /σ = 400, 350, 300, 250, 220, 198, 190 и 180.

были смоделированы. Для удобства сравнения и обсуждения частные значения линейной плотности l , соответствующие каждой длине канала L , приведены в табл. 1 вместе с соответствующими значениями числовой плотности дисков ρ = Nσ ² / ( HL ) и коэффициент упаковки η = Nπσ ² /(4 HL ), поскольку последние часто используются в литературе по квазиодномерным системам.Прогоны моделирования с более крупными системами до N = 2000 также были выполнены и правильно указаны в тексте. На протяжении всей статьи диаметр жесткого ядра диска σ используется как единица длины, а время выражается в единицах (β м σ ² ) ^1/2 . При моделировании использовалось β = σ = м = 1, где β = 1/ кт , а м — масса диска.

Таблица 1 . Параметры плотности (доля упаковки η, числовая плотность ρ и линейная плотность l ) квазиодномерной системы жесткого диска с шириной канала H /σ = 1.5 и варьировали длину канала L для случая N = 200 дисков.

Первоначально выбранные N дисков располагались случайным образом внутри канала наименьшей длины L , т. е. наибольшей рассматриваемой плотности. Затем путем увеличения длины канала L были получены начальные конфигурации дисков для более низких плотностей. Для обработки столкновений жестких дисков друг с другом и с жесткими стенками канала мы используем алгоритм событийной молекулярной динамики (МД) [27, 28].Согласно этому методу, температура поддерживается постоянной за счет соответствующего масштабирования величины скоростей каждого жесткого диска таким образом, чтобы кинетическая энергия системы соответствовала теореме о равнораспределении. Направления скоростей дисковых частиц в начале каждого прогона выбирались случайным образом. Прежде чем вычислять средние значения для статических величин, мы провели МД-моделирование с заданными скоростями, как описано выше, чтобы уравновесить систему.

Коллективная динамика исследована путем расчета функций корреляции плотность-плотность, энергия-энергия, продольная (L) и поперечная (T) ток–ток во времени.Чтобы получить одинаково выбранные во времени позиции жестких дисков, т. Е. Траектории дисков, позиции жестких дисков между событиями столкновения были интерполированы. Действуя таким образом, для систем N = 200, 400 и 1000 жестких дисков мы записали траектории и скорости вдоль траектории для каждого жесткого диска, всего сбросив 100 000 конфигураций для систем N = 200 частиц, но 40 000 конфигураций для систем N = 400 частиц, и только 20 000 конфигураций для систем N = 1 000 частиц с фиксированным сокращенным интервалом времени 0.01.

Для каждой конфигурации были отобраны следующие компоненты Фурье. Фурье-компонента плотности частиц

n(k,t)=1N∑i=1Neikxi(t),    (4)

продольной составляющей плотности тока

JL(k,t)=1N∑i=1Nvx,i(t)eikxi(t),    (5)

и поперечной составляющей плотности тока

JT(k,t)=1N∑i=1Nvy,i(t)eikxi(t),    (6)

, а также с плотностью энергии

e(k,t)=1N∑i=1Nεikin(t)eikxi(t). (7)

Вот x _{I I вдоль канала, V x, I ( T ), V y, I ( t ) — компоненты скорости и -го диска вдоль канала и перпендикулярно каналу соответственно, а εikin — кинетическая энергия i -го диска в момент времени t . Волновой вектор k определяется вдоль оси канала x , совместимой с периодичностью окна моделирования, как с м = 1, 2, 3, …. Отметим, что из-за ненулевой ширины канала H положения и скорости частиц в квазиодномерных системах имеют две составляющие: вдоль ( x ) и перпендикулярно ( y ) каналу.Однако мы используем только волновые векторы, выбранные вдоль канала. Причина в том, что поперечные коллективные возбуждения в атомистических системах могут распространяться, если в поперечном коллективном движении участвуют хотя бы две частицы, т. е. волновое число меньше π/σ. В случае узкого канала шириной H = 1,5σ наименьшее волновое число k y = 2π/ H слишком велико.}

Имея фурье-компоненты энергии и плотности частиц, несложно вычислить фурье-компоненты плотности тепла [24]

h(k,t)=e(k,t)-fne(k)fnn(k)n(k,t).(8)

Здесь F _NE ( K ) и F _{NN NN ( K ) ≡ S ( K ) являются статическими корреляторами плотности энергии и плотности плотности, соответственно, тогда как S ( k ) является статическим структурным фактором.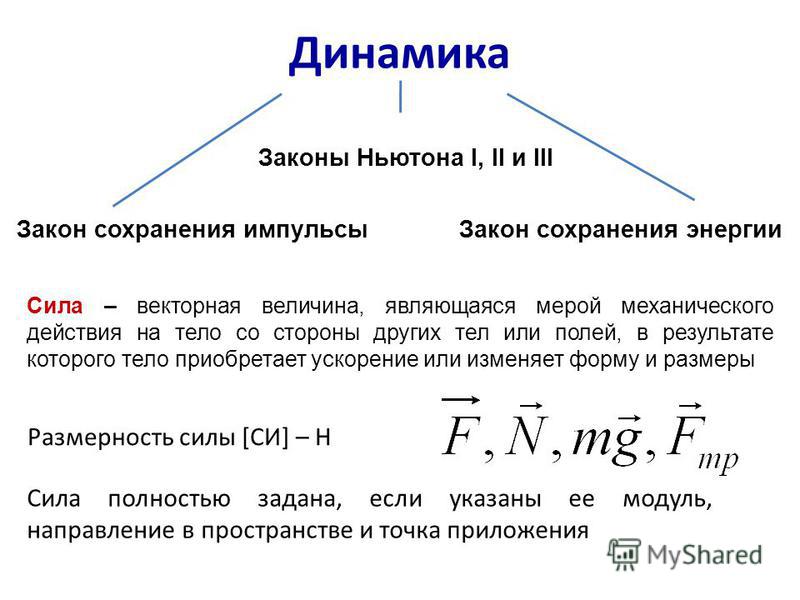 Флуктуации плотности тепла позволяют рассчитать зависящую от волнового числа удельную теплоемкость при постоянном объеме C v ( k ), которая в длинноволновом пределе стремится к своему макроскопическому значению.Другой важной величиной, которую можно получить из наблюдаемой динамики плотности тепла, является отношение типа Ландау–Плачека, которое дает информацию о доле вклада релаксационных и распространяющихся процессов в удельную теплоемкость C v [24, 29] .}

Определенные выше нестационарные компоненты Фурье соответствующих плотностей, уравнения 4 — 8, описывают флуктуации сохраняющихся величин в одноатомных жидкостях и образуют набор гидродинамических переменных макроскопической коллективной динамики.Имея динамические переменные (4–8), мы рассчитали зависящую от времени корреляционную функцию плотность–плотность

Fnn(k,t)=〈n(-k,t)n(k,t=0)〉,    (9)

зависящие от времени продольные и поперечные корреляционные функции ток-ток,

FJJL/T(k,t)=〈JL/T(-k,t)JL/T(k,t=0)〉,    (10)

и функция автокорреляции плотности тепла, зависящая от времени,

Fhh(k,t)=〈h(-k,t)h(k,t=0)〉.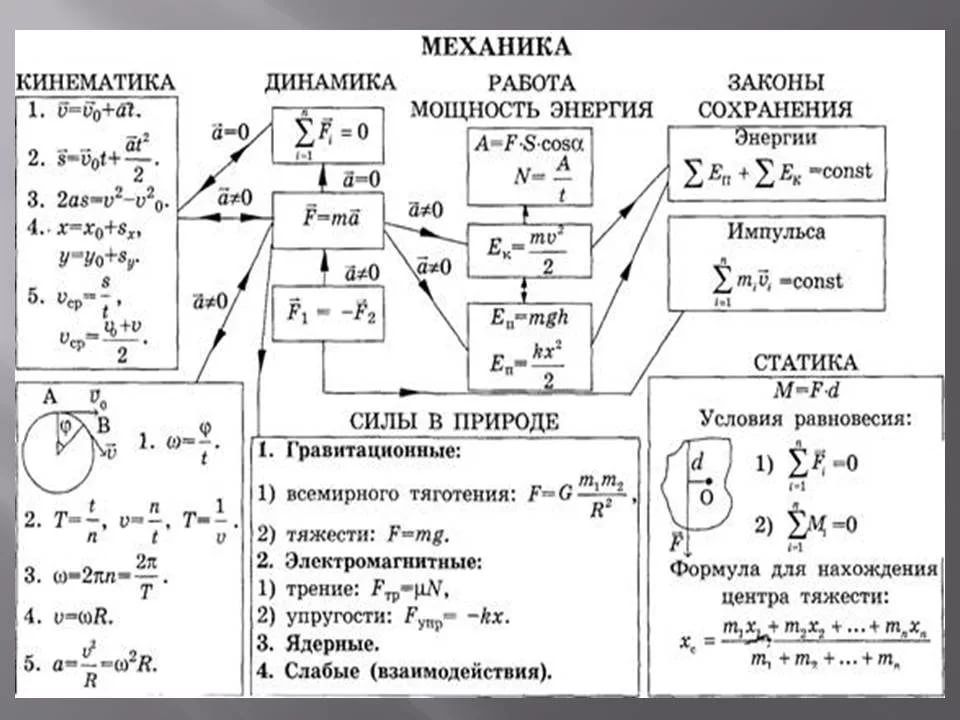 (11)

В дальнейшем корреляционные функции (9–11) использовались для численного преобразования Фурье-время с целью получения динамических структурных факторов плотность–плотность S ( k , ω), продольных/поперечных токовых спектральных функций, C ^{L / T} ( k , ω) и динамический структурный коэффициент тепло-плотности S _{hh ω15} ( ,

).

3. Результаты

Система жестких дисков в узком жесткостенном канале является анизотропной [5]. Анизотропия ожидается из-за настройки системы L >> H , что приводит к двум различным компонентам давления, то есть продольному, P _L = F _{L 6 H} , и поперечные, P _T = F _T / L .Здесь F _L и F _T — сила на единицу поперечного сечения, действующая по длине канала L , а сила на отрезке горизонтальной стенки длиной L /( Nσ ) = 1/ l соответственно. Эти силы имеют энтропийное происхождение и довольно чувствительны, чтобы их можно было оценить с помощью компьютерного моделирования. К счастью, эти силы могут быть найдены из аналитической канонической статистической суммы квазиодномерной системы жестких дисков, описанной в [10].

На рисунке 2 представлены зависимости P _{L ( л ) и P T ( л ), а также F L ( л ) и F T ( l ) для трех значений ширины канала, H = σ + h , где h зафиксировано на: 1D корпус; б) ч /σ = 0,5, что далеко как от нижнего 1D, так и от верхнего однорядного предела; в) ч /σ = 0.866, что очень близко к граничной ширине h/σ=3/2~0,866025 однофайловой системы. При низкой линейной плотности поперечная сила F T не зависит от плотности, что означает, что движение вертикальных дисков является баллистическим, вертикальный свободный пробег максимален, т. е. H − σ, диски подпрыгивают между каналами стены и не сталкиваются с другими дисками. Так как при той же малой линейной плотности l ≲ 0,8 поперечная сила меньше для более широкого канала, частота подпрыгивания диска между горизонтальными стенками также должна быть ниже для более широких каналов.}

Рисунок 2 . Зависимость от плотности продольных (L) и поперечных (T) давлений и сил в квазиодномерной системе жестких дисков с различной шириной канала (C) рассчитано с использованием аналитической канонической статистической суммы [10].

Видим, что при малых плотностях поперечное давление P _T больше, чем вдоль канала.Это связано с тем, что в этом случае P _L определяется большим расстоянием между дисками вдоль канала, а P _T определяется малым радиусом поперечного движения, ограниченным сверху H − о. По мере увеличения линейной плотности до l ≥ 1 диски начинают насаживаться друг на друга, длина свободного пробега по вертикали уменьшается, а поперечное давление и сила быстро увеличиваются. Для ч /σ = 0,866, рисунок 2C, это приводит к тому, что P _T всегда выше, чем P _L .Однако для более узких каналов с h /σ = 0,141 и h /σ = 0,5, рис. 2А,Б, прежде чем это произойдет, при определенном значении линейной плотности, разном для каждой ширины канала H , зазоры между дисками и стенками в поперечном направлении и зазоры между соседними дисками вдоль канала становятся равными, а давления на вертикальной и горизонтальной границах совпадают.

Профили распределения плотности, n _y ( y ), в поперечном y -направлении, полученные как из аналитической статистической суммы [10], так и из моделирования MD для квазиодномерной системы жесткого диска ширины H /σ = 1.5, показаны на рис. 3. В то время как линейная плотность низкая, l ≲ 0,8, система примерно однородна поперек канала, так как профили плотности соответствующей линейной плотности л . Напротив, при увеличении линейной плотности л > 1 распределение диска поперек канала имеет тенденцию к увеличению в областях, близких к стенкам канала, и уменьшению в средней части канала.Для наибольшей изученной линейной плотности l = 1,111 профиль плотности n _y ( y ) имеет почти δ-образную форму в непосредственной близости от стенок канала и практически исчезает в других местах.

Рисунок 3 . Профиль поперечной плотности n _y ( y ) квазиодномерной системы жестких дисков с шириной канала H /σ = 1,5 и различной линейной плотностью диска l : 1—1.111; 2—1,053; 3 — 0,909; 4—0,5. Символы соответствуют данным моделирования МД, а сплошные линии являются результатом аналитической канонической статистической суммы [10].

Продольный статический структурный фактор, S ( k ), рассчитывается из моделирования методом МД стандартным способом как мгновенно-временной коррелятор плотность-плотность,

S(k)≡fnn(k)=〈n(-k,0)n(k,0)〉. (12)

На рисунке 4 показаны изменения первого пика S ( k ) при уменьшении линейной плотности l .Что касается коллективной динамики, то одним из наиболее важных признаков является расположение K _max главного пика S ( k ), так как значение k = K _max имеет смысл границы псевдозоны Бриллюэна в рассматриваемой квазиодномерной жидкости жесткого диска при определенной плотности. В этой области волновых чисел имеет место де-Женновское замедление флуктуаций плотности, что в конечном итоге отражается в длинных хвостах корреляционных функций плотность-плотность во времени.Видно, что при линейных плотностях l > 1 структурный фактор S ( k ) типичен для искаженных кристаллов с основным пиком в виде сдвинутой дельта-функции. Для линейных плотностей л < 1 наблюдается типичный флюидоподобный структурный фактор. В неупорядоченных системах, где имеет место структурный переход, можно обнаружить разные наклоны основного пика S ( k ) по обе стороны от перехода [30]. На рисунке 5 показано положение основного пика K _max продольного статического структурного фактора S ( k ) как функция линейного размера L системы, пропорциональная обратной 1/ л линейной плотности.Положение главного пика меняется от К _max ≈ 7 для случая L /σ = 180 (наибольшая линейная плотность l = 1,111) до значения К _max ≈ 4,5 для L /σ = 400 (наименьшая рассматриваемая линейная плотность l = 0,5). Действительно, можно видеть излом в поведении положений максимумов, который возникает в области линейных плотностей 0,8 < l < 1,01. Согласно рис. 2Б, этот диапазон линейных плотностей соответствует в нашей системе термодинамическому состоянию, где поперечное давление P _T ниже продольного давления P _L .Стоит отметить, что в квазиодномерной системе с шириной канала H /σ = 1,866 происходит последнее новее, т. е. всегда P _T > P _{L 9002C (см. рис. ), при этом имеется диапазон линейных плотностей 0,93 ≲ l ≲ 1,01, где поперечная сила F T несколько меньше продольной силы F L 6 9. Этот диапазон плотности соответствует диапазону доли упаковки от η = 0.35 до 0,45 (см. рис. 10 в [9]), где зависимость среднеквадратичного смещения от времени начинает приобретать степенной характер из-за медленной диффузии дефектов зигзагообразного расположения дисков, предложенного в [12]. ] как механизм α-релаксации.}

Рисунок 4 . Статический структурный фактор, S ( k ) квазиодномерной системы жестких дисков с шириной канала H /σ = 1,5, рассчитанный в соответствии с определяющим уравнением 12 с использованием 100 000 конфигураций N = 200, сгенерированных МД. диски.Последовательность панелей (А–Н) соответствует уменьшению линейной плотности от л = 1,111 (А) до 0,5 (Н) согласно Таблице 1.

Рисунок 5 . Зависимость положения главного пика K _max статического структурного фактора S ( k ) квазиодномерных жестких дисков с шириной канала H /σ = 1,5 от длины канала L , что обратно пропорционально 1/ l линейной плотности.

Динамику одной частицы можно изучать с помощью автокорреляционных функций скоростей

ψ(t)=〈v(t)·v(t=0)〉〈v(0)·v(0)〉. (13)

Автокорреляционные функции скоростей уже были получены с помощью молекулярно-динамического моделирования объемных трехмерных твердых сфер [31] и двумерных жестких дисков [22]. В обоих случаях авторы обнаружили, что существует значение коэффициента упаковки (η = 0,45 для 3D-случая и η = 0,65 для 2D-жестких дисков), выше которого автокорреляционная функция скорости на коротких промежутках времени развивает отрицательную минимальную сигнализацию зарождающегося каркаса.В нашем случае анизотропная квазиодномерная система жесткого диска показывает существенно разное поведение для направлений вдоль и поперек канала. На рисунке 6 мы показываем автокорреляционную функцию скорости ψ( t ), ее компоненты xx и yy и их зависимость от плотности диска. Компонент xx , ψ _xx ( t ), в квазиодномерной системе жесткого диска ведет себя так же, как и в объемной двумерной системе жесткого диска [22].Он имеет длинные хвосты при малых линейных плотностях l ≲ 0,667 и переходит в неглубокий отрицательный минимум при наибольшей из изученных линейных плотностей l = 1,111 (доля упаковки η = 0,582) за счет столкновений с ближайшими соседями.

Рисунок 6 . Автокорреляционная функция скорости, ψ( t ) (A) и ее продольная ( xx направление вдоль канала) (B) и поперечная ( yy направление поперек канала) (C) компоненты для квазиодномерной системы жестких дисков с шириной канала H /σ = 1.5 при разных линейных плотностях л = 1,111( л = 180), 1,053(190), 1,01(198), 0,909(220), 0,667(300) и 0,5(400).

Влияние отражений от жестких стенок канала хорошо видно в поперечной составляющей ψ _yy ( t ) автокорреляционной функции скорости. Нас удивило, что характерное колебание ψ _yy ( t ) за счет отражений от стенок изменило свою форму, особенно для промежуточной плотности l = 1.01. К меньшим временам оно становилось более мелким, превращаясь для наиболее плотной системы л = 1,111 в очень высокочастотное сильно затухающее колебание. Этот эффект гораздо лучше виден в спектре Фурье Z~yy(ω) функции ψ _yy ( t ), показанном на рис. = 1,01 для смещения в сторону более высоких частот с увеличением затухания колебаний. Это означает, что при высоких плотностях зигзагообразная структура жестких дисков предотвращает их отражение от обеих стенок канала.Вместо этого при зигзагообразном порядке жесткие диски отражаются от одной ближайшей стены и от двух ближайших зигзагообразных соседей.

Рисунок 7 . Фурье-спектр Z~yy(ω) автокорреляционной функции поперечной скорости, ψ _yy ( t ), показанный на рисунке 6C, при различных линейных плотностях ), 1,053 (190), 1,01 (198), 0,909 (220) и 0,5 (400).

xx — и yy -компоненты автокорреляционной функции скорости в квазиодномерной системе до сих пор обсуждались только для случая твердых ядерных частиц, взвешенных в вязкоупругом жидком растворителе [32].Подобно нашему рисунку 6B, авторы наблюдали отрицательный минимум и отрицательный длинный хвост асимптотической формы ~ − t ^−3/2 для компоненты, параллельной оси канала. Они также пришли к выводу, что оба вывода имеют место только для липких граничных условий и не возникают, если растворитель может скользить по стенкам. Наше обнаружение отрицательного минимума автокорреляционной функции скорости на рисунке 6B при самой высокой изученной линейной плотности l = 1,111 имеет совершенно другую природу, поскольку наша система состоит исключительно из жестких дисков, которые баллистически летают между ударами о твердые препятствия. Мы попытались оценить экспоненты для отрицательного долговременного хвоста ψ _xx ( t ). Однако даже в нашем случае сохраненных 100 000 конфигураций с N = 200 частиц шум в хвостах был очень сильным, что не позволяло надежно оценить показатели степени. Это показывает, что решеточное моделирование Больцмана [32] является более подходящим инструментом для этой цели, чем ньютоновское моделирование МД.

Коллективную динамику обычно изучают с помощью анализа временных корреляционных функций, которые хранят всю информацию о коллективных возбуждениях в системе и их связи.До сих пор коллективная динамика в макроскопических масштабах в объемных системах была хорошо изучена, но в литературе практически отсутствует информация о коллективных возбуждениях в ограниченных низкоразмерных системах, состоящих исключительно из твердых частиц. Временные корреляции в последнем случае могут существенно отличаться от таковых в объемных системах. Простой пример этой разницы виден в поперечной динамике рассматриваемой квазиодномерной системы жестких дисков, которая при наименьшем волновом числе, доступном в наших симуляциях, всегда показывает затухающие колебания из-за отражения от жестких стенок канала. Напротив, в объемных трехмерных системах твердых сфер и двумерных жестких дисках, где действует макроскопическая гидродинамика, не существует поперечных возбуждений при малых волновых числах, доступных при моделировании. На рис. 8 видно, что изменение коллективных поперечных токовых автокорреляционных функций с плотностью диска практически такое же, как и для одночастичных yy -скоростных корреляций. Это свидетельствует о том, что основной вклад в поперечные корреляционные функции ток–время вносят отражения частиц от жестких стенок канала.

Рисунок 8 . Коллективная временная корреляционная функция поперечного импульса в квазиодномерной системе жестких дисков с шириной канала H /σ = 1,5, рассчитанная при наименьших волновых числах k _мин , доступных при моделировании, и для различных линейных плотностей l = 1,111( л = 180), 1,053(190), 1,01(198), 0,909(220), 0,667(300) и 0,5(400). Стандартной гидродинамической формой корреляционной функции поперечного тока во времени в жидкостях является одноэкспоненциальная.

Корреляционные функции продольного течения и времени позволяют оценить скорость звука для наименьших волновых чисел, доступных при моделировании. На рис. 9 представлена ​​полученная зависимость скорости звука от длины канала L , пропорциональная обратной 1/ l линейной плотности (см. табл. 1). Как и ожидалось, скорость звука монотонно уменьшается с увеличением длины канала, т. е. с уменьшением плотности.

Рисунок 9 .Зависимость скорости звука c _s в квазиодномерной системе жесткого диска с шириной канала H /σ = 1,5 от длины канала L , обратно пропорциональная 1/ l линейной плотность.

Дисперсия продольных и поперечных возбуждений в исследуемой квазиодномерной системе жестких дисков была получена из положений пиков продольных и поперечных токовых спектральных функций которые представляют собой преобразование Фурье во времени продольных/поперечных функций корреляции ток-течение, полученных по МД, FJJL/T(k,t). Используя хорошо зарекомендовавшую себя методологию [24], последние были проанализированы на предмет положения их пиков, которые для различных волновых чисел k определяют дисперсию ω _{L / T} ( k ) продольных и поперечные возбуждения. Типичные формы спектральной функции C ^{L / T} ( k , ω) показаны на рис. 10 для системы N = 200 частиц и линейной плотности l = 1.01. Поскольку формы спектральных функций зашумлены, чтобы определить положение их пиков и максимумов, мы использовали стандартную аппроксимацию Безье для зашумленных данных. Моделирование с большим числом частиц позволило нам получить доступ к меньшим волновым числам, в то время как дисперсионные соотношения в пределах погрешностей остались прежними.

Рисунок 10 . Типичные продольные (L) и поперечные (T) спектральные функции токов, C ^{L / T} ( k , ω), в длинноволновой области при k _мин = 2π/ L (A) и для волнового числа k = 17 k _min (B) для системы из N = 200 дисков и линейной плотности л 90. 01. В (A) поперечная спектральная функция была умножена на коэффициент 100 для удобства восприятия. Звездочки, соединенные синими линиями, показывают аппроксимацию Безье, примененную для оценки положения пика зашумленных спектральных функций.

На рис. 11 показаны дисперсии ω _L/T ( k ) продольных и поперечных возбуждений в квазиодномерной системе жесткого диска. Части рисунков 11A,B представляют данные для линейных плотностей l < 1. На первый взгляд, в этом случае дисперсия ω _L ( k ) продольных возбуждений в квазиодномерной системе жесткого диска очень похожа на это уже наблюдалось для системы 2D жестких дисков [22].При малой линейной плотности, л = 0,5, дисперсия ω _л ( к ) лишь незначительно отклоняется от монотонности. Но как только линейная плотность увеличивается, l = 0,909, она показывает четко выраженный минимум в районе значений волнового числа k ~ 6, связанный с положением главного пика K _max продольного структурного фактора S ( k ), рассмотренных на рис. 4, 5. Отклонение от гидродинамического закона дисперсии в длинноволновом пределе для обеих рассматриваемых плотностей остается «отрицательным».«Отрицательная» дисперсия относится к отрицательному отклонению дисперсионной кривой ω _L ( k ) на границе гидродинамического режима от линейного гидродинамического закона дисперсии акустических мод в рассматриваемой квазиодномерной жесткой системе. Эти эффекты аналогичны тем, которые наблюдаются в системе 2D жестких дисков с увеличением плотности [22]. Напротив, дисперсия ω _T ( k ) поперечных возбуждений существенно отличается от таковой в случае двумерной системы жестких дисков [22].А именно, для обеих линейных плотностей l < 1 мы наблюдаем достаточно пологую форму кривой ω _T ( k ) при пониженной частоте ~10 с тенденцией к более высоким значениям частоты с увеличением линейной плотности. В двумерной системе жесткого диска поперечные возбуждения имеют акустическую природу. Кроме того, поперечные возбуждения отсутствуют при низких плотностях и наблюдается длинноволновая щель распространения, когда они начинают появляться при более высоких плотностях. Поэтому вполне естественно приписать плоскую поперечную моду в квазиодномерной системе жестких дисков отражениям дисков от жестких стенок канала.Этот вопрос более подробно обсуждается ниже.

Рисунок 11 . Дисперсия продольных (L) и поперечных (T) возбуждений, ω _L ( k ) и ω _T ( k ), в квазиодномерной системе жесткого диска с шириной канала H H /σ = 1,5 при линейной плотности диска л = 0,5 (А) , 0,909 (Б) , 1,01 (В) и 1,111 (Г) . Штриховые прямые в области малых к соответствуют гидродинамическому закону дисперсии ω = с _с к с соответствующей скоростью звука с _с , показанной на рис. 9.Исходные данные для деталей (C,D) были взяты из нашей предыдущей статьи [33].

Части (c) и (d) рисунка 11 показывают аналогичные данные для дисперсий ω _L/T ( k ) продольных и поперечных возбуждений, но для диапазона линейных плотностей l > 1. Что касается дисперсии продольных возбуждений, ω _L ( k ), мы видим тенденции, уже наблюдавшиеся на рис. минимумы углубляются, достигая нулевых значений частоты при плотности ρ = 1.111 и смещается в сторону больших значений волнового числа k . Последнее снова согласуется со сдвигом для положения K _max первого пика продольного структурного фактора S ( k ) на рисунках 4, 5; сохраняется и «отрицательная» дисперсия в длинноволновой области. Такое поведение ω _L ( k ) напоминает таковое для упорядоченных твердых тел и интерпретируется в [33] как следствие возникновения зигзагообразного упорядочения в сжатой квазиодномерной системе. Дисперсия поперечных возбуждений на рис. 11В,Г также не показывает заметных изменений при изменении линейной плотности до l = 1,01. Однако он показывает резкие изменения при самой высокой рассматриваемой линейной плотности l = 1,111. А именно: (i) происходит резкое увеличение частоты ω _T до ~70; 2) сама дисперсионная кривая ω _T ( k ) имеет пузыревидную форму за счет расщепления на низкочастотную и высокочастотную ветви в области значений k , совпадающих с положением максимума дисперсии ω _L ( k ), что предполагает возможность продольно-поперечной связи возбуждения на атомном уровне в сжатой почти зигзагообразно упорядоченной квазиодномерной системе жесткого диска.

МД-моделирование позволяет изучать флуктуации плотности тепла в системе и их влияние на коллективную динамику. Напомним, что адиабатическое распространение звука в жидкостях вызывает небольшие отклонения локальной температуры и мгновенных градиентов температуры, которые вызывают процессы релаксации локальной температуры через температуропроводность.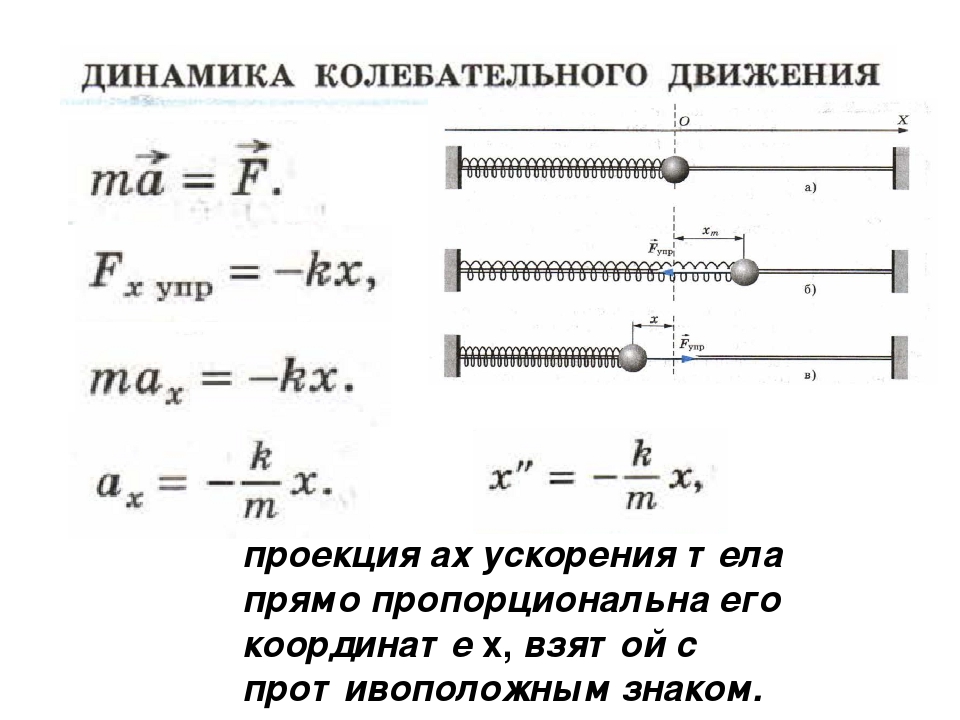 Эти релаксационные процессы непосредственно связаны с флуктуациями энтропии и обусловливают центральный пик динамических структурных факторов S ( k , ω).На рис. 12 показаны динамические структурные факторы S ( k , ω), а также динамические факторы плотности тепла S _hh ( k , ω) для трех самых низких волновых чисел в квазиодномерная система жесткого диска при максимальной линейной плотности l = 1,111. В обоих типах спектральных функций боковые пики обусловлены продольными акустическими возбуждениями, а центральный пик для жидкого состояния обусловлен флуктуациями энтропии. В нашем случае замкнутой, почти зигзагообразной структуры при линейной плотности л = 1.111 (длина канала L /σ = 180 и ширина H /σ = 1,5), центральные пики S ( k , ω) и S _{hh 9,0016 9002 ω) свидетельствуют об одних и тех же температурных (иногда называемых энтропийными) процессах релаксации, характерных для жидкого состояния. Мы рассчитали S hh ( k , ω) и для более низких плотностей и наблюдали практически такую ​​же форму S hh ( k , k , центральный и боковой пики по сравнению с более высокими плотностями.}

Рисунок 12 . Динамический структурный фактор, S ( k , ω), и динамические факторы плотности тепла, S _hh ( k , ω), квазиодномерной системы жесткого диска с шириной канала H /σ = 1,5 получено из моделирования методом МД при наибольшей рассматриваемой линейной плотности l = 1,111 для трех наименьших волновых чисел k ₁ < k ₂ 2 3 k 900

4. Обсуждение

В плотных, почти твердотельных состояниях квазиодномерной системы жесткого диска мы наблюдали быстрое увеличение поперечной частоты ω _T ( k ) в длинноволновой области k ~ 0 от ω _T ~ 12 для линейной плотности l = 1,01 на рисунке 11C до частоты ω _T ~ 70 для линейной плотности l = 1,111 на рисунке 11D.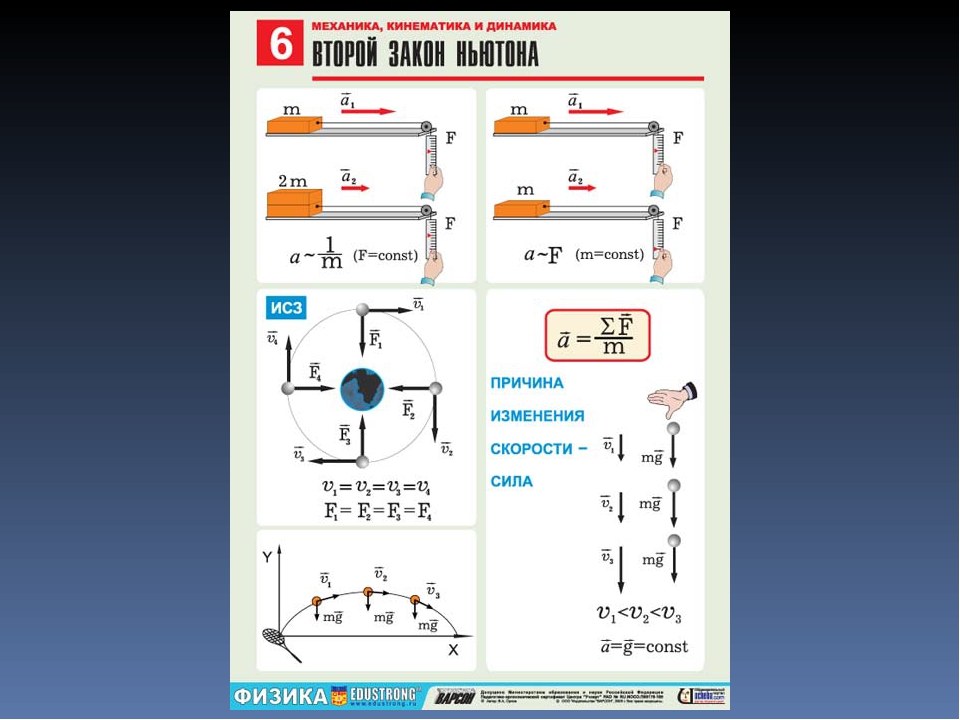 Неглубокий минимум на профиле ω _T ( k ), наблюдаемый при линейной плотности l = 1.01 при волновых числах k ~ K _max /2, также углубляется и становится хорошо развитой. Однако в конце концов частота ω _T ( k ) при k ~ K _max /2 разделяется на высокочастотную и низкочастотную ветви при линейной плотности l = 1,111, как показано на рис. Рисунок 11D. Наблюдаемое изменение дисперсии ω _T ( k ) поперечных возбуждений при изменении системы от разреженной к плотной можно объяснить формированием зигзагообразной структуры.Поперечная низкочастотная мода, обусловленная подпрыгиванием между двумя жесткими стенками, трансформируется в высокочастотные поперечные колебания между одной стенкой и ближайшими соседями в зигзагообразной структуре. Это также подтверждается поведением поперечной составляющей автокорреляционной функции скорости ψ _yy ( t ) на рисунке 6C. Вдохновленный этим интригующим поведением, один из нас разработал аналитическую теорию [10] этой системы, которая предполагает, что она связана с развивающимися оконными дефектами в расположении зигзагообразных дисков [33].Представление о дефектах такого рода (дефект — это локальная бесупаковка) было введено [12] и использовано [7–9, 12–14] для описания стеклообразной динамики в терминах состояний в клетке и без клетки в дисковых конструкциях в квазипространстве. -1D система жесткого диска с шириной канала H /σ = 1,866. В [33] такие дефекты были связаны с максимальным контактным расстоянием двух дисков вдоль канала, равным диаметру диска σ; в [10] их распределение найдено аналитически как функция линейной плотности.Что касается плотностей l > 1, горизонтальное контактное расстояние между дисками и фактическое горизонтальное расстояние между ближайшими соседними дисками очень близки, это распределение может хорошо отражать фактическое расстояние между дисками Δ _x , что поддерживается по данным компьютерного моделирования.

При плотной/плотной упаковке диски образуют идеальный зигзаг. По мере ослабления удержания тенденция к увеличению энтропии приводит к появлению все большего числа оконных дефектов, через которые пары соседних дисков освобождаются и меняются вертикальными положениями (рис. 13).Это теоретическое предсказание [10] было подтверждено данными моделирования МД для распределения фактических расстояний Δ _x между следующими соседними дисками (рис. 14) и согласуется с более ранним результатом [8]. При высокой линейной плотности л = 1,111 они распределяются вокруг Δ _х /σ ~ 0,89, близкого к минимально возможному контактному расстоянию вдоль поры, 3/2≈0,87σ. Однако при несколько меньшей линейной плотности л = 1,053, кроме уширения максимума при Δ _x /σ ~ 0.92 мы видим появление острого подпика при Δ _х /σ = 1. В отличие от широкого максимума, смещающегося в сторону больших Δ _х , подпик всегда остается при Δ _х /σ = 1, хотя его форма меняется: он становится все более выраженным и, наконец, превышает основной пик, сигнализируя о приближении к жидкоподобному состоянию. Это указывает на исключительную роль, которую играет расстояние между центрами следующего соседнего диска Δ _x = σ.А именно, создание окон шириной с диаметр диска σ (σ-окна) в зигзагообразном массиве, ни шире, ни уже, является наиболее эффективным способом набрать энтропию, разблокировав два диска и заставив их распространить свое удивление на всю ширину канала. . Описанный механизм захвата/отторжения диска соседями в квазиодномерной системе жесткого диска принципиально отличается от такового в квазиодномерной системе с дальнодействующим экранированным электростатическим отталкиванием в пылевой плазме [20], где частицы остаются на конечных расстояниях, а зигзаг может даже трансформироваться в прямую линию.

Рис. 13. Слева : Перестановка дисков в поре, которая создает окно для двух дисков, чтобы поменяться местами по вертикали. Верхняя панель: диск в поре на среднем расстоянии вдоль поры, которое меньше диаметра диска σ, и диски не могут поменяться вертикальными положениями. Чтобы диск 1 опустился, диски слева и справа от него становятся более плотными. Средняя панель: Диск 1 опускается через окно размером σ между дисками 2 и 3. Теперь диск 2 может подняться между дисками 4 и 1.Нижняя панель: Произведен обмен вертикальными положениями дисков 1 и 2. Теперь диск 4 потенциально может съехать вниз. Справа : Репрезентативные снимки конфигураций дисков, полученные в результате MD-моделирования квазиодномерной системы жестких дисков с шириной канала H /σ = 1,5 для иллюстрации схем перестановки дисков. Показаны четыре самые высокие рассматриваемые линейные плотности сверху вниз: l = 1,111, 1,053, 1,01, 0,909, которые обсуждаются на рисунке 14.Закрашенные кружки обозначают диски, которые находятся в клетке и не могут поменяться местами по вертикали.

Рисунок 14 . Распределение фактических горизонтальных расстояний, Δ _x , между ближайшими соседними дисками в квазиодномерной системе жестких дисков с шириной канала H /σ = 1,5 при линейных плотностях дисков l = 1,111(1), 1,053( 2), 1,01(3), 0,909(4) и 0,5(5), полученные при моделировании МД.

В чисто одномерной системе с жестким диском вертикальное движение отсутствует.В плотно упакованной квазиодномерной жесткой дисковой системе шириной H /σ = 1,5 этому также препятствует полный каркас, но в конечном итоге он появляется по мере ослабления удержания. Так как при достаточно малой плотности возможно вертикальное движение дисков от одной стенки к другой, то здесь ожидается некоторый вклад в закон дисперсии от почти баллистических поперечных колебаний между стенками. Поскольку это происходит от максимального вертикального пути H − σ, этот вклад ω _T1 ( k ) в частоту ω _T ( k ) при низкой плотности должен быть минимально возможным.Однако при высокой плотности σ-окна встречаются редко, и диски могут отскакивать не более чем между одной стенкой и срединной плоскостью, поэтому ожидается, что самая низкая поперечная частота ω _T2 для более высоких плотностей будет примерно в два раза выше, чем для низкой плотности, ω _{. T2} ~ 2ω _T1 . Частота ω _T2 связана с максимальным расстоянием Δ _x в ядрах окон, которые требуют локального сжатия и должны приводить к высокочастотным продольным и поперечным флуктуациям.Таким образом, можно ожидать, что самая низкая поперечная частота ω _T2 и самые высокие продольная и поперечная частоты появятся вблизи одинаковых волновых чисел k . Кроме того, групповая скорость в этом диапазоне волновых чисел должна быть равна нулю, поскольку окна не переносятся волнами. Дисперсия продольных и поперечных возбуждений в квазиодномерной системе жесткого диска, полученная в результате моделирования методом МД, соответствует этой картине (рис. 11C, D). Для линейной плотности л = 1.01 пик при Δ _х = σ (рис. 14) свидетельствует о том, что σ−окна в зигзагообразной структуре хорошо развиты, порядок диска узкий, а частоту ω _T1 можно отождествить с практически k — независимая поперечная частота ω _T ( K _max /2) ~ 10 на рисунке 11C. В то же время при линейной плотности l = 1,111, когда σ−окна практически отсутствуют (рис. 14), поперечный спектр распадается на самый низкий, ω _T2 ~ 20 ≈ 2ω _T1 , и самый высокий частота, ω _T ~ 100, при волновых числах k , где продольная частота максимальна (см. рис. 11D).При волновых числах k ~ K _max /2 кривые ω _T1 ( k ) и ω _T2 ( k ) являются плато, что указывает на нулевые групповые скорости. Непрерывные продольная и поперечная моды при погонной плотности л = 1,111 связаны с колебаниями на коротком свободном пробеге взаимно защемленных дисков у стенок. Таким образом, основные свойства ω _T ( k ), непосредственно связанные с вертикальным движением, согласуются с представлениями о роли σ-окон в зигзагообразном расположении.

Представленная выше интерпретация данных компьютерного моделирования в терминах вертикального движения диска также согласуется и хорошо иллюстрируется теоретической зависимостью полной поперечной силы F _T ( l ) на рис. 2Б. Действительно, как обсуждалось выше, для низкой линейной плотности l поперечная сила F _T постоянна, что означает, что вертикальное движение является баллистическим, поскольку свободный путь и свободное время максимальны.Напротив, при высокой линейной плотности l поперечная сила F _T резко возрастает с l , расположение дисков близко к плотному зигзагу, они не могут пересекать среднюю линию канала, поэтому что свободный пробег и время в лучшем случае составляют половину их максимальных значений. Наконец, эта картина явно соответствует распределению плотности диска по каналу на рисунке 3.

В заключение мы хотели бы указать на новое и неожиданное развитие, вытекающее из приведенных выше исследований коллективных возбуждений.Речь идет о возможном сценарии Костерлица-Таулесса в квазиодномерной системе жесткого диска [33]. В 2D-системах плавление протекает по сценарию Костерлица-Таулесса [34]: в кристалле появляются дефекты, и их количество непрерывно растет от нуля при нулевой температуре до тех пор, пока состояние не станет жидким. Именно так ведет себя число оконных дефектов при зигзагообразном расположении [7, 9, 10, 12]: оно равно нулю только при плотной упаковке и плавно увеличивается с уменьшением плотности. Но в сценарии Костерлица-Таулесса важно, чтобы пространственные корреляции уменьшались по степенному закону при высоких плотностях и экспоненциально при более низких плотностях.В то же время известно, что если статистическая сумма системы обладает свойством передаточной матрицы, что, как принято считать, имеет место для квазиодномерной системы с жестким диском, то корреляции могут затухать только экспоненциально. Наш поиск другого поведения корреляции мотивирован следующим образом. Во-первых, наши уже опубликованные [33, 35] и предварительные результаты молекулярной динамики для описанной здесь системы указывают на возможность степенного распада. Во-вторых, в Приложении к [10] показано, что свойство матрицы переноса может быть не столь универсальным для квазиодномерных систем, что оставляет место для альтернативной теории. Работа продолжается.

Заявление о доступности данных

Необработанные данные, подтверждающие выводы этой статьи, будут предоставлены авторами без неоправданных оговорок.

Вклад авторов

AH и AT разработали модель и вычислительную основу. AH выполнила моделирование МД, управляемое событиями, для создания траекторий частиц. Компания AT выполнила МД-моделирование распределения частиц, управляемое событиями. ТБ использовал траектории, сгенерированные МД, и выполнил численные расчеты свойств коллективной динамики.В.П. внес свой вклад в интерпретацию поперечных режимов возбуждения с точки зрения оконных дефектов и связи между поперечным движением диска и полными силами и давлениями на границах канала. AT руководил проектом и написал рукопись при поддержке VP, TB и AH. Все авторы обсудили результаты и внесли свой вклад в окончательный вариант рукописи.

Финансирование

ТБ и АТ были поддержаны NRFU Project 2020.02/0115. Работа ВП была поддержана ВК 202 НАН Украины и НИФУ Проект 2020. 01/0144.

Конфликт интересов

Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Ссылки

1. Лёвен Х. Веселье с твердыми сферами. В: Мекке К.Р., Стоян Д., ред. Статистическая физика и пространственная статистика . Берлин: Спрингер (2000). п. 297–331.

Академия Google

2. Баркер Дж. Статистическая механика почти одномерных систем. Austr J Phys . (1962) 15:127–34. дои: 10.1071/PH620127

Полнотекстовая перекрестная ссылка | Академия Google

4. Тонкс Л. Полное уравнение состояния одно-, двух- и трехмерных газов жестко-упругих сфер. Физическая версия . (1936) 50:955–63. doi: 10.1103/PhysRev.50.955

Полнотекстовая перекрестная ссылка | Академия Google

5. Кофке Д., Пост А. Твердые частицы в узких порах. Решение трансфер-матрицы и периодический узкий ящик.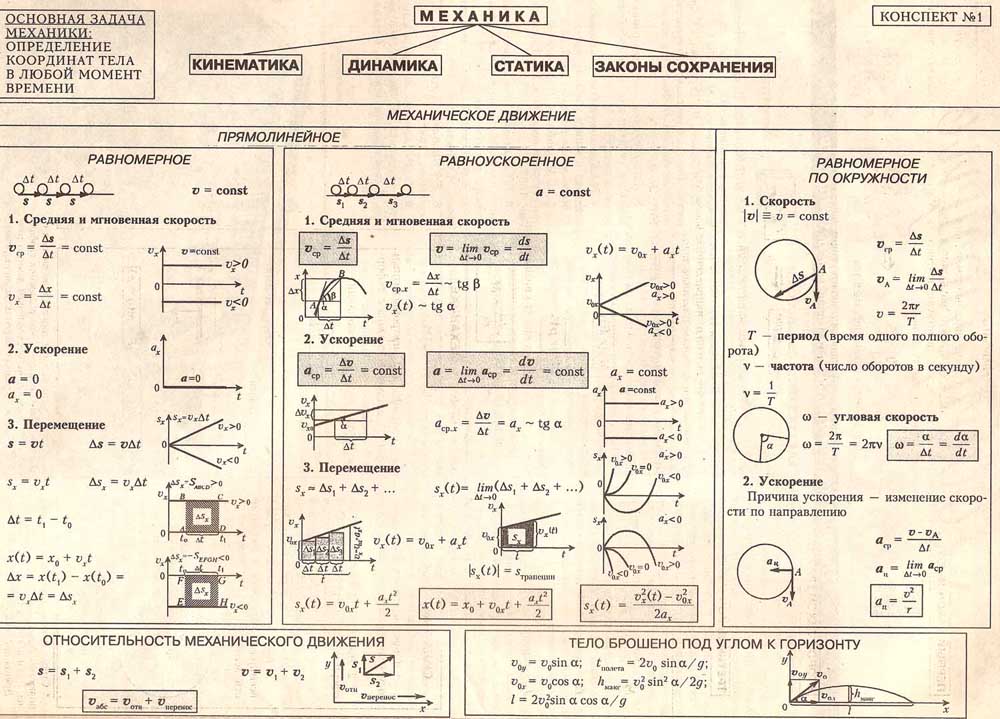 J Chem Phys .(1993) 98:4853–61. дои: 10.1063/1.464967

Полнотекстовая перекрестная ссылка | Академия Google

6. Варга С., Балло Г., Гурин П. Структурные свойства жестких дисков в узкой трубке. J Stat Mech Theory Exp . (2011) 153:P11006. дои: 10.1088/1742-5468/2011/11/P11006

Полнотекстовая перекрестная ссылка | Академия Google

8. Годфри М.Дж., Мур М.А. Понимание идеального стеклования: уроки исследования равновесия жестких дисков в канале. Физическая версия E .(2015) 91:022120. doi: 10.1103/PhysRevE.91.022120

Реферат PubMed | Полный текст перекрестной ссылки | Академия Google

11. Форстер С., Мукамель Д., Пош Х.А. Жесткие диски в узких каналах. Физическая версия E . (2004) 69:022125. doi: 10.1103/PhysRevE.69.066124

Полнотекстовая перекрестная ссылка | Академия Google

12. Боулз Р.К., Сайка-Воевода И. Ландшафты, динамическая неоднородность и кинетическая фасилитация в простой внерешеточной модели. Физическая версия E . (2006) 73:011503.doi: 10.1103/PhysRevE.73.011503

Реферат PubMed | Полный текст перекрестной ссылки | Академия Google

13. Хикс С.Л., Уитли М.Дж., Годфри М.Дж., Мур М.А. Переход Гарднера в физических измерениях. Phys Rev Lett . (2018) 120:225501. doi: 10.1103/PhysRevLett.120.225501

Полнотекстовая перекрестная ссылка | Академия Google

15. Шарбонно П., Курчан Дж., Паризи Г., Урбани П., Зампони Ф. Стеклянные переходы и переходы помех: от точных результатов к конечномерным описаниям. Annu Rev Cond Matter Phys . (2017) 8: 265–88. doi: 10.1146/annurev-conmatphys-031016-025334

Полнотекстовая перекрестная ссылка | Академия Google

16. Fois E, Gamba A, Tabacchi G, Quartieric S, Vezzalini G. О коллективных свойствах молекул воды в одномерных цеолитовых каналах. Физ Хим Хим Физ . (2001) 3:4158–63. дои: 10.1039/b102231h

Полнотекстовая перекрестная ссылка | Академия Google

17. Кофингер Дж., Хаммер Г., Деллаго С. Однорядная вода в нанопорах. Физ Хим Хим Физ . (2011) 13:15403–17. дои: 10.1039/c1cp21086f

Полнотекстовая перекрестная ссылка | Академия Google

19. Mark D, Haeberle S, Roth G, von Stetten F, Zengerle R. Микрожидкостные платформы «лаборатория на кристалле»: требования, характеристики и приложения. Chem Soc Rev . (2010) 39:1153–82. дои: 10.1039/b820557b

Полнотекстовая перекрестная ссылка | Академия Google

20. Coste C, Delfau JB, Saint Jean M. Продольная и поперечная одиночная диффузия в квазиодномерных системах. Biophys Rev Lett . (2014) 9:333–48. дои: 10.1142/S17

014400025

Полнотекстовая перекрестная ссылка | Академия Google

21. Дайсон Ф.Дж. Существование фазового перехода в одномерном изинговском ферромагнетике. Общинная математика, физика . (1969) 12:91–107. дои: 10.1007/BF01645907

Полнотекстовая перекрестная ссылка | Академия Google

24. Брик Т., Руокко Г., Скопиньо Т. Соотношение Ландау-Плачека для динамики плотности тепла и его применение к теплоемкости жидкостей. J Chem Phys . (2013) 138:034502. дои: 10.1063/1.4774406

Реферат PubMed | Полный текст перекрестной ссылки | Академия Google

25. Truskett TM, Torquato S, Sastry S, Debenedetti PG, Stillinger FH. Структурный предшественник заморозки в системах жестких дисков и жестких сфер. Физическая версия E . (1998) 58:3083–8. doi: 10.1103/PhysRevE.58.3083

Полнотекстовая перекрестная ссылка | Академия Google

26. Уэрта А., Хендерсон Д., Трохимчук А. Замораживание двумерных жестких дисков. Физическая версия E . (2006) 74:061106. doi: 10.1103/PhysRevE.74.061106

Полнотекстовая перекрестная ссылка | Академия Google

27. Олдер Б.Дж., Уэйнрайт Т.Э. Исследования по молекулярной динамике: общий метод. J Chem Phys . (1959) 31:459–66. дои: 10.1063/1.1730376

Полнотекстовая перекрестная ссылка | Академия Google

28. Донев А., Торквато С., Стиллинджер Ф.Х. Моделирование молекулярной динамики на основе списка соседей для несферических твердых частиц. I. Алгоритмические детали. J Вычислительная физика . (2005) 202:737–64. doi: 10.1016/j.jcp.2004.08.014

Полнотекстовая перекрестная ссылка | Академия Google

29. Брык Т., Скопиньо Т., Руокко Г. Теплоемкость жидкостей: гидродинамический подход. Cond Matt Phys . (2015) 18:13606. doi: 10.5488/CMP.18.13606

Полнотекстовая перекрестная ссылка | Академия Google

30. Gorelli FA, De Panfilis S, Bryk T, Ulivi L, Garbarino G, Parisiades P, et al. Превращение простого в сложное в жидком рубидии. J Phys Chem Lett . (2018) 9: 2909–13. doi: 10.1021/acs.jpclett.8b01094

Полнотекстовая перекрестная ссылка | Академия Google

31. Уильямс С.Р., Брайант Г., Снук И.К., ван Меген В. Автокорреляционные функции скоростей жидкостей твердых сфер: долговременные хвосты при переохлаждении. Phys Rev Lett . (2006) 96:087801. doi: 10.1103/PhysRevLett.96.087801

Полнотекстовая перекрестная ссылка | Академия Google

32. Hagen MHJ, Pagonabarraga I, Lowe CP, Frenkel D. Алгебраическое затухание флуктуаций скорости в замкнутой жидкости. Phys Rev Lett . (1997) 78:3785–8. doi: 10.1103/PhysRevLett.78.3785

Полнотекстовая перекрестная ссылка | Академия Google

33. Хуэрта А., Брык Т., Пергаменщик В.М., Трохимчук А. Переход типа Костерлица-Таулесса в клетке-распаковке в квазиодномерной системе жесткого диска. Phys Rev Res . (2020) 2:033351. doi: 10.1103/PhysRevResearch.2.033351

Полнотекстовая перекрестная ссылка | Академия Google

34. Костерлиц Ю.М., Таулесс Д.Дж. Упорядочение, метастабильность и фазовые переходы в двумерных системах. J Phys C Физика твердого тела . (1973) 6:1181–203. дои: 10.1088/0022-3719/6/7/010

Реферат PubMed | Полный текст перекрестной ссылки | Академия Google

35. Хуэрта А. , Брык Т., Трохимчук А. Поперечные возбуждения и зигзагообразный переход в квазиодномерной системе жесткого диска. Препринт arXiv arXiv:1970v1. (2019).

Академия Google

PHYS 200 — Лекция 9 — Вращения, часть I: Динамика твердых тел

PHYS 200 — Лекция 9 — Вращения, часть I: Динамика твердых тел

Глава 1.Введение в твердые тела; Вращение твердых тел [00:00:00]

Профессор Рамамурти Шанкар: Итак, это новая тема под названием «Физика или динамика твердых тел». Итак, твердое тело — это то, что не изгибается, не меняет своей формы, когда к нему прилагаются силы, и одним из примеров может быть десятицентовик, монета или метровая палка. Конечно, никто не является абсолютно жестким. Изогнуть всегда можно что угодно, но возьмем то приближение, которое имеем в руках, совершенно твердое тело.Техническое определение твердого тела состоит в том, что если вы укажете пару точек, расстояние между ними не изменится во время движения тела. Итак, динамика твердых тел в трех измерениях довольно сложна, потому что я хочу, чтобы вы сейчас представили не точечную массу, а какой-то объект определенной формы, как этот парень. Вы берете это; вы подбрасываете его в воздух; вы можете видеть, что он делает что-то довольно сложное.

На самом деле мы можем охарактеризовать его действия с помощью двух выражений.Я думаю, вы можете догадаться, что они собой представляют. Во-первых, если бы это была точечная масса, то точечная масса будет просто двигаться вперед и назад или вверх и вниз. Он будет делать то, что называется «переводами». Он пойдет из одного места в другое, может быть, по прямой, может, по кривой. Но на самом деле у точечной массы нет никакой дополнительной информации; Вы должны сказать мне, где он находится и как быстро он движется. Вот и вся история. Но если у вас есть такое тело, недостаточно сказать мне, где оно находится, потому что, если я подброшу это в воздух, вы можете себе представить, что когда оно движется по какой-то параболической траектории, в одно мгновение ластик может выглядеть вот так, в следующее мгновение мгновенное и ластик могут выглядеть так; Итак, мы говорим, что он перемещается и вращается. Неочевидная теорема состоит в том, что все, что тело делает от одного мгновения к другому, может быть достигнуто путем его сначала перемещения, а затем легкого вращения, чтобы привести его к желаемой конфигурации. Другими словами, вы можете перейти отсюда сюда путем перевода с последующим поворотом.

Итак, перенос — это то, что мы изучали все время, потому что для точечных частиц нет понятия вращения. Они берут точечную массу и вращают ее. Вы даже не знаете, что он вращается. У него нет внутренних переменных, так что это была проблема, на которой мы сосредоточились, но теперь мы собираемся распространить наше исследование на объекты, которые имеют размер и форму, следовательно, которые имеют ориентацию.Недостаточно сказать, что футбол здесь. Мяч мог быть здесь, но его длинный острый конец мог быть направлен вверх вниз или из стороны в сторону. Итак, что мы хотим сделать, так это разбить проблему на две части. Мы хотим сосредоточиться на теле, которое только вращается, но не перемещается. Как только мы отточим наши навыки, мы вернем способность тела переводить.

Итак, сначала мы сосредоточимся на теле, которое не может перемещаться. Итак, это означает, что вы берете тело и захватываете в нем одну точку; затем вы можете спросить: «Что он может сделать, если я возьму в нем одно очко?» Что ж, любое его движение будет таким, что эта точка не будет двигаться.Теперь, в трех измерениях, если вы возьмете футбольный мяч и зафиксируете определенную точку, он может вращаться по-разному. Но в любой момент вы можете показать, что он будет делать. Это должно быть вращение вокруг оси, проходящей через точку, где вы его захватываете, потому что, если он вращается вокруг оси, точки на оси не двигаются, а точка, где вы его захватываете, лучше лежит на ось. Теперь это тоже довольно сложно. Вы понимаете, почему я дал вам небольшую предосторожность. Трудно представить эти вещи.

Итак, я снова хочу взять простейшую возможную задачу; затем делайте это все более и более сложным. Что ж, вы могли бы сказать, что самое простое, чем вы занимались весь семестр, — это рассматривать вещи в одном измерении. Но это оказывается слишком мало. Если вы находитесь в одном измерении и у вас твердое тело — кстати, твердое тело означает не только протяженное, но и действительно жесткое. Например, если вы возьмете кошку или змею, змею вы можете схватить за одну точку, но змея не просто вращается вокруг одной точки, верно, пытается укусить вас, пытается двигаться; змея не твердое тело.Мертвая змея может быть твердым телом. Живая змея — определенно не твердое тело. Теперь вы должны помнить, что я дал вам передышку, изучая твердые тела, но на самом деле реальные тела могут не только раскачиваться, скручиваться и поворачиваться, они также могут вибрировать и двигать руками. Это намного сложнее, поэтому мы не будем туда лезть, а попробуем взять самое простое твердое тело. Но я сказал, что если я возьму твердое тело в одном измерении, оно вообще не сможет вращаться, потому что в одном измерении нет места для вращения.Можно только туда-сюда. Итак, чтобы показать вам, что есть какая-то новая возможность, я должен перейти по крайней мере в два измерения.

Вот пример, когда одного измерения недостаточно. Итак, я собираюсь представить твердые тела, живущие в плоскости доски. Один из способов сделать это — взять кусок металла, просто вырезать форму, и получится твердое тело. И, конечно, это имеет небольшую толщину, потому что все, что вы делаете из материи, имеет некоторую толщину, по крайней мере, в один атом толщиной, но представьте, что толщина пренебрежимо мала, так что это как кусок металла, кусок фольги или что-то в этом роде, но жесткое, и это твердое тело мы будем изучать.Это твердое тело может двигаться в плоскости доски и вращаться, но мы собираемся захватить его в одной точке. Итак, давайте выберем здесь какой-нибудь момент. Если я возьму его в этот момент и спрошу вас: «Что может сделать этот парень?» Итак, представьте, что вы протыкаете его через доску и говорите: «Хорошо, делай, что хочешь». Вы понимаете, что все, что он может сделать, это вращаться вокруг оси, проникая в эту точку.

Итак, допустим при t = 0 тело выглядело вот так, чуть позже оно будет выглядеть повернутым.Я должен сказать вам, что он делает в данный момент. Я должен рассказать вам, как он ориентирован. Итак, что мы делаем для этого, так это проводим через точку вращения некоторую линию. Вы можете выбрать любую линию, которая вам нравится. Выберите такую ​​линию, и мы скажем, какой угол образует эта линия со стандартным выбранным направлением, обычно с осью x . Итак, если я дам вам θ , я думаю, вам придется подумать об этом, и вы должны согласиться, что я сказал вам, где находится тело. Вы можете реконструировать все, верно, потому что эта точка прибита; он не может двигаться.Вы берете тело; вы поворачиваете его на угол θ .

Другими словами, вот вопрос. Предположим, что вы не в этой комнате; вы находитесь в другой комнате, и я хочу рассказать вам, что делает твердое тело. Какую информацию я должен сообщить вам, не видя фотографии? Я утверждаю, что если я скажу вам, как линия была проведена в теле, что вы делаете раз и навсегда, линейчатая линия, то я скажу, что линейчатая линия образует угол θ с осью x .Я полагаю, вы можете представить в другой комнате, что делает это тело, и в этом смысл фразы: «Я дал полную информацию». Конечно, это не полная динамическая информация, потому что она также зависит от того, насколько быстро он вращается. Но если просто сказать, что аналог того, где находится тело в одном измерении, это угол θ . Итак, вы обнаружите, что мы собираемся установить аналогию между одномерным перемещением и двухмерным вращением. Вы обнаружите, что аналогия очень полезна.Итак, я собираюсь использовать кусок доски, где я буду продолжать рисовать эту аналогию. Я делаю это потому, что количество вещей, которые вам нужно запомнить, уменьшится, если вы математически сопоставите эту проблему с проблемой перевода в одном измерении.

Глава 2. Вращение с точки зрения параметров окружности и радиана [00:08:15]

Другими словами, в одном измерении, когда тело движется, x говорит вам, где оно находится, верно? Я даю вам число, 3, или 91 561 π 91 562, или -14; ты знаешь, где это.Для этого твердого тела, живущего в плоскости доски, этот угол θ говорит вам, что тело делает. Таким образом, хотя тело находится в двух измерениях, вам нужен этот угол θ , чтобы сказать вам, какова его ориентация. Вам не нужны два числа; одно число говорит вам, что делает твердое тело. Так что чуть позже его можно было повернуть на угол Δθ . Это аналог того, что он переместился с 91 561 x 91 562 на 91 561 x 91 562 + 91 561 Δx 91 562.

Первое, что вам нужно сделать, это как вы хотите измерить θ ? Для x знаем, договорились.Мы собираемся измерять в метрах θ , стандартное предпочтение для людей с элементарным статусом — измерять его в градусах. Вы измеряете его в градусах, и когда тело совершает один полный оборот, вы любите говорить, что оно повернулось на угол в 360 градусов. Теперь это не предпочтительный способ измерения углов в более продвинутой динамике. Мы собираемся использовать что-то еще. Вы можете себе представить, что это такое. Вы знаете, к чему я клоню. aКто-нибудь знает, куда я иду?

Студенты: радиана.

Профессор Рамамурти Шанкар: радиана. Я иду к радианам, и вы можете спросить себя, зачем кому-то думать о радианах? Что не так с 360 градусов? Я имею в виду, во всех учебниках, во всех романах говорится: «Когда я шел по ложному пути, я делал разворот на 180 градусов». Правильно? Итак, все знают. На самом деле, я видел книгу скрипача, в которой говорилось: «Я делал все не так, и я сделал 360». Итак, вы понимаете, что 360 на самом деле не способ изменить вашу жизнь, но среди физиков это вызвало отклик.В физике 360 действительно не тривиальная вещь. Оказывается, частицы в мире делятся на бозоны и фермионы, причем половина частиц — бозоны, а примерно половина — фермионы. Электрон — это фермион; световой квант — это бозон, фотон. Для всех парней, которые являются фотонами или бозонами, если вы повернете их на 360, они вернутся к тому, что они делают. Оказывается, когда вы повернете электрон на 360, все числа вычитаются из этих чисел, и только когда вы повернетесь на 720, вы вернетесь к тому, что делаете.Так что вполне возможно, что этот человек имел в виду такое поведение; может быть, она была фермионом, но это то, что он сказал: «Я сделал 360». Я прошел через 360 много раз, поэтому, если вы используете его, вам лучше подкрепить его той информацией, которую я дал, иначе вы просто ошибетесь в два раза. В любом случае, 360 — это очень хорошо. Я думаю, что вавилонянам нравилось число 360 по многим причинам. Он делится на целую кучу чисел. Легко разделить на более мелкие части. По-моему, в некоторых инженерных кругах круг — это 400 и что-то еще, какая-то другая инженерная степень.Итак, вы можете решить, что такое круг, но нам нравится радиан.

Итак, давайте спросим: «Почему нам нравится радиан?» Для этого я хочу, чтобы вы взяли точку здесь, на расстоянии r от центра, и позволили ей переместиться в новое место под углом Δθ . Вы согласны с тем, что если твердое тело вращается, этот парень будет пересекать окружность радиусом r . Поскольку это твердое тело, оно не может изменить расстояние от этой точки. Итак, мы идем по кругу, и я спрашиваю вас, насколько велик этот отрезок, эта длина дуги ΔS , которую он прошел, когда он повернулся на угол Δθ .Итак, один из способов вычислить это — посмотреть, если бы я сделал полный круг, я бы сделал 2 πR . r — расстояние этой точки в твердом теле от центра. Я не прошел расстояние 2 πr , но я прошел Δθ , поэтому доля круга, который я проехал, равна Δθ на 360, если θ измеряется в градусах; Итак, позвольте мне указать, что таким образом. Итак, мы можем написать π на 180 Δθ умножить на r .

Если вы измерили θ в градусах, вот что вам нужно сделать, чтобы преобразовать угловой ход в фактическое расстояние по касательной к окружности.Линейное расстояние, которое вы проходите, связано с углом, на который вы поворачиваетесь, расстоянием r от центра и вот этим числом. Поэтому люди говорят: «Послушайте, почему бы нам не упростить жизнь, назвав θ умножить на π /180 в качестве нового угла». И назовем это Δθ умножить на r . Таким образом, Δθ, без маленького нуля сверху, с этого момента обозначает радианы, и это связано с θ , поэтому, если вы проигнорируете Δ , θ само по себе будет θ в градусах, № /180.Тогда преимущество заключается в том, что расстояние, которое вы преодолеваете, — линейное расстояние, которое вы проходите, — имеет простое соотношение с углом, под которым вы перемещаетесь, длиной плеча r от центра. Итак, вам не нужно носить с собой эти 180 и π и все такое, вы можете написать простой результат. Но теперь, когда вы делаете это, вы измеряете его в радианах, так что вы должны иметь представление о том, насколько велик радиан. Ну, полный круг, если пройти полный круг; расстояние, которое вы проедете, должно быть 2 πr , поэтому полный круг будет Δ θ = 2 π .Итак, круг стоит 2 π радиана; 2 π равно 6. Итак, один радиан составляет примерно 1/6 от 360, что составляет 60 градусов.

Реальный ответ близок к 58 с чем-то градусам. Кажется, это странная вещь для выбора. Странно только если начать с 360 градусов. Но если вы встретили людей из чужой культуры, вам просто нужно пойти в супермаркет, чтобы столкнуться с этими людьми, эти люди могут вообще не использовать 360; 360 — это человеческий артефакт, в 360 нет ничего особенного, независимого от нашей собственной культуры или предубеждений.Это может быть связано с тем, сколько у нас пальцев. Это может быть связано с тем, сколько длится год и так далее. Но в числе 360 нет ничего естественного. С другой стороны, 2 π , я полагаю, было бы обнаружено в любой развитой цивилизации. Если вы не вычислили π , вы не развитая цивилизация. Если вы не поняли 2, вы сильно отстали. Итак, вы знаете 2, и вы знаете π , и это то, что будут использовать другие культуры, другие планеты и галактики.Это единица измерения, которую мы любим использовать.

Вы снова и снова будете находить людей, использующих естественные для нас единицы измерения. Но позже, если вы захотите общаться с людьми на другой планете, вам придется использовать другую длину. Например, рост человека или длина руки Наполеона — это не очень хорошие единицы измерения, потому что, если у вас нет Наполеона в прошлом, вы не знаете, о чем говорите. Но если вы измеряете расстояния в единицах атома водорода, атомов водорода во всей Вселенной, это будет естественная шкала длины.В старые времена это была очень популярная тема. Когда они запускают ракету или закапывают что-то под землей, чтобы инопланетяне узнали об этом, вы хотите показать, какого мы роста; бесполезно давать ответ в метрах, футах или чем-то еще. Но если вы сможете каким-то образом связать свой размер и размер атома водорода, то это число будет иметь смысл для людей всех цивилизаций, потому что атомы водорода удобно производятся и разбросаны по всей вселенной, и они имеют одинаковый размер. В любом случае, это длинная вещь о радианах, поэтому мы любим использовать радианы.

Вы должны знать несколько популярных углов в радианах. Я буду использовать только радианы большую часть времени. Вы должны знать, что круг равен 2 π ; π — это половина круга, а π /2 — четверть круга, и когда вы находитесь на 90 градусов, это π /2; это то, что вы должны знать.

Как только вы запишете это таким образом, давайте получим еще один очень полезный результат. Возьмите расстояние, которое он проходит по касательной, за время, за которое он это делает.Это фактическая тангенциальная скорость или величина скорости в тангенциальном направлении. Я думаю, вы все согласны с этим; это то, что мы с вами подразумеваем под скоростью. Если в какой-то момент этот кусок образца просто оторвался и отлетел, он будет лететь с той же скоростью. Эта штука, у нас есть для нее символ, ω , а ω называется угловой скоростью и измеряется в радианах в секунду.

Итак, вы можете рассчитать угловую скорость для разных вещей. Например, какова угловая скорость Луны при ее обращении вокруг Земли? Ну, угловая скорость будет один оборот за 28 дней, верно? Один оборот равен 2 π радиан.В 28 дней вы делаете 28 раз 24 раза 3600; это столько радиан в секунду. Или есть полотно бензопилы, и бензопила вращается с некоторым числом оборотов в минуту — может быть, 3000 оборотов в минуту — вы можете перевести обороты в минуту в обороты в секунду, но вы должны помнить, что каждый оборот равен 2 π радианам. Итак, угловая скорость лопасти, вращающейся с частотой f , равна 2 πf . Вы это понимаете? f — это количество полных оборотов, которые он делает.Следовательно, если вы укажете на ней точку, она пройдет 2 91 561 πf 91 562 радиан. Итак, в словаре появился второй элемент, который представляет собой скорость, которая равна dx/dt , теперь заменена угловой скоростью, которая составляет dθ/dt . Это аналогия, кстати. Это поможет вам сказать, что ω похоже на скорость в старые времена, когда все двигалось вперед и назад. Но теперь они ходят по кругу, но и здесь есть понятие скорости, но она не в метрах в секунду, она измеряется в радианах в секунду.

Вот что вам, ребята, нужно держать в голове очень четко. Я могу только сказать об этом вам, но я не могу сделать это за вас. Это ω — аналог обычной скорости, но здесь это тоже реальная скорость, старая добрая скорость, это тангенциальная скорость точек, являющихся частью вращающегося твердого тела. Этого нет в моем словаре, но это очень полезный результат. Тангенциальная скорость — это угловая скорость, умноженная на расстояние этой точки от центра вращения.Таким образом, твердое тело в целом имеет единую угловую скорость. Вот что значит быть жестким. Все это вращается. Вы не можете сказать, что угловая скорость такая-то здесь и такая-то там; это свойство всего тела. С линейной скоростью не везде одинаково; точки рядом здесь за одно и то же время уходят так далеко, а точки рядом здесь за одно и то же время уходят так далеко. Следовательно, линейная скорость увеличивается от центра. Угловая скорость постоянна, а твердое тело не может иметь двух угловых скоростей.Он может иметь только одну угловую скорость.

Глава 3. Радиальное и тангенциальное вращение при постоянном ускорении [00:19:57]

Итак, что мы делаем, так это говорим: ладно, давайте возьмем задачу, в которой угловая скорость сама по себе изменяется. Хорошо, это аналог высказывания о том, что существует скорость изменения скорости, и здесь у нас есть величина, называемая α , которая представляет собой скорость изменения угловой скорости или вторую скорость изменения угла, и это обозначается по α .Итак, если вы взяли одну из этих вращающихся циркулярных пил, и она вращалась с определенной скоростью, и из-за трения, скажем, она замедлялась, или когда вы включаете двигатель, она ускорялась, предположим, вы только что повернули Выключите двигатель пилы, и он ускорит свое вращение, вы должны четко понимать, что ускорение деталей — это пильный диск, хорошо? Я пытаюсь нарисовать для вас одну из этих пил, и она крутится. Если вы выбираете точку, скажем, на окружности; Вы помните, давно мы узнали, что даже если он движется с постоянной скоростью, постоянной угловой скоростью, он имеет тангенциальную скорость, которая составляет ω умножить на r .И из-за этого у него будет ускорение к центру, центростремительное ускорение, которое равно v ² /r , и вы можете записать это как ω ² r . Это одно ускорение, которое он имеет, даже если он вращается с постоянной скоростью. Но я говорю, что у него может быть и тангенциальное ускорение, если ко всему прочему меняется сама угловая скорость.

Что ж, давайте переварим это. Это не слишком сложно, но я хочу, чтобы вы, ребята, поняли.Если он вращается с постоянной скоростью ω , мы узнали, что все, что движется по кругу, имеет старомодное линейное ускорение по направлению к центру, которое равно v ² /r . Но мы поняли, что v в тангенциальном направлении равно ωr , поэтому, если вы подставите это — если хотите, можете назвать это v тангенциальным — это даст мне ω ² r , это просто v ² / р . Но если вы затормозите это, ускорив или замедлив его, оно будет иметь вдобавок ускорение в этом направлении.Итак, ускорение точки на краю или в любом другом месте может иметь две составляющие. Тангенциальный будет там, только если вы ускорите или замедлите вращающийся диск, а радиальный будет всегда, пока он вращается.

Хорошо, раз у вас есть этот словарь, у вас может быть целая куча аналогичных величин. Например, если вы сосредоточитесь на задачах, где тело имеет постоянный угол ускорения α , что вы можете сказать? Ну, вы уже можете сказать, что θ будет θ ₀ + ω ₀ + ½ αt ² .Это потому, что θ ведет себя так же, как x . Если x имеет постоянное ускорение a , мы все знали, что x равно начальным x + начальная скорость, умноженная на время плюс ½ при ² . Точно так же угол, на который он поворачивается, будет начальным углом. Начальная угловая скорость умножается на t плюс что-то, включающее t ² . Это только в том случае, если α является константой, точно так же, как я надеюсь, вы, ребята, знаете, что это верно только в том случае, если a является константой.Хорошо, теперь я собираюсь продолжить аналогию и спросить, какова кинетическая энергия твердого тела, когда оно вращается? Да?

Студент: Не могли бы вы объяснить [неразборчиво]

Профессор Рамамурти Шанкар: Здесь?

Студент: Нет, ускорение с α .

Профессор Рамамурти Шанкар: Здесь?

Студент: Рядом с пилой.

Профессор Рамамурти Шанкар: О, здесь?

Студент: Вверх.

Профессор Рамамурти Шанкар: Этот?

Студент: Ага.

Профессор Рамамурти Шанкар: Хорошо, я говорю, если у вас есть вращающийся диск, возьмите любую точку на вращающемся диске, даже если диск движется с постоянной угловой скоростью, у него есть тангенциальная скорость и направление скорость постоянно меняется. Это самая старая вещь, которую мы изучили, поэтому она имеет ускорение по направлению к центру. Но это не угловое ускорение; это просто стандартное ускорение к центру всего, что движется по кругу.Это всегда будет там. Но кроме того, если вы ускорите или замедлите эту скорость вращения диска, вы также получите тангенциальное ускорение, которое равно α умножить на r . Пока не ясно или? Это ускорение неспециалисты знают. Если вы находитесь на вращающейся платформе, и кто-то ускорил скорость вращения, вы заметите, что движетесь быстрее. Это ускорение в тангенциальном направлении. Ускорение по направлению к центру — более сложный процесс, который мы изучили, и он связан с тем, что скорость — это вектор, а не скаляр.Итак, если направление меняется, мы связываем с этим ускорение, и оно такое же реальное, как и любое другое ускорение; для этого нужна сила.

Может быть, лучше спросить вас так. Предположим, что это маленькое пятнышко — это вы, хорошо? Вы застряли на вращающемся лезвии бензопилы и цепляетесь за него изо всех сил. Какую силу нужно приложить, чтобы удержаться на этом вращающемся лезвии? Это может не случиться с вами и со мной, но если вы находитесь в организованной преступности, это не очень необычная ситуация.Вы можете столкнуться со всевозможными механизмами, и вы хотите знать, что я делаю, чтобы остаться. Ну, Ньютон говорит вам ответ. Ньютон говорит, что если вы хотите быть на этом вращающемся лезвии бензопилы, за ваше ускорение по направлению к центру нужно платить, и если лезвие набирает скорость, за это тоже нужно платить. Это чистое ускорение; что, раз ваша масса будет силой, которая должна быть применена к вам. Итак, вы будете цепляться за него с этой силой, а эта сила, в свою очередь, по третьему закону будет приложена к вам диском.

Например, предположим, что это вид сверху на вращающуюся платформу. Вы просто стоите, а платформа вращается. Вы можете спросить: «Какая сила трения мне нужна, чтобы оставаться на платформе?» Ну, вам нужна сила, чтобы обеспечить вас ma , и я говорю вам, что ваш a состоит из двух частей. Даже если карусель вращается с постоянной скоростью, вам понадобится сила трения, направленная к центру, чтобы согнуть вас в круг. Теперь, если поверх него, карусель начинает увеличивать свою скорость, или уменьшать ее скорость.Нам также понадобится тангенциальная составляющая силы, чтобы обеспечить тангенциальное ускорение.

Хорошо, теперь это кинематика вращения при постоянном угловом ускорении, которая математически идентична этой, потому что математически, если вы знаете d ² θ/dt ² равно α , ответ такой же, как d ² x/dt ² = a . Вы меняете символы, вы получаете тот же ответ. Итак, вы можете представить множество проблем, которые мне не хочется делать.Я думаю, вы, ребята, легко с этим справитесь. Лучше сосредоточусь на более сложных.

Например, полотно бензопилы, вращающееся со скоростью 3600 об/мин, замедляется с некоторой скоростью α . Сколько времени нужно, чтобы прийти в себя? Ну, для этого вы напишите вторую формулу, ω = ω ₀ + αt . Это аналог v = v ₀ + at . А вы начинаете с каких-то ω ₀ , тормозите; α это отрицательное число, вы видите, в какое время это ω становится 0; вот когда это прекратится.Другой результат, который я буду использовать сегодня, таков: Это аналог v ² = v ₀ ² + 2 a(x — x ₀ ) . Это говорит о том, что если тело имеет ускорение α , то оно, конечно, будет набирать скорость, и квадрат конечной скорости связан с квадратом начальной угловой скорости плюс умноженное на 2 ускорение, умноженное на угол поворота.Итак, это аналогия, поэтому нам не нужно заново изобретать все эти вещи. Они просто исходят из того факта, что математически одинаковые вещи имеют одинаковые математические результаты. Они подчиняются одному и тому же уравнению; у них одинаковые результаты.

Глава 4. Момент инерции, угловой момент, кинетическая энергия [00:28:34]

Хорошо, теперь найдем кинетическую энергию твердого тела. У него есть масса, и если он вращается, все маленькие атомы, составляющие тело, движутся, и у них есть свои собственные ½ mv ² .И мы хотим спросить: «Какова сумма ½ 91 561 mv 90 129 2 90 130 91 562, сложенная по всем частицам?» Для этого удобно взять следующее более простое твердое тело. Возьмем твердое тело, взяв массу m ₁ на расстоянии r ₁ , соединенное с некоторой центральной ступицей безмассовым стержнем, и вы берете другую массу, и вы берете третью массу. Это м ₂ , на расстоянии r ₂ , там м ₃ , на расстоянии r ₃ , и так далее.Вы можете создать твердое тело, моделируя его таким простым способом. Если вы немного более абстрактны, вы можете взять сплошное твердое тело и сделать то же самое; но начнем с простого. Вот твердое тело, три жестких стержня с массами м ₁ , м ₂ , м ₃ , и вот оно прибито гвоздями и там через доску проходит шпажка, и вещи могут только вращаться вокруг этого.

Кстати, я должен сказать вам условность ω .В одномерном движении скорость положительна, вы движетесь вправо, а отрицательная — вы движетесь влево. Что касается угловой скорости, у нас должно быть соглашение о том, что положительно, а что отрицательно. Эта вещь, которая вращается, может вращаться только по часовой стрелке или против часовой стрелки. Оказывается, ω положительно для против часовой стрелки. Это просто соглашение, которое люди используют. На самом деле, вы заметили, как я нарисовал твердое тело, когда делал Δθ , у меня было вращение против часовой стрелки.Это предпочтительное направление для измерения угла θ от оси x .

Хорошо, давайте возьмем твердое тело. Он вращается с общей угловой скоростью. Надеюсь, вы все понимаете, что значит быть жестким. Итак, у всех одинаковая угловая скорость ω . Итак, какова кинетическая энергия этого объекта? Ну, это кинетическая энергия каждой массы, суммированная по всем массам i , m _i v _i ² .Теперь, какова скорость каждого объекта? Если взять это тело м ₁ , то его скорость обязательно перпендикулярна линии, соединяющей его с точкой вращения. Этот движется сюда; он не может двигаться по соединяющей его линии, потому что если это так, то это не твердое тело. Для твердого тела все расстояния сохраняются. Итак, вы не приближаетесь к центру и не уходите далеко от центра. Итак, все, что вы можете сделать, это вращаться вокруг центра. Итак, скорость этого парня v ₁ = ωr ₁ .Скорость этого парня, v ₂ , равна ωr ₂ и так далее. Итак, вы можете добавить все это. И что вы получаете? Вы получаете ½ суммы по i m _i r _i ² ω ² . И надо сделать суммирование по всем телам. В моем примере суммирование идет от 1 до 3. У вас может быть от 1 до бесконечности и от 1 до миллиона; это не имеет значения. Это кинетическая энергия.

Вы следите за этим? Это не новая кинетическая энергия; это то, что мы знаем как кинетическую энергию, всего ½ mv ² на каждую часть, из которой состоит твердое тело.Для удобства я решил, что твердое тело состоит из дискретного набора масс. Но теперь, если вы обратите внимание, переходя от 1 к 3, м ₁ и м ₂ и м ₃ — это три разных числа. Мы не знаем, что такое массы. r ₁ и r ₂ и r ₃ — это три разных числа. мы не знаем; каждый из них может находиться на разном расстоянии от начала координат.Но ω не имеет нижнего индекса i ; нет ничего под названием ω для этого и ω для того. На все есть только один ω . Итак, вы можете вытащить это из суммы и записать так. Затем ответ запишем как идентичный ½ Iω ² и дадим этому I имя; I называется моментом инерции. Итак, продолжая аналогию, эта плата будет использоваться для аналогии, у нас было K = ½ mv ² .Тем не менее, мы можем иметь K = ½ Iω ² , а I называется моментом инерции.

Итак, момент инерции определяется не только массами, составляющими тело, но и тем, насколько они удалены от центра. Если бы все массы просто упали на вершину центра, у тела не было бы момента инерции. Он будет весить столько же; момент инерции исчезнет. И точно так же, если масса рассредоточена, момент инерции больше. Например, если я стою здесь, а вы подходите и решаете меня закрутить, я стою вот так, вы пытаетесь меня закрутить, я высовываю руки, мой момент инерции изменился, потому что сумма моя масса теперь дальше от оси вращения.Итак, момент инерции зависит от расположения масс. Мы берем твердое тело; это не похоже на танцоров на льду, которые делают это. Мы говорим о твердом теле; следовательно, момент инерции постоянен. Но для нахождения момента инерции требуется расчет.

И вот еще что важно. Если я решу повернуть тело относительно нового места, скажем, вокруг этой точки, момент инерции изменится, потому что изменятся все расстояния r . Момент инерции. Если кто-то скажет: «Вот массы, вот где они, пожалуйста, найдите мне момент инерции», вы скажете: «Я не могу этого сделать.Вы скажете: «Я не могу этого сделать, пока вы не скажете мне точку, вокруг которой вы планируете вращать тело. Пока это не дано, я не могу сказать вам, что такое момент инерции». Следовательно, момент инерции относится к точке, и нет ничего, что можно было бы назвать массой относительно точки. Масса — это просто масса. Момент инерции зависит от точки, относительно которой вы вычисляете момент инерции; это переменная. Также стоит знать, что если тело вращается вокруг массы m ₃ , то m ₃ не дает вклада в момент инерции; это из.Все, что находится на оси, не участвует. Вещи, находящиеся дальше, вносят больший вклад пропорционально своей массе, пропорционально квадрату расстояния от оси.

Итак, это мой словарь. Итак, кто играет роль массы? Массу играет момент инерции. У него есть килограммы, метры в квадрате, и никто не дал им названия. Например, метр Ньютона, умноженный на джоуль, называется джоулем. Вы можете спросить, ну, это килограмм на метр в квадрате, может быть, это чье-то имя.До сих пор он не был назван в честь кого-либо, он просто называется ньютон-метр в квадрате. Итак, это будет аналог массы в нашем мире вращений. Вы помните, в мире вращения [поправка: нужно было сказать «перевод»] мы определяем нечто, называемое импульсом, то есть массой, умноженной на скорость. Здесь мы собираемся назвать то, что называется угловым моментом, будет I умножить на ω . Это L называется угловым моментом.

Один чрезвычайно важный момент, на который вы, ребята, должны обратить внимание, это то, что все концепции, которые я использую, такие как масса и энергия, это те же самые старые концепции, которые мы изучали ранее.Тот факт, что это вращающееся тело, ничего не меняет, ясно? Кинетическая энергия по-прежнему означает то же самое; это 91 561 K 91 562, хотя и выглядит совсем по-другому, на самом деле является ½ 91 561 mv 90 129 2 90 130 91 562 каждой части тела, суммированной по телам. Итак, это L называется угловым моментом. Потребуется некоторое время, чтобы к этому привыкнуть, но сейчас это произведение момента инерции и угла скорости. Итак, теперь ищем самое важное уравнение в механике, которое равно F = ma .Это будет равнозначно какому-то таинственному объекту. Теперь вы должны быть в состоянии угадать, что находится справа, хорошо? Вы уже должны знать, что по аналогии это можно записать как dL/dt , если хотите, скорость изменения импульса, или как I умножить на α ; это не имеет значения.

Надеюсь, вы понимаете, что если вы возьмете скорость изменения импульса, вы получите мА , потому что, когда вы берете производную, м не меняется.Аналогично здесь, если вы возьмете dL/dt , I не изменится, ω изменится, чтобы дать вам dω/dt , что равно α . I не меняется, потому что при вращении тела, конечно, частицы в теле движутся, но их расстояние от точки вращения не меняется. Несмотря на то, что тела перемещаются в новые места, r ² остаются прежними, потому что они просто вращаются. Вот почему в производной по времени не нужно брать производную по времени от момента инерции.

Но мы не знаем, кто будет играть роль слева, хорошо? Итак, мы собираемся найти это. Мы собираемся найти аналог этому. Итак, я собираюсь рассказать вам, что есть много способов узнать это. Это гораздо более тонкий вопрос, чем принято считать, о том, что такое правильный закон. Вы можете услышать, что закон утверждается довольно часто, но некоторые рассуждения, стоящие за ним, неверны. Итак, позвольте мне рассказать вам один способ добраться до закона. Надеюсь, вы знаете, на что я смотрю. Я пытаюсь выяснить, какая сущность возможна для скорости изменения углового момента или каков аналог левой части для мА .Я знаю, что правая сторона Iα . По аналогии, кто слева? Во-первых, совершенно очевидно, что если вы хотите, чтобы угловой момент тела изменился, ω должно измениться. Вы можете видеть, если что-то крутится на каком-то фиксированном ω , вы хотите изменить это, вы должны толкнуть или потянуть или что-то сделать. Итак, очевидно, вы собираетесь приложить силу, но то, что появляется слева, — это не просто сила, а что-то еще, и мы выясним, что это за что-то.И это делается с помощью следующего устройства.

Я собираюсь использовать старую добрую теорему об энергии работы, которая гласит: когда сила действует на тело, работа, которую оно совершает, то есть произведение силы на пройденное им расстояние, равна изменению кинетической энергии. Это стандартная теорема об энергии работы, которую мы установили. Итак, если вы возьмете твердое тело, подобное этому, и давайте применим его к твердому телу, я просто возьму более простой случай твердого тела с этими двумя массами, м ₂ и м ₁ ; это не имеет значения.Теперь я прикладываю силу F перпендикулярно этому телу на расстоянии r от точки вращения. И пусть оно поворачивает тело в это время; допустим, тело перемещается на величину Δθ . Может быть, я должен нарисовать вам лучшую картину, потому что это очень, очень важно. Итак, вот тело; Я просто взял самый простой, с двумя массами, м ₁ , м ₂ . Я просто собираюсь толкнуть его сюда и решаю толкнуть его в этом направлении, а он находится на расстоянии r от точки вращения.И пусть он повернется на небольшой угол и придет в это положение, а этот угол равен Δθ . Какую работу совершает эта сила? Я собираюсь записать это, но я хочу, чтобы вы подумали об этом. Работа, совершаемая силой, равна произведению силы на расстояние, на которое она переместилась. И в основном, я спрашиваю вас, каково это расстояние, которое он прошел, и если вы вообще помните что-нибудь из того, что я делал ранее, это примерно такая длина дуги, которую мы видели, равна r умножить на Δθ .

Другими словами, если вы приложите силу F и повернете тело на Δθ , расстояние, которое вы фактически переместите, составит r Δθ ; Итак, это сила, умноженная на расстояние. Это должно быть равно изменению кинетической энергии. Оно должно быть равно изменению кинетической энергии. Кинетическая энергия, напомню, равна ½ Iω ² . Следовательно, изменение кинетической энергии составит ½ I(ω ² — ω ₀ ² ) .Кстати, это два очень соседних момента времени. Если в соседние моменты времени в течение этого короткого промежутка времени можно считать, что тело имеет постоянное ускорение; следовательно, α является константой. Итак, по этой формуле вы также можете рассчитать, когда α является постоянным, точка. В реальном теле, когда оно вращается, α не обязательно должно быть постоянным, но для достаточно малого интервала, сколь угодно малого, мы можем применить формулу, которая работает, когда α является постоянным.В этом случае вы запишете это как ½ умножить на 2 α умножить на угол поворота. Правильно? Посмотрите вот на эту формулу. Я имею в виду этот результат, ω в конечном квадрате — ω в начальном квадрате в 2 раза α раза больше изменения угла. Итак, я хочу, чтобы вы затем приравняли эту работу к этому изменению кинетической энергии. Я хочу, чтобы вы приравняли этого парня к этому парню, и мы получим отличный результат: F умножить на r = I умножить на α . Iα это мА ; это то, что я ищу.Итак, вот этот парень, Fr , является аналогом силы, и называется он крутящим моментом.

Очень важно отметить, что крутящий момент, создаваемый этой силой, равен произведению силы на расстояние от точки вращения, и я говорю только о внешней силе. В стержне также действуют внутренние силы. Каждую часть стержня тащит за собой другая часть стержня, но такой анализ с точки зрения сил можно провести, но это очень сложно и сложно.Гораздо проще смотреть на энергию там, где энергия изменяется только за счет внешних сил. Если вы смотрите только на силы, вы должны быть осторожны. Эта точка вращения также прикладывает силу к стержню, но он не движется и не выполняет никакой работы. Итак, единственная внешняя сила, которую я применяю, отвечает за изменение кинетической энергии. Внутри стержня действуют другие силы. Другими словами, эта масса будет набирать скорость не потому, что я прямо толкаю ее. Я, наверное, толкаю эту часть стержня, а она толкает соседнюю часть, и она, наконец, толкает эту.Итак, я не применяю закон силы напрямую к этой массе. Я говорю, что бы ни происходило внутри, мне все равно; произведение внешней силы на расстояние представляет собой изменение кинетической энергии объекта. Да?

Ученик: Но как ты говоришь угловатый [неразборчиво]

Профессор Рамамурти Шанкар: Нет, я сказал, что эта величина, изменение кинетической энергии, является конечной кинетической энергией, ½ умноженной на ω ² минус начальная кинетическая энергия; но окончательный / начальный, когда стержень был там и стержень немного повернулся.

Студент: Правильно.

Профессор Рамамурти Шанкар: Хорошо.

Студент: Итак, вы говорите, что это 2 α из [неразборчиво]

Профессор Рамамурти Шанкар: Правильно.

Студент: Вы сказали, что нужно что-то делать со скоростью [неразборчиво]

Профессор Рамамурти Шанкар: Здесь. Нет, я использовал это уравнение, изменение, ω ² в конце минус ω ² в начале, в 2 раза превышает ускорение и угол ускорения, умноженные на θ — θ не является изменением θ за это время, правильно.Другими словами, эту формулу можно использовать даже для конечных периодов времени при условии, что α постоянно. Мы применяем его в течение крошечного периода времени, достаточно малого, чтобы мы могли поверить, что ускорение в течение этого крошечного периода равно некоторому числу α . Итак, это ω ² — ω ₀ ² действительно так, если вы хотите изменить ω ² , и это пропорционально α , умноженному на изменение угла. Итак, α не является константой; α может меняться от момента к моменту.Но в этот момент, в зависимости от сил, будет примерно 91 561 α 91 562, а эта штука, называемая крутящим моментом, равна 91 561 I 91 562 умножить на 91 561 α 91 562. Теперь, я думаю, совершенно ясно, что если бы у меня было несколько сил, действующих на тело, то крутящий момент был бы F _i r _i , и есть только одна последняя оговорка по этому поводу, одна последняя оговорка, которая что на практике силы, которые используются для вращения тела, не всегда могут быть перпендикулярны. Вы можете применить силу в каком-то другом направлении, вот так.

Глава 5. Теорема о крутящем моменте и рабочей энергии [00:46:47]

Теперь вы должны понять, что крутящий момент — это способность изменять вращательное состояние тела, и мы понимаем, что он зависит от силы, которую вы прикладываете, и зависит от того, насколько далеко эта сила находится от точки вращение. Итак, если у вас есть дверь, вы пытаетесь открыть дверь, вот дверь, вот петли, и вы хотите открыть эту дверь, применив силу. Возникает вопрос: «Куда поставить дверную ручку?» Хорошо? Вы вдруг изобрели дверь, подумали о петлях, но так и не придумали, куда поставить дверную ручку.Ты спросишь себя: «Ну, у меня полная свобода, может быть, будет красиво, если я поставлю ее рядом с петлями», тогда ты поймешь, что есть части вселенной, такие как Земля Дебилов, куда, если вы пойдете, все петли, все дверные ручки здесь, и они говорят: «Вы знаете, мы прилагаем много усилий, мы ничего не добьемся. Что случилось?» Что ж, мы понимаем, что в то время как сила — это все в линейном движении, сила — это не все во вращательном движении. Если вы хотите, чтобы ваши деньги стоили того, вы должны взять дверную ручку как можно дальше и положить ее ближе к концу.

Ну ладно, разберетесь. Затем вы приходите и говорите: «Хорошо, я поставил дверную ручку в нужном месте, откройте дверь», — и таким образом вы применяете огромную силу. И снова разочарование, опять никаких результатов, вы говорите: «Я иду как можно дальше от шарнира», и до вас доходит, что если вы действительно хотите, чтобы что-то шло, вы должны действительно браться за дело. линию разделения между местом, где он вращается, и местом, где вы прикладываете силу, и приложите силу перпендикулярно ей.Любая часть, параллельная ему, ничего не делает, если только вы не сорвете ее с петель. Вы не хотите этого делать. Так вот, здесь у этой силы есть бесполезная часть, а есть полезная часть, и бесполезная часть, пытающаяся сдернуть стержень с петель, будет уравновешена силой со стороны шарниров, потому что стержень – это жесткий стержень, он не собирается двигаться. Но тот, что перпендикулярен стержню, может фактически поворачивать стержень, не влияя на жесткость.

Итак, здесь нам нужен дополнительный коэффициент, который равен sin θ _i , где θ _i определяется следующим образом.Если вы находитесь в точке r _i и прикладываете силу F таким образом, θ — это угол между линией, соединяющей точку приложения силы, и направлением силы. Вы находитесь здесь, и вас разделяет этот вектор, и как угол между этим вектором разделения и силой, этот угол θ может варьироваться от силы к силе. Но эта сила F _i угол может быть θ _i . Это окончательная формула для крутящего момента, хорошо? Итак, мы построили все части, и это окончательный ответ.Это определение крутящего момента, и теперь с этим крутящим моментом мы можем заполнить словарь и сказать, что хотим. В левой части находится крутящий момент, где крутящий момент определяется как F _i r _i sin θ _i . F sin θ — это всего лишь составляющая силы, перпендикулярная разделению r . Вот что делает F sin θ . Надеюсь, вы это видите. Если у вас есть сила, действующая таким образом, то F cos θ — это та часть, которая не годится, а F sin θ — та часть, которая хороша для вращения.Кроме того, если вы хотите, с точки зрения проделанной работы, вы хотите, чтобы сила умножилась на пройденное расстояние. Пройденное расстояние только в этом направлении. В этом направлении нет пройденного расстояния. Таким образом, пройденное расстояние равно F скалярному произведению с направлением, в котором вы движетесь, и это относится только к силе, перпендикулярной разделению, а не к той части, которая параллельна.

В любом случае, я надеюсь, мы интуитивно понимаем, почему именно этот парень отвечает за вращение объектов. Вы хотите что-то повернуть вокруг какой-то оси, у вас есть определенная сила, лучше всего прикладывать силу как можно дальше от точки вращения.Другими словами, предположим, что мы хотим, чтобы задний конец этого стола оставался неподвижным, но я хочу повернуть его таким образом. Тогда я говорю, я думаю, мы все знаем, что мы хотим начать продвигаться здесь. Кроме того, мы не хотим прикладывать силу так или иначе, мы хотим прикладывать силу перпендикулярно. Если по какой-то причине мы привязаны к веревке и можем тянуть только в этом направлении, то составляющую силы в этом направлении следует сбрасывать со счетов, бесполезно, это та часть, которая вращается, и та часть, которая также делает работу.Любая сила, перпендикулярная движению, не будет совершать никакой работы. Любая сила, перпендикулярная смещению, не будет совершать никакой работы. Это твердое тело может находиться в этом положении только позже, поэтому перемещение является тангенциальным направлением, и только сила в тангенциальном направлении способствует работе. И в моем рабочем аргументе энергии это то, что приходит сюда. Вот почему вы придумали такое определение крутящего момента.

Итак, у нас есть все необходимое для этого. Напишу еще кое-что по аналогии.Работа, совершаемая силой, смещающей тело на величину dx , такова. Работа, совершаемая крутящим моментом, будет τ раза — думаю, вы догадываетесь, что я хочу туда поставить — dθ или Δθ . Когда крутящий момент поворачивает тело на угол 91 561 Δθ 91 562 , то совершаемая работа равна 91 561 τ 91 562 умножить на 91 561 Δθ 91 562 . Вы можете видеть, что даже здесь вы можете записать проделанную работу как F умножить на r умножить на Δθ ; но это крутящий момент, это Δθ .Так что очень полезно знать. Итак, если вы, ребята, собираетесь рассуждать по аналогии, я бы попросил вас узнать аналоги, только тогда вы можете решать задачи. Итак, давайте привыкнем к этой формуле, ΔW = τ Δθ . Я покажу вам один пример.

Предположим, у меня есть стержень, свисающий с потолка. Ну допустим он безмассовый и на дне масса m и длина какая-то L ; это маятник. Итак, я возьму этот маятник и переведу его в это положение на угол θ ₀ , который, к сожалению, θ ₀ обозначает конечный угол.Я хочу знать, сколько работы я делаю; это то, что мы собираемся вычислить. Итак, мы занимаем какое-то промежуточное положение, когда находимся здесь. Какая сила действует на этого парня? Этот стержень не имеет массы; сила на этом составляет мг . Если этот угол равен θ , вы можете видеть, что этот угол равен θ , поэтому мг cos θ действует таким образом, а мг sin θ действует таким образом. Чтобы удержать маятник от падения, когда угол равен θ , я должен приложить в этом направлении тангенциальную силу величиной мг sin θ .Надеюсь, вы это видите. мг cos θ будет обеспечиваться стержнем. Поскольку стержень является твердым телом, он не позволит массе двигаться в этом направлении. Он обеспечит любую силу, необходимую для удержания массы в радиальном движении. В тангенциальном направлении, чтобы удержать его от соскальзывания в исходное положение, я должен приложить силу мг sin θ . Таким образом, крутящий момент, который я применяю, составляет 91 561 мг sin θ 91 562, умноженный на 91 561 L 91 562. Итак, я сделал все это, взяв силу, найдя составляющую силы, перпендикулярную предмету, и уравновешивая ее противодействующей силой.Вы также можете сказать, что крутящий момент, который я должен применить, на самом деле составляет мг , что является силой, R , которая здесь равна L , и синус угла между ними. Как бы мы это ни писали, это крутящий момент.

Давайте найдем работу, совершаемую этим крутящим моментом, когда я поворачиваю его от начального угла до некоторого конечного угла. Это будет мгл sin θ dθ от 0 до некоторого конечного угла θ ₀ . Я просто говорю, что проделанная работа равна сумме τ Δθ по всем углам; значит интегрировать.Итак, вам нужно вернуться к своим вычислениям, и вы должны помнить, что интеграл от sin θ равен — cos θ , и вы хотите начать с θ = 0 до θ равно некоторый конечный угол θ ₀ . И если вы запустите его, вы обнаружите, что это мгл умножить на 1 — cos θ . Итак, это работа, проделанная для того, чтобы взять маятник, который является горизонтальным, который является вертикальным, и повернуть его на угол θ ₀ . Я собираюсь провести перекрестную проверку, чтобы сказать вам, что это работает с другой точки зрения.Эта масса была здесь внизу, теперь она забралась туда. Итак, вы можете спросить: «Что случилось с работой, которую я сделал?»

Возвращаясь к теореме о рабочей энергии, возьмем здесь эту массу. На него действовали силы. Одним из них был стержень, но сила стержня всегда была перпендикулярна движению вот этого боба, так что он не мог совершать никакой работы. Единственная работа была сделана мной. Что случилось с моей работой? Работа, которую я проделал, должна заключаться в изменении общей энергии тела, но груз не двигался ни до, ни после, потому что я прилагаю как раз нужную силу, чтобы нейтрализовать гравитацию; Я скорости не давал.Итак, должно быть, потенциальная энергия этого боба, когда он здесь, должна объяснить работу, которую я проделал. Это именно то, что есть, потому что позвольте мне переписать это как [ мг ] — мгл + мгл cos θ . Но, может быть, мы увидим, что это мг + мгл. Этот, я думаю, лучше всего записать как L — L cos θ , и вы, ребята, сможете увидеть, что происходит. L это расстояние здесь, L cos θ это расстояние, и L — L cos θ это увеличение высоты этого боба.Эта высота здесь на самом деле равна L — L cos θ , потому что если это L , а это θ , то это L cos θ до этой точки. Итак, это всего лишь 91 561 мг 91 562 умножить на 91 561 ч 91 562 , и вот куда пошла твоя работа.

Итак, в чем смысл этого упражнения? Это упражнение предназначено для того, чтобы вы привыкли к понятию расчета проделанной работы не как сила, умноженная на расстояние, а как крутящий момент, умноженный на угол. И вот проблема, когда сам крутящий момент меняется с углом.Крутящий момент сам по себе является функцией θ , поэтому вам нужно выполнить интеграл, и вот как вы получите работу. Итак, теперь у нас есть все необходимое оборудование, есть все оборудование, необходимое для кинематики или динамики твердых тел в этой аналогии.

Итак, позвольте мне подытожить, что это такое. У вас твердое тело; у него есть момент инерции; у него есть угловая скорость. Произведение этих двух называется угловым моментом, L , и чтобы его изменить, нужно приложить крутящий момент.Чтобы найти крутящий момент, найдите все внешние силы, действующие на тело, умножьте каждую силу на расстояние от точки вращения, но составляющая каждой силы, перпендикулярная линии разделения, умноженная на расстояние разделения, это Fr sin θ и сложите его. Опять же, когда вы делаете крутящие моменты, вы должны подать знак. Если крутящий момент стремится повернуть тело против часовой стрелки, мы будем считать его положительным, а если крутящий момент стремится повернуть тело по часовой стрелке, мы будем считать его отрицательным.Итак, вполне возможно, что в данном теле могут быть крутящие моменты, пытающиеся двигать его в разных направлениях. Так, например, в простейшем твердом теле, состоящем, скажем, из двух масс, вы могли бы толкать туда, а я мог бы толкать туда. Мы все пытаемся повернуть их в противоположные стороны. Крутящий момент, который вы прикладываете, будет равен вашей силе, умноженной на это расстояние; это называется положительным, потому что вы движетесь против часовой стрелки. Крутящий момент, который я применяю, будет моей силой, умноженной на меньшее расстояние, и это будет считаться отрицательным, потому что это по часовой стрелке.И вы добавите их; вы получите чистый крутящий момент. Этот чистый крутящий момент вызовет ускорение этого гантелеподобного объекта.

Какое ускорение это вызовет? Это будет моя сила, умноженная на мое расстояние, sin θ равно 1 минус ваша сила, умноженная на расстояние, на котором вы это делаете, умноженная на момент инерции. Момент инерции для простой проблемы м ₁ R _{1 2 + M 2 R 2} R ₂ ² , если это м ₁ , и это R ₁ , а это м ₂ и это расстояние r ₂ .Итак, это самая простая задача, которую вы можете решить в динамике твердого тела. Возьмем пару сил, вычислим моменты, разделим на момент инерции и получим угол ускорения. Если крутящий момент постоянный, его трудно поддерживать. Что мне нужно сделать, чтобы сохранить постоянный крутящий момент? Я должен начать бегать с этим, когда он вращается, и вы можете себе представить, как я это делаю; тогда крутящий момент будет постоянным, αa будет постоянным, α постоянным, как постоянным , и вы сможете решить всю кучу проблем, которые вы, ребята, делали раньше.Хорошо, теперь есть одно техническое препятствие, которое вам нужно преодолеть, если вы хотите заниматься динамикой твердого тела, и это знать, как вычислить момент инерции для всех видов объектов. Если я дам вам 37 масс, каждая из которых находится на расстоянии r от точки вращения, это тривиальная вещь. Сделайте mr ² для каждого и добавьте его. Но вот объекты, которые вам могут быть даны, не дискретный набор масс, а непрерывная капля. Как и в случае с центром масс, когда у вас была связка масс, вы взяли м ₁ x ₁ + m ₂ x ₂ + m ₃ x ₃ и так далее. на.Но если у вас есть непрерывный стержень, вы должны сделать интеграл. Так что здесь тоже придется делать интеграл.

Глава 6. Расчет момента инерции: примеры для стержня, диска и т. д. [01:01:36]

Итак, давайте возьмем некоторые твердые тела и попробуем найти момент инерции, которые являются твердыми телами, которые непрерывны. Итак, вот кольцо радиусом r и массой M . Это не диск, несмотря на то, как он выглядит. Это кольцо, и я хочу найти его момент инерции.Итак, вам нужно подумать о том, что вы будете делать. Итак, вы на секунду задумайтесь, и я скажу вам, как я это сделаю, разбив его на крошечные части, каждая из которых достаточно мала, чтобы я мог рассмотреть точку. Этот крошечный кусочек имеет массу Δm _i , а i изменяется от 1, 2, 3, 4 до любого значения, 10 миллионов, пока я не обойду круг. Момент инерции будет равен — я использую Δm _i , чтобы сказать вам, что это крошечная масса для этого сечения. Но что такое r ² ? Если я планирую вращать его вокруг этой точки, я планирую вращать вокруг этой точки; это же r ² для всех.Итак, вы можете вытащить это из суммирования, и вы просто получите Mr ² . Итак, это очень простая проблема. Это так же просто, как и эта задача, но у вас явно была только одна масса и вся она находилась на расстоянии r от точки вращения, это Mr ² . Здесь вы разложили массу, но, к счастью, разложили ее таким образом, что каждая ее часть находится на одинаковом расстоянии r от центра, поэтому суммировать очень легко. Вытащите r ² , просуммируйте по массе и получите общую массу.Затем мы собираемся сделать… Есть вопросы по этому поводу? Все будет строиться на понимании этого. Итак, для кольца это момент инерции, который равен г ² .

А теперь я хочу сделать следующее. Хочу взять диск сейчас радиусом r ; Я должен вычислить сумму Mr ² для каждой массы в задаче. Итак, здесь вы должны организовать свое мышление. Я планирую сделать момент инерции через центр. Во-первых, если бы я вам не сказал момент инерции, через который вы даже не можете начать; Говорю вам, я хочу это через центр.Если мы хотим, чтобы он проходил через центр, у нас есть возможность представить его как составленный из целой группы концентрических колец, каждое из которых имеет радиус r и толщину dr . Если вы можете найти момент инерции этой крошечной заштрихованной области, я суммирую все маленькие шайбы, кольца, которые у меня есть, чтобы заполнить весь диск. Итак, каков момент инерции этого кольца? Ну, я уже сказал вам. Если кольцо имеет массу M , то M ² — это момент инерции этого кольца.Итак, вопрос: «Какова масса заштрихованной области?» Очевидно, что r ² , который мы используем, — это r , на котором он сидит. Но какую массу я должен использовать? Ну, что касается массы, которую я должен использовать, я утверждаю, что если общая масса равна [М], то умноженное на [должно быть сказано «больше»] πR ² — это масса на единицу площади. Затем мне нужна площадь этой заштрихованной области. Это сложная часть. У вас есть это? Да?

Студент: 2 πrdr .

Профессор Рамамурти Шанкар: Правильно, давайте спросим, ​​почему это 2 πrdr . Если вы возьмете это кольцо, ножницами вырежете его и раскроете, оно будет выглядеть как длинный прямоугольник, толщина которого будет dr ; его длина будет 2 πr . Итак, 2 πrdr — это то, что говорит вклад, вот dr . Теперь вы должны добавить это ко всему. Сложение — это то, что мы делаем, выполняя интеграл.Теперь я не хочу делать этот интеграл; вы, ребята, можете хотя бы догадаться, что произойдет. В ответе не будет π ; π больше нет. У вас есть rr ² это r ³ , r ⁴ /4 и если вы объедините это с этим, вы получите это MR ^{2 90 Итак, момент инерции диска равен MR 2 /2. Это потому, что если я приду и скажу вам момент… предположим, я где-то сделал расчет с ошибкой, и я сказал, что это MR 2 , вы поймете, что я ошибаюсь? И почему вы будете утверждать, что это не может быть правильным ответом? Да?}

Студент: Ну, это как кольцо, но радиусы меньше.

Профессор Рамамурти Шанкар: Правильно. Другими словами, его ответ, правильный ответ, если это MR ² значит вся масса находится на расстоянии R ² . Но мы знаем, что часть массы находится намного ближе к центру. На самом деле, некоторые из них находятся прямо в центре, поэтому вы не можете получить один и тот же R ² в качестве вклада от всех частей. Некоторые будут на 0 расстоянии; некоторые будут на полном расстоянии. Итак, всякий раз, когда вы определяете момент инерции для диска, он должен выглядеть как MR ² , умноженное на число, которое определенно меньше 1.Получается половина; если бы мы получили третий или четвертый, вы бы не знали, что это явно неправильно. Но если я получил 1 впереди или, что еще хуже, если я получил 2 раза MR ² , то вы знаете, что я сделал ошибку.

Хорошо, теперь последний из объектов, на которые я хочу посмотреть сегодня, это жезл, который я хочу взять. Это на самом деле тот пример, который довольно часто делается в качестве первого примера, но я сделаю это сейчас. Итак, вот жезл, хорошо? У него длина L , масса M , а я говорю, каков момент инерции? Вы знаете, что вы могли бы сделать? Какой первый вопрос вы зададите, когда я скажу: «Каков момент инерции?

Ученик: Примерно в какой точке?

Профессор Рамамурти Шанкар: Примерно в какой точке, верно? Пока я не скажу вам этого, вы не можете начать.Итак, я скажу: «Давайте найдем момент инерции вокруг этого конца». Итак, что вы должны представить в этом случае: вы втыкаете сюда гвоздь, и парень вращается вот так по большому кругу с центром в нем. Если вы воткнули гвоздь через эту середину, это уже другая история, и ответ будет другим. Итак, что я делаю, так это беру расстояние x . Беру полоску толщиной dx . Эта полоска достаточно мала, чтобы я мог предположить, что это точечная масса. Следовательно, момент инерции этой крошечной части будет выглядеть как квадрат расстояния, умноженный на массу этой крошечной части.Масса крошечной порции выглядит так. Дайте-ка подумать; это масса на единицу длины, это длина, это масса объекта. Затем я должен сделать интеграл от 0 до L . Ну, х ² даст мне х ³ /3. Это даст мне ML ² /3, а это момент инерции стержня. Опять же, это выглядит как ML ² , перед ним должно быть число меньше 1, потому что, если вы измеряете отсюда, то дальше всего вы можете быть L ; многие ребята были намного ближе.Итак, средневзвешенное значение квадрата расстояния не может равняться всем L ² ; это должно быть что-то меньше, чем L ² . Тот факт, что это 1/3, — это, конечно, то, ради чего вы делаете всю работу.

Студент: Вам также понадобится L .

Профессор Рамамурти Шанкар: Простите?

Студент: И L тоже.

Профессор Рамамурти Шанкар: Вы забыли здесь L ?

Студент: Ага.

Профессор Рамамурти Шанкар: Кроме того, размерность момента инерции должна быть равна произведению конечной массы на длину в квадрате. Да? Вас это не устраивает?

Студент: Нет, я не.

Профессор Рамамурти Шанкар: Вы согласны, хорошо. Слушай, иногда я ошибаюсь в этих вещах, так что ты всегда должен следить за этим. Последнее, что я хочу сделать, это найти… Что ж, когда я говорю, что последнее, что я хочу сделать, я не имею в виду, что я не хочу этого делать, я просто говорю, что я близок к концу. день.Последнее, что я сейчас вычислю, это момент инерции вокруг центра. Посмотрим, что произойдет. Это тот же интеграл, x ² , dx/L , M/L , но диапазон интегрирования для x теперь будет идти от -L /2 до + L / 2 . Затем я упрощаю свою жизнь, записывая ее как 2 M/L умножить на x ² dx от 0 до L /2. Это то, что я призываю вас делать все время.Если интеграл является четной функцией x , а именно -x дает столько же, сколько +x , то вы можете взять половину причины интегрирования и удвоить ответ. Вы можете сделать это, только если это четная функция, так что если x и – да?

Ученик: Почему это все еще больше L , если вы подставите x к другому?

Профессор Рамамурти Шанкар: О, простите, вы абсолютно правы. Способ сделать это будет здесь.Видишь ли, ты продолжаешь пытаться, ты поймаешь меня. Это верно, это правильно. Итак, давайте сделаем это сейчас, 2 M/L , ладно, теперь я очень волнуюсь, потому что это L ³ , это X ³ /3, но то, что кубируется это L /2, и это дает мне ML ² /12. Таким образом, момент инерции не является фиксированным числом. Он стал намного меньше, когда я взял его вокруг центра масс. Когда я взял его по левому краю, я получил ML ² /3; Я пошел в середину, у меня получилось ML ² /12.Я думаю, довольно ясно, что я иду отсюда, я сокращаю ответ. Так что, когда я продолжу, он станет еще меньше. Вот где ваш здравый смысл подскажет вам, что если вы получили какой-то ответ оттуда, вы получите такой же ответ отсюда, и вы достигнете наилучшего возможного момента инерции, какой только можете. Вы должны быть в состоянии рассуждать интуитивно, и если вы проведете расчет, он окажется таким же.

Теперь нужно проверить, если вы это сделаете, момент инерции вокруг одного конца равен моменту инерции вокруг центра за вычетом массы, умноженной на ( L /2) ² .Это то, что вы можете проверить на самом деле. Просто возьмите числа, которые я вам дал, и вы обнаружите, что этот ответ плюс M умножить ( L /2) ² будет равен этому ответу. И это очень общая теорема, о которой я расскажу в следующий раз. Если вы знаете момент инерции через центр масс, все готово, хорошо? Если мне нужен момент инерции через любую другую точку, я беру момент инерции через центр масс и добавляю к нему общую массу объекта и квадрат расстояния, на которое вы заставили меня переместить мою ось, что здесь оказывается L /2.Я, конечно, докажу это; Я не хочу давать вам ничего без доказательств. На самом деле, в нашем классе мы можем убедиться, что это правда. Это справедливо не только для стержня, но и для диска. Это верно для любого объекта в двух измерениях, что если вы получили момент инерции этого существа через центр масс, и вы хотите, чтобы он прошел через эту точку, просто возьмите ответ через центр масс и добавьте к нему Md ² где d это расстояние.Это будет доказано в следующий раз. Хорошо, вы знаете, что на этой неделе мы встречаемся в понедельник, среду и пятницу.

[конец стенограммы]

Наверх

Теория динамики | Механика | Упражнения по физике

 

Динамика — это часть физики, описывающая эволюцию физической системы во времени в связи с причинами изменений физического и/или двигательного состояния.

Целью

Dynamics является описание факторов, которые могут вызывать изменения в физической системе, их количественная оценка и составление уравнений движения или уравнений эволюции для этой операционной системы.

 

Законы динамики: Они были сформулированы Исааком Ньютоном и благодаря им мы можем предсказывать движение тела, если знаем его текущее состояние и силы, действующие на него.

• Закон инерции: «Если результат действия сил, действующих на тело, равен нулю или не существует никакой внешней силы, то если тело находится в состоянии покоя, оно будет продолжать это делать, и если он двигался прямолинейным равномерным движением, оно и дальше будет двигаться тем же движением.
• Закон фундаментальной динамики: «Если на тело действует равнодействующая сила, оно приобретает ускорение, прямо пропорциональное приложенной силе, поскольку масса тела является константой пропорциональности. Это ускорение имеет то же направление, что и результирующая сила
.

Биопрофе |Теория динамики| 01

• Принцип действия и противодействия: «Если одно тело действует с силой на другое тело, то это тело в то же время действует на первое с такой же силой и направлением, но противоположным.

Биопрофе |Теория динамики| 02

Знак минус означает противоположное направление. Силы не аннулируются, потому что они действуют на разные тела.

 

Закон Гука: Тело упруго, когда оно восстанавливает свою форму после прекращения действия деформировавших его сил. В случае пружины деформация (удлинение) прямо пропорциональна приложенной силе.
Упругие тела имеют пределы упругости, в пределах которых выполняется закон Гука, при выходе за эти пределы тело не подчиняется этому закону и его деформация может быть постоянной.
На этом законе основан динамометр.

 

 

ОБЗОР ФОРМУЛЫ:

 

Фундаментальное уравнение динамики

Биопрофе |Теория динамики| 03

 

Центростремительные и центробежные силы

Биопрофе |Теория динамики| 04

 

Напряжение

 

Объект, который поднимается

Биопрофе |Теория динамики| 05

 

Объект, который падает

Биопрофе |Теория динамики| 06

 

Машина Этвуда

Биопрофе |Теория динамики| 07

 

Трение (µ = коэффициент трения; N = нормальная сила)

Биопрофе |Теория динамики| 08

 

Трение о горизонтальную плоскость

Биопрофе |Теория динамики| 09

 

Трение о наклонную плоскость

Биопрофе |Теория динамики| 10

 

Радиус кривизны с наклоном и трением

Биопрофе |Теория динамики| 11

 

Механический импульс

Биопрофе |Теория динамики|12

 

Линейный импульс или количество движения

Биопрофе |Теория динамики|13

 

Теорема о механическом импульсе

Биопрофе |Теория динамики|14

 

Угловой или кинетический импульс

Биопроф |Теория динамики|15

 

Теорема об угловом моменте

Биопроф |Теория динамики|16

 

Закон Гука

Биопрофе |Теория динамики|17

 

 

 

 

 

 

Лаборатория химической физики | НИДДК

Секция биофизической химии

Уильям А.Итон, доктор медицины, доктор философии, заслуженный исследователь Национального института здравоохранения, Начальник отдела

Исследования в этом разделе в течение многих лет были посвящены термодинамике, кинетике и механизму образования волокон гемоглобина S, а также его связи с патофизиологией и терапией серповидно-клеточной анемии. Опыт, накопленный в этом исследовании, в настоящее время используется для разработки чувствительных и высокопроизводительных анализов серповидно-клеточных эритроцитов для скрининга соединений, которые можно было бы использовать в качестве специфического лекарства от серповидно-клеточной анемии.Первоначальный скрининг сосредоточен на библиотеках лекарств, которые уже прошли клинические испытания.

Секция биофизической спектроскопии ядерного магнитного резонанса

Адриан Бакс, доктор философии, заслуженный исследователь Национального института здравоохранения, Начальник отдела

Секция биофизической спектроскопии ядерного магнитного резонанса разрабатывает новые методы и подходы для определения структуры и динамики биологически активных молекул.Конкретные проекты сосредоточены на разработке методов повышения точности определения биомолекулярных структур по данным ЯМР. Работа в этой области делает упор на разработку более совершенных методов измерения межпротонных расстояний и двугранных углов с помощью NOE и J связей. Мы также разрабатываем количественную связь между молекулярной структурой и химическими сдвигами/анизотропией химических сдвигов.

Секция вычислительной биофизики

Роберт Б.Бест, доктор философии, Начальник отдела

Молекулярное моделирование вместе с теорией является очень многообещающим инструментом для получения механистической информации о сворачивании и неправильном фолдинге белков, а также о функциях как свернутых, так и внутренне неупорядоченных белков. С этой целью Секция вычислительной биофизики разрабатывает крупнозернистые и всеатомные модели моделирования, а также методы повышения эффективности моделирования. Эти модели можно применять для помощи в интерпретации экспериментов, предоставляя подробную информацию, которую было бы трудно определить на основе одного эксперимента.

Секция молекулярной и структурной биофизики

Г. Мариус Клор, доктор медицины, доктор философии, FRS, заслуженный исследователь NIH, Начальник отдела

Секция молекулярной и структурной биофизики изучает структуру и динамику белков, комплексов белок-белок и комплексов белок-нуклеиновая кислота с помощью многомерной спектроскопии ядерного магнитного резонанса (ЯМР), а также разрабатывает и применяет новые ЯМР и вычислительные методы, чтобы помочь в эти исследования.Особое внимание уделяется комплексам, участвующим в передаче сигнала и регуляции транскрипции, а также СПИДу и связанным со СПИДом белкам. В последнее время основное внимание уделяется разработке новых методов ЯМР для обнаружения, визуализации и характеристики переходных, малонаселенных состояний макромолекул. Такие состояния, невидимые для обычных биофизических методов, включая кристаллографию, электронную микроскопию и спектроскопию одиночных молекул, играют критическую роль в распознавании макромолекул, индуцированном аллостерией подборе, конформационном отборе и молекулярной сборке.

Раздел наноразмерной динамики одиночных молекул

Куан Ван, доктор философии, исследователь штата Штадтман, Исполняющий обязанности начальника отдела

В разделе динамики одиночных молекул в наномасштабе разрабатываются новые методы визуализации разнообразных биологических процессов на уровне отдельных молекул. Быстрое управление с обратной связью используется для удержания отдельной биомолекулы в водном растворе (ловушка ABEL) для изучения биохимической динамики, неограниченной диффузией.Научные интересы включают структурную гетерогенность биомолекул, сборку/разборку многосубъединичных ферментов и посттрансляционные модификации. Раздвигая границы существующих модальностей одиночных молекул и расширяя размерность измерений, обеспечиваются подробные наблюдения за действиями и взаимодействиями биомолекул в режиме реального времени, по одной молекуле за раз. Количественное физическое моделирование и симуляции проводятся для понимания этих богатых наборов данных с целью выявления биофизических принципов, лежащих в основе биологической функции.

Секция одномолекулярной биофизики

Хой Сунг Чунг, доктор философии, Начальник отдела

Секция биофизики одиночных молекул изучает конформационную динамику белков с помощью флуоресцентной спектроскопии одиночных молекул. Понимание молекулярных механизмов биохимических реакций с участием макромолекул, таких как белки и нуклеиновые кислоты, требует характеристики конформационного разнообразия в процессе в дополнение к термодинамике и кинетике.Мы разрабатываем и используем методы многоцветной флуоресцентной спектроскопии и визуализации одной молекулы для изучения гетерогенности в различных процессах, включая укладку, связывание и агрегацию белков.

Секция твердотельного ядерного магнитного резонанса и биомолекулярной физики

Роберт Тыко, доктор философии, Начальник отдела

Секция ядерного магнитного резонанса твердого тела и биомолекулярной физики под руководством Роберта Тыко разрабатывает методы твердотельного ЯМР для структурных исследований биополимеров и применяет эти методы к задачам биофизической химии и структурной биологии.Методы твердотельного ЯМР предоставляют структурную информацию на атомном уровне в системах, которые не могут быть охарактеризованы другими структурными методами, включая рентгеновскую дифракцию и ЯМР в жидком состоянии.

Секция теоретической биофизической химии

Аттила Сабо, доктор философии, заслуженный исследователь Национального института здравоохранения, Начальник отдела

Исследования в секции теоретической биофизической химии направлены на преодоление разрыва между теорией и экспериментом.Мы разрабатываем теории, необходимые для анализа и интерпретации как одномолекулярных оптических (где результат представляет собой последовательность фотонов разных цветов), так и механических (где результат представляет собой кривую сила-расширение) экспериментов. Целью нашей работы является получение как кинетической, так и термодинамической информации. Кроме того, одним из наших долгосрочных интересов является понимание роли диффузии в определении скорости химических реакций, включая связывание лиганда и белок-белковую ассоциацию.

Секция сверхбыстрой биофизической химии

Филип Анфинруд, доктор философии, Начальник отдела

Секция сверхбыстрой биофизической химии исследует взаимосвязь между структурой, динамикой и функцией белка с помощью сверхбыстрой лазерной спектроскопии с временным разрешением и рентгеновской кристаллографии. В этих экспериментальных методах используется сверхкороткий лазерный импульс «накачки» (короче 10–13 секунд) для запуска фотофизической или фотохимической реакции, а также «зондовый» импульс с различной задержкой, который измеряет спектральную или структурную эволюцию белка.Этот метод «насос-зонд» предоставляет средства для получения «моментальных снимков» белка, когда он выполняет предназначенную ему функцию. Отслеживая изменения, которые происходят с течением времени, от фемтосекунд до миллисекунд, мы стремимся создать основу для понимания того, как белки выполняют предназначенные для них задачи с высокой эффективностью и избирательностью. Исследователи секции используют этот метод для изучения различных модельных систем, включая лиганд-связывающие белки гема и их мутанты, бактериородопсин и фотоактивный желтый белок.Используя микрофокусирующий фемтосекундный спектрометр, способный исследовать динамику белков в небольших кристаллах, исследователи могут сравнивать динамику в растворе и кристаллах. Это позволяет оценить степень влияния контактов кристаллов на динамику белка. Более того, сверхбыстрые исследования фотофизики белков привели к созданию более эффективных протоколов фотоактивации хромофоров, тем самым улучшив качество рентгеновских структур с временным разрешением.

Изучение динамики с помощью онлайн-курсов, занятий и уроков

Что такое динамика?

Динамика — это раздел классической механики, касающийся движения и того, как взаимодействуют силы, влияющие на движение.Наше понимание исходит из законов движения Ньютона в рамках его классических законов физики. Исследователи изучают, как процессы могут развиваться и изменяться с течением времени. Законы движения Ньютона включают в себя первый закон движения или инерции, с которого начинается наше понимание, приводящее ко второму закону движения систем. Динамика в первую очередь связана с этим вторым законом, хотя вся серия дает информацию для нашего понимания. Динамика делится на две категории: линейную и вращательную. Линейная динамика касается таких принципов, как инерция, смещение и скорость, в то время как вращательная динамика включает в себя такие вещи, как крутящий момент, угловое смещение, центростремительная сила и угловой момент.Изучение сил позволяет нам проводить исследования и строить структуры классических тел. Это помогает нам отвечать на вопросы, когда мы не можем наблюдать за ответами напрямую, и помогает нам понять все, что мы видим вокруг себя. Это также информирует системную динамику или наше понимание нарастания и распада систем в движении. Эти исследования показывают скорость изменений с течением времени и помогают нам планировать.

Learn Dynamics

EdX.org предлагает курсы, предназначенные для ознакомления вас с принципами набора законов Ньютона для движения в сотрудничестве с ведущими мыслителями в этой области.Вы можете узнать, что вам нужно для исследования и применения этих законов в вашей области исследования. Занятия составлены так, чтобы соответствовать вашему расписанию, и вы можете посещать их, не выходя из дома. В некоторых случаях они имеют право на кредит и сертификацию.

Курсы и сертификаты по динамике

Массачусетский технологический институт предлагает ряд курсов по динамике, от базовых до продвинутых. Вы можете узнать о вращательном движении, потенциальной энергии и силе трения применительно к движущимся телам. Их серия является отличным учебником по ньютоновской физике, изложенной в Principia, и ведет к работам вне традиционной физики, таким как теории относительности Эйнштейна и квантовая механика.Вы также можете пройти специальное обучение, такое как «Системная динамика для медицинских наук» в Университете Витватерсранда в Йоханнесбурге, которое описывает рост, колебания и распад систем в рамках медицинских исследований. EPFL предлагает курс нейронной динамики, описывающий электромагнитные импульсы на уровне нейронов с помощью биофизического моделирования. Он информирует о биомедицинских исследованиях, а курс знакомит студентов со стохастическими процессами и дифференциальными уравнениями.

Постройте карьеру с помощью Dynamics

Курсы edX помогут вам познакомиться с классическими принципами законов движения Ньютона.Движение объектов дает нам информацию о системах и помогает нам логически исследовать физический мир, системы и даже миры, которые мы не можем видеть. Используйте свое новообретенное понимание, чтобы начать карьеру, и позвольте edX помочь вам найти путь.

Сила и законы движения Ньютона — физика Колледжа Дугласа 1108 Пользовательский учебник, зима 2021 г., текущий

Рисунок 1. Законы движения Ньютона описывают движение по траектории дельфина. (кредит: Jin Jang)

Движение привлекает наше внимание.Движение само по себе может быть красивым, заставляя нас восхищаться силами, необходимыми для достижения эффектного движения, например, дельфина, выпрыгивающего из воды, или прыгуна с шестом, или полета птицы, или орбиты спутника. Изучением движения является кинематика, но кинематика только описывает способ движения объектов — их скорость и их ускорение. Динамика рассматривает силы, влияющие на движение движущихся объектов и систем. Законы движения Ньютона лежат в основе динамики.Эти законы являются примером широты и простоты принципов, по которым функционирует природа. Они также являются универсальными законами в том смысле, что они применимы к аналогичным ситуациям как на Земле, так и в космосе.

Законы движения Исаака Ньютона (1642–1727) были лишь частью монументального труда, сделавшего его легендарным. Развитие законов Ньютона знаменует собой переход от эпохи Возрождения к современной эпохе. Этот переход характеризовался революционным изменением взглядов людей на физическую вселенную.На протяжении многих веков естествоиспытатели обсуждали природу Вселенной, в основном основываясь на определенных правилах логики, при этом большое значение придавалось мыслям более ранних классических философов, таких как Аристотель (384–322 до н.э.). Среди многих великих мыслителей, внесших свой вклад в это изменение, были Ньютон и Галилей.

Рисунок 2. Монументальный труд Исаака Ньютона «Philosophiae Naturalis Principia Mathematica» был опубликован в 1687 году. В нем были предложены научные законы, которые до сих пор используются для описания движения объектов.(Фото: Служба общественной документации Университета Страсбурга)

Галилей сыграл важную роль в установлении наблюдения как абсолютного определяющего фактора истины, а не «логического» аргумента. Использование Галилеем телескопа было его самым заметным достижением в демонстрации важности наблюдения. Он обнаружил спутники, вращающиеся вокруг Юпитера, и сделал другие наблюдения, несовместимые с некоторыми древними идеями и религиозными догмами. По этой причине и из-за того, как он обращался с власть имущими, Галилей был осужден инквизицией и наказан.Последние годы своей жизни он провел под домашним арестом. Поскольку другие до Галилея также сделали открытия, наблюдая природу вселенной, и поскольку повторные наблюдения подтвердили открытия Галилея, его работу нельзя было замалчивать или отрицать.{-9}\textbf{м}}[/латекс] в диаметре).Эти ограничения определяют область классической механики, как обсуждалось в главе 1 «Введение в природу науки и физики». В начале 20 века Альберт Эйнштейн (1879–1955) разработал теорию относительности и вместе со многими другими учеными разработал квантовую теорию. Эта теория не имеет ограничений, присутствующих в классической физике. Все ситуации, которые мы рассматриваем в этой главе, относятся к области классической физики.

УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ: ФИЛОСОФИЯ ПРОШЛОГО И НАСТОЯЩЕГО




Важность наблюдения и понятие причины и следствия не всегда так укоренялись в человеческом мышлении.Это осознание было частью эволюции современной физики от натурфилософии. Достижения Галилея, Ньютона, Эйнштейна и других были ключевыми вехами в истории научной мысли. Большинство научных теорий, описанных в этой книге, произошли от работ этих ученых.

Кинематика, динамика и структура физической теории

Куриэль, Эрик (2016) Кинематика, динамика и структура физической теории. [Препринт]

Аннотация

Каждая физическая теория имеет (по крайней мере) две различные формы математических уравнений для представления целевых систем: динамическую (уравнения движения) и кинематическую (кинематические ограничения). Кинематические связи отличаются от уравнений движения тем, что их конкретная форма фиксирована раз и навсегда, независимо от взаимодействий, в которые вступает система.Напротив, конкретная форма уравнений движения системы существенно зависит от конкретного взаимодействия, в которое вступает система. Все современные представления о структуре и семантике физической теории трактуют динамику, т. е. уравнения движения, как наиболее важную черту теории для целей ее философского анализа. Наоборот, я утверждаю, что именно кинематические ограничения наиболее важным образом определяют структуру и эмпирическое содержание физической теории: они функционируют как необходимые предварительные условия для надлежащего применения теории; они различают типы физических систем; они необходимы для того, чтобы уравнения движения были корректными или хотя бы убедительными; и они направляют экспериментатора в разработке инструментов для измерения и наблюдения.