Энергия: потенциальная и кинетическая энергия
Слово «энергия» в переводе с греческого означает «действие». Энергичным мы называем человека, который активно двигается, производя при этом множество разнообразных действий.
Энергия в физике
И если в жизни энергию человека мы можем оценивать в основном по последствиям его деятельности, то в физике энергию можно измерять и изучать множеством различных способов. Ваш бодрый друг или сосед, скорее всего, откажется повторить тридцать-пятьдесят раз одно и то же действие, когда вдруг вам взбредет на ум исследовать феномен его энергичности.
А вот в физике вы можете повторять почти любые опыты сколь угодно много раз, производя необходимые вам исследования. Так и с изучением энергии. Ученые-исследователи изучили и обозначили множество видов энергии в физике. Это электрическая, магнитная, атомная энергия и так далее. Но сейчас мы поговорим о механической энергии. А конкретнее о кинетической и потенциальной энергии.
Кинетическая и потенциальная энергия
В механике изучают движение и взаимодействие тел друг с другом. Поэтому принято различать два вида механической энергии: энергию, обусловленную движением тел, или кинетическую энергию, и энергию, обусловленную взаимодействием тел, или потенциальную энергию.
В физике существует общее правило, связывающее энергию и работу. Чтобы найти энергию тела, надо найти работу, которая необходима для перевода тела в данное состояние из нулевого, то есть такого, при котором его энергия равна нулю.
Потенциальная энергия
В физике потенциальной энергией называют энергию, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела. То есть, если тело поднято над землей, то оно обладает возможностью падая, произвести какую-либо работу.
И возможная величина этой работы будет равна потенциальной энергии тела на высоте h. Для потенциальной энергии формула определяется по следующей схеме:
A=Fs=Fт*h=mgh, или Eп=mgh,
где Eп потенциальная энергия тела,
m масса тела,
h — высота тела над поверхностью земли,
g ускорение свободного падения. 2) / 2 ,
2) / 2 ,
где Eк кинетическая энергия тела,
m масса тела,
v скорость тела.
Из формулы видно, что чем больше масса и скорость тела, тем выше его кинетическая энергия.
Каждое тело обладает либо кинетической, либо потенциальной энергией, либо и той, и другой сразу, как, например, летящий самолет.
Формула энергии в физике всегда показывает, какую работу совершает или может совершить тело. Соответственно, единицы измерения энергии такие же, как и работы джоуль (1 Дж).
Нужна помощь в учебе?
Предыдущая тема: Коэффициент полезного действия механизмов: расчет, формула + примеры
Следующая тема:   Превращение энергии: закон сохранения энергии
«Демон» Максвелла – шутка или реальность? — Энергетика и промышленность России — № 08 (124) апрель 2009 года — WWW.EPRUSSIA.RU
Газета «Энергетика и промышленность России» | № 08 (124) апрель 2009 года
Группа инженеров сконструировала гидравлическую турбину для получения энергии из безнапорного потока текущей воды (свободно-поточный гидроагрегат). Однако при замере мощности вдруг выяснилось, что энергии она дает больше, чем по расчетам.
Однако при замере мощности вдруг выяснилось, что энергии она дает больше, чем по расчетам.
Известно, что движущийся поток воды имеет кинетическую энергию, которую из этого потока можно извлечь (что и делают свободно-поточные турбины). Однако извлечь из потока всю его кинетическую энергию невозможно. Для этого его бы пришлось полностью остановить, и он уже перестал бы быть текущим потоком. Поэтому скорость потока воды на выходе рабочего органа турбины меньше, чем на входе, и именно этой разницей и определяется эффективность установки. При входящей скорости, равной 1 м/c, и выходящей 0,5 м/с, мы сможем забрать у потока 75 процентов его кинетической энергии (у реальных свободно-поточных турбин эта цифра еще меньше):
(Eвх – Eвых)/Eвх = (V2вх – V2вых)/V2вх.
Но, как говорилось выше, созданная машина выдавала энергии даже больше, чем полная кинетическая энергия потока.
Откуда же взялась дополнительная энергия, полученная от машины?
Кинетическая или потенциальная?
Давайте представим себе кубометр воды размером 1 метр x 1 метр x 1 метр, движущийся со скоростью 1 м/c. Его кинетическая энергия не вызывает сомнений:
Ek = m x V2/2 = 1000 (кг) x 1 (м/с)2/2 = 500 (Дж)
Однако есть еще и давление верхних слоев воды на нижние (потенциальная энергия). И если мы позволим растечься этому кубу воды, мы сможем ее извлечь. С учетом того, что центр масс этого куба находится на половине его высоты, то есть h = 0,5 метра, она равна:
Ep = m x g x h = 1000 (кг) x 9,8 (м/c2) x 0,5 (метров) = 4900 (Дж)
То есть потенциальная энергия этого кубометра воды почти в 10 раз превышает его кинетическую энергию. Нетрудно посчитать, что при скорости, равной 0,5 м/с, эта разница увеличивается до 40 раз!
Таким образом, мы видим, что в текущем потоке, кроме кинетической энергии, существует и потенциальная энергия, величина которой зависит от глубины потока. Но ее эксергия (то есть та часть энергии, которая может быть извлечена и которая в состоянии совершить работу) при обычных условиях равна нулю. Ведь вокруг любого объема воды находится точно такая же по свойствам (глубина, скорость, температура) вода.
Но ее эксергия (то есть та часть энергии, которая может быть извлечена и которая в состоянии совершить работу) при обычных условиях равна нулю. Ведь вокруг любого объема воды находится точно такая же по свойствам (глубина, скорость, температура) вода.
Теперь давайте представим, что мы извлекаем из кубометра воды, движущегося в потоке, часть его кинетической энергии и затрачиваем ее на «отодвигание» соседнего с ним кубометра воды. То есть, притормаживая движущийся выше по течению объем воды, мы будем ускорять следующий за ним (ниже по течению). Вследствие этого между ними возникнет разница в уровнях, и появляется потенциальная энергия разницы этих уровней, которую можно из потока извлечь. Возникает следующий вопрос: будет ли количество извлеченной потенциальной энергии больше, меньше или равно энергии, затраченной на ускорение второй части воды, то есть, иными словами, на увеличение его кинетической энергии?
Расчеты для гидротурбины
Прибегнем к услугам математики. Для примера рассмотрим машину, позволяющую разгонять выходящий поток воды за счет частичного отбора энергии у входящего потока. То есть это машина с положительной обратной связью между энергиями входящего и выходящего потоков. Кстати, машина, работающая именно на этом принципе, и была изобретена учеными (см. начало статьи).
Для примера рассмотрим машину, позволяющую разгонять выходящий поток воды за счет частичного отбора энергии у входящего потока. То есть это машина с положительной обратной связью между энергиями входящего и выходящего потоков. Кстати, машина, работающая именно на этом принципе, и была изобретена учеными (см. начало статьи).
Принцип работы установки следующий. Рабочие органы входного потока извлекают часть кинетической энергии из потока и передают ее при помощи обратной связи рабочим элементам выходного потока, дополнительно ускоряющим выходной поток. Поскольку расход воды, входящий в установку, равен выходящему и скорость вытекающего потока выше, чем входящего, то площадь сечения выходящего потока будет меньше, чем входящего. Следовательно, его глубина будет меньше, чем глубина входящего потока на величину h. Вследствие этого возникает потенциальная энергия разницы уровней горизонтов входящего и выходящего потоков.
Энергетический баланс установки следующий: E = Eh + Ek1 – Ek2
Суммарная энергия установки будет равна потенциальной энергии разницы уровней бьефов плюс кинетической энергии входного потока минус кинетической энергии выходного.
E = M x (g x h + (V12 x (1 – (h2 / (h2 – h) 2) / 2)
или
E = M x (g x h2 x (1 – V1 / V2) + (V12 – V22) / 2),
где M – масса воды, входящая в установку в некоторую единицу времени, равная плотности воды, умноженной на активную площадь входного потока и умноженной на его скорость.
Необходимо отметить, что все математические выкладки основаны строго на уравнении Бернулли (законе сохранения энергии) и уравнении неразрывности потока (законе сохранения массы).
Извлечение энергии без затрат извне
Далее начинается самое интересное. Видно, что в уравнении левая часть в скобке будет линейно возрастать в зависимости от h или по гиперболе для V2, а правая будет убывать, причем по параболе. Кто же перетянет? Построим зависимость энергии от перепада уровней h. График сделаем для различных величин входной скорости V1, приняв ее за константу.
Парадоксально! График зависимости энергии от перепада уровней имеет экстремум. Причем на восходящей ветви баланс энергии будет положительным (коэффициент мощности > 1), то есть извлекаемая потенциальная энергия будет больше затрачиваемой на ускорение выходящего потока кинетической, и установка будет саморазгоняться, пока не достигнет максимума. Энергия, выдаваемая установкой в этой точке, будет превышать кинетическую энергию входного потока в несколько раз. А при определенных условиях в десятки и даже сотни раз!
Причем на восходящей ветви баланс энергии будет положительным (коэффициент мощности > 1), то есть извлекаемая потенциальная энергия будет больше затрачиваемой на ускорение выходящего потока кинетической, и установка будет саморазгоняться, пока не достигнет максимума. Энергия, выдаваемая установкой в этой точке, будет превышать кинетическую энергию входного потока в несколько раз. А при определенных условиях в десятки и даже сотни раз!
При этом скорость выходящего потока будет существенно (порой в 2 – 3 раза) выше скорости входящего, а, следовательно, кинетическая энергия выходящего потока в 4 – 9 раз выше кинетической энергии входящего. Более того, не все «в порядке» и с входной скоростью. Она также имеет экстремум.
Как ни парадоксально, но существует оптимальная скорость входного потока, при превышении которой мощность установки будет резко падать. Это связано с существенными затратами энергии на разгон уже и без того быстродвижущегося потока. Подобная машина сама для себя создает подпор и в состоянии извлекать потенциальную энергию из объекта без затрат энергии извне.
Мифология или наука?
Вам это ничего не напоминает?
Наиболее сведущие в физике сразу воскликнут: «Да ведь это же «демон Максвелла»! Пресловутый и неуловимый! Многие скажут, что Максвелл предложил своего «демона» для термодинамики, а здесь мы оперируем гидродинамикой. Да, но смысл от этого не меняется – мы можем извлечь из объекта (в данном случае – потока жидкости) потенциальную энергию, которую при обычных условиях извлечь невозможно, – и при этом ничего не затрачивая (даже не строя плотины!).
Правда, извлечь можно все же не всю потенциальную энергию. Во-первых, глубина выходящего потока не равна нулю. Во-вторых, часть извлеченной потенциальной энергии переходит в дополнительную кинетическую энергию, выплескиваемую с этим потоком. А она ведь даже больше, чем кинетическая энергия входящего потока. Но это – та плата, которую мы должны отдать «демону», чтобы он согласился работать на нас.
Может возникнуть вопрос: «А как же тогда выходящий поток, имеющий уменьшенную глубину, сопрягается с окружающим его потоком воды с нормальной, неизмененной глубиной?». Тут стоит как раз вспомнить, что скорость выходящего потока выше, чем окружающей среды, и вследствие эффекта эжекции возникает так называемый «гидравлический прыжок», который выравнивает несоответствия кинетической и потенциальной энергий двух потоков. Этот «прыжок» по сути представляет собой бурун, завихрение в потоке.
Тут стоит как раз вспомнить, что скорость выходящего потока выше, чем окружающей среды, и вследствие эффекта эжекции возникает так называемый «гидравлический прыжок», который выравнивает несоответствия кинетической и потенциальной энергий двух потоков. Этот «прыжок» по сути представляет собой бурун, завихрение в потоке.
Вывод из всего вышеописанного невозможно переоценить. В природе существует процесс, позволяющий извлекать не извлекаемую прежде потенциальную энергию из любого ее имеющего объекта, и он найден! Это – принцип положительной обратной связи с возможностью передачи энергии между разными потоками энергоносителя. И есть возможность получения бесплатной, экологически чистой энергии из окружающей среды, предсказанная великим английским ученым Джеймсом Максвеллом еще в 1871 году в виде шуточного демона. Может быть, именно поэтому это всегда и воспринималось не более чем шутка великого ученого?
Или это все же реальность?
С термодинамикой и аэродинамикой, правда, пока еще не все ясно, но, поскольку этот процесс существует в гидродинамике, то он должен существовать и в любой другой отрасли физики.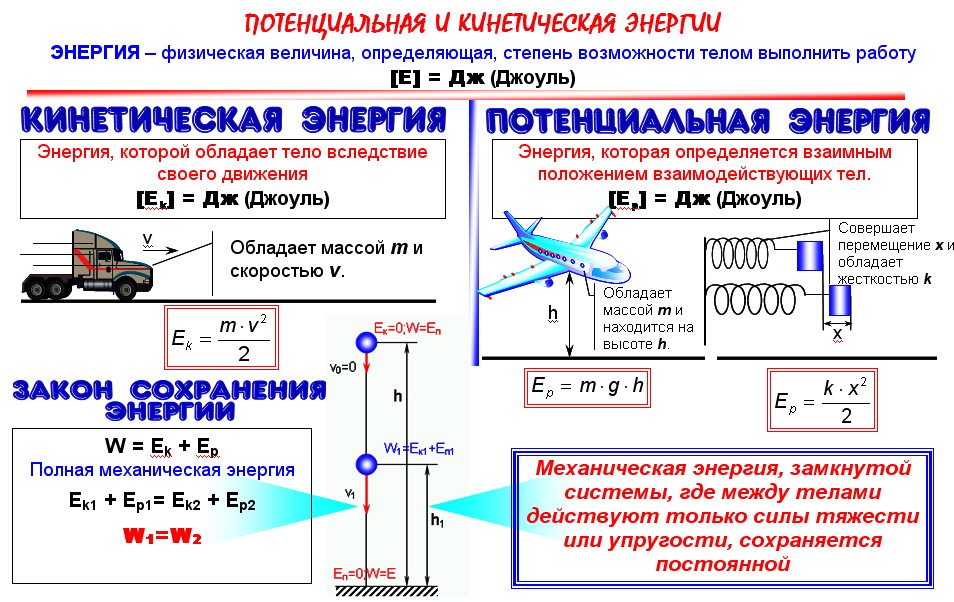 Некоторые разработки в термо- и аэродинамике уже имеются. Но, даже если этот процесс не будет найден для них в ближайшее время и поиск его затянется еще на десяток лет, то, как минимум, использование его гидродинамической интерпретации уже сейчас сулит человечеству огромные дивиденды в виде бесплатной энергии и чистой атмосферы.
Некоторые разработки в термо- и аэродинамике уже имеются. Но, даже если этот процесс не будет найден для них в ближайшее время и поиск его затянется еще на десяток лет, то, как минимум, использование его гидродинамической интерпретации уже сейчас сулит человечеству огромные дивиденды в виде бесплатной энергии и чистой атмосферы.
В заключение хотелось бы отметить, что все вышеприведенные расчеты сделаны для идеальной жидкости, а на способ получения энергии и расчета устройств, использующих этот принцип, а также на конструкцию этих устройств поданы международные патентные заявки.
Что такое кинетическая и потенциальная энергия для «чайников»?
Кинетическая энергия — это энергия движения тела. Соотвественно, если у нас есть какой-то объект, обладающий хоть какой-то массой и хоть какой-то скоростью, то он и обладает кинетической энергией. Однако относительно разных систем отсчета эта кинетическая энергия у одного и того же объекта может быть разной.
Пример. Есть бабушка, которая относительно земли нашей планеты находится в состоянии покоя, то есть не движется и, скажем, сидит на остановке в ожидании своего автобуса. Тогда относительно нашей планеты ее кинетическая энергия равна нулю. Но если посмотреть на эту же бабушку с Луны или с Солнца, относительно которых можно наблюдать движение планеты и, соответственно, этой бабушки, которая находится на нашей планете, то бабушка уже будет обладать кинетической энергией относительно упомянутых небесных тел. И тут приезжает автобус. Эта самая бабушка быстро встает и бежит занимать положенное ей место. Теперь относительно планеты она уже не в покое, а вполне себе движется. А значит и обладает кинетической энергией. И чем толще бабушка и быстрее, тем больше ее кинетическая энергия.
Есть бабушка, которая относительно земли нашей планеты находится в состоянии покоя, то есть не движется и, скажем, сидит на остановке в ожидании своего автобуса. Тогда относительно нашей планеты ее кинетическая энергия равна нулю. Но если посмотреть на эту же бабушку с Луны или с Солнца, относительно которых можно наблюдать движение планеты и, соответственно, этой бабушки, которая находится на нашей планете, то бабушка уже будет обладать кинетической энергией относительно упомянутых небесных тел. И тут приезжает автобус. Эта самая бабушка быстро встает и бежит занимать положенное ей место. Теперь относительно планеты она уже не в покое, а вполне себе движется. А значит и обладает кинетической энергией. И чем толще бабушка и быстрее, тем больше ее кинетическая энергия.
Есть несколько фундаментальных видов энергии — основных. Расскажу, например, про механические. К ним относятся энергия кинетическая, которая зависит от скорости и массы объекта, энергия потенциальная, которая зависит от того, где вы возьмете нулевой уровень потенциальной энергии, и от того положения, где находится этот объект относительно нулевого уровня потенциальной энергии. То есть потенциальная энергия — энергия, зависящая от положения объекта. Эта энергия характеризует работу, совершаемую полем, в котором находится объект, по его перемещению.
То есть потенциальная энергия — энергия, зависящая от положения объекта. Эта энергия характеризует работу, совершаемую полем, в котором находится объект, по его перемещению.
Пример. Несете вы в руках огромную коробку и падаете. Коробка лежит на полу. Выходит, что нулевой уровень потенциальной энергии у вас будет находится, соответственно, на уровне пола. Тогда верхняя часть коробки будет обладать большей потенциальной энергией, так как она находится выше пола и выше нулевого уровня потенциальной энергии.
Глупо говорить про энергию, не упомянув закон о ее сохранении. Таким образом, по закону сохранения энергии, эти два ее вида, описывающих состояние объекта, ни откуда не берутся и никуда не исчезают, а только переходят друг в друга.
А вот и пример. Падаю я с высоты дома, изначально имея потенциальную энергию относительно земли в момент перед прыжком, а моя кинетическая энергия пренебрежимо мала, поэтому можем приравнять её к нулю. Вот я отрываю ножки от карниза и моя потенциальная энергия начинает уменьшаться, так как высота, на которой я нахожусь, становится все меньше и меньше. В этот же момент при падении вниз я постепенно приобретаю кинетическую энергию, так как падаю вниз все с большей скоростью. В момент падения я уже обладаю максимальной кинетической энергией, но потенциальная равно нулю, такие дела.
В этот же момент при падении вниз я постепенно приобретаю кинетическую энергию, так как падаю вниз все с большей скоростью. В момент падения я уже обладаю максимальной кинетической энергией, но потенциальная равно нулю, такие дела.
Масса, энергия, импульс и закон сохранения / Хабр
Множество непонятных свойств мира связаны с природой массы и энергии (а также импульса). Все мы слышали эти слова и у многих из нас есть туманное представление об их значении. Конечно, значений у слов «масса» и «энергия» в английском и других языках довольно много. К сожалению, ни одно из них не совпадает с теми, что имеют в виду физики. Попробуйте отставить в сторону эти значения слов и поработать с точными физическими понятиями – иначе вы полностью запутаетесь.
Необходимо отметить, что не стоит при словосочетании «масса и энергия» вспоминать другую популярную пару, «вещество и энергия». Многие люди упоминают последнее словосочетания так, будто вещество и энергия – это две стороны одной медали. Но это не так. Вещество и энергия относятся к разным категориям, как яблоки и орангутанги. Вещество, не важно, как его определять – это класс объектов, существующих во Вселенной, а масса и энергия – это не объекты, а свойства, которыми эти объекты обладают. Масса и энергия глубоко переплетены друг с другом, и заслуживают общего объяснения.
Но это не так. Вещество и энергия относятся к разным категориям, как яблоки и орангутанги. Вещество, не важно, как его определять – это класс объектов, существующих во Вселенной, а масса и энергия – это не объекты, а свойства, которыми эти объекты обладают. Масса и энергия глубоко переплетены друг с другом, и заслуживают общего объяснения.
Чтобы понять массу и энергию, необходимо добавить к ним импульс и обсудить различия и связи этих величин.
Энергия
У слова «энергия» есть множество значений. Когда мы заболеваем, то говорим о том, что у нас не осталось энергии, имея в виду силу и мотивацию. Когда мы говорим, что у кого-то полно энергии, мы имеем в виду его высокую активность. Мы жалуемся на рост цен на энергию, имея в виду топливо. Мы говорим о духовной энергии как о чём-то неизмеримом, но важном, возможно, о некоей форме харизмы. И все эти понятия перекликаются друг с другом, поэтому мы и выбираем одно слово для их описания. Но в физике энергия – это совсем другое.
 С точки зрения физики ошибочно будет смешивать одно из этих определений с физическим. В физике нужно придерживаться физического термина, чтобы не получить неправильные ответы и не запутаться вконец.
С точки зрения физики ошибочно будет смешивать одно из этих определений с физическим. В физике нужно придерживаться физического термина, чтобы не получить неправильные ответы и не запутаться вконец.К несчастью, понятие «энергии» в физике очень сложно описать так, как это делают словари – короткой содержательной фразой. Но не подумайте плохого – всё дело в несовершенстве естественного языка, а не в том, что понятие энергии в физике расплывчато. В любой заданной физической системе совершенно понятно, какова её энергия, как в смысле её экспериментального измерения, так и в смысле расчётов (при наличии описывающих систему уравнений).
Одна из причин, по которым энергию так сложно описать – она может принимать множество форм, и не все из них просто понять. Вот три наиболее часто встречающихся разновидности:
1. Энергия может быть заключена в массе объекта. Здесь я называю такой вариант «энергией массы» (благодаря известному уравнению E=mc2 энергия связывается с массой. Также она называется «энергия покоя», поскольку это энергия объекта, находящегося в покое, то есть, без движения).
Также она называется «энергия покоя», поскольку это энергия объекта, находящегося в покое, то есть, без движения).
2. Во-вторых, энергия бывает связанной с движением объекта. Здесь я называю её «энергией движения», а технический термин для этого – кинетическая энергия. Этот вариант интуитивно легко воспринять, поскольку у быстро движущихся объектов энергия больше, чем у медленно движущихся. Кроме того, у тяжёлого объекта энергия движения больше, чем у лёгкого, движущегося с той же скоростью.
3. Энергия может храниться во взаимоотношении объектов (и обычно называется «потенциальной»). Она хранится в растянутой пружине, в воде за дамбой, в гравитационном взаимодействии Земли и Солнца, во взаимодействиях атомов в молекуле. Существует множество способов хранения энергии. Звучит расплывчато, но в этом виноват язык. В любом из перечисленных случаев существуют точные формулы, описывающие сохранённую в системе энергию и хорошо определённые пути её измерения.
С третьим типом энергии связано то, что я буду называть энергией взаимодействия, и это наиболее запутанное понятие из всех. В отличие от энергии массы и энергии движения, которые всегда больше или равны нулю, энергия взаимодействий может быть положительной и отрицательной. Пока я оставлю эту тему, но мы к ней ещё вернёмся.
В отличие от энергии массы и энергии движения, которые всегда больше или равны нулю, энергия взаимодействий может быть положительной и отрицательной. Пока я оставлю эту тему, но мы к ней ещё вернёмся.
Энергия – это особая величина огромной важности для физики. Причина такой важности – в том, что она «сохраняется». Что же это означает?
Если вы начнёте наблюдение с объекта или с набора объектов – назовём их «системой объектов» – обладающих определённым количеством энергии в начальный момент (не забудьте подсчитать всю энергию – массы, движения, сохранённую энергию всех типов, и т.п.), а затем части системы будут взаимодействовать только друг с другом и более ни с чем, тогда в конце наблюдения общее количество энергии, которым обладают эти объекты, будет тем же, что и в начале. Общая энергия системы сохраняется – её общее количество не меняется. Она может менять форму, но если отслеживать все разновидности, то в конце её будет столько же, сколько и в начале.
Это правило работает, даже если некоторые объекты будут исчезать и уступать место другим, к примеру, если одна частица в системе распадётся на две других, вливающихся в систему.
Почему энергия сохраняется? Из-за математического принципа, соотносящего тот факт, что законы природы со временем не меняются, с существованием сохраняющейся величины, которую мы по определению называем «энергией».
Самым известным и общим определением этого принципа мы обязаны Эмми Нётер, одной из величайших математических физиков предыдущего столетия, современнице Эйнштейна. Некоторые члены физического и математического сообщества относились к ней с глубоким уважением, но в то время в своей родной Германии она страдала от дискриминации по половому и национальному признаку (там блокировали попытки присвоить ей звание профессора в Гёттингене, и оттуда ей пришлось бежать после того, как к власти пришли нацисты). Эмигрировав в США, всего после двух лет преподаваний в колледже Брин-Мар (который по сию пору принимает для обучения только женщин), она умерла от онкологического заболевания.
Знаменитая теорема Нётер (реально это две тесно связанных теоремы) говорит нам, что если в законах природы существует симметрия – в нашем случае это значит, что законы природы одинаковы в любой момент времени – то из этого следует сохранение некоей величины – в нашем случае, энергии.
Более того, теорема в точности сообщает нам, что это за величина – каковы различные формы энергии, для заданной системы объектов, которые необходимо сложить, чтобы получить общую энергию. Именно поэтому физики всегда точно знают, что такое энергия, и почему её легче получить при помощи уравнений, чем определить словами.
Импульс
С импульсом дело обстоит примерно таким же образом, что и с энергией. Законы природы везде одинаковые. Грубо говоря, эксперименты дают одни и те же ответы, проводите ли вы их к северу или к югу отсюда, к западу или востоку, на вершине здания или в глубокой шахте. Выберите любое направление в пространстве. Тогда, согласно Нётер, импульс вдоль этого направления сохраняется. Поскольку в пространстве есть три измерения, то можно двигаться в трёх разных независимых направлениях и существуют три независимых закона сохранения. Выбрать можно три любых направления, при условии, что они разные. К примеру, можно выбрать в качестве трёх законов сохранения импульсы в направлениях север-юг, запад-восток и вверх-вниз.
 Или можно выбрать три других – по направлению к и от Солнца, вдоль орбиты Земли в обе стороны, и вверх и вниз по отношению к плоскости Солнечной системы. Ваш выбор не имеет значения, ибо импульс сохраняется вдоль любого направления.
Или можно выбрать три других – по направлению к и от Солнца, вдоль орбиты Земли в обе стороны, и вверх и вниз по отношению к плоскости Солнечной системы. Ваш выбор не имеет значения, ибо импульс сохраняется вдоль любого направления.Простейшая форма импульса возникает благодаря простому движению объектов, и это примерно то, что можно представить себе интуитивно: если объект двигается в определённом направлении, то у него есть импульс в этом направлении, и чем быстрее он двигается, тем больше этот импульс. А у более тяжёлого объекта импульс больше, чем у лёгкого, если они двигаются с одинаковыми скоростями.
Одно из интересных следствий этого сохранения: если у вас имеется неподвижная система из объектов (то есть, система в целом не двигается, если усреднить все движения составляющих её объектов), тогда она будет оставаться неподвижной, если только ей не придаст движение какое-либо внешнее воздействие. Причина в том, что у неподвижной системы суммарный импульс равен нулю, и поскольку импульс сохраняется, он останется равным нулю навсегда, если только не вмешается что-либо извне системы.
Масса, и её связь с энергией и импульсом
Теперь обратимся к массе
К сожалению, с массой связано много путаницы – после выхода работы Эйнштейна по теории относительности некоторое время существовало два понятия массы. И только одно из них (то, на котором остановился сам Эйнштейн, и которое иногда называют «инвариантной массой» или «массой покоя», чтобы отличить её от уже ставшего архаичным термина «релятивистская масса»), до сих пор используют в физике частиц. В отдельной статье я поясню это более подробно.
Рис. 1
Под массой m, которую я использую в статьях, подразумевается та масса, что непосредственно связывает энергию и импульс. Для объекта, двигающегося без воздействия внешних сил (не взаимодействующего значительно с другими объектами), Эйнштейн предположил (и это было подтверждено экспериментами), что его энергия E, импульс p и масса m удовлетворяют простому пифагорову равенству:
Помните старика Пифагора, утверждавшего, что для прямоугольного треугольника со сторонами A и B и гипотенузой C выполняется равенство ? Это связь того же типа – см. рис. 1. У нас с – постоянная скорость, которая, как мы увидим, служит универсальным пределом скорости. Также мы увидим, почему её называют «скоростью света».
рис. 1. У нас с – постоянная скорость, которая, как мы увидим, служит универсальным пределом скорости. Также мы увидим, почему её называют «скоростью света».
Согласно уравнениям Эйнштейна, скорость объекта, делённая на предел скорости с, это просто отношение pc к Е:
То есть отношение горизонтального катета к гипотенузе. Оно также равно синусу угла α на рис. 1. Вот так вот, граждане. А поскольку катеты прямоугольного треугольника всегда короче гипотенузы (синус любого угла всегда меньше или равен 1), скорость любого объекта не может превышать с, универсальный предел скорости. С увеличением скорости объекта фиксированной массы p и E становятся очень большими (рис. 2), но E всегда больше pc, поэтому v всегда меньше c!
Рис. 2
Теперь обратите внимание, что если объект не двигается, то его импульс p равен нулю, и отношение в уравнении 1 сводится к:
Знаменитая формула Эйнштейна, связь массы с фиксированным количеством энергии (то, что я называю энергией массы), это просто утверждение, соответствующее тому, что когда треугольник вырождается в вертикальную линию, как на рис. 3 слева, его гипотенуза становится такой же длины, как вертикальный катет. При этом оно не означает, что энергия всегда равна массе, помноженной на квадрат с. Это работает только для покоящегося объекта с нулевым импульсом.
3 слева, его гипотенуза становится такой же длины, как вертикальный катет. При этом оно не означает, что энергия всегда равна массе, помноженной на квадрат с. Это работает только для покоящегося объекта с нулевым импульсом.
Рис. 3
Ещё одно интересное наблюдение: для безмассовой частицы вертикальный катет треугольника нулевой, а гипотенуза и горизонтальный катет совпадают, как на рис. 3. В таком случае E равняется pc, что означает, что v/c = 1, или v = c. Видно, что безмассовая частица (к примеру, фотон, частица света) неизбежно перемещается со скоростью с. Поэтому скорость света такая же, как универсальный предел скорости, с.
С другой стороны, если взять обладающую массой частицу, как на рис. 4, то неважно, насколько большим вы делаете импульс и энергию, E всегда будет немного больше, чем p*c, поэтому скорость всегда будет меньше с. Безмассовые частицы обязаны перемещаться с максимальной скоростью. Скорость массивных частиц должна быть меньше.
Рис. 4. Здесь «>>» означает «гораздо больше»
4. Здесь «>>» означает «гораздо больше»
Представьте себе другой пограничный случай, медленно (по сравнению со скоростью света) движущийся массивный объект, к примеру, автомобиль. Поскольку его скорость v гораздо меньше с, его импульс p умноженный на c будет гораздо меньше E, и, как видно из рис. 5, E будет немногим больше, чем mc2. Поэтому энергия движения медленного объекта E — mc2 гораздо меньше, чем энергия его массы mc2, а у быстрого объекта энергию движения можно сделать сколь угодно большой, как мы видели на рис. 4.
Один тонкий момент: импульс – это не только число, но и вектор. У него есть величина и направления. Он направлен в сторону движения частицы. Когда я пишу «p», я указываю только величину. Во многих случаях необходимо отслеживать и направление импульса, хотя в уравнении №1, связывающем импульс с энергией и массой, этого делать не нужно.
Рис. 5
Ещё один тонкий момент: я использовал треугольники и простейшую тригонометрию, поскольку она известна всем из школы. Экспертам же нужно быть осторожнее – правильно понять уравнения Эйнштейна можно, используя гиперболические функции, обычно не встречающиеся дилетантам, но крайне важные для понимания структуры теории, и делающие более понятными такие вещи, как сложение скоростей, сжатие расстояний и т.п. Не претендующие на экспертизу люди могут это игнорировать.
Экспертам же нужно быть осторожнее – правильно понять уравнения Эйнштейна можно, используя гиперболические функции, обычно не встречающиеся дилетантам, но крайне важные для понимания структуры теории, и делающие более понятными такие вещи, как сложение скоростей, сжатие расстояний и т.п. Не претендующие на экспертизу люди могут это игнорировать.
Но скорость же относительна?..
Если вы внимательно читали текст, вас уже может кое-что удивить. Вы знаете, что скорость частицы – или чего угодно, движущегося медленнее света – зависит от точки зрения.
Если вы сидите дома и читаете книгу, вы скажете, что скорость книги нулевая (и относительно вас она действительно покоится), следовательно, у неё нет импульса и энергии движения, только энергия массы. Но если бы я стоял на Луне, то я напомнил бы вам, что Земля вертится, поэтому это вращение увлекает и вас, и двигает вас относительно меня со скоростью в сотни километров в час. Так что вы с вашей книгой обладали бы импульсом с моей точки зрения.
Кто же прав?
Вариант относительности согласно Галилею – первый принцип относительности – утверждает, что правы мы оба. Вариант относительности Эйнштейна соглашается с точкой зрения Галилея в том, что правы оба, но вносит важные корректировки в то, как обозначили бы последователи Галилея энергию, импульс и массу книги, помещая эти величины в пифагорово соотношение уравнения №1.
Но если правы все, какую E и какой p мне нужно подставить в соотношение энергии/импульса/массы, ? Подставить E и p, измеренные вами, читающим книгу, то есть E = mc2 и p = 0? Или подставить E и p, которыми обладает книга с моей точки зрения, когда вы двигаетесь вместе с Землёй?
В ответе на этот вопрос содержится вся суть уравнения Эйнштейна №1. Каждый наблюдатель измерит разные величины E и p для книги, в зависимости от того, как быстро книга будет двигаться относительно него. Но для всех наблюдателей уравнение будет верным!
Магия! А на самом деле, гениальность – мысль, пришедшая в 1905 году, о том, как можно заменить набор уравнений, предложенных Ньютоном и его последователями, новым удивительным набором уравнений, всё ещё совпадающим со всеми предыдущими экспериментами, но оказавшимся более точным представлением реальности. Сложно представить, как сильно нужно было изменить образ мышления, чтобы додуматься до этого, пока не разберёшься с тем, сколько всего во время формирования новой теории могло пойти не так, и сколько других различных уравнений, содержащих противоречия с математикой или с предыдущими экспериментами, можно было бы предложить (а люди их предлагали). Мне, к примеру, постоянно приходят работы начинающих физиков, пытающихся «исправить» уравнения Эйнштейна, но я никогда не видел, чтобы кто-нибудь из них проверил свои уравнения на внутреннюю непротиворечивость. Это очень сложная задача и причина неудачи большинства теорий.
Сложно представить, как сильно нужно было изменить образ мышления, чтобы додуматься до этого, пока не разберёшься с тем, сколько всего во время формирования новой теории могло пойти не так, и сколько других различных уравнений, содержащих противоречия с математикой или с предыдущими экспериментами, можно было бы предложить (а люди их предлагали). Мне, к примеру, постоянно приходят работы начинающих физиков, пытающихся «исправить» уравнения Эйнштейна, но я никогда не видел, чтобы кто-нибудь из них проверил свои уравнения на внутреннюю непротиворечивость. Это очень сложная задача и причина неудачи большинства теорий.
Но как тогда могут сохраняться энергия и импульс?
Погодите-ка, – скажете вы, когда ваша голова уже готова будет взорваться и забрызгать всё вокруг мозгами (я и сам помню это ощущение), – но энергия и импульс должны сохраняться! Так как же могут разные наблюдатели не соглашаться с тем, что они собой представляют?
Тут есть ещё больше магии, которая, кстати, была ещё до Эйнштейна. Поверьте мне, Вселенная – очень, очень хитроумный бухгалтер, и, несмотря на то, что разные наблюдатели не будут соглашаться по поводу энергии, имеющейся у объекта или системы объектов, они все согласятся, что эта энергия не меняется со временем. То же касается и импульса.
Поверьте мне, Вселенная – очень, очень хитроумный бухгалтер, и, несмотря на то, что разные наблюдатели не будут соглашаться по поводу энергии, имеющейся у объекта или системы объектов, они все согласятся, что эта энергия не меняется со временем. То же касается и импульса.
А вот масса очень сильно отличается от энергии и импульса. Во-первых, масса не сохраняется. В природе есть множество процессов, изменяющих общую массу системы: к примеру, массивная частица Хиггса может распадаться на два безмассовых фотона. С массой не связана симметрия, и поэтому у Нётер нет для нас закона сохранения. Во-вторых, в отличие от энергии и импульса, чьи величины зависят от наблюдателя (в частности, от его скорости по отношению к измеряемым объектам), все наблюдатели согласятся с величиной массы m объекта. А это вовсе не очевидно, и происходит так оттого, как ужасно хитроумно работают уравнения Эйнштейна.
Итак, что мы имеем
На текущий момент у нас несколько, на первый взгляд, противоречивых знаний.
 Мы знаем, что:
Мы знаем, что:• Энергия и импульс изолированной физической системы сохраняются (общая энергия и общий импульс изолированной системы не меняются со временем) с точки зрения любого наблюдателя.
• Разные наблюдатели, движущиеся относительно друг друга, по-разному оценят величины энергии и импульса системы!
• Сумма масс объектов, составляющих систему, не сохраняется, она может меняться.
• Но все наблюдатели согласятся с величиной массы объекта.
К этому списку нужно добавить ещё два факта и два вывода:
Масса физической системы объектов не равна сумме масс объектов, составляющих эту систему.
Вместо этого масса физической системы, по поводу которой согласятся все наблюдатели, определяется её энергией и импульсом, и удовлетворяет своему варианту уравнения №1:
Получается, что дополнительный закон сохранения не нужен, и что хотя сумма масс объектов, составляющих систему, не сохраняется, масса системы сохраняется, поскольку она связана через уравнение №1′ с энергией и импульсом системы, которые сохраняются.
Масса системы объектов – это единственный пункт нашего списка, одновременно и сохраняющийся, и не являющийся предметом споров наблюдателей.
Нужно лишь помнить, что масса системы объектов – это не сумма масс объектов, составляющих систему, а то, что задано уравнением №1′.
Чем пытаться объяснить это, просто посмотрим, как это работает. Яркий пример стоит тысячи слов. Давайте в качестве примера системы рассмотрим самую модную штуку, а именно, частицу Хиггса (обладающую массой в 126 ГэВ/с2), и посмотрим, как различные утверждения, сделанные выше, работают при её распаде на два фотона.
Одна частица Хиггса, два фотона и три наблюдателя
Рис. 6. Три наблюдателя смотрят на частицу Хиггса. По отношению к ней Петя (Peter) не двигается, Маша (Marie) двигается вниз, а Костя (Chris) двигается влево.
Давайте посмотрим на то, как частица Хиггса распадается на два фотона, с точки зрения трёх разных наблюдателей. Они изображены на рис. 6 вместе с частицей Хиггса, на которую они смотрят. Конечно, они не могут увидеть её глазами, ибо она существует слишком малый отрезок времени и она слишком мала. Им необходимо использовать какое-либо научное оборудование. Для Пети частица Хиггса не двигается. Маша двигается вниз относительно Пети. Костя двигается влево относительно Пети. Значит, для Маши частица Хиггса двигается вверх, а для Кости – вправо. Три наблюдателя видят, как частица распадается согласно рис. 7. Петя видит, что Хиггс распадается на два фотона одинаковых энергий, один из которых двигается вверх, а другой – вниз. Маша видит, что Хиггс распадается на два фотона различных энергий, и у двигающегося вверх энергии больше, чем у двигающегося вниз. Костя видит, как Хиггс распадается на два фотона, направляющихся вправо вверх и вправо вниз. Давайте посчитаем, какие энергии и импульсы присвоят Хиггсу и двум фотонам наблюдатели, и как каждый из них придёт к выводу о сохранении энергии и импульса в процессе распада.
Конечно, они не могут увидеть её глазами, ибо она существует слишком малый отрезок времени и она слишком мала. Им необходимо использовать какое-либо научное оборудование. Для Пети частица Хиггса не двигается. Маша двигается вниз относительно Пети. Костя двигается влево относительно Пети. Значит, для Маши частица Хиггса двигается вверх, а для Кости – вправо. Три наблюдателя видят, как частица распадается согласно рис. 7. Петя видит, что Хиггс распадается на два фотона одинаковых энергий, один из которых двигается вверх, а другой – вниз. Маша видит, что Хиггс распадается на два фотона различных энергий, и у двигающегося вверх энергии больше, чем у двигающегося вниз. Костя видит, как Хиггс распадается на два фотона, направляющихся вправо вверх и вправо вниз. Давайте посчитаем, какие энергии и импульсы присвоят Хиггсу и двум фотонам наблюдатели, и как каждый из них придёт к выводу о сохранении энергии и импульса в процессе распада.
Распад неподвижной частицы Хиггса
Для начала разберём частицу Хиггса с точки зрения Пети.
 Петя смотрит (при помощи измерительных приборов) на частицу Хиггса, и что же он видит? (Я буду ставить чёрточку над всем, что видит Петя, и потом мы сравним это с наблюдениями Маши и Кости). Хиггс не двигается, значит, его импульс равен нулю, и согласно уравнению №1 у него, с его массой m = 126 ГэВ/c2 энергия будет
Петя смотрит (при помощи измерительных приборов) на частицу Хиггса, и что же он видит? (Я буду ставить чёрточку над всем, что видит Петя, и потом мы сравним это с наблюдениями Маши и Кости). Хиггс не двигается, значит, его импульс равен нулю, и согласно уравнению №1 у него, с его массой m = 126 ГэВ/c2 энергия будетТеперь, согласно сохранению энергии и импульса, система, состоящая из частицы Хиггса, сохранит всю энергию и импульс после распада. И это будет так, пока никакая внешняя сила не будет воздействовать на Хиггса. Вы можете спросить, нужно ли нам волноваться по поводу земного притяжения, ведь гравитация и будет внешним воздействием, способным менять импульс. Отвечу, что за то краткое время, которое нужно Хиггсу на распад, влияние гравитации будет столько малым, что если бы я рассказал вам, какое оно на самом деле мелкое, вы бы захихикали. Забудьте об этом.
Итак, когда Хиггс распадается, энергии частиц, составляющих его остатки, должны в сумме дать 126 ГэВ, а импульс частиц (учитывая, что импульс – это не только величина, но и направление — вектор) в сумме даст ноль.
Два безмассовых фотона, на которые распадается Хиггс, могут разлететься в любых направлениях, но чтобы упростить пример, представим, что они разлетятся вертикально – один вверх, а другой, отскочив от него, вниз. (Чуть позже обсудим, почему они должны разлетаться в противоположных направлениях).
Каким импульсом обладают фотоны? Это просто. Во-первых, общий импульс системы – сумма импульсов двух фотонов – должен быть нулевым, поскольку у Хиггса до распада был нулевой импульс (с точки зрения Пети). Теперь у каждого из фотонов есть импульс определённой величины и направления. В сумме они могут давать ноль только одним способом – если они равной величины и противоположного направления. Если один идёт вверх, другой должен идти вниз, и величина их должна быть одинаковой.
Рис. 8: что видит Петя
Во-вторых, общая энергия системы – это сумма энергий двух фотонов. Это происходит потому, что между ними нет никакой энергии взаимодействия (кроме крайне малого гравитационного притяжения, о котором можно забыть). Конечно, раз у них нет масс, то вся их энергия заключается в энергии движения. Кроме того, в случае для безмассовой частицы уравнение №1 говорит о том, что E = p c, где p – величина импульса. Из-за этого два фотона с одинаковыми импульсами должны обладать и одинаковыми энергиями. А поскольку две эти энергии в сумме должны дать энергию частицы Хиггса, то энергия каждого фотона должна равняться половине энергии частицы Хиггса.
Конечно, раз у них нет масс, то вся их энергия заключается в энергии движения. Кроме того, в случае для безмассовой частицы уравнение №1 говорит о том, что E = p c, где p – величина импульса. Из-за этого два фотона с одинаковыми импульсами должны обладать и одинаковыми энергиями. А поскольку две эти энергии в сумме должны дать энергию частицы Хиггса, то энергия каждого фотона должна равняться половине энергии частицы Хиггса.
А поскольку для безмассовой частицы p = E/c, то
И это отображено на рис. 8.
Энергия и импульс сохраняются, а масса – нет, поскольку у фотонов нет массы, а у Хиггса была. А что по поводу массы системы? Какова масса системы из двух фотонов? Ненулевая. Очевидно, какая она. Точно так же, как и для самого Хиггса (из которого и состояла изначально вся система), система из двух фотонов обладает той же энергией и импульсом, что были у Хиггса:
А поскольку для Пети ,
Что и есть масса Хиггса. Масса системы не изменилась за время распада, как и ожидалось.
Наблюдатель, для которого Хиггс движется вверх
Маша движется вниз по отношению к Пете, так что с её точки зрения Петя и Хиггс двигаются вверх. Допустим, что Хиггс двигается со скоростью v = 0,8 c, то есть 4/5 скорости света, относительно неё. В отличие от Пети, с точки зрения Маши Хиггс обладает ненулевым импульсом, а импульсы у фотонов оказываются разными по величине, но по-прежнему разнонаправленными – в результате чего сумма их импульсов будет ненулевой.
Рис. 9: как Маша видит распад частицы Хиггса
Как посчитать, какими импульсом и энергией обладает Хиггса и два фотона, на которые он распадается, с точки зрения Маши? Для этого нам понадобится ещё один набор простых уравнений Эйнштейна. Допустим, с точки зрения некоего наблюдателя объект обладает импульсом p и энергией E. Тогда с точки зрения другого наблюдателя, движущегося со скоростью v по направлению движения объекта (или против него), импульс и энергия объекта будут выражаться следующим образом:
Где γ удовлетворяет ещё одному пифагорову уравнению:
согласно Эйнштейну. Это позволяет нам выполнять преобразования между тем, что видит Петя, и тем, что видит Маша (или любой другой наблюдатель, двигающийся со скоростью v). То, что мы обнаружим, показано на рис. 9.
Это позволяет нам выполнять преобразования между тем, что видит Петя, и тем, что видит Маша (или любой другой наблюдатель, двигающийся со скоростью v). То, что мы обнаружим, показано на рис. 9.
Чтобы сравнить наблюдения Маши с наблюдениями Пети, нам понадобятся v и γ. Я утверждаю, что если v=4/5 c, то γ = 5/3.
Проверим, используя уравнение №5: 1 = (4/5)2 + (3/5)2 = 16/25 + 9/25 = 25/25
Петя говорит, что у Хиггса . Что насчёт Маши? Она говорит, что:
Петя утверждает, что у двух фотонов , и для каждого из них E = p c. Теперь мы можем подсчитать, что видит Маша, используя уравнения №4 и №4.
Работает! Энергия сохраняется и с точки зрения Марии, ибо
Импульс тоже сохраняется:
Масса системы совпадает с массой Хиггса до и после распада, поскольку до и после распада
Что, согласно уравнению №1′, приводит массу системы вновь к , как и у Пети, поскольку
Наблюдатель, с точки зрения которого Хиггс движется вправо
Что у нас с Костей? Костя двигается влево относительно Пети, допустим, со скоростью v=4/5 c, так что относительно Кости Хиггс (и Петя) двигаются вправо со скоростью v=4/5 c.
 Те же расчёты, что мы делали для Маши, показывают, что энергия Хиггса , но, в отличие от Маши, для которой Хиггс двигается вверх, для Кости импульс Хиггса направлен вправо. Это изображено на рис. 10.
Те же расчёты, что мы делали для Маши, показывают, что энергия Хиггса , но, в отличие от Маши, для которой Хиггс двигается вверх, для Кости импульс Хиггса направлен вправо. Это изображено на рис. 10.
Рис. 10
Хиггс распадается на два фотона. Если с точки зрения Пети фотоны двигаются вверх и вниз, то для Кости, наблюдающего, как Хиггс и Петя двигаются вправо, один из фотонов двигается вправо вверх, а другой – вправо вниз. Какие у них тогда будут импульс и энергия?
Через уравнения №4 и №5 нам этого не узнать, поскольку они предназначаются для случаев, когда частица и наблюдатель двигаются в одном направлении. Для нашего случая уравнения будут такими:
Эти уравнения будут проще, чем кажутся, поскольку с точки зрения Пети, у p нет компоненты, двигающейся слева направо, и весь импульс идёт вверх или вниз. Так что Костя наблюдает следующие величины для Хиггса:
А у фотона, идущего вверх
Для второго фотона формулы те же, только его вертикальная составляющая направлена вниз. Заметьте, что для обоих фотонов E = p c, согласно теореме Пифагора для размера p у каждого из импульсов – согласно врезке на рис. 10
Заметьте, что для обоих фотонов E = p c, согласно теореме Пифагора для размера p у каждого из импульсов – согласно врезке на рис. 10
И вновь Костя наблюдает другие величины энергии и импульса, по сравнению с Петей и Машей. Но и для Кости энергия и импульс всё равно сохраняются. Также Костя наблюдает, что у системы с двумя фотонами масса совпадает с массой Хиггса. Почему? Общая вертикальная часть импульса системы нулевая, она взаимно уничтожается. Горизонтальная часть импульса системы равна 168 ГэВ/с. Общая энергия системы 210 ГэВ. Это то же, что наблюдала Маша, за исключением того, что у неё импульс системы шёл вверх, а не вправо. Но направление импульса не влияет на уравнение №1′. Там играет роль только его величина. Так что, как и Маша, Костя видит, что масса системы из двух протонов получается , равной массе первичной частицы Хиггса.
Итог
Итак, мы видим, что наблюдают три разных наблюдателя. Их наблюдения:
• разнятся по поводу того, какие у Хиггса энергия и импульс,
• разнятся в части энергии и импульса обоих фотонов,
• согласуются по поводу сохранения энергии и импульса при распаде,
• следовательно, они согласны, что при этом сохраняется масса системы,
• соглашаются, что масса системы равна 126 ГэВ/c2,
• и более того, что сумма масс объектов системы не сохраняется, а уменьшается с 126 ГэВ/c2 до нуля.
И это не случайно. Эйнштейн из предыдущих экспериментов знал, что энергия и импульс сохраняются, поэтому он искал и нашёл уравнения, сохраняющие эту особенность мира. Также в процессе он обнаружил, что масса системы должна удовлетворять уравнению №1′.
Бонус: как это используется в поисках частицы Хиггса
Учёные:
• наблюдают столкновения протонов, в результате которых рождается два фотона;
• подсчитывают массу системы из двух фотонов (на техническом жаргоне это называется инвариантная масса пары фотонов).
Когда в результате эксперимента получается частица Хиггса, распадающаяся на два фотона, то вне зависимости от того, в каком направлении и с какой скоростью двигается частица по отношению к лаборатории, система из двух фотонов, на которую она распадётся, всегда будет обладать массой, равной массе частицы Хиггса, произведшей их на свет! Поэтому, в отличие от случайных процессов, в результате которых получается система из двух фотонов случайной массы, частицы Хиггса всегда будут порождать систему из двух фотонов одной и той же массы. Поэтому, если в результатах эксперимента появятся частицы Хиггса, и если они иногда будут распадаться на два фотона, то мы увидим пик от распадов Хиггса, возвышающийся над гладким фоном из других случайных процессов. Так и произошло в эксперименте на БАК!
Поэтому, если в результатах эксперимента появятся частицы Хиггса, и если они иногда будут распадаться на два фотона, то мы увидим пик от распадов Хиггса, возвышающийся над гладким фоном из других случайных процессов. Так и произошло в эксперименте на БАК!
Свободное качение
1. Установление взаимосвязей
(5-10 мин.)
Дима и Катя, как обычно, спорят. Они мастерят тележки, чтобы посмотреть, которая из них укатится дальше, съехав со стартовой горки в их Презеленом парке.
Катя говорит, что если она дополнительно нагрузит свою тележку пассажиром (это будет Пес Барбос), то тележка поедет дальше, потому что станет тяжелее. А Дима считает, что он уедет дальше
на легкой тележке, поскольку тяжелые грузы труднее передвигать. Еще он предпочитает ездить на колесах большего размера, но Катя сомневается, что это ему поможет.
Так какая же тележка поедет дальше – легкая или тяжелая, с большими или с маленькими колесами? Давайте выясним!
2. Конструирование
Конструирование
(20-25 мин.)
Постройте стартовую горку
Проведите линию старта на расстоянии 1 м от одного из краев планки. Другой ее конец приподнимите так, чтобы старт располагался на
высоте 15 см от пола.
Зачем нам нужна стартовая линия?
Она необходима для того, чтобы все испытания проводились в одинаковых условиях: все тележки будут съезжать по одной и той же наклонной плоскости.(пандусу) с одной и той же отметки.
Полезный совет
Если планка слишком толстая, то тележка может «плюхнуться» с нее на пол. Положите лист картона, чтобы сделать переход от планки к полу плавным.
Соберите тележку
(Технологические карты 3A и 3B, с. 6, шаг 12)
Испытайте тележку на пандусе. Плавно ли едет модель? Если нет, отрегулируйте все оси и втулки так, чтобы колеса крутились плавно. Проверьте также, плотно ли прилегают друг к другу всеэлементы конструкции.
Разметьте шкалу
Разметьте голубой пластиковый диск или вырежьте такой же диск из бумаги. Нанесите разметку шкалы и прикрепите поверх голубого пластикового диска.
Нанесите разметку шкалы и прикрепите поверх голубого пластикового диска.
3. Рефлексия
(20-25 мин.)
Измерьте рулеткой расстояние, которое проедет пустая тележка, результат сравните с положением указателя на шкале. Запишите пройденный путь, а место, где тележка остановилась, отметьте ЛЕГО®-кирпичиком. Сделайте не меньше трех замеров, как того требует методика научного эксперимента, чтобы получить достоверный результат.
Тележка без груза должна проехать приблизительно 160 см. При этом указатель сделает больше одного оборота вокруг шкалы. Точность шкалы составляет несколько сантиметров.
Стираемым маркером отметьте на пластиковой шкале положение указателя, соответствующее пройденному расстоянию в 1 м. Еще раз спустите тележку с пандуса и посмотрите по шкале, проехала ли она 160 см – указатель должен сделать один полный оборот и пройти еще немного больше половины циферблата (шкалы). Проведите несколько испытаний. Теперь нет необходимости измерять пройденный тележкой путь рулеткой или сантиметром – просто считывайте показания со шкалы.
Полезный совет
Обратите внимание: один оборот указателя вокруг шкалы почти точно соответствует пройденному расстоя- нию в 1 м. Это означа-ет, что указатель будет находиться на нулевой отметке, когда тележка достигнет пола.
Нагрузите тележку – поставьте на нее груз ЛЕГО (с. 7, шаг 13). Подумайте, как далеко укатится тележка в этом случае – отметьте место ее предполагаемой остановки еще одним кирпичиком. После этого проведите испытание.
На этот раз тележка уедет почти в два раза дальше. Груз, «падающий» вместе с тележкой, придает ей вдвое большую энергию движения (кинетическую энергию). Однако следует учитывать, что при увеличении нагрузки возрастает и трение на осях, а это замедляет движение тележки.
Что вы можете отметить в поведении указателя (стрелки)?
Указатель делает больше одного оборота вокруг шкалы. Вам нужно посчитать количество его оборотов.
Проведите несколько испытаний, чтобы результат ваших наблюдений был достоверным.
Знаете ли вы?
Масса пустой тележки около 58 г, а ЛЕГО-груза – 53 г, то есть почти
такая же!
Димина Теория большого колеса
Уедет ли тележка на больших колесах дальше, чем на маленьких? Наденьте большие колеса на заднюю ось и спустите тележку с горки (с. 7, шаг 14).
Сначала испытайте пустую тележку (с. 7, шаг 14), а затем – тележку с грузом (с. 8, шаг 15).
Как правило, массивная тележка на больших колесах проезжает большее расстояние. Это можно объяснить двумя причинами: 1) чем больше масса, тем больше энергия, 2) задняя ось вращается медленнее, трение меньше.
Не забывайте сбрасывать показание счетчика – устанавливать указатель (стрелку) на начальное (нулевое) положение – перед каждым испытанием!
Знаете ли вы?
Масса каждого большого колеса примерно 16 г, а маленького – 8 г.
4. Развитие
(25-30 мин.)
Расширенная шкала
(Технологическая карта 3B, с. 12, шаг 12) Замените 8-зубое колесо на 24-зубое. Как вы думаете, какое расстояние проедет тележка к тому
12, шаг 12) Замените 8-зубое колесо на 24-зубое. Как вы думаете, какое расстояние проедет тележка к тому
моменту, когда указатель сделает один полный оборот?
Тележка проедет 3 м. Новое зубчатое колесо имеет в три раза больше зубьев, чем прежнее, маленькое. 8-зубое колесо должно было вращаться в 3 раза быстрее, чтобы «поспеть» за 24-зубым колесом, которое сделало один оборот. Теперь нужно будет откалибровать шкалу так, чтобы можно было измерять расстояние до 3 м.
Более крутой спуск
Сначала попробуйте предположить, а затем проверьте, что произойдет, если сделать спуск вдвое круче.
При этом удвоится потенциальная и кинетическая энергия, но трение на осях не станет в два раза больше.
Кинетический песок — что это такое?
Перейти в общий каталог:
Многие яркие воспоминания из детства связаны с летним раздольем, пляжем, лепкой песчаных замков, песочными баталиями. Современные дети, несмотря на изобилие технологически продвинутых игрушек, которые теснятся на полках магазинов, в качестве любимого места для игр выбирают песочницу. Но песок на улице открыт для доступа не только ребятам, но и животным, становясь из-за этого местом возможного скопления болезнетворных микроорганизмов, аллергенов. Прекрасная альтернатива ему – кинетический песок. Это принципиально новый материал для игры и творчества, учебного и познавательного процесса. Песочница с кинетическим песком не просто очередной экспонат в коллекции малыша.
Но песок на улице открыт для доступа не только ребятам, но и животным, становясь из-за этого местом возможного скопления болезнетворных микроорганизмов, аллергенов. Прекрасная альтернатива ему – кинетический песок. Это принципиально новый материал для игры и творчества, учебного и познавательного процесса. Песочница с кинетическим песком не просто очередной экспонат в коллекции малыша.
Что это такое? На первый взгляд — обычный мелкозернистый песок, каким покрыты пляжи и морское дно, который встречается на детских площадках. Но если присмотреться, взять его в руки, сразу можно отметить его необычные особенности.
Это уникальный продукт, обладающий всеми свойствами знакомого с детства материала для игр и творчества. На 98% кинетический песок состоит из обычного кварцевого песка, остальные 2% составляет добавка, используемая в легкой и пищевой промышленности, фармакологии. Этот факт дает гарантию экологической чистоты материала игрушки, ее безвредности для ребенка. Его состав абсолютно не токсичен, не вызывает аллергии и не поддерживает развитие микроорганизмов.
Этот факт дает гарантию экологической чистоты материала игрушки, ее безвредности для ребенка. Его состав абсолютно не токсичен, не вызывает аллергии и не поддерживает развитие микроорганизмов.
Производит оригинальный Kinetic Sand компания Waba Fun в Швеции, что само по себе является показателем высокого уровня продукции, так как эта страна славится щепетильным отношением к качеству и экологичности выпускаемых товаров, безопасности для здоровья маленьких потребителей.
Песок сертифицирован в Украине, Европе и США. Торговая марка Waba Fun известна во всем мире благодаря своим оригинальным игрушкам и товарам для детского развития. Она давно успела завоевать расположение и авторитет у потребителей. За время своего существования ее товары получили более 20 наград.
Кинетический песок позволяет лепить различные фигуры, строить замки или просто делать пасочки, но в отличие от простого песка, набранного в песочнице во дворе, он не липнет, не пачкает руки и одежду. Просыпанный песок не разлетается, а остается в виде компактной массы. Кстати, благодаря этому им практически невозможно засорить глаза, что любят делать некоторые озорники. Поиграв с песком, его легко собрать, просто скатав в шар, чтобы далее использовать повторно.
Кстати, благодаря этому им практически невозможно засорить глаза, что любят делать некоторые озорники. Поиграв с песком, его легко собрать, просто скатав в шар, чтобы далее использовать повторно.
Связующий компонент обеспечивает особенные свойства песка: сыпучесть и одновременно его податливость, его плотную, но в то же время пушистую консистенцию. При просеивании песчинки приходят в движение и пытаются разъединиться под силой земного притяжения, но благодаря специальной составляющей не сообщаются, образуя полимерные нити длиной 1-2 мм. Они практически невидимы, за счет их удивительного свойства кинетический песок льется, словно тонкая струя воды.
Кинетический песок кажется влажным на ощупь, не высыхает со временем и остается рассыпчатым. В свободно насыпанном состоянии песок создает впечатление мягкого, рыхлого и пористого. В то же время изделия из него могут сохранять форму на протяжении продолжительного времени.
Песочница – одна из излюбленных забав малышей, несмотря на свою незатейливость и простоту. Во что можно играть в кинетической песочнице? Полет фантазии тут безграничен. Ведь в песке можно создать целую жизнь.
Во что можно играть в кинетической песочнице? Полет фантазии тут безграничен. Ведь в песке можно создать целую жизнь.
Кинетический песок можно мять, лепить из него песочные скульптуры. С помощью формочек для песка, которые также продаются, можно делать пасочки, выкладывать треки и пускать по ним машинки. Специальные формочки «Строим замок» помогут создавать крепости и строить целые города, а набор раскопки динозавра даст почувствовать себя настоящим археологом.
На таком песке, рассыпанном в песочнице, легко рисовать следы животных и птиц. Можно изображать несложные картины, а можно выдумывать с помощью взрослых целые сюжеты. Его можно гладить, перебирать, сжимать в ладонях, наблюдая, как он оживает прямо на глазах, меняя свою консистенцию.
Процесс игры с кинетическим песком – не просто занимательное занятие, но также способ развития творческих способностей ребенка, и даже метод, используемый психологами и психотерапевтами в коррекции различных расстройств. Песочная терапия давно перестала являться просто методикой, но стала отдельным направлением в психотерапии. Ее смысл заключается в том, что наше бессознательное проявляется в символах внешнего мира. Через способность создавать фигуры на песке человек передает свои скрытые переживания, проявляет неразрешенные внутренние конфликты, страхи. А воплотив смутные образы из бессознательного в жизнь, придавая им форму, он становится на путь исцеления.
Ее смысл заключается в том, что наше бессознательное проявляется в символах внешнего мира. Через способность создавать фигуры на песке человек передает свои скрытые переживания, проявляет неразрешенные внутренние конфликты, страхи. А воплотив смутные образы из бессознательного в жизнь, придавая им форму, он становится на путь исцеления.
Многие психологи используют терапию песком для лечения страхов, фобий, неврозов (читать «Песочная терапия для детей»). Игры с кинетическим песком помогают оптимизировать эмоциональный фон, справиться с травматическими переживаниями, побороть такие негативные поведенческие проявления как гиперактивность, агрессивность, замкнутость. Кроме того песок прекрасно развивает мелкую моторику, поэтому игры с ним советуют для детей с задержкой речи.
Для работы с кинетическим песком или живым песком или умным песком не обязательны особые навыки, художественные способности. Лепить можно все, что заблагорассудиться, не опасаясь неэстетичности результатов своего творчества. И в этом заключается еще одно преимущество песочной терапии – принятие ребенком себя, повышение его самооценки и веры в свои возможности.
И в этом заключается еще одно преимущество песочной терапии – принятие ребенком себя, повышение его самооценки и веры в свои возможности.
Чем покорит кинетический песок детей? С ним легко играть, стоить, ваять. Он не рассыпается и держит нужную форму. Он чистый и приятый на ощупь. Это своя собственная песочница дома.
Преимущества такой уникальной игрушки для родителей. Песок не пачкает все вокруг: ковер, одежду, заигравшегося ребенка. Благодаря своим компонентам в его составе не размножаются патогенные организмы, он абсолютно безвреден для детского здоровья.
Занятия с таким песком снимают напряжение и усталость, поэтому даже взрослому будет полезно повозиться у песочницы после рабочего дня. Процесс постройки песочных скульптур является хорошей возможностью просто отдохнуть и расслабиться. Родители могут поучаствовать в играх с кинетическим песком, извлекая из занятий пользу для себя.
Хранить кинетический песок легко, он не портится и не высыхает. Для удобства рекомендуется после игры поместить песок в контейнер для хранения.
Готовые наборы для игры с песком – замечательный подарок ребенку. Будь то дома или в детском саду, песочные занятия проходят интересно и весело. Время на них летит незаметно, так как нет ничего более захватывающего и увлекательного, чем сотворить своими руками свой собственный мир.
Сертифицирован ли кинетический песок Waba Fun Kinetic Sand?
Компания Waba Fun получила все необходимые сертификаты и разрешения в Европейском Союзе и США, где нормы для детской продукции очень строги.
Мы же в соответствие с законодательством Украины получили сертификат соответствия украинского образца и заключение санитарно-эпидемиологической службы Украины.
На рынке Украины появилось много подделок Кинетического песка из Китая, о том чем они отличаются от оригинального песка читайте в статье «Кинетический песок: оригинал против аналога».
Где можно купить кинетический песок:
Купить песок можете в нашем магазине, у нас широчайший ассортимент песочниц, формочек для песка, постоянно проводятся акции на комплекты готовые для игры и обучения. У нас бесплатная доставка по Киеву и Украине при заказе от 500 грн.
У нас бесплатная доставка по Киеву и Украине при заказе от 500 грн.
Заходите в наш раздел «Кинетический песок Waba Fun Kinetic Sand» выбирайте и покупайте!
Мы гарантируем — Ваш ребенок и Вы останетесь довольны покупкой и обязательно к нам вернетесь!
Приятного Вам творчества!
Клиника промышленной медицины | Память, причины ее нарушений, и методы тренировки памяти
Память — это психическое свойство человека, способность к накоплению (запоминанию) хранению и воспроизведению опыта и информации. Память — это способность вспоминать отдельные переживания из прошлого, осознавая не только само переживание, а его место в истории нашей жизни, его размещение во времени и пространстве. Память трудно свести к одному понятию. Но подчеркнем, что память — это совокупность процессов и функций, которые расширяют познавательные возможности человека. Память охватывает все впечатления об окружающем мире, которые возникают у человека. Память — это сложная структура нескольких функций или процессов, обеспечивающих фиксацию прошлого опыта человека. Память можно определить как психологический процесс, выполняющий функции запоминания, сохранения и воспроизведения материала. Три указанных функции являются основными для памяти.
Память — это сложная структура нескольких функций или процессов, обеспечивающих фиксацию прошлого опыта человека. Память можно определить как психологический процесс, выполняющий функции запоминания, сохранения и воспроизведения материала. Три указанных функции являются основными для памяти.
Еще один важный факт: память хранит, восстанавливает очень разные элементы нашего опыта: интеллектуальный, эмоциональный и моторно-двигательный. Память о чувствах и эмоциях может сохраняться даже дольше, чем интеллектуальная память о конкретных событиях.
Наиболее важные черты, неотъемлемые характеристики памяти — это длительность, быстрота, точность, готовность, объём (запоминания и воспроизведения). От этих характеристик зависит то, насколько продуктивна память человека.
1. Объём — способность одновременно сохранять значительный объём информации. Средний объём памяти — 7 элементов (единиц) информации.
2. Быстрота запоминания отличается у разных людей. Скорость запоминания можно увеличить с помощью специальной тренировки памяти.
Скорость запоминания можно увеличить с помощью специальной тренировки памяти.
3. Точность проявляется в припоминании фактов и событий, с которыми сталкивался человек, а также в припоминании содержания информации. Эта черта очень важна в обучении.
4. Длительность – способность в течение долгого времени сохранять пережитый опыт. Очень индивидуальное качество: некоторые люди могут вспомнить лица и имена школьных друзей спустя много лет (развита долговременная память), некоторые забывают их спустя всего несколько лет. Длительность памяти имеет выборочный характер.
5. Готовность к воспроизведению — способность быстро воспроизводить в сознании человека информацию. Именно благодаря этой способности мы можем эффективно использовать приобретенный раньше опыт.
Виды и формы памяти
Существуют разные классификации видов человеческой памяти:
1. По участию воли в процессе запоминания.
2. По психической активности, которая преобладает в деятельности.
3. По продолжительности сохранения информации.
4. По сути предмета и способа запоминания.
5. По характеру участия воли.
6. По характеру целевой деятельности память подразделяют на непроизвольную и произвольную.
1) Непроизвольная память означает запоминание и воспроизведение автоматически, без всяких усилий.
2) Произвольная память подразумевает случаи, когда присутствует конкретная задача, и для запоминания используются волевые усилия.
Доказано, что непроизвольно запоминается материал, который интересен для человека, который важен, имеет большое значение.
По характеру психической деятельности, с помощью которой человек запоминает информацию, память делят на двигательную, эмоциональную (аффективную), образную и словесно-логическую.
1. Двигательная (кинетическая) память есть запоминание и сохранение, а при необходимости, воспроизведение многообразных, сложных движений. Эта память активно участвует в развитии двигательных (трудовых, спортивных) умений и навыков. Все ручные движения человека связаны с этим видом памяти. Эта память проявляется у человека раньше всего, и крайне необходима для нормального развития ребенка.
Эта память активно участвует в развитии двигательных (трудовых, спортивных) умений и навыков. Все ручные движения человека связаны с этим видом памяти. Эта память проявляется у человека раньше всего, и крайне необходима для нормального развития ребенка.
2. Эмоциональная память – память на переживания. Особенно этот вид памяти проявляется в человеческих взаимоотношениях. Как правило, то, что вызывает у человека эмоциональные переживания, запоминается им без особого труда и на длительный срок. Доказано, что существует связь между приятностью переживания, и тем, как оно удерживается в памяти. Приятные переживания удерживаются гораздо лучше, чем неприятные. Человеческая память вообще оптимистична по природе. Человеку свойственно забывать неприятное; воспоминания о страшных трагедиях, с течением времени, утрачивают свою остроту.
Данный вид памяти играет важную роль в мотивации человека, а проявляет себя эта память очень рано: в младенчестве (около 6 мес.).
3. Образная память — связана с запоминанием и воспроизведением чувственных образов предметов и явлений, их свойств, отношений между ними. Данная память начинает проявляться к возрасту 2-х лет, и достигает своей высшей точки к юношескому возрасту. Образы могут быть разными: человек запоминает как образы различных предметов, так и общее представление о них, с каким-то абстрактным содержанием. В свою очередь, образную память делят по виду анализаторов, которые участвуют при запоминании впечатлений человеком. Образная память может быть зрительной, слуховой, обонятельной, осязательной и вкусовой.
Образная память — связана с запоминанием и воспроизведением чувственных образов предметов и явлений, их свойств, отношений между ними. Данная память начинает проявляться к возрасту 2-х лет, и достигает своей высшей точки к юношескому возрасту. Образы могут быть разными: человек запоминает как образы различных предметов, так и общее представление о них, с каким-то абстрактным содержанием. В свою очередь, образную память делят по виду анализаторов, которые участвуют при запоминании впечатлений человеком. Образная память может быть зрительной, слуховой, обонятельной, осязательной и вкусовой.
У разных людей более активны разные анализаторы, но у большинства людей лучше развита зрительная память.
Зрительная память связана с сохранением и воспроизведением зрительных образов. Люди с развитой зрительной памятью обычно имеют хорошо развитое воображение и способны «видеть» информацию, даже когда она уже не воздействует на органы чувств. Зрительная память очень важна для людей некоторых профессий: художников, инженеров, конструкторов. Упомянутое раньше эйдетическое зрение, или феноменальная память, также характеризуется богатым воображением, обилием образов.
Зрительная память очень важна для людей некоторых профессий: художников, инженеров, конструкторов. Упомянутое раньше эйдетическое зрение, или феноменальная память, также характеризуется богатым воображением, обилием образов.
Слуховая память — это хорошее запоминание и точное воспроизведение разнообразных звуков: речи, музыки. Такая память особенно необходима при изучении иностранных языков, музыкантам, композиторам.
Осязательная, обонятельная и вкусовая память – это примеры памяти, (существуют и другие виды, которые не будут упомянуты), не играющей существенной роли в жизни человека, т. к. возможности такой памяти очень ограниченны и ее роль – это удовлетворение биологических потребностей организма. Эти виды памяти развиваются особенно остро у людей определенных профессий, а также в особых жизненных обстоятельствах (классические примеры: слепорожденные и слепоглухонемые).
4. Словесно-логическая память — это разновидность запоминания, когда большую роль в процессе запоминания играет слово, мысль, логика. В данном случае человек старается понять усваиваемую информацию, прояснить терминологию, установить все смысловые связи в тексте, и только после этого запомнить материал. Людям с развитой словесно-логической памятью легче запоминать словесный, абстрактный материал, понятия, формулы. Этим типом памяти, в сочетании со слуховой, обладают ученые, а так же опытные лекторы, преподаватели вузов и т. д. Логическая память при ее тренировке дает очень хорошие результаты, и более эффективна, чем простое механическое запоминание. Некоторые исследователи считают, что эта память формируется и начинает «работать» позже других видов. П. П. Блонский называл ее » память-рассказ». Она имеется у ребенка уже в 3-4 года, когда начинают развиваться самые основы логики. Развитие логической памяти происходит с обучением ребенка основам наук.
В данном случае человек старается понять усваиваемую информацию, прояснить терминологию, установить все смысловые связи в тексте, и только после этого запомнить материал. Людям с развитой словесно-логической памятью легче запоминать словесный, абстрактный материал, понятия, формулы. Этим типом памяти, в сочетании со слуховой, обладают ученые, а так же опытные лекторы, преподаватели вузов и т. д. Логическая память при ее тренировке дает очень хорошие результаты, и более эффективна, чем простое механическое запоминание. Некоторые исследователи считают, что эта память формируется и начинает «работать» позже других видов. П. П. Блонский называл ее » память-рассказ». Она имеется у ребенка уже в 3-4 года, когда начинают развиваться самые основы логики. Развитие логической памяти происходит с обучением ребенка основам наук.
По продолжительности сохранения информации:
1) Мгновенная или иконическая память
Данная память удерживает материал, который был только что получен органами чувств, без какой-либо переработки информации. Длительность данной памяти — от 0,1 до 0,5 с. Часто, в этом случае, человек запоминает информацию без сознательных усилий, даже против своей воли. Это память-образ.
Длительность данной памяти — от 0,1 до 0,5 с. Часто, в этом случае, человек запоминает информацию без сознательных усилий, даже против своей воли. Это память-образ.
Человек воспринимает электромагнитные колебания, изменения давления воздуха, изменение положения объекта в пространстве, придавая им определённое значение. Стимул всегда несёт в себе определённую информацию, специфичную лишь для него. Воздействующие на рецептор в сенсорной системе физические параметры стимула преобразуются в определённые состояния центральной нервной системы (ЦНС). Установление соответствия между физическими параметрами стимула и состоянием ЦНС невозможно без работы памяти. Данная память проявляется у детей еще в дошкольном возрасте, но с годами ее значение для человека возрастает.
2) Кратковременная память
Сохранение информации в течение короткого промежутка времени: в среднем около 20 с. Этот вид запоминания может происходить после однократного или очень краткого восприятия. Эта память работает без сознательного усилия для запоминания, но с установкой на будущее воспроизведение. В памяти сохраняются самые существенные элементы воспринятого образа. Кратковременная память «включается», когда действует, так называемое, актуальное сознание человека (т.е. то, что осознается человеком и как-то соотносится с его актуальными интересами и потребностями).
Эта память работает без сознательного усилия для запоминания, но с установкой на будущее воспроизведение. В памяти сохраняются самые существенные элементы воспринятого образа. Кратковременная память «включается», когда действует, так называемое, актуальное сознание человека (т.е. то, что осознается человеком и как-то соотносится с его актуальными интересами и потребностями).
Информация вводится в кратковременную память с помощью обращения внимания на нее. Например: человек, сотни раз видевший свои наручные часы, может не ответить на вопрос: «Какой цифрой — римской или арабской — изображена на часах цифра шесть?». Он никогда целенаправленно не воспринимал этот факт и, таким образом, информация не отложилась в кратковременной памяти.
Объем кратковременной памяти очень индивидуален, и существуют разработанные формулы и методы для ее измерения. В связи с этим необходимо сказать о такой ее особенности, как свойство замещения. Когда индивидуальный объем памяти переполняется, новая информация частично замещает уже хранящуюся там, а прежняя информация часто безвозвратно исчезает. Хорошим примером могут быть трудности при запоминании обилия фамилий и имён людей, с которыми мы только что познакомились. Человек способен удержать в кратковременной памяти не больше имен, чем позволяет его индивидуальный объем памяти.
Хорошим примером могут быть трудности при запоминании обилия фамилий и имён людей, с которыми мы только что познакомились. Человек способен удержать в кратковременной памяти не больше имен, чем позволяет его индивидуальный объем памяти.
Сделав сознательное усилие, можно удержать информацию в памяти дольше, что обеспечит её перевод в оперативную память. Это лежит в основе запоминания путем повторения.
На самом деле, кратковременная память играет важнейшую роль. Благодаря кратковременной памяти перерабатывается громадный объём информации. Сразу же отсеивается не нужная и остается то, что потенциально полезно. В результате, не происходит перегрузки долговременной памяти излишними сведениями. Кратковременная память организовывает мышление человека, так как мышление «черпает» информацию и факты именно из кратковременной и оперативной памяти.
3) Оперативная память – это память, рассчитанная на сохранение информации в течение определённого, заранее заданного срока. Срок хранения информации колеблется от нескольких секунд до нескольких дней.
Срок хранения информации колеблется от нескольких секунд до нескольких дней.
После решения поставленной задачи информация может исчезнуть из оперативной памяти. Хорошим примером может быть информация, которую пытается вложить в себя студент на время экзамена: четко заданы временные рамки и задача. После сдачи экзамена снова наблюдается полная «амнезия» по данному вопросу. Этот вид памяти является, как бы переходным от кратковременной к долговременной, так как включает в себя элементы и той, и другой памяти.
4) Долговременная память — память, способная хранить информацию в течение неограниченного срока.
Эта память начинает функционировать не сразу после того, как был заучен материал, а спустя некоторое время. Человек должен переключиться с одного процесса на другой: с запоминания на воспроизведение. Эти два процесса несовместимы и их механизмы полностью разные.
Интересно, что чем чаще воспроизводится информация, тем прочнее она закрепляется в памяти. Иными словами, человек может в любой нужный момент припомнить информацию с помощью усилия воли. Интересно заметить, что умственные способности не всегда являются показателем качества памяти. Например, у слабоумных людей, иногда встречается феноменальная долговременная память.
Иными словами, человек может в любой нужный момент припомнить информацию с помощью усилия воли. Интересно заметить, что умственные способности не всегда являются показателем качества памяти. Например, у слабоумных людей, иногда встречается феноменальная долговременная память.
Почему же для восприятия информации необходима способность к её сохранению? Это объясняется двумя основными причинами. Во-первых, человек имеет дело в каждый момент времени лишь с относительно небольшими фрагментами внешнего окружения. Чтобы интегрировать эти разделённые во времени воздействия в целостную картину окружающего мира, эффекты предшествовавших событий при восприятии последующих должны быть, так сказать, «под рукой». Вторая причина связана с целенаправленностью нашего поведения. Приобретаемый опыт должен запоминаться в таком виде, чтобы его можно было успешно использовать для последующей регуляции направленных на достижение сходных целей форм поведения. Хранящаяся в памяти человека информация оценивается им с точки зрения значения её для управления поведением и в соответствии с этой оценкой удерживается в различной степени готовности.
Человеческая память ни в малейшей степени не пассивный хранитель информации – это активная деятельность.
Большинство людей периодически сетуют на свою «девичью» память. Как правило, они практически не расстаются с ежедневниками, в которых тщательно вписывают все свои планы на будущий день. Однако трудности подстерегают повсюду. Иногда невозможность вспомнить чье-то имя может поставить в достаточно неловкую ситуацию.
Как развить память у взрослого?
Подобный вопрос периодически задают себе забывчивые люди. И те, кто не только ищут ответ, но и начинают внедрять все рекомендации в жизнь, со временем замечают прекрасный результат.
Причины плохой памяти
С возрастом у людей ухудшается способность к запоминанию, а также появляется рассеянность. Человеку необходимо держать к голове слишком много информации, из-за чего он иногда забывает самые очевидные факты. Но дело не только в этом. Чем старше становится человек, тем хуже его способность рассуждать здраво. Причины плохой памяти у взрослых сокрыты как в возрастных изменениях, так и в неправильном образе жизни, стрессах, плохом сне и многом другом. Нервных клеток становится меньше, и наряду с этим человеку все труднее вникать во что-то новое. Плохая память у взрослого может являться следствием некоторых заболеваний. Отмечается, что на способность запоминания, а также мышление, неблагоприятно влияют: высокое давление; атеросклероз; диабет; полнота. Иногда ухудшение запоминания может быть следствием развивающейся болезни Альцгеймера.
Причины плохой памяти у взрослых сокрыты как в возрастных изменениях, так и в неправильном образе жизни, стрессах, плохом сне и многом другом. Нервных клеток становится меньше, и наряду с этим человеку все труднее вникать во что-то новое. Плохая память у взрослого может являться следствием некоторых заболеваний. Отмечается, что на способность запоминания, а также мышление, неблагоприятно влияют: высокое давление; атеросклероз; диабет; полнота. Иногда ухудшение запоминания может быть следствием развивающейся болезни Альцгеймера.
Методы улучшения памяти
Удивительную способность можно натренировать, как, например, мышцу тела. Для этого нужно делать специальные упражнения для памяти. У взрослых, конечно, тренировка потребует определенных усилий. Ведь легче всего это происходит в детском возрасте. Малыши стараются запомнить все, что попадается им на глаза.
Упражнения для памяти у взрослых
Нагрузка на память школьника уже достаточно существенна. Но когда человек заканчивает учиться и начинает работать, его память больше не поддается систематической тренировке. Жизнь становится более скучной и обыденной. Для того чтобы память продолжала развиваться, человек должен получать впечатления. Хорошо, если происходят различные приятные события, и люди стараются их не забыть.
Жизнь становится более скучной и обыденной. Для того чтобы память продолжала развиваться, человек должен получать впечатления. Хорошо, если происходят различные приятные события, и люди стараются их не забыть.
Влияние табака
Прежде всего необходимо избавиться от пагубного влияния никотина. Многочисленные исследования подтвердили, что табак достаточно сильно ухудшает способность запоминать. Если сравнить человека, который тренирует память и при этом курит, и другого, который не работает над способностью запоминать, но и вредной привычки у него нет, то окажется, что у первого результат лучше. Однако если их условия уравнять, то окажется, что табак все же ухудшает память. Исследования показали, что курящие студенты хуже справляются с заданиями, чем некурящие. Хотя табак имеет свойство мгновенно повышать концентрацию внимания, однако это быстро проходит.
Влияние алкоголя
Гибкий ум невозможно сохранить, принимая спиртосодержащие напитки. Ведь они также ослабляют память. Даже малая доза спиртного снижает способность запоминать. Систематический его прием лишает человека возможности фиксировать что-то в памяти. Поэтому тем людям, которые задумываются о том, как развить память у взрослого, следует отказаться от спиртного. методики развития памяти у взрослых Рекомендуется исключить все виды алкоголя перед ответственным мероприятием, на котором необходимо что-то запоминать.
Даже малая доза спиртного снижает способность запоминать. Систематический его прием лишает человека возможности фиксировать что-то в памяти. Поэтому тем людям, которые задумываются о том, как развить память у взрослого, следует отказаться от спиртного. методики развития памяти у взрослых Рекомендуется исключить все виды алкоголя перед ответственным мероприятием, на котором необходимо что-то запоминать.
Медикаментозные препараты
Прием некоторых лекарств также может влиять на запоминание и даже вызывать провалы в памяти. К ним относятся различные успокаивающие или возбуждающие препараты, а также обезболивающие, антигистаминные и противовоспалительные средства.
Основные рекомендации
Существуют правила, позволяющие памяти всегда оставаться в рабочем состоянии: обогащать кровь кислородом; обязательно хорошо высыпаться; не злоупотреблять алкоголем и табаком; отказаться (по возможности) от лекарств, снижающих память.
Методики запоминания от гениев
Психолог Карл Сишор считает, что обычный человек использует свою память только на 10%, в то время как 90% остаются без применения. Мало кто знает, что практически все методики развития памяти у взрослых базируются на трех природных законах запоминания. Речь идет про эмоции, ассоциации и повторения. Знание этих правил способно помочь как в обыденной жизни, так и в ответственных ситуациях.
Мало кто знает, что практически все методики развития памяти у взрослых базируются на трех природных законах запоминания. Речь идет про эмоции, ассоциации и повторения. Знание этих правил способно помочь как в обыденной жизни, так и в ответственных ситуациях.
Закон эмоций гласит, что для лучшего запоминания достаточно получить яркие впечатления о заданном предмете. Самым известным человеком, использовавшим данное правило, был Рузвельт. Он всегда сохранял отличную концентрацию внимания. Все, что он прочитывал, запоминал почти дословно. Секрет данной методики развития памяти у взрослых сокрыт в необходимости полностью сосредоточиться, хотя бы ненадолго, на нужной информации. Именно в этом случае она запомнится лучше, чем если долго размышлять о ней и отвлекаться.
Удивительную методику оставил после себя Наполеон. Он отлично помнил на смотре войск расположение каждого своего бойца и его фамилию. Секрет его запоминания имени человека состоял в том, чтобы получить о нем более яркое впечатление. Например, спросив, как пишется его фамилия.
Например, спросив, как пишется его фамилия.
Президент Линкольн имел свою методику запоминания: он читал вслух то, что было важно помнить. Получается, что нужно задействовать как можно больше органов чувств. Это позволяет достаточно эффективно повлиять на развитие памяти у взрослых. Упражнения, которые строятся на задействовании нескольких чувств, рекомендуются большинством психологов. К примеру, чтобы запомнить, достаточно записать, а затем мысленно представить написанное.
Марк Твен часто читал лекции. Чтобы запомнить длинный текст, он записывал пару слов с начала каждого абзаца. Перед выступлением Твен повторял всю лекцию, используя эту шпаргалку. Но затем ему пришла в голову другая идея — и он стал рисовать то, что ему нужно было запомнить. Таким образом, гении прошлого смогли воплотить все три закона запоминания.
Как развить память у взрослого: упражнения для тренировки
Тренировка памяти у взрослых должна начинаться со следующих упражнений: 5-10 секунд сохраняйте полностью свободный от мыслей ум. Это необходимо для тренировки концентрации внимания. Во время данного процесса не должно возникать какого-либо напряжения: нервного либо психического. С пяти секунд очень важно постепенно дойти до тридцати секунд непрерывного нахождения в этом состоянии.
Это необходимо для тренировки концентрации внимания. Во время данного процесса не должно возникать какого-либо напряжения: нервного либо психического. С пяти секунд очень важно постепенно дойти до тридцати секунд непрерывного нахождения в этом состоянии.
Очень важно развивать не только зрительную или слуховую способность запоминания, но и другие виды. Также нужно помнить, что краткосрочная и долгосрочная память в одинаковой мере необходимы человеку.
Зрительную память можно натренировать, если пытаться запомнить внешность проходящих мимо людей. Достаточно мимолетного взгляда на человека, идущего навстречу, и затем нужно попробовать представить себе его облик во всех деталях.
Очень полезно время от времени спрашивать себя, как выглядит обертка любимой конфеты, что там изображено.
Можно пытаться представить, что вы видели, когда проходили в очередной раз мимо магазина, какая там была вывеска. При этом нужно стараться вспомнить все до мельчайших подробностей.
Для того чтобы улучшить звуковую память, достаточно регулярно читать вслух либо учить стихотворения с ребенком. Пропойте только что прослушанную мелодию. В уличном шуме старайтесь расслышать обрывки фраз и зафиксировать их в памяти.
Принимая пищу, вообразите себя дегустатором, который досконально запоминает вкус блюда. Ассоциируйте каждое кушанье с чем-либо. Играйте на угадывание блюда с закрытыми глазами.
В парфюмерном магазине брызгайте понравившиеся духи на тест-полоску. Затем пытайтесь вспомнить их название. Тренируйтесь со всеми окружающими вас запахами. Можно начать с более простых ароматов, далее переходите к более сложным.
Попробуйте развить числовую память. Для того чтобы запомнить целую комбинацию, нужно всего лишь выбросить калькулятор. Для начала можно просто определять в магазине сдачу при каждой покупке. Расчеты в уме очень тренируют память, связанную с числами. Попробуйте определить цену на каждый продукт.
Считайте свои шаги, например, от входа в квартиру до двери лифта. Можно попробовать запомнить, сколько раз вам приходится прокрутить лампу в патроне, прежде чем она будет закручена достаточно туго. причины плохой памяти у взрослых.
Все виды памяти прекрасно развиваются при помощи любых видов настольных игр. Ускорить мыслительные процессы можно при помощи шахмат и шашек, игральных карт, домино.
Отлично натренировать память поможет разгадывание кроссвордов, а также всяческие головоломки.
Оригами улучшает механическую память. Различные виды рукоделия, типа вязания, вышивки и рисования, улучшают мелкую моторику и концентрацию на деталях.
При недостаточном эффекте от самостоятельных занятий необходимо обратиться к специалистам: неврологу или психиатру.
Кроме этого, в г. Оренбурге по адресу: ул. Пролетарская, д. 153 работает «Школа для пациентов с проблемами памяти». Занятия проходят каждую вторую среду месяца. Запись по телефону (3532) 40-20-11.
Запись по телефону (3532) 40-20-11.
Памятью обладают все. У некоторых людей отмечается просто феноменальная способность к запоминанию. Другие сознаются в том, что являются обладателями «дырявой» головы. По мнению психологов, людей с плохой памятью крайне мало. При этом очень много тех, кто не умеет правильно ее использовать или не знает, как развить память у взрослого.
Статья подготовлена врачом-неврологом высшей квалификационной категории Гранкиным С. А.
При подготовке статьи использовались материалы сайта:
http://fb.ru/article/162910/kak-razvit-pamyat-u-vzroslogo-uprajneniya-dlya-trenirovki-obzor-luchshih-metodik-po-razvitiyu-pamyati
http://fb.ru/, Обзор лучших методик по развитию памяти, Елена Билецкая, December 29, 2014
химической кинетики | Определение, уравнения и факты
Химическая кинетика , раздел физической химии, который занимается изучением скорости химических реакций. Ее следует противопоставить термодинамике, которая имеет дело с направлением, в котором происходит процесс, но сама по себе ничего не говорит о его скорости. Термодинамика — это стрела времени, а химическая кинетика — это часы времени. Химическая кинетика относится ко многим аспектам космологии, геологии, биологии, инженерии и даже психологии и, таким образом, имеет далеко идущие последствия.Принципы химической кинетики применимы как к чисто физическим процессам, так и к химическим реакциям.
Ее следует противопоставить термодинамике, которая имеет дело с направлением, в котором происходит процесс, но сама по себе ничего не говорит о его скорости. Термодинамика — это стрела времени, а химическая кинетика — это часы времени. Химическая кинетика относится ко многим аспектам космологии, геологии, биологии, инженерии и даже психологии и, таким образом, имеет далеко идущие последствия.Принципы химической кинетики применимы как к чисто физическим процессам, так и к химическим реакциям.
Британская викторина
Подводки к химии
Возможно, вы знаете, что элементы составляют воздух, которым мы дышим, и воду, которую мы пьем, но знаете ли вы о них больше? Какой элемент почти такой же легкий, как водород? Что вы называете смесью двух химических элементов? Узнайте ответы в этой викторине.
Одна из причин важности кинетики заключается в том, что она предоставляет доказательства механизмов химических процессов. Помимо научного интереса, знание механизмов реакции имеет практическое применение при принятии решения о том, какой способ вызвать реакцию является наиболее эффективным. Многие коммерческие процессы могут происходить с использованием альтернативных путей реакции, и знание механизмов позволяет выбирать условия реакции, которые благоприятствуют одному пути по сравнению с другим.
Помимо научного интереса, знание механизмов реакции имеет практическое применение при принятии решения о том, какой способ вызвать реакцию является наиболее эффективным. Многие коммерческие процессы могут происходить с использованием альтернативных путей реакции, и знание механизмов позволяет выбирать условия реакции, которые благоприятствуют одному пути по сравнению с другим.
Химическая реакция — это, по определению, реакция, в которой химические вещества преобразуются в другие вещества, что означает, что химические связи разрываются и образуются, так что взаимное расположение атомов в молекулах изменяется. В то же время происходят сдвиги в расположении электронов, образующих химические связи. Поэтому описание механизма реакции должно касаться движений и скоростей атомов и электронов. Подробный механизм, с помощью которого происходит химический процесс, называется реакционным путем или путем.
Огромный объем работы, проделанной в области химической кинетики, привел к выводу, что некоторые химические реакции протекают в один этап; они известны как элементарные реакции. Другие реакции проходят в несколько стадий и называются ступенчатыми, сложными или сложными. Измерения скорости химических реакций в ряде условий могут показать, идет ли реакция в одну или несколько стадий. Если реакция ступенчатая, кинетические измерения подтверждают механизм отдельных элементарных шагов.Информация о механизмах реакции также предоставляется некоторыми некинетическими исследованиями, но мало что может быть известно о механизме до тех пор, пока не будет исследована его кинетика. Даже в этом случае всегда должно оставаться некоторое сомнение относительно механизма реакции. Исследование, кинетическое или иное, может опровергнуть механизм, но никогда не может установить его с абсолютной уверенностью.
Другие реакции проходят в несколько стадий и называются ступенчатыми, сложными или сложными. Измерения скорости химических реакций в ряде условий могут показать, идет ли реакция в одну или несколько стадий. Если реакция ступенчатая, кинетические измерения подтверждают механизм отдельных элементарных шагов.Информация о механизмах реакции также предоставляется некоторыми некинетическими исследованиями, но мало что может быть известно о механизме до тех пор, пока не будет исследована его кинетика. Даже в этом случае всегда должно оставаться некоторое сомнение относительно механизма реакции. Исследование, кинетическое или иное, может опровергнуть механизм, но никогда не может установить его с абсолютной уверенностью.
Скорость реакции определяется скоростью, с которой образуются продукты и расходуются реагенты (реагирующие вещества).Для химических систем обычно имеют дело с концентрациями веществ, которые определяются как количество вещества в единице объема. Скорость может быть определена как концентрация вещества, которое потребляется или производится в единицу времени. Иногда удобнее выражать скорость как количество молекул, образовавшихся или потребленных за единицу времени.
Скорость может быть определена как концентрация вещества, которое потребляется или производится в единицу времени. Иногда удобнее выражать скорость как количество молекул, образовавшихся или потребленных за единицу времени.
Полезная мера скорости — это период полураспада реагента, который определяется как время, которое требуется для того, чтобы половина исходного количества вступила в реакцию.Для особого типа кинетического поведения (кинетика первого порядка; см. Ниже Некоторые кинетические принципы) период полураспада не зависит от начального количества. Обычный и простой пример периода полураспада, не зависящего от начального количества, — это радиоактивные вещества. Уран-238, например, распадается с периодом полураспада 4,5 миллиарда лет; Из первоначального количества урана половина этого количества распадется за этот период времени. Такое же поведение наблюдается во многих химических реакциях.
Даже когда период полураспада реакции меняется в зависимости от начальных условий, часто бывает удобно указать период полураспада, имея в виду, что это применимо только к конкретным начальным условиям. Рассмотрим, например, реакцию, в которой газообразные водород и кислород соединяются с образованием воды; химическое уравнение: 2H 2 + O 2 → 2H 2 O. Если газы смешать вместе при атмосферном давлении и комнатной температуре, то в течение длительного времени ничего наблюдаемого не произойдет.Однако реакция все же происходит с периодом полураспада, который оценивается более чем в 12 миллиардов лет, что примерно соответствует возрасту Вселенной. Если искра проходит через систему, реакция происходит с взрывной силой с периодом полураспада менее одной миллионной секунды. Это яркий пример большого диапазона скоростей, с которыми связана химическая кинетика. Есть много возможных процессов, которые протекают слишком медленно, чтобы их можно было изучить экспериментально, но иногда их можно ускорить, часто путем добавления вещества, известного как катализатор.Некоторые реакции протекают даже быстрее, чем водородно-кислородный взрыв — например, сочетание атомов или молекулярных фрагментов (называемых свободными радикалами), при котором все, что происходит, — это образование химической связи.
Рассмотрим, например, реакцию, в которой газообразные водород и кислород соединяются с образованием воды; химическое уравнение: 2H 2 + O 2 → 2H 2 O. Если газы смешать вместе при атмосферном давлении и комнатной температуре, то в течение длительного времени ничего наблюдаемого не произойдет.Однако реакция все же происходит с периодом полураспада, который оценивается более чем в 12 миллиардов лет, что примерно соответствует возрасту Вселенной. Если искра проходит через систему, реакция происходит с взрывной силой с периодом полураспада менее одной миллионной секунды. Это яркий пример большого диапазона скоростей, с которыми связана химическая кинетика. Есть много возможных процессов, которые протекают слишком медленно, чтобы их можно было изучить экспериментально, но иногда их можно ускорить, часто путем добавления вещества, известного как катализатор.Некоторые реакции протекают даже быстрее, чем водородно-кислородный взрыв — например, сочетание атомов или молекулярных фрагментов (называемых свободными радикалами), при котором все, что происходит, — это образование химической связи. Некоторые современные кинетические исследования связаны с еще более быстрыми процессами, такими как разрушение высокоэнергетических и, следовательно, переходных молекул, в которых задействовано время порядка фемтосекунд (фс; 1 фс = 10 –15 секунды).
Некоторые современные кинетические исследования связаны с еще более быстрыми процессами, такими как разрушение высокоэнергетических и, следовательно, переходных молекул, в которых задействовано время порядка фемтосекунд (фс; 1 фс = 10 –15 секунды).
Измерение медленных реакций
Лучший способ изучить чрезвычайно медленные реакции — это изменить условия так, чтобы реакции происходили в разумные сроки.Одна из возможностей — повышение температуры, которое может сильно повлиять на скорость реакции. Если температура водородно-кислородной смеси повышается примерно до 500 ° C (900 ° F), реакция происходит быстро, и ее кинетика изучается в этих условиях. Когда реакция происходит в измеримой степени в течение минут, часов или дней, измерения скорости просты. Количества реагентов или продуктов измеряются в разное время, и скорости легко рассчитываются на основе результатов.В настоящее время разработано множество автоматизированных систем для измерения скорости таким образом.
Kinetics Type — обзор
Chain Type Kinetics.
Кинетика цепного типа, вероятно, наиболее изученная и наиболее изученная кинетическая система. С виниловыми реагентами реакцию можно понять с точки зрения трех основных реакций. Используя свободнорадикальный процесс с использованием инициатора, I, мономера M и свободного радикала с помощью символа «w», мы можем описать эти три группы.
Инициирование
(2) R * + M → R − M * или просто M *
Поскольку энергия активации для разложения выше, чем для добавления R * к M, первым шагом является определение скорости шаг с соответствующей константой скорости k d , так что скорость образования радикальных цепочек инициатора равна
Это выражение обычно модифицируют, чтобы отразить, что два активных свободных радикала создаются для каждого разложения I путем включения «2» .Кроме того, все R * не создают растущие полимерные цепи свободных радикалов, поэтому добавляется некоторый фактор f, который представляет собой долю цепей, которые действительно начинают рост цепи. Таким образом, скорость образования радикалов обычно дается как
Таким образом, скорость образования радикалов обычно дается как
Распространение
M − M − M * + M → M − M − M − M * Etc.
Поскольку экспериментально установлено, что скорости добавления различные мономеры растущей цепи свободных радикалов подобны, обычно всю последовательность размножения следует рассматривать следующим образом.
(6) M * + M → M *
с соответствующим выражением скорости для распространения цепи (p)
Завершение
Завершение обычно осуществляется с помощью двух механизмов
(8) комбинация M * + M * → M − M
и
(9) диспропорционирование M * + M * → M + M
Соответствующее скоростное выражение для прерывания (tr) равно
(10) Ratetr = 2ktr [M *] [M *]
«2» добавляется для распознавания того факта, что задействованы две растущие цепи, которые уничтожаются каждый раз, когда происходит завершение.
Скорость использования мономера может быть описана как
(11) Скорость = kp [M *] [M] + ki [R *] [M]
, где k i — удельная константа скорости для мономера -потребляющий этап инициации.
Поскольку большая часть потребления мономера происходит на стадии роста или размножения, вторым членом можно пренебречь, получая
Хотя это простое выражение скорости, концентрацию свободнорадикального мономера нелегко измерить. Таким образом, типичная кинетическая обработка ищет способ описать скорость реакции в терминах более легко измеримых значений.
Экспериментально установлено, что общее количество «живых» или растущих свободнорадикальных цепей обычно примерно постоянное в процессе полимеризации, так что скорость инициирования и распространения одинакова.
(13) ki [R *] [M] = 2ktr [M *] [M *]
Кроме того, R * не меняется со временем, так что два выражения скорости для реакций инициирования, включающих создание и кончина R * равны друг другу.
Управляя уравнениями 13 и 14, можно получить выражение для [M *], которое содержит легко измеряемые величины, которые можно заменить на [M *].
(15) Ratep = kp [M⋅] [M] = kp [M] (kdf [l] / kt) 1/2
Кинетические выражения для реакций конденсации аналогичны кинетическим выражениям для большинства других кислотно-основных реакций Льюиса. . Для образования сложных полиэфиров в результате реакции двухосновной кислоты A и диола B в отсутствие добавленных катализаторов было установлено, что выражение скорости равно
. Для образования сложных полиэфиров в результате реакции двухосновной кислоты A и диола B в отсутствие добавленных катализаторов было установлено, что выражение скорости равно
Rate = k [A] [B] и где [A] = [B] выражение принимает вид
(16) Rate = k [A] [B], а где [A] = [B], выражение принимает вид Rate = k [A] 2
Учитывая, что «p» — это степень реакция, так что «1-p» представляет собой долю функциональных групп, которые не прореагировали, мы имеем при интеграции и последующем замещении
(17) kt = (1 / [At]) — (1 / [Ao])
и что
(18) [At] = [Ao] (1-p)
, что дает после перегруппировки
Таким образом, существует линейная зависимость 1/1-p от времени.
Молекулярная масса полимера весьма чувствительна к присутствию примесей в ступенчатых процессах. Это демонстрируется в следующем расчете. Степень полимеризации, DP или количество повторяющихся звеньев определяется как
Умножение уравнения 19 на [A o ] и перегруппировка дает
Объединение этого с уравнением 18 дает
Таким образом, высокая чистота и высокая степень реакции являются необходимо для получения высокомолекулярных полимеров.
Кинетика | Энциклопедия.com
Химическая кинетика — это исследование скорости химических реакций. Такие скорости реакции варьируются от почти мгновенных, как при взрыве, до почти незаметно медленных, как при коррозии. Целью химической кинетики является прогнозирование состава реакционных смесей как функции времени, понимание процессов, происходящих во время реакции, и определение факторов, контролирующих ее скорость.
Скорости и законы скорости
Скорость химической реакции определяется как скорость изменения концентрации одного из ее компонентов, либо реагента, либо продукта.Таким образом, экспериментальное исследование скорости реакции зависит от возможности отслеживать изменение концентрации во времени. Классические процедуры для реакций, протекающих за часы или минуты, используют различные методы определения концентрации, такие как спектроскопия , и электрохимия. Спектроскопически изучаются очень быстрые реакции. Спектроскопические процедуры доступны для мониторинга реакций, которые инициируются быстрым импульсом электромагнитного излучения и заканчиваются за несколько фемтосекунд (1 фс = 10 −15 с).
Анализ кинетических данных обычно осуществляется путем установления закона скорости , математического выражения скорости в терминах концентраций реагентов (а иногда и продуктов) на каждой стадии реакции. Например, можно обнаружить, что скорость потребления реагента пропорциональна концентрации реагента, и в этом случае закон скорости равен
Скорость = k [Реагент]
, где [Реагент] обозначает концентрацию реагента и k называется константой скорости.Константа скорости не зависит от концентрации каких-либо компонентов в реакционной смеси, но зависит от температуры. Реакция с законом скорости этой формы классифицируется как закон скорости первого порядка . В более общем смысле, реакция с законом скорости формы
Скорость = k [Реагент A] a [Реагент B] b …
считается порядка a в A порядка b в B и иметь общий порядок a + b +….Некоторые законы скорости намного сложнее, чем эти два простых примера, и многие из них связаны с концентрациями продуктов.
Преимущество определения порядка реакции состоит в том, что все реакции с одним и тем же законом скорости (но с разными характеристическими константами скорости) ведут себя одинаково. Например, концентрация реагента в реакции первого порядка экспоненциально спадает со временем со скоростью, определяемой константой скорости
[Reactant] = [Reactant] 0 e −kt
где [Реагент] 0 — начальная концентрация реагента.С другой стороны, все реакции второго порядка приводят к следующей зависимости концентрации от времени:
На рисунке 1 показана зависимость от времени, предсказываемая этими выражениями. Обычно сообщают о временной зависимости реакций первого порядка в терминах периода полураспада 90–150, t ½ , реагента, времени, необходимого для того, чтобы его концентрация упала до половины от исходного значения. Для реакции первого порядка (но не для других порядков)
Таким образом, реакции с большими константами скорости имеют короткие периоды полураспада.
Механизмы реакций
Определение закона скорости дает ценную информацию о механизме реакции, последовательности элементарных шагов, посредством которых происходит реакция. Цель состоит в том, чтобы определить механизм реакции путем построения закона скорости, который он подразумевает. Эту процедуру можно упростить, указав этап , определяющий скорость, реакции, самый медленный этап в последовательности, определяющей общую скорость. Таким образом, если предложенный механизм — A → B, за которым следует B → C, и первый намного быстрее, чем последний, то общая скорость реакции будет равна скорости A → B, поскольку после образования B он сразу преобразуется в C.
В общем, для механизма, состоящего из многих шагов (включая их обратную), построение общего закона скорости довольно сложно, требуя аппроксимации или компьютера для численного анализа. Одним из распространенных приближений
является допущение устойчивого состояния , , в котором чистая скорость образования любого промежуточного звена (B в данном примере) установлена равной нулю. Однако опасность использования кинетической информации для определения механизма реакции состоит в том, что несколько механизмов могут привести к одному и тому же закону скорости, особенно когда получены приблизительные решения.По этой причине предполагаемый механизм реакции должен подтверждаться дополнительными доказательствами.
Однако опасность использования кинетической информации для определения механизма реакции состоит в том, что несколько механизмов могут привести к одному и тому же закону скорости, особенно когда получены приблизительные решения.По этой причине предполагаемый механизм реакции должен подтверждаться дополнительными доказательствами.
Происхождение скоростей реакций
После того, как механизм реакции идентифицирован, внимание обращается на молекулярные свойства, которые определяют значения констант скорости, которые возникают на отдельных элементарных стадиях. Ключ к разгадке вовлеченных факторов дается экспериментальным наблюдением, что константы скорости многих реакций зависят от температуры в соответствии с выражением Аррениуса
, где E a называется энергией активации .
Простейшей моделью, которая учитывает выражение Аррениуса, является теория столкновений скоростей реакции газ- фаза , в которой предполагается, что реакция происходит, когда две молекулы реагента сталкиваются, по крайней мере, с минимальной кинетической энергией (которая равна отождествляется с энергией активации, рисунок 2). Более сложной теорией является теория активированного комплекса (также известная как теория переходного состояния ), в которой предполагается, что реагенты сталкиваются друг с другом, образуют разрыхленный кластер атомов, а затем распадаются на продукты.
Более сложной теорией является теория активированного комплекса (также известная как теория переходного состояния ), в которой предполагается, что реагенты сталкиваются друг с другом, образуют разрыхленный кластер атомов, а затем распадаются на продукты.
Реакции в растворах требуют более детального рассмотрения, чем реакции в газах. Необходимо различать реакции, контролируемые диффузией, и реакции
, контролируемые активацией. В реакции, управляемой диффузией, скорость регулируется способностью реагентов мигрировать через растворитель и встречаться друг с другом. В реакции, управляемой активацией, скорость регулируется способностью реагентов, которые встретились друг с другом, приобретать достаточно энергии для реакции.
Скорость реакции также можно увеличить, найдя катализатор , вещество, которое принимает участие в реакции, обеспечивая альтернативный путь с более низкой энергией активации, но регенерируется в процессе и поэтому не расходуется. Катализ — это основа химической промышленности, и прилагаются огромные усилия для обнаружения или изготовления эффективных и экономичных катализаторов. Это также основа жизни, потому что биологические катализаторы, известные как ферменты (сложные белковые молекулы), контролируют почти все аспекты функционирования организма.
Катализ — это основа химической промышленности, и прилагаются огромные усилия для обнаружения или изготовления эффективных и экономичных катализаторов. Это также основа жизни, потому что биологические катализаторы, известные как ферменты (сложные белковые молекулы), контролируют почти все аспекты функционирования организма.
см. Также Катализ и катализаторы; Ферменты; Физическая химия.
Питер Аткинс
Библиография
Аткинс, Питер и де Паула, Хулио (2002). Физическая химия. Нью-Йорк: W.H. Фримен.
Аткинс, Питер и Джонс, Лоретта (2001). Химические основы. Нью-Йорк: W.H. Фримен.
Лайдлер, К. Дж. (1987). Химическая кинетика. Нью-Йорк: Харпер и Роу.
Пиллинг, М. Дж., И Сикинс, П.W. (1996). Кинетика реакций. Лондон: Издательство Оксфордского университета.
| Ресурсы базы данных кинетики Поиск простой реакции База данных поисковых реакций Поиск по библиографической базе данных Установить настройки единиц измерения Обратная связь Отправить статью Оцените наши продукты и услуги Цитата Справка Другие базы данных Программа стандартных справочных данных NIST Интернет-книга по химии NIST База данных кинетики решений NDRL-NIST База данных сравнительных и контрольных показателей по вычислительной химии NIST Справочник NIST по константам, единицам и неопределенности Подробнее. Административные ссылки Домашняя страница DOC Домашняя страница NIST Домашняя страница MML Отделение химических наук | База данных химической кинетики NIST включает практически всю зарегистрированную кинетику. результаты для термических газофазных химических реакций. База данных предназначена для искать данные кинетики на основе конкретных задействованных реагентов, для реакции, приводящие к указанным продуктам, для всех реакций отдельные виды или различные их комбинации.В дополнение библиографию можно искать по имени автора или комбинации имен. В база данных содержит более 38000 отдельных записей реакций для более чем 11700 различные пары реагентов. Эти данные были взяты из более чем 12000 статьи с литературным освещением до начала 2000 г. Записи констант скорости для указанной реакции можно найти путем поиска
База данных реакций. Возвращаются все записи констант скорости для этой реакции,
со ссылкой на «Подробности» этой записи. Каждая запись константы скорости содержит следующую информацию (если таковая имеется):
 В настоящее время это включает прямые ссылки на
соответствующая страница веб-книги NIST для всех веществ, для которых такая ссылка
возможное. На это указывает подчеркивание и выделение вида. В
WebBook предоставляет термодинамические, спектральные и другие данные о видах. Заметка
ссылка на веб-книгу открывается в вашем браузере как новый фрейм. В настоящее время это включает прямые ссылки на
соответствующая страница веб-книги NIST для всех веществ, для которых такая ссылка
возможное. На это указывает подчеркивание и выделение вида. В
WebBook предоставляет термодинамические, спектральные и другие данные о видах. Заметка
ссылка на веб-книгу открывается в вашем браузере как новый фрейм. |
| Ресурсы базы данных кинетики Поиск простой реакции База данных поисковых реакций Поиск по библиографической базе данных Установить настройки единиц измерения Обратная связь Отправить статью Оцените наши продукты и услуги Цитата Справка Другие базы данных Программа стандартных справочных данных NIST Интернет-книга по химии NIST База данных кинетики решений NDRL-NIST База данных сравнительных и контрольных показателей по вычислительной химии NIST Справочник NIST по константам, единицам и неопределенности Подробнее. Административные ссылки Домашняя страница DOC Домашняя страница NIST Домашняя страница MML Отделение химических наук |
Версия данных 2015.09 Обобщение данных кинетики газофазных реакцийУведомление: Сейчас мы принимаем запросы для извлечения данных кинетики из журнальных статей и других ссылок.Если вы найдете статью, воспользуйтесь ссылкой «Отправить статью» слева. который был пропущен в базе данных. Вы можете запросить абстракцию нового публикация. База данных реакций Форма быстрого поискаВведите реагент (ы) и / или продукт (ы) в поля ниже. Поля могут оставьте пустым.
 .. .. Форма расширенного поиска реакции Форма библиографического поиска Добро пожаловать Начало работы Источники и история Свяжитесь с нами Конфиденциальность |
Полимеры | Бесплатный полнотекстовый | Интерпретация и физический смысл кинетических параметров, полученных из изоконверсионного кинетического анализа полимеров
3.1.3. Эффективная энергия активации
Применение принципа изоконверсии к автокаталитической модели Кислого и Камала приводит к уравнениям (9) — (11) [11,12]:Eα = k1 (T) E1 + k2 (T) E2αmk1 (T) + k2 (T) αm
(9)
Eα = A1exp (−E1 / RT) E1 + A2exp (−E2 / RT) E2αmA1exp (−E1 / RT) + A2exp (−E2 / RT) αm
(10)
Eα = (A1 / A2) ехр (−E1 / RT) E1 + ехр (−E2 / RT) E2αm (A1 / A2) ехр (−E1 / RT) + ехр (−E2 / RT) αm
(11)
Эти уравнения показывают, что эффективная энергия активации зависит как от температуры, так и от степени превращения. Энергии активации некаталитических (E 1 ) и катализированных (E 2 ) реакций получают путем нелинейной аппроксимации уравнения (11) зависимости эффективной энергии активации от температуры. Подгонка осуществляется в интервале, где реакция химически контролируется (обычно для α около 0,3–0,5), и приводит к энергиям активации E 1 и E 2 [11,12]. Обратите внимание, что при низкой степени превращения (α → 0) эффективная энергия активации E α дает оценку энергии активации некаталитической реакции E 1 .Применение принципа изоконверсии к диффузионной модели приводит к уравнениям (12) — (14) [11,12]:
Энергии активации некаталитических (E 1 ) и катализированных (E 2 ) реакций получают путем нелинейной аппроксимации уравнения (11) зависимости эффективной энергии активации от температуры. Подгонка осуществляется в интервале, где реакция химически контролируется (обычно для α около 0,3–0,5), и приводит к энергиям активации E 1 и E 2 [11,12]. Обратите внимание, что при низкой степени превращения (α → 0) эффективная энергия активации E α дает оценку энергии активации некаталитической реакции E 1 .Применение принципа изоконверсии к диффузионной модели приводит к уравнениям (12) — (14) [11,12]:Eα = k (T) ED + kD (T, α) E2k (T) + kD (T, α)
(12)
Eα = A2exp (−E2 / RT) ED + D0exp (−ED / RT + Kα) E2A2exp (−E2 / RT) + D0exp (−ED / RT + Kα)
(13)
Eα = (A2 / D0) ехр (−E2 / RT) ED + ехр (−ED / RT + Kα) E2 (A2 / D0) ехр (−E2 / RT) + ехр (−ED / RT + Kα)
(14)
Нелинейная аппроксимация уравнения (14) реализуется в интервале, где реакция контролируется диффузией, и приводит к энергиям активации E 2 и E D .
 Это было впервые выведено из единственного анализа зависимости E α , полученного из измерений DSC и позже подтвержденного TMDSC и реологическими измерениями [12,16].Рисунок 1 иллюстрирует корреляцию между снижением E α и комплексной теплоемкостью (C p *), приписываемой стеклованию. Витрификация во время изотермического сшивания может быть обнаружена с помощью реометрии или измерений TMDSC [16,17]. После этой стадии молекулярная подвижность значительно снижается, и реакция контролируется диффузией. В неизотермическом режиме значения E α , полученные в конце реакции, очень низкие (10–20 кДж моль · 1 ). , и не соответствуют энергии активации какой-либо химической реакции, такой как добавление первичного и вторичного амина или этерификация (рис. 2).Фактически, эти значения соответствуют диффузии небольших молекул, таких как непрореагировавшие сегменты цепи полимерной цепи [19]. В точке гелеобразования растущие отдельные макромолекулы соединяются в единую сеть, так что эпоксидная система теряет способность течь, однако она все еще способна к дальнему перемещению сегментов полимерной цепи, если температура повышается, как в неизотермической условия.
Это было впервые выведено из единственного анализа зависимости E α , полученного из измерений DSC и позже подтвержденного TMDSC и реологическими измерениями [12,16].Рисунок 1 иллюстрирует корреляцию между снижением E α и комплексной теплоемкостью (C p *), приписываемой стеклованию. Витрификация во время изотермического сшивания может быть обнаружена с помощью реометрии или измерений TMDSC [16,17]. После этой стадии молекулярная подвижность значительно снижается, и реакция контролируется диффузией. В неизотермическом режиме значения E α , полученные в конце реакции, очень низкие (10–20 кДж моль · 1 ). , и не соответствуют энергии активации какой-либо химической реакции, такой как добавление первичного и вторичного амина или этерификация (рис. 2).Фактически, эти значения соответствуют диффузии небольших молекул, таких как непрореагировавшие сегменты цепи полимерной цепи [19]. В точке гелеобразования растущие отдельные макромолекулы соединяются в единую сеть, так что эпоксидная система теряет способность течь, однако она все еще способна к дальнему перемещению сегментов полимерной цепи, если температура повышается, как в неизотермической условия. В данном случае это приводит к увеличению E α -зависимости в конце реакции вместо тенденции к уменьшению, наблюдаемой для реакций, контролируемых движением малых молекул [20,21].Это объясняется расстеклованием и / или реактивацией химической реакции из-за увеличения молекулярной подвижности. Раскрывание можно обнаружить по увеличению комплексной теплоемкости C p *, измеренной TMDSC. Пример представлен на рисунке 2, где расстекловывание происходит при температуре выше 140 ° C. Стоит отметить, что этот температурный диапазон полностью согласуется с увеличением E α , приписываемым реактивации химических реакций (Рисунок 2).Согласие между E α -зависимостью и вариациями C p *, представленными на рисунках 1 и 2, является замечательным и подтверждает, что зависимость E α отражает изменение в общем механизме полимеризации. для этой системы сообщалось, что гелеобразование происходит при α около 0,55 при температуре 124 ° C, а стеклование при α около 0,90 при температуре 146 ° C [16].
В данном случае это приводит к увеличению E α -зависимости в конце реакции вместо тенденции к уменьшению, наблюдаемой для реакций, контролируемых движением малых молекул [20,21].Это объясняется расстеклованием и / или реактивацией химической реакции из-за увеличения молекулярной подвижности. Раскрывание можно обнаружить по увеличению комплексной теплоемкости C p *, измеренной TMDSC. Пример представлен на рисунке 2, где расстекловывание происходит при температуре выше 140 ° C. Стоит отметить, что этот температурный диапазон полностью согласуется с увеличением E α , приписываемым реактивации химических реакций (Рисунок 2).Согласие между E α -зависимостью и вариациями C p *, представленными на рисунках 1 и 2, является замечательным и подтверждает, что зависимость E α отражает изменение в общем механизме полимеризации. для этой системы сообщалось, что гелеобразование происходит при α около 0,55 при температуре 124 ° C, а стеклование при α около 0,90 при температуре 146 ° C [16]. Эти значения полностью согласуются с данными рисунка 2.Температура 124 ° C соответствует началу снижения C p *, а температура 146 ° C соответствует минимуму E α (обратите внимание, что для неизотермических условий скорости нагрева, используемые для оценки E α выше, чем скорость, используемая для измерения C p *, что вызывает небольшой сдвиг значений E α в сторону более высокой температуры). При температуре выше 140–150 ° C происходит расстекловывание, о чем свидетельствует повышение C p *, и химические реакции возобновляются.Контроль диффузии мономеров в конце реакции значительно снижается, когда наноглины добавляются к эпокси-аминной системе (DGEBA / 1,3-фенилендиамин) [22]. Молекулярная подвижность выше в конце реакции для смесей, содержащих глину, независимо от природы ионов алкиламмония, присутствующих в галереях глины, что отражено более низким снижением E α , характерным для контроля диффузии.
Эти значения полностью согласуются с данными рисунка 2.Температура 124 ° C соответствует началу снижения C p *, а температура 146 ° C соответствует минимуму E α (обратите внимание, что для неизотермических условий скорости нагрева, используемые для оценки E α выше, чем скорость, используемая для измерения C p *, что вызывает небольшой сдвиг значений E α в сторону более высокой температуры). При температуре выше 140–150 ° C происходит расстекловывание, о чем свидетельствует повышение C p *, и химические реакции возобновляются.Контроль диффузии мономеров в конце реакции значительно снижается, когда наноглины добавляются к эпокси-аминной системе (DGEBA / 1,3-фенилендиамин) [22]. Молекулярная подвижность выше в конце реакции для смесей, содержащих глину, независимо от природы ионов алкиламмония, присутствующих в галереях глины, что отражено более низким снижением E α , характерным для контроля диффузии. Используя метод, предложенный Сбирраццуоли, основанный на уравнениях (11) и (14), были получены энергии активации, согласующиеся для некатализированной и катализированной реакции [13].Кроме того, было показано, что добавление модифицированной глины вызывает меньше неэффективных ударов, а реактивность увеличивается за счет повышения эффективности столкновений [13]. Для химически контролируемой части реакции высокое увеличение эффективности столкновений присоединения амина, инициированного донором протона, приводит к усилению раскрытия цикла. В части реакции, контролируемой диффузией, предэкспоненциальный фактор, рассчитанный согласно описанному безмодельному методу, также увеличивается за счет добавления модифицированной глины и объясняется значительным увеличением частоты диффузионных скачков (1000 раз) [10,13].Аналогичный результат был получен для полимеризации фурфурилового спирта (FA) в присутствии органически модифицированного монтмориллонита [23]. Поскольку соответствие одной зависимости E α может привести к нескольким наборам коррелированных предэкспоненциальных факторов (A 1 , A 2 , D 0 ), предпочтительно использовать сначала зависимость E α для получения начальных значений и использования соотношений (A 1 / A 2 , A 2 / D 0 ) в качестве ограничений [13].
Используя метод, предложенный Сбирраццуоли, основанный на уравнениях (11) и (14), были получены энергии активации, согласующиеся для некатализированной и катализированной реакции [13].Кроме того, было показано, что добавление модифицированной глины вызывает меньше неэффективных ударов, а реактивность увеличивается за счет повышения эффективности столкновений [13]. Для химически контролируемой части реакции высокое увеличение эффективности столкновений присоединения амина, инициированного донором протона, приводит к усилению раскрытия цикла. В части реакции, контролируемой диффузией, предэкспоненциальный фактор, рассчитанный согласно описанному безмодельному методу, также увеличивается за счет добавления модифицированной глины и объясняется значительным увеличением частоты диффузионных скачков (1000 раз) [10,13].Аналогичный результат был получен для полимеризации фурфурилового спирта (FA) в присутствии органически модифицированного монтмориллонита [23]. Поскольку соответствие одной зависимости E α может привести к нескольким наборам коррелированных предэкспоненциальных факторов (A 1 , A 2 , D 0 ), предпочтительно использовать сначала зависимость E α для получения начальных значений и использования соотношений (A 1 / A 2 , A 2 / D 0 ) в качестве ограничений [13]. Таким образом, уравнения (11) и (14) были предложены Сбирраццуоли [13], чтобы уменьшить степень свободы и избежать получения локальных минимумов при применении нелинейной минимизации. Получаются только соотношения. Затем значения A 1 , A 2 , D 0 получаются путем подбора экспериментальных скоростей и уравнений (10) и (13) в качестве дополнительных ограничений [24]. Использование скорости реакции при постоянном значении степени превращения [dα / dt] α, i (см. Уравнение (6) ссылки [11]) упрощает вычисления, поскольку меньшее количество точек участвует в минимизация [11].Эти данные ([dα / dt] α, i ) автоматически вычисляются при использовании метода Фридмана. Для химически контролируемой части изученной реакции было обнаружено очевидное противоречие [13]. Реакция с наночастицами начиналась при более низкой температуре, а значения E α были выше. Это объясняется более высокими значениями предэкспоненциального множителя при введении наночастиц.
Таким образом, уравнения (11) и (14) были предложены Сбирраццуоли [13], чтобы уменьшить степень свободы и избежать получения локальных минимумов при применении нелинейной минимизации. Получаются только соотношения. Затем значения A 1 , A 2 , D 0 получаются путем подбора экспериментальных скоростей и уравнений (10) и (13) в качестве дополнительных ограничений [24]. Использование скорости реакции при постоянном значении степени превращения [dα / dt] α, i (см. Уравнение (6) ссылки [11]) упрощает вычисления, поскольку меньшее количество точек участвует в минимизация [11].Эти данные ([dα / dt] α, i ) автоматически вычисляются при использовании метода Фридмана. Для химически контролируемой части изученной реакции было обнаружено очевидное противоречие [13]. Реакция с наночастицами начиналась при более низкой температуре, а значения E α были выше. Это объясняется более высокими значениями предэкспоненциального множителя при введении наночастиц. Действительно, более высокое значение A приводило к увеличению скорости реакции, что компенсировало увеличение E (уравнение (1)).Это экспериментальное наблюдение было позже подтверждено с использованием модельных данных [11]. Это моделирование подтвердило актуальность использования изоконверсионного анализа для определения этапов, ограничивающих скорость в сложных (многоступенчатых) реакциях. Эти примеры иллюстрируют важность вычисления предэкспоненциальной зависимости фактора (lnA α -зависимость) без использования модели с использованием эффекта компенсации в дополнение к E α . Затем, как только зависимости E α и A α были определены, эффективная константа скорости (k ef ) и математическая функция, относящаяся к механизму f (α), могут быть оценены для каждой степени преобразования.Эти параметры затем используются для определения изменений в этапах ограничения скорости и для понимания механизма реакции. Механистическое понимание было получено для полимеризации цианатных эфиров с различными мостиковыми фрагментами ((CH 3 ) 2 C, S и O) с использованием изоконверсионного кинетического анализа.
Действительно, более высокое значение A приводило к увеличению скорости реакции, что компенсировало увеличение E (уравнение (1)).Это экспериментальное наблюдение было позже подтверждено с использованием модельных данных [11]. Это моделирование подтвердило актуальность использования изоконверсионного анализа для определения этапов, ограничивающих скорость в сложных (многоступенчатых) реакциях. Эти примеры иллюстрируют важность вычисления предэкспоненциальной зависимости фактора (lnA α -зависимость) без использования модели с использованием эффекта компенсации в дополнение к E α . Затем, как только зависимости E α и A α были определены, эффективная константа скорости (k ef ) и математическая функция, относящаяся к механизму f (α), могут быть оценены для каждой степени преобразования.Эти параметры затем используются для определения изменений в этапах ограничения скорости и для понимания механизма реакции. Механистическое понимание было получено для полимеризации цианатных эфиров с различными мостиковыми фрагментами ((CH 3 ) 2 C, S и O) с использованием изоконверсионного кинетического анализа. Обнаружена более высокая реакционная способность мономера с серной мостиковой связью по сравнению с его аналогом с углеродным мостиком. Это было объяснено более высоким значением предэкспоненциального фактора для стадии реакции, катализируемой металлом, из-за более высокой поляризуемости, которая вызывает более сильное межмолекулярное взаимодействие между молекулами и способствует предпочтительной ориентации реагирующих мономеров [24].Granando et al. сообщили о квазипостоянном значении E α для сшивки резольной системы фенол – формальдегид (PF), которое было приписано одностадийному механизму конденсации метилольной группы [25]. Они пришли к выводу, что режим, контролируемый диффузией, гораздо менее ограничивает, чем в эпоксидных системах, где кинетика отверждения резко замедляется. Эту систему сравнивали со сшивкой резола фенол-терефталевый альдегид (ПТПА), которая демонстрирует более сложный механизм.Первое плато E α было приписано конденсации вторичного спирта на фенолах, за которым последовало небольшое снижение, связанное со сдвигом в механизме полимеризации, от первой реакции к присоединению к фенолу второй альдегидной функции для однократно прореагировавший ТФК.
Обнаружена более высокая реакционная способность мономера с серной мостиковой связью по сравнению с его аналогом с углеродным мостиком. Это было объяснено более высоким значением предэкспоненциального фактора для стадии реакции, катализируемой металлом, из-за более высокой поляризуемости, которая вызывает более сильное межмолекулярное взаимодействие между молекулами и способствует предпочтительной ориентации реагирующих мономеров [24].Granando et al. сообщили о квазипостоянном значении E α для сшивки резольной системы фенол – формальдегид (PF), которое было приписано одностадийному механизму конденсации метилольной группы [25]. Они пришли к выводу, что режим, контролируемый диффузией, гораздо менее ограничивает, чем в эпоксидных системах, где кинетика отверждения резко замедляется. Эту систему сравнивали со сшивкой резола фенол-терефталевый альдегид (ПТПА), которая демонстрирует более сложный механизм.Первое плато E α было приписано конденсации вторичного спирта на фенолах, за которым последовало небольшое снижение, связанное со сдвигом в механизме полимеризации, от первой реакции к присоединению к фенолу второй альдегидной функции для однократно прореагировавший ТФК. Незначительное увеличение E α во время более поздней стадии отверждения PF и PTFA было отнесено к диффузионным ограничениям из-за образования трехмерной сшитой сетки.Кинетика полимеризации фурфурилового спирта (FA) в полифурфуриловый спирт (PFA) с органически модифицированным монтмориллонитом (Nanomer I30E) при кислотном катализе изучалась как методами ДСК, так и реометрией [26]. ДСК может определять остаточное тепло после отверждения, но, как правило, нелегко использовать эти данные для расчета кинетических параметров, особенно при высоких степенях сшивания. В этом случае реометрия может быть эффективным методом после окончания реакций, протекающих в высоковязкой среде.При полимеризации FA в PFA образуется вода, что затрудняет реологические измерения. Таким образом, для низких температур предпочтение отдается ДСК, а при высоких температурах реология более подходит, когда цель состоит в том, чтобы использовать эти данные для выполнения сложных вычислений, требующих данных высокого качества.
Незначительное увеличение E α во время более поздней стадии отверждения PF и PTFA было отнесено к диффузионным ограничениям из-за образования трехмерной сшитой сетки.Кинетика полимеризации фурфурилового спирта (FA) в полифурфуриловый спирт (PFA) с органически модифицированным монтмориллонитом (Nanomer I30E) при кислотном катализе изучалась как методами ДСК, так и реометрией [26]. ДСК может определять остаточное тепло после отверждения, но, как правило, нелегко использовать эти данные для расчета кинетических параметров, особенно при высоких степенях сшивания. В этом случае реометрия может быть эффективным методом после окончания реакций, протекающих в высоковязкой среде.При полимеризации FA в PFA образуется вода, что затрудняет реологические измерения. Таким образом, для низких температур предпочтение отдается ДСК, а при высоких температурах реология более подходит, когда цель состоит в том, чтобы использовать эти данные для выполнения сложных вычислений, требующих данных высокого качества. Идеальная преемственность между значениями E α , полученными с помощью DSC, и реометрическими данными, представленными на рисунке 3, является дополнительным доказательством физического смысла полученных значений E α .Действительно, зависимость E от α не может быть определена с помощью ДСК при высокой температуре, потому что в конце реакции, когда материал сильно сшит, не обнаруживается сигнал, однако оставшееся сшивание системы при нагревании может быть адекватно определено. с помощью реометрических измерений и зависимости E от α , рассчитанной с использованием этого метода. В этом случае параметр X уравнения (6), используемый для отслеживания остаточной реакции, происходящей в каучуковом состоянии, представляет собой модуль упругости G ’.Полимеризация FA в PFA с малеиновым ангидридом (MA) в качестве кислотного инициатора была изучена методами DSC и DMA [27]. ДСК использовали для контроля реакции в жидком состоянии, в то время как ДМА выполняли на отвержденных материалах путем нагревания образцов от 20 до 350 ° C после остаточных реакций, происходящих в твердом состоянии.
Идеальная преемственность между значениями E α , полученными с помощью DSC, и реометрическими данными, представленными на рисунке 3, является дополнительным доказательством физического смысла полученных значений E α .Действительно, зависимость E от α не может быть определена с помощью ДСК при высокой температуре, потому что в конце реакции, когда материал сильно сшит, не обнаруживается сигнал, однако оставшееся сшивание системы при нагревании может быть адекватно определено. с помощью реометрических измерений и зависимости E от α , рассчитанной с использованием этого метода. В этом случае параметр X уравнения (6), используемый для отслеживания остаточной реакции, происходящей в каучуковом состоянии, представляет собой модуль упругости G ’.Полимеризация FA в PFA с малеиновым ангидридом (MA) в качестве кислотного инициатора была изучена методами DSC и DMA [27]. ДСК использовали для контроля реакции в жидком состоянии, в то время как ДМА выполняли на отвержденных материалах путем нагревания образцов от 20 до 350 ° C после остаточных реакций, происходящих в твердом состоянии. Увеличение модуля упругости наблюдалось для всех систем в диапазоне от 170 до 290 ° C, в то время как на первых кривых нагрева ДСК не было зарегистрировано теплового события при температуре выше 220 ° C.Таким образом, это увеличение было связано с остаточными сшивками, возникающими в каучуковом состоянии после интенсивного постотверждения. Зависимость эффективной энергии активации (E α ), как функция температуры, вычисленная из измерений прямого доступа к памяти, показывает возрастающие значения, что соответствует кинетическому контролю за счет диффузии длинных полимерных цепей (Рисунок 4). По мере того как материал PFA постепенно сшивается в твердом состоянии, молекулярная подвижность становится более ограниченной, что приводит к увеличению энергии активации.Значения ниже в присутствии растворителей, что свидетельствует о том, что в этом случае цепи менее ограничивают. Более примечательно, что существует полная непрерывность между зависимостями E α , полученными для полимеризации из жидкого состояния (измерения DSC), и зависимостями, полученными для дополнительных поперечных связей, происходящих в каучуковом состоянии (измерения DMA), окончательные значения реакция, начиная с жидкого состояния, хорошо согласуется с первыми значениями реакции, начиная с каучукообразного состояния.
Увеличение модуля упругости наблюдалось для всех систем в диапазоне от 170 до 290 ° C, в то время как на первых кривых нагрева ДСК не было зарегистрировано теплового события при температуре выше 220 ° C.Таким образом, это увеличение было связано с остаточными сшивками, возникающими в каучуковом состоянии после интенсивного постотверждения. Зависимость эффективной энергии активации (E α ), как функция температуры, вычисленная из измерений прямого доступа к памяти, показывает возрастающие значения, что соответствует кинетическому контролю за счет диффузии длинных полимерных цепей (Рисунок 4). По мере того как материал PFA постепенно сшивается в твердом состоянии, молекулярная подвижность становится более ограниченной, что приводит к увеличению энергии активации.Значения ниже в присутствии растворителей, что свидетельствует о том, что в этом случае цепи менее ограничивают. Более примечательно, что существует полная непрерывность между зависимостями E α , полученными для полимеризации из жидкого состояния (измерения DSC), и зависимостями, полученными для дополнительных поперечных связей, происходящих в каучуковом состоянии (измерения DMA), окончательные значения реакция, начиная с жидкого состояния, хорошо согласуется с первыми значениями реакции, начиная с каучукообразного состояния. Комбинация данных DSC и DMA позволяет изучить кинетику полимеризации и получить информацию о механизме в широком диапазоне температур, начиная от жидкого состояния и заканчивая твердым состоянием. Эта идеальная непрерывность является дополнительным показателем физического смысла полученных кинетических параметров (Рисунок 4). Об увеличении зависимости E от α , приписываемой кинетическому контролю посредством диффузии длинных полимерных цепей, также сообщалось для сшивания DGEBA. с диамином, а также для полимеризации 2-гидроксиэтилметакрилата [20,21].Как уже упоминалось, возрастающая зависимость ожидается, когда процесс будет определяться диффузией больших молекул, таких как полимерные цепи или их длинные участки. Разница между уменьшающимися до очень низких значений (5 кДж моль -1 ), полученными для сшивки системы FA / I30E (Рисунок 3), и возрастающими до высоких значений (220 кДж моль -1 ), полученными для FA Система / MA (уже вылеченная) (рисунок 4) также иллюстрирует это утверждение [23,26,27].
Комбинация данных DSC и DMA позволяет изучить кинетику полимеризации и получить информацию о механизме в широком диапазоне температур, начиная от жидкого состояния и заканчивая твердым состоянием. Эта идеальная непрерывность является дополнительным показателем физического смысла полученных кинетических параметров (Рисунок 4). Об увеличении зависимости E от α , приписываемой кинетическому контролю посредством диффузии длинных полимерных цепей, также сообщалось для сшивания DGEBA. с диамином, а также для полимеризации 2-гидроксиэтилметакрилата [20,21].Как уже упоминалось, возрастающая зависимость ожидается, когда процесс будет определяться диффузией больших молекул, таких как полимерные цепи или их длинные участки. Разница между уменьшающимися до очень низких значений (5 кДж моль -1 ), полученными для сшивки системы FA / I30E (Рисунок 3), и возрастающими до высоких значений (220 кДж моль -1 ), полученными для FA Система / MA (уже вылеченная) (рисунок 4) также иллюстрирует это утверждение [23,26,27]. В случае системы FA / I30E модуль упругости достигает плато, и система находится в стеклообразном состоянии [23,26], в то время как для системы FA / MA модуль упругости начинает расти при высоких температурах, когда химические реакции повторно активируются.Зависимость E α уменьшается, когда скорость становится ограниченной из-за диффузии небольших молекул или коротких сегментов полимерной цепи, в то время как зависимость E α увеличивается, когда скорость ограничивается подвижностью длинных сегментов полимера. цепи [3]. ДСК со стохастической модуляцией температуры выявила стеклование и расстекловывание, которые могут происходить во время сшивания [16,28]. Стеклование вызывает переход от химического контроля к диффузионному, что приводит к снижению зависимости E α .В неизотермических условиях система может расстекловываться после стеклования, что приводит к реактивации остаточных химических реакций, что приводит к усилению зависимости E α (рисунок 2) [20].
В случае системы FA / I30E модуль упругости достигает плато, и система находится в стеклообразном состоянии [23,26], в то время как для системы FA / MA модуль упругости начинает расти при высоких температурах, когда химические реакции повторно активируются.Зависимость E α уменьшается, когда скорость становится ограниченной из-за диффузии небольших молекул или коротких сегментов полимерной цепи, в то время как зависимость E α увеличивается, когда скорость ограничивается подвижностью длинных сегментов полимера. цепи [3]. ДСК со стохастической модуляцией температуры выявила стеклование и расстекловывание, которые могут происходить во время сшивания [16,28]. Стеклование вызывает переход от химического контроля к диффузионному, что приводит к снижению зависимости E α .В неизотермических условиях система может расстекловываться после стеклования, что приводит к реактивации остаточных химических реакций, что приводит к усилению зависимости E α (рисунок 2) [20]. Подобные выводы были сделаны при анализе E α — зависимости, возникающие в результате полимеризации эпоксидированного льняного масла (ELO) с тремя различными дикарбоновыми кислотами на биологической основе, т.е. себациновой кислотой, субериновой кислотой и янтарной кислотой, используемыми в качестве сшивающих агентов [29]. Вязкость, измеренная неизотермической динамической реометрией ELO, отвержденного субериновой или себациновой кислотами, показывает плато в конце полимеризации, в то время как при использовании янтарной кислоты это не так.В этом случае кривая вязкости неуклонно растет, а зависимость E от α показывает увеличение в конце реакции. Напротив, когда ELO отверждается субериновой или себациновой кислотой, зависимости E α снижаются до низких значений в результате перехода к контролю диффузии малых непрореагировавших молекул, и химические реакции не активируются при высоких температурах в этом кейс. В этом исследовании определение E α , lnA α и f (α) было выполнено без предположения о механизме реакции.
Подобные выводы были сделаны при анализе E α — зависимости, возникающие в результате полимеризации эпоксидированного льняного масла (ELO) с тремя различными дикарбоновыми кислотами на биологической основе, т.е. себациновой кислотой, субериновой кислотой и янтарной кислотой, используемыми в качестве сшивающих агентов [29]. Вязкость, измеренная неизотермической динамической реометрией ELO, отвержденного субериновой или себациновой кислотами, показывает плато в конце полимеризации, в то время как при использовании янтарной кислоты это не так.В этом случае кривая вязкости неуклонно растет, а зависимость E от α показывает увеличение в конце реакции. Напротив, когда ELO отверждается субериновой или себациновой кислотой, зависимости E α снижаются до низких значений в результате перехода к контролю диффузии малых непрореагировавших молекул, и химические реакции не активируются при высоких температурах в этом кейс. В этом исследовании определение E α , lnA α и f (α) было выполнено без предположения о механизме реакции. В самом деле, оценка кинетического триплета полностью без использования моделей может позволить по-новому взглянуть на механизм реакции. Это было достигнуто путем сочетания кинетического анализа, FTIR и химико-реологических исследований. Последовательность выводов, сделанных с помощью этих различных методов анализа сложного механизма полимеризации, поразительна. Было показано, что ранняя стадия реакции контролируется автокаталитической стадией, которая возникает в результате увеличения количества гидроксильных групп в реакционной среде для трех исследуемых систем, т.е.е., ELO / янтарная, ELO / суберическая и ELO / себациновая. Образование достаточного количества β-гидроксиэфиров играет основную роль при низкой вязкости. Для ELO / Suberic и ELO / Sebacic перенос непрореагировавших молекул и / или их концентрация в каучуковом состоянии определяют и объясняют замедление скорости реакции в конце реакции. С янтарной кислотой реакция начинается при более низкой температуре и скорость реакции выше на ранних стадиях реакции, тогда как кажущаяся энергия активации выше.
В самом деле, оценка кинетического триплета полностью без использования моделей может позволить по-новому взглянуть на механизм реакции. Это было достигнуто путем сочетания кинетического анализа, FTIR и химико-реологических исследований. Последовательность выводов, сделанных с помощью этих различных методов анализа сложного механизма полимеризации, поразительна. Было показано, что ранняя стадия реакции контролируется автокаталитической стадией, которая возникает в результате увеличения количества гидроксильных групп в реакционной среде для трех исследуемых систем, т.е.е., ELO / янтарная, ELO / суберическая и ELO / себациновая. Образование достаточного количества β-гидроксиэфиров играет основную роль при низкой вязкости. Для ELO / Suberic и ELO / Sebacic перенос непрореагировавших молекул и / или их концентрация в каучуковом состоянии определяют и объясняют замедление скорости реакции в конце реакции. С янтарной кислотой реакция начинается при более низкой температуре и скорость реакции выше на ранних стадиях реакции, тогда как кажущаяся энергия активации выше. Опять же, это кажется противоречивым. Расчеты показали, что это явление связано с более высокой частотой диффузионных скачков, что выражается более высокими значениями предэкспоненциального члена. Для системы ELO / янтарная кислота вязкость выше в конце процесса, и только повышение температуры позволяет увеличить диффузию. В конце процесса вязкость высока, а количество и эффективность столкновений между молекулами низки, и только повышение температуры позволяет увеличить диффузию.Предэкспоненциальный фактор намного ниже для более длинных цепей (например, себациновой и суберической), что приводит к гораздо более выраженной разнице в значениях k (T) между ELO / янтарной и двумя другими системами. Такая разница между эффективностью столкновения длинных и коротких цепочек как-то компенсируется влиянием механизма реакции f (α). Спектр FTIR системы ELO / янтарная не выделяет оставшуюся карбоновую кислоту после сшивания. Это согласуется с более низкими значениями f (α) для этой системы, что свидетельствует о все более низкой концентрации карбоксильной группы в конце реакции.
Опять же, это кажется противоречивым. Расчеты показали, что это явление связано с более высокой частотой диффузионных скачков, что выражается более высокими значениями предэкспоненциального члена. Для системы ELO / янтарная кислота вязкость выше в конце процесса, и только повышение температуры позволяет увеличить диффузию. В конце процесса вязкость высока, а количество и эффективность столкновений между молекулами низки, и только повышение температуры позволяет увеличить диффузию.Предэкспоненциальный фактор намного ниже для более длинных цепей (например, себациновой и суберической), что приводит к гораздо более выраженной разнице в значениях k (T) между ELO / янтарной и двумя другими системами. Такая разница между эффективностью столкновения длинных и коротких цепочек как-то компенсируется влиянием механизма реакции f (α). Спектр FTIR системы ELO / янтарная не выделяет оставшуюся карбоновую кислоту после сшивания. Это согласуется с более низкими значениями f (α) для этой системы, что свидетельствует о все более низкой концентрации карбоксильной группы в конце реакции. Сильное уменьшение члена f (α) объясняет более низкие значения скорости реакции для янтарной кислоты. Увеличение вязкости после плато стеклования для ELO / Succinic предполагает продолжение дополнительных поперечных связей. Поскольку температура постоянно увеличивается, могут происходить некоторые химические реакции. Это явление связано с кооперативным движением длинных полимерных цепей, образующихся во время сшивания, и энергетический барьер выше по сравнению с низкими значениями, полученными для диффузии небольших непрореагировавших молекул в случае себациновой и субериновой кислот.Напротив, вязкость достигает плато для систем ELO / Suberic и ELO / Sebacic в конце реакции, где оставшиеся карбоновые кислоты все еще присутствуют, как показывают измерения FTIR. Тем не менее, эти частицы неспособны реагировать из-за плохого транспорта этих более длинных цепей, что согласуется с контролем диффузии, о чем свидетельствует снижение E α и A α до низких значений в конце реакции.
Сильное уменьшение члена f (α) объясняет более низкие значения скорости реакции для янтарной кислоты. Увеличение вязкости после плато стеклования для ELO / Succinic предполагает продолжение дополнительных поперечных связей. Поскольку температура постоянно увеличивается, могут происходить некоторые химические реакции. Это явление связано с кооперативным движением длинных полимерных цепей, образующихся во время сшивания, и энергетический барьер выше по сравнению с низкими значениями, полученными для диффузии небольших непрореагировавших молекул в случае себациновой и субериновой кислот.Напротив, вязкость достигает плато для систем ELO / Suberic и ELO / Sebacic в конце реакции, где оставшиеся карбоновые кислоты все еще присутствуют, как показывают измерения FTIR. Тем не менее, эти частицы неспособны реагировать из-за плохого транспорта этих более длинных цепей, что согласуется с контролем диффузии, о чем свидетельствует снижение E α и A α до низких значений в конце реакции. Это полностью согласуется с переходом от химического к диффузионному контролю малых молекул при отверждении с помощью субериновой и себациновой кислот и с диффузионным контролем движений длинноцепочечных сегментов при отверждении янтарной кислотой.Гумины — это материал, полученный из биомассы, побочный продукт кислотно-катализируемого превращения целлюлозы и гемицеллюлозы в платформенные химические вещества. Значения E α , рассчитанные на основе неизотермических реометрических данных для гуминов и гуминов с кислотным инициатором (моногидрат п-толуолсульфоновой кислоты; pTSA), показывают убывающие зависимости (рис. 5). Первое резкое снижение было связано с автокаталитическим этапом. Первое значение 110 кДж моль · 1 представляет энергию активации некаталитического сшивания сырых гуминов.Второй этап определяется при α> 0,35, и на этом этапе вязкость сильно увеличивается. Уменьшение до 25 кДж · моль · 1 хорошо согласуется с контролем диффузии в конце реакции.
Это полностью согласуется с переходом от химического к диффузионному контролю малых молекул при отверждении с помощью субериновой и себациновой кислот и с диффузионным контролем движений длинноцепочечных сегментов при отверждении янтарной кислотой.Гумины — это материал, полученный из биомассы, побочный продукт кислотно-катализируемого превращения целлюлозы и гемицеллюлозы в платформенные химические вещества. Значения E α , рассчитанные на основе неизотермических реометрических данных для гуминов и гуминов с кислотным инициатором (моногидрат п-толуолсульфоновой кислоты; pTSA), показывают убывающие зависимости (рис. 5). Первое резкое снижение было связано с автокаталитическим этапом. Первое значение 110 кДж моль · 1 представляет энергию активации некаталитического сшивания сырых гуминов.Второй этап определяется при α> 0,35, и на этом этапе вязкость сильно увеличивается. Уменьшение до 25 кДж · моль · 1 хорошо согласуется с контролем диффузии в конце реакции. Для α> 0,8 достигнутая высокая температура может увеличить молекулярную подвижность, способствуя реактивации химических реакций, а скорость контролируется движениями более длинных сегментов цепи, таким образом, E α увеличивается [30]. Для гуминов с системой pTSA реакции инициирования протекают при значительно более низких температурах и с меньшим значением E α , что хорошо согласуется с ускоряющим эффектом pTSA.Кроме того, результирующее уменьшение E α хорошо согласуется с данными, полученными с помощью изотермической ДСК, и комплексной теплоемкости (C p *), полученной с помощью квазиизотермической ДСК с стохастической температурной модуляцией (TOPEM © ) [30 ].
Для α> 0,8 достигнутая высокая температура может увеличить молекулярную подвижность, способствуя реактивации химических реакций, а скорость контролируется движениями более длинных сегментов цепи, таким образом, E α увеличивается [30]. Для гуминов с системой pTSA реакции инициирования протекают при значительно более низких температурах и с меньшим значением E α , что хорошо согласуется с ускоряющим эффектом pTSA.Кроме того, результирующее уменьшение E α хорошо согласуется с данными, полученными с помощью изотермической ДСК, и комплексной теплоемкости (C p *), полученной с помощью квазиизотермической ДСК с стохастической температурной модуляцией (TOPEM © ) [30 ].Что такое химическая кинетика?
Химическая кинетика — это изучение химических процессов и скоростей реакций. Это включает в себя анализ условий, которые влияют на скорость химической реакции, понимание механизмов реакции и переходных состояний, а также формирование математических моделей для прогнозирования и описания химической реакции. Скорость химической реакции обычно измеряется в секундах -1 , однако кинетические эксперименты могут длиться несколько минут, часов или даже дней.
Скорость химической реакции обычно измеряется в секундах -1 , однако кинетические эксперименты могут длиться несколько минут, часов или даже дней.
Также известен как
Химическую кинетику можно также назвать кинетикой реакции или просто «кинетикой».
История химической кинетики
Область химической кинетики возникла из закона действия масс, сформулированного в 1864 году Петером Вааге и Като Гульдбергом. Закон действия масс гласит, что скорость химической реакции пропорциональна количеству реагентов.Якоб Вант Хофф изучал химическую динамику. Его публикация 1884 года «Этюды динамической химии» привела к получению Нобелевской премии по химии 1901 года (это был первый год присуждения Нобелевской премии). Некоторые химические реакции могут включать сложную кинетику, но основные принципы кинетики изучаются в средней школе и на уроках химии в колледже.
Ключевые выводы: химическая кинетика
- Химическая кинетика или кинетика реакций — это научное исследование скорости химических реакций.
 Это включает в себя разработку математической модели для описания скорости реакции и анализ факторов, влияющих на механизмы реакции.
Это включает в себя разработку математической модели для описания скорости реакции и анализ факторов, влияющих на механизмы реакции. - Питер Вааге и Като Гулдберг являются пионерами в области химической кинетики, описав закон действия масс. Закон действия масс гласит, что скорость реакции пропорциональна количеству реагентов.
- Факторы, влияющие на скорость реакции, включают концентрацию реагентов и других частиц, площадь поверхности, природу реагентов, температуру, катализаторы, давление, наличие света и физическое состояние реагентов.
Тарифные законы и тарифные константы
Экспериментальные данные используются для определения скоростей реакций, из которых выводятся законы скорости и константы скорости химической кинетики с применением закона действия масс. Законы скорости позволяют выполнять простые вычисления для реакций нулевого порядка, реакций первого и второго порядка.
- Скорость реакции нулевого порядка постоянна и не зависит от концентрации реагентов.

скорость = k - Скорость реакции первого порядка пропорциональна концентрации одного из реагентов:
скорость = k [A] - Скорость реакции второго порядка пропорциональна квадрату концентрации единственный реагент или продукт концентрации двух реагентов.
коэффициент = k [A] 2 или k [A] [B]
Законы скорости для отдельных шагов должны быть объединены, чтобы вывести законы для более сложных химических реакций. Для этих реакций:
- Есть этап определения скорости, который ограничивает кинетику.
- Уравнение Аррениуса и уравнения Эйринга можно использовать для экспериментального определения энергии активации.
- Стационарные приближения могут применяться для упрощения закона скорости.
Факторы, влияющие на скорость химической реакции
Химическая кинетика предсказывает, что скорость химической реакции будет увеличиваться за счет факторов, которые увеличивают кинетическую энергию реагентов (до определенного предела), что приводит к увеличению вероятности взаимодействия реагентов друг с другом. Точно так же можно ожидать, что факторы, уменьшающие вероятность столкновения реагентов друг с другом, снизят скорость реакции. Основными факторами, влияющими на скорость реакции, являются:
Точно так же можно ожидать, что факторы, уменьшающие вероятность столкновения реагентов друг с другом, снизят скорость реакции. Основными факторами, влияющими на скорость реакции, являются:
- концентрация реагентов (увеличение концентрации увеличивает скорость реакции)
- температура (повышение температуры увеличивает скорость реакции до определенного предела)
- присутствие катализаторов (катализаторы предлагают механизм реакции, требующий более низкой активации энергии, поэтому присутствие катализатора увеличивает скорость реакции)
- физическое состояние реагентов (реагенты в одной фазе могут вступать в контакт посредством теплового воздействия, но площадь поверхности и перемешивание влияют на реакции между реагентами в разных фазах)
- давление (для реакций с участием газов повышение давления увеличивает столкновения между реагентами, увеличивая скорость реакции)
Обратите внимание, что хотя химическая кинетика может предсказать скорость химической реакции, она не определяет степень, в которой реакция происходит. Термодинамика используется для предсказания равновесия.
Термодинамика используется для предсказания равновесия.
Источники
- Espenson, J.H. (2002). Химическая кинетика и механизмы реакций (2-е изд.). Макгроу-Хилл. ISBN 0-07-288362-6.
- Guldberg, C.M .; Вааге, П. (1864 г.). «Исследования по аффинити» Forhandlinger i Videnskabs-Selskabet i Christiania
- Горбань, А.Н .; Яблонский. Г. С. (2015). Три волны химической динамики. Математическое моделирование природных явлений 10 (5).
- Laidler, K. J. (1987). Химическая кинетика (3-е изд.). Харпер и Роу. ISBN 0-06-043862-2.
- Steinfeld J. I., Francisco J. S .; Хасе В. Л. (1999). Химическая кинетика и динамика (2-е изд.). Прентис-Холл. ISBN 0-13-737123-3.

 Конструирование
Конструирование ..
..
 ..
.. Это включает в себя разработку математической модели для описания скорости реакции и анализ факторов, влияющих на механизмы реакции.
Это включает в себя разработку математической модели для описания скорости реакции и анализ факторов, влияющих на механизмы реакции.